Расчёт магнитных полей с помощью закона
Расчёт магнитных полей с помощью закона
Био–Савара–Лапласа
Индукция магнитного поля отрезка прямолинейного проводника с током
Для всех бесконечно малых элементов dl отрезка векторы dl и rлежат в плоскости листа. Поэтому векторы dB, созданные в выбранной нами точке различными элементами проводника направлены одинаково – перпендикулярно плоскости листа. Следовательно, сложение векторов dB можно заменить сложением их модулей dB.
Из рисунка видно, что r = b/sina
(b – расстояние от проводника до инте-ресующей нас точки), и
.
Тогда индукция, созданная элементом проводника dl, равна
.
Индукция магнитного поля, созданного всем проводником, может быть найдена как интеграл от dB в пределах от a1 до + a2:
Иногда удобнее воспользоваться другим выражением:
(обратите внимание на рисунок, показывающий углы q1 и q2).
Обратите также внимание на то, что если точка расположена так, как показано на следующем рисунке, то q2 меняет знак и формула для расчёта магнитного поля прямолинейного отрезка записывается следующим образом:
.
Индукция магнитного поля бесконечно длинного
Прямолинейного проводника с током
Если длина прямого проводника бесконечно велика, то a1 = 0, а a2 = p.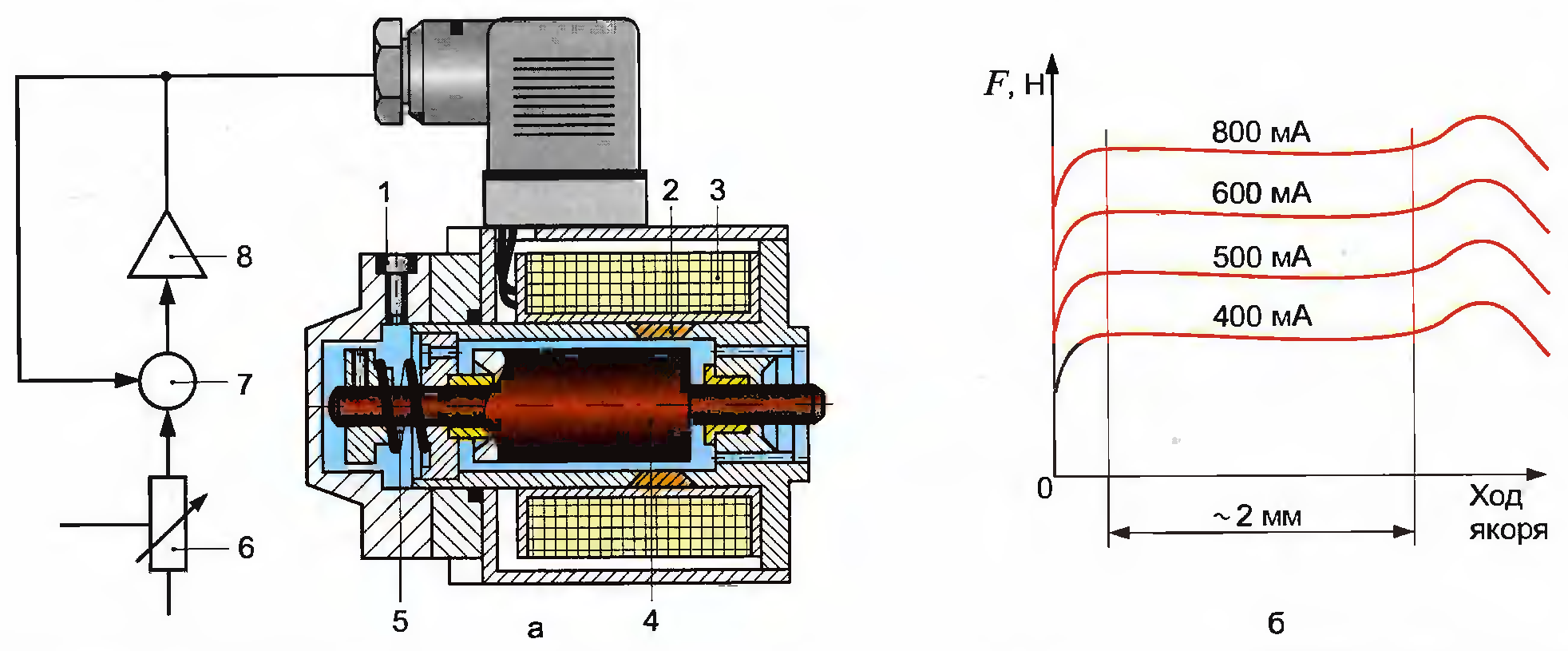
В этом случае индукция магнитного поля, созданного проводником, будет равна
.
Таким образом, индукция магнитного поля, созданного бесконечно длинным проводником прямо пропорциональна току в проводнике и обратно пропорциональна расстоянию от проводника до интересующей нас точки.
Дополнительно рассмотрим магнитное поле, созданное бесконечным проводником, который изогнут под прямым углом.
Ограничимся получением расчётной формулы для точки А, расположенной на продолжении одной из половин проводника.
Участок DB в точке А не создаёт магнитного поля, так как для него a1 и a2 равны 0.
Для участка ВС a1 = 900, a2 = -1800. Поэтому индукция, созданная этим участком, равна
.
Таким образом, индукция магнитного поля в точке А равна половине индукции, созданной прямым бесконечно длинным проводником с таким же током.
Сила Лоренца
Экспериментально установлено, что на заряд, движущийся в магнитном поле, действует сила. Эту силу принято называть силой Лоренца:
.
Модуль силы Лоренца
,
где a – угол между векторами v и B.
Направление силы Лоренца зависит от направления вектора . Его можно определить с помощью правила правого винта или правила левой руки. Но направление силы Лоренца не обязательно совпадает с направлением вектора !
Дело в том, что сила Лоренца равна результату произведения вектора [v, В] на скаляр q. Если заряд положительный, то Fл параллельна вектору [v, В]. Если же q < 0, то сила Лоренца противоположна направлению вектора [v, В] (см. рисунок).
рисунок).
Если заряженная частица движется параллельно силовым линиям магнитного поля, то угол a между векторами скорости и магнитной индукции равен нулю. Следовательно, сила Лоренца на такой заряд не действует (sin 0 = 0, Fл = 0).
Если же заряд будет двигаться перпендикулярно силовым линиям магнитного поля, то угол a между векторами скорости и магнитной индукции равен 900. В этом случае сила Лоренца имеет максимально возможное значение: Fл = qvB.
Сила Лоренца всегда перпендикулярна скорости движения заряда. Это означает, что сила Лоренца не может изменить величину скорости движения, но изменяет её направление.
Поэтому в однородном магнитном поле заряд, влетевший в магнитное поле перпендикулярно его силовым линиям, будет двигаться по окружности.
Если на заряд действует только сила Лоренца, то движение заряда подчиняется следующему уравнению, составленному на основе второго закона Ньютона: ma = Fл. не будет меняться по величине, но будет непрерывно изменяться её направление. За счёт этой компоненты заряд будет двигаться по окружности, плоскость ко-торой перпендикулярна силовым линиям.
не будет меняться по величине, но будет непрерывно изменяться её направление. За счёт этой компоненты заряд будет двигаться по окружности, плоскость ко-торой перпендикулярна силовым линиям.
Заряженная частица одновременно будет участвовать в этих движениях, поэтому её траектория будет представлять собой винтовую линию.
Радиус винтовой линии будет равен .
Период обращения заряженной частицы равен времени, за которое она пройдёт один виток, .
Шаг винтовой линии равен расстоянию, которое заряд пройдёт за один период: L = v||T.
Рассмотрим два одноимённых заряда, движущихся с одинаковой скоростью v вдоль параллельных прямых.
За счёт кулоновского взаимодействия они отталкиваются с силой .
Каждый из зарядов создаёт магнитное поле. Следовательно, на заряды действует сила Лоренца.
Заряд q1 создаёт магнитное поле, индукция которого направлена на нас (см. рисунок), и по модулю равна
рисунок), и по модулю равна
.
Тогда сила Лоренца, действующая на второй заряд, по модулю равна
и направлена так, как показано на рисунке справа.
Отношение силы Лоренца к кулоновской силе равно
.
Значения величин eо и mо связаны между собой соотношением , где с – скорость света в вакууме. Поэтому
.
Таким образом, в рассматриваемой ситуации сила Лоренца меньше кулоновской и возрастает по мере роста скорости движения заряда. Это ещё раз указывает на релятивистский характер магнитного взаимодействия.
Сила Ампера
Если проводник с током поместить в магнитное поле, то на каждый электрон, направленно движущийся в проводнике, действует сила Лоренца.
Действие этой силы передаётся всему проводнику. В результате на проводник с током, находящийся в магнитном поле, будет действовать некоторая сила.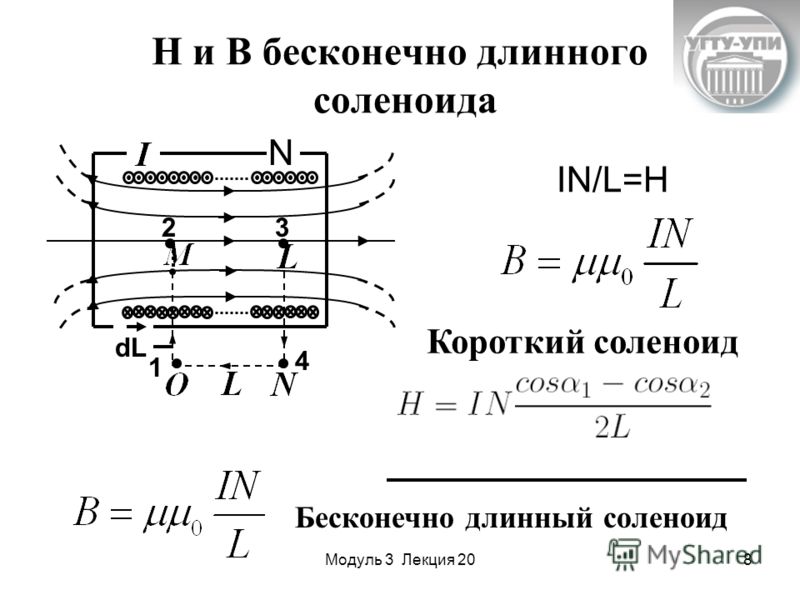 Найдём её величину.
Найдём её величину.
Для этого выделим элементарный участок проводника dl.
В нём имеется n.S.dl свободных электронов (n – концентрация свободных носителей заряда в проводнике, S – площадь поперечного сечения проводника, dl – длина элементарного участка). На каждый из электронов действует сила .
Результирующая сила dF, действующая на элемент проводника, равна сумме сил, действующих на все электроны в участке dl:
;
поскольку q.n.v = j, постольку сила dF равна
.
Это и есть выражение для расчёта силы Ампера, т. е. силы, действующей на элемент проводника с током, находящийся в магнитном поле.
Направление силы Ампера совпадает с направлением вектора и может быть определено по правилу правого винта для векторного произведения (или по правилу левой руки).
Для вычисления силы, действующей на весь проводник, необходимо взять интеграл от dF по длине проводника:
.
Теперь рассмотрим два параллельных проводника с токами I1 и I2, расположенных на расстоянии b друг от друга.
Первый проводник создаёт магнитное поле, индукция которого
.
В этом поле на единицу длины второго проводника действует сила, равная
.
Такая же по величине сила действует и на первый проводник. Легко увидеть, что если токи направлены в одну сторону, проводники притягиваются, если же токи противоположны, то проводники отталкиваются.
В магнитном поле
Рассмотрим контур из П-образного проводника и подвижной перемычки длиной l, находящийся в однородном магнитном поле.
Пусть в этом контуре источником ЭДС поддерживается постоянный ток I.
В результате взаимодействия с магнитным полем на перемычку будет действовать сила F = I [l, B]. Под действием этой силы перемычка будет двигаться вправо.
При смещении перемычки на dh сила F совершит работу dA = = Fdh = I[l, B]dh = IB[dh, l] = IBdS = IdФ, где dФ = BdS – магнитный поток через элементарную поверхность площадью dS.
Магнитным потоком называется скалярная величина, равная скалярному произведению вектора магнитной индукции на площадь элементарной поверхности dS, пронизываемой магнитным полем.
Из приведённых выше выкладок видно, что вектор элементарной поверхности dS = [dh, l] перпендикулярен поверхности dS и определяется по правилу правого винта для векторного произведения.
Размерность магнитного потока [Ф] = [B][dS] = Тл.м2 = Вб
(вебер).
Магнитный поток через конечную площадку S равен Ф .
Таким образом работа, совершаемая при перемещении проводника с током в магнитном поле, определяется выражением
Ф
и равна произведению силы тока в проводнике на приращение магнитного потока, вызванное перемещением проводника.
В данном случае dФ есть поток вектора магнитной индукции через площадь, пройденную перемычкой в процессе её движения.
Теперь рассмотрим жёсткий замкнутый контур с током I, перемещающийся в магнитном поле.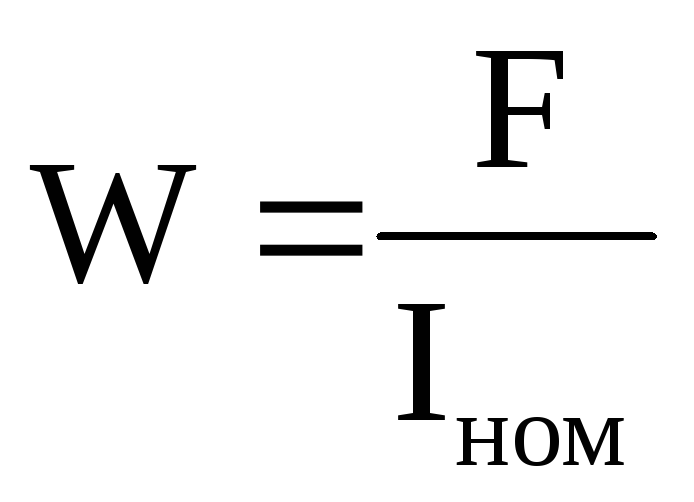
Выделим бесконечно малый элемент контура dl. При его перемещении на расстояние dh магнитное поле совершает работу dА¢ = IdФ¢, где dА¢ – работа по перемещению элемента контура dl на расстояние dh, а dФ¢ – поток вектора магнитной индукции через площадь, пройденную элементом контура dl.
Работа по перемещению всего контура на dh
,
где dФ – магнитный поток через площадь, пройденную всеми элементами контура dl
Работа по перемещению контура на конечное расстояние
,
где Ф2 и Ф1 – значения магнитного потока через контур в начальном и конечном положениях контура.
Необходимо отметить, что последний результат имеет общий характер, он не зависит от того, как именно изменялось положение контура в пространстве.
Закон полного тока
Рассмотрим магнитное поле, созданное бесконечным прямым проводником с током I.
Как было установлено ранее, силовые линии такого тока – окружности с центром на проводнике, а индукция магнитного поля .
Вычислим для этого поля циркуляцию вектора магнитной индукции , т. е. интеграл от скалярного произведения вектора магнитной индукции на элемент контура dl, взятый по некоторому замкнутому контуру.
Для этого прежде всего необходимо выбрать контур.
В данном случае удобнее всего в качестве контура выбрать окружность, совпадающую с силовой линией магнитного поля.
Для такого контура Bdl = Bdl, так как в любой точке В параллелен dl и косинус угла между этими векторами равен единице. Поэтому
.
Таким образом, циркуляция вектора В оказалась равна произведению магнитной постоянной на ток, охваченный контуром интегрирования:
.
Можно показать, что полученный результат не связан с формой контура интегрирования и имеет общий характер.
Если магнитное поле создано несколькими токами, то индукция магнитного поля в любой точке может быть найдена на основе принципа суперпозиции , где Вi– индукция магнитного поля, созданного i-м проводником с током.
Циркуляция каждого из векторов Вi будет равна произведению силы i-го тока на магнитную постоянную .
В свою очередь циркуляция вектора В по замкнутому контуру будет равна
,
т. е. циркуляция вектора магнитной индукции по контуру, охватывающему несколько токов, равна произведению mо на алгебраическую сумму токов, охваченных этим контуром.
Полученное выражение для циркуляции вектора магнитной индукции имеет общий характер и называется законом полного тока*.
Знак тока в алгебраической сумме определяется простым правилом: ток, охватываемый контуром, положителен, если его направление совпадает с направлением положитель-ной нормали к контуру (см. рисунок).
Направление положительной нормали определяется правилом правого винта: если правый винт вращать по выбранному направлению обхода контура, то направление поступательного движения винта покажет направление положительной нормали n.
Закон полного тока удобно использовать для расчёта магнитных полей, созданных токами, которым свойственна симметрия (см. следующий раздел).
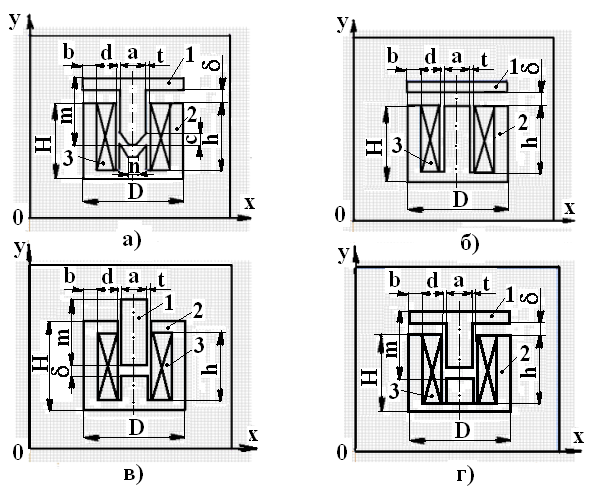
Магнитное поле тороида
Тороидом называется соленоид, свёрнутый в кольцо.
Поскольку тороид симметричен относительно оси, проходящей через его центр перпендикулярно плоскости, в которой лежит тороид, то и магнитное поле должно быть симметрично относительно этой оси. Следовательно, силовые линии магнитного поля в тороиде также должны быть симметричны относительно той же самой оси.
Следовательно, силовые линии магнитного поля в тороиде также должны быть симметричны относительно той же самой оси.
В качестве контура интегрирования удобно выбрать окружность, совпадающую с какой-либо силовой линией магнитного поля.
В этом случае циркуляция вектора магнитной индукции (направления В и dl во всех точках контура совпадают, поэтому скалярное произведение Bdl равно произведению их модулей; магнитная индукция во всех точках контура одинакова, следовательно, её можно вынести за знак интеграла).
Ток, охваченный контуром, , где N – число витков тороида.
Тогда в соответствии с законом полного тока
и
.
Обратите внимание: магнитная индукция поля внутри тороида зависит от расстояния между центром тороида и точкой внутри него. Величина В обратно пропорциональна расстоянию r.
Можно показать, что поле вне тороида равно нулю (примерно так же, как это было сделано в предыдущем разделе для поля вне соленоида).
Индуктивность соленоида
Рассмотрим произвольный замкнутый контур с током I. В соответствии с законом Био–Савара–Лапласа индукция магнитного поля, созданного контуром, прямо пропорциональна силе тока в проводнике.
Магнитный поток, охваченный контуром, прямо пропорционален индукции магнитного поля внутри контура и его площади .
Если охваченная контуром площадь неизменна, то величина магнитного потока прямо пропорциональна В и, следовательно, силе тока в контуре I
Ф = LI.
Коэффициент пропорциональности L называется коэффициентом индуктивности, или индуктивностью контура.
Индуктивность является размерным коэффициентом пропорциональности. В системе СИ размерность индуктивности [L] = Гн (генри).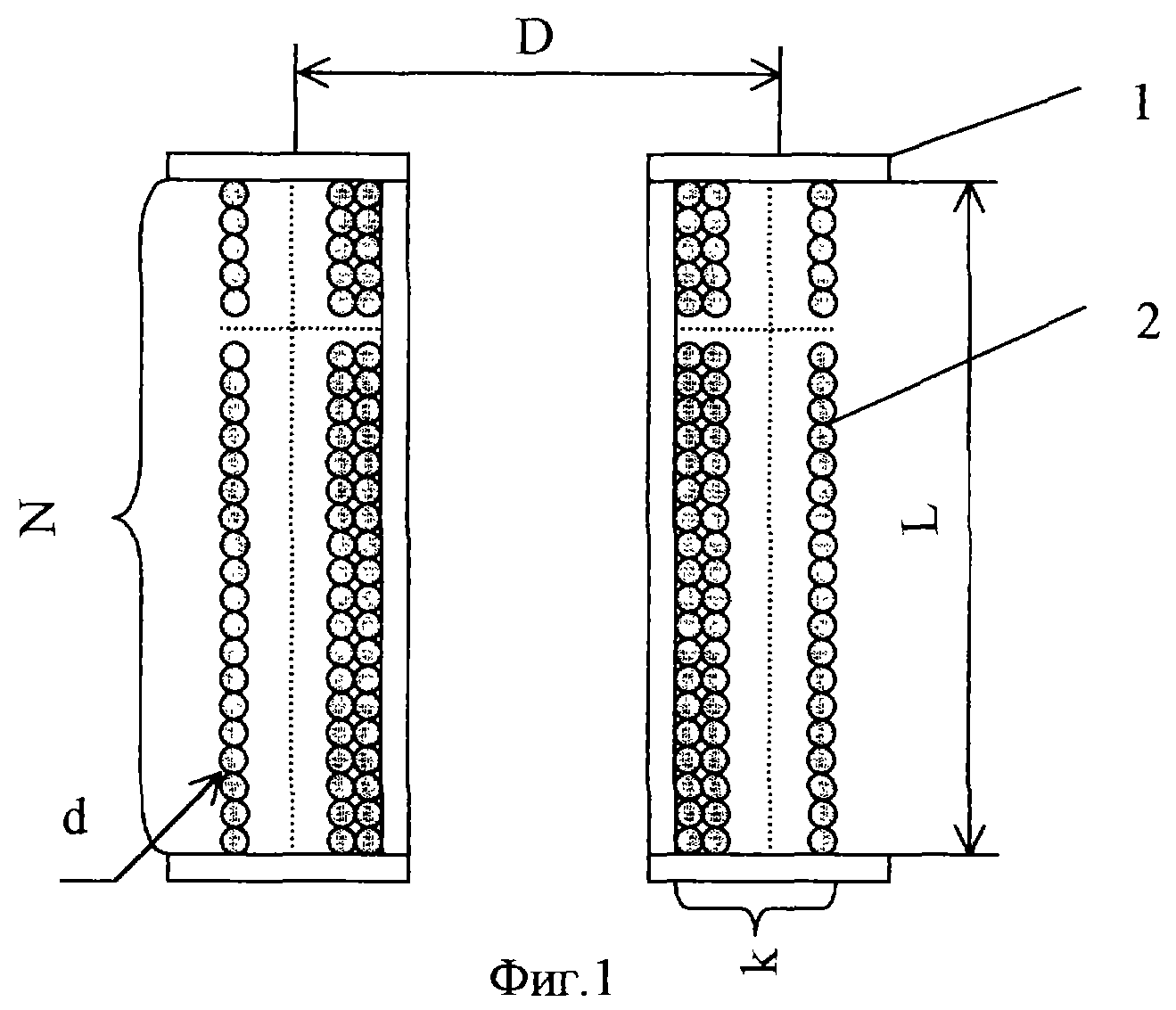
Найдём выражение для расчёта индуктивности соленоида.
Как показано в разд. 3.11.1, магнитная индукция поля внутри соленоида В = mоnI.
Магнитный поток через один виток соленоида Ф = mоnIS =
= , где l длина соленоида, N – количество витков соленоида на длине l, S – площадь витка соленоида.
Магнитный поток через N витков соленоида равен .
Это означает, что для соленоида
и отсюда индуктивность соленоида
,
где V – объём соленоида.
Таким образом, индуктивность соленоида без сердечника определяется плотностью витков и объёмом соленоида.
Магнитное поле в веществе
Магнитное поле создаётся электрическим током.
Если один ток создаёт магнитное поле в вакууме, а второй, такой же – в веществе, то созданные ими магнитные поля будут разными. Причём в некоторых веществах магнитное поле будет слабее поля в вакууме, в других – сильнее.
Причём в некоторых веществах магнитное поле будет слабее поля в вакууме, в других – сильнее.
По соотношению поля в веществе и в вакууме вещества делят на три класса: диамагнетики, парамагнетики и ферромагнетики.
В данном разделе будут рассмотрены причины, по которым разные вещества намагничиваются по-разному.
Намагничивание магнетика
Всякое вещество является магнетиком. Это значит, что всякое вещество способно намагничиваться, т. е. под действием внешнего магнитного поля в нём возникает дополнительное, собственное магнитное поле. Другими словами – индукция магнитного поля внутри магнетика В складывается из индукции внешнего поля Во и индукции собственного поля В¢:
В = Во+В¢.
Механизм намагничивания вещества был раскрыт французским учёным Андре Мари Ампером, который предположил, что во всех молекулах вещества циркулируют круговые токи. Каждый такой ток создаёт магнитное поле. Но, поскольку в отсутствие магнитного поля молекулярные токи ориентируются хаотически, суммарное магнитное поле всех этих токов равно нулю.
Каждый такой ток создаёт магнитное поле. Но, поскольку в отсутствие магнитного поля молекулярные токи ориентируются хаотически, суммарное магнитное поле всех этих токов равно нулю.
Появление внешнего магнитного поля вызывает упорядочение ориентации молекулярных круговых токов, в результате чего суммарное магнитное поле молекулярных токов становится отличным от нуля, а магнетик – намагниченным.
Намагничивание магнетика количественно характеризуют намагниченностью J, которая определяется выражением
,
где – суммарный магнитный момент всех молекул, находящихся в элементарном объёме DV в окрестности интересующей нас точки.
Размерность вектора намагниченности [J] = [pm]/[V] =
А.м2/м3 = А/м.
Итак, намагничивание вещества есть результат упорядочивания ориентации молекулярных токов внешним магнитным полем. Условно это можно представить так, как показано на рисунке.
Условно это можно представить так, как показано на рисунке.
Как видно из рисунка, токи внутри объёма магнетика компенсируют друг друга.
Токи же, выходящие на боковую поверхность, компенсироваться не будут.
Поэтому намагничение вещества можно трактовать как результат появления на боковой поверхности магнетика макроскопического тока намагничивания I¢.
Магнитомеханические явления
В атоме любого вещества электроны движутся вокруг ядра. Для объяснения магнитных явлений можно считать, что электрон вращается по круговой орбите. Угловая скорость электрона направлена так, как показано на рисунке (направление можно определить с помощью правила правого винта).
Движение электрона упорядочено. Поэтому орбитальное движение электрона можно трактовать как электрический ток.
Электрон движется по круговой орбите, поэтому созданный ток является круговым. Поскольку электрон имеет отрицательный заряд, направление созданного им тока противоположно направлению вращения электрона.
Поскольку электрон имеет отрицательный заряд, направление созданного им тока противоположно направлению вращения электрона.
Этот круговой ток обладает магнитным моментом pm = IS, направление которого показано на рисунке.
Если вещество находится в магнитном поле, на электрон действует вращательный момент M = [pm, B] (см. разд. 3.6).
Направление вектора момента силы определяется по правилу правого винта для векторного произведения. В данном случае вектор М направлен так, как показано на рисунке справа.
_________________________
*На самом деле циркуляция вектора Н зависит не только от тока проводимости, но и от конвекционного тока (пример – движение заряженных капель дождя) и тока смещения (будет рассмотрен позже)
.
Расчёт магнитных полей с помощью закона
Био–Савара–Лапласа
Читайте также:
Применение закона полного тока для расчета магнитных полей – поле бесконечного соленоида с постоянным током.
Соленоидом будем называть систему круговых концентрических проводников радиусом R
Пусть по соленоиду (т.е. по каждому из концентрических проводников) течет постоянный ток силой I- будем вычислять магнитное поле соленоида
По закону полного тока
где N – число витков (концентрических проводников)
И после несложных вычислений для величины индукции магнитного поля внутри соленоида получим
где n – число витков на единицу длины
Направлен вектор B по оси Z по правилу правого винта
Теорема Гаусса для магнитного поля.
Найдем дивергенцию индукции магнитного поля
По правилам повторного применения оператора
В результате, получаем уравнение.
называемое теоремой Гаусса для магнитного поля в дифференциальной форме
Сравнивая это уравнение с теоремой Гаусса для электростатического поля,
сформулируем физический смысл уравнения (теоремы Гаусса для магнитного поля)
Магнитных зарядов НЕ существует
Проинтегрируем уравнение по всему окружающему пространству – получим теорему Гаусса для магнитного поля в интегральной форме
Поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю.
Магнитный момент.
Согласно постулату Ампера элементарным объектом, создающим магнитное поле, является элементарный виток с током или элементарный магнит – магнитный диполь.
По определению, вектор элементарного магнитного момента dµ элементарного кругового витка с током I равен
Здесь dS – вектор площади витка с током Постулат Ампера позволяет определить векторный потенциал магнитного поля в любой точке A через геометрические параметры контура Перепишем эту формулу для элементарного поля dAA(r) элементарного магнитного момента dµ — при вычислении воспользуемся формулой (следствие из теоремы Стокса)
Очевидно, эта формула справедлива не только для элементарного контура с током, но и для элементарного магнита.
Магнитная восприимчивость
Из уравнения для индукции магнитного поля B получим
Тогда, учитывая, что для однородного изотропного магнетика,
для намагниченности M можно написать
Введем обозначение
Тогда получим, что намагниченность M, в точке заданной точке однородного изотропного магнетика пропорциональна напряженности магнитного поля H в этой точке
где — магнитная восприимчивость вещества (магнетика)
Закон полного тока для магнитного поля в магнетике
Как и прежде, найдем ротор индукции магнитного поля
И согласно уравнению Пуассона для магнитного поля в магнитной среде
В результате, получаем уравнение,
называемое законом полного тока для магнитной среды в дифференциальной форме. Однако в такой форме закон полного тока не отражает особенностей магнитного поля для магнитной среды
Однако в такой форме закон полного тока не отражает особенностей магнитного поля для магнитной среды
Преобразуем уравнение
Введем обозначение
Величину H называют вектором напряженности магнитного поля.
В однородном изотропном магнетике
— магнитная проницаемость вакуума, µ — магнитная проницаемость магнетика.
С обозначением, закон полного тока для магнитного поля в магнетке принимает вид
Интегрируя это уравнение по контуру L, охватывающему площадь S (с использованием теоремы Стокса) получим закон полного тока в интегральной форме для магнитного поля в магнетике.
Циркуляция вектора напряженности магнитного поля H по замкнутому контуру L пропорциональна алгебраической сумме токов, охватываемых контуром
ИЗМЕРЕНИЕ ИНДУКТИВНОСТИ СОЛЕНОИДОВ — Студопедия.Нет
Приборы и принадлежности: генератор сигналов звуковой частоты, цифровой вольтметр,
ключ, два соленоида.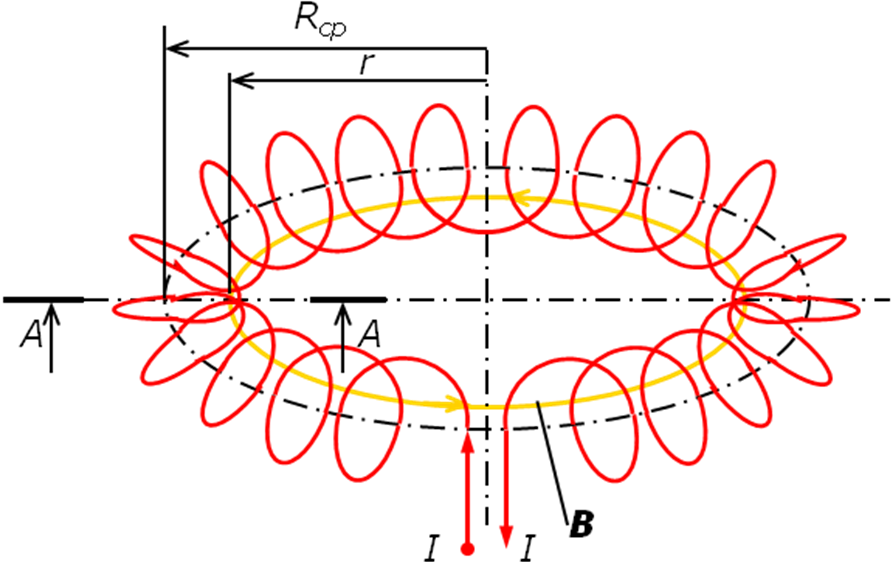
Краткая теория
При изменении магнитного потока через поверхность, ограниченную замкнутым контуром, в этом контуре возникает электродвижущая сила :
( — время). (1)
Магнитный поток Ф равен , (2)
где — проекция вектора индукции магнитного поля на нормаль к плоскости контура, а интегрирование проводится по поверхности S, ограниченой этим контуром (рис. I).
Пусть изменение магнитного потока вызвано изменением внешнего магнитного поля, деформацией или перемещением конура. Тогда явление возникновения электродвижущей силы (ЭДС) в контуре называется электромагнитной индукцией. Если же изменяющийся магнитный поток создается током I ,протекающим по контуру, то явление возникновения ЭДС в этом же контуре называется самоиндукцией. Как ЭДС индукции, так и ЭДС самоиндукции определяется по формуле (1). Ток в контуре создает поле, поток вектора магнитной индукции которого через поверхность, ограниченную этим контуром, (магнитный поток) равен
(3)
Коэффициент пропорциональности между током и магнитным потоком называется индуктивностью контура.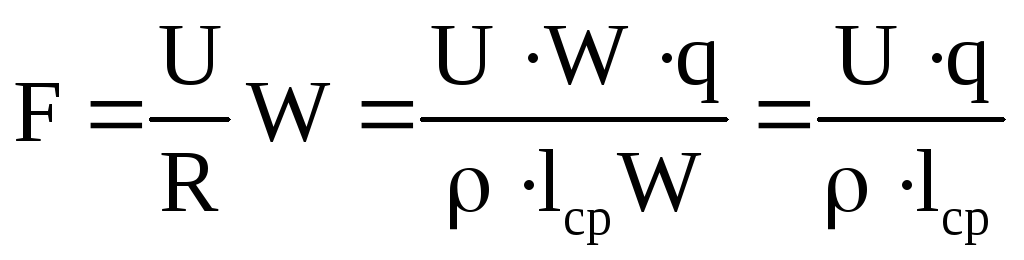 Индуктивность зависит от геометрических характеристик контура с током и магнитных свойств среды, в которой он находится. Если L не изменяется с течением времени, то, подставив (3) в (I), получим следующее выражение для ЭДС самоиндукции в контуре:
Индуктивность зависит от геометрических характеристик контура с током и магнитных свойств среды, в которой он находится. Если L не изменяется с течением времени, то, подставив (3) в (I), получим следующее выражение для ЭДС самоиндукции в контуре:
. (4)
Суммарный магнитный поток через все витки соленоида (потокосцепление) также пропорционален силе тока в нем. Поэтому формула (3) остается справедливой и для
соленоида, если в ней магнитный поток через виток заменить на , а под понимать индуктивность всего соленоида. Суммарная ЭДС самоиндукции в соленоиде, индуктивность которого , определяется формулой (4).
Обычно любой элемент электрической цепи в некоторой степени обладает активным сопротивлением , индуктивностью , и емкостью . Идеализированный элемент, у которого , а , называется идеальной индуктивностью; элемент, у которого , а ― идеальным активным сопротивлением. Аналогично определяется идеальная емкость.
Аналогично определяется идеальная емкость.
При последовательном соединении двух идеальных индуктивностей и суммарная индуктивность системы определяется соотношением
, (5)
а в случае их параллельного соединения ¾ формулой
. (6)
Докажем формулу (6). Пусть , и I2 — сила тока, соответственно, через соединение индуктивностей, через первую и через вторую индуктивности (рис. 2). Тогда I=I1+I2 , то есть изменения этих токов связаны соотношением
. (7)
Так как активное сопротивление идеальных индуктивностей равно нулю, то из закона Ома для неоднородного участка цепи следует, что
. (8)
Здесь ― разность потенциалов между точками А и В (рис. 2), а , и ― ЭДС самоиндукции 1ой и 2ой индуктивности и их соединения. Поделим (7) на и воспользуемся формулой (8):
. (9)
(9)
Выразив , и в (9) с помощью формулы (4), получим искомую формулу (6).
Измерение индуктивности соленоида:
Если через идеальную индуктивность идет переменный ток , то, согласно (4), в ней возникает ЭДС самоиндукции
, (10)
где и ― частота и амплитуда колебаний силы тока, а ― начальная фаза этих колебаний. Разность потенциалов между концами идеальной индуктивности равна взятой с обратным знаком ЭДС самоиндукции, возникающей в ней (см. (8)). Поэтому, согласно (10), ее амплитуда определяется выражением
. (11)
Для идеальной индуктивности коэффициент пропорциональности между амплитудой разности потенциалов и амплитудой силы тока называется индуктивным сопротивлением. Из (11) следует, что индуктивное сопротивление равно
. (12)
Реальный соленоид имеет как индуктивность L, так и активное сопротивление . Его можно рассматривать как последовательное соединение идеальной индуктивности L и идеального активного сопротивления . Подключим соленоид к генератору, активное сопротивление которого R , а ЭДС изменяется с частотой (рис. 3), и рассмотрим частотную зависимость разности потенциалов между концами этого соленоида (точки 1 и 2 на рис. 3). Пусть одновременно выполняются два условия: и . Первое условие означает, что соленоид можно считать идеальной индуктивностью и рассчитывать амплитуду разности потенциалов по формуле (11). При выполнении второго условия можно пренебречь вкладом индуктивного сопротивления соленоида в полное сопротивление цепи, вследствие чего амплитуда силы тока в цепи не зависит от частоты :
Его можно рассматривать как последовательное соединение идеальной индуктивности L и идеального активного сопротивления . Подключим соленоид к генератору, активное сопротивление которого R , а ЭДС изменяется с частотой (рис. 3), и рассмотрим частотную зависимость разности потенциалов между концами этого соленоида (точки 1 и 2 на рис. 3). Пусть одновременно выполняются два условия: и . Первое условие означает, что соленоид можно считать идеальной индуктивностью и рассчитывать амплитуду разности потенциалов по формуле (11). При выполнении второго условия можно пренебречь вкладом индуктивного сопротивления соленоида в полное сопротивление цепи, вследствие чего амплитуда силы тока в цепи не зависит от частоты :
. (13)
Здесь, и — амплитуда ЭДС и активное сопротивление генератора. Подставив (13) в (11), получим следующее соотношение для амплитуды разности потенциалов:
. (14)
Формула (14) остается справедливой, если в ней амплитуды разности потенциалов и ЭДС заменить их действующими значениями и . После перехода к действующим значениям (14) принимает вид
После перехода к действующим значениям (14) принимает вид
(15)
где при неизменных характеристиках генератора А=const. Таким образом, если и , то, согласно (15), действующее значение разности потенциалов между концами соленоида линейно зависит от частоты . Линейный участок зависимости используется в данной работе для измерения индуктивности соленоида.
Порядок выполнения работы
1. Установите переключатель формы сигнала генератора, расположенный внизу слева, в верхнее положение (~). Это обеспечивает синусоидальное изменение ЭДС генератора с течением времени.
2. Подсоедините выход генератора «земля», “20” (ослабление в dB)[1] к средним клеммам ключа 1, 2.
3. К этим же клеммам (1, 2) подсоедините цифровой вольтметр. Выходы «земля» генератора и вольтметра, которые обозначаются ┴ или ╧, должны быть подсоединены к одной и той же клемме ключа.
4. К крайним клеммам ключа (3, 4) подсоедините соленоид.
5. Разомкните ключ.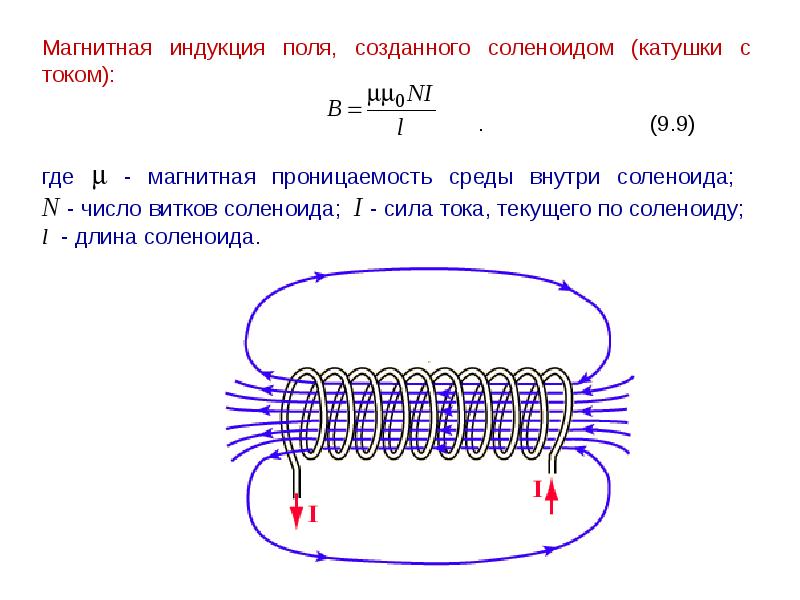 Включите генератор. Установите регулятор частоты генератора на 2000 Гц. Используя тумблер генератора «регулятор выхода» , установите показание цифрового вольтметра примерно на 0.6 В. Запишите это значение (действующее значение ЭДС генератора ).
Включите генератор. Установите регулятор частоты генератора на 2000 Гц. Используя тумблер генератора «регулятор выхода» , установите показание цифрового вольтметра примерно на 0.6 В. Запишите это значение (действующее значение ЭДС генератора ).
6. Замкните ключ. Теперь цифровой вольтметр показывает действующее значение разности потенциалов между концами соленоида . Измерьте его величину при значениях частоты генератора равных 1000, 2000, 3000, 4000, 5000 Гц. Данные занесите в таблицу.
7. Разомкните ключ и отсоедините соленоид от ключа.
8. Поочередно подсоединяя к крайним клеммам ключа (3, 4), сначала второй соленоид, а затем последовательно и параллельно соединенные два соленоида, повторите измерения согласно пункту 6.
9. Постройте графики для каждого соленоида и их соединений. Имейте в виду, что каждый график – это прямая, наиболее близко отстоящая от экспериментальных точек и проходящая через 0.
10. Определяя и с помощью графиков, рассчитайте индуктивность соленоидов и их соединений по формуле
(Гн),
которая следует из формулы (15) ( 500 Ом ).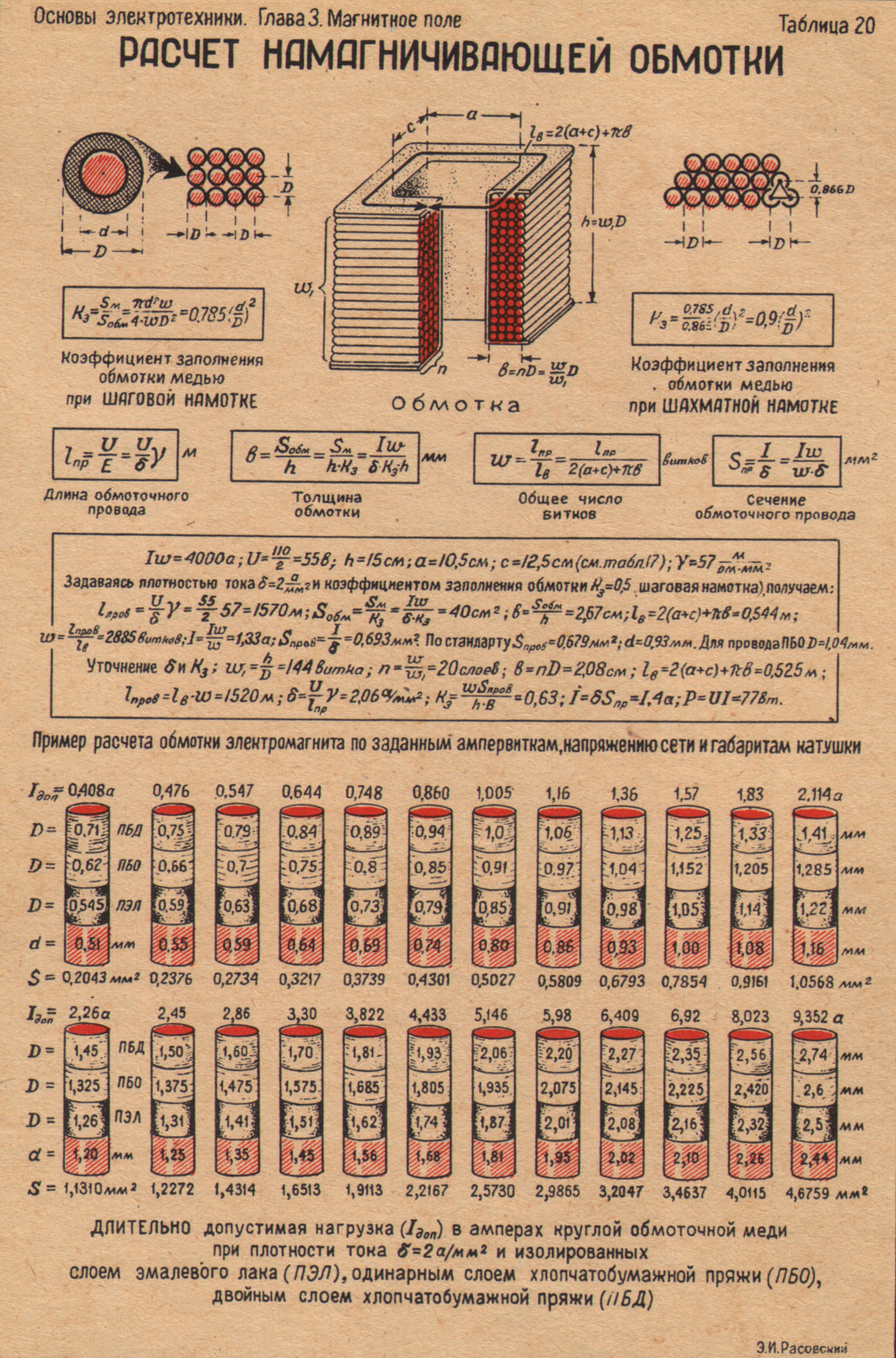
11. Оцените погрешность измерения индуктивности по формуле
,
где =1 мВ – систематическая погрешность измерения действующих значений разности потенциалов и ЭДС вольтметром, а =100 Гц – систематическая погрешность задания частоты генератора. Согласно приведенной формуле, для уменьшения погрешности, и следует определять с использованием точек экспериментальной прямой, которые максимально удалены друг от друга.
12. Используя значения индуктивности соленоидов и , полученные экспериментально, рассчитайте индуктивность их параллельного и последовательного соединений и по формулам (6) и (5) и сравните результаты расчетов с соответствующими измеренными значениями.
| , В | , Гц | L, Гн
(эксперимент) | L, Гн
по форм. (5) и (6) | |
| 1ый соленоид | 1) …
… 5) … | 1) …
… 5) … |
| |
| 2ой соленоид | 1) …
… 5) … | 1) …
… 5) … |
| |
| Последовательное
Соединение | 1) …
… 5) … | 1) …
… 5) … | ||
| Параллельное соединение | 1) …
… 5) … | 1) …
… 5) … |
Контрольные вопросы
1. Что такое магнитный поток? Чему равна ЭДС индукции?
Что такое магнитный поток? Чему равна ЭДС индукции?
2. Сформулируйте правило Ленца и приведите соответствующий пример.
3. Что такое индуктивность? Почему при изменении силы тока в соленоиде в нем возникает ЭДС? Чему она равна?
4. Сформулируйте правило Ленца применительно к явлению самоиндукции.
5. Получите формулу для индуктивности последовательного соединения идеальных индуктивностей.
6. Покажите, что амплитуда ЭДС самоиндукции в соленоиде является линейной функцией частоты колебаний силы тока в нем, если амплитуда колебаний силы тока не изменяется при изменении частоты.
Литература
6. Скорохватов Н.А. Курс лекций по электромагнетизму. М: МИИГАиК, 2006.
7. Савельев И.В., Курс общей физики, т. 2 (любое издание).
8. Трофимова Т.И., Курс физики (любое издание).
Лабораторная работа № 257
% PDF-1.4
%
3197 0 объект
>
endobj
xref
3197 88
0000000016 00000 н.
0000002954 00000 н.
0000003102 00000 п.
0000003924 00000 н.
0000004037 00000 н.
0000004487 00000 н.
0000004913 00000 н.
0000005027 00000 н.
0000005501 00000 н.
0000005586 00000 н.
0000005993 00000 н.
0000006509 00000 н.
0000006915 00000 н.
0000007030 00000 н.
0000007146 00000 н.
0000027058 00000 п.
0000027760 00000 п.
0000027848 00000 н.
0000028509 00000 п.
0000048139 00000 п.
0000067752 00000 п.
0000067927 00000 н.
0000082840 00000 п.
0000102300 00000 н.
0000102442 00000 н.
0000102818 00000 п.
0000102993 00000 п.
0000103161 00000 п.
0000103764 00000 н.
0000103938 00000 н.
0000104425 00000 н.
0000104454 00000 п.
0000105035 00000 н.
0000105180 00000 н.
0000105382 00000 п.
0000108232 00000 н.
0000127903 00000 н.
0000128094 00000 н.
0000128391 00000 н.
0000131373 00000 н.
0000131740 00000 н.
0000132352 00000 н.
0000132543 00000 н.
0000132710 00000 н.
0000133162 00000 п.
0000146945 00000 н.
0000147494 00000 н.
0000149535 00000 н.
0000165037 00000 н.
0000169451 00000 н.
0000169533 00000 н.
0000174539 00000 н.
0000174610 00000 н.
0000177757 00000 н.
0000178174 00000 н.
0000178450 00000 н.
0000181256 00000 н.
0000181443 00000 н.
0000181626 00000 н.
0000181933 00000 н.
0000229480 00000 н.
0000229551 00000 н.
0000229633 00000 н.
0000230117 00000 н.
0000230398 00000 н.
0000230559 00000 н.
0000230588 00000 н.
0000230895 00000 н.
0000230983 00000 п.
0000231295 00000 н.
0000231561 00000 н.
0000231869 00000 н.
0000231955 00000 н.
0000232487 00000 н.
0000232763 00000 н.
0000233072 00000 н.
0000256613 00000 н.
0000278854 00000 н.
0000319485 00000 н.
0000360498 00000 н.
0000360816 00000 н.
0000364030 00000 н.
0000416171 00000 п.
0000419385 00000 п.
0000480787 00000 п.
0000484001 00000 н.
0000002721 00000 н.
0000002101 00000 п.
трейлер
] / Назад 1074371 / XRefStm 2721 >>
startxref
0
%% EOF
3284 0 объект
> поток
hb«b` €
% PDF-1.4
%
2424 0 объект
>
endobj
xref
2424 73
0000000016 00000 н.
0000002450 00000 н.
0000002610 00000 н.
0000003283 00000 н.
0000003777 00000 н.
0000004330 00000 н.
0000004506 00000 н.
0000005210 00000 н.
0000005813 00000 н.
0000005991 00000 н.
0000006367 00000 н.
0000006854 00000 н.
0000006969 00000 н.
0000007085 00000 п.
0000007198 00000 н.
0000007312 00000 н.
0000007397 00000 н.
0000007909 00000 н.
0000008296 00000 н.
0000008786 00000 н.
0000008874 00000 н.
0000009491 00000 п.
0000010111 00000 п.
0000010203 00000 п.
0000010742 00000 п.
0000011024 00000 п.
0000011340 00000 п.
0000012003 00000 п.
0000012205 00000 п.
0000015055 00000 п.
0000023132 00000 п.
0000023662 00000 п.
0000023874 00000 п.
0000026989 00000 п.
0000027381 00000 п.
0000027847 00000 п.
0000040595 00000 п.
0000058736 00000 п.
0000076199 00000 п.
0000094235 00000 п.
0000111446 00000 н.
0000111640 00000 н.
0000128284 00000 н.
0000130895 00000 п.
0000147522 00000 н.
0000150253 00000 н.
0000154783 00000 н.
0000154962 00000 н.
0000159974 00000 н.
0000160015 00000 н.
0000196959 00000 н.
0000197142 00000 н.
0000197449 00000 н.
0000197553 00000 н.
0000197926 00000 н.
0000198208 00000 н.
0000198527 00000 н.
0000199077 00000 н.
0000199349 00000 н.
0000227757 00000 н.
0000227798 00000 н.
0000256632 00000 н.
0000256673 00000 н.
0000281869 00000 н.
0000281910 00000 н.
0000317833 00000 н.
0000317874 00000 н.
0000318192 00000 н.
0000321585 00000 н.
0000378799 00000 н.
0000382184 00000 п.
0000002227 00000 н.
0000001794 00000 н.
трейлер
] / Назад 751469 / XRefStm 2227 >>
startxref
0
%% EOF
2496 0 объект
> поток
hb«f`hd`c` Ā
Часто задаваемые вопросы о соленоиде постоянного тока
| Компания TDS Co.LTD./Top Страница
Соленоид работает под напряжением, а плунжер притягивается и намагничивается.
Плунжер возвращается в исходное положение с помощью внешней нагрузки, такой как возвратная пружина.
Элементы, которые необходимо учитывать для освобождения плунжера, следующие.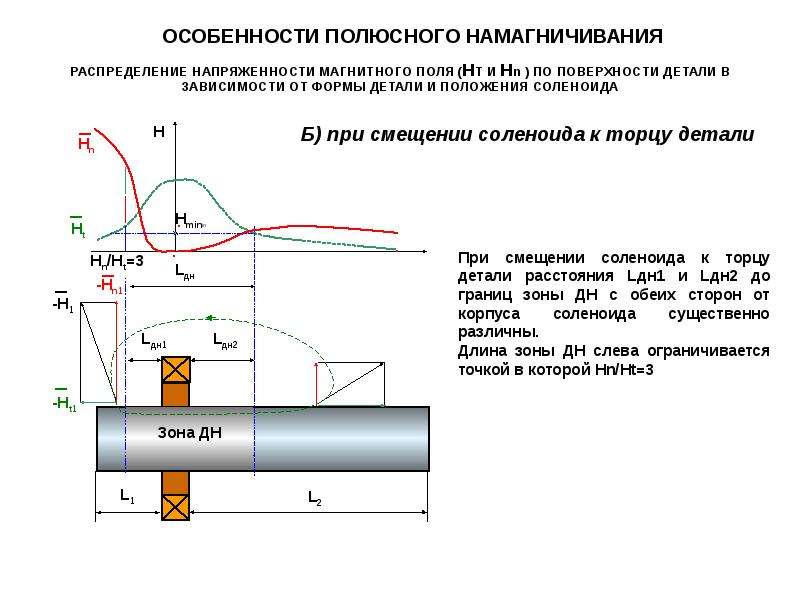
(1) Ток
(2) Ход
(3) Остаточная удерживающая сила (остаточный магнетизм)
(4) Возвратная нагрузка
Ниже приводятся подробные пояснения.
(1) Ток
1 、 Убедитесь, что ток не течет.
Независимо от направления тока (+ или -), даже при небольшом токе сила тяги соленоида может стать больше, чем обратная нагрузка.
2 、 Даже после отключения питания катушка генерирует противоэлектродвижущую силу из-за изменения тока, вызывая переходное явление.
Таким образом, текущий поток не будет нулевым в течение от нескольких до нескольких десятков миллисекунд.
В это время соленоид является магнитным и не возвращается, если обратная нагрузка меньше тягового усилия.
(2) Ход
Плунжер вернется в исходное положение через некоторое время.
Когда во время обратного движения течет ток для следующего рывка, плунжер не может полностью вернуться, но будет вытянут.
(3) Остаточная удерживающая сила (остаточный магнетизм)
Магнетизм остается в металлических частях соленоидов даже после того, как текущий ток становится равным нулю, что является остаточным магнетизмом, создающим удерживающую силу.
Когда остаточная удерживающая сила превышает возвратную нагрузку, плунжер не возвращается.
Если монтажная часть соленоида сделана из железа, остаточная удерживающая сила станет еще больше из-за его остаточного магнетизма.
(4) Возвратная нагрузка
Возвратная нагрузка должна быть больше, чем (1) и (3), и особое внимание требуется для сценариев и ② ниже.
① Если ожидается трение между плунжером и его направляющей трубой или механическое трение, в зависимости от ориентации соленоида при работе в горизонтальном направлении.
② Если соленоид установлен в приложении таким образом, что его возвратная нагрузка меньше из-за того, что направление силы тяжести плунжера и направление обратной нагрузки различны.
Измерение тока в соленоидах для автомобильных систем управления
Соленоиды в автомобильных системах управления
Соленоид — это линейный двигатель с фиксированным диапазоном хода. Соленоиды могут быть разработаны для простых двухпозиционных приложений, действующих как реле. Например, они используются таким образом в пускателях и дверных замках .
С другой стороны, линейный соленоид или пропорциональный , соленоид — это соленоид, положение которого можно точно контролировать.Они используются для управления поршнями и клапанами для точного управления давлением или расходом жидкости в таких приложениях, как трансмиссия , и , впрыск топлива .
Коробки передач
требуют точного и плавного управления давлением на муфты для переключения передач и для управления блокирующим преобразователем крутящего момента. Коробки передач с электронным управлением могут содержать более восьми линейных соленоидов, каждый из которых требует плавного и точного управления.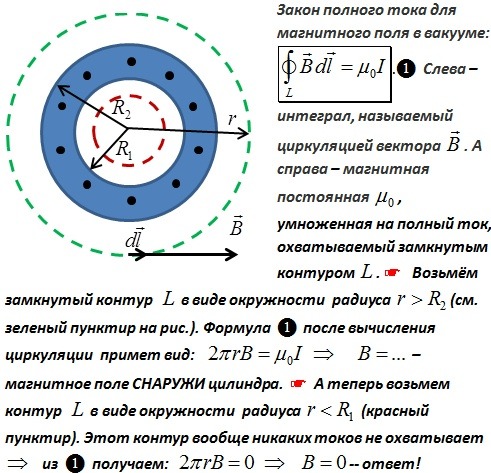 Для систем впрыска дизельного топлива с системой Common Rail с давлением, превышающим 2000 фунтов на квадратный дюйм, может потребоваться один линейный соленоид на цилиндр — и один на топливном насосе — для точной регулировки давления для поддержания предсказуемого расхода топлива в форсунках.
Для систем впрыска дизельного топлива с системой Common Rail с давлением, превышающим 2000 фунтов на квадратный дюйм, может потребоваться один линейный соленоид на цилиндр — и один на топливном насосе — для точной регулировки давления для поддержания предсказуемого расхода топлива в форсунках.
Пример: электронное управление коробкой передач
Автоматическая трансмиссия — это система, в которой электронное управление в значительной степени заменяет механическое управление из-за улучшения качества движения и топливной экономичности. Предыдущие улучшения в топливной экономичности и ускорении произошли с введением блокирующего преобразователя крутящего момента. Совсем недавно комбинация программного и аппаратного обеспечения с использованием соленоидов с электронным управлением позволила упростить настройку алгоритмов переключения передач и обеспечила дополнительные преимущества в отношении плавности и качества переключения передач.
В целом электронное управление трансмиссией позволяет создать более простую, надежную и менее дорогостоящую электромеханическую систему. Электронные системы управления трансмиссией улучшают управление точками переключения трансмиссии с менее резким переключением передач и улучшенной плавностью переключения. Кроме того, гибкость электронного управления позволяет лучше адаптироваться к меняющимся условиям. Электронное управление точками переключения передач с более высокой разрешающей способностью обеспечивает лучшее ускорение, улучшенную экономичность, лучший контроль нагрузки и снижение выбросов с минимальными усилиями водителя.Кроме того, электронное управление позволяет трансмиссии переключаться более плавно при изменении нагрузки и ускорения.
Электронные системы управления трансмиссией улучшают управление точками переключения трансмиссии с менее резким переключением передач и улучшенной плавностью переключения. Кроме того, гибкость электронного управления позволяет лучше адаптироваться к меняющимся условиям. Электронное управление точками переключения передач с более высокой разрешающей способностью обеспечивает лучшее ускорение, улучшенную экономичность, лучший контроль нагрузки и снижение выбросов с минимальными усилиями водителя.Кроме того, электронное управление позволяет трансмиссии переключаться более плавно при изменении нагрузки и ускорения.
С помощью электронной системы управления можно влиять на алгоритм управления переключением с помощью множества входных сигналов, помимо скорости вала, вакуума и входного сигнала привода. Некоторые из этих параметров включают опережение зажигания, параметры форсунки, датчики входной скорости, выбор переключения по проводам, скорость двигателя, положение дроссельной заслонки, скорость / блокировку гидротрансформатора, температуру ATF, температуру двигателя, датчики пробуксовки колес и инерционные датчики. Комбинирование этих типов входных данных позволяет получить широкий спектр точек оптимизации переключения, адаптированных к общим условиям эксплуатации. Для наиболее эффективного использования этих входных сигналов необходима система, в которой используется точное и плавно регулируемое электронное управление точками переключения передач и скоростью переключения.
Комбинирование этих типов входных данных позволяет получить широкий спектр точек оптимизации переключения, адаптированных к общим условиям эксплуатации. Для наиболее эффективного использования этих входных сигналов необходима система, в которой используется точное и плавно регулируемое электронное управление точками переключения передач и скоростью переключения.
Гидравлическое управление по-прежнему используется для переключения передач в автоматической коробке передач с электронным управлением. В отличие от механической системы, электронное управление гидравликой в электромеханической системе осуществляется линейными соленоидами, которые изменяют гидравлическое давление, прикладываемое к исполнительным механизмам, прикрепленным к блокам сцепления.Для того, чтобы это работало, чрезвычайно важно иметь точный и повторяемый контроль открытия соленоида, что, в свою очередь, позволяет точно и с повторяемостью контролировать точки переключения передач за счет применения точного количества гидравлической жидкости.
Определение положения соленоида
Положение линейного соленоида регулируется по контуру обратной связи. Например, давление на выходе клапана можно отслеживать и использовать в качестве сигнала обратной связи для сравнения с уставкой, регулируя рабочий цикл широтно-импульсной модуляции (ШИМ) для управления соленоидом.Однако измерение давления на выходе может оказаться трудным, непрактичным или очень дорогостоящим.
Практическая альтернатива — установить положение соленоида путем измерения тока через соленоид. Это возможно, потому что сила, создаваемая механической нагрузкой на соленоид, прямо пропорциональна магнитному полю, которое, в свою очередь, прямо пропорционально току через катушку. Пропорциональное управление соленоидом достигается за счет баланса сил между нагрузкой пружинного типа и магнитным полем соленоида, который можно определить путем измерения тока через соленоид.
ШИМ-управление соленоидом
Электромагнит приводится в действие с помощью генерируемого микроконтроллером входного сигнала с широтно-импульсной модуляцией для быстрого размыкания и замыкания переключателя на полевом транзисторе последовательно с соленоидом и источником напряжения (аккумулятором автомобиля).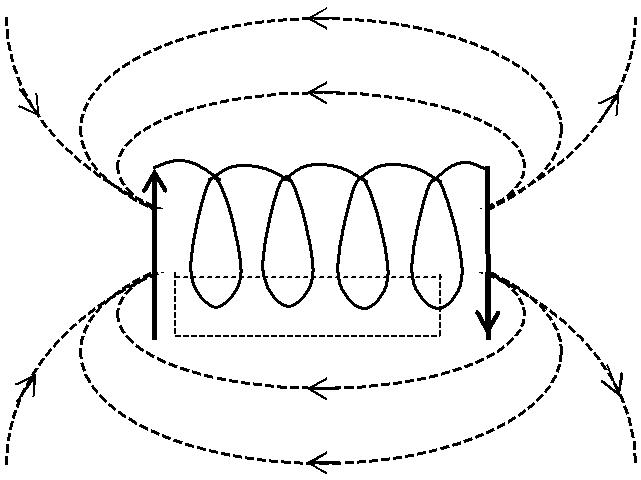 Среднее напряжение определяется отношением времени на формы волны к периоду импульса. Изменения длительности импульса и механической нагрузки соленоида вызывают изменение среднего тока, протекающего через соленоид. Средний ток указывает на величину движения соленоида и, следовательно, на давление и расход жидкости.
Среднее напряжение определяется отношением времени на формы волны к периоду импульса. Изменения длительности импульса и механической нагрузки соленоида вызывают изменение среднего тока, протекающего через соленоид. Средний ток указывает на величину движения соленоида и, следовательно, на давление и расход жидкости.
Взаимосвязь между перемещением соленоида и средним током для конкретной формы сигнала ШИМ устанавливается с помощью характеристики . Хотя это правда, что магнитная сила напрямую связана с током, протекающим через соленоид, фактическая механическая сила и движение не так тесно связаны, поскольку они зависят от конструкции соленоида и характера нагрузки. Таким образом, требуется характеристика, чтобы соотнести средний ток с открытием соленоида.
Например, коэффициент ШИМ должен быть увеличен при первом включении соленоида для преодоления статического трения. Как только статическое трение преодолевается, используется другое соотношение ШИМ для его перемещения внутрь и наружу.
Измерение тока через катушку
Таким образом, ток является важным показателем состояния соленоида. Самый эффективный метод измерения тока соленоида — это измерение напряжения на резистивном шунте, подключенном последовательно с соленоидом, батареей и переключателем.Существует несколько различных способов настройки этой последовательной цепи для переключения и измерения напряжения.
Датчик тока низкой стороны с приводом высокого давления
Схема на Рисунке 1 показывает переключатель, подключенный к стороне высокого напряжения (незаземленной) батареи последовательно с катушкой соленоида и заземленным резистивным шунтом. Перевернутый диод подключен к катушке для фиксации (т. Е. Короткого замыкания) индуктивного напряжения, генерируемого катушкой, когда ток отключается от .Использование заземления для шунта позволяет использовать недорогой операционный усилитель с разными характеристиками синфазного сигнала в электронном блоке управления (ЭБУ) для измерения напряжения на шунте.
Рис. 1. Электронный блок управления с переключением на стороне высокого и низкого давления.
При рассмотрении этого подхода проектировщик должен учитывать следующие недостатки:
- Рециркулирующий ток соленоида не учитывается при измерении, поэтому эта схема обеспечивает неточное измерение среднего тока через катушку соленоида.Ток рециркуляции соленоида может помочь в обнаружении состояния соленоида; если некоторые из обмоток начали закорачиваться, состояние можно увидеть, измерив пассивно контролируемый рециркуляционный ток.
- Поскольку переключатель находится в верхнем положении, его дороже покупать и ездить. Привод PWM требует тщательного преобразования уровня между логическим выходом микроконтроллера и вентилем.
- Требуется дополнительная схема для обнаружения короткого замыкания на землю, поскольку токи короткого замыкания не проходят через шунт.Повреждение проводки и полевого транзистора может произойти, если короткое замыкание на землю (рис. 1) не обнаружено.
- Измерение может быть нестабильным, потому что на практике заземление не является идеальным универсальным соединением , графически отображенным как маленький перевернутый треугольник. В реальном приложении «земля» на самом деле не может быть заземлением . Падения напряжения, вызванные токами между землей операционного усилителя и заземлением шунта, могут вызвать значительные ошибки.
Измерение тока на стороне высокого давления с помощью переключателя на стороне низкого давления
Лучшим методом управления соленоидом является использование переключателя с заземлением (рис. 2), что позволяет использовать менее дорогой переключатель низкого напряжения.
Возможна значительно лучшая диагностика, так как в измерение включен рециркуляционный ток соленоида. Кроме того, привод дешевле, потому что нет необходимости выполнять преобразование уровня в ворота.
Рис. 2. Электронный блок управления с переключением на стороне низкого давления и датчиком высокого давления.
Однако усилитель должен иметь высокий уровень подавления синфазного сигнала и должен выдерживать значительное синфазное напряжение (CMV). Уровень напряжения на шунте в этом примере варьируется от напряжения батареи до падения напряжения батареи и диода.Вот объяснение: когда переключатель замкнут, уровень синфазного напряжения на шунте остается на уровне напряжения батареи с низким сопротивлением. Когда переключатель размыкается, напряжение на соленоиде меняется на противоположное из-за индуктивности соленоида и заставляет уровень синфазного напряжения включать падение ограничивающего диода — пока протекает переходный ток — перед установкой на напряжение батареи.
Важным преимуществом этого метода возбуждения является то, что он позволяет обнаруживать короткое замыкание на землю, потому что ток на стороне высокого напряжения протекает через шунт, как показано на рисунке 2.
Ключевой проблемой при использовании этого метода измерения тока является то, что сторона высокого напряжения батареи всегда подключена к соленоиду. Это может привести к неожиданному переключению соленоида при периодическом замыкании на массу. Кроме того, постоянное наличие напряжения на соленоиде может со временем вызвать чрезмерную коррозию.
Измерение тока на стороне высокого давления с помощью переключателя на стороне высокого давления
Конфигурация, которая сводит к минимуму возможность неожиданного срабатывания соленоида и чрезмерной коррозии, показана на рисунке 3, где и переключатель, и шунт подключены со стороны высокого напряжения.Это снимает напряжение батареи с соленоида, когда переключатель выключен , предотвращая повреждение от потенциальных коротких замыканий на землю, и позволяет включить рециркулирующий ток в измерение. Напряжение аккумулятора снимается с нагрузки, когда переключатель разомкнут, поэтому коррозионные эффекты, вызванные перепадом напряжения, устраняются.
Рисунок 3. Электронный блок управления с электромагнитным клапаном на стороне низкого давления и переключением и датчиком высокого давления.
В этом случае, однако, изменение напряжения на соленоиде при размыкании переключателя вызовет гораздо более широкий разброс синфазного напряжения, от напряжения на высокой стороне батареи до падения напряжения на одном диоде ниже земли (обратное напряжение ограничено зажимной диод).Таким образом, усилитель, используемый в этом приложении, должен обеспечивать точное измерение шунтирующего напряжения (тока), игнорируя большие, быстрые колебания синфазного напряжения, когда переключатель выходит из положения .
Как и в случае с переключением на стороне низкого напряжения и конфигурацией считывания на стороне высокого напряжения (Рисунок 2), можно измерить замыкание на землю, поскольку весь ток соленоида со стороны высокого напряжения протекает через шунт, как показано на Рисунке 3.
Простая схема измерения тока на стороне высокого давления
К счастью, дифференциальный усилитель с однополярным питанием AD8200 со всеми необходимыми для этого приложения свойствами — в едином корпусе ИС — можно приобрести у Analog Devices.На рисунке 4 показан пример применения AD8200 в ЭБУ для измерения тока на стороне высокого напряжения в этом типе приложений. Здесь AD8200 используется для усиления и фильтрации небольшого дифференциального напряжения от шунта, подавляя при этом большие синфазные колебания, упомянутые выше. AD8200 можно использовать в любой из конфигураций, показанных ранее.
Рис. 4. Электронный блок управления, использующий AD8200, с соленоидом на стороне низкого давления и переключением и измерением на стороне высокого давления.
AD8200 использует один источник питания +5 В и имеет диапазон входного синфазного напряжения от –2 В до +24 В с сбросом нагрузки до +44 В.Если требуется более высокий синфазный диапазон, рекомендуется использовать другой член семейства AD8200, например AD8205, с диапазоном CMV от –2 В до +65 В и коэффициентом усиления 50; или AD8206 с диапазоном CMV от –2 В до +65 В и коэффициентом усиления 20 (такое же усиление, как у AD8200).
Рисунок 5. Функциональная блок-схема AD8200.
На рис. 5 представлена функциональная блок-схема внутренней проводки AD8200. Прежде чем разрабатывать дифференциальный усилитель с использованием недорогого операционного усилителя и некоторых внешних резисторов, примите во внимание, что для достижения характеристик, необходимых для измерения тока соленоида с достаточной точностью для приложения управления, требуется схема, построенная с резисторами, которые точно согласованы с точностью до 0.01%. AD8200 имеет внутренние резисторы с лазерной подстройкой, которые обеспечивают такой уровень точности при работе как с переменным, так и с постоянным напряжением. Типичный дрейф смещения и усиления в корпусе SOIC составляет 6 мкВ / ° C и 10 ppm / ° C соответственно. Устройство также обеспечивает минимальное подавление синфазного сигнала 80 дБ от постоянного тока до 10 кГц.
Помимо поставки в корпусе SOIC, AD8200 также доступен в форме кристалла. Оба варианта корпуса рассчитаны на широкий диапазон температур, что делает AD8200 хорошо подходящим для использования во многих автомобильных и промышленных платформах.Корпус SOIC рассчитан на диапазон от –40 ° C до + 125 ° C, а матрица — от –40 ° C до + 150 ° C.
AD8200 также имеет доступный извне резистор 100 кОм на выходе предусилителя, который можно использовать с внешней емкостью для фильтров нижних частот, а также с внешними резисторами для установления коэффициентов усиления, отличных от предварительно установленного коэффициента усиления 20.
Приложение
Механическая коробка передач
В более старом методе управления точками переключения передач использовались сложные гидравлические цепи, зависящие от скорости.Переключение происходило за счет изменения гидравлического давления в сложном корпусе клапана. Гидравлическое давление регулировалось регулятором, прикрепленным к выходному валу. Центробежная сила перемещала регулятор, выпуская трансмиссионное масло и увеличивая давление в корпусе клапана. Метод адаптации к изменяющимся условиям движения обычно заключался в принудительном переключении трансмиссии на пониженную передачу при сильном ускорении или нагрузке с помощью механических приводов.
Когда водителю требовалось большее ускорение, требование обычно передавалось через механизм переключения на пониженную передачу, состоящий из стержня, идущего от рычага управления дроссельной заслонкой в моторном отсеке к стороне трансмиссии.Шток перемещал рычаг, перекрывая ряд каналов в корпусе дроссельной заслонки. Это заставляло трансмиссию переключаться на пониженную передачу при резком ускорении, пока на скорости регулятор не перекрыл механизм понижающей передачи.
Адаптация к изменениям нагрузки осуществлялась с помощью модулятора вакуума. С увеличением нагрузки на двигатель изменение вакуума заставляло шток входить или выходить из корпуса клапана, изменяя точку переключения трансмиссии и скорость переключения. Несмотря на то, что эти методы управления точками переключения передач и плавностью переключения передач работали, мало что можно было сделать для настройки этих параметров для более изменчивых условий из-за характеристик механической системы, используемой для управления ими.