Разность потенциалов в физике это: 30. Потенциал. Разность потенциалов. Потенциальность электрического поля. Работа электрического поля.

Разность потенциалов электрического поля в физике

Разность потенциалов электрического поля

Потенциал электростатического поля в данной точке численно равен работе, которую совершают силы поля при перемещении единичного положительного заряда из данной точки в бесконечность.
То есть

где — потенциал, — работа, — положительный заряд.

Потенциал — величина скалярная. Потенциал считается положительным, если перемещение положительного единичного заряда из данной части поля в бесконечность совершается силами поля, и отрицательным, если силы поля препятствуют такому перемещению.

Поскольку работа в силовом поле равна разности потенциальных энергий двух точек поля, между которыми осуществляется перемещение, то

Работа равна разности энергий конечной и начальной точек, взятой с противоположным знаком: Потенциальная энергия точки в бесконечности принята равной нулю: — потенциальная энергия рассматриваемой точки поля. Выбор нулевого уровня потенциала произволен, так как физический смысл имеет не сам потенциал, а разность потенциалов, или напряжение поля.

Разность потенциалов (напряжение) между двумя точками поля равна отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:

(3.3)

Поскольку работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, совершаемую полем по перемещению единичного заряда.

Если имеется несколько точечных зарядов, то потенциал поля в некоторой точке пространства определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в этой точке:

(3.4)

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, для любых точек которой разность потенциалов равна нулю. Это значит, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряжённости электрического поля перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.
Вектор напряжённости (как и сила ) перпендикулярен эквипотенциальным поверхностям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.

В однородном электрическом поле напряжённость во всех точках одинакова, и работа по перемещению заряда параллельно на расстояние между двумя точками с потенциалами и равна:

(3.5)

или

(3.6)

Таким образом, напряжённость поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.

Единицей напряжения (разности потенциалов) является вольт. Согласно формуле (3. 3), Разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.

Эта лекция взята со страницы лекций по всем темам предмета физика:

Предмет физика

Возможно эти страницы вам будут полезны:

Потенциал электростатического поля и разность потенциалов

Потенциал электростатического поля и разность потенциалов

Подробности

Просмотров: 590

«Физика — 10 класс»

Обладает ли электрическое поле энергией? В чём это выражается?

Как рассчитать энергию поля?

В механике взаимное действие тел друг на друга характеризуют силой и потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряжённость поля — это силовая характеристика. Теперь введём энергетическую характеристику — потенциал.

Потенциал поля.

Работа любого электростатического поля при перемещении в нём заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля.

На замкнутой траектории работа электростатического поля всегда равна нулю.

Поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю, называют потенциальным.

Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.

Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А = — (W_п2 — W_п1) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой (14.14).

Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля (см. формулу (14.14)), так и для неоднородного. Следовательно, отношение потенциальной энергии к заряду не зависит от помещённого в поле заряда.

Это позволяет ввести новую количественную характеристику поля — потенциал, не зависящую от заряда, помещённого в поле.

Для определения значения потенциальной энергии, как мы знаем, необходимо выбрать нулевой уровень её отсчёта. При определении потенциала поля, созданного системой зарядов, как правило, предполагается, что потенциал в бесконечно удалённой точке поля равен нулю.

Потенциалом точки электростатического поля называют отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.

Согласно данному определению потенциал равен:

Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:

Напряжённость поля — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.

Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине (см. рис. 14.31), то согласно формулам (14.14) и (14.15) потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:

Разность потенциалов.

Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю.

Изменение потенциала не зависит от выбора нулевого уровня отсчёта потенциала.

Так как потенциальная энергия Wn = дчр, то работа сил поля равна:

А = — (W_п2 — W_п1) = -q(φ₂ — φ₁) = q(φ₁ — φ₂) = qU.         (14.17)

Здесь

U = φ₁ — φ₂ —         (14.18)

разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.

Разность потенциалов называют также напряжением.

Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:

Если за нулевой уровень отсчёта потенциала принять потенциал бесконечно удалённой точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.

Единица разности потенциалов.

Единицу разности потенциалов устанавливают с помощью формулы (14.19). В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах.

Разность потенциалов между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В): 1 В = 1 Дж/1 Кл.

Выразим единицу разности потенциалов через основные единицы СИ. Так как

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Электростатика — Физика, учебник для 10 класса — Класс!ная физика

Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

Элеком37, Потенциал. Разность потенциалов. Напряжение. физика.

Потенциал. Разность потенциалов. Напряжение.

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом
поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно
бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

          φ – потенциал электрического поля.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

Потенциал и разность потенциалов. Связь между напряженностью электрического поля и разностью потенциалов. Конденсаторы. | Поурочные планы по физике 8 класс

Потенциал и разность потенциалов. Связь между напряженностью электрического поля и разностью потенциалов. Конденсаторы.

27.02.2014

11083

0

Цель: доказать, что
электростатическое поле потенциально. дать понятие потенциала электрического
поля. Побуждать учащихся к
преодолению трудностей в процессе умственной деятельности, воспитать интерес к
физике.

Ход урока

I. Организационный момент

II.    Проверка
домашнего задания

1. Как обнаружить существование электрического поля?

2. Дайте определение напряженности электрического
поля. Какова единица напряженности.

3. Как напряженность электрического заряда зависит от
расстояния?

4. Где начинается и где заканчивается линия
напряженности электростати­ческого поля?

5. Какое электрическое поле называется однородным?

6. Сформируйте принцип суперпозиции электростатических
полей.

III.  Физический
диктант.

Электрическое поле

См. раздел «Самостоятельные и контрольные работы»

. Ответы: 1. Вещество, поле. 2. Электростатическим.
3- Заряд. 4. Действие на электрические заряды. 5. Кулоновская.
6. Напряженность электрического поля.

IV.Изучение нового материала

При перемещении тока между двумя точками в
гравитационном поле работа силы тяжести не зави­сит от формы траектории его
движения. Силы гравитационного и электрическо­го взаимодействия имеют
одинаковую зависимость от расстояния, и векторы сил направлены вдоль прямой,
соединяющей точечные тела.

Можно предположить, что при перемещении заряда в
электростатическом поле из одной точки в другую работа сил электрического поля
не зависит от формы.

Пусть q перемещается в электрическом поле из т. М в т. N по
траектории MBN, при этом совершается работа А_г Теперь вернем заряд в начальную
точку по траектории NCM. Внешние силы должны совершить работу А₂, а работа поля
А₂ — -А; тогда А- А, + А₂ => A — 0.

Работа электрических сил по любой замкнутой траектории
равна нулю.

Пусть заряд q перемещается в однородном
электрическом поле из т. В в т. Д

Если работа не зависит от формы траектории, то работу
мож­но найти как разность потенциальных энергий в начале и в конце траектории.

Потенциалом электрического поля в данной точке
называется отношение потенциальной энергии, которой обладает пробный заряд,
помещенный в дан­ную точку поля, к этому заряду Тогда: А = q (e, — е₂).

В международной системе единиц, единицей потенциала
служит [В] вольт.

1В — это разность потенциалов двух точек
электрического поля, при переходе между которыми заряда в I Кл поле совершает работу 1 Дж.

Поверхность, во всех точках которой потенциал
электрического поля имеет одинаковые значения, называется эквипотенциальной
поверхностью.

Между двумя любыми точками на эквипотенциальной
поверхности раз­ность потенциалов равна нулю, поэтому работа сил электрического
поля при любом перемещении заряда эквипотенциальной поверхности равна нулю.
Значит, вектор силы F перпендикулярен вектору
перемещения. Линии на­пряженности электростатического поля перпендикулярны
эквипотенциаль­ной поверхности.

Эквипотенциальными поверхностями точечного заряда
являются сферы, в центре которых расположен заряд.

Потенциал — величина скалярная.

Для накопления значительных разноименных электрических
зарядов приме­няются конденсаторы.

Конденсаторы — это система из двух проводников
(обкладок), разделенных диэлектриком, толщина которого мала по сравнению с
линейными размерами проводников. Плоский конденсатор представляет собой две
плоские металличес­кие пластины, разделенные слоем диэлектрика. Напряженность
поля между пластинами . Физическая величина, определяемая отношением заряда q к

разности потенциалов Де между обкладками конденсатора,
называется электроемкостью

Единица электроемкости в системе СИ — фарад  Ф

Электроемкость плоского конденсатора можно увеличить
путем увеличения площади обкладок, уменьшая расстояние между ними и применяя
диэлектрики с большими значениями диэлектрической проницаемости.

Электроемкость уединенной среды радиусом R:

Электроемкость шара зависит от его радиуса и не
зависит от заряда на его поверхности.

1Ф — электроемкость очень большой величины: такой
электроемкостью об­ладает сфера 9 • 10¹¹ км, что в 13 раз превышает
радиус Солнца.

Виды конденсаторов: воздушный,
бумажный, слюдяной, электростатический.

Назначение:

1. Накапливать на короткое время заряд или энергию для
быстрого измене­ния потенциала.

2. Не пропускать постоянный ток.

3. В радиотехнике — колебательный контур, выпрямитель.

4. Фототехника.

V. Повторение изученного

1. Что понимают под работой электрического поля?

2. Как понимать выражение «электрическое поле
потенциально»?

3. Какие поля называют потенциальными?

4. Как связанно изменение потенциальной энергии с
работой?

5. Чему равна потенциальная энергия заряженной частицы
в однородном поле?

6. От чего зависит работа по перемещению заряда из
одной точки поля в другую?

7. Чему равна работа по перемещению заряда по
замкнутому контуру?

8. Напишите формулу работы по перемещению заряда в
электрическом поле.

 9. Что
называется потенциалом электрического поля?

10. Какая формула выражает смысл этого понятия?

11. Что называют разностью потенциалов между двумя
точками поля?

12. Какая формула выражает смысл этого понятия?

13. Для чего предназначены конденсаторы?

14. Как устроен конденсатор?

15. Что называется электроемкостью?

16. В каких единицах выражается электроемкость?

17. От чего зависит электроемкость конденсатора?

Домашнее задание

§  33-34
Упражнение 16

Потенциал электростатического поля. Разность потенциалов

На прошлом уроке мы с вами говорили о том, что на помещённый
в электростатическое поле пробный заряд, будет действовать сила, под действием
которой заряд способен перемещаться вдоль линии напряжённости поля. Иными
словами, электростатическое поле способно совершать работу, значение которой
пропорционально величине переносимого заряда и зависит только от того, из какой
и в какую точку поля заряд переносится:

При этом на замкнутой траектории работа сил
электростатического поля равна нулю.

Напомним, что если работа сил поля не зависит от формы
траектории и на замкнутой траектории равна нулю, то такое поле называется потенциальными.
Следовательно, точечный заряд, находящийся в любой точке электростатического
поля, обладает потенциальной энергией взаимодействия с этим полем, значение
которой определяют относительно произвольно выбираемой нулевой точки (чаще
всего, это бесконечно удалённая точка поля). В нулевой точке потенциальную
энергию заряда в поле принимают равной нулю. Тогда потенциальная энергия
взаимодействия точечного заряда с электростатическим полем равна работе,
которую совершили бы силы поля при перемещении данного заряда из указанной
точки поля в нулевую точку:

Из этого определения следует, что величина потенциальной энергии
заряда в электростатическом поле пропорционально значению этого заряда:

Иными словами, если мы будем вносить в одну и туже точку
электростатического поля пробные заряды, значения которых будут отличаться в
два, три, четыре и так далее раз, то потенциальные энергии этих зарядов будут
отличаться во столько же раз.

Однако, отношение потенциальной энергии пробного заряда в
поле к значению этого заряда для данной точки поля остаётся неизменным:

Отношение потенциальной энергии пробного заряда,
помещённого в данную точку поля, к величине этого заряда, называется
потенциалом электростатического поля в данной точке пространства:

Обозначать потенциал мы будем греческой буквой «Фи» (φ).

Вы уже знаете, что силовой характеристикой электрического
поля является напряжённость. Потенциал же характеризует энергетическое
состояние поля в данной точке пространства.

Поскольку потенциальная энергия заряда в электростатическом
поле зависит от выбора нулевой точки, то эта зависимость сохраняется и для
потенциала. Если принять, что на бесконечно большом расстоянии от источника
поле отсутствует, то потенциал поля в данной точке численно равен работе,
совершаемой при перемещении пробного заряда из данной точки поля в бесконечность
(то есть в нулевую точку):

Найдём формулу, по которой можно рассчитать потенциал
электростатического поля, создаваемого точечным зарядом, на некотором
расстоянии от него. Для этого запишем формулу для определения работы
электростатического поля:

Здесь r — это расстояние от создающего поле заряда до
исследуемой точки поля. А модуль напряжённости поля прямо пропорционален модулю
этого заряда и обратно пропорционален квадрату расстояния между зарядом и
точкой, в которой определяют значение напряжённости:

Перепишем формулу для потенциала поля с учётом наших
рассуждений.

После упрощения, получим формулу, по которой можно рассчитать
потенциал электростатического поля точечного заряда на заданном расстоянии от
него. Из формулы видно, что знак заряда-источника поля определяет знак
потенциала этого поля.

По этой же формуле можно рассчитывать и потенциал поля,
создаваемого равномерно заряженной проводящей сферой в точках, находящихся вне
сферы. Для точек же, находящихся на поверхности и внутри сферы, в знаменателе
формулы «Эр малое» заменяется на радиус сферы:

Если электростатическое поле создаётся системой зарядов, то
имеет место принцип суперпозиции: потенциал такого поля в любой точке пространства
равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом
системы в отдельности:

Зная потенциал поля в данной точке, можно рассчитать
потенциальную энергию заряда, помещённого в эту точку:

На прошлом уроке мы с вами отмечали тот факт, что работа
сил электростатического поля по перемещению электрического заряда из начальной
точки в конечную равна изменению потенциальной энергии, взятому с обратным
знаком:

Давайте выразим потенциальную энергию через потенциалы поля в
соответствующих точках:

Подставим значения потенциальных энергий в формулу для работы.

Как видно из полученной формулы, работа поля по перемещению
заряда из одной его точки в другую пропорциональна значению переносимого заряда
и разности потенциалов начальной и конечной точек.

А теперь давайте разделим выражение для работы на величину
переносимого заряда q₀:

Скалярная физическая величина, численно равная отношению
работы сил поля по перемещению заряда между данными точками поля к величине
этого заряда, называется разностью потенциалов.

Как и изменение потенциальной энергии, разность
потенциалов не зависит от выбора нулевой точки.

Из определения следует, что единицей разности потенциалов в
СИ является Дж/Кл. Эта единица называется вольтом, в честь итальянского учёного
Алессандро Джузеппе Антонио Анастасио Джероламо Умберто Вольта.

1 В — это разность потенциалов между двумя такими точками
электростатического поля, при перемещении между которыми заряда в 1 Кл силами
поля совершается работа 1 Дж.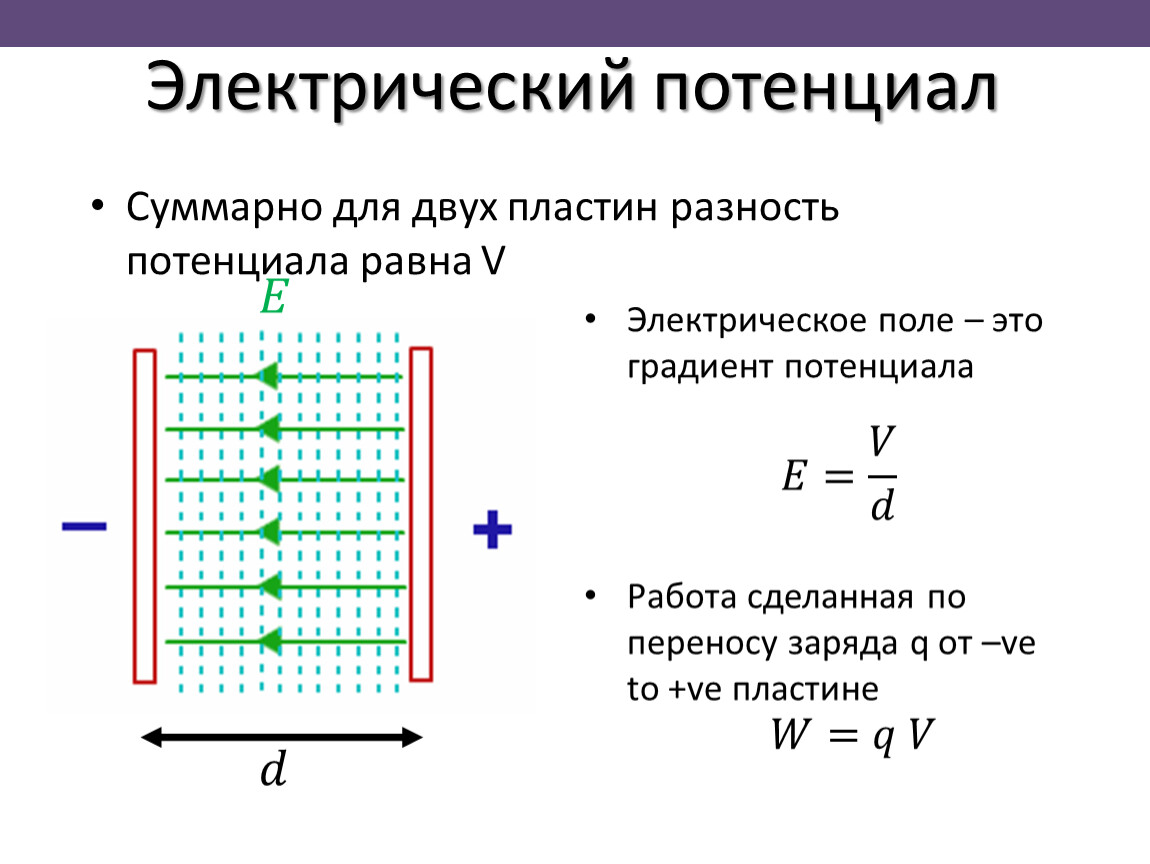

Как вы, наверное, догадались, разность потенциалов очень
часто называют напряжением.

То есть напряжение между двумя точками поля определяется
работой сил этого поля по перемещению заряда 1 Кл из одной точки в другую. В
электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.

Для закрепления нового материала, решим с вами несколько
задач. Задача 1. В центре проводящей сферы с равномерно распределённым
положительным зарядом в 45 нКл находится металлический шарик с отрицательным
зарядом, модуль которого равен 17 нКл. Определите потенциал электростатического
поля в точке, находящейся вне сферы на расстоянии 30 м от её центра.

Задача 2. Электрон влетает в однородное
электростатическое поле по направлению силовой линии. Определите потенциал точки
поля, в которой электрон поменяет направление движения, если в точке поля с
потенциалом 1 В его скорость равнялась 300 км/с.

Потенциальная энергия заряженного тела. Потенциал и разность потенциалов.

Электростатическое
поле — электрическое поле неподвижного заряда. Электрическая сила,
действующая на заряд, перемещает его, совершая работу. В однородном
электрическом поле Fэл = qE — постоянная величина

А₁₂ =
Fs ^.Cos (F,s) = qEΔd

А₂₃ = 0, т.к.  Cos 90^о = 0

А₃₄ =
— qEΔd,  т.к.  Cos 180^о
= -1

А₄₁ = 0, т.к.  Cos 270^о = 0

А₁₂₃₄₁ = А₁₂  + А₂₃  + А₃₄  + А₄₁ = 0

Работа электрического поля не зависит от формы траектории и на
замкнутой траектории равна нулю. Поля, обладающие таким свойством, называют потенциальными.
Потенциальный характер, в частности, имеет электростатическое поле точечного
заряда.

Электростатическая
энергия — потенциальная энергия системы заряженных тел (т.к. они
взаимодействуют и способны совершить работу).

А = qEΔd = qE(d₁ – d₂)
= — (qEd₂ – qEd₁)

Работу
потенциального поля можно выразить через изменение потенциальной энергии. Так
как работа поля не зависит от формы траектории, то  A = — ΔW_п
= — (W_п2 — W_п1) справедлива
для любого электростатического поля. Но только в случае однородного поля
потенциальная энергия выражается формулой W_п = qEd.
Если поле совершает положительную работу (вдоль силовых линий), то
потенциальная энергия заряженного тела уменьшается (но согласно закону
сохранения энергии увеличивается кинетическая энергия) и наоборот.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

— энергетическая
характеристика электростатического поля.

— равен отношению
потенциальной энергии заряда в поле к этому заряду.

— скалярная
величина, определяющая потенциальную энергию заряда в любой точке эл. поля.

φ = W / q = const     [φ] = Дж / Кл =
1В

φ – скаляр; φ >
0, если +q,  φ < 0, если –q.

φ = ± φ₁
± φ₂ ± φ₃     принцип
суперпозиции.

Величина
потенциала считается относительно выбранного нулевого уровня.

РАЗНОСТЬ ПОТЕНЦИАЛОВ (или иначе НАПРЯЖЕНИЕ)

— это разность
потенциалов в начальной и конечной точках траектории заряда.

А = -(W_п2 — W_п1) = -(q φ₂
 — qφ₁) = q(φ₁  — φ₂)

φ₁  — φ₂ = U = A / q;  [U] = Дж / Кл = В

Напряжение U между двумя точками равно разности
потенциалов этих точек и равно работе поля по перемещению единичного заряда.

СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ

A = q E Δd; A = qU => E = U / Δd.      [E] = B / м   

Чем меньше
меняется потенциал на отрезке пути, тем меньше напряженность поля. Напряженность электростатического поля направлена в сторону уменьшения
потенциала.

ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ

— поверхности,
все точки которых имеют одинаковый потенциал

для однородного
поля — это плоскость                                               для поля
точечного заряда — это концентрические

                                                                                                                                                                                        сферы.

Эквипотенциальные поверхности
перпендикулярны силовым линиям и  φ₁
= φ₂ = φ_{3  = …}  

Эквипотенциальная
поверхность имеется у любого проводника в электростатическом
поле, т.к. силовые линии перпендикулярны поверхности проводника. Все точки
внутри проводника имеют одинаковый потенциал. Напряженность внутри проводника равна
0, значит и разность потенциалов внутри равна 0.

Разность потенциалов — Энциклопедия по машиностроению XXL

Температуру металлов измеряют обычно при помощи термопары. Принцип измерения температуры следующий. Термопара состоит из двух проволок разных металлов, сваренных в одном конце (так( называемый горячий спай ), два других конца подключены к гальванометру или другому прибору (например, потенциометру), измеряющему ток очень малой разности потенциалов .  [c.114]

При разности потенциалов на электродах происходит ионизация межэлектродного промежутка. Когда напряжение достигнет определенного значения, в среде между электродами образуется канал проводимости, по которому устремляется электрическая энергия в виде импульсного искрового или дугового разряда. При высокой концентрации энергии, расходуемой за 10″ —10 с, мгновенная плотность тока в канале проводимости достигает 8000—10 ООО А/мм , в результате чего температура на поверхности обрабатываемой заготовки-электрода возрастает до 10 ООО—12 ООО °С. При этой температуре мгновенно оплавляется и испаряется элементарный объем металла и на обрабатываемой поверхности заготовки образуется лунка. Удаленный металл застывает в диэлектрической жидкости в виде гранул диаметром 0,01—0,005 мм.  [c.401]

Если А /iq, то в этих условиях электроны быстро проходят через слой окисла благодаря туннельному эффекту, оставляя позади себя ионы металла и переводя хемосорбированный кислород в ионы O , а в пленке устанавливается разность потенциалов V, которая считается постоянной, и поле с напряженностью F = V/h.  [c.51]

Величина С выражает емкость конденсатора, который при разности потенциалов между обкладками Va несет заряд, равный заряду двойного слоя.  [c.167]

Общий сложный процесс электрохимической коррозии металла состоит из последовательных более простых процессов (стадий) анодного, катодного и процесса протекания электрического тока. Установившаяся скорость этого сложного процесса, соответствующая силе коррозионного тока /, определяется торможением протекания тока на отдельных стадиях, т. е. сопротивлением его отдельных стадий (7 , Рд, Р ), на преодоление которых расходуется начальная разность потенциалов электродных процессов обр =  [c.274]

Для величины максимальной разности потенциалов между основным металлом и центром включения получаем  [c.275]

Электрический ток передается в металлах движением электронов, образующих электронный газ. При отсутствии внешнего электрического поля электроны движутся во всех направлениях, и это движение электронов проводимости носит неупорядоченный характер. Под влиянием же разности потенциалов, приложенной к металлу извне, появляется направленное движение электронов. Движение электронов и осуществляет передачу электричества. Чем слабее электроны связаны с атомами, тем больше будет электропроводность металла.  [c.10]

При погружении металла в раствор электролита между поверхностью металла и электролитом возникает разность потенциалов, называемая потенциалом электрода.  [c.19]

Из рассмотренной схемы взаимодействия между металлом и электролитом (см. рис. 8), вытекает, что причиной возникновения электродных потенциалов является перенос ионов из металла в раствор и обратно. Электродные потенциалы являются энергетической характеристикой двойных слоев, представляя собой меру энергии, нужную для перехода ионов в раствор или в обратном направлении. Когда двойной электрический слой достигает разности потенциалов, при которой энергетический уровень ионов в металле и растворе сравняется, процесс перехода ионов прекращается (устанавливается равновесие).  [c.19]

При погружении в раствор электролита двух разных металлов, соединенных проводником, по последнему проходит ток вследствие наличия в образовавшемся гальваническом элементе электродвижущей силы. Каждый гальванический элемент характеризуется определенной электродвижущей силой 7, численно равной разности потенциалов между его электродами в разомкнутом состоянии, т. е. при условии, что сила тока в цепи равна нулю,  [c.27]

Определение потенциала отдельного электрода производят, как это описано выше, путем измерения разности потенциалов гальванического элемента, составленного из электрода сравнения с точно известным и постоянным значением потенциала и электрода, потенциал которого определяется. При измерении потенциалов через измеряемую цепь не должен проходить электрический ток. Это реализуется в компенсационной электрической схеме, на которой основано действие всех потенциометров.  [c.28]

Схема изменения разности потенциалов в коррозионном элементе прн его замыкании показана на рис. 12. На рис. 13 даны типичные кривые изменения потенциала анода и катода короткозамкнутого коррозионного элемента во времени.  [c.32]

Наиболее простой вид имеет поляризационная диаграмма в случае, когда не тормозится ни анодный, ни катодный процесс (рис. 19, а). Разность потенциалов между действующими анодом и катодом остается постоянной во времени, а величина коррозионного тока определяется омическим сопротивлением цепи. Это — случай омического контроля процесса.  [c.50]

Это уравнение показывает, что скорость электрохимической коррозии будет тем больше, чем больше начальная разность потенциалов (э. д. с.) коррозионного элемента, чем меньше сопротивление системы и чем меньше поляризуемости электродов.  [c.54]

Различие в природе электролитов может создать разность электродных потенциалов металлов в 0,3 в. Имеются указания, что различие в степени аэрации вызывает еще большую э. д. с., равную 0,9 в. Все эти причины, а в ряде случаев действие находящихся в грунте микроорганизмов способствуют разрушению подземных металлических сооружений. Развитию коррозии подземных сооружений также способствует наличие на их поверхности прокатной окалины. В отдельных случаях разность потенциалов между окалиной и основным металлом достигает 0,45 в. На процессы подземной коррозии оказывают влияние самые разнообразные факторы, к числу которых относятся, помимо указанных выше, температура, электропроводность, воздухопроницаемость грунта, состав грунтовых вод и др. Поэтому очень трудно выделить и изучить влияние каждого фактора в отдельности.  [c.184]

В начальный момент ( 3 О) разность потенциалов электродов наибольшая.  [c.31]

По нихромовому стержню диаметром й = Ъ мм и длиной ( = 420 мм проходит электрический ток. Разность потенциалов на концах стержня u=IO В.  [c.27]

На диаграмме рис. 6.1 показано распределение потенциала Е(Т) для пары проводников из разных материалов А и В, спаи которых имеет температуру Гг, а оба свободных конца — одинаковую температуру Го. Рабочий спай и свободные концы находятся в области с постоянной температурой, а оба проводника проходят через одинаковое температурное поле. Для измерения термоэлектрической разности потенциалов между свобод-  [c.268]

Е — разность потенциалов на концах нагревателя.  [c.520]

Вернемся к частному случаю, когда между основанием газожидкостного слоя и его свободной поверхностью поддерживается постоянная разность потенциалов (т. е. газожидкостная система находится в поле плоского конденсатора), и проанализируем условие устойчивого равномерного всплывания пузырьков газа. В рассматриваемом случае 3=0, у = 9. Условие существования режима равномерного всплывания пузырьков (5. 7. 9) перепишем в следующем виде  [c.234]

При трансформаторном типе связи в одной подсистеме включается зависимый источник разности потенциалов. Этот источник зависит от разности потенциалов на зависимом источнике потока, установленном в  [c. 85]

При г и р а т о р н о м типе связи в обеих физических подсистемах включаются зависимые источники одного вида либо типа разности потенциалов, либо типа потока. Источники разности потенциалов зависят от потока через источник в другой подсистеме (рис. 2.15, а), источники потока зависят от разности потенциалов на источнике в другой подсистеме (рис. 2.15,6). Такой вид связи характерен при взаимодействии механической и гидравлической или пневматической подсистем.  [c.87]

Особенность строения металлических веществ заключается в том, что ОИН все построены в основном из таких атомов, у которых внешние электроны слабо связаны с ядром. Это обусловливает и особый характер химического взаимодействия атомов металла, и металлические свойства. Электроны имеют отрицательный заряд, и достаточно создать ничтожную разность потенциалов, чтобы началось перемещение электронов по направлению к положите.льио заряженному полюсу, создающее электрический ток. EioT почему металлы пв-ляются хорошими проводниками электрического тока, а неметаллы ими нэлектрическим свойством металлов является также и то, что с повышением температуры у всех без исключения металлов элокт]) -проводность уменьшается.  [c.14]

В установках для электромно-лучевой сварки электроны эмит-тируются на катоде / электронной пушки формируются в пучок электродо.м 2, расположенным неносредственно за катодом ускоряются под действием разности потенциалов между катодом и анодом 3, составляющей 20—150 кВ и выше, затем фокусируются в виде луча и направляются специальной отклоняющей магнитной системой 5 па обрабатываемое изделие в. На формирующий электрод 2 подается отрицательный или нулевой по отношению к катоду потенциал. Фокусировкой достигается высокая удельная мощность (до 5-10 кВт/м и выше). Ток электронного луча невелик (от нескольких миллиампер до единиц ампер).  [c.203]

Схема установки для электронно-лучевой обработки (электронная пушка) показана на рис. 7.14. В вакуумной камере 1 установки вольфрамовый катод И, питаемый от исючкика тока, обеспечивает эмиссию свободных электронов. Электроны формируются в пучок специальным электродом и под действием электрического поля, создаваемого высокой разностью потенциалов между катодом И анодом 10, ускоряются в осевом направлении. Луч электронов проходит систему юстировки 9, диафрагму 8, корректор изображения 7 и систему магнитных линз 6, которые окончательно  [c.413]

Гальванический элемент принято (Международной конвенцией в Стокгольме в 1953 г.) записывать так, чтобы электрод сравнения всегда был слева, а за э. д. с. ячейки Е принимать разность потенциалов правого и левого электродов, т. е. = — Vn- Если левым электродом служит стандартный водородный электрод, (pH, = 1 атм, ан+ = 1), то э. д. с. элемента равналю величине и по знаку электродному потенциалу правого (исследуемого) электрода по водородной шкале, т. е.  [c.150]

Источником э. д. с. между металлами при V (0), по теории А. Н. Фрумкина, могут быть контактная разность потенциалов, а также адсорбция ионов и полярных молекул. Разность потенциалов нулевых зарядов двух металлов должна быть приблизи-  [c.162]

Все это справедливо и для электрохимического коррозионного процесса, протекание которого аналогично работе короткозамкнутого гальванического элемента возникающий из-за наличия начальной разности потенциалов катодной и анодной реакций Е обр = ( Joep—( а)обр процесс электрохимической коррозии сопровождается перетеканием электрического тока от анодных участков к катодным в металле и от катодных участков к анодным в электролите, которое вызывает поляризацию на обоих участках. Эти явления дополнительно тормозят протекание коррозионного процесса.  [c.193]

Описанный выше метод может быть использован и при наличии поляризационных кривых, полученных упрощенным методом, при котором измеряют силу тока / и разность потенциалов ДУ между двумя одинаковыми электродами из одного и того же металла, помещенными в электролит и одновременно катодно- и анодно-поляризуемыми от внешнего источника тока. Измерение омического сопротивления электролита исследуемой двухэлектродной системы / внутр с помощью мостика переменного тока позволяет определить омическое падение потенциала в электр05ште измерительной ячейки АУ = внутр/ и рассчитать поляризационный сдвиг потенциалов  [c.286]

Анализ субкритического развития трещины начинается с определения момента ее старта, который контролируется параметром Ji . Существуют различные методы испытаний для определения he. Прямые методы разности потенциалов, разгрузки, акустической эмиссии позволяют с помощью одного образца непосредственно фиксировать момент старта трещины и величину бхс, далее посредством пересчета определять he [134, 135, 219]. Недостатки этих методов заключаются в том, что приходится использовать довольно сложное оборудование кроме того, имеются материалы, у которых трудно дифференцировать изменение податливости образца, обусловленное текучестью или стартом трещины [13. Косвенные методы (испытания по ГОСТ 25. 508—85 [143], ASTM Е399—74 [419], методы Гриффитса [330], Бигли—Лэндеса [350]) определения he требуют испытаний нескольких образцов с различными уровнями нагружения. В результате этих испытаний строится /н-кривая. Далее путем графических построений определяется величина he.  [c.260]

Так как электродные потенциалы играют очень большую роль в коррозионных процессах, то весьма важно знать значения этих потенциалов, а отсюда и действигельную разность потенциалов между металлом и раствором электролита. Однако абсолютные значения потенциалов до сих пор не удалось определить. Нет достаточно надежных методов экспериментального измерения или теоретического вычисления абсолютных значений потенциалов, и вместо абсолютных электродных потенциалов измеряют относительные, пользуясь для этого так называемыми электродами сравнения. Этот принцип определения значений электродных потенциалов основан на том, что если определить э. д. с. коррозионных элементов, составленных последовательно из большинства технических металлов и какого-нибудь одного, одинакового во всех случаях электрода, потенциал которого условно принят за нуль, то измеренные э. д. с. указанных элементов позволят сравнить электрохимическое поведение различных металлов. В качестве основного электрода сравнения принят так называемый стандартный водородный электрод, представляющий собой электрод из черненой (платинированной) платины, погруженный в раствор кислоты с активностью ионов Н+, равной 1 г пон1л. Через раствор продувается водород под давлением 1,01.3-10 н м -. Пузырьки водорода адсорбируются на платине, образуя как бы водородную пластинку, которая, подобно металлу, обменивает с раствором положительные ионы. На рис. 10 показано, как составляется цепь из водородного электрода и другого электрода при измерении относительных электродных потенциалов.  [c.23]

При применении бронз следует иметь в виду, что контакт бронз с другими цветными металлами (с цинком, свинцом, алюминием и др.) нежелателен вследствие возникновения больщой разности потенциалов между ними. По этой причине не рекомендуется пайка бронзы оловом или третником. Недопустим также контакт бронзы с углеродистой сталью.  [c.252]

Так как частные производные каждой из рассмотренных характеристических функций U V, S), / р, S), F T, V) и Z(/j, Т) полностью определяют все термодинамические свойства системы, то эти функции по аналогии с механикой, где работа в поле постоянных сил числе1Шо равна разности потенциалов в начальной и конечной точках пути, называют термодинамическими потенциалами. Разность значений в двух состояниях любой из этих функций при обратимом процессе представляет собой полезную работу, совершенную системой.  [c.149]

Используя уравнения (5. 7. 1)—(5. 7. 6), можно решить задачу о стационарном одномерном изотермическом всплывании недефор-мируемых пузырей в слое несжимаемой жидкости при условии, что между основанием слоя и его свободной поверхностью поддерживается постоянной разность потенциалов Драсхода газа ( р = Рор5 -г р=сопз1 и электрических характеристик фаз. Одним из таких режимов является всплывание пузырей газа с постоянной скоростью и [80]  [c.230]

П.лотность заряда определялась по току насыщения, измеряемому при помощи массивного двойного зонда (способного выдержать воздействие потока твердых частиц и их отложение на его поверхности) с охлаяедаемыми водой медными электродами диаметром 19 мм и зазором 3 мм (разность потенциалов около 3 в). Ток 0,001—1,0 ма был измерен микроамперметром Кейтли. Зонд установлен таким образом, чтобы его рабочие поверхности были пара.члельны направлению струи. Эта мера позволяет уменьшить до минимума накопление твердых частиц на поверхности зонда. Перемещения зонда преобразовывались во временную зависимость для струи при помощи измерений скорости струи насадком полного давления и температуры газа термоэлектрическим зондом. Эти зонды перемещались вдоль оси струи. Температура твердых частиц измерялась пирометром.  [c.458]

Независимые источинки используются для моделирования постоянных воздействий на объект, например сила тяжести может быть отражена постоянным источником силы, напряжение нитаиия электронной схемы — источником типа разности потенциалов и т. д.  [c.75]

Разность электрических потенциалов

Когда мы поднимали объект против силы тяжести, применяя силу на расстоянии, мы действительно работали, чтобы передать этому объекту гравитационную потенциальную энергию. Та же концепция применима и к электрическим полям. Если вы перемещаете заряд против электрического поля, вы должны приложить силу на некотором расстоянии, поэтому вы совершаете работу и сообщаете ему электрическую потенциальную энергию. Работа, совершаемая на единицу заряда при перемещении заряда между двумя точками в электрическом поле, известна как разность электрических потенциалов , (В) .Единицами электрического потенциала являются вольты, где вольт равен 1 джоулю на кулон. Следовательно, если вы совершили работу в 1 Дж, перемещая заряд в 1 кулон в электрическом поле, разность электрических потенциалов между этими точками составила бы 1 вольт. Это дается:

В в этой формуле — это разность потенциалов (в вольтах), Вт — это работа или электрическая энергия (в джоулях), а q — ваш заряд (в кулонах). Давайте рассмотрим пример задачи.

Вопрос: Разность потенциалов 10.0 вольт существует
между двумя точками А и В на электрическом
поле. Какова величина заряда, который
требуется 2,0 × 10 ^–2 джоулей работы, чтобы переместить его из
от А до Б?

Ответ:

Когда имеешь дело с электростатикой, часто количество электрической энергии или работы, совершаемой над зарядом, составляет очень маленькую долю джоуля. Работать с такими малыми числами обременительно, поэтому физики разработали альтернативную единицу измерения электрической энергии и работы, которая может быть более удобной, чем джоуль.Эта единица, известная как электрон-вольт (эВ), представляет собой количество работы, совершаемой при перемещении элементарного заряда через разность потенциалов в 1 В. Таким образом, один электрон-вольт эквивалентен одному вольту, умноженному на один элементарный заряд (в кулонах): 1 эВ = 1,6*10 ^-19 Дж.

Вопрос: Заряд 2*10 ^-3 Кл проходит через разность потенциалов 10 вольт в электрическом поле. Какая работа в электрон-вольтах потребовалась для перемещения этого заряда?

Ответ:

Параллельные пластины

Если вы знаете разность потенциалов между двумя параллельными пластинами, вы можете легко рассчитать напряженность электрического поля между пластинами.Пока вы не находитесь рядом с краем пластин, электрическое поле между пластинами постоянно, а его напряженность определяется выражением:

Обратите внимание, что при разности потенциалов V в вольтах и ​​расстоянии между пластинами в метрах единицами измерения напряженности электрического поля являются вольты на метр [В/м]. Ранее мы заявили, что единицами измерения напряженности электрического поля являются ньютоны на кулон [Н/Кл]. Легко показать, что эти единицы эквивалентны:

Вопрос: Какая электрическая единица эквивалентна одному джоулю?

1. вольт/метр
2. ампер * вольт
3. вольт / кулон
4. Кулон*вольт

Ответ: (4) Кулон*вольт

 

Давайте попробуем другую примерную задачу:

Вопрос: На схеме изображены два электрона,
e ₁ и e ₂ , расположенные между двумя противоположными
заряженные параллельные пластины.Сравните величину силы, действующей на
электрическое поле на e ₁ на величину
сила электрического поля, действующая на e ₂ .

Ответ: Сила одинакова, потому что электрическое поле одинаково для обоих зарядов, так как электрическое поле постоянно между двумя параллельными пластинами.

Эквипотенциальные линии

Подобно топографической карте, на которой показаны линии одинаковой высоты или равной гравитационной потенциальной энергии, мы можем составить карту электрического поля и соединить точки с равным электрическим потенциалом.Эти линии, известные как эквипотенциальные линии, всегда пересекают линии электрического поля под прямым углом и показывают положения в пространстве с постоянным электрическим потенциалом. Если вы перемещаете заряженную частицу в пространстве, и она всегда остается на эквипотенциальной линии, никакой работы не будет.

Напряжение и разность потенциалов | IOPSpark

Напряжение/разность потенциалов

Электричество и магнетизм

Напряжение и разность потенциалов

Учебное руководство

за
11-14

Настаивай… и получай

Совет учителя: Слово напряжение более понятно, чем словосочетание разность потенциалов , поэтому, вероятно, его достаточно для детей 11–14 лет. Более сложная разработка, которая оправдывает термин разность потенциалов , вероятно, не подходит для класса 11–14 лет. Падения и повышения напряжения, позже называемые падениями и подъемами потенциала, по аналогии с гравитационной разностью потенциалов, также лучше пока исключить из классной комнаты. Действительно, сама идея разности потенциалов сложна для учащихся старше 16 лет. Мы бы предложили оставить аналогию с холмами на потом. Возможно, есть смысл тонко ввести его в обучение 14–16 лет.Но следует опасаться сложностей, так как электрические горки бывают только при наличии петли с током в элементах цепи. Это не очень похоже на круговой маршрут в сопках, где есть холмы, есть ли на пути поток пешеходов или нет. Всегда нужно следить за тем, чтобы не увести учеников по ложному следу, вводя недоразвитую аналогию.

Совет учителя: Отношение напряжения к мощности, как то, что происходит теперь в цепи, может быть более выгодным подходом. Введите его в качестве второго фактора, определяющего яркость лампочки: вам нужно будет указать как напряжение, так и силу тока.

Потенциальная разница — главы 1-17 физики колледжа

Резюме

• Дайте определение электрического потенциала и электрической потенциальной энергии.
• Опишите взаимосвязь между разностью потенциалов и электрической потенциальной энергией.
• Объясните электрон-вольт и его использование в субмикроскопическом процессе.
• Определить электрическую потенциальную энергию, зная разность потенциалов и величину заряда.

Когда свободный положительный заряд [латекс]\boldsymbol{q}[/латекс] ускоряется электрическим полем, как показано на рисунке 1, ему придается кинетическая энергия. Этот процесс аналогичен ускорению объекта гравитационным полем. Это похоже на то, как будто заряд спускается с электрического холма, где его электрическая потенциальная энергия преобразуется в кинетическую энергию. Давайте исследуем работу, совершаемую электрическим полем над зарядом [латекс]\boldsymbol{q}[/латекс] в этом процессе, чтобы мы могли разработать определение электрической потенциальной энергии.

Рис. 1. Заряд, ускоренный электрическим полем, аналогичен массе, спускающейся с холма. В обоих случаях потенциальная энергия переходит в другую форму. Работа совершается силой, но поскольку эта сила консервативна, мы можем написать Вт = –ΔPE .

Электростатическая или кулоновская сила является консервативной, что означает, что работа, выполненная над [латексом]\boldsymbol{q}[/латекс], не зависит от пройденного пути.Это в точности аналогично гравитационной силе в отсутствие диссипативных сил, таких как трение. Когда сила консервативна, можно определить потенциальную энергию, связанную с силой, и обычно легче иметь дело с потенциальной энергией (поскольку она зависит только от положения), чем напрямую вычислять работу.

Мы используем буквы PE для обозначения электрической потенциальной энергии, которая измеряется в джоулях (Дж). Изменение потенциальной энергии, [латекс]\boldsymbol{\Delta\textbf{PE}}[/латекс], имеет решающее значение, поскольку работа, выполняемая консервативной силой, является отрицательной величиной изменения потенциальной энергии; то есть [латекс]\boldsymbol{W = — \Delta \textbf{PE}}[/латекс].Например, работа [латекс]\boldsymbol{W}[/латекс], совершаемая для ускорения положительного заряда из состояния покоя, положительна и является результатом потери PE, или отрицательная [латекс]\boldsymbol{ \Delta \textbf{PE} }[/латекс]. Перед [latex]\boldsymbol{ \Delta \textbf{PE}}[/latex] должен стоять знак минус, чтобы [latex]\boldsymbol{W}[/latex] был положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и рассчитав работу, необходимую для перемещения заряда в другую точку.

Потенциальная энергия

[латекс]\boldsymbol{W =- \Delta\textbf{PE}}[/латекс].Например, работа [латекс]\boldsymbol{W}[/латекс], совершаемая для ускорения положительного заряда из состояния покоя, положительна и является результатом потери PE, или отрицательная [латекс]\boldsymbol{ \Delta \textbf{PE} }[/латекс]. Перед [latex]\boldsymbol{\Delta \textbf{PE}}[/latex] должен стоять знак минус, чтобы [latex]\boldsymbol{W}[/latex] был положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и рассчитав работу, необходимую для перемещения заряда в другую точку.

Гравитационная потенциальная энергия и электрическая потенциальная энергия совершенно аналогичны.Потенциальная энергия учитывает работу, выполняемую консервативной силой, и дает дополнительное представление об энергии и преобразовании энергии без необходимости иметь дело с силой напрямую. Например, гораздо чаще используется понятие напряжения (связанное с потенциальной электрической энергией), чем непосредственное рассмотрение кулоновской силы.

Прямой расчет работы, как правило, затруднен, поскольку [латекс]\boldsymbol{ W = Fd \;\textbf{cos} \theta }[/latex], а также направление и величина [латекс]\boldsymbol{F}[/latex] ] может быть сложным для нескольких зарядов, для объектов необычной формы и на произвольных путях. Но мы знаем, что, поскольку [latex]\boldsymbol{F = qE}[/latex], работа и, следовательно, [latex]\boldsymbol{\Delta \textbf{PE}}[/latex], пропорциональна тестовый заряд [латекс]\boldsymbol{q}[/латекс]. Чтобы иметь физическую величину, независимую от пробного заряда, мы определяем электрический потенциал [латекс]\boldsymbol{V}[/латекс] (или просто потенциал, поскольку понимается электричество) как потенциальную энергию на единицу заряда:

[латекс]\boldsymbol{V =}[/латекс] [латекс]\boldsymbol{\frac{\textbf{PE}}{q}} .[/латекс]

Электрический потенциал

Это электрическая потенциальная энергия на единицу заряда.

[латекс]\boldsymbol{V =}[/латекс] [латекс]\boldsymbol{\frac{\textbf{PE}}{q}}[/латекс]

Поскольку PE пропорциональна [latex]\boldsymbol{q}[/latex] , зависимость от [latex]\boldsymbol{q}[/latex] отменяется. Таким образом, [latex]\boldsymbol{V}[/latex] не зависит от [latex]\boldsymbol{q}[/latex]. Изменение потенциальной энергии [латекс]\boldsymbol{ \Delta \textbf{PE}}[/latex] имеет решающее значение, поэтому нас интересует разность потенциалов или разность потенциалов [латекс]\boldsymbol{ \Delta \textbf{ V}}[/latex] между двумя точками, где

[латекс]\boldsymbol{ \Delta \textbf{V} = \textbf{V}_{\textbf{B}} — \textbf{V}_{\textbf{A}} =}[/latex] [латекс ]\boldsymbol{\frac{\Delta \textbf{PE}}{q}} . [/латекс]

Таким образом, разность потенциалов между точками A и B, [латекс]\boldsymbol{V_{\textbf{B}} — V_{\textbf{A}}}[/latex], определяется как изменение потенциальной энергии заряд [латекс]\boldsymbol{q}[/латекс] переместился из А в В, разделенный на заряд. Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

[латекс]\boldsymbol{1 \textbf{V} = 1}[/латекс] [латекс]\boldsymbol{\frac{\textbf{J}}{\textbf{C}}}[/латекс]

Разница потенциалов

Разность потенциалов между точками A и B, [латекс]\boldsymbol{V_{\textbf{B}} — V_{\textbf{A}}}[/latex], определяется как изменение потенциальной энергии заряд [латекс]\boldsymbol{q}[/латекс] переместился из А в В, разделенный на заряд.Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

[латекс]\boldsymbol{1 \textbf{V} = 1}[/латекс] [латекс]\boldsymbol{\frac{\textbf{J}}{\textbf{C}}}[/латекс]

Знакомый термин «напряжение» является общим названием разности потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, подразумевается разность потенциалов между двумя точками. Например, у каждой батареи есть две клеммы, а ее напряжение — это разность потенциалов между ними.Более того, точка, которую вы выбираете как ноль вольт, является произвольной. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный нуль, например, уровень моря или, возможно, пол лекционного зала.

Таким образом, связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением

.

[латекс]\boldsymbol{\Delta V =}[/латекс] [латекс]\boldsymbol{\frac{\Delta \textbf{PE}}{q}}[/латекс] [латекс]\текст{и} \ ;\boldsymbol{\Delta \textbf{PE} = \textbf{q} \Delta \textbf{V}} .[/латекс]

Разность потенциалов и электрическая потенциальная энергия

Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением

.

[латекс]\boldsymbol{\Delta V =}[/латекс] [латекс]\boldsymbol{\frac{\Delta \textbf{PE}}{q}}[/латекс] [латекс]\текст{и} \ ;\boldsymbol{\Delta \textbf{PE} = q \Delta V}. [/latex]

Второе уравнение эквивалентно первому.

Напряжение не совпадает с энергией. Напряжение – это энергия на единицу заряда.Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), однако один из них хранит гораздо больше энергии, чем другой, поскольку [латекс]\boldsymbol{ \Delta \textbf{PE} = q \Delta V}[/latex]. Автомобильный аккумулятор может передавать больше заряда, чем аккумулятор мотоцикла, хотя оба являются аккумуляторами на 12 В.

Расчет энергии

Предположим, у вас есть мотоциклетный аккумулятор на 12,0 В, способный обеспечить заряд 5000 Кл, и автомобильный аккумулятор на 12,0 В, способный обеспечить заряд 60 000 Кл.Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда соответствует трем значащим цифрам.)

Стратегия

Если мы говорим, что у нас есть аккумулятор на 12,0 В, это означает, что его клеммы имеют разность потенциалов 12,0 В. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов 12,0 В, и заряду сообщается изменение потенциальной энергии, равное [латекс]\boldsymbol{\Delta \textbf{PE} = q \Delta V} .[/латекс]

Итак, чтобы найти выходную энергию, мы умножаем перемещаемый заряд на разность потенциалов.

Раствор

Для аккумулятора мотоцикла [латекс]\boldsymbol{q = 5000 \;\textbf{C}}[/латекс] и [латекс]\boldsymbol{\Delta V = 12,0 \;\textbf{V}}[/латекс ]. Суммарная энергия, отдаваемая аккумулятором мотоцикла, составляет

.

[латекс]\begin{array}{r @{{}={}} l} \boldsymbol{\Delta \textbf{PE}_{\textbf{цикл}}} & \boldsymbol{(5000 \;\textbf {C})(12,0 \;\textbf{V})} \\[1em] & \boldsymbol{(5000 \;\textbf{C})(12,0 \;\textbf{J} / \textbf{C}) } \\[1em] & \boldsymbol{6.5 \;\textbf{J}} \end{массив}[/latex]

Обсуждение

Хотя напряжение и энергия связаны, это не одно и то же. Напряжения батарей идентичны, но энергия, выдаваемая каждой из них, совершенно разная. Учтите также, что по мере разрядки аккумулятора часть его энергии расходуется внутри, и напряжение на его клеммах падает, например, когда фары тускнеют из-за низкого заряда автомобильного аккумулятора. Энергия, поставляемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.

Обратите внимание, что энергии, рассчитанные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для батареи отрицательно, так как она теряет энергию. Эти батареи, как и многие электрические системы, на самом деле перемещают отрицательный заряд, в частности электроны. Батареи отталкивают электроны от своих отрицательных клемм (A) через любую задействованную схему и притягивают их к своим положительным клеммам (B), как показано на рисунке 2. Изменение потенциала составляет [латекс]\boldsymbol{\Delta V = V_{\ textbf{B}} — V_{\textbf{A}} = +12 \;\textbf{V}}[/latex] и заряд [latex]\boldsymbol{q}[/latex] отрицателен, так что [ латекс]\boldsymbol{\Delta \textbf{PE} = q \Delta V}[/latex] имеет отрицательное значение, что означает, что потенциальная энергия батареи уменьшилась, когда [latex]\boldsymbol{q}[/latex] переместился из от А до Б.

Рисунок 2. Аккумулятор перемещает отрицательный заряд от отрицательной клеммы через фару к положительной клемме. Соответствующие комбинации химических веществ в батарее разделяют заряды так, что на отрицательной клемме появляется избыток отрицательного заряда, который отталкивается ею и притягивается к избыточному положительному заряду на другой клемме. С точки зрения потенциала, положительная клемма находится под более высоким напряжением, чем отрицательная. Внутри батареи движутся как положительные, так и отрицательные заряды.

Сколько электронов проходит через фару каждую секунду?

Когда автомобильный аккумулятор на 12,0 В питает одну фару мощностью 30,0 Вт, сколько электронов проходит через нее каждую секунду?

Стратегия

Чтобы найти количество электронов, мы должны сначала найти заряд, который переместился за 1,00 с. Перемещенный заряд связан с напряжением и энергией через уравнение [латекс]\жирныйсимвол{\Delta\textbf{PE} = q \Delta V}[/латекс]. Лампа мощностью 30,0 Вт потребляет 30,0 Дж в секунду. Поскольку батарея теряет энергию, мы имеем [латекс]\boldsymbol{ \Delta \textbf{PE} = -30.0 \;\textbf{J}}[/latex] и, поскольку электроны движутся от отрицательного вывода к положительному, мы видим, что
[латекс]\boldsymbol{\Delta V = +12,0 \; V}[/латекс].

Раствор

Чтобы найти перемещенный заряд [латекс]\boldsymbol{q}[/latex], решаем уравнение [латекс]\boldsymbol{\Delta \textbf{PE} = q \Delta V}[/latex]:

[латекс]\boldsymbol{q =}[/латекс] [латекс]\boldsymbol{\frac{\Delta \textbf{PE}}{\Delta V}}.[/latex]

Вводя значения для [latex]\boldsymbol{\Delta \textbf{PE}}[/latex] и [latex]\boldsymbol{\Delta \textbf{V}}[/latex], мы получаем

[латекс]\boldsymbol{q =}[/латекс] [латекс]\boldsymbol{\frac{-30.{19} \;\textbf{электроны.}}[/latex]

Обсуждение

Это очень большое число. Неудивительно, что мы обычно не наблюдаем отдельных электронов, когда их так много в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих случаях были отрицательными. Положительный заряд, движущийся в направлении, противоположном направлению отрицательного заряда, часто производит идентичные эффекты; это затрудняет определение того, что движется или движутся ли оба.

Энергия, приходящаяся на электрон, очень мала в макроскопических ситуациях, как в предыдущем примере, — крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на одну частицу (электрон, протон или ион), может иметь большое значение. Например, даже крошечной доли джоуля может быть достаточно для того, чтобы эти частицы разрушили органические молекулы и нанесли вред живым тканям. Частица может нанести ущерб при прямом столкновении или создать вредное рентгеновское излучение, которое также может нанести ущерб.Полезно иметь единицу энергии, связанную с субмикроскопическими эффектами. На рис. 3 показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как в телевизионной трубке старой модели или в осциллографе. Электрон получает кинетическую энергию, которая затем преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что нисходящий для электрона восходящий для положительного заряда.) Поскольку энергия связана с напряжением соотношением [латекс]\boldsymbol{ \Delta \textbf{PE} = q \Delta V}[/latex], мы можем думать о джоуль как кулон-вольт.

Рисунок 3. Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя металлическими пластинами. Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов 5000 В производит электроны с энергией 5000 эВ.

В субмикроскопическом масштабе удобнее определить единицу энергии, называемую электрон-вольт (эВ), которая представляет собой энергию, переданную основному заряду, ускоренному за счет разности потенциалов в 1 В. {-19} \;\textbf{J}.} \end{массив}[/latex]

Электрон, ускоренный разностью потенциалов в 1 В, получает энергию 1 эВ. Отсюда следует, что электрон, ускоренный через 50 В, получает энергию 50 эВ. Разность потенциалов 100 000 В (100 кВ) даст электрону энергию 100 000 эВ (100 кэВ) и так далее. Точно так же ион с двойным положительным зарядом, ускоренный до 100 В, получит энергию 200 эВ. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.

Соединения: энергоблоки

Электрон-вольт (эВ) является наиболее распространенной единицей энергии для субмикроскопических процессов. Это будет особенно заметно в главах, посвященных современной физике. Энергия настолько важна для очень многих предметов, что существует тенденция определять специальную единицу измерения энергии для каждой основной темы. Есть, например, калории для пищевой энергии, киловатт-часы для электрической энергии и термы для энергии природного газа.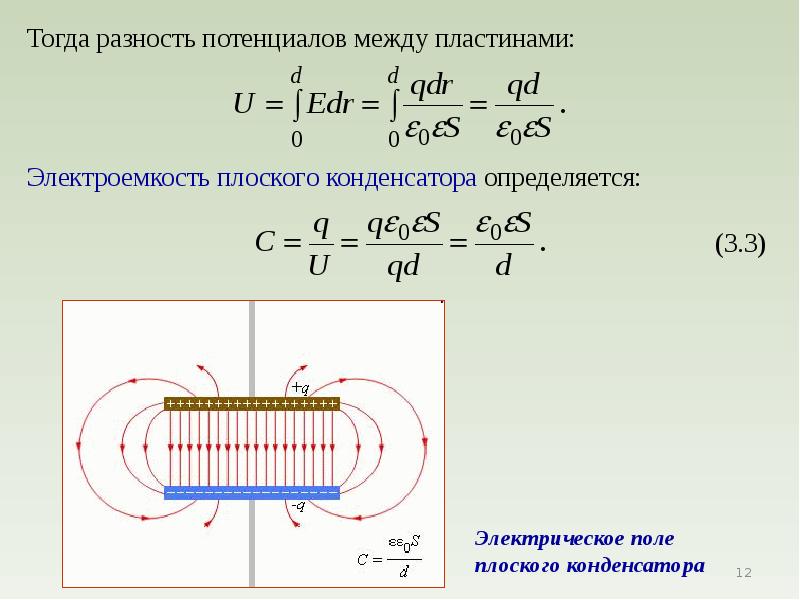

Электрон-вольт обычно используется в субмикроскопических процессах — химические валентные энергии, молекулярные и ядерные энергии связи входят в число величин, часто выражаемых в электрон-вольтах.Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускоряется из состояния покоя через разность потенциалов 30 кВ, ему придается энергия 30 кэВ (30 000 эВ), и он может расщепить до 6000 этих молекул [латекса]\boldsymbol{(30 000 \;\ textbf{эВ} \div 5 \;\textbf{эВ на молекулу} = 6000 \;\textbf{молекул})}[/latex]. Энергия ядерного распада составляет порядка 1 МэВ (1 000 000 эВ) на событие и, таким образом, может привести к значительным биологическим повреждениям.

Полная энергия системы сохраняется, если нет чистого прибавления (или вычитания) работы или теплопередачи. Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия является константой.

Механическая энергия – это сумма кинетической энергии и потенциальной энергии системы; то есть [латекс]\жирныйсимвол{\textbf{KE} + \textbf{PE} = \textbf{константа}}[/латекс]. Потеря PE заряженной частицы становится увеличением ее KE.Здесь РЕ — электрическая потенциальная энергия. Сохранение энергии выражается в форме уравнения как

[латекс]\boldsymbol{\textbf{KE} + \textbf{PE} = \textbf{константа}}[/latex]

или

[латекс]\boldsymbol{\textbf{KE}_{\textbf{i}} + \textbf{PE}_{\textbf{i}} = \textbf{KE}_{\textbf{f}} + \ textbf{PE}_{\textbf{f}},}[/латекс]

, где i и f обозначают начальные и конечные условия. Как мы уже много раз убеждались, рассмотрение энергии может дать нам понимание и облегчить решение проблем.

Электрическая потенциальная энергия, преобразованная в кинетическую энергию

Рассчитайте конечную скорость свободного электрона, ускоренного из состояния покоя при разности потенциалов 100 В. (Предположим, что это числовое значение имеет точность до трех значащих цифр.)

Стратегия

У нас есть система только с консервативными силами. Если предположить, что электрон ускоряется в вакууме и пренебречь силой гравитации (мы проверим это предположение позже), вся электрическая потенциальная энергия преобразуется в кинетическую энергию. 2}{2}}.6 \;\textbf{m}/ \textbf{s}} \end{массив} .[/latex]

Обсуждение

Обратите внимание, что и заряд, и начальное напряжение отрицательны, как на рис. 3. Из обсуждений в главе 18 «Электрический заряд и электрическое поле» мы знаем, что электростатические силы на малых частицах обычно очень велики по сравнению с силой гравитации. Большая конечная скорость подтверждает, что гравитационной силой здесь действительно можно пренебречь. Большая скорость также указывает на то, насколько легко ускорять электроны при малых напряжениях из-за их очень малой массы.Напряжения, намного превышающие 100 В в этой задаче, обычно используются в электронных пушках. Эти более высокие напряжения создают настолько большие скорости электронов, что необходимо учитывать релятивистские эффекты. Вот почему в этом примере рассматривается (точно) низкое напряжение.

• Электрический потенциал – это потенциальная энергия на единицу заряда.
• Разность потенциалов между точками A и B, [латекс]\boldsymbol{V_{\textbf{B}} -V _{\textbf{A}}}[/latex], определяемая как изменение потенциальной энергии заряда [латекс]\boldsymbol{q}[/латекс], перемещенный из А в В, равен изменению потенциальной энергии, деленному на заряд. Разность потенциалов обычно называют напряжением, обозначаемым символом
  [латекс]\жирныйсимвол{\ Дельта \textbf{V}}[/latex].{-19} \;\textbf{J}.} \end{массив}[/latex]

• Механическая энергия представляет собой сумму кинетической энергии и потенциальной энергии системы, то есть [латекс]\boldsymbol{\textbf{KE} + \textbf{PE}}[/latex]. Эта сумма является константой.

Концептуальные вопросы

1: Напряжение — это обычное слово для обозначения разности потенциалов. Какой термин является более описательным, напряжение или разность потенциалов?

2: Если напряжение между двумя точками равно нулю, можно ли перемещать между ними пробный заряд, совершая нулевую чистую работу? Обязательно ли это можно сделать без приложения силы? Объяснять.

3: Какая связь между напряжением и энергией? Точнее, какова связь между разностью потенциалов и электрической потенциальной энергией?

4: Напряжения всегда измеряются между двумя точками. Почему?

5: Как связаны единицы вольт и электронвольт? Чем они отличаются?

Задачи и упражнения

1: Найдите отношение скоростей электрона и отрицательного иона водорода (имеющего лишний электрон), ускоренных при одинаковом напряжении, при нерелятивистских конечных скоростях.{-27} \;\textbf{kg}}[/latex]. (a) Рассчитайте его кинетическую энергию в джоулях при 2,00% скорости света. б) Сколько это в электрон-вольтах? в) Какое напряжение потребуется для получения этой энергии?

4: Комплексные концепции
Однозарядные ионы газа ускоряются из состояния покоя напряжением 13,0 В. При какой температуре средняя кинетическая энергия молекул газа будет такой же, как у этих ионов?

5: Integrated Concepts
Предполагается, что температура вблизи центра Солнца составляет 15 миллионов градусов Цельсия [латекс]\boldsymbol{(1.{\ circ} \ textbf {C})} [/ латекс]. При каком напряжении должен быть ускорен однозарядный ион, чтобы его энергия равнялась средней кинетической энергии ионов при данной температуре?

6: Integrated Concepts
(a) Какова средняя выходная мощность сердечного дефибриллятора, рассеивающего 400 Дж энергии за 10,0 мс? (b) Почему дефибриллятор, учитывая большую выходную мощность, не вызывает серьезных ожогов?

7: Интегрированные концепции
Молния ударяет в дерево, перемещая 20.{\ circ} \textbf{C}}[/latex]. а) Какой заряд переносится батареей? б) Сколько электронов течет в секунду, если для нагревания формулы требуется 5,00 мин? (Подсказка: предположим, что удельная теплоемкость детского питания примерно такая же, как удельная теплоемкость воды.)

9: Интегрированные концепции
Автомобиль с аккумуляторным питанием использует систему 12,0 В. Найдите заряд, который должны иметь аккумуляторы, чтобы разогнать автомобиль массой 750 кг из состояния покоя до 25,0 м/с, заставить его подняться на [латекс]\boldsymbol{2. {-12} \;\textbf{m}}[/latex], найдя напряжение одного на этом расстоянии и умножив его на заряд другого. б) При какой температуре атомы газа будут иметь среднюю кинетическую энергию, равную этой необходимой электрической потенциальной энергии?

11: Необоснованные результаты
(a) Найдите напряжение вблизи металлического шара диаметром 10,0 см, на котором имеется 8,00 Кл избыточного положительного заряда. б) Что неразумного в этом результате? (c) Какие предположения ответственны?

12: Создайте свою собственную задачу
Рассмотрим аккумулятор, используемый для питания сотового телефона.Постройте задачу, в которой вы определяете энергию, которая должна быть предоставлена ​​батареей, а затем вычисляете количество заряда, которое она должна быть в состоянии переместить, чтобы обеспечить эту энергию. Среди вещей, которые следует учитывать, — потребности в энергии и напряжение батареи. Возможно, вам придется заглянуть вперед, чтобы интерпретировать характеристики батареи производителя в ампер-часах как энергию в джоулях.

Глоссарий

электрический потенциал

потенциальная энергия на единицу заряда

разность потенциалов (или напряжение)

изменение потенциальной энергии заряда, перенесенного из одной точки в другую, деленное на заряд; единицами разности потенциалов являются джоули на кулон, известные как вольт

.

электрон-вольт

энергия, переданная основному заряду, ускоренному разностью потенциалов в один вольт

механическая энергия

сумма кинетической энергии и потенциальной энергии системы; эта сумма является константой

Решения

Задачи и упражнения

1: 42.{12} \;\textbf{V}}[/латекс]

(b) Это напряжение очень высокое. Сфера диаметром 10,0 см никогда не сможет поддерживать такое напряжение; это разрядится.

(c) Заряд в 8,00 Кл больше заряда, чем может разумно накопиться на сфере такого размера.

Объяснение урока: Разность электрических потенциалов

В этом объяснении мы узнаем, как определить разность электрических потенциалов и как разность электрических потенциалов на компоненте в цепи создает ток в этом компоненте.

Разность электрических потенциалов (или просто «разность потенциалов») — одно из самых важных понятий, которые мы используем, когда говорим об электричестве. Понимание разности потенциалов необходимо, если мы хотим описать, как работают цепи и электрические устройства.

Чтобы понять разницу потенциалов, нам нужно посмотреть, как заряд может течь в определенных материалах. Электрические устройства полагаются на поток заряда через компоненты. Этот поток заряда называется током .Материалы, пропускающие через себя ток (например, медь), известны как проводники .

Давайте подробнее рассмотрим, как ведут себя проводники. Проводник состоит из положительно заряженных атомных ядер (показаны красным) и отрицательно заряженных электронов (показаны синим). Атомные ядра неподвижны.

Напомним, что объекты с противоположными зарядами притягиваются друг к другу, а объекты с одинаковым зарядом отталкиваются. Во многих материалах отрицательные электроны сильно притягиваются к положительным ядрам, что означает, что каждый электрон остается тесно связанным с одним из неподвижных ядер.Но это не относится к проводникам! Проводники содержат электроны, способные свободно двигаться. Это означает, что когда мы говорим, что в проводнике течет 90 522 электронов 90 523, 90 523 течет 90 523 электронов.

Все электроны отрицательно заряжены, что означает, что они отталкиваются друг от друга. Это означает, что они стремятся рассредоточиться и держаться как можно дальше друг от друга.

Мы знаем, что поток электронов необходим для электрических устройств. Но какие вызывают поток электронов? Давайте представим, что мы добавили несколько дополнительных электронов на левый конец нашего проводника.

Теперь, когда мы добавили дополнительные электроны, мы можем видеть, что они «сгруппированы» слева. Все эти электроны отталкивают друг друга, поэтому они рассредоточиваются, чтобы уйти друг от друга. Хотя отдельные электроны могут двигаться с разной скоростью и в разных направлениях, существует общий поток электронов слева направо.

(Здесь можно вспомнить, что в физике часто говорят о « условный ток ». Условный ток определяется в направлении, противоположном реальному потоку электронов.Итак, в этом примере, где электроны текут вправо, мы бы сказали, что направление условного тока — влево.)

Итак, какое отношение все это имеет к разности потенциалов? Что ж, когда электроны «сгруппированы», мы видели, что они естественным образом рассредоточиваются, чтобы равномерно заполнить доступное пространство. В данном случае это заставляет электроны двигаться слева направо. Всякий раз, когда электроны заставляют двигаться из одной точки в другую, мы можем сказать, что между этими точками существует разность потенциалов .Другими словами, разность потенциалов описывает, как жесткие электроны перемещаются из одной точки в другую.

Разность потенциалов всегда измеряется между двумя точками. Когда между двумя точками существует разность потенциалов, это означает, что заряд будет стремиться перетекать из одной точки в другую. В этом примере «группирование» электронов, которые отталкивают друг друга, означает, что существует разность потенциалов между левым и правым концами проводника.

В этом случае, как только электроны переместились и рассредоточились, больше нет ничего, что заставляло бы их течь в каком-либо конкретном направлении.Итак, как только это произошло, больше нет разности потенциалов между концами проводника.

Пример 1: Описание эффектов разности потенциалов внутри проводника

На рисунке показаны электроны и атомные ядра в сечении медной проволоки. Синие кружки представляют электроны, а красные кружки представляют атомные ядра.

Между левым и правым концами провода устанавливается разность электрических потенциалов. Какое из следующих утверждений лучше всего описывает то, что произойдет в проводе?

1. Ничего не произойдет.
2. Электроны будут двигаться вне провода.
3. Электроны будут двигаться к центру провода.
4. Электроны начнут двигаться к одному концу провода.

Ответ

Во-первых, отметим, что провода являются проводниками. Это означает, что электроны в проводе могут свободно перемещаться по нему.

Глядя на схему, мы видим, что электроны более или менее равномерно распределены по всему проводнику. Это означает, что если мы просто следуем диаграмме, мы можем предположить, что ничего не произойдет!

Однако в этом вопросе нам сказали , что между левым и правым концами проводника создается разность потенциалов.Нам не нужно знать, что такое причина этой разности потенциалов. Чтобы ответить на вопрос, нам нужно знать, как разность потенциалов повлияет на электроны в проводнике.

Напомним, что разность потенциалов всегда измеряется между двумя точками. Наличие разности потенциалов между этими двумя точками означает, что ток будет течь из одной точки в другую, если это возможно.

Тот факт, что нам говорят, что между двумя концами есть разность потенциалов, достаточен для того, чтобы сделать вывод, что электроны будут течь от одного конца провода к другому, если смогут, и их ничто не остановит.Другими словами, правильный вариант D: электроны начнут двигаться к одному концу провода.

Пример 2: Определение направления тока, вызванного разностью потенциалов

На рисунке показаны электроны и атомные ядра в отрезке медной проволоки. Синие кружки представляют электроны, а красные кружки представляют атомные ядра.

Между левым и правым концами провода устанавливается разность электрических потенциалов. Это создает в нем электрический ток.Какая из стрелок лучше всего показывает направление тока в проводе?

Ответ

Здесь нам говорят, что между левым и правым концами показанного провода возникает разность потенциалов. Наличие разности потенциалов между двумя точками означает, что электроны будут стремиться течь из одной точки в другую. Другими словами, будет ток из одной точки в другую.

В этом случае, поскольку между концами провода существует разность потенциалов, мы знаем, что это создаст ток от одного конца провода к другому.Однако мы не знаем, какое направление это будет: правое или левое.

Глядя на варианты ответов, мы видим, что мы не можем выбрать вариант «слева». Это означает, что мы знаем, что правильный ответ iii: ток пойдет вправо.

Разность потенциалов измеряется в вольтах и ​​обозначается символом V. Мы также используем символ 𝑉 для обозначения разности потенциалов в уравнениях. По этой причине разность потенциалов часто называют «напряжением».

Некоторые устройства способны создавать разность потенциалов.Одной из самых распространенных в физике является ячейка . Мы можем думать о клетке как об устройстве, которое выталкивает электроны из одного вывода и притягивает их к другому.

Если мы соединим клеммы ячейки токопроводящим проводом, как показано на принципиальной схеме ниже, в проводе возникнет ток в направлении, указанном стрелками.

На следующей схеме показана та же цепь с подключенной к ней лампочкой.

Если к этой цепи подключить электрическую лампочку, то разность потенциалов между клеммами элемента будет создавать ток через лампочку, заставляя ее загореться.

Подавая на цепь разность потенциалов, ячейка должна совершить работу над электронами в цепи. Это еще один способ сказать, что клетка должна передать 90 522 энергии 90 523 электронам, чтобы они двигались по цепи. Величина разности потенциалов, измеряемая в вольтах, описывает количество энергии, которое будет воздействовать на каждую единицу заряда, проходящего по цепи.

Вольт можно также выразить в джоулях (единица энергии) на кулон (единица заряда):
1=1/.VJC

Это означает, что, например, батарея с разностью потенциалов между клеммами 9 вольт будет расходовать 9 джоулей энергии на каждый кулон заряда, который она перемещает по цепи. Ячейка с более высокой разностью потенциалов между ее клеммами будет выполнять больше работы на каждую единицу заряда: она сильнее толкает электроны и обычно производит больший ток.

Ключевые точки

• Разность электрических потенциалов всегда измеряется между двумя точками. Он описывает, как жесткие электроны перемещаются из одной точки в другую.
• Электроны в проводниках могут свободно перемещаться. Если между двумя точками есть разность потенциалов и эти точки соединены проводником, заряд будет течь от одной точки к другой.
• Разность потенциалов измеряется в вольтах, что может быть представлено символом V.
• Мы также можем думать о разности потенциалов как о количестве энергии, используемой для перемещения вольта заряда между двумя точками. 1 вольт равен 1 джоулю на кулон.

Разность потенциалов или напряжение

разница в электричестве
потенциальная энергия единичного заряда между двумя точками
в электрическом
поле называется разностью электрических потенциалов.

Это
также определяется как; количество работы, совершаемой для перемещения единицы
положительный заряд от
точка с более низким потенциалом в точку с более высоким потенциалом
против статического электрического поля. То
точка, в которой единица заряда имеет меньшую потенциальную энергию, равна
называется нижним потенциалом. Аналогичным образом точка в
единица заряда которой имеет большую потенциальную энергию, называется высшим
потенциал.Разность электрических потенциалов также называется
напряжения или электрического давления.

рассмотреть
две различные точки А и В в электрическом поле
положительный заряд Q как
показано на рисунке (1). Здесь точка А намного
ближе к заряду Q, чем точка B. Пусть единичный заряд
помещен в точку B. Эта единица заряда имеет электрический потенциал
энергия V _B .

В
чтобы переместить единичный положительный заряд из точки B в точку A
необходимо совершить работу над единичным положительным зарядом против электрического
поле. Если работа совершается над единицей заряда, то энергия
перейдет в единицу заряда и начнет движение из точки
B в точку A. Значит, в точке A единица измерения
заряд приобретает электрическую потенциальную энергию, как показано на
рис (2).Величина электрического потенциала единицы заряда при
точка А есть V _A .

количество потенциальной электрической энергии, полученной единицей заряда от
точка B к точке A называется разностью потенциалов.
Следовательно, разность потенциалов между точкой B и точкой
А есть V _A – V _B .

Электрический
разность потенциалов может быть математически записана как

Если
работа в один джоуль совершается для перемещения заряда в один кулон из
одной точки (более низкий потенциал) в другую (более высокий потенциал),
разность потенциалов между этими двумя точками составляет 1В.в
аналогично, если
Для перемещения заряда на один кулон совершается работа 5 джоулей.
из точки с более низким потенциалом в точку с более высоким
потенциал, разница потенциалов между этими двумя
точек составляет 5В. Однако один джоуль работы выделяется как
тепла, если один кулон заряда перемещается из точки
с более высоким потенциалом в точку с более низким потенциалом.

Электрический
разность потенциалов между двумя точками измеряется в
вольт. Один вольт равен одному джоулю на кулон. А
вольтметр можно использовать для измерения разности потенциалов
между двумя точками. Как правило, заземление или нулевой потенциал
воспринимается как одна общая точка отсчета.

Что такое физика разности потенциалов? – СидмартинБио

Что такое физика разности потенциалов?

Определение разности потенциалов: разность потенциалов между двумя точками, которая представляет собой работу или энергию, выделяемую при передаче единицы количества электричества из одной точки в другую.

Что вы подразумеваете под разностью потенциалов?

Разность потенциалов — это разница в количестве энергии, которой обладают носители заряда между двумя точками цепи. Разность потенциалов в один вольт равна энергии в один джоуль, используемой одним кулоновским зарядом, когда он течет между двумя точками цепи.

Что такое разность электрических потенциалов в физике?

Разность электрических потенциалов, также известная как напряжение, представляет собой внешнюю работу, необходимую для переноса заряда из одного места в другое место в электрическом поле.Разность электрических потенциалов — это изменение потенциальной энергии, испытываемое пробным зарядом, значение которого равно +1.

Что означает PD в физике?

Разность электрических потенциалов
Когда электроны проходят через компонент, совершается работа. Часть энергии электронов передается компоненту. Это вызывает разницу в энергии на компоненте, известную как разность электрических потенциалов (p. d.)

.

Какова разность потенциалов для класса 10?

Разность потенциалов — это напряжение на клеммах батареи, а электродвижущая сила — это разность потенциалов между клеммами батареи при отсутствии тока во внешней цепи и при разомкнутой цепи.

Что такое 10-й класс разности потенциалов?

Ответ: Разность потенциалов между любыми двумя точками определяется как количество работы, совершаемой при перемещении единицы заряда из одной точки в другую. дв=двдк.

Что такое 10-й класс разности потенциалов?

Какая потенциальная разница в физике 12 класса?

Подсказка: Разность потенциалов — это разница в количестве энергии, которой обладают носители заряда между двумя точками цепи. Разница потенциалов (стр.г.) ​​и называется также напряжением.

Как найти разность потенциалов?

Умножьте величину тока на величину сопротивления в цепи. Результатом умножения будет разность потенциалов, измеряемая в вольтах. Эта формула известна как закон Ома, V = IR.

Как найти разность потенциалов?

Какое уравнение для разности потенциалов?

Формула для измерения разности потенциалов: V=W/Q, известная как закон Ома.В этом уравнении V равно разности потенциалов, W — переданная энергия или проделанная работа, а Q — количество заряда.

Что такое потенциал в физике?

Потенциал означает способность и в физике способность системы совершать работу. Существует множество систем, и вы можете рассматривать все, что находится в равновесии с окружающей их средой, например, вы сидите на стуле и не двигаетесь.

В чем разница между наукой и физикой?

Физика – это наука «А».Наука рассматривает гораздо больше, чем физика сама по себе. В то время как биология ИСПОЛЬЗУЕТ физику, она также использует химию, чтобы ответить на многие вопросы. Астрономия использует физику, и она МОЖЕТ использовать биологию и химию, когда решает, кого отправить в космос, но пока это довольно обособленная наука.

Какие существуют виды физики?

Существует только один тип физики, есть только разные разделы физики, такие как ядерная физика, физика элементарных частиц, статистическая физика, квантовая механика, физика твердого тела или физика конденсированного состояния.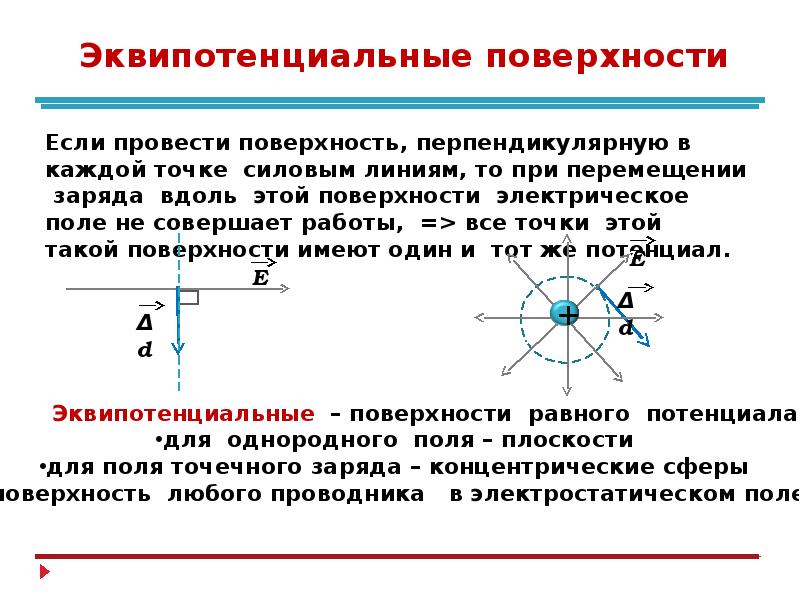

GCSE PHYSICS — Электричество — В чем потенциальная разница? — Что такое напряжение?

GCSE PHYSICS — Электричество — В чем потенциальная разница? — Что такое напряжение? — ОГЭ НАУКА.

gcsescience.com

5

gcsescience.com

Электричество

Что такое потенциал
Разница или напряжение?

Разность потенциалов
(или стр.г.) ​​- это другое слово для обозначения напряжения.
Вы можете использовать любой термин для обозначения одного и того же, но чаще всего
.
экзаменационные вопросы используют разность потенциалов, а не
Напряжение.

Разность потенциалов
(напряжение) источника питания
электрическое давление
, которое вызывает ток
течь
в цепи.
Удвоение
напряжение питания удвоится
электрический ток.

Что такое вольт?

Сила
источник питания (ячейка или батарея) дает сумму
энергии на каждый кулон заряда
в электрической цепи.

Энергия измеряется в
джоули.
6 вольт
клетка отдает 6 джоулей энергии
каждый кулон.

1 вольт = 1
джоуль на кулон.

Слово «за» означает «разделенный
по»,
поэтому напряжение = энергия ÷
обвинение.

Это уравнение
возможно
переставить, чтобы получить
энергия = напряжение x
обвинение. Е = В х
Вопрос

Так как Q =
я х т,
если мы напишем I x t
вместо Q
в приведенном выше уравнении получаем
Е = В х я
х т.
энергия = напряжение x ток
х раз.

Мы также можем использовать слово работа
вместо слова энергия
потому что работа сделана
= переданная энергия

, так что вы можете увидеть уравнение
энергия = напряжение x
заряд    E = V x
Q
пишется как
работа
= напряжение x заряд    Вт
= В х
Вопрос

Просмотреть все
уравнения для электричества.

Как измеряется разница потенциалов?

Разность потенциалов
измеряется с помощью вольтметра.

Схема слева показывает разность потенциалов ячейки.
Это называется поставка
Напряжение. Обозначение схемы
для вольтметра представляет собой кружок с буквой
В внутри.
Вольтметр всегда подключен
параллельно компоненту.
Говорят, что вольтметр подключен.
через компонент.
Мы используем слово «через» для обозначения
«параллельно с».

Цепь справа
имеет вольтметр, подключенный через
лампу.Это скажет вам, сколько джоулей
энергия переводится
из электрической энергии в
световая энергия (+ тепло)
на каждый кулон
обвинение
который проходит через лампу.

Показание 6 вольт говорит вам, что 6 джоулей энергии составляют
передается за каждый кулон, проходящий через
фонарь.

Показание 10 вольт говорит вам, что 10 джоулей энергии составляют
передается за каждый кулон, проходящий через
фонарь.

Ссылки

Электричество

Вопросы по пересмотру

gcsescience.com

Викторина по физике

Показатель

Викторина по электричеству

gcsescience.com

Дом

GCSE Химия

GCSE Физика

Авторское право © 2015 gcsescience.ком. Все права защищены.

.