Схема логического элемента и: Логические элементы и их релейные эквиваленты

Логические элементы и их релейные эквиваленты

С помощью логических элементов довольно легко реализуются функции алгебры логики, которая является костяком устройств автоматики и вычислительных машин. Логические элементы могут реализовываться огромным количеством способов в зависимости от надобности и состоять из полупроводниковых, релейных, интегральных, пневматических и других элементов и схем.

Между величинами, входящими и выходящими из логического элемента, существует определенная зависимость, которая называется функциональной и обозначается как y = f(x) для устройств с одной переменной и как y = f(x₁, x₂) для устройств с двумя переменными величинами. В этой записи Х называют независимую переменную или аргумент, а Y – зависимая переменная, так как ее значение напрямую зависит от значения аргумента Х.

Ниже показана таблица логических элементов и эквивалентных им положений контактов реле:

Функция повторения

Реализуется логическим элементом повторителем (пункт 1 в таблице). Повторитель можно сравнить с нормально открытым контактом реле. При открытом контакте Х=0 и, соответственно Y=0, то есть цепь находится в непроводящем состоянии, а при закрытом наоборот Х=1 и Y=1, то есть цепь находится в проводящем состоянии.

Функция отрицания

Реализует данную функцию логический элемент НЕ или как его часто называют – инвертор (пункт 2 в таблице). Его сравнивают с нормально закрытым контактом реле, когда при отсутствии напряжения на катушке управления (Х=0) его контакт находится в проводящем состоянии (Y=1). При подаче напряжения на катушку (Х=1) контакт размыкается и разрывает цепь (Y=0).

Функция логического сложения

В схемотехнике носит название дизъюнкция или функция ИЛИ (пункт 3 в таблице). Реализуема эта функция логическим элементом дизъюнктором. Суть данной операции заключается в логическом суммировании входных сигналов X для получения результирующего сигнала на выходе Y. Описывается данная зависимость простой формулой X₁ + X₂ = Y. Вот примеры – 0+0=1, 1+0=1,0+1=1,1+1=1. На примере обычного реле – это два параллельно подключенных нормально разомкнутых контакта. Если один контакт разомкнут, то проводимость цепи обеспечит второй, замкнутый контакт. Для того что бы цепь оказалась разорванной, необходимо разомкнуть оба контакта.

Функция логического умножения

В схемотехнике носит название конъюнкция или функция И (пункт 4 в таблице). Реализует ее специальный логический элемент – конъюктор. Данная функция – логическое перемножение сигналов:

Если сравнить с реле – то это два последовательно включенные нормально открытые контакты. А при таком подключении контактов реле проводимость можно получить только в случае, когда оба контакта замкнуты.

Функция равнозначности

Имеет следующий вид — X₁≡X₂ = Y или в виде логических символов: 0≡0 =1; 1≡0 = 0; 0≡1 = 0; 1≡1 = 1.

Значения 1 будет только при условии, что X₁ = X₂. Эквивалентом в релейной схеме будет два последовательно включенных переключающихся контакта (пункт 5 в таблице).

Функция неравнозначности

Противоположная функции равнозначности (пункт 6 в таблице) и часто носит название функции сложности по модулю m2:

Глава 3. Построение схем на логических элементах

Основные логические функции и их реализация в

Электронных устройствах

Элемент ИЛИ.

 

Устройства ЧПУ, как любые цифровые устройства, включая ЭВМ, состоят из основных логических элементов и элементов памяти. К основным логическим элементам относятся физические элементы, реализующие логические функции «ИЛИ», «И», «НЕ», т. е. осуществляющие логические суммирование, умножение и отрицание. Элементы памяти также могут состоять из этих же логических элементов, соединенных в триггеры.

Узлы цифровых устройств реализуются в виде серийно выпускаемых стандартных логических элементов, образующих их элементную базу, которая состоит из серии функционально различных логических элементов. Эти элементы конструктивно оформлены в одинаковых корпусах, содержащих несколько логических элементов, которые устанавливают на блоках, панелях или платах (в зависимости от конструкции этих элементов) и соединяют между собой внешним монтажом. Основным свойством логических элементов определенной серии является возможность их последовательного включения, в связи с чем предусмотрен одинаковый уровень их входных и выходных сигналов. Из основных логических элементов можно построить любую сколь угодно сложную схему, реализующую любую логическую функцию. Например, можно построить логические схемы со многими входами и выходами, служащие для преобразования кодов из одной формы в другую.

Логические элементы (узлы) предназначены для, выполнения различных логических (функциональных) операций над дискретными сигналами при двоичном способе их представления.

Преимущественное распространение получили логические элементы потенциального типа. В них используются дискретные сигналы, нулевому значению которых соответствует уровень низкого потенциала, а единичному значению — уровень высокого потенциала (отрицательного или положительного). Связь потенциального логического элемента с предыдущим и последующими узлами в системе осуществляется непосредственно, без применения реактивных компонентов. Благодаря этому преимуществу именно потенциальные логические элементы нашли почти исключительное применение в интегральном исполнении в виде микросхем. С позиций использования логических микросхем потенциального типа и проводится далее рассмотрение логических элементов. Логические биполярные микросхемы чаще выполняют на транзисторах типа n-p-n с напряжением питания E_ti>0. Этим объясняется, что используемые здесь сигналы имеют положительную полярность. Уровню высокого положительного потенциала («1») на выходе соответствует закрытое состояние транзистора, а уровню низкого потенциала («0») — его открытое состояние. С этой точки зрения, в частности, и следует понимать действие сигнала на входе логического элемента, имеющего непосредственную связь с другими элементами в конкретной схеме. Для упрощения уровень низкого потенциала сигнала полагаем равным нулю, а процесс перехода транзистора из одного состояния в другое — достаточно быстрым.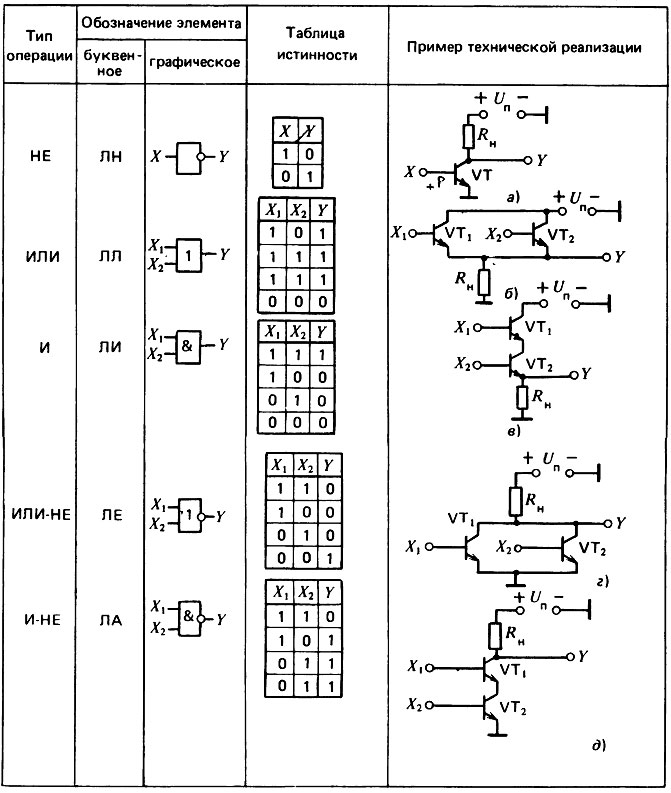

Логические интегральные микросхемы являются элементами, на основе которых выполняются схемы цифровой техники, в частности, применяемые в устройствах систем ЧПУ.

Логический элемент ИЛИ. Логический элемент ИЛИ имеет несколько входов и один общий выход. Его условное обозначение показано на рис.3.1, а.

Логический элемент ИЛИ выполняет операцию логического сложения (дизъюнкции):

(3.1)

где F — функция; х₁, х₂, х₃,…, х_n— аргументы (переменные, двоичные сигналы на входах).

Здесь функция F=0, когда все ее аргументы равны нулю, и F=1 при одном, нескольких или всех аргументах, равных единице. Работу схемы двухвходового логического элемента ИЛИ иллюстрируют таблица истинности и временные диаграммы, приведенные на рис.3.1,б, в. Моделью двухвходового элемента ИЛИ может служить схема с двумя параллельно включенными ключами. Если оба ключа выключены (аргументы равны нулю), то напряжение на выходе равно нулю и F=0. При одном или двух включенных ключах напряжение на выходе равно Е и F=1.

 

Рис.3.1. Условное обозначение логического элемента ИЛИ (а), его таблица истинности и временное диаграммы (б, в)

 

Наиболее просто элемент ИЛИ реализуется на диодах (рис.3.2). Значение F=1 на выходе создается передачей входного сигнала вследствие отпирания соответствующего диода. К диодам, для которых входной сигнал равен нулю, прикладывается обратное напряжение, и они находятся в закрытом состоянии.

Рис.3.2. Схема логического элемента ИЛИ на диодах

 

На практике возможны случаи, когда число входов используемого логического элемента ИЛИ превышает количество входных сигналов. Неиспользуемые входы заземляют. Тем самым исключается возможность прохождения помех через элемент ИЛИ от наводок по неиспользованным входам.

 

Элементы И, НЕ.

 

Логический элемент И. Логический элемент И также имеет несколько входов и один выход. Его условное обозначение показано на рис.3.3, а.

Логический элемент И выполняет операцию логического умножения (конъюнкции):

(3.2)

 

 

 

Рис.3.3. Условное обозначение логического элемента И (а),

его таблица истинности и временные диаграммы (б, в)

 

Здесь функция F=0, если один из ее аргументов равен нулю, и F=1 при всех аргументах, равных единице.

Работу схемы двухвходового логического элемента И иллюстрируют таблица истинности и временные диаграммы, приведенные на рис.3.3,б,в. Элемент И является схемой совпадения: сигнал «1» на выходе появляется при совпадении сигналов «1» на всех входах. Моделью двухвходового элемента И может служить схема с двумя последовательно включенными ключами и источником питания. Простейшая схема элемента И на диодах приведена на рис.3.4. Отличие от схемы элемента ИЛИ (см. рис.3.2) заключается в изменении полярности включения диодов и наличии резистора R подключенного к шине «+» источника питания. Схема работает следующим образом. При всех входных сигналах, равных единице, на катодах диодов имеется положительный потенциал относительно общей точки и все диоды закрыты. На выходе схемы создается напряжение ER₂/(R₁+R₂), определяющее F=1. При нулевом значении сигнала хотя бы на одном из входов соответствующий диод будет проводить ток и шунтировать резистор R₂, выполняющий, как и резистор R в схеме рис. 3.2, роль нагрузки. Напряжение на выходе при этом определяется падением напряжения на открытом диоде и близко к нулю (F=0). Увеличение числа входов с нулевым значением сигнала приводит только к увеличению числа проводящих диодов, а функция F остается равной нулю.

Рис.3.4. Схема логического элемента И на диодах

 

В случае применения логического элемента И, имеющего число входов, большее количества входных сигналов, неиспользуемые входы элемента соединяют с шиной «+» источника питания (подают сигнал логической «1»).

Диоды неиспользуемых входов будут находиться в закрытом состоянии. Это уменьшает вероятность прохождения помех на выход элемента И от наводок по неиспользованным входам. Поведение логического элемента будет зависеть от комбинации входных сигналов.

Логический элемент НЕ. Логический элемент НЕ имеет один вход и один выход. Его условное обозначение показано на рис.3.5,а.

Элемент НЕ выполняет операцию инверсии (отрицания), в связи с чем его часто называют логическим инвертором.

Сигналу х=0 на входе соответствует F=1 и, наоборот, при x=1 F=0.

Работу схемы логического элемента НЕ иллюстрируют таблица истинности и временные диаграммы, приведенные на рис.3.5,б,в. Логический элемент НЕ представляет собой ключевую схему на транзисторе (рис.3.6). При х=0 (U_вх=0) транзистор закрыт, напряжение u_кэ=Е_к, т.е. F=1. При х=1 (U_вх=U_вхотп) транзистор открыт, напряжение F=0. Открытое состояние транзистора обеспечивается заданием тока базы, вводящего транзистор в режим насыщения.

Рис.3.5. Условное обозначение логического элемента НЕ (а), его

таблица истинности и временные диаграммы (б, в)

Рис.3.6. Схема логического элемента НЕ

 

Элементы ИЛИ-НЕ, И-НЕ.

 

Логический элемент ИЛИ-НЕ. Условное обозначение логического элемента ИЛИ-НЕ показано на рис. 3.7,а. Он объединяет элементы ИЛИ и НЕ с очередностью проведения операций, показанной в таблице истинности рис.3.7,б. В связи с этим входным сигналам, равным единице, соответствует логический «0» на выходе, а при нулевых сигналах на всех входах F=1. Функциональная операция, выполняемая элементом ИЛИ-НЕ при n входах, определяется выражением

(3.3)

На рис.3.8,а приведена схема логического элемента ИЛИ-НЕ, представляющая собой последовательное соединение элемента ИЛИ на диодах и элемента НЕ. Логические схемы подобного сочетания определяют, в частности, класс элементов так называемой диодно-транзисторной логики (ДТЛ). Принцип действия элемента ясен из диаграмм рис.3.8,б, где показаны сигналы x₁ и х₂ на входах, сигнал у на выходе элемента ИЛИ и выходная функция F.

 

 

а) б)

Рис. 3.7. Условное обозначение логического элемента ИЛИ-НЕ (а),

его таблица истинности (б)

а) б)

Рис. 3.8. Схема логического элемента ИЛИ-НЕ ДТЛ (а)

и его временные диаграммы (б)

 

 

Логический элемент И-НЕ. Условное обозначение логического элемента И-НЕ показано на рис.3.9,а. Ему эквивалентна структурная схема, показанная на рис.3.9,б. Логической «1» на всех информационных входах соответствует логический «0» на выходе элемента. При логическом «0» на одном из входов создается логическая «1» на выходе. Для двухвходового элемента И-НЕ сказанное отражено в таблице истинности на рис.3.9,в. Логическая функция элемента И-НЕ при n входах отвечает выражению

(3.4)

На рис.3.10,а приведена схема логического элемента И-НЕ ДТЛ. Принцип действия элемента иллюстрируют временные диаграммы рис.3.10,б. При логических «1» на обоих входах диоды Д₁, Д₂ закрыты. В схеме образуется цепь + Е_И — R_G — Д¢— Д², которая обеспечивает протекание тока базы E_H/R₆ транзистора. Транзистор открыт и насыщен, F=0.

 

 

Рис.3.9. Условное обозначение логического элемента И-НЕ (а),

его функциональный эквивалент (б) и таблица истинности (в)

 

 

Рис.3.10. Схема логического элемента И-НЕ ДТЛ (а) и его временные диаграммы (б)

 

При логическом «0» на одном из входов (например, x₁) открывается диод этого входа (Д₁). Образуется цепь, в которой ток резистора R_б (рис.3.10,а) протекает через открытый диод (Д₁) и источник сигнала логического «0» (x₁). При этом цепь Д’ — Д» — эмиттерный переход транзистора — оказывается шунтированной цепью с проводящим диодом. Ток базы транзистора равен нулю, транзистор закрыт, F=1.

Поскольку напряжение на открытом диоде входной цепи, а также напряжение входа логического «0» реально больше нуля, точка у на рис.3.10,а имеет некоторый положительный потенциал относительно эмиттера транзистора. В отсутствие диодов Д’, Д» это могло бы привести к отпиранию транзистора. При их введении напряжение между точкой у и эмиттером транзистора будет приложено к диодам, а напряжение U_бэ транзистора близко к нулю.

Наличие усилительного элемента, транзистора, в логических микросхемах ИЛИ-НЕ и И-НЕ классов ДТЛ и ТТЛ определяет такое их важное преимущество, как сохранение неизменного уровня напряжения, соответствующего логической «1», в процессе передачи сигнала при их последовательном соединении. В связи с этим указанные элементы, а также элемент НЕ являются базовыми в микросхемотехнике. В общем корпусе выпускаемых микросхем обычно содержится несколько элементов одного типа.

Функцию И-НЕ называют функцией Шеффера (штрихом Шеффера) и обозначают в виде у=x₁|x₂, а функцию ИЛИ-НЕ — функцией Пирса (стрелкой Пирса) и обозначают в виде . Базис И-НЕ называют базисом Шеффера, а базис ИЛИ-НЕ — базисом Пирса.

Логическое устройство, реализованное в базисе И-НЕ (ИЛИ-НЕ), имеет преимущества по сравнению с устройством, реализованным в базисе И, ИЛИ, НЕ:

уменьшение номенклатуры элементов до одного типа, что упрощает компоновку устройства и его ремонт;

наличие в каждом элементе инвертора (усилителя), который компенсирует затухание потенциалов при передаче их через коныонктор или дизъюнктор элемента. Благодаря этому не накапливается затухание сигнала при прохождении его через ряд последовательно включенных элементов, что могло бы вызвать снижение уровня U₁ (лог. 1). Кроме того, инвертор увеличивает нагрузочную способность элемента: подключение допустимого числа других элементов к его выходу не вызывает заметного умень­шения на нем уровней потенциалов (что важно для U₁), а наличие емкости на выходе не вызывает длительного переходного процесса при смене потенциалов.

 

Цифровые компараторы

 

Цифровой компаратор предназначен для сравнения двух двоичных чисел (компарировать — сравнивать). Он имеет две группы входов. На одну из них поступают разряды первого числа А, на другую группу — разряды второго числа В. Появление лог.1 на одном из трех выходов компаратора фиксирует результат сравнения. На одном выходе она устанавливается при равенстве чисел (А=В), на другом — при А>В, на третьем — при А<В.

Сравнение одноразрядных чисел на равенство может осуществлять элемент «Равнозначность», а на неравенство — элемент «Неравнозначность» (см. п.2.3.2). Для сравнения многоразрядных чисел они дополняются элементами других типов.

Цифровой компаратор можно использовать, например, в системах автоматического контроля и регулирования. При этом число А является параметром некоторого процесса, а число В — порогом (уставкой), которого (в соответствии с условиями задачи) этот параметр не должен превосходить или опускаться ниже его. На рис.4.12 приведена классификация цифровых компараторов. Наряду с цифровыми существуют и аналоговые компараторы.

Рис.3.11. Классификация компараторов

 

Структура компаратора.

 

В табл.3.1 показана связь между сигналами на выходах и входах компаратора при сравнении одноразрядных чисел а и в, которые могут быть равны единице или нулю. На соответствующем выходе появляется лог.1, когда в должном соотношении находятся коды на входах. Так, если а=1, b=1 (числа одинаковы), то функция, характеризующая равенство чисел, F_a=b=1, а функции, характеризующие их неравенство, F_a>b=0 и F_a<b=0.

Таблица 3.1

Связь между входными и выходными сигналами компаратора

Входы	Выходы
A	B	Fa>b	Fa=b	Fa<b

 

Аналогично заполняются другие строки таблицы. По правилам алгебры логики из табл.3.1 можно записать следующие логические функции, характеризующие соотношения одноразрядных чисел:

; ; .

Если значения а и b таковы, что правые части функций равны 1, то соотношения, указанные в индексах левых частей, выполняются. Если правые части функций равны 0, то соотношения между а и в противоположны указанным.

Схема одноразрядного компаратора, реализующая приведенные функции, изображена на рис.3.12.

На рис.3.13 приведены условное обозначение компараторов и способ наращивания их разрядности. Каждый из изображенных компараторов предназначен для сравнения двух 4-разрядных слов и имеет выходы А>В, А=В и А<В. Аналогичные входы служат для наращивания разрядности компараторов. Результат сравнения младших разрядов отражается на выходах компаратора К₁: на одном из них появляется единица, на других присутствуют нули.

Рис.3.12. Схема одноразрядного компаратора

 

Компаратор К₂ воспринимает этот результат как единую пару младших разрядов, с учетом которой формируется окончательный результат сравнения. Подобным образом можно осуществлять дальнейшее наращивание разрядности. Указанные потенциалы на входах компаратора К₁ младших разрядов обеспечивают правильное функционирование многокаскадного компаратора на данных микросхемах.

Рис.3.13. Условное обозначение компараторов и способ

наращивания их разрядности

Читайте также:





Урок 8.3 — Логические элементы

8.3. Логические элементы

Все, абсолютно все электронные компоненты, обрабатывающие цифровые сигналы, состоят из небольшого набора одинаковых «кирпичиков». В микросхемах малой степени интеграции могут быть единицы и десятки таких элементов, а в современных процессорах их может быть очень и очень много. Они называются логические элементы. Логическим элементом называется электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами.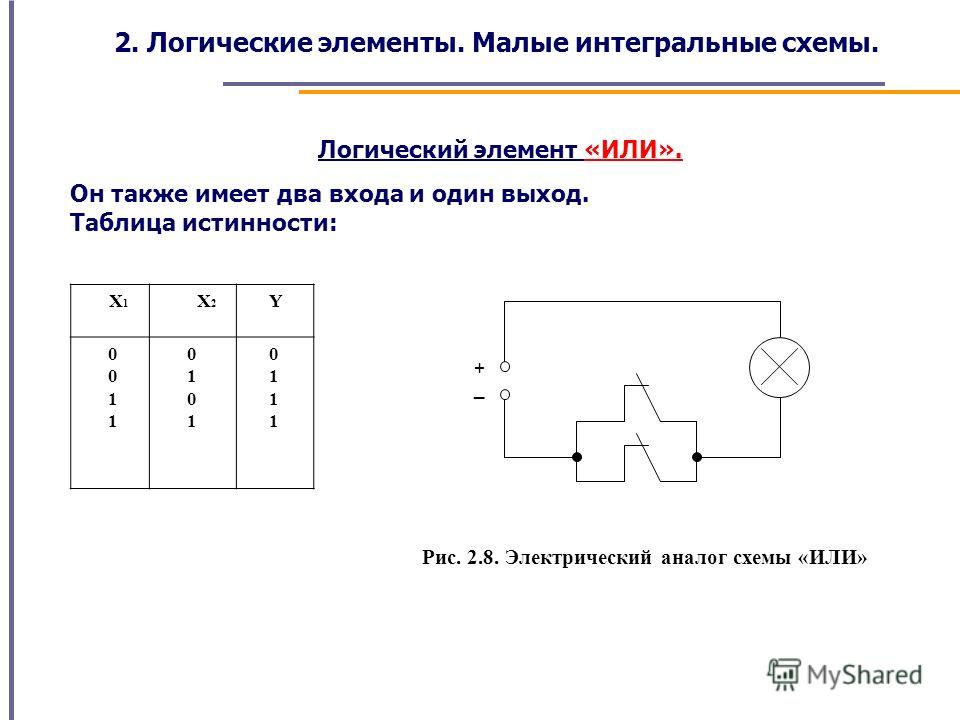 Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.

Тем не менее, принцип работы цифровой логики остается неизменным – на входе логического элемента (входов может быть несколько)  должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.

Конечно, логические элементы строятся, в свою очередь, из уже рассмотренных в предыдущих уроках резисторов, транзисторов и других электронных компонентов, но с точки зрения разработки цифровых схем именно логический элемент является их «элементарной» частицей.

 При анализе работы логических элементов используется так называемая булева алгебра . Начала этого раздела математики было изложено в работах Джорджа Буля – английского математика и логика 19-го века, одного из основателей математической логики.   Основами булевой алгебры являются высказывания, логические операции, а также функции и законы. Для понимания принципов работы логических элементов нет необходимости изучать все тонкости булевой алгебры, мы освоим ее основы в процессе обучения с помощью таблиц истинности.

Еще несколько замечаний. Логические элементы (как, впрочем, и другие элементы электронных схем) принято обозначать  так, чтобы входы были слева, а выходы справа. Число входов может быть, вообще говоря, любым, отличным от нуля. Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.

Какие же бывают логические элементы?

Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.

 

Элемент «И» (AND), он же конъюнктор, выполняет операцию логического умножения:

Условное обозначение — Таблица истинности

Здесь изображен логический элемент «2И» (цифра перед буквой «И» означает число входов).  Знак  & (амперсант) в левом верхнем углу прямоугольника  указывает, что это логический элемент «И». Первые две буквы обозначения  DD1.2  указывают на то, что это цифровая микросхема (Digital), цифра слева от  точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.

Состояние входов в таблице обозначаются «0» и «1» («ложь» и «истина»). Из таблицы видно, что выход «Y» будет иметь состояние «1» только в том случае, когда на обоих входах «Х1» и «Х2» будут «1». Это легко запомнить: умножение на «0» всегда дает «0».

 

Элемент «ИЛИ» (OR), он же дизъюнктор, выполняет операцию логического сложения:

Условное обозначение — Таблица истинности

Состояние «1»  на выходе будет всегда, пока есть хотя бы одна «1» на входах.

 

Элемент «НЕ» (NOT), он же инвертор, выполняет операцию логического отрицания:

Условное обозначение — Таблица истинности

Состояние на входе обратно состоянию на входе.

Вот из этих трех элементов строятся все цифровые устройства!

Рассмотрим еще три логических элемента, которые можно получить, комбинируя уже рассмотренные. В силу исторически сложившихся схемотехнических решений эти скомбинированные схемы тоже считаются логическими элементами.

 

Элемент «И-НЕ» (NAND), конъюнктор с отрицанием:

Условное обозначение — Таблица истинности

Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» будет единица. И наоборот.

 

Элемент «ИЛИ-НЕ» (NOR), дизъюнктор с отрицанием:

Условное обозначение — Таблица истинности

 

Элемент работает так же как и «ИЛИ», но с инверсией выхода.

 

Элемент «Исключающее ИЛИ» (XOR), сумматор по модулю 2:

Условное обозначение — Таблица истинности

В этом элемента «1» на выходе будет только тогда, когда на входах разные состояния.

На таких элементах  строят сумматоры двоичных многоразрядных чисел. Для этого используется еще один дополнительный выход, на котором при появлении на входах двух «1» появляется сигнал переноса разряда.

Мы рассмотрели логические элементы, которые применяются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут делать одну крайне важную работу  – они не умеют хранить информацию.   Для хранения используется более сложный класс устройств, называемый элементами с памятью или конечными автоматами. В этот класс входят триггеры, регистры, счетчики, шифраторы (дешифраторы), мультиплексоры (демультиплексоры) и сумматоры. Некоторый из этих устройств мы рассмотрим в следующем уроке.

 

Диодные логические элементы ИЛИ, И — Студопедия

Логические элементы могут работать как с положительными напряжениями, так и с отрицательными напряжениями. На рис.10.3 приведены временные диаграммы таких напряжений.

Рис.10.3. Временные диаграммы работы логических элементов с положительными и отрицательными напряжениями

Логические элементы ИЛИ и И можно реализовать с помощью диодов.

На рисунках 10.4 и 10.5 приведены электрические схемы логических элементов ИЛИ, построенных на диодах с использованием положительных и отрицательных напряжений.

Рассмотрим работу схемы рис.10.4. Если на входы диодов х1 и х2 подавать сигналы лог. 0 , то диоды VD1 и VD2 будут закрыты и на выходе y cхемы появится лог.0 . Если на один из входов, например на Вх.1, подать положительное напряжение лог.1, а на Вх.2 – лог.0, то диод VD1 откроется и через нагрузку пойдёт ток, на выходе y появится сигнал лог.1. При этом диод VD2 будет закрыт.

Рис.10.4. Диодная схема логического элемента ИЛИ с положительными

напряжениями

Рис.10.5. Диодная схема логического элемента ИЛИ с отрицательными

напряжениями

Аналогично работает схема, приведённая на рис.10.5. Входные и выходные сигналы схемы будут соответствовать таблице истинности:

На рис.10.6 изображена электрическая схема логического элемента И, построенная на диодах VD1, VD2 и ограничительном резисторе R. Cхема питается от источника постоянного тока.

Если логические сигналы на одном из входов х1 и х2 или на двух входах элемента соответствуют лог. 0, то сигнал на выходе схемы будет также равен лог.0. Это происходит потому, что один из диодов или оба диода будут открыты и ток проходит от +E через резистор R, один или два диода, вход или два входа элемента к -E. При этом внутренние сопротивления входов малы Rвн.вх.<Rн. Если на входах х1 и х2 появятся сигналы лог.1, то на выходе y элемента также появляется сигнал лог.1, так как диоды VD1, VD2 закрыты положительными напряжениями входных сигналов.

Рис.10.6. Электрическая диодная схема логического элемента И

Входные и выходные сигналы схемы будут соответствовать таблице истинности:

Логический элемент И-НЕ транзисторно-транзисторной логики — Студопедия

Логический элемент НЕ реализуется с помощью биполярного транзистора n-p-n cтруктуры. Принципиальная электрическая схема транзисторного логического элемента НЕ и его таблица истинности приведены на рис. 10.7.

Схема работает следующим образом. Если на вход x логического элемента подать сигнал лог.0, то транзистор VT будет закрыт и на выходе y появится сигнал лог.1, так как всё напряжение будет падать на закрытом транзисторе. При подаче на вход x логического элемента сигнала лог.1, транзистор VT открывается и на выходе y появится сигнал лог.0, при этом всё напряжение падает на резисторе Rк.

При использовании логических элементов транзисторно-транзисторной логики, построенной с помощью биполярных транзисторов n-p-n cтруктуры, реализуется операция И-НЕ. На рис.10.8 приведена электрическая схема логического элемента И-НЕ и таблица истинности. Схема состоит из двух логических элементов И и НЕ, соединённых последовательно. Транзисторный элемент И имеет несколько входов. На схеме рассматриваются только два из эмиттерных входов х1 и х2 транзистора VT1, коллектор которого соединён с базой инвертора, построенного на транзисторе VT2.

Рис.10.7. Принципиальная электрическая схема транзисторного логического элемента НЕ и его таблица истинности

Рис.10.8. Электрическая схема логического элемента И-НЕ и его таблица истинности

Схема работает следующим образом. Если на входы х1 и х2 транзистора VT1 поступают сигналы лог.0 или на одном из этих входов присутствует сигнал лог.1, то базовый ток пройдет через сопротивление базы транзистора к эмиттерным входам (входу) от “+” источника питания к его “–“. При этом, транзистор VT2 будет закрыт и на его выходе y присутствует cигнал лог.1. Если на входы х1 и х2 транзистора VT1 поступают положительные сигналы лог.1, то в этом случае закрываются эмиттерные входы тразистора VT1 и базовый ток течет через коллектор тразистора VT1 к базе тразистора VT2, открывая его. При этом на выходе у тразистора VT2 появится синал лог.0.

10.5. Логический элемент ИЛИ-НЕ эмиттерно-связанной логики

На рис.10.9 изображена электрическая схема логического элемента ИЛИ-НЕ, построенного на транзисторах n-p-n cтруктуры, и его таблица истинности. Если на

входах х1 и х2 транзисторов VT1, VT2 присутствуют входные сигналы лог.0, то эти транзисторы будут закрыты и сопротивление между их коллекторами и эмиттерами будет бесконечным. При этом коллекторная цепь этих транзисторов будет иметь положительный потенциал, то есть инвертированный сигнал ИЛИ, который будет поступать на вход транзистора VT3. На выходе у транзистора VT3, работающего в режиме повторителя, появится сигнал лог.1.

В случае поступления на входы х1 и х2 транзисторов VT1, VT2 положительных сигналов лог.1 или на одном из этих входов присутствует сигнал лог.1, то их коллекторные цепи будут иметь отрицательный потенциал. При этом транзисторы VT1, VT2 (или один из них) открываются, и сопротивление цепи коллектор-эмиттер будет равно нулю. Так как Rк>Rэ1, то на общем коллекторном выходе транзисторов VT1, VT2 появится отрицательный потенциал, который поступит на вход транзистора VT3 и закроет его. Сигнал на выходе y транзистора VT3 будет иметь лог.0. Фактически транзистор VT3 является повторителем действия выходного сигнала транзисторов VT1 и VT2, работающих в режиме операции ИЛИ-НЕ.

Рис.10.9. Электрическая схема логического элемента ИЛИ-НЕ и его таблица истинности

НОУ ИНТУИТ | Лекция | Простейшие логические элементы

Аннотация: В лекции рассматриваются принципы работы, характеристики и типовые схемы включения простейших логических
элементов — инверторов, буферов, элементов И и ИЛИ, а также приводятся схемотехнические решения, позволяющие
реализовать на их основе часто встречающиеся функции.

Изучение базовых элементов цифровой электроники мы начнем с наиболее простых, а затем будем рассматривать все более
сложные. Примеры применения каждого следующего элемента будут опираться на все элементы, рассмотренные ранее.
Таким образом, будут постепенно даны главные принципы построения довольно сложных цифровых устройств.

Логические элементы (или, как их еще называют, вентили, «gates») — это наиболее простые цифровые микросхемы.
Именно в этой простоте и состоит их отличие от других микросхем. Как правило, в одном корпусе микросхемы может
располагаться от одного до шести одинаковых логических элементов. Иногда в одном корпусе могут располагаться и
разные логические элементы.

Обычно каждый логический элемент имеет несколько входов (от одного до двенадцати) и один выход. При этом
связь между выходным сигналом и входными сигналами (таблица истинности) предельно проста. Каждой
комбинации входных сигналов элемента соответствует уровень нуля или единицы на его выходе. Никакой
внутренней памяти у логических элементов нет, поэтому они относятся к группе так называемых комбинационных
микросхем. Но в отличие от более сложных комбинационных микросхем, рассматриваемых в следующей лекции,
логические элементы имеют входы, которые не могут быть разделены на группы, различающиеся по выполняемым ими
функциям.

Главные достоинства логических элементов, по сравнению с другими цифровыми микросхемами, — это их высокое
быстродействие (малые времена задержек), а также малая потребляемая мощность (малый ток потребления). Поэтому
в тех случаях, когда требуемую функцию можно реализовать исключительно на логических элементах, всегда имеет
смысл проанализировать этот вариант. Недостаток же их состоит в том, что на их основе довольно трудно реализовать
сколько-нибудь сложные функции. Поэтому чаще всего логические элементы используются только в качестве дополнения к
более сложным, к более «умным» микросхемам. И любой разработчик обычно стремится использовать их как можно меньше
и как можно реже. Существует даже мнение, что мастерство разработчика обратно пропорционально количеству используемых
им логических элементов. Однако это верно далеко не всегда.

Инверторы

Самый простой логический элемент — это инвертор (логический элемент НЕ, «inverter»), уже упоминавшийся
в
«Базовые понятия цифровой электроники»
. Инвертор выполняет простейшую логическую функцию — инвертирование, то есть изменение
уровня входного сигнала на противоположный. Он имеет всего один вход и один выход. Выход инвертора может
быть типа 2С или типа ОК. На рис. 3.1 показаны условные обозначения инвертора, принятые у нас и за рубежом,
а в табл. 3.1 представлена таблица истинности инвертора.

Рис.
3.1.
Условные обозначения инверторов: зарубежные (слева) и отечественные (справа)

В одном корпусе микросхемы обычно бывает шесть инверторов. Отечественное обозначение микросхем инверторов
— «ЛН». Примеры: КР1533ЛН1 (SN74ALS04) — шесть инверторов с выходом 2С, КР1533ЛН2 (SN74ALS05) —
шесть инверторов с выходом ОК. Существуют также инверторы с выходом ОК и с повышенным выходным током
(ЛН4), а также с повышенным выходным напряжением (ЛН3, ЛН5). Для инверторов с выходом ОК необходимо
включение выходного нагрузочного резистора pull-up. Его минимальную величину можно рассчитать очень
просто: R < U/I_OL, где U — напряжение питания, к которому подключается резистор. Обычно величина
резистора выбирается порядка сотен Ом — единиц кОм.

Таблица
3.1.
Таблица истинности инвертора

Вход	Выход
0	1
1	0

Две основные области применения инверторов — это изменение полярности сигнала и изменение полярности
фронта сигнала (рис. 3.2). То есть из положительного входного сигнала инвертор делает отрицательный
выходной сигнал и наоборот, а из положительного фронта входного сигнала — отрицательный фронт
выходного сигнала и наоборот. Еще одно важное применение инвертора — буферирование сигнала (с инверсией),
то есть увеличение нагрузочной способности сигнала. Это бывает нужно в том случае, когда какой-то сигнал
надо подать на много входов, а выходной ток источника сигнала недостаточен.

Рис.
3.2.
Инверсия полярности сигнала и инверсия полярности фронта сигнала

Основные логические ворота с таблицами истинности

В наши дни компьютеры стали неотъемлемой частью жизни, поскольку они выполняют множество задач и операций за довольно короткий промежуток времени. Одна из наиболее важных функций ЦП компьютера — выполнение логических операций с использованием оборудования, такого как интегральные схемы, электронные схемы и программные технологии. Но как это оборудование и программное обеспечение выполняют такие операции — загадка. Чтобы лучше понять такую ​​сложную проблему, мы должны познакомиться с термином «логическая логика», разработанным Джорджем Булем.Для простой операции компьютеры используют двоичные цифры, а не цифровые. Все операции выполняются воротами базовой логики.

Basic Logic Gates

Что такое Logic Gate

Логический вентиль — это базовый строительный блок цифровой схемы, которая имеет два входа и один выход. Связь между i / p и o / p основана на определенной логике. Эти затворы реализованы с помощью электронных ключей типа транзисторов, диодов. Но на практике базовые логические вентили строятся с использованием технологии CMOS, полевых транзисторов и полевых транзисторов MOSFET (Metal Oxide Semiconductor FET).Логические вентили используются в микропроцессорах, микроконтроллерах, встроенных системных приложениях, а также в электронных и электрических схемах проекта. Основные логические элементы делятся на семь категорий: AND, OR, XOR, NAND, NOR, XNOR и NOT. Эти логические вентили с их символами логических вентилей и таблицами истинности объясняются ниже.

Логический вентиль

Логический вентиль

И вентиль

Логический вентиль И представляет собой цифровой логический вентиль с ‘n’ i / ps и одним o / p, который выполняет логическое соединение на основе комбинаций его входов.Выход этого вентиля истинен только тогда, когда все входы истинны. Когда один или несколько входов i / ps логического элемента И являются ложными, тогда только выход логического элемента И является ложным. Таблица символов и истинности логического элемента И с двумя входами показана ниже.

Логический элемент И и его таблица истинности

Логический элемент ИЛИ

Логический элемент ИЛИ — это цифровой логический вентиль с n i / ps и одним o / p, который выполняет логическое соединение на основе комбинаций его входов. Элемент ИЛИ истинен только тогда, когда один или несколько входов истинны.Если все i / ps логического элемента ложны, то ложным является только выход логического элемента ИЛИ. Таблица символов и истинности логического элемента ИЛИ с двумя входами показана ниже.

Логический элемент ИЛИ и его таблица истинности

Логический элемент НЕ

Элемент НЕ — это цифровой логический вентиль с одним входом и одним выходом, который управляет инверторной операцией входа. Выход элемента НЕ является обратным входу. Когда вход логического элемента НЕ истинен, тогда выход будет ложным, и наоборот. Таблица символов и истинности логического элемента НЕ с одним входом показана ниже.Используя этот вентиль, мы можем реализовать вентили ИЛИ и И-НЕ.

Шлюз НЕ и его таблица истинности

Шлюз И-НЕ

Логический вентиль И-НЕ — это цифровой логический вентиль с ‘n’ i / ps и одним o / p, который выполняет операцию вентиль И, за которым следует вентиль НЕ. вентиль НЕ разработан путем объединения вентилей И и НЕ. Если вход логического элемента И-НЕ высокий, то выход элемента будет низким. Ниже показаны символы и таблица истинности логического элемента И-НЕ с двумя входами.

Шлюз И-НЕ и его таблица истинности

Шлюз ИЛИ

Элемент ИЛИ-НЕ — это цифровой логический вентиль с n входами и одним выходом, который выполняет операцию логического элемента ИЛИ, за которым следует вентиль НЕ.Ворота NOR разработаны путем объединения ворот OR и NOT. Когда любой из i / ps логического элемента ИЛИ-НЕ истинен, тогда выход логического элемента ИЛИ-НЕ будет ложным. Таблица символов и истинности вентиля ИЛИ-НЕ с таблицей истинности показана ниже. Шлюз

ИЛИ-ИЛИ и его таблица истинности

Шлюз исключающего ИЛИ

Элемент исключающего ИЛИ — это цифровой логический вентиль с двумя входами и одним выходом. Краткая форма этих ворот — Ex-OR. Он работает на основе операции логического элемента ИЛИ. . Если на любом из входов этого логического элемента высокий уровень, то на выходе элемента EX-OR будет высокий уровень.Символы и таблица истинности EX-OR показаны ниже.

Элемент EX-OR и его таблица истинности

Элемент Exclusive-NOR

Элемент Exclusive-NOR — это цифровой логический элемент с двумя входами и одним выходом. Краткая форма этих ворот — Ex-NOR. Он работает на основе работы логического элемента ИЛИ-НЕ. Когда на обоих входах этого логического элемента высокий уровень, тогда выход элемента ИСКЛЮЧАЮЩЕЕ НЕ будет высоким. Но если какой-либо из входов высокий (но не оба), то выход будет низким. Символ и таблица истинности EX-NOR показаны ниже.

Шлюз EX-NOR и его таблица истинности

Применение логических вентилей в основном определяется на основе их таблицы истинности, т. Е. Их режима работы. Базовые логические вентили используются во многих схемах, таких как кнопочный замок, охранная сигнализация с включением света, предохранительный термостат, автоматическая система полива и т. Д.

При использовании комбинации базовых логических вентилей часто выполняются расширенные операции. Теоретически нет предела количеству ворот, которые можно одеть за одно устройство.Однако в приложении существует ограничение на количество ворот, которые могут быть упакованы в данную физическую зону. Массивы блока логических вентилей находятся в цифровых интегральных схемах (ИС). По мере развития технологии ИС желаемый физический объем для каждого отдельного шлюза уменьшается, и цифровые устройства эквивалентного или меньшего размера становятся способными выполнять более сложные операции с постоянно увеличивающейся скоростью.

Это все о базовых логических элементах, которые включают в себя элемент И, элемент ИЛИ, элемент И-НЕ, элемент ИЛИ-НЕ, элемент ИСКЛЮЧАЮЩЕЕ ИЛИ и элемент ИСКЛЮЧАЮЩЕЕ ИЛИ.В этом случае вентили И, НЕ и ИЛИ являются основными логическими вентилями. Используя эти вентили, мы можем создать любой логический вентиль, комбинируя их. Где ворота NAND и NOR называются универсальными воротами. Эти ворота имеют особое свойство, с помощью которого они могут создавать любое логическое логическое выражение, если они спроектированы надлежащим образом. Кроме того, по любым вопросам, касающимся этой статьи или проектов в области электроники, просьба оставлять свои отзывы, комментируя их в разделе комментариев ниже.

Основные типы логических вентилей и структурные блоки »Электроника

— обзор различных типов логических элементов и строительных блоков цифровых схем, которые доступны.

---

Логический / цифровой дизайн Включает:
Типы логических вентилей
Таблица логической истинности
Как преобразовать вентили NAND / NOR с помощью инверторов
RS Вьетнамки
RS-триггер с синхронизацией по фронту
Программируемый инвертор
Делитель частоты типа D

---

Цифровая электроника работает с числами.

Это достигается путем представления чисел в цифровой форме и использования логических операций для обеспечения необходимой обработки.

Для этого можно использовать большое количество различных типов логических элементов и строительных блоков цифровых схем.

Эта цифровая схема сегодня составляет основу многих электронных устройств. Несмотря на то, что многие логические схемы или цифровые схемы содержатся в больших интегральных схемах, применяются те же основные функции. Единственное отличие — количество схем, содержащихся в большом блоке.

Базовый логический вентиль и типы схем

Существует множество стандартных строительных блоков или базовых типов логических элементов, которые можно использовать.

• Буфер: Возможно, логический вентиль неправильного типа в строгом смысле слова, но иногда вентиль может быть введен в качестве буфера по разным причинам.
  Логический буферный символ логического буфера

  Иногда могут быть введены буферы, чтобы обеспечить более высокую выходную способность, для ускорения фронта логического сигнала или иногда для добавления небольшой задержки. В связи с этим буферы используются более широко, чем можно было бы ожидать на первый взгляд.

• НЕ: Элемент НЕ, возможно, является самым простым типом логического элемента.Он берет сингл и инвертирует его. Используя этот логический вентиль или логическую схему, логическая «1» становится логическим «0», а логический «0» становится логической «1».
  Обозначение схемы логического инвертора

  Логический вентиль НЕ — бесценный тип логического элемента, который широко используется в логических схемах. Часто два гейта вместе могут использоваться, когда не требуется инверсия, но требуется небольшая задержка. Этот метод может работать, когда нет буферов.

• AND / NAND: Логические вентили AND и NAND обычно рассматриваются вместе, потому что выход одного из них является инверсным по отношению к другому.Основная функция логического элемента этого типа такая же. В вентиле типа AND выдает на выходе «1» только тогда, когда оба входа равны «1», в противном случае — «0». Логический вентиль типа И-НЕ производит обратное.
  Обозначение логической схемы логического И
  Обозначение логической схемы И-НЕ

  Затворы И и И-НЕ, возможно, являются наиболее широко используемой формой логических схем. Из двух наиболее часто встречается вентиль NAND.

• OR / NOR: Логические элементы ИЛИ и ИЛИ — еще одна форма логических элементов, которые образуют один из основных строительных блоков цифровой технологии.Элемент ИЛИ выдает логическую «1», когда на одном из других входов (или на обоих входах) высокий уровень.

  Точно так же вентиль ИЛИ-ИЛИ является обратным этому и переходит в низкий уровень, «0», когда один или другой вход (или оба входа) имеют высокий уровень.

  Символ логической схемы ИЛИ
  Символ логической схемы ИЛИ-ИЛИ

  Как и вентиль И-НЕ, вентиль ИЛИ-НЕ является более широко используемым из этой пары логических вентилей.

• Исключающее ИЛИ / ИЛИ: Логический вентиль типа исключающее ИЛИ или ИЛИ используется, когда изменение выхода требуется только тогда, когда один или другой вход имеет высокий уровень, а не оба.
  Логический символ логической схемы исключающего ИЛИ
  Логический символ исключающей логической схемы ИЛИ

  Хотя более широко используется более привычный стандартный тип логического элемента ИЛИ или ИЛИ-ИЛИ, существуют некоторые обстоятельства, когда требуется исключающее ИЛИ или ИЛИ.

• RS Flip-Flop: Инициалы RS-триггера обозначают Set-Reset. Этот тип логического элемента или схемы имеет два входа: установка и сброс. Как и следовало ожидать, этот тип логической схемы устанавливается при срабатывании одного входа и сбрасывается при срабатывании другого. Подробнее о RS Flip Flop
• Триггер D-типа: Триггер D-типа можно назвать формой или типом логической схемы. Это разновидность триггера, который передает входные данные на выход на границе тактового сигнала. Это особенно полезная форма триггера, которая находит множество применений в различных приложениях.
• J-K Flip Flop: J-K Flip-flop — самый универсальный из основных триггеров, и его можно настроить для работы в различных режимах.
• Счетчик: Счетчики широко используются в различных формах логических схем. По сути, они принимают последовательность импульсов и, в зависимости от их коэффициента деления, выдают импульс после того, как введено заданное количество импульсов.

Дополнительные темы по цифровой логике и встраиваемым системам:
Программирование ПЛИС
Встроенные системы
Как работает компьютер

Основы проектирования логических схем
Рекомендации по проектированию логики / схем

Вернуться в меню Цифра / Логика / Обработка.. .

Логические ворота

• Изучив этот раздел, вы должны уметь:
• Опишите действие логических вентилей.
• • AND, OR, NAND, NOR, NOT, XOR и XNOR.
• • Использование логических выражений.
• • Использование таблиц истинности.
• Разберитесь в использовании универсальных ворот.
• • NAND.
• • NOR.
• Распознавать общие микросхемы серии 74, содержащие стандартные логические элементы.

Логические ворота

Семь базовых логических вентилей

Цифровая электроника полагается на действия всего семи типов логических вентилей, называемых И, ИЛИ, И-НЕ (Не И), ИЛИ (Не ИЛИ), XOR (Исключающее ИЛИ), XNOR (Исключающее ИЛИ) и НЕ.

Поскольку в двоичной логике есть только два состояния, 1 и 0 или «включено и выключено», НЕ в мире двоичной логики означает «противоположное».Если что-то не 1, это должно быть 0, если оно не включено, оно должно быть выключено. Таким образом, NAND (не AND) просто означает, что вентиль NAND выполняет функцию, противоположную вентилю AND.

Логический вентиль — это небольшая транзисторная схема, в основном тип усилителя, который реализован в различных формах внутри интегральной схемы. Каждый тип ворот имеет один или несколько (чаще всего два) входа и один выход.

Принцип работы состоит в том, что схема работает всего на двух уровнях напряжения, называемых логическим 0 и логической 1.Когда любой из этих уровней напряжения подается на входы, выход затвора реагирует, принимая уровень 1 или 0, в зависимости от конкретной логики затвора. Логические правила для каждого типа ворот могут быть описаны по-разному, с помощью письменного описания действия, с помощью таблицы истинности или с помощью оператора булевой алгебры.

Логические операторы используют буквы из начала алфавита, такие как A, B, C и т. Д., Для обозначения входных данных и буквы из второй половины алфавита, очень часто X или Y и иногда Q или P для обозначения выхода.Буквы сами по себе не имеют никакого значения, кроме обозначения различных точек в цепи. Затем буквы соединяются символом, обозначающим логическое действие ворот.

Символ • обозначает И, хотя во многих случаях символ • может быть опущен. (A • B может также записываться как AB или A.B)

+ обозначает ИЛИ

⊕ означает XOR (Исключающее ИЛИ)

Хотя символы • и + такие же, как и символы, используемые в нормальной алгебре для обозначения произведения (умножения) и суммы (сложения) соответственно, в двоичной логике символ + не совсем соответствует сумме.В цифровой логике 1 + (ИЛИ) 1 = 1, но двоичная сумма 1 + 1 = 10 ₂ , поэтому в цифровой логике + всегда следует рассматривать как ИЛИ.

Три дополнительных типа логических вентилей дают выход, который является инвертированной версией трех основных функций вентилей, перечисленных выше, и они обозначены полосой, нарисованной над оператором с использованием символов И, ИЛИ или ИСКЛЮЧАЮЩЕЕ ИЛИ для обозначения И-НЕ, ИЛИ ИЛИ и XNOR.

A • B означает A AND B, но A • B означает A NAND B

Например:

Элемент И дает выход логической 1, когда вход A И вход B находятся на уровне логической 1, но элемент И-НЕ дает выход логического 0 для тех же условий входа.Также, если вентиль И дает логический ноль для конкретной входной комбинации, вентиль И-НЕ даст логическую 1. Таким образом, буква «N» в имени логического элемента или полоса над логическим выражением указывает на то, что логика выхода «инвертирована». . В цифровой логике NAND — это NOT AND или противоположность AND. Точно так же NOR — это «NOT» OR, а XNOR — это «NOT» XOR.

Последний тип ворот, вентиль НЕ или инвертор, представляет собой единственный входной вентиль, у которого есть выход, имеющий противоположное логическое состояние или инверсию входа.

Таблица 2.1.1 показывает каждый из семи основных логических вентилей, которые могут быть проиллюстрированы либо традиционным символом ANSI «Отличительной формы», либо новым прямоугольным символом IEC, а также письменным описанием его логической функции в сравнении с его булевым уравнением.

Рис. 2.1.1 Логические вентили семейства TTL IC серии 74

Логические ИС

Рис. 2.1.1 иллюстрирует выбор основных логических вентилей, которые доступны от ряда производителей в стандартных семействах интегральных схем.Каждое семейство логики спроектировано таким образом, чтобы вентили и другие логические ИС в этом семействе (и других связанных семействах) можно было легко комбинировать и встраивать в более крупные логические схемы для выполнения сложных функций с минимумом дополнительных компонентов.

Как правило, стандартные логические вентили доступны в 14- или 16-контактных микросхемах DIL (двойная линия). Количество вентилей на IC варьируется в зависимости от количества входов на вентиль. Обычно используются вентили с двумя входами, но если требуется только один вход, например, в вентилях 7404 NOT (или инверторе), 14-контактная ИС может вмещать 6 (или шестнадцатеричных) вентилей.Наибольшее количество входов на один вентиль находится на вентиле И-НЕ 74133 с 13 входами, который размещен в 16-выводном корпусе.

Таблицы данных

7400 Четыре входа NAND, 2 входа

7402 Quad 2 входа NOR вентили

7404 Затворы Hex NOT (инверторы)

7408 Quad 2 входа И вентили

7432 Quad 2 входа ИЛИ вентили

7486 Четыре входа XOR, 2 входа

747266 Quad 2 входа XNOR вентили

74133 Одиночный логический элемент И-НЕ с 13 входами

Как работают логические вентили

Фиг.2.1.2 Логические функции

С помощью Рис. 2.1.2 вы можете проверить работу основных логических вентилей. Интерактивная анимация позволяет вам выбрать любой из 7 основных ворот на верхней панели и нажать переключатели A и B, чтобы проверить его работу. Используйте анимацию, чтобы познакомиться с работой каждого из ворот, сравнивая результаты, которые вы видите, с предоставленными таблицами истинности. Чтобы легко понять более сложные цифровые схемы, важно создать хорошее представление об ожидаемом выходе каждого логического элемента для любого возможного входа.

Логические функции

На рис. 2.1.2 также показано, как семь основных логических функций могут быть описаны с помощью «таблицы истинности», чтобы показать взаимосвязь между выходом (X) и всеми возможными комбинациями входов для входов A и B, показанных в виде четырехзначного двоичного файла. считайте от 00 до 11. Каждая диаграмма показывает условия входа и выхода для одной из семи логических функций в форме двух входов. Однако некоторые типы ворот также доступны с большим количеством входов (например, от 3 до 13). Для этих ворот таблицы истинности должны быть расширены, чтобы включать все возможные входные условия.

Универсальные ворота

Поскольку вентили производятся в форме ИС, обычно содержащей от двух до шести вентилей одного типа, часто неэкономично использовать полную ИС из шести вентилей для выполнения определенной логической функции. Лучшим решением может быть использование только одного типа ворот для выполнения любых необходимых логических операций. Два типа вентилей, И-НЕ и ИЛИ-ИЛИ, часто используются для выполнения функций любых других стандартных вентилей, путем соединения нескольких из этих «универсальных» вентилей в комбинационную схему.Хотя может показаться неэффективным использование нескольких универсальных вентилей для выполнения функции одного логического элемента, если в одной или нескольких ИС И ИЛИ и ИЛИ ИС имеется несколько неиспользуемых вентилей, они могут использоваться для выполнения других функций, таких как И или ИЛИ. вместо использования дополнительных микросхем для выполнения этой функции. Этот метод особенно полезен при разработке сложных ИС, где целые схемы внутри ИС могут быть изготовлены с использованием одного типа затвора.

На рис. 2.1.3 от a до g показано, как можно использовать вентили NAND для получения любой из стандартных функций, используя только этот тип единственного логического элемента.

Рис. 2.1.3 Создание любой логической функции с использованием шлюза NAND

Функция НЕ

а. Соединение входов логического элемента И-НЕ вместе создает функцию НЕ.

г. В качестве альтернативы функция НЕ может быть реализована путем использования только 1 входа и постоянного подключения другого входа к логической 1.

И функция

г. Добавление функции НЕ (инвертора) к выходу логического элемента И-НЕ создает функцию И.

ИЛИ Функция

г.Инвертирование входов в логический элемент И-НЕ создает функцию ИЛИ.

Функция NOR

e. Использование функции НЕ для инвертирования вывода функции ИЛИ создает функцию ИЛИ.

Функция XOR

ф. Четыре логических элемента NAND (одна микросхема), подключенные, как показано, создают функцию XOR (а микросхема Quad NAND примерно на 15% дешевле, чем микросхема Quad XOR).

Функция XNOR

г. Инвертирование вывода функции XOR создает функцию XNOR.

Подобные преобразования могут быть достигнуты с использованием вентилей ИЛИ-ИЛИ, но поскольку вентили И-НЕ являются, как правило, наименее дорогими ИС, преобразования, показанные на рис.2.1.3 используются чаще. Причиной таких преобразований обычно является стоимость. Это может показаться не очень полезным, поскольку ни одна из основных микросхем серии 74 не является дорогостоящей, но, когда должно быть изготовлено несколько тысяч единиц конкретной схемы, небольшая экономия затрат и места на печатных платах за счет максимального использования неиспользуемых вентилей. в ИС с несколькими затворами может стать очень важным.

Логические ворота

В реальном мире цифровые устройства не являются абстрактными логическими выражениями булевой алгебры, а являются аппаратными реализациями этих выражений.Логические выражения транслируются в структуры устройства, называемые логическими вентилями , . Логический вентиль является как символическим представлением логической операции, так и при использовании в цифровой электронике может быть реальной схемой в оборудовании. Один логический вентиль обычно состоит из нескольких транзисторов, разделенных пространством со многими другими в интегральной схеме.

Каждый из основных операторов, о которых мы узнали в разделе выражений, имеет символ ворот. Символ занимает место оператора, а переменные являются входными данными для логического элемента.Значение, полученное в результате выражения уравнения, является выходом ворот. Выход элемента может быть конечным результатом или может быть подключен как вход к еще одному элементу.

Символы ворот

Логические элементы — это символы, которые могут напрямую заменять выражение в логической арифметике. У каждого есть своя форма, чтобы показать свою особую функцию. Входы (булевы переменные) вводятся слева от символа, а выходные данные уходят справа. При объединении несколько ворот могут образовать сложную логическую систему оценки, имеющую множество входов и выходов.Цифровые компьютеры созданы путем соединения тысяч или миллионов этих ворот вместе.

Элемент НЕ

Элемент НЕ представляет собой стрелку вперед с маленьким кружком на выходе. Круглая часть символа говорит о том, что вывод отрицает ввод.

вентиль OR

Th вентиль OR имеет изогнутую входную сторону и остроконечный выход.

Логический элемент И

Логический элемент И имеет плоскую входную сторону и круглую выходную сторону.

Элемент исключающего ИЛИ (XOR)

Символ логического элемента ИСКЛЮЧАЮЩЕЕ ИЛИ аналогичен вентилю ИЛИ, но имеет дополнительную изогнутую линию, пересекающую входы.

Комбинированная логика

Когда вы соединяете несколько вентилей вместе, у вас есть комбинированная логическая система или комбинаторная логика . Для разработки комбинированной логической системы мы можем использовать таблицы истинности для сопоставления логических выходов для различных входных условий. Булевы выражения записываются из условий в таблице.Затем мы можем напрямую преобразовать выражение в схему логических вентилей.

Возможно, вы помните, что еще в булевых элементах мы видели, что в коде для XOR не было оператора. Он был составлен с помощью комбинации операторов AND, OR и NOT:

  пусть A = false
пусть B = false
пусть Q = (A || B) &&! (A && B)  

Давайте сопоставим входные и выходные условия в таблице истинности для комбинированной логической системы для XOR. Мы найдем все условия, которые вызывают истинный результат , и создадим для них логическое выражение.

А	B	A ⊕ B
Ф.	Ф	Ф
Ф.	Т	Т
т	Ф	Т
т	Т	Ф

Есть два условия, при которых столбец результата имеет истинных значений. Первое условие: A является ложным и B является истинным , что выражается как ~ A · B .Второе условие: A — это истинный , а B — false , что выражается как A · ~ B . Наше выражение XOR — true , когда одно из этих условий true , которое записывается как:

A ⊕ B = (~ A · B) + (A · ~ B)

В коде это выражение формируется с помощью следующих логических блоков:

  пусть A = false
пусть B = false
пусть Q = (! A && B) || (A &&! B)  

Покрытие уравнения до логических вентилей дает следующую диаграмму.Обратите внимание, как каждый вентиль «связывает» переменные вместе, как и логические блоки в приведенном выше коде.

Однако, если мы возьмем два других неиспользуемых условия из таблицы истинности, которые делают операцию XOR ложной , мы можем составить отрицательное уравнение для XOR, называемое NXOR:

~ (A ⊕ B) = (~ A · ~ B) + (A · B)

Чтобы вернуться к A ⊕ B , мы должны отрицать это отрицательное уравнение. Затем, с помощью Thereom Де Моргана, мы получаем другое уравнение для XOR, но оно все еще логически эквивалентно исходному.

A ⊕ B = (A + B) · ~ (A · B)

Когда это уравнение преобразуется в логические вентили, их на один вентиль меньше, чем на первой диаграмме.

Эта диаграмма менее сложна, чем первая. Уменьшение количества вентилей для достижения одного и того же логического результата — одна из основных целей проектирования цифровой логики. Для электронных устройств это позволяет большему количеству вентилей использовать ограниченное пространство на интегральной схеме.

Electronics Club — Logic Gates

Electronics Club — Logic Gates — символы, таблицы истинности, НЕ, И, ИЛИ, ИЛИ, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ, комбинации, подстановка

Символы | Таблицы истинности |
ИС | НЕ | И | NAND |
ИЛИ | NOR | EX-OR | EX-NOR |
Комбинации | Подставляя

Следующая страница: Счетные схемы

Введение

Логические вентили обрабатывают сигналы, которые представляют истинных или ложных .Обычно положительное напряжение питания + Vs соответствует истине, а 0 В — ложному.
Другие термины, используемые для истинного и ложного состояний, показаны в таблице, лучше всего знать их все.

Ворота идентифицируются по их функции: НЕ, И,
ИЛИ, ИЛИ, ИЛИ,
EX-OR и EX-NOR.
Заглавные буквы обычно используются, чтобы прояснить, что этот термин относится к логическому элементу.

Обратите внимание, что логические вентили не всегда требуются, потому что простые логические функции
могут выполняться переключателями или диодами, например:

Логические состояния
Истина	Ложь
1	0
Высокий		Выкл.

---

Символы логического элемента

Есть две серии символов для логических вентилей. традиционных символов имеют отличительные
формы, благодаря которым их легко узнать, они широко используются в промышленности и образовании.
Символы МЭК (Международная электротехническая комиссия)
представляют собой прямоугольники с символом внутри, показывающим функцию ворот. Они редко используются, несмотря на
их официальный статус, но вам, возможно, потребуется узнать их для экзамена.

Традиционный

МЭК

Входы и выходы

Шлюз

имеет два или более входа, кроме элемента НЕ, у которого только один вход.Все ворота имеют только один выход. Обычно буквы A, B, C и так далее используются для обозначения входов, а Q используется для обозначения вывода.
На этой странице входы показаны слева, а выход — справа.

Обратный круг (o)

Некоторые символы ворот имеют кружок на выходе, что означает, что их функция включает
инвертирует вывода. Это эквивалентно пропусканию выхода через вентиль НЕ.
Например, символ логического элемента И-НЕ ( N, или И ), показанный справа, одинаков.
как символ логического элемента И, но с добавлением инвертирующего круга на выходе.

---

Таблицы истинности

Таблица истинности — хороший способ показать функцию логического элемента.
Он показывает состояния вывода для всех возможных комбинаций состояний ввода.
Символы 0 (ложь) и 1 (истина) обычно используются в таблицах истинности.
В примере таблицы истинности показаны входы и выход логического элемента И.

Ниже приведены сводные таблицы истинности, показывающие состояния вывода для
все типы ворот с 2 и 3 входами. Это может быть полезно, если вы пытаетесь выбрать
подходящие ворота.

9037 1

Вход A	Вход B	Выход Q
0	0	0
0	1	0
	0	0	0
1	1

Сводные таблицы истинности

В этих сводных таблицах истинности ниже показаны состояния выходов для всех типов вентилей с 2 ​​и 3 входами.
Обратите внимание, что ворота EX-OR и EX-NOR могут иметь только 2 входа.

6

6

Сводка для всех вентилей с 2 ​​входами
Входы		Выход каждого вентиля
A	B	и	NAND	OR	NOR	EX-OR	EX-NOR
0	0
0	0	1	0	1	0	1
0	1	0	1	1	0	1	0
1	0	0	1	1	0	1	0
1	1	1	0	1	0	0	1

Сводка для всех вентилей с 3 входами
Входы			Выходы каждого вентиля
A	B	C	И	NAND	OR	NOR
0	0	0	0	1	0	1
0	0	1	0	1	1	0
0	1	0	0	1	1	0
0	1	1	0	1	1	0
1	0	0	0	1	1	0
1	0	1	0	1	1	0
1	1	0	0	1	1	0
1	1	1	1	0	1	0

---

---

Логические ИС

Логические вентили доступны на ИС (микросхемах), которые обычно содержат несколько вентилей.
того же типа, например, ИС 4001 содержит четыре логических элемента ИЛИ-НЕ с 2 входами.Существует несколько семейств логических ИС, которые можно разделить на две группы:
серии 4000 и серии 74

Для сравнения различных семейств см. Страницу ИС.

Семейства 4000 и 74HC лучше всего подходят для проектов с батарейным питанием, потому что они
будут работать с хорошим диапазоном питающих напряжений и потреблять очень мало энергии.
Однако, если вы используете их для проектирования схем и исследования логических вентилей
помните, что все неиспользуемые входы ДОЛЖНЫ быть подключены к источнику питания
питание (либо + Vs, либо 0V) , это применимо, даже если эта часть IC не используется в цепи!

Дополнительная информация: ИС серии 4000 | ИС 74 серии

Rapid Electronics:
4000 серия |
74 серии

---

НЕ вентиль (инвертор)

Элемент НЕ может иметь только один вход, а выход является обратным входу.Элемент НЕ также называется инвертором.

Выход Q является истинным, когда вход A НЕ истинен: Q = НЕ

Традиционный символ

Символ МЭК

---

И ворота

Логический элемент И может иметь два или более входов, его выход будет истиной, если все входы верны.
Выход Q является истинным, если оба входа A и вход B истинны: Q = A AND B

9037 1

Вход A	Вход B	Выход Q
0	0	0
0	1	0
	0	0	0
1	1

Традиционный символ

Символ МЭК

---

вентиль NAND

NAND = N или И .Это логический элемент И с инвертированным выходом, как показано буквой «o» на выходе символа.
Логический элемент И-НЕ может иметь два или более входов, его выход истинен, если НЕ все входы истинны.
Выход Q является истинным, если вход A И вход B НЕ оба истинны:
Q = НЕ (А И В)

9037 1

Вход A	Вход B	Выход Q
0	0	1
0	1	1
1
1	0

Традиционный символ

Символ МЭК

---

ИЛИ ворота

Логический элемент ИЛИ может иметь два или более входов, его выход истинен, если хотя бы один вход истинен.Выход Q является истинным, если вход A ИЛИ вход B истинен (или оба из них истинны):
Q = A ИЛИ B

9037 1

Вход A	Вход B	Выход Q
0	0	0
0	1	1
1
1	1

Традиционный символ

Символ МЭК

---

NOR ворота

NOR = N или OR .Это логический элемент ИЛИ с инвертированным выходом, как показано буквой «o» на выходе символа.
У логического элемента ИЛИ-НЕ может быть два или более входов, его выход будет истиной, если ни один из входов не верен.
Выход Q является истинным, если НЕ входы A ИЛИ B истинны:
Q = НЕ (A ИЛИ B)

9037 1

Вход A	Вход B	Выход Q
0	0	1
0	1	0
1	0

Традиционный символ

Символ МЭК

---

Выход EX-OR

EX включительно- OR .Это похоже на логический элемент ИЛИ, но за исключением того, что оба входа истинны.
Выход истинен, если входы A и B — РАЗНЫЕ . Ворота EX-OR могут иметь только 2 входа.
Выход Q является истинным, если любой вход A истинен ИЛИ вход B истинен,
, но не тогда, когда они оба верны :
Q = (A И НЕ B) ИЛИ (B И НЕ A)

9037 1

Вход A	Вход B	Выход Q
0	0	0
0	1	1
1
1	0

Традиционный символ

Символ МЭК

---

Выход EX-NOR

EX включительно — NOR .Это вентиль EX-OR с инвертированным выходом, как показано буквой «o» на выходе символа. Ворота EX-NOR могут иметь только 2 входа.
Выход Q является истиной, если входы A и B — это ТО ЖЕ (оба истинны или оба ложны):
Q = (A И B) ИЛИ (НЕ A И НЕ B)

9037 1

Вход A	Вход B	Выход Q
0	0	1
0	1	0
1	1

Традиционный символ

Символ МЭК

---

Комбинации логических вентилей

Логические вентили можно комбинировать для выполнения более сложных функций.

Например, чтобы создать выходной сигнал Q, который является истинным только тогда, когда вход A является истинным, а вход B — ложным,
мы можем объединить вентиль НЕ и вентиль И, как показано.

Q = A И НЕ B

Разработка функции калитки

Таблицы истинности могут использоваться для определения функции комбинации ворот, такой как система, показанная ниже:

Начните с создания таблицы, показывающей все возможные комбинации входов (A, B и C в этом примере)
с достаточным количеством дополнительных столбцов для каждого промежуточного вывода (D и E в этом примере), а также для окончательного вывода (Q).Затем определите все промежуточные состояния вывода, заполняя таблицу по ходу дела.
Эти промежуточные выходы формируют входы для следующих ворот (или ворот), поэтому вы можете использовать их для работы.
выводит следующий вывод (ы), в этом примере это конечный вывод (Q).

D = НЕ (A ИЛИ B)
E = B AND C
Q = D OR E = (НЕ (A OR B)) OR (B AND C)

Таблица истинности показывает промежуточные выходы D и E, а также окончательный результат Q.

9075

Входы			Выходы
A	B	C	D	E	Q
0	0	0	1	0	1
0	0	1	1
0	1	0	0	0	0
0	1	1	0	1	1
0	0	0
1	0	1	0	0	0
1	1		0
1	1	1	0	1	1

---

---

Замена одного типа ворот на другой

Логические вентили доступны на ИС, которые обычно содержат несколько вентилей одного типа,
например, четыре логических элемента И-НЕ с 2 входами или три шлюза И-НЕ с 3 входами.Это может быть расточительным, если
требуется только несколько ворот, если все они не одного типа. Чтобы не использовать слишком много
IC вы можете уменьшить количество входов затвора или заменить один тип затвора другим.

Уменьшение количества входов

Количество входов в вентиль можно уменьшить, соединив два (или более) входа вместе.
На схеме показан логический элемент И с 3 входами, работающий как логический элемент И с 2 входами.

Создание гейта НЕ из логического элемента И-НЕ или НЕ-НЕ

При уменьшении логического элемента НЕ-И или ИЛИ-НЕ до одного входа создается вентиль НЕ.На схеме это показано для логического элемента И-НЕ с 2 входами.

Любые ворота могут быть построены из ворот NAND или NOR

Помимо создания ворот НЕ, ворота И-НЕ или ИЛИ-НЕ можно комбинировать для создания ворот любого типа!
Это позволяет построить схему только с одним типом логических элементов, NAND или NOR.
Например, вентиль И — это вентиль И-НЕ, а затем вентиль НЕ (чтобы отменить функцию инвертирования).
Обратите внимание, что элементы И и ИЛИ нельзя использовать для создания других ворот, потому что в них отсутствует функция инвертирования (НЕ).

Чтобы изменить тип ворот , например изменить OR на AND, вы должны сделать три вещи:

• Инвертировать (НЕ) каждый вход.
• Изменить тип ворот (ИЛИ на И или И на ИЛИ)
• Инвертировать (НЕ) вывод.

Например, логический элемент ИЛИ может быть построен из входов NOTed, подаваемых в логический элемент И-НЕ (И + НЕ).

---

эквиваленты ворот NAND

Приведенные ниже схемы показывают, как использовать логические элементы И-НЕ для создания вентилей НЕ, И, ИЛИ и ИЛИ:

НЕ сделано из одного логического элемента NAND:

И состоит из двух ворот NAND:

ИЛИ из трех ворот NAND:

NOR состоит из четырех вентилей NAND:

---

Подстановка вентилей в примерную логическую систему

Эта система имеет 3 разных логических элемента (ИЛИ, И и ИЛИ), поэтому требуется три ИС, по одной для каждого типа ворот.

Чтобы перепроектировать эту систему с использованием вентилей NAND, начните только с замены каждого
гейт с его эквивалентом логического элемента NAND, как показано ниже:

Затем упростите систему, удалив соседние пары вентилей НЕ (отмечены X выше).
Это может быть сделано, потому что вторые ворота НЕ отменяют действие первых:

Последняя система имеет пять логических элементов NAND и требует двух микросхем (по четыре логических элемента на каждой микросхеме).
Это лучше, чем исходная система, которая требовала трех микросхем (по одной для каждого типа ворот).

Замена вентилей NAND (или NOR) не всегда увеличивает количество вентилей,
но когда это происходит (как в этом примере), увеличение обычно составляет только одно или два входа.
Настоящее преимущество заключается в уменьшении количества требуемых микросхем за счет использования только одного типа ворот.

---

Следующая страница: Счетные схемы | Исследование

---

Политика конфиденциальности и файлы cookie

Этот сайт не собирает личную информацию.
Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет
используется только для ответа на ваше сообщение, оно не будет передано никому.На этом веб-сайте отображается реклама, если вы нажмете на
рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден.
Рекламодателям не передается никакая личная информация.
Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации.
Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов.
(включая этот), как объяснил Google.Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста
посетите AboutCookies.org.

electronicsclub.info © Джон Хьюс 2020

Веб-сайт размещен на Tsohost

Цифровые логические ворота, часть I

		Логические ворота
		Логический вентиль — это электронная схема / устройство, которое принимает логические решения.Чтобы прийти к такому решению, чаще всего используются логические вентили ИЛИ, И, НЕ, ИЛИ и ИЛИ. Ворота NAND и NOR называются универсальными воротами. Элемент исключающее ИЛИ — это еще один логический элемент, который может быть построен с использованием элементов И, ИЛИ и НЕ.
		Логические вентили имеют один или несколько входов и только один выход. Выход активен только для определенных комбинаций входов. Логические вентили — это строительные блоки любой цифровой схемы.Логические вентили также называют переключателями. С появлением интегральных схем переключатели были заменены схемами TTL (Transistor Transistor Logic) и схемами CMOS. Здесь я привожу примеры схем построения простых ворот.
		Символьная логика
		Булева алгебра получила свое название от математика Джорджа Буля. Символическая логика использует значения, переменные и операции.
		инверсия
		Маленький кружок на входе или выходе означает инверсию.См. Примеры вентилей NOT, NAND и NOR, приведенные ниже.
		Шлюз с несколькими входами
		Учитывая законы коммутативности и ассоциативности, многие логические вентили могут быть реализованы с более чем двумя входами, а из-за недостатка места в схемах, обычно с несколькими входами, создаются сложные вентили.Вы встретите такие ворота в реальном мире (возможно, вы могли бы проанализировать библиотеку ASIC, чтобы найти это).
		Тип ворот
		И ИЛИ НЕ BUF NAND NOR XOR XNOR
		И Ворота
		Элемент И выполняет логическое умножение, широко известное как функция И.Логический элемент И имеет два или более входа и один выход. Выход логического элемента И ВЫСОКИЙ только тогда, когда все его входы ВЫСОКОЕ (т.е. даже если один вход НИЗКИЙ, выход будет НИЗКИЙ).
		Если X и Y — два входа, то выход F может быть представлен математически как F = X.Y, здесь точка (.) Обозначает операцию AND. Таблица истинности и символ логического элемента И показаны на рисунке ниже.
		Символ
		Таблица истинности
		х Y F = (X.Y) 0 0 0 0 1 0 1 0 0 1 1 1
		Два входа логического элемента И, использующие логику «диод-резистор», показаны на рисунке ниже, где X, Y — входы, а F — выход.
		Схема
		Если X = 0 и Y = 0, то оба диода D1 и D2 смещены в прямом направлении, и, таким образом, оба диода проводят и понижают F.
		Если X = 0 и Y = 1, D2 имеет обратное смещение, поэтому не проводит.Но D1 смещен в прямом направлении, поэтому проводит и, следовательно, тянет F на низком уровне.
		Если X = 1 и Y = 0, D1 имеет обратное смещение, поэтому не проводит. Но D2 смещен в прямом направлении, поэтому проводит и, следовательно, тянет F на низком уровне.
		Если X = 1 и Y = 1, то оба диода D1 и D2 имеют обратное смещение, и, таким образом, оба диода находятся в отсечке, и, следовательно, нет падения напряжения на F.Таким образом, F ВЫСОКИЙ.
		Коммутатор Представление AND Gate
		На рисунке ниже X и Y — это два переключателя, которые подключены последовательно (или просто каскадно) со светодиодом нагрузки и батареей-источником. Когда оба переключателя замкнуты, ток течет на светодиод.
		Три входа И вентиль
		Поскольку мы уже видели, как работает вентиль И, я просто перечислю таблицу истинности логического элемента И с тремя входами. На рисунке ниже показаны его символы и таблица истинности.
		Схема
		Таблица истинности
		х Y Z F = X.Y.Z 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1
		OR Выход
		Элемент ИЛИ выполняет логическое сложение, широко известное как функция ИЛИ.Логический элемент ИЛИ имеет два или более входа и один выход. Выход логического элемента ИЛИ ВЫСОКИЙ только тогда, когда любой из его входов ВЫСОКИЙ (т.е. даже если один вход ВЫСОКИЙ, выход будет ВЫСОКИЙ).
		Если X и Y — два входа, то выход F можно математически представить как F = X + Y. Здесь знак плюса (+) обозначает операцию ИЛИ. Таблица истинности и обозначение ворот ИЛИ показаны на рисунке ниже.
		Символ
		Таблица истинности
		х Y F = (X + Y) 0 0 0 0 1 1 1 0 1 1 1 1
		Два входа ИЛИ, использующие логику «диод-резистор», показаны на рисунке ниже, где X, Y — входы, а F — выход.
		Схема
		Если X = 0 и Y = 0, то оба диода D1 и D2 имеют обратное смещение, и, таким образом, оба диода находятся в отсечке, и, следовательно, F имеет низкий уровень.
		Если X = 0 и Y = 1, D1 имеет обратное смещение, поэтому не проводит.Но D2 смещен в прямом направлении, поэтому проводит и, таким образом, переводит F в ВЫСОКОЕ.
		Если X = 1 и Y = 0, D2 имеет обратное смещение, поэтому не проводит. Но D1 смещен в прямом направлении, поэтому проводит и, таким образом, переводит F в ВЫСОКИЙ уровень.
		Если X = 1 и Y = 1, то оба диода D1 и D2 смещены в прямом направлении и, таким образом, оба диода проводят, и, следовательно, F имеет ВЫСОКИЙ уровень.
		Switch Представление OR Gate
		На рисунке X и Y — два переключателя, которые были подключены параллельно, и они подключены последовательно со светодиодом нагрузки и батареей-источником. Когда оба переключателя разомкнуты, ток не течет на светодиод, но когда любой переключатель замкнут, ток течет.
		Три входа ИЛИ вентиль
		Поскольку мы уже видели, как работает вентиль ИЛИ, я просто перечислю таблицу истинности логического элемента ИЛИ с 3 входами.На рисунке ниже показаны его схема и таблица истинности.
		Схема
		Таблица истинности
		х Y Z F = X + Y + Z 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1

.