|
1. |
Меры длины. Задача
|
2 |
|
2. |
Единицы времени
|
4 |
|
3. 
|
Интервал времени
|
2 |
|
4. |
Преобразование единиц длины
|
4 |
|
5. 
|
Меры длины
|
4 |
|
6. |
Преобразование миллиметров в другие меры длины
|
4 |
|
7. 
|
Меры площади
|
3 |
|
8. |
Из аров в другие меры площади
|
5 |
|
9. 
|
Округление десятичных долей
|
1 |
|
10. |
Округление мер
|
3 |
|
11. 
|
Интервал времени
|
2 |
|
12. |
Високосный год
|
1 |
|
13. 
|
Меры времени
|
1 |
|
14. |
Измерение времени
|
2 |
Международная система единиц (СИ) | Диаэм
Единицы измерения
Международная система единиц (СИ) (фр. Le Système International d’Unités (SI)) — система единиц физических величин, современный вариант метрической системы.
Le Système International d’Unités (SI)) — система единиц физических величин, современный вариант метрической системы.
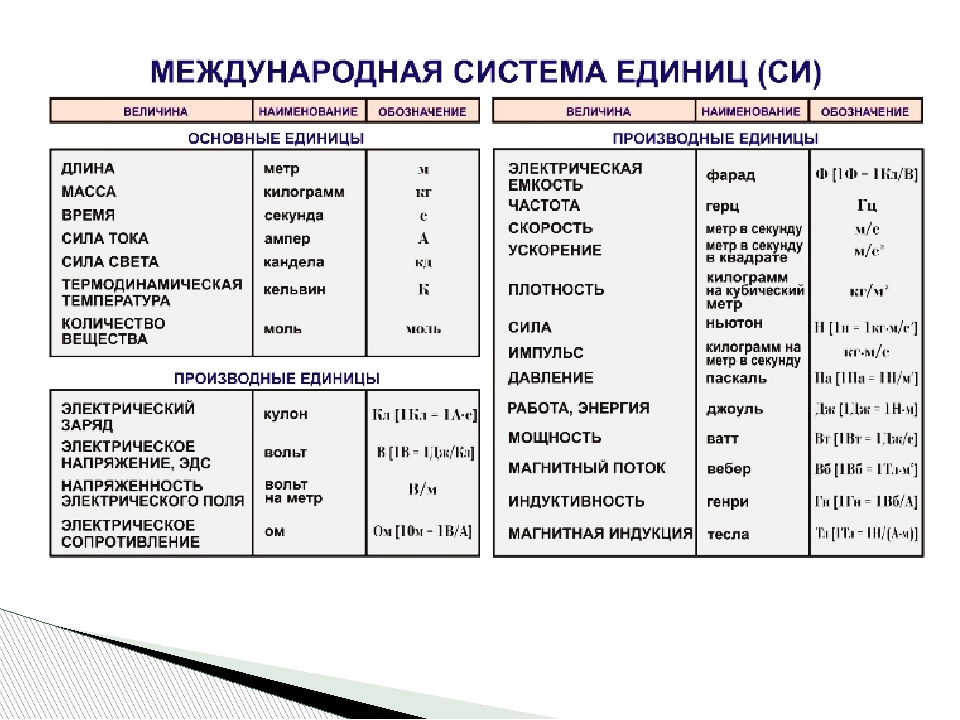
СИ определяет семь основных и производные единицы физических величин (далее — единицы), а также набор приставок. Установлены стандартные сокращённые обозначения для единиц и правила записи производных единиц.
Основные единицы: килограмм, метр, секунда, ампер, кельвин, моль и кандела.
Основные единицы системы СИ
|
|
|
| ||
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производные единицы системы СИ
|
|
|
| ||
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¹) — Шкалы Кельвина и Цельсия связаны между собой следующим образом: °C = K — 273,15
Кратные единицы — единицы, которые в целое число раз превышают основную единицу измерения некоторой физической величины.
Международная система единиц (СИ) рекомендует следующие десятичные приставки для обозначений кратных единиц:
|
|
|
| ||
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дольные единицы составляют определённую долю (часть) от установленной единицы измерения некоторой величины.
Международная система единиц (СИ) рекомендует следующие приставки для обозначений дольных единиц:
|
|
|
| ||
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Система СИ
К оглавлению. ..
..
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры.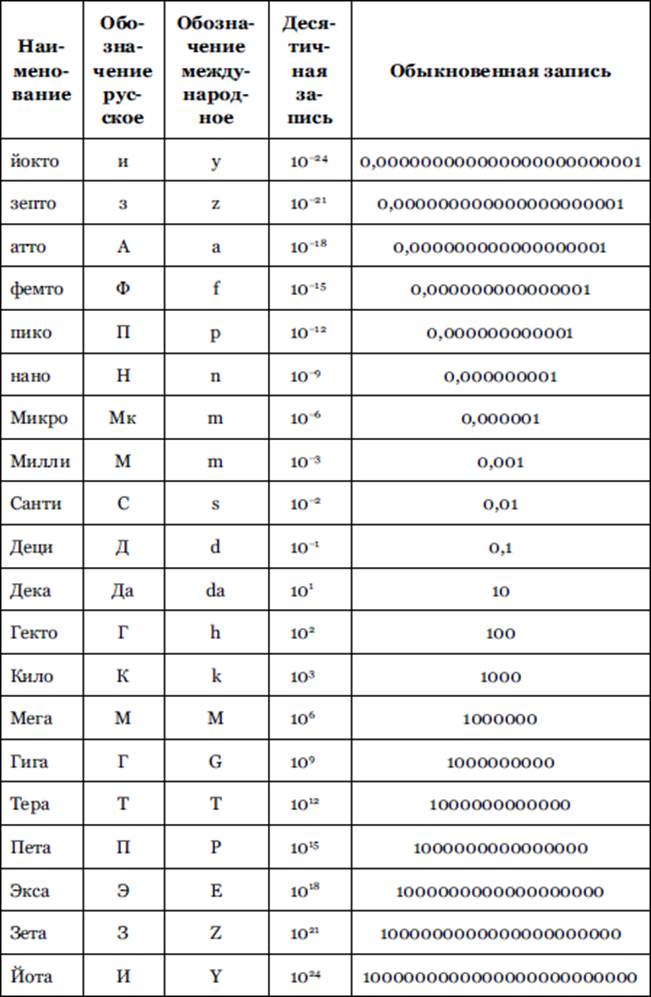 Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве.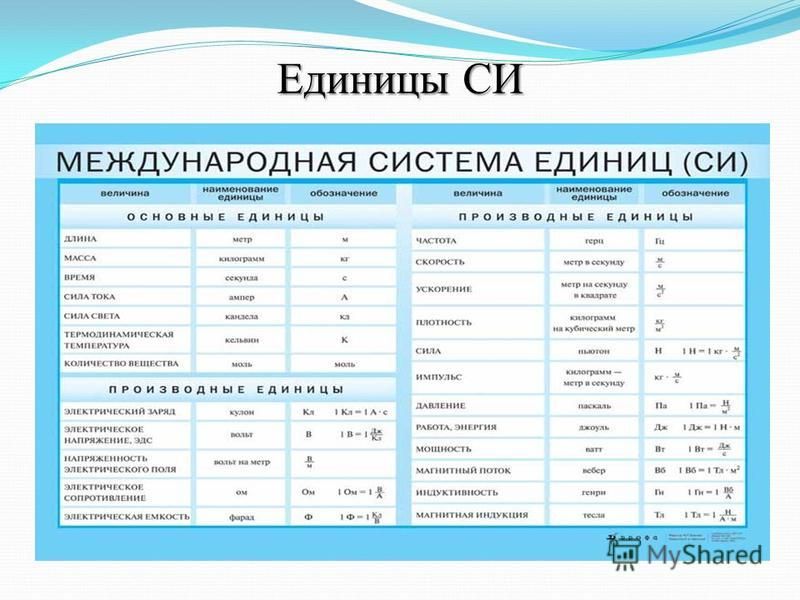 Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку.
 Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях. - И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным./177f2936fcd4422.s.siteapi.org/img/21253690f46666ab7f96df52866c1e0eaa2e506e.jpg) Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи.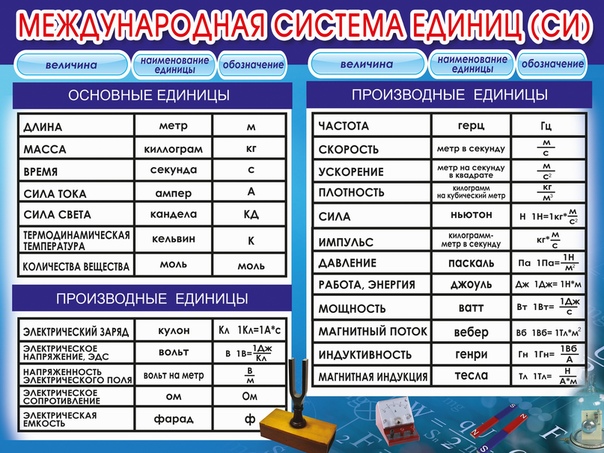 Вариантов 2: вверх или вниз.
Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали.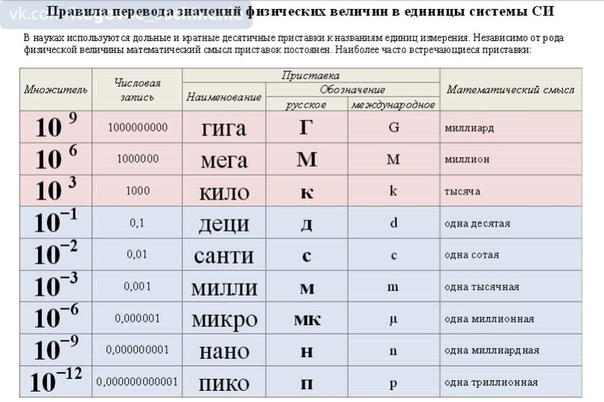 Тогда этот угол будет находиться из соотношения:
Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Перевод единиц
В этом уроке мы научимся переводить физические величины из одной единицы измерения в другую.
Перевод единиц измерения длины
Из прошлых уроков мы знаем, что основные единицы измерения длины это:
- миллиметры;
- сантиметры;
- дециметры;
- метры;
- километры.
Любая величина, которая характеризует длину, может быть переведена из одной единицы измерения в другую.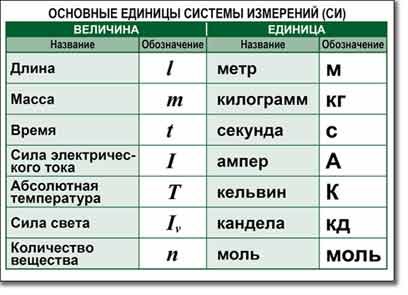
Кроме того, при решении задач по физике, обязательно нужно соблюдать требования международной системы СИ. То есть если длина дана не в метрах, а в другой единице измерения, то её обязательно нужно перевести в метры, поскольку метр является единицей измерения длины в системе СИ.
Чтобы переводить длину из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения. То есть нужно знать, что к примеру один сантиметр состоит из десяти миллиметров или один километр состоит из тысячи метров.
Покажем на простом примере, как можно рассуждать при переводе длины из одной единицы измерения в другую. Предположим, что имеется 2 метра и нужно перевести их в сантиметры.
Сначала нужно узнать сколько сантиметров содержится в одном метре. В одном метре содержится сто сантиметров:
1 м = 100 см
Если в 1 метре содержится 100 сантиметров, то сколько сантиметров будет содержаться в двух метрах? Ответ напрашивается сам — 200 см. А эти 200 см получаются, если 2 умножить на 100.
Значит, чтобы перевести 2 метра в сантиметры, нужно 2 умножить на 100
2 × 100 = 200 см
Теперь попробуем перевести те же 2 метра в километры. Сначала надо узнать сколько метров содержится в одном километре. В одном километре содержится тысяча метров:
1 км = 1000 м
Если один километр содержит 1000 метров, то километр который содержит только 2 метра будет намного меньше. Чтобы его получить нужно 2 разделить на 1000
2 : 1000 = 0,002 км
Поначалу бывает трудно запомнить, какое действие применять для перевода единиц — умножение или деление. Поэтому на первых порах удобно пользоваться следующей схемой:
Суть данной схемы заключается в том, что при переходе из старшей единицы измерения в младшую применяется умножение. И наоборот, при переходе из младшей единицы измерения в более старшую применяется деление.
Стрелки, которые направлены вниз и вверх указывают на то, что осуществляется переход из старшей единицы измерения в младшую и переход из младшей единицы измерения в более старшую соответственно. В конце стрелки указывается какую операцию применить: умножение или деление.
В конце стрелки указывается какую операцию применить: умножение или деление.
Например, переведём 3000 метров в километры, пользуясь данной схемой.
Итак, мы должны перейти из метров в километры. Другими словами, перейти из младшей единицы измерения в более старшую (километр старше метра). Смотрим на схему и видим, что стрелка указывающая переход из младших единиц в более старшие, направлена вверх и в конце стрелки указано, что мы должны применить деление:
Теперь нужно узнать, сколько метров содержится в одном километре. В одном километре содержится 1000 метров. А чтобы узнать, сколько километров составляют 3000 таких метров, нужно 3000 разделить на 1000
3000 : 1000 = 3 км
Значит, при переводе 3000 метров в километры, получим 3 километра.
Попробуем перевести те же 3000 метров в дециметры. Здесь мы должны перейти из старших единиц в младшие (дециметр младше метра). Смотрим на схему и видим, что стрелка указывающая переход из старших единиц в младшие, направлена вниз и в конце стрелки указано, что мы должны применить умножение:
Теперь нужно узнать, сколько дециметров в одном метре. В одном метре 10 дециметров.
В одном метре 10 дециметров.
1 м = 10 дм
А чтобы узнать сколько таких дециметров в трёх тысячах метрах, нужно 3000 умножить на 10
3000 × 10 = 30 000 дм
Значит при переводе 3000 метров в дециметры, получим 30000 дециметров.
Перевод единиц измерения массы
Из прошлых уроков мы знаем, что основные единицы измерения массы это:
- миллиграммы;
- граммы;
- килограммы;
- центнеры;
- тонны.
Любая величина, которая характеризует массу, может быть переведена из одной единицы измерения в другую.
Кроме того, при решении задач по физике, обязательно нужно соблюдать требования международной системы СИ. То есть если масса дана не в килограммах, а в другой единице измерения, то её обязательно нужно перевести в килограммы, поскольку килограмм является единицей измерения массы в системе СИ.
Чтобы переводить массу из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения. То есть нужно знать, что к примеру один килограмм состоит из тысячи граммов или один центнер состоит из ста килограммов.
То есть нужно знать, что к примеру один килограмм состоит из тысячи граммов или один центнер состоит из ста килограммов.
Покажем на простом примере, как можно рассуждать при переводе массы из одной единицы измерения в другую. Предположим, что имеется 3 килограмма и нужно перевести их в граммы.
Сначала нужно узнать сколько граммов содержится в одном килограмме. В одном килограмме содержится тысяча граммов:
1 кг = 1000 г
Если в 1 килограмме 1000 граммов, то сколько граммов будут содержаться в трёх таких килограммах? Ответ напрашивается сам — 3000 граммов. А эти 3000 граммов получаются путем умножения 3 на 1000. Значит, чтобы перевести 3 килограмма в граммы, нужно 3 умножить на 1000
3 × 1000 = 3000 г
Теперь попробуем перевести те же 3 килограмма в тонны. Сначала нужно узнать сколько килограммов содержатся в одной тонне. В одной тонне содержится тысяча килограмм:
1 т = 1000 кг
Если одна тонна содержит 1000 килограмм, то тонна которая содержит только 3 килограмма будет намного меньше. Чтобы её получить нужно 3 разделить на 1000
Чтобы её получить нужно 3 разделить на 1000
3 : 1000 = 0,003 т
Как и в случае с переводом единиц измерения длины, на первых порах удобно пользоваться следующей схемой:
Данная схема позволит быстро сориентироваться какое действие выполнить для перевода единиц — умножение или деление.
Например, переведём 5000 килограмм в тонны, пользуясь данной схемой.
Итак, мы должны перейти из килограммов в тонны. Другими словами, перейти из младшей единицы измерения в более старшую (тонна старше килограмма). Смотрим на схему и видим, что стрелка указывающая переход из младших единиц в более старшие, направлена вверх и в конце стрелки указано, что мы должны применить деление:
Теперь нужно узнать сколько килограмм содержатся в одной тонне. В одной тонне содержится 1000 килограмм. А чтобы узнать, сколько тонн составляет 5000 килограмм, нужно 5000 разделить на 1000
5000 : 1000 = 5 т
Значит, при переводе 5000 килограмм в тонны, получается 5 тонн.
Попробуем перевести 6 килограммов в граммы. В данном случае мы переходим из старшей единицы измерения в младшую. Поэтому будем применять умножение.
Сначала надо узнать сколько граммов содержится в одном килограмме. В одном килограмме содержится тысяча граммов:
1 кг = 1000 г
Если в 1 килограмме 1000 граммов, то в шести таких килограммах будет в шесть раз больше граммов. Значит 6 нужно умножить на 1000
6 × 1000 = 6000 г
Значит, при переводе 6 килограммов в граммы, получим 6000 грамм.
Перевод единиц измерения времени
Из прошлых уроков мы знаем, что основные единицы измерения времени это:
- секунды;
- минуты;
- часы;
- сутки.
Любая величина, которая характеризует время, может быть переведена из одной единицы измерения в другую.
Кроме того, при решении задач по физике, обязательно нужно соблюдать требования международной системы СИ. То есть если время дано не в секундах, а в другой единице измерения, то его обязательно нужно перевести в секунды, поскольку секунда является единицей измерения времени в системе СИ.
Чтобы переводить время из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения времени. То есть нужно знать, что к примеру один час состоит из шестидесяти минут или одна минута состоит из шестидесяти секунд и т.д.
Покажем на простом примере, как можно рассуждать при переводе времени из одной единицы измерения в другую. Предположим, что требуется перевести 2 минуты в секунды.
Сначала надо узнать сколько секунд содержится в одной минуте. В одной минуте содержатся шестьдесят секунд:
1 мин = 60 с
Если в 1 минуте 60 секунд, то сколько секунд будет в двух таких минутах? Ответ напрашивается сам — 120 секунд. А эти 120 секунд получаются путём умножения 2 на 60. Значит, чтобы перевести 2 минуты в секунды, нужно 2 умножить на 60
2 × 60 = 120 с
Теперь попробуем перевести те же 2 минуты в часы. Поскольку мы переводим минуты в часы, то сначала надо узнать сколько минут содержится в одном часе. В одном часе содержится шестьдесят минут:
1 ч = 60 м
Если один час содержит 60 минут, то час который содержит только 2 минуты будет намного меньше. Чтобы его получить нужно 2 минуты разделить на 60
Чтобы его получить нужно 2 минуты разделить на 60
При делении 2 на 60 получается периодическая дробь 0,0 (3). Эту дробь можно округлить до разряда сотых. Тогда получим ответ 0,03
2 : 60= 0,03 ч
При переводе единиц измерения времени также применима схема, подсказывающая что применять — умножение или деление:
Например, переведём 25 минут в часы, пользуясь данной схемой.
Итак, мы должны перейти из минут в часы. Другими словами, перейти из младшей единицы измерения в более старшую (часы старше минут). Смотрим на схему и видим, что стрелка указывающая переход из младших единиц в более старшие, направлена вверх и в конце стрелки указано, что мы должны применить деление:
Теперь нужно узнать, сколько минут содержится в одном часе. В одном часе содержится 60 минут. А час, который содержит только 25 минут будет намного меньше. Чтобы его найти, нужно 25 разделить на 60
При делении 25 на 60 получается периодическая дробь 0,41 (6). Эту дробь можно округлить до разряда сотых. Тогда получим ответ 0,42
Эту дробь можно округлить до разряда сотых. Тогда получим ответ 0,42
25 : 60 = 0,42 ч
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Единицы СИ — Класс!ная физика
Единицы СИ
Знаете ли вы?
Старые единицы измерения — ЧЕТВЕРИКИ, СТЯГИ, ОСЬМИНЫ, РОГОЖИ
Вплоть до 17 века весовые меры на Руси употреблялись редко. С помощью весовых единиц исчислялись в 16 веке, пожалуй, только масло, конопля, сало, мед и некоторые другие товары.
Вместо весовых мер широко применялись меры вместимости.
Рожь, овес, ячмень, лук, мелкую рыбу, известь измеряли четвертями, осьминами, четвериками.
Четверть равнялась 2 осьминам, 8 четверикам. В конце 17 века четверть соответствовала 8 пудам, отсюда осьмина — 4 пудам, четверик — 1 пуду.
В конце 17 века четверть соответствовала 8 пудам, отсюда осьмина — 4 пудам, четверик — 1 пуду.
Единицами измерения соли были рогожа (около 18—25 пудов), пошев (около 15 пудов), мех (до 7 пудов).
Мясо исчислялось стягами, полтями, тушами, сено — возами, копнами, стогами, острамками, необмолоченный хлеб — сотницами и овинами, рыба — возами, бочками, властями, прутами, звеньями, металл — крицами и прутами.
Эти единицы измерения были общеупотребительными мерами Московского государства.
Кроме них в то время были в ходу сохранившиеся от далекого прошлого местные меры.
Так, в Новгороде Великом зерно измеряли не общеупотребительными четвертями, а коробьями, в Пскове — зобнями; в Белозерском уезде вместе с четвериком использовалась одинаковая по величине единица измерения — маленка, в Вологодском уезде — лукошко.
Единицей измерения соли в Пермском крае был сапец, в Новгородских землях — луб и сугреб, в Двинском уезде— пуз.
Местными единицами измерения сена в Белозерье были волочуга и провозок.
С течением времени большая часть этих старых мер объема выпадает из обращения, входят в употребление пуды, фунты, гривенки, золотники, почки; потом граммы, килограммы, центнеры, тонны.
Но еще в первой половине 20 века продолжали использоваться некоторые старые единицы вместимости. Пережитком старых единиц измерения остался осьминный мешок. Сено предпочитали продавать возами, стогами, необмолоченный хлеб — овинами.
Однако самой устойчивой оказалась старая единица вместимости — мера (1 пуд). С помощью ее измерялись не только зерно, но и вообще сыпучие тела.
Слово «мера» не было общеупотребительной единицей измерения сыпучих тел. В 16-17 веках оно употреблялось со значением «сосуд для измерения сыпучих тел».
Стремясь сделать меры сыпучих тел везде одинаковыми, правительство рассылало образцы мер, то есть медные сосуды, по которым на местах делались деревянные копии.
На севере в городах, расположенных по Северной Двине, слово «мера» означало не только сосуд для измерения, но и единицу емкости для сыпучих тел, то есть величину содержимого этого сосуда.
С 1679 года правительство начинает рассылать в качестве образца меры только медный четверик, вмещавший около пуда. С этого времени слово «мера» стало обозначать единицу емкости сыпучих тел, равную пуду.
| Физические величины. 7 класс | ||||
| Название величины | Обозначение | Единица измерения | Расчетная формула | Прибор для измерения |
| Длина | a, l | м, метр | — | линейка, рулетка, штангенциркуль, микрометр |
| Ширина | b | м, метр | — | линейка, рулетка, штангенциркуль, микрометр |
| Высота | с, h | м, метр | — | линейка, рулетка, штангенциркуль, микрометр |
| Площадь | S | м2, метр в квадрате | S=a·b | расчетная величина |
Объем тв.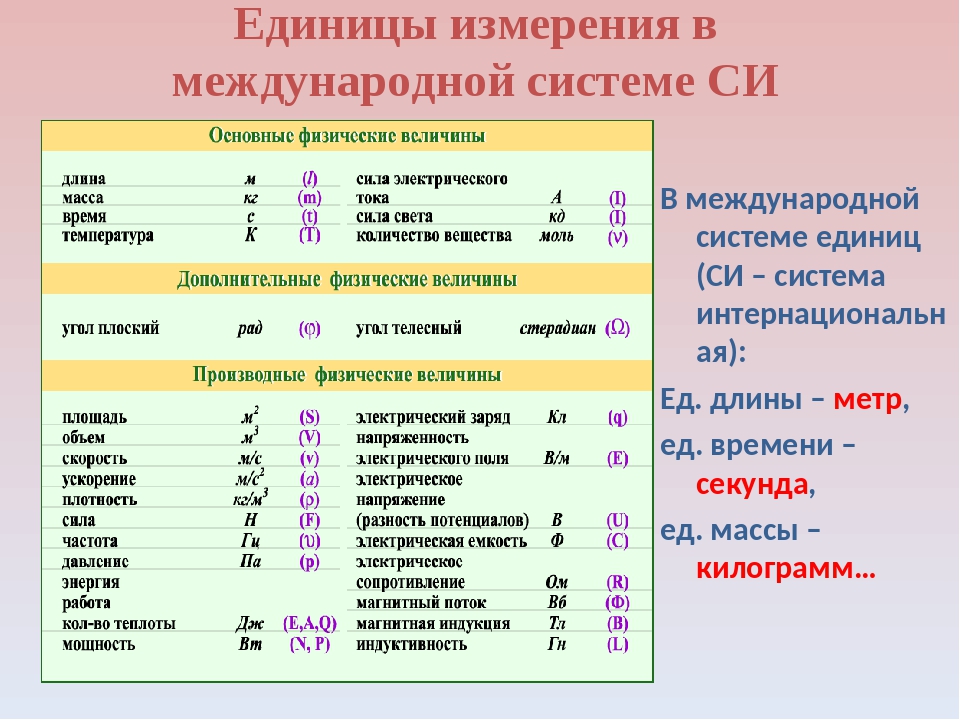 тел тел | V |
м3, метр в кубе
| V=a·b·c | расчетная величина |
| жидкостей | V | л, литр | 1 л=1 дм3=0,001 м3 | мерный стакан (мензурка) |
| Температура | t° | °С, градус Цельсия | — | термометр |
| Время | t | с, секунда | — | часы, секундомер |
| Путь | s | м, метр | — | линейка, рулетка, штангенциркуль, микрометр |
| Скорость | v | м/с, метр на секунду | v=s/t | спидометр |
| Масса | m | кг, килограмм | — | весы |
| Плотность | ρ | кг/м3, килограмм на метр в кубе | ρ=m/V | расчетная величина |
| Сила | F | H, Ньютон | — | динамометр |
| тяжести | Fтяж | Н, Ньютон | F=m·g | динамометр |
| упругости | Fупр | Н, Ньютон | F=k·Δl | динамометр |
| трения | Fтр | Н, Ньютон | F=μ·N | динамометр |
| нормального давления | N | Н, Ньютон | N=m·g | динамометр |
| равнодействующая | R | Н, Ньютон | R=F1+F2 R=F2-F1 | динамометр |
| Архимеда | FА | Н, Ньютон | FА=g·ρж·Vт | динамометр |
| Ускорение свободного падения | g | Н/кг, Ньютон на килограмм | g=9,8 Н/кг | постоянная величина |
| Жесткость | k | Н/кг, Ньютон на килограмм | — | табличные значения |
| Удлинение | Δl | м, метр | — | линейка, рулетка, штангенциркуль, микрометр |
| Коэффициент трения | μ | безразмерная | — | табличные значения |
| Вес тела | Р | Н, Ньютон | P=m·g | динамометр |
| Давление | p | Па, Паскаль | p=F/S | манометр |
| атмосферное | p | мм рт.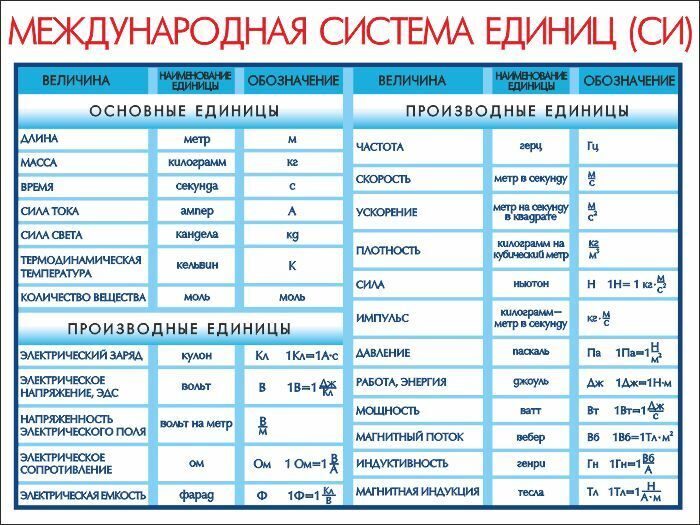 ст., миллиметр ртутного столба ст., миллиметр ртутного столба | 1 мм рт. ст.=133,3 Па | барометр, барометр-анероид |
| Механическая работа | А | Дж, Джоуль | А=F·s | расчетная величина |
| Мощность | N | Вт, Ватт | N=A/t | расчетная величина |
| Момент силы | М | Н·м, Ньютон-метр | М=F·l | расчетная величина |
| КПД (коэффициент полезного действия) | η | %, процент | η=(Ап/Аз)100% | расчетная величина |
| Энергия | Е | Дж, Джоуль | расчетная величина | |
| кинетическая | Ек | Дж, Джоуль | Ек=m·v2/2 | расчетная величина |
| потенциальная | Еп | Дж, Джоуль | Eп=m·g·h | расчетная величина |
Физические величины.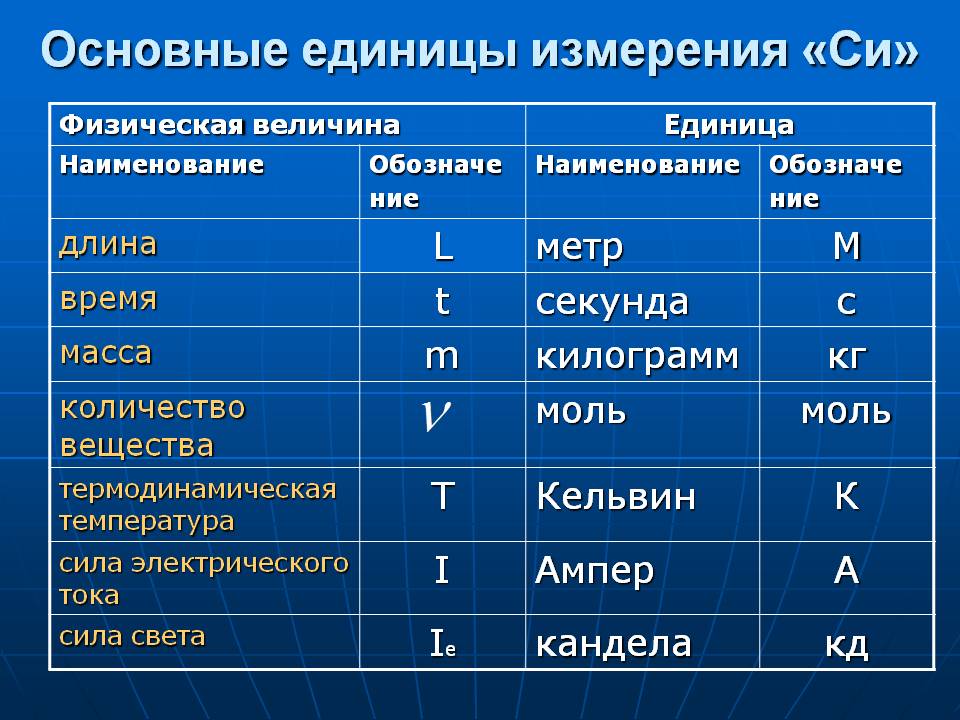 8 класс 8 класс | ||||
| Количество теплоты | Q | Дж, Джоуль | — | расчетная величина |
| Удельная теплоемкость | с | Дж/(кг·0С), Джоуль на килограмм-градус Цельсия | — | табличные значения |
| Удельная теплота сгорания | q | Дж/кг, Джоуль на килограмм | табличные значения | |
| Удельная теплота плавления | λ | Дж/кг, Джоуль на килограмм | табличные значения | |
| Влажность | φ | %, проценты | φ=(ρ/ρ0)·100% | гигрометр, психрометр |
| Удельная теплота парообразования и конденсации | L | Дж/кг, Джоуль на килограмм | табличные значения | |
| Электрический заряд | q | Кл, Кулон | электромер | |
| Сила тока | I | А, Ампер | I=q/t | амперметр |
| Электрическое напряжение | U | В, Вольт | u=A/q | вольтметр |
| Электрическое сопротивление | R | Ом, Ом | R=ρl/S | расчетная величина, омметр |
| Удельное сопротивление | ρ | Ом·мм2/м, Ом-миллиметр в квадрате на метр | табличные значения | |
| Работа электрического тока | А | Дж, Джоуль; кВт·ч, киловатт в час | A=IUt | электросчетчик |
| Мощность электрического тока | Р | Вт, Ватт | P=IU | ваттметр |
| Показатель преломления | n | безразмерная | n=sin α/sin β | расчетная величина |
| Фокусное расстояние | F | м, метр | линейка, рулетка, штангенциркуль, микрометр | |
| Оптическая сила линзы | D | дптр, диоптрия | D=1/F | расчетная величина |
Физические величины.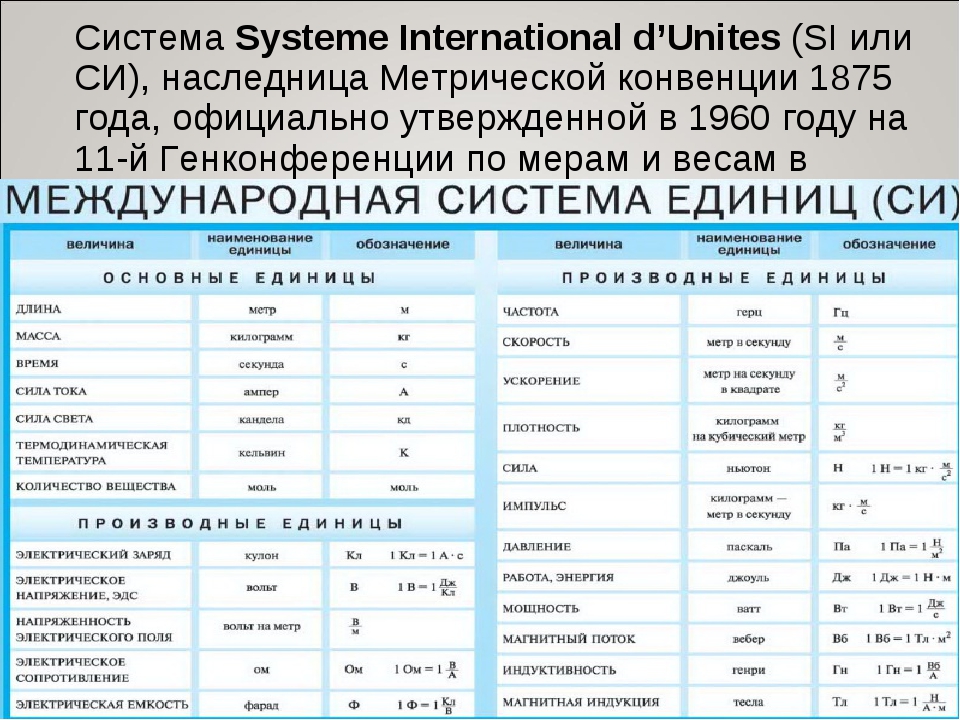 9 класс 9 класс | ||||
| Перемещение | s | м, метр | линейка, рулетка, штангенциркуль, микрометр | |
| Координаты | x, y | м, метр | ||
| Ускорение | а | м/с2, метр на секунду в квадрате | a=(v-v0)/t | расчетная величина |
| Ускорение свободного падения | g | м/с2, метр на секунду в квадрате | g=9,806 м/с2 | постоянная величина |
| Гравитационная постоянная | G | Н·м2/кг2, Ньютон-метр квадратный на килограмм в квадрате | G=6.67·10-11 Н·м2/кг2 | постоянная величина |
| Расстояние, радиус | r, R | м, метр | линейка, рулетка, штангенциркуль, микрометр | |
| Импульс тела | p | кг·м/с, килограмм-метр на секунду | p=mv | расчетная величина |
| Период колебания | Т | с, секунда | секундомер | |
| Частота колебания | ν | Гц, Герц | ν=1/Т | частотомер |
| Амплитуда колебаний | А | м, метр | линейка, рулетка, штангенциркуль, микрометр | |
| Фаза колебаний | φ | рад, радиан | ||
| Длина волны | λ | м, метр | λ=vT | линейка, рулетка, штангенциркуль, микрометр |
| Громкость | сон, Б, сон, бел (дБ, децибел) | субъективное ощущение | ||
| Магнитная индукция | В | Тл, Тесла | B=F/I·l | |
| Магнитный поток | Φ | Вб, Вебер | ||
| Электрическая ёмкость | С | Ф, Фарада | C=U/q | |
| Индуктивность | L | Гн, Генри | ||
| Постоянна Планка | h | |||
| Скорость света | с | м/с, метр в сеунду | 3·108 м/с | постоянная величина |
| Поглощенная доза излучения | D | Гр, Грэй, Р рентген | D=E/m | 1 Гр≈100 Р |
| Эквивалентная доза | Н | Зв, зиверт | H=D·K | |
Системы измерения в физике
- Образование
- Наука
- Физика
- Системы измерения в физике
Стивен Хольцнер
Чтобы сохранить одинаковые измерения вместе, физики и математики сгруппировали их в измерительных систем .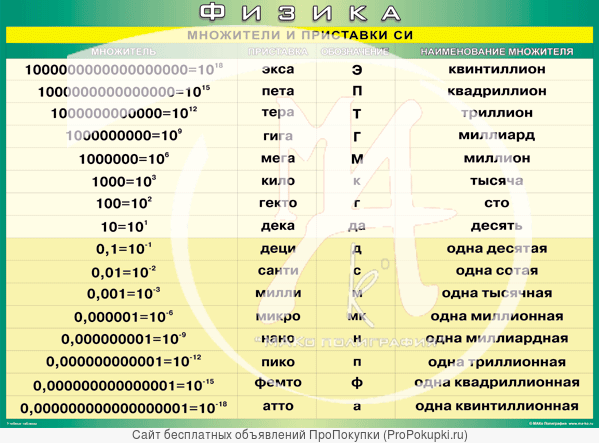 Самая распространенная система измерения, которую вы видите на начальном этапе физики, — это система метр-килограмм-секунда (MKS), называемая SI (сокращенно от Système International d’Unités, Международная система единиц), но вы также можете прийти по системе фут-фунт-секунда (FPS).
Самая распространенная система измерения, которую вы видите на начальном этапе физики, — это система метр-килограмм-секунда (MKS), называемая SI (сокращенно от Système International d’Unités, Международная система единиц), но вы также можете прийти по системе фут-фунт-секунда (FPS).
В таблице перечислены основные единицы измерения в системе MKS вместе с их сокращениями.
| Измерение | Блок | Аббревиатура |
|---|---|---|
| Длина | метр | м |
| Масса | килограмм | кг |
| Время | секунд | с |
| Усилие | ньютон | N |
| Энергия | джоуль | Дж |
| Давление | паскаль | Па |
| Электрический ток | ампер | A |
| Плотность магнитного потока | тесла | т |
| Электрический заряд | кулон | С |
Поскольку в разных системах измерения используются разные стандартные длины, вы можете получить несколько разных чисел для одной части задачи, в зависимости от используемого вами измерения. Например, если вы измеряете глубину воды в бассейне, вы можете использовать систему измерения MKS, которая дает вам ответ в метрах, или менее распространенную систему FPS, и в этом случае вы определяете глубину воды. вода в ногах.
Например, если вы измеряете глубину воды в бассейне, вы можете использовать систему измерения MKS, которая дает вам ответ в метрах, или менее распространенную систему FPS, и в этом случае вы определяете глубину воды. вода в ногах.
Дело? При работе с уравнениями придерживайтесь одной и той же системы измерения на протяжении всей задачи. Если вы этого не сделаете, ваш ответ будет бессмысленной мешаниной, потому что вы меняете мерные палочки для нескольких предметов, пытаясь прийти к единому ответу.Смешивание размеров вызывает проблемы — представьте, что вы выпекаете пирог, в котором рецепт требует 2 стакана муки, но вместо этого вы используете 2 литра.
Об авторе книги
Стивен Хольцнер, доктор философии, работал редактором журнала PC Magazine и работал на факультете Массачусетского технологического института и Корнельского университета. Он написал Physics II For Dummies , Physics Essentials For Dummies и Quantum Physics For Dummies .
Physics — документация SymPy 1.6.2
Модуль, помогающий решать задачи по физике
Содержание¶
- Водородные волновые функции
- Матрицы
- Алгебра Паули
- Список литературы
- Квантовый гармонический осциллятор в 1-D
- Квантовый гармонический осциллятор в трехмерном пространстве
- Второе квантование
- Символы Вигнера
- Ссылки
- Авторские права и авторские права
- Системы единиц
- Философия систем единиц
- Размеры
- Кол-во
- Необходимость справки
- Литература
- Примеры
- Размерный анализ
- Уравнение с величинами
- Размеры и система размеров
- Префиксы единиц
- Агрегаты и системы единиц
- Физические величины
- Преобразование величин
- Философия систем единиц
- Физика высоких энергий
- Гамма-матрицы
- Примеры
- Гамма-матрицы
- Модуль вектора физики
- Ссылки по физике / вектор
- Руководство по вектору
- Vector & ReferenceFrame
- Вектор: кинематика
- Возможные проблемы / Расширенные темы / Будущие функции по физике / Векторный модуль
- Функциональность скалярных и векторных полей
- Vector API
- Основные классы
- Кинематика (строки документации)
- Печать (строки документации)
- Основные функции (строки документации)
- Строки документации для основных функций поля
- Классическая механика
- Вектор
- Механика
- Руководство по механике
- Массы, инерции, частицы и твердые тела в физике / механике
- Метод Кейна в физике / механике
- Метод Лагранжа в физике / механике
- Символьные системы в физике / механике
- Линеаризация в физике / механике
- Примеры по физике / механике
- Возможные проблемы / Расширенные темы / Будущие функции в области физики / механики
- Ссылки по физике / механике
- Autolev Parser
- Механика SymPy для пользователей Autolev
- Механика API
- Масса, инерция и частицы, твердые тела (строки документации)
- Метод Кейна и метод Лагранжа (строки документации)
- SymbolicSystem (строки документации)
- Линеаризация (строки документации)
- Манипуляции с выражением (строки документации)
- Печать (строки документации)
- Корпус (строки документации)
- Квантовая механика
- Квантовые функции
- Антикоммутатор
- Коэффициенты Клебша-Гордана
- Коммутатор
- Константы
- Кинжал
- Внутренний продукт
- Тензорный продукт
- Состояния и операторы
- Декартовы операторы и состояния
- Гильбертово пространство
- Оператор
- Функции оператора / государственного помощника
- Qapply
- Представляют
- Вращение
- Государство
- Quantum Computing
- Схема
- Схема
- Ворота
- Алгоритм Гровера
- QFT
- Кубит
- Алгоритм Шора
- Аналитические решения
- Частица в коробке
- Квантовые функции
- Модуль оптики
- Gaussian Optics
- Средний
- Поляризация
- Примеры
- Коммунальные услуги
- Волны
- Системы единиц
- Философия систем единиц
- Размеры
- Кол-во
- Необходимость справки
- Литература
- Примеры
- Размерный анализ
- Уравнение с
- Философия систем единиц
| Учебные программы и стандарты | ||||
|---|---|---|---|---|
| Стандарты | Стандарты уровня 1 | Стандарты уровня 2 | Стандарты уровня 3 | |
| Физические матрицы | NCEA по TKI Physics | Матрица и руководство по дистанционной оценке физики (PDF, 171 КБ) | ||
| Учебное пособие по TKI | Все уровни | |||
| Ресурсы для стандартов внутренней оценки | ||||
| Разъяснения | Все уровни | |||
| Образцы студенческих работ | Все уровни | |||
| Шаблоны сбора оценочных доказательств | Все уровни | |||
| Национальный доклад модератора | Все уровни | |||
| Ресурсы и условия оценки TKI | Уровень 1 | Уровень 2 | Уровень 3 | |
| Войдите в свою учетную запись Facebook, чтобы просмотреть страницу Physics на Facebook | Щелкните здесь, чтобы просмотреть основные сведения об оценке и модерации | |||
| Ресурсы для стандартов внешней оценки | ||||
| Спецификации оценки | Уровень 1 | Уровень 2 | Уровень 3 | |
| Шаблоны сбора доказательств оценки | Все уровни | |||
| Экзаменационные работы и образцы | Уровень 1 | Уровень 2 | Уровень 3 | |
| График оценки | Уровень 1 | Уровень 2 | Уровень 3 | |
| Отрезки | Уровень 1 | Уровень 2 | Уровень 3 | |
| Отчеты об оценке | Уровень 1 | Уровень 2 | Уровень 3 | |
| Экзаменационные документы на Просроченные стандарты | Эти ресурсы были удалены, так как стандарты истекли и были заменены новыми стандартами и ресурсами. | |||

 Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.