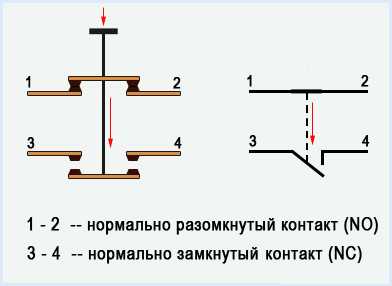
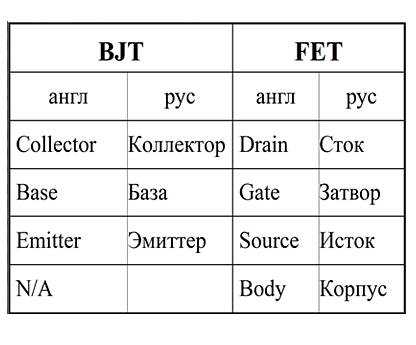
Сила Ампера. Правило левой руки. Сила ампера определение и формула

43. Сила Ампера. Сила Лоренца

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.

Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:

F=B.I.ℓ.sin α — закон Ампера.

Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:

Если вектор vчастицы перпендикуляренвектору В,то частица описывает траекторию в виде окружности:

Роль центростремительной силы играет сила Лоренца:

При этом радиус окружности: ,

Если вектор скорости и частицы не перпендикулярен В, то частица описывает траекторию в виде винтовой линии (спирали).

44. Теорема о циркуляции вектора магнитной индукции. Применение теоремы о циркуляции вектора магнитной индукции для расчета поля прямого тока. Циркуляция вектора магнитной индукции через замкнутый контур=произведению магнитной постоянной на алгебраическую сумму токов, охватываемых контуром.

∫BdL=μ0I; I=ΣIi

I1>0 I2<0

Теорема говорит о том, что магнитное поле не является потенциальным, а является вихревым.

Применение в тетради

45. Закон электромагнитной индукции. Правило Ленца

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции εинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Эта формула носит название закона Фарадея.

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.

Правило Ленца отражает тот экспериментальный факт, что εиндивсегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

εi=-N, гдеN- кол-во витков

Способ возникновения ЭДС:

1.рамка неподвижна, но изменяется магнитный поток за счёт движения ккатушки или за счет изменения силы тока в ней.

2.рамка перемещается в поле непожвижной катушки.

46. Явление самоиндукции.

Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется явлением самоиндукции.

Магнитный поток, обусловленный собственным током контура (сцепленный с контуром), пропорционален магнитной индукции, которая, в свою очередь, по закону Био-Савара-Лапласа, пропорциональна току.

, где L –коэффициент самоиндукции или индуктивность, «геометрическая» характеристика проводника, так как зависит от его формы и размеров, а также от магнитных свойств среды.

47. Уравнения Максвелла в интегральной форме. Свойства уравнений Максвелла.

Закон Гаусса Поток электрической индукции через замкнутую поверхность s пропорционален величине свободного заряда, находящегося в объёме v, который окружает поверхность s.

Закон Гаусса для магнитного поля Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).

Закон индукции Фарадея Изменение потока магнитной индукции, проходящего через незамкнутую поверхность, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре, который является границей поверхности.

Теорема о циркуляции магнитного поля

Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность , пропорциональны циркуляции магнитного поля на замкнутом контуре, который является границей поверхности.

Свойства уравнений Максвелла.

А. Уравнения Максвелла линейны. Они содержат только первые производные полейEиBпо времени и пространственным координатам, а так же первые степени плотности электрических зарядов ρ и токов γ. Свойство линейности уравнений непосредственно связано с принципом суперпозиции.

Б. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда:

∫pdv=const

В. Уравнения Максвелла выполняются во всех инерциальных системах отсчёта. Они являются релятивистски-инвариантными, что подтверждается опытными данными.

Г. О симметрииуравнений Максвелла.

Уравнения не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет магнитных зарядов. Вместе с тем в нейтральной однородной среде, где ρ = 0 и j=0 ,уравнения Максвелла приобретают симметричный вид, т.е.Eтак связано с(dB/dt) , какBсdE/dt.

Различие только в знаках перед производными(dB/dt) и(dD/dt) показывает, что линии вихревого электрического поля, индуцированного уменьшением поляB, образуют с вектором(dB/dt) левовинтовую систему, в то время как линии магнитного поля, индуцируемого изменениемD, образуют с вектором (dD/dt) правовинтовую систему.

Д. Об электромагнитных волнах.

Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение электрического поля, в свою очередь, возбуждает магнитное поле. За счёт непрерывного взаимопревращения они и должны сохранятся. Поля такого рода называются электромагнитными волнами. Выяснилось также, что ток смещения(dD/dt) играет в этом явлении первостепенную роль.

studfiles.net

Сила Ампера | Virtual Laboratory Wiki

Сила $ d\vec F $, с которой магнитное поле действует на элемент $ d\vec l $ проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока $ I $ в проводнике и векторному произведению элемента длины $ d\vec l $ проводника на магнитную индукцию $ \vec B $:

$ d\vec F = I[d\vec l, \vec B] $.

Сила Ампера/рамка

Направление силы $ d\vec F $ определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

$ dF = I B dl \sin\alpha\, $,

где $ \alpha $ — угол между векторами магнитной индукции и тока.

Сила $ dF $ максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ($ \alpha = 90^\circ, \sin\alpha = 1 $):

$ dF_{max} = IBdl\, $.

Два параллельных проводника Править

Файл:AtractionTwoWires.svg

Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии $ r $ друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи $ I_1 $ и $ I_2 $. Требуется найти силу, действующую на единицу длины проводника.

Бесконечный проводник с током $ I_1 $ в точке на расстоянии $ r $ создаёт магнитное поле с индукцией:

$ B_1(r) = \frac{\mu_0}{4\pi}\frac{2I_1}{r} $ (по закону Био — Савара — Лапласа).

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

$ d\vec F_{1-2} = I_2[d\vec l, \vec B_1(r)] $

По правилу буравчика, $ d\vec F_{1-2} $ направлена в сторону первого проводника (аналогично и для $ d\vec F_{2-1} $, а значит, проводники притягиваются).

Модуль данной силы ($ r $ — расстояние между проводниками):

$ dF_{1-2} = \frac{\mu_0}{4\pi}\frac{2 I_1 I_2}{r} dl $

Интегрируем, учитывая только проводник единичной длины (пределы $ l $ от 0 до 1):

$ F_{1-2} = \frac{\mu_0}{4\pi}\frac{2 I_1 I_2}{r} $

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Сила Ампера. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

ru.vlab.wikia.com

Сила Ампера. Правило левой руки | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Магнитное поле действует на проводник с током. Силу, которая возникает при этом, называют силой Ампера.

Сила Ампера действует на проводник с током в магнитном поле.

Исследуем, от чего зависит модуль и направление данной силы. С этой целью используем установку, в которой прямолинейный проводник подвешен на тонких проволочках в магнитном поле постоянного магнита (рис. 6.16). Гибкие проволочки, присоединенные к концам проводника, позволяют включать его в электрическую цепь, сила тока в которой регулируется с помощью реостата и измеряется амперметром.

Легкая, но жесткая тяга соединяет проводник с чувствительным измерителем силы.

Замкнув электрическую цепь, в которую входит исследуемый проводник, увидим, что он отклонится от положения равновесия, а измеритель покажет определенное значение силы. Увеличим силу тока в проводнике в 2 раза и увидим, что сила, действующая на проводник, также увеличится в 2 раза. Любые другие изменения силы тока в проводнике вызовут соответствующие изменения силы, которая действует на проводник. Сопоставление полученных результатов позволяет сделать вывод, что сила F, действующая в магнитном поле на проводник с током, пропорциональна силе тока I в нем:

F ~ I.

Сила Ампера пропорциональна силе тока в проводнике.

Рис. 6.16. Установка для измерения силы Ампера, действующей на прямой проводник с током в магнитном поле

Расположим еще один магнит рядом с первым. Длина той части проводника, которая находится в магнитном поле, увеличится приблизительно в 2 раза. Значение силы, действующей на проводник, также увеличится приблизительно в два раза. Таким образом, сила F, действующая на проводник с током в магнитном поле, пропорциональна длине части проводника Δl, которая находится в магнитном поле:

F ~ Δl.

Сила Ампера пропорциональна длине активной части проводника.

Сила увеличится также тогда, когда применим другой, более «сильный» магнит с большей магнитной индукцией. Это позволяет сделать вывод о зависимости силы F от магнитной индукции поля B:

F ~ B. Материал с сайта http://worldofschool.ru

Рис. 6.17. С помощью левой руки можно определить направление силы Ампера

Максимальной сила будет тогда, когда между магнитной индукцией и проводником угол α = 90°. Если же этот угол равен нулю, то есть магнитная индукция будет параллельной проводнику, то сила будет равна нулю. Отсюда нетрудно сделать вывод о зависимости силы Ампера от угла между магнитной индукцией и проводником.

Окончательно формула для расчета силы Ампера будет иметь вид

FА = BIΔl • sin α.

Направление силы Ампера определяется по правилу левой руки (рис. 6.17).

Правило левой руки. Если левую руку разместить так, чтобы линии магнитной индукции входили в ладонь, а четыре пальца показывали направление тока, то отставленный большой палец покажет направление силы, действующей на проводник с током в магнитном поле.

На этой странице материал по темам:

От каких величин зависит сила ампера
Реакция разложения перманганата калия уравнение
Правило ампера
Правило лівої руки фізика закон ампера
Закон ампера правило левой руки конспект

Вопросы по этому материалу:

Какое явление описывает сила Ампера?
Какой может быть установка для исследования силы Ампера?
От каких величин зависит сила Ампера?
Как определяется направление силы Ампера?

worldofschool.ru

46.6 Сила Ампера. | FizPortal

46.6 Сила Ампера.

Основное свойство магнитного поля − воздействие на движущиеся электрически заряженные частицы, использовано нами для определения векторной характеристики поля − вектора магнитной индукции. В основу определения этой физической величины мы положили механический момент, действующий на малый контур с током. Но поле действует с некоторой силой на каждую движущуюся заряженную частицу, на каждый участок проводника с током. Сейчас мы получим выражение для силы, действующей на небольшой участок проводника с током, которая называется силой А.М. Ампера. Выделим на участке цепи, по которой протекает электрический ток силой I, малый прямолинейный участок длиной Δl. Далее нам будет удобно характеризовать этот участок вектором элемента тока IΔl, направленным вдоль выделенного участка цепи. Ранее мы подчеркивали, что создать такой уединенный элемент тока невозможно, так постоянный ток может существовать только в замкнутой цепи. Поэтому проверить правильность выражения, для силы, действующей на элемент тока, можно только по тем следствия, которые следуют из формулы для силы. Фактически мы так и поступим − запишем формулу для силы, а затем на ее основании получим выражения, для момента силы, действующей на контур с током. Опыты А.М. Ампера и его последователей свидетельствуют, что сила, действующая на проводник с током, во-первых, пропорциональна силе тока и длине проводника (что очевидно), во-вторых, перпендикулярна проводнику1. Разумно предположить, что эта сила пропорциональная индукции магнитного поля. Наконец, опыт показывает, что на ток, текущий параллельно силовым линиям магнитного поля, никакая сила не действует. Следовательно, величина силы должна быть пропорциональна компоненте поля, перпендикулярной направлению тока (рис. 418).

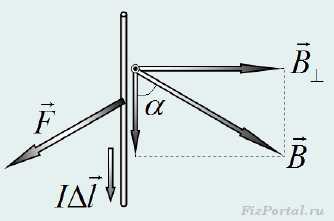рис. 418 Таким образом, мы приходим к формуле для вычисления модуля силы Ампера где B⊥ = Bsinα − компонента вектора индукции поля, перпендикулярная направлению тока, α − угол между вектором индукции и направлением тока. Обратим внимание, что вектор силы Ампера перпендикулярен векторам индукции поля и элемента тока, поэтому в векторной форме выражение для рассматриваемой силы можно представить в виде векторного произведения Для правильного определения направления силы Ампера полезно запомнить, что векторы (именно в таком порядке) ориентированы также как оси декартовой системы координат Ox, Oy, Oz в традиционном изображении (рис. 419).рис. 419 Кстати, такая ориентация традиционно называется правой тройкой (а система координат − правой) − поворот от первого вектора ко второму, со стороны третьего происходит против часовой стрелки. Для тех, кто не в состоянии разобраться в операции векторного произведения, придумано правило левой руки2 (рис. 420):

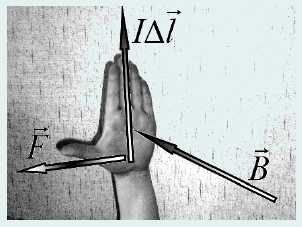рис. 420 Для определения направления силы Ампера, необходимо расположить кисть левой руки так, чтобы силовые линии магнитного поля входили в ладонь, четыре пальца были направлены вдоль направления тока, тогда отставленный на 90° большой палец укажет направление силы Ампера. Рассмотрим теперь силы, действующие на прямоугольный контур с током ABCD, длины сторон которого обозначим a и b. Для простоты, будем считать, что вектор индукции B однородного магнитного поля лежит в плоскости контура и перпендикулярен одной из сторон контура (рис. 421).

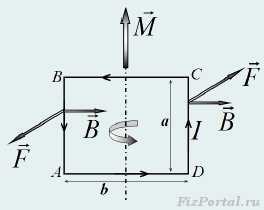рис. 421 На стороны контура BC и DA сила Ампера не действует, силы, действующие на стороны AB и CD, направлены перпендикулярно плоскости контура в противоположные стороны, их модули равны F = IBa. Эти силы образуют пару сил, момент которой не зависит от выбора оси вращения. Поэтому в качестве произвольной оси выберем прямую, параллельную сторонам AB и CD и проходящую через центр контура. Вектор момента силы ориентирован вдоль этой оси и по модулю равен где S = ab − площадь контура. Полученное выражение для вектора момента силы, действующего со стороны магнитного поля совпадает с выражением, использованном нами для определения вектора индукции поля, что доказывает справедливость формулы (12) для силы Ампера.

Задание для самостоятельной работы. 1. Докажите, что для произвольного контура и его произвольной ориентации выражение (2) для силы Ампера приводит к правильному выражению для момента силы, действующему на контур. Воспользуйтесь подсказкой, что произвольный контур можно представить в виде наложения прямоугольных контуров (рис. 422).

рис. 422 В заключение данного раздела укажем, что способ получения формулы для силы Ампера нельзя считать математически выводом. Фактически это угадывание формулы, приводящей к правильному выражению для момента силы, действующей на контур, которая верна «по определению» − по определению вектора магнитной индукции. Конечно, здесь используются и экспериментально проверенные факты: пропорциональность силы Ампера Силе тока и ее перпендикулярность направлению тока − все остальное является следствием определения вектора индукции. Кроме того, при разложении вектора индукции на две составляющие мы неявно использовали принцип суперпозиции для индукции магнитного поля, о котором подробнее будет сказано ниже. 1Этот факт был воспринят его открывателями как чрезвычайно странный и удивительный. К началу XIX века физики привыкли к центральным силам, направленным вдоль линии, соединяющей малые тела, подобно гравитационным и электростатическим силам.2Для того чтобы определить, какая рука левая полезно следующее правило: расположите две руки на краю стола ладонями вниз и запомните, что на левой руке большой палец справа!

fizportal.ru

Сила Ампера.

Радио Сила Ампера.

Количество просмотров публикации Сила Ампера. - 504

Наименование параметра	Значение
Тема статьи:	Сила Ампера.
Рубрика (тематическая категория)	Радио

Сила, действующая на прямолинейный провод с током в магнитном поле, принято называть силой Ампера и определяется законом Ампера.

1. Направление силы Ампера определяется правилом левой руки. В случае если ладонь левой руки расположить так, чтобы перпендикулярная проводу составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по току в проводе, то отогнутый на 90° большой палец покажет направление силы Ампера (рис.12.1).

2. Величина силы Ампера определяется по формуле:

, (12.1)

где l - длина провода; a - угол между направлением тока в проводе и вектором магнитной индукции; В – величина магнитной индукции. В случае если уголa =90° , то сила Ампера принимает максимальное значение . В случае если расположить провод с током в магнитном поле так, чтобы сила Ампера была максимальна, и измерить эту силу, то величину магнитной индукции можно рассчитать по формуле:

. (12.2)

Единица измерения магнитной индукции получила название тесла (Тл): 1Тл = 1Н/А.м.

Сила Ампера. - понятие и виды. Классификация и особенности категории "Сила Ампера." 2014, 2015.

Работа силы Ампера. Сила Ампера. проводящий ползунок AC, которому

Транскрипт

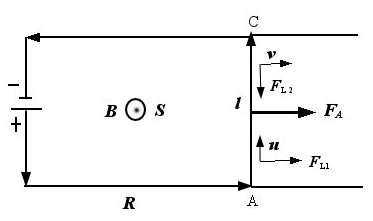
1 Работа силы Ампера Напомню, что сила Ампера, действующая на элемент линейного тока, дается формулой (1) Посмотрим на рисунок По двум неподвижным горизонтальным проводникам (рельсам) может свободно перемещаться проводящий ползунок AC, которому соответствует вектор Все проводники образуют замкнутую цепь с током, помещенную в магнитное поле Положительное направление обхода указано стрелками на проводниках, и ему соответствует направление нормали к поверхности, натянутой на контур, показанное на рисунке вектором площади («на нас») 1 Вектор задает положение ползунка, скорость которого Будем считать поле однородным, тогда интегрирование соотношения (1) по отрезку дает (2) Если ток положителен и направление магнитного поля совпадает с направлением нормали, 2 то эта сила (см рис) направлена вправо Еще заметим, что (3) При движении проводника сила Ампера производит работу Поскольку мы считаем поле однородным, то скалярное произведение есть поток вектора магнитной индукции, и производимую силой Ампера элементарную работу можно переписать так: (4) Пусть поток вектора в начальный, а в конечный моменты времени Тогда полная работа силы Ампера при постоянном токе есть Сила Ампера Элементарная работа силы Ампера 1 Напомню, что 2 На рисунке поле тоже направлено «на нас», но все последующие формулы верны для произвольного направления вектора 1

2 (5) Формулы (4) и (5) для работы силы Ампера, выраженной через изменение потока магнитной индукции, оказываются справедливыми при любой деформации контура с током в магнитном поле На нашем рисунке при выбранных направлениях поля и обхода контура и при положительном токе работа силы Ампера положительна, если проводник движется вправо При этом, как легко проверить, поток магнитной индукции увеличивается, так что положительной оказывается и работа, вычисленная по формулам (4) и (5) Наша картинка показывает, как энергия источника тока преобразуется в механическую работу, однако это еще не двигатель нет цикличности процесса Впрочем, это легко исправить, например, изогнув полозья так, чтобы получилось движение по окружности Если чуть-чуть задуматься о наших результатах, то неминуемо возникнет следующий вопрос Сила Лоренца не может совершать работу, сила Ампера сумма сил Лоренца, действующих на носители заряда Как же получается, что она совершает работу? Ответ очень прост Если проводник движется, то в силу Ампера входят только части сил Лоренца В самом деле, это, где скорость заряда вдоль проводника с током (в нашем случае ), но есть еще другая составляющая силы Лоренца, где скорость движения проводника Суммарная работа этих двух составляющих равна нулю В самом деле, используя свойство смешанного произведения, имеем Сила направлена на нашем рисунке вправо, она и дает вклад в силу Ампера (см рисунок) А что же делает сила? Если считать, что носители тока имеют положительный заряд, то она направлена вниз, а поскольку в этом случае скорость направлена в ползунке вверх (по току), то эта сила препятствует току, ее работа отрицательна 1 Источнику ЭДС для поддержания тока приходится компенсировать эту работу Как мы видим, сила Лоренца играет хитрую роль: она одной «рукой» забирает энергию у источника ЭДС, а другой совершает механическую работу Работа силы Ампера Отрицательная работа силы Лоренца Роль силы Лоренца 1 Если заряд носителей тока отрицателен (электроны), то изменяется как направление силы, так и скорости, поэтому все выводы остаются такими же 2

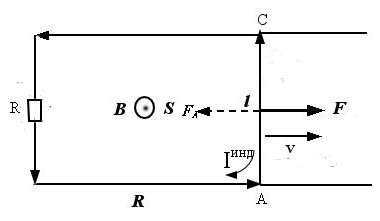
3 Электромагнитная индукция ЭДС индукции при движении проводника в магнтном поле «Вредная» для двигателя часть силы Лоренца представляет собой не что иное, как стороннюю силу, приводящей к отрицательной ЭДС Несколько изменим рисунок: уберем источник тока, явно укажем сопротивление и приложим внешнюю силу, под действием которой ползунок приходит в движение Его скорость, как и раньше, обозначим Мы сохраняем все остальные условия предыдущего параграфа, так что поток вектора магнитной индукции увеличивается На носитель заряда действует сила Лоренца, это сторонняя сила и ее поле есть ЭДС этой силы называется ЭДС индукции и вычисляется по определению: (6) Эта формула полезна во многих случаях В частности, если скорость перпендикулярна полю, то можно написать, (6а) где знак определяется по формуле (6) или с использованием правила Ленца, о котором мы поговорим чуть позже Однако продолжим цепочку вычислений (6) [ ] Сила Лоренца сторонняя сила ЭДС индукции 3

4 Итак, (7) Знак «минус» соответствует тому, что ЭДС индукции включена против выбранного положительного направления обхода контура 1 Ток индукции также направлен в отрицательную сторону Раз по контуру протекает ток, то возникает ситуация «проводник с током в магнитном поле», рассмотренная в предыдущем параграфе, стало быть, появляется сила Ампера, показанная на рисунке пунктирной линией 2 Эта сила направлена против внешней силы, вызывающей движение ползунка, тем самым препятствуя причине вызывающей ток индукции Этот вывод обобщает правило Ленца Индукционный ток всегда направлен так, чтобы препятствовать причине, его вызывающей Движение проводника первоначальная причина, но оно приводит к изменению потока магнитной индукции Проверьте, что создаваемое индукционным током поле препятствует этому изменению Можно сказать, что знак «минус» в формуле для тока индукции (8) математически отображает правило Ленца Пусть теперь в магнитном поле перемещается рамка с током как целое со скоростью На рисунке показана простейшая ситуация, и видно, что если магнитное поле однородное, то полная ЭДС индукции равна нулю: 3 В неоднородном же поле для этого случая получаем (см (6а)) (8) Закон Фарадея Индукционный ток Правило Ленца 1 Если, конечно, поток магнитной индукции увеличивается, как в нашем примере 2 Ее направление противоположно направлению силы Ампера предыдущего параграфа потому, что ток индукции отрицателен 3 ЭДС индукции на нашей картинке наводится только в проводниках длиной 4

5 Вычислим теперь производную по времени от потока магнитной индукции, учитывая, что : Сравнивая два последних равенства, убеждаемся, что опять выполняется закон Фарадея (7) Можно показать, что он справедлив и при произвольной форме контура с током В обоих рассмотренных случаях в роли сторонней силы выступает сила Лоренца Пусть в контуре, движущемся со скоростью в неоднородном поле, горит лампочка Ясно, что она будет гореть и для наблюдателя, движущегося вместе с контуром Иначе говоря, перейдем в ИСО, привязанную к этому контуру Раз лампочка горит, значит и в этой ИСО есть ЭДС индукции, но ведь в ней контур неподвижен, и нет никаких сил Лоренца! Изменение потока магнитной индукции есть, потому что поле меняется во времени, но само это изменение не может быть причиной возникновение ЭДС, нужна сторонняя сила Приходится признать, что для возникновения ЭДС в неподвижном контуре, пронизываемом изменяющимся во времени магнитным полем, должна быть сила, действующая на заряды, но которую мы пока не знаем Что это за сила объясняет первое положение теории Максвелла Любое изменяющееся во времени магнитное поле порождает в пространстве изменяющееся во времени вихревое электрическое поле такое, что циркуляция его по любому контуру определяется скоростью изменения потока вектора магнитной индукции через любую поверхность, границей которой служит этот контур: (9) Если контур неподвижен и не деформируется, то (10) Здесь контур воображаемый, «вспомогательный», но если он совпадает с реальным проводящим контуром, то сразу получается закон Фарадея, поскольку вихревое электрическое поле и есть то поле сторонней силы, кото- 5 1-ое положение теории Максвелла Вихревое электрическое поле как поле сторонней силы

6 рое нам было необходимо для объяснения явления электромагнитной индукции в покоящемся контуре: Таким образом, в зависимости от выбора ИСО в роли сторонней силы явления электромагнитной индукции может выступать либо сила Лоренца (двигающийся проводник), либо сила, действующая на заряд со стороны вихревого электрического поля (покоящийся контур) 1 В любом случае справедлив закон Фарадея (7) Как видно из уравнения (8), сила со стороны вихревого электрического поля может совершать работу по замкнутому контуру Применим к левой части уравнения (10) теорему Стокса: Две стороны одной медали, так что это уравнение примет вид, и (в силу произвольности поверхности интегрирования) получаем (11) Вспомним еще теорему Гаусса (12) и, применив к левой ее части теорему Остроградского Гаусса, Уравнение Максвелла (эм индукция) получим, Опять же в силу произвольности, но теперь объема интегрирования, получаем (14) Уравнение Максвелла (источники поля) 1 Либо их комбинация 6

7 Уравнения (11) и (14) входят в систему уравнений Максвелла и описывают возникновение электрического поля Они же в интегральной форме даются формулами (10) и (12) Вместо уравнения (14) часто используется уравнение, получающееся в точности так же из теоремы о потоке вектора электрического смещения Самоиндукция Вернемся к контуру с током (при обсуждении этих вопросов его часто называют «витком с током») и посмотрим, что будет происходить, если ток в нем изменяется Ток создает магнитное поле, и, конечно есть поток магнитной индукции через поверхность, ограниченную рассматриваемым контуром Этот поток пропорционален протекающему току: 1 (15а) Коэффициент называется индуктивностью или коэффициентом самоиндукции и определяется только свойствами самого контура (его геометрией, материалом) При изменении тока возникает ЭДС, которая в данном случае называется ЭДС самоиндукции Явлением самоиндукции называется появление ЭДС индукции в контуре за счет изменения тока в нем самом Для ЭДС самоиндукции из закона Фарадея получаем (16) Витки с током обычно оказываются соединены последовательно, когда провод наматывают на катушку Пусть площадь витка есть, полное число витков равно, а их плотность (число витков на единицу длины ) (17) Магнитное поле внутри длинного соленоида с обмоткой мы уже вычислили: (18) Индуктивность контура Явление самоиндукции ЭДС самоиндукции 1 Здесь и далее мы считаем, что нет каких-либо ферромагнитных материалов 7

8 Благодаря однородности поля поток через один виток вычисляется легко Можно было бы вычислить ЭДС самоиндукции в одном витке, а затем умножить ее на полное число витков Однако, чтобы сохранить соотношение (16), поступают по-другому Назовем потокосцеплением величину и несколько изменим определение индуктивности (15а), полагая (15б) Тогда для катушки справедлива формула (16), но для определения индуктивности нужно вычислить потокосцепление Сравнивая последнее равенство с определением (15), видим, что индуктивность соленоида есть Потокосцепление Определение индуктивности в общем случае Индуктивность соленоида или, учитывая (17), (19) где объем соленоида Энергия магнитного поля Любой контур с током (в том числе, конечно, и катушка) обладаут некоторой энергией Это следует из следующего опыта В некоторый момент времени отключим источник ЭДС, замкнув при этом контур Ток не прекратится мгновенно, а некоторое время его будет поддерживать ЭДС самоиндукции Запасенную энергию можно вычислить как работу, которую совершает ЭДС индукции при изменении тока от начального значения до нуля Элементарная работа есть так что запасенная энергия определяется интегрированием:, Энергия контура с током 8

9 Попробуем переписать это выражение так, чтобы в него не входили ни ток, ни индуктивность 1 Для этого выразим эти величины через другие параметры с помощью сосоотношений (18) и (19) соответственно Получим Скоро мы убедимся, что вся эта энергия действительно заключена в магнитном поле Наиболее общая формула для плотности энергии магнитного поля выглядит так:, а магнитная энергия, заключенная в объеме пространства, находится интегрированием по этому объему: Плотность энергии магнитного поля Энергия магнитного поля Взаимная индукция Взаимной индукцией называется явление возникновения ЭДС индукции в одном контуре при изменении тока в другом У магнитного поля, создаваемого током, есть поток 2 магнитной индукции через первый контур, пропорциональный этому току, Коэффициент пропорциональности называется коэффициентом взаимной индукции В первом контуре наводится ЭДС индукции Аналогично, во втором контуре наводится ЭДС индукции при изменении тока в первом контуре:, где коэффициент взаимной индукции определяет поток магнитной индукции поля, создаваемого первым током, через второй контур: Взаимная индукция Коэффициент взаимной индукции 1 Подобным образом мы уже действовали при обсуждении энергии конденсатора в лекции 4 2 В общем случае надо говорить о потокосцеплении 9

10 Терема взаимности утверждает, что 10

docplayer.ru

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

Сила Ампера. Правило левой руки. Сила ампера определение и формула

43. Сила Ампера. Сила Лоренца

45. Закон электромагнитной индукции. Правило Ленца

46. Явление самоиндукции.

47. Уравнения Максвелла в интегральной форме. Свойства уравнений Максвелла.

Сила Ампера | Virtual Laboratory Wiki

Два параллельных проводника Править

Сила Ампера. Правило левой руки | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

От каких величин зависит сила ампера

Реакция разложения перманганата калия уравнение

Правило ампера

Правило лівої руки фізика закон ампера

Закон ампера правило левой руки конспект

Какое явление описывает сила Ампера?

Какой может быть установка для исследования силы Ампера?

От каких величин зависит сила Ампера?

Как определяется направление силы Ампера?

46.6 Сила Ампера. | FizPortal

46.6 Сила Ампера.

Сила Ампера.

Радио Сила Ампера.

Читайте также

Работа силы Ампера. Сила Ампера. проводящий ползунок AC, которому

Транскрипт

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация