Сила, Давление — Формулы по физике
По
рыхлому снегу человек идёт с большим трудом, глубоко проваливаясь при
каждом шаге. Но, надев лыжи, он может идти, почти не проваливаясь в
него. Почему? На лыжах или без лыж человек действует на снег с одной и
той же силой, равной своему весу. Однако действие этой силы в обоих
случаях различно, потому что различна площадь поверхности, на которую
давит человек, с лыжами и без лыж. Площадь поверхности лыж почти в 20
раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на
каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз
меньшей, чем стоя на снегу без лыж.
Ученик,
прикалывая кнопками газету к доске, действует на каждую кнопку с
одинаковой силой. Однако кнопка, имеющая более острый конец, легче
входит в дерево.
Значит,
результат действия силы зависит не только от её модуля, направления и
точки приложения, но и от площади той поверхности, к которой она
приложена (перпендикулярно которой она действует).
Этот вывод подтверждают физические опыты.
Опыт.Результат действия данной силы зависит от того, какая сила действует на единицу площади поверхности.
По
углам небольшой доски надо вбить гвозди. Сначала гвозди, вбитые в
доску, установим на песке остриями вверх и положим на доску гирю. В этом
случае шляпки гвоздей лишь незначительно вдавливаются в песок. Затем
доску перевернем и поставим гвозди на острие. В этом случае площадь
опоры меньше, и под действием той же силы гвозди значительно углубляются
в песок.
Опыт. Вторая иллюстрация.
От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы.
В
рассмотренных примерах силы действовали перпендикулярно поверхности
тела. Вес человека был перпендикулярен поверхности снега; сила,
действовавшая на кнопку, перпендикулярна поверхности доски.
Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением.
Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности:
давление = сила / площадь.
Обозначим величины, входящие в это выражение: давление — p, сила, действующая на поверхность, — F и площадь поверхности — S.
Тогда получим формулу:
p = F/S
Понятно, что бóльшая по значению сила, действующую на ту же площадь, будет производить большее давление.
За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м2 перпендикулярно этой поверхности.
Единица давления — ньютон на квадратный метр ( 1 Н / м2 ). В честь французского ученого Блеза Паскаля она называется паскалем (Па). Таким образом,
1 Па = 1 Н / м2 .
Используется также другие единицы давления: гектопаскаль (гПа) и килопаскаль (кПа).
1 кПа = 1000 Па;
1 гПа = 100 Па;
1 Па = 0,001 кПа;
1 Па = 0,01 гПа.
Пример.
Рассчитать давление, производимое на пол мальчиком, масса которого 45
кг, а площадь подошв его ботинок, соприкасающихся с полом, равна 300 см2.
Запишем условие задачи и решим её.
Дано: m = 45 кг, S = 300 см2; p = ?
В единицах СИ: S = 0,03 м2
Решение:
p = F/S,
F = P,
P = g·m,
P = 9,8 Н · 45 кг ≈ 450 Н,
p = 450/0,03 Н / м2 = 15000 Па = 15 кПа
‘Ответ’: p = 15000 Па = 15 кПа
Способы уменьшения и увеличения давления.
Тяжелый
гусеничный трактор производит на почву давление равное 40 — 50 кПа, т.
е. всего в 2 — 3 раза больше, чем давление мальчика массой 45 кг. Это
объясняется тем, что вес трактора распределяется на бóльшую площадь за
счёт гусеничной передачи. А мы установили, что чем больше площадь опоры, тем меньше давление, производимое одной и той же силой на эту опору.
В
зависимости от того, нужно ли получить малое или большое давление,
площадь опоры увеличивается или уменьшается. Например, для того, чтобы
грунт мог выдержать давление возводимого здания, увеличивают площадь
нижней части фундамента.
Шины
грузовых автомобилей и шасси самолетов делают значительно шире, чем
легковых. Особенно широкими делают шины у автомобилей, предназначенных
для передвижения в пустынях.
Тяжелые
машины, как трактор, танк или болотоход, имея большую опорную площадь
гусениц, проходят по болотистой местности, по которой не пройдет
человек.
С
другой стороны, при малой площади поверхности можно небольшой силой
произвести большое давление. Например, вдавливая кнопку в доску, мы
действуем на нее с силой около 50 Н. Так как площадь острия кнопки
примерно 1 мм2, то давление, производимое ею, равно:
p = 50 Н/ 0, 000 001 м2 = 50 000 000 Па = 50 000 кПа.
Для
сравнения, это давление в 1000 раз больше давления, производимого
гусеничным трактором на почву. Можно найти еще много таких примеров.
Лезвие
режущих и острие колющих инструментов (ножей, ножниц, резцов, пил, игл и
др.) специально остро оттачивается. Заточенный край острого лезвия
имеет маленькую площадь, поэтому при помощи даже малой силы создается
большое давление, и таким инструментом легко работать.
Режущие
и колющие приспособления встречаются и в живой природе: это зубы,
когти, клювы, шипы и др. — все они из твердого материала, гладкие и
очень острые.
Давление
Известно, что молекулы газа беспорядочно движутся.
Опыт. Здесь мы узнаем, что газ давит на стенки сосуда по всем направлениям одинаково.
Мы
уже знаем, что газы, в отличие от твердых тел и жидкостей, заполняют
весь сосуд, в котором находятся. Например, стальной баллон для хранения
газов, камера автомобильной шины или волейбольный мяч. При этом газ
оказывает давление на стенки, дно и крышку баллона, камеры или любого
другого тела, в котором он находится. Давление газа обусловлено иными
Давление газа обусловлено иными
причинами, чем давление твердого тела на опору.
Известно,
что молекулы газа беспорядочно движутся. При своем движении они
сталкиваются друг с другом, а также со стенками сосуда, в котором
находится газ. Молекул в газе много, поэтому и число их ударов очень
велико. Например, число ударов молекул воздуха, находящегося в комнате, о
поверхность площадью 1 см2 за
1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной
молекулы мала, но действие всех молекул на стенки сосуда значительно, —
оно и создает давление газа.
Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.
Рассмотрим
следующий опыт. Под колокол воздушного насоса поместим резиновый шарик.
Он содержит небольшое количество воздуха и имеет неправильную форму.
Затем насосом откачиваем воздух из-под колокола. Оболочка шарика, вокруг
которой воздух становится все более разреженным, постепенно раздувается
и принимает форму правильного шара.
Как объяснить этот опыт?
Для хранения и перевозки сжатого газа используются специальные прочные стальные баллоны.
В
нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика
внутри и снаружи. При откачивании воздуха число молекул в колоколе
вокруг оболочки шарика уменьшается. Но внутри шарика их число не
изменяется. Поэтому число ударов молекул о внешние стенки оболочки
становится меньше, чем число ударов о внутренние стенки. Шарик
раздувается до тех пор, пока сила упругости его резиновой оболочки не
станет равной силе давления газа. Оболочка шарика принимает форму шара.
Это показывает, что газ давит на ее стенки по всем направлениям одинаково.
Иначе говоря, число ударов молекул, приходящихся на каждый квадратный
сантиметр площади поверхности, по всем направлениям одинаково.
Одинаковое давление по всем направлениям характерно для газа и является
следствием беспорядочного движения огромного числа молекул.
Попытаемся
уменьшить объем газа, но так, чтобы масса его осталась неизменной. Это
значит, что в каждом кубическом сантиметре газа молекул станет больше,
плотность газа увеличится. Тогда число ударов молекул о стенки
увеличится, т. е. возрастет давление газа. Это можно подтвердить опытом.
На рисунке а изображена
стеклянная трубка, один конец которой закрыт тонкой резиновой пленкой. В
трубку вставлен поршень. При вдвигании поршня объем воздуха в трубке
уменьшается, т. е. газ сжимается. Резиновая пленка при этом выгибается
наружу, указывая на то, что давление воздуха в трубке увеличилось.
Наоборот,
при увеличении объема этой же массы газа, число молекул в каждом
кубическом сантиметре уменьшается. От этого уменьшится число ударов о
стенки сосуда — давление газа станет меньше. Действительно, при
вытягивании поршня из трубки объем воздуха увеличивается, пленка
прогибается внутрь сосуда. Это указывает на уменьшение давления воздуха в
трубке. Такие же явления наблюдались бы, если бы вместо воздуха в
трубке находился бы любой другой газ.
Итак, при
уменьшении объема газа его давление увеличивается, а при увеличении
объема давление уменьшается при условии, что масса и температура газа
остаются неизменными.
А
как изменится давление газа, если нагреть его при постоянном объеме?
Известно, что скорость движения молекул газа при нагревании
увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда
чаще. Кроме того, каждый удар молекулы о стенку будет сильнее.
Вследствие этого, стенки сосуда будут испытывать большее давление.
Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.
Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.
Для
хранения и перевозки газов их сильно сжимают. При этом давление их
возрастает, газы необходимо заключать в специальные, очень прочные
баллоны. В таких баллонах, например, содержат сжатый воздух в подводных
В таких баллонах, например, содержат сжатый воздух в подводных
лодках, кислород, используемый при сварке металлов. Конечно же, мы
должны навсегда запомнить, что газовые баллоны нельзя нагревать, тем
более, когда они заполнены газом. Потому что, как мы уже понимаем, может
произойти взрыв с очень неприятными последствиями.
Закон Паскаля.
Давление передается в каждую точку жидкости или газа.
Давление поршня передается в каждую точку жидкости, заполняющей шар.
Теперь газ.
В
отличие от твердых тел отдельные слои и мелкие частицы жидкости и газа
могут свободно перемещаться относительно друг друга по всем
направлениям. Достаточно, например, слегка подуть на поверхность воды в
стакане, чтобы вызвать движение воды. На реке или озере при малейшем
ветерке появляется рябь.
Подвижностью частиц газа и жидкости объясняется, что давление, производимое на них, передается не только в направлении действия силы, а в каждую точку. Рассмотрим это явление подробнее.
На рисунке, а изображен
сосуд, в котором содержится газ (или жидкость). Частицы равномерно
распределены по всему сосуду. Сосуд закрыт поршнем, который может
перемещаться вверх и вниз.
Прилагая
некоторую силу, заставим поршень немного переместиться внутрь и сжать
газ (жидкость), находящийся непосредственно под ним. Тогда частицы
(молекулы) расположатся в этом месте более плотно, чем прежде(рис, б).
Благодаря подвижности частицы газа будут перемещаться по всем
направлениям. Вследствие этого их расположение опять станет равномерным,
но более плотным, чем раньше (рис, в). Поэтому давление газа всюду
возрастет. Значит, добавочное давление передается всем частицам газа или
жидкости. Так, если давление на газ (жидкость) около самого поршня
увеличится на 1 Па, то во всех точках внутри газа
или жидкости давление станет больше прежнего на столько же. На 1 Па
увеличится давление и на стенки сосуда, и на дно, и на поршень.
Давление, производимое на жидкость или газ, передается на любую точку одинаково во всех направлениях.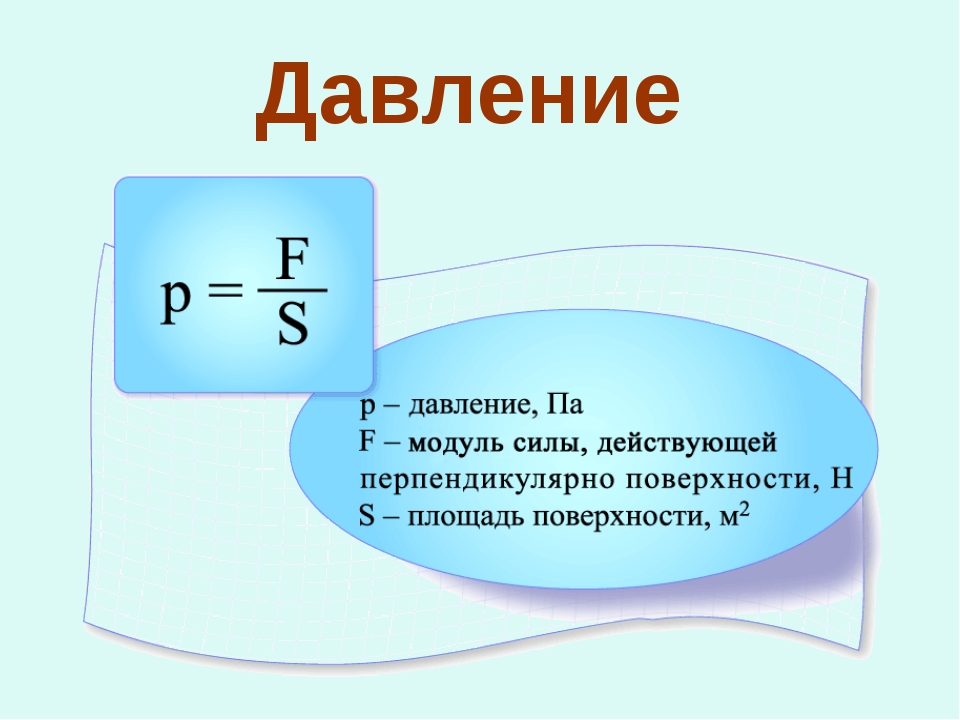
Это утверждение называется законом Паскаля.
На основе закона Паскаля легко объяснить следующие опыты.
На
рисунке изображен полый шар, имеющий в различных местах небольшие
отверстия. К шару присоединена трубка, в которую вставлен поршень. Если
набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех
отверстий шара. В этом опыте поршень давит на поверхность воды в
трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его
давление другим слоям, лежащим глубже. Таким образом, давление поршня
передается в каждую точку жидкости, заполняющей шар. В результате часть
воды выталкивается из шара в виде одинаковых струек, вытекающих из всех
отверстий.
Если
шар заполнить дымом, то при вдвигании поршня в трубку из всех отверстий
шара начнут выходить одинаковые струйки дыма. Это подтверждает, что и газы передают производимое на них давление во все стороны одинаково.
Давление в жидкости и газе.
Под действием веса жидкости резиновое дно в трубке прогнется.
На
жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому,
каждый слой жидкости, налитой в сосуд, своим весом создает давление,
которое по закону Паскаля передается по всем направлениям.
Следовательно, внутри жидкости существует давление. В этом можно
убедиться на опыте.
В
стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой
пленкой, нальем воду. Под действием веса жидкости дно трубки прогнется.
Опыт
показывает, что, чем выше столб воды над резиновой пленкой, тем больше
она прогибается. Но всякий раз после того, как резиновое дно прогнулось,
вода в трубке приходит в равновесие (останавливается), так как, кроме
силы тяжести, на воду действует сила упругости растянутой резиновой
пленки.
По мере опускания трубки | резиновая пленка постепенно выпрямляется. | Силы, действующие на резиновую пленку, | одинаковы с обеих сторон. |
Иллюстрация.
Дно отходит от цилиндра вследствие давления на него силы тяжести.
Опустим
трубку с резиновым дном, в которую налита вода, в другой, более широкий
сосуд с водой. Мы увидим, что по мере опускания трубки резиновая пленка
постепенно выпрямляется. Полное выпрямление пленки показывает, что
силы, действующие на нее сверху и снизу, равны. Наступает полное
выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают.
Такой
же опыт можно провести с трубкой, в которой резиновая пленка закрывает
боковое отверстие, как это показано на рисунке, а. Погрузим эту трубку с
водой в другой сосуд с водой, как это изображено на рисунке, б.
Мы заметим, что пленка снова выпрямится, как только уровни воды в
трубке и сосуде сравняются. Это означает, что силы, действующие на
резиновую пленку, одинаковы со всех сторон.
Возьмем
сосуд, дно которого может отпадать. Опустим его в банку с водой. Дно
при этом окажется плотно прижатым к краю сосуда и не отпадет. Его
прижимает сила давления воды, направленная снизу вверх.
Будем
осторожно наливать воду в сосуд и следить за его дном. Как только
уровень воды в сосуде совпадет с уровнем воды в банке, оно отпадет от
сосуда.
В
момент отрыва на дно давит сверху вниз столб жидкости в сосуде, а снизу
вверх на дно передается давление такого же по высоте столба жидкости,
но находящейся в банке. Оба эти давления одинаковы, дно же отходит от
цилиндра вследствие действия на него собственной силы тяжести.
Выше были описаны опыты с водой, но если взять вместо воды любую другую жидкость, результаты опыта будут те же.
Итак, опыты показывают, что внутри
жидкости существует давление, и на одном и том же уровне оно одинаково
по всем направлениям. С глубиной давление увеличивается.
Газы
в этом отношении не отличаются от жидкостей, ведь они тоже имеют вес.
Но надо помнить, что плотность газа в сотни раз меньше плотности
жидкости. Вес газа, находящегося в сосуде, мал, и его «весовое» давление
Вес газа, находящегося в сосуде, мал, и его «весовое» давление
во многих случаях можно не учитывать.
1. |
Давление твердого тела (определение)
Иллюстрированное и озвученное определение понятия давления твердого тела.
| Тип: И
| |
Скачать (архив, | |||
2. |
Понятие давления (интерактивная модель эксперимента)
Моделирование экспериментального выяснения зависимости давления от площади, на которую действует сила и от величины этой силы (на примере грузов, помещаемых на поршень в цилиндре с газом).
| Тип: И
| |
Скачать (архив, | |||
3. |
Вычисли давление книги на стол (задача)
Предназначена для отработки умения решать задачи на нахождение давления, оказываемого твердым телом на опору.
| Тип: П
| |
Скачать (архив, | |||
4. |
Зависимость давления от силы и площади (интерактивная модель эксперимента)
Моделирование экспериментального исследования зависимости давления твердого тела от силы и площади (платформа с опорами помещается в емкость с песком, можно изменять количество грузов на платформе и форму ее опор – острые или тупые).
| Тип: И
| |
Скачать (архив, | |||
5. |
Понятие давления (интерактивная модель эксперимента)
Моделирование экспериментального выяснения зависимости давления от площади, на которую действует сила, и от величины этой силы (на примере грузов, помещаемых на поршень в цилиндре с газом).
| Тип: И
| |
Скачать (архив, | |||
6. |
Давление твердого тела (определение)
Иллюстрированное и озвученное определение понятия давления твердого тела.
| Тип: И
| |
Скачать (архив, | |||
7. |
Давление в 1 Па (рисунок)
Иллюстрация к рассказу о понятии давления и давления в 1 Па (кусочек фольги массой 0,1 г и размером 1см х 1см лежит на столе).
| Тип: И
| |
Скачать (архив, |
Физика — сила и давление
Когда объект либо отталкивается, либо вытягивается, называется силой.
Движение, генерируемое в объекте, происходит из-за действия силы.
Приложенная сила заставляет стол двигаться в заданном направлении.
Сила силы обычно выражается величиной.
Сила также имеет направление; аналогично, если изменяется величина или направление, это напрямую влияет на силу.
Если сила прикладывается в направлении, противоположном направлению движения, то это приводит к уменьшению скорости движения объекта.
Если объект находится в движении, то внешняя сила может измениться в состоянии или направлении движения этого объекта.
Состояние движения объекта объясняется его скоростью и направлением движения.
Состояние «покоя» объекта считается нулевой скоростью, так как —
Объект не может двигаться сам по себе.
Объект не может изменить свою скорость сам по себе.
Объект не может изменить свое направление сам по себе.
Объект не может измениться сам по себе.
Сила может заставить объект двигаться от отдыха.
Сила может изменить скорость движущегося объекта.
Сила может изменить направление движущегося объекта.
Сила может изменить форму объекта.
Сила, вызванная действием мышц, известна как мышечная сила .
Некоторая сила, уменьшающая скорость движущегося объекта, известна как « трение» . Например, движущееся колесо на дороге; как только источник силы перестает работать, колесо останавливается из-за трения.
Сила, приложенная заряженным телом к другому заряженному или незаряженному телу, известна как « электростатическая сила» .
Объекты или вещи, которые падают на землю, поскольку земля притягивает их к себе; эта сила известна как сила тяжести или гравитации .
Сила гравитации применима ко всем объектам. Фактически, каждый объект в этой вселенной, независимо от его размера и формы, оказывает некоторую силу на любой другой объект. Это происходит только из-за « гравитационной силы» .
Сила, действующая на единицу площади поверхности, называется давлением (давление = сила / площадь, на которую она действует).
Если площадь меньше, то давление на поверхность будет больше; например, это причина того, что область одного конца гвоздя заострена (для оказания достаточного давления), а другой конец больше (как показано на рисунке ниже).
Эта оболочка воздуха известна как атмосфера, которая простирается на много километров над поверхностью земли.
Давление, оказываемое воздухом, известно как атмосферное давление .
Давление внутри наших тел точно равно атмосферному давлению и аннулирует давление, действующее извне (см. Изображение ниже).
Жидкости и газы также оказывают давление на стенки соответствующих емкостей.
Урок по теме: «Давление и сила давления»
Цели:
- Образовательные: сформировать общие
представления о давлении, силе давления,
формирование практических навыков вычисления
давления; - Развивающие: развитие экспериментальных
умений, навыков, логического мышления,
обоснование своих высказываний, развитие
навыков работы в паре, обосновывать
необходимость увеличения или уменьшения
давления; - Воспитательные: формирование навыков
самостоятельной работы, воспитание стремления к
учению, умения напряженно трудиться, воспитание
чувства коллективизма при работе в парах.
Тип рассматриваемого урока: изучение
нового материала.
Форма урока: комбинированный урок.
Место урока в учебном плане. Тема
“давление и сила давления” рассматриваются в
разделе “Давление твердых тел, жидкостей и
газов”. Эта тема в разделе первая и является
наиболее интересной для учащихся (т.к. большая
связь изучаемого материала с жизнью, техникой),
поэтому на изучение этой темы необходимо 2 часа.
Основное содержание изучаемого материала задают
учебная программа и обязательный минимум
содержания образования по физике.
Методы: словесные, наглядные,
практические.
Оборудование:
- стенд-выставка режущих и колющих инструментов;
- презентация в Power Point, лабораторные динамометры,
бруски, линейки, кнопки.
План урока:
| 1. Этап организации начала урока – | 1 мин. |
| 2. Этап подготовки к активному и
сознательному усвоению нового материала – | 7 мин. |
| 3. Этап усвоения новых знаний (сила
давления, формула давления, единицы измерения давления) – | 20мин. |
| 4. Путешествие в биологию – | 6 мин. |
| 5. Мир техники – | 6 мин. |
| 6. “Знакомые буквы” – | 2 мин. |
| 7. Экспериментальные задания. – | 15 мин. |
| 8. Тестовые задания. – | 13 мин. |
| 9. Подведение итогов – | 5 мин. |
| 10. Домашнее задание. – | 5 мин. |
Эпиграф к уроку: “Знание только тогда
знание, когда оно приобретено усилиями мысли, а
не памяти” (А.Н. Толстой).
Ход урока
1. Этап организации урока.
2. Этап подготовки к активному и
сознательному усвоению материала.
Учитель обращает внимание учащихся на
иллюстрацию к произведению Мамина-Сибиряка
“Серая шейка” (см. Слайд №1
Слайд №1
презентации) и зачитывает отрывок из этого
произведения: “…Лиса действительно пришла
через несколько дней, села на берегу и опять
заговорила:
— Cоскучилась я по тебе, уточка…Выходи сюда; а не
хочешь, так я сама к тебе приду. Я не спесива…
И Лиса принялась ползти осторожно по льду к
самой полынье. У Серой Шейки замерло сердце…”.
Вопрос. Почему лиса осторожно ползла по
льду? (Выслушиваем ответы)
Учитель. Чтобы ответить на этот
вопрос, необходимо познакомиться с темой
“Давление и сила давления”. Слово “давление”
вам хорошо известно. Вы понимаете смысл
следующих предложений:
- Давление резко падает, возможны осадки.
- Защитники команды “Динамо” не выдержали
давления нападающих “Спартака”. - У больного внезапно повысилось давление.
- “Наутилус” скользнул в бездонные глубины,
несмотря на огромное давление внешней среды. - – Это была женщина, – сказал комиссар Мегре, –
только тонкий каблук женских туфель мог
произвести такое большое давление.
Во всех этих предложениях слово “давление”
использовано в разных ситуациях и имело разное
значение. Мы рассмотрим давление с точки зрения
физики. Для этого пригласим помощника на урок.
Дети мёда захотели – сгиньте, вьюги и
метели,
Чтобы добрая пчела в гости на урок зашла.
Сегодня главным героем нашего урока будет
пчела.
Перед вами слайд (слайд №2),
на котором изображен цветик-семицветик, лепестки
у которого не простые, посмотрите,
1 лепесток – Формулы давления, сила давления.
2 лепесток – Единицы давления.
3 лепесток – Путешествие в биологию.
4 лепесток – Мир техники.
5 лепесток – “Знакомые буквы”
6 лепесток – Экспериментальные задания.
7 лепесток – Тестовые задания.
После изучения темы должны будете знать:
- определение силы давления,
- определение давления,
- единицы измерения давления;
уметь:
- применять формулу давления при решении задач.
3. Этап усвоения новых знаний.
Учитель: (Пчела на слайде по щелчку мыши
перелетает на первый лепесток) на первом
лепестке. (Фронтальная беседа по вопросам)
- Что такое сила?
- Какие силы мы изучили?
- От чего зависит результат действия силы? (За
правильный ответ ученик получает жетон).
Учитель дает определение силы давления: силу,
прикладываемую перпендикулярно поверхности,
называют силой давления на эту поверхность,
учащиеся работают с ОК (см.
приложение).
Учитель. Рассмотрим пример (кнопка на
лепестке): по свежевыпавшему снегу с горы
скатывается мальчик, неожиданно падает, и лыжи
скатываются вниз. Поднявшись на ноги, мальчик
спускается за лыжами, при этом его ноги глубоко
вязнут в снегу.
Вопрос: почему мальчик на лыжах
не проваливается в снег, а без лыж проваливается?
Учащиеся делают вывод, что в обоих случаях
мальчик действует на снег с одной и той же силой,
но результат действия силы разный,
следовательно, (учитель подводит к мысли)
результат действия зависит еще от какой-то
величины.
Учитель: Что изменилось после падения
мальчика? Учащиеся делают вывод, что изменилась
площадь опоры мальчика на снег. Когда мальчик
стоит на лыжах, то площадь опоры больше, чем без
лыж.
Учитель: Результат действия силы
зависит от:
1 – значения силы давления;
2 – площади поверхности, перпендикулярно
которой действует сила давления.
(Учащиеся работают с ОК.)
Учитель: величина, которая показывает, какая
сила давления действует на каждую единицу
площади поверхности, называется давлением.
;
P – давление
Fд – сила давления
S – площадь опоры.
– чтобы давление нам получить,
нужно силу давления на площадь делить!
Проведем качественный анализ данной формулы.
Вопрос 1. Сила давления не
изменяется, а площадь опоры увеличивается. Как
изменится давление? Почему? (Давление
уменьшится, т. к. давление обратно
пропорционально площади).
Вопрос 2. Площадь опоры не меняется,
а сила давления увеличивается. Как изменится
давление? Почему? (Давление увеличится, т.к.
давление прямо пропорционально силе давления).
Учащиеся делают вывод, что при одной и той же
силе давление больше в том случае, когда площадь
опоры меньше, и, наоборот, чем больше площадь
опоры, тем давление меньше.
Учитель:
Проникнуть в тело цель твоя – сведи опору
до нуля.
Идя гулять зимою в лес, ты увеличь опору S.
(Для усвоения смысла формулы давления твердого
тела).
Для создания наглядных образов учитель
знакомит учащихся с различным давлением,
встречающимся в технике, природе и быту (таблица 6
стр.84 учебник Физика – 7 кл.)
Учащиеся работают с ОК (работа с треугольником).
Вопрос 1. Как можно найти силу
давления, зная давление и площадь поверхности, к
которой приложена сила? (Fд=p*S)
Вопрос 2. Как найти площадь
поверхности, к которой приложена сила, зная силу
давления? (S=Fд/p)
Учитель. Выведем единицу
Выведем единицу
измерения давления. (Пчела на слайде перелетает
на второй лепесток по щелчку мыши).
| Дано: |
|
| S=1м2 | |
| Fд=1Н |
|
| p-? |
1 Па – это такое давление, которое производит
сила давления в 1 Н, действующая на поверхность
площадью 1 м2 перпендикулярно этой
поверхности.
1 гПа – 100 Па
1 кПа – 1000 Па
1 МПа – 1000 000 Па
Вопрос. Что означает запись: р=15 000Па, р=5000Па?
(15 000 ПА – это такое давление, которое
производит сила давления в 15 000 Н, действующая
на поверхность площадью 1м2
перпендикулярно этой поверхности.)
Учитель.
Моря и пустыни, Земля и Луна
Свет Солнца и снега лавины…
Природа сложна, но Природа одна.
Законы природы – едины!
Совершим путешествие в биологию (пчела на
слайде перелетает на третий лепесток по щелчку
мыши).
В Амазонке есть пиранья –
С виду рыбка так себе.
Если сунешь палец в воду,
Перекусит вмиг его.
Вопрос: почему пиранья может
перекусить палец человека?
Вот верблюд, а на верблюде
Возят кладь и ездят люди.
Он живет среди пустынь,
Ест невкусные кусты,
Он в работе круглый год…
Почему же на верблюде возят кладь и ездят люди?
(Площадь поверхности конечностей верблюда
велика, а давление, оказываемое на песок,
невелико, поэтому верблюд не проваливается в
песок. )
)
Ёж сердитый, серый ёж,
Ты куда, скажи, идёшь?
Ты колючий весь такой, что не взять тебя рукой!
Почему же ёж колючий?
(Площадь поверхности иголок мала, а давление
велико.)
Пчелка – труженик известный,
Дарит людям мёд и воск,
А врагам покажет жало,
Будут помнить целый год!
Почему жало пчелы оказывает на кожу человека
очень большое давление? (Жало пчелы имеет малую
площадь поверхности, а давление, оказываемое на
кожу человека, велико.)
Как-то раз спросили розу:
Отчего, чаруя око,
Ты колючими шипами
Нас царапаешь жестоко?
(Площадь поверхности шипов розы мала, а
давление велико.)
Вернемся к героям “Серой Шейки”. Почему лиса
осторожно ползла по льду? (Лиса выбрала такой
способ передвижения, чтобы увеличить площадь
поверхности, а давление, производимое на лед,
уменьшить.)
Учитель: Хитрая лиса знала формулу
давления! Мы убедились в справедливости этой
формулы в природе – иглы, клюквы, когти, зубы,
клыки, жала. Но. “Душа науки – это практическое
применение её открытий” (У.Томсон).
Совершим экскурсию в мир техники.
(Пчела перелетает на четвертый лепесток по
щелчку мыши.)
Мы знаем, что, чем больше площадь опоры, тем
меньше давление, производимое данной силой, и,
наоборот, с уменьшением площади опоры (при
неизменной силе) давление возрастает. Поэтому, в
зависимости от того, хотят ли получить малое или
большое давление, площадь опоры увеличивают или
уменьшают. (Учащиеся работают с ОК – способы
изменения давления). Шины грузовых автомобилей и
шасси самолетов делают значительно шире, чем
легковых. Особенно широкими шины делают у
автомобилей, предназначенных для передвижения в
пустынях. Тяжелые машины, такие как трактор, танк
Тяжелые машины, такие как трактор, танк
или болотоход, могут проезжать по болотистой
местности, по которой не всегда пройдет человек.
Почему? (Тяжелые машины, имея большую опорную
площадь, оказывают небольшое давление.)
Учитель обращает внимание учащихся на выставку
режущих и колющих предметов и инструментов.
Вопрос: Почему режущие и колющие инструменты оказывают
на тело очень большое давление? (Площадь
поверхности режущих и колющих инструментов мала,
а давление велико.)
Учитель. Мы убедились в
справедливости формулы давления в природе и
технике.(Пчела перелетает на пятый лепесток по
щелчку мыши.)
Игра “Знакомые буквы”.
На доске записаны буквы – обозначения
физических величин: p, m, F, l, V. Ваша задача:
послушав пословицы, поставить им в соответствие
одну их этих величин.
Пословицы:
- Шила в мешке не утаишь.
- Ежа голыми руками не возьмёшь.
- Палец в рот не клади.
(Давление)
Учитель. “Знания, не рожденные опытом,
матерью всякой достоверности, бесплодны и полны
ошибок”. (Пчела по щелчку мыши перелетает на 6
лепесток.)
Экспериментальные задания.
1. Задача. Вдавливая кнопку в доску, мы
действуем на нее силой 50Н, площадь острия кнопки
0,000 001м2. Определите давление, производимое
кнопкой.
| Дано: | Решение: |
| Fд=50Н |
[p]=Па. |
| S=0,000 001м2 | |
| р=? | (Па) |
Ответ: 50 МПа.
2. Вычислить давление твердого тела на
опору.(Работа в парах.)
Оборудование: динамометр, линейка
измерительная, деревянный брусок.
Порядок выполнения работы.
- Измерьте силу давления бруска на стол (вес
бруска). - Измерьте длину, ширину и высоту бруска.
- Используя все полученные данные, вычислите
площади наибольшей и наименьшей граней бруска. - Рассчитайте давление, которое производит
брусок на стол наименьшей и наибольшей гранями. - Результаты запишите в тетрадь.
- На основе полученных результатов сформируйте
вывод.
Учащиеся записывают результаты опытов на доске
и делают вывод о зависимости давления от площади
поверхности опоры.
Учитель.
Чтоб пчеле продолжить путь
Надо знанья почерпнуть.
Мы листочки открываем
И работу выполняем.
(Пчела перелетает на 7 лепесток по щелчку мыши.)
“Тестовые задания”.
Итог урока
- С какой физической величиной вы познакомились
сегодня на уроке? - Какую силу называют силой давления?
- Что такое давление?
- Единицы давления?
- Единицы давления в СИ?
Оценки за урок: Учитываются
результаты теста, жетоны.
Выводится итоговая оценка за урок.
Учитель обращает внимание учеников на эпиграф к
уроку.
Домашнее задание: §32б33; стр.85
(экспериментальное задание).
Дополнительное задание. “Почему
заостренные предметы колючи. Наподобие
Левиафана”, Занимательная физика. Я.И.Перельман.
Список использованной литературы.
- Физика – 7 кл.
 С.В.Громов, Н.А.Родина. Москва.
С.В.Громов, Н.А.Родина. Москва.
“Просвещение”,2000 г. - Урок физики в современной школе. Творческий
поиск учителей. Составитель Э.М.Браверман под
редакцией В.Г.Разумовского. Москва,
“Просвещение”, 1993 г. - Проверка знаний учащихся по физике (6-7кл.)А.В.
Постников, Москва, “Просвещение”, 1986г. - Газета “Физика” № 45, 2004г.
- Журнал “Физика в школе” № 8, 2002г.
- Хрестоматия по литературе. 1-4кл. Ростов-на-Дону.
АО”Книга”, 1997г.
Сила нормального давления определение
сила нормального давления это
Автор Ўлия Прудникова задал вопрос в разделе Естественные науки
Что такое сила нормального давления? Чему она равна? В учебнике написано: Сила нормального давления N всегда перпендикул и получил лучший ответ
Ответ от Leonid[гуру]
Опечатка. Должно быть N=mg.
А определение дано верно. Если сила давления направлена под углом к поверхности, то её можно разложить на две составляющие: одна по касательной (параллельно поверхности, если она плоская) , другая – перпендикулярно касательной, то есть по нормали. Вот её и называют силой нормального давления.
Leonid
Высший разум
(381255)
Я где-то писал про давление? Прочтите внимательнее – у меня именно про СИЛУ давления ведле и говорится.
Проделаем опыт. Возьмем небольшую доску, в углы которой вбиты четыре гвоздя, и поместим ее остриями вверх на песок. Сверху на нее положим гирю (рис. 81). Мы увидим, что шляпки гвоздей лишь незначительно вдавятся в песок. Если же мы перевернем доску и снова поставим ее (вместе с гирей) на песок, то теперь гвозди войдут в него значительно глубже (рис. 82). В обоих случаях вес доски был одним и тем же, однако эффект оказался разным. Почему? Вся разница в рассматриваемых случаях заключалась в том, что площадь поверхности, на которую опирались гвозди, в одном случае была больше, а в другом меньше. Ведь сначала песка касались шляпки гвоздей, а затем их острия.
Ведь сначала песка касались шляпки гвоздей, а затем их острия.
Мы видим, что результат воздействия зависит не только от силы, с которой тело давит на поверхность, но и от площади этой поверхности. Именно по этой причине человек, способный скользить по рыхлому снегу на лыжах, сразу же проваливается в него, как только их снимет (рис. 83). Но дело не только в площади. Важную роль играет и величина прикладываемой силы. Если, например, на ту же. доску (см. рис. 81) положить еще одну гирю, то гвозди (при той же площади опоры) погрузятся в песок еще глубже.
Силу, прикладываемую перпендикулярно поверхности, называют силой давления на эту поверхность.
Силу давления не следует путать с давлением. Давление — это физическая величина, равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности:
,(32.1)
р — давление, F — сила давления, S — площадь.
Итак, чтобы определить давление, надо силу давления разделить на площадь поверхности, на которую оказывается давление.
При одной и той же силе давление больше в том случае, когда площадь опоры меньше, и, наоборот, чем больше площадь опоры, тем давление меньше.
В тех случаях, когда силой давления является вес находящегося на поверхности тела ( F = P = mg ), давление, оказываемое телом, можно найти по формуле
Если давление р и площадь S известны, то можно определить силу давления F ; для этого надо давление умножить на площадь:
Сила давления (как и любая другая сила) измеряется в ньютонах. Давление же измеряется в паскалях. Паскаль (1 Па) — это такое давление, которое производит сила давления в 1 Н, будучи приложенной к поверхности площадью 1 м 2 :
Используются также другие единицы давления — гектопаскаль (гПа) и килопаскаль (кПа):
1 гПа = 100 Па, 1 кПа = 1000 Па.
1. Приведите примеры, показывающие, что результат действия силы зависит от площади опоры, на которую действует эта сила. 2. Почему человек, идущий на лыжах, не проваливается в снег? 3. Почему острая кнопка легче входит в дерево, чем тупая? 4. Что называют давлением? 5. Какие вы знаете единицы давления? 6. Чем отличается давление от силы давления? 7. Как можно найти силу давления, зная давление и площадь поверхности, к которой приложена сила?
2. Почему человек, идущий на лыжах, не проваливается в снег? 3. Почему острая кнопка легче входит в дерево, чем тупая? 4. Что называют давлением? 5. Какие вы знаете единицы давления? 6. Чем отличается давление от силы давления? 7. Как можно найти силу давления, зная давление и площадь поверхности, к которой приложена сила?
Давление – это отношение силы, которая действует перпендикулярно на поверхность, к площади этой поверхности. Измеряется давление в паскалях (1 Па – такое давление, которое сила в 1 ньютон производит при ее приложении к поверхности площадью в один квадратный метр).
Сила давления – это такая сила, которую оказывает давление на определенную поверхность. Она измеряется в ньютонах (1 Н). Чем меньше площадь поверхности, на которую это давление оказывается, тем меньше может быть прилагаемая сила, с помощью которой можно добиться ожидаемого эффекта.
Сила давления действует на поверхность перпендикулярно ей. Ее нельзя отождествлять с давлением. Чтобы определить давление, нужно его силу разделить на площадь поверхности, на которую оно оказывается. Если приложить одинаковую силу для воздействия на поверхности разной площади, то давление будет больше там, где меньше площадь опоры. Если известно давление и площадь поверхности, то узнать силу давления можно, умножив давление на площадь.
Сила нормального давления всегда обязательно направлена перпендикулярно той поверхности, на которую оно оказывает воздействие. По третьему закону Ньютона она равняется силе реакции опоры по ее модулю.
Роль силы давления способна играть любая сила. Это может быть вес, который деформирует опору, или сила, прижимающая какое-либо тело к определенной поверхности, и так далее.
При соприкосновении с твердыми телами жидкости действуют на них с определенной силой, которую так и называют – сила давления. В быту ощутить воздействие такой силы можно, прикрыв пальцем отверстие крана, из которого идет вода. Если в резиновый баллон налить ртуть, что можно увидеть, что его стенки начнут выпирать наружу. Сила давления жидкости может оказывать воздействие также и на другие жидкости.
Сила давления жидкости может оказывать воздействие также и на другие жидкости.
При соприкосновении твердых тел сила упругости возникает при изменении их формы или объема. В жидкостях такие силы при изменении формы не возникают. Отсутствие упругости по отношению к изменениям формы обусловливает подвижность жидкостей. При сжатии же жидкостей (изменении их объемов) силы упругости будут проявляться. Именно они и называются силой давления. То есть, если жидкость действует на соприкасающиеся с ней другие тела с силой давления, значит, она находится в сжатом состоянии. Чем более сжата жидкость, тем более сильными будут возникающие в результате этой силы давления.
В результате сжатия плотность веществ увеличивается, поэтому жидкости обладают упругостью, проявляющейся по отношению к их плотности. Если сосуд закрыть поршнем и поместить сверху груз, то при опускании поршня жидкость начнет сжиматься. В ней возникнет сила давления, которая уравновесит вес поршня с находящимся на нем грузом. Если продолжать увеличивать нагрузку на поршень, жидкость будет продолжать сжиматься, а увеличивающаяся сила давления будет направлена на уравновешивание нагрузки.
Все жидкости (в большей или же меньшей степени) способны сжиматься, поэтому есть возможность измерить степень их сжатия, которая соответствует определенной силе давления.
Чтобы уменьшить давление на поверхность, в случае если невозможно уменьшить силу, необходимо увеличить площадь опоры. И наоборот, для увеличения давления нужно уменьшить площадь, на которую действует его сила.
Молекулы газа не связаны (либо слишком слабо связаны) между собой силой взаимодействия. Поэтому они движутся хаотично, практически свободно, заполняя весь объем предоставленного им сосуда. В связи с этим свойства газа отличаются от свойств жидкостей. У газов плотность зависит от давления в гораздо большей степени, чем у жидкостей. Общим между ними является то, что давление как жидкости, так и газа не зависит от формы сосуда, в который они могут быть помещены.
Как обозначается сила давления в физике
1. Давление = отношение силы, действующей на поверхность перпендикулярно этой поверхности, к площади этой поверхности.
Единица давления в СИ = 1Па (паскаль) .
Обиходная (особенно в технике) единица давления = 1атм (примерно, давление земной атмосферы) = 100000Па.
2. Сила давления – это сила, которая оказывает давление на какую-либо поверхность.
Для уменьшения давления в том случае, если силу уменьшить невозможно, увеличивают площадь опоры.
В тех случаях, когда бывает необходимо увеличить давление, уменьшают площадь поверхности, на которую действует сила давления.
3. Закон Паскаля: «жидкости и газы передают оказываемое на них давление без изменения в каждую точку жидкости или газа».
4. Основное свойство жидкостей и газов – передавать давление без изменения по всем направлениям – лежит в основе конструкции гидравлических и пневматических устройств и машин.
Во сколько раз площадь одного поршня больше площади другого, во столько же раз гидравлическая машина дает выигрыш в силе.
5. Давление на глубине жидкости не зависит от площади поверхности, а зависит от плотности жидкости и от глубины:
6. Свойство сообщающихся сосудов: поверхности жидкости в сообщающихся сосудах устанавливаются на одном уровне.
Но поверхности разных жидкостей, плотности которых отличаются, устанавливаются в сообщающихся сосудах на разных уровнях!
Сосуды, соединенные между собой, называются сообщающимися.
7. Действие простейшего U-образного жидкостного манометра основано на свойстве сообщающихся сосудов.
Представьте себе заполненный воздухом герметичный цилиндр, с установленным сверху поршнем. Если начать давить на поршень, то объем воздуха в цилиндре начнет уменьшаться, молекулы воздуха станут сталкиваться друг с другом и с поршнем все интенсивнее, и давление сжатого воздуха на поршень возрастет.
Если поршень теперь резко отпустить, то сжатый воздух резко вытолкнет его вверх. Это произойдет потому, что при неизменной площади поршня увеличится сила, действующая на поршень со стороны сжатого воздуха. Площадь поршня осталась неизменной, а сила со стороны молекул газа увеличилась, соответственно увеличилось и давление.
Это произойдет потому, что при неизменной площади поршня увеличится сила, действующая на поршень со стороны сжатого воздуха. Площадь поршня осталась неизменной, а сила со стороны молекул газа увеличилась, соответственно увеличилось и давление.
Или другой пример. Стоит человек на земле, стоит обеими стопами. В таком положении человеку комфортно, он не испытывает неудобств. Но что случится, если этот человек решит постоять на одной ноге? Он согнет одну из ног в колене, и теперь будет опираться на землю только одной стопой. В таком положении человек ощутит определенный дискомфорт, ведь давление на стопу увеличилось, причем примерно в 2 раза. Почему? Потому что площадь, через которую теперь сила тяжести придавливает человека к земле, уменьшилась в 2 раза. Вот пример того, что такое давление, и как легко его можно обнаружить в обычной жизни.
Давление в физике
С точки зрения физики, давлением называют физическую величину, численно равную силе, действующей перпендикулярно поверхности на единицу площади данной поверхности. Поэтому, чтобы определить давление в некоторой точке поверхности, нормальную составляющую силы, приложенной к поверхности, делят на площадь малого элемента поверхности, на который данная сила действует. А для того чтобы определить среднее давление по всей площади, нормальную составляющую действующей на поверхность силы нужно разделить на полную площадь данной поверхности.
Измеряется давление в системе СИ в паскалях (Па). Эта единица измерения давления получила свое название в честь французского математика, физика и литератора Блеза Паскаля, автора основного закона гидростатики — Закона Паскаля, гласящего, что давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях. Впервые единица давления «паскаль» была введена в обращение во Франции в 1961 году, согласно декрету о единицах, спустя три столетия после смерти ученого.
Один паскаль равен давлению, которое вызывает сила в один ньютон, равномерно распределенная, и направленная перпендикулярно к поверхности площадью в один квадратный метр.
В паскалях измеряют не только механическое давление (механическое напряжение), но и модуль упругости, модуль Юнга, объемный модуль упругости, предел текучести, предел пропорциональности, сопротивление разрыву, сопротивление срезу, звуковое давление и осмотическое давление. Традиционно именно в паскалях выражаются важнейшие механические характеристики материалов в сопромате.
Атмосфера техническая (ат), физическая (атм), килограмм-сила на квадратный сантиметр (кгс/см2)
Кроме паскаля для измерения давления применяют и другие (внесистемные) единицы. Одной из таких единиц является «атмосфера» (ат). Давление в одну атмосферу приблизительно равно атмосферному давлению на поверхности Земли на уровне Мирового океана. На сегодняшний день под «атмосферой» понимают техническую атмосферу (ат).
Техническая атмосфера (ат) — это давление, производимое одной килограмм-силой (кгс), распределенной равномерно по площади в один квадратный сантиметр. А одна килограмм-сила, в свою очередь, равна силе тяжести, действующей на тело массой в один килограмм в условиях ускорения свободного падения, равного 9,80665 м/с2. Одна килограмм-сила равна таким образом 9,80665 ньютон, а 1 атмосфера оказывается равной точно 98066,5 Па. 1 ат = 98066,5 Па.
В атмосферах измеряют, например, давление в автомобильных шинах, например рекомендованное давление в шинах пассажирского автобуса ГАЗ-2217 равно 3 атмосферам.
Есть еще «физическая атмосфера» (атм), определяемая как давление ртутного столба, высотой 760 мм на его основание при том, что плотность ртути равна 13595,04 кг/м3, при температуре 0°C и в условиях ускорения свободного падения равного 9,80665 м/с2. Так выходит, что 1 атм = 1,033233 ат = 101 325 Па.
Что касается килограмм-силы на квадратный сантиметр (кгс/см2), то эта внесистемная единица давления с хорошей точностью равна нормальному атмосферному давлению, что бывает иногда удобно для оценок различных воздействий.
Внесистемная единица «бар» равна приблизительно одной атмосфере, но является более точной — ровно 100000 Па. В системе СГС 1 бар равен 1000000 дин/см2. Раньше название «бар» носила единица, называемая сейчас «бария», и равная 0,1 Па или в системе СГС 1 бария = 1 дин/см2. Слово «бар», «бария» и «барометр» происходят от одного и того же греческого слова «тяжесть».
В системе СГС 1 бар равен 1000000 дин/см2. Раньше название «бар» носила единица, называемая сейчас «бария», и равная 0,1 Па или в системе СГС 1 бария = 1 дин/см2. Слово «бар», «бария» и «барометр» происходят от одного и того же греческого слова «тяжесть».
Часто для измерения атмосферного давления в метеорологии используют единицу мбар (миллибар), равную 0,001 бар. А для измерения давления на планетах где атмосфера очень разряженная — мкбар (микробар), равный 0,000001 бар. На технических манометрах чаще всего шкала имеет градуировку именно в барах.
Миллиметр ртутного столба (мм рт. ст.), миллиметр водяного столба (мм вод. ст.)
Внесистемная единица измерения «миллиметр ртутного столба» равна 101325/760 = 133,3223684 Па. Обозначается «мм рт.ст.», но иногда ее обозначают «торр» – в честь итальянского физика, ученика Галилея, Эванджелисты Торричелли, автора концепции атмосферного давления.
Образовалась единица в связи с удобным способом измерения атмосферного давления барометром, у которого ртутный столб пребывает в равновесии под действием атмосферного давления. Ртуть обладает высокой плотностью около 13600 кг/м3 и отличается низким давлением насыщенного пара в условиях комнатной температуры, поэтому для барометров в свое время и была выбрана именно ртуть.
На уровне моря атмосферное давление равно приблизительно 760 мм рт.ст., именно это значение и принято считать теперь нормальным атмосферным давлением, равным 101325 Па или одной физической атмосфере, 1 атм. То есть 1 миллиметр ртутного столба равен 101325/760 паскаль.
В миллиметрах ртутного столба измеряют давление в медицине, в метеорологии, в авиационной навигации. В медицине кровное давление измеряют в мм рт.ст, в вакуумной технике приборы для измерения давления градуируются в мм рт.ст, наряду с барами. Иногда даже просто пишут 25 мкм, подразумевая микроны ртутного столба, если речь идет о вакуумировании, а измерения давления осуществляют вакуумметрами.
В некоторых случаях используют миллиметры водяного столба, и тогда 13,59 мм вод. ст = 1мм рт.ст. Иногда это более целесообразно и удобно. Миллиметр водяного столба, как и миллиметр ртутного столба — внесистемная единица, равная в свою очередь гидростатическому давлению 1 мм столба воды, которое этот столб оказывает на плоское основание при температуре воды столба 4°С.
ст = 1мм рт.ст. Иногда это более целесообразно и удобно. Миллиметр водяного столба, как и миллиметр ртутного столба — внесистемная единица, равная в свою очередь гидростатическому давлению 1 мм столба воды, которое этот столб оказывает на плоское основание при температуре воды столба 4°С.
ФИЗИКА. — ФИЗИКА. 1. Предмет и структура физики Ф. наука, изучающая простейшие и вместе с тем наиб. общие свойства и законы движения окружающих нас объектов материального мира. Вследствие этой общности не существует явлений природы, не имеющих физ. свойств … Физическая энциклопедия
ФИЗИКА — наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, св ва и строение материи и законы её движения. Понятия Ф. и её законы лежат в основе всего естествознания. Ф. относится к точным наукам и изучает количеств … Физическая энциклопедия
ФИЗИКА — ФИЗИКА, наука, изучающая совместно с химией общие законы превращения энергии и материи. В основе обеих наук лежат два основных закона естествознания закон сохранения массы (закон Ломоносова, Лавуазье) и закон сохранения энергии (Р. Майер, Джауль… … Большая медицинская энциклопедия
Физика звёзд — Физика звезд одна из отраслей астрофизики, изучающая физическую сторону звезд (масса, плотность, …). Содержание 1 Размеры, массы, плотность, светимость звезд 1.1 Масса звёзд … Википедия
Физика — I. Предмет и структура физики Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения. Поэтому понятия Ф. и сё законы лежат в основе всего… … Большая советская энциклопедия
Давление высокое — в широком смысле давление, превышающее атмосферное; в конкретных технических и научных задачах давление, превышающее характерное для каждой задачи значение. Столь же условно встречающееся в литературе подразделение Д. в. на высокие и… … Большая советская энциклопедия
ФИЗИКА — (от древнегреч. physis природа). Древние называли физикой любое исследование окружающего мира и явлений природы. Такое понимание термина физика сохранилось до конца 17 в. Позднее появился ряд специальных дисциплин: химия, исследующая свойства… … Энциклопедия Кольера
physis природа). Древние называли физикой любое исследование окружающего мира и явлений природы. Такое понимание термина физика сохранилось до конца 17 в. Позднее появился ряд специальных дисциплин: химия, исследующая свойства… … Энциклопедия Кольера
ФИЗИКА ВЫСОКИХ ДАВЛЕНИЙ — исследование влияния, оказываемого на вещество очень высокими давлениями, а также создание методов получения и измерения таких давлений. История развития физики высоких давлений удивительный пример необычайно быстрого прогресса в науке,… … Энциклопедия Кольера
Физика твёрдого тела — Физика твёрдого тела раздел физики конденсированного состояния, задачей которого является описание физических свойств твёрдых тел с точки зрения их атомарного строения. Интенсивно развивалась в XX веке после открытия квантовой механики.… … Википедия
Физика низких температур — Содержание 1 Методы получения 1.1 Испарение жидкостей … Википедия
Глава 9. Гидростатика
Для решения задач на гидростатику необходимо знать определения плотности и давления, уметь находить давление в покоящейся жидкости, возникающее благодаря притяжению этой жидкости к Земле (гидростатическое давление), а также находить силы, с которыми жидкости действуют на погруженные в них тела (силу Архимеда). Кратко сформулируем эти определения и законы.
Плотностью тела называется отношение
(9.1) |
где — масса тела, — его объем. Очевидно, отношение (9.1) имеет смысл массы единицы объема тела. Если тело однородно, то плотность (9.1) является характеристикой не тела, а вещества, из которого оно состоит. Действительно, для тел, состоящих из одного и того же вещества масса пропорциональна объему, и отношение (9.1) одинаково у всех этих тел.
Для характеристики воздействия жидкости или газа на стенки сосудов вводят понятие давления жидкости или газа, которое определяется как отношение силы , действующей на элемент стенки сосуда со стороны жидкости или газа, к величине площади этого элемента :
(9. |
Важным свойством давления является то обстоятельство, что хотя оно и определяется через элемент площади стенки сосуда, от этого элемента давление (9.2) не зависит, а является характеристикой только жидкости или газа. Действительно, сила, действующая со стороны жидкости на элемент площади дна сосуда или стенки сосуда, пропорциональна площади этого элемента, и потому отношение (9.2) от не зависит. Отметим, что хотя давление и определяется через векторную величину — силу, давление — величина не векторная. Как показывает опыт, отношение (9.2) не зависит не только от величины площадки , но и от ее ориентации в пространстве. Другими словами, жидкость, будучи сжатой, оказывает воздействие во всех направлениях. Последнее утверждение и говорит о невекторном характере давления и называется законом Паскаля.
В жидкости, находящейся в каком-либо сосуде в поле силы тяжести, благодаря ее притяжению к Земле, возникает давление. Это давление называется гидростатическим. Можно доказать, что гидростатическое давление жидкости не зависит от формы сосуда, в котором она находится, а зависит только от глубины. Гидростатическое давление жидкости плотности на глубине равно
(9.3) |
где — ускорение свободного падения. Если на поверхность жидкости действует атмосферный воздух, то давление жидкости на глубине будет складываться из атмосферного давления и гидростатического давления (9.3).
Благодаря зависимости гидростатического давления жидкости от глубины возникает своеобразный эффект выталкивания тел, погруженных в жидкость, из этой жидкости. Действительно, в жидкости, находящейся в поле силы тяжести, возникает гидростатическое давление, и жидкость оказывает воздействие на поверхность тела, опущенного в жидкость. При этом силы, действующие на боковые поверхности тела, компенсируют друг друга. Однако из-за зависимости гидростатического давления от глубины, сила, действующая на более глубокую (нижнюю) поверхность тела, больше силы, действующей на верхнюю поверхность (см. рисунок), и на тело действует результирующая сила, направленная вертикально вверх. Эта сила называется выталкивающей силой или силой Архимеда. Можно доказать, что на тело, целиком погруженное в жидкость, действует выталкивающая сила
рисунок), и на тело действует результирующая сила, направленная вертикально вверх. Эта сила называется выталкивающей силой или силой Архимеда. Можно доказать, что на тело, целиком погруженное в жидкость, действует выталкивающая сила
(9.4) |
где — плотность жидкости, — объем тела. Если тело погружено в жидкость не целиком, то выталкивающая сила также определяется формулой (9.4), но вместо объема тела в нее входит объем погруженной в жидкость части тела.
С помощью формулы (9.4) можно установить условие плавания тел. Тело будет плавать, если сила Архимеда будет больше действующей на тело силы тяжести
где — плотность тела. Отсюда получаем, что тело плавает, если плотность жидкости больше плотности тела
(9.5) |
Рассмотрим теперь задачи.
В задаче 9.1.1 с использованием формулы (9.3) для гидростатического давления находим
(ответ — 4).
Поскольку высота уровней жидкости в сосудах (в задаче 9.1.2) и их плотности одинаковы, то давление жидкости около дна обоих сосудов одинаково (ответ 3).
В задаче 9.1.3 давление жидкости около дна сосудов одинаково (одинаковы плотности и уровень жидкостей), поэтому сила, действующая на дно, больше для того сосуда, площадь дна которого больше, а меньше для того, площадь дна которого меньше. Поэтому (правильный ответ — 2).
Чтобы найти силу, действующую на небольшую поверхность внутри жидкости, нужно найти гидростатическое давление жидкости на той глубине, на которой находится рассматриваемая поверхность, и умножить это давление на площадь поверхности. Поэтому для крана из задачи 9.1.4 получаем
Поэтому для крана из задачи 9.1.4 получаем
(ответ 4).
Бытовой насос (задача 9.1.5) поднимает воду благодаря создаваемому им избыточному давлению. Ясно, что вода в трубках насоса будет подниматься до тех пор, пока ее гидростатическое давление не компенсирует избыточное давление насоса. Поэтому насос сможет поднять воду на следующую высоту
где — избыточное давление, созданное насосом, — плотность воды, — ускорение свободного падения (правильный ответ — 3).
Поскольку бруски в задаче 9.1.6 изготовлены из одинакового материала, у них одинаковые плотности, и, следовательно, отношение их масс равно отношению их объемов. А поскольку объем второго бруска вчетверо больше объема первого, то и его масса вчетверо больше массы первого, т.е. равна 40 г (ответ 3).
Пусть размер меньшего ребра бруска в задаче 9.1.7 — . Тогда размеры остальных сторон — и . Следовательно, площади граней бруска равны , и . Поэтому давления бруска на стол, когда он лежит на разных гранях, равны (начиная с наименьшего):
т.е. относятся друг к другу так же, как и длины сторон 1:2:3 (ответ 1).
В сообщающихся сосудах жидкость занимает такое положение, что ее давление в обоих коленах одинаково. Поэтому в задаче 9.1.8 имеем с использованием формулы для гидростатического давления
Отсюда находим
(правильный ответ — 4).
Поскольку плотность натрия 950 кг/м3 (задача 9.1.9) меньше плотности воды 1000 кг/м3, то натрий плавает на поверхности воды (ответ 1).
На льдину (задача 9.1.10) действуют сила тяжести и сила Архимеда. Условие равновесия льдины дает
(1) |
где — плотность воды, — объем погруженной в воду части льдины, — ее масса. Поскольку, где — плотность льда, — объем льдины, из формулы (1) получаем
Отсюда находим, что отношение объема погруженной в воду части льдина к ее объему равно отношению плотностей льда и воды
(ответ 2). Таким образом, девять десятых частей плавающей льдины находятся под водой.
Поскольку тело в задаче 9.2.1 плавает в жидкости, выталкивающая сила Архимеда равна действующей на тело силе тяжести — 10 Н (ответ 1).
Весом тела называется сила, с которой тело действует на опору (сила реакции опоры). На тело, полностью погруженное в воду, действуют сила тяжести , выталкивающая сила Архимеда и сила реакции. Для силы реакции (веса тела) из условия равновесия тела имеем
где и — плотности жидкости и тела, — объем тела (обратим внимание читателя на то, что согласно этой формуле вес тела в жидкости уменьшается). Отсюда находим
(задача 9.2.2 — ответ 3).
Из условия равновесия коробки, плавающей на поверхности воды (задача 9.2.3), следует, что сила тяжести равна силе Архимеда , где — масса тела, — плотность воды, — объем погруженной части коробки, который можно выразить через площадь дна коробки и глубину его погружения в воду см3. Отсюда получаем для массы коробки = 500 г (ответ 2).
При решении задачи 9. 2.4 школьники часто допускают ошибку, говоря, что выталкивающая сила равна нулю, так как шар, наполненный воздухом, находясь в воздухе, «всплывать» не будет. Последнее утверждение, конечно, правильно, а первое — нет. Шар, наполненный воздухом, не «всплывает» в воздухе не потому, что выталкивающая сила не действует, а потому, что она меньше силы тяжести. Выталкивающая сила действует на тело со стороны жидкости или газа и никак не может зависеть от того, что внутри этого тела, воздух или, напрмер, гелий, с которым шар всплывал бы. Для выталкивающей силы имеем согласно закону Архимеда Н (ответ 1).
2.4 школьники часто допускают ошибку, говоря, что выталкивающая сила равна нулю, так как шар, наполненный воздухом, находясь в воздухе, «всплывать» не будет. Последнее утверждение, конечно, правильно, а первое — нет. Шар, наполненный воздухом, не «всплывает» в воздухе не потому, что выталкивающая сила не действует, а потому, что она меньше силы тяжести. Выталкивающая сила действует на тело со стороны жидкости или газа и никак не может зависеть от того, что внутри этого тела, воздух или, напрмер, гелий, с которым шар всплывал бы. Для выталкивающей силы имеем согласно закону Архимеда Н (ответ 1).
На поплавок из задачи 9.2.5 действуют силы: тяжести , Архимеда , натяжения лески (см. рисунок). Используя стандартное выражение для силы Архимеда (9.4), получаем из условия равновесия поплавка
где — плотность воды, и — масса и объем поплавка. Выражая массу поплавка через его плотность и объем и учитывая, что по условию плотность воды вдвое больше плотности поплавка , получим 10 Н (ответ 1).
В задаче 9.2.6 умышленно дано много лишних данных. Поскольку и в воде, и в керосине мяч плавает, то архимедова сила и в том, и в другом случае уравновешивает силу тяжести мяча (ответ 2).
Несмотря на то, что тело в задаче 9.2.7 не касается дна и стенок сосуда, суммарная сила, действующая на левую чашку весов, увеличится. Действительно, при опускании тела в воду возникает сила Архимеда, действующая со стороны воды на тело, но при этом и тело действует на воду, причем эта сила направлена вертикально вниз и равна силе Архимеда. Чтобы весы остались в равновесии на правую чашку весов надо положить такой груз, сила тяжести которого равна этой силе, т.е. груз с массой , где — плотность воды, — объем тела. А поскольку плотность тела по условию вчетверо больше плотности воды, то (ответ 1).
Для нахождения давления жидкости, в которой плавают те или иные тела, существует следующий прием.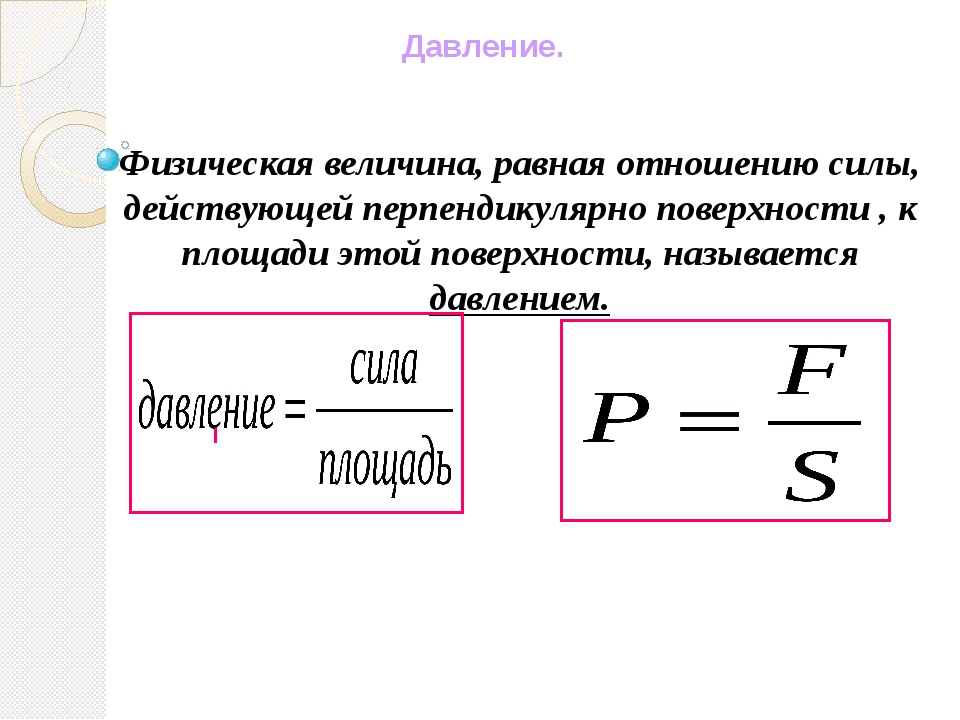 Если мысленно удалить тело из жидкости и заполнить освободившееся место той же жидкостью, то силы, действующие со стороны жидкости на стенки сосуда не изменяться. Действительно, на плавающее тело со стороны жидкости и со стороны тела на жидкость действует сила , где — плотность жидкости, — объем погруженной в жидкость части тела. Таким образом, тело действует на жидкость с той же силой, с которой на нее действовала бы жидкость, занимающая объем погруженной в воду части тела. Поэтому если вытащить тело из жидкости и заполнить освободившееся место жидкостью, то не меняется уровень жидкости, не меняются также все силы, действующие внутри жидкости. Поэтому если в жидкости плавает тело, то независимо от параметров этого тела (массы, плотности, объема), давление жидкости на глубине равно , причем отсчитывается от поверхности жидкости с плавающим в ней телом. Поэтому в задаче 9.2.8 надо найти, на сколько поднимется уровень воды в сосуде, а затем и связанное с этим повышением уровня избыточное гидростатическое давление около дна. Очевидно, что в цилиндрическом сосуде площадью сечения уровень воды поднимется на такую величину , что , где — объем погруженной в воду части тела. Находя величину из условия равновесия тела и закона Архимеда, получим . Поэтому гидростатическое давление воды около дна вырастет на величину (ответ 1).
Если мысленно удалить тело из жидкости и заполнить освободившееся место той же жидкостью, то силы, действующие со стороны жидкости на стенки сосуда не изменяться. Действительно, на плавающее тело со стороны жидкости и со стороны тела на жидкость действует сила , где — плотность жидкости, — объем погруженной в жидкость части тела. Таким образом, тело действует на жидкость с той же силой, с которой на нее действовала бы жидкость, занимающая объем погруженной в воду части тела. Поэтому если вытащить тело из жидкости и заполнить освободившееся место жидкостью, то не меняется уровень жидкости, не меняются также все силы, действующие внутри жидкости. Поэтому если в жидкости плавает тело, то независимо от параметров этого тела (массы, плотности, объема), давление жидкости на глубине равно , причем отсчитывается от поверхности жидкости с плавающим в ней телом. Поэтому в задаче 9.2.8 надо найти, на сколько поднимется уровень воды в сосуде, а затем и связанное с этим повышением уровня избыточное гидростатическое давление около дна. Очевидно, что в цилиндрическом сосуде площадью сечения уровень воды поднимется на такую величину , что , где — объем погруженной в воду части тела. Находя величину из условия равновесия тела и закона Архимеда, получим . Поэтому гидростатическое давление воды около дна вырастет на величину (ответ 1).
Из условия равновесия плавающего тела следует, что его масса равна массе воды в объеме погруженной части тела. . Поэтому суммарная масса воды и деревянного тела в одном ведре и суммарная масса воды и пенопластового тела в другом в задаче 9.2.9 равна массе воды в полном ведре, т.е. одинакова в обоих ведрах. Поэтому правильный ответ в этой задаче — 3.
Когда внутрь плиты из задачи 9.2.10 вставляют более плотное тело, возникает дополнительное гравитационное взаимодействие между жидкостью и плитой. Если до этого на каждый элемент жидкости действовала гравитационная сила, направленная вертикально вниз, то после этого возникает дополнительная сила, направленная к центру тела (см. рисунок, на котором нарисованы силы, действующие на выделенный элемент жидкости). К каким последствиям для расположения жидкости на плите это приведет? Легко сообразить, что уровень жидкости в области над телом повысится. Действительно, поверхность жидкости всегда расположена перпендикулярно приложенным силам (иначе жидкость будет течь), поэтому она расположится так, как показано на рисунке. Другими словами, более массивное тело, вставленное внутрь плиты, благодаря дополнительному гравитационному взаимодействию «натянет» жидкость со всех сторон, и ее уровень над телом поднимется. Поэтому правильный ответ в задаче — 3.
рисунок, на котором нарисованы силы, действующие на выделенный элемент жидкости). К каким последствиям для расположения жидкости на плите это приведет? Легко сообразить, что уровень жидкости в области над телом повысится. Действительно, поверхность жидкости всегда расположена перпендикулярно приложенным силам (иначе жидкость будет течь), поэтому она расположится так, как показано на рисунке. Другими словами, более массивное тело, вставленное внутрь плиты, благодаря дополнительному гравитационному взаимодействию «натянет» жидкость со всех сторон, и ее уровень над телом поднимется. Поэтому правильный ответ в задаче — 3.
Давление | Физика
Цели обучения
К концу этого раздела вы сможете:
- Определите давление.
- Объясните взаимосвязь между давлением и силой.
- Рассчитайте силу с учетом давления и площади.
Вы, несомненно, слышали, что слово давление используется в отношении крови (высокое или низкое кровяное давление) и погоды (погодные системы высокого и низкого давления).Это только два из многих примеров давления в жидкости. Давление P определяется как
[латекс] P = \ frac {F} {A} \\ [/ latex]
, где F — сила, приложенная к области A , перпендикулярной силе.
Давление
Давление определяется как сила, деленная на площадь, перпендикулярную силе, к которой прилагается сила, или
[латекс] P = \ frac {F} {A} \\ [/ latex]
Данная сила может иметь существенно различный эффект в зависимости от области, на которую действует сила, как показано на рисунке 1.{5} {\ text {Pa}} \\ [/ latex].
фунтов на квадратный дюйм (фунт / дюйм 2 или фунт / кв. Дюйм) все еще иногда используется как мера давления в шинах, а миллиметры ртутного столба (мм рт. Ст.) Все еще часто используются для измерения артериального давления. Давление определяется для всех состояний вещества, но особенно важно при обсуждении жидкостей.
Рис. 1. (a) Хотя человек, которого ткнули пальцем, может раздражаться, сила не имеет длительного эффекта. (б) Напротив, та же сила, приложенная к области размером с острый конец иглы, достаточно велика, чтобы повредить кожу.
Пример 1. Какую силу оказывает давление?
Астронавт работает за пределами Международной космической станции, где атмосферное давление практически равно нулю. Манометр на ее баллоне с воздухом показывает 6,90 × 10 6 Па. Какую силу воздух внутри баллона оказывает на плоский конец цилиндрического баллона — диск диаметром 0,150 м?
Стратегия
Мы можем найти прилагаемую силу из определения давления, данного в [latex] P = \ frac {F} {A} \\ [/ latex], при условии, что мы можем найти область действия A .{5} \ text {N} \ end {array} \\ [/ latex].
Обсуждение
Ух ты! Неудивительно, что танк должен быть сильным. Поскольку мы нашли F = PA , мы видим, что сила давления прямо пропорциональна площади воздействия, а также самому давлению.
Сила, действующая на конец резервуара, перпендикулярна его внутренней поверхности. Это направление обусловлено тем, что сила создается статической или неподвижной жидкостью. Мы уже видели, что жидкости не могут выдерживать поперечные (боковые) усилия ; они не могут также оказывать усилие сдвига .Давление жидкости не имеет направления, будучи скалярной величиной. Силы давления имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности. (См., Например, шину на рисунке 2.) Наконец, обратите внимание, что давление действует на все поверхности. Пловцы, как и покрышка, ощущают давление со всех сторон. (См. Рисунок 3.)
Рис. 2. Давление внутри этой шины оказывает силы, перпендикулярные всем поверхностям, с которыми она контактирует. Стрелки показывают характерные направления и величины сил, действующих в различных точках. Обратите внимание на то, что статические жидкости не вызывают сдвиговых усилий.
Обратите внимание на то, что статические жидкости не вызывают сдвиговых усилий.
Рис. 3. На этого пловца оказывается давление со всех сторон, так как вода текла бы в пространство, которое он занимает, если бы его там не было. Стрелки показывают направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы снизу больше из-за большей глубины, что дает чистую восходящую или выталкивающую силу, которая уравновешивается весом пловца.
Исследования PhET: свойства газа
Накачивайте молекулы газа в ящик и смотрите, что происходит, когда вы изменяете объем, добавляете или убираете тепло, меняете гравитацию и многое другое.Измерьте температуру и давление и узнайте, как свойства газа меняются по отношению друг к другу.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
Концептуальные вопросы
1. Как давление связано с остротой ножа и его режущей способностью?
2. Почему тупая игла для подкожных инъекций болит больше, чем острая?
3. Внешняя сила на одном конце воздушного резервуара была рассчитана в Пример 1: Расчет силы, прилагаемой воздухом .Как уравновешивается эта сила? (Танк не ускоряется, поэтому сила должна быть сбалансирована.)
4. Почему статические жидкости всегда действуют перпендикулярно поверхности?
5. В отдаленном месте недалеко от Северного полюса в озере плавает айсберг. Рядом с озером (предположим, что оно не замерзло) на суше находится ледник сопоставимых размеров. Если оба куска льда растают из-за повышения глобальной температуры (и весь растаявший лед уйдет в озеро), какой кусок льда даст наибольшее повышение уровня воды в озере, если таковое имеется?
6.Как бег по мягкому грунту и ношение мягкой обуви снижают нагрузку на ступни и ноги?
7. Танцы на пальцах ног (как в балете) намного тяжелее воздействуют на пальцы ног, чем при обычном танце или ходьбе.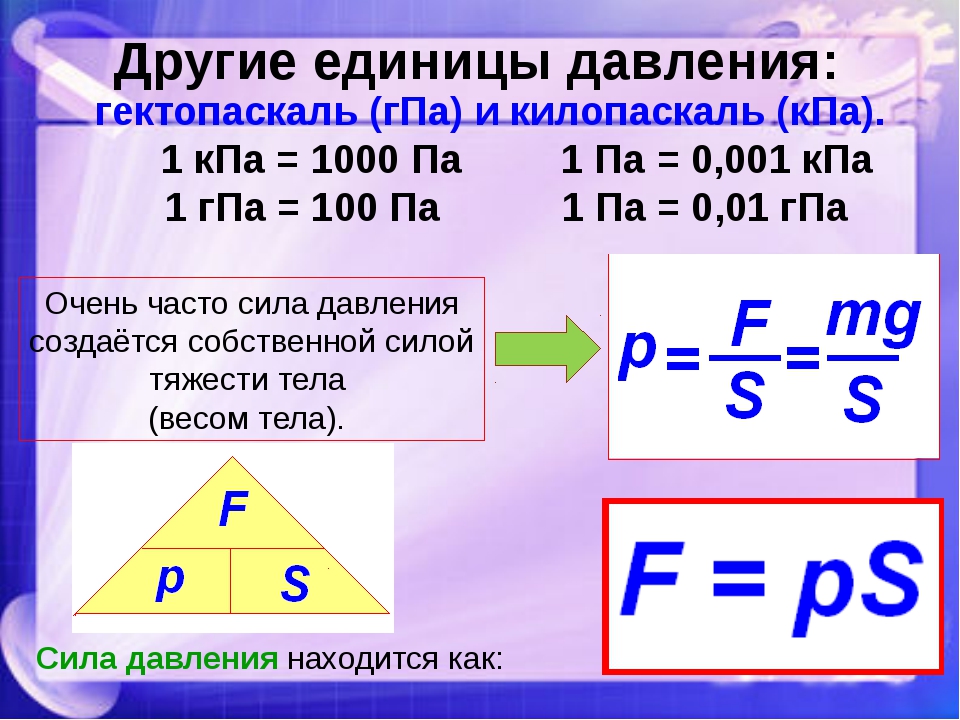 Объясните с точки зрения давления.
Объясните с точки зрения давления.
8. Как преобразовать единицы давления, такие как миллиметры ртутного столба, сантиметры водяного столба и дюймы ртутного столба, в такие единицы, как ньютоны на квадратный метр, не прибегая к таблице коэффициентов преобразования давления?
Задачи и упражнения
1.Когда женщина идет, весь ее вес на мгновение ложится на пятку ее туфель на высоком каблуке. Вычислите давление, оказываемое пяткой на пол, если ее площадь составляет 1,50 см 2 , а масса женщины составляет 55,0 кг. Выразите давление в Па. (На заре коммерческих рейсов женщинам не разрешалось носить обувь на высоком каблуке, потому что полы самолетов были слишком тонкими, чтобы выдерживать такое большое давление.)
2. Давление, которое игла фонографа оказывает на пластинку, на удивление велико.Если эквивалент 1,00 г поддерживается иглой, острие которой представляет собой круг радиусом 0,200 мм, какое давление будет оказано на запись в Н / м 2 ?
3. Кончики гвоздей оказывают огромное давление, когда по ним ударяют молотком, потому что они оказывают большую силу на небольшой площади. Какую силу необходимо приложить к гвоздю с круглым наконечником диаметром 1,00 мм, чтобы создать давление 3,00 × 10 9 Н / м 2 (Это высокое давление возможно, потому что молоток, ударяющий по гвоздю, останавливается в такое короткое расстояние.)
Глоссарий
- давление:
- Сила на единицу площади, перпендикулярная силе, на которую действует сила
Избранные решения проблем и упражнения
1. 3,59 × 10 6 Па; или 521 фунт / дюйм 2
3. 2.36 × 10 3 N
аэродинамических сил
аэродинамических сил
Когда два твердых объекта взаимодействуют в механическом процессе, силы
передаются или применяются в точке контакта.Но когда
твердый объект взаимодействует с жидкостью, вещи сложнее
описать, потому что жидкость может изменять свою форму. Для твердого тела
Для твердого тела
погруженный в жидкость, «точка контакта» — это каждая точка на
поверхность тела. Жидкость может обтекать тело и поддерживать
физический контакт во всех точках. Передача или применение
механические силы между твердым телом и жидкостью возникают на каждом
точка на поверхности тела. И передача происходит через
давление жидкости.
Изменение давления
Величина силы, действующей на небольшой участок
объект равен давлению, умноженному на площадь сечения. Быстрый
Проверка единиц показывает, что давление (сила / площадь), умноженное на площадь, дает
сила. Как описано на слайде давления жидкости, давление является
скалярная величина, связанная с импульсом молекул жидкости.
Поскольку сила является векторной величиной, имея
как по величине, так и по направлению, мы должны определить направление
сила.Давление действует перпендикулярно (или перпендикулярно) твердой поверхности.
объекта. Итак, направление силы на небольшом участке
объект расположен по нормали к поверхности. Обозначим это
направление письмом н .
Нормальное направление
изменяется от передней части профиля к задней и сверху к
дно. Чтобы получить чистую механическую силу по всему твердому телу
объект, мы должны суммировать вклады всех небольших разделов.Математически суммирование обозначается греческой буквой
сигма ()
Аэродинамическая сила F равна сумме произведения
давление p, умноженное на площадь A, в нормальном направлении.
F = p * A * n
В пределе бесконечно малых участков это дает
интеграл давления, умноженный на площадь вокруг замкнутого
поверхность. Если давление на замкнутой поверхности постоянно, существует
нет результирующей силы, потому что сумма направлений
нормальная сумма равна нулю.(Для каждого небольшого раздела есть еще один
небольшой участок, нормальные точки которого прямо противоположны
направление.)
Определения подъемной силы и сопротивления
Для движущейся жидкости скорость будет иметь разные значения при разных
места вокруг тела.
Местное давление связано с
местная скорость, поэтому
давление также будет меняться вокруг закрытого
поверхность и результирующая сила. Суммирование (или
интегрируя) давление, перпендикулярное поверхности, умноженное на площадь
вокруг тела создает чистую силу .
Поскольку жидкость находится в движении, мы можем определить
направление потока по ходу движения. Составляющая чистой силы
перпендикулярно (или перпендикулярно) направлению потока называется
поднимать; составляющая чистой силы вдоль
направление потока называется сопротивлением. Эти
являются определениями. На самом деле существует единая, чистая, интегрированная сила.
вызванные колебаниями давления вдоль тела.Это аэродинамическая сила
действует через среднее место изменения давления, которое называется
центр давления.
Распределение скорости
Для идеальной жидкости без
пограничные слои,
поверхность объекта — это
рационализировать.
Если скорость мала и нет энергии
добавлен к потоку, мы можем использовать Бернулли
уравнение вдоль линии тока к
определить распределение давления для известной скорости
распределение.Если пограничные слои присутствуют, дела обстоят немного
более запутанный, так как внешний поток реагирует на край
пограничный слой, а давление на поверхность накладывается со стороны
край пограничного слоя. Если пограничный слой отделяется от
поверхность, это становится еще более запутанным. Как мы определяем
распределение скорости вокруг тела? Задание скорости — это
источник ошибки в двух наиболее популярных
неверные теории подъемника.
Чтобы правильно определить распределение скоростей, мы должны решить
уравнения, выражающие сохранение
масса,
импульс, и
энергия для жидкости, проходящей через объект.
Сводка
Итак, чтобы подвести итог, для любого объекта, погруженного в жидкость,
механические силы передаются в каждой точке на поверхности
тело. Силы передаются через давление, которое действует
перпендикулярно поверхности. Чистую силу можно найти по формуле
Чистую силу можно найти по формуле
интегрируя (или суммируя) давление, умноженное на площадь вокруг
всю поверхность. Для движущегося потока давление будет изменяться от точки
в точку, потому что скорость меняется от точки к точке.Для некоторых
простые задачи потока, мы можем определить распределение давления (и
чистая сила), если мы знаем распределение скоростей, используя
Уравнение Бернулли.
Экскурсии с гидом
В начало
Перейти к …
- Руководство для начинающих Домашняя страница
byTom
Бенсон
Присылайте предложения / исправления по адресу: benson @ grc.nasa.gov
Сила и давление в жидкостях
Три общих состояния или фазы материи — твердое, жидкое и газообразное. solid сохраняет фиксированную форму и размер; даже при приложении большой силы твердое тело не может легко изменить форму или объем. Жидкость не сохраняет фиксированную форму, но принимает форму своего контейнера; Как и твердые тела, он не сжимается легко, но его объем может заметно измениться, если приложить очень большую силу.У газа нет фиксированной формы или объема; он расширяется и заполняет свой контейнер.
Например, когда в автомобильную шину нагнетается воздух, он не концентрируется внизу, как жидкость, а заполняет весь объем шины. Поскольку жидкости и газы не имеют фиксированной формы, они обладают способностью течь; именно поэтому они обычно называются жидкостями .
Плотность и удельный вес
Плотность является характерным свойством каждого вещества и дает представление о том, насколько тяжелы атомы и насколько они близки: одна и та же масса разных веществ занимает разные объемы.
d = M / V
Удельный вес вещества определяется как отношение плотности к плотности воды при 4,0 ° C. Удельный вес (GE) — это чистое число без размеров и единиц. Поскольку плотность воды составляет 1,00 г / см 3 = 1,00 x 10 3 кг / м 3 , удельный вес любого вещества в точности равен его плотности в г / см 3 или 10 — 3 , умноженное на его плотность, выраженную в кг / м 3 .
Поскольку плотность воды составляет 1,00 г / см 3 = 1,00 x 10 3 кг / м 3 , удельный вес любого вещества в точности равен его плотности в г / см 3 или 10 — 3 , умноженное на его плотность, выраженную в кг / м 3 .
Bioprofe | Сила и давление в жидкостях | 01
Давление
Твердое тело при контакте с другим телом оказывает на его поверхность силу, пытаясь проникнуть через него. Деформирующий эффект этой силы или проникающая способность зависит от интенсивности силы и площади контакта. Давление — это величина, которая измеряет эту емкость.
P = F / S
Единицей измерения в Международной системе является Паскаль (Па = 1 Н / м 2 )
В случае твердых тел и жидкостей, приложение внешней силы к движущейся стенке контейнера, содержащего жидкость, создает давление, которое сжимает ее.Сила, распределенная по поверхности подвижной стенки, дает значение давления. Объем, занимаемый жидкостью, уменьшается с увеличением давления. В жидкостях усвояемость практически нулевая.
Даже без внешней силы вес жидкости оказывает гидростатическое давление на ее нижние слои. Это давление создает силу, действующую изнутри жидкости наружу и перпендикулярно всем стенкам емкости.
Bioprofe | Сила и давление в жидкостях | 02
Давление является скаляром, не имеет направления или смысла, но сила, которая создается против стенок, является вектором, имеет направление, перпендикулярное поверхности, и направление наружу.
Понятие давления особенно полезно при изучении жидкостей. Это экспериментальный факт, что жидкость оказывает давление во всех направлениях. Это хорошо известно пловцам и дайверам, которые ощущают давление воды всеми частями своего тела. В определенной точке покоящейся жидкости давление одинаково во всех направлениях. Если бы это было не так, результирующая сила не была бы равна нулю и двигалась бы до тех пор, пока давление не сравнялось бы.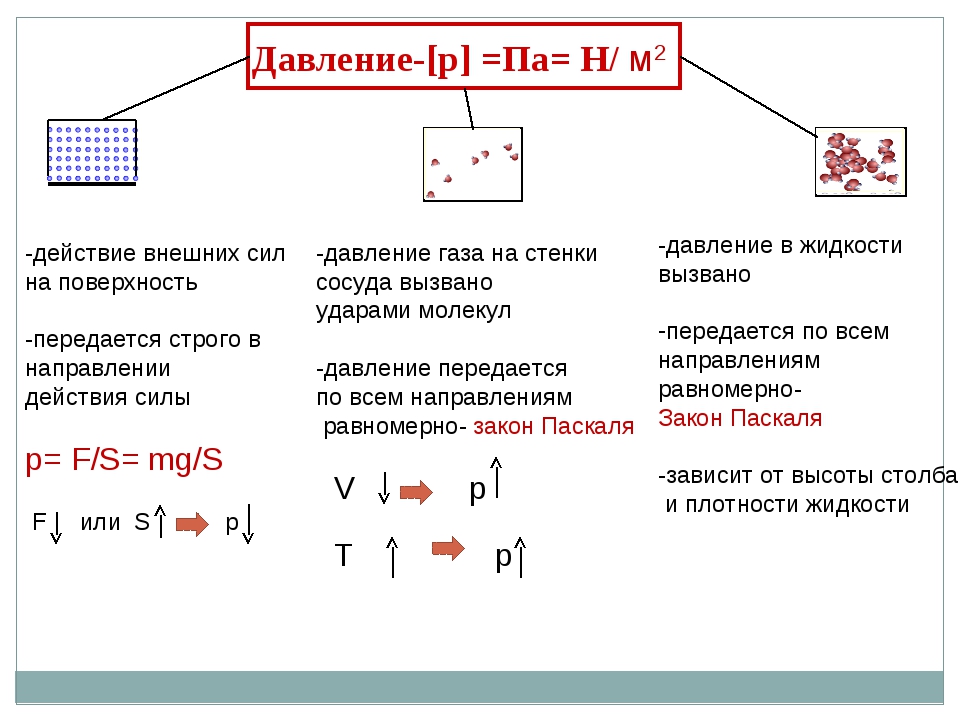 Если жидкость не течет, то давления должны быть равными.
Если жидкость не течет, то давления должны быть равными.
Еще одним важным свойством покоящейся жидкости является то, что сила, обусловленная ее давлением, всегда действует перпендикулярно любой поверхности, которая с ней контактирует. Если бы существовала составляющая силы, параллельная поверхности, согласно третьему закону Ньютона, поверхность оказывала бы силу, противоположную силе жидкости, которая, в свою очередь, также имела бы составляющую, параллельную поверхности. Этот компонент заставил бы жидкость течь, что противоречит нашей гипотезе о том, что жидкость находится в состоянии покоя.Итак, давление перпендикулярно поверхности.
Атмосферное давление, гидростатическое давление и манометрическое давление
Давление атмосферы Земли, атмосферное давление, , как и в любой другой жидкости, уменьшается по мере уменьшения глубины (или увеличения высоты). Но земная атмосфера несколько сложнее, потому что не только плотность воздуха меняется с высотой, но и нет определенной внешней поверхности, по которой вы можете измерить высоту «h» по следующему уравнению:
P = dgh
Тем не менее, мы можем рассчитать приблизительную разницу давлений между двумя высотами с помощью следующего уравнения:
Bioprofe | Сила и давление в жидкостях | 03
Давление воздуха в определенном месте незначительно меняется в зависимости от климата.На уровне моря атмосферное давление в среднем составляет 1,013 × 10 5 Н / м 2 . Это значение используется для определения другой часто используемой единицы давления: атмосферы (сокращенно атм).
Bioprofe | Fuerza y Presión en Fluidos | 03
Другой единицей давления, которая иногда используется, является бар, который определяется как 1,00 × 10 5 Н / м 2 = 100 кПа. Таким образом, нормальное атмосферное давление немного больше 1 бара.
Hydrostatics обрабатывает жидкости в состоянии покоя.Жидкость, заключенная в емкость, создает давление в ее груди и оказывает давление на стенки, которые ее содержат.
Гидростатическое давление в точке внутри жидкости прямо пропорционально плотности жидкости d, глубине h и силе тяжести места g.
P = dgh
Жидкости также оказывают давление на любое тело, погруженное в них. Давление будет тем больше, чем плотнее жидкость и чем больше глубина. Все точки, расположенные на одной глубине, имеют одинаковое давление.
Мы можем проверить, что гидростатическое давление увеличивается при спуске внутрь жидкости, поскольку скорость, с которой жидкость выходит, тем больше, чем дальше делается отверстие в боковой стенке контейнера, так как:
Bioprofe | Сила и давление в жидкостях | 01
Давление на стенки увеличивается вниз, а следовательно, и сила, действующая на них. Если мы просверливаем отверстия на разной глубине, выходная скорость увеличивается с увеличением глубины.
Bioprofe | Сила и давление в жидкостях | 05
Давление из-за веса атмосферы действует на все объекты, погруженные в этот огромный океан воздуха, включая наши тела.Как получается, что человеческий организм выдерживает такое огромное давление? Ответ заключается в том, что живые клетки поддерживают внутреннее давление, которое точно уравновешивает внешнее давление. Давление внутри воздушного шара также уравновешивает давление за его пределами из-за атмосферы. Благодаря своей жесткости автомобильная шина может выдерживать давление, намного превышающее внешнее давление.
Однако следует соблюдать осторожность при определении давления в шинах, поскольку все манометры, включая манометры, измеряют давление, превышающее атмосферное.Это давление называется манометрическим. Таким образом, чтобы получить абсолютное давление P, к манометрическому давлению P M :
необходимо прибавить атмосферное давление P A .
Bioprofe | Сила и давление в жидкостях | 06
Принцип Паскаля
Атмосфера оказывает давление на все объекты, с которыми она контактирует, включая другие жидкости. Через него передается внешнее давление, действующее на жидкость. Принцип Паскаля гласит, что « давление, приложенное к точке статической и несжимаемой жидкости, заключенной в контейнер, полностью передается во все точки жидкости ».
Через него передается внешнее давление, действующее на жидкость. Принцип Паскаля гласит, что « давление, приложенное к точке статической и несжимаемой жидкости, заключенной в контейнер, полностью передается во все точки жидкости ».
Если внешняя сила F действует на поршень секции S, давление возникает во всей массе жидкости.
P = F / S
Bioprofe | Сила и давление в жидкостях | 07
Давление, как мы уже говорили ранее, является скалярной величиной, у него нет определенного направления, но внутренняя сила, которую оно производит, представляет собой вектор, перпендикулярный поверхности, на которую оно действует. Поэтому во время ожидания он перпендикулярен в каждой точке внутренней поверхности.
Струя жидкости не выходит с большей силой через внутреннее отверстие, как можно было бы подумать, когда внешняя сила толкает плунжер в этом направлении, но она выходит через все отверстия с одинаковой скоростью.
Bioprofe | Сила и давление в жидкостях | 08
Есть несколько устройств, использующих принцип Паскаля, например, гидравлические тормоза автомобиля и гидравлическая рампа или хорошо известный «гидравлический домкрат».
Гидравлический домкрат используется в мастерских для подъема автомобилей.Это бак, к которому подключены два поршня разного сечения S 1 и S 2 . Давление, оказываемое плунжером при надавливании на поверхность жидкости, полностью передается на всю жидкость. В точках рядом с двумя поршнями давление одинаковое. Р 1 = Р 2 .
Bioprofe | Сила и давление в жидкостях | 09
Сила F 1 , приложенная к маленькому поршню, применяется с усиленным коэффициентом k , так что: F 2 в большом поршне составляет k · F1.Помимо усиления значение F 1 меняет свое направление использования, потому что F 2 будет там, где мы подключаемся к резервуару второго поршня.
Bioprofe | Сила и давление в жидкостях | 10
Плавучесть и принцип Архимеда
Объекты, погруженные в жидкость, кажутся меньше, чем когда они находятся вне жидкости. Например, камень, который с трудом можно было оторвать от земли, будет легче подниматься со дна ручья.Когда камень превышает поверхность воды, он кажется намного тяжелее. Многие предметы, например дерево, плавают на поверхности воды. Это два примера плавучести или плавучести . В каждом из них сила тяжести действует вниз, но, кроме того, жидкость оказывает плавающую силу вверх.
Сила плавучести возникает из-за того, что давление жидкости увеличивается с глубиной. Таким образом, давление вверх, оказываемое на нижнюю поверхность погруженного объекта, больше, чем давление вниз на его верхнюю поверхность.После различных исследований Архимед достиг своего принципа, в котором: «Каждое тело, погруженное в жидкость, испытывает вертикальную силу, направленную вверх, равную весу жидкости, которая вытесняет погруженную часть тела».
Bioprofe | Сила и давление в жидкостях | 11
Если используется вода:
Bioprofe | Сила и давление в жидкостях | 12
Как выселенная масса равна погруженному объему тела по плотности (m = V · d):
Bioprofe | Сила и давление в жидкостях | 13
В наши дни мы используем этот принцип с воздушными шарами или лодками.Подъем воздушного шара происходит потому, что его внутренняя плотность меньше плотности воздуха, а вес вытесненного воздуха больше, чем сумма веса внутреннего газа, корзины, балласта и веревок.
Лодки плавают, потому что они вытесняют воду, равную весу самой лодки. Для обеспечения равновесия и отсутствия колебаний, помимо равенства веса тела и тяги, требуется, чтобы центр тяжести тела и погруженной части оставался на одной и той же вертикали.Если вес и толчок не в вертикальном направлении, возникает пара сил.
15.1: Давление — Physics LibreTexts
Давление, оказываемое силой \ (\ vec F \) на поверхность с площадью \ (A \), является скалярной величиной \ (P \), определяемой как:
\ [\ begin {Выровнено} P = \ frac {F _ {\ perp}} {A} \ end {Выровнено} \]
где \ (F_ {⊥} \) — составляющая силы, перпендикулярная поверхности. Единицей измерения давления в системе СИ является Паскаль (Па). Давление связано с площадью \ (A \), на которую действует сила, и может рассматриваться как мера того, насколько сконцентрирована эта сила.Например, сила \ (10 \ text {N} \), приложенная через иглу (небольшая область), приведет к гораздо большему давлению, чем если бы эта сила была приложена плоской рукой (большая площадь).
Единицей измерения давления в системе СИ является Паскаль (Па). Давление связано с площадью \ (A \), на которую действует сила, и может рассматриваться как мера того, насколько сконцентрирована эта сила.Например, сила \ (10 \ text {N} \), приложенная через иглу (небольшая область), приведет к гораздо большему давлению, чем если бы эта сила была приложена плоской рукой (большая площадь).
Когда сила действует на жидкость, она создает давление, которое мы моделируем как повсюду в жидкости . Для каждого элемента в жидкости давление окружающей жидкости оказывает на элемент внутреннюю силу со всех направлений (см. Рисунок \ (\ PageIndex {1} \)). В качестве реакции элемент прилагает внешнюю силу во всех направлениях, и эти силы действуют на соседние элементы.
Это в некоторой степени аналогично натяжению, которое существует повсюду в веревке, когда каждый элемент веревки испытывает силы от соседних элементов веревки, которые пытаются «разорвать его». Давление можно рассматривать как «отрицательное» натяжение, когда материал под давлением испытывает силы, пытающиеся сжать элемент на себя, а не пытаться разорвать его. Чтобы создать натяжение в канате, нужно приложить к веревке внешнюю силу (чтобы растянуть ее), так что веревка будет оказывать внутреннюю силу в ответ.Чтобы создать давление в жидкости, нужно приложить к жидкости внутреннюю силу, которая затем в качестве реакции оказывает внешнюю силу.
Если мы рассмотрим небольшой кубический объем жидкости, как показано в центре рисунка \ (\ PageIndex {1} \), этот элемент жидкости будет испытывать внутренние силы во всех направлениях от давления в окружающей жидкости, как показано стрелки. Если силы от давления не приводят к действию результирующей силы на элемент жидкости, то мы говорим, что жидкость находится в гидростатическом равновесии, и элемент жидкости будет покоиться в инерциальной системе отсчета.
Рисунок \ (\ PageIndex {1} \): Небольшой элемент внутри жидкости под давлением не будет испытывать результирующей силы от давления в жидкости, поскольку сила, связанная с давлением в жидкости, действует во всех направлениях.
Рассмотрим вместо этого элемент жидкости, который находится на краю емкости для жидкости (например, чашка с водой), как показано на рисунке \ (\ PageIndex {2} \).
Рис. \ (\ PageIndex {2} \): На краю контейнера небольшой элемент жидкости будет оказывать внешнее усилие на контейнер, а контейнер будет оказывать внутреннее усилие на элемент жидкости.
В этом случае на правой стороне жидкостного элемента нет текучей среды, которая оказывала бы силу, направленную влево. Если элемент жидкости находится в равновесии, это должен быть контейнер, который оказывает эту силу, контейнер \ (\ vec F \), на жидкость. Согласно третьему закону Ньютона элемент жидкости воздействует на сосуд с внешней стороны. Это верно для всех точек на поверхности контейнера, которые все испытывают внешнюю силу от давления жидкости. Если давление на поверхности постоянно, величина внешней силы на поверхности будет равна давлению жидкости, умноженному на площадь этой поверхности.
Если вы поместите пустую запечатанную жестяную банку под воду, вода окажет давление на все поверхности жестяной банки, что приведет к действию внутренней силы на все поверхности жестяной банки. Если давление воды будет достаточно высоким, консервная банка раздавится. Если, с другой стороны, консервная банка наполнится водой, она не раздавится, так как вода внутри жестяной банки будет иметь такое же давление, что и вода вне жестяной банки, и будет оказывать такое же чистое внешнее усилие. на всех поверхностях жестяной банки.Чистая сила на каждой поверхности банки будет равна нулю, и консервная банка не будет раздавлена, независимо от того, насколько велико давление воды.
В общем, если имеется граница раздела с жидкостью по обе стороны от нее с разными давлениями, именно разница в давлении по обе стороны от границы раздела определяет результирующую силу, действующую на границу раздела, а не абсолютное давление.
Упражнение \ (\ PageIndex {1} \)
Вы кладете жестяную банку на стол и используете насос для создания вакуума внутри банки. Вы замечаете, что консервная банка раздавливается. Какое объяснение правильное?
Вы замечаете, что консервная банка раздавливается. Какое объяснение правильное?
- Вытягивая воздух из банки, вы также втягиваете его стенки.
- Вы понижаете давление внутри банки, так что воздух снаружи банки оказывает на банку большую внутреннюю силу, чем внешнюю силу воздуха внутри банки.
- Вы понижаете давление внутри банки, чтобы воздух внутри банки оказывал тянущее усилие на стенки банки.
- Все вышеперечисленное — действительные способы смоделировать это.
- Ответ
Эффект гравитации
Обсуждая рисунок \ (\ PageIndex {1} \), мы утверждали, что жидкость оказывает равное усилие со всех направлений на элемент жидкости, так что результирующая сила на элементе жидкости равна нулю. Это не совсем правильно при наличии силы тяжести, когда элемент жидкости будет иметь вес. Таким образом, если жидкий элемент должен находиться в равновесии, восходящая сила (и давление) от текучей среды ниже должны быть выше, чем со стороны текучей среды над текучим элементом.
На рисунке \ (\ PageIndex {3} \) показан элемент жидкости, имеющий высоту \ (h \) и площадь поверхности \ (A \) в горизонтальной плоскости. Давление \ (P_ {2} \) в текучей среде ниже элемента текучей среды должно быть выше давления \ (P_ {1} \) над элементом текучей среды, если элемент текучей среды находится в равновесии.
Рисунок \ (\ PageIndex {3} \): В присутствии силы тяжести давление под элементом жидкости должно быть больше, чтобы элемент жидкости оставался в равновесии.
Элемент жидкости имеет общую массу \ (м \), определяемую по формуле:
\ [\ begin {align} m = \ rho V = \ rho Ah \ end {align} \]
где \ (V = Ah \) — объем жидкости, а \ (ρ \) — ее плотность.
Чистая (горизонтальная) сила, прилагаемая внешней жидкостью к жидкостному элементу, равна нулю вдоль вертикальных поверхностей. Пусть \ (P_ {1} \) будет давлением в жидкости над элементом жидкости, а \ (P_ {2} \) будет давлением ниже элемента жидкости. Если мы выберем ось y, которая положительна вверх, и элемент жидкости не ускоряется в вертикальном направлении, тогда компонент y второго закона Ньютона, записанный для элемента жидкости, будет:
Если мы выберем ось y, которая положительна вверх, и элемент жидкости не ускоряется в вертикальном направлении, тогда компонент y второго закона Ньютона, записанный для элемента жидкости, будет:
\ [\ begin {align} & \ sum F_ {y} = F_ {2} -F_ {1} -mg = 0 \\ & P_ {2} A-P_ {1} A-mg = 0 \\ & P_ { 2} A-P_ {1} A- \ rho Ahg = 0 \\ & \, следовательно, P_ {2} -P_ {1} = \ rho gh \ end {align} \]
, где мы использовали тот факт, что сила, возникающая в результате давления, определяется давлением, умноженным на площадь, на которую оно действует.Таким образом, мы находим, что разница в давлении из-за силы тяжести в жидкости между двумя положениями, \ (y_ {2} \) и \ (y_ {1} \), определяется выражением:
\ [P (y_ {2}) — P (y_ {1}) = — \ rho g (y_ {2} -y_ {1}) \]
, где ось \ (y \) определена так, чтобы увеличиваться в направлении вверх. Поскольку давление в жидкости зависит от ее местоположения, мы говорим, что в жидкости существует «градиент давления».
Упражнение \ (\ PageIndex {2} \)
Рисунок \ (\ PageIndex {4} \): удерживание воды в вертикальной соломке.
Вы закрываете пальцем верхний конец соломинки, а затем вынимаете соломинку из стакана с водой. Как лучше всего описать, почему вода остается в соломинке (Рисунок \ (\ PageIndex {4} \)) до того, как вы отпустите палец?
- Внутри соломинки не должно быть вакуума; если палец не будет удален, чтобы впустить воздух, чтобы заменить воду, вода останется в соломе.
- Над водой создается небольшой вакуум, который всасывает воду вверх и предотвращает ее падение.
- Давление воздуха в соломке под водой выше, чем давление воздуха в соломке над водой.
- Давление воздуха в соломке под водой ниже, чем давление воздуха в соломе над водой.
- Ответ
Мы предположили, что плотность жидкости \ (ρ \) постоянна и жидкость не может сжиматься. Это очень хорошее приближение для жидкости, такой как вода, но не для газа, плотность которого будет зависеть от его давления.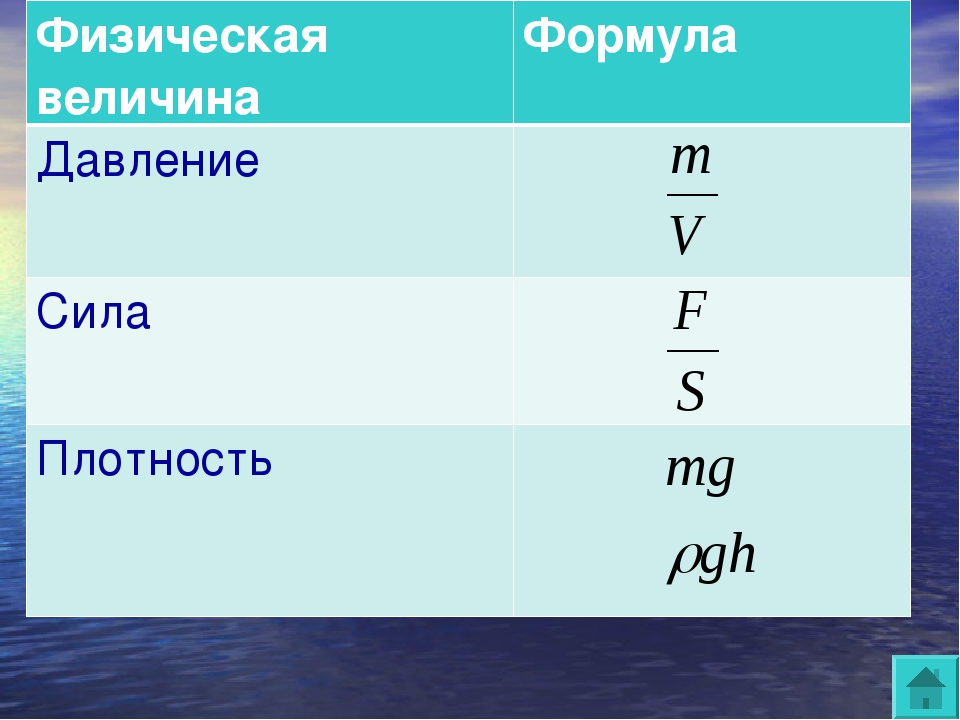 Если бы жидкостью был газ (например, столб воздуха в нашей атмосфере), и плотность, и давление изменились бы в зависимости от высоты. Мы можем легко учесть это в нашей модели, если учесть, что элемент жидкости имеет очень маленькую высоту, \ (dy \), вместо конечной высоты, \ (h \), как в приведенном выше выводе. Элемент жидкости бесконечно малой высоты \ (dy \) показан на рисунке \ (\ PageIndex {5} \).
Если бы жидкостью был газ (например, столб воздуха в нашей атмосфере), и плотность, и давление изменились бы в зависимости от высоты. Мы можем легко учесть это в нашей модели, если учесть, что элемент жидкости имеет очень маленькую высоту, \ (dy \), вместо конечной высоты, \ (h \), как в приведенном выше выводе. Элемент жидкости бесконечно малой высоты \ (dy \) показан на рисунке \ (\ PageIndex {5} \).
Рисунок \ (\ PageIndex {5} \): градиент давления от силы тяжести на бесконечно малом элементе жидкости.
На очень малой высоте \ (dy \) плотность жидкости \ (ρ \) можно считать постоянной, а бесконечно малый элемент жидкости будет иметь массу \ (dm \):
\ [\ begin {Выровнено} dm = \ rho Ady \ end {Выровнено} \]
Мы можем смоделировать давление, оказываемое жидкостью над элементом жидкости, как \ (P + dP \), а давление, оказываемое жидкостью ниже, как \ (P \), где \ (dP \) — небольшое (отрицательное) изменение давления 1 . Компонент \ (y \) Второго закона Ньютона, записанный для бесконечно малого жидкого элемента, имеет следующий вид:
\ [\ begin {align} \ sum F_ {y} = PA- (P + dP) A-dmg & = 0 \\ PA-PA-dPA- \ rho адыгский & = 0 \\ \ поэтому — dP — \ rho gdy & = 0 \ end {align} \]
Таким образом, мы можем определить, как давление изменяется с высотой, \ (y \):
\ [\ frac {dP} {dy} = — \ rho g \]
Это говорит нам, что скорость изменения давления с увеличением \ (y \) отрицательна; другими словами, давление уменьшается с увеличением высоты, как мы уже сделали.{y_ {2}} \ rho gdy \ end {align} \]
Если плотность \ (ρ \) постоянна, то это приводит к Уравнению 15.1.1 . Обратите внимание, что до сих пор мы только смоделировали, как давление в жидкости изменяется с высотой, но мы не определили абсолютное давление в жидкости.
Пример \ (\ PageIndex {1} \)
Если мы предположим, что плотность воздуха пропорциональна его давлению, как плотность воздуха изменяется с высотой?
Решение :
Мы знаем, что скорость изменения давления с высотой (положение \ (y \), где положительное значение \ (y \) определяется как направленное вверх) определяется выражением:
\ [\ begin {выравнивается} \ frac {dP} {dy} = — \ rho g \ end {выравнивается} \]
Так как мы можем предположить, что плотность пропорциональна давлению, мы можем ввести произвольную константу, \ (a \), и заявить, что:
\ [\ begin {align} \ rho & = aP \\ \ следовательно \ frac {dP} {dy} & = \ frac {d} {dy} \ frac {1} {a} \ rho = \ frac {1 } {a} \ frac {d \ rho} {dy} \ end {align} \]
, где постоянная \ (a \) может быть вычислена, если мы знаем давление и плотность в какой-то момент. {5} \ text {Па} \).Если атмосферное давление на поверхности океана равно \ (P_ {0} \), то давление на некоторой глубине, \ (h \), определяется по формуле:
{5} \ text {Па} \).Если атмосферное давление на поверхности океана равно \ (P_ {0} \), то давление на некоторой глубине, \ (h \), определяется по формуле:
\ [\ начало {выровнено} P (h) = P_ {0} + \ rho gh \ end {выровнено} \]
где \ (ρ \) — плотность воды. Как следствие, давление в жидкости на любой глубине \ (h \) одинаково везде на этой глубине в жидкости.
Упражнение \ (\ PageIndex {3} \)
Рисунок \ (\ PageIndex {7} \): Три стакана разной формы.
Вы наполняете три стакана на рисунке \ (\ PageIndex {7} \) так, чтобы жидкость достигла высоты h над дном стакана.Что вы можете сказать о давлении жидкости на дно каждого стакана?
- Наибольшее значение для стекла \ (A \).
- Это самый высокий показатель для стекла \ (В \).
- Это самый высокий показатель для стекла \ (С \).
- Он одинаков для всех очков.
- Это то же самое для всех очков, если пренебречь атмосферным давлением.
- Ответ
Пример \ (\ PageIndex {2} \)
Рисунок \ (\ PageIndex {8} \): сила, действующая на поршень гидравлического подъемника, чтобы оживить массу \ (M \).
Гидравлический подъемник использует принцип Паскаля, чтобы использовать небольшую силу для приложения большой силы. Гидравлический подъемник на рисунке \ (\ PageIndex {8} \) показывает подъемник, который создается за счет наличия жидкости между двумя вертикальными подвижными поршнями. Поршни имеют цилиндрическую форму с диаметром поперечного сечения \ (D \) и \ (D / 2 \). На поршень большего диаметра помещается груз \ (M \). Какова величина силы \ (\ vec F \), которая должна быть приложена к меньшему поршню, чтобы поднять массу \ (M \)?
Решение :
Если к маленькому поршню приложить силу \ (\ vec F \), то давление в жидкости увеличится на:
\ [\ begin {align} \ Delta P = \ frac {F} {A} = \ frac {F} {\ pi \ frac {D ^ {2}} {4}} = \ frac {4F} {\ пи D ^ {2}} \ end {align} \]
Это приведет к появлению направленной вверх силы \ (\ vec F ‘\) на большой поршень с величиной:
. {2} = 4F \ конец {выровнен} \]
{2} = 4F \ конец {выровнен} \]
Таким образом, сила, действующая на большой поршень, будет в четыре раза больше, чем на маленький поршень.Нужно только приложить силу величиной \ (Mg / 4 \), чтобы поднять массу \ (M \).
Измерение давления
В этом разделе мы описываем, как можно разработать приборы для измерения давления. Самым простым устройством является манометр, который состоит из U-образной трубки, заполненной жидкостью известной плотности \ (ρ \), как показано на рисунке \ (\ PageIndex {9} \).
Рисунок \ (\ PageIndex {9} \): Манометр может измерять разницу между давлением \ (P \) и атмосферным давлением, \ (P_ {0} \).Эта разница называется «манометрическим давлением».
Манометр можно использовать для измерения давления \ (P \) относительно атмосферного давления, \ (P_ {0} \). Один конец трубки открыт для атмосферного давления, а другой подключен к жидкости (например, газу), для которой мы хотим измерить давление. Если измеряемое давление превышает атмосферное давление, жидкость в манометре будет испытывать большую направленную вниз силу на стороне измеряемого давления, чем на стороне, открытой для атмосферного давления, как показано на рисунке \ (\ PageIndex {9 } \).Будет разница, \ (h \), в уровне жидкости на каждой стороне трубы, которая прямо пропорциональна разнице давления между двумя сторонами трубы.
Рассмотрим точку в жидкости в точке \ (B \) на рисунке \ (\ PageIndex {9} \), где давление равно \ (P_ {B} = P \), давление, которое необходимо измерить. Точка в жидкости в точке \ (A \), которая находится на той же высоте в жидкости, должна иметь то же давление, что и точка \ (B \). Мы можем записать давление в точке \ (A, P_ {A} \) как сумму атмосферного давления и давления водяного столба высотой \ (h \):
\ [\ begin {Выровнено} P_ {A} = P_ {0} + \ rho gh \ end {Выровнено} \]
Поскольку оно также должно быть равно давлению в точке \ (B \), мы можем найти разницу между давлением, которое мы хотим измерить, и атмосферным давлением:
\ [\ begin {выровнено} P_ {A} & = P_ {B} \\ P_ {0} + \ rho gh & = P \\ \, следовательно, P-P_ {0} & = \ rho gh \ end {выровнено } \]
Разница между давлением и атмосферным давлением называется «манометрическим давлением», и это все, что мы можем измерить, если не знаем абсолютного значения атмосферного давления. При использовании манометра манометрическое давление определяется как \ (ρgh \), тогда как «абсолютное давление», \ (P \), задается путем добавления атмосферного давления к манометрическому давлению, \ (P = P_ {0} + ρgh \). Большинство устройств для измерения давления («манометры») измеряют давление относительно атмосферного, используя аналогичный механизм.
При использовании манометра манометрическое давление определяется как \ (ρgh \), тогда как «абсолютное давление», \ (P \), задается путем добавления атмосферного давления к манометрическому давлению, \ (P = P_ {0} + ρgh \). Большинство устройств для измерения давления («манометры») измеряют давление относительно атмосферного, используя аналогичный механизм.
Атмосферное давление в определенном месте на Земле меняется в зависимости от погоды. Барометр — это прибор, предназначенный для измерения атмосферного давления. Простой барометр можно построить из манометра с закрытым концом, как показано на рисунке \ (\ PageIndex {10} \).
Рисунок \ (\ PageIndex {10} \): барометр, созданный на основе мамометра для измерения относительных изменений атмосферного давления.
Один конец манометра опломбирован в день, когда атмосферное давление, скажем, \ (P_ {0} \), а другой конец трубки остается открытым. Разница высот \ (h \) между жидкостью по обе стороны от трубы является мерой того, насколько отличается текущее атмосферное давление \ (P_ {1} \) от давления \ (P_ {0 } \), когда манометр был опломбирован. На рисунке \ (\ PageIndex {10} \) барометр показан в день, когда атмосферное давление ниже, чем в день закрытия манометра.Разница давлений определяется по формуле:
\ [\ begin {Выровнено} P_ {1} = P_ {0} + \ rho gh \ end {Выровнено} \]
, если мы определим \ (h \) как положительное, когда сторона с давлением \ (P_ {0} \) выше (поэтому \ (h \) отрицательна на рисунке \ (\ PageIndex {10} \) и \ (P_ {1} \) меньше \ (P_ {0} \)).
Мы также можем измерить абсолютное атмосферное давление, если откачим воздух из запечатанного конца трубки, так что \ (P_ {0} = 0 \). При этом разница в высоте жидкости по обе стороны от манометра является мерой абсолютного атмосферного давления.{2})} = 10,3 \ text {m} \ end {align} \]
Обсуждение :
Разница в высоте составляет примерно \ (10 \ text {m} \) при номинальном атмосферном давлении. Это означает, что манометр должен быть по крайней мере такой высоты, чтобы измерять абсолютное атмосферное давление, что непрактично конструировать! Если вместо этого использовать жидкость с более высокой плотностью, чем у воды, то эту высоту можно существенно уменьшить. Традиционно в барометрах используется ртуть, плотность которой составляет (\ (ρ_ {Hg} = 13.{3} \)), так что перепад высот при номинальном атмосферном давлении составляет \ (760 \ text {мм} \). Это гораздо более простой инструмент в изготовлении (не считая соображений безопасности при использовании ртути). По этой причине часто используемой единицей давления является «мм рт. Ст.», Что соответствует разнице высот в манометре, построенном с использованием ртути.
Это означает, что манометр должен быть по крайней мере такой высоты, чтобы измерять абсолютное атмосферное давление, что непрактично конструировать! Если вместо этого использовать жидкость с более высокой плотностью, чем у воды, то эту высоту можно существенно уменьшить. Традиционно в барометрах используется ртуть, плотность которой составляет (\ (ρ_ {Hg} = 13.{3} \)), так что перепад высот при номинальном атмосферном давлении составляет \ (760 \ text {мм} \). Это гораздо более простой инструмент в изготовлении (не считая соображений безопасности при использовании ртути). По этой причине часто используемой единицей давления является «мм рт. Ст.», Что соответствует разнице высот в манометре, построенном с использованием ртути.
Упражнение \ (\ PageIndex {4} \)
Рисунок \ (\ PageIndex {12} \): барометр Торричелли.
Вы создаете барометр Торричелли, как показано на рисунке \ (\ PageIndex {12} \), для измерения абсолютного атмосферного давления.Герметичная вертикальная трубка имеет пространство наверху, которое вакуумируется (нулевое давление), так что атмосферное давление на емкость с жидкостью заставляет жидкость подниматься по трубке на высоту \ (h \), которая пропорциональна атмосферному давлению. давление. Если вы используете оливковое масло в качестве жидкости, что вы можете сказать о высоте \ (h \) при номинальном атмосферном давлении?
- Это больше, чем \ (10.3 \ text {m} \).
- Это равно \ (10.3 \ text {m} \).
- Меньше \ (10.3 \ текст {m} \).
- Недостаточно информации, чтобы сказать.
- Ответ
Сноски
1. Мы поместили \ (dP \) в верхнюю часть жидкости, хотя давление выше в нижней части жидкости, потому что ось \ (y \) увеличивается вверх. Нас действительно интересует изменение давления \ (dP \), которое соответствует изменению высоты \ (dy \) в положительном направлении \ (y \).
Динамика — Давление
Динамика — Давление
Что такое давление?
Чтобы свести к минимуму путаницу, вероятно, лучше избегать
обсуждение давления в целом — но, наверное, уже слишком поздно — вы
наверное уже запутались в вопросе силы и давления!
Возможно, вы думаете, что сила и давление на самом деле одно и то же,
нравится масса и инерция. Извиняюсь!
Извиняюсь!
Давление зависит от приложенной силы — больше силы означает
больше давления. На самом деле давление прямо пропорционально силе.
Однако давление НЕ то же самое, что сила.
Давление также зависит от области, к которой прилагается сила.
Больше площади означает меньшее давление — на самом деле давление обратно пропорционально
пропорционально площади:
Единицы давления:
Единицей давления в системе СИ является Паскаль — сила в 1 Ньютон.
нанесенный на площадь 1 квадратный метр создает давление 1
Паскаль, поэтому Паскаль (сокращенно Па) — это очень небольшое давление.Другая распространенная единица давления — фунты на квадратный дюйм (psi).
Нормальное атмосферное давление (1 атмосфера, сокращенно атм) = 14,7
psi = 1,0 x 10 5 Па. Метеорологи используют единицу давления
исходя из высоты столба ртути, на которую давление будет
поддержка, поэтому в сводках погоды вы часто слышите атмосферное давление
указывается в «дюймах ртутного столба», где 1 атм = 29,9 дюйма ртутного столба.
Разница между силой и
Давление:
Когда к объекту прилагается сила, давление также оказывается на
объект, но сила и давление — это не одно и то же.Вот
«мысленный эксперимент», чтобы проиллюстрировать разницу. Предположим, что вы
будут воздействовать на вашего партнера по лаборатории силой в 5 Ньютонов, и
предположим, у вашего партнера есть следующий выбор:
- Сила 5 Ньютонов, приложенная острием штифта.
- Сила 5 Ньютонов, приложенная к плоской стороне Физики
книга.
Если предположить, что ваш партнер по лаборатории не ОЧЕНЬ странный, что
она выбирает? Конечно же, книга! Но почему? И булавка, и книга
приложит ту же силу, и она получит такое же ускорение
от любой силы.Ну, потому что сила, приложенная к булавке, будет
больно — сильно — и сила, приложенная к книге, не будет.
Хотя и булавка, и книжка имеют одинаковое усилие, они
оказывают очень разное давление. Давление зависит от количества
сила и площадь, к которой приложена сила. Больше силы — больше
давление. Больше площади — меньше давления. На самом деле давление прямо
пропорциональна силе и обратно пропорциональна площади.
Force сообщает вам, как объект будет
ускоряться .Давление
расскажет, как будет выглядеть .
или:
Сила ускоряется. Снижение давления.
Примеры давления
Пример 1: Почему острый нож режет лучше, чем тупой
нож?
на диаграмме справа показаны острый нож и тупой нож, соприкасающийся с
поверхность (может быть, хороший, сочный стейк!). Вы знаете, что острый нож
режет более эффективно — Почему?
Обратите внимание, что острый нож имеет очень маленькую площадь контакта с
поверхность, в то время как тупой нож имеет гораздо большую площадь контакта.Если оба ножа нажимаются с одинаковой силой, острый нож
будет оказывать большее давление на поверхность, чем тупой нож
— и снижение давления.
Итак, если вы «застряли» с тупым ножом, придется много потрудиться.
больше силы, чтобы создать достаточное давление, чтобы разрезать стейк,
Правильно?
Пример 2: коньки и обувь
Почему
люди должны использовать коньки? Почему обувь не работает так же
Что ж?
Посмотрите на диаграмму справа, на которой слева изображена обувь.
и конек справа.Нисходящая сила, которую вы прикладываете к
лед в любом случае (при условии, что вы стоите на двух ногах) будет
половина вашего веса.
Обратите внимание, однако, что обувь распределяет усилие на
большая площадь, чем у конька. Это означает, что коньк
давление на лед намного выше, чем у обуви — оно такое высокое
давление, которое делает возможным катание на коньках!
Пример 3: Почему удобная мягкая кровать?
Почему (большинству людей!) Удобнее лечь на
мягкий матрас, чем лечь на пол?
Прежде всего, на чем бы вы ни лежали, оно должно подниматься вверх.
(нормальная) сила, равная вашему весу, чтобы поддерживать вас.Таким образом, мягкий матрас и твердый пол поднимаются вверх одинаково.
сила на вас. Однако матрас соответствует вашей форме, поэтому
он оказывает опорную силу на большей площади, чем пол.
Поэтому матрас оказывает на вас меньшее давление, чем пол.
Давление болит.
, последнее обновление 27 декабря 2005 г., автор: JL
Stanbrough
Как разница давлений вызывает силу?
Простое давление — это (по определению) просто сила на единицу площади.Предположим, у вас есть коробка, и вы ставите ее в воздух. Затем воздух вдавливается в коробку. Он толкает с каждой стороны с силой, равной давлению, умноженному на площадь стороны, и с направлением силы, перпендикулярным стороне.
Если внутри коробки также есть воздух, он создает свое собственное давление, которое противодействует атмосфере, но если внутри коробки ничего нет, коробка, скорее всего, рухнет. Вы можете продемонстрировать это с помощью пустой банки из-под газировки с небольшим количеством воды на дне.Если вы нагреете банку над пламенем так, чтобы она была наполнена водяным паром, а затем переверните ее вверх дном в холодную воду, банку раздавит атмосфера. Пар внутри банки быстро конденсируется, и давление внутри банки падает. Давление снаружи из атмосферы остается таким же сильным, а сам материал банки недостаточно прочен, чтобы противодействовать внешнему давлению воздуха, поэтому банка раздавливается.
Вернитесь к ящику, сидящему в воздухе. Предположим, что давление в передней части коробки несколько выше, чем в задней.Тогда сила спереди больше, чем сила сзади. Коробка будет ускорена назад — в том направлении, в котором действует большая сила. (Обратите внимание, что давление на переднюю часть коробки толкает коробку назад, как если бы вы давили на переднюю часть автомобиля, вы толкаете ее назад.)
Обычная ситуация, в которой возникает эта разница давлений, — это жидкость в гравитационном поле, таком как атмосфера или океан. В этом случае сама жидкость удерживается разницей давления.Это называется гидростатическим равновесием. Мы можем представить себе воображаемую коробку, состоящую только из самой жидкости. Давление есть со всех сторон, но снизу немного больше, чем сверху, поэтому чистая сила направлена вверх. С другой стороны, сила тяжести направлена вниз, и они просто компенсируются.
В этом случае сама жидкость удерживается разницей давления.Это называется гидростатическим равновесием. Мы можем представить себе воображаемую коробку, состоящую только из самой жидкости. Давление есть со всех сторон, но снизу немного больше, чем сверху, поэтому чистая сила направлена вверх. С другой стороны, сила тяжести направлена вниз, и они просто компенсируются.
Представьте себе длинный ряд таких ящиков под океаном. Давление под каждой коробкой всегда немного выше, когда вы спускаетесь вниз, поэтому давление нарастает. Давление — это просто вес столба воды, деленный на площадь столба (плюс давление на поверхности.) Глубоко под водой это давление очень высокое.
Когда градиент давления сдвигается в сторону, а не вверх / вниз, ничто не может противодействовать силе, поэтому равновесие больше не существует. В этом случае жидкость будет двигаться. В общем, быстро движущаяся жидкость имеет низкое давление, а медленно движущаяся жидкость имеет более высокое давление, потому что при переходе от медленного к быстрому вы ускоряетесь, поэтому у вас должно быть высокое давление позади вас и низкое давление перед вами. Однако это всего лишь эвристика, и фактическое давление зависит от других факторов, таких как роль трения, температуры и т. Д.
Как рассчитать давление в резервуаре
Обновлено 22 декабря 2020 г.
Автор S. Hussain Ather
Гидростатическое давление, или давление, которое жидкость оказывает в равновесии в определенной точке жидкости под действием силы тяжести, увеличивается на более низких глубинах поскольку жидкость может оказывать большее усилие от жидкости выше этой точки.
Вы можете рассчитать гидростатическое давление жидкости в резервуаре как силу, приходящуюся на площадь для площади дна резервуара, выраженную по формуле давление = сила / единицы площади.В этом случае сила будет представлять собой вес, который жидкость оказывает на дно резервуара из-за силы тяжести.
Если вы хотите найти чистую силу, зная ускорение и массу, вы можете вычислить ее как F = ma в соответствии со вторым законом Ньютона.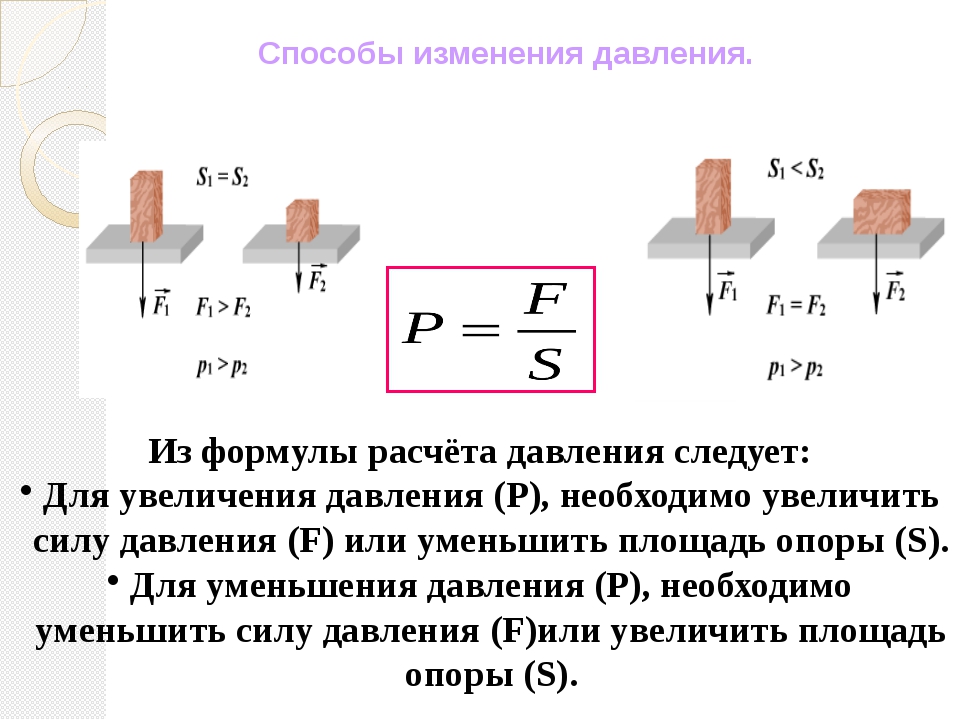 Для силы тяжести ускорение — это постоянная ускорения свободного падения, g . Это означает, что вы можете рассчитать это давление как
Для силы тяжести ускорение — это постоянная ускорения свободного падения, g . Это означает, что вы можете рассчитать это давление как
P = \ frac {mg} {A}
для массы м в килограммах, площади A футов 2 или 2 м, и g как гравитационная постоянная ускорения (9.81 м / с 2 , 32,17405 фут / с 2 ).
Это дает вам приблизительный способ определения сил между частицами для жидкости в резервуаре, но предполагает, что сила тяжести является точной мерой силы между частицами, вызывающей давление.
Если вы хотите принять во внимание дополнительную информацию, используя плотность жидкости, вы можете рассчитать гидростатическое давление жидкости по формуле P = ρ gh , в которой P — гидростатическое давление жидкости (в Н / м 2 , Па, фунт-сила / фут 2 , или фунт-сила / фут), ρ («rho») — плотность жидкости (кг / м 3 или пробок / фут 3 ), g — ускорение свободного падения (9.81 м / с 2 , 32,17405 фут / с 2 ) и h — высота столба жидкости или глубина, на которой измеряется давление.
Давление, формула жидкости
Эти две формулы выглядят одинаково, потому что в них используется один и тот же принцип. Вы можете вывести P = ρ gh из P = мг / А , используя следующие шаги для получения формулы давления для жидкостей:
- P = мг / А
- P = ρgV / A : заменить массу м на плотность ρ , умноженную на объем V .
- P = ρ g h : замените V / A на высоту h , потому что V = A x h .
Для газа в баллоне вы можете определить давление, используя закон идеального газа PV = nRT для давления P в атмосферах (атм), объема V в м 3 , число молей n , газовая постоянная R 8,314 Дж / (моль · К) и температура T в Кельвинах.



 С.В.Громов, Н.А.Родина. Москва.
С.В.Громов, Н.А.Родина. Москва.
 2)
2)