Как изменяется сила тока при параллельном соединении. Последовательное и параллельное соединение проводников
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.
На рисунке 78, а изображена цепь последовательного соединения двух электрических ламп, а на рисунке 78, б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.
Рис. 78. Последовательное включение лампочек и источников питания
Последовательно соединены, например, аккумулятор, лампа, два амперметра и ключ в цепи, изображённой на рисунке 62 (см. § 38).
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же
, т. е.
А чему равно сопротивление последовательно соединённых проводников?
Соединяя проводники последовательно, мы как бы увеличиваем длину проводника.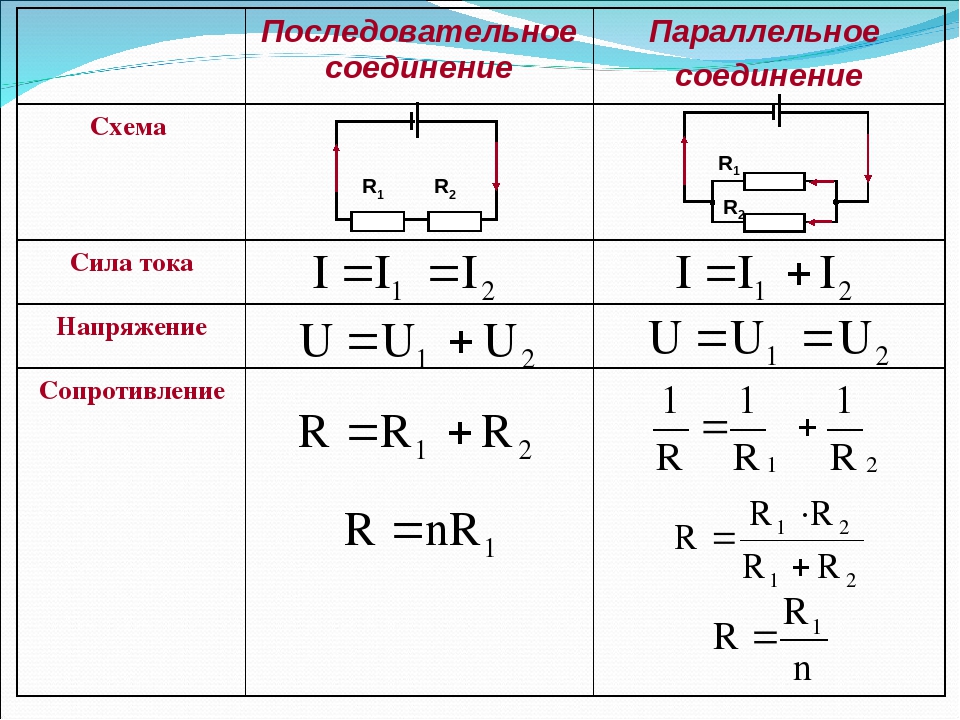 Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников
(или отдельных участков цепи):
Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:
U 1 = IR 1 , U 2 = IR 2 .
Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи
:
Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.
Пример 1
. Два проводника сопротивлением R 1 = 2 Ом, R 2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим её.
Вопросы
- Какое соединение проводников называют последовательным? Изобразите его на схеме.
- Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
- Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
- Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
Упражнение
- Цепь состоит из двух последовательно соединённых проводников, сопротивление которых 4 и 6 Ом. Сила тока в цепи 0,2 А.
 Найдите напряжение на каждом из проводников и общее напряжение.
Найдите напряжение на каждом из проводников и общее напряжение. - Для электропоездов применяют напряжение 3000 В. Как можно использовать для освещения вагонов лампы, рассчитанные на напряжение 50 В каждая?
- Две одинаковые лампы, рассчитанные на 220 В каждая, соединены последовательно и включены в сеть с напряжением 220 В. Под каким напряжением будет находиться каждая лампа?
- Электрическая цепь состоит из источника тока — батареи аккумуляторов, создающей в цепи напряжение 6 В, лампочки от карманного фонаря сопротивлением 13,5 Ом, двух спиралей сопротивлением 3 и 2 Ом, ключа и соединительных проводов. Все детали цепи соединены последовательно. Начертите схему цепи. Определите силу тока в цепи, напряжение на концах каждого из потребителей тока.
1 Какое надо взять сопротивление R, чтобы можно было включить в сеть с напряжением V=220 В лампу, рассчитанную на напряжение Vо = 120 В и ток Iо = 4 А?
2 Две дуговые лампы и сопротивление R соединены последовательно и включены в сеть с напряжением V=110В. Найти сопротивление R, если каждая лампа рассчитана на напряжение Vо = 40 В, а ток в цепи I=12 А.
Найти сопротивление R, если каждая лампа рассчитана на напряжение Vо = 40 В, а ток в цепи I=12 А.
Напряжение на сопротивлении
По закону Ома
3 Для измерения напряжения на участке цепи последовательно включены два вольтметра (рис. 88). Первый вольтметр дал показание V1 = 20 В, второй- V2 = 80 В. Найти сопротивление второго вольтметра R2, если сопротивление первого вольтметра R1 = 5 кОм.
Через вольтметры протекает один и тот же ток I. Так как вольтметр показывает напряжение на собственном сопротивлении, то
и сопротивление второго вольтметра
4 Реостат из железной проволоки, миллиамперметр и источник тока включены последовательно. При температуре to = 0° С сопротивление реостата Ro = 200 Ом. Сопротивление миллиамперметра R = 20 Ом, его показание Iо = 30 мА. Какой ток It будет показывать миллиамперметр, если реостат нагреется до температуры t = 50° С? Температурный коэффициент сопротивления железа .
Последовательное и параллельное соединения проводников. Добавочные сопротивления и шунты
Добавочные сопротивления и шунты
5 Проводник с сопротивлением R = 2000 Ом состоит из двух последовательно соединенных частей: угольного стержня и проволоки, имеющих температурные коэффициенты сопротивления . Какими следует выбрать сопротивления этих частей, чтобы общее сопротивление проводника R не зависело от температуры?
При температуре t общее сопротивление последовательно включенных частей проводника с сопротивлениями R1 и R2 будет
где R10 и R20 — сопротивления угольного стержня и проволоки при t0=0° С. Общее сопротивление проводника не зависит от температуры, если
В этом случае при любой температуре
Из последних двух уравнений найдем
6 Составить такую схему электропроводки для освещения одной лампочкой коридора, которая позволяет включать и выключать свет независимо в любом конце коридора.
Схемы электропроводки, позволяющие включать и выключать лампочку в любом конце коридора, показаны на рис. 347. У концов коридора устанавливаются два переключателя П1 и П2 каждый из которых имеет два положения.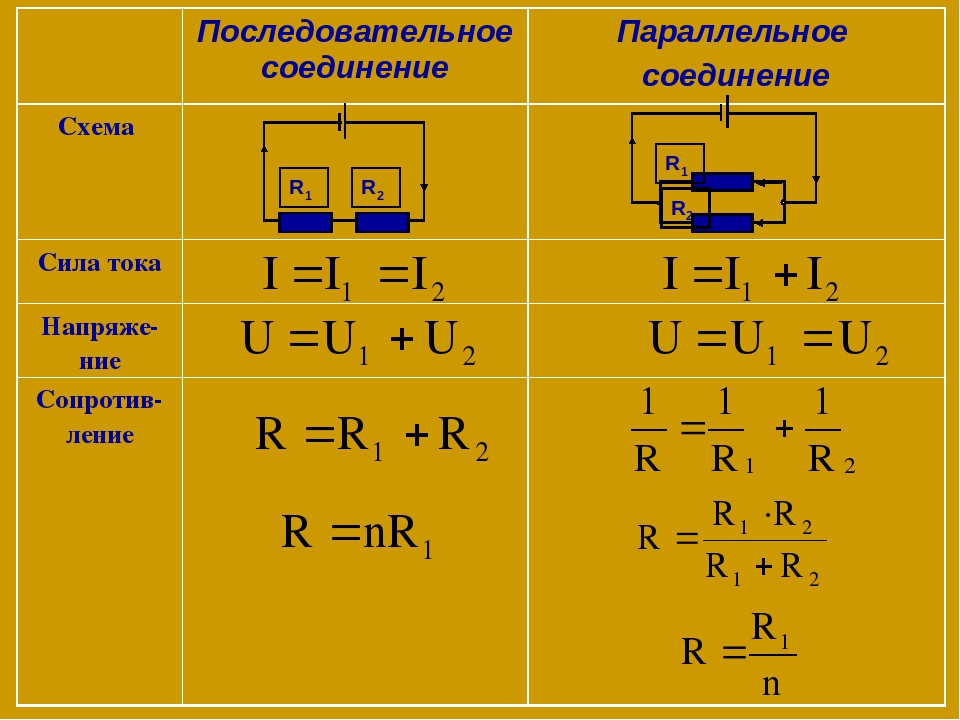 В зависимости от расположения выводов от сети может оказаться выгоднее с точки зрения экономии проводов вариант а) или б).
В зависимости от расположения выводов от сети может оказаться выгоднее с точки зрения экономии проводов вариант а) или б).
7 В сеть с напряжением V= 120 В включены две электрические лампочки с одинаковыми сопротивлениями R = 200 Ом. Какой ток пойдет через каждую лампочку при их параллельном и последовательном соединениях?
I1 = V/R=0,6 А при параллельном соединении; I2=V/2R=0,3 А при последовательном соединении.
8 Реостат со скользящим контактом, соединенный по схеме, приведенной на рис. 89, является потенциометром (делителем напряжения). При перемещении движка потенциометра снимаемое с него напряжение Vx изменяется от нуля до напряжения на клеммах источника тока V. Найти зависимость напряжения Vx от положения движка. Построить график этой зависимости для случая, когда полное сопротивление потенциометра Ro во много раз меньше сопротивления вольтметра r.
Пусть при данном положении движка сопротивление участка ах потенциометра равно rх (рис. 89). Тогда общее сопротивление этого участка и вольтметра (они соединены параллельно) а сопротивление остальной части потенциометра xb равно Таким образом, полное сопротивление между точками а и b будет
Тогда общее сопротивление этого участка и вольтметра (они соединены параллельно) а сопротивление остальной части потенциометра xb равно Таким образом, полное сопротивление между точками а и b будет
Ток в цепи I= V/R. Напряжение на участке ах
Так как по условию R0
т.е. напряжение Vх пропорционально сопротивлению rх. В свою очередь сопротивление rх пропорционально длине участка ах.
На рис. 348 сплошная прямая показывает зависимость Vx от rх, штрихпунктирная линия — зависимость Vx от rх, когда R0~r, т. е. когда в выражении для Vх нельзя пренебречь первым членом в знаменателе. Эта зависимость не является линейной, однако и в этом случае Vx изменяется в пределах от нуля до напряжения на клеммах источника V.
9 Найти сопротивление R биметаллического (железо- медь) провода длины l=100м. Диаметр внутренней (железной) части провода d=2 мм, общий диаметр провода D = 5 мм. Удельные сопротивления железа и меди . Для сравнения найти сопротивления железного и медного проводов Яж и Rм диаметра D и длины l.
Площади сечения железной и медной частей провода
(рис. 349). Их сопротивления
Сопротивление R биметаллического провода находится по формуле параллельного соединения проводников:
Сопротивления железного и медного проводов диаметра D и длины l
10 Найти общее сопротивление проводников, включенных в цепь по схеме, изображенной на рис. 90, если сопротивления R1= = R2 = R5 = Я6 = 1 Ом, R3 = 10 Ом, R4 = 8 Ом.
11 Общее сопротивление двух последовательно соединенных проводников R=5 Ом, а параллельно соединенных Rо=1,2 Ом. Найти сопротивление каждого проводника.
При последовательном соединении двух проводников с сопротивлениями R1 и R2 их общее сопротивление
а при параллельном соединении
Согласно известному свойству приведенного квадратного уравнения (теорема Виета) сумма корней этого уравнения равна второму его коэффициенту с обратным знаком, а произведение корней-свободному члену, т. е. R1 и R2 должны быть корнями квадратного уравнения
Подставив значения Rо и R, найдем R1 = З Ом и R2 = 2 0м (или R1 =2 Ом и R2 = 3 Ом).
12 К проволочному кольцу в двух точках присоединены подводящие ток провода. В каком отношении делят точки присоединения длину окружности кольца, если общее сопротивление получившейся цепи в n = 4,5 раза меньше сопротивления проволоки, из которой сделано кольцо?
Точки присоединения подводящих проводов делят длину окружности кольца в отношении 1:2, т. е. отстоят друг от друга по дуге на 120град.
13 В цепи, изображенной на рис. 91, амперметр показывает ток I=0,04 А, а вольтметр — напряжение V=20 В. Найти сопротивление вольтметра R2, если сопротивление проводника R1 = 1 кОм.
14 Найти сопротивление R1 лампочки по показаниям вольтметра (V=50 В) и амперметра (I=0,5 А), включенных по схеме, изображенной на рис. 92, если сопротивление вольтметра R2 = 40 кОм.
Ток в общей цепи I=I1+I2, где I1 и I2 — токи, текущие через лампочку и вольтметр. Так как
Пренебрегая током I2 = 1,25мА по сравнению с I=0,5 А получим по приближенной формуле
то же значение сопротивления лампочки: R1 = 100 Ом.
15 Найти сопротивление проводника R1 по показаниям амперметра (I=5 А) и вольтметра (V=100В), включенных по схеме, изображенной на рис. 93, если сопротивление вольтметра R2 = 2,5 кОм. Какова будет ошибка в определении R1, если, предположив, что , при расчетах пренебречь током, текущим через вольтметр?
Показание вольтметра
где I1 и I2-токи, текущие через сопротивление и вольтметр. Общий ток
Если пренебречь током I2 по сравнению с I, то искомое сопротивление
Ошибка в определении R`1 будет
Учитывая, что
найдем относительную ошибку:
16 К источнику тока с напряжением V присоединены последовательно два проводника с одинаковыми сопротивлениями R. Какова будет разница в показаниях вольтметров с сопротивлениями R и 10R, если их поочередно подключать к концам одного из проводников?
Вольтметры с сопротивлениями R и 10R показывают напряжения
поэтому разница в показаниях вольтметров
17 К источнику тока с напряжением V= 12 В присоединены две лампочки (рис. 94). Сопротивления участков цепи r1 = r2 = r3 = r4 = г = 1,5 Ом. Сопротивления лампочек R1 = R2 = R = 36 Ом. Найти напряжение на каждой лампочке.
94). Сопротивления участков цепи r1 = r2 = r3 = r4 = г = 1,5 Ом. Сопротивления лампочек R1 = R2 = R = 36 Ом. Найти напряжение на каждой лампочке.
18 В схеме, изображенной на рис. 95, напряжение источника тока V=200 В, а сопротивления проводников R1=60Ом, R2 = R3 = 30 Ом. Найти напряжение на сопротивлении R1.
19 Электрическая цепь состоит из источника тока с напряжением V=180В и потенциометра с полным сопротивлением R = 5 кОм. Найти показания вольтметров, присоединенных к потенциометру по схеме, изображенной на рис. 96. Сопротивления вольтметров R1=6 кОм и R2 = 4кОм. Движок x стоит посередине потенциометра.
20 Три резистора включены по схеме, изображенной на рис. 97. Если резисторы включены в цепь в точках а и b, то сопротивление цепи будет R = 20 Ом, а если в точках а и с, то сопротивление цепи будет Rо = 15 Oм. Найти сопротивления резисторов R1, R2, R3, если R1=2R2.
Эквивалентные схемы включения изображены на рис. 350. Сопротивления реостатов
350. Сопротивления реостатов
21 На сколько равных частей нужно разрезать проводник, имеющий сопротивление R = 36 Ом, сопротивление его частей, соединенных параллельно, было Ro — 1 Ом?
Весь проводник имеет сопротивление R = nr, где r-сопротивление каждой из п равных частей проводника. При параллельном соединении п одинаковых проводников их общее сопротивление R0 = r/n. Исключая r, получим
n может быть лишь целым положительным числом, большим единицы. Поэтому решения возможны только в случаях, когда R/Rо = 4, 9, 16, 25, 36,… В нашем случае
22 Из проволоки сделан каркас в форме куба (рис. 98), каждое ребро которого имеет сопротивление r. Найти сопротивление R этого каркаса, если ток I в общей цепи идет от вершины А к вершине В.
На участках Аа и bВ (рис. 351), ввиду равенства сопротивлений ребер куба и их одинакового включения, ток I равномерно разветвляется по трем ветвям и поэтому в каждой из них равен I/3. На участках ab ток равен I/6, так как в каждой точке а ток вновь разветвляется по двум ребрам с равными сопротивлениями и все эти ребра включены одинаково.
Напряжение между точками А и В складывается из напряжения на участке Аа, напряжения на участке ab и напряжения на участке bВ:
23 Из проволоки, единица длины которой имеет сопротивление Rl, сделан каркас в форме окружности радиуса r, пересеченной двумя взаимно перпендикулярными диаметрами (рис. 99). Найти сопротивление Rx каркаса, если источник тока подключен к точкам c и d.
Если источник тока подключен к точкам с и d, то напряжения на участках da и ab равны, поскольку проволока
однородна. Следовательно, разность потенциалов между точками а и b равна нулю. Ток на этом участке отсутствует. Поэтому наличие или отсутствие контакта в точке пересечения проводников ab и cd безразлично. Сопротивление Rx, таким образом, представляет собой сопротивление трех параллельно включенных проводников: cd с сопротивлением 2rR1, cad и cbd с одинаковыми сопротивлениями prR1. Из соотношения
24 Провод длины L=1 м сплетен из трех жил, каждая из которых представляет собой кусок неизолированной проволоки с сопротивлением единицы длины Rl = 0,02 Ом/м.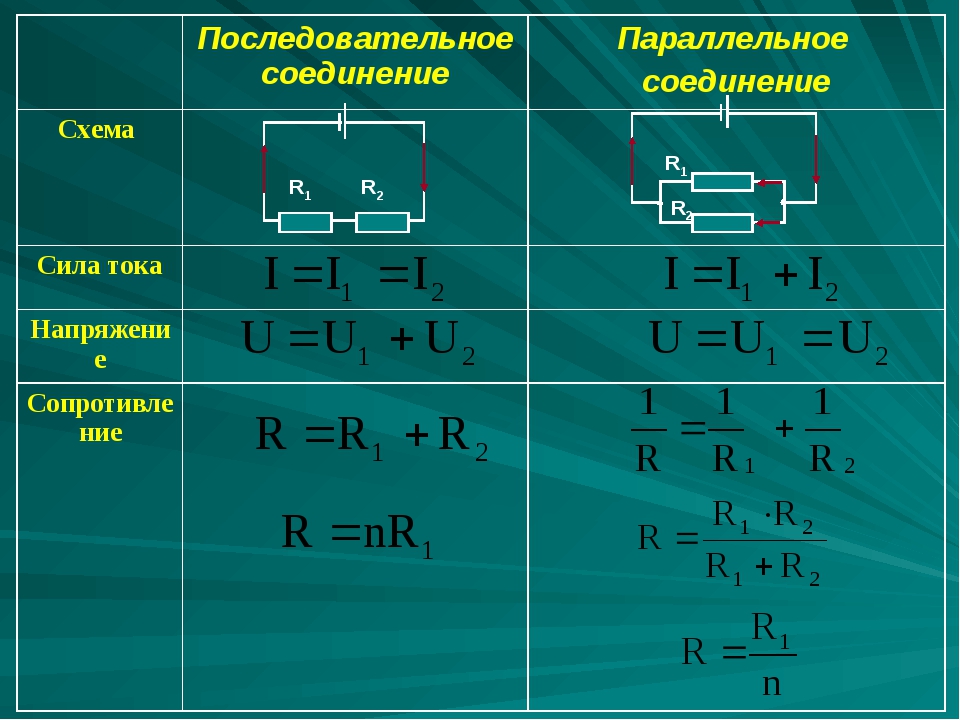 На концах провода создано напряжение V=0,01 В. На какую величину DI изменится ток в этом проводе, если от одной жилы удалить кусок длины l=20 см?
На концах провода создано напряжение V=0,01 В. На какую величину DI изменится ток в этом проводе, если от одной жилы удалить кусок длины l=20 см?
25 Источник тока первоначально присоединяют к двум соседним вершинам проволочной рамки в форме правильного выпуклого n-угольника. Затем источник тока присоединяют к вершинам, расположенным через одну. При этом ток уменьшается в 1,5 раза. Найти число сторон n-угольника.
26 Как надо соединить четыре проводника с сопротивлениями R1 = 10м, R2 = 2 0м, R3 = 3 Ом и R4 = 4 0м, чтобы получить сопротивление R = 2,5 Ом?
Сопротивление R = 2,5 Ом достигается, когда проводники включены по схеме сметанного соединения (рис. 352).
27 Найти проводимость k цепи, состоящей из двух последовательных групп параллельно включенных проводников. Проводимости каждого проводника первой и второй групп равны k1=0,5Cм и k2 = 0,25 См. Первая группа состоит из четырех проводников, вторая- из двух.
28 Вольтметр рассчитан на измерение напряжений до максимального значения Vо = 30 В. При этом через вольтметр идет ток I=10 мА. Какое добавочное сопротивление Rд нужно присоединить к вольтметру, чтобы им можно было измерять напряжения до V=150В?
При этом через вольтметр идет ток I=10 мА. Какое добавочное сопротивление Rд нужно присоединить к вольтметру, чтобы им можно было измерять напряжения до V=150В?
Для измерения вольтметром более высоких напряжений, чем те, на которые рассчитана шкала, необходимо включить последовательно с вольтметром добавочное сопротивление Rд (рис. 353). Напряжение на этом сопротивлении Vд=V-Vо; поэтому сопротивление Rд=(V-Vо)/I=12 кОм.
29 Стрелка миллиамперметра отклоняется до конца шкалы, если через миллиамперметр идет ток I=0,01 А. Сопротивление прибора R = 5 0м. Какое добавочное сопротивление Rд нужно присоединить к прибору, чтобы его можно было использовать в качестве вольтметра с пределом измерения напряжений V= 300 В?
Для измерения прибором напряжений, не превышающих V, необходимо последовательно с ним включить такое добавочное сопротивление Rд, чтобы V=I(R + Rд), где I-максимальный ток через прибор; отсюда Rд= V/I-R30 кОм.
30 Вольтметр, соединенный последовательно с сопротивлением R1 = 10 кОм, при включении в сеть с напряжением V=220 В показывает напряжение V1 = 70 В, а соединенный последовательно с сопротивлением R2, показывает напряжение V2 = 20 В.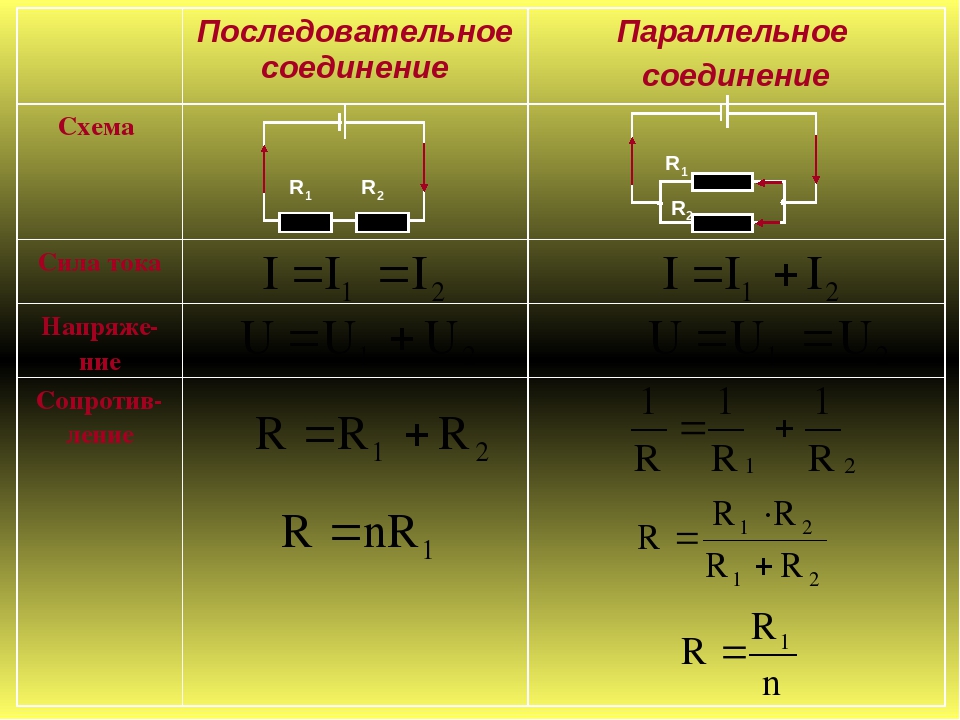 Найти сопротивление R2.
Найти сопротивление R2.
31 Вольтметр с сопротивлением R = 3 кОм, включенный в городскую осветительную сеть, показал напряжение V=125В. При включении вольтметра в сеть через сопротивление Ro его показание уменьшилось до Vо = 115 В. Найти это сопротивление.
Городская осветительная сеть представляет собой источник тока, обладающий внутренним сопротивлением, намного меньшим сопротивления вольтметра R. Поэтому напряжение V=125 В, которое показывал вольтметр при непосредственном включении в сеть, равно напряжению источника тока. Это значит, что оно не изменяется и при включении вольтметра в сеть через сопротивление Rо. Поэтому V=I(R + Rо), где I=Vо/R — ток, текущий через вольтметр; отсюда Rо = (V-Vо)R/Vо = 261 Ом.
32 Вольтметр с сопротивлением R = 50 кОм, подключенный к источнику тока вместе с добавочным сопротивлением Rд = 120 кОм, показывает напряжение Vо =100 В. Найти напряжение V источника тока.
Ток, текущий через вольтметр и добавочное сопротивление, I=Vо/R. Напряжение источника тока V=I(R+Rд)= (R+Rд)Vо/R = 340 В.
33 Найти показание вольтметра V с сопротивлением R в цепи, изображенной на рис. 100. Ток до разветвления равен I, сопротивления проводников R1 и R2 известны.
34 Имеется прибор с ценой деления i0=1 мкА/дел и числом делений шкалы N= 100. Сопротивление прибора R = 50 Ом. Как этот прибор приспособить для измерения токов до значения I=10 мА или напряжений до значения V= 1 В?
Для измерения более высоких токов чем те, на которые рассчитана шкала, параллельно прибору включается шунт с сопротивлением
для измерения напряжений последовательно с прибором включается добавочное сопротивление — ток, текущий через прибор при максимальном отклонении стрелки,
Напряжение на его клеммах в этом случае.
35 Миллиамперметр с пределом измерения токов I0 = 25 мА необходимо использовать как амперметр с пределом измерения токов I=5 А. Какое сопротивление Rш должен иметь шунт? Во сколько раз уменьшается чувствительность прибора? Сопротивление прибора R=10 Oм.
При включении параллельно прибору шунта (рис. 354) ток I должен делиться так, чтобы через миллиамперметр протекал ток Iо. Через шунт при этом течет ток Iш, т.е. I=Iо + Iш. Напряжения на шунте и на миллиамперметре равны: IоR = IшRш; отсюда
354) ток I должен делиться так, чтобы через миллиамперметр протекал ток Iо. Через шунт при этом течет ток Iш, т.е. I=Iо + Iш. Напряжения на шунте и на миллиамперметре равны: IоR = IшRш; отсюда
Rш=IоR/(I-Iо)0,05 Ом. Чувствительность прибора уменьшается, а цена деления прибора увеличивается в n=I/Iо=200 раз.
36 Амперметр с сопротивлением R = 0,2 Ом, накоротко присоединенный к источнику тока с напряжением V=1,5B, показывает ток I=5А. Какой ток I0 покажет амперметр, если его зашунтировать сопротивлением Rш=0,1 Ом?
37 При шунтировании гальванометра сопротивлениями R1, R2 и R3 в них ответвляется 90%, 99% и 99,9% тока I общей цепи. Найти эти сопротивления, если сопротивление гальванометра R = 27 Ом.
Так как шунты присоединяются к гальванометру параллельно, то условие равенства напряжений на гальванометре и на шунтах дает
38 Миллиамперметр с числом делений шкалы N=50 имеет цену деления i0 = 0,5 мА/дел и сопротивление R = 200 Ом. Как этот прибор приспособить для измерения токов до значения I= 1 А?
Наибольший ток, протекающий через прибор, Iо = iоN. Для измерения токов, значительно превышающих ток Iо, необходимо параллельно прибору включить шунт, сопротивление которого Rш значительно меньше сопротивления миллиамперметра R:
Для измерения токов, значительно превышающих ток Iо, необходимо параллельно прибору включить шунт, сопротивление которого Rш значительно меньше сопротивления миллиамперметра R:
39 К амперметру с сопротивлением R = 0,1 Ом подключен шунт с сопротивлением Rш= 11,1 мОм. Найти ток, текущий через амперметр, если ток в общей цепи I=27 А.
Ток, текущий через шунт, Iш = I-Iо. Падения напряжения на шунте и амперметре равны: IшRш = IоR; отсюда Iо=IRш/(R+Rш) =2,7 А.
Содержание:
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.

- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
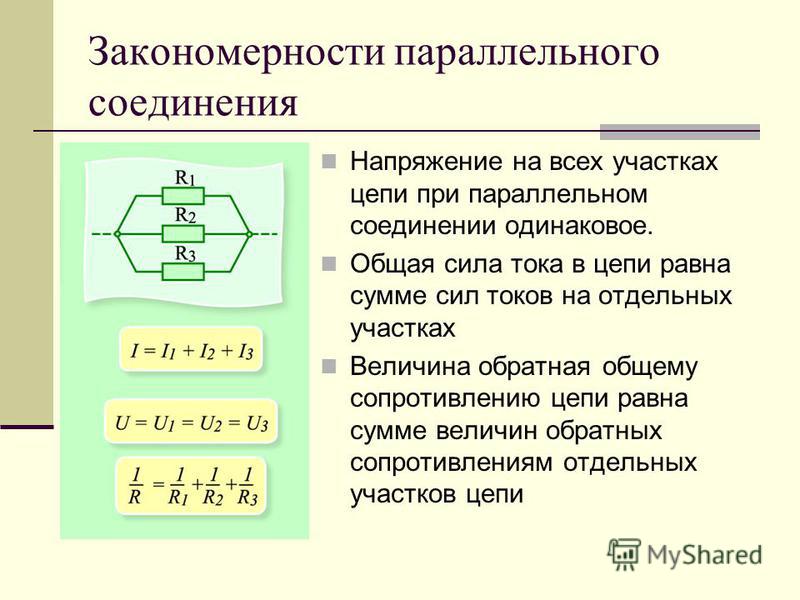
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой.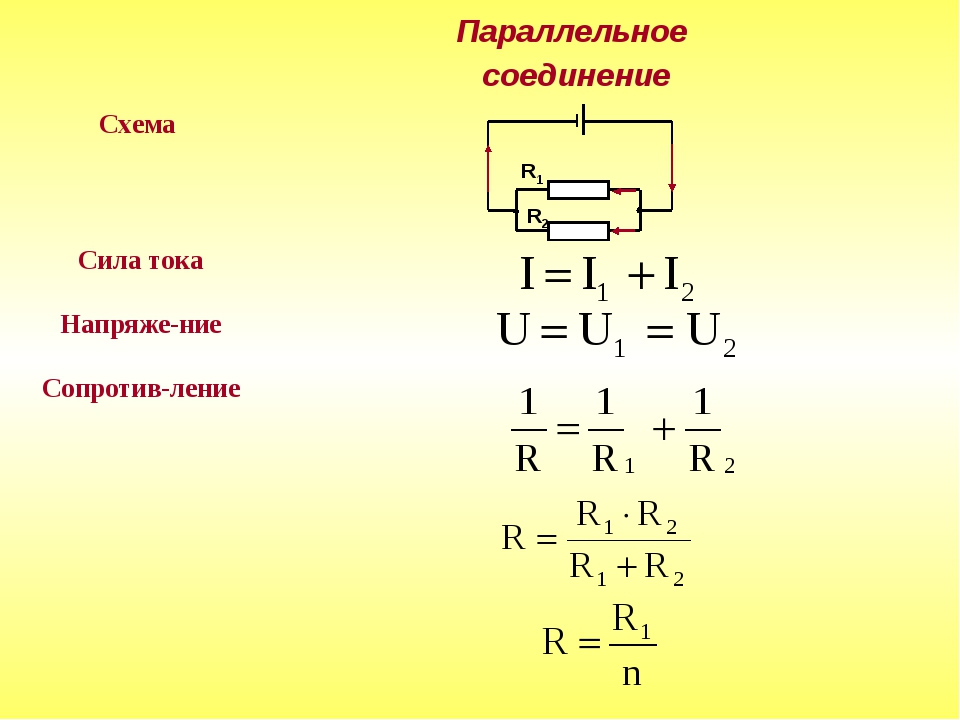 Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.

- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U 1
+ U 2
+ U 3 или
IR экв
= IR 1
+ IR 2
+ IR 3 ,
откуда
следует
R экв
= R 1
+ R 2
+ R 3 .
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением R экв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
и
по вышеприведенным формулам рассчитывают
падение напряжений U 1 ,
U 2 ,
U 3
на соответствующих участках электрической
цепи (рис. 1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I 1
+ I 2
+ I 3 ,
т.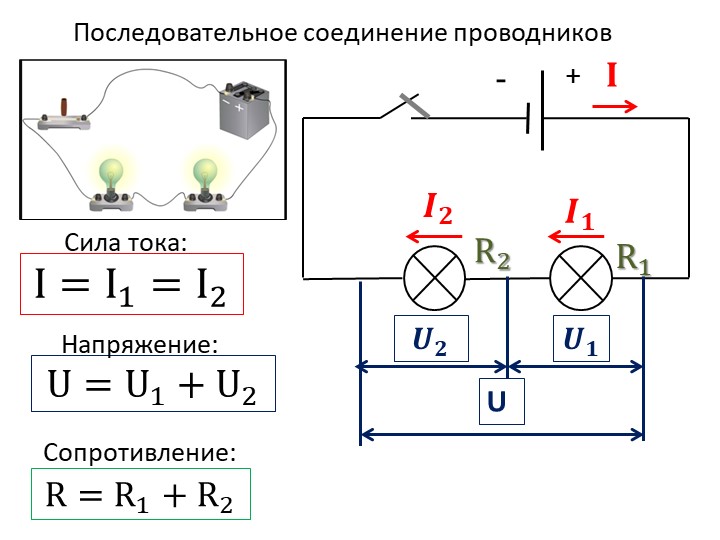 е.
е.
откуда
следует, что
.
В
том случае, когда параллельно включены
два сопротивления R 1
и R 2 ,
они заменяются одним эквивалентным
сопротивлением
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
g экв
= g 1
+ g 2
+ g 3 .
По
мере роста числа параллельно включенных
потребителей проводимость цепи g экв
возрастает, и наоборот, общее сопротивление
R экв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IR экв
= I 1 R 1
= I 2 R 2 =
I 3 R 3 .
Отсюда
следует, что
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R.
Сопротивления R 4
и R 5
включены параллельно, тогда сопротивление
участка цепи cd равно:
.
В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
На
схеме (рис. 1.8) сопротивление R 3
и R cd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
На
схеме (рис. 1.9) сопротивление R 2
и R ad
соединены параллельно, тогда сопротивление
участка цепи аb равно
.
Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R 1
и R ab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
Рис. | Рис. |
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
R экв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ
ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение
синусоидальной ЭДС. . Основные
характеристики синусоидального тока
Основным
преимуществом синусоидальных токов
является то, что они позволяют наиболее
экономично осуществлять производство,
передачу, распределение и использование
электрической энергии. Целесообразность
их использования обусловлена тем, что
коэффициент полезного действия
генераторов, электрических двигателей,
трансформаторов и линий электропередач
в этом случае оказывается наивысшим.
Для
получения в линейных цепях синусоидально
изменяющихся токов необходимо, чтобы
э. д. с. также изменялись по синусоидальному
закону. Рассмотрим процесс возникновения
синусоидальной ЭДС. Простейшим генератором
синусоидальной ЭДС может служить
прямоугольная катушка (рамка), равномерно
вращающаяся в однородном магнитном
поле с угловой скоростью ω
(рис. 2.1, б
).
Пронизывающий
катушку магнитный поток во время вращения
катушки abcd
наводит (индуцирует) в ней на основании
закона электромагнитной индукции
ЭДС е
.
Нагрузку подключают к генератору с
помощью щеток 1
,
прижимающихся к двум контактным кольцам
2
,
которые, в свою очередь, соединены с
катушкой. Значение наведенной в катушке
abcd
э. д. с. в каждый момент времени
пропорционально магнитной индукции В
,
размеру активной части катушки l
= ab
+ dc
и нормальной составляющей скорости
перемещения ее относительно поля v
н
:
e
= Blv
н
(2. 1)
1)
где
В
и l
— постоянные величины, a v
н
— переменная, зависящая от угла α. Выразив
скорость v н
через линейную скорость катушки v
,
получим
e
= Blv·sinα
(2.2)
В
выражении (2.2) произведение Blv
= const. Следовательно, э. д. с., индуцируемая
в катушке, вращающейся в магнитном поле,
является синусоидальной функцией угла
α
.
Если
угол α = π/2
,
то произведение Blv
в формуле (2.2) есть максимальное
(амплитудное) значение наведенной э. д.
с. E m
= Blv
.
Поэтому выражение (2.2) можно записать в
виде
e
= E
m
sinα
(2.3)
Так
как α
есть угол поворота за время t
,
то, выразив его через угловую скорость
ω
,
можно записать α
= ωt
, a формулу
(2.3) переписать в виде
e
= E
m
sinωt
(2.4)
где
е
— мгновенное значение э. д. с. в катушке;
α = ωt
— фаза, характеризующая значение э. д.
д.
с. в данный момент времени.
Необходимо
отметить, что мгновенную э. д. с. в течение
бесконечно малого промежутка времени
можно считать величиной постоянной,
поэтому для мгновенных значений э. д.
с. е
,
напряжений и
и токов i
справедливы законы постоянного тока.
Синусоидальные
величины можно графически изображать
синусоидами и вращающимися векторами.
При изображении их синусоидами на
ординате в определенном масштабе
откладывают мгновенные значения величин,
на абсциссе — время. Если синусоидальную
величину изображают вращающимися
векторами, то длина вектора в масштабе
отражает амплитуду синусоиды, угол,
образованный с положительным направлением
оси абсцисс, в начальный момент времени
равен начальной фазе, а скорость вращения
вектора равна угловой частоте. Мгновенные
значения синусоидальных величин есть
проекции вращающегося вектора на ось
ординат. Необходимо отметить, что за
положительное направление вращения
радиус-вектора принято считать направление
вращения против часовой стрелки. На
На
рис. 2.2 построены графики мгновенных
значений э. д. с. е
и е»
.
Если
число пар полюсов магнитов p
≠ 1
, то за
один оборот катушки (см. рис. 2.1) происходит
p
полных циклов изменения э. д. с. Если
угловая частота катушки (ротора) n
оборотов в минуту, то период уменьшится
в pn
раз. Тогда частота э. д. с., т. е. число
периодов в секунду,
f
= Pn
/ 60
Из
рис. 2.2 видно, что ωТ
= 2π
, откуда
ω
= 2π / T = 2πf
(2.5)
Величину
ω
,
пропорциональную частоте f и равную
угловой скорости вращения радиус-вектора,
называют угловой
частотой.
Угловую частоту выражают в радианах в
секунду (рад/с) или в 1 / с.
Графически
изображенные на рис. 2.2 э. д. с. е
и е»
можно описать выражениями
e
= E
m
sinωt;
e» = E»
m
sin(ωt
+ ψ
e»
)
.
Здесь
ωt
и ωt + ψ
e»
— фазы, характеризующие значения э. д.
д.
с. e
и e»
в заданный момент времени; ψ
e»
— начальная фаза, определяющая значение
э. д. с. е»
при t = 0. Для э. д. с. е
начальная фаза равна нулю (ψ
e
= 0
). Угол ψ
всегда отсчитывают от нулевого значения
синусоидальной величины при переходе
ее от отрицательных значений к
положительным до начала координат (t =
0). При этом положительную начальную
фазу ψ
(рис. 2.2) откладывают влево от начала
координат (в сторону отрицательных
значений ωt
),
а отрицательную фазу — вправо.
Если
у двух или нескольких синусоидальных
величин, изменяющихся с одинаковой
частотой, начала синусоид не совпадают
по времени, то они сдвинуты друг
относительно друга по фазе, т. е. не
совпадают по фазе.
Разность
углов φ
,
равная разности начальных фаз, называют
углом сдвига
фаз. Сдвиг фаз
между одноименными синусоидальными
величинами, например между двумя э. д.
с. или двумя токами, обозначают α
.
Угол сдвига фаз между синусоидами тока
и напряжения или их максимальными
векторами обозначают буквой φ
(рис. 2.3).
Когда
для синусоидальных величин разность
фаз равна ±π
,
то они противоположны
по фазе, если
же разность фаз равна ±π/2
,
то говорят, что они находятся в квадратуре.
Если для синусоидальных величин одной
частоты начальные фазы одинаковы, то
это означает, что они совпадают
по фазе.
Синусоидальные
напряжение и ток, графики которых
представлены на рис. 2.3, описываются
следующим образом:
u
= U
m
sin(ω
t
+
ψ
u
)
;
i
= I
m
sin(ω
t
+
ψ
i
)
, (2.6)
причем
угол сдвига фаз между током и напряжением
(см. рис. 2.3) в этом случае φ
= ψ
u
— ψ
i
.
Уравнения
(2.6) можно записать иначе:
u
= U
m
sin(ωt
+ ψ
i
+ φ)
; i
= I
m
sin(ωt
+ ψ
u
— φ)
,
поскольку
ψ
u
= ψ
i
+ φ
и ψ
i
= ψ
u
— φ
.
Из
этих выражений следует, что напряжение
опережает по фазе ток на угол φ
(или ток отстает по фазе от напряжения
на угол φ
).
Формы
представления синусоидальных электрических
величин.
Любая,
синусоидально изменяющаяся, электрическая
величина (ток, напряжение, ЭДС) может
быть представлена в аналитическом,
графическом и комплексном видах.
1).
Аналитическая
форма представления
I
= I
m
·sin(ω·t
+ ψ
i
),
u
= U
m
·sin(ω·t
+ ψ
u
),
e
= E
m
·sin(ω·t
+ ψ
e
),
где
I
,
u
,
e
– мгновенное значение синусоидального
тока, напряжения, ЭДС, т. е. Значения в
рассматриваемый момент времени;
I
m
,
U
m
,
E
m
– амплитуды синусоидального тока,
напряжения, ЭДС;
(ω·t
+ ψ
)
– фазовый угол, фаза; ω
= 2·π/Т
– угловая частота, характеризующая
скорость изменения фазы;
ψ
i ,
ψ
u ,
ψ
e
– начальные фазы тока, напряжения, ЭДС
отсчитываются от точки перехода
синусоидальной функции через нуль к
положительному значению до начала
отсчета времени (t
= 0). Начальная фаза может иметь как
Начальная фаза может иметь как
положительное так и отрицательное
значение.
Графики
мгновенных значений тока и напряжения
показаны на рис. 2.3
Начальная
фаза напряжения сдвинута влево от начала
отсчёта и является положительной ψ
u
> 0, начальная фаза тока сдвинута вправо
от начала отсчёта и является отрицательной
ψ
i
φ
.
Сдвиг фаз между напряжением и током
φ
= ψ
u
– ψ
i
= ψ
u
– (- ψ
i)
= ψ
u
+ ψ
i .
Применение
аналитической формы для расчёта цепей
является громоздкой и неудобной.
На
практике приходится иметь дело не с
мгновенными значениями синусоидальных
величин, а с действующими. Все расчёты
проводят для действующих значений, в
паспортных данных различных
электротехнических устройств указаны
действующие значения (тока, напряжения),
большинство электроизмерительных
приборов показывают действующие
значения. Действующий ток является
эквивалентом постоянного тока, который
за одно и то же время выделяет в резисторе
такое же количество тепла, как и переменный
ток. Действующее значение связано с
Действующее значение связано с
амплитудным простым соотношением
2).
Векторная
форма представления синусоидальной
электрической величины – это вращающийся
в декартовой системе координат вектор
с началом в точке 0, длина которого равна
амплитуде синусоидальной величины,
угол относительно оси х – её начальной
фазе, а частота вращения – ω
= 2πf
.
Проекция данного вектора на ось у в
любой момент времени определяет
мгновенное значение рассматриваемой
величины.
Рис.
2.4
Совокупность
векторов, изображающих синусоидальные
функции, называют векторной диаграммой,
рис. 2.4
3).
Комплексное
представление синусоидальных электрических
величин сочетает наглядность векторных
диаграмм с проведением точных аналитических
расчётов цепей.
Рис.
2.5
Ток
и напряжение изобразим в виде векторов
на комплексной плоскости, рис.2.5 Ось
абсцисс называют осью действительных
чисел и обозначают +1
,
ось ординат называют осью мнимых чисел
и обозначают +j
.
(В некоторых учебниках ось действительных
чисел обозначают Re
,
а ось мнимых – Im
).
Рассмотрим векторы U
и I
в момент времени t
= 0. Каждому из этих векторов соответствует
комплексное число, которое может быть
представлено в трех формах:
а).
Алгебраической
U
= U
’+
jU
«
I
= I
’
– jI
«,
где
U
«,
U
«,
I
«,
I
»
– проекции векторов на оси действительных
и мнимых чисел.
б).
Показательной
где
U
,
I
– модули (длины) векторов; е
– основание натурального логарифма;
поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
в).
Тригонометрической
U
= U
·(cosψ
u
+ j
sinψ
u)
I
= I
·(cosψ
i
– j
sinψ
i).
При
решении задач в основном применяют
алгебраическую форму (для операций
сложения и вычитания) и показательную
форму (для операций умножения и деления).
Связь между ними устанавливается
формулой Эйлера
е
j
·ψ
=
cosψ
+ j
sinψ
.
Неразветвлённые
электрические цепи
Основы > Задачи и ответы > Постоянный электрический ток
Последовательное и параллельное соединения источников тока
Правило Кирхгофа
1
Найти разность потенциалов между точками а и
b
в схеме, изображенной на рис. 118. Э. д. с. источников тока
e
1
=
1
В и
e
2
=1,3 В, сопротивления резисторов
R
1 = 10
Ом и
R
2 = 5 Ом.
Решение:
Поскольку
e
2
>
e
1
то ток I будет идти в направлении, указанном на рис. 118, при этом разность потенциалов между точками а и b
2
Два элемента с э. д. с.
e
1
=
1
,5
B и
e
2
r1
=0,6
Ом и
r
2 = 0,4 Ом соединены по схеме, изображенной на рис. 119. Какую разность потенциалов между точками а и b покажет вольтметр, если сопротивление вольтметра велико по сравнению с внутренними сопротивлениями элементов?
Решение:
Поскольку
e
2
>
e
1
, то ток I будет идти в направлении, указанном на рис. 119. Током через вольтметр пренебрегаем ввиду
119. Током через вольтметр пренебрегаем ввиду
того, что его сопротивление велико по сравнению с внутренними сопротивлениями элементов. Падение напряжения на внутренних сопротивлениях элементов должно равняться разности э. д. с. элементов, так как они включены навстречу друг другу:
отсюда
Разность потенциалов между точками а и b (показание вольтметра)
3
Два элемента с э. д. с.
e
1
=1.4B и
e
2
= 1,1 В и внутренними сопротивлениями
r
=0,3 Ом и
r
2 = 0,2 Ом замкнуты разноименными полюсами (рис. 120). Найти напряжение на зажимах элементов. При каких условиях разность потенциалов между точками а и
b
равна нулю?
Решение:
4
Два источника тока с одинаковыми э. д. с.
e
= 2 В и внутренними сопротивлениями
r1
=0,4 Ом и
r
2 = 0,2 Ом соединены последовательно. При каком внешнем сопротивлении цепи R напряжение на зажимах одного из источников будет равным нулю?
Решение:
Ток в цепи
(рис.361). Напряжения на зажимах источников тока
Решая первые два уравнения при условии V1=0, получим
Условие V2=0 неосуществимо, так как совместное решение первого и третьего уравнений приводит к значению R
5
Найти внутреннее сопротивление
r1
первого элемента в схеме, изображенной на рис. 121, если напряжение на его зажимах равно нулю. Сопротивления резисторов
121, если напряжение на его зажимах равно нулю. Сопротивления резисторов
R
1 = ЗОм,
R
2 = 6 0м, внутреннее сопротивление второго элемента
r
2 = 0,4 Ом, э. д. с. элементов одинаковы.
Решение:
Ток в общей цепи
По условию задачи напряжение на зажимах первого элемента
отсюда
6
При каком соотношении между сопротивлениями резисторов R
1
, R2, R3 и внутренними сопротивлениями элементов
r1,
r2
(рис. 122) напряжение
на зажимах одного из элементов будет равно нулю? Э. д. с. элементов одинаковы.
Решение:
7
Два генератора с одинаковыми э. д. с.
e
= 6 В и внутренними сопротивлениями
r1
=0,5 Ом и
r2
= 0,38 Ом включены по схеме, изображенной на рис. 123. Сопротивления резисторов R
1
= 2 Ом, R2 = 4 Ом,
R3
= 7 Ом. Найти напряжения V
1
и V2 на зажимах генераторов.
Решение:
Ток в общей цепи
где внешнее сопротивление цепи
Напряжения на зажимах первого и второго генератора
напряжение на зажимах второго генератора
8
Три элемента с э. д. с.
д. с.
e
1
= 2,2 В,
e
2
=
1
,1 В и
e
3
= 0,9 В и внутренними сопротивлениями r
1
= 0,2 Ом,
r
2 = 0,4 Ом и
r
з = 0,5 Ом включены в цепь последовательно. Внешнее сопротивление цепи R=
1
Ом. Найти напряжение на зажимах каждого элемента.
Решение:
По закону Ома для полной цепи ток
Напряжение на зажимах каждого элемента равно разности э. д. с. и падения напряжения на внутреннем сопротивлении элемента:
Напряжение на зажимах батареи элементов равно падению напряжения на внешнем сопротивлении цепи:
Напряжение на зажимах третьего элемента оказалось отрицательным, так как ток определяется всеми сопротивлениями цепи и суммарной э.д.с, а падение напряжения на внутреннем сопротивлении r3 больше, чем э.д.с.
e
3
.
9
Батарея из четырех последовательно включенных в цепь элементов с э. д. с.
e
= 1,25 В и внутренним сопротивлением
r
= 0,1 Ом питает два параллельно соединенных проводника с сопротивлениями
R1
= 50 Ом и
R
2 = 200 Ом. Найти напряжение на зажимах батареи.
Найти напряжение на зажимах батареи.
Решение:
10
Сколько одинаковых аккумуляторов с э. д. с.
e
=
1
,25B и внутренним сопротивлением
r
= 0,004 Ом нужно взять, чтобы составить батарею, которая давала бы на зажимах напряжение V=
11
5 В при токе
I
=25 А?
Решение:
Напряжение на зажимах батареи
Следовательно,
11
Батарея из
n
= 40 последовательно включенных в цепь аккумуляторов с э. д. с.
e
= 2,5 В и внутренним сопротивлением
r
= 0,2 Ом заряжается от сети с напряжением V=121 В. Найти зарядный ток, если последовательно в цепь введен проводник с сопротивлением
R
= 2 Ом.
Решение:
12
Два элемента с э. д. с.
e
1
= 1,25 В и
e
2
= 1,5 В и одинаковыми внутренними сопротивлениями
r
= 0,4 Ом соединены параллельно (рис. 124). Сопротивление резистора
R
= 10 Ом. Найти токи, текущие через резистор и каждый элемент.
Решение:
Падение напряжения на резисторе, если токи текут в направлениях, указанных на рис. 124,
124,
Учитывая, что I=I1+I2, находим
Заметим, что I1
13
Два элемента с э. д. с.
e
1
=6 В и
e
2
= 5 В и внутренними сопротивлениями
r1
= 1 Ом и
r2
= 20м
соединены по схеме, изображенной на рис. 125. Найти ток, текущий через резистор с сопротивлением
R
= 10 Ом.
Решение:
Выбрав направления токов, указанные на рис. 362, составим уравнения Кирхгофа. Для узла b имеем I1+I2-I=0; для контура abef (обход по часовой стрелке)
и для контура bcde (обход против часовой стрелки)
Из этих уравнений найдем
14
Три одинаковых элемента с э. д. с.
e
= 1,6 В и внутренним сопротивлением
r
=0,8 Ом включены в цепь по схеме, изображенной на рис. 126. Миллиамперметр показывает ток
I
=100 мА. Сопротивления резисторов
R
1 = 10Ом и
R2
= 15 0м, сопротивление резистора
R
неизвестно. Какое напряжение V показывает вольтметр? Сопротивление вольтметра очень велико, сопротивление миллиамперметра пренебрежимо мало.
Решение:
Внутреннее сопротивление элементов
Сопротивление параллельно включенных резисторов
Общая э. д. с. элементов
д. с. элементов
e
0
=2
e
Согласно закону Ома для полной цепи
15
Сопротивления резисторов R
1
и
R
2 и э. д. с.
e
1
и
e
2
источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с.
e
3
третьего источника ток через резистор R3 не течет?
Решение:
Выберем направления токов I1, I2 и I3 через резисторы R1, R2 и R3, указанные на рис. 363. Тогда I3=I1+I2. Разность потенциалов между точками а и b будет равна
Если
Исключая I1 находим
16
Цепь из трех одинаковых последовательно соединенных элементов с э.д.с.
e
и внутренним сопротивлением
r
замкнута накоротко (рис. 128). Какое
напряжение покажет вольтметр, подключенный к зажимам одного из элементов?
Решение:
Рассмотрим ту же схему без вольтметра (рис. 364). Из закона Ома для полной цепи находим
Из закона Ома для участка цепи между точками а и b получим
Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.
Поэтому вольтметр будет показывать напряжение, равное нулю.
17
Источник тока с э.д.с.
e
0
включен в схему, параметры которой даны на рис. 129. Найти э.д.с.
e
источника тока и направление его подключения
к выводам а и
b
, при которых ток через резистор с сопротивлением R2 не идет.
Решение:
Подключим источник тока к выводам а и b и выберем направления токов, указанные на рис. 365. Для узла е имеем I=I0+I2. При обходе контуров aefb и ecdf по часовой стрелке получим
Используя условие I2 = 0, находим
Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.
18
Два элемента с одинаковыми э.д.с.
e
включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента
равно 2/3. Найти внутренние сопротивления элементов
r1
и
r
2, если
r
1=2
r
2.
Решение:
19
Два одинаковых элемента с э.д.с.
e
=
1
,5 В
и внутренним сопротивлением
r
= 0,2 Ом замкнуты на
резистор, сопротивление которого составляет в одном
случае R1=0,2
Oм, В другом —
R
2 = 20
Ом.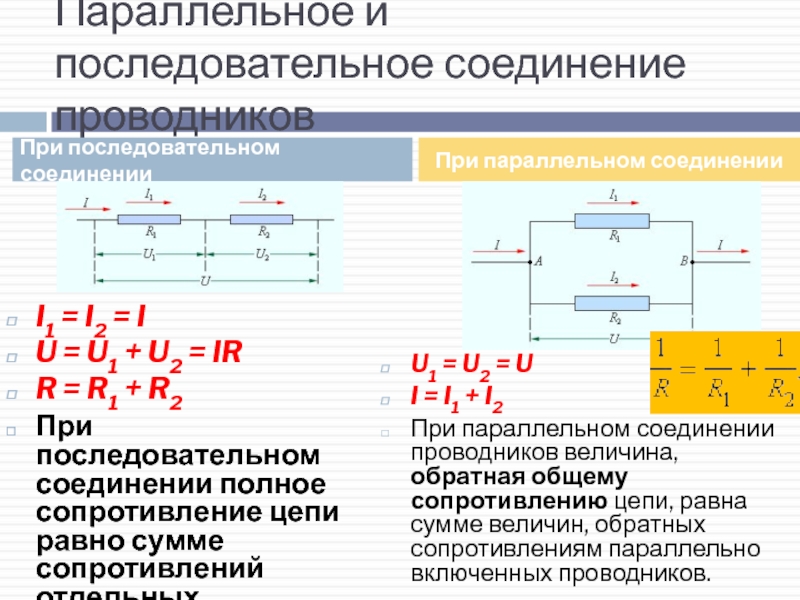 Как нужно
Как нужно
соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?
Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и
e
при последовательном соединении они равны 2r и 2
e
. Через резистор R при этом текут токи
Отсюда видно, что I2>I1, если R/2+rr. Поэтому ток больше при последовательном соединении.
20
Два элемента с э.д.с.
e
1
=4В и
e
2
= 2В
и внутренними сопротивлениями
r1
= 0,25 Ом
и
r
2 = 0,75 Ом включены в схему, изображенную на
рис. 130. Сопротивления резисторов
R1
= 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ.
Найти заряд на конденсаторе.
Решение:
21
К батарее из двух параллельно включенных элементов
с э.д.с.
e
1
и
e
2
и внутренними
сопротивлениями
r1
и
r
2 подключен резистор с сопротивлением R. Найти ток
I
, текущий через резистор R, и токи
I1
и
I
2 в первом и втором элементах. При каких
условиях токи в отдельных цепях могут быть равными
нулю или изменять свое направление на обратное?
Решение:
Выберем направления токов, указанные на рис. 366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим
366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим
Из этих уравнений находим
Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие
Ток I1=0 при
а ток I2 = 0 при
Токи I1 и I2 имеют направления, указанные на рис.366, если
Они меняют свое направление при
22
Батарея из
n
одинаковых аккумуляторов,
соединенных в одном случае последовательно, в другом- параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через
резистор, в обоих случаях будет один и тот же?
Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R
№
r, задача не имеет решения ( n
=1).
23
Батарея из
n
= 4 одинаковых элементов с внутренним сопротивлением
r
=2 Ом, соединенных в одном случае
последовательно, в другом — параллельно, замыкается на резистор с сопротивлением
R
=10Ом.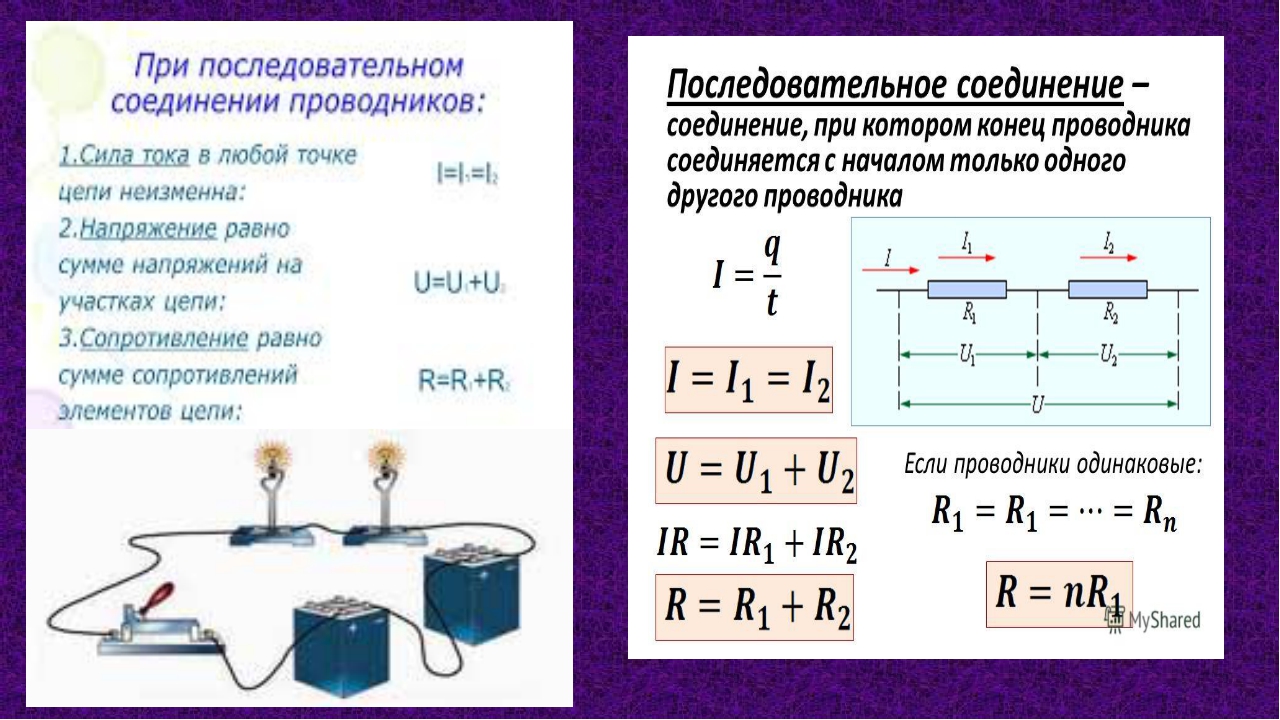 Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с
Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с
R
и
r.
Решение:
где V1 — показание вольтметра при последовательном соединении элементов, V2-при параллельном.
24
Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если
n
=10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э.д.с. элемента
e
= 2 В, его внутреннее сопротивление
r
= 0,2 Ом.
Решение:
25
Батарея составлена из N=600 одинаковых
элементов так, что п групп соединены последовательно
и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента
e
= 2 В, его
внутреннее сопротивление
r
= 0,4 Ом. При каких значениях
n
и
m
батарея, будучи замкнута на внешнее
сопротивление R = 0,6 Ом, отдаст во внешнюю цепь
максимальную мощность? Найти при этом ток, текущий
через сопротивление R.
Решение:
Общее число элементов N=nm (рис. 367). Ток во внешней цепи
367). Ток во внешней цепи
где r/
m
— внутреннее сопротивление группы из т параллельно соединенных элементов, а
n
r/
m
— внутреннее сопротивление
n
групп, соединенных последовательно. Максимальная мощность (см. задачу 848) отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов
n
r/
m
, т. е.
При этом через сопротивление R течет точек I=46 А.
26
Емкость аккумулятора
=80
А
Ч
ч. Найти емкость батареи из
n
=
3
таких аккумуляторов, включенных последовательно и параллельно.
Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора:
При параллельном соединении
n
аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в
n
раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:
е. емкость батареи в п раз больше емкости отдельного аккумулятора:
Заметим, однако, что энергия
отдаваемая батареей в цепь, и при последовательном и при параллельном соединении
n
аккумуляторов в
n
раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в
n
раз больше э. д. с. одного аккумулятора, а при параллельном соединении э.д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в
n
раз.
27
Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора
Qo
=64
А
Ч
ч
.
Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость
Три параллельно включенные группы дают общую емкость батареи
28
Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви
I
=0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.
Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.
Решение:
29
Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока
e
1
= 6,5 В и
e
2
= 3,9 В. Сопротивления резисторов R1=R2=R3=R4=R5=R6=R=10 Ом.
Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I1 + I2 — I3 = 0 для узла b;
I3 — I4 — I5 =0 для узла h; I5 — I1 — I6 = 0 для узла f: при этом
Для контура abfg (обход по часовой стрелке),
Для контура bcdh (обход против часовой стрелки) и
для контура hdef (обход по часовой
стрелке). Решая эту систему уравнений с учетом, что все сопротивления одинаковы и равны R=10 Ом, получим
Отрицательные значения токов I2, I4 и I6 показывают, что при данных э.д.с. источников и сопротивлениях резисторов эти токи текут в стороны, противоположные указанным на рис. 133.
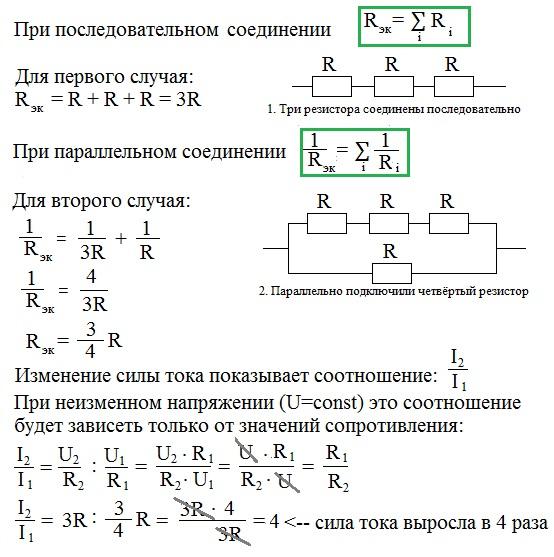
При параллельном соединении ток. Соединение резисторов параллельно и последовательно
Возьмем три постоянных сопротивления R1, R2 и R3
и включим их в цепь так, чтобы конец первого сопротивления R1
был соединен с началом второго сопротивления R
2, конец второго — с началом третьего R
3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1
1
).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2
и U3 = IR3
или
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I
за скобки, получим IR = I(R1 + R2 + R3)
.
Поделив теперь обе части равенства на I
, будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1
== 10 Ом, R
2 = 20 Ом и R
3 = 50 Ом). Соединим их последовательно (рис. 2
Соединим их последовательно (рис. 2
) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R
= 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи : 60 / 80
= 0
,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U
1 = 0,75х 10 = 7,5 В, U
2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U
= 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1
и I
2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1
, а во второй — I
2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I
до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки.
I = I1 + I2
Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи
.
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3
, непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1
и U2 на сопротивлениях R1
и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2
,
где U — напряжение на зажимах источника тока; U1
— падение напряжения на сопротивлении R1
, U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR
.
Поэтому для каждой ветви можно написать: U1 = I1R1
и U2 = I2R2
, но так как U1
= U2, то и I1R1 = I2R2
.
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1
т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей.
Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1
и R
2, подключенных к источнику тока. Пусть R1
= 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 =
U / R1 = 3 / 10 = 0
,3 А = 300 мА
I
2 =
U / R
2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1
+I2
= 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1
== 10 Ом вдвое меньше R
2 = 20 Ом, при этом I1
= 300 мА вдвое больше I2
= 150 мА. Общий ток в цепи I
= 450 мА разветвился на две части так, что большая его часть (I1
= 300 мА) пошла через меньшее сопротивление (R1
= 10 Ом), а меньшая часть (R2
= 150 мА) -через большее сопротивление (R
2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления.
Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R
, где I
— ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1
, I2 = U2 / R2
, где I1
и I
2 — токи в ветвях; U1
и U2 — напряжение на ветвях; R1
и R2
— сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2
, то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U
(1 / R1 +
1 / R2
)
Разделив теперь обе части равенства на U
, будем окончательно иметь 1 / R
=
1 / R1 +
1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению
, мы можем сказать, что в полученной формуле 1 / R —
проводимость внешней цепи; 1 / R1
проводимость первой ветви; 1 / R2-
проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2
= 20 Ом и R3
= 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5
).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R
=
1 / R1 +
1 / R2
, можем написать 1 / R
=
1 / R1 +
1 / R2 +
1 / R3
и, подставляя известные величины, получим 1 / R
=
1 /
10 +
1 /
20 +
1 /
60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6
Следовательно, эквивалентное сопротивление
R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений
, т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3
равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1
Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1
,2 А I
2 = U/R
2 = 12 /
20 = 1
,6 А I
3 = U/R1 = 12 /
60 =
0,2
А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3
=1,2 + 0,6 + 0,2 =
2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U
/
R
= 12 / 6 = 2
А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1
и R2
, то формулу 1 / R
=
1 / R1 +
1 / R2
можно преобразовать так: 1/R = (R2 + R1) / R1 R2
и, решая равенство относительно R, получить R = R1
х R2 /
(R1 + R2
), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Знаете ли Вы,
что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, «мысленный эксперимент» фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей «мысленных экспериментов» является обман слушателя или читателя путем замены настоящего физического эксперимента его «куклой» — фиктивными рассуждениями под честное слово без самой физической проверки.
Таким образом, основной задачей заявителей «мысленных экспериментов» является обман слушателя или читателя путем замены настоящего физического эксперимента его «куклой» — фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, «мысленными экспериментами» привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие «фантики» от настоящих ценностей.
Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: «Если факт не соответствует теории — измените факт» (В другом варианте » — Факт не соответствует теории? — Тем хуже для факта»).
Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: «Если факт не соответствует теории — измените факт» (В другом варианте » — Факт не соответствует теории? — Тем хуже для факта»).
Максимально, на что может претендовать «мысленный эксперимент» — это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.
В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.
п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.
Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.
Последовательное соединение
Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т. д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.
Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания.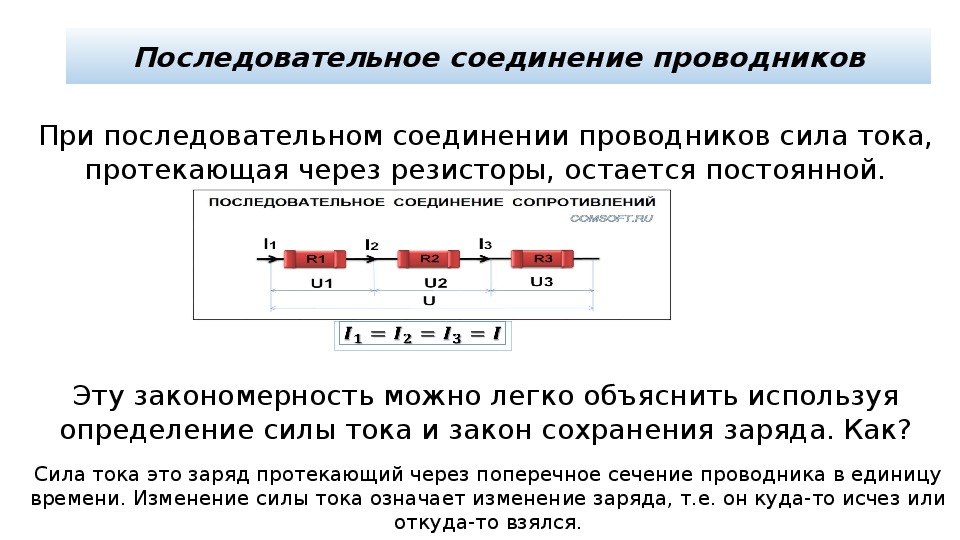 Для простоты здесь и далее изобразим источник в виде гальванического элемента.
Для простоты здесь и далее изобразим источник в виде гальванического элемента.
Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:
Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.
Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.
Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.
Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.
Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.
В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.
К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.
Параллельное соединение
Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.
Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.
Здесь I — ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.
Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:
Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.
Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.
Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.
Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.
В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях. Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.
Сравнение последовательных и параллельных цепей
Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно. При этом вся цепь может быть образована из разных соединений таких частей между собой.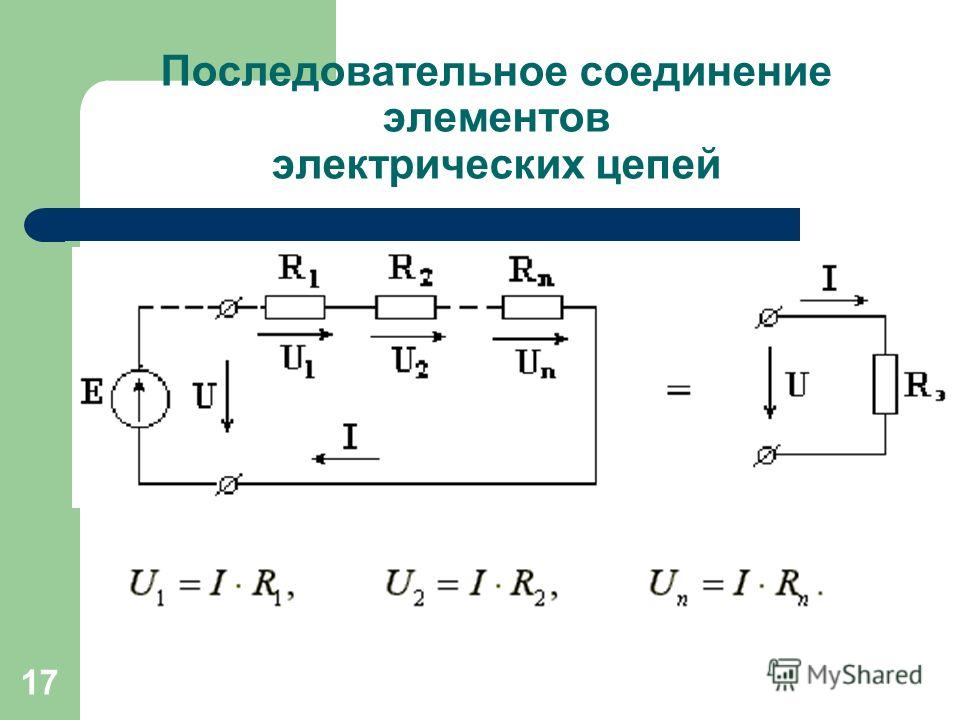 Для примера рассмотрим схему:
Для примера рассмотрим схему:
Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.
Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.
Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.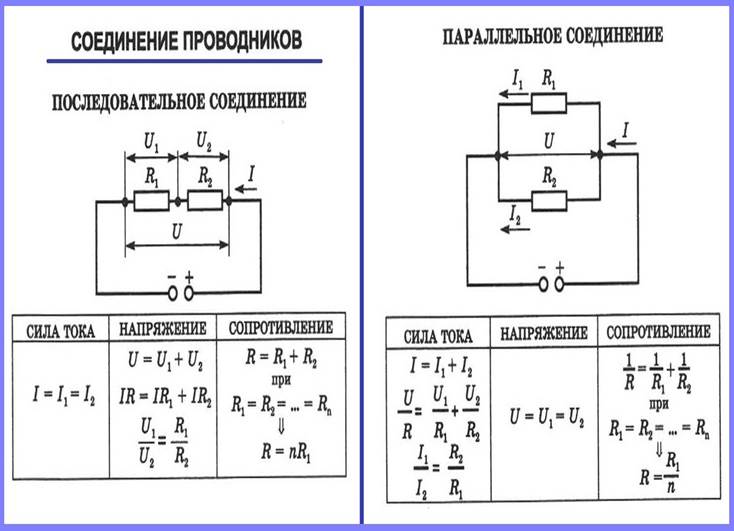
Андрей Повный
Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
- Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
- Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
- Внешняя часть цепи, где заряды движутся, увлекаемые полем.
- Внутренняя часть цепи, где заряды движутся против напряженности.
Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
Приведем некоторые тезисы касательно рассматриваемой тематики:
- При последовательном включении суммируются сопротивления, при параллельном — проводимости:
- Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
- Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
- Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот.
 При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
- Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
- Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Если нам надо, чтобы электроприбор работал, мы должны подключить его к . При этом ток должен проходить через прибор и возвращаться вновь к источнику, то есть цепь должна быть замкнутой.
Но подключение каждого прибора к отдельному источнику осуществимо, в основном, в лабораторных условиях. В жизни же приходится иметь дело с ограниченным количеством источников и довольно большим количеством потребителей тока. Поэтому создают системы соединений, позволяющие нагрузить один источник большим количеством потребителей. Системы при этом могут быть сколь угодно сложными и разветвленными, но в их основе лежит всего два вида соединения: последовательное и параллельное соединение проводников. Каждый вид имеет свои особенности, плюсы и минусы. Рассмотрим их оба.
Последовательное соединение проводников
Последовательное соединение проводников – это включение в электрическую цепь нескольких приборов последовательно, друг за другом. Электроприборы в данном случае можно сравнить с людьми в хороводе, а их руки, держащие друг друга – это провода, соединяющие приборы. Источник тока в данном случае будет одним из участников хоровода.
Электроприборы в данном случае можно сравнить с людьми в хороводе, а их руки, держащие друг друга – это провода, соединяющие приборы. Источник тока в данном случае будет одним из участников хоровода.
Напряжение всей цепи при последовательном соединении будет равно сумме напряжений на каждом включенном в цепь элементе. Сила тока в цепи будет одинакова в любой точке. А сумма сопротивлений всех элементов составит общее сопротивление всей цепи. Поэтому последовательное сопротивление можно выразить на бумаге следующим образом:
I=I_1=I_2=⋯=I_n ; U=U_1+U_2+⋯+U_n ; R=R_1+R_2+⋯+R_n ,
Плюсом последовательного соединения является простота сборки, а минусом – то, что если один элемент выйдет из строя, то ток пропадет во всей цепи. В такой ситуации неработающий элемент будет подобен ключу в выключенном положении. Пример из жизни неудобства такого соединения наверняка припомнят все люди постарше, которые украшали елки гирляндами из лампочек.
Если в такой гирлянде выходила из строя хотя бы одна лампочка, приходилось перебирать их все, пока не найдешь ту самую, перегоревшую. В современных гирляндах эта проблема решена. В них используют специальные диодные лампочки, в которых при перегорании сплавляются вместе контакты, и ток продолжает беспрепятственно проходить дальше.
В современных гирляндах эта проблема решена. В них используют специальные диодные лампочки, в которых при перегорании сплавляются вместе контакты, и ток продолжает беспрепятственно проходить дальше.
Параллельное соединение проводников
При параллельном соединении проводников все элементы цепи подключаются к одной и той же паре точек, можно назвать их А и В. К этой же паре точек подключают источник тока. То есть получается, что все элементы подключены к одинаковому напряжению между А и В. В то же время ток как бы разделяется на все нагрузки в зависимости от сопротивления каждой из них.
Параллельное соединение можно сравнить с течением реки, на пути которой возникла небольшая возвышенность. Вода в таком случае огибает возвышенность с двух сторон, а потом вновь сливается в один поток. Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.
Напряжение тока в каждой отдельной ветви будет равно общему напряжению в цепи. Общий ток цепи будет складываться из токов всех отдельных ветвей. А вот общее сопротивление цепи при параллельном соединении будет меньше сопротивления тока на каждой из ветвей. Это происходит потому, что общее сечение проводника между точками А и В как бы увеличивается за счет увеличения числа параллельно подключенных нагрузок. Поэтому общее сопротивление уменьшается. Параллельное соединение описывается следующими соотношениями:
U=U_1=U_2=⋯=U_n ; I=I_1+I_2+⋯+I_n ; 1/R=1/R_1 +1/R_2 +⋯+1/R_n ,
где I — сила тока, U- напряжение, R – сопротивление, 1,2,…,n – номера элементов, включенных в цепь.
Огромным плюсом параллельного соединения является то, что при выключении одного из элементов, цепь продолжает функционировать дальше. Все остальные элементы продолжают работать. Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.
Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.
Нужна помощь в учебе?
Предыдущая тема: Расчёт сопротивления проводников и реостаты: формулы
Следующая тема:   Работа и мощность тока
Вконтакте
Одноклассники
Google+
Параллельное и последовательное соединение. Последовательное и параллельное соединения проводников
В физике изучается тема про параллельное и последовательное соединение, причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.
Как различить эти два соединения?
Внимательно посмотрите на схему.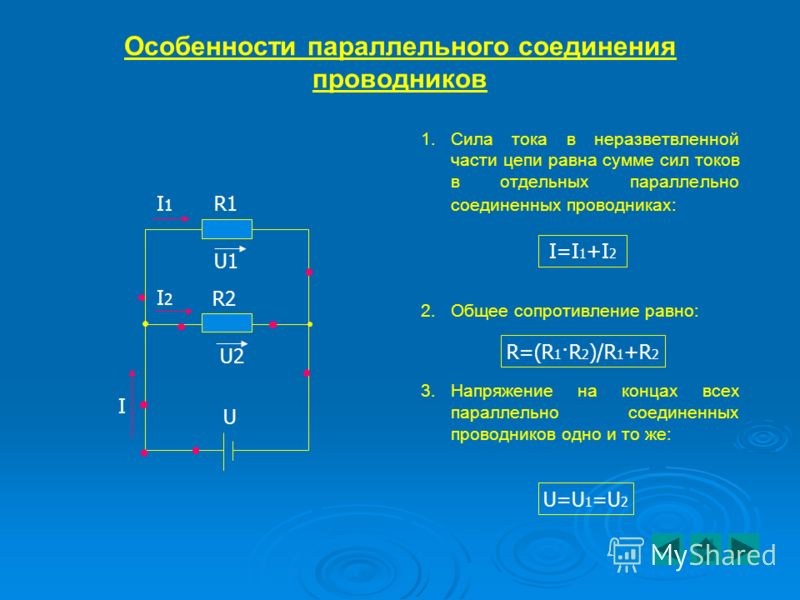 Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину силы тока в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
I общ = I 1 = I 2
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при параллельном соединении проводников:
I общ = I 1 + I 2
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
U общ = U 1 + U 2, где U — обозначение, принятое для электрического напряжения.
Другая ситуация складывается, если рассматривается параллельное соединение резисторов. Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
U общ = U 1 = U 2
Формулы для электрического сопротивления
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — Iобщ * Rобщ = I1 * R1 + I2 * R2;
- параллельно необходимо пользоваться формулой для силы тока — Uобщ / Rобщ = U1 / R1 + U2 / R2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны.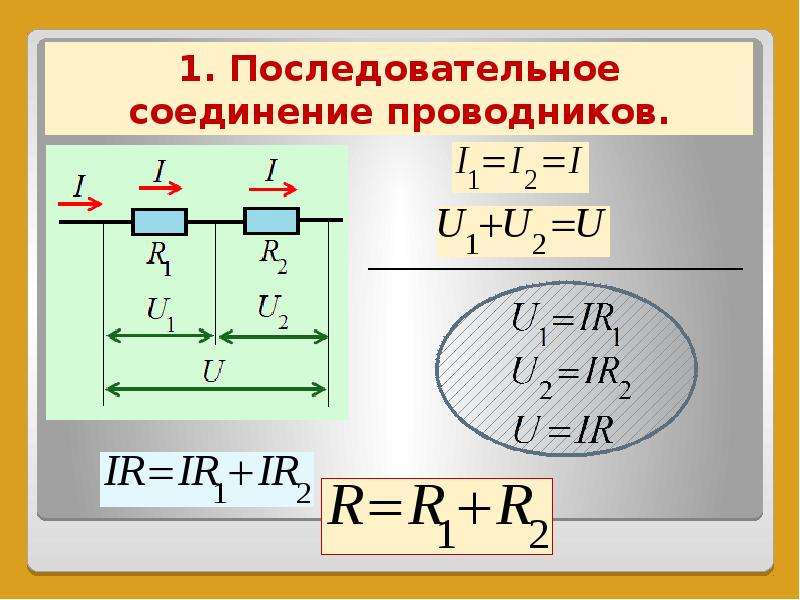 Значит, их можно сократить. То есть получаются такие выражения:
Значит, их можно сократить. То есть получаются такие выражения:
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).
При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу.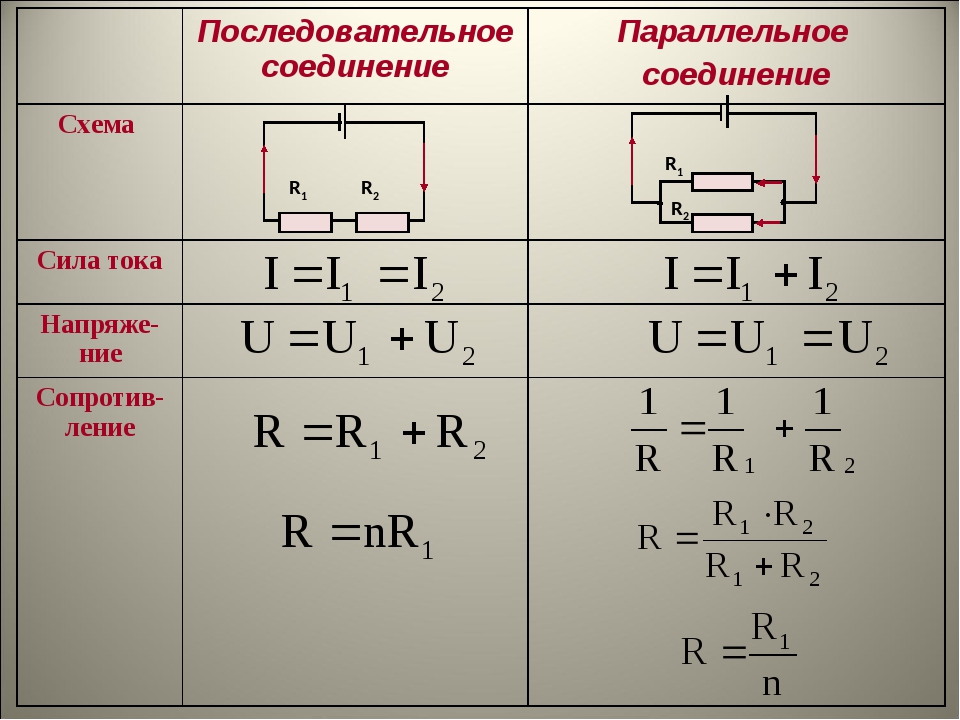 Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.
Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2.
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2.
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Как влияет соединение проводников на ремонт новогодней гирлянды?
Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.
Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.
Что происходит с цепью, если в нее включены не резисторы, а конденсаторы
При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
q общ = q 1 = q 2.
Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С. В ней С — емкость конденсатора.
Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:
С = q / (U 1 + U 2).
Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С 1 + 1 / С 2.
Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное.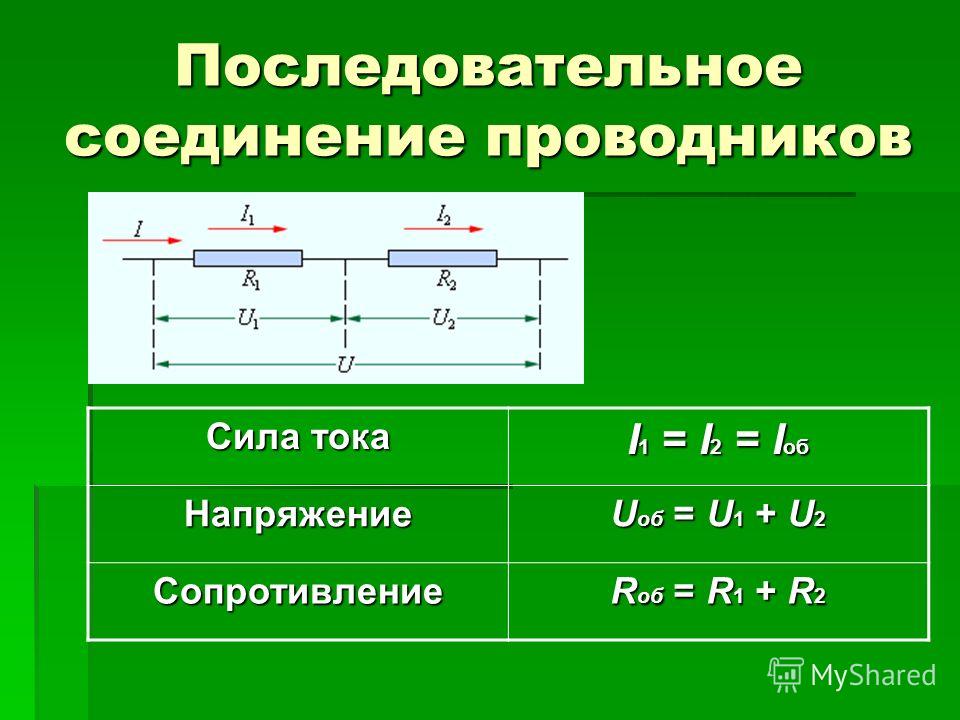 Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
С = (q 1 + q 2 ) / U.
То есть эта величина считается, как сумма каждого из использованных в соединении приборов:
С = С 1 + С 2.
Как определить общее сопротивление произвольного соединения проводников
То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.
Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).
Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.
Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.
Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.
Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:
- сначала ту, которая приведена для последовательного соединения;
- потом для параллельного;
- и снова для последовательного.
Подобным образом можно развернуть любую, даже очень сложную схему.
Задача на последовательное соединение проводников
Условие. В цепи друг за другом подсоединены две лампы и резистор.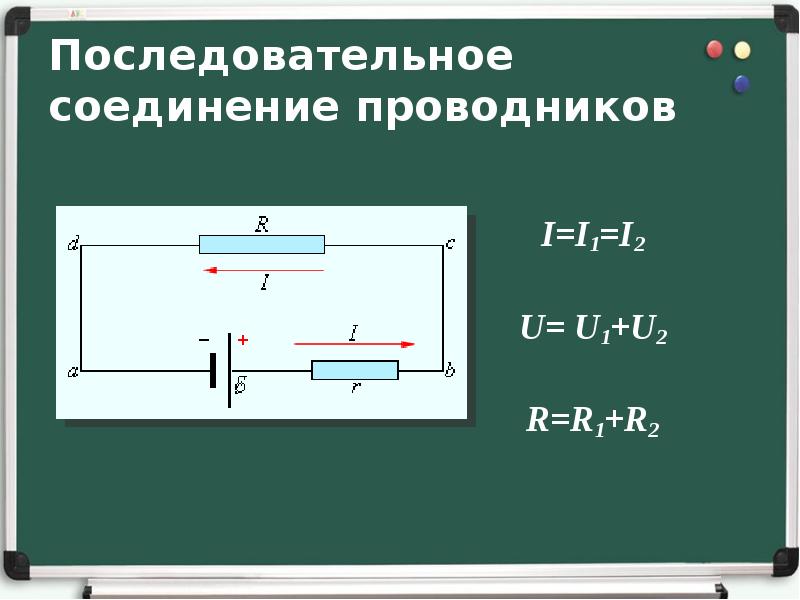 Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?
Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?
Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.
Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.
Ответ. Сопротивление резистора равно 2,5 Ом.
Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.
Решение. Проще начать с параллельного подключения. В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.
Таким образом, общая емкость оказывается равной 75 мкФ.
Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.
Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.
Соединение элементов питания и батарей
Источники напряжения обычно называют источниками питания. Для увеличения тока или напряжения, а может и того и другого источники питания (элементы, батареи) могут соединяться вместе. Существует три типа соединения элементов питания:
1. Последовательное соединение элементов.
2. Параллельное соединение элементов.
3. Последовательно-параллельное (смешанное) соединение элементов.
Последовательное соединение элементов.
При последовательном соединении элементов питания выделяются две схемы: последовательно-дополняющая и последовательно-препятствующая.
В последовательно-дополняющей схеме положительный вывод первого элемента питания соединяется с отрицательным выводом второго элемента питания; положительный вывод второго элемента питания соединяется с отрицательным выводом третьего элемента питания и т.д. (рисунок 3.11.)
Рисунок 3.11.Последовательное соединение элементов питания.
При таком соединении источников питания через все элементы будет течь одинаковый ток:
Iобщ=I1=I2=I3
Индексы в обозначениях токов указывают на номера отдельных источников питания (элементов или батарей питания)
А полное напряжение при последовательном соединении равно сумме напряжений (ЭДС) отдельных элементов:
Еобщ = Е1 + Е2 + Е3.
При последовательно-препятствующем включении источников питания, они соединяются друг с другом одноименными выводами. Но на практике такая схема не применяется или применяется, но очень редко.
Параллельное соединение элементов.
При параллельном соединении элементов питания, их одноименные выводы соединяются вместе, то есть плюс к плюсу, минус к минусу (рис 3. 12).
12).
Рисунок 3.11.Параллельное соединение элементов питания.
В этом случае общий ток будет равен сумме токов каждого элемента:
Iобщ=I1+I2+I3
Общее напряжение при параллельном включении источников питания будет равно напряжению каждого отдельного источника.
Еобщ = Е1 = Е2 = Е3.
Последовательно-параллельное соединение элементов напряжения.
Источники питания включают по последовательно-параллельной схеме для увеличения, как тока, так и напряжения. При этом основываются на том, что параллельное включение увеличивает силу тока, а последовательное увеличивает общее напряжение. На рисунке 3.13 показаны примеры последовательно-параллельных схем включения элементов питания.
Рисунок 3.11.Последовательно-параллельное соединение элементов питания.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Расчет напряжения при последовательном соединении.
 Соединение резисторов
Соединение резисторов
Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.
Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.
Параллельное подключение
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым — во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.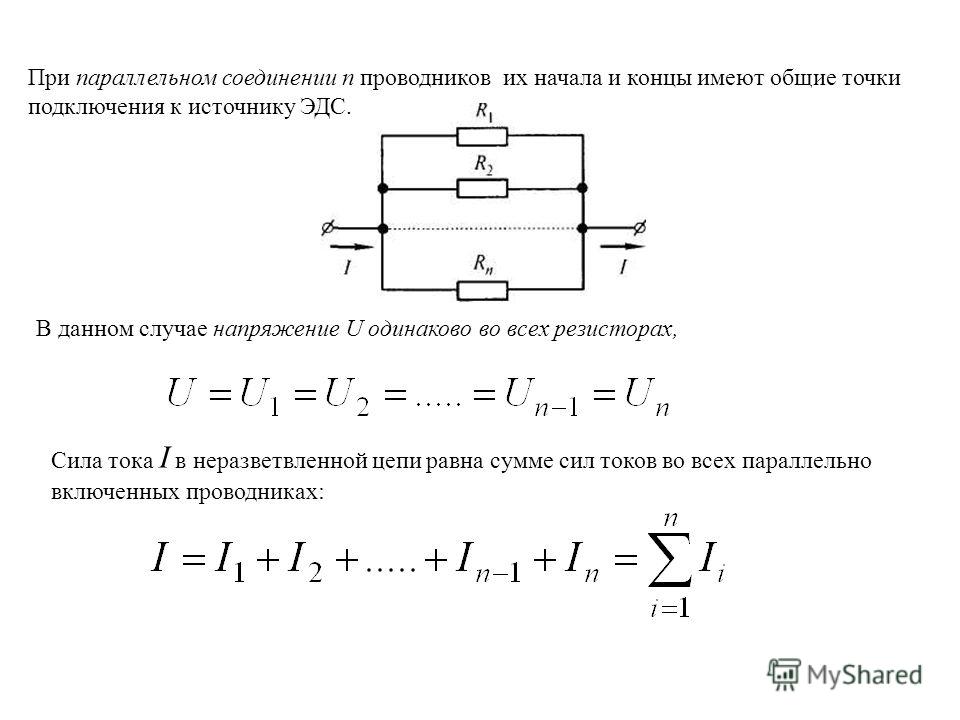
Последовательное подключение
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.
Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.
В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов.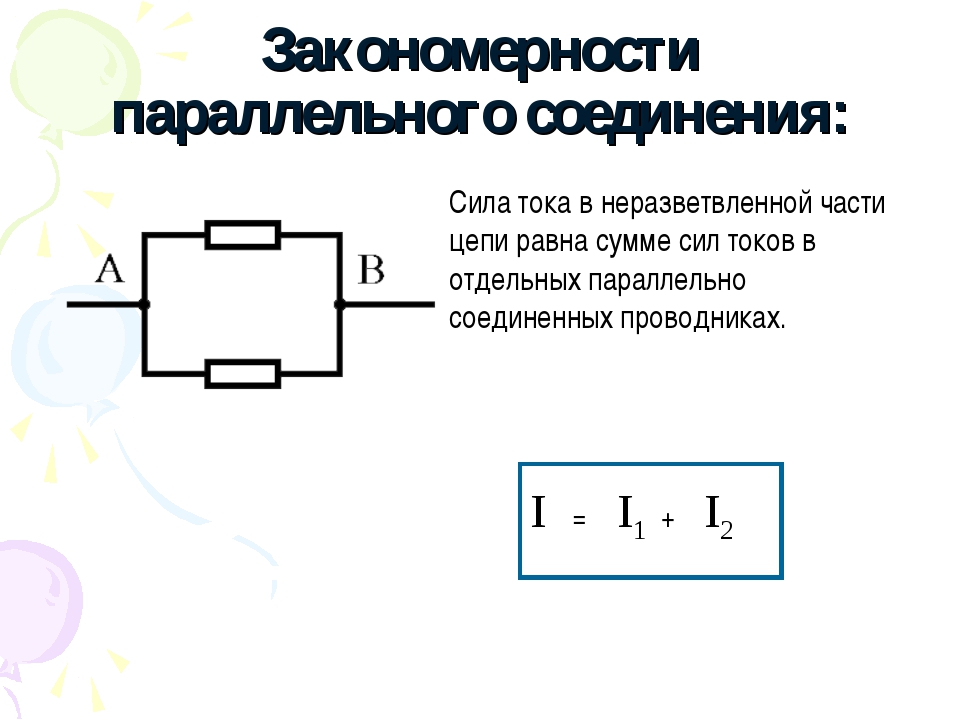 В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
Подключение светодиодов
Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. во многом зависит от напряжения источника тока.
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.
При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А). Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь.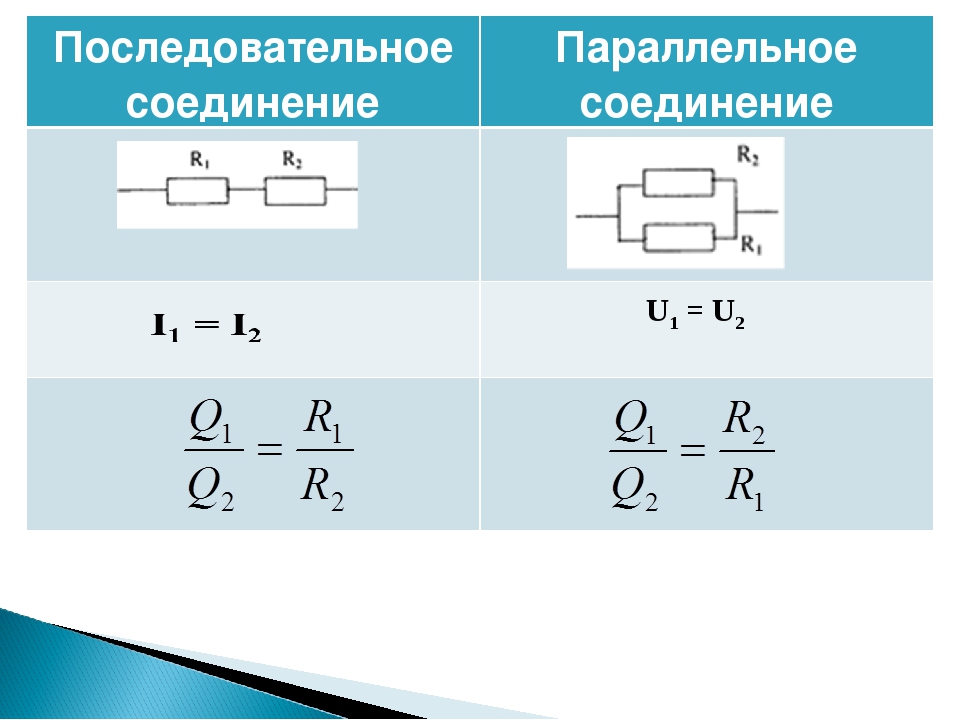 И она может быть только последовательной.
И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R
= 1/U
, где
R
= 1
Ом
А мощность будет выделяться P
=
I
*
U
,
то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G
, по аналогии с сопротивлением R
и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I
=
U
*
G
&
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.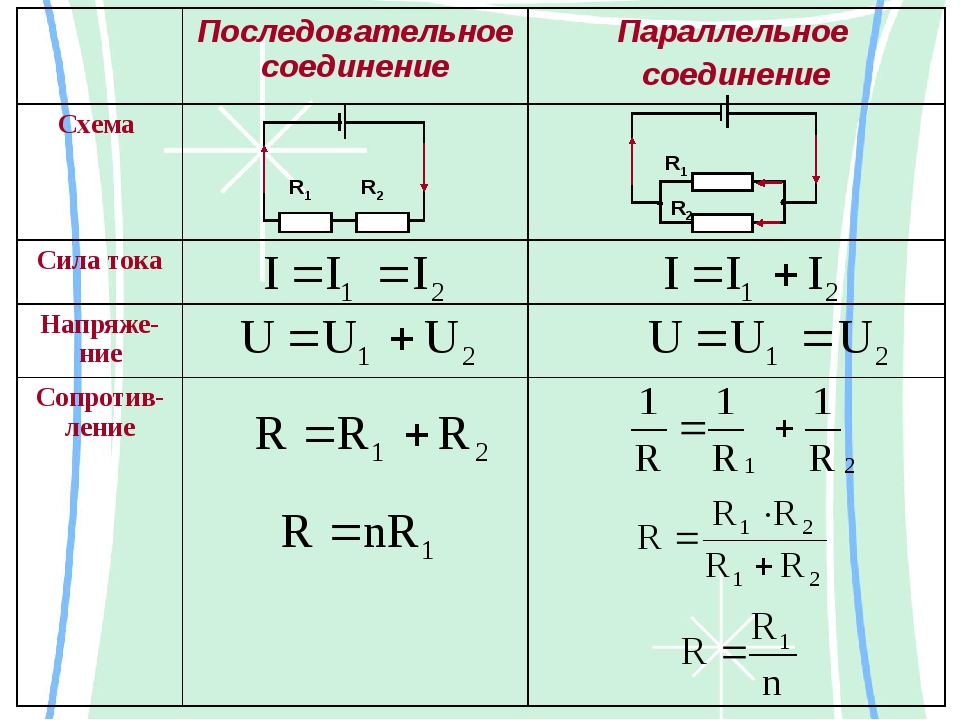
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Содержание:
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.

- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.

- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Содержание:
В электрических цепях используются различные типы соединений. Основными являются последовательные, параллельные и смешанные схемы подключений. В первом случае используется несколько сопротивлений, соединенных в единую цепочку друг за другом. То есть, начало одного резистора соединяется с концом второго, а начало второго — с концом третьего и так далее, до любого количества сопротивлений. Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках. Для определения и сравнения других параметров электрической цепи, следует рассматривать и остальные виды соединений, обладающие собственными свойствами и характеристиками.
Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках. Для определения и сравнения других параметров электрической цепи, следует рассматривать и остальные виды соединений, обладающие собственными свойствами и характеристиками.
Последовательное и параллельное соединение сопротивлений
Любая нагрузка обладает сопротивлением, препятствующим свободному течению электрического тока. Его путь проходит от источника тока, через проводники к нагрузке. Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.
В большинстве электрических цепей применяются медные проводники. Каждая цепь содержит приемники энергии — нагрузки, обладающие различными сопротивлениями. Параметры соединения лучше всего рассматривать на примере внешней цепи источника тока, состоящей из трех резисторов R1, R2, R3. Последовательное соединение предполагает поочередное включение этих элементов в замкнутую цепь.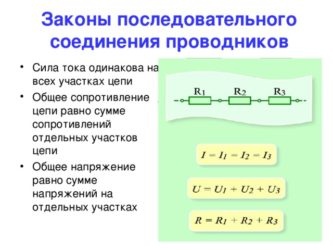 То есть начало R1 соединяется с концом R2, а начало R2 — с концом R3 и так далее. В такой цепочке может быть любое количество резисторов. Эти символы используют в расчетах .
То есть начало R1 соединяется с концом R2, а начало R2 — с концом R3 и так далее. В такой цепочке может быть любое количество резисторов. Эти символы используют в расчетах .
На всех участках будет одинаковой: I = I1 = I2 = I3, а общее сопротивление цепи составит сумму сопротивлений всех нагрузок: R = R1 + R2 + R3. Остается лишь определить, каким будет при последовательном соединении. В соответствии с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.
При постоянном значении напряжения, ток при последовательном соединении будет находиться в зависимости от сопротивления цепи. Поэтому при изменении сопротивления хотя-бы на одной из нагрузок, произойдет изменение сопротивления во всей цепи. Кроме того, изменятся ток и напряжение на каждой нагрузке. Основным недостатком последовательного соединения считается прекращение работы всех элементов цепи, при выходе из строя даже одного из них.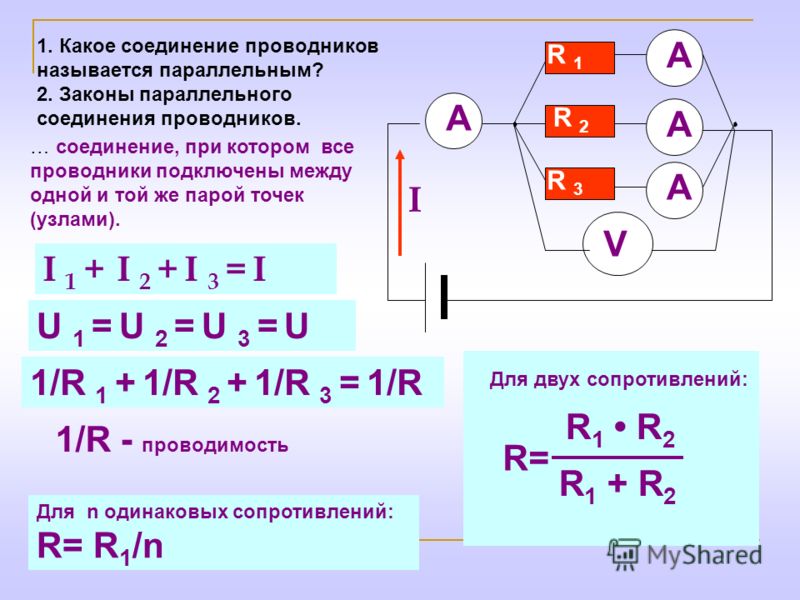
Совершенно другие характеристики тока, напряжения и сопротивления получаются при использовании параллельного соединения. В этом случае начала и концы нагрузок соединяются в двух общих точках. Происходит своеобразное разветвление тока, что приводит к снижению общего сопротивления и росту общей проводимости электрической цепи.
Для того чтобы отобразить эти свойства, вновь понадобится закон Ома. В данном случае сила тока при параллельном соединении и его формула будет выглядеть так: I = U/R. Таким образом, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n. Это указывает на обратно пропорциональное распределение токов в нагрузках по отношению к сопротивлениям этих нагрузок. То есть, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться. В виде формул все характеристики отображаются следующим образом: сила тока — I = I1 + I2 + I3, напряжение — U = U1 = U2 = U3, сопротивление — 1/R = 1/R1 + 1/R2 + 1/R3.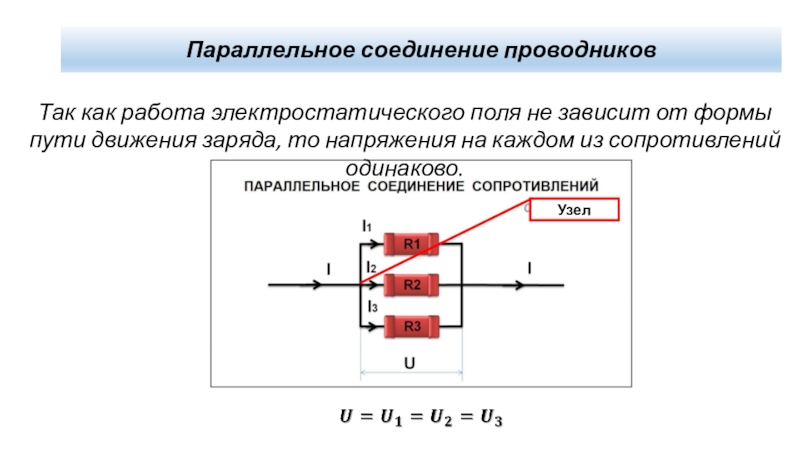
При неизменном значении напряжения между элементами, токи в этих резисторах не имеют зависимости друг от друга. Если один или несколько резисторов будут выключены из цепи, это никак не повлияет на работу других устройств, остающихся включенными. Данный фактор является основным преимуществом параллельного соединения электроприборов.
В схемах обычно не используется только последовательное соединение и параллельное соединение сопротивлений, они применяются в комбинированном виде, известном как . Для вычисления характеристик таких цепей применяются формулы обоих вариантов. Все расчеты разбиваются на несколько этапов, когда вначале определяются параметры отдельных участков, после чего они складываются и получается общий результат.
Законы последовательного и параллельного соединения проводников
Основным законом, применяемым при расчетах различных видов соединений, является закон Ома. Его основным положением является наличие на участке цепи силы тока, прямо пропорциональной напряжению и обратно пропорциональной сопротивлению на данном участке.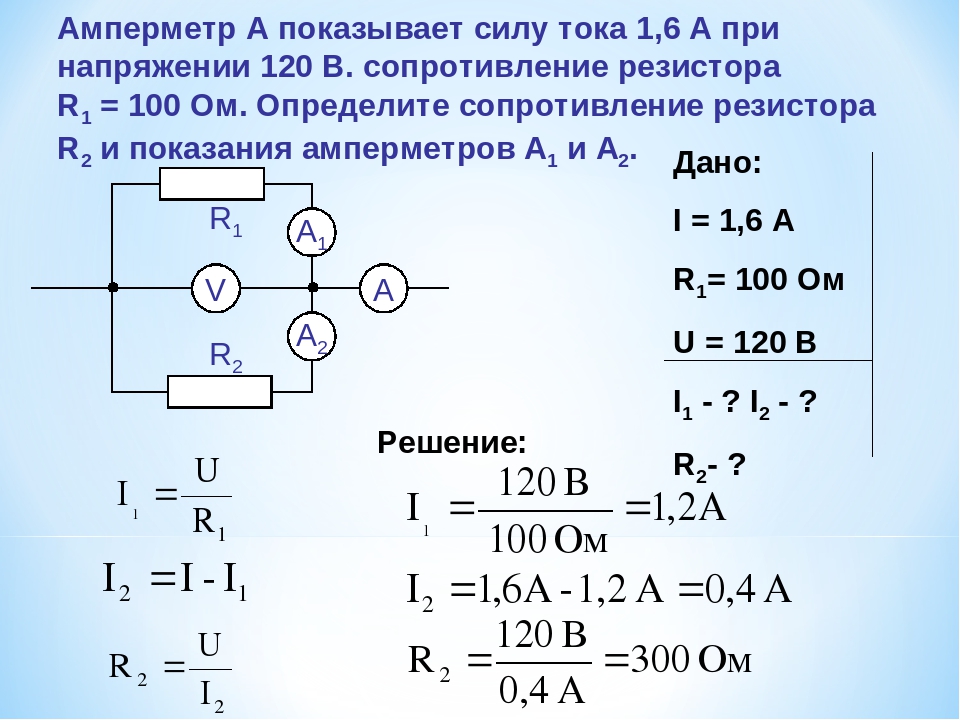 В виде формулы этот закон выглядит так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно или параллельно. Порядок вычислений и зависимость всех параметров от закона Ома наглядно показаны на рисунке. Отсюда выводится и формула последовательного соединения.
В виде формулы этот закон выглядит так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно или параллельно. Порядок вычислений и зависимость всех параметров от закона Ома наглядно показаны на рисунке. Отсюда выводится и формула последовательного соединения.
Более сложные вычисления с участием других величин требуют применения . Его основное положение заключается в том, что несколько последовательно соединенных источников тока, будут обладать электродвижущей силой (ЭДС), составляющей алгебраическую сумму ЭДС каждого из них. Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если выполняется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n. Эти положения актуальны не только для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.
В том случае, когда ЭДС источников будет иметь разное значение, для расчетов силы тока на различных участках цепи применяются дополнительные правила Кирхгофа.
Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы. Некоторые решают проблемы параллельного и последовательного соединения проводников методом «тыка», для многих «несгораемая» гирлянда является необъяснимой, но привычной аксиомой. Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом. Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Основные электрические величины цепи
Для того чтобы выяснить, как то или иное соединение проводников повлияет на характеристики схемы, необходимо определиться с величинами, которые характеризуют любую электрическую цепь. Вот основные из них:
Взаимная зависимость электрических величин
Теперь необходимо определиться
, как все вышеперечисленные величины зависят одна от другой. Правила зависимости несложны и сводятся к двум основным формулам:
Правила зависимости несложны и сводятся к двум основным формулам:
Здесь I – ток в цепи в амперах, U – напряжение, подводимое к цепи в вольтах, R – сопротивление цепи в омах, P – электрическая мощность цепи в ваттах.
Предположим, перед нами простейшая электрическая цепь, состоящая из источника питания с напряжением U и проводника с сопротивлением R (нагрузки).
Поскольку цепь замкнута, через нее течет ток I. Какой величины он будет? Исходя из вышеприведенной формулы 1, для его вычисления нам нужно знать напряжение, развиваемое источником питания, и сопротивление нагрузки. Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
220 / 100 = 2,2 А.
Какова мощность этого паяльника
? Воспользуемся формулой 2:
2,2 * 220 = 484 Вт.
Хороший получился паяльник, мощный, скорее всего, двуручный. Точно так же, оперируя этими двумя формулами и преобразуя их, можно узнать ток через мощность и напряжение, напряжение через ток и сопротивление и т.
д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:
60 / 220 = 0,27 А или 270 мА.
Сопротивление спирали лампы в рабочем режиме:
220 / 0,27 = 815 Ом.
Схемы с несколькими проводниками
Все рассмотренные выше случаи являются простыми – один источник, одна нагрузка. Но на практике нагрузок может быть несколько, и соединены они бывают тоже по-разному. Существует три типа соединения нагрузки:
- Параллельное.
- Последовательное.
- Смешанное.
Параллельное соединение проводников
В люстре 3 лампы, каждая по 60 Вт. Сколько потребляет люстра? Верно, 180 Вт. Быстренько подсчитываем сначала ток через люстру:
180 / 220 = 0,818 А.
А затем и ее сопротивление:
220 / 0,818 = 269 Ом.
Перед этим мы вычисляли сопротивление одной лампы (815 Ом) и ток через нее (270 мА). Сопротивление же люстры оказалось втрое ниже, а ток — втрое выше. А теперь пора взглянуть на схему трехрожкового светильника.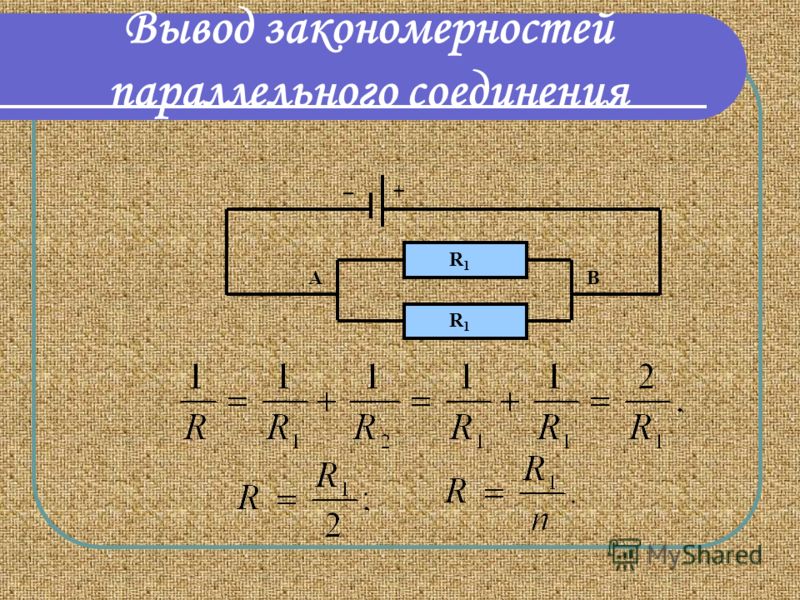
Все лампы в нем соединены параллельно и подключены к сети. Получается, при параллельном соединении трех ламп общее сопротивление нагрузки уменьшилось втрое? В нашем случае — да, но он частный – все лампы имеют одинаковые сопротивление и мощность. Если каждая из нагрузок будет иметь свое сопротивление, то для подсчета общего значения простого деления на количество нагрузок мало. Но и тут есть выход из положения – достаточно воспользоваться вот этой формулой:
1/Rобщ. = 1/R1 + 1/R2 + … 1/Rn.
Для удобства использования формулу можно легко преобразовать:
Rобщ. = (R1*R2*… Rn) / (R1+R2+ … Rn).
Здесь Rобщ
. – общее сопротивление цепи при параллельном включении нагрузки. R1 … Rn – сопротивления каждой нагрузки.
Почему увеличился ток, когда вы включили параллельно три лампы вместо одной, понять несложно – ведь он зависит от напряжения (оно осталось неизменным), деленного на сопротивление (оно уменьшилось). Очевидно, что и мощность при параллельном соединении увеличится пропорционально увеличению тока.
Последовательное соединение
Теперь настала пора выяснить, как изменятся параметры цепи, если проводники (в нашем случае лампы) соединить последовательно.
Расчет сопротивления при последовательном соединении проводников исключительно прост:
Rобщ. = R1 + R2.
Те же три шестидесятиваттные лампы, соединенные последовательно, составят уже 2445 Ом (см. расчеты выше). Какими будут последствия увеличения сопротивления цепи? Согласно формулам 1 и 2 становится вполне понятно, что мощность и сила тока при последовательном соединении проводников упадет. Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Общее напряжение, приложенное ко всей цепи, так и осталось 220 В. Но оно поделилось между каждой из ламп пропорционально их сопротивлению! Поскольку лампы у нас одинаковой мощности и сопротивления, то напряжение поделилось поровну: U1 = U2 = U3 = U/3.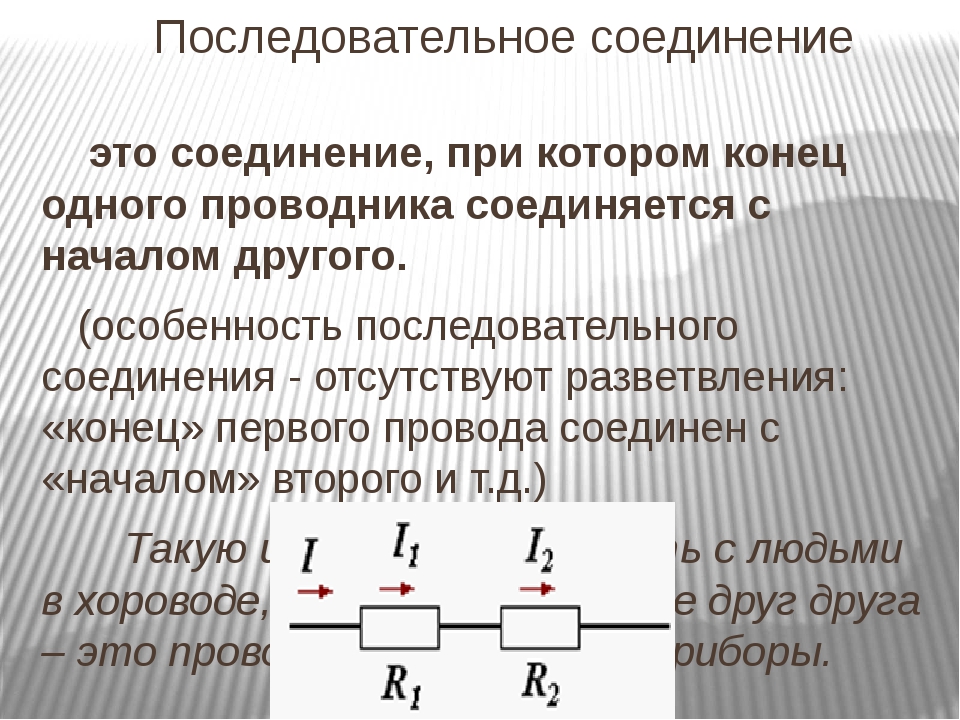 То есть на каждую из ламп подается теперь втрое меньшее напряжение, вот почему они светятся так тускло. Возьмете больше ламп – яркость их упадет еще больше. Как рассчитать падение напряжения на каждой из ламп, если все они имеют различные сопротивления? Для этого достаточно четырех формул, приведенных выше. Алгоритм расчета будет следующим:
То есть на каждую из ламп подается теперь втрое меньшее напряжение, вот почему они светятся так тускло. Возьмете больше ламп – яркость их упадет еще больше. Как рассчитать падение напряжения на каждой из ламп, если все они имеют различные сопротивления? Для этого достаточно четырех формул, приведенных выше. Алгоритм расчета будет следующим:
- Измеряете сопротивление каждой из ламп.
- Рассчитываете общее сопротивление цепи.
- По общим напряжению и сопротивлению рассчитываете ток в цепи.
- По общему току и сопротивлению ламп вычисляете падение напряжения на каждой из них.
Хотите закрепить полученные знания
? Решите простую задачу, не заглядывая в ответ в конце:
В вашем распоряжении есть 15 однотипных миниатюрных лампочек, рассчитанных на напряжение 13,5 В. Можно ли из них сделать елочную гирлянду, подключаемую к обычной розетке, и если можно, то как?
Смешанное соединение
С параллельным и последовательным соединением проводников вы, конечно, без труда разобрались. Но как быть, если перед вами оказалась примерно такая схема?
Но как быть, если перед вами оказалась примерно такая схема?
Смешанное соединение проводников
Как определить общее сопротивление цепи? Для этого вам понадобится разбить схему на несколько участков. Вышеприведенная конструкция достаточно проста и участков будет два — R1 и R2,R3. Сначала вы рассчитываете общее сопротивление параллельно соединенных элементов R2,R3 и находите Rобщ.23. Затем вычисляете общее сопротивление всей цепи, состоящей из R1 и Rобщ.23, соединенных последовательно:
- Rобщ.23 = (R2*R3) / (R2+R3).
- Rцепи = R1 + Rобщ.23.
Задача решена, все очень просто. А теперь вопрос несколько сложнее.
Сложное смешанное соединение сопротивлений
Как быть тут? Точно так же, просто нужно проявить некоторую фантазию. Резисторы R2, R4, R5 соединены последовательно. Рассчитываем их общее сопротивление:
Rобщ.245 = R2+R4+R5.
Теперь параллельно к Rобщ.245 подключаем R3:
Rобщ.2345 = (R3* Rобщ.245) / (R3+ Rобщ. 245).
245).
Rцепи = R1+ Rобщ.2345+R6.
Вот и все!
Ответ на задачу о елочной гирлянде
Лампы имеют рабочее напряжение всего 13.5 В, а в розетке 220 В, поэтому их нужно включать последовательно.
Поскольку лампы однотипные, напряжение сети разделится между ними поровну и на каждой лампочке окажется 220 / 15 = 14,6 В. Лампы рассчитаны на напряжение 13,5 В, поэтому такая гирлянда хоть и заработает, но очень быстро перегорит. Чтобы реализовать задумку, вам понадобится минимум 220 / 13,5 = 17, а лучше 18-19 лампочек.
Параллельные цепи – Основное электричество
Параллельная схема, вероятно, является наиболее распространенным типом схемы, с которой вы столкнетесь. Нагрузки в системах распределения электроэнергии в основном так или иначе соединены параллельно друг другу.
Строительство параллельной цепи
Параллельная цепь строится путем соединения клемм всех отдельных нагрузочных устройств таким образом, чтобы на каждом компоненте появлялось одинаковое значение напряжения.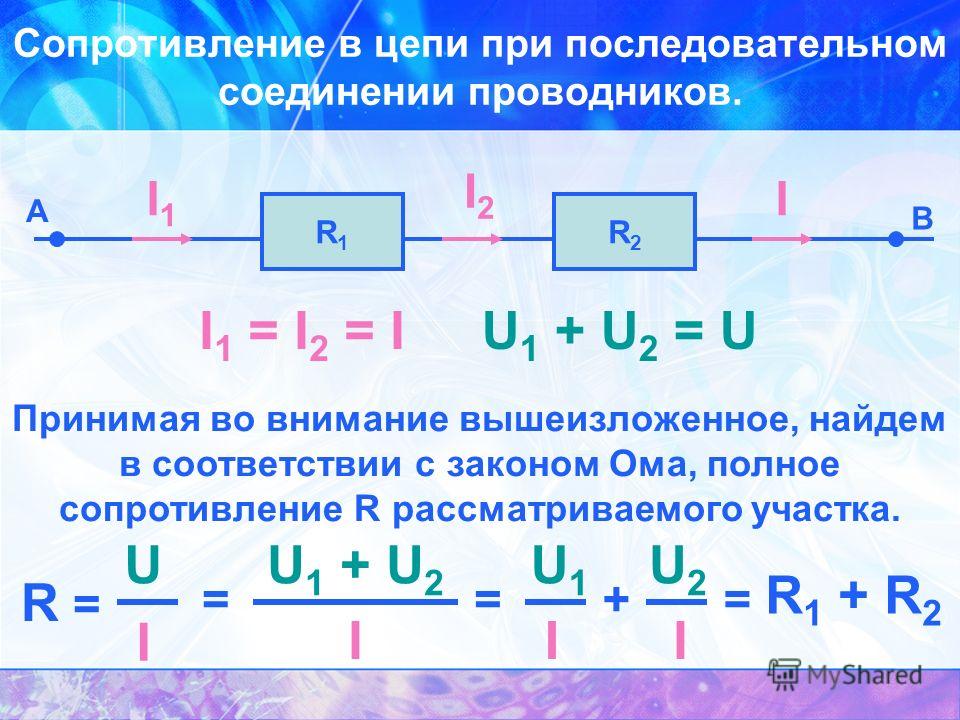
Рисунок 19. Параллельная цепь
- Напряжение на каждой ветви одинаковое.
- Есть три отдельных пути (ветви) для протекания тока, каждый из которых выходит из отрицательной клеммы и возвращается к положительной клемме.
В отличие от последовательной цепи, ток по-прежнему течет к остальным устройствам в цепи, если какая-либо ветвь или компонент в параллельной цепи разомкнуты.
Три закона параллельной цепи
Во всех параллельных цепях существуют три основных соотношения, касающиеся напряжения, тока и сопротивления.
Напряжение
В параллельной цепи каждый нагрузочный резистор действует как независимая ветвь цепи, и благодаря этому каждая ветвь «видит» все напряжение питания.
Суммарное напряжение параллельной цепи имеет то же значение, что и напряжение на каждой ветви.
Это отношение может быть выражено как:
ЭТ = Е1 = Е2 = Е3…
Рис. 20. Протекание тока в параллельной цепи
20. Протекание тока в параллельной цепи
В приведенной выше схеме напряжение в каждой ветви равно 120 В.
Текущий
Параллельная цепь имеет более одного пути для протекания тока. Количество токовых путей определяется количеством параллельно соединенных нагрузочных резисторов.
Общий ток в параллельной цепи представляет собой сумму токов отдельных ответвлений.
Это отношение в параллельной цепи выражается как:
ИТ = И1 + И2 + И3…
Чтобы найти общий ток, необходимо сначала определить токи отдельных ветвей, используя закон Ома:
I1 = 120 В/ 20 Ом = 6 А
I2 = 120 В/ 40 Ом = 3 А
I3 = 120 В/ 60 Ом = 2 А
IT = 6 А + 3 А + 2 А = 11 А
Сопротивление
Всякий раз, когда большее количество сопротивлений подключается параллельно, они уменьшают общее сопротивление цепи.
Чистое сопротивление параллельной цепи всегда меньше, чем любое из значений сопротивления по отдельности.
Общее сопротивление обычно определяется по обратному уравнению:
1/RT = 1/R1 + 1/R2 + 1/R3…
Использование кнопки инверсии вашего калькулятора может упростить вычисление общего сопротивления.
Параллельные цепи постоянного тока и последовательно-параллельные цепи постоянного тока и переменного тока и напряжения
Параллельные цепи постоянного тока
Цепь, в которой два или более электрических сопротивления или нагрузки подключены к одному и тому же источнику напряжения, называется параллельной цепью.Основное различие между последовательной цепью и параллельной цепью заключается в том, что для тока в параллельной цепи предусмотрено более одного пути. Каждый из этих параллельных путей называется ветвью. Минимальные требования к параллельной цепи следующие:
- Источник питания
- Проводники
- Сопротивление или нагрузка для каждого пути тока
- Два или более пути прохождения тока
На рис. параллельная схема.Ток, вытекающий из источника, делится в точке А на схеме и проходит через R 1 и R 2 . Чем больше ветвей добавляется в схему, тем больше путей для тока источника обеспечивается.
параллельная схема.Ток, вытекающий из источника, делится в точке А на схеме и проходит через R 1 и R 2 . Чем больше ветвей добавляется в схему, тем больше путей для тока источника обеспечивается.
Рисунок 12-96. Базовая параллельная схема.
Падение напряжения
Первое, что нужно понять, это то, что напряжение на любой ветви равно напряжению на всех других ветвях.
Полное параллельное сопротивление
Параллельная цепь состоит из двух или более резисторов, соединенных таким образом, что ток проходит через все резисторы одновременно.Это устраняет необходимость прохождения тока через один резистор перед прохождением через следующий. При параллельном соединении резисторов общее сопротивление цепи уменьшается. Общее сопротивление параллельной комбинации всегда меньше сопротивления наименьшего резистора в цепи. В последовательной цепи ток должен проходить через резисторы по одному. Это дало сопротивление току, равное сумме всех сопротивлений. В параллельной цепи ток имеет несколько резисторов, через которые он может проходить, фактически уменьшая общее сопротивление цепи по отношению к любому одному значению резистора.
В параллельной цепи ток имеет несколько резисторов, через которые он может проходить, фактически уменьшая общее сопротивление цепи по отношению к любому одному значению резистора.
Величина тока, проходящего через каждый резистор, зависит от его индивидуального сопротивления. Общий ток цепи равен сумме токов во всех ветвях. Осмотром можно определить, что общий ток больше, чем у любой данной ветви. Используя закон Ома для расчета общего сопротивления на основе приложенного напряжения и общего тока, можно определить, что общее сопротивление меньше любой ветви.
Например, если имеется цепь с резистором 100 Ом и резистором 5 Ом; хотя точное значение необходимо рассчитать, все же можно сказать, что комбинированное сопротивление между ними меньше 5 Ом.
Резисторы, включенные параллельно
Формула для полного параллельного сопротивления выглядит следующим образом:
Если взять обратную величину двух сторон, то общая формула для полного параллельного сопротивления будет следующей:
Два резистора, включенных параллельно
Как правило, более удобно рассматривать одновременно только два резистора, поскольку такая установка используется в обычной практике. Любое количество резисторов в цепи можно разбить на пары. Поэтому наиболее распространенным методом является использование формулы для двух параллельных резисторов.Объединение членов в знаменателе и переписывание: Проще говоря, это означает, что общее сопротивление для двух резисторов, включенных параллельно, равно произведению обоих резисторов, деленному на сумму двух резисторов. По приведенной ниже формуле рассчитайте общее сопротивление.
Любое количество резисторов в цепи можно разбить на пары. Поэтому наиболее распространенным методом является использование формулы для двух параллельных резисторов.Объединение членов в знаменателе и переписывание: Проще говоря, это означает, что общее сопротивление для двух резисторов, включенных параллельно, равно произведению обоих резисторов, деленному на сумму двух резисторов. По приведенной ниже формуле рассчитайте общее сопротивление.
Источник тока
Источник тока — это источник энергии, который обеспечивает постоянную величину тока для нагрузки даже при изменении сопротивления нагрузки. Общее правило, которое следует помнить, заключается в том, что общий ток, создаваемый параллельными источниками тока, равен алгебраической сумме отдельных источников.
Закон тока Кирхгофа
Закон тока Кирхгофа можно сформулировать следующим образом: сумма токов, поступающих в узел или узел, равна сумме токов, вытекающих из этого же узла или узла. Соединение можно определить как точку в цепи, где сходятся два или более пути цепи. В случае параллельной цепи это точка в цепи, где соединяются отдельные ветви. См. пример на Рисунке 12-97. Точка A и точка B представляют собой два соединения или узла в цепи с тремя резистивными ответвлениями между ними.
Соединение можно определить как точку в цепи, где сходятся два или более пути цепи. В случае параллельной цепи это точка в цепи, где соединяются отдельные ветви. См. пример на Рисунке 12-97. Точка A и точка B представляют собой два соединения или узла в цепи с тремя резистивными ответвлениями между ними.
Рис. 12-97. Текущий закон Кирхгофа.
Источник напряжения обеспечивает общий ток I T в узел А. В этот момент ток должен разделиться, вытекая из узла А в каждую из ветвей, в соответствии со значением сопротивления каждой ветви. Закон тока Кирхгофа гласит, что входящий ток должен равняться выходному току. Следуя току через три ветви и обратно в узел B, общий ток I T , входящий в узел B и выходящий из узла B, такой же, как и ток, который вошел в узел A.Затем ток возвращается к источнику напряжения. На рис. 12-98 показано, что токи отдельных ветвей составляют:
Рис. 12-98. Токи отдельных ветвей.
Общий ток, поступающий в узел А, равен сумме токов ветвей, которая равна: I T = I 1 + I 2 Суммарный ток, поступающий в узел B, также одинаков.
На рис. 12-99 показано, как определить неизвестный ток в одной ветви. Обратите внимание, что общий ток в соединении трех ветвей известен.Известны два ответвленных тока. Преобразовав общую формулу, можно определить ток во второй ветви.
Рисунок 12-99. Определение неизвестной цепи в ответвлении 2.
Делители тока
Теперь легко увидеть, что параллельная цепь является делителем тока. Как показано на рис. 12-96, через каждый из двух резисторов протекает ток.
Рисунок 12-96. Базовая параллельная схема.
Поскольку на оба резистора параллельно подается одинаковое напряжение, токи ветвей обратно пропорциональны омическим значениям резисторов.Ветви с более высоким сопротивлением имеют меньший ток, чем ветви с более низким сопротивлением. Например, если значение сопротивления R 2 вдвое больше, чем у R 1 , ток в R 2 составляет половину от тока R 1 . Все это можно определить по закону Ома. По закону Ома ток через любую из ветвей может быть записан как: Источник напряжения появляется на каждом из параллельных резисторов, а R X представляет любой из резисторов. Напряжение источника равно произведению полного тока на общее параллельное сопротивление.
Эта формула является общей формулой делителя тока. Ток через любую ветвь равен общему параллельному сопротивлению, деленному на сопротивление отдельной ветви, умноженному на общий ток.
Последовательно-параллельные цепи постоянного тока
Большинство цепей, с которыми сталкивается технический специалист, не являются простыми последовательными или параллельными цепями. Цепи обычно представляют собой комбинацию обоих, известных как последовательно-параллельные цепи, которые представляют собой группы, состоящие из резисторов, соединенных параллельно и последовательно.Пример схемы такого типа можно увидеть на рис. 12-100. Хотя последовательно-параллельная схема может сначала показаться сложной, к этим схемам можно применить те же правила, которые использовались для последовательных и параллельных цепей.
Рисунок 12-100. Последовательно-параллельные схемы.
Источник напряжения подает ток на резистор R 1 , затем на группу резисторов R 2 и R 3 и затем на следующий резистор R 4 перед возвратом к источнику напряжения.Первым шагом в процессе упрощения является выделение группы R 2 и R 3 и признание того, что они представляют собой параллельную сеть, которую можно свести к эквивалентному резистору. Используя формулу для параллельного сопротивления,
R 2 и R 3 можно сократить до R 23 . На рис. 12-101 показана эквивалентная схема с тремя последовательно соединенными резисторами. Общее сопротивление цепи теперь можно просто определить, сложив номиналы резисторов R 1 , R 23 и R 4 .
Рисунок 12-101. Эквивалентная схема с тремя последовательно соединенными резисторами.
Определение полного сопротивления
Более количественный пример определения полного сопротивления и тока в каждой ветви комбинированной цепи показан в следующем примере. [Рис. 12-102]Рис. 12-102. Определение полного сопротивления.
Первым шагом является определение тока в соединении А, ведущем в параллельную ветвь. Для определения I T необходимо знать общее сопротивление R T всей цепи.Общее сопротивление цепи определяется как:
Теперь, когда общее сопротивление R T определено, можно определить общее I T . Используя закон Ома:
Ток через параллельные ветви R 2 и R 3 можно определить с помощью правила делителя тока, рассмотренного ранее в тексте. Напомним, что:
Теперь, используя закон тока Кирхгофа, можно определить ток в отрасли с R 3 .
Переменный ток (AC) и напряжение
Переменный ток (AC) в значительной степени заменил постоянный ток (DC) в коммерческих энергосистемах по ряду причин.Его можно передавать на большие расстояния легче и экономичнее, чем постоянное, поскольку переменное напряжение можно повышать или понижать с помощью трансформаторов.
Поскольку все больше и больше агрегатов в самолетах эксплуатируются от электричества, требования к питанию таковы, что благодаря использованию переменного тока можно реализовать ряд преимуществ. Можно сэкономить место и вес, поскольку устройства переменного тока, особенно двигатели, меньше и проще, чем устройства постоянного тока. В большинстве двигателей переменного тока щетки не требуются, и устраняются проблемы коммутации на большой высоте.Автоматические выключатели удовлетворительно работают под нагрузкой на больших высотах в системе переменного тока, в то время как в системах постоянного тока искрение настолько сильное, что автоматические выключатели необходимо часто заменять. Наконец, большинство самолетов, использующих 24-вольтовую систему постоянного тока, имеют специальное оборудование, для которого требуется определенное количество переменного тока с частотой 400 циклов.
Сравнение переменного и постоянного тока
Многие принципы, характеристики и эффекты переменного тока аналогичны принципам постоянного тока. Точно так же есть ряд отличий.Постоянный ток постоянно течет только в одном направлении с постоянной полярностью. Он изменяет величину только тогда, когда цепь размыкается или замыкается, как показано на форме сигнала постоянного тока на Рисунке 12-103. АС через равные промежутки времени меняет направление, увеличивается с определенной скоростью от нуля до максимальной положительной силы и снова уменьшается до нуля; затем течет в обратном направлении, аналогично увеличиваясь до максимального отрицательного значения и снова уменьшаясь до нуля. На рис. 12-103 сравниваются формы сигналов постоянного и переменного тока.
Рисунок 12-103. Кривые постоянного и переменного напряжения.
Поскольку переменный ток постоянно меняет направление и интенсивность, в цепях переменного тока имеют место следующие два эффекта (будут обсуждаться позже), которые не возникают в цепях постоянного тока:
- Индуктивное реактивное сопротивление
- Емкостное реактивное сопротивление в параллельных цепях (источники, формула и способ добавления)
Что такое параллельное напряжение?
Параллельная цепь или параллельное соединение относится к случаю, когда два или более электрических устройства соединены вместе в расположении рядом друг с другом в цепи.В связи с этим каждое устройство находится в своей отдельной ветке. Напряжение (то есть разность потенциалов) является причиной того, что ток проходит через замкнутую цепь. В этой статье будет подробно рассмотрено напряжение в параллельной цепи .
Цепь с источником напряжения и 3 параллельными резисторами
Наличие нескольких ответвлений в цепи означает, что существует несколько путей для перемещения заряда во внешнюю цепь. Когда заряд достигает узла или места разветвления, он выбирает, через какую ветвь он должен пройти на своем пути, чтобы вернуться к терминалу с низким потенциалом.
Рассмотрим замкнутую цепь источника напряжения и резистора. В этой цепи ток будет течь по единственному доступному пути. Затем в той же схеме мы добавляем еще два резистора параллельно первому резистору.
Это приводит к тому, что ток проходит по нескольким путям, а не по одному пути для достижения терминала с низким потенциалом. Итак, с увеличением количества ветвей общее сопротивление уменьшается и очевидно, что ток в цепи увеличивается.
То есть весь ток будет суммой различных токов через три резистора. Здесь в параллельной схеме мы видим, что существует не более двух наборов электрически общих точек. Это; A и H, B и G, C и F, D и E в схеме, показанной ниже. Напряжение, измеряемое в общих точках за все время, должно быть одинаковым.
На двух приведенных выше рисунках сначала показана замкнутая цепь с источником напряжения и одним резистором. Второй представляет собой параллельную цепь из 3 резисторов и источника напряжения.
Напряжение в этой цепи одинаково для каждой из трех ветвей, а также совпадает с напряжением источника. Формально, то есть:
Полный ток в данной параллельной цепи представлен I total . Формула для этого дается как.
Полное или эффективное сопротивление данной параллельной цепи описывается приведенной ниже формулой.
Таким образом, можно сделать вывод, что при добавлении дополнительных ветвей в конкретную параллельную цепь общий ток будет увеличиваться, а цепь перегружаться.
Преимущества параллельных цепей
Когда мы хотим подключить две лампочки к одной батарее, у нас есть два варианта. Либо он может быть подключен в массив или параллельно. Если мы соединим его в массив, две лампочки окажутся на одном и том же проводящем пути между двумя клеммами батареи. Проблемы с этим подключением следующие
- Мы не можем включить или использовать одну лампочку.
- Обе лампы будут тусклыми, так как они используют один и тот же источник.
- Если неисправна одна лампочка, это повлияет на всю цепь.
Далее, если мы подключим две лампочки рядом или параллельно, две лампочки получат полное напряжение батареи. Таким образом, результатом будут следующие преимущества.
- Обе лампочки получают полное напряжение аккумулятора.
- Мы можем работать с двумя лампочками по отдельности.
- Обе лампочки будут ярко гореть при включении.
- Если неисправна одна лампочка, ее можно удалить или отремонтировать.Таким образом, вся схема не будет затронута.
Параллельные цепи в доме
Все наши бытовые приборы соединены параллельно друг с другом. Вот почему мы можем управлять каждым устройством отдельно, не затрагивая другие. Например, мы можем включить стиральную машину, не включая микроволновую печь или телевизор.
Мы знаем, что в нашем доме электрические кабели состоят из трех проводов: под напряжением, нейтрали и земли. В этот момент мы игнорируем землю и просто концентрируемся на проводе под напряжением и нейтральном проводе.
Напряжение присутствует на проводе под напряжением и на нейтральном проводе, который, в конечном счете, подключен к электростанции. Каждая розетка в нашем доме подключена к этим живым и нейтральным проводам. Когда мы втыкаем металлический штырь прибора в эту розетку, он создает электрическое соединение с этой розеткой.
Каждый прибор имеет собственное соединение между токоведущим и нулевым проводом. Таким образом, когда мы включаем устройство, на нем будет присутствовать все напряжение, и им можно будет управлять отдельно.
Применение параллельного напряжения
Применение параллельного напряжения включает:
GCSE PHYSICS — Electricity — What Is Current in Parallel Circuit? — Как рассчитать ток в параллельной цепи
GCSE PHYSICS — Электричество — Что такое ток в параллельной цепи? — Как рассчитать ток в параллельной цепи — GCSE SCIENCE.
gcsescience.com
21
наука.ком
Электричество
Параллельно
ЦепиКакой ток в
Параллельная цепь?1. В
параллельной цепи ток зависит от сопротивления
отделение (см.
расчет ниже).2. Всего
ток течет в
на ветви
равно общему току, протекающему
из ветвей.
На схеме ниже
А 1 = А 5Как рассчитать ток в
Параллельная цепь.Ток при А 2 , протекающий через резистор 2 Ом
можно найти с помощью уравнения V
= я
х Р.Уравнение можно изменить, чтобы получить ток
.
= напряжение
÷ сопротивление
я =
В
÷руб.
Если напряжение питания
12 вольт,я =
В ÷
Р= 12 ÷ 2
= 6 ампер.
См. следующую страницу для расчета текущего
в
два других резистора и общее
ток в цепи.Вы получите тот же ответ для
ток в
2
Ом
резистор,
являются ли другие резисторы
или нет
подключен в цепь.
Для параллельной схемы
выше, каждый
компонент ведет себя
как будто это
подключен самостоятельно к
ячейке и не знает о
другие компоненты.
Посмотреть лампы
в параллельной цепи.Ссылки
Электричество
Параллельные цепи
Вопросы по пересмотру
gcsescience.ком
Викторина по физике
Показатель
Викторина по электричеству
gcsescience.com
Дом
GCSE Химия
GCSE Физика
Авторское право © 2015 gcsescience.com. Все права защищены.
Параллельные цепи — преимущества, мощность, ток, напряжение и эффективное сопротивление
Введение
В этом уроке мы рассмотрим параллельные схемы.Мы увидим, почему они так распространены. Мы также рассмотрим напряжение, мощность, ток и эффективное сопротивление.
Упражнение, показывающее, что лампочки, подключенные параллельно, дают одинаковую яркость, потому что они всегда подключены к одному и тому же напряжению.
Преимущество параллельных цепей перед последовательными
Если мы хотим подключить две лампочки к одной и той же батарее, очевидным способом будет их последовательное соединение. Это означает, что обе лампочки находятся на одном и том же проводящем пути от одной клеммы батареи к другой.
Проблема с последовательным подключением двух лампочек заключается в том, что обе лампочки тусклые, и если выключить одну лампочку, то обе гаснут.
Анимация, показывающая, что ток, потребляемый батареей, увеличивается по мере того, как большее количество компонентов подключается параллельно.
Параллельное подключение ламп имеет два преимущества.
- Все они получают полное напряжение батареи, поэтому все они яркие
- Все они находятся в собственной проводящей петле, так что вы можете выключить одну лампочку, не затрагивая другие.
Параллельные цепи в доме
Дома все ваши приборы соединены параллельно друг с другом. Это означает, что все они получают полное сетевое напряжение, и вы можете включить телевизор, не включая микроволновую печь.
Анимация, показывающая, как все наши бытовые приборы соединены параллельно друг с другом.
Как это работает?
Электрические кабели в вашем доме состоят из трех проводов. На данный момент мы проигнорируем землю и сосредоточимся только на двух из них: живом и нейтральном.В Европе живой цвет коричневый, а нейтральный синий. В США живой может быть черным, красным или желтым; и нейтральный, как правило, белый или белый с желтыми полосами.
Между фазой и нейтралью есть напряжение, потому что они косвенно связаны с электростанцией. Каждая электрическая розетка в вашем доме подключена к фазе и нейтрали. Металлические контакты вилки обеспечивают электрическое соединение с розеткой. Провод, опять же с токоведущими и нейтральными проводами, соединяет вилку с вашим прибором.
Каждое устройство имеет собственное соединение между фазой и нейтралью, поэтому каждое устройство можно включать отдельно, и на него подается все напряжение.
Параллельное добавление всегда увеличивает общий ток
Несмотря на то, что все приборы в вашем доме подключены к одному и тому же напряжению, все они потребляют разные токи. Электрическая духовка быстро передает энергию, поэтому потребляемый ею ток будет большим. Телевизор передает энергию довольно медленно, поэтому потребляемый им ток будет довольно мал.
Упражнение, чтобы визуализировать, как ток, потребляемый от батареи, увеличивается, когда дополнительный компонент добавляется параллельно.
Все эти токи должны добавляться в источник питания, поскольку он должен обеспечивать их все одновременно. Чем больше приборов подключено, тем больше потребляемый ток.
Почему ток не «расщепляется» в местах соединения в параллельных цепях
Довольно часто говорят, что ток разделяется на соединениях в параллельных цепях, но вам нужно быть очень осторожным с этой идеей.Часто это может привести к неправильному представлению о постоянном токе.
Анимация, объясняющая, почему лучше не думать о разделении тока в местах соединения.
Первое, что нужно помнить, это то, что заряды не начинаются с батареи, а затем текут по пустым проводам, пока они не дойдут до соединения, а затем нужно решить, что делать. Заряды уже есть везде в цепи, и все они начинают очень медленно течь везде одновременно.
Другая проблема заключается в том, что нет течения.Чем больше вещей вы подключаете параллельно, тем больше ток, потребляемый от источника питания. Один и тот же ток не просто делится по-разному.
Иногда проще думать о компонентах как об активных вещах, требующих тока от источника питания. Если схема устроена так, что иногда эти токи должны протекать по одному проводу, их нужно сложить.
Расчет токов в параллельных цепях
Когда лампы соединены параллельно, напряжение на них должно быть одинаковым.Вы можете относиться к ним так, как если бы они были в своей собственной цепи (что, если вы относитесь к цепи как к смысловой петле, так и есть).
Анимации показывают, как рассчитывать токи в параллельных цепях.
Если лампы разные, то лампочка с меньшим сопротивлением будет потреблять больший ток и будет ярче. Это просто закон Ома: малое сопротивление означает большой ток.
Это стратегия:
- рассчитать ток через каждую лампочку по закону Ома
- сложите токи, чтобы найти ток, потребляемый от батареи
Вы можете рассчитать ток, используя уравнение закона Ома V = IR.Сначала вам нужно переставить его так, чтобы I = V / R, и помните, что V — это просто напряжение батареи.
Параллельное добавление всегда снижает эффективное сопротивление
Батарея параллельной цепи не «знает», что к ней подключено. Все, что он чувствует, это общее сопротивление (или, если хотите, общий спрос на ток). Сопротивление, которое испытывает батарея, называется эффективным сопротивлением цепи.
Анимация объясняющая параллельные сопротивления как дырки в ванне.
По мере того, как вы добавляете все больше и больше компонентов параллельно, ток, потребляемый от источника, становится все больше и больше. Если ток увеличивается, сопротивление должно уменьшаться. Таким образом, добавляя сопротивления, вы фактически уменьшаете эффективное сопротивление, что кажется странным.
Не имеет значения, насколько велико сопротивление, добавление его параллельно всегда снижает эффективное сопротивление. Есть пара аналогий для объяснения этого.
Если у вас есть ванна с отверстием на дне, она будет опорожняться.Если вы добавите еще одно отверстие, каким бы маленьким оно ни было, ванна всегда будет опорожняться быстрее.
Или подумайте об огромной толпе, покидающей спортивный стадион через главные ворота. Если открыть хотя бы маленькую боковую калитку, количество людей, покидающих стадион каждую минуту, увеличивается.
Эмпирические правила расчета эффективного сопротивления параллельных цепей
Графика, иллюстрирующая некоторые эмпирические правила для эффективного сопротивления параллельных цепей.
- Общее сопротивление всегда меньше наименьшего сопротивления (потому что вы всегда можете представить, что сначала строите цепь с наименьшим сопротивлением, а затем эффективное сопротивление продолжает уменьшаться по мере добавления больших сопротивлений).
- Два одинаковых резистора имеют эффективное сопротивление, равное половине их значения (поскольку добавление второго сопротивления удваивает ток, поэтому сопротивление уменьшается вдвое).
- Три одинаковых резистора имеют эффективное сопротивление в три раза меньше их номинала и так далее.
- Параллельное очень большое сопротивление и очень маленькое сопротивление имеют эффективное сопротивление, которое немного меньше, чем у малого сопротивления (маленькое сопротивление похоже на большую дыру в ванне, добавление еще одной крошечной дырочки все равно немного увеличивает общую скорость потока). )
Игра Попрактикуйтесь в определении эффективного сопротивления параллельных резисторов.Проведите космоход над черной дырой, используя только квадраты с эффективным сопротивлением менее 10 Ом.
Расчет эффективного сопротивления параллельных цепей
Анимация, показывающая, как использовать формулу для расчета эффективного сопротивления.
Формула для расчета эффективного сопротивления параллельных цепей выглядит довольно сложной, поэтому, возможно, параллельные цепи часто преподаются после последовательных цепей, хотя параллельные цепи гораздо более распространены и гораздо полезнее.
Эту формулу довольно легко вывести, если вы не возражаете против дробей.
Использовать формулу не так уж сложно. Просто подставьте свои значения сопротивления, а затем сложите дроби.
Осторожно, после сложения дробей вы получите не R эффективное , а 1/R эффективное , поэтому вам нужно перевернуть результат, чтобы найти эффективное сопротивление.
В качестве проверки убедитесь, что результат меньше наименьшего сопротивления.
Расчет эффективного сопротивления путем расчета общего потребляемого тока
График поясняющий, как рассчитать эффективное сопротивление, вычислив общий ток, потребляемый от батареи.
Вместо использования формулы мы можем рассчитать общий ток, потребляемый от источника питания, а затем использовать R эффективное = V батареи /I общее для расчета эффективного сопротивления.
Это фактически то, что делает формула, но иногда вопрос даст вам токи через компоненты, а не их сопротивления, поэтому быстрее использовать этот метод, а не сначала вычислять сопротивления, а затем использовать формулу.
Назад к краткому описанию электричества
резисторов в параллельных схемах
сумма токов в параллельной сети можно рассчитать как
I = I 1 + I 2 + … + I N (1)
где
I N = Параллельный ток (AMPS)
I = Сумма токов (AMPS)
Общее сопротивление в параллельной цепи можно рассчитать как
1 / R = 1 / R 1 + 1 / R 2 + … + 1 / R N (2)
, где
R N = Параллельное сопротивление (Ом, Ом)
R = Общее сопротивление в параллельной сети (Ом, Ом)
Пример — параллельная сеть
Общее сопротивление в сети с тремя резисторами R 1 = 10 Ом, R 2 = 20 Ом и R 3 = 50 30 Ом можно рассчитать как
1 / R = 1 / (10 Ом) + 1 / (20 Ом) + 1 / (30 Ом)
= 0.183 (1 / Ω)
R = 1/0.182 R = 1/0.183 R = 1/0.183
= 5.46 (Ω)
, подключенный к батарею 12 V Сумма токов можно рассчитать
I = U / R
= (12 В) / (5.46 Ω)
= 2.2 AMPS)
Ток через каждый резистор может быть рассчитан как
I 1 = U / R 1
= (12 В) / (10 Ом)
= 1.2 (AMPS)
I 2 = U / R 2 = U / R 2
= (12 В) / (20 Ω)
= 0,6 (AMPS)
I 3 = U / r 3 3
= (12 В) / (30 Ом)
= 0,4 (AMPS)
Резисторы параллельно и результирующие резисторы
Два резистора параллельно — устойчивость к диапазону 1 — 100 Ом
Полученное сопротивление (Ω) (Ω) (Ω) R2
( Ω )R1 ( ω ) 1 1.5 2.2 3.3 4.7 6 10 9
68 9 1 0.5 0.6 0.69 0.77 0.83 0.87 0.87 0.91 0.93 0,95 0,97 0.98 0.98 0.99 1,5 0.6 0.75 0.89 1.03 1.14 1.22 1.30 1.36 1,40716 1,45 2 0.69 0.89 1.1 1.32 1.50 1.66 1.82 1.92 1.92 2.0 2.06 2.10 2.13 3.3 0,77 1.03 1.32 1.65 1.94 2.22 2.48 2.70 2,87 300716 4 9 0.83 0 1.14 1.50 1.94 2,35 2.78 3.20 3.58 3.58 3.87 4.12 4,27 4.39 6.8 0.87 1.22 1.66 2.22 2.22 3.40 3.40 4.05 4,68 5.19 5.64 6.18 10 9 0,91 1.82 2.48 3.20 4.05 5.05 5.0 6.0 6.9 7.7 8.3 8.7 15 0.93 1.36 1.92 1.92 3.58 4.68 6.0 70 80716 11.4 12.2 22 0,95 1.40 2,00916 3.87 5.19 5.19 6.9 8.9 11.0 13.2 15,0 16.6 33 1.43 2.06 2.06 3.0 4.12 5.64 70716 9 9.4 22.2 47 0,98 1.45 4,27 5.94 5.94 8.3 11.4 15.0 19.4 19.4 23,5 27.8 68
0.99 1.46 2.13 3.14 3.14 4.39 6.18 8.7 12.2 16.6 22.2 Скачать и печатные резисторы на параллельном диаграмме
Урок Урок Параллельные цепи | Nagwa
В этом объяснителе мы научимся рассчитывать разность потенциалов, ток и сопротивление в разных точках простых параллельных цепей.
На приведенной ниже схеме показана схема, состоящая из ячейки и резистора. Разность потенциалов, обеспечиваемая ячейкой, равна 𝑉, ток в цепи
равно 𝐼, а сопротивление резистора равно 𝑅.В приведенной выше схеме есть только один путь, по которому могут течь электроны, чтобы двигаться от одного конца ячейки к другому. Однако в приведенной ниже схеме
есть два пути, по которым электроны могут течь, чтобы двигаться от одного конца ячейки к другому.Путь между двумя терминалами ячейки разветвляется на две ветви в точке A. Пути снова соединяются в точке B. На каждом пути есть резистор.
Когда существует несколько различных путей, по которым электроны могут пройти между выводами ячейки, как этот, мы говорим, что эта часть цепи
это параллельно . Если в цепи есть элементы, включенные последовательно и параллельно, то она называется комбинированной схемой. Когда все компоненты цепи
соединены только параллельными соединениями, это называется параллельной цепью.Давайте рассмотрим пример.
Пример 1: Идентификация компонентов, соединенных параллельно
На схеме показаны четыре цепи. Какая цепь содержит два резистора, включенных параллельно?
Ответ
Компоненты соединены параллельно , если они находятся на разных путях цепи.
В цепи а есть два резистора, но они находятся на одном пути, а не на разных. Электроны, идущие от одного конца клетки к другому, должны пройти через
оба резистора.Следовательно, они последовательно, а не параллельно.Схема b очень похожа на схему; единственное отличие состоит в том, что компоненты размещены на разных сторонах диаграммы. Это не влияет
независимо от того, соединены ли компоненты последовательно или параллельно, эти компоненты также соединены последовательно.В схеме d есть два возможных пути движения электронов между клеммами ячейки, но один путь проходит через лампочку, а другой — через лампочку.
два резистора последовательно.Резисторы параллельны лампочке, но не друг другу.В схеме c также есть два возможных пути движения электронов, каждый из которых содержит резистор. Эти резисторы включены параллельно.
Правильный ответ: схема c.
Определить, где именно начинается и где заканчивается параллельная цепь, может быть непросто. Рассмотрим следующие параллельные схемы.
Несмотря на то, что кажется, что они начинаются и заканчиваются в разных местах, эти схемы эквивалентны.Обведенная площадь обоих точно такая же: раскол, с 𝑅
на одном пути и 𝑅 на другом, то оба пути в конце сходятся.Пока пути, по которым проходят токи, одинаковы, цепи эквивалентны. На схеме ниже есть еще две схемы, которые эквивалентны.
Ориентация компонентов не имеет значения, если схема может быть описана одинаково — в данном случае это разделение на два пути,
один содержит 𝑅, а другой 𝑅, которые затем снова собираются вместе.На приведенной ниже схеме показаны четыре полностью эквивалентные схемы с двумя резисторами и лампочкой.
Эти схемы эквивалентны, поскольку компоненты соединены параллельно. Все они могут быть описаны как раздвоение пути, одно из которых содержит
два резистора, а другой содержит лампочку, а затем пути снова собираются вместе. На рисунке ниже это описание показано визуально с использованием двух схем.Давайте рассмотрим пример.
Пример 2: определение эквивалентных схем цепей
На схеме показаны четыре цепи с компонентами, соединенными параллельно.Какие две схемы эквивалентны?
Ответ
Рассмотрим пути в этих цепях. Цепь а имеет разделение с резистором 10 Ом.
на одном пути и лампочка и резистор 20 Ом на другом.Цепь b имеет разделение с резистором 20 Ом на одном пути и лампочкой и
Резистор 10 Ом с другой стороны.Цепь c сначала имеет резистор 20 Ом, а затем разделяется на две цепи с лампочкой на одной и другой
резистор 10 Ом с другой стороны.Примечательно, что это не настоящая параллельная схема, а скорее комбинированная схема,
так как он имеет компоненты как последовательно, так и параллельно.Цепь d разделена, с резистором 10 Ом на одном пути и лампочкой и
резистор 20 Ом с другой стороны.Если ток проходит по одному и тому же пути через одни и те же компоненты, цепи эквивалентны. Два, которые описываются одинаково, это a и d.
В параллельной цепи разность потенциалов на каждой параллельной ветви будет одинаковой.Независимо от значений сопротивления компонентов на этих путях,
разность потенциалов на каждом из них будет одинаковой. На приведенной ниже диаграмме показаны два вольтметра, измеряющие разность потенциалов на двух резисторах.Если 𝑅 равно 1 Ом и 𝑅 равно 1 000 Ом,
не важно. Разность потенциалов между ними составляет 20 В.Правило: Разность потенциалов между компонентами, включенными параллельно
Разность потенциалов на каждой ветви параллельной цепи одинакова:
𝑉=𝑉=𝑉=….Давайте рассмотрим пример.
Пример 3. Поиск потенциальных различий между компонентами, включенными параллельно
На схеме показаны два резистора, подключенных параллельно к ячейке. Если разность потенциалов на 3 Ом
резистор 18 В, какова разность потенциалов на
резистор 6 Ом?Ответ
Разность потенциалов между параллельными компонентами определяется правилом
𝑉=𝑉=𝑉=….Для этой схемы с двумя компонентами правило выглядит так
𝑉=𝑉.Нам дано значение разности потенциалов на резисторе 3 Ом, 𝑉,
быть 18 В. Разность потенциалов на резисторе 6 Ом
тогда должно быть одинаково: 18 В.В отличие от разности потенциалов на разных ветвях, которая одинакова для каждой ветви, ток в каждой ветви может быть разным.
Напомним, что сопротивление — это противодействие потоку электрического заряда. Если одна ветвь имеет большее сопротивление, чем другая, заряду будет труднее течь по ней.
и поэтому ток в нем будет слабее, а ток в другом ответвлении сильнее.Однако все электроны из ячейки должны пройти по одной из ветвей. Следовательно, суммарный ток по всем ветвям будет равен
к току до того, как путь цепи разделился.На приведенной ниже диаграмме общий ток 𝐼total равен сумме токов в отдельных ветвях, 𝐼
и 𝐼.Правило: Суммарный ток в параллельных цепях цепи
Суммарный ток параллельных компонентов, 𝐼total, равен сумме токов в каждой цепи:
𝐼=𝐼+𝐼+𝐼+…, всего
где 𝐼, 𝐼, 𝐼 и т. д. — токи на определенном пути.Точный способ разделения тока зависит от сопротивления каждого пути. На приведенной ниже диаграмме показана цепь, которая разделена на три пути с током в каждом.
Нам дан общий ток 𝐼общий и ток в двух путях вдоль резисторов 𝑅
и 𝑅. Мы можем использовать их, чтобы найти ток через крайний левый путь, 𝐼.Суммарный ток в цепи равен 9 А. Средний путь можно назвать 𝐼, а крайний правый
путь 𝐼, равный 5 A и 1 A соответственно.Мы можем использовать правило для полного тока вдоль параллельных путей, чтобы представить это как уравнение:
𝐼=𝐼+𝐼+𝐼.totalПодставляя наши известные значения тока, уравнение становится
(9)=𝐼+(5)+(1)9=𝐼+6.AAAAAAЧтобы найти 𝐼, нам нужно вычесть 6 А с обеих сторон:
9−6=𝐼+6−63=𝐼.AAAAAИтак, ток по крайнему левому пути, 𝐼, равен 3 А.
Предположим теперь, что нам не задан ток по пути, как в диаграмма ниже.
Мы можем определить, сколько тока проходит по каждому пути, сравнив значения сопротивления.На приведенной выше схеме резисторы имеют одинаковое значение
сопротивления 𝑅. Это означает, что ток будет равномерно разделен между двумя путями:
𝐼=𝐼.Итак, глядя на общий ток,
𝐼=𝐼+𝐼.totalПодстановка всех токов на 𝐼, поскольку они одинаковы, дает нам
𝐼=𝐼+(𝐼)𝐼=2𝐼.totaltotalЧтобы найти 𝐼, мы просто делим обе части на 2:
𝐼2=2𝐼2𝐼2=𝐼.totaltotalТаким образом, отдельные пути имеют половину общего тока. Суммарный ток равен 8 А, поэтому
𝐼2=4.totalAПоскольку 𝐼 и 𝐼 равны друг другу, они оба равны 4 А.
Давайте рассмотрим несколько примеров вопросов.
Пример 4. Определение токов через компоненты, соединенные параллельно
Схема, показанная на схеме, состоит из двух резисторов, подключенных параллельно к ячейке. Значение 𝐼total равно
до 30 А. Каково значение 𝐼?Ответ
Суммарный ток в цепи с параллельными элементами определяется по правилу
𝐼=𝐼+𝐼+𝐼+….totalТолько для двух компонентов на разных путях это правило становится
𝐼=𝐼+𝐼.totalДва резистора на дорожках в этой цепи одинаковы, поэтому ток распределяется между ними поровну. Это означает, что текущий 𝐼
то же, что и 𝐼:
𝐼=𝐼.Подстановка этого соотношения в правило для полного тока дает
𝐼=(𝐼)+𝐼𝐼=2𝐼.totaltotalТеперь, чтобы найти 𝐼, разделим обе части на 2:
𝐼2=2𝐼2.totalЭто приводит к тому, что 2 в правой части уравнения отменяется, оставляя
𝐼2=𝐼.totalСуммарный ток равен 30 А. Подстановка этого значения дает значение 𝐼:
(30)2=15.AAИтак, значение 𝐼 равно 15 А.
Чтобы проследить, как ток изменяется в зависимости от сопротивления пути, мы должны сначала посмотреть, как найти общее сопротивление компонентов, включенных параллельно. .
Правило: общее сопротивление компонентов, расположенных параллельно
Для ряда компонентов, расположенных параллельно, общее сопротивление 𝑅total равно
1𝑅=1𝑅+1𝑅+1𝑅+…, всего
где 𝑅 — сопротивление первой составляющей, 𝑅 — второй и т. д.Давайте используем это уравнение только с двумя резисторами, 𝑅 и 𝑅, чтобы продемонстрировать, как найти 𝑅общий
сам по себе. Это делает уравнение
1𝑅=1𝑅+1𝑅.totalМы можем взять обратное значение обеих частей, чтобы получить 𝑅total в левой части:
1=1+.totalДеление на дробь равносильно умножению на знаменатель, поэтому левая часть становится
1=1×𝑅1=𝑅.totaltotaltotalЭто делает уравнение
𝑅=1+.totalТеперь умножим обе части на 𝑅𝑅; поскольку это всего лишь один, он сохранит 𝑅полный член в левой части:
𝑅×𝑅𝑅=1+×𝑅𝑅.totalДробь означает, что верх и низ будут распределяться поперек для дроби в правой части:
𝑅×1=1×𝑅𝑅+𝑅=𝑅+.totaltotal𝑅 больше 𝑅, поэтому уравнение теперь равно единице
𝑅=𝑅1+.totalТеперь умножим обе части на 𝑅𝑅:
𝑅×𝑅𝑅=𝑅1+×𝑅𝑅.totalУмножая 𝑅 сверху и снизу для правой части, получаем
𝑅×1=𝑅×𝑅𝑅1+.total𝑅 распределяется по знаменателю:
𝑅=𝑅𝑅𝑅+.total𝑅𝑅 в знаменателе равно 1, что дает
𝑅=𝑅𝑅(𝑅+𝑅).totalТаким образом, при наличии двух резисторов это уравнение можно использовать для определения общего сопротивления цепи.
Правило: полное сопротивление двухкомпонентной параллельной цепи
Когда два компонента проходят параллельные пути, общее сопротивление 𝑅total равно
𝑅=𝑅𝑅(𝑅+𝑅), всего
где 𝑅 — сопротивление первого компонента, а 𝑅 — сопротивление второго компонента.В приведенной ниже схеме мы можем вычислить 𝑅total, используя это правило.
Примем 𝑅 за 5 Ом и 𝑅 за 20 Ом. Ввод этих значений в уравнение для полного сопротивления дает
𝑅=(5)(20)(5)+(20)=100(25).totalΩΩΩΩΩΩДеление на омы отменяет квадрат в омах
член в числителе, дающий общее сопротивление как
100(25)=4.ΩΩΩРассмотрим пример.
Пример 5. Определение того, как изменяется ток в зависимости от количества параллельных путей в цепи
Учащийся устанавливает цепь, показанную на схеме.Изначально переключатель разомкнут. Когда ученик замкнет переключатель, будет ли ток течь через
схема увеличения или уменьшения?Ответ
Чтобы определить полный ток в цепи, можно применить закон Ома к току:
𝐼=𝑉𝑅.Разность потенциалов в этой цепи фиксируется ячейкой, но сопротивление может изменяться, когда путь снизу закрыт. Назовем резисторы
как 𝑅 и 𝑅 нравится так.Первоначально, когда переключатель разомкнут, в нижней ветви этой цепи отсутствует ток.Все электроны из клетки будут проходить только через
𝑅. Таким образом, полное сопротивление можно описать как
𝑅=𝑅.totalКогда ключ замкнут, в ветвях, содержащих как 𝑅, так и 𝑅, будет ток. Напомним, что общая
сопротивление в цепи с двумя параллельными резисторами определяется по уравнению
𝑅=𝑅𝑅(𝑅+𝑅).totalТеперь, независимо от значения 𝑅, общее сопротивление будет уменьшаться. Это потому, что умножение 𝑅
на 𝑅, то деление на сумму всегда будет меньше, чем 𝑅 само по себе:
𝑅>𝑅𝑅(𝑅+𝑅).Чтобы убедиться в этом, предположим, что 𝑅 равно 1 Ом, и проверим 𝑅
как 0,1 Ом и 1 000 Ом:
𝑅=1.ΩЗаменив 0,1 Ω на 𝑅, общее сопротивление 𝑅total станет
𝑅𝑅(𝑅+𝑅)(1)(0,1)((0,1)+(1))=0,099.ΩΩΩΩΩΩΩТеперь попробуем подставить 1 000 Ом вместо 𝑅:
(1)(1000)((1000)+(1))=0,999.ΩΩΩΩΩΩМы видим, что в обоих этих случаях окончательный результат меньше, чем просто 𝑅.
Значит, если общее сопротивление уменьшается, то по закону Ома общий ток в цепи должен увеличиваться, так как ток обратно пропорционален
к сопротивлению:
𝐼=𝑉𝑅.Правильный ответ: ток увеличивается при замыкании ключа.
Теперь, когда мы видим, как работают ток, сопротивление и разность потенциалов в параллельных цепях, мы можем использовать эти правила, чтобы найти нужные значения в цепи.
Давайте рассмотрим пример.
Пример 6. Определение значений разности потенциалов и тока для компонентов, соединенных параллельно
Схема, показанная на схеме, состоит из двух резисторов, подключенных параллельно к ячейке.Значение тока, даваемое вторым амперметром,
𝐼 равно 3 А. Каково значение 𝐼total?Ответ
Мы знаем, что в параллельной цепи полный ток равен сумме всех токов в параллельных цепях. Таким образом, для этой цепи полный ток равен
𝐼=𝐼+𝐼.totalЭто означает, что мы должны найти ток второго пути, 𝐼, поэтому мы можем добавить его к 𝐼 и найти общий ток. Мы можем сделать это, рассмотрев потенциальные различия на каждом пути.
Нам не известна разность потенциалов клетки, но мы знаем, что разность потенциалов одинакова на обоих путях:
𝑉=𝑉.Это дает возможность использовать закон Ома, чтобы связать два пути вместе. Однако прежде чем мы это сделаем, предположим, что резистор вдоль
путь 𝐼 — это 𝑅, а путь 𝐼 — это 𝑅.Разность потенциалов на первом пути, используя закон Ома, можно записать как
𝑉=𝐼𝑅
и второй путь как
𝑉=𝐼𝑅,
но поскольку 𝑉=𝑉, мы можем связать эти уравнения как
𝐼𝑅=𝐼𝑅.Теперь мы можем найти искомое значение 𝐼, разделив обе части на 𝑅:
𝐼𝑅𝑅=𝐼𝑅𝑅.Отмена слева дает
𝐼=𝐼𝑅𝑅.𝐼 равно 3 А, 𝑅 равно 4 Ом,
и 𝑅 равно 12 Ом. Подставляя эти значения в уравнение, получаем
𝐼=(3)(12)(4).AΩΩТеперь мы разделим единицы измерения омов, сократив их как в числителе, так и в знаменателе, что даст
𝐼=(3)(3)𝐼=9.

 Найдите напряжение на каждом из проводников и общее напряжение.
Найдите напряжение на каждом из проводников и общее напряжение.

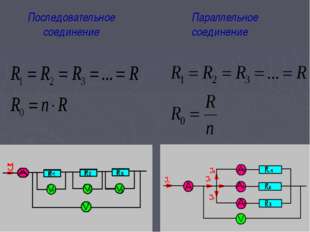 При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.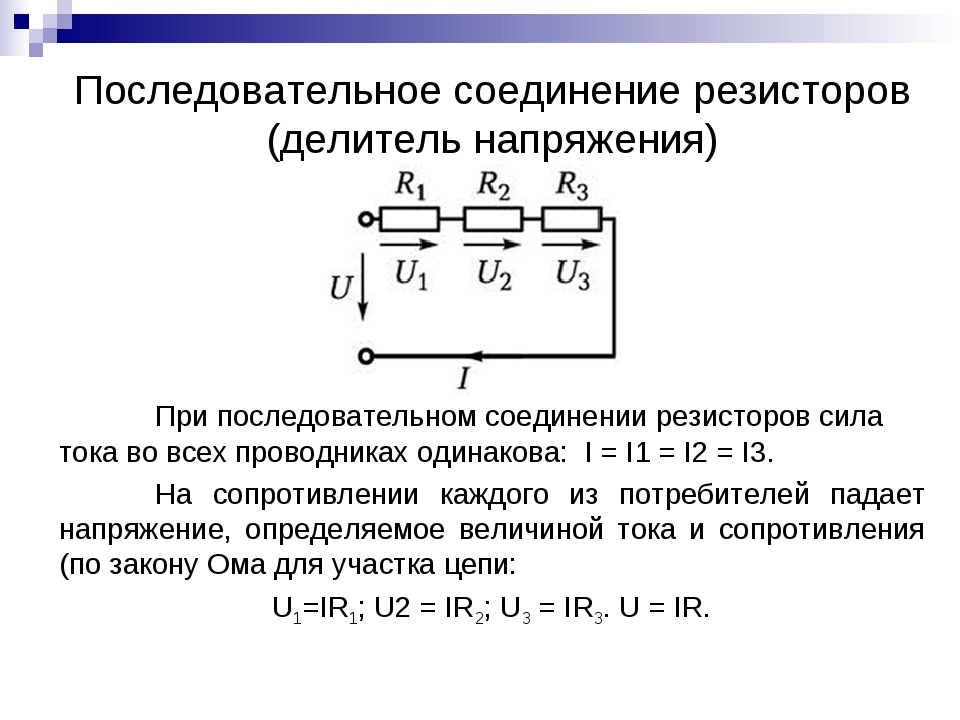
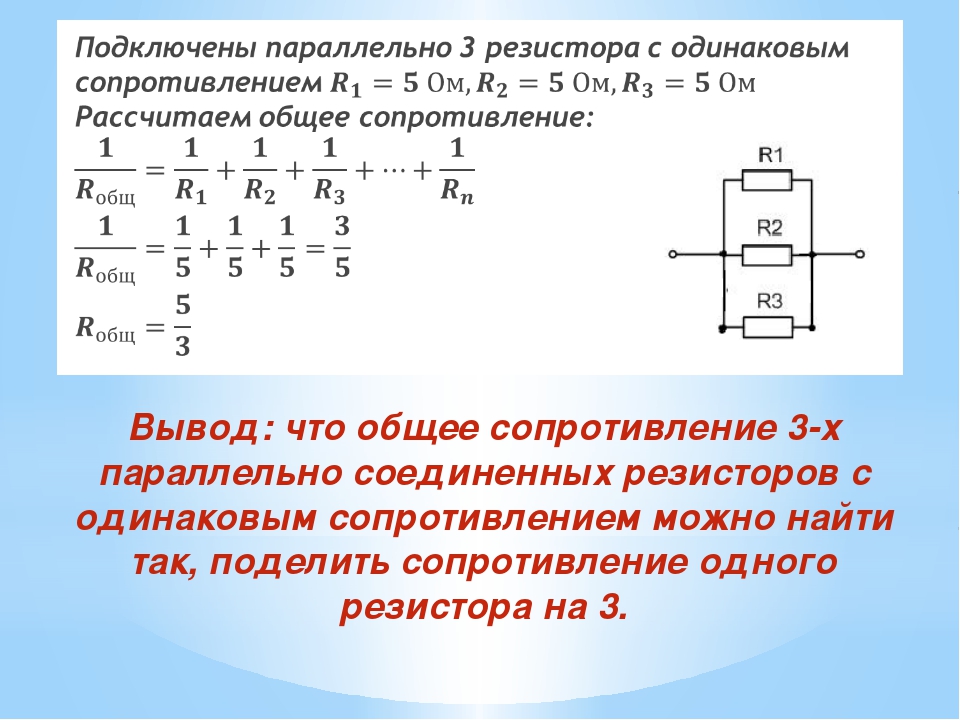
 д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:
д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе: