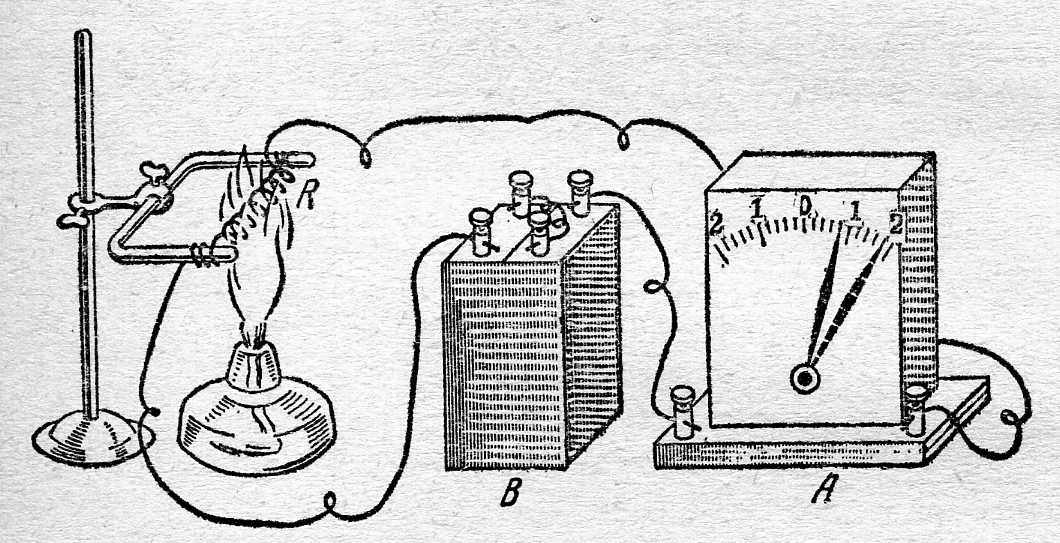
Изучаем зависимость изменения сопротивления от температуры
При нагревании проводника мы наблюдаем зависимость электрического сопротивления от температуры. Изменение температуры проводника вызывает изменение его сопротивления.
С одной стороны, повышение температуры проводника вызывает увеличение числа столкновений электронов с молекулами, благодаря чему уменьшается средняя скорость движения электронов в проводнике, т. е. при том же напряжении уменьшается ток. Следовательно, увеличение температуры может привести к увеличению сопротивления.
С другой стороны, повышение температуры может привести к возрастанию числа свободных электронов и ионов в единице объема проводника. Это обстоятельство способствует увеличению тока. Следовательно, повышение температуры может привести к уменьшению сопротивления проводника.
В зависимости от преобладания той или иной причины с увеличением температуры сопротивление проводника может или увеличиваться (металлы), или уменьшаться (электролиты, уголь), или оставаться практически неизменным (сплавы — манганин, константан).
С достаточной точностью в пределах от 0 до 100° С относительное приращение сопротивления металлических проводников можно считать пропорциональным изменению температуры, т. е.:
где:
альфа — температурный коэффициент сопротивления, равный относительному изменению сопротивления проводника при повышении температуры на 1° С;
t — разность температур (T2 — T1)
R0 — сопротивление, соответствующее начальной температуре T1
R — сопротивление, соответствующее температуре после нагрева T2
Значение температурного коэффициента сопротивления некоторых проводников указано в таблице.
Температурный коэффициент сопротивления химически чистых металлов близок к 0,004 1/С, т. е. при изменении температуры на 1° С их сопротивление изменяется на 0,4%. У некоторых сплавов (константан, манганин) температурный коэффициент сопротивления очень мал, наряду с этим указанные сплавы обладают относительно большим удельным сопротивлением.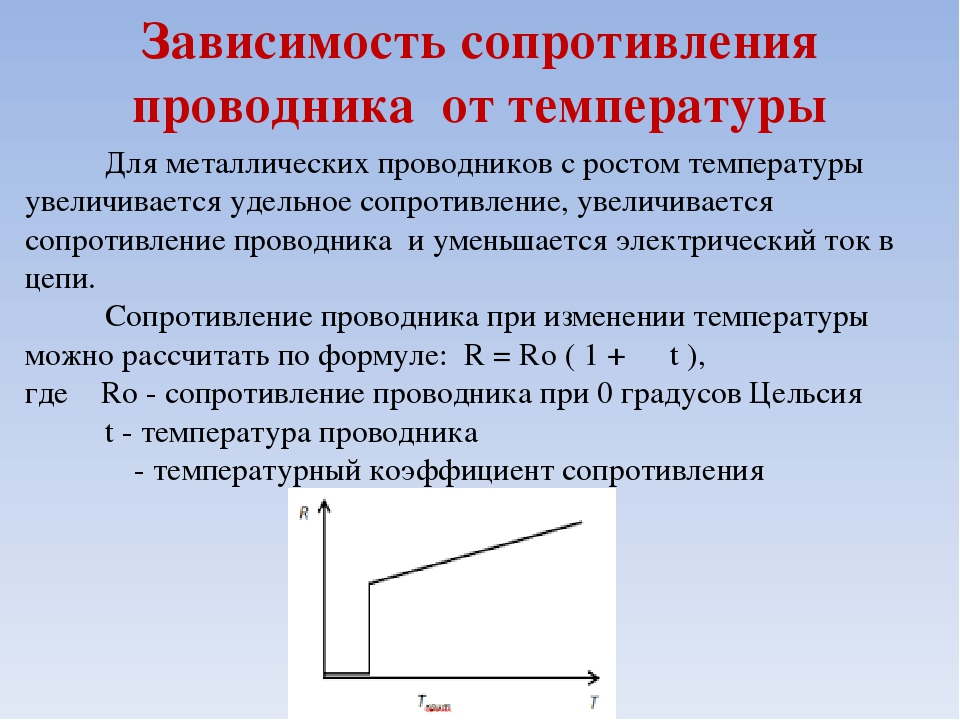 По этим причинам они используются для изготовления образцовых мер сопротивления, магазинов сопротивления, применяются для изготовления шунтов и добавочных сопротивлений к из-мерительным приборам и т. д.
По этим причинам они используются для изготовления образцовых мер сопротивления, магазинов сопротивления, применяются для изготовления шунтов и добавочных сопротивлений к из-мерительным приборам и т. д.
Уголь и электролиты имеют отрицательный температурный коэффициент сопротивления.
Проект по физике «Исследование зависимости электрического сопротивления проводника от температуры»
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа с. Усть-Курдюм Саратовского района Саратовской области»
_____________________________________________________________________________________________
Саратовская область, Саратовский район, с. Усть-Курдюм, ул. Б.Советская 66; т. (8-452)276-268,
e-mail: [email protected]
Исследовательская работа
«Исследование зависимости электрического сопротивления проводника от температуры»
Выполнили: Семёнова Т.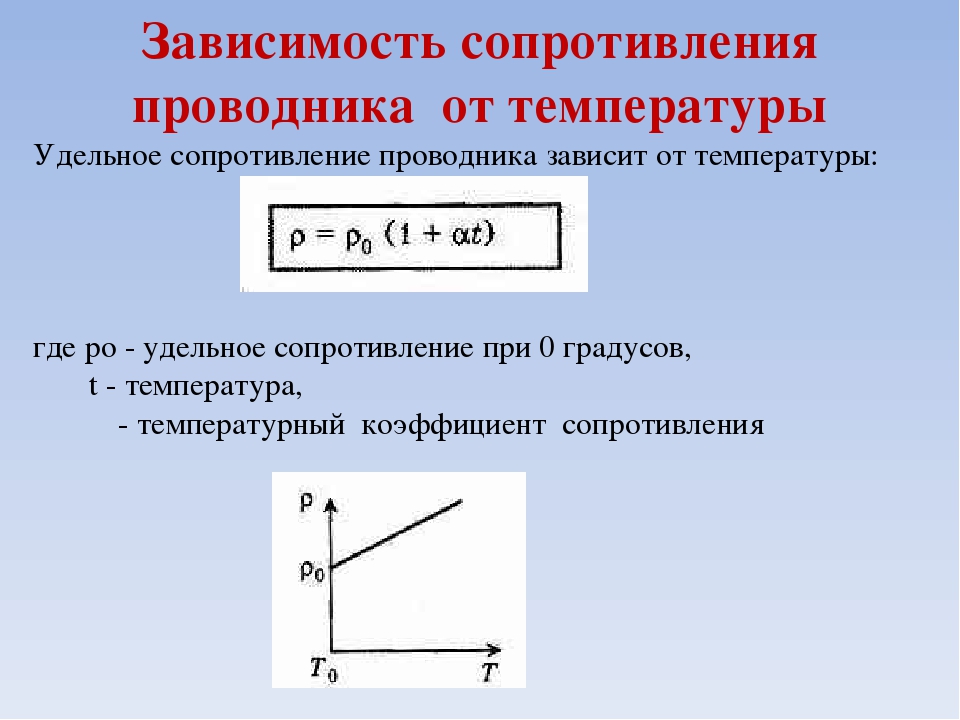 И- учитель физики
И- учитель физики
Степанова Яна- ученица 8 класса
2018 год
Оглавление
Введение………………………………………………….3
Глава 1 Зависимость сопротивления металлических проводников от температуры……………………………………………..5
1.1 История происхождения закона Ома………………….5
1.2 Температурный коэффициент электрического сопротивления……6
Глава 2 Исследования проводников…………………………10
Заключение………………………………………….15
Источники…………………………………………….. 16
Введение
Основным законом электротехники, при помощи которого можно изучать и рассчитывать электрические цепи, является закон Ома, устанавливающий соотношение между током, напряжением и сопротивлением. Необходимо отчетливо понимать его сущность и уметь правильно пользоваться им при решении практических задач. Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.
Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.
Данная исследовательская работа служит дополнением расширяющие рамки школьной программы, и посвящена закону Ома и температурному коэффициенту. Выбор темы не случаен, основным поводом послужило, что на практике при использовании ламп накаливания в цепи, при увеличение напряжения на лампе например в два раза не приводит к увеличению тока в два раза, как мы уже знаем данное условие противоречит выполняемости закона Ома. Значит -закон Ома не всегда справедлив. Хотим заметить, в школьном курсе физики данному моменту не уделено должного внимания.
В этой связи весьма важным представляется проанализировать перечисленных выше фактов и выявить решение проблемы, как методом изучения дополнительной литературы, так и рассмотреть практически. Такова цель настоящей работы.
Задачи:
Выявить влияние фактора температуры проводника на его электрическое сопротивление и соблюдение выполнения закона Ома от данного обстоятельства.
Объектом исследования является определяющая связь электрического напряжения с силой тока, протекающего в проводнике, и сопротивлением проводника, и его температурой.
Методы исследования:
анализ литературы;
моделирование;
обобщение.
Практическая значимость работы заключается в дополнительном представлении учащимся, что закон Ома не является фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников, но перестающим соблюдаться в ряде ситуаций.
Зависимость сопротивления металлических проводников от температуры.
История происхождения закона Ома
Большой в клад в формирование взаимосвязи силы тока, напряжения и сопротивление проводника внес немецкий физик Георг Симон Ом. Он руководствовался следующей идеей. Если над проводником, по которому проходит ток, подвесить на упругой нити магнитную стрелку, то угол поворота стрелки даст информацию о токе, об его изменениях при вариации элементов замкнутой цепи. Ом обратился к идее Кулона и построил крутильные весы. Магнитная стрелка оказалась точным и чувствительным гальванометром. В первых опытах, результаты которых Ом опубликовал в 1825 г., наблюдалась «потеря силы» (уменьшение угла отклонения стрелки) с увеличением длины проводника, подключенного к полюсам вольтова столба (поперечное сечение проводника было постоянным). Поскольку не было единиц измерения, пришлось выбрать эталон — «стандартную проволоку». В качестве зависимой переменной фигурировало уменьшение силы, действующей на магнитную стрелку. Опыты обнаружили закономерное уменьшение этой силы при увеличении длины проводника. Функция получила аналитическое выражение, но Ом не претендовал на установление закономерности, потому что гальванический элемент не давал постоянной ЭДС.
Он руководствовался следующей идеей. Если над проводником, по которому проходит ток, подвесить на упругой нити магнитную стрелку, то угол поворота стрелки даст информацию о токе, об его изменениях при вариации элементов замкнутой цепи. Ом обратился к идее Кулона и построил крутильные весы. Магнитная стрелка оказалась точным и чувствительным гальванометром. В первых опытах, результаты которых Ом опубликовал в 1825 г., наблюдалась «потеря силы» (уменьшение угла отклонения стрелки) с увеличением длины проводника, подключенного к полюсам вольтова столба (поперечное сечение проводника было постоянным). Поскольку не было единиц измерения, пришлось выбрать эталон — «стандартную проволоку». В качестве зависимой переменной фигурировало уменьшение силы, действующей на магнитную стрелку. Опыты обнаружили закономерное уменьшение этой силы при увеличении длины проводника. Функция получила аналитическое выражение, но Ом не претендовал на установление закономерности, потому что гальванический элемент не давал постоянной ЭДС.
Большое внутренние сопротивление источника ЭДС, препятствовало исследованиям так, как сопротивление внешней цепи, которая использовались в опытах имела малые значения. Успех дальнейших экспериментов Ома решило открытие термоэлектричества. Ом использовал термопару висмут — медь; один спай помещался в лед, другой — в кипящую воду. Чувствительность «гальванометра» пришлось, естественно, увеличить. Процедура измерений заключалась в следующем. Восемь испытуемых проводников поочередно включались в цепь. В каждом случае фиксировалось отклонение магнитной стрелки. В следующей работе (1826 г.) Ом вводит понятие «электроскопической силы», пользуется понятием силы тока и записывает закон для участка цепи уже в форме, близкой к современной:
где X — сила тока, k — проводимость, w — поперечное сечение проводника, а — электроскопическая сила (электрическое напряжение на концах проводника), l — длина проводника. Несмотря на убедительные экспериментальные данные, проверка закона Ома продолжалась почти в течение всего XIX века.
Температурный коэффициент электрического сопротивления
Как мы уже знаем сопротивление проводников зависит от вещества, из которого они изготовлены, и их геометрических размеров
R = ρ • l / S,
где ρ — удельное сопротивление вещества, из которого изготовлен проводник; l —длина проводника; S — площадь поперечного сечения проводника.
Сопротивление проводников входит в закон Ома для однородного участка цепи I = U / R, из которого и может быть определено R = U / I.
Из последней формулы выходит, что сопротивление проводника постоянно, поскольку, в соответствии с законом Ома, во сколько раз увеличиваем напряжение на концах проводника, во столько же раз возрастает и сила тока в нем. Все выше описанное также экспериментально было подтверждено на практических опытах
Но практике также выявилось, что можно наблюдать и другие явления. Составив электрическую цепь, схема которой показана на рис. 1. В этой цепи есть источник тока с регулированным напряжением, электрическая лампа, например автомобильная, вольтметр и амперметр, показывающие напряжение на лампе и силу тока в ней. Устанавливаем на лампе напряжение U1 и отмечаем силу тока I1. Если теперь увеличить напряжение, например в 2 раза (U2 = 2U1), то по закону Ома и сила тока должна увеличиться в 2 раза (I2 = 2I1). Однако амперметр показывает силу тока значительно меньшую, чем 2I1. Следовательно, в данном случае закон Ома не выполняется.
Составив электрическую цепь, схема которой показана на рис. 1. В этой цепи есть источник тока с регулированным напряжением, электрическая лампа, например автомобильная, вольтметр и амперметр, показывающие напряжение на лампе и силу тока в ней. Устанавливаем на лампе напряжение U1 и отмечаем силу тока I1. Если теперь увеличить напряжение, например в 2 раза (U2 = 2U1), то по закону Ома и сила тока должна увеличиться в 2 раза (I2 = 2I1). Однако амперметр показывает силу тока значительно меньшую, чем 2I1. Следовательно, в данном случае закон Ома не выполняется.
Рис. 1. Электрическая цепь с лампой накала
Возникло несоответствие между нашими предшествующими знаниями и новым для вас фактом — закон Ома не всегда справедлив.
Анализ дополнительной литературы и сети интернет существенно расширил наши познания в изученных закономерностях. Еще Ом в своих работах описывал об изменении проводящих свойств металлов как при нагревании так и при остывании. Нами была найдена зависимость сопротивления проводников от температуры, отличной от стандартной, которую можно выразить через следующую формулу:
Еще Ом в своих работах описывал об изменении проводящих свойств металлов как при нагревании так и при остывании. Нами была найдена зависимость сопротивления проводников от температуры, отличной от стандартной, которую можно выразить через следующую формулу:
Константа «альфа» (α) известна как температурный коэффициент сопротивления, который равен относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на единицу. Так как все материалы обладают определенным удельным сопротивлением (при температуре 20 ° С), их сопротивление будет изменяться на определенную величину в зависимости от изменения температуры. Для чистых металлов температурный коэффициент сопротивления является положительным числом, что означает увеличение их сопротивления с ростом температуры. Для таких элементов, как углерод, кремний и германий, этот коэффициент является отрицательным числом, что означает уменьшение их сопротивления с ростом температуры. У некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, что означает крайне малое изменение их сопротивления при изменении температуры.
У некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, что означает крайне малое изменение их сопротивления при изменении температуры.
Теперь возникает вопрос почему так происходит, что с ростом температуры проводника ухудшаются его проводящие свойства. Как мы уже знаем высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока. Значит, теперь можем сделать вывод, что структура кристаллической решётки влияет на прохождение заряжённых частиц, а как мы уже знаем с ростом температуры происходит увеличение кинетической энергии, тем самым колебания ионных узлов решетки становятся значительными, влияя на периодичность структуры, образуя преграду для прохождения упорядоченного потока электронов, и этим увеличивая сопротивление проводника.
Значит, теперь можем сделать вывод, что структура кристаллической решётки влияет на прохождение заряжённых частиц, а как мы уже знаем с ростом температуры происходит увеличение кинетической энергии, тем самым колебания ионных узлов решетки становятся значительными, влияя на периодичность структуры, образуя преграду для прохождения упорядоченного потока электронов, и этим увеличивая сопротивление проводника.
Полупроводники в свою очередь при низких температурах наоборот страдают недостатком носителей электрических зарядов. По этому при их нагревании количество носителей возрастает, что приводит к снижению сопротивления. Если иметь в виду, что размеры металлов при нагревании изменяются мало, то соответствующую формулу можно записать и для удельного сопротивления металлических проводников
ρ = ρ0(1 + αt°).
Тщательные исследования показывают, что сопротивление металлических проводников зависит от их температуры практически линейно и график такой зависимости представлен на рис.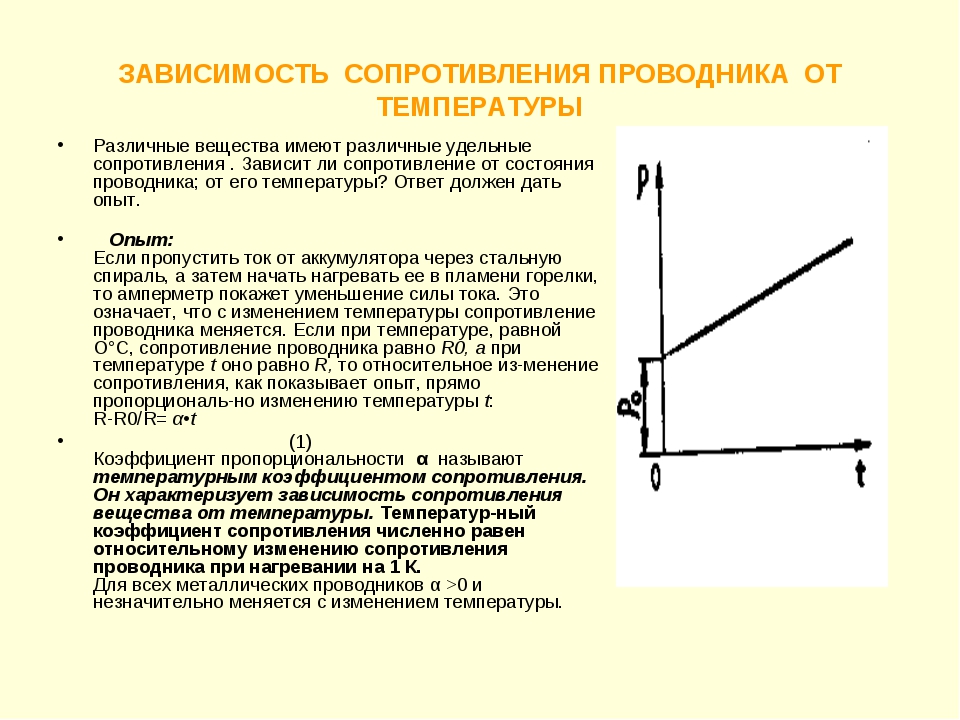 2.
2.
Рис 2. График зависимости сопротивления металлического проводника от температуры.
Исследования проводников
Одним из возможных способов изучения и демонстрации зависимости электрического сопротивления проводника от температуры может служить лабораторная установка. Такая установка была реализована по схеме (рис. 1.) и в ее состав вошли:
регулируемый низковольтный источник напряжения
автомобильная лампа накаливания на 12 вольт
в качестве вольтметра использовался цифровой мультиметр VC9808
роль амперметра выполнил цифровой мультиметр DT-832
Рис. 1. Электрическая цепь с лампой накала
В ходе эксперимента была составлена вольт- амперная характеристика (таблица 1) , которая потвердела выше изложенные доводы.
Таблица 1. Результаты измерений вольт- амперной характеристики.
График изменения тока цепи от напряжения:
На данном графике красной линией показана зависимость тока от напряжения согласно расчетным данным по закону Ома для участка цепи без учета температурного коэффициента, как мы видим он линейный, что согласовается с формулой. Синяя линия показывает результат реальной вольт- амперной характеристики, которая имеет нелинейную зависимость. Сделаем некоторые выводы относительно проделанной работы. В ходе опыта бросается в глаза, что при увеличенном напряжении лампа светится ярче, чем в первом случае. Это является свидетельством того, что температура спирали лампы во втором случае выше, чем в первом. Значит температура влияет на сопротивление проводника, таким образом, чем выше нагрев, тем выше его сопротивление. В нашем случае сопротивление возросло в 11 раз. Для полного убеждения в нашем проведенном опыте, была собрана еще одна схема рис 2.
Рисунок 2. Исследование зависимости сопротивления металлического проводника от температуры.
Установка представляет собой стальную пружину подключенную к омметру, которую нагревают при помощи пламени свечи. При нагревании спирали пламенем было зафиксировано увеличение сопротивления с 1,1 Ом до 2 Ом. Значит таким образом получили еще одно подтверждение термозависимости электрического сопротивления проводников.
Было проверено еще одно утверждение, что сопротивление растет практически линейно при возрастании температуры. Вооружившись таблицей температурных коэффициентов с учетом, что нить лампы накаливания вольфрамовая применив полученную формулу имеем следующие данные.таб.2.
Формула для расчета температуры
( – 1/α)-Т0= Т
Проводник
α, на градус Цельсия
Никель
0,005866
Железо
0,005671
Молибден
0,004579
Вольфрам
0,004403
Алюминий
0,004308
Медь
0,004041
Серебро
0,003819
Платина
0,003729
Золото
0,003715
Цинк
0,003847
Сталь (сплав)
0,003
Нихром (сплав)
0,00017
Нихром V (сплав)
0,00013
Манганин (сплав)
0,000015
Константан (сплав)
0,000074
Таблица 2. Температура накала нити при разных значениях напряжения
Температура накала нити при разных значениях напряжения
Как можно заметить наш график зависимости электрического сопротивления от температуры имеет линейный вид, а значит очередной этап опыта подтвердился.
Заключение
Целью данной работы являлось оптимально изучить закон Ома для участка цепи с точки зрения нагревания проводников. Опытным путем удалось выявить, что термическая нестабильность может существенно повлиять на сопротивление проводников, а свою очередь на конечный результат. Исследование также выявило, что существуют сплавы, которые мало подвержены изменению своего сопротивления (используются в точных приборах). Были сделаны выводы, что лампы накаливания имеют нелинейную вольт-амперную характеристику, поэтому не могут использоваться для демонстрации линейной (закон Ома) зависимости тока от напряжения
Работу в целом можно рассматривать как определенный этап на пути развития, пригодного для учебных целей. Полученные в ней результаты могут оказаться полезными для продолжения исследований и конструирования в деле познания законов электричества.
Полученные в ней результаты могут оказаться полезными для продолжения исследований и конструирования в деле познания законов электричества.
Физика — 9
Здесь R0 – сопротивление проводника при температуре 0°C (273K), R — сопротивление проводника при температуре t (T), αt – разность температур, равная разности конечной и начальной температуры проводника (αt = t конечная – t началльная), α – температурный коэффициент сопротивления.
• Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании его на 1°C (1K):
α =
R — R 0
R 0 αt
=
R — R 0
R 0 αT
. (1.2)
(1.2)
Относительное изменение сопротивления проводника прямо пропорционально изменению температуры:
R — R 0
R 0
= αΔt = αΔT
. (1.3)
Для чистых металлов температурный коэффициент сопротивления (α) всегда больше 0 и равен нижеприведенному значению:
α ≈ 1
273 1
°C = 1
273 1
K.
Аналогично выражению (1.1) можно записать формулу для температурной зависимости и удельного сопротивления металлического проводника:
ρ = ρ 0 (1 + αΔt) или ρ = ρ 0 (1 + αΔt) (1.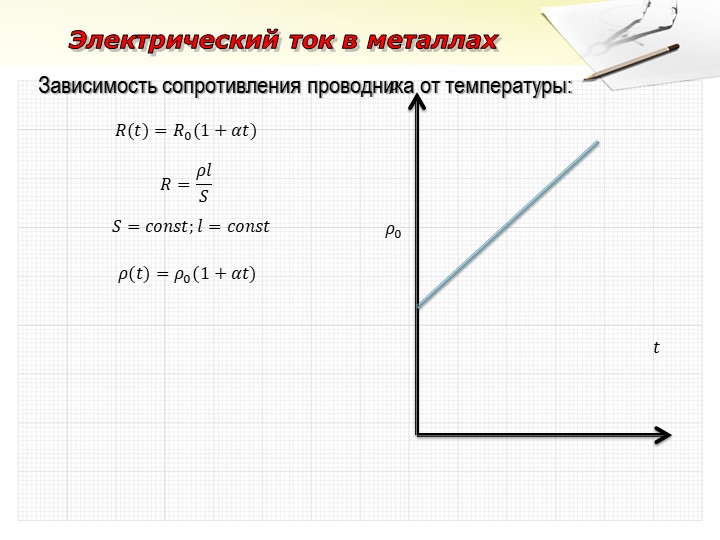 4)
4)
Зависимость сопротивления металлов от температуры используется в специальных приборах, например, в термометрах сопротивления (c). Эти термометры, изготовленные из чистых металлов, дают возможность измерять очень высокие или очень низкие температуры. Например, платиновый термометр может измерять температуру в интервале –264°C ÷ 1064°C, а медный термометр — в интервале –50°C ÷ 180°C.
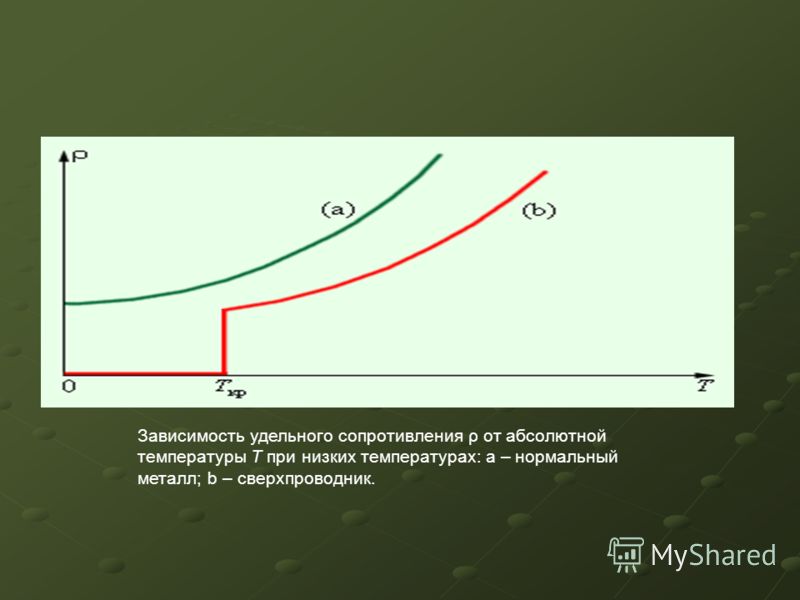
Возможно ли получить металлический проводник с такой высокой электропроводностью, чтобы сопротивление можно было считать равным нулю? При очень низких температурах у некоторых металлических проводников сопротивление скачкообразно падает до нуля. Этот эффект в металлах в 1911 году впервые обнаружил голландский ученый Камерлинг-Оннес. Он экспериментально определил, что сопротивление ртути при температуре 4,15 К скачкообразно падает до нуля. В дальнейшем в результате многочисленных исследований это свойство было обнаружено у многих проводников.
В дальнейшем в результате многочисленных исследований это свойство было обнаружено у многих проводников.
• Температура, при которой электрическое сопротивление проводника падает до нуля, называется критической температурой, а электропроводность при этой температуре называется сверхпроводимостью (d).
Если создать электрический ток в таком сверхпроводящем проводнике, то ток в нем может существовать долгое время даже после удаления источника тока.
Зависимость удельного сопротивления полупроводника от температуры
Зависимость удельного сопротивления полупроводника от температуры
[c.196]
Зависимость удельного сопротивления полупроводников от температуры и освещения. Опыты показывают, что при нагревании электрическое сопротивление полупроводниковых кристаллов уменьшается (рис. 157). Уменьшение электрического сопротивления полупроводников при нагревании объясняется тем, что с повышением температуры кристалла число освобождающихся
[c.156]
Опыты показывают, что при нагревании электрическое сопротивление полупроводниковых кристаллов уменьшается (рис. 157). Уменьшение электрического сопротивления полупроводников при нагревании объясняется тем, что с повышением температуры кристалла число освобождающихся
[c.156]
Зависимость удельного сопротивления полупроводника от температуры может быть выражена экспоненциальной функцией
[c.207]
Рассмотрим теперь аналогичные характеристики электронных полупроводников. Эти. материалы обычно имеют удельные сопротивления в пределах от —10 дд юэ ом см при 0° С, т. е. значительно более высокие, чем у металлов, но гораздо более низкие, чем у изоляторов. На фиг. 1 приведены кривые зависимости удельного сопротивления р от температуры Т для двух типичных образцов полупроводников. Из кривых видно, что удельное [c.159]
Таким образом, изменение удельного сопротивления полупроводника с собственной проводимостью в зависимости от температуры дается выражением
[c. 197]
197]
Обычно к проводникам относят вещества с удельным сопротивлением менее 10 Ом -м, а к диэлектрикам — с р более 10 Ом -м удельное сопротивление полупроводников составляет 10″ —10 Ом -м. Однако при классификации веществ по электрическим свойствам кроме значения р необходимо учитывать и физическую природу электропроводности, в частности вид свободных носителей заряда и характер зависимости р от температуры. [c.7]
Качественное объяснение этих свойств графита было получено в результате расчетов, произведенных с помощью зонной модели [36, 37]. Установлено, что в направлении, параллельном слоям атомов углерода, вершина заполненной зоны электронных уровней касается дна проводящей зоны. Поэтому проводимость графита в этом направлении должна быть такой же, как и у полупроводника с собственной проводимостью при стремлении к нулю ширины запрещенной зоны. На основании расчетов, произведенных для чистого поликристаллического графита [36, 38], следует, что величина удельного сопротивления р изменяется при низких температурах пропорционально 1/Г.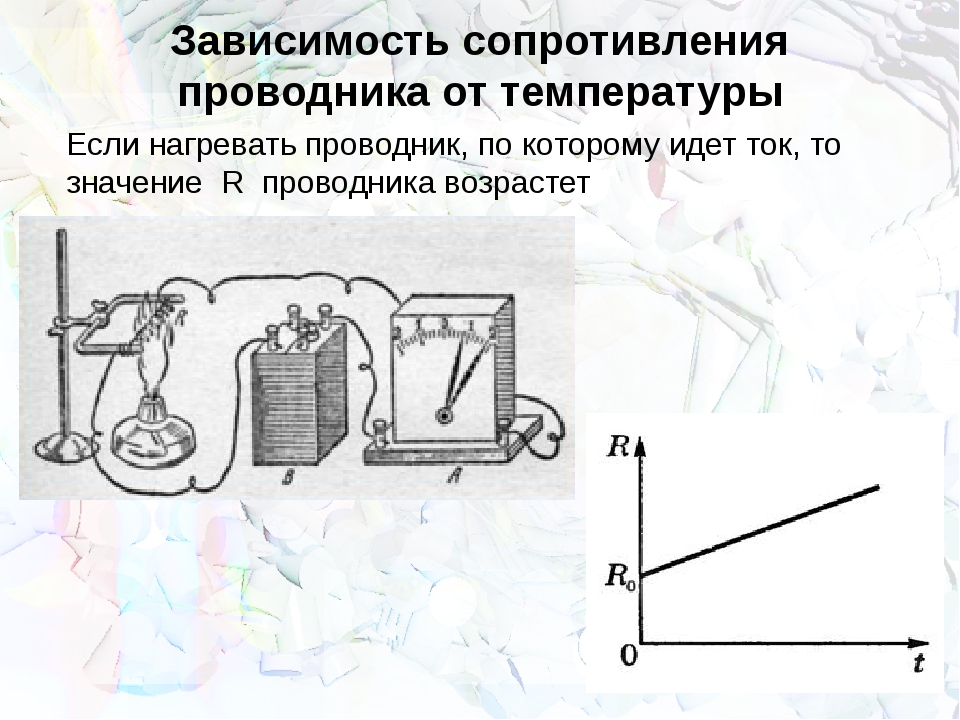 Присутствие химических загрязнений и физических неоднородностей приводит к появлению дополнительных уровней в месте соприкосновения заполненной валентной и пустой проводящей зон, в результате чего характер зависимости удельного сопротивления от температуры изменяется. Для графита с небольшим содержанием примеси величина удельного сопротивления должна возрастать при понижении температуры и принимать конечные значения при 0° К. Образцы очень загрязненного примесями графита должны обладать слабо выраженными. металлическими свойствами и иметь положительный температурный коэффициент даже при самых низких температурах.
[c.172]
Присутствие химических загрязнений и физических неоднородностей приводит к появлению дополнительных уровней в месте соприкосновения заполненной валентной и пустой проводящей зон, в результате чего характер зависимости удельного сопротивления от температуры изменяется. Для графита с небольшим содержанием примеси величина удельного сопротивления должна возрастать при понижении температуры и принимать конечные значения при 0° К. Образцы очень загрязненного примесями графита должны обладать слабо выраженными. металлическими свойствами и иметь положительный температурный коэффициент даже при самых низких температурах.
[c.172]
Контролируемое введение примесей в полупроводник позволяет в очень широких пределах изменять как удельное сопротивление, так и степень его зависимости от температуры. Если в полупроводник добавляется очень небольшое количество [c.197]
В разд. 5.1 показано, как влияет на свойства полупроводника введение небольшого количества примеси. Зависимость сопротивления от температуры чрезвычайно чувствительна к количеству и качеству вводимой примеси, что может использоваться для получения желаемых характеристик. Из рис. 5.7 видно, что для термометрических целей более всего интересны области III и IV. Хотя наклоном кривой и абсолютным значением удельного сопротивления можно в какой-то степени управлять, высокая чувствительность обоих этих параметров к малым изменениям концентрации примеси мешает получать
[c.235]
5.1 показано, как влияет на свойства полупроводника введение небольшого количества примеси. Зависимость сопротивления от температуры чрезвычайно чувствительна к количеству и качеству вводимой примеси, что может использоваться для получения желаемых характеристик. Из рис. 5.7 видно, что для термометрических целей более всего интересны области III и IV. Хотя наклоном кривой и абсолютным значением удельного сопротивления можно в какой-то степени управлять, высокая чувствительность обоих этих параметров к малым изменениям концентрации примеси мешает получать
[c.235]
Цель лабораторной работы — определение зависимости величины удельного электрического сопротивления твердых проводников и полупроводников от изменения температуры с использованием стандартных методов. [c.141]
Полупроводниками называют вещества, удельное сопротивление которых при нормальной температуре находится между значениями удельных сопротивлений проводников и диэлектриков (в диапазоне от до 10 °. ..10 Омом). Основным свойством полупроводника является зависимость его электропроводности от воздействия температуры, электрического поля, излучения и других факторов. Полупроводники в отличие от проводников имеют отрицательный коэффициент температурного удельного сопротивления, электропроводность полупроводников с увеличением температуры растет экспоненциально.
[c.334]
..10 Омом). Основным свойством полупроводника является зависимость его электропроводности от воздействия температуры, электрического поля, излучения и других факторов. Полупроводники в отличие от проводников имеют отрицательный коэффициент температурного удельного сопротивления, электропроводность полупроводников с увеличением температуры растет экспоненциально.
[c.334]
На рис. 16 и 17—представлены величины удельного сопротивления карбида кремния в зависимости от давления, а на рис. 17 — в зависимости от зернистости. Электросопротивление полупроводников, как правило, снижается с повышением температуры, уменьшается под воздействием сильного электрического поля и увеличивается в магнитном поле [27]. [c.98]
Характер отклонения кривой зависимости 1п р от 1/7 от линейности для типичного термистора показывает, что удельное сопротивление термистора зависит от температуры так же, как удельное сопротивление примесного полупроводника, для которого наблюдается зависимость вида
[c. 165]
165]
Недостатками всех ферритов являются хрупкость и возможность обработки только шлифованием, а также резко выраженная зависимость магнитных свойств от температуры и механических воздействий. Ферриты являются магнитными полупроводниками и, следовательно, с ростом температуры их удельное сопротивление уменьшается, что вызывает увеличение потерь на вихревые токи. [c.86]
Прежде чем перейти к подробному обсуждению зависимости удельного сопротивления металлов и полупроводников от температуры, коснемся особенностей поведения концентрированных сплавов. Введение значительного количества примесных атомов в твердый раствор приводит к искажению кристаллической решетки. Вследствие этого появляется дополнительный вклад в рассеяние. Его величина почти не зависит от температуры и может во много раз превышать долю электрон-фонон-ного рассеяния в чистом металле. Изменение остаточного удельного сопротивления неупорядоченного сплава Си—Аи в зави-
[c. 191]
191]
Типичные температурные зависимости удельного сопротивления р полупроводниковых керамических сегнетоэлектриков приведены на рис. 21.17. Вдали от точки Кюри р снижается с ростом температуры, как и у других диэлектриков и полупроводников, однако в определенном интервале в окрестности точки Кюри наблюдается резкий аномальный рост р. Величина р увеличивается в тысячи, а иногда и миллионы раз. Это и есть позисторный эффект. Область положительного ТКр находится в области перестройки решетки при фазовом переходе. Если перестройка решетки происходит в узком интервале температур (четкий фазовый переход), то р увеличивается скачкообразно (кривые 1, 2, 5). В случае же сегнетоэлектриков с размытым фазовым переходом увеличение р с температурой плавное и происходит во всем интервале температур раз.мытия перехода (кривые 3, 4). [c.226]
Удельное сопротивление полупроводников является величиной изменчивой, зависящей от наличия примесей в материале и от технологии изготовления (многие полупроводники изготовляются посредством измельчения, смешения, прессования составных частей и последующего обжига, т. е. приемами керамической технологии (см. гл. 8). Как уже упоминалось, сопротивление полупроводников зависит от температуры в некоторых апучаях эта зависимость выражена весьма заметно, и такие полупроводники могут применяться в качестве элементов электрических устройств, для которых важна зависимость сопротивления от температуры ( т е р м о с о п р о т и в л е н и я ), В ряде случаев сопротивление полупроводников сильно зависит от освещенности, уменьшаясь при повышении последней такие полупроводники используются в качестве фотосопротивлений. Некоторые материалы типа полупроводников резко изменяют сопротивление в зависимости от величины приложенного напряжения, являясь нелинейными сопротивлениями . Полупроводники используются в качестве электронагревательных элемен-
[c.193]
е. приемами керамической технологии (см. гл. 8). Как уже упоминалось, сопротивление полупроводников зависит от температуры в некоторых апучаях эта зависимость выражена весьма заметно, и такие полупроводники могут применяться в качестве элементов электрических устройств, для которых важна зависимость сопротивления от температуры ( т е р м о с о п р о т и в л е н и я ), В ряде случаев сопротивление полупроводников сильно зависит от освещенности, уменьшаясь при повышении последней такие полупроводники используются в качестве фотосопротивлений. Некоторые материалы типа полупроводников резко изменяют сопротивление в зависимости от величины приложенного напряжения, являясь нелинейными сопротивлениями . Полупроводники используются в качестве электронагревательных элемен-
[c.193]
Простая модель электронного газа, созданная Друде в 1900 г., успещно предсказала законы Ома и Видемана — Франца. Однако она не объяснила зависимость электропроводности от температуры, а также магнитные свойства и малую величину электронной теплоемкости по сравнению с классическим значением 3/ . В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления).
[c.187]
В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления).
[c.187]
Существует класс полупроводниковых приборов, выполненных на основе смешанных окислов переходных металлов, которые известны под общим названием термисторов. Термин термистор происходит от слов термочувствительный резистор .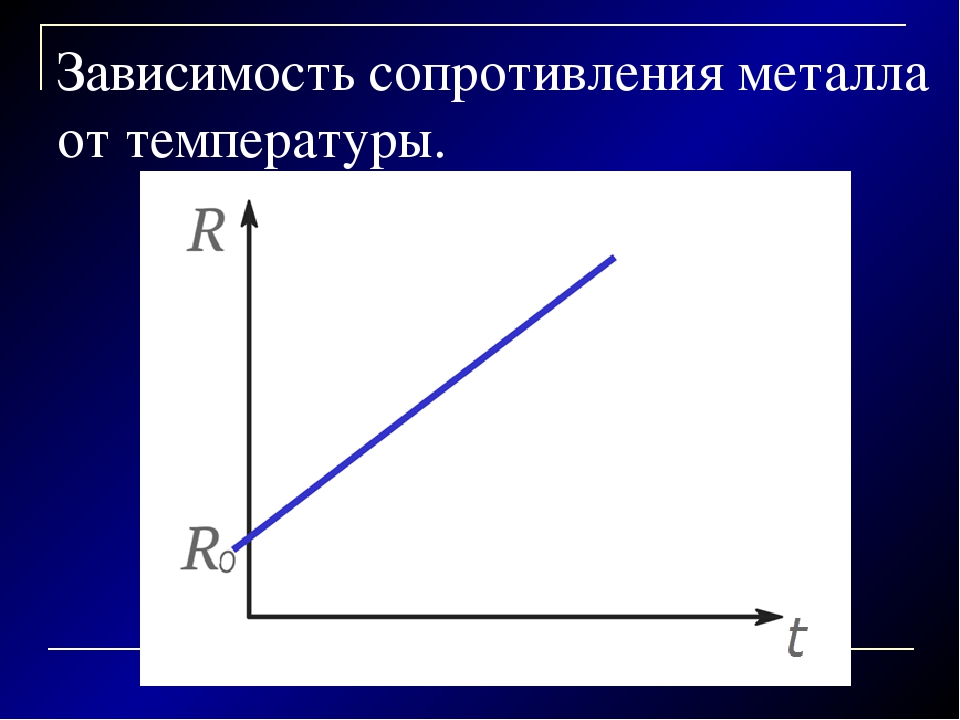 Толчком к разработке термисторов послужила необходимость компенсировать изменение параметров электронных схем под влиянием колебаний температуры. Первые термисторы изготавливались на основе двуокиси урана ПОг, но затем в начале 30-х годов стали использовать шпинель MgTiOз. Оказалось, что удельное сопротивление MgTiOз и его температурный коэффициент сопротивления (ТКС) легко варьируются путем контролируемого восстановления в водороде и путем изменений концентрации MgO по сравнению со стехиометрической. Использовалась также окись меди СиО. Современные термисторы [60, 61] почти всегда представляют собой нестехиометрические смеси окислов и изготавливаются путем спекания микронных частиц компонентов в контролируемой атмосфере. В зависимости от того, в какой атмосфере происходит спекание (окислительной или восстановительной), может получиться, например, полупроводник п-типа на поверхности зерна, переходящий в полупроводник р-типа в глубине зерна, со всеми вытекающими отсюда последствиями для процессов проводимости.
Толчком к разработке термисторов послужила необходимость компенсировать изменение параметров электронных схем под влиянием колебаний температуры. Первые термисторы изготавливались на основе двуокиси урана ПОг, но затем в начале 30-х годов стали использовать шпинель MgTiOз. Оказалось, что удельное сопротивление MgTiOз и его температурный коэффициент сопротивления (ТКС) легко варьируются путем контролируемого восстановления в водороде и путем изменений концентрации MgO по сравнению со стехиометрической. Использовалась также окись меди СиО. Современные термисторы [60, 61] почти всегда представляют собой нестехиометрические смеси окислов и изготавливаются путем спекания микронных частиц компонентов в контролируемой атмосфере. В зависимости от того, в какой атмосфере происходит спекание (окислительной или восстановительной), может получиться, например, полупроводник п-типа на поверхности зерна, переходящий в полупроводник р-типа в глубине зерна, со всеми вытекающими отсюда последствиями для процессов проводимости. Помимо характера проводимости в отдельном зерне, на проводимость материала оказывают существенное влияние также процессы на границах между спеченными зернами. Высокочастотная дисперсия у термисторов, например, возникает вследствие того, что они представляют собой сложную структуру, образованную зонами плохой проводимости на границах зерен и зонами относительно высокой проводимости внутри зерен.
[c.243]
Помимо характера проводимости в отдельном зерне, на проводимость материала оказывают существенное влияние также процессы на границах между спеченными зернами. Высокочастотная дисперсия у термисторов, например, возникает вследствие того, что они представляют собой сложную структуру, образованную зонами плохой проводимости на границах зерен и зонами относительно высокой проводимости внутри зерен.
[c.243]
Ниже будет рассмотрено изменение электросопротивления с температурой для некоторых типов угольных термометров сопротивления. Даже качественное совпадение с тем, что дает зонная теория, наблюдается только в отдельных случаях. Для некоторых образцов величина удельного сопротивления р увеличивается почти экспоненциально при понижении температуры, указывая на то, что имеет место термическая активация носителей тока. Однако из этого не следует, что весь объем графита является элементарным полупроводником и что теоретическое предсказание оказывается несостоятельным. Характер изменения величины электросопротивления с температурой может быть объяснен тем, что частицы графита, входящие в состав образца, обычно находятся в плохом контакте друг с другом или с металлическими контактами. Поэтому носители должны быть тер.мически активированы для преодоления значительных энергетических барьеров. Этот процесс активации может привести к такой зависимости электросопротивления от температуры, которая наблюдалась выше. Очевидно, что способ изготовления угольных сопротивлений играет наиболее важную, хотя и трудно определимую роль при получении желаемых характеристик.
[c.173]
Характер изменения величины электросопротивления с температурой может быть объяснен тем, что частицы графита, входящие в состав образца, обычно находятся в плохом контакте друг с другом или с металлическими контактами. Поэтому носители должны быть тер.мически активированы для преодоления значительных энергетических барьеров. Этот процесс активации может привести к такой зависимости электросопротивления от температуры, которая наблюдалась выше. Очевидно, что способ изготовления угольных сопротивлений играет наиболее важную, хотя и трудно определимую роль при получении желаемых характеристик.
[c.173]
Пленки больщинства металлов (например, благородных металлов и неферромагнитных металлов переходной группы) толщиной в несколько сот ангстрем имеют удельное электросопротивление, величина которого изменяется с изменением температуры так же, как и у сплошных металлов. Однако пленки этих металлов толщиной в несколько ангстрем имеют большое удельное электросопротивление и большой отрицательный температурный коэффициент. Зависи.мость сопротивления этих пленок от те.мпературы в широком интервале температур описывается уравнением, характерным для примесных полупроводников. Энергия активации в сильной степени зависит от состава пленок и их толщины. Для пленок значительной толщины, но еще не настолько толстых, чтобы появились типичные металлические свойства, зависимость сопротивления от температуры оказывается более сложной. Характеристики этих пленок и воспроизводимость их свойств сильно зависят от способа приготовления пленки, от присутствия сорбируе.мых газов, а в некоторых случаях — от старения и отжига.
[c.181]
Зависи.мость сопротивления этих пленок от те.мпературы в широком интервале температур описывается уравнением, характерным для примесных полупроводников. Энергия активации в сильной степени зависит от состава пленок и их толщины. Для пленок значительной толщины, но еще не настолько толстых, чтобы появились типичные металлические свойства, зависимость сопротивления от температуры оказывается более сложной. Характеристики этих пленок и воспроизводимость их свойств сильно зависят от способа приготовления пленки, от присутствия сорбируе.мых газов, а в некоторых случаях — от старения и отжига.
[c.181]
Выше приведено значение удельного сопротивления германия весьма высокой чистоты, близкое к значению собственного со-ттротивления германия. Примеси сильно понижают удельное сопротивление германия. С увеличением температуры удельное электросопротивление германия (как и у всех полупроводников) понижается. Характерна зависимость электросопротивления германия от давления. [c.376]
[c.376]
Удельное электрическое сопротивление любого радиоматериала в значительной степени зависит от температуры (рис. 1). Так, у проводников с повышением температуры удельное сопротивление возрастает. Это связано с более интенсивным колебанием атомов в узлах кристаллической решетки проводника, что мешает направленному перемещению свободных электронов В связи с этим общее и удельное электрические сопротивления проводников увеличиваются. У полупроводников и диэлектриков, наоборот, с возрастанием температуры общее и удельное сопротивления уменьшаются. Это объясняется увеличением энергии носителей элек-Рис. 1. Зависимость удель- тоических зяпялов ного электрического сопро- трических зарядов. [c.6]
Измерение электрофизических свойств Ag2Se показало, что при комнатной температуре селенид серебра является электронным полупроводником с удельным сопротивлением 10-10 ом-см, подвижностью электронов 2050 см (в-сек). Термоэлектродвижущая сила селенида в зависимости от способа приготовления колеблется от 140 до 160 мв град [42]. Теплопроводность АдгЗе при комнатной температуре минимальная при 40°С 5на имеет максимальную величину, составляющую 3-10 з кал (см-сек-град).
[c.109]
Термоэлектродвижущая сила селенида в зависимости от способа приготовления колеблется от 140 до 160 мв град [42]. Теплопроводность АдгЗе при комнатной температуре минимальная при 40°С 5на имеет максимальную величину, составляющую 3-10 з кал (см-сек-град).
[c.109]
Перейдем теперь к рассмотрению менее изученного класса жидкостей с высоким удельным электрическим сопротивлением. Чистый селен изучали в течение долгого времени. По сравнению с другими жидкими полупроводниками молекулярная структура селена хорошо изучена. Жидкая сера очень похожа на жидкий селен, и было показано, что обе эти жидкости состоят из смеси цепных молекул и восьмичленных колец (а возможно и больших колец). Концентрация колец увеличивается с понижением температуры, и имеется критическая температура, ниже которой существуют только кольцевые молекулы. Критическая температура экспериментально наблюдалась только для жидкой серы для селена расчетное значение этой температуры лежит ниже точки затвердевания. Теория равновесия связей для этих жидкостей разработана очень хорошо [78, 104], и эта теория является прототипом теории для сплавов Т1—Те, описанной в гл. 7, 3. Для настоящего обсуждения достаточно отметить, что средняя длина цепи уменьшается с температурой, а концентрация разрушенных связей описывается с помощью константы равновесия с энергией активации Еа, которая была определена различными способами. Эйзенберг и Тобольски [78] на основе данных по вязкости оценили d = 0,54 эВ. Разорванные связи являются парамагнитными центрами, и определение их концентрации в зависимости от температуры методом электронного спинового резонанса дало значение магнитной восприимчивости [175] привело к значению Еа==0,87 эВ.
[c.210]
Теория равновесия связей для этих жидкостей разработана очень хорошо [78, 104], и эта теория является прототипом теории для сплавов Т1—Те, описанной в гл. 7, 3. Для настоящего обсуждения достаточно отметить, что средняя длина цепи уменьшается с температурой, а концентрация разрушенных связей описывается с помощью константы равновесия с энергией активации Еа, которая была определена различными способами. Эйзенберг и Тобольски [78] на основе данных по вязкости оценили d = 0,54 эВ. Разорванные связи являются парамагнитными центрами, и определение их концентрации в зависимости от температуры методом электронного спинового резонанса дало значение магнитной восприимчивости [175] привело к значению Еа==0,87 эВ.
[c.210]
На первых порах накопление достоверной информации о полупроводниках существенно задерживалось тем обстоятельством, что экспериментальные данные чрезвычайно чувствительны к чистоте образца. Примером может служить фиг. 28.2, где изображенно удельное сопротивление германия в зависимости от Т для различных концентраций примесей. Отметим, что даже столь малые концентрации, как несколько примесей на 10 атомов, могут приводить к заметным эффектам и сопротивление может изменяться при данной температуре в 10 раз при изменении концентрации примесей только в 10 раз. Отметим также, что при повышении температуры сопротивление образца с заданной концентрацией примесей достигает значения, лежащего на общей для всех образцов кривой. Это предельное сопротивление, которое имел бы, очевидно, идеальный, совершенно чистый образец, носит название собственного сопротивления.
[c.186]
Отметим, что даже столь малые концентрации, как несколько примесей на 10 атомов, могут приводить к заметным эффектам и сопротивление может изменяться при данной температуре в 10 раз при изменении концентрации примесей только в 10 раз. Отметим также, что при повышении температуры сопротивление образца с заданной концентрацией примесей достигает значения, лежащего на общей для всех образцов кривой. Это предельное сопротивление, которое имел бы, очевидно, идеальный, совершенно чистый образец, носит название собственного сопротивления.
[c.186]
Физика_8.3А_8 класс_8.4.2.16_Краткосрочный план
1.
Организация к уроку. Знакомство с ЦО, целями
обучения.
2.
Деление на группы.
3.
Актуализация знаний учащихся. Вопросы для группы:
1)
Чтотакоеэлектрическийток?
2)
Какие условия необходимы, чтобы эл. ток возник и существовал длительное
время?
3)
Какие величины связывает закон Ома?
4)
От чего и как зависит сопротивление проводника?
5)
Сформулируйтеопределениеэлектрическогосопротивления?
4.
Решениезадач
4.1 Используя карточки, соберите таблицу
Название | Формула |
|
|
|
|
|
|
|
|
|
|
1)
Закон ОмаI =
2)
Сила тока I =
3)
Напряжение U=
4)
Электродвижущая сила
5)
Электрическое сопротивление R=
4.2Решение задач в группах. Деление на
новые группы.
Каждая группа разбирает 1 задачу
1.
Рассчитайте сопротивление никелиновой проволоки длиной 400 см и
площадью поперечного сечения 0, 5 мм2?
2.
Какой электрический заряд пройдет за 3 мин через амперметр при силе
тока в цепи 200 мА?
3.
Какую работу совершит ток силой 3 А за 10 мин при напряжении на
участке цепи 15 В?
4.
Определите сопротивление электрической лампы, сила тока в которой 500
мА, при напряжении 0,12 кВ.
5.
Сопротивление алюминиевого провода длиной 0,9 км и сечением 10
мм2 равно 2,5 Ом. Определите его удельное сопротивление.
5.
Новая тема. Создание проблемной ситуации: А как вы думаете,
зависит ли сопротивление металлического проводника от температуры?
6.
Постановка опыта:Включим в цепь, содержащую батарею аккумуляторов,
стальную спираль (см. рис.) последовательно с ней включим лампу, по свечению которой
можно судить об изменении силы тока в цепи (вместо лампы можно использовать
амперметр демонстрационный).Нагревая спираль при помощи горелки, видим. Что
яркость лампы уменьшилась.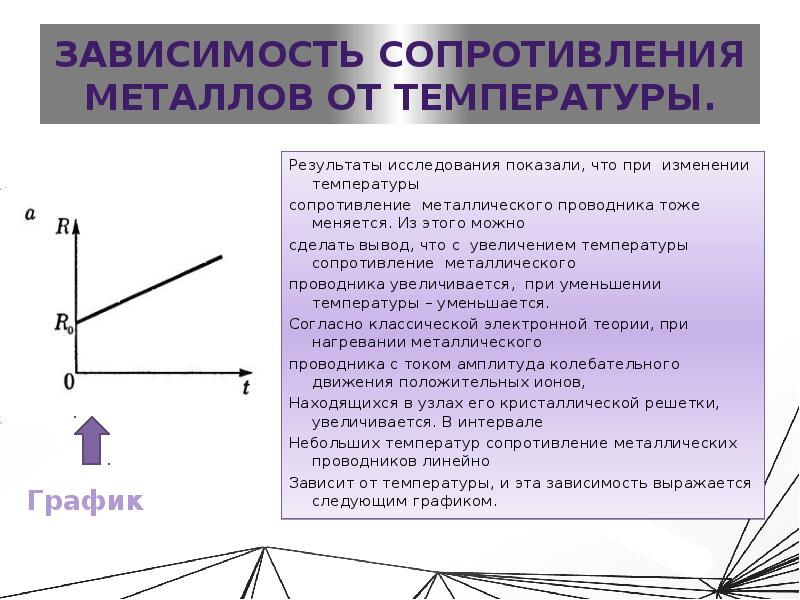 Следовательно, ток в цепи уменьшился. Значит, при
Следовательно, ток в цепи уменьшился. Значит, при
нагревании стального проводника сопротивление проводника увеличивается.
Заменяя стальную спираль другими металлическими проводниками, можно убедиться
в том, что при повышении температуры сопротивление всех
металлических проводников растет.
Ожидаемые результаты:
Ученики наблюдают и делают
вывод:
1) при нагревании
металлического проводника сопротивление его увеличивается.
2)При повышении температуры
сопротивление всех металлических проводников растет, но у одних рост
сопротивления сильнее, чем у других.
7. Работа
с таблицей «Температурный коэффициент сопротивления металлов и сплавов»
8. Объяснение
учителяоб опытах и электронной теории. Вклады ученых в исследование этого
вопроса.
9. Анализ
формул
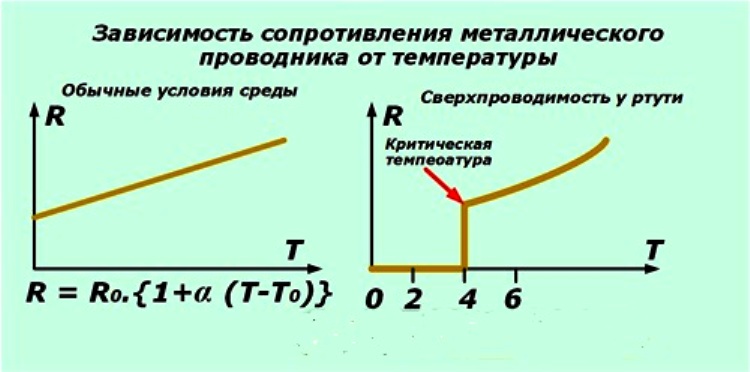
зависимости удельного сопротивления и сопротивления проводника от температуры:
и графическое выражение зависимости
сопротивления
проводника от температуры:
10. Просмотр
Просмотр
видео
по новой теме: «Сверхпроводимость»
11. Обсуждение в
группах (перекресток вопросов)
12. Перестановка
групп
13. Решитезадачи:
1) Каков
температурный коэффициент электрического сопротивления материала проводника,
если при нагревании от 0°С до 100°С его электрическое сопротивление
увеличилось на 0,001?
2) Электрическое
сопротивление вольфрамовой нити электрической лампы при 0 °С равно 3,6 Ом. Найдитеэлектрическоесопротивлениенитипри 2700К.
3)
Объяснение
решенных задач в группах.
Критерии оценивания:
1)
Оформление
2)
Перевод в Си
3)
Знание формулы
4)
Применение формулы
5)
Вычисление и ответ
График зависимости сопротивления металлического проводника от температуры. Зависимость электрического сопротивления от температуры
Удельное сопротивление зависит не только от рода вещества, но и от его состояния, в частности, от температуры. Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:
Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:
Он даёт относительное приращение сопротивления при увеличении температуры на один градус.
Температурный коэффициент сопротивления для данного вещества различен при разных температурах. Это показывает, что удельное сопротивление изменяется с температурой не по линейному закону, а зависит от неё более сложным образом.
ρ=ρ 0 (1+αt) (14.12)
где ρ 0 – удельное сопротивление при 0ºС, ρ – его значение при температуре tºС.
Температурный коэффициент сопротивления может быть как положительным, так и отрицательным. У всех металлов сопротивление увеличивается с увеличением температуры, а следовательно для металлов
α >0. У всех электролитов в отличии от металлов сопротивление при нагревании всегда уменьшается. Сопротивление графита с повышением температуры также уменьшается. Для таких веществ α
На основании электронной теории электропроводности металлов можно объяснить зависимость сопротивления проводника от температуры. С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (14.7), видим, что электропроводимость пропорциональна концентрации электронов проводимости и средней длине свободного пробега
С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (14.7), видим, что электропроводимость пропорциональна концентрации электронов проводимости и средней длине свободного пробега
, т.е. чем больше
, тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости
. Тепловая скорость при повышении температуры возрастает пропорционально , что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
При очень низких температурах порядка 1-8ºК сопротивление некоторых веществ резко падает в миллиарды раз и практически становится равным нулю.
Это явление, впервые открыто голландским физиком Г.Камерлинг-Оннесом в 1911 г.. называется сверхпроводимостью
.
В настоящее время сверхпроводимость установлена у целого ряда чистых элементов (свинца, олова, цинка, ртути, алюминия и др), а также у большого числа сплавов этих элементов друг с другом и с другими элементами. На рис. 14.3 схематически показана зависимость сопротивления сверхпроводников от температуры.
Теория сверхпроводимости была создана в 1958 г. Н.Н. Боголюбовым. Согласно этой теории, сверхпроводимость – это движение электронов в кристаллической решётке без соударений друг с другом и с атомами решётки. Все электроны проводимости движутся как один поток невязкой идеальной жидкости, не взаимодействуя между собой и с решёткой, т.е. не испытывая трения. Поэтому сопротивление сверхпроводников равно нулю. Сильное магнитное поле, проникая в сверхпроводник, отклоняет электроны, и, нарушая «ламинарное течение» электронного потока, вызывает соударение электронов с решёткой, т.е. возникает сопротивление.
В сверхпроводящем состоянии между электронами происходит обмен квантами энергии, что приводит к созданию между электронами сил притяжения, которые больше кулоновских сил отталкивания. При этом образуются пары электронов (куперовские пары) с взаимно скомпенсированными магнитными и механическими моментами. Такие пары электронов движутся в кристаллической решётке без сопротивления.
При этом образуются пары электронов (куперовские пары) с взаимно скомпенсированными магнитными и механическими моментами. Такие пары электронов движутся в кристаллической решётке без сопротивления.
Одним из важнейших практических применений сверхпроводимости является применение её в электромагнитах со сверхпроводящей обмоткой. Если бы не существовало критического магнитного поля, разрушающего сверхпроводимость, то с помощью таких электромагнитов можно было бы получать магнитные поля в десятки и сотни миллионов ампер на сантиметр. Получать такие большие постоянные поля с помощью обычных электромагнитов невозможно, так как для этого потребовались бы колоссальные мощности, и был бы практически невозможен отвод тепла, выделяемого при поглощении обмоткой столь больших мощностей. В сверхпроводящем электромагните расход мощности источника тока ничтожен, а расход мощности на охлаждение обмотки до гелиевой температуре (4,2ºК) на четыре порядка ниже, чем в обычном электромагните, создающем такие же поля. Сверхпроводимость применяется и для создания систем памяти электронных математических машин (криотронные элементы памяти).
Сверхпроводимость применяется и для создания систем памяти электронных математических машин (криотронные элементы памяти).
В 1853 г. Видеман и Франц опытным путём установили, что отношение теплопроводности λ к электропроводности γ для всех метал лов при одной и той же температуре одинаково и пропорционально их термодинамической температуре.
Это заставляет предполагать, что теплопроводность в металлах, так же как и электропроводность, обусловлена движением свободных электронов. Будем считать, что электроны подобны одноатомному газу, коэффициент теплопроводности которого, согласно кинетической теории газов, равен
Одна из характеристик любого проводящего электрический ток материала — это зависимость сопротивления от температуры. Если ее изобразить в виде графика на где по горизонтальной оси отмечаются промежутки времени (t), а по вертикальной — значение омического сопротивления (R), то получится ломаная линия. Зависимость сопротивления от температуры схематично состоит из трех участков. Первый соответствует небольшому нагреву — в этом время сопротивление изменяется очень незначительно. Так происходит до определенного момента, после которого линия на графике резко идет вверх — это второй участок. Третья, последняя составляющая — это прямая, уходящая вверх от точки, на которой остановился рост R, под относительно небольшим углом к горизонтальной оси.
Первый соответствует небольшому нагреву — в этом время сопротивление изменяется очень незначительно. Так происходит до определенного момента, после которого линия на графике резко идет вверх — это второй участок. Третья, последняя составляющая — это прямая, уходящая вверх от точки, на которой остановился рост R, под относительно небольшим углом к горизонтальной оси.
Физический смысл данного графика следующий: зависимость сопротивления от температуры у проводника описывается простым до тех пор, пока величина нагрева не превысит какое-то значение, характерное именно для данного материала. Приведем абстрактный пример: если при температуре +10°C сопротивление вещества составляет 10 Ом, то до 40°C значение R практически не изменится, оставаясь в пределах погрешности измерений. Но уже при 41°C возникнет скачок сопротивления до 70 Ом. Если же дальнейший рост температуры не прекратится, то на каждый последующий градус придутся дополнительные 5 Ом.
Данное свойство широко используется в различных электротехнических устройствах, поэтому закономерно привести данные по меди как одному из самых распространенных материалов в Так, для медного проводника нагрев на каждый дополнительный градус приводит к росту сопротивления на полпроцента от удельного значения (можно найти в справочных таблицах, приводится для 20°C, 1 м длины сечением 1 кв. мм).
мм).
При возникновении в металлическом проводнике появляется электрический ток — направленное перемещение элементарных частиц, обладающих зарядом. Ионы, находящиеся в узлах металла, не в состоянии долго удерживать электроны на своих внешних орбитах, поэтому они свободно перемещаются по всему объему материала от одного узла к другому. Это хаотичное движение обусловлено внешней энергией — теплом.
Хотя факт перемещения налицо, оно не является направленным, поэтому не рассматривается в качестве тока. При появлении электрического поля электроны ориентируются в соответствии с его конфигурацией, формируя направленное движение. Но так как тепловое воздействие никуда не исчезло, то хаотично перемещающиеся частицы сталкиваются с направленными полем. Зависимость сопротивления металлов от температуры показывает величину помех прохождению тока. Чем больше температура, тем выше R проводника.
Очевидный вывод: снижая степень нагрева, можно уменьшить и сопротивление. Явление сверхпроводимости (около 20°K) как раз и характеризуется существенным снижением теплового хаотичного движения частиц в структуре вещества.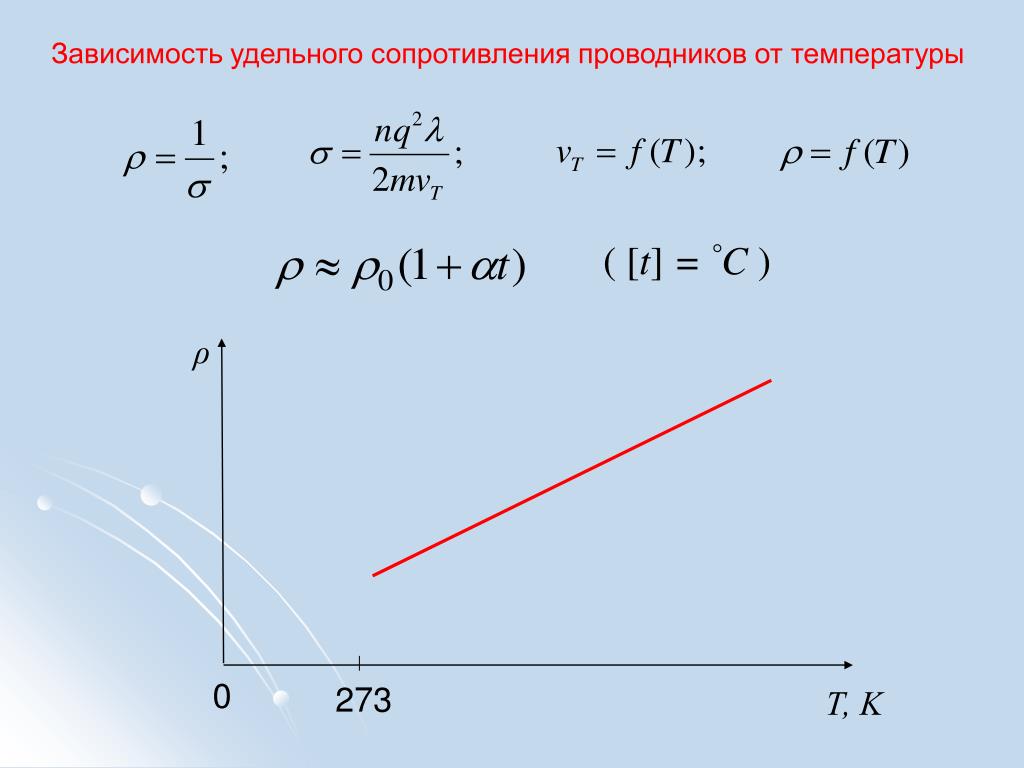
Рассматриваемое свойство проводящих материалов нашло широкое применение в электротехнике. Например, зависимость от температуры используется в электронных датчиках. Зная ее значение для какого-либо материала, можно изготовить терморезистор, подключить его к цифровому или аналоговому считывающему устройству, выполнить соответствующую градуировку шкалы и использовать в качестве альтернативы В основе большинства современных термодатчиков заложен именно такой принцип, ведь надежность выше, а конструкция проще.
Кроме того, зависимость сопротивления от температуры дает возможность рассчитывать нагрев обмоток электродвигателей.
§3. Зависимость сопротивления проводника от температуры. Сверхпроводники
С увеличением температуры сопротивление проводника возрастает по линейному закону
где
R
0
— сопротивление при
t
=0° С;
R
— сопротивление при температуре
t
,
α
— термический коэффициент сопротивления, показывает как меняется сопротивление проводника при изменении температуры на 1 градус.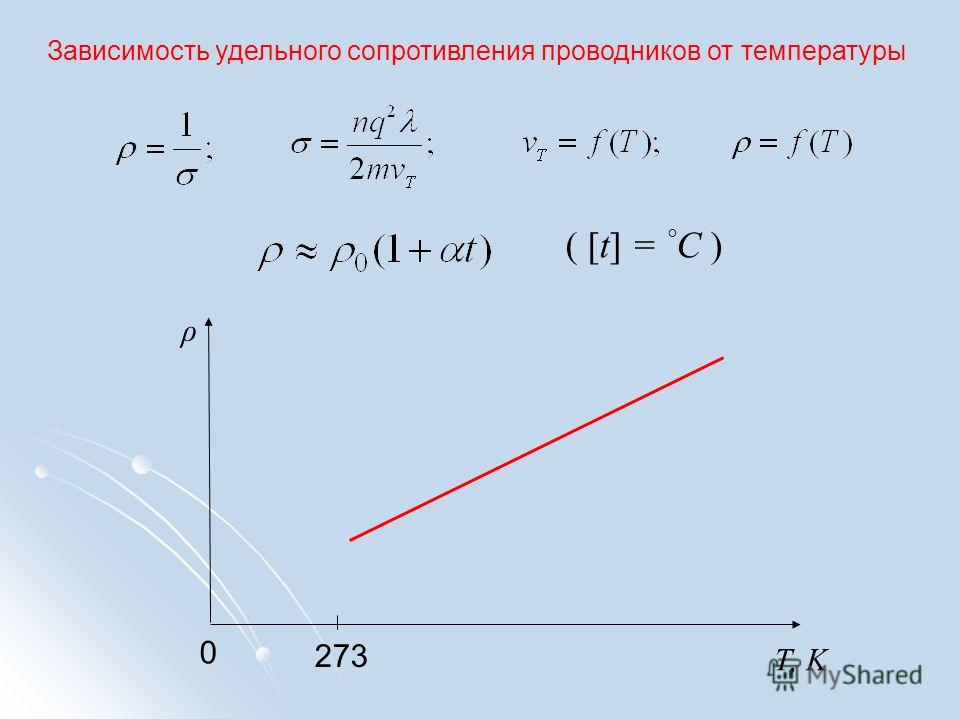 Для чистых металлов при не очень низких температурах , т.е. можно записать
Для чистых металлов при не очень низких температурах , т.е. можно записать
При определенных температурах (0,14-20 К), называемых «критическими» сопротивление проводника резко уменьшается до 0 и металл переходит в сверхпроводящее состояние. Впервые в 1911 г. Это обнаружил Камерлинг-Оннес для ртути. В 1987 г. разработаны керамики, переходящие в сверхпроводящее состояние при температурах превышающих 100 К, так называемые высокотемпературные сверхпроводники — ВТСП.
§4 Элементарная классическая теория электропроводности металлов
Носителями тока в металлах являются свободные электроны, т.е. электроны слабо связанные с ионами кристаллической решетки металла. Наличие свободных электронов объясняется тем, что при образовании кристаллической решетки металла при сближении изолированных атомов валентные электроны, слабо связанные с атомными ядрами, отрываются от атома металла, становятся «свободными», обобществленными, принадлежащими не отдельному атому, а всему веществу, и могут перемещаться по всему объему. В классической электронной теории эти электроны рассматриваются как электронный газ, обладающий свойствами одноатомного идеального газа.
В классической электронной теории эти электроны рассматриваются как электронный газ, обладающий свойствами одноатомного идеального газа.
Электроны проводимости в отсутствии электрического поля внутри металла хаотически двигаются и сталкиваются с ионами кристаллической решетки металла. Тепловое движение электронов, являясь хаотическим, не может, привести к возникновению тока. Средняя скорость теплового движения электронов
при Т = 300 К.
2. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Выразим силу и плотность тока через скорость v упорядоченного движения электронов в проводнике.
За время dt через поперечное сечение S проводника пройдет
N
электронов
,
;
следовательно, даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов , обуславливавшего электрический ток, значительно меньше их скорости теплового движения .
длина цепи, с = 3·10 8 м/с — скорость света в вакууме. Электрический ток возникает в цепи практически одновременно с ее замыканием.
2. Средняя длина свободного пробега электронов λ по порядку величины должна быть равна периоду кристаллической решетки металла λ
≅
10 -10 м.
3.
С ростов температуры увеличивается амплитуда колебаний ионов кристаллической решетки и электрон чаше сталкивается с колеблющимися ионами, поэтому его длина свободного пробега уменьшается, а сопротивление металла растет,
Недостатки классической теории электропроводности металлов:
1.
(1)
т.к. ~ ,
n
и λ
≠
f
(T
)
ρ
~
,
т.е. из классической теории электропроводности следует, что удельное сопротивление пропорционально корню квадратному из температуры, а из опыта следует, что оно линейно зависит от температуры,
ρ
~ Т
2. Дает неправильное значение молярной теплоемкости металлов. Согласно закону Дюлонга и Пти С μ = 3
R
, а по классической теории С = 9 / 2
R
=С
μ
ионной решетки
= 3
R
+ С
μ
дноатомного электронного газа
= 3/2
R
.
3. Средняя длина свободного пробега электронов из формулы (1) при подстановке экспериментального значения ρ и теоретического значения дает 10 -8 , что на два порядка больше средней длины пробега принимаемой в теории (10 -10).
§5. Работа и мощность тока. Закон Джоуля -Ленца
Т.к. заряд переносится в проводнике под действием электроста-тического поля, то его работа равна
МОЩНОСТЬ
— работа, совершаемая в единицу времени
[Р]=Вт (Ватт).
Если ток проходит по неподвижному проводнику, то вся работа тока идет на нагревание металлического проводника, и по закону сохранения энергии
Закон Джоуля-Ленца.
УДЕЛЬНОЙ МОЩНОСТЬЮ
тока называется количество теплоты, выделенное в единице объема, проводника за единицу времени.
Закон Джоуля-Ленца в дифференциальной форме.
§6 Правила Кирхгофа для разветвленных цепей
Любая точка разветвленной цепи, в которой сходится не менее трех проводников, с током называется УЗЛОМ.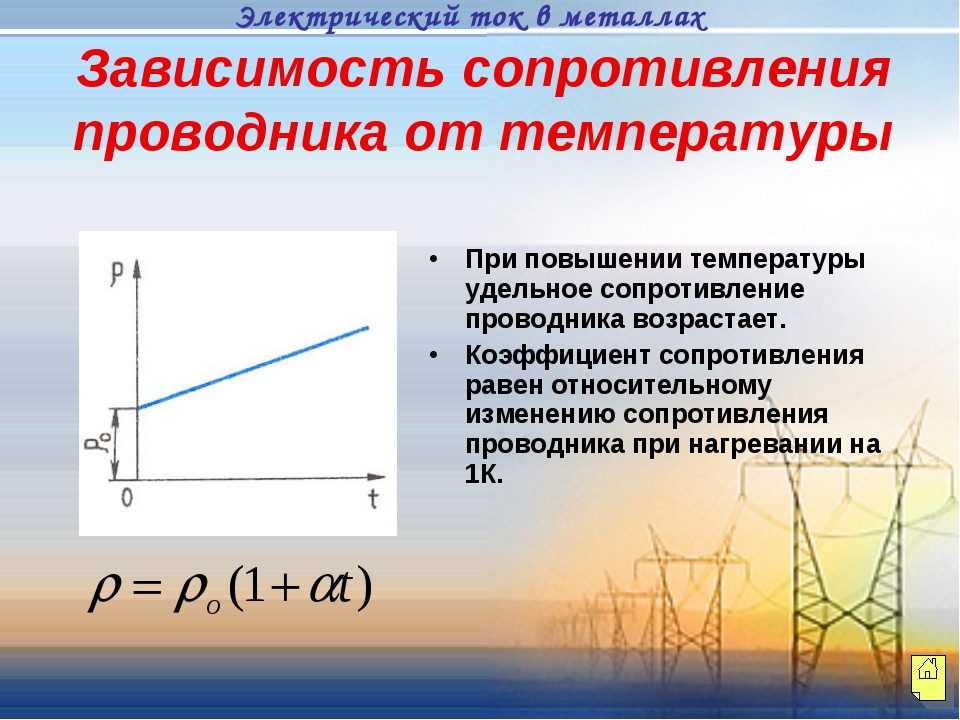 При этом ток, входящий в узел, считается положительным, а выходящий — отрицательный,
При этом ток, входящий в узел, считается положительным, а выходящий — отрицательный,
ПЕРВОЕ ПРАВИЛО КИРХГОФА: алгебраическая сумма токов, сходящихся в узле, равна нулю.
Первое правило Кирхгофа вытекает из закона сохранения заряда (заряд, вошедший в узел, равен вышедшему заряду).
ВТОРОЕ ПРАВИЛО КИРХГОФА: в либом замкнутом контуре произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС. встречающихся в контуре.
При расчете сложных цепей пстоянного тока с применением правил Кирхгофа необходимо:
Число независимых уравнений, составленных в соответствии с первым и вторым правилом Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы ЭДС и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи.
Как зависит от температуры сопротивление газов.
 Зависимость сопротивления проводника от температуры. Сверхпроводимость
Зависимость сопротивления проводника от температуры. Сверхпроводимость
Каждое вещество имеет свое удельное сопротивление. Причем сопротивление будет зависеть от температуры проводника. Убедимся в этом, проведя следующий опыт.
Пропустим ток через стальную спираль. В цепи со спиралью подключим последовательно амперметр . Он покажет некоторое значение. Теперь будем нагревать спираль в пламени газовой горелки. Значение силы тока, которое покажет амперметр, уменьшится. То есть, сила тока будет зависеть от температуры проводника.
Изменение сопротивления в зависимости от температуры
Пусть при температуре 0 градусов, сопротивление проводника равняется R0, а при температуре t сопротивление равно R, тогда относительное изменение сопротивления будет прямо пропорционально изменению температуры t:
В данной формуле а — коэффициент пропорциональности, который называют еще температурным коэффициентом. Он характеризует зависимость сопротивления, которым обладает вещество, от температуры.
Температурный коэффициент сопротивления
численно равен относительному изменению сопротивления проводника при нагревании его на 1 Кельвин.
Для всех металлов температурный коэффициент больше нуля.
При изменениях температуры он будет незначительно меняться. Поэтому, если изменение температуры невелико, то температурный коэффициент можно считать постоянным, и равным среднему значению из этого интервала температур.
Растворы электролитов с ростом температуры сопротивление уменьшается. То есть для них температурный коэффициент будет меньше нуля.
Сопротивление проводника зависит от удельного сопротивления проводника и от размеров проводника. Так как размеры проводника при нагревании меняются незначительно, то основной составляющей изменения сопротивления проводника является удельное сопротивление.
Зависимость удельного сопротивления проводника от температуры
Попытаемся найти зависимость удельного сопротивления проводника от температуры.
Подставим в полученную выше формулу значения сопротивлений R=p*l/S R0=p0*l/S.
Получим следующую формулу:
Данная зависимость представлена на следующем рисунке.
Попробуем разобраться, почему увеличивается сопротивление
Когда мы повышаем температуру, то увеличивается амплитуда колебаний ионов в узлах кристаллической решетки. Следовательно, свободные электроны будут чаще с ними сталкиваться. При столкновении они будет терять направленность своего движения. Следовательно, сила тока будет уменьшаться.
>>Физика: Зависимость сопротивления проводника от температуры
Различные вещества имеют разные удельные сопротивления (см. § 104). Зависит ли сопротивление от состояния проводника? от его температуры ? Ответ должен дать опыт.
Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать ее в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.
Если при температуре, равной 0°С, сопротивление проводника равно R 0
, а при температуре t
оно равно R
, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t
:
Коэффициент пропорциональности α
называют температурным коэффициентом сопротивления
. Он характеризует зависимость сопротивления вещества от температуры. Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К.
Для всех металлических проводников коэффициент α
> 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов α ≈
1/273 K -1 . У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается
. Для них α
α ≈
-0,02 K -1 .
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счет изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (16.1) подставить значения
. Вычисления приводят к следующему результату:
Так как α
мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис.16.2
).
Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решетки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения. Хотя коэффициент α
довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока более чем в 10 раз.
У некоторых сплавов, например у сплава меди с никелем (константан), температурный коэффициент сопротивления очень мал: α
≈ 10 -5 K -1 ; удельное сопротивление константана велико: ρ
≈ 10 -6 Ом м. Такие сплавы используют для изготовления эталонных сопротивлений и добавочных сопротивлений к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления
. Обычно в качестве основного рабочего элемента такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.
Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Удельное сопротивление металлов растет линейно с увеличением температуры. У растворов электролитов оно уменьшается при увеличении температуры.
У растворов электролитов оно уменьшается при увеличении температуры.
???
1. Когда электрическая лампочка потребляет большую мощность: сразу после включения ее в сеть или спустя несколько минут?
2. Если бы сопротивление спирали электроплитки не менялось с температурой, то ее длина при номинальной мощности должна быть большей или меньшей?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Содержание урока
конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку,
Опыт
в соответствии с общими соображениями § 46 показывает, что сопротивление
проводника зависит также и от его температуры.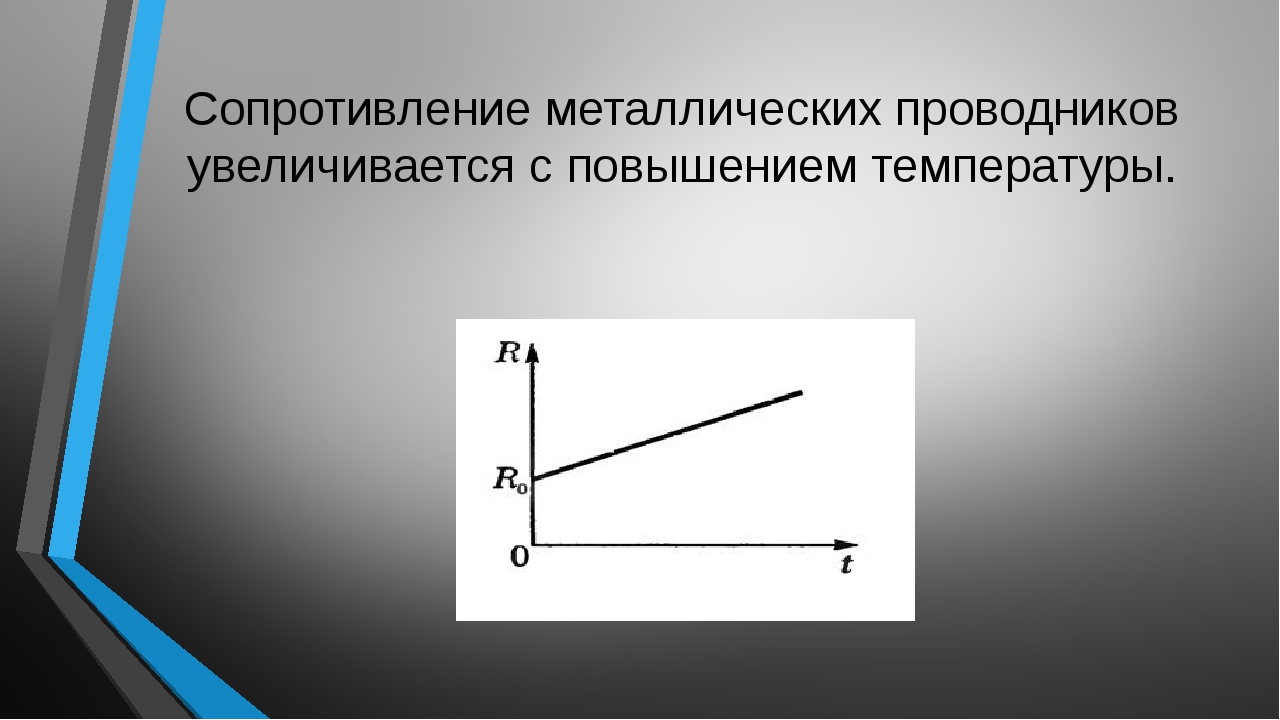
Намотаем
в виде спирали несколько метров тонкой (диаметра 0,1-0,2 мм) железной проволоки
1 и включим ее в цепь, содержащую батарею гальванических элементов 2 и
амперметр 3 (рис. 81). Сопротивление этой проволоки подберем таким, чтобы при
комнатной температуре стрелка амперметра отклонялась почти на всю шкалу.
Отметив показания амперметра, сильно нагреем проволоку при помощи горелки. Мы
увидим, что по мере нагревания ток в цепи уменьшается, а значит, сопротивление
проволоки при нагревании увеличивается. Такой результат получается не только с
железом, но и со всеми другими металлами. При повышении температуры
сопротивление металлов увеличивается. У некоторых металлов это увеличение
значительно: у чистых металлов при нагревании на 100°С оно достигает 40-50%; у
сплавов оно обычно бывает меньше. Есть специальные сплавы, у которых
сопротивление почти не меняется при повышении температуры; таковы, например,
константан (от латинского слова constans – постоянный) и манганин.
Константан употребляется для изготовления некоторых измерительные приборов.
Рис. 81. Опыт, показывающий
зависимость сопротивления проволоки от температуры. При нагревании
сопротивление проволоки увеличивается: 1 – проволока, 2 – батарея
гальванических элементов, 3 – амперметр
Иначе
меняется при нагревании сопротивление электролитов. Повторим описанный опыт, но
введем в цепь вместо железной проволоки какой-нибудь электролит (рис. 82). Мы
увидим, что показания амперметра при нагревании электролита все время
увеличиваются, а значит, сопротивление электролитов при повышении температуры
уменьшается. Отметим, что сопротивление угля и некоторых других материалов
также уменьшается при нагревании.
Рис. 82. Опыт, показывающий
зависимость сопротивления электролита от температуры. При нагревании
сопротивление электролита уменьшается: 1 – электролит, 2 – батарея
гальванических элементов, 3 – амперметр
Зависимость
сопротивления металлов от температуры используется для устройства термометров
сопротивления. В простейшем виде это – намотанная на слюдяную пластинку тонкая
платиновая проволока (рис. 83), сопротивление которой при различных
83), сопротивление которой при различных
температурах хорошо известно. Термометр сопротивления помещают внутрь тела,
температуру которого желают измерить (например, в печь), а концы обмотки
включают в цепь. Измеряя сопротивление обмотки, можно определить температуру.
Такие термометры часто применяются для измерения очень высоких и очень низких
температур, при которых ртутные термометры уже неприменимы.
Рис. 83. Термометр сопротивления
Приращение
сопротивления проводника при его нагревании на 1°С, разделенное на
первоначальное сопротивление, называется температурным коэффициентом
сопротивления и обычно обозначается буквой . Вообще говоря, температурный
коэффициент сопротивления сам зависит от температуры. Величина имеет одно
значение, например, если мы будем повышать температуру от 20 до 21°С, и другое
при повышении температуры от 200 до 201°С. Но во многих случаях изменение в довольно
широком интервале температур незначительно, и можно пользоваться средним
значением в
этом интервале. Если сопротивление проводника при температуре равно , а при
Если сопротивление проводника при температуре равно , а при
температуре равно
, то
среднее значение
. (48.1)
Обычно
в качестве принимают
сопротивление при температуре 0°С.
Таблица
3. Среднее значение температурного коэффициента сопротивления некоторых
проводников (в интервале от 0 до 100 °С)
Вещество | Вещество | ||
Вольфрам | |||
Константан | |||
Манганин |
В
табл. 3 приведены значения для некоторых проводников.
3 приведены значения для некоторых проводников.
48.1.
При включении электрической
лампочки сила тока в цепи в первый момент отличается от силы тока, который
течет после того, как лампочка начнет светиться. Как изменяется ток в цепи с
угольной лампочкой и лампочкой, имеющей металлическую нить накаливания?
48.2.
Сопротивление выключенной
электрической лампочки накаливания с вольфрамовой нитью равно 60 Ом. При полном
накале сопротивление лампочки возрастает до 636 Ом. Какова температура
накаленной нити? Воспользуйтесь табл. 3.
48.3.
Сопротивление электрической печи
с никелиновой обмоткой в ненагретом состоянии равно 10 Ом. Каково будет
сопротивление этой печи, когда обмотка ее нагреется до 700°С? Воспользуйтесь
табл. 3.
Частицы проводника (молекулы, атомы, ионы), не участвующие в образовании тока, находятся в тепловом движении, а частицы, образующие ток, одновременно находятся в тепловом и в направленном движениях под действием электрического поля. Благодаря этому между частицами, образующими ток, и частицами, не участвующими в его образовании, происходят многочисленные столкновения, при которых первые отдают часть переносимой ими энергии источника тока вторым. Чем больше столкновений, тем меньше скорость упорядоченного движения частиц, образующих ток. Как видно из формулы I = enνS
Благодаря этому между частицами, образующими ток, и частицами, не участвующими в его образовании, происходят многочисленные столкновения, при которых первые отдают часть переносимой ими энергии источника тока вторым. Чем больше столкновений, тем меньше скорость упорядоченного движения частиц, образующих ток. Как видно из формулы I = enνS
, снижение скорости приводит к уменьшению силы тока. Скалярная величина, характеризующая свойство проводника уменьшать силу тока, называется сопротивлением проводника.
Из формулы закона Ома сопротивление Ом — сопротивление проводника, в котором получается ток силой в 1 а
при напряжении на концах проводника в 1 в.
Сопротивление проводника зависит от его длины l, поперечного сечения S и материала, который характеризуется удельным сопротивлением Чем длиннее проводник, тем больше за единицу времени столкновений частиц, образующих ток, с частицами, не участвующими в его образовании, а поэтому тем больше и сопротивление проводника. Чем меньше поперечное сечение проводника, тем более плотным потоком идут частицы, образующие ток, и тем чаще их столкновения с частицами, не участвующими в его образовании, а поэтому тем больше и сопротивление проводника.
Чем меньше поперечное сечение проводника, тем более плотным потоком идут частицы, образующие ток, и тем чаще их столкновения с частицами, не участвующими в его образовании, а поэтому тем больше и сопротивление проводника.
Под действием электрического поля частицы, образующие ток, между столкновениями движутся ускоренно, увеличивая свою кинетическую энергию за счет энергии поля. При столкновении с частицами, не образующими ток, они передают им часть своей кинетической энергии. Вследствие этого внутренняя энергия проводника увеличивается, что внешне проявляется в его нагревании. Рассмотрим, изменяется ли сопротивление проводника при его нагревании.
В электрической цепи имеется моток стальной проволоки (струна, рис. 81, а). Замкнув цепь, начнем нагревать проволоку. Чем больше мы ее нагреваем, тем меньшую силу тока показывает амперметр. Ее уменьшение происходит от того, что при нагревании металлов их сопротивление увеличивается. Так, сопротивление волоска электрической лампочки, когда она не горит, приблизительно 20 ом
, а при ее горении (2900° С) — 260 ом
.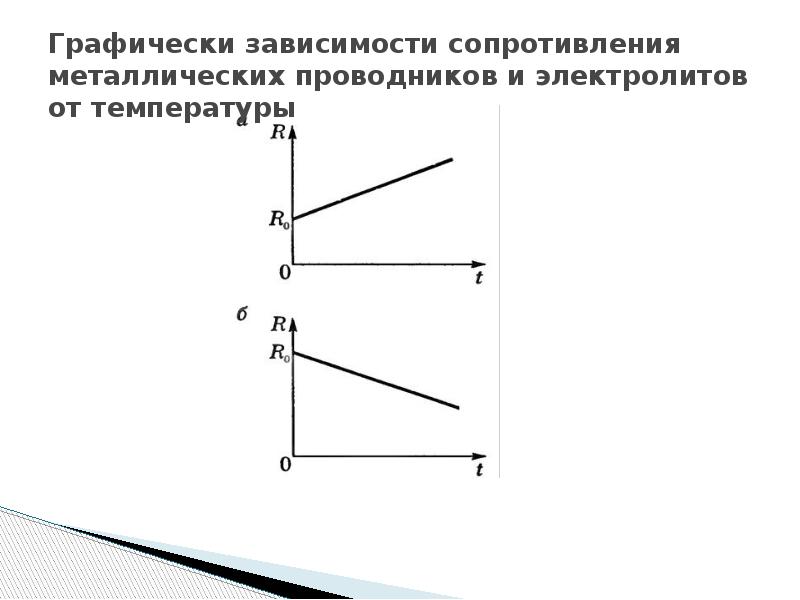 При нагревании металла увеличивается тепловое движение электронов и скорость колебания ионов в кристаллической решетке, в результате этого возрастает число столкновений электронов, образующих ток, с ионами. Это и вызывает увеличение сопротивления проводника * . В металлах несвободные электроны очень прочно связаны с ионами, поэтому при нагревании металлов число свободных электронов практически не изменяется.
При нагревании металла увеличивается тепловое движение электронов и скорость колебания ионов в кристаллической решетке, в результате этого возрастает число столкновений электронов, образующих ток, с ионами. Это и вызывает увеличение сопротивления проводника * . В металлах несвободные электроны очень прочно связаны с ионами, поэтому при нагревании металлов число свободных электронов практически не изменяется.
* (Исходя из электронной теории, нельзя вывести точный закон зависимости сопротивления от температуры. Такой закон устанавливается квантовой теорией, в которой электрон рассматривается как частица, обладающая волновыми свойствами, а движение электрона проводимости через металл — как процесс распространения электронных волн, длина которых определяется соотношением де Бройля.
)
Опыты показывают, что при изменении температуры проводников из различных веществ на одно и то же число градусов сопротивление их изменяется неодинаково. Например, если медный проводник имел сопротивление 1 ом
, то после нагревания на 1°С
он будет иметь сопротивление 1,004 ом
, а вольфрамовый — 1,005 ом.
Для характеристики зависимости сопротивления проводника от его температуры введена величина, называемая температурным коэффициентом сопротивления. Скалярная величина, измеряемая изменением сопротивления проводника в 1 ом, взятого при 0° С, от изменения его температуры на 1° С, называется температурным коэффициентом сопротивления α
. Так, для вольфрама этот коэффициент равен 0,005 град -1
, для меди — 0,004 град -1 .
Температурный коэффициент сопротивления зависит от температуры. Для металлов он с изменением температуры меняется мало. При небольшом интервале температур его считают постоянным для данного материала.
Выведем формулу, по которой рассчитывают сопротивление проводника с учетом его температуры. Допустим, что R 0
— сопротивление проводника при 0°С
, при нагревании на 1°С
оно увеличится на αR 0
, а при нагревании на t°
— на αRt°
и становится R = R 0 + αR 0 t°
, или
Зависимость сопротивления металлов от температуры учитывается, например при изготовлении спиралей для электронагревательных приборов, ламп: длину проволоки спирали и допускаемую силу тока рассчитывают по их сопротивлению в нагретом состоянии.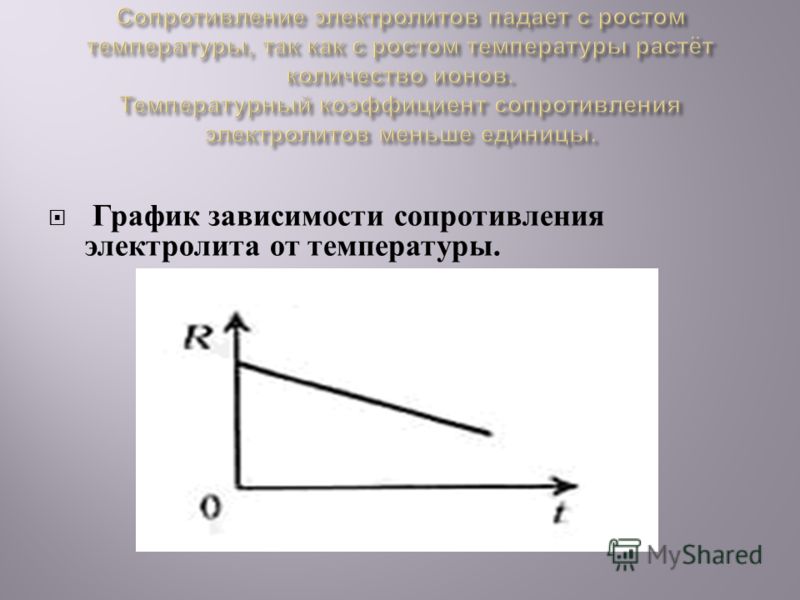 Зависимость сопротивления металлов от температуры используется в термометрах сопротивления, которые применяются для измерения температуры тепловых двигателей, газовых турбин, металла в доменных печах и т. д. Этот термометр состоит из тонкой платиновой (никелевой, железной) спирали, намотанной на каркас из фарфора и помещенной в защитный футляр. Ее концы включаются в электрическую цепь с амперметром, шкала которого проградуирована в градусах температуры. При нагревании спирали сила тока в цепи уменьшается, это вызывает перемещение стрелки амперметра, которая и показывает температуру.
Зависимость сопротивления металлов от температуры используется в термометрах сопротивления, которые применяются для измерения температуры тепловых двигателей, газовых турбин, металла в доменных печах и т. д. Этот термометр состоит из тонкой платиновой (никелевой, железной) спирали, намотанной на каркас из фарфора и помещенной в защитный футляр. Ее концы включаются в электрическую цепь с амперметром, шкала которого проградуирована в градусах температуры. При нагревании спирали сила тока в цепи уменьшается, это вызывает перемещение стрелки амперметра, которая и показывает температуру.
Величина, обратная сопротивлению данного участка, цепи, называется электрической проводимостью проводника
(электропроводностью). Электропроводность проводника Чем больше проводимость проводника, тем меньше его сопротивление и тем лучше он проводит ток. Наименование единицы электропроводности Проводимость проводника сопротивлением 1 ом
называется сименс.
При понижении температуры сопротивление металлов уменьшается. Но есть металлы и сплавы, сопротивление которых при определенной для каждого металла и сплава низкой температуре резким скачком уменьшается и становится исчезающе малым — практически равным нулю (рис. 81, б). Наступает сверхпроводимость
Но есть металлы и сплавы, сопротивление которых при определенной для каждого металла и сплава низкой температуре резким скачком уменьшается и становится исчезающе малым — практически равным нулю (рис. 81, б). Наступает сверхпроводимость
— проводник практически не обладает сопротивлением, и раз возбужденный в нем ток существует долгое время, пока проводник находится при температуре сверхпроводимости (в одном из опытов ток наблюдался более года). При пропускании через сверхпроводник тока плотностью 1200 а / мм 2
не наблюдалось выделения количества теплоты. Одновалентные металлы, являющиеся наилучшими проводниками тока, не переходят в сверхпроводящее состояние вплоть до предельно низких температур, при которых проводились опыты. Например, в этих опытах медь охлаждали до 0,0156°К,
золото — до 0,0204° К.
Если бы удалось получить сплавы со сверхпроводимостью при обычных температурах, то это имело бы огромное значение для электротехники.
Согласно современным представлениям, основной причиной сверхпроводимости является образование связанных электронных пар. При температуре сверхпроводимости между свободными электронами начинают действовать обменные силы, отчего электроны образуют связанные электронные пары. Такой электронный газ из связанных электронных пар обладает иными свойствами, чем обычный электронный газ — он движется в сверхпроводнике без трения об узлы кристаллической решетки.
При температуре сверхпроводимости между свободными электронами начинают действовать обменные силы, отчего электроны образуют связанные электронные пары. Такой электронный газ из связанных электронных пар обладает иными свойствами, чем обычный электронный газ — он движется в сверхпроводнике без трения об узлы кристаллической решетки.
Сопротивление металлов связано с тем, что электроны, движущиеся в проводнике, взаимодействуют с ионами кристаллической решетки и теряют при этом часть энергии, которую они приобретают в электрическом поле.
Опыт показывает, что сопротивление металлов зависит от температуры. Каждое вещество можно характеризовать постоянной для него величиной, называемой температурным коэффициентом сопротивления α
.
Этот коэффициент равен относительному изменению удельного сопротивления проводника при его нагревании на 1 К: α =
где ρ 0 — удельное сопротивление при температуре T 0 = 273 К (0°С), ρ — удельное сопротивление при данной температуре T.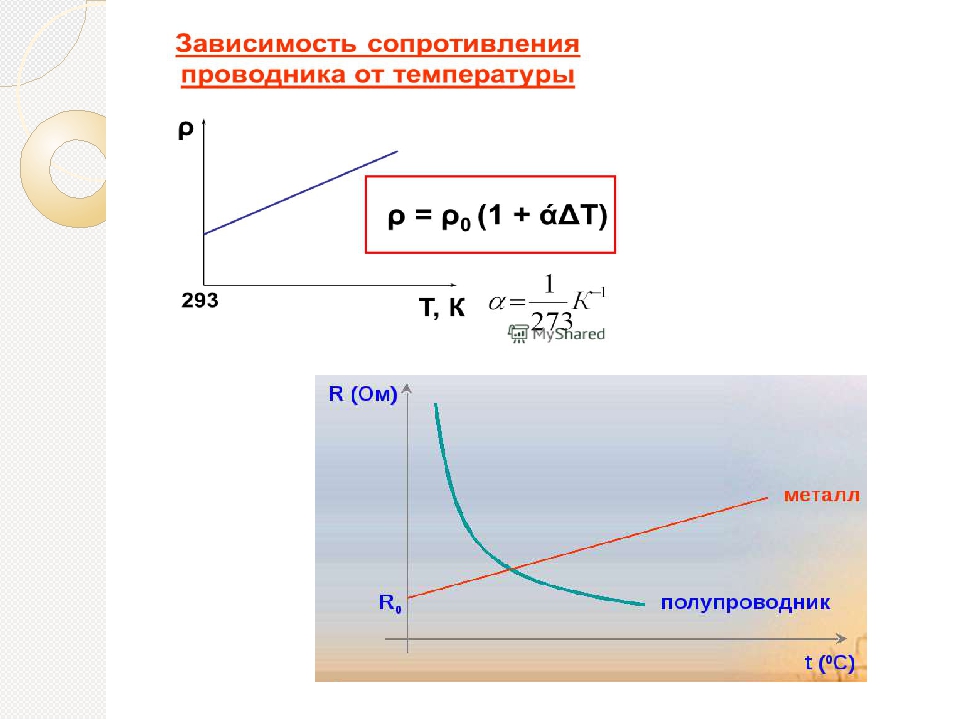 Отсюда зависимость удельного сопротивления металлического проводника от температуры выражается линейной функцией: ρ = ρ 0 (1+ αT).
Отсюда зависимость удельного сопротивления металлического проводника от температуры выражается линейной функцией: ρ = ρ 0 (1+ αT).
Зависимость сопротивления от температуры выражается такой же функцией:
R = R 0 (1+ αT).
Температурные коэффициенты сопротивления чистых металлов сравнительно мало отличаются друготдруга и примерно равны 0,004 K -1 . Изменение сопротивления проводников при изменении температуры приводит к тому, что их вольт-амперная характеристика не линейна. Это особенно заметно в тех случаях, когда температура проводников значительно изменяется, например при работе лампы накаливания. На рисунке приведена ее вольт — амперная характеристика. Как видно из рисунка, сила тока в этом случае не прямо пропорциональна напряжению. Не следует, однако, думать, что этот вывод противоречит закону Ома. Зависимость, сформулированная в законе Ома, справедлива только при постоянном сопротивлении.
Зависимость сопротивления металлических проводников от температуры используют в различных измерительных и автоматических устройствах. Наиболее важным из них является термометр сопротивления
Наиболее важным из них является термометр сопротивления
. Основной частью термометра сопротивления служит платиновая проволока, намотанная на керамический каркас. Проволоку помещают в среду, температуру которой нужно определить. Измеряя сопротивление этой проволоки и зная ее сопротивление при t 0 = 0 °С (т. е. R 0),
рассчитывают по последней формуле температуру среды.
Сверхпроводимость.
Однако до конца XIX в. нельзя было проверить, как зависит сопротивление проводников от температуры в области очень низких температур. Только в начале XX в. голландскому ученому Г. Камерлинг-Оннесу удалось превратить в жидкое состояние наиболее трудно конденсируемый газ — гелий. Температура кипения жидкого гелия равна 4,2 К. Это и дало возможность измерить сопротивление некоторых чистых металлов при их охлаждении до очень низкой температуры.
В 1911г работа Камерлинг-Оннеса завершилась крупнейшим открытием. Исследуя сопротивление ртути при ее постоянном охлаждении, он обнаружил, что при температуре 4,12 К сопротивление ртути скачком падало до нуля. В дальнейшем ему удалось это же явление наблюдать и у ряда других металлов при их охлаждении до температур, близких к абсолютному нулю. Явление полной потери металлом электрического сопротивления при определенной температуре получило название сверхпроводимости.
В дальнейшем ему удалось это же явление наблюдать и у ряда других металлов при их охлаждении до температур, близких к абсолютному нулю. Явление полной потери металлом электрического сопротивления при определенной температуре получило название сверхпроводимости.
Не все материалы могут стать сверхпроводниками, но их число достаточно велико. Однако у многих из них было обнаружено свойство, которое значительно препятствовало их применению. Выяснилось, что у большинства чистых металлов сверхпроводимость исчезает, когда они находятся в сильном магнитном поле. Поэтому, когда по сверхпроводнику течет значительный ток, он создает вокруг себя магнитное поле и сверхпроводимость в нем исчезает. Всё же это препятствие оказалось преодолимым: было выяснено, что некоторые сплавы, например ниобия и циркония, ниобия и титана и др., обладают свойством сохранять свою сверхпроводимость при больших значениях силы тока. Это позволило более широко использовать сверхпроводимость.
Сопротивление в зависимости от температуры — сопротивление различных материалов
Сопротивление — это препятствие для потока электронов в материале.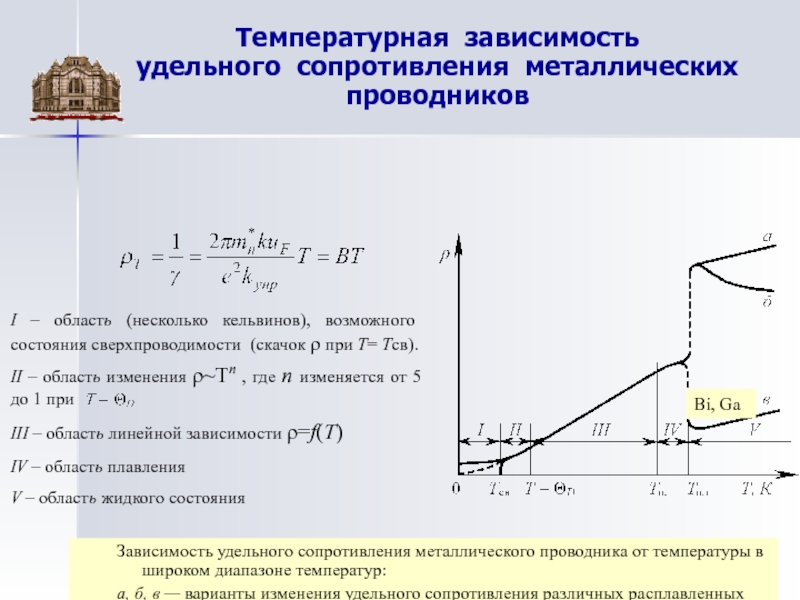 Когда к проводнику прикладывается разность потенциалов, она способствует движению электронов, в то время как сопротивление препятствует движению электронов. Комбинация этих двух факторов представляет собой скорость, с которой заряд течет между двумя клеммами.
Когда к проводнику прикладывается разность потенциалов, она способствует движению электронов, в то время как сопротивление препятствует движению электронов. Комбинация этих двух факторов представляет собой скорость, с которой заряд течет между двумя клеммами.
Когда к веществу прикладывается напряжение, возникает электрический ток.Напряжение, приложенное к веществу через него, прямо пропорционально току.
V∝I
Константа пропорциональности называется удельным сопротивлением металлов.
V=RI
Следовательно, сопротивление определяется как отношение напряжения, приложенного к веществу, к силе тока. Сопротивление измеряется в омах (Ом).
Единица сопротивления
Исходя из концепции сопротивления, можно сказать, что единицей электрического сопротивления является вольт на ампер.Одна единица сопротивления — это сопротивление, которое позволяет одной единице тока протекать через себя, когда к ней приложена одна единица разности потенциалов.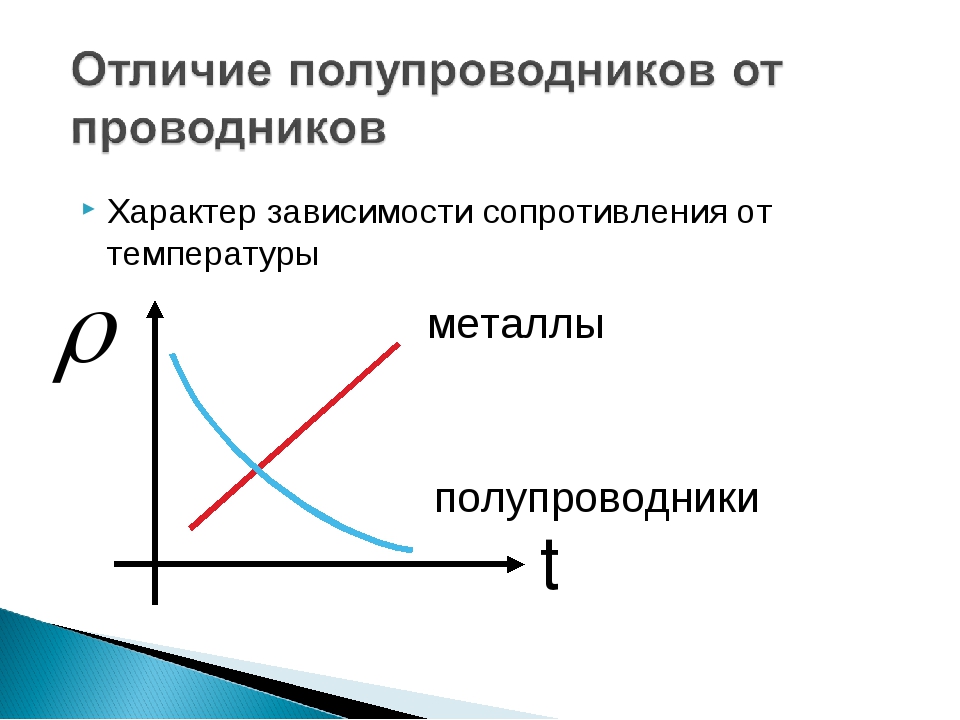 Единица сопротивления на вольт на ампер называется ом (Ом).
Единица сопротивления на вольт на ампер называется ом (Ом).
Сопротивление различных материалов
Проводники: Материалы с очень низким сопротивлением потоку электронов. Серебро является хорошим проводником электричества, но из-за высокой стоимости редко используется в электрических системах.Алюминий является хорошим проводником и широко используется в качестве проводника из-за его низкой стоимости и доступности.
Полупроводники. Материалы с умеренным значением сопротивления (не очень высоким и не очень низким) при комнатной температуре называются полупроводниками. Есть несколько применений полупроводников, например, для изготовления электронных устройств. Кремний и германий — два материала, которые в основном используются в полупроводниках.
Изоляторы: Материалы с очень высоким сопротивлением потоку электронов.
 Эти материалы являются очень плохими проводниками электричества и в основном используются в электрических системах для предотвращения утечки тока. Слюда, фарфор, бумага, сухая древесина, минеральное масло, газообразный азот, воздух и т. д. являются хорошими примерами изоляторов.
Эти материалы являются очень плохими проводниками электричества и в основном используются в электрических системах для предотвращения утечки тока. Слюда, фарфор, бумага, сухая древесина, минеральное масло, газообразный азот, воздух и т. д. являются хорошими примерами изоляторов.
Сопротивление в зависимости от температуры
Общее правило гласит, что сопротивление увеличивается в проводниках с повышением температуры и уменьшается с повышением температуры в изоляторах. В случае полупроводников, как правило, сопротивление полупроводника уменьшается с повышением температуры.Но нет простого математического соотношения для описания этой зависимости между сопротивлением и температурой для различных материалов с помощью графиков.
Для проводника: Валентная зона и зона проводимости перекрывают друг друга в случае проводника. Итак, зона проводимости проводника содержит избыточные электроны.
 Поглощая энергию, больше электронов перейдет из валентной зоны в зону проводимости, когда вы повысите температуру.
Поглощая энергию, больше электронов перейдет из валентной зоны в зону проводимости, когда вы повысите температуру.Для полупроводников: проводимость полупроводникового материала увеличивается с повышением температуры.По мере повышения температуры самые внешние электроны приобретают энергию, и, таким образом, получая энергию, самые внешние электроны покидают оболочку атома.
Что такое удельное сопротивление?
Удельное сопротивление — это в основном количественное значение сопротивления, обеспечиваемого любым материалом. Хотя материалы сопротивляются протеканию электрического тока, некоторые лучше проводят его, чем другие. Удельное сопротивление — это показатель, который позволяет сравнивать, как различные материалы пропускают или сопротивляются протеканию тока.
Единицей удельного сопротивления в СИ является ом⋅метр (Ом⋅м), обычно обозначаемый греческой буквой ρ, ро.
Удельное сопротивление материала может быть определено через сопротивление (R), длину (L) и площадь материала (A).
ρ=RA/L
Из уравнения видно, что сопротивление можно изменять, регулируя ряд параметров.
Удельное сопротивление в зависимости от температуры
Удельное сопротивление материалов зависит от температуры как ρt = ρ0 [1 + α (T – T0).Это уравнение, которое показывает зависимость между удельным сопротивлением и температурой.
ρt = ρ0 [1 + α (t — t0)
ρ0 — удельное сопротивление при стандартной температуре
ρt — удельное сопротивление при T0 C
T0 — эталонная температура
α — температурный коэффициент удельного сопротивления
Здесь зависимость между удельным сопротивлением и температурой с графиками.

Для проводников: Говорят, что проводники имеют положительную ко-температуру, эффективную для металлов или проводников. Положительное значение равно α. Для большинства металлов удельное сопротивление увеличивается линейно с повышением температуры примерно на 500 K.
Для полупроводников: Удельное сопротивление полупроводника уменьшается с повышением температуры. Говорят, что у них отрицательный температурный коэффициент. Таким образом, температурный коэффициент удельного сопротивления α отрицателен.
Изоляторы: Для изоляторов с повышением температуры увеличивается проводимость материала. Когда проводимость материала увеличивается, мы знаем, что удельное сопротивление уменьшается, и тем самым увеличивается ток. А некоторые изоляторы превращаются в проводники при высоких температурах при комнатной температуре.
 Имеют отрицательный температурный коэффициент.
Имеют отрицательный температурный коэффициент.
Забавные факты
Основной причиной использования резистора в качестве электрического компонента является сопротивление электричеству.
Значение резистора легко измерить омметром или мультиметром.
Изучение электричества и мощности в физике является наиболее интересной главой, если хорошо поняты соответствующие понятия и формулы. Веб-сайт Vedantu очень красиво и естественно объясняет течение тока и его силу сопротивления, чтобы ученики могли легко их понять. Эксперты подготовили специальные видеоролики о том, как все это работает, и очень хорошо объяснили концепции.Студенты могут просто обратиться к этим материалам, доступным в Интернете, и хорошо подготовиться к экзаменам.
Сопротивление определяется как мера противодействия протеканию тока, индуцированного напряжением в электрической цепи. Сопротивление измеряется в омах, что обозначается греческой буквой омега (Ом).
 Сила, например трение, действует против направления движения тела и имеет тенденцию предотвращать или замедлять движение тела. Простым примером сопротивления может быть ребенок, сражающийся с похитителем, или ветер с крыльями самолета.
Сила, например трение, действует против направления движения тела и имеет тенденцию предотвращать или замедлять движение тела. Простым примером сопротивления может быть ребенок, сражающийся с похитителем, или ветер с крыльями самолета.Если вы знаете общий ток и напряжение во всей цепи, присутствующей в какой-либо конкретной области, вы можете найти общее сопротивление, используя
Закон Ома: R = V / I.
Например, параллельная цепь имеет напряжение 9 вольт и общий ток 3 ампера. Общее сопротивление RT = 9 вольт / 3 ампера = 3 Ом.
Сопротивление в зависимости от температуры
По мере повышения температуры количество фононов увеличивается, а вместе с ним и вероятность столкновения электронов и фононов.Таким образом, когда температура повышается, сопротивление увеличивается. Для некоторых материалов удельное сопротивление является линейной функцией температуры. Удельное сопротивление проводника увеличивается с температурой.

Влияние температуры на сопротивление
- Изучив этот раздел, вы должны уметь:
- • Описать влияние температуры на сопротивление проводника.
- • Опишите влияние температуры на сопротивление изолятора.
- • Определите отрицательные и положительные температурные коэффициенты.
Как температура влияет на сопротивление
Хотя сопротивление проводника изменяется в зависимости от размера проводника (например, более толстые провода имеют меньшее сопротивление току, чем более тонкие провода), сопротивление проводника также изменяется при изменении температуры. Можно ожидать, что это произойдет, потому что при изменении температуры размеры проводника будут изменяться по мере его расширения или сжатия.
Однако материалы, классифицируемые как ПРОВОДНИКИ, имеют тенденцию УВЕЛИЧИВАТЬ свое сопротивление при повышении температуры.
 Однако ИЗОЛЯТОРЫ могут УМЕНЬШАТЬ свое сопротивление при повышении температуры. Материалы, используемые для практических изоляторов (стекло, пластмасса и т. д.), демонстрируют заметное падение сопротивления только при очень высоких температурах. Они остаются хорошими изоляторами при всех температурах, с которыми они могут столкнуться при использовании.
Однако ИЗОЛЯТОРЫ могут УМЕНЬШАТЬ свое сопротивление при повышении температуры. Материалы, используемые для практических изоляторов (стекло, пластмасса и т. д.), демонстрируют заметное падение сопротивления только при очень высоких температурах. Они остаются хорошими изоляторами при всех температурах, с которыми они могут столкнуться при использовании.Таким образом, эти изменения сопротивления нельзя объяснить изменением размеров вследствие теплового расширения или сжатия.Фактически для данного размера проводника изменение сопротивления происходит главным образом за счет изменения удельного сопротивления материала и вызывается изменяющейся активностью атомов, составляющих материал.
Температура и атомная структура
Причины этих изменений удельного сопротивления можно объяснить, рассматривая протекание тока через материал. Поток тока на самом деле представляет собой движение электронов от одного атома к другому под действием электрического поля.Электроны представляют собой очень маленькие отрицательно заряженные частицы, и они будут отталкиваться отрицательным электрическим зарядом и притягиваться положительным электрическим зарядом.
 Следовательно, если к проводнику (положительному на одном конце и отрицательному на другом) приложен электрический потенциал, электроны будут «мигрировать» от атома к атому к положительному выводу.
Следовательно, если к проводнику (положительному на одном конце и отрицательному на другом) приложен электрический потенциал, электроны будут «мигрировать» от атома к атому к положительному выводу.Однако только некоторые электроны могут свободно мигрировать. Другие внутри каждого атома так крепко привязаны к своему конкретному атому, что даже электрическое поле не может их сместить.Таким образом, ток, протекающий в материале, обусловлен движением «свободных электронов», и количество свободных электронов в любом материале по сравнению с теми, которые прочно связаны со своими атомами, определяет, является ли материал хорошим проводником (много свободных электронов) или хороший изолятор (почти нет свободных электронов).
Воздействие тепла на атомную структуру материала заставляет атомы вибрировать, и чем выше температура, тем сильнее вибрируют атомы.
В проводнике, по которому уже протекает большое количество свободных электронов, вибрация атомов вызывает много столкновений между свободными электронами и захваченными электронами.
 Каждое столкновение использует некоторую энергию свободного электрона и является основной причиной сопротивления. Чем больше атомов толкаются в материале, тем больше возникает столкновений и, следовательно, тем больше сопротивление току.
Каждое столкновение использует некоторую энергию свободного электрона и является основной причиной сопротивления. Чем больше атомов толкаются в материале, тем больше возникает столкновений и, следовательно, тем больше сопротивление току.Однако в изоляторе ситуация несколько иная. Свободных электронов так мало, что почти не может протекать ток. Почти все электроны прочно связаны внутри своего конкретного атома. Нагрев изоляционного материала вызывает вибрацию атомов, и при достаточном нагреве атомы вибрируют достаточно сильно, чтобы высвободить некоторые из своих захваченных электронов, создавая свободные электроны, которые становятся носителями тока.Поэтому при высоких температурах сопротивление изолятора может падать, причем в некоторых изоляционных материалах весьма резко.
В материале, сопротивление которого ПОВЫШАЕТСЯ с повышением температуры, говорят, что материал имеет ПОЛОЖИТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ.
Когда сопротивление ПАДАЕТ при повышении температуры, говорят, что материал имеет ОТРИЦАТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ.

Как правило, проводники имеют ПОЛОЖИТЕЛЬНЫЙ температурный коэффициент, в то время как (при высоких температурах) изоляторы имеют ОТРИЦАТЕЛЬНЫЙ температурный коэффициент.
Различные материалы в каждой группе имеют разные температурные коэффициенты. Материалы, выбранные для изготовления резисторов, используемых в электронных схемах, представляют собой тщательно отобранные проводники с очень низким положительным температурным коэффициентом. При использовании резисторы, изготовленные из таких материалов, будут иметь очень незначительное увеличение удельного сопротивления и, следовательно, их сопротивления. Использование таких материалов для изготовления резисторов создает компоненты, значение которых изменяется незначительно в заданном диапазоне температур.
Материалы, выбранные в качестве изоляторов, будут иметь очень низкий ОТРИЦАТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ в своем рабочем диапазоне температур.
Температурная зависимость удельного сопротивления полупроводников | Блог системного анализа
Ключевые выводы
При повышении температуры удельное сопротивление металла увеличивается, придавая ему положительный температурный коэффициент сопротивления.

Полупроводники имеют отрицательный температурный коэффициент сопротивления.
Удельное сопротивление внешних полупроводников больше, чем собственных полупроводников.
Температурная зависимость удельного сопротивления полупроводников играет важную роль в их применении в электронике
Электропроводность описывает легкость прохождения электрического тока через материал и является важным параметром материала . Проводники – это материалы, пропускающие через себя ток.Те, которые блокируют ток, называются изоляторами. Есть материалы, которые попадают между проводниками и изоляторами, когда ток, протекающий по ним, принимается за относительный параметр. Такие материалы известны как полупроводники.
Во всех этих материалах протекание тока может быть напрямую связано с проводимостью материала, которая является обратной величиной удельного сопротивления.
 Удельное сопротивление является свойством материала и зависит от температуры. Температурная зависимость удельного сопротивления полупроводников играет существенную роль в их применении в электронике.В этой статье мы рассмотрим, почему это так.
Удельное сопротивление является свойством материала и зависит от температуры. Температурная зависимость удельного сопротивления полупроводников играет существенную роль в их применении в электронике.В этой статье мы рассмотрим, почему это так.Что такое удельное сопротивление?
Удельное сопротивление является неотъемлемым свойством материала. Это константа для материала при данной температуре. Удельное сопротивление материала можно определить как сопротивление материала единицы площади поперечного сечения и единицы длины. Удельное сопротивление материала не зависит от его длины и площади.
Соотношение между сопротивлением материала и удельным сопротивлением: материал.Единицей удельного сопротивления является ом-метр.
Электропроводность обратна удельному сопротивлению. Когда удельное сопротивление материала высокое, его проводимость очень низкая, и наоборот. Учитывая это соотношение, можно сказать, что удельное сопротивление металлов или проводников очень низкое.
 Располагая материалы в порядке возрастания удельного сопротивления, порядок: проводники, полупроводники и изоляторы.
Располагая материалы в порядке возрастания удельного сопротивления, порядок: проводники, полупроводники и изоляторы.Далее мы рассмотрим, как температура влияет на удельное сопротивление.
Температурная зависимость удельного сопротивления
Удельное сопротивление материала зависит от температуры.Температурная зависимость удельного сопротивления различна для проводников, полупроводников и диэлектриков. Давайте обсудим, как изменяется удельное сопротивление в проводниках и изоляторах, прежде чем обсуждать полупроводники.
Проводники
В проводниках при повышении температуры атомы начинают сильно вибрировать, что приводит к столкновению свободных электронов и других электронов. Это столкновение вызывает потерю энергии свободными электронами, которые ответственны за ток. Уменьшение движения или скорости дрейфа электронов из-за утечки энергии увеличивает удельное сопротивление проводников, особенно металлов.
 С повышением температуры удельное сопротивление металла также увеличивается, что придает ему положительный температурный коэффициент сопротивления. При высоких температурах удельное сопротивление проводника увеличивается, а проводимость уменьшается.
С повышением температуры удельное сопротивление металла также увеличивается, что придает ему положительный температурный коэффициент сопротивления. При высоких температурах удельное сопротивление проводника увеличивается, а проводимость уменьшается.Изоляторы
Изоляторы смещаются в зону проводимости при повышении температуры. Удельное сопротивление изолятора уменьшается с температурой, что приводит к увеличению проводимости. Изоляторы имеют отрицательный температурный коэффициент сопротивления.
Далее мы исследуем температурную зависимость удельного сопротивления полупроводников.
Температурная зависимость удельного сопротивления полупроводников
В полупроводниках энергетическая щель между зоной проводимости и валентной зоной уменьшается с повышением температуры. Валентные электроны в полупроводниковом материале получают энергию, чтобы разорвать ковалентную связь и перейти в зону проводимости при высоких температурах.
 Это создает больше носителей заряда в полупроводнике при высоких температурах.Более высокая концентрация носителей заряда снижает удельное сопротивление полупроводника. Поскольку удельное сопротивление полупроводника уменьшается с повышением температуры, он становится более проводящим. Полупроводник обладает отличной проводимостью при высоких температурах.
Это создает больше носителей заряда в полупроводнике при высоких температурах.Более высокая концентрация носителей заряда снижает удельное сопротивление полупроводника. Поскольку удельное сопротивление полупроводника уменьшается с повышением температуры, он становится более проводящим. Полупроводник обладает отличной проводимостью при высоких температурах.На приведенном ниже графике показана зависимость между удельным сопротивлением и температурой в полупроводнике. Полупроводники имеют отрицательный температурный коэффициент сопротивления. Это свойство используется для применения полупроводников в электронике.При приложении внешнего напряжения температура полупроводникового кристалла увеличивается, что, в свою очередь, увеличивает плотность в нем термически генерируемых носителей. Генерируется больше электронно-дырочных пар, что позволяет легко протекать току через полупроводник.
Удельное сопротивление в зависимости от температуры в полупроводниках
Характеристики полупроводника улучшаются путем легирования его донорными или акцепторными примесями.
 Такие полупроводники называются внешними полупроводниками.Удельное сопротивление примесных полупроводников больше, чем у собственных (нелегированных или чистых) полупроводников.
Такие полупроводники называются внешними полупроводниками.Удельное сопротивление примесных полупроводников больше, чем у собственных (нелегированных или чистых) полупроводников.Температурная зависимость удельного сопротивления полупроводников очень полезна; используемая нами сегодня полупроводниковая электроника возможна только благодаря отрицательному температурному коэффициенту сопротивления. Cadence предлагает набор инструментов для проектирования и анализа, помогающих создавать твердотельные электронные схемы.
Подпишитесь на нашу рассылку, чтобы быть в курсе последних обновлений. Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, поговорите с нашей командой экспертов.
Изменение температуры и сопротивление | IOPSpark
Температурная зависимость сопротивления
Электричество и магнетизм
Изменение температуры и сопротивление
Практическая деятельность
за
14-16Практический класс
Исследование изменения сопротивления провода при его нагревании.

Аппаратура и материалы
- Источник питания, низкое напряжение, постоянный ток, напр. 12 В, 4 А не менее
- Реостат (10 — 20 Ом) на ток не менее 5 А
- Алюминиевый контейнер (например, одноразовый пищевой контейнер)
- Амперметр, от 0 до 5 А, постоянный ток
- Вольтметр, от 0 до 10 В, постоянный ток
- Провода, 4 мм, 6 шт.
- Зажимы типа «крокодил», 2 шт.
- Катушка медной проволоки (см. техническое примечание)
Здоровье и безопасность и технические примечания
Провод с полиуретановым покрытием может выделять опасные пары при перегреве.Окна лаборатории должны быть открыты, чтобы уменьшить риск.
Ознакомьтесь с нашим стандартным руководством по охране труда и технике безопасности
Катушка должна быть свободно намотана из 1 м медного провода с полиуретановым покрытием (30 или 33 SWG).
 Снимите покрытие с концов, чтобы обеспечить электрический контакт с помощью зажимов типа «крокодил».
Снимите покрытие с концов, чтобы обеспечить электрический контакт с помощью зажимов типа «крокодил».Процедура
- Соберите простую последовательную цепь с длинными выводами к свободно намотанной катушке медного провода.
- Отрегулируйте источник питания, чтобы ток в катушке составлял около 4-5 ампер.Выключите цепь как можно скорее.
- Примерно через минуту катушка остынет до комнатной температуры. Снова включите цепь. Снимите показания амперметра и вольтметра несколько раз в течение следующих полминуты или около того. За это время катушка нагревается и ток меняется довольно быстро.
- Повторите эксперимент с катушкой медной проволоки, подвешенной в воде в контейнере. Воду следует очень хорошо перемешивать. Будьте осторожны, чтобы избежать короткого замыкания катушки, используя деревянную палочку от леденца или шпатель в качестве мешалки.
Учебные заметки
- Учащиеся записывают пары показаний тока и разности потенциалов с катушкой в воздухе, а затем строят характеристику ток/разность потенциалов.
 Это не прямая линия, показывающая постоянное сопротивление, а скорее кривая, показывающая, что сопротивление провода увеличивается с температурой.
Это не прямая линия, показывающая постоянное сопротивление, а скорее кривая, показывающая, что сопротивление провода увеличивается с температурой. - Когда эксперимент повторяется со змеевиком в водяной бане, так что его температура остается постоянной, характеристический график представляет собой прямую линию, показывающую, что сопротивление остается постоянным.Чистые металлы подчиняются закону Ома, когда их температура остается постоянной. Проволока, изготовленная из таких сплавов, как проволока из константана или эврика (состоящая из 60 % меди и 40 % никеля}, рассчитана на очень малый температурный коэффициент удельного сопротивления. Поэтому их не нужно помещать в ванну с постоянной температурой, чтобы показать омическое поведение
- Этот эксперимент можно использовать для обучения идее достоверности научных результатов. Результаты могут быть признаны недействительными, если на результаты влияет неконтролируемый фактор.
 В этом случае температура провода является фактором, влияющим на измерения его сопротивления.
В этом случае температура провода является фактором, влияющим на измерения его сопротивления. - Обсудите, как это можно учесть. Один из подходов (как обсуждалось выше) состоит в том, чтобы поддерживать постоянную температуру проволоки, погружая ее в водяную баню. В качестве альтернативы можно было бы использовать приведенный выше график p.d./ток для определения сопротивления провода, когда по нему не течет ток, потому что тогда нет эффекта нагрева. Объясните, что сопротивление провода равно p.d. разделить на ток; я.е. это градиент линии от начала координат до точки на графике. Поместите линейку на график через начало координат и проведите через самую высокую точку графика. Линейка имеет большой градиент. Двигайтесь вниз по графику от точки к точке, показывая, что градиент уменьшается. Вблизи начала координат график почти прямой (или вы можете использовать идею касательной к графику). Таким способом можно определить сопротивление провода, когда он не нагревается током.
- Этот эксперимент можно расширить, включив в него исследование влияния температуры на сопротивление в диапазоне от 0°C до 100°C с использованием водяной бани.
 Если учащиеся знакомы с экспериментальным наблюдением закона Шарля, вы можете попросить их экстраполировать свой график зависимости сопротивления от температуры, чтобы найти приблизительную температуру, при которой сопротивление провода будет равно нулю. Для чистого металла сопротивление уменьшается приблизительно линейно по направлению к температуре, близкой к 0 К. (Температурный коэффициент сопротивления многих чистых металлов близок к 0,004 К-1, поэтому график сопротивления/температуры экстраполируется обратно к 1/0,004 = 250 К.) Вы могли бы связать это с идеей, что сопротивление чистого металла при комнатной температуре определяется вибрацией ионов, и это уменьшится до нуля вблизи 0 К.
Если учащиеся знакомы с экспериментальным наблюдением закона Шарля, вы можете попросить их экстраполировать свой график зависимости сопротивления от температуры, чтобы найти приблизительную температуру, при которой сопротивление провода будет равно нулю. Для чистого металла сопротивление уменьшается приблизительно линейно по направлению к температуре, близкой к 0 К. (Температурный коэффициент сопротивления многих чистых металлов близок к 0,004 К-1, поэтому график сопротивления/температуры экстраполируется обратно к 1/0,004 = 250 К.) Вы могли бы связать это с идеей, что сопротивление чистого металла при комнатной температуре определяется вибрацией ионов, и это уменьшится до нуля вблизи 0 К.
Расширение «Как работает наука»:
Этот эксперимент был проверен на безопасность в октябре 2006 г.
Повышение температуры проводника из-за изменения тока в проводниках
%PDF-1.
 6
6
%
27 0 объект
>
эндообъект
29 0 объект
>поток
1998-03-10T10:53:08Z2010-11-09T09:53:44-06:002010-11-09T09:53:44-06:00Acrobat Distiller 2.0 для MacintoshConductor, Temperature, Rise, Due, Current, Changes, Conductors, Test, Methodapplication/pdf- Повышение температуры проводника из-за изменения тока в проводниках
- Проводник
- Температура
- Подъем
- Долг
- Текущий
- Изменения
- Проводники
- Тест
- Метод
- Установка оборудования (химический стакан, мешалка, блок питания)
- Подготовка программного обеспечения Logger Pro для сбора данных
- Измерение сопротивления и разницы температур
когда вода нагревается от комнатной температуры почти до кипения - Сохранить данные этого прогона
- Измерение сопротивления и разницы температур
как вода потом остывает - Сохранить данные этого прогона
- Построение графиков зависимости сопротивления от разницы температур
за каждый прогон; подгонка прямой линией к соответствующим данным на
каждый график - Используйте параметры линейной подгонки для расчета
температурный коэффициент меди
UUID: e5505c33-ce19-48a5-89c4-4d5f9883a4abuuid: 5057cda7-6fe9-4368-9938-71b7fc027705
конечный поток
эндообъект
10 0 объект
>
эндообъект
2 0 объект
>
эндообъект
11 0 объект
>
эндообъект
17 0 объект
>
эндообъект
18 0 объект
>поток
ph@i@P@2E1 vdFl GἜ!$RTNlpr9E29,m&z4(jM,A8D»QHaTI\A/ӪMo9gI&hڪغcHE@h7
ir8@Q,@j2z}%»v 3ʆ0hP!FR!b)*aG&
/’vF%/-Ɠ9eF~1F|0
Pe9?q@t:NFit%+8Ppz*+ZAB+s^$J4LT3 *Dix^$07rנ2!svЭk2#h>8dij
g’+ħ:f20Jƕ32Hjz0)
,JR9!7R0(s)LCKztŸl㳌Ø2Գ>дj2KT5b6p7Ӏ1-&94GZ*N*nԻӸ9c?cPJf(«tApl1
Tq(rRSp,li~FtG:Hu/8 7B=AB餋
诲ʈo’4’6gvcbJHfg*=偮]B. %a!eӸ%t»{@oW)7_:,pBi3 ;ΨRbo7uǤ
%a!eӸ%t»{@oW)7_:,pBi3 ;ΨRbo7uǤ
Влияние температуры на удельное сопротивление металлов или проводников, полупроводников и изоляторов
Поскольку удельное сопротивление материала указано как
ρ=м/нэ 2 т
Это показывает, что удельное сопротивление связано с числовой плотностью n свободных электронов в материале и временем релаксации t. Изменение удельного сопротивления материала в зависимости от температуры различно для разных материалов и обсуждается ниже:
(a) Металлы : В большинстве металлов плотность свободных электронов n не изменяется с температурой, но повышение температуры увеличивает амплитуду колебаний ионов решетки металла.Поэтому столкновения свободных электронов с ионами или атомами при дрейфе к положительному концу проводника учащаются, что приводит к уменьшению времени релаксации. Таким образом, удельное сопротивление проводника увеличивается с повышением температуры. При низкой температуре удельное сопротивление увеличивается при большей мощности Тл
Установлено, что температурная зависимость удельного сопротивления металла определяется соотношением
ρ = ρ 0 [1+α t (Т-Т 0 )]
Где ρ и ρ 0 — удельное сопротивление при температуре T и T 0 соответственно, а α t называется температурным коэффициентом удельного сопротивления.
Или α r = (ρ – ρ 0 )/ ρ 0 (T-T 0 )=d ρ/dT03 (9 0)
Таким образом, α r определяется как относительное изменение удельного сопротивления (dρ / ρ 0 ) на единицу изменения температуры (dT)
Для проводников. Величина α r положительна, показывая, что их удельное сопротивление увеличивается с повышением температуры. Для большинства металлов удельное сопротивление линейно увеличивается с повышением температуры в диапазоне температур около 500 К выше комнатной температуры.
(b) Полупроводники: В случае полупроводников значение α r отрицательно. Это означает, что удельное сопротивление полупроводников уменьшается с ростом температуры.
(c) Изоляторы: Удельное сопротивление увеличивается экспоненциально с понижением температуры в случае полупроводников.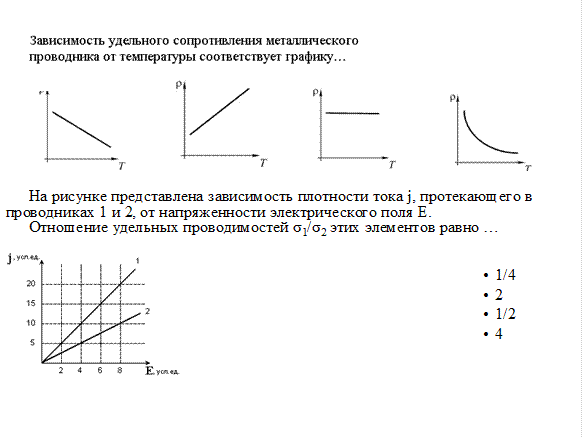 Она становится бесконечно большой при температуре, близкой к абсолютному нулю, т. е. проводимость почти равна нулю при ok.
Она становится бесконечно большой при температуре, близкой к абсолютному нулю, т. е. проводимость почти равна нулю при ok.
Температурная зависимость удельного сопротивления полупроводников и изоляторов определяется по формуле:
ρ = ρ 0 e E g /2kT
Где K= постоянная Больцмана
(1.381*10 -23 j моль -1 k -1 )
T= абсолютная температура
E g = Ширина запрещенной зоны между зоной проводимости и валентной зоной или энергия активации для проводимости
Классификация непроводящих материалов на изоляторы и полупроводники зависит от E g .
(i) Если E g = 1 эВ, значение удельного сопротивления не очень велико, поэтому материалы называются полупроводниками.
(ii) Если E g ≥1 эВ, значение удельного сопротивления очень велико, и материалы называются изоляторами.
Просмотры сообщений:
1305
Температурный коэффициент сопротивления
Температурный коэффициент сопротивления
Температурный коэффициент сопротивления
НАЗНАЧЕНИЕ:
Для исследования изменения сопротивления
моток проволоки в зависимости от температуры
катушка разнообразная.
В ЧЕМ СМЫСЛ?
Чтобы увидеть, что сопротивление действительно меняется с температурой,
и получить некоторое представление о размере этого изменения
для типичного проводника.
ПРЕДПОСЫЛКИ ЧТЕНИЯ:
Катнелл и Джонсон 20.3. Обратите внимание на уравнение 20.5.
КОНТРОЛЬНЫЙ СПИСОК ЭКСПЕРИМЕНТОВ
ТЕОРИЯ:
Когда существует разность потенциалов V на
длина металлического проводника наблюдается, что
в проводнике текут отрицательные заряды,
от низкого до высокого электрического потенциала из-за электрического
поле, связанное с разностью потенциалов. Поток заряда, называемый током, I , принимается равным
Поток заряда, называемый током, I , принимается равным
положительный
в направлении движения положительных зарядов под действием электрического поля.
В реальной жизни во многих электрических цепях используются токи, вызванные
движения электронов, имеющих отрицательный заряд;
следовательно, фактическое направление движения заряженных частиц
проходит против к направлению тока.
Наблюдается линейная зависимость между током
через и разность потенциалов через
проводник.Это соотношение, называемое законом Ома,
часто указывается как
В = Я * Р
но также может быть записано как
В
Р = --- (1)
я
где Р
это
сопротивление в омах:
1 вольт
1 Ом = ---------
1 ампер
Для проводника одинакового сечения (например, проволоки или стержня)
можно рассчитать сопротивление по свойствам его материала:
ро * л
R = --------- (2)
площадь
где
rho = удельное сопротивление материала (Ом-метры)
L = длина проводника (метры)
площадь = площадь поперечного сечения (метры * метры)
Для большинства материалов удельное сопротивление изменяется с температурой. Если диапазон температур не слишком велик, удельное сопротивление является линейным.
Если диапазон температур не слишком велик, удельное сопротивление является линейным.
функция температуры, T , и может быть выражена как
rho(T) = rho(T0) * [1 + a(T - T0)] (3)
где
T0 = эталонная температура (градусы Цельсия)
T = интересующая температура (градусы Цельсия)
rho(T0) = удельное сопротивление при стандартной температуре (ом-метры)
rho(T) = удельное сопротивление при интересующей температуре (ом-метры)
a = температурный коэффициент удельного сопротивления (1/градус Цельсия)
Когда
таблицы для нескольких различных материалов,
как указано в вашем учебнике, эталонная температура равна
обычно 20 С.В этом эксперименте мы будем использовать то же значение.
При изменении температуры проводника его сопротивление изменяется за счет
- температурная зависимость удельного сопротивления
- тепловое расширение проводника
Для меди, которую вы будете использовать в этом эксперименте,
эффекты теплового расширения больше
чем в 200 раз меньше, чем влияние изменения удельного сопротивления.
Мы можем полностью игнорировать эффекты теплового расширения.
в этом эксперименте
учитывая точность наших измерительных приборов.Поскольку только изменение
важное значение имеет удельное сопротивление материала.
общее сопротивление проводника имеет аналогичную зависимость
по температуре:
R(T) = R(T0) * [1 + a(T - T0)]
= R(T0) + R(T0)*a*(T - T0) (4)
где
T0 = эталонная температура (градусы Цельсия)
T = интересующая температура (градусы Цельсия)
R(T0) = сопротивление при эталонной температуре (Ом)
R(T) = сопротивление при интересующей температуре (Ом)
a = температурный коэффициент удельного сопротивления (1/градус Цельсия)
Температурный коэффициент и такой же, как
то, что указано выше для удельного сопротивления.
Если сопротивление проводника измеряется в нескольких
температуры, график данных
будет линейным с наклоном
а * Р(Т0)
и вертикальная точка пересечения T0 R(T0).
ПРОЦЕДУРА:
Меры предосторожности:
Не прикасайтесь к горячим частям устройства!
В этом эксперименте вы определите сопротивление
катушка медного провода, в то время как его
температура варьируется от комнатной до температуры, близкой к температуре кипения.Сопротивление будет
рассчитывается на основе измерения потенциала
разница между катушкой и измерение
ток, проходящий через катушку.
Разность потенциалов и температура будут
измеряется автоматически компьютером через датчики
подключен к интерфейсу.
Ток будет подаваться от источника постоянного тока
(источник питания постоянного тока) и измеряется с помощью
цифровой мультиметр.
- Налейте в стакан примерно 200 мл водопроводной воды.
и поместите его на нагревательную пластину.Установите на место колпачок, удерживающий резистор и датчик температуры.
убедившись, что резистор и датчик температуры
(расположен на конце зонда)
находятся рядом друг с другом и достаточно погружены в воду.
- Датчик температуры измеряет температуру воды.
Температура катушки будет такой же, как и температура
воды при условии, что она находится в тепловом равновесии с
вода.
Включите и настройте магнитную мешалку на скорость,
правильно перемешивайте воду, пока она нагревается, не создавая турбулентности. - Включите питание. Убедитесь, что цифровой мультиметр
настроен на чтение постоянного тока.Персонал склада должен был установить для вас источник питания,
поэтому вам не придется вносить какие-либо коррективы.
Однако, если он был неправильно отрегулирован, вам может потребоваться
настроить элементы управления следующим образом:- полностью повернуть все ручки против часовой стрелки (в ноль)
- поверните верхнюю ручку напряжения примерно на 1/2 оборота по часовой стрелке
(таким образом, маленькая белая линия на ручке перемещается примерно на 12 часов) - медленно поверните ручку «точной регулировки» тока (крайняя слева) по часовой стрелке,
пока вы смотрите на дисплей мультиметра - остановитесь, когда на дисплее мультиметра появится около 80.
 При этой настройке единицами измерения на дисплее являются миллиампер.
При этой настройке единицами измерения на дисплее являются миллиампер.
так что ток будет около 80 миллиампер.
То
индикатор постоянного тока (красный свет) должен гореть на
переднюю панель блока питания. Если горит зеленый свет,
ваша схема получает постоянное напряжение , а не постоянное
текущий ; попросите лаборанта исправить ситуацию. - Найдите на рабочем столе папку с надписью
Эксперименты ; внутри вы должны найти предмет под названием
Сопротивление vs.Температура.
Используйте его для запуска приложения, которое считывает датчики.Датчики должны были быть установлены персоналом склада.
На всякий случай их нужно отрегулировать:- В меню выберите «Настройка», затем «Датчики».
- Щелкните на канале 2 и установите для датчика значение «Необработанное напряжение».
в диапазоне 0-5 вольт.
- Нажмите на Ch3 и выберите «Температура нержавеющей стали».
из меню датчика.
Вы можете увидеть сообщение об ошибке «Конфликт датчиков».Исправьте
Датчик Ch2, используя раскрывающееся меню справа, чтобы выбрать
«Необработанное напряжение, 0–5 В», затем нажмите «ОК». Сообщение об ошибке должно исчезнуть.
Вы должны рассчитать значения
- (T — T0) , где T0 – эталонная температура
(обычно комнатная температура, около 20-25 градусов Цельсия) - сопротивление R(T) в зависимости от температуры
Для этого должна быть настроена программа Logger Pro
поэкспериментируйте, когда начнете.Вам нужно будет только внести две небольшие корректировки в его значения по умолчанию.
- Датчики будут измерять температуру, T , но вы
необходимо использовать разницу температур, T — T0 , в вашем
анализ. Итак, создайте новый столбец данных для «Разницы температур»:- В меню выберите Данные , Новый столбец , затем
Формула.
- Заполните параметры (длинное имя, короткое имя и единицы измерения)
на разницу температур. - Выберите Определение , чтобы построить уравнение для расчета
(Т — Т0) .
Имена переменных из предыдущего
столбцы в электронной таблице перечислены в разделе переменных.
Обратите внимание, что определяющее уравнение делает
не используйте знак равенства, а имена переменных заключаются в кавычки.
Вы должны построить запись следующим образом: «Температура» — 20,0
- В меню выберите Данные , Новый столбец , затем
- Во-вторых, вам может понадобиться немного изменить используемую формулу
для расчета сопротивления.- Проверьте показания мультиметра тока через ваш
схема. Он покажет ток в миллиамперах, который
должно быть около 80 мА. - Найдите столбец данных под названием Сопротивление . Выбирать
Изменить столбец . - Выберите Определение : оно должно включать
уравнение для расчета R(T) .
Ваша запись должна выглядеть примерно так: «Потенциал»/0,080.
Знаменатель должен быть током, протекающим через ваш
цепи, измеряется в амперах (не миллиамперах).Если ваш ток не совсем равен значению в знаменателе,
измените уравнение так, чтобы оно содержало ваш фактический ток в амперах.
- Проверьте показания мультиметра тока через ваш
На этом этапе вы должны увидеть красный . Соберите .
кнопка в верхней части экрана, рядом с элементами управления меню
Файл, Редактировать, и т. д. Если вы не видите Соберите
кнопку, затем Сохранить текущую сессию в файл на диске,
затем закройте и перезапустите Logger Pro .Это известная ошибка 🙁
Сбор данных № 1 (резистор прогревается)
- Включите нагреватель на уровень 5, чтобы начать нагревать воду.
Подождите примерно одну минуту, чтобы
изменение температуры воды идет полным ходом.
Начните принимать данные, нажав на кнопку
Собрать кнопку или выбрать (из меню) Эксперимент,
затем Сбор данных .
- Через 10–12 минут температура воды должна
достигать примерно 35 градусов С.Это хороший момент, чтобы остановиться.
Кнопка Стоп будет
завершить сбор данных до указанного времени, если это необходимо.
Не позволяйте воде нагреваться выше 50 градусов C!
Сбор данных № 2 (резистор остывает)
- Не прикасаться к горячим предметам!
- Выключить нагрев.
- Подождите 3 минуты, пока вода не начнет остывать.
- Поскольку процесс охлаждения протекает медленнее, чем процесс нагрева,
уменьшите частоту дискретизации примерно до четверти предыдущего значения. - Соберите данные в течение примерно 20 минут.
- Если аппарат можно отрегулировать так, чтобы
зазор между стаканом и крышкой (при сохранении резистора
и датчик температуры погружен),
температура будет снижаться быстрее. - Получите еще один набор данных, пока вода (и резистор) остынет.

ГРАФИК
Вы должны построить графики зависимости сопротивления от температуры.
Создайте отдельные графики для процессов прогрева и охлаждения.Вы можете использовать компьютерные графики в своем отчете для этого
лаборатории, или вы можете построить их вручную.
Если вы хотите сделать графики на компьютере, вы можете сделать это в течение
программа Logger Pro . Иметь ввиду:
- Не позволяйте компьютеру «соединять точки»
(неудачная установка по умолчанию). Постройте свой
данные с помощью «точечных протекторов». - Щелчок по метке оси позволяет отобразить другую переменную.
- Оси могут масштабироваться автоматически или вручную;
дважды щелкните по оси графика, чтобы изменить масштаб или диапазон.Выберите ограничения, которые подходят для ваших данных. - Доступен изогнутый фитинг.
- Графики можно распечатать на принтере в лаборатории.
Вы также можете экспортировать свой набор данных в другую программу и сделать
сюжеты с ним, если хотите.
Вам следует рассмотреть возможность сохранения каждого «запуска» на дискету.
Не сохраняйте файл на компьютере
жесткий диск.
Сохранить как создает файл, который впоследствии можно открыть с помощью Logger ProДанные можно экспортировать в виде текстового файла для использования в других приложениях.Лучший способ сделать это — вырезать и вставить:
щелкните любую запись в области таблицы данных в Logger Pro,
затем «Выбрать все» и «Копировать» в меню «Правка».
Откройте другую программу (например, Excel или Блокнот )
и «Вставьте» в него столбцы данных.Команда Logger Pro Экспорт должна произвести хороший
простой текстовый файл ASCII со всеми данными… но появляется
игнорировать некоторые столбцы данных!АНАЛИЗ:
Постройте график сопротивления противтемпературы на линейной миллиметровой бумаге.
Подгоните линию к данным на этом графике,
желательно с помощью какой-нибудь компьютерной программы, которая вычисляет метод наименьших квадратов.

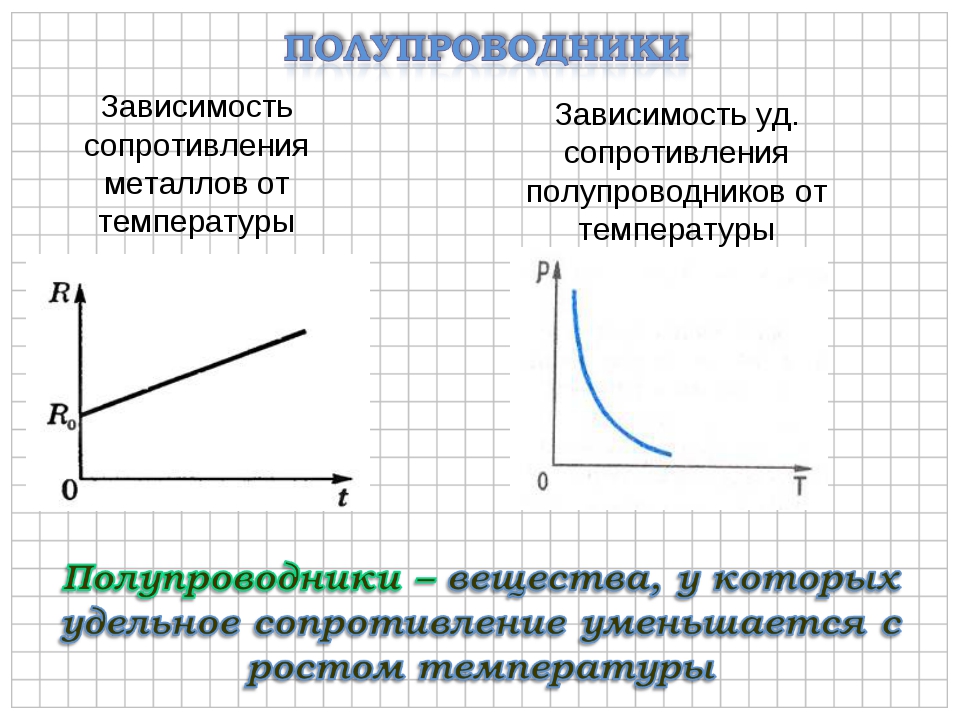 Эти материалы являются очень плохими проводниками электричества и в основном используются в электрических системах для предотвращения утечки тока. Слюда, фарфор, бумага, сухая древесина, минеральное масло, газообразный азот, воздух и т. д. являются хорошими примерами изоляторов.
Эти материалы являются очень плохими проводниками электричества и в основном используются в электрических системах для предотвращения утечки тока. Слюда, фарфор, бумага, сухая древесина, минеральное масло, газообразный азот, воздух и т. д. являются хорошими примерами изоляторов. Поглощая энергию, больше электронов перейдет из валентной зоны в зону проводимости, когда вы повысите температуру.
Поглощая энергию, больше электронов перейдет из валентной зоны в зону проводимости, когда вы повысите температуру.
 Имеют отрицательный температурный коэффициент.
Имеют отрицательный температурный коэффициент. Сила, например трение, действует против направления движения тела и имеет тенденцию предотвращать или замедлять движение тела. Простым примером сопротивления может быть ребенок, сражающийся с похитителем, или ветер с крыльями самолета.
Сила, например трение, действует против направления движения тела и имеет тенденцию предотвращать или замедлять движение тела. Простым примером сопротивления может быть ребенок, сражающийся с похитителем, или ветер с крыльями самолета.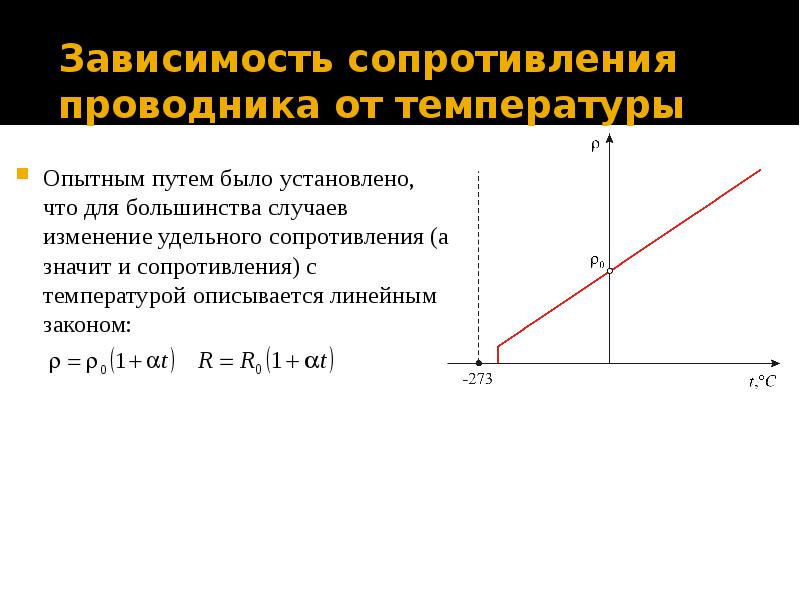
 Однако ИЗОЛЯТОРЫ могут УМЕНЬШАТЬ свое сопротивление при повышении температуры. Материалы, используемые для практических изоляторов (стекло, пластмасса и т. д.), демонстрируют заметное падение сопротивления только при очень высоких температурах. Они остаются хорошими изоляторами при всех температурах, с которыми они могут столкнуться при использовании.
Однако ИЗОЛЯТОРЫ могут УМЕНЬШАТЬ свое сопротивление при повышении температуры. Материалы, используемые для практических изоляторов (стекло, пластмасса и т. д.), демонстрируют заметное падение сопротивления только при очень высоких температурах. Они остаются хорошими изоляторами при всех температурах, с которыми они могут столкнуться при использовании.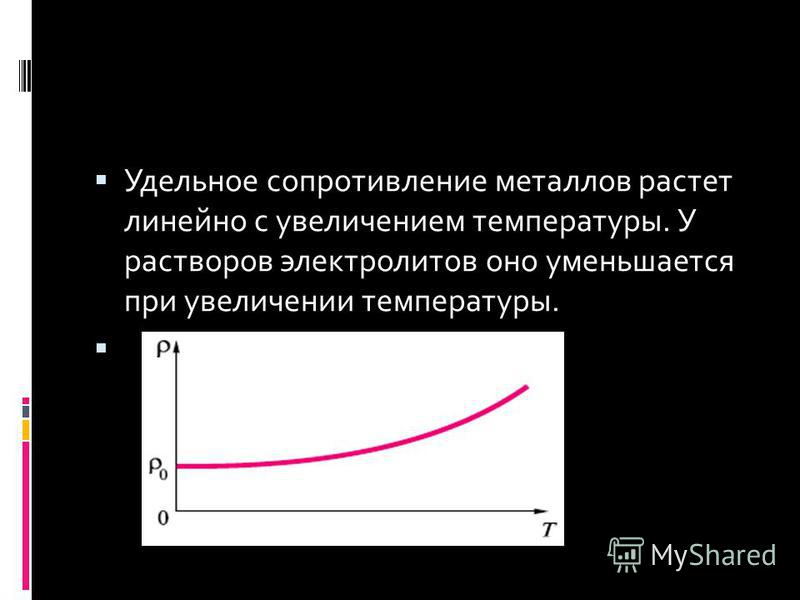 Следовательно, если к проводнику (положительному на одном конце и отрицательному на другом) приложен электрический потенциал, электроны будут «мигрировать» от атома к атому к положительному выводу.
Следовательно, если к проводнику (положительному на одном конце и отрицательному на другом) приложен электрический потенциал, электроны будут «мигрировать» от атома к атому к положительному выводу.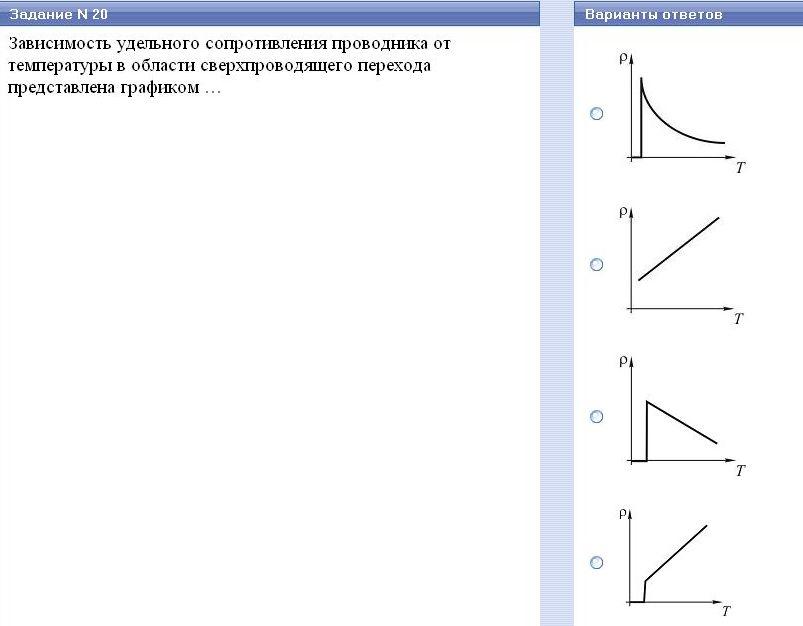 Каждое столкновение использует некоторую энергию свободного электрона и является основной причиной сопротивления. Чем больше атомов толкаются в материале, тем больше возникает столкновений и, следовательно, тем больше сопротивление току.
Каждое столкновение использует некоторую энергию свободного электрона и является основной причиной сопротивления. Чем больше атомов толкаются в материале, тем больше возникает столкновений и, следовательно, тем больше сопротивление току.

 Удельное сопротивление является свойством материала и зависит от температуры. Температурная зависимость удельного сопротивления полупроводников играет существенную роль в их применении в электронике.В этой статье мы рассмотрим, почему это так.
Удельное сопротивление является свойством материала и зависит от температуры. Температурная зависимость удельного сопротивления полупроводников играет существенную роль в их применении в электронике.В этой статье мы рассмотрим, почему это так. Располагая материалы в порядке возрастания удельного сопротивления, порядок: проводники, полупроводники и изоляторы.
Располагая материалы в порядке возрастания удельного сопротивления, порядок: проводники, полупроводники и изоляторы.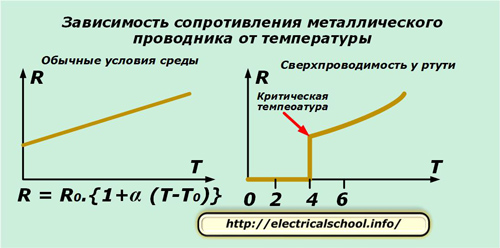 С повышением температуры удельное сопротивление металла также увеличивается, что придает ему положительный температурный коэффициент сопротивления. При высоких температурах удельное сопротивление проводника увеличивается, а проводимость уменьшается.
С повышением температуры удельное сопротивление металла также увеличивается, что придает ему положительный температурный коэффициент сопротивления. При высоких температурах удельное сопротивление проводника увеличивается, а проводимость уменьшается. Это создает больше носителей заряда в полупроводнике при высоких температурах.Более высокая концентрация носителей заряда снижает удельное сопротивление полупроводника. Поскольку удельное сопротивление полупроводника уменьшается с повышением температуры, он становится более проводящим. Полупроводник обладает отличной проводимостью при высоких температурах.
Это создает больше носителей заряда в полупроводнике при высоких температурах.Более высокая концентрация носителей заряда снижает удельное сопротивление полупроводника. Поскольку удельное сопротивление полупроводника уменьшается с повышением температуры, он становится более проводящим. Полупроводник обладает отличной проводимостью при высоких температурах. Такие полупроводники называются внешними полупроводниками.Удельное сопротивление примесных полупроводников больше, чем у собственных (нелегированных или чистых) полупроводников.
Такие полупроводники называются внешними полупроводниками.Удельное сопротивление примесных полупроводников больше, чем у собственных (нелегированных или чистых) полупроводников.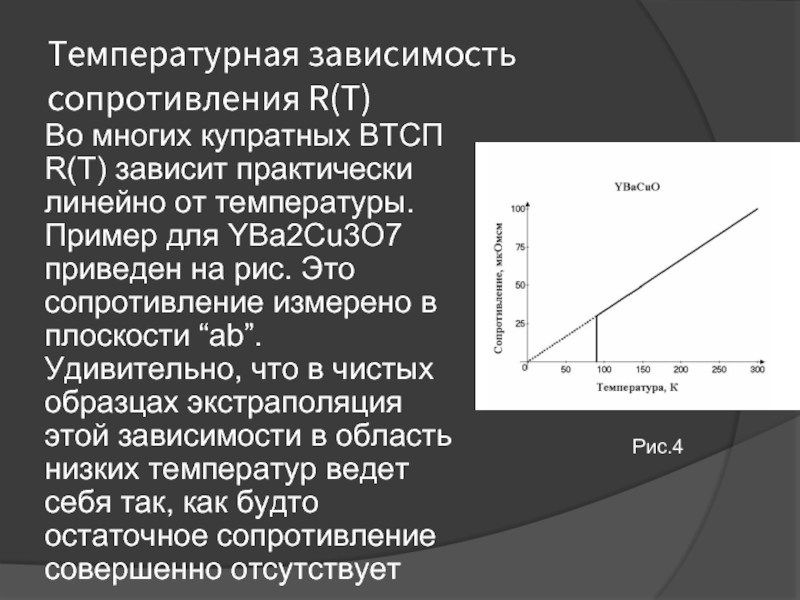
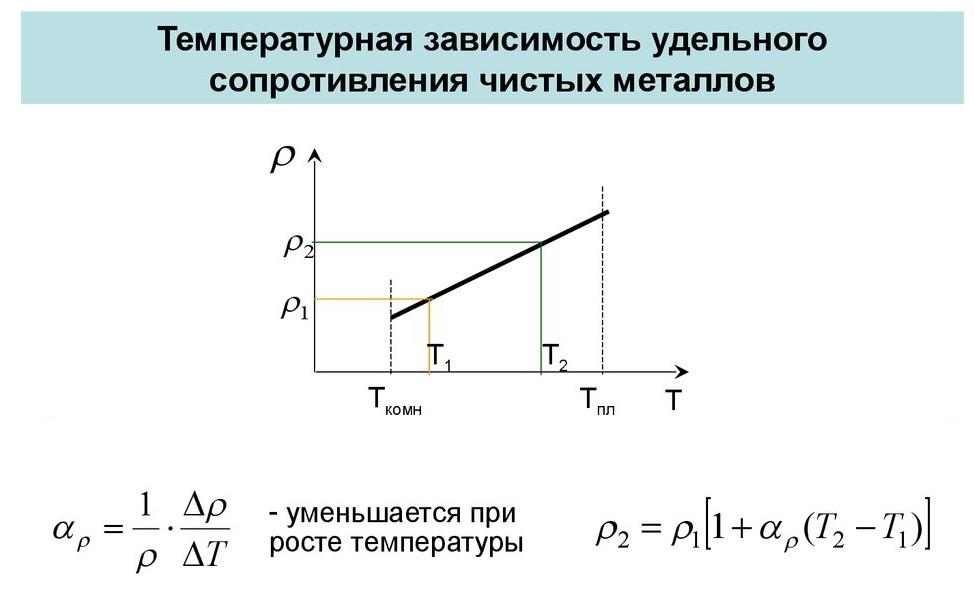 Снимите покрытие с концов, чтобы обеспечить электрический контакт с помощью зажимов типа «крокодил».
Снимите покрытие с концов, чтобы обеспечить электрический контакт с помощью зажимов типа «крокодил». Это не прямая линия, показывающая постоянное сопротивление, а скорее кривая, показывающая, что сопротивление провода увеличивается с температурой.
Это не прямая линия, показывающая постоянное сопротивление, а скорее кривая, показывающая, что сопротивление провода увеличивается с температурой. В этом случае температура провода является фактором, влияющим на измерения его сопротивления.
В этом случае температура провода является фактором, влияющим на измерения его сопротивления. Если учащиеся знакомы с экспериментальным наблюдением закона Шарля, вы можете попросить их экстраполировать свой график зависимости сопротивления от температуры, чтобы найти приблизительную температуру, при которой сопротивление провода будет равно нулю. Для чистого металла сопротивление уменьшается приблизительно линейно по направлению к температуре, близкой к 0 К. (Температурный коэффициент сопротивления многих чистых металлов близок к 0,004 К-1, поэтому график сопротивления/температуры экстраполируется обратно к 1/0,004 = 250 К.) Вы могли бы связать это с идеей, что сопротивление чистого металла при комнатной температуре определяется вибрацией ионов, и это уменьшится до нуля вблизи 0 К.
Если учащиеся знакомы с экспериментальным наблюдением закона Шарля, вы можете попросить их экстраполировать свой график зависимости сопротивления от температуры, чтобы найти приблизительную температуру, при которой сопротивление провода будет равно нулю. Для чистого металла сопротивление уменьшается приблизительно линейно по направлению к температуре, близкой к 0 К. (Температурный коэффициент сопротивления многих чистых металлов близок к 0,004 К-1, поэтому график сопротивления/температуры экстраполируется обратно к 1/0,004 = 250 К.) Вы могли бы связать это с идеей, что сопротивление чистого металла при комнатной температуре определяется вибрацией ионов, и это уменьшится до нуля вблизи 0 К. 6
6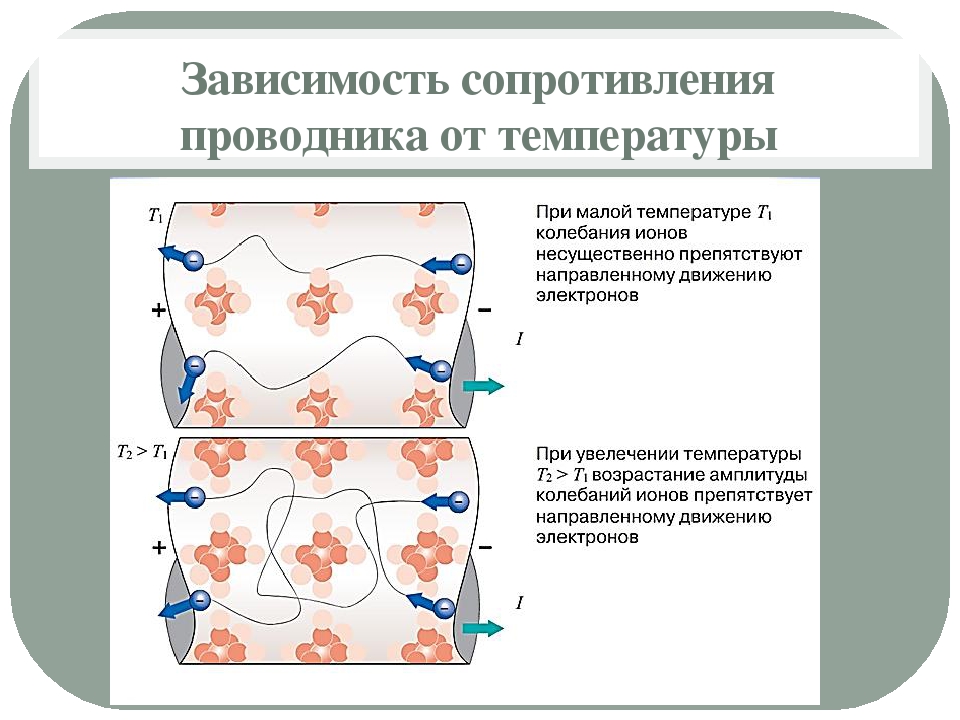
 При этой настройке единицами измерения на дисплее являются миллиампер.
При этой настройке единицами измерения на дисплее являются миллиампер.