Перевод из одной системы счисления в другую
Для перевода чисел из одной системы счисления в другую необходимо владеть основными сведениями о системах счисления и
форме представления чисел в них.
Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой
системы счисления. В общем случае положительное число X в позиционной системе с основанием s
может быть представлено в виде полинома:
где s — база системы счисления, — цифры,
допустимые в данной системе счисления . Последовательность
образует целую часть X, а последовательность
— дробную часть X.
В вычислительной технике наибольшее применение нашли двоичная (BIN — binary),
и двоично кодированные системы счисления: восьмеричная (OCT — octal), шестнадцатеричная (HEX — hexadecimal) и двоично-кодированная десятичная (BCD — binary coded decimal).
В дальнейшем для обозначения используемой системы счисления число будет заключаться в скобки, а
в индексе указано основание системы. Число X по основанию s будет обозначено
.
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.
Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только
две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент
с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.
Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.
Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления
представляет собой целую степень двойки: —
для восьмеричной и — для шестнадцатеричной.
В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:
В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Пример записи числа в шестнадцатеричной системе:
Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.
Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением
(запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа).
Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой
осуществляется сравнительно просто. Действительно, поскольку для восьмеричного числа каждый разряд представляется
группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад),
то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от
разделительной запятой вправо и влево. При этом, в случае необходимости, добавляют нули слева от целой части
и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или
шестнадцатеричной цифрой (см. таблицу).
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.
Соответствие между цифрами в различных системах счисления
| DEC | BIN | OCT | HEX | BCD |
| 0 | 0000 | 0 | 0 | 0000 |
| 1 | 0001 | 1 | 1 | 0001 |
| 2 | 0010 | 2 | 2 | 0010 |
| 3 | 0011 | 3 | 3 | 0011 |
| 4 | 0100 | 4 | 4 | 0100 |
| 5 | 0101 | 5 | 5 | 0101 |
| 6 | 0110 | 6 | 6 | 0110 |
| 7 | 0111 | 7 | 7 | 0111 |
| 8 | 1000 | 10 | 8 | 1000 |
| 9 | 1001 | 11 | 9 | 1001 |
| 10 | 1010 | 12 | A | 0001 0000 |
| 11 | 1011 | 13 | B | 0001 0001 |
| 12 | 1100 | 14 | C | 0001 0010 |
| 13 | 1101 | 15 | D | 0001 0011 |
| 14 | 1110 | 16 | E | 0001 0100 |
| 15 | 1111 | 17 | F | 0001 0101 |
Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой
двоичных цифр, причём незначащие нули слева и справа отбрасываются.
Для рассмотренных ранее примеров это выглядит следующим образом:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.
В двоично-десятичной системе вес каждого разряда равен степени 10, как в десятичной системе,
а каждая десятичная цифра кодируется четырьмя двоичными цифрами. Для записи десятичного числа в BCD-системе
Для записи десятичного числа в BCD-системе
достаточно заменить каждую десятичную цифру эквивалентной четырёхразрядной двоичной комбинацией:
Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что
это не двоичный эквивалент числа. Это видно из следующего примера:
Пусть X — число в системе счисления с основанием s, которое требуется
представить в системе с основанием h. Удобно различать два случая.
В первом случае
и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования
состоит в представлении числа в виде
многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления
с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный
приём иллюстрируют следующие примеры:
.
.
В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.
Во втором случае ()
удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел
и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части
переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.
Перевод целых чисел
Правила перевода целых чисел становится ясным из общей формулы записи числа
в произвольной позиционной системе. Пусть число
в исходной системе счисления s имеет вид .
Требуется получить запись числа в системе счисления с основанием h:
.
Для нахождения значений разделим
этот многочлен на h:
.
Как видно, младший разряд
, то есть , равен первому остатку.
Следующий значащий разряд определяется
делением частного на h:
.
Остальные также
вычисляются путём деления частных до тех пор, пока
не станет равным нулю.
Для перевода целого числа из s-ичной системы счисления в h-ичную
необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h)
до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит
последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в
последовательности, обратной их получению.
Пример 1. Перевести число 75 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы.
Решение:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.
Перевод правильных дробей
Правильную дробь ,
имеющую в системе с основанием s вид ,
можно выразить в системе счисления с основанием h как многочлен вида
Старшая цифра может быть
найдена умножением этого многочлена на h, т.е.
Если это произведение меньше 1, то цифра равна 0,
если же оно больше или равно 1, то цифра равна
целой части произведения. Следующая цифра справа
определяется путём умножения дробной части указанного выше произведения на h и выделения
его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь
по основанию h конечным набором цифр.
Для перевода правильной дроби из системы счисления
с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части
получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных
произведений дают последовательность цифр дроби в h-системе счисления.
Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения
не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в
h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления
будет последовательности целых частей полученных произведений, записанных в порядке их получения и
изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p
знаков после запятой равняется .
Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы счисления.
* В двоичную систему:
Ответ:
** В восьмеричную систему:
Ответ:
*** В шестнадцатеричную систему:
Ответ: так как , то
Поделиться с друзьями
Перевод чисел между системами счисления, основания которых равно степени числа 2
Перевод чисел между системами счисления, основания которых равны значениям степеней числа 2 (т. е. P = 2 n), можно произвести по более простым алгоритмам. Получим эти правила.
Перевод между двоичной и восьмеричной системами счисления
Определим информационный вес двоичной цифры. Так как алфавит двоичной системы содержит две цифры (0 и 1), то используя формулу Хартли, имеем:
N = 2 i, 2 = 2 i, откуда i = 1 бит
Аналогично для восьмеричной цифры:
N = 2 i, 8 = 2 i, 2 3 = 2 i, откуда i = 3 бит
Нетрудно заметить, что информационный вес восьмеричной цифры в три раза больше двоичного. Поэтому каждой восьмеричной цифре можно поставить в соответствие группу из трех двоичных разрядов (триаду):
Поэтому каждой восьмеричной цифре можно поставить в соответствие группу из трех двоичных разрядов (триаду):
0 – 000, 1 – 001, 2 – 010, 3 – 011, 4 – 100, 5 – 101, 6 – 110, 7 – 111
Последнее утверждение позволяет сформулировать алгоритм перевода двоичного числа в восьмеричную систему счисления:
- Разбить двоичное число на триады, справа налево.
- Если в правой группе меньше трех цифр, то добавить ведущие нули.
- Каждую триаду перевести в восьмеричную систему счисления.
- Записать полученные цифры в соответствующих разрядах восьмеричного числа.
Пример. Перевести двоичное число 10111011102 в восьмеричную систему счисления.
Для решения задачи воспользуемся выше приведенным алгоритмом:
- 1.011.101.110
- 001.011.101.110
- 1 3 5 6
- 10111011102 = 13568
Ответ. 1356
Алгоритм перевода восьмеричного числа в двоичную систему счисления:
- Разбить двоичное число на триады, справа налево.
- Поставить в соответствие каждой восьмеричной цифре двоичную триаду.
- Соединить триады и записать двоичное число.
- Удалить (если существуют) незначащие нули.
Пример. Перевести восьмеричное число 2578 в двоичную систему счисления.
Используем алгоритм, приведенный выше:
- 010.101.111
- 010101111
- 10101111
Таким образом, 2578 = 101011112
Ответ. 10101111
Перевод между двоичной и шестнадцатеричной системами счисления
Определим информационный вес шестнадцатеричной цифры:
N = 2 i, 16 = 2 i, 2 4 = 2 i, откуда i = 4 бит
Итак, информационный вес шестнадцатеричной цифры в четыре раза больше двоичного. Значит, каждой цифре шестнадцатеричной системы счисления можно поставить в соответствие группу из четырех двоичных разрядов (тетраду):
0 – 000, 1 – 001, 2 – 010, 3 – 011, 4 – 100, 5 – 101, 6 – 110, 7 – 111
8 – 0111, 9 – 1001, A – 1010, B – 1011, C – 1100, D – 1101, E – 1110, F – 1111
Алгоритм перевода двоичного целого числа в шестнадцатеричную систему счисления:
- Разбить двоичное число на тетрады, справа налево.

- Если в правой группе меньше четырех цифр, то добавить ведущие нули.
- Каждую тетраду перевести в шестнадцатеричную систему счисления.
- Записать полученные цифры в соответствующих разрядах шестнадцатеричного числа.
Пример. Перевести двоичное число 10011011102 в шестнадцатеричную систему счисления.
Воспользуемся выше приведенным алгоритмом:
- 10.0110.1110
- 0010.0110.1110
- 2 6 E
- 10011011102 = 26E16
Ответ. 26E
Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления:
- Поставить в соответствие каждой шестнадцатеричной цифре двоичную тетраду.
- Соединить тетрады и записать двоичное число.
- Удалить (если существуют) незначащие нули.
Пример. Перевести шестнадцатеричное число 3AC16 в двоичную систему счисления.
Используем алгоритм, приведенный выше:
- 0011.1010.1100
- 001110101100
- 1110101100
Таким образом, 3AC16 = 11101011002
Ответ. 1110101100
Перевод чисел в различных системах счисления
Перевод чисел в различных системах счисления
Перевод чисел в различных системах счисления.
Для перевода числа из десятичной системы счисления в систему счисления с
другим основанием поступают следующим образом:
а) Для перевода целой части числа его делят нацело на основание системы,
фиксируя остаток. Если неполное частное не равно нулю продолжают делить его
нацело. Если равно нулю остатки записываются в обратном порядке.
б) Для перевода дробной части числа ее умножают на основание системы
счисления, фиксируя при этом целые части полученных произведений. Целые
части в дальнейшем умножении не участвуют. Умножение производиться до
получения 0 в дробной части произведения или до заданной точности
вычисления.
в) Ответ записывают в виде сложения переведенной целой и переведенной
дробной части числа.
Пример:
перевод чисел из десятичной системы счисления в двоичную систему
счисления.
Перевести число 75,375 в двоичную систему счисления.
а) переведем в двоичную систему целую часть — 75
75 : 2 = 37 ( 1 )
37 : 2 = 18 ( 1 )
18 : 2 = 9 ( 0 )
9 : 2 = 4 ( 1 )
4 : 2 = 2 ( 0 )
2 : 2 = 1 ( 0 )
1 : 2 = 0 ( 1 )
Закончив деление, запишем остатки в обратном порядке, и получим
искомый результат:
75=10010112
б) переведем в двоичную систему дробную часть — 0,375
0,375
2
0,750
2
1,500
2
1,000
Выделенные числа запишем в естественном порядке и получим дробное число в
двоичной системе счисления:
0,375 = 0,0112
в) получив целую и дробную части числа в двоичном виде (75=10010112
и 0,375 = 0,0112 ) можем сделать вывод:
75,375=75+0,375 = 10010112+0,0112=1001011,0112,
значит 75,375=1001011,0112
Пример:
перевод чисел из десятичной системы счисления в шестнадцатеричную систему
счисления.
Представить десятичное число 157,23 в шестнадцатеричной системе счисления.
Целая часть числа равна 157, дробная — 0,23.
а) переведем в двоичную систему целую часть — 157
157 : 16 = 9 (13 или D)
9 : 16 = 0 ( 9 )
Закончив деление, запишем остатки в обратном порядке, и получим
искомый результат:
157=9D 16
а) переведем в двоичную систему дробную часть — 0,23.
Результат умножения 0,23 на 16 равен 3,68. Целая часть этого числа равна
3, значит первый коэффициент дробной части равен 3. Дробная часть равна 0,68.
Снова умножим ее на основание системы: 0,68*16=10,88. Целая часть равна 10 или в
шестнадцатеричной системе А. Дробная часть равна 0,88, она опять
умножается на 16 и так далее.
Выпишем весь процесс:
0,23 * 16 = 3,68 ( 3 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
0,08 * 16 = 1,28 ( 1 )
0,28 * 16 = 4,48 ( 4 )
0,48 * 16 = 7,68 ( 7 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
0,08 * 16 = 1,28 ( 1 )
0,28 * 16 = 4,48 ( 4 )
0,48 * 16 = 7,68 ( 7 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
Замечаем, что последовательность чисел 0,68; 0,88; 0,08; 0,28; 0,48 повторилась
уже 2 раза и начинается в третий раз.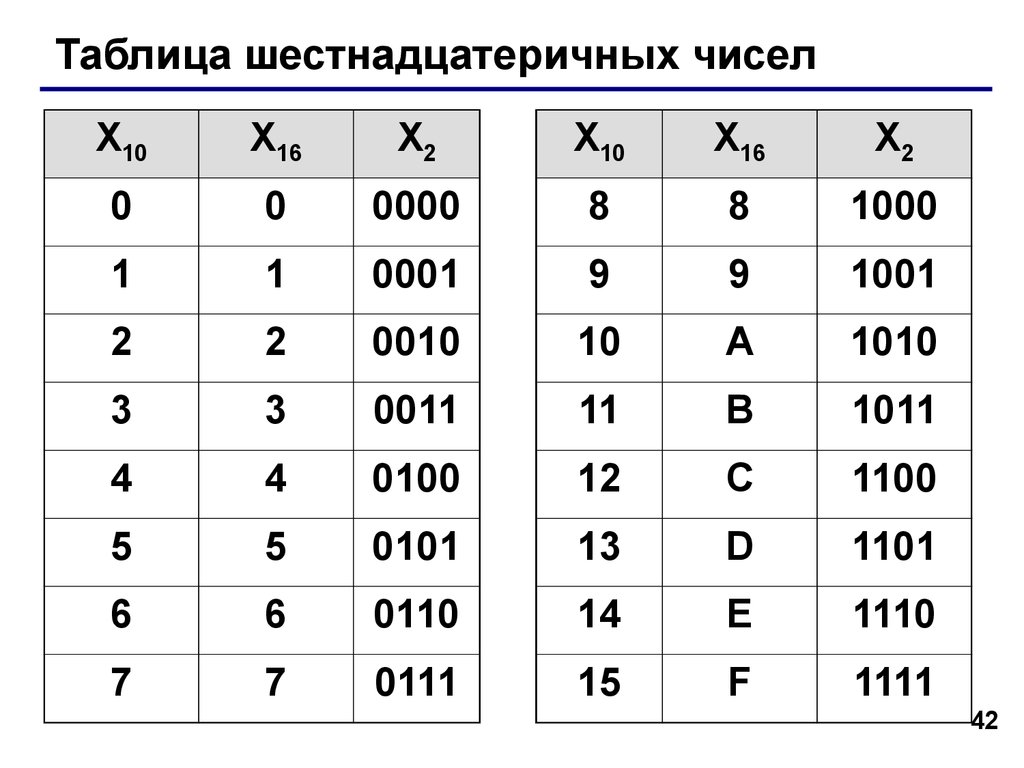 Получается бесконечная шестнадцатеричная
Получается бесконечная шестнадцатеричная
дробь в которой период (бесконечно повторяемая последовательность цифр)
заключен в скобки:
157,23=9D,3(АЕ147)16
Для перевода числа в десятичную систему счисления из системы счисления с другим
основанием каждый коэффициент переводимого числа умножается на основание системы
в степени соответствующей этому коэффициенту и полученные результаты
складываются.
Пример:
перевод чисел из двоичной системы счисления в десятичную систему
счисления
Перевести число 1001011,0112 в десятичную систему счисления
1001011,0112 = 1*26+0*25+0*24+1*23+0*22+1*21+1*20+0*2-1+1*2-2+1*2-3
=64+8+2+1+0,25+0,125=75,375
Двоичная система проста, так как использует две цифры, но громоздка. В
десятичной хранить числа в памяти возможно, но сложен перевод из десятичной в
двоичную и обратно и занимает много времени. Необходима система счисления
компактнее двоичной, но с более простым переводом.
23 = 8 0, 1, 2, 3, 4, 5, 6, 7.
Для перевода из двоичной системы счисления в восьмеричную необходимо разбить
данное двоичное число вправо и влево от запятой на триада ( три цифры ) и
представить каждую триаду соответствующим восьмеричным кодом. При невозможности
разбиения на триады допускается добавление нулей слева в целой записи числа и
справа в дробной части числа. Для обратного перевода каждую цифру восьмеричного
числа представляют соответствующей триадой двоичного кода.
|
|
|
|
| |
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Пример:
перевод чисел из двоичной системы счисления в восьмеричную систему
счисления.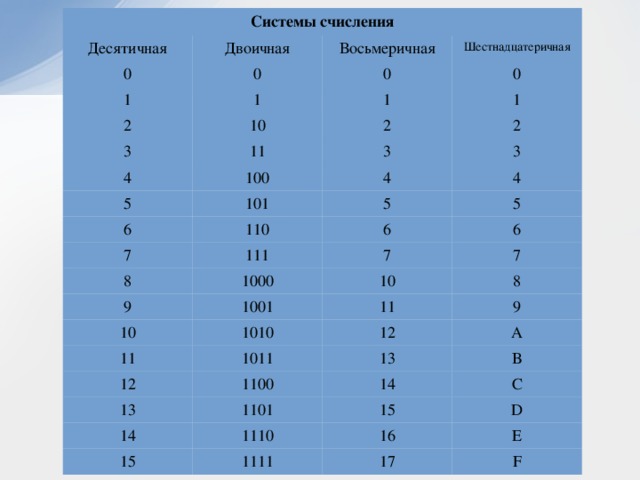
Переведем число 1001011,0112 в восьмеричную систему счисления.
Разобьем данное число на триады, приписав слева недостающие нули:
001 001 011 , 011
1 1 3 , 3
и заменим каждую триаду соответствующим восьмеричным кодом (см. таблицу). Можем
сделать вывод:
1001011,0112 = 113,38
Пример:
перевод чисел из восьмеричной системы счисления в двоичную систему
счисления.
Переведем число 347,258 в двоичную систему счисления. Каждую цифру
восьмеричного числа заменим соответствующей триадой (см. таблицу).
3 4 7 , 2 5
011 100 111 , 010 101
Запишем ответ, удалив нули слева в записи числа:
347,258 = 11100111,0101012
Восьмеричная система компактнее двоичной и с более простым переводом чисел,
однако, современные требования к ЭВМ заставили создавать шестнадцатеричную
систему счисления.
24 = 16 1, 2, 3, 4, 5, 6, 7, 8, 9,
A,
B,
C,
D,
E,
F.
Правило перевода из двоичной системы счисления в шестнадцатеричную: разбить
двоичное число вправо и влево от запятой на тетрады ( по 4 цифры ) и представить
каждую тетраду соответствующим шестнадцатеричным кодом. При невозможности
разбиения на тетрады допускается добавление нулей слева в целой записи числа и
справа в дробной части числа. Для обратного перевода каждую цифру
Для обратного перевода каждую цифру
шестнадцатеричного числа представляют тетрадой двоичного кода.
Пример:
перевод чисел из двоичной системы счисления в шестнадцатеричную систему
счисления.
Переведем число 1001011,0112 в шестнадцатеричную систему счисления.
Разобьем данное число на тетрады, приписав слева в целой части, и справа в
дробной части недостающие нули:
0100 1011, 0110
4 В , 6
и заменим каждую тетраду соответствующим шестнадцатеричным кодом (см. таблицу).
Можем сделать вывод:
1001011,0112 = 4В,616
Пример:
перевод чисел из шестнадцатеричной системы счисления в двоичную систему
счисления.
Переведем число А4F,C516 в двоичную систему счисления. Каждую цифру
шестнадцатеричного числа заменим соответствующей тетрадой (см. таблицу).
A
4
F
,
C
5
1010 0100 1111 , 1100 0101
Запишем ответ, удалив нули слева в записи числа:
A4F,C516 = 101001001111,110001012
В МЕНЮ
Используются технологии uCoz
Информатик БУ — Кратко о системах счисления
Система счисления – это способ записи чисел с помощью символов. Мы все привыкли использовать десять различных знаков для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такая система счисления называется десятичной. Один знак числа называется цифрой.
Мы все привыкли использовать десять различных знаков для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такая система счисления называется десятичной. Один знак числа называется цифрой.
Основание системы счисления – это количество знаков, используемых для записи числа в этой системе. Основанием системы счислений, как правило, может являться любое натуральное число (например, шумеры использовали шестидесятеричную систему счисления), но сегодня наиболее распространены (кроме десятичной) двоичная, восьмеричная и шестнадцатеричная. Основание системы счисления указывается подстрочным знаком после числа, например 1012.
Разряд числа – это место цифры в числе. В зависимости от количества разрядов мы называем числа двузначными, трёхзначными, четырёхзначными и т.д.
Двоичная система счисления
Популярность двоичной системы в информатике обусловлена тем, что для записи чисел используется всего две цифры: 0 и 1. Это соответствует значению одного бита, который тоже может принимать значения 0 и 1. Поэтому во многих случаях один разряд двоичного числа называют битом. А так как в вычислительной технике информация передаётся в битах, то и числа удобнее передавать в виде двоичного (бинарного) кода.
Простой пример. IP-адрес компьютера состоит из четырёх байт, разделенных точками, к примеру:
192.168.0.1
Почему байты записаны в виде чисел? Если перевести байты этого IP-адреса в биты (двоичную систему), мы получим четыре восьмизначных двоичных числа:
11000000. 10101000.00000000.00000001
Двоичные числа состоят из восьми разрядов, а байт равен восьми битам.
Восьмеричная система счисления
Двоичная система счисления удобна для компьютера, но не очень удобна для людей, так как числа, записанные в ней, получаются очень большими по размеру. Представьте, десятичное число 10000000 в двоичной системе выглядит как 100110001001011010000000, не очень удобно, согласитесь?
Поэтому была введена восьмеричная система счисления. Восьмеричная система отличается от десятичной тем, что двоичные числа очень удобно приводить к основанию 8, а восьмеричные – к основанию 2. С десятичной всё немного сложнее. Для перевода используется таблица триад (в правом нижнем углу сайта есть кнопочка, можете посмотреть, а почитать про правила перевода можно здесь).
Восьмеричная система отличается от десятичной тем, что двоичные числа очень удобно приводить к основанию 8, а восьмеричные – к основанию 2. С десятичной всё немного сложнее. Для перевода используется таблица триад (в правом нижнем углу сайта есть кнопочка, можете посмотреть, а почитать про правила перевода можно здесь).
Шестнадцатеричная система счисления
Помните, что один разряд двоичной системы – это один бит? А два разряда шестнадцатеричной системы – это один байт. В современных компьютерах информация кодируется в байтах, поэтому во многих случаях удобно использовать шестнадцатеричную систему.
В шестнадцатеричной системе шестнадцать разрядов: цифры от 0 до 9, и буквы от A до F (где буквы от A до F – десятичные числа от 10 до 15 соответственно).
Шестнадцатеричную систему используют в низкоуровневом программировании, в компьютерном дизайне широко используются шестнадцатеричные коды цвета, в некоторых кодировках символы кодируются именно с помощью шестнадцатеричной системы… В общем, штука полезная:).
Одно из заданий ЕГЭ предыдущих лет было как раз на знание шестнадцатеричных цветовых кодов.
Пример: нужно определить, какой цвет зашифрован кодом #00FF00 в палитре RGB.
Решение: Данный код является кодом цвета в палитре RGB, то есть первые два разряда – Red, вторые два разряда – Green, третьи два разряда – Blue:
#00FF00
Получается, что красного цвета — 0, синего цвета – 0, а зелёного – FF, то есть 255 в десятичной системе счисления (максимальное двузначное шестнадцатеричное число). То есть это код чистого зелёного цвета.
Подобные коды вы можете встретить, к примеру, в палитре цветов Adobe Photoshop, или при разработке внешнего вида сайта, когда для различных элементов дизайна необходимо указать код цвета.
Шестнадцатиричная система счисления | Практическая электроника
В прошлой статье мы с Вами разбирали двоичную и двоично-десятичную систему счисления. С помощью калькулятора Windows мы переводили числа из двоичной системы в десятичную. Представьте себе, что нам надо перевести число из десятичной в двоичную систему счисления. Такое безобидное число, как 9999 в двоичной системе будет выглядеть уже как 10 0111 0000 1111. Не очень то и удобно, так ведь? С такими числами работает только компьютер и другие цифровые девайсы.
С помощью калькулятора Windows мы переводили числа из двоичной системы в десятичную. Представьте себе, что нам надо перевести число из десятичной в двоичную систему счисления. Такое безобидное число, как 9999 в двоичной системе будет выглядеть уже как 10 0111 0000 1111. Не очень то и удобно, так ведь? С такими числами работает только компьютер и другие цифровые девайсы.
Системы счисления
Если подробнее вдаваться в компьютерные системы, то комп даже на знает, что такое единичка, а что такое ноль. Это для нас понятно, что единичка – это “ДА” , “ИСТИНА”, а ноль это – “НЕТ”, “ЛОЖЬ”. В компьютерах, микропроцессорах, микроконтроллерах да и во всех цифровых микросхемах используются другие понятия единицы и нуля. Напряжение есть и оно соответствует норме – это ЕДИНИЧКА, напряжение маленькое или его нет – это НОЛЬ. Именно так и оперируют цифровые микросхемы и вся сложнейшая цифровая электроника ;-). ЕДИНИЦА И НОЛЬ! 🙂
А вам слабо написать программу на единичках и нулях? Я думаю, это не под силу даже самому наяренному программеру в мире. Люди недолго думали и для удобства написания чисел придумали сначала восьмеричную систему счисления, а потом и шестнадцатеричную. Если помните, в двоичной системе счисления только два знака: 1 и 0. В десятичной – 10 знаков: 0 1 2 3 4 5 6 7 8 9, восьмеричной системе счисления используются только 8 знаков: 0 1 2 3 4 5 6 7. В шестнадцатеричной системе счисления знаков целых 16 штук! Чтобы не мудрить, взяли первые 9 знаков от десятичной системы счисления, а остальные от английского алфавита. Итого – 0 1 2 3 4 5 6 7 8 9 A B C D E F – ровненько 16 знаков.
Почему раньше не использовали десятичную систему вместо восьмеричной? Ведь в десятичной было на два знака больше? Все упиралось в байты. Как вы помните, 8 бит – это один Байт. Именно поэтому было удобно использовать восьмеричную и шестнадцатеричную системы счисления, кратную восьмерке, чем десятеричную. В последнее время самая крутая считается шестнадцатеричная система счисления. Именно она в большинстве используется в микроконтроллерах и в других цифровых микросхемах.
В последнее время самая крутая считается шестнадцатеричная система счисления. Именно она в большинстве используется в микроконтроллерах и в других цифровых микросхемах.
Перевод из одной системы счисления в другую
Как же нам переводить числа из одной системы счисления в другую? Здесь все просто, следуем примеру из второй главы, где написано, как использовать калькулятор Windows для перевода чисел из десятичной системы в двоичную. С помощью этого калькулятора мы также можем переводить числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и обратно. Запускаем наш калькулятор, пишем от балды число “123” в десятичной системе счисления. Для этого ставим маркер на “Dec” и для красоты “1 байт”.
Для того, чтобы перевести это число в двоичную систему счисления, ставим маркер на “Bin” и получаем число “123” в двоичной системе счисления.
Для перевода в восьмеричную систему ставим маркер на “Oct”.
Ну и для перевода в шестнадцатеричную систему ставим маркер на “Hex”.
Все операции взаимозаменяемы. Это значит, что мы можем перевести число из двоичной в шестнадцатеричную, из восьмеричной в двоичную и так далее. Чтобы не спутать системы счисления и знать, какое число записано, после каждого записанного числа снизу ставится его индекс системы счисления. Например:
7ВС16 – значит число записано в шестнадцатеричной системе счисления
10112 – в двоичной системе
4578 – в восьмеричной системе
998510 – в десятеричной системе.
СИСТЕМЫ СЧИСЛЕНИЯ | Наука и жизнь
В повседневной жизни мы, как правило, пользуемся десятичной системой счисления. Но это лишь одна из многих систем, которая получила свое распространение, вероятно, по той причине, что у человека на руках 10 пальцев. Однако эта система не всегда удобна. Так, в вычислительной технике применяется двоичная система счисления.
Системой счисления называют совокупность приемов и правил наименования и обозначения чисел, с помощью которых можно установить взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов.
В разные исторические периоды развития человечества для подсчетов и вычислений использовались те или иные системы счисления. Например, довольно широко была распространена двенадцатеричная система. Многие предметы (ножи, вилки, тарелки, носовые платки и т. д.) и сейчас считают дюжинами. Число месяцев в году двенадцать. Двенадцатеричная система счисления сохранилась в английской системе мер (например, 1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам).
В древнем Вавилоне существовала весьма сложная шестидесятеричная система. Она, как и двенадцатеричная система, в какой-то степени сохранилась и до наших дней (например, в системе измерения времени: 1 час = 60 минутам, 1 минута = 60 секундам, аналогично в системе измерения углов: 1 градус = 60 минутам, 1 минута = 60 секундам).
У некоторых африканских племен была распространена пятеричная система счисления, у ацтеков и народов майя, населявших в течение многих столетий обширные области американского континента, — двадцатеричная система. У некоторых племен Австралии и Полинезии встречалась двоичная система.
Десятичная система возникла в Индии. Впоследствии ее стали называть арабской потому, что она была перенесена в Европу арабами. Цифры, которыми мы теперь пользуемся, — арабские.
В разное время существовали и другие записи цифр, в настоящее время почти забытые. Однако до сих пор мы иногда встречаемся с записью чисел с помощью букв латинского алфавита, например на циферблатах часов, в книгах для обозначения глав или частей, на деловых бумагах для обозначения месяцев и т.д.
В вычислительной технике применяется двоичная система счисления. Основанием этой системы является число 2. Это означает, что для представления любого числа используются только две цифры, 0 и 1. Целесообраз ность применения двоичной системы в цифровой электронике объясняется тем, что базовый элемент любой электронной схемы имеет два состояния, которым можно приписать значения 0 и 1.
Рассмотрим для примера двоичное число 110010. Единицы и нули в двоичном числе называют разрядами (битами), а положение каждого бита определяет величину показателя степени основания 2, причем старший значащий разряд находится в числе слева, как и в десятичной системе, а младший — справа. Таким образом двоичное число 110010 в десятичной системе равно 1x25+1x24 +0x23+0x22 +1x21+0x20 = 50. Обратное преобразование целого числа производится методом последовательного деления на 2 до тех пор, пока частное от деления не станет равным 1. Число в двоичной системе счисления записывается в виде остатков от деления, начиная с последнего частного, справа налево.
Единицы и нули в двоичном числе называют разрядами (битами), а положение каждого бита определяет величину показателя степени основания 2, причем старший значащий разряд находится в числе слева, как и в десятичной системе, а младший — справа. Таким образом двоичное число 110010 в десятичной системе равно 1x25+1x24 +0x23+0x22 +1x21+0x20 = 50. Обратное преобразование целого числа производится методом последовательного деления на 2 до тех пор, пока частное от деления не станет равным 1. Число в двоичной системе счисления записывается в виде остатков от деления, начиная с последнего частного, справа налево.
Фибоначчиева система счисления — Задачи
Как известно, последовательность Фибоначчи начинается с двух чисел 0 и 1 и каждый последующий член последовательности получается как сумма двух предыдущих. Например, третий член последовательности это 1 (1=1+0), четвёртый — 2 (2=1+1), пятый — 3 (3=2+1) и т.д.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Fib(i) | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
Рисунок 1 — Первые числа последовательности Фибоначчи
Эта последовательность проявляется очень часто и в нашей жизни и в природе и имеет большое значение. А знаете ли Вы, что все положительные целые числа можно представить как сумму чисел из последовательности Фибоначчи? Более того, все натуральные числа можно представить при помощи последовательности Фибоначчи, причём без повторений. Например: 13 может быть представлено из указанного множества как {13}, {5,8} или {2,3,8} а 17 представлено как {1,3,13} или {1,3,5,8}. Так как все числа обладают этим свойством (может у Вас есть желание доказать это?), то этот набор является хорошим способом для использования в качестве «базы» (основания системы счисления) для представления чисел. Но, как мы видели выше, некоторые числа могут быть представлены более чем одним способом суммой чисел из последовательности Фибоначчи. Как нам выйти из этой ситуации? Очень просто! Для этого достаточно наложить ограничение, что для предоставления числа нельзя использовать два соседних элемента из последовательности Фибоначчи! Это ограничение объясняется тем, что сумма двух соседних членов последовательности Фибоначчи сама является членом последовательности Фибоначчи.
Например: 13 может быть представлено из указанного множества как {13}, {5,8} или {2,3,8} а 17 представлено как {1,3,13} или {1,3,5,8}. Так как все числа обладают этим свойством (может у Вас есть желание доказать это?), то этот набор является хорошим способом для использования в качестве «базы» (основания системы счисления) для представления чисел. Но, как мы видели выше, некоторые числа могут быть представлены более чем одним способом суммой чисел из последовательности Фибоначчи. Как нам выйти из этой ситуации? Очень просто! Для этого достаточно наложить ограничение, что для предоставления числа нельзя использовать два соседних элемента из последовательности Фибоначчи! Это ограничение объясняется тем, что сумма двух соседних членов последовательности Фибоначчи сама является членом последовательности Фибоначчи.
Теперь, когда мы знаем всё изложенное выше, мы можем предложить хороший способ предоставления любого целого положительного числа. Для этого мы будем использовать двоичную последовательность (только нулей и единиц). Например, 17 = 1 + 3 + 13 (мы должны помнить, что нельзя использовать два последовательных числа Фибоначчи). Будем использовать ноль в записи, если очередное число из последовательности Фибоначчи не используется, и единицу для тех что используются. Тогда, 17 = 100101 (ведущие нули должны быть опущены). На рисунке 2 подробно показано, как получена эта запись и что означают нули и единицы в приведённой выше записи. Для лучшего понимания этой схемы обратим внимание на тот факт, что не использование двух соседних чисел Фибоначчи означает, что двоичная последовательность не будет иметь двух подряд идущих единиц. Используя приведённое представление числа, мы будем говорить, что мы используем Фибоначчиеву систему счисления и записывать его как 17 = 100101 (fib).
Используя приведённое представление числа, мы будем говорить, что мы используем Фибоначчиеву систему счисления и записывать его как 17 = 100101 (fib).
Рисунок 2 — Объяснение представления числа 17 в Фибоначчиевой системе счисления
Ваша задача состоит в записи заднного десятичного числа в Фибоначчиевой системе счисления.
Входные данные
В первой строке входных данных задано единственное натуральное число N, указывающее на количество примеров в тесте (1 ≤ N ≤ 500).
Следующие N строк содержат по одному положительному целому числу, не превышающему 100 000 000. Числа могут быть поданы в произвольном порядке.
Выходные данные
Вы должны вывести по одной строке для каждого из N чисел, полученных во входных данных, в следующем формате: «DEC_BASE = FIB_BASE (fib)«. DEC_BASE это заданное оригинальное число в десятичной системе счисления, а FIB_BASE соответственно — его представление в Фибоначчиевой системе счисления. Образец вывода приведён в примере выходных данных.
Лимит времени 1 секунда
Лимит использования памяти 64 MiB
Что такое система счисления? — Определение, факты и примеры
Система счисления
Десятичная система счисления:
Десятичная система счисления состоит из 10 цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 и является наиболее часто используемой системой счисления. Мы используем комбинацию этих 10 цифр для образования всех остальных чисел. Значение цифры в числе зависит от ее положения в номере. Таблица значений десятичной системы счисления выглядит так:
Каждое место слева в десять раз больше, чем место справа от него, то есть, когда мы перемещаемся справа налево, разрядное значение увеличивается в десять раз с каждым местом.
Десятичная система счисления также называется системой счисления с основанием 10.
Число 49 365 читается как сорок девять тысяч триста шестьдесят пять, где значение 4 — сорок тысяч, 9 — девять тысяч, 3 — триста, 6 — шестьдесят и 5 — пять.
Двоичная система счисления
В двоичной системе счисления мы используем только две цифры 0 и 1. Это означает двойную систему счисления.
Пример двоичного числа: 1011; 101010; 1101101
Каждая цифра двоичного числа называется битом.Итак, двоичное число 101 имеет 3 бита. 499787080
В компьютерах и других цифровых устройствах используется двоичная система. В двоичной системе счисления используется основание 2.
Шестнадцатеричная система счисления
Слово шестнадцатеричный происходит от шестнадцатеричного значения 6 и десятичного значения 10. Итак, в шестнадцатеричной системе счисления 16 цифр. Он состоит из цифр от 0 до 9 и первых 5 букв алфавита:
В таблице ниже числа от 1 до 20 показаны в десятичном, двоичном и шестнадцатеричном формате.
Десятичное | двоичный | Шестнадцатеричный |
0 | 0 | 0 |
1 | 1 | 1 |
2 | 10 | 2 |
3 | 11 | 3 |
4 | 100 | 4 |
5 | 101 | 5 |
6 | 110 | 6 |
7 | 111 | 7 |
8 | 1000 | 8 |
9 | 1001 | 9 |
10 | 1010 | 10 |
11 | 1011 | А |
12 | 1100 | Б |
13 | 1101 | С |
14 | 1110 | D |
15 | 1111 | E |
16 | 10000 | Ф |
17 | 10001 | 11 |
18 | 10010 | 12 |
19 | 10011 | 13 |
20 | 10100 | 14 |
Интересные факты
|
Натуральные, целые, рациональные, иррациональные, действительные и другие числа
Натуральные числа
натуральных (или , считая ) чисел — 1,2,3,4,5 и т. Д.
много натуральных чисел.Набор натуральных чисел, {1,2,3,4,5, …},
иногда для краткости пишут N .
Целые числа — натуральные числа вместе с 0.
(Примечание: некоторые учебники не согласны с этим и говорят, что натуральные числа включают 0.)
Сумма
любые два натуральных числа также являются натуральными числами (например, 4 + 2000 = 2004), а произведение любых двух натуральных чисел
натуральное число (4 × 2000 = 8000). Этот
однако это неверно для вычитания и деления.
Целые числа
целых чисел — это набор действительных чисел, состоящий из натуральных чисел, их аддитивных обратных чисел и нуля.
{…, — 5, −4, −3, −2, −1,0,1,2,3,4,5, …}
Набор целых чисел иногда
написано J или Z для краткости.
сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это не относится к делению … просто попробуйте 1 ÷ 2.
Рациональные числа
рациональных чисел — это
те числа, которые можно выразить как отношение между
два целых числа.Например, дроби 13 и −11118 являются
рациональное число. Все целые числа входят в рациональные числа,
поскольку любое целое число z можно записать как отношение z1.
Все десятичные дроби, которые заканчиваются, являются рациональными числами (с версии 8.27 можно записать как 827100.) Десятичные дроби
которые после некоторой точки имеют повторяющийся узор, также являются рациональными:
например,
0,0833333 …. = 112.
Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их
сумма, разница, произведение и частное также являются рациональным числом
(пока мы не делим на 0).
Иррациональные числа
Иррациональное число — это число, которое нельзя записать в виде отношения (или дроби). В десятичной форме он никогда не заканчивается и не повторяется. В
древние греки обнаружили, что не все числа рациональны; там
— это уравнения, которые нельзя решить с помощью отношений целых чисел.
Первое такое уравнение
для изучения было 2 = x2. Что
само число раз равно 2?
2 является
около 1,414, поскольку 1,4142 = 1,999396, что близко к
2. Но вы никогда не попадете точно, возведя дробь в квадрат (или завершив
десятичная дробь).Квадратный корень из 2 — иррациональное число, то есть его
десятичный эквивалент продолжается вечно, без повторяющегося образца:
2 = 1,41421356237309 …
Другой известный иррациональный
числа золотое сечение , число с большим
значение для биологии:
1 + 52 = 1,61803398874989 …
π (пи),
отношение длины окружности к ее диаметру:
π = 3,141558979 …
и е,
самое важное число в исчислении:
е = 2.71828182845904 …
Иррациональные числа можно далее разделить на алгебраических чисел, которые являются решениями некоторого полиномиального уравнения (например, 2 и золотое сечение), и трансцендентных чисел, которые не являются решениями какого-либо полиномиального уравнения. π и e оба трансцендентны.
Реальные числа
Действительные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» в числовой строке.Существует бесконечно много действительных чисел, как и бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел на больше бесконечности.
«Меньше»,
или счетных бесконечности целых чисел и
rationals иногда называют ℵ0 (alef-naught),
и бесчисленных бесконечности реалов
называется ℵ1 (алеф-он).
Есть еще «большие» бесконечности,
но для этого вам следует взять курс теории множеств!
Комплексные числа
Комплексные числа
— множество {a + bi | a и b — действительные числа}, где i — мнимая единица, −1.(нажмите здесь, чтобы
подробнее о мнимых числах и операциях с комплексными числами).
Комплексные числа включают набор действительных чисел. Действительные числа в сложной системе записываются в виде a + 0i = a. реальное число.
Этот набор иногда бывает
записывается как C для краткости. Набор комплексных чисел
важно, потому что для любого полинома p (x) с коэффициентами действительного числа все решения p (x) = 0 будут в C .
За пределами …
Есть и «большие» наборы
чисел, используемых математиками.Кватернионы ,
открытые Уильямом Х. Гамильтоном в 1845 году, образуют систему счисления с тремя
разные мнимые единицы!
Система счисления | математика | Britannica
Система счисления , любой из различных наборов символов и правила их использования для представления чисел, которые используются для обозначения количества объектов в данном наборе. Таким образом, идея «единства» может быть представлена римской цифрой I, греческой буквой альфа α (первая буква), используемой в качестве числительного, еврейской буквой алеф (первая буква), используемой в качестве числа, или современная цифра 1, которая имеет индуистско-арабское происхождение.
Подробнее по этой теме
математика: Система счисления и арифметические операции
Египтяне, как и римляне после них, выражали числа по десятичной схеме, используя отдельные символы для 1, 10, 100, 1000, …
Далее следует краткое описание систем счисления. Для дальнейшего обсуждения, см. цифры и системы счисления: Системы счисления.
Очень вероятно, что самой ранней системой письменных символов в древней Месопотамии была система символов для чисел. Современные системы счисления — это системы счисления. То есть значение символа зависит от положения или места символа в представлении; например, 2 из 20 и 200 представляют две десятки и две сотни соответственно. Большинство древних систем, таких как египетская, римская, еврейская и греческая системы счисления, не имели позиционной характеристики, что усложняло арифметические вычисления.Однако в других системах, включая вавилонскую, по одной версии китайской и индийской, а также в системе майя, действительно использовался принцип числовой стоимости. Наиболее часто используемая система счисления — десятичная позиционная система счисления, десятичная относится к использованию 10 символов — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 — для построения всех чисел. Это было изобретение индейцев, усовершенствованное средневековым исламом. В компьютерах и информатике используются две другие общие системы позиционирования, а именно двоичная система с двумя символами 0, 1 и шестнадцатеричная система с ее 16 символами 0, 1, 2,…, 9, A, B,… , Ф.
Границы | Роль приблизительной системы счисления в различных математических навыках в классах
Введение
Приблизительная система счисления (ANS) — это ментальная система, отвечающая за представление и обработку информации о числовой величине (De Smedt et al., 2013; Libertus, 2015). Утверждалось, что ANS помогает детям формировать неточные численные оценки, которые позже активируются и используются при сравнении величин (Siegler and Lortie-Forgues, 2014) и в обучении математике (см. Clements and Sarama, 2007; Feigenson et al., 2013; Либертус, 2015; Mussolin et al., 2016, для обзоров). Однако гораздо меньше известно об условиях, при которых два наиболее известных аспекта ВНС (символическая и несимвольная оценка) предсказывают математические навыки. Таким образом, это исследование было направлено на изучение того, как два аспекта ВНС (символическая и несимвольная оценка) способствуют разным математическим навыкам (ранние математические навыки, числовые операции, решение математических задач и беглость вычислений) в разных классах (детский сад, 2 класс). , и класс 4).
Приближенная система счисления состоит из двух аспектов: несимвольной оценки и символьной оценки. Несимвольная оценка относится к обработке количеств и числовых значений без использования цифр (Smets et al., 2015). Он возникает уже в возрасте 6 месяцев, когда младенцы различают большие соотношения двух массивов (например, 6:12; Libertus and Brannon, 2010), и продолжает развиваться до взрослого возраста, когда люди используют это знание для различения между меньшие отношения (например,г., 0,9: 1; Price et al., 2012). В свою очередь, символическая оценка относится к отображению цифр в количественном измерении, например, в приближении количества точек на картинке и расположения числа на числовой прямой (Booth and Siegler, 2006). Предполагается, что числа мысленно представляются вдоль линии мысленных чисел (Siegler and Lortie-Forgues, 2014), а представление чисел становится более точным, переходя от логарифмической формы к линейной по мере того, как дети становятся старше (Siegler and Booth, 2004; Фризо-ван ден Бос и др., 2015). Мета-анализ выявил значительную корреляцию между двумя аспектами ВНС и математикой (Chen and Li, 2014; Fazio et al., 2014; Schneider et al., 2018a). Например, Чен и Ли (2014) оценили среднюю корреляцию между несимвольными оценками и математикой в 0,24, а Шнайдер и др. (2018a) сообщили о средней корреляции между символической оценкой и математикой 0,44.
Однако метаанализ также выявил большую неоднородность корреляций.Возможное объяснение этой неоднородности может заключаться в том, что два аспекта ВНС по-разному влияют на математические навыки в разных классах. Чтобы обозначить это, в исследовании следует изучить роль обоих аспектов ВНС в математике на разных уровнях обучения (что мы сделали в нашем исследовании). Кроме того, также возможно, что влияние уровня обучения взаимодействует с типом математических навыков, оцениваемых в различных исследованиях. Математические навыки включают широкий спектр навыков, таких как ранние математические навыки (например,g., счет и знание чисел), числовые операции (то есть способность использовать алгоритмы для решения письменной арифметики), беглость вычислений (способность быстро извлекать арифметические факты из памяти) и решение математических задач (способность применять математические концепции и арифметика для решения контекстных задач). Некоторые исследователи (Libertus et al., 2013; Wang et al., 2016) утверждали, что несимволическая оценка может помочь детям усвоить знания, связанные с числами, такие как концепции чисел, взаимосвязи между числами, и, таким образом, быть более важными для ранних математических способностей.В более поздние годы символическая оценка может помочь детям понять символическую арифметику и облегчить запоминание ответов на арифметические задачи (Siegler and Braithwaite, 2017) и, таким образом, будет более важной в математике в старших классах. Недавно Tosto et al. (2017) также утверждали, что после автоматизации арифметических навыков ни несимволические, ни символические оценки не должны играть важной роли. Это должно особенно повлиять на беглость вычислений, поскольку дети (особенно китайцы) начинают эффективно выполнять простые вычисления уже в 1-м классе (например.г., Deng et al., 2015; Cui et al., 2017).
Лишь несколько исследований также сравнивали эффекты как символической, так и несимволической оценки в одном и том же исследовании (например, Sasanguie et al., 2012, 2013; Jordan et al., 2013; Lyons et al., 2014; Cirino et al., 2014; Cirino et al., 2012, 2013; Jordan et al., 2013; Lyons et al., 2014; Cirino et al., 2012, 2013; Jordan et al., 2013; Lyons et al., 2014; Cirino et al. др., 2016; Tosto et al., 2017). Большинство этих исследований показали, что числовая линейная оценка однозначно объясняет математические навыки после контроля несимволических оценок (например, Sasanguie et al., 2012; Jordan et al., 2013; Lyons et al., 2014; Cirino et al., 2016; Tosto et al., 2017), но ни в одном из этих исследований не изучалось, как два навыка ANS объясняют первые математические навыки. Хотя несимволическая оценка, по-видимому, менее важна для изучения математики в школьные годы, как уже говорилось выше, она может однозначно объяснить математические навыки в ранние годы.
Интересно, что в большинстве предыдущих исследований, посвященных роли ВНС в математике, не учитывались эффекты ключевых когнитивных предикторов математики, таких как невербальный интеллект или исполнительное функционирование.Управляющее функционирование, когнитивные навыки, задействованные в целенаправленной деятельности, включают торможение и рабочую память (например, Miyake et al., 2000; Lehto et al., 2003), оба из которых являются важными коррелятами математических навыков (например, Swanson, 2006; Bull et al., 2008; Lan et al., 2011; Cragg et al., 2017; см. Обзор Bull and Lee, 2014). Исполнительное функционирование также может способствовать несимволической и символической оценке (например, Xenidou-Dervou et al., 2013; Wong et al., 2016; Peng et al., 2017; Zhu et al., 2017; Пурпура и Симмс, 2018). Подавление может потребоваться для подавления нечисловых характеристик стимула и сосредоточения внимания на величине (Starr et al., 2017), а рабочая память может потребоваться для хранения символической или несимвольной информации при быстром сравнении двух массивов объектов (Xenidou -Dervou et al., 2013) и удержании границ или референтных точек и их соответствующих значений в задачах числовой прямой (Schneider et al., 2018b). Следовательно, связь между остротой зрения ВНС и математикой может быть объяснена исполнительными функциями.Прайс и Уилки (2017), например, обнаружили, что торможение и рабочая память частично опосредуют связь между остротой ВНС (как несимвольной, так и символической оценкой) и математическими навыками.
Также обратите внимание, что большинство предыдущих исследований ВНС проводилось в западных странах, и гораздо меньше известно о роли остроты ВНС в изучении математики в странах Восточной Азии (например, в Китае). Система знаков в китайском языке относительно прозрачна (например, «(десять-один)» для одиннадцати), что может облегчить китайским детям изучение символических чисел (Miller et al., 2005). Более легкое освоение символических чисел на китайском языке может привести к тому, что несимволическая оценка будет менее важной в изучении математики. Есть основания полагать, что несимволическая и символическая оценка может играть в Китае иную роль, чем в западных странах. На сегодняшний день лишь несколько исследований изучали влияние символической или несимволической оценки на математику у китайских детей (см. Lonnemann et al., 2011; He et al., 2016; Wang et al., 2016; Wong et al. ., 2016; Zhang et al., 2016; Cui et al., 2017; Peng et al., 2017; Zhu et al., 2017), и ни одно из этих исследований не изучало, как символическая и несимволическая оценка предсказывает различные математические навыки как в раннем, так и в последующем начальном школьном возрасте.
Таким образом, настоящее исследование было направлено на изучение влияния обоих аспектов ВНС (символическая и несимволическая оценка) на различные математические навыки (начальные математические навыки, числовые операции, решение математических задач и беглость расчетов) в разных классах в Китае.Основываясь на результатах предыдущих исследований (Jordan et al., 2013; Lyons et al., 2014; Wong et al., 2016; Tosto et al., 2017; Zhu et al., 2017), мы предположили, что:
1) Эффекты символической и несимволической оценки будут различаться в зависимости от уровня обучения. Несимвольная оценка однозначно предсказывает математические навыки только в детском саду, в то время как символическая оценка однозначно предсказывает математические навыки на всех уровнях обучения.
2) Несимвольные и символьные оценки предсказывают различные математические навыки.Несимвольная оценка предскажет первые математические навыки, то есть счет, знание символьных чисел и арифметику, а символьная оценка предскажет все математические навыки, за исключением беглости вычислений.
Материалы и методы
Участников
Участниками были 100 детей из детского сада (53 девочки и 47 мальчиков; средний возраст = 66,53 месяца, SD = 3,31), 107 детей из 2 класса (60 девочек и 47 мальчиков; средний возраст = 92,16 месяцев, SD = 3.96) и 104 ребенка из 4 класса (59 девочек и 44 мальчика; средний возраст = 115,75 месяцев, SD = 3,62). Дети были набраны на добровольной основе из двух детских садов и трех начальных школ в Шанхае, Китай. Школы, которые участвовали в нашем исследовании, обслуживают в основном семьи среднего класса, а демографические данные являются репрезентативными для населения в целом в Шанхае (Национальное статистическое бюро в Шанхае, 2017). Все дети были носителями китайского языка, и ни у одного из них не было диагностировано интеллектуальных, сенсорных или поведенческих расстройств.Перед тестированием было получено согласие родителей и одобрение этических норм Шанхайского педагогического университета.
Материалы
Общие когнитивные способности
Невербальный интеллект
невербальных матриц из системы когнитивной оценки версии 2 (CAS-2; Naglieri et al., 2014) использовался для оценки невербального интеллекта. Детям предлагали различные геометрические рисунки, в которых отсутствовала одна часть, и их просили выбрать недостающую часть из шести вариантов.Задача была прервана после четырех последовательных ошибок. Результатом было правильное общее количество (макс. = 44). Сообщается, что валидность критерия находится в диапазоне от 0,57 до 0,65 (Naglieri et al., 2014). Коэффициент надежности альфа Кронбаха в текущем исследовании составил 0,85 в детском саду, 0,91 во 2-м классе и 0,90 в 4-м классе.
Исполнительная деятельность
Ингибирование
Expressive Attention, заимствованный из CAS-2 (Naglieri et al., 2014), использовался для оценки детского торможения.Две версии (5–7 лет и 8–18 лет) использовались, чтобы избежать эффекта потолка / пола. Версия, используемая для детей 2-х и 4-х классов, аналогична тесту Штрупа с цветными словами (Stroop, 1935) и включает три страницы. На первой странице детей попросили произнести вслух названия цветных квадратов (например, синий, желтый, красный и зеленый), а на второй детям было предложено назвать цветные символы (например, «,» желтый) . На третьей странице детям были представлены 40 цветных символов, каждый из которых был напечатан цветом, отличным от цветного символа [e.г., «(желтый)» напечатано синими чернилами]. Их попросили как можно быстрее прочитать вслух цвет чернил, которыми были напечатаны символы. Было проведено практическое испытание из 8 пунктов, чтобы убедиться, что дети поняли инструкции перед тестированием. Коэффициент соотношения был рассчитан путем деления количества правильных ответов на время до окончания наименования всех 40 пунктов. Сообщается, что валидность критерия находится в диапазоне от 0,69 до 0,73 (Naglieri et al., 2014). Коэффициент надежности Кронбаха в текущем исследовании был равен 0.86 учеников 2 и 4 классов.
Версия для школьников 5–7 лет использовалась в детском саду и также включала три страницы. На каждой странице детям показывали рисунки животных, включая маленьких животных (бабочка, мышь, птица и лягушка) и больших животных (слон, кит, лошадь и медведь), и их просили сказать вслух, маленькое ли каждое животное или большое. так быстро, как могли. На первой странице рисунки животных были напечатаны в едином размере, а на второй странице большие животные были напечатаны в большом размере, а маленькие животные — в маленьком.На третьей странице большие животные были напечатаны в маленьком размере, а маленькие животные — в большом, и детям было предложено назвать рисунок животного на основе их фактического размера, а не на основе размера, который они были напечатаны. Оценка представляла собой количество правильных ответов на третьей странице, разделенное на время, необходимое для завершения наименования элементов. Сообщается, что валидность критерия находится в диапазоне от 0,51 до 0,67 (Naglieri et al., 2014). Коэффициент надежности Кронбаха в текущем исследовании составил 0,81.
Оперативная память
цифр в прямом направлении от CAS-2 (Naglieri et al., 2014) использовалась для оценки рабочей памяти детей. Испытание состоит из 2–9 пролетов с четырьмя испытаниями на каждом отрезке. Числа представлялись устно со скоростью одно число в секунду, а затем детей просили повторить эти числа в том же порядке. Испытание было прекращено, когда в каждом пролете было допущено по три ошибки. Счет был последним, которого достигли дети. Сообщается, что валидность критерия находится в диапазоне от 0,40 до 0,64 (Naglieri et al., 2014). Коэффициент надежности Кронбаха в текущем исследовании был равен 0.88, 0,89 и 0,88 в детском саду, 2 и 4 классе соответственно.
Навыки математики
Ранние математические навыки
Тест на ранние математические способности (ТЕМА-3; Гинзбург и Баруди, 2003) использовался для измерения начальных математических навыков детских садов. ТЕМА-3 включает 72 пункта по счету, знанию символических чисел и арифметике. Тест был прерван после четырех последовательных ошибок, и общая оценка детей была правильной. Было обнаружено, что ТЕМА-3 значительно коррелирует с другими математическими тестами, такими как подтест по математике в тесте на успеваемость детей младшего возраста и пересмотренный ключевой математический анализ (диапазон — от 0.54 до 0,91; Гинзбург и Баруди, 2003). Коэффициент надежности Кронбаха в текущем исследовании составил 0,88.
Числовые операции
Числовые операции, заимствованные из WIAT-III (Wechsler Individual Achievement Test-Third Edition; Wechsler, 2009), использовались для оценки навыков детей в области числовых операций в неограниченных условиях. Задания были расположены в порядке возрастания сложности, и детей просили решать их один за другим. Тест был прерван после четырех последовательных ошибок, и общее количество баллов участника было правильным.Было обнаружено, что числовые операции значительно коррелируют с другими математическими мерами, такими как числовые операции в WIAT-II и Math Reasoning ( — диапазон от 0,71 до 0,81; Wechsler, 2009). Коэффициент надежности Кронбаха в текущем исследовании составил 0,80 и 0,89 для 2 и 4 классов соответственно.
Решение математических задач
Решение математических задач, заимствованное из WIAT-III (Wechsler Individual Achievement Test-Third Edition; Wechsler, 2009), использовалось для оценки решения математических задач.Пункты задания были расположены по возрастающей сложности (не более 72). Детей просили решать эти задачи один за другим в неограниченных условиях. Тест был прерван после четырех последовательных ошибок, и общее количество баллов участника было правильным. Было обнаружено, что решение математических задач значительно коррелирует с другими математическими мерами, такими как числовые операции и математические рассуждения (диапазон — от 0,75 до 0,84; Wechsler, 2009). Коэффициент надежности Кронбаха в текущем исследовании был равен 0.88, 0,90 и 0,90 в детском саду, 2 и 4 классе соответственно.
Беглость расчетов
«Беглость математики» из WIAT-III (Wechsler Individual Achievement Test — Third Edition; Wechsler, 2009) использовался для оценки беглости расчетов детей. Это задание включает в себя три подтеста: беглость сложения (например, 5 + 1 = 6), беглость вычитания (например, 4-2 = 2) и беглость умножения (например, 2 × 3 = 6). Детей попросили записать ответы на 48 вопросов в каждом субтесте, как только они смогут в течение 1 минуты.Оценка участника складывалась из результатов трех субтестов. Было обнаружено, что свободное владение математикой значительно коррелирует с другими математическими показателями, такими как числовые операции и математические рассуждения (диапазон — от 0,55 до 0,64; Wechsler, 2009). Zhu et al. (2017) сообщили, что надежность внутренней согласованности для беглости математики составила 0,88 и 0,93 для 2 и 4 классов соответственно.
Приблизительная система счисления
Несимвольная оценка
Точечная оценка, адаптированная из Halberda and Feigenson (2008), использовалась для оценки задачи несимвольной оценки на компьютере.Во время тестирования на экране появятся две картинки. На каждой картинке было несколько случайных точек (10–30 точек). Количество точек на двух картинках было разным. Во 2-х и 4-х классах детей просили решить, какая фотография набрала больше баллов, в течение 2-х секундного ограничения. В детском саду на принятие решения детям давали 3 секунды. В задание входили 6 практических заданий и 24 тестовых задания. Оценка участника — это процент правильных ответов по 24 пунктам. Задача использовалась в нескольких предыдущих исследованиях на китайском языке, показавших хорошие психометрические свойства (например,г., Cui et al., 2017; Чжу и др., 2017; Cheng et al., 2018). Коэффициент надежности альфа Кронбаха в текущем исследовании составил 0,69, 0,77 и 0,72 для детского сада, 2 и 4 класса соответственно.
Символьная оценка
Оценка
Числовая линия была заимствована у Опфера и Зиглера (2007) и использовалась для измерения символической оценки детей. Версия для Grade 2 и Grade 4 проводилась на 8-дюймовом планшете. На панели отображалась линия. 0 был отмечен слева от линии, а 100 был отмечен справа.Во время тестирования на экране появлялось число, и детей просили оценить, в каком положении находится это число в диапазоне от 0 до 100, и отметить позицию на линии. Пункты включали 26 номеров: 3, 4, 6, 8, 12, 17, 20, 21, 23, 25, 29, 33, 39, 43, 48, 50, 52, 57, 61, 64, 72, 79, 81, 84, 90 и 96. Пункты были представлены в случайном порядке. В детском саду задание числовой линии давалось в виде задания с бумагой и карандашом. Фактическая длина линии составляла 24 см, и она использовалась для обозначения расстояния от 0 до 10.Пункты включали девять чисел: 1, 2, 3, 4, 5, 6, 7, 8 и 9. Формула для расчета окончательной оценки была следующей: | Оценка — Количество оценок | Шкала оценки. Эта задача использовалась в предыдущих исследованиях на китайском языке, показавших хорошие психометрические свойства (например, Siegler and Mu, 2008; Laski, Yu, 2014; Zhu et al., 2017). Коэффициент надежности альфа Кронбаха в нашей выборке составил 0,72, 0,80 и 0,69 для детского сада, 2 и 4 класса соответственно.
Процедуры
Дети прошли индивидуальное тестирование подготовленными аспирантами в тихой комнате своей школы.Тестирование проводилось в два сеанса по 30–40 мин каждое. Сессия A включала тесты по математике [решение математических задач, числовые операции, свободное владение математикой (только во 2 и 4 классах), ТЕМА-3 (только в детском саду)]. Сессия B включала когнитивные тесты (невербальные матрицы, выразительное внимание и размах цифр вперед) и задачи ANS (оценка точек и оценка числовой линии). Половина детей в каждом классе выполняла сначала Сессию А, а затем Сессию Б. Другая половина выполняла занятия в обратном порядке.
Результаты
Предварительный анализ данных
Таблица 1 показывает описательную статистику (среднее значение, стандартное отклонение, диапазон, эксцесс и асимметрию) для всех показателей в нашем исследовании. Распределение числовых операций и точечной оценки было искажено в положительную сторону, и поэтому было применено логарифмическое преобразование. После преобразования журнала их распределения были нормализованы, и преобразованные баллы использовались в дальнейших анализах.
ТАБЛИЦА 1. Описательная статистика для всех показателей, использованных в нашем исследовании.
Соотношения между мерами
Коэффициенты корреляции между всеми переменными в детском саду, классе 2 и классе 4 представлены в таблицах 2, 3. В детском саду как числовая, так и точечная оценка значимо коррелировали со всеми математическими навыками ( — — От 0,43 до -0,55). Во 2-м классе оценка числовой линии значительно коррелировала с решением математических задач ( r = -0.52) и беглость математики ( r = -0,21). В 4 классе оценка числовой линии значительно коррелировала с решением математических задач ( r = -0,28) и числовыми операциями ( r = -0,27). Точечная оценка достоверно не коррелировала с каким-либо заданием по математике во 2 и 4 классах.
ТАБЛИЦА 2. Корреляции между переменными в детском саду.
ТАБЛИЦА 3. Корреляции между переменными для Уровня 2 (ниже диагонали) и Уровня 4 (выше диагонали).
Результаты регрессионного анализа
Иерархический регрессионный анализ был впоследствии проведен в пределах каждого класса для изучения уникального вклада двух аспектов ANS в результаты математики [решение математических задач, числовые операции, беглость математики (оценивается только в 2 и 4 классах) и TEMA (оценивается только в детский сад)]. В каждой модели возраст и пол были введены в уравнение регрессии на этапе 1 в качестве контрольных переменных. Общие когнитивные способности (невербальный интеллект, торможение и рабочая память) были введены в уравнение регрессии на этапе 2, а оценка числовой линией и оценка точки были введены на этапе 3 уравнения регрессии в виде блока.
Таблицы 4–6 показывают стандартизованные бета-коэффициенты, R 2 изменений и уровни значимости регрессионных моделей для каждого класса. В детском саду два аспекта ANS составляли уникальную дисперсию в решении математических задач [5%, но только точечная оценка имела значительный эффект (β = -0,190, p <0,01)], числовые операции [4%, но только точка оценка оказала значительный эффект (β = -0,192, p <0,05)], и TEMA-3 [17%, обе оценки числовой прямой (β = -0.358, p <0,001) и точечная оценка (β = -0,246, p <0,01) имели значительный эффект] после учета возраста, пола, невербального интеллекта, торможения и рабочей памяти. Во 2-м классе ANS объясняет уникальную дисперсию в решении математических задач [14%, но только эффекты оценки числовой прямой были значительными (β = -0,444, p <0,001)], но не в числовых операциях и беглости математики. В 4-м классе ANS объясняет уникальную дисперсию в решении математических задач [5%, но только эффекты оценки числовой прямой были значительными (β = -0.184, p <0,05)], но не в математике. Прогнозирующий эффект оценки числовой прямой на числовые операции также был значительным (β = -0,203, p <0,05).
ТАБЛИЦА 4. Результаты иерархического регрессионного анализа для прогнозирования решения математических задач в детском саду, 2 и 4 классы
ТАБЛИЦА 5. Результаты иерархического регрессионного анализа, прогнозирующего числовые операции в детском саду 2 и 4 класса.
ТАБЛИЦА 6. Результаты анализа иерархической регрессии для прогнозирования TEMA и беглости математики (MF) в детском саду, 2 и 4 классы
Обсуждение
Целью этого исследования было изучить, как два аспекта ANS (symbolin) предсказывают разные математические навыки в разных классах в Китае. В целом, наши результаты показали, что взаимосвязь между остротой ВНС и математическими навыками зависит от типа аспекта ВНС, типа оцениваемого математического результата и уровня обучения.Среди детских садов несимволическая оценка однозначно предсказывала первые математические навыки, числовые операции и решение математических задач. Символическая оценка объяснила уникальную дисперсию только в начальных математических навыках. Символьное оценивание также предсказывало решение математических задач среди второклассников и числовых операций среди четвероклассников.
В соответствии с нашими ожиданиями, несимволическая оценка внесла уникальный вклад в развитие математических навыков только в детском саду.Это повторяет результаты более ранних исследований, которые показали, что несимволическая оценка играет уникальную роль в ранних математических навыках (например, Clements and Sarama, 2007; Inglis et al., 2011; Desoete et al., 2012; Xenidou-Dervou et al. др., 2016; Старр и др., 2017). Как пишет Xenidou-Dervou et al. (2016) отметили, что начало формального математического образования может привести к тому, что символическая оценка станет важным показателем математических навыков. Следует отметить, что несимвольное оценивание в детском саду внесло существенный вклад в развитие начальных математических навыков, помимо числовых операций и решения математических задач, что повторяет результаты недавнего метаанализа (Schneider et al., 2017). Schneider et al. (2017) обнаружили, что корреляция между несимвольными оценками и ранними математическими навыками была выше, чем между несимвольными оценками и навыками формальной математики, такими как арифметика. Предыдущие исследования также показали, что несимволическая оценка сильно коррелирует с ранними числовыми навыками, такими как счет и несимволическая арифметика (Gilmore et al., 2007; Libertus et al., 2013; van Marle et al., 2014).
Символьная оценка внесла уникальный вклад в решение математических задач во 2 и 4 классах и в числовые операции в 4 классе.Влияние оценки числовой прямой на числовые операции и решение математических задач соответствует результатам предыдущих исследований (например, Jordan et al., 2013; Tosto et al., 2017; Zhu et al., 2017). Было удивительно, что символьная оценка не объясняет однозначно числовые операции в классе 2, хотя это согласуется с данными Гири (2011), который обнаружил, что оценка числовой прямой в классе 1 не позволяет одновременно прогнозировать числовые операции. Это предполагает, что символическая оценка может быть более важной при изучении более сложной арифметики, такой как дроби.Учащиеся 4-х классов, изучающие китайский язык, изучают дроби (Шанхайская муниципальная комиссия по образованию, 2004 г.) и, таким образом, решают задачи с дробями в задаче числовых операций. Предыдущие исследования показали, что оценка числовой прямой очень важна для обучения дробным знаниям (Jordan et al., 2013; Hansen et al., 2015), так как это может дать детям преимущество в изучении понятий дробей. Jordan et al. (2013) также утверждали, что знание дробей может облегчить оценку числовой прямой, поскольку дети могут использовать стратегии пропорциональности в задании числовой прямой, например, мысленно разделить линию на четверти, чтобы получить более точную оценку (Siegler and Opfer, 2003).
В отличие от наших ожиданий, символьная оценка однозначно объясняла только ТЕМА-3, но не числовые операции или решение математических задач среди детсадовцев. Это может быть связано с тем, что ранние математические задачи включали такие элементы, как сравнение чисел, а знание чисел тесно связано с эффективностью вычисления числовой линии. Дети в детском саду учились наносить символические цифры на уже существующие несимволические представления (Barth et al., 2005; Mundy and Gilmore, 2009), и, таким образом, оценка числовой прямой коррелировала с ранними математическими навыками.Другая причина может заключаться в том, что ранние математические навыки могут способствовать выполнению задач числовой прямой. Предыдущие исследования показали, что маленькие дети обычно используют стратегии, основанные на счете, при размещении числа на числовой прямой (Petitto, 1990; Schneider et al., 2008), и, таким образом, дети с лучшими навыками счета могут более точно оценивать задачи числовой прямой.
Символьная оценка не позволила однозначно предсказать беглость вычислений среди детей школьного возраста, что соответствовало результатам предыдущих исследований (Sasanguie et al., 2013; Чжу и др., 2017). Например, Sasanguie et al. (2013) обнаружили, что числовая линия среди детей 1–3 классов однозначно предсказывала их успеваемость в комплексном тесте достижений по математике через год, но не могла предсказать их результативность в арифметическом тесте с ограничением по времени. Однако Zhu et al. (2017) обнаружили, что оценка числовой прямой во 2-м, а не в 4-м классе однозначно предсказывала беглость параллельных вычислений после контроля общих когнитивных способностей. Возможное объяснение может заключаться в том, что Zhu et al.(2017) не включили несимвольные оценки в свое исследование. Альтернативное объяснение может заключаться в том, что мы использовали точность оценки числовой линии, в то время как беглость вычислений оценивала скорость арифметики, которая может влиять на скорость активации представлений чисел. Холлоуэй и Ансари (Holloway and Ansari, 2009) обнаружили, что эффект расстояния в задаче символического сравнения (рассчитанный на основе оценок точности детей младшего возраста) не коррелировал с беглостью вычислений, в то время как эффект расстояния, вычисленный на основе показателей времени ответа, однозначно объяснял беглость вычислений.Как отмечает Tosto et al. (2017) утверждали, ограниченная роль символической оценки в беглости вычислений может указывать на то, что символическая оценка может быть менее важной для арифметики, когда вычисление достигнет автоматического уровня.
Стоит упомянуть некоторые ограничения настоящего исследования. Во-первых, кросс-секционный дизайн этого исследования не позволяет нам сделать выводы о причинно-следственных связях между двумя аспектами ВНС и математическими навыками. Направление их взаимосвязи следует изучить дополнительно, поскольку недавние исследования также показали, что математические навыки могут повысить остроту зрения ВНС (например,г., Фризо-ван ден Бос и др., 2015). Во-вторых, в нашем исследовании мы не оценивали роль домашней среды для чтения. Предыдущие исследования показали, что домашняя математическая среда является важным предиктором успеваемости детей по математике (например, Manolitsis et al., 2013; Deng et al., 2015), а занятия по математике дома могут также способствовать несимволическим и символическим оценкам детей. (например, Mutaf-Yildiz et al., 2018). В будущих исследованиях следует изучить влияние домашней среды, в которой учатся считать, на остроту остроты зрения ВНС и математические навыки.
Заключение
Взятые вместе, наши результаты показали, что два аспекта ВНС по-разному влияют на математические навыки в разные периоды обучения: несимволическая оценка была однозначно связана с математическими навыками в детском саду, тогда как символическая оценка была однозначно связана с математическими навыками в начальной школе. Эти результаты предполагают, что разные типы остроты зрения ВНС следует использовать для прогнозирования математических навыков в разные периоды обучения и, возможно, для выявления детей из группы риска по математическим трудностям.Кроме того, меры по развитию у детей математических навыков должны быть нацелены на различные аспекты ВНС у детей младшего и школьного возраста.
Заявление об этике
Это исследование было проведено в соответствии с рекомендациями Этического руководства по защите человеческих субъектов исследования, Комитета по академической этике Шанхайского педагогического университета. Протокол был одобрен Комитетом по академической этике Шанхайского педагогического университета. Родители всех детей дали письменное согласие в соответствии с Хельсинкской декларацией.
Авторские взносы
DC, GG, WW и YL разработали исследование. WW, DC и LZ собрали данные, подготовили данные для анализа и написали рукопись. GG, DC, WW и YL отредактировали рукопись.
Финансирование
Это исследование было поддержано грантом Национального фонда естественных наук Китая (грант № 31600906), грантом Общего проекта Шанхайской муниципальной комиссии по образованию (C16011) и грантом Китайского института при университете Альберты. .
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Мы хотели бы поблагодарить Zhang Meixia, Luo Qin, Su Hong-Ying, Liang Dandan и Zha Ling из Шанхайского педагогического университета за их помощь в сборе данных.
Сноски
- Это потому, что китайские дети посещают детский сад в возрасте 3 лет и остаются в детском саду в течение 3 лет, прежде чем перейти в 1 класс.В детском саду учатся выполнять несложные вычисления.
- Этот временной предел был определен на основе проведенного нами пилотного исследования, а также на основе временного ограничения, использованного в предыдущих исследованиях с детьми того же возраста, что и наш (например, Fazio et al., 2014; Libertus et al., 2016 ).
Список литературы
Барт, Х., Ла Монт, К., Липтон, Дж., И Спелк, Э. С. (2005). Абстрактное число и арифметика у дошкольников. Proc. Natl. Акад. Sci. НАС.А. 102, 14116–14121. DOI: 10.1073 / pnas.0505512102
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Булл Р., Эспи К. А. и Вибе С. А. (2008). Кратковременная память, рабочая память и исполнительные функции у дошкольников: продольные предикторы математических достижений в возрасте 7 лет. Dev. Neuropsychol. 33, 205–228. DOI: 10.1080 / 87565640801982312
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Бык, Р., и Ли, К. (2014). Исполнительное функционирование и достижения в математике. Child Dev. Перспектива. 8, 36–41. DOI: 10.1111 / cdep.12059
CrossRef Полный текст | Google Scholar
Чен, К., и Ли, Дж. (2014). Связь между индивидуальными различиями в остроте несимволических чисел и математическими способностями: метаанализ. Acta Psychol. 148, 163–172. DOI: 10.1016 / j.actpsy.2014.01.016
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ченг, Д., Сяо, К., Чен, К., Цуй, Дж., И Чжоу, X. (2018). Дислексия и дискалькулия характеризуются общим дефицитом зрительного восприятия. Dev. Neuropsychol. 43, 497–507. DOI: 10.1080 / 87565641.2018.1481068
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чирино, П. Т., Толар, Т. Д., Фукс, Л. С., и Хьюстон-Уоррен, Э. (2016). Когнитивные и числительные предикторы математических навыков в средней школе. J. Exp. Child Psychol. 145, 95–119. DOI: 10.1016 / j.jecp.2015.12.010
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Клементс, Д. Х., и Сарама, Дж. (2007). «Изучение математики в раннем детстве», в Second Handbook of Research on Mathematics Teaching and Learning , Vol. 1, изд. Ф. К. Лестер-младший (Нью-Йорк, Нью-Йорк: Издательство информационного века), 461–555.
Google Scholar
Крэгг, Л., Кибл, С., Ричардсон, С., Рум, Х. Э., и Гилмор, К. (2017). Прямое и косвенное влияние управляющих функций на успеваемость по математике. Познание 162, 12–26. DOI: 10.1016 / j.cognition.2017.01.014
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Цуй, Дж., Георгиу, Г. К., Чжан, Ю., Ли, Ю., Шу, Х., и Чжоу, X. (2017). Изучение взаимосвязи между быстрым автоматическим называнием и беглостью арифметики у китайских детей детского сада. J. Exp. Child Psychol. 154, 146–163. DOI: 10.1016 / j.jecp.2016.10.008
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Де Смедт, Б., Ноэль, М. П., Гилмор, К., и Ансари, Д. (2013). Как навыки обработки символических и несимволических числовых величин соотносятся с индивидуальными различиями в математических способностях детей? Обзор данных, полученных от мозга и поведения. Trends Neurosci. Educ. 2, 48–55. DOI: 10.1016 / j.tine.2013.06.001
CrossRef Полный текст | Google Scholar
Дэн, С.П., Силинскас, Г., Вэй, В., и Георгиу, Г.К. (2015). Перекрестная взаимосвязь между домашней учебной средой и академической успеваемостью по китайскому языку. Ранний ребенок. Res. Q. 33, 12–20. DOI: 10.1016 / j.ecresq.2015.05.001
CrossRef Полный текст | Google Scholar
Desoete, A., Ceulemans, A., De Weerdt, F., and Pieters, S. (2012). Можем ли мы предсказать нарушения математической обучаемости на основе символьных и несимволических сравнительных задач в детском саду? Результаты длительного исследования. Br. J. Educ. Psychol. 82, 64–81. DOI: 10.1348 / 2044-8279.002002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фацио, Л.К., Бейли Д. Х., Томпсон К. А. и Сиглер Р. С. (2014). Отношения различных типов представлений числовой величины друг к другу и к математическим достижениям. J. Exp. Child Psychol. 123, 53–72. DOI: 10.1016 / j.jecp.2014.01.013
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фейгенсон Л., Либертус М. Э. и Халберда Дж. (2013). Связь между интуитивным чувством числа и способностями к формальной математике. Child De. Перспектива. 7, 74–79. DOI: 10.1111 / cdep.12019
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фризо-ван ден Бос, И., Крезберген, Э. Х., Ван Луит, Дж. Э., Ксениду-Дерву, И., Йонкман, Л. М., Ван дер Шут, М. и др. (2015). Продольное развитие оценки числовой прямой и успеваемости по математике у детей младшего школьного возраста. J. Exp. Child Psychol. 134, 12–29. DOI: 10.1016 / j.jecp.2015.02.002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гинзбург, Х.П., Баруди А. Дж. (2003). TEMA: Test of Early Mathematics Ability , 3rd Edn. Остин, Техас: PRO-ED.
Google Scholar
Халберда Дж. И Фейгенсон Л. (2008). Изменение в развитии остроты «чувства числа»: приблизительная числовая система у 3-, 4-, 5- и 6-летних и взрослых. Dev. Psychol. 44, 1457–1465. DOI: 10.1037 / a0012682
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хансен, Н., Джордан, Н.C., Fernandez, E., Siegler, R. S., Fuchs, L., Gersten, R., et al. (2015). Общие и математические предикторы знания дробей шестиклассниками. Cogn. Dev. 35, 34–49. DOI: 10.1016 / j.cogdev.2015.02.001
CrossRef Полный текст | Google Scholar
Хе Й., Чжоу Х., Ши Д., Сун Х., Чжан Х. и Ши Дж. (2016). Новые данные о причинно-следственной связи между остротой зрения по приблизительной системе счисления (ВНС) и арифметическими способностями у учащихся начальной школы: продольный анализ с перекрестным запаздыванием. Фронт. Psychol. 7: 1052. DOI: 10.3389 / fpsyg.2016.01052
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Холлоуэй, И. Д., и Ансари, Д. (2009). Отображение числовых величин на символы: эффект числового расстояния и индивидуальные различия в успеваемости детей по математике. J. Exp. Child Psychol. 103, 17–29. DOI: 10.1016 / j.jecp.2008.04.001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Инглис, М., Аттридж, Н., Бэтчелор, С., и Гилмор, К. (2011). Острота невербальных чисел коррелирует с достижениями в символической математике: но только у детей. Психон. Бык. Ред. 18, 1222–1229. DOI: 10.3758 / s13423-011-0154-1
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Джордан, Н. К., Хансен, Н., Фукс, Л. С., Зиглер, Р. С., Герстен, Р., и Миклос, Д. (2013). Предикторы развития понятий и процедур дробей. J. Exp. Child Psychol. 116, 45–58. DOI: 10.1016 / j.jecp.2013.02.001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лан, X., Легар, К. Х., Пониц, К. К., Ли, С., и Моррисон, Ф. Дж. (2011). Изучение связей между подкомпонентами исполнительной функции и академической успеваемостью: кросс-культурный анализ китайских и американских дошкольников. J. Exp. Child Psychol. 108, 677–692. DOI: 10.1016 / j.jecp.2010.11.001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ласки, Э.В., Ю. К. (2014). Оценка числовой линии и мысленное сложение: изучение потенциальной роли языка и образования. J. Exp. Child Psychol. 117, 29–44. DOI: 10.1016 / j.jecp.2013.08.007
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Lehto, J. E., Juujärvi, P., Kooistra, L., and Pulkkinen, L. (2003). Размеры исполнительного функционирования: данные детей. Br. J. Dev. Psychol. 21, 59–80. DOI: 10.1348 / 026151003321164627
CrossRef Полный текст | Google Scholar
Либертус, М.Е. (2015). Роль навыков интуитивной аппроксимации для школьных математических способностей. Mind Brain Educ. 9, 112–120. DOI: 10.1111 / mbe.12072
CrossRef Полный текст | Google Scholar
Либертус, М. Э., Фейгенсон, Л., и Халберда, Дж. (2013). Является ли приблизительная точность чисел стабильным показателем математических способностей? Учиться. Индивидуальный. Dif. 25, 126–133. DOI: 10.1016 / j.lindif.2013.02.001
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Либертус, М.Э., Одич Д., Фейгенсон Л. и Халберда Дж. (2016). Точность сопоставления числовых слов и приблизительной системы счисления предсказывает формальные математические способности детей. J. Exp. Child Psychol. 150, 207–226. DOI: 10.1016 / j.jecp.2016.06.003
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лоннеманн, Дж., Линкерсдёрфер, Дж., Хассельхорн, М., и Линдберг, С. (2011). Символьные и несимволические эффекты расстояния у детей и их связь с арифметическими навыками. J. Neurolinguistics 24, 583–591. DOI: 10.1016 / j.jneuroling.2011.02.004
CrossRef Полный текст | Google Scholar
Лайонс, И. М., Прайс, Г. Р., Вессен, А., Бломерт, Л., и Ансари, Д. (2014). Числовые предикторы успешности арифметики в 1–6 классах. Dev. Sci. 17, 714–726. DOI: 10.1111 / desc.12152
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Манолитсис, Г., Георгиу, Г. К., и Цираки, Н. (2013). Изучение влияния домашней грамотности и навыков счета на чтение и математику в раннем возрасте. Ранний ребенок. Res. Q. 28, 692–703. DOI: 10.1016 / j.ecresq.2013.05.004
CrossRef Полный текст | Google Scholar
Миллер К. Ф., Келли М. и Чжоу X. (2005). «Изучение математики в Китае и США: кросс-культурное понимание природы и курса математического развития дошкольников», в Handbook of Mathematical Cognition , ed. Дж. И. Д. Кэмпбелл (Нью-Йорк, Нью-Йорк: Psychology Press), 163–177.
Google Scholar
Мияке, А., Фридман, Н. П., Эмерсон, М. Дж., Витцки, А. Х., Хауэртер, А., и Вейджер, Т. Д. (2000). Единство и разнообразие исполнительных функций и их вклад в сложные задачи «лобной доли»: анализ скрытых переменных. Cogn. Psychol. 41, 49–100. DOI: 10.1006 / cogp.1999.0734
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Манди, Э., и Гилмор, К. К. (2009). Детское отображение символьных и несимволических представлений числа. J. Exp.Child Psychol. 103, 490–502. DOI: 10.1016 / j.jecp.2009.02.003
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Муссолин, К., Найс, Дж., Лейберт, Дж., И Контент, А. (2016). Как приблизительные и точные числовые навыки связаны друг с другом в процессе разработки: обзор. Dev. Ред. 39, 1–15. DOI: 10.1016 / j.dr.2014.11.001
CrossRef Полный текст | Google Scholar
Мутаф-Йылдыз, Б., Сасанги, Д., Де Смедт, Б., и Рейнвоет, Б.(2018). Частота домашних занятий по математике дифференцированно связана с базовыми навыками обработки чисел и счета у детсадовцев. Фронт. Psychol. 9: 340. DOI: 10.3389 / fpsyg.2018.00340
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Наглиери, Дж. А., Дас, Дж. П., и Гольдштейн, С. (2014). CAS2: Система когнитивной оценки. Остин, Техас: Pro-Ed.
Google Scholar
Пэн, П., Ян, X., и Мэн, X. (2017).Связь между приблизительной системой счисления и ранней арифметикой: посредническая роль числовых знаний. J. Exp. Child Psychol. 157, 111–124. DOI: 10.1016 / j.jecp.2016.12.011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Прайс, Г. Р., Палмер, Д., Баттиста, К., и Ансари, Д. (2012). Несимволическое сравнение числовой величины: надежность и валидность различных вариантов задач и показателей результатов и их связь с арифметическими достижениями у взрослых. Acta Psychol. 140, 50–57. DOI: 10.1016 / j.actpsy.2012.02.008
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Прайс, Г. Р., Уилки, Э. Д. (2017). Когнитивные механизмы, лежащие в основе отношения между обработкой несимволических и символических величин и их отношения к математике. Cogn. Dev. 44, 139–149. DOI: 10.1016 / j.cogdev.2017.09.003
CrossRef Полный текст | Google Scholar
Пурпура, Д. Дж., И Симмс, В. (2018).Примерное развитие системы счисления в дошкольном учреждении: какие факторы предсказывают изменение? Cogn. Dev. 45, 31–39. DOI: 10.1016 / j.cogdev.2017.11.001
CrossRef Полный текст | Google Scholar
Сасанги, Д., Гебель, С. М., Молл, К., Сметс, К., и Рейнвоет, Б. (2013). Приближенное чувство числа, обработка символьных чисел или отображение числа в пространство: что лежит в основе достижений математики? J. Exp. Child Psychol. 114, 418–431. DOI: 10.1016 / j.jecp.2012.10.012
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Сасанги, Д., Van den Bussche, E., and Reynvoet, B. (2012). Предикторы достижений по математике? Данные лонгитюдного исследования. Mind Brain Educ. 6, 119–128. DOI: 10.1111 / j.1751-228X.2012.01147.x
CrossRef Полный текст | Google Scholar
Шнайдер М., Берес К., Кобан Л., Мерц С., Сьюзан Шмидт С., Стрикер Дж. И др. (2017). Связь обработки несимволических и символических числовых величин с математической компетенцией: метаанализ. Dev. Sci. 20: e12372. DOI: 10.1111 / desc.12372
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шнайдер М., Хайне А., Талер В., Торбейнс Дж., Де Смедт Б., Вершаффель Л. и др. (2008). Подтверждение движений глаз как меры развивающегося у детей начальной школы чувства числа. Cogn. Dev. 23, 409–422. DOI: 10.1016 / j.cogdev.2008.07.002
CrossRef Полный текст | Google Scholar
Шнайдер, М., Мерц, Дж., Наклейка, Дж., Де Смедт, Б., Torbeyns, J., Verschaffel, L., et al. (2018a). Связь оценки числовой линии с математической компетентностью: метаанализ. Child Dev. doi: 10.1111 / cdev.13068 [Epub перед печатью]. DOI: 10.1111 / cdev.13068
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шнайдер М., Томпсон К. А. и Риттл-Джонсон Б. (2018b). «Ассоциации сравнения величин и числовой оценки с математической компетентностью: сравнительный обзор», в Cognitive Development from a Strategy Perspective: Festschrift for Robert S.Siegler , изд. П. Лемэр (Лондон: Psychology Press), 100–119.
Google Scholar
Шанхайская муниципальная комиссия по образованию (2004 г.). Шанхайский стандарт учебной программы начальной и средней школы математики (пробная версия). Шанхай: Шанхайское образовательное издательство.
Зиглер, Р.С., Лорти-Форгез, Х. (2014). Интегративная теория численного развития. Child Dev. Перспектива. 8, 144–150. DOI: 10.1111 / cdep.12077
CrossRef Полный текст | Google Scholar
Зиглер, Р.С., Му Ю. (2008). Китайские дети преуспевают в решении новых задач по математике еще до начальной школы. Psychol. Sci. 19, 759–763. DOI: 10.1111 / j.1467-9280.2008.02153.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Зиглер Р. С. и Опфер Дж. Э. (2003). Развитие численного оценивания: свидетельство множественных представлений числовой величины. Psychol. Sci. 14, 237–250. DOI: 10.1111 / 1467-9280.02438
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Смец, К., Sasanguie, D., Szücs, D., and Reynvoet, B. (2015). Влияние различных методов построения несимволических стимулов при оценке и сравнении численности. J. Cogn. Psychol. 27, 310–325. DOI: 10.1080 / 20445911.2014.996568
CrossRef Полный текст | Google Scholar
Старр А., Де Винд Н. К. и Браннон Э. М. (2017). Вклад числовой остроты и нечисловых характеристик стимулов в развитие чувства числа и символических математических достижений. Познание 168, 222–233. DOI: 10.1016 / j.cognition.2017.07.004
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Струп, Дж. Р. (1935). Исследования вмешательства в серийных словесных реакций. J. Exp. Psychol. 18, 643–662. DOI: 10.1037 / h0054651
CrossRef Полный текст | Google Scholar
Суонсон, Х. Л. (2006). Поперечные и инкрементные изменения рабочей памяти и решение математических задач. J. Educ. Psychol. 98, 265–281. DOI: 10.1037 / 0022-0663.98.2.265
CrossRef Полный текст | Google Scholar
Национальное бюро статистики в Шанхае (2017). Шанхайский статистический ежегодник, 2017 г. Пекин: China Statistics Press.
Tosto, M. G., Petrill, S. A., Malykh, S., Malki, K., Haworth, C., Mazzocco, M. M., et al. (2017). Чувство чисел и математика: что, когда и как? Dev. Psychol. 53, 1924–1939. DOI: 10.1037 / dev0000331
PubMed Аннотация | CrossRef Полный текст | Google Scholar
ван Марле, К., Чу, Ф. В., Ли, Ю., Гири, Д. С. (2014). Острота примерной системы счисления и количественное развитие дошкольников. Dev. Sci. 17, 492–505. DOI: 10.1111 / desc.12143
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ван, Л., Сунь, Ю., и Чжоу, X. (2016). Связь между приблизительной остротой зрения системы счисления и математическими достижениями: влияние беглости речи. Фронт. Psychol. 7: 1966. DOI: 10.3389 / fpsyg.2016.01966
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Векслер, Д.(2009). Весы памяти Векслера: Техническое и пояснительное руководство WMS-IV. Сан-Антонио, Техас: Пирсон.
Вонг, Т. Т. Я., Хо, К. С. Х., Танг, Дж. (2016). Связь между ANS и навыками символической арифметики: посредническая роль отображений число-число. Contemp. Educ. Psychol. 46, 208–217. DOI: 10.1016 / j.cedpsych.2016.06.003
CrossRef Полный текст | Google Scholar
Xenidou-Dervou, I., De Smedt, B., van der Schoot, M., and van Lieshout, E.С. (2013). Индивидуальные различия в успеваемости по математике в детском саду: интегративные роли навыков приближения и рабочей памяти. Учиться. Индивидуальный. Dif. 28, 119–129. DOI: 10.1016 / j.lindif.2013.09.012
CrossRef Полный текст | Google Scholar
Xenidou-Dervou, I., Molenaar, D., Ansari, D., van der Schoot, M., and van Lieshout, E.C. (2016). Несимволические и символические навыки сравнения величин как продольные предикторы математических достижений. Учиться.Instr. 50, 1–13. DOI: 10.1016 / j.learninstruc.2016.11.001
CrossRef Полный текст | Google Scholar
Чжан, Ю., Чен, К., Лю, Х., Цуй, Дж., И Чжоу, X. (2016). Обработка как несимвольных, так и символьных величин важна для арифметических вычислений, но не для математических рассуждений. J. Cogn. Psychol. 28, 807–824. DOI: 10.1080 / 20445911.2016.1205074
CrossRef Полный текст | Google Scholar
Системы счисления
Обзор
Эта страница посвящена системам счисления.Вы уже знакомы по крайней мере с одной системой счисления — десятичной системой счисления, которую мы используем каждый день — на работе или за покупками — даже во время досуга (подумайте о многих играх и спортивных мероприятиях, связанных с хронометражом или счетом). ). На протяжении всей письменной истории появилось множество различных систем счисления. Здесь нас в первую очередь интересуют те, с которыми мы встретимся в контексте математики, науки и техники.
Существует множество различных систем счисления, основное различие между которыми заключается в количестве используемых символов (называемых основанием или основанием системы счисления).Десятичные числа имеют основание десять , двоичные числа (которые очень важны в вычислениях) имеют основание два , восьмеричные числа имеют базу восемь , а шестнадцатеричные числа имеют базу шестнадцать .
В вычислениях используются двоичные, восьмеричные и шестнадцатеричные числа. Шестнадцатеричные числа особенно важны в области вычислений, поскольку они обеспечивают удобный способ выражения двоичных значений.Каждая шестнадцатеричная цифра может использоваться для представления группы из четырех двоичных цифр (или битов ), а пара шестнадцатеричных цифр может использоваться для представления байтов (группа из восьми двоичных цифр).
Символы, используемые в большинстве стран западного мира для выражения числовых значений, являются версией индуистско-арабской системы счисления, позиционной десятичной системы счисления , разработанной индуистскими и индийскими математиками в девятом веке, позже принятой арабскими математиками и принятой в их во многие части Европы.В системе десять символов, каждый из которых представляет одно из десяти целых значений от 0 до 9.
Символы, используемые для представления цифр, важны только в том смысле, что они обеспечивают способ идентификации различных числовых значений с целью передачи их другим. Свойства данной системы счисления зависят только от количества различных используемых символов и от того, является ли система счисления позиционной.
Цифры, используемые в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления, приведены ниже.Обратите внимание, что шестнадцатеричная система счисления использует первые шесть букв алфавита (A-F) для представления чисел от десять до пятнадцать (10-15).
| Система счисления | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Двоичный | 1 | 0 | ||||||||||||||
| восьмеричный | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | ||||||||
| Десятичный | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | ||||||
| Десятичный | F | E | D | С | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Десятичные числа
Обычно предполагается, что использование системы счисления, основанной на десяти символах (десятичная система счисления , ), основано на том факте, что ранний человек впервые научился считать, используя пальцы обеих рук, что позволило им считать до десять с относительной легкостью.
Все интересующие нас системы счисления (включая десятичную систему счисления, с которой большинство из нас знакомо) являются позиционными. Рассмотрим для примера число 123,456. Это число с плавающей запятой , то есть оно имеет дробную часть, представленную цифрами, которые появляются справа от десятичной запятой (термин «с плавающей запятой» просто означает, что десятичная запятая (или точка счисления ) может размещать в любом месте относительно значащих цифр номера).
Число в первой позиции перед десятичной точкой (3) представляет собой значение 3 × 10 0 (три, умноженное на десять до нулевой степени), что равняется трем, поскольку любое число в степени нуля равно единице. Число во второй позиции слева от десятичной точки (2) представляет собой значение 2 × 10 1 или 20 (любое число в степени единицы само по себе). Цифра в третьей позиции слева от десятичной точки (1) представляет значение 1 × 10 2 , или сто.
Каждую цифру в десятичном числе необходимо умножить на десять в степени, которая зависит от позиции цифры в числе, относительно десятичной точки, отделяющей целую часть числа от дробной части (если есть). Положение важно, потому что оно определяет величину значения, представленного каждой цифрой. Три цифры справа от десятичной точки в приведенном выше примере (4, 5 и 6) представляют значения 4 × 10 -1 , 5 × 10 -2 и 6 × 10 -3 соответственно.
Восьмеричные числа
Восьмеричная система счисления, как следует из названия, имеет основание восемь (8). В ней используются те же первые восемь цифр, что и в десятичной системе счисления (от 0 до 7). Восьмеричная система счисления больше не широко используется в вычислениях (или где-либо еще в этом отношении), но когда-то она была популярна, потому что все восьмеричные цифры могли быть представлены с использованием всего трех битов.
Некоторые ранние мэйнфреймы и миникомпьютеры были построены на основе 36-битной архитектуры. Восьмеричный код часто использовался для хранения цифровой информации, потому что группировка из трех битов довольно хорошо вписывалась в слово из тридцати шести битов. Восьмеричные цифры и их двоичные представления показаны ниже.
0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111
Подобно шестнадцатеричной и двоичной системах счисления, используемым в современных компьютерах, восьмеричные числа часто требовались для представления десятичных значений.Выше мы видели, что представляет собой число 123,456 в десятичной системе счисления. Каждая цифра представляет собой некоторую степень, кратную десяти, в зависимости от ее положения относительно точки счисления. Что бы представляла эта же последовательность чисел, если бы вместо десятичной системы счисления мы использовали восьмеричную систему счисления? Давайте узнаем.
Чтобы преобразовать это значение в его десятичный эквивалент, нам нужно сложить значения цифр:
123.456 8 = 1 × 8 2 + 2 × 8 1 + 3 × 8 0 + 4 × 8 -1 + 5 × 8 -2 + 6 × 8 -3
123,456 8 = 64 + 16 + 3 + 0,5 + 0,078125 + 0,01171875
123,456 8 = 83,58984375
Как видите, эта последовательность цифр представляет собой совсем другое восьмеричное значение. Обратите внимание: когда мы пишем десятичное число, мы обычно не указываем явно, что это десятичное число.Однако при написании чисел в других основаниях иногда рекомендуется указывать используемую числовую основу, чтобы избежать путаницы. Мы можем сделать это, добавив нижний индекс после числа, как показано ниже:
123,456 8
Мы видели, что преобразование восьмеричных чисел в десятичные относительно просто. Преобразование восьмеричных чисел в двоичные стало еще проще. Мы видели, что каждая цифра восьмеричного числа умножается на степень восьми, а восемь равняется двум в степени трех:
8 = 2 3
Каждая дополнительная цифра при движении справа налево в двоичном числе представляет собой последовательную степень двойки.Точно так же каждая дополнительная цифра при движении справа налево в восьмеричном числе представляет собой последовательную степень восьми. Это означает, что сдвиг на одну позицию влево в восьмеричном числе эквивалентен сдвигу на три позиции влево в двоичном числе.
Значение может быть не сразу очевидным — возможно, вам придется подумать над этим некоторое время. Важно понимать, что для преобразования восьмеричного числа в его двоичный эквивалент мы просто заменяем каждую восьмеричную цифру тремя двоичными цифрами, которые ее представляют (мы видели их, перечисленные выше).Преобразуем восьмеричное число 123,456 в двоичное:
Следовательно:
123,456 8 = 1010011,10010111 2
Обратите внимание, что мы удалили два начальных нуля и конечный ноль из двоичного результата. Вы должны увидеть, что обратный процесс (преобразование двоичных чисел в их восьмеричное представление) — это просто вопрос замены каждой группы из трех двоичных цифр ее восьмеричным представлением.Преобразуем двоичное число 111110101.10001101 в восьмеричное:
Следовательно:
111110101.10001101 2 = 765.432 8
Единственное, с чем вам нужно быть осторожным, — это убедиться, что вы разбили двоичное число на правильные трехзначные группы (при необходимости добавьте начальные или конечные нули, чтобы завершить левую и крайнюю правую группы двоичных цифр.
Преобразование восьмеричных чисел в шестнадцатеричные нельзя выполнить напрямую — это двухэтапный процесс. Первый шаг — преобразовать восьмеричное число в его десятичный эквивалент, как показано выше. Второй шаг — преобразовать полученное десятичное число в шестнадцатеричное (см. Ниже).
Шестнадцатеричные числа
Шестнадцатеричная система счисления (или основание шестнадцати) — это позиционная система счисления, которая представляет числовые значения с использованием шестнадцати символов — от 0 до 9 для значений от нуля до девяти и A, B, C, D, E и F для представления чисел. без десяти пятнадцать.По этой причине считается, что его основание равняется шестнадцати. Шестнадцатеричные числа выражаются как последовательность из одной или нескольких шестнадцатеричных цифр, за которыми следует строчная буква «h» или иногда нижний индекс 16, чтобы указать, что они на самом деле являются шестнадцатеричными числами (с основанием шестнадцати). Вот десятичное число сто шестьдесят пять (165), выраженное в виде шестнадцатеричного числа:
A5h
Как и в знакомой нам десятичной системе, положение каждой цифры в шестнадцатеричном числе определяет ее значение.В то время как каждая позиция в десятичном числе представляет некоторую степень десяти, однако каждая позиция в шестнадцатеричном числе представляет степень шестнадцати. В таблице ниже показаны числа от 0 до 63 (с десятичным основанием) в виде шестнадцатеричных чисел.
| Шестигранник | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | С | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| декабрь | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Шестигранник | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1Б | 1С | 1D | 1E | 1 этаж |
| декабрь | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| Шестигранник | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 2A | 2B | 2C | 2D | 2E | 2F |
| декабрь | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |
| Шестигранник | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 3A | 3B | 3C | 3D | 3E | 3F |
| декабрь | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 |
Десятичное число тридцать девять (39), выраженное шестнадцатеричным числом (27h), таким образом:
2 × 16 1 + 7 × 16 0 = 32 + 7 = 39
Шестнадцатеричная цифра в крайней правой позиции любого шестнадцатеричного целого числа содержит наименьшее значение (с максимальным значением пятнадцать).Самая левая шестнадцатеричная цифра имеет максимальное значение, которое отражает ее положение относительно самой правой цифры и будет кратным некоторой степени шестнадцати, большей нуля. Значение самой левой шестнадцатеричной цифры (при условии, что мы игнорируем ведущие нули) всегда превышает суммарное значение всех цифр справа от нее. По этой причине общая величина шестнадцатеричного числа всегда определяется позицией самой левой цифры.
Дроби также могут быть представлены с помощью шестнадцатеричных цифр, как и действительные (дробные) числа.Как и действительные числа с основанием десять, дробная часть шестнадцатеричного числа следует за точкой. В десятичной системе счисления мы называем это десятичной точкой. В шестнадцатеричной системе счисления мы называем это шестнадцатеричной точкой .
В десятичной системе число в первой позиции после десятичной точки умножается на 10 -1 (0,1), цифра во второй позиции после десятичной точки умножается на 10 -2 (0.01) и так далее. Дробная часть шестнадцатеричного числа работает по тому же принципу, за исключением того, что цифра в первой позиции, следующей за двоичной точкой, умножается на 16 -1 (от 0,0625 до десятичного основания), цифра во второй позиции после двоичной точки. умножается на 16 -2 (0,003
по основанию десять) и т. д.
Обратите внимание, что, в то время как каждая последующая положительная степень шестнадцати имеет значение в шестнадцать раз больше, чем ее предшественник, каждая последующая отрицательная степень шестнадцати имеет одну шестнадцатую значение своей предшественницы.Анатомия реального шестнадцатеричного числа проиллюстрирована ниже.
Анатомия реального шестнадцатеричного числа
Поскольку так легко представить группы из четырех двоичных цифр с помощью шестнадцатеричных цифр, шестнадцатеричная система счисления часто используется для представления двоичных значений в областях вычислительной техники и цифровой электроники. Байтовые значения, которые могут представлять десятичные числа в диапазоне от 0 до 255, часто выражаются с помощью пары шестнадцатеричных цифр в диапазоне от 00h до FFh.Шестнадцатеричные числа также обычно используются для представления адресов памяти в программах на языке ассемблера.
Двоичные числа
Важность двоичной системы счисления, которая, как следует из названия, состоит только из двух символов (0 и 1), заключается в том, что это единственная система счисления, которую современные цифровые компьютеры действительно «понимают». Следует помнить, что в основе этих устройств лежит центральный процессор (ЦП), который по сути представляет собой конечный автомат, состоящий из транзисторов и микросхем, которые обеспечивают сотни миллионов взаимосвязанных высокоскоростных переключателей.Состояние каждого отдельного переключателя может быть включено или выключено, поэтому каждый переключатель может представлять только единицу или ноль.
Хотя компьютеры могут обрабатывать огромные объемы данных и выполнять миллионы вычислений в секунду, все основные машинные операции, которые достигают этого, основаны на манипулировании двоичными значениями с использованием различных типов логических схем. Даже данные, хранящиеся в оперативной памяти (RAM) и на магнитных или оптических дисках, физически хранятся как двоичные данные — миллиарды отдельных двоичных цифр («битов»), все из которых имеют значение 0 или 1.
В то время как целочисленные значения в других системах счисления могут быть точно представлены с использованием двоичной системы счисления, многие действительные числа (числа с дробными значениями) не могут. Таким образом, такие значения являются приблизительными, хотя достигаемая степень точности увеличивается с количеством битов, используемых в их представлении, за счет увеличения объема памяти в рабочей памяти или на диске.
Поскольку двоичная (или основанная на двух) система счисления представляет числовые значения с использованием всего двух символов (0 и 1), считается, что она имеет основание системы счисления, равное двум.Двоичные числа выражаются как последовательность двоичных цифр, иногда за которыми следует нижний индекс 2, чтобы указать, что они на самом деле являются двоичными числами. Вот десятичное число сто семьдесят (170), выраженное в виде двоичного числа:
10101010 2
Как и в знакомой нам десятичной системе, положение каждой цифры в двоичном числе определяет его значение.В то время как каждая позиция в десятичном числе представляет некоторую степень десяти, однако каждая позиция в двоичном числе представляет степень двойки. В таблице ниже показаны числа от 0 до 15 (с основанием десять) как 4-битные двоичные числа (пятнадцать — это наибольшее число, которое может быть выражено четырьмя двоичными цифрами).
| Двоичный | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| декабрь | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
| Двоичный | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | ||||||||
| декабрь | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||||||
Десятичное число 13 может быть выражено как двоичное число следующим образом:
1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 8 + 4 + 0 + 1 = 13
Двоичная цифра в самой правой позиции любого двоичного целого числа содержит наименьшее значение (с максимальным значением, равным единице) и иногда называется младшим значащим битом (LSB).Самая левая двоичная цифра имеет максимальное значение, которое отражает ее положение относительно младшего разряда, и будет представлять собой некоторую степень двойки больше нуля.
Крайняя левая двоичная цифра (при условии, что мы игнорируем ведущие нули) иногда называется старшим значащим битом (MSB), и ее значение всегда превышает суммарное значение всех битов справа от нее. По этой причине общая величина двоичного числа всегда определяется позицией самого левого (ненулевого) бита.
Дроби также могут быть представлены двоичными цифрами, как и действительные (дробные) числа. Как и действительные числа с основанием десять, дробная часть двоичного числа следует за точкой счисления. В десятичной системе счисления мы называем это десятичной точкой, но в двоичной системе счисления мы называем это двоичной точкой .
В десятичной системе число в первой позиции после десятичной точки умножается на 10 -1 (0.1) цифра во второй позиции после десятичной точки умножается на 10 -2 (0,01) и т. Д. Дробная часть двоичного числа работает по тому же принципу, за исключением того, что цифра в первой позиции, следующей за двоичной точкой, умножается на 2 -1 (от 0,5 до десятичного), цифра во второй позиции после двоичной точки. умножается на 2 -2 (0,25 с точностью до десяти) и т. д.
Обратите внимание, что в то время как каждая последующая положительная степень двойки имеет двойное значение своего предшественника, каждая последующая отрицательная степень двойки имеет половину значения своего предшественника.Анатомия реального двоичного числа проиллюстрирована ниже.
Анатомия реального двоичного числа
Из вышесказанного видно, что преобразование двоичных чисел в десятичные относительно просто. Просто сложите степени двойки, представленные каждой двоичной цифрой (это работает для двоичных целых чисел, дробей и действительных чисел).
Когда вы думаете об этом, почти столь же очевидным является тот факт, что точность, с которой действительные числа и дроби (с основанием десять) могут быть преобразованы в двоичные, часто будет зависеть от количества битов, доступных для представления дробной части числа.Чем больше количество используемых битов, тем точнее будет результат (с точки зрения вычислений, более высокая точность означает больший объем памяти, необходимый для хранения результата).
Преобразование двоичных чисел в шестнадцатеричные стало еще проще, и это позволяет нам представлять двоичные значения гораздо более удобным для человека способом. Мы уже видели таблицу, содержащую десятичные целые (целые числа) значения от нуля до пятнадцати (0–15) и их двоичные эквиваленты.Давайте теперь посмотрим на двоичные эквиваленты шестнадцати цифр, используемых в шестнадцатеричной системе (0–9, A – F):
| Двоичный | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестигранник | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
| Двоичный | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | ||||||||
| Шестигранник | 8 | 9 | A | B | С | D | E | F | ||||||||
Мы видели, что каждая цифра в шестнадцатеричном числе умножается на степень шестнадцати, а шестнадцать равно двум в степени четырех:
16 = 2 4
Каждая дополнительная цифра при движении справа налево в двоичном числе представляет собой последовательную степень двойки.Точно так же каждая дополнительная цифра при движении справа налево в шестнадцатеричном числе представляет собой последовательную степень шестнадцати. Это означает, что сдвиг на одну позицию влево в шестнадцатеричном числе эквивалентен сдвигу на четыре позиции влево в двоичном числе.
Значение может быть не сразу очевидным — возможно, вам придется подумать над этим некоторое время. Важно понимать, что для преобразования двоичного числа в его шестнадцатеричный эквивалент достаточно просто заменить каждую группу из четырех двоичных цифр ее шестнадцатеричным представлением.Преобразуем двоичное число 110111110101.100011010011 в шестнадцатеричное:
Следовательно:
110111110101.100011010011 2 = DF5.8D3h
Единственное, с чем вам нужно быть осторожным, это убедиться, что вы разбили двоичное число на правильные четырехзначные группы (при необходимости добавьте начальные или конечные нули, чтобы завершить левую и крайнюю правую группы двоичных цифр.Кстати, если вы хотите проверить какой-либо из примеров преобразования, приведенных на этой странице, вы можете найти здесь удобный онлайн-инструмент для преобразования:
Набор инструментов кодера — преобразование чисел
Преобразование из шестнадцатеричного в двоичное — это просто вопрос обратного процесса. Другими словами, мы просто заменяем каждую цифру шестнадцатеричного числа четырьмя двоичными цифрами, которые ее представляют.После того, как мы выполнили преобразование, мы можем безопасно удалить все нули в начале и в конце. Преобразуем шестнадцатеричное число F08.7A5h в двоичное:
Следовательно:
F08.7A5h = 111100001000.011110100101 2
Преобразование десятичного числа в восьмеричное
Один из методов, который можно использовать для преобразования десятичного числа в его восьмеричный эквивалент, — выполнить целочисленное деление с использованием восьми в качестве делителя.Преобразуемое число делится на восемь, а остаток записывается в крайней правой позиции (восьмеричной цифрой). Целочисленный результат деления затем снова делится на восемь, а остаток записывается (снова как восьмеричная цифра) слева от восьмеричной цифры, полученной на предыдущем шаге. Этот процесс повторяется до тех пор, пока целочисленный результат деления не станет нулевым. Пример послужит иллюстрацией процесса. Чтобы преобразовать десятичное число 16895 в восьмеричное, выполните следующие действия:
| Целочисленное деление | Целочисленное значение | Остаток | Восьмеричное |
|---|---|---|---|
| 16895 ÷ 8 | 2,111 | 7 | 7 8 |
| 2,111 ÷ 8 | 7 8 | ||
| 263 ÷ 8 | 32 | 7 | 7 8 |
| 32 ÷ 8 | 4 | 0 | 0 8 |
| 4 ÷ 8 | 0 | 4 | 4 8 |
Следовательно:
16 895 10 = 40777 8
Мы можем выполнить относительно простой процесс, который мы уже видели, чтобы преобразовать число обратно в десятичное (и в то же время подтвердить, что полученный ответ правильный).Просто умножьте каждую шестнадцатеричную цифру на соответствующую степень шестнадцати и сложите полученные десятичные значения, как показано ниже:
4 × 8 4 + 0 × 8 3 + 7 × 8 2 + 7 × 8 1 + 7 × 8 0
= 4 × 4,096 + 0 × 512 + 7 × 64 + 7 × 8 + 7 × 1
= 16,384 + 0 + 448 + 56 + 7
= 16,895 10
Преобразование десятичного числа в шестнадцатеричное
Один из методов, который можно использовать для преобразования десятичного числа в его шестнадцатеричный эквивалент, заключается в выполнении целочисленного деления с использованием шестнадцати в качестве делителя.Преобразуемое число делится на шестнадцать, а остаток записывается в крайнем правом положении (в виде шестнадцатеричной цифры). Целочисленный результат деления затем снова делится на шестнадцать, а остаток записывается (снова как шестнадцатеричная цифра) слева от шестнадцатеричной цифры, полученной на предыдущем шаге. Этот процесс повторяется до тех пор, пока целочисленный результат деления не станет нулевым. Пример послужит иллюстрацией процесса. Чтобы преобразовать десятичное число 13,337 в шестнадцатеричное, выполните следующие действия:
| Целочисленное деление | Целочисленное значение | Остаток | Hex |
|---|---|---|---|
| 13,337 ÷ 16 | 833 | 9 | 9h |
| 833 ÷ 16 | 52 | 1h 900 | |
| 52 ÷ 16 | 3 | 4 | 4 часа |
| 3 ÷ 16 | 0 | 3 | 3 часа |
Следовательно:
13 337 10 = 3419 ч
Мы можем выполнить относительно простой процесс, который мы уже видели, чтобы преобразовать число обратно в десятичное (и в то же время подтвердить, что полученный ответ правильный).Просто умножьте каждую шестнадцатеричную цифру на соответствующую степень шестнадцати и сложите полученные десятичные значения, как показано ниже:
3 × 16 3 + 4 × 16 2 + 1 × 16 1 + 9 × 16 0
= 3 × 4096 + 4 × 256 + 1 × 16 + 9 × 1
= 12 288 + 1,024 + 16 + 9
= 13,337 10
Преобразование десятичных чисел в двоичные
Преобразование десятичных чисел в двоичные не так просто, но не так уж и сложно.Чтобы упростить задачу, мы будем иметь дело с целыми числами и дробями (или целыми числами и дробными частями действительных чисел) отдельно. Начнем с двоичных целых чисел («целое» — это имя, которое мы используем для целого числа). Описанный здесь метод — один из нескольких, которые можно использовать, но, вероятно, он самый простой. Чтобы преобразовать десятичное число n в двоичное, выполните следующие действия:
- Разделите n на два и запишите остаток (ноль или один).
- Если результат предыдущего шага больше нуля, разделите его на два и запишите остаток. В противном случае переходите к шагу 4.
- Повторите шаг 2.
- Запишите последовательность значений остатка в обратном порядке.
Следующий пример должен прояснить этот процесс. Мы собираемся преобразовать десятичное число сто шестьдесят девять (169) в его двоичный эквивалент.
| Целочисленное деление | Целочисленное значение | Остаток | Бит |
|---|---|---|---|
| 169 ÷ 2 | 84 | 1 | LSB |
| 84 ÷ 2 | 42 | 0 | — |
| 42 ÷ 2 | 21 | 0 | — |
| 21 ÷ 2 | 10 | 1 | — |
| 10 ÷ 2 | 5 | 0 | — |
| 5 ÷ 2 | 2 | 1 | — |
| 2 ÷ 2 | 1 | 0 | — |
| 1 ÷ 2 | 0 | 1 | MSB |
Двоичное число считывается из столбца остатка, начиная с самого нижнего бита (самый старший бит , , или MSB) и заканчивая самым верхним битом (младший бит , , или LSB), что дает нам двоичное значение:
169 10 = 10101001 2
Преобразование десятичных дробей в двоичные — аналогичный процесс.Как и в случае с целочисленным преобразованием, описанным выше, метод, показанный ниже, не единственный доступный, но относительно прост в использовании. Его можно использовать для дробных значений, выраженных в виде собственных дробей (например, 3 / 4 ) или десятичных дробей (например, 0,75). Чтобы преобразовать десятичную дробь в двоичную, действуйте следующим образом:
- Начните с записи двоичной точки, перед которой стоит ноль.
- Умножьте дробное значение на два.
- Если результат меньше единицы, добавьте ноль.
- Если результат один, добавьте единицу и переходите к шагу 7.
- Если результат больше единицы, добавьте единицу и отбросьте целую часть результата, чтобы создать новое дробное значение.
- Перейти к шагу 2.
- Стоп.
В следующем примере показано, как работает этот процесс. Мы собираемся преобразовать дробь 1 / 3 в ее двоичный эквивалент.
| Дробь × 2 | Результат | <1 или> 1? | Двоичная дробь |
|---|---|---|---|
| 1 / 3 × 2 | 2 / 3 | <1 (добавить 0) | 0,0 |
| 2 / × 2 | 1 1 / 3 | > 1 (добавить 1) | 0.01 |
| 1 / 3 × 2 | 2 / 3 | <1 (добавить 0) | 0,010 |
| 2 / 3 × 2 | 1 1 / 3 | > 1 (добавить 1) | 0,0101 |
| 1 / 3 × 2 | 2 / 3 | <1 (добавить 0) | 0,010 |
| 2 / 3 × 2 | 1 1 / 3 | > 1 (добавить 1) | 0.0101 |
Быстро должно быть очевидно, что преобразовываемая десятичная дробь в этом случае представлена повторяющимся двоичным шаблоном . Следовательно, точность преобразования будет зависеть от того, сколько битов доступно для хранения дробного значения. В этом случае мы разрешили шесть битов справа от двоичной точки, что дает нам двоичное значение:
0,010101 2
Обратите внимание, что 1 / 3 , выраженный в виде десятичной дроби, равен 0.333, и точность десятичного представления, таким образом, зависит от количества двоичных цифр, следующих за точкой счисления. Поэтому при выполнении вычислений с использованием дробных значений всегда рекомендуется определять степень точности, требуемую для ответа. Для двоичных вычислений обычно существует верхний предел количества бит, доступных для дробной части результата.
Система счисления.Все мы работали с числами… | пользователя ABHISHEK | The Startup
ПРЕОБРАЗОВАНИЕ СИСТЕМЫ НОМЕРА
Как мы интерпретируем число в другой системе счисления? Что ж, для нас (на данный момент) интерпретация числа из другой системы означает знание его значения в нашей хорошо известной десятичной системе счисления, поскольку это система, которую мы знали до сих пор. Мы научимся читать разные числа в разных системах так же, как мы научились читать десятичные числа. Как мы читаем такое число, как 9,05,000 ? Мы начинаем с самой правой цифры и берем его базовое значение как 1 (10⁰), и каждый раз, когда мы перемещаем одну цифру влево, базовое значение увеличивается в 10 раз (10¹, 10² и так далее…) от предыдущего базового значения, верно? И, наконец, мы суммируем произведение всех цифр на их соответствующее базовое значение.Что ж, это делается одинаково во всех системах счисления.
- Двоичные числа — Давайте возьмем двоичное число 101010 .
Представление двоичного числа в виде десятичного числа
Чтобы преобразовать число в десятичную систему, мы начинаем с самой правой цифры (обычно известной как младший значащий бит или LSB ). На соседнем изображении мы видим базовое значение каждой цифры. Мы увеличиваем его так же, как и для десятичной системы счисления, двигаясь влево.Но, поскольку наша база в этом случае равна 2, наше базовое значение увеличивается на 2⁰, 2¹, 2² и так далее… по мере того, как мы идем влево. Таким образом, наше двоичное число — 101010 можно преобразовать в десятичную систему счисления, используя базовое значение каждой цифры, умножая его на соответствующую цифру и просуммировав их все. Таким образом, 101010 в двоичном формате эквивалентно —
(0 x 2⁰) + (1 x 2¹) + (0 x 2²) + (1 x 2³) + (0 x 2⁴) + (1 x 2⁵) = 42.
- Шестнадцатеричные числа — Возьмем шестнадцатеричное число — 5C8A .
Представление шестнадцатеричного числа в виде десятичного числа
Мы преобразуем это число в десятичное эквивалентное число так же, как и раньше. Мы начинаем с LSB и принимаем начальное базовое значение равным 16⁰. Увеличиваем его точно так же, двигаясь влево. Таким образом, наше базовое значение будет 16⁰, 16¹, 16² и так далее… по мере того, как мы идем влево. Одно небольшое отличие состоит в том, что у нас есть буквы от A до F в нашем шестнадцатеричном формате. Мы просто считаем их числами после 9, то есть A-10, B-11, C-12, D-13, E-14, F-15.Итак, давайте преобразуем 5C8A в шестнадцатеричном формате в его эквивалентное десятичное число —
(10 x 16⁰) + (8 x 16¹) + (12 x 16²) + (5 x 16³) = 23690
И, наконец, восьмеричный (как вы уже догадались, они имеют основание 8) преобразуются в десятичный формат таким же образом. Имея знания, которые вы приобрели до сих пор, попробуйте и посмотрите, сможете ли вы теперь преобразовать его самостоятельно!
| Смысл номера | ||||||||||||||||||||||||||||||||||
Чувство числа — это не способность считать, а способность распознать изменения в небольшой коллекции.Некоторые виды животных на это способны. Если изменить количество детенышей у материнского животного, это заметят все млекопитающие и большинство птиц. Млекопитающие имеют более развитый мозг и вырастают меньше детенышей, чем другие виды, но лучше заботятся о своем потомстве в течение гораздо более длительного периода времени. Многие птицы хорошо умеют считать. Если в гнезде четыре яйца, одно можно безопасно взять, но когда два удалены, птица обычно дезертирует.Птица может отличить двоих от трех. 1 Эксперимент, проведенный с щеглом, показал способность различать груды семян: три от одного, три от двух, четыре от двух, четыре от трех и шесть от трех. Щеглы почти всегда путали пять и четыре, семь и пять, восемь и шесть, десять и шесть. В другом эксперименте участвовал оруженосец, который пытался застрелить ворону, устроившую свое гнездо на сторожевой башне его поместья.Сквайр пытался удивить ворона, но при его приближении ворона уходила, наблюдала издали и не возвращалась, пока человек не покинул башню. Затем оруженосец взял с собой в башню еще одного человека. Один человек ушел, а другой остался, чтобы забрать ворону, когда она вернется в гнездо, но ворона не обманулась. Ворона держалась подальше, пока не вышел другой мужчина. На следующий день эксперимент повторили с тремя мужчинами, но ворона не вернулась в гнездо. На следующий день четыре человека попытались, но только на следующий день с пятью людьми ворона вернулась в гнездо, а один человек все еще был в башне. 2 В мире насекомых одиночная оса, казалось, имела лучшее чувство числа. Мать-оса откладывает яйца в отдельные клетки и снабжает каждое яйцо несколькими живыми гусеницами, которыми кормятся детеныши, когда вылупляются. Некоторые виды ос всегда дают пять гусениц, другие — двенадцать, а третьи — до двадцати четырех гусениц на клетку. Одиночная оса из рода Eumenus поместит пять гусениц в клетку, если это будет самец (самец меньше), и десять гусениц в клетку самки.Эта способность кажется инстинктивной, а не усвоенной, поскольку поведение ос связано с основной жизненной функцией. 3 Можно было подумать, что у людей есть очень хорошее чувство числа, но, как оказалось, у людей нет. Эксперименты показали, что средний человек имеет чувство числа около четырех. 4 Сегодняшним группам людей в мире, которые не разработали счетчик по пальцам, трудно определить количество четыре. Они склонны использовать величины один, два и многие, включая четыре. Маленькие дети в возрасте около четырнадцати месяцев почти всегда будут замечать что-то, чего не хватает в группе, с которой они знакомы. Ребенок того же возраста обычно может снова собирать предметы, которые снова были разделены в одну группу. Но способность ребенка воспринимать числовые различия в людях или объектах вокруг него или ее очень ограничена, когда их число превышает три или четыре. 5 Так что же отличает людей от остального животного царства? Он может включать в себя много вещей, но умение считать — одна из них.Счету, который обычно начинается с кончика наших рук или пальцев, обычно обучает другой человек или, возможно, обстоятельства. Это то, к чему мы никогда не должны относиться легкомысленно, поскольку это помогло человечеству развиваться бесчисленным количеством способов. Чувство чисел — это то, что есть у многих существ в этом мире так же хорошо, как и у нас. Хотя, как мы видим, наши человеческие способности не намного лучше, чем способности обычных ворон. Мы рождены с чувством числа, но мы учимся считать. 1 Данциг, стр. 1. 2 Dantzig, p. 3. 3 Infrah, p. 4. 4 Данциг, стр. 5. 5 Infrah, p. 6. | ||||||||||||||||||||||||||||||||||
Предоставлено Брюсом Уайтом | ||||||||||||||||||||||||||||||||||
Ссылки:
| ||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | ||||||||||||||||||||||||||||||||||
| Quipu — система подсчета инков | ||||||||||||||||||||||||||||||||||
Представьте себе, если хотите, высокоразвитую цивилизацию. Эта цивилизация правит более чем миллионом людей, они построили огромные города, разработали обширные дорожные системы, справедливо относились к своим гражданам и построили каменные стены настолько плотно, что даже лезвие ножа не могло пройти между огромными валунами.А теперь представьте, что вы можете делать все это без письменности. Это была древняя южноамериканская цивилизация Империи инков. Высокоразвитая цивилизация, способная отслеживать все важные факты, необходимые для управления такой огромной империей. Они сделали это с помощью инструмента запоминания, сделанного из завязанных узлов, который называется кипу. Люди, отвечающие за поддержание кипу, были известны как «кипу камайочс» или «хранители кипу». Поскольку у них не было письменности и осталось очень мало древних кипу, мы можем только предполагать, для чего на самом деле использовалось кипу.К счастью, кипу все еще используются сегодня, поэтому мы сможем узнать о древних, посмотрев, как используются современные. Объедините это с устными традициями, и окажется, что они использовались для учета количества вещей. Остается еще одна загадка: какую базу использовали инки? Все их соседи использовали базу 60, но, похоже, инки использовали базу 10. Недавние открытия, пока еще не подтвержденные, подтверждают эту теорию. Для наших целей предположим, что это была база 10. Сделать кипу было легко. Тонкие струны были обвиты вокруг более крупного шнура. Затем вокруг более тонких ниток завязывались узлы цветной нити или веревки. Где были размещены сучки, указывала стоимость. Чем ближе к большому шнуру был завязан узел, тем больше его стоимость. То, как был завязан узел, и использованный цвет может иметь значение, но без письменного языка мы просто не знаем. Некоторые найденные кипу были длиной несколько футов, поэтому для кипу камайока было очень важно запомнить, кто, где и что на каждой струне, и ее расположение на более крупном шнуре. | ||||||||||||||||||||||||||||||||||
Предоставлено Стивеном Таком | ||||||||||||||||||||||||||||||||||
| Ссылки. Макинтайр, Лорен. Затерянная империя инков, National Geographic, декабрь 1973 г., 729–766. | ||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||
| Дроби и Древний Египет | ||||||||||||||||||||||||||||||||||
Древние египтяне понимали дроби, однако они не писали простые дроби как 3/5 или 4/9 из-за ограничений в обозначениях.Египетский писец записывал дроби с числителем 1. Они использовали иероглиф «открытый рот» над числом, чтобы указать обратное. Цифра 5, записанная как дробь 1/5, будет записана. Есть некоторые исключения. Существовал специальный иероглиф для 2/3, и некоторые свидетельства того, что 3/4 также имел особый иероглиф. Все остальные дроби записывались как сумма дробей единиц. Например, 3/8 было записано как 1/4 + 1/8. У египтян была потребность в дробях, таких как разделение еды, припасов, поровну или в определенном соотношении.Например, разделение 3 буханок между 5 мужчинами потребует доли 3/5. По мере того, как возникали новые ситуации, египтяне разработали специальные методы работы с обозначениями, которые у них уже были, что означало, что дробь выражалась как сумма единичной дроби. Сегодня, когда появляются новые концепции, математики придумывают новые обозначения, чтобы справиться с ситуацией. Дроби были настолько важны для египтян, что из 87 задач Математического папируса Райнда только шесть не включали дроби.Поскольку египтяне выполняли свои операции умножения и деления путем удвоения и деления вдвое, было необходимо иметь возможность удваивать дроби. Писцы создавали таблицы с вычислением дробей и целых чисел. Эти таблицы будут использоваться в качестве справочных, чтобы храмовый персонал мог произвести дробное деление на еду и припасы. | ||||||||||||||||||||||||||||||||||
Предоставлено Одри Смолли | ||||||||||||||||||||||||||||||||||
| Ссылки. Жиллингс, Ричард Дж. Математика во времена фараонов. (1982), Дувр. | ||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||
| Система счисления майя | ||||||||||||||||||||||||||||||||||
Система счисления майя восходит к четвертому веку и была примерно на 1000 лет более развитой, чем европейцы того времени. Эта система уникальна для нашей нынешней десятичной системы с основанием 10, поскольку майя использовали десятичную систему с основанием 20.Считается, что эта система использовалась, потому что, поскольку майя жили в таком теплом климате и редко приходилось носить обувь, общее количество пальцев рук и ног составляло 20, что делало систему работоспособной. Поэтому двумя важными маркерами в этой системе являются 20, которые относятся к пальцам рук и ног, и пять, которые относятся к количеству цифр на одной руке или ноге. В системе майя использовалась комбинация двух символов. Точка (.) Использовалась для обозначения единиц (от одного до четырех), а тире (-) использовалась для обозначения пяти.Считается, что майя, возможно, использовали счеты из-за использования их символов, и, следовательно, может существовать связь между японцами и некоторыми американскими племенами (Ortenzi, 1964). Майя написали свои числа вертикально, а не горизонтально, с наименьшим номиналом внизу. Их система была настроена таким образом, что первые пять значений были основаны на множителях 20. Это были 1 (20 0 ), 20 (20 1 ), 400 (20 2 ), 8000 (20 ). 3 ) и 160 000 (20 4 ).В арабской форме мы используем разряды 1, 10, 100, 1000 и 10 000. Например, число 241083 можно вычислить и записать следующим образом: Это число, написанное на арабском языке, будет 1.10.2.14.3 (Маклиш, 1991, стр. 129). Майя также были первыми, кто символизировал концепцию ничто (или нуля). Самым распространенным символом была ракушка (), но было несколько других символов (например, голова). Интересно узнать, что вместе со всеми великими математиками и учеными, существовавшими в Древней Греции и Риме, именно индейцы майя независимо придумали этот символ, который обычно означал завершение, а не ноль или ничего.Ниже представлены визуальные изображения различных чисел и того, как они были бы написаны: В таблице ниже представлены некоторые числа майя. В левом столбце указан десятичный эквивалент каждой позиции числа майя. Помните, что числа читаются снизу вверх. Под каждым числом майя находится его десятичный эквивалент. Было высказано предположение, что для обозначения единиц могли использоваться счетчики, такие как зерно или галька, а для обозначения пятерок — короткая палка или стручок фасоли.С помощью этой системы штрихов и точек можно было легко сложить вместе, в отличие от таких систем счисления, как у римлян, но, к сожалению, от этой формы записи не осталось ничего, кроме системы счисления, относящейся к календарю майя. Для дальнейшего изучения: календарь на 360 дней также произошел от индейцев майя, которые фактически использовали основание 18 при работе с календарем. Каждый месяц состоял из 20 дней от 18 месяцев до года. Осталось пять дней в конце года, который сам по себе был месяцем, полным опасностей и неудач.Таким образом, майя изобрели календарь на 365 дней, вращающийся вокруг Солнечной системы. | ||||||||||||||||||||||||||||||||||
Предоставлено Микель Мерсер | ||||||||||||||||||||||||||||||||||
Ссылки.
| ||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||
| Египетская система счисления | ||||||||||||||||||||||||||||||||||
Как мы узнаем, что такое египетский язык чисел? Он был найден на надписях на камнях стен памятников древности.Цифры также были найдены на керамике, известняковых бляшках и на хрупких волокнах папируса. Язык состоит из иероглифов, графических знаков, которые представляют людей, животных, растения и числа. Египтяне использовали письменную нумерацию, которая была заменена иероглифическим письмом, что позволяло им записывать целые числа до 1 000 000. Он имеет десятичную основу и учитывает аддитивный принцип. В этой записи для каждой степени десяти был специальный знак.Для I — вертикальная линия; для 10 — знак в виде перевернутой буквы U; на 100 — спиральный канат; за 1000 — цветок лотоса; за 10 000 — поднятый, слегка согнутый палец; на 100 000 головастик; а для 1000000 — джинн на коленях с поднятыми руками. Эта иероглифическая нумерация была письменной версией конкретной системы счета с использованием материальных объектов. Чтобы представить число, знак для каждого десятичного порядка повторялся столько раз, сколько необходимо. Чтобы облегчить чтение повторяющихся знаков, они были размещены группами по два, три или четыре и расположены вертикально. Пример 1. При записи чисел первым будет записан самый большой десятичный порядок. Цифры были написаны справа налево. Пример 2. 46,206 =
Сложение и вычитание Для этого египтяне использовали те же методы, что и современные математики.Египтяне добавляли путем комбинирования символов. Они объединят все единицы () вместе, затем все десятки () вместе, затем все сотни () и т. Д. Если у писца будет более десяти единиц (), он заменит эти десять единиц на. Он будет продолжать делать это до тех пор, пока количество оставшихся единиц не станет меньше десяти. Этот процесс был продолжен для десятков, заменив десять десятков на и т. Д. Например, если бы писец хотел сложить 456 и 265, его задача выглядела бы так:
Затем писец объединял все похожие символы, чтобы получить что-то вроде следующего Затем он заменил одиннадцать единиц () единицей () и десятью . Вычитание выполнялось почти так же, как и мы, за исключением того, что когда нужно заимствовать, это делается путем написания десяти символов вместо одного. Умножение Египетский метод умножения довольно умен, но может занять больше времени, чем современный метод.Вот как они умножили бы 5 на 29
При умножении они начинали с числа, которое они умножали на 29, и удваивали его для каждой строки. Затем они вернулись и выбрали числа в первом столбце, которые в сумме составили первое число (5).Они использовали распределительное свойство умножения над сложением. Отдел То, как они делали деление, было похоже на их умножение. Для задачи 98/7 они думали об этой проблеме как о том, что 7 умноженное на какое-то число равно 98. И снова задача решалась по столбцам.
На этот раз отмечены числа в правом столбце, сумма которых равна 98, затем соответствующие числа в левом столбце суммируются, чтобы получить частное. Итак, ответ равен 14. 98 = 14 + 28 + 56 = 7 (2 + 4 + 8) = 7 * 14. | ||||||||||||||||||||||||||||||||||
| Предоставлено Ллойдом Холтом | ||||||||||||||||||||||||||||||||||
Рекомендации:
| ||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | ||||||||||||||||||||||||||||||||||
| Греческая система счисления | ||||||||||||||||||||||||||||||||||
Греческая система нумерации основывалась исключительно на их алфавите. Греческий Например, представлено число 849 Первоначальный греческий алфавит состоял из 27 букв и был написан слева. Если вы заметили, у греков не было символа нуля. Они могли натянуть эти Вот представления для 1000, 2000 и числа, которое мы дали выше 849. Это отлично подходит для меньших чисел, но как насчет больших чисел? Здесь | ||||||||||||||||||||||||||||||||||
| Предоставил Эрик Сорум | ||||||||||||||||||||||||||||||||||
Рекомендации: Бертон, Дэвид М.История математики — Введение. Дубьюк, Айова: Уильям | ||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | ||||||||||||||||||||||||||||||||||
| Вавилонская система счисления | ||||||||||||||||||||||||||||||||||
Вавилоняне жили в Месопотамии, которая находится между реками Тигр и Евфрат. Они начали систему нумерации около 5000 лет назад.Это одна из старейших систем нумерации. Первая математика восходит к древней стране Вавилон, в третьем тысячелетии до нашей эры. Таблицы были самым выдающимся достижением вавилонян, которое помогало им решать задачи. Одна из вавилонских табличек, Плимптон 322, датируемая периодом между 1900 и 1600 годами до нашей эры, содержит таблицы троек Пифагора для уравнения a 2 + b 2 = c 2 . В настоящее время находится в британском музее. Набу-риманни и Кидину — два единственных известных математика из Вавилонии. Однако о них известно немногое. Историки считают, что Набу-Риманни жил около 490 г. до н.э., а Кидину — около 480 г. до н.э. Вавилонская система счисления начиналась со счетных отметок, как и большинство древних математических систем. Вавилоняне разработали форму письма, основанную на клинописи. Клинопись в переводе с латыни означает «клиновидная форма». Они написали эти символы на влажных глиняных табличках, обожженных на жарком солнце.Многие тысячи этих планшетов все еще существуют. Вавилоняне использовали стилиста для печати символов на глине, поскольку изогнутые линии не могли быть нарисованы. У вавилонян была очень продвинутая система счисления даже по сегодняшним меркам. Это была система с основанием 60 (шестнадцатеричная), а не десятичная (десятичная). База десять — это то, что мы используем сегодня. Вавилоняне делили день на двадцать четыре часа, каждый час на шестьдесят минут и каждую минуту на шестьдесят секунд.Эта форма счета просуществовала четыре тысячи лет. У любого числа меньше 10 клин был направлен вниз. Пример: 4 Число 10 символизировалось клином, указывающим налево. Пример: 20 Числа меньше 60 были составлены путем объединения символов 1 и 10. Пример: 47 Как и в нашей системе счисления, в вавилонской системе счисления использовались единицы, то есть десятки, сотни, тысячи. Пример: 64 Однако у них не было символа для нуля, но они использовали идею нуля. Когда они хотели выразить ноль, они просто оставляли пробел в написанном числе. Когда они писали «60», они ставили одинарный клин на втором месте числа. Когда они писали «120», они ставили две отметки клина на втором месте. Ниже приведены несколько примеров больших чисел.
| ||||||||||||||||||||||||||||||||||
| Предоставлено Джереми Траутманом | ||||||||||||||||||||||||||||||||||
Рекомендации:
| ||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | ||||||||||||||||||||||||||||||||||
| Откуда произошли числа? | ||||||||||||||||||||||||||||||||||
Тысячи лет назад не существовало чисел, представляющих два или три.Вместо этого для представления чисел использовались пальцы, камни, палки или глаза. Не было ни часов, ни календарей, чтобы отслеживать время. Солнце и луна использовались, чтобы различать 13:00 и 16:00. У большинства цивилизаций не было слов для обозначения чисел больше двух, поэтому им приходилось использовать знакомую им терминологию, например, стада овец, груды зерна или множество людей. В числовой системе не было необходимости, пока группы людей не образовали кланы, деревни и поселения и не начали систему бартера и торговли, которая, в свою очередь, не создавала спроса на валюту.Как бы вы отличили пять от пятидесяти, если бы могли использовать только вышеуказанную терминологию? Не было бумаги и карандашей для расшифровки чисел. Были изобретены и другие методы для общения и обучения системам счисления. Вавилоняне штамповали числа в глине, используя палку и вдавливая ее в глину под разными углами или давлением, а египтяне рисовали на керамике и вырезали числа на камне. Вместо чисел использовались числовые системы, состоящие из символов.Например, египтяне использовали следующие числовые символы: От Эстер Ортенци, Числа в древности. Мэн: У китайцев была одна из самых старых систем счисления, основанная на палках, положенных на таблицы для представления расчетов. Это выглядит следующим образом: От Дэвида Смита и Джекутиэля Гинзбурга, «Числа и цифры». Примерно с 450 г. до н.э. у греков было несколько способов написания чисел, наиболее распространенным способом было использование первых десяти букв алфавита для обозначения первых десяти чисел.Чтобы различать цифры и буквы, они часто ставили отметку (/ или) возле каждой буквы: От Дэвида Смита и Джекутиэля Гинзбурга, «Числа и цифры». Римская система счисления используется до сих пор, хотя символы время от времени менялись. Римляне часто писали четыре как IIII вместо IV, I из V. Сегодня римские цифры используются для обозначения числовых глав книг или для основных частей контуров.Самые ранние формы римских числовых значений: От Дэвида Смита и Джекутиэля Гинзбурга, «Числа и цифры». Цифры на пальцах использовались древними греками, римлянами, европейцами в средние века, а затем и азиатами. |


