Билет 12
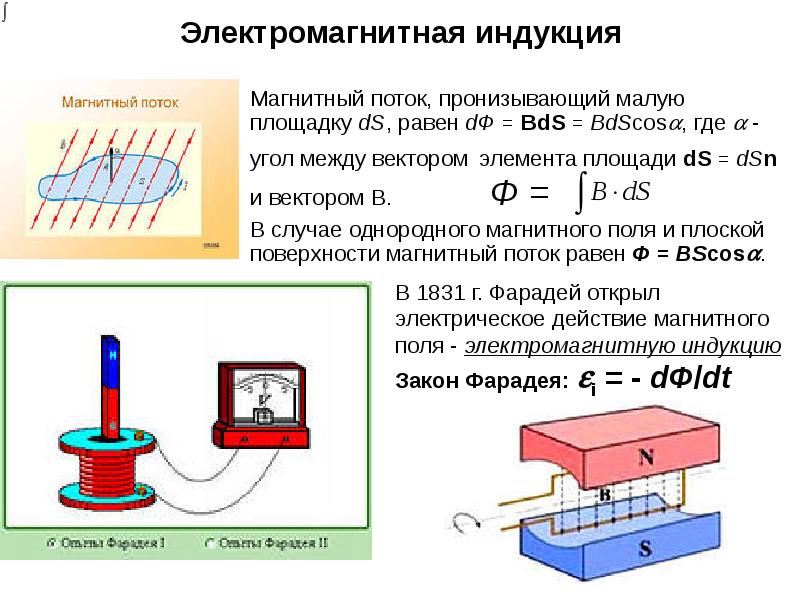
Магнитный поток
и способы его изменения.
Явление
электромагнитной индукции. Закон
электромагнитной индукции. Величина
ЭДС индукции движущегося проводника.
Магнитный поток
Ф через поверхность S
– скалярная физическая величина, равная
произведению модуля магнитной индукции
на площадь поверхности и на косинус
угла между нормалью к поверхности и
вектором магнитной индукции.
Ф=ВScos
Единица измерения
– 1 Вб.
1 Вб
– это такой магнитный поток который
создаётся магнитным полем с индукцией
1 Тл через плоскую поверхность площадью
1 м2, расположенную перпендикулярно
вектору магнитной индукции.
Магнитный поток
характеризует число линий магнитной
индукции, пронизывающих поверхность
S.
Магнитный поток
может изменяться
при изменении: 1) магнитной индукции; 2)
площади контура; 3) угла ,
т. е. ориентации контура в магнитном
е. ориентации контура в магнитном
поле.
При изменении
магнитного потока через замкнутый
контур в этом контуре возникает
индукционный
ток. Протекание
тока возможно в том случае, если на
свободные заряды действуют сторонние
силы. Следовательно, при изменении
магнитного потока через поверхность,
ограниченную замкнутым контуром, в этом
контуре возникают сторонние силы,
характеризуемые ЭДС, называемой ЭДС
индукции.
Величина индукционного
тока не зависит от причины изменения
магнитного потока, а зависит от скорости
изменения магнитного потока.
Закон Фарадея
для электромагнитной индукции.
ЭДС
индукции в замкнутом контуре равна
скорости изменения потока магнитной
индукции через поверхность, ограниченную
контуром, взятой со знаком «-».
Знак минус
объясняется правилом Ленца, которое
определяет направление индукционного
тока.
Правило Ленца.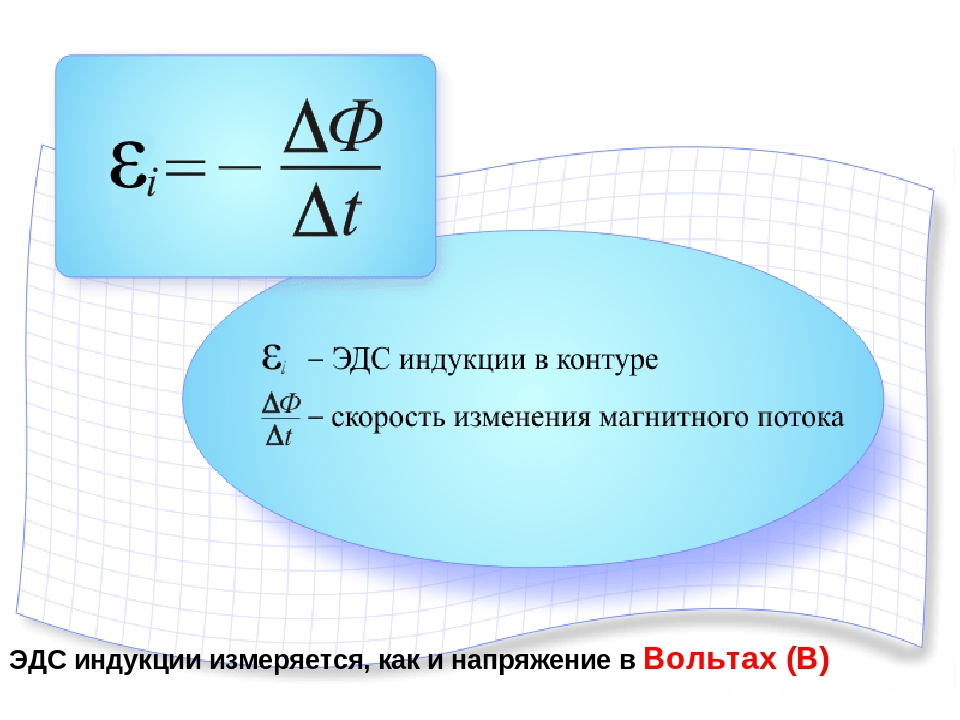
ЭДС индукции
создаёт в замкнутом контуре такой
индукционный ток, который своим магнитным
полем стремится компенсировать изменение
потока внешнего магнитного поля.
Причина возникновения
ЭДС индукции в замкнутом контуре зависит
от того, каким образом изменился поток.
Возникновение ЭДС
в движущемся проводнике
объясняется действием на свободные
заряды силы Лоренца. Величина ЭДС
индукции движущегося проводника равна
i=
B l v sin
где В –
индукция магнитного поля, l
– длина проводника, v
– скорость проводника,
—
угол
между векторами скорости и магнитной
индукции.
Направление
индукционного тока в
контуре с перемещающимся проводником
можно определить с помощью правила
правой руки.
Если правую руку
расположить вдоль проводника так, чтобы
линии магнитной индукции входили в
ладонь, а отогнутый большой палец
показывал направление движения
проводника, то четыре вытянутых пальца
укажут направление индукционного тока
в проводнике.
Возникновение ЭДС
в неподвижном замкнутом проводнике,
находящимся в изменяющемся магнитном
поле, объясняется возникновением
вихревого электрического поля.
Вихревое
электрическое поле появляется при
изменении магнитного поля и существует
независимо от того, имеется ли в данной
точке пространства замкнутый проводник
или нет. Силовые линии этого поля
замкнуты.
Билет 13
Потокосцепление
и индуктивность. Явление самоиндукции.
Величина ЭДС самоиндукции. Энергия
магнитного поля.
Электрический
ток, проходящий по замкнутому контуру,
создаёт в окружающем пространстве
магнитное поле, часть линий которого
пересекает поверхность, ограниченную
этим же контуром. Таким образом,
получается, что контур пронизывается
своим собственным потоком. Величина
потока пропорциональна величине
магнитной индукции, которая в свою
очередь пропорциональна силе тока,
протекающего по контуру. Следовательно,
величина потока прямопропорциональна
силе тока.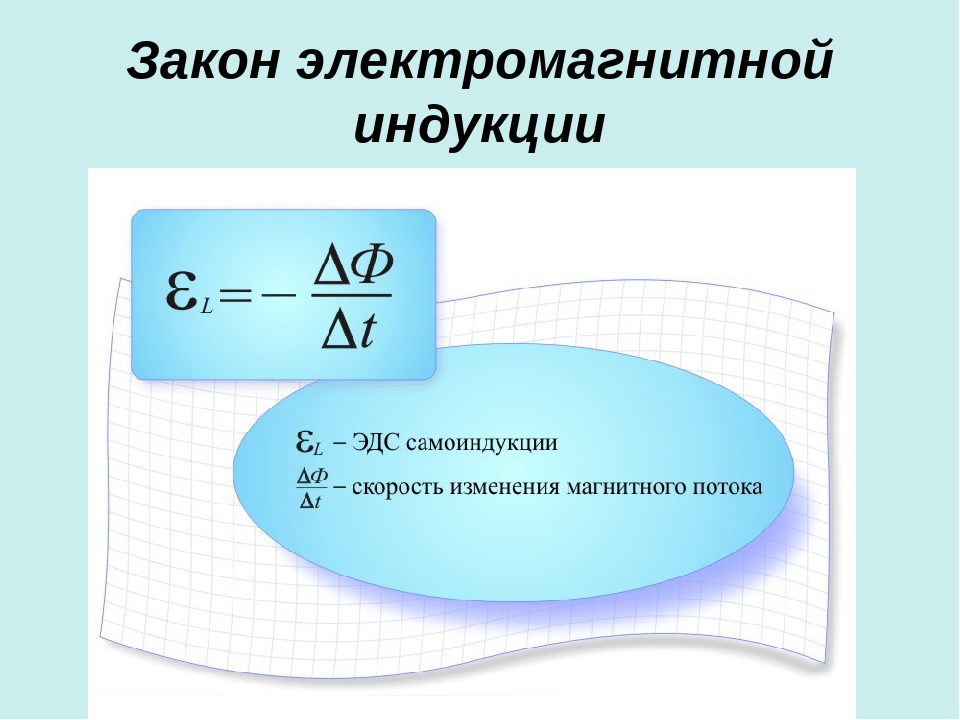
Ф
Ф=LI
где коэффициент
пропорциональности L
– называется индуктивностью
контура.
Индуктивность
зависит от размеров и формы проводника,
от магнитных свойств среды, в которой
находится проводник.
Индуктивность
– скалярная
физическая величина, равная собственному
магнитному потоку, пронизывающему
контур, при силе тока в контуре 1 А.
Единица
измерения индуктивности1
генри.
1 Гн – это
индуктивность такого контура, в котором
при силе тока 1 А возникает магнитный
поток через контур, равный 1 Вб.
Магнитный поток
через один виток соленоида Ф=ВS,
а через N
витков
полный магнитный поток, который называется
потокосцеплением,
равен
=ВSN
Так
как модуль магнитной индукции магнитного
поля внутри соленоида
Сравнивая
полученное выражение для потокосцеления
иLI,
получим формулу для расчёта индуктивности
соленоида.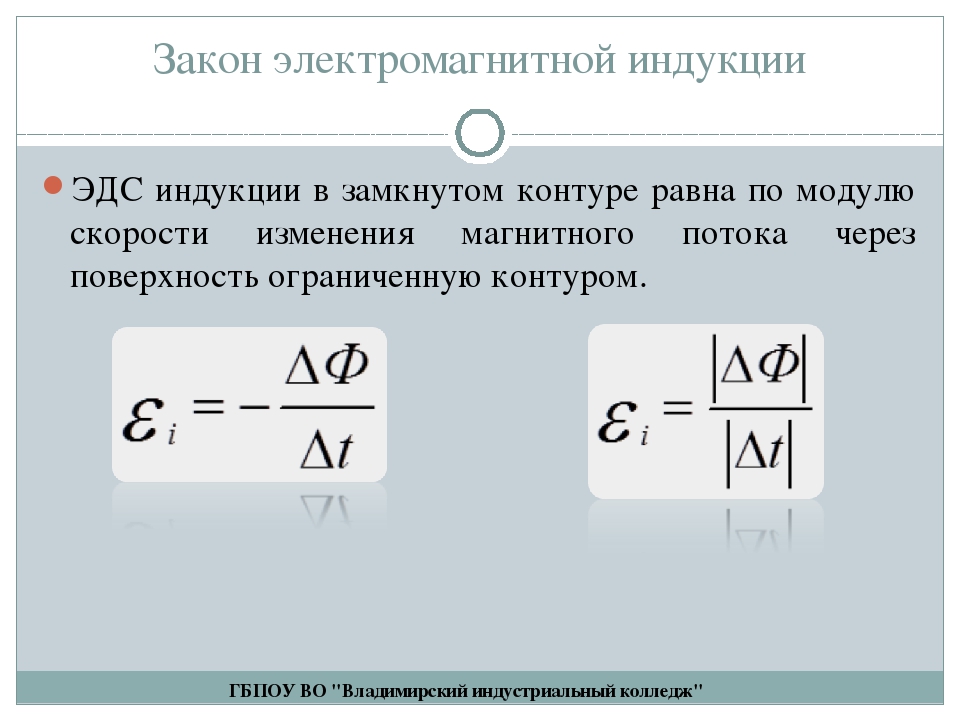
где N
– количество витков соленоида, S
– площадь витка, l
– длина соленоида.
Если ток, протекающий
в контуре, начинает изменяться, то
изменяется и создаваемое им магнитное
поле, а следовательно, и магнитный поток,
пронизывающий контур. Согласно закону
Фарадея, в контуре возникает ЭДС индукции,
которая называется ЭДС
самоиндукции.
Знак
«-» соответствует правилу Ленца.
Отсюда следует,
что индуктивность численно равна ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1 А за 1 с.
Подключим контур
к источнику тока. В контуре за счёт
разности потенциалов на зажимах источника
начинается перемещение зарядов. Ток в
контуре возрастает. Следовательно, в
контуре возникает ЭДС самоиндукции,
препятствующая нарастанию тока. Работа
источника тока по преодолению ЭДС
самоиндукции и установлению тока идёт
на создание магнитного поля.
Магнитное поле,
также как электрическое, является
носителем энергии. Энергия
Энергия
магнитного поля равна работе сторонних
сил источника против ЭДС самоиндукции.
При
отключении контура от источника тока
возникает ЭДС самоиндукции и по контуру
протекает индукционный ток. В результате
выделения теплоты Джоуля-Ленца, контур
нагревается. Следовательно, энергия
магнитного поля переходит во внутреннюю
энергию проводника.
Объёмной
плотностью энергии
называется энергия, заключённая в
единице объёма
3. Электромагнетизм. Электричество и магнетизм. Физика. Курс лекций
3.1. Электромагнетизм
3.2. Взаимодействие токов
3.3. Принцип суперпозиции
3.4. Закон Био-Савара-Лапласа
3.4.1. Магнитное поле проводника с током
3.4.2. Применение закона Био-Савара-Лапласа для анализа магнитных полей проводников с током различной конфигурации. Конечный и бесконечный прямолинейный проводник с током
3.
4.3. Магнитное поле кругового проводника с током
3.4.4. Магнитное поле вдали от центра контура с током
3.4.5. Магнитное поле соленоида
3.5. Магнитный поток
3.6. Напряженность магнитного поля
3.7. Силы, действующие в магнитном поле
3.7.1. Сравнение электрической и магнитной сил
3.8. Взаимодействие параллельных проводников с током
3.9. Закон Ампера
3.10. Работа по перемещению проводника стоком в магнитном поле
3.11. Действие магнитного поля на контур с током
3.12. Магнитный момент контура с током
3.13. Явление электромагнитной индукции. ЭДС электромагнитной индукции
3.14. Явление взаимоиндукции
3.15. Явление самоиндукции
3.16. Вихревые токи. Токи Фуко
3.17. Энергия магнитного поля
3.18.
Плотность энергии магнитного поля
3.19. Единицы измерения магнитных величин
3.20. Магнетики. Вещества в магнитном поле
3.21. Движение зарядов в магнитном поле
3.22. Уравнения Максвелла. Обобщение теории магнитного поля
3.23. Анализ массово-зарядового состояния элементарных частиц
3.24. Приложение к теореме Остроградского-Гаусса
3.25. Первое уравнение Максвелла
3.26. Второе уравнение Максвелла
3.27. Третье уравнение Максвелла
3.28. Четвертое уравнение Максвелла
3.29. Анализ III и IV уравнений
3.1. Электромагнетизм
Электромагнетизм — это раздел электричества, рассматривающий воздействие движущихся зарядов на движущиеся заряды.
Движение заряда может быть равномерным (I закон Ньютона). Если к такому заряду привязать систему отсчета, то в этой системе заряд не движется.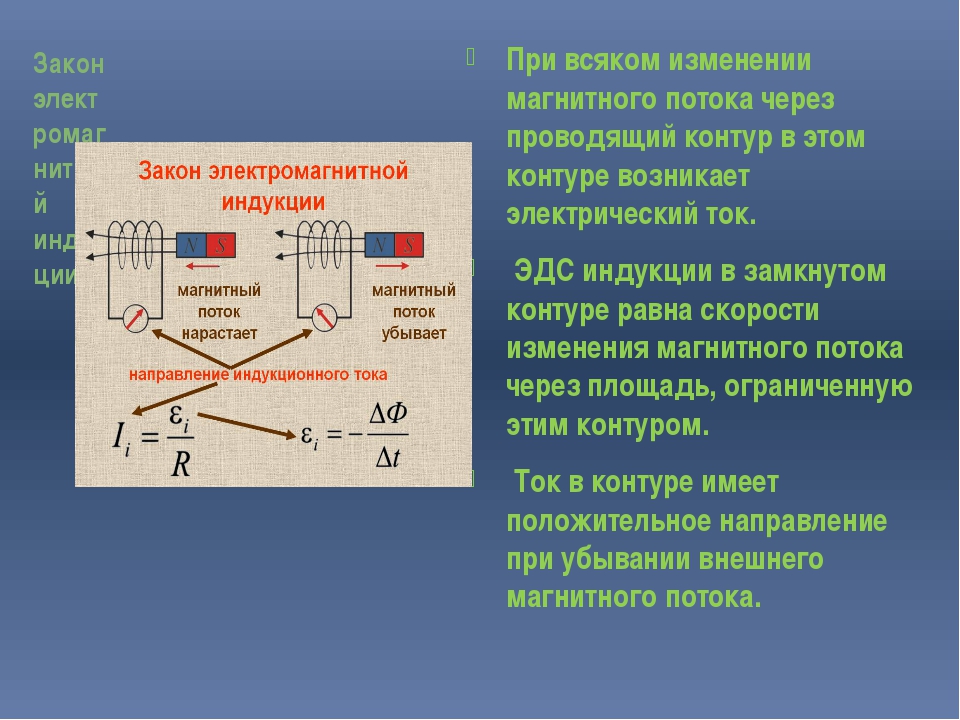 Таким образом, если другая заряженная частица движется параллельно первой с той же скоростью и в том же направлении, то между ними не будет магнитного взаимодействия, а только кулоновское взаимодействие. Итак, чтобы магнитное взаимодействие проявилось, частицы должны двигаться или с разной скоростью или в разном направлении.
Таким образом, если другая заряженная частица движется параллельно первой с той же скоростью и в том же направлении, то между ними не будет магнитного взаимодействия, а только кулоновское взаимодействие. Итак, чтобы магнитное взаимодействие проявилось, частицы должны двигаться или с разной скоростью или в разном направлении.
Связь характеристик магнитного поля:
B = µ0*H; где B — индукция магнитного поля; H — напряженность магнитного поля; µ0 = 1,16 * 10-6
Для того, чтобы заряды направленно двигались в пространстве, необходимо наличие проводящей среды, специально ориентированной в пространстве.
3.2. Взаимодействие параллельных токов
Закон Фарадея:
, где µ — магнитная характеристика среды, называемая магнитной проницаемостью.
Направление токов влияет на силу взаимодействия.
По аналогии с электростатикой, где сила определяет напряженность, а напряженность — индукцию, в магнетизме напряженность и индукция — силовые характеристики. Принято в электростатике основной силовой характеристикой считать напряженность, а в магнетизме — индукцию.
Правило буравчика:
Если ток направлен по закрутке буравчика, то шляпка вращается по силовой линии. В каждой точке пространства направление силовых линий совпадает с направление касательной. Таким образом, силовые линии магнитного поля являются замкнутыми.
3.3. Принцип суперпозиции
Примем на рисунке направление токов перпендикулярно плоскости рисунка. Тогда в точках:
A:Bрез = B1 + B2 D:Bрез = B1 — B2 C:Bрез= Принято, направление линий, перпендикулярных плоскости рисунка, изображать: Д — от нас, — к нам.
3. 4. Закон Био-Савара–Лапласа
4. Закон Био-Савара–Лапласа
3.4.1. Магнитное поле проводника с током
В общем случае для определения магнитного поля от произвольного проводника с произвольным знаком протекания тока проводим дифференцирование. Определяем полную индукцию, как сумму элементарных индукций от элементов тока dl, содержащих dq движущегося заряда.
Согласно последнему утверждению, совпадает с перпендикуляром к плоскости, образованной векторами cкорости и радиус- вектора
Пользуясь известными формулами, получим:
Последняя формула и есть закон Био-Савара-Лапласа для определения магнитной индукции для проводника с током.
3.4.2. Применение закона Био-Савара-Лапласа для анализа магнитных полей проводников с током различной конфигурации. Конечный и бесконечный прямолинейный проводник с током
Примем условиями: . Тогда Переведем в скалярную форму и выразим геометрические величины через один параметр, параметр a: ; Используем условия геометрии: при условии, что: Подставляя полученное в формулу для dB, получаем:
Тогда Переведем в скалярную форму и выразим геометрические величины через один параметр, параметр a: ; Используем условия геометрии: при условии, что: Подставляя полученное в формулу для dB, получаем:
Это выражение для составляющей магнитного поля в точке p элемента проводника с током dl. Тогда полное магнитное поле проводника с током в искомой точке принимает вид:
Назовем предельные углы α1 и α2 как углы, под которыми из искомой точки видны концы проводника, создающего магнитное поле. Тогда для конечного проводника с током это будет выглядеть так:
. Если проводник бесконечен, т.е. , то: ; . Тогда .
3.4.3. Магнитное поле кругового проводника с током
Направление магнитного поля (B) внутри кругового проводника с током также подчиняется правилу буравчика (шляпка как ток, буравчик как индукция). Магнитное поле элемента dl кругового проводника с током:
Тогда для замкнутого проводника с током в центре витка магнитное поле определится как: — Магнитная индукция кругового проводника (контура) с током в центре контура.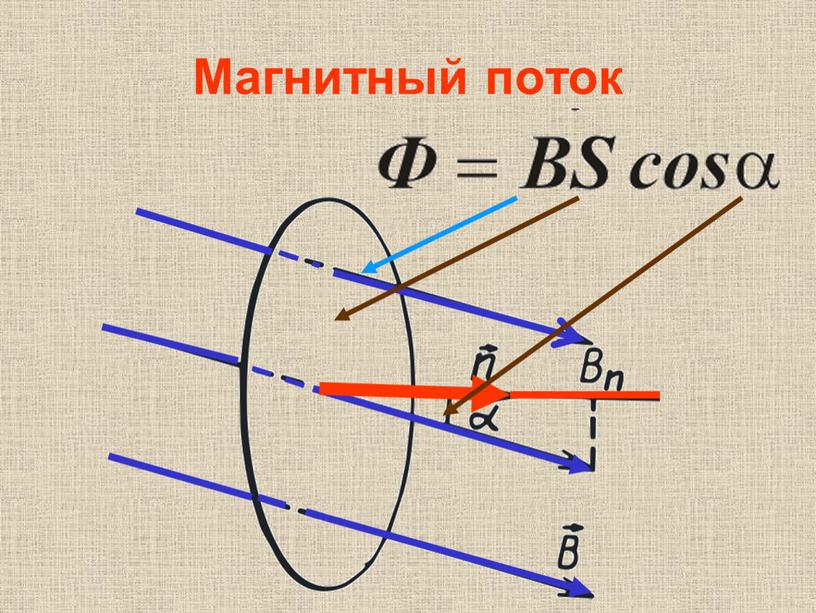
3.4.4. Магнитное поле вдали от центра контура с током
Элементы контура с током dl создают в точке А элементарные индукции dB, являющиеся трехмерным образованием в виде конуса, который дает результирующую B, равную:
Это магнитное поле на оси контура с током. При : (смотри формулу для центра контура)
3.4.5. Магнитное поле соленоида
Если контура с током последовательно соединить в одном месте пространства, то такое образование называется соленоидом.
В таком соленоиде магнитные потоки от последовательно соединенных контуров суммируются. Так как магнитные силовые линии замкнутые, то внутри соленоида число силовых линий равно числу силовых линий всего соленоида.
А раз объем внутри соленоида ограничен, то можно сказать, что магнитное поле сконцентрировано внутри соленоида, снаружи рассеяно, и магнитные силовые линии внутри соленоида параллельны между собой и поле внутри соленоида считается однородным, вне соленоида — неоднородным. Величина магнитной индукции внутри соленоида записывается так:
Величина магнитной индукции внутри соленоида записывается так:
, где μ — среда внутри соленоида, N — число витков соленоида, l — длина соленоида. Если обозначить — удельное число витков
3.5. Магнитный поток
По теореме Остроградского-Гаусса в общем случае поток любого вектора через поверхность S численно равен
Индукция — вектор в пространстве, поэтому можно применить понятие потока индукции . Если площадь фигуры, пересекающей силовые линии магнитного поля — площадь контура, по которому протекает ток, тогда — магнитный поток контура с током. Если имеется множество последовательно соединенных контуров, то есть соленоид, то общее количество магнитных силовых линий равно сумме силовых линий, образованных каждым контуром.
. Эта величина называется потокосцепление =NФвитков =Ф.
3.6. Напряженность магнитного поля
Зная, что , а магнитная индукция для бесконечного прямолинейного проводника с током равна . Аналогично: Для конечного проводника: В центре контура с током: . На оси кругового витка:
Аналогично: Для конечного проводника: В центре контура с током: . На оси кругового витка:
3.7. Силы, действующие в магнитном поле
Сила Лоренца — сила, действующая со стороны магнитного поля на движущийся заряд. Эмпирически получаем F В векторной форме F, а в скалярной форме .
Принято правило левой руки (для “+” заряда для нахождения направления силы Лоренца): если вектор входит в ладонь, вектор направлен по отогнутым пальцам, то направлена, как показывает большой палец. Правило правой руки для отрицательного заряда аналогично. Если на заряд действуют и электрическая и магнитная силы, то в этом случае сила Лоренца равна в векторной форме:
. Результат действия этих двух сил будет зависеть от их ориентации в пространстве.
3.7.1. Сравнение электрической и магнитной сил
Сравним взаимодействие зарядов (сила Кулона) и токов, образованных этими зарядами (сила ампера) в параллельных проводниках.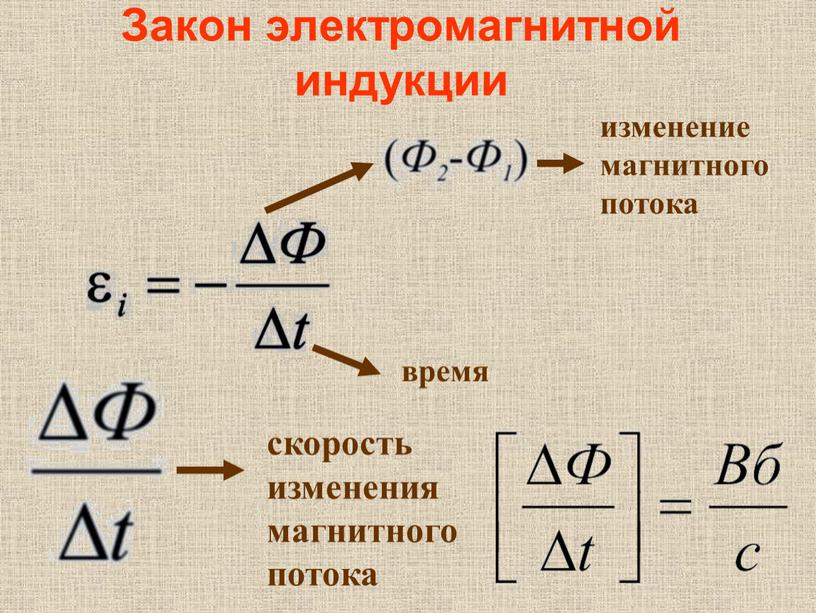
Магнитное поле, действующее на заряд, создается другим зарядом, движущимся относительно первого. Предположим, что ν1=ν2, заряды находятся на расстоянии r друг от друга. Возьмем перпендикулярно , то есть , тогда по закону Био-Савара-Лапласа выражаем с учетом этого получили выражение для Fэ/Fм. Известно, что . Пусть среда вакуум. Тогда если ε=1, μ=1,
Получим .
Следствия:
- Электрическая сила больше магнитной
- Магнитная сила принимает существенные значения, когда скорости зарядов близки к скорости света. Если бы С
- Поскольку скорость света конечна, магнитная сила релятивистская, то есть проявляет себя при скоростях, близких к скорости света.
3.8. Взаимодействие параллельных проводников с током
Вблизи каждого проводника с током формируется магнитное поле (сила, действующая на проводник с током, определяется по правилу левой руки: магнитные силовые линии входят в ладонь, ток по вытянутым пальцам, тогда сила направлена по отогнутому большому пальцу)
Два близко расположенных проводника с током притягиваются, с противоположным направлением токов — отталкиваются. Силы магнитного и электрического взаимодействия между движущимися зарядами противоположны.
Силы магнитного и электрического взаимодействия между движущимися зарядами противоположны.
3.9. Закон Ампера
Касается действия силы на проводник с током со стороны магнитного поля. Ориентируем проводник в соответствии с направлением тока.
Если проводник прямолинейный, то мы можем проинтегрировать по всей длине проводника. — закон Ампера в интегральной форме. — закон Ампера в скалярной форме.
Сила Ампера указывает величину и направление силы, действующей на проводник с током I, длиной l помещенный в однородное магнитное поле. Направление задается правилом левой руки ( — в ладонь, — вдоль пальцев, — вдоль большого пальца).
3.10. Работа по перемещению проводника с током в магнитном поле
Длина проводника l, и перемещается он слева направо. Тогда работа по перемещению элемента проводника с током на расстояние dr равна:
.
Условия перемещения:
- магнитное поле и проводник в пространстве взаимно перпендикулярны, .
- Направление перемещения проводника параллельно силе, вдоль которой мы совершаем работу по перемещению. То есть
- — площадочка, заметаемая элементом проводника с током dl при его перемещении на dr. Тогда поток векторов B, проходящих через эту площадку:
Работа по перемещению проводника с током в магнитном поле определяется величиной тока, величиной магнитной индукции и площадью закрываемой (заметаемой) проводником при движении. Она также определяется величиной тока и магнитным потоком, проходящим через площадь, закрываемую проводником при движении.
3.11. Действие магнитного поля на контур с током
Для удобства предположим, что контур имеет прямоугольную форму.
1) Пусть dl перпендикулярен B, т. е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, указаны на рисунке.
е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, указаны на рисунке.
Если контур с током расположен перпендикулярно силовым линиям, то действие поля выражается в сжимании и разжимании контура. Если же контур состоит из упругого проводника, то внешнего изменения положения в пространстве не будет.
2) площадь контура с током параллельна силовым линиям. То есть нормаль плоскости контура перпендикулярна вектору магнитной индукции.
Тогда силы Ампера на каждом участке:
I. Sin=1, FA≠0, сила направлена от нас.
II, IV. Sin=0, FA=0, То есть на элемент контура с током лежащим вдоль силовых линий FA не действует.
III Sin=1, FA≠0, сила направлена к нам. Тогда если контур с током закрепить в точках A и B ,то при таком расположении его в магнитном поле он будет вращаться, то есть на него действует момент силы.
3.12. Магнитный момент контура с током
Пусть r — плечо силы. (См. предыдущий рисунок) .
. Если FA перпендикулярна r, тогда Sin=1. Это момент силы, действующий на I или III участок контура. Площадь S — между линией A B и участком тока I или III.
Поскольку в каждой из противоположных сторон контура действует самостоятельная сила Ампера, то за площадь для суммарного момента сил принимается не половина, а вся площадь контура. Тогда вводится понятие магнитного момента контура с током как собственной характеристики контура, которая численно равна произведению P=IS, где S это вся площадь контура. Направление магнитного момента задается нормалью контура с током
Тогда полный момент силы, действующий на контур с током в магнитном поле, численно равен: .
3.13. Явление электромагнитной индукции. ЭДС электромагнитной индукции
Проводник, по которому не пропускают ток, помещаем в магнитное поле. Будем перемещать проводник перпендикулярно вектору магнитного поля. По закону Лоренца так как . Мы получили, что свободные заряды, которые, по определению, имеются в проводнике, будут перемещаться вдоль проводника. В результате перераспределения зарядов в проводнике при их движении на концах проводника возникает разность потенциалов, которая создает электрическое поле в проводнике: . Тогда напряженность электрического поля в проводнике
Будем перемещать проводник перпендикулярно вектору магнитного поля. По закону Лоренца так как . Мы получили, что свободные заряды, которые, по определению, имеются в проводнике, будут перемещаться вдоль проводника. В результате перераспределения зарядов в проводнике при их движении на концах проводника возникает разность потенциалов, которая создает электрическое поле в проводнике: . Тогда напряженность электрического поля в проводнике
Если подключим гальванометр, то можно выразить напряженность через напряжение . В равновесии Fл=Fк. То есть: . Если закон перемещения проводника в магнитном поле произволен, то разбиваем все перемещение на отрезки dr: , где dS=drℓ — площадь, заметаемая проводником при перемещении. Правило Фарадея: величина разности потенциалов, возникающих на концах проводника при его перемещении в магнитном поле прямо пропорциональна скорости изменения магнитного потока.
Если концы проводника замкнуты между собой, то в цепи протекает ток так, если бы проводник являлся источником тока. Тогда по закону Ампера сила, действующая на проводник с током в магнитном поле (правило левой руки) направлена в сторону, противоположную перемещению проводника в магнитном поле, то есть эта сила препятствует перемещению. Тогда:
Тогда по закону Ампера сила, действующая на проводник с током в магнитном поле (правило левой руки) направлена в сторону, противоположную перемещению проводника в магнитном поле, то есть эта сила препятствует перемещению. Тогда:
- разность потенциалов, возникающих на концах проводника, называют ЭДС магнитной индукции.
- поскольку ЭДС вызывает силы, препятствующие движению проводника, то в законе Фарадея ставят знак “минус” (правило Ленца):
3.14. Явление электромагнитной индукции (взаимоиндукции)
В 1831 году Фарадей установил, что если изменять магнитный поток, проходящий через контур, то в этом контуре возникает ЭДС, препятствующая изменению внешнего магнитного поля. Пусть есть контур I, к которому подключен гальванометр, и контур II, к которому подключен резистор, и источник ЭДС.
- силовые линии II проводника пересекают первый контур. Если менять величину тока во II контуре, то меняется B2 , то есть магнитный поток, создаваемый вторым контуром также меняется.
 И по закону Фарадея в первом контуре возникает ЭДС.
И по закону Фарадея в первом контуре возникает ЭДС. - Удаление или приближение второго контура также вызывает ЭДС в первом.
- Можно поворачивать контура относительно друг друга, чтобы вызвать ЭДС в I контуре.
- Вызвать ЭДС можно также изменением магнитной среды, которая находится между контурами.
Приложение:
- Контуры с током, близко расположенные друг с другом называют связанными.
- Влияние одного контура на другой возможно только, если ток в контурах переменный (принцип трансформатора). Для усиления взаимодействия используют последовательно соединенные контура – соленоиды.
Пусть:
Соленоид 1 содержит N витков, а соленоид, II: N2 витков. S — поперечное сечение соленоида.
Если в соленоиде I изменить величину тока, то в соленоиде II возникает ЭДС, равная:
Если в каждом из контуров соленоида возникает ЭДС, то результирующая ЭДС соленоида будет равна произведению числа витков соленоида на ЭДС одного витка:
то есть: , где L12 — коэффициент взаимной индукции первого соленоида относительно второго.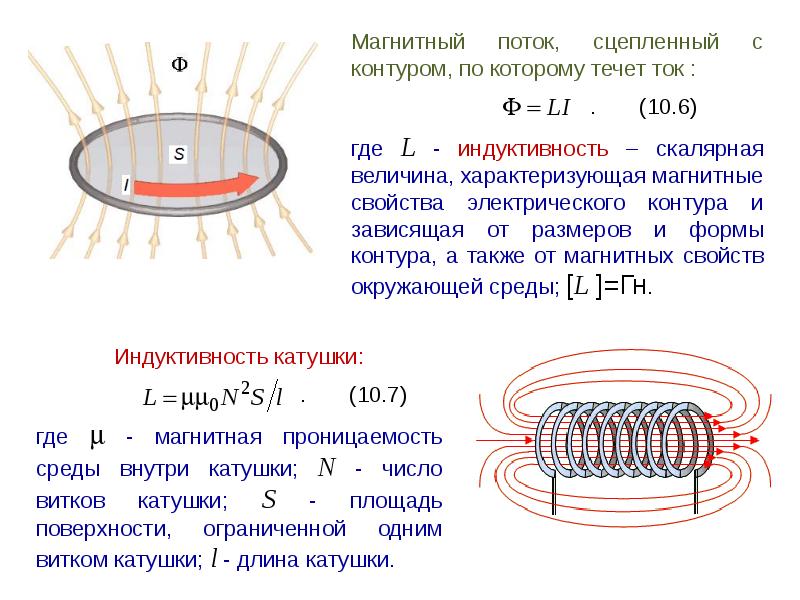
Если источник неэлектрических сил подключить ко второму соленоиду, а гальванометр к первому, то ЭДС, возникающую в первом соленоиде можно будет рассчитать аналогично:
, где — коэффициент взаимоиндукции II-ого соленоида относительно первого. Таким образом L21=L12
3.15. Явление самоиндукции
Возьмем один соленоид. Если в таком соленоиде изменять величину тока, то в контуре соленоида возникает ЭДС, стимулирующая магнитное поле, и препятствующая изменению тока в соленоиде.
— коэффициент самоиндукции, связывающий ЭДС электромагнитной индукции и ток. Его называют индуктивностью соленоида.
Индуктивность — характеристика соленоида, связывающая скорость изменения тока в соленоиде с препятствующей ей ЭДС и определяемая только геометрическим устройством соленоида.
— аналогия со вторым законом Ньютона. — вторая производная заряда, аналогично в механике — вторая производная пути. Тогда закон электромагнитной индукции похож на — второй закон механики Ньютона. аналогичные характеристики
— вторая производная заряда, аналогично в механике — вторая производная пути. Тогда закон электромагнитной индукции похож на — второй закон механики Ньютона. аналогичные характеристики
3.16. Вихревые токи или токи Фуко
В связанных контурах для передачи энергии переменного электрического тока из одного участка цепи в другой, часто используются магнитопроводящие среды.
При подаче переменного напряжения (тока) на первый 1 соленоид со второго 2 можно снять переменное напряжение (ток) противоположного направления (закон Фарадея-Ленца) Так как магнитное поле замкнутое, то сердечники делаются сплошными, чтобы избежать потери магнитного поля. Тогда сам сердечник создает замкнутый контур, по которому может протекать электрический ток. Если сопротивление сердечника мало, то по закону Джоуля-Ленца количество теплоты, выделившейся на этом сердечнике, будет велико. То есть . Эта теплота отбирается от энергии переменного электрического тока, подаваемого на соленоид. Для того, чтобы избежать паразитных тепловых потерь, магнитнопроводящие сердечники делаются из специального металла, обладающего большим сопротивлением (углеродистая сталь — пермаллой, ферритовые сплавы).
Для того, чтобы избежать паразитных тепловых потерь, магнитнопроводящие сердечники делаются из специального металла, обладающего большим сопротивлением (углеродистая сталь — пермаллой, ферритовые сплавы).
Если в связанных между собой механических частях какой- либо установки присутствуют электрические цепи с переменным током, то для предотвращения перемещения одной механической части относительно другой( когда их невозможно закрепить жестко) подвижные части делают в виде электрической цепи. ЭДС препятствует изменению магнитного поля, вызываемого движением. Возникающая ЭДС создает собственное магнитное поле, препятствующее движению механической детали. Таким образом, её движение ограничено. Это явление называют током Фуко.
Индуцирование переменного тока и напряжения используется для создания переменных токов и напряжений в местах, недоступных человеку (в вакуумных устройствах, где требуется разогреть какую-либо деталь).
Пропуская переменный ток по наружному соленоиду мы индуцируем электрический ток внутри вакуумного объема и так как соленоид внутри замкнут сам на себя, то энергия тока второго соленоида переходит в тепловую энергию. Такие устройства называют индукционными печами (температура достигает в них ≈1000С).
Такие устройства называют индукционными печами (температура достигает в них ≈1000С).
3.17. Энергия магнитного поля
Как любое поле, магнитное поле обладает энергией. Легче всего исследуется однородное магнитное поле, которое находится в соленоиде.
При замкнутом ключе внутри соленоида накапливается магнитная энергия. Если величину тока не менять в стационарных условиях, то часть тока идет через нагрузку, например, лампочку Л, другая часть через соленоид L.
При выключении ЭДС батареи в момент времени ток, протекающий в соленоиде, уменьшается и вызывает ЭДС электромагнитной индукции, препятствующую этому уменьшению. Эта ЭДС стремиться поддержать ток на нагрузке.
Поэтому величина тока на приборе плавно уменьшиться. Это происходит за счет энергии магнитного поля, накопленной в соленоиде.
Можно записать работу по переносу заряда для поддержания тока в цепи при выключении ключа, которая происходит за счет энергии магнитного поля, запасенной в соленоиде.
а так, как (Закон Фарадея-Ленца) и dq=Idt,
то — закон сохранения энергии.
Тогда полная энергия магнитного поля:
— полная магнитная энергия, запасенная в соленоиде с индуктивностью L. Аналогична ситуация с включением.
Схема включения цепи с соленоидом. Время релаксации τ — время, необходимое для установления в рабочих цепях режима равновесной (стационарной) работы.
3.18. Плотность энергии магнитного поля
Плотность энергии магнитного поля – количество магнитной энергии в единице объема соленоида: где Итак: аналогично: .
3.19. Единицы измерения магнитных величин
-
- Магнитный момент: , где — единичный вектор, нормаль к площади контура, определяющий ее ориентацию в пространстве.
- Магнитная индукция: так как (см. § 12), то — тесла.
- Магнитный поток Ф: .
- Потокосцепление
- Индуктивность — коэффициент, зависящий от геометрических размеров соленоида.

- Напряженность магнитного поля для витка с током или для соленоида .
- Магнитная проницаемость m — показывает, во сколько раз магнитное поле в среде отличается от магнитного поля в вакууме.- для среды. — безразмерная.
- Магнитная постоянная
Аналогия: магнитное поле ↔ механика
Аналогия между силой и ЭДС заключается в том, что сила есть вектор и направление его действия в пространстве легко установить, а ЭДС — скаляр, и направление его действия на изменение тока в цепи указывается знаком “-”
3.20. Магнетики. Вещества в магнитном поле
Вещества, способные намагничиваться и влиять на направление вектора магнитной индукции внешнего поля B, называются магнетиками.
Способность намагничиваться — создание собственного магнитного поля в веществе, которое или усиливает, или уменьшает внешнее магнитное поле.
Собственные магнитные свойства вещества определяются электронами, связанными с атомами. Строение атома подразумевает наличие электрона e, вращающегося вокруг ядра. Магнитный момент электрона , то есть каждая орбита электрона в атоме обладает собственным магнитным моментом и создает собственное магнитное поле. В целом в веществе суммарные магнитные моменты электронов в атоме расположены хаотично и их сумма зачастую равна нулю.
Под действием внешнего магнитного поля собственные магнитные поля, созданные электронами, упорядочиваются. Это и есть явление намагниченности. Оно может сохраняться после снятия магнитного поля, а может и исчезать. У ферромагнетиков оно сохраняется, а у диа и парамагнетиков исчезает.
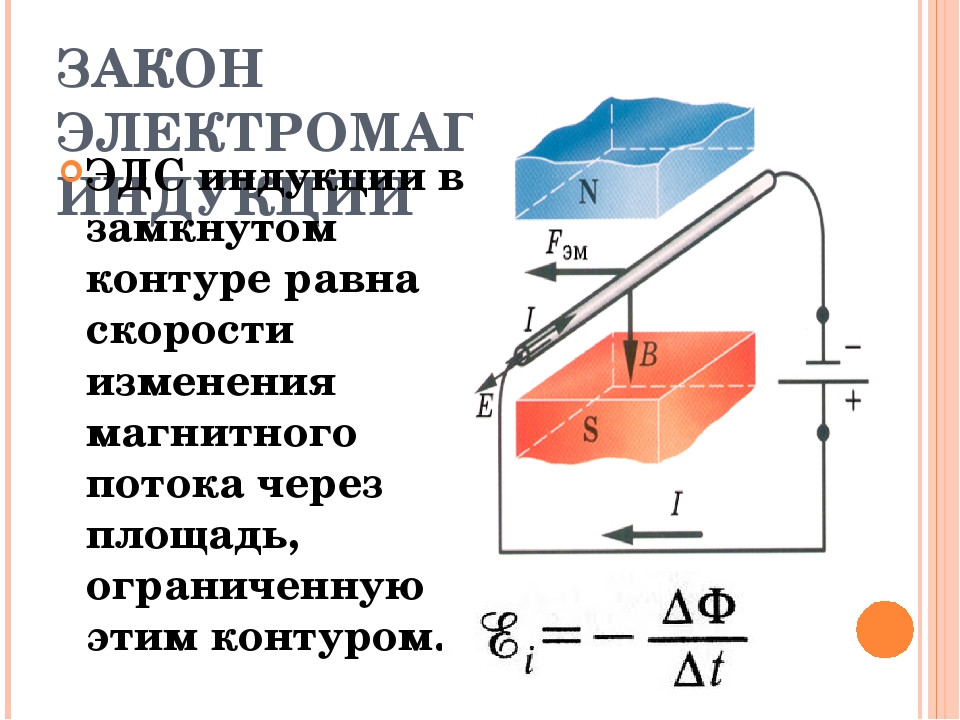
В результате поле равно: , где каппа — магнитная восприимчивость, которая определяется внешним воздействием, а и — магнитные моменты электронных орбит.
; — магнитная проницаемость.
.
Для разных веществ значение может принимать как положительные, так и отрицательные значения. В большинстве веществ собственные магнитные моменты атомов (молекул) не зависят друг от друга и хаотично расположены в пространстве. Если к такому веществу приложить внешнее поле, то собственный магнитный момент каждого атома стремится, как волчок, выровнять положение оси вращения вдоль силовых линий внешнего поля.
Bвне — индукция внешнего магнитного поля, Pm- собственный магнитный момент атома.
Изменение собственной оси вращения (собственного магнитного момента) относительно вектора магнитной индукции (внешнего поля) называется прецессией.
Собственный механический момент или количество движения Ls (спин)
Механические моменты электронов в атоме могут отличаться только направлением движения по орбите (вдоль и против часовой стрелки).
- Если внешнее магнитное поле затрачивает энергию на прецессию, то её результирующее магнитное поле ослабляется.
 Такие вещества называют диа–магнетиками: .
Такие вещества называют диа–магнетиками: . - В некоторых веществах внешнее магнитное поле не затрачивает энергию на прецессию, а разворачивает весь атом так, чтобы его собственное магнитное поле совпадало с внешним магнитным полем. Эти вещества -парамагнетики. Для них .
Парамагнетики
Стрелками укажем магнитные моменты отдельных атомов.
Ферромагнетики.
Для объяснения ферромагнетизма вводим понятие доменов. Домен — совокупность атомов с одинаковым направлением собственных магнитных полей. Подобные совокупности атомов требуют меньше энергии для образования доменов, т.е. энергетически более выгодны по сравнению с разрозненными атомами. В целом собственное магнитное поле вещества равно нулю. Под действием внешнего магнитного поля домены могут увеличиваться за счет других доменов вплоть до поглощения неориентированных доменов, то есть все пространство вещества заполняется доменами, ориентированными вдоль поля. При снятии внешнего поля обратной переориентации не происходит, так как это энергетически не выгодно. В этом случае магнитная восприимчивость составляет тысячи и десятки тысяч единиц. Оказывается, реакция вещества на воздействие внешнего магнитного поля носит нелинейный характер. Это определяется способностью собственных магнитных моментов переориентироваться во внешнем магнитном поле. Сначала идёт резкое изменение ориентации во внешнем магнитном поле, магнитные моменты ориентируются вдоль силовых линий магнитного поля. Дальнейшее увеличение магнитного поля не изменяет намагниченность, так как все магнитные моменты уже ориентированы вдоль поля. Зависимость результирующего магнитного поля в веществе в целом в зависимости от внешнего поля носит характер гистерезиса.
При снятии внешнего поля обратной переориентации не происходит, так как это энергетически не выгодно. В этом случае магнитная восприимчивость составляет тысячи и десятки тысяч единиц. Оказывается, реакция вещества на воздействие внешнего магнитного поля носит нелинейный характер. Это определяется способностью собственных магнитных моментов переориентироваться во внешнем магнитном поле. Сначала идёт резкое изменение ориентации во внешнем магнитном поле, магнитные моменты ориентируются вдоль силовых линий магнитного поля. Дальнейшее увеличение магнитного поля не изменяет намагниченность, так как все магнитные моменты уже ориентированы вдоль поля. Зависимость результирующего магнитного поля в веществе в целом в зависимости от внешнего поля носит характер гистерезиса.
B1 — остаточная индукция. H1 — коэрцетивная сила.
B1 — в веществе остается собственное магнитное поле без внешнего магнитного поля H1 = 0, (так создаются постоянные магниты).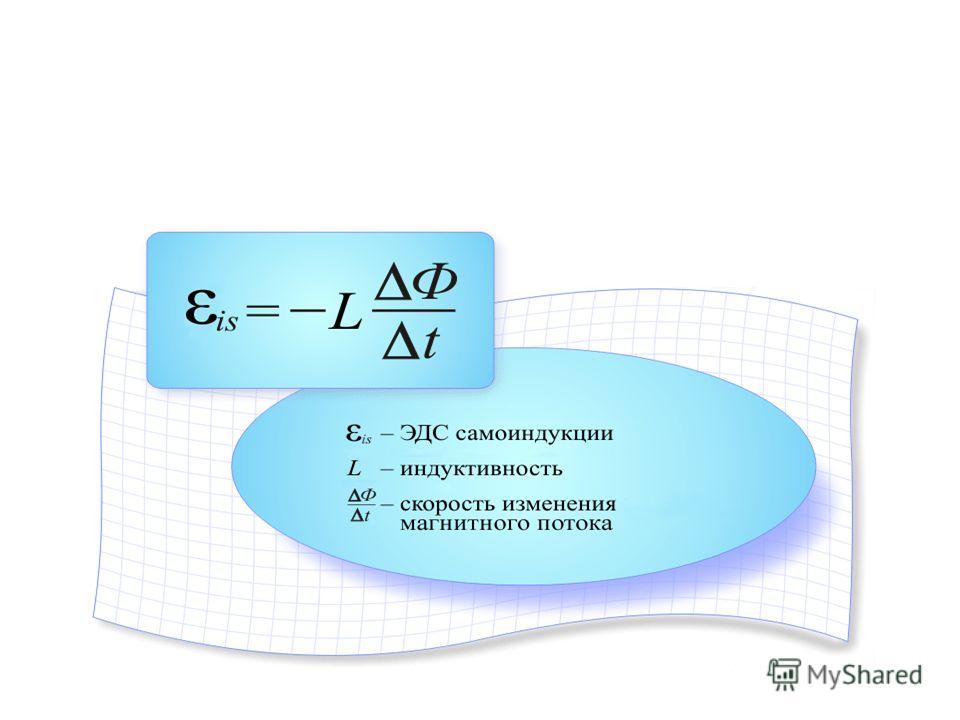
H1 — внешнее поле, необходимое для снятия собственной намагниченности, B1=0. Эта величина называется коэрцетивная сила.
Анализ петли гистерезиса см. в разделе “Сегнетоэлектрики”. Если коэрцетивная сила велика, то говорят, что ферромагнетик жёсткий, если мала — то мягкий.
3.21. Движение зарядов в магнитном поле
1) Вектор скорости перпендикулярен силовым линиям.
направленная перпендикулярно скорости – центростремительная.
Скорость изменяется только по направлению, но не по величине. Сила Лоренца, действующая на движущуюся частицу в магнитном поле, закручивает траекторию движения в окружность, то есть появляется центростремительное ускорение: значит v изменяется только по направлению, но не по величине. Тогда приравняем
,
где Т – период обращения заряда по орбите
2) угол между направлением скорости и силовыми линиями не равен 90 градусам.
, 0<α<90
Дальнейший анализ траектории движения частицы относительно вектора скорости аналогичен пункту 1).
Здесь сила Лоренца
. Новой характеристикой здесь является l — шаг спирали.
Приложение:
- если частица движется вдоль силовых линий магнитного поля, то сила Лоренца равна нулю.
- Если частица неподвижна в магнитном поле, то сила Лоренца также равна нулю.
3.22. Уравнение Максвелла. Обобщение теории магнитного поля (обобщение электродинамики)
Имеется замкнутый контур и внешнее магнитное поле, меняющееся во времени. Если внешнее магнитное поле создается соленоидом с током, то изменение магнитного поля через контур произойдет, если
- в соленоид вносим сердечник,
- меняем ток в этом соленоиде,
- изменяем положение соленоида относительно контура.

Тогда в контуре появляется ЭДС по закону Фарадея-Ленца, препятствующая изменению внешнего магнитного поля, то есть стрелка прибора, который можно подключить к контуру, отклоняется, в контуре идет движении зарядов, то есть появляется электрический ток. Так как до включения магнитного поля заряды в проводнике находились в неподвижности, значит после включения поля сила Лоренца не должно действовать на заряды. Откуда же берется ЭДС? Единственным объяснением появления ЭДС в контуре, то есть движения зарядов, является появление электрического поля, сила Кулона которого заставляет заряды двигаться. Напряженность такого поля
Не зная источника внешнего магнитного поля можно записать для ЭДС в контуре
Примем
— оператор дифференцирования по координатам (декартовым или полярным). Аналогично
. Окончательно имеем:
Напряжение, выраженное через законы электростатики, и ЭДС, возникшее в контуре, есть одно и то же. Тогда интегралы равны между собой, а, следовательно, и подинтегральные выражения равны.
Тогда интегралы равны между собой, а, следовательно, и подинтегральные выражения равны.
. Здесь отображена связь между неоднородным электрическим полем и переменным магнитным.
3.23. Анализ массово-зарядового состояния (q/m) элементарных частиц
С поверхности вещества испаряют часть атомов или молекул. Как правило, при этом такие атомы обладают зарядовыми свойствами. Далее эти атомы ускоряются в электрическом поле E, и движущийся поток атомов пропускают через магнитное поле B. По закону Лоренца эти заряды в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах оседают атомы разных зарядов. По степени отклонения атомов от прямолинейного распространения можно судить о заряде атома.
Частицы в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах, например:
Заряд q= 1e – в точке 2 на экране.
Заряд q=2e – в точке 1 на экране.
Процесс разделения частиц по зарядам называется сепарированием, а прибор, анализирующий состав этих пучков — масспектрограф.
3.24. Приложение к теореме Остроградского-Гаусса
Для любого вектора a можно записать его поток:
Так как интегрирование и дифференцирование по сути своей противоположные операции, то можно записать, например:
Интегрирование и дифференцирование по одному и тому же параметру по сути взаимно компенсирующие операции. Тогда можно записать для вектора а:
Где dV=dx*dy*dz.
А так же:
Таким образом, можно связать линейный, поверхностный и объемный интегралы, т.е. можно переходить от линейного к поверхностному, и от поверхностного к объёмному интегралу.
Приложение к теореме Остроградского-Гаусса мы используем при рассмотрении уравнений Максвелла.
3.25. I-ое уравнение Максвелла
Итак, мы из предыдущих параграфов (§ 22, 24) получаем закон Фарадея-Ленца:
ЭДС, возникающая в контуре при изменении магнитного поля, регистрируется гальванометром как напряжение на концах проводника контура. Тогда приравняем подинтегральные выражения.
.
Переменное магнитное поле породило неоднородное электрическое поле, которое создало электрический ток, создающий собственное поле, препятствующее (знак “-“) изменению внешнего магнитного поля (закон сохранения энергии). Это и есть I-ое уравнение Максвелла.
3.26. II-ое уравнение Максвелла
Используем соленоид для создания магнитного поля. r- радиус соленоида, l — его длина, N — число витков, n — удельное число витков соленоида. Запишем напряженность соленоида
.
Если предположим, что соленоид намотан в один слой и витки плотно прилегают друг к другу, то — толщина одного витка. Тогда можно считать d, как элемент l, или d=dl.
Тогда можно считать d, как элемент l, или d=dl.
Продифференцируем левую и правую часть по координатам.
— площадь сечения проводника, из которого сделан соленоид. По определению
, плотность тока
Если внутри соленоида находится среда с μ>1, то магнитное поле в соленоиде усиливается за счет электрического поля, обусловленного протекающим по проводнику током. Так как среда в соленоиде непроводящая, то электрическое поле вызывает в этой среде только смещение зарядов (смотри раздел “диэлектрики”). Тогда плотность тока зарядов проводимости и смещенных зарядов в самом общем случае, когда есть и свободные и связанные заряды
.
Как и в диэлектриках смещение зарядов вызывается электрической индукцией, а именно . Тогда имеем — второе уравнение Максвелла, которое говорит, что электрическое поле, которое вызывало в проводнике электрический ток проиндуцировало в среде усиление магнитного поля, то есть сформировало его.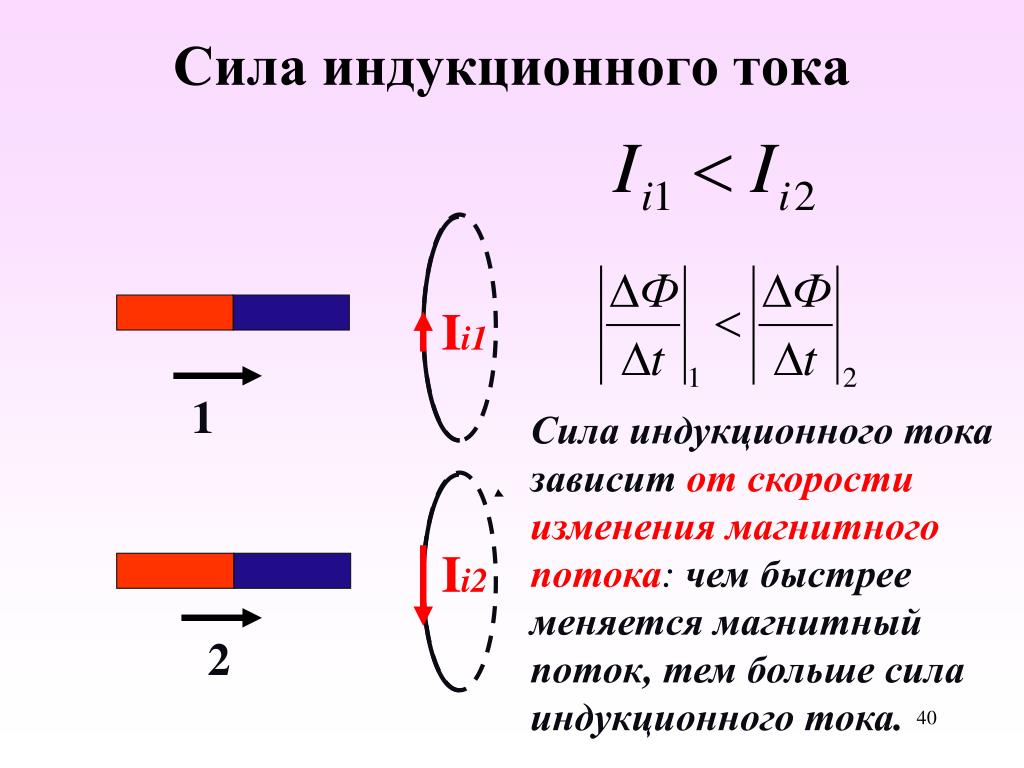
В I уравнении знак “-” означает, что переменное магнитное поле вызывает электрический ток, который генерирует магнитное поле, препятствующее изменению внешнего магнитного поля. Это связанно с законом сохранения энергии. Во II уравнении минус не ставится, так как за направление электрического тока принято движение положительных зарядов, а реально движутся отрицательные.
3.27. III-e уравнение Максвелла
В системе зарядов поток векторов напряженности по теореме Остроградского-Гаусса равен Если заряды распределены произвольно в пространстве, то введем понятие объемная плотность заряда: Тогда по теореме Гаусса Иначе говоря По приложению к т. О.-Г. перейдем от поверхностного к объемному интегралу. Это и есть III-е уравнение Максвелла. Из него следует, что источником электрического поля являются заряды.
3.28. IV уравнение Максвелла
Если есть соленоид, по которому течет ток, то соленоид формирует магнитное поле. Принцип силовых линий магнитного поля B — замкнутость. Найдем поток векторов B, который по теореме Остроградского есть . Полный поток векторов найдем, замкнув соленоид поверхностью S.
Принцип силовых линий магнитного поля B — замкнутость. Найдем поток векторов B, который по теореме Остроградского есть . Полный поток векторов найдем, замкнув соленоид поверхностью S.
Чтобы посчитать этот поток, мы должны учесть как входящие, так и выходящие через поверхность S силовые линии B магнитного поля. Результатом является компенсация этих линий, то есть общий поток равен нулю, т.к. количество входящих и выходящих линий B через поверхность S одинаково из-за замкнутости линий. Используя приложение к теореме перейдем от поверхностного интеграла к объемному
Отсюда следует, что в объеме, в котором находится соленоид, как источник магнитного поля, нет зарядов. Это IV уравнение Максвелла.
3.29. Анализ III и IV уравнений
Из III уравнения Максвелла следует, что в объеме, из которого исходят силовые линии электрического поля, находятся электрические заряды, а из IV следует, что объем, из которого исходят силовые линии магнитного поля не содержит зарядов магнитного поля.
Это доказательство того, что в природе не существует магнитных зарядов, соответственно, нет потенциала магнитного поля.
Итак, рассмотренные 4 уравнения Максвелла считаются основными, но есть еще три дополнительных.
Эти уравнения соединяют свойства электрических и магнитных полей в вакууме и средах.
Первые два уравнения Максвелла получены из поверхностных интегралов, для которых важно задать направление силовых линий, значит, в уравнениях обязательно отмечается векторность полей.
(I).
(II)
А III и IV уравнения – количественные, то есть скалярные уравнения.
или умножив это уравнение на получим (III).
И наконец (IV).
Система уравнений Максвелла отображает единую теорию электромагнитного поля и показывает, что оно есть единое поле, то есть электрического поля не существует без магнитного, а магнитное поле не существует без электрического. Можно ещё сказать, что переменное магнитное поле порождает неоднородное электрическое, а переменное электрическое поле порождает неоднородное магнитное поле.
Можно ещё сказать, что переменное магнитное поле порождает неоднородное электрическое, а переменное электрическое поле порождает неоднородное магнитное поле.
Магнитный поток как физическая величина характеризуется
Автор На чтение 13 мин. Опубликовано
Магнитный поток Ф — скалярная физическая величина численно равная произведению магнитной индукции на площадь поверхности ограниченной замкнутым контуром. Измеряется в веберах Вб.
Наглядно магнитный поток можно представить как совокупность магнитных линий, пересекающих площадку S.
Если вектор магнитной индукции не перпендикулярен к площадке, то необходимо определить перпендикулярную к площадке нормальную составляющую Bn вектора магнитной индукции (рис. ). Магнитный поток
В общем случае при вычислении магнитного потока через произвольную поверхность в неоднородном поле поверхность следует разделить на бесконечно малые плоские элементы площадью dS. В пределах каждой из элементарных площадок магнитную индукцию можно считать одинаковой. Поэтому поток через отдельную элементарную площадку
В пределах каждой из элементарных площадок магнитную индукцию можно считать одинаковой. Поэтому поток через отдельную элементарную площадку
Магнитный поток через произвольную поверхность находится суммированием (интегрированием) элементарных потоков:
Магнитный поток через замкнутую поверхность равен нулю, т. е.
так как магнитные линии замкнутые и каждая линия, входящая в замкнутую поверхность, должна из нее выйти.Так же поток через контур равен нулю,если контур располагается параллельно магнитному полю.
Магнитный поток необходимо знать или предварительно определить при анализе работы и расчете режима самых разных электротехнических приборов, устройств и установок.
Наблюдение за спектрами
В соответствии с плотностью линий магнитного поля (МП) можно увидеть величину вектора индукции, а согласно направленности силовых рядов — его течение. Наблюдение за спектрами постоянного тока и катушки на самом деле показывает, что при удалении проводника индукция МП уменьшается и довольно быстро.
Магнитный фон называется:
- С различным выведением в разных точках — гетерогенным. Неоднородный фон — это часть прямолинейного и радиального тока, вне соленоида, неизменённого магнита и т. д.
- С индукцией во всех точках — однородным полем. Графически такой МФ представлен силовыми линиями, которые считаются равноотстоящими параллельными частями. Этот случай является фоном изнутри длинного соленоида, а также полем между близкими соседними плоскими наконечниками электромагнита.
Произведение индукции поля, проникающего в контур от его области, называется потоком МИ или элементарным МП. Определение было дано и изучено британским физиком Фарадеем. Он отметил, что эта концепция на самом деле позволяет глубже рассмотреть совместный характер магнитных и электрических явлений.
Обозначая поток буквой f, площадью контура S и углом между направлением вектора индукции B и нормальной частью n к области α, можно написать магнитный поток формулой:
МП является скалярным размером. Например, поскольку плотность силовых рядов случайного магнитного поля равна его индукции, он уравнивается всему количеству линий, которые проникают в цепь. С изменением поля поток, который пронизывает контур, также меняется.
Например, поскольку плотность силовых рядов случайного магнитного поля равна его индукции, он уравнивается всему количеству линий, которые проникают в цепь. С изменением поля поток, который пронизывает контур, также меняется.
Единица измерения магнитного потока — вебер. Определение СИ струи считается линия, площадь которой 1 м², оказавшаяся на равномерном фоне с индукцией 1 Вт / м2 и перпендикулярная вектору. Это устройство будет обозначаться:
1 Вт = 1 Вт / м2 — 1 м².
Особенности течения
Скорость изменения магнитного потока генерирует электронный фон, имеющий замкнутые блоки питания (вихревое поле). Этот фон рассматривается в проводнике как циркуляция внешних сил. Это явление называется электрической индукцией, а мощность, которую можно определить, генерируемая в этом случае, является индуцированной ЭДС поверхности.
Поток подчёркивает вероятность характеристики всего магнита или видов других источников МП. Если индукция выдвигает на первый план вероятность, характерную её эффекту в любой отдельной точке, поток будет целым. Это вторая по значимости особенность поля. Если МИ функционирует как силовая часть МП, поток считается её энергетической линией.
Возвращаясь к экспериментам, можно сказать, что фактически любая электромагнитная катушка может рассматриваться как 1 закрытая. Это схема, по которой будет течь магнитный поток вектора индукции, тогда ток МИ электронов будет замечен при потокосцеплении.
Таким образом, непосредственно под действием струи в замкнутом проводнике образуется электронный фон. И в течение этого времени он будет генерировать ток.
Магнитная индукция
Согласно прогрессивным научным представлениям об электрических явлениях, МП неразрывно связан с током и не может присутствовать без него. Невозможно предположить электроток без МП. В том числе в случае неизменного магнита связывают этот фон с молекулярными линиями.
Если в место, где находится МП, поставить иглу, она стремится заимствовать определённое состояние, которое фактически показывает ориентационные качества МП. Скоординированное направление в этой точке места должно учитывать пункт назначения, где установлена ось, — это свободноподвешенная бесконечно небольшая магнитная стрелка, середина которой выровнена с точкой начального места. При этом из 2 возможных направлений вдоль оси стрелки МП символически присваивается назначение от южного конца на север.
Можно получить более яркое представление о направленности поля, если имеется ряд линий, где оси всех стрелок будут относительно касательными. Эти части называются магнитными магистралями.
Набор рядов упоминается как МП. Если бесконечно уменьшать площадь контура, притягивая его к точке, можно прийти к выражению для бесконечно малой стадии d, T активно в контуре маленькой области s, где угол P имеет конкретное значение между нормальностью к плоскости и небольшого контура. В этом случае направлением поля будет точка места, где расположено малое очертание.
Удар на плоскую цепь с током
В таких условиях коэффициент B принимается как характеристика интенсивности МП в этой точке места и называется индукцией МП. Она считается величиной, объединяющей назначение вектора МИ с направлением магнитного поля в этой точке места.
МП, характеризующийся на некоторых участках одинаковым значением вектора МИ, называется равномерным МП. Индукция в международной системе (СИ) измеряется в единицах Тесла (TL). МИ однородного МП составляет 1 т, если она воздействует на плоскую электронную последовательность площадью 5 ‘= 1 м и током 7 = 1 А, расположенную так, что магнитные доли лежат в плоскости цепи p = 0,5 n sin p = 1 с коэффициентом t = 1 Нм.
Область места любой части, что связана с конкретным вектором, называется полем. Понятие строк широко используется для визуального представления ВП. В случае с линейным полем можно увидеть линию, так как сам вектор ориентирован тангенциально в любой точке. Трубчатая линия представляет собой область узла, ограниченную обилием соседних рядов, проделанных сквозь закрытое очертание. Представление векторного поля часто используется при описании различных взаимодействий тела. В частности, в отображении МП упоминается фон вектора магнитной индукции, определяющий в нём части и трубки МИ.
Электрическая зависимость
Британский физик Майкл Фарадей не сомневался в единственной природе явлений магнетизма в своей теореме. Изменяющийся во времени фон создаёт электронный и магнитный вид. В 1831 году Фарадей обнаружил появление индукции, которая легла в основу устройства для генераторов, преобразующих механическую энергию в электронную. А в 1835 г. немецкий математик Карл Гаусс определил аксиому, описывающую обозначение и зависимость напряжённости поля от величины заряда.
Появление электрической индукции замечено в появлении тока в проводящей цепи, которая либо лежит на изменяющемся во времени фоне, либо движется на непременном участке таким образом, что фактически число магнитных витков проникает в контуры трансформаций.
Для своих многочисленных экспериментов Фарадей воспользовался двумя катушками, магнитом, переключателем постоянного тока и гальванометром. Электронный поток мог зависеть и намагничивать кусок железа.
В результате экспериментов Фарадея были заложены основные особенности возникновения электрической индукции, и ток появляется:
- в одной из катушек во время замыкания или размыкания электронной цепи внутри другой части;
- когда энергия протекает в одном из элементов с поддержкой реостата;
- при перемещении катушек относительно друг друга;
- когда неизменный магнит движется относительно.
В замкнутом проводящем контуре ток появляется, когда число линий магнитной индукции изменяется, создавая плоскость, ограниченную цепью. И чем раньше перевести количество рядов МИ, тем больше генерируется индукционный ток в рамке. Это является основной причиной конфигурации численности последовательностей индукции.
Явление позволяет содержать и изменять число линий МИ, делая плоскость площадки, ограниченной неподвижной проводящей цепью, из-за конфигурации тока в катушке, расположенной рядом. Происходит максимальное изменение количества последовательностей МИ из-за смещения схемы на неоднородном фоне, плотность линий которого может изменяться на месте.
Однородное магнитное поле (МП), существующее в некотором объёме, называется так, потому что оно одинаково во всех его точках. Если рассмотреть определённую плоскость, расположенную под прямым углом к магнитным линиям поля, то количество линий, пронизывающих её, можно вычислить. Поток магнитной индукции, формула которого выведена немецким физиком Вильгельмом Вебером, является искомой величиной.
Что такое магнитный поток
Проводя опыты и работая в сфере магнитных явлений, Вебер дал определение магнитному потоку. Он охарактеризовал его, как меру силы и протяжённости МП. Это одна из физических величин, которую можно найти, зная модуль вектора магнитной индукции В→ (ВМИ). Знать также нужно площадь пересекаемой поверхности и синус угла между ВМИ и нормалью к плоскости.
Единицы измерения
Магнитный поток обозначают буквой Φ, измеряется в веберах (Вб). Единица названа по фамилии учёного. Так, 1 Вб характеризует магнитный поток Φ, создаваемый магнитным полем, имеющим индукцию в одну теслу (1 Тл), пронизывающий плоскость площадью в один квадратный метр (1 м²), с учётом того, что эта поверхность расположена под прямым углом к ВМИ (В→).
Измерительные приборы
Магнитные потоки, определимые с помощью специальных приборов – флюксметров, измеряются и в лабораторных, и в полевых условиях. Приборы ещё называют веберметрами. Особенностью такого измерительного аппарата магнитоэлектрической системы (МЭС) является то, что ток подводится к перемещающейся бескаркасной рамке через спирали, не имеющие момента противодействия (безмоментные).
Внимание! В тот момент, когда ток отсутствует, указатель прибора не имеет фиксированного положения в пределах шкалы.
Прибор состоит из следующих деталей, отмеченных на рис. выше:
- испытуемый постоянный магнит – 1;
- рамка измерительная – 2;
- рамка прибора – 3;
- магнит прибора – 4;
- рамка корректирующего устройства – 5;
- головка регулировки корректирующей рамки – 6;
- переключатель «работа – коррекция» – 7.
Флюксметр не может измерять слабые МП из-за низкой чувствительности.
Теорема Гаусса для магнитной индукции
Великий немецкий учёный Карл Гаусс, который отличился в математике, физике и астрономии, вывел закон (теорему) в области магнетизма. Он доказал, что, в отличие от электрического поля, создаваемого электрическими зарядами, МП не создаётся зарядами магнитными. Их попросту не существует в классической электродинамике.
Информация.Теорема, которую вывел Гаусс, принадлежит к главным законам электродинамики и является частью системы уравнений Максвелла. Она описывает соотношение между потоком напряжённости электрополя, п
Физика для науки и техники II
из отдела академических технологий на Vimeo.
Пример — конечная скорость
Рассмотрим интересный пример, связанный с двигательной ЭДС. Предположим, что у нас есть наклонная рельсовая система, которая составляет угол Теты с горизонтом. И вдоль этого рельса у нас есть подвижная токопроводящая планка. Что-то вроде этого. И мы прикладываем магнитное поле, направленное в этом направлении.Другими словами, она перпендикулярна полу. И этот подвижный рельс, конечно, когда мы его отпускаем, предполагая, что рельс не имеет трения, он скользит вниз по этому рельсу. Теперь, когда он скользит вниз, он в конечном итоге достигнет предельной скорости. А давайте попробуем определить эту предельную скорость.
Допустим, длина рельса равна l. И, во-первых, как только мы отпустим этот поручень, он, конечно, начнет скользить вниз под действием гравитационной силы, действующей вдоль наклона.Что ж, по мере того, как он скользит вниз, площадь проводящей петли будет становиться все меньше и меньше. Это означает, что магнитный поток через эту область будет становиться все меньше и меньше. Итак, мы собираемся закончить с изменением магнитного потока через область, окружающую проводящую петлю бидуса [sp]. Следовательно, из [??] мы получим наведенную ЭДС и, следовательно, индуцированный ток. И этот ток будет течь в таком направлении, что будет противодействовать его причине. Причина заключается в уменьшении магнитного потока из-за уменьшения площади, окружающей проводящую петлю бидуса, когда стержень скользит вниз.Что ж, в этом случае индуцированный ток проявится так, что он будет пытаться противодействовать своей причине, или он будет пытаться компенсировать это уменьшение, и он может сделать это только путем создания магнитного поля. Что будет в некотором роде, добавив в это поле. Ну, конечно, в этом поле оно не будет точно в том же направлении, потому что это поле на самом деле не перпендикулярно этой поверхности; поверхность, окруженная проводящей петлей. Но чтобы снова попытаться скомпенсировать это магнитное поле, оно должно быть каким-то образом в этом направлении.И если мы применим правило правой руки, удерживая большой палец в направлении направленного потока тока, и мы хотим, чтобы магнитное поле выходило из плоскости, окруженной этой петлей. Следовательно, b должен быть, скажем, штрихом b, магнитное поле индуцированного тока через эту петлю должно указывать что-то вроде этого, чтобы связанный ток протекал против часовой стрелки по этой петле от линии Лэнда. Закон. Итак, как только этот ток индуцируется, мы собираемся получить ситуацию, когда проводник с током во внешнем магнитном поле этого b.Это будет генерировать силу, и эта сила будет исходить от il cross b, удерживая большой палец правой руки в потоке направленного тока и изгибаясь к внешнему магнитному полю b. il cross b будет генерировать примерно такую силу в этом направлении. И эта сила, следовательно, составляющая этой силы будет уравновешивать гравитационную силу, действующую вдоль наклонной плоскости, и в результате этого баланса сила на стержне будет равна 0, когда он скользит вниз. Итак, он достигнет предельной скорости.Другими словами, в этот момент, в этот момент его ускорение будет равно 0.
Чтобы увидеть ориентацию этих сил, давайте введем систему координат. А также посмотрите на проблему с этой точки зрения. И, следовательно, если мы посмотрим на проблему спереди, вот наклонная плоскость с углом Тета. И, давайте посмотрим, вот стержень сидит здесь, и теперь ток i выходит из плоскости в этой точке. И силы, действующие на эту систему, у нас есть mg из-за веса гравитационного поля этого стержня.И мы собираемся ввести такую систему координат, чтобы она была перпендикулярна наклонной плоскости. А также параллельно наклонной плоскости. И если вы сделаете это, параллельно наклонной плоскости вот так, и это одна сила из-за силы тяжести, действующей в нисходящем направлении. Конечно, у нас будет сила, действующая на этот скользящий стержень, токопроводящий стержень, из-за внешнего магнитного поля B. И с этой точки зрения, i l выходит наружу, b находится в плоскости, направленной вверх.i l cross b, таким образом, даст нам силу. Магнитная сила, действующая в этом направлении. Назовем это f sub b. Относительно этой системы координат у нас будут две составляющие этих сил. Взяв проекцию mg в направлении X вдоль наклонной плоскости. Другой компонент этого, если этот угол равен Theta, следовательно, этот угол также будет Theta, потому что они будут иметь взаимно перпендикулярные стороны. Эта сторона перпендикулярна этой стороне, а эта сторона перпендикулярна этой стороне.Итак, это конгруэнтные углы, и поэтому эти два угла будут равны друг другу. Итак, сила вдоль наклонной плоскости, составляющая mg вдоль наклонной плоскости с использованием этого прямоугольного треугольника, будет равна mg sin Theta. И, конечно же, у нас есть его компонент в вертикальном направлении, а именно этот. И для другой силы, опять же, если этот угол равен Theta, мы можем легко увидеть, что этот угол и этот угол равны друг другу. Это тоже будет Тета. Итак, если мы возьмем проекцию этой силы, опять же, в направлении наклонной плоскости, мы закончим тем, что этот компонент будет выровнен таким образом, а другой компонент будет в том же направлении.С компонентом MG перпендикулярно наклонной плоскости. Таким образом, всякий раз, когда эти две силы становятся равными друг другу, результирующая сила вдоль наклонной плоскости будет равна 0. Это означает, что ускорение будет равно 0. Таким образом, скорость объекта при его скольжении будет равна постоянная и, следовательно, это то, что мы называем предельной скоростью. И это то, что мы хотели бы вычислить. V-образная клемма при опускании токопроводящей шины — это вопросительный знак. Итак, это токопроводящая шина, а это токопроводящая шина длиной l.Хорошо, если мы, конечно, запишем, вертикальные силы или перпендикулярные силы относительно наклонной плоскости будут уравновешены нормальной силой, создаваемой из-за конуса поверхностей. Другими словами, из-за сил контакта между штангой и наклонной плоской поверхностью. И поскольку у нас нет трения, мы предполагаем, что трение между стержнем и рельсом равно 0, поэтому мы не собираемся в конечном итоге получить силу трения. Тогда это единственные силы, действующие на систему.Поскольку в этом перпендикулярном направлении нет движения, естественно, эта нормальная сила будет равна сумме этих двух компонентов. И снова система теперь движется с постоянной скоростью по наклонной плоскости. Следовательно, составляющая магнитной силы вдоль наклонной плоскости должна быть равна составляющей веса этого стержня вниз по наклонной плоскости.
Если мы запишем это здесь или просто запишем результирующие силы, действующие на систему, сумма сил вдоль, скажем, назвав это направление как x, а другое направление как y, вдоль x даст us mg sin Theta, это в положительном направлении x минус компонент x магнитной силы, и то, что здесь используется этот прямоугольный треугольник, косинус теты, должно складываться в массу, умноженную на ускорение в направлении x из закона Ньютона.И мы хотим, чтобы это ускорение было 0. Вот что произойдет с конечной скоростью. Следовательно, все это уравнение будет равно 0. Точно так же некоторые силы в направлении y будут давать нам нормальную силу, которая находится в положительном направлении y и минус mg cos Theta. Составляющая ipsa b вдоль направления y равна, или, скажем, отрицательному направлению y, и это будет минус fb sin Theta и будет равно массе, умноженной на ускорение вдоль направления y. В этом направлении нет движения, поэтому подпункт Y также равен 0.И это результирующие силы, действующие на стержень, когда он скользит вниз. Назовем это уравнение номером 1, а это уравнением номер 2. Из уравнения номер 1 мы можем сказать, что mg sin Theta будет равно fb cos Theta. fb равно idl cross b, интегрированному по длине этого токоведущего провода. Теперь, конечно, на эти сегменты рельса будет действовать магнитная сила, но очевидно, что они будут иметь противоположные направления с равными величинами. Таким образом, они в основном отменят, а также это фиксированный рельс, и то же самое здесь, тогда эти силы будут уравновешены силами реакции.Что ж, если мы посмотрим сюда, величина этой силы будет равна величине idl, умноженной на величину косинуса угла между этими двумя векторами. Что ж, опять же, с нашего вида спереди, idl выходит из плоскости и магнитное поле находится в этом направлении. Направление вверх и idl выходит из плоскости, поэтому угол между этими двумя векторами составляет 90 градусов. Итак, у нас здесь sin 90 и sin 90 равен 1, и мы собираемся интегрировать все это по длине этой движущейся полосы.Следовательно, границы будут идти от 0 до l. Величина f sub b тогда будет равна постоянной i, b будет постоянной, если не считать интер-свечения. Интер-свечение от 0 до l даст нам ibl.
Теперь давайте попробуем получить значение i. Допустим, r представляет собой сопротивление ползунка. В этом случае шина i будет равна, согласно закону Ома, наведенной ЭДС, деленной на это полное сопротивление. Индуцированная ЭДС отрицательна по отношению к изменению потока во времени.Конечно, этот отрицательный знак связан с направлением потока тока, и поэтому нас интересует абсолютное значение скорости изменения потока. Phi sub b в тот момент времени, когда рельс скользит вниз, будет равно, скажем так, этому расстоянию, другими словами, если вы просто возьмете, например, фотографию со вспышкой, когда она замедляется, оно будет равно b точка a. Другими словами, область, окруженная этой проводящей петлей. И это будет равно ширине для постепенного смещения этого.l умножить на dx, другими словами, d pi b инкрементное изменение потока будет равно b dot da, и это будет равно величине d, величине da умноженной на cos угла между этими двумя векторами. Чтобы увидеть этот угол, вернемся снова к нашей диаграмме. Итак, мы наблюдаем, как стержень скользит вниз, он будет испытывать изменение, скажем, некоторого расстояния в dx, когда он скользит вниз вдоль этого направления x, и в этот момент изменение потока будет таким же большим, как это подметаемая площадь.Которая будет равна b от b, точка da, и что da будет равно l умноженным на dx, а площадь вектора этой области будет перпендикулярна этому, поэтому это будет вектор примерно так. Хорошо, перпендикулярно этому региону. И вектор магнитного поля в этой точке указывает в эту сторону, поэтому мы говорим об этом угле как об угле между b и da. В нашем трехмерном изображении b вид спереди находится в этом направлении, da будет перпендикулярно области, окруженной этой петлей.Другими словами, он будет перпендикулярен этой наклонной плоскости. Итак, da будет указывать вот так, и угол между этими двумя векторами снова будет равен Theta. Потому что этот угол равен этому углу. Спускаясь вниз, мы получаем величину b, умноженную на величину косинуса теты. Или b, умноженное на da, будет ldx умноженным на косинус теты. Если мы посмотрим на скорость изменения потока, d Phi b по сравнению с dt, тогда будет равно b, умноженному на l, умноженному на dx, по dt, умноженному на косинус теты. Таким образом, только изменение количества равно dx относительно времени.b и длина стержня и угол между b и da, Theta остается постоянным. Но dx over dt — это скорость скольжения этой полосы вниз. Таким образом, это становится равным b умноженным на l умноженным на v умноженным на косинус теты. Итак, как только мы определим d Phi по dt, тогда индуцированный ток будет равен, согласно закону Ома, эпсилону по сопротивлению, blv косинус Theta по r. Теперь, если мы вернемся к уравнению 1, которое в конечном итоге дало нам это выражение здесь, mg sin Theta равно fb cos Theta. Скажем, от 1, mg sin Theta равно f sub b, умноженному на cos Theta, а f sub b в явном виде равно ibl.Теперь у нас есть cos Theta. Следовательно, mg sin Theta равно 4i. Мы можем записать его эквивалент blv cos Theta, разделенный на r, и в уравнении мы получим еще b, еще l, еще cos Theta. Другими словами, эта часть является явной формой тока. Следовательно, это уравнение принимает форму: mg sin Theta равно b квадрат l квадрат, v умноженный на cos квадрат Theta, деленный на r. Если вы решите это выражение для скорости или конечной скорости, она будет равна mgr sin Theta, деленному на b квадрат l квадрат и cos квадрат Theta.Итак, это все заданные величины: масса стержня, ускорение свободного падения, сопротивление контура, угол наклона плоскости, внешнее магнитное поле и длина движущегося стержня. Следовательно, конечная скорость этой штанги при движении вниз по наклонной плоскости будет равна этой величине.
23.1 Индуцированная ЭДС и магнитный поток — College Physics
23.1 Индуцированная ЭДС и магнитный поток — College Physics | OpenStaxSkip к контенту
- Предисловие
- 1 Введение: Природа науки и физики
- Введение в науку и область физики, физических величин и единиц измерения
- 1.1 Физика: Введение
- 1.2 Физические величины и единицы
- 1.3 Точность, прецизионность и значащие числа
- 1.4 Приближение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в Одномерная кинематика
- 2.1 Смещение
- 2.2 Векторы, скаляры и системы координат
- 2.3 Время, скорость и скорость
- 2.4 Ускорение
- 2.5 Уравнения движения для постоянного ускорения в одном измерении
- 2.6 Основы решения проблем для одномерной кинематики
- 2.7 Падающие объекты
- 2.8 Графический анализ одномерного движения
- Глоссарий
- Краткое содержание раздела
- Концептуальный Вопросы
- Задачи и упражнения
- 3 Двумерная кинематика
- Введение в двумерную кинематику
- 3.1 Кинематика в двух измерениях: введение
- 3.2 Сложение и вычитание векторов: графические методы
- 3.3 Сложение и вычитание векторов: аналитические методы
- 3.4 Движение снаряда
- 3.5 Добавление скоростей
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- 4 Динамика: сила и законы движения Ньютона
- Введение в динамику: законы движения Ньютона
- 4.1 Развитие концепции силы
- 4.2 Первый закон движения Ньютона: инерция
- 4.3 Второй закон движения Ньютона: концепция системы
- 4.4 Третий закон движения Ньютона: симметрия сил
- 4.5 Примеры нормального движения, напряжения и другие сил
- 4.6 Стратегии решения проблем
- 4.7 Дальнейшие применения законов движения Ньютона
- 4.8 Расширенная тема: Четыре основных силы — Введение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- 5 Дальнейшие применения законов Ньютона: трение, сопротивление и упругость
- Введение: дальнейшие применения законов Ньютона
- 5.1 Трение
- 5.2 Силы сопротивления
- 5.3 Упругость: напряжение и деформация
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- 6 Равномерное круговое движение и гравитация
- Введение в однородное круговое движение и гравитацию
- 6,1 Угол вращения и угловая скорость
- 6,2 Центростремительное ускорение
- 6,3 Центростремительная сила
- 6,4 Фиктивные силы и неинерциальные системы координат: сила Кориолиса
- 6.5 Универсальный закон тяготения Ньютона
- 6.6 Спутники и законы Кеплера: аргумент в пользу простоты
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Проблемы и упражнения
- 7 Работа, энергия и энергетические ресурсы
- Введение в Работа, энергия и энергетические ресурсы
- 7.1 Работа: научное определение
- 7.2 Кинетическая энергия и теорема работы-энергии
- 7.3 Гравитационная потенциальная энергия
- 7.4 Консервативные силы и потенциальная энергия
- 7.5 Неконсервативные силы
- 7.6 Сохранение энергии
- 7.7 Энергия
- 7.8 Работа, энергия и мощность у людей
- 7.9 Использование энергии в мире
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- 8 Линейный импульс и столкновения
- Введение в линейный импульс и столкновения
- 8.1 Линейный импульс и сила
- 8.2 Импульс
- 8.3 Сохранение импульса
- 8.4 Упругие столкновения в одном измерении
- 8.5 Неупругие столкновения в одном измерении
- 8.6 Столкновения точечных масс в двух измерениях
- 8.7 Введение в ракетное движение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в статику и крутящий момент
- 9.1 Первое условие равновесия
- 9.2 Второе условие равновесия
- 9.3 Стабильность
- 9.4 Приложения статики, включая стратегии решения проблем
- 9.5 Простые механизмы
- 9.6 Силы и моменты в мышцах и суставах
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- 10 Вращательное движение и угловой момент
- Введение во вращательное движение и угловой момент
- 10.1 Угловое ускорение
- 10.2 Кинематика вращательного движения
- 10.3 Динамика вращательного движения: вращательная инерция
- 10.4 Кинетическая энергия вращения: новый взгляд на работу и энергию
- 10,5 Угловой момент и его сохранение
- 10,6 Столкновения протяженных тел в двух измерениях
- 10.7 Гироскопические эффекты: векторные аспекты углового момента
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в статику жидкости
- 11.1 Что такое жидкость?
- 11.2 Плотность
- 11.3 Давление
- 11.4 Изменение давления по глубине в жидкости
- 11.5 Принцип Паскаля
- 11.6 Манометрическое давление, абсолютное давление и измерение давления
- 11.7 Принцип Архимеда
- 11.8 Когезия и адгезия в жидкостях : Поверхностное натяжение и капиллярное действие
Плотность магнитного потока
Плотность магнитного потока
В международной системе (СИ) единицей измерения плотности магнитного потока является тесла (Тл).
Магнитное поле в один тесла относительно велико. Вот почему магнитные поля также выражаются в милтеслах (мТл) и микротеслах (мкТл).
1 T = 1 000 мТл = 1 000 000 мкТл
Для облегчения сравнений GreenFacts систематически использовал единицу mT в своих сводках статических полей.
Типичные значения для статических магнитных полей
(наиболее часто используемые единицы отмечены серым цветом)
| Магнитный поле | Т | мТ | мкТл |
| Земли напряженность магнитного поля при его поверхность | 0.035- 0,070 мТл | 35–70 мкТл | |
| Внутри электропоезда | до 0,002 Т | до 2 mT | до 2000 мкТл |
| алюминий производство | вверх до 0.06 Т | до 60 mT | до 60000 мкТл |
| Магнитный Резонансная томография (МРТ) сканер, используемый в клинических условиях | 0,2 — 3 т | 200- 3000 мТ | |
| Поля Сообщается, что вызывает головокружение и фосфены в людях, перемещающихся в них | выше 2-3 Т | выше 2000-3000 mT | |
| Поля для которых последствия для здоровья имеют изучено на данный момент | вверх к 8 Т | до 8000 mT | |
| Самый сильный поля, которые сейчас разрабатываются для клиническая визуализация | до 9.4 Т | до 9400 mT |
В Международной системе (СИ) одна тесла (1 Тл) определяется как напряженность поля, генерирующая один ньютон силы на ампер тока на метр проводника:
T = Nw · A-1 · м-1 = кг · с-2 · A-1
Международное бюро мер и весов (BIPM) предоставляет дополнительную информацию о Международной системе единиц (SI) на сайте www.bipm.org/en/si/ и префиксы Международной системы единиц (СИ) на сайте www.bipm.fr/en/si/prefixes.html
Связанная публикация :
Другие рисунки и таблицы в этой публикации :
Таблица 1: Рекомендации по исследованию
Статические электрические поля телевизоров и экранов компьютеров
Плотность магнитного потока
ОПРЕДЕЛЕНИЕ | |||
| Магнитный поток (Df) равен общему количеству магнитных силовые линии, проходящие через область A любого форма. | |||
ПОЯСНЕНИЕ | |||
Рассмотреть Флюс | |||
Df = или | |||
| Сейчас поток по всей площади A — это сумма потоков через все элементы DA т.е. | |||
f = Df 1 + Df 2 f = или | |||
| Агрегат магнитного потока WEBER. | |||
ПОТОК | |||
ОПРЕДЕЛЕНИЕ: | |||
| f = S Это Принимая f = BS или или Единица B | |||
| Плотность потока на небольшом элементе занимаемой площади перпендикулярно полю магнитное поле индикации.т.е. | |||
B = Df / DA | |||
| Для последняя информация, бесплатные компьютерные курсы и важные заметки посетите: www.citycollegiate.com | |||
Дизайн громкоговорителей HiFi
Основные сведения о громкоговорителях
Есть много разных типов драйверов, но все они в основном работают одинаково.
вещь: создавать звуковые волны.Безусловно, наиболее распространенным типом водителя является движущийся
катушка электродинамического поршневого привода. Он имеет подвижную часть, называемую диафрагмой, которая
действует как поршень, нагнетая воздух и тем самым создавая звуковые волны. Обычный
Диафрагма для вуфера — бумажный диффузор. Обычная диафрагма твитера — это
тканевый купол. Драйверы
бывают разных размеров, потому что сделать их практически невозможно.
поршневой драйвер, который может воспроизводить звуковые волны в диапазоне от 20 Гц до 20 кГц
частотный диапазон человеческого слуха.Для воспроизведения низких частот драйверу необходимо
иметь большую диафрагму и достаточную массу, чтобы резонировать на низкой частоте. Чтобы
воспроизводить высокие частоты, драйвер должен иметь небольшую диафрагму с низким
масса. Очевидно, что эти требования противоречат друг другу, поэтому водители обычно
предназначен для воспроизведения только части звука.
Твитеры — это драйверы меньшего размера, поскольку они производят самые высокие частоты с
самые короткие длины волн. НЧ-динамики — самые большие динамики, так как они производят
самые низкие частоты с самыми длинными волнами.
Существуют также среднечастотные динамики различных размеров, воспроизводящие средние частоты.
частоты между твитером и вуфером. Среднечастотные драйверы используются в
многополосные динамики с тремя и более размерами драйверов.У некоторых есть открытая спина и
у некоторых есть запечатанные спины.
Помимо разного размера, есть еще одно очень существенное различие.
между твитером и вуфером. Твитер обычно имеет герметичную заднюю часть, в то время как
НЧ динамик обычно имеет открытую спинку. Твитер издает звук с герметичной задней стенкой.
волны только с лицевой стороны.Низкочастотный динамик излучает звуковые волны с обеих сторон
и оборотная сторона.
Чтобы понять, как работают колонки, сначала нужно понять, как
звук
работает.
Внутри вашего уха находится очень тонкий кусок кожи, называемый барабанной перепонкой.Когда ваш
барабанная перепонка вибрирует, ваш мозг интерпретирует вибрации как звук — вот как вы
слышать. Быстрые изменения давления воздуха — наиболее частая причина вибрации вашего
барабанная перепонка.
Объект издает звук, когда он вибрирует в воздухе (звук также может проходить через
жидкости и твердые вещества, но воздух является средством передачи, когда мы слушаем
динамики).Когда что-то вибрирует, оно перемещает частицы воздуха вокруг себя. Те
частицы воздуха, в свою очередь, перемещают частицы воздуха вокруг себя, неся импульс
вибрация в воздухе как движущаяся помеха.
Чтобы увидеть, как это работает, давайте посмотрим на простой вибрирующий объект — колокол. когда
вы звоните в колокольчик, металл быстро вибрирует — прогибается и выходит наружу.Когда это
прогибается с одной стороны, он выталкивает частицы окружающего воздуха на этом
боковая сторона. Эти частицы воздуха затем сталкиваются с частицами перед ними,
которые сталкиваются с частицами перед ними и так далее. Когда колокол
отклоняется, он втягивает в себя эти окружающие частицы воздуха, создавая каплю в
давление, которое притягивает больше окружающих частиц воздуха, что создает еще одну
падение давления, которое втягивает частицы, которые находятся еще дальше, и так далее.Это понижение давления называется разрежением .
Таким образом, вибрирующий объект посылает волну давления
колебание
через атмосферу. Когда волна колебаний достигает вашего уха, оно вибрирует
барабанная перепонка вперед и назад. Наш мозг интерпретирует это движение как звук.
Дифференцирующий звук:
Мы слышим разные звуки от разных вибрирующих объектов из-за вариаций
в:
- Частота звуковой волны — более высокая частота волны просто означает, что воздух
давление колеблется быстрее.Мы слышим это как более высокий тон. Когда там
чем меньше колебаний во времени, тем ниже высота звука. - Уровень атмосферного давления — это амплитуда волны, которая определяет, как
громкий звук есть. Звуковые волны с большей амплитудой перемещают наше ухо
барабаны больше, и мы регистрируем это ощущение как более высокую громкость.
Звук распространяется волнами колебаний давления воздуха, и мы слышим звуки
по-разному в зависимости от частоты и амплитуды этих волн. Мы также
узнали, что микрофоны преобразовывают звуковые волны в электрические сигналы, которые
можно закодировать на компакт-диски, кассеты, пластинки и т. д.Игроки конвертируют это хранилище
информацию обратно в электрический ток для использования в стереосистеме.
Диафрагма:
Говорящий — это, по сути, последняя машина перевода — обратная сторона
микрофон. Он принимает электрический сигнал и переводит его обратно в физический
вибрации для создания звуковых волн.Когда все работает как надо,
динамик производит почти те же вибрации, что и микрофон изначально
записаны и закодированы на ленте, CD, LP и т. д.
Драйвер генерирует звуковые волны путем быстрой вибрации гибкого
конус , или
диафрагма .
- Конус , обычно изготовленный из бумаги, пластика или металла,
прикреплен к
широкий конец подвески. - Узкий конец конуса подключен к голосу
катушка . - Катушка прикреплена к корзине при помощи крестовины , a
кольцо
гибкий материал. Паук удерживает катушку на месте, но позволяет
свободно двигаться вперед и назад.
Подвеска или подвес представляет собой обод
гибкий материал
который позволяет конусу двигаться и прикреплен к металлической раме водителя,
позвонил в корзину
Некоторые драйверы имеют купол вместо диффузора.Купол — это просто
диафрагма
который расширяется, а не сужается.
Звуковая катушка:
Звуковая катушка — это основной электромагнит. Когда электрический ток протекает через
в
звуковая катушка меняет направление, полярная ориентация катушки меняется на противоположную.
Пропускание электрического тока через провод создает магнитное поле вокруг катушки,
намагничивая металл, вокруг которого он намотан.Поле действует так же, как магнитное поле
вокруг постоянного магнита: имеет полярную ориентацию — «северный» конец и «южный» конец
— и его привлекают железные предметы. Но в отличие от постоянного магнита в электромагните
вы можете изменить ориентацию полюсов. Если вы измените направление тока,
северный и южный концы переключателя электромагнита.
Именно это и делает сигнал — он постоянно меняет направление потока
электричество .Если вы когда-либо подключали стереосистему, то знаете, что есть два выходных провода для
каждый динамик — обычно черный и красный.
По сути, усилитель постоянно переключает электрический сигнал, колеблется
между положительным зарядом и отрицательным зарядом на красном проводе. Поскольку электроны всегда текут
в том же направлении между положительно заряженными частицами и отрицательно заряженными частицами,
ток, проходящий через динамик, движется в одну сторону, а затем меняет направление и течет в другую
путь.Этот переменный ток вызывает изменение полярной ориентации электромагнита.
сам много раз в секунду.
Магниты:
Так как же колебания заставляют катушку динамика двигаться вперед и назад? Электромагнит есть
находится в постоянном магнитном поле, создаваемом постоянным магнитом . Эти
два магнита
— электромагнит и постоянный магнит — взаимодействуют друг с другом, как любые два магнита.Положительный конец электромагнита притягивается к отрицательному полюсу постоянного
магнитное поле, а отрицательный полюс электромагнита отталкивается от постоянного магнита.
отрицательный полюс. Когда меняется полярная ориентация электромагнита, меняется и направление
отталкивание и притяжение. Таким образом, переменный ток постоянно меняет магнитную
силы между звуковой катушкой и постоянным магнитом.Это толкает катушку вперед и назад
стремительно, как поршень.
Когда электрический ток, протекающий через звуковую катушку, меняет направление, катушка
полярная ориентация меняется на противоположную. Это изменяет магнитные силы между звуковой катушкой и
постоянный магнит, перемещающий катушку и прикрепленную диафрагму вперед и назад.
Когда катушка движется, она толкает и тянет диффузор динамика.Это вибрирует воздух впереди
динамика, создавая звуковые волны. Электрический звуковой сигнал также можно интерпретировать как
волна . Частота и амплитуда этой волны, которая представляет собой
оригинальный звук
волна, определяет скорость и расстояние, на которое движется звуковая катушка. Это, в свою очередь, определяет
частота и амплитуда звуковых волн, создаваемых диафрагмой.
Драйверы разных размеров лучше подходят для определенных диапазонов частот. Именно по этой причине,
громкоговорители обычно делят широкий частотный диапазон между несколькими
драйверы . В
в следующем разделе мы узнаем, как динамики делят частотный диапазон, и посмотрим
у основных типов драйверов, используемых в громкоговорителях.
Громкоговорители с подвижной катушкой
Драйверы громкоговорителей с подвижной катушкой используются уже несколько десятилетий. Они были
Первоначально изобретен Келлогом и Райсом (около 1920 г.). Вид движущейся катушки в разрезе
Типичный для современных конструкций драйвер динамика показан на рис. 1.0
Рис. 1.0
Поведение водителя регулируется основными принципами
физика.На выводы драйвера подается переменный ток. Эти выводы
подключен к проводу, который оборачивается вокруг формирователя катушки, создавая так называемый голос
катушка. Катушка имеет связанные с ней электрическое сопротивление и индуктивность. это
расположен в зазоре между полым цилиндрическим магнитом (например, северным полюсом)
и цельный цилиндрический полюсный наконечник (например, южный полюс).Последний расположен внутри
полый формирователь катушек. Ток, подаваемый на звуковую катушку, течет по кругу вокруг
обмотки. Структура магнита обеспечивает магнитный поток через катушку с полем
линии, идущие перпендикулярно направлению тока.
Как хорошо известно при изучении электромагнетизма, если ток течет в
При наличии магнитного поля создается сила Лоренца.Применительно к геометрии
драйвер громкоговорителя с подвижной катушкой, ортогонально ориентированная сила Лоренца упрощает
произведение эффективной плотности магнитного потока на эффективную длину катушки в
поле и ток, текущий в катушке. Поскольку приложенный ток чередуется, Лоренц
сила также чередуется, заставляя звуковую катушку (и все, что к ней прикреплено) колебаться
аналогичным образом.
Звуковая катушка прикреплена к каркасу, который прикреплен к диффузору или диафрагме.
Этот узел диафрагмы удерживается на месте системой подвески, которая центрирует голос
катушка в зазоре магнита. Подвесные системы обычно состоят из двух отдельных гибких
Компоненты: окантовка и паук. Эти разнесенные компоненты служат для ограничения
колебания конуса для движения вдоль одной оси и создания возвращающей силы для возврата
конус в исходное положение.Система подвески имеет податливость и сопротивление
связанные с ним. Конус, формирователь катушки, звуковая катушка, части системы подвески и
Подводящие провода идеально перемещаются по фазе как сосредоточенные элементы с определенной эффективной массой.
Колебания конуса вызывают колебания давления воздуха, которые расходятся от
драйвер как звуковые волны.
Краткая история разработки моделирования громкоговорителей с подвижной катушкой
Драйверы громкоговорителей с подвижной катушкой изучаются в течение многих лет.Маклахан первый
разработал уравнения для громкоговорителей с подвижной катушкой в 1930-х годах.
В 1940-х годах
Олсон представил аналогичные схемы, которые представляют несколько областей движущейся катушки.
Водитель. Позже, в 1954 году, Беранек продолжил разработки Олсона в его
разработка частичного решения отклика фазоинверторной акустической системы.
В 1958 году Новак представил обобщенную теорию конструкции и характеристик
вентилируемые и закрытые корпуса громкоговорителей. Тем не менее, Тиле обычно считают
of as первым, кто разработал полную процедуру синтеза для громкоговорителей с прямым излучателем.
Работа Тиле была первоначально опубликована в Трудах Института радио за 1961 год.
Инженеры.Затем он был перепечатан в журнале Journal of the Audio Engineering 1971 года.
Общество (JAES).
Между 1968 и 1972 годами Бенсон опубликовал серию статей.
опираясь на предыдущую работу. Работа, проделанная Бенсоном, была мало известна до Смолла.
сослался на его работу. Небольшие публикации в международных изданиях
JAES, что принесло признание усилиям Бенсона и Смолла.Фундаментальный набор параметров, которые описывают модель сосредоточенных элементов
Громкоговоритель с подвижной катушкой получил название Thiele / Small Parameters в
признание их работы.
Знание этих параметров необходимо при проектировании
полные акустические системы.
Драйвер громкоговорителя
Электрическая энергия, передаваемая от усилителя, преобразуется в кинетическую энергию как
диффузор громкоговорителя перемещается внутрь и наружу посредством электромеханического преобразования.
Звуковая катушка прикреплена к конусу , , в свою очередь,
проводился в
Стальная корзина и прикрепленная к подвесу . Поток генерируется
с помощью магнита и направляется стальными пластинами и полюсным наконечником
эффективно формируя
магнитная цепь.По мере прохождения через катушку переменного тока взаимодействие с
в
поток, создаваемый магнитом , вызывает силу. В общем-то
паук необходим для центрирования звуковой катушки в зазоре, эти
обычно изготавливаются из хлопка, отжатого паром. Катушка и магнит
также поддерживается в чистоте с помощью защитного колпачка .Конус обычно
изготовлены из бумаги, прессованной паром, через конусы из полипропилена, кевлара и даже из углеродного волокна
может быть использован. В результате поршневое действие
конуса вызывает изменение давления воздуха перед ним, производя
звуковая энергия. Хорошо спроектированный динамик может иметь эффективность только около 5%,
другими словами, 20 Вт электроэнергии от усилителя могут
в результате получается 1 ватт звуковой мощности.
Чувствительность динамика
Уточняем чувствительность
громкоговорителя с точки зрения дБ SPL для входа 2,83 В.
уровень звукового давления измеряется по оси в безэховых условиях при
расстояние 1 метр от динамика.
2,83 Вольт соответствует напряжению на стандартном 8-омном динамике с мощностью 1 Вт.
Итак, если мы измеряем 0,2 Па при одном вольте, какова чувствительность динамиков?
= 80 дБ
Изменение SPL при подаче 2,83 В = 9,04 дБ
, т. Е. 89,04 дБ на расстоянии 1 м при входе 2,83 В
На приведенном ниже графике показана типичная чувствительность широкого диапазона современных динамиков
Обычно 88 дБ / 2.83 В на расстоянии 1 м
Плоские колонки 80 дБ / 2,83 В @ 1 м
Профессиональные мониторы 95 дБ / 2,83 В @ 1 м
Использование пикового отклика или измерения с широкополосным шумом может привести к ошибочно высоким
чувствительность.
Измерение с B-взвешиванием дает более точную картину с учетом субъективных
громкость.
Примечание чувствительность не обязательно
руководство по тому, насколько хорош спикер. Например, динамик PA будет иметь
чувствительность около 115 дБ, поэтому качество звука жертвуется ради высокого
выход. И наоборот, хороший монитор может быть спроектирован так, чтобы обеспечивать ровную частоту.
ответ с компонентами, которые также снижают чувствительность.
Старая система
Старше
система указала эффективность в довольно необычных агрегатах
дБ SPL / Вт / м, где мощность — это входная электрическая мощность.Старший
система по-прежнему довольно популярна, поэтому о ней стоит знать.
Изменение входной МОЩНОСТИ при соотношении P приведет к увеличению излучаемого звука
уровень давления
10 log (коэффициент P )
, поскольку скорость и звуковое давление пропорциональны напряжению,
тогда как мощность пропорциональна квадрату напряжения).
Это означает, например, что динамик
при чувствительности 100 дБ / Вт / м питается от 50Вт, результирующий SPL равен
100 + 10 * ЖУРНАЛ (50/1)
= 100 + 17 = 117 дБ / Вт / м
Хотя до сих пор широко используемый КПД не так полезен, как чувствительность к напряжению
поскольку входную мощность трудно измерить, данный входной импеданс равен частоте
зависимы, поэтому, например, более низкая частота будет иметь меньшее сопротивление
и потреблять больше энергии, следовательно, быть менее эффективным.Также современный твердотельный
усилители — это источники напряжения, подающие ток по запросу, поэтому мощность меньше
важнее, чем дБ для вольт.
Частотная характеристика
Результирующий SPL для динамика с питанием
в диапазоне (развертке) узких полос частот — это частотная характеристика.
Частотная характеристика часто обозначается как максимальное отклонение SPL в пределах
указанный диапазон.Например…
Частотный диапазон от 20 Гц до 20 кГц
Часто производители также предоставляют график частотной характеристики…
дБ от частоты.
В идеале у динамика должна быть плоская
отклик в широком диапазоне.Обычно более резкий ответ на
беднее динамик.
Разные типы динамиков будут
имеют разные ответы в соответствии с их применением, например
- Студийные мониторы требуют ровного отклика
- PA Динамики требуют высокой чувствительности за счет частотной характеристики
- Сабвуферам требуется улучшенный бас
отклик за счет высоких частот
Улучшение низких частот
Низкочастотную характеристику громкоговорителя можно улучшить, используя обратное излучение.К сожалению, излучение спереди и сзади в противофазе — нам нужно
«фазоинвертор» до того, как можно будет добавить переднюю
и обратное излучение конструктивно.
Такая стратегия реализована в семействе громкоговорителей с фазоинвертором.
кожухи, которые пропускают переднее и заднее излучение низкочастотных
блок (ы) через акустическую фазоинвертирующую сеть.
Семейство фазоинверторов включает
- корпус линии передачи
- корпус фазоинвертора
- Радиатор вспомогательный НЧ
Наиболее важным представителем семейства фазоинверторов является:
Корпус фазоинвертора
В корпусе с фазоинвертором громкоговоритель внутренне возбуждает резонатор Гельмгольца.Это
акустическая сеть, имеющая амплитуду и фазу
реакция резонансной системы второго порядка (которая дает инверсию фазы
выше резонанса).
Корпус фазоинвертора представляет собой закрытый корпус с
«порт» в одной из стенок корпуса.Порт — трубка,
открыть с одного конца во внутренний объем корпуса и открыть с
другой конец в место для прослушивания. Воздух в порту движется как единый
«сосредоточенная масса», которая подпрыгивает вверх и вниз на пружине, образованной
объемом воздуха, захваченного в корпусе, что дает системе секунду
заказать резонансное поведение.
Начиная с резонансной частоты вверх, излучение порта и излучение динамика
в фазе (, поэтому они добавляют конструктивно, давая больше басов ).Ниже
резонанс, излучение порта и динамика не в фазе (, поэтому они
добавить деструктивно, давая меньше басов, чем закрытый ящик ) На резонансной частоте
отклик порта намного больше, чем отклик динамика (потому что обратная нагрузка, представленная
громкоговоритель максимален на резонансе порта.
АЧХ динамика и порта в
корпус фазоинвертора показан отдельно на рисунке ниже….
Направленность
На низких частотах распространение звука
всенаправленный (распространяется во всех направлениях) для высоких частот
распространение звука становится гораздо более направленным. Это верно для
динамики, где размещение сабвуферов менее важно, чем выше
частотомеры.
Это может быть показано для громкоговорителя путем нанесения
кривая равного SPL, следовательно, представляющая фронт распространяющейся волны.
Низкая частота
Высокая частота
Эти графики созданы с помощью Visaton BoxSim (немецкое приложение для Windows)
По мере увеличения частоты фронт распространяющейся волны
распадается на доли.Передняя доля несет большую часть звуковой энергии.
Это имеет важное значение для стерео
звуковые системы и микширование, поскольку слушателя меньше волнует, где
низкочастотные звуки соответствуют высокочастотным звукам.
На странице калькулятора вы найдете 24
Калькулятор-модули …
Бесплатный двоичный переводчик | Перевести двоичный код в текст
Инструменты для AshBox
РАССЧИТАТЬ
- android dpi калькулятор
- калькулятор площади
- калькулятор площади комнаты
- ручной калькулятор
- калькулятор сжигания калорий
- калькулятор автокредитования
- калькулятор разрешения chmod
- калькулятор окружности
- проблема слова монеты
- составное имя и формула
- конвертировать архивы
- калькулятор кредитной карты
- калькулятор уменьшения долга
- калькулятор времени загрузки
- анализатор заголовка электронной почты
- калькулятор серии Фибоначчи
- калькулятор финансовой экономии
- калькулятор дробей
- преобразование дроби в процент
- бесплатный калькулятор ставок
- калькулятор FRM
- калькулятор числа фронта
- калькулятор расхода газа
- калькулятор gpa
- хеш-калькулятор
- ie калькулятор
- калькулятор неупругих столкновений
- калькулятор инвестиций
- калькулятор времени выполнения
- калькулятор високосного года
- матричный калькулятор
- миллиметровый калькулятор комиссии
- калькулятор молярной массы
- калькулятор осмотического давления
- калькулятор избыточного веса
- калькулятор предсказателя овуляции
- генератор паролей
- процентов калькулятор ошибок
- калькулятор периметра
- калькулятор пикселей и соотношения сторон
- калькулятор возраста планеты
- простое число
- преобразователь квадратного уравнения
- научный калькулятор
- преобразователь прямолинейного графика
- калькулятор разницы во времени
- калькулятор подсказки
- калькулятор верхнего слоя почвы
- Калькулятор тригонометрии
- Калькулятор объема
- Калькулятор охлаждения ветром
9 0025 калькулятор индекса насыщения по Ланжелье
КОНВЕРТ
- преобразователь в алфавитном порядке
- преобразователь количества вещества
- преобразователь угла
- преобразователь углового ускорения
- преобразователь единиц площади
- преобразователь астрономических единиц
- двоичный преобразователь
- преобразователь сахара в крови
- преобразователь brix в baume
- преобразователь теплотворной способности
- конвертер единиц емкости
- конвертер единиц заряда
- конвертер единиц ткани для мужчин
- конвертер единиц ткани для женщин
- конвертер цветовых кодов
- конвертер проводимости
- конвертер электропроводности
- конвертер единиц кухонной единицы
- конвертер валют
- единиц тока преобразователь
- преобразователь передачи данных
- преобразователь единиц плотности
- преобразователь разрешения цифрового изображения
- преобразователь цифровой памяти
- преобразователь электрического поля
- преобразователь единиц электрического потенциала
- преобразователь энергии
.

 4.3. Магнитное поле кругового проводника с током
4.3. Магнитное поле кругового проводника с током Плотность энергии магнитного поля
Плотность энергии магнитного поля 4. Закон Био-Савара–Лапласа
4. Закон Био-Савара–Лапласа И по закону Фарадея в первом контуре возникает ЭДС.
И по закону Фарадея в первом контуре возникает ЭДС.
 Такие вещества называют диа–магнетиками: .
Такие вещества называют диа–магнетиками: .