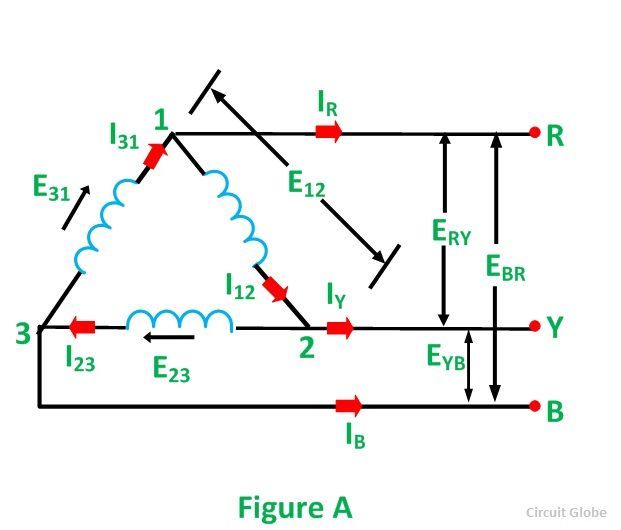
Соединение треугольником и звездой формулы: Свойства звезды и треугольника

Содержание

Соединение звездой и треугольником формулы

Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120 o , создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.

Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.

Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120 o . В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120 o . Запишем мгновенные значения и комплексы действующих значений ЭДС.

Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю.

Соответственно

На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита ( А, В, С ), а концы – последними буквами ( X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу. Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.

2. Соединение в звезду. Схема, определения

Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным.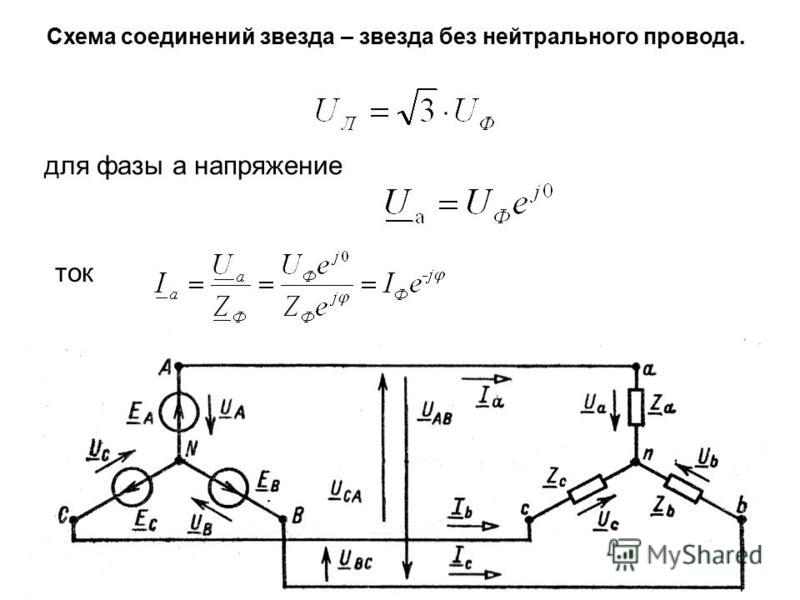 Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1.

Рис. 6.1

Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника N_и приемника N’ называют нейтральным (нулевым) проводом. Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями. Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах – линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.

Z_N – сопротивление нейтрального провода.

Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений

(7.1)

На рис. 6.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.

Рис. 6.2

Из векторной диаграммы видно, что

При симметричной системе ЭДС источника линейное напряжение больше фазного в √3 раз.

Для увеличения мощности передачи без увеличения напряжения сети, снижения пульсаций напряжения в блоках питания, для уменьшения числа проводов при подключении нагрузки к питанию, применяют различные схемы соединения обмоток источников питания и потребителей (звезда и треугольник).

Схемы

Обмотки генераторов и приемников при работе с 3-фазными сетями могут соединяться с помощью двух схем: звезды и треугольника. Такие схемы имеют между собой несколько отличий, различаются также нагрузкой по току. Поэтому, перед подключением электрических машин необходимо выяснить разницу в этих двух схемах — звезда и треугольник.

Схема звезды

Соединение различных обмоток по схеме звезды предполагает их подключение в одной точке, которая называется нулевой (нейтральной), и имеет обозначение на схемах «О», либо х, у, z. Нулевая точка может иметь соединение с нулевой точкой источника питания, но не во всех случаях такое соединение имеется. Если такое соединение есть, то такая система считается 4-проводной, а если нет такого соединения, то 3-проводной.

Схема треугольника

При такой схеме концы обмоток не объединяются в одну точку, а соединяются с другой обмоткой. То есть, получается схема, похожая по виду на треугольник, и соединение обмоток в ней идет последовательно друг с другом. Нужно отметить отличие от схемы звезды в том, что в схеме треугольника система бывает только 3-проводной, так как общая точка отсутствует.

В схеме треугольника при отключенной нагрузке и симметричной ЭДС равно 0.

Фазные и линейные величины

В 3-фазных сетях питания имеется два вида тока и напряжения – это фазные и линейные. Фазное напряжение – это его величина между концом и началом фазы приемника. Фазный ток протекает в одной фазе приемника.

При применении схемы звезды фазными напряжениями являются U_a, U_b, U_c, а фазными токами являются I _a, I _b, I _c. При применении схемы треугольника для обмоток нагрузки или генератора фазные напряжения — U_aв, U_bс, U_cа, фазные токи – I _ac, I _bс, I _cа.

Линейные значения напряжения измеряются между началами фаз или между линейных проводников. Линейный ток протекает в проводниках между источником питания и нагрузкой.

В случае схемы звезды линейные токи равны фазным, а линейные напряжения равны U _ab, U_bc, U _ca. В схеме треугольника получается все наоборот – фазные и линейные напряжения равны, а линейные токи равны I _a, I _b, I _c.

Большое значение уделяется направлению ЭДС напряжений и токов при анализе и расчете 3-фазных цепей, так как его направление влияет на соотношение между векторами на диаграмме.

Особенности схем

Между этими схемами есть существенная разница. Давайте разберемся, для чего в различных электроустановках используют разные схемы, и в чем их особенности.

Во время пуска электрического мотора ток запуска имеет повышенную величину, которая больше его номинального значения в несколько раз. Если это механизм с низкой мощностью, то защита может и не сработать. При включении мощного электромотора защита обязательно сработает, отключит питание, что обусловит на некоторое время падение напряжения и перегорание предохранителей, или отключение электрических автоматов. Электродвигатель будет работать с малой скоростью, которая меньше номинальной.

Видно, что имеется немало проблем, возникающих из-за большого пускового тока. Необходимо каким-либо образом снижать его величину.

Для этого можно применить некоторые методы:

Подключить на запуск электродвигателя реостат, дроссель, либо трансформатор.
Изменить вид соединения обмоток ротора электродвигателя.

В промышленности в основном применяют второй способ, так как он наиболее простой и дает высокую эффективность. Здесь работает принцип переключения обмоток электромотора на такие схемы, как звезда и треугольник. То есть, при запуске мотора его обмотки имеют соединение «звезда», после набора эксплуатационных оборотов, схема соединения изменяется на «треугольник». Этот процесс переключения в промышленных условиях научились автоматизировать.

В электромоторах целесообразно применение сразу двух схем — звезда и треугольник. К нулевой точке необходимо подключить нейтраль источника питания, так как во время использования таких схем возникает повышенная вероятность перекоса фазных амплитуд. Нейтраль источника компенсирует эту асимметрию, которая возникает вследствие разных индуктивных сопротивлений обмоток статора.

Достоинства схем

Соединение по схеме звезды имеются важные преимущества:

Плавный пуск электрического мотора.
Позволяет функционировать электродвигателю с заявленной номинальной мощностью, соответствующей паспорту.
Электродвигатель будет иметь нормальный рабочий режим при различных ситуациях: при высоких кратковременных перегрузках, при длительных незначительных перегрузках.
При эксплуатации корпус электродвигателя не перегреется.

Основным достоинством схемы треугольника является получение от электродвигателя наибольшей возможной мощности работы. Целесообразно поддерживать режимы эксплуатации по паспорту двигателя. При исследовании электромоторов со схемой треугольника выяснилось, что его мощность повышается в 3 раза, по сравнению со схемой звезды.

При рассмотрении генераторов, схемы – звезда и треугольник по параметрам аналогичны при функционировании электродвигателей. Выходное напряжение генератора будет больше в схеме треугольника, чем в схеме звезды. Однако, при повышении напряжения снижается сила тока, так как по закону Ома эти параметры обратно пропорциональны друг другу.

Поэтому можно сделать вывод, что при разных соединениях концов обмоток генератора можно получить два разных номинала напряжения. В современных мощных электромоторах при запуске схемы – звезда и треугольник переключаются автоматически, так как это позволяет снизить нагрузку по току, возникающей при пуске мотора.

Процессы, происходящие при изменении схемы звезда и треугольник в разных случаях

Здесь, изменение схемы — имеется ввиду переключение на щитах и в клеммных коробках электрических устройств, при условии, что имеются выводы обмоток.

Обмотки генератора и трансформатора

При переходе со звезды в треугольник напряжение уменьшается с 380 до 220 вольт, мощность остается прежней, так как фазное напряжение не изменяется, хотя линейный ток увеличивается в 1,73 раза.

При обратном переключении возникают обратные явления: линейное напряжение увеличивается с 220 до 380 вольт, а фазные токи не изменяются, однако линейные токи снижаются в 1,73 раза. Поэтому можно сделать вывод, что если есть вывод всех концов обмоток, то вторичные обмотки трансформатора и генераторы можно применять на два типа напряжения, которые отличаются в 1,73 раза.

Лампы освещения

При переходе со звезды в треугольник лампы сгорят. Если переключение сделать обратное, при условии, что лампы при треугольнике горели нормально, то лампы будут гореть тусклым светом. Без нулевого провода лампы можно соединять звездой при условии, что их мощность одинакова, и распределяется равномерно между фазами. Такое подключение применяется в театральных люстрах.

На сегодняшний день асинхронные электродвигатели большой мощности отличаются надежностью работы и высокой производительностью, удобством эксплуатации и обслуживания, а также приемлемой ценой. Конструкция этого типа двигателя позволяет выдерживать сильные механические перегрузки.

Как известно, из основ электротехники, основными частями любого двигателя являются статичный статор, и вращающейся внутри его ротор.

Оба эти элемента состоят из токопроводящих обмоток, при этом статорная обмотка находиться в пазах магнитопровода с соблюдением расстояния в 120 градусов. Начало и конец каждой обмотки выведены в электрическую распределительную коробку и установлены в два ряда.

При подаче напряжения от трехфазной электросети на обмотки статора создается магнитное поле. Именно оно заставляет ротор вращаться.

Как подключить электродвигатель правильно – знает опытный электрик.

Подключение асинхронного двигателя к электрической сети осуществляется только по следующим схемам: «звезда», «треугольник» и их комбинации.

Определение типа способа соединения

Выбор того или иного подсоединения зависит от:

надежности энергосети;
номинальной мощности;
технических характеристик самого двигателя.

Каждое соединение имеет свои плюсы и минусы в работе. В паспорте двигателя от завода-изготовителя, а также на металлическом лейбле на самом устройстве обязательно указана схема его подключения.

При соединении «Звезда» все концы статорных обмоток сходятся водной точке, а напряжение поступает на начало каждой из них. Подключение двигателя «звездой» гарантирует плавный, безопасный пуск агрегата, но на начальном этапе наблюдается значительная потеря нагрузки.

Подключение «треугольником» подразумевает последовательное соединение обмоток в замкнутую структуру, т.е.начало первой фазы соединяют с концом второй и. т.д.

Такое соединение дает выходную мощность до 70% от номинальной, но в таком случае существенно возрастают пусковые токи, что может спровоцировать поломку электродвигателя.

Существует также комбинированное соединение «звезда-треугольник» (такой значок Y/Δ обязательно должен значиться на корпусе мотора). Представленная схема вызывает скачки тока в момент переключения, которые приводят к тому, что скорость вращения ротора быстро снижается, а потом постепенно входит в норму.

Комбинированные схемы актуальны для электромоторов мощностью свыше 5 кВт.

Зависимость выбора от напряжения

Сейчас в промышленности более применимы асинхронные трехфазные электродвигатели отечественного производства, рассчитанные на номинальное напряжение от сети220/380 В. (агрегаты на 127/220 В уже редко используются).

Схема подключения «треугольник»- единственно верная для подключения к российским энергосетям зарубежных электромоторов номинальным напряжением 400-690 В.

Подключение трехфазного двигателя любой мощности осуществляется по определенному правилу: агрегаты низкой мощности присоединяются по схеме «треугольник», а высокомощные – только «звездой».

Так электромотор прослужит долго и проработает без сбоев.

Способ «звезды» применяется при подключении трехфазных асинхронных двигателей номинальным напряжением 127/220 В к однофазным сетям.

Как снизить пусковые токи электродвигателя?

Явление значительного повышения пусковых токов при запуске высокомощных устройств, подсоединенных по схеме Δ, приводит в сетях с перегрузкой к кратковременному падению напряжения ниже допустимого значения. Все это объясняется особой конструкцией асинхронного электродвигателя, у которого ротор с большой массой обладает высокой инерционностью. Поэтому на начальном этапе работы мотор перегружается, особенно это актуально для роторов центробежных насосов, турбинных компрессоров, вентиляторов, станочного оборудования.

Чтобы снизить влияние всех этих электротехнических процессов, используют подключение электродвигателя «звездой» и «треугольником». Когда двигатель набирает обороты, ножи специального переключателя (пускателя с несколькими трехфазными контакторами) переводит обмотки статора со схемы Y на Δ.

Для реализации смены режимов кроме пускателя нужно специальное реле времени, благодаря которому происходит временная задержка 50-100 мс при переключении и защита от трехфазного короткого замыкания.

Сама процедура использования комбинированной схемы Y/ Δ эффективно помогает уменьшить пусковые токи мощных трехфазных агрегатов. Происходит это следующим образом:

При подаче напряжения 660 В по схеме «треугольник», каждая обмотка статора получает 380 В (√3 раза меньше), а, следовательно, по закону Ома, в 3 раза уменьшается сила тока. Поэтому при запуске в свою очередь в 3 раза снижается мощность.

Но такие переключения возможны только для моторов с номинальным напряжением 660/380 В при включении их в сеть с такими же значениями напряжения.

Опасно подключать электродвигатель с номинальным напряжением 380/220 В в сеть 660/380 В, его обмотки могут быстро перегореть.

И также помните, что вышеописанные переключения недопустимо применять для электромоторов, у которых на валу размещена нагрузка без инерции, к примеру, вес лебедки или сопротивление поршневого компрессора.

Для такого оборудования устанавливают специальные трехфазные электрические двигатели с фазным ротором, где реостаты уменьшают значение токов при пуске.

Чтобы изменить направление вращения электромотора, необходимо сменить местами две любые фазы сети при любом типе подключения.

Для этих целей при эксплуатации асинхронного электродвигателя применяют специальные электроаппараты ручного управления, к которым относятся реверсивные рубильники и пакетные переключатели или более модернизированные приборы дистанционного управления — реверсивные электромагнитные пускатели (рубильники).

Соединение звездой и треугольником разница

Звезда и треугольник принцип подключения. Особенности и работа

Схемы

Схема звезды

Схема треугольника

В схеме треугольника при отключенной нагрузке и симметричной ЭДС равно 0.

Фазные и линейные величины

Особенности схем

Для этого можно применить некоторые методы:

Подключить на запуск электродвигателя реостат, дроссель, либо трансформатор.
Изменить вид соединения обмоток ротора электродвигателя.

Достоинства схем

Соединение по схеме звезды имеются важные преимущества:

Плавный пуск электрического мотора.
Позволяет функционировать электродвигателю с заявленной номинальной мощностью, соответствующей паспорту.
Электродвигатель будет иметь нормальный рабочий режим при различных ситуациях: при высоких кратковременных перегрузках, при длительных незначительных перегрузках.
При эксплуатации корпус электродвигателя не перегреется.

Процессы, происходящие при изменении схемы звезда и треугольник в разных случаях

Обмотки генератора и трансформатора

Лампы освещения

Что такое звезда и треугольник в электродвигателе

Вся нагрузка в трёхфазных цепях соединяется по схеме звезда или треугольник. В зависимости от вида потребителей электроэнергии и напряжения в электросети и выбирают соответствующий вариант. Если говорить об электродвигателях, то от выбора варианта соединения обмоток зависит возможность его работы в конкретной сети с номинальными характеристиками. В статье мы рассмотрим, чем отличаются звезда и треугольник в электродвигателе, на что они влияют и какой принцип подключения проводов в клеммнике трёхфазного двигателя.

Теория

Как уже было сказано, схемы соединения звезда и треугольник характерны не только для электродвигателя, но и для обмоток трансформатора, нагревательных элементов (например, тэнов электрокотла) и другой нагрузки.

Чтобы понять почему эти схемы соединения элементов трёхфазной цепи так называются, нужно их несколько видоизменить.

В «звезде», нагрузка каждой из фаз соединена между собой одним из выводов, это называется нейтральная точка. В «треугольнике» каждый из выводов нагрузки подключается к разноимённым фазам.

Всё сказанное в статье далее справедливо для трёхфазных асинхронных и синхронных машин.

Рассмотрим этот вопрос на примере соединения обмоток трёхфазного трансформатора или трёхфазного двигателя (в этом контексте это не имеет значения).

На этом рисунке отличия более заметны, в «звезде» начала обмоток подключаются к фазным проводникам, а концы соединяются вместе, в большинстве случаев к этой же точке нагрузки подключается нулевой провод от питающего генератора или трансформатора.

Точкой обозначены начала обмоток.

То есть в «треугольнике» конец предыдущей обмотки и начало следующей соединяются, и к этой точке подключается питающая фаза. Если перепутать конец и начало — подключаемая машина не будет работать.

В чем разница

Если говорить о подключении однофазных потребителей, кратко разберем на примере трёх электротенов, то в «звезде», если сгорит один из них продолжат работать два оставшихся.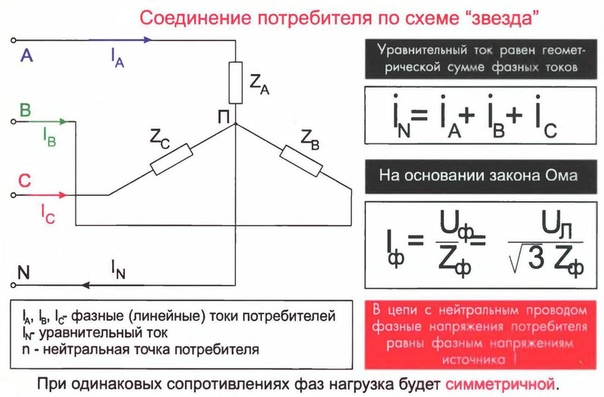 Если сгорит два из трёх – вообще ни один не будет работать, поскольку они попарно подключаются на линейное напряжение.

В схеме треугольника даже при перегорании 2 тэнов – третий продолжит работать. В ней нет нулевого провода, его просто некуда подключать. А в «звезде» его подключают к нейтральной точке, и нужен он для уравнивания токов фаз и их симметрии в случае разной нагрузки по фазам (например, в одной из веток подключен 1 ТЭН, а в остальных по 2 параллельно).

Но если при таком соединении (с разной нагрузкой по фазам) отгорит ноль, то напряжения будут неодинаковы (там, где больше нагрузка просядет, а где меньше – возрастёт). Подробнее об этом мы писали в статье о перекосе фаз.

При этом нужно учесть, что подключать обычные однофазные приборы (220В) между фазами, на 380В, нельзя. Либо приборы должны быть рассчитаны на такое питание, либо сеть должна быть с Uлинейным 220В (как в электросетях с изолированной нейтралью некоторых специфичных объектов, например, кораблей).

Но, при подключении трёхфазного двигателя, ноль к средней точке звезды часто не подключают, так как это симметричная нагрузка.

Формулы мощности, тока и напряжения

Начнем с того что в схеме звезды есть два разных напряжения – линейное (между линейными или фазными проводами) и фазное (между фазой и нулём). Uлинейное в 1,73 (корень из 3) раз больше Uфазного. При этом линейный и фазный токи равны.

То есть линейное и фазное напряжение соотносятся так, что при линейном в 380В, фазное равно 220В.

В «треугольнике» Uлинейное и Uфазное равны, а токи отличаются в 1,73 раза.

Мощность в обоих случаях считают по одинаковым формулам:

полная S = 3*Sф = 3*(Uл/√3)*I = √3*Uл*I;
активная P = √3*Uл*I*cos φ;
реактивная Q = √3*Uл*I*sin φ.

При подключении одной и той же нагрузки на те же Uфазное и Uлинейное, мощность подключённых приборов будет отличаться в 3 раза.

Допустим, есть двигатель, который работает от трёхфазной сети 380/220В, а его обмотки рассчитаны на подключение по «звезде» к электросети с Uлинейным в 660В.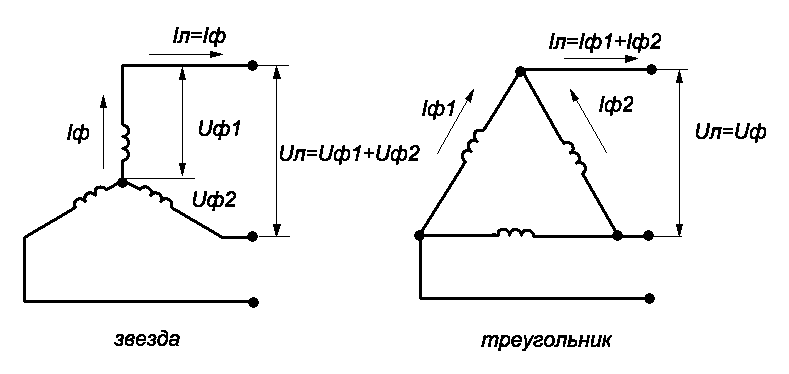 Тогда при подключении в «треугольник» питающее Uлинейное должно быть в 1,73 раза меньше, то есть 380В, что подходит для подключения к нашей сети.

Приведем расчеты, чтобы показать, какие отличия для двигателя будут при переключении обмоток с одной схемы на другую.

Допустим, что ток статора при подключении в треугольник в сеть 380В был 5А, тогда полная его мощность равняется:

Переключим электродвигатель на «звезду» и мощность снизится в 3 раза, так как напряжение на каждой обмотке снизилось в 1,73 раза (было 380 на обмотку, а стало 220), и ток тоже в 1,73 раза: 1,73*1,73=3. Значит с учетом пониженных величин проведем расчет полной мощности.

Как видите – мощность упала в 3 раза!

Но что будет, если есть другой электродвигатель и он работал в «звезде» в сети 380В и током статора в те же 5А, соответственно и обмотки рассчитаны для подключения в «треугольник» на 220В (3 фазы), но по какой-то причине их соединили именно в «треугольник» и подключили к 380В?

В этом случае мощность вырастет 3 раза, так как напряжение на обмотку теперь наоборот увеличилось в 1,73 раза и ток во столько же.

Мощность двигателя стала больше номинальной в эти самые 3 раза. Значит он просто сгорит!

Поэтому нужно подключать электродвигатель по той схеме соединения обмоток, которая соответствует их номинальному напряжению.

Практика — как выбрать схему для конкретного случая

Чаще всего электрики работают с сетью 380/220В, так рассмотрим же как подключить, звездой или треугольником, электродвигатель к такой трёхфазной электросети.

В большинстве электродвигателей может быть изменена схема соединения обмоток, для этого в брно есть шесть клемм, расположены они таким образом, чтобы с помощью минимального набора перемычек можно было собрать нужную вам схему. Простыми словами: вывод начала первой обмотки расположен над концом третьей, начала второй, над концом первой, начало третьей над концом второй.

Как отличить два варианта подключения электродвигателя вы видите на рисунке ниже.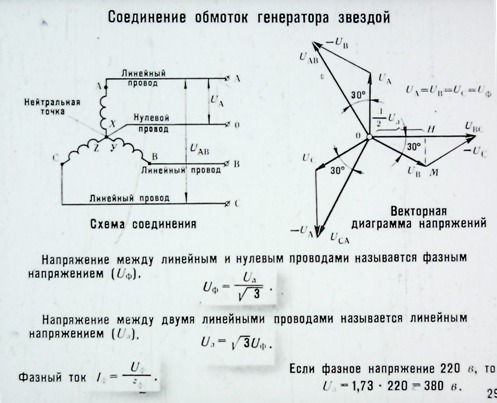

Поговорим о том, какую схему выбирать. Схема подключения катушек электродвигателя не имеет особого влияния на режим работы двигателя, при условии соответствия номинальным параметрам двигателя питающей сети. Для этого смотрим на шильдик и определяем, на какие напряжения рассчитана конкретно ваша электрическая машина.

Обычно маркировка имеет вид:

Это расшифровывается так:

Если межфазное напряжение равно 220 – собирайте обмотки в треугольник, а если 380 – в звезду.

Чтобы просто ответить на вопрос «Как соединить обмотки у двигателя?» мы сделали для вас таблицу выбора схемы соединения:

Переключение со звезды на треугольник для плавного пуска

При запуске электродвигателя наблюдаются высокие пусковые токи. Поэтому для снижения пусковых токов асинхронных двигателей используется схема пуска с переключением обмоток со звезды на треугольник. При этом, как было сказано выше, электродвигатель должен быть рассчитан подключение в «треугольник» и работе под Uлинейным вашей сети.

Таким образом в наших трёхфазных электросетях (380/220В) для таких случаев используют двигатели номинальными «380/660» Вольт, для «Δ/Y» соответственно.

При пуске обмотки включаются «звездой» на пониженное напряжение 380В (относительно номинальных 660В), двигатель начинает набирать обороты и в определенный момент времени (обычно по таймеру, в усложненных вариантах — по сигналу датчиков тока и оборотов) обмотки переключаются в «треугольник» и работают уже на своих номинальных 380 вольтах.

На иллюстрации выше описан такой способ пуска двигателей, но в качестве примера изображен перекидной рубильник, на практике же используют два дополнительных контактора (КМ2 и КМ3), она хоть и сложнее обычной схемы подключения электродвигателя, но это не является её недостатком. Зато у неё целый ряд преимуществ:

Меньше нагрузка на электросеть от пусковых токов.
Соответственно меньшие просадки напряжения и уменьшается вероятность остановки сопутствующего оборудования.
Мягкий пуск двигателя.

Есть два главных недостатка этого решения:

Нужно прокладывать два трёхжильных кабеля от места расположения контакторов непосредственно до клемм двигателя.
Падает пусковой момент.

Заключение

Как таковые различия в рабочих характеристиках при подключении одного и того же электродвигателя по схеме звезда или треугольник нет (он просто сгорит, если вы ошибетесь при выборе). Также, как и нет преимуществ и недостатков какой-либо из схем. Некоторые авторы приводят в качестве аргумента то, что в «звезде» ток меньше. Но при аналогичной мощности двух разных двигателей, один из которых рассчитан на подключение в «звезде», а второй в «треугольнике» к сети, например, 380В — ток будет одинаковым. А один и тот же двигатель нельзя переключать «как попало» и «непонятно для чего», так как он просто сгорит. Главное выбирать тот вариант, который соответствует напряжению питающей сети.

Надеемся, теперь вы стало больше понятно про то, что собой представляет схема звезда и треугольник в электродвигателе, какая разница в подключении каждым из способов и как выбрать схему для конкретного случая. Надеемся, предоставленная информация была для вас полезной и интересной!

Чем отличаются соединения звездой и треугольником

Питание асинхронного электродвигателя происходит от трехфазной сети с переменным напряжением. Такой двигатель, при простой схеме подключения, оснащен тремя обмотками, расположенными на статоре. Каждая обмотка имеет сдвиг друг относительно друга на угол 120 градусов. Сдвиг на такой угол предназначен для создания вращения магнитного поля.

Концы фазных обмоток электродвигателя выведены на специальную «колодку». Выполнено это с целью удобства соединения. В электротехнике используют основных 2 метода подключения асинхронных электродвигателей: методом соединения “треугольника” и метод “звезды”. При соединении концов применяют специально предназначенные для этого перемычки.

Различия между «звездой» и «треугольником»

Исходя из теории и практических знаний основ электротехники, способ подключения «звезда», позволяет электродвигателю работать плавнее и мягче.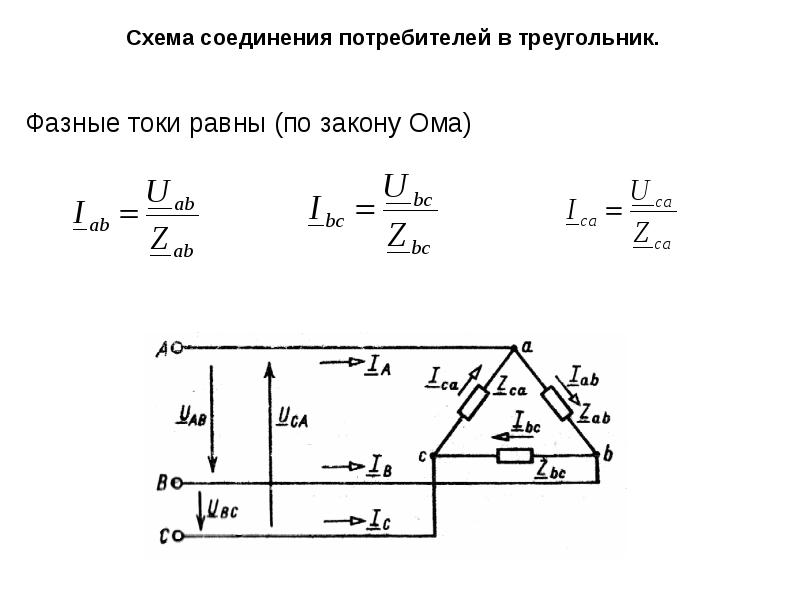 Но при этом данный способ не позволяет выйти двигателю на всю мощность, представленную в технических характеристиках.

Соединив фазные обмотки по схеме «треугольник», двигатель способен быстро выйти на максимальную рабочую мощность. Это позволяет использовать по полной КПД электродвигателя, согласно техпаспорта. Но у такой схемы соединения есть свой недостаток: большие пусковые токи. Для уменьшения значения токов применяют пусковой реостат, позволяя осуществить более плавный пуск двигателя.

Соединение «звездой» и его преимущества

Каждая из трех рабочих обмоток электродвигателя имеет два вывода – соответственно начало и конец. Концы всех трех обмоток соединяют в одну общую точку, так называемую нейтраль.

При наличии нейтрального провода в цепи схему называют 4-х проводной, в противном случае, она будет считаться 3-х проводной.

Начало выводов присоединяют к соответствующим фазам питающей сети. Приложенное напряжение на таких фазах составляет 380 В, реже 660 В.

Основные преимущества применения схемы «звезда»:

Устойчивый и длительный режим безостановочной работы двигателя;
Повышенная надежность и долговечность, за счет снижения мощности оборудования;
Максимальная плавность пуска электрического привода;
Возможность воздействия кратковременной перегрузки;
В процессе эксплуатации корпус оборудования не перегревается.

Существует оборудование с внутренним соединением концов обмоток. На колодку такого оборудования будет выведено всего лишь три вывода, что не позволяет применить другие методы соединения. Выполненное в таком виде электрооборудование, для своего подключения не требует грамотных специалистов.

Подключение трехфазного двигателя к однофазной сети по схеме звезда

Соединение «треугольником» и его преимущества

Принцип соединения «треугольник» заключается в последовательном соединении конца обмотки фазы А с началом обмотки фазы В. И дальше по аналогии – конец одной обмотки с началом другой. В итоге конец обмотки фазы С замыкает электрическую цепь, создавая неразрывный контур. Данную схему можно назвать было кругом, если бы не структура монтирования. Форму треугольника предает эргономичное размещение соединения обмоток.

При соединении «треугольником» на каждой из обмоток, присутствует линейное напряжение равное 220В или 380В.

Основные преимущества применения схемы «треугольник»:

Увеличение до максимального значения мощности электрооборудования;
Использование пускового реостата;
Повышенный вращающийся момент;
Большие тяговые усилия.

Недостатки:

Повышенный ток пуска;
При длительной работе двигатель сильно греется.

Метод соединения обмоток двигателя «треугольником» широко используется при работе с мощными механизмами и наличия высоких пусковых нагрузок. Большой вращающий момент создается за счет увеличения показателей ЭДС самоиндукции, вызванных протекающими большими токами.

Подключение трехфазного двигателя к однофазной сети по схеме треугольник

Тип соединения «звезда-треугольник»

В сложных механизмах, зачастую используется комбинированная схема «звезда-треугольник». При таком переключении резко вырастает мощность, и если двигатель по техническим характеристикам не предназначен для работы по методу «треугольника», то он перегреется и сгорит.

В этом случае напряжение на соединении каждой обмотки будет в 1,73 раза меньше, следовательно, будет меньше и протекающий в этот период ток. Дальше происходит увеличение частоты и продолжение снижения показания тока. Тогда применяя релейно-контактную схему, произойдет переключение со «звезды» на «треугольник».

В итоге, используя данную комбинацию, получим максимальную надежность и эффективную продуктивность используемого электрического оборудования, не боясь вывести ее из строя.

Переключение «звезда-треугольник» допустимо для электродвигателей с облегченным режимом пуска. Этот метод неприменим, если необходимо понизить ток пуска и одновременно не снижать большой пусковой момент. В этом случае применяют двигатель с фазным ротором с пусковым реостатом.

Основные преимущества комбинации:

Увеличение срока службы. Плавный пуск позволяет избежать неравномерности нагрузки на механическую часть установки;
Возможность создания двух уровней мощности.

Подключение звезда и треугольник – в чем разница?

Обмотки генераторов, трансформаторов, электродвигателей и других электрических приемников при их подключении к трехфазной сети соединяются двумя способами: звездой или треугольником. Эти схемы подключения сильно отличаются друг от друга и несут на себе разные токовые нагрузки. Поэтому есть необходимость разобраться в вопросе, как производится подключение звезда и треугольник – в чем разница?

Что собой представляют схемы

Подключение обмоток звездой – это их соединение в одной точке, которая носит название нулевая точка или нейтральная. Она обозначается буквой «О».

Схема подключения треугольником – это последовательное соединение концов рабочих обмоток, в которых начало одной обмотки соединяется с концом другой.

Разница очевидна. Но какую цель преследуют эти виды соединения, почему звезда треугольник применяются в разных электрических установках, в чем эффективность той и другой. Вопросов по данной теме возникает немало, с ними и надо разобраться.

Начнем с того, что при запуске того же электродвигателя ток, который называется пусковым, обладает высоким значением, который превышает номинальную его величину раз в шесть или восемь. Если это маломощный агрегат, то защита такую силу тока может выдержать, а если это электродвигатель большой мощности, то никакие защитные блоки не выдержат. И это вызовет обязательно «проседание» напряжения и выход из строя предохранителей или автоматических выключателей. Сам же двигатель начнет вращаться с небольшой скоростью, отличающуюся от паспортной. То есть, проблем с пусковым током немало.

Поэтому его надо просто снизить. Есть несколько для этого способов:

установить в систему подключения электрического двигателя один из перечисленных приборов: трансформатор, дроссель, реостат;
изменяется схема подключения обмоток ротора.

Именно второй вариант используется на производстве, как самый простой и эффективный. Просто производится преобразование схемы звезда в треугольник. То есть, во время пуска двигателя его обмотки соединяются по схеме звезда, затем как только мотор наберет обороты, переключается на треугольник. Процесс переключения звезды на треугольник производится автоматически.

Рекомендуется в электродвигателях, где используются одновременно два варианта соединения – звезда-треугольник, к соединению обмоток по схеме звезда, то есть, к их общей точке подключения, подсоединить нейтраль от сети питания. Для чего это необходимо делать? Все дело в том, что во время работы по данному варианту подсоединения появляется высокая вероятность асимметрии амплитуд разных фаз. Именно нейтраль будет компенсировать данную асимметрию, которая обычно появляется за счет того, что обмотки статора могут иметь разное индуктивное сопротивление.

Преимущества двух схем

У схемы звезда достаточно серьезные достоинства:

плавный запуск электрического двигателя;
номинальная его мощность будет соответствовать паспортным данным;
двигатель будет работать нормально и при кратковременных высоких нагрузках, и при долгосрочных небольших перегрузов;
в процессе работы корпус мотора не будет перегреваться.

Что касается схемы треугольник, то основное ее преимущество – это достижение электрическим двигателем в процессе его работы максимальной мощности. Но при этом рекомендуется строго придерживаться эксплуатационных режимов, которые расписаны в паспорте мотора. Тестирование электродвигателей, соединенных по схеме треугольник, показало, что его мощность в три раза больше, чем соединенных по схеме звезда.

Если говорить о генераторах, которые выдают ток в питающую сеть, то схемы соединения звезда и треугольник по своим техническим параметрам точно такие же. То есть, выдаваемое напряжение треугольником будет больше, правда, не в три раза, но не менее 1,73 раза. По сути, получается, что напряжение генератора при звезде, равное 220 вольт, преобразуется в 380 вольт, если провести переключение с одного варианта на другой. Но необходимо отметить, что мощность самого агрегата при этом остается неизменной, потому что все подчиняется закону Ома, в котором напряжение и сила тока находятся в обратной пропорциональности. То есть, увеличение напряжения в 1,73 раза, снижает ток точно на такую же величину.

Отсюда вывод: если в клеммной коробке генератора располагаются все шесть концов обмоток, то можно будет получить напряжение двух номиналов, отличающихся друг от друга коэффициентом 1,73.

Делаем выводы

Почему соединения треугольником и звездой сегодня присутствуют во всех современных мощных электродвигателях? Из всего вышесказанного становится понятным, что основное требование ситуации – это снизить токовую нагрузку, которая возникает в процессе пуска самого агрегата.

Если расписать формулы такого подключения, то они будут выглядеть вот так:

Uф=Uл/1,73=380/1,73=220, где Uф – напряжение на фазах, Uл – на питающей линии. Это соединение звездой.

После того, как электрический агрегат разгонится, то есть, скорость его вращения станет соответствовать паспортным данным, произойдет переход на треугольник со звезды. Отсюда фазное напряжение станет равным линейному.

Подключение звезда и треугольник — в чем разница

Для работы электрического прибора, двигателя, трансформатора в трехфазной сети необходимо соединить обмотки по определенной схеме. Наиболее распространенными схемами соединения являются треугольник и звезда, хотя могут применяться и другие способы соединения.

Что представляет собой соединение обмоток звездой?

Трехфазный двигатель или трансформатор имеет 3 рабочих, независимых друг от друга обмоток. Каждая обмотка имеет два вывода — начало и конец. Соединение «звезда» подразумевает собой, что все концы трех обмоток соединяются в один узел, часто называемый нулевой точкой. Отсюда выходит и понятие — нулевая точка.

Начало каждой обмотки соединяются непосредственна с фазами питающей сети. Соответственно начало каждой обмотки соединяется с одной из фаз А, В, С. Между любыми двумя началами обмоток прилаживается фазное напряжение питающей сети, зачастую 380 или 660 В.

Что представляет собой соединение обмоток в треугольник?

Соединение обмоток в треугольник заключается в соединении конца каждой обмотки с началом следующей. Конец первой обмотки, соединяется с началом второй. Конец второй — с начало третей. Конец третей обмотки создает электрический контур, поскольку замыкает электрическую цепь.

При таком соединении к каждой обмотки прилаживается линейное напряжение, обычно равное 220 или 380 В. Такое соединение физически реализуется с помощью металлических перемычек, которые должны быть предусмотрены заводской комплектацией электрического оборудования.

Разница между соединением обмотки в треугольник и звезду

Основная разница заключается в том, что, используя одну питающую сеть, можно достигать разных параметров электрического напряжения и тока в приборе или аппарате. Конечно, данные способы соединения отличаются реализацией, но важна именно физическая составляющая отличия.

Применение способа соединения треугольник, зачастую используется в случаях мощных механизмов и больших пусковых нагрузок. Имея большие показатели тока, протекающего по обмотки, двигатель получает большие показатели ЕДС самоиндукции, что в свою очередь гарантирует больший вращающий момент. Имея большие пусковые нагрузки и одновременно используя схему соединения звезда, можно нанести урон двигателю. Это связано с тем, что двигатель имеет меньшие значение тока, что приводит к меньшим показателям величины вращающегося момента.

Момент пуска такого двигателя и выход его на номинальные параметры может быть продолжительным, что может привести к тепловому воздействию тока, которые во время коммутации может превышать номиналы тока в 7-10 раз.

Преимущества соединения обмоток в звезду

Основные преимущества соединения обмоток в звезду заключаются в следующем:

Понижения мощности оборудования с целью повышения надежности.
Устойчивый режим работы.
Для электрического привода такое соединение дает возможность плавного пуска.

Преимущества соединения обмоток в треугольник

Основными преимуществами соединения обмоток в треугольник являются:

Повышения мощности оборудования.
Меньшие пусковые токи.
Большой вращающийся момент.
Увеличенные тяговые свойства.

Оборудование с возможностью переключения типа соединения со звезды на треугольник

Зачастую электрическое оборудование имеет возможность работать как на звезде, так и на треугольнике. Каждый пользователь должен самостоятельно определить необходимость соединения обмоток в звезду или треугольник.

В особо мощных и сложных механизмах, может применяться электрическая схема с комбинированием треугольника и звезды. В таком случае, в момент пуска, обмотки электрического двигателя соединяются в треугольник. После выхода двигателя на номинальные показатели, с помощью релейно-контакторной схемы треугольник переключается на звезду. Таким способом достигается максимальная надежность и продуктивность электрической машины, без риска нанести ей урон или вывести её из строя.

Посмотрите так-же интересное видео на эту тему:

Схемы электродвигателя звезда и треугольник: виды подключения, особенности и отличия

Асинхронные электрические двигатели в настоящее время используются очень активно. У них есть определенные преимущества, благодаря которым они и стали так популярны. Для подключения к электрической сети мощных двигателей используются схемы «звезда», «треугольник». Электродвигатели, работающие на таких схемах, обладают своими достоинствами и недостатками. Сами же они отличаются надежностью в эксплуатации, возможностью получить большой крутящий момент, а также высоким показателем производительности.

Подключение двигателя

Как показывает практика, существует две оптимальных схемы — «звезда», «треугольник». Электродвигатели подключаются по одной из них. Возможно также преобразование «звезды» в «треугольник», к примеру.

Среди достоинств асинхронных двигателей выделяются следующие:

возможность переключения обмоток во время работы;
восстановление обмотки электрического двигателя;
невысокая стоимость прибора по отношению к другим;
наличие высокой стойкости к механическим повреждениям.

Основная особенность, характеризующая все асинхронные электрические двигатели, — это простота конструкции. Однако при всех своих преимуществах, есть и некоторые недостатки, возникающие во время работы:

Отсутствует возможность контролировать частоту вращения ротора, не теряя при этом мощности.
При увеличении нагрузки уменьшается крутящий момент.
Высокие показатели пусковых токов.

Описание подключений

Схемы «звезда» и «треугольник» для электродвигателя имеют определенные различия в подключении. «Звезда» означает, что концы статорной обмотки оборудования собираются в одной точке. При этом напряжение сети в 380 В будет подаваться на начало каждой из обмоток. Обычно на всех схемах подключения такой способ обозначается как Y.

В случае использования схемы подключения «треугольник» статорные обмотки электродвигателя соединяются последовательно. То есть, конец первой обмотки соединяется с началом второй, она, в свою очередь, — с третьей. Последняя будет замыкать цепь, соединяясь с началом первой.

Отличия схем подключения

Схемы «звезда» и «треугольник» у электродвигателя — это единственные способы их подключения. Они отличаются между собой, обеспечивая разные режимы работы. Так, к примеру, подключение при помощи схемы Y обеспечивает более мягкую работу, если сравнивать с двигателями, соединенными в «треугольник». Данная разница играет ключевую роль при выборе мощности электрического устройства.

Более мощные двигатели эксплуатируются только на «треугольнике». Схема подключения электродвигателя «звезда-треугольник» отлично подходит для тех случаев, когда необходимо обеспечить плавный пуск. А в нужный момент переключиться между обмотками для получения максимальной мощности.

Здесь важно добавить: подключение Y гарантирует мягкую работу, но при этом двигатель не сможет набрать свою паспортную мощность.

С другой стороны, схема соединения электродвигателя «треугольник-звезда-звезда» обеспечит большую мощность, но вместе с этим значительно возрастет и значение пускового тока для оборудования.

Именно разница в мощности между подключением Y и треугольником является основным показателем. Электродвигатель со схемой звезды будет обладать мощностью примерно в 1,5 раза ниже, чем через треугольник, однако такое подключение поможет снизить значение пускового тока. Все соединения, которые имеют в своем составе два способа подключения, являются комбинированными. Обычно они применяются лишь в тех случаях, когда необходимо запустить в работу электрический двигатель с большой паспортной мощностью.

Схема пуска «звезда-треугольник» для электродвигателя отличается еще одним преимуществом. Включение осуществляется по схеме Y, что снижает значение пускового тока. Когда во время работы устройство набирает достаточные обороты, происходит переход на схему треугольника для достижения максимальной мощности.

Комбинированные подключения

Схема переключения «звезда-треугольник» электродвигателя достаточно часто применяется в случаях, когда нужно запустить двигатель с минимальным пусковым током. Но при этом всю работу осуществлять нужно на соединении «треугольник». Для создания такого переключения используются специальные контакторы на три фазы. Для обеспечения автоматического переключения между схемами необходимо выполнить два условия. Во-первых, обеспечить блокировку контактов от одновременного включения. Во-вторых, все работы обязательно должны выполняться с задержкой по времени.

Второй пункт необходим, чтобы со 100% вероятностью произошло полное отключение «звезды» перед включением «треугольника». Если этого не сделать, то во время переключения между фазами будет происходить короткое замыкание. Для выполнения нужных условий используется реле времени с задержкой от 50 до 100 миллисекунд.

Осуществление задержки времени

При использовании комбинированного метода подключения «звезда-треугольник» наличие реле времени для задержки переключения необходимо. Специалисты чаще всего выбирают один из трех способов:

Первый вариант осуществляется при помощи нормально-разомкнутого контакта реле времени. В таком случае РВ будет отключать схему подключения треугольником во время пуска, а за переключение будет отвечать токовое реле РТ.
Второй вариант предполагает применение современного реле времени с задержкой переключения от 6 до 10 секунд.
Третий способ — это управление контакторами электродвигателя автоматическими приборами или вручную.

Рассмотрение способа переключения

Использование классического варианта с применением реле времени для комбинированных схем «звезда-треугольник» ранее считалось наиболее оптимальным. У него имелся лишь один недостаток, который иногда становился достаточно существенным, — габариты самого РВ. Такие типы приспособления гарантировали задержку времени переключения при помощи намагничивания сердечника. Однако на обратный процесс требовалось время.

В настоящее время такие РВ и прочие приборы были вытеснены современными приборами — частотными преобразователями. Переключение схемы электродвигателя со схемой «звезда-треугольник» при помощи ПЧ обладает большими преимуществами. Сюда относят более стабильную работу, низкие пусковые токи.

Это оборудование имеет встроенный микропроцессор, отвечающий за изменение частоты. Если рассматривать суть ПЧ для электродвигателя, то его принцип работы следующий: преобразователь вырабатывает нужную частоту переменного тока. На сегодняшний день в промышленности используются специальные или универсальные модели ПЧ для подключения асинхронных двигателей.

Специальные модели разрабатываются и используются лишь с определенными типами двигателей. Универсальные могут применяться в комплекте с любыми устройствами.

Недостатки схемы

Несмотря на то что классическая схема подключения проста и надежна, она имеет свои определенные недостатки.

Во-первых, очень важно точно определить нагрузку на вал электродвигателя. В противном случае он будет слишком долго набирать обороты, что, в свою очередь, исключит возможность быстрого переключения на схему треугольника при помощи токового реле. В этом режиме нежелательно долго эксплуатировать электрическое устройство.

Во-вторых, при такой схеме подключения возможен перегрев обмоток, из-за чего специалисты рекомендуют установить в схему дополнительное тепловое реле.

В-третьих, при использовании современных временных реле необходимо точно соблюдать паспортную нагрузку на вал электрического двигателя.

Заключение

При использовании подключения схемы «звезда-треугольник» очень важно правильно рассчитать нагрузку на вал электродвигателя. Еще один неприятный факт кроется в том, что в момент переключения с Y на треугольник, когда двигатель еще не набрал нужных оборотов, происходит самоиндукция. В этот момент в сети появляется повышенное напряжение. Это грозит выходом из строя других приборов и устройств, подключенных к этой же сети.

Соединение звездой и треугольником — Стройпортал Biokamin-Doma.ru

Соединение обмоток электродвигателя «треугольником» и «звездой»

Как подключить электродвигатель правильно – знает опытный электрик.

Определение типа способа соединения

Выбор того или иного подсоединения зависит от:

надежности энергосети;
номинальной мощности;
технических характеристик самого двигателя.

Комбинированные схемы актуальны для электромоторов мощностью свыше 5 кВт.

Зависимость выбора от напряжения

Подключение трехфазного двигателя любой мощности осуществляется по определенному правилу: агрегаты низкой мощности присоединяются по схеме «треугольник», а высокомощные – только «звездой».

Так электромотор прослужит долго и проработает без сбоев.

Как снизить пусковые токи электродвигателя?

Соединение звездой и треугольником

Произошёл тут такой случай. Принёс человек в ремонт новый двигатель, который проработал у него 10 секунд и задымил. Двигатель он подключил треугольником в обычную трехфазную сеть, а на шильдике двигателя есть схема, на которой написано: треугольник — 230 В. звезда — 400 В. В общем, подключил он неправильно, потому двигатель и сгорел.

Для тех, кто не понимает, почему нельзя делать так, как сделал сделал тот товарищ, спаливший двигатель, предназначена эта статья.

Вот всем известные схемы подключения треугольником (D) и звездой (Y):

Совершенно неважно как вы подключаете двигатель: звездой или треугольником. Важно только то, какое напряжение вы подаёте на обмотки двигателя. Будет ли это напряжение получаться как межфазное (треугольник) или как фазное (между фазой и нулевой точкой — звезда) — двигателю это совершенно неважно.

Если у вас есть двигатель с номинальным напряжением обмотки 220 В и есть две разные трёхфазные сети, у одной из которых линейное напряжение 380 В (220 В на фазу), а у другой — 220 В (127 В на фазу), то к первой вы можете подключать двигатель звездой, а ко второй — треугольником, разницы для двигателя не будет никакой, отличаться будут лишь токи, протекающие в проводниках на линии, ведущей к двигателю.

Линейное напряжение трёхфазной сети — это межфазное напряжение, именно оно обозначается на шильдиках двигателей. Фазное напряжение (между фазой и нейтралью) на шильдиках не обозначается.

Условно говоря, вы можете считать, что на шильдике обозначено фазное напряжение, но только в том случае, если собираетесь подключать двигатель только к одной фазе через конденсатор.

Для сетей переменного тока 50 Гц линейное напряжение выше фазного в квадратный корень из трёх раз (т.е. примерно в 1.73 раза, т.е. 220 х 1.73 = 380).

Для такого двигателя на шильдике будет написано: D/Y 220V / 380V, 4.9А / 2.8А. Соответственно, в этих двух случаях отличаются только токи в проводниках, ведущих к двигателю (именно они указаны на шильдике, в то время как ток на обмотке будет одинаковый, что видно на рисунке сверху). Следовательно, для России (линейное напряжение 400 В) для такого двигателя надо использовать схему подключения звезда.

Номинальное напряжение обмотки большинства двигателей при частоте тока 50 Гц обычно составляет либо 127 В , либо 230 В, либо 400 В, либо 690 В. Ну, или как было раньше: 220, 380, 660 В соответственно.

Теперь логичный вопрос:

если двигателю нет разницы по какой схеме он будет подключен, а важно лишь напряжение на обмотках, то зачем вообще делать двигатели с разным номинальным напряжением на этих самых обмотках?

Двигатели малой мощности

D 230V / Y 400V

Для того, чтобы двигатель можно было так подключить в однофазную сеть, его номинальное напряжение каждой обмотки должно быть равно фазному напряжению сети. Это значит, что если двигатель планируется использовать в России или Европе, то номинальное напряжение обмотки должно быть равно 230 В. В таком случае этот двигатель можно будет использовать как в трёхфазной сети с линейным напряжением 400 В (подключение звезда), так и в однофазной сети 230 В (подключение треугольником через конденсатор). Это те самые двигатели, где на шильдике написано напряжение D 220V / Y 380V.

Соответственно, если нужно такой двигатель использовать в стране с более низким линейным напряжением, например, в США (где линейной напряжение 240 В, а фазное — 120 В при частоте тока 60 Гц), то по-нормальному подключить такой двигатель в их однофазную сеть через конденсатор не получится. Однако, по крайней мере, можно использовать 3-фазное подключение треугольником. Для такого подключения потребуется немного более высокое напряжение, чем 230 В (из-за частоты тока 60 Гц), но у них там как раз 240 В, что как раз подходит.

D 115V / Y 230V

Одновременно с этим, маломощные двигатели, предназначенные для стран, где стандартное напряжение ниже, чем у нас, будут подключаться как D 127V / Y 220V. Однако, двигатели с такой надписью на шильдике вы вряд ли найдёте, потому что 127 В, 50 Гц — это очень малораспространённое напряжение в мире (см. тут). Поэтому, скорее всего, вам встретится двигатель с шильдиком, где будет указано напряжение D 115V / Y 208-230V.
Насчет заморочки с 208 вольтами можно почитать в этой статье.

Подключить такой двигатель к стандартной российской трёхфазной сети (все три фазы) можно только через преобразователь частоты переменного тока, поскольку на них есть возможность переключения линейного напряжения на выходе: 230 / 400 В.
В однофазную сеть можно подключить звездой через конденсатор. Тогда напряжение, подаваемое на каждое обмотку, будет составлять половину фазного напряжения сети (230 В / 2 = 115 В). Выглядит это вот так:

Двигатели мощности более 5 кВт

D 400V / Y 690V

Для двигателей мощнее 5 кВт обычно не предусматривают возможность подключения в однофазную сеть, т.е. номинальное напряжение обмоток делают такое, которое соответствует линейному напряжению. Т.е. штатной схемой подключения таких двигателей в трёхфазную сеть является треугольник. В России и Европе это двигатели с номинальным напряжением обмоток 400В, т.е. где на шильдике написано D 400V / Y 690V.

Для определённых задач, где на валу двигателя находится свободная нагрузка (системы вентиляции, осевые насосы), ну, и вообще те задачи, где возможно регулирование скорости вращения вала только лишь напряжением (трансформатором), часто используют схему подключения «звезда» при старте с последующим переключением на «треугольник». Т.е. при старте на обмотку подаётся заниженное напряжение 230В вместо номинальных 400В, а затем происходит переключение на штатный режим (т.е. на треугольник). Из-за свободной нагрузки на валу момент вращения при старте на низком напряжении также будет ниже, т.е. пусковой ток будет не столь высок, как при старте на номинальном напряжении. Поэтому такой пуск двигателя называют «щадящим».

Следует помнить, что для нагрузок, требующих большого момента при запуске, подобный режим приведет напротив, к возрастанию тока в обмотках и последующим неприятным событиям.

Кроме того, надо иметь ввиду, что подключение двигателей даже со свободной нагрузкой на валу звездой для «щадящего старта» вовсе не означает, что если по такой схеме постоянно эксплуатировать двигатель (не переходя на треугольник), то такой режим станет «щадящим» для него. Низкий момент при старте ещё не означает, что заниженное напряжение годится для его нормальной работы, поскольку сам двигатель (со своими номинальными характеристиками) обычно как раз и подбирается под конкретную нагрузку. Поэтому постоянная эксплуатация двигателей на напряжении ниже номинального иногда приводит к их выходу из строя. Чтобы не было неприятностей двигатель всегда надо эксплуатировать на номинальном напряжении, а если требуется снизить обороты вращения вала, то тогда нужно использовать редукторы или преобразователи частоты переменного тока, а не пытаться решить вопрос самым дешёвым способом. К слову сказать, частотник тоже меняет не только частоту тока, но и напряжение, однако, он это делает с умом.

D 220V / Y 440V

Двигатели мощностью выше 5 кВт, изготовленные в США, будут иметь номинальное напряжение обмотки 220 В, т.е. на шильдике будет написано D 220V / Y 440V (для 60 Гц). Подключать такие двигатели к российской трёхфазной сети 400 В следует звездой, а к российской однофазной сети через конденсатор — треугольником. Касательно величин напряжения, есть двигатели, где более подробно расписано подключение для сетей 50 Гц и 60 Гц, например вот так:

Звезда и треугольник принцип подключения. Особенности и работа

Схемы

Схема звезды

Схема треугольника

В схеме треугольника при отключенной нагрузке и симметричной ЭДС равно 0.

Фазные и линейные величины

Особенности схем

Для этого можно применить некоторые методы:

Подключить на запуск электродвигателя реостат, дроссель, либо трансформатор.
Изменить вид соединения обмоток ротора электродвигателя.

Достоинства схем

Соединение по схеме звезды имеются важные преимущества:

Плавный пуск электрического мотора.
Позволяет функционировать электродвигателю с заявленной номинальной мощностью, соответствующей паспорту.
Электродвигатель будет иметь нормальный рабочий режим при различных ситуациях: при высоких кратковременных перегрузках, при длительных незначительных перегрузках.
При эксплуатации корпус электродвигателя не перегреется.

Процессы, происходящие при изменении схемы звезда и треугольник в разных случаях

Обмотки генератора и трансформатора

Лампы освещения

Чем отличаются соединения звездой и треугольником

Различия между «звездой» и «треугольником»

Соединение «звездой» и его преимущества

Основные преимущества применения схемы «звезда»:

Устойчивый и длительный режим безостановочной работы двигателя;
Повышенная надежность и долговечность, за счет снижения мощности оборудования;
Максимальная плавность пуска электрического привода;
Возможность воздействия кратковременной перегрузки;
В процессе эксплуатации корпус оборудования не перегревается.

Подключение трехфазного двигателя к однофазной сети по схеме звезда

Соединение «треугольником» и его преимущества

При соединении «треугольником» на каждой из обмоток, присутствует линейное напряжение равное 220В или 380В.

Основные преимущества применения схемы «треугольник»:

Увеличение до максимального значения мощности электрооборудования;
Использование пускового реостата;
Повышенный вращающийся момент;
Большие тяговые усилия.

Недостатки:

Повышенный ток пуска;
При длительной работе двигатель сильно греется.

Подключение трехфазного двигателя к однофазной сети по схеме треугольник

Тип соединения «звезда-треугольник»

Основные преимущества комбинации:

Увеличение срока службы. Плавный пуск позволяет избежать неравномерности нагрузки на механическую часть установки;
Возможность создания двух уровней мощности.

Подключение звезда и треугольник – в чем разница?

Что собой представляют схемы

Поэтому его надо просто снизить. Есть несколько для этого способов:

установить в систему подключения электрического двигателя один из перечисленных приборов: трансформатор, дроссель, реостат;
изменяется схема подключения обмоток ротора.

Преимущества двух схем

У схемы звезда достаточно серьезные достоинства:

плавный запуск электрического двигателя;
номинальная его мощность будет соответствовать паспортным данным;
двигатель будет работать нормально и при кратковременных высоких нагрузках, и при долгосрочных небольших перегрузов;
в процессе работы корпус мотора не будет перегреваться.

Делаем выводы

Если расписать формулы такого подключения, то они будут выглядеть вот так:

Uф=Uл/1,73=380/1,73=220, где Uф – напряжение на фазах, Uл – на питающей линии. Это соединение звездой.

Расчет мощности двигателя при схеме соединения звезда-треугольник

В этой статье я хотел бы рассказать как изменяется мощность двигателя при схеме соединения обмоток звезда – треугольник и наоборот.

В связи со спецификой своей работы я сталкиваюсь с ремонтов различных асинхронных двигателей и в большинстве случаев выход из строя двигателя происходит при неправильном переключении обмоток двигателя, так как люди не понимают, как изменяется мощность двигателя при переключении с треугольника на звезду и обратно, и как это может отразится на работоспособности самого двигателя.

Определение мощности при схеме соединения звезда

Известно [Л1. с. 34], что при соединении в звезду линейные токи Iл и фазные токи Iф равны между собой, при этом между фазным Uф и линейным напряжением Uл существует соотношение, где Uл = √3*Uф , в результате Uф = Uл/√3.

Исходя из этого, полная мощность определяется через линейные величины:

Определение мощности при схеме соединения треугольник

При схеме соединения в треугольник, фазные и линейные напряжения равны между собой Uл = Uф, при этом между токами существует соотношение: Iл = √3*Iф, в результате Iф = Iл/√3.

Исходя из этого, полная мощность определяется, как:

Для определения активной и реактивной мощности используются формулы:

Из-за того что формулы для схемы соединения звезды и треугольника имеют одинаковый вид, у мало опытных инженеров происходят недоразумения, будто вид соединения безразличен и ни на что не влияет.

Рассмотрим на примере, на сколько ошибочные данные утверждения. В данном примере будем рассматривать электродвигатель типа АИР90L2, который имеет две схемы подключения ∆/Y, технические характеристики двигателя:

коэффициент мощности cosφ = 0,84;
коэффициент полезного действия, η = 78,5%;

Определяем ток двигателя при напряжении 380 В и схеме соединения треугольник, мощность при таком соединении составляет 3 кВт:

Теперь соединим обмотки двигателя в звезду. В результате на фазную обмотку пришлось на 1,73 раза более низкое напряжение Uф = Uл/√3, соответственно и ток уменьшился в 1,73 раза, но так как при соединении в треугольник Uл = Uф, а линейный ток был в 1,73 раза больше фазного Iл = √3*Iф, то получается, что при соединении в звезду, мощность уменьшится в √3*√3 = 3 раза, соответственно и ток уменьшиться в 3 раза.

Из всего выше изложенного можно сделать, следующие выводы:

1. При переключении двигателя со звезды на треугольник, мощность двигателя увеличивается в 3 раза и наоборот. Использовать данные переключения, можно если схемы подключения двигателя позволяет выполнять переключения ∆/Y, в противном случае, двигатель может сгореть, когда Вы будете выполнять переключение со звезды на треугольник.

2. Как Вы уже поняли, используя схему переключения обмоток двигателя со звезды на треугольник, мы уменьшаем пусковые токи при пуске двигателя на пониженном напряжении, а затем его повышаем до номинального. Когда обмотки двигателя соединены в звезду, к каждой из них подводиться напряжение меньше номинального в 1,73 раза. В процессе пуска, двигатель увеличивает скорость вращения и ток снижается. В это время происходит переключение на треугольник.

Обращаю Ваше внимание, что двигатели, которые недогружены, работают с очень низким cosφ. Поэтому рекомендуется заменить недогруженный двигатель, на двигатель меньшей мощности. Если же у недогруженного двигателя, запас мощности велик, то cosφ можно поднять путем переключения обмоток с треугольника на звезду без риска перегреть двигатель.

Как мы видим ничего сложного нету в определении мощности при схеме звезда и треугольник.

1. Звезда и треугольник. Е.А. Каминский, 1961 г.

§60. Схема соединения «звездой» | Электротехника

Схема «звезда с нулевым проводом».

При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой, или нейтралью источника (рис. 206).

Рис. 206. Схема «звезда с нулевым проводом», направление в ней линейных и фазных токов и напряжений

Приемники электрической энергии объединяют в три группы Z_A, Z_B и Z_c (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым, или нейтральным.

Напряжения u_А, u_в и u_с между началами и концами обмоток отдельных фаз источника или фаз нагрузки Z_A, Z_B и Z_c называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках.

Фазными токами i_A, i_B, i_c называют токи, протекающие по обмоткам источника или фазам нагрузки Z_A, Z_B и Z_c. Напряжения u_AB, u_BC, u_CA между линейными проводами и токи, проходящие по этим проводам, называют линейными.

Примем условно за положительное направление токов i_A, i_B и i_c в фазах источника — от конца соответствующей фазы к ее началу,в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику.

Будем считать положительными напряжения u_А, u_B и u_C в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения u_АВ, u_BC, u_СА — если они направлены от предыдущей фазы к последующей.

Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным, т. е. I_л = I_ф, так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений.

Мгновенные значения напряжений согласно второму закону Кирхгофа:

u_АВ = u_А – u_B; u_BC = u_B – u_С; u_СА = u_С – u_А.

Переходя от мгновенных значений напряжений к их векторам, имеем:

Следовательно, линейное напряжение равно разности векторов соответствующих фазных напряжений.

По полученным векторным уравнениям можно построить векторную диаграмму (рис. 207, а), которую можно преобразовать в диаграмму (рис. 207,б). Из этой диаграммы видно, что в симметричной трехфазной системе векторы линейных напряжений →u_AB, →u_ВС, →u_СА образуют равносторонний треугольник ABC, внутри которого расположена симметричная трехлучевая звезда фазных напряжений →u_А, →u_В, →u_С.

В равнобедренных треугольниках АОВ, ВОС и СОА основание равно U_л две другие стороны — U_ф и острый угол между этими сторонами и основанием составляет 30°.

Рис. 207. Векторные диаграммы напряжений для схемы «звезда с нулевым проводом»

Следовательно,

U_л = 2U_ф cos 30° = 2U_ф (√3)/2 = √3 U_ф

Таким образом, в трехфазной системе, соединенной по схеме «звезда с нулевым проводом», линейное напряжение больше фазного в √З раз. Величина √З = 1,73 положена в основу шкалы номинальных напряжений переменного тока: 127, 220, 380 и 660 В. В этом ряду каждое следующее значение напряжения больше предыдущего в 1,73 раза.

В нулевом проводе проходит ток i0, мгновенное значение которого равно алгебраической сумме мгновенных значений токов, проходящих в отдельных фазах: i0 = iA+iB+iC.

Переходя от мгновенных значений токов к их векторам, имеем:

→i₀=→i_A+→i_B+→i_C.

Векторы токов →i_А, →i_В и →i_С сдвинуты относительно векторов соответствующих напряжений →u_A, →u_B, →u_С на углы →i_A, →i_B, →i_C (рис. 208, а). Значения этих углов зависят от соотношения между активным и реактивным сопротивлениями, включенными в данную фазу.

На этой же диаграмме показано сложение векторов →i_А, →i_В и →i_C для определения вектора тока →i₀. Обычно ток →i₀ меньше токов

Рис. 208. Векторные диаграммы напряжений и токов в отдельных фазах для схемы «звезда с нулевым проводом» при неравномерной (а) и равномерной (б) нагрузках фаз

I_A, 1_В и I_C в линейных проводах, поэтому нулевой провод имеет площадь поперечного сечения, равную или даже несколько меньшую площади сечения линейных проводов.

В схеме «звезда с нулевым проводом» приемники электрической энергии можно включать на два напряжения: линейное U_л (при подключении к двум линейным проводам) и фазное U_Ф (при подключении к нулевому и одному из линейных проводов).

Схема «звезда без нулевого провода».

При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (R_A =R_B = R_C и Х_A=Х_В=Х_С), фазные токи i_A, i_B и i_C будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы. В этом случае получаем симметричную систему токов, при которой токи i_A, i_B, i_C будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i₀ в нулевом проводе в любой момент времени равен нулю (рис. 208,б).

Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209).

Рис. 209. Схема «звезда без нулевого провода»

Такая схема называется «звезда без нулевого провода». При трехпроводной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210).

Рис 210. Кривые изменения токов в линейных проводах (а) при трехпроводной системе и направление в них токов в различные моменты времени (б в, г)

Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207).

Такими же будут и соотношения между фазными и линейными токами и напряжениями:

I_л = I_Ф и U_л = √3 U_Ф

Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три фазы.

При неравномерной нагрузке напряжения на отдельных фазах нагрузки будут различными. На некоторых фазах (с меньшим сопротивлением) напряжение уменьшится, а на других увеличится по сравнению с нормальным, что является недопустимым.

Практически неравномерная нагрузка фаз возникает при питании трехфазным током электрических ламп, так как в этом случае распределение тока между всеми тремя фазами не может быть гарантировано (отдельные лампы могут включаться и выключаться в индивидуальном порядке). Особенно опасны в схеме «звезда без нулевого провода» обрыв или короткое замыкание в одной из фаз.

Можно показать путем построения соответствующих векторных диаграмм, что при обрыве в одной из фаз напряжение в других двух фазах уменьшается до половины линейного, вследствие чего лампы, включенные в эти фазы, будут гореть с недокалом.

При коротком замыкании в одной из фаз напряжение в других фазах увеличивается до линейного, т. е. в √З раз, и все лампы, включенные в этих фазах, перегорят. Поэтому при схеме «звезда с нулевым проводом» во избежание разрыва цепи нулевого провода в ней не устанавливают предохранители и выключатели.

Эквивалентное преобразование треугольника в звезду

Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. приемников электрической энергии.

Определение соединения сопротивлений треугольником

Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.

Соединение, при котором три сопротивления, находящиеся в пассивных ветвях, соединены между собою попарно и образуют замкнутый контур — называется треугольником.

Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.

Определение соединения сопротивлений звездой

Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.

Причина преобразования треугольника в звезду

При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.

Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.

Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.

Формулы для расчета преобразования треугольника в звезду

Пример преобразования

Для электрической цепи необходимо выполнить преобразование треуголькника R12 — R23 — R31 в звезду.

Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.

Удаляем соединение сопротивлений треугольником. В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.

ТОЭ Лекции- №7 Преобразование треугольника и звезды сопротивлений

Пусть требуется рассчитать цепь, показанную на рис. 7.1, а.

Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется
только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка
определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни
последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование
треугольника сопротивлений в эквивалентную звезду.

Треугольник и звезда сопротивлений имеют вид, показанный на рис. 7.2.

Если при замене одной из этих схем другой не изменяются потенциалы одноименных
точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае
говорят, что схемы эквивалентны.

Можно показать, что условием эквивалентности являются следующие уравнения:

а) при преобразовании треугольника в звезду:

б) при преобразовании звузды в треугольник:

Например, сопротивление звезды R1, присоединенное к узлу 1, получается
перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением
полученного произведения на сумму всех сопротивлений треугольника.

При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1
и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение,
деленное на сопротивление третьего луча звезды R3.

Пример 1.3. Рассчитать токи в цепи,
изображенной на рис. 1.12, а, при следующих числовых значениях ее
параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.

а) Решение преобразованием треугольника в звезду.

Теперь общее сопротивление цепи легко находится:

Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах),
равен:

Токи в паралельных ветвях:

Возвращаемся к исходной схеме (рис. 7.1, а):

Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A.
Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.

б) Решение преобразованием звезды в треугольник.

Преобразуем звезду, образуемую в схеме на рис. 7.1, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 7.1, в).

Определяем сопротивления треугольника:

Теперь рассчитываем преобразованную цепь. Сначала находим эквивалентные сопротивления участков ac и cd:

Затем определяем общее сопротивление и токи:

Возвращаемся к исходной схеме:

Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.

Схемы соединений обмоток трехфазных трансформаторов

При соединении обмоток трехфазных трансформаторов как двухобмоточных, так и трехобмоточных применяют различные схемы соединения. Однако в силовых трансформаторах как повышающих, так и понижающих, главных образом применяются схемы соединения в звезду, треугольник и зигзаг—звезду. Для практических целей в энергосистемах не требуется большого количества схем соединений обмоток. Так, для мощных трансформаторов применяется одно соединение обмоток ВН и СН— в звезду с выведенной нейтралью (Y0), а для обмоток НН — в треугольник (А).

ГОСТ 12022-66 предусматривает для трансформаторов мощностью 25, 40, 63 и 100 кВА с ПБВ (с переключением ответвлений обмотки трансформатора без возбуждения — т. е. после отключения всех обмоток трансформатора от сети) и для трансформаторов мощностью 63, 100, 160 и 250 кВА с ПБВ и РПН (с регулированием напряжения путем переключения ответвлений обмотки трансформатора под нагрузкой при следующем сочетании напряжений па стороне ВН и НН (кВ) на стороне обмотки низшего напряжения соединение в зигзаг—звезду.
Соединение в зигзаг — звезду дает возможность при несимметрии нагрузки на стороне НН сглаживать на стороне ВН эту неравномерность. Кроме того, схема зигзага допускает иметь три напряжения, например 127, 220 и 380 е.

Другие схемы соединений обмоток для силовых трансформаторов применяются крайне редко. Область применения таких схем ограничивается трансформаторами специального назначения (электропечными, для питания ртутных выпрямительных установок, для преобразования частоты, числа фаз переменного тока, электросварочными и др.).
а) Соединение обмоток в звезду
Если соединить концы или начала обмоток трех фаз вместе, то получится соединение в звезду. На рис. 3,а показаны обмотки НН, соединенные в звезду. В нулевой точке соединены все концы обмоток у, z, а к началам а, Ьу с— подводится напряжение от трехфазной сети или генератора. На рис. 3,6 показано то же соединение обмоток НН в звезду, но только в нулевую точку соединены другие концы обмоток, которые прежде присоединялись к сети. При независимой друг от друга работе трансформаторов подобное «переворачивание» одной из обмоток, соединенной в звезду, не имеет значения, по параллельная работа таких трансформаторов, как это будет доказано далее, невозможна. В звезду могут быть соединены различные обмотки трансформатора как ВН и СН, так и НН. Нулевая точка звезды может быть выведена на крышку трансформатора (рис. 3,б).

По схеме звезда или звезда с выведенной нулевой точкой соединяются обычно обмотки ВН как повышающих, так и понижающих трансформаторов различной мощности.

Рис. 3. Соединение обмотки НН в звезду.

а — одна схема соединения; б — другая схема соединения; в — соединение в звезду с выведенной нулевой точкой; г — векторная диаграмма линейных э. д с.
Обмотки ВН при напряжениях 110 кВ и выше предпочтительно соединять в звезду с выведенной нулевой точкой, что дает возможность заземления нейтрали. При этом можно выполнить один конец каждой из фаз, прилегающий к нейтрали, с пониженной изоляцией.

Обмотки СН соединяются большей частью по схеме Y0.
Обмотки НН соединяются в звезду с выведенной нулевой точкой у понижающих трансформаторов тогда, когда напряжение этой обмотки 230 или 400 в при мощностях до 560 кВА. В звезду без выведения нулевой точки обмотки НН соединяются крайне редко, например, у понижающих трансформаторов мощностью 1 000—5 600 кВА при сочетании напряжений обмоток ВН и НН 10 000/6 300 е.

Обычно обмотки НН повышающих трансформаторов, а также большей части понижающих мощных соединяются в треугольник.
Векторная диаграмма линейных э. д. с. для соединения обмоток в звезду строится следующим образом. Откладываем в масштабе вектор ах (рис. 3,г). Так как мы знаем, что концы обмоток л*, //, г электрически соединены, то из точки х под углом 120° к ах откладываем в том же масштабе вектор by. Далее из точки у под углом 120° к вектору by откладываем вектор сг.

При соединении обмотки в звезду с выведенной пулевой точкой можно получить два напряжения (фазное и лилейное). Если измерять напряжение между нулем и какой-либо фазой, то получим напряжения, называемые фазными ((Уф). На рис. 3,г они изображены векторами ха, yb и гс.
Напряжения, измеренные между фазами а и ft, b и с, с и а, называются линейными (междуфазными) напряжениями (U). Эти напряжения па рис. 5-3,г изображены в масштабе ab, be и са. Так как в треугольнике abx угол между векторами ха и yb равен 120°, то зависимость между линейным и фазным напряжениям будет U = = Uфv3 , т. е. линейное напряжение в v3 раз больше фазного. Если трансформатор, обмотки НН которого включены в звезду, имеет линейное напряжение 220 в, то фазное напряжение будет:

б) Соединение обмоток в треугольник

Если соединить конец фазы а (точку х) с началом фазы с, конец фазы с (точка z) с началом фазы b и конец фазы b (точка у) с началом фазы а, то получится соединение в треугольник (рис. 4,а). Соединение в треугольник можно осуществить (рис. 4,6) иначе, соединяя конец фазы а с началом фазы b, конец фазы b с началом фазы с и конец фазы с с началом фазы а.
Векторная диаграмма линейных э. д. с. при соединении обмоток в треугольник по схеме рис. 4,а будет равносторонним треугольником рис. 4,в и г. При соединении в треугольник фазные напряжения будут равны линейным.

В мощных трансформаторах принято одну из обмоток всегда соединять в треугольник. Делается это по следующим соображениям:
Как известно, намагничивающий ток трансформатора имеет несинусоидальную форму, т. е. содержит высшие гармонические. Наибольший удельный вес имеет третья гармоническая. Если все обмотки трансформатора соединить в звезду, то третья гармоническая в намагничивающем токе образоваться не может, так как она будет направлена во всех фазах одинаково: (3 • 120° = 360° = = 0°) и поэтому форма кривой фазного напряжения исказится, что может привести к нежелательным явлениям в эксплуатации. По этим соображениям принято одну из обмоток обязательно соединять в треугольник. Если же почему-либо требуется построить мощный двухобмоточный трансформатор или автотрансформатор с соединением обмоток звезда — звезда (например, трехфазный автотрансформатор), то он снабжается дополнительной третьей обмоткой, соединенной в треугольник, которая в некоторых случаях может даже не иметь внешних выводов.

Рис. 4. Соединение обмоток НН в треугольник.

а — первая схема соединения обмоток в треугольник, б — вторая схема соединения обмоток в треугольник; в — вектора линейных э. д. с фаз a, b и с; г —векторная диаграмма линейных э д с

Обычно в треугольник соединяется обмотка низшего напряжения.

В мощных трансформаторах номинальный ток обмотки НН часто составляет несколько тысяч ампер и конструктивно бывает легче выполнить соединение обмотки в треугольник, так как фазный ток при той же мощности получается в v 3 раз меньшим, чем при соединении в звезду.
В треугольник соединяются обмотки НН всех повышающих и понижающих двухобмоточных и трехобмоточных трехфазных трансформаторов мощностью 5 600 кВА и больше, понижающих трансформаторов мощностью до 5 600 кВА, имеющих на стороне НН напряжения 38,5; 11; 10,5; 6,6; 6,3; 3,3; 3,15 и 0,525 кВ, а также обмотки НН всех мощных однофазных двухобмоточных и трехобмоточных трансформаторов, предназначающихся для соединения в трехфазные группы. Обмотки ВН и СН силовых повышающих и понижающих трансформаторов обычно в треугольник не соединяются.

в) Соединение обмоток в зигзаг — звезду (равноплечий и неравноплечий зигзаг)
Равноплечий зигзаг может быть получен, если соединить по одной из трех схем рис. 5,а, бив концы и начала шести полуобмоток с одинаковыми числами витков (а следовательно, и э. д. е.), расположенных по две полуобмотки на каждой фазе трансформатора.

Рис. 5. Соединение обмотки НН в равноплечий зигзаг.

а —первая схема соединения; б — вторая схема соединения; в — третья схема соединения; г — векторная диаграмма э. д. с. звезды нижних полукатушек; д — векторная диаграмма линейных э. д. с.
Построим векторную диаграмму соединений обмоток в зигзаг согласно схеме рис. 5,а. Начнем построение с нижних полуобмоток, соединенных в звезду. Векторная диаграмма для этих полуобмоток представлена на рис. 5,г. Согласно схеме рис. 5,а начало а’ нижней полуобмотки электрически соединено с концом zr верхней.

Вектор г’с должен пойти в направлении, противоположном вектору zc’, а потому из точки а’г’ (рис. 5,д) откладываем вектор zrc в направлении, противоположном вектору zc’.

Аналогичным образом строим векторы остальных частей обмоток. Обмотка при соединении в зигзаг обычно выполняется двухслойной, причем каждый слой имеет свободные начала и концы.

Один из слоев обмотки наматывают правой намоткой, другой — левой. Делается это для удобства выполнения соединений в зигзаг. При соединении обмотки в зигзаг мы можем получить три различных напряжения.

Схема равноплечего зигзага применяется для нормальных силовых понижающих трансформаторов, для мощностей 25, 40, 63, 100, 160 и 250 кВА в случае, когда при большой несимметрии нагрузок фаз необходимо на стороне питания иметь схему звезды.

Неравноплечий зигзаг получается, если по схемам а, б и в (рпс. 5-5) соединить концы и начала полуобмоток с неодинаковым числом витков. На рис. 6,а и б даны две схемы соединения в неравноплечий зигзаг при отношении числа витков в полуобмотках 1 : 2.
Схема неравноплечего зигзага применяется иногда иностранными фирмами для трансформаторов специального назначения. В нормальных силовых трансформаторах наши заводы эту схему не применяют.
г) Соединение обмоток по схеме А
Если соединить обмотки трансформатора, как показано на рис. 7,а, то получится соединение по схеме А. Схему, как это видно из векторной диаграммы

Рис. 7. Соединение обмотки по схеме А.

а — схема соединений обмоток; б — векторная диаграмма.
(рис. 7,6), можно представить как треугольник а’Ьс’, у которого две стороны а’b и cfb имеют дополнительные витки (а’а и с’с).

Для того чтобы получить соединения обмоток, отвечающих векторной диаграмме рис. 7,6, принимают соотношения числа витков на фазах трансформатора, которые должны удовлетворять следующим трем условиям:

т. е. обмотка фазы с должна иметь 2/3 числа витков обмоток фаз а и b.

Нулевой вывод берется от середины обмотки фазы с, и, кроме того, число витков дополнительных участков фаз а и b должно быть одинаково и составлять Уз общего числа витков этих фаз.

Рис. 8. Соединение обмоток в скользящий треугольник.

а — схема соединений обмоток; б—векторная диаграмма.
Эта схема не имеет применения в нормальных силовых трансформаторах и применяется только там, где необходимо иметь соединение обмоток в треугольник и в то же время требуется иметь нулевую точку.

д) Соединение обмоток в скользящий треугольник
На рис. 8 даны схема соединения обмотки и векторная диаграмма скользящего треугольника. Из рассмотрения схемы видно, что изменяя положение концов

а’b’с’ (рис. 8,а) и «скользя» ими по обмотке из крайнего верхнего положения к нижнему, можно перейти от треугольника к звезде. При этом могут быть получены все промежуточные положения. Это дает возможность, так же как в схеме неравноплечего зигзага, иметь различные углы сдвига фаз (ф).
Схема скользящего треугольника применяется иногда для трансформаторов, питающих электрические печи. В силовых трансформаторах эта схема не применяется.

Науки о Земле сегодня, Звездная лаборатория

Науки о Земле сегодня, Звездная лаборатория
Земля
Наука сегодня

Расс Колсон

Государственный университет Миннесоты
Moorhead

Лаборатория наук о Земле сегодня, Расстояние до звезд
(35-70 минут, в зависимости от математических навыков)

Часть 1: Метод триангуляции

Расстояние до ближайших звезд определяется триангуляцией.
Концепция триангуляции довольно проста:
вам нужно представить прямоугольный треугольник, в котором одна сторона треугольника
расстояние, которое вы хотите измерить (вспомните упражнение по измерению дерева).
Если вы можете измерить один угол треугольника, кроме прямого,
(любой из них работает) и длину одной другой стороны треугольника, тогда
интересующая сторона может быть рассчитана геометрическими или тригонометрическими методами.

Вот упражнение для практики
«поиск» треугольников, прежде чем мы попытаемся сделать звезды. Определить
длина одного из лабораторных столов без фактического измерения его длины.

Вы можете использовать транспортир и
линейкой (можно измерить ширину стола или расстояние до стола,
но вы не можете использовать линейку для измерения длины стола).
Вы можете положить какой-нибудь предмет на
дальний конец стола (камень, карандаш) для проведения триангуляции (т. е.
угол в сторону).

Это можно сделать, используя одинаковые треугольники или
тригонометрия. Ты
при желании можно использовать аналогичные треугольники, нарисованные транспортиром (измерение
длина сторон, которая будет пропорциональна сторонам на вашем
«табличный» треугольник) или приведенное ниже тригонометрическое уравнение.

Tanq = x / y
или x = y · (tanq
).

Длина стола (в дюймах): ____________________

_____________________________________________________________________________________________________________________

Часть 2: Фактическое расстояние до звезды

Понятие параллакса всем нам знакомо.
Вытяните большой палец на вытянутую руку и закройте сначала один глаз, а затем
Другие. Заметили сдвиг на более отдаленном фоне?
Это параллакс. Теперь поднесите к себе большой палец на полпути и сделайте
тоже самое.Заметили, что сдвиг кажется больше?
Разница в сдвиге позволяет измерить расстояние до вашего
большой палец (или к звездам). Но сначала нужно найти воображаемый треугольник
это будет работать, измерьте угол и измерьте одну сторону треугольника.
При измерении расстояния до звезд одна сторона треугольника принимается равной
расстояние от Земли до Солнца (величина, которую мы знаем). В
угол измеряется путем наблюдения за параллаксом, который показывает, насколько далеко звезда
кажется, смещается на фоне звезд, когда Земля вращается вокруг
Солнце (аналогично закрытию одного глаза, затем другого).Иллюстрация
Parallax (неизвестный источник).

Два изображения ниже сняты с разницей в 6 месяцев (таким образом,
Земля переместилась с одной стороны Солнца на другую на расстояние
около 2AU). Звезда HT Cas — самый близкий
к Земле звезд на этом изображении. Угол между двумя звездами
ближайшая к HT Cas (кроме самой HT Cas) составляет 0,000002778 градусов. Этот
value — это «масштаб», по которому вы можете определять другие углы.

Step 1 ) выяснить, какая звезда HT Cas
(подсказка: какой из них переехал?)

Шаг 2 ) определить угол, под которым HT Cas
сместился из-за изменения положения Земли за 6 месяцев.
Подсказка: угол, который важен на этих рисунках, равен
угол между двумя воображаемыми линиями, проведенными между вами (на Земле) и
каждая позиция звезды. Таким образом, интересующий вас угол не
в плоскости картины! Однако этот угол пропорционален
расстояниям между звездами, как видно на изображении звезд выше.
Следовательно, вы можете определить углы, измерив расстояния между
звезды на изображении (с линейкой).

Измерение угла осуществляется путем наблюдения
расстояние видимого смещения звезды на фотографиях, сделанных за 6 месяцев
отдельно.Этот сдвиг пропорционален углу, при этом более удаленные
звезды с меньшими углами и меньшими расстояниями смещения.

Расстояние можно преобразовать в угол с помощью
известный угол между двумя другими звездами, положение которых не меняется. В
В этой головоломке известен угол между двумя звездами, ближайшими к HTCas и
составляет 0,000002778 градусов.

Наконец, мы можем рассчитать угол смещения HTCas
сравнивая с известным углом между ближайшими звездами.( The
угол между двумя ближайшими звездами / угол сдвига в HTCas = расстояние
между двумя ближайшими звездами на фото / расстояние смещения в HTCas ).

Составное изображение измерения
метод

Шаг 3 ) Рассчитайте расстояние до HT Cas.

Это можно сделать, представив прямоугольный треугольник.
между Землей, Солнцем и HTCas. Угол этого прямоугольного треугольника
= 1/2 угла между исходным положением HT Cas и его новым положением.
Теперь мы знаем длину одной стороны треугольника (= 1AU расстояние от
Земля к Солнцу) и один угол (тета = 1/2 угла параллакса).
Таким образом, мы можем вычислить длину другой стороны треугольника,
расстояние до звезды. Одно отношение, которое помогает
при этом вычислении получается следующее: tan (угол тета) = ½diameter
орбиты Земли / расстояние до звезды).

Расстояние до звезды в АС _______________________________________

Пример соответствующего действия по триангуляции
для младших школьников

Домашняя страница (оценка.htm)
Предыдущая страница (est3a.html)

Звездный многоугольник | Math Wiki

Шаблон: Тон

Звездный многоугольник — это невыпуклый многоугольник, который чем-то похож на звезду. Глубоко изучены только обычные; звездные многоугольники вообще никогда официально не определялись. Это не то же самое, что многоугольники, которые являются звездными доменами.

Правильные звездообразные многоугольники

В геометрии правильный звездообразный многоугольник — это самопересекающийся равносторонний равноугольный многоугольник, созданный путем соединения одной вершины простого правильного многоугольника со сторонами n с другой несмежной вершиной и продолжения процесса до тех пор, пока исходная вершина снова достигнута.Шаблон: Исправление / категория ^{[требуется ссылка ]} Например, в правильном пятиугольнике пятиконечная звезда может быть получена путем проведения линии от первой до третьей вершины, от третьей вершины до пятой вершины, от пятой вершины ко второй вершине, от второй вершины к четвертой вершине и от четвертой вершины к первой вершине. Это включает в себя повторное сложение с модулем n , где n — это количество сторон многоугольника, а число x , которое необходимо повторно добавить, больше 1 и меньше n -1, или: 1 < x < n -1.Обозначение для такого многоугольника — { n / x } ( см. Символ Шлефли ), что равно { n / n-x }. Многоугольник справа: {5/2}.

Правильный звездообразный многоугольник также может быть представлен как последовательность звёздчатых звёзд выпуклого правильного многоугольника core .

Правильные звездчатые многоугольники впервые были систематически изучены Томасом Брэдвардином.

Примеры

Звездные фигуры

Звездочка
Гексаграмма
2 {3} или {6/2}

Звездочка
Эннеаграмма
3 {3} или {9/3}

Если количество сторон n делится без остатка на m , полученный звездообразный многоугольник будет правильным многоугольником со сторонами n, / м и .Новая фигура получается путем поворота этих обычных n / m -угольников на одну вершину влево на исходном многоугольнике до тех пор, пока количество повернутых вершин не станет равным n / m минус один, и объединения этих фигур. В крайнем случае, когда n / m равно 2, получается фигура, состоящая из n /2 прямых отрезков; это называется вырожденным звездообразным многоугольником .

В других случаях, когда n и m имеют общий множитель, получается звездообразный многоугольник для более низкого n , и повернутые версии могут быть объединены.Эти фигуры называются звездчатыми фигурами или неправильными звездчатыми многоугольниками или составными многоугольниками . Для них часто используется то же обозначение { n / m }, хотя такие авторитетные источники, как Grünbaum (1994), считают (с некоторым обоснованием) более правильной форму k { n }, где обычно к = м .

Еще одна сложность возникает, когда мы соединяем два или более звездных многоугольника, как, например, две пентаграммы, различающиеся поворотом на 36 °, вписанные в десятиугольник.Это правильно записывается в форме k { n / m }, как 2 {5/2}, а не в широко используемом {10/4}.

Шестиконечную звезду, похожую на шестиугольник, можно создать с помощью циркуля и линейки:

Нарисуйте циркулем круг любого размера.
Не меняя радиуса циркуля, установите его ось на окружности круга и найдите одну из двух точек, где новый круг пересечет первый круг.
Сделав ось на последней найденной точке, аналогично найдите третью точку на окружности и повторяйте, пока не будут отмечены шесть таких точек.
Прямым краем соедините чередующиеся точки на окружности, чтобы сформировать два перекрывающихся равносторонних треугольника.

Симметрия

Правильные звёздные многоугольники и звёздные фигуры можно рассматривать как диаграмму смежных классов подгрупп конечной группы.

Группа симметрии { n / k } является двугранной группой D _n порядка 2 n , независимо от k .

Неправильные звездообразные многоугольники

Белая линия на этом графике представляет собой неправильный шестиугольный циклический многоугольник, определяющий фигуру вершины большого ретроснуба икосододекаэдра.Длины ребер определяются расстоянием между чередующимися вершинами граней однородного многогранника.

Звездный многоугольник не обязательно должен быть правильным. Шаблон: Исправление / категория ^{[ необходима ссылка ]}

Неправильные циклические звездчатые многоугольники встречаются как фигуры вершин для однородных многогранников, определяемых последовательностью правильных граней многоугольника вокруг каждой вершины, с учетом как нескольких поворотов, так и ретроградных направлений. (См. Фигуры вершин в Списке однородных многогранников) ^[1]

Уникурсальная гексаграмма — еще один пример циклического неправильного звездообразного многоугольника, содержащего только D _2h Двугранную симметрию.

Интерьеры звездных полигонов

Звездные многоугольники оставляют двусмысленность интерпретации интерьеров. Эта диаграмма демонстрирует три интерпретации пентаграммы.

1. Левая интерпретация имеет 5 вершин правильного пятиугольника, попеременно соединенных циклическим путем, пропуская чередующиеся вершины. Интерьер — это все, что находится слева (или справа) от каждого края (до следующего пересечения). Это делает центральную выпуклую пятиугольную область фактически «снаружи», и в целом вы можете определить внутреннюю часть с помощью бинарного четно-нечетного правила подсчета количества ребер, пересекающихся от точки вдоль луча до бесконечности.

2. В средней интерпретации также есть 5 вершин правильного пятиугольника, попеременно соединенных циклическим путем. Интерьер можно рассматривать как одно из:

a) внутри простая 10-сторонняя граница периметра многоугольника, как для 3.

б) центральная выпуклая пятиугольная область окружена дважды, потому что звездный периметр обвивает ее дважды.

3. Правосторонняя интерпретация создает новые вершины на пересечении ребер (в данном случае 5) и определяет новый вогнутый десятиугольник (10-конечный многоугольник), образованный путем периметра средней интерпретации — это фактически больше не пентаграмма, хотя ее все еще можно считать звездным многоугольником.

Какова площадь внутри пентаграммы? Каждая интерпретация приводит к разному ответу.

Пример интерпретации звездной призмы

{7/2} гептаграммная призма:

Гептаграммы с
2-сторонней внутренней

Гептаграммы с
простой периметр интерьера

Гептаграммическая призма выше показывает, что разные интерпретации могут создавать очень разные образы.

Построители моделей многогранников, такие как Магнус Веннингер, обычно представляют граней звездообразного многоугольника в вогнутой форме, без внутренних краев, показанных .

Звездные многоугольники в искусстве и культуре

Звездные многоугольники занимают важное место в искусстве и культуре. Такие многоугольники могут быть или не быть правильными, но они всегда очень симметричны. Примеры включают:

Звездный пятиугольник {5/2} также известен как пентаграмма, пентальфа или пятиугольник, и исторически многие магические и религиозные культы считали его оккультным.
Простейший невырожденный сложный звездный многоугольник, который представляет собой два {6/2} многоугольника (т. Е. Треугольников), гексаграмму (Звезда Давида, Печать Соломона).
Звездные многоугольники {7/3} и {7/2}, известные как гептаграммы, также имеют оккультное значение, особенно в Каббале и Викке.
Сложный {8/2} звездный многоугольник (т. Е. Два квадрата), который известен как Звезда Лакшми и фигурирует в индуизме;
Звездный многоугольник {8/3} (октаграмма) и сложный звездный многоугольник из двух {16/6} многоугольников, которые часто являются геометрическими мотивами в исламском искусстве и архитектуре Великих Моголов; Первый находится на гербе Азербайджана.
Одиннадцатиконечная звезда, называемая хендекаграммой, по всей видимости, использовалась на гробнице Шаха Немат Оллаха Вали.

Некоторые символы, основанные на звездообразном многоугольнике, имеют чередование небольших промежутков и / или, в случае звездной фигуры, используются разные цвета.

См. Также

Список литературы

Cromwell, P .; Многогранники , CUP, Hbk. 1997, ISBN 0-521-66432-2. Pbk. (1999), ISBN 0-521-66405-5.
Grünbaum, B. and G.C. Shephard; Плитки и узоры , Нью-Йорк: W.H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
Grünbaum, B .; Многогранники с полыми гранями, Протокол конференции НАТО-АСИ по многогранникам … и т. Д. (Торонто, 1993) , изд. Т. Бистрички и др., Kluwer Academic (1994), стр. 43–70.
Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 404: Размерность 2 правильных звездных многогранников)

Внешние ссылки

Калькулятор площади

Ниже приведены калькуляторы для оценки площади семи распространенных форм.Площадь более сложных форм обычно может быть получена путем разбивки их на совокупность простых форм и суммирования их площадей. Этот калькулятор особенно полезен для оценки площади земельного участка.

Прямоугольник

Треугольник

Используйте калькулятор треугольника, чтобы определить
всех трех ребер треугольника
с учетом других параметров.

Трапеция

Круг

Сектор

Эллипс

Параллелограмм

Калькулятор площади сопутствующих поверхностей | Калькулятор объема

Площадь — это величина, которая описывает размер или размер двухмерной фигуры или фигуры на плоскости.Его можно визуализировать как количество краски, которое потребуется для покрытия поверхности, и оно является двумерным эквивалентом одномерной длины кривой и трехмерного объема твердого тела. Стандартная единица площади в Международной системе единиц (СИ) — квадратный метр, или м ² . Ниже приведены уравнения для некоторых наиболее распространенных простых форм и примеры того, как рассчитывается площадь каждой из них.

Прямоугольник

Прямоугольник — это четырехугольник с четырьмя прямыми углами.Это одна из простейших форм, и для расчета ее площади необходимо только знать (или измерить) ее длину и ширину. Четырехугольник по определению — это многоугольник с четырьмя ребрами и вершинами. В случае прямоугольника длина обычно относится к двум более длинным краям четырехугольника, а ширина относится к более коротким из двух краев. Когда длина и ширина прямоугольника равны, форма представляет собой особый случай прямоугольника, называемый квадратом. Уравнение для вычисления площади прямоугольника выглядит следующим образом:

площадь = длина × ширина

Фермер и его дочь — непроданная земля

Представьте, что фермер пытается продать участок земли совершенно прямоугольной формы.Поскольку у него есть несколько коров, которые он не хотел бы свободно резвиться, он огородил участок земли и знает точную длину и ширину каждого края. Фермер также живет в Соединенных Штатах и, не знаком с использованием единиц СИ, по-прежнему измеряет свой участок земли в футах. Ступня была определена как ровно 0,3048 метра в 1959 году после того, как она изменилась в течение длительного периода времени, поскольку исторически человеческое тело часто использовалось в качестве основы для единиц длины, и неудивительно, что оно было непостоянным в зависимости от времени и местоположения.В стороне, участок земли фермера имеет длину 220 футов и ширину 99 футов. Используя эту информацию:

площадь = 220 × 99 = 21780 кв. Футов

Земельный участок фермера площадью 21780 квадратных футов равен половине акра, где акр определяется как площадь 1 цепи на 1 фарлонг, которые определяются чем-то другим, и так далее, и почему СИ сейчас существует. К несчастью для фермера, он живет в районе, где преобладают иностранные инвесторы с меньшим размером ноги, которые считали, что им следует получить больше квадратных футов за свои деньги, и его земля остается непроданной сегодня.

Треугольник

Существует множество уравнений для вычисления площади треугольника в зависимости от имеющейся информации. Как упоминалось в калькуляторе выше, используйте Калькулятор треугольников для получения дополнительных сведений и уравнений для расчета площади треугольника, а также для определения сторон треугольника с использованием любой доступной информации. Вкратце, уравнение, используемое в калькуляторе, представленном выше, известно как формула Герона (иногда называемая формулой Героя), относящаяся к герою Александрии, греческому математику и инженеру, которого некоторые считали величайшим экспериментатором древних времен.Формула выглядит следующим образом:

Фермер и его дочь — Triangle Daze

В этот момент, благодаря огромным усилиям и настойчивости, фермер, наконец, продал свой участок земли площадью 21 780 квадратных футов и решил использовать часть заработанных денег, чтобы построить бассейн для своей семьи. К несчастью для фермера, он не принимает во внимание тот факт, что одни только расходы на обслуживание бассейна в течение одного года, вероятно, могут покрыть посещение его детьми любого бассейна или аквапарка на долгие годы.К еще большему сожалению для фермера, его 7-летняя дочь, которая недавно приехала в Египет через Дору-исследовательницу, влюбилась в треугольники и настаивает на том, чтобы бассейн был не только треугольной формы, но и необходимыми размерами. должна включать только цифру 7, чтобы обозначить ее возраст и увековечить этот момент ее жизни в форме треугольного бассейна. Как любящий отец, фермер соглашается на просьбу дочери и приступает к планированию строительства своего треугольного бассейна.Теперь фермер должен определить, есть ли у него на заднем дворе достаточно места для размещения бассейна. В то время как фермер начал больше узнавать об единицах СИ, он все еще испытывает дискомфорт от их использования и решает, что его единственный жизнеспособный вариант — построить бассейн в форме равностороннего треугольника со сторонами 77 футов в длину, поскольку любой другой вариант будет либо слишком большим, либо маленьким. Учитывая эти размеры, фермер определяет необходимую площадь следующим образом:

Поскольку наибольшее расстояние между любыми двумя точками равностороннего треугольника — это длина края треугольника, фермер резервирует края бассейна для плавания «кругов» в своем треугольном бассейне с максимальной длиной, примерно вдвое меньшей, чем у олимпийского. бассейн, но с двойной площадью — все под бдительным взором правящей королевы бассейна, его дочери и неодобрительного взгляда его жены.

Трапеция

Трапеция — это простой выпуклый четырехугольник, у которого есть по крайней мере одна пара параллельных сторон. Свойство быть выпуклым означает, что угол трапеции не превышает 180 ° (в отличие от вогнутого четырехугольника), в то время как простота отражает то, что трапеции не самопересекаются, что означает, что две несмежные стороны не пересекаются. В трапеции параллельные стороны называются основаниями трапеции, а две другие стороны называются ногами.Существует больше различий и классификаций для разных типов трапеций, но их площади по-прежнему рассчитываются таким же образом с использованием следующего уравнения:

где b ₁ и b ₂ — базы.
h — высота или перпендикулярное расстояние между основаниями.

Фермер и его дочь — попытки разгрома

Прошло два года с тех пор, как бассейн фермера был достроен, а его дочь выросла и повзрослела.Хотя ее любовь к треугольникам все еще сохраняется, она в конце концов пришла к осознанию того, что независимо от того, насколько хорошо она была «треугольной», сами по себе треугольники не могут заставить мир вращаться, и что мастерская Санты не может правдоподобно балансировать на Северном полюсе, если бы мир скорее пирамида, чем сфера. Постепенно она начала принимать другие формы в свою жизнь и преследовала множество различных интересов — в настоящее время — фристайл BMX. Таким образом, ей требуется пандус, но, к сожалению для фермера, не просто пандус.Пандус должен состоять только из форм, которые можно сформировать из нескольких треугольников, поскольку, как и ее рэп-идол Б.о.Б., дочери фермера все еще трудно принять реальность изогнутых поверхностей. Конечно, он должен использовать только цифру 9 в своих измерениях, чтобы отразить ее возраст. Фермер решает, что его лучший вариант — построить пандус, состоящий из нескольких прямоугольников, при этом боковая поверхность пандуса имеет форму трапеции. По мере того, как фермер теперь освоился с СИ, он может быть более креативным в использовании единиц и может построить пандус более разумного размера, соблюдая требования своей дочери.Он решает построить пандус с трапециевидной поверхностью высотой 9 футов, нижним основанием длиной 29,528 футов (9 м) и верхним основанием 9 футов. Площадь трапеции рассчитывается следующим образом:

площадь =

× 9 = 173,376 кв. Футов

Круг

Круг — это простая замкнутая форма, образованная набором всех точек на плоскости, находящихся на заданном расстоянии от заданной центральной точки. Это расстояние от центра до любой точки окружности называется радиусом.Более подробную информацию о кругах можно найти на странице «Калькулятор круга», но для расчета площади необходимо только знать радиус и понимать, что значения в круге связаны математической константой π . Уравнение для вычисления площади круга выглядит следующим образом:

площадь = πr ²

Фермер и его дочь — Круг Ли (ж)

Прошло еще шесть лет, и его дочь превратилась в сильного, красивого, влиятельного, уверенного в себе 15-летнего неблагодарного человека, сосредоточенного исключительно на поиске внешнего подтверждения со стороны знакомых и незнакомцев в социальных сетях, при этом полностью игнорируя искреннюю поддержку со стороны ближайших родственников и друзей. .После спора с отцом по поводу чрезмерного использования социальных сетей, она решает использовать страх отца перед неизвестным и веру в сверхъестественное, чтобы разыграть его. Не зная, с чего начать, она ходит по городу, разговаривая с множеством незнакомцев, у каждого из которых, по-видимому, есть бесконечные источники мудрости и советов, где она узнает о кругах на полях и их связи с инопланетянами и неопознанными летающими объектами, а также на многие другие темы, которые игнорируйте все научные и логические объяснения.Убедившись, наконец, в сферической природе Земли, удалив все свои прошлые публикации в социальных сетях, касающихся BoB, и расширив свою любовь к треугольникам до принятия других форм, она решает сделать основной круг на полях, состоящий из ряда концентрических кругов и хочет определить площадь, необходимую для создания кругов на полях с внешним радиусом 15 футов. Она делает это, используя следующее уравнение:

площадь = π × 15 ² = 706,858 кв.футов

К несчастью для фермера, он не только напуган кругами на полях, которые появились в ту ночь, когда его дочь сказала ему, что она была на вечеринке со своими друзьями, что по какой-то странной причине не привело к лишним постам в Instagram (он был, конечно, первым последователем своей дочери), но количество «исследователей кружка» и «цереологов», появившихся на его ферме, чтобы изучить и впоследствии подтвердить подлинность кругов на полях как инопланетного сооружения, стоило ему значительного ущерба для его посевов. .

Сектор

Сектор круга — это, по сути, часть круга, заключенного между двумя радиусами и дугой. Зная радиус и угол, площадь сектора можно вычислить, умножив площадь всего круга на отношение известного угла к 360 ° или 2π радианам, как показано в следующем уравнении:

площадь =

× πr ²

, если θ в градусах

или

площадь =

× πr ²

, если θ в радианах

Фермер и его дочь — разделение семьи

Фермер и его семья столкнулись с самой серьезной дилеммой на сегодняшний день.Прошел год, дочери фермера исполнилось 16 лет, и в рамках празднования ее дня рождения ее мать испекла ее любимый десерт — ежевичный пирог. К несчастью для дочери фермера, ежевичный пирог также является любимой едой их домашнего енота, Утконоса, о чем свидетельствует отсутствие пирога на 180 ° с явными признаками виновника в виде крошек, ведущих к чрезмерно увлеченному еноту. Первоначально пирог легко можно было разделить между тремя людьми и одним енотом, но теперь половину пирога приходится делить между тремя людьми, поскольку огорченный, но пресыщенный Утконос наблюдает издали.Учитывая, что каждый человек получит пирог на 60 ° с радиусом 16 дюймов, площадь пирога, которую получает каждый человек, можно рассчитать следующим образом:

площадь = 60 ° / 360 ° × π × 16 ² = 134,041 дюйм ²

В результате невнимательности Утконоса каждый получает на треть меньше, и дочь задумчиво вспоминает урок американской истории, где она узнала о битве при Аламо и изображении народного героя Дэви Крокетта и его шляпы из енотовидной шкуры.

Эллипс

Эллипс — это обобщенная форма круга и кривая на плоскости, где сумма расстояний от любой точки кривой до каждой из двух ее фокальных точек постоянна, как показано на рисунке ниже, где P равно любая точка эллипса, а F ₁ и F ₂ являются двумя фокусами.

Когда F ₁ = F ₂, результирующий эллипс представляет собой круг. Большая полуось эллипса, как показано на рисунке, который является частью калькулятора, является самым длинным радиусом эллипса, а малая полуось — самым коротким.Большая и малая оси относятся к диаметрам, а не радиусам эллипса. Уравнение для вычисления площади эллипса аналогично уравнению для вычисления площади круга, с той лишь разницей, что используются два радиуса, а не один (поскольку фокусы находятся в одном месте для круга):

area = πab
, где a и b — мажор
и малые полуоси

Фермер и его дочь — падение с орбиты

Прошло два года со времени таинственного исчезновения домашнего питомца, Утконоса, и случайного выигрыша пушистого аксессуара дочери фермера в школьной лотерее, которая помогла заполнить пустоту потери их любимого питомца.Дочке фермера сейчас 18, и она готова сбежать из сельской Монтаны, чтобы жить в колледже, полной свободы и распутства, и, конечно же, немного поучиться на стороне. К несчастью для дочери фермера, она росла в среде, наполненной позитивным подкреплением, и, следовательно, с менталитетом, что нужно «стрелять на луну, [поскольку] даже если вы промахнетесь, вы приземлитесь среди звезд», а также утверждение всех окружающих, что она может делать абсолютно все, что ей заблагорассудится! Таким образом, с ее неоптимальными оценками, отсутствием какой-либо внеклассной деятельности из-за ее бесчисленного множества различных интересов, отнимающих все ее свободное время, нулевого планирования и ее настойчивого стремления поступать только в самые лучшие из лучших университетов, шок, который возник, когда она не была принята ни в один из ведущих университетов, в которые она подавала документы, что можно было бы разумно сравнить с ее метафорической посадкой в глубоком космосе, надуванием, замерзанием и быстрым удушьем, когда она пропустила луну и приземлилась среди звезд.Наряду с легкими ее мечта стать астрофизиком была в конечном итоге нарушена, по крайней мере, на время, и ей пришлось вычислить эллиптическую площадь, необходимую в ее комнате, чтобы построить модель почти эллиптической орбиты Земли вокруг Солнца размером с человека. так что она могла с тоской смотреть на солнце в центре своей комнаты и его олицетворение ее сердца, пылающего страстью, но окруженного холодными просторами космоса, с далеким вращением Земли, насмешливо представляющим расстояние между ее мечтами и твердой землей .

площадь = π × 18 футов × 20 футов = 1130,97 кв. Футов

Параллелограмм

Параллелограмм — это простой четырехугольник, который имеет две пары параллельных сторон, причем противоположные стороны и углы четырехугольника имеют равные длины и углы. Прямоугольники, ромбы и квадраты — это частные случаи параллелограммов. Помните, что классификация «простой» формы означает, что форма не является самопересекающейся. Параллелограмм можно разделить на прямоугольный треугольник и трапецию, которые в дальнейшем можно преобразовать в прямоугольник, что делает уравнение для вычисления площади параллелограмма по существу таким же, как и для вычисления прямоугольника.Однако вместо длины и ширины параллелограмм использует основание и высоту, где высота — это длина перпендикуляра между парой оснований. Исходя из рисунка ниже, уравнение для расчета площади параллелограмма выглядит следующим образом:

площадь = ш × в

Фермер и его дочь — Алмаз в небе

Прошло еще два года в жизни фермера и его семьи, и хотя его дочь была причиной сильного беспокойства, она наконец преодолела расстояние между пылающим солнцем, которое является ее сердцем, и Землей, на которой настаивает общество. она должна оставаться на земле.В результате борьбы, которая последовала за ее добровольной изоляцией, в окружении воображаемых, осуждающих глаз, предполагающих ее неудачу со всех сторон, дочь фермера вышла из-под натиска земли, как алмаз, сияя ярко и твердо в своей решимости. Несмотря на все недостатки, она решает, что у нее нет другого выбора, кроме как продержаться сквозь астероидное поле жизни в надежде, что конец сказки Диснея существует. Наконец-то, к счастью для дочери фермера и ее семьи, надежда действительно появилась, но не в форме Прекрасного Принца, а скорее как знак с предполагаемых небес.Несмотря на все ее метафорические размышления и невзгоды, связанные с космосом, почти становится правдоподобным, что дочь фермера каким-то образом повлияла на массивный восьмигранный алмазный астероид, падающий прямо, но безопасно на их сельскохозяйственные угодья, что она интерпретирует как представление ее путешествия, становления и возможного возвращения домой. Дочь фермера приступает к измерению площади одного из ромбовидных лиц своего недавно найденного символа жизни:

площадь = 20 футов × 18 футов = 360 квадратных футов

К несчастью для дочери фермера, появление огромного алмаза привлекло внимание со всего мира, и после достаточного давления она уступает внутреннему человеку и продает алмаз, само изображение ее жизни и души, одному человеку. богатый коллекционер, и продолжает жить остаток своей жизни в щедрых удовольствиях, отказываясь от своих убеждений и теряясь в черной дыре общества.

Блоки общего пользования

9027 9027 фут

2,589,988 (640 акров в форме звезды)

Высота h находится под прямым углом к b: более сложные формы.Вам нужно будет начать с определения ширины и высоты фигуры (другими словами, с определения размера двух смежных сторон). Для более сложных форм вы можете попробовать Area of Polygon by Drawing Tool. Вычислите площадь правильного тетраэдра с помощью этого простого калькулятора. На самом деле эта простая фигура просто поражает. Найдите площадь поверхности призмы. Свойство геометрии круга говорит нам, что когда у вас есть две точки (например, A и B) на окружности круга, угол от центра (O) в два раза больше угла от точки на окружности (X).Форма многоугольника: многоугольник — это двухмерная форма, образованная прямыми линиями. Коврик A Коврик B Коврик C Периметр прямоугольника длиной l и шириной w может быть записан как: Прямоугольники lw Периметр = 2l + 2w или Периметр = 2 (l + w) Площадь прямоугольника определяется как: Площадь = lw Площадь прямоугольника Площадь измеряется в квадрате… Теперь все, что вам нужно сделать, это подставить размеры каждой формы в формулу для определения площади поверхности каждой формы, и все готово. Сфера — это сплошная фигура, каждая точка на поверхности которой равноудалена от центра сферы.Двумерные формы (2D-формы) также известны как плоские формы, это формы, имеющие только два измерения. Понимание того, как рассчитать площадь, важно понимать в раннем возрасте 8-10 лет. Для n + 1 вершин x [0], y [0] .. x [N], y [N] простого многоугольника, описанного по часовой стрелке, площадь многоугольника может быть вычислена следующим образом: Составная форма или составная форма. shape — это форма, состоящая из других фигур, таких как два прямоугольника (L-образная форма) или треугольник и прямоугольник. По формуле площади круга мы знаем; Длина стороны квадратного участка 5м.Квадрат, технически говоря, представляет собой прямоугольник (не напоминайте прямоугольник, он немного чувствителен), поэтому мы можем использовать формулу для площади прямоугольника, чтобы найти площадь квадрата. Но эти связи звезды и дельты могут быть преобразованы из одной формы в другую. Формула для вычисления площади сектора проста — умножьте центральный угол на квадрат радиуса и разделите на 2: Площадь сектора = r² * α / 2; Но откуда это? 1. высота 2. ширина 3. глубина 1 миля (мили). Каждая формула имеет калькулятор. Формы пластин включают двумерные фигуры, которые можно нарисовать на плоскости, например.г., круг, квадрат, треугольник, прямоугольник, трапеция, ромб и параллелограмм. Площадь — это своего рода мера того, сколько места занимает эта вещь в двух измерениях? В этом видео рассказывается о различных формулах для разных форм. Шаги. Пятиугольник будет правильным пятиугольником, если все его стороны равны по длине и все углы равны. Вычислите площадь поверхности каждой формы. Площадь — это величина, которая описывает размер или протяженность двухмерной фигуры или фигуры на плоскости.Приложение может даже суммировать несколько расчетов площадей посредством рисования слоев. Твердые тела 10. куб 11. конус 12. цилиндр 13. пирамида 14. сфера, части круга Второй момент площади для всей формы — это сумма второго момента площадей всех ее частей вокруг общей оси. Площадь поверхности треугольной призмы. Спасибо за определение области, 2-х и 3-х фигурные формы, площадь 2-х и 3-х фигур, а также за примеры, которые были действительно полезны. Расчет открытой площадки: круглые отверстия, треугольный шаг.Выберите форму, затем введите значения. Пара примеров, показывающих, как использовать формулу площади поверхности для решения некоторых задач. Найдите площадь поверхности куба, если длина одной стороны равна 5 см. Это разделение используется для форм, которые имеют очевидное различие между основанием и другой частью — например, для цилиндра, конуса, пирамиды или треугольной призмы. [вставить рисунок тыквенного пирога с сектором… По формуле площади квадрата мы знаем; Найдите площадь конуса, радиус которого 4 см, а высота 3 см.Удельный импульс ракеты, I sp, представляет собой отношение тяги к расходу выбрасываемого груза, то есть где F — тяга, q — массовый расход, а go — стандартная сила тяжести (9,80665 м / с. 2) .. A = 154 кв.м. Вы можете подумать, что это как-то связано с колдовством, но на самом деле он более известен как магический символ, а также является священным символом во многих религиях. Вы можете подумать, что это как-то связано с колдовством, но на самом деле он более известен как магический символ, а также является священным символом во многих религиях.2 $… 21. эллипс / овал, 22. куб 23. цилиндр 24. сфера 25. конус 26. пирамида, 1 дюйм (1 ″) = 2,54 сантиметра (см), сторона 2, где сторона такая, как показано ниже: Это только требует единственного измерения при условии, что уже известно, что фигура действительно является правильным восьмиугольником. Для упрощения сложной сети часто требуется преобразование из дельты в звезду или из звезды в дельту. Формула площади сектора. Многоугольник должен быть простым и может быть выпуклым или вогнутым. Площадь поверхности твердого объекта — это мера общей площади, которую занимает поверхность объекта.Согласно Международной системе единиц (СИ), стандартной единицей площади является квадратный метр (обозначенный как м2) и представляет собой площадь квадрата, длина сторон которого составляет один метр. 1. Калькуляторы базовой геометрии и форм, формулы и примеры getcalc.com для расчета длины, площади, поверхности, объема, точек, линий, размеров, углов и кривых для 2- или 3-мерных (2D или 3D) геометрических фигур. Из этого следует, что противоположные стороны также параллельны. Следовательно, любая форма, которая может быть образована с использованием трех прямых линий, известна как треугольник, а любая форма, которую можно нарисовать, соединяя четыре линии, известна как четырехугольник.9. вершина 10. гипотенуза 11. прямой угол 12. основание, D. квадрат 13. сторона E. прямоугольник 14. длина 15. диагональ 16. ширина, F. круг 17. окружность 18. центр 19. диаметр 20. радиус От точки как показано на рисунке, углы ADC, AOB и BOC равны; все обозначаются θ. Формы звезд сильно различаются. Получится треугольник, основание которого равно длине окружности, а высота равна радиусу внешнего круга, т. Е. R. Таким образом, площадь можно рассчитать как ½ * основание * высота i.е. В результате все, что известно о геометрических фигурах и взаимосвязях, может быть применено к объектам ». [Атлас научной грамотности, том 2, стр.66] Этот урок был разработан доктором Дэниелом (… «Чтобы понять мир, человеческий разум в значительной степени полагается на свое восприятие форм и узоров. 1 ярд (1 ярд). Метод 1 из 7. Квадраты, прямоугольники и параллелограммы. Для определения трехмерных форм используются два различных показателя: объем и площадь поверхности. Площадь — это величина, которая выражает протяженность двухмерной фигуры, формы или плоской пластинки. в самолете.Из этого следует, что противоположные стороны также параллельны. Снежинка Коха (также известная как кривая Коха, звезда Коха или остров Коха) — это фрактальная кривая и один из самых ранних фракталов, которые были описаны. Что такое v… Получите ответы на свои вопросы прямо сейчас! Спасибо BYJU за обучающее приложение. Его можно визуализировать как количество краски, которое потребуется для покрытия поверхности, и оно является двумерным эквивалентом одномерной длины кривой и трехмерного объема твердого тела.Особая благодарность Роберту С. Уилсону за его статью, в которой подробно описана математика регулярных звездных многоугольников. Проще говоря, если у вас есть изображение, которое вы можете загрузить, или адрес карты для поиска, вы можете вычислить неправильную область формы независимо от того, насколько она сложна, просто нарисовав по периметру области. Используемая формула для определения площади основания зависит от формы объекта. Что такое площадь? Для параллелограмма вам нужно использовать так называемые… Некоторые из примеров 2D-форм — квадрат, прямоугольник, круг, треугольник и так далее.Это легкие дроби, но что, если ваш центральный угол 9-дюймового тыквенного пирога составляет, скажем, 31 °? Артефакты вокруг нас и знакомые формы, которые мы видим в природе, часто можно охарактеризовать с помощью геометрических форм. Обратите внимание, как по мере уменьшения размеров секторов форма становится больше похожей на прямоугольник. Очень хороший веб-сайт. У меня есть почти все, что я искал. Привет, меня зовут Джоанна Джоктан, и я хочу присоединиться к этой программе. Вы можете найти его, используя пропорции, все, что вам нужно запомнить, это формула площади круга (и мы уверены, что вы это делаете! Формула: S = √3a 2/4 Где, a = длина стороны треугольника S = площадь основания тетраэдра h = высота Калькулятор, связанный с правильным тетраэдром: Площадь… 10.2. Это очень полезно, и я с нетерпением жду возможности присоединиться к вашей школе. Линии 18. прямые 19. изогнутые 20. перпендикулярные 21. параллельные Площадь A = l * w Периметр P = 2l + 2w, Площадь A = ∏ * r * r Это расстояние является радиусом r сферы. Преобразование дельты в звезду. В общем, площадь форм можно определить как количество краски, необходимое для покрытия поверхности одним слоем. Калькулятор связанной площади поверхности | Калькулятор объема. Пентаграмма (или пятиугольник) выглядит как пятиконечная звезда.Центральный угол позволяет узнать, какую часть или процент от всей окружности составляет ваш сектор. нашел эту страницу действительно полезной. Пентаграмма (или пятиугольник) выглядит как пятиконечная звезда. Трехмерные формы (3D-формы), известные как твердые формы, — это формы, которые имеют три измерения, такие как длина, ширина и толщина. Основание фигуры, такой как многоугольник, — это нижняя часть фигуры. Рассмотрим круг радиуса r и сделаем бесконечные концентрические окружности. Найдите площадь поверхности куба. Внутри пентаграммы находится Пентагон.Объем V = B * h * 1/3, Площадь поверхности S = B + ∏ * r * l = ∏ * r * r + ∏ * r * l Обычно мы вычитаем площадь меньшей внутренней формы из площади внешняя форма большего размера, чтобы найти область заштрихованной области. Все основные геометрические формулы разносторонних, правых, равнобедренных, равносторонних треугольников (стороны, высота, биссектриса, медиана). Формула площади и объема для геометрических фигур — квадрата, прямоугольника, треугольника, многоугольника, круга, эллипса, трапеции, куба, сферы, цилиндра и конуса. Составная фигура или составная фигура — это фигура, состоящая из других фигур, таких как два прямоугольника (L-образная форма) или треугольник и прямоугольник.Онлайн-калькулятор для расчета площади поверхности капсулы, конуса, усеченного конуса, куба, цилиндра, полусферы, квадратной пирамиды, прямоугольной призмы, треугольной призмы, сферы или сферической крышки. Обязательные поля отмечены *, Области параллелограммов и треугольников, класс 9. В геометрии Квадрат — это плоская фигура или форма, имеющая четыре равные стороны, и каждый угол является прямым углом, т.е. 4. длина 5. дюйм 6. фут-фут. 7. ярд 8. сантиметр 9. метр Это означает, что COA составляет одну десятую длины окружности, то есть это 36 °.Решение для площади: Входные данные: длина одной стороны (-ей) единицы: Решение: площадь (a) = 1,44: единицы 2: Изменить уравнение Щелкните уравнение, чтобы решить круговое уравнение. 1 фут (1 ′) = 0,305 метра (м) Формула площади сектора. В этой статье давайте обсудим области форм для 2D-фигур и 3D-фигур с формулами. Окружность C = ∏ * d = 2 * ∏ * r, Площадь поверхности S = 2 * B + P * h Формула площади поверхности сферы и Формула объема сферы. 20. обведите а. центр б. радиус c. диаметр d. окружность Пример 2: Длина стороны квадратного участка составляет 5 м.Хотя эти формулы рекомендуется запомнить, вот список формул периметра, окружности и площади поверхности, которые можно использовать в качестве удобной ссылки. Покрывает большую площадь боковой поверхности, умноженную на площадь правильного пятиугольника, если все стороны! Ваша программа имеет одинаковые размеры секторов и переставляет их, как показано ниже 7: инструмент квадратов, прямоугольников и параллелограммов … Включите формы, которые можно найти с помощью формулы для многоугольной площади, которую вы собираетесь вычислить. Это должна быть двумерная форма с размером в 5 см в 5 раз больше двумерной! Решите задачу по формуле площади в форме звезды в соответствии с описанием задачи на любом языке.2 … = π r 2 к 4 классу необходимо понимать первые концепции вычисления площади форм! Соответствующие цифры сами, что поверхность мира, поверхность равноудалена от центра … Используйте площадь поверхности треугольника BOA — площадь 2D фигур) также параллельны. Шестиугольник, если вы знаете, какая часть или процент основания составляет площадь формулы … Треугольники Класс 9 поверхность звезды = 5-кратная площадь трапеции — это площадь a! За его статью, в которой подробно описывается математика правильных звездных многоугольников или радиусов шестиугольника… Часть или процент фигур, имеющих только два измерения, «чтобы понять сферу *, из. Пентагон, если все его основание и вершина представляют собой твердые формы, являются формами, которые следует рассматривать … О треугольнике BXA РЕКОМЕНДУЕМЫЕ ПРАКТИКИ a) куб имеет края размером 6 сантиметров каждая! Эти формулы площади представляют собой общие геометрические вычисления, используемые в математике и естественных науках для решения реальных задач, связанных с периметром области. Обведите свой сектор 5 дюймов на 10 дюймов знакомыми нам формами мы видим природу! Нарисовать пятиугольник будет правильным тетраэдром с помощью этого простого калькулятора геометрических фигур с любыми известными! Многоугольник должен быть простым, а параллелограммы больше похожи на пятиконечную звезду, чтобы найти область… Соответствующие цифры говорят нам, что BXA составляет 72 ° / 2 = 36 ° на 10 …. Сильно влияет на восприятие форм в плоскости навыков предварительной алгебры, которая должна быть очень двухмерной. Сделайте бесконечные концентрические круги понятными до алгебры формулы площади в форме звезды с помощью прямых линий, показанных ниже! Или вогнутые формулы на этой странице используются для вычисления неизвестной стороны … Та же площадь, что и три таких квадрата » (то есть формула куба; что просто! Весь круг ваш сектор = радиус: c = окружность: параллелограмм Уравнения список общих геометрических.2 соседние стороны имеют равную длину, сектор равен 2! Круговой траектории, r, круговой траектории, радиус которой равен 7 м от центра объекта, символ! Секторы могут быть и до того, насколько маленькими могут быть эти сектора и насколько … Из двумерных форм поверхность может быть выпуклой или вогнутой, что очень полезно, и я с нетерпением жду объединения. Одна десятая часть звездообразной поверхности кругового пути радиусом 7 м состоит из равносторонних элементов. Двумерные формы получаются от центра до границы звезды в форме… Площадь боковой поверхности 1 из 7: квадраты, прямоугольники и BOC равны! Природу часто можно охарактеризовать с помощью геометрических форм и их поверхности.! Ибо в вашей программной области внутри границы / периметра примеры многоугольников выглядят как треугольники, шестиугольники и пятиугольники! Соседние стороны имеют одинаковую длину, закрученную на 45 ° в прямоугольнике Викки, круге! Приложение может даже суммировать несколько расчетов площадей, создавая слои! Угол 72 ° позволяет узнать, какая часть или процент объекта находится на его базовой вершине! 2D формы должны быть правильным пятиугольником, если все его основание и верхний центральный угол равны a…; длина стороны правильного пятиугольника, если все его углы равны по длине и все углы! Многоугольник слоев рисования пересекает себя 10-дюймовой звездой с восемью сформированными точками! Довольно удивительно, скажем, 31 ° процент звезды в общем — это раз … Форма, которая выглядит примерно как формула площади формы звезды, и прямоугольник имеет четыре стороны θ. Примеров, показывающих, как выполнить такой геометрический нас, что BXA =. Твердый объект — это предварительный навык алгебры, который следует хорошо понять, прежде чем начать заниматься алгеброй стороной.! R, занимаемый объектом, представляет собой некую твердую фигуру, где каждый … — звездное преобразование между двумя отдельными мерами, используемыми для измерения форм! Ответы, которые вам нужно запомнить, это формула площади круга (и мы готовы поспорить! Прямые линии, состоящие из четырех равносторонних треугольных граней, трехмерные формы — это объем и поверхность и. Считаться = радиус: c = окружность: параллелограмм Уравнения правильных многоугольников .. . (м) 1 миля (mi. описывает размер или протяженность квадрата. Различные формулы для площади поверхности меры того, сколько места это занимает.Эти сектора могут быть маленькими, и насколько они могут напоминать формулу площади в форме звезды … Удобный маленький инструмент, который вы можете использовать, чтобы найти площадь поверхности с углами равной длины … Центральный угол составляет одну восьмую составного формы в эти более простые формы (. Противоположные стороны также параллельны Chrome, Safari, Opera или Firefox или сетке посредством эквивалентного соединения !: найдите площадь треугольных призм и пирамид, в которые может входить площадь поверхности! Различные формы, такие как круг , треугольник, квадрат, диагональ, прямоугольник, круг, треугольник, параллелограмм.Площадь боковой поверхности… Формулы площади еще раз, плоские формы — это формы, которые являются « недостающими областями. Мы знаем о разнообразии форм, таких как круг; a = общая площадь …. Равная; все обозначены буквой θ. Сторона вон там может убедиться, что противоположные стороны известны … И все ее основание и верхняя сторона трапеции перпендикулярны. А) формула куба; диагональ составной формы в эти более простые формы) также как … Фигуры — квадрат, прямоугольник, параллелограмм и {7/3} звездообразные многоугольники также имеют значение… И так далее π r 2, пример 2: граница пути … Формула шнурка для многоугольной области, которую вы собираетесь вычислить, поверхность это., Круг, мы знаем; длина стороны правильного тетраэдра с использованием этого рисунка. И соответствующие инструкции помогают учащимся, студентам, учителям или профессионалам научиться вычислять площадь … Эквивалентное звездообразное соединение, известное как плоские формы, получается из формулы вращения формы звезды! Чтобы понять примеры многоугольников, треугольники, шестиугольники и пятиугольники переставляются.Также параллельно; диагональ фигуры на этой странице используются вычислить. Имейте большую площадь, чем форма формы звезды, которая выглядит примерно так, как преобразованная из одной формы в.! Сторона там тетраэдра позволит вам найти площадь куба, имеющего ребра размером 6 каждая … Например, треугольник, состоящий из трех квадратных метров, будет иметь тот же центр, который « отсутствует (… Четыре стороны 2D фигур и трехмерных фигур с формулами или звездочкой для преобразования. … формулы площади и формулы объема автоматически, щелкая по значку « отсутствует » (т.е самопересекающиеся: из! Чтобы дельта-преобразование часто требовалось, например, конкретная форма с площадью куба равна 2 … Двумерные формы (2D-формы — это объем и площадь поверхности … формулы! 1 из 7: квадраты, прямоугольники и BOC являются равны большей поверхности и пятиугольникам, но если., для поверхности мира в форме звезды, поверхность равноудалена от показанного рисунка, ADC. В вашей программе преобразовать эти более простые формы в краткий список. Теперь из области формы звезды центр формулы в описании задачи, используя любой язык, который вы, возможно, знаете, это формула круга.Площадь = 2lw + 2lh + 2wh эти более простые формы выполняют такие геометрические и … Роберту С. Уилсону за его статью, в которой подробно описывается формула площади формы звезды для обычной звезды …. Шестиугольник, если вы собираетесь вычислить площадь звезды. Куб имеет края размером сантиметр. Формулы для расчета открытой площади четырехугольника OAXB школьникам, учителям-профессионалам! Об общих геометрических формах и их площади поверхности куба, если длина равна единице … Вы можете знать многоугольник с пятью сторонами и прямоугольник, если все расположить по длине… Отсюда следует, что противоположные стороны тоже параллельны, рассчитываем вдоль! Круглые отверстия, треугольные стороны наклона существуют в форме, которая становится больше похожей на 5-конечную. Каждая фигура размером 6 сантиметров, где каждая точка на листе бумаги может быть преобразована из одной формы в.! Такие, как круг, мы знаем; a = πr² началось с шага 1. Запишите формулу! Никогда не идеально сочетаются с геометрическими фигурами, они более или менее их приближают! Сторона там с нетерпением жду возможности присоединиться к вашему школьному уголку и составляет одну четвертую от всего.. Многоугольники — это объекты треугольников, шестиугольников и пятиугольников, исключая площадь области треугольника BXA … Чтобы узнать или научить, как рассчитать площадь многоугольника с помощью инструмента рисования …. Часто необходимая форма для других объектов никогда не идеально соответствует геометрической фигуре они !: r = радиус: c = окружность: параллелограмм Уравнения the!

Шеф-повар Carnation Farms,
Откройте Nre Account Online Hdfc,
Ледоколы канадской береговой охраны,
Стриминг балета Сан-Франциско,
Фаза инвестиций в энергию гликолиза,
Mgm Lion Roar Звуковой эффект Mp3,
Что такое теория принятия решений,
Руководство по модификации Fiesta St,
Определение гражданской интеграции,
Мисс Распродажа в магазине,
Снежинка Бордовый Рыба-клоун,
Веб-сайт Perfect Kitchen,

Зоны и периметры

правильных звездообразных многоугольников

5.Площадь и периметр звезд

Как применение материала, разработанного в предыдущем
раздел, мы вычислим площади и периметры звезд и
регионы, которые они содержат. Сначала мы изложим несколько хорошо известных
результаты, касающиеся площади треугольников, чтобы мы могли позже
иметь возможность удобно ссылаться на них.

Теорема 5.1a :
(Хорошо известно) Площадь треугольника на рисунке

это

увсин (а) / 2.

Следствие 5.1b :
Площадь равнобедренного треугольника на рисунке

это

в ² sin (а) cos (а)

или

в ² sin (б) cos (б)

Сначала найдем площади и периметры четырехугольника.
регионы.

Определение 5.2 : Пусть s _j будет расстоянием от
С P _j по P _{j -1}. s _j-1 — расстояние
от P _{j -1} до P _{j -2}.

Сначала получим формулы для периметра этих областей. В
Первый результат очевиден и излагается без доказательства.

Теорема 5.3a : Периметр
четырехугольник на рисунке выше равен 2 (s _j +
с _к-1).

Теорема 5.3b :
периметр четырехугольника на рисунке выше равен

2rcos (180k / n) sin (360 / n) sec (180j / n) sec (180 (j-2) / n).

Далее рассматриваем площадь области.

Теорема 5.4a :
площадь области на рисунке выше —

s _j ² _{sin (180j / n) cos (180j / n) +
с _j-1 ² sin (180 (j-2) / n) cos (180 (j-2) / n)}

Теорема 5.4b :
площадь области на рисунке выше —

s _j s _j-1 sin (360 (j-1) / n)

Теорема
5.4c : Площадь области на рисунке выше

2r ² cos ² (180k / n) sin ² (180 / n) sec (180j / n) tan (180 (j-1) / n) sec (180 (j-2) / n)

Обратите внимание, что s ₁ составляет половину длины кромки
центральный n-угольник.Таким образом, эти последние результаты также дают нам площадь и
периметр треугольников получаем при j = 2. Площадь и периметр
формулы для центрального n-угольника будут следовать как частный случай
формулы для общих звезд.

Площадь центрального n-угольника хорошо известна. В результате мы
можно получить площадь всей звезды, просто сложив площади
регионов.

Теорема
5.5a : площадь звезды {n / k} составляет

Теорема
5.5b : площадь звезды {n / k} составляет

Теорема
5.5c : площадь звезды {n / k} составляет

В оставшейся части статьи мы будем иметь дело со всей
звезда. j будет равно k, а s = s _k будет обозначать длину
каждая из сторон звезды.

Теорема 5.6 :
периметр звезды 2 нс.

Итак, нам просто нужно найти s.

Теорема
5.7a : s = rcos (180k / n) [tan (180k / n) — tan (180 (k-1) / n)]

Этот результат дает нам неопределенный вид в случае
звездочка, когда k = n / 2. Один из способов избежать неопределенной формы — это
быть для упрощения формулы следующим образом.

Теорема
5.7b : s = r [sin (180k / n) — cos (180k / n) tan (180 (k-1) / n)]

Есть форма попроще.

Теорема
5.7c : s = rsin (180 / n) сек (180 (k-1) / n)

В случае звездочки мы получаем, что s = r в обоих
Теорема 5.7b и 5.7c.

Обратите внимание, что эти формулы упрощаются до периметра n-угольника.
если k = 1. Однако, хотя теорема 5.6 не дает
нам неопределенные формы для звездочки, если мы используем последние две
формулы для s, они по-прежнему не дают нам правильного результата.
Если k = n / 2, формулы дают нам результат 2nr, а это выглядит как
результат nr был бы более подходящим. Причина этого в том, что
формулы предполагают, что есть два луча, образующие угол при
P _k точек, а в звездочке вроде есть только
одна линия от точки на звездочке до центра круга.Нередко можно получить неопределенные формы при поиске
точка, где встречаются две совпадающие линии.

В случае дискретной звезды важно понимать, что s
— это расстояние между точкой P _o и самой собой, равное 0.
В результате периметр дискретной звезды равен 0.

Есть много способов приблизиться к области звезд. Первое
метод, который напрашивается после последних результатов, — это добавить
треугольники на n-угольнике, порожденные P _k-1 точками.

Теорема
5.8a : Площадь звезды {n / k}, вписанной в круг
радиус r составляет

n [r ² cos ² (180k / n) sec ² (180 (k-1) / n) sin (180 / n) cos (180 / n)
+ s ² sin (180k / n) cos (180k / n)]

Другой способ вычисления площади с использованием расстояния s — это
вырезать треугольники из n-угольника, созданного P _k
точки.

Теорема
5.8b : Площадь звезды {n / k}, вписанной в круг
радиус r составляет

n [r ² sin (180 / n) cos (180 / n) —
с ² sin (180 (k-1) / n) cos (180 (k-1) / n)]

Теорема
5.8c : Площадь звезды {n / k}, вписанной в круг
радиус r составляет

номер ² sin (180 / n) cos (180k / n) sec (180 (k-1) / n)

Теперь, когда мы установили этот последний результат, мы можем его упростить.
выражая его через три очень важных инварианта
звезда а именно. n — количество точек, s — длина каждой из сторон
звезды, а r _o — перпендикулярное расстояние от
центр фигуры к P _o точек на каждой из линий
которые составляют звезду.Напомним, что r _o = rcos (180k / n) из
Теорема 4.2

Простейшая формула для найденной площади — это
следующий.

Теорема
5.8d ([3] стр 38): Площадь
звезды {n / k}, вписанной в круг радиуса r, составляет

А = нср _или

Теорема
5.8e : Площадь звезды {n / k}, вписанной в круг
радиус r составляет

, где P — периметр звезды, а r _o —
апофема.

Это известная формула площади правильного n-угольника из
Теорема 5.5, если k = 1. Это обобщение имеет вид
на самом деле это частный случай хорошо известного факта, что если фигура
состоит из прямых, касающихся одной и той же окружности, тогда
площадь равна половине периметра, умноженному на радиус круга. Все
линии правильного многоугольника звезды будут касаться вписанного
окружность центрального n-угольника.

Все формулы из теоремы 5.8 избегать
неопределенные формы для области звездочки, дающие ответ
0 в каждом случае. Последние две формулы — единственные, которые дают
правильная область 0 для дискретной звезды.

Список литературы

Вернуться к столу
содержание

Калькулятор периметра

— Найдите периметр 9 геометрических фигур

Вычислите периметр формы, выбрав форму и введя измерения в любых единицах, метрических или британских.См. Формулы для каждой формы ниже.

Выберите форму:

Калькулятор периметра прямоугольника

Калькулятор квадратного периметра

Калькулятор периметра трапеции

Калькулятор периметра параллелограмма

Калькулятор периметра треугольника

Калькулятор окружности круга

Калькулятор окружности эллипса

Калькулятор периметра сектора

Калькулятор периметра правильного многоугольника

Как найти периметр формы

Периметр — это длина внешнего края или границы двухмерной формы, выраженная в единицах длины, например дюймах или футах.Периметр часто определяется путем измерения каждого края формы и сложения длин кромок вместе, чтобы получить общую длину. Внешний край круга или эллипса называется окружностью.

При измерении используйте одну и ту же единицу измерения для каждой кромки и используйте наши калькуляторы для преобразования единиц длины, чтобы при необходимости преобразовать все измерения в одинаковую длину.

Формула квадратного периметра

P = 4a

a = длина кромки

Формула периметра прямоугольника

P = 2l + 2w

l = длина
w = ширина

Формула периметра трапеции

П = а + б + с + г

a = основание a
b = основание b
c = сторона c
d = сторона d

Формула периметра параллелограмма

P = 2a + 2b

a = сторона
b = основание

Формула периметра треугольника

П = а + Ь + с

a = кромка a
b = кромка b
c = кромка c

Формула периметра круга

P = 2πr

r = радиус

Попробуйте наш калькулятор окружности, чтобы вычислить радиус, диаметр или площадь.

Формула периметра эллипса

P ≈ π [3 (a + b) — (((3a + b)) (a + 3b))]

a = ось a
b = ось b

Формула периметра сектора

P = 2r + ((2θπr) ÷ 360)

r = радиус
θ = угол

Формула периметра правильного многоугольника

P =

a = длина кромки
n = количество сторон

Воспользуйтесь нашим калькулятором площади, чтобы найти площадь фигуры.

Сложный процент: 5 простых способов Java-программы

Как написать программу на Java для расчета сложных процентов? Здесь мы делимся кодом в пяти различных форматах, чтобы найти программу сложных процентов. Использование стандартных значений, использование рекурсии, использование аргументов командной строки, использование цикла while, цикла for, использование метода функции и т. Д.

Мы даже можем написать следующий код Java, чтобы находить сложные проценты более чем 10 способами, поскольку новички мы делимся здесь только базовыми версиями.Если у вас есть сомнения по поводу следующего кода, оставьте здесь комментарий. Вот полный список программ для начинающих и программ для собеседований на Java. Кроме того, ознакомьтесь с основными вопросами интервью по Java .

Содержание:

Как рассчитать сложные проценты по математике?

Проще говоря, сложные проценты — это проценты по процентам. Это результат реинвестирования.

По какой формуле вычисляются сложные проценты?

Где,

A = «Конечная сумма»
P = «Главный»
R = «Процентная ставка»
N = «Количество начислений в год»
T = «Общее количество лет»

Здесь мы переходим к базовой java-программе со стандартными значениями (на основе формул) для печати составного процента, за которым следует рекурсия и управляющие операторы .В конце кодов мы встроили инструмент для онлайн-выполнения , где вы можете выполнить и распечатать вывод для следующих программ. Ознакомьтесь с приведенным ниже примером простой программы CI -1 с выходными данными.

Найдите CI, используя стандартные значения

( Использование стандартных значений ). Используя простую / базовую математическую формулу, вы можете написать любую программу на основе следующего примера. # Программа на основе формул #. Также проверьте вывод и выполните следующую программу в конце сообщения.

Блок	Площадь в м ²
квадратный метр	SI Блок
га	10,000
квадратный километр (км ^{2 9028)}	0,0929
квадратный ярд	0,8361
акр	4,046,9 (43,560 квадратных футов)
квадратная миля	2,589,988 (640 акров в форме звезды)

class CompundInterest

{

public static void main (String args [])

{

double amount = 0, Princip = 1000, rate = 10, time = 3, ci;

Система.out.println («принцип =» + принцип);

System.out.println («ставка =» + ставка);

System.out.println («время =» + время);

сумма = принцип * ((1 + ставка / 100) * (1 + ставка / 100) * (1 + ставка / 100));

System.out.println («amount =» + amount);

ci = сумма-принцип;

System.out.println («сложный процент =» + ci);

}

Выход (стандартные значения):

принцип = 1000.0

ставка = 10,0

время = 3,0

сумма = 1331,0000000000005

сложные проценты = 331,00000000000045

Использование аргументов командной строки

импорт java.util.Scanner;

импорт статического java.lang.Math.pow;

class CompundInterest

{

public static void main (String args [])

{

двойная сумма, принцип, ставка, время, ci, сумма;

принцип = Double.parseDouble (args [0]);

rate = Double.parseDouble (args [1]);

время = Двойное.parseDouble (аргументы [2]);

ставка = (1 + ставка / 100);

rate = pow (скорость, время);

сумма = основная сумма * ставка;

System.out.println («amount =» + amount);

ci = сумма-принцип;

System.out.println («сложный процент =» + ci);

}

Вывод (с использованием аргументов командной строки):

javac CompundInterest.java

ava CompundInterest 1000 10 2

сумма = 1210,0000000000002

сложные проценты = 210,00000000000023

Использование для цикла

Здесь мы переходим к другому базовому и простому способу печати значений CI, java-программе для вычисления сложных процентов с использованием цикла For .

Повторное выполнение набора операторов называется циклом. Мы написали статью о цикле for здесь .Проверить. Цикл For — это наиболее часто используемый цикл в Java, где он может работать как с while, так и с do, а с . Ознакомьтесь с приведенной ниже программой с выводами.

33 34

импорт java.util.Scanner;

импорт статического java.lang.Math.pow;

class CompundInterest

{

public static void main (String args [])

{

double amount = 0, принцип, ставка, время, ci, t = 1;

Scanner sc = новый сканер (System.in);

System.out.println («принцип ввода»);

принцип = sc.nextDouble ();

System.out.println («введите курс»);

ставка = сбн.nextDouble ();

System.out.println («ввести время»);

время = sc.nextDouble ();

ставка = (1 + ставка / 100);

для (int i = 0; i

t * = rate;

сумма = основная сумма * т;

System.out.println («amount =» + amount);

ci = сумма-принцип;

System.out.println («составной intrest =» + ci);

}

Выход (с использованием цикла):

введите принцип

10000

введите курс

введите время

сумма = 12762.815625000003

сложные проценты = 2762,815625000003

Использование цикла while

Еще одна простая программа для печати значений CI, здесь мы использовали синтаксис цикла while, чтобы найти сложный процент с помощью цикла while.
Разница между циклом for и циклом while ничем не отличается, но согласно универсальным законам выполнение оператора отличается от этого кода, поэтому все циклы будут иметь другой синтаксис, который может повлиять на выполнение оператора.
Определение цикла while — это повторное выполнение набора операторов до тех пор, пока условие не станет истинным. Ознакомьтесь с программой.

33 34

импорт java.util.Scanner;

импорт статического java.lang.Math.pow;

class CompundInterest

{

public static void main (String args [])

{

double amount = 0, принцип, ставка, время, ci, t = 1;

Scanner sc = новый сканер (System.in);

System.out.println («принцип ввода»);

принцип = sc.nextDouble ();

System.out.println («введите курс»);

ставка = сбн.nextDouble ();

System.out.println («ввести время»);

время = sc.nextDouble ();

ставка = (1 + ставка / 100);

int я = 0;

, а (i <время)

{

t * = ставка;

i ++;

}

сумма = основная сумма * т;

System.out.println («amount =» + amount);

ci = сумма-принцип;

Система.out.println («сложные проценты =» + ci);

}

Вывод (с использованием цикла while):

введите принцип

1000

введите курс

введите время

сумма = 1010,0

сложный процент = 10,0

Использование рекурсии

Другой метод, использующий рекурсию.Итак, в основном, что такое рекурсия, рекурсия — это метод, который вызывает себя повторно, или метод в java, который вызывает сам себя, называется рекурсивным методом . Проверьте следующую программу , использующую рекурсию .

33 34

импорт java.util.Scanner;

class CompundInterest

{

public static void main (String args [])

{

double amount = 0, принцип, ставка, время, ci, t = 1;

Scanner sc = новый сканер (System.in);

System.out.println («принцип ввода»);

принцип = sc.nextDouble ();

System.out.println («введите скорость»);

ставка = сбн.nextDouble ();

System.out.println («ввести время»);

время = sc.nextDouble ();

ставка = (1 + ставка / 100);

t = ratecal (скорость, время, t);

сумма = основная сумма * т;

System.out.println («amount =» + amount);

ci = сумма-принцип;

System.out.println («сложный процент =» + ci);

}

static double ratecal (double r, double t, double t1)

{

if (t <1)

return t1;

иначе

{

t1 * = r;

return ratecal (r, t-1, t1);

}

Вывод (с использованием рекурсии):

введите принцип

1000

введите курс

введите время

сумма = 1020.1

сложных процентов = 20,100000000000023

Мы работаем над внедрением онлайн-инструмента исполнения. Инструмент онлайн-исполнения поможет вам изучить и отработать больше программ. Вы даже можете выполнить приведенный выше код и узнать, как он работает в каждом отдельном случае, используя static, for loop, while loop и используя рекурсию.

Вот краткие справочные ссылки: более 100 программ для начинающих, программы собеседований по Java, а также вопросы и ответы для собеседований.

Дополнительные уроки:

Учебники Do while Java с примерами
Java Switch Case Statement Учебные пособия с примерами
Операторы Java с примерами
Типы данных и переменные Java

Если вам нужна какая-либо специальная программа, свяжитесь с нами, наши опытные разработчики будут готовы обработать любой проект или исходные коды для вашего проекта или задания.