Сопротивление проводников параллельное и последовательное: Последовательное и параллельное соединение проводников — урок. Физика, 8 класс.

Последовательное и параллельное соединение проводников. Физика, 8 класс: уроки, тесты, задания.

1.	Закономерности физических величин Сложность: лёгкое	1
2.	Соединение потребителей в быту Сложность: лёгкое	1
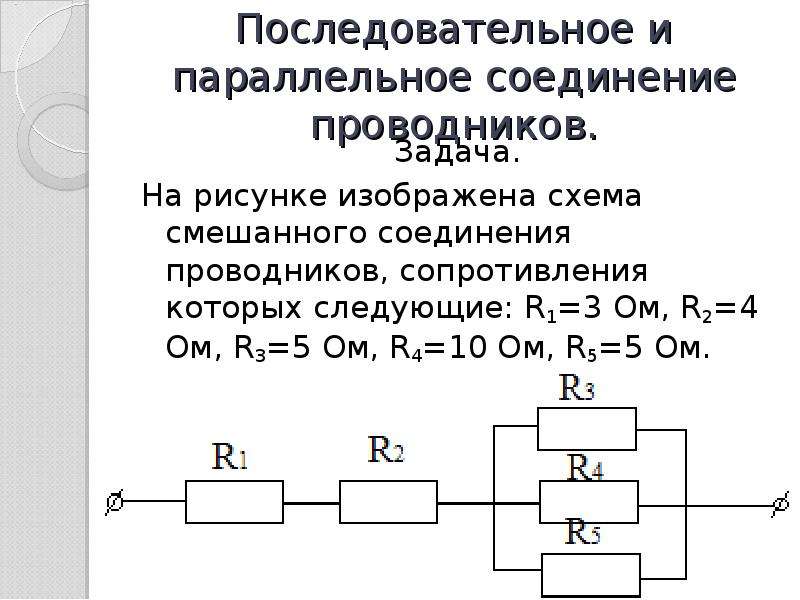
3.	Напряжение на резисторах при параллельном соединении Сложность: лёгкое	1
4.	Сопротивление ступенчатого реостата Сложность: лёгкое	1
5.	Расчёт количества потребителей при параллельном соединении Сложность: среднее	1
6.	Расчёт количества потребителей при последовательном соединении Сложность: среднее	1
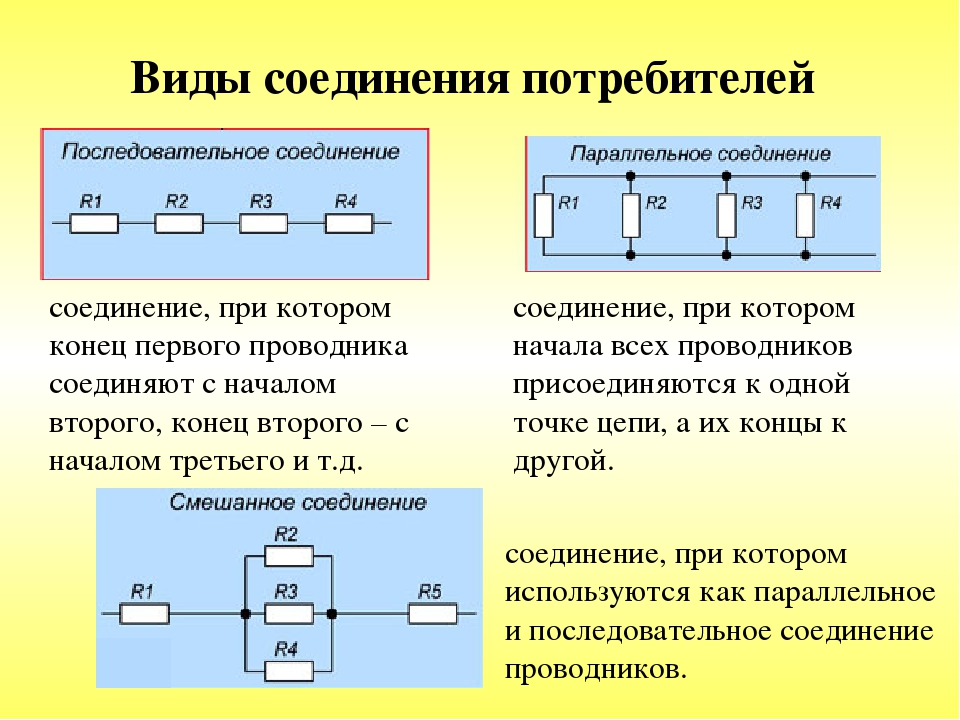
7.	Последовательное соединение двух проводников (вычисление величин) Сложность: среднее	6
8.	Параллельное соединение двух проводников Сложность: среднее	6
9.	Последовательное соединение трёх проводников 1 Сложность: среднее	8
10.	Последовательное соединение трёх проводников 2 Сложность: среднее	8
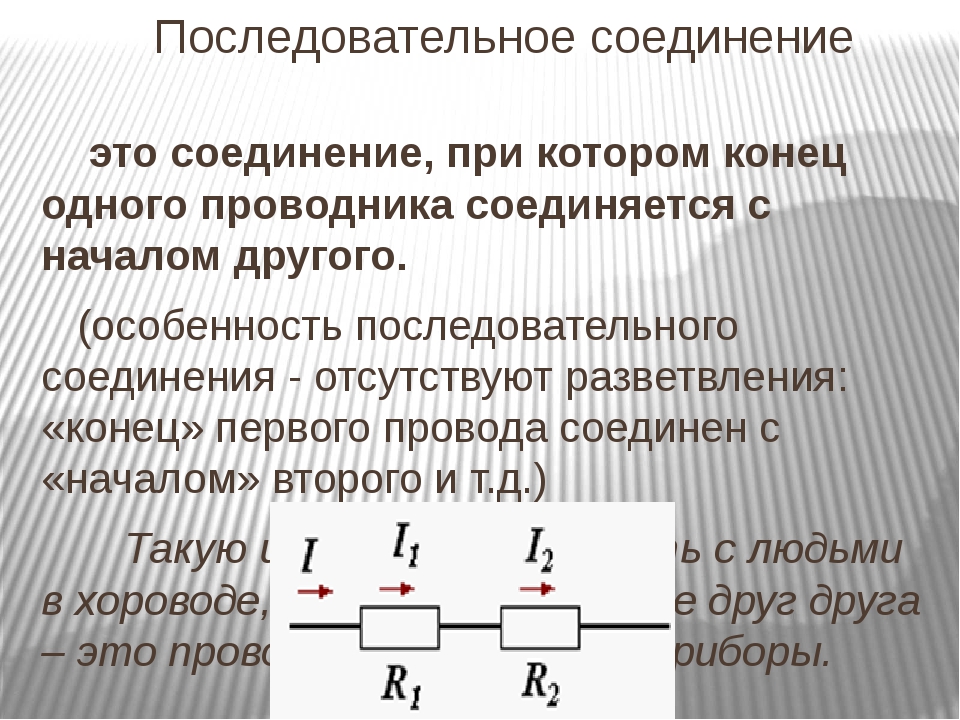
11.	Последовательное соединение трёх проводников 3 Сложность: среднее	8
12.	Напряжение на резисторах при последовательном соединении Сложность: среднее	1
13.	Параллельное соединение трёх проводников 1 Сложность: среднее	8
14.	Параллельное соединение трёх проводников 2 Сложность: среднее	8
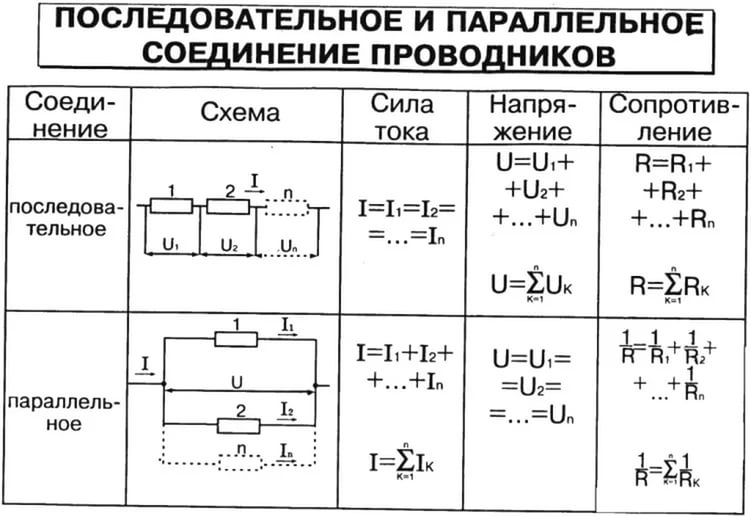
15.	Параллельное соединение трёх проводников 3 Сложность: среднее	8
16.	Параллельное соединение трёх проводников 4 Сложность: среднее	8
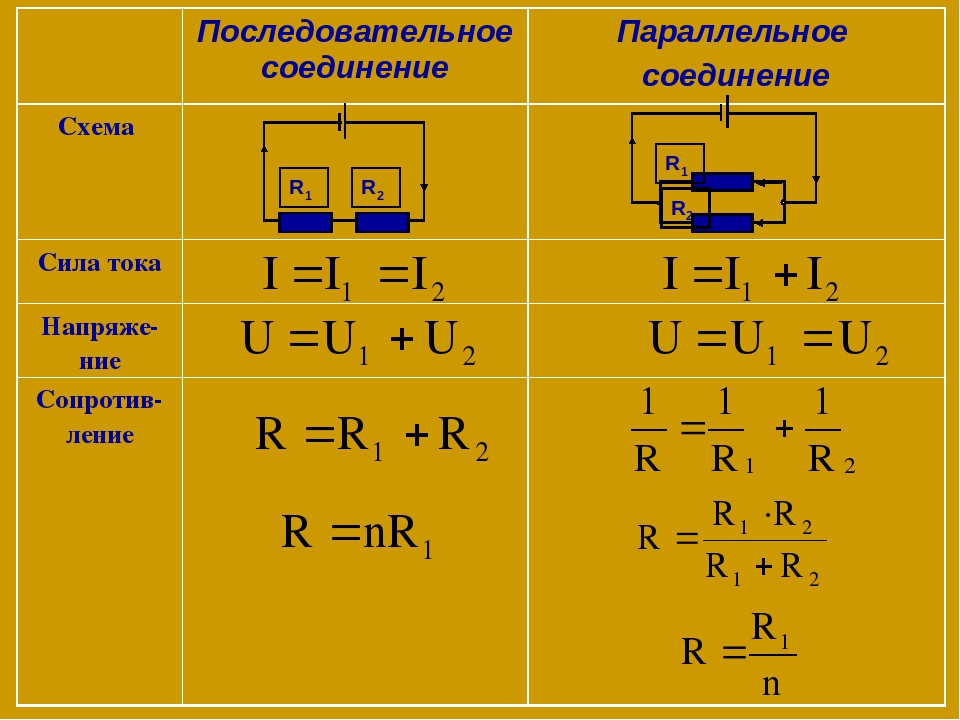
17.	Сравнение сопротивлений проводников, соединённых последовательно Сложность: среднее	1
18.	Сравнение физических величин при параллельном соединении проводников Сложность: среднее	2
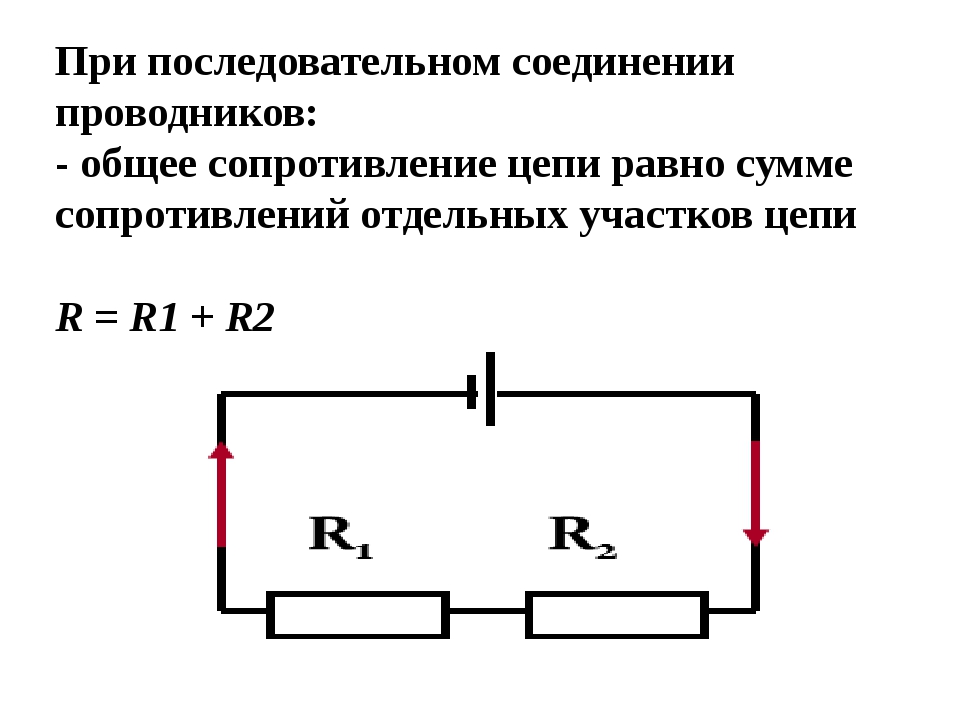
19.	Сравнение физических величин при последовательном соединении проводников Сложность: среднее	2
20.	Сопротивление второго проводника Сложность: среднее	1
21.	Последовательное соединение двух проводников Сложность: среднее	6
22.	Последовательное соединение Сложность: среднее	2
23.	Электрические цепи Сложность: среднее	1
24.	Электрические цепи Сложность: среднее	1
25.	Параллельное соединение Сложность: среднее	2
26.	Электрические цепи Сложность: среднее	2
27.	Параллельное соединение Сложность: среднее	1
28.	Вычисление силы тока в смешанном соединении Сложность: сложное	1

Сопротивление проводников. Последовательное и параллельное соединение проводников

Электрическое сопротивление R — физическая скалярная величина, характеризующая свойство проводника уменьшать скорость упорядоченного движения свободных носителей зарядов в проводнике. Обозначается сопротивление буквой R. В СИ единицей сопротивления проводника является ом (Ом).

1 Ом — сопротивление такого проводника, сила тока в котором равна 1 А при напряжении на нем 1 В.

Физическую величину G, обратную сопротивлению, называют электрической проводимостью G=1/R.

Удельное сопротивление проводника — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника, изготовленного из данного вещества и имеющего длину 1 м и площадь поперечного сечения 1 м2, или сопротивлению куба с ребром 1 м. Единицей удельного сопротивления в СИ является ом-метр (Ом·м).

Удельное сопротивление металлического проводника зависит от

концентрации свободных электронов в проводнике;

интенсивности рассеивания свободных электронов на ионах кристаллической решетки, совершающих тепловые колебания;

интенсивности рассеивания свободных электронов на дефектах и примесях кристаллической структуры.

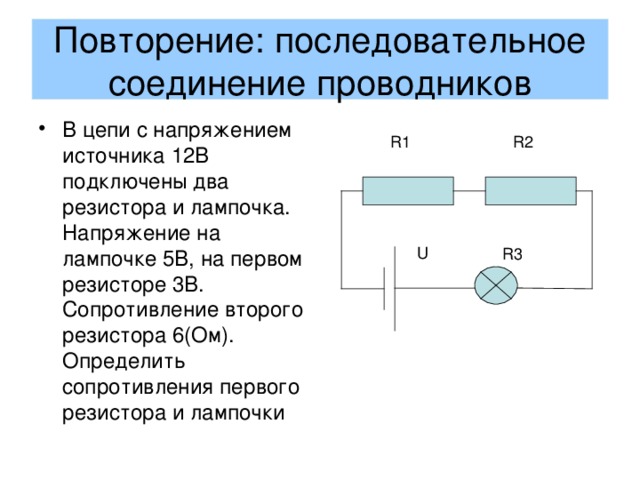
Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников сила тока во всех проводниках одинакова:

По закону Ома, напряжения U1 и U2 на проводниках равны

Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:

Где R – электрическое сопротивление всей цепи. Отсюда следует:

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении напряжения U1 и U2 на обоих проводниках одинаковы:

Сумма токовI1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Изучение последовательного и параллельного сопротивления проводников. | Учебно-методическое пособие на тему:

Лабораторная работа №9-10.

Изучение последовательного и параллельного сопротивления проводников.

Цель работы: экспериментально проверить справедливость законов последовательного и параллельного соединения проводников.

Оборудование:  источник тока, два проволочных резистора, амперметр, вольтметр, ключ замыкания тока, реостат, комплект соединительных проводников. (Виртуальный стенд)

Краткая теория для проверки соотношений при последовательном соединении проводников.
При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочерёдно друг за другом.Сила тока в последовательно соединённых  проводниках одинакова, т. е.

I1 = I2 = I.        

В проводниках электрический заряд в случае постоянного тока не накапливается, и через любое поперечное сечение проводника за определённое время проходит один и тот же заряд. Напряжение на концах рассматриваемого участка цепи складывается из напряжений на первом и втором проводниках:

U = U1 + U2.

Экспериментально — расчётная часть

1.Законы последовательного соединения проводников:

U=U1+U2,

R=R1+R2,

U1/U2=R1/R2.

Схема электрической цепи показана на рисунке.

1. Соберите электрическую цепь (см. рис.1) и с помощью реостата установите стрелку амперметра на определенное деление.
2. Измерьте вольтметром напряжение в общей цепи и на отдельных потребителях.

Ход работы

1. Рассчитайте сопротивление каждого резистора и общее сопротивление в цепи
2. Проверьте законы последовательного соединения проводников (см. п.1)

Краткая теория для проверки соотношений при параллельном соединении проводников.
При параллельном соединение двух проводников 1 и 2 сопротивлениями R1 и R2.  В этом случае электрический ток I разветвляется на две части. Силу тока в первом и втором проводниках обозначим через I1 и I2. Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не накапливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время.

Следовательно, I = I1 + I2.        

Напряжение U на концах проводников, соединённых параллельно, одинаково, так как они присоединены к одним и тем же точкам цепи.

Применяя закон Ома для всего участка в целом и для участков проводников сопротивлениями R1 и R2, можно доказать, что напряжения на параллельно соединённых проводниках равны: I1R1 = I2R2.

Общее сопротивление цепи 

2. Законы параллельного соединения проводников

U1=U2=U​.

I1/I2=R1/R2.

Схема электрической цепи показана на рисунке.

3. Соберите электрическую цепь (см. рис.2)
4. Измерьте вольтметром напряжение в общей цепи и силу тока общую и на отдельных потребителях.

1. Рассчитайте сопротивление каждого резистора и общее сопротивление в цепи
2. Проверьте законы последовательного соединения проводников (см. п.2)

Контрольные вопросы:

1. Какие сопротивления можно получить, имея три резистора по 6 кОм?
2. Сопротивление одного из последовательно включенных проводников в п раз больше сопротивления другого. Во сколько раз изменится сила тока в цепи (напряжение постоянно), если эти проводники включить параллельно?
3. Какую гидродинамическую аналогию можно использовать для моделирования последовательного и параллельного соединения проводников?
4. Как зависит мощность, выделяемая в проводниках с током, от типа их соединения?
5. Как соединены потребители электроэнергии в квартирах? Почему?
6. Как соединены лампочки в елочной гирлянде?

Рекомендуемый видео материал

http://genby.ru/tv.php?c=wU-TSa2-U5w

http://school-collection.edu.ru/

Последовательное и параллельное соединение — Википедия

Материал из Википедии — свободной энциклопедии

Последовательное соединение проводников.
Параллельное соединение проводников.

Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включённых проводников.

Последовательное соединение

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I=I1=I2=⋯=In{\displaystyle I\mathrm {=} I_{1}=I_{2}=\cdots =I_{n}} (так как сила тока определяется количеством электронов, проходящим через поперечное сечение проводника, и если в цепи нет узлов, то все электроны в ней будут течь по одному проводнику).

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника питания, равно сумме напряжений на отдельных участках цепи: U=U1+U2+⋯+Un{\displaystyle U\mathrm {=} U_{1}+U_{2}+\cdots +U_{n}}.

Резисторы

R=R1+R2+⋯+Rn{\displaystyle R=R_{1}+R_{2}+\cdots +R_{n}}

Катушка индуктивности

L=L1+L2+⋯+Ln{\displaystyle L=L_{1}+L_{2}+\cdots +L_{n}}

Электрический конденсатор

1C=1C1+1C2+⋯+1Cn{\displaystyle {\frac {1}{C}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}}.

Мемристоры

M=M1+M2+⋯+Mn{\displaystyle M=M_{1}+M_{2}+\cdots +M_{n}}

Выключатели

Цепь замкнута, когда замкнуты все выключатели. Цепь разомкнута, когда разомкнут хотя бы один выключатель. (См.также Логическая операция И).

Параллельное соединение

Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках: I=I1+I2+⋯+In{\displaystyle I\mathrm {=} I_{1}+I_{2}+\cdots +I_{n}}

Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: U=U1=U2=⋯=Un{\displaystyle U\mathrm {=} U_{1}=U_{2}=\cdots =U_{n}}

Резисторы

При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость 1R{\displaystyle {\frac {1}{R}}} складывается из проводимостей каждого резистора 1Ri{\displaystyle {\frac {1}{R_{i}}}})

Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.

Доказательство

Для двух параллельно соединённых резисторов их общее сопротивление равно: R=R1R2R1+R2{\displaystyle R={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}}.

Если R1=R2=R3=…=Rn{\displaystyle R_{1}=R_{2}=R_{3}=…=R_{n}}, то общее сопротивление равно: R=R1n{\displaystyle R={\frac {R_{1}}{n}}}.

При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.

Катушка индуктивности

1Ltotal=1L1+1L2+⋯+1Ln{\displaystyle {\frac {1}{L_{\mathrm {total} }}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}

Электрический конденсатор

Исследование сопротивлений проводников при параллельном и последовательном

Колледж экономики, права и информатики

Отчет по лабораторной работе

По дисциплине

«Электротехнические основы источников питания»

студент 25 группы

Лабораторная работа №1

«Измерение зависимости сопротивления реальных проводников от их геометрических параметров и удельных сопротивлений материалов»

Цель:определить удельное сопротивление проводника и сравнить его с табличным значением.

2) L = 100м; S=0.1мм 2

6) P=0.0724*100/0.1=0.0000724мОм=0.0724Ом*мм 2 /м

8) ρ_ср=0,0731 Ом*мм 2 /м

Табличное значение для никеля ρ

Определили удельное сопротивление проводника и сравнили его с табличными данными, в итоге мы получили приблизительное значения. Произошли расхождения в результате погрешности в измерениях и погрешности в вычислениях.

Ответы на контрольные вопросы:

1. Что называют удельным сопротивлением проводника?

Постоянный параметр для определенного вещества, определяющийся произведением сопротивления на длину и деленным на площадь поперечного сечения проводника

2. Как зависит сопротивление проводника от его длины?

Сопротивление прямо пропорционально его длине

3. По какой формуле можно рассчитать удельное сопротивление проводника?

4. В каких единицах измеряется удельное сопротивление проводника?

Лабораторная работа №2

«Исследование сопротивлений проводников при параллельном и последовательном соединении»

Цель:изучить законы протекания тока через последовательно и параллельно соединенные проводники и определить формулы расчета сопротивлений таких участков

По данным измерений

По данным расчета :

Теоретические расчеты частично потверждают практический данные

5)I(Rac)=0.315 A I=0.136 A I (R_CD)=0.181A

6)I=1.5/4.76=0.315 A I+I=0.136+0.181=0.317

Ответы на контрольные вопросы:

1. Может ли сопротивление участка двух параллельно соединненых проводников быть больше (меньше) любого из них? Объясните ответ.

Может быть меньше, так как 1/R_общ=1/R1+1/R₂

2. Какие законы сохранения используются для вывода формул сопротивления параллельного и последовательного соединения проводников?

Первый и второй законы Кирхгофа

3. Проанализируйте аналогию между приводимыми здесь формулами и формулой для расчета сопротивления одного проводника через его геометрические параметры: . В чем заключается эта аналогия?

Аналогичная пропорция R=U/I можно привести к U=p*L и I=S

Лабораторная работа №3

«ЭДС и внутреннее сопротивление источников постоянного тока. Закон Ома для полной цепи»

Цель:определить сопротивление источника цепи и его ЭДС

3. V=0.950 B I=0.33 A

5) R= (0,75-0,6)/(0,24-0,29)=0,3 Ом

Ответы на контрольные вопросы:

1. Сформулируйте закон Ома для полной цепи.

Сила тока пропорциональна ЭДС и обратно пропорциональна сумме внутреннего и внешнего сопротивлений.

2. Чему равна ЭДС источника при разомкнутой цепи?

В таком случае ЭДС равна напряжению

3. Чем обусловлен внутреннее сопротивление источника тока?

Отношению изменения силы тока к изменению напряжения

4. Чем измеряется сила тока короткого замыкания батарейки?

Отношением ЭДС в внутреннему сопротивлению

Лабораторная работа № 4

«Исследование сложных цепей постоянного электрического тока»

Цель:изучить приемы расчета сложных электрических цепей постоянного тока.

Вывод: Разность потенциалов в точках О и О ’ равна 0, и ток тоже равен 0. Замкнутое и разомкнутое состояние не влияют на работу схемы

Ответы на контрольные вопросы:

1. Какие свойства схемы могут оказаться полезными при расчете сложных схем?

Из симметрии ясно, что токи через элементы CO и DO должны быть одинаковы и равны токам, текущим через элементы OF и OE. А раз так, то в точке О цепь можно разорвать, при этом токи через элементы сетки не изменятся:

2. Между какими точками схемы, изображенной на рисунке 3, напряжение равно нулю?

3. Исследуйте аналогичным способом сопротивление между противоположными вершинами проволочного куба? Чему равно сопротивление между этими точками?

Пусть сопротивление одного ребра куба = r, тогда

R_AB= + + =

Лабораторная работа №5

«Мощность в цепи постоянного тока»

Цель:изучить законы выделения мощности в цепях постоянного тока и согласования источников тока с нагрузкой.

Вывод: При сопротивлении нагрузки0,65 ОмМощность, отдаваемая источником питания будет максимальна.

Чем ниже сопротивление нагрузки, тем больше теряется мощности.

Оптимальное сопротивление нагрузки ≥ внутреннему сопротивлению источника питания.

Ответы на контрольные вопросы:

1. Почему при увеличении сопротивления нагрузки напряжение на ней растет?

По закону Ома, напряжение прямо пропорционально сопротивлению.

2. Объясните, почему выделяемая на нагрузке мощность мала, если сопротивление нагрузки сильно отличается от внутреннего сопротивления источника? Обратите внимание на формулы для силы тока (1) и напряжения (2) на нагрузке.

По формуле видно, что мощность обратно пропорциональная сумме сопротивлений нагрузки и источника питания, таким образом, наибольшая мощность будет выделяться на нагрузке при равенстве этих сопротивлений.

Лабораторная работа № 6.

«Принцип работы плавких предохранителей в электрических цепях»

Цель:рассчитать предохранители для защиты электронной сети с напряжением 220 В, питающей осветительные и электронагревательные приборы.

U генератора = 220В

Р лампочек = 60 Вт и 150 Вт

Р нагревательных приборов = 600Вт и 1000Вт

Рабочее напряжение = 240В

Вывод: Номинальный ток вставки должен удовлетворять требованию Iвст>Ip.

Каждый предохранитель сработал лишь тогда, когда будет превышение тока плавкой вставки на участке в цепи, который он защищает, величина тока предохранителя должна быть больше расчетного тока участка цепи.

Ответы на контрольные вопросы:

1. Какова цель установки предохранителей в электрических цепях?

Предохранитель необходим для защиты электрической цепи

2. Как рассчитать номинальный ток плавкой вставки предохранителя?

Рассчитать по формуле I=P/U

3. Почему правилами техники безопасности запрещается установка так называемых «жучков» – случайно выбранных проводников вместо целых предохранителей?

Потому, что случайно выбранные проводники могу не расплавиться при критической силе тока.

ЦЕЛЬ РАБОТЫ: определить общее сопротивление двух последовательно соединенных проволочных резисторов.

ОБОРУДОВАНИЕ: ЛИП, 3 вольтметра, амперметр, 2 реостата, соединительные провода.

Теория:

1. сила тока во всех последовательно соединенных участках цепи одинакова
I=I₁+I₂
2. напряжение в цепи, состоящей из нескольких последовательно соединенных участков,
равно сумме напряжений на каждом участке U=U₁+U₂
3. сопротивление цепи, состоящей из нескольких последовательно соединенных участков,
равно сумме сопротивлений каждого участка R=R₁+R₂

Ход работы:

1. Расположите на столе приборы в соответствии со схемой.

2. Соберите цепь по схеме, соблюдая полярность подключаемых приборов.

3. Запишите показания амперметра и трех вольтметров.

4. Используя закон Ома для участка цепи

рассчитайте сопротивление:

· сопротивление первого резистора

· сопротивление второго резистора

· общее сопротивление цепи по двум формулам

и

5. Занесите результаты измерений и вычислений в таблицу:

6. Сравните результаты вычислений общего сопротивления и сделайте вывод

ОТЧЁТ РАБОТЫ:

1. Произвести все расчёты лабораторной работы.

2. Сделать вывод работы.

3. Способ подключения амперметра, вольтметра.

4. Единицы измерения силы тока, напряжения.

5. Закон Ома для участка цепи.

6. Формулы вычисления силы тока, напряжения и сопротивления при параллельном соединении проводников.

Литература:

· Г.Я.Мякишев, Физика учебник 10 кл. 2010 г.

Исследование параллельного соединения проводников»

ЦЕЛЬ РАБОТЫ: определить общее сопротивление двух параллельно соединенных

Проволочных резисторов.

ОБОРУДОВАНИЕ: ЛИП, вольтметр, 3 амперметра, 2 реостата, соединительные провода.

Теория:

1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках

2. напряжение на всех параллельно соединенных участках цепи одинаково

U=U₁+U₂
3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению:(R-сопротивлениепроводника,1/R – электрическая проводимость проводника)

Если в цепь включены параллельно только два сопротивления, то:

Ход работы:

1. Расположите на столе приборы в соответствии со схемой.

2. Соберите цепь по схеме, соблюдая полярность подключаемых приборов.

3. Запишите показания трех амперметров и вольтметра.

4. Используя закон Ома для участка цепи

ü 1 участка

ü 2 участка

ü общее сопротивление по двум формулам

и

5. Занесите результаты измерений и вычислений в таблицу:

6. Сравните результаты вычислений общего сопротивления и сделайте вывод.

ОТЧЁТ РАБОТЫ:

1. Произвести все расчёты лабораторной работы.

2. Сделать вывод работы.

3. Метод измерения силы тока, напряжения.

4. Единицы измерения силы тока, напряжения, сопротивления.

5. Закон Ома для участка цепи.

6. Формулы вычисления силы тока, напряжения и сопротивления при последовательном соединении проводников.

Литература:

· Г.Я.Мякишев, Физика учебник 10кл. 2010 г.

Папиллярные узоры пальцев рук – маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Материал содержит описание лабораторной работы по проверке основных соотношений для последовательного и параллельного соединения проводников. Данный материал используется для работы со студентами дистанционно и с категорией студентов с ОВЗ.

Скачать:

Предварительный просмотр:

Лабораторная работа №9-10.

Изучение последовательного и параллельного сопротивления проводников.

Цель работы: экспериментально проверить справедливость законов последовательного и параллельного соединения проводников.

Оборудование: источник тока, два проволочных резистора, амперметр, вольтметр, ключ замыкания тока, реостат, комплект соединительных проводников. (Виртуальный стенд)

Краткая теория для проверки соотношений при последовательном соединении проводников.
При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочерёдно друг за другом.Сила тока в последовательно соединённых проводниках одинакова, т. е.

В проводниках электрический заряд в случае постоянного тока не накапливается, и через любое поперечное сечение проводника за определённое время проходит один и тот же заряд. Напряжение на концах рассматриваемого участка цепи складывается из напряжений на первом и втором проводниках:

Экспериментально – расчётная часть

1. Законы последовательного соединения проводников:

Схема электрической цепи показана на рисунке.

1. Соберите электрическую цепь (см. рис.1) и с помощью реостата установите стрелку амперметра на определенное деление.
2. Измерьте вольтметром напряжение в общей цепи и на отдельных потребителях.

Сила тока в цепи

1. Рассчитайте сопротивление каждого резистора и общее сопротивление в цепи
2. Проверьте законы последовательного соединения проводников (см. п.1)

Краткая теория для проверки соотношений при параллельном соединении проводников.
При параллельном соединение двух проводников 1 и 2 сопротивлениями R1 и R2. В этом случае электрический ток I разветвляется на две части. Силу тока в первом и втором проводниках обозначим через I1 и I2. Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не накапливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время.

Следовательно, I = I1 + I2.

Напряжение U на концах проводников, соединённых параллельно, одинаково, так как они присоединены к одним и тем же точкам цепи.

Применяя закон Ома для всего участка в целом и для участков проводников сопротивлениями R1 и R2, можно доказать, что напряжения на параллельно соединённых проводниках равны: I1R1 = I2R2.

Общее сопротивление цепи

1. Законы параллельного соединения проводников

Последовательное и параллельное соединение резисторов

Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также – это база для расчета более сложных схем.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.

Рис. Последовательное подключение.

Обозначение:

Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим. Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях – складываем, в параллельных – это обратно пропорциональная величина.

Параллельное соединение

Рис. Параллельное подключение.

Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах – //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.
Более наглядно это можно представить в виде формул:
1. Каждый вид соединения находится под одинаковым напряжением:
U = U1 = U2;
2. Суммарная сила тока равняется суммарному значению тока каждого участка
I = I1 + I2;
3. Сопротивление цепи равно сумме величина обратных сопротивлению участка:
1/R = 1/R1 + 17R2 + . . . + 1/Rn;
4. Сила тока пропорциональна сопротивлению каждого участка
I1/I2=R2/R1.
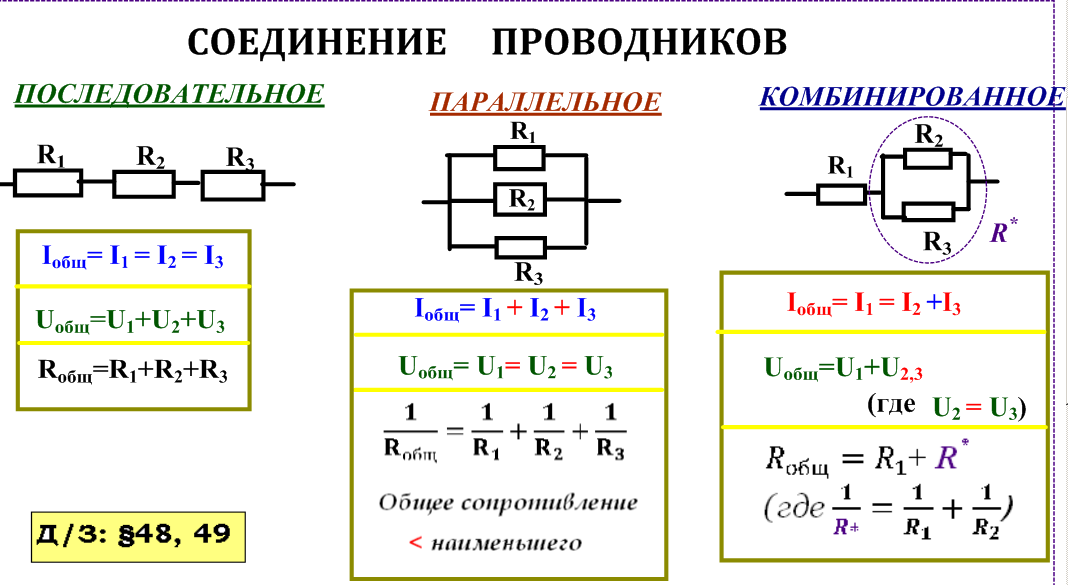
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.

Смешанное подключение

Рис. Смешанное подключение резисторов

В электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока.
При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.

Основные законы электротехники, наиболее часто используемые для расчетов

Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи

Закон Ома

Напряжение находится по закону Ома по формуле I=U/R – чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.

Законы Кирхгофа

Первый закон

Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.

Рис. иллюстрация к пояснению действия первого закона Кирхгофа.

Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю.
Если посмотреть на схему, I1 – это ток, который заходит в узел, I2 и I3 – это электроны, которые вытекают из него.
Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.

Второй закон Кирхгофа.

Рис. иллюстрация к пояснению действия второго закона Кирхгофа.

Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
E1- Е2 = – UR1 – UR2 или E1 = Е2 – UR1 – UR2.

Параллельное и последовательное соединение резисторов,  решение задач

Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.

Рис. Порядок замещения при расчете сложных позиций более простыми.

Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).

Теперь образовалась ситуация – включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.

Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

Схема с подключением сопротивлений «треугольником»

Рис. Расчетная схема соединения резисторов в треугольник.

Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.

Рассмотрим на примере рисунка расчет резисторов по этому подключению.
Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.

Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.

Проведем несложные вычисления учитывая, что
R1, R2, R4, R5 равняется 1 Ом. R3, R7 – 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.

Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.

Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом.
И последнее – Rэ123 4 5 с R6 – параллельное.

Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.

Расчет последовательного и параллельного подключения резисторов онлайн

Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие. Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах. Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.

Также такая форма расчета подойдет и для проверки результатов решения учебных задач.

Последовательное и параллельное соединение резисторов и конденсаторов

Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.

Рис. Замещения последовательно включенных элементов.

Определение этому элементу можно дать следующее: Конденсатор – это совокупность проводящих тел служащий для накопления электрического заряда.
Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной – по форме пластин разделяется и тип конденсатора.

Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.

Устройство конденсатора

Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.

Типовые схемы подключения конденсаторов

Рассмотрим различные виды подключения конденсатора.

Последовательное

Первый вид — это последовательное соединение.
Предположим, что емкость этих конденсаторов будут равны. Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами,  сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним. У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается,  U эк = U1 + U2+ … Un.

Параллельное

Второй тип подключения конденсаторов – это соединение в паралель

Рис. Схема замещения элементов, включенных в параллель.

Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.

У элементов в // емкость складывается Сэ = C1 + C2 + … C n.
Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
Uэ = U1 = U2 =… = Un – это особенность параллельного подсоединения всех элементов цепи.

Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.

Рис. Расчетные позиции элементов при различном включении.

Простая позиция, которая не требует преобразования №1 – последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3,  подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.

Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3
Сэ = 100 + 200 + 500 = 800 мФ.

Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.

Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф.
Практическая задача решена.

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

Текст 4. Проводники и изоляторы

Проводники — это материалы с низким сопротивлением, поэтому ток легко проходит через них. Чем ниже сопротивление материала, тем больше тока может пройти через него.

Наиболее распространенными проводниками являются металлы. Лучшие из них — серебро и медь. Преимущество меди в том, что она намного дешевле серебра. Таким образом, медь широко используется для производства проводов. Одна из общих функций проводников — это подключение источника напряжения к сопротивлению нагрузки.Поскольку проводники из медной проволоки имеют очень низкое сопротивление, в них создается минимальное падение напряжения. Таким образом, все приложенное напряжение может создавать ток в сопротивлении нагрузки.

Следует учитывать, что большинство материалов меняют значение сопротивления при изменении температуры.

Металлы повышают свое сопротивление при повышении температуры, тогда как углерод снижает свое сопротивление при повышении температуры. Таким образом, металлы имеют положительный температурный коэффициент сопротивления, а углерод — отрицательный температурный коэффициент.Чем меньше температурный коэффициент или чем меньше изменение сопротивления при изменении температуры, тем совершеннее материал сопротивления.

Материалы, имеющие очень высокое сопротивление, называются изоляторами. Ток через изоляторы проходит с большим трудом.

Наиболее распространены изоляторы воздушные, бумажные, резиновые, пластмассовые.

Любой изолятор может проводить ток, если к нему приложено достаточно высокое напряжение. К изоляторам необходимо приложить токи большой силы, чтобы они стали проводящими.Чем выше сопротивление изолятора, тем больше должно быть приложенное напряжение.

Когда изолятор подключен к источнику напряжения, он накапливает электрический заряд, и на изоляторе создается потенциал. Таким образом, изоляторы выполняют две основные функции:

для изоляции проводящих проводов и, таким образом, для предотвращения короткого замыкания между ними и

для хранения электрического заряда при подаче напряжения.

1. Найдите ответы на эти вопросы в тексте выше:

1.Какие материалы называют проводниками?

2. В чем преимущество меди перед серебром?

3. Какая наиболее распространенная функция проводников?

4. Почему в медных проводниках возникает минимальное падение напряжения?

5. Какая связь между значением сопротивления и температурой углерода?

6. Какие материалы называются изоляторами?

7. Какие изоляторы наиболее распространены?

8.Каковы две основные функции изоляторов?

2. Дополните предложения правильным вариантом:

1. Изоляторы — это материалы, имеющие а) низкое сопротивление.

б) высокое сопротивление.

2. Ток легко проходит по проводникам а).

б) с большим трудом.

3. Медь и серебро — а) общие проводники.

б) изоляторы общие.

4. Воздух, бумага и пластмассы — это а) обычные изоляторы.

б) общие жилы.

5. При подаче высокого напряжения. а) не проводит ток

изолятор б) он проводит ток.

6. Изоляторы используются а) для накопления электрического заряда.

б) для снижения напряжения.

c) для предотвращения короткого замыкания между проводками

провода

8.Углерод снижает свое сопротивление а) при повышении температуры.

б) при понижении температуры.

9. Металлы имеют а) положительный температурный коэффициент

сопротивление

б) отрицательный температурный коэффициент

сопротивление

Текст 5. Электрогенераторы и двигатели

Устройство для преобразования механической энергии в электрическую называется генератором.Функция двигателя прямо противоположна, то есть он преобразует электрическую энергию в механическую. Огромная энергия паровых двигателей, газовых двигателей и водяных турбин теперь может быть преобразована в электричество и передана на многие мили. Генератор произвел революцию в современной промышленности, давая дешевую электроэнергию.

Основными частями генератора являются: а) магнитное поле, создаваемое постоянными магнитами или электромагнитами; и б) подвижная катушка из медной проволоки, называемая якорем, намотанная на драм.

Генераторы

D. используются для электролитических процессов. Большой д. c. генераторы используются в определенных производственных процессах, таких как производство стали. Генераторы малой мощности используются для различных специальных целей, таких как сварочные, автомобильные генераторы, освещение поездов, системы связи и т. Д.

Текст 6. D.c. электродвигатели

Существует большое разнообразие d. c. и а. c. моторы. Существуют параллельные двигатели, серийные двигатели, синхронные двигатели, асинхронные двигатели, одно-, двух- и трехфазные двигатели.Они используются для привода различных машин.

Двигатели постоянного тока бывают трех основных типов и названы в соответствии с тем, как их катушки возбуждения соединены с якорем. Они названы соответственно: серия, шунт и составной.

В серийных двигателях обмотки возбуждения и якорь соединены последовательно друг с другом. Весь ток, который проходит через якорь, проходит через катушки возбуждения. Поэтому обмотки возбуждения состоят из нескольких витков толстого провода.При запуске под большой нагрузкой последовательный двигатель потребляет большой ток, чтобы обеспечить необходимый крутящий момент.

Катушки возбуждения параллельных двигателей подключены непосредственно к щеткам, следовательно, к ним приложено напряжение фольги сети. Шунтирующий двигатель можно назвать двигателем постоянной скорости, и он подходит для привода станков, токарных станков. деревообрабатывающие станки и любые станки, требующие постоянной скорости.

Составной двигатель имеет как шунтирующие, так и последовательные обмотки возбуждения и, следовательно, имеет природу обоих типов двигателей.

Текст 7. A.c. электродвигатели

Двигатели для цепей переменного тока могут быть однофазными или многофазными (двух- или трехфазными). Их снова можно разделить на два вида, названных соответственно: I. Синхронные; II. Не- или асинхронные, обычно называемые асинхронными двигателями.

Наиболее широко используемый a. c. Двигатель представляет собой асинхронный двигатель, показанный на рис. 2. Он состоит из двух основных частей: а) неподвижной обмотки или статора, который создает вращающееся магнитное поле, и б) вращающейся части двигателя, т.е.е. ротор. Ротор коммерческого а. c. Двигатель состоит из железного сердечника с большими медными стержнями, размещенными в пазах по окружности и соединенными с обоих концов с медными кольцами. Это называется ротор с короткозамкнутым ротором. Когда ротор помещается во вращающееся магнитное поле, в нем индуцируется большой ток.

A. c. Двигатели по конструкции в точности аналогичны двигателям переменного тока. генераторы и могут называться инвертированными генераторами переменного тока, поскольку одна и та же машина может использоваться либо как генератор, либо как двигатель.

Синхронные двигатели очень подходят для больших мощностей, когда машину можно запустить без нагрузки, а после запуска работать в течение длительного времени.

Для питания сетей постоянного тока питание в первую очередь исходит от источника переменного тока и преобразуется в постоянный ток синхронными преобразователями или мотор-генераторными установками.

1. Добавьте английские эквиваленты к следующему:

,

Текст 8.Линии трансмиссии

Энергосистема — это соединение электростанций высоковольтными линиями электропередачи. В настоящее время электричество передается на большие расстояния, и длина передающих линий электропередачи варьируется от области к области.

Система проводов называется линией электропередачи, если она не имеет параллельных ветвей, и сетью электропитания, если она имеет параллельные ветви.

По своему назначению линии электропередач и сети подразделяются на линии передачи и распределения.

Линии передачи служат для доставки энергии от станции к распределительным центрам. Линии распределения поставляют мощность от распределительных центров к нагрузкам.

Линии также подразделяются на: 1) служебные; 2) закрытый; 3) кабель (под землей).

Воздушные линии включают линейные провода, изоляторы и опоры. Проводники присоединяются к изоляторам, а они — к опорам. Чем больше сопротивление, тем выше тепловые потери в проводящих проводах.Для уменьшения потерь можно использовать понижающий трансформатор.

Внутренние линии включают проводники, шнуры и автобусы. Проводник может включать один провод или комбинацию проводов, не изолированных друг от друга. Они поставляют электрический ток потребителям.

Что касается линий метро, ​​то они используются в городских районах. Соответственно, они используются в городах и поселках, а также на территориях промышленных предприятий.

Сопротивление последовательно и параллельно

Последнее обновление: 15 июня 2020 г., Teachoo

Электрическая цепь в серии

Преимущества

• В этом случае легче включить или выключить все соединенные между собой приборы.
• Кроме того, это безопаснее, поскольку через цепь протекает меньше тока.
• Он используется, когда сотни или тысячи лампочек должны использоваться вместе (чтобы один и тот же ток проходил через все, и они могли включаться и выключаться вместе).
• Пример — световое украшение Дивали

Недостаток

• Если один электроприбор перестанет работать из-за какой-либо неисправности, то все остальные перестанут работать.
• Все электроприборы имеют только один выключатель, из-за которого их нельзя включать и выключать по отдельности.
• Все устройства не получают одинаковое напряжение, так как напряжение делится последовательно.
• Эквивалентное сопротивление увеличивается слишком сильно, из-за чего величина протекающего тока становится очень маленькой.

Электрическая цепь параллельно

Использует

Обычно используется в домах для подключения лампочек и различной бытовой техники.

Каждое устройство имеет отдельный выключатель, который можно включать и выключать по мере необходимости.

Преимущества

Даже если один электроприбор перестает работать из-за какого-либо дефекта, все остальные приборы работают нормально.

Отдельный прибор можно выключить или включить отдельно

Каждый электроприбор получает такое же напряжение, как и линия электропитания.

Поскольку общее сопротивление цепи уменьшается, устройства могут потреблять больше тока для работы.

Недостатки

Этот метод становится неудобным в использовании, если необходимо включить или выключить тысячи лампочек / приборов.

Это менее безопасно, так как через цепь может проходить больше тока.

Различают последовательную и параллельную комбинацию резисторов.

Вопросы

Вопрос 18 (c) NCERT —

Почему для бытовых цепей не используется последовательное соединение?

Посмотреть ответ

Q3 Стр. 216 —

Каковы преимущества подключения электрических устройств параллельно к батарее вместо их последовательного подключения?

Посмотреть ответ

Подпишитесь на наш канал Youtube — https: // you.трубка / teachoo

Физика для науки и техники II

из отдела академических технологий на Vimeo.

Пример — последовательное и параллельное соединение сопротивлений

Хорошо. Давайте рассмотрим пример, связанный с подключением сопротивлений. Предположим, у нас есть несколько сопротивлений, которые соединены таким образом. Сюда подключается R 1, R 2, а здесь подключается R 3.Здесь R, 4, а здесь сопротивление R 6, которое в конечном итоге подключено к сопротивлению R 7 здесь. Затем, допустим, мы применяем разность потенциалов ко всей комбинации, соединив концы этих соединений с выводами электродвижущей силы, которая генерирует ε вольт.

Давайте посмотрим, вопрос в том, какая мощность рассеивается через каждое сопротивление? Теперь, чтобы иметь возможность определить мощность, если вы помните, что она была равна рассеиваемой мощности — давайте использовать индекс рассеиваемой мощности — была равна i в 2 раза больше сопротивления R .Квадрат тока, проходящего через сопротивление, умноженный на значение сопротивления этого резистора, даст нам, сколько энергии преобразуется в тепло за каждую секунду.

Ну, очевидно, что числовые значения наших сопротивлений даны. Скажем, R 1 равно 2 Ом, R 2 равно 6 Ом и R 3 равно 12 Ом. R 4 равен 4 Ом, а R 6 равен 10 Ом и, наконец, R 7 равен 3 Ом.Итак, зная числовые значения этих сопротивлений, следовательно, если мы сможем определить количество тока, протекающего через каждый резистор, то мы сможем определить мощность, рассеиваемую через каждый резистор.

Хорошо. Чтобы сделать это, сначала мы попытаемся определить эквивалентное сопротивление цепи, а затем проследим его, чтобы иметь возможность определить ток, протекающий через каждое сопротивление. Если мы вспомним закон Ома, который был просто равен, из определения сопротивления, и это было равно отношению разности потенциалов между двумя точками к величине тока, проходящего через эти точки.

Когда мы смотрим на этот закон, мы видим, что для определения любой из этих величин, напряжения, тока, сопротивления, нам необходимо знать две другие из этих величин. Итак, мы собираемся попытаться определить эти величины, поскольку сопротивления даны, мы попытаемся определить ток, и, чтобы иметь возможность сделать это, нам нужно определить разность потенциалов на каждом резисторе. Таким образом, применяя свойства, связанные с параллельным и последовательным подключением, мы определим эти величины, следовательно, в конечном итоге ток через каждое сопротивление, и как только мы это определим, мы сможем вычислить рассеиваемую мощность.

Хорошо. Если мы посмотрим на нашу схему, мы увидим, что сначала эти три сопротивления R 2, R 3 и R 4 соединены параллельно. Сначала отметим точки соединения. Это те моменты, в которых мы заканчиваем с diff

экзамен по физике 2 Карточки

Срок Что из следующего не является вектором? А) электрическая сила В) электрическое поле В) электрическое напряжение; D) силовая линия	Определение
Срок Один джоуль на кулон равен А) ньютон. B) вольт. С) электрон-вольт. D) фарад.	Определение
Срок Два идентичных алюминиевых объекта изолированы от своего окружения. Объект А имеет сеть заряд лишних электронов. Объект Б заземлен. Какой объект имеет более высокий потенциал? А) А В) В C) Оба имеют одинаковый потенциал. D) не может быть определено без дополнительной информации	Определение B) Объект B, заземленный объект, имеет более высокий потенциал.
Член Для протона, движущегося в направлении электрического поля A) его потенциальная энергия увеличивается, а его электрический потенциал уменьшается. B) его потенциальная энергия уменьшается, а его электрический потенциал увеличивается. C) его потенциальная энергия увеличивается, а его электрический потенциал увеличивается. D) его потенциальная энергия уменьшается, а его электрический потенциал уменьшается.	Определение D) его потенциальная энергия уменьшается, а его электрический потенциал уменьшается.
Член Для электрона, движущегося в направлении, противоположном электрическому полю A) его потенциальная энергия увеличивается, а его электрический потенциал уменьшается. B) его потенциальная энергия уменьшается, а его электрический потенциал увеличивается. C) его потенциальная энергия увеличивается, а его электрический потенциал увеличивается. D) его потенциальная энергия уменьшается, а его электрический потенциал уменьшается	Определение B) его потенциальная энергия уменьшается, а его электрический потенциал увеличивается
Термин Несколько электронов помещены на полую проводящую сферу.Они A) слипаются на внешней поверхности сферы. B) слипаются на внутренней поверхности сферы. C) равномерно распределяются по внешней поверхности сферы. D) равномерно распределяются по внутренней поверхности сферы.	Определение C) становятся равномерно распределенными на внешней поверхности сферы.
Условие Небольшой заряженный шар ускоряется от состояния покоя до скорости v за счет разности потенциалов 500 В.Если разность потенциалов изменена на 2000 В, какая будет новая скорость мяча? A) v В) 2в C) 4v D) 16В	Определение
Термин Поверхность, на которой все точки имеют одинаковый потенциал, обозначается как . А) поверхность с постоянной электрической силой. В) поверхность постоянного электрического поля. C) эквипотенциальная поверхность. D) поверхность эквивалентности.	Определение C) эквипотенциальная поверхность
Условие Отрицательный заряд перемещается из точки A в точку B по эквипотенциальной поверхности. A) Отрицательный заряд выполняет работу по перемещению из точки A в точку B. B) Требуется работа, чтобы переместить отрицательный заряд из точки A в точку B. C) Требуется и выполняется работа по перемещению отрицательного заряда из точки A в точка Б. D) Перемещение отрицательного заряда из точки A в точку B не требуется.	Определение D) Для перемещения отрицательного заряда из точки A в точку B не требуется никаких действий
Клемма Эквипотенциальная поверхность должна быть A) параллельно электрическому полю в любой точке. B) перпендикулярно электрическому полю в любой точке.	Определение B) эквипотенциальная поверхность должна быть перпендикулярна электрическому полю в любой точке.
Термин Энергия, приобретаемая частицей, несущей заряд, равный заряду электрона, в результате , движущийся через разность потенциалов в один вольт, обозначается как . А) джоуль. В) электрон-вольт. В) протон-вольт. D) кулон.	Определение
Срок Электрон-вольт — это единица А) напряжение. В) ток. С) мощность. D) энергия.	Определение D) электрон-вольт — единица энергии
Срок Один электрон-вольт соответствует А) 8.0 * 10-20 Дж. В) 1,6 * 10-19 Дж. C) 9,5 * 10-17 Дж. D) 1,9 * 10-16 Дж	Определение
Клемма Абсолютный потенциал на расстоянии 2,0 м от положительного точечного заряда составляет 100 В. Что такое абсолютный потенциал на расстоянии 4,0 м от того же точечного заряда? А) 25 В В) 50 В C) 200 В D) 400 В	alexxlab Посмотреть все записи автора alexxlab → Вам также может понравиться Сварочные аппараты аргон: Доступ с вашего IP-адреса временно ограничен — Авито 05.10.202024.03.2021 Схема замещения участка эц: Электрические схемы замещения 01.05.202122.11.2020 Скорость света в вакууме км в час: Скорость света в километры в час 19.04.202113.11.2020 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт