Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор
Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор
03.04.18
Данный текст является расширенным и углубленным вариантом моей старой заметки на сайте we.easyelectronics.ru.
Введение
В рамках данной заметки рассмотрим способы вычисления среднего и среднеквадратичного значений тока и напряжения. При этом для простоты ограничимся формами сигнала, характерными для импульсных источников питания. Обращаю ваше внимание – все формулы, приводимые в заметке, даются без выводов, дабы не забивать головы читателей мутной и не особо нужной херней. С другой стороны, если кому-то интересно, откуда данные формулы взялись – можно скачать файл, в котором приведены все необходимые выводы с пояснениями.
Основные определения
Будучи в недавнем прошлом яростным разработчиком всевозможных импульсных источников питания (ИИП), интересовался всяким по данной теме (да и сейчас, бывает, трясу стариной). В частности, весьма важными мне всегда казались такие характеристики сигнала, как среднее и среднеквадратичное значение токов и напряжений в различных точках схемы, поскольку при расчетах ИИП данные параметры используются сплошь и рядом. Чтобы понять, где могут быть полезны данные характеристики, сначала определимся с тем, что мы под ними понимаем.
Естественно, существуют строгие «математические» определения как для среднего, так и для среднеквадратичного значений физических величин, периодически изменяющихся во времени по некоторому закону. Однако, больно уж они мутные и абстрактные, и, на мой взгляд, нужны только при выводе формул. Разработчику же гораздо важнее понимать физический смысл используемых в расчетах величин, поэтому приводимые ниже определения среднего и среднеквадратичного значений будут носить сугубо прикладной характер.
Разработчику же гораздо важнее понимать физический смысл используемых в расчетах величин, поэтому приводимые ниже определения среднего и среднеквадратичного значений будут носить сугубо прикладной характер.
Среднее значение переменного тока или напряжения (во вражеских терминах AVG) – это просто их постоянная составляющая. Поэтому вполне очевидно, что среднее значение широко применяется при расчетах схем, выделяющих из переменного сигнала постоянный уровень. Простейший понижающий преобразователь (Step-Down) с LC-фильтром на выходе, RC-цепочка, призванная выделить постоянное напряжение из поступающего на вход ШИМ-сигнала – всё это примеры того, где без использования среднего значения физической величины ничего толком не посчитаешь.
Среднеквадратичное (действующее, эффективное) значение определяется немного сложнее. Как известно, любой переменный ток (напряжение), проходя через активную линейную нагрузку (например, резистор), выделяет на ней некоторое количество тепла. Но так поступает не только переменный сигнал – постоянный ток тоже будет греть резистор.
Но так поступает не только переменный сигнал – постоянный ток тоже будет греть резистор.
Так вот, среднеквадратичное значение переменного тока или напряжения (во вражеских терминах RMS) – это такой постоянный ток (напряжение), который за одинаковый промежуток времени нагреет один и тот же резистор точно так же, как и исходный переменный сигнал. Поэтому одно из важнейших применений среднеквадратичного значения – расчет потерь и соответствующего нагрева для различных элементов силовых цепей ИИП. Хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.
В общем, среднее и среднеквадратичное значения используются довольно часто.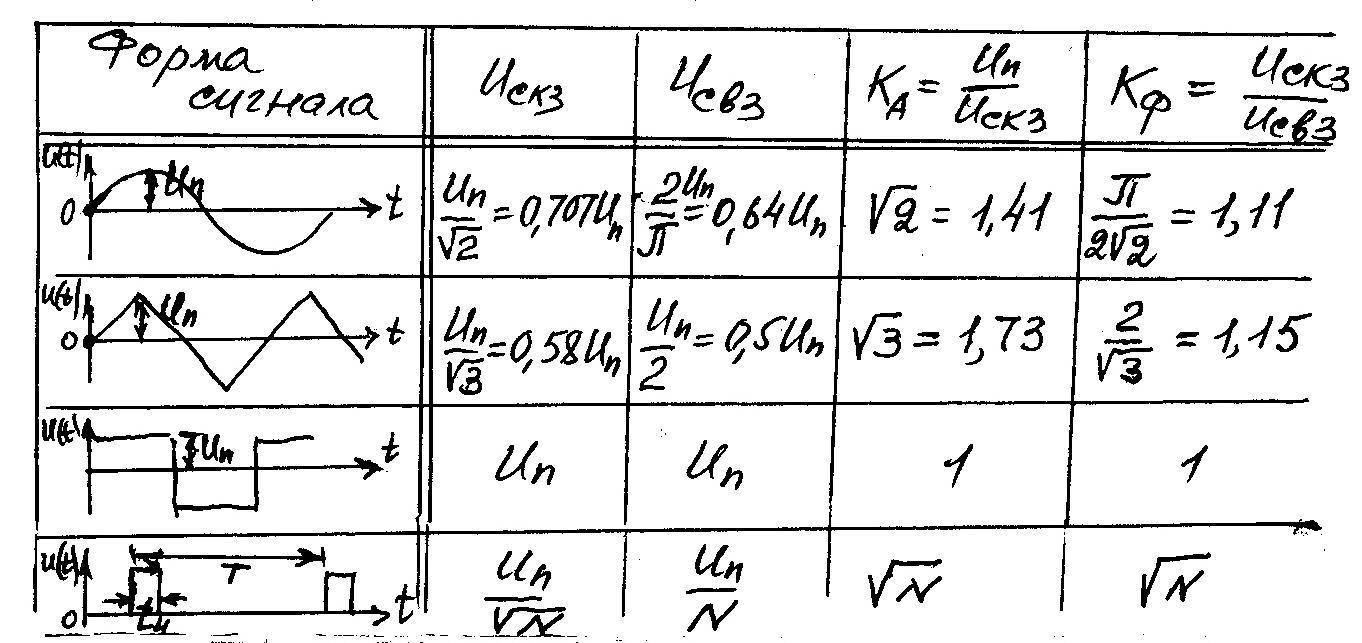 Поэтому неплохо было бы уметь их рассчитывать для любого сигнала, который может нам встретиться в импульсном источнике питания. При этом лично я разделяю токи и напряжения в ИИП на две большие группы: сигналы с простой формой (элементарные) и сигналы со сложной формой (т.е. те, которые могут быть представлены в виде суммы нескольких элементарных). И поскольку принципы расчета среднего и среднеквадратичного значений для этих двух групп немного отличаются, предлагаю рассмотреть их по отдельности.
Поэтому неплохо было бы уметь их рассчитывать для любого сигнала, который может нам встретиться в импульсном источнике питания. При этом лично я разделяю токи и напряжения в ИИП на две большие группы: сигналы с простой формой (элементарные) и сигналы со сложной формой (т.е. те, которые могут быть представлены в виде суммы нескольких элементарных). И поскольку принципы расчета среднего и среднеквадратичного значений для этих двух групп немного отличаются, предлагаю рассмотреть их по отдельности.
Сигналы простой формы
У сигналов простой формы вычислить среднее и среднеквадратичное значение довольно легко – для этого надо всего лишь взять соответствующую формулу и подставить в нее нужные значения. Чтобы постоянно не шариться по различным справочникам, я завел себе специальную табличку, в которую свел расчетные формулы для наиболее часто встречающихся элементарных сигналов:
• прямоугольника:
• треугольника:
• трапеции:
• и пилы:
(данные формулы, кстати, взяты не с потолка – их вывод при желании можно посмотреть в специальной заметке-пояснении).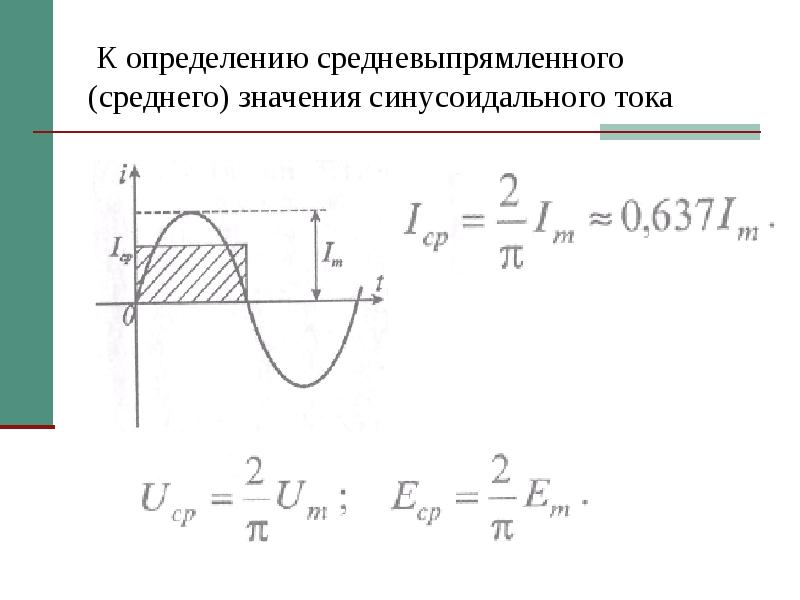
Здесь хотелось бы заострить внимание на нескольких моментах. Во-первых, на приведенных выше рисунках рассматривается по два варианта каждого из простейших сигналов: «в общем виде» и «без смещения». При этом с точки зрения разработчика импульсных источников питания наиболее интересным обычно является именно второй вариант, поэтому для него и даны отдельные формулы (чтобы постоянно не подставлять С=0 в «общие» выражения). Во-вторых, пилообразное напряжение, вообще говоря, является сложным сигналом, поскольку может быть представлено в виде суммы двух простых (либо трапеций, либо треугольников). Однако, пила настолько часто встречается при расчетах ИИП, а выражения AVG и RMS для нее настолько лаконичны и красивы, что я в результате включил-таки ее в список сигналов, среднее и среднеквадратичное значение которых вычисляется тупо всего по одной формуле. Ну и в-третьих, вышеприведенная таблица, в принципе, могла бы состоять всего из одной трапеции, ибо из нее легко получить как прямоугольник, так и треугольник, поставляя соответствующие значения «H», «L» и «C». Однако практика показала, что постоянно этим заниматься весьма муторно, ибо мы рассчитываем источник, а не тренируем математические навыки. Поэтому в итоге я себе выписал готовые формулы AVG и RMS для прямоугольника и треугольника, что оказалось весьма и весьма удобным. Ну а в целом – как ни странно, представленные выше формулы для элементарных сигналов покрывают, наверное, 75-80% всех потребностей разработчика импульсных источников питания, что весьма немало. Однако, всё многообразие токов и напряжений в ИИП отнюдь не ограничивается вышеупомянутыми четырьмя (и даже тремя, если не учитывать пилу) формами. Поэтому рано или поздно любой разработчик импульсников сталкивается с необходимостью вычисления среднего и среднеквадратичного значения сложного сигнала (яркий пример – расчет пуш-пула).
Однако практика показала, что постоянно этим заниматься весьма муторно, ибо мы рассчитываем источник, а не тренируем математические навыки. Поэтому в итоге я себе выписал готовые формулы AVG и RMS для прямоугольника и треугольника, что оказалось весьма и весьма удобным. Ну а в целом – как ни странно, представленные выше формулы для элементарных сигналов покрывают, наверное, 75-80% всех потребностей разработчика импульсных источников питания, что весьма немало. Однако, всё многообразие токов и напряжений в ИИП отнюдь не ограничивается вышеупомянутыми четырьмя (и даже тремя, если не учитывать пилу) формами. Поэтому рано или поздно любой разработчик импульсников сталкивается с необходимостью вычисления среднего и среднеквадратичного значения сложного сигнала (яркий пример – расчет пуш-пула).
Сигналы сложной формы
Как было сказано выше, сигналы сложной формы – это такие, которые могут быть представлены в виде суммы нескольких элементарных сигналов. Применительно к импульсным источникам питания в качестве последних выступают прямоугольник, треугольник или трапеция, и значительно реже – синус, косинус и прочая «плавная» херня. Отметим, что в данном случае, в отличие от простейших форм, нахождение аналитических выражений для среднего и среднеквадратичного значений обычно превращается в неблагодарное занятие. Например, для вывода «среднеквадратичной» формулы нам надо разбить сложный сигнал на несколько простейших, а затем извлечь квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений (думаю, даже понять, о чем говорится в данном предложении, у вас получится далеко не сразу). Найти среднее значение сложного сигнала немного проще (надо просто просуммировать средние «элементарные» значения), однако поверьте – сделать из этого удобоваримую формулу в подавляющем большинстве случаев не удается:
Применительно к импульсным источникам питания в качестве последних выступают прямоугольник, треугольник или трапеция, и значительно реже – синус, косинус и прочая «плавная» херня. Отметим, что в данном случае, в отличие от простейших форм, нахождение аналитических выражений для среднего и среднеквадратичного значений обычно превращается в неблагодарное занятие. Например, для вывода «среднеквадратичной» формулы нам надо разбить сложный сигнал на несколько простейших, а затем извлечь квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений (думаю, даже понять, о чем говорится в данном предложении, у вас получится далеко не сразу). Найти среднее значение сложного сигнала немного проще (надо просто просуммировать средние «элементарные» значения), однако поверьте – сделать из этого удобоваримую формулу в подавляющем большинстве случаев не удается:
К счастью, готовая формула для нахождения AVG и RMS сложного сигнала обычно не требуется. Чаще всего нам надо просто узнать среднее или среднеквадратичное значение тока (напряжения) именно для нашего конкретного случая, а не вывести аналитическое выражение на все случаи жизни. А это существенно упрощает задачу, ибо посчитать числовое значение AVG или RMS для каждого элементарного сигнала на соответствующем временно́м интервале не так уж и сложно. В качестве примера можно рассмотреть нахождение среднего и среднеквадратичного значения напряжения, характерного для пушпульной, полумостовой и полномостовой схем (данный расчет есть и в специальной заметке-пояснении):
Чаще всего нам надо просто узнать среднее или среднеквадратичное значение тока (напряжения) именно для нашего конкретного случая, а не вывести аналитическое выражение на все случаи жизни. А это существенно упрощает задачу, ибо посчитать числовое значение AVG или RMS для каждого элементарного сигнала на соответствующем временно́м интервале не так уж и сложно. В качестве примера можно рассмотреть нахождение среднего и среднеквадратичного значения напряжения, характерного для пушпульной, полумостовой и полномостовой схем (данный расчет есть и в специальной заметке-пояснении):
Как следует из предпоследнего рисунка, для начала нам надо разбить исходный сигнал на элементарные. Очевидно, что это будут три трапеции и один прямоугольник:
Дальше нам надо посчитать среднее и среднеквадратичное значение каждого из четырех элементарных сигналов, для чего воспользуемся формулами из вышеприведенной таблицы. Начнем с первого из них — трапеции №1. Как видно из последнего рисунка, это трапеция без смещения с параметрами
Начнем с первого из них — трапеции №1. Как видно из последнего рисунка, это трапеция без смещения с параметрами
H1=11;
L1=9;
C1=0;
tИ1=0,15∙T.
Поэтому в соответствии с формулами для трапеции, приведенными выше, будем иметь:
Сигнал №2 – это тоже трапеция без смещения. Параметры данной трапеции будут таковы:
H2=21;
L2=19;
C2=0;
tИ2=0,50∙T – 0,15∙T = 0,35∙T.
Поэтому среднее и среднеквадратичное значение второго сигнала составят соответственно
Трапеция №3 полностью совпадает с трапецией №1, просто она сдвинута вправо на полпериода. Поэтому как параметры третьего сигнала, так и его среднее и среднеквадратичное значения будут равны соответствующим значениям первого сигнала:
Поэтому как параметры третьего сигнала, так и его среднее и среднеквадратичное значения будут равны соответствующим значениям первого сигнала:
H3= H1=11;
L3= L1=9;
C3= C1=0;
tИ3= tИ1= 0,65∙T – 0,50∙T = 0,15∙T.
Ну и остался сигнал №4. Данный сигнал представляет собой прямоугольник с параметрами
H4=0,5;
C4=0;
tИ4=1,00∙T – 0,65∙T = 0,35∙T.
И после использования формул для вычисления среднего и среднеквадратичного значения сигнала №4, получим следующее:
Теперь у нас есть все данные для нахождения AVG и RMS исходного сигнала. Как было сказано выше, среднее значение находится как сумма средних значений элементарных сигналов, на которые был разложен «исходник», а среднеквадратичное – как квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений. То есть в нашем случае будем иметь
Как было сказано выше, среднее значение находится как сумма средних значений элементарных сигналов, на которые был разложен «исходник», а среднеквадратичное – как квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений. То есть в нашем случае будем иметь
Для проверки полученного результата используем широко распространенное бесплатное ПО LTSpice IV от компании Linear Technology Corporation (LTC). Сгенерировав сигнал с требуемыми параметрами, измерим в эмуляторе среднее и среднеквадратичное его значение за 5 периодов:
Как видим, результаты работы эмулятора полностью совпадают с расчетными AVG и RMS, т.е. предложенный способ вычисления среднего и среднеквадратичного значений для сложного сигнала вполне имеет право на жизнь. Более того, способ этот довольно прост и не требует от разработчика ИИП никаких особых математических навыков. С другой стороны, муторность рассмотренного алгоритма также налицо. Лично меня дичайше бесит постоянно считать на калькуляторе и выписывать на бумажку средние и среднеквадратичные значения для всех элементарных сигналов, на которые раскладывается исходный, а пото́м складывать их на том же калькуляторе (и это в лучшем случае, ибо если требуется RMS, всё становится еще волшебнее). Поэтому я принял решение сделать себе некий инструмент, упрощающий жизнь разработчика ИИП, которым и хотел бы поделиться с читателями.
С другой стороны, муторность рассмотренного алгоритма также налицо. Лично меня дичайше бесит постоянно считать на калькуляторе и выписывать на бумажку средние и среднеквадратичные значения для всех элементарных сигналов, на которые раскладывается исходный, а пото́м складывать их на том же калькуляторе (и это в лучшем случае, ибо если требуется RMS, всё становится еще волшебнее). Поэтому я принял решение сделать себе некий инструмент, упрощающий жизнь разработчика ИИП, которым и хотел бы поделиться с читателями.
Калькулятор
Данный инструмент – это такая специальная «программа» (cko4aTb бесплатно). «Программа» представляет собой обычный экселовский файл (т.к. программист я тот еще), поэтому для работы нам потребуется «Excel» (у меня вот такой: Microsoft® Excel 2002 (10.4302.2625)). Изначальная и основная задача рассматриваемой «программы» – отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период), а также вычисление среднего и среднеквадратичного значений для этого сигнала.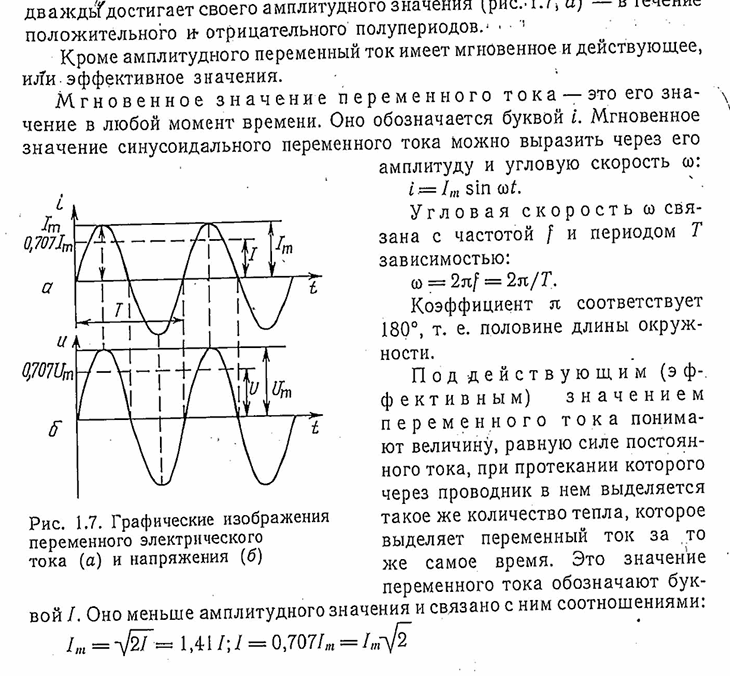 Также «программа» умеет рисовать переменную составляющую заданной трапеции (она получается если из исходного сигнала вычесть постоянную составляющую) и вычислять ее RMS-значение (это уж так, чисто на всякий случай). Ну и еще предлагаемый софт позволяет быстро посчитать среднее и среднеквадратичное значения для сложного сигнала, состоящего максимум из 16-ти различных элементарных (большее количество в реальной жизни вряд ли потребуется):
Также «программа» умеет рисовать переменную составляющую заданной трапеции (она получается если из исходного сигнала вычесть постоянную составляющую) и вычислять ее RMS-значение (это уж так, чисто на всякий случай). Ну и еще предлагаемый софт позволяет быстро посчитать среднее и среднеквадратичное значения для сложного сигнала, состоящего максимум из 16-ти различных элементарных (большее количество в реальной жизни вряд ли потребуется):
Почему в качестве основы взята именно трапеция? Потому что, как было сказано выше, из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник и треугольник:
Ну а уж на основе этих базовых сигналов можно сляпать и пилу, и напряжение на стоке ключа во флайбэке, и то, что творится на вторичке пушпула и многое другое.
Пользоваться «программой» очень просто. Исходные данные для трапеции вводятся слева в ячейки, выделенные зеленым цветом. После этого чуть ниже можно посмотреть на форму сигнала с введенными параметрами, а еще ниже отобразятся рассчитанные среднее и среднеквадратичное значения этого сигнала. За переменную составляющую трапеции отвечает правый нижний угол экрана (здесь рисуется ее график и рассчитывается значение RMS). Ну а для работы со сложным сигналом предназначен правый верхний угол. Здесь в ячейки, выделенные зеленым цветом, вводятся средние и среднеквадратичные значения элементарных сигналов, из которых состоит «исходник», а ниже рассчитываются уже́ его собственные AVG и RMS.
Исходные данные для трапеции вводятся слева в ячейки, выделенные зеленым цветом. После этого чуть ниже можно посмотреть на форму сигнала с введенными параметрами, а еще ниже отобразятся рассчитанные среднее и среднеквадратичное значения этого сигнала. За переменную составляющую трапеции отвечает правый нижний угол экрана (здесь рисуется ее график и рассчитывается значение RMS). Ну а для работы со сложным сигналом предназначен правый верхний угол. Здесь в ячейки, выделенные зеленым цветом, вводятся средние и среднеквадратичные значения элементарных сигналов, из которых состоит «исходник», а ниже рассчитываются уже́ его собственные AVG и RMS.
Отмечу, что на всю «программу» наложена магическая защита, позволяющая редактировать только те ячейки, которые можно. При необходимости защита снимается элементарно («Сервис» => «Защита» => «Снять защиту листа»), однако делать это не рекомендую: можно по дури снести какую-нибудь нужную формулу, восстанавливать которую – лишний геморрой.
Вот, в принципе, и всё описание представленной «программы». Несмотря на свою простоту и очевидность, данный софт довольно существенно помогает и экономит время при расчетах ИИП (ну, во всяком случае, у меня происходит именно так). Например, на расчет среднего и среднеквадратичного значения сложного сигнала, приведенного в предыдущем пункте, понадобится менее минуты. Последовательность действий проста – вводим параметры первой трапеции, затем переписываем рассчитанные для нее значения AVG и RMS в ячейки секции сложного сигнала. Затем то же самое проделываем для остальных трех элементарных функций, из которых состоит «исходник». Всё, остальное «программа» сделает сама, не надо никаких шаманств с бумажками и калькуляторами:
Ну а у меня на сегодня всё. Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!
Обсудить эту заметку можно
здесь
Ссылки по теме, документация
Заметка-пояснение с выводом формул и примером расчета среднего и среднеквадратичного значений сложного сигнала:
• AVG_RMS.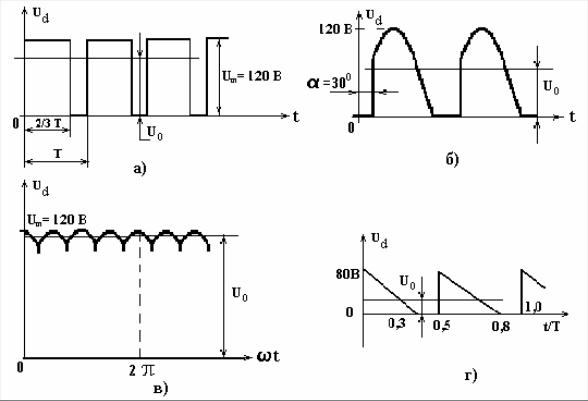 pdf;
pdf;
Калькулятор для упрощения вычислений среднего и среднеквадратичного значений простых и сложных сигналов:
• AVG_RMS_Calc.xls;
Среднеквадратичное значение — ток — Большая Энциклопедия Нефти и Газа, статья, страница 1
Среднеквадратичное значение — ток
Cтраница 1
Среднеквадратичное значение тока берется исходя из того, что тепловые потери пропорциональны квадрату тока.
[2]
Среднеквадратичное значение тока электродвигателя, приведенное к одному из стандартных значений относительной продолжительности включения ( ПВ 15, 25 и 40 %), не должно превышать номинального тока катушки, приведенного в табл. 2.2. При малых нагрузках магнитный поток может оказаться недостаточным для срабатывания магнита.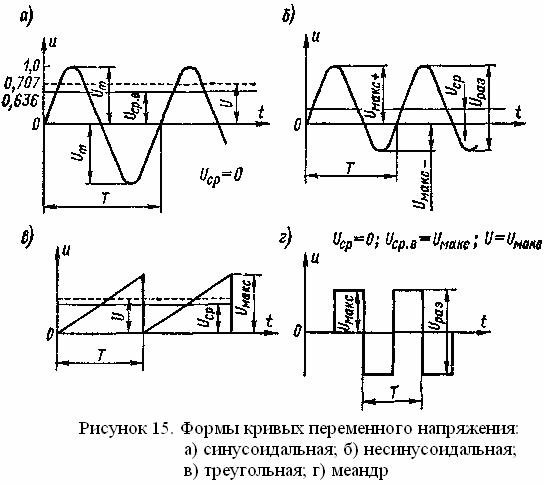 Поэтому обычно такие магниты устанавливают на тормозах механизмов, для которых нагрузка и величина тока меняются мало ( например, механизмы передвижения и поворота) или в которых цепь возбуждения является самостоятельной и ток в ней не уменьшается ниже определенного значения.
Поэтому обычно такие магниты устанавливают на тормозах механизмов, для которых нагрузка и величина тока меняются мало ( например, механизмы передвижения и поворота) или в которых цепь возбуждения является самостоятельной и ток в ней не уменьшается ниже определенного значения.
[3]
Рассчитанное среднеквадратичное значение тока двигателя находится в допустимых пределах, так как номинальный ток двигателя / дв.
[4]
Нужно отметить, что хотя среднеквадратичное значение тока правильно определяет потери в меди обмоток, оно далеко не всегда достаточно точно определяет повышение температуры обмоток. Если, например, нагрузка в течение длительного времени превышает номинальную, то действительное превышение температуры может значительно превосходить величину, подсчитанную по среднегеометрическому значению тока.
[5]
Наибольшим током термической устойчивости / т называется наибольшее среднеквадратичное значение тока за промежуток времени i.
[6]
Действующее значение тока первичной обмотки трансформатора определяется как среднеквадратичное значение токов, пересчитанных из вторичной обмотки в первичную, с учетом длительности протекания тока в каждой секции вторичной цепи трансформатора.
[7]
Наиболее характерны циклические перегрузки, показанные на рис. 5.5. Среднеквадратичное значение тока / 0 ( Т и 1 — длительность и ток в период нагрузки, Тч — время бестоковой паузы) не должно превышать номинальное значение тока / Н0м, допустимое в ста-дионарном тепловом режиме.
[9]
При этом за время работы преобразователя в режиме перегрузок среднеквадратичное значение тока за любые 30 мин ( время усреднения) не должно превышать номинальный ток преобразователя, а если в течение этих 30 мин происходит 100 % — тая перегрузка, то время усреднения должно быть 5 мин.
[10]
Среднеквадратичное значение — ток — Большая Энциклопедия Нефти и Газа, статья, страница 2
Среднеквадратичное значение — ток
Cтраница 2
С некоторой степенью приближения можно оценить эффект периодически меняющейся нагрузки, заменив ее среднеквадратичным значением тока. Этот метод, по существу, состоит в том, что действительная периодически меняющаяся нагрузка заменяется постоянной нагрузкой, эквивалентной действительной в отношении средних потерь. При этом очень упрощается вычисление превышения температуры.
[17]
Зависимости М и / от скорости изображены на рис. 10.98, там же указаны среднеквадратичное значение тока / д и среднее значение момента Мер.
[18]
Если Кф 1 05, то при определении потерь в — линии необходимо принимать среднеквадратичное значение тока нагрузка за расчетный период, определяемое так же, как и для трансформатора ( стр.
[20]
Вместе с тем в последние годы часто предлагается принимать за номинальный ток быстродействующих предохранителей среднеквадратичное значение тока в циклическом режиме, при котором гарантируется отсутствие разрушений предохранителя в течение заданного срока службы.
[21]
Для каждсй серии или даже типа разъединителей завод-изготовитель устанавливает наибольший ток термической устойчивости — наибольшее среднеквадратичное значение тока за промежуток времени, соответствующий термическому эффекту тока короткого замыкания, выдерживаемого разъединителем в течение этого же промежутка времени без нагрева токоведущих частей до температур, превышающих допустимые при токах короткого замыкания, и без повреждений, препятствующих дальнейшей исправной работе разъединителя.
[22]
При такой величине максимальный сдвиг фаз дает амплитудную величину тока в 2 3 раза больше среднеквадратичного значения тока. Амплитудное значение в 2 3 раза может быть определено то выражениям ( 2) или ( 3), по.
[23]
Для фотодиодов и фототранзисторов характерны резкие всплески тока, амплитуда которых в 3 — 6 раз больше среднеквадратичного значения тока шумов. Поэтому при приеме слабых световых сигналов фотоэлектрическая схема должна реагировать не на амплитуду сигналов, а на их действующее значение.
[24]
При этом перегрузки имеют циклический характер и за время цикла, состоящего из перегрузки и паузы, среднеквадратичное значение тока не должно пре
Бюджетный вариант измерения TrueRMS / Хабр
Вступление
Измерение trueRMS переменного напряжения — задача не совсем простая, не такая, какой она кажется с первого взгляда. Прежде всего потому, что чаще всего приходится измерять не чисто синусоидальное напряжение, а нечто более сложное, усложнённое наличием гармоник шумов.
Поэтому соблазнительно простое решение с детектором среднего значения с пересчётом в ср.кв. значения не работает там, где форма сигнала сильно отличается от синусоидальной или просто неизвестна.
Профессиональные вольтметры ср. кв. значения — это достаточно сложные устройства как по схемотехнике, так и по алгоритмам [1,2]. В большинстве измерителей, которые носят вспомогательный характер и служат для контроля функционирования, такие сложности и точности не требуются.
Также требуется, чтобы измеритель мог быть собран на самом простом 8-битном микроконтроллере.
Общий принцип измерения
Пусть имеется некое переменное напряжение вида, изображённого на рис. 1.
Квазисинусоидальное напряжение имеет некий квазипериод T.
Преимущество измерения среднеквадратичного значения напряжения в том, что в общем случае время измерения не играет большой роли, оно влияет только на частотную полосу измерения. Большее время даёт большее усреднение, меньшее даёт возможность увидеть кратковременные изменения.
Базовое определение ср. кв. значения выглядит вот таким образом:
где u(t) — мгновенное значение напряжения
T — период измерения
Таким образом, время измерения может быть, вообще говоря, любым.
Для реального измерения реальной аппаратурой для вычисления подинтегрального выражения необходимо проквантовать сигнал с некоторой частотой, заведомо превосходящей не менее, чем в 10 раз частоту квазисинусоиды. При измерении сигналов с частотами в пределах 20 кГц это не представляет проблемы даже для 8-битных микроконтроллеров.
Другое дело, что все стандартные контроллеры имеют однополярное питание. Поэтому измерить мгновенное переменное напряжение в момент отрицательной полуволны не представляется возможным.
В работе [3] предложено довольно остроумное решение, как внести постоянную составляющую в сигнал. Вместе с тем в том решении определение момента, когда стоит начать или закончить процесс вычисления ср. кв. значения представляется довольно громоздким.
В данной работе предлагается метод преодоления этого недостатка, а также вычисление интеграла с большей точностью, что позволяет снизить число точек выборки до минимума.
Особенности аналоговой части измерителя
На рис. 2 показано ядро схемы предварительной аналоговой обработки сигнала.
Сигнал поступает через конденсатор C1 на усилитель-формирователь, собранный на операционном усилителе DA1. Сигнал переменного напряжения замешивается на неинвертирующем входе усилителя с половиной опорного напряжения, которое используется в АЦП. Напряжение выбрано 2.048 В, поскольку в компактных устройствах часто используется напряжение питания +3.6 В и менее. В иных случаях удобно использовать 4.048 В, как в [3].
С выхода усилителя-формирователя через интегрирующую цепочку R3-C2 сигнал поступает на вход АЦП, который служит для измерения постоянной составляющей сигнала (U0). C усилителя-формирователя сигнал U’ — это измеряемый сигнал, сдвинутый на половину опорного напряжения. Таким образом, чтобы получить переменную составляющую, достаточно вычислить разность U’-U0.
Сигнал U0 используется также в качестве опорного для компаратора DA2. При переходе U’ через значение U0 компаратор вырабатывает перепад, который используется для формирования процедуры прерывания для сбора измерительных отсчётов.
Важно, что во многие современные микроконтроллеры встроены как операционные усилители, так и компараторы, не упоминая АЦП.
Базовый алгоритм
На рис. 3 дан базовый алгоритм для случая измерения величины переменного напряжения с основной частотой 50 Гц.
Запуск измерения может осуществляться по любому внешнему событию вплоть до кнопки, нажимаемой вручную.
После запуска в первую очередь измеряется постоянная составляющая во входном сигнале АЦП, а затем контроллер переходит в ожидание положительного перепада на выходе компаратора. Как только прерывание по перепаду наступает, контроллер делает выборку из 20 точек с временным шагом, соответствующим 1/20 квазипериода.
В алгоритме написано X мс, поскольку низкобюджетный контроллер имеет собственное время задержки. Чтобы измерение происходило в правильные моменты времени, необхоимо учитывать эту задержку. Поэтому реальная задержка будет меньше 1 мс.
В данном примере задержка соответствует измерениям квазисинусоид в диапазоне 50 Гц, но может быть любой в зависимости от квазипериода измеряемого сигнала в пределах быстродействия конкретного контроллера.
При измерениях ср.кв. значения напряжения произвольного квазипериодического сигнала, если априори неизвестно, что это за сигнал, целесообразно измерить его период, используя встроенный в контроллер таймер и тот же выход компаратора. И уже на основании этого замера устанавливать задержку при осуществлении выборки.
Вычисление среднеквадратичного значения
После того, как АЦП создал выборку, имеем массив значений U'[i], всего 21 значение, включая значение U0. Теперь, если применить формулу Симпсона (точнее, Котеса) для численного интергрирования, как наиболее точную для данного применения, то получим следующее выражение:
где h — шаг измерения, а нулевой компонент формулы отсутствует, поскольку он равег 0 по определению.
В результате вычисления мы получим значение интеграла в чистом виде в формате отсчётов АЦП. Для перевода в реальные значения полученное значение нужно промасштабировать с учётом величины опорного напряжения и поделить на интервал времени интегрирования.
где Uоп — опорное напряжение АЦП.
Если всё пересчитать в мВ, K приблизительно равняется просто 2. Масштабный коэффициент относится к разностям в квадратных скобках. После пересчёта и вычисления S делим на интервал измерения. С учётом множителя h фактически получаем деление на целое число вместо умножения на h с последующим делением на интервал времени измерения.
И в финале извлекаем квадратный корень.
И вот тут самое интересное и сложное наступает. Можно, разумеется, использовать плавающую точку для вычислений, поскольку язык C это допускает даже для 8-битных контроллеров, и производить вычисления непосредственно по приведённым формулам. Однако скорость расчёта упадёт существенно. Также можно выйти за пределы весьма небольшого ОЗУ микроконтроллера.
Чтобы такого не было, нужно, как верно указано в [3], использовать фиксированную точку и оперировать максимум 16-битными словами.
Автору эту проблему удалось решить и измерять напряжение с погрешностью Uоп/1024, т.е. для приведённого примера с точностью 2 мВ при общем диапазоне измерения ±500 мВ при напряжении питания +3.3 В, что достаточно для многих задач мониторинга процессов.
Программная хитрость состоит в том, чтобы все процессы деления, по возможности, делать до процессов умножения или возведения в степень, чтобы промежуточный результат операций не превышал 65535 (или 32768 для действий со знаком).
Конкретное программное решение выходит за рамки данной статьи.
Заключение
В данной статье рассмотрены особенности измерения среднеквадратичных значений напряжения с помощью 8-битных микроконтроллеров, показан вариант схемной реализации и основной алгоритм получения отсчётов квантования реального квазисинусоидального сигнала.
Ссылки
- Преобразователь среднеквадратического значения напряжения
- Цифровой вольтметр
- Метод измерения действующего значения напряжения с применением МК
Как измерить среднеквадратичное значение тока или напряжения?
Измерение тока и напряжения произвольной формы
В радиолюбительской практике иногда возникает необходимость измерить ток или напряжение, форма которых сильно отличается от синусоидальной. Подобные измерения могут потребоваться, например, когда нужно измерить мощность системного блока компьютера или другого устройства с импульсным источником питания.
Однако большинство бюджетных любительских тестеров могут с достаточной точностью измерять ток и напряжение только синусоидальной формы. Подробнее на https://oldoctober.com/ru/
Приборы позволяющие измерять токи и напряжения произвольной формы дороги, да и необходимость в подобных измерениях возникает крайне редко.
Между тем, прибор позволяющий производить такие измерения можно изготовить самому за каких-нибудь полчаса.
Самые интересные ролики на Youtube
Прибор для измерения напряжения произвольной формы.
Работа прибора основано на том, что световой поток лампы накаливания пропорционален силе протекающего через неё тока, а инертность нити накала лампы обеспечивает правильное считывание показаний с фотодатчика. https://oldoctober.com/ru/
Первый раз, я собрал такой прибор для измерения напряжения накала кинескопа, когда это напряжение начали получать от трансформатора строчной развёртки. В приборе использованы лампы СМН-6-20-1, хотя можно использовать любые другие с малыми токами.
Две шестивольтовые лампы включены последовательно, чтобы продлить их срок службы.
Технические данные миниатюрных ламп накаливания с малым током потребления приведены в конце статьи.
Фотодиод ФД-263 такой, как использовался в системах дистанционного управления телевизорами.
Измерительная головка на 20 — 100 µA.
Для калибровки прибора достаточно подключить его к источнику питания постоянного тока напряжением 6,3 Вольта и установить стрелку в середину шкалы, до совмещения с одной из рисок, при помощи резистора R1 .
Для удобства работы, измерительная головка встроена в корпус прибора. Однако, с таким же успехом, в качестве измерительной головки можно использовать мультиметр или стрелочный тестер.
Лампы и фотоприёмник заключены в трубку из алюминиевой фольги для увеличения светового потока.
Прибор для измерения силы тока произвольной формы.
Другой раз мне понадобился подобный прибор для измерения потребляемой мощности системных блоков компьютеров.
Форма тока, протекающего через входные цепи импульсного блока питания, так сильно отличается от синусоидальной, что при измерении тока обычными любительскими тестерами и мультиметрами, ошибка может достигать 180%.
На картинке осциллограмма тока протекающего во входных цепях импульсного источника питания.
Прибор работает по тому же принципу, что и предыдущий, только вместо напряжения измеряет ток.
Величину шунтирующего резистора R1 нужно подобрать в зависимости от измеряемого тока.
Я использовал для диапазона 20 – 170 Ватт – 4,7 Ом, а для 100 – 250 Ватт – 1,8 Ом (мощность резисторов 5 – 10 Ватт).
Фотоприёмник VD – фотодиод ФД-263.
Лампа EL1 и фотодиод VD1 впаяны в отрезок макетной платы и помещены в пластиковый светонепроницаемый контейнер чёрного цвета от фотоплёнки.
Переключатель S1 (КМ-1-1) — очень важная часть прибора. Чтобы обеспечить достаточную точность измерений, пропускать ток через шунтирующий резистор и лампу, следует только на то короткое время, в которое производится измерение.
Дело в том, что при длительном горении лампы, нагревается колба лампы, фотоприёмник да и сам корпус, что приводит к погрешности в измерениях.
Кроме всего, переключатель S1 защищает лампу от броска тока, который происходит в момент включения нагрузки. Пусковой ток импульсного блока питания ПК может превышать 60 Ампер.
Для замера напряжения на фотодиоде используется бюджетный цифровой мультиметр. Замеры нужно производить с точностью до 0,001 Вольта.
Прибор можно откалибровать по точкам, подключив к источнику постоянного тока. Для удобства можно построить номограммы, наподобие тех, что представлены ниже, а можно просто измерить переменный ток, а затем найти ему соответствие, используя источник постоянного тока.
По представленным номограммам видно в каком диапазоне напряжений возможно использовать указанный фотоприёмник, это примерно от 0,008 до 0,4 Вольта.
Калибровочная таблица для измерителя тока произвольной формы.
По этой таблице легко откалибровать прибор для измерения мощности. Контрольные точки выбраны через каждые 10 Ватт. Это ссылка, по которой можно скачать версию этой таблицы для печати в формате «doc».
| Мощность
(W) | Ток (А) (U=220V) | Напряжение
(V) при R балл. = …… Ом | Напряжение
(V) при R балл. = …… Ом |
| 25 | 0,11 | ||
| 30 | 0,14 | ||
| 40 | 0,18 | ||
| 50 | 0,23 | ||
| 60 | 0,27 | ||
| 70 | 0,32 | ||
| 80 | 0,36 | ||
| 90 | 0,41 | ||
| 100 | 0,45 | ||
| 110 | 0,50 | ||
| 120 | 0,55 | ||
| 130 | 0,59 | ||
| 140 | 0,64 | ||
| 150 | 0,68 | ||
| 160 | 0,73 | ||
| 170 | 0,77 | ||
| 180 | 0,82 | ||
| 190 | 0,86 | ||
| 200 | 0,91 | ||
| 210 | 0,95 | ||
| 220 | 1,00 | ||
| 230 | 1,05 | ||
| 240 | 1,09 | ||
| 250 | 1,14 | ||
| 260 | 1,18 | ||
| 270 | 1,23 | ||
| 280 | 1,27 | ||
| 290 | 1,32 | ||
| 300 | 1,36 | ||
| 310 | 1,41 | ||
| 320 | 1,45 | ||
| 330 | 1,50 | ||
| 340 | 1,55 | ||
| 350 | 1,59 |
Таблица параметров миниатюрных ламп с малым током потребления.
| Тип лампы | Параметры | Ресурс | Размеры (мм) | |||
|---|---|---|---|---|---|---|
| V | mA | Лм | Диаметр | Длина/Длина выводов | ||
| СМН 1,5-12 | 1,5 | 12 | 0,04 | 40 | 0.85 | 3.5/60 |
| СМН 6-20 | 6 | 20 | 0.25 | 600 | 3.2 | 9 |
| СМН 6-20-1 | 6 | 20 | 0.25 | 600 | 3.2 | 7/27 |
| СМН 6,3-20 | 6 | 20 | 0.26 | 600 | 3.2 | 9 |
| СМН 6,3-20-2 | 6 | 20 | 0.26 | 600 | 3.2 | 7/27 |
| СМН 6,3-20-3 | 6 | 20 | 0.2 | — | 3.2 | 14 |
| СМН 12-5 | 12 | 5 | 0.002 | 500 | 3.2 | 8/37 |
В столбике «Длина», через дробь, обозначены длина колбы (в знаменателе) и длина выводов (в числителе) для ламп с гибкими выводами.
Недостатки конструкции.
Если при измерении напряжения высокой частоты, предложенный метод лишён существенных недостатков, то точность измерения тока низкой частоты напрямую зависит от инертности нити накала лампы.
Использование лампы с большим номинальным током приводит к ошибкам из-за быстрого нагрева содержимого светонепроницаемого контейнера, а с малым — к ошибкам вызванным недостаточной инертностью нити накала.
Если при измерении тока или напряжения низкой частоты требуется гарантированная погрешность менее 10%, то стоит подумать о более серьёзном приборе.
Близкие темы.
Как самому изготовить киловольтметр.
Подключение непривычных нагрузок и источнику бесперебойного питания (UPS).
Выбор источника бесперебойного питания (ИБП) исходя из мощности нагрузки.
7 Апрель, 2009 (10:29) в
Измерения
Переменный ток
Переменный ток все время изменяет свое направление в отличие от постоянного, который протекает только в одном направлении. Постоянный ток вырабатывают батареи и источники постоянного тока, а переменный – генераторы сигналов и государственные энергетические системы.
Синусоидальные колебания
Форма переменного тока или напряжения может принимать самые различные виды. Наиболее распространенной является синусоидальная форма переменного напряжения или тока (рис. 2.1). Синусоидальное колебание имеет два максимальных значения, или пика: положительный пик и отрицательный. Пиковое значение называется также амплитуде синусоиды. Значение синусоидального напряжения, измеренное от пика до пика (размах), является разностью потенциалов между положительным пиком и отрицательным.
Размах = Положительная амплитуда + Отрицательная амплитуда = Удвоенная амплитуда.
Рис. 2.1. Синусоидальные колебания переменного тока
Среднеквадратическое значение
Постоянный ток имеет постоянное значение, и это значение можно использовать во всех вычислениях. Значение же переменного тока изменяется во времени. Чтобы преодолеть эту трудность, за «постоянное» значение переменного тока приняли и используют его среднеквадратическое значение.
Среднеквадратическое значение переменного тока является эквивалентом значения постоянного тока, при котором вырабатывается такая же мощность, что и при исходном значении переменного тока. Если известно среднеквадратическое значение переменного тока, то его можно использовать для вычисления мощности так же, как если бы это было постоянное напряжение или ток. Например:
Мощность пост. тока = Постоянный ток х Постоянное напряжение;
Мощность перем. Тока = Среднеквадр. значение тока х Среднеквадр. значение напряжения.
Значения переменного тока и напряжения всегда задают в виде среднеквадратической величины, за исключением специально оговоренных случаев.
Пример 1
Какое сопротивление имеет домашний электрический обогреватель мощностью 1 кВт?
Решение
Домашние обогреватели работают от сетевого напряжения, имеющего среднеквадратическое значение 240 В (в России 220 В. — Прим. перев.). Мощность, потребляемая обогревателем, составляет 1 кВт = 1000 Вт. Из формулы P = V2/R определяем
P = V2/R = 240*240/1000 = 57, б Ом.
Соотношение между пиковыми и среднеквадратическими значениями
Среднеквадратическое значение сигнала переменного тока зависит от его формы. Так, среднеквадратическое значение синусоидального сигнала составляет 0,707 его пикового значения (амплитуды). Заметим, что это справедливо только для синусоидального сигнала. Например, если амплитуда синусоидального сигнала Vр = 10 В, то его среднеквадратическое значение составит Vср.кв. = 0,707 * Vр = 0,707 * 10 = 7,07 В (см. рис. 2.2). Из соотношения Vср.кв. = 0,707 * Vр следует, что
Vр = 1/0,707 * Vср.кв. = 1,414 * Vср.кв.
Рис. 2.2. Среднеквадратическое значение синусоидального сигнала.
Рис. 2.3. Постоянная составляющая сигнала переменного тока.
Постоянная составляющая в сигнале переменного тока
До сих пор мы имели дело с сигналами переменного тока, которые не содержали постоянной составляющей. Рассмотрим два синусоидальных сигнала, изображенных на рис. 2.3. Левый сигнал не имеет постоянной составляющей, и его положительный пик равен отрицательному. Правый же сигнал содержит составляющую постоянного тока величиной 5 В.
Постоянная составляющая переменного тока называется также средним, или усредненным значением сигнала переменного тока.
Определим постоянную составляющую сигнала, имеющего прямоугольную форму (рис. 2.4).
Рис. 2.4.
1. Сначала определим положение нулевого уровня.
2. Вычислим площадь А1, лежащую выше нулевого уровня:
А1 = 4*1 = 4.
3. Вычислим площадь А2, лежащую ниже нулевого уровня:
А2 = 2*1 = 2.
4. Вычислим суммарную площадь:
А1 – А2 = 4 – 2 = 2.
5. Отсюда среднее значение напряжения за период равно
Суммарная площадь/Время периода = 2/3 = 0,67 В.
Среднеквадратическое значение сложных сигналов
Как уже говорилось, соотношение
Среднеквадратическое значение = 0,707 амплитуды
справедливо только для синусоидальных сигналов. Среднеквадратическое значение сигналов, имеющих другую форму, может быть определено следующим образом.
1. Определить площадь сигнала за один период. Заметим, что при определении площади отрицательное значение превращается в положительное.
2. Определить среднее значение площади сигнала за период.
3. Вычислить квадратный корень из средней площади сигнала за период.
Определим среднеквадратическое значение сигнала, имеющего форму меандра (рис. 2.5(а)). Площадь положительного полупериода этого сигнала равна 3 * 3 = 9. Площадь отрицательного полупериода составля¬ет (-3) * (-3) = 9. Среднее значение площади за период, следовательно, равно 9. Отсюда среднеквадратическое значение напряжения будет корень из 9 = 3 В.
Рис. 2.5. Сравнение среднеквадратических значений
прямоугольного и синусоидального сигналов.
Для сравнения определим среднеквадратическое значение синусоидального напряжения, имеющего значение положительной и отрицательной амплитуды +3 В и –3 В соответственно (рис. 2.5(б)): 0,707 * 3 В = 2,12 В.
Как видим, прямоугольный сигнал имеет большее среднеквадратическое значение. Это объясняется тем, что площадь под прямоугольной огибающей больше, чем площадь под синусоидой, хотя оба сигнала имеют одинаковые значения положительного и отрицательного пиков. В данном случае среднеквадратическое значение прямоугольного сигнала равно его пиковому значению.
На рис. 2.6 изображен прямоугольный сигнал, имеющий только положительные значения. Среднеквадратическое значение этого сигнала меньше его пикового значения.
При однополупериодном выпрямлении среднеквадратическое значение напряжения равно половине его амплитуды.
При двухполупериодном выпрямлении среднеквадратическое значение такое же, как у полной синусоиды, т. е. 0,707 амплитуды (рис. 2.7), поскольку при вычислении среднеквадратического значения положительная полуволна сигнала идентична отрицательной, положительный полупериод идентичен отрицательному.
Заметим, что постоянная составляющая, или среднее значение сигнала, это просто усредненное значение напряжения за один период, не имеющее никакого отношения к среднеквадратическому значению.
Рис. 2.6. Среднеквадратическое значение прямоугольного сигнала, имеющего только положительную полярность.
Рис. 2.7. (а) При однополупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,5 амплитуды.
(б) При двухполупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,707 амплитуды.
В этом видео наглядно рассказывается о типах тока, в том числе о переменном токе:
Добавить комментарий
Ток
rms — это … Что такое ток rms?
Токовые клещи — Для регистрации токовых клещей в нейронах см. Электрофизиология # Токовые клещи. В электротехнике и электронике токовые клещи или токовые щупы — это электрическое устройство, имеющее две губки, которые открываются для зажима вокруг электрического…… Wikipedia
RMS Titanic — пассажирский лайнер олимпийского класса, принадлежавший компании White Star Line и построенный на верфи Harland and Wolff в Белфасте, Ирландия (ныне Северная Ирландия).В ночь на 14 апреля 1912 года во время своего первого рейса «Титаник» столкнулся с айсбергом и затонул…… Wikipedia
RMS Queen Mary — это океанский лайнер, курсировавший в Северной Атлантике с 1936 по 1967 год по линии Cunard Line (затем Cunard White Star Line). Построенный Джоном Брауном и компанией, Клайдбанк, Шотландия, он был спроектирован как первое из запланированных Cunard двух кораблей еженедельно… Wikipedia
RMS Carpathia — трансатлантический пассажирский пароход компании Cunard Line, построенный Swan Hunter Wigham Richardson.»Карпатия» начала свое первое плавание в 1903 году и прославилась спасением выживших с корабля «Титаник» после того, как он затонул 15 апреля 1912 года. История RMS…… Википедия
RMS Sylvania — океанский лайнер, построенный в 1957 году компанией John Brown Co (Clydebank), Глазго, Шотландия, для судоходной компании Cunard Line из Великобритании. Это было последнее судно Cunard Line, построенное специально для трансатлантических переходов. Сайт…… Wikipedia
RMS Segwun — небольшой пароход, построенный в 1887 году для круизов по озерам Мускока, в округе Мускока, Онтарио, Канада.Мускока — курортная зона с множеством озер и рек. В начале 20 века Мускока была плохо обслужена дорогами. Отдыхающие были…… Википедия
RMS St. Helena (1989) — RMS St. Helena — это грузовое и пассажирское судно, которое обслуживает британскую заморскую территорию острова Святой Елены. Он курсирует между Кейптауном и островом Святой Елены, время от времени посещая зависимые территории острова Вознесения. Он также посещает Портленд, в…… Wikipedia
RMS Queen Mary 2 — RMS Queen Mary 2 (QM2) — это океанский лайнер Cunard Line, названный в честь более раннего лайнера Cunard Queen Mary, который, в свою очередь, был назван в честь Марии Текской, королевы-консорта Георга V.На момент ее постройки в 2003 году Chantiers de l…… Wikipedia
RMS Empress of Britain (1931) — RMS Empress of Britain был океанским лайнером, построенным между 1928 и 1931 годами на верфи Джона Брауна в Шотландии, принадлежавшей Canadian Pacific Steamship Company. Этот корабль является вторым из трех судов CP, получивших название Empress of Britain [Первый SS…… Wikipedia
Датчик тока — Датчик тока — это устройство, которое определяет электрический ток (переменный или постоянный) в проводе и генерирует сигнал, пропорциональный ему.Сгенерированный сигнал может быть аналоговым напряжением, током или даже цифровым выходом. Затем его можно использовать для отображения…… Wikipedia
Переменный ток — (зеленая кривая). Горизонтальная ось измеряет время; по вертикали, току или напряжению. В переменном токе (AC, также AC) движение электрического заряда периодически меняет направление. В постоянном токе (DC, также dc) поток электрического заряда… Wikipedia
Объяснение действующего значения напряжения и тока
переменного тока
Электричество и магнетизм
Объяснение действующего значения напряжения и тока
Методические указания
для 14-16
Есть много способов объяснить среднеквадратичное значение напряжения и тока на разных уровнях сложности для студентов продвинутого уровня.
- Для простейшего уровня скажем, что вы измеряете ток (или разность потенциалов) через крошечные интервалы времени. Возведите каждое значение в квадрат, сложите квадраты (все положительные) и разделите на количество выборок, чтобы найти средний квадрат или средний квадрат. Затем извлеките из этого квадратный корень. Это среднее значение
(среднеквадратичное).
- Для тех, кто знаком с графиками функций синуса и косинуса, можно попробовать следующий алгебраический метод.
- I = I 0 sinω t и I 2 = I 0 2 sin 2 ω
7 t
- Эффект нагрева зависит от I 2 R , поэтому требуется среднее значение I 2 , а не среднее значение I .
- Чтобы найти среднеквадратичное значение, вам нужно среднее значение sin 2 с течением времени.
- График sinω t и график cosω t выглядят одинаково, за исключением смещения начала координат. Поскольку это одна и та же модель, sin 2 ω t и cos 2 ω t имеют одинаковое среднее значение с течением времени.
- Но sin 2 ω t + cos 2 ω t = 1. Следовательно, средние значения любого из них должны быть 1/2.
- Следовательно, действующее значение I 0 sinω t должно быть I 0 √ 2
- Среднеквадратичное значение составляет 0,707 пикового значения, а пиковое значение — 1,41 раза больше значения, отображаемого вольтметром. Пиковое значение для сети 230 В составляет 325 В.
- В качестве альтернативы: построить график sin 2 θ. Разрежьте график пополам и переверните одну половину вверх ногами или скопируйте на прозрачную пленку и совместите вместе. Две половины точно совпадают, показывая, что среднее значение равно 1/2.
- Обратите внимание, что при использовании несглаженного выпрямителя переменного тока
от простого источника питания оценка мощности, полученная путем умножения показаний вольтметра постоянного тока с подвижной катушкой и амперметра с подвижной катушкой, вероятно, будет почти на 20% меньше. Это связано с тем, что каждый измеритель с подвижной катушкой измеряет простое среднее по времени неровностей за полупериод, а не среднеквадратичное значение.
Например, предположим, что существует 8 временных интервалов, как показано на диаграмме выше:
| Значения | 7 | 10 | 7 | 0 | -7 | -10 | -7 | 0 |
| Квадраты | 49 | 100 | 49 | 0 | 49 | 100 | 49 | 0 |
Сумма квадратов = 396
Среднее значение квадратов = 396/8 = почти 50
Квадратный корень ~ 7
С большим количеством интервалов среднеквадратичное значение оказывается равным
(пиковое значение) √ 2 = пиковое значение 1.41 = 0,707 пиковое значение
Умноженные действующие значения тока и напряжения дают фактическую мощность. Это жизненно важная часть при проведении количественных экспериментов с мощностью и энергией, таких как удельная теплоемкость.В лучшем случае значения составляют только 80% от стоимости.
Измерение действующих значений напряжения и тока
ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ (ТОКА)
Стандартные классические измерения значений напряжения (тока) основаны на двух основных методах: «средний» или «эффективный».
«Среднее» значение функции времени — это чистая площадь функции, вычисленная за определенный интервал времени, деленная на этот интервал времени.
В частности,
(Уравнение 1)
Если напряжение (ток) является постоянным или периодическим, то измерение его среднего значения не зависит от интервала, в течение которого выполняется измерение.Если, с другой стороны, функция напряжения (тока) неограниченно растет с течением времени, среднее значение зависит от интервала измерения и не обязательно будет постоянным, то есть среднего значения не существует. К счастью, в практическом мире электричества значения напряжения (тока) не растут безмерно и, следовательно, имеют хорошие средние значения. Это результат того, что реальные источники напряжения (тока) обычно либо; (1) батареи с постоянными или медленно (экспоненциально) убывающими значениями, (2) ограниченные синусоидальные функции времени или (3) комбинации вышеперечисленного.Синусоидальные функции с постоянной амплитудой имеют чистое нулевое среднее значение за интервалы времени, которые равны целым кратным синусоидальному периоду. Более того, средние значения могут быть вычислены по бесконечному количеству интервалов, которые не равны синусоидальному периоду. Эти средние значения также равны нулю. Хотя среднее значение ограниченной синусоидальной функции равно нулю, «эффективное» значение не равно нулю. Например, электрические водонагреватели очень хорошо работают на синусоидальных напряжениях с нулевыми средними значениями.
ЭФФЕКТИВНОЕ ЗНАЧЕНИЕ
«Эффективное» значение симметричных периодических функций напряжения (тока) от времени основано на концепции «нагревательной способности». Рассмотрим испытательное приспособление, показанное на рисунке 1.
Рисунок 1: Испытательное приспособление
Этот сосуд изолирован и наполнен некоторой стабильной жидкостью (например, трансформаторным маслом), способной достичь термодинамического равновесия.Если к внутреннему нагревателю сосуда приложить напряжение постоянного тока Vx, температура жидкости повысится. В конце концов, электрическая энергия, приложенная к этому сосуду, установит состояние равновесия, при котором подводимая энергия равна потерянной энергии (теплу), а жидкость в сосуде достигнет равновесной температуры, Tx градусов.
Затем в этом экспериментальном сценарии замените источник постоянного напряжения Vx изменяющимся во времени напряжением, которое не увеличивается без ограничений. В конце концов, через некоторое время Tfinal снова установится тепловое равновесие.Если это условие равновесия устанавливает ту же температуру Tx, которая была достигнута ранее с приложенным напряжением постоянного тока Vx, то можно сказать, что «эффективное» значение этой изменяющейся во времени функции равно Vx.
Отсюда и определение «действующей стоимости».
Уравнение 2 иллюстрирует это тепловое равновесие.
(Уравнение 2)
Если V (t) является периодической функцией времени с периодом цикла Tp, а T final является целым числом «n», умноженным на период (n * Tp), то интеграл по T final равен n умноженный на интеграл по Tp.Результаты этих замен показаны в уравнении 3.
(Уравнение 3)
Уравнение 3 показывает, что эффективная эквивалентная нагревательная способность ограниченной периодической функции напряжения (тока) может быть определена всего за один цикл.
Это уравнение известно как старая знакомая форма «квадрат R oot из M ean (средний) S quared»; отсюда и название: « RMS ».
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ УРАВНЕНИЯ «RMS»
Следующие результаты могут быть получены прямым применением уравнения 3.
- Синусоидальная функция, пик Vp
- Симметричная периодическая импульсная волна, пик Vp
- Несимметричная периодическая импульсная волна, все положительные пики Vp, с рабочим циклом D
- Симметричная периодическая треугольная волна, пик Vp
- Двухполупериодная выпрямленная синусоида, пиковое Vp
- Полуволновая выпрямленная синусоида, пиковое Vp
Примечание: Эти примеры показывают, что форма периодической функции может определять ее среднеквадратичное значение.Пик (пик) зависимости напряжения (тока) от времени, деленный на √ 2
часто по ошибке используется для расчета среднеквадратичного значения. Этот метод может привести к ошибкам, и его явно следует избегать.
ЭФФЕКТИВНЫЕ (СКЗ) ЗНАЧЕНИЯ КОМПЛЕКСНЫХ ФУНКЦИЙ
Чрезвычайно полезный факт при определении значений RMS состоит в том, что любая ограниченная периодическая функция времени с хорошим поведением может быть выражена, например, как среднее значение плюс сумма синусоид (теорема Фурье);
(Уравнение 4)
Где ωo — радианная частота V (t), а An, Bn, Ao — коэффициенты амплитуды Фурье.
Когда этот ряд подставляется в интегральное выражение Уравнение 2 для RMS, получается следующее;
(Уравнение 5)
Примечание: (A n ) 2 и (B n ) 2 /2 — квадраты среднеквадратичных значений для каждого n -го компонента Sin и косинуса.
Важный вывод:
Ограниченная периодическая функция времени имеет среднеквадратичное значение, равное квадратному корню из суммы квадрата среднеквадратичного значения каждого отдельного компонента.
ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
На рисунке 2 показаны составные кривые, образованные добавлением двух синусоид, одна с частотой 60 Гц и одна с частотой 180 Гц. Кривая 1 соответствует нулевой разности фаз, а кривая 2 — разности фаз 90 градусов.
Конкретно;
Кривая 1 V (t) = 170 * Sin (377 * t) + 50 * Sin (1131 * t)
Кривая 2 V (t) = 170 * Sin (377 * t) + 50 * Cos (1131 * t)
Примечание: Форма составной кривой определяется гармониками фазы и частоты.
Рисунок 2:
Фундаментальный с третьей гармоникой Добавлен
Кривая 2170 * Sin (377 * t) + 50 * Cos (1131 * t)
Кривая 1170 * Sin (377 * t) + 50 * Sin (1131 * t)
Промышленные синусоидальные функции напряжения (тока) часто содержат гармоники, которые влияют на форму волны и пиковые (пиковые) значения. Например, кривая 2 типична для токов намагничивания в трансформаторах и двигателях 60 Гц.В недорогих устройствах для считывания среднеквадратичных значений часто используются схемы выпрямителя, которые фиксируют пиковое значение, которое затем масштабируется на 0,707 и отображается как среднеквадратичное значение. Очевидно, что этот метод может дать неверные показания RMS.
В этом примере использование Vpeak ÷ √2 явно дает неверные значения.
Кривая 1: 203 * 0,707 = 144 вольт, не соответствует действительности RMS
Кривая 2: 155 * 0,707 = 110 вольт, неверно RMS
Правильное среднеквадратичное значение для обеих этих составных синусоидальных функций:
[(170) 2 /2 + (50) 2 /2] 1/2 = 125.3 вольта RMS
Таблица 1 иллюстрирует два примера вычислений RMS с использованием индивидуальных коэффициентов Фурье и уравнения 5. Примером является двухполупериодная выпрямленная пиковая синусоида с напряжением 1 вольт. Обратите внимание, что для функции двухполупериодного выпрямления измерительному устройству, необходимому для получения показаний RMS с погрешностью 0,01%, требуется полоса пропускания, которая включает пятую (5) гармонику, и разрешение для считывания уровней 10 мВ.
Другой пример, проиллюстрированный в Таблице 1, представляет собой пиковую функцию напряжения 1 В.В этом примере измерительному устройству для пилообразной функции, необходимому для получения показаний RMS с погрешностью 0,3%, требуется полоса пропускания, которая включает двадцать пятую (25) гармонику, и разрешение для считывания уровней 10 мВ.
Предположим, в целях иллюстрации, что пульсации переменного тока на выходе постоянного тока выпрямителя могут быть аппроксимированы пилообразной функцией. Таблица 1 показывает, что для измерения с погрешностью 0,3% среднеквадратичных пульсаций переменного тока на выходе постоянного тока выпрямителя 20 кГц, измерительное устройство должно иметь полосу пропускания более 500 кГц и разрешение для считывания уровней напряжения на 40 дБ (100 микровольт). для пиковой пульсации 10 мВ).Этот пример ясно показывает, что форма сигнала вместе с шириной полосы измерения и разрешением чрезвычайно важны для определения точности измерения истинного среднеквадратичного значения.
Любое устройство измерения «истинного среднеквадратичного значения» должно быть способно точно реализовать уравнение 3. Тонкость этого утверждения состоит в том, что электронная реализация уравнения 3 требует, чтобы устройство имело очень большую полосу пропускания и было способно определять малые величины.
КРЕСТ-ФАКТОР
Еще одним показателем качества, часто используемым для характеристики периодической временной функции напряжения (тока), является пик-фактор (CF).Пик-фактор для конкретной формы волны определяется как пиковое значение, деленное на среднеквадратичное значение. В частности,
ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ДЛЯ СКОРОСТИ ДАННЫХ
Для истинных измерений среднеквадратичных значений требуются измерительные приборы, которые точно реализуют уравнение 3, «уравнение среднеквадратичных значений».
Эти устройства должны иметь широкую полосу пропускания и хорошее разрешение низкого уровня, чтобы поддерживать высокий коэффициент амплитуды.
Dataforth разработал три продукта, которые удовлетворяют этим требованиям; модули ввода SCM5B33, DSCA33 и 8B33 True RMS.Эти продукты обеспечивают изоляционный барьер 1500 В среднеквадратичного значения между входом и выходом.
SCM5B33 Изолированный входной модуль True RMS
- Интерфейсы Среднеквадратичное напряжение (0 — 300 В) или действующий ток (0 — 5 А)
- разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (расширенный диапазон до 20 кГц)
- Совместимость со стандартными трансформаторами тока и напряжения
- Промышленный стандартный выход 0-1 мА, 0-20 мА, 4-20 мА, 0-5 В или 0-10 В постоянного тока
- ± 0.25% заводская калибровка точности (класс точности 0,2)
- Изоляция непрерывного трансформатора 1500 В среднекв.
- Защита входа от перегрузки до 480 В макс. (Пиковый и постоянный ток) или 10 А среднеквадратичного значения в непрерывном режиме
- ANSI / IEEE C37.90.1 Защита от переходных процессов
- Сертификат CSA, соответствие CE и ATEX
DSCA33 Изолированный формирователь входного сигнала истинного среднеквадратичного значения
- Интерфейсы Среднеквадратичное напряжение (0 — 300 В) или действующий ток (0 — 5 А)
- разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (работа в расширенном диапазоне до 20 кГц)
- Совместимость со стандартными трансформаторами тока и напряжения
- Промышленный стандартный выход 0-1 мА, 0-20 мА, 4-20 мА, 0-5 В или 0-10 В постоянного тока
- ± 0.25% заводская калибровка точности (класс точности 0,2)
- ± 5% Регулируемые ноль и диапазон
- Изоляция трансформатора 1500Vrms
- Защита входа от перегрузки до 480 В (пиковое напряжение переменного и постоянного тока) или 10 А RMS в непрерывном режиме
- ANSI / IEEE C37.90.1 Защита от переходных процессов
- легко устанавливается на стандартную DIN-рейку
- Зарегистрировано в C-UL-US
- Соответствие CE и ATEX
8B33 Миниатюрный модуль ввода True RMS
- Интерфейсы для среднеквадратичного напряжения (0-300 В) или среднеквадратичного тока (0-1 А)
- разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (расширенный диапазон до 10 кГц)
- Совместимость со стандартными трансформаторами тока и напряжения
- Промышленный стандартный выход от 0 до 5 В постоянного тока
- ± 0.25% заводская калибровка точности
- Изоляция трансформатора 1500Vrms
- Защита входа от перегрузки до 350 В среднеквадратического значения (пиковое значение переменного и постоянного тока) или 2 А постоянного тока
- 120 дБ CMR
- 70 дБ ЯМР при 60 Гц
- ANSI / IEEE C37.90.1 Защита от переходных процессов
- CE соответствует требованиям
- Зарегистрировано в C-UL-US
- Ожидается соответствие ATEX
- Типы модулей Mix and Match на задней панели
Лучшее значение среднеквадратичного значения тока — Отличные предложения по среднеквадратичному току от продавцов со всего мира
Отличные новости !!! Вы находитесь в нужном месте для текущего значения действующего значения.К настоящему времени вы уже знаете, что что бы вы ни искали, вы обязательно найдете это на AliExpress. У нас буквально тысячи отличных продуктов во всех товарных категориях. Ищете ли вы товары высокого класса или дешевые и недорогие оптовые закупки, мы гарантируем, что он есть на AliExpress.
Вы найдете официальные магазины торговых марок наряду с небольшими независимыми продавцами со скидками, каждый из которых предлагает быструю доставку и надежные, а также удобные и безопасные способы оплаты, независимо от того, сколько вы решите потратить.
AliExpress никогда не уступит по выбору, качеству и цене. Каждый день вы будете находить новые онлайн-предложения, скидки в магазинах и возможность сэкономить еще больше, собирая купоны. Но вам, возможно, придется действовать быстро, поскольку этот максимальный среднеквадратичный ток в кратчайшие сроки станет одним из самых востребованных бестселлеров. Подумайте, как вы, друзья, будете завидовать, когда скажете им, что получили текущую сумму на AliExpress.Благодаря самым низким ценам в Интернете, дешевым тарифам на доставку и возможности получения на месте вы можете еще больше сэкономить.
Если вы все еще не уверены в текущих продажах и думаете о выборе аналогичного товара, AliExpress — отличное место для сравнения цен и продавцов. Мы поможем вам разобраться, стоит ли доплачивать за высококачественную версию или вы получаете столь же выгодную сделку, приобретая более дешевую вещь.А если вы просто хотите побаловать себя и потратиться на самую дорогую версию, AliExpress всегда позаботится о том, чтобы вы могли получить лучшую цену за свои деньги, даже сообщая вам, когда вам будет лучше дождаться начала рекламной акции. и ожидаемая экономия.AliExpress гордится тем, что у вас всегда есть осознанный выбор при покупке в одном из сотен магазинов и продавцов на нашей платформе. Реальные покупатели оценивают качество обслуживания, цену и качество каждого магазина и продавца.Кроме того, вы можете узнать рейтинги магазина или отдельных продавцов, а также сравнить цены, доставку и скидки на один и тот же продукт, прочитав комментарии и отзывы, оставленные пользователями. Каждая покупка имеет звездный рейтинг и часто имеет комментарии, оставленные предыдущими клиентами, описывающими их опыт транзакций, поэтому вы можете покупать с уверенностью каждый раз. Короче говоря, вам не нужно верить нам на слово — просто слушайте миллионы наших довольных клиентов.
А если вы новичок на AliExpress, мы откроем вам секрет.Непосредственно перед тем, как вы нажмете «купить сейчас» в процессе транзакции, найдите время, чтобы проверить купоны — и вы сэкономите еще больше. Вы можете найти купоны магазина, купоны AliExpress или собирать купоны каждый день, играя в игры в приложении AliExpress. Вместе с бесплатной доставкой, которую предлагают большинство продавцов на нашем сайте, вы сможете приобрести rms current по самой выгодной цене.
У нас всегда есть новейшие технологии, новейшие тенденции и самые обсуждаемые лейблы.На AliExpress отличное качество, цена и сервис всегда в стандартной комплектации. Начните самый лучший шоппинг прямо здесь.
Лучшее значение текущих СКЗ — Отличные предложения на текущие СКЗ от глобальных продавцов текущих СКЗ
Отличные новости !!! Вы находитесь в нужном месте для текущей компании. К настоящему времени вы уже знаете, что что бы вы ни искали, вы обязательно найдете это на AliExpress.У нас буквально тысячи отличных продуктов во всех товарных категориях. Ищете ли вы товары высокого класса или дешевые и недорогие оптовые закупки, мы гарантируем, что он есть на AliExpress.
Вы найдете официальные магазины торговых марок наряду с небольшими независимыми продавцами со скидками, каждый из которых предлагает быструю доставку и надежные, а также удобные и безопасные способы оплаты, независимо от того, сколько вы решите потратить.
AliExpress никогда не уступит по выбору, качеству и цене. Каждый день вы будете находить новые онлайн-предложения, скидки в магазинах и возможность сэкономить еще больше, собирая купоны. Но вам, возможно, придется действовать быстро, так как это самое популярное на данный момент среднеквадратичное значение вскоре станет одним из самых востребованных бестселлеров. Подумайте, как вам будут завидовать друзья, когда вы скажете им, что у вас есть текущий торговый центр на AliExpress.Благодаря самым низким ценам в Интернете, дешевым тарифам на доставку и возможности получения на месте вы можете еще больше сэкономить.
Если вы все еще не уверены в текущих торговых точках и думаете о выборе аналогичного товара, AliExpress — отличное место для сравнения цен и продавцов. Мы поможем вам разобраться, стоит ли доплачивать за высококачественную версию или вы получаете столь же выгодную сделку, приобретая более дешевую вещь.А если вы просто хотите побаловать себя и потратиться на самую дорогую версию, AliExpress всегда позаботится о том, чтобы вы могли получить лучшую цену за свои деньги, даже сообщая вам, когда вам будет лучше дождаться начала рекламной акции. и ожидаемая экономия.AliExpress гордится тем, что у вас всегда есть осознанный выбор при покупке в одном из сотен магазинов и продавцов на нашей платформе. Реальные покупатели оценивают качество обслуживания, цену и качество каждого магазина и продавца.Кроме того, вы можете узнать рейтинги магазина или отдельных продавцов, а также сравнить цены, доставку и скидки на один и тот же продукт, прочитав комментарии и отзывы, оставленные пользователями. Каждая покупка имеет звездный рейтинг и часто имеет комментарии, оставленные предыдущими клиентами, описывающими их опыт транзакций, поэтому вы можете покупать с уверенностью каждый раз. Короче говоря, вам не нужно верить нам на слово — просто слушайте миллионы наших довольных клиентов.
А если вы новичок на AliExpress, мы откроем вам секрет.Непосредственно перед тем, как вы нажмете «купить сейчас» в процессе транзакции, найдите время, чтобы проверить купоны — и вы сэкономите еще больше. Вы можете найти купоны магазина, купоны AliExpress или собирать купоны каждый день, играя в игры в приложении AliExpress. Вместе с бесплатной доставкой, которую предлагают большинство продавцов на нашем сайте, вы сможете приобрести current rms по самой выгодной цене.
У нас всегда есть новейшие технологии, новейшие тенденции и самые обсуждаемые лейблы.На AliExpress отличное качество, цена и сервис всегда в стандартной комплектации. Начните самый лучший шоппинг прямо здесь.
Пиковое, среднее значение и среднеквадратичное напряжение
Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эквивалентом переменного тока и постоянного напряжения.
Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эффективным или тепловым значением переменного тока, эквивалентно напряжению постоянного тока, которое будет обеспечивать такое же количество тепловыделения в резисторе, как и напряжение переменного тока. если применяется к тому же резистору.
RMS не является «средним» напряжением, и его математическое отношение к пиковому напряжению зависит от типа сигнала. Среднеквадратичное значение — это квадратный корень из среднего (среднего) значения функции квадрата мгновенных значений.
Поскольку переменное напряжение повышается и падает со временем, для получения заданного среднеквадратичного напряжения требуется больше переменного напряжения, чем для постоянного. Например, для достижения среднеквадратичного значения 120 В (0,707 x169) потребуется пиковое значение переменного тока 169 вольт.
В этом примере величина нагрева напряжения 169 переменного тока эквивалентна значению нагрева источника постоянного тока на 120 вольт.Большинство мультиметров, будь то вольтметры или амперметры, измеряют среднеквадратичное значение, принимая чисто синусоидальную форму волны.
Важные термины, которые следует запомнить
Пиковое напряжение (Vp)
Максимальное мгновенное значение функции, измеренное от нулевого напряжения. Для показанной выше формы волны пиковая амплитуда и пиковое значение одинаковы, поскольку среднее значение функции равно нулю вольт.
Пиковое напряжение (В пик-пик)
Полное напряжение между положительным и отрицательным пиками формы волны; то есть сумма величин положительного и отрицательного пиков.
RMS напряжение (Vrms)
Среднеквадратичное или эффективное значение сигнала.
Среднее напряжение (Vavg)
Уровень формы волны, определяемый условием, что область, ограниченная кривой выше этого уровня, в точности равна области, ограниченной кривой ниже этого уровня.
Важные уравнения, которые следует запомнить
- Впик x 0,707 = Среднеквадратичное значение
- Vrms = 1,11 x Vavg
- 1.414 x Vrms = Vp
- Vavg = 0,637 x Vp
В
Дополнительная литература / Источники
.
