Расчет среднего и среднеквадратичного значений тока/напряжения. Среднеквадратичный ток

Расчет среднего и среднеквадратичного значений тока/напряжения

. .Вот здесь есть расширенный и углубленный вариант данной заметки . .

Будучи в очень недавнем прошлом яростным разработчиком всевозможных импульсных источников питания, интересовался всяким по данной теме. В частности – вычислением среднего (AVG, Average) и среднеквадратичного (действующего, эффективного, RMS) значений напряжений и (особенно) токов, живущих в разрабатываемом источнике. Для тех, кто не помнит/не знает – напомню определение среднеквадратичного значения тока/напряжения из Википедии:

Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока

Посему, хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. И про выпрямители во вторичной цепи – та же песня. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.

Или, например, делаем могучий источник с высоким КПД. Чтобы оптимально спроектировать обмотку магнитного элемента требуются уже среднее значение тока и среднеквадратичное значение переменной составляющей. В общем – куда ни плюнь, везде фигурируют RMS и AVG (среднее значение, а не антивирус, это важно). Поэтому было принято решение сделать себе некий инструмент, упрощающий жизнь разработчика импульсных источников питания. Вот этим инструментом я и хочу поделиться с общественностью – вдруг кому пригодится.

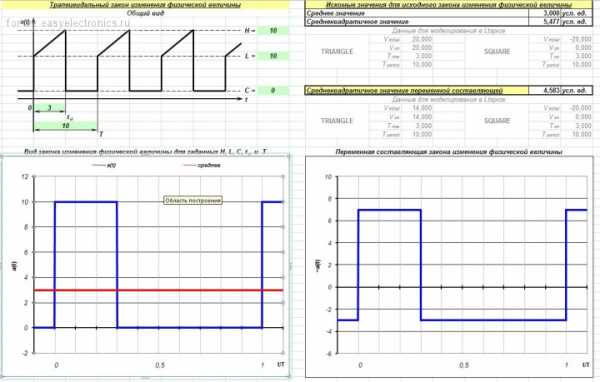
Как нетрудно заметить, данный инструмент («программа») представляет собой обычный Экселовский файл, поскольку в «компьютерном» программировании я вообще ничего не понимаю. В задачу рассматриваемой «программы» входит отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период) и отрисовка формы переменной составляющей заданного сигнала. Также «программа» умеет вычислять среднее и среднеквадратичное значения заданного сигнала и RMS-значение его переменной составляющей. Исходные данные вводятся слева в ячейки, выделенные зеленым цветом (на рисунке обведены красным). Рассчитанные значения AVG и RMS, а также среднеквадратичное значение переменной составляющей заданного сигнала отображаются в правой стороне экрана (обведены синим). Ну а картинки рисуются в нижней части экрана: слева – исходный сигнал, справа – его переменная составляющая.

В нагрузку к «программе» идет короткая заметка, в которой выводятся (а не берутся невесть откуда) расчетные формулы для основных форм сигналов в импульсных источниках питания (трапеции, прямоугольника, треугольника, пилы). Также в этой короткой заметке рассмотрен пример расчета AVG и RMS значений сложного сигнала.

Почему в качестве основы взята именно трапеция? Потому, что из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник

и треугольник

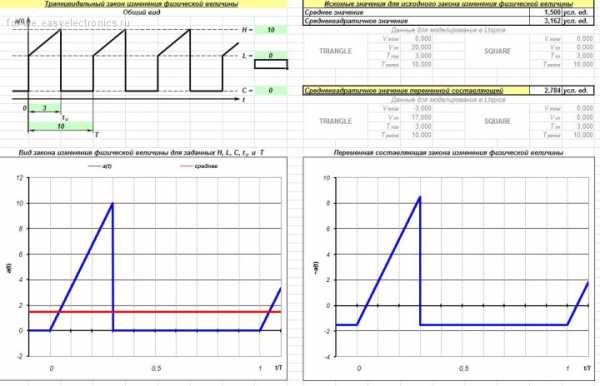
А уж на основе этих базовых сигналов можно сляпать и пилу

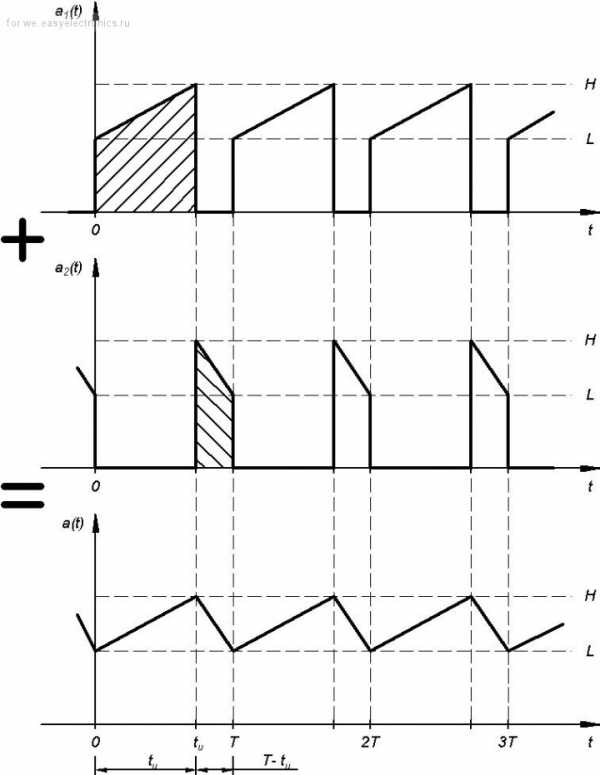
и даже то, что творится на вторичке пушпула:

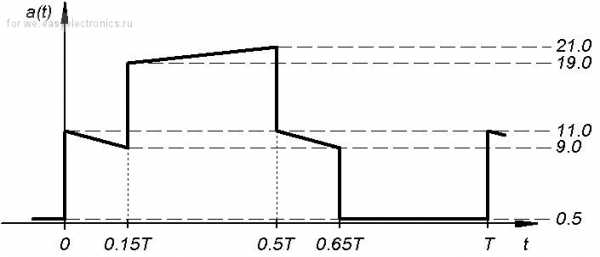
И еще много чего. Пример же расчета среднего и среднеквадратичных значений для сложных (т.е., составленных из простейших) сигналов, повторюсь, есть в короткой заметке-нагрузке. Хотя, если кого-то заинтересует данный аспект, могу впоследствие осветить его и в этом топике.

Вот, в принципе, и всё описание представленной «программы». Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!

Примечание: все вопросы лучше валить в камменты после заметки, так как не факт, что я смогу на них на все ответить. А вот шансы на то, что в сообществе найдется более прошаренный человек по твоей теме — довольно хорошие. Но уж если зарегистрироваться на сайте совсем никак — можно воспользоваться возможностями электрической почты: [email protected]

Содержание архива (также прилеплен к заметке):AVG_RMS.zip:Среднее_и_среднеквадратичное_Трапеция.xls – собственно, «программа» для расчета AVG и RMS в формате Microsoft Excel;Среднее и среднеквадратичное.pdf – короткая заметка-нагрузка с выводом расчетных формул и с примером расчета AVG и RMS значений сложного сигнала.

we.easyelectronics.ru

Среднеквадратичное значение напряжения | Практическая электроника

Что же из себя представляет среднеквадратичное значение напряжения и как его замерить? Давайте разберем значение этого термина. Поможет нам в этих делах наш осциллограф OWON SDS6062 , Блок питания, а также ЛАТР (Лабораторный автотрансформатор).

Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт:

Вот ее характеристики: рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.

Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I — сила тока, можно найти I. Значит I=P/U=21/12=1,75 Ампер.

Ладно, с лампочкой разобрались. Давайте ее зажгем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы

Подаем напряжение с блока питания на лампу и вуаля!

Замеряем напряжение на клеммах-крокодилах блока питания с помощью Мультиметра . Ровненько 12 Вольт, как и предполагалось.

К этим же клеммах цепляем и наш осцил

Смотрим осциллограмму на осцилле:

Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени у нас напряжение остается таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.

Замеряем Силу тока, как правильно замерить силу тока в цепи, можно узнать, прочитав статью Как измерить ток и напряжение мультиметром?.

Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить на погрешность прибора или на лампочку ;-).

Теперь начинается самое интересное. Берем наш ЛАТР

Ставим прибор на измерение переменного напряжения и выставляем с помощью крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.

Цепляем осциллограф к клеммах ЛАТРа, не забывая на осцилле выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

Смотрим, сколько силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.

Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение зажигали одну и ту же лампочку, которая кушала одну и ту же мощность. Значит эта осциллограмма

и вот эта осциллограмма

Значит они чем то похожи? Но чем???

Cреднеквадратичное значение напряжения — это такое значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении. То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном. То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.

Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала любой частоты равняется максимальной его амплитуде, поделенной на корень из двух

Стоп! Мы ведь не разобрали, что такое максимальная амлитуда! Давайте взглянем на осциллограмму и сразу все поймем:

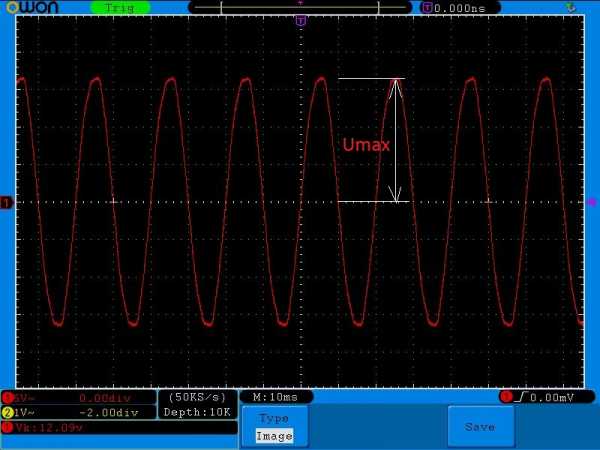
Ну что, догнали, что такое Umax? Если даже посчитать по клеточкам и глянуть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то Umax=17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉

Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение. Максимальная амплитуда этих 220 Вольт равняется 220х1,41=310 Вольт.

Где же среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот же они!

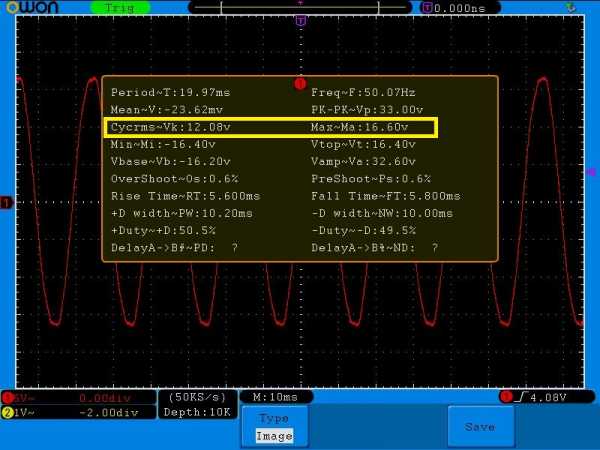
Vk — это и есть среднеквадратичное напряжение этого сигнала.

Ma — это и есть Umax.

Конечно, 16,6/1,41=11,8 Вольт, а он пишет 12,08 Вольт. Думаю, это связано с тем, что в синусоиде есть небольшие искажения, поэтому измерения немного неточные.

Итак, внимание! Кто первый напишет среднеквадратичное значение напряжения этого сигнала, получит 100 руб на мобилу 😉

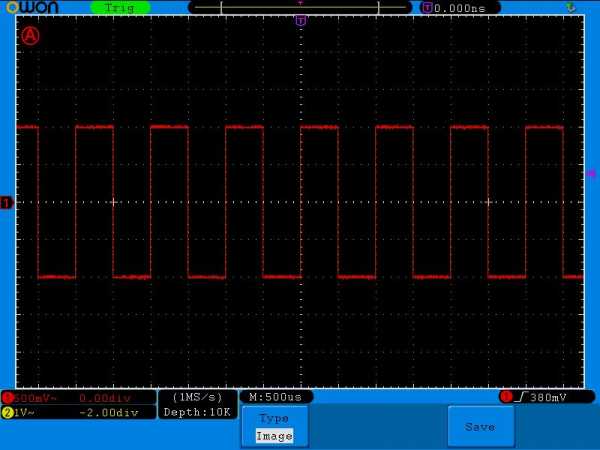
Конкурс уже давненько прошел и первая в комментах ответила Ирина Молчалина и выиграла 100 руб ;-). Правильный ответ 1 Вольт. Почему именно так, читаем эту статью.

www.ruselectronic.com

Переменный ток

Переменный ток все время изменяет свое направление в отличие от постоянного, который протекает только в одном направлении. Постоянный ток вырабатывают батареи и источники постоянного тока, а переменный – генераторы сигналов и государственные энергетические системы.

Синусоидальные колебания

Форма переменного тока или напряжения может принимать самые различные виды. Наиболее распространенной является синусоидальная форма переменного напряжения или тока (рис. 2.1). Синусоидальное колебание имеет два максимальных значения, или пика: положительный пик и отрицательный. Пиковое значение называется также амплитуде синусоиды. Значение синусоидального напряжения, измеренное от пика до пика (размах), является разностью потенциалов между положительным пиком и отрицательным.Размах = Положительная амплитуда + Отрицательная амплитуда = Удвоенная амплитуда.

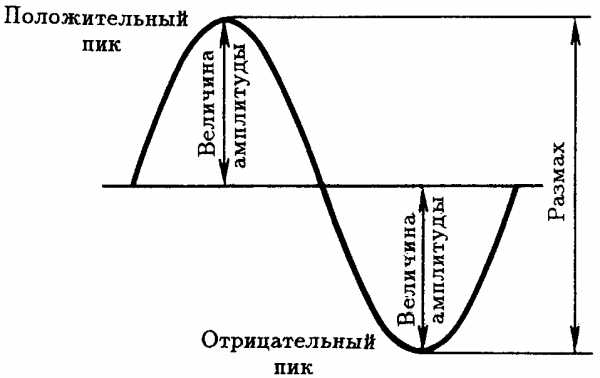
Рис. 2.1. Синусоидальные колебания переменного тока

Среднеквадратическое значение

Постоянный ток имеет постоянное значение, и это значение можно использовать во всех вычислениях. Значение же переменного тока изменяется во времени. Чтобы преодолеть эту трудность, за «постоянное» значение переменного тока приняли и используют его среднеквадратическое значение.Среднеквадратическое значение переменного тока является эквивалентом значения постоянного тока, при котором вырабатывается такая же мощность, что и при исходном значении переменного тока. Если известно среднеквадратическое значение переменного тока, то его можно использовать для вычисления мощности так же, как если бы это было постоянное напряжение или ток. Например:

Мощность пост. тока = Постоянный ток х Постоянное напряжение;Мощность перем. Тока = Среднеквадр. значение тока х Среднеквадр. значение напряжения.

Значения переменного тока и напряжения всегда задают в виде среднеквадратической величины, за исключением специально оговоренных случаев.Пример 1Какое сопротивление имеет домашний электрический обогреватель мощностью 1 кВт?РешениеДомашние обогреватели работают от сетевого напряжения, имеющего среднеквадратическое значение 240 В (в России 220 В. — Прим. перев.). Мощность, потребляемая обогревателем, составляет 1 кВт = 1000 Вт. Из формулы P = V2/R определяем

P = V2/R = 240*240/1000 = 57, б Ом.

Соотношение между пиковыми и среднеквадратическими значениями

Среднеквадратическое значение сигнала переменного тока зависит от его формы. Так, среднеквадратическое значение синусоидального сигнала составляет 0,707 его пикового значения (амплитуды). Заметим, что это справедливо только для синусоидального сигнала. Например, если амплитуда синусоидального сигнала Vр = 10 В, то его среднеквадратическое значение составит Vср.кв. = 0,707 * Vр = 0,707 * 10 = 7,07 В (см. рис. 2.2). Из соотношения Vср.кв. = 0,707 * Vр следует, что

Vр = 1/0,707 * Vср.кв. = 1,414 * Vср.кв.

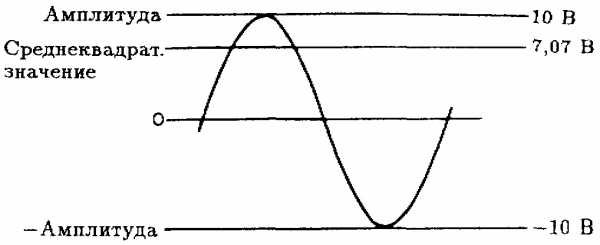
Рис. 2.2. Среднеквадратическое значение синусоидального сигнала.

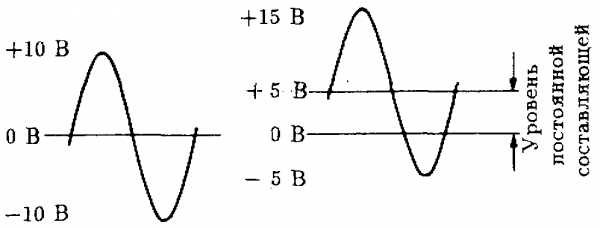
Рис. 2.3. Постоянная составляющая сигнала переменного тока.

Постоянная составляющая в сигнале переменного тока

До сих пор мы имели дело с сигналами переменного тока, которые не содержали постоянной составляющей. Рассмотрим два синусоидальных сигнала, изображенных на рис. 2.3. Левый сигнал не имеет постоянной составляющей, и его положительный пик равен отрицательному. Правый же сигнал содержит составляющую постоянного тока величиной 5 В.Постоянная составляющая переменного тока называется также средним, или усредненным значением сигнала переменного тока.Определим постоянную составляющую сигнала, имеющего прямоугольную форму (рис. 2.4).

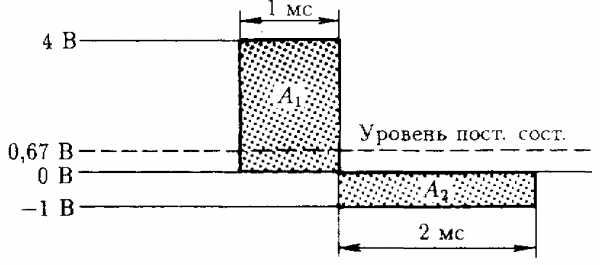
Рис. 2.4.

1. Сначала определим положение нулевого уровня.2. Вычислим площадь А1, лежащую выше нулевого уровня:А1 = 4*1 = 4.

3. Вычислим площадь А2, лежащую ниже нулевого уровня:А2 = 2*1 = 2.

4. Вычислим суммарную площадь:А1 – А2 = 4 – 2 = 2.

5. Отсюда среднее значение напряжения за период равноСуммарная площадь/Время периода = 2/3 = 0,67 В.

Среднеквадратическое значение сложных сигналов

Как уже говорилось, соотношениеСреднеквадратическое значение = 0,707 амплитудысправедливо только для синусоидальных сигналов. Среднеквадратическое значение сигналов, имеющих другую форму, может быть определено следующим образом.1. Определить площадь сигнала за один период. Заметим, что при определении площади отрицательное значение превращается в положительное.2. Определить среднее значение площади сигнала за период.3. Вычислить квадратный корень из средней площади сигнала за период.Определим среднеквадратическое значение сигнала, имеющего форму меандра (рис. 2.5(а)). Площадь положительного полупериода этого сигнала равна 3 * 3 = 9. Площадь отрицательного полупериода составля¬ет (-3) * (-3) = 9. Среднее значение площади за период, следовательно, равно 9. Отсюда среднеквадратическое значение напряжения будет корень из 9 = 3 В.

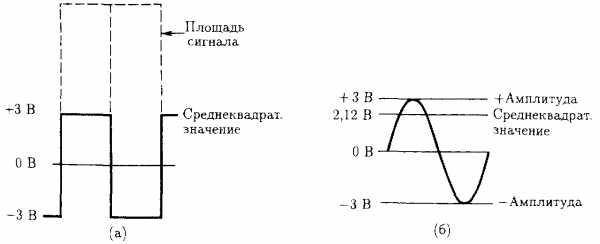
Рис. 2.5. Сравнение среднеквадратических значенийпрямоугольного и синусоидального сигналов.

Для сравнения определим среднеквадратическое значение синусоидального напряжения, имеющего значение положительной и отрицательной амплитуды +3 В и –3 В соответственно (рис. 2.5(б)): 0,707 * 3 В = 2,12 В.

Как видим, прямоугольный сигнал имеет большее среднеквадратическое значение. Это объясняется тем, что площадь под прямоугольной огибающей больше, чем площадь под синусоидой, хотя оба сигнала имеют одинаковые значения положительного и отрицательного пиков. В данном случае среднеквадратическое значение прямоугольного сигнала равно его пиковому значению.

На рис. 2.6 изображен прямоугольный сигнал, имеющий только положительные значения. Среднеквадратическое значение этого сигнала меньше его пикового значения.При однополупериодном выпрямлении среднеквадратическое значение напряжения равно половине его амплитуды.При двухполупериодном выпрямлении среднеквадратическое значение такое же, как у полной синусоиды, т. е. 0,707 амплитуды (рис. 2.7), поскольку при вычислении среднеквадратического значения положительная полуволна сигнала идентична отрицательной, положительный полупериод идентичен отрицательному.Заметим, что постоянная составляющая, или среднее значение сигнала, это просто усредненное значение напряжения за один период, не имеющее никакого отношения к среднеквадратическому значению.

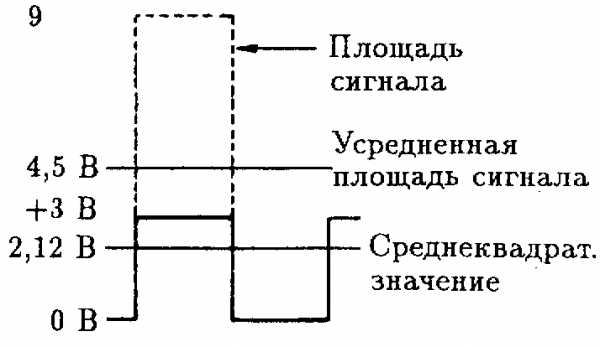
Рис. 2.6. Среднеквадратическое значение прямоугольного сигнала, имеющего только положительную полярность.

Рис. 2.7. (а) При однополупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,5 амплитуды.(б) При двухполупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,707 амплитуды.

В этом видео наглядно рассказывается о типах тока, в том числе о переменном токе:

Добавить комментарий

radiolubitel.net

Среднеквадратичное значение (СКЗ). Действующее или эффективное значение. Root-mean-square (RMS)

Среднеквадратичное значение (СКЗ). Действующее или эффективное значениеИстинное среднеквадратичное значение (ИСКЗ)

Root-mean-square (RMS) − среднеквадратичное значение – англ.True Root-Mean-Square (TRMS) − истинное среднеквадратичное значение – англ.

Для любой периодической функции (например, тока или напряжения) вида f = f(t) среднеквадратичное значение функции определяется как:

Если функция задана в виде суммы гармоник (как например в случае тока нелинейной нагрузки)

то действующее значение периодической несинусоидальной функции выражается формулой

Поскольку Fn − амплитуда n-ой гармоники, то Fn / √2 − действующее значение гармоники. Таким образом, полученное выражение показывает, что действующее значение периодической несинусоидальной функции равно корню квадратному из суммы квадратов действующих значений гармоник и квадрата постоянной слагающей.

Например если, несинусоидальный ток выражается формулой:

то среднеквадратичное значение тока равно:

Все приведённые выше соотношения используются при вычислении в тестерах измеряющих ИСКЗ, в цепях измерения тока ИБП, в анализаторах сети и в др. оборудовании.

Истинное среднеквадратичное значение (ИСКЗ), True Root-Mean-Square (TRMS)

Большинство простых тестеров не могут точно измерять среднеквадратичное значение несинусоидального сигнала (то есть сигнала с большими гармоническими искажениями, например, прямоугольной формы). Они правильно определяют СКЗ напряжения только для синусоидальных сигналов. Если таким прибором измерить СКЗ напряжения прямоугольной формы, то показание будет ошибочным. Причина ошибки – обычные тестеры при вычислении учитывают основную гармонику (для обычной сети – 50 Гц), но не берут в расчет высшие гармоники сигнала.

Для решения данной проблемы существуют особые приборы, точно измеряющие СКЗ с учётом высших гармоник (обычно до 30-50 гармоник). Они маркируются символом TRMS или ИСКЗ (true root-mean-square) – истинное среднеквадратичное значение, True RMS, истинное СКЗ.

Так, например, обычный тестер может измерить с ошибкой напряжение на выходе ИБП с аппроксимированной синусоидой, в то время как тестер «APPA 106 TRUE RMS MULTIMETER» измеряет напряжение (СКЗ) правильно.

Замечания

Для синусоидального сигнала, фазное напряжение в сети (нейтраль – фаза, phase voltage) равно:

UСКЗф = Uмаксф / (√2)

Для синусоидального сигнала, линейное напряжение в сети (фаза – фаза, interlinear voltage) равно:

UСКЗл = Uмаксл / (√2)

Соотношение между фазным и линейным напряжением:

UСКЗл = UСКЗф * √3

Обозначения:

ф – линейное (напряжение)

л – фазное (напряжение)

СКЗ – среднеквадратичное значение

макс – максимальное или амплитудное значение (напряжения)

Примеры:

Фазному напряжению 220 В соответствует линейное напряжение 380 В

Фазному напряжению 230 В соответствует линейное напряжение 400 В

Фазному напряжению 240 В соответствует линейное напряжение 415 В

Фазное напряжение:

Напряжение в сети 220 В (СКЗ), - амплитудное значение напряжения около ±310 В

Напряжение в сети 230 В (СКЗ), - амплитудное значение напряжения около ±325 В

Напряжение в сети 240 В (СКЗ), - амплитудное значение напряжения около ±340 В

Линейное напряжение:

Напряжение в сети 380 В (СКЗ), - амплитудное значение напряжения около ±537 В

Напряжение в сети 400 В (СКЗ), - амплитудное значение напряжения около ±565 В

Напряжение в сети 415 В (СКЗ), - амплитудное значение напряжения около ±587 В

Ниже приведён обычный пример фазных напряжений в 3-фазной сети:

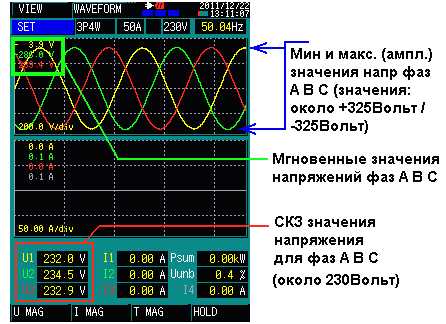[1] Г.И. Атабеков Основы Теории Цепей с.176, 434 с.

www.xn--80aacyeau1asblh.xn--p1ai

Среднеквадратичное значение - ток - Большая Энциклопедия Нефти и Газа, статья, страница 1

Среднеквадратичное значение - ток

Cтраница 1

Среднеквадратичное значение тока берется исходя из того, что тепловые потери пропорциональны квадрату тока. [2]

Среднеквадратичное значение тока электродвигателя, приведенное к одному из стандартных значений относительной продолжительности включения ( ПВ 15, 25 и 40 %), не должно превышать номинального тока катушки, приведенного в табл. 2.2. При малых нагрузках магнитный поток может оказаться недостаточным для срабатывания магнита. Поэтому обычно такие магниты устанавливают на тормозах механизмов, для которых нагрузка и величина тока меняются мало ( например, механизмы передвижения и поворота) или в которых цепь возбуждения является самостоятельной и ток в ней не уменьшается ниже определенного значения. [3]

Рассчитанное среднеквадратичное значение тока двигателя находится в допустимых пределах, так как номинальный ток двигателя / дв. [4]

Нужно отметить, что хотя среднеквадратичное значение тока правильно определяет потери в меди обмоток, оно далеко не всегда достаточно точно определяет повышение температуры обмоток. Если, например, нагрузка в течение длительного времени превышает номинальную, то действительное превышение температуры может значительно превосходить величину, подсчитанную по среднегеометрическому значению тока. [5]

Наибольшим током термической устойчивости / т называется наибольшее среднеквадратичное значение тока за промежуток времени i. [6]

Действующее значение тока первичной обмотки трансформатора определяется как среднеквадратичное значение токов, пересчитанных из вторичной обмотки в первичную, с учетом длительности протекания тока в каждой секции вторичной цепи трансформатора. [7]

Наиболее характерны циклические перегрузки, показанные на рис. 5.5. Среднеквадратичное значение тока / 0 ( Т и 1 - длительность и ток в период нагрузки, Тч - время бестоковой паузы) не должно превышать номинальное значение тока / Н0м, допустимое в ста-дионарном тепловом режиме. [9]

При этом за время работы преобразователя в режиме перегрузок среднеквадратичное значение тока за любые 30 мин ( время усреднения) не должно превышать номинальный ток преобразователя, а если в течение этих 30 мин происходит 100 % - тая перегрузка, то время усреднения должно быть 5 мин. [10]

Предельным током термической устойчивости аппарата / пт, называется наибольшее среднеквадратичное значение тока за промежуток времени, соответствующий термическому эффекту тока короткого замыкания, выдерживаемого аппаратом в течение того же промежутка времени без нагрева токоведущих частей до температур, превышающих допустимые при токах короткого замыкания, и без повреждений, препятствующих дальнейшей исправной работе аппарата. [11]

Защита от токовой перегрузки должна быть выбрана так, чтобы среднеквадратичное значение тока, проходящего через управляемый вентиль, не превышало допустимой величины. Пик тока после зажигания управляемого вентиля ограничивается входной индуктивностью. Входная индуктивность состоит из индуктивности питающего трансформатора и реактора, включенного на выходе выпрямителя. [13]

Угол отклонения стрелки определяется некоторым средним усилием, величина которого пропорциональна среднеквадратичному значению тока или напряжения. Следовательно, при включении электромагнитных приборов в цепь переменного тока они измеряют действующие значения тока или напряжения. [15]

Страницы: 1 2 3

www.ngpedia.ru

Основные понятия в электроизмерениях | РОБОТОША

Не всегда для проведения измерений требуется только правильно подключить измерительный прибор. Очень важно ответить себе на вопрос: зачем я это измеряю? Для измерения тока при проверке выделения тепла в проводе требуется один параметр, для измерения тока, чтобы определить уровень заряда конденсатора или батареи — совсем другой.

Параметры могут быть выражены в виде средней величины, среднеквадратического значения (RMS, Root Mean Square), мгновенного или пикового значения. Важен не только тип нагрузки, но также, имеем мы дело с переменным или постоянным током и как выглядит форма напряжения и тока. Тесно связаными с понятиями напряжения и тока являются мощность и энергия.

Мгновенные значения

Мгновенные ток , напряжение и мощность — это значения, соответствующие конкретному моменту времени . Любой сигнал состоит из бесконечного числа мгновенных значений. В случае с напряжением это записывается как .

Рассмотрим цепь, состоящую из последовательно соединененных резистора и катушки индуктивности, подключенных к источнику синусоидального напряжения с пиковым напряжением и частотой Гц.

Синусоидальное напряжение, как функцию времени, в этом случае, можно записать как:

(1)

Ток имеет максимальное значение и сдвинут на по отношению к напряжению:

(2)

Мощность, как функция времени, представляет собой соответствующие мгновенные значения напряжения и тока:

(3)

На рисунке ниже представлены графики напряжения, тока и мощности.

Для примера линией серого цвета показаны мгновенные значения для момента времени мс:

v (4.2) = 2.906 В

i (4.2) = 0.538 А

p (4.2) = 1.563 Вт

В определенный момент времени, мгновенные напряжение и ток всегда можно умножить, рассчитав мгновенную мощность.

Напряжение, ток и мощность как функции времени

Средние значения

Средние значения — это наиболее часто часто используемые параметры.

Если мультиметр устанавливается для измерения значений на постоянном токе, измеряются средние значения напряжения и тока. Кроме того, если мультиметр работает в режиме измерений постоянного тока, то для сигналов на переменном токе также будут измерены средние значения напряжения или тока. В случае симметричного переменного напряжения, мультиметр покажет , что является правильным значением.

Напряжение и ток

Среднее значение является суммой всех произведений мгновенных значений , деленное на число произведенных измерений. Если измерения производятся бесконечное число раз, то мы можем перейти к пределу, в котором промежуток времени измерения → 0 и сумма превратится в интеграл. В общем виде:

(4)

Для напряжения мы получим:

(5)

Мультиметр

Как упоминалось ранее, мультиметр, переведонный в режим измерений на постоянном токе, измеряет среднее значение напряжения или тока. В цифровых приборах, это среднее получается с помощью RC-фильтра. Входной сигнал непрерывно усредняется по постоянной времени . В виде формулы:

(6)

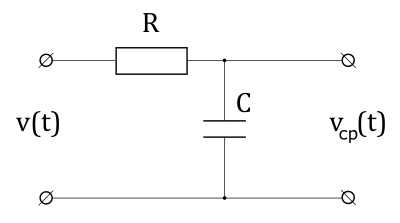
Усреднение напряжения RC-фильтром

Энергия и мощность

Уравнение (3) показывает, что результатом произведения мгновенного напряжения и тока является мгновенная мощность . Если просуммировать мгновенную мощность, умноженную на бесконечно малое время , то результатом будет энергия. Так как :

(7)

Действительно, энергия есть мощность, умноженная на время: , и энергетические пакеты можно всегда сложить для расчета полной энергии.

В качестве примера, опять возьмем последовательное соединение катушки индуктивности и резистора. На рисунке ниже черной линией показана динамика энергии во времени, рассчитанная в соответствии с уравнением (7).

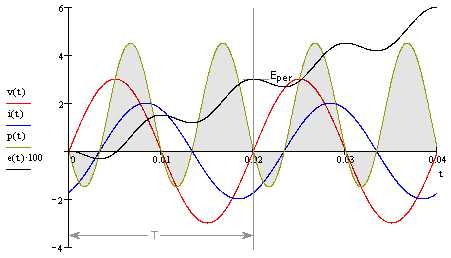
Энергия как функция времени

Кривая мощности в случае напряжения и тока переменной полярности, также имеет периодическое изменение амплитуды с удвоенной частотой. Поскольку энергия рассеивается на сопротивлении, область серого цвета положительных значений кривой мощности больше, чем отрицательной области.

Значение энергии (черная линия) в любой момент времени равно площади под кривой мощности до этого момента. Хорошо видно, что энергия периодически возрастает сильнее, чем падает в результате амплитудной асимметрии кривой мощности относительно оси .

На рисунке показан период времени . Энергия внутри этого временного интервала , которая поступила в систему обозначена и вычисляется следующим образом:

(8)

Средняя мощность за определенный период времени равна общему количеству энергии, за это время, деленному на время измерений:

(9)

Если это подставить в уравнение (8), среднюю мощность можно вычислить для любой формы сигнала.

(10)

Это уравнение получено в соответствии с (4). Активная мощность всегда является средней мощностью.

Это уравнение для расчета средней рассеиваемой мощности всегда справедливо, потому что расчет основан на мгновенных значениях. Не имеет значения, является ток постоянным или переменным, как выглядит форма напряжения и тока и есть ли сдвиг фаз между напряжением и током.

Уравнение для расчета средней мощности лежит в основе метода, применяемого в измерителях мощности. Счетчики электроэнергии дома и на предприятиях работают в соответствии с уравнением (8), которое можно переписать в виде:

(11)

Верхний предел в интеграле — момент времени, в который счетчик энергии считывает значение.

Эффективные (RMS) значения

Среднеквадратическим (RMS), или эффективным значением является значение напряжения или тока, при котором на нагрузке рассеивается та же мощность, что и при постоянном напряжении или токе.При переменном напряжении с эффективным значением 230В будет выделяться такое же количество тепла на нагрузке, как и при постоянном напряжении 230В. Действующее значение относится только к выделению тепла на резистивной нагрузке. Для примера, значение RMS тока полезно для измерения напряжения под нагрузкой в проводе (= резистивная), но не для измерения зарядного тока батареи или конденсатора (= поток электронов).

Среднеквадратическое значение

RMS является аббревиатурой от Root Mean Square, что буквально переводится как среднеквадратическое значение.

Над напряжением или током, как функциями времени, для вычисления значения RMS последовательно проводятся три математические операции: возведение в квадрат, усреднение и извлечение квадратного корня. Почему так?

Мощность, выделяемая на резисторе, подключенным к источнику напряжения:

(12)

Для мгновенных мощности и напряжения:

(13)

Вычисление средней мощности как функции времени показано в (10). можем подстваить из (13):

(14)

Так как — константа, то ее можно вынести за интеграл:

(15)

Перенеся напряжение в уравнении (12) в левую часть, мы можем расчитать напряжение по средней мощности и сопротивлению:

(16)

Затем, вычисленную среднюю мощность из (15), подставим в уравнение (16):

(17)

Сократив значения сопротивлений , получим:

(18)

Хорошо видно, что это уравнение состоит из трех частей: квадрата , среднего и квадратного корня.

В приведенных выше выкладках вычислялось значение напряжения на резисторе. Аналогично можно сделать и для тока через резистор:

(19)

Большинство мультиметров не может вычислить эффективное значение измеряемого напряжения. Чтобы узнать среднеквадратическое значение, обычно необходим специальный прибор.

На рисунке ниже показано, как вычисляет измеряемое напряжение прибор True RMS (истинные среднеквадратические значения). True RMS прибор, на практике, использует несколько иной метод работы, в котором необходим только один умножитель. Аналоговые умножители должны иметь очень низкий температурный дрейф и смещение, что делает эти инструменты достаточно дорогими.

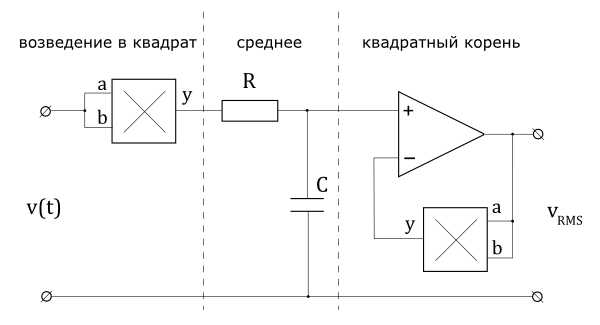
Аналоговая схема получения RMS-значений

Кроме того, можно сделать расчет RMS программным путем с последовательных цифровых значений измеряемых напряжений. Этот подход обычно используется в мультиметрах и цифровых осциллографах.

Псевдо RMS

Большинство мультиметров не измеряет RMS-значений, когда выбран режим переменного тока. Тем не менее, они, кажется, дают эффективные значения при измерениях переменных напряжений и токов. Но отображаемые значения действительны только при измерениях синусоидального сигнала.

Простой прибор сначала выпрямляет измеряемый сигнал. Затем RC-фильтр нижних частот выделяет среднее значение, которое масштабируется таким образом, что прибор показывает эффективное значение. В виде уравнения:

(20)

Недостатком такого подхода является то, что это подходит только для синусоидальных сигналов. Для любой другой формы сигнала будет получено ошибочное эффективное значение.

Номинальная мощность?

Особенно в аудиотехнике широко используется термин «Номинальная мощность» или . Это по определению ошибочный термин.

Чуть выше, говоря про энергию и мощность, показано, что рабочая мощность рассчитывается из общего количества энергии, деленного на время за которое эта энергия измеряется, см. уравнение (9). Полная энергия определяется путем суммирования всех мгновенный пакетов энергии , см. уравнение (11). Это единственно правильный путь для расчета активной мощности.

Как выше указано, эффективное значение эквивалентно постоянному напряжению или току, при которых выделится такая же мощность на том же сопротивлении. Этот показатель рассчитывается как квадратный корень из среднего значения квадрата мгновенного напряжения (или тока). Нет причин думать, что эти три математические операции должны производиться для мгновенной мощности. Это было бы бессмысленное значение.

Чтобы проиллюстрировать это, приведу расчет для синусоидального напряжения с амплитудой В и частотой 1кГц.

Для представленного ниже графика сопротивление нагрузки Ом.

График напряжения и тока

Во-первых, вычислим эффективное напряжение для временной функции . В результате, имеем хорошо известное уравнение:

Далее, вычислим среднеквадратическое значение тока как функции времени . Оно равно:

Затем, вычислим тремя различными способами активную мощность, используя RMS-значения напряжения и тока:

Для проверки, вычислим среднюю мощность для временной функции :

И, наконец, попробуем формально подойти к задаче, и вычислить номинальную мощность:

Полученный результат (0.153Вт) значительно отличается от предыдущих трех (0.125Вт). Это подтверждает некорректность применения последней формулы.

В приведенном выше примере используются синусоидальные напряжение и ток. Но форма напряжения и тока, а также вид нагрузки и возможный фазовый сдвиг фазы принципиально не меняют ситуацию.

Активная мощность всегда является средней мощностью. Номинальная мощность — бессмысленное число.

Еще по этой теме

Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.

robotosha.ru

Среднеквадратичное значение - ток - Большая Энциклопедия Нефти и Газа, статья, страница 1

Среднеквадратичное значение - ток

Cтраница 1

Страницы: 1 2 3

Расчет среднего и среднеквадратичного значений тока/напряжения. Среднеквадратичный ток