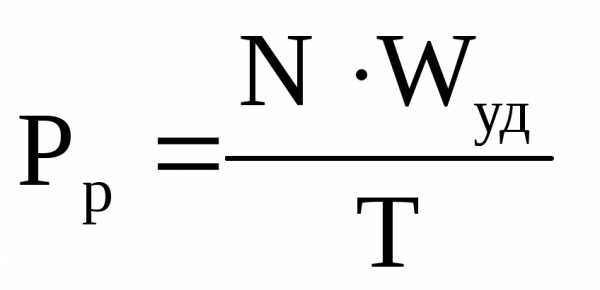Таблица истинности онлайн с примерами - логика. Таблица истинности логические операции

Таблица истинности онлайн с примерами

Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Например, они принимают значения «истина» либо «ложь» (true либо false, 1 либо 0).

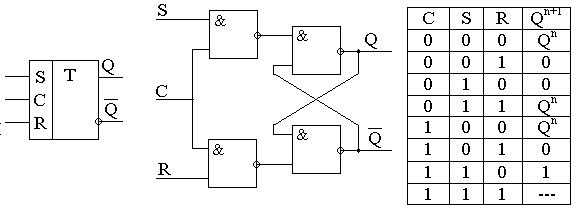
Таблицы истинности применяются для определения значения какого-либо высказывания для всех возможных случаев значений истинности высказываний, которые его составляют. Количество всех существующих комбинаций в таблице находится по формуле N=2*n; где N - общее количество возможных комбинаций, n - число входных переменных. Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы описать работу логических схем.

Таблицы истинности для основных функций

Примеры: конъюнкция - 1&0=0, импликация - 1→0=0.

Порядок выполнения логических операций

Инверсия; Конъюнкция; Дизъюнкция; Импликация; Эквиваленция; Штрих Шеффера; Стрелка Пирса.

Последовательность построения (составления) таблицы истинности:

https://uchim.org/matematika/tablica-istinnosti - uchim.org

1. Определить количество N используемых переменных в логическом выражении.
2. Вычислить количество всевозможных наборов значений переменных M = 2N , равное количеству строк в таблице.
3. Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.
4. Озаглавить столбцы таблицы названиями переменных и названиями логических операций.
5. Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.
6. Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.
7. Заполнить окончательный столбец значений для функции F.

Таким образом, можно составить (построить) таблицу истинности самостоятельно.

Составить таблицу истинности онлайн

Заполните поле ввода и нажмите OK. T - истина, F - ложь. Рекомендуем добавить страницу в закладки или сохранить в социальной сети.

Обозначения

1. Множества или выражения большими буквами латинского алфавита: A, B, C, D...
2. A' - штрих - дополнения множеств
3. && - конъюнкция ("и")
4. || - дизъюнкция ("или")
5. ! - отрицание (например, !A)
6. \cap - пересечение множеств \cap
7. \cup - объединение множеств (сложение) \cup
8. A&!B - разность множеств A∖B=A-B
9. A=>B - импликация "Если ..., то"
10. AB - эквивалентность

Всё для учебы » Математика в школе » Таблица истинности онлайн с примерами - логика

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

uchim.org

Таблицы истинности. Логические функции. Основные логические операции

Приведем примеры, предложений не являющихся высказываниями: «Посмотрите в окно.» «Который час?»

«2x+7>12»

Еще раз подчеркнем, что отличительным признаком любого высказывания является его свойство быть истинным или ложным, а этим свойством три вышеприведенных предложения не обладают.

Используя простые высказывания, можно образовыватьсложные, или составные, высказывания, в которые простые входят в качестве элементарных составляющих. В образовании сложных высказываний используются слова:и, или, тогда и только тогда, когда (в том и только в том случае), если …, то …, нет. Рассмотрим несколько примеров сложных высказываний. Рассмотрим несколько примеров сложных высказываний:

«Если идет дождь, то солнце не светит.» « Если ветер дует, то нет дождя.»

Основная задача логики высказываний заключается в том, чтобы на основании истинности или ложности простых высказываний определить истинность или ложность сложных высказываний.

Условимся, простые высказывания называть логическими переменными и обозначать большими буквами и, если высказывание истинно, будем писатьA=1, а если ложно, тоA=0.

Использование 0 и 1 подчеркивает некоторое соответствие между значениями логических переменных и функций в алгебре логики и цифрами в двоичной системе счисления. Это позволяет описывать работу логических схем ЭВМ и проводить их анализ и синтез с помощью математического аппарата алгебры логики.

Любое устройство ЭВМ, выполняющее действия над двоичными числами, можно рассмотреть как некоторый функциональный преобразователь. Причем числа на входе — значения входных логических переменных, а число на выходе — значениелогической функции, которое получено в результате выполнения определенных операций. Таким образом, этот преобразователь реализует некоторую логическую функцию.

Значения	логической	функции для разных	X				F(X,Y,Z)
			Y
сочетаний значений входных			Z
переменных	— или, как	это иначе называют,

наборов входных переменных — обычно задаются специальной таблицей. Такая таблица называется таблицей истинности. Количество наборов входных переменных (Q) можно определить по формуле:

Q=2n, гдеn — количество входных переменных.

Простейшим примером логической функции является функция одной переменной .

Аргумент			Функция
X	F0 ( X)	F1 (X)		F2 (X)	F3 ( X)
0	0	0		1	1
1	0	1		0	1

F0 (X ) — константа 0;

F1 (X ) — переменнаяX;

F2 (X ) — инверсияX;

F3 ( X ) — константа 1.

studfiles.net

Логические операции, таблицы истинности.

Поиск Лекций

Определение информации, основные свойства.

Обычно под информацией понимается совокупность сведений, расширяющая представление об объектах и явлениях окружающей среды, их свойствах, состоянии и взаимосвязях.

 

Информации обладает следующими свойствами:

- запоминаемость, то есть способность воспринять информацию и хранить ее

продолжительное время;

- передаваемость, то есть способность информации к копированию – восприятием

ее другой системой без искажения;

- воспроизводимость характеризует неиссякаемость и неистощимость

информации, то есть при копировании информация остается тождественной себе;

свойство воспроизводимости не является базовым и тесно связано с передаваемостью;

- преобразуемость – это способность информации менять способ и форму своего

существования.

 

Три концепции информации.

- концепция предложена американским ученым Клодом Шенноном и

отражает количественно-информационный подход . Информация определяется , как мера неопределенностей, состояний или событий.

-Информация, как атрибут материи. Информация создает представление о:

-природе

-структуре

-упорядоченности

-разноообразии

-Логико-семантический(смысловой). Информация рассматривается, как данные, которые используются для ориентирования, активные действия или упражнения.

Измерение информации, два подхода.

-Вероятностный подход

N состояний.

P=m/N i-состояния-Pi

Hi= -количество информации i состояния.

H= - общее количество информации

-Формула Хартли

H= . Если N=2, то H=1 бит.

8бит=1байт

1024байт=1кбайт.

 

Двоичная, десятичная и шестнадцатеричная системы

 

- двоичная n = 2; используемый алфавит: A = {0, 1}; например, 01110002;

- десятичная n = 10; используемый алфавит: A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};

например, 10210; в дальнейшем числа без указания основания системы счисления будем

считать десятичными;

- шестнадцатеричная n = 16; используемый алфавит: A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,

A, B, C, D, E, F}; цифры A, B, C, D, E, F имеют десятичные количественные эквиваленты

10, 11, 12, 13, 14, 15 соответственно; например, AB034D16.

Перевод целых чисел

Правила перевода числа в другую, не десятичную систему счисления различаются

для целых и дробных чисел.

Перевод целого числа X осуществляется по следующему алгоритму:

1) получить цифру числа n-ой системы счисления как остаток от деления числа X

на основание новой системы счисления n; полученную цифру приписать слева от

имеющихся цифр;

2) принять за X частное от деления числа X на основание системы счисления n;

3) выполнять шаги 1-2, пока X <> 0.

 

Перевод дробных чисел из n-й в десятичную систему счисления - вещественное

число переводится из n-й в десятичную систему счисления с использованием

формализованного представления числа.

Перевод дробных чисел с нулевой целой частью из десятичной в n-ую систему

счисления - дробное число X, у которого целая часть равна 0, переводится из десятичной в

n-ую систему счисления по следующему алгоритму:

1) умножить X на n;

2) получить цифру как целую часть числа X и приписать ее справа от имеющихся

цифр;

3) обнулить целую часть числа X;

4) выполнять шаги 1-3, пока X <> 0 (при точном переводе) или до получения

нужного количества цифр в дробной части (при приближенном переводе с заданной

точностью).

Логические основы ЭВМ.

Логические операции, таблицы истинности.

1. Отрицание X (со штрихом сверху)

Отрицание X (NOT, читается «не X») – это высказывание, которое истинно, если X

ложно, и ложно, если X истинно.

2. Конъюнкция XY (X&Y, X^Y).

Конъюнкция XY (AND, логическое умножение, «X и Y») – это высказывание, которое

истинно только в том случае, если X истинно и Y истинно.

3. Дизъюнкция X+Y (X\/Y).

Дизъюнкция X+Y (OR, логическая сумма, «X или Y или оба») – это высказывание,

которое ложно только в том случае, если X ложно и Y ложно.

4. Стрелка Пирса X стрелка вниз Y.

Стрелка Пирса X  Y (NOR (NOT OR), ИЛИ-НЕ) – это высказывание, которое истинно

только в том случае, если X ложно и Y ложно.

5. Штрих Шеффера X | Y.

Штрих Шеффера X | Y (NAND (NOT AND), И-НЕ) – это высказывание, которое ложно

только в том случае, если X истинно и Y истинно.

Определить значения логических операций при различных сочетаниях аргументов

можно из таблицы истинности.

poisk-ru.ru

---

• 
  Какие цифровые устройства вам известны
• 
  Сварочный инвертор своими руками схемы
• 
  Расчет электрических нагрузок
• 
  Нет отопления в квартире куда жаловаться
• 
  Переделать в сетевой шуруповерт
• 
  Солнце доклад
• 
  Магнит что такое
• 
  Чем грэс отличается от тэц
• 
  Си система единиц
• 
  Как закрепить кабель на столбе
• 
  Изу импульсное зажигающее устройство