Основы логики. Логические операции и таблицы истинности
Содержание:
На данной странице будут рассмотренны 5 логических операций:
конъюнкция,
дизъюнкция,
инверсия,
импликация и
эквивалентность,
которых Вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных
логических выражениях и представим таблицы истинности для каждой логической операции. Советуем Вам
воспользоваться нашими программами для решения задач по математике,
геометрии и
теории вероятности.
Помоми большого количества программ для решения задач на сайте работает
форум, на котором Вы всегда можете
задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать
истинно оно или ложно (истина (логическая 1), ложь (логический 0)).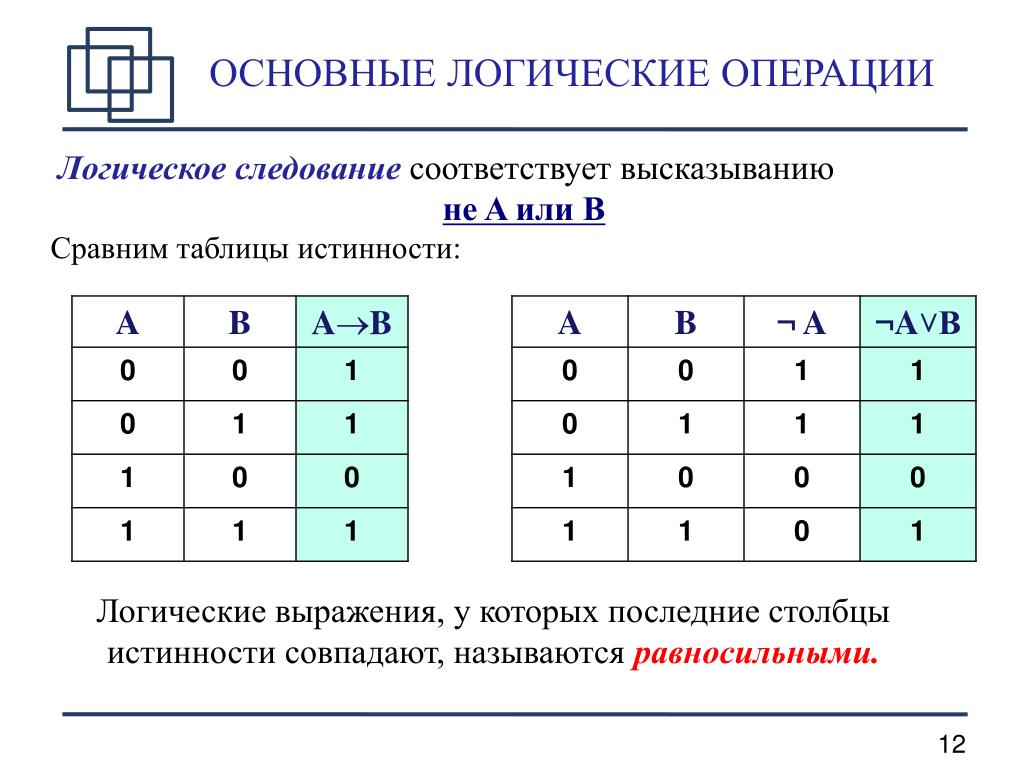
Логические операции — мыслительные действия, результатом которых является изменение
содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами,
обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать
одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или
нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
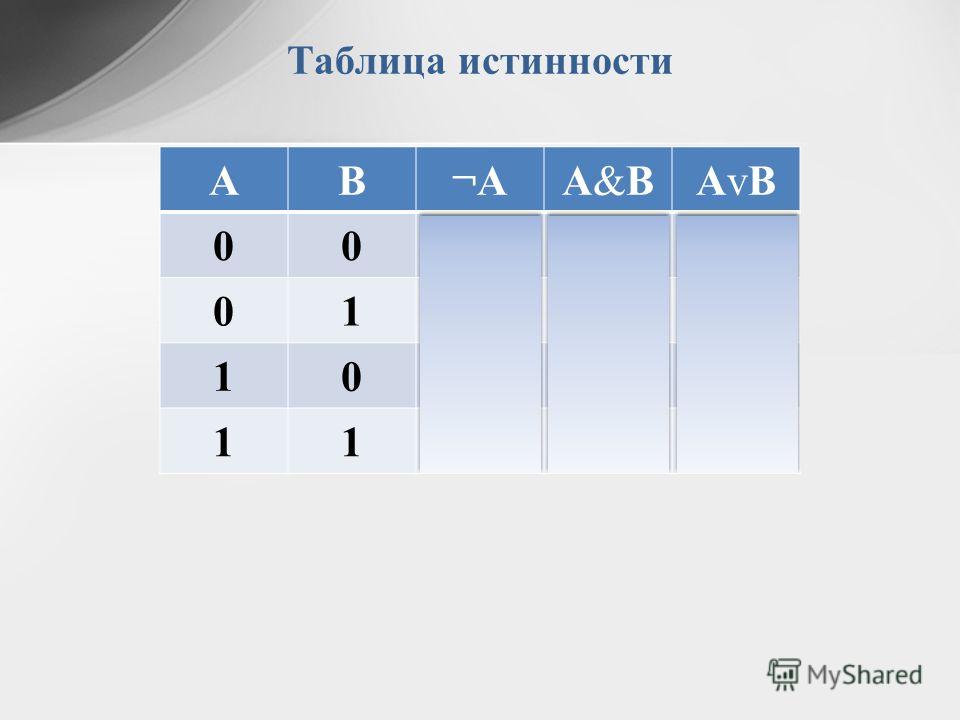
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда
оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из
простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат
отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова,
Другими простыми слова,
данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
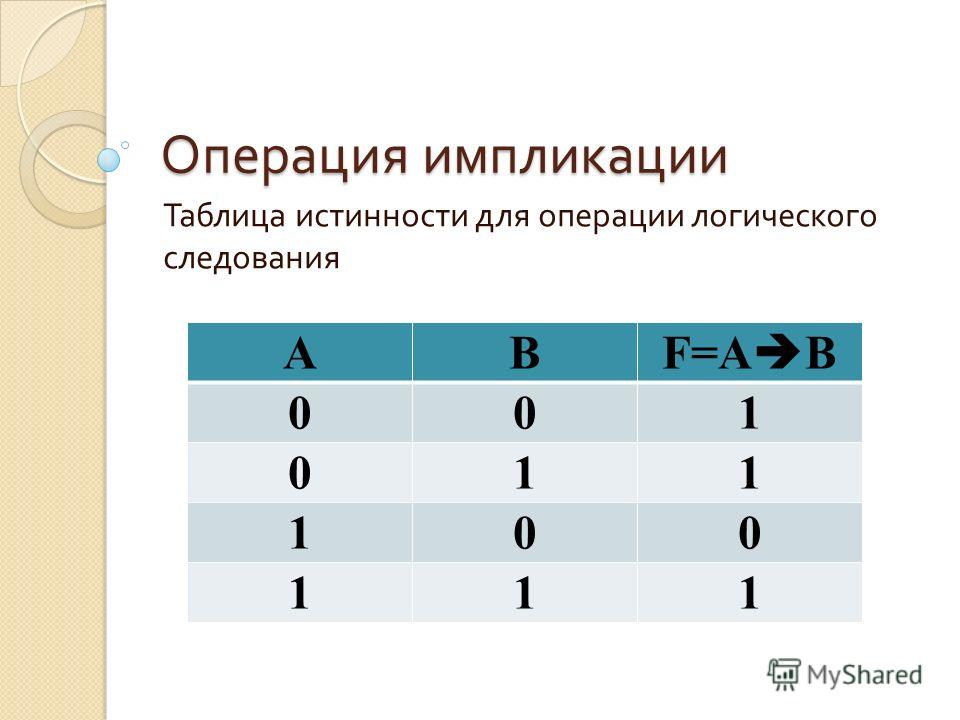
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины
следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А),
а второе (В) является следствием.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда
и только тогда, когда оба простых логических выражения имеют одинаковую истинность.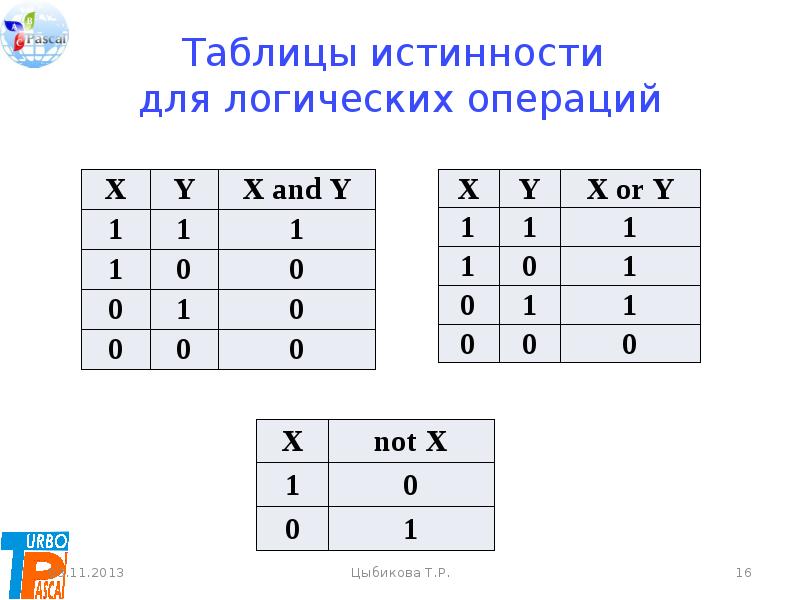
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Слишком сложно?
Основы логики. Логические операции и таблицы истинности не по зубам? Тебе ответит эксперт через 10 минут!
Основы логики. Логические операции и таблицы истинности
Основы логики. Логические операции и таблицы истинности
На данной странице будут рассмотрены 6 логических операций: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность и исключающие или, которых вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции.
Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции.
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.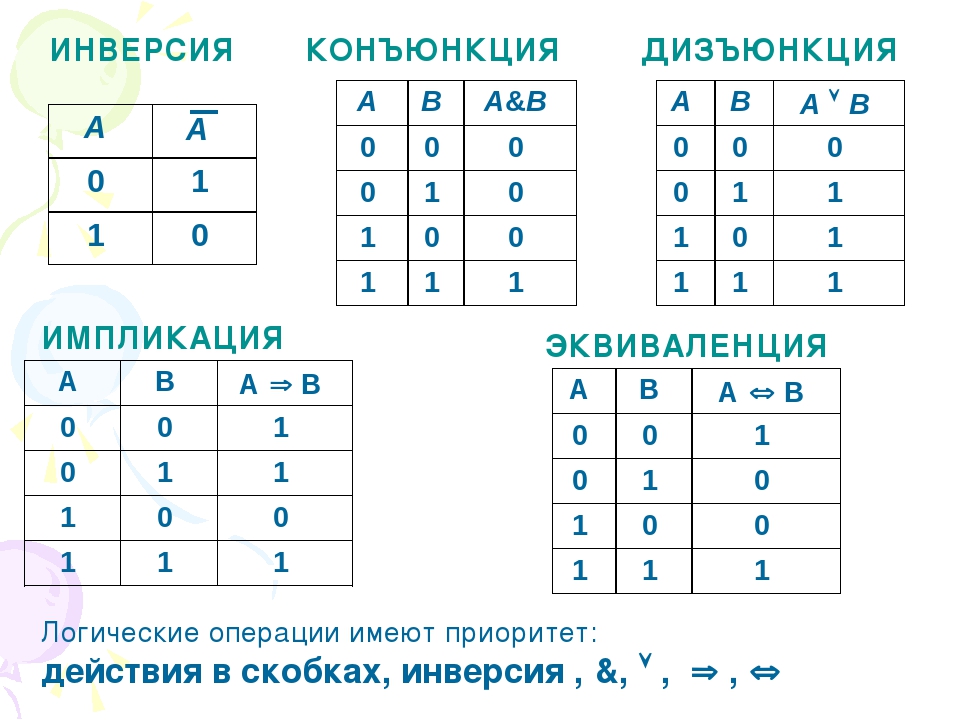
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬A.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
«A ↔ B» истинно тогда и только тогда, когда А и B равны.
Обозначение: F = A ↔ B.
Таблица истинности для эквивалентности
«A ⊕ B» истинно тогда, когда истинно А или B, но не оба одновременно.
Эту операцию также называют «сложение по модулю два».
Поскольку таблица истинности выражения состоит из строк со всеми возможными комбинациями значений переменных, она полностью определяет значение выражения.
Истинность составных высказываний, образованных в результате выполнения каких-либо логических операций над простыми высказываниями, зависит только от истинности исходных высказываний. Чаще всего для установления значений сложных высказываний используют таблицы истинности.
|
Таблица истинности — это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию, и значениями функции. |
Рассмотрим построение таблиц истинности на примере операций, рассмотренных в предыдущем разделе. Начнем с унарной операции отрицания Ā. Поскольку операция выполняется над одним операндом (A), принимающим всего два значения ( 1-истина; 0-ложь), таблица будет иметь три строки и два столбца.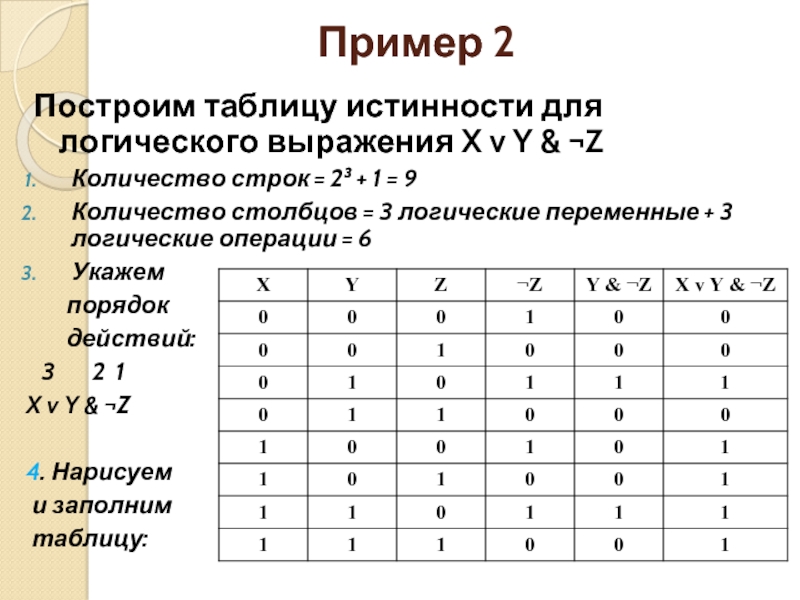 В заголовке таблицы укажем высказывание A и результат отрицания Ā, как показано на рисунке.
В заголовке таблицы укажем высказывание A и результат отрицания Ā, как показано на рисунке.
Далее в первом столбце разместим все возможные значения высказывания A, а во втором — значения логической функции Ā, как показано на рисунке.
Приведем таблицу истинности логического умножения (конъюнкции).
| A | B | A Λ B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Заметим, что составное высказывание A Λ B истинно только в том случае, когда истинны ода высказывания и A, и B.
Таблица истинности логического сложения приведена на следующем рисунке.
| A | B | A V B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Составное высказывание A V B ложно лишь в случае, когда оба операнда ложны.
Таблица истинности импликации, выглядит следующим образом.
| A | B | A - B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Составное высказывание A - B ложно лишь в случае, когда ложь имплицируется истиной. Таблица истинности эквивалентности представлена на следующем рисунке.
Таблица истинности эквивалентности представлена на следующем рисунке.
| A | B | A ~ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Составное высказывание A ~ B истинно в том случае, когда значения операндов совпадают. Полезно иметь под рукой сводную таблицу истинности.
| Сводная таблица истинности | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Заметим, что таблицы истинности находят широкое применение для
|
Два сложных высказывания называют эквивалентными , если совпадают их таблицы истинности. | |
|
Высказывания, истинность которых постоянна и не зависит от истинности входящих в них простых высказываний, а определяется только их структурой, называются тождественными или тавтологиями.
| |
Ефимова Елена Виленьевна, учитель информатики МБОУ «Основная общеобразовательная школа №3» г.Киселевск Кемеровской области
Алгебра высказываний. Логические выражения и таблицы истинности.
(Примечание: полноценные таблицы, диаграммы, рисунки, схемы, кроссворд находятся во вложении к публикации)
Цели урока: закрепление знаний учащихся по теме “Основы логики”, познакомить учащихся с основными понятиями алгебры высказываний.
Задачи урока:
обучающие – дать учащимся представление о подходах к пониманию алгебры высказываний; познакомить с основными логическими операциями; научить строить по логическим выражениям таблицы истинности;
развивающие – развитие познавательного интереса учащихся; памяти; внимания; обучение рациональным способам построения таблиц истинности; развитие логического мышления; выработка рефлексивных навыков оценки собственной мыслительной деятельности через экспериментальное получение результатов; формирование навыков эвристического мышления.
воспитательные – воспитание чувства ответственности, аккуратности, трудолюбия; сочетание индивидуальной и коллективной работы; ответственность за выполнение домашнего задания.
Тип урока: урок формирования знаний, умений с элементами практики, систематизация изученного материала.
Вид урока: сдвоенный, продолжительность 80 минут.
Возраст учащихся: 11 класс.
Оборудование:
— программы Microsoft Excel и NumLock Calculator 3. 2
2
— раздаточный материал (теория по теме, практическая работа, карточки с самостоятельной работой)
— слайды с ответами к самостоятельной работе
Оформление доски: доска разделена на две части – в правой части кроссворд, слева – домашнее задание и приоритет логических операций (на плакате).
1. Организационный момент – 5 минут.
2. Повторение и актуализация знаний по теме ”Логика”.
3. Лекция – беседа (тема ”Логика высказываний).
4. Повторение и актуализация знаний по теме “ Microsoft Excel”.
5. Практическая работа по теме урока.
6. Решение задачи с использованием программы NumLock Calculator 3.2.
7.Лекция – беседа (тема “Логические выражения и таблицы истинности”).
8. Решение задачи на построение таблиц истинности.
9. Самостоятельная работа по теме урока.
10. Домашнее задание.
11. Подведение итогов урока.
1. Подготовка учащихся к уроку, сообщение темы и целей проведения урока.
2. Повторение пройденного материала по предыдущей теме проводится в виде кроссворда:
1. Форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определённым правилам логического вывода получается новое знание о предметах реального мира.
2. Высказывание, состоящее из простых высказываний.
3. Наука об общих операциях, которые могут выполняться над различными математическими объектами.
4. Форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от других предметов.
5. Форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и соотношениях между ними.
6. Мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения посредством других, ранее обоснованных выводов.
Наука о способах и формах мышления.
3. Алгебра в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и так далее). Объектами алгебры логики являются высказывания.
Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт – истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Аристотель – основоположник логики};
B = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному – 0.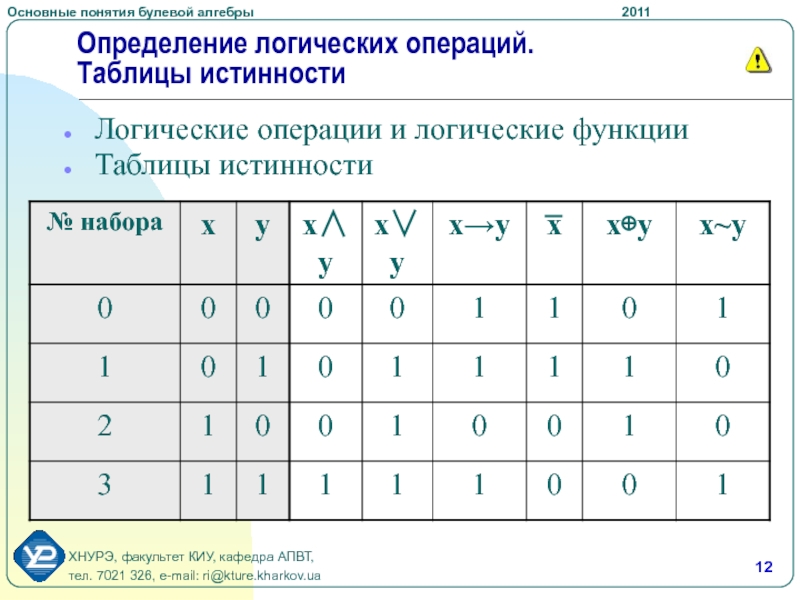 Таким образом, А = 1, В = 0.
Таким образом, А = 1, В = 0.
Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.
Логическая операция КОНЪЮНКЦИЯ (логическое умножение):
- в естественном языке соответствует союзу и;
- в алгебре высказываний обозначение &;
- в языках программирования обозначение And.
Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.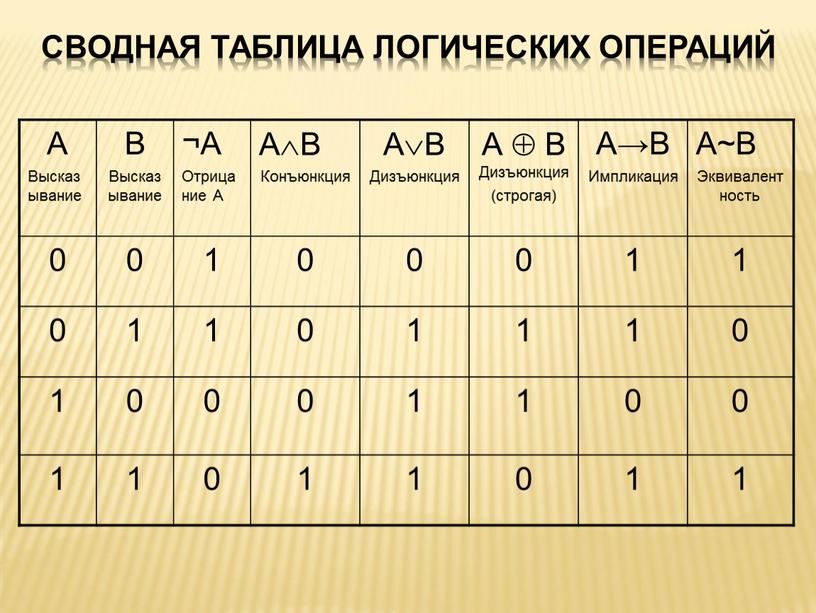
В алгебре множеств конъюнкции соответствует операция пересечения множеств, то есть множеству, получившемуся в результате умножения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
|
Таблица истинности
|
Диаграмма Эйлера-Венна
| ||
|
А
|
В
|
А&B
|
|
|
0
|
0
|
0
| |
|
0
|
1
|
0
| |
|
1
|
0
|
0
| |
|
1
|
1
|
1
| |
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):
- в естественном языке соответствует союзу или;
- обозначение ?;
- в языках программирования обозначение Or.

Дизъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, то есть множеству, получившемуся в результате сложения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
|
Таблица истинности
|
Диаграмма Эйлера-Венна
| ||
|
А
|
В
|
А?B
|
|
|
0
|
0
|
0
| |
|
0
|
1
|
1
| |
|
1
|
0
|
1
| |
|
1
|
1
|
1
| |
Логическая операция ИНВЕРСИЯ (отрицание):
- в естественном языке соответствует словам неверно, что… и частице не;
- обозначение ;
- в языках программирования обозначение Not.

Инверсия – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, то есть множеству, получившемуся в результате отрицания множества А, соответствует множество , дополняющее его до универсального множества.
|
Таблица истинности
|
Диаграмма Эйлера-Венна
| ||
|
А
|
не А
|
|
|
|
0
|
1
|
| |
|
1
|
0
|
| |
|
|
|
| |
4. Для закрепления теоретического материала данной части урока проводится практическая работа с использованием программы Microsoft Excel, которая изучалась ранее. Именно поэтому необходимо повторить знания по теме Microsoft Excel в виде опроса по основным понятиям:
Для закрепления теоретического материала данной части урока проводится практическая работа с использованием программы Microsoft Excel, которая изучалась ранее. Именно поэтому необходимо повторить знания по теме Microsoft Excel в виде опроса по основным понятиям:
а) для чего предназначены электронные таблицы;
б) из каких элементов состоит электронная таблица;
в) как можно определить адрес ячейки;
г) как ввести нужную информацию в любую ячейку;
д) как исправить или отредактировать данные в ячейке;
е) что значит выделить ячейку ли сделать её активной;
ж) как можно скопировать формулу в другие ячейки;
з) как осуществить ввод функции с помощью мастера функций.
- Откройте программу Microsoft Excel.
- Выделите ячейки A1, B1, C1 (для этого нажав на кнопку мыши внутри ячейки А1, протяните мышь до ячейки С1).
- Нажмите на панели инструментов кнопку «Объединить и поместить в центре»: (если этой кнопки не видно, нажмите )
- Напишите в объединенной ячейке слово «Конъюнкция».

- В столбцах А и В введите значения логических аргументов (см. рис. ниже).
- Аналогично объедините ячейки E1, F1, G1 и напишите слово «Дизъюнкция». Введите также значения логических аргументов.
- Аналогично сделайте для Инверсии (см. рис.).
- Сделайте активной ячейку С2 и выполните команду Вставка – Функция. В разделе «Категория» выберите «Логические», а в разделе «Функция» – «И», нажмите ОК. Сдвиньте вниз серую панель (взявшись за нее в любом месте и потянув вниз), так, чтобы были видны заполненные ячейки.
- Щелкните по ячейке А2 – в окне «Логическое1» появится адрес А2, затем поставьте курсор в окошко «Логическое2» и щелкните по ячейке В2 – в окошке появится адрес В2, нажмите ОК.
- В ячейке С2 появилось значение ЛОЖЬ, а в строке формул (наверху) мы видим формулу =И(А2;В2). Теперь эту формулу надо скопировать в нижние три ячейки. Для этого ухватите за маркер в правом нижнем углу ячейки (при этом курсор приобретет форму маленького черного крестика) и потяните вниз на три ячейки (там тоже появятся значения логической функции).
 Аналогично проделайте для Дизъюнкции (в столбце G) и для Инверсии (в столбце J).
Аналогично проделайте для Дизъюнкции (в столбце G) и для Инверсии (в столбце J). - Теперь займемся оформлением таблиц. Выделите диапазон ячеек А1:С5 и нажмите кнопку «Границы»: . Аналогично сделайте границы для остальных таблиц.
- Выделите строки со 2-й по 5-ю (протянув мышкой по номерам строк — с левой стороны) и нажмите кнопку «По центру»: .
- Раскрасим таблицы. Выделите диапазон А2:С5 и нажмите кнопку «Цвет заливки»: , выберите бледно-зеленый цвет. Заголовок таблицы раскрасьте в изумрудный цвет, а цвет текста в заголовке сделайте белым (с помощью кнопки «Цвет шрифта»: ). Увеличьте размер шрифта в заголовке до 12 и сделайте его полужирным.
- Аналогичные операции проделайте с остальными таблицами.
- Выделите первую таблицу и, взявшись за рамку этой таблицы, перетащите ее вниз-вправо так, чтобы ее верхний левый угол был в ячейке В4. Вторую таблицу перетяните в ячейку F4, а третью – в J4.

- Уменьшите ширину столбца А (для этого возьмитесь за границу между названиями столбцов А и В и потяните ее влево). Аналогично уменьшите ширину столбцов Е и I.
- Объедините ячейки В2:К2 и напишите (заглавными буквами) общий заголовок «Л О Г И Ч Е С К И Е О П Е Р А Ц И И». Сделайте его красного цвета, размером 12, полужирным.
- У вас должно получиться следующее: (СМОТРИТЕ ВЛОЖЕНИЕ)
6. Решение задачи с использованием программы NumLock Calculator 3.2.
Пример1. Определите истинность составного высказывания: ( & ) & (C ?D), состоящего из простых высказываний с использованием программы NumLock Calculator 3.2.
А = {Принтер – устройство вывода информации},
В = {Процессор – устройство хранения информации},
С = {Монитор – устройство вывода информации},
D = {Клавиатура – устройство обработки информации}.
Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний: А = 1, В = 0, С = 1, D = 0.
Определим теперь истинность составного высказывания, используя таблицы истинности логических операций:
( & ) &(1? 0) = (0&1) & (1? 0) = 0
Составное высказывание ложно.
Проверим правильность полученного результата с использованием NumLock Calculator — это специальная программа, позволяющая проверить совпадение правильности значения составного логического выражения с вычесленным алгебраически.
|
|
Определение истинности составного логического высказывания с использованием NumLock Calculator.
| |
|
1
|
Запустить программу NumLock Calculator.
| |
|
2
|
Установить удобный вид калькулятора командой [Вид калькулятора-Универсальный].
| |
|
3
|
Ввести составное логическое выражение, подставив в него значения простых логических выражений.
|
|
|
4
|
Нажать кнопку “=”, получим значение (0) составного логического выражения, которое совпадает с вычисленным алгебраически.
| |
Составное высказывание ложно.
7.Лекция – беседа.
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.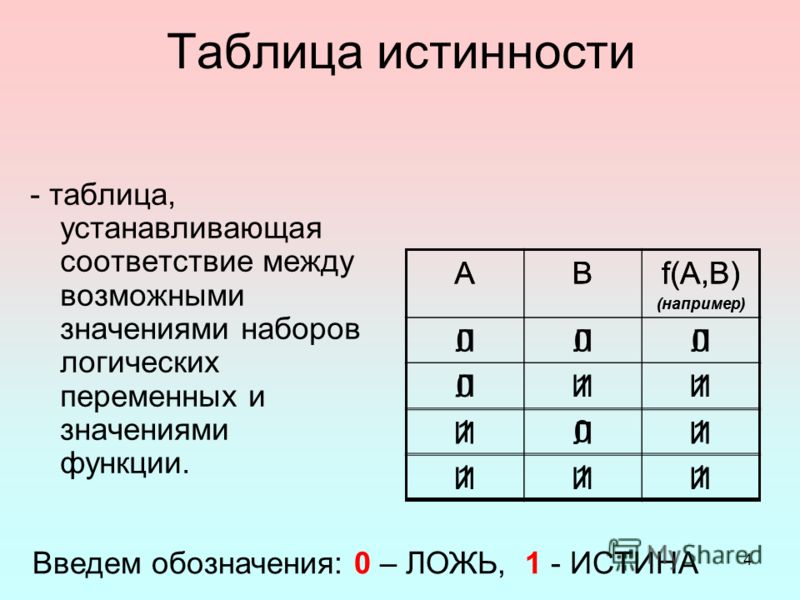
Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.
1) подсчитать количество переменных n в логическом выражении;
2) определить число строк в таблице, которое равно m = 2n;
3) подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;
4) ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
5) заполнить столбцы входных переменных наборами значений;
6) провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.
Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;
б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц , начиная с группы нулей;
в) продолжать деление колонок значений последующих переменных на 8, 16 и т. д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
8. Решение задач на построение таблиц истинности.
Пример2. Для формулы A & ( B ? & ) построить таблицу истинности алгебраически и с использованием электронных таблиц.( алгебраическое решение выполняет учащийся на доске, с использованием электронных таблиц – все вместе на компьютерах).Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8. Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.
|
|
A
|
B
|
C
|
|
|
&
|
B ? ( & )
|
A&(B ? & )
|
| |
|
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
| |
|
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
| |
|
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
| |
|
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
| |
|
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
| |
|
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
| |
|
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
| |
|
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
| |
|
|
Построение таблицы истинности логического выражения с использованием электронных таблиц программы Microsoft Excel.
| |||||||||
|
1
|
Запустить программу Microsoft Excel.
| |||||||||
|
2
|
Создать заголовки и ввести в столбцы A, B, и С значения логических аргументов, а в столбцы D, E, F, G, H соответствующие логические функции. Для ввода логических функций воспользоваться командой [Вставка-Функция или использовать Мастер функций].
| |||||||||
|
4
|
После ввода аргументов и формул на листе появится таблица истинности логического выражения.
| |||||||||
|
5
|
Переименовать лист Лист1 в Таблицу истинности и сохранить в файле log.
| |||||||||
9. Самостоятельная работа по всей теме урока проводится на компьютере и состоит из двух заданий. Всего – три варианта карточек.
Задание 1
Даны простые высказывания:
А = {Принтер – устройство ввода информации},
В = {Процессор – устройство обработки информации},
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.
Определите истинность составного высказывания А & & (C ? D), ис- пользуя таблицы истинности логических операций, а правильность полученного результата проверить с использованием программы NumLock Calculator.
Задание 2
Для формулы (А ? ) ? C & построить таблицу истинности алгебраически и с использованием электронных таблиц.
Задание 1
Даны простые высказывания:
А = {Принтер – устройство ввода информации},
В = {Процессор – устройство обработки информации},
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.
Определите истинность составного высказывания (А?В) ? &D, ис- пользуя таблицы истинности логических операций, а правильность полученного результата проверить с использованием программы NumLock Calculator.
Задание 2
Для формулы B & (A ? & ) построить таблицу истинности алгебраически и с использованием электронных таблиц.
Задание 1
Даны простые высказывания:
А = {Принтер – устройство ввода информации},
В = {Процессор – устройство обработки информации},
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.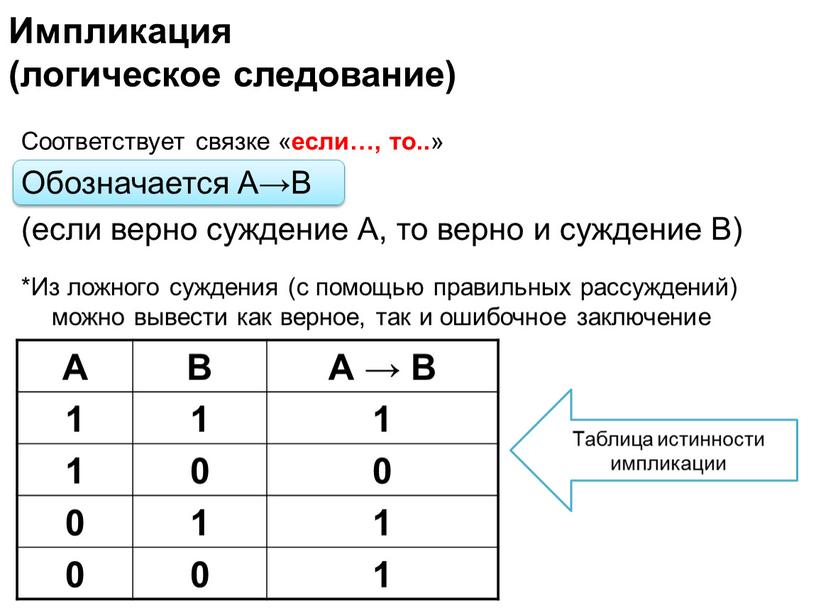
Определите истинность составного высказывания ( ? ) & (C ? D), ис- пользуя таблицы истинности логических операций, а правильность полученного результата проверить с использованием программы NumLock Calculator.
Задание 2
Для формулы B & ( ? C ) ? построить таблицу истинности алгебраически и с использованием электронных таблиц.
10. Домашнее задание.
Доделать задание самостоятельной работы ( для тех, кто не успел), учить – материал конспекта и изучить § 35 стр.197- 201 (А.Г. Гейн, А.И. Сенокосов “ Информатика”).
11. Подведение итогов урока.
Оценка знаний учащихся по новой теме с учётом знаний по предыдущим темам ( повторение ), а также краткое сообщение о теме следующего урока.
(Примечание: полноценные таблицы, диаграммы, рисунки, схемы, кроссворд находятся во вложении к публикации)
Логические операции
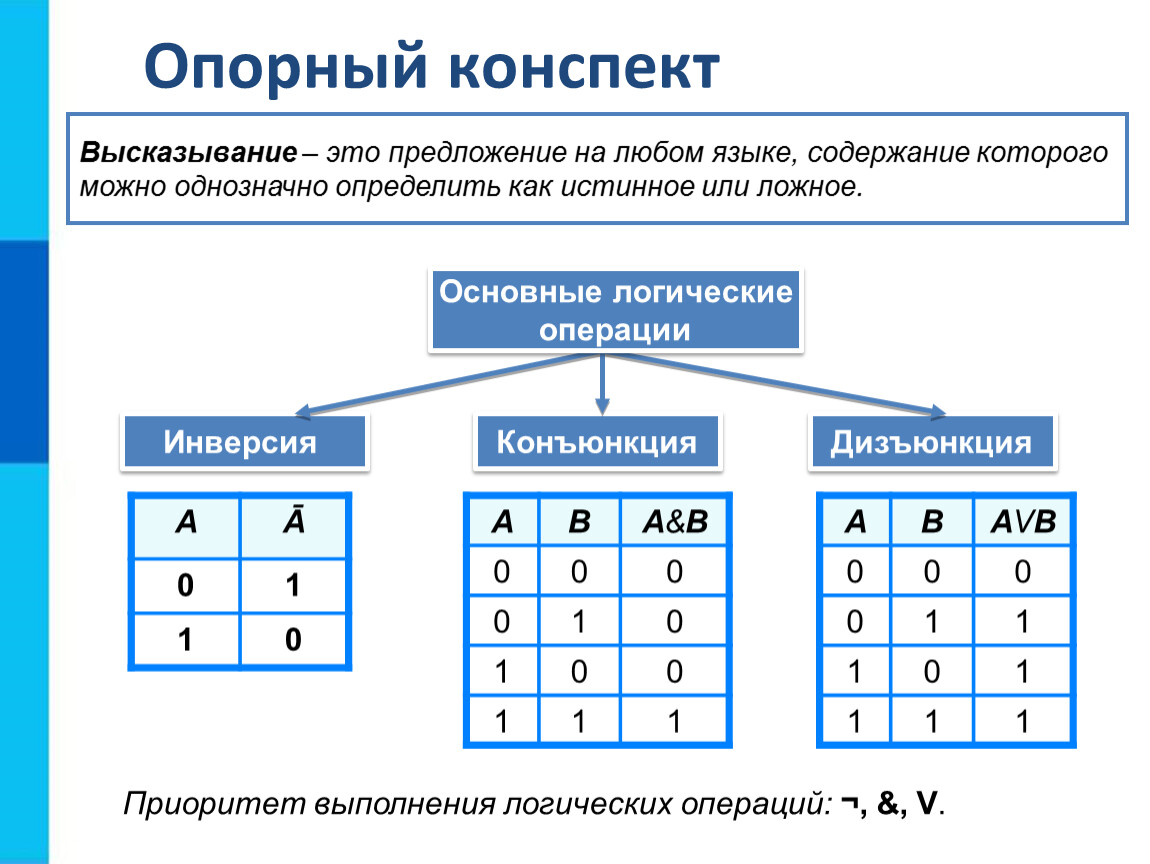
Чаще всего используются следующие логические операции:
- инверсия (отрицание, логическое не),
- конъюнкция (логическое и),
- дизъюнкция (логическое или),
- импликация (следование),
- эквивалентность (тождество).

Рассмотрим каждую из них подробно. Для описания используем диаграммы Эйлера-Венна и таблицы истинности.
| Логическая операция/ соответствие в русском языке | Обозначение | Диаграмма Эйлера-Венна | Таблица истинности | ||
|---|---|---|---|---|---|
| инверсия (отрицание, логическое «НЕ»)/ «…не…», «неверно, что…» | ¬ | A | ¬A | ||
| 0 | 1 | ||||
| 1 | 0 | ||||
| конъюнкция (логическое «И»)/ «. | Λ, & | A | B | AΛB | |
| 0 | 0 | 0 | |||
| 0 | 1 | 0 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | |||
| дизъюнкция (логическое «ИЛИ») «. | V | A | B | AVB | |
| 0 | 0 | 0 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 1 | |||
| импликация (следование)/ «если…,то…», «когда. | → | A | B | A→B | |
| 0 | 0 | 1 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | |||
| эквивалентность (тождество) «тогда и только тогда, когда» | ↔, ≡ | A | B | A↔B | |
| 0 | 0 | 1 | |||
| 0 | 1 | 0 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | |||
Основные логические операции: инверсия, конъюнкция, дизъюнкция.
Остальные логические операции можно выразить через них:
A→B=¬AVB;
A↔B=(AΛB)V(¬AΛ¬B).
Порядок выполнения логических операций в выражении (от наибольшего приоритета к наименьшему):
инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
Пример:
AV¬BΛC→D↔E.
Порядок выполнения:
- ¬B
- (¬B)ΛC
- AV((¬B)ΛC)
- (AV((¬B)ΛC))→D
- ((AV((¬B)ΛC))→D)↔E
Перейти к решению задач на алгебру логики из демо ЕГЭ
Разбор задания 2 ЕГЭ. Построение таблиц истинности логических выражений. Часть 1. | Учи Урок информатики
Основано на: демонстрационных вариантах ЕГЭ по информатике за 2015 год, на учебнике Босовой Людмилы Леонидовны
Задание:
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
x1
x2
x3
x4
x5
x6
x7
x8
F
0
1
0
1
0
1
1
1
1
Каким выражением может быть F?
1) x1 /\ ¬x2 /\ x3 /\ ¬x4 /\ x5 /\ x6 /\ ¬x7 /\ ¬x8
2) x1 \/ x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
3) ¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\ x7 /\ x8
4) x1 \/ ¬x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
В решении заданий ЕГЭ по информатике № 2 согласно Спецификации КИМ 2015 года к ЕГЭ по ифнорматике тестируются знания по пунктам:
- Высказывания, логические операции, кванторы, истинность высказывания.

- Умения строить модели объектов, систем и процессов в виде таблицы истинности для логического высказывания
На выполнение задания №2 ЕГЭ по информатике отводится 3 минуты.
Для решения этого задания нам необходимо вспомнить теорию в области Высказываний и логических операций (тема 9-го класа).
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Примеры:
- Солнце вращается вокруг земли (НЕТ, ложное высказывание)
- Земля круглая (ДА, истинное высказывание)
- 2+2=4 (ДА)
- 2>6 (НЕТ)
Побудительные и вопросительные предложения высказываниями не являются. Например, не являются высказываниями такие предложения, как: «Запишите задание на каникулы», «Как пройти в магазин?», «Кто там?».
В алгебре логики высказывания обозначают буквами (например X1, x2, C, A, B) и называют логическими переменными. При этом если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно — нулём (В = 0). 0 и 1, обозначающие значения логических переменных, называются логическими значениями.
При этом если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно — нулём (В = 0). 0 и 1, обозначающие значения логических переменных, называются логическими значениями.
Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций. Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.
Конъюнкция
Рассмотрим два высказывания: А = «Основоположником алгебры логики является Джордж Буль», В = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике». Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания. Самостоятельно установите истинность или ложность трёх рассмотренных высказываний.
Самостоятельно установите истинность или ложность трёх рассмотренных высказываний.
Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Для записи конъюнкции используются следующие знаки: /\ , `*`, И, &, Например: А/\В, А*В, А И В, А&В. Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:
В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы А и В), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00, 01, 10, 11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов.
Иначе конъюнкцию называют логическим умножением. Подумайте почему.
Дизъюнкция
Рассмотрим два высказывания: А = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», В = «Лейбниц является основоположником бинарной арифметики».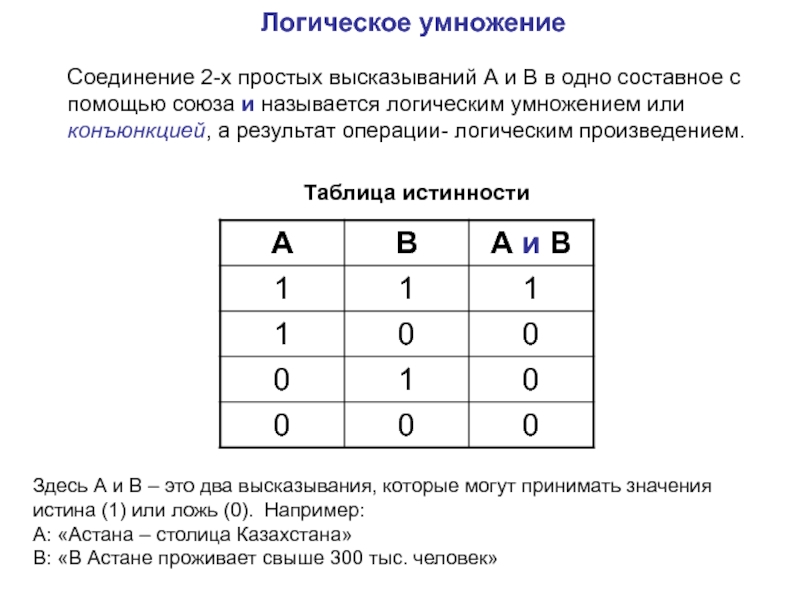 Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.
Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.
Самостоятельно установите истинность или ложность трёх рассмотренных высказываний.
Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Для записи дизъюнкции используются следующие знаки: V, |, ИЛИ, +. Например: АVВ, А|В, А ИЛИ В, А+В. Дизъюнкция определяется следующей таблицей истинности:
Иначе дизъюнкцию называют логическим сложением.
Проболжение читайте в части Номер два. Разбор задания 2 ЕГЭ. Построение таблиц истинности логических выражений. Часть 2.
Пожалуйста, оцените статью
4. 16 из 5. (Всего голосов:262)
16 из 5. (Всего голосов:262)
Все статьи раздела
Логические операторы — Python
Мы уже умеем писать функции, которые проверяют одиночные условия. Теперь научимся строить составные условия.
Хороший пример: проверка пароля. Предположим, что некий сайт при регистрации требует, чтобы пароль был длиннее восьми символов и короче двадцати символов. Да, ограничение выглядит странно, но бывает и такое.
В математике мы бы написали 8 < x < 20, но во многих языках программирования так сделать нельзя. К счастью, Python такие составные условия писать позволяет. И всё же на минутку мы забудем о такой возможности. Попробуем сделать два отдельных логических выражения и соединить их специальным оператором «И»:
Пароль длиннее 8 символов И пароль короче 20 символов.
Вот функция, которая принимает пароль и говорит, соответствует ли он условиям (True) или не соответствует (False):
def is_correct_password(password):
length = len(password)
return length > 8 and length < 20
print(is_correct_password('qwerty')) # => False
print(is_correct_password('qwerty1234')) # => True
print(is_correct_password('zxcvbnmasdfghjkqwertyui')) # => False
and — означает «И» (в математической логике это называют конъюнкцией).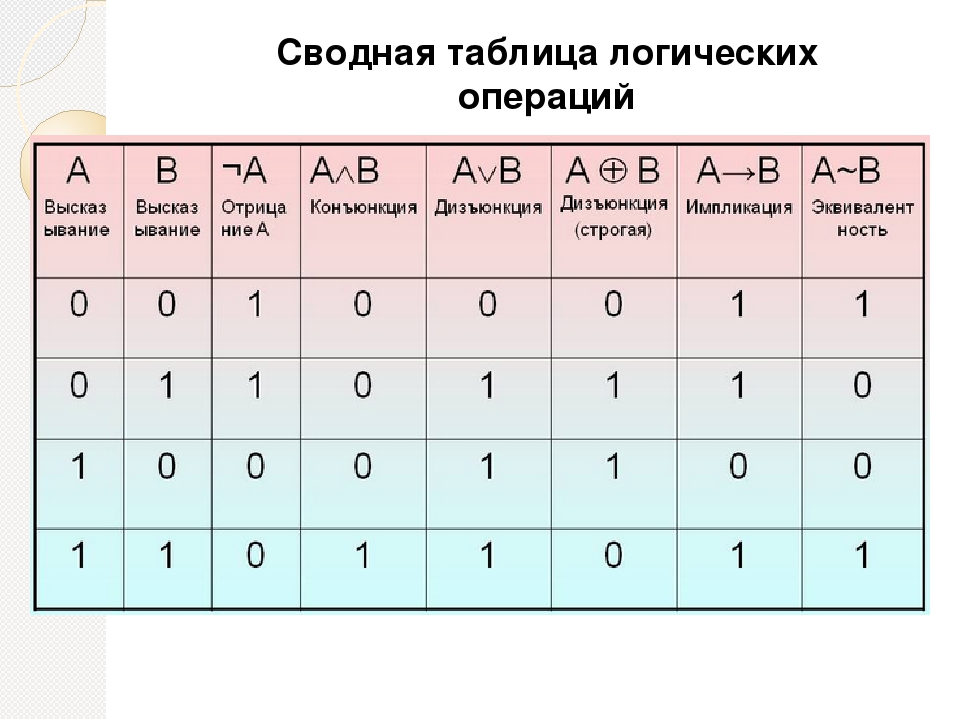 Всё выражение считается истинным, только если истинен каждый операнд — каждое из составных выражений. Иными словами,
Всё выражение считается истинным, только если истинен каждый операнд — каждое из составных выражений. Иными словами, and означает «и то, и другое».
Приоритет этого оператора ниже, чем приоритет операторов сравнения, поэтому выражение length > 8 and length < 20 отрабатывает правильно без скобок.
Кроме and часто используется оператор or — «ИЛИ» (дизъюнкция). Он означает «или то, или другое, или оба». То есть выражение a or b считается истинным, если хотя бы один из операндов (a или b или одновременно все операнды) является истинным. Иначе выражение ложное.
Операторы можно комбинировать в любом количестве и любой последовательности, но когда одновременно встречаются and и or, то приоритет лучше задавать скобками. Ниже пример расширенной функции определения корректности пароля:
def has_special_chars(str):
# проверяет содержание специальных символов в строке
def is_strong_password(password):
length = len(password)
# Скобки задают приоритет. Понятно что к чему относится.
return (length > 8 and length < 20) or has_special_chars(password)
Понятно что к чему относится.
return (length > 8 and length < 20) or has_special_chars(password)
Другой пример. Мы хотим купить квартиру, которая удовлетворяет условиям: площадь от 100 кв. метров и больше на любой улице ИЛИ площадь от 80 кв. метров и больше, но на центральной улице Main Street.
Напишем функцию, проверяющую квартиру. Она принимает два аргумента: площадь (число) и название улицы (строку):
def is_good_apartment(area, street):
return area >= 100 or (area >= 80 and street == 'Main Street')
print(is_good_apartment(91, 'Queens Street')) # => False
print(is_good_apartment(78, 'Queens Street')) # => False
print(is_good_apartment(70, 'Main Street')) # => False
print(is_good_apartment(120, 'Queens Street')) # => True
print(is_good_apartment(120, 'Main Street')) # => True
print(is_good_apartment(80, 'Main Street')) # => True
Область математики, в которой изучаются логические операторы, называется булевой алгеброй.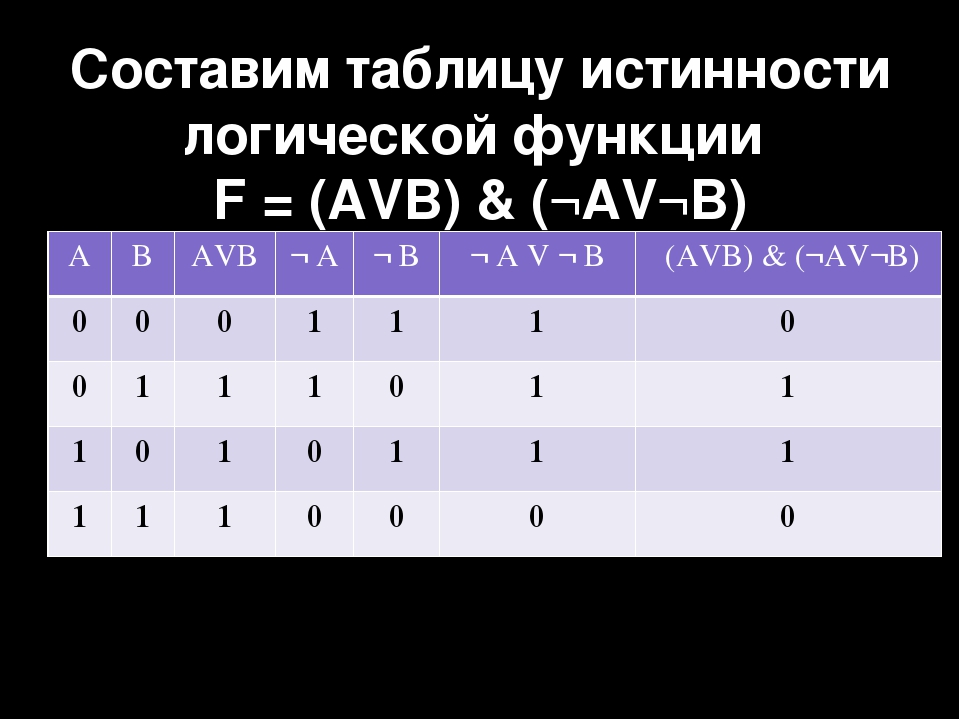 Ниже показаны «таблицы истинности» — по ним можно определить, каким будет результат применения оператора:
Ниже показаны «таблицы истинности» — по ним можно определить, каким будет результат применения оператора:
И
and
| A | B | A and B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | False |
ИЛИ
or
| A | B | A or B |
|---|---|---|
| True | True | True |
| True | False | True |
| False | True | True |
| False | False | False |
Задание
Джон поручил Сэму реализовать автоматическое распознавание солдат Ланнистеров на видео. Идея автоматизировать дозор крепости казалась ему привлекательной. В процессе работы Сэму понадобилось написать функцию, которая определяет, Ланнистер ли перед ним или нет. Немного подумав, Сэм выделил следующие правила определения Ланнистера:
В процессе работы Сэму понадобилось написать функцию, которая определяет, Ланнистер ли перед ним или нет. Немного подумав, Сэм выделил следующие правила определения Ланнистера:
Если у солдата доспехи красного цвета И нет щита
ИЛИ
если у солдата есть щит с изображением льва
то это Ланнистер.
Напишите функцию is_lannister_soldier(), которая принимает на вход два аргумента:
- Цвет доспехов (строка). Если доспехи красные, то строка
red. None, если щита нет. Строкаlion, если щит есть, и на нём изображен лев.
Функция возвращает True, если распознан Ланнистер, и False, если не распознан.
Примеры вызова:
is_lannister_soldier('red', 'man') # False
is_lannister_soldier('blue', 'lion') # True
Когда будете проверять на равенство None, делайте так, как принято в настоящем коде на Python: shield is None — код будет выглядеть профессионально! Дело в том.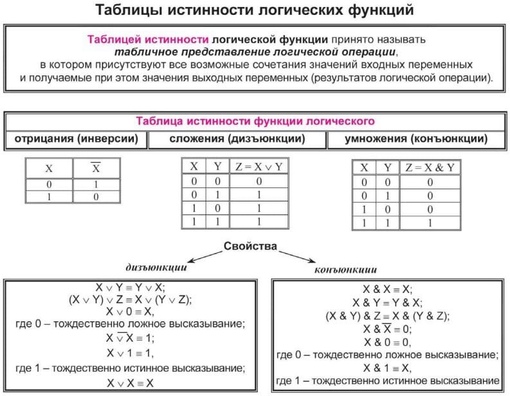 что
что is работает быстрее в случае некоторых специальных значений вроде None, True и False.
Советы
Определения
Логические операторы — операторы «И» (
and), ИЛИ (or), позволяющие создавать составные логические условия.
Нашли ошибку? Есть что добавить? Пулреквесты приветствуются https://github.com/hexlet-basics
таблиц истинности пяти общих логических связок или операторов
В этом уроке мы собираемся построить пять (5) общих логических связок или операторов. Они считаются обычными логическими связками, потому что они очень популярны, полезны и всегда преподаются вместе.
Прежде чем мы начнем, я предлагаю вам просмотреть другой мой урок, ссылка на который показана ниже.
Этот вводный урок о таблицах истинности содержит предварительные знания или информацию, которые помогут вам лучше понять содержание этого урока.
Введение в таблицы истинности, утверждения и связки
Ле начинает с перечисления пяти (5) общих логических связок.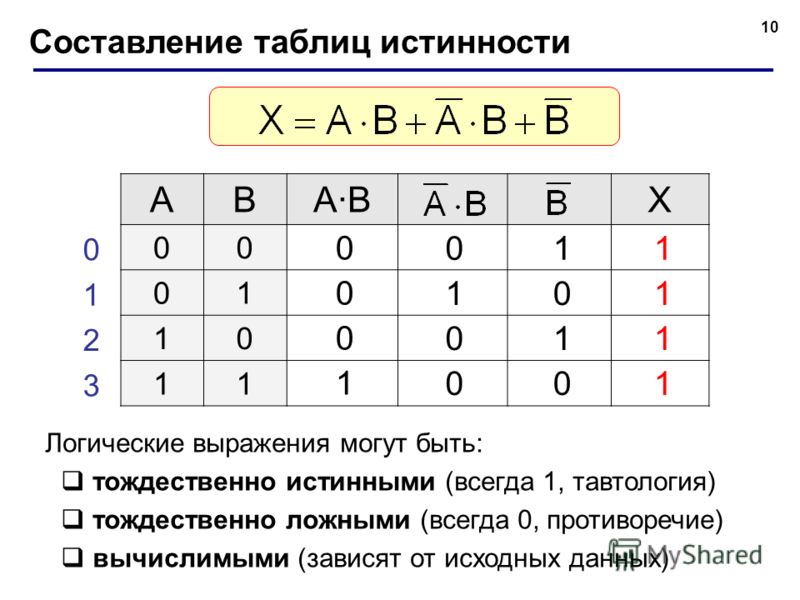
Пять (5) общих логических связок или операторов
- Логическое отрицание
- Логическое соединение (И)
- Логическая дизъюнкция (включающее ИЛИ)
- Логическое следствие (условное)
- Логическое биконусное (двойное следствие)
I. Таблица истинности логического отрицания
Отрицание утверждения также является утверждением со значением истинности, которое прямо противоположно исходному утверждению.Например, отрицание утверждения символически записывается как
~ \ large {P} или \ large {\ neg P}.
~ {P} или {\ neg P} читается как «не P.»
Помните: Оператор отрицания, обозначаемый символом ~ или \ neg, принимает значение истинности исходного утверждения, а затем выводит значение, прямо противоположное его значению истинности. Другими словами, отрицание просто меняет значение истинности данного утверждения. Таким образом, если утверждение P истинно, то значение истинности его отрицания ложно. Таким же образом, если P ложно, истинное значение его отрицания истинно.
Таким же образом, если P ложно, истинное значение его отрицания истинно.
II. Таблица истинности логического соединения
Соединение — это тип составного утверждения, состоящего из двух предложений (также известных как простые утверждения), соединенных оператором AND.
Символ, который используется для представления логического оператора AND или оператора соединения, — \ color {red} \ Large {\ wedge}. Это похоже на перевернутую букву V.
Если у нас есть два простых оператора P и Q, и мы хотим сформировать составной оператор, соединенный оператором AND, мы можем записать его как:
\ large {P \ wedge Q} .
{P \ wedge Q} читается как «P и Q».
Помните: Значение истинности составного утверждения P \ wedge Q истинно только в том случае, если значения истинности P и Q оба истинны. В противном случае P \ wedge Q ложно.
Обратите внимание в таблице истинности ниже, что, когда P истинно, а Q истинно, P \ wedge Q истинно. Однако остальные три комбинации предложений P и Q неверны.
Однако остальные три комбинации предложений P и Q неверны.
III. Таблица истинности логической дизъюнкции
Дизъюнкция — это разновидность составного оператора, который состоит из двух простых операторов, образованных путем соединения операторов с оператором ИЛИ.
В операторе дизъюнкции используется OR. Это означает «один или другой» или оба.
Символ, который используется для обозначения оператора ИЛИ или логической дизъюнкции, — \ color {red} \ Large {\ vee}. Он напоминает букву V алфавита.
Два предложения P и Q, соединенные оператором OR, чтобы сформировать составное утверждение, записываются как:
\ large {P \ vee Q}.
{P \ vee Q} читается как «P или Q».
Запомните: Значение истинности составного утверждения P \ vee Q истинно, если значение истинности любого из двух простых утверждений P и Q истинно.Moreso, P \ vee Q также истинно, когда истинные значения обоих утверждений P и Q истинны.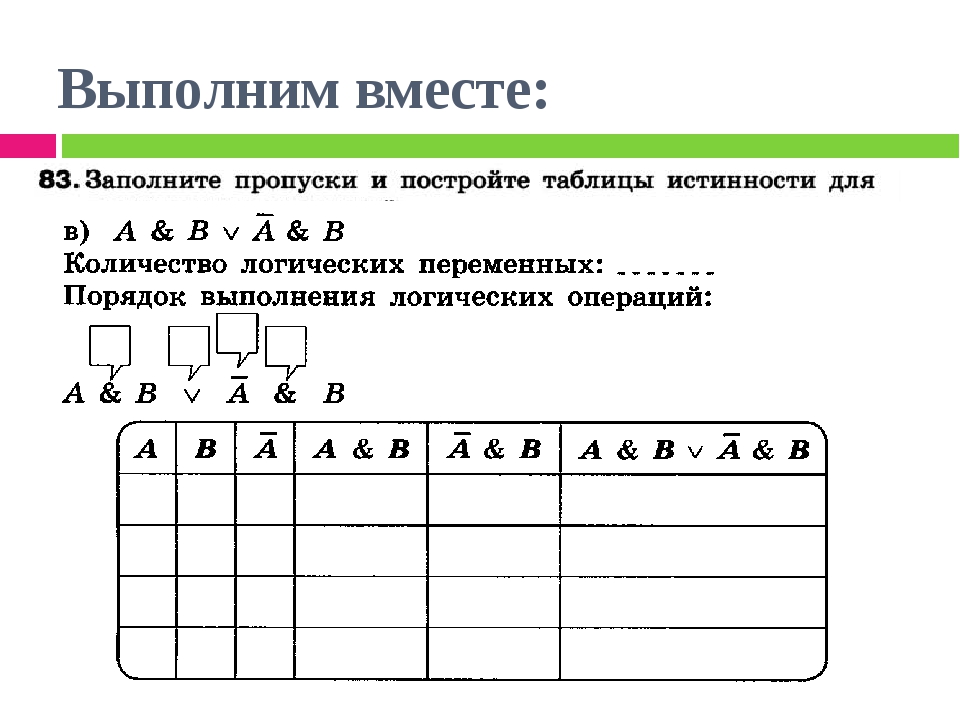 Однако единственный раз, когда оператор дизъюнкции P \ vee Q ложен, происходит, когда значения истинности P и Q ложны.
Однако единственный раз, когда оператор дизъюнкции P \ vee Q ложен, происходит, когда значения истинности P и Q ложны.
IV. Таблица истинности логического следствия
Импликация (также известная как условный оператор ) — это тип составного оператора, который формируется путем соединения двух простых операторов с помощью связки или оператора логической импликации.
Символ, который используется для представления оператора логической импликации, — это стрелка, указывающая вправо, то есть стрелка вправо.
Когда два простых оператора P и Q соединяются оператором импликации, мы имеем:
\ Large {P \ to Q}.
- где P известна как гипотеза
- где Q известна как заключение
Есть много способов, как читать условные {P \ to Q}. Ниже приведены некоторые из немногих распространенных.
{P \ to Q} читается как «P подразумевает Q».
{P \ to Q} читается как «Если P, то Q».
{P \ to Q} читается как «P, только если Q».
{P \ to Q} читается как «Если P достаточно для Q».
{P \ to Q} читается как «Q необходим для P».
{P \ to Q} читается как «Q следует из P».
{P \ to Q} читается как «Q, если P».
Помните: Значение истинности составного оператора P \ to Q истинно, когда истинны оба простых утверждения P и Q.Более того, P \ to Q всегда верно, если P ложно. Единственный сценарий, в котором P \ to Q ложно, происходит, когда P истинно, а Q ложно.
V. Таблица истинности логической биконусной или двойной импликации
Двойная импликация (также известная как двухусловный оператор ) — это тип составного оператора, который формируется путем соединения двух простых операторов с биконусным оператором. Двуусловный оператор на самом деле представляет собой комбинацию условного оператора и его обратного.
Двузначный оператор обозначается двунаправленной стрелкой.
Когда вы соединяете два простых утверждения (также известных как молекулярные утверждения) с биконусным оператором, мы получаем:
\ Large {P \ leftrightarrow Q}
{P \ leftrightarrow Q} читается как «P, если и только если Q. »
- где P известен как антецедент
- где Q известен как консеквент
Помните: Значение истинности биконусного утверждения P \ leftrightarrow Q истинно, когда оба простых утверждения P и Q являются одновременно правда или оба ложь.В противном случае P \ leftrightarrow Q ложно.
Возможно, вас также заинтересует:
Введение в таблицы истинности, утверждения и логические связки
Обратное, обратное и противоположное условное утверждение
Введение в таблицы истины и логическую алгебру | Бретт Берри | Math Hacks
Таблица истинности — это удобный небольшой логический прибор, который используется не только в математике, но также в компьютерных науках и философии, что делает его отличным междисциплинарным инструментом. Обозначения могут отличаться в зависимости от того, в какой дисциплине вы работаете, но основные концепции остаются теми же.
Обозначения могут отличаться в зависимости от того, в какой дисциплине вы работаете, но основные концепции остаются теми же.
Этот учебник даст вам знания, необходимые для понимания символической логики. Мы начнем с определения общих операторов, а в следующей статье я покажу вам, как анализировать более сложное логическое утверждение.
→ Для получения дополнительных уроков по математике, посетите Math Hacks на YouTube! ←
Булева алгебра — это ветвь алгебры, которая включает в себя логические значения или истинные и ложные значения.Обычно они обозначаются как T или 1 для истинного и F или 0 для ложного . Используя эту простую систему, мы можем свести сложные утверждения в удобоваримые логические формулы.
Унарные операторы — это самые простые операции, потому что они могут применяться к одному значению True или False.
Идентификатор
Идентификатор — наш тривиальный случай. В нем указано, что True — это правда, а False — это ложь.
Отрицание
Оператор отрицания обычно обозначается тильдой (~) или ¬ .Он отрицает или меняет истинную ценность чего-либо.
Мы можем показать эту взаимосвязь в таблице истинности. Таблица истинности — это способ организации информации для перечисления всех возможных сценариев.
Назовем первый столбец p для предложения. Во втором столбце мы применяем оператор к p, в данном случае это ~ p (читай: не p). Итак, как вы можете видеть, если наша посылка начинается как Истина, и мы ее отрицаем, мы получаем Ложь, и наоборот.
Таблица истинности для логического отрицания в обозначениях TF и 01
Logical True и Logical False
Это довольно странные операции.Логическая истина всегда приводит к Истине, а логическая ложь всегда приводит к Ложи, независимо от посылки. Эти операции часто называют «всегда истинными» и «всегда ложными».
Эти операции часто называют «всегда истинными» и «всегда ложными».
Logical True (он же «всегда верно») в нотациях TF и 01 Логический False (он же «всегда false») в нотациях TF и 01
Для двоичных операторов требуются два предложения. Мы будем использовать p и q в качестве примеров предложений.
AND
Оператор AND (символически: ∧), также известный как логическое соединение , требует, чтобы как p, так и q были True, чтобы результат был True.Во всех остальных случаях возвращается False. Логически это то же самое, что и пересечение двух множеств в диаграмме Венна.
Таблицы истинности, тавтологии и логические эквивалентности
Таблицы истинности, тавтологии и логические эквивалентности
Математики обычно используют двузначное число .
логика : Каждое утверждение либо Истина , либо
Неверно . Это называется
Закон Исключенного Среднего .
Утверждение в логике предложений строится из простых утверждений с использованием
логические связки,,, и.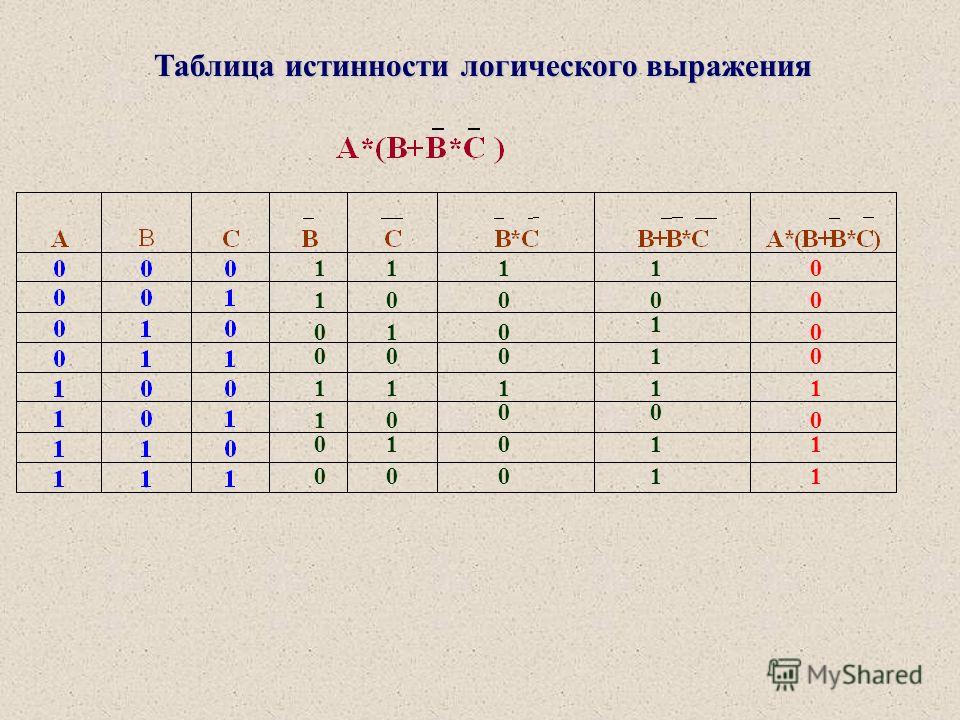 Правда или ложь
Правда или ложь
утверждения, построенного с помощью этих связок, зависит от истины или
ложность его составляющих.
Например, составной оператор строится с использованием логических связок, и. Правда или
ложь зависит от правды
или ложность P, Q и R.
Таблица истинности показывает, как правда или ложь
составного утверждения зависит от истинности или ложности простого
утверждения, из которых он построен.Итак, мы начнем с рассмотрения
таблицы истинности для пяти логических связок.
Вот таблица отрицания:
Эта таблица проста для понимания. Если P истинно , его отрицание
является ложным . Если P ложно , то истинно .
должно быть истинным , когда и P, и Q равны
истина и ложь иначе:
равно истинно , если либо P равно истинно , либо Q равно
правда (или оба — помните, что мы используем «или»
в инклюзивном смысле).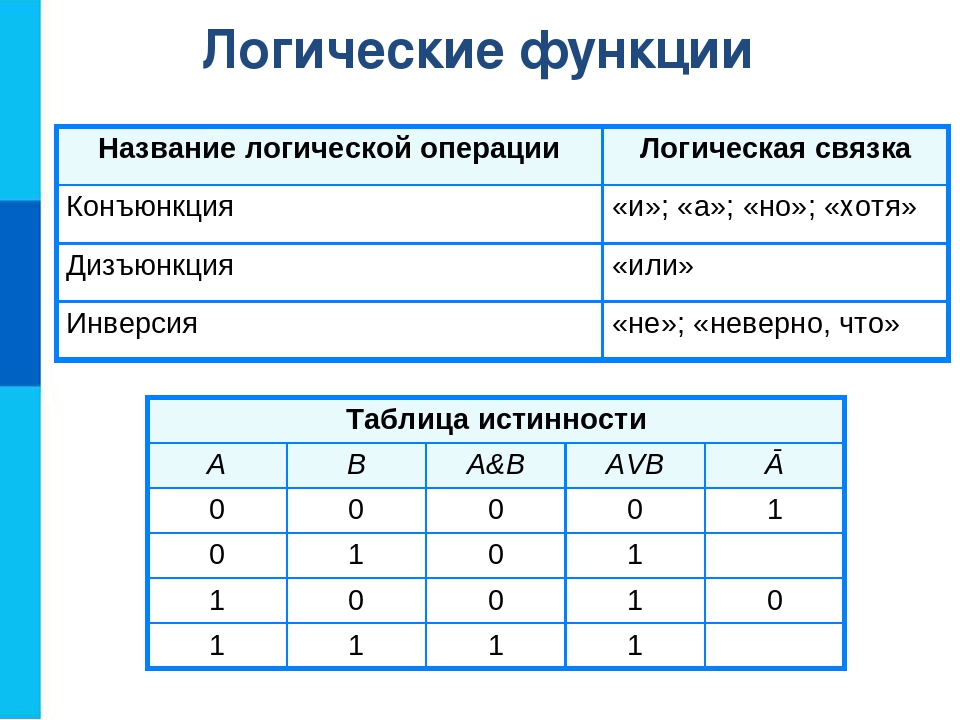 Только ложь , если и P, и Q равны
Только ложь , если и P, и Q равны
ложь .
Вот таблица для логического вывода:
Чтобы понять, почему эта таблица такая, как она есть, рассмотрим следующие
пример:
«Если вы получите пятерку, то я дам вам доллар».
Утверждение будет истинным , если я сдержу свое обещание и
ложь , если я этого не сделаю.
Предположим, что истинно , что вы получили A, и это истинное
что я даю вам доллар.Поскольку я сдержал свое обещание, подразумевается
правда . Это соответствует первой строке в таблице.
Предположим, что истинно , что вы получили A, но это ложь
что я даю вам доллар. Поскольку я не сдержал свое обещание,
подразумевается ложный . Это соответствует второму
строка в таблице.
Что, если вы получите пятерку неверно? Независимо от того, даю ли я вам
доллар, я не нарушил свое обещание. Таким образом, значение не может быть
Таким образом, значение не может быть
false, поэтому (поскольку это двузначная логика) оно должно быть истинным. Этот
объясняет последние две строки таблицы.
означает, что P и Q равны
эквивалент . Таким образом, двойное значение истинно , если P и
Q оба являются истинными или если P и Q оба ложны ;
в противном случае двойная импликация ложна.
Вы должны помнить — или уметь строить — таблицы истинности
для логических связок.Вы будете использовать эти таблицы для построения
таблицы для более сложных предложений. Проще продемонстрировать
что делать, чем описывать словами, чтобы вы увидели порядок действий
отработано в примерах.
Замечание. (а) Когда вы конструируете истину
таблицу, вы должны рассмотреть все возможные назначения True (T) и
Ложь (F) для операторов компонентов. Например, предположим, что
операторы компонентов — это P, Q и R. Каждый из этих операторов может быть
либо правда, либо ложь, значит, есть возможности.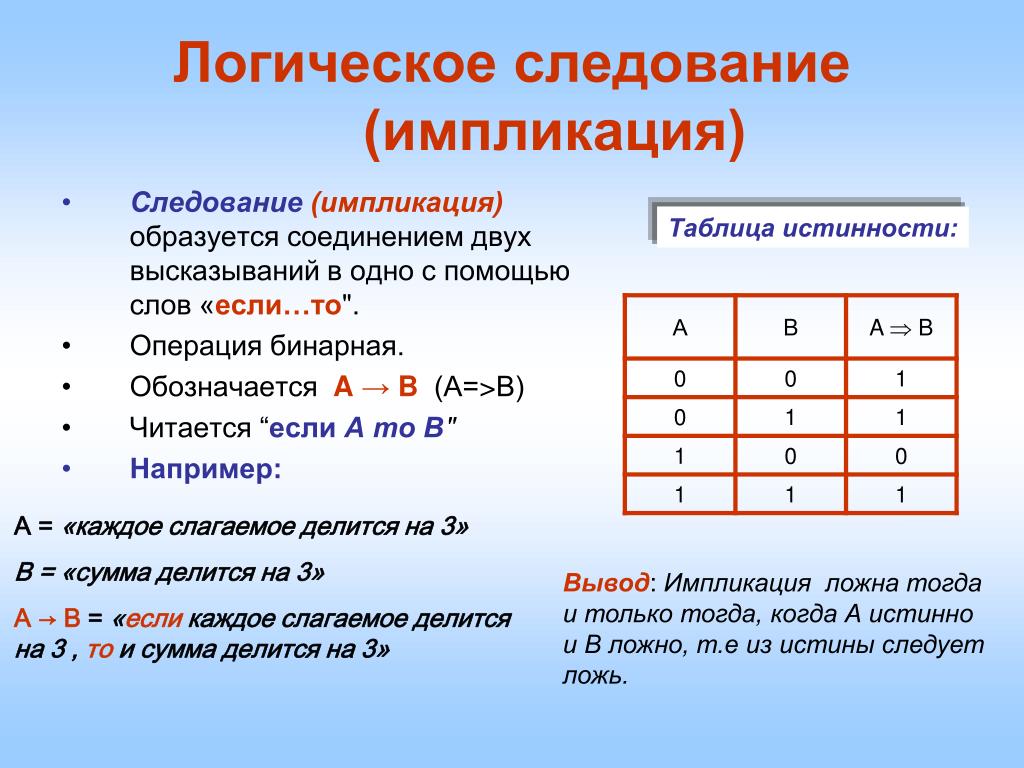
Когда вы перечисляете возможности, вы должны присваивать значения истинности
к операторам компонентов систематическим образом, чтобы избежать дублирования
или упущение. Самый простой подход — использовать
лексикографическая упорядоченность . Таким образом, для составного оператора с
три компонента P, Q и R, я бы перечислил возможности этого
путь:
б) Существуют разные способы составления таблиц истинности. Вы можете для
например, запишите значения истинности «под» логическим
связки составного высказывания, постепенно наращивая
столбец для «первичной» связки.
Я напишу подробности, построив столбцы для каждого
«кусок» составного высказывания и постепенно наращивая
к составному оператору. Любой стиль хорош, пока ты показываешь
достаточно работы, чтобы оправдать ваши результаты.
Пример. Постройте таблицу истинности для
формула.
Сначала я перечисляю все альтернативы для P и Q.
Затем в третьем столбце я перечисляю значения на основе значений P.Я использую таблицу истинности для
отрицание: когда P истинно, ложно, а когда P ложно,
правда.
В четвертом столбце я перечисляю значения для. Убедитесь сами, что это только ложь
(«F»), если P истинно («T») и Q ложно
(«F»).
Пятый столбец дает значения для моего составного выражения. Это «и»
(третий столбец) и (четвертый
столбец). «И» верно, только если обе части
«и» верны; в противном случае это ложь. Я смотрю на
третья и четвертая колонки; если оба верны («T»), я ставлю T
в пятом столбце, иначе я поставил F.
Тавтология — это формула, которая «всегда
истина «— то есть верно для каждого назначения истины
ценности к его простым компонентам. Вы можете думать о тавтологии как о
правило логики .
Противоположность тавтологии —
противоречие , формула, которая «всегда ложна». В
В
другими словами, противоречие ложно для каждого приписывания истины
ценности к его простым компонентам.
Пример. Показать, что это тавтология.
Я составляю таблицу истинности и показываю, что формула всегда верна.
Последний столбец содержит только буквы T. Следовательно, формула представляет собой
тавтология.
Пример. Постройте таблицу истинности для.
Вы можете видеть, что построение таблиц истинности для утверждений с множеством
связок или множества простых утверждений довольно утомительно и
подвержен ошибкам.Хотя могут быть некоторые применения этого (например, для
цифровых схем), в какой-то момент лучше всего было бы написать
программа для построения таблиц истинности (и это, безусловно, было сделано).
Дело здесь в том, чтобы понять, как истинное значение сложного
утверждение зависит от истинности его простых утверждений и
его логические связки.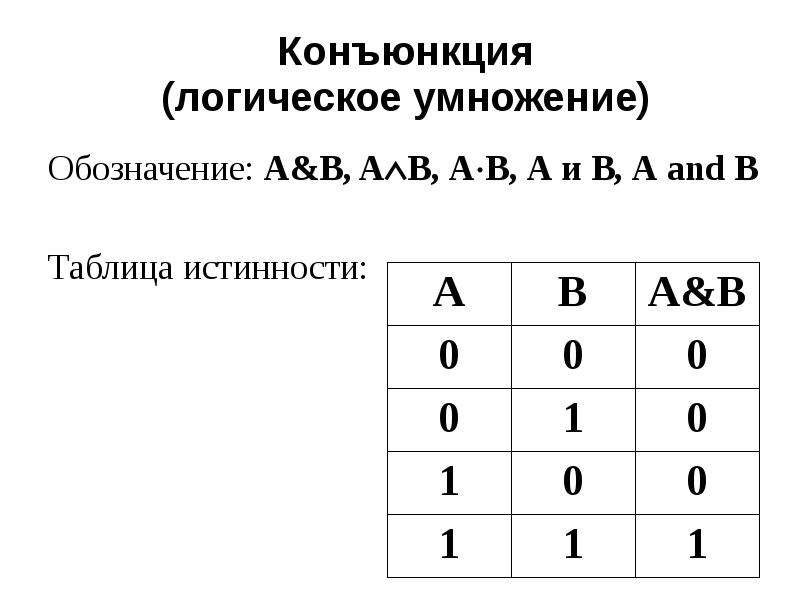 В большинстве работ математики обычно не
В большинстве работ математики обычно не
используйте операторы, которые очень сложны с логической точки зрения
Посмотреть.
Пример. (a) Предположим, что P ложно и истинно. Скажите, истинно ли Q, ложно или истинно
значение не может быть определено.
(b) Предположим, что это неверно. Рассказывать
является ли Q истинным, ложным или его истинное значение не может быть определено.
(a) Поскольку истинно, либо P истинно, либо истинно. Поскольку P ложно, должно быть верно. Следовательно, Q должно быть ложным.
(b) Утверждение «если-то» неверно, когда часть «если»
истина, а часть «тогда» — ложь.Поскольку ложно, верно. Утверждение «и» верно только
когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.
Пример. Предположим
» » правда.
«» ложно.
«У Кэлвина Баттерболла фиолетовые носки» — правда.
Определите истинность утверждения
Пусть для простоты
P = «».
Q = «».
R = «У Кэлвина Баттерболла фиолетовые носки».
Я хочу определить истинное значение. Поскольку мне были даны конкретные значения истинности для P, Q,
и R, я установил таблицу истинности с единственной строкой, используя данную
значения для P, Q и R:
Следовательно, утверждение истинно .
Пример. Определите истинное значение
утверждение
Утверждение «» ложно. Ты не можешь сказать
есть ли в заявлении «Икабод Ксеркс шоколад»
кексы «верно или неверно, но это не имеет значения.Если
«если» часть утверждения «если-то» ложна,
тогда утверждение «если-то» верно. (Проверить правду
таблица, если вы не уверены в этом!)
данное утверждение должно быть верным.
Два оператора X и Y логически равны
эквивалент , если это тавтология. Другой способ сказать
это: Для каждого присвоения значений истинности простому элементу
операторы , составляющие X и Y, операторы X и Y имеют
идентичные значения истинности.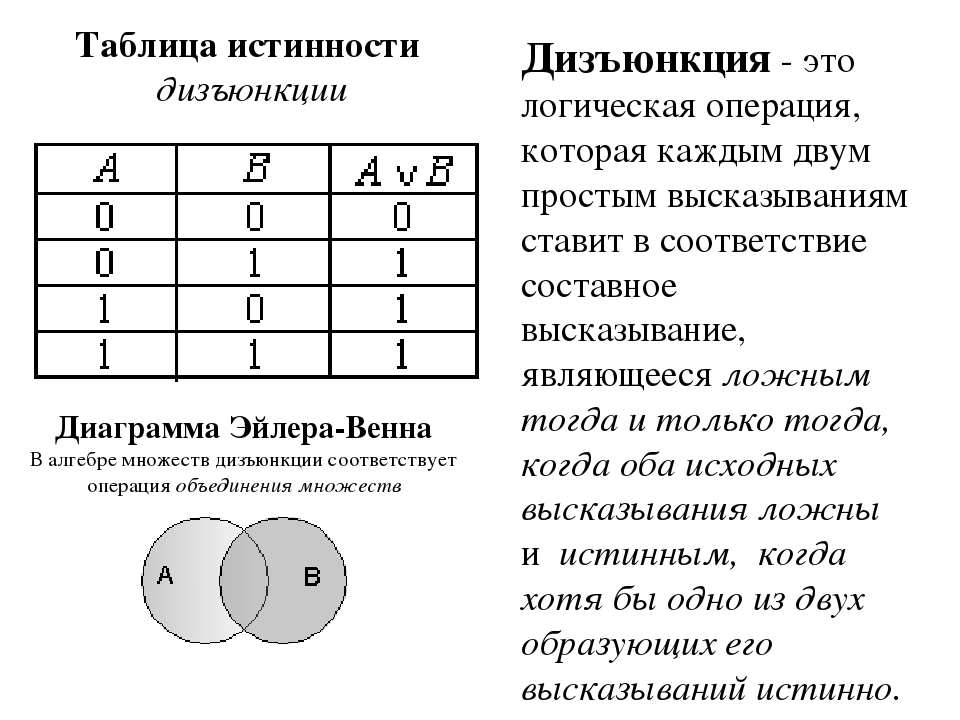
С практической точки зрения вы можете заменить выражение в
доказательство любым логически эквивалентным утверждением.
Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить
таблица истинности, чтобы проверить, является ли тавтология — это
есть ли «все Т в столбце».
Однако проще создать таблицу, содержащую X и Y, а затем
проверьте, совпадают ли столбцы для X и для Y.
Пример. Покажите, что и логически эквивалентны.
Поскольку столбцы для и идентичны, два оператора логически
эквивалент.Эта тавтология называется условной .
Дизъюнкция . Вы можете использовать эту эквивалентность для замены
условно дизъюнкцией.
Существует бесконечное количество тавтологий и логических эквивалентностей;
Я перечислил несколько ниже; более обширный список приведен в конце
эта секция.
Когда тавтология имеет форму двусмысленного выражения, два утверждения
которые составляют двусмысленность, логически эквивалентны. Следовательно, вы
Следовательно, вы
может заменить одну сторону на другую без изменения логического
смысл.
Вам часто потребуется отрицать математическое утверждение. К
посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символическое
заявления.
Пример. Запишите отрицание
следующие утверждения, упрощающие, так что только простые утверждения
отрицается.
(а)
(б)
(а) Я отвергаю данное утверждение, затем упрощаю, используя логические
эквивалентности. Я привел названия логических эквивалентов на
правильно, чтобы вы могли видеть, какие из них я использовал.
(б)
Я показал это и
логически эквивалентен в предыдущем примере.
В следующих примерах мы будем отрицать утверждения, написанные словами.
Это более типично для того, что вам нужно делать по математике. В
идея состоит в том, чтобы преобразовать слово-утверждение в символическое утверждение, тогда
используйте логические эквиваленты, как мы делали в последнем примере.
Пример. Используйте закон ДеМоргана, чтобы написать
отрицание следующего утверждения, упрощая так, чтобы
отрицаются только простые утверждения:
«Кальвина нет дома, или Бонзо в кино.»
Пусть C будет утверждением «Кальвин дома» и пусть B будет
заявление «Бонзо в движении». Данное заявление
. Я должен опровергнуть это утверждение,
затем упростите:
Результат: «Кальвин дома, а Бонзо нет в доме.
фильмы ».
Пример. Используйте закон ДеМоргана, чтобы написать
отрицание следующего утверждения, упрощая так, чтобы
отрицаются только простые утверждения:
«Если Фиби покупает пиццу, то Кэлвин покупает попкорн.»
Пусть P будет утверждением «Фиби покупает пиццу» и пусть C будет
заявление «Кэлвин покупает попкорн». Данное заявление
. Чтобы упростить отрицание, я буду использовать тавтологию условного дизъюнкции , которая говорит
То есть я могу заменить на (или наоборот).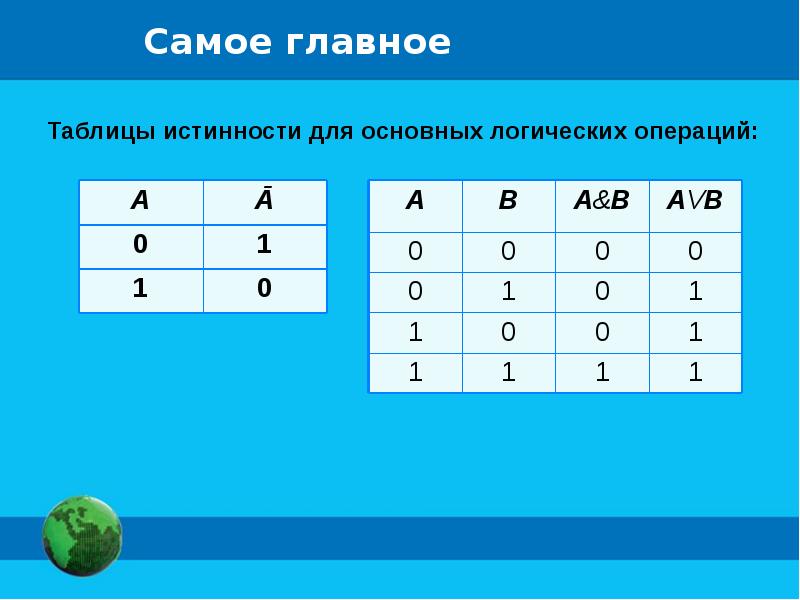
Итак, вот отрицание и упрощение:
Результат: «Фиби покупает пиццу, а Кэлвин не покупает.
Попкорн».
Далее мы применим нашу работу с таблицами истинности и отрицательными утверждениями к
задачи, связанные с построением обратного, обратного и
противоположность утверждению «если-то».
Пример. Заменить следующую инструкцию на
его противоположность:
«Если x и y рациональны, то рационально».
В силу противоположной эквивалентности это утверждение совпадает с утверждением
«Если не рационально, значит, это не так
что и x, и y рациональны «.
Это правильный ответ в его нынешнем виде, но мы можем выразить его в
немного лучший способ, который удаляет некоторые явные отрицания.
Большинству людей легче понять положительное утверждение, чем
отрицательное заявление.
По определению действительное число — это иррациональное , если
это не рационально. Так что я мог бы заменить часть «если» в
Так что я мог бы заменить часть «если» в
противоположно выражению «иррационально».
«Тогда» часть контрапозитива — это отрицание
«и» заявление.Вы можете повторить это так: «Это не
случай, когда и x рационально, и y рационально «. (Слово
«оба» гарантирует, что отрицание применимо ко всему
«И», а не только «х рационально».)
По закону ДеМоргана это эквивалентно: «x нерационально или
y нерационально «. В качестве альтернативы я мог бы сказать:» x есть
иррационально или y иррационально ».
Объединив все вместе, я мог бы выразить контрапозитив как:
«Если иррационально, то либо x иррационально
или y иррационально «.
(Как обычно, я добавил слово «либо», чтобы было ясно, что
часть «затем» — это целое выражение «или».)
Пример. Покажите, что обратное и
обратное условное выражение логически эквивалентно.
Позвольте быть условным. Обратное. Обратное.
Я мог бы показать, что обратное и обратное эквивалентны
построение таблицы истинности для. Вместо этого я воспользуюсь некоторыми известными тавтологиями.
Вместо этого я воспользуюсь некоторыми известными тавтологиями.
Начать с:
Помните, что я могу заменить выражение логическим
эквивалент.Например, на последнем шаге я заменил Q, потому что два оператора эквивалентны
Двойное отрицание.
Пример. Предположим, x — действительное число. Учитывать
заявление
«Если, то.»
Постройте обратное, обратное и противоположное.
Определите истинность или ложность четырех утверждений —
исходное утверждение, обратное, обратное и противоположное
— используя свои знания алгебры.
Обратное — «Если, то».
Обратное — «Если, то».
Противоположным является «Если, то».
Исходное утверждение неверно:, но. Поскольку исходное утверждение эквивалентно
контрапозитивный, контрапозитивный тоже должен быть ложным.
Верно и обратное. Обратное логически эквивалентно
обратное, значит, верно и обратное.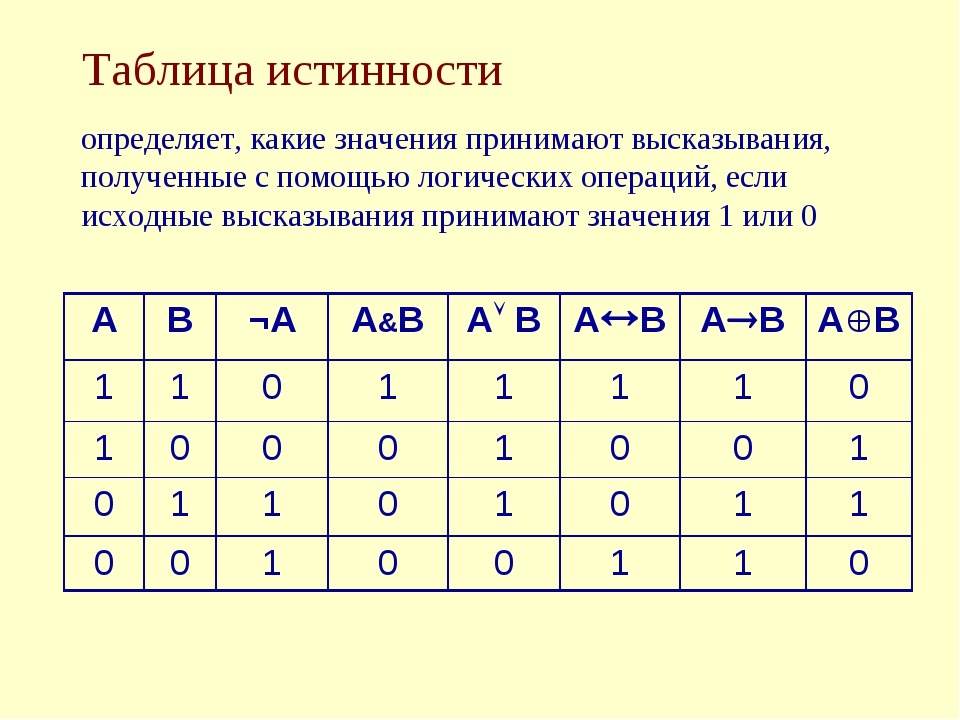
\новая страница
\ centerline {\ bigssbold Список тавтологий}
Контактная информация
Домашняя страница Брюса Икенаги
Авторские права 2019 Брюс Икенага
% PDF-1.5
%
2 0 obj
>
/ Метаданные 5 0 R
/ StructTreeRoot 6 0 R
>>
endobj
5 0 obj
>
транслировать
2017-09-07T07: 54: 05-04: 002017-09-07T07: 54: 16-04: 00Microsoft® Word 2013Microsoft® Word 2013application / pdf
конечный поток
endobj
22 0 объект
>
транслировать
xkoF ~ 澹! r ^ m ^} i? (HD ꏼ} | i !, ٙ a. P2n? o RU 鮾 =? {3ɦdphYAdf2eFDu_l {~ fWDҮfB> Ωg | e_ | XFx `sJ d? j: S> njzxfJTN> nZ ڟ 0 xs7ec? w C @ bqB: @ 1C2H) * d.x ف G, ‘uG!
P2n? o RU 鮾 =? {3ɦdphYAdf2eFDu_l {~ fWDҮfB> Ωg | e_ | XFx `sJ d? j: S> njzxfJTN> nZ ڟ 0 xs7ec? w C @ bqB: @ 1C2H) * d.x ف G, ‘uG!
lͳ 😕 ] -MnyD
Пропозициональная логика
Пропозициональная логика
Логические выражения
Мы можем определять логические выражения, используя рекурсивное определение:
- Пропозициональные переменные (значение ИСТИНА или ЛОЖЬ)
а пропозициональные константы ИСТИНА и ЛОЖЬ являются логическими выражениями. - Если LE1 и LE2 — логические выражения, то
LE1 AND LE2 — логическое выражение, значение которого ИСТИНА, если
оба LE1 и LE2 имеют значение ИСТИНА,
и ЛОЖЬ в противном случае. - Если LE1 и LE2 — логические выражения, то
LE1 OR LE2 — логическое выражение, значение которого ИСТИНА, если
либо LE1, либо LE2 имеют значение TRUE,
и ЛОЖЬ в противном случае. - Если LE1 является логическим выражением, тогда НЕ LE1 является логическим выражением,
чье значение ИСТИНА, если LE1 имеет значение ЛОЖЬ, и ЛОЖЬ в противном случае.
Уровни приоритета логических операторов:
- НЕ
- И
- ИЛИ
Присваивая значения переменным в логическом выражении,
мы также присваиваем значение самому выражению.
Пример: задано выражение «(p AND q) OR r»,
если p = TRUE, q = TRUE и r = FALSE, то значение выражения — TRUE.
Логические функции и таблицы истинности
Смысл (или значение) логического выражения — логическое
функция из множества возможных присвоений истинностных значений
для переменных в выражении к значениям {TRUE, FALSE}.
Пример: используя выражение «(p AND q) OR r», мы можем описать
логическая функция, определяющая значение выражения
путем рассмотрения всех комбинаций присвоений значений для p, q и r.
p q r (p AND q) ИЛИ r
------------------------------
Т Т Т Т
Т Т Ф Т
Т Ф Т Т
T F F F
F T T T
F T F F
F F T T
F F F F
Приведенная выше таблица с описанием логической функции «(p AND q) OR r»
называется таблицей истинности .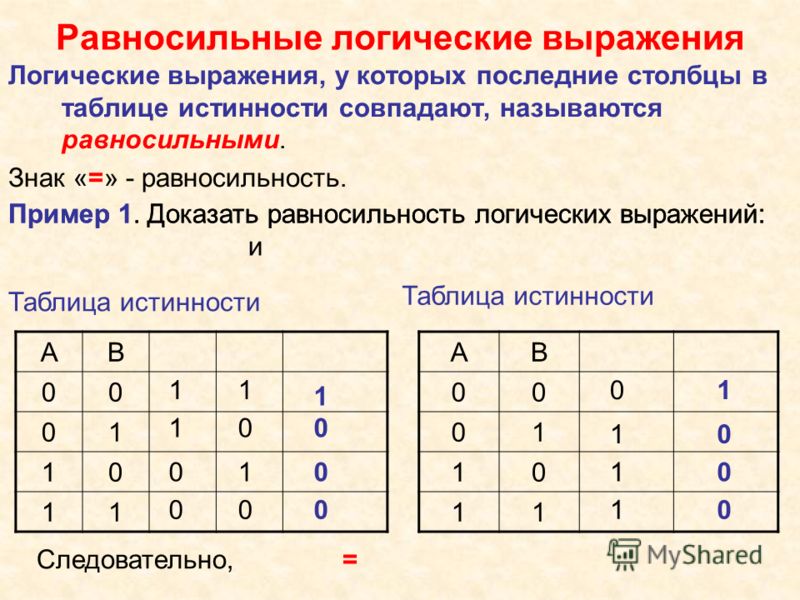 N строк.N различных булевых функций от N переменных.
N строк.N различных булевых функций от N переменных.
Вот некоторые дополнительные функции двух переменных, которые
часто используются:
p q p-> q p == q p NAND q p NOR q
-------------------------------------------
0 0 1 1 1 1
0 1 1 0 1 0
1 0 0 0 1 0
1 1 1 1 0 0
Комментарии к этим функциям:
- Следствие: «p -> q» или «p подразумевает q»
означает, что всякий раз, когда p истинно, q тоже.Единственный способ «p -> q» может иметь значение FALSE, если p — TRUE, а q — FALSE. - Эквивалентность: «p == q» означает
что p и q имеют одинаковое значение. - И-НЕ: «p NAND q» то же самое, что «NOT (p AND q)».
- NOR: «p NOR q» — это то же самое, что «NOT (p OR q)».
- Приоритет (от высшего к низшему):
НЕ, И-НЕ, ИЛИ, И, ИЛИ, ->, ==.
Вычисление выражений с таблицами истинности
Мы можем вычислить значение выражения, используя таблицы истинности.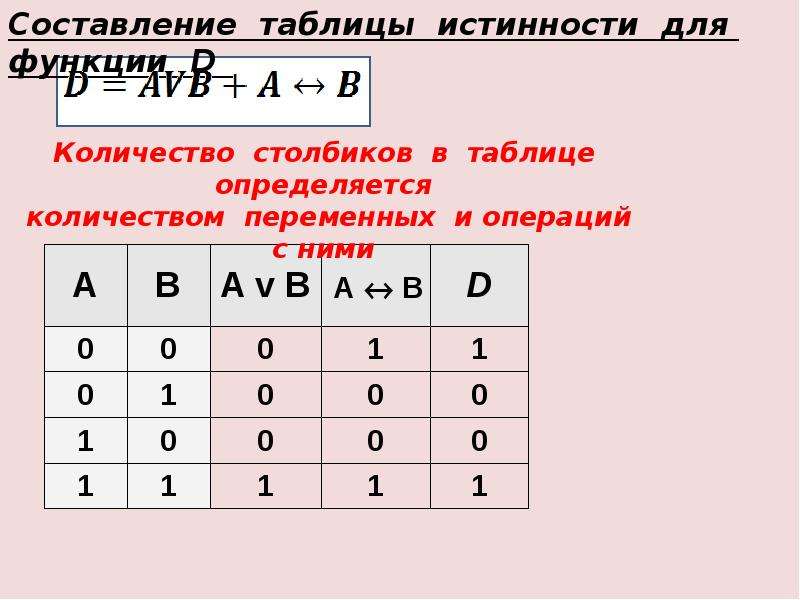 Создаем таблицу для всех возможных значений переменных,
Создаем таблицу для всех возможных значений переменных,
и все подвыражения в выражении.
Вычислите значение следующего выражения E для всех
возможные присвоения истинности: (p -> q) -> (q -> r)
p q r p-> q q-> r E
---------------------------
0 0 0 1 1 1
0 0 1 1 1 1
0 1 0 1 0 0
0 1 1 1 1 1
1 0 0 0 1 1
1 0 1 0 1 1
1 1 0 1 0 0
1 1 1 1 1 1
Обратите внимание, что столбец для значения q-> r такой же
как столбец для значения всего выражения E.Мы установили эквивалентность этих двух столбцов,
что значит:
(p -> q) -> (q -> r) == q-> r.
Генерация выражений из функций
Нам часто дают логическую функцию в виде таблицы истинности.
и должен получить соответствующее логическое выражение.
Например, цифровые схемы построены из цифровых
элементы, которые вычисляют основные логические операции
(например, НЕ и И-НЕ).
Для конкретной функции, выраженной в виде результатов
присвоения переменных (например, схема, которая добавляет два
битов вместе и производит сумму и бит переноса, все
что выражается в форме таблицы истинности), мы бы
как соответствующее логическое выражение, так что мы
может построить схему для функции.
Мы можем построить такое логическое выражение непосредственно из
таблица истинности для функции.
Результирующее выражение использует в качестве операторов только AND, OR и NOT.
Исключительное Или: выражение из таблицы истинности
Исключающее ИЛИ (XOR) — еще одна хорошо известная функция двух переменных.
Таблица истинности для XOR:
p q XOR
---------------
0 0 0
0 1 1
1 0 1
1 1 0
Мы можем построить выражение для XOR в терминах AND, OR и
НЕ, используя следующие рассуждения:
- Вторая строка говорит нам, что p XOR q TRUE
когда p — ЛОЖЬ, а q — ИСТИНА. Другими словами,
Другими словами,
p XOR q истинно, если НЕ p И q истинно. - Третья строка сообщает нам, что p XOR q истинно
когда p — ИСТИНА, а q — ЛОЖЬ. Другими словами,
p XOR q истинно, если p AND NOT q истинно. - Другие строки говорят нам, что p XOR q имеет значение FALSE в
все остальные случаи. - Итак, p XOR q ИСТИНА, если НЕ p И q ИСТИНА,
или если p AND NOT q истинно.
Из вышеизложенного мы определяем, что следующее
логическое выражение для функции p XOR q:
(НЕ p И q) ИЛИ (p И НЕ q)
Конъюнктивные и дизъюнктивные нормальные формы
Логическое выражение находится в дизъюнктивной нормальной форме
если оно выражено как сумма (ИЛИ) произведений (И).То есть логическое выражение B находится в дизъюнктивной нормальной форме
если это написано как:
A1 ИЛИ A2 ИЛИ A3 ИЛИ ... An
где каждый Ai выражается как
T1 И T2 И . .. И Tm
.. И Tm
где каждый Ti — простая переменная,
или отрицание (НЕ) простой переменной.
Каждый из терминов Ai называется minterm .
Логическое выражение находится в конъюнктивной нормальной форме
если оно выражено как произведение (И) сумм (ИЛИ).То есть логическое выражение B находится в конъюнктивной нормальной форме
если это написано как:
O1, O2, O3, и ...
где каждый Oi выражается как
Т1 ИЛИ Т2 ИЛИ ... ИЛИ Tm
где каждый Ti — простая переменная,
или отрицание (НЕ) простой переменной.
Каждый из терминов Oi называется maxterm .
Нормальные формы в таблицах истинности
Конъюнктивные и дизъюнктивные нормальные формы
двойственны друг другу;
любой из них может использоваться для генерации логического выражения
из таблицы истинности.
С помощью этих нормальных форм мы можем быть более точными
о том, как сгенерировать логическое выражение из таблицы истинности.
Чтобы построить логическое выражение в дизъюнктивной нормальной форме из
таблица истинности:
- Создайте minterm для каждой строки таблицы, где функция истинна.
- Для каждой переменной, значение которой равно 1 в этой строке, мы включаем
переменная в minterm; если переменная в этой строке равна 0,
мы включаем отрицание переменной в minterm. - Выражение состоит из ИЛИ всех минтермов.
Конечно, мы могли бы построить выражение в дизъюнктивном нормальном
форма с использованием maxterms и И.
Логическое выражение для сумматора
Двоичный сумматор целых чисел может быть построен из ряда
однобитовых сумматоров.
Однобитовый сумматор принимает два однобитовых операнда (x и y)
и бит переноса из предыдущего однобитового сумматора (ci),
и производит сумму этих бит,
и выносной бит (со).
Мы можем определить булеву функцию, соответствующую сумматору
в виде таблицы истинности.
Затем мы можем построить логические выражения для s и co,
из которого мы могли бы построить схему.
x y ci co s --------------------- 0 0 0 0 0 0 0 1 0 1 с: НЕ x И НЕ y И ci 0 1 0 0 1 с: НЕ x И y И НЕ ci 0 1 1 1 0 co: НЕ x, y и ci 1 0 0 0 1 с: x И НЕ y И НЕ ci 1 0 1 1 0 co: x И НЕ y И ci 1 1 0 1 0 co: x И y И НЕ ci 1 1 1 1 1 co, s: x, y и ci
Логическое выражение для s:
(НЕ x И y И ci) ИЛИ (x И НЕ y И ci) ИЛИ (x AND y И НЕ ci) ИЛИ (x AND y AND ci)
Логическое выражение для co:
(НЕ x И НЕ y И ci) ИЛИ (НЕ x И Y И НЕ ci) ИЛИ (x И НЕ y И НЕ ci) ИЛИ (x И y И ci)
Полнота логических операторов
Предыдущее построение логического выражения из
таблица истинности показала, как представить любую логическую функцию
как сумма произведений или произведение сумм.
Поскольку мы можем представить любую логическую функцию, используя И, ИЛИ,
и НЕ, эти операторы образуют полный набор для
Булевы функции.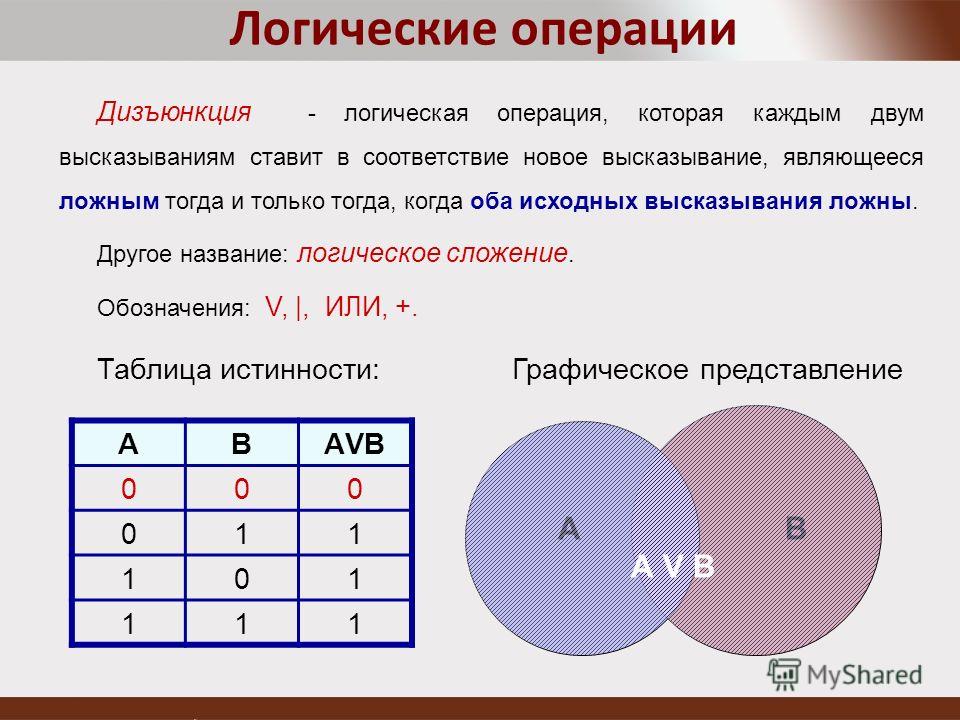
Мы можем показать, что одного оператора NAND достаточно
для генерации каждой логической функции, показывая, как
реализовать И, ИЛИ, и НЕ с точки зрения NAND.
p q p NAND 1 q NAND 1 p NAND q E1 E2
--------------------------------------------
0 0 1 1 1 0 0
0 1 1 0 1 0 1
1 0 0 1 1 0 1
1 1 0 0 0 1 1
E1: p AND q == ((p NAND q) НЕ ИСТИНА)
E2: p ИЛИ q == ((p НЕ И ИСТИНА) ИЛИ (q НЕ И ИСТИНА))
E3: (НЕ p) == (p НЕ ИСТИНА)
Подобная конструкция может использоваться, чтобы показать, что NOR
также достаточно для генерации каждой логической функции.
Таким образом, мы можем генерировать цифровые схемы для любой булевой функции
используя только операторы NAND или NOR (или компоненты).
Тавтологии
Тавтология — это логическое выражение, которое всегда ИСТИНА,
независимо от присвоения значений истинности переменным
в выражениях.
Примеры тавтологий:
- ИСТИНА
- ИСТИНА ИЛИ p
- p ИЛИ НЕ p
- НЕ (p И НЕ p)
- p == p
- (p OR q) == p OR (НЕ p AND q)
- (p == q) -> (p -> q)
Если мы сможем установить, что «LE1 == LE2» является тавтологией,
тогда независимо от того, какие значения мы присваиваем переменным в LE1 и LE2,
мы знаем, что «LE1 == LE2» имеет значение ИСТИНА.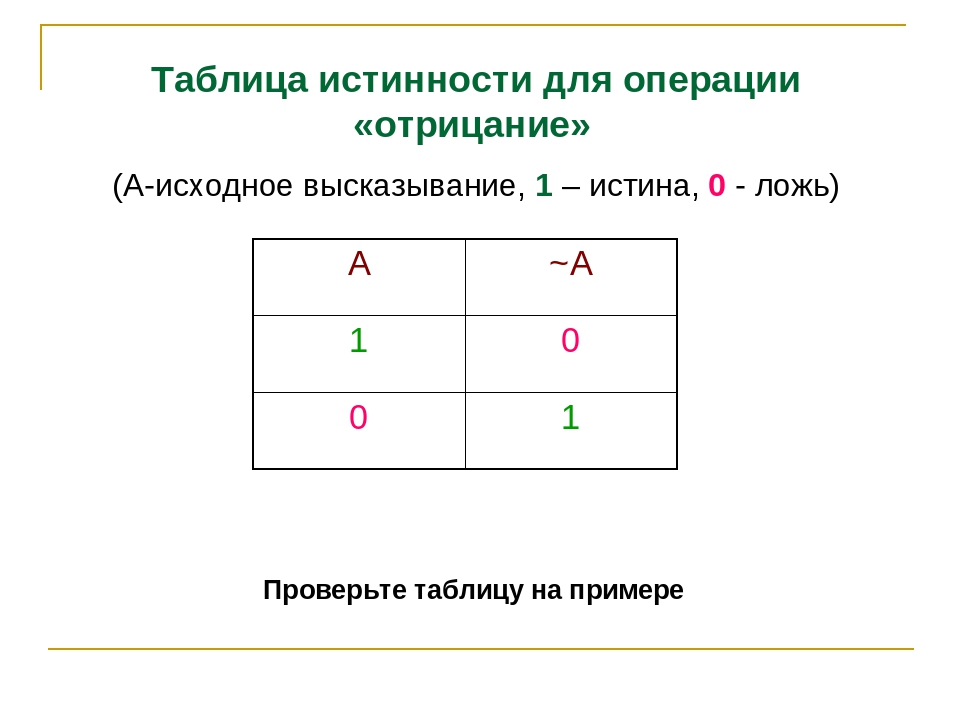
Если «LE1 == LE2» — тавтология, то мы можем заменить LE2 на LE1.
(или наоборот) в любом выражении,
без изменения значения выражения.
Задача тавтологии
Интересный вопрос — задать ли данное логическое
выражение — тавтология.
Этот вопрос известен как «проблема тавтологии».
Чтобы решить проблему тавтологии, нам достаточно построить
таблица истинности логического выражения.kn) время, т.е. экспоненциальное время.
Не существует известного алгоритма решения проблемы тавтологии, который
занимает меньше экспоненциального времени. Такие проблемы называются
«трудноразрешимыми», потому что в крупных случаях эти проблемы
не могут быть решены в разумные сроки.
Другой такой неразрешимой проблемой является «проблема выполнимости».
который спрашивает, есть ли присвоение значений истинности
переменные в логическом выражении, которое делает выражение ИСТИННЫМ.Не существует известного алгоритма решения этой проблемы, более того
эффективнее, чем перебор всех возможных комбинаций
присвоения истинности для переменных.
Краткое содержание главы
Глава 7
Логика высказываний — это изучение того, как простые высказывания (базовые компоненты в логике высказываний) изменяются, чтобы сформировать составные высказывания, и того, как истина является функцией простых высказываний и составляющих элементов.Простое утверждение — это такой оператор, в котором нет другого оператора в качестве компонента. Составной оператор — это оператор, в состав которого входит хотя бы один простой оператор.
Чтобы облегчить изучение логики высказываний, утверждения обычного языка переводятся в нотацию логики высказываний. В логической записи используются заглавные буквы, A – Z для обозначения простых утверждений и логические операторы для обозначения составных элементов. Существует пять символов логического оператора: тильда , точка , клин , подкова и тройная черта.
Тильда — символ отрицания. Слово «не» и фраза «это не тот случай» используются для отрицания следующего за ними утверждения (мы называем их использование «отрицанием»). Точка — это символ соединения, который соединяет два различных утверждения (называемых «конъюнктами»). Дизъюнкция — это составное утверждение, в котором есть два разных утверждения (называемых «дизъюнкциями»), соединенных символом клина. В обычном языке слово «если» обычно предшествует условному условию: «только если» обычно предшествует следствию условного.Символ подковы используется для перевода условного оператора. Двухусловное выражение — это составное выражение, состоящее из двух условных операторов: одно обозначается словом «если», а другое — фразой «только если».
Когда мы конструируем составные утверждения, мы стремимся создавать правильно сформированные формулы, которые являются грамматически правильными формами составных утверждений. Каждый составной оператор, содержащий два или более операторов, имеет главный оператор.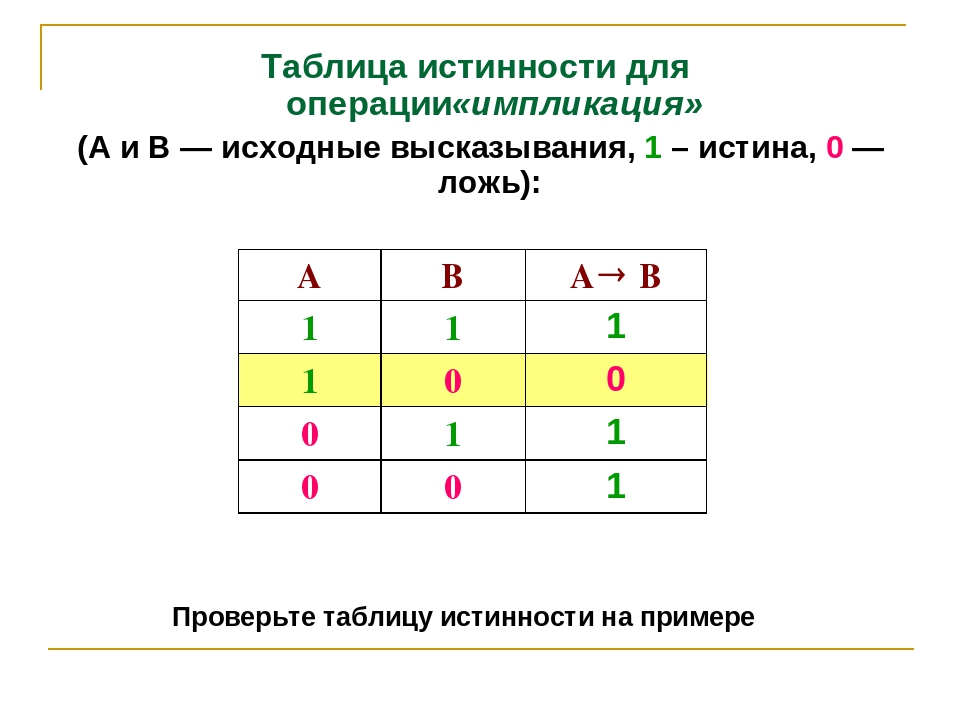 Это логический оператор, в диапазоне которого находится самый большой компонент или компоненты составного оператора.
Это логический оператор, в диапазоне которого находится самый большой компонент или компоненты составного оператора.
Каждое утверждение имеет значение истинности, то есть каждое утверждение истинно или ложно. Значение истинности сложного предложения с функцией истинности определяется значениями истинности его компонентов и определениями задействованных логических операторов. Любое сложное суждение с функциональной истинностью, которое может быть определено таким образом, называется «функцией истинности».
Определения истинности для логических операторов отображаются как формы утверждений в таблице истинности. Форма оператора — это набор переменных оператора и логических операторов.Таблица истинности — это набор значений истинности для сложного предложения с функциональной истинностью, который отображает для каждого возможного случая, как значение истинности предложения определяется значениями истинности его простых компонентов.
Важно знать следующие концепции, связанные с использованием и результатами таблиц истинности:
Инклюзивная дизъюнкция: обе дизъюнкции могут быть истинными одновременно.

Исключительная дизъюнкция: когда оба дизъюнкта не могут быть истинными одновременно.
Порядок операций: порядок обработки логических операторов в предложении с функцией истинности; это пошаговый метод создания полной таблицы истинности.
Условные утверждения: утверждения, которые не обязательно истинны или ложны (иногда они верны, иногда ложны).
Неконфликтные утверждения: утверждения, при которых значения истинности в главном столбце оператора не зависят от значений истинности составных частей.
Тавтология: утверждение, которое обязательно верно.
Внутреннее противоречие: утверждение, которое обязательно ложно.
Логически эквивалентно: Когда два функциональных утверждения истинности кажутся разными, но имеют идентичные таблицы истинности.
Противоречивые утверждения: два утверждения, которые имеют противоположные значения истинности в каждой строке соответствующих таблиц истинности.

Согласованные утверждения: два (или более) утверждения, которые содержат по крайней мере одну строку в соответствующих таблицах истинности, где основные операторы истинны.
Несогласованные утверждения: два (или более) утверждения, у которых нет ни одной строки в соответствующих таблицах истинности, где основные операторы истинны.
Форма аргумента: набор логических операторов и переменных оператора, в котором последовательная замена переменных оператора операторами приводит к получению аргумента.
Modus ponens : Действительная форма аргумента (также называемая , подтверждающая антецедент ).
Ошибка подтверждения консеквента: неверная форма аргумента; это формальная ошибка.
Modus tollens : Действительная форма аргумента (также называемая , отрицающая консеквент ).
Ошибка отрицания антецедента: неверная форма аргумента; это формальная ошибка.

Раздел 1.1
Раздел 1.1
Логические формы и эквиваленты
Логическая форма и логика
Эквивалентность | Определения | Сложный
Заявления | Таблицы истинности
Логическая эквивалентность | Законы ДеМоргана
| Таблица логических эквивалентов
Логический
Форма и логическая эквивалентность
Содержание утверждения не совпадает с его логической формой.Например,
рассмотрите 2 следующих утверждения:
Если Салли просыпается поздно или опаздывает на автобус,
она опоздает на работу. Поэтому, если Салли приходит на работу вовремя, она
не просыпалась поздно и не опаздывала на автобус.
Если x — действительное число такое, что x <-2 или x>
2, то x 2 > 4. Следовательно, если x 2 < 4, то
x > -2 и x < 2.
Логический анализ не помогает определить достоинства аргумента.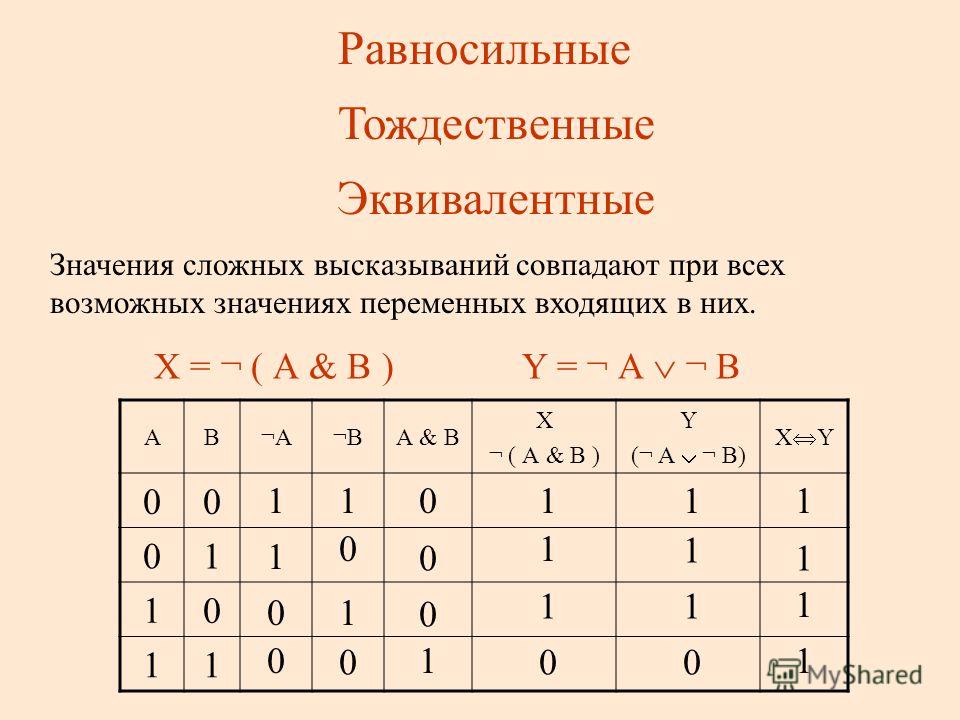 Вместо
Вместо
это помогает проанализировать форму аргумента, чтобы определить, является ли
Вывод следует из истинности предыдущих утверждений. В то время как
содержание двух приведенных выше утверждений различно, их логическая форма
похожий.
Пусть p означает утверждения «Салли поздно просыпается».
и «x — действительное число такое, что x <-2».
Пусть q означает утверждения «Салли опаздывает на автобус».
и «x — действительное число такое, что x> -2».
Пусть r означает утверждения «Салли опаздывает на работу».
и «x 2 > 4».
Тогда общая форма для обоих приведенных выше аргументов:
Если p или q, то r.
Следовательно, если не r, то не p и не q.
| Практические упражнения |
| Д Е Ф И Н И Т И Я С | |
| Аргумент: | последовательность утверждений, направленных на доказательство истины утверждения или утверждения.  |
| Заявление: | предложение, которое истинно или ложно, но не то и другое. Это также называется предложением. |
| Отрицание: | , если p — переменная оператора, отрицание p — это «не p », обозначается ~ p . Если р верно, то ~ p ложно. |
| Соединение: | , если p и q — переменные инструкции, то соединение p и q составляет « p и q «, обозначено pq . Соединение истинно только тогда, когда истинны обе переменные. Если 1 или обе переменные ложны, pq ложно. |
| Дизъюнкция: | , если p и q — переменные инструкции, то дизъюнкция p и q равна « p или q «, обозначено pq .  Дизъюнкция истинна, если истинны одна или обе переменные. pq ложно, только если обе переменные ложны. |
| Тавтология: | Форма утверждения, которая всегда верна. Правда делает не полагаться на значения отдельных утверждений, замененных переменные оператора, но на логической структуре самого оператора. (т.е. вы получите пятерку в этом классе или нет). |
| Противоречие: | Форма заявления, которая всегда является ложной. Как тавтология, ложность заключается не в отдельных переменных утверждения, а в логическая структура самого высказывания.(т.е. я всегда вру.) |
Составные отчеты
используйте символы (логические
И), (логическое ИЛИ),
и ~ (НЕ) для построения сложных логических операторов из более простых.
Пусть p = «жарко» и q = «солнечно». Тогда
заявление «Не жарко, но солнечно». можно написать
символически:
| ~ п в |
| Практические упражнения |
Однако утверждения должны иметь четко определенные истинностные значения
— они должны быть истинными или ложными.Истинность утверждения может быть выражена
по таблице истинности . А
таблица истинности для данного утверждения отображает результирующие значения истинности для различных
комбинации значений истинности для переменных. Правда соединения
утверждение может быть логически выведено, используя известные значения истинности для различных
части заявления.
| Таблица истинности для ~ стр. | Таблица истинности для pq | Таблица истинности для pq | |||||
| п. | ~ стр. | п. | q | уп. | п. | q | уп. |
| Т | Факс | Т | Т | Т | Т | Т | Т |
| Ф. | Т | Т | Факс | Факс | Т | Факс | Т |
| Факс | Т | Факс | Факс | Т | Т | ||
| Факс | Факс | Факс | Факс | Факс | Факс | ||
| Практические упражнения |
Логическая эквивалентность:
Два оператора логически эквивалентны
тогда и только тогда, когда их результирующие формы логически эквивалентны, когда идентичны
переменные оператора используются для представления операторов компонентов.
Две формы операторов логически эквивалентны тогда и только тогда, когда их
итоговые таблицы истинности идентичны для каждого варианта переменных утверждения.
| п | q | уп. | qp |
| Т | Т | Т | Т |
| Т | Факс | Факс | Факс |
| Факс | Т | Факс | Факс |
| Факс | Факс | Факс | Факс |
Другие логически эквивалентные утверждения включают:
Для проверки логической эквивалентности двух утверждений постройте
таблица истинности, которая включает каждую переменную для оценки, а затем проверьте
чтобы увидеть, эквивалентны ли результирующие значения истинности двух утверждений.
Законы ДеМоргана
Отрицание конъюнкции (логическое И) двух операторов
логически эквивалентен дизъюнкции (логическое ИЛИ) каждого оператора
отрицание.Звучит глупо, но это означает, что «не
(A и B) « логически эквивалентно », а не
А или нет В ».
Аналогично, отрицание дизъюнкции 2 утверждений
логически эквивалентен соединению отрицания каждого утверждения. Положить
просто «не (A или B)» логически
эквивалент «не A и не B» .
Символически это можно записать как
Эти два утверждения логически эквивалентны
(щелкните здесь для определения), и это можно проверить
с помощью таблицы истинности.
Таблица логики
Эквиваленты:
Следующая таблица может использоваться для сокращения составных операторов до
более простые формы. Для заданных переменных оператора p, q, и r ,
тавтология t и противоречие c, следующее
правила логического удержания:
Логические эквиваленты могут использоваться для упрощения форм выписок и подтверждения
или опровергнуть эквивалентность, чтобы создать эффективный и логически правильный компьютер
программ или для помощи в проектировании цифровых логических схем.
Чтобы упростить эквивалентность, начните с одной стороны уравнения и попытайтесь
заменить его части эквивалентными выражениями. Продолжайте делать это, пока
вы достигли желаемой формы заявления.
| Практические упражнения |
.

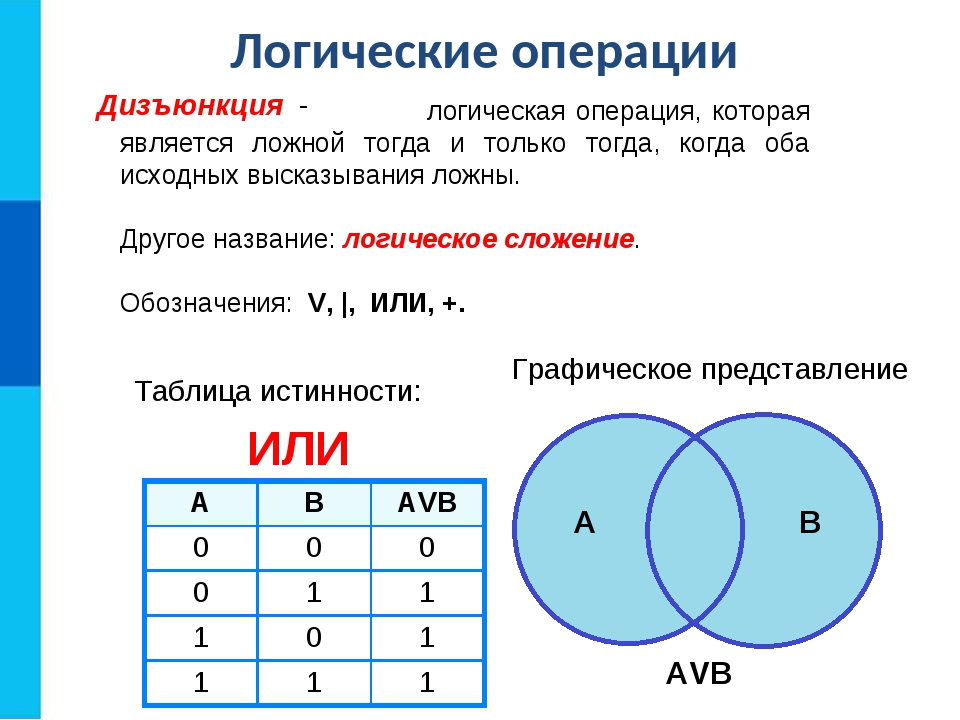
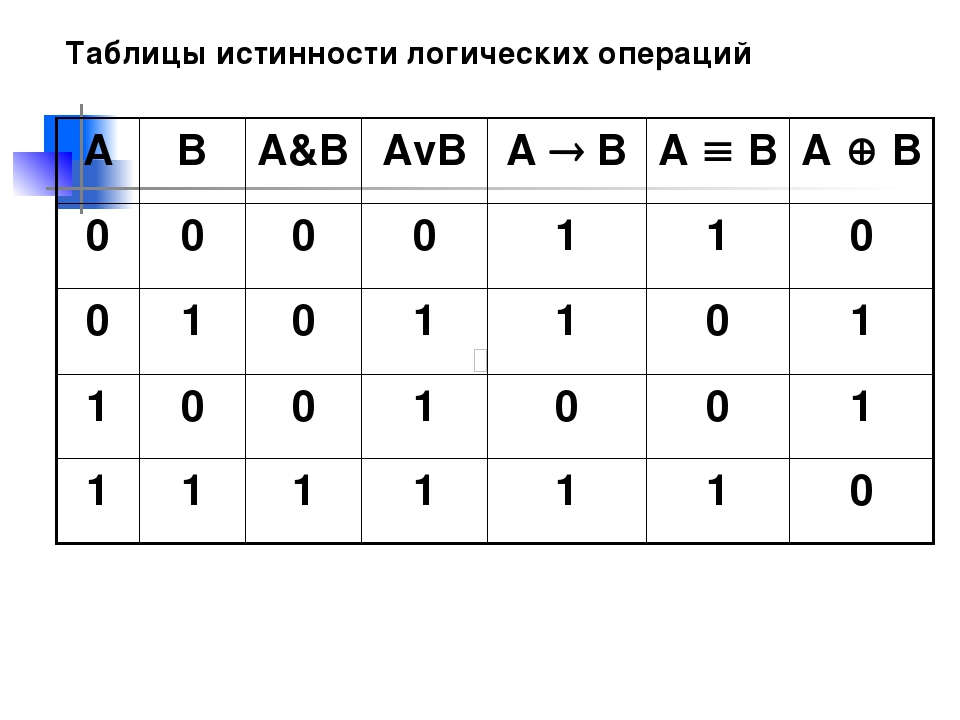
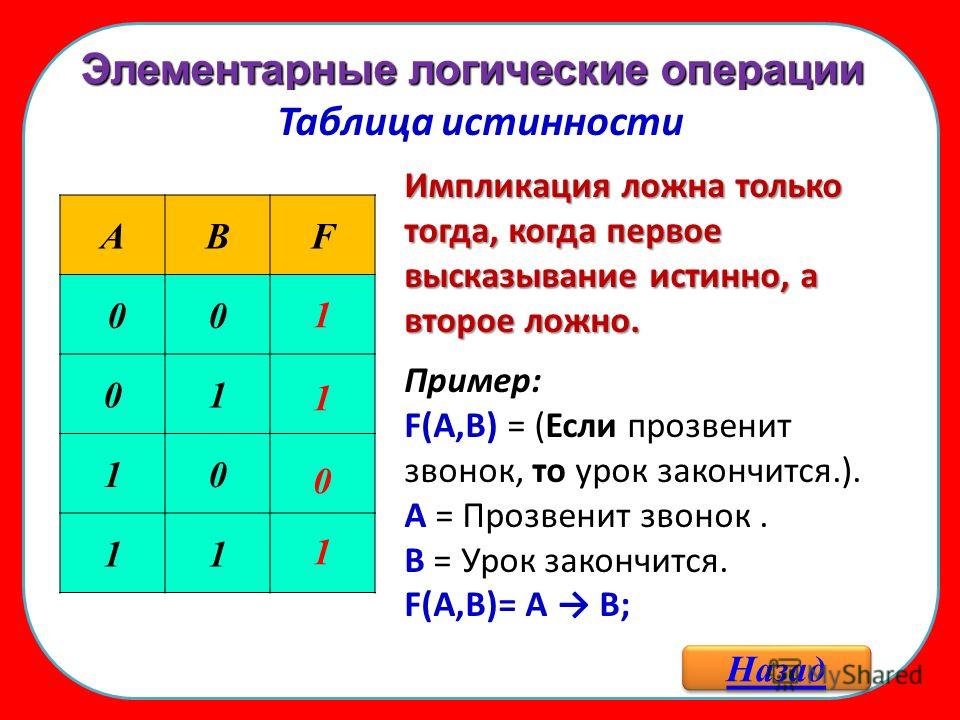
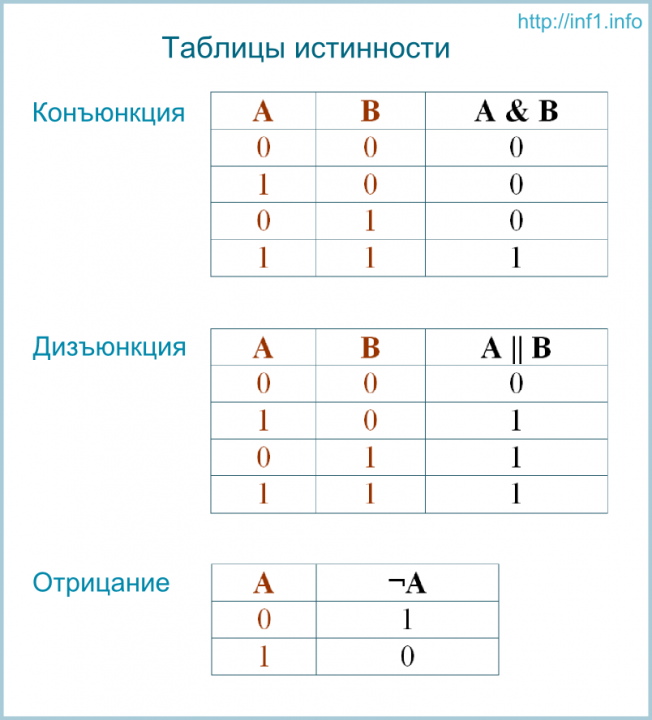
 Аналогично проделайте для Дизъюнкции (в столбце G) и для Инверсии (в столбце J).
Аналогично проделайте для Дизъюнкции (в столбце G) и для Инверсии (в столбце J).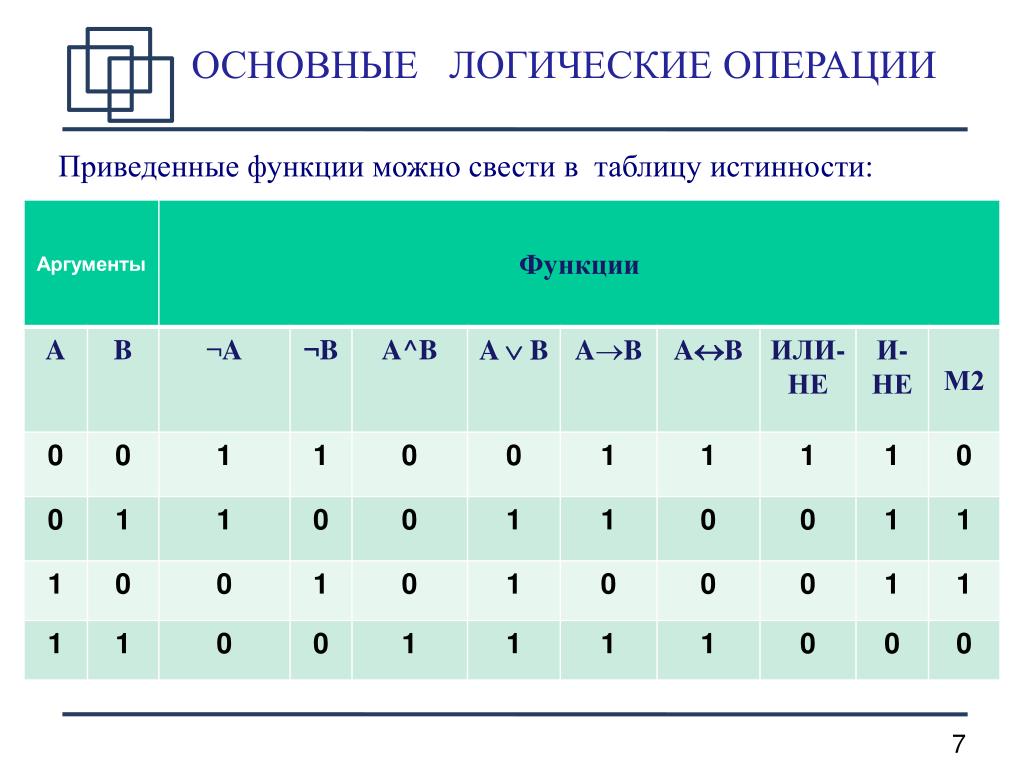
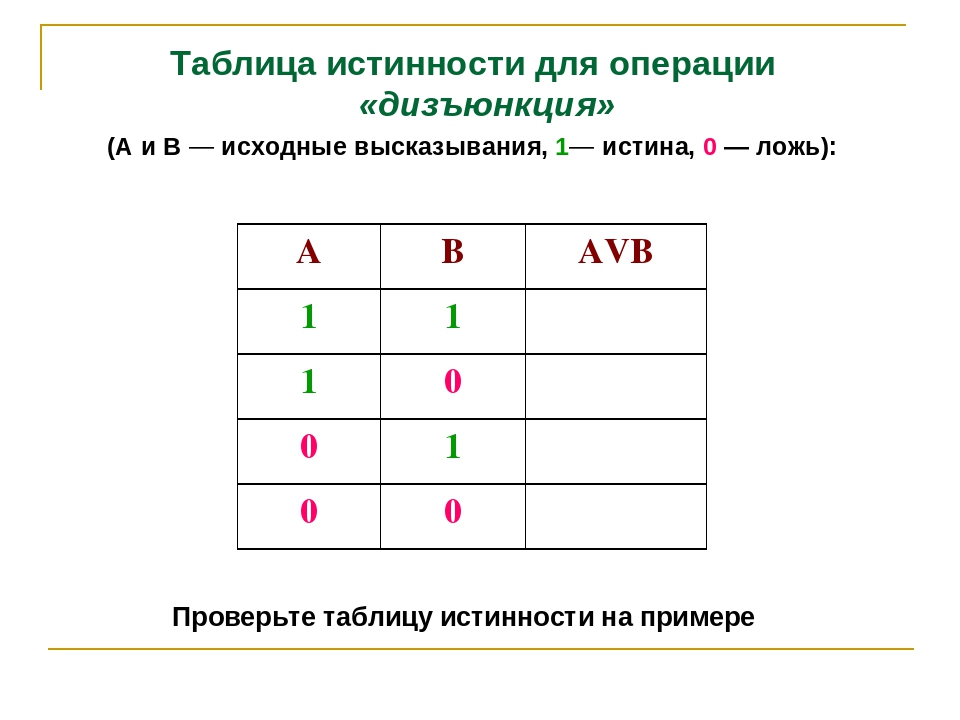
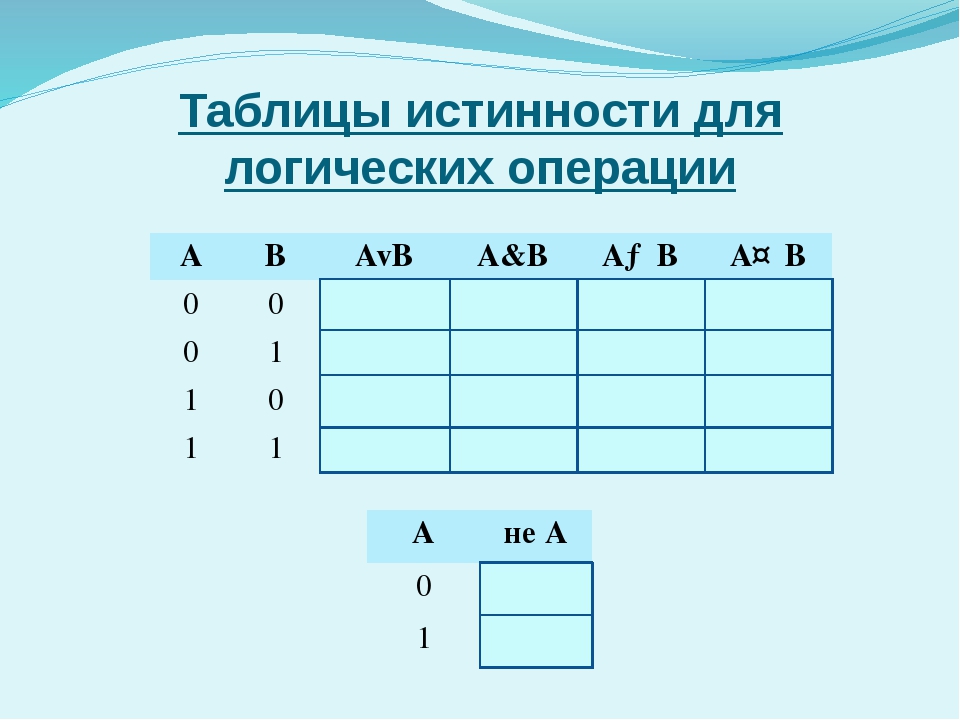
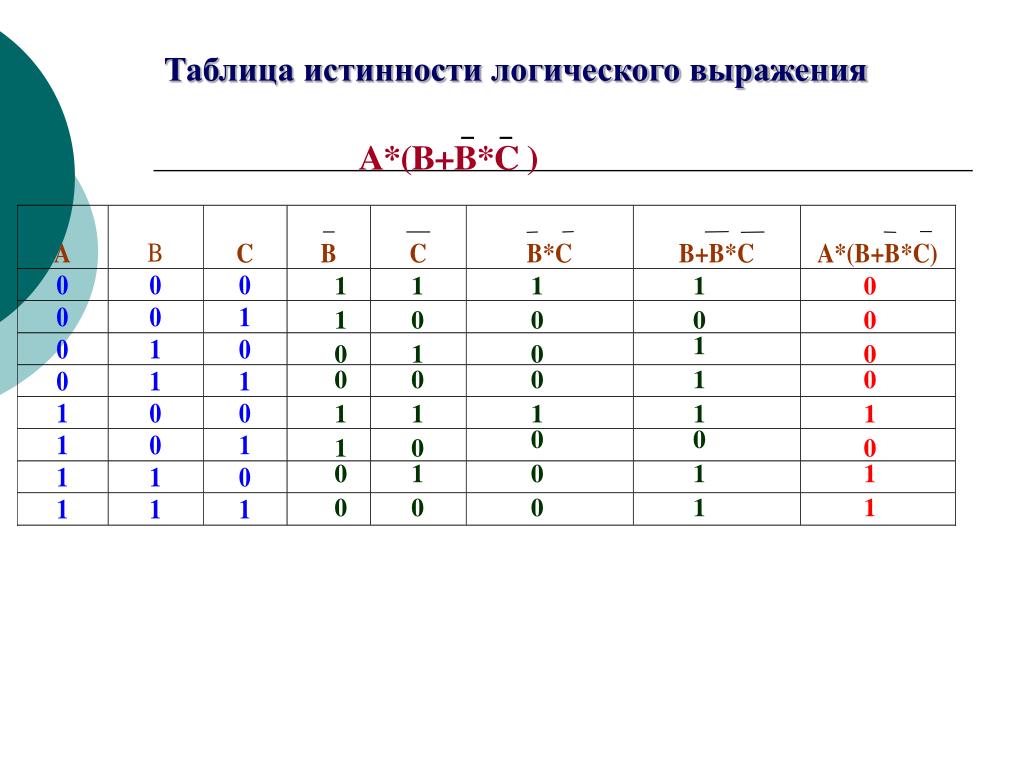 xlc .
xlc .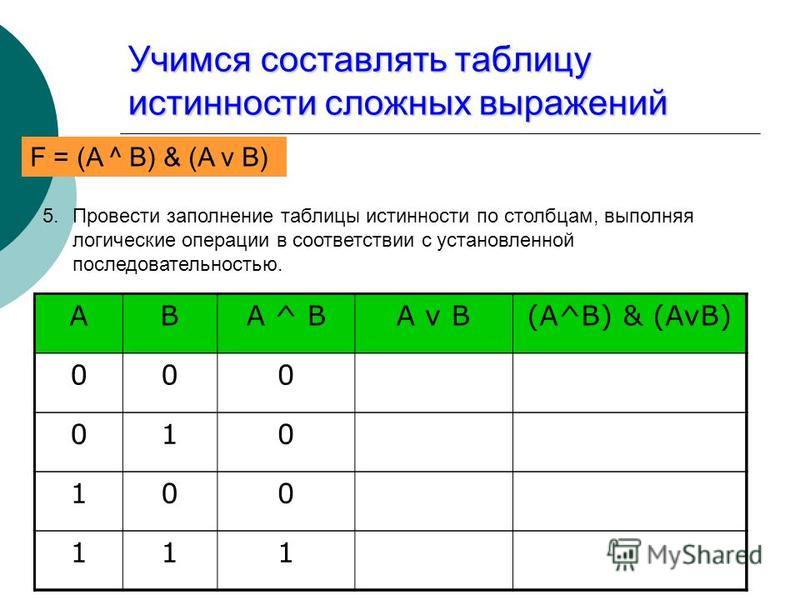
 ..и…»
..и…» ..или…», «…либо…»
..или…», «…либо…» .., тогда…»
.., тогда…»
 Понятно что к чему относится.
return (length > 8 and length < 20) or has_special_chars(password)
Понятно что к чему относится.
return (length > 8 and length < 20) or has_special_chars(password)
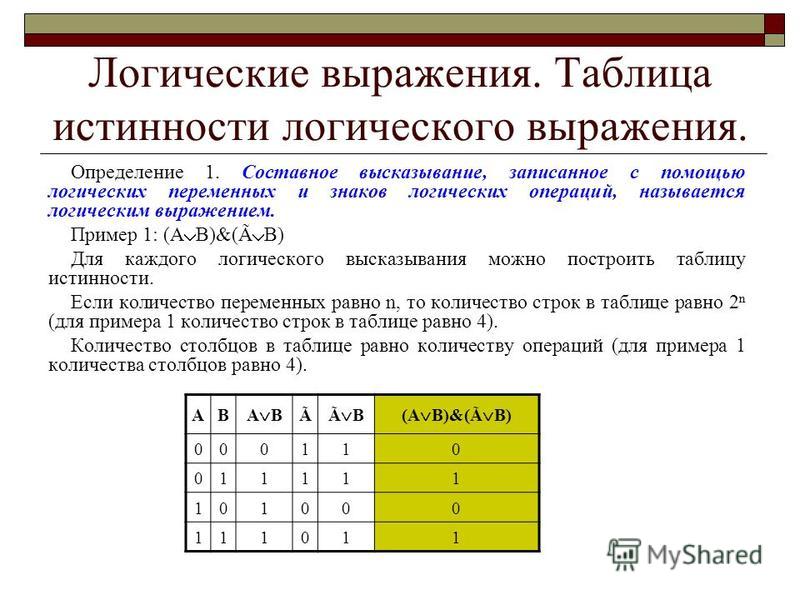
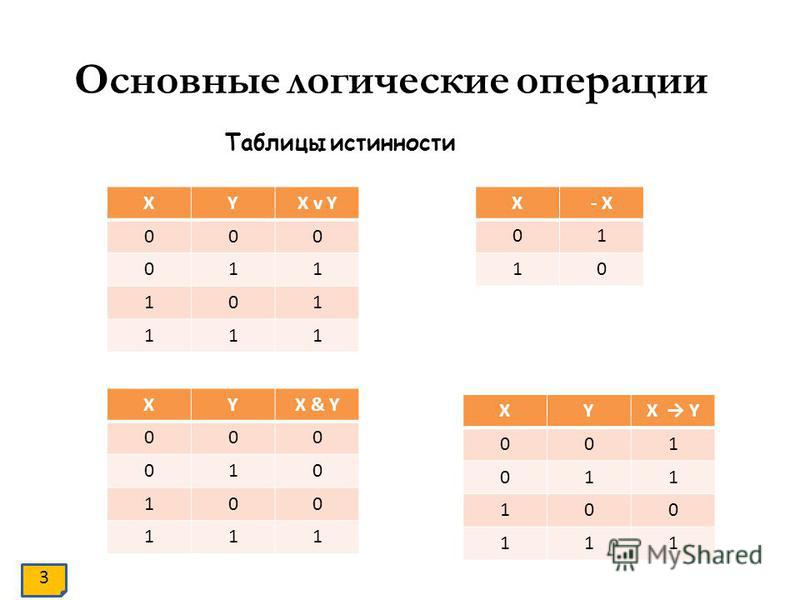 Другими словами,
Другими словами,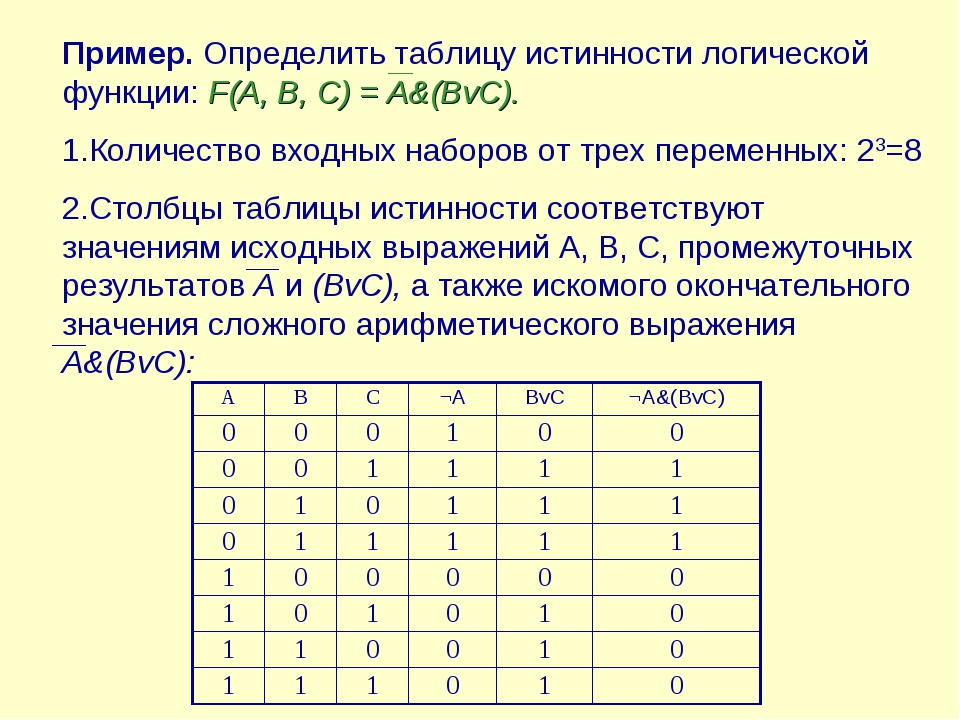 .. И Tm
.. И Tm