18.02.2025
Разное

Тангенс угла определение: определения, формулы, примеры, угол поворота

alexxlabАвтор: alexxlab

Содержание

Тангенс — что это такое? Таблица тангенсов и котангенсов

Тангенс (tg) — это отношение синуса к косинусу (tgα = sinα / cosα). Либо отношение противолежащего катета (дальнего/противоположного) к прилежащему (который находится рядом с углом).

В этом треугольнике тангенс угла вычисляется по этой формуле:

Обратите внимание, что в вычислении принимают участие только катеты, гипотенузы здесь нет (противолежащий делится на прилежащий — это тангенс острого угла прямоугольного треугольника).

Например:

Вычислите длину стороны BC, зная, что tan α = 0,4:

tan α = противолежащий катет / прилежащий катет = BC / AB = x / 15 <=>

<=> x / 15 = 0,4 <=> x = 15 * 0,4 <=> x = 6

Ответ: BC = 6 см.

Таблица тангенсов и котангенсов (главных углов от 0° до 360°)

α градусов0°30°45°60°90°180°270°360°
α радиан0π/6π/4π/3π/2π3π/22π
tg α0√3/31√3–0–0
ctg α–√31√3/30–0–

Основные тригонометрические тождества

Что такое синус?

Синус угла (sin) — это отношение противолежащего катета (который находится напротив угла) к гипотенузе (самой длинной стороне, находится напротив прямого угла).

В нашем примере sin α = BC/AC.

Что такое косинус?

Косинус угла (cos) — это отношение прилежащего катета (находится рядом с углом) к гипотенузе (самой длинной стороне, находится напротив прямого угла). В нашем примере cos α = AB/AC.

Что такое котангенс?

Котангенс угла (ctg) — это отношение прилежащего катета (который находится рядом с углом) к противолежащему (напротив угла). В нашем примере ctg α = AB / BC. Обратите внимание, что котангенс — это как «тангенс наоборот» (прилежащий делится на противолежащий), т. е. ctg α = AB / BC, а tg α = BC / AB (противолежащий делится на прилежащий).

Что такое секанс?

Секанс (sec или sec x) — это отношение гипотенузы (самой длинной стороны, напротив прямого угла) к прилежащему катету (рядом с углом) острого угла в прямоугольном треугольнике. Ещё секанс определяется формулой:

Что такое гипотенуза и катет?

Гипотенуза — это та сторона, которая находится напротив прямого угла (она самая длинная), в нашем треугольнике это сторона AC.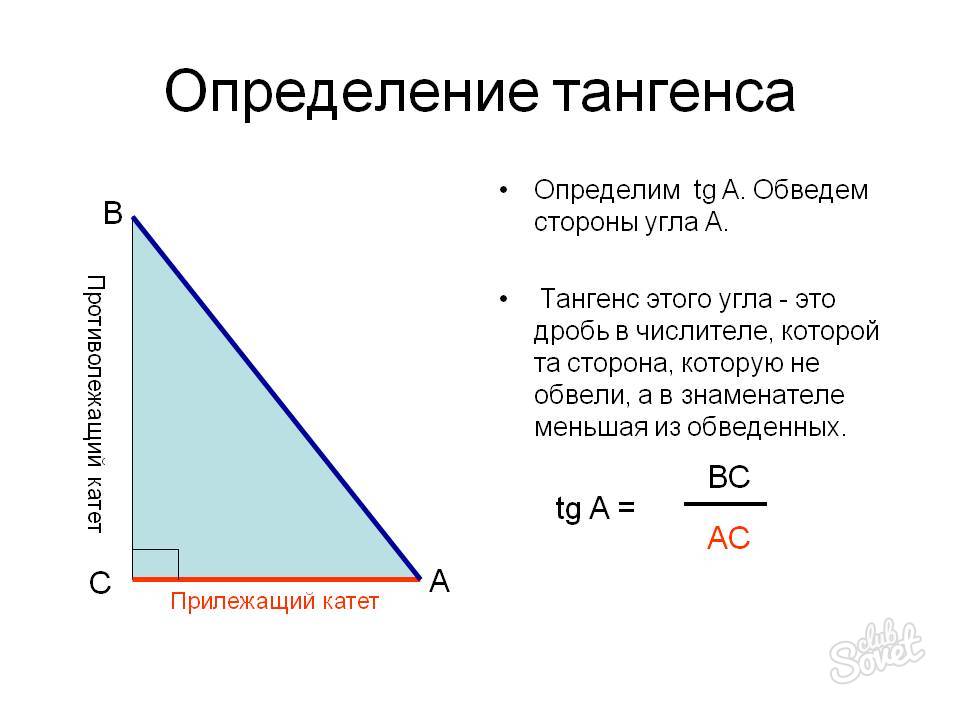 Катеты — это две другие стороны, которые находятся рядом с прямым углом, в нашем треугольнике это стороны BC и AB:

Узнайте про Теорему Пифагора, Теорему косинусов и Гиперболу в математике

Дата обновления 08/10/2020.

Другие значения и понятия, которые могут вас заинтересовать

Тригонометрические функции

В школьной программе изучаются четыре тригонометрических функции — синус, косинус, тангенс и котангенс. В этой статье мы рассмотрим графики и основные свойства этих функций.

1. Начнем с построения графика функции y = sin x.

Выберем подходящий масштаб. По оси X: три клетки примем за (это примерно полтора). Тогда — одна клеточка, — две клетки.
По оси Y : две клетки примем за единицу.

Область определения функции y = sin x — все действительные числа, поскольку значение sin α можно посчитать для любого угла α.

Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.

Можем добавить, для большей плавности графика, точки и . В них значение синуса равно
Соединим полученные точки плавной кривой.

Мы помним, что . Это значит, что
Получается часть графика, симметричная той, которую нарисовали раньше.

Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть

Это значит, что функция y = sin x является периодической. Мы уже построили уча-сток графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:

Синусоида построена.
Перечислим основные свойства функции y = sin x.

1) D(y): x ∈ R, то есть область определения — все действительные числа.

2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = sin x равно единице, а наименьшее — минус единице.

3) Функция y = sin x — нечетная. Ее график симметричен относительно нуля.

4) Функция y = sin x — периодическая. Ее наименьший положительный период равен 2π.

2. Следующий график: y = cos x. Масштаб — тот же. Отметим на графике точки, в которых косинус является рациональным числом:

Поскольку cos (−x) = cos x, график будет симметричен относительно оси Y , то есть левая его часть будет зеркальным отражением правой.

Функция y = cos x — тоже периодическая. Так же, как и для синуса, ее значения повторяются через 2πn. «Копируем» участок графика, который уже построили, и повторяем периодически.

Перечислим основные свойства функции y = cos x.

1) D(y): x ∈ R, то есть область определения — все действительные числа.

2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = cos x равно единице, а наименьшее — минус единице.

3) Функция y = cos x — четная. Ее график симметричен относительно оси Y .

4) Функция y = cos x — периодическая. Ее наименьший положительный период равен 2π.

Отметим еще одно свойство. Графики функций y = sin x и y = cos x весьма похожи друг на друга. Можно даже сказать, что график косинуса получится, если график синуса сдвинуть на влево. Так оно и есть — по одной из формул приведения,.

Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!

Функции синус и косинус идеально подходят для описания колебаний и волн — то есть процессов, повторяющихся во времени.

По закону синуса (или косинуса) происходят колебания маятника или груза на пружине. Переменный ток (тот, который в розетке) выражается формулой I(t) = I cos(ωt+α). Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того — объекты микромира (например, электрон) проявляют волновые свойства.

3. Перейдем к графику функции y = tg x.

Чтобы построить его, воспользуемся таблицей значений тангенса. Масштаб возьмем тот же — три клетки по оси X соответствуют , две клетки по Y — единице. График будем строить на отрезке от 0 до π. Поскольку tg (x + πn) = tg x, функ-ция тангенс также является периодической. Мы нарисуем участок длиной π, а затем периодически его повторим.

Непонятно только, как быть с точкой . Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к , то есть к 90 градусам?

Чтобы ответить на этот вопрос, возьмем значение x, близкое к , и посчитаем на калькуляторе значения синуса и косинуса этого угла. Пусть .

Синус угла — это почти 1. Точнее, sin = 0,9998. Косинус этого угла близок к нулю. Точнее, cos = 0,0175.

Тогда
график уйдет на 59 единиц (то есть на 118 клеток) вверх. Можно сказать, что если x стремится к (то есть к , значение функции y = tg x стремится к бесконечности.

Аналогично, при x, близких к , график тангенса уходит вниз, то есть стремится к минус бесконечности.

Осталось только «скопировать» этот участок графика и повторить его с периодом π.

Перечислим свойства функции y = tg x.

1) .
Другими словами, тангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.

3) Функция y = tg x — нечетная. Ее график симметричен относительно начала координат.

4) Функция y = tg x — периодическая. Ее наименьший положительный период равен π.

5) Функция y = tg x возрастает при то есть на каждом участке, на котором она непрерывна.

4. График функции y = ctg x строится аналогично. Вот он:

1) .
Другими словами, котангенс не определен для где n ∈ Z.
2) Область значений E(y) — все действительные числа.

3) Функция y = сtg x — нечетная. Ее график симметричен относительно начала координат.

4) Функция y = сtg x — периодическая. Ее наименьший положительный период равен π.

5) Функция y = сtg x убывает при то есть на каждом участке, на котором она непрерывна.

Тангенс угла онлайн. Таблица тангенсов. Формула тангенса угла.

Тангенс угла через градусы, минуты и секунды

&plus;−

Тангенс угла через десятичную запись угла

Определение тангенса

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

tg(α) = sin(α)/cos(α)

tg(α) = 1/ctg(α)

Таблица тангенсов в радианах

tg(0°) = 0tg(π/12) = tg(15°) = 0.2679491924tg(π/6) = tg(30°) = 0. 5773502692tg(π/4) = tg(45°) = 1tg(π/3) = tg(60°) = 1.732050808tg(5π/12) = tg(75°) = 3.732050808tg(π/2) = tg(90°) = ∞tg(7π/12) = tg(105°) = -3.732050808tg(2π/3) = tg(120°) = -1.732050808tg(3π/4) = tg(135°) = -1tg(5π/6) = tg(150°) = -0.5773502692tg(11π/12) = tg(165°) = -0.2679491924tg(π) = tg(180°) = 0tg(13π/12) = tg(195°) = 0.2679491924tg(7π/6) = tg(210°) = 0.5773502692tg(5π/4) = tg(225°) = 1tg(4π/3) = tg(240°) = 1.732050808tg(17π/12) = tg(255°) = 3.732050808tg(3π/2) = tg(270°) = ∞tg(19π/12) = tg(285°) = -3.732050808tg(5π/3) = tg(300°) = -1.732050808tg(7π/4) = tg(315°) = -1tg(11π/6) = tg(330°) = -0.5773502692tg(23π/12) = tg(345°) = -0.2679491924

Таблица Брадиса тангенсы

tg(0) = 0tg(120) = -1.732050808tg(240) = 1.732050808
tg(1) = 0.01745506493tg(121) = -1.664279482tg(241) = 1.804047755
tg(2) = 0.03492076949tg(122) = -1.600334529tg(242) = 1.880726465
tg(3) = 0. 05240777928tg(123) = -1.539864964tg(243) = 1.962610506
tg(4) = 0.06992681194tg(124) = -1.482560969tg(244) = 2.050303842
tg(5) = 0.08748866353tg(125) = -1.428148007tg(245) = 2.144506921
tg(6) = 0.1051042353tg(126) = -1.37638192tg(246) = 2.246036774
tg(7) = 0.1227845609tg(127) = -1.327044822tg(247) = 2.355852366
tg(8) = 0.1405408347tg(128) = -1.279941632tg(248) = 2.475086853
tg(9) = 0.1583844403tg(129) = -1.234897157tg(249) = 2.605089065
tg(10) = 0.1763269807tg(130) = -1.191753593tg(250) = 2.747477419
tg(11) = 0.1943803091tg(131) = -1.150368407tg(251) = 2.904210878
tg(12) = 0.2125565617tg(132) = -1.110612515tg(252) = 3.077683537
tg(13) = 0.2308681911tg(133) = -1. 07236871tg(253) = 3.270852618
tg(14) = 0.2493280028tg(134) = -1.035530314tg(254) = 3.487414444
tg(15) = 0.2679491924tg(135) = -1tg(255) = 3.732050808
tg(16) = 0.2867453858tg(136) = -0.9656887748tg(256) = 4.010780934
tg(17) = 0.3057306815tg(137) = -0.9325150861tg(257) = 4.331475874
tg(18) = 0.3249196962tg(138) = -0.9004040443tg(258) = 4.704630109
tg(19) = 0.3443276133tg(139) = -0.8692867378tg(259) = 5.144554016
tg(20) = 0.3639702343tg(140) = -0.8390996312tg(260) = 5.67128182
tg(21) = 0.383864035tg(141) = -0.8097840332tg(261) = 6.313751515
tg(22) = 0.4040262258tg(142) = -0.7812856265tg(262) = 7.115369722
tg(23) = 0.4244748162tg(143) = -0.7535540501tg(263) = 8. 144346428
tg(24) = 0.4452286853tg(144) = -0.726542528tg(264) = 9.514364454
tg(25) = 0.4663076582tg(145) = -0.7002075382tg(265) = 11.4300523
tg(26) = 0.4877325886tg(146) = -0.6745085168tg(266) = 14.30066626
tg(27) = 0.5095254495tg(147) = -0.6494075932tg(267) = 19.08113669
tg(28) = 0.5317094317tg(148) = -0.6248693519tg(268) = 28.63625328
tg(29) = 0.5543090515tg(149) = -0.600860619tg(269) = 57.28996163
tg(30) = 0.5773502692tg(150) = -0.5773502692tg(270) = ∞
tg(31) = 0.600860619tg(151) = -0.5543090515tg(271) = -57.28996163
tg(32) = 0.6248693519tg(152) = -0.5317094317tg(272) = -28.63625328
tg(33) = 0.6494075932tg(153) = -0.5095254495tg(273) = -19.08113669
tg(34) = 0. 6745085168tg(154) = -0.4877325886tg(274) = -14.30066626
tg(35) = 0.7002075382tg(155) = -0.4663076582tg(275) = -11.4300523
tg(36) = 0.726542528tg(156) = -0.4452286853tg(276) = -9.514364454
tg(37) = 0.7535540501tg(157) = -0.4244748162tg(277) = -8.144346428
tg(38) = 0.7812856265tg(158) = -0.4040262258tg(278) = -7.115369722
tg(39) = 0.8097840332tg(159) = -0.383864035tg(279) = -6.313751515
tg(40) = 0.8390996312tg(160) = -0.3639702343tg(280) = -5.67128182
tg(41) = 0.8692867378tg(161) = -0.3443276133tg(281) = -5.144554016
tg(42) = 0.9004040443tg(162) = -0.3249196962tg(282) = -4.704630109
tg(43) = 0.9325150861tg(163) = -0.3057306815tg(283) = -4.331475874
tg(44) = 0. 9656887748tg(164) = -0.2867453858tg(284) = -4.010780934
tg(45) = 1tg(165) = -0.2679491924tg(285) = -3.732050808
tg(46) = 1.035530314tg(166) = -0.2493280028tg(286) = -3.487414444
tg(47) = 1.07236871tg(167) = -0.2308681911tg(287) = -3.270852618
tg(48) = 1.110612515tg(168) = -0.2125565617tg(288) = -3.077683537
tg(49) = 1.150368407tg(169) = -0.1943803091tg(289) = -2.904210878
tg(50) = 1.191753593tg(170) = -0.1763269807tg(290) = -2.747477419
tg(51) = 1.234897157tg(171) = -0.1583844403tg(291) = -2.605089065
tg(52) = 1.279941632tg(172) = -0.1405408347tg(292) = -2.475086853
tg(53) = 1.327044822tg(173) = -0.1227845609tg(293) = -2.355852366
tg(54) = 1.37638192tg(174) = -0. 1051042353tg(294) = -2.246036774
tg(55) = 1.428148007tg(175) = -0.08748866353tg(295) = -2.144506921
tg(56) = 1.482560969tg(176) = -0.06992681194tg(296) = -2.050303842
tg(57) = 1.539864964tg(177) = -0.05240777928tg(297) = -1.962610506
tg(58) = 1.600334529tg(178) = -0.03492076949tg(298) = -1.880726465
tg(59) = 1.664279482tg(179) = -0.01745506493tg(299) = -1.804047755
tg(60) = 1.732050808tg(180) = 0tg(300) = -1.732050808
tg(61) = 1.804047755tg(181) = 0.01745506493tg(301) = -1.664279482
tg(62) = 1.880726465tg(182) = 0.03492076949tg(302) = -1.600334529
tg(63) = 1.962610506tg(183) = 0.05240777928tg(303) = -1.539864964
tg(64) = 2.050303842tg(184) = 0. 06992681194tg(304) = -1.482560969
tg(65) = 2.144506921tg(185) = 0.08748866353tg(305) = -1.428148007
tg(66) = 2.246036774tg(186) = 0.1051042353tg(306) = -1.37638192
tg(67) = 2.355852366tg(187) = 0.1227845609tg(307) = -1.327044822
tg(68) = 2.475086853tg(188) = 0.1405408347tg(308) = -1.279941632
tg(69) = 2.605089065tg(189) = 0.1583844403tg(309) = -1.234897157
tg(70) = 2.747477419tg(190) = 0.1763269807tg(310) = -1.191753593
tg(71) = 2.904210878tg(191) = 0.1943803091tg(311) = -1.150368407
tg(72) = 3.077683537tg(192) = 0.2125565617tg(312) = -1.110612515
tg(73) = 3.270852618tg(193) = 0.2308681911tg(313) = -1.07236871
tg(74) = 3.487414444tg(194) = 0.2493280028tg(314) = -1. 035530314
tg(75) = 3.732050808tg(195) = 0.2679491924tg(315) = -1
tg(76) = 4.010780934tg(196) = 0.2867453858tg(316) = -0.9656887748
tg(77) = 4.331475874tg(197) = 0.3057306815tg(317) = -0.9325150861
tg(78) = 4.704630109tg(198) = 0.3249196962tg(318) = -0.9004040443
tg(79) = 5.144554016tg(199) = 0.3443276133tg(319) = -0.8692867378
tg(80) = 5.67128182tg(200) = 0.3639702343tg(320) = -0.8390996312
tg(81) = 6.313751515tg(201) = 0.383864035tg(321) = -0.8097840332
tg(82) = 7.115369722tg(202) = 0.4040262258tg(322) = -0.7812856265
tg(83) = 8.144346428tg(203) = 0.4244748162tg(323) = -0.7535540501
tg(84) = 9.514364454tg(204) = 0.4452286853tg(324) = -0.726542528
tg(85) = 11.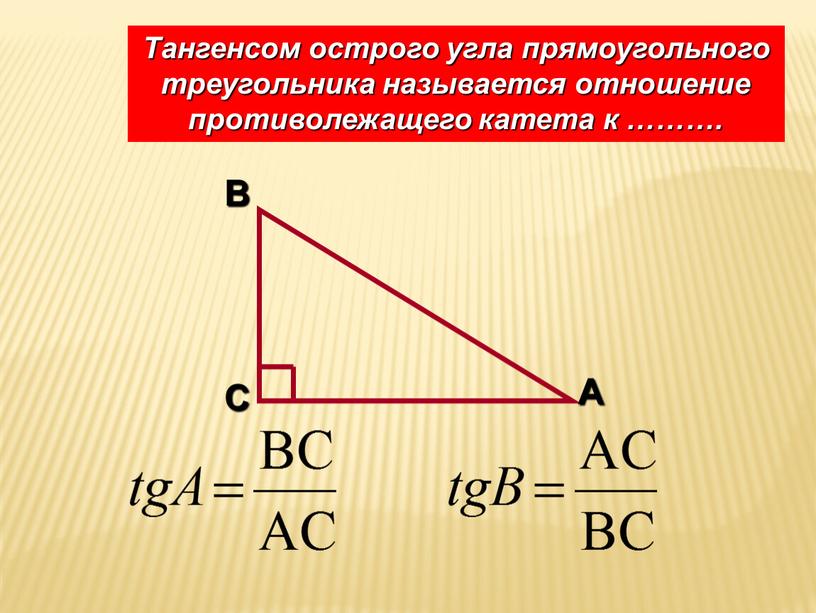 4300523tg(205) = 0.4663076582tg(325) = -0.7002075382
tg(86) = 14.30066626tg(206) = 0.4877325886tg(326) = -0.6745085168
tg(87) = 19.08113669tg(207) = 0.5095254495tg(327) = -0.6494075932
tg(88) = 28.63625328tg(208) = 0.5317094317tg(328) = -0.6248693519
tg(89) = 57.28996163tg(209) = 0.5543090515tg(329) = -0.600860619
tg(90) = ∞tg(210) = 0.5773502692tg(330) = -0.5773502692
tg(91) = -57.28996163tg(211) = 0.600860619tg(331) = -0.5543090515
tg(92) = -28.63625328tg(212) = 0.6248693519tg(332) = -0.5317094317
tg(93) = -19.08113669tg(213) = 0.6494075932tg(333) = -0.5095254495
tg(94) = -14.30066626tg(214) = 0.6745085168tg(334) = -0.4877325886
tg(95) = -11.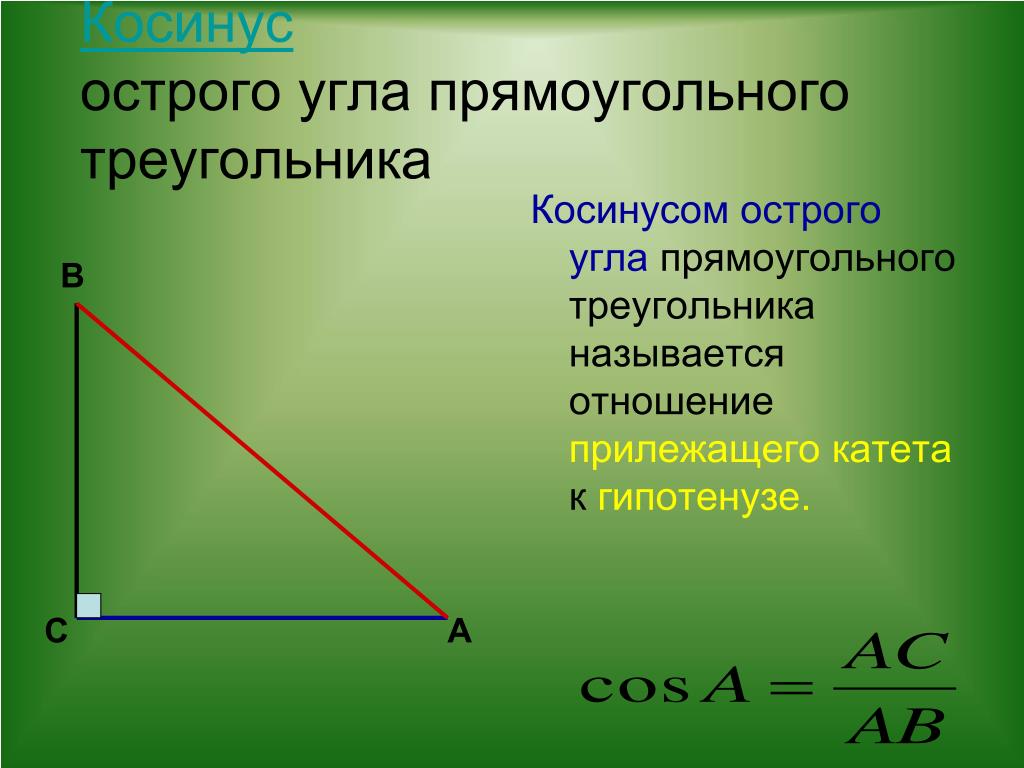 4300523tg(215) = 0.7002075382tg(335) = -0.4663076582
tg(96) = -9.514364454tg(216) = 0.726542528tg(336) = -0.4452286853
tg(97) = -8.144346428tg(217) = 0.7535540501tg(337) = -0.4244748162
tg(98) = -7.115369722tg(218) = 0.7812856265tg(338) = -0.4040262258
tg(99) = -6.313751515tg(219) = 0.8097840332tg(339) = -0.383864035
tg(100) = -5.67128182tg(220) = 0.8390996312tg(340) = -0.3639702343
tg(101) = -5.144554016tg(221) = 0.8692867378tg(341) = -0.3443276133
tg(102) = -4.704630109tg(222) = 0.9004040443tg(342) = -0.3249196962
tg(103) = -4.331475874tg(223) = 0.9325150861tg(343) = -0.3057306815
tg(104) = -4.010780934tg(224) = 0.9656887748tg(344) = -0.2867453858
tg(105) = -3. 732050808tg(225) = 1tg(345) = -0.2679491924
tg(106) = -3.487414444tg(226) = 1.035530314tg(346) = -0.2493280028
tg(107) = -3.270852618tg(227) = 1.07236871tg(347) = -0.2308681911
tg(108) = -3.077683537tg(228) = 1.110612515tg(348) = -0.2125565617
tg(109) = -2.904210878tg(229) = 1.150368407tg(349) = -0.1943803091
tg(110) = -2.747477419tg(230) = 1.191753593tg(350) = -0.1763269807
tg(111) = -2.605089065tg(231) = 1.234897157tg(351) = -0.1583844403
tg(112) = -2.475086853tg(232) = 1.279941632tg(352) = -0.1405408347
tg(113) = -2.355852366tg(233) = 1.327044822tg(353) = -0.1227845609
tg(114) = -2.246036774tg(234) = 1.37638192tg(354) = -0.1051042353
tg(115) = -2. 144506921tg(235) = 1.428148007tg(355) = -0.08748866353
tg(116) = -2.050303842tg(236) = 1.482560969tg(356) = -0.06992681194
tg(117) = -1.962610506tg(237) = 1.539864964tg(357) = -0.05240777928
tg(118) = -1.880726465tg(238) = 1.600334529tg(358) = -0.03492076949
tg(119) = -1.804047755tg(239) = 1.664279482tg(359) = -0.01745506493

Тангенс 292 градусов
Тангенс минус 207 градусов
Тангенс 226 градусов
Тангенс 269 градусов
Тангенс минус 191 градуса

Котангенс угла онлайн. Таблица котангенсов. Формула котангенса угла.

Котангенс угла через градусы, минуты и секунды

&plus;−

Котангенс угла через десятичную запись угла

Определение котангенса

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

tg(α) = cos(α)/sin(α)

сtg(α) = 1/tg(α)

Таблица котангенсов в радианах

ctg(0°) = ∞ctg(π/12) = ctg(15°) = 3. 732050808ctg(π/6) = ctg(30°) = 1.732050808ctg(π/4) = ctg(45°) = 1ctg(π/3) = ctg(60°) = 0.577350269ctg(5π/12) = ctg(75°) = 0.2679491924ctg(π/2) = ctg(90°) = 0ctg(7π/12) = ctg(105°) = -0.2679491924ctg(2π/3) = ctg(120°) = -0.577350269ctg(3π/4) = ctg(135°) = -1ctg(5π/6) = ctg(150°) = -1.732050808ctg(11π/12) = ctg(165°) = -3.732050808ctg(π) = ctg(180°) = ∞ctg(13π/12) = ctg(195°) = 3.732050808ctg(7π/6) = ctg(210°) = 1.732050808ctg(5π/4) = ctg(225°) = 1ctg(4π/3) = ctg(240°) = 0.577350269ctg(17π/12) = ctg(255°) = 0.2679491924ctg(3π/2) = ctg(270°) = 0ctg(19π/12) = ctg(285°) = -0.2679491924ctg(5π/3) = ctg(300°) = -0.577350269ctg(7π/4) = ctg(315°) = -1ctg(11π/6) = ctg(330°) = -1.732050808ctg(23π/12) = ctg(345°) = -3.732050808

Таблица Брадиса котангенсы

ctg(0) = ∞ctg(120) = -0.577350269ctg(240) = 0.577350269
ctg(1) = 57.28996162ctg(121) = -0.6008606192ctg(241) = 0.5543090515
ctg(2) = 28.63625328ctg(122) = -0. 6248693519ctg(242) = 0.5317094318
ctg(3) = 19.08113669ctg(123) = -0.6494075931ctg(243) = 0.5095254494
ctg(4) = 14.30066626ctg(124) = -0.6745085166ctg(244) = 0.4877325885
ctg(5) = 11.4300523ctg(125) = -0.7002075381ctg(245) = 0.466307658
ctg(6) = 9.514364451ctg(126) = -0.7265425283ctg(246) = 0.4452286853
ctg(7) = 8.144346428ctg(127) = -0.7535540499ctg(247) = 0.4244748162
ctg(8) = 7.115369723ctg(128) = -0.7812856266ctg(248) = 0.4040262259
ctg(9) = 6.313751516ctg(129) = -0.8097840329ctg(249) = 0.383864035
ctg(10) = 5.67128182ctg(130) = -0.8390996309ctg(250) = 0.3639702343
ctg(11) = 5.144554017ctg(131) = -0.869286738ctg(251) = 0.3443276133
ctg(12) = 4.704630109ctg(132) = -0. 9004040442ctg(252) = 0.3249196963
ctg(13) = 4.331475875ctg(133) = -0.9325150862ctg(253) = 0.3057306815
ctg(14) = 4.010780934ctg(134) = -0.9656887746ctg(254) = 0.2867453857
ctg(15) = 3.732050808ctg(135) = -1ctg(255) = 0.2679491924
ctg(16) = 3.487414443ctg(136) = -1.035530314ctg(256) = 0.2493280028
ctg(17) = 3.270852618ctg(137) = -1.07236871ctg(257) = 0.2308681911
ctg(18) = 3.077683537ctg(138) = -1.110612515ctg(258) = 0.2125565617
ctg(19) = 2.904210878ctg(139) = -1.150368407ctg(259) = 0.1943803091
ctg(20) = 2.747477419ctg(140) = -1.191753593ctg(260) = 0.1763269807
ctg(21) = 2.605089065ctg(141) = -1.234897157ctg(261) = 0.1583844403
ctg(22) = 2.475086854ctg(142) = -1. 279941632ctg(262) = 0.1405408347
ctg(23) = 2.355852366ctg(143) = -1.327044822ctg(263) = 0.1227845609
ctg(24) = 2.246036774ctg(144) = -1.37638192ctg(264) = 0.1051042353
ctg(25) = 2.14450692ctg(145) = -1.428148007ctg(265) = 0.08748866355
ctg(26) = 2.050303841ctg(146) = -1.482560969ctg(266) = 0.06992681193
ctg(27) = 1.962610505ctg(147) = -1.539864964ctg(267) = 0.05240777928
ctg(28) = 1.880726465ctg(148) = -1.600334529ctg(268) = 0.0349207695
ctg(29) = 1.804047755ctg(149) = -1.664279482ctg(269) = 0.01745506493
ctg(30) = 1.732050808ctg(150) = -1.732050808ctg(270) = 0
ctg(31) = 1.664279482ctg(151) = -1.804047755ctg(271) = -0.01745506493
ctg(32) = 1.600334529ctg(152) = -1.880726465ctg(272) = -0.0349207695
ctg(33) = 1.539864964ctg(153) = -1.962610505ctg(273) = -0.05240777928
ctg(34) = 1.482560969ctg(154) = -2.050303841ctg(274) = -0.06992681193
ctg(35) = 1.428148007ctg(155) = -2.14450692ctg(275) = -0.08748866355
ctg(36) = 1.37638192ctg(156) = -2.246036774ctg(276) = -0.1051042353
ctg(37) = 1.327044822ctg(157) = -2.355852366ctg(277) = -0.1227845609
ctg(38) = 1.279941632ctg(158) = -2.475086854ctg(278) = -0.1405408347
ctg(39) = 1.234897157ctg(159) = -2.605089065ctg(279) = -0.1583844403
ctg(40) = 1.191753593ctg(160) = -2.747477419ctg(280) = -0.1763269807
ctg(41) = 1.150368407ctg(161) = -2.904210878ctg(281) = -0.1943803091
ctg(42) = 1.110612515ctg(162) = -3.077683537ctg(282) = -0.2125565617
ctg(43) = 1.07236871ctg(163) = -3.270852618ctg(283) = -0.2308681911
ctg(44) = 1.035530314ctg(164) = -3.487414443ctg(284) = -0.2493280028
ctg(45) = 1ctg(165) = -3.732050808ctg(285) = -0.2679491924
ctg(46) = 0.9656887746ctg(166) = -4.010780934ctg(286) = -0.2867453857
ctg(47) = 0.9325150862ctg(167) = -4.331475875ctg(287) = -0.3057306815
ctg(48) = 0.9004040442ctg(168) = -4.704630109ctg(288) = -0.3249196963
ctg(49) = 0.869286738ctg(169) = -5.144554017ctg(289) = -0.3443276133
ctg(50) = 0.8390996309ctg(170) = -5.67128182ctg(290) = -0.3639702343
ctg(51) = 0.8097840329ctg(171) = -6.313751516ctg(291) = -0.383864035
ctg(52) = 0.7812856266ctg(172) = -7.115369723ctg(292) = -0.4040262259
ctg(53) = 0.7535540499ctg(173) = -8.144346428ctg(293) = -0.4244748162
ctg(54) = 0.7265425283ctg(174) = -9.514364451ctg(294) = -0.4452286853
ctg(55) = 0.7002075381ctg(175) = -11.4300523ctg(295) = -0.466307658
ctg(56) = 0.6745085166ctg(176) = -14.30066626ctg(296) = -0.4877325885
ctg(57) = 0.6494075931ctg(177) = -19.08113669ctg(297) = -0.5095254494
ctg(58) = 0.6248693519ctg(178) = -28.63625328ctg(298) = -0.5317094318
ctg(59) = 0.6008606192ctg(179) = -57.28996162ctg(299) = -0.5543090515
ctg(60) = 0.577350269ctg(180) = ∞ctg(300) = -0.577350269
ctg(61) = 0.5543090515ctg(181) = 57.28996162ctg(301) = -0.6008606192
ctg(62) = 0.5317094318ctg(182) = 28.63625328ctg(302) = -0.6248693519
ctg(63) = 0.5095254494ctg(183) = 19.08113669ctg(303) = -0.6494075931
ctg(64) = 0.4877325885ctg(184) = 14.30066626ctg(304) = -0.6745085166
ctg(65) = 0.466307658ctg(185) = 11.4300523ctg(305) = -0.7002075381
ctg(66) = 0.4452286853ctg(186) = 9.514364451ctg(306) = -0.7265425283
ctg(67) = 0.4244748162ctg(187) = 8.144346428ctg(307) = -0.7535540499
ctg(68) = 0.4040262259ctg(188) = 7.115369723ctg(308) = -0.7812856266
ctg(69) = 0.383864035ctg(189) = 6.313751516ctg(309) = -0.8097840329
ctg(70) = 0.3639702343ctg(190) = 5.67128182ctg(310) = -0.8390996309
ctg(71) = 0.3443276133ctg(191) = 5.144554017ctg(311) = -0.869286738
ctg(72) = 0.3249196963ctg(192) = 4.704630109ctg(312) = -0.9004040442
ctg(73) = 0.3057306815ctg(193) = 4.331475875ctg(313) = -0.9325150862
ctg(74) = 0.2867453857ctg(194) = 4.010780934ctg(314) = -0.9656887746
ctg(75) = 0.2679491924ctg(195) = 3.732050808ctg(315) = -1
ctg(76) = 0.2493280028ctg(196) = 3.487414443ctg(316) = -1.035530314
ctg(77) = 0.2308681911ctg(197) = 3.270852618ctg(317) = -1.07236871
ctg(78) = 0.2125565617ctg(198) = 3.077683537ctg(318) = -1.110612515
ctg(79) = 0.1943803091ctg(199) = 2.904210878ctg(319) = -1.150368407
ctg(80) = 0.1763269807ctg(200) = 2.747477419ctg(320) = -1.191753593
ctg(81) = 0.1583844403ctg(201) = 2.605089065ctg(321) = -1.234897157
ctg(82) = 0.1405408347ctg(202) = 2.475086854ctg(322) = -1.279941632
ctg(83) = 0.1227845609ctg(203) = 2.355852366ctg(323) = -1.327044822
ctg(84) = 0.1051042353ctg(204) = 2.246036774ctg(324) = -1.37638192
ctg(85) = 0.08748866355ctg(205) = 2.14450692ctg(325) = -1.428148007
ctg(86) = 0.06992681193ctg(206) = 2.050303841ctg(326) = -1.482560969
ctg(87) = 0.05240777928ctg(207) = 1.962610505ctg(327) = -1.539864964
ctg(88) = 0.0349207695ctg(208) = 1.880726465ctg(328) = -1.600334529
ctg(89) = 0.01745506493ctg(209) = 1.804047755ctg(329) = -1.664279482
ctg(90) = 0ctg(210) = 1.732050808ctg(330) = -1.732050808
ctg(91) = -0.01745506493ctg(211) = 1.664279482ctg(331) = -1.804047755
ctg(92) = -0.0349207695ctg(212) = 1.600334529ctg(332) = -1.880726465
ctg(93) = -0.05240777928ctg(213) = 1.539864964ctg(333) = -1.962610505
ctg(94) = -0.06992681193ctg(214) = 1.482560969ctg(334) = -2.050303841
ctg(95) = -0.08748866355ctg(215) = 1.428148007ctg(335) = -2.14450692
ctg(96) = -0.1051042353ctg(216) = 1.37638192ctg(336) = -2.246036774
ctg(97) = -0.1227845609ctg(217) = 1.327044822ctg(337) = -2.355852366
ctg(98) = -0.1405408347ctg(218) = 1.279941632ctg(338) = -2.475086854
ctg(99) = -0.1583844403ctg(219) = 1.234897157ctg(339) = -2.605089065
ctg(100) = -0.1763269807ctg(220) = 1.191753593ctg(340) = -2.747477419
ctg(101) = -0.1943803091ctg(221) = 1.150368407ctg(341) = -2.904210878
ctg(102) = -0.2125565617ctg(222) = 1.110612515ctg(342) = -3.077683537
ctg(103) = -0.2308681911ctg(223) = 1.07236871ctg(343) = -3.270852618
ctg(104) = -0.2493280028ctg(224) = 1.035530314ctg(344) = -3.487414443
ctg(105) = -0.2679491924ctg(225) = 1ctg(345) = -3.732050808
ctg(106) = -0.2867453857ctg(226) = 0.9656887746ctg(346) = -4.010780934
ctg(107) = -0.3057306815ctg(227) = 0.9325150862ctg(347) = -4.331475875
ctg(108) = -0.3249196963ctg(228) = 0.9004040442ctg(348) = -4.704630109
ctg(109) = -0.3443276133ctg(229) = 0.869286738ctg(349) = -5.144554017
ctg(110) = -0.3639702343ctg(230) = 0.8390996309ctg(350) = -5.67128182
ctg(111) = -0.383864035ctg(231) = 0.8097840329ctg(351) = -6.313751516
ctg(112) = -0.4040262259ctg(232) = 0.7812856266ctg(352) = -7.115369723
ctg(113) = -0.4244748162ctg(233) = 0.7535540499ctg(353) = -8.144346428
ctg(114) = -0.4452286853ctg(234) = 0.7265425283ctg(354) = -9.514364451
ctg(115) = -0.466307658ctg(235) = 0.7002075381ctg(355) = -11.4300523
ctg(116) = -0.4877325885ctg(236) = 0.6745085166ctg(356) = -14.30066626
ctg(117) = -0.5095254494ctg(237) = 0.6494075931ctg(357) = -19.08113669
ctg(118) = -0.5317094318ctg(238) = 0.6248693519ctg(358) = -28.63625328
ctg(119) = -0.5543090515ctg(239) = 0.6008606192ctg(359) = -57.28996162

Котангенс минус 68 градусов
Котангенс 161 градуса
Котангенс минус 209 градусов
Котангенс минус 49 градусов
Котангенс минус 176 градусов

Синус угла онлайн. Таблица синусов. Формула синуса угла.

Синус угла через градусы, минуты и секунды

&plus;−

Синус угла через десятичную запись угла

Как найти угол зная синус этого угла

У синуса есть обратная тригонометрическая функция — arcsin(y)=x

sin(arcsin(y))=y

Пример sin(30°) = 1/2; arcsin(1/2) = 30°

Рассчитать арксинус

Определение синуса

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

sin(α) = BC/AB

sin(-α) = -sin(α)

Периодичность синуса

Функция y = sin(x) периодична, с периодом 2π

sin(α ± 2π) = sin(α)

Пример sin(5π) = sin(4π + π) = sin(π)

Таблица синусов в радианах

sin(0°) = 0sin(π/12) = sin(15°) = 0.2588190451sin(π/6) = sin(30°) = 0.5sin(π/4) = sin(45°) = 0.7071067812sin(π/3) = sin(60°) = 0.8660254038sin(5π/12) = sin(75°) = 0.9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105°) = 0.9659258263sin(2π/3) = sin(120°) = 0.8660254038sin(3π/4) = sin(135°) = 0.7071067812sin(5π/6) = sin(150°) = 0.5sin(11π/12) = sin(165°) = 0.2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0.2588190451sin(7π/6) = sin(210°) = -0.5sin(5π/4) = sin(225°) = -0.7071067812sin(4π/3) = sin(240°) = -0.8660254038sin(17π/12) = sin(255°) = -0.9659258263sin(3π/2) = sin(270°) = -1sin(19π/12) = sin(285°) = -0.9659258263sin(5π/3) = sin(300°) = -0.8660254038sin(7π/4) = sin(315°) = -0.7071067812sin(11π/6) = sin(330°) = -0.5sin(23π/12) = sin(345°) = -0.2588190451

Таблица Брадиса синусы

sin(0) = 0sin(120) = 0.8660254038sin(240) = -0.8660254038
sin(1) = 0.01745240644sin(121) = 0.8571673007sin(241) = -0.8746197071
sin(2) = 0.0348994967sin(122) = 0.8480480962sin(242) = -0.8829475929
sin(3) = 0.05233595624sin(123) = 0.8386705679sin(243) = -0.8910065242
sin(4) = 0.06975647374sin(124) = 0.8290375726sin(244) = -0.8987940463
sin(5) = 0.08715574275sin(125) = 0.8191520443sin(245) = -0.906307787
sin(6) = 0.1045284633sin(126) = 0.8090169944sin(246) = -0.9135454576
sin(7) = 0.1218693434sin(127) = 0.79863551sin(247) = -0.9205048535
sin(8) = 0.139173101sin(128) = 0.7880107536sin(248) = -0.9271838546
sin(9) = 0.156434465sin(129) = 0.7771459615sin(249) = -0.9335804265
sin(10) = 0.1736481777sin(130) = 0.7660444431sin(250) = -0.9396926208
sin(11) = 0.1908089954sin(131) = 0.7547095802sin(251) = -0.9455185756
sin(12) = 0.2079116908sin(132) = 0.7431448255sin(252) = -0.9510565163
sin(13) = 0.2249510543sin(133) = 0.7313537016sin(253) = -0.956304756
sin(14) = 0.2419218956sin(134) = 0.7193398003sin(254) = -0.9612616959
sin(15) = 0.2588190451sin(135) = 0.7071067812sin(255) = -0.9659258263
sin(16) = 0.2756373558sin(136) = 0.6946583705sin(256) = -0.9702957263
sin(17) = 0.2923717047sin(137) = 0.6819983601sin(257) = -0.9743700648
sin(18) = 0.3090169944sin(138) = 0.6691306064sin(258) = -0.9781476007
sin(19) = 0.3255681545sin(139) = 0.656059029sin(259) = -0.9816271834
sin(20) = 0.3420201433sin(140) = 0.6427876097sin(260) = -0.984807753
sin(21) = 0.3583679495sin(141) = 0.629320391sin(261) = -0.9876883406
sin(22) = 0.3746065934sin(142) = 0.6156614753sin(262) = -0.9902680687
sin(23) = 0.3907311285sin(143) = 0.6018150232sin(263) = -0.9925461516
sin(24) = 0.4067366431sin(144) = 0.5877852523sin(264) = -0.9945218954
sin(25) = 0.4226182617sin(145) = 0.5735764364sin(265) = -0.9961946981
sin(26) = 0.4383711468sin(146) = 0.5591929035sin(266) = -0.9975640503
sin(27) = 0.4539904997sin(147) = 0.544639035sin(267) = -0.9986295348
sin(28) = 0.4694715628sin(148) = 0.5299192642sin(268) = -0.999390827
sin(29) = 0.4848096202sin(149) = 0.5150380749sin(269) = -0.9998476952
sin(30) = 0.5sin(150) = 0.5sin(270) = -1
sin(31) = 0.5150380749sin(151) = 0.4848096202sin(271) = -0.9998476952
sin(32) = 0.5299192642sin(152) = 0.4694715628sin(272) = -0.999390827
sin(33) = 0.544639035sin(153) = 0.4539904997sin(273) = -0.9986295348
sin(34) = 0.5591929035sin(154) = 0.4383711468sin(274) = -0.9975640503
sin(35) = 0.5735764364sin(155) = 0.4226182617sin(275) = -0.9961946981
sin(36) = 0.5877852523sin(156) = 0.4067366431sin(276) = -0.9945218954
sin(37) = 0.6018150232sin(157) = 0.3907311285sin(277) = -0.9925461516
sin(38) = 0.6156614753sin(158) = 0.3746065934sin(278) = -0.9902680687
sin(39) = 0.629320391sin(159) = 0.3583679495sin(279) = -0.9876883406
sin(40) = 0.6427876097sin(160) = 0.3420201433sin(280) = -0.984807753
sin(41) = 0.656059029sin(161) = 0.3255681545sin(281) = -0.9816271834
sin(42) = 0.6691306064sin(162) = 0.3090169944sin(282) = -0.9781476007
sin(43) = 0.6819983601sin(163) = 0.2923717047sin(283) = -0.9743700648
sin(44) = 0.6946583705sin(164) = 0.2756373558sin(284) = -0.9702957263
sin(45) = 0.7071067812sin(165) = 0.2588190451sin(285) = -0.9659258263
sin(46) = 0.7193398003sin(166) = 0.2419218956sin(286) = -0.9612616959
sin(47) = 0.7313537016sin(167) = 0.2249510543sin(287) = -0.956304756
sin(48) = 0.7431448255sin(168) = 0.2079116908sin(288) = -0.9510565163
sin(49) = 0.7547095802sin(169) = 0.1908089954sin(289) = -0.9455185756
sin(50) = 0.7660444431sin(170) = 0.1736481777sin(290) = -0.9396926208
sin(51) = 0.7771459615sin(171) = 0.156434465sin(291) = -0.9335804265
sin(52) = 0.7880107536sin(172) = 0.139173101sin(292) = -0.9271838546
sin(53) = 0.79863551sin(173) = 0.1218693434sin(293) = -0.9205048535
sin(54) = 0.8090169944sin(174) = 0.1045284633sin(294) = -0.9135454576
sin(55) = 0.8191520443sin(175) = 0.08715574275sin(295) = -0.906307787
sin(56) = 0.8290375726sin(176) = 0.06975647374sin(296) = -0.8987940463
sin(57) = 0.8386705679sin(177) = 0.05233595624sin(297) = -0.8910065242
sin(58) = 0.8480480962sin(178) = 0.0348994967sin(298) = -0.8829475929
sin(59) = 0.8571673007sin(179) = 0.01745240644sin(299) = -0.8746197071
sin(60) = 0.8660254038sin(180) = 0sin(300) = -0.8660254038
sin(61) = 0.8746197071sin(181) = -0.01745240644sin(301) = -0.8571673007
sin(62) = 0.8829475929sin(182) = -0.0348994967sin(302) = -0.8480480962
sin(63) = 0.8910065242sin(183) = -0.05233595624sin(303) = -0.8386705679
sin(64) = 0.8987940463sin(184) = -0.06975647374sin(304) = -0.8290375726
sin(65) = 0.906307787sin(185) = -0.08715574275sin(305) = -0.8191520443
sin(66) = 0.9135454576sin(186) = -0.1045284633sin(306) = -0.8090169944
sin(67) = 0.9205048535sin(187) = -0.1218693434sin(307) = -0.79863551
sin(68) = 0.9271838546sin(188) = -0.139173101sin(308) = -0.7880107536
sin(69) = 0.9335804265sin(189) = -0.156434465sin(309) = -0.7771459615
sin(70) = 0.9396926208sin(190) = -0.1736481777sin(310) = -0.7660444431
sin(71) = 0.9455185756sin(191) = -0.1908089954sin(311) = -0.7547095802
sin(72) = 0.9510565163sin(192) = -0.2079116908sin(312) = -0.7431448255
sin(73) = 0.956304756sin(193) = -0.2249510543sin(313) = -0.7313537016
sin(74) = 0.9612616959sin(194) = -0.2419218956sin(314) = -0.7193398003
sin(75) = 0.9659258263sin(195) = -0.2588190451sin(315) = -0.7071067812
sin(76) = 0.9702957263sin(196) = -0.2756373558sin(316) = -0.6946583705
sin(77) = 0.9743700648sin(197) = -0.2923717047sin(317) = -0.6819983601
sin(78) = 0.9781476007sin(198) = -0.3090169944sin(318) = -0.6691306064
sin(79) = 0.9816271834sin(199) = -0.3255681545sin(319) = -0.656059029
sin(80) = 0.984807753sin(200) = -0.3420201433sin(320) = -0.6427876097
sin(81) = 0.9876883406sin(201) = -0.3583679495sin(321) = -0.629320391
sin(82) = 0.9902680687sin(202) = -0.3746065934sin(322) = -0.6156614753
sin(83) = 0.9925461516sin(203) = -0.3907311285sin(323) = -0.6018150232
sin(84) = 0.9945218954sin(204) = -0.4067366431sin(324) = -0.5877852523
sin(85) = 0.9961946981sin(205) = -0.4226182617sin(325) = -0.5735764364
sin(86) = 0.9975640503sin(206) = -0.4383711468sin(326) = -0.5591929035
sin(87) = 0.9986295348sin(207) = -0.4539904997sin(327) = -0.544639035
sin(88) = 0.999390827sin(208) = -0.4694715628sin(328) = -0.5299192642
sin(89) = 0.9998476952sin(209) = -0.4848096202sin(329) = -0.5150380749
sin(90) = 1sin(210) = -0.5sin(330) = -0.5
sin(91) = 0.9998476952sin(211) = -0.5150380749sin(331) = -0.4848096202
sin(92) = 0.999390827sin(212) = -0.5299192642sin(332) = -0.4694715628
sin(93) = 0.9986295348sin(213) = -0.544639035sin(333) = -0.4539904997
sin(94) = 0.9975640503sin(214) = -0.5591929035sin(334) = -0.4383711468
sin(95) = 0.9961946981sin(215) = -0.5735764364sin(335) = -0.4226182617
sin(96) = 0.9945218954sin(216) = -0.5877852523sin(336) = -0.4067366431
sin(97) = 0.9925461516sin(217) = -0.6018150232sin(337) = -0.3907311285
sin(98) = 0.9902680687sin(218) = -0.6156614753sin(338) = -0.3746065934
sin(99) = 0.9876883406sin(219) = -0.629320391sin(339) = -0.3583679495
sin(100) = 0.984807753sin(220) = -0.6427876097sin(340) = -0.3420201433
sin(101) = 0.9816271834sin(221) = -0.656059029sin(341) = -0.3255681545
sin(102) = 0.9781476007sin(222) = -0.6691306064sin(342) = -0.3090169944
sin(103) = 0.9743700648sin(223) = -0.6819983601sin(343) = -0.2923717047
sin(104) = 0.9702957263sin(224) = -0.6946583705sin(344) = -0.2756373558
sin(105) = 0.9659258263sin(225) = -0.7071067812sin(345) = -0.2588190451
sin(106) = 0.9612616959sin(226) = -0.7193398003sin(346) = -0.2419218956
sin(107) = 0.956304756sin(227) = -0.7313537016sin(347) = -0.2249510543
sin(108) = 0.9510565163sin(228) = -0.7431448255sin(348) = -0.2079116908
sin(109) = 0.9455185756sin(229) = -0.7547095802sin(349) = -0.1908089954
sin(110) = 0.9396926208sin(230) = -0.7660444431sin(350) = -0.1736481777
sin(111) = 0.9335804265sin(231) = -0.7771459615sin(351) = -0.156434465
sin(112) = 0.9271838546sin(232) = -0.7880107536sin(352) = -0.139173101
sin(113) = 0.9205048535sin(233) = -0.79863551sin(353) = -0.1218693434
sin(114) = 0.9135454576sin(234) = -0.8090169944sin(354) = -0.1045284633
sin(115) = 0.906307787sin(235) = -0.8191520443sin(355) = -0.08715574275
sin(116) = 0.8987940463sin(236) = -0.8290375726sin(356) = -0.06975647374
sin(117) = 0.8910065242sin(237) = -0.8386705679sin(357) = -0.05233595624
sin(118) = 0.8829475929sin(238) = -0.8480480962sin(358) = -0.0348994967
sin(119) = 0.8746197071sin(239) = -0.8571673007sin(359) = -0.01745240644

Похожие калькуляторы

Тригонометрия для чайников. Урок1. Тригонометрия с нуля

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

 

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

 

Синус угла – отношение противолежащего катета к гипотенузе.

sinα=Противолежащий катетгипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cosα=Прилежащий катетгипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tgα=Противолежащий катетПрилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctgα=Прилежащий катетПротиволежащий катет

 

Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:

sin∠A=CBAB

cos∠A=ACAB

tg∠A=sin∠Acos∠A=CBAC

ctg∠A=cos∠Asin∠A=ACCB

sin∠B=ACAB

cos∠B=BCAB

tg∠B=sin∠Bcos∠B=ACCB

ctg∠B=cos∠Bsin∠B=CBAC

 

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат. 

Такая окружность пересекает ось х в точках (−1;0) и (1;0), ось y в точках (0;−1) и (0;1)

На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами (1;0), – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠SOA, обозначим его за α. Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠SOA=α=∪SA.

 

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).

 

Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.

Рассмотрим прямоугольный треугольник AOB:

cosα=OBOA=OB1=OB

sinα=ABOA=AB1=AB

Поскольку OCAB – прямоугольник, AB=CO.

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

 

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90°:

 

Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x.Косинус тупого угла отрицательный.

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0° до 180°. Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x.  (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0°,30°,45°,60°,90°,120°,135°,150°,180°. Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.

 

Координата по оси x – косинус угла, координата по оси y – синус угла.

Пример:

cos150°=−32

sin150°=12

 

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.

 

sin2α+cos2α=1

Данное тождество – теорема Пифагора в прямоугольном треугольнике OAB:

 

AB2+OB2=OA2

sin2α+cos2α=R2

sin2α+cos2α=1

 

0° 30° 45° 60° 90°
sinα 0 12 22 32 1
cosα 1 32 22 12 0
tgα 0 33 1 3 нет
ctgα нет 3 1 33 0

 

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

 

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin180°=sin(180°−0°)=sin0°

sin150°=sin(180°−30°)=sin30°

sin135°=sin(180°−45°)=sin45°

sin120°=sin(180°−60°)=sin60°

 

cos180°=cos(180°−0°)=−cos0°

cos150°=cos(180°−30°)=−cos30°

cos135°=cos(180°−45°)=−cos45°

cos120°=cos(180°−60°)=−cos60°

 

Рассмотрим тупой угол β:

 

Для произвольного тупого угла β=180°−α всегда будут справедливы следующие равенства:

sin(180°−α)=sinα

cos(180°−α)=−cosα

tg(180°−α)=−tgα

ctg(180°−α)=−ctgα

 

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

 

asin∠A=bsin∠B=csin∠C

 

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

 

asin∠A=bsin∠B=csin∠C=2R

 

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

 

a2=b2+c2−2bc⋅cos∠A

b2=a2+c2−2ac⋅cos∠B

c2=a2+b2−2ab⋅cos∠C

 

Модуль геометрия: задания, связанные с тригонометрией.

 

Скачать домашнее задание к уроку 1.

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

 

определение тангенса по The Free Dictionary

Тогда я подбросил ему йоркера, который он пропустил, и он улетел по касательной, как только добрался до дерева, но иногда он хочет уйти по касательной, может быть, просто потому, что ему суждено проложить дорогу и, возможно, также, что каким бы глупым ни был «прямой» практичный человек, ему иногда приходит в голову мысль, что дорога почти всегда куда-то ведет и что конечный пункт, к которому она ведет, менее важен, чем процесс ее создания. и что самое главное — спасти воспитанное дитя от презрения к инженерии и тем самым уступить место фатальному безделью, которое, как мы все знаем, является матерью всех пороков.Видите ли, европейская война потребовала использования большого количества самолетов, и поскольку их пилотам часто приходится сражаться, и поэтому они не могут уделять все свое внимание машинам, необходим какой-то автоматический стабилизатор, чтобы предотвратить их. Поворачивая черепаху или уходя по неверному пути. Достаточно того, что буревестник вращался где-то между темно-карминовым и бледно-синим, и это отвлекло мои мысли на земном касании. Я поблагодарил Бога за то, что в этих широтах нет больших морских птиц; ни ястребов, ни альбатросов, ни кур-мысов.В результате этих противоречивых влияний возникла линия, которая могла стать касательной. Но было очевидно, что снаряд не упадет прямо на Луну; потому что его нижняя часть из-за своего веса должна быть повернута к ней. Пони побежал под острым углом, чтобы осмотреть фонарный столб на противоположной стороне дороги, а затем ушел по касательной к другому фонарю. — пост с другой стороны. Существа всегда уходят в какую-нибудь фантастическую работу или нелепые рассуждения, полностью противоречащие «пригодности вещей» и не имеющие никакого дела, которое можно было бы рассматривать как бизнес.Судно, казалось, по касательной к ее прежнего курса и прыгнул почти мгновенно из поля зрения в fog.His вылетающими по касательной был бесспорно natural.The француз, который был на ногах, в акте вытекающая из саней Он также совершил воздушный полет, во многом в той позе, которую принимают мальчики, когда играют в прыгуны, и, улетев по касательной к изгибу своего курса, вошел в сугроб прямо перед головой, где он остался, две лапы на высоких лапах, как чучела на кукурузном поле.Начните прямо сейчас с того самого дальнего западного пути, который не останавливается у Миссисипи или Тихого океана и не ведет к изношенным Китаю или Японии, а ведет по прямому, касательному к этой сфере, летом и зимой, днем ​​и ночью, заходит солнце, луна вниз, и наконец земля тоже. «Скажи!» Билли ушел по касательной. «К следующей зиме, когда все гудит и выглядит как корабль, что с нами делать, чтобы навестить Кармел?

Синус, косинус, тангенс

Три функции, но та же идея.

Прямой треугольник

Синус, косинус и тангенс — основные функции, используемые в тригонометрии, они основаны на прямоугольном треугольнике.

Прежде чем углубляться в функции, полезно присвоить имя каждой стороне прямоугольного треугольника:

  • «Противоположно» противоположно углу θ
  • «Соседний» примыкает (рядом) к углу θ
  • «Гипотенуза» — длинная

Соседний всегда находится рядом с углом

И Напротив находится напротив угла

Синус, косинус и тангенс

Синус , Косинус и Касательная (часто сокращается до sin , cos и tan ), каждый — это отношение сторон прямоугольного треугольника :

Для заданного угла θ каждое отношение остается неизменным
независимо от того, насколько большой или малый треугольник

Для их расчета:

Разделите длину одной стороны на другую

Пример: Что такое синус 35 °?

Используя этот треугольник (длины до одного десятичного знака):

sin (35 °) = Напротив Гипотенуза
= 2.8 4,9
= 0,57 …
cos (35 °) = Соседний Гипотенуза
= 4,0 4,9
= 0,82 …
загар (35 °) = Напротив Соседний
= 2.8 4,0
= 0,70 …

Размер не имеет значения

Треугольник может быть большим или маленьким, а соотношение сторон остается неизменным .

Только угол меняет соотношение.

Попробуйте перетащить точку «A», чтобы изменить угол, и точку «B», чтобы изменить размер:

На хороших калькуляторах есть sin, cos и tan, чтобы облегчить вам задачу.Просто вставьте угол и нажмите кнопку.

Но все же нужно помнить , что они означают !

В форме изображения:

Практика здесь:

Sohcahtoa

Как запомнить? Думайте «Sohcahtoa» !

Работает так:

Soh …

S ine = O pposite / H ypotenuse

…ка …

C osine = A djacent / H ypotenuse

… toa

T angent = O pposite / A djacent

Вы можете узнать больше о sohcahtoa … запомните это, это может помочь на экзамене!

Углы от 0 ° до 360 °

Перемещайте мышь, чтобы увидеть, как разные углы (в радианах или градусах) влияют на синус, косинус и тангенс.

В этой анимации гипотенуза равна 1, образуя единичную окружность.

Обратите внимание, что соседняя сторона и противоположная сторона могут быть положительными или отрицательными, что также приводит к изменению синуса, косинуса и тангенса между положительными и отрицательными значениями.

«Почему sin и
tan не пошли на вечеринку?»
«… всего cos !»

Примеры

Пример: каковы синус, косинус и тангенс 30 °?

Классический треугольник 30 ° имеет гипотенузу длины 2, противоположную сторону длины 1 и смежную сторону
√3:

Теперь мы знаем длины, можем вычислить функции:

Синус

sin (30 °) = 1/2 = 0.5

Косинус

cos (30 °) = 1,732 / 2 = 0,866 …

Касательная

тангенс угла (30 °) = 1 / 1,732 = 0,577 …

(возьмите калькулятор и проверьте его!)

Пример: каковы синус, косинус и тангенс угла 45 °?

Классический треугольник 45 ° имеет две стороны 1 и гипотенузу √2:

Синус

sin (45 °) = 1/1.414 = 0,707 …

Косинус

cos (45 °) = 1 / 1,414 = 0,707 …

Касательная

тангенс угла (45 °) = 1/1 = 1

Почему?

Почему эти функции важны?

  • Потому что они позволяют нам вычислять углы, когда мы знаем стороны
  • И они позволяют нам определять стороны, когда мы знаем углы

Пример: используйте синусоидальную функцию , чтобы найти «d»

Мы знаем:

  • Кабель образует угол 39 ° с дном
  • Кабель имеет длину 30 метров .

И мы хотим знать «d» (расстояние вниз).

Начать с: sin 39 ° = противоположно / гипотенуза

sin 39 ° = d / 30

Поменять местами стороны: d / 30 = sin 39 °

С помощью калькулятора найдите sin 39 °: d / 30 = 0,6293 …

Умножаем обе стороны на 30: d = 0,6293… x 30

d = 18,88 с точностью до 2 знаков после запятой.

Глубина «d» составляет 18,88 м

Упражнение

Попробуйте это бумажное упражнение, в котором вы можете вычислить синусоидальную функцию.
для всех углов от 0 ° до 360 °, а затем нарисуйте результат.Это поможет вам понять эти относительно
простые функции.

Вы также можете увидеть графики синуса, косинуса и тангенса.

И поиграйте с пружиной, создающей синусоидальную волну.

Менее распространенные функции

Чтобы завершить картину, есть еще 3 функции, в которых мы разделяем одну сторону на другую, но они не так часто используются.

Они равны 1, деленному на cos , 1, деленному на sin , и 1, деленному на tan :

Секущая функция:

 сек ( θ ) = Гипотенуза Соседний (= 1 / cos)

Функция косеканса:

 csc ( θ ) = Гипотенуза Напротив (= 1 / sin)

Функция котангенса:

 детская кроватка ( θ ) = Соседний Напротив (= 1 / tan)

Функция тангенса в прямоугольных треугольниках — Тригонометрия

Функция тангенса в прямоугольных треугольниках — Тригонометрия — Math Open Reference

(См. Также Касательная к кругу).В
прямоугольный треугольник,
тангенс угла — это длина противоположной стороны, деленная на длину
соседняя сторона.

Попробуй это
Перетащите любой
вершину треугольника и посмотрите, как вычисляется касательная к A и C.

Касательная функция вместе с
синус и косинус — один из трех наиболее распространенных
тригонометрические функции.
В любом прямоугольном треугольнике
тангенс угла — это длина противоположной стороны (O), деленная на длину
соседняя сторона (A).В формуле он записывается просто как «загар».

Часто вспоминается как «SOH» — что означает
Синус
Напротив
Гипотенуза.

См. SOH CAH TOA.

В качестве примера предположим, что мы хотим найти тангенс угла C на рисунке выше (сначала нажмите «сбросить»).
Из приведенной выше формулы мы знаем, что тангенс угла — это противоположная сторона, деленная на соседнюю.
Противоположная сторона — это AB и имеет длину 15. Соседняя сторона — это BC длиной 26. Таким образом, мы можем написать

Это деление на калькуляторе оказывается равным 0.577.
Таким образом, мы можем сказать: « Тангенс C равен 0,5776 » или

Пример — использование касательной для определения длины стороны

Если мы посмотрим на общее определение —

мы видим, что есть три переменные: размер угла x и длины двух сторон (противоположной и смежной).
Итак, если у нас есть два из них, мы можем найти третий.

На рисунке выше нажмите «Сброс». Представьте, что мы не знаем длины стороны BC.
Мы знаем, что касательная к A (60 °) — это противоположная сторона (26), разделенная соседней стороной AB — той, которую мы пытаемся найти.Из нашего калькулятора мы находим, что загар 60 ° равен 1,733, поэтому мы можем написать

Транспонирование:

что составляет 26, что соответствует цифре выше.

Функция арктангенса — arctan

Для каждой тригонометрической функции, такой как tan, существует обратная функция, которая работает наоборот.
Эти обратные функции имеют то же имя, но с дугой впереди.
Таким образом, загар — это арктан и т.д.

Когда мы видим «арктангенс А», мы интерпретируем его как «угол, тангенс которого равен А».

загар 60 = 1.733 Означает: тангенс 60 градусов равен 1,733
арктан 1,733 = 60 Означает: угол, тангенс которого равен 1,733, равен 60 градусам.

Мы используем его, когда знаем, что такое тангенс угла, и хотим узнать фактический угол.

См. Также определение арктангенса и
Обратные функции — тригонометрия

Большие и отрицательные углы

В прямоугольном треугольнике два переменных угла всегда меньше 90 °.
(См. Внутренние углы треугольника).Но на самом деле мы можем найти тангенс любого угла, независимо от его размера, а также тангенс отрицательных углов.
Подробнее об этом см. Функции больших и отрицательных углов.

При использовании этого способа мы также можем построить график касательной функции. См. Раздел Построение касательной функции.

Производная tan (x)

В расчетах производная tan (x) равна сек 2 (x) .
Это означает, что при любом значении x скорость изменения или наклона tan (x) составляет сек 2 (x) .

Подробнее об этом см.
Производные тригонометрических функций вместе с производными других тригонометрических функций.
См. Также Оглавление по исчислению.

Другие темы по тригонометрии

Уголки

Тригонометрические функции

Решение задач тригонометрии

Исчисление

(C) Открытый справочник по математике, 2011 г.

Все права защищены.

Определение касательной к окружности

Определение касательной к окружности — Math Open Reference

Линия, которая касается дуги или окружности только в одной точке.

(См. Также функцию тангенса (загар) в прямоугольном треугольнике — тригонометрия).

Попробуйте это Перетащите оранжевую точку. Синяя линия всегда будет касательной к окружности.

Синяя линия на рисунке выше называется «касательной к окружности c».
Другими словами, синяя линия «тангенциальна» к окружности c. (Произносится «тан-ген-шулл»).

Линия едва касается круга в одной точке. Если бы линия была ближе к центру круга,
он разрезал бы круг в двух местах и ​​затем был бы назван
секущий.Фактически, вы можете думать о касательной как о предельном случае секущей.
По мере того, как секущая линия удаляется от центра круга, две точки, где она пересекает круг, в конечном итоге сливаются в одну, и линия становится касательной к окружности.

Как видно на рисунке выше, касательная линия всегда находится под прямым углом к ​​радиусу в точке контакта.

Касательные к двум окружностям

Для двух окружностей есть прямые, которые касаются их обоих одновременно.

Если круги разделены (не пересекаются), есть четыре возможных общих касательных:

Если два круга соприкасаются только в одной точке, есть три возможных касательных, общих для обоих:

Если два круга соприкасаются только в одной точке, причем один внутри другого, есть только одна линия, касательная к обоим:

Если круги перекрываются, то есть пересекаются в двух точках, есть две касательные, общие для обеих:

Если окружности лежат одна внутри другой, общих для них обоих нет касательных.Касательная к внутреннему кругу будет
секущая внешнего круга.

Строительство

Другие определения

  • В тригонометрии тангенс угла в прямоугольном треугольнике — это отношение противоположной стороны к соседней стороне.
    См. Функцию тангенса (загар) в прямоугольном треугольнике — тригонометрия.
  • В исчислении прямая касается кривой, если
    в единственной точке контакта он имеет тот же наклон, что и кривая.

Другие темы в круге

Общие

Уравнения окружности

Углы по окружности

Дуги

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

Функция тригонометрии arctan () — арктангенс — определение математического слова

Функция тригонометрии arctan () — арктангенс — определение математического слова — Math Open Reference

Функция арктангенса — это функция, обратная касательной.

Возвращает угол, тангенс которого является заданным числом.

Попробуй это
Перетащите любой
вершине треугольника и посмотрите, как вычисляется угол C с помощью функции arctan ().

Для каждой тригонометрической функции существует обратная функция, которая работает наоборот.
Эти обратные функции имеют то же имя, но с дугой впереди.
(На некоторых калькуляторах кнопка arctan может быть помечена как атан, а иногда
загар -1 .)
Таким образом, тангенс, обратный tan, равен arctan и т. Д. Когда мы видим «arctan x», мы понимаем его как «угол, тангенс которого равен x»

загар 30 = 0,577 Означает: тангенс 30 градусов равен 0,577
арктан 0.577 = 30 Означает: угол, тангенс которого равен 0,577, равен 30 градусам.

Используйте arctan, если вы знаете тангенс угла и хотите узнать фактический угол.
См. Также Обратные функции — тригонометрия

Пример — использование arctan для нахождения угла

На приведенном выше рисунке нажмите «Сброс».
Нам известны длины сторон, но нам нужно найти величину угла C.

Мы знаем, что

поэтому нам нужно знать угол, тангенс которого равен 0,577, или формально:

С помощью калькулятора находим arctan 0.577 — 30 °.

Большие и отрицательные углы

Напомним, что мы можем применить
Триггерные функции на любой угол, включая большие и отрицательные углы. Но когда мы
Рассмотрим обратную функцию, и мы столкнемся с проблемой, потому что существует бесконечное количество углов, имеющих одинаковую касательную.
Например, 45 ° и 360 + 45 ° будут иметь одинаковую касательную. Подробнее об этом см.
Обратные тригонометрические функции.

Чтобы решить эту проблему,
спектр
обратных триггерных функций ограничены
таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.

Ареал и область действия arctan

Напомним, что область определения функции — это набор допустимых входных данных для нее. Диапазон — это набор возможных выходов.

Для y = arctan x:

Диапазон
Домен Все вещественные числа

Условно диапазон arctan ограничен от -90 ° до + 90 ° * .

Итак, если вы используете калькулятор для решения, скажем, arctan 0.55, из бесконечного числа возможностей он вернет 28,81 °,
тот, который находится в диапазоне функции.

* Собственно, -90 ° и + 90 ° сами по себе не входят в диапазон. Это потому, что функция tan имеет значение
бесконечность при этих значениях. Но значения чуть ниже них находятся в диапазоне, например +89.9999999. Но для простоты объяснения
мы говорим, что диапазон составляет ± 90 °.

Что попробовать

  1. На рисунке выше нажмите «сбросить» и «скрыть детали».
  2. Отрегулируйте треугольник до нового размера
  3. Используя функцию arctan, вычислите значение угла C из длин сторон
  4. Щелкните «Показать подробности», чтобы проверить ответ.

Другие темы по тригонометрии

Уголки

Тригонометрические функции

Решение задач тригонометрии

Исчисление

(C) Открытый справочник по математике, 2011 г.

Все права защищены.

Определение

в кембриджском словаре английского языка

Щелкните стрелки, чтобы изменить направление перевода.

  • Двуязычные словари


  • Английский французский
    Французский – английский

  • Английский – немецкий
    Немецкий – английский

alexxlab

Посмотреть все записи автора alexxlab →

Вам также может понравиться

Усилитель на телевизионную антенну: как выбрать, рейтинг лучших для DVB-T2

Частота в сети 220 в россии: Почему в США напряжение в сетях 110 В, а в России 220 В?

Реле контроллер: Цифровой ПИД Контроллер Температуры REX-C100 + реле SSR-40DA + теплоотвод + термопара K 1 м

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *