| Развернуть структуру обучения | Свернуть структуру обучения |
|
Тригонометрический круг тангенса. Тригонометричне коло тангенса
Значения функции тангенса угла (tg α)
Смотрите также:
Теорема косинусов. Описание курса | Тригонометрические соотношения в прямоугольном треугольнике
|
1.2.1 Синус, косинус, тангенс, котангенс произвольного угла
Видеоурок: Синус, косинус, тангенс и котангенс угла
Лекция: Синус, косинус, тангенс, котангенс произвольного угла
Синус, косинус произвольного угла
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР, который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ. Так как окружность имеет радиус, равный единице, то ОР = R = 1.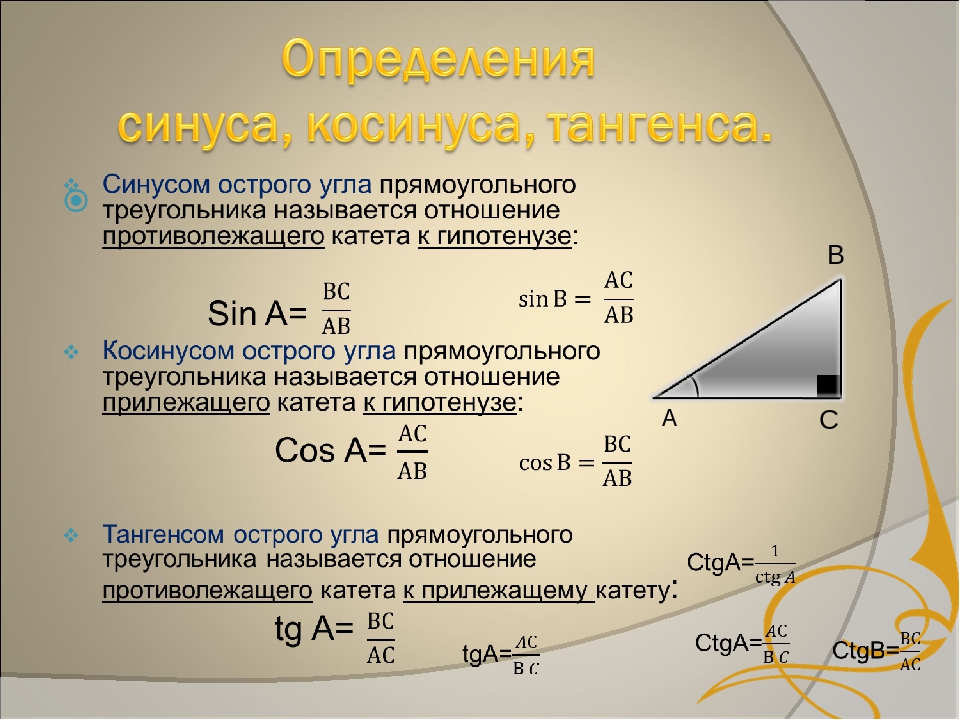
Если с точки Р опустить перпендикуляр на ось ОХ, то получим прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным, если же он двигается против движения часовой стрелки — положительным.
Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1, то sin(α) = y0.
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.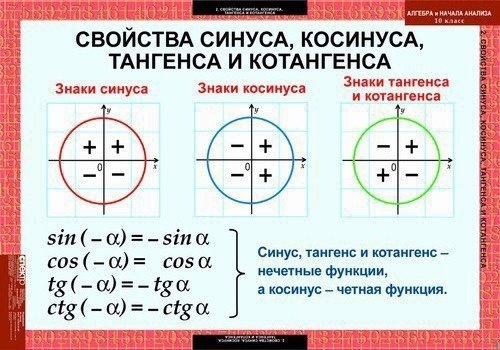
Косинусом угла данной окружности, образованного радиусом-вектором ОР, является абсцисса точки Р вектора на окружности.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1, то cos(α) = x0.
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов.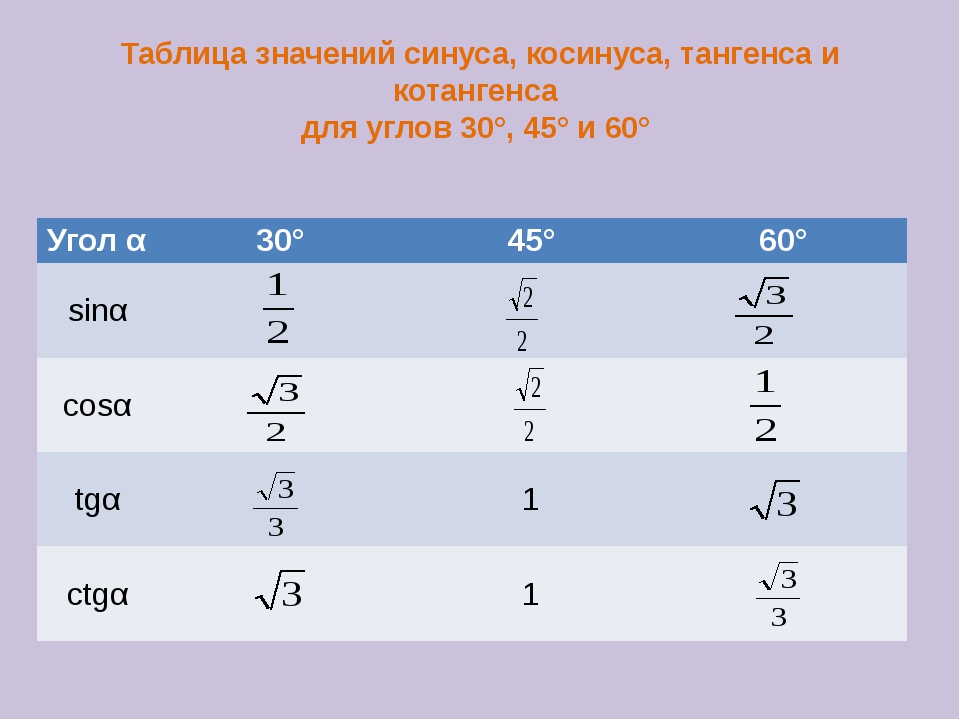 Все остальные значения тангенс принимать может.
Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
Котангенсом произвольного угла называется отношение косинуса к синусу.
Рассматривая прямоугольный треугольник — отношение прилежащего катета к противолежащему, то есть абсциссы к ординате.
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.
Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.
Все перечисленные функции являются периодичными. Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.
норма у трансформатора, формулы для измерения
Измерение тангенса угла различных диэлектрических потерь трансформатора – необходимая процедура, влияющая на эффективность работы оборудования. Потерями диэлектрического типа называют энергию, которая ушла под воздействием работы электрического поля. При этом способность механизма освобождать энергию характеризуется углом или его тангенсом диэлектрических потерь (зависит от ситуации и схемы измерения).
Потерями диэлектрического типа называют энергию, которая ушла под воздействием работы электрического поля. При этом способность механизма освобождать энергию характеризуется углом или его тангенсом диэлектрических потерь (зависит от ситуации и схемы измерения).
Как определить тангенс угла диэлектрических потерь
В силовых трансформаторах тангенс угла рассчитывается как диэлектрик конденсатора. Берется в расчет угол, который дополняет до прямого, основной угол между сдвигами фаз тока и напряжения.
Расположенный внутри этих плоскостей угол и является искомым диэлектрических потерь.
Для измерения принимают, что конденсатор относится к идеальному типу. Он может быть включен последовательным образом, то есть в последовательно включенным сопротивлением активной нагрузки, или по параллельной схеме. Для первой мощность составит Р=(U2ωtgδ)/(1+tg2δ), а для второй — Р=U2ωtgδ. Угол по этим расчетам вычислить несложно, зная емкость конденсатора и показатели сопротивления.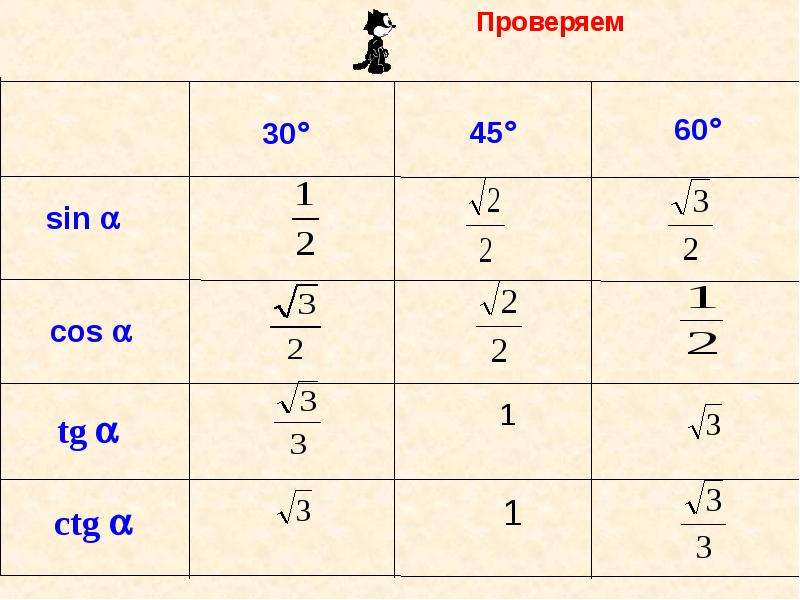 Обычно значение его не превышает десятых или сотых долей единицы, определяется в графиках процентами. При этом увеличиваются, если увеличивается напряжение и частота работы. Для снижения коэффициента используются изоляционные материалы.
Обычно значение его не превышает десятых или сотых долей единицы, определяется в графиках процентами. При этом увеличиваются, если увеличивается напряжение и частота работы. Для снижения коэффициента используются изоляционные материалы.
Что такое мостовая схема
Мостовая схема представляет собой тип соединения, при котором есть мостовая составляющая между двумя точками, которая не соединяет непосредственным образом источники. При равных значениях сопровождения в диагонали тока нет, поэтому удается добиться равнозначности.
Какие значения используют для расчёта
Мостовые схемы дают возможность проводить измерения различных по типам приборов с показателями от 10-8 до 1010 Ом, с высокой точностью (обычно погрешность вычислений составляет до двух девятых процента). Для расчетов необходимы значения сопротивлений отдельных и полного, сопротивления.
Формула расчета
Обычно мостовые схемы используются для вычисления характеристик конденсаторов с минимальными энергетическим тратам. Равновесие мостов рассчитывается по стандартной формуле:
Искомый тангенс, если рассчитывать по формуле равновесия, составит tgδ=ωCxRx=ωCNRN.
Что способствует повышению диэлектрических потерь
Норма диэлектрических потерь прописывается в инструкции к определенному прибору. Есть факторы, вызывающие колебания и отклонения от нормы (обычно это повышение). Различают несколько типов:
- за чет электропроводности сквозного типа;
- ионизирующие;
- резонансные;
- обусловленные поляризацией.
Если частотный и температурный график зависимости понятен интуитивно, то дело обстоит иначе с другими факторами, приводящими к негативному явлению. Обратите внимание, что нагревание трансформаторного масла приводит к более интенсивному смещению, иногда даже смещаются заряды диэлектрика. При стабильных низких показателях температуры вязкость не меняется, следовательно, нет смещения диполей.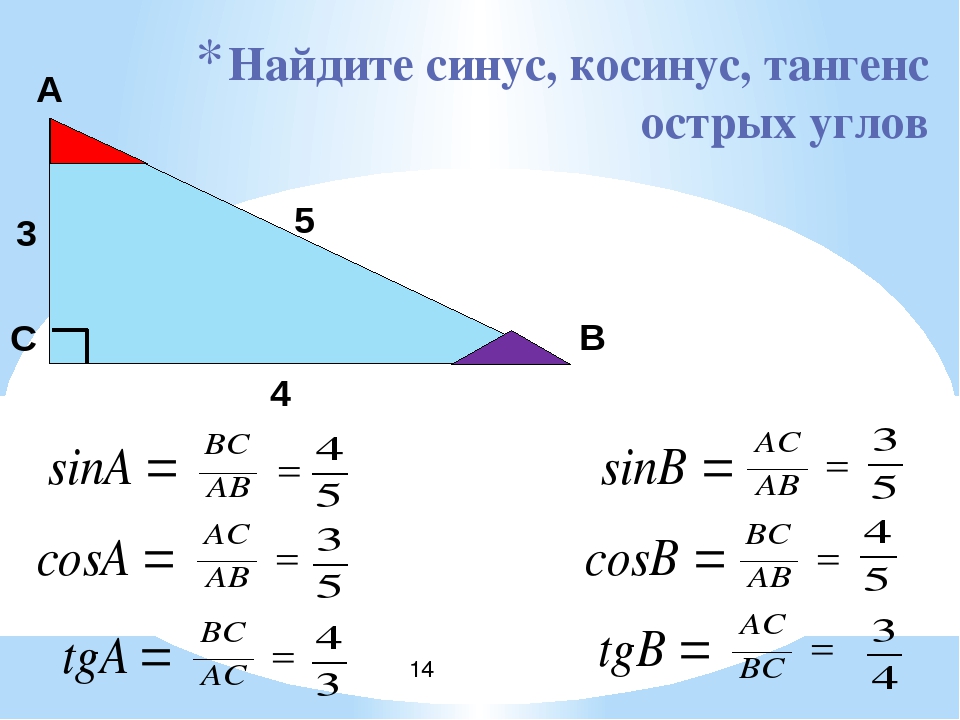
А вот увеличение частоты обуславливает улучшенную проводимость. Показатели тока емкостного могут смещать диполи, при больших показателях уменьшается трение. Рост угла вызывает и проявление влаги в любом виде (это может быть и газообразное состояние). Приводит к повышению показателя ионизация, при этом увеличивается рост напряжения.
Факторы, которые увеличивают тангенс угла диэлектрических потерь
Специалисты выделяют несколько факторов, которые приводят к увеличению тангенса. На первый взгляд они кажутся несущественными, но в итоге обуславливают эффективность работы трансформатора.
Наличие мыла в маслах
Мыло в маслах, которые используются для смазки обмоток трансформатора, приводят к изменению численного показателя. Это объясняется тем, что мыло провоцирует дополнительное увлажнение, приводящие к снижению удельного сопротивления.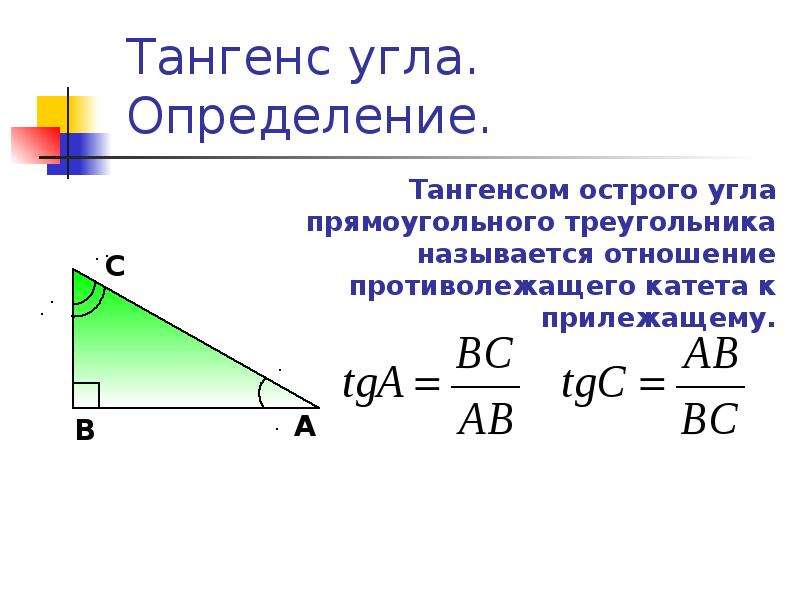 Нюансы увеличивают проводимость, что влияет на рост тангенса.
Нюансы увеличивают проводимость, что влияет на рост тангенса.
Образования кислых продуктов старения
Кислотные продукты старения вызывают порчу вторичной и первичной обмотки. В свою очередь уменьшается проводимость, образуются дополнения на кристаллических решетках. Изменение в худшую сторону физико-технических характеристик диэлектрика приводит у увеличению потерь.
Одной из важнейших задач при использовании транспорта является уменьшение угла. Это позволит оптимизировать работы и избежать траты энергии в холостую.
Как найти угол по тангенсу
В комментариях к тригонометрической таблице меня спросили, как перевести в градусы tg@= 4,99237? В общем виде вопрос заключается в том, как найти угол по тангенсу? Для решения этой задачи мы будем использовать калькулятор. Поскольку математики никогда не ставили перед собой задачи навести порядок в математике, то углы и сегодня измеряются в самых разных единицах измерения. Наиболее популярны среди математиков градусная и радианная меры углов. Мы тоже найдем решение как в градусах, так и в радианах. Благо, на калькуляторе они есть.
Мы тоже найдем решение как в градусах, так и в радианах. Благо, на калькуляторе они есть.
Сначала мы найдем угол по тангенсу в градусах. Для этого в правом верхнем углу калькулятора нужно установить специальный пыптик в положение Deg 360, что соответствует градусам. Дальше кнопочками вводим число 4,99237. Вот что у нас должно получиться.
После этого нужно нажать кнопочку арктангенс. Именно эта математическая ерунда превращает значение тангенса в угол. На калькуляторе эта хитрая обратная тригонометрическая функция (как её величают математики) замаскирована под кнопочку tan в степени минус 1, то есть тангенс в минус первой степени. После нажатия этой кнопочки восторженный калькулятор на все лады расхваливает нашу мудрость и всеми возможными способами сообщает нам, что мы таки ковырнули арктангенс, а не что нибудь другое. Об этом свидетельствует название функции atan (4.99237) в окошке калькулятора. Для особо одаренных здесь же буковками написано Arc tangent.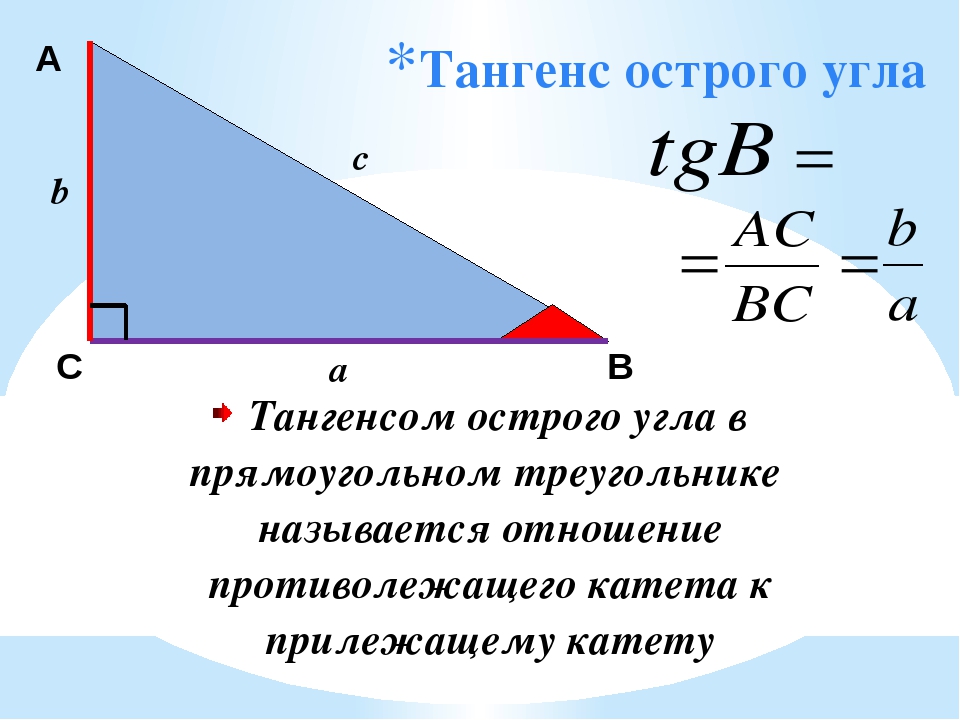 Правда, особо одаренным нужно ещё знать английский язык, для того, чтобы понять всю глубину восторга калькулятора.
Правда, особо одаренным нужно ещё знать английский язык, для того, чтобы понять всю глубину восторга калькулятора.
«А где же угол?» — спросите вы и будете правы. Угла нет, не смотря на все наши старания. Для превращения восторга калькулятора в математический результат нужно ещё нажать здоровенную кнопку равно, обозначенную двумя горизонтальными палочками =. Вот теперь мы нашли угол по тангенсу в градусах. Он равняется 78,6732 (ну, и так далее) градусов.
Для полного счастья, можно пролить бальзам на душу математиков, разложив эту десятичную форму записи градусов на градусы, минуты и секунды. Для этого дробную часть числа умножаем на 60 и получаем количество минут в дробном хвосте градусов.
0,6732 * 60 = 40,392′
Подобную процедуру повторяем с минутами. Дробную часть минут умножаем на 60 и получаем секунды.
0,392 * 60 = 23,52″
Процедуру можно повторять и дальше до бесконечности, но, к счастью, математики до этого ещё не додумались. По этому на секундах мы и остановимся. Ничего, что секунды у нас получились с дробным хвостиком. Математики к таким хвостам относятся терпимо. В итоге, полнометражная версия полученного нами угла в градусной мере углов выглядит следующим образом:
По этому на секундах мы и остановимся. Ничего, что секунды у нас получились с дробным хвостиком. Математики к таким хвостам относятся терпимо. В итоге, полнометражная версия полученного нами угла в градусной мере углов выглядит следующим образом:
78 градусов 40′ 23,52″
В слух эта магическая надпись произносится так: «78 градусов, 40 минут, 23 целых и 52 сотых секунды». Аминь!
Нет, ещё не «Аминь!». Теперь нужно выковырять из калькулятора этот же угол, только в радианах. Процедура добывания угла точно такая же, как и для градусов, с той только разницей, что в самом начале мы на калькуляторе нажимаем соседний пыптик Rad 2п. Повинуясь нашей воле, калькулятор добросовестно выдаст нам результат в радианах. Вот как это будет выглядеть.
Как видите, в радианах мы получили всего-навсего 1,3731 радиан. И за что математики так любят радианы? Ведь, плюнуть не на что. Ну, да Бог с ними, с этими математиками.
Тригонометрия — что такое синус, косинус и тангенс?
Знаете ли вы, что два угла, находящиеся внутри одного прямоугольного треугольника, сказали друг другу? Первый угол звучит так: «Привет, Тельма (или это Тета?), Я не хочу уходить по касательной, но каков твой синус?» На что второй угол отвечает: «Фил (или это Фи?), Я не знаю, зачем ты вообще спрашиваешь, мой синус, очевидно, такой же, как твой косинус!»
Хорошо, может быть, это не лучшая шутка в мире, но как только вы поймете синусы и косинусы, это будет немного забавно.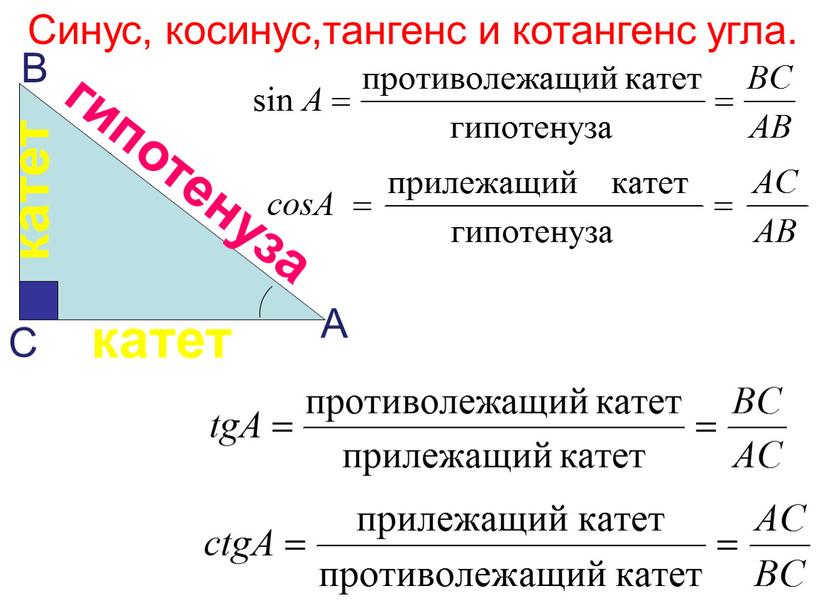 Конечно, это означает, что если вы не знаете разницы между синусом и косинусом, вы в настоящее время оставлены в метафорическом холоде.
Конечно, это означает, что если вы не знаете разницы между синусом и косинусом, вы в настоящее время оставлены в метафорическом холоде.
Ясно, что мы не можем допустить этого — и не будем! Потому что сегодня мы узнаем все о синусах, косинусах и касательных.
Резюме: тригонометрия и треугольники
Когда мы говорили о мире тригонометрии, мы узнали, что часть математики, называемая тригонометрией, имеет дело с треугольниками.И, в частности, это та часть математики, которая занимается выяснением отношений между тремя сторонами и тремя углами, составляющими каждый треугольник.
Особый интерес для нас представляет особый тип треугольников, известный как прямоугольные треугольники. Каждый прямоугольный треугольник имеет один угол в 90 градусов (например, угол квадрата или прямоугольника) и два угла, каждый из которых находится в диапазоне от 0 до 90 градусов (при этом, как мы поговорим в будущем, сумма всех трех углов составляет 180 градусов).
Для нашего обсуждения синуса, косинуса и тангенса (которые, не волнуйтесь, не так сложны, как кажутся), важно, чтобы у нас был способ обозначать стороны прямоугольных треугольников.
Как мы узнали в прошлый раз, самая длинная сторона треугольника известна как его «гипотенуза». Сторона, противоположная углу, на который мы смотрим, известна как «противоположная» сторона (логически). А сторона, прилегающая к углу, на который мы смотрим (тот, который не является гипотенузой), называется «прилегающей» стороной.
Синус, косинус и тангенс
Теперь, когда все эти предварительные сведения с радостью попадают в наш растущий фонд математических знаний, мы, наконец, готовы заняться значением синуса, косинуса и тангенса. Вот ключевая идея:
Соотношения сторон прямоугольного треугольника полностью определяются его углами.
Соотношения сторон прямоугольного треугольника полностью определяются его углами.
Другими словами, значение, которое вы получаете, когда делите длины любых двух сторон прямоугольного треугольника — скажем, длину стороны, противоположной одному из его углов, деленную на его гипотенузу, — полностью высечено в камне, как только углы высечены в камне.
Почему? Что ж, если углы фиксированные, увеличение или уменьшение треугольника не влияет на относительную длину его сторон. Но даже незначительное изменение углов треугольника дает! Если вам нужно что-то убедительное, попробуйте нарисовать несколько собственных треугольников, и вы убедитесь, что это действительно правда.
Итак, тот факт, что у треугольника три стороны, означает, что есть также три возможных отношения длин сторон треугольника. И, как вы, возможно, уже догадались, эти три соотношения — не что иное, как известные тригонометрические функции синуса, косинуса и тангенса.
Что такое SOH-CAH-TOA?
Синус одного из углов прямоугольного треугольника (часто сокращенно «грех») — это отношение длины стороны треугольника, противоположной углу, к длине гипотенузы треугольника. Косинус (часто сокращенно «cos») — это отношение длины стороны, прилегающей к углу, к длине гипотенузы. А касательная (часто сокращенно «загар») — это отношение длины стороны, противоположной углу, к длине смежной стороны.
Так как это немного сложно запомнить, добрые люди на протяжении веков придумали удобную мнемонику, которая поможет вам (и бесчисленным поколениям детей в школе) выйти из школы. Все, что вам нужно запомнить, это SOH-CAH-TOA. Другими словами:
- SOH → sin = «противоположный» / «гипотенуза»
- CAH → cos = «смежный» / «гипотенуза»
- TOA → tan = «напротив» / «рядом»
Реальная тригонометрия
Вам может быть интересно, как тригонометрия применима в реальной жизни.Как вы будете использовать синус, косинус и тангенс вне класса и почему это актуально?
Есть несколько карьерных путей, которые приводят к постоянному использованию этих уравнений. Например, предположим, что вы звукорежиссер, работающий над продюсированием нового альбома известного исполнителя. Вы знаете, что звук распространяется волнами, и инженеры могут управлять этими волнами (измеряя и применяя тригонометрию) для создания различных звуков, генерируемых компьютером.
Что делать, если вы архитектор, которому нужно знать высоту существующего здания в районе, который вам назначен? Вы можете использовать расстояние до здания и угол подъема, чтобы определить высоту.Вы даже можете использовать триггер, чтобы определить, под каким углом солнце будет попадать в здание или комнату.
Строители также используют синус, косинус и тангенс. Им нужно измерить размеры участков, углы кровли, высоту стен и ширину пола и многое другое.
Следователи на месте преступления используют тригонометрию для определения углов траектории пули, причины аварии или направления падения объекта.
А как насчет места преступления? Следователи могут использовать тригонометрию для определения углов траектории пули, причины аварии или направления упавшего объекта.
НАСА использует синус, косинус и тангенс. Физики и астронавты часто используют манипуляторы для выполнения заданий в космосе и используют тригонометрию, чтобы определить, куда и как переместить руку для выполнения своей задачи.
Думаете об изучении морской биологии? В этой карьере синус, косинус и тангенс иногда используются для определения размера крупных морских существ на расстоянии, а также для расчета уровней освещенности на определенных глубинах, чтобы увидеть, как они влияют на фотосинтез.
В десятках профессий тригонометрия используется в повседневных задачах.Итак, вы можете перестать говорить такие вещи, как «Я никогда не буду использовать тригонометрию в реальном мире ».
Что дальше?
Хотя все эти разговоры об углах и сторонах прямоугольных треугольников и их соответствии друг другу благодаря красоте и великолепию тригонометрии действительно прекрасны, это может оставить вас в недоумении по поводу «Почему?». «Какие?» и когда?» всего этого. Под этим я подразумеваю:
- Почему это полезно в реальном мире?
- Для чего нужны кнопки sin, cos и tan на моем калькуляторе? (А как они работают?)
- Когда я действительно смогу вычислить синус или косинус?
Это, разумеется, очень важные (и очень разумные) вопросы. И это тоже очень важные вопросы, на которые нужно ответить. Именно эту задачу мы начнем выполнять в следующий раз.
И это тоже очень важные вопросы, на которые нужно ответить. Именно эту задачу мы начнем выполнять в следующий раз.
Измерение углов
Измерение углов
Понятие угла
Понятие угла — одно из самых важных понятий в геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении и углов.
Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше.Каждый градус делится на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. |
Части градуса теперь обычно обозначаются десятичной дробью.Например, семь с половиной градусов теперь обычно пишут как 7.5 & deg.
Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), с одной стороны угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. 1 ° равняется π /180 радиан а также 1 радиан равен 180/ π градусов Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор. |
Краткая заметка по истории радианов
Хотя слово «радиан» было придумано Томасом Мьюром и / или Джеймсом Томпсоном примерно в 1870 году, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей книге Elements of Algebra явно сказал, что углы измеряются длиной дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией.
e iθ = cos θ + i sin θ
где θ — это то, что позже было названо радианами измерения угла.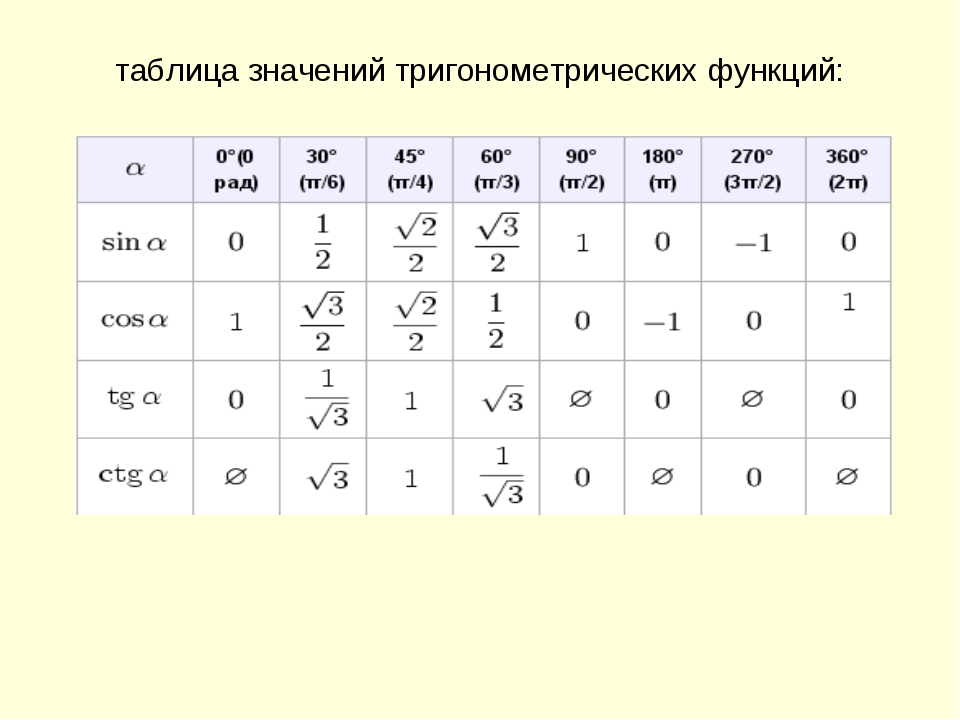 К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда приводится в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, тогда мера в радианах равна 1.5.
Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает то же число, что и приведенное выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r, в умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть окружности, ограниченная двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, когда он измеряется в радианах.Так как площадь всего круга составляет πr 2 , а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтому
Общие углы
Ниже приведена таблица общих углов для измерения в градусах и радианах. Обратите внимание, что измерение в радианах дано в единицах π . Его, конечно, можно было бы дать десятичной дроби, но радианы часто появляются с коэффициентом π
.
| Уголок | градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С. Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). Он дал свои задачи с точностью до пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь использовать таблицу синус-косинусов, таблицу касательных, таблицу логарифмов, таблицу log-sin-cos и таблицу log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на утомительных вычислениях.
Кроули написал книгу « Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). Он дал свои задачи с точностью до пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь использовать таблицу синус-косинусов, таблицу касательных, таблицу логарифмов, таблицу log-sin-cos и таблицу log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на утомительных вычислениях.
Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, , чтобы найти длину переходящей дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов.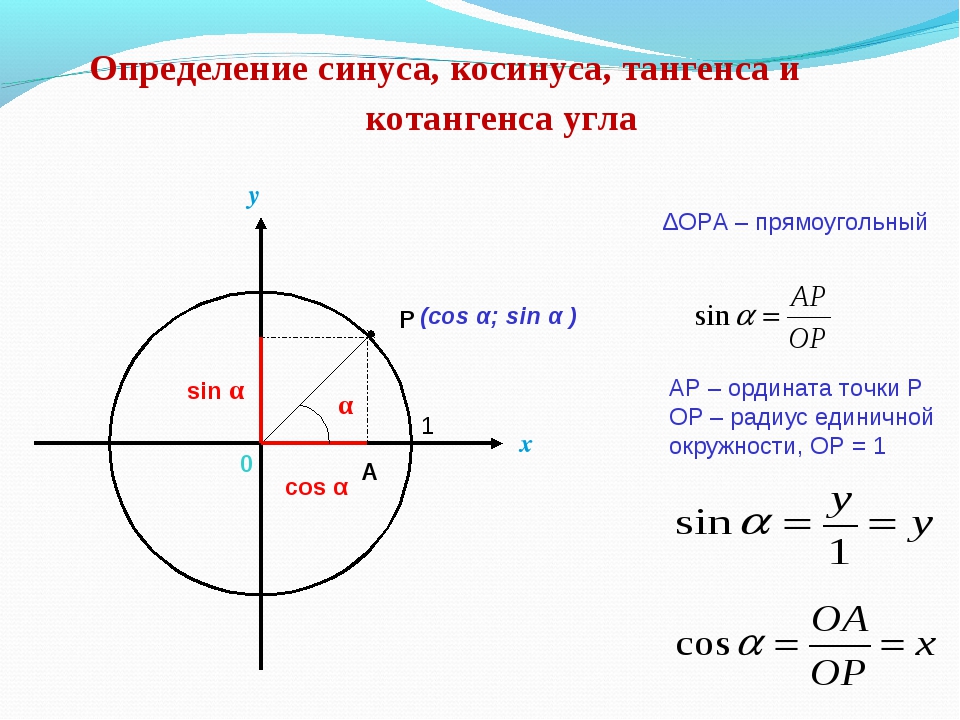 Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623 разделить на π и умножить на 180 дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286, умноженное на 60, равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 «.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус.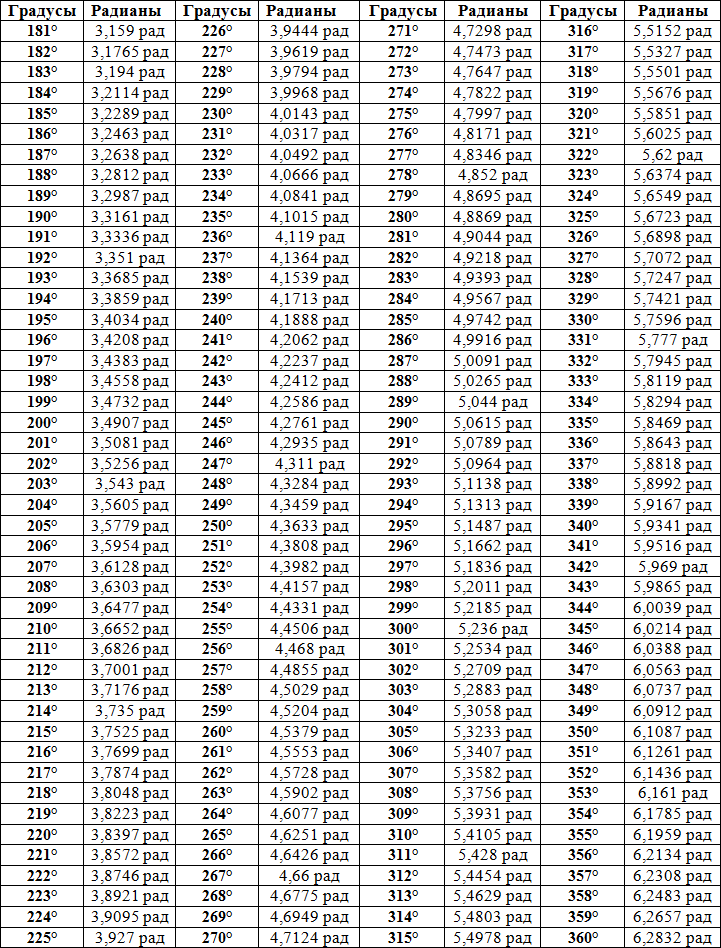 Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас получился круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко.) Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.
2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776
Идиомы по The Free Dictionary
(выкл.) По касательной
Обращение к теме или темам, не относящимся к основному обсуждению. Я попытался решить проблему клиента, но она продолжала отклоняться от темы, и я не мог понять, в чем была ее настоящая жалоба. В середине нашего разговора о моих финансах мой советник коснулся текущих событий.
лететь по касательной
Чтобы начать обсуждение или обсуждение темы, которая отличается от основной дискуссии или не имеет отношения к ней. Я попытался решить проблему клиента, но она продолжала улетать, и я не мог понять, в чем была ее настоящая жалоба. В середине нашего разговора о моих финансах мой советник улетел, не зная о текущих событиях.
go (off) on a tangent
Для начала обсуждения или обсуждения темы или тем, не относящихся к основному обсуждению.Я попытался решить проблему клиента, но она продолжала отклоняться от темы, и я не мог понять, в чем была ее настоящая жалоба.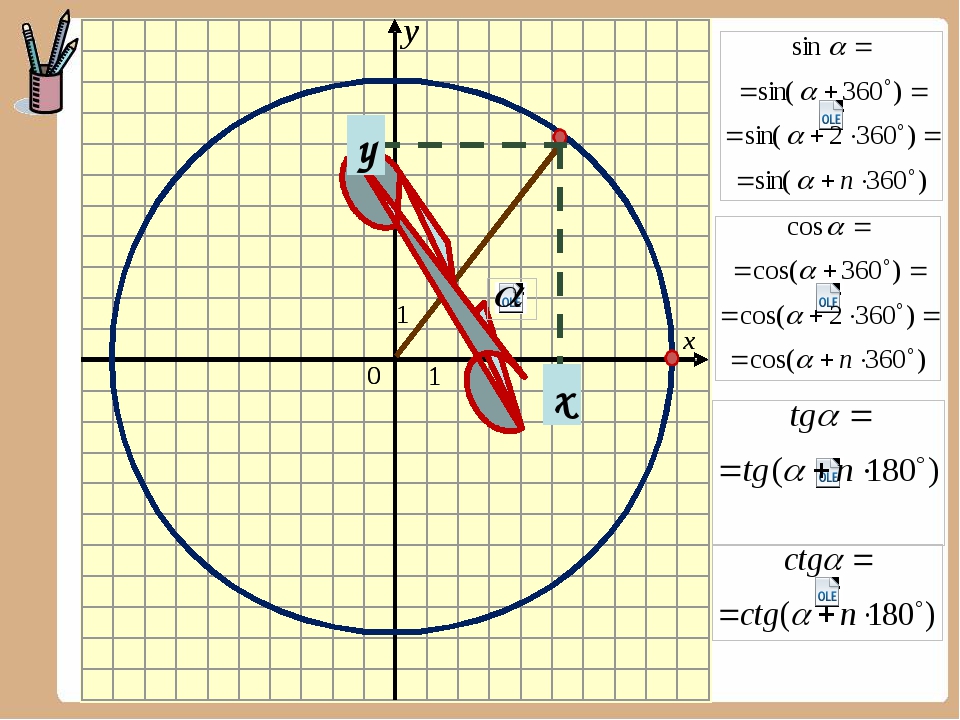 В середине нашего разговора о моих финансах мой советник коснулся текущих событий.
В середине нашего разговора о моих финансах мой советник коснулся текущих событий.
взорваться
1. Взрывное устройство, взорваться. Бегать! Бомба в здании могла взорваться в любой момент!
2. Из аварийного сигнала — переход в активное состояние, обычно приводящее к громкому шуму или другой индикации. Все здание пришлось эвакуировать из-за срабатывания пожарной сигнализации.В банке сработала тихая сигнализация, лучше проверим.
3. Отбыть. Если вы хотите, чтобы мама что-то для вас купила, лучше поговорите с ней, прежде чем она пойдет в магазин.
4. Прекратить работу. Вам лучше пойти поищите кофе в другом отделе — наш котелок сгорел еще до того, как он заварился. Электроэнергия отключилась несколько часов назад — почему они так долго не включали ее?
5. Случиться. Учитывая все проблемы, которые у нас были до этого, удивительно, что наша вечеринка прошла так хорошо!
6.Срок годности истекает после еды или питья. «Off» в этом использовании означает испорченный или гнилой. Не ешьте эти остатки — им неделя и они определенно ушли.
Не ешьте эти остатки — им неделя и они определенно ушли.
7. Прекратить прием лекарства, которое указано после «выключено». Разве врач не сказал вам, что вы должны постепенно прекращать прием таких лекарств?
8. Быть очень злым и враждебным, часто неожиданно. Босс просто зашел ко мне в офис и бросился на меня без видимой причины. Каждый раз, когда я поднимаю эту тему, он просто уходит.
9. Чтобы поговорить о чем-то подробно. Дедушка так долго ушел в политику, что наш обед остыл.
10. Умереть. На Рождество мне очень не хватает родственников, уехавших раньше нас.
11. сленг До оргазма. Не думаю, что снова пересплю с ним — в последний раз я не уходил.
по касательной.
Для начала обсуждения или обсуждения темы или тем, не относящихся к основному обсуждению. Я попытался решить проблему клиента, но она продолжала уходить по касательной, и я не мог понять, в чем была ее настоящая жалоба.В середине нашего разговора о моих финансах мой советник ушел, не обращая внимания на текущие события.
выкл. По касательной
По ходу обсуждения, которое не имеет отношения к обсуждаемой теме или расходится с ней. В первую очередь слышно в Великобритании. Если мы будем продолжать отклоняться от темы, мы никогда не пройдем через эту встречу. Невозможно поговорить с мамой, потому что она всегда идет вразрез.
Словарь идиом Farlex. © 2015 Farlex, Inc, все права защищены.
перейти
1. Лит. [для взрывного устройства] для взрыва. Фейерверк прошел по расписанию. Бомба взорвалась и нанесла большой ущерб.
2. Лит. [для звукового устройства], чтобы издавать шум. Будильник сработал в шесть часов. Сирена срабатывает каждый день в полдень.
3. Рис. [для события], которое должно произойти или произойти. Вечеринка прошла по плану. Ваше медицинское обследование прошло так хорошо, как вы надеялись?
уйти
(самому) уйти в уединение; изолировать себя.Она ушла одна, где ее никто не нашел. Я должен уйти и подумать об этом.
Я должен уйти и подумать об этом.
уйти
(во что-то) уйти во что-то; уйти и пойти во что-нибудь. Ушел в армию. Вы ожидаете, что я просто уйду в мир и зарабатываю на жизнь?
уходит по касательной
Рис. , чтобы следовать несколько связанному или несоответствующему курсу, игнорируя основной предмет. Не уходите по касательной. Придерживайтесь своей работы. В тот момент, когда мы начали разговор, Генри задумался о высокой стоимости жизни.
уйти (у кого-то)
уйти с кем-нибудь. Том только что ушел с Мэгги. Думаю, Мария куда-то ушла с Фредом.
Словарь американских идиом и фразовых глаголов Макгроу-Хилла. © 2002 McGraw-Hill Companies, Inc.
взорвалось
1. Взрыв, детонация; также шуметь, издавать звук, особенно резко. Например, Я слышал выстрел из пистолета или Сирены сработали в полдень . Это выражение появилось в конце 1500-х и привело примерно к 1700 году к связанному с ним с полувзводом , теперь означающему «действовать преждевременно», но первоначально относящемуся к скольжению курка ружья, так что ружье стреляет (срабатывает) неожиданно. .
.
2. Уходи, уходи, особенно внезапно, как в Не сходи с ума , или Ушли, не попрощавшись . [c. 1600]
3. Придерживаться ожидаемого плана или хода событий, добиться успеха, как в Проект прошел гладко . [Вторая половина 1700-х годов]
4. Ухудшается по качеству, как в Это молоко, кажется, уходит с . [Конец 1600-х годов]
5. Die. Шекспир использовал этот смысл в Macbeth (5: 9): «Я бы хотел, чтобы друзья, которых мы пропустили, благополучно прибыли.-Некоторые должны уйти ».
6. Испытайте оргазм. Д.Х. Лоуренс использовал этот жаргонный смысл в Lady Chatterley’s Lover (1928):« Вы не могли уйти одновременно … ». вероятно, сегодня редко. Также см. выход, деф. 8. 8. сойти с головы . Провести по голове. Также см. последующие идиомы, начинающиеся с , уходят с .
по касательной
Внезапное отступление или изменить курс, как в . За профессором сложно уследить, он всегда идет по касательной . Эта фраза часто встречается в идиомах fly off или go off on a касательная , как и в . Свидетель был убедительным, пока он не ушел на касательной . Это выражение относится к геометрической касательной — линии или кривой, которые касаются, но не пересекаются с другой линией или кривой. [Вторая половина 1700-х годов]
Эта фраза часто встречается в идиомах fly off или go off on a касательная , как и в . Свидетель был убедительным, пока он не ушел на касательной . Это выражение относится к геометрической касательной — линии или кривой, которые касаются, но не пересекаются с другой линией или кривой. [Вторая половина 1700-х годов]
Словарь идиом «Американское наследие®» Кристин Аммер. Авторское право © 2003, 1997 Траст Кристин Аммер 1992. Опубликовано Houghton Mifflin Harcourt Publishing Company.Все права защищены.
уходит по касательной
БРИТАНСКИЙ, АМЕРИКАНСКИЙ или
выходит по касательной
БРИТАНСКИЙ
1. Если человек или кусок письма уходит по касательной или уходит по касательной , они начинают говорить или думать о чем-то, что напрямую не связано с тем, что они говорили или думали раньше. Наш учитель иногда уходил по касательной, совершенно не связанной с учебником. Примечание. Иногда вместо идут и другие глаголы.Юмор часто бывает немного натянутым, и тема книги время от времени отклоняется от темы.
2. Если кто-то уходит по касательной или уходит по касательной , они начинают вести себя совершенно иначе, чем раньше, или делать что-то совершенно отличное от того, что они делали раньше. Полагаю, я пытался приспособиться, но потом я пошел вразрез, переехав в Лондон, чтобы изучать драму. Примечание. В геометрии касательная — это прямая линия, которая касается кривой в одной точке, но не пересекает ее.
Словарь идиом COBUILD Collins, 3-е изд. © HarperCollins Publishers 2012
летят / летят по касательной
( британский английский ) ( американский английский переходят по касательной) внезапно переходят от разговора или размышлений об одном к разговору или размышлению о другом профессор усердно работает над проблемой по физике, в следующий раз он ушел по касательной и говорит о пчелах.
Касательная — это прямая линия, которая касается внешней стороны кривой, но не пересекает ее.
Словарь идиом для партнеров Farlex © Farlex 2017
go off
v.
1. Чтобы уйти: все дети ушли играть в парк. Не сходи с ума — позволь мне объяснить!
2. Прекратить работу. Особенно часто используются электрические устройства: внезапно погас свет, и сразу же началось представление.
3. Произойти или восприниматься как произошедшее определенным образом: я думаю, наша вечеринка прошла очень хорошо!
4. Придерживаться ожидаемого развития событий или ожидаемого плана: проект прошел гладко.
5. Чтобы прекратить прием лекарств или лекарств: она отказалась от обезболивающих через несколько недель после операции.
6. Шуметь; звук: Сирена срабатывает каждый день в полдень.
7. Подрываться; взорваться: если вы нажмете эту красную кнопку, бомба взорвется.
8. ушел на Чтобы начать много говорить о чем-то: Он ушел под серию оправданий за свое плохое поведение.
9. перейти на Чтобы ругать кого-то прямо и громко: Моя босс действительно обиделась на меня, когда узнала, что я забыл позвонить по телефону.
Словарь фразовых глаголов American Heritage®. Авторские права © 2005 издательской компании Houghton Mifflin Harcourt. Опубликовано Houghton Mifflin Harcourt Publishing Company. Все права защищены.
См. Также:
Касательные к окружностям Секущие и касательные к окружностям Секущая 2 точки пересечения Касательная 1 точка пересечения Точка касательности.
Презентация на тему: «Касательные к окружностям Секущие и касательные к окружностям Секущие 2 точки пересечения Касательная 1 точка пересечения Точка касания» — стенограмма презентации:
1
2
Касательные к кругам
3
Секущие и касательные Секущие 2 точки пересечения Касательная 1 точка пересечения Точка касания
4
Радиусы _ | _ Хорда Что бы вы сделали по поводу следующей диаграммы? П А Б Х Р
5
Радиусы _ | _ Хорда Что бы вы сделали по поводу следующей диаграммы? P A B X R AX XB? Докажите это!
6
Радиусы и касательная.

 «Тангенс» дословно переводится с латинского как «касающийся».
«Тангенс» дословно переводится с латинского как «касающийся».
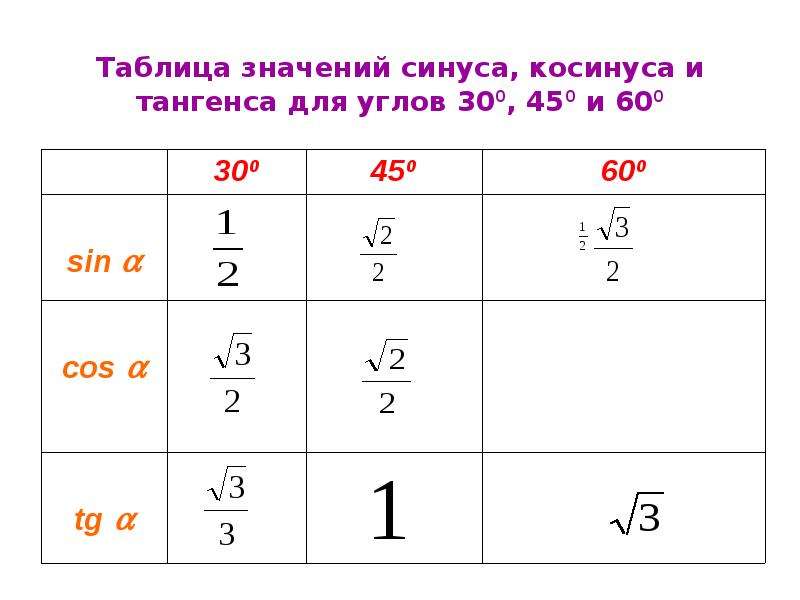 При этом подразумевается, что, используя базовое свойство функции тангенса tg α = BC / AC (см. выше рисунок с обозначениями сторон), можно легко найти размеры треугольника или иной геометрической фигуры. Однако, на практике, именно это простейшее свойство тангенса и вызывает трудности при решении.
При этом подразумевается, что, используя базовое свойство функции тангенса tg α = BC / AC (см. выше рисунок с обозначениями сторон), можно легко найти размеры треугольника или иной геометрической фигуры. Однако, на практике, именно это простейшее свойство тангенса и вызывает трудности при решении. За положительное направление линии тангенсов берут направление снизу вверх.
За положительное направление линии тангенсов берут направление снизу вверх.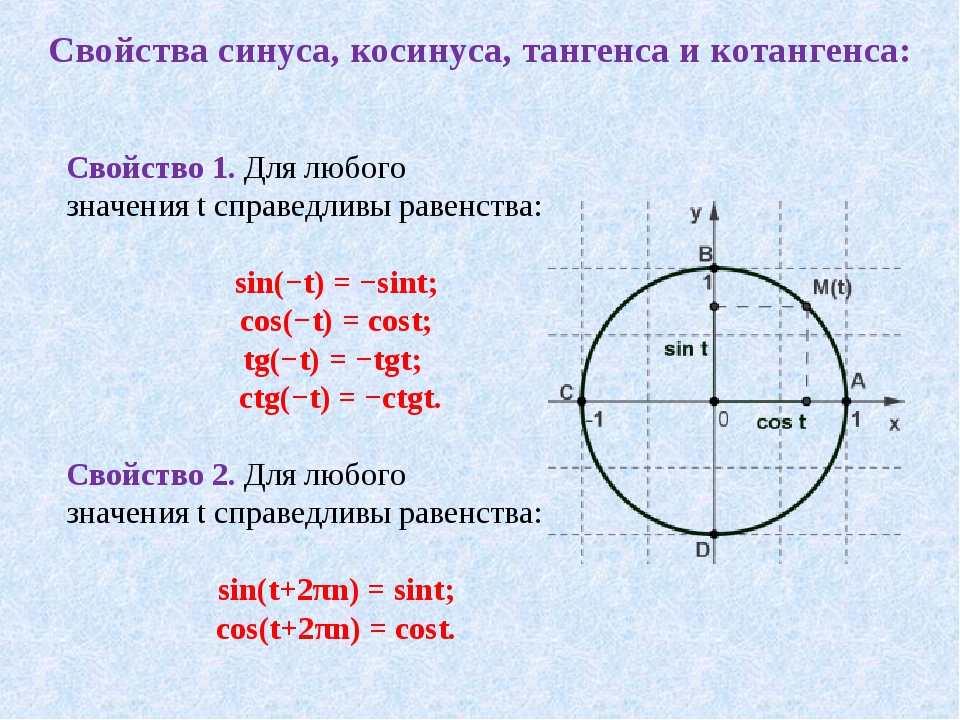 За позитивний напрямок лінії тангенсів беруть напрямок знизу вгору.
За позитивний напрямок лінії тангенсів беруть напрямок знизу вгору. Для более простого визуального запоминания, там где функция тангенса принимает положительные значения, tg α обозначен красным цветом, а там, где отрицательные — синим.
Для более простого визуального запоминания, там где функция тангенса принимает положительные значения, tg α обозначен красным цветом, а там, где отрицательные — синим. Пример решения задачи |
Пример решения задачи | Каждая минута далее делится на 60 равных частей, называемых секунды, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 дюймов. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды.
Каждая минута далее делится на 60 равных частей, называемых секунды, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 дюймов. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно,
Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно,