Что такое полная, активная и реактивная мощность?
ЧТО ТАКОЕ ПОЛНАЯ, АКТИВНАЯ И РЕАКТИВНАЯ МОЩНОСТЬ? ОТ СЛОЖНОГО К ПРОСТОМУ.
В повседневной жизни практически каждый сталкивается с понятием «электрическая мощность», «потребляемая мощность» или «сколько эта штука «кушает» электричества». В данной подборке мы раскроем понятие электрической мощности переменного тока для технически подкованных специалистов и покажем на картинке электрическую мощность в виде «сколько эта штука кушает электричества» для людей с гуманитарным складом ума :-). Мы раскрываем наиболее практичное и применимое понятие электрической мощности и намеренно уходим от описания дифференциальных выражений электрической мощности.
ЧТО ТАКОЕ МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА?
В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для практических расчётов бесполезна. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность (Real Power)
Единица измерения — ватт (русское обозначение: Вт, киловатт — кВт; международное: ватт -W, киловатт — kW).
Среднее за период Τ значение мгновенной мощности называется активной мощностью, и
выражается формулой:
В цепях однофазного синусоидального тока , где υ и Ι это среднеквадратичные значения напряжения и тока, а φ — угол сдвига фаз между ними.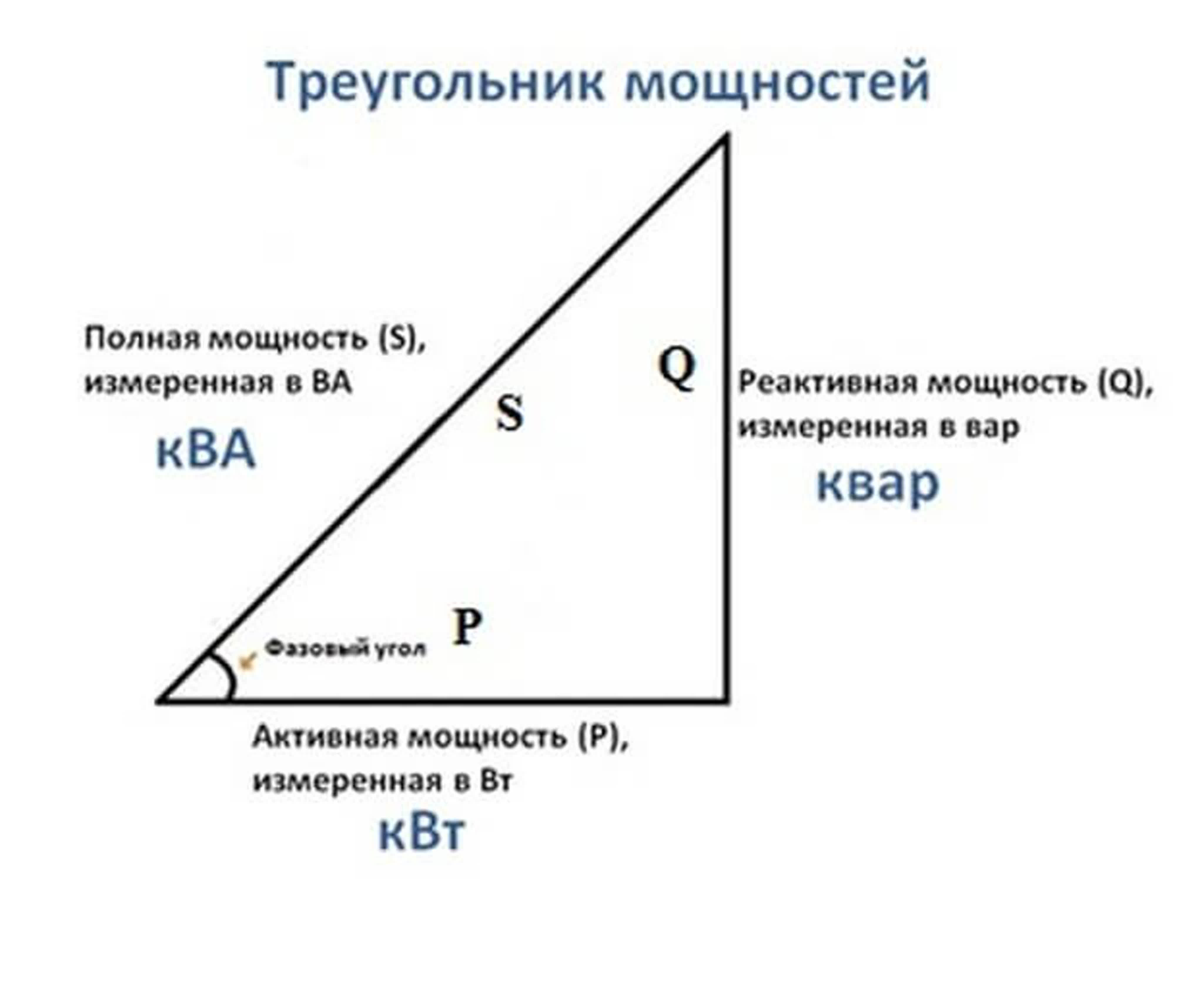 Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S, активная связана соотношением .
Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S, активная связана соотношением .
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.
Реактивная мощность (Reactive Power)
Единица измерения — вольт-ампер реактивный (русское обозначение: вар, кВАР; международное: var).
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними:
(если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью P соотношением: .
Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до минус 90° является отрицательной величиной. В соответствии с формулой
Величина sin φ для значений φ от 0 до минус 90° является отрицательной величиной. В соответствии с формулой
реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например,асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения
Полная мощность (Apparent Power)
Единица полной электрической мощности — вольт-ампер (русское обозначение: В·А, ВА, кВА-кило-вольт-ампер; международное: V·A, kVA).
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: ; соотношение полной мощности с активной и реактивной мощностями выражается в следующем виде: где P — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q›0, а при ёмкостной Q‹0).Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Визуально и интуитивно-понятно все вышеперечисленные формульные и текстовые описания полной, реактивной и активной мощностей передает следующий рисунок 🙂
Специалисты компании НТС-групп (ТМ Электрокапризам-НЕТ) имеют огромный опыт подбора специализированного оборудования для построения систем обеспечения жизненно важных объектов бесперебойным электропитанием. Мы умеем максимально качественно учитывать множество электрических и эксплуатационных параметров, которые позволяют выбрать экономически обоснованный вариант построения системы бесперебойного электропитанияс применением стабилизаторов напряжения, топливных электростанций, источников бесперебойного питания и др. сопутствующего оборудования.
© Материал подготовлен специалистами компании НТС-групп (ТМ Электрокапризам-НЕТ) с использованием информации из открытых источников, в т. ч. из свободной энциклопедии ВикипедиЯ https://ru.wikipedia.org
ч. из свободной энциклопедии ВикипедиЯ https://ru.wikipedia.org
как найти, формула расчёта, в чем измеряется
Все мы ежедневно сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической инструкции указана мощность. Сегодня мы разберемся что же это такое, узнаем виды и способы расчета.
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.
В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).
Рассчитывается по формуле: P = U⋅I⋅cosφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.
ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73
Понятие реактивной мощности
Реактивная «вредная» мощность — это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.
Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.
Обозначается эта величина латинской буквой Q.
ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).
Рассчитывается по формуле:
Q = U⋅I⋅sinφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.
ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.
Емкостные и индуктивные нагрузки
Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.
Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.
ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.
Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.
Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.
ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.
Коэффициент мощности cosφ
Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.
Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.
ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.
Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.
Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.
Понятие полной мощности. Треугольник мощностей
Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.
Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.
S = U⋅I
ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).
Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.
Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.
Как найти активную, реактивную и полную мощности. Пример расчета
Пример расчета
Все расчеты строятся на указанных ранее формулах и треугольнике мощностей. Давайте рассмотрим задачу, наиболее часто встречающуюся на практике.
Обычно на электроприборах указана активная мощность и значение коэффициента cosφ. Имея эти данные несложно рассчитать реактивную и полную составляющие.
Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.
Далее, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.
Как измеряют cosφ на практике
Значение коэффициента cosφ обычно указано на бирках электроприборов, однако, если необходимо измерить его на практике пользуются специализированным прибором – фазометром. Также с этой задачей легко справится цифровой ваттметр.
Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.
- Если необходимо скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий противоположно уже функционирующему прибору. Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
- Если необходимо скорректировать проблемы нелинейности в схему вводят пассивный корректор коэффициента cosφ, к примеру, это может быть дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой.
Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.
Что такое треугольник мощностей и каково его назначение?
Треугольник мощностей представляет собой прямоугольный треугольник, показывающий соотношение между активной, реактивной и полной мощностью.
Когда каждая составляющая тока (активная составляющая (Icosϕ) или реактивная составляющая (Isinϕ)) умножается на напряжение U, получается треугольник мощности, показанный на рисунке ниже:
Мощность, которая фактически потребляется или используется в цепи переменного тока, называется активной мощностью или реальной мощностью. Она измеряется в ваттах (Вт), киловаттах (кВт) или МВт.
Мощность, которая протекает в линиях переменного тока, но не выполняет полезной работы, называется реактивной мощностью. Реактивная мощность измеряется в вольт-амперах (ВАр) реактивных, киловольт-амперах реактивных (кВАр) или МВАр.
Произведение среднеквадратичного значения напряжения и тока известно как полная мощность. Она измеряется в вольт-амперах (ВА), кВА или МВА.
Следующий пункт показывает взаимосвязь между электрическими величинами и объясняется графическим представлением под названием треугольник мощностей, показанным выше.
- Когда активная составляющая тока умножается на напряжение цепи U, получается активная мощность.
 Именно она создает крутящий момент в двигателе, нагревает резистор и выполняет другую полезную работу. Она измеряется ваттметром.
Именно она создает крутящий момент в двигателе, нагревает резистор и выполняет другую полезную работу. Она измеряется ваттметром. - Когда реактивная составляющая тока умножается на напряжение цепи, получается реактивная мощность. Она определяет коэффициент мощности сети. Она не выполняет полезную работу, а только перегоняется по сети, создавая препятствия для полезной мощности.
- Когда общий ток цепи (активный и реактивный) умножается на напряжение — мы получаем полную мощность.
Коэффициент мощности (cos φ) может быть определен из треугольника мощностей путем вычисления отношений активной мощности к полной:
Как мы знаем, обычная мощность означает произведение напряжения и тока, но в цепи переменного тока, за исключением чисто резистивной нагрузки, обычно существует разность фаз между напряжением и током, и поэтому произведение напряжения и тока не отражает реальной или активной мощности в цепи.
Активная, реактивная и полная мощность
В отличии от сетей постоянного тока, где мощность имеет выражение и не изменяется во времени, в сетях переменного тока это не так.
Мощность в цепи переменного тока также есть переменной величиной. На любом участке цепи в любой момент времени t она определяется как произведение мгновенных значений напряжения и тока.
Рассмотрим, что представляет активная мощность
В цепи с чисто активным сопротивлением она равна:
Если принять и тогда выйдет:
Где
Исходя из выражений выше — активная энергия состоит из двух частей — постоянной и переменной , которая меняется с двойной частотой. Среднее ее значение
График Р(ωt)
Отличие реактивной мощности от активной
В цепи, где есть реактивное сопротивление (возьмем для примера индуктивное) значение мгновенной мощности равно:
Соответственно и в итоге получим:
Данное выражение показывает, что реактивная энергия содержит только переменную часть, которая изменяется с двойной частотой, а ее среднее значение равно нулю
График q(ωt)
Если ток и напряжение имеют синусоидальную форму и сеть содержит элементы типа R-L или R-C, то в таких сетях кроме преобразования энергии в активном элементе R вдобавок еще и изменяется энергия электрического и магнитного полей в реактивных элементах L и C.
В таком случае полная мощность сети будет равна сумме:
Что такое полная мощность на примере простой R-L цепи
Графики изменения мгновенных значений u,i:
Графики изменения мгновенных значений u,i:
φ — фазовый сдвиг между током и напряжением
Уравнение для S примет следующий вид
Подставим вместо и заменим амплитудные значения на действующие:
Значение S рассматривается как сумма двух величин , где
и — мгновенные активные и реактивные мощности на участках R-L.
Графики p,q,s:
Как видим из графика, наличие индуктивной составляющей повлекло за собой появление отрицательной части в полной мощности (заштрихованная часть графика), что снижает ее среднее значение. Это происходит из-за фазового сдвига, в какой-то момент времени ток и напряжение находятся в противофазе, поэтому появляется отрицательное значение S.
Итоговые выражения для действующих значений:
Активная составляющая сети выражается в ваттах (Вт), а реактивная в вольт-амперах реактивных (вар).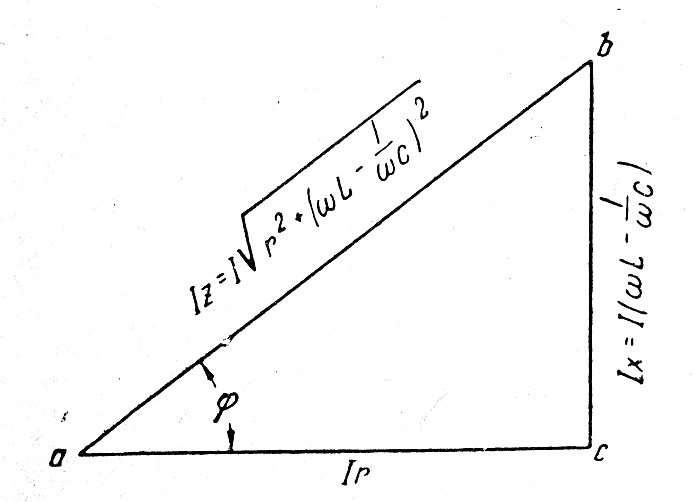
Полная мощность сети S, обусловлена номинальными данными генератора. Для генератора она обусловлена выражением:
Для нормальной работы генератора ток в обмотках и напряжение на зажимах не должны превышать номинальные значения Iн, Uн. Для генератора значения P и S одинаковы, однако все-таки на практике условились S выражать в вольт-амперах (ВА).
Также энергию сети можно выразить через каждую составляющую отдельно:
Где S, P, Q – соответственно активное, реактивное и полное сопротивление сети. Они образуют треугольник мощностей:
Треугольник мощностей с преобладающей индуктивной нагрузкой
Если вспомнить теорему Пифагора, то из прямоугольного треугольника можно получить такое выражение:
Реактивная составляющая в треугольнике является положительной (QL), когда ток отстает от напряжения, и отрицательной (QC), когда опережает:
Треугольник мощностей с преобладающей емкостной нагрузкой
Для реактивной составляющей сети справедливо алгебраическое выражение:
Из чего следует что индуктивная и емкостная энергия взаимозаменяемы. То есть если вы хотите уменьшить влияние индуктивной части цепи, вам необходимо добавить емкость, и наоборот. Ниже пример данной схемы :
То есть если вы хотите уменьшить влияние индуктивной части цепи, вам необходимо добавить емкость, и наоборот. Ниже пример данной схемы :
Схема компенсации реактивной составляющей
Векторная диаграмма показывает влияние конденсатора на cosφ. Как видно, что при включении конденсатора cosφ2> cosφ1 и Iл<I.
Векторная диаграмма
Связь между полной и реактивной энергии выражается:
Отсюда:
сosφ – это коэффициент мощности. он показывает какую долю от полной энергии составляет активная энергия. Чем ближе он к 1, тем больше полезной энергии потребляется из сети.
Выводы о трех составляющих цепи переменного тока
В отличии от цепей постоянного тока, цепи переменного напряжения имеют три вида мощности – активная, реактивная, полная. Активная энергия, как и в цепях постоянного тока, выполняет полезную работу. Реактивная – не выполняет ничего полезного, а только снижает КПД сети, греет провода, грузит генератор. Полная – сумма активной и реактивной, она равна мощности сети. Индуктивная составляющая реактивной энергии может быть скомпенсирована емкостной. На практике в промышленности это реализовано в виде конденсаторных установок.
Полная – сумма активной и реактивной, она равна мощности сети. Индуктивная составляющая реактивной энергии может быть скомпенсирована емкостной. На практике в промышленности это реализовано в виде конденсаторных установок.
Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. (Лекция №7)
Передача энергии w по электрической цепи (например, по линии электропередачи),
рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также
и другие виды преобразования энергии характеризуются интенсивностью, с которой
протекает процесс, то есть тем, сколько энергии передается по линии в единицу
времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи
или преобразования энергии называется мощностью р. Сказанному соответствует
математическое определение:
| . | (1) |
Выражение для мгновенного значения мощности в электрических цепях имеет вид:
. | (2) |
Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током
за , получим:
| . | (3) |
Итак, мгновенная мощность имеет
постоянную составляющую и гармоническую составляющую, угловая частота которой
в 2 раза больше угловой частоты напряжения и тока.
Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда
u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике
противоположны, энергия возвращается из двухполюсника источнику питания.
Такой возврат энергии источнику происходит за счет того, что энергия периодически
запасается в магнитных и электрических полях соответственно индуктивных и емкостных
элементов, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику
в течение времени t равна .
Среднее за период значение мгновенной мощности называется активной мощностью .
Принимая во внимание, что , из (3) получим:
| . | (4) |
Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной
(иначе двухполюсник будет генерировать энергию), поэтому , т.е. на входе пассивного двухполюсника
. Случай Р=0, теоретически возможен для двухполюсника,
не имеющего активных сопротивлений, а содержащего только идеальные индуктивные
и емкостные элементы.
1. Резистор (идеальное активное сопротивление).
Здесь напряжение и ток (см. рис. 2) совпадают
по фазе , поэтому мощность всегда положительна, т.е. резистор
потребляет активную мощность
2. Катушка индуктивности (идеальная индуктивность)
При идеальной индуктивности ток отстает от напряжения по фазе на .
Поэтому в соответствии с (3) можно записать
.
Участок 1-2: энергия , запасаемая в магнитном поле катушки, нарастает.
Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.
3. Конденсатор (идеальная емкость)
Аналогичный характер имеют процессы и для идеальной емкости. Здесь . Поэтому из (3) вытекает, что
. Таким образом, в катушке индуктивности
и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит
необратимого преобразования энергии в другие виды энергии. Здесь происходит
только циркуляция энергии: электрическая энергия запасается в магнитном поле
катушки или электрическом поле конденсатора на протяжении четверти периода,
а на протяжении следующей четверти периода энергия вновь возвращается в сеть.
В силу этого катушку индуктивности и конденсатор называют реактивными элементами,
а их сопротивления ХL и ХС , в отличие от активного сопротивления
R резистора, – реактивными.
Интенсивность обмена энергии принято характеризовать наибольшим значением скорости
поступления энергии в магнитное поле катушки или электрическое поле конденсатора,
которое называется реактивной мощностью.
В общем случае выражение для реактивной мощности имеет вид:
| (5) |
Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем
токе (емкостная нагрузка- ). Единицу мощности в применении
к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).
В частности для катушки индуктивности имеем:
, так как .
.
Из последнего видно, что реактивная мощность для идеальной катушки индуктивности
пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично
можно получить для идеального конденсатора:
.
Полная мощность
Помимо понятий активной и реактивной мощностей в электротехнике широко используется
понятие полной мощности:
| . | (6) |
Активная, реактивная и полная мощности связаны следующим соотношением:
| . | (7) |
Отношение активной мощности к полной называют коэффициентом мощности.
Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между
током и напряжением. Итак,
| . | (8) |
Комплексная мощность
Активную, реактивную и полную мощности можно определить, пользуясь комплексными
изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:
Пусть , а . Тогда комплекс полной мощности:
| , | (9) |
где — комплекс, сопряженный с комплексом
.
.
Комплексной мощности можно поставить в
соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка),
для которого имеем:
Применение статических конденсаторов для повышения cos
Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный
ток, не совершая полезной работы, приводит к дополнительным потерям в силовом
оборудовании и, следовательно, к завышению его установленной мощности. В этой
связи понятно стремление к увеличению в силовых электрических цепях.
Следует указать, что подавляющее большинство потребителей (электродвигатели,
электрические печи, другие различные устройства и приборы) как нагрузка носит
активно-индуктивный характер.
Если параллельно такой
нагрузке (см. рис. 5), включить конденсатор
С, то общий ток , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. увеличивается, а общая величина
тока (а следовательно, потери) уменьшается при постоянстве активной мощности . На этом основано применение конденсаторов
для повышения .
Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения
до значения ?
Разложим на активную и реактивную составляющие. Ток через конденсатор
компенсирует часть реактивной составляющей тока
нагрузки :
| ; | (10) |
| ; | (11) |
| . | (12) |
Из (11) и (12) с учетом (10) имеем
,
но , откуда необходимая для повышения
емкость:
. | (13) |
Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и может служить
критерием правильности расчета электрической цепи.
а) Постоянный ток
Для любой цепи постоянного тока выполняется соотношение:
| (14) |
Это уравнение представляет собой математическую форму записи баланса мощностей:
суммарная мощность, генерируемая источниками электрической энергии, равна суммарной
мощности, потребляемой в цепи.
Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку
активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых
больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том,
что соответствующие источники работают в режиме потребителей энергии (например,
заряд аккумулятора).
б) Переменный ток.
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей
равна сумме всех потребляемых активных мощностей, т.е.
| (15) |
В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство
опустим), что баланс соблюдается и для реактивных мощностей:
| , | (16) |
где знак “+” относится к индуктивным элементам , “-” – к емкостным .
Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому
выражению баланса мощностей в цепях синусоидального тока (без учета взаимной
индуктивности):
или
.
Литература
- Основы теории цепей: Учеб.
 для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Что такое активная мощность?
- Что такое реактивная мощность, с какими элементами она связана?
- Что такое полная мощность?
- Почему необходимо стремиться к повышению коэффициента мощности ?
- Критерием чего служит баланс мощностей?
- К источнику с напряжением подключена активно-индуктивная
нагрузка, ток в которой . Определить активную, реактивную
и полную мощности. - В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности
L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность
Напряжение на зажимах ветви U=100 B, а потребляемая мощность
Р=120 Вт. Определить сопротивления R и XL элементов ветви. - Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора
и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с
резистором I2=4 A. Определить сопротивления R и XC элементов цепи.
Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.
Ответ: R=30 Ом; XL=40 Ом.
Ответ: R=10 Ом; XС=7,5 Ом.
Активная и реактивная мощность. За что платим и работа
Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять. Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной. Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр. ).
).
Кроме активной электроэнергии существует еще и реактивная. Это та часть полной энергии, которая не расходуется на полезную работу. Как понятно из вышесказанного, полная мощность – это активная и реактивная мощность в целом.
Активная и реактивная мощность
В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков. Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии. Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю.
Активная мощность
Существуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.
Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность . Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети. Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).
Реактивная мощность
Иногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой. Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности. В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т. п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).
п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).
Реактивная емкостная мощность
Красивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор. Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет. Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке. Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.
Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения. Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному). Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т.е. на четверть периода.
Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности.
Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр). Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.
Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.
Реактивная индуктивная мощность
Если в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.
На практике хорошим приближением чисто индуктивной нагрузки является работающий без нагрузки трансформатор (или стабилизатор напряжения с автотрансформатором). Хорошо сконструированный трансформатор на холостом ходу потребляет очень мало активной мощности, потребляя мощность в основном реактивную.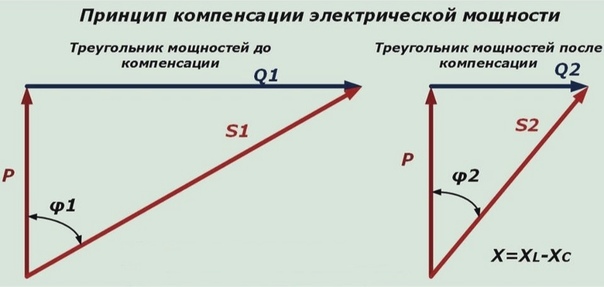
Реальные потребители электрической энергии и полная электрическая мощность
Из рассмотрения особенностей емкостной и индуктивной нагрузки возникает интересный вопрос – что произойдет, если емкостную и индуктивную нагрузку включить одновременно и параллельно. Ввиду их противоположной реакции на приложенное напряжение, эти две реакции начнут компенсировать друг друга. Суммарная нагрузка окажется только емкостной или индуктивной, и в некотором идеальном случае удастся добиться полной компенсации. Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи. Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.
Вернемся к реальным потребителям электрической энергии. В быту мы пользуемся в основном потребителями чисто активной мощности (примеры приведены выше), и смешанной активно-индуктивной. Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники. Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности. Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.
Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники. Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности. Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.
Таинственный «косинус фи»
Отношение активной мощности к полной называется в электротехнике «косинусом фи». Обозначается cos φ. Это отношение называется также и коэффициентом мощности. Нетрудно видеть, что для случая чисто активной нагрузки, где полная мощность совпадает с активной, cos φ = 1. Для случаев чисто емкостной или индуктивной нагрузок, где нулю равна активная мощность, cos φ = 0.
В случае смешанной нагрузки значение коэффициента мощности заключается в пределах от 0 до 1.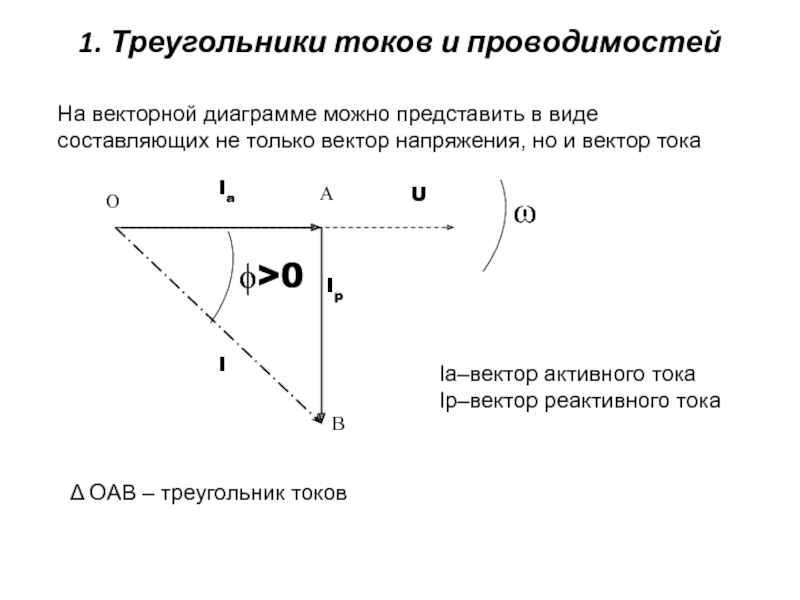 Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.
Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.
За что платим?
И, наконец, самый интересный вопрос – за какой вид энергии платит потребитель. Исходя из того, что реактивная составляющая суммарной энергии не приносит потребителю никакой пользы, при этом долю периода реактивная энергия потребляется, а долю отдается, платить за реактивную мощность незачем. Но бес, как известно, кроется в деталях. Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».
Таким образом, заставить потребителя платить за потребляемую реактивную индуктивную мощность вполне справедливо. Это побуждает потребителя компенсировать реактивную составляющую своей нагрузки, а, поскольку эта составляющая в основном индуктивная, компенсация заключается в подключении конденсаторов наперед рассчитанной емкости.
Потребитель находит возможность платить меньше
Если потребителем оплачивается отдельно потребляемая активная и реактивная мощность. Он готов идти на дополнительные затраты и устанавливать на своем предприятии батареи конденсаторов, включаемые строго по графику в зависимости от средней статистики потребления электроэнергии по часам суток.
Существует также возможность установки на предприятии специальных устройств (компенсаторов реактивной мощности), подключающих конденсаторы автоматически в зависимости от величины и характера потребляемой в данный момент мощности. Эти компенсаторы позволяют поднять значение коэффициента мощности с 0,6 до 0,97, т.е. практически до единицы.
Принято также, что если соотношение потребленной реактивной энергии и общей не превышает 0,15, то корпоративный потребитель от оплаты за реактивную энергию освобождается.
Что же касается индивидуальных потребителей, то, ввиду сравнительно невысокой потребляемой ими мощности, разделять счета на оплату потребляемой электроэнергии на активную и реактивную не принято. Бытовые однофазные счетчики электрической энергии учитывают лишь активную мощность электрической нагрузки, за нее и выставляется счет на оплату. Т.е. в настоящее время даже не существует технической возможности выставить индивидуальному потребителю счет за потребленную реактивную мощность.
Особых стимулов компенсировать индуктивную составляющую нагрузки у потребителя нет, да это и сложно осуществить технически. Постоянно подключенные конденсаторы при отключении индуктивной нагрузки будут бесполезно нагружать подводящую электропроводку. За электросчетчиком (перед счетчиком тоже, но за то потребитель не платит), что вызовет потребление активной мощности с соответствующим увеличением счета на оплату, а автоматические компенсаторы дороги и вряд ли оправдают затраты на их приобретение.
Другое дело, что производитель иногда устанавливает компенсационные конденсаторы на входе потребителей с индуктивной составляющей нагрузки. Эти конденсаторы, при правильном их подборе, несколько снизят потери энергии в подводящих проводах, при этом несколько повысив напряжение на подключенном электроприборе за счет уменьшения падения напряжения на подводящих проводах.
Но, что самое главное, компенсация реактивной энергии у каждого потребителя, от квартиры до огромного предприятия, снизит токи во всех линиях электропитания, от электростанции до квартирного щитка. За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.
Похожие темы:
Мгновенная мощность
В отличие от цепей постоянного тока, где мощность в течение определенного промежутка времени остается неизменной, в цепях переменного тока дело обстоит иначе. Так как ток и напряжение постоянно меняют своё значение, то и мощность соответственно будет меняться в каждый момент времени. Такая мощность называется мгновенной.
Мгновенной мощностью p(t) называют произведение приложенного к цепи мгновенного напряжения u(t) на мгновенное значение тока i(t) в этой цепи.
График мгновенной мощности представлен на рисунке ниже
Мощность обозначена заштрихованной областью. Знак мощности зависит от сдвига фаз между током и напряжением. В данном случае в цепи присутствуют только активные сопротивления, которые не создают сдвига фаз, поэтому мощность имеет только положительные значения.
Рассмотрим другой график
На данном графике имеются области отрицательных значений мгновенной мощности. Такой график может соответствовать цепи, в которой присутствуют конденсатор или катушка, причем положительные участки — это мощность, которая пошла в цепь и рассеялась на сопротивлении, либо запаслась в качестве энергии полей конденсаторов или катушек, а отрицательные участки это мощность, которая была возвращена обратно источнику.
Активная мощность
Чтобы понять какое количество энергии потребляет источник, целесообразнее взять среднюю мощность за период. Для этого вернемся к первому графику.
На графике мгновенной мощности выделяют прямоугольник со сторонами T и Pm/2. Часть графика, которая находится выше линии Pm/2 точно укладывается в незаштрихованную часть прямоугольника. Таким образом, с помощью линии Pm/2 мы можем определить среднюю мощность за период, которая называется активной мощностью. Активная мощность – это полезная мощность, которая идет на преобразование в другие виды энергии.
В нашем случае сдвиг фаз равен нулю, поэтому коэффициент мощности равен единице, но в случаях с реактивными элементами нужно этот момент учитывать.
Активная мощность измеряется в ваттах – Вт.
cosφ – коэффициент мощности, который показывает отношение активной мощности к полной мощности.
Реактивная мощность
Реактивная мощность – это энергия, которая периодически циркулирует между источником и приемником. Реактивная мощность возникает потому, что конденсатор и катушка способны накапливать энергию, а затем снова отдавать её в сеть. На практике от реактивной мощности зачастую стараются избавиться.
Реактивная мощность измеряется в вольт амперах реактивных – ВАр.
Полная мощность
Полная мощность — это максимальное значение активной мощности.
Полная мощность измеряется в вольт-амперах — ВА.
Для наглядного представления существует треугольник мощностей, в котором гипотенузой является полная мощность, а катетами – активная и реактивная составляющие.
Читайте также — Последовательная RL-цепь
Что такое треугольник силы? — Активная, реактивная и полная мощность
Треугольник мощности представляет собой прямоугольный треугольник, показывающий соотношение между активной мощностью, реактивной мощностью и полной мощностью.
Когда каждая составляющая тока, которая является активной составляющей (Icosϕ) или реактивной составляющей (Isinϕ), умножается на напряжение V, получается треугольник мощности, показанный на рисунке ниже:
Мощность, которая фактически потребляется или используется в цепи переменного тока, называется истинной мощностью или активной мощностью или реальной мощностью.Он измеряется в киловаттах (кВт) или МВт.
Мощность, которая течет вперед и назад, что означает, что она движется в обоих направлениях в цепи или реагирует на нее, называется Реактивная мощность . Реактивная мощность измеряется в киловольт-амперах, реактивная (кВАр) или МВАр.
Произведение среднеквадратичного значения напряжения и тока известно как кажущаяся мощность . Эта мощность измеряется в кВА или МВА.
Следующая точка показывает взаимосвязь между следующими величинами и объясняется графическим представлением, называемым треугольником мощности, показанным выше.
- Когда активная составляющая тока умножается на напряжение цепи V, получается активная мощность. Именно эта мощность создает крутящий момент в двигателе, нагревает нагреватель и т. Д. Эта мощность измеряется ваттметром.
- Когда реактивная составляющая тока умножается на напряжение цепи, получается реактивная мощность. Эта мощность определяет коэффициент мощности, и она течет вперед и назад по цепи.
- Когда ток в цепи умножается на напряжение в цепи, получается полная мощность.
- Из треугольника мощности, показанного над мощностью, коэффициент может быть определен путем взятия отношения истинной мощности к полной мощности.
Как мы знаем, просто мощность означает произведение напряжения и тока, но в цепи переменного тока, за исключением чисто резистивной цепи, обычно существует разность фаз между напряжением и током, и поэтому VI не дает реальной или истинной мощности в цепи.
Активная, реактивная и полная мощность
Требуемый источник питания электрической цепи зависит от
- активной мощности — фактическая потребляемая мощность электрического сопротивления в цепи
- реактивная мощность — мнимая индуктивная и емкостная потребляемая мощность в цепи
Требуемый источник питания называется полной мощностью и представляет собой комплексное значение, которое может быть выражено в виде треугольника Пифагора, как показано на рисунке ниже.
Полная мощность — S
Полная мощность — это мощность, подаваемая в электрическую цепь (обычно от поставщика энергии в сеть) для покрытия реальной и реактивной мощности, потребляемой нагрузкой.
Полная мощность может быть рассчитана как
S = (Q 2 + P 2 ) 1/2 (1)
, где
S = полная мощность, подаваемая в цепь ( вольт-ампер, ВА)
Q = потребляемая реактивная мощность в нагрузке (вольт-ампер, реактивная, ВА)
P = активная потребляемая мощность в нагрузке (ватты, Вт)
Полная мощность измеряется в вольт-амперах (ВА) — напряжение системы переменного тока, умноженное на текущий ток.Полная мощность — это комплексное значение и векторная сумма активной и реактивной мощности, как показано на рисунке выше.
Однофазный ток
S = UI (2a)
где
U = электрический потенциал (В)
I = ток (A)
Трехфазный ток
S = 3 1/2 UI
= 1.732 U I (2b)
Active Power — P
Active — или Real или True — мощность выполняет фактическую работу в нагрузке. Активная мощность измеряется в Вт (Вт) и — это мощность, потребляемая электрическим сопротивлением.
- Истинная мощность — это ток в фазе с напряжением, умноженный на напряжение
Однофазный ток
P = UI cos φ
= UI PF (3a)
, где
φ = фазовый угол между электрическим потенциалом (напряжением) и током
PF = cos φ
= коэффициент мощности
Трехфазный ток
P = 3 1/2 UI cos φ
= 1.732 U I PF (3b)
Постоянный ток
P = U I (3c)
Реактивная мощность — Q
Реактивная мощность — это мнимая или комплексная мощность в емкостной или индуктивной нагрузке. Реактивная мощность представляет собой обмен энергией между источником питания и реактивными нагрузками, при котором полезная мощность не увеличивается и не теряется. Чистая средняя реактивная мощность равна нулю. Реактивная мощность накапливается и разряжается асинхронными двигателями, трансформаторами, соленоидами и конденсаторами.Чистая катушка индуктивности и чистый конденсатор не потребляют никакой энергии, поскольку в течение полупериода, какая бы мощность ни принималась от источника этими компонентами, та же самая мощность возвращается к источнику.
Реактивная мощность должна быть минимизирована, поскольку она увеличивает общий ток, протекающий в электрической цепи, не создавая никакой работы для нагрузки. Повышенные реактивные токи приводят только к невосстановимым потерям мощности из-за сопротивления линии электропередачи.
Увеличение реактивной и полной мощности приведет к уменьшению коэффициента мощности — PF .
Реактивная индуктивная мощность измеряется в реактивных вольт-амперах (ВАР).
- Реактивная мощность — это ток, не совпадающий по фазе с напряжением, умноженным на напряжение
Однофазный ток
Q = UI sin φ (4a)
, где
φ = фазовый угол
Трехфазный ток
Q = 3 1/2 UI sin φ
= 1.732 UI sin φ (4b)
11.2: Истинная, реактивная и полная мощность
Реактивная мощность
Мы знаем, что реактивные нагрузки, такие как катушки индуктивности и конденсаторы, рассеивают нулевую мощность, но тот факт, что они понижают напряжение и потребляют ток, создает обманчивое впечатление, что они на самом деле рассеивают мощность. Эта «фантомная мощность» называется реактивной мощностью , и она измеряется в единицах, называемых вольт-ампер-реактивная мощность (ВАР), а не в ваттах.Математическим обозначением реактивной мощности является (к сожалению) заглавная буква Q.
.
Истинная сила
Фактическая мощность, используемая или рассеиваемая в цепи, называется истинной мощностью и измеряется в ваттах (как всегда, обозначается заглавной буквой P).
Полная мощность
Комбинация реактивной мощности и истинной мощности называется кажущейся мощностью , и она является произведением напряжения и тока цепи без учета фазового угла.Полная мощность измеряется в единицах Вольт-Ампер (ВА) и обозначается заглавной буквой S.
Расчет реактивной, истинной или полной мощности
Как правило, истинная мощность является функцией рассеивающих элементов схемы, обычно сопротивления (R). Реактивная мощность зависит от реактивного сопротивления цепи (X). Полная мощность — это функция полного сопротивления цепи (Z). Поскольку для расчета мощности мы имеем дело со скалярными величинами, любые комплексные начальные величины, такие как напряжение, ток и импеданс, должны быть представлены их полярными величинами , а не действительными или мнимыми прямоугольными составляющими.Например, если я вычисляю истинную мощность по току и сопротивлению, я должен использовать полярную величину для тока, а не просто «реальную» или «мнимую» часть тока. Если я рассчитываю полную мощность по напряжению и импедансу, обе эти ранее комплексные величины должны быть уменьшены до их полярных величин для скалярной арифметики.
Существует несколько уравнений мощности, связывающих три типа мощности с сопротивлением, реактивным сопротивлением и импедансом (все с использованием скалярных величин):
Обратите внимание, что существует два уравнения для расчета истинной и реактивной мощности.Для расчета полной мощности доступны три уравнения, P = IE подходит для только для этой цели. Изучите следующие схемы и посмотрите, как эти три типа мощности взаимосвязаны: чисто резистивная нагрузка на рисунке ниже, чисто реактивная нагрузка на рисунке ниже и резистивная / реактивная нагрузка на рисунке ниже.
Только резистивная нагрузка
Истинная мощность, реактивная мощность и полная мощность для чисто резистивной нагрузки.
Только реактивная нагрузка
Истинная мощность, реактивная мощность и полная мощность для чисто реактивной нагрузки.
Активная / реактивная нагрузка
Истинная мощность, реактивная мощность и полная мощность для резистивной / реактивной нагрузки.
Треугольник власти
Эти три типа мощности — истинная, реактивная и полная — связаны друг с другом в тригонометрической форме. Мы называем это треугольником мощности : (рисунок ниже).
Треугольник мощности, связывающий кажущуюся мощность с реальной мощностью и реактивной мощностью.
Используя законы тригонометрии, мы можем найти длину любой стороны (количество любого типа мощности), учитывая длины двух других сторон или длину одной стороны и угол.
Обзор
- Мощность, рассеиваемая нагрузкой, обозначается как истинная мощность . Истинная мощность обозначается буквой P и измеряется в ваттах (Вт).
- Мощность, просто поглощаемая и возвращаемая нагрузкой из-за ее реактивных свойств, обозначается как реактивной мощностью .Реактивная мощность обозначается буквой Q и измеряется в вольт-амперных реактивных единицах (ВАР).
- Полная мощность в цепи переменного тока, как рассеиваемая, так и поглощенная / возвращаемая, обозначается как полная мощность . Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).
- Эти три типа мощности тригонометрически связаны друг с другом. В прямоугольном треугольнике P = смежная длина, Q = противоположная длина и S = длина гипотенузы.Противоположный угол равен фазовому углу импеданса цепи (Z).
Активная, реактивная и полная мощность
Многие практические схемы содержат комбинацию резистивных, индуктивных и емкостных элементов. Эти элементы вызывают фазовый сдвиг между параметрами электропитания, такими как напряжение и ток.
Из-за поведения напряжения и токов, особенно при воздействии на эти компоненты, количество мощности может иметь разные формы.
В цепях переменного тока амплитуды напряжения и тока будут непрерывно изменяться с течением времени. Поскольку мощность равна напряжению, умноженному на ток, она будет максимальна, когда токи и напряжения выровнены друг с другом.
Это означает, что нулевая и максимальная точки на осциллограммах тока и напряжения возникают одновременно. Это можно назвать полезной мощностью.
В случае элементов индуктивности или конденсатора существует 90 0 фазовый сдвиг между напряжением и током.Таким образом, мощность будет иметь нулевое значение каждый раз, когда напряжение или ток будут иметь нулевое значение.
Это нежелательное состояние, поскольку с нагрузкой не выполняется никаких работ, даже если источник вырабатывает энергию. Эта мощность называется реактивной мощностью. Давайте кратко обсудим эти формы мощности в электрических цепях переменного тока.
Питание в цепях переменного тока
Мощность в любой электрической цепи может быть получена путем умножения значений напряжения и тока в этой цепи.Это применимо как для цепей постоянного, так и для переменного тока.
т.е. мощность = (текущее значение) x (значение напряжения)
P = V x I
Мощность измеряется в ваттах. В цепях постоянного тока и цепях чистого переменного тока без каких-либо нелинейных компонентов формы сигналов тока и напряжения «синфазны».
Таким образом, мощность в любой момент времени в этой цепи получается путем умножения напряжения и тока. Однако в случае цепей переменного тока этого не будет (как уже упоминалось выше о существовании фазового сдвига).
Рассмотрим приведенную выше схему, в которой переменный ток подается на нагрузку. Напряжения и токи в цепи заданы как
v = Vm sin ωt ⇒ v = √2 V sin ωt
i = Im sin ωt ⇒ i = √2 I sin (ωt ± ϕ)
Где V (= Vm / √2) и I (= Im / √2) — среднеквадратичные значения приложенного напряжения и тока, протекающего по цепи, соответственно. Φ — это разность фаз между напряжением и током, для которой знак + указывает начальный фазовый угол, а отрицательный — отстающий фазовый угол.
Тогда мгновенная мощность, передаваемая на нагрузку от источника, определяется выражением
p = vi = 2 VI sin wt sin (ωt ± ϕ)
= VI (cos ϕ — cos (2ωt ± ϕ)
p = VI cos ϕ (1 — cos 2wt) ± VI sin ϕ sin2wt
Приведенное выше уравнение мощности состоит из двух членов, а именно:
- Член, пропорциональный VI cos ϕ, который пульсирует вокруг среднего значения VI cos ϕ
- A член пропорциональный VI sin ϕ, пульсирующий с удвоенной частотой питания, производя в среднем ноль за цикл.
Итак, в цепях переменного тока есть 3 формы мощности. Это
- Активная мощность или Истинная мощность или Активная мощность
- Реактивная мощность
- Полная мощность
Активная мощность
Фактическое количество мощности, рассеиваемой или выполняющей полезную работу в цепи, называется активной или истинной или реальный сила. Он измеряется в ваттах, а в энергосистемах практически измеряется в кВт (киловаттах) и МВт (мегаваттах).
Обозначается буквой P (заглавная) и соответствует среднему значению p = VI cos ϕ.Это желаемый результат электрической системы, которая управляет цепью или нагрузкой.
P = VI cos ϕ
Реактивная мощность
Среднее значение второго члена в приведенном выше производном выражении равно нулю, поэтому мощность, вносимая этим членом, равна нулю. Составляющая, пропорциональная VI sin ϕ, называется реактивной мощностью и обозначается буквой Q.
Хотя это мощность, но не измеряется в ваттах, поскольку это неактивная мощность и, следовательно, она измеряется в Вольт-ампер-реактивный (ВАР).Значение этой реактивной мощности может быть отрицательным или положительным в зависимости от коэффициента мощности нагрузки.
Это связано с тем, что индуктивная нагрузка потребляет реактивную мощность, а емкостная нагрузка генерирует реактивную мощность.
Q = VI sin ϕ
Значение реактивной мощности
Реактивная мощность — это одна из составляющих полной мощности, которые перемещаются вперед и назад в цепи или линии. Это можно назвать скоростью изменения энергии по отношению ко времени, которая продолжает течь от источника к реактивным компонентам в течение положительного полупериода и обратно к компонентам от источника во время отрицательного цикла.Следовательно, нагрузка никогда не расходуется.
В обычном смысле эта фиктивная мощность вовсе не мощность, а всего лишь подобная мощности мера реактивной составляющей тока. Если имеется избыточное количество реактивной мощности, коэффициент мощности значительно снижается. Такой низкий коэффициент мощности нежелателен с точки зрения эффективности работы и эксплуатационных затрат.
А также эта мощность заставляет потреблять дополнительный ток от источника питания, что приводит к дополнительным потерям и большей мощности оборудования.Вот почему эту мощность в шутливой форме называют холестерином линий электропередач.
Чтобы минимизировать потери и увеличить мощность имеющегося оборудования, коммунальные предприятия используют методы компенсации VAR или оборудование коррекции коэффициента мощности. Как правило, эти методы компенсации реактивной мощности реализуются на стороне нагрузки.
Однако эта реактивная мощность полезна для создания необходимых магнитных полей для работы индуктивных устройств, таких как трансформаторы, двигатели переменного тока и т. Д.Это также помогает регулировать напряжение в мощных механизмах электропитания.
Полная мощность
Сложная комбинация истинной или активной мощности и реактивной мощности называется полной мощностью. Без учета фазового угла произведение напряжения и тока дает полную мощность. Полная мощность полезна для оценки силового оборудования.
Его также можно выразить как квадрат тока, умноженный на импеданс цепи. Он обозначается буквой S и измеряется в вольт-амперах (ВА), практические единицы включают в себя кВА (киловольт-вольт-амперы) и МВА (мегавольт-амперы).
Полная мощность = действующее значение напряжения × действующее значение тока
Полная мощность, S = V × I
В сложной форме S = VI *
S = V ∠0 0 I ∠ ϕ (для запаздывающего тока нагрузки)
S = VI ∠ ϕ
S = VI cos ϕ + jV I sin ϕ
S = P + jQ
или S = I 2 Z
Треугольник мощности
Соотношение между активной, реактивной и полной мощностью может быть выражено представлением величин в виде векторов, что также называется методом степенного треугольника, как показано ниже.На этой векторной диаграмме напряжение рассматривается как опорный вектор. Векторная диаграмма напряжения и тока является основой для формирования треугольника мощности.
На рисунке (а) ток отстает от приложенного напряжения на угол ϕ. Горизонтальная составляющая тока равна I cos ϕ, а вертикальная составляющая тока — I sin ϕ. Если каждый вектор тока умножить на напряжение V, получится треугольник мощности, как показано на рисунке (b).
Активная мощность обеспечивается составляющей I cos ϕ по фазе с напряжением, в то время как реактивная мощность создается квадратурной составляющей.
Следовательно, полная мощность или гипотенуза треугольника получается путем векторного комбинирования активной и реактивной мощности.
Используя теорему Пифагора, сумма квадратов двух смежных сторон (активная мощность и реактивная мощность) равна квадрату диагонали (полная мощность). т.е.
(Полная мощность) 2 = (Фактическая мощность) 2
S 2 = P 2 + Q 2
S = √ ((Q 2 + P 2 ))
Где
S = полная мощность, измеренная в киловольт-амперах, кВА
Q = реактивная мощность, измеренная в киловольт-амперах, реактивная, кВАр
P = активная мощность, измеренная в киловаттах, кВт
В единицах резистивной, индуктивной и элементы полного сопротивления, формы мощности могут быть выражены как
Активная мощность = P = I 2 R
Реактивная мощность = Q = I 2 X
Полная мощность = S = I 2 Z
Где
X — индуктивность
Z — полное сопротивление.
Коэффициент мощности
Коэффициент мощности — это косинусоидальный угол между напряжением и током. Коэффициент мощности может быть выражен в терминах рассмотренных выше форм мощности. Рассмотрим треугольник мощности на рисунке выше, в котором коэффициент мощности представляет собой отношение активной мощности к полной мощности. Коэффициент мощности определяет эффективность схемы.
Коэффициент мощности (PF) = (Активная мощность в ваттах) / (Полная мощность в ваттах)
PF = VI cos ϕ / VI
PF = cos ϕ
Пример проблемы
Если источник питания переменного тока 100 В , 50 Гц подключен к нагрузке с сопротивлением 20 + j15 Ом.Затем рассчитайте ток, протекающий по цепи, активную мощность, полную мощность, реактивную мощность и коэффициент мощности.
Учитывая, что Z = R + jXL = 20 + j 15 Ом
Преобразуя импеданс в полярную форму, мы получаем
Z = 25 ∠36,87 Ом
Ток, протекающий по цепи,
I = V / Z = 100∠0 0 /25 ∠36,87
I = 4 ∠ – 36,87
Активная мощность, P = I 2 R = 42 × 20 = 320 Вт
Или P = VI cos ϕ = 100 × 4 × cos (36.87) = 320,04 ≈ 320 Вт
Полная мощность, S = VI = 100 × 4 = 400 ВА
Реактивная мощность, Q = √ (S 2 — P 2 )
= √ (400 2 — 320 2 ) = 240 VAr
Коэффициент мощности, PF = cos ϕ = cos 36,87 = 0,80 с запаздыванием.
Треугольники мощности и импеданса — тригонометрия и генерация однофазного переменного тока для электриков
Это тот момент, когда я попрошу вас взять меня за руку и поверить мне. Хорошо, тебе не нужно брать меня за руку, но ты должен мне доверять.Мы собираемся начать использовать некоторые термины, прежде чем полностью углубиться в их теорию. Я обещаю, что мы более подробно рассмотрим эти концепции в будущих уроках.
При работе с цепями постоянного тока единственное, что препятствует току, — это сопротивление в цепи.
Рис. 20. Резистивная цепь постоянного тока
Как мы узнаем в следующих разделах, переменный ток добавляет компонент, который также противодействует току. Это называется реактивным сопротивлением и проходит под углом 90 градусов к сопротивлению цепи.Это означает, что их невозможно арифметически сложить; это должно быть сделано с использованием теоремы Пифагора. Когда вы складываете эти два вместе, вы получаете полное сопротивление протеканию тока, называемое импедансом .
Рис. 21. Индуктивная цепь постоянного тока
Треугольник, который образуется при добавлении сопротивления к реактивному сопротивлению, известен как треугольник импеданса .
Рис. 22. Треугольник полного сопротивления
В треугольнике полного сопротивления сопротивление (r) всегда находится в нижней части треугольника, реактивное сопротивление (x) всегда идет сбоку, а гипотенуза всегда является сопротивлением (z).
При работе с чисто резистивной схемой рассеиваемая мощность находится в форме тепла или света и измеряется в ваттах и известна как истинная или активная мощность . Это продукт I 2 R.
Рисунок 23. Цепь резистивной мощности
В цепи переменного тока с индуктивностью все еще присутствуют ватты. При прохождении тока через реактивное сопротивление также присутствует реактивная мощность. Эта мощность называется реактивной мощностью , а также мощностью без ваттной мощности или квадратурной мощностью .Его единица — варс.
Рис. 24. Индуктивная цепь питания
Подобно треугольнику импеданса, мы не можем просто сложить две мощности вместе, чтобы получить общую мощность. Их необходимо добавить, используя теорему Пифагора. Их сумма равна полной мощности (ВА).
Рис. 25. Треугольник мощности
При расчете реактивной мощности мы все еще можем использовать формулы мощности. Нам просто нужно использовать их с реактивным сопротивлением вместо сопротивления.
- I 2 X = Варс
- E 2 (напряжение индуктора) / X = Варс
- I x E (напряжение индуктора) = Варс
Помните
При построении треугольника импеданса или мощности резистивная составляющая всегда идет в нижней части треугольника, а реактивная составляющая всегда идет сбоку.
Калькулятор степенного треугольника
Треугольник мощности показывает соотношение между реактивной, активной и полной мощностью в цепи переменного тока.
Важные термины
- Реальная мощность (P) — Измеряется в ваттах, определяет мощность, потребляемую резистивной частью цепи. Также известная как истинная или активная мощность, выполняет реальную работу в электрической цепи.
- Реактивная мощность (Q) — Измеренная в ВАХ мощность, потребляемая в цепи переменного тока, которая не выполняет никакой полезной работы, вызванной индукторами и конденсаторами. Реактивная мощность противодействует действию реальной мощности, забирая мощность из цепи для использования в магнитных полях.
- Полная мощность (S) — произведение среднеквадратичного напряжения и действующего тока, протекающего в цепи, содержит активную и реактивную мощность.
- Коэффициент мощности (q) — Отношение активной мощности (P) к полной мощности (S), обычно выражаемое в виде десятичного или процентного значения. Коэффициент мощности определяет фазовый угол между сигналами тока и напряжения. Чем больше фазовый угол, тем больше реактивная мощность.
Важные формулы
- Реальная мощность (P) = VIcosq, Вт (Вт)
- Реактивная мощность (Q) = VIsinq, Реактивная мощность вольт-ампер (VAr)
- Полная мощность (S) = VI, Вольт-амперы (ВА)
- Коэффициент мощности (q) = P / S
- ВА = Вт / cosq
- ВА = VAR / sinq
- VAR = VA * sinq
- VAR = W * tanq
- Вт = ВА * cosq
- Вт = VAR / tanq
- Sin (q) = Противоположно / Гипотенуза = Q / S = VAr / VA
- Cos (q) = Соседний / Гипотенуза = P / S = Вт / ВА = коэффициент мощности, p.f.
- Желто-коричневый (q) = Напротив / Соседний = Q / P = VAr / W
Дополнительная литература
Активная, реактивная и полная мощность
В этом блоге мы поймем концепцию активной, реактивной и полной мощности. Мы также изучим мгновенную мощность. Мы также увидим, как активная, реактивная и полная мощность связаны друг с другом, что объясняется треугольником мощности. Итак, в конце этого блога мы рассмотрим Треугольник власти.Следовательно, в этом блоге есть о чем рассказать. Итак, начнем.
Для инженера-электрика очень важно знать активную, реактивную и полную мощность, потому что этот раздел является одним из строительных блоков энергосистемы.
Активная, реактивная и полная мощность проявляется только в случае цепей переменного тока, а не в случае цепей постоянного тока, потому что все мы знаем, что формы сигналов напряжения и тока синусоидальны в случае цепей переменного тока.
Вот почему мы изучаем активную, реактивную и полную мощность в цепях переменного тока только не в цепях постоянного тока.В цепях постоянного тока мы изучаем мощность постоянного тока.
Прежде чем изучать активную, реактивную и полную мощность, мы должны знать, «что такое мгновенная мощность?»
МГНОВЕННАЯ СИЛА
Мощность, которая измеряется в конкретный момент времени, известна как Мгновенная мощность.
(ИЛИ)
Умножение напряжения и тока в определенный момент времени известно как мгновенной мощности.
Чтобы понять концепцию мгновенной мощности, давайте рассмотрим форму волны некоторой цепи, показанной на диаграмме ниже.
В момент t 1
P 1 = V 1 (+ ve) * I 1 (-ve) = -ve
Мгновенная мощность P 1 в момент t 1 отрицательна.
В момент t 2
P 2 = V 2 (+ ve) * I 2 (+ ve) = + ve
Мгновенная мощность P 2 в момент t 2 положительна.
Из приведенного выше примера мы можем сказать, что
- Мгновенная мощность может быть положительной и отрицательной.
Что такое положительная сила и отрицательная сила?
Положительная мощность
Когда мощность течет от источника к нагрузке в цепи, мощность называется Положительная мощность.
Отрицательная мощность
В некоторых ситуациях мощность может течь от нагрузки к источнику.В этом случае мощность известна как отрицательная мощность .
- Отрицательная мощность индуцируется в цепи в случае индуктивной нагрузки, емкостной нагрузки и при наличии некоторых нелинейных устройств, таких как выпрямительный мост.
АКТИВНАЯ МОЩНОСТЬ
Чтобы понять концепцию активной мощности, давайте возьмем пример чисто резистивной цепи.
На принципиальной схеме чисто резистивная нагрузка питается от источника переменного тока с напряжением В и током в цепи I.
В случае чисто резистивной нагрузки напряжение и ток остаются в одной фазе, как показано на векторной диаграмме. Это означает, что формы сигнала как напряжения, так и тока достигают своего положительного и отрицательного пика одновременно, и обе формы сигнала пересекают нулевое значение в один и тот же момент времени, и это можно проверить на формах сигналов, приведенных ниже.
Теперь мы увидим полярность мгновенной мощности в разные моменты времени.
В момент t 1
P 1 = V 1 (+ ve) * I 1 (+ ve) = + ve
В момент t 2
P 2 = V 2 (-ve) * I 2 (-ve) = + ve
Следовательно, в случае чисто резистивной нагрузки мощность всегда положительна в каждый момент времени, что означает, что мощность всегда течет от источника к нагрузке.Этот тип мощности известен как активная мощность .
Свойства активной мощности
- Активная мощность всегда положительная.
- Активная мощность не меняет своего направления, как вы можете видеть на осциллограмме.
- Всегда перетекает от источника к нагрузке.
- Активная мощность всегда отвечает за полезную работу, например: свет, звук, движение и т. Д.
- Она обозначается буквой «P» и измеряется в «Вт».{\ circ}} \)
- \ (\ Rightarrow P = VI \ quad Watts \)
РЕАКТИВНАЯ МОЩНОСТЬ
Мы поймем концепцию реактивной мощности с помощью чисто индуктивной цепи.
На принципиальной схеме чисто индуктивная нагрузка питается от источника переменного тока с напряжением В и током в цепи I.
В случае чисто индуктивной нагрузки ток отстает от напряжения питания на 90 o , как показано на векторной диаграмме.
Это означает, что форма волны тока достигает своего положительного пика, отрицательного пика и пересекает нулевое значение 90 o после формы волны напряжения. Ниже приведены кривые напряжения, тока и мощности для чисто индуктивной нагрузки.
Теперь мы увидим полярность мгновенной мощности в разные моменты времени.
В момент t 1
P 1 = V 1 (+ ve) * I 1 (-ve) = -ve
В момент t 2
P 2 = V 2 (-ve) * I 2 (-ve) = + ve
Следовательно, в случае чисто индуктивной нагрузки мощность может быть как положительной, так и отрицательной.Это означает, что мощность движется вперед и назад между источником и нагрузкой точно так же, как маятник, без выполнения какой-либо полезной работы в системе. Этот тип мощности известен как реактивная мощность .
Теперь давайте посмотрим, что происходит в случае чисто емкостной нагрузки .
В случае чисто емкостной нагрузки ток опережает напряжение на 90 o , что означает, что форма волны тока достигает своего положительного пика, отрицательного пика и нулевого значения 90 o до формы волны напряжения.Векторная диаграмма и формы сигналов для чисто емкостной нагрузки приведены ниже.
На графике мощности видно, что мощность также является положительной и отрицательной, что означает, что мощность колеблется между источником и нагрузкой, не выполняя никакой полезной работы. Этот тип мощности известен как реактивная мощность .
Если мы внимательно рассмотрим формы сигналов мощности как в случае чисто индуктивной, так и чисто емкостной нагрузки, мы обнаружим, что величина положительной и отрицательной мощности абсолютно одинакова.
Следовательно, средняя мощность в случае чисто индуктивной нагрузки и чисто емкостной нагрузки равна нулю.
Почему мощность течет назад и вперед в случае индуктивных и емкостных нагрузок?
Во время положительного полупериода, когда мощность положительная, то есть мощность течет от источника к нагрузке, конденсатор накапливает энергию в виде электрического поля.
Во время отрицательного полупериода электрическое поле конденсатора схлопывается, и вся энергия, накопленная в конденсаторе, отправляется обратно к источнику, и мощность начинает течь от нагрузки к источнику.Следовательно, мы получаем отрицательную мощность.
Аналогичным образом, в случае индуктивной нагрузки, в течение положительного полупериода, когда мощность положительная, т. Е. Мощность течет от источника к нагрузке, индуктор накапливает энергию в виде магнитного поля.
Во время отрицательного полупериода магнитное поле индуктора схлопывается, и вся энергия, накопленная в индукторе, высвобождается и отправляется обратно к источнику, и мощность начинает течь от нагрузки к источнику. {\ circ}} \)
ВНЕШНЯЯ МОЩНОСТЬ
Случаи, которые мы видели до сих пор (чисто резистивная, чисто индуктивная и чисто емкостная нагрузка), являются стандартными случаями.
На самом деле, большинство нагрузок, которые мы используем в нашей повседневной жизни (например: электрический вентилятор, электрический утюг, асинхронный двигатель и т. Д.), Представляют собой комбинацию резистивной и индуктивной нагрузки. Некоторые нагрузки также могут представлять собой комбинацию резистивной и емкостной нагрузки, но большинство бытовых и промышленных нагрузок представляют собой смесь резистивной и индуктивной нагрузки.
Общая схема для смеси резистивной и индуктивной нагрузки показана на схеме.
Резистивный компонент потребляет активную мощность, а индуктивный компонент потребляет реактивную мощность.Таким образом, общая мощность, отдаваемая источником, представляет собой комбинацию активной и реактивной мощности, и эта мощность известна как полная мощность .
В случае комбинации резистивной и индуктивной нагрузки, ток отстает от напряжения питания на угол \ (\ phi \), что означает, что форма волны тока достигает своего положительного пика, отрицательного пика и нулевого значения с фазовой задержкой \ (\ phi \) От формы сигнала напряжения.
Векторная диаграмма и формы сигналов для смеси резистивной и индуктивной нагрузки приведены ниже.
На диаграмме формы сигнала мы можем видеть, что мощность бывает положительной и отрицательной из-за наличия активной и реактивной мощности в цепи. Кроме того, величина положительной мощности больше, чем величина отрицательной мощности.
Следовательно, средняя мощность в этом случае не будет равна нулю и, следовательно, мы получим некоторую мощность от системы. Но в этом случае средняя мощность меньше по сравнению со средней мощностью чисто резистивной цепи.
Свойства полной мощности
- Полная мощность — это комбинация активной и реактивной мощности.{2} \)
СИЛОВОЙ ТРЕУГОЛЬНИК
Треугольник мощности — это прямоугольный треугольник, который показывает соотношение между активной, реактивной и полной мощностью.
Основание, нормаль и гипотенуза прямоугольного треугольника обозначают активную, реактивную и полную мощность соответственно.
Чтобы получить треугольник мощности, мы будем использовать векторную диаграмму смеси резистивной и емкостной нагрузки.
В случае сочетания резистивной и емкостной нагрузки ток опережает напряжение питания на некоторый угол \ (\ phi \).Теперь ток можно разделить на две перпендикулярные составляющие, которые равны
- \ (I \ cos {\ phi} \) = Составляющая тока (I), которая находится в фазе с напряжением питания (В).
- \ (I \ cos {\ phi} \) известен как Активная или Ваттная составляющая тока (I)
- \ (I \ sin {\ phi} \) = Составляющая тока (I) что на 90 o не совпадает по фазе с напряжением питания (В).

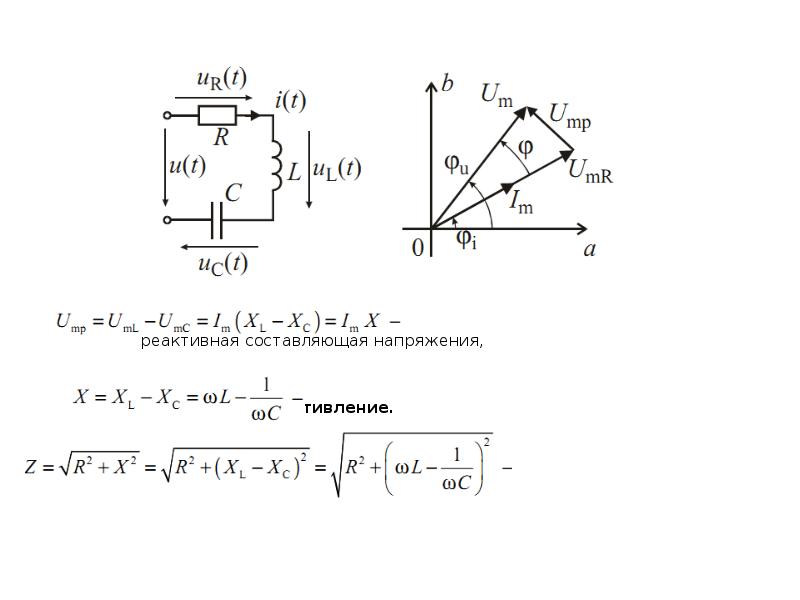 Именно она создает крутящий момент в двигателе, нагревает резистор и выполняет другую полезную работу. Она измеряется ваттметром.
Именно она создает крутящий момент в двигателе, нагревает резистор и выполняет другую полезную работу. Она измеряется ваттметром. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
 Напряжение на зажимах ветви U=100 B, а потребляемая мощность
Напряжение на зажимах ветви U=100 B, а потребляемая мощность