Репетитор-онлайн — подготовка к ЦТ
Магнитное поле создается постоянными магнитами, движущимися зарядами (токами) и характеризуется вектором магнитной индукции B→.
Магнитное поле — форма материи, посредством которой осуществляется магнитное взаимодействие между движущимися зарядами (токами).
Магнитная индукция — векторная физическая величина, модуль которой равен максимальному вращающему моменту, действующему на рамку с током, деленному на модуль магнитного момента этой рамки:
B=MmaxPm,
где M
max — модуль максимального вращающего момента; P
m
— модуль магнитного момента рамки с током.
Направления векторов B→, M→max и P→m связаны правилом правого винта. В Международной системе единиц магнитная индукция измеряется в теслах (1 Тл).
Силовые линии магнитного поля — линии вектора магнитной индукции B→; с помощью силовых линий производится изображение магнитного поля. Силовые линии магнитного поля являются замкнутыми.
Магнитный момент контура с током — векторная физическая величина, модуль которой равен произведению силы тока в контуре на площадь, ограниченную этим контуром:
P
m
= IS,
где I — сила тока в контуре; S — площадь, ограниченная этим контуром.
Направление вектора магнитного момента P→m связано с направлением тока правилом правого винта. В Международной системе единиц магнитный момент измеряется в амперах, умноженных на квадратный метр (1 A ⋅ м2).
Механический вращающий момент, действующий на рамку с током, помещенную в магнитное поле, — векторное произведение магнитного момента на индукцию магнитного поля:
M→=[P→m, B→],
где P→m — магнитный момент рамки с током; B→ — вектор индукции магнитного поля.
Магнитное поле оказывает ориентирующее действие на рамку с током. Направление механического вращающего момента M→ определяется правилом правого винта.
Поток вектора магнитной индукции через некоторую площадку — скалярная физическая величина, равная скалярному произведению вектора магнитной индукции B→ на вектор S→:
Ф=B→⋅S→=BScosα,
где S→=S⋅n→; n→ — единичный вектор нормали (перпендикуляра) к площадке; α — угол между векторами B→ и S→.
В Международной системе единиц поток измеряется в веберах (1 Вб).
Магнитный поток, сцепленный с контуром, — скалярная физическая величина, равная произведению индуктивности контура на силу тока в данном контуре:
Фs
= LI,
где L — индуктивность контура.
В Международной системе единиц поток, сцепленный с контуром, также измеряется в веберах (1 Вб).
Индуктивность контура — скалярная физическая величина, равная отношению потока, сцепленного с данным контуром, к силе тока в нем:
L=ФsI,
где Фs
— поток, сцепленный с контуром.
В Международной системе единиц индуктивность измеряется в генри (1 Гн).
Индуктивность является собственной характеристикой данного контура; она определяется его геометрическими размерами и формой, а также магнитными свойствами среды, в которую помещен этот контур.
Явление электромагнитной индукции заключается в появлении вихревого электрического поля и, как следствие, индукционного тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего площадку, ограниченную данным контуром.
Явление самоиндукции состоит в появлении индукционного тока в замкнутом проводящем контуре при изменении магнитного потока, сцепленного с данным контуром.
Закон Фарадея: ЭДС электромагнитной индукции (самоиндукции) в контуре равна скорости изменения магнитного потока через поверхность, ограниченную этим контуром:
ℰi=−limΔt→0ΔФΔt,
где ΔФ/Δt — скорость изменения магнитного потока; наличие минуса объясняется правилом Ленца.
Правило Ленца: индукционный ток всегда направлен таким образом, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
Индукция магнитного поля это векторная физическая величина
Тест по физике Основы электродинамики. Магнитное поле для 11 класса с ответами. Тест включает 2 варианта, в каждом по 6 заданий.
1 вариант
A1. Индукция магнитного поля — это векторная физическая величина, равная отношению:
1) силы, действующей на элемент длины проводника, помещенный в данную точку поля, к произведению силы тока на длину элемента
2) силы тока, действующей на элемент длины проводника, помещенный в данную точку поля, к произведению силы на длину элемента
3) напряжения, действующего на элемент длины проводника, помещенный в данную точку поля, к произведению силы тока на длину элемента
4) напряжения, действующего на элемент длины проводника, помещенный в данную точку поля, к произведению работы тока на длину элемента
А2. При увеличении тока в контуре в 4 раза индукция магнитного поля:
1) увеличится в 4 раза
2) уменьшится в 4 раза
3) увеличится в 16 раз
4) не изменится
А3. Три частицы влетели в однородное магнитное поле. На рисунке траектории их движения показаны штриховой линией.
Линии магнитной индукции направлены от наблюдателя. Отрицательный заряд имеет:
1) только частица 1
2) только частица 2
3) только частица 3
4) частицы 2 и 3
А4. Доказательством реальности существования магнитного поля может служить:
1) наличие источника поля
2) отклонение заряженной частицы, движущейся в поле
3) взаимодействие двух проводников с током
4) существование электромагнитных волн
В1. Горизонтальный проводник длиной l = 0,20 м и массой m = 0,01 кг, подвешенный на двух тонких нитях, находится в однородном вертикальном магнитном поле с индукцией В = 0,25 Тл. На какой угол α от вертикали отклонятся нити, если по проводнику пропустить ток I = 2,0 А?
C1.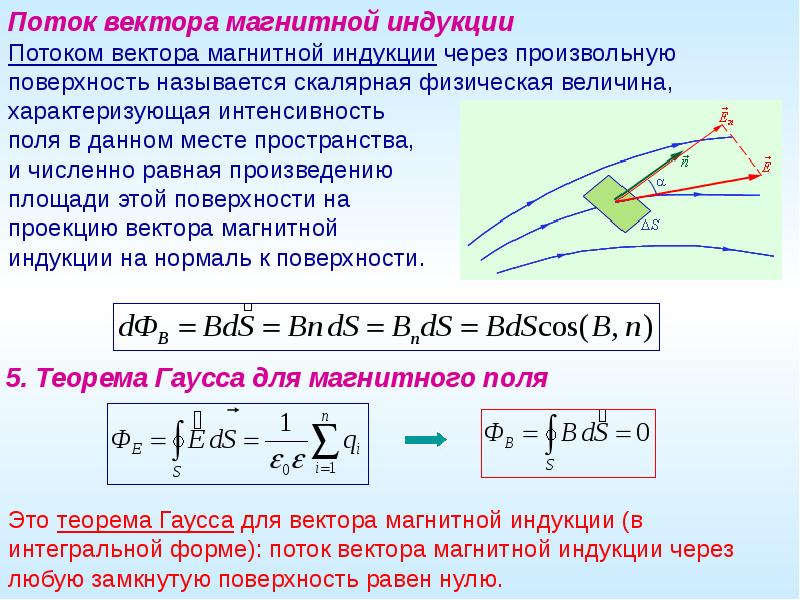 Протон с энергией W = 1,0 МэВ влетел в однородное магнитное поле, перпендикулярное линиям индукции. Какой должна быть минимальная протяженность поля l в направлении движения протона, чтобы направление его движения изменилось на противоположное? (Магнитная индукция поля В = 1 Тл.)
Протон с энергией W = 1,0 МэВ влетел в однородное магнитное поле, перпендикулярное линиям индукции. Какой должна быть минимальная протяженность поля l в направлении движения протона, чтобы направление его движения изменилось на противоположное? (Магнитная индукция поля В = 1 Тл.)
2 вариант
A1. Индукция магнитного поля показывает, чему равна:
1) сила, действующая на элемент проводника с током единичной длины, если по нему идет ток единичной силы
2) сила, действующая на проводник с током, если по нему идет ток единичной силы
3) сила тока, действующая на элемент проводника с током единичной длины
4) сила тока, действующая на проводник с током единичной длины
А2. На рисунке изображен проводник с током. Символ «+» означает, что ток в проводнике направлен от наблюдателя. Куда направлен вектор магнитной индукции поля в точке а?
1) только в направлении 1
2) только в направлении 2
3) в направлении 1 или 3
4) только в направлении 4
А3. В горизонтально расположенном проводнике длиной 50 см и массой 10 г сила тока равна 20 А. Найдите индукцию магнитного поля, в которое нужно поместить проводник, чтобы сила тяжести уравновесилась силой Ампера.
1) 10 -2 Тл
2) 10 Тл
3) 0,1 мТл
4) 100 Тл
А4. Для двух параллельных проводников, находящихся в вакууме, модуль силы взаимодействия между элементами токов, на которые можно разложить любые участки проводников, прямо пропорционален токам, протекающим по проводникам, длинам элементов и обратно пропорционален квадрату расстояния между ними — гласит закон:
1) Ампера
2) Фарадея
3) Ленца
4) Ньютона
В1. На горизонтальных рельсах, расстояние между которыми l = 60 см, перпендикулярно им стоит стержень. Определите силу тока I, который надо пропустить по стержню, чтобы он начал двигаться. Рельсы и стержень находятся в однородном вертикальном поле с индукцией B = 0,6 Тл. Масса стержня m = 0,5 кг, коэффициент трения стержня о рельсы µ = 0,1.
Рельсы и стержень находятся в однородном вертикальном поле с индукцией B = 0,6 Тл. Масса стержня m = 0,5 кг, коэффициент трения стержня о рельсы µ = 0,1.
C1. Электрон, ускоренный разностью потенциалов U = 400 В, влетел в однородное магнитное поле с индукцией В = 1,5 мТл и описал дугу окружности. Найдите радиус этой окружности R.
Ответы на тест по физике Основы электродинамики. Магнитное поле для 11 класса
1 вариант
А1-1
А2-2
А3-1
А4-2
В1. 45°
С1. 14 см
2 вариант
А1-1
А2-1
А3-1
А4-1
В1. 1,4 А
С1. 4,5 см
Вектор магнитной индукции (В) – это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.
Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:
где Мо – магнитная постоянная, R – расстояние, I – сила тока в проводнике.
Магнитная индукция – это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.
Единица магнитной индукции – тесла (Тл).
Магнитная индукция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .
В вакууме B = μH.
Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).
Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции.
Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.
| Рисунок– Электрический ток (I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника. | Рисунок – Правило буравчика |
Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.
На практике удобно пользоваться следующим правилом: Если обхватить соленоид (катушку) правой рукой так, что бы четыре пальца были направлены по току, то отогнутый большой палец покажет направление магнитного поля внутри соленоида.
Рисунок 3.2 – А) Образование магнитного потока в соленоиде
Б) Схема полей в соленоиде при протекании по обмотке переменного тока
Единица измерения В в СИ – тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8841 – | 7555 – или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.
В – физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).
Магнитная индукция – векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:
Единица магнитной индукции. В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:
Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера FА = IBlsin a , а сила Лоренца действует на движущийся заряд:
где a – угол между векторами B и v .
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует силам , постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:
В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,
Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.
Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.
Если напряженность электрического поля равна нулю, то сила Лоренца л равна магнитной силе м :
Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.
Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S – величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором и нормалью к поверхности:
Ф=BScos
В СИ единица магнитного потока 1 Вебер (Вб) – магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:
Электромагнитная индукция-явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.
Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Опыты Фарадея показали, что сила индукционного тока Ii в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции , пронизывающих поверхность, ограниченную этим контуром.
Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:
Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции εi.
По закону Ома для замкнутой цепи
Так как R не зависит от , то
ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.
Закон электромагнитной индукции
ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:
Опыт показывает, что магнитный поток Ф , связанный с контуром, прямо пропорционален силе тока в этом контуре:
Индуктивность контура L – коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.
Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.
Самоиндукция – явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.
Самоиндукция – частный случай электромагнитной индукции.
Индуктивность – величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.
Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :
Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.
ЭДС самоиндукции имеет в этом случае постоянное значение:
где I – начальное значение тока, t – промежуток времени, за который сила тока убывает от I до 0.
За время t в цепи проходит электрический заряд q = Icpt . Так как Icp = (I + 0)/2 = I/2 , то q=It/2 . Поэтому работа электрического тока:
Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:
Таким образом, снова получаем:
Пример. Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?
Энергия магнитного поля катушки W 1 = LI 1 2 /2. По определению, индуктивность катушки L = Ф/I 1. Следовательно,
Ответ: энергия поля равна 8,6 Дж; при уменьшении тока вдвое она уменьшится в 4 раза.
Магнитное поле. Магнитный поток.Свойства магнитного поля.
Магнитное поле
Уже в VI в. до н.э. в Китае было известно, что некоторые руды обладают способностью притягиваться друг к другу и притягивать железные предметы. Куски таких руд были найдены возле города Магнесии в Малой Азии, поэтому они получили название магнитов.
Посредством чего взаимодействуют магнит и железные предметы? Вспомним, почему притягиваютсянаэлектризованные тела? Потому что около электрического заряда образуется своеобразная форма материи -электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют магнитным полем.
Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами (северный и южный). Разноименные магнитные полюса притягиваются, а одноименные — отталкиваются.
Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии — северный полюс (North), входят магнитные линии в южный полюс (South).
Магнитное поле можно сделать «видимым» с помощью железных опилок.
Магнитное поле проводника с током
А теперь о том, что обнаружили Ханс Кристиан Эрстед и Андре Мари Ампер в 1820 г. Оказывается, магнитное поле существует не только вокруг магнита, но и любого проводника с током. Любой провод, например, шнур от лампы, по которому протекает электрический ток, является магнитом! Провод с током взаимодействует с магнитом (попробуйте поднести к нему компас), два провода с током взаимодействуют друг с другом.
Оказывается, магнитное поле существует не только вокруг магнита, но и любого проводника с током. Любой провод, например, шнур от лампы, по которому протекает электрический ток, является магнитом! Провод с током взаимодействует с магнитом (попробуйте поднести к нему компас), два провода с током взаимодействуют друг с другом.
Силовые линии магнитного поля прямого тока — это окружности вокруг проводника.
Направление вектора магнитной индукции
Направление магнитного поля в данной точке можно определить как направление, которое указывает северный полюс стрелки компаса, помещенного в эту точку.
Направление линий магнитной индукции зависит от направления тока в проводнике.
Определяется направление вектора индукции по правилу буравчика или правилу правой руки.
Вектор магнитной индукции
Индукция магнитного поля бесконечного прямолинейного проводника с током на расстоянии r от него:
Индукция магнитного поля в центре тонкого кругового витка радиуса r:
Индукция магнитного поля соленоида (катушка, витки которой последовательно обходятся током в одном направлении):
Принцип суперпозиции
Если магнитное поле в данной точке пространства создается несколькими источниками поля, то магнитная индукция — векторная сумма индукций каждого из полей в отдельности
Магнитный поток
Нормаль — перпендикуляр к плоскости контура.
Анализ формулы позволяет заключить, что магнитный поток изменится, если изменить угол наклона контура, площадь контура, интенсивность магнитного поля.
Контур — замкнутый провод. При изучении магнитного поля контур «усиливают», используя катушку.
Магнитная индукция формула единица измерения
Единица измерения магнитной индукции
Тесла — единица измерения магнитной индукции в системе СИ
Единица магнитной индукции ($overline$) в международной системе единиц (СИ) называется тесла (Тл), по имени сербского ученого Н. 3Тл$. Магнитное поле Земли может существенно отличаться в зависимости от местоположения на планете, оно составляет порядка $approx $10 мкТл.
3Тл$. Магнитное поле Земли может существенно отличаться в зависимости от местоположения на планете, оно составляет порядка $approx $10 мкТл.
Гаусс — единица измерения магнитной индукции в системе единиц СГС
В системе единиц СГС (сантиметр, грамм, секунда) единицей измерения магнитной индукций служит гаусс (Гс). Соотношение между гауссом и тесла:
Данная единица измерения именована в честь немецкого ученого К.Ф. Гаусса.
Используя основные единицы системы СГС, единица измерения магнитной индукции выражается как:
Примеры задач с решением
Задание. Получите единицу измерения магнитной индукции в Международной системе единиц, используя формулу, связывающую ее с магнитным потоком ($Ф$).
Решение. По условию задачи в качестве основы для ее решения используем выражение:
где$ Ф$- поток вектора магнитной индукции через площадку S;$ S$ — величина площади площадки; $alpha $ — угол между направлением нормали к площади S и направлением вектора магнитной индукции. Выразим модуль вектора магнитной индукции из формулы (1.1), имеем:
Учитывая, что в системе СИ $$ — величина безразмерная, поток вектора магнитной индукции измеряется в веберах (Вб):
а единицы измерения площади:
Ответ. Мы получили, что тесла — единица измерения магнитной индукции, и ее можно выразить как: $Тл=frac$
Задание. Определите размерность индукции магнитного поля, используя формулу для модуля $overline$ кругового витка с током.
Решение. Найдем величину вектора магнитной индукции в центре кругового вика с током (рис.1).
Получим формулу для вычисления модуля вектора магнитной индукции в центре витка с током $I$, будем считать, что радиус витка равен R, виток находится в вакууме. Выделим элементарный участок кругового тока ($dl$) (см. рис.1). Величина индукции в очке О от избранного элемента $dl$ равна (из закона Био-Савара — Лапласа):
Для нашего случая все элементы $dl$ перпендикулярны соответствующим радиус-векторам, соединяющим их с точкой, где мы ищем поле, значит $=1. $ Кроме того для всех участков витка $r=R.$ Выражение (2.1) преобразуется к виду:
$ Кроме того для всех участков витка $r=R.$ Выражение (2.1) преобразуется к виду:
Все элементы кругового тока будут образовывать вектор, направленный по оси X (рис.1). Для нахождения полного поля перейдем к интегралу:
[B=ointlimits_L_0 >Рассмотрим единицы измерения правой части выражения (2.3), имеем:
Ответ. Мы получили, что тесла можно выразить как: $Тл=frac$
Магнитная индукция
Магнитное поле, так же как и электрическое поле, является одной из сторон электромагнитного поля и представляет собой один из видов материи. Оно возникает, например, при движении электрических зарядов и, в частности, вокруг проводов с током. Магнитное поле обладает энергией называемой энергией магнитного поля, которая проявляет себя различным образом, например в действии одного провода с током на другой провод с током, находящийся в магнитном поле первого, или в действии магнитного поля проводника с током на магнитную стрелку.
Направление, которое указывается северным кон цом магнитной стрелки, установившейся под дей ствием сил магнитного поля, принимается за направление магнитного поля.
Рис. 3-1. Правило буравчика.
Магнитное поле изображается магнитными линиями (линиями магнитной индукции), Они проводятся так, чтобы направление касательной в каждой точке линии совпадало с направлением поля.
Направление магнитного поля связано с направлением тока. Эта связь устанавливается правилом буравчика: если поступательное движение буравчика совпадает с направлением тот (рис 3-1), то направление вращения рукоятки буравчика укажет направление магнитных линий. Иногда лучше пользоваться другой формулировкой этого правила: если направление вращения рукоятки буравчика совпадает с направлением тока в контуре (рис. 3-2), то поступательное движение его укажет направление магнитных линий, пронизывающих поверхность, ограниченную контуром.
Поместим в магнитное поле перпендикулярно его направлению участок прямолинейного провода длиной l, по которому проходит ток I (рис. 3-3).
3-3).
Из опыта можно убедиться, что на участок провода будет действовать сила F, по величине пропорциональная току, длине участка проводника и интенсивности магнитного поля, которая характеризуется величиной магнитной индукции В.
Таким образом, сила
Рис. 3-2. Правило буравчика для коль цевого тока.
Из написанного следует, что
т. е. магнитная индукция измеряется отношением механической силы, действующей на участок провода, по которому проходит ток, к произведению тока и длины участка про вода, причем провод должен быть расположен перпендикулярно направлению поля.
В международной системе единиц (СИ) сила измеряется в ньютонах, ток — в амперах, длина — в метрах, поэтому единица измерения магнитной индукции
Единица вольт-секунда называется в е б е р (вб), а вебер, деленный на квадратный метр, — тесла (тл),
Кроме единицы тесла, иногда применяется гаусс (гс) — единица магнитной индукции, не принадлежащая к системе
1 гс — 10 -4 тл, или 1 тл = 10 4 гс.
Рис. 3-3. Провод с током в магнитном поле.
Магнитная индукция — векторная величина. Направление вектора магнитной индукции совпадает с направлением поля в данной точке.
Магнитное поле, во всех точках которого векторы магнитной индукции одинаковы по величине и параллельны друг другу, называется однородным.
Магнитные линии можно использовать не только для указания направления поля, но и для характеристики его интенсивности. Для этого условно через единичную площадку, перпендикулярную к направлению поля, проводят число линий, равное или пропорциональное величине магнитной индукции в данном месте поля.
Произведение магнитной индукции В на площадь S, перпендикулярную к вектору магнитной индукции, называется магнитным потоком, т. е.
Так как магнитная индукция измеряется в теслах (тл), а площадь — в квадратных метрах, и учитывая, что 1 тл = 1вб : 1м2 получим, что магнитный поток измеряется в веберах:
Более мелкой единицей магнитного потока, не относящейся к системе СИ, является максвелл
1 мкс = 10 -8 вб = 1 гс•см 2 .
Так как магнитная индукция характеризуется числом магнитных линий, проходящих через единицу площади поверхности, перпендикулярной направлению поля, то магнитный поток будет характеризоваться числом линий, проходящих через площадь S.
Статья на тему Магнитная индукция
Что такое магнитная индукция
В этой статье мы постараемся разобраться в том, что такое магнитная индукция, как она связана с магнитным полем, какое отношение имеет магнитная индукция к току, и как действует на ток. Вспомним основные правила, определяющие направление индукционных линий, а также отметим некоторые формулы, которые помогут в решении задач магнитостатики.
Силовой характеристикой магнитного поля в выбранной точке пространства является магнитная индукция В. Эта векторная величина определяет силу, с которой магнитное поле действует на движущуюся в нем заряженную частицу. Если заряд частицы равен q, ее скорость равна v, а индукция магнитного поля в данной точке пространства равна В, то на частицу в данной точке со стороны магнитного поля действует сила, равная:
Таким образом, В — это вектор, величина и направление которого таковы, что сила Лоренца, действующая на движущийся заряд со стороны магнитного поля равна:
Здесь альфа — это угол между вектором скорости и вектором магнитной индукции. Вектор силы Лоренца F перпендикулярен вектору скорости и вектору магнитной индукции. Его направление для случая движения положительно заряженной частицы в однородном магнитном поле определяется правилом левой руки:
«Если левую руку расположить так, чтобы вектор магнитной индукции входил в ладонь, а четыре вытянутых пальца были направлены по направлению движения положительно заряженной частицы, то отогнутый на 90 градусов большой палец покажет направление силы Лоренца».
Поскольку ток в проводнике является движением заряженных частиц, то магнитную индукцию можно определить и как отношение максимального механического момента, действующего со стороны однородного магнитного поля на рамку с током, к произведению силы тока в рамке на площадь рамки:
Магнитная индукция — фундаментальная характеристика магнитного поля, как напряженность для электрического поля . В системе СИ магнитная индукция измеряется в тесла (Тл), в системе СГС — в гауссах (Гс). 1 тесла = 10000 гаусс. 1 Тл — это индукция такого однородного магнитного поля, в котором на рамку площадью 1 м2, по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.
В системе СИ магнитная индукция измеряется в тесла (Тл), в системе СГС — в гауссах (Гс). 1 тесла = 10000 гаусс. 1 Тл — это индукция такого однородного магнитного поля, в котором на рамку площадью 1 м2, по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.
Кстати, индукция магнитного поля Земли на широте 50° в среднем составляет 0,00005 Тл, а на экваторе — 0,000031 Тл. Вектор магнитной индукции всегда направлен по касательной к магнитной силовой линии.
Контур, помещенный в однородное магнитное поле, пронизывается магнитным потоком Ф, — потоком вектора магнитной индукции. Величина магнитного потока Ф зависит от направления вектора магнитной индукции относительно контура, от его величины, и от площади контура, пронизываемого линиями магнитной индукции. Если вектор В будет перпендикулярен площади контура, то магнитный поток Ф, пронизывающий контур, будет максимальным.
Сам термин индукция происходит от латинского «индукцио», что означает «наведение» (например, навести на мысль – то есть вызвать мысль). Синонимы: наведение, возникновение, образование. Не путать с явлением электромагнитной индукции.
Проводник с током имеет вокруг себя магнитное поле. Открыл магнитное поле электрического тока в 1820 году датский физик Ханс Кристиан Эрстед. Для определения направления силовых линий индукции магнитного поля В электрического тока I, текущего по прямолинейному проводнику, пользуются правилом правого винта или буравчика:
«Направление вращения рукоятки буравчика показывает направление линий магнитной индукции В, а поступательное движение буравчика тогда соответствует направлению тока в проводнике.»
При этом величина магнитной индукции B на расстоянии R от проводника с током I может быть найдена про формуле:
где магнитная постоянная:
Если линии напряженности электростатического поля Е начинаясь на положительных зарядах, заканчиваются на отрицательных, то линии магнитной индукции B замкнуты всегда. В отличие от электрических зарядов, магнитных зарядов, которые бы создавали полюса подобно электрическим зарядам, в природе не обнаружено.
В отличие от электрических зарядов, магнитных зарядов, которые бы создавали полюса подобно электрическим зарядам, в природе не обнаружено.
Теперь несколько слов о постоянных магнитах. Еще в начале 19 века, французский исследователь и физик-естествоиспытатель Андре-Мари Ампер выдвинул гипотезу о молекулярных токах. Согласно Амперу, движения электронов вокруг атомных ядер порождают элементарные токи, которые в свою очередь создают вокруг себя элементарные магнитные поля. И если кусок ферромагнетика поместить во внешнее магнитное поле, то эти микроскопические магнитики сориентируются во внешнем поле, и кусок ферромагнетика станет магнитом.
Вещества с большим значением остаточной намагниченности, такие как сплав неодим-железо-бор, позволяют сегодня получать мощные постоянные магниты. Неодимовые магниты теряют не более 1-2 % своей намагниченности за 10 лет. Но их можно легко размагнитить, нагрев до температуры +70°C и более.
Надеемся, что данная статья помогла Вам получить общее представление о том, что такое магнитная индукция и откуда на возникает.
Вектор магнитной индукции
Вектор магнитной индукции (В) — это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.
Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:
где Мо — магнитная постоянная, R — расстояние, I — сила тока в проводнике.
Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.
Единица магнитной индукции — тесла (Тл).
Магнитная индукция
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .
В вакууме B = μH.
Более конкретно,
— это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора
перпендикулярно им обоим и направлено по правилу буравчика).
Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции.
Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.
| Рисунок– Электрический ток (I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника. | Рисунок – Правило буравчика |
Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.
На практике удобно пользоваться следующим правилом: Если обхватить соленоид (катушку) правой рукой так, что бы четыре пальца были направлены по току, то отогнутый большой палец покажет направление магнитного поля внутри соленоида.
Рисунок 3.2 – А) Образование магнитного потока в соленоиде
Б) Схема полей в соленоиде при протекании по обмотке переменного тока
Единица измерения В в СИ — тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9656 —
9656 —
| 7533 — или читать все.
188.64.174.65 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Электромагнитная индукция
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ) , площади поверхности ( S ) , пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec ) и ( vec ) .
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
 В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_ ) , возникающая в катушке с индуктивностью ( L ) , по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ) , создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
Что такое магнитная индукция
Магнитная индукция – что это такое простым языком
Магнитная индукция – одна из основных характеристик магнитного поля. Представляет собой векторную величину и характеризует силу магнитного действия поля на перемещающиеся внутри него заряженные частицы.
Физический смысл
С научной точки зрения данное явление можно объяснить таким образом. В основе любого металла лежит кристаллическая решётка. В этой кристаллической решётке содержатся отрицательно заряженные частицы – электроны. В ситуации, когда на проводник не оказывается никакого внешнего магнитного воздействия, заряженные частицы находятся в состоянии полного покоя.
Но в ситуации, когда проводник подпадает под воздействие магнитного поля переменной направленности, эти частицы приходят в движение. Прибор для создания магнитного поля и наблюдения явления индукции в лабораторных условиях состоит из металлической катушки, и перемещающегося в ней постоянного магнита. В результате перемещения внутри металла образуется электроток. Сила возникающего в катушке электротока зависит от нескольких факторов:
- Свойств металла, из которого сделана катушка.
- Свойств магнита, перемещающегося внутри катушки.
- Скорости движения катушки и магнита относительно друг друга.
В результате воздействия силового поля магнита на кристаллическую решётку катушки, электроны, содержащиеся в ней, разворачиваются на определённый угол, выстраиваясь вдоль направления силовых линий поля.
И чем сильнее магнитное воздействие, тем большее число электронов внутри металла поворачиваются, однороднее становится их положение в кристаллической решётке. При этом магнитные поля отдельных частиц не нейтрализуют друг друга, а наоборот, усиливают и формируют единое магнитное поле.
Формула и обозначения
Обозначается магнитная индукция латинским символом «В», и определяет силу внешнего влияния, оказываемого магнитным полем на заряженные частицы – в нашем случае электроны, обозначаемые «q», – в некоторой точке. Скорость движения заряженных частиц обозначается буквой «U».
Скорость движения заряженных частиц обозначается буквой «U».
Сама физическая формула магнитной индукции выглядит следующим образом:
- Fмач– наибольшая сила, воздействующая на проводник.
- L – его длина.
- I – сила тока заряженных частиц в металле.
Единицей индукции в международной системе СИ является «тесла», сокращённо в русском варианте «Тл», в международном – «Т». Это название дано в честь сербского учёного Н. Теслы. В старой метрической системе СГС единица индукции обозначалась в честь германского физика «гаусс»: Гс – среди русскоязычных учёных, и G – в интернациональном варианте.
Магнитное поле
Под данным термином в физике подразумевается некое силовое поле, оказывающее определённое влияние на перемещающиеся заряженные частицы, и на прочие тела, имеющие определённый магнитный момент. Воздействие оказывается не зависимо от того, находятся ли эти частицы в состоянии покоя, либо же в движении. Кроме вектора магнитной индукции, дополнительной характеристикой поля выступает векторный потенциал. Он носит альтернативный характер, но при этом, в физическом смысле, неразрывно связан с магнитной индукцией.
Для поля, действующего в абсолютном вакууме, главной характеристикой обычно выбирается не индукция, а его напряжённость, обозначаемая Н. Однако, подобная замена в сфере действия земного магнитного поля уже не имеет особого смысла, в связи с чем, в практических опытных измерениях и наблюдениях за основную характеристику магнитного поля всё же принимается вектор магнитной индукции.
Фактически, магнитное поле допустимо определить, как особую материю, с помощью которой происходит взаимодействие меж некими заряженными элементарными частицами, передвигающимися с определённой скоростью.
При этом не стоит путать магнитную и электромагнитную индукцию. Под электромагнитной индукцией понимается закономерность, установленная англичанином М. Фарадеем. Суть закономерности состоит в возникновении электромагнитного силового поля под действием переменного электротока, протекающего в замкнутом проводниковом контуре. В контуре возникает определённая движущая сила, в свою очередь, порождающая индукционный ток. Магнитное поле, наряду с электрическим полем, выступает как одна из двух частей электромагнитного поля.
Под электромагнитной индукцией понимается закономерность, установленная англичанином М. Фарадеем. Суть закономерности состоит в возникновении электромагнитного силового поля под действием переменного электротока, протекающего в замкнутом проводниковом контуре. В контуре возникает определённая движущая сила, в свою очередь, порождающая индукционный ток. Магнитное поле, наряду с электрическим полем, выступает как одна из двух частей электромагнитного поля.
Теория о постоянных магнитах, своим воздействием вызывающих возникновение индукции, была разработана французским физиком А-М. Ампером, в честь него позднее была названа единица мощности электротока. Он впервые установил, что движения электронов вокруг центра атома в итоге порождают микроскопические, или элементарные магнитные поля. Также им был открыто свойство металлических проводников сохранять магнитные свойства некоторое время после прекращения воздействия на них магнитным полем.
Вектор напряженности магнитного поля
Для описания магнитного поля используются две его основные характеристики — индукция B→ и напряженность H→. Эти величины связаны между собой. Рассмотрим, что такое напряженность магнитного поля, чему она равна, каков физический смысл этой величины.
Напряженность магнитного поля
Определение
Напряженность магнитного поля — векторная физическая величина, в общем случае равная разности векторов индукции магнитного поля B→ и намагниченности Pm→.
Напряженность обозначается буквой Н→. Единица измерения напряженности магнитного поля в системе СИ — ампер на метр (Амперметр).
Формула напряженности магнитного поля:
Н→=1μ0B→-Pm→.
Здесь коэффициент μ0 — магнитная постоянная. μ0=1,25663706 НА2.
Физический смысл напряженности магнитного поля
Индукция магнитного поля — силовая характеристика. Индукция определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью.
Индукция определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью.
Напряженность поля характеризует густоту силовых линий (линий магнитной индукции).
Физический смысл напряженности магнитного поля
В вакууме или при отсутствии среды, способной к намагничиванию (например, в воздухе) напряженность магнитного поля совпадает с магнитной индукцией с точностью до коэффициента μ0.
В средах, способных к намагничиванию (магнетиках) напряженность несет смысл как бы «внешнего поля». Она совпадает с вектором магнитной индукции, который был бы, если бы магнетика не было.
Циркуляция вектора напряженности магнитного поля
Существует теорема о циркуляции магнитного поля. Это одна из основных теорем электродинамики, сформулированная Анри Ампером. Ее также иногда называют теоремой или законом Ампера. Теорема о циркуляции магнитного поля — своеобразный аналог теоремы Гаусса о циркуляции вектора напряженности электрического поля.
Теорема о циркуляции магнитного поля
Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов проводимости, охваченных контуром, по которому рассматривается циркуляция.
∮H→dr→=∑Im
Пример
Определить циркуляцию вектора напряженности для замкнутого контура L.
I1=5A, I2=2A, I3=10A, I4=1A.
По теореме о циркуляции:
∮H→dr→=∑Im
Рассматриваемый контур охватывает токи I1, I2, I3.
Подставим значения c учетом указанных на рисунке направлений токов и вычислим циркуляцию:
∮H→dr→=∑Im=5A12A+10A=13A.
Магнитное поле — вихревое поле, которое не является потенциальным. Циркуляция вектора напряженности в общем случае отлична от нуля.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Единица измерения индукции магнитного поля в международной системе …
10. Единица измерения индукции магнитного поля в Международной системе — …
Единица измерения индукции магнитного поля в Международной системе — …
А) Ом. Б) Кл. В) Н. Г) Тл.
11. Индукция магнитного поляпоказывает, чему равна сила …
А) Действующая на элемент проводника с током единичной длины, если по нему идет ток единичной силы.
Б) Действующая на проводник с током, если по нему идет ток единичной силы.
В) Тока, действующая на элемент проводника с током единичной длины.
Г) Тока, действующая на проводник с током единичной длины.
12. Сила, действующая со стороны магнитного поля на отдельно взятую движущуюся заряженную частицу, называется …
А) Силой Ампера.
Б) Силой Архимеда.
В) Силой взаимодействия.
Г) Силой Лоренца.
13. При увеличении тока в контуре в 4 раза, индукция магнитного поля …
А) Увеличится в 4 раза.
Б) Уменьшится в 4 раза.
В) Увеличится в 16 раз.
Г) Не изменится.
14. Единица измерения магнитного потока в Международной системе — …
А) Тл. Б) Омм. В) Вб. Г) А.
15. На рисунке изображен проводник с током. Символ «+» означает, что ток в проводнике направлен от наблюдателя. Укажите направление вектора магнитной индукции поля в точке а.
А) Только 1.
Б) Только 2.
В) 1 или 3.
Г) Только 4.
16. На рисунке изображены линии индукции магнитного поля прямого проводника с током и показано положение точек 1, 2, 3. Сравните индукции магнитного поля в этих точках.
А) В > В> В.
Б) В.
В) В= В= В.
Г) Нет правильного ответа.
17. Магнитный поток, пронизывающий катушку, изменяется со временем так, как показано на рисунке. Укажите промежуток времени, при котором модуль ЭДС индукции имеет максимальное значение.
А) От 0 до 5 с.
Б) От 5 до 10 с.
В) От 10 до 20 с.
Г) Везде одинаков.
18. За 2 с магнитный поток, пронизывающий проволочную рамку, увеличивается с 4 до 12 Вб. Модуль ЭДС индукции, наведенный в рамке, равен …
Модуль ЭДС индукции, наведенный в рамке, равен …
А) 8 В. Б) 4 В. В) 12 В. Г) 16 В.
19. Если силу тока в катушке увеличить вдвое, то энергия магнитного поля …
А) Увеличится в 2 раза.
Б) Уменьшится в 2 раза.
В) Не изменится.
Г) Увеличится в 4 раза.
20. Три частицы влетели в однородное магнитное поле. На рисунке траектории их движения показаны штриховой линией. Линии магнитной индукции направлены от наблюдателя. Отрицательный заряд имеет …
А) Только 1.
Б) Только 2.
В) Только 3.
Г) 2 и 3.
21. Магнит вводится в алюминиевое кольцо так, как показано на рисунке. Направление тока в кольце указано стрелкой. Каким полюсом магнит вводится в кольцо?
А) Положительным.
Б) Отрицательным.
В) Северным.
Г) Южным.
22. В горизонтально расположенном проводнике длиной 50 см и массой 10 г сила тока равна 20 А. Найдите индукцию магнитного поля, в которое нужно поместить проводник, чтобы сила тяжести уравновесилась силой Ампера.
А) 10 Тл. Б) 10 Тл. В) 0,1 мТл. Г) Нет правильного ответа.
23.Когда металлический стержень присоединили к одному из полюсов источника тока, то вокруг него образовалось … поле.
А) Электрическое.
Б) Магнитное.
В) Электрическое и магнитное.
Г) Нет правильного ответа.
24. Диамагнетики – этовещества, у которых магнитная проницаемость…
А) Больше единицы и они слабо втягиваются в магнитное поле.
Б) Очень большая.
В) Меньше единицы и они слабо выталкиваются из магнитного поля.
Г) Очень маленькая.
25. Три одинаковые катушки включены последовательно в электрическую цепь постоянного тока. Катушка 1 без сердечника, в катушке 2 – сердечник из кобальта, в катушке 3 – сердечник из трансформаторной стали. В какой из катушек индукция магнитного поля будет наименьшей? Магнитная проницаемость воздуха равна 1, кобальта – 175, трансформаторной стали – 8000.
А) 1. Б) 2. В) 3. Г) Индукция магнитного поля во всех катушках одинакова.
Тест № 9 Электромагнитная индукция.
1. Индукционный ток – это направленное движение …
А) Заряженных частиц, по своим действиям в принципе не отличается от электрического тока, проявляется за счет сил неэлектрического происхождения.
Б) Нейтральных частиц, по своим действиям в принципе не отличается от электрического тока, проявляется за счет сил электрического происхождения.
В) Заряженных частиц, по своим действиям отличается от электрического тока, проявляется за счет сил неэлектрического происхождения.
Г) Нейтральных частиц, по своим действиям в принципе отличается от электрического тока, проявляется за счет сил электрического происхождения.
2. На каком опыте можно показать возникновение индукционного тока?
А) Проводник, концы которого присоединены к гальванометру, надо поместить в магнитное поле.
Б) Проводник, концы которого присоединены к гальванометру, надо двигать вдоль магнитных линий.
В) Магнит или проводник, концы которого присоединены к гальванометру, надо двигать так, чтобы магнитные линии пересекали проводник.
Г) Нет правильного ответа.
3. Какую задачу ставил перед собой Фарадей, приступаяк работе, которая привела его к открытию явления электромагнитной индукции?
А) С помощью электрического тока получить магнитное поле.
Б) Превратить магнетизм в электричество.
В) С помощью электрического поля получить ток
Г) Нет правильного ответа.
4. Магнитный поток – этофизическая величина, равная …
А) Отношению модуля вектора индукции магнитного поля на площадь контура, пронизываемого этим магнитным полем к синусу угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной контуром.
Б) Произведению модуля вектора индукции магнитного поля на площадь контура, пронизываемого этим магнитным полем и на косинус угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной контуром.
В) Произведению модуля вектора индукции магнитного поля на площадь контура, пронизываемого этим магнитным полем и на синус угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной контуром.
Г) Отношению вектора индукции магнитного поля на площадь контура, пронизываемого этим магнитным полем к косинусу угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной контуром.
5. Единица измерения магнитного потока в Международной системе — …
А) Тл. Б) Омм. В) Вб. Г) А.
6.Из предложенных вариантов выберите выражение магнитного потока.
А) ВSsin . Б) . В) ВScos . Г) Нет правильного ответа.
7. На острие укреплено коромысло с двумя уравновешивающими друг друга кольцами, изготовленными из немагнитного металла, например, алюминия. Одно кольцо сплошное, другое – разрезанное. Будем вдвигать в кольца постоянный магнит, при этом …
А)Сплошное и разрезанное кольца – оттолкнутся.
Б) Сплошное — оттолкнется, а разрезанное – нет.
В) Оба кольца останутся в первоначальном положении.
Г) Разрезанное оттолкнется, а сплошное – нет.
8. Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он был вызван, – это …
А) Правило правой руки.
Б) Правило левой руки.
В) Правило буравчика.
Г) Правило Ленца.
9. Направление индукционного тока зависит …
А) От направления магнитной индукции поля, пронизывающего контур.
Б) От направления силовых линий.
В) От магнитного потока.
Г) Нет правильного ответа.
10. Электромагнитной индукцией называют явление возникновения …
А) Магнитного поля вокруг проводника при прохождении по нему электрического тока.
Б) Электрического тока в проводнике, пересекающем магнитные линии.
В) Электрического тока в проводнике.
Г) Правильного ответа нет.
11. Физическая величина, равная отношению работы сторонних сил по перемещению электрического заряда по электрической цепи к величине этого заряда, называется …
А) Электродвижущей силой.
Б) Электромагнитной индукцией.
В) Магнитным потоком.
Г) Правильного ответа нет.
12. Из предложенных вариантов выберите выражение закона электромагнитной индукции.
А) . Б) -. В) . Г) -.
13. Кто придал закону электромагнитной индукции именно такой вид: ?
А) М. Фарадей. Б) Х. Эрстед. В) А. Ампер. Г) Д. Максвелл.
14.Работа трансформатора основана на явлении …
А) Самоиндукции.
Б) Электромагнитной индукции.
В) Магнитной индукции.
Г) Нет правильного ответа.
15. ЭДС, вырабатываемая генератором, зависит от …
А) Периода.
Б) Индукции магнитного поля.
В) Частоты вращения рамки в магнитном поле.
Г) Нет правильного ответа.
16. Явление возникновения ЭДС индукции в катушке, по которой протекает переменный ток, называется…
А) Самоиндукцией.
Б) Электродвижущей силой.
В) Электромагнитной индукцией.
Г) Нет правильного ответа.
17. Из предложенных вариантов выберите выражение индуктивности.
А) . Б) . В) ФI. Г) Нет правильного ответа.
18. Индуктивность численно равна …
А) Магнитному потоку, охватываемому проводником, если сила тока, протекающая по проводнику, равна 1 А.
Б) Силе тока, протекающей по проводнику, если магнитный поток, охватываемый проводником, равен 1 Вб.
В) Магнитному потоку, охватываемому проводником, при изменении силы тока на 1 А за 1 с.
Г) Силе тока, протекающей по проводнику, если магнитная индукция равна 1 Тл.
19. . Что такое k?
А) Коэффициент пропорциональности.
Б) Коэффициент трансформации.
В) Постоянная Больцмана.
Г) Нет правильного ответа.
20. Если силу тока в катушке увеличить вдвое, то энергия магнитного поля …
А) Увеличится в 2 раза.
Б) Уменьшится в 2 раза.
В) Не изменится.
Г) Увеличится в 4 раза.
21. Какой магнитный поток возникает в контуре индуктивностью 3 мГн при силе тока 15 мА?
А) 45 мкВб. Б) 45 Вб. В) 45 мВб. Г) Нет правильного ответа.
22. Чему равна ЭДС самоиндукции в катушке с индуктивностью 0,4 Гн при равномерном уменьшении силы тока с 15 до 10 А за 0,2 с?
А) 0. Б) 10 В. В) 50 В. Г) 0,4 В.
23. По катушке индуктивностью L — 0,6 Гн течет ток I = 15 А, а по катушке с индуктивностью L = 15 Гн течет ток I = 0,6 А. Сравните энергии магнитного поля этих катушек.
А) W = W.
Б) W > W.
В) W.
Г) W = W = 0.
24. В катушке с индуктивностью 0,3 Гн сила тока равна 3 мА. Энергия магнитного поля этой катушки равна …
А) 1,35 Дж. Б) 1,35 мкДж. В) 0,45 мДж. Г) Нет правильного ответа.
25. Прямой проводник длиной 80 см движется в магнитном поле со скоростью 36 км/ч под углом 30° к вектору магнитной индукции. В проводнике возникает ЭДС 5 мВ. Магнитная индукция равна …
А) 1,25 мТл.
Б) 3 мТл.
В) 0,8 кТл.
Г) Нет правильного ответа.
Тест № 10. Основы молекулярно – кинетической теории строения вещества.
1. Выберите правильное утверждение:
А) Молекулы одного и того же вещества различны.
Б) Молекулы одного и того же вещества одинаковы.
В) При нагревании тела молекулы вещества увеличиваются в размерах.
Г) При нагревании тела увеличивается масса молекул.
2. Явление диффузии доказывает…
А) Только факт существования.
Б) Только факт движения молекул.
В) Факт существования и движения молекул.
Г) Факт взаимодействия молекул.
3. Опытным обоснованием существования промежутков между молекулами является…
А) Диффузия.
Б) Броуновское движение.
В) Испарение жидкости.
Г) Наблюдение с помощью оптического микроскопа.
4. Броуновское движение — это…
А) Проникновение молекул одного вещества в промежутки между молекулами другого вещества..
Б) Отрыв молекул с поверхности жидкости или твердых тел.
В) Хаотическое тепловое движение взвешенных частиц в жидкостях или газах.
Г) Движение молекул, объясняющее текучесть жидкости.
5. Выберите величину, которая соответствует порядку значения массы молекулы или соединения.
А) 10 кг. Б) 10 кг. В) 10 кг. Г) 10кг.
6. Физическая величина, определяемая числом структурных элементов, содержащихся в системе, называется…
А) Молярной массой.
Б) Относительной молекулярной массой.
В) Количеством вещества.
Г) Нет правильного ответа.
7. Молярная масса – это физическая величина, …
А)Определяемая отношением массы вещества к его количеству.
Б) Определяемая числом структурных элементов, содержащихся в системе.
В) Равная отношению массы молекулы данного вещества к 1/12 атома углерода.
Г) Определяемая произведением массы вещества к его количеству.
8. Единица измерения количества вещества в Международной системе — …
А) Моль. Б) кг. В) . Г) Моль.
9. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде …
А) 12 массой 0,012 кг.
Б) 14 массой 0,014 кг.
В) 16 массой 0,016 кг.
Г) 18 массой 0,018 кг.
10. Выберите из предложенных ответов выражение, позволяющее рассчитать число молекул данного вещества.
А) . Б) . В) . Г) .
11. Масса углекислого газа (CO) равна…
А) 7,3 кг.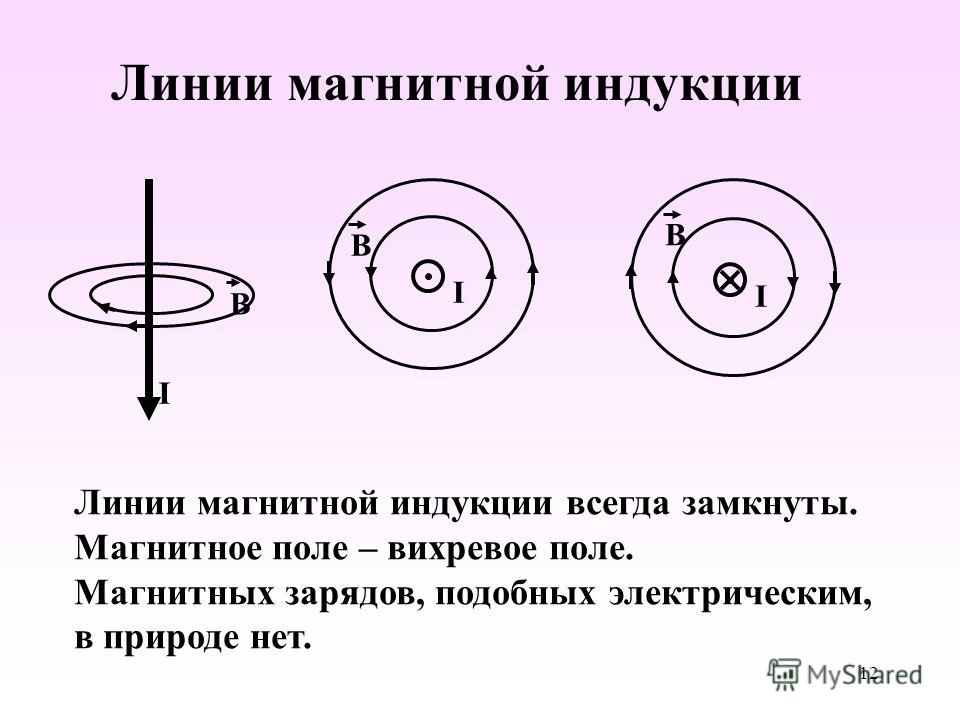
Б) 7,3 кг.
В) 7,3 кг.
Г) 7,310 кг.
12. В … состоянии молекулы движутся равномерно и прямолинейно до столкновения друг с другом.
А) Газообразном.
Б) Жидком.
В) Твердом.
Г) Кристаллическом.
13. В опыте Штерна пары раскаленного металла проводника М оседали на вращающемся внешнем цилиндре (в т. О молекулы оседали при неподвижном цилиндре). Скорость молекул, осевших в точке 1 …
А) Наименьшая.
Б) Наибольшая.
В) Средняя.
Г) Может быть любой.
14. Графики 1, 2, 3 характеризуют распределение молекул газа по скоростям ( кривая Максвелла). Сравните температуру газов.
А) Т.
Б) Т.
В) Т>Т>Т.
Г) Т>Т.
15. Разрушение твердых веществ является доказательством …
А) Существования сил взаимодействия между молекулами.
Б) Движения молекул.
В) Существования самих молекул.
Г) Броуновского движения.
16. Количество вещества определяется выражением …
А) . Б) . В) . Г) .
17. Единица измерения молярной массы в Международной системе — …
А) Моль. Б) кг. В) . Г) Моль.
18. Молярная масса показывает, …
А) Сколько молей находится в однородном веществе.
Б) Сколько молекул находится в однородном веществе.
В) Какова масса одного моля однородного вещества.
Г) Сколько молекул не находится в однородном веществе.
19. Число Авогадро равно…
А) 6,02 моль.
Б) 6,02 моль.
В) 6,02 кг.
Г) Нет правильного ответа.
20. Количество вещества, содержащееся в алюминиевой отливке массой 2,7 кг, равно …
А) 0,1 моль. Б) 10 моль. В) 100 моль. Г) 100 кг.
21. Число молекул, содержащихся в 56 г азота, равно …
А) 0. Б) 5. В) 12. Г) 12.
22. Масса молекулы воды равна…
А) 3 кг.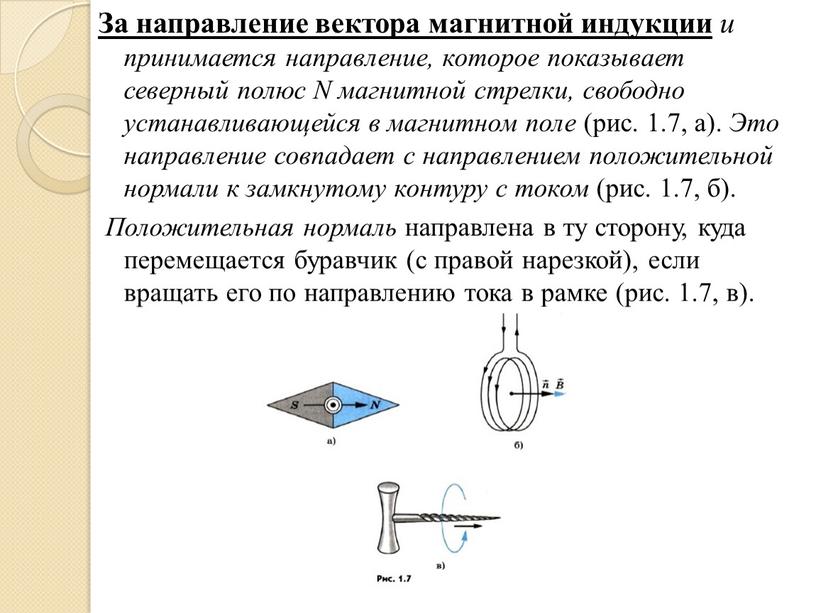 Б) 0,3 кг. В) 0,3 кг. Г) 3 кг.
Б) 0,3 кг. В) 0,3 кг. Г) 3 кг.
23.Массу одной молекулы определяет выражение…
А) . Б) . В) . Г) .
24. Укажите величину, соответствующую порядку линейных размеров молекул веществ.
А) 10 кг. Б) 10 кг. В) 10 кг. Г) 10кг.
25. Какой объем занимает 1 моль любого вещества в газообразном состоянии при нормальных условиях ( р = 101,325 Па и t = 0°)?
А) 23,4 л.
Б) 22,4 л.
В) 22,4 кг.
Г) 22,4 г.
Коды правильных ответов
Тест №1 Кинематика
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | А | А | Б | А | Г | А | А | В | Г | Г | В | В | Г | В | А | Б | В | В | А | Б | Г | В | А | Б | Г |
Тест№2 Динамика
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | А | Б | В | В | Б | Б | Г | В | Б | В | Г | А | Г | В | В | В | Б | Б | А | В | Г | А | А | В | В |
Тест №3. Законы сохранения в механике.
Законы сохранения в механике.
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | Б | В | А | А | А | Г | А | Б | Б | В | А | Б | В | В | Б | В | А | Б | Г | Б | В | Б | Б | Г | А |
Тест№4 Механические колебания и волны.
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | А | В | Г | Б | А | А | Г | Б | А | Г | А | Б | В | Б | Б | А | А | Б | В | Б | Б | А | В | Б | А |
Тест №5 Электростатика
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | Г | А | Б | А | Б | А | В | А | Б | Г | В | А | Б | В | Б | А | Г | А | А | В | Г | А | В | Г | А |
Тест №6 Постоянный электрический ток
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | Г | В | В | Г | Б | В | Г | А | А | Г | Б | А | А | В | А | Б | В | Б | В | А | Г | В | Б | А | Г |
Тест №7 Электрический ток в средах.
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | Б | А | А | В | А | В | А | Б | А | А | Б | А | А | Б | В | Г | А | А | В | Б | Г | Б | Г | А | А |
Тест №8 Магнитостатика
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | Б | А | Б | Г | В | В | Б | А | Б | Г | А | Г | Б | В | А | А | А | Б | Г | А | В | А | А | В | А |
Тест №9 Электромагнитная индукция.
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | А | Б | А | В | В | А | Б | Г | А | В | А | Г | Г | Б | В | А | Б | А | Б | Г | А | Б | Б | Б | А |
Тест №10 Основы молекулярно – кинетической теории строения вещества.
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Ответ | Б | Б | А | В | Б | В | А | Г | А | Б | Г | А | А | Б | В | Б | В | В | Б | В | Г | А | Г | Г | Б |
FIZIKA_2_otvety_na_voprosy — Стр 2
2. Что такое электрический ток.
Что такое электрический ток.
Электрическим током называется
упорядоченное движение электрических
зарядов. За направление тока принимают
направление движения положительных
зарядов, которое противоположно
направлению движения отрицательных
зарядов. Различают: ток проводимости
(ток в проводниках), конвекционный ток
и ток в вакууме.
3. Назовите характеристики электрического
тока и их единицы измерения. Количественной
характеристикой электрического тока
служит сила тока I
–скалярная физическая величина,
равная отношению заряда dq,
переносимого через поперечное сечение
проводника за интервал времени dt,
к этому интервалу времени:
.
В международной системе единиц СИ
сила тока измеряется в амперах (А).
В
качестве характеристики, задающей
распределение силы тока по поперечному
сечению проводника служит вектор
плотности тока
.
Плотностью электрического тока
называется вектор
,
совпадающий с направлением электрического
тока в рассматриваемой точке и численно
равный отношению силы тока dI
сквозь малый элемент поверхности,
перпендикулярной направлению тока, к
площади dS⊥
этого элемента:
.
Единицей измерения плотности тока
является А/м2.
4. Назовите условия, выполнение которых
необходимо для протекания в цепи
электрического тока. Условия,
необходимые для проявления и существования
электрического тока проводимости в
среде: а) наличие в среде свободных
носителей заряда, т.е. заряженных частиц,
способных перемещаться. В металле это
электроны проводимости; в электролитах
– положительные и отрицательные ионы;
в газах – положительные, отрицательные
ионы и электроны. б) наличие в
среде электрического поля, энергия
которого затрачивалась бы на перемещение
электрических зарядов. Для того, чтобы
ток был длительным, энергия электрического
поля должна все время пополняться, т. е.
е.
нужен источник электрической энергии
– устройство, в котором происходит
преобразование какого-либо вида энергии
в энергию электрического тока.
5. Какие силы по своей природе не могут
быть сторонними. Если
в цепи на носители тока действуют только
силы
электростатического поля (кулоновские),
то происходит перемещение носителей
(они предполагаются положительными) от
точек с большим потенциалом к точкам с
меньшим потенциалом. Это приведет к
выравниванию потенциалов во всех точках
цепи и к исчезновению электрического
поля. Поэтому для существования
постоянного тока необходимо наличие в
цепи устройства, способного создавать
и поддерживать разность потенциалов
за счет работы сил
не электростатического
происхождения.
Такие устройства называются источниками
тока. Силы
не электростатического происхождения,
действующие на заряды со стороны
источников тока, называются сторонними.
Эти силы могут быть обусловлены
химическими процессами, диффузией
носителей тока в неоднородной среде
или через границу двух разнородных
веществ, электрическими полями,
порождаемыми меняющимся во времени
магнитным полем.
6. Чему равна циркуляция вектора
напряженности сторонних сил. Вне
источника напряженность поля сторонних
сил отсутствует, т.е. равна нулю, поэтому
при перемещении положительного заряда
по замкнутой цепи работу сторонних сил
можно представить как интеграл по всему
замкнутому контуру
(
– напряженность поля сторонних сил,
определяемая сторонней силой, действующей
на единичный положительный заряд внутри
источника). Отсюда ЭДС, действующая в
замкнутой цепи — циркуляция вектора
напряженности поля сторонних сил:
.
Если цепь разомкнута, то ЭДС останется
по величине такой же, поскольку
определяется только на промежутке
источника тока.
7. Запишите обобщенный закон Ома (закон
Ома для неоднородного участка цепи).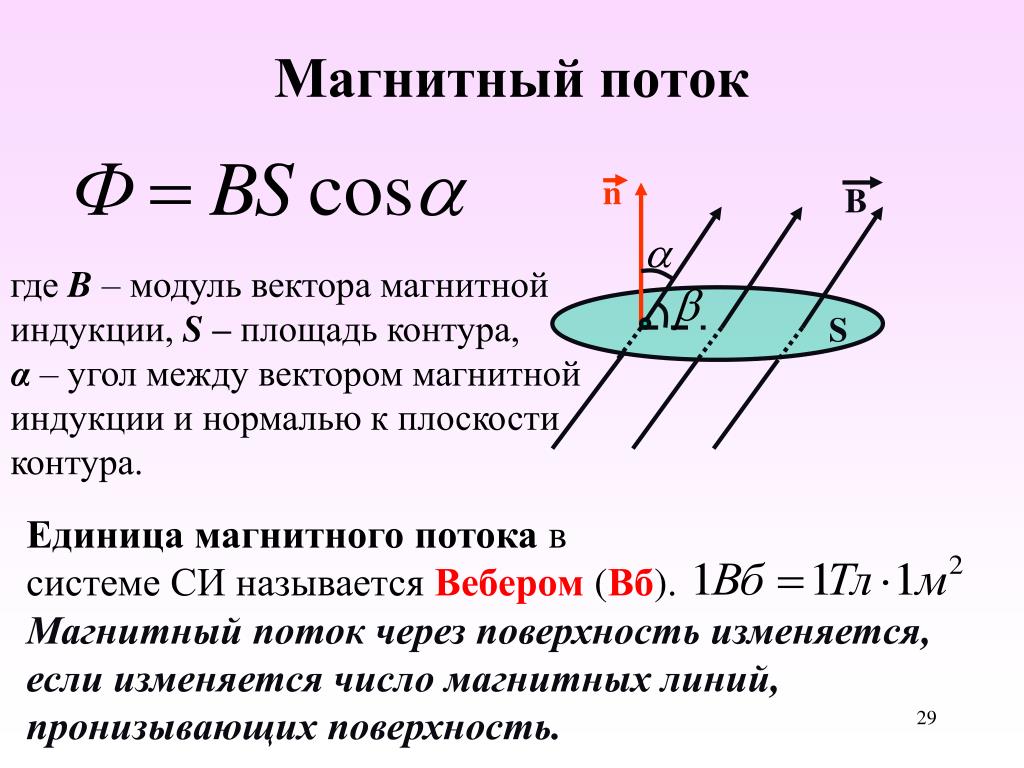
Для неоднородного участка цепи
(участка, содержащего ЭДС), закон Ома
записывается в следующей форме:
.
Это соотношение принято называть
обобщенным законом Ома. Обобщенный
закон Ома выражает закон сохранения
энергии применительно к участку цепи
постоянного тока. Он в равной мере
справедлив как для пассивных участков
(не содержащих ЭДС), так и для активных.
8. Запишите закон Ома для замкнутой
цепи. Закон Ома для замкнутой цепи,
содержащей источник ЭДС, запишется в
виде:
. Эта формула выражает закон Ома
для полной цепи: Сила тока в полной цепи
равна электродвижущей силе источника,
деленной на сумму сопротивлений
однородного и неоднородного участков
цепи.
9. Сформулируйте и запишите формулу
закона Джоуля-Ленца (в интегральной или
дифференциальной форме). Независимо
друг от друга Джоуль и Ленца показали,
что при протекании тока, в проводнике
выделяется количество теплоты:
(работа электрического тока,
протекающего по неподвижному проводнику
с сопротивлением, преобразуется в тепло,
выделяющееся на проводнике).
Если ток изменяется со временем, то
.
Это закон Джоуля-Ленца в интегральной
форме. Отсюда видно, что нагревание
происходит за счет работы, совершаемой
силами поля над зарядом.
Закон
Джоуля-Ленца в дифференциальной форме
выражен следующей формулой:
(удельная тепловая мощность тока
пропорциональна квадрату плотности
электрического тока и удельному
сопротивлению среды в данной точке).
Приведенные
формулы справедливы для однородного
участка цепи и для неоднородного при
условии, что действующие в них сторонние
силы имеют нехимическое происхождение.
10.
Дайте определение вектора магнитной
индукции, назовите ее размерность и
приведите соответствующие формулы
(через силу Ампера и через вращающийся
момент). Вектор магнитной индукции
— векторная физическая величина,
являющаяся силовой характеристикой
магнитного поля в данной точке
пространства. Вектор магнитной индукции
Вектор магнитной индукции
определяет силы, действующие на токи
или движущиеся заряды в магнитном поле.
В СИ единицей измерения магнитной
индукции является тесла: 1 Тл = Дж/А·м2
= Н·м/А·м2 = Н/А·м Силовое
действие магнитного поля может
обнаруживаться по действию силы Ампера
на прямолинейный проводник с током и
по вращающемуся действию на замкнутый
контур. При исследовании магнитного
поля с помощью прямолинейного проводника
с током магнитная индукция определяется
следующим образом: модуль магнитной
индукции равен отношению максимального
значения модуля силы Ампера F,
действующий на проводник с током, к силе
тока I в проводнике
и его длине l:
. При исследовании магнитного поля
с помощью контура с током магнитная
индукция определяется следующим образом:
модуль вектора индукции
равен отношению максимального вращающегося
момента сил М, действующего на рамку
с током со стороны магнитного поля, к
произведению силы тока I
в рамке на ее площадь S:
.
11. Что называется магнитным моментом
контура с током. (приведите соответствующий
момент). Магнитный
момент контура с током (магнитный
дипольный момент) — основная
векторная величина,
характеризующая магнитные
свойства вещества:
,
где I — сила тока
в контуре, S — площадь
поверхности контура (рамки),
— единичный вектор
нормали к поверхности рамки. Направление
вектора
совпадает с направлением положительной
нормали к контуру.
12. Запишите закон Био-Савара-Лапласа
(формула и расшифровка всех величин,
входящих в нее, привести рисунок).
Закон Био —
Савара — Лапласа
для проводника с током I,
элемент которого
l
создает в некоторой
точке А
индукцию поля
,
записывается в виде
, где
— магнитная постоянная, d
— вектор, по модулю равный
длине dl
элемента проводника
и совпадающий по направлению с током,
— радиус-вектор, проведенный
из элемента d
проводника в точку А
поля, r
— модуль радиуса-вектора
.
Направление d
перпендикулярно d
и r,
т. е. перпендикулярно плоскости, в
которой они лежат, и совпадает с
касательной к линии магнитной
индукции. Это направление может быть
найдено по правилу нахождения линий
магнитной индукции (правилу правого
винта): направление вращения головки
винта дает направление d,
если поступательное движение винта
соответствует направлению тока в
элементе.
13. Приведите формулировку и математическую
запись в интегральной форме закона
полного тока (теорема о циркуляции) для
магнитного поля в вакууме.
Закон полного
тока для магнитного поля в вакууме
(теорема о циркуляции вектора
):
циркуляция вектора
по произвольному
замкнутому контуру равна произведению
магнитной постоянной 0
на алгебраическую сумму токов,
охватываемых этим контуром:
,
где n
— число проводников
с токами, охватываемых контуром L
произвольной формы.
Каждый ток учитывается
столько раз, сколько раз он охватывается
контуром. Положительным считается
ток, направление которого связано с
направлением обхода по контуру
правилом правого винта; ток противоположного
направления считается отрицательным.
14. Поток вектора магнитной индукции
(определение, математическая запись),
размерность.
Потоком вектора магнитной
индукции (магнитным
потоком) через площадку dS
называется скалярная
физическая величина,
равная dФB
==
Bn
dS
, где Bn
= Вcos
— проекция вектора
на направление нормали к площадке dS
(
— угол между векторами
и
),
dS
= dSn
— вектор, модуль которого равен dS,
а направление совпадает с направлением
нормали
к площадке. Поток
Поток
вектора
может быть как положительным, так и
отрицательным в зависимости от знака
cos
(определяется выбором положительного
направления нормали
).
Поток вектора
связывают с контуром, по которому течет
ток. В таком случае положительное
направление нормали к контуру нами уже
определено, оно связывается с током
правилом правого винта. Таким образом,
магнитный поток, создаваемый контуром
через поверхность, ограниченную им
самим, всегда положителен. Поток вектора
магнитной индукции
через произвольную поверхность S
равен
=
Для однородного поля и
плоской поверхности, расположенной
перпендикулярно вектору
,
Bn= B
= const
и
=
ВS.
Из этой формулы
определяется единица магнитного потока
вебер (Вб):
1 Вб — магнитный поток, проходящий через
плоскую поверхность площадью 1 м2,
расположенную перпендикулярно
однородному магнитному полю, индукция
которого равна 1 Тл (1 Вб = 1 Тл·м2).
15. Приведите формулировку и математическую
запись в интегральной форме теоремы
Остроградского – Гаусса для магнитного
поля. Теорема Гаусса для вектора
:
поток вектора
магнитной индукции через любую замкнутую
поверхность равен нулю:
Эта теорема
отражает факт отсутствия магнитных
зарядов, вследствие чего линии магнитной
индукции не имеют ни начала, ни конца и
являются замкнутыми.
16. Запишите закон Ампера для силы
взаимодействия двух параллельных токов.
Два параллельных тока
одинакового направления притягиваются
друг к другу с силой
dF
=
Если токи
имеют противоположные направления,
то, используя правило
левой руки, можно показать, что между
ними действует сила
отталкивания, определяемая
приведенной формулой.
17. Запишите закон Ампера для элемента
проводника с током в магнитном поле в
векторной форме. Магнитное поле
Магнитное поле
оказывает на рамку с током ориентирующее
действие. Следовательно, вращающий
момент, испытываемый рамкой, есть
результат действия сил на отдельные ее
элементы. Обобщая результаты исследования
магнитного поля на различные проводники
с током, Ампер установил, что сила
,
с которой магнитное поле действует на
элемент проводника d
с током, находящегося в магнитном
поле, равна
,
где
– вектор, по модулю равный d
и совпадающий по направлению с током,
– вектор магнитной индукции. Направление
вектора
может быть найдено по общим правилам
векторного произведения, откуда следует
правило левой руки: если ладонь левой
руки расположить так, чтобы в нее входил
вектор
,
а четыре вытянутых пальца расположить
по направлению тока в проводнике, то
отогнутый большой палец покажет
направление силы, действующей на ток.
18. Запишите выражение для силы Лоренца.
Опыт показывает, что магнитное поле
действует не только на проводники с
током, но и на отдельные заряды, движущиеся
в магнитном поле. Сила, действующая на
электрический заряд q,
движущийся в магнитном поле со скоростью
,
называется силой Лоренца и
выражается формулой
,
где
– индукция магнитного поля, в котором
заряд движется. Направление силы Лоренца
определяется с помощью правила левой
руки: если ладонь левой руки расположить
так, чтобы в нее входил вектор
,
а четыре вытянутых пальца направить
вдоль вектора
(для q > 0 направления
совпадают, для q <
0 – противоположны), то отогнутый большой
палец покажет направление силы,
действующей на положительный заряд.
19. Запишите выражение для работы,
которая совершается при перемещении
проводника с током в магнитном поле.
Работа по перемещению проводника с
током в магнитном поле равна произведению
силы тока на магнитный поток, пересеченный
движущимся проводником:
.
Формула справедлива и для произвольного
направления вектора
.
20. Запишите выражение для работы,
которая совершается при перемещении
контура с током в магнитном поле. Работа
по перемещению замкнутого контура с
током в магнитном поле равна произведению
силы тока в контуре на изменение
магнитного потока, сцепленного с
контуром:
.
Формула остается справедливой для
контура любой формы в произвольном
магнитном поле.
21.
Запишите выражение для индукции
магнитного поля (B)
в центре кругового витка с током I
и радиусом R.
Магнитная индукция поля в центре
кругового проводника с током равна
, где
– магнитная постоянная, μ — магнитная
проницаемость среды, в которой находится
проводник, I – сила
тока в проводнике, R
– радиус кругового витка.
22.
Запишите выражение для индукции
магнитного поля (B),
создаваемого прямым бесконечным
проводником с током в произвольной
точке. Для прямолинейного бесконечно
длинного проводника с током симметрия
линий напряженности и индукции в
изотропной среде позволяет определить
величину магнитного поля в любой точке
на расстоянии R от
оси проводника. Линии напряженности и
магнитной индукции поля прямолинейного
проводника представляют собой
концентрические окружности, лежащие в
плоскостях, перпендикулярных проводнику.
Вдоль линии напряженность (индукция)
магнитного поля одинакова и циркуляция
равна произведению напряженности
(индукции) на длину линии. Соответственно
магнитная индукция поля прямого тока
равна
, где
– магнитная постоянная, μ — магнитная
проницаемость среды, в которой находится
проводник, I – сила
тока в проводнике, R
– расстояние до проводника.
23.
Что называется вектором намагниченности
(J). (формула,
размерность).
Вещество, помещенное во внешнее
магнитное поле, намагничивается. Степень
намагничения вещества принято
характеризовать вектором намагничения
.
Вектором намагниченности
(намагничения) называется физическая
величина, численно равная суммарному
магнитному моменту единицы объема
вещества:
, где
– физически бесконечно малый объем,
взятый в окрестности рассматриваемой
точки,
– магнитный момент отдельной молекулы.
Суммирование производится по всем
молекулам, заключенным в объеме
.
В СИ имеет название ампер на метр и
обозначается А/м.
24. Запишите формулу, связывающую
магнитную индукцию В в
магнетике с магнитной проницаемостью
и напряженностью магнитного поля Н в
этом магнетике.
Вектор напряженности
магнитного поля
является дополнительным вектором к
силовому вектору индукции магнитного
поля
.
Векторы
и
между собой связаны наподобие векторов
напряженности электрического поля
и электрического смещения
.
А именно, для однородной
изотропной среды вектор магнитной
индукции связан с вектором напряженности
следующим соотношением:
,
где 0
— магнитная
постоянная,
— безразмерная величина — магнитная
проницаемость среды,
показывающая, во
сколько раз магнитное поле макротоков
усиливается за
счет поля микротоков среды. Таким
образом, напряженность магнитного поля
есть вектор, имеющий то же направление,
что и вектор
,
но в
раз меньший по модулю (в анизотропных
средах векторы
и
,
вообще говоря, не совпадают по направлению).
25. Запишите формулу, связывающую
векторы намагниченности и напряженности
магнитного поля. Вектор намагниченности
принято связывать не с магнитной
индукцией, а с напряженностью поля.
Вектор намагничения пропорционален
напряженности магнитного поля
,
вызывающего намагничение
,
где
– характерная для данного магнетика
величина, называемая магнитной
восприимчивостью вещества, численно
равная величине вектора намагниченности
магнетика при напряженности магнитного
поля равной единице. Следовательно,
магнитная восприимчивость парамагнетиков
положительна (
), диамагнетиков – отрицательна (
).
26.
Сформулируйте закон полного тока
(теорема о циркуляции) для магнитного
поля в веществе и запишите его
математическое выражение в интегральной
форме.
Теорема о циркуляции
вектора магнитной индукции (закон
полного тока): циркуляция
вектора магнитной индукции по произвольному
замкнутому контуру
равна
произведению магнитной постоянной
μ0 на
алгебраическую сумму токов, охватываемых
этим контуром:
,
где n — число
проводников с токами, которые охватываются
контуром L
любой формы. Каждый ток в уравнении
учитывается столько раз, сколько раз
он охватывается контуром. Ток считается
положительным, если его направление
образует с направлением обхода по
контуру правовинтовую систему;
отрицательным считается ток противоположного
направления. Закон
полного тока является интегральной
формулировкой закона Био-Савара и входит
в систему уравнений Максвелла.
27. Назовите типы магнетиков. В
зависимости от знака и величины магнитной
восприимчивости все магнетики
подразделяются на три группы: 1)
диамагнетики, у которых χ отрицательна
мала по абсолютной величине (
;
2)
парамагнетики, у которых χ тоже
невелика, но положительна
(3)
ферромагнетики, у которых χ положительна
и достигает очень больших значений
(1).
Кроме того, в отличие от диа- и
парамагнетиков, для которых χ не зависти
от
,
восприимчивость ферромагнетиков
является функцией напряженности
магнитного поля.
28. Что называется спином электрона.
Существование собственных моментов
электрона первоначально пытались
объяснить, рассматривая электрон как
заряженный шарик, вращающийся вокруг
своей оси. В соответствии с этим
собственный механический момент
электрона получил название СПИН (от
англ. to spin
– вращаться). Однако вскоре обнаружилось,
что такое представление приводит к ряду
противоречий, и от гипотезы о «вращающемся»
электроне пришлось отказаться. В
настоящее время принимается, что
собственный механический момент (спин)
и связанный с ним собственный (спиновый)
магнитный момент являются такими же
неотъемлемыми свойствами электрона,
как и его масса и заряд. И так, электрон,
обладающий собственным механическим
моментом импульса
, называется спином. Спину электрона
соответствует собственный (спиновый)
магнитный момент
.
Проекция спина на направление вектора
может принимать только одно из следующих
двух значений
, где ħ =
( h – постоянная
Планка),
– магнетон Бора, являющийся единицей
магнитного момента электрона.
29. Приведите закон преломления линий
вектора
на границе раздела двух магнетиков.
Вблизи поверхности раздела двух
магнетиков векторы
и
должны удовлетворять определенным
граничным условиям, которые вытекают
из соотношений
B
= 0,
= j. В соответствии с тем,
чтоB
= 0, поток вектора
через любую замкнутую поверхность равен
нулю. Сосчитаем поток вектора
через поверхность малого цилиндра,
охватывающего границу раздела 2-х сред:
=0,
где S — площадь основания цилиндра,
— площадь боковой поверхности. Устремляя
высоту цилиндра h → 0 и,
→
0 получаем на границе:
и, учитывая, что
и
— противоположно направленные нормали,
и вводя общую нормаль, имеем:
Итак: нормальные составляющие вектора
непрерывны на границе раздела двух
магнетиков.
Магнитное индукционное поле — обзор
4.14 Парамагнитные и ферромагнитные материалы
В парамагнитном материале атомы содержат постоянные магнитные дипольные моменты, возникающие из спина и орбитального углового момента электронов. К кристаллу прикладывается внешнее магнитное поле с индукцией B, где магнитная восприимчивость χm — это константа пропорциональности между вектором намагниченности M (объемной плотностью магнитных диполей) и напряженностью магнитного поля H, так что
(4.182) M = χmH
Эта линейная зависимость от χm применима только к линейным магнитным материалам. В вакууме χm = 0, а в немагнитных материалах он обычно очень мал, в диапазоне от 10-4 до 10-5; например, χm = −0,94 × 10−5 для меди.
Магнитное поле индукции B представляет собой сумму вектора намагниченности M материала и напряженности внешнего магнитного поля H, где сумма умножается на константу проницаемости вакуума μ0, где
(4,183) B = μ0 ( H + M)
Индукционное магнитное поле B возникает из-за микроскопических (атомных) и макроскопических (проволочные) токов; тогда как напряженность магнитного поля H возникает только из-за макроскопических токов.Индукционное магнитное поле B будет стремиться выровнять дипольные моменты, потому что энергия меньше для параллельного выравнивания диполей. Индуцированное магнитное поле выровненных магнитных диполей M добавляет к приложенному извне магнитному полю H. Таким образом, магнитное поле составляет
(4,184) B = μ0 (1 + χm) H
Относительная проницаемость материала μr определяется как
(4,185) μr = 1 + χm
Материалы с относительной проницаемостью μr <1 являются диамагнитными. Материалы с μr> 1, но с μrÀ1 парамагнитны.Материалы с μrÀ1 являются ферромагнитными, а ферромагнитные материалы нелинейны, поэтому χm и μr меняются в зависимости от напряженности приложенного магнитного поля H.
Магнитная проницаемость μ определяется как
(4,186) μ = μ0μr
В линейных магнитных материалах, константа пропорциональности между индукционным магнитным полем B и напряженностью приложенного магнитного поля H — это магнитная проницаемость μ, где
(4,187) B = μH
В нелинейных магнитных материалах, таких как кобальт, никель и мягкое железо, проницаемость μ изменяется в зависимости от напряженности приложенного магнитного поля H, где μ может быть большим и иметь репрезентативные значения в диапазоне от 250 для кобальта, 600 для никеля и 5000 для мягкого железа.
Тепловое движение атомов, которое имеет тенденцию хаотизировать ориентацию диполей, должно преодолеваться приложенным магнитным полем или более низкими температурами. Восприимчивость при низких температурах и магнитных полях подчиняется закону Кюри, где для постоянной C характеристика материала равна
(4,188) χ = CT
Ферромагнетизм — это намагниченность, которая возникает в небольших областях материала без применения внешнего магнитного поля. поле. В ферромагнетиках естественная намагниченность, возникающая из-за неспаренных электронных спинов, достигает максимума при T = 0K и спадает до нуля при температуре Кюри TC.При температурах выше TC ферромагнитный материал становится парамагнитным, и его магнитная восприимчивость подчиняется модифицированному соотношению Кюри, в котором
(4.189) χ = CT − TC
Для температур ниже TC закон ферромагнетика Кюри больше не применим, потому что тогда материал становится ферромагнитным с постоянной намагниченностью. Ферромагнитный материал не намагничен в одном и том же направлении по всему объему, а скорее имеет множество меньших областей или доменов. Каждый домен полностью намагничен в одном направлении, но ориентация доменов случайна, так что направление намагничивания меняется от одного домена к другому.Случайная ориентация доменов происходит потому, что случайные домены создают более низкое энергетическое состояние, чем полностью выровненные домены. Приложенное магнитное поле в некоторой степени выравнивает эти домены, так что их магнитные поля более выровнены, тем самым увеличивая магнитное поле материала в целом. Увеличение приложенного магнитного поля сверх магнитного поля насыщения не приводит к дальнейшему увеличению намагниченности материала, поскольку домены достигают максимально возможного взаимного выравнивания. Когда внешнее магнитное поле удаляется, домены и их границы не возвращаются полностью к своей исходной ориентации, и, таким образом, домены проявляют гистерезис.Единственными ферромагнитными элементами являются железо, кобальт, никель, гадолиний и диспрозий.
Напомним, что идентичные атомные электроны должны быть неразличимы (следовательно, полная волновая функция должна быть симметричной), но составляющие пространственные и спиновые волновые функции могут быть симметричными или асимметричными, если произведение волновых функций спиновой и пространственной составляющих равно асимметричный. В трехмерных кристаллических полосах, где имеет место ферромагнитное действие, и в других неферромагнитных парамагнитных элементах кулоновское отталкивание между парой электронов имеет тенденцию перемещать электроны дальше друг от друга в антисимметричное пространственное состояние с минимальной энергией.Эта асимметрия полной волновой функции требует симметричного состояния спина, в котором спины неспаренных электронов ориентированы в одном направлении. Таким образом, кулоновская сила, которая раздвигает электроны для минимизации энергии, затем приводит к их параллельному выравниванию спинов в парамагнитных и ферромагнитных материалах.
Обменная сила или взаимодействие между пространственной и спиновой составляющими волновой функции для двух или более электронов отвечает за эту связь электронных спинов с параллельным выравниванием в парамагнитных и ферромагнитных материалах.В случае ферромагнетиков 3-D полоса заполнена не полностью, близкое расположение атомов железа делает неразличимыми электроны соседних атомов, а обменное взаимодействие теперь распространяется на электроны соседних атомов. Для поддержания полной асимметричной волновой функции для набора электронов, принадлежащих близко расположенным соседним атомам, которые имеют перекрывающиеся d-оболочки неспаренных электронов, есть две возможности. В ферромагнитном случае (например, для атомов железа) пространственная волновая функция может быть асимметричной, а функция спина — симметричной.В этом случае кулоновская энергия сводится к минимуму за счет разделения электронов, но разделение позволяет неспаренным электронам иметь параллельные спины. Другая возможность состоит в том, что пространственная волновая функция будет симметричной, а электроны локализованы вместе, и, следовательно, их спиновая волновая функция должна быть антисимметричной, что требует, чтобы спины электронов были антипараллельны. Возможность антиферромагнетизма не минимизирует кулоновскую энергию в железе и не возникает.Однако такие материалы, как MnO 2 , являются антиферромагнитными.
Что означает вектор магнитного поля?
Зачем нужны векторы?
Векторы представляют собой набор физических величин, которым для полного описания величины требуются как величина (или длина), так и направление (пространственная ориентация). Возьмем, к примеру, реальную жизненную ситуацию. Вы спрашиваете, сколько шариков у меня в сумке. Я говорю, что это 10. Достаточно цифры «10» для ответа.А теперь задам другой вопрос. Как далеко отсюда твой дом? Вы, наверное, сказали бы около 20 км; не только 20. Необходимо включить дополнительные «км», чтобы полностью определить решение. Теперь мы спрашиваем, как добраться до вашего дома? Конечно, вам нужна помощь в направлениях на север, юг, восток, запад.
Аналогично некоторым физическим величинам. Упоминание только их количества кажется бессмысленным. Мы называем эти величины векторами. Эти величины требуют направления (представленного стрелками) вдоль каждой координаты плюс значение, принятое в некоторой точке, представленное точкой пробела.
Магнитное поле — вектор?
Ответ — нет. На самом деле это псевдовектор. Рассмотрим прямой длинный провод с током и постоянный ток, протекающий по нему. Это создаст магнитное поле, при этом силовые линии образуют замкнутые контуры или концентрические кольца вокруг провода. Как указать направление замкнутого контура. На самом деле силовые линии даже не циркулируют. Тогда как мы узнаем, что силовые линии имеют изгиб?
Как магнитное поле стало векторным?
Проделайте тот же эксперимент, что и упомянутый выше.Сначала заставьте ток течь вверх по проводу. Он будет генерировать магнитное поле в некоторой точке рядом с проводом, направление которого можно измерить с помощью компаса. Сохраняйте положение компаса фиксированным (т. Е. Расстояние между проводом и компасом). Стрелка компаса отклоняется в направлении линии поля в этой точке (которую мы представляем, проводя касательную к петле в этой точке). Теперь поменяйте направление тока. Удивительно, но вы видите, что стрелка компаса отклоняется в противоположном направлении.Что это означает? Это означает, что даже если силовые линии не циркулируют, их направление должно быть указано, чтобы указывать направление потока тока и, таким образом, силу, действующую на движущийся заряд. Итак, мы предположили, что если положительный ток движется вверх по проводу, силовые линии магнитного поля изгибаются против часовой стрелки. Если он течет вниз, силовые линии изгибаются по часовой стрелке.
Вот почему мы говорим, что магнитное поле является псевдовектором.
Специальные символы — гипертекст по физике
Это условные обозначения, используемые в этой книге.
Период
Вязкость
| символ | количество | символ | шт. |
|---|---|---|---|
| r , r | положение, разделение, радиус, радиус кривизны | м | метр |
| с , с | перемещение, расстояние | м | метр |
| θ , φ , | угол, угловое перемещение, угловое разделение, угол поворота | рад | радиан |
| x , y , z | декартовы координаты | м | метр |
| î , 94 , k | декартовых единичных векторов | безразмерный | |
| r , θ, φ | сферические координаты | м, | метр, радиан |
| r̂, θ̂, φ̂ | сферические единичные векторы | безразмерный | |
| ρ, φ, z | цилиндрические координаты | м, | метр, радиан |
| ρ̂, φ̂, ẑ | цилиндрических единичных векторов | безразмерный | |
| № | нормальный единичный вектор | безразмерный | |
| t̂ | тангенциальный единичный вектор | безразмерный | |
| ч | высота, глубина | м | метр |
| ℓ, л | длина | м | метр |
| г | расстояние, отрыв, толщина | м | метр |
| т | толщина | м | метр |
| D | диаметр | м | метр |
| С | окружность | м | метр |
| А , А | площадь, площадь поперечного сечения, площадь проекции, площадь поверхности | м 2 | квадратных метров |
| В | том | м 3 | куб.м |
| т | время, продолжительность | с | секунды |
| т | , периодическое время | с | секунды |
| τ | постоянная времени | с | секунды |
| f | частота | Гц | герц |
| ω | угловая частота | рад / с | радиан в секунду |
| символ | количество | символ | шт. |
| v , v | скорость, скорость | м / с | метра в секунду |
| a , a | ускорение | м / с 2 | метр в секунду в квадрате |
| a c , a c | центростремительное ускорение, центробежное ускорение | м / с 2 | метр в секунду в квадрате |
| г , г | гравитационное поле, ускорение свободного падения | м / с 2 | метр в секунду в квадрате |
| м | масса | кг | килограмм |
| F , F | сила | N | ньютон |
| F г , | сила тяжести, вес | N | ньютон |
| F n , | нормальная сила, нормальная | N | ньютон |
| F f , | Сила трения (статическая, кинетическая) | N | ньютон |
| μ с , μ k | коэффициент трения (статический, кинетический) | безразмерный | |
| p , p | импульс | кг м / с | килограмм-метр в секунду |
| Дж , Дж | импульс | Н с | ньютон секунда |
| Вт | работа | Дж | джоуль |
| E | энергия, общая энергия | Дж | джоуль |
| K , | кинетическая энергия (поступательная, вращательная) | Дж | джоуль |
| U , | потенциальная энергия (гравитационная, пружинная) | Дж | джоуль |
| V г | гравитационный потенциал | Дж / кг | джоуль на килограмм |
| η | КПД | безразмерный | |
| п. | мощность | Вт | ватт |
| ю , ю | скорость вращения, частота вращения | рад / с | радиан в секунду |
| α , α | ускорение вращения | рад / с 2 | радиан на секунду в квадрате |
| τ , τ | крутящий момент | Н м | Ньютон-метр |
| Я | момент инерции | кг м 2 | килограмм метр в квадрате |
| л , л | Угловой момент | кг м 2 / с | килограмм-метр в секунду |
| H , H | угловой импульс | Н м | ньютон-метр секунда |
| к | жесткость пружины | Н / м | ньютон на метр |
| п. | давление | Па | паскаль |
| σ | нормальное напряжение | Па | паскаль |
| τ | напряжение сдвига | Па | паскаль |
| ρ | плотность, объемно-массовая плотность | кг / м 3 | килограмм на кубический метр |
| σ | удельная масса поверхности, поверхностная плотность массы | кг / м 2 | килограмм на квадратный метр |
| λ | линейная массовая плотность | кг / м | килограмм на метр |
| F B , | Плавучесть, подъемная сила | N | ньютон |
| q м | массовый расход | кг / с | килограмм в секунду |
| q В | объемный расход | м 3 / с | кубометров в секунду |
| F D , | сопротивление, аэродинамическое сопротивление, сопротивление воздуха | N | ньютон |
| C , C D | Коэффициент аэродинамического сопротивления, коэффициент аэродинамического сопротивления | безразмерный | |
| η | , динамическая вязкость | Па с | паскаль секунда |
| ν | кинематическая вязкость | м 2 / с | квадратных метра в секунду |
| млн лет | Машинный номер | безразмерный | |
| Re | число Рейнольдса | безразмерный | |
| Fr | номер фронта | безразмерный | |
| E | Модуль Юнга, модуль упругости | Па | паскаль |
| G | Модуль сдвига, модуль жесткости | Па | паскаль |
| К | Модуль объемной упругости, модуль сжатия | Па | паскаль |
| ε | линейная деформация | безразмерный | |
| γ | деформация сдвига | безразмерный | |
| θ | объемная деформация | безразмерный | |
| γ | Поверхностное натяжение | Н / м | ньютон на метр |
| символ | количество | символ | шт. |
| т | температура | К | кельвина |
| α | линейное расширение, коэффициент линейного теплового расширения | К -1 | обратный кельвин |
| β | объемное расширение, коэффициент объемного теплового расширения | К -1 | обратный кельвин |
| Q | тепло | Дж | джоуль |
| с | удельная теплоемкость, удельная теплоемкость | Дж / кг K | джоуль на килограмм кельвина |
| л | скрытая теплота, удельная скрытая теплота | Дж / кг | джоуль на килограмм |
| n | количество вещества | моль | |
| № | количество частиц | безразмерный | |
| п. | тепловой поток | Вт | ватт |
| к | теплопроводность | Вт / м K | ватт на метр кельвина |
| ε | излучательная способность | безразмерный | |
| U | внутренняя энергия | Дж | джоуль |
| S | энтропия | Дж / К | джоуль на кельвин |
| Вт | пути, количество одинаковых микросостояний | безразмерный | |
| COP | КПД | безразмерный | |
| символ | количество | символ | шт. |
| q , Q | заряд, электрический заряд | С | кулон |
| ρ | Плотность заряда, объемная плотность | С / м 3 | кулонов на кубический метр |
| σ | поверхностная плотность заряда, поверхностная плотность заряда | С / м 2 | кулонов на квадратный метр |
| λ | линейная плотность заряда | С / м | кулонов на метр |
| F E , F E | электрическая сила, электростатическая сила | N | ньютон |
| E , E | электрическое поле | Н / З, В / м | ньютон на кулон, вольт на метр |
| Φ E | электрический поток | Н · м 2 / C, В · м | Ньютон-метр в квадрате на кулон, вольтметр |
| U , U E | потенциальная энергия, электрическая потенциальная энергия | Дж | джоуль |
| В, В E | напряжение, потенциал, электрический потенциал | В | вольт |
| ℰ | Электродвижущая сила, ЭДС | В | вольт |
| С | емкость | F | фарад |
| κ | диэлектрическая проницаемость | безразмерный | |
| Я | ток, электрический ток | А | ампер |
| р , р | сопротивление, электрическое сопротивление, внутреннее сопротивление | Ом | Ом |
| ρ | удельное сопротивление | Ом · м | Омметр |
| G | проводимость | S | siemens |
| σ | проводимость | См / м | сименс на метр |
| F B , F B | магнитная сила | N | ньютон |
| B , B | магнитное поле | т | тесла |
| Φ B | магнитный поток | Вт | Вебер |
| № | количество витков | безразмерный | |
| n | витка на единицу длины, плотность витков | м −1 | обратный счетчик |
| η | Плотность энергии | Дж / м 3 | джоуль на кубический метр |
| S , S | вектор пойнтинга, интенсивность | Вт / м 2 | ватт на квадратный метр |
| символ | описание | ||
| + | плюс, сложение, плюс | ||
| – | минус, вычесть, минус | ||
| ± | неопределенность, погрешность, плюс-минус | ||
| · | умножение, точка, скалярное произведение, скалярное произведение | ||
| × | умножение, крест, векторное произведение, векторное произведение | ||
| ÷, / | делить | ||
| x 2 | квадрат | ||
| x 3 | куб | ||
| √ | корень квадратный, корень, корень | ||
| ∛ | кубический корень | ||
| 1 x , x -1 | обратная, обратная | ||
| = | равно, равенство | ||
| ≈ | примерно равно | ||
| ∝ | пропорционально | ||
| ≠ | не равно, неравенство | ||
| ~ | на заказ, тильда | ||
| < | менее | ||
| > | больше | ||
| ≤ | меньше или равно | ||
| ≥ | больше или равно | ||
| ⇒, | логическое следствие | ||
| ⇔ | логическая эквивалентность | ||
| … | и так далее, многоточие | ||
| ∴ | следовательно | ||
| f ( x ) | функция | ||
| грех | синус | ||
| cos | косинус | ||
| желто-коричневый | касательная | ||
| синх | гиперболический синус | ||
| кош | гиперболический косинус | ||
| танх | гиперболический тангенс | ||
| x̂ | единичный вектор, шляпа, циркумфлекс | ||
| ∥ | параллельно | ||
| ⟂ | перпендикуляр | ||
| х | среднее, среднее, античастица, столбик, линия над чертой | ||
| x | медиана, суперсимметричная частица, тильда | ||
| ⟨⟩ | среднее по времени, среднее по ансамблю, скобка | ||
| p ( x ) | распределение вероятностей, функция плотности вероятности | ||
| ∆ | приращение, изменение, дельта | ||
| г | дифференциал, d | ||
| ∂ | частичный дифференциал, d частичный | ||
| ∇ | градиент, дель | ||
| ∇ · | расхождение, деление, точка | ||
| ∇ × | локон, дель-крест | ||
| ∇ 2 | лапласиан, дель-квадрат | ||
| ∑ | суммирование, сигма | ||
| ∫ | интегральный | ||
| ∬ | двойной интеграл | ||
| ∭ | тройной интеграл | ||
| ∮ | контур интегральный | ||
| ∯ | Поверхность интегральная | ||
| ∰ | интегральный объем | ||
| ∞ | бесконечность | ||
| ℵ 0 | трансфинитное число, алеф ноль |
23.1 Индуцированная ЭДС и магнитный поток — Физика колледжа, главы 1-17
23 Электромагнитная индукция, цепи переменного тока и электрические технологии
Индуцированная ЭДС и магнитный поток
- Рассчитайте поток однородного магнитного поля через петлю произвольной ориентации.
- Опишите методы создания электродвижущей силы (ЭДС) с помощью магнитного поля или магнита и проволочной петли.
Аппарат, использованный Фарадеем для демонстрации того, что магнитные поля могут создавать токи, проиллюстрирован в [ссылка].Когда переключатель замкнут, в катушке в верхней части железного кольца создается магнитное поле, которое передается катушке в нижней части кольца. Гальванометр используется для обнаружения любого тока, наведенного в катушке внизу. Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр обнаруживает ток в одном направлении в катушке внизу. (Вы также можете наблюдать это в физической лаборатории.) Каждый раз, когда переключатель открывается, гальванометр обнаруживает ток в противоположном направлении.Интересно, что если переключатель остается замкнутым или разомкнутым в течение некоторого времени, через гальванометр нет тока. Замыкание и размыкание переключателя индуцирует ток. Это изменение магнитного поля, которое создает ток. Более важным, чем текущий ток, является вызывающая его ЭДС . Ток является результатом ЭДС, индуцированной изменяющимся магнитным полем , независимо от того, есть ли путь для протекания тока.
Аппарат Фарадея для демонстрации того, что магнитное поле может производить ток. Изменение поля, создаваемого верхней катушкой, вызывает ЭДС и, следовательно, ток в нижней катушке. Когда переключатель разомкнут и замкнут, гальванометр регистрирует токи в противоположных направлениях. Когда переключатель остается замкнутым или разомкнутым, через гальванометр не течет ток.
Эксперимент, который легко проводится и часто проводится в физических лабораториях, проиллюстрирован в [ссылка]. ЭДС индуцируется в катушке, когда стержневой магнит вставляется и выходит из нее.ЭДС противоположных знаков создаются движением в противоположных направлениях, и ЭДС также меняются на противоположные за счет изменения полюсов. Те же результаты будут получены, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, и когда магнит неподвижен относительно катушки, ЭДС отсутствует.
Движение магнита относительно катушки создает ЭДС, как показано на рисунке. Такие же ЭДС возникают при перемещении катушки относительно магнита. Чем больше скорость, тем больше величина ЭДС, а при отсутствии движения ЭДС равна нулю.
Метод индукции ЭДС, используемый в большинстве электрических генераторов, показан в [ссылка]. Катушка вращается в магнитном поле, создавая ЭДС переменного тока, которая зависит от скорости вращения и других факторов, которые будут исследованы в следующих разделах. Обратите внимание, что генератор очень похож по конструкции на двигатель (другая симметрия).
Вращение катушки в магнитном поле создает ЭДС. Это основная конструкция генератора, в котором работа, выполняемая по вращению катушки, преобразуется в электрическую энергию.Обратите внимание, что генератор очень похож по конструкции на двигатель.
Итак, мы видим, что изменение величины или направления магнитного поля вызывает ЭДС. Эксперименты показали, что существует критическая величина, называемая магнитным потоком, ΦΦ размер 12 {Φ} {}, определяемая соотношением
.
Φ = BAcosθ, Φ = BAcosθ, размер 12 {Φ = курсив «BA» «cos» θ} {}
, где BB, размер 12 {B} {} — напряженность магнитного поля на площади AA, размер 12 {A} {} , под углом θθ к перпендикуляру к области, как показано в [ссылка]. Любое изменение магнитного потока ΦΦ размером 12 {Φ} {} индуцирует ЭДС. Этот процесс определяется как электромагнитная индукция. Единицы магнитного потока ΦΦ размер 12 {Φ} {} — T⋅m2T⋅m2 размер 12 {T cdot m rSup {size 8 {2}}} {}. Как видно из [ссылка], Bcosθ = BBcosθ = B, размер 12 {B ”cos” θ = B rSub {size 8 {ortho}}} {} ⊥ , что является составной частью BB размером 12 {B} { } перпендикулярно области AA размер 12 {A} {} . Таким образом, магнитный поток равен Φ = B⊥AΦ = B⊥A размером 12 {Φ = B rSub {size 8 {ortho}} A} {}, произведению площади и составляющей магнитного поля, перпендикулярной ей.
Магнитный поток ΦΦ размером 12 {Φ} {} связан с магнитным полем и площадью, на которой оно существует. Поток Φ = BAcosθΦ = BAcosθ size 12 {Φ = ital «BA» «cos» θ} {} связан с индукцией; любое изменение ΦΦ размера 12 {Φ} {} индуцирует ЭДС.
Вся индукция, включая приведенные до сих пор примеры, возникает из-за некоторого изменения магнитного потока ΦΦ размер 12 {Φ} {} . Например, Фарадей изменил BB размером 12 {B} {} и, следовательно, ΦΦ размера 12 {Φ} {} при открытии и закрытии переключателя в своем устройстве (показано в [ссылка]).Это также верно для стержневого магнита и катушки, показанных на [ссылка]. При вращении катушки генератора угол θθ размера 12 {θ} {} и, следовательно, ΦΦ размера 12 {Φ} {} изменяется. Насколько велика ЭДС и какое направление она принимает, зависит от изменения ΦΦ размера 12 {Φ} {} и от того, как быстро это изменение будет выполнено, как будет рассмотрено в следующем разделе.
- Ключевой величиной в индукции является магнитный поток ΦΦ размер 12 {Φ} {} , определяемый как Φ = BAcosθΦ = BAcosθ размер 12 {Φ = ital «BA» «cos» θ} {}, где BB размер 12 {B} {} — напряженность магнитного поля над площадью AA размером 12 {A} {} под углом θθ размером 12 {θ} {} с перпендикуляром к площади.
- Единицы магнитного потока ΦΦ размер 12 {Φ} {} — T⋅m2T⋅m2 размер 12 {T cdot m rSup {размер 8 {2}}} {}.
- Любое изменение магнитного потока ΦΦ размер 12 {Φ} {} вызывает ЭДС — процесс определяется как электромагнитная индукция.
Каким образом многоконтурные катушки и железное кольцо в версии аппарата Фарадея, показанной в [ссылка], улучшают наблюдение наведенной ЭДС?
Когда магнит вставляется в катушку, как в [link] (a), в каком направлении сила, прилагаемая катушкой к магниту? Нарисуйте диаграмму, показывающую направление тока, индуцируемого в катушке, и создаваемое ею магнитное поле, чтобы обосновать вашу реакцию.Как величина силы зависит от сопротивления гальванометра?
Объясните, как магнитный поток может быть равен нулю, когда магнитное поле не равно нулю.
Наведена ли ЭДС в катушке [ссылка], когда она растягивается? Если да, укажите причину и укажите направление индуцированного тока.
Круглая катушка с проволокой натягивается в магнитном поле.
Какое значение магнитного потока в катушке 2 в [link] из-за катушки 1?
(а) Плоскости двух катушек перпендикулярны.(б) Проволока перпендикулярна плоскости катушки.
Какое значение имеет магнитный поток, проходящий через катушку в [link] (b) из-за провода?
Глоссарий
- магнитный поток
- величина магнитного поля, проходящего через конкретную область, вычисленная с помощью Φ = BAcosθΦ = BAcosθ размер 12 {Φ = ital «BA» «cos» θ} {}, где BB размер 12 {B} {} — магнитное поле прочность по площади AA размер 12 {A} {} под углом θθ размер 12 {θ} {} с перпендикуляром к площади
- электромагнитная индукция
- процесс наведения ЭДС (напряжения) с изменением магнитного потока
вектор | Определение, физика и факты
Вектор , в физике величина, которая имеет как величину, так и направление.Обычно он представлен стрелкой, направление которой совпадает с направлением количества, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, у него нет позиции. То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
В отличие от векторов, обычные величины, которые имеют величину, но не направление, называются скалярами. Например, смещение, скорость и ускорение — векторные величины, а скорость (величина скорости), время и масса — скаляры.
Чтобы считаться вектором, величина, имеющая величину и направление, также должна подчиняться определенным правилам комбинирования. Одним из них является сложение векторов, символически записываемое как A + B = C (векторы обычно обозначаются жирным шрифтом). С геометрической точки зрения векторную сумму можно визуализировать, поместив хвост вектора B в начало вектора A и нарисовав вектор C, начиная с хвоста A и заканчивая в голове B, так, чтобы он завершал треугольник. Если A, B и C — векторы, должна быть возможность выполнить ту же операцию и получить тот же результат (C) в обратном порядке, B + A = C.Величины, такие как смещение и скорость, обладают этим свойством (законом коммутативности), но есть величины (например, конечные вращения в пространстве), которые не являются векторами и, следовательно, не являются векторами.
векторный параллелограмм для сложения и вычитания
Один из методов сложения и вычитания векторов состоит в том, чтобы соединить их хвосты вместе, а затем подвести еще две стороны, чтобы сформировать параллелограмм. Вектор от их хвостов к противоположному углу параллелограмма равен сумме исходных векторов.Вектор между их головами (начиная с вычитаемого вектора) равен их разности.
Encyclopdia Britannica, Inc.
Другими правилами обработки векторов являются вычитание, умножение на скаляр, скалярное умножение (также известное как скалярное произведение или внутреннее произведение), векторное умножение (также известное как перекрестное произведение) и дифференцирование. . Нет операции, соответствующей делению на вектор. См. Векторный анализ для описания всех этих правил.
Правило правой руки для векторного векторного произведения
Обычное, или точечное, произведение двух векторов — это просто одномерное число или скаляр. Напротив, перекрестное произведение двух векторов приводит к другому вектору, направление которого ортогонально обоим исходным векторам, как показано правилом правой руки. Величина или длина вектора векторного произведения равна v w sin θ , где θ — это угол между исходными векторами v и w .
Британская энциклопедия, Inc.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишись сейчас
Хотя векторы математически просты и чрезвычайно полезны при обсуждении физики, они не были разработаны в их современной форме до конца XIX века, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (из США и Англии соответственно) применили векторный анализ в своих исследованиях. чтобы помочь выразить новые законы электромагнетизма, предложенные Джеймсом Клерком Максвеллом.
2.5: Плотность магнитного потока — Engineering LibreTexts
Плотность магнитного потока — это векторное поле, которое мы идентифицируем с помощью символа \ ({\ bf B} \) и которое имеет единицы СИ в тесла (Т). Прежде чем предложить формальное определение, полезно рассмотреть более широкую концепцию магнитного поля .
Магнитные поля являются неотъемлемым свойством некоторых материалов, особенно постоянных магнитов. Основное явление, вероятно, знакомо и показано на рисунке \ (\ PageIndex {1} \).У стержневого магнита есть «полюса», обозначенные как «N» («север») и «S» («юг»). N-конец одного магнита притягивает S-конец другого магнита, но отталкивает N-конец другого магнита и так далее. Существование векторного поля очевидно, поскольку наблюдаемая сила действует на расстоянии и утверждается в определенном направлении. В случае постоянного магнита магнитное поле возникает из-за механизмов, происходящих в масштабе атомов и электронов, составляющих материал. Эти механизмы требуют некоторого дополнительного объяснения, которое мы пока отложим.
Рисунок \ (\ PageIndex {1} \): свидетельство векторного поля из наблюдений силы, воспринимаемой стержневыми магнитами справа в присутствии стержневых магнитов слева. (CC BY 3.0; Ю. Цинь).
Магнитные поля также появляются при наличии тока. Например, обнаружено, что катушка с проводом, по которой проходит ток, влияет на постоянные магниты (и наоборот) так же, как постоянные магниты влияют друг на друга. Это показано на рисунке \ (\ PageIndex {2} \). Из этого мы заключаем, что основной механизм тот же — i.е. векторное поле, создаваемое токонесущей катушкой, представляет собой то же явление, что и векторное поле, связанное с постоянным магнитом. Каким бы ни был источник, теперь мы заинтересованы в количественной оценке его поведения.
Рисунок \ (\ PageIndex {2} \): Доказательство того, что ток также может создавать магнитное поле. (CC BY 4.0; Ю. Цинь).
Для начала рассмотрим действие магнитного поля на электрически заряженную частицу. Во-первых, представьте себе область свободного пространства без электрических или магнитных полей. Затем представьте, что появляется заряженная частица.Эта частица не будет испытывать силы. Далее появляется магнитное поле; возможно, это связано с постоянным магнитом или током поблизости. Эта ситуация показана на рисунке \ (\ PageIndex {2} \) (вверху). Тем не менее, к частице не приложена сила. Фактически, ничего не происходит, пока частица не придет в движение. На рисунке \ (\ PageIndex {3} \) (внизу) показан пример. Внезапно частица воспринимает силу. Мы скоро перейдем к деталям о направлении и величине, но основная идея теперь очевидна.Магнитное поле — это то, что прилагает к движущейся заряженной частице силу, отличную от силы, связанной с электрическим полем (фактически, в дополнение к ней).
Рисунок \ (\ PageIndex {3} \): сила, воспринимаемая заряженной частицей, которая (вверху) неподвижна и (внизу) движется со скоростью \ (\ mathbf {v} = \ hat {\ mathbf {z}} v \ ), которая перпендикулярна плоскости этого документа и по направлению к читателю (CC BY 4.0; Y. Qing).
Стоит отметить, что движущаяся одиночная заряженная частица представляет собой простейшую форму тока.Помните также, что для того, чтобы магнитное поле влияло на частицу, необходимо движение. Следовательно, не только ток является источником магнитного поля, магнитное поле также оказывает влияние на ток. Суммируя:
Магнитное поле описывает силу, действующую на постоянные магниты и токи в присутствии других постоянных магнитов и токов.
Итак, как мы можем количественно определить магнитное поле? Ответ из классической физики включает другое экспериментально выведенное уравнение, которое предсказывает силу как функцию заряда, скорости и векторного поля \ ({\ bf B} \), представляющего магнитное поле.Вот оно: сила, приложенная к частице, несущей заряд \ (q \), равна
.
\ [\ mathbf {F} = q \ mathbf {v} \ times \ mathbf {B} \ label {m0005_eFqvB} \]
где \ ({\ bf v} \) — скорость частицы, а «\ (\ times \)» обозначает перекрестное произведение. Перекрестное произведение двух векторов находится в направлении, перпендикулярном каждому из двух векторов, поэтому сила, создаваемая магнитным полем, перпендикулярна как направлению движения, так и направлению, в котором указывает магнитное поле.
Читатель будет вправе задаться вопросом, почему сила, создаваемая магнитным полем, должна перпендикулярно к \ ({\ bf B} \). В таком случае, почему сила должна зависеть от \ (\ bf v \)? Это вопросы, на которые классическая физика не дает очевидных ответов. Эффективные ответы на эти вопросы требуют концепций квантовой механики, где мы обнаруживаем, что магнитное поле является проявлением фундаментальной электромагнитной силы , удачно названной .Электромагнитная сила также усиливает электрическое поле, и только ограниченная интуиция, основанная на классической физике, заставляет нас воспринимать электрические и магнитные поля как отдельные явления. Для наших настоящих целей — и для наиболее часто встречающихся инженерных приложений — нам не нужны эти концепции. Достаточно принять эту кажущуюся странность как факт и действовать соответственно.
Анализ размеров \ ref {m0005_eFqvB} показывает, что \ ({\ bf B} \) имеет единицы измерения (N \ (\ cdot \) s) / (C \ (\ cdot \) m).В системе СИ эта комбинация единиц известна как тесла (Т).
Мы называем \ ({\ bf B} \) плотностью магнитного потока , и поэтому тесла — это единица плотности магнитного потока. Здесь уместно задать вопрос: что делает это плотностью потока? Короткий ответ заключается в том, что эта терминология несколько произвольна и на самом деле даже не является общепринятой. В инженерной электромагнетизме предпочтение называть \ ({\ bf B} \) «плотностью потока» объясняется тем, что мы часто обнаруживаем, что интегрируем \ ({\ bf B} \) по математической поверхности.2 \)) представляет собой описание магнитного поля, которое можно определить как решение уравнения \ ref {m0005_eFqvB}.
Рисунок \ (\ PageIndex {4} \): Магнитное поле стержневого магнита, иллюстрирующее силовые линии. (CC BY 4.0; Ю. Цин).
При описании магнитных полей мы иногда ссылаемся на концепцию силовой линии , определяемую следующим образом:
Линия магнитного поля — это кривая в пространстве, очерченная в направлении, в котором указывает вектор магнитного поля.
Эта концепция проиллюстрирована на рисунке \ (\ PageIndex {4} \) для постоянного стержневого магнита и на рисунке \ (\ PageIndex {5} \) для токонесущей катушки.
Рисунок \ (\ PageIndex {5} \): Магнитное поле токонесущей катушки, иллюстрирующее силовые линии. (CC BY 4.0; Ю. Цин).
Силовые линии магнитного поля примечательны по следующей причине:
Линия магнитного поля всегда образует замкнутый контур.
В некотором смысле это верно даже для силовых линий, которые кажутся прямыми (например, линии вдоль оси стержневого магнита и катушки на рисунках \ (\ PageIndex {4} \) и \ (\ PageIndex {5) } \), поскольку силовая линия, уходящая в бесконечность в одном направлении, снова появляется из бесконечности в противоположном направлении.
Авторы и ссылки
Введение в векторную графику и масштабатор Примечания, видео, контроль качества и тесты | 11 класс> Физика> Скаляры и векторы
Введение в Vector и Scaler
Физическая величина
Измеримая величина, определяющая законы физики, называется физической величиной. Физические величины делятся на два типа:
- Скалярная физическая величина: Некоторые физические величины полностью описываются только числовыми значениями (с указанием единиц измерения) и складываются в соответствии с обычными правилами алгебры.В качестве примера масса системы описывается, говоря, что она составляет 3 кг. Если два тела, одно из которых имеет массу 3 кг, а другое — 4 кг, сложить вместе, чтобы образовать составную систему, общая масса системы станет 3 кг + 4 кг = 7 кг. Такие величины называются скалярами. Физическая величина, которая имеет величину, но не имеет направления, называется скалярной величиной. Пример: длина, масса, время, площадь, температура, электрический ток, давление, работа, энергия, электрический поток, магнитный поток и т. Д.Скалярные величины можно складывать или вычитать, используя простой алгебраический метод. [Если изменение скалярной величины очень мало, то есть → 0, то это изменение можно рассматривать как векторную величину].
- Векторная физическая величина: Полное описание определенных физических величин, числовое значение (с указанием единиц измерения), а также направление в пространстве. Скорость частицы является примером такого рода. Физическая величина, которая имеет как величину, так и направление, называется векторной величиной.Пример: смещение, скорость, ускорение, сила, вес, импульс, импульс, магнитное поле, электрическое поле, гравитационное поле и т. Д. Векторные величины не могут быть добавлены или вычтены простым алгебраическим методом, но могут быть добавлены или вычтены с помощью геометрического метода, такого как в виде закона вектора треугольника, закона вектора параллелограмма, закона вектора многоугольника и т. д.
Графическое представление вектора
Векторная величина может быть представлена графически с помощью прямой линии со стрелкой, как показано на рисунке.Длина прямой линии дает величину вектора, а стрелка указывает его направление. Начальная точка, такая как «О», называется хвостом, а конечная точка, такая как «А», называется головой.
Обозначение вектора
Векторная величина может быть записана в виде алфавита (строчного или заглавного) со стрелкой, например
Пример: \ (\ overrightarrow {OA}, \ overrightarrow {OB}, \ overrightarrow {OC } \)
\ (\ vec a, \ vec b, \ vec c \)
\ (\ vec A, \ vec B, \ vec C \)
Разница между скалярными и векторными величинами
С.N | Скалярные величины | Векторные величины | |
1. | Физическая величина, которая имеет величину, но не имеет направления, называется скалярной величиной. Пример: длина, масса, время, площадь, температура и т. Д. | 1. | Физическая величина, которая имеет как величину, так и направление, называется векторной величиной. Пример: смещение, скорость, ускорение и т. Д. |
2. | Скалярные величины изменяются только с изменением величины. | 2. | Векторные величины изменяются с изменением либо величины, либо направления, либо одновременно величины и направления. |
3. | Скалярные величины можно складывать или вычитать согласно обычным правилам алгебры. | 3. | Векторные величины нельзя складывать или вычитать согласно обычным правилам алгебры. |
4. | Обозначаются обычными буквами. | 4. | Они представлены полужирными буквами или буквами со стрелкой над ними, например \ (\ vec A \) читается как вектор A. |
Типы вектора
- Единичный вектор: Вектор, имеющий единицу величины 1, известен как единичный вектор.Единичный вектор может быть записан в виде алфавита со шляпой или кепкой. Пример: $$ \ widehat A = \ frac {\ vec A} {\ lvert A \ rvert} $$ Направление единичного вектора — вдоль его вектора.
- Нулевой или нулевой вектор: Вектор, имеющий нулевую величину, называется нулевым вектором. Направление нулевого вектора не определено и обозначается как \ (\ vec A \).
- Параллельные векторы: Векторы, имеющие одинаковое направление, называются параллельными векторами. Здесь \ (\ vec A \) и \ (\ vec B \) — параллельные векторы.
- Равные векторы: Два вектора, имеющие одинаковую величину и направление, называются равными векторами. Здесь \ (\ vec A \) и \ (\ vec B \) — равные векторы.
- Противоположные векторы: Векторы, имеющие одинаковую величину, но противоположное направление, называются противоположными векторами. Здесь \ (\ vec A \) и — \ (\ vec A \) — противоположные векторы.
- Коллинеарные векторы: Векторы, проходящие через одну и ту же прямую линию, называются коллинеарными векторами.Здесь \ (\ vec A \) и \ (\ vec B \), \ (\ vec P \) и \ (\ vec Q \) — коллинеарные векторы.
- Копланарные векторы: Векторы, лежащие в одной плоскости, называются копланарными векторами. Здесь \ (\ vec A \) и \ (\ vec B \) — копланерные векторы
- Полярные векторы: Вектор, который производит линейный эффект при воздействии на тело, называется полярным вектором. Пример: сила, количество движения и т. Д.
- Осевые векторы: Вектор, который производит эффект поворота при воздействии на тело, называется осевым вектором.Пример: угловой момент, крутящий момент и т. Д.
- Правильные векторы: Векторы, отличные от нулевых векторов, называются собственными векторами.
Необходимое условие, чтобы физическая величина была вектором: Должен иметь величину и направление.

 В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.