Виды энергии в механике закон сохранения энергии: Законы сохранения. Работа и мощность. Теория, Формулы, Шпаргалка

Урок 11. Лекция 11. Работа. Мощность. Энергия. Закон сохранения энергии

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.

Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы  и вектором перемещения (или скорости).

A = Fs cos α

Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.

В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

[1 Дж=1 Н·м]

Работа силы, совершаемая в единицу времени, называется мощностью.

Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

 N=A/t

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

Внесистемная единица мощности 1 л.с.=735 Вт

Связь между мощностью и скоростью при равномерном движении:

N=A/t  так как   A=FScosα      тогда   N=(FScosα)/t, но S/t = v   следовательно

N=Fvcos α

В технике используются единицы работы и мощности:

1 Вт·с = 1 Дж;     1Вт·ч = 3,6·10³ Дж;      1кВт·ч = 3,6·10⁶ Дж

Если тело способно совершить работу, то говорят, что оно обладает энергией.

 Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.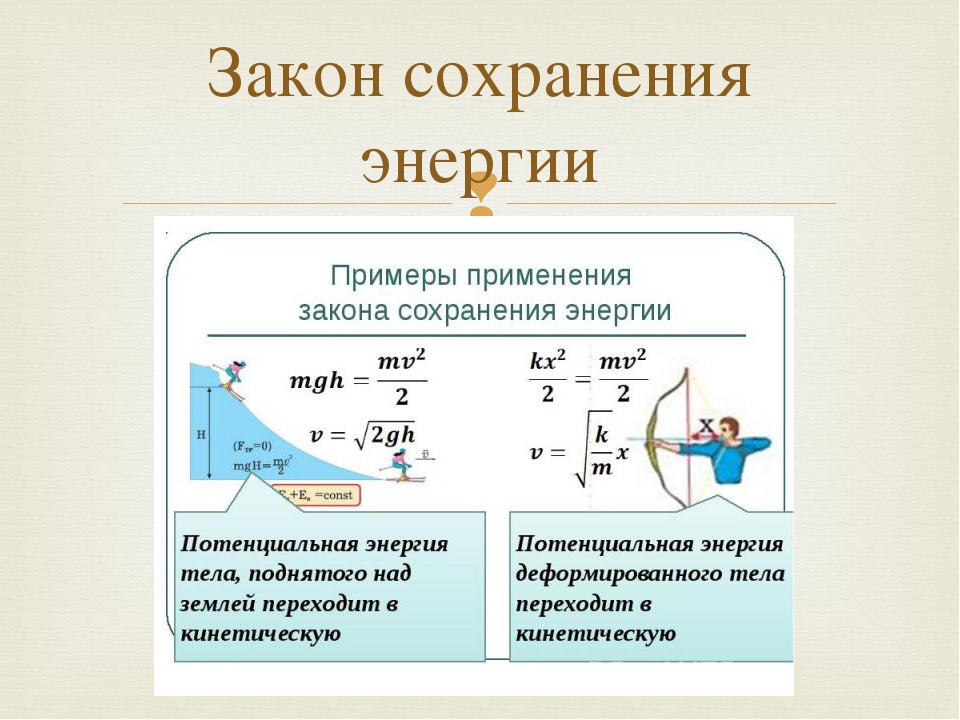

Обозначается  Е Единица энергии в СИ  [1Дж = 1Н*м]

Механическая работа есть мера изменения энергии в различных процессах А = ΔЕ.

Различают два вида механической энергии – кинетическая Ек и потенциальная Еp энергия.

Полная механическая энергия тела равна сумме его кинетической и потенциальной энергий

Е = Ек + Еp

Кинетическая энергия – это энергия тела, обусловленная его движением.

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью  равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

Если тело движется со скоростью , то для его полной остановки необходимо совершить работу

Наряду с кинетической энергией или энергией движения в физике важную роль играет понятиепотенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела. 

Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю.

Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Потенциальная энергия тела в поле силы тяжести (потенциальная энергия тела, поднятого над землёй):

Ep = mgh

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Понятие потенциальной энергии можно ввести и для упругой силы. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.

Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях упругая сила совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :

где k – жесткость пружины.

Растянутая (или сжатая) пружина способна привести в движ

§2.8 Закон сохранения энергии в механике

В
1018 г.Эмми Нётер, немецкий физик и
математик, доказал фундаментальную
теорему физики, которую в упрощённом
виде можно сформулировать так: каждому
свойству симметрии пространства и
времени соответствует свой закон
сохранения. В частности, как следует из
теоремы (теоремы
Нётер)
однородности времени должен соответствовать
закон
сохранения энергии: при
любых процессах, происходящих в замкнутой
консервативной системе, её полная
механическая энергия не изменяется.

Элементарная
работа потенциальных сил равна взятому
с обратным знаком эле­ментарному
изменению потенциальной энергии dA=
-dE_п
. Так как иных сил в системе нет, то та
же элементарная работа равна элементарному
изменению кинетической энергии dA=
dE_к.
По­этому можем записать

-dE_п
= dE_к

dE_к
+ dE_п
= 0,

d(Е_к
+ Е_п)
= 0. (2.34)

Обозначим

Е_к
+ Е_п
= Е (2.35)

здесь
Е — полная
механическая энергия.
Из (2.39) видим, что полная механическая
энергия остается постоянной:

E=const
(2.36)

При
решении задач в механике удобно
пользоваться законом сохранения энергии
в виде

ΔE_к
= ΔE_п
или Е_к1
+ Е_п1
= Е_к2
+ Е_п2.
(2.37)

здесь Е_к1
и Е_п1,
— соответственно кинетическая и
потенциальная энергии тела (системы) в
начальном положении; Е_к2
и Е_п2
— то же для конечного положения тела
(системы).

Закон
сохранения энергии в механике является
частным случаем более общего закона
сохранения и превращения энергии,
который является одним из основных
законов природы.

В
земных условиях невозможно указать
консервативную систему, хотя бы потому,
что всегда действуют силы трения и
сопротивления (диссипативные силы),
происходит уменьшение механической
энергии (диссипация энергии). В этом
случае механическая энергия уже не
будет оставаться постоянной; она будет
изменяться, и её изменение, как это видно
из формулы (2.38)
будет складываться из изменения
кинетической энергии ΔE_к,
и изменения потенциальной энергии ΔE_п
:

ΔЕ=
ΔE_к,+
ΔE_п. .
(2.38)

Учитывая
соотношения (2.27)
и (2.32),
выражающие теорему о кинетической и
потенциальной энергиях, последнее
равенство можно переписать так:

ΔЕ=
А_пот+А_дис-А_пот=
А_дис.
(2.39)

Изменение
полной механической энергии неконсервативной
системы равно сумме работы диссипативных
сил.

Так
как диссипативные силы направлены
противоположно перемещению, то работа
этих сил отрицательна и, следовательно,
механическая энергия системы уменьшается.

§2.9 Столкновение тел

Столкновение
тел – одно из наиболее часто встречающихся
явлений в жизни. При столкновении
происходит их кратковременное
взаимодействие, сопровождающееся как
деформацией, так и изменением направления
их движения. Особый интерес представляют
два вида столкновений – абсолютно
упругий и абсолютно неупругий удары.

Простейшим
видом соударения является центральный
удар тел. При этом ударе тела движутся
только поступательно, их скорость
направлена по прямой, соединяющей центры
масс.

Абсолютно
неупругий удар.
Так
называется столкновение двух тел, в
результате которого они соединяются
вместе и движутся дальше как одно целое.
Например, столкновение слипающихся
пластилиновых шариков; попадание
ружейной пули в ящик с песком и т.д.

Пусть
один из шаров массойm₁
догоняет другой массой m₂
(рис. 2.12).

Можно
записать

m₁υ₁+m₂υ₂=(m₁+m₂)υ
(2.40)

откуда

(2.41)

здесь
υ₁
и υ₂
— скорости взаимодействующих шаров до
удара; υ — их скорость после удара.

Направления
векторов скоростей в общем случае
определяются правилом:
скорости положительны, если направлены
вдоль оси ОХ, и отрицательны, если
направлены противоположно.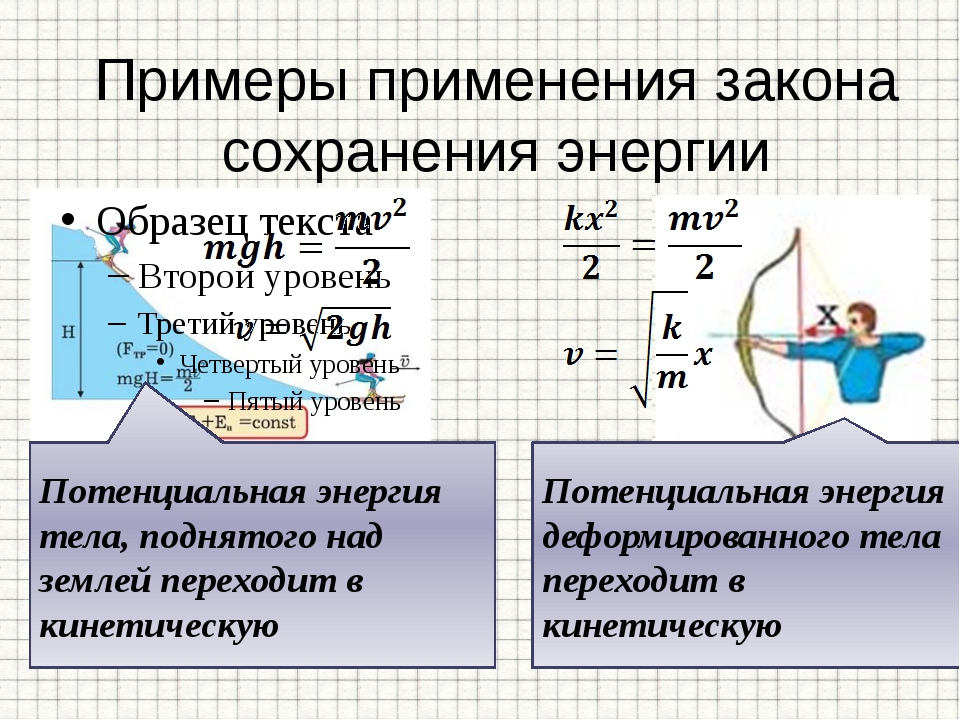

Рассмотрим
несколько частных случаев.

1.
Если массы шаров равны (m₁
= m₂),
то из (2.45) получим

(2.42)

2.
Удар шара о стенку. Неподвижное тело
(стенка) (υ₂
= 0) значительно массивнее шара (m₂
» m₁),
тогда

(2.43)

т.е.
налетевшее тело остановится после
абсолютно неупругого удара, при этом
υ₂
считаем
не слишком большой.

При
абсолютно неупругом ударе механическая
энергия шаров не сохраняется, так как
в системе действуют диссипативные силы
и происходит потеря кинетической
энергии, в результате чего механическая
энергия системы уменьшается, переходя
во внутреннюю энергию ΔЕ сталкивающихся
тел (которые при этом нагреваются). Но
закон сохранения полной энергии
выполняется, т.е. сумма всех видов энергии
замкнутой системы тел до и после
столкновений остаётся неизменной:

(2. 44)

Абсолютно
упругий удар.
Так
называется столкновение тел, в результате
которого не происходит соединения тел
в одно целое и их внутренние энергии
остаются неизменными. При абсолютно
упругом ударе сохраняется не только
импульс, но и механическая энергия
системы.

К
абсолютно упругому удару можно применить
закон сохранения механической энергии:

(2.45)

где
m₁
и m₂
— массы взаимодействующих шаров; υ₁,
υ₂
– их скорости до удара; u₁,
u₂—
после удара.

По
тем же причинам, которые были изложены
для абсолютно неупругого удара, к этому
случаю можно применить и закон сохранения
импульса:

m₁υ₁+
m₂υ₂
=
m₁
u₁+
m₂
u₂

(2.46)

Решая
совместно уравнения (2. 49) и (2.50), получим

(2.47)

(2.48)

2.3. Работа и механическая энергия. Механика. Физика. Курс лекций

2.3.1. Работа постоянной и переменной силы. Мощность. Потенциальные (консервативные) и непотенциальные силы

2.3.2. Энергия

2.3.3. Кинетическая энергия

2.3.4. Потенциальная энергия

2.3.5. Закон сохранения механической энергии

2.3.6. Сравнение кинематических и динамических характеристик поступательного и вращательного движений

2.3.7. Применение законов сохранения в теории ударов тел

2.3.1. Работа постоянной и переменной силы. Мощность. Потенциальные (консервативные) и непотенциальные силы

В физике работа неразрывно связана с изменением состояния тела или системы. Это изменение может выражаться самым различным образом: а) тело приобретает другую скорость, б) тело поднимается на другой уровень, в) тело деформируется, г) тело заряжается, д) тела намагничивается и т.д. Состояние механической системы (или тела) характеризуется одновременным заданием координат и скоростей всех точек системы (или тела) и может изменяться в процессе движения.

Процесс изменения характера движения тела происходит при его силовом взаимодействии с другими телами. Для количественного описания процесса вводят понятия силы и работы, совершаемой силой.

1. Если на тело действует постоянная сила F (Рисунок 13), и это приводит к перемещению ∆ r тела, то элементарной работой ∆А постоянной силы называется скалярное произведение вектора силы F и вектора перемещения ∆r:

∆А = (F∙∆r) = ½ F½½∆ r½ cos a ,

где a — угол между направлениями векторов силы F и перемещения ∆r, ( F∙ ∆r) – скалярное произведение двух векторов (см. [8]).

Рисунок 13 — Перемещение тела под действием постоянной силы.

Работа ∆А — скаляр. Если угол a — острый, то ∆А положительная величина, и говорят, что сила совершает работу. Если угол a — тупой, то ∆А — отрицательная величина, и говорят, что работа совершается против действия силы. Если a = 90⁰, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.

2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 90⁰), то работа ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом.

На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F _i и ∆ r _i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F _i на своем малом участке (Рисунок 14):

А = ∆А₁ + ∆А₂ +….+ ∆А _N = ( F₁∙∆ r₁) + (F ₂∙∆ r₂) + …+( F _N∙∆ r_N) = ( F_i∙∆ r_i),

где i = 1,2…… N — номер элементарного участка траектории.

Рисунок 14 — График зависимости силы от пути.

На участке ∆r _i силу F_i можно считать постоянной, тогда элементарная работа ∆А_i на участке ∆r _i равна ∆А_i= F_i∙∆ r _i и равна площади заштрихованной фигуры на рисунке 14.

А=∆А_i — это работа силы F на участке r, равна она численно площади S фигуры, ограниченной кривой зависимости F(х) и осью Х.

3. Примеры вычисления работы.

а) Тело, поднятое над землей на высоту h, падает на землю (без трения) из точки В в точку С и возвращается обратно (Рисунок 15). Определить работу силы по замкнутому пути.

Сила, действующая на тело, постоянна и равна силе притяжения тела к Земле (сила тяжести). Работа этой силы на участке ВС равна .

Чтобы поднять тело без ускорения из точки С в точку В, надо приложить к телу силу, равную силе тяжести, но противоположно направленную, и работа на участке пути СВ равна (работа совершается против силы тяжести).

Полная работа на участке (ВС+СВ) равна нулю.

Рисунок 15. Падение тела с высоты h (a) и поднятие тела на высоту h (б)

б) Пружину длиной l₁ растягиваем до длины l₂.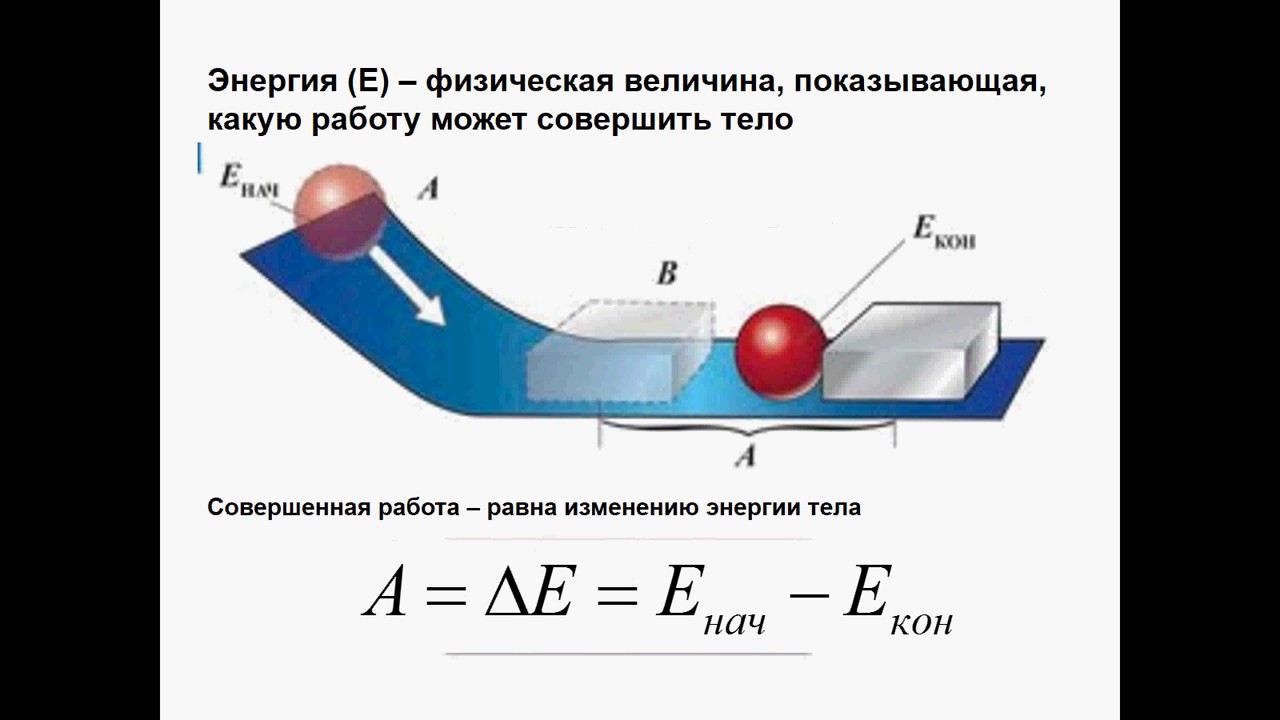 Какая работа при этом совершается?

Пусть х — длина, на которую растянута пружина, отсчет х от положения равновесия (Рисунок 16). При этом на пружину будет действовать упругая сила, старающаяся вернуть пружину в состояние равновесия, что соответствует минусу в формуле F = — kх (закон Гука). Если растянуть пружину еще на малую длину ∆х, надо совершить элементарную работу ∆А = — kх∙ ∆х.

Возникающая упругая сила будет переменной, т.к. она зависит от длины, на которую растягивают пружину. Для определения работы, которую надо затратить для растяжения пружины от длины l₁ до l₂, надо воспользоваться операцией интегрирования:

Работа силы упругости определяется только начальным и конечным положением пружины.

Рисунок 16. Сжатие пружины

4. Полная работа внешних сил при вращательном движении тела равна произведению момента этих сил относительно оси вращения на угол поворота тела за время действия сил. ∆ A= М∆.

И момент сил, и угловое перемещение (равное по модулю углу поворота) — векторы, направленные вдоль оси вращения. Если направление этих векторов совпадает, то ∆ A>0. Если направление этих векторов противоположное, то ∆ A<0.

5. Силы, работа которых определяется только начальной и конечной точками их приложений, и не зависят ни от вида траектории, ни от характера движения тела, называются консервативными или потенциальными силами.

Другое определение для этих сил таково. Силы, работа которых по замкнутой траектории равна нулю, называются потенциальными.

Соответственно, если работа силы по замкнутой траектории не равна нулю, то такая сила неконсервативная ( непотенциальная).

К непотенциальным силам относятся силы трения и силы, величина которых зависит от скорости движения точки (тела).

Сила тяжести и сила упругости являются потенциальнымисилами (см. приведенные выше примеры).

2.3.2. Энергия

1. Наиболее общим определением понятия энергии можно считать то, которое связано с понятием состояния системы (или тела). Энергия всегда является функцией состояния системы (тела). В любом состоянии система имеет определенное значение энергии и может сохранять это состояние, а значит и энергию этого состояния, сколь угодно долго. Для перехода системы (тела) в другое состояние должна быть совершена работа.

Физическая величина, характеризующая способность тела или системы тел совершить работу, называется энергией.

Состояние системы (тела) может меняться в процессе движений. Формы движений в природе различны. Для количественного сравнения разных форм движений и служит понятие энергии. Поэтому можно дать другое определение для энергии.

Энергией называется физическая величина, являющаяся общей мерой различных форм движения материи.

Различают виды энергии механическую, внутреннюю, электромагнитную, химическую, ядерную и т.д.

Механическая энергия может быть обусловлена или движением тела с некоторой скоростью (кинетическая энергия), или расположением данного тела в системе других тел определенной конфигурации (потенциальная энергия) W_мех. = W_кин. + W_пот..

2.3.3. Кинетическая энергия

1. Кинетической энергией тела называется энергия его механического движения.

Изменение кинетической энергии тела под действием силы равно работе этой силы.

Физическая величина называется кинетической энергией, а величина , равная разности кинетических энергий конечного состояния системы (индекс 2) и начального состояния (индекс 1), называется приращанием кинетической энергии.

Если на тело действуют несколько сил, и каждая из них совершает работу, и в результате этого меняется кинетическая энергия тела, то полная работа равна алгебраической сумме работ всех сил, действующих на тело. Энергия тела меняется за счет совершения работы.

Итак, связь работы и кинетической энергии задается соотношением:

А_{всех сил} = ∆ W_кин = ( W_кин)_кон. — ( W_кин.) _нач.,

т.е. работа всех сил равна изменению кинетической энергии тела (или системы).

Работа — мера изменения энергии (физический смысл работы).

2. Кинетическая энергия вращающегося тела.

Твердое тело вращается вокруг неподвижной оси. Полная кинетическая энергия вращающегося тела равна:

,

где I — момент инерции тела относительно оси вращения.

2.3.4. Потенциальная энергия

1. Потенциальная энергия — энергия, определяемая взаимным расположением тел или отдельных частей тела относительно друг друга.

Когда меняется конфигурация системы тел или частиц одного тела относительно друг друга, должна совершаться работа.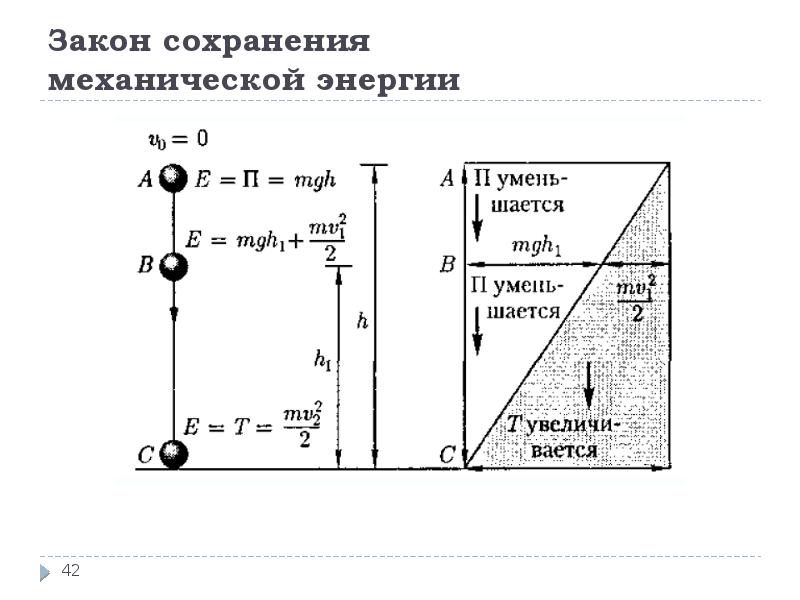

Пространство, в каждой точке которого на тело действует определенная сила, называется физическим или силовым полем.

Поэтому когда тело перемещается вблизи Земли, то говорят, что тело двигается в силовом поле тяготения Земли или в потенциальном поле Земли. Потенциальная энергия тяготения равна (W_пот)_тяг. = mgh,

h — расстояние между телом и Землей.

В растянутой (или сжатой) пружине на каждую ее точку действует сила упругости, в этом случае можно говорить о потенциальном поле упругости. Потенциальная энергия упругости равна ( W_пот) _упр. = ( kl²)/2, l — длина растянутой пружины, отсчет х от положения равновесия.

При делении сил, действующих на тело, на внешние и внутренние рассмотренные в примерах сила тяготения (в системе «тело — Земля») и сила упругости растянутой (сжатой) пружины можно отнести к внутренним силам. Поэтому верно утверждение, что каждой конфигурации произвольной системы частиц присуща своя собственная потенциальная энергия, и работа всех внутренних потенциальных сил, приводящая к изменению этой конфигурации, равна взятому со знаком минус приращению ( убыли) потенциальной энергии системы.

2.3.5. Закон сохранения механической энергии системы

Обобщая материал, рассмотренный в данной главе, можно основные выводы сформулировать так:

1) Приращение кинетической энергии системы равно произведенной работе всех сил, приложенных к системе.

А_{всех сил} = ∆ W_кин = ( W_кин)_кон. — ( W_кин.) _нач.

2) Все силы, действующие на систему можно разделить на внешние и внутренние. Внутренние силы можно разделить на потенциальные и непотенциальные (к последним относятся силы трения и сопротивления). Тогда А_{всех сил} = А_внеш. + _.А_пот. + А_тр.

3) Работа потенциальных внутренних сил равна приращению потенциальной энергии системы, взятому со знаком минус.

А_пот. = — ∆ W_пот = ( W_пот) _нач. — ( W_пот.)_кон..

4) Полная механическая энергия система равна сумме кинетической и потенциальной энергии системы.

W_мех. = W_кин. + W_пот..

Суммируя все эти положения и сделав соответствующие преобразования, получим

∆ W_мех. =( W_мех) _кон. — (W_мех.) _нач = А_внеш. + А_тр.

Если внешние силы на систему не действуют, то система называется замкнутой или изолированной и А_внеш. = 0. С замкнутой системой мы работали при рассмотрении законов сохранения импульса (ЗСИ) и момента импульса (ЗСМИ).

Если внутри системы действуют только потенциальные силы, а сил трения и сопротивления нет, то А_тр. = 0.

И тогда ∆ W_мех. = ( W_мех) _кон. — (W_мех.) _нач. = 0 и выполняется закон сохранения механической энергии ( ЗСЭ_мех):

Полная механическая энергия замкнутой системы, в которой не действуют силы трения, остается постоянной, независимо от взаимодействий внутри системы.

W_мех. = ( W_мех) _кон. = (W_мех.) _нач = const.

Если система замкнутая, но в ней действуют силы трения, то

∆ W_мех. = ( W_мех) _кон. — ( W_мех.) _нач. = А_тр.

Так как работа силы трения всегда отрицательна, то ее действие приводит к уменьшению полной механической энергии системы:

( W_мех) _кон. < ( W_мех.) _нач..

2.3.6. Сравнение кинематических и динамических характеристик поступательного и вращательного движений

Воспользуемся аналогией записи кинематических и динамических характеристик, законов поступательного и вращательного движений(см. таблицу 3).

Таблица 3. Сравнение кинематических и динамических характеристик поступательного и вращательного движений.

2.3.7. Применение законов сохранения в теории ударов тел

Ударом называется явление конечного изменения скоростей твердых тел за весьма малый промежуток времени при их столкновении.

Поведение соударяющихся тел можно рассчитать с помощью законов сохранения. Потенциальная энергия взаимодействующих тел не учитывается.

Абсолютно неупругий удар — удар, в результате которого тела после столкновения двигаются с одинаковыми скоростями. Поведение тел при таких ударах может быть описано моделью, называемой абсолютно неупругое тело.

Рассмотрим центральный неупругий удар двух шаров массой m₁ и m₂. Скорости шаров лежат на одной линии, соединяющей их центры: v₁ и v₂ — скорости шаров до удара, v — общая скорость шаров после удара. ЗСИ в векторной форме имеет вид:

m₁∙ v₁ + m₂∙ v₂ = ( m₁ + m₂)∙ v

Если v₁ и v₂ имеют одинаковые направления, то ЗСИ примет вид:

m₁∙ v₁ + m₂∙ v₂ = ( m₁ + m₂)∙v.

Если шары двигаются навстречу друг другу, тогда

m₁∙ v₁ — m₂∙ v₂ = ( m₁ + m₂)∙v

Закон сохранения механической энергии при таком ударе не выполняется, но с учетом энергии, затраченной на деформацию тел, общий закон сохранения энергии имеет вид:

Абсолютно упругий удар — такое кратковременное взаимодействие тел, при котором в обоих взаимодействующих телах не остается никаких деформаций. Поэтому кинетическая энергия, которой тела обладали до взаимодействия, превращается в кинетическую энергию тех же тел после взаимодействия.

Поведение тел при таких ударах может быть описано моделью, называемой абсолютно упругое тело.

Рассмотрим центральный упругий удар двух шаров массой m₁ и m₂. Скорости шаров лежат на одной линии, соединяющей их центры: v₁ и v₂ — скорости шаров до удара, u₁ и u₂ — скорости шаров после удара.

(ЗСИ) m₁∙ v₁ + m₂∙ v₂ = m₁∙ u₁ + m₂∙ u₂

( ЗСЭ_мех)

В ЗСИ надо учитывать направления скоростей до удара. Значения и направления скоростей после удара получаются при решении приведенной выше системы двух уравнений.

Закон сохранения энергии — Эко-свет

Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) физической системы сохраняется с течением времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.

Фундаментальный смысл закона сохранения энергии

Закон сохранения энергии — «фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) физической системы сохраняется с течением времени». Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.

С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени и в этом смысле является универсальным, то есть присущим системам самой разной физической природы. Другими словами, для каждой конкретной замкнутой системы, вне зависимости от её природы можно определить некую величину, называемую энергией, которая будет сохраняться во времени. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.

Однако в различных разделах физики по историческим причинам закон сохранения энергии формулируется по-разному, в связи с чем говорится о сохранении различных видов энергии. Например, в термодинамике закон сохранения энергии выражается в виде первого начала термодинамики.

Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то более правильным является его именование не законом, а принципом сохранения энергии.

С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.

Согласно теореме Нётер каждому закону сохранению ставится в соответствие некая симметрия уравнений, описывающих систему. В частности, закон сохранения энергии эквивалентен однородности времени, то есть независимости всех законов, описывающих систему, от момента времени, в который система рассматривается.

Вывод этого утверждения может быть произведён, например, на основе лагранжева формализма. Если время однородно, то функция Лагранжа, описывающая систему, не зависит явно от времени, поэтому полная её производная по времени имеет вид:

Здесь — функция Лагранжа, — обобщённые координаты и их первые и вторые производные по времени соответственно. Воспользовавшись уравнениями Лагранжа, заменим производные на выражение:

Перепишем последнее выражение в виде

Сумма, стоящая в скобках, по определению называется энергией системы и в силу равенства нулю полной производной от неё по времени она является интегралом движения (то есть сохраняется).

История открытия закона сохранения и превращения энергии

В 1841 г. русский ученый Ленц и англичанин Джоуль почти одновременно и независимо друг от друга экспериментально доказали, что теплота может быть создана за счет механической работы. Джоуль определил механический эквивалент тепла. Эти и другие исследования подготовили открытие закона сохранения и превращения энергии. В 1842—1845 г.г. немецкий ученый Р. Майер сформулировал этот закон на основе обобщения данных естествознания о механическом движении, электричестве, магнетизме, химии и даже физиологии человека. Одновременно в Англии (Гров) и в Дании (Кольдинг) были высказаны аналогичные идеи. Несколько позднее этот закон разрабатывал Гельмгольц (Германия)

Воззрения на теплоту как форму движения мельчайших «нечувствительных» частиц материи высказывались еще в XVII в. Ф. Бэкон, Декарт, Ньютон, Гук и многие другие приходили к мысли, что теплота связана с движением частиц вещества []. Но со всей полнотой и определенностью эту идею разрабатывал и отстаивал Ломоносов. Однако он был в одиночестве, его современники переходили на сторону концепции теплорода, и, как мы видели, эта концепция разделялась многими выдающимися учеными XIX столетия.

Успехи экспериментальной теплофизики, и прежде всего калориметрии, казалось, свидетельствовали в пользу теплорода. Но тот же XIX в. принес наглядные доказательства связи теплоты с механическим движением. Конечно, факт выделения тепла при трении был известен с незапамятных времен. Сторонники теплоты усматривали в этом явлении нечто аналогичное электризации тел трением — трение способствует выжиманию теплорода из тела. Однако в 1798 г. Бенжамен Томпсон (1753―1814), ставший с 1790 г. графом Румфордом, сделал в мюнхенских военных мастерских важное наблюдение: при высверливании канала в пушечном стволе выделяется большое количество тепла. Чтобы точно исследовать это явление, Румфорд проделал опыт по сверлению канала в цилиндре, выточенном из пушечного металла. В высверленный канал помещали тупое сверло, плотно прижатое к стенкам канала и приводившееся во вращение. Термометр, вставленный в цилиндр, показал, что за 30 минут операции температура поднялась на 70 градусов Фаренгейта. Румфорд повторил опыт, погрузив цилиндр и сверло в сосуд с водой. В процессе сверления вода нагревалась и спустя 2,5 часа закипала. Этот опыт Румфорд считал доказательством того, что теплота является формой движения.

Опыты по получению теплоты трением повторил Дэви. Он плавил лед трением двух кусков друг о друга. Дэви пришел к выводу, что следует оставить гипотезу о теплороде и рассматривать теплоту как колебательное движение частиц материи.

По Майеру, все движения и изменения в мире порождаются «разностями», вызывающими силы, стремящиеся уничтожить эти разности. Но движение не прекращается, потому что силы неуничтожаемы и восстанавливают разности. «Таким образом, принцип, согласно которому раз данные силы количественно неизменны, подобно веществам, логически обеспечивает нам продолжение существования разностей, а значит, и материального мира». Эта формулировка, предложенная Майером, легко уязвима для критики. Не определено точно понятие «разность», неясно, что понимается под термином «сила». Это предчувствие закона, а не самый еще закон. Но из дальнейшего изложения понятно, что под силой он понимает причину движения, которое измеряется произведением массы на скорость. «Движение, теплота и электричество представляют собою явления, которые могут быть сведены к одной силе, которые измеряются друг другом и переходят друг в друга по определенным законам». Это вполне определенная и ясная формулировка закона сохранения и превращения силы, т.е. энергии.

Задавшись целью применить идеи механики в физиологии, Майер начинает с выяснения понятия силы. И здесь он вновь повторяет мысль о невозможности возникновения движения из ничего, сила — причина движения, а причина движения является неразрушимым объектом. Эта формулировка поразительно напоминает формулировку «всеобщего закона» Ломоносова, распространяемого им «и на самые правила движения». Заметим, что выдвижение Ломоносовым и Майером всеобщего закона сохранения в качестве «верховного закона природы» принято современной наукой, которая формулирует многочисленные конкретные законы сохранения в качестве основной опоры научного исследования. Майер подробно подсчитывает механический эквивалент теплоты из разности теплоемкостей газа (этот подсчет нередко воспроизводится в школьных учебниках физики) и находит его, опираясь на измерения Делароша и Берара, а также Дюлонга, определивших отношение теплоемкостей для воздуха равным 367 кгс-м/ккал.

Майер закончил развитие своих идей к 1848 г., когда в брошюре «Динамика неба в популярном изложении» он поставил и сделал попытку решить важнейшую проблему об источнике солнечной энергии. Майер понял, что химическая энергия недостаточна для восполнения огромных расходов энергии Солнца. Но из других источников энергии в его время была известна только механическая энергия. И Майер сделал вывод, что теплота Солнца восполняется бомбардировкой его метеоритами, падающими на него со всех сторон непрерывно из окружающего пространства. Он признает, что открытие сделано им случайно (наблюдение на Яве), но «оно все же моя собственность, и я не колеблюсь защищать свое право приоритета». Майер указывает далее, что закон сохранения энергии, «а также численное выражение его, механический эквивалент теплоты, были почти одновременно опубликованы в Германии и Англии». Он указывает на исследования Джоуля и признает, что Джоуль «открыл безусловно самостоятельно» закон сохранения и превращения энергии и что «ему принадлежат многочисленные важные заслуги в деле дальнейшего обоснования и развития этого закона». Но Май ер не склонен уступать свое право на приоритет и указывает, что из самих его работ видно, что он не гонится за эффектом. Это, однако, не означает отказа от прав на свою собственность.

Задолго до Джоуля исследования были начаты петербургским академиком Э.Х. Ленцем, который опубликовал свою работу в 1843 г. под заглавием «О законах выделения тепла гальваническим током». Ленц упоминает о работе Джоуля, публикация которого опередила публикацию Ленца, но считает, что, хотя его результаты в «основном совпадают с результатами Джоуля», они свободны от тех обоснованных возражений, которые вызывают работы Джоуля.

Ленц тщательно продумал и разработал методику эксперимента, испытал и проверил тангенс-гальванометр, служивший у него измерителем тока, определил применяемую им единицу сопротивления (напомним, что закон Ома к этому времени еще не вошел во всеобщее употребление), а также единицы тока и электродвижущей силы, выразив последнюю через единицы тока и сопротивления. Ленц тщательно изучил поведение сопротивлений, в частности исследовал вопросе существовании так называемого «переходного сопротивления» при переходе из твердого тела в жидкость. Это понятие вводилось некоторыми физиками в эпоху, когда закон Ома еще не был общепризнанным. Затем он перешел к основному эксперименту, результаты которого сформулировал в следующих двух положениях: нагревание проволоки гальваническим током пропорционально сопротивлению проволоки; нагревание проволоки гальваническим током пропорционально квадрату служащего для нагревания тока. Точность и обстоятельность опытов Ленца обеспечили признание закона, вошедшего в науку под названием закона Джоуля — Ленца.

Джоуль сделал свои эксперименты по выделению тепла электрическим током исходным пунктом дальнейших исследований выяснения связи между теплотой и работой. Уже на первых опытах он стал догадываться, что теплота, выделяемая в проволоке, соединяющей полюсы гальванической батареи, порождается химическими превращениями в батарее, т. е. стал прозревать энергетический смысл закона. Чтобы выяснить далее вопрос о происхождении «джоулева тепла» (как теперь называется теплота, выделяемая электрическим током), он стал исследовать теплоту, выделяемую индуцированным током. В работе «О тепловом эффекте магнитоэлектричества и механическом эффекте теплоты», доложенной на собрании Британской Ассоциации в августе 1843 г., Джоуль сформулировал вывод, что теплоту можно создавать с помощью механической работы, используя магнитоэлектричество (электромагнитную индукцию), и эта теплота пропорциональна квадрату силы индукционного тока.

Вращая электромагнит индукционной машины с помощью падающего груза, Джоуль определил соотношение между работой падающего груза и теплотой, выделяемой в цепи. Он нашел в качестве среднего результата из своих измерений, что «количество тепла, которое в состоянии нагреть один фунт воды на один градус Фаренгейта, может быть превращено в механическую силу, которая в состоянии поднять 838 фунтов на вертикальную высоту в один фут». Переводя единицы фунт и фут в килограммы и метры и градус Фаренгейта в градус Цельсия, найдем, что механический эквивалент тепла, вычисленный Джоулем, равен 460 кгс-м/ккал. Этот вывод приводит Джоуля к другому, более общему выводу, который он обещает проверить в дальнейших экспериментах: «Могучие силы природы… неразрушимы, и… во всех случаях, когда затрачивается механическая сила, получается точное эквивалентное количество теплоты». Он утверждает, что животная теплота возникает в результате химических превращений в организме и что сами химические превращения являются результатом действия химических сил, возникающих из «падения атомов» Таким образом, в работе 1843 г. Джоуль приходит к тем же выводам, к которым ранее пришел Майер.

Джоуль продолжал свои эксперименты и в 60-х и в 70-х годах. В 1870 г. он вошел в состав комиссии по определению механического эквивалента теплоты. В состав этой комиссии входили В. Томсон, Максвелл и другие ученые. Но Джоуль не ограничился работой экспериментатора. Он решительно встал на точку зрения кинетической теории теплоты и стал одним из основоположников кинетической теории газов. Об этой работе Джоуля будет сказано позднее. В отличие от своих предшественников Гельмгольц связывает закон с принципом невозможности вечного двигателя (peгрetuum mobile). Этот принцип принимал еще Леонардо да Винчи, ученые XVII в. (вспомним, что Стевин обосновал закон наклонной плоскости невозможностью вечного движения), и, наконец, в XVIII в. Парижская Академия наук отказалась рассматривать проекты вечного двигателя. Гельмгольц считает принцип невозможности вечного двигателя тождественным принципу, что «все действия в природе можно свести на притягательные или отталкивательные силы». Материю Гельмгольц рассматривает как пассивную и неподвижную. Для того чтобы описать изменения, происходящие в мире, ее надо наделить силами как притягательными, так и отталкивательными. «Явления природы, — пишет Гельмгольц, — должны быть сведены к движениям материи с неизменными движущими силами, которые зависят только от пространственных взаимоотношений». Разными путями шли открыватели закона сохранения и превращения энергии к его установлению. Майер, начав с медицинского наблюдения, сразу рассматривал его как глубокий всеобъемлющий закон и раскрывал цепь энергетических превращений от космоса до живого организма. Джоуль упорно и настойчиво измерял количественное соотношение теплоты и механической работы. Гельмгольц связал закон с исследованиями великих механиков XVIII в. Идя разными путями, они наряду со многими другими современниками настойчиво боролись за утверждение и признание закона вопреки противодействию цеховых ученых. Борьба была нелегкой и порой принимала трагический характер, но она окончилась полной победой. Наука получила в свое распоряжение великий закон сохранения и превращения энергии.

Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) физической системы сохраняется с течением времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.

Однако в различных разделах физики по историческим причинам закон сохранения энергии формулируется по-разному, в связи с чем говорится о сохранении различных видов энергии. Например, в термодинамике закон сохранения энергии выражается в виде первого начала термодинамики. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то более правильным является его именование не законом, а принципом сохранения энергии.

В 1841 г. русский ученый Ленц и англичанин Джоуль почти одновременно и независимо друг от друга экспериментально доказали, что теплота может быть создана за счет механической работы. Джоуль определил механический эквивалент тепла. Эти и другие исследования подготовили открытие закона сохранения и превращения энергии. В 1842—1845 г.г. немецкий ученый Р. Майер сформулировал этот закон на основе обобщения данных естествознания о механическом движении, электричестве, магнетизме, химии и даже физиологии человека. Одновременно в Англии (Гров) и в Дании (Кольдинг) были высказаны аналогичные идеи. Несколько позднее этот закон разрабатывал Гельмгольц (Германия) Разными путями шли открыватели закона сохранения и превращения энергии к его установлению

Механическая энергия. Закон изменения (сохранения) механической энергии. Физика. 1 курс НПО и СПО. — Закон сохранения и превращения энергии..

Комментарии преподавателя

Рассмотрим замкнутую механическую систему тел, состоящую из капли дождя и Земли, которая обладает как потенциальной энергией (тела взаимодействуют друг с другом), так и кинетической энергией (тела системы могут двигаться).

Предположим, в какой-то момент времени кинетическая энергия капли равна Ек1, а потенциальная – Еп1.

Кинетическая и потенциальная энергии капли в другой момент времени соответственно равны Ек2 и Еп2.

Согласно теореме об изменении кинетической энергии работа, совершенная силой тяжести, действующей на каплю, равна изменению его кинетической энергии

А =Еk2 – Ek1                   (1)

Эта же работа равна изменению потенциальной энергии капли, взятой с противоположным знаком:

A = –(En2 –En1)              (2)

В левых частях уравнений (1) и (2) стоит одна и та же величина, в таком случае и правые части уравнений должны быть равны

Еk2 – Ek1 = –(En2 –En1)                (3)

Из уравнения (3) следует вывод: когда кинетическая энергия увеличивается на некоторую величину, на такую же величину уменьшается потенциальная энергия, и наоборот. Энергия не создается и не уничтожается, а происходит превращение одного вида энергии в другой. Запишем равенство (3) в другой форме:

En1 + Ek1 = En2 + Еk2                    (4)

В левой части равенства (4) записана сумма потенциальной и кинетической энергии, то есть полной механической энергии Е системы тел в какой-то момент времени. В правой части записана эта же энергия в другой момент времени, тогда

E = En + Еk = const                      (5)

Равенства (4) и (5) позволяют сформулировать закон сохранения энергии: полная механическая энергия замкнутой системы тел, в которой действуют консервативные силы (тяготения или упругости), остается постоянной. Энергия не создается и не уничтожается, а только превращается из одного вида в другой: из кинетической энергии в потенциальную и наоборот.

Для системы тел лыжница – Земля, в которой действует сила тяжести, закон сохранения механической энергии можно записать так:

Или

Уравнение (6) позволяет найти скорость камня v2 на высоте h3, если известна начальная скорость v1 камня на исходной высоте h2.

Для системы, состоящей из тела массой m и пружины жесткостью k, растянутой на расстояние Dl, закон сохранения механической энергии имеет вид:

Закон сохранения механической энергии выполняется в том случае, когда малы силы трения, сопротивления и ими пренебрегают. Чем отличается сила трения от консервативных сил тяжести и упругости?

Работа силы тяжести и силы упругости может быть и положительной, и отрицательной.

Закон сохранения механической энергии

сбережения энергии | Определение и примеры

Посмотрите, как маятник, вращающийся в шине, демонстрирует закон сохранения энергии

Объяснение принципа сохранения энергии.

Encyclopædia Britannica, Inc. Посмотреть все видео по этой статье

Сохранение энергии , физический принцип, согласно которому энергия взаимодействующих тел или частиц в замкнутой системе остается постоянной. Первым видом энергии, который был распознан, была кинетическая энергия или энергия движения.В некоторых столкновениях частиц, называемых упругими, сумма кинетической энергии частиц до столкновения равна сумме кинетической энергии частиц после столкновения. Понятие энергии постепенно расширялось и включало другие формы. Кинетическая энергия, теряемая телом, замедляющимся при движении вверх против силы тяжести, считалась преобразованной в потенциальную энергию или запасенную энергию, которая, в свою очередь, преобразуется обратно в кинетическую энергию по мере того, как тело ускоряется во время возвращения на Землю. .Например, когда маятник движется вверх, кинетическая энергия преобразуется в потенциальную. Когда маятник ненадолго останавливается в верхней точке своего колебания, кинетическая энергия равна нулю, а вся энергия системы находится в потенциальной энергии. Когда маятник опускается обратно, потенциальная энергия преобразуется обратно в кинетическую энергию. В любое время сумма потенциальной и кинетической энергии постоянна. Однако трение замедляет самые тщательно сконструированные механизмы, постепенно рассеивая их энергию.В 1840-х годах было окончательно показано, что понятие энергии можно расширить, включив в него тепло, генерируемое трением. Истинно сохраняемая величина — это сумма кинетической, потенциальной и тепловой энергии. Например, когда блок скользит по склону, потенциальная энергия превращается в кинетическую. Когда трение замедляет блок до остановки, кинетическая энергия преобразуется в тепловую. Энергия не создается и не разрушается, а просто меняет формы, переходя от потенциальной к кинетической и тепловой энергии.Эта версия принципа сохранения энергии, выраженная в самой общей форме, является первым законом термодинамики. Концепция энергии продолжала расширяться, включая энергию электрического тока, энергию, запасенную в электрическом или магнитном поле, и энергию в топливе и других химических веществах. Например, автомобиль движется, когда химическая энергия бензина преобразуется в кинетическую энергию движения.

Британская викторина

Викторина «Все о физике»

Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.

С появлением физики относительности (1905 г.) масса впервые была признана эквивалентом энергии. Полная энергия системы высокоскоростных частиц включает не только их массу покоя, но также очень значительное увеличение их массы вследствие их высокой скорости. После открытия теории относительности принцип сохранения энергии получил альтернативное название — сохранение массы-энергии или сохранение полной энергии.

Когда казалось, что принцип не работает, как это было в применении к типу радиоактивности, называемому бета-распад (спонтанный выброс электронов из атомных ядер), физики признали существование новой субатомной частицы, нейтрино, которая должна была унести недостающей энергии, а не отвергать принцип сохранения.Позже нейтрино было обнаружено экспериментально.

Однако энергосбережение — это больше, чем общее правило, которое остается в силе. Можно показать математически, что это следует из единообразия времени. Если бы один момент времени отличался от любого другого момента, идентичные физические явления, происходящие в разные моменты времени, потребовали бы разного количества энергии, так что энергия не будет сохраняться.

Получите эксклюзивный доступ к контенту из нашего первого издания 1768 с вашей подпиской.Подпишитесь сегодня

Механика 1: Сохранение энергии и импульса

1 Механика: сохранение энергии и импульса Если определенная величина, связанная с системой, не изменяется во времени. Мы говорим, что она сохраняется, а система обладает законом сохранения.Законы сохранения важны, поскольку они могут значительно упростить решение проблем. Например, они могут избавить от необходимости решать дифференциальные уравнения, чтобы найти движение, или, по крайней мере, упростить процедуру интегрирования (это обязательно должно привлечь ваше внимание). Первый закон сохранения, который мы изучим, — это закон сохранения полной энергии. Сохранение энергии для консервативных силовых полей. Рассмотрим частицу массы m, движущуюся под действием консервативного силового поля, т.е.е., силу можно записать как F = V для некоторой скалярной функции V. Ссылаясь на рис., мы предполагаем, что масса m частицы постоянна, и что в моменты времени t и t 2 она находится в точках P и P 2, соответственно, и движущиеся со скоростями v = dr v 2 = dr2 в точках P и P 2 соответственно. и z PC rikjr 2 P 2 yx Рисунок: Мы уже доказали, что полная работа, совершаемая силой при перемещении частицы от P к P 2 по кривой C, определяется разностью кинетических энергий в P 2 и P, я.е., W = 2 мв2 2 2 мв2. Если сила консервативна, мы доказали, что полная работа, совершаемая силой при перемещении частицы от P к P 2 вдоль кривой C, определяется разностью потенциальных энергий в P и P 2, т. Е. Задавая эти два выражения равенство дает: W = V (P) V (P 2). или 2 mv2 2 2 mv2 = V (P) V (P 2), 2 mv2 2 + V (P 2) = 2 mv2 + V (P). () Мы называем сумму кинетической и потенциальной энергии частицы полной энергией или просто энергией частицы. Поскольку путь C и точки P и P 2 были полностью произвольными, () говорит, что под действием консервативного силового поля частица движется так, что ее полная энергия никогда не изменяется.Это закон сохранения энергии, действующий для консервативных сил.

2 Постоянные силы консервативны. Мы рассмотрели ряд задач, касающихся движения частицы под действием только постоянного силового поля. Мы хотим явно показать, что постоянные силы консервативны. Это сразу означает, что энергия сохраняется. Мы воспользуемся этим фактом и вернемся к этим проблемам и покажем, что учет энергосбережения значительно упрощает их решение.Предположим, что поле постоянной силы имеет следующий вид: F = Ai + Bj + Ck, где A, B и C — константы (действительные числа). Чтобы показать, что F консервативен, нам нужно только показать, что F = 0. Однако это должно быть очевидно, поскольку ротор вектора включает частные производные вектора. Этот вектор постоянен, поэтому все частные производные равны нулю. Поскольку F консервативен, его можно представить как (отрицательный) градиент потенциальной функции. Давайте теперь вычислим потенциал.Однако давайте упростим задачу, предположив, что F отличен от нуля только в одном из координатных направлений, скажем, в k. Тогда имеем или F = Ck = V = V x i V y j V z k, 0 = V x, 0 = V y, C = V z. Первые два из этих уравнений подразумевают, что V (x, y, z) не зависит от x или y (мы могли этого ожидать, почему?). Следовательно, мы можем проинтегрировать последнее уравнение и получить: V = Cz + c, где c — неизвестная, и произвольная постоянная интегрирования (произвольная в том смысле, что ее выбор не влияет на силу).Поэтому давайте сделаем выбор. Предположим, мы выбрали V = 0 при z = z 0. Тогда имеем: и, следовательно: 0 = Cz 0 + c, или c = Cz 0, V = C (z z 0). Если мы рассмотрим важный случай постоянной гравитационной силы F = mgk, тогда связанный потенциал будет: V = mg (z z 0). (2) Движение в одном измерении в консервативном силовом поле. Рассмотрим уравнения Ньютона в одном измерении, где сила задается консервативным силовым полем, т.е. m d2 s 2 = V (s), s (t 0) = s 0, ṡ (t 0) = v 0. (3) Мы знаем, поскольку сила консервативна, что частица движется таким образом, что энергия сохраняется, т.е.е., 2 мṡ2 + V (s) = E, (4) 2

3 где E — постоянная, называемая энергией. Повторюсь, любое решение (3) должно удовлетворять (4). Но как начальные условия решения (3) проявляются в (4)? Через постоянную E. Eq. (4) выполняется для всех точек решения (3), включая начальную точку (начальные условия). Следовательно, константа E может быть выражена через (постоянное) начальное условие (3) путем подстановки начальных условий (3) в (4).Теперь (4) может помочь нам решить (3), позволяя пропустить одно интегрирование. Вот что мы имеем в виду. Уравнение (4) можно переписать как: или, ds 2 = ± E V (s), (5) m s (t) ds 2 t ± s (t 0) E V (s) =. (6) m t 0 Если мы можем сделать этот интеграл (инвертировать его), мы будем решать для s (t). Следовательно, сохранение энергии сводит решение обыкновенного дифференциального уравнения второго порядка к интегрированию дифференциального уравнения первого порядка. Вычисление интеграла существенно зависит от V (s), и, к сожалению, для большинства функций V (s) мы не можем вычислить интеграл аналитически.Также есть знак ±. Правильный выбор должен быть сделан при извлечении квадратного корня и зависит от конкретного рассматриваемого приложения. Сохранение импульса. Пока мы обсуждаем сохранение, мы можем также выделить сохранение количества движения, хотя мы действительно уже открыли его, как это выражено в законах Ньютона. Вспомните второй закон Ньютона в форме импульса: dp = F, (7) где F — векторная сумма всех сил. Теперь предположим, что все силы равны нулю.Тогда мы имеем: dp = 0, (8) что говорит о том, что импульс постоянен во времени, если нет результирующих сил, т.е. импульс сохраняется в отсутствие сил. Теперь мы можем вернуться к нескольким примерам и задачам, приведенным ранее, и решить их, используя закон сохранения энергии. предыдущая задача Объект массы m отбрасывается вертикально вверх от поверхности Земли с начальной скоростью v 0 k (v 0> 0). Мы предполагаем, что единственной силой, действующей на объект, является гравитация, см. Рис. 2. F = -mgk z m r i k O j y x Рис. 2: 3

4 Найдите :.максимальная достигнутая высота, 2. скорость как функция расстояния от исходной точки. Мы видели, что потенциальная энергия, связанная с силой тяжести, определяется выражением: V = mg (z z 0), (9) где z 0 — исходное положение. Мы выберем это так, чтобы частица имела нулевую потенциальную энергию при z = 0, т. Е. Выберем z 0 = 0. При таком выборе нам известна полная энергия при z = 0. Она просто задается кинетической энергией 2 mv2. 0. Что теперь характеризует полную энергию на максимальной высоте? На максимальной высоте скорость равна нулю, поэтому полная энергия определяется потенциальной энергией mgz max.Таким образом, приравнивание полной энергии при z = 0 к полной энергии при z max дает: 2 mv2 0 = mgz max,

консервация_энергии

Закон сохранения энергии

Энергия и теплофизика

Практическая деятельность
для 14-16

Демонстрация

Машины позволяют перемещать большую силу, используя малую, но они не умножают энергию.Эта демонстрация представляет собой отличное введение в принцип сохранения энергии.

Аппаратура и материалы

• Масса, 1/2 кг, 4
• Доска деревянная (от 2 м до 3 м x 15 см x 2 см)
• Кирпич или брусок в качестве опоры
• Шкив одинарный
• Шкив двойной
• Шнур
• Ассорти из масс для весов
• Метрическая линейка
• Ретортная стойка и втулка
• Гвоздь, 15 см
• Измеритель силы, показания до 10 Н

Примечания по охране труда и технике безопасности

Хотя доска не очень тяжелая, безопаснее перемещать ее по одному человеку с каждого конца.

Прочтите наше стандартное руководство по охране труда

Процедура

1. Установите большие качели на скамейке, используя деревянную доску и кирпич или деревянный брусок в качестве точки опоры. Уравновешивайте нагрузки в соотношении 10: 1 с двух сторон качелей. Вам нужно будет потренироваться в этом заранее, так как нагрузки, необходимые для легкого перемещения качели, будут зависеть от трения в опоре, которую вы используете.
2. Используйте линейку измерителя, чтобы измерить, как далеко каждый груз перемещается по вертикали, когда вы наклоняете качели.При этом соотношении вы должны обнаружить, что маленький груз перемещается в 10 раз дальше большого груза. Теперь вы можете рассчитать дополнительную энергию, запасенную гравитационно (сила x расстояние, перемещенное по вертикали) каждым из весов. Как описано в обучающей записке, суть в том, чтобы сравнить их.
3. Установите систему шкивов, как показано на схеме.