Катушка индуктивности. Описание, характеристики, формула расчета
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Паяльный фен YIHUA 8858
Обновленная версия, мощность: 600 Вт, расход воздуха: 240 л/час…
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
где R является собственным сопротивлением обмотки.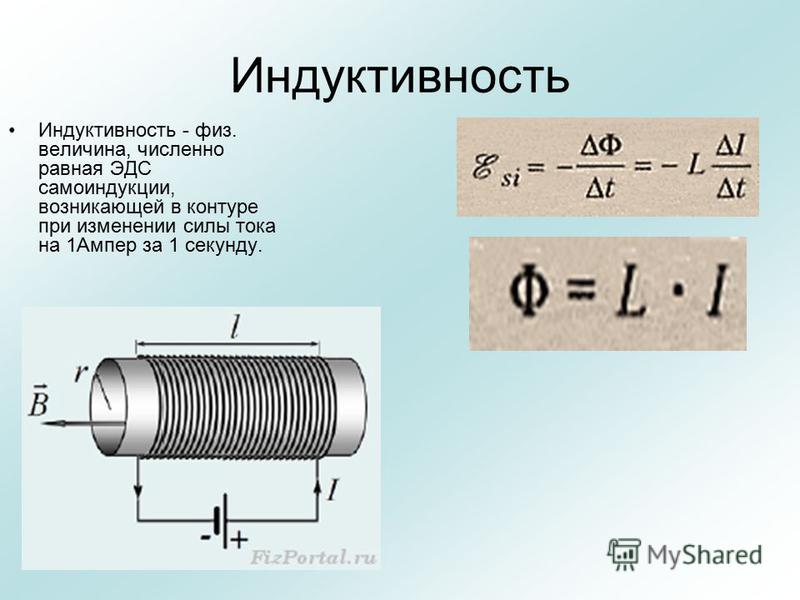
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
формула расчета. Измерение индуктивности. Индуктивность контура
Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.
Электрическая цепь и индуктивность
Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.
Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.
Самоиндукция и измерение индуктивности
Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:
Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Как найти индуктивность
Формула, которая является простейшей для нахождения величины, следующая:
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
«Катушка ниток»
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от «витков в квадрате».
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате.
 В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Соленоид
Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:
Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.
В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:
- Первая способна контролировать линейное давление.
- Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.

- Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
- Четвертая управляется гидравлическим способом или клапанами.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Работа на постоянном и переменном токе
Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:
где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.
Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:
Чтобы вычислить в этом случае индуктивность, формула используется следующая:
где L показывает значение индуктивности, а E – запасающую энергию.
ЭДС самоиндукции возникает при изменении тока в соленоиде.
В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.
Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.
Колебательные контуры
Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:
где XL показывает реактивное сопротивление катушки, а W — круговая частота.
Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:
Xc = 1 : W х C.
Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.
В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.
При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:
При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.
В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.
Работа конденсатора
Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.
Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.
Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.
Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:
- Конденсаторы с газообразным диэлектриком.
- Вакуумные.
- С жидким диэлектриком.
- С твердым неорганическим диэлектриком.
- С твердым органическим диэлектриком.
- Твердотельные.
- Электролитические.
Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:
- Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.

- Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
- Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
Явление самоиндукции — определение, формулы, примеры
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Магнитный поток
Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.
Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.
Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению:
- модуля вектора магнитной индукции B,
- площади поверхности S, которую пронизывает поток,
- и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).
Магнитный поток Ф — магнитный поток [Вб] B — магнитная индукция [Тл] S — площадь пронизываемой поверхности [м2] n — вектор нормали (перпендикуляр к поверхности) [-] |
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.
Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.
Вот что показали эти опыты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока различается при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока.
 При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Самоиндукция
Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.
Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток [Вб] L — индуктивность контура [Гн] I — сила тока в контуре [А] |
Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.
Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.
Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.
Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:
Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:
- первая лампа загорится практически сразу,
- вторая лампа загорится с заметным запаздыванием.
При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.
ЭДС самоиндукции ξis — ЭДС самоиндукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность [Гн] |
Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.
При решении расчетных задач знак минуса не учитывается.
Индуктивность
Индуктивность — это способность катушки, контура или проводника с током накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.
Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.
Можно ли увеличивать индуктивность катушки?
Конечно! Можно увеличить число витков, например. Или поместить в центр катушки железный сердечник.
Как работает катушка
Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.
Если поместить проводник в переменное поле — в нем возникнет ток.
Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.
Задачка раз
На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.
Решение
За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:
Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.
Задачка два
По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб. Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?
Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?
Решение
При протекании тока через катушку индуктивности возникает магнитный поток, численно равный Ф = LI.
Отсюда индуктивность катушки равна:
Тогда для достижения значений потока вектора магнитной индукции в 6 мВб ток будет равен:
Ответ: для достижения значений потока вектора магнитной индукции в 6 мВб необходим ток в 3 А.
формула. Измерение индуктивности. Индуктивность контура. Наука техника технологии
Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.
Электрическая цепь и индуктивность
Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.
Самоиндукция и измерение индуктивности
Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:
Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Как найти индуктивность
Формула, которая является простейшей для нахождения величины, следующая:
где F — магнитный поток, I — ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
«Катушка ниток»
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк — это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
где I характеризует силу тока, U — показывает напряжение, R — сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка — источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN 2 R 2: 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N 2 R 2: 2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.

- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от «витков в квадрате».
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Соленоид
Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:
Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом — ярмом.
В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом — ярмом.
В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:
- Первая способна контролировать линейное давление.
- Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
- Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
- Четвертая управляется гидравлическим способом или клапанами.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
где µ0 показывает магнитную проницаемость вакуума, n — это число витков, V — объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
где S — это площадь поперечного сечения, а l — длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Работа на постоянном и переменном токе
Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:
где µ0 — это магнитная проницаемость вакуума, n — это число витков, а I — значение тока.
Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:
где L показывает значение индуктивности, а E — запасающую энергию.
ЭДС самоиндукции возникает при изменении тока в соленоиде.
В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.
Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для в
Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для в
Колебательные контуры
Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить формула используется следующая:
где XL показывает реактивное сопротивление катушки, а W — круговая частота.
Если используется реактивное то формула будет выглядеть следующим образом:
Важными характеристиками колебательного контура являются резонансная частота, и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.
Третья характеристика определяет амплитуду и ширину резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.
При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:
На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:
При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.
Работа конденсатора
Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.
Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.
Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.
Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:
- Конденсаторы с газообразным диэлектриком.
- Вакуумные.
- С жидким диэлектриком.
- С твердым неорганическим диэлектриком.
- С твердым органическим диэлектриком.

- Твердотельные.
- Электролитические.
Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:
- Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.
- Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
- Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
- Ce = C: (1 — 4Π 2 f 2 LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f — это частота, L — индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида — апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
где Lk показывает индуктивность устройства, Lp -пакета, Lm — главных шин, а Lb — индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc: n + µ0 l х d: (3b) + Lb,
где l — длина шин, b — ее ширина, а d — расстояние между шинами.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга
. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Индуктивность
Любая катушка индуктивности обладает индуктивностью
. Индуктивность катушки измеряется в Генри
(Гн), обозначается буковкой L
и замеряется с помощью LC — метра .
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
где
В — магнитное поле, Вб
I —
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф)
. Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I),
Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I),
а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается, то магнитное поле сжимается.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции.
Эта зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома :
Согласно Закону Ома :
где
I
— сила тока в катушке, А
U
— напряжение в катушке, В
R
— сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока.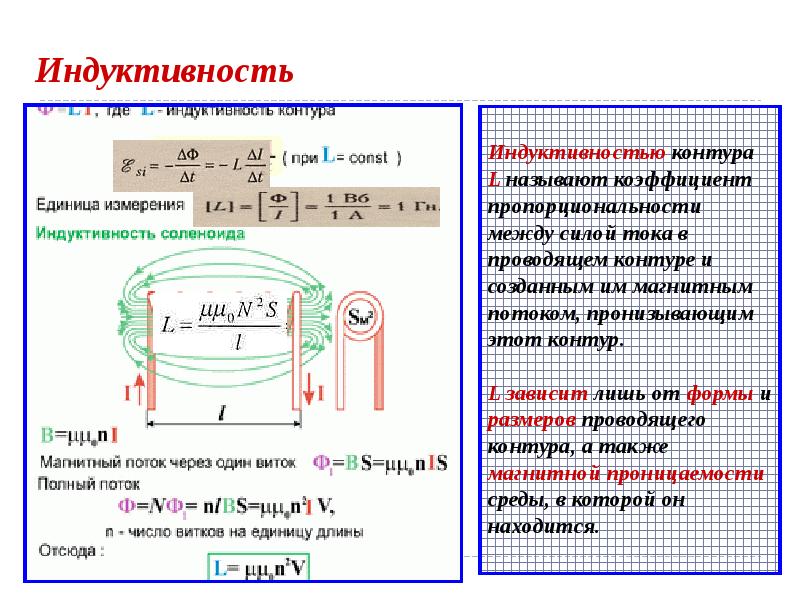 При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником
. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух — это немагнитный сердечник:-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы.
Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссели
Также есть особый вид катушек индуктивностей. Это так называемые . Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей — это . Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Опыты с катушкой
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине.
Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
где
1 — это каркас катушки
2 — это витки катушки
3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Замеряем индуктивность
15 микрогенри
Отдалим витки катушки друг от друга
Замеряем снова
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Замеряем
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате».
Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек
При последовательном соединении индуктивностей
, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении
получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате.
Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Рис. 4.12.
Рис. 4.13
если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения.
Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L
Индуктивность обозначается буквой L
, единицей ее измерения является генри (Гн).
Постоянная времени RС
-цепи
На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е
т. е. ЭДС или напряжения источника питания.
Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е
, называется постоянной времени контура или цепи.
Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4. 14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.
14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.
Рис. 4.14.
Кривые заряда (а) и разряда (б) конденсатора, где t —
постоянная времени.
Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой
где t —
постоянная времени в секундах, С
— емкость в фарадах, R —
сопротивление, выраженное в омах.
Например, для случая С
= 10мкФ и R
=
10 кОм постоянная времени цепи равна
На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.
Рис. 4.15.
Постоянная времени
RL
-цепи
Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L
соединена последовательно с резистором R
, имеющим сопротивление 1 кОм. В момент замыкания ключа S
В момент замыкания ключа S
ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R
станет равным приложенному напряжению Е.
Установившееся значение тока равно
E/
R =
20 В/1 кОм = 20 мА.
Скорость изменения тока в цепи зависит от конкретных значений R
и L
. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/
R
где L
выражается в генри, а R —
в омах. В этом случае постоянная времени получается в секундах.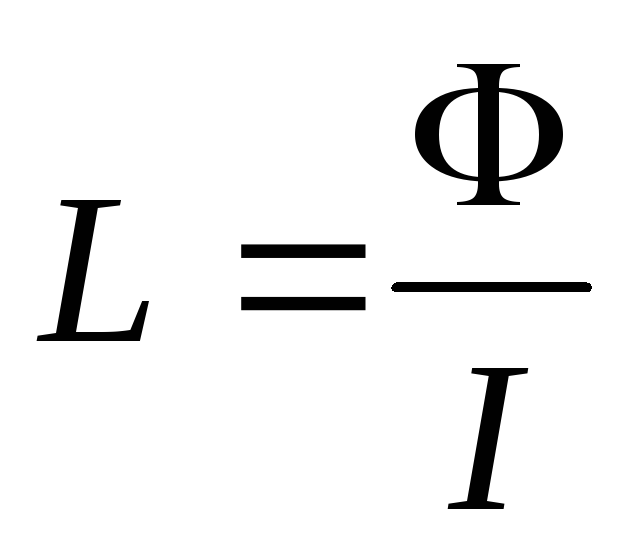 Используя значения L
Используя значения L
и R
, указанные на рисунке, получаем
Следует заметить, что, чем больше R
, тем меньше L/R
и тем быстрее изменяется ток в цепи.
Рис. 4.16.
Рис. 4.17.
Сопротивление по постоянному току
Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего диэлектрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.
Векторное представление
Сигнал синусоидальной формы может быть представлен в виде вектора ОА, вращающегося против часовой стрелки с угловой скоростью ω
= 2πf
, где f
– частота сигнала (рис. 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω
= 2πf
. Это означает, что угол между этими векторами
Рис. 4.18.
Рис. 4.19.
Разность фаз. Вектор ОА опережает вектор ОВ
(или вектор ОВ отстает от вектора ОА) на угол θ
.
изменяться не будет.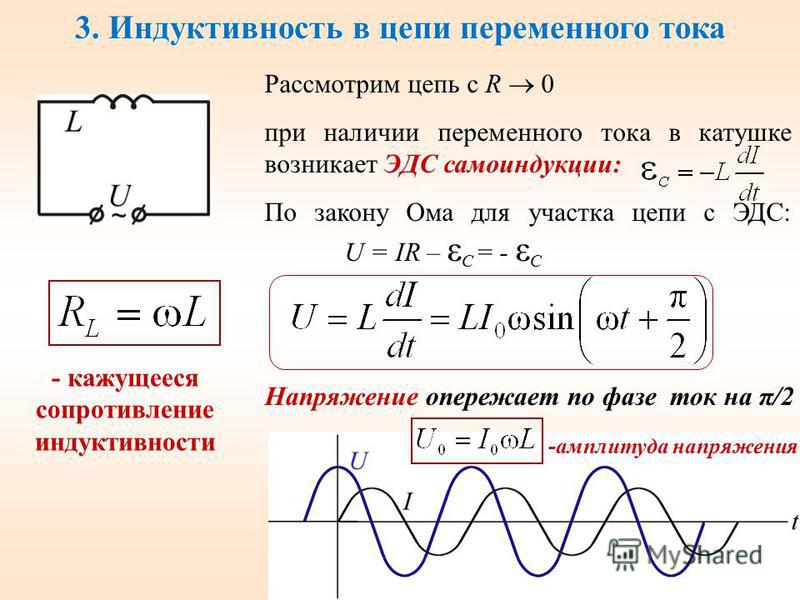 Говорят, что вектор ОА опережает вектор ОВ на угол θ
Говорят, что вектор ОА опережает вектор ОВ на угол θ
, а вектор ОВ отстает от вектора ОА на угол в.
На рис. 4.19(б) эти сигналы развернуты во времени.
Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f
, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α
и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.
В этом видео рассказывается о катушке индуктивности:
Магнитное поле внутри длинного соленоида однородно. Кроме того, зачастую соленоидом
называют устройство, выполняющую механическую работу за счёт магнитного поля при втягивании ферромагнитного сердечника, или электромагнитом
. В электромагнитных реле называют обмоткой реле
, реже — электромагнитом.
При использовании для накопления энергии называют индукционным накопителем
.
Конструкция
Для увеличения индуктивности часто имеют замкнутый или разомкнутый ферромагнитный сердечник, помехоподавляющие дроссели высокочастотных помех имеют ферродиэлектрические сердечники: ферритовые , флюкстроловые, из карбонильного железа. Дроссели, предназначенные для сглаживания пульсаций промышленной и звуковой частот имеют сердечники из электротехнических сталей или магнитомягких сплавов (пермаллоев). Также сердечники используют для изменения индуктивности катушек в небольших пределах изменением положения сердечника относительно обмотки, как правило, ферромагнитного сердечника. На СВЧ , когда ферродиэлектрики теряют высокую магнитную проницаемость и резко увеличиваются потери, для этой цели применяются металлические (латунные) сердечники.
Свойства катушки индуктивности
Свойства катушки индуктивности:
- Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки.

- Сопротивление (модуль импеданса) катушки растет с увеличением частоты текущего через неё тока.
- Катушка индуктивности при протекании тока запасает энергию в своем магнитном поле. При отключении внешнего источника тока катушка отдаст запасенную энергию, стремясь поддержать величину тока в цепи. При этом напряжение на катушке нарастает, вплоть до пробоя изоляции или возникновения дуги на коммутирующем ключе.
Индуктивность катушки пропорциональна линейным размерам катушки, магнитной проницаемости сердечника и квадрату числа витков намотки. Индуктивность катушки, намотанной на тороидальном сердечнике:
где — магнитная постоянная
— относительная магнитная проницаемость материала сердечника (зависит от частоты)
— площадь сечения сердечника
— длина средней линии сердечника
— число витков
При последовательном соединении катушек общая индуктивность равна сумме индуктивностей всех соединённых катушек:
При параллельном соединении катушек общая индуктивность равна:
Сопротивление потерь
Потери в проводах
Потери в проводах вызваны тремя причинами:
- Провода обмотки обладают омическим (активным) сопротивлением.

- Сопротивление провода обмотки возрастает с ростом частоты, что обусловлено скин-эффектом . Суть эффекта состоит в вытеснении тока в поверхностные слои провода. Как следствие, уменьшается полезное сечение проводника и растет сопротивление.
- В проводах обмотки, свитой в спираль, проявляется эффект близости, суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к периферии намотки. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведёт к дополнительному возрастанию сопротивления провода.
Потери в диэлектрике
Потери в диэлектрике (изоляции проводов и каркасе катушки) можно отнести к двум категориям:
- Потери от диэлектрика межвиткового конденсатора (межвитковые утечки и прочие потери характерные для диэлектриков конденсаторов).
- Потери обусловленные магнитными свойствами диэлектрика (эти потери аналогичны потерям в сердечнике).
В общем случае можно заметить, что для современных катушек общего применения потери в диэлектрике чаще всего пренебрежимо малы.
Потери в сердечнике
Потери в сердечнике складываются из потерь на вихревые токи , потерь на перемагничивание ферромагнетика гистерезис .
Потери на вихревые токи
Переменное магнитное поле индуцирует вихревые ЭДС в окружающих проводниках, например в сердечнике, экране и в проводах соседних витков. Возникающие при этом вихревые токи (токи Фуко) становятся источником потерь из-за омического сопротивления проводников.
Добротность
С сопротивлениями потерь тесно связана другая характеристика — добротность . Добротность катушки индуктивности определяет отношение между активным и реактивным сопротивлениями катушки. Добротность равна
Иногда потери в катушке характеризуют тангенсом угла потерь (величина, обратная добротности) — сдвигом фаз тока и напряжения катушки в цепи синусоидального сигнала относительно π/2 — для идеальной катушки.
На частотах ниже собственного резонанса этот эффект проявляется в падении добротности с ростом частоты.
Для увеличения частоты собственного резонанса используют сложные схемы намотки катушек, разбиение одной обмотки на разнесённые секции.
Температурный коэффициент индуктивности (ТКИ)
ТКИ — это параметр, характеризующий зависимость индуктивности катушки от температуры.
Балластный дроссель. Ранее применявшаяся в качестве реактивного сопротивления для люминесцентных ламп катушка индуктивности
См. также
Примечания
Ссылки
| Пассивные твердотельные | Резистор · Переменный резистор · Подстроечный резистор · Варистор · Конденсатор · Переменный конденсатор · Подстроечный конденсатор · Катушка индуктивности · Кварцевый резонатор · Предохранитель · Самовосстанавливающийся предохранитель · Трансформатор |
|---|---|
| Активные твердотельные | Диод · Светодиод · Фотодиод · Полупроводниковый лазер · Диод Шоттки · Стабилитрон · Стабистор · Варикап · Вариконд · Диодный мост · Лавинно-пролётный диод · Туннельный диод · Диод Ганна Транзистор · Биполярный транзистор · Полевой транзистор · КМОП-транзистор · Однопереходный транзистор · Фототранзистор · Составной транзистор · Баллистический транзистор Интегральная схема · Цифровая интегральная схема · Аналоговая интегральная схема Тиристор · Симистор · Динистор · Мемристор |
| Пассивные вакуумные | Бареттер |
| Активные вакуумные и газоразрядные | Электронная лампа · Электровакуумный диод · |
Катушка индуктивности
является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля.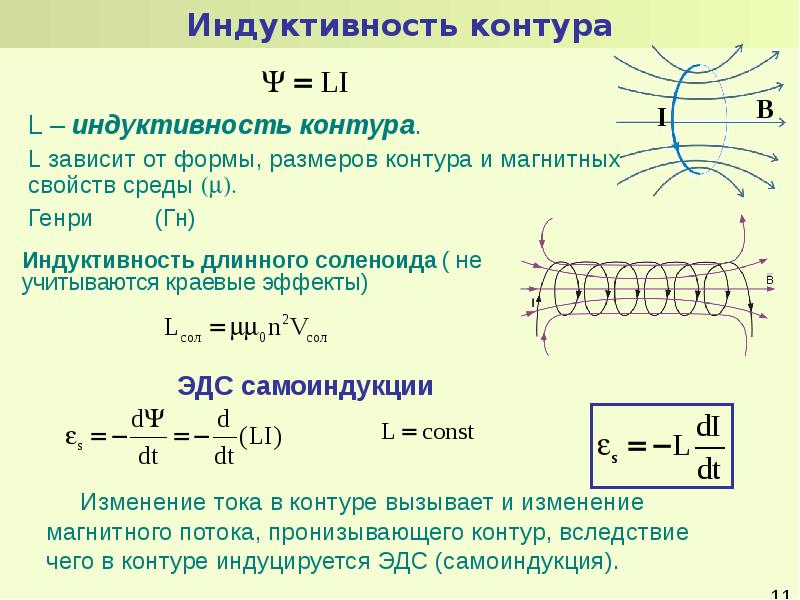 Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.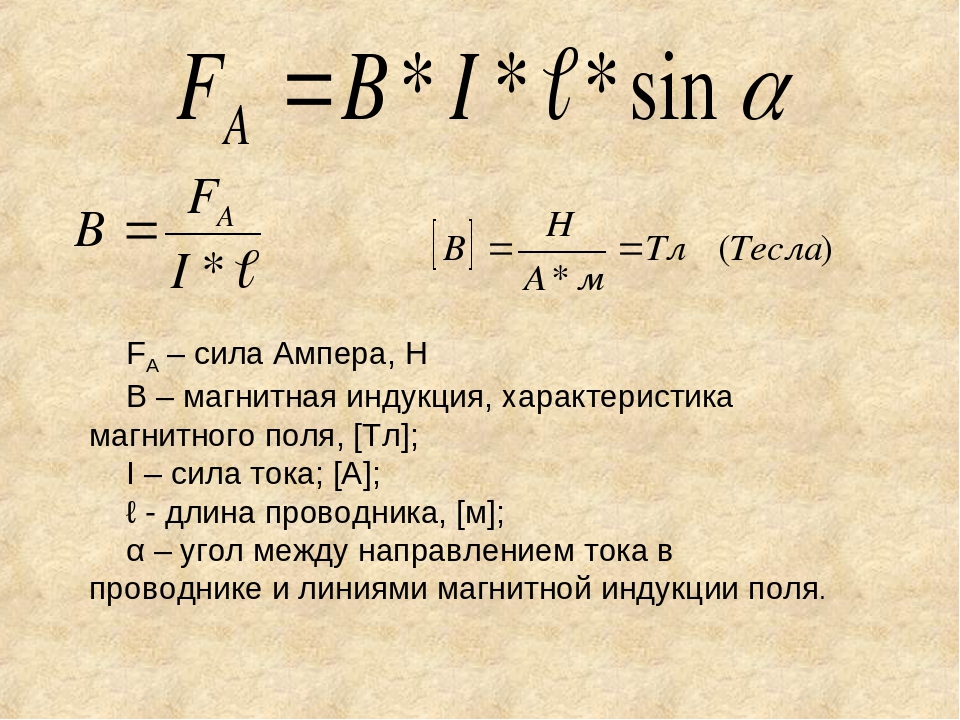
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
где R является собственным сопротивлением обмотки.
Катушка индуктивности. Формула индуктивности
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2)
- l = длина катушки в метрах (м)
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют , являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Самоиндукция. Индуктивность. Энергия магнитного поля тока
Самоиндукция. Индуктивность. Энергия магнитного поля тока
- Подробности
- Просмотров: 639
Самоиндукция
Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.
При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.
Это явление называется самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции
Проявление явления самоиндукции
Замыкание цепи
При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т. е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.
Размыкание цепи
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключении ярко вспыхивает.
Вывод:
в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).
ИНДУКТИВНОСТЬ
От чего зависит ЭДС самоиндукции?
Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).
ЭДС САМОИНДУКЦИИ
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии.
В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока.
Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ
по теме «Электромагнитная индукция»
1. Перечислить 6 способов получения индукционного тока.
Перечислить 6 способов получения индукционного тока.
2. Явление электромагнитной индукции (определение).
3. Правило Ленца.
4. Магнитный поток ( определение, чертеж, формула, входящие величины, их ед. измерения).
5. Закон электромагнитной индукции (определение, формула).
6. Свойства вихревого электрического поля.
7. ЭДС индукции проводника, движущегося в однородном магнитном поле ( причина появления, чертеж, формула, входящие величины, их ед. измерения).
8. Самоиндукция (кратко проявление в электротехнике, определение).
9. ЭДС самоиндукции (ее действие и формула).
10. Индуктивность (определение, формулы, ед. измерения).
11. Энергия магнитного поля тока (формула, откуда появляется энергия м. поля тока, куда пропадает при прекращении тока).
Электромагнитное поле — Класс!ная физика
Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера —
Действие магнитного поля на движущийся заряд. Магнитные свойства вещества —
Магнитные свойства вещества —
Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца —
ЭДС электромагнитной индукции. Вихревое электрическое поле —
ЭДС индукции в движущихся проводниках
—
Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе
Основные формулы и методические рекомендации по решению задач на электромагнитную индукцию
«Превратить
магнетизм в электричество…»
Майкл
Фарадей
Данная
тема будет посвящена рассмотрению основных формул и методических рекомендаций по
решению задач на электромагнитную индукцию
Рассмотрим
основные понятия электромагнитной индукции. Магнитный поток – это
скалярная физическая величина, численно равная произведению модуля вектора
магнитной индукции на площадь поверхности, ограниченной контуром, и на косинус
угла между нормалью к поверхности и направлением линий магнитной индукцией.
Изменение
магнитного потока влечет за собой такое явление, как электромагнитная индукция.
Чем быстрее изменяется магнитный поток, тем большая сила тока возникает в
замкнутом контуре.
В
результате явления электромагнитной индукции, в контуре возникает электродвижущая
сила – она так и называется ЭДС индукции.
Поскольку
сила тока связана с индукцией порождаемого им магнитного поля, а магнитная
индукция, в свою очередь, связана с магнитным потоком, возникает явление
самоиндукции. Самоиндукция – это явление возникновения ЭДС индукции в
проводящем контуре при изменении протекающего через контур тока. То есть, при
изменении силы тока, в цепи возникает индукционный ток, который стремится
препятствовать этому изменению. В связи с этим, вводится такая величина, как индуктивность
– коэффициент пропорциональности между электрическим током, текущим в
каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через
поверхность, краем которой является этот контур. Иными словами, индуктивность
Иными словами, индуктивность
характеризует способность проводника влиять на быстроту установления тока в
цепи. Она, конечно, обнаруживает себя только при изменении силы тока в цепи.
Сведём
в таблицу основные формулы по рассматриваемой теме.
|
Формула
|
Описание
|
|
|
Магнитный
|
|
|
ЭДС
|
|
|
ЭДС
|
|
|
Коэффициент
|
|
|
ЭДС
|
|
|
Индуктивность
|
|
|
Энергия
|
|
|
Энергия
|
Методические
рекомендации по решению задач на электромагнитную индукцию
1.
Установить причину изменения магнитного потока через контур. Исходя из формулы,
причиной может стать либо изменение магнитной индукции поля, либо изменение
площади контура, а также угла между направлением линий магнитной индукции и
нормалью к плоскости контура (чаще всего, это поворот рамки с током).
2.
Записать закон электромагнитной индукции (закон Фарадея).
3.
Если речь идет о поступательном движении проводника, применить формулу, по
которой вычисляется ЭДС индукции в движущемся проводнике.
4.
Определить изменение магнитного потока, рассматривая его в выбранные моменты
времени t1
и t2
(как правило, это должны быть те моменты времени, которые описываются в
задаче).
5.
Подставить найденное выражение для изменения магнитного потока в закон Фарадея.
При необходимости, используя дополнительные уравнения, составить систему и
решить её относительно искомых величин.
Оценка индуктивности элементов топологии печатных плат / Хабр
Предисловие
В поисках ответов на вопросы, возникающие при проектировании печатных плат, мною был изучен значительный объём литературы – как больших монографий, так и отдельных технических статей. За исключением, наверное, нескольких статей, это была англоязычная литература. Я подумал, а почему бы не оформить накопившийся опыт в виде практического руководства, которое может оказаться полезным как начинающим, так и, надеюсь, более опытным отечественным разработчикам. Начиная, я думал о распространении ценной информации, а краем мысли и о вкладе в отрасль в целом. Настоящая публикация открывает целую серию статей, в которых с практической точки зрения будут рассмотрены основные задачи, возникающие при разработке печатных плат, и в систематизированном виде изложены ключевые рекомендации с обязательным указанием их физических основ и условий применимости.
Последние два фактора очень важны, так как рекомендация отдельно, сама по себе может принести вреда больше, чем пользы. В условиях ускорения вывода радиоэлектронной продукции на рынок производители микросхем стремятся дать потребителю готовые решения в виде отладочных и оценочных плат, инструкций в документации, а также выпускают руководства, содержащие набор рекомендаций разработчикам с краткими пояснениями (например, [1] от Texas Instruments). Эти рекомендации перетекают из руководства в руководство, теряя свои основы и границы применимости и в итоге, как говорится в одной из статей [2] на сайте LearnEMC:
Худшие печатные платы, что нам доводилось видеть, были разработаны инженерами, которые пытались обеспечить соответствие всем пунктам списка рекомендаций по повышению ЭМС печатных плат.
Ряд рекомендаций противоречит друг другу, а некоторые продолжают использоваться, несмотря на то, что они устарели. Вот почему я призываю экспертное сообщество к обсуждению, обратной связи как положительной, так и отрицательной, к конструктивной критике, основанной на реальном опыте проектирования печатных плат. С одной общей максималистской целью – докопаться до истины, до базовых практических принципов.
С одной общей максималистской целью – докопаться до истины, до базовых практических принципов.
Индуктивность и электромагнитная индукция
Первая публикация не случайно посвящена индуктивности. Понимание физических основ индуктивности критически важно, так как с индуктивностью (а точнее, с паразитной индуктивностью) топологии печатной платы связаны многие проблемы ЭМИ и ЭМС, о которых будет говориться в последующих статьях цикла. О сложности вопроса можно судить по нечёткой терминологии, когда одним термином «индуктивность» называют величины хоть и связанные, но имеющие совершенно разный математический и физический смысл: индуктивность выводов корпуса, индуктивность катушки, паразитная индуктивность конденсатора ESL, индуктивность петли и т.п.
Согласно классическому определению [3] индуктивность – это коэффициент пропорциональности между силой постоянного тока в тонком замкнутом проводящем контуре и магнитным потоком через этот контур. Первое, на что необходимо обратить внимание, – индуктивность определена для замкнутого контура. В определении также говорится о полном магнитном потоке, разберёмся с ним. Движущийся электрический заряд порождает магнитное поле, а магнитное поле вокруг электрического тока – суперпозиция (векторная сумма) магнитных полей отдельных зарядов. Для наглядного изображения магнитных полей используются силовые линии. Направление касательной к силовой линии в каждой точке совпадает с направлением вектора магнитного поля в этой точке. Например, для тока в длинном прямолинейном проводе силовые линии – это концентрические окружности, плоскость которых перпендикулярна проводу, а направление определяется известным «правилом правой руки» (рис. 1). С помощью силовых линий можно судить и об относительной напряжённости магнитного поля – она тем выше, чем выше плотность силовых линий (число линий через единицу перпендикулярной им площади). Далее, поток магнитного поля B – это поверхностный интеграл напряжённости магнитного поля:
В определении также говорится о полном магнитном потоке, разберёмся с ним. Движущийся электрический заряд порождает магнитное поле, а магнитное поле вокруг электрического тока – суперпозиция (векторная сумма) магнитных полей отдельных зарядов. Для наглядного изображения магнитных полей используются силовые линии. Направление касательной к силовой линии в каждой точке совпадает с направлением вектора магнитного поля в этой точке. Например, для тока в длинном прямолинейном проводе силовые линии – это концентрические окружности, плоскость которых перпендикулярна проводу, а направление определяется известным «правилом правой руки» (рис. 1). С помощью силовых линий можно судить и об относительной напряжённости магнитного поля – она тем выше, чем выше плотность силовых линий (число линий через единицу перпендикулярной им площади). Далее, поток магнитного поля B – это поверхностный интеграл напряжённости магнитного поля:
где поверхность
S
определяется контуром тока. Следовательно, поток магнитного поля пропорционален числу силовых линий магнитного поля через поверхность
Следовательно, поток магнитного поля пропорционален числу силовых линий магнитного поля через поверхность
S
и определение индуктивности можно привести к более удобному с практической точки зрения виду:
Индуктивность пропорциональна числу силовых линий магнитного поля, которые пересекают поверхность, определяемую контуром тока, при величине тока в 1 А.
Изменение силы тока приводит к пропорциональному изменению напряжённости магнитного поля, которое
условно
можно представить как изменение количества силовых линий вокруг проводника. Такой подход к пониманию индуктивности, описанный Эриком Богатиным [4, 5], был подвергнут аргументированной критике со стороны не менее авторитетного автора, Клэйтона Пола [6, 7]. Действительно, силовые линии – это абстракция и никто не определяет индуктивность с помощью подсчёта их количества (которое, очевидно, бесконечно). Однако такое наглядное представление упрощает понимание многих закономерностей, связанных с магнитным полем. В то время как теоретическая физика стремится к поиску универсального уравнения, описывающего все взаимодействия, для практических целей ищутся приближённые аналитические соотношения, обладающие невысокой вычислительной сложностью. На практике никто не начинает анализ электрической цепи с составления уравнений Максвелла для её участков. Даже несмотря на появление САПР, снимающих вопрос вычислительной сложности, необходимость упрощённых соотношений сохраняется, так как они дают качественное понимание основных закономерностей и позволяют выполнять первоначальные оценочные инженерные расчёты.
В то время как теоретическая физика стремится к поиску универсального уравнения, описывающего все взаимодействия, для практических целей ищутся приближённые аналитические соотношения, обладающие невысокой вычислительной сложностью. На практике никто не начинает анализ электрической цепи с составления уравнений Максвелла для её участков. Даже несмотря на появление САПР, снимающих вопрос вычислительной сложности, необходимость упрощённых соотношений сохраняется, так как они дают качественное понимание основных закономерностей и позволяют выполнять первоначальные оценочные инженерные расчёты.
Следует сделать одно важное замечание: индуктивность не зависит от величины тока и определяется конфигурацией линий тока в проводнике. Часто в подобной формулировке говорится об определяющем значении геометрии проводника, но такая формулировка не учитывает тот эффект, что распределение тока в проводнике не всегда равномерное – на него влияет частота тока (скин-эффект) и близость других проводников с током. Наиболее простой для получения аналитических соотношений случай – это равномерное распределение тока по сечению проводника и все известные аналитическое соотношения получены с учётом этого предположения. На практике указанные эффекты мало влияют на значение индуктивности и использование этих формул расчёта индуктивности обеспечивает достаточную для практических задач точность.
Наиболее простой для получения аналитических соотношений случай – это равномерное распределение тока по сечению проводника и все известные аналитическое соотношения получены с учётом этого предположения. На практике указанные эффекты мало влияют на значение индуктивности и использование этих формул расчёта индуктивности обеспечивает достаточную для практических задач точность.
Рассмотрим физическое явление, связанное с индуктивностью, которое и определяет её основополагающую роль в вопросах ЭМС и ЭМИ. Открыто оно Майклом Фарадеем и носит название электромагнитной индукции. Согласно одноимённому закону, при изменении потока магнитного поля ΦB через замкнутый контур в нём возникает ЭДС:
В терминах силовых линий это означает (помним об условности этого подхода):
Изменение количества силовых линий через замкнутый контур приводит к возникновению в нём напряжения ЭДС.
Изменение это может быть вызвано любой из причин: изменение силы тока в самом проводнике, изменение силы тока в соседнем проводнике, изменение геометрии контура или его ориентации в магнитном поле, нахождение контура в переменном магнитном поле, изменение расстояния до другого контура с током и т. п.
п.
Частичная индуктивность – удобный инструмент
Прежде чем перейти к формулам, проведём разграничение между разными типами «индуктивностей» и уточним терминологию (рис. 2). Если рассчитывается магнитный поток через контур, вызванный только током в самом контуре, то говорят о собственной индуктивности контура
L
(англ. loop inductance, self-inductance). Если учитывается магнитный поток через контур, вызванный только током в другом контуре, то это взаимная индуктивность контуров
M
(англ. loop mutual inductance, mutual inductance). С практической точки зрения важен вопрос, чему равно напряжение ЭДС индукции на конкретном участке контура электрической цепи. Но для этого нужно связать с этим участком значение индуктивности, а индуктивность контура в этом смысле неделима. Поэтому был разработан математический аппарат расчёта частичной собственной индуктивности участка контура
LP
(англ. partial self-inductance) и частичной взаимной индуктивности двух участков одного или разных контуров
MP
(англ. partial mutual inductance). Они рассчитываются так, что учитывается магнитное поле, вызванное только током этого участка, словно остальная часть контура не существует. Иначе это можно представить следующим образом – остальная часть контура замещается бесконечно длинными подводящим проводами и контур, через который вычисляется магнитный поток, определяется так, как на
partial mutual inductance). Они рассчитываются так, что учитывается магнитное поле, вызванное только током этого участка, словно остальная часть контура не существует. Иначе это можно представить следующим образом – остальная часть контура замещается бесконечно длинными подводящим проводами и контур, через который вычисляется магнитный поток, определяется так, как на
рис. 2
.
Зная значения частичных собственных и взаимных индуктивностей отдельных участков контура может быть получено значение индуктивности любой их комбинации, в том числе и всего контура:
здесь
LiP
– собственная индуктивность i-го участка,
MijP
– взаимная индуктивность i-го и j-го участков, знак которой положителен, если токи в участках сонаправлены и отрицателен в противном случае. Взаимная индуктивность обладает свойством симметрии, то есть
MijP = MjiP
, для участков, перпендикулярных друг другу, взаимная индуктивность равна нулю. Если в расчёте учитывается только ток рассматриваемого составного участка, то указанная формула даёт его частичную индуктивность, если же во второй сумме учитывается влияние всего контура, то полученное значение – полная индуктивность участка (англ. total inductance, net inductance) (рис. 3).
Если в расчёте учитывается только ток рассматриваемого составного участка, то указанная формула даёт его частичную индуктивность, если же во второй сумме учитывается влияние всего контура, то полученное значение – полная индуктивность участка (англ. total inductance, net inductance) (рис. 3).
Именно полная индуктивность определяет падение напряжение на участке при изменении тока
I
в контуре:
Из формулы для полной индуктивности участка прямоугольного контура
L1NET
на рис. 3 видно, что это значение тем меньше, чем больше взаимная индуктивность этого участка с противоположным ему
M13P
. Именно поэтому сближение сигнальной дорожки и опорного слоя рекомендуется как мера снижения шумов в опорном слое.
Частичная индуктивность параллельного соединения двух участков рассчитывается по формуле:
которая только в случае, когда взаимная индуктивность пренебрежимо мала (значительно удалённые проводники), превращается в известную формулу для параллельного соединения катушек индуктивности. В случае идентичных проводников (например, два одинаковых переходных отверстия) формула принимает вид:
В случае идентичных проводников (например, два одинаковых переходных отверстия) формула принимает вид:
то есть индуктивность уменьшается в два раза только для проводников, расстояние между которыми достаточно велико, чтобы пренебречь их взаимной индуктивностью.
Расчётные формулы
В таблице 1 на схематических изображениях стрелкой указано направление тока, распределение которого равномерно по сечению. Так как именно распределение тока определяет индуктивность, важно соотносить распределение тока в рассматриваемой структуре печатной платы с указанной в таблице. Другим условием применимости формул, о котором нельзя забывать, является требование малости характерных размеров проводника
l
по сравнению с длиной волны
λ
(по крайней мере,
l<λ/10
), так как при этом ток во всех точках проводника можно считать одинаковым. К слову, точно такое же ограничение накладывается и на применимость модели электрических цепей с сосредоточенными параметрами.
Таблица 1. Формулы для оценки индуктивности элементов топологии печатной платы1.
Примечания к таблице 1:
1. Для среды с относительной магнитной проницаемостью
μr
= 1.
2. В расчёте на единицу длины.
3. Формула иногда применяется для оценки собственной индуктивности переходного отверстия между двумя сплошными слоями в предположении, что возвратный ток смещения равномерно распределён вокруг отверстия.
4. Формула может применяться для оценки собственной индуктивности пары переходных отверстий (например, обеспечивающих соединение блокировочного конденсатора).
5. Формула может применяться для оценки собственной индуктивности переходного отверстия.
6. Формула может применяться для оценки взаимной индуктивности параллельных переходных отверстий.
7. Габариты сплошных проводящих слоёв должны быть достаточно велики, чтобы не ограничивать распределение тока между переходными отверстиями.
Примеры
С использованием математического аппарата частичной индуктивности участков цепи и приведённых приближённых аналитических формул можно проводить оценку индуктивности участков топологии печатной платы и варьировать их геометрические параметры для снижения паразитной индуктивности. А следовательно, снижения искажений сигнала, шумов и ЭМИ – вопросов, которые будут рассматриваться в последующих статьях цикла. Полезно также произвести расчёт для типовых применяемых элементов топологии печатной платы, чтобы в дальнейшем при трассировке с ними ассоциировалось оценочное значение паразитной индуктивности. Для примера в таблице 2 представлены значения паразитной индуктивности элементов топологии соединения конденсатора подсистемы питания при различных параметрах геометрии (рис. 4).
А следовательно, снижения искажений сигнала, шумов и ЭМИ – вопросов, которые будут рассматриваться в последующих статьях цикла. Полезно также произвести расчёт для типовых применяемых элементов топологии печатной платы, чтобы в дальнейшем при трассировке с ними ассоциировалось оценочное значение паразитной индуктивности. Для примера в таблице 2 представлены значения паразитной индуктивности элементов топологии соединения конденсатора подсистемы питания при различных параметрах геометрии (рис. 4).
Литература
[1] PCB Design Guidelines For Reduced EMI. Texas Instruments, 1999.
[2] Why You Should Be Cautious about Using EMC Design Rules. LearnEMC, 2017.
[3] Сивухин Д. В. Общий курс физики. Т. III. Электричество. Изд. 4-е. М.: Физматлит, 2004.
[4] Bogatin E. What is Inductance? Printed Circuit Design & Manufacture, 2007.
[5] Bogatin E. Signal and power integrity — simplified. 2 nd ed. Pearson, 2004.
[6] Paul C. R. What Do We Mean By “Inductance”? Part I: Loop Inductance.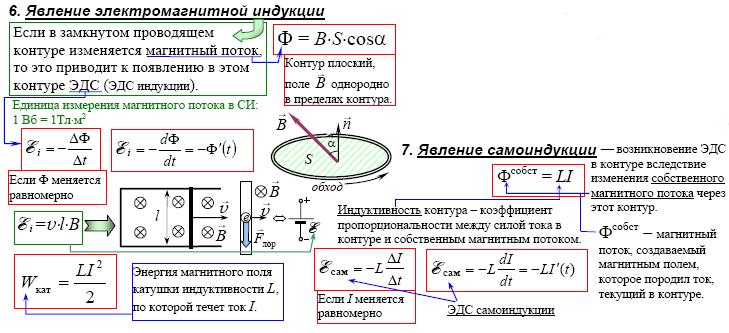 IEEE Practical Papers, 2007.
IEEE Practical Papers, 2007.
[7] Paul C. R. Inductance: loop and partial. Wiley, 2010.
Статья была впервые опубликована в журнале «Компоненты и технологии» 2017, №11. Публикация на «Geektimes» согласована с редакцией журнала.
Катушка индуктивности и индуктивность – формулы и уравнения
Катушка индуктивности и формулы и уравнения индуктивности
Следующие формулы и уравнения можно использовать для расчета индуктивности и связанных с ней величин различных форм катушек индуктивности следующим образом.
Индуктивность индуктора:
Индуктивность индуктора из основной формулы индуктора:
Напряжение на дросселе:
Ток индуктора:
Где
- В — напряжение на катушке индуктивности
- L — индуктивность катушки индуктивности в Генри
- Di/dt — мгновенная скорость изменения тока через индуктор.

- i от до = ток в момент времени t = 0.
Реактивное сопротивление катушки индуктивности:
Индуктивное сопротивление – это сопротивление индуктора переменному току переменного тока, которое зависит от его частоты f и измеряется в Омах так же, как сопротивление. Индуктивное реактивное сопротивление рассчитывается с использованием:
X Д = ωL = 2π f Д
Где
- X L — индуктивное реактивное сопротивление
- f — применяемая частота
- L — индуктивность в Генри
Коэффициент качества индуктора:
Эффективность катушки индуктивности известна как добротность и измеряется:
QF = X L /ESR
Где
- X L — индуктивное реактивное сопротивление
- ESR — эквивалентное последовательное сопротивление цепи.

Коэффициент рассеяния катушки индуктивности:
Это значение, обратное коэффициенту добротности, показывает мощность, рассеиваемую внутри индуктора, и определяется как:
DF = тангенс δ = ESR/X L
Где
- DF — коэффициент рассеяния
- δ — угол между емкостной реактивностью победителя и отрицательной осью.
- X C — емкостное реактивное сопротивление
- ESR — эквивалентное последовательное сопротивление цепи.
Энергия, запасенная в индукторе:
Энергия E, запасенная в катушке индуктивности, определяется как:
Е = ½ литра 2
Где
- E – энергия в джоулях
- L — индуктивность в Генри
- i — сила тока в амперах
Похожие сообщения:
Средняя мощность индуктора
Средняя мощность катушки индуктивности определяется по формуле:
P av = Li 2 / 2t
Где
- t = время в секундах.

Ток катушки индуктивности во время зарядки/разрядки:
Как и конденсатору, катушке индуктивности требуется до 5 постоянных времени для полной зарядки или разрядки, за это время ток можно рассчитать по формуле:
Во время зарядки:
Мгновенный ток катушки индуктивности во время зарядки определяется по формуле:
Во время разрядки:
Ток во время разрядки в любое время t определяется как:
Где
- I C ток катушки индуктивности
- I 0 ток в момент времени t=0
- t — время, прошедшее после подачи тока.
- τ = L/R — это постоянная времени контуры RL
Похожие сообщения:
Формулы индуктивности
Индуктивность спиральной катушки «Формула Уилера»
Где:
- L — индуктивность
- R это радиус
- n — количество витков
- ч это высота
Формула индуктивности спиральной катушки
Где:
- ИЛИ — внешний радиус в дюймах
- IR — самый внутренний радиус в дюймах
Длина провода спиральной катушки Формула
Формула индуктивности конической катушки
Где:
- θ — угол вне конуса (примем, что θ ≈ 15°)
Связанные формулы и уравнения Сообщений:
Катушки индуктивности и расчеты индуктивности Формулы Уравнения
Типы корпусов индукторов
Катушки индуктивности — это пассивные устройства, используемые в электронных схемах для хранения энергии в форме
магнитного поля. Они являются дополнением к конденсаторам, которые хранят энергию в виде электрического поля. Ан
Они являются дополнением к конденсаторам, которые хранят энергию в виде электрического поля. Ан
идеальный индуктор эквивалентен короткому замыканию (0 Ом) для постоянного тока (DC),
и представляет противодействующую силу (реактивное сопротивление) переменным токам (AC), которая зависит
на частоте тока. Реактивное сопротивление (противодействие протеканию тока) индуктора
пропорциональна частоте тока, протекающего через него. Индукторы иногда
называются «катушками», потому что большинство катушек индуктивности физически состоят из спиральных секций.
провода.
Свойство индуктивности, противодействующее изменению тока, используется для
целью предотвращения прохождения сигналов с более высокой частотной составляющей во время
пропускание сигналов низкочастотных составляющих. Вот почему катушки индуктивности иногда
называются «дросселями», поскольку они эффективно подавляют более высокие частоты. Общий
применение дросселя в цепи смещения радиоусилителя, где коллектор
транзистор должен питаться постоянным напряжением, не допуская ВЧ (радиочастоты)
сигнал от проведения обратно в источник постоянного тока.
При использовании в
серия (левый рисунок) или
параллельно (правый рисунок) со своей цепью
комплимент, конденсатор, комбинация индуктора и конденсатора образует цепь, которая резонирует
на определенной частоте, которая зависит от значений каждого компонента. В сериале
цепи полное сопротивление протеканию тока на резонансной частоте равно нулю с идеальными составляющими.
В параллельной цепи (справа) полное сопротивление протеканию тока бесконечно с идеальными компонентами.
Реальные катушки индуктивности из физических компонентов
проявляют больше, чем просто чистую индуктивность, когда присутствуют в цепи переменного тока.Общая схема
Модель тренажера показана слева. Он включает реальный идеальный индуктор с параллельным
резистивный компонент, реагирующий на переменный ток. Резистивный компонент постоянного тока
последовательно с идеальной катушкой индуктивности, а через всю катушку подключен конденсатор.
сборки и представляет собой емкость, присутствующую из-за близости обмоток катушки.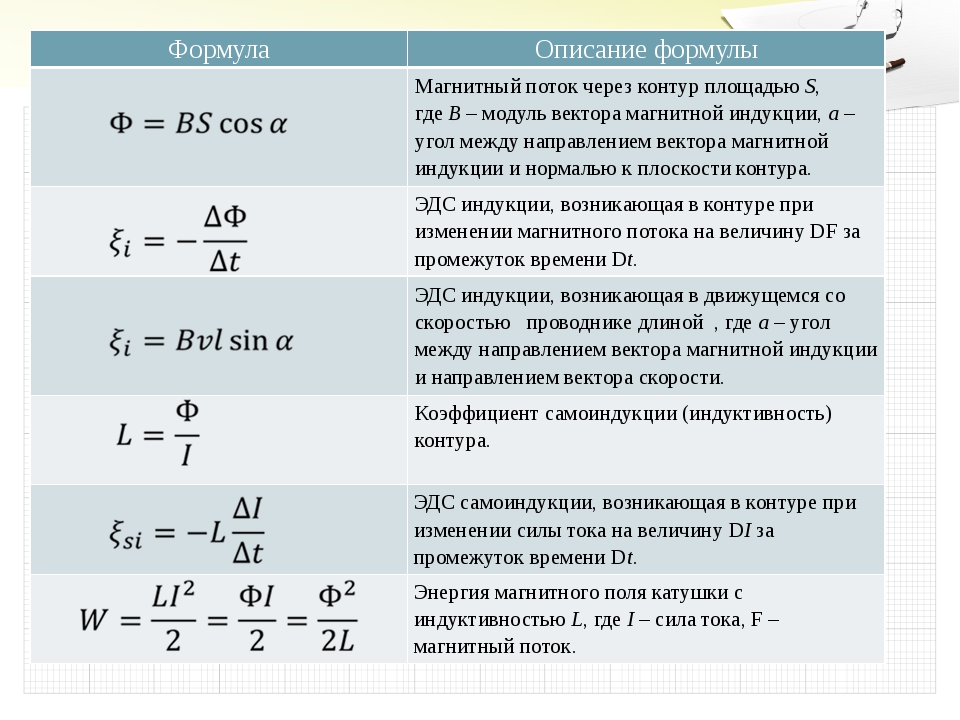
Симуляторы типа SPICE используют эту или даже более сложную модель для облегчения более
точные расчеты в широком диапазоне частот.
Связанные страницы в RF Cafe
— Катушки индуктивности и
Расчет индуктивности
— Преобразование индуктивности
—
Стандартные значения индуктора
—
Поставщики индукторов
HamWaves.com
на сайте есть очень сложный калькулятор индуктивности катушки, который позволяет ввести
диаметр проводника.
Уравнения (формулы) для соединения катушек индуктивности последовательно и параллельно приведены ниже.Приведены дополнительные уравнения для катушек индуктивности различных конфигураций.
Катушки индуктивности с последовательным соединением
Суммарная индуктивность последовательно соединенных катушек индуктивности равна сумме индивидуальных
индуктивности. Сохраняйте единицы измерения постоянными.
Плотно намотанный тороид
Прямоугольное сечение
Индуктивность коаксиального кабеля
Индуктивность прямого провода
Эти уравнения применимы, когда
длина провода намного больше диаметра провода (см.
диаметр провода здесь).Справочник ARRL
представляет уравнение для единиц дюймов и мкФ:
Для более низких частот — примерно до УКВ используйте эту формулу:
Выше ОВЧ скин-эффект приводит к тому, что ¾ в верхнем уравнении приближается к единице (1), поэтому
используйте это уравнение:
Прямой провод, параллельный плоскости заземления, с одним заземленным концом
Справочник ARRL представляет это уравнение для прямого провода, подвешенного над землей.
плоскость, с одним концом, заземленным на плоскость:
а = радиус проволоки,
l = длина провода параллельно плоскости заземления
h = высота провода над плоскостью заземления
до низа провода
Индуктивность параллельной линии
Многослойная индуктивность с воздушным сердечником
Уилера
Формула:
Параллельно соединенные катушки индуктивности
Суммарная индуктивность параллельно соединенных катушек индуктивности равна обратной
сумма обратных величин отдельных индуктивностей.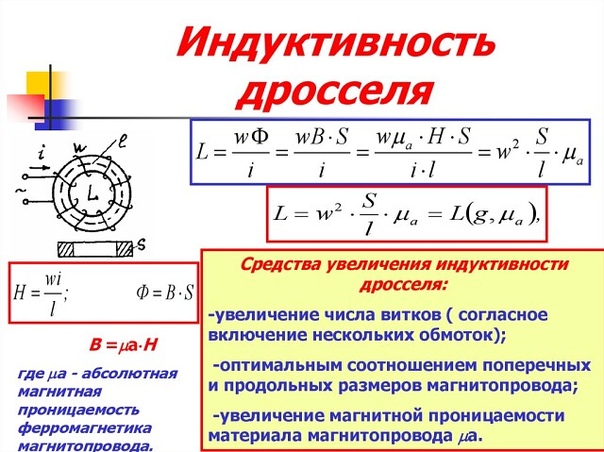 Сохраняйте единицы измерения постоянными.
Сохраняйте единицы измерения постоянными.
Константы и переменные формулы индуктивности
Следующие физические константы и механические размерные переменные применяются к уравнениям
на этой странице. Единицы для уравнений указаны в скобках в конце уравнений;
например, средние длины
в дюймах, а индуктивность в генри. Если единицы измерения не указаны, то можно использовать любые
до тех пор, пока они непротиворечивы для всех сущностей; т. е. все счетчики, все мкГн и т. д.
C = емкость
L = индуктивность
N = количество витков
Вт = энергия
ε r
= относительная диэлектрическая проницаемость (безразмерная)
ε 0
= 8.85 x 10 -12 Ф/м (диэлектрическая проницаемость в свободном пространстве)
µ r
= относительная проницаемость (безразмерная)
µ 0
= 4π
x 10 -7 Гн/м (проницаемость свободного пространства)
1 метр = 3,2808 фута <—> 1 фут = 0,3048 метра
1 мм =
0,03937 дюйма <—> 1 дюйм = 25,4 мм
Также точки (не путать с десятичными точками)
используются для обозначения умножения во избежание двусмысленности.
Индуктивное сопротивление
Индуктивное сопротивление (X L , в Ом) пропорционально частоте (ω,
в радианах/сек или f в Гц) и индуктивность (L в генри). Чистая индуктивность имеет фазу
угол 90° (напряжение опережает ток с фазовым углом 90°).
Энергия, запасенная в индукторе
Энергия (Вт, в джоулях), запасенная в катушке индуктивности, равна половине произведения индуктивности
(L, в генри) и ток (I, в амперах) через устройство.
Напряжение на дросселе
Свойство катушки индуктивности противодействовать изменению тока вызывает встречную ЭДС
(напряжение) для формирования на его клеммах, противоположных по полярности приложенному напряжению.
Коэффициент добротности индуктора
Добротность представляет собой безразмерное отношение реактивного сопротивления к сопротивлению в катушке индуктивности.
Индуктивность однослойной круглой катушки
Уилера
Формула для d >> a:
Обычно для a = радиус провода:
Примечание.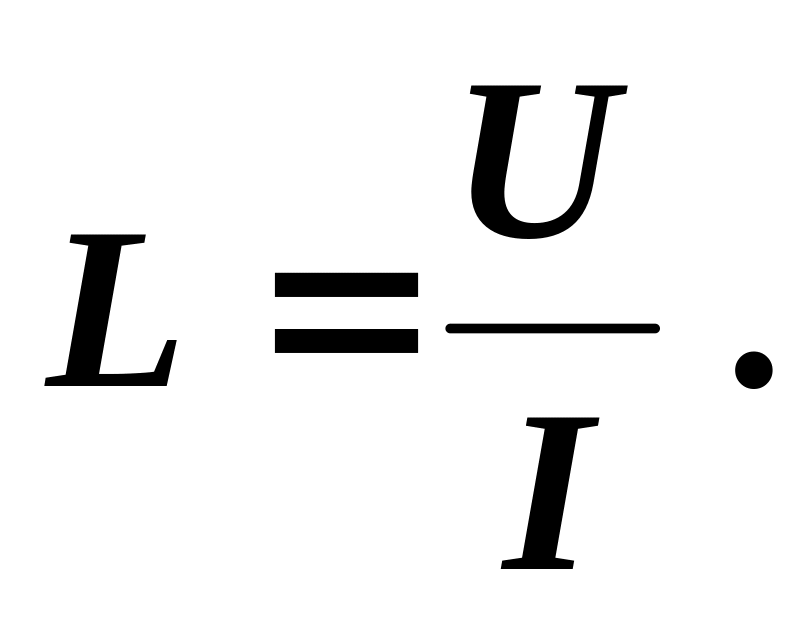 Если длина выводов значительна, используйте расчет прямой проволоки, чтобы добавить
Если длина выводов значительна, используйте расчет прямой проволоки, чтобы добавить
индуктивность.
Поиск эквивалента «R
Q »
С момента
«Q» индуктора — это отношение реактивной составляющей к резистивной,
эквивалентная схема может быть определена с резистором, включенным параллельно катушке индуктивности. Этот
Уравнение справедливо только для одной частоты «f» и должно быть рассчитано для каждой частоты.
представляет интерес.
Микроволны101 | Индуктор Математика
Нажмите здесь, чтобы перейти на нашу главную страницу индуктора
В марте 2016 г. наши друзья из Keysight Technologies предоставили нам видео о том, как моделировать спиральные катушки индуктивности.Спасибо, KeySight!
Ниже приведен указатель нашего математического обсуждения катушек индуктивности:
Индуктивное реактивное сопротивление
Индуктивность линии передачи (отдельная страница)
Индуктивность соленоида
Спиральный индуктор (проволока)
Спиральные индукторы на подложке (Новинка марта 2016 г.
!)
Тороидальная индуктивность
Индуктивность проволочного соединения (теперь на отдельной странице)
Индуктивность воздушного моста (отдельная страница)
Индуктивность через отверстие (отдельная страница)
Индуктивность проволочного соединения (отдельная страница)
Постоянное и ВЧ сопротивление катушек индуктивности
Резонансы
Индуктивное реактивное сопротивление
Используйте наш калькулятор реактивного сопротивления, если вам интересна эта тема!
Ниже показано известное уравнение для индуктивного сопротивления.Обратите внимание, что индуктивное сопротивление положительно, противоположная полярность емкостного сопротивления. На диаграмме Смита это означает, что последовательная индуктивность имеет тенденцию сдвигать коэффициент отражения по часовой стрелке.
Более полезная форма уравнения индуктивного реактивного сопротивления приведена ниже, где частота выражена в ГГц, а индуктивность – в наногенри. К счастью, все эти десятичные знаки просто компенсируют друг друга!
К счастью, все эти десятичные знаки просто компенсируют друг друга!
Индуктивность соленоида
Соленоид представляет собой цилиндрическую форму, обмотанную проволокой для создания индуктивности.Он может иметь однослойную обмотку или многослойную, а также может использовать воздушный сердечник или сердечник с высокой магнитной проницаемостью для увеличения индуктивности. Наиболее полезными (читай, что «самая высокая добротность») соленоидами для микроволновых приложений являются миниатюрные однослойные катушки индуктивности с воздушным сердечником. Графика ниже предоставлена Sebastian. Большое спасибо!
Классическая формула для однослойной индуктивности (воздушный сердечник) называется формулой Уилера, которая восходит к временам радио 1920-х годов:
где:
L = индуктивность в микро-Генри (не в нано-Генри!)
N= количество витков провода
R= радиус катушки в дюймах
H= высота катушки в дюймах
Вот он в пересчете на D, диаметр катушки:
(Эта формула была исправлена 9 апреля 2006 г. благодаря КБ!)
благодаря КБ!)
Формула Уиллера не учитывает диаметр проволоки и расстояние между витками.В формуле Уилера витки касаются друг друга, но предполагается, что некоторая изоляция предотвращает короткое замыкание. На практике необходимо некоторое расстояние между витками, чтобы уменьшить межвитковую емкость и увеличить рабочую частоту. Посмотрим правде в глаза, Уилера не интересовала точность нанокатушек Генри для микроволнового оборудования.
Предположительно более точный метод расчета индуктивности однослойных индукторов с воздушным сердечником для микроволновых компонентов можно найти на веб-сайте Microwave Components Incorporated:
где:
L = индуктивность в нано-Генри
N = количество витков провода
D = внутренний диаметр катушки (дюймы)
D1 = диаметр неизолированного провода (дюймы)
S = расстояние между витками (дюймы)
Используя формулу MCI, применяемую к проводу 47 калибра (1. диаметр оголенного провода 2 мил) и расстояние между витками 0,5 мил, обернув витки вокруг штифтовых тисков 20 мил, вы можете получить следующие значения воздушной катушки:
диаметр оголенного провода 2 мил) и расстояние между витками 0,5 мил, обернув витки вокруг штифтовых тисков 20 мил, вы можете получить следующие значения воздушной катушки:
1 виток = 2 нГн
2 витка = 5 нГн
3 витка = 8 нГн
4 витка = 12 нГн
5 витков = 16 нГн
6 витков = 20 нГн
7 витков = 25 нГн
8 витков = 305 2 нГн 9 витки = 35 нГн
10 витков = 40 нГн
Нажмите здесь, чтобы перейти к нашей таблице американских калибров проводов (AWG).
Спиральный индуктор (проволока)
Эта формула и график также были предоставлены Себастьяном (единицы измерения также являются микро-Генри): Должны признать, что мы лично не проверяли некоторые формулы на этой странице на соответствие измеренным данным.Также обратите внимание, что любая модель катушки индуктивности, не учитывающая паразитную емкость и сопротивление, будет иметь ограниченную точность на микроволновых частотах.
Спиральные индукторы на подложке
Спиральные катушки индуктивности
часто используются в конструкциях MIC, MMIC и RFIC, особенно на частотах ниже 18 ГГц. Катушки индуктивности могут быть прямоугольными или круглыми, если вы знаете, как их моделировать. Модель с сосредоточенными элементами спиральной катушки индуктивности может иметь множество конденсаторов и резисторов для учета всех паразитных явлений, которые делают ее все менее и менее идеальной по мере увеличения частоты.Моделирование катушки индуктивности требует хороших извлеченных данных об одном или нескольких значениях катушки индуктивности, что приводит к масштабируемой модели, позволяющей прогнозировать характеристики произвольных значений катушки индуктивности, необходимые для вашего проекта.
Хотите немного больше практического описания того, как моделировать спиральные катушки индуктивности? Посмотрите это видео на ТОЧНО ЭТОМ. Франц Сишка из SisConsult знакомит вас с полной моделью спирального индуктора с сосредоточенными элементами, включая скин-эффекты, вихревые токи подложки и связь с металлическим экраном 1. Программа Keysight для определения характеристик и анализа интегральных схем (IC-CAP) используется для подгонки двух примеров измерений. Элементы настраиваются вручную с последующей оптимизацией. Предоставляются методы проверки модели, и файлы примеров можно скачать.
Программа Keysight для определения характеристик и анализа интегральных схем (IC-CAP) используется для подгонки двух примеров измерений. Элементы настраиваются вручную с последующей оптимизацией. Предоставляются методы проверки модели, и файлы примеров можно скачать.
Тороидальная индуктивность
Тороид похож на соленоид, но имеет форму пончика. Еще не все!
Постоянное и ВЧ сопротивление катушек индуктивности
Расчет сопротивления постоянному току спиральной катушки индуктивности прост, и разработчики часто упускают его из виду до тех пор, пока не построят схему усилителя, и в первой итерации эта часть не сместится правильно.Вам нужно знать поверхностное сопротивление вашей металлизации в омах на квадрат и вычислить количество квадратов в катушке индуктивности. Количество квадратов — это общая длина (если вы ее размотали), деленная на ширину, и может легко исчисляться сотнями для большой катушки индуктивности.
При расчете ВЧ-сопротивления вам, возможно, придется учитывать эффект глубины скин-слоя.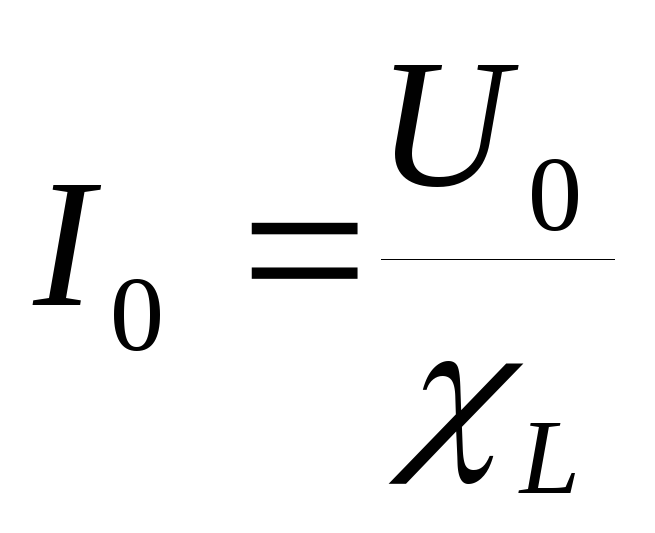
Показанная ниже модель является классической моделью для спиральных индукторов. Вычисление элементов не так просто, как вы могли бы надеяться.
Резонансы индуктора
Еще не все!
Самоиндукция – определение, формула, единица измерения и часто задаваемые вопросы
Давайте рассмотрим волшебство концепции самоиндукции.
Рассмотрим катушку и пропустим через нее ток, не только ток, но и переменный ток.
Теперь из-за изменяющегося тока в нем индуцируется дополнительный ток, т. е. наведенный ток.
Итак, вы знаете, что означает этот наведенный ток?
Ну, индуцированный ток неосязаем, и свойство катушки генерировать его из-за изменяющегося тока, подаваемого нами через батарею.
Разве это не так просто?
Однако наше внимание сосредоточено на собственной индуктивности, поэтому давайте вернемся к рассмотрению этой магической концепции.
Итак, что вы наблюдали в этом явлении и почему оно волшебное?
Итак, волшебство заключается в следующем: пропуская ток через катушку, она индуцирует внутри себя ток, известный как самоиндуцируемый. Вот почему это явление известно как самоиндукция.
Собственная индуктивность катушки
Рассмотрим катушку и подачу тока через нее.Подаваемый ток является первичным током, и здесь мы рассмотрим два случая:
Подаваемый ток увеличивается, и
Подаваемый ток уменьшается.
Случай а: Рассмотрим катушку, в которой первичный (подаваемый) ток увеличивается в направлении, как показано ниже на диаграмме.
(изображение скоро будет загружено)
Как известно, возрастающий (изменяющийся) ток сам по себе порождает индуктивный ток, т.е.е., ток самоиндукции и внутри себя, но который течет в направлении, противоположном направлению подаваемого тока. Направление этого самоиндуцированного тока описано на диаграмме ниже.
Направление этого самоиндуцированного тока описано на диаграмме ниже.
(изображение будет загружено в ближайшее время)
Этот индуцированный ток препятствует любому изменению (или увеличению тока) того тока, из-за которого он возникает.
Теперь возьмем другой случай:
Случай b: Рассмотрим катушку, в которой ток уменьшается, здесь происходит то, что этот индуцированный ток способствует изменению (или уменьшению) приложенного тока.
Это означает, что индуцированный ток течет в направлении приложенного тока и способствует его увеличению.
(изображение скоро будет загружено)
Мы поняли, что индуцированный ток препятствует увеличению тока и поддерживает его уменьшение.
(изображение скоро будет загружено)
Что такое собственная индуктивность?
Рассмотрим круг, в котором изменение тока создает магнитное поле (B).
Направление этого поля можно определить, согнув пальцы правой руки, и мы получим направление B, которое указывает внутрь, что можно увидеть в виде крестиков на диаграмме ниже:
(изображение будет скоро выложу)
Теперь при увеличении тока увеличиваются и силовые линии магнитного поля.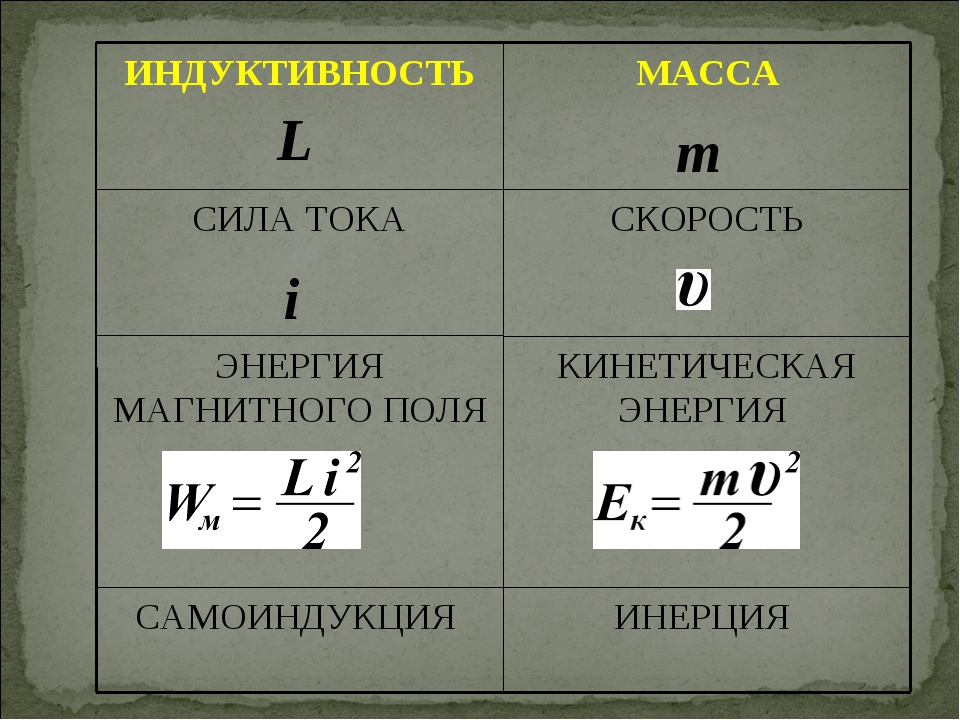 Это означает, что B α i.
Это означает, что B α i.
Из-за увеличения B увеличивается также поток (ΦB).
Как только поток увеличивается, то по закону индукции Фарадея в этой катушке возникает ЭДС индукции.
По закону Ленца,
ЭДС индукции представляет собой разность потенциалов между двумя точками этой катушки, из-за которой генерируется индукционный ток. Этот индуцированный ток уменьшит первичный ток. Направление его наружу, т. е. противоположно направлению В.
Этот ток создает свой поток, который противостоит потоку (ΦB), из-за которого он был создан.
Итак, это явление самоиндукции.
Формула собственной индуктивности
Рассмотрим катушку с током, имеющую N число витков, как показано ниже:
(изображение будет загружено в ближайшее время)
Катушки, это будет:
Φt (общий поток) = Nφ, и
Φt α I
на удаление знака пропорциональности, мы получаем
Φt = li ⇒ l = \ \ \ frac {n \ phi t} {i}\]
Где L — коэффициент собственной индуктивности.
Здесь L — константа, не зависящая от Φ и i. Скорее это зависит от следующего:
Геометрия,
Форма и
Размер индуктора (катушки).
Это означает, что индуктивность не изменяется при увеличении или уменьшении при изменении Φ и i.
Единица измерения собственной индуктивности
Единица измерения собственной индуктивности — Вебер/Ампер или Генри «H».
Размер собственной индуктивности [ML 2 T -2 A -2 ].
Коэффициент собственной индуктивности Определение
По закону Фарадея ЭДС \[e = -\frac{\Phi T}{dt}\]
Итак, \[e = |- L \frac{di} {дт} | \Rightarrow L = \frac{e}{|\frac{di}{dt}|}\]
Если значение изменения тока или di/dt равно 1 Ампер/сек, то L = e. Это определение коэффициента собственной индуктивности.
Это определение коэффициента собственной индуктивности.
Мы знаем, что индуктивность — это свойство электрического проводника, благодаря которому изменение силы тока вызывает ЭДС.
Самоиндукция и взаимная индукция
С.№ | Самоиндукция | Взаимная индукция |
1. Определение | самоиндукция. | Если скорость изменения тока вызывает ЭДС индукции в соседней катушке, то это взаимоиндукция. |
2. Формула | \[e = — L \frac{di}{dt}\], и \[L = \frac{e}{|di/dt|}\] Для N витков в катушке \[L = \frac{N \Phi T}{i}\] | Если ток течет в первичной катушке, то коэффициент взаимной индукции, \[ M = \frac{N_{2} \Phi_{12}}{i_{1}}\] Если ток течет во вторичной обмотке, то \[M = \frac{N_{1} \Phi_{ 21}}{i_{2}}\] |
(PDF) Проверка правильности формул взаимной индуктивности для круглых нитей накала с поперечным и угловым смещением используя подход магнитного векторного потенциала
.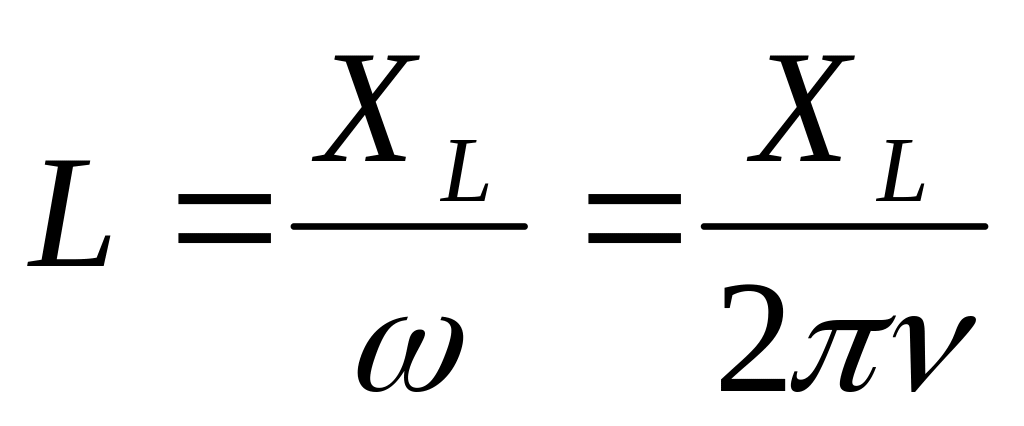 Мы прояснили некоторую предыдущую работу по
Мы прояснили некоторую предыдущую работу по
той же теме, в которой была представлена неверная формула для
расчета взаимной индуктивности между круговыми нитями с
параллельными осями в воздухе.
ССЫЛКИ
1. Максвелл Дж. К., Трактат об электричестве и магнетизме, Dover
Publications INC, New York, 1954 (перепечатка с оригинала
1873).
2. Баттерворт, С., «О коэффициентах взаимной индукции
эксцентриковых катушек», Философский журнал, серия 6, том.31, 443–
454, 1916.
3. Snow, C., Formulas for Compacitance and Inductance,
National Bureau of Standards Circular 544, Washington DC,
Dec. 1954.
4.Growver, FW, «Расчет взаимной индуктивности
круглых нитей накала в любых желаемых положениях», Proceedings of the
IRE, 620–629, октябрь 1944 г.
5. Grover, FW, Inductance Calculations, Dover, New York. , 1964.
6. Калантаров П.П.L., Расчеты индуктивности, National Power Press,
Москва, 1955.
7. Дуайт, Х.Б., Электрические катушки и проводники, McGraw-Hill
Book Company, INC., Нью-Йорк, 1945.
8. Ким , KB, E. Levi, Z. Zabar, and L. Birenbaum, «Взаимная
индуктивность некоаксиальных круглых катушек с постоянной плотностью тока
», IEEE Trans. Маг., Том. 33, No. 5, 3916–3921, сентябрь 1997 г.
9. Abramowitz, M. and IA Stegun, Handbook of Mathematical
Functions, Series 55, 595, National Bureau of Standards Applied
Mathematics, Washington DC, дек.1972.
. 10. Градштейн И.С., Ризик И.М. Таблицы интегралов, рядов и произведений
. Довер, Нью-Йорк, 1972.
. Расчет
для некоаксиальных круглых воздушных катушек с параллельными осями»,
Progress In Electro Magnetics Research, PIER 91, 287–301, 2009.
катушки и плоские катушки», IEEE
Trans.Маг., Том. 44, № 4, 453–462, апрель 2008 г.
Преобразователь случайных чисел | Онлайн-конвертеры единиц измерения Конвертер длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиПреобразователь угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер момента импульсаИмпульсПреобразователь крутящего моментаКонвертер удельной энергии, теплоты сгорания (на массу)Конвертер удельной энергии, теплоты сгорания (на объем)Температура Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Конвертер nsityПреобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибра проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахКонвертер магнитодвижущей силы КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Этот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовать множество единиц измерения из одной системы в другую. Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах. Вы можете использовать этот онлайн-конвертер для преобразования нескольких сотен единиц (включая метрические, британские и американские) в 76 категориях или нескольких тысяч пар, включая ускорение, площадь, электрическую энергию, силу, длину, свет, массу, массовый расход, плотность, удельный объем, мощность, давление, напряжение, температура, время, крутящий момент, скорость, вязкость, объем и производительность, объемный расход и многое другое. Общие конвертеры единицКонвертер длины и расстояния : метр, километр, сантиметр, миллиметр, нанометр, ярд, фут, дюйм, парсек, световой год, астрономическая единица, лунное расстояние (от Земли до Луны), лига , миля, морская миля (международная), сажень, кабельтовая (международная), точка, пиксель, калибр, планковская длина… Конвертер массы : грамм, килограмм, миллиграмм, тонна (метрическая), фунт, унция, стоун (США), стоун (Великобритания), карат, гран, талант (греческое библейское), драхма (греческое библейское), денарий (библейский римлянин), шекель (библейский иврит), планковская масса, масса протона, атомная единица массы, масса электрона (покой), масса Земли, масса Солнца. Конвертер площади : миллиметр², сантиметр², метр², километр², гектар, акр, дюйм², фут², ярд², миля², сарай, круговой дюйм, поселок, руд, стержень², окунь², усадьба, полюс², сабин, арпен, куэрда, верста квадратная, аршин квадратный, фут квадратный, сажень квадратная, площадь планка… Конвертер единиц объема и кулинарных единиц измерения : метр³, километр³, миллиметр³, литр, гектолитр, миллилитр, капля, баррель (масло), баррель (США) ), баррель (Великобритания), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), баррель (нефть), баррель (США), баррель (Великобритания ), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), ярд³, фут³, дюйм³, регистровая тонна, 100 кубических футов. Преобразователь температуры : кельвин, градус Цельсия, градус Фаренгейта, градус Ранкина, градус Реомюра, планковская температура. Давление, напряжение, модуль Юнга Конвертер единиц : паскаль, килопаскаль, мегапаскаль, миллипаскаль, микропаскаль, нанопаскаль, техническая атмосфера, стандартная атмосфера, тысяч фунтов/кв. дюйм, ньютон/метр², бар, миллибар, килограмм-сила/метр², грамм- сила/сантиметр², тонна-сила (короткая)/фут², фунт-сила/фут², миллиметр ртутного столба (0°C), дюйм ртутного столба (32°F), сантиметр водяного столба (4°C), фут водяного столба (4°C) м морской воды… Преобразователь энергии и работы : джоуль, килоджоуль, мегаджоуль, миллиджоуль, мегаэлектрон-вольт, электрон-вольт, эрг, киловатт-час, мегаватт-час, ньютон-метр, килокалория (ИТ), калория (пищевая), БТЕ (ИТ), мега БТЕ (ИТ), тонна-час (охлаждение), тонна нефтяного эквивалента, баррель нефтяного эквивалента (США), мегатонна, тонна (ВВ), килограмм тротила, дина-сантиметр, грамм-сила-сантиметр, килограмм-сила-метр, килопонд-метр, фут-фунт, дюйм-фунт, планковская энергия. Преобразователь мощности : ватт, киловатт, мегаватт, милливатт, лошадиная сила, вольт-ампер, ньютон-метр/секунда, джоуль/секунда, мегаджоуль/секунду, килоджоуль/секунду, миллиджоуль/секунду, джоуль/час, килоджоуль/час, эрг/секунду, Btu (IT)/час, килокалорию (IT)/час… Конвертер силы : ньютон, килоньютон, миллиньютон, дина, джоуль/метр, джоуль/сантиметр, грамм-сила, килограмм-сила, тонна-сила (короткая), кип-сила, килофунт-сила, фунт-сила сила, унция-сила, фунтал, фунт-фут/секунда², пруд, стен, грав-сила, миллиграмм-сила… Конвертер времени : секунда, миллисекунда, наносекунда, пикосекунда, минута, час, день, неделя, месяц, год, десятилетие, столетие, тысячелетие, планковское время, год (юлианский), год (високосный), год (тропический), год (сидерический), год (григорианский), две недели, встряска… Преобразователь линейной скорости и скорости : метр/секунда, километр/час, километр/секунда, миля/час, фут/секунда, миля/секунда, узел, узел (Великобритания), скорость света в вакууме, космическая скорость — первая, Космическая скорость — вторая, Космическая скорость — третья, Скорость Земли, Скорость звука в чистой воде, Мах (стандарт СИ), Мах (20°C и 1 атм), ярд/сек. Угол Конвертер : градус, радиан, град, гон, минута, секунда, знак, мил, оборот, круг, оборот, квадрант, прямой угол, секстант. Конвертер топливной экономичности, расхода топлива и экономии топлива : метр/литр, километр/литр, миля (США)/литр, морская миля/литр, морская миля/галлон (США), километр/галлон (США), литр/100 км, галлон (США)/миля, галлон (США)/100 миль, галлон (Великобритания)/миля, галлон (Великобритания)/100 миль… Преобразователь чисел : двоичный, восьмеричный, десятичный, шестнадцатеричный, по основанию 3, по основанию 4, по основанию 5, по основанию 6, по основанию 7, по основанию 9, по основанию 10, по основанию 11, по основанию 12, по основанию 13, по основанию 14, по основанию 15, по основанию 20, по основанию 21, по основанию 22, по основанию 23, по основанию 24, по основанию 28, по основанию 30, по основанию 32, по основанию 34, по основанию 36… Преобразователь единиц хранения информации и данных : бит, байт, слово, четверное слово, MAPM-слово, блок, килобит (10³ бит), кибибит, кибибайт, килобайт (10³ байт), мегабайт (10⁶ байт), гигабайт (10⁹ байт), терабайт (10¹² байт), петабайт (10¹⁵ байт), эксабайт (10¹⁸ байт), дискета (3,5 ED), дискета (5,25 HD), Zip 250, Jaz 2GB, CD (74 минут), DVD (2 слоя 1 сторона), диск Blu-ray (однослойный), диск Blu-ray (двухслойный). Курсы обмена валют : евро, доллар США, канадский доллар, британский фунт, японская иена, швейцарский франк, аргентинское песо, австралийский доллар, бразильский реал, болгарский лев, чилийское песо, китайский юань, чешская крона, датская крона, египетский фунт, венгерский форинт, исландская крона, индийская рупия, индонезийская рупия, новый израильский шекель , Иорданский динар, Малайзийский ринггит, Мексиканское песо, Новозеландский доллар, Норвежская крона, Пакистанская рупия, Филиппинское песо, Румынский лей, Российский рубль, Саудовский риал, Сингапурский доллар, Южноафриканский рэнд, южнокорейская вона, шведская крона, новый тайваньский доллар, тайский бат, турецкая лира, украинская гривна… Размеры женской одежды и обуви : Женские платья, костюмы и свитера, женская обувь, женские купальники, размер букв, бюст, дюймы, естественная талия, дюймы, заниженная талия, дюймы, бедра, дюймы, бюст, сантиметры, Естественная талия, сантиметры, Заниженная талия, сантиметры, Бедра, сантиметры, Длина стопы, мм, Торс, дюймы, США, Канада, Великобритания, Европа, Континенталь, Россия, Япония, Франция, Австралия, Мексика, Китай, Корея. Размеры мужской одежды и обуви : Мужские рубашки, мужские брюки, размер мужской обуви, буквенный размер, шея, дюймы, грудь, дюймы, рукав, дюймы, талия, дюймы, шея, сантиметры, грудь, сантиметры, Рукав, сантиметры, Талия, сантиметры, Длина стопы, мм, Длина стопы, дюймы, США, Канада, Великобритания, Австралия, Европа, Континентальная, Япония, Россия, Франция, Италия, Испания, Китай, Корея, Мексика… МеханикаПреобразователь угловой скорости и частоты вращения : радиан/секунда, радиан/день, радиан/час, радиан/минута, градус/день, градус/час, градус/минута, градус/секунда, оборот/ день, оборот/час, оборот/минута, оборот/секунда, оборот/год, оборот/месяц, оборот/неделя, градус/год, градус/месяц, градус/неделя, радиан/год, радиан/месяц, радиан/неделя. Преобразователь ускорения : дециметр/секунда², метр/секунда², километр/секунда², гектометр/секунда², декаметр/секунда², сантиметр/секунда², миллиметр/секунда², микрометр/секунда², нанометр/секунда², пикометр/секунда², фемтометр/секунда² , аттометр/секунда², гал, галилео, миля/секунда², ярд/секунда², фут/секунда², дюйм/секунда², ускорение свободного падения, ускорение свободного падения на Солнце, ускорение свободного падения на Меркурии, ускорение свободного падения на Венере , ускорение свободного падения на Луне, ускорение свободного падения на Марсе, ускорение свободного падения на Юпитере, ускорение свободного падения на Сатурне. Конвертер плотности : килограмм/метр³, килограмм/сантиметр³, грамм/метр³, грамм/сантиметр³, грамм/миллиметр³, миллиграмм/метр³, миллиграмм/сантиметр³, миллиграмм/миллиметр³, экзаграмм/литр, петаграмм/литр, тераграмм /литр, гигаграмм/литр, мегаграмм/литр, килограмм/литр, гектограмм/литр, декаграмм/литр, грамм/литр, дециграмм/литр, сантиграмм/литр, миллиграмм/литр, микрограмм/литр, нанограмм/литр, пикограмм/литр , фемтограмм/литр, аттограмм/литр, фунт/дюйм³… Конвертер удельного объема : метр³/килограмм, сантиметр³/грамм, литр/килограмм, литр/грамм, фут³/килограмм, фут³/фунт, галлон (США) )/фунт, галлон (Великобритания)/фунт. Преобразователь момента инерции : килограмм-метр², килограмм-сантиметр², килограмм-миллиметров², грамм-сантиметр², грамм-миллиметр², килограмм-сила-метр-секунда², унция-дюйм², унция-сила-дюйм-секунда², фунт-фут², фунт-сила-фут-секунда², фунт-дюйм² , фунт-сила, дюйм, секунда², слизняк, фут². Преобразователь момента силы : ньютон-метр, килоньютон-метр, миллиньютон-метр, микроньютон-метр, тонно-сила (короткий) метр, тонно-сила (длинный) метр, тонно-сила (метрический) метр, килограмм-силомер, грамм-сила-сантиметр, фунт-сила-фут, фунт-фут, фунт-дюйм. Импульс : килограмм-метр в секунду, ньютон-секунда, килоньютон-секунда, килограмм-метр в минуту, килограмм-метр в час, грамм-сантиметр в секунду, ньютон-минута, ньютон-час, дина-минута, грамм-сила-секунда, килограмм-сила-секунда, тонна-сила-минута, фунт-фут в секунду, слаг-фут в минуту, фунт-сила-час, кип-минута, планковский импульс, мегаэлектронвольт импульса… Импульс : ньютон-секунда, меганьютон-секунда, миллиньютон-секунда, килограмм-метр в секунду, килограмм-метр в минуту, килограмм-метр в час, грамм-сантиметр в секунду, ньютон-минута, ньютон-час, дина -минута, грамм-сила-секунда, килограмм-сила-секунда, тонна-сила-минута, фунт-фут в секунду, слаг-фут в минуту, фунт-сила-час, кип-секунда, кип-минута, кип-час ., грамм-сила-сантиметр, грамм-сила-миллиметр, унция-сила-фут, унция-сила-дюйм, фунт-сила-фут, фунт-сила-дюйм. Термодинамика. Теплота Удельная энергия, теплота сгорания (на массу) Перевод единиц Btu (th)/фунт, килограмм/джоуль, килограмм/килоджоуль, грамм/калория (IT), грамм/калория (th), фунт/Btu (IT), фунт/Btu (th), фунт/лошадиная сила-час, грамм /лошадиная сила (метрическая)-час, грамм/киловатт-час. Удельная энергия, теплота сгорания (на объем) Перевод единиц : джоуль/метр³, джоуль/литр, мегаджоуль/метр³, килоджоуль/метр³, килокалория (ИТ)/метр³, калория (ИТ)/сантиметр³, терм/фут³, терм/галлон (Великобритания), БТЕ (IT)/фут³, БТЕ (терм.)/фут³, CHU/фут³, метр³/джоуль, литр/джоуль, галлон (США)/лошадиная сила-час, галлон (США)/лошадиная сила (метрическая )-час. Преобразователь теплопроводности : ватт/метр/K, ватт/сантиметр/°C, киловатт/метр/K, калория (ИТ)/секунда/сантиметр/°C, калория (терм)/секунда/сантиметр/°C , килокалория (ИТ)/час/метр/°C, килокалория (терм.)/час/метр/°C, БТЕ (IT) дюйм/секунда/фут²/°F, БТЕ (терм.) дюйм/секунда/фут²/°F , Btu (IT) фут/час/фут²/°F, Btu (TH) фут/час/фут²/°F, BTU (IT) дюйм/час/фут²/°F, BTU (TH) дюйм/час/фут²/ °F. Конвертер удельной теплоемкости : джоуль/килограмм/K, джоуль/килограмм/°C, джоуль/грамм/°C, килоджоуль/килограмм/K, килоджоуль/килограмм/°C, калория (ИТ)/грамм/° C, калория (IT)/грамм/°F, калория (TH)/грамм/°C, килокалория (IT)/килограмм/°C, килокалория (TH)/килограмм/°C, килокалория (IT)/килограмм/K , килокалория (терм. Преобразователь плотности теплового потока : ватт/метр², киловатт/метр², ватт/сантиметр², ватт/дюйм², джоуль/секунда/метр², килокалория (IT)/час/метр², килокалория (IT)/час/фут², калория (IT)/минута/сантиметр², калория (IT)/час/сантиметр², калория (й)/минута/сантиметр², калория (теплая)/час/сантиметр², дина/час/сантиметр, эрг/час/миллиметр², фут-фунт/ минута/фут², лошадиная сила/фут², лошадиная сила (метрическая)/фут², БТЕ (ИТ)/секунда/фут², БТЕ (ИТ)/минута/фут², БТЕ (ИТ)/час/фут², БТЕ (й)/секунда/дюйм² , БТЕ (й)/секунда/фут², БТЕ (й)/минута/фут², БТЕ (й)/час/фут², CHU/час/фут². Преобразователь коэффициента теплопередачи : ватт/метр²/K, ватт/метр²/°C, джоуль/секунда/метр²/K, килокалория (IT)/час/метр²/°C, килокалория (IT)/час/фут² /°C, БТЕ (ИТ)/секунда/фут²/°F, БТЕ (терм.)/секунда/фут²/°F, БТЕ (ИТ)/час/фут²/°F, БТЕ (терм. Гидравлика — жидкостиПреобразователь объемного расхода : метр³/сек, метр³/день, метр³/час, метр³/минута, сантиметр³/день, сантиметр³/час, сантиметр³/минута, сантиметр³/секунда, литр/день, литр/час, литр/минута, литр/секунда, миллилитр/день, миллилитр/час, миллилитр/минута, миллилитр/секунда, галлон (США)/день, галлон (США)/час, галлон (США)/минута, галлон (США)/секунда, галлон (Великобритания)/день, галлон (Великобритания)/час, галлон (Великобритания)/минута, галлон (Великобритания)/секунда, килобаррель (США)/день, баррель (США)/день… Конвертер массового расхода : килограмм/секунда, грамм/секунда, грамм/минута, грамм/час, грамм/день, миллиграмм/минута, миллиграмм/час, миллиграмм/день, килограмм/минута, килограмм/час , килограмм/день, эксаграмм/секунда, петаграмм/секунда, тераграмм/секунда, гигаграмм/секунда, мегаграмм/секунда, гектограмм/секунда, декаграмм/секунда, дециграмм/секунда, сантиграмм/секунда, миллиграмм/секунда, микрограмм/секунда, тонна (метрическая)/секунда, тонна (метрическая)/минута, тонна (метрическая)/час, тонна (метрическая)/день. Конвертер молярного расхода : моль/секунду, экзамол/секунду, петамоль/секунду, терамол/секунду, гигамоль/секунду, мегамоль/секунду, киломоль/секунду, гектомоль/секунду, декамоль/секунду, децимоль/секунду, сантимоль/секунду, миллимоль/секунду, микромоль/секунду, наномоль/секунду, пикомоль/секунду, фемтомоль/ секунда, аттомоль/секунда, моль/минута, моль/час, моль/день, миллимоль/минута, миллимоль/час, миллимоль/день, киломоль/минута, киломоль/час, киломоль/день. Преобразователь массового потока : грамм в секунду/метр², килограмм/час/метр², килограмм/час/фут², килограмм/секунда/метр², грамм/секунда/сантиметр², фунт/час/фут², фунт/секунда/фут². Конвертер молярной концентрации : моль/метр³, моль/литр, моль/сантиметр³, моль/миллиметр³, киломоль/метр³, киломоль/литр, киломоль/сантиметр³, килломоль/миллиметр³, миллимоль/метр³, миллимоль/литр, миллимоль/ сантиметр³, миллимоль/миллиметр³, моль/дециметр³, молярный, миллимолярный, микромолярный, наномолярный, пикомолярный, фемтомолярный, аттомолярный, зептомолярный, йоктомолярный. Конвертер массовой концентрации в растворе : килограмм/литр, грамм/литр, миллиграмм/литр, часть/миллион, гран/галлон (США), гран/галлон (Великобритания), фунт/галлон (США), фунт/галлон галлон (Великобритания), фунт/миллион галлонов (США), фунт/миллион галлонов (Великобритания), фунт/фут³, килограмм/метр³, грамм/100 мл. Конвертер динамической (абсолютной) вязкости : паскаль-секунда, килограмм-сила-секунда/метр², ньютон-секунда/метр², миллиньютон-секунда/метр², дина-секунда/сантиметр², пуаз, экзапуаз, петапуаз, терапуаз, гигапуаз, мегапуаз, килопуаз, гектоуравновешенность, декауаз, деципуаз, сантипуаз, миллипуаз, микроуравновешенность, наноуравновешенность, пикоуравновешенность, фемтоуравновешенность, атоуравновешенность, фунт-сила-секунда/дюйм², фунт-сила-секунда/фут², фунт-секунда/фут², грамм/сантиметр/секунда., килостокс, гектостокс, декастокс, декастокс, сантистокс, миллистокс, микростокс, наностокс, пикостокс, фемтостокс, аттостокс. Преобразователь поверхностного натяжения : ньютон/метр, миллиньютон/метр, грамм-сила/сантиметр, дина/сантиметр, эрг/сантиметр², эрг/миллиметр², фунт/дюйм, фунт-сила/дюйм. Акустика — звукПреобразователь чувствительности микрофона : децибел относительно 1 вольта на 1 паскаль, децибел относительно 1 вольта на 1 микропаскаль, децибел относительно 1 вольта на 1 дин на квадратный сантиметр, децибел относительно 1 вольта на 1 микробар, вольт на паскаль, милливольт на паскаль, микровольт на паскаль. Преобразователь уровня звукового давления (SPL) : ньютон на квадратный метр, паскаль, миллипаскаль, микропаскаль, дина/квадратный сантиметр, бар, миллибар, микробар, уровень звукового давления в децибелах. Фотометрия — светПреобразователь яркости : кандела/метр², кандела/сантиметр², кандела/фут², кандела/дюйм², килокандела/метр², стильб, люмен/метр²/стерадиан, люмен/сантиметр²/стерадиан, люмен/фут²/ стерадиан, нит, миллинит, ламберт, миллиламберт, фут-ламберт, апостильб, блондель, брил, скот. Конвертер силы света : кандела, свеча (немецкий), свеча (Великобритания), десятичная свеча, свеча (пентан), пентановая свеча (мощность 10 свечей), свеча Хефнера, единица Карселя, десятичное число бужей, люмен/стерадиан, свеча (Международный). Преобразователь освещенности : люкс, метр-свеча, сантиметр-свеча, фут-свеча, фот, нокс, кандела стерадиан/метр², люмен/метр², люмен/сантиметр², люмен/фут², ватт/сантиметр² (при 555 нм) . Преобразователь частоты и длины волны : герц, экзагерц, петагерц, терагерц, гигагерц, мегагерц, килогерц, гектогерц, декагерц, децигерц, сантигерц, миллигерц, микрогерц, наногерц, пикогерц, фемтогерц, аттогерц, цикл/секунду, длина волны в экзаменах , длина волны в петаметрах, длина волны в тераметрах, длина волны в гигаметрах, длина волны в мегаметрах, длина волны в километрах, длина волны в гектометрах, длина волны в декаметрах… Конвертер оптической силы (диоптрий) в фокусное расстояние : Оптическая сила (диоптрийная сила или преломляющая сила) линзы или другой оптической системы — это степень, в которой система сводит или расходит свет. Он рассчитывается как величина, обратная фокусному расстоянию оптической системы, и измеряется в обратных метрах в СИ или чаще в диоптриях (1 диоптрия = м⁻¹). , килокулон, милликулон, микрокулон, нанокулон, пикокулон, абкулон, EMU заряда, статкулон, ESU заряда, Франклин, ампер-час, миллиампер-час, ампер-минута, ампер-секунда, фарадей (на основе углерода 12), элементарный обвинение. Преобразователь электрического тока : ампер, килоампер, миллиампер, биот, абампер, ЭВС тока, статампер, ЭСУ тока, СГС э.м. ед., СГС у.с. ед., микроампер, наноампер, планковский ток. Конвертер линейной плотности тока : ампер/метр, ампер/сантиметр, ампер/дюйм, абампер/метр, абампер/сантиметр, абампер/дюйм, эрстед, гильберт/сантиметр, ампер/миллиметр, миллиампер/метр, миллиампер/дециметр , миллиампер/сантиметр, миллиампер/миллиметр, микроампер/метр, микроампер/дециметр, микроампер/сантиметр, микроампер/миллиметр. Преобразователь плотности поверхностного тока : ампер/метр², ампер/сантиметр², ампер/дюйм², ампер/мил², ампер/круговой мил, абампер/сантиметр², ампер/миллиметр², миллиампер/миллиметр², микроампер/миллиметр², килоампер/миллиметр², миллиампер/сантиметр², микроампер/сантиметр², килоампер/сантиметр², ампер/дециметр², миллиампер/дециметр², микроампер/дециметр², килоампер/дециметр². Преобразователь напряженности электрического поля : вольт/метр, киловольт/метр, киловольт/сантиметр, вольт/сантиметр, милливольт/метр, микровольт/метр, киловольт/дюйм, вольт/дюйм, вольт/мил, абвольт/сантиметр, статвольт /сантиметр, статвольт/дюйм, ньютон/кулон, вольт/микрон. Преобразователь электрического потенциала и напряжения : вольт, милливольт, микровольт, нановольт, пиковольт, киловольт, мегавольт, гигавольт, теравольт, ватт/ампер, абвольт, EMU электрического потенциала, статвольт, ESU электрического потенциала, планковское напряжение. Преобразователь электрического сопротивления : ом, мегом, микроом, вольт/ампер, обратный сименс, абом, EMU сопротивления, статом, ESU сопротивления, квантованное сопротивление Холла, импеданс Планка, миллиом, килоом. Преобразователь удельного электрического сопротивления : ом-метр, ом-сантиметр, ом-дюйм, микроом-сантиметр, микроом-дюйм, абом-сантиметр, статом-сантиметр, круговой мил ом/фут, ом кв.миллиметр на метр. Преобразователь электрической проводимости : сименс, мегасименс, килосименс, миллисименс, микросименс, ампер/вольт, мхо, геммо, микромо, абмо, статмо, квантованная холловская проводимость. Преобразователь удельной электропроводности : сименс/метр, пикосименс/метр, мОм/метр, мОм/сантиметр, абмо/метр, абмо/сантиметр, статмо/метр, статмо/сантиметр, сименс/сантиметр, миллисименс/метр, миллисименс/ сантиметр, микросименс/метр, микросименс/сантиметр, единица электропроводности, коэффициент проводимости, частей на миллион, шкала 700, частей на миллион, шкала 500, частей на миллион, шкала 640, TDS, частей на миллион, шкала 640, TDS, частей на миллион, шкала 550, TDS, частей на миллион, шкала 500, TDS, частей на миллион, шкала 700. Преобразователь емкости : фарад, эксафарад, петафарад, терафарад, гигафарад, мегафарад, килофарад, гектофарад, декафарад, децифарад, сантифарад, миллифарад, микрофарад, нанофарад, пикофарад, фемтофарад, аттофарад, кулон/вольт, абфарад, EMU , статфарад, ЕСУ емкости. Преобразователь индуктивности : генри, эксагенри, петагенри, терагенри, гигагенри, мегагенри, килогенри, гектогенри, декагенри, децигенри, сантигенри, миллигенри, микрогенри, наногенри, пикогенри, фемтогенри, аттогенри, вебер/ампер EMU, индуктивности, , статенри, ЭСУ индуктивности. Преобразователь реактивной мощности переменного тока : вольт-ампер реактивный, милливольт-ампер реактивный, киловольт-ампер реактивный, мегавольт-ампер реактивный, гигавольт-ампер реактивный. Преобразователь американского калибра проводов : Американский калибр проводов (AWG) — это стандартизированная система калибров проводов, используемая в Соединенных Штатах и Канаде для определения диаметров цветных электропроводящих проводов, включая медь и алюминий. Чем больше площадь поперечного сечения провода, тем выше его пропускная способность по току.Чем больше номер AWG, также называемый калибром провода, тем меньше физический размер провода. Наибольший размер AWG — 0000 (4/0), а наименьший — 40. В этой таблице перечислены размеры и сопротивления AWG для медных проводников. Используйте закон Ома для расчета падения напряжения на проводнике. Магнитостатика, магнетизм и электромагнетизмПреобразователь магнитного потока : вебер, милливебер, микровебер, вольт-секунда, единица измерения полюса, мегалиния, килолиня, линия, максвелл, тесла-метр², тесла-сантиметр², гаусс-сантиметр², квант магнитного потока. Преобразователь плотности магнитного потока : тесла, вебер/метр², вебер/сантиметр², вебер/дюйм², максвелл/метр², максвелл/сантиметр², максвелл/дюйм², гаусс, линия/сантиметр², линия/дюйм², гамма. Радиация и радиологияМощность поглощенной дозы излучения, общая мощность дозы ионизирующего излучения : грей/сек, экзагрей/сек, петагрей/сек, терагрэй/сек, гигагрей/сек, мегагрей/сек, килогрей/сек, гектогрей /секунда, декагрей/секунда, децигрей/секунда, сантигрей/секунда, миллигрей/секунда, микрогрей/секунда, наногрей/секунда, пикогрей/секунда, фемтогрей/секунда, аттогрей/секунда, рад/секунда, джоуль/килограмм/секунда, ватт /килограмм, зиверт/секунда, миллизиверт/год, миллизиверт/час, микрозиверт/час, бэр/секунда, рентген/час… Радиоактивность. Конвертер радиоактивного распада : беккерель, петабеккерель, терабеккерель, гигабеккерель, мегабеккерель, килобеккерель, миллибеккерель, кюри, килокюри, милликюри, микрокюри, нанокюри, пикокюри, резерфорд, одна/секунда, распад/секунда, распад/минута. Преобразователь радиационной экспозиции : кулон/килограмм, милликулон/килограмм, микрокулон/килограмм, рентген, миллирентген, микрорентген, рентген ткани, Паркер, респ. Радиация. Конвертер поглощенной дозы : рад, миллирад, джоуль/килограмм, джоуль/грамм, джоуль/сантиграмм, джоуль/миллиграмм, грей, экзагрей, петагрей, терагрей, гигагрей, мегагрей, килогрей, гектогрей, декагрей, децигрей, сантигрей, миллигрей, микрогрей , наногрей, пикогрей, фемтогрей, аттогрей, зиверт, миллизиверт, микрозиверт… Разные конвертерыКонвертер метрических префиксов : нет, йотта, зетта, экза, пета, тера, гига, мега, кило, гекто, дека , деци, санти, милли, микро, нано, пико, фемто, атто, зепто, йокто. Преобразователь передачи данных : бит/секунду, байт/секунду, килобит/секунду (SI по умолчанию), килобайт/секунду (SI по умолчанию), кибибит/секунду, кибибайт/секунду, мегабит/секунду (SI по умолчанию) , мегабайт в секунду (по SI), мебибит в секунду, мебибайт в секунду, гигабит в секунду (по SI), гигабайт в секунду (по SI), гибибит в секунду, гибибайт в секунду, терабит в секунду (по SI по умолчанию) .), терабайт/секунду (SI по умолчанию), тебибит/секунду, тебибайт/секунду, ethernet, ethernet (быстрый), ethernet (гигабит), OC1, OC3, OC12, OC24, OC48… Типография и цифровая Конвертер единиц измерения изображения : твип, метр, сантиметр, миллиметр, символ (X), символ (Y), пиксель (X), пиксель (Y), дюйм, пика (компьютер), пика (принтер), точка (DTP/PostScript) ), точка (компьютерная), точка (принтерная), en, cicero, em, Didot точка. Конвертер единиц измерения объема пиломатериалов : кубический метр, кубический фут, кубический дюйм, досковые футы, тысяча досковых футов, шнур, шнур (80 футов³), кордовые футы, кунит, поддон, поперечная стяжка, перекидная стяжка. Калькулятор молярной массы : Молярная масса — это физическое свойство, которое определяется как масса вещества, деленная на количество вещества в молях. Другими словами, это масса одного моля определенного вещества. Периодическая таблица : Периодическая таблица представляет собой список всех химических элементов, расположенных слева направо и сверху вниз по их атомному номеру, электронным конфигурациям и повторяющимся химическим свойствам, организованным в виде таблицы, так что элементы с аналогичные химические свойства отображаются в вертикальных столбцах, называемых группами.Некоторые группы имеют имена, а также номера. Например, все элементы 1-й группы, кроме водорода, являются щелочными металлами, а элементы 18-й группы — благородными газами, которые ранее назывались инертными газами. Различные строки таблицы называются периодами, потому что такое расположение отражает периодическое повторение сходных химических и физических свойств химических элементов по мере увеличения их атомного номера. Элементы одного периода имеют одинаковое количество электронных оболочек. Вам трудно перевести единицу измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут получите ответ от опытных технических переводчиков. |
Индуктивность — Энциклопедия Нового Света
| Электромагнетизм | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Электричество · Магнетизм | |||||||||
Магнитостатика
| |||||||||
Электродинамика
| |||||||||
Тензоры в теории относительности
| |||||||||
Индуктивность — это свойство электрической цепи, при котором изменение тока, протекающего по цепи, вызывает появление электродвижущей силы (ЭДС), которая противодействует изменению тока.В электрических цепях любой электрический ток ( я {\ displaystyle i}) создает магнитное поле вокруг проводника с током, создавая общий магнитный поток ( Φ {\ displaystyle \ Phi}), действующий на цепь. Этот магнитный поток имеет тенденцию противодействовать изменениям потока, генерируя напряжение (противоЭДС), которое противодействует или имеет тенденцию уменьшать скорость изменения тока. Отношение магнитного потока к току называется собственной индуктивностью , которую обычно называют просто индуктивностью цепи.
Свойство индуктивности особенно заметно и полезно в виде электрических устройств, известных как катушки индуктивности . Катушка индуктивности часто представляет собой катушку проволоки, намотанную на материал, называемый сердечником . Когда через катушку пропускают электрический ток, вокруг нее образуется магнитное поле, и это поле заставляет индуктор сопротивляться изменениям величины проходящего через него тока.
Катушки индуктивности
имеют различные практические применения. Например, в сочетании с конденсаторами они используются в качестве дросселей в источниках питания и для создания настроенных цепей для радиоприема и вещания.Кроме того, катушки индуктивности используются в трансформаторах для электрических сетей и в качестве накопителей энергии в некоторых импульсных источниках питания.
Свойство индуктивности используется при использовании электрических устройств, известных как катушки индуктивности , некоторые из которых показаны здесь.
Символы и единицы
Термин «индуктивность» был придуман Оливером Хевисайдом в феврале 1886 года. [2] [3]
В честь Джозефа Генри единица индуктивности была названа Генри (H):
- 1 H = 1 вебер на ампер (Вб/А).
Индуктивность является мерой количества ЭДС, генерируемой при единичном изменении тока. Например, индуктор с индуктивностью 1 генри создает ЭДС в 1 вольт, когда ток через индуктор изменяется со скоростью 1 ампер в секунду.
Определения
Количественное определение (собственной) индуктивности проволочной петли в единицах СИ (веберах на ампер):
- L = NΦi {\ displaystyle \ displaystyle L = {\ frac {N \ Phi} {i}}}
, где Φ {\ displaystyle \ Phi} обозначает магнитный поток через площадь, охваченную контуром, а N это количество витков провода.Таким образом, потокосцепление λ = NΦ{\ displaystyle \ lambda = N \ Phi}
- NΦ=Li{\displaystyle \displaystyle N{\Phi}=Li}.
Однако могут быть вклады от других цепей. Рассмотрим, например, две цепи C1{\displaystyle C_{1}}, C2{\displaystyle C_{2}}, по которым проходят токи i1{\displaystyle i_{1}}, i2{\displaystyle i_{2}}. Потокосцепления C1 {\ displaystyle C_ {1}} и C2 {\ displaystyle C_ {2}} определяются выражением
- N1Φ1 = L11i1 + L12i2, {\ displaystyle \ displaystyle N_ {1} \ Phi _ {1} = L_ {11} i_ {1} + L_ {12} i_ {2},}
- N2Φ2=L21i1+L22i2.{\ displaystyle \ displaystyle N_ {2} \ Phi _ {2} = L_ {21} i_ {1} + L_ {22} i_ {2}.}
Согласно приведенному выше определению, L11 {\ displaystyle L_ { 11}} и L22{\displaystyle L_{22}} — собственные индуктивности C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}} соответственно. Можно показать (см. ниже), что два других коэффициента равны: L12 = L21 = M {\ displaystyle L_ {12} = L_ {21} = M}, где M {\ displaystyle M} называется взаимной индуктивностью . пары цепей.
Количество витков N1{\displaystyle N_{1}} и N2{\displaystyle N_{2}} встречается несколько асимметрично в приведенном выше определении.{K}L_{m,n}i_{m}i_{n}}
для энергии магнитного поля, создаваемого электрическими цепями K{\displaystyle K}, где in{\displaystyle i_{n}} ток в n-й цепи. Это уравнение является альтернативным определением индуктивности, которое также применяется, когда токи не ограничиваются тонкими проводами, так что не сразу ясно, какая область охватывается цепью, и как следует определять магнитный поток через цепь.
Определение, напротив, является более прямым и более интуитивным.Можно показать, что эти два определения эквивалентны, приравняв производную W по времени и переданную системе электрическую мощность.
Свойства индуктивности
Взятие производной по времени от обеих частей уравнения дает NΦ=Li{\displaystyle N\Phi =Li}:
- NdΦdt = Ldidt + dLdti {\ displaystyle N {\ frac {d \ Phi} {dt}} = L {\ frac {di} {dt}} + {\ frac {dL} {dt}} i \,}
В большинстве физических случаев индуктивность постоянна во времени, поэтому
- NdΦdt = Ldidt{\ displaystyle N {\ frac {d \ Phi} {dt}} = L {\ frac {di} {dt}}}
По закону индукции Фарадея имеем:
- NdΦdt = -E = v {\ displaystyle N {\ frac {d \ Phi} {dt}} = — {\ mathcal {E}} = v}
, где E {\ displaystyle {\ mathcal {E} }} — электродвижущая сила (ЭДС), а — индуцированное напряжение.{t}v(\tau)d\tau +i(0)}
Вместе эти уравнения утверждают, что при постоянном приложенном напряжении v, ток изменяется линейно, со скоростью пропорциональной приложенному напряжению, но обратно пропорционально индуктивности.{2}} — энергия магнитного поля, создаваемого током.
Анализ векторной цепи и импеданс
Эквивалентный импеданс индуктивности с помощью векторов определяется по формуле:
- ZL=V/I=jLω{\displaystyle Z_{L}=V/I=jL\omega \,}
где
- j — воображаемая единица,
- L — индуктивность,
- — угловая частота,
- f это частота и
- Lω =XL{\displaystyle L\omega \=X_{L}} — индуктивное сопротивление.
ω = 2πf {\ displaystyle \ omega = 2 \ pi f \,}
ЭДС индукции
Поток Φi {\displaystyle \Phi _{i}\ \!} через i -ю цепь в наборе определяется выражением:
- Φi = ∑jMijIj = LiIi + ∑j≠iMijIj {\ displaystyle \ Phi _ {i} = \ sum _ {j} M_ {ij} I_ {j} = L_ {i} I_ {i} + \ sum _ { j \ neq i} M_ {ij} I_ {j} \,}
, так что ЭДС индукции E {\ displaystyle {\ mathcal {E}}} конкретной цепи, i , в любой заданной set может быть задан непосредственно:
- E=-dΦidt=-ddt(LiIi+∑j≠iMijIj)=-(dLidtIi+dIidtLi)-∑j≠i(dMijdtIj+dIjdtMij).{\ displaystyle {\ mathcal {E}} = — {\ frac {d \ Phi _ {i}} {dt}} = — {\ frac {d} {dt}} \ left (L_ {i} I_ {i } + \ sum _ {j \ neq i} M_ {ij} I_ {j} \ right) = — \ left ({\ frac {dL_ {i}} {dt}} I_ {i} + {\ frac {dI_ {i}}{dt}}L_{i}\right)-\sum _{j\neq i}\left({\frac {dM_{ij}}{dt}}I_{j}+{\frac { dI_{j}}{dt}}M_{ij}\right).}
Связанные катушки индуктивности
Принципиальная схема представления взаимно индуцирующих катушек индуктивности. Две вертикальные линии между индукторами указывают на сплошной сердечник , вокруг которого намотаны провода индуктора.«n:m» показывает отношение количества витков левого индуктора к количеству витков правого индуктора. На этом рисунке также показано точечное соглашение.
Взаимная индуктивность возникает, когда изменение тока в одном индукторе индуцирует напряжение в другом соседнем индукторе. Это важно как механизм работы трансформаторов, но он также может вызвать нежелательную связь между проводниками в цепи.
Взаимная индуктивность, M , также является мерой связи между двумя индукторами.Взаимная индуктивность по цепи i по цепи j определяется двойным интегралом по формуле Неймана, см. # Методика расчета
Взаимная индуктивность также имеет отношение:
- M21=N1N2P21{\displaystyle M_{21}=N_{1}N_{2}P_{21}\!}
где
- M21{\displaystyle M_{21}} — это взаимная индуктивность, а нижний индекс определяет отношение напряжения, индуцированного в катушке 2, к току в катушке 1.
- N1{\displaystyle N_{1}} — количество витков в катушке 1,
- N2{\displaystyle N_{2}} — количество витков в катушке 2,
- P21{\displaystyle P_{21}} — магнитная проницаемость пространства, занимаемого потоком.
Взаимная индуктивность также связана с коэффициентом связи . Коэффициент связи всегда находится в диапазоне от 1 до 0 и является удобным способом указать связь между определенной ориентацией катушки индуктивности и произвольной индуктивностью:
- M = kL1L2 {\ displaystyle M = k {\ sqrt {L_ {1} L_ {2}}} \!}
где
- k — коэффициент связи и 0 ≤ k ≤ 1,
- L1{\displaystyle L_{1}} — индуктивность первой катушки, а
- L2{\displaystyle L_{2}} — индуктивность второй катушки.
После определения этого коэффициента взаимной индуктивности M его можно использовать для прогнозирования поведения цепи:
- V1 = L1dI1dt + MdI2dt {\ displaystyle V_ {1} = L_ {1} {\ frac {dI_ {1}} {dt}} + M {\ frac {dI_ {2}} {dt}}}
где
- В — напряжение на интересующей катушке индуктивности,
- L1{\displaystyle L_{1}} — индуктивность интересующей катушки индуктивности,
- dI1/dt{\displaystyle dI_{1}/dt} — производная по времени тока через интересующую катушку индуктивности,
- M{\displaystyle M} — взаимная индуктивность, а
- dI2/dt{\displaystyle dI_{2}/dt} – это производная по времени тока через индуктор, соединенный с первым индуктором.
Когда одна катушка индуктивности тесно связана с другой катушкой индуктивности через взаимную индуктивность, например, в трансформаторе, напряжения, токи и число витков могут быть связаны следующим образом:
- Vs = VpNsNp {\ displaystyle V_ {s} = V_ {p} {\ frac {N_ {s}} {N_ {p}}}}
, где
- Vs{\displaystyle V_{s}} — напряжение на вторичной катушке индуктивности,
- Vp{\displaystyle V_{p}} — напряжение на первичной катушке индуктивности (подключенной к источнику питания),
- Ns{\displaystyle N_{s}} – число витков вторичной катушки индуктивности, а
- Np{\displaystyle N_{p}} — число витков первичной катушки индуктивности.
Обратно ток:
- Is=IpNpNs{\displaystyle I_{s}=I_{p}{\frac {N_{p}}{N_{s}}}}
где
- Is{\displaystyle I_{s}} — ток через вторичную катушку индуктивности,
- Ip{\displaystyle I_{p}} — ток через первичную катушку индуктивности (тот, что подключен к источнику питания),
- Ns{\displaystyle N_{s}} – число витков вторичной катушки индуктивности, а
- Np{\displaystyle N_{p}} — число витков первичной катушки индуктивности.
Обратите внимание, что мощность через один индуктор такая же, как мощность через другой. Также обратите внимание, что эти уравнения не работают, если оба трансформатора принудительно подключены (с источниками питания).
Когда любая сторона трансформатора является настроенной цепью, величина взаимной индуктивности между двумя обмотками определяет форму кривой частотной характеристики. Хотя границы не определены, это часто называют слабой, критической и чрезмерной связью. Когда две настроенные цепи слабо связаны взаимной индуктивностью, полоса пропускания будет узкой.По мере увеличения взаимной индуктивности полоса пропускания продолжает расти. Когда взаимная индуктивность увеличивается выше критической точки, пик на кривой отклика начинает падать, и центральная частота будет затухать сильнее, чем ее прямые боковые полосы. Это известно как избыточная связь.
Методы расчета
Взаимная индуктивность
Взаимная индуктивность по цепи i по цепи j определяется двойным интегралом по формуле Неймана
- Мий = Б.CE ; 04π∮Ci∮Cjdsi⋅dsj|Rij|{\displaystyle M_{ij}={\frac {\mu _{0}}{4\pi}}\oint _{C_{i}}\oint _ {C_{j}}{\frac {\mathbf {ds} _{i}\cdot \mathbf {ds} _{j}}{|\mathbf {R} _{ij}|}}}
константа г. до н.э. ;0{\displaystyle \mu _{0}} — проницаемость свободного пространства (4π{\displaystyle \pi} × 10 -7 Гн/м), Ci{\displaystyle C_{i}} и Cj{ \displaystyle C_{j}} — кривые, натянутые проводами, Rij{\displaystyle R_{ij}} — расстояние между двумя точками. См. вывод этого уравнения.
Самоиндуктивность
Формально собственная индуктивность проволочной петли определяется приведенным выше уравнением: i = j .
Однако теперь 1 / R {\ displaystyle 1 / R} становится сингулярным, а конечный радиус a {\ displaystyle a} и
необходимо учитывать распределение тока в проводе. Остается вклад
из интеграла по всем точкам, где |R|≥a/2{\displaystyle |R|\geq a/2} и поправочный член,
- Ljj=L=( г. до н.э.E. ;04π∮C∮C′ds⋅ds′|R|)|R|≥a/2+ г. до н. э. ; 02πlY {\ displaystyle L_ {jj} = L = \ left ({\ frac {\ mu _ {0}} {4 \ pi}} \ oint _ {C} \ oint _ {C’} {\ frac { \mathbf {ds} \cdot \mathbf {ds} ‘}{|\mathbf {R} |}}\right)_{|\mathbf {R} |\geq a/2} +{\ frac {\mu _ {0}}{2\pi}}lY}
Здесь a{\displaystyle a} и l{\displaystyle l} обозначают радиус и длину провода, а Y{\displaystyle Y} – константа, зависящая от в
распределение тока в проводе: Y = 0 {\ displaystyle Y = 0}, когда ток течет по поверхности провода.
(скин-эффект), Y = 1/4 {\ displaystyle Y = 1/4}, когда ток по проводу однороден.Вот вывод этого уравнения.
Метод изображений
В некоторых случаях разные распределения тока генерируют одно и то же магнитное поле в некотором сечении пространства. Этот факт можно использовать для определения собственных индуктивностей (метод изображений). В качестве примера рассмотрим:
- A) Провод на расстоянии d/2{\displaystyle d/2} перед идеально проводящей стеной (которая является обратной)
- B) Два параллельных провода на расстоянии d{\displaystyle d} с противоположным током
Магнитное поле двух систем совпадает (в полупространстве).Таким образом, энергия магнитного поля и индуктивность системы В в два раза больше, чем у системы А.
Самоиндукция простых электрических цепей в воздухе
Самоиндукцию многих типов электрических цепей можно привести в замкнутом виде. Примеры приведены в таблице.
| Тип | Индуктивность / г. {2}} {3l }}\left\{-8w+4{\frac {\sqrt {1+m}}{m}}\left(K\left({\frac {m}{1+m}}\right)-\ влево (1-м \ вправо) E \ влево ({\ гидроразрыва {м} {1 + м}} \ вправо) \ вправо) \ вправо \}} =r2N2πl(1−8w3π+w22−w44+5w616−35w864+.{2}} | |
|---|---|---|
| Коаксиальный кабель, высокочастотный | l2πlna1a{\ displaystyle {\ frac {l} {2 \ pi}} \ ln {\ frac {a_ {1}} {a}}} | a 1 : Внешний радиус a: Внутренний радиус l{\displaystyle l}: Длина |
| Круглая петля | р⋅ (ln8ra−2 + Y) {\ displaystyle r \ cdot \ left (\ ln {\ frac {8r} {a}} -2 + Y \ right)} | r: радиус петли a: радиус проволоки |
| Прямоугольник | 1π (bln2ba+dln2da−(b+d)(2−Y)+2b2+d2−b⋅arsinhbd−d⋅arsinhdb) {\ displaystyle {\ frac {1} {\ pi }} \ left (b \ ln {\ frac {2b} {a}} + d \ ln {\ frac {2d} {a}} — \ left (b + d \ right) \ left (2-Y \ right) ) +2 {\ sqrt {b ^ {2} + d ^ {2}}} -b \ cdot \ operatorname {arsinh} {\ frac {b} {d}} -d \ cdot \ operatorname {arsinh} {\ frac {d}{b}}\right)} | b, d: длина границы d >> a, b >> a a: радиус проволоки |
| Пара параллельных проводов | lπ (lnda + Y) {\ displaystyle {\ frac {l} {\ pi}} \ left (\ ln {\ frac {d} {a}} + Y \ right)} | a: радиус провода d: расстояние, d ≥ 2a l{\displaystyle l}: длина пары |
| Пара параллельных проводов , высокая частота | l2πarcosh (d22a2−1) {\ displaystyle {\ frac {l} {2 \ pi}} \ operatorname {arcosh} \ left ({\ frac {d ^ {2}} {2a ^ {2}}} — 1\справа)} | a: радиус провода d: расстояние, d ≥ 2a l{\displaystyle l}: длина пары |
| Провод параллельно идеально токопроводящая стена | l2π (ln2da + Y) {\ displaystyle {\ frac {l} {2 \ pi}} \ left (\ ln {\ frac {2d} {a}} + Y \ right)} | a: радиус провода d: расстояние, d ≥ a l{\displaystyle l}: длина |
| Провод, параллельный проводящей стене , высокочастотный | l4πarcosh (2d2a2−1) {\ displaystyle {\ frac {l} {4 \ pi}} \ operatorname {arcosh} \ left ({\ frac {2d ^ {2}} {a ^ {2}}} — 1\справа)} | a: радиус провода d: расстояние, d ≥ a l{\displaystyle l}: длина |
Константа Б.CE ;0{\displaystyle \mu _{0}} — проницаемость свободного пространства (4π{\displaystyle \pi} × 10 -7 Гн/м).
Для высоких частот электрический ток течет по поверхности проводника.
(скин-эффект), и в зависимости от геометрии иногда приходится различать
низкочастотные и высокочастотные индуктивности.
Это цель константы Y:
Y=0, когда ток равномерно распределен по поверхности провода (скин-эффект),
Y=1/4, когда ток равномерно распределен по сечению провода.В высокочастотном случае при сближении проводников по их поверхности протекает дополнительный экранирующий ток, и выражения, содержащие Y, становятся недействительными.
Индуктивность соленоида
Соленоид представляет собой длинную тонкую катушку, т.е. катушку, длина которой намного больше диаметра. В этих условиях и без использования какого-либо магнитного материала плотность магнитного потока внутри катушки практически постоянна и определяется выражением
- Б= Б.CE ;0Ni/l{\displaystyle \displaystyle B=\mu _{0}Ni/l}
, где г. до н.э. ;0{\displaystyle \mu _{0}} — проницаемость свободного пространства, N{\displaystyle N} количество витков, i{\displaystyle i} ток и l{\displaystyle l} длина катушка. Без учета концевых эффектов полный магнитный поток через катушку получается путем умножения плотности потока B {\ displaystyle B} на площадь поперечного сечения A {\ displaystyle A} и количество витков N {\ displaystyle N}:
- Φ= Б.{2}А/л.}
Это, а также индуктивность более сложных форм можно получить из уравнений Максвелла. Для жестких катушек с воздушным сердечником индуктивность зависит от геометрии катушки и количества витков и не зависит от тока.
Аналогичный анализ применим к соленоиду с магнитным сердечником, но только если длина катушки намного больше, чем произведение относительной магнитной проницаемости магнитного сердечника на диаметр. Это ограничивает простой анализ сердечниками с низкой проницаемостью или чрезвычайно длинными тонкими соленоидами.{2}A/l.}
Обратите внимание, что поскольку проницаемость ферромагнитных материалов изменяется в зависимости от приложенного магнитного потока, индуктивность катушки с ферромагнитным сердечником обычно зависит от силы тока.
Индуктивность коаксиальной линии
Пусть внутренний проводник имеет радиус ri{\displaystyle r_{i}} и магнитную проницаемость до н.э. ;i{\displaystyle \mu _{i}}, пусть диэлектрик между внутренним и внешним проводником имеет проницаемость г. до н.э. ;d{\displaystyle \mu _{d}}, а внешний проводник имеет внутренний радиус ro1{\displaystyle r_{o1}}, внешний радиус ro2{\displaystyle r_{o2}} и магнитную проницаемость Б.{2}}}\right)-{\frac {\mu _{o}}{8\pi }}}
Однако для типичного применения коаксиальной линии нас интересует передача (непостоянного тока) сигналов на частоты, для которых резистивным скин-эффектом нельзя пренебречь. В большинстве случаев члены внутреннего и внешнего проводника пренебрежимо малы, и в этом случае можно аппроксимировать
- dLdl≈ г. до н.э. ; d2πlnro1ri {\ displaystyle {\ frac {dL} {dl}} \ приблизительно {\ frac {\ mu _ {d}} {2 \ pi}} \ ln {\ frac {r_ {o1}} {r_ {i}}}}
См. также
Примечания
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Гриффитс, Дэвид Дж.1999. Введение в электродинамику, 3-е изд. Река Аппер-Сэдл, Нью-Джерси: Прентис-холл. ISBN 013805326X.
- Гровер, Фредерик Уоррен. 1962. Расчеты индуктивности, рабочие формулы и таблицы . Нью-Йорк: Довер. OCLC 299921393.
- Хевисайд, Оливер. 1894. Электротехнические документы. Нью-Йорк: Макмиллан.
- Хьюз, Эдвард и др. 2002. Электрические и электронные технологии, , 8-е изд. Харлоу: Прентис Холл. ISBN 058240519X.
- Wangsness, Roald K. 1986. Электромагнитные поля, , 2-е изд. Нью-Йорк: Уайли. ISBN 0471811866.
Внешние ссылки
Все ссылки получены 2 марта 2018 г.
Кредиты
New World Encyclopedia писатели и редакторы переписали и дополнили статью Википедии
в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства.Упоминание должно быть выполнено в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в New World Encyclopedia :
Примечание. На использование отдельных изображений, которые лицензируются отдельно, могут распространяться некоторые ограничения.
.


 В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

 При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.







 !)
!) Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических приставокКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических приставокКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
 .. сухой (США), пинта сухой (США), кварт сухой (США), пек (США), пек (Великобритания), бушель (США), бушель (Великобритания), кор (библейский), гомер (библейский), ефа (библейский ), сеах (библейский), омер (библейский), каб (библейский), бревно (библейский), метр кубический.
.. сухой (США), пинта сухой (США), кварт сухой (США), пек (США), пек (Великобритания), бушель (США), бушель (Великобритания), кор (библейский), гомер (библейский), ефа (библейский ), сеах (библейский), омер (библейский), каб (библейский), бревно (библейский), метр кубический. ..
.. ..
.. ..
.. ..
..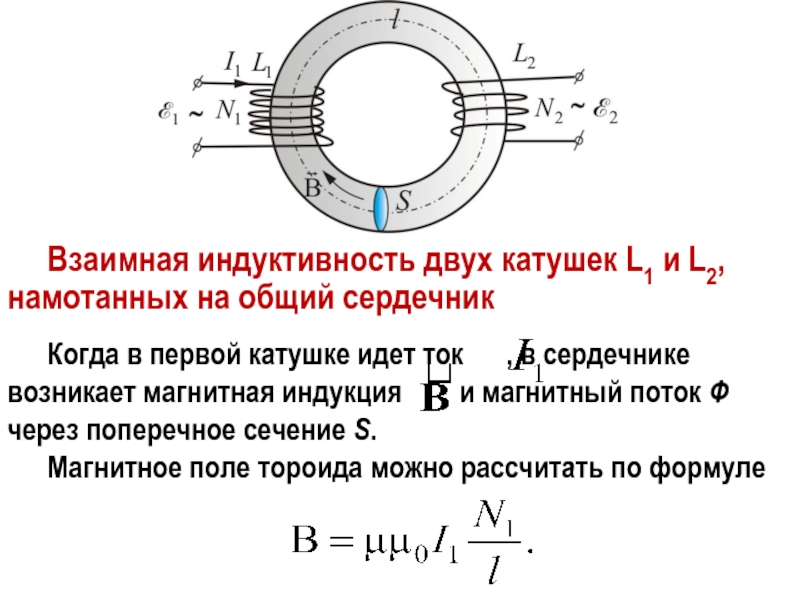 .
.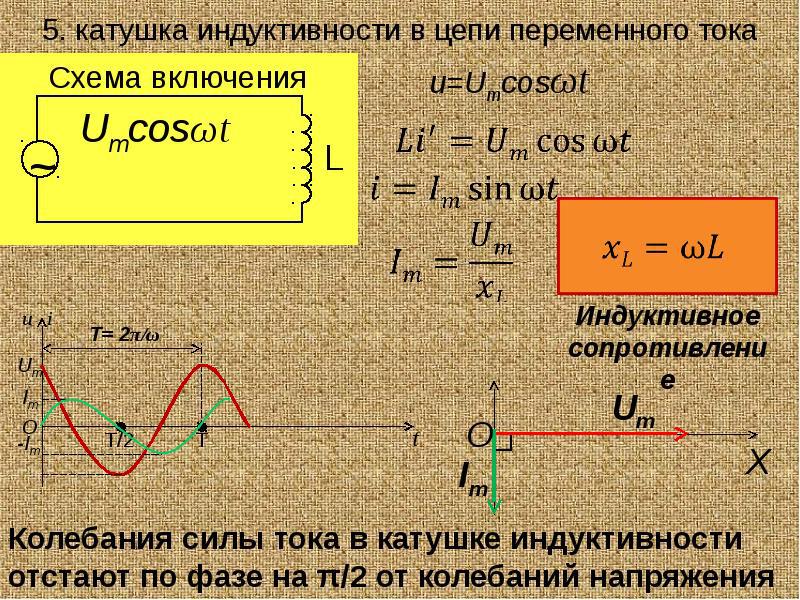

 )/килограмм/K, килограмм-сила-метр/килограмм/K, фунт-сила-фут/фунт/°R, Btu (IT)/фунт/°F, Btu (th)/фунт/°F, Btu (IT)/фунт/°R, Btu (th)/фунт/°R, Btu (IT)/фунт/°C, CHU/фунт/°C.
)/килограмм/K, килограмм-сила-метр/килограмм/K, фунт-сила-фут/фунт/°R, Btu (IT)/фунт/°F, Btu (th)/фунт/°F, Btu (IT)/фунт/°R, Btu (th)/фунт/°R, Btu (IT)/фунт/°C, CHU/фунт/°C. )/час/фут²/° F, CHU/час/фут²/°C.
)/час/фут²/° F, CHU/час/фут²/°C. ..
..