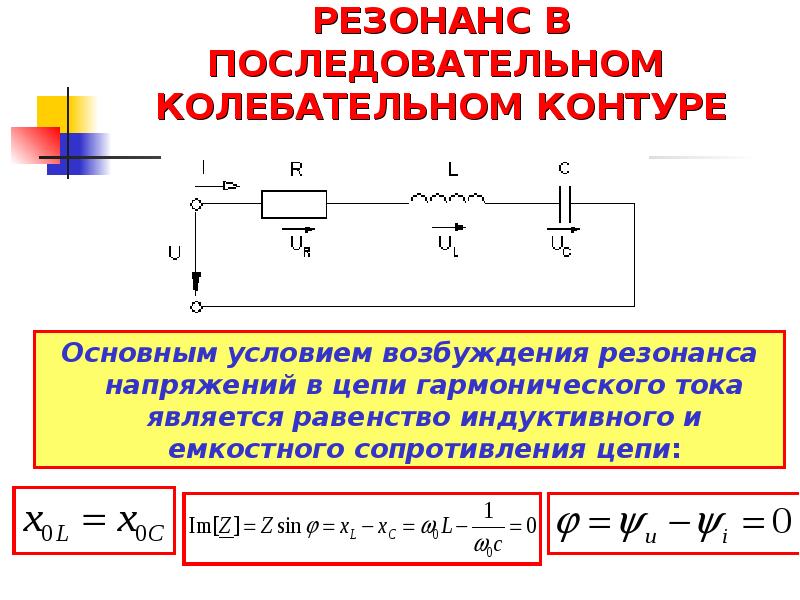
Резонанс напряжений в последовательном колебательном контуре
В радиотехнике широкое применение имеют электрические цепи, составленные из катушки индуктивности и конденсатора. Такие цепи в радиотехнике называются колебательными контурами. Источник переменного тока к колебательному контуру может быть присоединен двумя способами: последовательно (рисунок 1а) и параллельно (рисунок 1б).
Рисунок 1. Схемотическое обозначение колебательного контура. а) последовательный колебательный контур; б) параллельный колебательный контур.
Рассмотрим поведение колебательного контура в цепи переменного тока при последовательном соединении контура и источника тока (рис 1а).
Мы знаем, что такая цепь оказывает переменному току реактивное сопротивление, равное:
где RL— активное сопротивление катушки индуктивности в ом;
ωL,-индуктивное сопротивление катушки индуктивности в ом;
1/ωC-емкостное сопротивление конденсатора в ом.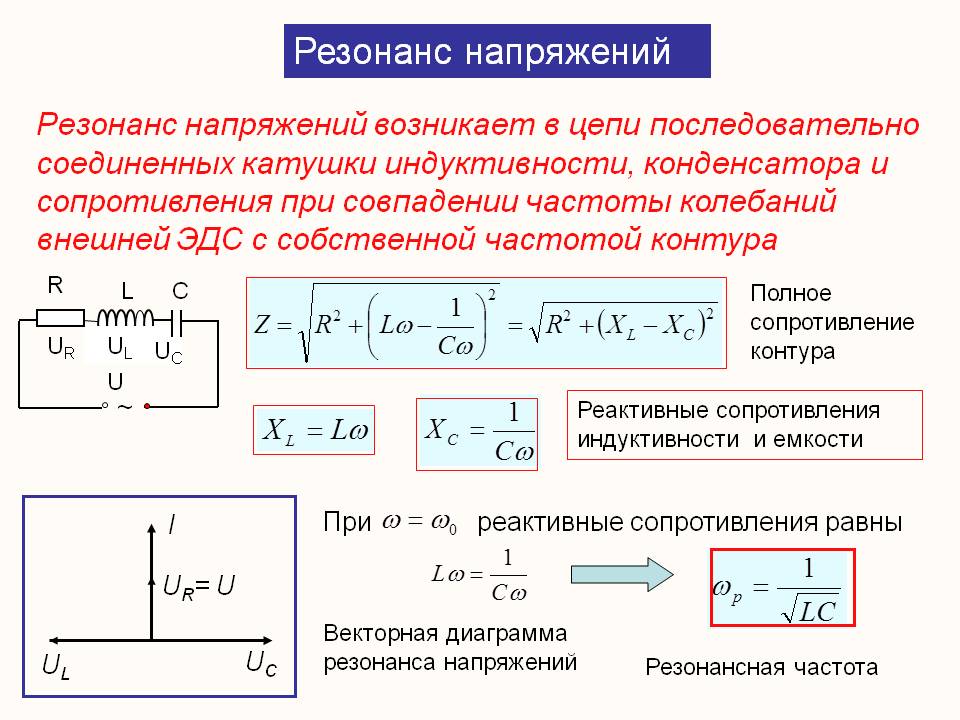
Активное сопротивление катушки RL практически очень мало изменяется при изменении частоты (если пренебречь поверхностным эффектом). Индуктивное и емкостное сопротивления в очень сильной степени зависят от частоты, а именно: индуктивное сопротивление ωL увеличивается прямо пропорционально частоте тока, а емкостное сопротивление 1/ωC уменьшается при повышении частоты тока, т. е. оно связано с частотой тока обратно пропорциональной зависимостью.
Отсюда непосредственно следует, что реактивное сопротивление последовательного колебательного контура также зависит от частоты, и колебательный контур будет оказывать токам разных частот неодинаковое сопротивление.
Если мы будем измерять реактивное сопротивление колебательного контура при различных частотах, то обнаружим, что в области низких частот сопротивление последовательного контура очень велико; при увеличении частоты оно уменьшается до некоторого предела, а затем начинает снова возрастать.
Объясняется это тем, что в области низких частот ток испытывает большое сопротивление со стороны конденсатора, при увеличении же частоты начинает действовать индуктивное сопротивление, компенсирующее действие емкостного сопротивления.
При некоторой частоте индуктивное сопротивление становится равным емкостному, т. е.
Они будут взаимно компенсировать друг друга и общее реактивное сопротивление контура станет равным нулю:
При этом реактивное сопротивление последовательного колебательного контура будет равно только его активному сопротивлению, так как
При дальнейшем повышении частоты ток будет испытывать все большее и большее сопротивление со стороны индуктивности катушки, при одновременном уменьшении компенсирующего действия емкостного сопротивления. Поэтому реактивное сопротивление контура начнет снова возрастать.
На рисунке 2а приведена кривая, показывающая изменение реактивного сопротивления последовательного колебательного контура при изменении частоты тока.
Рисунок 2. Резонанс напряжений. а) зависимость изменения полного сопротивления от частоты; б) зависимость реактивного сопротивления от активного сопротивления контура; в) кривые резонанаса.
Частота тока, при которой сопротивление колебательного контура делается наименьшим, называется частотой резонанса или резонансной частотой колебательного контура.
При резонансной частоте имеет место равенство:
пользуясь которым, нетрудно определить частоту резонанса:
(1)
Единицами в этих формулах служат герцы, генри и фарады.
Из формулы (1) видно, что чем меньше величины емкости и самоиндукции колебательного контура, тем больше будет его резонансная частота.
Величина активного сопротивления RL не влияет на резонансную частоту, однако от нее зависит характер изменения Z. На рисунке 2б приведен ряд графиков изменения реактивного сопротивления колебательного контура при одних и тех же величинах L и С, но при разных RL. Из этого рисунка видно, что чем больше активное сопротивление последовательного колебательного контура, тем тупее становится кривая изменения реактивного сопротивления.
На рисунке 2б приведен ряд графиков изменения реактивного сопротивления колебательного контура при одних и тех же величинах L и С, но при разных RL. Из этого рисунка видно, что чем больше активное сопротивление последовательного колебательного контура, тем тупее становится кривая изменения реактивного сопротивления.
Теперь рассмотрим, как будет изменяться сила тока в колебательном контуре, если мы будем изменять частоту тока. При этом мы будем считать, что напряжение, развиваемое источником переменного тока, остается все время одним и тем же.
Так как источник тока включен последовательно с L и С контура, то сила тока, протекающего через катушку и конденсатор, будет тем больше, чем меньше реактивное сопротивление колебательного контура в целом, так как
Отсюда непосредственно следует, что при резонансе сила тока в колебательном контуре будет наибольшей. Величина тока при резонансе будет зависеть от напряжения источника переменного тока и от активного сопротивления контура:
На рисунке 2г изображен ряд графиков изменения силы тока в последовательном колебательном контуре при изменении частоты тока так называемых кривых резонанса. Из этого рисунка видно, что чем больше активное сопротивление контура, тем тупее кривая резонанса.
Из этого рисунка видно, что чем больше активное сопротивление контура, тем тупее кривая резонанса.
При резонансе сила тока может достигать огромных значений при сравнительно малой внешней ЭДС. Поэтому падения напряжения на индуктивном и емкостном сопротивлениях контура, т. е. на катушке и на конденсаторе, могут достигать очень больших величии и далеко превосходить величину внешнего напряжения.
Последнее утверждение на первый взгляд может показаться несколько странным, однако нужно помнить, что фазы напряжений на емкостном и индуктивном сопротивлениях сдвинуты друг относительно друга на 180°, т. е. мгновенные значения напряжений на катушке и конденсаторе направлены всегда в противоположные стороны. Вследствие этого большие напряжения, существующие при резонансе внутри контура на его катушке и конденсаторе, ничем не обнаруживают себя вне контура, взаимно компенсируя друг друга.
Разобранный нами случай последовательного резонанса называется резонансом напряжений, так как в этом случае в момент резонанса имеет место резкое увеличение напряжения на L и С колебательного контура.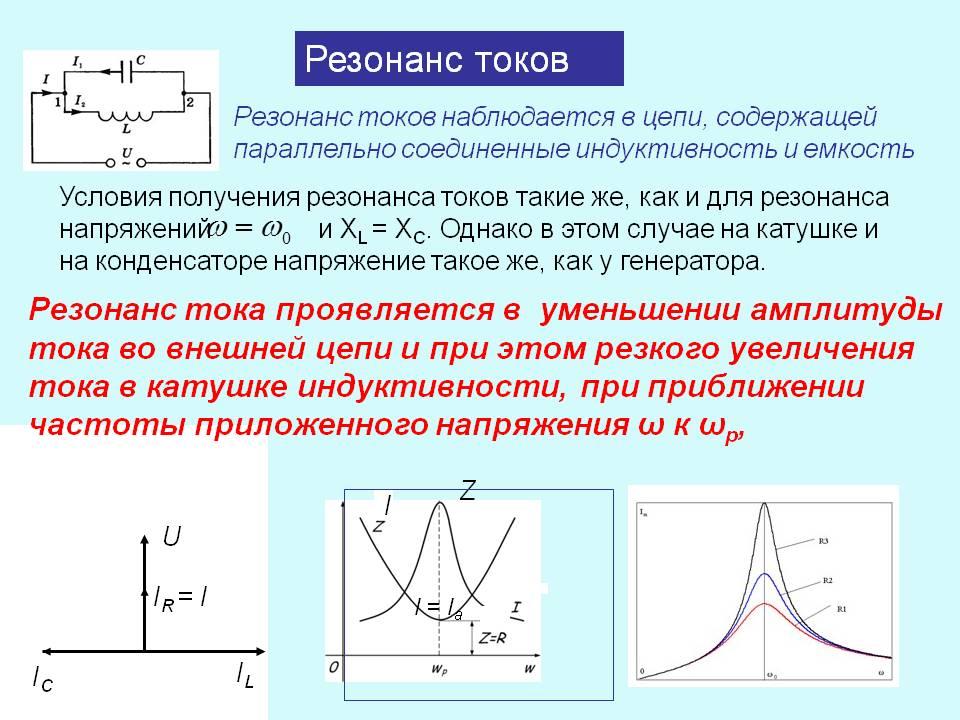
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
И составление отчета по работе
При последовательном соединении участков электрической цепи полное сопротивление всей цепи
(1.1)
и определяется из выражения (1.2)
где r — активное сопротивление всей цепи; x – реактивное сопротивление всей цепи.
Таблица 1.2
Результаты измерений в неразветвленной цепи
| № п/п |
Характер нагрузки |
Измеренные величины |
Примечание | ||||
| U, B | I, A | P, Вт | Uk, B | Uc, B | |||
| Катушка индуктивности и конденсатор | xk < xc(Cmin= ) | ||||||
| xk = xc (Cp= ) | |||||||
| xk > xc (Cmax= ) | |||||||
| Катушка индуктивности | |||||||
| Конденсатор | Cmin= | ||||||
| Ламповый реостат |
Активное сопротивление катушки вычисляется по формуле:
(1. 3)
3)
где Рk — активная мощность, потребляемая катушкой индуктивности, в опытах 1, 2, 3 и 4 равная активной мощности всей цепи Р.
Реактивное (индуктивное) сопротивление катушки определяется следующим образом:
(1.4)
где — полное сопротивление катушки индуктивности.
Индуктивность катушки вычисляется по формуле:
(1.5)
где ω, с-1 — круговая частота напряжения питания; f = 50 Гц — циклическая частота напряжения питания.
Реактивное (емкостное) сопротивление конденсатора можно вычислить следующим образом:
(1.6)
Емкость конденсатора определяется по формуле:
. (1.7)
Коэффициенты мощности всей цепи cosφ и катушки индуктивности cosφк вычисляются по формулам:
(1.8)
(1.9)
Составляющие напряжения катушки Uak — активная и реактивная Upk — определяются по формулам:
(1. 10)
10)
Активное сопротивление лампового реостата определяется по данным опыта 6 как
(1.11)
Реактивное сопротивление всей цепи при последовательном соединении катушки индуктивности и конденсатора можно определить по формуле:
. (1.12)
Рассчитанные значения параметров цепи записать в табл. 1.3.
По результатам измерений и расчетным данным строятся векторные диаграммы. На рис. 1.2 приведен пример построения векторной диаграммы.
Рис. 1.2. Пример построения векторной диаграммы для последовательного соединения катушки индуктивности и конденсатора
Таблица 1.3
Параметры неразветвленной цепи
| № п/п | Ламповый реостат | Катушка индуктивности | Конденса-тор | Вся цепь | ||||||||||
| rr, Ом | rk, Ом | xk, Ом | zk, Ом | cosφk | L, мГн | Uak, B | Upk, B | xc,Ом | C, мкФ | r, Ом | x, Ом | z,Ом | cosφ | |
. .. ..
|
При построении векторных диаграмм для последовательного соединения элементов электрической цепи за исходный вектор принимается вектор тока. Векторы напряжений откладываются в масштабе, общем для всех напряжений. Вектор Ūr совпадает по направлению с вектором тока, а вектор Ūс отстает от вектора тока на угол π/2. Вектор напряжения Ūk строится как векторная сумма вектора активной составляющей Ūаk, совпадающего по фазе с вектором тока, и вектора индуктивной составляющей Ūpk, опережающего вектор тока на угол π/2.
Вектор приложенного к схеме напряжения Ū равен векторной сумме векторов напряжений на отдельных элементах цепи.
При последовательном соединении катушки индуктивности и конденсатора и условии
хk = хс . (1.13)
наступает резонанс напряжений.
В этом режиме цепь ведет себя как активное сопротивление:
(1.14)
При резонансе напряжений, в случае если реактивные сопротивления катушки индуктивности и конденсатора значительно больше активного сопротивления цепи, на катушке индуктивности и конденсаторе возникают перенапряжения, величина которых существенно больше напряжения питания, что может привести к пробою изоляции и выходу из строя этих элементов.
В отчете привести:
– принципиальные схемы с необходимыми пояснениями;
– паспортные данные приборов;
– таблицы и расчетные формулы;
– резонансную кривую;
– векторные диаграммы для режимов, указанных преподавателем.
Вопросы для самоконтроля
1. Как зависят хk и хс от частоты?
2. Как найти полное сопротивление последовательной цепи, в случае если известно сопротивление отдельных элементов?
Как найти полное сопротивление последовательной цепи, в случае если известно сопротивление отдельных элементов?
3. Что такое коэффициент мощности?
4. Как можно изменить коэффициент мощности всей цепи?
5. Вследствие чего ток в цепи при резонансе напряжений имеет наибольшее значение?
6. Что такое резонанс напряжений и каковы его характерные особенности?
7. Каков знак φ при хk > хс , хk < хс?
Возможен ли электрический резонанс в данных схемах. Резонансные явления в электрических цепях. Резонанс в идеальной цепи
Резонанс в электрической цепи возникает при резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определенной резонансной частотой системы. Это происходит тогда, когда два элемента противоположного характера компенсируют эффект друг друга в цепи.
RLC-цепь
Схема RLC – это электрическая цепь с последовательно или параллельно соединенными элементами:
- резистора,
- индуктора,
- конденсатора.

Название RLC связано с тем, что эти буквы являются обычными символами электрических элементов: сопротивления, индуктивности и емкости.
Векторная диаграмма последовательной RLC-цепи представлена в одном из трех вариантов:
- индуктивном,
- емкостном,
- активном.
В последнем варианте при нулевом сдвиге фаз, равенстве индуктивного и емкостного сопротивлений возникает резонанс напряжений.
Электрический резонанс
В природе бывают резонанс токов и резонанс напряжений. Наблюдаются они в цепи с параллельным и последовательным соединением элементов R, L и С. Резонансная частота одинакова для обеих цепей, она находится из условия противоположности сопротивлений реактивных элементов и вычисляется по нижеследующей формуле.
Векторные диаграммы практически идентичны, только сигналы отличаются. В последовательном контуре резонируют напряжения, в параллельном – ток. Но если отступиться от резонансной частоты такая симметрия естественно нарушится. В первом случае сопротивление возрастет, во втором – уменьшится.
В первом случае сопротивление возрастет, во втором – уменьшится.
Резонанс напряжений, достигающих максимальной амплитуды
На картинке ниже представлена векторная диаграмма цепи последовательного контура, где:
- I – вектор общего тока;
- Ul – опережает I на 900;
- UС – отстает от I на 900;
- UR – синфазно I.
Из трех векторов напряжения (Ul, UС, UR) два первых взаимно компенсируют друг друга. Они между собой:
- противоположны по направлению,
- равны по амплитуде,
- отличаются по фазе на пи.
Получается, что напряжение по второму закону Кирхгофа приложено только к резистору. В этот момент:
- импеданс последовательного контура на резонансной частоте минимален и равен просто R;
- так как сопротивление цепи минимальное, то соответственно ток по амплитуде максимальный;
- также приблизительно максимальны напряжения на индуктивности и на емкости.
Если рассматривать отдельно последовательный контур LC, то он даёт нулевое сопротивление на резонансной частоте:
Важно!
Когда установился гармонический режим c резонансной частотой, в контуре происходит следующее: источник обеспечивает установившуюся амплитуду колебаний; мощность источника расходуется лишь на нагрев резистора.
Резонанс токов через реактивные элементы
Диаграмма параллельного контура на той же частоте. Поскольку все элементы соединены параллельно, то диаграмму лучше начать строить с общего напряжения.
- U – вектор общего тока;
- Ic – опережает U на 900;
- IU – отстает от U на 900;
- Ток в резисторе (IR) синфазен общему напряжению.
Поскольку сопротивления реактивности по модулю равны, то и амплитуды токов
Ic
и
Iu
:
- одинаковы;
- достигают максимальной амплитуды.
Получается, что по первому закону Кирхгофа IR равен току источника. Другими словами, ток источника течет только через резистор.
Если рассматривать отдельно параллельный контур LC, то на резонансной частоте его сопротивление бесконечно большое:
Когда установится гармонический режим
c
резонансной частотой, в контуре происходит следующее:
- источник обеспечивает установившуюся амплитуду колебаний;
- мощность источника тока расходуется лишь на пополнение потерь в активном сопротивлении.

Двойственность RLC-контуров
Таким образом, можно сделать сравнительный вывод:
- У последовательной RLC цепи импеданс минимален на резонансной частоте и равен активному сопротивлению контура;
- У параллельной RLC цепи импеданс максимален на резонансной частоте и равен так называемому сопротивлению утечки, фактически тоже активному сопротивлению контура.
Для того чтобы предуготовить условия для резонанса тока или напряжения, требуется проверить электрическую цепь с целью предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимую часть необходимо приравнять к нулю.
Для информации.
Напряжения в последовательной цепи ведут себя очень похоже токам параллельной цепи на резонансной частоте, в этом проявляется двойственность RLC-контуров.
Применение резонансного явления
Хорошим примером применения резонансного явления может служить электрический резонансный трансформатор, разработанный изобретателем Николой Тесла ещё в 1891 году. Тесла проводил эксперименты с различными конфигурациями, состоящими в сочетании из двух, а иногда трех резонансных электрических цепей.
Тесла проводил эксперименты с различными конфигурациями, состоящими в сочетании из двух, а иногда трех резонансных электрических цепей.
Для информации.
Термин «катушки Теслы» применяются к ряду высоковольтных резонансных трансформаторов. Устройства используются для получения высокого напряжения, низкого тока, высокой частоты переменного тока.
В то время как обычный трансформатор предназначен для эффективной передачи энергии с первичной на вторичную обмотку, резонансный трансформатор предназначен для временного хранения электрической энергии. Устройство управляет воздушным сердечником резонансно настроенного трансформатора для получения высоких напряжений при малых токах. Каждая обмотка имеет емкость и функционирует как резонансный контур.
Чтобы произвести наибольшее выходное напряжение, первичный и вторичный контуры настроены в резонанс друг с другом. Оригинальные схемы изобретателя применяются как простые разрядники для возбуждения колебаний с помощью настроенных трансформаторов. В более сложных конструкциях используют транзисторные или тиристорные выключатели.
В более сложных конструкциях используют транзисторные или тиристорные выключатели.
Для информации.
Трансформатор Теслы основан на использовании резонансных стоячих электромагнитных волн в катушках. Своеобразный дизайн катушки продиктован необходимостью достигнуть низкого уровня резистивных потерь энергии (высокая добротность) на высоких частотах, что приводит к увеличению вторичных напряжений.
Электрический резонанс – одно из самых распространенных в мире физических явлений, без которого не было бы TV, диагностических мед. аппаратов. Одни из самых полезных видов резонанса в электрической цепи – это резонанс токов и резонанс напряжений.
Видео
Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением
. Входные реактивные сопротивление и проводимость равны нулю:
x = ImZ =
0 и B = ImY =
0. Цепь носит чисто активный характер:
Z = R
; сдвиг фаз отсутствует (j =
0).
Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 2.42, а
).
Рис. 2.42. Векторные диаграммы при резонансе напряжений (а) и токов (б)
Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q
, определяется величинами индуктивного (или емкостного) и активного сопротивлений
Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать нескольких сотен единиц.
Из условия (2.33) следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз.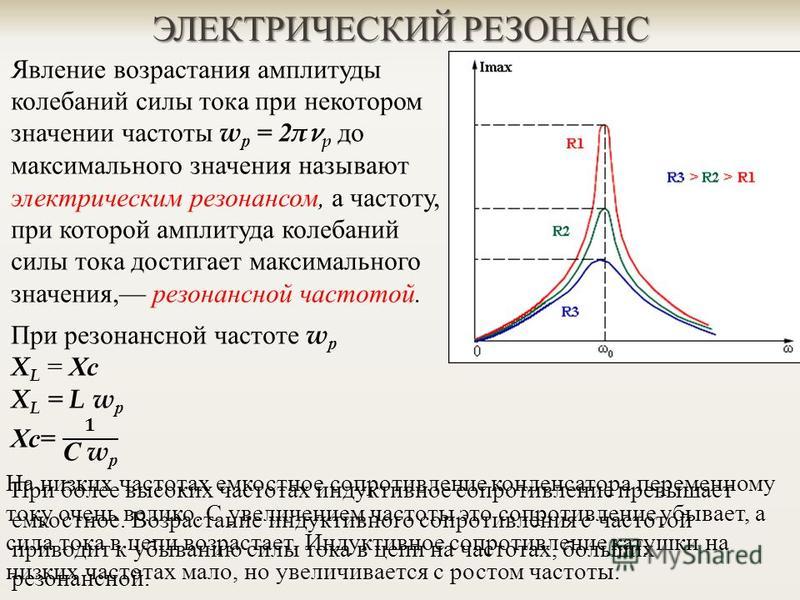 Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 2.43). Емкость , при которой наступает резонанс, можно определить из формулы (2.33):
Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 2.43). Емкость , при которой наступает резонанс, можно определить из формулы (2.33):
Если, например, индуктивность контура L =
0,2 Гн, то при частоте 50 Гц, резонанс наступит при емкости
Рис. 2.43. Зависимости параметров режима от емкости
Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R
, L
и C
(рис. 2.31, а
). Векторная диаграмма ее резонансного режима приведена на рис. 2.42, б
.
Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления
(рис. 2.44, а
).
Рис. 2.44. Разветвленная цепь (а
) и ее эквивалентная схема (б
)
Для нее условием резонанса является равенство нулю ее реактивной проводимости: ImY =
0
. Это равенство означает, что мы должны мнимую часть комплексного выражения Y
приравнять к нулю.
Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:
Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:
Или . (2.34)
Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B 1
и B 2
. Заменяя схему на рис. 2.44, а
эквивалентной (рис. 2.44, б
), параметры которой вычисляем по формуле (2.31), и используя условие резонанса(B = B 1 – B 2 =
0), снова приходим к выражению (2.34).
Схеме на рис. 2.44, б
соответствует векторная диаграмма, приведенная на рис. 2.45.
Резонанс в разветвленной цепи называется резонансом токов
. Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.
Рис. 2.45. Векторная диаграмма резонансного режима разветвленной цепи
Пример 2. 23.
23.
Считая R 2
и x 3
известными, определить величину x 1
, при которой в цепи наступит резонанс напряжений (рис. 2.46, а
). Для резонансного режима построить векторную диаграмму.
В том случае, когда электрическая цепь содержит элементы с емкостными, а также с индуктивными свойствами может возникнуть режим резонанса. Кроме того, резонанс в электрической цепи появляется в случае совпадения по фазе тока и напряжения. Реактивное сопротивление и проводимость на входе имеют нулевое значение. Полностью отсутствует сдвиг фаз, и цепь становится активной.
Причины резонанса
Резонанс напряжений появляется в случае последовательного соединения участков, содержащих сопротивления индуктивного и емкостного характера, а также резисторы. Такая простая цепь очень часто носит название последовательного или параллельного контура.
В резонансном контуре вовсе не обязательно присутствие резистивного сопротивления. Тем не менее, его необходимо учитывать при определении сопротивления проводников. Таким образом, резонансный режим полностью зависит от параметров и свойств электрической цепи. На него никак не влияют внешние источники электрической энергии.
Таким образом, резонансный режим полностью зависит от параметров и свойств электрической цепи. На него никак не влияют внешние источники электрической энергии.
Для того, чтобы определить условия, при которых возникает режим резонанса, необходимо проверить электрическую цепь с целью определения ее проводимости или комплексного . Кроме того, её мнимая часть должна быть выделена и приравнена к нулю.
Характеристики резонанса
Все параметры, входящие в цепь, и присутствующие в полученном уравнении, так или иначе, влияют на показатели, характеризующие резонансные явления. В зависимости от параметров, входящих в состав уравнения, решение может иметь несколько различных вариантов. При этом, все решения будут соответствовать собственному варианту и в дальнейшем обретать физический смысл.
В различных видах электро цепей, явление резонанса рассматривается, как правило, при анализе в случае нескольких вариантов. В этих же случаях может проводиться синтез цепи, в котором заранее заданы резонансные параметры.
Электрические цепи которые имеют большое количество связей и реактивных элементов, представляют собой серьезную проблему при проведении анализа. Их никогда не используют при синтезе с заранее заданными свойствами, поскольку далеко не всегда возможно получение желаемого результата. Поэтому, в практической деятельности производится исследование двухполюсных приборов самых простых конструкций и на основании полученных данных проводится создание более сложных цепей с заранее заданными параметрами.
Таким образом, резонанс электрической цепи представляет собой достаточно сложное явление, благодаря использованию в ней определенных элементов. Учет этого явления позволяет наиболее полно определить параметры и прочие характеристики.
Резонансы токов и напряжений
Начнём с основных определений.
Определение 1
Резонанс — это явление, при котором частота колебаний какой-либо системы увеличивается колебаниями внешней силы.
Вынужденные колебания, источником которых является внешняя сила, увеличивают даже те колебания, амплитуда которых имеет довольно небольшие значения. Максимальный резонанс с наибольшей амплитудой возможен именно при совпадении частот внешнего воздействия и рассматриваемой системы.
Максимальный резонанс с наибольшей амплитудой возможен именно при совпадении частот внешнего воздействия и рассматриваемой системы.
Примером резонанса является раскачивание моста ротой солдат. Частота шага солдат, являющаяся по отношению к мосту примером вынужденных колебаний, при этом синхронизирована и может совпасть с собственной частотой колебаний моста. В результате мост может разрушиться.
Электрический резонанс в физике считается одним из распространенных в мире физических явлений, без которого было бы невозможным, например, телевидение и диагностика с помощью медицинских аппаратов.
Одними из наиболее полезных видов резонанса в электрической цепи являются:
- резонанс токов;
- резонанс напряжений.
Возникновение резонанса в электрической цепи
Замечание 1
Возникновению резонанса в электрической цепи способствует резкое увеличение амплитуды стационарных собственных колебаний системы при условии совпадения частоты внешней стороны воздействия и соответствующей колебательной резонансной частоты системы.
Схема $RLC$ представляет электрическую цепь с соединенными последовательным или параллельным образом элементами (резистора, индуктора, конденсатора). Название $RLC$ состоит из простых символов электрических элементов: сопротивления, емкости, индуктивности.
Векторная диаграмма последовательной $RLC$-цепи представлена в одной из трех вариаций:
- емкостной;
- активной;
- индуктивной.
В последней вариации резонанс напряжений возникает при условии нулевого сдвига фаз, и совпадении значений индуктивного и емкостного сопротивлений.
Резонанс напряжений
При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может возникать такое физическое явление, как резонанс напряжений. Колебания источника напряжения в этом случае будут равны по частоте колебаниям контура. При этом известна как полезность (например, в радиотехнике) этого явления, так и негативные последствия (для электрических установок большой мощности), например, при резком скачке напряжения в системах возможно возникновение неисправности или даже пожара. 2L}$
2L}$
Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется максимальной и равной:
Это предполагает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по своему значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, существенно превосходящее напряжение на зажимах цепи.
Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:
$Q = \frac{U_c0}{U}$
Величина $Q$ характеризует резонансные свойства контура, называясь при этом добротностью контура. Также резонансные свойства характеризуются величиной $\frac{1}{Q}$, то есть — затуханием контура.
Резонанс токов через реактивные элементы
Резонанс токов появляется в электроцепях цепях переменного тока при условии параллельного соединения ветвей с разнохарактерными реактивными сопротивлениями. В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее собственной реактивной емкостной проводимости, т.е. $BL = BC$.
В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее собственной реактивной емкостной проводимости, т.е. $BL = BC$.
Колебания контура, частота которых имеет определённое значение, в данном случае совпадают по частоте с источником напряжения.
Простейшей электроцепью, в которой мы наблюдаем резонанс токов, считается цепь с параллельным соединением конденсатора с катушкой индуктивности.
Поскольку сопротивления реактивности равнозначны по модулю, амплитуды токов $I_c$ и $I_u$ будут одинаковыми и смогут достигать максимальной амплитуды. На основании первого закона Кирхгофа $IR$ равен току источника. Ток источника, иными словами, протекает только через резистор. При рассмотрении отдельного параллельного контура $LC$, на резонансной частоте его сопротивление оказывается бесконечно большим: $ZL = ZC$. При установлении гармонического режима с резонансной частотой, в контуре наблюдается обеспечение источником установившейся определенной амплитуды колебаний, а мощность источника тока при этом расходуется исключительно на пополнение потерь в активном сопротивлении.
Таким образом, у последовательной $RLC$ цепи импеданс оказывается минимальным на резонансной частоте и равным активному сопротивлению контура. В то же время, у параллельной $RLC$ цепи импеданс максимальный на резонансной частоте и считается равным сопротивлению утечки, фактически также активному сопротивлению контура. С целью обеспечения условий для резонанса силы тока или напряжения, требуется проверка электрической цепи для предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимая часть должна приравниваться к нулю.
Применение явления резонанса
Хороший пример использования резонансного явления представляет электрический резонансный трансформатор, разработанный Николой Тесла ещё в 1891 году. Ученый проводил эксперименты на разных конфигурациях, состоящих в сочетании из двух, а зачастую и трех резонансных электроцепей.
Замечание 2
Термин «катушки Теслы» применяют к высоковольтным резонансным трансформаторам. Устройства используют при получении высокого напряжения, частоты переменного тока. Обычный трансформатор необходим для эффективной передачи энергии с первичной на вторичную обмотку, резонансный используется для временного хранения электроэнергии.
Обычный трансформатор необходим для эффективной передачи энергии с первичной на вторичную обмотку, резонансный используется для временного хранения электроэнергии.
Устройство отвечает за управление воздушным сердечником настроенного резонансно трансформатора с целью получения высоких напряжений при малых значениях силы токов. Каждая обмотка обладает емкостью и функционирует в качестве резонансного контура. Для произведения наибольшего выходного напряжения первичный и вторичный контуры настраивают в резонанс друг с другом.
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений
и резонанс токов
.
Резонанс напряжений возникает в последовательной RLC-цепи .
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=w р, а следовательно и индуктивного и емкостного сопротивлений x L =x C . Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке U L и на конденсаторе U C будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке U L и на конденсаторе U C будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения U C и U L могут быть намного больше, чем напряжение , что опасно для цепи.
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=w р, следовательно проводимости B L =B C . То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.
Выразим резонансную частоту
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Поделись статьей:
Похожие статьи
Рабочий лист резонанса
— Электрические цепи переменного тока
Позвольте электронам сами дать вам ответы на ваши собственные «практические проблемы»!
Примечания:
По моему опыту, студентам требуется много практики с анализом цепей, чтобы стать профессионалом. С этой целью инструкторы обычно предоставляют своим ученикам множество практических задач, над которыми нужно работать, и дают ученикам ответы, с которыми они могут проверить свою работу. Хотя такой подход позволяет студентам овладеть теорией схем, он не дает им полноценного образования.
С этой целью инструкторы обычно предоставляют своим ученикам множество практических задач, над которыми нужно работать, и дают ученикам ответы, с которыми они могут проверить свою работу. Хотя такой подход позволяет студентам овладеть теорией схем, он не дает им полноценного образования.
Студентам нужна не только математическая практика. Им также нужны настоящие практические схемы построения схем и использование испытательного оборудования. Итак, я предлагаю следующий альтернативный подход: ученики должны построить свои собственные «практические задачи» с реальными компонентами и попытаться математически предсказать различные значения напряжения и тока. Таким образом, математическая теория «оживает», и учащиеся получают практические навыки, которых они не достигли бы, просто решая уравнения.
Еще одна причина для использования этого метода практики — научить студентов научному методу : процессу проверки гипотезы (в данном случае математических предсказаний) путем проведения реального эксперимента. Студенты также разовьют реальные навыки поиска и устранения неисправностей, поскольку они время от времени допускают ошибки при построении схем.
Студенты также разовьют реальные навыки поиска и устранения неисправностей, поскольку они время от времени допускают ошибки при построении схем.
Выделите несколько минут времени со своим классом, чтобы ознакомиться с некоторыми «правилами» построения схем, прежде чем они начнутся. Обсудите эти проблемы со своими учениками в той же сократической манере, в которой вы обычно обсуждаете вопросы рабочего листа, вместо того, чтобы просто говорить им, что они должны и не должны делать. Я никогда не перестаю удивляться тому, насколько плохо студенты понимают инструкции, представленные в типичном формате лекции (монолог преподавателя)!
Отличный способ познакомить студентов с математическим анализом реальных цепей — попросить их сначала определить значения компонентов (L и C) на основе измерений переменного напряжения и тока.Самая простая схема, конечно же, представляет собой отдельный компонент, подключенный к источнику питания! Это не только научит студентов правильно и безопасно настраивать цепи переменного тока, но также научит их измерять емкость и индуктивность без специального испытательного оборудования.
Примечание по реактивным компонентам: используйте качественные конденсаторы и катушки индуктивности, а для источника питания постарайтесь использовать низкие частоты. Небольшие понижающие силовые трансформаторы хорошо подходят для катушек индуктивности (по крайней мере, два индуктора в одном корпусе!), Пока напряжение, приложенное к любой обмотке трансформатора, меньше номинального напряжения этого трансформатора для этой обмотки (во избежание насыщения сердечника ).
Примечание для тех инструкторов, которые могут жаловаться на «потраченное впустую» время, необходимое ученикам для построения реальных схем вместо того, чтобы просто математически анализировать теоретические схемы:
Какова цель студентов, посещающих ваш курс?
Если ваши ученики будут работать с реальными схемами, им следует по возможности учиться на реальных схемах. Если ваша цель — обучить физиков-теоретиков, то во что бы то ни стало придерживайтесь абстрактного анализа! Но большинство из нас планирует, чтобы наши ученики что-то делали в реальном мире с образованием, которое мы им даем. «Потраченное впустую» время, потраченное на создание реальных схем, принесет огромные дивиденды, когда им придет время применить свои знания для решения практических задач.
«Потраченное впустую» время, потраченное на создание реальных схем, принесет огромные дивиденды, когда им придет время применить свои знания для решения практических задач.
Кроме того, когда студенты создают свои собственные практические задачи, они учатся выполнять первичных исследований , тем самым давая им возможность продолжить свое образование в области электротехники / электроники в автономном режиме.
В большинстве наук реалистичные эксперименты намного сложнее и дороже, чем электрические схемы. Профессора ядерной физики, биологии, геологии и химии хотели бы, чтобы их студенты применяли передовую математику в реальных экспериментах, не представляющих опасности для безопасности и стоивших меньше, чем учебник.Они не могут, но вы можете. Воспользуйтесь удобством, присущим вашей науке, и заставит ваших учеников практиковать математику на множестве реальных схем!
Q-фактор
и полоса пропускания резонансной цепи | Резонанс
Коэффициент добротности или качества резонансного контура является мерой «качества» или качества резонансного контура. Более высокое значение этого показателя качества соответствует более узкой полосе пропускания, что желательно во многих приложениях. Более формально Q — это отношение накопленной мощности к мощности, рассеиваемой в реактивном сопротивлении и сопротивлении цепи, соответственно:
Более высокое значение этого показателя качества соответствует более узкой полосе пропускания, что желательно во многих приложениях. Более формально Q — это отношение накопленной мощности к мощности, рассеиваемой в реактивном сопротивлении и сопротивлении цепи, соответственно:
Q = P сохранено / P рассеивается = I 2 X / I 2 R Q = X / R где: X = емкостное или индуктивное реактивное сопротивление при резонансе R = последовательное сопротивление.
Эта формула применима к последовательным резонансным цепям, а также к параллельным резонансным цепям, если сопротивление включено последовательно с индуктором. Так обстоит дело в практических приложениях, поскольку нас больше интересует сопротивление катушки индуктивности, ограничивающее Q.
Примечание: Некоторый текст может отображать местами X и R в формуле «Q» для параллельного резонансного контура. Это верно для большого значения R параллельно с C и L. Наша формула верна для небольшого R, идущего последовательно с L.
Наша формула верна для небольшого R, идущего последовательно с L.
Практическое применение «Q» состоит в том, что напряжение на L или C в последовательном резонансном контуре в Q раз больше общего приложенного напряжения. В параллельном резонансном контуре ток через L или C в Q раз больше общего приложенного тока.
Резонансные цепи серии
Последовательный резонансный контур выглядит как сопротивление на резонансной частоте. Поскольку определение резонанса — X L = X C , реактивные компоненты нейтрализуются, оставляя только сопротивление, чтобы вносить вклад в импеданс.
Импеданс также минимален в резонансе. Ниже резонансной частоты последовательный резонансный контур выглядит емкостным, поскольку полное сопротивление конденсатора увеличивается до значения, превышающего уменьшающееся индуктивное реактивное сопротивление, оставляя чистое емкостное значение.
Выше резонанса индуктивное реактивное сопротивление увеличивается, емкостное реактивное сопротивление уменьшается, оставляя чистую индуктивную составляющую.
ПРИМЕЧАНИЕ:
При резонансе последовательный резонансный контур выглядит чисто резистивным.Ниже резонанса он выглядит емкостным. Выше резонанса он кажется индуктивным. Ток максимален при резонансе, импеданс минимален. Ток устанавливается величиной сопротивления. Выше или ниже резонанса сопротивление увеличивается.
Импеданс минимален при резонансе в последовательном резонансном контуре.
Пик резонансного тока может быть изменен путем изменения последовательного резистора, который изменяет добротность. Это также влияет на ширину кривой.Схема с низким сопротивлением и высокой добротностью имеет узкую полосу пропускания по сравнению с схемой с высоким сопротивлением и низкой добротностью.
Ширина полосы по добротности и резонансной частоте:
BW = f c / Q Где f c = резонансная частота Q = добротность
Резонансный контур с высокой добротностью имеет узкую полосу пропускания по сравнению с контуром с низкой добротностью
Ширина полосы измеряется между точками амплитуды тока 0,707. Точки тока 0,707 соответствуют точкам половинной мощности, поскольку P = I 2 R, (0,707) 2 = (0,5).
Точки тока 0,707 соответствуют точкам половинной мощности, поскольку P = I 2 R, (0,707) 2 = (0,5).
Полоса пропускания Δf измеряется между точками амплитуды 70,7% последовательного резонансного контура.
BW = Δf = f h -f l = f c / Q Где: f h = край верхней полосы f l = край нижней полосы f l = f c - Δf / 2 f h = f c + Δf / 2 Где f c = центральная частота (резонансная частота)
На рисунке выше 100% текущая точка составляет 50 мА.Уровень 70,7% составляет 0,707 (50 мА) = 35,4 мА. Верхний и нижний края полосы, считанные с кривой, составляют 291 Гц для f и 355 Гц для f h . Полоса пропускания составляет 64 Гц, а точки половинной мощности составляют ± 32 Гц от центральной резонансной частоты:
.
BW = Δf = f h -f l = 355-291 = 64 f l = f c - Δf / 2 = 323-32 = 291 f h = f c + Δf / 2 = 323 + 32 = 355
Так как BW = fc / Q:
Q = f c / ЧБ = (323 Гц) / (64 Гц) = 5
Параллельные резонансные схемы
Полное сопротивление параллельного резонансного контура максимально на резонансной частоте. Ниже резонансной частоты параллельный резонансный контур выглядит индуктивным, поскольку импеданс катушки индуктивности ниже, и на нее потребляется большая часть тока.
Ниже резонансной частоты параллельный резонансный контур выглядит индуктивным, поскольку импеданс катушки индуктивности ниже, и на нее потребляется большая часть тока.
Выше резонанса емкостное реактивное сопротивление уменьшается, потребляя больший ток, таким образом, принимая емкостную характеристику.
Параллельный резонансный контур является резистивным при резонансе, индуктивным ниже резонанса, емкостным выше резонанса.
Полное сопротивление является максимальным при резонансе в параллельном резонансном контуре, но уменьшается выше или ниже резонанса.Напряжение достигает пика при резонансе, поскольку напряжение пропорционально импедансу (E = IZ).
Параллельный резонансный контур: Пики импеданса при резонансе.
Низкая добротность из-за высокого сопротивления, включенного последовательно с катушкой индуктивности, дает низкий пик на широкой кривой отклика для параллельного резонансного контура. Высокая добротность обусловлена низким последовательным сопротивлением катушки индуктивности. Это дает более высокий пик на более узкой кривой отклика. Высокая добротность достигается за счет наматывания на индуктор большего диаметра (меньшего сечения) провода с меньшим сопротивлением.
Высокая добротность обусловлена низким последовательным сопротивлением катушки индуктивности. Это дает более высокий пик на более узкой кривой отклика. Высокая добротность достигается за счет наматывания на индуктор большего диаметра (меньшего сечения) провода с меньшим сопротивлением.
Параллельный резонансный отклик зависит от добротности.
Ширина полосы параллельного резонансного отклика измеряется между точками половинной мощности. Это соответствует точкам напряжения 70,7%, поскольку мощность пропорциональна E 2 . ((0.707) 2 = 0.50) Поскольку напряжение пропорционально импедансу, мы можем использовать кривую импеданса.
Полоса пропускания, Δf измеряется между 70.Точки полного сопротивления 7% параллельного резонансного контура.
На рисунке выше точка 100% импеданса составляет 500 Ом. Уровень 70,7% составляет 0707 (500) = 354 Ом. Верхний и нижний края полосы, считанные с кривой, составляют 281 Гц для fl и 343 Гц для fh. Полоса пропускания составляет 62 Гц, а точки половинной мощности составляют ± 31 Гц от центральной резонансной частоты:
Полоса пропускания составляет 62 Гц, а точки половинной мощности составляют ± 31 Гц от центральной резонансной частоты:
.
BW = Δf = f h -f l = 343-281 = 62 f l = f c - Δf / 2 = 312-31 = 281 f h = f c + Δf / 2 = 312 + 31 = 343
Q = fc / BW = (312 Гц) / (62 Гц) = 5
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Резонанс в управляемой цепи RLC
Резонанс в управляемой цепи RLC
За последние несколько недель в лекции было обсуждено несколько схем.В цепи, состоящей
катушки индуктивности и конденсатора (LC) энергия будет колебаться между двумя элементами, сначала
сохраняется в магнитном поле индуктора, а затем в электрическом поле конденсатора.
Более реалистичная схема (RLC) включает эффекты сопротивления, и в этом случае сохраненная
энергия уменьшается, поскольку некоторые переходят на резистивный нагрев. Формулы для напряжений и токов
в схемах RLC объединяет синусоидальную функцию и экспоненту с затуханием.
Схема, которую мы рассмотрим сегодня, имеет источник питания переменного тока, добавляющий энергию в схему.Концептуально мы можем представить ребенка на качелях. Взрослый толкает ребенка на
правильная частота, ребенок будет подниматься все выше и выше. Если взрослый плохо справляется
толкать (то есть толкать в неподходящее время), движению ребенка не поможет
толкать. Лучшее время для толчка будет соответствовать собственной частоте замаха, так как
определяется длиной качелей и силой тяжести.
В терминах электрической цепи мы можем записать формулу падения напряжения около
последовательная цепь:
V всего = V L + V R + V C ,
Где V L — напряжение на катушке индуктивности, V R — напряжение на резисторе, а V C
напряжение на конденсаторе.Так как В итого должно быть равно входному напряжению, мы
можно написать:
V Sin (вес) = L dI / dt + RI + q / C
Или:
V Sin (wt) = L d 2 q / dt 2 + R dq / dt + q / C.
Формулы, удовлетворяющие этому дифференциальному уравнению второго порядка, приведены на рисунке 1.
Рисунок 1 — Формулы для управляемой цепи RLC
Обычный подход к решению дифференциального уравнения — использовать векторную диаграмму
подход.Фазоры связывают напряжение на элементе схемы с протекающим током.
через это. У резисторов ток и напряжение совпадают по фазе, в индукторах фаза напряжения опережает
ток на π / 2, а в конденсаторах фаза напряжения отстает от тока на π / 2.
Ток в цепи максимизируется, когда угловая частота равна
к (LC) -0,5 . Это известно как «резонансная частота». Когда мы удаляемся от
резонансная частота, отклик цепи упадет.Мы будем зондировать
Схема RLC с разными частотами и установим кривую отклика. Ширина
пика вокруг резонансной частоты измеряется «Q», качество
схема. Математически Q = ω o L / R, где ω o — резонансная частота.
Экспериментально Q = ω o / (ω 2 — ω 1 ), где ω 2 и ω 1 — частоты, где
мощность в цепи составляет 1/2 ее пикового значения.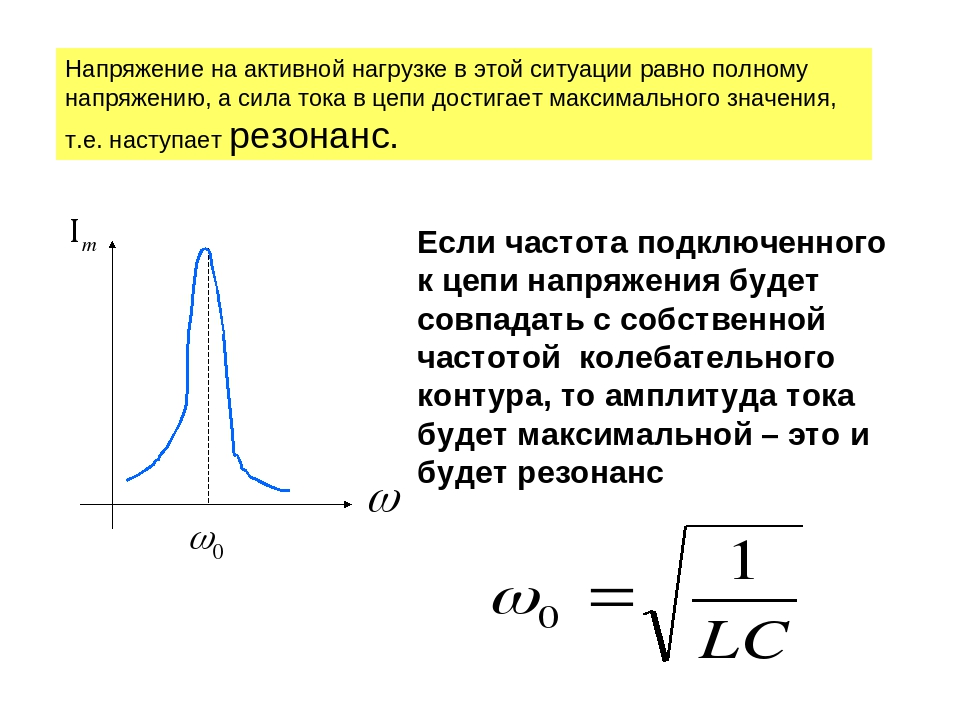 Поскольку мощность связана с квадратом тока, и
Поскольку мощность связана с квадратом тока, и
поскольку ток пропорционален напряжению в резисторе, если ω o — пиковая частота
тогда ω 1 и ω 2 — частоты по обе стороны от напряжения
через резистор есть.707 пикового значения,
Процедура:
Поместите Т-образный соединитель на выход вашего функционального генератора. Отправьте один выход на первый канал
вашего осциллографа. Убедитесь, что вы видите на телескопе синусоидальную волну.
Следующим шагом является подключение цепи RCL. Используйте индуктор на плате RLC
и подключите его последовательно с конденсатором. Завершите схему, подключив резистор
последовательно. См. Рисунок 2. Попросите инструктора проверить вашу схему перед включением.
сила.В этой лаборатории вы будете использовать индуктор 8,2 мГн. Ваш выбор для
резистор 10 Ом, 33 Ом и 100 Ом, а для конденсатора 100 мкФ и 330 мкФ. Прежде чем вы придете в
лаборатории, определите хорошие значения для C и R, чтобы получить резонансную частоту, которую вы можете
сгенерируйте с помощью генератора функций и пика, достаточно узкого для измерения.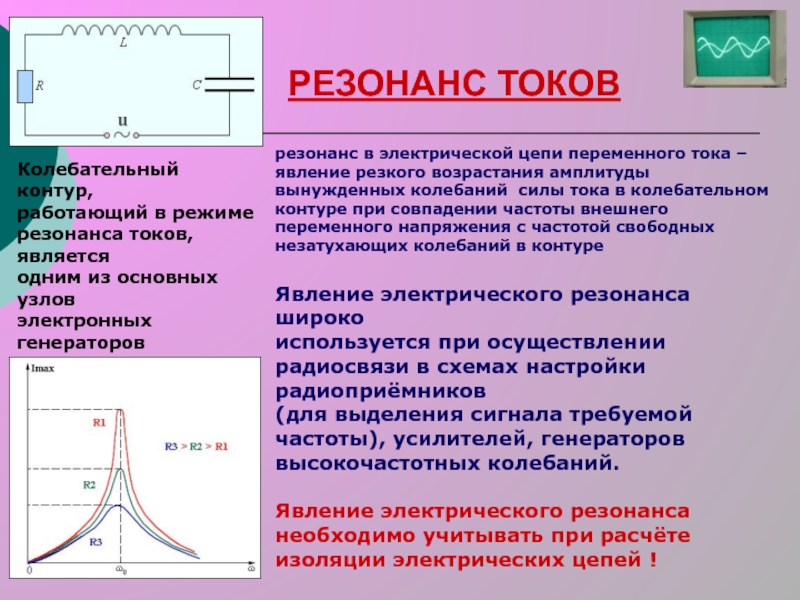 Рисование векторных диаграмм
Рисование векторных диаграмм
предлагаемой схемы в вашем ноутбуке на ω o , ω 1 и ω 2 с
как можно подробнее.
Рисунок 2 — Электропроводка, вид сбоку
Измерьте напряжение на резисторе на втором канале осциллографа.Через закон Ома
это дает ток через цепь. Если вы просматриваете оба канала, вы должны увидеть экран
как на рисунке 3.
Рисунок 3 — Осциллограф с управляющим напряжением и напряжением на резисторе
Не снимайте данные о напряжении в своем ноутбуке, постройте резонансную кривую цепи RLC.
Вам нужно будет использовать логарифмическую шкалу для вашей частоты. Принесите следующие
миллиметровка в лабораторию
(указывает, если вы дождетесь, пока лаборатория напечатает это). Если вы не знаете, как использовать бумагу для полулоготипа,
см. следующий праймер.Обратите внимание, что в
В нашей лаборатории независимой переменной является частота, которая будет охватывать несколько десятилетий. Следовательно, логарифмический масштаб
будет по оси абсцисс.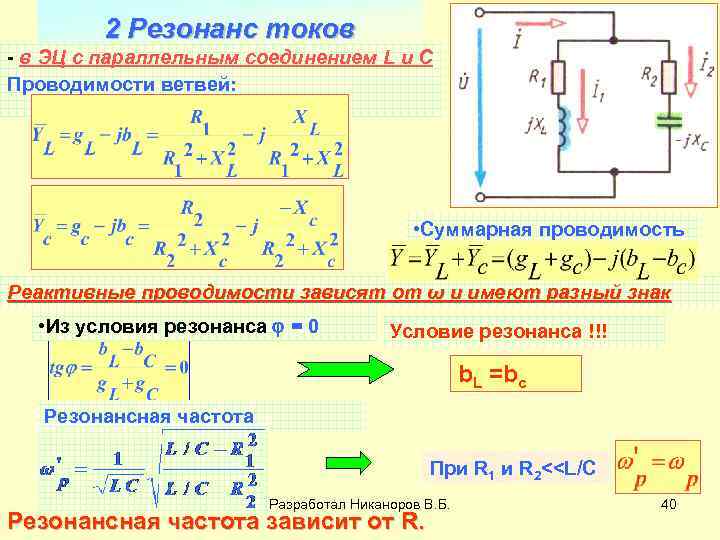
Резкость пика измеряется величиной, известной как «Q». Что вы измеряете
значение Q? Соответствует ли это теоретическому значению
Q = ω o L / R?
Прокомментируйте относительную фазу управляющего напряжения и тока в цепи как
функция частоты. Можете ли вы придумать нематематическое объяснение поведения?
Емкостное реактивное сопротивление — обзор
Символ реактивного сопротивления.
Символ емкостного реактивного сопротивления.
Символ индуктивного реактивного сопротивления.
Система демодуляции цветного ТВ, в которой два повторно вставленных сигнала поднесущей 3,58 МГц отличаются примерно на 60 °, а не на обычные 90 °. Напряжения R — Y, B — Y и G — Y выводятся из демодулированных сигналов, и эти напряжения управляют тремя пушками кинескопа. Важным преимуществом этой системы является то, что схема приемника проще, чем требуется при I- и Q-демодуляции.
Важным преимуществом этой системы является то, что схема приемника проще, чем требуется при I- и Q-демодуляции.
1. Референтная ось в кристалле кварца. 2. Горизонтальная ось в системе прямоугольных координат. 3. Направление по горизонтали или слева направо в двумерной системе координат. X-X обозначает одно направление, в котором следует метод пошагового повторения.
Радиочастотный диапазон от 5200 до 11000 МГц с длинами волн 5.От 77 до 2,75 см.
Прямоугольный кристаллический стержень, обычно вырезанный из Z-образного сечения, вытянутый параллельно X и с краями, параллельными X, Y и Z.
Конденсатор для подавления радиопомех, предназначенный для применений, в которых отказ конденсатора не приведет к опасности поражения электрическим током.
Кристалл, вырезанный так, что его основные поверхности перпендикулярны электрической оси (X) исходного кристалла кварца.
Инертный газ, используемый в некоторых тиратронах и других газовых трубках.
Источник некогерентного белого света высокой интенсивности; он работает путем разряда конденсатора через ксеноновую трубку. Такое устройство часто используется в качестве источника излучения накачки для различных лазеров с оптическим возбуждением.
Устройство для печати оптического изображения на бумаге; светлые и темные области представлены электростатически заряженными и незаряженными участками на бумаге.Порошковые чернила, присыпанные пылью на бумаге, прилипают к заряженным участкам и впоследствии растворяются в бумаге под воздействием тепла.
Ксерографическая запись.
1. Эта ветвь электростатической электрофотографии, в которой изображения формируются на фотопроводящей изолирующей среде с помощью инфракрасного, видимого или ультрафиолетового излучения. Затем среду присыпают порошком, который прилипает только к электростатически заряженному изображению.Затем применяется тепло, чтобы сплавить порошок в постоянное изображение. 2. Процесс печати электростатической электрофотографии, в котором используется фотопроводящая изолирующая среда в сочетании с инфракрасным, видимым или ультрафиолетовым излучением для создания структур скрытого электростатического заряда для достижения наблюдаемых данных.
Затем среду присыпают порошком, который прилипает только к электростатически заряженному изображению.Затем применяется тепло, чтобы сплавить порошок в постоянное изображение. 2. Процесс печати электростатической электрофотографии, в котором используется фотопроводящая изолирующая среда в сочетании с инфракрасным, видимым или ультрафиолетовым излучением для создания структур скрытого электростатического заряда для достижения наблюдаемых данных.
Эта ветвь электростатической электрофотографии, в которой узор из изоляционного материала на проводящей среде используется для формирования структур электростатического заряда для использования при копировании.
Процесс печати электростатической электрофотографии, в котором используется светопроводящая изолирующая среда в сочетании с рентгеновскими или гамма-лучами для создания структур скрытого электростатического заряда для достижения наблюдаемого рисунка.
Оборудование, использующее принципы электростатики и фотопроводимости для записи рентгеновских изображений на сенсибилизированную пластину через короткое время после экспонирования.
Сокращенное обозначение трансформатора.
Сокращенное обозначение транзистора.
Экранированный трехжильный микрофонный штекер или розетка с фиксатором для разблокировки пальцами для предотвращения случайного извлечения. Стандартный разъем для профессиональных пользователей микрофонов.
Аббревиатура передатчика.Также сокращенно trans или xmtr.
Сокращенное обозначение передачи.
Аббревиатура передатчика. Также сокращенно транс или xmitter.
Также сокращенно транс или xmitter.
Передатчик выключен.
Датчик включен.
Частица, имеющая такой же отрицательный заряд, что и электрон, но масса между электроном и протоном.Он создается космическим излучением, падающим на молекулы газа или фактически составляющим часть космических лучей.
Рентгеновская трубка и принадлежности к ней, включая рентгеновский аппарат.
1. Использование рентгеновских лучей для изучения расположения атомов в кристалле. 2. Изучение структуры кристаллических материалов с использованием взаимодействия рентгеновских лучей и электронной плотности кристалла (дифракции).
Устройство, обнаруживающее неоднородности поверхности и объема твердых тел с помощью рентгеновских лучей.
Камера, которая направляет пучок рентгеновских лучей на образец неизвестного материала и позволяет полученным дифрагированным лучам воздействовать на полосу пленки.
Картина, полученная на пленке, экспонированной с помощью рентгеновской дифракционной камеры.Он состоит из частей кругов с разным расстоянием между ними в зависимости от исследуемого материала.
Прибор, который определяет положение электрических осей кристалла кварца путем отражения рентгеновских лучей от атомных плоскостей кристалла.
Также называемые рентгеновскими лучами. Проникающее излучение, подобное свету, но имеющее гораздо более короткие длины волн (от 10 –7 до 10 –10 см).Обычно они генерируются при бомбардировке металлической мишени потоком высокоскоростных электронов.
Прибор, который используется для построения диаграмм дифракции рентгеновских лучей, например рентгеновский спектрометр с фотографическими или другими регистрирующими устройствами.
1. Прибор для получения спектра рентгеновского излучения и измерения длин волн его компонентов. 2. Прибор, предназначенный для получения рентгеновского спектра материала в качестве помощи в его идентификации.Этот метод особенно полезен, когда материал не может быть физически разрушен.
Расположение пучка рентгеновских лучей в порядке длины волны.
Бесконтактный толщиномер, используемый для измерения и индикации толщины движущегося холоднокатаного стального листа в процессе прокатки. Рентгеновский луч, направленный через лист, поглощается пропорционально толщине материала и его атомному номеру, и измерение количества поглощения дает непрерывное указание толщины листа.
Вакуумная трубка, в которой рентгеновские лучи производятся путем бомбардировки мишени высокоскоростными электронами, ускоренными электростатическим полем.
Также известен как антикатод. Электрод или электродная секция, на которую фокусируется электронный луч и излучает рентгеновские лучи.
Аббревиатура для кварцевого стабилизатора.
Аббревиатура кристалла.
Одна из двух составляющих, на которые магнитное поле Земли делит радиоволну в ионосфере. Другой компонент — обыкновенная, или О- волна.
Кристалл, ограненный таким образом, что его характеристики находятся между кристаллами X- и Y-огранки.
1. Устройство, используемое вместе с компьютером для нанесения координатных точек в виде графика. 2. Компьютерное устройство вывода, которое реагирует на цифровые сигналы предварительно записанных и / или обработанных данных путем распечатки линейных сегментов. Эти данные, которые могут включать буквенно-цифровые символы, диаграммы, таблицы или рисунки, загружаются из памяти компьютера со скоростью, достаточно низкой для плоттера. XY-плоттер нельзя использовать для прямой записи аналоговых сигналов без дигитайзеров.
Устройство, используемое вместе с компьютером для нанесения координатных точек в виде графика. 2. Компьютерное устройство вывода, которое реагирует на цифровые сигналы предварительно записанных и / или обработанных данных путем распечатки линейных сегментов. Эти данные, которые могут включать буквенно-цифровые символы, диаграммы, таблицы или рисунки, загружаются из памяти компьютера со скоростью, достаточно низкой для плоттера. XY-плоттер нельзя использовать для прямой записи аналоговых сигналов без дигитайзеров.
1.Регистратор, который отслеживает на диаграмме отношения между двумя переменными, ни одна из которых не является временем. Иногда диаграмма перемещается, и одна из переменных контролируется так, что взаимосвязь действительно увеличивается пропорционально времени. 2. Регистратор, в котором два сигнала записываются одновременно одним пером, которое приводится в движение в одном направлении (ось X) одним сигналом, а в другом направлении (ось Y) — вторым сигналом. 3. Регистратор данных, который используется для записи изменения одного параметра по отношению к другому.Например, изменение давления в зависимости от температуры. Для этих самописцев доступен широкий спектр преобразователей для преобразования физических параметров в электрические сигналы, которые можно использовать в самописце. Датчики давления, термопары, тензодатчики и акселерометры — вот несколько примеров. 4. Тип регистратора, который реагирует на поступающие аналоговые сигналы по мере их появления. Сигналы печатаются на графике заранее определенного размера, который может охватывать тестовые периоды от нескольких секунд до целого года. XY-рекордер записывает непрерывные линии.Кроме того, скорость отклика прибора важна для точности записи.
3. Регистратор данных, который используется для записи изменения одного параметра по отношению к другому.Например, изменение давления в зависимости от температуры. Для этих самописцев доступен широкий спектр преобразователей для преобразования физических параметров в электрические сигналы, которые можно использовать в самописце. Датчики давления, термопары, тензодатчики и акселерометры — вот несколько примеров. 4. Тип регистратора, который реагирует на поступающие аналоговые сигналы по мере их появления. Сигналы печатаются на графике заранее определенного размера, который может охватывать тестовые периоды от нескольких секунд до целого года. XY-рекордер записывает непрерывные линии.Кроме того, скорость отклика прибора важна для точности записи.
Переключатель с дистанционным управлением, расположенный так, что дворники перемещаются вперед и назад по горизонтали.
Напряжение и ток в последовательной резонансной цепи
Напряжение и ток в последовательной резонансной цепи:
Изменение импеданса и тока в зависимости от частоты напряжения и тока в последовательной резонансной цепи показано на рис. 8.7.
8.7.
На резонансной частоте емкостное реактивное сопротивление равно индуктивному реактивному сопротивлению, и, следовательно, полное сопротивление минимально. Из-за минимального импеданса через цепь протекает максимальный ток. График изменения тока в зависимости от частоты.
Падение напряжения на сопротивлении, индуктивности и емкости также зависит от частоты. При f = 0 конденсатор действует как разомкнутая цепь и блокирует ток. На конденсаторе появляется полное напряжение источника.По мере увеличения частоты X C уменьшается, а X L увеличивается, вызывая уменьшение общего реактивного сопротивления X C — X L . В результате сопротивление уменьшается, а ток увеличивается. По мере увеличения тока V R также увеличивается, а V C и V L увеличиваются.
Когда частота достигает своего резонансного значения f r , импеданс равен R, и, следовательно, ток достигает своего максимального значения, а V R имеет максимальное значение.
По мере увеличения частоты выше резонанса X L продолжает увеличиваться, а X C продолжает уменьшаться, вызывая увеличение общего реактивного сопротивления X L —X C . В результате происходит увеличение импеданса и уменьшение тока. По мере уменьшения тока V R также уменьшается, и как V C , так и V L уменьшаются. Когда частота становится очень высокой, ток приближается к нулю, и V R , и V C приближаются к нулю, а V L приближается к V S .
Отклик различных напряжений с частотой показан на рис. 8.8.
Падение сопротивления достигает максимума, когда f = f r . Максимальное напряжение на конденсаторе возникает при f = f c . Точно так же максимальное напряжение на катушке индуктивности возникает при f = f L .
Падение напряжения на катушке индуктивности
.
где
Чтобы получить условие максимального напряжения на катушке индуктивности, мы должны взять производную приведенного выше уравнения по частоте и сделать ее равной нулю.
Если мы решим для ω, мы получим значение ω, когда V L является максимальным.
Из этого
Аналогично напряжение на конденсаторе
Для получения максимального значения dV c / dω = 0
Если мы решим для ω, мы получим значение ω, когда V C является максимальным.
Из этого
Максимальное напряжение на конденсаторе ниже резонансной частоты; и максимальное напряжение на катушке индуктивности возникает выше резонансной частоты.
15.5 Резонанс в цепи переменного тока — University Physics Volume 2
Задачи обучения
К концу этого раздела вы сможете:
- Определите пиковую резонансную угловую частоту переменного тока для цепи RLC
- Объясните ширину кривой зависимости средней мощности от угловой частоты и ее значение, используя такие термины, как полоса пропускания и коэффициент качества
В последовательной цепи RLC , показанной на рисунке 15. 11, амплитуда тока определяется уравнением 15.10,
11, амплитуда тока определяется уравнением 15.10,
I0 = V0R2 + (ωL − 1 / ωC) 2. I0 = V0R2 + (ωL − 1 / ωC) 2.
15.15
Если мы можем изменять частоту генератора переменного тока, сохраняя при этом постоянную амплитуду его выходного напряжения, то ток изменится соответствующим образом. График зависимости I0I0 от ωω показан на рисунке 15.17.
Фигура
15,17
На резонансной частоте контура RLC , ω0 = 1 / LC, ω0 = 1 / LC, амплитуда тока имеет максимальное значение.
В «Колебаниях» мы встретили похожий график, на котором амплитуда затухающего гармонического осциллятора была построена в зависимости от угловой частоты синусоидальной движущей силы (см. «Принудительные колебания»).Это сходство — больше, чем просто совпадение, как было показано ранее применением правила петли Кирхгофа к схеме на рис. 15.11. Это дает
Ldidt + iR + qC = V0sinωt, Ldidt + iR + qC = V0sinωt,
15,16
или
Ld2qdt2 + Rdqdt + 1Cq = V0sinωt, Ld2qdt2 + Rdqdt + 1Cq = V0sinωt,
, где мы заменили dq (t) / dt на i (t). Сравнение уравнения 15.16 и, из «Колебаний», «Затухающие колебания» для затухающего гармонического движения ясно демонстрирует, что управляемая последовательная цепь RLC является электрическим аналогом управляемого затухающего гармонического генератора.
Сравнение уравнения 15.16 и, из «Колебаний», «Затухающие колебания» для затухающего гармонического движения ясно демонстрирует, что управляемая последовательная цепь RLC является электрическим аналогом управляемого затухающего гармонического генератора.
Резонансная частота f0f0 цепи RLC — это частота, при которой амплитуда тока является максимальной, и цепь будет колебаться, если не будет управляться источником напряжения. При осмотре это соответствует угловой частоте ω0 = 2πf0ω0 = 2πf0, при которой импеданс Z в уравнении 15.15 является минимальным, или когда
и
Это резонансная угловая частота контура. Подставляя ω0ω0 в уравнение 15.9, уравнение 15.10 и уравнение 15.11, находим, что при резонансе
ϕ = tan − 1 (0) = 0, I0 = V0 / R и Z = R. ϕ = tan − 1 (0) = 0, I0 = V0 / R и Z = R.
Следовательно, в резонансе цепь RLC является чисто резистивной, с приложенной ЭДС и током в фазе.
Что происходит с мощностью при резонансе? Уравнение 15.14 говорит нам, как средняя мощность, передаваемая от генератора переменного тока комбинации RLC , изменяется в зависимости от частоты. Кроме того, PavePave достигает максимума, когда Z , который зависит от частоты, является минимумом, то есть когда XL = XCandZ = R.XL = XC и Z = R. Таким образом, при резонансе средняя выходная мощность источника в последовательной цепи RLC является максимальной. Из уравнения 15.14 этот максимум составляет Vrms2 / R.Vrms2 / R.
Рисунок 15.18 представляет собой типичный график зависимости PavePave от ωω в области максимальной выходной мощности. Ширина полосы ΔωΔω резонансного пика определяется как диапазон угловых частот ωω, в котором средняя мощность PavePave превышает половину максимального значения Pave.Pave. Резкость пика описывается безразмерной величиной, известной как добротность Q схемы. По определению
По определению
Q = ω0Δω, Q = ω0Δω,
15,18
где ω0ω0 — резонансная угловая частота. Высокое значение Q указывает на резкий пик резонанса. Мы можем дать Q в терминах параметров схемы как
Фигура
15,18
Как и ток, средняя мощность, передаваемая от генератора переменного тока к цепи RLC , достигает пика на резонансной частоте.
Резонансные цепи обычно используются для пропуска или отклонения выбранных частотных диапазонов.Это делается путем регулировки значения одного из элементов и, следовательно, «настройки» схемы на определенную резонансную частоту. Например, в радиоприемнике приемник настраивается на желаемую станцию путем регулировки резонансной частоты его схемы в соответствии с частотой станции. Если схема настройки имеет высокое значение Q , она будет иметь небольшую полосу пропускания, поэтому сигналы от других станций на частотах, даже немного отличающихся от резонансной частоты, имеют высокий импеданс и не проходят через схему. Сотовые телефоны работают аналогичным образом, передавая сигналы с частотой около 1 ГГц, которые настраиваются цепью индуктивности и конденсатора. Одним из наиболее распространенных применений конденсаторов является их использование в схемах синхронизации переменного тока, основанное на достижении резонансной частоты. Металлоискатель также использует сдвиг резонансной частоты при обнаружении металлов (рис. 15.19).
Сотовые телефоны работают аналогичным образом, передавая сигналы с частотой около 1 ГГц, которые настраиваются цепью индуктивности и конденсатора. Одним из наиболее распространенных применений конденсаторов является их использование в схемах синхронизации переменного тока, основанное на достижении резонансной частоты. Металлоискатель также использует сдвиг резонансной частоты при обнаружении металлов (рис. 15.19).
Фигура
15,19
Когда металлоискатель приближается к куску металла, самоиндукция одной из его катушек изменяется.Это вызывает сдвиг резонансной частоты цепи, содержащей катушку. Этот сдвиг фиксируется схемой и передается дайверу через наушники. (кредит: модификация работы Эрика Липпманна, ВМС США)
Пример
15.4
Резонанс в цепи серии
RLC
(a) Какова резонансная частота цепи, использующей значения напряжения и LRC, соединенные последовательно из Примера 15.1? (b) Если генератор переменного тока настроен на эту частоту без изменения амплитуды выходного напряжения, какова амплитуда тока?
Стратегия
Резонансная частота для цепи RLC рассчитывается по уравнению 15. 17, что является результатом баланса реактивных сопротивлений конденсатора и катушки индуктивности. Поскольку цепь находится в резонансе, сопротивление равно сопротивлению. Затем максимальный ток рассчитывается делением напряжения на сопротивление.
17, что является результатом баланса реактивных сопротивлений конденсатора и катушки индуктивности. Поскольку цепь находится в резонансе, сопротивление равно сопротивлению. Затем максимальный ток рассчитывается делением напряжения на сопротивление.
Решение
- Резонансная частота находится из уравнения 15.17:
f0 = 12π1LC = 12π1 (3,00 × 10–3H) (8,00 × 10–4F) = 1,03 × 102 Гц. f0 = 12π1LC = 12π1 (3,00 × 10–3H) (8,00 × 10–4F) = 1,03 × 102 Гц. - В резонансе полное сопротивление цепи является чисто резистивным, а амплитуда тока равна
I0 = 0.100 В 4,00 Ом = 2,50 × 10–2 А. I0 = 0,100 В 4,00 Ом = 2,50 × 10–2 А.
Значение
Если бы цепь не была настроена на резонансную частоту, нам потребовалось бы полное сопротивление всей цепи для расчета тока.
Пример
15.5
Передача мощности в цепи серии
RLC при резонансе
(a) Какова резонансная угловая частота цепи RLC с R = 0,200 Ом, R = 0,200 Ом, L = 4,00 × 10–3H, L = 4,00 × 10–3H и C = 2,00 × 10–6F ? C = 2,00 × 10−6F? (b) Если источник переменного тока постоянной амплитуды 4. На эту частоту установлено 00 В. Какова средняя мощность, передаваемая в цепь? (c) Определите Q и полосу пропускания этой цепи.
На эту частоту установлено 00 В. Какова средняя мощность, передаваемая в цепь? (c) Определите Q и полосу пропускания этой цепи.
Стратегия
Резонансная угловая частота рассчитывается по уравнению 15.17. Средняя мощность рассчитывается на основе действующего значения напряжения и сопротивления в цепи. Добротность рассчитывается по уравнению 15.19 и зная резонансную частоту. Полоса пропускания рассчитывается по уравнению 15.18 с учетом коэффициента качества.
Решение
- Резонансная угловая частота равна
ω0 = 1LC = 1 (4,00 × 10–3H) (2,00 × 10–6F) = 1,12 × 104рад / с. ω0 = 1LC = 1 (4,00 × 10–3H) (2,00 × 10–6F) = 1,12 × 104рад / с. с. - На этой частоте средняя мощность, передаваемая в цепь, является максимальной. это
Pave = Vrms2R = [(1/2) (4.00V)] 20.200Ω = 40.0W. Pave = Vrms2R = [(1/2) (4.00V)] 20.200Ω = 40.0W. - Добротность схемы составляет
Q = ω0LR = (1,12 × 104рад / с) (4,00 × 10–3H) 0,200 Ом = 224. Q = ω0LR = (1,12 × 104рад / с) (4,00 × 10–3H) 0,200 Ом = 224.
Q = ω0LR = (1,12 × 104рад / с) (4,00 × 10–3H) 0,200 Ом = 224.
Затем находим для пропускной способности
Δω = ω0Q = 1.12 × 104рад / с224 = 50,0рад / с. Δω = ω0Q = 1,12 × 104рад / с224 = 50,0рад / с.
Значение
Если требуется более узкая полоса пропускания, могут помочь более низкое сопротивление или более высокая индуктивность. Однако более низкое сопротивление увеличивает мощность, передаваемую в схему, что может быть нежелательно, в зависимости от максимальной мощности, которая может быть передана.
Проверьте свое понимание
15,6
Проверьте свое понимание В схеме на рисунке 15.11 L = 2,0 × 10–3H, L = 2,0 × 10–3H, C = 5.0 × 10–4F, C = 5,0 × 10–4F и R = 40 Ом, R = 40 Ом. а) Что такое резонансная частота? (б) Какое сопротивление цепи при резонансе? (c) Если амплитуда напряжения составляет 10 В, что такое и ( t ) в резонансе? (d) Частота генератора переменного тока теперь изменена на 200 Гц. Рассчитайте разность фаз между током и ЭДС генератора.
Рассчитайте разность фаз между током и ЭДС генератора.
Проверьте свое понимание
15,7
Проверьте свое понимание Что происходит с резонансной частотой цепи серии RLC , когда следующие величины увеличиваются в 4 раза: (а) емкость, (б) самоиндукция и (в) сопротивление?
Проверьте свое понимание
15.8
Проверьте свое понимание Резонансная угловая частота цепи серии RLC составляет 4,0 × 102рад / с. 4,0 × 102рад / с. Источник переменного тока, работающий на этой частоте, передает в схему среднюю мощность 2,0 × 10–2 Вт2,0 × 10–2 Вт. Сопротивление цепи составляет 0,50 Ом 0,50 Ом. Напишите выражение для ЭДС источника.
Увеличение напряжения
- • Опишите увеличение напряжения и коэффициент добротности в цепях серии LCR.

- • Рассчитайте увеличение напряжения по соответствующим формулам.
В ответах на вычисления в примере 9.2.2 должно быть заметно, что на резонансной частоте схемы r 107 кГц, реактивные напряжения на L и C равны, и каждое из них больше, чем напряжение питания цепи В S 100 В.
Это возможно, потому что в резонансе напряжение (В C = 199.56 В) на конденсаторе, находится в противофазе к напряжению (В L = 199,56 В) на индуктивности. Поскольку эти два напряжения равны и противоположны по фазе, они полностью компенсируют друг друга, оставляя только напряжение питания, развиваемое на импедансе цепи, которое в резонансе совпадает с общим сопротивлением 320 + 18 = 338 Ом.
На резонансной частоте ток в цепи имеет максимальное значение около 296 мА. Из-за эффекта компенсации фазы при резонансе два реактивных напряжения V C и V L «исчезли»! Это оставляет ток питания I S , эффективно протекающий через R, и сопротивление индуктора R L последовательно.
В этом примере влияние внутреннего сопротивления катушки индуктивности 18 Ом на V L настолько мало (0,03 В), что им можно пренебречь, а значение V L TOT совпадает с величиной V L примерно при 199,6 В. . .
Поскольку полное сопротивление цепи меньше, чем емкостное или индуктивное реактивное сопротивление при резонансе, напряжение питания 100 В (развиваемое на сопротивлении цепи) меньше любого из противостоящих реактивных напряжений V C или V L .Этот эффект, когда реактивные напряжения внутренних компонентов больше, чем напряжение питания, называется УВЕЛИЧЕНИЕМ НАПРЯЖЕНИЯ.
Это может быть очень полезным свойством и используется, например, в антенных каскадах радиоприемников, где последовательная цепь, резонансная на частоте принимаемой передачи, используется для увеличения амплитуды напряжения принимаемого сигнала напряжения перед тем, как оно подается на любые транзисторные усилители в схеме.
Увеличение напряжения, которое происходит при резонансе, обозначается символом Q, а «Q Factor» (увеличение напряжения) цепей полосового фильтра LC и полосового стопорного фильтра, например, управляет «отклонением», отношением желаемого к нежелательному. частоты, которые могут быть достигнуты схемой.
Эффекты увеличения напряжения особенно полезны, поскольку они могут обеспечить увеличение сигналов напряжения переменного тока с использованием только пассивных компонентов, то есть без необходимости в каком-либо внешнем источнике питания.
В некоторых случаях увеличение напряжения также может быть опасным. В оборудовании, работающем от сети (линии) высокого напряжения, имеющем индуктивность и емкость, при проектировании необходимо соблюдать осторожность, чтобы гарантировать, что цепь не резонирует на частотах, слишком близких к частоте сети (линии).Если это произойдет, в оборудовании могут возникнуть чрезвычайно высокие реактивные напряжения, что приведет к катастрофическим последствиям для схемы и / или пользователя.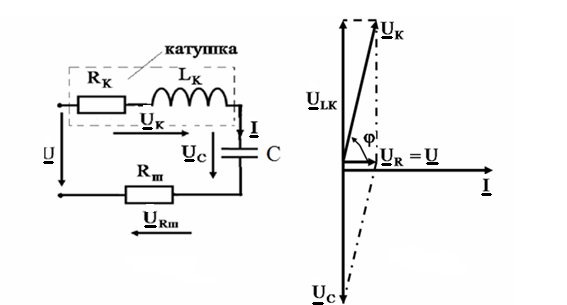
Коэффициент добротности можно рассчитать по простой формуле. Отношение напряжения питания V S к любому из (равных) реактивных напряжений V C или V L будет в том же соотношении, что и полное сопротивление цепи (R) к любому из реактивных сопротивлений (X C или X L ) в резонансе.Отношение реактивного напряжения V L к напряжению питания V S представляет собой коэффициент увеличения Q.
Формула для определения Q (увеличения напряжения) использует отношение индуктивного реактивного сопротивления к общему сопротивлению цепи.
Где X L — это индуктивное реактивное сопротивление при резонансе , равное 2πƒ r L, а R — ОБЩЕЕ сопротивление цепи. Обратите внимание, что Q не имеет единиц измерения (вольт, ом и т. Д.), Так как это ОТНОШЕНИЕ
.


 Q = ω0LR = (1,12 × 104рад / с) (4,00 × 10–3H) 0,200 Ом = 224.
Q = ω0LR = (1,12 × 104рад / с) (4,00 × 10–3H) 0,200 Ом = 224.