как связаны между собой напряжение, ток и сопротивление
Добавлено 30 сентября 2020 в 00:30
Сохранить или поделиться
Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.
Без упоминания двух конкретных точек термин «напряжение» не имеет значения.
Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:
| Величина | Символ | Единица измерения | Сокращение единицы измерения |
|---|---|---|---|
| Ток | I | Ампер | А |
| Напряжение | V | Вольт | В |
| Сопротивление | R | Ом | Ом |
«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.
Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.
Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.
Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Формула закона Ома
Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
\[E=IR\]
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:
Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:
\[I = \frac{E}{R}\]
\[R = \frac{E}{I}\]
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:
Рисунок 1 – Пример простой схемы
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы
Какая величина тока (I) в этой цепи?
\[I = \frac{E}{R} = \frac{12 \ В}{3 \ Ом} = 4 \ А\]
Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи
Известны напряжение источника и ток в цепи
Какое сопротивление (R) оказывает лампа?
\[R = \frac{E}{I} = \frac{36 \ В}{4 \ А} = 9 \ Ом\]
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы
Какое напряжение обеспечивает батарея?
\[E = IR = (2 \ А)(7 \ Ом) = 14 \ В\]
Метода треугольника закона Ома
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 5 – Треугольник закона Ома
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Рисунок 6 – Закон Ома для определения R
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Рисунок 7 – Закон Ома для определения I
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
Рисунок 8 – Закон Ома для определения E
В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Резюме
- Напряжение измеряется в вольтах, обозначается буквами «E» или «V».
- Сила тока измеряется в амперах, обозначается буквой «I».
- Сопротивление измеряется в омах, обозначается буквой «R».
- Закон Ома: E = IR; I = E/R; R = E/I
Оригинал статьи:
Теги
Закон ОмаЗарядКулонОбучениеСила токаСопротивлениеСхемотехникаЭлектрический токЭлектрическое напряжение
Сохранить или поделиться
Закон Ома для участка цепи
Закон Ома для участка цепи — это основной закон в электротехнике. Он устанавливает связь между током, сопротивлением и напряжением. С его помощью можно изучить и рассчитать электрические цепи. Важно не просто выучить закон Ома, а понять его, как он применяется на самом деле. Так как довольно часто происходят ошибки в его применении на практике, из-за не правильного его использования.
Важно не просто выучить закон Ома, а понять его, как он применяется на самом деле. Так как довольно часто происходят ошибки в его применении на практике, из-за не правильного его использования.
Закон Ома определение — ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Стоит поднять напряжение, проходящее по электро цепи, ток так же поднимется догнав напряжение. Подняв сопротивление в цепи, ток снизится во столько же раз, во сколько поднялось сопротивление. Это можно увидеть на простом примере, взять простую трубу и пустить через нее поток воды, чем выше давление тем сильнее поток воды, если же встречается сопротивление то поток воды значительно теряет свою скорость.
В математике принято считать: сопротивление проводника, в котором во время напряжения 1В протекает ток 1А — равняется 1Ом.
Закон Ома формула — расшифровывается как определение тока в амперах с помощью деления напряжения на сопротивление в омах.
I=U/R
Правильные вычисления по закону Ома будут только тогда , когда напряжение отражается в вольтах, сопротивление в Омах, ток в амперах. При использовании различных версий данных величин, следует их преобразовывать в нужные для вычисления величины.
Данный закон одинаков для всего участка цепи. В случае выяснения напряжения на конкретном участке, нужно будет брать размеры всех величин именно с этого участка.
Данный закон можно рассмотреть на примерах:
1)Определим ток в лампе с сопротивлением 2,5ОМ и напряжении 5В. Разделим 5 / 2,5 получим ток = 2А
2) Вычисляем, так же ток в лампе. с напряжением 500В и сопротивлением 0,5мОм (в Омах получается 500000). Разделим 500 / 500000 получим ток = 0,001А либо 1мА.
Когда ток и сопротивление известны, напряжение так же находят с помощью закона Ома. С помощью формулы:
U = IR
Из чего мы видим, напряжение в концах участка цепи ровно пропорционально току и сопротивлению.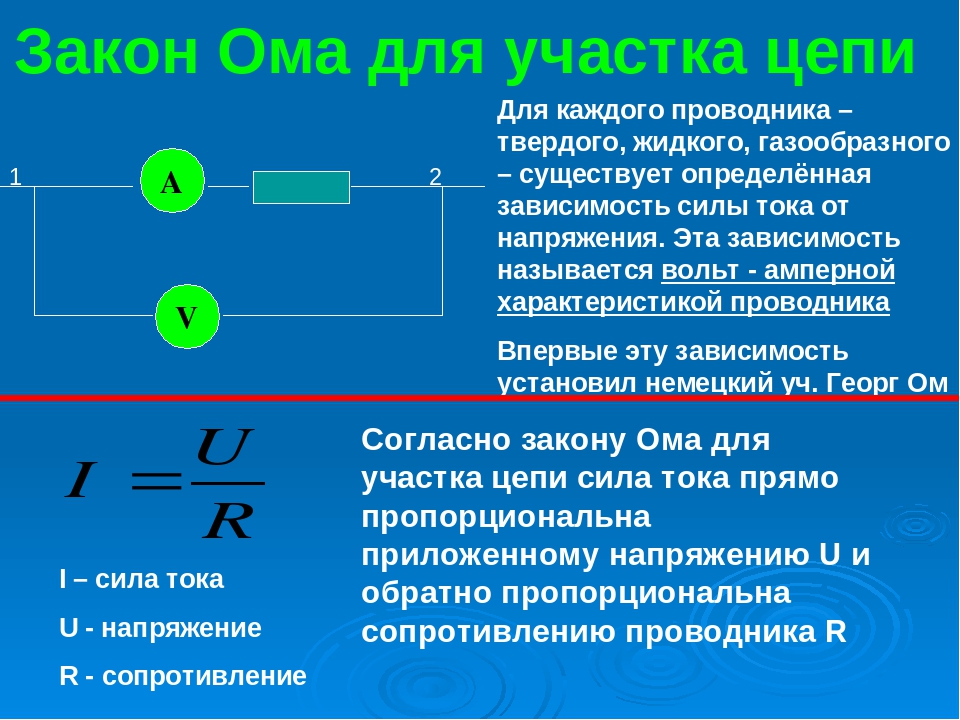 Так как увеличение тока без изменения сопротивления, возможно только при увеличения напряжения. Следовательно, постоянное сопротивление большему току, преследует большое напряжение. Если использовать постоянно одинаковый ток с разным сопротивлением, с большим сопротивлением нужно большее напряжение.
Так как увеличение тока без изменения сопротивления, возможно только при увеличения напряжения. Следовательно, постоянное сопротивление большему току, преследует большое напряжение. Если использовать постоянно одинаковый ток с разным сопротивлением, с большим сопротивлением нужно большее напряжение.
Вычисление напряжения можно рассмотреть на примере:
Вычислить напряжение с током = 5мАм (0,005А), сопротивление 10кОм (10000 Ом). Умножаем ток * напряжение = 50В.
Связь между током и напряжением называется — сопротивление. Увеличивается напряжение так же происходит и увеличение тока, ровно тоже происходит при уменьшении. Соотношение между напряжением и током = сопротивлению, которое не меняется. При рассмотрении двух участков с одинаковым током и разным напряжением, ясно, что в участке с большим напряжением, большее сопротивление. В случае же когда напряжение одинаково, а ток разный, то на участке где меньшее количество тока будет большее сопротивление.
Вычисление сопротивления можно рассмотреть на примере:
Найти сопротивление, имея напряжение 40В и ток 50мАм (0,05А). Поделим 40/0,05 сопротивление = 800 Ом.
Заметка: Интересуют двухуровневые натяжные потолки SATIN.BY. Перейдите по ссылке натяжной потолок (http://satin.by/natjazhnye-potolki.html) и узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
09-д. Закон Ома для участка цепи
§ 09-д. Закон Ома для участка цепи
В § 8-и мы начали знакомство с физической величиной «электрическое сопротивление». Продолжим его – проделаем опыт. Нам потребуются источник электроэнергии, амперметр, вольтметр, реостат и два резистора (две нихромовые спирали) с различными сопротивлениями.
Соберём цепь, как показано на рисунке слева или на схеме в конце параграфа. Перемещая движок реостата, поочерёдно установим значения силы тока 0,4 А, 0,6 А, 0,8 А, 1 А. Запишем показания амперметра и вольтметра в таблицу. Повторим опыт, заменив резистор, и дополним таблицу:
Запишем показания амперметра и вольтметра в таблицу. Повторим опыт, заменив резистор, и дополним таблицу:
Примеры экспериментальных значений силы тока и напряжения на двух различных проводниках: равным силам токов соответствуют различные напряжения.
| Первый резистор | Второй резистор | |||||||
| I , A | 0,4 | 0,6 | 0,8 | 1,0 | 0,4 | 0,6 | 0,8 | 1,0 |
| U , В | 1,6 | 2,4 | 3,2 | 4,0 | 2,4 | 3,6 | 4,8 | 6,0 |
| Поделив напряжение на силу тока, обнаружим закономерность: | ||||||||
| R = U/I | 4 | 4 | 4 | 4 | 6 | 6 | 6 | 6 |
Закономерность в том, что вне зависимости от значений напряжения и силы тока их частное остаётся постоянным для каждого резистора. Проверьте: после деления каждого числа строки (U, В) на расположенное над ним число строки (I, А) получаются одинаковые результаты во всех колонках левой половины таблицы: 4 В/А и во всех колонках правой половины таблицы: 6 В/А. Это показывает, что величина R является характеристикой именно изучаемого участка цепи – резистора.
Проверьте: после деления каждого числа строки (U, В) на расположенное над ним число строки (I, А) получаются одинаковые результаты во всех колонках левой половины таблицы: 4 В/А и во всех колонках правой половины таблицы: 6 В/А. Это показывает, что величина R является характеристикой именно изучаемого участка цепи – резистора.
Заметим, что эта закономерность всегда справедлива для металлических проводников в твёрдом или жидком состоянии; для других проводников она справедлива не всегда. Однако величину R, равную отношению U/I, всегда называют электрическим сопротивлением проводника независимо от его материала и состояния, а 1 В/А называют 1 Ом. Следовательно, 1 Ом – сопротивление такого проводника, в котором возникнет ток 1 А, если на концах проводника напряжение 1 В.
Связь между величинами U, I, R обычно записывается в виде формулы, известной как закон Ома для участка цепи:
Закон Ома для участка цепи: сила тока в твёрдом металлическом проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению этого проводника.
| I = | U | I – сила тока в участке цепи, А | |||
| R |
Чтобы выяснить, как следует прочитать эту формулу, вспомним знания по алгебре о видах пропорциональности величин.
Пояснение прямой и обратной пропорциональностей величин в законе Ома для участка цепи.
| прямая пропорциональность: | Y = k · X | → | I = 1/R · U |
| обратная пропорциональность: | Y = k / X | → | I = U / R |
Из первой строки следует: при постоянном сопротивлении величина 1/R тоже постоянна, поэтому сила тока прямо пропорциональна напряжению на концах участка цепи. Из второй строки: при постоянном напряжении сила тока обратно пропорциональна сопротивлению участка цепи. Объединяя это, получаем формулировку закона Ома для участка цепи: сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению этого участка.
Из второй строки: при постоянном напряжении сила тока обратно пропорциональна сопротивлению участка цепи. Объединяя это, получаем формулировку закона Ома для участка цепи: сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению этого участка.
Примечание. С точки зрения алгебры, формулу закона Ома можно записать в такой форме: U=I·R. Применим её для изучения цепи, изображённой на схеме. Допустим, клеммы A и B присоединены к источнику с напряжением 10 В, однако вольтметр позволяет измерить напряжение не более 6 В (см. рисунок в начале параграфа). Поэтому нам нужно создать падение напряжения на реостате на 4 В или более. Как это сделать? Чем правее мы смещаем движок, тем больше сопротивление реостата, и, согласно формуле U=I·R, больше напряжение на реостате, которое и называют падением напряжения. В результате на резисторе напряжение снижается и может стать менее 6 В, что нам и нужно.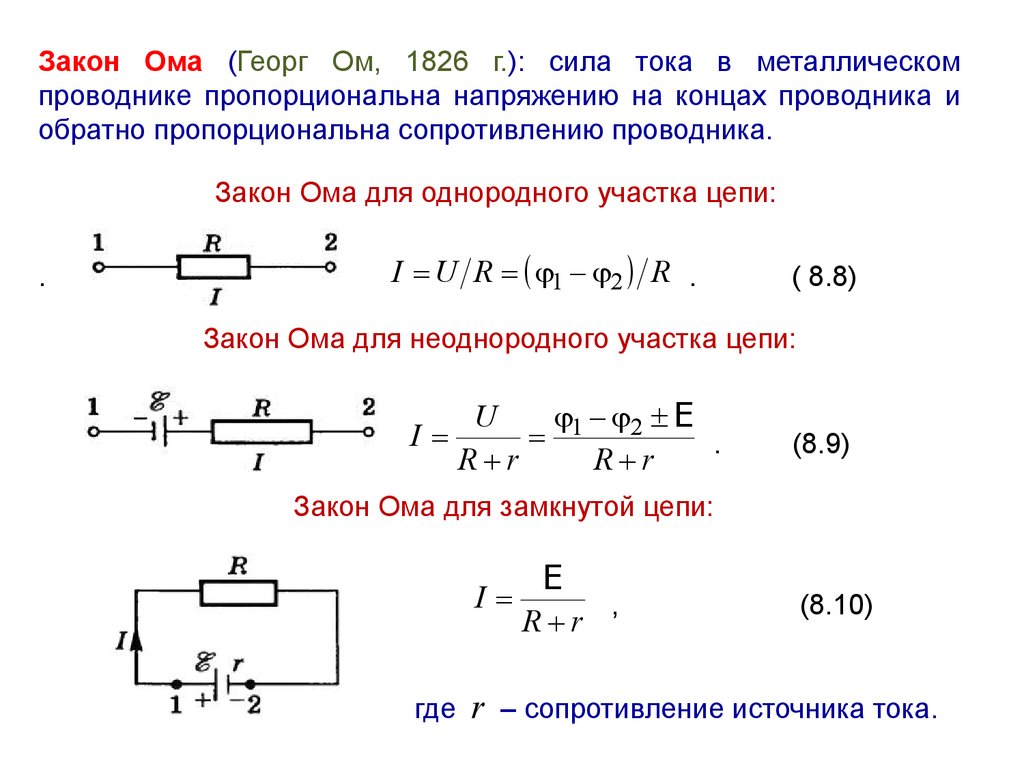
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Закон Ома для участка цепи или первый закон Ома
В этой главе мы поговорим о законе Ома и рассмотрим закон Ома для участка цепи с резисторами, это то, что мы должны знать в первую очередь в электричестве, потому что резисторы — это самые простые для изучения диполи.
Сопротивление и закон Ома
Электрическое сопротивление — это диполь, который включается в цепь. Он характеризуется величиной, называемой сопротивлением R.
Оно выражается в Ом. Например, R = 20 Ом или R = 3,5 Ом.
В отличие от токов и напряжений сопротивление всегда положительно!
Он представлен следующим прямоугольником:
Участок цепи с двумя резисторами
Здесь, поскольку есть два сопротивления, они были отмечены R 1 и R 2.
Ток, протекающий через сопротивление один и тот же до и после его пересечения, поскольку мы находимся на одном проводе.
С другой стороны, потенциал (напряжение) до и после различается: следовательно, существует разность потенциалов и, следовательно, напряжение.
Это напряжение иногда обозначают U R, чтобы мы понимали, что это напряжение на резисторе:
напряжение на резисторе
Это напряжение связано со значением сопротивления R и силой тока по формуле, называемой законом Ома для участка цепи:
Закон Ома для участка цепи
Внимание!
Эта формула действительна ТОЛЬКО для резисторов, но не для катушек, конденсаторов, генераторов или любых других диполей.
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению U. Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению.
Это важное соотношение известно как закон Ома для участка цепи. Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Сопротивление проводников
Если напряжение управляет током, что ему мешает? Электрическое свойство, которое тормозит ток (грубо похож на трение и сопротивление воздуха) называется сопротивлением R. Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току.
Георг Симон Ом
Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых справедлив закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R , которое не зависит от напряжения U и тока I. Объект с простым сопротивлением называется резистором, даже если его сопротивление невелико.
Сопротивление варьируется на много порядков. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. Сопротивление между руками и ногами у человека может составлять 10 5 Ом, в то время как сопротивление сердца человека составляет около 10 3 Ом. Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 -5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит.
Тесты по закону Ома MCQ с ответами • Закон Ома
Тест
по закону Ома — это простой тест, предназначенный для проверки вашего знания закона Ома.
1. Утверждение, которое правильно представляет закон Ома:
- В = ИК
- В = R / I
- R = VI
- I = R / V
- Правильный ответ: 1. V = IR
2. Резистор 10 Ом питается от батареи 5 В. Ток, протекающий через источник:
Резистор 10 Ом питается от батареи 5 В. Ток, протекающий через источник:
- 10 А
- 50 А
- 2 А
- 0.5 А
- Правильный ответ: 4. 2 A
- Решение: От I = V / R = 5-В / 10 Ом = 0,5 A
3. Если V = 50 В и I = 5 А, то R = ___:
- 50 Ом
- 5 Ом
- 10 Ом
- 2 Ом
- Правильный ответ: 3. 10 Ом
- Решение: от R = V / I = 50 В / 5A = 10 Ом
4. Если P = 50 Вт и R = 2 Ом, то I = ___?
- 50 А
- 5 А
- 10 А
- 2 А
- Правильный ответ: 3.5 А
- Решение: Из I = √ (P / R) = √ (50 В / 2A) = √25 A = 5 A
5. Единица напряжения:
- Вольт
- Ватт
- Кулон
- ампер
- Правильный ответ: 1. Вольт
6. Единица тока:
- Вольт
- Ватт
- Кулон
- ампер
- Правильный ответ: 4.
 Ампер
Ампер
- Правильный ответ: 4.
7. Единица мощности:
- Вольт
- Ватт
- Кулон
- ампер
- Правильный ответ: 2.Ватт
8. Единица сопротивления:
- Вольт
- Ватт
- Ом
- ампер
9. Если V = 10 В и R = 15 кОм, то I = ___?
- 0,666 мА
- 666 мкА
- 0,66 А
- а и б
- Правильный ответ: 4. a & b
- Решение: Здесь I = V / R = 10 В / 15 кОм = 0,666 мА = 666 мкА
10. Если I = 5 А и R = 10 Ом, то P = ___?
- 50 Вт
- 250 Вт
- 350 Вт
- 500 Вт
- Правильный ответ: 2.250 ватт
- Решение: Здесь P = I2R = (5 A) 2 * 10 Ω = 250 Вт
11. Компоненты, которые подчиняются закону Ома, известны как:
- Резисторы
- Омические компоненты
- Неомические компоненты
- Ни один из этих
- Правильный ответ: 2.
 Омические составляющие
Омические составляющие
- Правильный ответ: 2.
12. Омические компоненты имеют кривую __________ V-I:
- Прямая линия VI, кривая
- Параболическая кривая VI
- Нелинейная кривая VI
- Синусоидальная кривая VI
- Правильный ответ: 1.Прямая линия VI кривая
Тест по закону Ома Численные задачи
13. Электрочайник с 50-омным нагревательным элементом питается от розетки на 230 В. Ток, протекающий через чайник:
- 0,217 А
- 4,6 А
- 10,86 А
- 11500 А
14. Водяной нагревательный стержень потребляет ток 10 А при подключении к определенному источнику питания. Сопротивление стержня 12 Ом. Напряжение источника:
- 1.2 В
- 120 В
- 1200 В
- Ни один из этих
15. Реле с сопротивлением 100 Ом требует для работы 50 мА. При подключении к источнику 4 В реле будет:
- Эксплуатация
- Не работает
- Правильный ответ: 2.
 Не работает
Не работает - Решение: При 4 В ток будет I = V / R = 40 мА, что недостаточно для работы
- Правильный ответ: 2.
16. Разность потенциалов на резисторе 5 кОм равна 12 В. Найдите ток, протекающий через резистор:
- 60 мА
- 2.4 мА
- 1,77 мА
- 0,998 мА
- Правильный ответ: 2. 2,4 мА
- Решение: I = V / R = 12 В / 5 кОм = 2,4 мА
17. Электрическая лампочка потребляет ток 5 А при подключении к розетке на 100 В, сопротивление лампы:
- 5 Ом
- 20 Ом
- 100 Ом
- 500 Ом
- Правильный ответ: 2. 20 Ом
18. Через неизвестный резистор протекает ток 5 мА, когда к нему приложено 10 вольт.Для того же резистора приложение 20 вольт приведет к протеканию тока:
- 2 мА
- 5 мА
- 10 мА
- 50 мА
- Правильный ответ: 3. 10 мА
- Решение: Здесь R = 10 В / 5 мА = 2 кОм, Теперь для 20 В, I = 20 В / 2 кОм = 10 мА
MCQ, включающие знание префиксов в законе Ома Викторина
Префиксы — это числа, представляющие математическую величину в степени десяти. Мы уже рассказали об основных приставках в статье закона Ома. В предыдущих разделах вводились два префикса «m» и «k». Этот раздел MCQ включает также другие префиксы. Приступим к обучению:
Мы уже рассказали об основных приставках в статье закона Ома. В предыдущих разделах вводились два префикса «m» и «k». Этот раздел MCQ включает также другие префиксы. Приступим к обучению:
19. Если I 1 = 50 мА, R 1 = 50 кОм, то V 1 = __:
- 1 кВ
- 2,5 кВ
- 5 кВ
- 10 кВ
- Правильный ответ: 2. 2,5 кВ
- Подсказка: 1k = 1000, 1m = 0,001
20.Если I 2 = 100 мкА, R 2 = 50 кОм, то V 2 = __:
- 5000 В
- 500 В
- 5 В
- 0,5 В
- Правильный ответ: 3. 5 В
- Подсказка: 1µ = 0,000 001
21. Если I 3 = 100 мкА, R 3 = 50 МОм, то V 3 = __:
- 5000 В
- 500 В
- 5 В
- 0,5 В
- Правильный ответ: 1. 5000 В
- Подсказка: 1M = 1 000 000
22. Если V 4 = 50 В, R 4 = 10 ГОм, то I 4 = __:
Если V 4 = 50 В, R 4 = 10 ГОм, то I 4 = __:
- 5 А
- 5 мА
- 5 мкА
- 5 нА
- Правильный ответ: 4. 5 нА
- Подсказка: 1G = 1 000 000 000, 1 n = 0 000 000 001
23. Если V 5 = 99 кВ, R 5 = 33 ГОм, то I 5 = __:
- 5 А
- 5 мА
- 5 мкА
- 5 нА
24. Если V 6 = 22 В, R 6 = 11 кОм, то I 6 = __:
- 5 А
- 5 мА
- 5 мкА
- 5 нА
- Правильный ответ: 4.5 нА
- Подсказка: 1G = 1 000 000 000, 1 n = 0 000 000 001
25. Если V 7 = 10 В, I 7 = 1 мкА, то R 7 = __:
- 10 кОм
- 10 МОм
- 0,1 кОм
- 0,1 МОм
- Правильный ответ: 4.10 МОм
27. Если V 8 = 15 кВ, I 8 = 2 нА, то R 7 = __:
- 7500 кОм
- 7500 ГОм
- 30 кОм
- 30 ГОм
- Правильный ответ: 4.
 7500 ГОм
7500 ГОм
- Правильный ответ: 4.
28. Если V 9 = 50 В, I 9 = 25 мкА, то R 9 = __:
- 2 МОм
- 2 ГОм
- 1250 МОм
- 1250 ГОм
Тесты на соответствие закону Ома MCQ с методикой цветового кодирования резисторов
Метод цветного кодирования используется для представления номиналов резисторов в виде цветных полос. Над корпусами резисторов спроектировано 4, 5 или 6 полос. Хотя чаще всего доступны 4-полосные резисторы, мы будем использовать их в следующих задачах.Первая и вторая полосы представляют собой числа, а третья и четвертая — множители.
29. Резистор имеет цветовую маркировку с четырьмя полосами, первая из которых коричневая, вторая — черная, третья — красная, а четвертая — золотая. Резистор подключается к источнику 10 В. Найдите ток, протекающий через резистор.
- 1 мА
- 10 мА
- 100 мА
- 1А
- Правильный ответ: 2.
 10 мА
10 мА - Решение: Резистор может иметь цветовую маркировку по таблице, как показано ниже.Это резистор на 1 кОм. Пренебрегая допуском, мы можем легко использовать выражение Ома I = V / R, чтобы найти ток.
- Правильный ответ: 2.
30 Если 1-я полоса = желтая; 2-я полоса = фиолетовый; 3-я полоса = коричневый; и V = 47 В, тогда I = ___?
- 0,1 А
- 0,1 мА
- 100 мА
- 470 мА
- Правильный ответ: 1. 0,1 A
- Решение: Из цветовой маркировки резисторов резистор 470 Ом. Теперь I = V / R = 47/470 = 0,1 А
31.Если 1-я полоса = красная; 2-я полоса = красный; 3-я полоса = красный; и V = 44 В, тогда I = ___?
- 20 А
- 20 мА
- 44 А
- 44 мА
- Правильный ответ: 2. 20 мА
- Решение: Из цветовой маркировки резисторов резистор 2,2 кОм. Теперь I = V / R = 44 / 2,2 k = 20 мА
32. Если 1-я полоса = Коричневая; 2-я полоса = черный; 3-я полоса = зеленый; и V = 50 В, тогда I = ___?
- 1 мА
- 100 мкА
- 5 мА
- 50 мкА
- Правильный ответ: 4.
 50 мкА
50 мкА - Здесь сопротивление = 1 МОм
- Правильный ответ: 4.
33. Если 1-я полоса = Коричневая; 2-я полоса = черный; 3-я полоса = коричневый; и I = 50 мА, затем, используя закон Ом , найти значение напряжения источника:
- 0,5 В
- 5 В
- 50 В
- 500 В
- Правильный ответ: 2. 5 В
- Здесь сопротивление = 100 Ом
34. Если 1-я полоса = Коричневая; 2-я полоса = черный; 3-я полоса = оранжевый; и I = 50 мА, затем, используя формулу закона Ома , найдите значение источника напряжения, питающего источник:
- 0.5 В
- 5 В
- 50 В
- 500 В
- Правильный ответ: 4. 500 В
- Здесь сопротивление = 10кОм
35. Если 1-я полоса = Оранжевый; 2-я полоса = оранжевый; 3-я полоса = оранжевый; и I = 10 мА, затем, используя формулу закона Ома , найдите значение источника напряжения, питающего источник:
- 3 В
- 33 В
- 330 В
- 500 В
- Правильный ответ: 3.
 330 В
330 В - Здесь сопротивление = 33кОм
- Правильный ответ: 3.
Проблемы для последовательных и параллельных цепей
Эта часть викторины включает в себя последовательные схемы.Последовательная схема состоит из двух или более, в которых голова одного соединяется с хвостом другого, и между ними нет другой связи. Чтобы решить такие схемы, просто добавьте резисторы и получите один эквивалентный резистор, а затем примените закон, чтобы найти ток или напряжение.
36. Два резистора номиналом 5 Ом и 10 Ом последовательно подключены к источнику 10 В. Найдите ток, протекающий по цепи:
- 0,66 А
- 1,5 А
- 2 А
- 2.5 А
- Правильный ответ: 1,5 A
- Решение: R всего = R 1 + R 2 = 5 Ом + 10 Ом = 15 Ом, теперь I = V / R всего = 10 В / 15 Ом = 0,66 A
37. Два резистора номиналом 18 Ом и 50 Ом подключены последовательно к неизвестному источнику. Амперметр подключен к цепи, которая показывает 2 А. Найдите входное напряжение в цепи:
Амперметр подключен к цепи, которая показывает 2 А. Найдите входное напряжение в цепи:
- 36 В
- 100 В
- 136 В
- 168 В
- Правильный ответ: 136 В
- Решение: R всего = R 1 + R 2 = 18 Ом + 50 Ом = 68 Ом, теперь V = I * R всего = 2A * 68 Ом = 136 В
Параллельная схема представляет собой конфигурацию, в которой головки двух резисторов соединены в общей точке, а выводы — в другой общей точке.Соединение двух или более резисторов параллельно следует простой формуле:
рандов всего = 1 / ((1/ 1 ) + (1/ 2 ))
38. Два параллельных резистора номиналом 28 Ом подключены параллельно. Общий ток, обеспечиваемый источником 28 В, составляет.
- 1 А
- 2 А
- 4 А
- 8 А
- Правильный ответ: 2. 2 A
- Решение: R всего = 1 / ((1/28 Ом) + (1/28 Ом)) = 14 Ом, I = V / R = 28/14 = 2 A
39. Два параллельных резистора номиналом 50 и 60 Ом подключены параллельно. Общий ток, обеспечиваемый источником 100 В, составляет:
Два параллельных резистора номиналом 50 и 60 Ом подключены параллельно. Общий ток, обеспечиваемый источником 100 В, составляет:
- 1,72 А
- 2,88 А
- 3,66 А
- 4,52 А
- Правильный ответ: 3. 66 A
- Решение: R всего = 1 / ((1/50 Ом) + (1/60 Ом)) = 27,27 Ом, I = V / R = 100 / 27,27 = 3,66 A
40. Повторите описанную выше проблему для резисторов номиналом 30 Ом каждое, когда источник составляет 60 В.
- 0,25 А
- 0,5 А
- 2 А
- 4 А
- Правильный ответ: 4. 4 A
ЗАКОН ОМА После прочтения этого раздела вы сможете сделать следующее:
Вероятно, наиболее важным математическим соотношением между напряжением, током и сопротивлением в электричестве является то, что называется «законом Ома». Человек по имени Джордж Ом опубликовал эту формулу в 1827 году на основе своих экспериментов с электричеством. Эта формула используется для расчета электрических величин, чтобы мы могли проектировать схемы и использовать электричество с пользой. Закон Ома показан ниже.
Давайте посмотрим, что говорит нам закон Ома. Вторая версия формулы говорит нам, что напряжение можно рассчитать, если известны ток и сопротивление в цепи. Из уравнения видно, что если ток или сопротивление в цепи увеличиваются (в то время как другое остается неизменным), напряжение также должно увеличиваться. Третья версия формулы говорит нам, что мы можем рассчитать сопротивление в цепи, если известны напряжение и ток. Если ток остается постоянным, увеличение напряжения приведет к увеличению сопротивления. В качестве альтернативы увеличение тока при поддержании постоянного напряжения приведет к уменьшению сопротивления. Как видите, напряжение, ток и сопротивление математически, а также физически связаны друг с другом. Мы не можем иметь дело с электричеством без учета всех трех этих свойств. (Символ Ом имеет вид подковы и изображен после «100» на диаграмме выше.) Обзор
|
Калькулятор закона Ома
|
Закон Ома гласит, что ток через проводник между двумя точками прямо пропорционален напряжению в этих двух точках.Закон был назван в честь немецкого физика Георга Ома, который в трактате, опубликованном в 1827 году, описал измерения приложенного напряжения и тока через простые электрические цепи, содержащие провода различной длины.
Закон Ома был, вероятно, самым важным из первых количественных описаний физики электричества. Сегодня мы считаем это почти очевидным. Когда Ом впервые опубликовал свою работу, это было не так. Закон Ома остается верным для среднего тока в случае обычных резистивных материалов.
Резисторы — это элементы схемы, которые препятствуют прохождению электрического заряда в соответствии с законом Ома, и имеют определенное значение сопротивления R .
Закон
Ома справедлив для цепей, содержащих только резистивные элементы (без емкости или индуктивности) для всех форм управляющего напряжения или тока, независимо от того, является ли управляющее напряжение или ток постоянным (DC) или изменяющимся во времени, например (AC). В любой момент времени для таких цепей действует закон Ома.
Резисторы, включенные последовательно или параллельно, могут быть сгруппированы в одно «эквивалентное сопротивление», чтобы применить закон Ома при анализе цепи.
Примечание: Сопротивление нельзя измерить в рабочей цепи, поэтому закон Ома особенно полезен, когда его нужно вычислить. Вместо того, чтобы отключать цепь для измерения сопротивления, технический специалист, т.е. инопланетянин, может определить R, используя вышеуказанный вариант закона Ома.
Теперь, если вы знаете напряжение (E) и сопротивление (R) и хотите знать ток (I), разделите (E) на (R) (см. Уравнение выше).
И если вы знаете ток (I) и сопротивление (R) и хотите знать напряжение (E), умножьте (I) x (R) (см. Уравнение выше).
Если вы знаете напряжение (В) и ток (I) и хотите узнать сопротивление (R), разделите (E) на (I) (см. Уравнение выше).
Цепи, как и вся материя, состоят из атомов.Атомы состоят из субатомных частиц:
- Протоны (с положительным электрическим зарядом)
- нейтронов (бесплатно)
- Электронов (отрицательно заряженных)
Атомы остаются связанными силами притяжения между ядром атома и электронами в его внешней оболочке. Под воздействием напряжения атомы в цепи начинают преобразовываться, и их компоненты проявляют потенциал притяжения, известный как разность потенциалов.Взаимно притянутые свободные электроны движутся к протонам, создавая поток электронов (ток) . Любой материал в цепи, который ограничивает этот поток, считается сопротивлением .
Что удерживает силы, связывающие всю материю вместе? Что поддерживает их постоянство? Щелкните по ссылкам ниже и узнайте на ICR.org
Субатомные частицы, часть 1: лептоны
Субатомные частицы, часть 2: Барионы, субстанция Космоса
Авторские права (c) 2016 AnyCalculator.com. Все права защищены. www.anycalculator.com.
Gen1.org (эволюция = миллионы лет + ваше воображение)
2.2.4 Закон Ома и почему мы заботимся о сопротивлении
Устройство, которое мы знаем как тостер, удивительно простое. Он состоит в основном из провода, по которому пропускается ток. Проволока нагревается, поджаривая хлеб. Это оно!
а почему нагревается провод? Ответ в том, что провод имеет некоторое сопротивление. Когда ток проходит через материал с некоторым сопротивлением, материал нагревается.Это тепло в первую очередь является рассеянием некоторой части электроэнергии, проходящей через материал. Это рассеяние мощности в виде тепла называется «потерями» в электросети.
Сопротивление материала, через который проходит ток, помогает определить потери, но это не единственный фактор. Напряжение, при котором мощность проходит через материал, также имеет значение, как и величина тока.
Эта связь четко резюмируется в законе Ома, который гласит, что напряжение равно произведению тока и сопротивления, или V = I × R.Закон Ома используется для определения величины напряжения, необходимого для перемещения заданного количества тока (I) через некоторый материал с заданным сопротивлением (R).
Между тем, вспомните наше определение мощности: P = I × V. По сути, это количество мощности, передаваемой в цепи, подобной той, что была в нашем последнем упражнении.
Мы можем включить закон Ома в наше определение мощности, чтобы получить:
P = I × V = I × (I × R) = I2 × R
Это уравнение описывает количество мощности, рассеиваемой в цепи.Он также описывает количество потерь. Таким образом, закон Ома говорит нам, что потери будут увеличиваться пропорционально квадрату тока. Таким образом, если мы сохраним постоянное напряжение и удвоим ток, потери увеличатся в четыре раза.
Чтобы понять важность этого, предположим, что мы пропускаем 1000 ампер тока через цепь с падением напряжения 100 В. Итак, у нас есть мощность 100 кВт. Потери в цепи будут пропорциональны I2 × R или 10002 × R
в этом случае.
Но, если бы нам нужно было 100 кВт мощности, мы могли бы сделать это по-другому, пропустив 100 А через цепь при напряжении 1000 В.Сопротивление в цепи не изменится, но потери в цепи теперь будут пропорциональны 100 2 × R.
Таким образом, увеличивая напряжение (и уменьшая ток) в 10 раз, мы уменьшили наши потери в 100 раз. Это объясняет причину, по которой у нас есть сеть переменного тока вместо сети постоянного тока. Помните, что в технологии питания постоянного тока Эдисона напряжение в источнике должно быть близко к напряжению в точке потребления.Но с помощью технологии переменного тока, разработанной Tesla и Westinghouse, мощность может генерироваться и передаваться при очень высоких напряжениях, а затем снижаться до более низких напряжений в точке потребления. Это имело два больших преимущества: во-первых, можно было существенно снизить потери при передаче, а во-вторых, для домов и предприятий было намного безопаснее использовать электроэнергию низкого напряжения, а не высокого.
закон Ома | Статья о законе Ома в The Free Dictionary
закон, который гласит, что постоянная плотность тока I в проводнике прямо пропорциональна разности потенциалов (напряжению) U между двумя фиксированными точками или поперечными сечениями проводника:
(1) RI = U
Константа пропорциональности R , которая зависит от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением, или просто сопротивлением данного участка проводника. дирижер.Закон Ома был открыт в 1826 году немецким физиком Г. С. Омом.
В общем случае связь между I и U нелинейна; однако на практике всегда можно предположить, что он линейный для определенного диапазона напряжений, и применить закон Ома для этого диапазона. Для металлов и их сплавов диапазон практически неограничен.
Закон Ома по форме (1) действителен для тех участков цепи, которые не содержат никаких источников электродвижущей силы (ЭДС).При наличии таких источников (аккумуляторные батареи, термопары или динамо-машины) закон Ома принимает вид
(2) RI = U + E
, где E — ЭДС всех источников, подключенных в секции схемы, которая рассматривается. Для замкнутой цепи закон Ома принимает следующий вид:
(3) R t I = E
, где R t = R + R i — полное сопротивление всей цепи, которое равно сумме внешнего сопротивления R цепи и внутреннего сопротивления R и источника ЭДС.Законы Кирхгофа обобщают закон Ома на случай разветвленных цепей.
Закон Ома также может быть записан в дифференциальной форме, который связывает плотность тока j и общую напряженность электрического поля для каждой точки проводника. Потенциальное электрическое поле напряженности E, создаваемое в проводниках микроскопическими зарядами — электронами и ионами — самих проводников, не может поддерживать установившееся движение свободных зарядов (ток), поскольку работа, совершаемая полем в замкнутом контуре, равна нулю. .Ток поддерживается неэлектростатическими силами различного происхождения (индукционные, химические, термические и т. Д.), Которые действуют в источниках ЭДС и могут быть представлены в виде некоторого эквивалентного непотенциального поля с напряженностью E ext , называемого внешним полем. В общем случае полная напряженность поля, действующего на заряды в проводнике, составляет E + E ext . Соответственно, дифференциальный закон Ома принимает вид
(4) ρj = E + E ext или j = σ (E + E ext )
где ρ — удельное электрическое сопротивление материала проводника, а σ = 1 / ρ — удельная электропроводность.
Закон Ома в сложной форме также действителен для синусоидальных квазистационарных токов:
(5) ZI = E
, где Z — полный комплексный импеданс, равный R + iX и R и iX — это сопротивление и реактивное сопротивление цепи соответственно. Если индуктивность L и емкость C присутствуют в цепи, несущей квазистационарный ток с частотой ω, тогда X = ω L — 1 / ω C.
СПИСОК ЛИТЕРАТУРЫ
Kursfiziki , vol. 2. Под редакцией Н. Д. Папалекси. Москва-Ленинград, 1948.
Калашников С.Г. Электричество. Москва, 1964. ( Общий курс физики , т. 2.)
Физические основы электротехники. Главный редактор Поливанов К.М. Москва-Ленинград, 1950.
Большая Советская Энциклопедия, 3-е издание (1970-1979). © 2010 The Gale Group, Inc. Все права защищены.
% PDF-1.4
%
256 0 объект
>
endobj
xref
256 85
0000000016 00000 н.
0000003095 00000 н.
0000003616 00000 н.
0000003652 00000 н.
0000004202 00000 н.
0000004358 00000 п.
0000004515 00000 н.
0000004659 00000 н.
0000004813 00000 н.
0000004957 00000 н.
0000005115 00000 п.
0000005271 00000 н.
0000005426 00000 н.
0000005477 00000 н.
0000005561 00000 н.
0000005934 00000 н.
0000005980 00000 н.
0000006563 00000 н.
0000007758 00000 н.
0000008947 00000 н.
0000010139 00000 п.
0000011336 00000 п.
0000011373 00000 п.
0000011410 00000 п.
0000011946 00000 п.
0000012281 00000 п.
0000017886 00000 п.
0000018354 00000 п.
0000018881 00000 п.
0000019231 00000 п.
0000019306 00000 п.
0000019866 00000 п.
0000020088 00000 н.
0000020535 00000 п.
0000021433 00000 п.
0000022144 00000 п.
0000022906 00000 п.
0000023627 00000 п.
0000024823 00000 п.
0000024907 00000 п.
0000025755 00000 п.
0000025994 00000 п.
0000026410 00000 п.
0000027070 00000 п.
0000027655 00000 п.
0000028263 00000 п.
0000028625 00000 п.
0000029394 00000 п.
0000029589 00000 п.
0000030351 00000 п.
0000031175 00000 п.
0000033868 00000 п.
0000039222 00000 п.
0000043089 00000 п.
0000046546 00000 п.
0000053941 00000 п.
0000054013 00000 п.
0000054191 00000 п.
0000054291 00000 п.
0000054412 00000 п.
0000054581 00000 п.
0000054689 00000 п.
0000054793 00000 п.
0000054957 00000 п.
0000055054 00000 п.
0000055175 00000 п.
0000055302 00000 п.
0000055441 00000 п.
0000055556 00000 п.
0000055697 00000 п.
0000055810 00000 п.

 Ампер
Ампер Омические составляющие
Омические составляющие Не работает
Не работает 7500 ГОм
7500 ГОм 10 мА
10 мА 50 мкА
50 мкА 330 В
330 В
 В первой версии формулы I = V / R закон Ома говорит нам, что электрический ток в цепи можно рассчитать, разделив напряжение на сопротивление. Другими словами, ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.Таким образом, увеличение напряжения приведет к увеличению тока, пока сопротивление остается постоянным. В качестве альтернативы, если сопротивление в цепи увеличивается, а напряжение не изменяется, ток будет уменьшаться.
В первой версии формулы I = V / R закон Ома говорит нам, что электрический ток в цепи можно рассчитать, разделив напряжение на сопротивление. Другими словами, ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.Таким образом, увеличение напряжения приведет к увеличению тока, пока сопротивление остается постоянным. В качестве альтернативы, если сопротивление в цепи увеличивается, а напряжение не изменяется, ток будет уменьшаться. Следует отметить, что закон Ома верен для полупроводников, но для широкого спектра материалов (например, металлов) сопротивление является фиксированным и не зависит от величины тока или величины напряжения.
Следует отметить, что закон Ома верен для полупроводников, но для широкого спектра материалов (например, металлов) сопротивление является фиксированным и не зависит от величины тока или величины напряжения.