Последовательное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.
Предположим известными параметры катушки R1, L и конденсатора R2, C; ток в цепи i = Imsinωt.
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цели
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
u = u1R + uL + uC + u2R,
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
U = U2R + UL + UC +U2R
Для построения векторной диаграммы находим:
U1R = IR1; U2R = IR2; UL = IXL; UC = IXC.
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:
1. ХL>ХC . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
Векторная сумма напряжений U1 + U2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: Ua = U1R + U2R.
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: Uр = UL — UC .
При одинаковом токе во всех элементах цепи UL>UC . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
где R = R1 + R2 и X = XL — XC общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
U = IZ; I = U/Z; Z = U/I.
Из треугольников напряжения и сопротивлений определяют следующие величины:
Угол сдвига по фазе между напряжением и током в цепи положительный (φ>0) (фазовые токи отсчитываются от вектора тока).
2. ХL< ХC Векторная диаграмма изображена на рис. 14.3, где UL<UC , поэтому общее напряжение отстает от тока на угол φ<0.
Реактивное сопротивление цепи носит емкостный характер.
Расчетные формулы для первого случая остаются без изменения и для второго случая.
3. XL = ХC . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: UL = UC (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.
Общее напряжение совпадает по фазе с током и равно по величине активной
составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
U = IR, или I = U/R.
В случае XL = ХC в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи с последовательном соединении конденсатора и катушки
Из треугольника напряжений легко получить треугольник мощностей из которого следуют уже известные формулы:
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ>0 Q>0; при φ<0 Q<0.
Активная мощность положительна при любом угле, так как cosφ = cos(-φ).
Полная мощность также всегда положительна. На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии (Р ≠ 0) и обменный процесс между генератором и приемником (Q ≠ 0 при φ ≠ 0).
На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии (Р ≠ 0) и обменный процесс между генератором и приемником (Q ≠ 0 при φ ≠ 0).
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при XL = ХС.
Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова.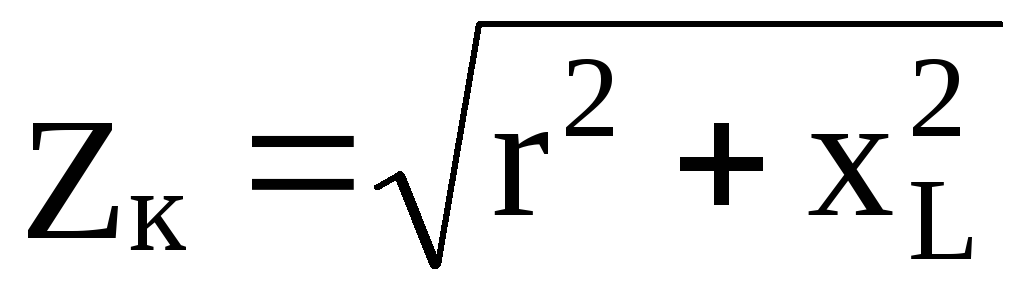 Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задачи по теме и пример решения задачи для схемы с последовательным соединением конденсатора и катушки
Полное сопротивление электрической цепи
Понятие тока и напряжения
Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.
В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.
Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.
Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.
Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.
При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.
Вычисление импеданса
Идеальные элементы
Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:
| zR=R{\displaystyle z_{R}=R} | (2) |
Конденсатор
Ток и напряжение для конденсатора связаны соотношением:
i(t)=CdUdt. (jω) =R+1jωC+jωL=R−jωC+jωL=R+j(−1ωC+ωL).{\displaystyle {\hat {Z}}(j\omega )\ =R+{\frac {1}{j\omega C}}+j\omega L=R-{\frac {j}{\omega C}}+j\omega L=R+j\left(-{\frac {1}{\omega C}}+\omega L\right).} (jω) =R+1jωC+jωL=R−jωC+jωL=R+j(−1ωC+ωL).{\displaystyle {\hat {Z}}(j\omega )\ =R+{\frac {1}{j\omega C}}+j\omega L=R-{\frac {j}{\omega C}}+j\omega L=R+j\left(-{\frac {1}{\omega C}}+\omega L\right).} | (8) |
Параллельное и последовательное соединение элементов
В разделе электротехники присутствует несколько вариантов того, как подключить детали в электрическую цепь. Есть параллельное и попеременное подсоединения. Их объединяет смешанная схема, которая представлена ниже.
Последовательное подключение — это когда все источники соединяются друг с другом последовательно. Получаемая цепь не обладает никакими разветвлениями. Сила тока в данном случае проходит через каждый источник. Она постоянная, общее напряжение одинаковое.
В случае препятствия резисторов заряду при последовательном подключении получится, что сопротивляемость будет равна сумме всех взаимозаменяемых пассивных элементов цепи. Рассчитывая параметры электротехнической схемы, не нужно применять частные параметры устройств. Их можно заменить одним значением, которое равно их суммарному показателю.
Их можно заменить одним значением, которое равно их суммарному показателю.
Обратите внимание! Польза взаимозаменяемости компонентов заключается в возможности замены нескольких пассивных элементов электрической сети одним. Соединение элементов
Соединение элементов
Параллельное подключение — это такое подсоединение источников, в котором входы всех устройств находятся в одних местах, а выходы — в других. Этими местами служат узлы.
В случае эквивалентного препятствия заряду при параллельном соединении определить его можно благодаря закону Ома с преобразованием формулировки подсчета. Так, сделать необходимый расчет можно, основываясь на следующей формуле: R · R / N·R = R / N.
Если это соединение нескольких индуктивных катушек, то их индуктивный показатель сопротивляемости будет рассчитываться по той же формуле, что для резисторных устройств.
Важно! В случае с параллельным подключением общий показатель будет меньше любого показателя резистора. При последовательном подсоединении все наоборот
Аналогия с электрическим сопротивлением проводника на примере резистора
Резистор — пассивный элемент, обладающий чисто активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения, а так же из-за того, что резистор является пассивным элементом (поскольку не содержит внутренних источников энергии). Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения U. Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения U, к току I (см. закон Ома для участка цепи):
Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения, а так же из-за того, что резистор является пассивным элементом (поскольку не содержит внутренних источников энергии). Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения U. Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения U, к току I (см. закон Ома для участка цепи):
- R=UI.{\displaystyle R={\frac {U}{I}}.}
Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:
сопротивление идеальной катушки индуктивности стремится к нулю:
- если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:
- U=;{\displaystyle U=0;}
- R=UI=I=;{\displaystyle R={\frac {U}{I}}={\frac {0}{I}}=0;}
сопротивление идеального конденсатора стремится к бесконечности:
- если приложить к конденсатору некоторое постоянное напряжение U, то при любом значении U, ток через конденсатор будет нулевым:
- I=;{\displaystyle I=0;}
- R=UI=U=∞.
 {\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}
{\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}
Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:
- напряжение между выводами катушки индуктивности не равно нулю;
- ток, протекающий через конденсатор, не будет равен нулю.
Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.
Было бы удобно иметь некоторый параметр аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.
Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитывается и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.
В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитывается и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.
Обобщенный импеданс в s-плоскости и преобразование Лапласа
Импедансы, определённые через комплексную частоту jω{\displaystyle j\omega }, позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной s=σ+jω{\displaystyle s=\sigma +j\omega } и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал fin(t){\displaystyle f_{in}(t)} из временного представления должен быть предварительно преобразован в комплексное представление Ft(s){\displaystyle F_{t}(s)} через прямое преобразование Лапласа:
- Ft(s)=∫∞fin(t)e−stdt.
 {-st}\,dt.}
{-st}\,dt.}
Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы H(s){\displaystyle H(s)}:
- Ft,H(s)=H(s) Ft(s).{\displaystyle F_{t,H}(s)=H(s)\ F_{t}(s).}
| Двухполюсник | Обобщённыйимпеданс |
|---|---|
| Резистор | R{\displaystyle R\,} |
| Катушкаиндуктивности | sL{\displaystyle sL\,} |
| Конденсатор | 1sC{\displaystyle {\frac {1}{sC}}\,} |
Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет R+sL{\displaystyle R+sL}.
Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:
- fF,H(t)=L−1H(s) Ft(s)=12πi∫σ1−j⋅∞σ1+j⋅∞estH(s) Ft(s)ds,{\displaystyle f_{F,H}(t)={\mathcal {L}}^{-1}={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}H(s)\ F_{t}(s)\,ds,}
- где σ1 {\displaystyle \sigma _{1}\ } — некоторое вещественное число, выбираемое из условий сходимости интеграла.

- Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение
Пассивный RС-фильтр нижних частот 1-го порядка
Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи HRC(s){\displaystyle H_{RC}(s)} такого делителя:
- HRC(s)=1sCR+1sC=1sRC+1=1sT+1,{\displaystyle H_{RC}(s)={\frac {1/sC}{R+1/sC}}={\frac {1}{sRC+1}}={\frac {1}{sT+1}},}
- где обозначено T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.
Ступенчатый входной сигнал можно выразить через функцию Хевисайда h(t){\displaystyle h(t)}:
- Uin(t)=U h(t),{\displaystyle U_{in}(t)=U_{0}\ h(t),}
- где U{\displaystyle U_{0}} — амплитуда ступеньки.
Преобразование Лапласа входного сигнала:
Fin(s)=LU h(t)=∫∞e−stUh(t)dt=Us. {-t/T}).}
{-t/T}).}
Таким образом, получен отклик цепи при нулевом начальном условии (UC={\displaystyle U_{C}=0} при t={\displaystyle t=0}), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.
Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.
Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.
Оцените статью:
6.4. Сопротивление в цепи синусоидального
тока
Если напряжение
подключить к сопротивлению R, то через него протекает ток
(6.7)
Анализ выражения (6. 7) показывает,
7) показывает,
что напряжение на сопротивлении и ток, протекающий через него, совпадают
по фазе.
Формула (6.7) в комплексной форме записи
имеет вид
(6.8)
где
и — комплексные
амплитуды тока и напряжения.
Комплексному уравнению (6.8) соответствует векторная
диаграмма (рис. 6.4).
Из анализа диаграммы следует, что векторы напряжения
и тока совпадают по направлению.
Сопротивление участка цепи постоянному току называется
омическим, а сопротивление того же участка переменному току — активным
сопротивлением.
Рис.6.4
Активное сопротивление больше омического из-за явления
поверхностного эффекта. Поверхностный эффект заключается в том, что
Поверхностный эффект заключается в том, что
ток вытесняется из центральных частей к периферии сечения проводника.
6.5. Индуктивная катушка
в цепи синусоидального тока
Сначала рассмотрим идеальную индуктивную
катушку, активное сопротивление которой равно нулю. Пусть по идеальной
катушке с индуктивностью L протекает синусоидальный ток .
Этот ток создает в индуктивной катушке переменное магнитное поле, изменение
которого вызывает в катушке ЭДС самоиндукции
(6.9)
Эта ЭДС уравновешивается напряжением,
подключенным к катушке: u = eL = 0.
(6.10)
Таким образом, ток в индуктивности
отстает по фазе от напряжения на 90o из-за явления самоиндукции.
Уравнение вида (6.10) для реальной катушки, имеющей
активное сопротивление R, имеет следующий вид:
(6.11)
Анализ выражения (6.11) показывает,
что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию
переменного тока, из-за чего ток в реальной индуктивной катушке отстает
по фазе от напряжения на некоторый угол φ (0oo), величина которого зависит от соотношения R и L.
Выражение (6.11) в комплексной форме записи имеет вид:
(6.12)
где ZL — полное комплексное
сопротивление индуктивной катушки ;
ZL — модуль комплексного
сопротивления;
— начальная фаза комплексного сопротивления;
—
индуктивное сопротивление (фиктивная величина, характеризующая реакцию
электрической цепи на переменное магнитное поле).
Полное сопротивление индуктивной катушки или модуль
комплексного сопротивления
.
Комплексному уравнению (6.12)
соответствует векторная диаграмма (рис.6.5).
Рис. 6.5
Из анализа диаграммы видно,
что вектор напряжения на индуктивности опережает вектор тока на 90o.
В цепи переменного тока напряжения на участках
цепи складываются не арифметически, а геометрически.
Если мы поделим стороны треугольника напряжений
на величину тока Im, то перейдем к подобному треугольнику
сопротивлений (рис. 6.6).
Из треугольника сопротивлений получим несколько формул:
;
;
Рис. 6.6
6.6
;
;
.
6.6. Емкость в цепи
синусоидального тока
Если к конденсатору емкостью C
подключить синусоидальное напряжение, то в цепи протекает синусоидальный
ток
;
. (6.13)
Из анализа выражений 6.13 следует,
что ток опережает напряжение по фазе на 90o.
Выражение (6.13) в комплексной
форме записи имеет вид:
, (6.14)
где
— емкостное сопротивление, фиктивная расчетная величина, имеющая размерность
сопротивления.
Если комплексное сопротивление
индуктивности положительно
, то комплексное
сопротивление емкости отрицательно
.
На рис. 6.7 изображена векторная
диаграмма цепи с емкостью.
Вектор тока опережает вектор напряжения на
90o.
Рис. 6.7
6.7. Последовательно
соединенные реальная индуктивная
катушка и конденсатор в цепи синусоидального тока
Катушка с активным сопротивлением
R и индуктивностью
L и конденсатор
емкостью С
включены последовательно (рис.6.8). В схеме протекает
синусоидальный ток
.
Определим напряжение на входе схемы.
В соответствии со вторым законом Кирхгофа,
(6. 15)
15)
Подставим эти формулы в
уравнение (6.15). Получим:
(6.16)
Из выражения (6.16) видно: напряжение в активном
сопротивлении совпадает по фазе с током, напряжение на индуктивности
опережает по фазе ток на 90o, напряжение по емкости отстает
по фазе от тока на 90o.
Запишем уравнение (6.16) в комплексной форме:
(6.17)
Рис. 6.8
Поделим левую и правую части
уравнения (6.17) на √2.
Получим уравнение для комплексов действующих
значений токов и напряжений
,
(6.18)
где
— комплексное сопротивление цепи;
— модуль комплексного
сопротивления, или полное сопротивление цепи;
— начальная фаза комплексного сопротивления.
При построении векторных
диаграмм цепи рассмотрим три случая.
- XL > XC, цепь носит индуктивный характер.
Векторы напряжений на индуктивности и емкости направлены в противоположные
стороны, частично компенсируют друг друга. Вектор напряжения на входе
схемы опережает вектор тока (рис.6.9). - Индуктивное сопротивление меньше емкостного. Вектор напряжения на
входе схемы отстает от вектора тока. Цепь носит емкостный характер
(рис.6.10). - Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности
и емкости полностью компенсируют друг друга. Ток в цепи совпадает
по фазе с входным напряжением. В электрической цепи наступает режим
резонансного напряжения (рис.6.11).
Ток в резонансном режиме
достигает максимума, так как полное сопротивление (z)
цепи имеет минимальное значение.
Условие возникновения резонанса: ,
отсюда резонансная частота равна
.
Из формулы следует,
что режима резонанса можно добиться следующими способами:
- изменением частоты;
- изменением индуктивности;
- изменением емкости.
В резонансном режиме входное напряжение
равно падению напряжения в активном сопротивлении. На индуктивности
и емкости схемы могут возникнуть напряжения, во много раз превышающие
напряжение на входе цепи. Это объясняется тем, что каждое напряжение
равно произведению тока I0 (а он наибольший), на соответствующее
индуктивное или емкостное сопротивление (а они могут быть большими).
.
Рис. 6.9
Рис. 6.10
Рис. 6.11
6.8. Параллельно соединенные
индуктивность, емкость
и активное сопротивление в цепи синусоидального тока
К схеме на рис. 6.12 подключено
синусоидальное напряжение . Схема состоит
из параллельно включенных индуктивности, емкости и активного сопротивления.
Определим ток на входе схемы.
В соответствии с первым законом Кирхгофа:
,
(6.19)
где
— активная проводимость.
Рис. 6.12
Подставим эти формулы в
уравнение (6.19). Получим:
, (6.20)
где
— индуктивная проводимость;
— емкостная проводимость.
Из уравнения (6.20) видно, что
ток в ветви с индуктивностью отстает по фазе от напряжения на 90o,
ток в ветви с активным сопротивлением совпадает по фазе с напряжением,
ток в ветви с емкостью опережает по фазе напряжение на 90o.
Запишем уравнение (6.20) в комплексной форме.
, (6.21)
где
— комплексная проводимость;
—
полная проводимость;
—
начальная фаза комплексной проводимости.
Построим векторные диаграммы,
соответствующие комплексному уравнению (6.21).
Рис. 6.13
Рис. 6.14
Рис. 6.15
В схеме на рис. 6.12
может возникнуть режим резонанса токов. Резонанс токов возникает тогда,
когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный
и емкостный токи, направленные в противоположные стороны, полностью
компенсируют друг друга. Ток в неразветвленной части схемы совпадает
по фазе с напряжением.
Из условия возникновения резонанса тока
получим формулу для резонансной частоты тока
.
В режиме резонанса тока
полная проводимость цепи — минимальна,
а полное сопротивление — максимально.
Ток в неразветвленной части схемы в
резонансном режиме имеет минимальное значение. В идеализированном случае
R = 0,
и .
Ток в неразветвленной части цепи I = 0. Такая
схема называется фильтр — пробкой.
6.9. Резонансный режим
в цепи, состоящей
из параллельно включенных реальной индуктивной
катушки и конденсатора
Комплексная
проводимость индуктивной ветви
где
— активная проводимость индуктивной катушки;
— полное сопротивление индуктивной катушки;
— индуктивная проводимость катушки;
— емкостная проводимость второй ветви.
В режиме резонансов
токов справедливо уравнение:
или
Из этого уравнения
получим формулу для резонанса частоты
(6.22)
На рисунке
6.16 изображена векторная диаграмма цепи в резонансном режиме.
Вектор тока I2 опережает вектор напряжения на
90o. Вектор тока I1 отстает от вектора напряжения
на угол φ,
где
.
Разложим вектор тока I1 на две взаимно
перпендикулярные составляющих, одна из них, совпадающая с вектором напряжения,
называется активной составляющей тока Iа1, другая — реактивной
составляющей тока Iр1.
Рис. 6.16
В режиме резонанса тока реактивная составляющая тока Iр1
и емкостный ток I2 , направленные в противоположные стороны,
полностью компенсируют друг друга, активная составляющая тока Iа1
совпадает по фазе с напряжением (рис. 6.17). Ток I в неразветвленной
части схемы совпадает по фазе с напряжением.
Рис.
6.17
Что такое активное реактивное и полное сопротивление. Реактивное сопротивление XL и XC. Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления
Итак, катушки индуктивности и конденсаторы препятствуют протеканию переменного тока. Такое сопротивление по переменному току носит название реактивного сопротивления
Х и измеряется в омах. Реактивное сопротивление
зависит как от величины индуктивности и емкости, так и от частоты сигнала.
Катушка индуктивности имеет индуктивное реактивное сопротивление VL равное
где f — частота в герцах, a L — индуктивность в генри.
Так как ω = 2πf, то можно записать XL = ωL. Например, реактивное сопротивление катушки с индуктивностью 10 мГн, на которую подается сигнал частотой 1 кГц, равно
XL = 2π*1*103*10 *10-3 = 62,8 Ом.
Реактивное сопротивление катушки индуктивности возрастает с увеличением частоты сигнала (рис. 4.26).
Конденсатор имеет емкостное сопротивление XC равное
где С — емкость в фарадах. Например, реактивное сопротивление конденсатора емкостью 1 мкФ, на который подается сигнал частотой 10 кГц, равно
Рис. 4.26. Зависимость индуктивного Рис. 4.27.
сопротивления от частоты.
Рис. 4.28. Векторная сумма емкостного (XC)
и индуктивного (XL) сопротивлений.
Рис. 4.29.
(а) Катушка индуктивности, соединенная последовательно с резистором R.
(б) Векторное представление R, XL и их векторной суммы Z
Реактивное сопротивление конденсатора уменьшается с увеличением частоты сигнала (рис. 4.27).
Результирующее сопротивление цепи, включающей в себя емкостное сопротивление XC и индуктивное сопротивление XL, равно векторной сумме XC и XL. Векторы XC и XL, как видно из рис. 4.28(б), находятся в противофазе, т. е. разность фаз между ними равна 1800. Поэтому результирующее сопротивление просто равно разности между XC и XL. Например, пусть XL = 100 Ом, а XC = 70 Ом. Тогда результирующее реактивное сопротивление Х = 100 – 70 = 30 Ом и является индуктивным так как XL больше, чем XС.
Импеданс
Результирующее сопротивление цепи, содержащей как активное, так и реактивное (индуктивное либо емкостное) сопротивление, носит название импеданса или полного сопротивления цепи.
Импеданс Z является векторной суммой реактивного сопротивления Х и активного сопротивления R.
Рассмотрим, например, схему, изображенную на рис. 4.29. Она включает в себя индуктивное сопротивление XL соединенное последовательно с резистором R. Как видно из рис. 4.29(б), вектор XL опережает вектор R на 90°. Импеданс равен
Если XL = 400 Ом и R = 300 Ом, то Z = 500 Ом.
Реактивное сопротивление
– электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I
в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию,
оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противо
общие сведения, зависимость от других величин и формулы расчета
Любое вещество, находясь в разнообразных состояниях, обладает определенным сопротивлением. В некоторых случаях возникает необходимость рассчитать полное сопротивление цепи или конкретного участка. В такой ситуации следует воспользоваться формулами. Кроме того, нужно понимать основной смысл сопротивления и электропроводимости, а также зависимость этих понятий от некоторых величин.
Физический смысл
Все вещества по проводимости электрического тока (ЭТ) делятся на проводники, полупроводники и диэлектрики. Проводниками являются элементы, хорошо проводящие ЭТ. Это обусловлено наличием свободных электронов (СЭ). Полупроводники — особая группа веществ, проводимость которых зависит от внешних факторов, например, от температуры, освещенности и т. д. Диэлектриками являются все вещества, которые не проводят ЭТ из-за отсутствия или недостаточного количества СЭ. Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.
Электронная конфигурация какого-либо элемента берется из таблицы Менделеева. Ток оказывает на проводник тепловое действие, так как происходит взаимодействие СЭ с кристаллической решеткой (КР).Они замедляются, но с течением времени под действием электромагнитного поля снова ускоряются, после чего процесс взаимодействия повторяется много раз.
Процесс взаимодействия свободных заряженных частиц с КР вещества называется электрическим сопротивлением проводника. Обозначается сопротивление или электропроводимость буквой R, единицей измерения этой величины является Ом.
Зависимость электропроводимости
R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.
Электрические величины
К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.
Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I. Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) — R внутреннее. Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).
Геометрические параметры и тип вещества
Если основными носителями заряда являются СЭ, а свойства проводимости прямо пропорционально зависят от их количества и структуры КР, то тип вещества является одним из факторов, влияющих на R проводника. Вещества и их составляющие элементы, имеющие различные электронные конфигурации, согласно таблице Менделеева обладают разными КР, что и обуславливается различным R.
Зависимость от материала выражается коэффициентом, обозначающимся p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.
Кроме того, от площади поперечного сечения (S) также зависит R проводника. Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить. Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:
- Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
- Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.
П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.
Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:
- Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат: S = sqr(a).
- Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле S = a * b.
Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:
- Визуально определить геометрическую фигуру при разрезе П.
- Найти в справочнике формулу S.
- Произвести измерения при помощи ШЦ необходимых величин.
- Подставить в формулу и вычислить S.
Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.
Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.
Температура проводника
Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.
На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания. Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры. При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.
В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П. По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры. В физике существует формула зависимости p = p0 * [1 + a * (t — 20)]. Буква а является температурным коэффициентом:
- для металлов а > 0;
- для электролитов a < 0.
Переменная t — температура П, p0 — удельное сопротивление, взятое из справочника для конкретного материала. Кроме того, p зависит еще и от деформации П, поскольку при этом КР меняет свою структуру. Это происходит в процессе обработки металла при низких температурах и давлении. Такая деформация является пластической, при ней искажается КР, и увеличивается R течения Э.
В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой. Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются. Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.
Конечную формулу можно записать в виде R = p0 * [1 + a * (t — 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.
Цепь переменного тока
Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:
- активным;
- индуктивным;
- емкостным;
- полным.
Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im. При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R. Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).
Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.
Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.
При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:
- w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
- C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.
Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt [sqr(R) + sqr (Xc — Xl)]. В ЦПТ величина Z зависит от:
- геометрии П;
- типа вещества, из которого сделан П;
- температуры;
- деформации различного вида;
- электрических показателей I, U, f, L, C и R.
Закон Ома для участка цепи принимает следующий вид: I = U / Z. Необязательно рассчитывать электропроводимость П, так как для этих целей существуют омметры. Расчет Xl и Xс следует производить самостоятельно.
Измерение сопротивления
На расчет R необходимо потратить определенное время. Эту задачу упрощает прибор, который называется омметром. Он состоит из цифрового или стрелочного индикатора. Практически все современные комбинированные приборы (мультиметры) оснащены функцией измерения R. Однако есть и специализированные устройства, применяющиеся для определенных целей, например, для измерения R изоляции жил кабеля. Этот тип прибора называется мегаомметром. Омметр применяется не только для измерения величины R, но и для прозвонки радиокомпонентов, кабелей, отдельных шлейфов и других элементов на исправность и обрыв цепи.
Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.
Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит. Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений. Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.
Катушка импеданса
— определение — английский
Примеры предложений с «катушкой импеданса», память переводов
tmClassChoking или импеданс катушкаspatents-wipoМагнитоимпедансный сенсорный элемент с электромагнитной катушкой и магнитоимпедансный датчик с электромагнитной катушкойpatents-wipoРегулируемый импеданс дросселя Ограничитель тока с шунтирующим сопротивлением с переменным импедансом Coilpatents-WIPO Физические свойства определяются на основе измерения электрического комплексного импеданса катушки и данных, коррелирующих физические свойства процесса с электрическим комплексным импедансом катушки.springer Эффекты собственных емкостей катушек и взаимных сопротивлений между катушками показаны с помощью числового примера. tmClassChoking катушки [импеданс] springerStreak артефакты, вызванные зажимами аневризмы и катушками, ухудшают качество изображения в многодетекторной компьютерной томографии (MDCT) .Common crawlAny. дефекты, которые изменяют течение вихревых токов, также изменяют импеданс катушек в зонде.Патенты-wipoМоделирование импеданса индукционной катушки с использованием параметров схемы замещения патенты-wipoУстройство для ограничения тока с переменным импедансом катушки пружина Изменение импеданса катушки определяется посредством анализа схем замещения с сосредоточенными параметрами. Обычное ползание Эти изменения импеданса катушек измеряются и используются для обнаружения дефектов в трубке. tmClass Трансформаторы, дросселирующие катушки [импеданс], преобразователи, поглотители перенапряжения, преобразователи мощности, выпрямители, инвертированные выпрямители, преобразователи, токоподводящие устройства, зарядные устройства, пружина солнечных батарей Измерения производятся по изменению комплексного импеданса этой катушки при включении электромагнита.WikiMatrix Коэффициент демпфирования (отношение выходного сопротивления (усилителя) к входному сопротивлению (звуковая катушка драйвера)) в любом случае подходит для хорошо спроектированных усилителей. вызывает параллельный резонанс. Патенты-WIPO Изобретение относится к дроссельной катушке, полное сопротивление которой может быть согласовано в определенных пределах с заданным импедансом, и к способу установки импеданса дроссельной катушки по изобретению.патент-wipo Когда светопропускающий слой смещается к катушке индуктивного сенсорного датчика, значение импеданса катушки индуктивного сенсорного датчика изменяется, и это изменение обнаруживается. spinger Проблема измерения частотно-зависимой катушки h.f. Также обсуждается импеданс .patents-wipoЭти резонансные частоты можно контролировать, регулируя импеданс катушки имплантата .patents-wipoПоверхность индуктивного питания включает в себя несколько первичных катушек, схему автоподстройки импеданса и другие схемы управления.tmClassCoils (Choking -) [импеданс] патенты-wipo В частности, первичный токоотвод от пневматического терминала регулируемой длины зажимается между пневматическим терминалом и кабельной катушкой на любой промежуточной длине, а зажим шунтируется к плоскости заземления ( например, заземление) через второй токоотвод с низким импедансом, в отличие от витого токоотвода с высоким импедансом, тем самым повышая эффективность токоотвода за счет уменьшения импеданса, наблюдаемого при ударе молнии, до плоскости заземления.
Показаны страницы 1. Найдено 237 предложения с фразой импедансная катушка.Найдено за 9 мс.Накопители переводов создаются человеком, но выравниваются с помощью компьютера, что может вызвать ошибки. Найдено за 1 мс.Накопители переводов создаются человеком, но выравниваются с помощью компьютера, что может вызвать ошибки. Они поступают из многих источников и не проверяются. Имейте в виду.
Электрическое сопротивление — Простая английская Википедия, бесплатная энциклопедия
Источник переменного тока прикладывает напряжение V {\ displaystyle \ scriptstyle V} через импеданс Z {\ displaystyle \ scriptstyle Z}, управляя током I {\ displaystyle \ scriptstyle I}.
Электрический импеданс — это величина сопротивления цепи изменению тока или напряжения.
Два основных способа записать импеданс:
(см. 2-й рисунок, «плоскость комплексного импеданса»)
- с сопротивлением «R» (действительная часть) и реактивным сопротивлением «X» (мнимая часть), например Z = 1 + 1j {\ displaystyle Z = 1 + 1j}
- с величиной и фазой (размером | Z | {\ displaystyle \ left \ vert Z \ right \ vert} и углом ∠θ {\ displaystyle \ angle \ theta}), например Z = 1.{\ circ}} (1,4 Ом при 45 градусах)
Импеданс и сопротивление очень похожи:
В случае сопротивления резистор сопротивляется любому току, протекающему через него. Чем выше сопротивление, тем выше напряжение, необходимое для достижения заданного тока. Формула:
V = R ∗ I {\ displaystyle V = R * I}, где V — напряжение, R — сопротивление, I — ток.
В случае импеданса катушка индуктивности сопротивляется изменениям тока, а конденсатор — изменениям напряжения.
Ключевое различие между сопротивлением и импедансом — это слово «изменение», скорость изменения влияет на импеданс. Обычно «изменение» выражается как частота, количество раз в секунду направление изменения тока или напряжения. Формулы следующие:
Для индуктора:
Z знак равно j2πfL {\ Displaystyle Z = j2 \ pi fL \,}
Для конденсатора:
Z = 1j2πfC {\ Displaystyle Z = {\ гидроразрыва {1} {j2 \ pi fC}}}
Где Z — символ импеданса, j — мнимое число -1 {\ displaystyle {\ sqrt {-1}}}, π {\ displaystyle \ pi} — константа пи, f — частота, L — индуктивность и C — емкость.Единицы измерения сопротивления и импеданса одинаковые, ом с символом Ω {\ displaystyle \ Omega} (заглавная омега).
Как видно из приведенных выше формул, полное сопротивление изменяется в зависимости от частоты, например, при нуле в герцах или постоянном токе, полное сопротивление катушки индуктивности равно нулю, как при коротком замыкании, а полное сопротивление конденсатора равно бесконечно, то же, что и при разомкнутой цепи. Большинство сигналов представляют собой сумму множества синусоидальных волн на разных частотах (подробнее см. Преобразование Фурье), и каждый из них испытывает разный импеданс.
Аналогично сопротивлению, чем выше импеданс, тем выше напряжение, необходимое для достижения заданного тока. Формула:
V = Z ∗ I {\ displaystyle V = Z * I}, где V — напряжение, Z — импеданс, а I — ток.
На физическом уровне многие вещи упрощаются:
- Сопротивление вызвано столкновениями электронов с атомами внутри резисторов.
- : полное сопротивление конденсатора вызвано созданием электрического поля.
- : полное сопротивление индуктора вызвано созданием магнитного поля.
Одно из важных различий между сопротивлением и импедансом состоит в том, что резистор рассеивает энергию, он нагревается, но индуктор и конденсатор накапливают энергию и могут возвращать эту энергию источнику, когда он выходит из строя.
Сигнал частично отражается туда, где изменяется импеданс.
Если импеданс источника, кабеля и нагрузки не равны, то часть сигнала отражается обратно в источник, теряя мощность и создавая помехи.Коэффициент отражения можно рассчитать с помощью:
- Γ = ZL − ZSZL + ZS {\ displaystyle \ Gamma = {Z_ {L} -Z_ {S} \ over Z_ {L} + Z_ {S}}}, где Γ {\ displaystyle \ Gamma} (заглавная гамма) — коэффициент отражения, ZS {\ displaystyle Z_ {S}} — это импеданс источника, ZL {\ displaystyle Z_ {L}} — импеданс нагрузки.
Любая среда, которая может иметь волну, имеет волновое сопротивление, даже пустое пространство (свет — это электромагнитная волна, и он может перемещаться в пространстве) имеет импеданс около 377 Ом {\ displaystyle \ Omega}.
На конденсаторе (вверху) напряжение (красный) изменяется на после тока (синий), на катушке индуктивности (внизу) оно с до . Разность фаз между напряжением и током составляет 1/4 длины волны.
На резисторе напряжение и ток одновременно повышаются и понижаются, они считаются синфазными, но с импедансом оно другое, напряжение смещено на 1/4 длины волны относительно тока в конденсаторе. , и вперед в катушку индуктивности.
1/4 длины волны обычно обозначается мнимым числом «j», что также эквивалентно смещению на 90 градусов.
Использование мнимого числа «j» значительно упрощает математику, это позволяет рассчитать общий импеданс так же, как это делается с резисторами, например, резистор плюс импеданс последовательно равен R + Z, а параллельно это (R * Z) / (R + Z).
Импеданс
— Викисловарь
Английский [править]
Этимология [править]
препятствие + -ance .Использование физики: придумано Оливером Хевисайдом в 1886 году.
Произношение [править]
Существительное [править]
импеданс ( счетное и несчетное , множественное импедансы )
- Акт воспрепятствования; то, что мешает; помеха.
- 2012 , Р. Крафтон Гиббс, Духовный рост: Логос 2, Том. 2, Написание Божьей Книги Жизни (страница 31)
- Таким образом, верное подчинение — это проявление любви перед Богом, когда мы готовимся ответить на Его Призыв к оружию, даже если Он не может отправить нас на передовую, если какая-то инвалидность или сопротивление Сатаны мешает нам действовать [… ]
- 2012 , Р. Крафтон Гиббс, Духовный рост: Логос 2, Том. 2, Написание Божьей Книги Жизни (страница 31)
- (физика) Мера противодействия протеканию переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивлений; отношение напряжения к току, рассматриваемое как комплексные величины.
- (физика) Величина, аналогичная электрическому импедансу в некоторой другой области энергии.
- (физика, обычно с «механическим») мера противодействия движению чего-либо, на которое действует сила; отношение силы к скорости, рассматриваемое как комплексные величины.
- (физика, обычно с «акустикой» или «звуком») отношение звукового давления к объемному расходу, рассматриваемое как комплексные величины.
- (по аналогии, программная инженерия, обычно с «несоответствием») мера противостояния, вызванного различиями между двумя парадигмами, особенно между объектно-ориентированной разработкой и реляционными базами данных.
- 1997 , Бхавани М.Thuraisingham, Системы управления данными: эволюция и взаимодействие → ISBN, CRC Press, стр. 33:
- Некоторые утверждают, что несоответствие импеданса затруднительно для программирования интенсивных приложений.
- 2002 , Джим Мелтон, Advanced SQL: 1999: Общие сведения об объектно-реляционных и других расширенных функциях → ISBN, Морган Кауфманн, стр. 353:
- Но несоответствие импеданса между SQL и Java было не лучше, чем между SQL и другими языками.
- 2004 , Скотт У. Амблер, The Object Primer: Agile Model-Driven Development with UML 2.0 → ISBN, Cambridge University Press, стр. 442:
- Почему существует технологическое несоответствие импеданса ?
- 1997 , Бхавани М.Thuraisingham, Системы управления данными: эволюция и взаимодействие → ISBN, CRC Press, стр. 33:
Примечания по использованию [править]
Импеданс повсеместно обозначается в технических работах символом Z , который часто используется как синоним этого слова даже в бегущем тексте.
Производные термины [править]
Связанные термины [править]
Переводы [править]
физика, мера противодействия течению тока
Импеданс катушки
— перевод на французский — примеры английский
Эти примеры могут содержать грубые слова на основании вашего поиска.
Эти примеры могут содержать разговорные слова, основанные на вашем поиске.
импеданс катушки метод обнаружения и метод обнаружения объектов и устройство, использующие те же
процесс обнаружения объекта impédance d’une bobine ainsi qu’appareil et procédé de detection d’un objet mettant en oeuvre celui-ci
индукция импеданс катушки моделирование с использованием параметров эквивалентной схемы
Импеданс катушки поочередно определяется для минимальной, средней и максимальной толщины слоя материала образца в приборе для отбора образцов в диапазоне дискретных частот.
Определите импеданс из bobine в одной серии дисков, выберите тур по минимальным, моим и максимальным кушетам материальных шантильонов в выборных наборах.
Предусмотрен датчик положения, превосходный по линейности сопротивления катушки
предварительное изобретение раскрывает и удерживает позицию, представленную на превосходной линии , импеданс на бобине
элемент связи, выполненный в виде катушки связи, и антенная катушка конфигурируются по-разному в зависимости от параметров катушки, влияющих на импеданс катушки .
l’élément de couplage, qui se présente sous la forme d’une bobine de couplage, et la bobine d’antenne sont conçus différemment en ce qui Concerne leurs paramètres de bobine ingant sur l ‘ impédance de bobine .
УСТРОЙСТВО ДЛЯ ОГРАНИЧЕНИЯ ТОКА, ИМЕЮЩЕЕ ПЕРЕМЕННОЕ ИМПЕДАНС КАТУШКИ
Заявляемый способ бесконтактного вихретокового контроля порошковых материалов состоит в помещении образца материала в диэлектрический пробоотборник, возбуждении исследуемого магнитного поля и в измерении импеданса катушки для измерения .
Dans ce procédé d’inspection sans contact par courants de Foucault on place l’échantillon dans un dispositif de sélection d’échantillons diélectrique.
Что такое дистанционное реле типа импеданса? — Определение, принцип работы и тип реле сопротивления .Это оборудование, управляемое напряжением.
Реле измеряет импеданс неисправной точки, если импеданс меньше, чем импеданс уставки реле, оно дает команду отключения на автоматический выключатель для замыкания их контактов. Реле импеданса непрерывно контролирует линейный ток и напряжение, протекающие через трансформатор тока и трансформатор тока соответственно. Если соотношение напряжения и тока меньше, чем реле начинает работать, реле начинает работать.
Принцип действия реле импеданса
В нормальном рабочем состоянии значение линейного напряжения больше тока.Но когда в линии возникает неисправность, величина тока возрастает, а напряжение становится меньше. Линейный ток обратно пропорционален импедансу линии передачи. Таким образом, сопротивление уменьшается, из-за чего реле импеданса начинает работать.
Рисунок ниже гораздо проще поясняет реле импеданса. Трансформатор напряжения подает напряжение в линию передачи, и ток течет через трансформатор тока. Трансформатор тока включен в цепь последовательно.
Считайте, что реле импеданса размещено на линии передачи для защиты линии AB. Z — полное сопротивление линии в нормальном рабочем состоянии. Если полное сопротивление линии падает ниже полного сопротивления Z, реле начинает работать.
Пусть, неисправность F1 возникла в линии AB. Эта неисправность снижает импеданс линии ниже установленного импеданса реле. Реле начинает работать и отправляет команду отключения на автоматический выключатель. Если повреждение вышло за пределы защитной зоны, контакты реле остаются незамкнутыми.
Рабочие характеристики реле полного сопротивления
Элементы управления напряжением и током являются двумя важными компонентами реле полного сопротивления. Текущий рабочий элемент генерирует отклоняющий момент, в то время как элемент накопления напряжения генерирует восстанавливающий момент. Уравнение крутящего момента реле показано на рисунке ниже
-K 3 — это пружина реле. V и I — это значения напряжения и тока.Когда реле находится в нормальном рабочем состоянии, чистый крутящий момент реле становится нулевым.
Если пренебречь эффектом регулирования пружины, уравнение принимает вид
Рабочие характеристики, касающиеся напряжения и тока, показаны на рисунке ниже. Пунктирная линия на изображении представляет рабочее состояние при постоянном сопротивлении линии.
Рабочие характеристики реле импеданса показаны на рисунке ниже.Область положительного крутящего момента реле полного сопротивления находится выше рабочей характеристики. В области положительного крутящего момента сопротивление линии больше, чем сопротивление неисправного участка. Аналогично, в отрицательной области полное сопротивление неисправной секции больше, чем полное сопротивление линии
.
Импеданс линии представлен радиусом окружности. Фазовый угол между осями X и R представляет положение вектора. Если импеданс линии меньше радиуса круга, тогда он показывает область положительного момента.Если полное сопротивление больше отрицательной области, то это область отрицательного момента.
Этот тип реле называется высокоскоростным реле.
Индукционное реле электромагнитного типа
В реле такого типа крутящий момент индуцируется электромагнитным воздействием на напряжение и ток. Эти моменты сравниваются. Рассмотрим схему индукционного реле электромагнитного типа. Соленоид B возбуждается напряжением, подаваемым от ПТ. Это напряжение развивает крутящий момент по часовой стрелке, и оно тянет плунжер P 2 вниз.Пружина соединяется с плунжером P 2 прикладывает к нему сдерживающую силу. Эта пружина создает механический крутящий момент по часовой стрелке.
Соленоид A создает другой крутящий момент по часовой стрелке и, таким образом, перемещает плунжер P 1 вниз. Электромагнитный возбуждается ТТ линий. Этот крутящий момент называется отклоняющим или захватывающим крутящим моментом.
Когда система исправна, контакты реле разомкнуты. Когда повреждение происходит в защитной зоне, ток в системе возрастает, из-за чего увеличивается ток через реле.Чем больше крутящий момент создается на соленоиде A. Восстанавливающий крутящий момент из-за напряжения уменьшается. Уравновешивающие рычаги реле начинают вращаться в обратном направлении, замыкая свои контакты.
Усилие соленоида A, т.е. (токовый элемент), пропорционально I 2 , а тяговое усилие соленоида B (элемент напряжения) — V 2 . Следовательно, реле сработает, когда
Значение констант k 1 и k 2 зависит от ампер-витков двух соленоидов и отношения измерительных трансформаторов.Установив ответвления на катушке, можно изменить настройку реле.
Ось Y показывает время срабатывания реле, а ось X представляет их полное сопротивление. Время работы реле остается постоянным. Значение напряжения и тока становится постоянным на заданном расстоянии, а после этого их значение становится бесконечным.
Реле импеданса индукционного типа
Принципиальная схема реле импеданса индукционного типа показана на рисунке ниже.Это реле состоит из элементов тока и напряжения. Реле имеет алюминиевый диск, который вращается между электромагнитами.
Верхний электромагнит имеет две отдельные обмотки. Первичная обмотка подключена ко вторичной обмотке трансформатора тока. Текущее значение обмотки изменяется с помощью перемычки, расположенной под реле.
Электромагниты реле соединяются последовательно друг с другом. Магнитный поток между электромагнитами создает крутящий момент, который вращает алюминиевый диск реле.Постоянный магнит обеспечивает управляющий и тормозной момент.
В нормальных рабочих условиях сила, действующая на якорь, превышает силу индукционного элемента, который удерживает контакты размыкания. При возникновении неисправности в системе алюминиевые диски начинают вращаться, и их вращение прямо пропорционально току электромагнита. Вращение дисковой пружины.
Угол поворота диска для срабатывания реле зависит от силы, действующей на их якорь.Сила, действующая на якорь, прямо пропорциональна приложенному напряжению.

 {\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}
{\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .} {-st}\,dt.}
{-st}\,dt.}