Задачи метод контурных токов: Метод контурных токов для расчёта электрических цепей

Содержание

Метод контурных токов для расчёта электрических цепей

При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов позволяет уменьшить количество решаемых уравнений.

В методе контурных токов уравнения составляются на основании второго закона Кирхгофа, причём их равно N_в – N_у + 1, где N_у – число узлов, N_в – число ветвей, т.е. количество совпадает с количеством уравнений, составляемых по второму закону Кирхгофа.

Опишем методику составления уравнений по методу контурных токов. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно направления контурных токов (рис. 2).

Рис. 2. Задание направления контурных токов в электрической цепи

Количество уравнений, составляемых по методу контурных токов, равно 3. Здесь контур с источником тока так же не рассматривается.

Составим уравнение для контура «1 к.». В контуре «1 к.» контурный ток I₁₁ протекает по всем сопротивлениям R₂, Z_L₁, Z_C₁. Кроме того, через сопротивление R2 протекает контурный ток смежного контура «2 к.» I₂₂, причём контурные токи I₁₁ и I₂₂ протекают в противоположных направлениях. Через индуктивное сопротивление Z_L₁ также протекает контурный ток I₃₃, причём контурные токи I₁₁ и I₃₃ также протекают в противоположных направлениях. Про составлении уравнения нужно сложить все падения напряжения (аналогично второму закону Кирхгофа), при этом необходимо учесть направление контурных токов: если контурные токи смежных контуров протекают в определённой ветви в одном направлении, то падение напряжения в этой ветви необходимо вносить со знаком «+», в противном случае – со знаком «-». Полученная сумма будет равна сумме ЭДС данного контура, при этом ЭДС берётся со знаком «+», если направление контурного тока совпадает с направлением ЭДС, в противном случае – со знаком «-».

Учитывая вышеизложенное, уравнение по методу контурных токов для контура «1 к.» будет выглядеть следующим образом:

(R₂ + Z_L₁ + Z_C₁) ∙ I₁₁ – R₂ ∙ I₂₂– Z_L₁ ∙ I₃₃ = E₁.

Аналогично составим уравнение для контура «2 к.». Необходимо учесть, что уравнение для контура с источником тока не составляется, но ток от источника тока также необходимо учитывать в уравнение аналогично контурным токам других контуров. Само уравнение будет выглядеть следующим образом:

–R₂ ∙ I₁₁ + (R₂ + R₄ + Z_C₂) ∙ I₂₂– Z_С₂ ∙ J₁ = E₂.

Для контура «3 к.»:

–Z_L₁ ∙ I₁₁ + (R₁ + R₃ + Z_L₁ + Z_L₂) ∙ I₃₃– R₃ ∙ J₁ = E₃.

В приведённых выше уравнениях Z_C = –1/(ωC), Z_L = ωL.

Таким образом, для того, чтобы найти искомые контурные токи, необходимо решить следующую систему уравнений, где слагаемые с силой тока источника тока перенесены в правую часть уравнений:

В данном случае это система из 3 уравнений с 3 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3;
>> A = [R2+Zl1+Zc1       -R2          -Zl1;
               -R2 R2+R4+Zc2             0;
              -Zl1         0 R1+R3+Zl1+Zl2];
>> b = [ E1;
E2 + Zc2*J1;
 E2 + R3*J1];
>> I = A\b

В результате получим вектор-столбец I токов из трёх элементов, состоящий из искомых контурных токов, при этом

I(1) = I₁₁, I(2) = I₂₂, I(3) = I₃₃.

Далее в схеме по рис. 2 расставим направления токов в ветвях (рис. 3).

Рис. 3. Задание направления токов в электрической цепи

Для определения токов в ветвях необходимо рассмотреть все контурные токи, которые протекают через данную ветвь. Видим, что через ветвь, где протекает ток I₁, проходит только один контурный ток I₁₁, и он сонаправлен, отсюда

I₁ = I₁₁.

Через ветвь, где протекает ток I₂, проходят контурные токи I₁₁ и I₂₂, причём ток I₁₁ совпадает с принятым направлением тока I₂, а ток I₂₂ – не совпадает. Те контурные токи, которые совпадают с принятым направлением, берутся со знаком «+», те, которые не совпадают – со знаком «-». Отсюда

I₂ = I₁₁ – I₂₂.

Аналогично для других ветвей

I₃ = I₂₂,

I₄ = – I₁₁ + I₃₃,

I₅ = I₂₂ – J₁,

I₆ = I₃₃,

I₇ = I₃₃ – J₁.

Итак, метод контурных токов позволяет рассчитывать меньшее количество сложных уравнений для расчёта аналогичной электрической цепи по сравнению с законами Кирхгофа.

Список использованной литературы

Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

калькулятор расчета, примеры применения метода

Все расчеты электрических схем базируются на простых формулах. Сложность и громоздкость вычислений зависят от сложности схем. Для упрощения расчетов без ущерба качеству разработано несколько методик, позволяющих сократить число вычислений до разумных пределов.

Основные формулы электротехники

Основные принципы

Любая электротехническая цепь состоит из участков (ветвей), образующих узлы и контуры. Для определения значений тока через любой элемент используют два закона Кирхгофа. Прямое составление уравнений дает систему с их максимальным количеством, равным количеству ветвей. В результате, если множество узлов цепи равно У, а число ветвей Р, то уравнения распределяются следующим образом:

Для узлов У-1 по закону Кирхгофа для токов;
Для ветвей Р-У+1 по закону Кирхгофа для напряжений.

Данное количество избыточно и приводит к образованию громоздкой системы уравнений большой размерности.

Для упрощения расчетов разработаны методики, которые позволяют сократить количество уравнений до приемлемых значений без снижения точности результатов. Наиболее простым является метод контурных токов.

Определение и суть метода контурных токов

По данному методу в исследуемой цепи выделяются независимые плоские замкнутые контуры, включающие все, без исключения, элементы. Предполагается, что в каждом контуре может протекать некоторый контурный ток. В том случае, если цепь с элементом принадлежит только одному контуру, то ток через входящие в нее элементы равен контурному. Если элемент охватывается несколькими контурами, то он в ней равен алгебраической (с учетом направления) сумме контурных токов.

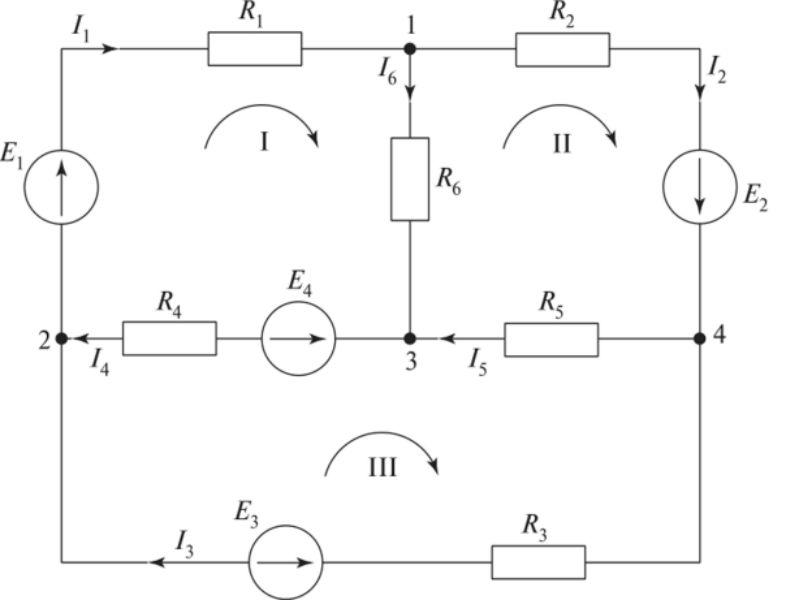
Разбиение цепи на контуры

Важно! Суммирование должно производиться строго с учетом направления движения при обходе контура. Знак «плюс» – при совпадении направления, «минус» – при противоположном.

При составлении уравнений учитываются входящие в схему источники ЭДС и тока.

На практике удобнее преобразовать идеальный источник тока в идеальный источник ЭДС. Преобразование выполняется согласно закона Ома:

U=I∙r, где r – внутреннее сопротивление источника тока (напряжения).

Методика расчета используется как в цепях постоянного, так и переменного напряжения. При расчетах цепей переменного напряжения с реактивными элементами используются комплексные величины, затем вычисляются мгновенные и амплитудные величины токов и напряжений и углы сдвига фаз между ними.

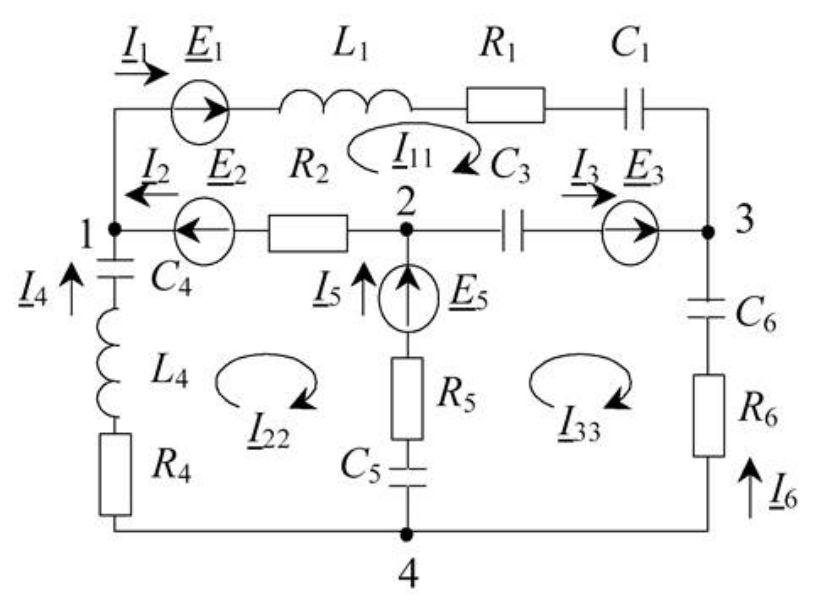
Цепь с реактивными элементами

Построение системы контуров

Основная сложность заключается в правильном выделении контуров. Количество контурных токов будет равняться числу выбранных контуров.

Важно! Каждый элемент схемы должен входить хотя бы в один контур.

Распространены две методики выбора контуров.

Использование планарных графов

Метод планарных графов применяется при ручном расчете, поскольку он наиболее прост и нагляден. Для построения плоского графа схему рисуют таким образом, чтобы не было взаимного пересечения ветвей. Получается, что схему можно разбить на несколько ограниченных участков, которые образуют контуры.

Рассматриваемая методика неприменима без дополнительных преобразований, если невозможно выразить схему в виде планарного графа.

Метод выделения максимального дерева

Метод выделения максимального дерева более абстрактный и используется при автоматизированных расчетах и наличия специализированных программ. Суть метода заключается в исключении из цепи некоторых ветвей в соответствии со строгими правилами, которые таковы:

При каждом шаге исключается только одна ветвь;
Исключение ветви не должно приводить к разбиению графа на несколько частей или к «висячим узлам»;
Количество удаленных звеньев равняется числу независимых контуров;
Подключение удаленной ветви образует соответствующий контур.

Построение системы уравнений

Построение системы уравнений по рассматриваемой методике выполняется по следующим правилам:

Для каждого выбранного контура задается направление обхода;
С левой стороны равенств записывается сумма всех произведений искомых токов в ветвях на сопротивление веток. В правую часть записывается сумма источников напряжений, присутствующих в контуре;
Если направление искомой величины или источника напряжения такое же, как у заданного направления обхода, то слагаемые пишутся со знаком «плюс», в ином случае они имеют отрицательное значение;
Значение токов в ветвях заменяют на их выражение через токи контура.

После выполнения арифметических действий (раскрытие скобок, приведение подобных слагаемых) получается система уравнений, в которых неизвестными величинами являются виртуальные контурные токи.

Решая систему уравнений, получают значения контурных, а затем искомых величин.

Оптимизированная процедура составления системы

По упрощенной методике поступают следующим образом:

В уравнениях в левой части записывают произведение суммы всех входящих в контур сопротивлений на контурный ток;
От полученного выражения вычитаются умноженные на сумму сопротивлений общей ветви соседние контурные токи;
Справа записывается сумма источников ЭДС контура.

Формальный подход

Формальный подход предполагает матричную форму записи системы уравнений. Для расчетов исходные данные записывают в матричной форме. Используются такие матрицы:

C – в которой i строк, соответствующих количеству контуров, и j столбцов по количеству ветвей;
Z – диагональная матрица сопротивлений, количество строк и столбцов которой соответствуют числу веток;
Ct – транспонированная матрица С;
I – матрица контурных величин;
J – матрица источников тока;
Е – матрица ЭДС.

При составлении матрицы С каждый элемент Сij:

0, если ветвь j не входит в контур;
-1, если ветвь входит в контур, направление тока противоположно контурному;
1 – то же самое, но направление тока совпадает с контурным.

В матрице Z диагональные элементы равняются сопротивлению участков, остальные приравниваются нулю.

Итоговая формула для расчетов имеет вид:

C∙Z∙Ct∙I=C(Z∙J+E).

Такая форма записи решения в матричной форме показывает, каким образом выполняются действия над составленными матрицами.

Пример системы уравнений

Ниже рассмотрен пример расчета конкретной схемы без учета номиналов элементов.

Пример решения

В заданной цепи выделяют три контура. Как выразить токи в ветвях через контурные:

i1=I1;
i2=I2;
i3=I3;
i4=I2+I3;
i5=I1+I2;
i6=I1-I3.

Как составить систему уравнений:

i1R1+i5R5+i6R6=E1;
i2R2+i4R4+i5R5=E2;
i3R3+i4R4-i6R6=0

Как подставить контурные значения:

I1R1+( I1+I2)R5+( I1-I3)R6=E1;
I2R2+( I2+I3)R4+( I1+I2)R5=E2;
I3R3+( I2+I3)R4-( I1-I3)R6=0

После преобразования получается необходимая система уравнений:

(R1+R5+R6)I1+R5I2+R6I3=E1;
R5I1+(R2+R4+R5)I2+R4I3=E2;
-R6I1+R4I2+(R3+R4+R6)I3=0.

Система из трех уравнений легко решается после подстановки известных параметров. Из полученных значений контурных токов затем можно найти искомые величины.

Данный пример решения задач по методу контурных токов показывает, что любую достаточно сложную схему можно существенно упростить для решения, руководствуясь указаниями.

Важно! Метод неприменим, если нет возможности преобразовать цепь без взаимного пересечения ветвей.

В некоторых случаях упростить схему можно путем преобразования ветвей, соединенных по схеме «звезда» в треугольник.

Точно такие же результаты получаются при использовании метода узловых потенциалов. В основе расчетов – поиск потенциала каждого узла (так называемый узловой потенциал). Существуют программы, позволяющие произвести онлайн расчет параметров по рассмотренным методам.

Видео

Пример решения задачи методом контурных токов

Скачайте приложение для онлайн решения разветвленной цепи. Вам потребуется только нарисовать схему в редакторе программы и задать численные значения элементов.
Программа сама выдаст подробное пошаговое решение как если бы вы сами делали это РГР.

Для электрической цепи рис. 1, выполнить следующее:

Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует.
Определить токи в ветвях методом контурных токов.
Построить потенциальную диаграмму для любого замкнутого контура, содержащего обе ЭДС.
Определить режимы работы активных элементов и составить баланс мощностей.

Значения ЭДС источников и сопротивлений приемников:
E1 = 130 В, Е2 = 110 В, R1 = 4 Ом, R2 = 8 Ом, R3 = 21 Ом, R4 = 16 Ом, R5 = 19 Ом, R6 = 16 Ом.

Смотрите также
Пример решения схемы методом контурных токов № 1
Пример решения схемы методом контурных токов № 2
Пример решения схемы методом контурных токов № 3
Пример решения схемы методом контурных токов № 4
Пример решения схемы методом контурных токов № 5
Посмотреть видео «Метод контурных токов 2» (пример решения конкретной задачи)

Рис. 1. Схема

Решение. Заказать работу! Решить онлайн! (New!!!)

1. Произвольно расставим направления токов в ветвях цепи, примем направления обхода контуров (против часовой стрелки), обозначим узлы.

Рис. 2

2. Для получения системы уравнений по законам Кирхгофа для расчета токов в ветвях цепи составим по 1-му закону Кирхгофа 3 уравнения (на 1 меньше числа узлов в цепи) для узлов 1,2,3:

По второму закону Кирхгофа составим m – (р – 1) уравнений (где m – кол-во ветвей, р – кол-во узлов ), т.е. 6 – (4 – 1) = 3 для контуров I11, I22, I33:

Токи и напряжения совпадающие с принятым направлением обхода с «+», несовпадающие с «-».
Т.е. полная система уравнений для нашей цепи, составленная по законам Кирхгофа:

3. Определим токи в ветвях методом контурных токов. Зададимся направлениями течения контурных токов в каждом контуре схемы и обозначим их I11, I22, I33 (см. рис. 2)

4. Определим собственные сопротивления трех контуров нашей цепи, а так же взаимное сопротивление контуров:

(Ом)
(Ом)
(Ом)
(Ом)
(Ом)
(Ом)

5. Составим систему уравнений для двух контуров нашей цепи:

Подставим числовые значения и решим.

(А)
(А)
(А)

Определим фактические токи в ветвях цепи:
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным
(А) направление тока потивоположно выбранному
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным

6. Проверим баланс мощностей:

(ВА)
Небольшая разница в полученных результатах является результатом погрешности при округлении числовых значений токов и сопротивлений.

7. Построим потенциальную диаграмму контура изображенного на рис. 3. В качестве начальной точки примем узел 1.

Рис.3

Для построения потенциальной диаграммы определим падения напряжения на каждом сопротивлении, входящем в выбранный контур.
(В)
(В)
(В)
(В)
Потенциал увеличивается если обход осуществляется против направления тока, и понижается если направление обхода совпадает с направлением тока. На участке с ЭДС потенциал изменяется на величину ЭДС. Потенциал повышается в том случае, когда переход от одной точки к другой осуществляется по направлению ЭДС и понижается когда переход осуществляется против направления ЭДС.

Рис. 4. Потенциальная диаграмма. ЗАКАЗАТЬ РАБОТУ!

Решить онлайн! (New!!!)

Методическая разработка урока «Метод контурных токов» (10 класс). Профильный уровень

Методическая разработка урока физики для профильного класса

(политехнический, физико-математический)

Урок 12/114 10 класс

Тема: Метод контурных токов.

Цели урока:

образовательная: научить учащихся производить расчеты сложных электрических цепей;
развивающая: сформировать умения анализировать, развитие логики мышления, поиска способов рационального решения физических задач;
воспитательная: воспитание мотивации учения.

Содержание урока:

Организационный момент
Проверка знаний.

Фронтальный опрос.

Вопросы:

Дайте определение узла электрической цепи. Начертите на доске электрический узел, укажите направление электрических токов в подводящих к узлу ветвях.
Сформулируйте первое правило Кирхгофа.
Запишите первое правило Кирхгофа для начерченного на доске (рис. 1) узла.

Рис. 1. Рис.2.

Какое соединение элементов электрической цепи можно считать ветвью?
Сформулируйте второе правило Кирхгофа, запишите второе правило Кирхгофа для предложенной схемы (рис. 2).
Объясните, как записать второе правило Кирхгофа, если в ветви находятся несколько источников тока?
Как влияет полярность включения источника тока в электрическую цепь на знак ЭДС в уравнении?

Индивидуальный опрос у доски с одновременным решением задачи № 1 в тетрадях учащихся.

ЗАДАЧА № 1.

В предложенной электрической цепи определите силу тока во всех резисторах, используя законы Кирхгофа.

Рис. 3

Решение задачи:

Напишем 1 закон Кирхгофа для узлов А, В, С:

А: I₁— I₂+ I₄ = 0;

В: I₅– I₁+ I₃ = 0;

С: I₆– I₄– I₅ = 0.

Выберем направление обхода контуров ADBA, BDCB и ABCA и напишем 2 закон Кирхгофа для этих контуров:

ADBA: ε₁= I₂^. R₂+ I₁^. R₁+ I₃^. R₃;

BDCB: ε₂= I₅^. R₅— I₃^. R₃+ I₆^. R₆;

ABCA : 0 = I₄^. R₄— I₁^. R₁– I₅^. R₅.

Подставим численные значения сопротивлений резисторов и источников тока в полученные уравнения и объединим их систему из шести уравнений с шестью неизвестными:

Выразим из наиболее простого уравнения системы один из неизвестных токов и, подставив это неизвестное в остальные уравнения, преобразуем уравнения системы с учетом полученного выражения, и, понижая с каждым преобразованием ранг системы уравнений, найдем численные значения неизвестных, входящих в эту систему уравнений:

Подставим полученные значения силы тока в резисторах в уравнения Кирхгофа, убедимся в правильности расчетов:

Изучение нового материала.

Вопросы: Расчет электрических цепей с помощью метода контурных токов.

Расчет электрической цепи методом контурных токов.

Для сравнения уровня сложности расчетов произведем расчет электрической цепи Рис. 3., предложенной в предыдущей задаче, методом контурных токов:

Основным достоинством, рассматриваемого метода расчета электрической цепи, метода контурных токов является то, что для вычисления силы токов в каждом элементе цепи количество уравнений в системе соответствует количеству контуров рассчитываемой электрической цепи. В нашем случае необходимо составить всего три уравнения, что в два раза меньше чем в системе уравнений рассчитываемой при использовании законов Кирхгофа.

Выберем в контурах ADBA, BDCB и ABCA произвольно направления контурных токов J₁, J₂и J₃. Составим систему из трех уравнений:

Подставив в полученную систему уравнений численные значения резисторов и ЭДС, рассчитаем контурные токи:

Сила тока в отдельных резисторах определяется как векторная сумма контурных токов, протекающих через эти резисторы:

I₁= J₁ – J₃ = 0,2 А; I₂ = J₁= 0,6 А;

I₃ = J₂ – J₁= 0,4 А; I₄ = J₃= 0,4 А;

I₅ = J₂ – J₃ = 0,6 А; I₆= J₂ = 1А.

Результаты расчета проверяются с помощью законов Кирхгофа.

Закрепление изученного материала.

Учащимся предлагается самостоятельно записать уравнения, необходимые для расчета следующей электрической цепи (рис. 4) методом контурных токов:

Рис. 4.

Для предложенной электрической цепи выберем 3 контура:

1 – контур: С, R₂ ,ε_1,R₁,А, R₃, С

2 – контур: С, R₃, А, R₄, В, R₆, D, R₅, С

3 – контур: D, R₆, В, R₇, ε_2,R₈, D

Составим уравнения согласно второму правилу Кирхгофа для выбранных контуров:

ε₁= J₁^.(R₁ + R₂ + R₃+ r₁) – J₂^.R₃ (1).

0 = J₂^.(R₃ + R₄ + R₅+ R₆) – J₁^.R₃ – J₃^.R₆ (2).

ε₂= J₃^.(R₆ + R₇ + R₈+ r₂) – J₂^.R₆ (3).

После решения системы трех уравнений с тремя неизвестными найдем токи в элементах цепи:

I₁ = I₂=J₁, I₃=J₁– J₂,

I₄ = I₅=J₂, I₃=J₁– J₂,

I₆= J₂– J₃, I₇ = I₈=J₃.

Самостоятельная работа учащихся по решению задач.

Используя метод контурных токов, вычислите численные значения силы тока в каждом элементе, найдите падение напряжения на всех резисторах, предложенной электрической цепи:

ЗАДАЧА № 2.

Рассчитайте электрическую цепь методом контурных токов:

Дано:

ε₁ = 50 В

ε₂= 40 В

R₁ = 7 Ом

R₂ = 10 Ом

R₃ = 6 Ом

r₁ = 3 Ом

r₂ = 4 Ом.

Определить:

I₁, I₂, I₃,

U₁, U₂, U₃.

РЕШЕНИЕ:

В цепи два простых контура. Выберем направление контурных токов J₁и J₂с учетом полярности ЭДС источников тока.

Для контура C,ε_1,r_1,R₁, A, R₂,C: ε₁= J₁^.(R₁ + R₂ + r₁) + J₂^.R₂ (1).

Для контура C, R₂, A, R₃, ε_1,r_1,,C: ε₂= J₂^.(R₃ + R₂ + r₂) + J₁^.R₂ (2).

Подставляя в выражения (1) и (2) численные значения сопротивления резисторов и ЭДС источников тока, получаем систему из двух уравнений:

50 = J₁^.(7 + 10 + 3) + J₂^.10, 5 = 2J₁ + J₂, J₁ = 2 А;

40 = J₂^.(6 + 10 + 4) + J₁^.10. 4 = 2J₂ + J₁. J₂= 1 А.

Рассчитаем токи в отдельных резисторах: I₁ = J₁ = 2А; I₂ = J₁ + J₂= 3А; I₃ = J₂ = 1А.

Рассчитаем падение напряжения на резисторах: U₁ = I₁^.R₁= 2^.7 = 14 B, U₂ = I₂^.R₂= 3^.10 = 30 B, U₃ = I₃^.R₃= 1^.6 = 6 B.

Ответ: I₁ = 2А; I₂ = 3А; I₃ = 1А. U₁ = 14 B, U₂ = 30 B, U₃ = 6 B.

Подведение итогов урока.
Задание на дом.

Рассчитайте методом контурных токов электрические цепи:

ЗАДАЧА № 1.

Дано:

ε₁ = 20 В

ε₂= 30 В

R₁ = 16 Ом

R₂ = 10 Ом

R₃ = 20 Ом

R₄ = 7 Ом

R₅ = 10 Ом

r₁ = 3 Ом

r₂ = 4 Ом.

Определить:

I₁, I₂, I₃, I₄, I₅,

U₁, U₂, U_3, U₄, U₅.

ЗАДАЧА № 2.

Дано:

ε₁ = 20 В

ε₂= 30 В

R₁ = 16 Ом

R₂ = 10 Ом

R₃ = 20 Ом

R₄ = 8 Ом

R₅ = 20 Ом

r₁ = 2 Ом

r₂ = 4 Ом.

Определить:

I₁, I₂, I₃, I₄, I₅,

U₁, U₂, U_3, U₄, U₅.

ЗАДАЧА № 3.

Дано:

ε₁ = 100 В

ε₂= 50 В

R₁ = 20 Ом

R₂ = 30 Ом

R₃ = 20 Ом

R₄ = 20 Ом

R₅ = 75 Ом

R₆ = 78 Ом

r₁ = 5 Ом

r₂ = 2 Ом.

Определить:

I₁, I₂, I₃, I₄, I₅, I₆,

U₁, U₂, U_3, U₄, U_5, U₆.

Практическая работа «Расчет сложных цепей постоянного тока методом контурных токов»

Практическая работа

«Расчет сложных цепей постоянного тока методом контурных токов»

1. Определить токи в ветвях схемы методом контурных токов.

2. Составить уравнение баланса мощностей.

рис.

Е₁, В

Е₂, В

Е₃, В

R₁, В

R₂, В

R₃, В

R₄, В

R₅, В

R₆, В

рис.1.

200

100

180

рис.2.

100

200

рис.3.

120

220

200

рис.4.

200

рис.1.

100

200

120

рис.2.

180

200

рис.3.

200

100

рис.4.

220

200

рис.1.

180

200

10.

рис.2.

200

120

100

11.

рис.3.

200

220

12.

рис.4.

200

13.

рис.1.

120

180

100

14.

рис.2.

100

150

15.

рис.3.

220

180

Методика решения:

Рис.1

Дано:

Е₁=100 В; R₂=5 Ом;

Е₂=120 В; R₃=16 Ом;

Е₃=200 В; R₄=21 Ом;

R₁=4 Ом; R₅=15 Ом;

R₆=23 Ом;

1. Определить токи в ветвях схемы методом контурных токов,

2. Составить уравнение баланса мощностей.

Решение:

1. Составим уравнение для каждого контура по 2 закону Кирхгофа.

2. Подставим исходные данные в полученную систему уравнений и решим ее относительно неизвестных I_к1, I_к2, I _к3:

Главный определитель:

= 40·36·49 + (-15) · (-5) · (-21) + (-15) · (-5) · (-21) — (-21) · 36· (-21) —

— (-15) · (-15) · 49 — (-5) · (-5) ·40 = 70560-1575-1575-15876-11025-1000 = 39509

Определитель по первому неизвестному:

= 100·36·49 + (-15) · (-5) · (-120) + (-80) · (-5) · (-21) — (-21) · 36· (-120)- (-15) · (-80) ·49 — (-5) · (-5) ·100 = 176400 – 9000 – 8400 – 90720 – 58800 – 1225 = 8255

Определитель по второму неизвестному:

= 40· (-80) · 49 + 100· (-5) · (-21) + (-15) · (-120) · (-21) — (-21) · (-80) · (-21) — 100· (-15) · 49 — (-5) · (-120) · 40 = -156800+10500-37800+35280+73500-24000 = -99320

А=-2,51 А

Определитель по третьему неизвестному:

= 40·36·(-120) + (-15) · (-80)·(-21) + (-15)·(-5)·100 — 100·36·(-21) —

— (-15)·(-15)·(-120) — (-80)·(-5)·40 = -172800 – 25200 + 7500 + 75600 + 27000 — 16000=-103900

А=-2,63А

3.Определим реальные токи в ветвях:

I₁= I_к₁= 0,21 A

I₂= I_к₂— I_к₃= -2,52 — (-2,63) = 0,11 A

I₃= I_к₂= -2,52 A (Ток I₃ направлен встречно I_к₂)

I₄= I_к₁-I_к₃= 0,18 — (-2,63) = 2,81 A

I₅= I_к₁— I_к₂= 0,18 — (-2,51)=2,69 A

I₆= I_к3= -2,63 A (Ток I₆ направлен встречно I_к3)

4. Составим уравнение баланса мощностей:

ΣР_ИСТ=ΣР_ПОТР

ΣР_ИСТ= Е₁I₁+Е₂I₂+Е₃I₃ =100·0,21+120·0,11+200·2,52=21+13,2+504=538,2 Вт;

ΣР_ПОТР= I₁²R ₁+ I₂²R₂+ I₃²R₃+ I₄²R₄+ I₅²R₅+ I₆²R₆= 0,21²·4 + 0,11²·5 + 2,52²·16 +

+2,81²·21+ 2,69²·15++2,63²·23 = 0,18 + 0,061+101,61 +165,82 +108,54+159,09=538,3 Вт

538,2 Вт ≈ 538,3 Вт

Таким образом, баланс мощностей выполняется.

Учебно-методический материал на тему: А21Практическая работа № 3 Тема: Расчет электрической цепи методом контурных токов. Цель работы: приобрести умения решения сложных цепей постоянного тока методом контурных токов.

Практическая работа № 3

Тема: Расчет электрической цепи методом контурных токов.

Цель работы: приобрести умения решения сложных цепей постоянного тока методом контурных токов.

Методика расчета цепи методом контурных токов

В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.

Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:

1 .Вычерчиваем принципиальную схему цепи и обозначаем все элементы.

2 .Определяем все независимые контуры.

3. Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.

4. По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

5. Решаем любым методом полученную систему относительно контурных токов и определяем их.

6. Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).

7 .Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.

При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.

Пример расчёта сложной цепи методом контурных токов

В цепи, изображённой на рисунке 1, рассчитать все токи методом контурных токов. Параметры цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.

Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов

Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).

По второму закону Кирхгофа относительно контурных токов составляем уравнения:

Решаем систему и получаем контурные токи I11 = I22 = 3 А.

Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов одинаковое – вертикально вверх.

Переходим от контурных токов к реальным. В первой ветви протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветви. В таком случае реальный ток I1 + I11 = 3 А.

Реальный ток второй ветви формируется двумя контурными I11 и I22. Ток I22 совпадает по направлению с реальным, а I11 направлен навстречу реальному. В результате I2 = I22 — I11 = 3 — 3 = 0А.

В третьей ветви протекает только контурный ток I22. Направление этого тока противоположно направлению реального, поэтому для I3 можно записать I3 = -I22 = -3А.

Следует отметить, как положительный факт, что в методе контурных токов по сравнению с решением по законам Кихгофа приходится решать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей.

Варианты схем цепи постоянного тока

1.5. Численные значения параметров цепи

Первая цифра варианта	, В	, Ом	, Ом	Вторая цифра варианта	, В	, Ом	, Ом	Третья цифра варианта	, В	, Ом	, Ом
1	50	10	5	1	80	40	25	1	120	40	100
2	75	25	10	2	120	20	10	2	80	10	20
3	100	50	50	3	30	5	40	3	30	5	50
4	25	25	40	4	40	10	50	4	75	25	10
5	80	20	25	5	50	25	40	5	90	10	50
6	120	40	20	6	75	25	100	6	110	10	25
7	30	10	50	7	80	10	20	7	45	5	25
8	100	5	40	8	90	5	25	8	70	10	40
9	150	50	5	9	60	20	50	9	125	25	40
0	40	20	20	0	25	5	50	0	50	50	20

№ по журналу	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
№ варианта для выбора задания	121	111	211	222	323	333	444	434	555	523	666	624	777	756	888	854	856

№ по журналу	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
№ варианта для выбора задания	999	965	907	000	190	265	785	945	367	863	549	675	189	239	378	320	136	610

Контрольные вопросы:

1.Что такое контур?

2.Что такое контурный ток?

3.Назовите основные пункты расчета цепи методом контурных токов?

4.Как осуществить переход от контурных токов к реальным?

Метод контурных токов. — Студопедия

Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m — количество ветвей, а n — количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.

Контурный ток — это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I₁₁, I₂₂ и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС — это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

Выполняем все поэтапно.

1. Произвольно выбираем направления действительных токов I₁-I₆.

2.Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

R₁₁=R₁+R₄+R₅=10+25+30= 65 Ом

R₂₂=R₂+R₄+R₆=15+25+35 = 75 Ом

R₃₃=R₃+R₅+R₆=20+30+35= 85 Ом

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

R₁₂=R₂₁=R₄=25 Ом

R₂₃=R₃₂=R₆=35 Ом

R₃₁=R₁₃=R₅=30 Ом

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E₁ этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.

5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.

Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

А для остальных

Метод

Mesh-Current (анализ петли) — Скачать PDF бесплатно

Эквивалентные схемы Thevenin

Эквивалентные схемы Hevenin Введение В каждой из этих задач нам показана схема и ее эквивалентная схема Hevenin или Norton.Эквивалентные схемы Хевенина и Нортона описываются с использованием трех

Дополнительная информация

МЕТОДЫ. C.T. Сковорода 1. C.T. Кастрюля

МЕТОДЫ АНАЛИЗА ЦЕПИ C.T. Часть 1 4.1 Введение 4.2 Метод узлового напряжения (узловой анализ) 4.3 Метод сеточного тока (анализ сетки) 4.4 Фундаментальный анализ петли 4.5 Фундаментальный разрез

Дополнительная информация

Схемы 1 M H Miller

Введение в теорию графов. Введение. Эти заметки представляют собой в первую очередь отступление от общих замечаний.Предмет является действенной методикой определения напряжений и токов

Дополнительная информация

Узловой и петлевой анализ

Узловой анализ и анализ контуров Процесс анализа схем иногда может быть сложной задачей. Изучение схемы с помощью методов узла или цикла может сократить время, необходимое для получения важных

Дополнительная информация

Анализ постоянного тока сетки

Анализ тока сетки постоянного тока Этот рабочий лист и все связанные файлы находятся под лицензией Creative Commons Attribution License, версия 1.0. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/1.0/,

Дополнительная информация

Текущий закон Кирхгофа (KCL)

Текущий закон Кирхгофа (KCL) I. Закон сохранения заряда (тока) (Закон Кирхгофа) Труба Труба Труба 3 Общий объем воды в секунду, протекающей по трубе = общий объем воды на

Дополнительная информация

Использование метода импеданса

Использование метода импеданса Метод импеданса позволяет нам полностью отказаться от подхода дифференциального уравнения для определения отклика цепей.По факту импедансный метод даже

Дополнительная информация

Студенческое исследование: схемы

Имя: Дата: Изучение учащимися: Схемы Словарь: амперметр, цепь, ток, омметр, закон Ома, параллельная цепь, сопротивление, резистор, последовательная цепь, напряжение Вопросы предварительных знаний (выполните

Дополнительная информация

Смещение делителя напряжения

Смещение делителя напряжения ENGI 242 ELEC 222 BJT Смещение 3 Для конфигураций смещения делителя напряжения Нарисуйте эквивалентную входную цепь Нарисуйте эквивалентную выходную цепь Запишите необходимые уравнения KVL и KCL Определите

Дополнительная информация

(6) (2) (-6) (- 4) (-4) (6) + (-2) (- 3) + (4) (3) + (2) (- 3) = -12-24 + 24 + 6 + 12 6 = 0

Глава 3 Домашнее задание Soluton P3.-, 4, 6, 0, 3, 7, P3.3-, 4, 6, P3.4-, 3, 6, 9, P3.5- P3.6-, 4, 9, 4 ,, 3, 40 ————————————————- — P 3.- Определите значения, 4, 3 и 6

Дополнительная информация

1 2 3 1 1 2 Икс = + Икс 2 + Икс 4 1 0 1

(d) Если вектор b является суммой четырех столбцов матрицы A, запишите полное решение Ax = b. 1 2 3 1 1 2 x = + x 2 + x 4 1 0 0 1 0 1 2. (11 баллов) Эта задача находит кривую y = C + D 2 t, которая

Дополнительная информация

Домашнее задание 03

Вопрос 1 (по 2 балла, если не указано иное) Домашнее задание 03 1.Блок питания 9 В постоянного тока вырабатывает 10 Вт в резисторе. Какой размах амплитуды должен быть источник переменного тока, чтобы генерировать тот же

Дополнительная информация

Графический метод: пример

Графический метод: пример. Рассмотрим следующую линейную программу: развернуть 4x 1 + 3x 2 При условии: 2x 1 + 3x 2 6 (1) 3x 1 + 2x 2 3 (2) 2x 2 5 (3) 2x 1 + x 2 4 (4) x 1, x 2 0, где для удобства

Дополнительная информация

Схемы усилителя BJT

Схемы усилителя JT Поскольку мы разработали различные модели для сигналов D (простая модель большого сигнала) и сигналов A (модель малого сигнала), анализ схем JT выполняется следующим образом: Анализ смещения D:

Дополнительная информация

Схемы усилителя BJT

Дополнительная информация

Последовательные и параллельные схемы

Последовательные и параллельные схемы. Компоненты схемы могут быть соединены последовательно или параллельно.При последовательном расположении компонентов они расположены на одной линии друг с другом, то есть соединены встык. Параллель

Дополнительная информация

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Системы линейных уравнений относятся к набору двух или более линейных уравнений, используемых для нахождения значений неизвестных переменных. Если система линейных уравнений состоит из двух уравнений

Дополнительная информация

Лаборатория физики законов Кирхгофа IX

Лаборатория физики законов Кирхгофа IX Цель В серии экспериментов, теоретические зависимости между напряжениями и токами в цепях, содержащих несколько батарей и резисторов в сети,

Дополнительная информация

Глава 7 Цепи постоянного тока

Глава 7 Цепи постоянного тока 7.Введение … 7-7. Электродвижущая сила … 7-3 7.3 Последовательные и параллельные резисторы … 7-5 7.4 Правила схемы Кирхгофа … 7-7 7.5 Измерения напряжения-тока … 7-9

Дополнительная информация

Последовательные и параллельные схемы

Последовательные и параллельные цепи Последовательные цепи постоянного тока Последовательная цепь — это цепь, в которой компоненты соединены в линию, один за другим, как железнодорожные вагоны на одной дороге.Есть

Дополнительная информация

Биполярные переходные транзисторы

Биполярные переходные транзисторы Физическая структура и символы NPN Эмиттер (E) n-тип Эмиттерная область p-типа Базовая область n-тип Коллекторная область Коллектор (C) B C Эмиттер-база-переход (EBJ) База (B) (a) Коллектор-база

Дополнительная информация

MEP Y9 Практическое пособие A

1 Основная арифметика 1.1 Двоичные числа Обычно мы работаем с числами с основанием 10. В этом разделе мы рассматриваем числа с основанием 2, часто называемые двоичными числами. В базе 10 мы используем цифры 0, 1, 2, 3, 4, 5,

Дополнительная информация

Рисунок 1. Модель диодной схемы.

Полупроводниковые приборы. Нелинейные приборы. Диоды. Введение. Диод представляет собой двухконтактный нелинейный прибор, вольт-амперная характеристика которого, помимо нелинейного поведения, также зависит от полярности.

Дополнительная информация

ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Имя: Дата: Курс и секция: Инструктор: ЭКСПЕРИМЕНТ 1 ПАРАЛЛЕЛЬНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА СЕРИИ 1 ЦЕЛИ 1. Проверить теоретический анализ последовательно-параллельных сетей с помощью прямых измерений. 2. Повышение квалификации

Дополнительная информация

5 Системы уравнений

Концепции систем уравнений: решения систем уравнений — системы, решающие графически и алгебраически — метод подстановки, решение систем — метод исключения, использующий -мерные графы для аппроксимации

Дополнительная информация

ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ

ВВЕДЕНИЕ ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ Студент познакомится с применением и анализом операционных усилителей в этом лабораторном эксперименте.Студент будет применять методы анализа схем

Дополнительная информация

MATH 185 ОБЗОР ГЛАВЫ 2

НАЗВАНИЕ МАТЕМАТИКА 18 ОБЗОР ГЛАВЫ Используйте наклон и точку пересечения для построения графика линейной функции. 1. F () = 4 — — Цель: (.1) Построить график линейной функции. Определить, является ли данная функция линейной или нелинейной.

Дополнительная информация

120 ГЛАВА 3 МЕТОДЫ УЗЛОВОГО И ПЕТЛЕВОГО АНАЛИЗА ОБЩИЕ ПРОБЛЕМЫ РАЗДЕЛ PDF Скачать бесплатно

Метод сеточного тока (анализ петли)

Метод Mesh-Current (анализ петли) Узловой анализ был разработан путем применения KCL на каждом нереференсном узле.Метод Mesh-Current разработан путем применения KVL вокруг сеток в цепи. Сетка петля

Дополнительная информация

Узловой и петлевой анализ

Дополнительная информация