примеры на последовательное, параллельное и смешанное соединение
Задания по электротехнике успешно даются только тем, кто может досконально разобраться в теме, нарисовать схему электроцепи и объяснить, каким образом в ней происходит взаимодействие между элементами. Ошибочно думать, что это очень сложный раздел физики, с которым под силу разобраться только электромеханикам. При желании эта тема доступна каждому среднестатистическому человеку. Давайте с ней разберемся!
Задания по электротехнике на тему «Конденсаторы»
Прежде чем приступать непосредственно к задачам, вспомним теорию.
Конденсатор — это два электрических проводника, разделенных между собой тонким слоем диэлектрика.
Проводники соединяют между собой с целью получить батареи. Существует 3 способа подключения конденсаторов:
- параллельное;
- последовательное;
- комбинированное.
Последовательным соединением называется подключение двух или более конденсаторов в цепь так, что каждый отдельный проводник соединен с другим только в одной точке.
Параллельным называется такое соединение конденсаторов, при котором все они подключены между одной и той же парой точек.
Комбинированное — это вид соединения, в котором часть проводников подключены параллельно, а часть — последовательно.
Знание каких формул и законов потребуется для решения
В зависимости от того, какой вид подключения проводников используется, по-разному будут определяться ключевые характеристики конденсаторов: емкость, заряд, напряжение.
Для решения заданий по данной теме в большинстве случаев понадобятся следующие формулы:
Источник: uk-parkovaya.ru
Предлагаем рассмотреть примеры решения типовых задач по данной теме со всеми необходимыми пояснениями, чтобы окончательно усвоить, как правильно разбирать такие задания.
Решение задач на параллельное соединение
Задача
Три проводника соединены между собой параллельно. Емкость первого равна 100 микрофарад, второго — 200 микрофарад, третьего — 500 микрофарад. Найдите общую емкость конденсаторов.
Решение
- Запишем известные вводные: C1=100 мкФ, C2=200 мкФ, C3=500 мкФ, C=?
- Так как соединение в цепи параллельное, общая емкость будет определяться по формуле: C=C1+C2+C3
- Подставляем числовые значения в формулу и получаем ответ: 800 мкФ.
Решение задач на последовательное соединение
Задача
Батарея состоит из двух конденсаторов, соединенных последовательно. Емкость первого — 4 мкФ, второго — 6 мкФ. Батарея заряжена до напряжения 220 Вольт. Определите емкость и заряд батареи.
Решение
- Запишем известные нам данные из условий задачи: C1=4 мкФ, C2=6 мкФ, U=220 В, C=? q=?
- Так как конденсаторы соединены последовательно, емкость батареи будет определяться по формуле: \(\frac1c=\frac1{c_1}+\frac1{c_2}\)
- Общий заряд батареи будет равен заряду первого и заряду второго проводника, т.
 е. q=q1=q2
е. q=q1=q2 - Ищем значение емкости батареи по указанной выше формуле, получаем значение, равное 2,4 мкФ.
- Заряд батареи можно вычислить по формуле: \(q=C\times U\)
- Подставляем числовые значения в формулу и получаем ответ: 528 мкКл.
Решение задач на смешанное соединение
Предлагаем рассмотреть более сложное задание, правильный ответ на которое включает в себя сразу четыре варианта решения:
Источник: bambookes.ru
Остались вопросы? Физика по-прежнему кажется сложным для понимания предметом? Вы не понимаете разницу между постоянным и переменным током? Не знаете откуда берется энергия? Обращайтесь за помощью в решении задач и подготовке докладов к специалистам нашего образовательного сервиса ФениксХелп. Для нас нет нелюбимых предметов и сложных тем!
Пример решения задачи по теме «Соединение конденсаторов» | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема:
Примеры решения задач по электродинамике
Рис.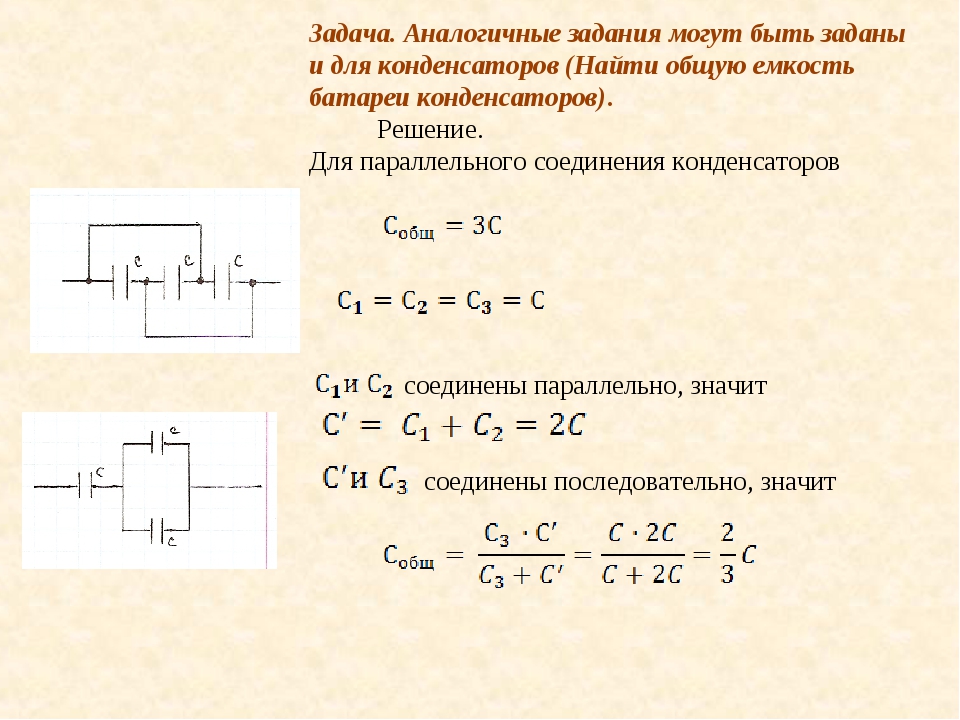 4.79. К задаче 4.79. К задаче |
Задача. Найти электроемкость системы конденсаторов, соединенных по схеме, показанной на рисунке 4.79. C1 = C2 = C4 = C5.
Решение.
Показанную на рис. 4.79 схему соединения конденсаторов можно изобразить иначе (рис. 4.80).
На схеме видно, что разность потенциалов между точками B и C равна нулю:
ΔφBC = 0.
| Рис. 4.80. К задаче |
Таким образом, ни один конденсатор, независимо от его электроемкости, присоединенный в точках B и C, не изменит электроемкости всей системы. Поэтому конденсатор C3 можно изъять из схемы и получить соединение по схеме рис. 4.81.
Общая электроемкость цепочки последовательно соединенных конденсаторов Q и C4 определится по формуле:
1 / C’ = 1 / C1 + 1 / C4,
или
C’ = C1C4 / (C1 + C4).
| Рис. 4.81. К задаче |
Такую же электроемкость будет иметь цепочка конденсаторов C2 и C5:
C’’ = C2C5 / (C2 + C5).
Вследствие параллельного соединения цепочек C1 — С4 и С2 — С5 их общая электроемкость Материал с сайта http://worldofschool.ru
C = С’ + C’’ = C1C4 / (C1 + C4) + C2C5 / (C2 + C5).
Если учесть, что C1 = C2 = C4 = C5, то получим
C = C12 / 2C1 + C12 / 2C1 = 2C12 / 2C1 = C1.
Ответ: общая электроемкость соединения конденсаторов равна C1.
На этой странице материал по темам:
Задачи с конденсаторами с решениями по схемам
Смешанное соединение трех конденсаторов решение задач
Задачи по теме конденсаторы электроемкость
Примеры по теме соединение конденсаторов
План конспект решение задач ао теме конденсаторы
Соединения конденсаторов и конденсаторные батареи
«Несовершенство
суждений –
наибольший
недостаток при
умственном
труде в любой области»
Майкл
Фарадей
Данная
тема посвящена решению задач на соединения конденсаторов и конденсаторные
батареи.
Задача
1.
Пять конденсаторов с одинаковой ёмкостью подключены параллельно друг другу,
образуя батарею. Определите ёмкость данной батареи, если при подключении к
Определите ёмкость данной батареи, если при подключении к
источнику тока с напряжением 50 В, заряд на обкладках каждого конденсатора
составляет 30 нКл.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
Запишем общее выражение для определения электроёмкости
При параллельном соединении
Т.к. по условию задачи заряд на обкладках каждого
|
|
|
Ответ:
3 нФ.
Задача
2.
Два подключенных последовательно конденсатора имеют ёмкости 200 мкФ и 400 мкФ.
Эти конденсаторы подключают к полюсам источника с напряжением 12 В и
максимально заряжают.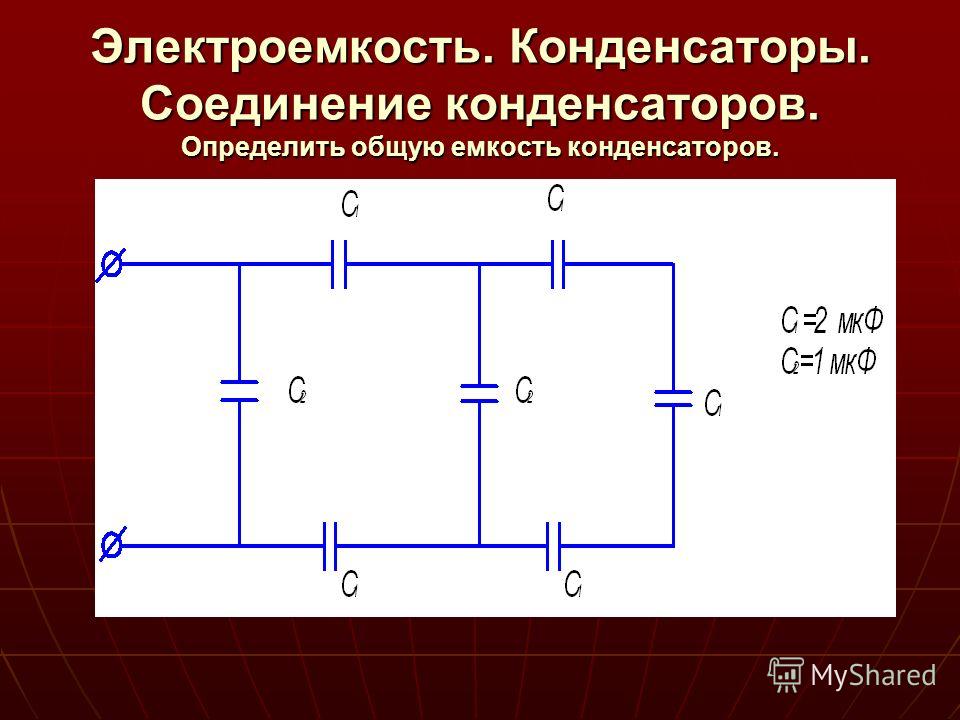 Найдите ток при разрядке батареи из этих конденсаторов,
Найдите ток при разрядке батареи из этих конденсаторов,
предполагая, что он постоянный, если разрядка занимает 20 мс.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
При последовательном соединении общая электроёмкость
Электроёмкость конденсатора в общем виде может быть
Из определения силы тока
Тогда получаем
|
|
|
Ответ:
80 мА.
Задача
3.
В приведённой схеме электроёмкость конденсатора C1
равна некоторому значению C0.
Ёмкость конденсатора C2
вдвое больше, а ёмкость конденсатора C3
‒
вчетверо больше и т. д. Найдите общую ёмкость участка цепи.
д. Найдите общую ёмкость участка цепи.
|
ДАНО:
|
РЕШЕНИЕ
Исходя из приведенного рисунка, имеется смешанное
Конденсаторы с емкостью C2
Тогда первоначальную схему можно заменить следующей
При параллельном соединении
Конденсаторы с ёмкостями С2,3, С4
Тогда имеющуюся схему можно заменить следующей
Конденсаторы с ёмкостями С1 и С2,3,4,5
|
|
|
Ответ:
Задача
4.
На схеме показано смешанное соединение конденсаторов и указаны электроёмкости
некоторых конденсаторов. Известно, что на конденсаторе с ёмкостью C1
напряжение равно 600 В,
а заряд – 600 нКл. Найдите общую электроёмкость данного участка, а также
общее напряжение на этом участке цепи.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
Электроёмкость конденсатора в общем виде рассчитывается по
Тогда электроёмкость первого конденсатора равна
Из рисунка видно, что конденсаторы С1 и С2
Таким образом, используя
При параллельном соединении
По закону сохранения заряда
Используя формулу для
При последовательном соединении
При параллельном соединении
При последовательном соединении
|
|
|
Ответ:
U = 6,35 В,
С = 12/127 мкФ.
Последовательное и параллельное соединение конденсаторов
На практике часто используются тела, обладающие малыми (и очень малыми) размерами, которые могут накопить большой заряд, при этом имея небольшой потенциал. Такие объекты называют конденсаторами. Одна из основных характеристик конденсатора – это его емкость. Имея в резерве набор конденсаторов, обладающих разными параметрами, можно расширить спектр величин емкостей и диапазон рабочих напряжений, если применять их соединения. Различают три типа соединений конденсаторов: последовательное, параллельное и смешанное (параллельное и последовательное).
Последовательное соединение конденсаторов
Последовательное соединение из конденсаторов изображено на рис. 1
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды. Электрическая емкость последовательного соединения конденсаторов вычисляется по формуле:
У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды. Электрическая емкость последовательного соединения конденсаторов вычисляется по формуле:
где – электрическая емкость i-го конденсатора.
Если емкости конденсаторов при последовательном соединении равны , то емкость последовательного их соединения составляет:
где N – количество последовательно соединенных конденсаторов. При этом предельное напряжение (U), которое выдержит подобная батарея конденсаторов составит:
где – предельное напряжение каждого конденсатора соединения. При последовательном соединении конденсаторов следует следить за тем, чтобы ни на один из конденсаторов батареи не падало напряжение, превышающее его максимальное рабочее напряжение.
Параллельное соединение конденсаторов
Параллельное соединение N конденсаторов изображено на рис. 2.
При параллельном соединении конденсаторов соединяют обкладки, обладающие зарядами одного знака (плюс с плюсом; минус с минусом). В результате такого соединения одна обкладка каждого конденсатора имеет одинаковый потенциал, например, , а другая . Разности потенциалов на обкладках всех конденсаторов при их параллельном соединении равны.
В результате такого соединения одна обкладка каждого конденсатора имеет одинаковый потенциал, например, , а другая . Разности потенциалов на обкладках всех конденсаторов при их параллельном соединении равны.
При параллельном соединении конденсаторов суммарная емкость соединения рассчитывается как сумма емкостей отдельных конденсаторов:
При параллельном соединении конденсаторов напряжение равно самой наименьшей величине рабочего напряжения конденсатора из состава рассматриваемого соединения.
Примеры решения задач
Открытый урок по физике Соединение конденсаторов и их признаки
ПЛАН УРОКА
Тема: «Соединение конденсаторов»
Класс: 10
Тип урока: Комбинированный урок
Цель урока:
Образовательная:
— Формирование умения решать задачи при различных способах соединения конденсаторов
Развивающая: развитие умения формулировать проблему, предлагать способы ее решения
Воспитывающая: воспитание дисциплинированности в ходе проведения урока
Оборудование: раздаточный материал
Ход урока:
1. Организационный момент
Организационный момент
Приветствие, запись даты и темы в журнале, отметить отсутствующих, объявление целей и хода урока
2.Постановка цели и задачи урока перед учениками:
Цель – освоить принципы нахождения параметров электрической цепи при различных способах соединения ее элементов
3.Проверка домашнего задания:
Проверка домашнего задания в виде взаимной проверки с помощью учителя.
Объяснение нового материала:
ПЛАН:
1.Последовательное соединение конденсаторов
2.Параллельное соединение конденсаторов
3.Смешанное соединение конденсаторов
4. примеры решения задач
5.Решение задач
6. Рефлексия
ВОПРОС 1 Последовательное Соединение конденсаторов
Если соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 1).
Рисунок 1. Последовательное соединение конденсаторов.
В случае последовательно соединенных конденсаторов одинаковы заряды на всех конденсаторах Q1 = Q2 =…= Qn Действительно, если мы поместим, например, заряд на левую обкладку первого конденсатора, то вследствие индукции на правой его обкладке возникнет заряд , а на левой обкладке второго конденсатора – заряд . Наличие этого заряда на левой обкладке второго конденсатора опять-таки вследствие индукции создает на правой его обкладке заряд , а на левой обкладке третьего конденсатора – заряд и т. Д. Таким образом, заряд каждого из последовательно соединенных конденсаторов равен . Напряжение же на каждом из этих конденсаторов определяется емкостью соответствующего конденсатора:
, , …, ,
где – емкость одного конденсатора. Суммарное напряжение между крайними (свободными) обкладками всей группы конденсаторов
.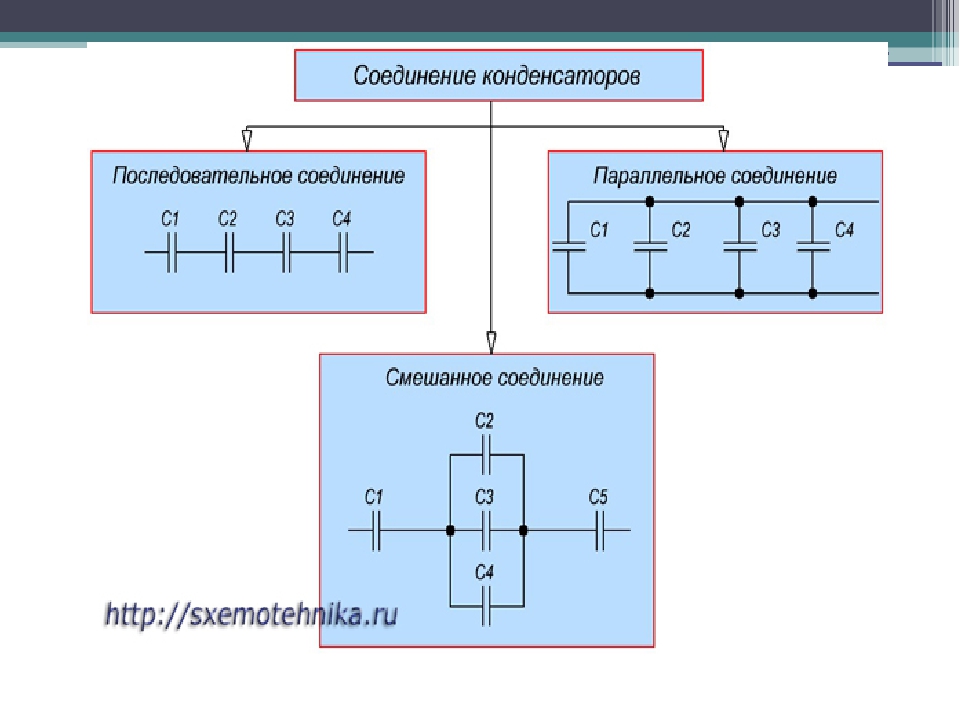
Следовательно, емкость всей системы конденсаторов
определяется выражением
.
Вопрос 2.
РИСУНОКМ 2
В случае параллельного соединения все конденсаторы заряжаются до одной и той же разности потенциалов , но заряды на них могут быть различными. Если емкости их равны , то соответствующие заряды будут
, , …, .
Общий заряд на всех конденсаторах
,
и, следовательно, емкость всей системы конденсаторов
.
Итак, емкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.
Из этой формулы видно, что емкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.
ВОПРОС 3
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 3 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 3. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 4.
Закрепление материала
Рассчитать ёмкость конденсаторов (раздать по два конденсатора каждой группе.
Рефлексия: самооценка
Домашнее задание_______________________
РАБОЧАЯ КАРТА УРОКА.
Фамилия, имя, группа.____________________________________________________
Домашнее
Задание
Изучение нового
материала.
Решение
задач.
Парная, групповая
работа.
Всего
баллов.
Оценка.
Электроника и электротехника Вариант 9 – Решение задач
| Дисциплина | Технические |
| Тип работы | Контрольные |
| Количество страниц | 22 |
| Год сдачи | 2017 |
| Номер работы | 1458 |
О работе
Оценка «отлично», качественное решение. Вы можете приобрести задания по отдельности, для этого обратитесь к нашему менеджеру.
Содержание
Контрольная работа. Вариант 9.
Задание № 1. Решить задачу по теме «Смешанное соединение конденсаторов» Дана батарея конденсаторов соединенных смешанным способом и подключенных к сети переменного тока напряжением 220В. Схема включения соответствует варианту задания и изображена на схемах 1.1 -1.25 в приложении А (страницы 34-35), по заданным в таблице 1.1 параметрам рассчитать:
Схема включения соответствует варианту задания и изображена на схемах 1.1 -1.25 в приложении А (страницы 34-35), по заданным в таблице 1.1 параметрам рассчитать:
1) Эквивалентную емкость батареи конденсаторов(Cэкв).
2) Заряд каждого конденсатора(q1, q2, q3, q4, q5).
3) Энергию каждого конденсатора(W1, W2, W3, W4, W5).
С1,мкФ | С2,мкФ | С3,мкФ | С4,мкФ | С5,мкФ | U, B |
14 | 14 | 6 | 6 | 30 | 220 |
Рис.1.9.
Решение.
Задание 2 Решить задачу на тему: «Простые цепи постоянного тока» Для электрической цепи постоянного тока, составленной из резистивных элементов, дана схема, изображенная на схемах 2.1-2.25 в приложение Б (страницы 36-38), по заданным в таблице 2. 1 параметрам рассчитать:
1 параметрам рассчитать:
1) Токи во всех ветвях схемы.
2) Падение напряжений на каждом из резисторов.
3) Мощность, развиваемую источником энергии (Рист) и мощность рассеиваемую на нагрузке (Рнаг).
4) Проверить правильность решения методом баланса мощностей.
R1,Ом | R2,Ом | R3,Ом | R4,Ом | R5,Ом | R6, Ом | R7,Ом | U,B |
1 | 3 | 5 | 10 | 12 | 7 | 4 | 10 |
Рис.2.9.
Решение.
Задание 3. Решить задачу на тему «Анализ электрической цепи постоянного тока методом законов Кирхгофа» Для электрической цепи, составленной из резистивных элементов и источников ЭДС постоянного напряжения, дана схема, изображенная на рисунках 3. 1 — 3.12 в приложении В (страница 39), по заданным в таблице 3.1 параметрам методом законов Кирхгофа определить:
1 — 3.12 в приложении В (страница 39), по заданным в таблице 3.1 параметрам методом законов Кирхгофа определить:
1)Токи во всех ветвях схемы (I1, I2, I3,).
2) Падение напряжений на каждом из резисторов (U1, U2, U3,).
3) Проверить правильность решения методом баланса мощностей.
R1,Ом | R2,Ом | R3,Ом | Е1,В | Е3,В | Рис. |
4 | 9 | 4 | 40 | 20 | 3.9 |
Рис.3.9.
Решение.
Задание 4
Решить задачу на тему: «Расчет однофазной электрической цепи переменного
тока»
Для однофазной электрической, цепи переменного тока, дана схема
изображенная на схемах 4.1-4.25 в приложение Г (страницы 40-41). По заданным в
таблице 3.1 параметрам рассчитать:
— для параллельного соединения резистора (R),катушки индуктивности(L),
конденсатора (C):
1)Токи в ветвях и в неразветвленной части цепи;
2) Активные мощности ветвей;
3)Углы сдвига фаз между током и напряжением первой и второй
ветвей и всей цепи;
4) Построить векторную диаграмму
R1,Ом | R2,Ом | С1,мкФ | С2,мкФ | U,В | Рис. |
7 | 14 | 35 | 40 | u=564sin628 | 4.9 |
Рис.4.9.
Решение.
Задание 5.
Вопрос 9. Что такое выпрямительный диод и его основные параметры?
Ответ
Вы можете убедиться в качестве данной работы. Часть контрольной представлена ниже:
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
- Подробности
- Просмотров: 1118
«Физика — 10 класс»
«Электроёмкость» — последняя тема раздела «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: закон сохранения электрического заряда, понятия напряжённости поля и потенциала, сведения о поведении проводников в электростатическом поле, о напряжённости поля в диэлектриках, о законе сохранения энергии применительно к электростатическим явлениям. Основной формулой при решении задач на электроёмкость является формула (14.22).
Основной формулой при решении задач на электроёмкость является формула (14.22).
Задача 1.
Электроёмкость конденсатора, подключённого к источнику постоянного напряжения U = 1000 В, равна C1 = 5 пФ. Расстояние между его обкладками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля.
Р е ш е н и е.
Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С2 — C)U = (nC1 — C1)U = (п — 1)С1U = 10-8 Кл.
Изменение энергии электрического поля
Задача 2.
Заряд конденсатора q = 3 • 10-8 Кл. Ёмкость конденсатора С = 10 пФ. Определите скорость, которую приобретает электрон, пролетая в конденсаторе путь от одной пластины к другой. Начальная скорость электрона равна нулю. Удельный заряд электрона
Р е ш е н и е.
Начальная кинетическая энергия электрона равна нулю, а конечная равна Применим закон сохранения энергии где А — работа электрического поля конденсатора:
Следовательно,
Окончательно
Задача 3.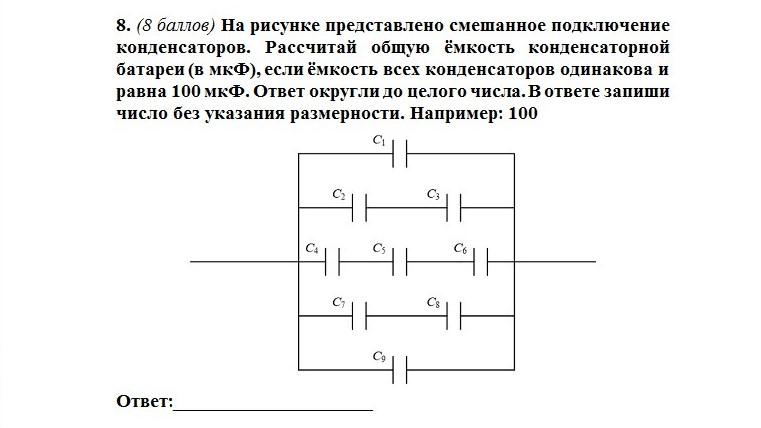
Четыре конденсатора ёмкостями С1 = С2 = = 1 мкФ, С3 = 3 мкФ, С4 = 2 мкФ соединены, как показано на рисунке 14.46. К точкам А и В подводится напряжение U = 140 В. Определите заряд q1 и напряжение U1, на каждом из конденсаторов.
Р е ш е н и е.
Для определения заряда и напряжения прежде всего найдём ёмкость батареи конденсаторов. Эквивалентная ёмкость второго и третьего конденсаторов С2,3 = С2 + С3, а эквивалентную ёмкость всей батареи конденсаторов, представляющей собой три последовательно соединённых конденсатора ёмкостями С1, С2,3, С4, найдём из соотношения
1/Cэкв = 1 /С1 + 1/С2,3 + 1 /С4, Сэкв = (4/7) • 10-6 Ф.
Заряды на этих конденсаторах одинаковы:
q1 = q2,3 = q4 = Сэкв = 8 • 10-5 Кл.
Следовательно, заряд первого конденсатора q1 = 8 • 10-5 Кл, а разность потенциалов между его обкладками, или напряжение, U1 = q1/С1 = 80 В.
Для четвёртого конденсатора аналогично имеем q4 = 8 • 10-5 Кл, U4 = q4/C4 = 40 В.
Найдём напряжение на втором и третьем конденсаторах: U2 = U3 = q2,3/C2,3 = 20 В.
Таким образом, на втором конденсаторе заряд q2 = C2U2 = 2 • 10-5 Кл, а на третьем конденсаторе q3 = C3U3 = 6 • 10-5 Кл. Отметим, что q2,3 = q2 + g3.
Задача 4.
Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке (14.47 а), если ёмкости конденсаторов известны.
Р е ш е н и е.
Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов.
В приведённой на рисунке (14.47, а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φA ≠ φB в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (14.47, б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и Сэкв определим по формуле 1/Сэкв = 1/2С1 + 1/2С2, откуда
Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (14.47, в). Конденсаторы С1 и С2 соединены последовательно, следовательно,
Эквивалентные конденсаторы с С’экв соединены параллельно, так что окончательно получим такое же выражение для эквивалентной ёмкости:
Задача 5.
Энергия плоского воздушного конденсатора W1 = 2 • 10-7 Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если:
1) конденсатор отключён от источника питания;
2) конденсатор подключён к источнику питания.
Р е ш е н и е.
1) Так как конденсатор отключён от источника питания, то его заряд q0 остаётся постоянным. Энергия конденсатора до заполнения его диэлектриком после заполнения где С2 = εС1.
Тогда
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Конденсаторы последовательно и параллельно – проблемы и решения
1.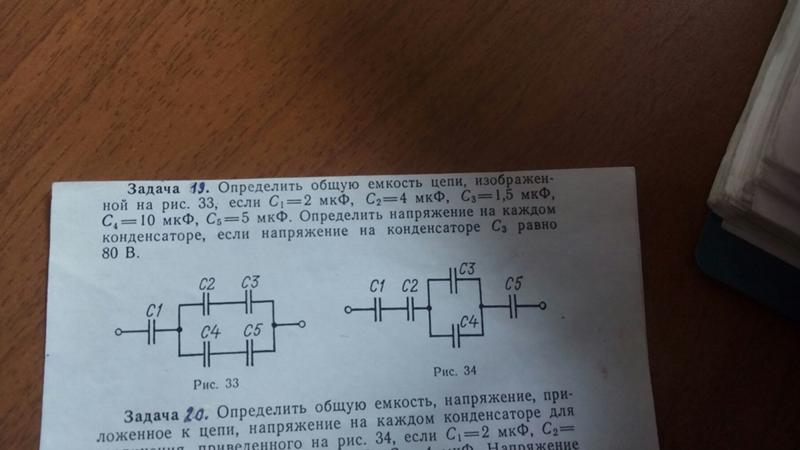 Три конденсатора, С 1 = 2 мкФ, С 2 = 4 мкФ, С 3 = 4 мкФ, соединены последовательно и параллельно. Определите емкость одного конденсатора, который будет иметь тот же эффект, что и их комбинация.
Три конденсатора, С 1 = 2 мкФ, С 2 = 4 мкФ, С 3 = 4 мкФ, соединены последовательно и параллельно. Определите емкость одного конденсатора, который будет иметь тот же эффект, что и их комбинация.
Известный :
Конденсатор С 1 = 2 мкФ
Конденсатор С 2 = 4 мкФ
Конденсатор С 3 = 4 мкФ
Разыскивается: Эквивалентная емкость (C)
Решение:
Конденсатор C 2 и C 3 соединены параллельно.Эквивалентная емкость:
C P = C 2 + C 3 = 4 + 4 = 8 мкФ
Конденсатор С 1 и С р соединены последовательно. Эквивалентная емкость:
1/C = 1/C 1 + 1/C P = 1/2 + 1/8 = 4/8 + 1/8 = 5/8
С = 8/5 мкФ
2. Пять конденсаторов, С 1 = 2 мкФ, С 2 = 4 мкФ, С 3 = 6 мкФ, С 4 = 5 мкФ, С 5 = 10 мкФ, соединены последовательно и параллельно.Определите емкость одного конденсатора, который будет иметь тот же эффект, что и их комбинация.
Пять конденсаторов, С 1 = 2 мкФ, С 2 = 4 мкФ, С 3 = 6 мкФ, С 4 = 5 мкФ, С 5 = 10 мкФ, соединены последовательно и параллельно.Определите емкость одного конденсатора, который будет иметь тот же эффект, что и их комбинация.
Известный :
Конденсатор С 1 = 2 мкФ
Конденсатор С 2 = 4 мкФ
Конденсатор С 3 = 6 мкФ
Конденсатор С 4 = 5 мкФ
Конденсатор С 5 = 10 мкФ
Разыскивается: Эквивалентная емкость (C)
Решение:
Конденсатор С 2 и С 3 соединены параллельно.Эквивалентная емкость:
С Р = С 2 + С 3
С Р = 4 + 6
С Р = 10 мкФ
Конденсатор С 1 , С Р , С 4 и С 5 соединены последовательно. Эквивалентная емкость:
Эквивалентная емкость:
1/К = 1/К 1 + 1/К P + 1/К 4 + 1/К 5
1/С = 1/2 + 1/10 + 1/5 + 1/10
1/С = 5/10 + 1/10 + 2/10 + 1/10
1/С = 9/10
С = 10/9 мкФ
3.С 1 = 3 мкФ, С 2 = 4 мкФ и С 3 = 3 мкФ, соединены последовательно и параллельно. Определить электрическую энергию в цепях.
Известный :
Конденсатор С 1 = 3 мкФ
Конденсатор С 2 = 4 мкФ
Конденсатор С 3 = 3 мкФ
Разыскивается: Эквивалентная емкость (C)
Решение:
Конденсатор С 2 и С 3 соединены параллельно.Эквивалентная емкость:
С Р = С 2 + С 3
С Р = 4 + 3
С Р = 7 мкФ
Конденсатор С 1 и С Р соединены последовательно. Эквивалентная емкость:
Эквивалентная емкость:
1/К = 1/К 1 + 1/К Р
1/С = 1/3 + 1/7
1/С = 7/21 + 3/21
1/К = 21.10
С = 21/10
С = 2,1 мкФ
С = 2.1 x 10 -6 F
Электроэнергия по цепям:
E = ½ C V 2
E = ½ (2,1 x 10 -6 )(12 2 )
Е = ½ (2,1 х 10 -6 )(144)
Е = (2,1 х 10 -6 )(72)
E = 151,2 х 10 -6 Дж
E = 1,5 х 10 -4 Дж
8.2 Конденсаторы последовательно и параллельно — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как определить эквивалентную емкость конденсаторов при последовательном и параллельном соединении
- Вычислить разность потенциалов на пластинах и заряд на пластинах для конденсатора в сети и определить чистую емкость сети конденсаторов
Несколько конденсаторов можно соединить вместе для использования в различных приложениях. Несколько соединений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Конденсаторы могут быть расположены в двух простых и распространенных типах соединений, известных как , серия и , параллельная , для которых мы можем легко рассчитать общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Несколько соединений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Конденсаторы могут быть расположены в двух простых и распространенных типах соединений, известных как , серия и , параллельная , для которых мы можем легко рассчитать общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Серийная комбинация конденсаторов
Рис. 8.11 показана последовательная комбинация трех конденсаторов, расположенных в ряд внутри цепи. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 8.1. При подключении этой последовательной комбинации к батарее с напряжением В каждый из конденсаторов приобретает одинаковый заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен +Q+Q, а заряд на пластине, подключенной к отрицательной клемме, равен -Q-Q.Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала V1=Q/C1V1=Q/C1 на одном конденсаторе может отличаться от падения потенциала V2=Q/C2V2=Q/C2 на другом конденсаторе, поскольку, как правило, конденсаторы могут иметь разные емкости. Последовательное соединение двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше, чем наименьшая из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательном соединении: То есть все конденсаторы в последовательном соединении имеют одинаковый заряд .
Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен +Q+Q, а заряд на пластине, подключенной к отрицательной клемме, равен -Q-Q.Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала V1=Q/C1V1=Q/C1 на одном конденсаторе может отличаться от падения потенциала V2=Q/C2V2=Q/C2 на другом конденсаторе, поскольку, как правило, конденсаторы могут иметь разные емкости. Последовательное соединение двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше, чем наименьшая из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательном соединении: То есть все конденсаторы в последовательном соединении имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи снимается с пластины первого конденсатора (обозначаем -Q-Q), он должен быть помещен на пластину второго конденсатора (обозначаем +Q), +Q) и так далее.
Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи снимается с пластины первого конденсатора (обозначаем -Q-Q), он должен быть помещен на пластину второго конденсатора (обозначаем +Q), +Q) и так далее.
Фигура
8.11
а) Три конденсатора соединены последовательно.Величина заряда на каждой пластине Å . (b) Цепь конденсаторов в (а) эквивалентна одному конденсатору, емкость которого меньше, чем у любой из отдельных емкостей в (а), а заряд на его обкладках равен Å .
Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны соответственно V1=Q/C1V1=Q/C1, V2=Q/C2V2=Q/C2 и V3=Q/C3V3=Q/C3.Эти потенциалы должны суммироваться с напряжением батареи, что дает следующий баланс потенциалов:
Потенциал В измеряется на эквивалентном конденсаторе, удерживающем заряд Q и имеющем эквивалентную емкость CSCS. Вводя выражения для V1V1, V2V2 и V3V3, получаем
Вводя выражения для V1V1, V2V2 и V3V3, получаем
QCS=QC1+QC2+QC3.QCS=QC1+QC2+QC3.
Отменяя заряд Q , получаем выражение, содержащее эквивалентную емкость CSCS трех последовательно соединенных конденсаторов:
1CS=1C1+1C2+1C3.1CS=1C1+1C2+1C3.
Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.
Комбинация серий
Для конденсаторов, соединенных последовательно, обратная величина эквивалентной емкости представляет собой сумму обратных величин отдельных емкостей:
1CS=1C1+1C2+1C3+⋯.1CS=1C1+1C2+1C3+⋯.
8,7
Пример
8.4
Эквивалентная емкость последовательной сети
Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1.000 мкФ 1000 мкФ, 5 000 мкФ 5 000 мкФ и 8 000 мкФ 8 000 мкФ.
Стратегия
Поскольку в этой цепи всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8. 7 с тремя членами.
7 с тремя членами.
Решение
Мы вводим данные емкости в уравнение 8.7:
1CS=1C1+1C2+1C3=11,000 мкФ+15,000 мкФ+18,000 мкФ1CS=1,325 мкФ.1CS=1C1+1C2+1C3=11,000 мкФ+15,000 мкФ+18,000 мкФ1CS=1,325 мкФ.
Теперь инвертируем этот результат и получаем CS=мкФ1,325=0,755мкФ.CS=мкФ1,325=0,755мкФ.
Значение
Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.
Параллельная комбинация конденсаторов
Параллельная комбинация трех конденсаторов, в которой одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рис. 8.12 (а). Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может хранить различный заряд. Чтобы найти эквивалентную емкость CPCP параллельной сети, заметим, что общий заряд Q , хранящийся в сети, представляет собой сумму всех отдельных зарядов:
В левой части этого уравнения мы используем соотношение Q=CPVQ=CPV, справедливое для всей сети.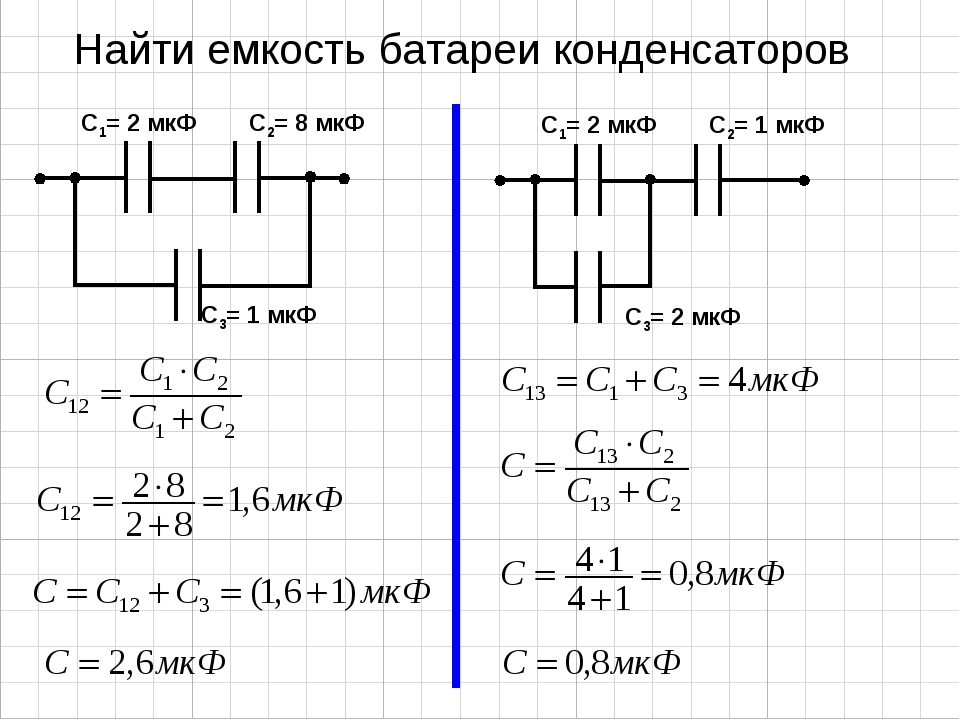 В правой части уравнения мы используем соотношения Q1=C1V, Q2=C2V, Q1=C1V, Q2=C2V и Q3=C3VQ3=C3V для трех конденсаторов в сети. Таким образом, мы получаем
В правой части уравнения мы используем соотношения Q1=C1V, Q2=C2V, Q1=C1V, Q2=C2V и Q3=C3VQ3=C3V для трех конденсаторов в сети. Таким образом, мы получаем
CPV=C1V+C2V+C3V.CPV=C1V+C2V+C3V.
Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:
Это выражение легко обобщается на любое количество конденсаторов, соединенных параллельно в сети.
Параллельная комбинация
Для конденсаторов, соединенных параллельно, эквивалентная (чистая) емкость представляет собой сумму всех отдельных емкостей в сети,
КП=С1+С2+С3+⋯.КП=С1+С2+С3+⋯.
8,8
Фигура
8.12
а) Три конденсатора соединены параллельно. Каждый конденсатор подключен непосредственно к аккумулятору. б) Заряд эквивалентного конденсатора равен сумме зарядов отдельных конденсаторов.
Пример
8,5
Эквивалентная емкость параллельной сети
Найдите общую емкость трех параллельно соединенных конденсаторов, если их отдельные емкости равны 1,0 мкФ,5. 0 мкФ и 8,0 мкФ. 1,0 мкФ, 5,0 мкФ и 8,0 мкФ.
0 мкФ и 8,0 мкФ. 1,0 мкФ, 5,0 мкФ и 8,0 мкФ.
Стратегия
Поскольку в этой цепи всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8.8 с тремя членами.
Решение
Ввод данных емкостей в уравнение 8.8 дает
CP=C1+C2+C3=1,0 мкФ+5,0 мкФ+8,0 мкФCP=14,0 мкФ. CP=C1+C2+C3=1,0 мкФ+5,0 мкФ+8,0 мкФСР=14,0 мкФ.
Значение
Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.
Сети конденсаторов обычно представляют собой некоторую комбинацию последовательных и параллельных соединений, как показано на рис. 8.13. Чтобы найти чистую емкость таких комбинаций, мы идентифицируем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
Фигура
8.13
а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов.(б) C1C1 и C2C2 соединены последовательно; их эквивалентная емкость CS.CS. (c) Эквивалентная емкость CSCS подключена параллельно C3.C3. Таким образом, эквивалентная емкость всей сети представляет собой сумму CSCS и C3.C3.
Пример
8,6
Эквивалентная емкость сети
Найдите общую емкость комбинации конденсаторов, показанной на рис. 8.13. Предположим, что емкости известны с точностью до трех знаков после запятой (C1=1,000 мкФ, C2=5,000 мкФ, (C1=1,000 мкФ, C2=5,000 мкФ, C3=8).000 мкФ).C3=8.000 мкФ). Округлите ответ до трех знаков после запятой.
Стратегия
Сначала мы определяем, какие конденсаторы подключены последовательно, а какие параллельно. Конденсаторы C1C1 и C2C2 включены последовательно. Их комбинация, обозначенная CS,CS, параллельна C3.C3.
Решение
Поскольку C1 и C2, C1 и C2 включены последовательно, их эквивалентная емкость CSCS получается с помощью уравнения 8. 7:
7:
1CS=1C1+1C2=11,000 мкФ+15,000 мкФ=1,200 мкФ⇒CS=0,833 мкФ.1CS=1C1+1C2=11,000 мкФ+15,000 мкФ=1,200 мкФ⇒CS=0,833 мкФ.
Емкость CSCS подключена параллельно с третьей емкостью C3C3, поэтому мы используем уравнение 8.8 найти эквивалент емкости C всей сети:
C=CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ.C=CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ.
Пример
8,7
Сеть конденсаторов
Определите чистую емкость C комбинации конденсаторов, показанной на рис. 8.14, когда емкости C1 = 12,0 мкФ, C2 = 2,0 мкФ, C1 = 12,0 мкФ, C2 = 2,0 мкФ и C3 = 4,0 мкФ3 = 4,0 мкФ. Когда на комбинации сохраняется разность потенциалов 12,0 В, найти заряд и напряжение на каждом конденсаторе.
Фигура
8.14
а) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.
Стратегия
Сначала мы вычисляем чистую емкость C23C23 параллельного соединения C2C2 и C3C3. Тогда C — это чистая емкость последовательного соединения C1C1 и C23C23. Мы используем соотношение C=Q/VC=Q/V, чтобы найти заряды Q1Q1, Q2Q2 и Q3Q3, а также напряжения V1V1, V2V2 и V3V3 на конденсаторах 1, 2 и 3 соответственно.
Тогда C — это чистая емкость последовательного соединения C1C1 и C23C23. Мы используем соотношение C=Q/VC=Q/V, чтобы найти заряды Q1Q1, Q2Q2 и Q3Q3, а также напряжения V1V1, V2V2 и V3V3 на конденсаторах 1, 2 и 3 соответственно.
Решение
Эквивалентная емкость для C2C2 и C3C3 равна
С23=С2+С3=2.0 мкФ + 4,0 мкФ = 6,0 мкФ. C23 = C2 + C3 = 2,0 мкФ + 4,0 мкФ = 6,0 мкФ.
Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,
1C=112,0 мкФ+16,0 мкФ=14,0 мкФ⇒C=4,0 мкФ.1C=112,0 мкФ+16,0 мкФ=14,0 мкФ⇒C=4,0 мкФ.
Рассмотрим эквивалентную комбинацию из двух конденсаторов на рис. 8.14(b). Поскольку конденсаторы соединены последовательно, они имеют одинаковый заряд Q1=Q23Q1=Q23. Кроме того, конденсаторы имеют общую разность потенциалов 12,0 В, поэтому
12,0 В=V1+V23=Q1C1+Q23C23=Q112,0 мкФ+Q16,0 мкФ⇒Q1=48,0 мкКл.12,0 В=V1+V23=Q1C1+Q23C23=Q112.0 мкФ+Q16,0 мкФ⇒Q1=48,0 мкКл.
Теперь разность потенциалов на конденсаторе 1 равна
.
V1=Q1C1=48,0 мкC12,0 мкФ=4,0 В. V1=Q1C1=48,0 мкC12,0 мкФ=4,0 В.
Поскольку конденсаторы 2 и 3 соединены параллельно, они имеют одинаковую разность потенциалов:
V2=V3=12,0В-4,0В=8,0В.V2=V3=12,0В-4,0В=8,0В.
Следовательно, заряды этих двух конденсаторов соответственно равны
Q2 = C2V2 = (2,0 мкФ) (8,0 В) = 16,0 мкКл, Q3 = C3V3 = (4,0 мкФ) (8,0 В) = 32,0 мкКл. Q2 = C2V2 = (2,0 мкФ) (8,0 В) = 16,0 мкКл, Q3 = C3V3=(4,0 мкФ)(8,0 В)=32,0 мкКл.
Значение
Как и ожидалось, чистая плата за параллельную комбинацию C2C2 и C3C3 составляет Q23=Q2+Q3=48.0 мкКл. Q23=Q2+Q3=48,0 мкКл.
Проверьте свое понимание
8,5
Проверьте свои знания Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что C1=1,0pFC1=1,0pF, C2=2,0pFC2=2,0pF, C3=4,0pFC3=4,0pF и C4=5,0pFC4=5,0pF. Найдите заряд каждого конденсатора, предполагая, что в каждой сети существует разность потенциалов 12,0 В.
19,6 Конденсаторы, включенные последовательно и параллельно — College Physics
Резюме
- Выведите выражения для полной емкости при последовательном и параллельном подключении.
- Определите последовательное и параллельное соединение конденсаторов.
- Рассчитайте эффективную емкость при последовательном и параллельном подключении по отдельным емкостям.
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены.Существует два простых и распространенных типа соединений, называемых последовательными и параллельными , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.
На рис. 1(а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением [latex]{C = \frac{Q}{V}}[/latex].
Обратите внимание на рис. 1, что противоположные заряды величиной [латекс]{Q}[/латекс] текут по обеим сторонам первоначально незаряженной комбинации конденсаторов при приложении напряжения [латекс]{В}[/латекс]. Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности.(См. рис. 1(b).) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине Å . (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.
Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [латекс]{С = \frac{Q}{V}}[/латекс] для [латекс]{В} [/latex] дает [latex]{V = \frac{Q}{C}}[/latex]. Таким образом, напряжения на отдельных конденсаторах равны [латекс]{V_1 = \frac{Q}{C_1}}[/latex], [латекс]{V_2 = \frac{Q}{C_2}}[/latex] и [ латекс]{V_3 = \frac{Q}{C_3}}[/латекс]. Общее напряжение представляет собой сумму отдельных напряжений:
[латекс] {V = V_1 + V_2 + V_3}.[/латекс]
Теперь, называя общую емкость [латекс]{C_S}[/латекс] последовательной емкостью, считайте, что
[латекс] {V =} [/латекс] [латекс] {\ гидроразрыва {Q} {C_S}} [/ латекс] [латекс] { = V_1 + V_2 + V_3}. [/латекс]
[/латекс]
Введя выражения для [латекс]{V_1}[/латекс], [латекс]{V_2}[/латекс] и [латекс]{V_3}[/латекс], мы получим
[латекс] {\ гидроразрыва {Q} {C_S} = \ гидроразрыва {Q} {C_1} + \ гидроразрыва {Q} {C_2} + \ гидроразрыва {Q} {C_3}}. [/латекс]
Отменяя [латекс]{Q}[/латекс], мы получаем уравнение для полной емкости в ряду [латекс]{C_S}[/латекс] равным
[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {C_1}} [/ латекс] [латекс] {+ } [/латекс] [латекс] {\ гидроразрыва {1} {C_2}} [/ латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {C_3}} [/латекс] [ латекс]{+ \cdots},[/латекс]
, где «…» означает, что выражение справедливо для любого количества последовательно соединенных конденсаторов.Выражение этой формы всегда приводит к тому, что общая емкость [латекс]{C_S}[/латекс] меньше любой из отдельных емкостей [латекс]{С_1}[/латекс], [латекс]{С_2}[/латекс]. ], …, как показано в следующем примере.
Суммарная емкость в серии,
C с
Суммарная емкость последовательно: [латекс]{\ гидроразрыва {1} {C_S} = \ гидроразрыва {1} {C_1} + \ гидроразрыва {1} {C_2} + \ гидроразрыва {1} {C_3} + \ cdots} [ /латекс]
Пример 1: Что такое последовательная емкость?
Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1.000, 5.000 и 8.000 [латекс]\mu \text{F}[/латекс].
Стратегия
Имея данные, общую емкость можно найти, используя уравнение для последовательной емкости.
Раствор
Ввод заданных емкостей в выражение для [латекс]{\ гидроразрыва {1} {C_S}} [/латекс] дает [латекс] {\ гидроразрыва {1} {C_S} = \ гидроразрыва {1} {C_1} + \ frac{1}{C_2} + \frac{1}{C_3}}[/latex].
[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1} {1.000 \;\mu \text{F}}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{5.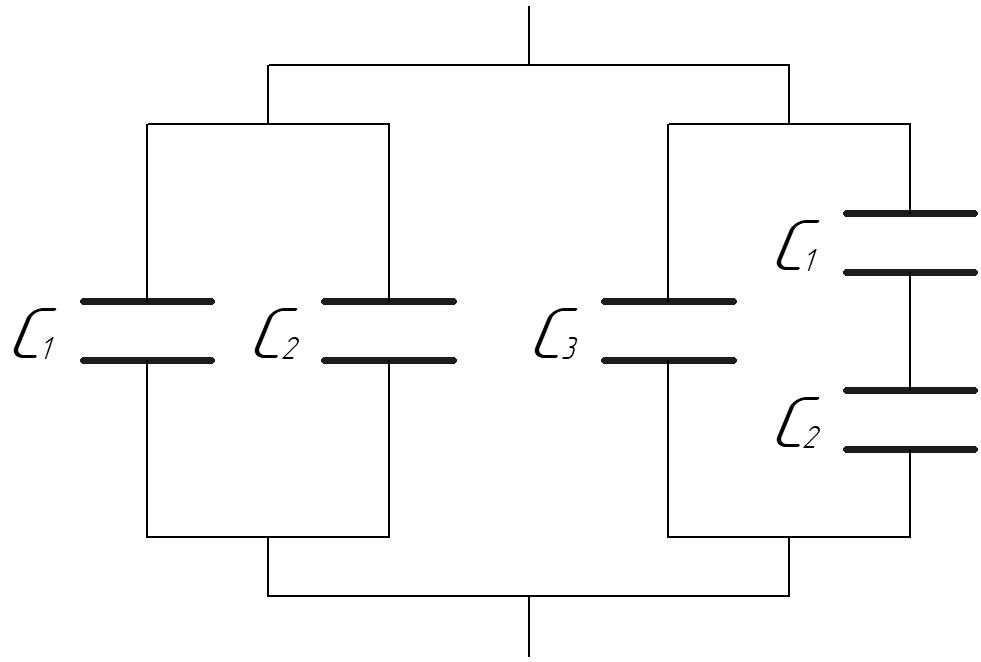 000 \;\text{F}}}[/latex] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {8.000 \; \ мю \ текст {F}}} [/ латекс] [латекс] {=}[/латекс] [латекс] { \frac{1.325}{\mu \text{F}}}[/latex]
000 \;\text{F}}}[/latex] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {8.000 \; \ мю \ текст {F}}} [/ латекс] [латекс] {=}[/латекс] [латекс] { \frac{1.325}{\mu \text{F}}}[/latex]
Инвертирование для нахождения [латекс]{C_S}[/латекс] дает [латекс]{C_S = \frac{\mu \text{F}}{1,325} = 0,755 \;\mu \text{F}}[/latex ].
Обсуждение
Суммарная последовательная емкость [латекс]{C_s}[/латекс] меньше наименьшей индивидуальной емкости, как и было обещано.При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,
[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {40} {40 \; \ мю \ текст {F}}} [/латекс] [латекс] {+}[/латекс] [латекс] {\ гидроразрыва {8} {40 \;\mu \ текст {F}}}[/латекс] [латекс] {+}[/латекс] [латекс] {\ гидроразрыва {5} {40 \; \ му \ текст {F}}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {53} {40 \; \ мю \текст{F}}},[/латекс]
так что
[латекс] {C_S =} [/ латекс] [латекс] {\ гидроразрыва {40 \; \ mu \ текст {F}} {53}} [/латекс] [латекс] {= 0. 755 \; \mu \text{F}}.[/latex]
755 \; \mu \text{F}}.[/latex]
На рис. 2(а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную общую емкость [латекс]{\текст{С}_{\текст{р}}}[/латекс], сначала отметим, что напряжение на каждом конденсаторе равно [латекс]{В}[/латекс], такие же, как и у источника, так как они подключены непосредственно к нему через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд [латекс]{Q}[/латекс] представляет собой сумму отдельных сборов:
[латекс] {Q = Q_1 + Q_2 + Q_3}.[/латекс]
Рис. 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.
(b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.
Используя соотношение [латекс]{Q = CV}[/латекс], мы видим, что общий заряд равен [латекс]{Q = C_{\text{p}}V}[/латекс], а отдельные заряды равны [латекс]{Q_1 = C_1 V}[/латекс] , [латекс]{Q_2 = C_2 V}[/латекс] , и [латекс]{Q_3 = C_3 V}[/латекс]. Ввод их в предыдущее уравнение дает
[латекс] {C_{\text{p}} V = C_1 V + C_2 V + C_3 V}.[/latex]
Исключая [латекс]{V}[/латекс] из уравнения, мы получаем уравнение для полной емкости параллельно [латекс]{С_{\текст{р}}}[/латекс]:
[латекс] {C_{\text{p}} = C_1 + C_2 + C_3 \cdots}[/латекс].
Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Снова « … » указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в приведенном выше примере были соединены параллельно, их емкость была бы
.
[латекс]{C_{\text{p}} = 1.000 \;\mu \text{F} + 5.000 \;\mu \text{F} + 8.000 \;\mu \text{F} = 14.000 \; \mu \text{F}}.[/latex]
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластин и, следовательно, большую емкость, как показано на рис. 2(b).
Общая емкость параллельно,
C p [латекс] {C _ {\ text {p}}} [/latex]
Суммарная емкость при параллельном соединении [латекс] {C_{\text{p}} = C_1 + C_2 + C_3 + \cdots}[/latex]
Более сложные соединения конденсаторов иногда могут представлять собой комбинации последовательного и параллельного соединения. (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.
Рис. 3. (а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C 1 и C 2 расположены последовательно; их эквивалентная емкость C S меньше, чем у любого из них. (c) Обратите внимание, что C S находится параллельно с C 3 . Таким образом, общая емкость равна сумме Кл С и Кл 3 .
(c) Обратите внимание, что C S находится параллельно с C 3 . Таким образом, общая емкость равна сумме Кл С и Кл 3 .
Смесь последовательной и параллельной емкости
Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех знаков после запятой ([latex]{C_1 = 1,000 \;\mu\text{F}}[/latex], [latex]{C_2 = 5.000 \;\mu \text{F}}[/latex] и [latex]{C_3 = 8.000 \;\mu \text{F}}[/latex]), и округлите ответ. до трех знаков после запятой.
Стратегия
Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы соединены последовательно, а какие — параллельно.Конденсаторы [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] включены последовательно. Их комбинация, обозначенная на рисунке [латекс]{C_S}[/латекс], параллельна [латекс]{С_3}[/латекс].
Раствор
Поскольку [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] соединены последовательно, их общая емкость определяется как [латекс]{\ гидроразрыва {1} {C_S} = \ гидроразрыва {1 {C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex]. Ввод их значений в уравнение дает
Ввод их значений в уравнение дает
[латекс] {\ гидроразрыва {1} {C_1}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {C_2}} [/ латекс] [латекс] {= }[/латекс] [латекс]{\ гидроразрыва {1} {1.000 \;\mu \text{F}}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{5.000 \;\mu \text{F}}}[/ латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {1.200} {\ mu \ text {F}}}. [/латекс]
Инвертирование дает
[латекс] {C_{\text{S}} = 0,833 \;\mu \text{F}} .[/latex]
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; таким образом, общая сумма составляет
[латекс]\begin{array}{r @{{}={}} l} {C_{\text{tot}}}\;= & {C_S + C_S} \\[1em]= & {0,833 \ ;\mu \text{F} + 8.000 \;\mu \text{F}} \\[1em]= & {8.833 \;\mu \text{F}}. \end{массив}[/латекс]
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям до тех пор, пока не будет получена сумма, может быть применен к более крупным комбинациям конденсаторов.
- Суммарная емкость последовательно [латекс] {\ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} C_3} + \cdots}[/латекс]
- Общая емкость параллельно [латекс] {C_{\text{p}} = C_1 + C_2 + C_3 + \cdots}[/latex]
- Если цепь содержит комбинацию конденсаторов, соединенных последовательно и параллельно, определите последовательные и параллельные части, вычислите их емкости, а затем найдите общую сумму.
Концептуальные вопросы
1: Если вы хотите хранить большое количество энергии в конденсаторной батарее, вы должны соединить конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
1: Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Комбинация последовательного и параллельного соединения конденсаторов.
2: Предположим, вам нужна батарея конденсаторов с общей емкостью 0. 750 F, и у вас есть множество конденсаторов по 1,50 мФ. Какое наименьшее число вы могли бы соединить вместе, чтобы достичь своей цели, и как бы вы их соединили?
750 F, и у вас есть множество конденсаторов по 1,50 мФ. Какое наименьшее число вы могли бы соединить вместе, чтобы достичь своей цели, и как бы вы их соединили?
3: Какую общую емкость можно получить, соединив [латекс]{5,00 \;\mu \text{F}}[/латекс] и [латекс]{8,00 \;\mu\text{F}} [/latex] конденсатор вместе?
4: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Комбинация последовательного и параллельного соединения конденсаторов.
5: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.
Рисунок 6. Комбинация последовательного и параллельного соединения конденсаторов.
6: необоснованные результаты
(a) Конденсатор из [латекса]{8,00 \;\mu \text{F}}[/latex] подключен параллельно другому конденсатору, что дает общую емкость [латекс]{5,00 \;\mu \text{ F}}[/латекс]. Какова емкость второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
Решения
Задачи и упражнения
1: [латекс]{0. 293 \;\mu \text{F}}[/латекс]
293 \;\mu \text{F}}[/латекс]
3: [латекс]{3.08 \;\mu \text{F}}[/латекс] в последовательном соединении, [латекс]{13.0 \;\mu \text{F}}[/латекс] в параллельном соединении
4: [латекс] {2,79 \;\mu \text{F}}[/латекс]
6: (a) [латекс]{-3.00 \;\mu \text{F}}[/латекс]
(b) У вас не может быть отрицательного значения емкости.
(c) Предположение о том, что конденсаторы были подключены параллельно, а не последовательно, было неверным.Параллельное соединение всегда дает большую емкость, а здесь предполагалась меньшая емкость. Это могло произойти только при последовательном соединении конденсаторов.
Электростатика :: Задача 8 — Онлайн задачи с решениями
Задача 8: Найдите эквивалентную емкость комбинации, показанной на следующей диаграмме.
Решение:
Шаг: 1
Обзор
Параллельная комбинация конденсаторов:
При параллельном соединении конденсаторов падение напряжения на каждом конденсаторе будет одинаковым.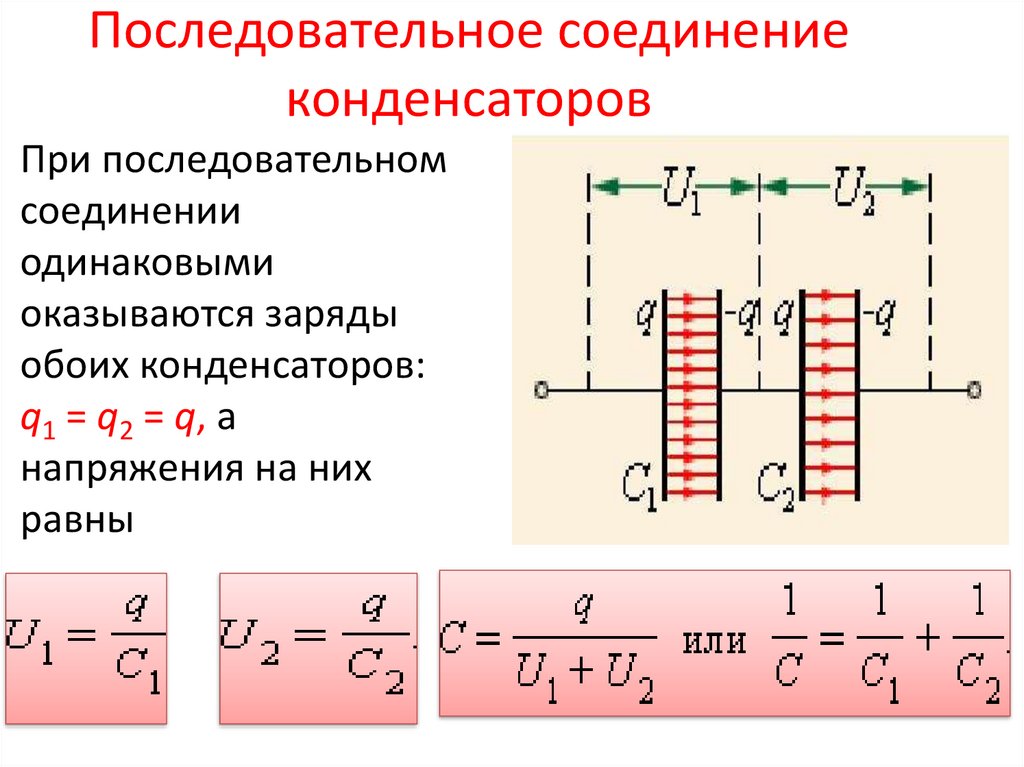 В то время как заряд будет разделен между каждым конденсатором в соответствии с его емкостью.
В то время как заряд будет разделен между каждым конденсатором в соответствии с его емкостью.
Предположим, что три конденсатора соединены параллельно с емкостями C 1 , C 2 и C 3 . Общая стоимость составит:
Q = Q 1 +Q 2 +Q 3
Так как Q=CV,
CV = C 1 V 1 +C 2 V 2 +C 3 V 3
мы знаем, что при параллельном объединении напряжение на каждом конденсаторе будет одинаковым, т.е. В 1 =В 2 =В 3 =В
CV = C 1 V + C 2 V + C 2 V + C 3 V
CV = (C 1 + C 2 + C 3 ) V
C = C 1 + C 2 +С 3
Из приведенного выше уравнения мы можем сделать вывод, что общая емкость при параллельном соединении представляет собой просто арифметическую сумму всех емкостей конденсаторов, соединенных параллельно.
Комбинация конденсаторов серии:
Когда конденсаторы соединены последовательно, каждый конденсатор сохраняет одинаковое количество заряда, а общее напряжение делится на каждый конденсатор.
Предположим, что три конденсатора соединены параллельно с емкостями C 1 , C 2 и C 3 . Суммарное напряжение будет:
В = В 1 + В 2 + В 3
Поскольку Q=CV, V=Q/C,
Q/C = Q 1 /C 1 + Q 2 /C 2 + Q 3 /C 3
В последовательном соединении каждый конденсатор хранит одинаковое количество заряда, поэтому Q 1 = Q 2 = Q 3 = Q
Q/C = Q/C 1 + Q/C 2 + Q/C 3
Q/C = Q(1/C 1 + 1/C 2 + 1/C 3 )
1/К = 1/К 1 + 1/К 2 + 1/К 3
Таким образом, в этой комбинации обратная величина полной емкости есть сумма обратных величин всех емкостей последовательно соединенных конденсаторов.
Шаг: 2
Расчет
Поскольку выше три выделенных конденсатора соединены последовательно, их эквивалентная емкость (C
x ) будет:
1/C x = 1/3 + 1/3 +1/3
1/C x = 3/3 = 1
C x = 1 мкф
После подстановки 1 мкф вместо трех последовательных конденсаторов мы видим, что теперь 1 мкф и 2 мкф включены параллельно, поэтому их эквивалент (C y ) будет:
C y = 1 + 2
C y = 3 мкф
Теперь, после дальнейшего упрощения, снова три конденсатора по 3 мкф соединены последовательно, поэтому их эквивалент (C z ) будет:
1/C z = 1/3 + 1/3 +1/3
1/C z = 3/3 = 1
C z = 1 мкф
Снова комбинация последовательных конденсаторов (1 мкф) и 2 мкф подключены параллельно, поэтому их эквивалент (C t ) будет:
C t = 1 + 2
C t = 3 мкФ
Теперь, наконец, три конденсатора соединены последовательно, поэтому их эквивалент будет:
.
1/C = 1/3 + 1/3 +1/3
1/C = 3/3 = 1
C = 1 мкф (Ans)
Комбинация конденсаторов | bartleby
Практическая задача s
Q1: Если пять различных конденсаторов соединены параллельно, каково будет их падение напряжения?
- Одинаковые
- разные
- не связаны с конденсаторами
- обратно пропорциональны емкости
Ответ: (a) Если четыре разных конденсатора соединены параллельно, падение напряжения на каждом конденсаторе будет одинаковым.
Q2: Если последовательно соединить три конденсатора, каков будет их заряд?
- разные
- одинаковые
- никак не связаны с емкостью
- бесконечное накопление заряда
Ответ: (b) Если три различных конденсатора соединены последовательно, заряд, накопленный на каждом конденсаторе, будет одинаковым. Все конденсаторы будут иметь одинаковое распределение заряда.
Q3: Если два конденсатора емкостью 5 Ф и 2 Ф соединены параллельно, какой будет эквивалентная емкость?
- 107 F
- 7 F
- 10 F
- 5 F
Ответ: (b) Формула для эквивалентной емкости в случае параллельной комбинации двух конденсаторов, скажем, C1 и C2, будет: C1+C2=5F+2F=7F
Следовательно, нашим правильным ответом будет 7 F.
Q4: Два конденсатора с емкостью 2 Ф и 6 Ф соединены последовательно. Какой будет эквивалентная емкость?
- 1,5 F
- 2,3 F
- 3,2 F
- 6 F
+16=812, следовательно, Ceq=1,5F
В5. Как ведет себя эффективная емкость двух или более одинаковых конденсаторов при последовательном соединении?
- остается прежним
- увеличивается
- уменьшается
- ничего не могу сказать
Ответ: (c) При последовательном соединении одинаковых конденсаторов эффективная емкость уменьшается.Это можно увидеть по формуле 1Ceq=1C+1C…..до n членов → Ceq=Cn. Следовательно, правильный вариант (с).
6 Общие проблемы с конденсаторами
physics.fisikastudycenter.com-Учебный метод изучения конденсатора в задачах и решениях. Будут обсуждаться нахождение эквивалентного конденсатора в последовательной и параллельной комбинации, накопленная энергия, разность потенциалов на конденсаторах, накопление электрического заряда, сферический конденсатор и емкость параллельных пластинчатых конденсаторов.
Задача 1
Дана схема, содержащая комбинацию трех конденсаторов X, Y и Z, см. рисунок ниже.
Если переключатель S включен, найдите:
a) эквивалентную емкость цепи (эквивалентный конденсатор)
b) электрический заряд, накопленный в цепи
c) электрический заряд, накопленный в конденсаторе Z, используйте принцип последовательного ряда
d) разность потенциалов на конденсаторе Z
e) разность потенциалов на конденсаторе X
f) разность потенциалов на конденсаторе Y
g) электрический заряд, накопленный в конденсаторе X
h) электрический заряд, накопленный в конденсаторе Y
i) электрический заряд, накопленный в конденсаторе Z
j) энергия накопленная в цепи
k) энергия, запасенная в конденсаторе X
l) энергия, запасенная в конденсаторе Y
m) энергия, запасенная в конденсаторе Z
Обсуждение
a) Сначала замените параллельную комбинацию X и Y ее эквивалентной емкостью, названной C xy :
Замена двух конденсаторов дает нам эквивалентную цепь в последовательной комбинации, затем найдите эквивалент для C xy и C z , два последовательно соединенных, называемых C eq или C tot :
b) Заряд, накопленный в цепи, или заряд в эквивалентной емкости; Q tot , C tot , умноженное на V tot
c) Заряд, накопленный в конденсаторе Z; Q z
При последовательном соединении заряд всех конденсаторов одинаков, он равен заряду эквивалентного конденсатора:
d) разность потенциалов на конденсаторе Z; V z
e) разность потенциалов между конденсаторами X и Z является одной и той же причиной параллельного соединения
f) разность потенциалов на Y такая же, как разность потенциалов на X
g) заряд в конденсаторе X, будьте осторожны, это не то же самое, что заряд в эквивалентном конденсаторе
h) заряд в конденсаторе Y
i) заряд в конденсаторе Z
j) энергия, накопленная в цепи
Используйте один из этих трех формул, чтобы получить запасенную энергию
Тогда
k) энергия, запасенная в конденсаторе X
l) энергия, запасенная в конденсаторе Y
90
Проблема 2
Учитывая три конденсатора в цепи ниже, источник напряжения составляет 24 вольта.
Если выключатель включен, найдите:
a) эквивалентную емкость цепи
b) электрический заряд, накопленный в цепи
c) электрический заряд, накопленный в конденсаторе Z
d) разность потенциалов на конденсаторе Z
e) разность потенциалов на конденсаторе X
f) разность потенциалов на конденсаторе Y
g) электрический заряд в конденсаторе X
h) электрический заряд в конденсаторе Y
i) энергия в цепи
j) энергия в конденсаторе X
k) энергия в конденсаторе Y
l) энергия, запасенная в конденсаторе Z
Попробуйте ..!!
Задача 3
Дан плоский конденсатор в вакууме. Пластины конденсатора расположены на расстоянии 2 см друг от друга и 50 см 2 площади каждой пластины. Через конденсатор подается разность потенциалов 120 вольт. Когда ε o равно 8,85 x 10 − 12 C 2 N − 1 − 2 , рассчитаем:
a) емкость конденсатора
b) заряд, накопленный в конденсаторе
c) величину электрического заряда в пространстве между двумя пластинами конденсатора
.
Задача 4
Пластинчатый конденсатор емкостью С в вакууме.Если затем между обкладками конденсатора вставить материал с его диэлектрической проницаемостью K = 2, найдите новую емкость конденсатора!
Ответ
Площадь и расстояние между пластинами конденсатора не меняются, поэтому новая емкость равна Если площадь пластин конденсатора увеличилась вдвое, а расстояние между двумя пластинами в 1,5 раза больше первоначального, найдите новую емкость конденсатора!
Ответ
Задача 6
Сферический конденсатор с радиусом 1.8 см. Когда 1/4πε o = 9 x 10 9 в международных единицах, найдите емкость этого сферического конденсатора!
Ответ
Емкость сферического конденсатора радиусом R :
Примеры
Примеры
Примеры
для конденсаторов
Пример №1
Проблема:
Рассмотрим два
пластины, разделенные d =1. 5 см , где
5 см , где
электрическое поле между ними составляет 100 В/м , а заряд
на пластинах 30,0 м С . Какова емкость?
Решение:
Емкость:
2.0Е-5
Ф
Пример №2
Проблема:
Рассмотрим
конденсатор из двух пластин 0,05 м 2
разделены 0.5 мм. Если емкость 3,0 нф ,
какова относительная проницаемость k материала между
тарелки?
Решение:
3,4
Пример №3
Задача: часть а.)
Что такое
емкость следующего сегмента цепи?
ДАННЫЕ: C 1 =C 2 =C 3 3
00
м ж
Решение:
Емкость двух в
параллель C 23 =C 2 +C 3
9.
Емкость всей цепи:
*** изменить C_34 на C_23 ***
2.0
( м Ф )
часть б.)
Если напряжение В аб
= 6.0 В применяется, какой заряд на каждом
конденсатор?
Решение:
Заряд на первом конденсаторе
такой же, как заряд всей комбинации, так как это
единственное, к чему подключен левый провод. Этот заряд
можно найти по емкости.
Платно Q 1
на противоположной стороне первого конденсатора, который должен
пришли в равной степени от следующих конденсаторов, так как они
равны друг другу.Следовательно,
.
Q 1
= 12 м С,
Q 2 = Q 3
= 6,0 м С
часть в.)
Что такое
напряжение на каждом конденсаторе?
Решение:
Использовать В i = Q i /C i .

 е. q=q1=q2
е. q=q1=q2
