Закон ома 1 определение: Закон Ома определение. Закон Ома для участка цепи

формулировка простыми словами, формула для первого, второго и третьего

Есть такие формулы и законы, которые люди узнают еще в школе, а помнят всю жизнь. Обычно это несложные уравнения, состоящие из двух-трех физических величин и объясняющие какие-то фундаментальные вещи в науке, основу основ. Закон Ома как раз такая штука.

Закон Ома: кто придумал, определение

Закон Ома — это основной закон электродинамики, который выводит взаимосвязь между ключевыми понятиями электрической цепи: силой тока, напряжением и сопротивлением.

Данную взаимозависимость выявил немецкий физик Георг Симон Ом в 1826 году. Несмотря на то, что этот закон является истинным законом природы, точность которого была многократно проверена и доказана позже, публикация работы Ома в 1827 году прошла незамеченной для научной общественности. И лишь в 1830-х гг., когда французский физик Пулье пришел к тем же самым выводам, что и Ом, работа немецкого ученого была оценена по достоинству.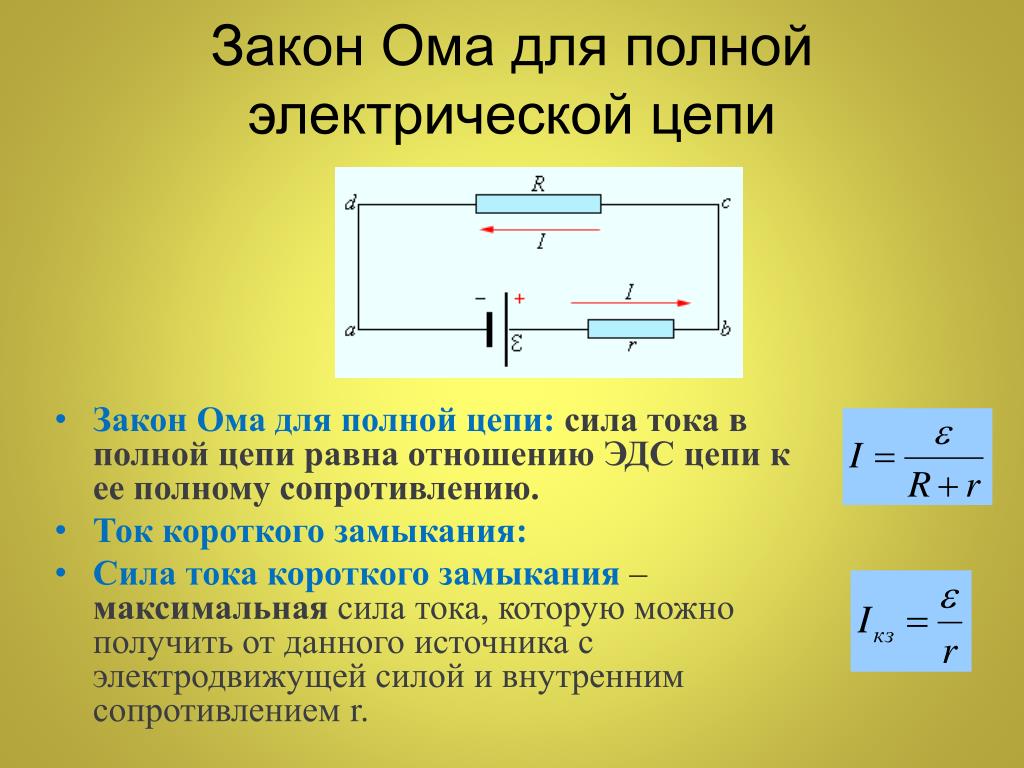

Установление закономерностей между основными параметрами электроцепи имеет огромное значение для науки. Ведь оно позволило количественно измерить свойства электрического тока.

Источник: rusenergetics.ru

Формулировки и основные формулы

Закон Георга Ома формулируется так: сила тока в проводнике прямо пропорциональна напряжению в проводнике и обратно пропорциональна сопротивлению этого проводника.

Пояснения к закону:

1. Чем выше напряжение в проводнике, тем выше будет и сила тока в этом проводнике.
2. Чем выше сопротивление проводника, тем меньше будет сила тока в нем.

Обозначение основных параметров, характеризующих электроцепь, известны всем с уроков физики в школе:

• I — сила электротока;
• U — напряжение;
• R — сопротивление.

Объяснение закона Ома в классической теории

Формула закона, известная всем со школьных лет, выглядит так:

\(I=\frac UR\)

Из нее легко выводятся формулы для определения \(U\):

\(U\;=I\times R\)

и для определения \(R\):

\(R=\frac UI\)

Единицами измерения силы тока являются амперы, напряжения — вольты, сопротивление измеряется в омах.

Данный закон верен для линейного участка цепи, на котором зафиксировано стабильное сопротивление.

Источник: dzgo.ru

Закон Ома для полной (замкнутой) цепи

Замкнутой или полной называется такая электрическая цепь, по которой проходит электроток.

Описание формулы этого закона для полной цепи выглядит так:

\(I=\frac\epsilon{R+r}\)

где \(\epsilon\) — это электродвижущая сила или напряжение источника питания, которое не зависит от внешней цепи;

\(R\) — сопротивление внешней цепи;

\(r\) — внутреннее сопротивление источника.

Источник: multiurok.ru

Использование закона Ома при параллельном и последовательном соединении

При последовательном соединении элементы цепи подключаются друг за другом последовательно. Так как такая электрическая цепь является неразветвленной, сила тока на каждом ее участке будет одинаковая. Пример последовательного соединения — лампочки в новогодней гирлянде.

При последовательном соединении элементов основные параметры электроцепи рассчитываются следующим образом:

• Сила тока по формуле: 

\(I=I_1=I_2=I_3\)

Где \(I\) — общая сила тока в электроцепи, \(I_1\) — сила тока первого участка, \(I_2\) — сила тока второго участка, \(I_3\) — сила тока третьего участка.

• Напряжение по формуле:

\(U=U_1+U_2+U_3\)

Где \(U\) — общее напряжение, \(U_1\) — напряжение первого участка, \(U_2\) — напряжение второго участка, \(U_3\) — напряжение третьего участка.

•  Сопротивление согласно формуле:

\(R=R_1+R_2+R_3\)

Где \(R\) — общее сопротивление в цепи, \(R_1\) — сопротивление первого участка, \(R_2\) — сопротивление второго участка, \(R_3\) — сопротивление третьего участка.

Подключая элементы в цепь параллельно, получают разветвленную электрическую цепь. Примером такого соединения является стандартная разводка электричества по квартире, когда в комнате одновременно можно включить несколько предметов бытовой техники и верхнее освещение.

При параллельном соединении элементов основные параметры электроцепи рассчитываются следующим образом:

\(I=I_1+I_2+I_3\)

Где \(I\) — общая сила тока в электроцепи, \(I_1, I_2, I_3\) — сила тока первого, второго и третьего участков соответственно.

\(U=U_1=U_2+U_3\)

Где \(U\) — общее напряжение, \(U_1, U_2, U_3\) — напряжение первого, второго и третьего участков соответственно.

• Сопротивление:

\(R=\frac{R_1\times R_2\times R_3}{R_1+R_2+R_3}\)

Где \(R\) — общее сопротивление в цепи, \(R_1, R_2, R_3\) — сопротивление первого, второго и третьего участков соответственно.

Закон Ома для переменного и постоянного тока

Для цепи постоянного тока правильными будут уже озвученные нами взаимосвязи основных параметров электроцепи:

Источник: en. ppt-online.org

При подключении к электроцепи источника переменного тока, сила электротока в цепи будет определяться по формуле:

\(I=\frac UZ\)

где \(Z\) — полное сопротивление или импеданс, который состоит из активной \((R)\) и реактивных составляющих (\(X_C\) — сопротивление емкости и \(X_L\) — сопротивление индуктивности).

Реактивное сопротивление цепи зависит:

• от значений реактивных элементов, 
• от частоты электротока;
• от формы тока в цепи. 

Источник: fizikaotfizika.ru

Закон Ома для однородного и неоднородного участка цепи

Закон Ома для однородного участка электроцепи представляет собой классическое выражение зависимости силы от напряжения и сопротивления:

\(I=\frac UR\)

В этом случае основной характеристикой проводника является сопротивление. От внешнего вида проводника зависит, как выглядит его кристаллическая решетка и какое количество атомов примесей содержит. От проводника зависит поведение электронов, которые могут ускоряться или замедляться.

Поэтому \(R\) зависит от вида проводника, точнее, от его сечения, длины и материала и определяется по формуле:

\(R=p\times\left(\frac lS\right)\)

где \(p\) — удельное сопротивление, \( l\) — это длина проводника, а \(S\) — площадь его сечения.

Под неоднородным участком цепи постоянного тока подразумевается такой промежуток цепи, на который помимо электрических зарядов воздействуют другие силы.

Источник: grabachapter.com

Как можно было убедиться, закон, открытый Георгом Омом, прост только на первый взгляд. Разобраться во всех тонкостях самостоятельно под силу далеко не каждому. Если столкнулись с трудностями в учебе и сложными для понимания темами, обращайтесь за помощью к образовательному ресурсу Феникс.Хелп. Квалифицированные эксперты помогут сдать в срок самую сложную работу.

1. Электрическое сопротивление. Закон Ома для участка электрической цепи

Соберём электрическую цепь, состоящую из источника тока (который позволяет плавно менять напряжение), амперметра, спирали из никелиновой проволоки (проводника), ключа и параллельно присоединённого к спирали вольтметра (схема этой цепи показана рядом, прямоугольником условно обозначен проводник).

Замкнём цепь и отметим показания приборов. Затем при помощи источника тока плавно изменим напряжение (лучше всего увеличить его вдвое). Напряжение на спирали при этом тоже увеличится вдвое, и амперметр покажет вдвое большую силу тока. Увеличивая напряжение в \(3\) раза, напряжение на спирали увеличивается втрое, во столько же раз увеличивается сила тока.
Таким образом, опыт показывает, что во сколько раз увеличивается напряжение, приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нём. Другими словами:

Обрати внимание!

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника.

Эту зависимость можно изобразить графически. Её называют зависимостью силы тока в проводнике от напряжения между концами этого проводника.

Включая в электрическую цепь источника тока различные проводники и амперметр, можно заметить, что при разных проводниках показания амперметра различны, т.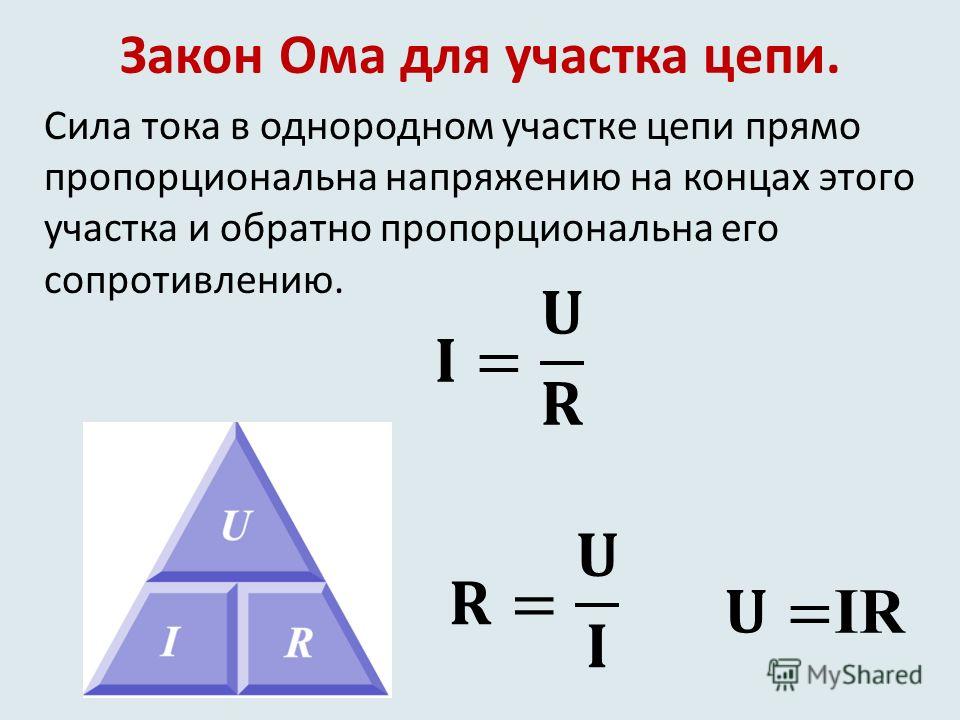 е. сила тока в данной цепи различна.

Графики тоже будут отличаться.

Вольтметр, поочерёдно подключаемый к концам этих проводников, показывает одинаковое напряжение. Значит, сила тока в цепи зависит не только от напряжения, но и от свойств проводников, включённых в цепь. Зависимость силы тока от свойств проводника объясняется тем, что разные проводники обладают различным электрическим сопротивлением.

Обрати внимание!

Электрическое сопротивление — физическая величина. Обозначается оно буквой R.

За единицу сопротивления принимают \(1\) ом — сопротивление такого проводника, в котором при напряжении на концах \(1\)вольт сила тока равна \(1\) амперу.

Кратко это записывают так: 1 Ом =1 В1 А.Применяют и другие единицы сопротивления: миллиом (мОм), килоом (кОм), мегаом (МОм).

\(1\) мОм = \(0,001\) Ом;

\(1\) кОм = \(1000\) Ом;

\(1\) МОм = \(1 000 000\) Ом.

Причина сопротивления заключается в следующем: электроны взаимодействуют с ионами кристаллической решётки металла. При этом замедляется упорядоченное движение электронов, и сквозь поперечное сечение проводника проходит за \(1\) с меньшее их число. Соответственно, уменьшается и переносимый электронами за \(1\) с заряд, т.е. уменьшается сила тока. Таким образом, каждый проводник как бы противодействует электрическому току, оказывает ему сопротивление. Итак:

Обрати внимание!

Причиной сопротивления является взаимодействие движущихся электронов с ионами кристаллической решётки.

Чтобы ответить на вопрос, как зависит сила тока в цепи от сопротивления, обратимся к опыту.

На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор. В эту цепь по очереди включают проводники, обладающие различным сопротивлением. Напряжение на концах проводника во время опыта поддерживается постоянным. За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром. Ниже приведены результаты опытов с тремя различными проводниками.

Обобщая результаты опытов, приходим к выводу, что:

Обрати внимание!

Сила тока в проводнике обратно пропорциональна сопротивлению проводника.

Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома — по имени немецкого учёного Георга Ома, открывшего этот закон в \(1827\) году.
Закон Ома читается так:

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

И записывается так:

I=UR,

где \(I\) — сила тока в участке цепи, \(U\) — напряжение на этом участке, \(R\) — сопротивление участка.

Зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах может быть показана графически:

Найти сопротивление экспериментально можно несколькими способами:

Где  — обозначение омметра в цепи (или мультиметра в режиме измерения сопротивления).

Источники:

Пёрышкин А.В. Физика, 8 класс// ДРОФА, 2013.

http://xn--h2adlho.xn--g1ababalj7azb.xn--p1ai/375/
http://radiolove. ucoz.com/index/ne_znaesh_zakona_oma_sidi_doma/0-8

Электрический ток. Закон Ома

При помещении изолированного проводника в электрическое поле E→ на свободные заряды q в проводнике будет действовать сила F→=qE→. Это провоцирует возникновение кратковременных перемещений свободных зарядов. Процесс завершается, когда собственное поле электрических зарядов будет компенсировано внешним. Электростатическое поле внутри проводника станет равным нулю.

Определение 1

Существуют определенные условия, при которых возникает непрерывное упорядоченное движение свободных носителей заряда. Оно получило название электрического тока.

За направление электрического тока принято брать направление движения положительных свободных зарядов. При наличии электрического поля произойдет возникновение электрического тока в проводнике.

Определение 2

Силой тока называют скалярную физическую величину I, равняющуюся отношению заряда ∆q, протекающего по сечению проводника за время ∆t:

I=∆q∆t

При неизменяемых силе тока и направлении за промежуток времени ток называют постоянным. Следует обращать внимание на его характеристики.

Рисунок 1.8.1. Упорядоченное движение электронов в металлическом проводнике и ток I. S – площадь поперечного сечения проводника, – электрическое поле.

Определение 3

В системе СИI измеряется в амперах (А), а единица измерения 1 А устанавливается по магнитному взаимодействию двух параллельных проводников.

Законы постоянного тока. Формулы

Определение 4

Постоянный электрический ток создается в замкнутой цепи, где свободные носители заряда проходят по замкнутым траекториям.

Разные точки цепи обладают неизменным по времени электрическим полем, исходя из основных законов постоянного тока. То есть в такой цепи оно ассоциируется с замороженным электростатическим полем. Когда электрический заряд перемещается по замкнутой траектории, то работа сил равняется нулю.

Определение 5

Чтобы постоянный ток имел место на существование, нужно наличие такого устройства в цепи, которое будет создавать и поддерживать разности потенциалов разных участков цепи при помощи работы сил неэлектростатического происхождения. Их называют источниками постоянного тока. Такие силы, действующие на свободные носители заряда со стороны источников тока, получили название сторонних сил.

Их природа различна. Гальванические элементы или аккумуляторы обладают сторонними силами, возникающими по причине электрохимических процессов. В генераторах это обстоит по-другому: появление сторонних сил возможно при движении проводников в магнитном поле. Источник тока сравним с насосом, перекачивающим жидкость замкнутой гидравлической системы. Электрические заряды внутри источника под действием сторонних сил движутся против сил электростатического поля. Именно поэтому замкнутая цепь может обладать постоянным током.

Перемещаясь по цепи постоянного тока, электрические заряды сторонних сил действуют на источники тока, то есть совершают работу.

Определение 6

Физическую величину, равную отношению сторонних сил Aст при перемещении заряда q от отрицательного полюса источника к положительной величине этого заряда, называют электродвижущей силой источника (ЭДС):

ЭДС=δ=Aстq.

Отсюда следует, что ЭДС определяется совершаемой сторонними силами работой при перемещении единичного положительного заряда. ЭДС измеряется в вольтах (В).

Если по замкнутой цепи движется единично положительный разряд, то работа сторонних сил равняется сумме ЭДС, которая действует в данной цепи с работой электростатического поля, имеющего значение 0.

Определение 7

Цепь с постоянной величиной тока следует разбивать на участки. Если на них отсутствует действие сторонних сил, тогда участки называют однородными, если присутствуют, то неоднородными.

Когда единичный положительный заряд перемещается по определенному участку цепи, то работу совершают кулоновские и сторонние силы. Запись работы электростатических сил равняется разности потенциалов ∆φ12=φ1-φ2 начальной и конечной точек неоднородного участка. Работу сторонних сил приравнивают к электродвижущей данного участка по закону Ома. Тогда полная работа запишется как:

U12=φ1-φ2+δ12.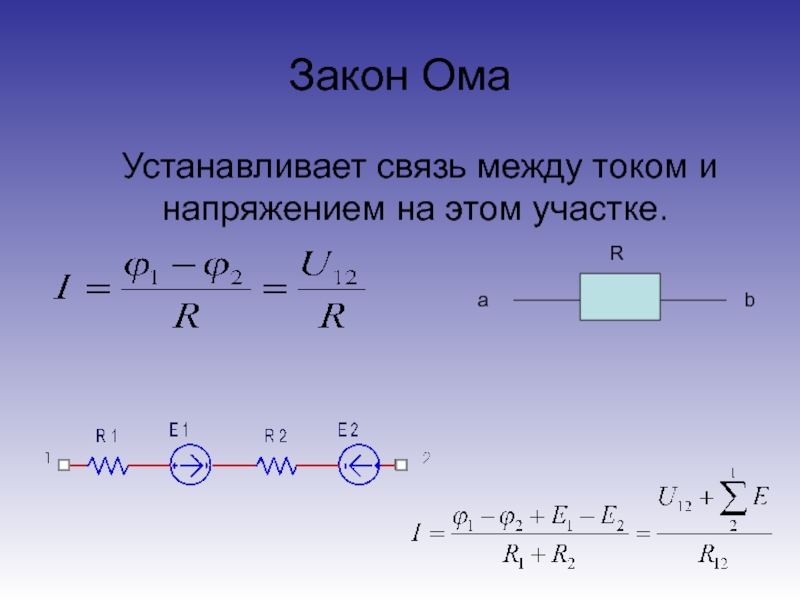

Величина U12 называется напряжением участка цепи 1-2. Если данный участок однородный, тогда напряжение фиксируется как разность потенциалов:

U12=φ1-φ2.

В 1826 году Г. Ом с помощью эксперимента установил, что сила тока I, текущая по однородному металлическому проводнику (отсутствие действия сторонних сил), пропорциональна напряжению на U концах проводника.

I=1RU или RI=U, где R=const.

Определение 8

R называют электрическим сопротивлением.

Проводник, имеющий электрическое сопротивление, получил название резистора.

Связь между R и I говорит о формулировке законе Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению.

Обозначение сопротивления по системе СИ выражается омами (Ом).

Если на участке цепи имеется сопротивление в 1 Ом, тогда при напряжении 1 В во время измерения возникает ток силой 1 А.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Электрический ток и его характеристики

Определение 9

Проводники, которые подчинены закону Ома, получили название линейных.

Для изображения графической зависимости силы тока I от U (графики называют вольт-амперными характеристиками, ВАХ) используется прямая линия, проходящая через начало координат.

Существуют устройства, не подчиняющиеся закону Ома. К ним относят полупроводниковый диод или газоразрядную лампу. Металлические проводники имеют отклонения от закона Ома при токах большой силы. Это связано с ростом температуры.

Определение 10

Участок цепи, содержащий ЭДС, позволяет записывать закон Ома таким образом:

IR=U12=φ1-φ2+δ=∆φ12+δ.

Формула получила название обобщенного закона Ома или закон Ома для неоднородного участка цепи.

Рисунок 1.8.2 показывает замкнутую цепь с постоянным током, причем ток цепи (cd) считается однородным.

Рисунок 1.8.2. Цепь постоянного тока.

Исходя из закона Ома IR=∆φcd, участок (ab) содержит источник тока с ЭДС, равной δ. Тогда для неоднородного участка формула примет вид Ir=∆φab+δ. Сумма обоих равенств дает в результате выражение I(R+r)=∆φcd+∆φab+δ. Но ∆φcd=∆φba=-∆φab, тогда I=δR+r.

Определение 11

Формула I=δR+r выражает закон Ома для полной цепи. Запишем ее, как определение: сила тока в полной цепи равняется электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.

Рисунок 1.8.2 говорит о том, что R неоднородного тела может быть рассмотрено как внутреннее сопротивление источника тока. Тогда (ab) участок будет являться внутренним участком источника.

Определение 12

При замыкании a и b с помощью проводника с малым по сравнению с внутренним сопротивлением источника получим, что в цепи имеется ток короткого замыкания Iкз=δr.

Сила тока короткого замыкания является максимальной, получаемой от источника с ЭДС и внутренним сопротивлением r. Если внутренне сопротивление мало, тогда ток короткого замыкания может вызвать разрушение электрической цепи или источника.

Пример 1

Свинцовые аккумуляторы автомобилей имеют силу тока короткого замыкания в несколько сотен ампер. Особую опасность представляют замыкания в осветительных сетях, которые имеют подпитку от подстанций. Во избежание разрушительных действий предусмотрены предохранители или автоматы для защиты сетей.

Чтобы при превышении допустимых значений силы тока не произошло короткого замыкания, используют внешнее сопротивление. Если сопротивление r равняется сумме внутреннего и внешнего сопротивления источника, сила тока не будет превышать норму.

При наличии разомкнутой цепи разность потенциалов на полюсах разомкнутой батареи равняется ее ЭДС. Когда внешнее R включено и ток I подается через батарею, то разность потенциалов на полюсах запишется, как ∆φba=δ-Ir.

Рисунок 1.8.3 дает точное схематическое изображение источника постоянного тока с ЭДС, равной δ, внутренним r в трех режимах: «холостой ход», работа на нагрузку, режим короткого замыкания. E→ является напряженностью внутри электрического поля внутри батареи, a – силами, действующими на положительные заряды, Fст→– сторонней силой. Исчезновение электрического поля возникает при коротком замыкании.

Рисунок 1.8.3. Схематическое изображение источника постоянного тока: 1 – батарея разомкнута;
2 – батарея замкнута на внешнее сопротивление R; 3 – режим короткого замыкания.

Вольтметр и амперметр

Определение 13

Применяются измерительные приборы для напряжения тока в электрических цепях, называемые вольтметрами и амперметрами.

Определение 14

Вольтметр измеряет разности потенциалов, приложенные к его клеммам.

Подключение к цепи производится параллельно. Каждый из приборов такого типа имеет внутреннее сопротивление RB. Чтобы перераспределение токов не было заметно, нужно проследить за тем, чтобы внутреннее сопротивление было больше, чем на участках подключаемой цепи. На рисунке 1.8.4 изображена такая цепь, тогда данное условие можно записать как RB≫R1.

Это означает, что ток IB=∆φcdRB, протекающий через вольтметр, меньше тока I=∆φcdR1, проходящего по заданному участку цепи.

Внутри прибора также не действуют сторонние силы, поэтому разность потенциалов его клемм совпадет со значением напряжения. Отсюда следует, что вольтметр измеряет напряжение.

Определение 15

Амперметр предназначается для измерения силы тока в цепи.

Его подключение к цепи производится последовательно для прохождения всего измеряемого тока. Внутреннее сопротивление прибора обозначается как RA. В отличие от вольтметра должно иметь малые значения относительно полного сопротивления цепи. На рисунке 1.8.4 показано, что сопротивление амперметра подходит к условию RA≪(r+R1+R2). При включении прибора ток в цепи не должен изменяться.

Измерительные приборы подразделяют на стрелочные и цифровые, последние из которых являются сложными электронными устройствами и способны давать максимально точные значения при измерении.

Рисунок 1.8.4. Включение амперметра (А) и вольтметра (В) в электрическую цепь.

Применение закона Ома на практике

Принцип работы омметра

Для выполнения замеров обычно используются магнитоэлектрические приборы, хотя в последнее время широко внедряются электронные (как аналоговые, так и цифровые).

В омметре магнитоэлектрической системы используется токоограничивающий резистор R, пропускающий через себя только миллиамперы и чувствительная измерительная головка (миллиамперметр). Она реагирует на протекание малых токов через прибор за счет взаимодействия двух электромагнитных полей от постоянного магнита N-S и поля, создаваемого током, проходящим через обмотку катушки 1 с токопроводящей пружинкой 2.

В результате взаимодействия сил магнитных полей происходит отклонение стрелки прибора на определенный угол. Шкала головки для облегчения работы сразу проградуирована в омах. При этом используется выражение сопротивления через ток по формуле 3.

У омметра для обеспечения точных замеров должно поддерживаться стабилизированное значение подаваемого напряжения от батареи питания. С этой целью применяется калибровка посредством использования добавочного регулировочного резистора R рег. С его помощью до начала измерения на схему ограничивается подача излишнего напряжения от источника, выставляется строго стабильная, нормируемая величина.

Определение напряжения с помощью закона Ома

Во время работ с электрическими схемами бывают случаи, когда необходимо узнать падение напряжения на каком-то элементе, например, резисторе, а известно его сопротивление, которое обычно маркируется на корпусе, и проходящий сквозь него ток. Для этого не обязательно подключать вольтметр, а достаточно воспользоваться расчетами по формуле 2.

В нашем случае для рисунка 3 проведем расчеты: U=2,5·4,8 =12 В.

Определение тока с помощью закона Ома

Этот случай описывает формула 3. Его используют для расчета нагрузок в электрических схемах, выбора сечений проводников, кабелей, предохранителей или защитных автоматов.

В нашем примере расчет выглядит так: I=12/4,8=2,5 А.

Шунтирование

Этот способ в электротехнике используют для исключения работы определенных элементов из схемы без их демонтажа. Для этого на ненужном резисторе замыкают накоротко проводником входящую и отходящую клеммы (на рисунке 1 и 2) — шунтируют.

В результате ток схемы выбирает для себя путь с меньшим сопротивлением через шунт и резко возрастает, а напряжение зашунтированного элемента падает до нуля.

Короткое замыкание

Этот режим является частным случаем шунтирования и, в общем-то, показан на рисунке выше, когда закоротка устанавливается на выходные клеммы источника. При его возникновении создаются очень опасные большие токи, способные поражать людей и сжигать не защищенное электрооборудование.

Для борьбы со случайно возникающими замыканиями в электрической сети используют защиты. На них выставляют такие уставки, которые не мешают работать схеме в нормальном режиме.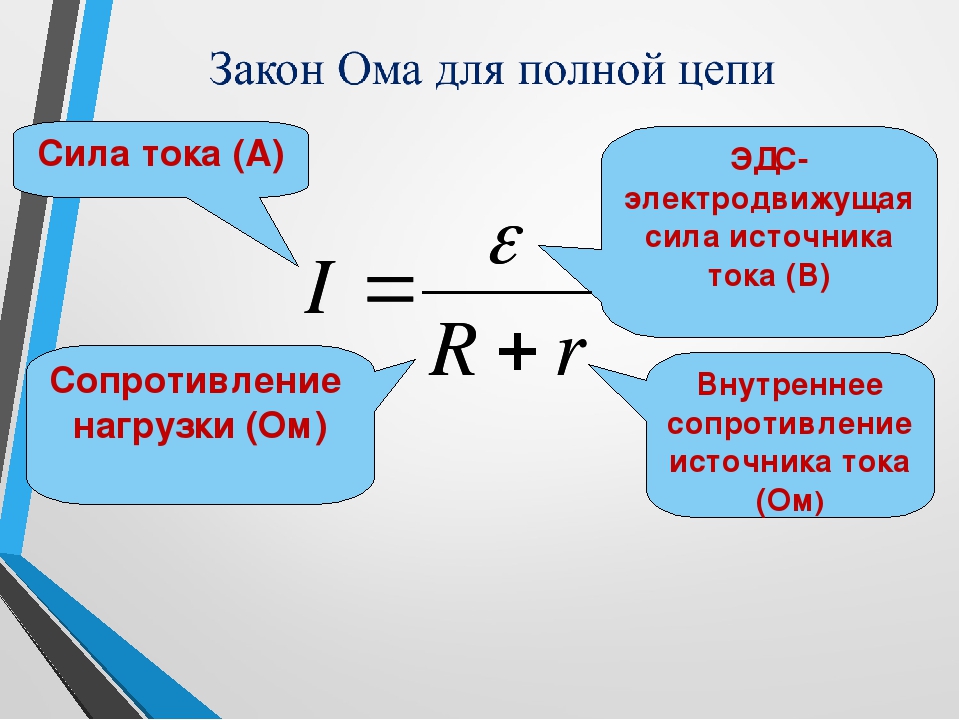 Они отключают питание только при аварийных случаях.

Например, если ребенок по неосторожности всунет в домашнюю розетку проволоку, то правильно настроенный автоматический выключатель вводного квартирного щита практически моментально отключит электроснабжение.

Все, что описано выше, относится к закону Ома для участка цепи постоянного тока, а не полной схемы, где процессов может быть значительно больше. Следует представлять, что это только небольшая часть применения его в электротехнике.

Закономерности, выявленные знаменитым ученым Георгом Симоном Омом между током, напряжением и сопротивлением по-разному описываются в различных средах и цепях переменного тока: однофазных и трехфазных.

Вот основные формулы, выражающие соотношения электрических параметров в металлических проводниках.

Более сложные формулы для проведения специальных расчетов закона Ома на практике.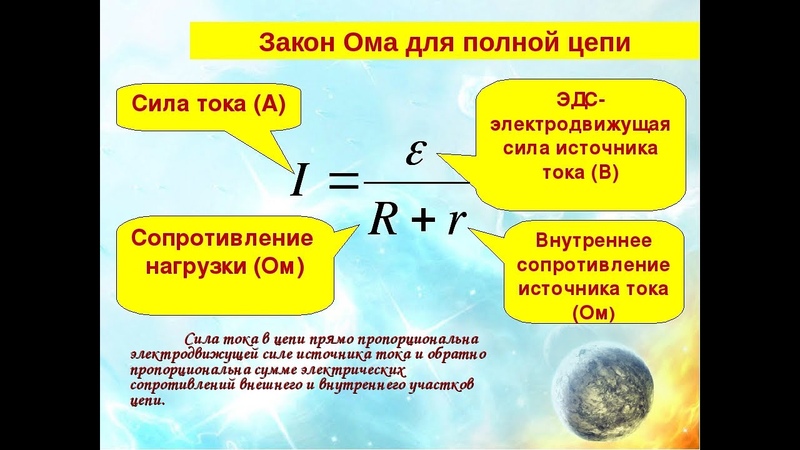  

Как видим, исследования, которые провел гениальный ученый Георг Симон Ом, имеют огромное значение даже в наше время бурного развития электротехники и автоматики.

Закон ома для замкнутого контура определение. Все виды законов ома

Вернёмся ещё раз к рис. 7.1. Здесь изображена
замкнутая проводящая цепь. На участке
цепи 1-а
-2 движение носителей заряда
происходит под действием только
электростатической силы=q
.
Такие участки называютсяоднородными
.

Совсем по-другому обстоят дела на участке
контура 2-b
-1. Здесь на
заряды действует не только электростатическая,
но и сторонняя сила. Полную силунайдем, сложив эти две:

.

Участок замкнутого контура, где наряду
с электростатической силой действуют
и сторонние силы, называют неоднородным
.

Можно показать, что на однородном участке
цепи средняя скорость направленного
движения носителей заряда пропорциональна
действующей на них силе.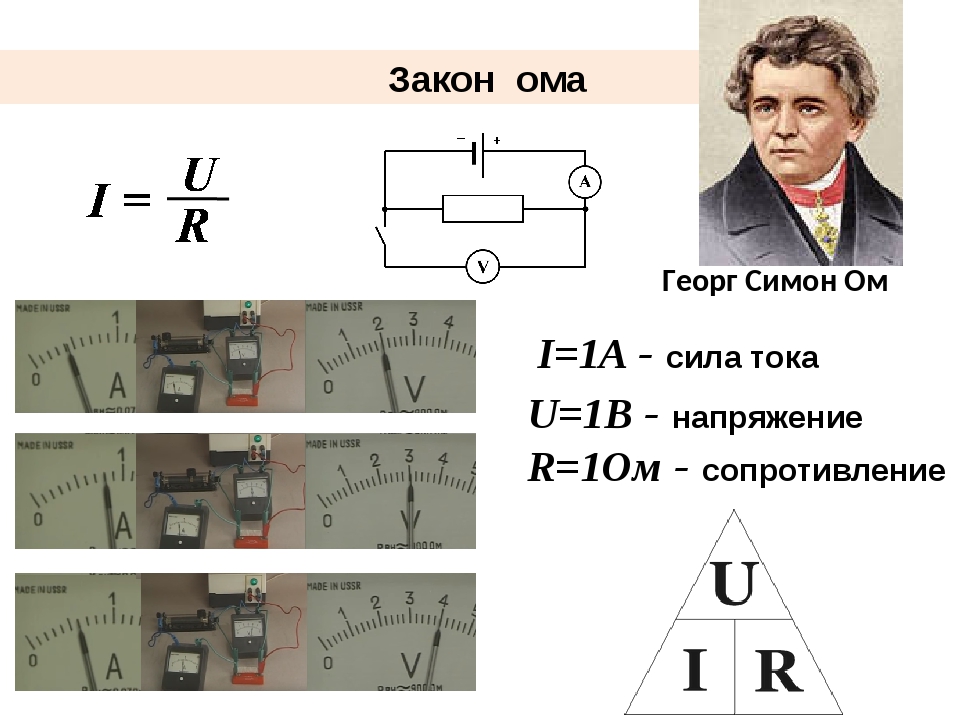 Для этого
достаточно сравнить формулы, полученные
на прошлой лекции:
=
(6.3) и=(6.13).

Пропорциональность скорости силе, а
плотности тока — напряжённости сохранится
и в случае неоднородного участка цепи.
Но теперь напряжённость поля равна
сумме напряжённостей электростатического
поля
и поля сторонних сил
:

. (7.5)

Это уравнение закона Ома в локальной
дифференциальной форме для неоднородного
участка цепи.

Теперь перейдём к закону Ома для
неоднородного участка цепи в интегральной
форме.

Выделим двумя близкими сечениями S
участокdl
трубки тока
(рис. 7.3.). Сопротивление этого участка:

,

а плотность тока можно связать с силой
тока:

.

Рис. 7.3.

Эти два выражения используем в уравнении
(7.5), спроецировав его предварительно
на линию тока:

Проинтегрировав последнее уравнение
по неоднородному участку 1-2, получим:

.

Произведение IR
1-2 =U
— напряжение на
участке 1-2;

первый интеграл справа
== 1 – 2 — разность потенциалов на концах
участка;

второй интеграл
== 1-2 — э.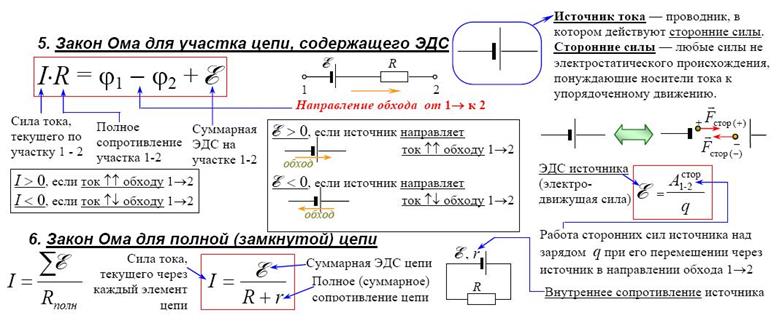 д.с.
источника тока.

Учтя всё это, конечный результат запишем
в виде:

. (7.6)

Это закон Ома для неоднородного участка
цепи в интегральной форме
. Обратите
внимание, что напряжение на неоднородном
участке цепиU
не
совпадает с разностью потенциалов на
его концах ( 1 – 2):

IR
1-2 =U
1-2 = ( 1 – 2)
+ 1-2 . (7.7)

Эти две величины равны только в случае
однородного участка, где источники тока
отсутствуют и  1-2 = 0. Тогда:

U
1-2 = 1 – 2 .

Для замкнутого контура уравнение закона
Ома (7.6) несколько видоизменяется, так
как разность потенциалов в этом случае
равна нулю:

. (7.8)

В законе Ома для
замкнутой цепи (7.8) R

— полное сопротивление контура,
складывающееся из внешнего сопротивления
цепи R
0
и внутреннего сопротивления источника
r
:

R
=R
0 +r
.

1. Правила Кирхгофа

Рассмотренные нами законы постоянного
тока позволяют рассчитать токи в сложных
разветвлённых электрических цепях. Эти
расчёты упрощаются, если пользоваться
правилами Кирхгофа.

Правил Кирхгофа два: правило токов
иправило напряжений
.

Правило токов относится к узлам цепи,
то есть, к таким точкам схемы, где сходятся
не менее трёх проводников (рис. 7.4.).
Правило токов гласит: алгебраическая
сумма токов в узле равняется нулю:

. (7.9)

Рис. 7.4.

При составлении соответствующего
уравнения, токи, втекающие в узел, берутся
со знаком плюс, а покидающие его — со
знаком минус. Так, для узла А
(рис.
7.3.) можно записать:

I
1 –I
2 –I
3 +I
4 –I
5 = 0.

Это первое правило Кирхгофа является
следствием уравнения непрерывности
(см. (6.7)) или закона сохранения электрического
заряда.

Правило напряжений
относится к
любому замкнутому контуру разветвлённой
цепи.

Выделим, например, в разветвлённой
сложной цепи замкнутый элемент 1-2-3-1
(рис. 7.5.). Произвольно обозначим в ветвях
контура направления токов I
1 ,I
2 ,I
3 .
Для каждой ветви запишем уравнение
закона Ома для неоднородного участка
цепи:

Участок

.

Здесь R
1 ,R
2 ,R
3 —полное
сопротивление соответствующих ветвей.
Сложив эти уравнения, получим формулу
второго правила Кирхгофа:

I
1 R
1 –I
2 R
2 –I
3 R
3 = 1 + 2 – 3 – 4 + 5 .

Правило напряжений формулируется
так: в любом замкнутом контуре
алгебраическая сумма падений напряжения
равна алгебраической сумме э.д.с.,
встречающихся в этом контуре:

. (7.10)

Рис. 7.5.

При составлении уравнения (7.10) второго
правила Кирхгофа задаются направлением
обхода: в нашем примере — по часовой
стрелке. Токи, совпадающие с направлением
обхода, берутся со знаком плюс (I
1),
токи противоположного направления —
со знаком минус (–I
2 ,
–I
3).

Э.д.с. источника берётся со знаком плюс,
если он создаёт ток, совпадающий с
направлением обхода (+ 1 ,
+ 2 , + 5).
В противном случае э.д.с. отрицательна
(– 3 , – 4).

В качестве примера составим уравнения
правил Кирхгофа для конкретной
электрической схемы — измерительного
моста Уитстона (рис. 7.6.). Мост образуют
четыре резистора R
1 ,R
2 ,R
3 ,R
4 . В точкахA
иB
к мосту подключен
источник питания (,r
), а в диагоналиBD

— измерительный гальванометр с
сопротивлениемR
g .

Рис. 7.6.

Во всех ветвях схемы произвольно
обозначим направления токовI
1 ,I
2 ,
I
3 ,
I
4 ,
I
g ,
I
 .

В схеме четыре узла: точки A
,B
,C
,D
. Для трёх из них
составим уравнения первого правила
Кирхгофа — правила токов:

точка А
: I

– I
1
– I
4
= 0; (1)

точка B
: I
1
– I
2
– I
g
= 0; (2)

точка D
: I
4
+ I
g
– I
3
= 0. (3)

Для трёх контуров цепи ABDA
,BCDB
иADC
A
составим уравнения второго правила
Кирхгофа. Во всех контурах направление
обхода по часовой стрелке.

ABDA
: I
1 R
1
+ I
g R
g
– I
4 R
4
= 0; (4)

BCDB
: I
2 R
2
– I
3 R
3
– I
g R
g
= 0; (5)

ADC
A
: I
4 R
4
+ I
3 R
3
+ I
 r

= . (6)

Таким образом, мы получили систему шести
уравнений, решая которую можно найти
все шесть неизвестных токов.

Но чаще мост Уитстона используется для
измерения неизвестного сопротивления
R
x
R
1 .
В этом случае резисторыR
2 ,R
3 иR
4 — переменные. Меняя их сопротивления,
добиваются того, чтобы ток в измерительной
диагонали моста оказался равным нулюI
g = 0. Это означает, что:

I
1 =I
2 см.
(1),

I
3 =I
4 см.(3),

I
1 R
1
= I
4 R
4 см.
(4),

I
2 R
2
= I
3 R
3 см.
(5).

Учитывая эти упрощающие обстоятельства,
приходим к выводу, что:

,

.

Замечательно, что для определения
неизвестного сопротивления нужно знать
лишь сопротивления резисторов моста
R
2 ,R
3 иR
4 . Э.д.с.
источника, его внутреннее сопротивление,
как и сопротивление гальванометра при
таком измерении не играют никакой роли.

часто находит применение в работе с электричеством. Благодаря закономерности, найденной немецким физиком Георгом Омом, сегодня мы можем рассчитать величину тока, протекающего в проводе или необходимую толщину провода для подключения к сети.

История открытия

Будущий ученый с малых лет интересовался . Он провел множество испытаний, связанных с . Ввиду несовершенства измерительных приборов того времени, первые результаты исследований были ошибочны и препятствовали дальнейшему развитию вопроса. Георг опубликовал первую научную работу, в которой описывал возможную связь между напряжением и силой тока. Последующие его работы подтвердили предположения, и Ом сформулировал свой знаменитый закон. Все труды были внесены в доклад 1826 года, но научное сообщество не заметило труды молодого физика.

Через пять лет, когда известный французский учёный Пулье пришел к такому же выводу, Георга Ома наградили медалью Копли, за внесение большого вклада в развитии физика как науки.

Сегодня закон Ома используется по всему миру, признанный истинным законом природы. .

Детальное описание

Закон Георга показывает значение электричества в определенной сети, имеющее зависимость от сопротивления к нагрузке и внутренним элементам источника питания. Рассмотрим это детально.

Условное устройство, использующее электроэнергию (например, звуковой динамик) при подключении к источнику питания образует замкнутую цепь (рисунок 1). Подсоединим динамик к аккумулятору. Следующий через динамик ток тоже следует через источник питания. Поток заряженных частиц встретит сопротивление провода и внутренней электроники устройства, а также сопротивление аккумулятора (электролит внутри банки оказывает определенное воздействие на электрический ток). Исходя из этого, значение сопротивления закрытой сети складывается из сопротивления:

• Источника питания;
• Электрического устройства.

Подключение условного электрического прибора (динамика) к источнику питания (автомобильному аккумулятору)

Первый параметр называют внутренним, второй – внешним сопротивлением. Противодействие источника электричества маркируется символом r.

Представим, что по сети источник питания/электрическое устройство проходит определённый ток T. Для сохранения стабильного значения электричества внешней сети, в соответствии с законом, на её окончаниях должна наблюдаться потенциальная разность, которая равна R*T. Ток такой же величины проходит и внутри цепи. Вследствие этого – сохранение постоянного значения электричества внутри сети требует потенциальной разности на окончаниях сопротивления r. Она, согласно закону, должна равняться T*r. При сохранении стабильного тока в сети, значение электродвижущей силы равно:

E=T*r+T*R

Из формулы следует, что ЭДС равна сумме падения напряжений во внутренней и внешней сети. Если вынести значение T за скобки, получим:

Е=
T(r+R)

T=E/(r+R)

Примеры задач на применение закона для соединенной сети

1)
К источнику ЭДС 15 В и сопротивлением 2 Ом подсоединен реостат с сопротивлением 5 Ом. Задача – вычислить силу тока и напряжение на зажимах.

Вычисление

• Представим закон Ома для соединенной сети: T=E/(r+R).
• Снижение напряжения вычислим по формуле: U= E-Tr=ER/(R+r).
• Подставим имеющиеся значения в формулу: T= (15 В)/((5+2) Ом) = 2.1 А, U=(15 В* 5 Ом)/(5+1) Ом = 12.5 В

Ответ: 2.1 А, 12.5 В.

2)
При подсоединении к гальваническим элементам резистора с сопротивлением 30 Ом, сила тока в сети приняла значение в 1.5 А, а при подсоединении такого же элемента с сопротивлением 15 Ом сила тока стала 2.5 А. Задача – узнать значение ЭДС и внутреннее сопротивление цепи из гальванических элементов.

Вычисление

• Запишем закон Георга Ома для соединённой сети: T=E/(r+R).
• Из него выведем формулы для внутреннего и внешнего сопротивления: E=T_1 R_1+T_1 r, E= T_2 R_2 + T 2r.
• Приравняем части формулы и вычислим внутреннее сопротивление: r=(T_1 R_1-T_2 R_2)/(T_2-T_1).
• Полученные значения подставим в закон: E=(T_1 T_2 (R_2-R_1))/(T_2-T_1).
• Проведем вычисления: r=(1.5 А∙30 Ом-2.5А∙15 Ом)/(2,5-1,5)А=7.5 Ом, E=(1.5 А∙2.5А(30-15)Ом)/((2.5-1.5)А)=56 В.

Ответ: 7.5 Ом, 56 В.

Сфера применения закона Ома для замкнутой цепи

Закон Ома – универсальный инструмент электрика. Он позволяет правильно рассчитать силу тока и напряжение в сети. В основе принципа работы некоторых устройств лежит закон Ома. В частности, предохранителей .

Короткое замыкание – случайное замыкание двух участков сети, не предусмотренное конструкцией оборудования и приводящее к неисправностям. Для предотвращения таких явлений используют специальные устройства, отключающие питание сети.

Если произойдет случайное замыкание цепи с большой перегрузкой, устройство автоматически прекратит подачу тока.

Закон Ома в данном случае находит место на участке цепи постоянного тока. В полной схеме процессов может быть гораздо больше. Многие действия при построении электрической сети или ее ремонте следует проводить с учетом закона Георга Ома.

Для полного изучения соотношения параметров тока в проводниках представлены формулы:

Более сложное выражение закона для практического применения:

Сопротивление представлено отношением напряжения к силе тока в цепи. Если напряжение увеличить в n раз, значение тока также увеличится в n раз.

Не менее известны в электротехнике труды Густава Киргофа. Его правила находят применения в расчетах разветвленных сетей. В основе этих правил лежит .

Труды ученого нашли применение при изобретении многих повседневных вещей, таких как лампы накаливания и электрические плиты. Современные достижения в электронике многим обязаны открытиям 1825 года.

то есть напряжение между полюсами источника

тока зависит от ЭДС и работы сторонних сил по перемещению единичного заряда от одного полюса источника к другому.

2. Сформулируйте и запишите закон Ома для замкнутой цепи

Сила тока в замкнутой электрической цепи пропорциональна ЭДС источника и обратно пропорционально сопротивлению цепи.

3. В чем различие встречного и согласованного включения последовательно соединенных источников тока?

Говорят, что 2-й источник включен встречно первому, если они, работая в одиночку, создают токи, идущие в одном направлении. 3-й источник включен согласованно с первым, если токи, создаваемые ими, направлены одинаково.

4. Сформулируйте закон Ома для замкнутой цепи с несколькими последовательно соединенными источниками тока. Приведите формулу этого закона.

Сила тока в замкнутой электрической цепи с последовательно соединенными источниками тока прямо пропорциональна сумме их

ЭДС и обратно пропорционально сопротивлению цепи.

5. Как определить направление тока в замкнутой цепи с несколькими последовательно соединенными источниками тока?

Если

то ток течет по часовой стрелке. В обратном случае — против часовой стрелки.

Рассмотрим простейшую систему проводников, содержащую источник тока (рис. III.29). Допустим, что в приборе потребляющем электрическую энергию, необходимо поддержат определенную силу тока причем электроны должны двигаться в направлении, указанном стрелками. Очевидно, что при переносе через электронов с общим зарядом, равным — электрические силы, действующие на электроны в направлении будут совершать положительную работу, которая, согласно формуле (1.42), зависит только от потенциалов начальной и конечной точек траектории переноса и равна

Для того чтобы поддержать потенциалы постоянными, источник тока должен непрерывно перебрасывать электроны обратно от точки 1 к точке 2. При этом необходимо преодолеть притяжение электронов к положительно заряженной точке 1 и отталкивание от отрицательно заряженной точки 2, т. е. преодолевать электростатическую силу направленную внутри источника от точки 2 к точке 1. Таким образом, источник тока должен приложить к электронам стороннюю силу направленную против электростатической силы

обусловленного столкновениями между электронами и атомами источника тока. При этих столкновениях теряется часть кинетической энергии упорядоченного движения электронов и поэтому, чтобы сохранить постоянной скорость этого движения, источник тока должен компенсировать указанную выше потерю энергии внутри самого источника.

Полная работа совершаемая сторонними силами внутри источника тока при переносе заряда из точки 1 в точку 2, равна сумме: 1) работы против электростатических сил действующих внутри источника тока, и 2) потери энергии электронов при их прохождении через источник тока:

Это соотношение выражает закон сохранения энергии. Очевидно, что работа сторонней силы равна работе совершаемой электростатическими силами вне источника тока. Это означает, что источник тока является также источником той энергии или работы, которая выделяется движущимися зарядами во внешнем участке цепи Для того чтобы поддержать потенциалы постоянными, источник тока должен непрерывно совершать работу компенсирующую потерю энергии во внешней цепи

Для оценки потери энергии электронов при их перемещении внутри самого источника тока необходима знать его электрическое сопротивление тогда, согласно формуле (2.13),

Полная работа сторонних сил на основании закона сохранения энергии (см. формулу (2.19))

Отношение работы, совершаемой сторонними силами внутри источника тока при перемещении через него заряда к величине этого заряда, называется электродвижущей силой (э. д. с.) этого источника тока и обозначается :

На основании закона Ома для участка цепи

Эта формула выражает закон Ома для замкнутого контура, по которому течет постоянный ток. Называя падением напряжения во внешних участках цепи, а падением напряжения внутри источника тока, можно закон Ома выразить иначе:

электродвижущая сила, действующая в замкнутой цепи, равна сумме падений напряжения в этой цепи.

Ежесекундная работа, совершаемая источником тока, т. е. его мощность,

Эта работа равна той энергии, которая ежесекундно выделяется на всех сопротивлениях цепи.

Если источник тока не замкнут, то упорядоченное движение зарядов через него не происходит и потеря энергии внутри источника тока отсутствует. Сторонняя сила может только вызвать скопление зарядов на полюсах источника тока. Это скопление прекратится, когда внутри источника между его полюсами появится электрическое поле в котором электростатическая сила сделается равной сторонней силе, т. е. Разность потенциалов между полюсами разомкнутого источника тока можно рассчитать по формуле (1.39):

причем интегрирование можно произвести вдоль любой линии, соединяющей полюсы источника тока. Подставим (пробный заряд, как обычно, положим положительным) и заменим на

Однако есть работа совершаемая сторонними силами против электростатических сил при переносе заряда из точки 2 в точку тогда, согласно указанному выше определению, э. д. с.

Таким образом, электродвижущая сила источника тока равна разности потенциалов на его полюсах в разомкнутом состоянии. Если же источник тока замкнуть на внешнюю цепь, то, согласно формуле (2.22), разность потенциалов между его полюсами будет меньше э. д. с. на величину падения напряжения внутри самого источника:

Допустим, в электрическом контуре (рис. II 1.30) имеются два источника тока, которые могут быть включены так, что сторонние силы в них действуют либо в одном либо в противоположных (б) направлениях. В первом случае (а) сторонние силы в обоих источниках действуют в направлении движении зарядов и совершают положительные работы Общая работа этих сил и тогда действующая в контуре э. д. с.

Энергия, выделяющаяся в контуре, равна сумме работ, совершаемых обоими источниками.

Во втором случае (б) у источника I сторонние силы действуют в направлении движения зарядов и совершают положительную работу; у источника II сторонние силы направлены против движения зарядов и совершают отрицательную работу. Суммарная работа сторонних сил в контуре и общая э. д. с. в контуре

Закон Ома для замкнутой цепи показывает — значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.

Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.

Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.

Формула закона Ома для замкнутой цепи записывается в следующем виде:

• I [А] – сила тока в цепи,
• ε [В] – ЭДС источника напряжения,
• R [Ом] – сопротивление всех внешних элементов цепи,
• r [Ом] – внутреннее сопротивление источника напряжения

Физический смысл закона

Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.

Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.

Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.

Примеры задач на применение закона Ома для замкнутой цепи

К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.

При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.

1. Закон Ома для участка цепи

понятие, формула, объяснение. Как запомнить формулы закона Ома

Закон
Ома для участка цепи: сила
тока
I


на участке электрической цепи прямо
пропорциональна напряжению
U


на концах участка и обратно пропорциональна
его сопротивлению

R.

Формула
закона:

I

=.
Отсюда запишем формулыU

=
IR


и R
=

.

Рис.1.
Участок
цепи
Рис.2.
Полная
цепь

Закон
Ома для полной цепи: сила
тока
I


полной электрической цепи
равнаЭДС
(электродвижущей силе) источника тока
Е
,
деленной на полное сопротивление цепи
(R
+ r).
Полное
сопротивление цепи равно сумме
сопротивлений внешней цепи R

и внутреннего r

источника тока.Формула
закона I
=




.
На
рис. 1 и 2 приведены схемы электрических
цепей.

3. Последовательное и параллельное соединение проводников

Проводники
в электрических цепях могут соединяться
последовательно

и параллельно
.
Смешанное соединение сочетает оба эти
соединения.

Сопротивление,при
включении которого
вместо всех других проводников,
находящихся между двумя точками цепи,
ток и напряжение остаются неизменными,
называют
эквивалентным
сопротивлением

этих
проводников.

Последовательное соединение

Последовательным
называется соединение, при котором
каждый
проводник соединяется только с одним
предыдущим и одним последующим
проводниками.

Как
следует из первого правила
Кирхгофа
,
при последовательном
соединении проводников сила электрического
тока, протекающего по всем проводникам,
одинакова (на основании закона сохранения
заряда).

1.
При последовательном соединении

проводников
(рис. 1)
сила
тока во всех проводниках одинакова:
I

1
=
I

2
=

I

3

=

I

Рис.
1.Последовательное
соединение двух проводников.

2.
Согласно закону Ома, напряженияU

1
иU

2
на
проводниках равны U

1
=
IR

1
,
U

2
=
IR

2
,
U

3
=
IR

3
.

Напряжение
при последовательном соединении
проводников равно сумме напряжений на
отдельных участках (проводниках)
электрической цепи.

U

=
U

1
+
U

2
+
U

3

Позакону
Ома, напряжения U
1,
U
2
на
проводниках равныU

1
=
IR

1
,
U

2
=
IR

2
,
В
соответствии вторым правилом Кирхгофа
напряжение на всем участке:

U

=
U

1
+
U

2
=
IR

1
+
IR

2

=

I(R

1
+

R

2
)=
I·R.

Получаем:
R

=
R

1
+
R

2

Общее
напряжение
U


на проводниках равно сумме напряжений
U

1
,
U

2
,
U

3

равно:
U

=
U

1
+
U

2
+
U

3
=
I

·

(R

1
+
R

2
+
R

3
)
=
IR

где
R

ЭКВ
–
эквивалентное

сопротивление всей цепи. Отсюда: R

ЭКВ

=
R

1
+
R

2
+
R

3

При
последовательном соединении эквивалентное
сопротивление цепи равно сумме
сопротивлений отдельных участков цепи:
R

ЭКВ
=
R

1
+
R

2
+
R

3
+…

Этот
результат справедлив для
любого числа

последовательно соединенных проводников.

Из
закона Омаследует:
при равенстве сил тока при последовательном
соединении:

I

=
,
I

=
.
Отсюда
=
или

=,
т. е. напряжения на отдельных участках
цепи прямо пропорциональны сопротивлениям
участков.

При
последовательном соединении n
одинаковых
проводников общее напряжение равно
произведению напряжению одного U 1
на
их количество n
:

U
ПОСЛЕД
=
n

·
U
1
.
Аналогично
для сопротивлений:

R

ПОСЛЕД

=

n

·

R

1

При размыкании
цепи одного из последовательно
соединенных потребителей ток исчезает
во всей цепи, поэтому последовательное
соединение на практике не всегда удобно.

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R
, но некоторые изменения и уточнения внести, думаю, стоит.

Возьмем замкнутую электрическую цепь (рисунок 1) и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е
).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R
, где

• I
  — ток, протекающий по участку цепи.
• R
  — сопротивление этого участка.
• φ1-φ2
  — разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы:
U=I*R

Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

• U 1 =I*R 1
• U 2 =I*R 2
• Un=I*Rn
• U=I*(R 1 +R 2 +…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U 1 +U 2 +…+Un
или U 1 /U 2 /…/Un=R 1 /R 2 /…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа .

ПРАВИЛО ЗНАКОВ ДЛЯ ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной (рис.3.1). В противном случае — ЭДС считается отрицательной (рис.3.2).

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E 1 +E 2 +…+En
, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E 1 +E 2 -E 3
.

При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ

Закон Ома для полной цепи — его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r)
.

Приведенная формула закона Ома содержит обозначение r
, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r — сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r
нельзя.

Как вариант можно рассмотреть случай, при котором R=0
(короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r
, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной.

Закон Ома рассмотрен здесь достоточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

© 2012-2019 г. Все права защищены.

Все представленные на этом сайте материалы имеют исключительно информационный характер и не могут быть использованы в качестве руководящих и нормативных документов

Физический закон , определяющий связь (или электрического напряжения) с силой тока , протекающего в проводнике , и сопротивлением проводника. Установлен Георгом Омом в 1826 году и назван в его честь.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига .

Если ток является синусоидальным с циклической частотой
ω
{\displaystyle \omega }

, а цепь содержит не только активные, но и реактивные компоненты (ёмкости , индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

U
=
I
⋅
Z
{\displaystyle \mathbb {U} =\mathbb {I} \cdot Z}

• U = U
  0 e
  i
  ωt
  
  — напряжение или разность потенциалов,
• I
  
  — сила тока,
• Z = Re
  −i
  δ
  — комплексное сопротивление (электрический импеданс),
• R
  = √ R a
  2 + R r
  2

  — полное сопротивление,

• R r
  = ωL
  − 1/(ωC
  )
  — реактивное сопротивление (разность индуктивного и емкостного),
• R а
  
  — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (R r
  /R a
  )
  — сдвиг фаз между напряжением и силой тока.{i(\omega t+\varphi)},}
  что
  Im
  ⁡
  U
  =
  U
  .
  {\displaystyle \operatorname {Im} \mathbb {U} =U.}
  Тогда все значения токов и напряжений в схеме надо считать как
  F
  =
  Im
  ⁡
  F
  {\displaystyle F=\operatorname {Im} \mathbb {F} }

  Для электрика и электронщика одним из основных законов является Закон Ома. Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов. Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни. Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.

  
  

  Историческая справка

  Год открытия Закон Ома — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника. Позже выяснилось, что третья составляющая – это не что иное, как сопротивление. Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.

  Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.

  Закон Ома для участка цепи

  Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:

  Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.

  Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.

  Внимание!
  Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.

  Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:

  f(x) = ky или f(u) = IR или f(u)=(1/R)*I
  

  Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:

  I=12 В/6 Ом=2 А

  Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.

  Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.

  Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:

  R провод =ρ(L/S)
  

  Где ρ – удельное сопротивление в Ом*мм 2 /м, L – длина в м, S – площадь поперечного сечения.

  Закон Ома для параллельной и последовательной цепи

  В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:

  Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток. При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:

  U эл =I*R элемента
  

  Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:

  1/R=1/R1+1/R2
  

  Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.

  Закон Ома для полной цепи

  Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:

  • напряжение, если это источник ЭДС;
  • силу тока, если это источник тока;

  Такой источник питания способен выдать любую мощность при неизменных выходных параметрах. В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.

  Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:

  I=ε/(R+r)
  

  Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.

  На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.

  Закон Ома в дифференциальной и интегральной форме

  Для однородного участка цепи приведенные выше формулы справедливы, для неоднородного проводника необходимо его разбить на максимально короткие отрезки, чтобы изменения его размеров были минимизированы в пределах этого отрезка. Это называется Закон Ома в дифференциальной форме.

  Иначе говоря: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.

  В интегральной форме:

  Закон Ома для переменного тока

  При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки R a и реактивное сопротивление X (или R r). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:

  1. Ток в цепи с индуктивностью не может измениться мгновенно.
  2. Напряжение в цепи с ёмкостью не может измениться мгновенно.

  Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.

  X L и X C – это реактивные составляющие нагрузки.

  В связи с этим вводится величина cosФ:

  Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.

  Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.

  При этом сопротивление представляют в комплексной форме:

  Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.

  Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».

  Как запомнить закон Ома

  Чтобы запомнить Закон Ома – можно заучить формулировку простыми словами типа:

  Чем больше напряжение – тем больше ток, чем больше сопротивление – тем меньше ток.
  

  Или воспользоваться мнемоническими картинками и правилами. Первая это представление закона Ома в виде пирамиды – кратко и понятно.

  Мнемоническое правило – это упрощенный вид какого-либо понятия, для простого и легкого его понимания и изучения. Может быть либо в словесной форме, либо в графической. Чтобы правильно найти нужную формулу – закройте пальцем искомую величину и получите ответ в виде произведения или частного. Вот как это работает:

  Вторая – это карикатурное представление. Здесь показано: чем больше старается Ом, тем труднее проходит Ампер, а чем больше Вольт – тем легче проходит Ампер.

  Закон Ома – один из основополагающих в электротехнике, без его знания невозможна бОльшая часть расчетов. И в повседневной работе часто приходится переводить или по сопротивлению определять ток. Совершенно не обязательно понимать его вывод и происхождение всех величин – но конечные формулы обязательны к освоению. В заключении хочется отметить, что есть старая шуточная пословица у электриков: «Не знаешь Ома – сиди дома».
  И если в каждой шутке есть доля правды, то здесь эта доля правды – 100%. Изучайте теоретические основы, если хотите стать профессионалом на практике, а в этом вам помогут другие статьи из нашего сайта.

  Нравится(0
  )
  Не нравится(0
  )

  Определение закона Ома

  | DeepAI

  Что такое закон Ома?

  Закон

  Ома гласит, что ток, протекающий через проводник в двух точках, прямо пропорционален напряжению при постоянном сопротивлении. Закон назван в честь немецкого физика Георга Ома, эксперименты которого легли в основу его основы. Закон Ома представлен уравнением I = V / R, где I — ток в амперах, V — напряжение, измеренное между двумя точками проводника, а R — сопротивление, определенное в Ом.Закон гласит, что сопротивление остается постоянным, независимо от силы тока. Закон Ома используется как общий принцип для понимания проводимости материалов в изменяющемся диапазоне электрических токов. Материалы можно определить как омические или неомические, в зависимости от того, соответствуют ли они нормам закона.

  Применение закона Ома

  Закон Ома иногда приводится в качестве примеров и обозначается в нескольких вариантах. Например, закон Ома можно определить как:

  I = V / R

  В = ИК

  R = V / I

  Взаимозаменяемость определений иногда отображается в виде трехстрочного треугольника с буквой V наверху и обозначениями I и R внизу.Взаимозаменяемое определение отображается как:

  Эти различные определения часто встречаются в процессе анализа схем. Анализ цепи — это напряжения и токи через каждый компонент в сети. Каждый компонент можно определить как омический или неомический.

  Закон Ома и линейные приближения

  Закон Ома можно визуализировать с помощью линейных функций. Если компонент действительно омический, его сопротивление не будет увеличиваться, независимо от увеличения или уменьшения напряжения.Короче говоря, отношение V к I постоянно, что приводит к прямой линии на графике. Если компонент неомический, то нанесенная на график линия может изгибаться, представляя непостоянное соотношение между током и напряжением. На графиках ниже показаны различия между омическими и неомическими компонентами.

  Автор Sbyrnes321 — Собственная работа, CC0, https://commons.wikimedia.org/w/index.php?curid=17718257

  Закон

  Ом

  • Изучив этот раздел, вы должны уметь:
  • Опишите закон Ома для металлических проводников:
  • • Сопротивление, напряжение и ток.
  • Определить:
  • Ом, Ампер и Вольт.

  Ом, вольт и ампер.

  Сопротивление проводника измеряется в Омах, а Ом — это единица измерения, названная в честь немецкого физика Джорджа Симона Ома (1787–1854 гг.), Который первым показал взаимосвязь между сопротивлением, током и напряжением. При этом он разработал свой закон, который показывает взаимосвязь между тремя основными электрическими свойствами сопротивления, напряжения и тока.Он демонстрирует одну из самых важных взаимосвязей в электротехнике и электронной технике.

  Закон Ома гласит: «В металлических проводниках при постоянной температуре и в нулевом магнитном поле протекающий ток пропорционален напряжению на концах проводника и обратно пропорционален сопротивлению проводника. »

  Проще говоря, при условии, что температура постоянна и электрическая цепь не подвержена влиянию магнитных полей, тогда:

  • В цепи с постоянным сопротивлением, чем больше напряжение, приложенное к цепи, тем больше будет протекать ток.

  • При постоянном напряжении, чем больше сопротивление цепи, тем меньше ток.

  Обратите внимание, что закон Ома гласит: «В металлических проводниках». Это означает, что закон применим для большинства металлических материалов, но не для всех. Например, вольфрам, используемый для накаливания накала лампочек, имеет сопротивление, которое изменяется в зависимости от температуры нити, отсюда в законе Ома ссылка на «при постоянной температуре». В электронике также используются компоненты, которые имеют нелинейную зависимость между тремя электрическими свойствами: напряжением, током и сопротивлением, но их можно описать разными формулами.Для большинства схем или компонентов, которые могут быть описаны законом Ома:

  Вместо того, чтобы пытаться запомнить весь закон Ома, три электрических свойства напряжения, тока и сопротивления отдельными буквами:

  Сопротивление обозначается буквой R и измеряется в единицах Ом, которые имеют символ Ω (греческая заглавная буква O).

  Напряжение обозначается буквой V (или иногда E, сокращением от Electromotive Force) и измеряется в вольтах, которые имеют символ V.

  Ток обозначается буквой I (не C, поскольку он используется для обозначения емкости) и измеряется в единицах ампер (часто сокращается до ампер), которые имеют символ A.

  Используя буквы V, I и R для обозначения соотношений, определенных в Законе Ома, дает три простые формулы:

  Каждый из них показывает, как найти значение любой из этих величин в цепи, если известны две другие. Например, чтобы найти напряжение V (в вольтах) на резисторе, просто умножьте ток I (в амперах), проходящий через резистор, на значение резистора R (в омах).

  Обратите внимание, что при использовании этих формул значения V I и R, записанные в формулу, должны быть в БАЗОВЫХ ЕДИНИЦАХ, то есть в ВОЛЬТАХ (не в милливольтах) в Ом (не в киломах) и в АМПЕРАХ (не в микроамперах) и т. Д.

  Вкратце 15 кОм (килоом) вводится как 15 EXP 03, а 25 мА (миллиампер) вводится как 25 EXP-03 и т. Д. Это проще всего сделать с помощью научного калькулятора.

  Как пользоваться калькулятором с инженерными обозначениями, широко используемыми в электронике, объясняется в нашем бесплатном буклете под названием «Подсказки по математике». Загрузите его со страницы загрузки.

  Определение сопротивления, ампера и напряжения

  1 Ом

  Может быть определено как «Величина сопротивления, которая создает разность потенциалов (p.d.) или напряжение в 1 вольт на нем, когда через него протекает ток в 1 ампер».

  1 АМПЕР

  Можно определить как «Величина тока, которая при прохождении через сопротивление 1 Ом создает разность потенциалов на сопротивлении 1 Вольт».

  (Хотя доступны более полезные определения ампера)

  1 ВОЛЬТ

  Можно определить как «Разность потенциалов (напряжений), возникающая на сопротивлении 1 Ом, через которое протекает ток в 1 Ампера.«

  Эти определения относятся к Вольтам, Амперам и Ом в пределах величин, описанных в Законе Ома, но также могут использоваться альтернативные определения с использованием других величин.

  ПОПРОБУЙТЕ ПРОСТЫЕ РАСЧЕТЫ, ИСПОЛЬЗУЯ Закон Ома.

  Закон

  Ома: что это такое и почему это важно?

  Обновлено 28 декабря 2020 г.

  Ли Джонсон

  Электрические цепи повсеместно встречаются в нашей повседневной жизни. От сложных интегральных схем, управляющих устройством, которое вы читаете в этой статье, до проводки, которая позволяет вам включать и выключать лампочку в вашем доме, вся ваша жизнь радикально изменилась бы, если бы вы не были окружены цепями повсюду. вы идете.

  Но большинство людей на самом деле не изучают мельчайших деталей того, как работают схемы, и довольно простые уравнения, такие как закон Ома, которые объясняют взаимосвязь между ключевыми понятиями, такими как электрическое сопротивление, напряжение и электрический ток. Однако более глубокое погружение в физику электроники может дать вам гораздо более глубокое представление об основных правилах, лежащих в основе большинства современных технологий.

  Что такое закон Ома?

  Закон Ома — одно из самых важных уравнений, когда дело доходит до понимания электрических цепей, но если вы собираетесь его понять, вам понадобится хорошее понимание основных концепций, которые он связывает: напряжение , ток и сопротивление .Закон Ома — это просто уравнение, описывающее соотношение между этими тремя величинами для большинства проводников.

  Напряжение — это наиболее часто используемый термин для обозначения разности электрических потенциалов между двумя точками, который обеспечивает «толчок», который позволяет электрическому заряду перемещаться по проводящей петле.

  Электрический потенциал — это форма потенциальной энергии, подобная гравитационной потенциальной энергии, и определяется как электрическая потенциальная энергия на единицу заряда. Единицей измерения напряжения в системе СИ является вольт (В), а 1 В = 1 Дж / Кл, или один джоуль энергии на кулон заряда.Иногда ее также называют электродвижущей силой , или ЭДС.

  Электрический ток — это скорость прохождения электрического заряда через заданную точку в цепи, в системе СИ единицей измерения является ампер (А), где 1 А = 1 Кл / с (один кулон заряда в секунду). Он имеет форму постоянного (DC) и переменного (AC) тока, и, хотя постоянный ток проще, цепи переменного тока используются для подачи энергии в большинство домашних хозяйств по всему миру, потому что его проще и безопаснее передавать на большие расстояния.

  Последняя концепция, которую вам необходимо понять, прежде чем приступить к изучению закона Ома, — это сопротивление, которое является мерой сопротивления току в цепи. Единицей измерения сопротивления в системе СИ является ом (в котором используется греческая буква омега, Ом), где 1 Ом = 1 В / А.

  Уравнение закона Ома

  Немецкий физик Георг Ом описал взаимосвязь между напряжением, током и сопротивлением в своем одноименном уравнении. Формула закона Ома:

  В = IR

  , где В, — напряжение или разность потенциалов, I — величина тока, а сопротивление R — окончательная величина.

  Уравнение можно легко переформулировать, чтобы получить формулу для расчета тока на основе напряжения и сопротивления или сопротивления на основе тока и напряжения. Если вам неудобно переставлять уравнения, вы можете найти треугольник закона Ома (см. Ресурсы), но это довольно просто для любого, кто знаком с основными правилами алгебры.

  Ключевыми моментами, которые показывает уравнение закона Ома, являются то, что напряжение прямо пропорционально электрическому току (поэтому, чем выше напряжение, тем выше ток), и этот ток обратно пропорционален сопротивлению (поэтому чем выше сопротивление, тем ниже электрический ток).

  Вы можете использовать аналогию с потоком воды, чтобы запомнить ключевые моменты, в основе которой лежит труба, один конец которой находится на вершине холма, а другой конец — внизу. Напряжение похоже на высоту холма (более крутой и высокий холм означает большее напряжение), текущий поток похож на поток воды (вода течет быстрее по крутому склону), а сопротивление похоже на трение между сторонами трубы. и вода (более тонкая труба создает большее трение и снижает скорость потока воды, как более высокое сопротивление для электрического тока).

  Почему важен закон Ома?

  Закон Ома жизненно важен для описания электрических цепей, поскольку он связывает напряжение с током, а значение сопротивления смягчает взаимосвязь между ними. Из-за этого вы можете использовать закон Ома для управления величиной тока в цепи, добавляя резисторы, чтобы уменьшить ток, и снимая их, чтобы увеличить величину тока.

  Его также можно расширить, чтобы описать электрическую мощность (скорость потока энергии в секунду), потому что мощность P = IV, и поэтому вы можете использовать ее, чтобы гарантировать, что ваша схема обеспечивает достаточно энергии, например, для 60-ваттного прибора.

  Для студентов-физиков наиболее важным в законе Ома является то, что он позволяет анализировать принципиальные схемы, особенно когда вы объединяете его с законами Кирхгофа, которые следуют из него.

  Закон Кирхгофа по напряжению гласит, что падение напряжения вокруг любого замкнутого контура в цепи всегда равно нулю, а закон тока утверждает, что величина тока, протекающего в переходе или узле в цепи, равна величине, вытекающей из Это. Вы можете использовать закон Ома с законом напряжения, в частности, для расчета падения напряжения на любом компоненте схемы, что является распространенной проблемой, возникающей в классах электроники.

  Примеры закона Ома

  Вы можете использовать закон Ома, чтобы найти любую неизвестную величину из трех, при условии, что вам известны две другие величины для рассматриваемой электрической цепи. Работа с некоторыми базовыми примерами показывает, как это делается.

  Во-первых, представьте, что у вас есть 9-вольтовая батарея, подключенная к цепи с общим сопротивлением 18 Ом. Сколько тока течет при подключении цепи? Изменив закон Ома (или используя треугольник), вы можете найти:

  \ begin {align} I & = \ frac {V} {R} \\ & = \ frac {9 \ text {V}} {18 \ текст {Ω}} \\ & = 0.5 \ text {A} \ end {align}

  Итак, 0,5 ампер тока течет по цепи. Теперь представьте, что это идеальная величина тока для компонента, который вы хотите запитать, но у вас есть только батарея на 12 В. Какое сопротивление нужно добавить, чтобы обеспечить оптимальное значение тока для компонента? Опять же, вы можете переставить закон Ома и решить его, чтобы найти ответ:

  \ begin {align} R & = \ frac {V} {I} \\ & = \ frac {12 \ text {V}} {0.5 \ text {A}} \\ & = 24 \ text {Ω} \ end {align}

  Итак, вам понадобится резистор 24 Ом для завершения вашей схемы.Наконец, каково падение напряжения на резисторе 5 Ом в цепи с током 2 А, протекающим через нее? На этот раз стандартная форма закона V = IR работает нормально:

  \ begin {align} V & = IR \\ & = 2 \ text {A} × 5 \ text {Ω} \\ & = 10 \ text {V} \ end {align}

  Омические и неомические резисторы

  Вы можете использовать закон Ома в огромном диапазоне ситуаций, но есть ограничения на его применимость — это не действительно фундаментальный закон физики. Закон описывает линейную зависимость между напряжением и током, но эта зависимость сохраняется только в том случае, если резистор или резистивный элемент схемы, с которым вы работаете, имеет постоянное сопротивление при различных значениях напряжения В и тока I .

  Материалы, которые подчиняются этому правилу, называются омическими резисторами, и хотя большинство физических проблем будут связаны с омическими резисторами, вы будете знакомы со многими неомическими резисторами из своей повседневной жизни.

  Лампочка — прекрасный пример неомического резистора. Когда вы строите график зависимости В от I для омических резисторов, он показывает полностью прямолинейную зависимость, но если вы сделаете это для чего-то вроде лампочки, ситуация изменится.По мере того как нить накала в лампе нагревается, сопротивление лампы увеличивается на , что означает, что график становится кривой, а не прямой линией, и закон Ома не действует.

  Закон первого Ома — MR WATT Shop

  Мы можем сказать, что в электрической цепи, если разность потенциалов, приложенная между двумя ее точками, равна 1 вольту, а частичное сопротивление участка между этими двумя точками составляет 1 Ом в этой электрической цепи. stretch циркулирует ток в 1 ампер.

  Закон Ома очень просто устанавливает отношения между тремя следующими электрическими величинами: напряжением (В), током (I) и сопротивлением (R)

  Этот закон был провозглашен известным немецким физиком Джорджем Саймоном Омом и, безусловно, является наиболее подходящим. важны из тех, что связаны с электричеством.

  Утверждение звучит точно так:

  «Сила тока в цепи прямо пропорциональна приложенному к ней напряжению и обратно пропорциональна сопротивлению самой цепи».

  Его математическое выражение:

  I = V / R

  , которое позволяет рассчитать ток, зная напряжение и сопротивление. Получено по этой формуле:

  V = I * R

  R = V / I

  , что позволяет определить напряжение или сопротивление, когда две другие величины известны.Если схема применяется к одному ф.э.м. (Электродвижущая сила) значения E, мы видим, что формула закона Ома принимает следующий вид:

  I = E / (R + r)

  где «r» — внутреннее сопротивление генератора. . Если мы рассмотрим схему с одним резистором и предположим, что разность потенциалов между клеммами A и B имеет значение V, ток, протекающий через сопротивление R, будет:

  I = V / R

  Тогда как с другой стороны, схема с двумя резисторами, питаемыми от ЭДС генератора E и внутренним сопротивлением r, если R1 и R2 являются внешними резисторами или нагрузкой, подключенными последовательно, мы будем иметь:

  I = E / (R1 + R2 + r)

  , что дает

  E = I (R1 + R2 + r) = I R1 + I R2 + I r.

  Продукты I R1, I R2 и I r (резисторы тока) соответственно выражают разность потенциалов, существующую между точками (AC) и (CB), а также внутреннее падение напряжения генератора.

  Мы видим, что ф.э.м. И приложенная к цепи сумма разностей парциальных потенциалов равна сумме, которую еще называют «падениями напряжения».

  Падения напряжения IR1 и IR2 возникают во внешней цепи и могут дать полезный эффект. Падение напряжения Ir возникает внутри генератора и не имеет значения.

  Предположим, что теперь переключатель разомкнут: в цепи нет тока и, поскольку I = 0, внутреннее падение напряжения будет нулевым, а ddp между двумя выводами A и B генератора будет равно ЭДС самого генератора. : VAB = E.

  Если вместо этого цепь замкнута и циркулирует ток I, между A и B будет разность потенциалов (ddp)

  VAB = E — I * r

  Другой случай, при котором возникает условие VAB = E, когда внутреннее сопротивление генератора равно нулю (r = 0).

  Несмотря на то, что большинство из нас знают и правильно используют «Закон Ома», мы не должны забывать, что есть люди, начинающие, которые, зная о существовании этого закона, не знают, как использовать его на практике, чтобы получить как можно больше преимуществ. .

  Мы обращаемся к симулятору за любыми примерами и приложениями.

  Закон Ома

  — обзор

  2.2 Электродинамика черной дыры

  Описание ЧД, которое мы приводим здесь, по сути, является «голографическим» по своей природе, поскольку оно будет заключаться в вырезании внутренней части ЧД и замене описания внутренней части Физика ЧД с помощью величин и явлений, происходящих целиком на «поверхности ЧД» (т.э., горизонт). Поверхность ЧД определяется как нулевая гиперповерхность, то есть поверхность, везде касательная к световому конусу, отделяющая область внутри ЧД от области снаружи. Как только что было сказано, мы игнорируем внутреннюю область, включая сингулярность пространства-времени, и рассматриваем физику во внешней области, дополняя ее подходящими «граничными эффектами» на горизонте. Эти граничные эффекты являются фиктивными и на самом деле не существуют на поверхности ЧД, но играют роль представления, в голографическом смысле, физики, происходящей внутри.В конце концов, у нас будет горизонт, набор поверхностных величин на горизонте и набор объемных свойств за пределами горизонта. Сначала рассмотрим уравнения Максвелла, а именно: F _мкВ = δ _μ A _v — δ _v A _μ и

  (2.32) μνFμν = 4πJμ, μμJμ = 0⋅

  Априори электромагнитное поле F _мкВ пронизывает все пространство-время, существующее как внутри, так и за пределами горизонта, и ток, т.е., истоковый член F _мкВ , несущий заряд, также распределяется как снаружи, так и внутри ЧД. Чтобы заменить внутреннюю электродинамику ЧД поверхностными эффектами, заменим реальный F _мкВ (x) на F _мкВ (x) Θ _H , где Θ _H — ступенчатая функция типа Хевисайда, равная 1 вне ЧД и 0 внутри. Затем рассмотрим, каким уравнениям удовлетворяет это электромагнитное поле, модифицированное 1 _H .Соответствующие модифицированные уравнения Максвелла содержат два типа источниковых членов:

  (2.33) ∇ν (FμνΘ) = (∇νFμν) Θ + Fμν∇vΘ = 4π (JμΘ + jvμ),

  , где мы ввели поверхность ЧД. ток jHμ as

  (2.34) jHμ = 14πFμν∇vΘ⋅

  Этот поверхностный ток содержит δ-функцию Дирака, которая ограничивает его горизонтом. Действительно, рассмотрим скалярную функцию ϕ (x) такую, что ϕ (x) = 0 на горизонте, при этом ϕ (x) <0 внутри ЧД и ϕ (x) > 0 вне его.Введенная выше-функция BH просто равна Θ _H = θ (ϕ (x)) , где θ обозначает стандартную ступенчатую функцию одной действительной переменной. Следовательно, градиент Θ _H читается как

  (2.35) ∂μΘH = ∂μθ (ϕ (x)) = δ (ϕ (x)) ∂μϕ,

  , где δ — (одномерный) обычный дираковский δ , так что δ (ϕ (x)) является δ-функцией с носителем на горизонте. С моральной точки зрения, градиент ∂ _μ ϕ дает вектор «нормальный к горизонту». В случае ЧД (в отличие от обычного случая гиперповерхности в евклидовом пространстве) существует дополнительная тонкость в точном определении нормали к горизонту.Горизонт представляет собой нулевую гиперповерхность, которая по определению нормальна к нулевому ковариантному вектору ℓ _μ , удовлетворяющему как ℓ _μ ℓ ^μ = 0, так и ℓ _μ d x ^μ = 0 для любого бесконечно малого смещения d x ^μ внутри гиперповерхности. Поскольку ℓ _μ является нулем, его нельзя нормализовать так же, как в евклидовом пространстве. Это приводит к неоднозначности физических наблюдаемых, связанных с ℓ _μ . В стационарно-осесимметричном пространстве-времени однозначно нормализуется ℓ _μ , требуя, чтобы соответствующий градиент направления ℓ ^μ ∂ _μ имел форму ∂ / ∂ t + Ω∂ / θϕ (с коэффициентом, равным члена, производного по времени).Мы будем предполагать (в общем нестационарном случае), что _μ нормировано, так что его нормализация совместима с обычной нормировкой при рассмотрении предельного случая стационарно-осесимметричных пространств-времени. В любом случае, при любой нормализации существует скаляр ω такой, что

  (2.36) ℓμ = ω∂μϕ,

  , и тогда мы можем определить «δ-функцию горизонта»

  (2.37) δH = 1ωδ (ϕ),

  , так что

  (2.38) ∂μΘH = ℓμδH⋅

  Тогда можно определить «плотность поверхностного тока ЧД»

  (2.39) Kμ = 14πFμνℓν⋅

  При таком определении ток ЧД jHμ имеет вид

  (2.40) jHμ = KμδH,

  и удовлетворяет

  (2.41) ∇μ (ΘHJμ + KμδH) = 0,

  , что является сохранением закон суммы внешнего объемного тока Θ _H J ^μ и граничного тока K ^μ δ _H В живописных терминах поверхностный ток K ^μ δ _H эффективно «замыкает» внешние линии тока, проходящие через ЧД (аналогично случаю, когда внешние токи вводятся в идеальный проводник и приводят к токам, текущим по его поверхности).Кроме того, уравнение. (2.39) показывает, что этот поверхностный ток связан с электромагнитными полями на горизонте. Таким образом, мы наделили горизонт поверхностными величинами, определенными однозначно и локально на горизонте.

  Прежде чем мы продолжим, мы вводим удобную систему координат для описания физики на горизонте общей ЧД. Мы предполагаем некоторую регулярную «срезку» горизонта и его окрестности некоторой (продвинутой) временной координатой типа Эддингтона-Финкельштейна t = x ⁰ .Затем мы предполагаем, что первая координата x ¹ такова, что она равна нулю на горизонте (например, r — r ₊ в случае Керра-Ньюмана). Наконец, x ^A для A = 2, 3 обозначают некоторые угловые координаты на двумерном пространственном срезе S _t ( x ⁰ = t) горизонта. В этой системе координат мы нормализуем ℓ ^μ так, чтобы

  (2.42) ℓμ∂μ = ∂∂t + vA∂∂xA⋅

  Здесь мы использовали тот факт, что «нормальный» вектор ℓ ^μ , будучи нулевым, также является касательной к горизонту, так что ℓ ^μ ∂ _μ — это общая комбинация ∂ / ∂ t и ∂ / ∂ x ^A , но не имеет составляющей вдоль «радиальной» (или «поперечной») координаты x ¹ . Поскольку ℓ ^μ является вектором, касательным к гиперповерхности, мы можем рассматривать его интегральные линии ℓ ^μ = dx ^μ / dt , которые лежат в пределах горизонта.Эти интегральные кривые называются образующими горизонта. Это нулевые геодезические кривые, полностью лежащие в пределах горизонта.

  Выражение (2.42) для направленного градиента вдоль ℓ ^μ предполагает, что v ^A следует интерпретировать как скорость некоторых «жидких частиц» на горизонте, которые являются «составными частями» нулевой мембраны. Подобно обычному описанию движения жидкости, нужно отслеживать изменения расстояния между двумя частицами жидкости, когда жидкость расширяется и сдвигается.Для обычной жидкости рассматривается градиент поля скорости, разбивая его на симметричную и антисимметричную части. Антисимметричная часть — это просто локальное вращение, которое не влияет на физику и может быть проигнорировано. Симметричная часть далее разделяется на ее следовую и бесследную части, а именно

  (2.43) 12 (∂ivj + ∂jvi) = σij + 1d∂⋅vδij,

  , где d — пространственный размер рассматриваемой жидкости (который в нашем случае будет d = 2). Здесь первый член описывает сдвиг, а второй — скорость расширения.Позже мы увидим, как определяются аналоги этих величин BH. А пока давайте рассмотрим расстояния на горизонте. Они измеряются с учетом ограничения горизонта метрики пространства-времени (которая, как предполагается, удовлетворяет уравнениям Эйнштейна). Поскольку мы рассматриваем нулевую гиперповерхность, имеем

  (2.44) ds2 | x1 = 0 = γAB (t, xC) (dxA-vAdt) (dxB-vBdt),

  , где vA = dxAdt. Обратите внимание, что d s ² является вырожденной метрикой: действительно, на (трехмерной) нулевой гиперповерхности нет направления реального времени (d s ² исчезает вдоль генераторов).Один имеет только два положительно определенных пространственных измерения вдоль, например, пространственные срезы S _t . Эта метрика описывает геометрию на горизонте, из которой можно вычислить элемент площади пространственных сечений S _t

  (2.45) dA = detγABdx2∧dx3⋅

  Плотность тока можно разложить K ^μ во временную составляющую σ _H = K ⁰ , и две пространственные компоненты K ^A , касательные к пространственным срезам S _t ( t = const.) горизонта,

  (2,46) Kμ∂μ = σH∂t + KA∂A

  , в котором ∂ _t = ℓ ^μ ∂ _μ — v _A ∂ _A , так что

  (2.47) Kμ∂μ = σHℓμ + (KA-σHvA) ∂A⋅

  Полный электрический заряд пространства-времени определяется поверхностным интегралом в ∞, скажем

  (2.48) Qtot = 14π∮ S∞12FμνdSμν⋅

  Этот результат можно переписать как сумму интеграла по поверхности на горизонте и интеграла по объему между горизонтом и ∞.dxσ = (nμℓv-nvℓμ) dA. Здесь n ^μ — второй нулевой вектор, который перпендикулярен горизонту и ортогонален пространственным сечениям S _t . Он нормализован таким образом, что n ^μ ℓ _μ = + 1. Используя приведенные выше определения для поверхностного тока ЧД, легко найти, что полный заряд ЧД можно переписать как

  (2,50) QH = HσHd. A,

  , где σ _H — временная составляющая поверхностного тока ЧД, представленная выше.Хотя априори ясный физический смысл имеет только интегрированный заряд ЧД, естественно рассматривать плотность σ _H , фигурирующую в приведенном выше интеграле поверхности, как определяющую распределение заряда на горизонте. Тогда связь

  (2,51) σH = Kμnμ = 14πFμνnμlν

  можно рассматривать как аналог результата σ = 14πEini, дающего распределение электрического заряда на металлическом объекте. Это снова можно рассматривать как часть голографического подхода, в котором внутренняя часть ЧД заменяется граничными эффектами.Эта аналогия распространяется на (пространственные) токи, текущие по поверхности ЧД. Действительно, используя закон сохранения μ (ΘHJμ + KμδH) = 0, который является просто тождеством Бианки, получаем

  (2.52) 1γ∂∂t (γσH) + 1γ∂∂xA (γKA) = — Jμℓμ⋅

  Это показывает математически точным образом, как внешний ток, введенный «обычно» в горизонт, «замыкается» на комбинацию токов, текущих вдоль горизонта, и / или увеличения локальной плотности заряда горизонта. Также можно ввести электромагнитную 2-форму и ограничить ее горизонтом.Затем он определяет электрические и магнитные поля на горизонте в соответствии с

  (2.53) 12Fμνdxμ∧dxν | H = EAdxA∧dt + B⊥dA⋅

  Взяв внешнюю производную левой части, мы получаем

  ( 2.54) ∇ × E → = -1γ∂t (γB⊥) ⋅

  , который связывает электрическое и магнитное поля на горизонте.

  Из различных формальных определений, приведенных выше, также получается следующее соотношение:

  (2,55) EA + εABB⊥vB = 4πγAB (KB-σHvB),

  или

  (2,56) E → + v → × B → ⊥ = 4π (K → -σHv →) ⋅

  Мы видим здесь аналог ЧД обычного закона Ома, связывающего электрическое поле с током (особенно в случае, когда v → 0, т.е.е., при отсутствии различных «эффектов конвекции», связанных со «скоростью» горизонта v →). Из этой формы закона Ома можно понять, что ЧД имеют удельное поверхностное электрическое сопротивление , равное ρ = 4π = 377 Ом [8,11].

  Приведем пример, в котором этот закон Ч. Ома можно «применить» к конкретной системе. Мы рассмотрим для простоты случай ЧД Шварцшильда и создадим электрическую цепь «на поверхности ЧД» путем инжекции на северном полюсе (через электрод, пронизывающий горизонт под полярным углом θ ₁ , скажем, θ ₁ «1) электрический ток I , и позволяя ему уйти ² с южного полюса (через электрод, проникающий через горизонт под полярным углом θ ₂ , скажем, с π — θ ₂ ≪ 1).Если рассматривать ЧД как мембрану с удельным поверхностным сопротивлением ρ, такая установка вызовет фиктивный электрический ток на горизонте, замыкая цепь между северным и южным полюсами. Связанный с текущим потоком на горизонте, между полюсами будет падение потенциала В, . Это падение потенциала просто дается обычным законом Ома, В = RI , то есть произведением тока I на «сопротивление» R:

  (2.57) V = -A0 (θ1) + A0 (θ2) = RI⋅

  Сопротивление BH R можно вычислить двумя разными способами: либо путем решения уравнений Максвелла на фоне Шварцшильда, либо путем вычислений в обычном евклидовом пространство, полное сопротивление сферической металлической оболочки с однородным удельным поверхностным сопротивлением ρ = 4π (путем разложения задачи на множество элементарных сопротивлений, некоторые из которых параллельны, а другие — последовательно). Оба метода дают один и тот же ответ, а именно:

  (2,58) R = 2lntanθ22tanθ12,

  , выраженное в единицах 30 Ом. ³ Этот результат говорит о том, что типичное полное удельное сопротивление ЧД составляет порядка 30 Ом. Вдобавок, если рассматривать вращающуюся ЧД, помещенную в магнитное поле, не совмещенную с ее осью вращения (поле, однородное на ∞, но искаженное на горизонте), можно ожидать, что на горизонте будут обнаружены вихревые токи, которые рассеивают энергия. Эти токи существуют, их можно вычислить, и они действительно тормозят вращение ЧД. В такой ситуации можно также найти крутящий момент, который восстанавливает выравнивание ЧД с полем [8].

  19,1 Закон Ома | Texas Gateway

  Постоянный и переменный ток

  Так же, как вода течет с большой высоты на низкую, электроны, которые могут свободно перемещаться, будут перемещаться из места с низким потенциалом в место с высоким потенциалом. Батарея имеет две клеммы с разным потенциалом. Если клеммы соединены проводом, электрический ток (заряды) будет течь, как показано на рисунке 19.2. Затем электроны будут перемещаться от низкопотенциальной клеммы батареи (отрицательный конец ) по проводу и попадут в высокопотенциальную клемму батареи (положительный конец ).

  Рис. 19.2 У батареи есть провод, соединяющий положительную и отрицательную клеммы, который позволяет электронам перемещаться от отрицательной клеммы к положительной.

  Электрический ток — это скорость, с которой движется электрический заряд. Большой ток, такой как тот, который используется для запуска двигателя грузовика, перемещает большую величину очень быстро, тогда как небольшой ток, такой как тот, который используется для работы портативного калькулятора, перемещает небольшое количество заряда медленнее. В форме уравнения электрический ток I определяется как

  , где ΔQΔQ — это количество заряда, которое проходит через данную область, а ΔtΔt — время, которое требуется заряду, чтобы пройти мимо этой области.Единицей измерения электрического тока в системе СИ является ампер (А), названный в честь французского физика Андре-Мари Ампера (1775–1836). Один ампер — это один кулон в секунду, или

  1 А = 1 Кл / с. 1 А = 1 Кл / с.

  Электрический ток, движущийся по проволоке, во многом похож на ток воды, движущийся по трубе. Чтобы определить поток воды через трубу, мы можем подсчитать количество молекул воды, которые проходят мимо данного участка трубы. Как показано на рисунке 19.3, электрический ток очень похож. Мы подсчитываем количество электрических зарядов, протекающих по участку проводника; в данном случае проволока.

  Рис. 19.3 Электрический ток, движущийся по этому проводу, — это заряд, который проходит через поперечное сечение A, деленный на время, необходимое этому заряду, чтобы пройти через участок A .

  Предположим, что каждая частица q на рисунке 19.3 несет заряд q = 1 нКл = 1 нКл, и в этом случае показанный общий заряд будет ΔQ = 5q = 5 нКДQ = 5q = 5 нКл. Если эти заряды пройдут мимо области A за время Δt = 1 нсΔt = 1 нс, то ток будет

  19,1I = ΔQΔt = 5 нКл1 нс = 5 А.I = ΔQΔt = 5 нКл1 нс = 5 А.

  Обратите внимание, что мы присвоили зарядам на рис. 19.3 положительный заряд. Обычно отрицательные заряды — электроны — являются подвижным зарядом в проводах, как показано на рисунке 19.2. Положительные заряды обычно застревают в твердых телах и не могут свободно перемещаться. Однако, поскольку положительный ток, движущийся вправо, совпадает с отрицательным током такой же величины, движущимся влево, как показано на рисунке 19.4, мы определяем обычный ток, который течет в том направлении, в котором протекал бы положительный заряд, если бы он мог двигаться. .Таким образом, если не указано иное, предполагается, что электрический ток состоит из положительных зарядов.

  Также обратите внимание, что один кулон — это значительная величина электрического заряда, поэтому 5 А — это очень большой ток. Чаще всего вы увидите ток порядка миллиампер (мА).

  Рис. 19.4 (a) Электрическое поле направлено вправо, ток движется вправо, а положительные заряды движутся вправо. (б) Эквивалентная ситуация, но с отрицательными зарядами, движущимися влево.Электрическое поле и ток по-прежнему справа.

  Snap Lab

  Vegetable Current

  Эта лабораторная работа помогает студентам понять, как работает ток. Учитывая, что частицы, заключенные в трубе, не могут занимать одно и то же пространство, толкание большего количества частиц в один конец трубы вытеснит такое же количество частиц из противоположного конца. Это создает поток частиц.

  Найдите солому и сушеный горох, которые могут свободно перемещаться в соломе. Положите соломинку на стол и засыпьте ее горошком.Когда вы вдавливаете одну горошину с одного конца, другая горошина должна выходить из другого конца. Эта демонстрация представляет собой модель электрического тока. Определите часть модели, которая представляет электроны, и часть модели, которая представляет собой подачу электроэнергии. В течение 30 секунд подсчитайте, сколько горошин вы можете протолкнуть через соломинку. Когда закончите, вычислите гороха текущий , разделив количество горошин на время в секундах.

  Обратите внимание, что поток гороха основан на том, что горох физически сталкивается друг с другом; электроны толкают друг друга за счет взаимно отталкивающих электростатических сил.

  Проверка захвата

  Предположим, через соломинку проходит четыре горошины в секунду. Если бы каждая горошинка несла заряд 1 нКл, какой электрический ток проходил бы через соломинку?

  1. Электрический ток будет равен заряду гороха, умноженному на 1 нКл / горох.
  2. Электрический ток будет равняться пиковому току, рассчитанному в лаборатории, умноженному на 1 нКл / горох.
  3. Электрический ток будет равняться гороховому току, рассчитанному в лаборатории.
  4. Электрический ток равен заряду горошины, разделенному на время.

  Направление обычного тока — это направление, в котором протекает положительный заряд . В зависимости от ситуации могут перемещаться положительные заряды, отрицательные заряды или и то, и другое. В металлических проводах, как мы видели, ток переносится электронами, поэтому отрицательные заряды движутся. В ионных растворах, таких как соленая вода, движутся как положительно заряженные, так и отрицательно заряженные ионы.То же самое и с нервными клетками. Чистые положительные токи относительно редки, но встречаются. История считает, что американский политик и ученый Бенджамин Франклин описал ток как направление, в котором положительные заряды проходят через провод. Он назвал тип заряда, связанный с электронами, отрицательным задолго до того, как стало известно, что они несут ток во многих ситуациях.

  Когда электроны движутся по металлической проволоке, они сталкиваются с препятствиями, такими как другие электроны, атомы, примеси и т. Д.Электроны рассеиваются от этих препятствий, как показано на рисунке 19.5. Обычно электроны теряют энергию при каждом взаимодействии. Таким образом, для поддержания движения электронов требуется сила, создаваемая электрическим полем. Электрическое поле в проводе направлено от конца провода с более высоким потенциалом к ​​концу провода с более низким потенциалом. Электроны, несущие отрицательный заряд, движутся в среднем (или дрейфуют на ) в направлении, противоположном электрическому полю, как показано на рисунке 19.5.

  Рис. 19.5. Свободные электроны, движущиеся в проводнике, совершают множество столкновений с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных электронов находится в направлении, противоположном электрическому полю. Столкновения обычно передают энергию проводнику, поэтому для поддержания постоянного тока требуется постоянный запас энергии.

  До сих пор мы обсуждали ток, который постоянно движется в одном направлении. Это называется постоянным током, потому что электрический заряд течет только в одном направлении.Постоянный ток часто называют током DC .

  Многие источники электроэнергии, такие как плотина гидроэлектростанции, показанная в начале этой главы, вырабатывают переменный ток, направление которого меняется взад и вперед. Переменный ток часто называют . Переменный ток . Переменный ток движется вперед и назад через равные промежутки времени, как показано на рисунке 19.6. Переменный ток, который исходит из обычной розетки, не меняет направление внезапно.Скорее, он плавно увеличивается до максимального тока, а затем плавно уменьшается до нуля. Затем он снова растет, но в противоположном направлении, пока не достигнет того же максимального значения. После этого он плавно уменьшается до нуля, и цикл начинается снова.

  Рисунок 19.6 При переменном токе направление тока меняется на противоположное через равные промежутки времени. График вверху показывает зависимость тока от времени. Отрицательные максимумы соответствуют движению тока влево.Положительные максимумы соответствуют течению, движущемуся вправо. Ток регулярно и плавно чередуется между этими двумя максимумами.

  Устройства, использующие переменный ток, включают пылесосы, вентиляторы, электроинструменты, фены и множество других. Эти устройства получают необходимую мощность, когда вы подключаете их к розетке. Настенная розетка подключена к электросети, которая обеспечивает переменный потенциал (потенциал переменного тока). Когда ваше устройство подключено к сети, потенциал переменного тока толкает заряды вперед и назад в цепи устройства, создавая переменный ток.

  Однако во многих устройствах используется DC, например в компьютерах, сотовых телефонах, фонариках и автомобилях. Одним из источников постоянного тока является аккумулятор, который обеспечивает постоянный потенциал (потенциал постоянного тока) между своими выводами. Когда ваше устройство подключено к батарее, постоянный потенциал подталкивает заряд в одном направлении через цепь вашего устройства, создавая постоянный ток. Другой способ получения постоянного тока — использование трансформатора, который преобразует переменный потенциал в постоянный. Маленькие трансформаторы, которые вы можете подключить к розетке, используются для зарядки вашего ноутбука, мобильного телефона или другого электронного устройства.Люди обычно называют это зарядным устройством или батареей , но это трансформатор, который преобразует напряжение переменного тока в напряжение постоянного тока. В следующий раз, когда кто-то попросит одолжить зарядное устройство для ноутбука, скажите им, что у вас нет зарядного устройства для ноутбука, но они могут одолжить ваш преобразователь.

  Рабочий пример

  Ток при ударе молнии

  Удар молнии может передать до 10201020 электронов из облака на землю. Если удар длится 2 мс, каков средний электрический ток в молнии?

  СТРАТЕГИЯ

  Используйте определение тока, I = ΔQΔtI = ΔQΔt.Заряд ΔQΔQ
  из 10201020 электронов составляет ΔQ = neΔQ = ne, где n = 1020n = 1020 — количество электронов, а e = −1.60 × 10−19 Ce = −1.60 × 10−19 C — заряд электрона. Это дает

  19,2 ΔQ = 1020 × (−1.60 × 10−19 ° C) = — 16,0 ° C ΔQ = 1020 × (−1,60 × 10−19 ° C) = — 16,0 ° C.

  Время Δt = 2 × 10–3 с Δt = 2 × 10–3 с — длительность удара молнии.

  Решение

  Ток при ударе молнии

  19,3I = ΔQΔt = −16,0 C2 × 10−3 с = −8 кAI = ΔQΔt = −16,0 C2 × 10−3 с = −8 кА.

  Обсуждение

  Отрицательный знак отражает тот факт, что электроны несут отрицательный заряд.Таким образом, хотя электроны текут от облака к земле, положительный ток должен течь от земли к облаку.

  Рабочий пример

  Средний ток для заряда конденсатора

  В цепи, содержащей конденсатор и резистор, зарядка конденсатора емкостью 16 мкФ с использованием батареи 9 В. занимает 1 мин. Какой средний ток в это время?

  СТРАТЕГИЯ

  Мы можем определить заряд конденсатора, используя определение емкости: C = QVC = QV.Когда конденсатор заряжается батареей 9 В, напряжение на конденсаторе будет V = 9 В = 9 В. Это дает заряд

  .

  Подставляя это выражение для заряда в уравнение для тока, I = ΔQΔtI = ΔQΔt, мы можем найти средний ток.

  Решение

  Средний ток

  19,5I = ΔQΔt = CVΔt = (16 × 10−6 F) (9 В) 60 с = 2,4 × 10−6 A = 2,4 мкА I = ΔQΔt = CVΔt = (16 × 10−6 F) (9 В) 60 с = 2,4 × 10-6 А = 2,4 мкА.

  Обсуждение

  Этот небольшой ток типичен для тока, встречающегося в таких цепях.

  Закон

  Ома | Определение | Формула | Приложения

  Определение закона Ома

  Закон Ома гласит, что ток в электрической цепи пропорционален приложенному напряжению и обратно пропорционален его сопротивлению.

  По мере увеличения напряжения в цепи (сопротивление остается постоянным) ток увеличивается на ту же величину. Следовательно, если напряжение удвоится, ток удвоится. Кроме того, величина тока в цепи обратно пропорциональна ее сопротивлению, когда напряжение остается неизменным.

  Другими словами, если сопротивление в цепи увеличивается, величина тока уменьшается. Например, если сопротивление увеличится в три раза, ток снизится до одной трети от исходного значения (напряжение останется постоянным).

  Формула закона Ома

  Закон Ома удобно выразить следующим простым уравнением:

  $ I (ампер) = \ frac {E \ text {} (вольт)} {R \ text {} (Ом )} \ text {} \ cdots \ text {} (1) $

  С помощью простой алгебры уравнение (1) можно переформулировать в терминах сопротивления или напряжения следующим образом:

  $ R = \ frac {E \ text { }} {I} \ text {} \ cdots \ text {} (2) $

  $ E = IR \ text {} \ cdots \ text {(3)} $

  Вот еще один способ выражения закона Ома:

  Электрическое давление в один вольт на сопротивлении в один ом вызовет протекание тока в один ампер.

  Закон Ома и нелинейные резисторы

  Поскольку R является постоянным, уравнение (3) представляет собой уравнение прямой линии, по этой причине резистор называется линейным резистором. График зависимости v от I показан на рисунке 1, который представляет собой линию, проходящую через начало координат с наклоном R. Очевидно, что прямая линия является единственным возможным графиком, для которого отношение v к I является постоянным для всех i.

  Рис. 1: вольт-амперная характеристика линейного резистора

  Резисторы, сопротивление которых не остается постоянным при разных токах на клеммах, известны как нелинейные резисторы.Для такого резистора сопротивление является функцией тока, протекающего в устройстве. Простым примером нелинейного резистора является лампа накаливания. Типичная вольт-амперная характеристика для этого устройства показана на рисунке 2, где мы видим, что график больше не является прямой линией. Поскольку R не является константой, анализ схемы, содержащей нелинейные резисторы, более труден.

  Рис. 2: типичная вольт-амперная характеристика для нелинейного резистора

  На самом деле все практические резисторы нелинейны, потому что электрические характеристики всех проводников зависят от факторов окружающей среды, таких как температура.Однако многие материалы очень близки к идеальному линейному резистору в желаемой рабочей области.

  Закон Ома: решение для тока

  Простая электрическая цепь показана в графической форме на рисунке 3, так что вы можете увидеть физическое соотношение нескольких компонентов. Вообще говоря, в работе с электроникой используются принципиальные схемы, а не графические схемы. Диаграмма, показанная на Рисунке 4, схематически представляет собой графическое изображение на Рисунке 3.

  Рис.3: Графическая схема простой электрической цепи

  Рис. 4: Принципиальная схема последовательной цепи

  Соблюдайте полярность соединений амперметра на рисунке 4. Обратите внимание, что положительный полюс амперметра подключается к положительному полюсу батареи. , в то время как отрицательная клемма подключается к резистору: также обратите внимание, что амперметр подключен последовательно с резистором, так что весь ток в цепи должен проходить через него. Поскольку амперметры имеют очень низкое сопротивление, они существенно не увеличивают сопротивление цепи.Если бы амперметр был случайно подключен параллельно (параллельно) батарее или резистору, на мгновение протек бы очень большой ток, который, вероятно, повредил бы измеритель.

  К аккумулятору подключен вольтметр для измерения напряжения аккумулятора. Поскольку вольтметры обычно являются приборами с очень высоким сопротивлением, они не потребляют значительного количества тока от батареи. Соблюдайте полярность подключения вольтметра. Положительный вывод подключается к положительной клемме аккумулятора, а отрицательный вывод подключается к отрицательной клемме аккумулятора.Следует помнить очень важное правило: вольтметры всегда подключаются параллельно источнику напряжения или нагрузке, а амперметры всегда подключаются последовательно с цепью или нагрузкой.

  Вот пример, чтобы проиллюстрировать, как можно использовать закон Ома для определения тока в последовательной цепи.

  Закон Ома Пример 1

  Определить ток в простой последовательной цепи, показанной на рисунке 4, по предоставленной информации?

  Решение

  Используйте формулу закона Ома для определения силы тока:

  $ I \ text {=} \ frac {E \ text {}} {R} $

  Замените известные значения в формулу:

  $ I = \ frac {12 \ text {}} {3} = 4A $

  Таким образом, 12 В, подключенное через сопротивление 3 Ом, дает ток 4 А через резистор.В этом случае амперметр покажет 4А.

  Закон Ома: определение сопротивления

  Сопротивление электрической цепи может быть легко определено с помощью формулы закона Ома, приведенной ранее, и решения для сопротивления следующим образом:

  $ R = \ frac {E \ text { }} {I} \ text {} $

  Эта формула говорит нам, что сопротивление в цепи обратно пропорционально величине тока. Если ток небольшой, сопротивление цепи должно быть большим, если предполагается, что напряжение остается постоянным.Следующий пример иллюстрирует использование этой формулы:

  Закон Ома Пример 2

  Ссылаясь на рисунок 5, определите омическое значение сопротивления нагрузки RL по приведенным данным.

  Рис.5: Определение сопротивления в последовательной цепи

  Решение

  Используйте уравнение (2) и подставьте известные значения:

  $ {{R} _ {L}} = \ frac {E \ text {}} {I} \ text {=} \ frac {10} {2} \ text {= 5} \ Omega \ text {} $

  Схема будет считаться схемой с относительно низким сопротивлением, поскольку ток 2А протекает только с Подано 10 В.

  Закон Ома: решение для напряжения

  Если сопротивление и ток цепи известны, вычислить величину приложенного напряжения несложно. Мы используем формулу закона Ома и решаем относительно напряжения:

  $ E = IR \ text {} $

  Из этой формулы мы видим, что напряжение — это произведение тока и сопротивления. Падение напряжения на сопротивлении или цепи будет напрямую зависеть от тока или сопротивления. Например, если ток через резистор удвоится, падение напряжения (IR-падение) удвоится.Или, если ток можно поддерживать на заданном уровне, но сопротивление удваивается, падение напряжения удваивается. В следующем примере показано, как рассчитать падение напряжения или IR.

  Закон Ома Пример 3

  Определите значение напряжения питания в цепи, показанной на рисунке 5, по предоставленной информации.

  Рис.6: Расчет E, когда известны R и I

  Решение

  $ E = IR = 2 * 50 = 100 В $

  Следовательно, из примера, мы видим, что для этого требуется питание 100 В. подайте ток 2А через резистор 50 Ом.Можно сказать, что падение напряжения IR на резисторе равно 100 В, как и у питания. На амперметре не происходит падения ИК-излучения, поскольку его сопротивление считается нулевым для всех практических целей.

  Графическое представление закона Ома

  Ранее мы узнали, что ток в цепи прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению. Если напряжение удвоить, ток увеличится в два раза, если сопротивление останется постоянным.Эта линейная зависимость показана верхней диагональной прямой линией на рисунке 7, которая представляет собой график уравнения I = V / R для сопротивления 20 Ом. Обратите внимание, что напряжение отложено по горизонтальной оси, а ток — по вертикальной оси.

  Рис. 7: Линейная зависимость между током и напряжением в цепи постоянного сопротивления

  Если бы мы приняли сопротивление нагрузки 40, а не 20 Ом, результатом была бы диагональная линия R = 40 Ом. Если использовалось сопротивление менее 20 Ом, результирующая линия была бы круче, чем линия для нагрузки 20 Ом.Кривые на рисунке 7 показывают прямую пропорциональность между напряжением и током для различных значений сопротивления нагрузки.

  Закон Ома Память AID

  Закон Ома можно легко запомнить с помощью простого вспомогательного средства запоминания, показанного на рисунке 8. Закрыв одну из букв, вы получите расположение двух других в правой части формула определения стоимости перепечатанного письма.

  • При наведении пальца на I дает E / R, указывая, что I = E / R.
  • Закрытие буквы E оставляет IR, показывая, что E является продуктом IR.
  • Точно так же, если R покрывается, E / I остается, что означает, что R равно E, деленному на I.

  Рис.8: Вспомогательное средство для изучения закона Ома

  Применение закона Ома

  1. Закон Ома полезен в линейных цепях для расчета напряжения, тока и сопротивления. Если мы знаем два из них
  2. Расчет мощности становится проще.

  https: // www.youtube.com/watch?v=OGI-065RhFo

  Проверьте свое понимание; ответьте на эти контрольные вопросы.

  1. Какова основная формула закона Ома? Каковы два вывода этой формулы?
  2. Какой ток течет в цепи с сопротивлением 100 В и сопротивлением 1000 Ом?
  3. Какое напряжение требуется для получения тока 2 А через 60 Ом?
  4. Какое сопротивление ограничит ток до 4 А в цепи с питанием 200 В?
  5. Сопротивление цепи остается прежним, но ток через резистор внезапно увеличивается втрое.