Урок физики в 8-м классе «Законы последовательного соединения проводников»
Цель:
- Изучить закономерности последовательного соединения потребителей тока.
- Раскрыть взаимозависимость I, U и R.
- Формировать умения рассчитывать электрические цепи с последовательным
соединением проводников.
Ход урока
Изучая тему «Электрический ток», мы встречались с целым рядом физических
величин. Назовите их пожалуйста ?
- Сила тока; обозначается буквой — I; единица измерения — 1А; прибор для определения – амперметр; физический
смысл — характеризует электрический ток. - Напряжение; обозначается буквой — U; единица измерения — 1В; прибор для определения – вольтметр; физический смысл
– характеризует электрическое поле. - Сопротивление; обозначается буквой — R; единица измерения – 1Ом; физический смысл – характеризует проводник.
- Физические величины: выражаются числом, их измеряют приборами, связь
между ними выражается математическим соотношением.
Физические величины сила тока, напряжение и сопротивление – связаны между
собой законом. Каким же?
- Закон Ома.
Как зависит сила тока от напряжения?
- Сила тока прямо пропорциональна напряжению на концах проводника, если
при этом сопротивление проводника не меняется. График (рис.1).
Как зависит сила тока от сопротивления?
- Сила тока в проводнике обратно пропорциональна сопротивлению проводника,
при условии, что напряжение не меняется. График (рис.2).
Так как сопротивление характеризует проводник значит оно зависит от ?
- Длинны проводника, площади сечения проводника, удельного сопротивления
проводника.
Эту зависимость можно выразить формулой. Какой?
- R =
Что такое электрическая цепь?
- Различные соединения источников и потребителей электрического тока.

Простейшую электрическую цепь составляют ?
- Источник, потребитель, ключ, провода.
Потребителей много, это показывает практика; часто приходится включать не
один, а несколько потребителей. Их можно включать разными способами. Какими ?
- Последовательно и параллельно.
Постройте в тетради схемы: 1 вариант – последовательного соединения
потребителей, 2 вариант – параллельного соединения потребителей. Затем
поменялись тетрадями взаимоконтроль.
И так тема нашего урока «Законы последовательного соединения
проводников»
Соберем схему (рис.3):
Что будет, если одну вывернуть?
- Если вывернуть одну лампу, о вторая тоже погаснет, т.к. цепь
разомкнется.
Вывод: особенность последовательного соединения — в ней отсутствуют
разветвления: «конец» первого провода соединен с «началом» второго и т.д.
Проверим на нашей цепи и по схеме в учебнике ( рис. 78 стр. 111)
78 стр. 111)
Выясним закономерности последовательного соединении:
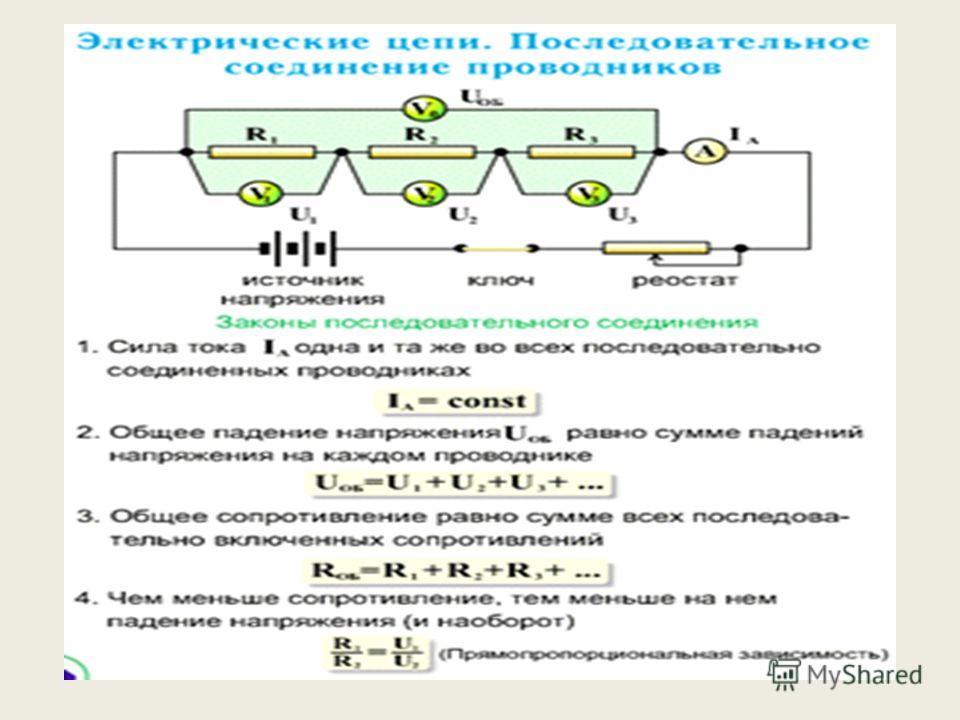
- Начнем с силы тока. В ходе лабораторной работы № 4 мы выяснили, что при
последовательном соединении сила тока в любых частях цепи одинакова:
I= I1 =I2 =I3
- А чему равно сопротивление последовательного соединённых проводников?
Соединяя проводники последовательно, мы как бы увеличивали длину проводника,
что же при этом можно сказать о сопротивлении цепи? Сопротивление становится
больше сопротивления одного проводника, т.к.
из этого можно сделать вывод: общее сопротивление цепи при последовательном
соединении равно сумме сопротивлений отдельных проводников
R=R1+R2+R3.
- Осталось выяснить вопрос с напряжением. Для этого воспользуемся законом
Ома (вспомним ещё раз его!).
Вывод: значит напряжение будет большим на проводнике с наибольшим
сопротивлением значит
U=U1+U2+U3
Полное напряжение в цепи при последовательном соединении равно сумме
напряжений на отдельных участках.
Эту формулу можно и вывести из закона Ома , т.е. доказать.
В ходе лабораторной работы № 5 «Измерение
напряжения на различных участках электрической цепи». Мы выяснили, что
напряжение на участке из двух спиралей было равно сумме напряжений на каждой
спирали.
U = U1+ U2
Все приведенные закономерности справедливы для любого числа последовательно
соединенных проводников.
Проверим экспериментально полученные соотношения. На опыте определим R
и U. При последовательно соединенных проводниках.
Соберем цепь (рис.4): амперметр, вольтметр, 2 спирали , источник тока,
реостат и ключ.
Амперметр – только
последовательно !!!
Вольтметр – только параллельно !!!
- Замкнем цепь.
- Определим показания амперметра (обратить внимание на цену деления!).
Везде одинаково. I = I1 = I2 = 1А - Подсоединим вольтметр (параллельно) к первой спирали. U1 =
2 В - Вычислим сопротивление:
- Подсоединим вольтметр (параллельно) ко второй спирали.
- Подсоединим вольтметр (параллельно) к двум спиралям.
- Вычислим напряжение: U = U1 + U2= 2В
+ 4В = 6 В
Что и требовалось доказать! Молодцы!
Урок 29. закон ома для участка цепи. соединения проводников — Физика — 10 класс
Физика, 10 класс
Урок 29. Закон Ома для участка цепи. Соединения проводников
Закон Ома для участка цепи. Соединения проводников
Перечень вопросов, рассматриваемых на уроке:
- условия, необходимые для существования электрического тока;
- постоянный электрический ток;
- закон Ома для участка цепи;
- формула расчета сопротивления проводника с учетом свойств материала проводника и его геометрических размеров;
- типы соединений проводников и формулы расчета параметров электрической цепи для каждого типа.
Глоссарий по теме.
Сила тока I — скалярная величина, равная отношению заряда q, прошедшего через поперечное сечение проводника, к промежутку времени t, в течение которого шёл ток.
Постоянный ток — электрический ток, не изменяющийся со временем.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом.
Параллельное соединение проводников. При параллельном соединении концы проводников присоединены к одной и той же паре точек.
При параллельном соединении концы проводников присоединены к одной и той же паре точек.
Смешанное соединение проводников — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Узел – это точка электрической цепи, где сходится не менее трех ветвей.
Свойство проводника ограничивать силу тока в цепи, то есть противодействовать электрическому току, называют электрическим сопротивлением проводника.
Резистор или проводник — элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления.
Основная и дополнительная литература по теме урока:
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 335 – 340.
2. Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009. – С. 105 – 109.
3. Элементарный учебник физики. Учебное пособие в 3 томах под редакцией академика Ландсберга Г.С.: Т.2. Электричество и магнетизм. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 110 – 115.
Учебное пособие в 3 томах под редакцией академика Ландсберга Г.С.: Т.2. Электричество и магнетизм. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 110 – 115.
4. Тульчинский М.Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 83 – 87.
5. Савельев И.В. Курс общей физики, том II. Электричество. М.: Изд. «Наука», 1970 г. С. 108.
Открытые электронные ресурсы:
http://kvant.mccme.ru/1979/02/elektrichestvo_ie_temperatura.htm
Теоретический материал для дополнительного изучения
Сложно представить нашу жизнь без электрического тока. Каждый день, не задумываясь, мы используем различные электрические приборы, в основе работы которых лежат простые и сложные электрические цепи. Какому закону подчиняются основные параметры электрических цепей? Как рассчитать эти цепи, чтобы приборы работали исправно?
Вы уже знаете, электрическим током называют упорядоченное (направленное) движение заряженных частиц.
Для возникновения и существования электрического тока в проводнике необходимо:
- наличие свободных заряженных частиц;
- сила, действующая на них в определённом направлении, то есть наличие электрического поля в проводнике.
Различают следующие действия электрического тока:
- тепловое ;
- химическое ;
- магнитное .
Постоянный ток — электрический ток, у которого сила тока и направление не изменяются со временем.
Сила тока I равна отношению электрического заряда q, прошедшего через поперечное сечение проводника, ко времени его прохождения t:
За направление электрического тока условно выбрано направление движения положительно заряженных частиц, то есть в сторону, противоположную направлению движения электронов.
Для каждого проводника – твердого, жидкого и газообразного – существует определённая зависимость силы тока от приложенной разности потенциалов (напряжения) на концах проводника.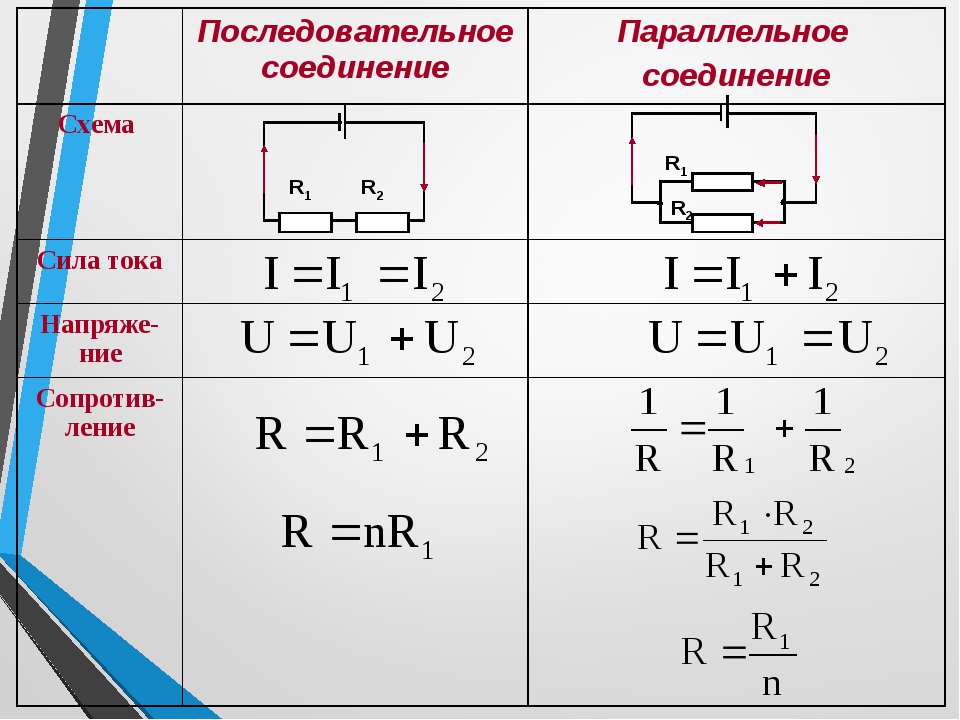 Эту зависимость выражает, так называемая, вольт-амперная характеристика проводника.
Эту зависимость выражает, так называемая, вольт-амперная характеристика проводника.
Для широкого класса проводников (в т. ч. металлов ) при неизменной температуре справедлив закон Ома для участка цепи:
Сила тока на участке цепи прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению этого участка цепи:
Закон имеет простую форму, но доказать экспериментально его справедливость довольно трудно.
Закон Ома является основой всей электротехники постоянных токов. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно.
Основная электрическая характеристика проводника – сопротивление. От этой величины зависит сила тока в проводнике при заданном напряжении. Причиной электрического сопротивления является взаимодействие электронов при их движении по проводнику с ионами кристаллической решетки. Сопротивление проводника зависит от свойств материала проводника и его геометрических размеров.
Электрическое сопротивление металлов прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения:
где величина ρ – удельное сопротивление проводника — величина, зависящая от рода вещества и его состояния (от температуры в первую очередь). Удельное сопротивление веществ приводятся в справочных таблицах.
Омметр – прибор для измерения сопротивления.
От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию. Для этого составляют электрические цепи различной сложности. Различают последовательное, параллельное, смешанное соединения проводников.
Последовательное соединение проводников. При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. Главная особенность последовательного соединения заключается в том, что через все проводники протекает одинаковый ток. Если через один проводник протекает ток определенной величины, то такой же ток протекает и через все остальные.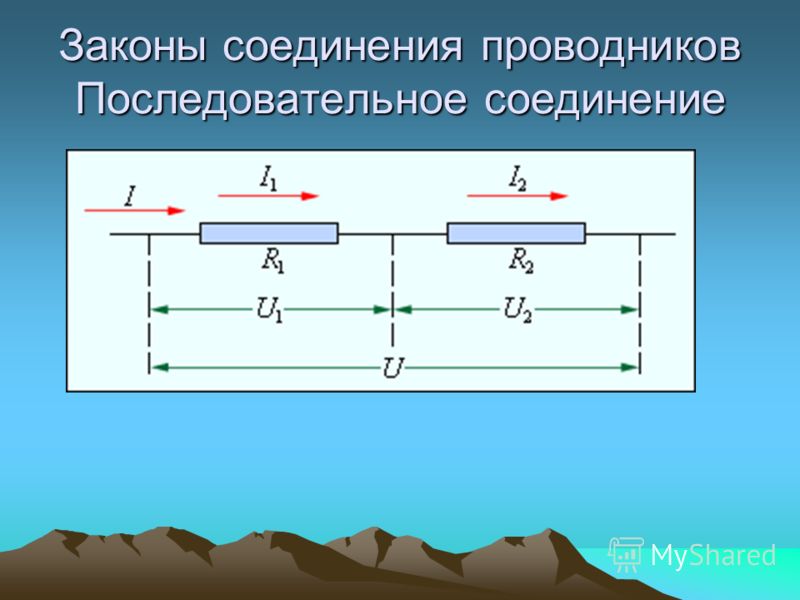 Если хотя бы в одном проводнике отсутствует ток, то он обязательно отсутствует и во всех остальных. Напряжение на концах последовательно соединенных проводников складывается. Полное сопротивление всего участка цепи при последовательном соединении равно сумме сопротивлений всех проводников.
Если хотя бы в одном проводнике отсутствует ток, то он обязательно отсутствует и во всех остальных. Напряжение на концах последовательно соединенных проводников складывается. Полное сопротивление всего участка цепи при последовательном соединении равно сумме сопротивлений всех проводников.
Последовательное соединение | |
Физическая величина | Формула |
Сила тока | I = I1 = I2 |
Напряжение | U = U1 + U2 |
Сопротивление | R = R1 + R2 |
Параллельное соединение проводников. При параллельном соединении концы проводников присоединены к одной и той же паре точек.
Параллельное соединение | |
Физическая величина | Формула |
Сила тока | I = I1 + I2 |
Напряжение | U = U1 = U2 |
Сопротивление | |
Узел – это точка электрической цепи, где сходится не менее трех ветвей.
Узел обозначается на схеме жирной точкой в том месте, где ветви соединяются между собой.
Смешанное соединение проводников.
Смешанным соединением проводников называют такое соединение, при котором в цепи присутствует и последовательное, и параллельное соединение.
Метод эквивалентных преобразований заключается в том, что электрическую цепь или ее часть заменяют более простой по структуре электрической цепью. При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными, т.е. такими, какими они были до преобразования. В результате преобразований расчет цепи упрощается и часто сводится к элементарным арифметическим операциям.
Расчет сопротивления сложной цепи:
Рези́стор или проводник — пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления.
Примеры и разбор решения заданий
1. Выберите один из 3 вариантов ответа:
Выберите один из 3 вариантов ответа:
При параллельном соединении проводников…
1) напряжение зависит от сопротивления на данном участке цепи
2) напряжение везде разное
3) напряжение везде одинаковое
Ответ: 3) напряжение везде одинаковое.
2. На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно 24 Ом. Чему равно полное сопротивление участка при замкнутом ключе К?
Решение.
После замыкания ключа схема будет представлять собой параллельное соединение резистора с двумя последовательно соединенными резисторами.
Полное сопротивление участка при замкнутом ключе равно
(R+R)R/((R+R) + R) = 2R/3 = 16 Ом.
Ответ: 16 Ом.
Элеком37, Закон Ома. Последовательное и параллельное соединение проводников.
Закон Ома. Последовательное и параллельное соединение проводников.
Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R, пропорциональна напряжению U на концах проводника:
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи:
Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи:
сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат.
Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома,
так как электрическое сопротивление металлических проводников растет с ростом температуры.
Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно. У каждого способа есть свои закономерности.
У каждого способа есть свои закономерности.
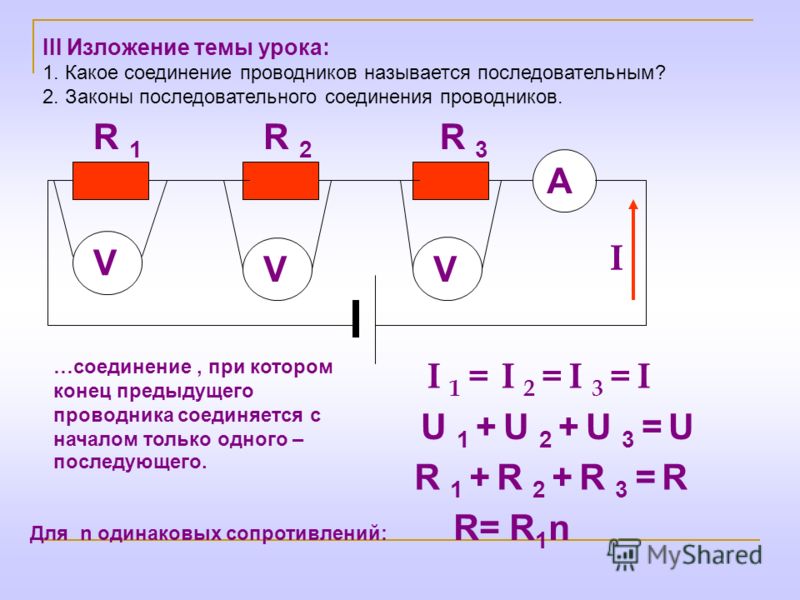
1. Закономерности последовательного соединения:
Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R, то общее сопротивление R0 находится по формуле:
2. Закономерности параллельного соединения:
Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R, то общее сопротивление R0 находится по формуле:
Электроизмерительные приборы
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB.
Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB.
Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA.
В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.
Законы соединения проводников. Последовательное и параллельное соединение проводников
Содержание:
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +
20, +
10, +
5, +
2, +
1% и так далее до величины +
0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
- P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
- P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
- P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
- P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A.
 На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R
= 1/U
, где
R
= 1
Ом
А мощность будет выделяться P
=
I
*
U
,
то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.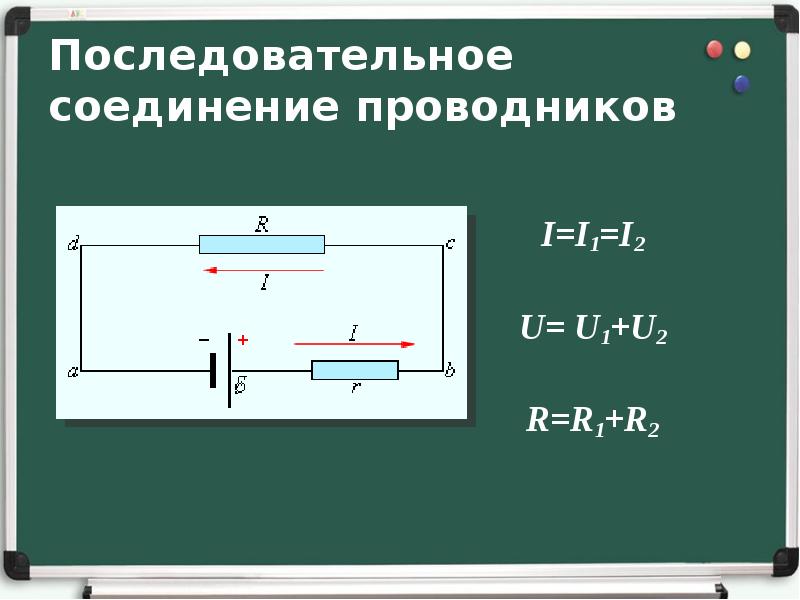
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G
, по аналогии с сопротивлением R
и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I
=
U
*
G
&
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих.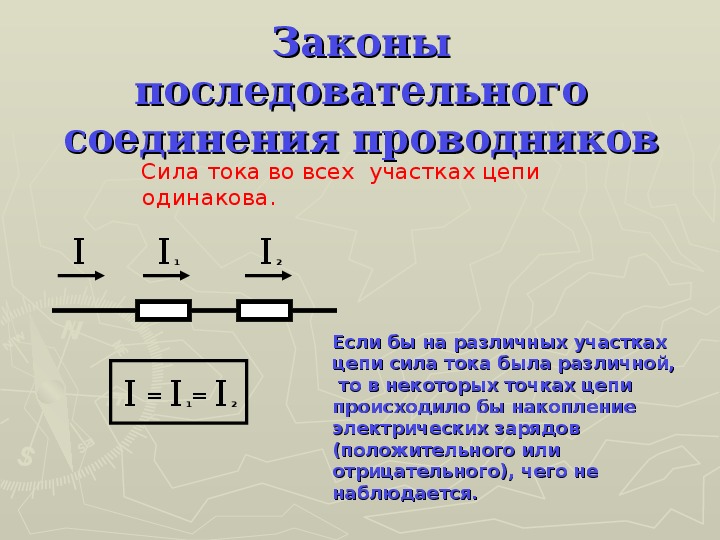 Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Содержание:
Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой.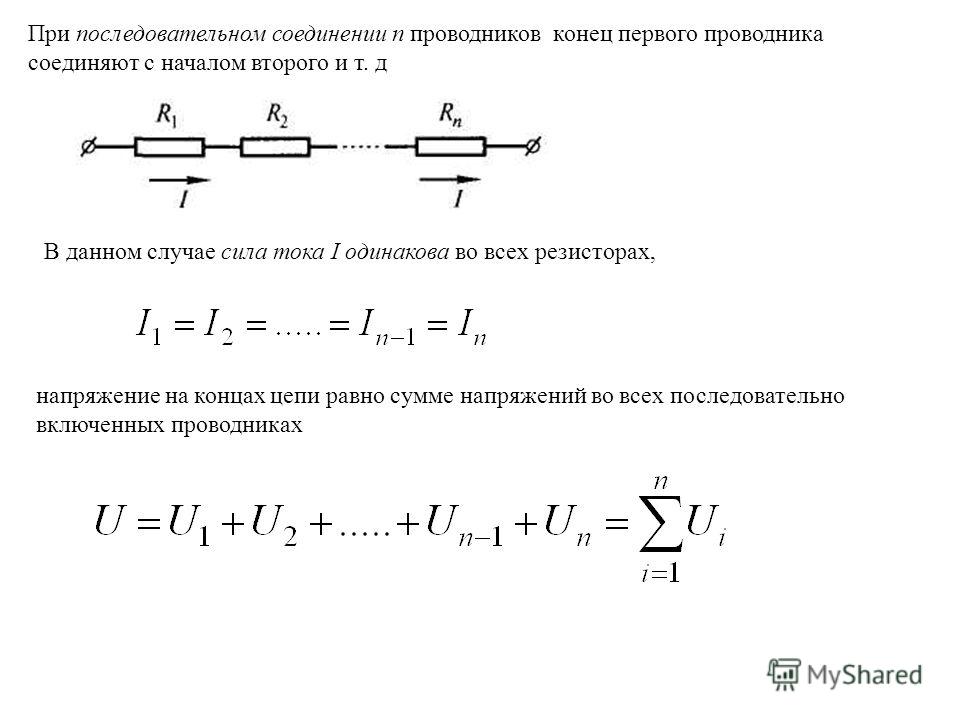 Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.
Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.
Способы подключения и их особенности
Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.
Последовательное соединение
Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы.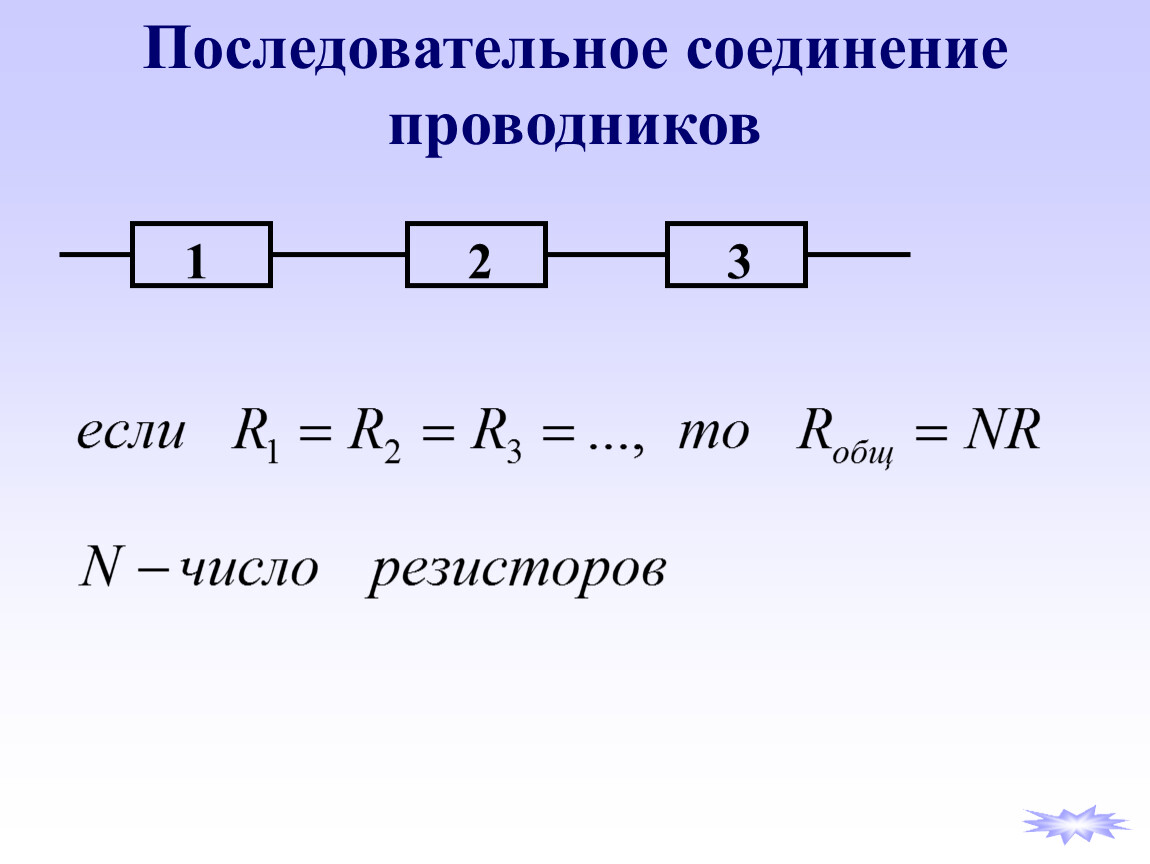 То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.
То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.
Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.
Параллельное соединение
Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.
Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.
Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.
Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.
Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.
Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь».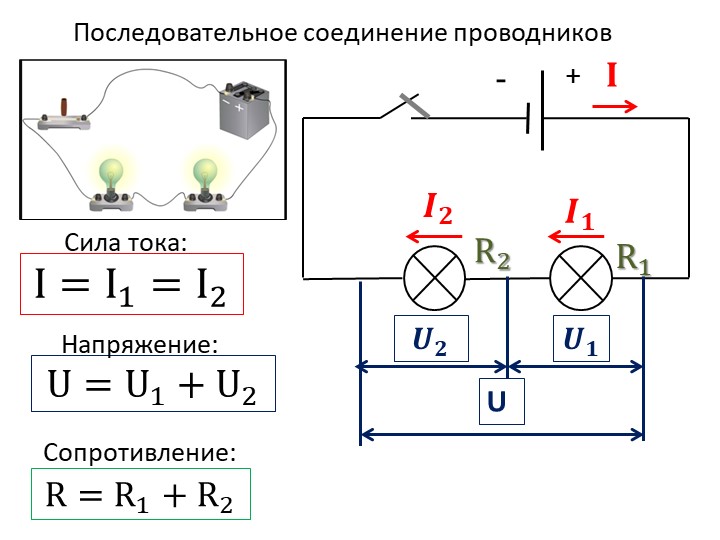 А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.
А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.
Последовательно-параллельное соединение
Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.
Подведем итог
Подводя итог всему вышеизложенному можно сделать следующие выводы:
- При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления.
 Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением. - При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
- Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
- Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
- Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.
В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.
А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U 1
+ U 2
+ U 3 или
IR экв
= IR 1
+ IR 2
+ IR 3 ,
откуда
следует
R экв
= R 1
+ R 2
+ R 3 .
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением R экв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
и
по вышеприведенным формулам рассчитывают
падение напряжений U 1 ,
U 2 ,
U 3
на соответствующих участках электрической
цепи (рис. 1.4).
1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I 1
+ I 2
+ I 3 ,
т.е.
откуда
следует, что
.
В
том случае, когда параллельно включены
два сопротивления R 1
и R 2 ,
они заменяются одним эквивалентным
сопротивлением
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
g экв
= g 1
+ g 2
+ g 3 .
По
мере роста числа параллельно включенных
потребителей проводимость цепи g экв
возрастает, и наоборот, общее сопротивление
R экв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IR экв
= I 1 R 1
= I 2 R 2 =
I 3 R 3 .
Отсюда
следует, что
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R.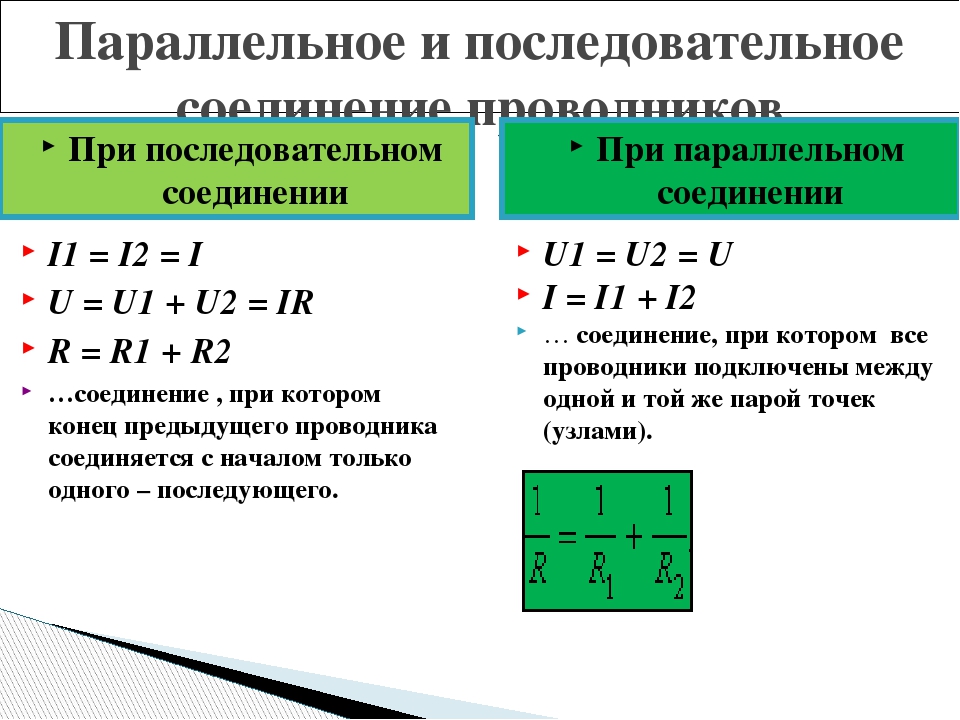
Сопротивления R 4
и R 5
включены параллельно, тогда сопротивление
участка цепи cd равно:
.
В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
На
схеме (рис. 1.8) сопротивление R 3
и R cd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
На
схеме (рис. 1.9) сопротивление R 2
и R ad
соединены параллельно, тогда сопротивление
участка цепи аb равно
.
Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R 1
и R ab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
Рис. | Рис. |
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
R экв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ
ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение
синусоидальной ЭДС. . Основные
характеристики синусоидального тока
Основным
преимуществом синусоидальных токов
является то, что они позволяют наиболее
экономично осуществлять производство,
передачу, распределение и использование
электрической энергии. Целесообразность
их использования обусловлена тем, что
коэффициент полезного действия
генераторов, электрических двигателей,
трансформаторов и линий электропередач
в этом случае оказывается наивысшим.
Для
получения в линейных цепях синусоидально
изменяющихся токов необходимо, чтобы
э. д. с. также изменялись по синусоидальному
закону. Рассмотрим процесс возникновения
синусоидальной ЭДС. Простейшим генератором
синусоидальной ЭДС может служить
прямоугольная катушка (рамка), равномерно
вращающаяся в однородном магнитном
поле с угловой скоростью ω
(рис. 2.1, б
).
Пронизывающий
катушку магнитный поток во время вращения
катушки abcd
наводит (индуцирует) в ней на основании
закона электромагнитной индукции
ЭДС е
.
Нагрузку подключают к генератору с
помощью щеток 1
,
прижимающихся к двум контактным кольцам
2
,
которые, в свою очередь, соединены с
катушкой. Значение наведенной в катушке
abcd
э. д. с. в каждый момент времени
пропорционально магнитной индукции В
,
размеру активной части катушки l
= ab
+ dc
и нормальной составляющей скорости
перемещения ее относительно поля v
н
:
e
= Blv
н
(2.1)
где
В
и l
— постоянные величины, a v
н
— переменная, зависящая от угла α. Выразив
скорость v н
через линейную скорость катушки v
,
получим
e
= Blv·sinα
(2.2)
В
выражении (2.2) произведение Blv
= const. Следовательно, э. д. с., индуцируемая
в катушке, вращающейся в магнитном поле,
является синусоидальной функцией угла
α
.
Если
угол α = π/2
,
то произведение Blv
в формуле (2.2) есть максимальное
(амплитудное) значение наведенной э. д.
д.
с. E m
= Blv
.
Поэтому выражение (2.2) можно записать в
виде
e
= E
m
sinα
(2.3)
Так
как α
есть угол поворота за время t
,
то, выразив его через угловую скорость
ω
,
можно записать α
= ωt
, a формулу
(2.3) переписать в виде
e
= E
m
sinωt
(2.4)
где
е
— мгновенное значение э. д. с. в катушке;
α = ωt
— фаза, характеризующая значение э. д.
с. в данный момент времени.
Необходимо
отметить, что мгновенную э. д. с. в течение
бесконечно малого промежутка времени
можно считать величиной постоянной,
поэтому для мгновенных значений э. д.
с. е
,
напряжений и
и токов i
справедливы законы постоянного тока.
Синусоидальные
величины можно графически изображать
синусоидами и вращающимися векторами.
При изображении их синусоидами на
ординате в определенном масштабе
откладывают мгновенные значения величин,
на абсциссе — время. Если синусоидальную
величину изображают вращающимися
векторами, то длина вектора в масштабе
отражает амплитуду синусоиды, угол,
образованный с положительным направлением
оси абсцисс, в начальный момент времени
равен начальной фазе, а скорость вращения
вектора равна угловой частоте. Мгновенные
Мгновенные
значения синусоидальных величин есть
проекции вращающегося вектора на ось
ординат. Необходимо отметить, что за
положительное направление вращения
радиус-вектора принято считать направление
вращения против часовой стрелки. На
рис. 2.2 построены графики мгновенных
значений э. д. с. е
и е»
.
Если
число пар полюсов магнитов p
≠ 1
, то за
один оборот катушки (см. рис. 2.1) происходит
p
полных циклов изменения э. д. с. Если
угловая частота катушки (ротора) n
оборотов в минуту, то период уменьшится
в pn
раз. Тогда частота э. д. с., т. е. число
периодов в секунду,
f
= Pn
/ 60
Из
рис. 2.2 видно, что ωТ
= 2π
, откуда
ω
= 2π / T = 2πf
(2.5)
Величину
ω
,
пропорциональную частоте f и равную
угловой скорости вращения радиус-вектора,
называют угловой
частотой.
Угловую частоту выражают в радианах в
секунду (рад/с) или в 1 / с.
Графически
изображенные на рис. 2.2 э. д. с. е
2.2 э. д. с. е
и е»
можно описать выражениями
e
= E
m
sinωt;
e» = E»
m
sin(ωt
+ ψ
e»
)
.
Здесь
ωt
и ωt + ψ
e»
— фазы, характеризующие значения э. д.
с. e
и e»
в заданный момент времени; ψ
e»
— начальная фаза, определяющая значение
э. д. с. е»
при t = 0. Для э. д. с. е
начальная фаза равна нулю (ψ
e
= 0
). Угол ψ
всегда отсчитывают от нулевого значения
синусоидальной величины при переходе
ее от отрицательных значений к
положительным до начала координат (t =
0). При этом положительную начальную
фазу ψ
(рис. 2.2) откладывают влево от начала
координат (в сторону отрицательных
значений ωt
),
а отрицательную фазу — вправо.
Если
у двух или нескольких синусоидальных
величин, изменяющихся с одинаковой
частотой, начала синусоид не совпадают
по времени, то они сдвинуты друг
относительно друга по фазе, т. е. не
е. не
совпадают по фазе.
Разность
углов φ
,
равная разности начальных фаз, называют
углом сдвига
фаз. Сдвиг фаз
между одноименными синусоидальными
величинами, например между двумя э. д.
с. или двумя токами, обозначают α
.
Угол сдвига фаз между синусоидами тока
и напряжения или их максимальными
векторами обозначают буквой φ
(рис. 2.3).
Когда
для синусоидальных величин разность
фаз равна ±π
,
то они противоположны
по фазе, если
же разность фаз равна ±π/2
,
то говорят, что они находятся в квадратуре.
Если для синусоидальных величин одной
частоты начальные фазы одинаковы, то
это означает, что они совпадают
по фазе.
Синусоидальные
напряжение и ток, графики которых
представлены на рис. 2.3, описываются
следующим образом:
u
= U
m
sin(ω
t
+
ψ
u
)
;
i
= I
m
sin(ω
t
+
ψ
i
)
, (2.6)
причем
угол сдвига фаз между током и напряжением
(см. рис. 2.3) в этом случае φ
рис. 2.3) в этом случае φ
= ψ
u
— ψ
i
.
Уравнения
(2.6) можно записать иначе:
u
= U
m
sin(ωt
+ ψ
i
+ φ)
; i
= I
m
sin(ωt
+ ψ
u
— φ)
,
поскольку
ψ
u
= ψ
i
+ φ
и ψ
i
= ψ
u
— φ
.
Из
этих выражений следует, что напряжение
опережает по фазе ток на угол φ
(или ток отстает по фазе от напряжения
на угол φ
).
Формы
представления синусоидальных электрических
величин.
Любая,
синусоидально изменяющаяся, электрическая
величина (ток, напряжение, ЭДС) может
быть представлена в аналитическом,
графическом и комплексном видах.
1).
Аналитическая
форма представления
I
= I
m
·sin(ω·t
+ ψ
i
),
u
= U
m
·sin(ω·t
+ ψ
u
),
e
= E
m
·sin(ω·t
+ ψ
e
),
где
I
,
u
,
e
– мгновенное значение синусоидального
тока, напряжения, ЭДС, т.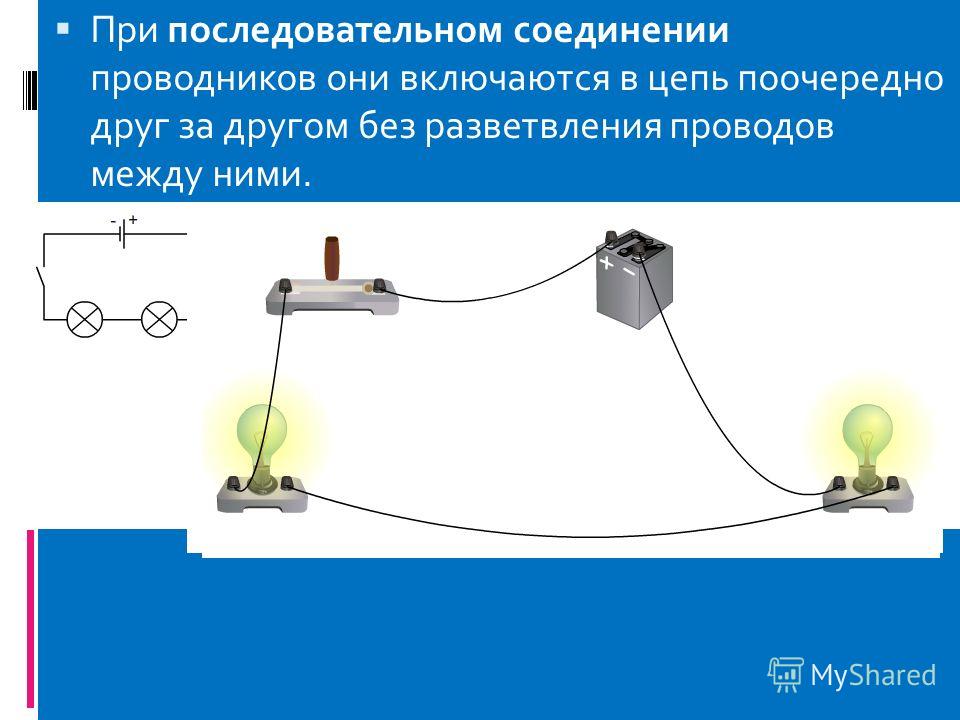 е. Значения в
е. Значения в
рассматриваемый момент времени;
I
m
,
U
m
,
E
m
– амплитуды синусоидального тока,
напряжения, ЭДС;
(ω·t
+ ψ
)
– фазовый угол, фаза; ω
= 2·π/Т
– угловая частота, характеризующая
скорость изменения фазы;
ψ
i ,
ψ
u ,
ψ
e
– начальные фазы тока, напряжения, ЭДС
отсчитываются от точки перехода
синусоидальной функции через нуль к
положительному значению до начала
отсчета времени (t
= 0). Начальная фаза может иметь как
положительное так и отрицательное
значение.
Графики
мгновенных значений тока и напряжения
показаны на рис. 2.3
Начальная
фаза напряжения сдвинута влево от начала
отсчёта и является положительной ψ
u
> 0, начальная фаза тока сдвинута вправо
от начала отсчёта и является отрицательной
ψ
i
φ
.
Сдвиг фаз между напряжением и током
φ
= ψ
u
– ψ
i
= ψ
u
– (- ψ
i)
= ψ
u
+ ψ
i .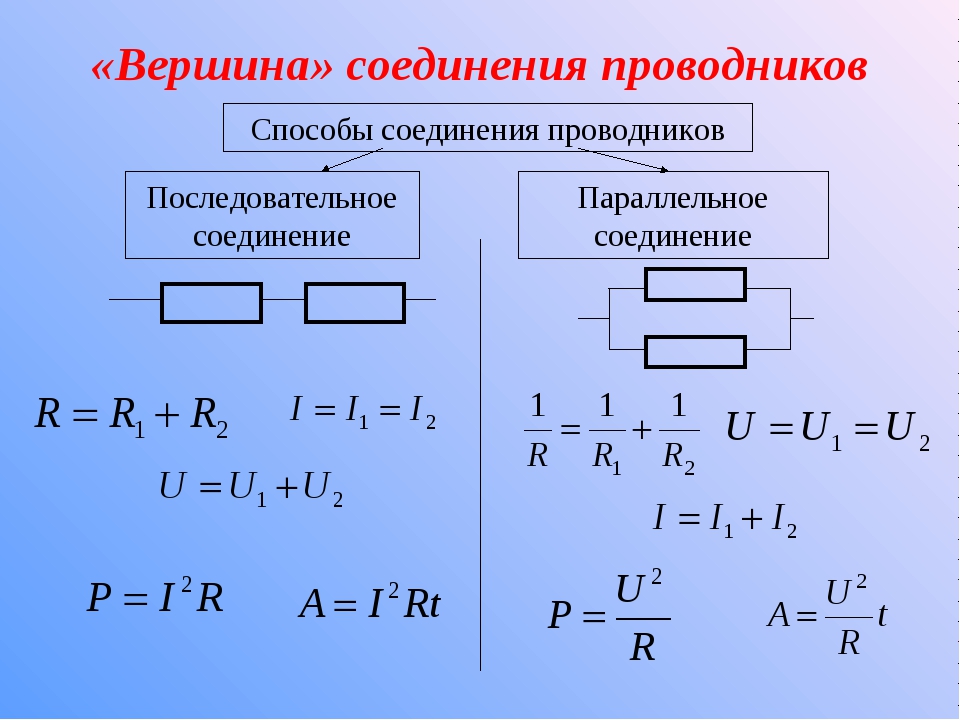
Применение
аналитической формы для расчёта цепей
является громоздкой и неудобной.
На
практике приходится иметь дело не с
мгновенными значениями синусоидальных
величин, а с действующими. Все расчёты
проводят для действующих значений, в
паспортных данных различных
электротехнических устройств указаны
действующие значения (тока, напряжения),
большинство электроизмерительных
приборов показывают действующие
значения. Действующий ток является
эквивалентом постоянного тока, который
за одно и то же время выделяет в резисторе
такое же количество тепла, как и переменный
ток. Действующее значение связано с
амплитудным простым соотношением
2).
Векторная
форма представления синусоидальной
электрической величины – это вращающийся
в декартовой системе координат вектор
с началом в точке 0, длина которого равна
амплитуде синусоидальной величины,
угол относительно оси х – её начальной
фазе, а частота вращения – ω
= 2πf
.
Проекция данного вектора на ось у в
любой момент времени определяет
мгновенное значение рассматриваемой
величины.
Рис.
2.4
Совокупность
векторов, изображающих синусоидальные
функции, называют векторной диаграммой,
рис. 2.4
3).
Комплексное
представление синусоидальных электрических
величин сочетает наглядность векторных
диаграмм с проведением точных аналитических
расчётов цепей.
Рис.
2.5
Ток
и напряжение изобразим в виде векторов
на комплексной плоскости, рис.2.5 Ось
абсцисс называют осью действительных
чисел и обозначают +1
,
ось ординат называют осью мнимых чисел
и обозначают +j
.
(В некоторых учебниках ось действительных
чисел обозначают Re
,
а ось мнимых – Im
).
Рассмотрим векторы U
и I
в момент времени t
= 0. Каждому из этих векторов соответствует
комплексное число, которое может быть
представлено в трех формах:
а).
Алгебраической
U
= U
’+
jU
«
I
= I
’
– jI
«,
где
U
«,
U
«,
I
«,
I
»
– проекции векторов на оси действительных
и мнимых чисел.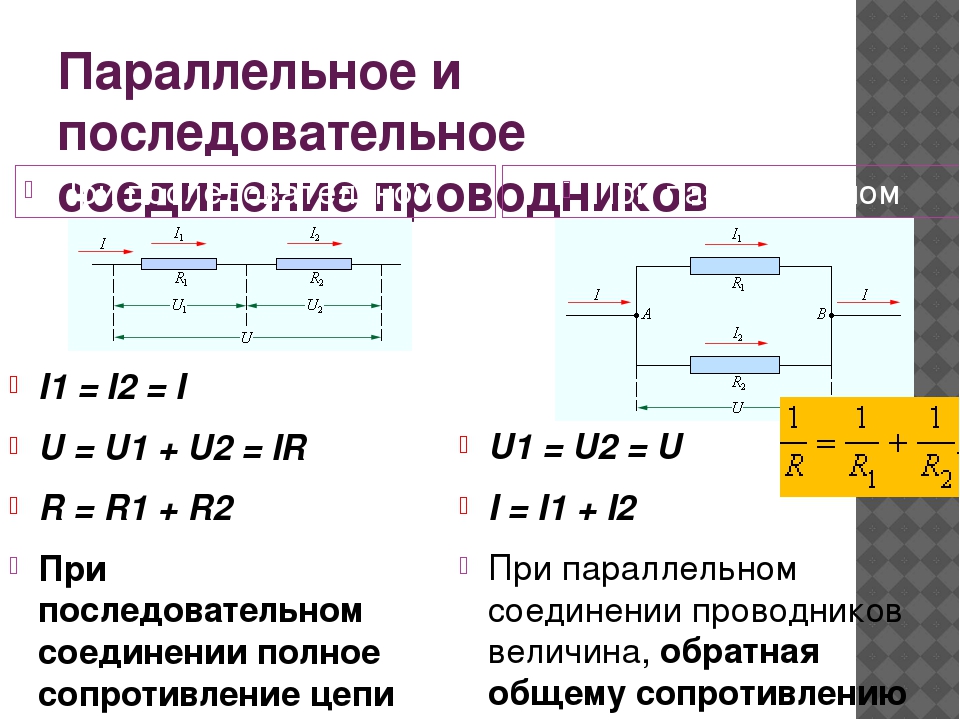
б).
Показательной
где
U
,
I
– модули (длины) векторов; е
– основание натурального логарифма;
поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
в).
Тригонометрической
U
= U
·(cosψ
u
+ j
sinψ
u)
I
= I
·(cosψ
i
– j
sinψ
i).
При
решении задач в основном применяют
алгебраическую форму (для операций
сложения и вычитания) и показательную
форму (для операций умножения и деления).
Связь между ними устанавливается
формулой Эйлера
е
j
·ψ
=
cosψ
+ j
sinψ
.
Неразветвлённые
электрические цепи
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2
на 3
и 47 Ом
и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно
учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом
и мощностью 1 Вт
. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А
), а сопротивление каждого из них равно 50 Ом
, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт
. В результате на каждом из них выделится по 0,5 Вт
В результате на каждом из них выделится по 0,5 Вт
мощности. В сумме это и будет тот самый 1 Вт
.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Последовательное соединение проводников определение. Чем отличается последовательное соединение от параллельного
Содержание:
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2.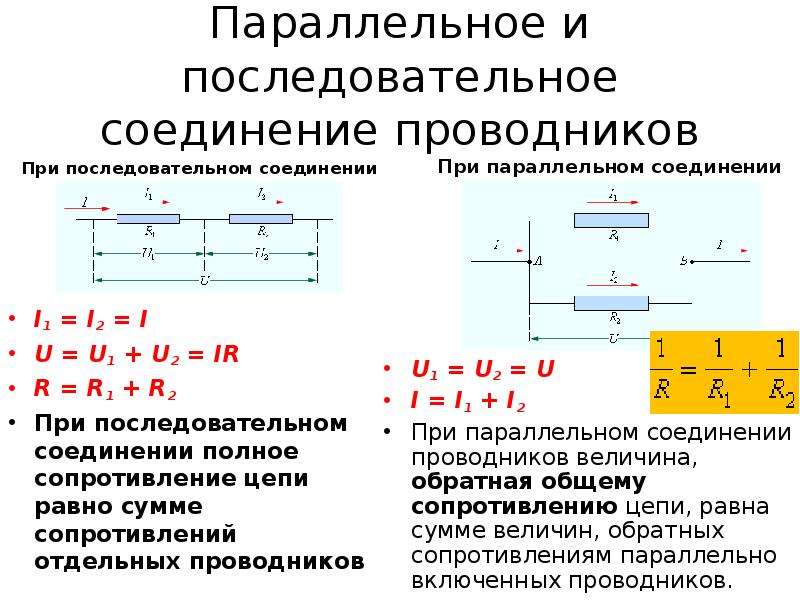 Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле.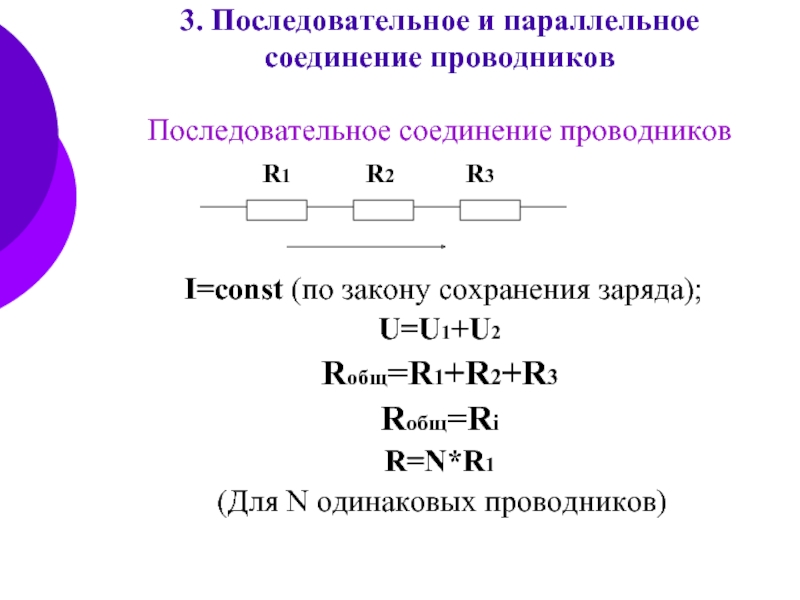 Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему.
 Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR. - Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.
Как различить эти два соединения?
Внимательно посмотрите на схему.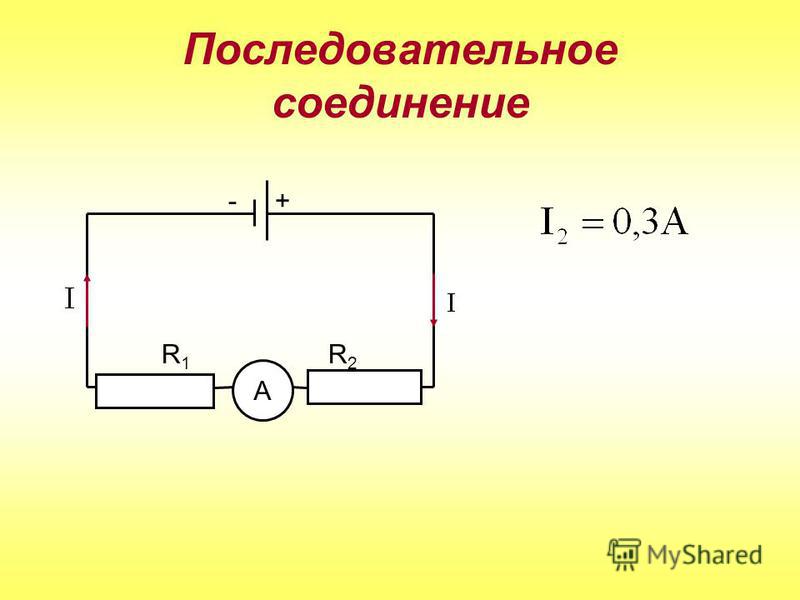 Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.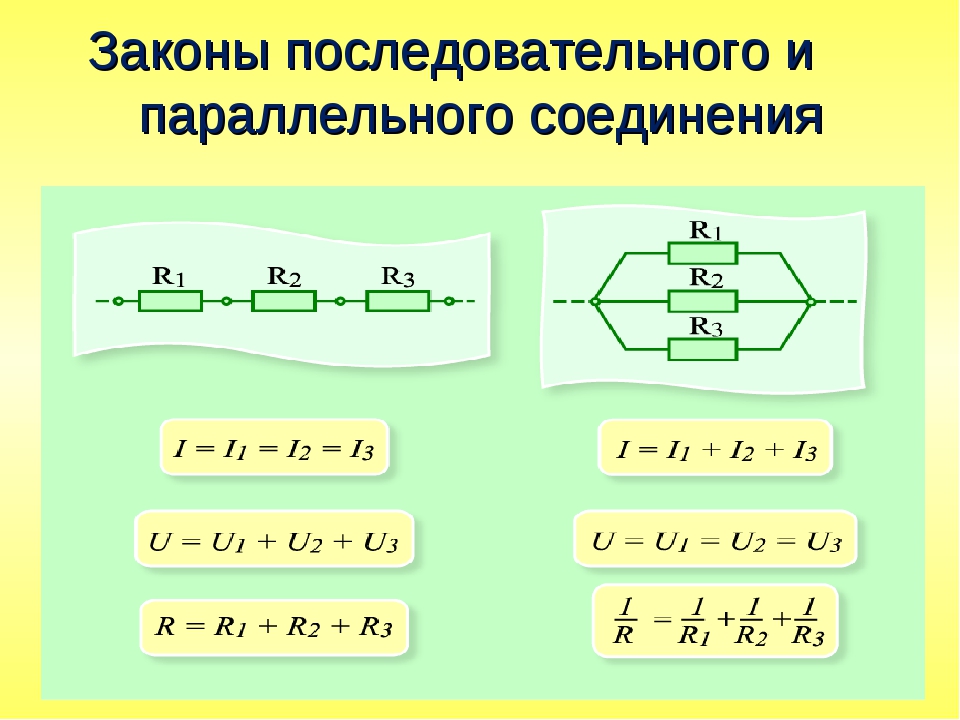
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
I общ = I 1 = I 2
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при :
I общ = I 1 + I 2
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.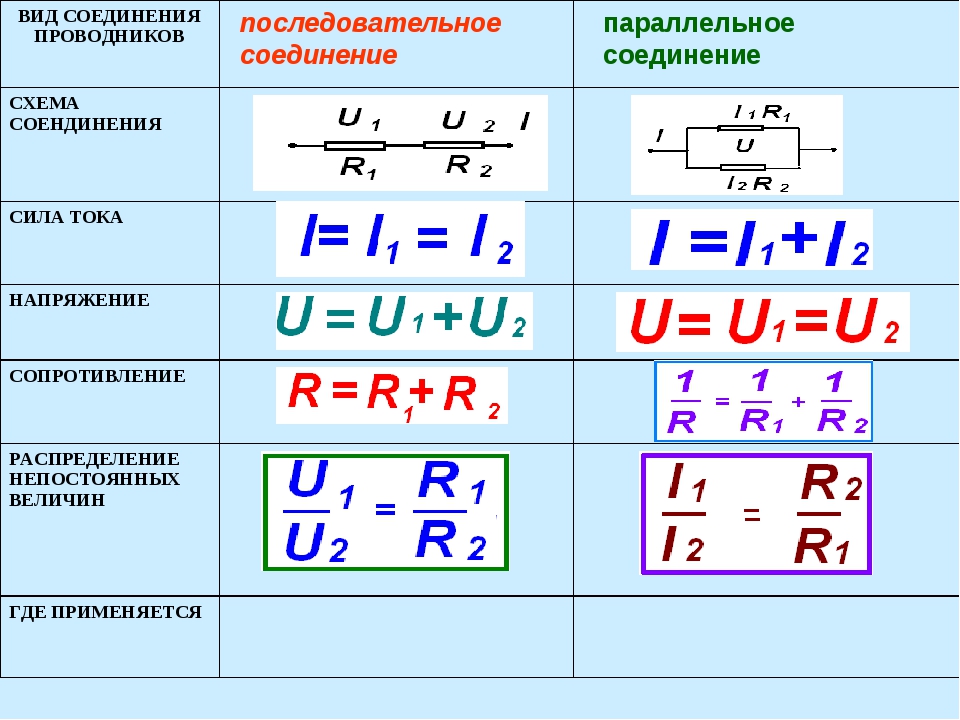
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
U общ = U 1 + U 2
, где U — обозначение, принятое для
Другая ситуация складывается, если рассматривается Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу.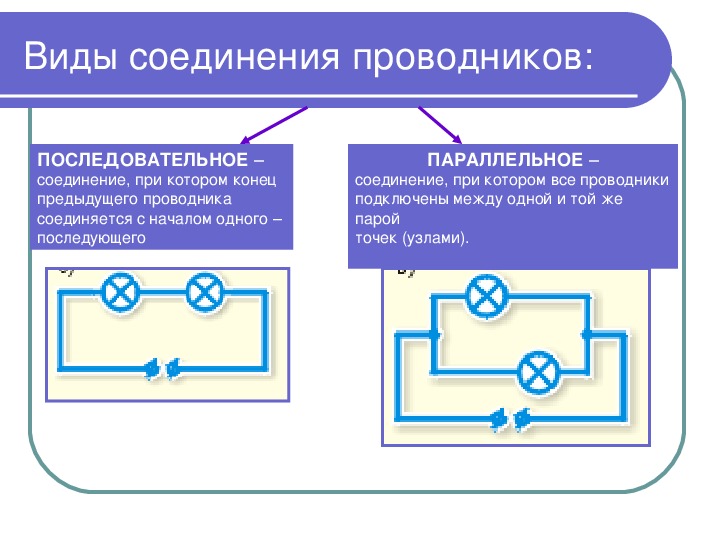 Формула общего напряжения такая:
Формула общего напряжения такая:
U общ = U 1 = U 2
Формулы для электрического сопротивления
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — I общ * R общ = I 1 * R 1 + I 2 * R 2;
- параллельно необходимо пользоваться формулой для силы тока — U общ / R общ = U 1 / R 1 + U 2 / R 2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).

При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t
, где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2 .
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I.
После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2 .
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Как влияет соединение проводников на ремонт новогодней гирлянды?
Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.
Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.
Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.
Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?
При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
q общ = q 1 = q 2 .
Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С.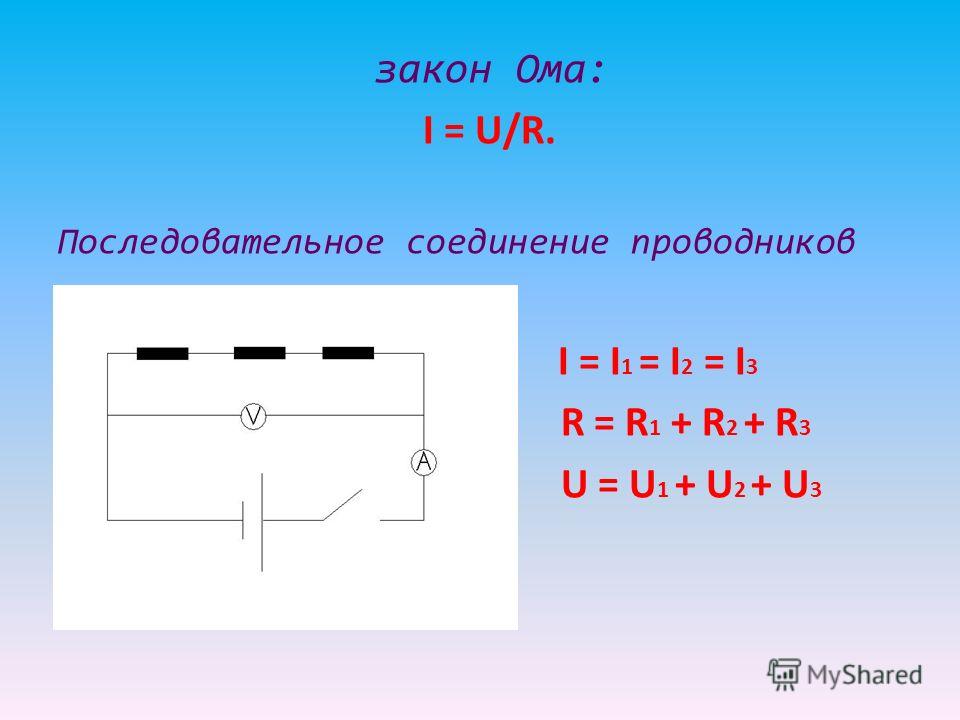
В ней С — емкость конденсатора.
Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:
С = q / (U 1 + U 2).
Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С 1 + 1 / С 2 .
Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
С = (q 1 + q 2) / U.
То есть эта величина считается, как сумма каждого из использованных в соединении приборов:
С = С 1 + С 2.
Как определить общее сопротивление произвольного соединения проводников?
То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.
Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.
Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).
Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.
Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.
Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:
Осталось применить формулы для расчета сопротивления:
- сначала ту, которая приведена для последовательного соединения;
- потом для параллельного;
- и снова для последовательного.
Подобным образом можно развернуть любую, даже очень сложную схему.
Задача на последовательное соединение проводников
Условие.
В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?
Решение.
Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.
Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.
Оно оказывается равным 2,5 Ом.
Ответ.
Сопротивление резистора равно 2,5 Ом.
Задача на параллельное и последовательное
Условие.
Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.
Решение.
Проще начать с В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.
Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.
Ответ.
Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение
– это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение
– это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение
– соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Содержание:
Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.
И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.
Способы подключения и их особенности
Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.
Последовательное соединение
Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.
Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.
Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.
Параллельное соединение
Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.
Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом.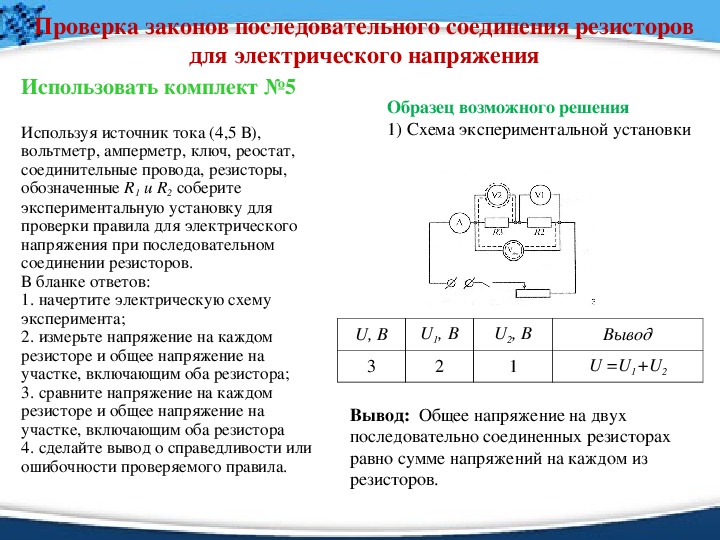 В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.
В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.
Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.
Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.
Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.
А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.
Последовательно-параллельное соединение
Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.
Подведем итог
Подводя итог всему вышеизложенному можно сделать следующие выводы:
- При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления.
 Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением. - При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
- Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
- Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
- Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.
В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения.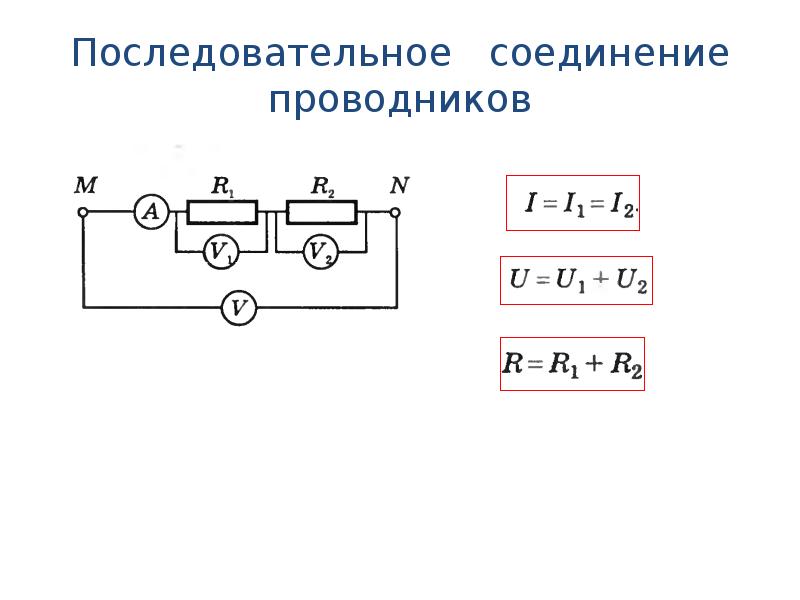 А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.
А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.
Всем доброго времени суток. В прошлой статье я рассмотрел , применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса , называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .
Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
Пример последовательного подключения приемников энергии.
В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления
Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.
Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями
где R – эквивалентное последовательное сопротивление.
Применение последовательного соединения
Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр
Делитель напряжения (слева) и потенциометр (справа).
В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.
Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.
Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже
Пример такого соединения показан на рисунке ниже
Пример параллельного соединения приемников энергии.
Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви
Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений
Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
Пример смешанного соединения приемников энергии.
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
В результате получили цепь из двух последовательных приемников энергии R 12 R 345 эквивалентное сопротивление и ток, протекающий через них, составит
Тогда падение напряжения по участкам составит
Тогда токи, протекающие через каждый приемник энергии, составят
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей.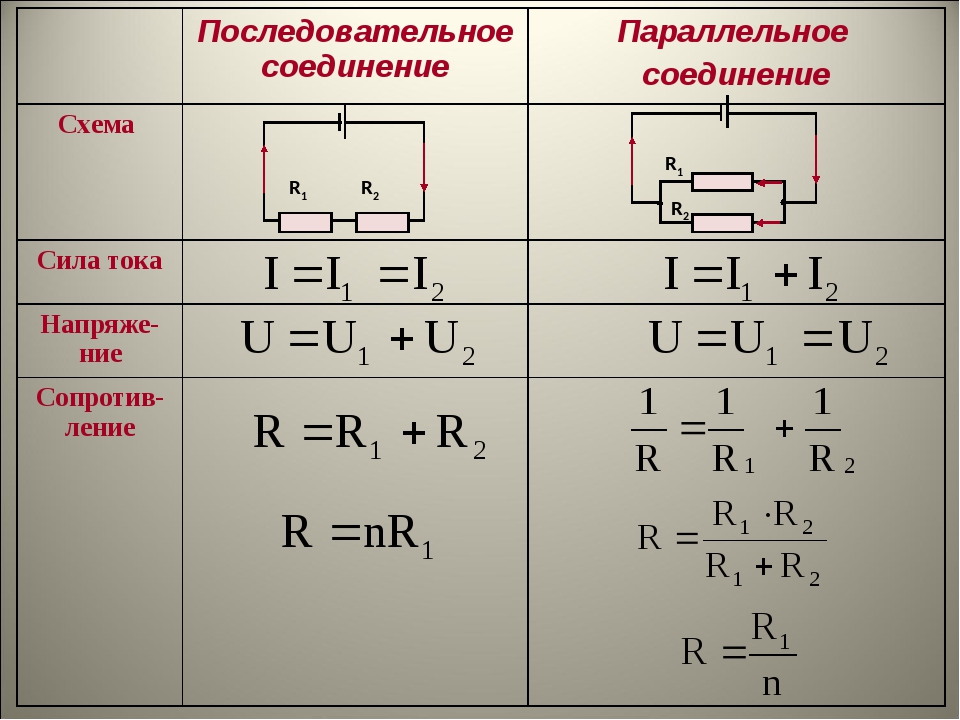 Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
Изображение первого закона Кирхгофа.
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи.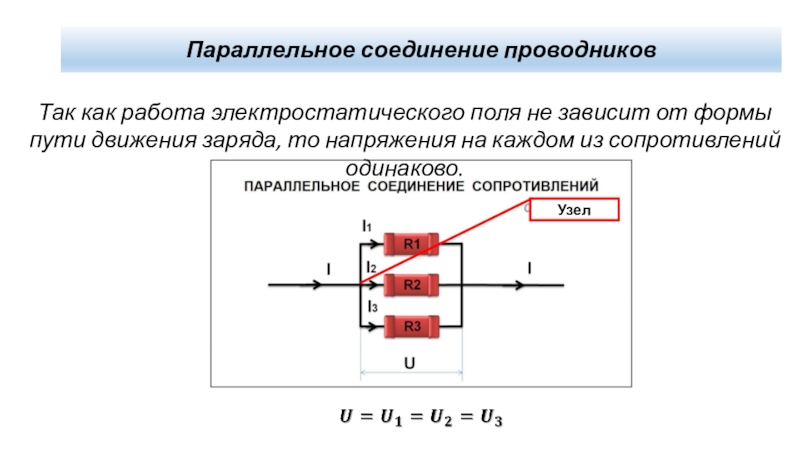 Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением
В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур
Схема, иллюстрирующая второй закон Кирхгофа.
Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид
Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.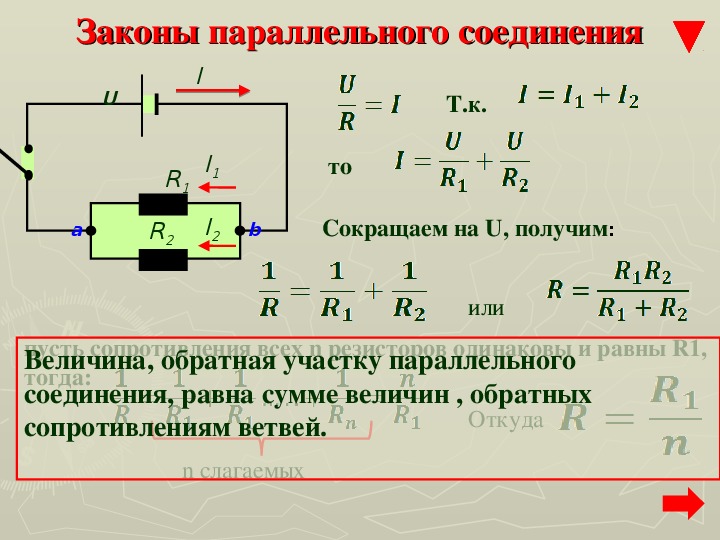
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.
Теория это хорошо, но без практического применения это просто слова.
В чем отличие последовательного соединения от параллельного. Соединения проводников
Ток в электроцепи проходит по проводникам от источника напряжения к нагрузке, то есть к лампам, приборам. В большинстве случаев в качестве проводника используются медные провода. В цепи может быть предусмотрено несколько элементов с разными сопротивлениями. В схеме приборов проводники могут быть соединены параллельно или последовательно, также могут быть смешанные типы.
Элемент схемы с сопротивлением называется резистором, напряжение данного элемента является разницей потенциалов между концами резистора. Параллельное и последовательное электрическое соединение проводников характеризуется единым принципом функционирования, согласно которому ток протекает от плюса к минусу, соответственно потенциал уменьшается. На электросхемах сопротивление проводки берется за 0, поскольку оно ничтожно низкое.
На электросхемах сопротивление проводки берется за 0, поскольку оно ничтожно низкое.
Параллельное соединение предполагает, что элементы цепы подсоединены к источнику параллельно и включаются одновременно. Последовательное соединение означает, что проводники сопротивления подключаются в строгой последовательности друг за другом.
При просчете используется метод идеализации, что существенно упрощает понимание. Фактически в электрических цепях потенциал постепенно снижается в процессе перемещения по проводке и элементам, которые входят в параллельное или последовательное соединение.
Последовательное соединение проводников
Схема последовательного соединения подразумевает, что они включаются в определенной последовательности один за другим. Причем сила тока во всех из них равна. Данные элементы создают на участке суммарное напряжение. Заряды не накапливаются в узлах электроцепи, поскольку в противном случае наблюдалось бы изменение напряжения и силы тока. При постоянном напряжении ток определяется значением сопротивления цепи, поэтому при последовательной схеме сопротивление меняется в случае изменения одной нагрузки.
Недостатком такой схемы является тот факт, что в случае выхода из строя одного элемента остальные также утрачивают возможность функционировать, поскольку цепь разрывается. Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки. Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.
Последовательная схема предполагает, что по причине одноуровневого подключения проводников их сопротивление в любой точки сети равно. Общее сопротивление равняется сумме уменьшения напряжений отдельных элементов сети.
При данном типе соединения начало одного проводника подсоединяется к концу другого. Ключевая особенность соединения состоит в том, что все проводники находятся на одном проводе без разветвлений, и через каждый из них протекает один электроток. Однако общее напряжение равно сумме напряжений на каждом. Также можно рассмотреть соединение с другой точки зрения – все проводники заменяются одним эквивалентным резистором, и ток на нем совпадает с общим током, который проходит через все резисторы. Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору. Так проявляется разность потенциалов на резисторе.
Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору. Так проявляется разность потенциалов на резисторе.
Использование последовательного подключения целесообразно, когда требуется специально включать и выключать определенное устройство. К примеру, электрозвонок может звенеть только в момент, когда присутствует соединение с источником напряжения и кнопкой. Первое правило гласит, что если тока нет хотя бы на одном из элементов цепи, то и на остальных его не будет. Соответственно при наличии тока в одном проводнике он есть и в остальных. Другим примером может служить фонарик на батарейках, который светит только при наличии батарейки, исправной лампочки и нажатой кнопки.
В некоторых случаях последовательная схема нецелесообразна. В квартире, где система освещения состоит из множества светильников, бра, люстр, не стоит организовывать схему такого типа, поскольку нет необходимости включать и выключать освещение во всех комнатах одновременно. С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.
С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.
Параллельное соединение проводников
В параллельной схеме проводники представляют собой набор резисторов, одни концы которых собираются в один узел, а другие – во второй узел. Предполагается, что напряжение в параллельном типе соединения одинаковое на всех участках цепи. Параллельные участки электроцепи носят название ветвей и проходят между двумя соединительными узлами, на них имеется одинаковое напряжение. Такое напряжение равно значению на каждом проводнике. Сумма показателей, обратных сопротивлениям ветвей, является обратной и по отношению к сопротивлению отдельного участка цепи параллельной схемы.
При параллельном и последовательном соединениях отличается система расчета сопротивлений отдельных проводников. В случае параллельной схемы ток уходит по ветвям, что способствует повышению проводимости цепи и уменьшает совокупное сопротивление. При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу .
При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу .
В каждой ветви предусмотрено по одному резистору, и электроток при достижении точки разветвления делится и расходится к каждому резистору, его итоговое значение равно сумме токов на всех сопротивлениях. Все резисторы заменяются одним эквивалентным резистором. Применяя закон Ома, становится понятным значение сопротивления – при параллельной схеме суммируются значения, обратные сопротивлениям на резисторах.
При данной схеме значение тока обратно пропорционально значению сопротивления. Токи в резисторах не взаимосвязаны, поэтому при отключении одного из них это никоим образом не отразится на остальных. По этой причине такая схема используется во множестве устройств.
Рассматривая возможности применения параллельной схемы в быту, целесообразно отметить систему освещения квартиры. Все лампы и люстры должны быть соединены параллельно, в таком случае включение и отключение одного из них никак не влияет на работу остальных ламп. Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.
Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.
Все электроприборы объединяются параллельно в электросеть с напряжением 220 В, затем они подключаются к . То есть все приборы подключаются независимо от подключения прочих устройств.
Законы последовательного и параллельного соединения проводников
Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.
При последовательной схеме имеется одинаковая сила тока во всех проводниках:
Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:
U1 = IR1, U2 = IR2.
Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:
U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.
В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:
А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:
Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.
Смешанное соединение проводников
Последовательная и параллельная схема соединения сопротивления могут сочетаться в одной электросхеме при необходимости. К примеру, допускается подключение параллельных резисторов по последовательной или их группе, такое тип считается комбинированным или смешанным.
В таком случае совокупное сопротивление рассчитывается посредством получения сумм значений для параллельного соединения в системе и для последовательного.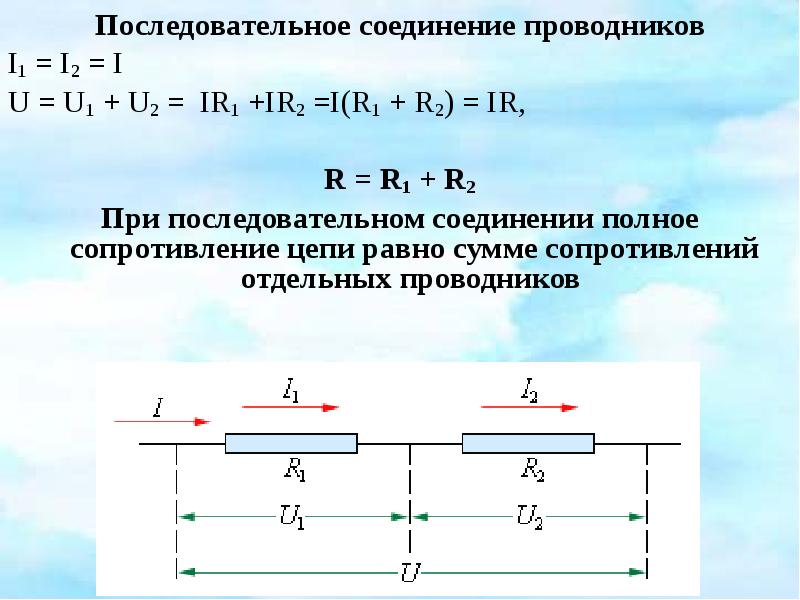 Сначала необходимо рассчитывать эквивалентные сопротивления резисторов в последовательной схеме, а затем элементов параллельного. Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.
Сначала необходимо рассчитывать эквивалентные сопротивления резисторов в последовательной схеме, а затем элементов параллельного. Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.
Итак, рассматривая типы подключений проводников в электроцепях и основываясь на законах их функционирования, можно полностью понять суть организации схем большинства бытовых электроприборов. При параллельном и последовательном соединениях расчет показателей сопротивления и силы тока отличается. Зная принципы расчета и формулы, можно грамотно использовать каждый тип организации цепей для подключения элементов оптимальным способом и с максимальной эффективностью.
Последовательным
называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи.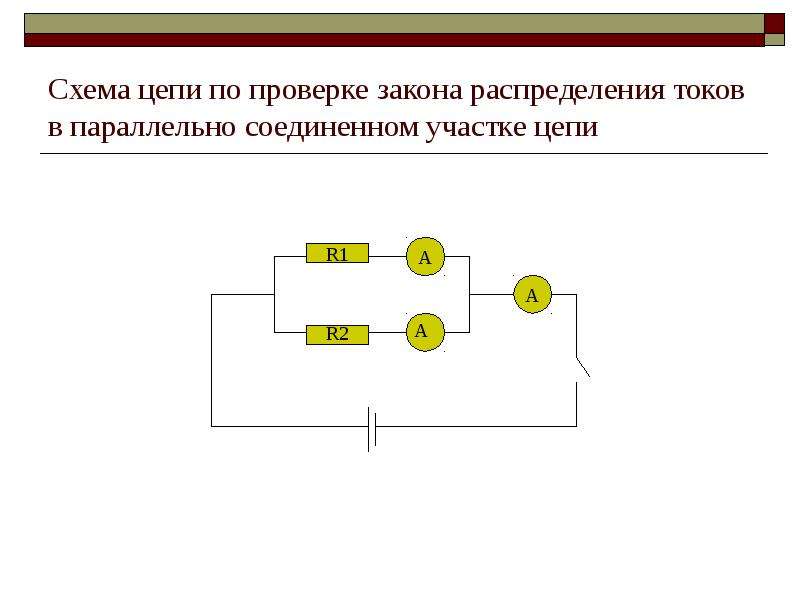 Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
\(~I = I_1 = I_2 .\)
Амперметр А
измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R
A → 0).
Включенные вольтметры V
1 и V
2 измеряют напряжение U
1 и U
2 на сопротивлениях R
1 и R
2 . Вольтметр V
измеряет подведенное к клеммам Μ
и N
напряжение U
. Вольтметры показывают, что при последовательном соединении напряжение U
равно сумме напряжений на отдельных участках цепи:
\(~U = U_1 + U_2 . \qquad (1)\)
Применяя закон Ома для каждого участка цепи, получим:
\(~U = IR ; \ U_1 = IR_1 ; \ U_2 = IR_2 ,\)
где R
— общее сопротивление последовательно соединенной цепи. Подставляя U
, U
1 , U
2 в формулу (1), имеем
\(~IR = IR_1 + IR_2 \Rightarrow R = R_1 + R_2 .\)
n
последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:
\(~R = R_1 + R_2 + \ldots R_n\) , или \(~R = \sum_{i=1}^n R_i .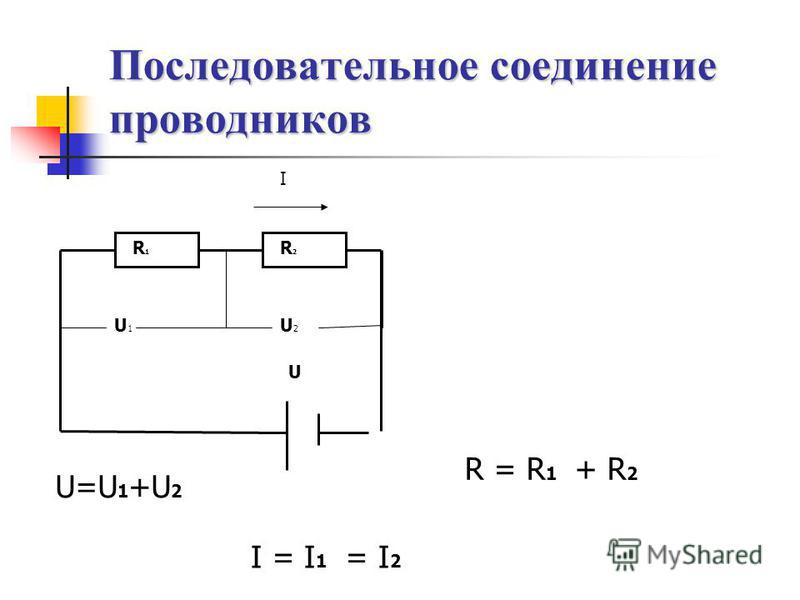 \)
\)
Если сопротивления отдельных резисторов равны между собой, т.е. R
1 = R
2 = … = R
n , то общее сопротивление этих резисторов при последовательном соединении в n
раз больше сопротивления одного резистора: R
= nR
1 .
При последовательном соединении резисторов справедливо соотношение \(~\frac{U_1}{U_2} = \frac{R_1}{R_2}\), т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.
Параллельным
называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ
и N
подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R
1 и R
2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:
\(~U = U_1 = U_2 . n \frac{1}{R_i} .\)
n \frac{1}{R_i} .\)
Если сопротивления всех n
параллельно соединенных резисторов одинаковы и равны R
1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .
Сопротивление цепи, состоящей из n
одинаковых параллельно соединенных резисторов, в n
раз меньше сопротивления каждого из них.
При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 257-259.
На уроке рассматривается параллельное соединение проводников. Изображается схема такого соединения, показывается выражение для вычисления силы тока в такой цепи. Также вводится понятие эквивалентного сопротивления, находится его значение для случая параллельного соединения.
Также вводится понятие эквивалентного сопротивления, находится его значение для случая параллельного соединения.
Соединения проводников бывают различные. Они могут быть параллельными, последовательными и смешанными. На данном уроке мы рассмотрим параллельное соединение проводников и понятие эквивалентного сопротивления.
Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. На схеме такое соединение обозначается следующим образом (рис. 1):
Рис. 1. Параллельное соединение трех резисторов
На рисунке изображены три резистора (прибор, основанный на сопротивлении проводника) с сопротивлениями R1, R2, R3. Как видим, начала этих проводников соединены в точке А, концы — в точке Б, а расположены они параллельно друг другу. Также в цепи может быть большее количество параллельно соединенных проводников.
Теперь рассмотрим следующую схему (рис. 2):
Рис. 2. Схема для исследования силы тока при параллельном соединении проводников
В качестве элементов цепи мы взяли две лампы (1а, 1б). Они также имеют свое сопротивление, поэтому мы их можем рассматривать наравне с резисторами. Эти две лампы соединены параллельно, соединяются они в точках А и Б. К каждой лампе подсоединен свой амперметр: соответственно, А 1 и А 2 . Также есть амперметр А 3 , который измеряет силу тока во всей цепи. В цепь еще входит источник питания (3) и ключ (4).
Они также имеют свое сопротивление, поэтому мы их можем рассматривать наравне с резисторами. Эти две лампы соединены параллельно, соединяются они в точках А и Б. К каждой лампе подсоединен свой амперметр: соответственно, А 1 и А 2 . Также есть амперметр А 3 , который измеряет силу тока во всей цепи. В цепь еще входит источник питания (3) и ключ (4).
Замкнув ключ, мы будем следить за показаниями амперметров. Амперметр А 1 покажет силу тока, равную I 1 , в лампе 1а, амперметр А 2 — cилу тока, равную I 2 , в лампе 1б. Что же касается амперметра А 3 , то он покажет силу тока, равную сумме токов в каждой отдельной взятой цепи, соединенных параллельно: I = I 1 + I 2 . То есть, если сложить показания амперметров А 1 и А 2 , то получим показания амперметра А 3 .
Стоит обратить внимание, что если одна из ламп перегорит, то вторая будет продолжать работать. При этом весь ток будет проходить через эту вторую лампу. Это очень удобно. Так, например, электроприборы в наших домах включаются в цепь параллельно.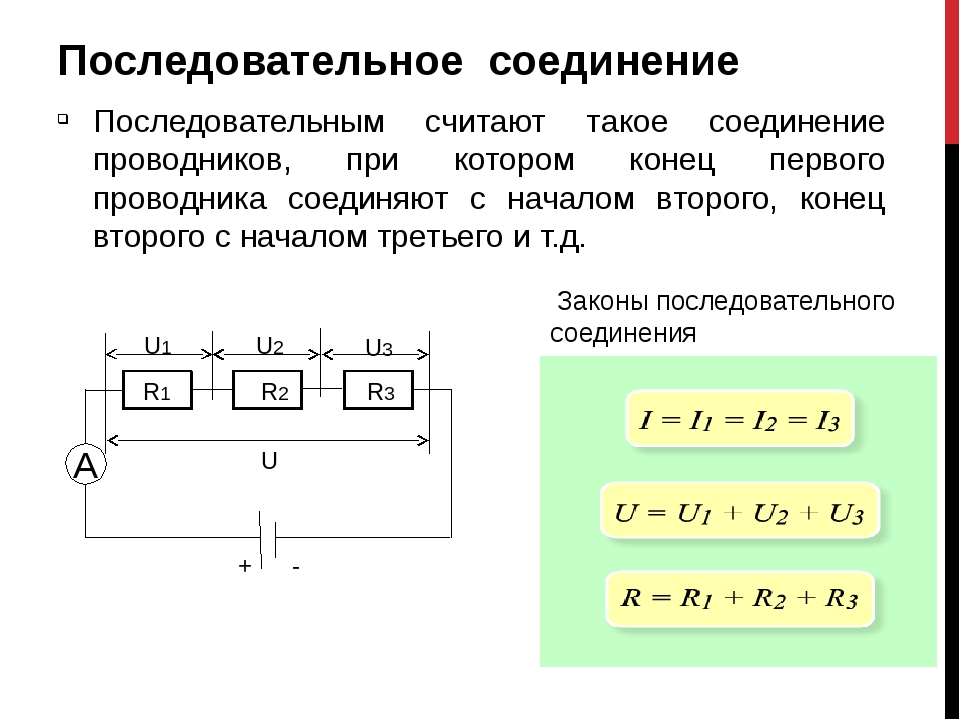 И если один из них выходит из строя, то остальные остаются в рабочем состоянии.
И если один из них выходит из строя, то остальные остаются в рабочем состоянии.
Рис. 3. Схема для нахождения эквивалентного сопротивления при параллельном соединении
На схеме рис. 3 мы оставили один амперметр (2), но добавили в электрическую цепь вольтметр (5) для измерения напряжения. Точки А и Б являются общими и для первой (1а), и для второй лампы (1б), а значит, вольтметр измеряет напряжение на каждой из этих ламп (U 1 и U 2) и во всей цепи (U). Тогда U = U 1 = U 2 .
Эквивалентным сопротивлением называется сопротивление, которое может заменить все элементы, входящие в данную цепь. Посмотрим, чему же оно будет равно при параллельном соединении. Из закона Ома можно получить, что:
В данной формуле R — эквивалентное сопротивление, R 1 и R 2 — сопротивление каждой лампочки, U = U 1 = U 2 — напряжение, которое показывает вольтметр (5). При этом мы используем то, что сумма токов в каждой отдельной цепи равна общей силе тока (I = I 1 + I 2). Отсюда можно получить формулу для эквивалентного сопротивления:
Если в цепи будет больше элементов, соединенных параллельно, то и слагаемых будет больше.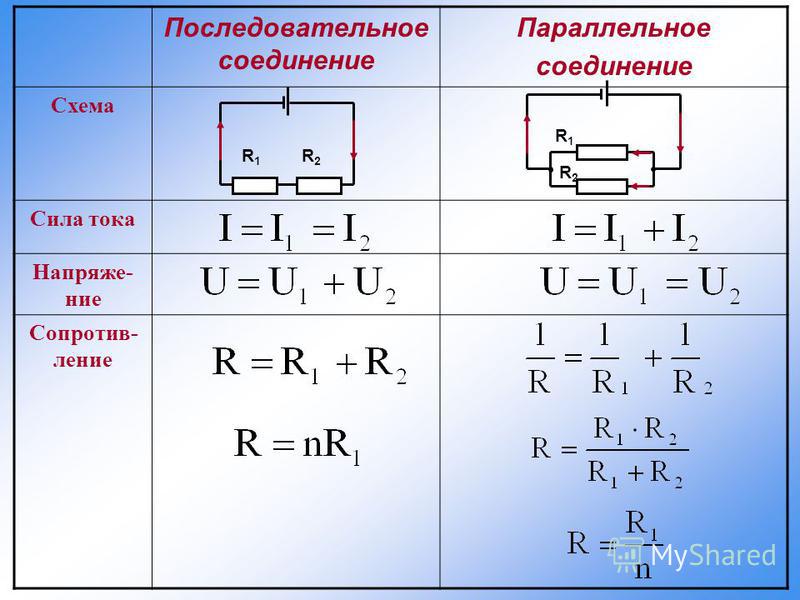 Тогда придется вспомнить, как работать с простыми дробями.
Тогда придется вспомнить, как работать с простыми дробями.
Стоить отметить, что при параллельном соединении эквивалентное сопротивление будет достаточно малым. Соответственно, сила тока будет достаточно большой. Это стоит учитывать при включении в розетки большого количества электрических приборов. Ведь тогда сила тока возрастет, что может привести к перегреванию проводов и пожарам.
На следующем уроке мы рассмотрим другой тип соединения проводников — последовательное.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. — М.: Мнемозина.
- Перышкин А.В. Физика 8. — М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. — М.: Просвещение.
- Физика ().
- Сверхзадача ().
- Интернет-портал Nado5.ru ().
Домашнее задание
- Стр. 114-117: вопросы № 1-6. Перышкин А.В. Физика 8. — М.: Дрофа, 2010.
- Могут ли быть параллельно соединены более трех проводников?
- Что случится, если одна из двух ламп, которые соединены параллельно, перегорит?
- Если к любой цепи параллельно подключить еще один проводник, всегда ли её эквивалентное сопротивление будет уменьшаться?
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U 1
+ U 2
+ U 3 или
IR экв
= IR 1
+ IR 2
+ IR 3 ,
откуда
следует
R экв
= R 1
+ R 2
+ R 3 .
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением R экв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
и
по вышеприведенным формулам рассчитывают
падение напряжений U 1 ,
U 2 ,
U 3
на соответствующих участках электрической
цепи (рис. 1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
1.6).
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I 1
+ I 2
+ I 3 ,
т.е.
откуда
следует, что
.
В
том случае, когда параллельно включены
два сопротивления R 1
и R 2 ,
они заменяются одним эквивалентным
сопротивлением
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
g экв
= g 1
+ g 2
+ g 3 .
По
мере роста числа параллельно включенных
потребителей проводимость цепи g экв
возрастает, и наоборот, общее сопротивление
R экв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IR экв
= I 1 R 1
= I 2 R 2 =
I 3 R 3 .
Отсюда
следует, что
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.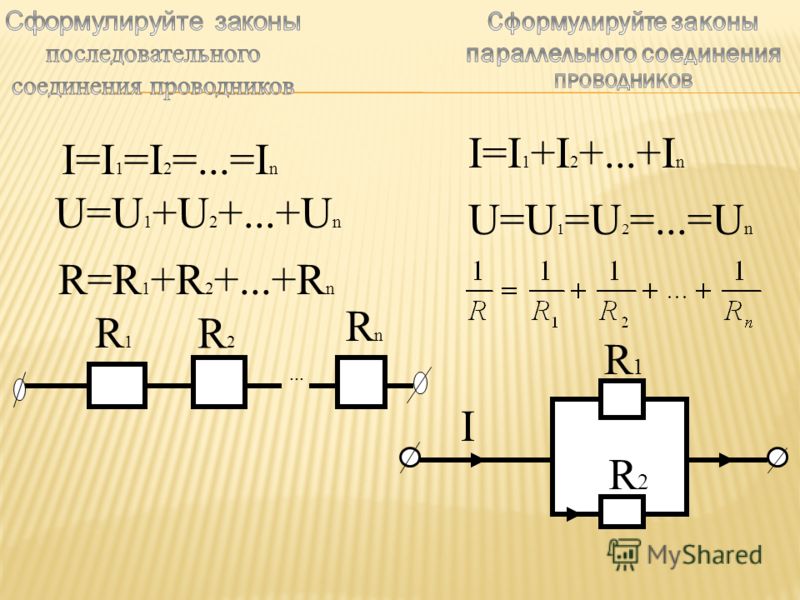
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R.
Сопротивления R 4
и R 5
включены параллельно, тогда сопротивление
участка цепи cd равно:
.
В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
На
схеме (рис. 1.8) сопротивление R 3
и R cd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
На
схеме (рис. 1.9) сопротивление R 2
и R ad
соединены параллельно, тогда сопротивление
участка цепи аb равно
.
Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R 1
и R ab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
Рис. | Рис. |
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
R экв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ
ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение
синусоидальной ЭДС. . Основные
характеристики синусоидального тока
Основным
преимуществом синусоидальных токов
является то, что они позволяют наиболее
экономично осуществлять производство,
передачу, распределение и использование
электрической энергии. Целесообразность
Целесообразность
их использования обусловлена тем, что
коэффициент полезного действия
генераторов, электрических двигателей,
трансформаторов и линий электропередач
в этом случае оказывается наивысшим.
Для
получения в линейных цепях синусоидально
изменяющихся токов необходимо, чтобы
э. д. с. также изменялись по синусоидальному
закону. Рассмотрим процесс возникновения
синусоидальной ЭДС. Простейшим генератором
синусоидальной ЭДС может служить
прямоугольная катушка (рамка), равномерно
вращающаяся в однородном магнитном
поле с угловой скоростью ω
(рис. 2.1, б
).
Пронизывающий
катушку магнитный поток во время вращения
катушки abcd
наводит (индуцирует) в ней на основании
закона электромагнитной индукции
ЭДС е
.
Нагрузку подключают к генератору с
помощью щеток 1
,
прижимающихся к двум контактным кольцам
2
,
которые, в свою очередь, соединены с
катушкой. Значение наведенной в катушке
abcd
э. д. с. в каждый момент времени
пропорционально магнитной индукции В
,
размеру активной части катушки l
= ab
+ dc
и нормальной составляющей скорости
перемещения ее относительно поля v
н
:
e
= Blv
н
(2.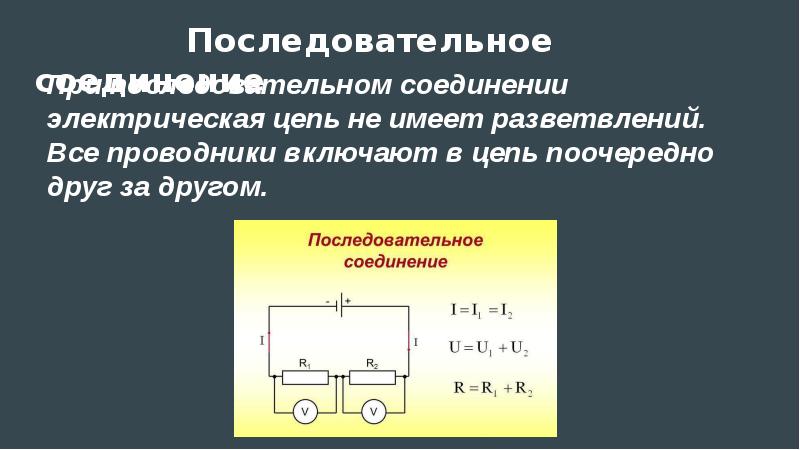 1)
1)
где
В
и l
— постоянные величины, a v
н
— переменная, зависящая от угла α. Выразив
скорость v н
через линейную скорость катушки v
,
получим
e
= Blv·sinα
(2.2)
В
выражении (2.2) произведение Blv
= const. Следовательно, э. д. с., индуцируемая
в катушке, вращающейся в магнитном поле,
является синусоидальной функцией угла
α
.
Если
угол α = π/2
,
то произведение Blv
в формуле (2.2) есть максимальное
(амплитудное) значение наведенной э. д.
с. E m
= Blv
.
Поэтому выражение (2.2) можно записать в
виде
e
= E
m
sinα
(2.3)
Так
как α
есть угол поворота за время t
,
то, выразив его через угловую скорость
ω
,
можно записать α
= ωt
, a формулу
(2.3) переписать в виде
e
= E
m
sinωt
(2.4)
где
е
— мгновенное значение э. д. с. в катушке;
α = ωt
— фаза, характеризующая значение э. д.
д.
с. в данный момент времени.
Необходимо
отметить, что мгновенную э. д. с. в течение
бесконечно малого промежутка времени
можно считать величиной постоянной,
поэтому для мгновенных значений э. д.
с. е
,
напряжений и
и токов i
справедливы законы постоянного тока.
Синусоидальные
величины можно графически изображать
синусоидами и вращающимися векторами.
При изображении их синусоидами на
ординате в определенном масштабе
откладывают мгновенные значения величин,
на абсциссе — время. Если синусоидальную
величину изображают вращающимися
векторами, то длина вектора в масштабе
отражает амплитуду синусоиды, угол,
образованный с положительным направлением
оси абсцисс, в начальный момент времени
равен начальной фазе, а скорость вращения
вектора равна угловой частоте. Мгновенные
значения синусоидальных величин есть
проекции вращающегося вектора на ось
ординат. Необходимо отметить, что за
положительное направление вращения
радиус-вектора принято считать направление
вращения против часовой стрелки. На
На
рис. 2.2 построены графики мгновенных
значений э. д. с. е
и е»
.
Если
число пар полюсов магнитов p
≠ 1
, то за
один оборот катушки (см. рис. 2.1) происходит
p
полных циклов изменения э. д. с. Если
угловая частота катушки (ротора) n
оборотов в минуту, то период уменьшится
в pn
раз. Тогда частота э. д. с., т. е. число
периодов в секунду,
f
= Pn
/ 60
Из
рис. 2.2 видно, что ωТ
= 2π
, откуда
ω
= 2π / T = 2πf
(2.5)
Величину
ω
,
пропорциональную частоте f и равную
угловой скорости вращения радиус-вектора,
называют угловой
частотой.
Угловую частоту выражают в радианах в
секунду (рад/с) или в 1 / с.
Графически
изображенные на рис. 2.2 э. д. с. е
и е»
можно описать выражениями
e
= E
m
sinωt;
e» = E»
m
sin(ωt
+ ψ
e»
)
.
Здесь
ωt
и ωt + ψ
e»
— фазы, характеризующие значения э. д.
д.
с. e
и e»
в заданный момент времени; ψ
e»
— начальная фаза, определяющая значение
э. д. с. е»
при t = 0. Для э. д. с. е
начальная фаза равна нулю (ψ
e
= 0
). Угол ψ
всегда отсчитывают от нулевого значения
синусоидальной величины при переходе
ее от отрицательных значений к
положительным до начала координат (t =
0). При этом положительную начальную
фазу ψ
(рис. 2.2) откладывают влево от начала
координат (в сторону отрицательных
значений ωt
),
а отрицательную фазу — вправо.
Если
у двух или нескольких синусоидальных
величин, изменяющихся с одинаковой
частотой, начала синусоид не совпадают
по времени, то они сдвинуты друг
относительно друга по фазе, т. е. не
совпадают по фазе.
Разность
углов φ
,
равная разности начальных фаз, называют
углом сдвига
фаз. Сдвиг фаз
между одноименными синусоидальными
величинами, например между двумя э. д.
с. или двумя токами, обозначают α
.
Угол сдвига фаз между синусоидами тока
и напряжения или их максимальными
векторами обозначают буквой φ
(рис. 2.3).
Когда
для синусоидальных величин разность
фаз равна ±π
,
то они противоположны
по фазе, если
же разность фаз равна ±π/2
,
то говорят, что они находятся в квадратуре.
Если для синусоидальных величин одной
частоты начальные фазы одинаковы, то
это означает, что они совпадают
по фазе.
Синусоидальные
напряжение и ток, графики которых
представлены на рис. 2.3, описываются
следующим образом:
u
= U
m
sin(ω
t
+
ψ
u
)
;
i
= I
m
sin(ω
t
+
ψ
i
)
, (2.6)
причем
угол сдвига фаз между током и напряжением
(см. рис. 2.3) в этом случае φ
= ψ
u
— ψ
i
.
Уравнения
(2.6) можно записать иначе:
u
= U
m
sin(ωt
+ ψ
i
+ φ)
; i
= I
m
sin(ωt
+ ψ
u
— φ)
,
поскольку
ψ
u
= ψ
i
+ φ
и ψ
i
= ψ
u
— φ
.
Из
этих выражений следует, что напряжение
опережает по фазе ток на угол φ
(или ток отстает по фазе от напряжения
на угол φ
).
Формы
представления синусоидальных электрических
величин.
Любая,
синусоидально изменяющаяся, электрическая
величина (ток, напряжение, ЭДС) может
быть представлена в аналитическом,
графическом и комплексном видах.
1).
Аналитическая
форма представления
I
= I
m
·sin(ω·t
+ ψ
i
),
u
= U
m
·sin(ω·t
+ ψ
u
),
e
= E
m
·sin(ω·t
+ ψ
e
),
где
I
,
u
,
e
– мгновенное значение синусоидального
тока, напряжения, ЭДС, т. е. Значения в
рассматриваемый момент времени;
I
m
,
U
m
,
E
m
– амплитуды синусоидального тока,
напряжения, ЭДС;
(ω·t
+ ψ
)
– фазовый угол, фаза; ω
= 2·π/Т
– угловая частота, характеризующая
скорость изменения фазы;
ψ
i ,
ψ
u ,
ψ
e
– начальные фазы тока, напряжения, ЭДС
отсчитываются от точки перехода
синусоидальной функции через нуль к
положительному значению до начала
отсчета времени (t
= 0). Начальная фаза может иметь как
Начальная фаза может иметь как
положительное так и отрицательное
значение.
Графики
мгновенных значений тока и напряжения
показаны на рис. 2.3
Начальная
фаза напряжения сдвинута влево от начала
отсчёта и является положительной ψ
u
> 0, начальная фаза тока сдвинута вправо
от начала отсчёта и является отрицательной
ψ
i
φ
.
Сдвиг фаз между напряжением и током
φ
= ψ
u
– ψ
i
= ψ
u
– (- ψ
i)
= ψ
u
+ ψ
i .
Применение
аналитической формы для расчёта цепей
является громоздкой и неудобной.
На
практике приходится иметь дело не с
мгновенными значениями синусоидальных
величин, а с действующими. Все расчёты
проводят для действующих значений, в
паспортных данных различных
электротехнических устройств указаны
действующие значения (тока, напряжения),
большинство электроизмерительных
приборов показывают действующие
значения. Действующий ток является
эквивалентом постоянного тока, который
за одно и то же время выделяет в резисторе
такое же количество тепла, как и переменный
ток.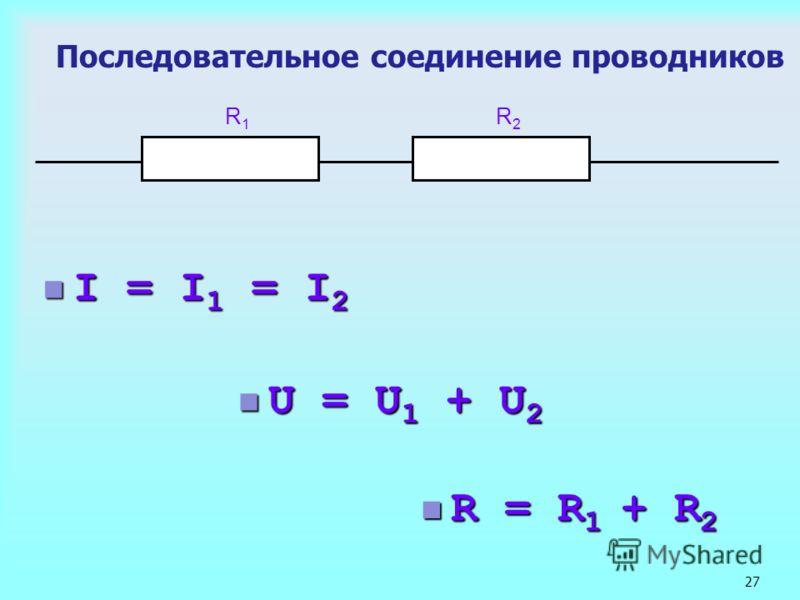 Действующее значение связано с
Действующее значение связано с
амплитудным простым соотношением
2).
Векторная
форма представления синусоидальной
электрической величины – это вращающийся
в декартовой системе координат вектор
с началом в точке 0, длина которого равна
амплитуде синусоидальной величины,
угол относительно оси х – её начальной
фазе, а частота вращения – ω
= 2πf
.
Проекция данного вектора на ось у в
любой момент времени определяет
мгновенное значение рассматриваемой
величины.
Рис.
2.4
Совокупность
векторов, изображающих синусоидальные
функции, называют векторной диаграммой,
рис. 2.4
3).
Комплексное
представление синусоидальных электрических
величин сочетает наглядность векторных
диаграмм с проведением точных аналитических
расчётов цепей.
Рис.
2.5
Ток
и напряжение изобразим в виде векторов
на комплексной плоскости, рис.2.5 Ось
абсцисс называют осью действительных
чисел и обозначают +1
,
ось ординат называют осью мнимых чисел
и обозначают +j
.
(В некоторых учебниках ось действительных
чисел обозначают Re
,
а ось мнимых – Im
).
Рассмотрим векторы U
и I
в момент времени t
= 0. Каждому из этих векторов соответствует
комплексное число, которое может быть
представлено в трех формах:
а).
Алгебраической
U
= U
’+
jU
«
I
= I
’
– jI
«,
где
U
«,
U
«,
I
«,
I
»
– проекции векторов на оси действительных
и мнимых чисел.
б).
Показательной
где
U
,
I
– модули (длины) векторов; е
– основание натурального логарифма;
поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
в).
Тригонометрической
U
= U
·(cosψ
u
+ j
sinψ
u)
I
= I
·(cosψ
i
– j
sinψ
i).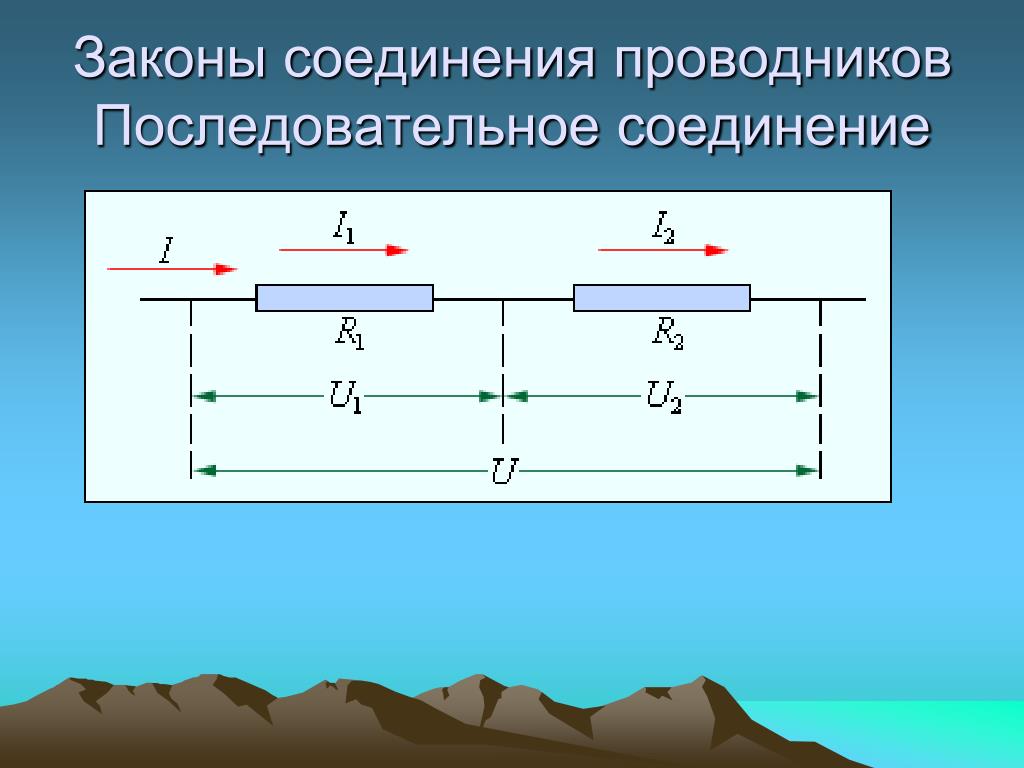
При
решении задач в основном применяют
алгебраическую форму (для операций
сложения и вычитания) и показательную
форму (для операций умножения и деления).
Связь между ними устанавливается
формулой Эйлера
е
j
·ψ
=
cosψ
+ j
sinψ
.
Неразветвлённые
электрические цепи
Содержание:
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.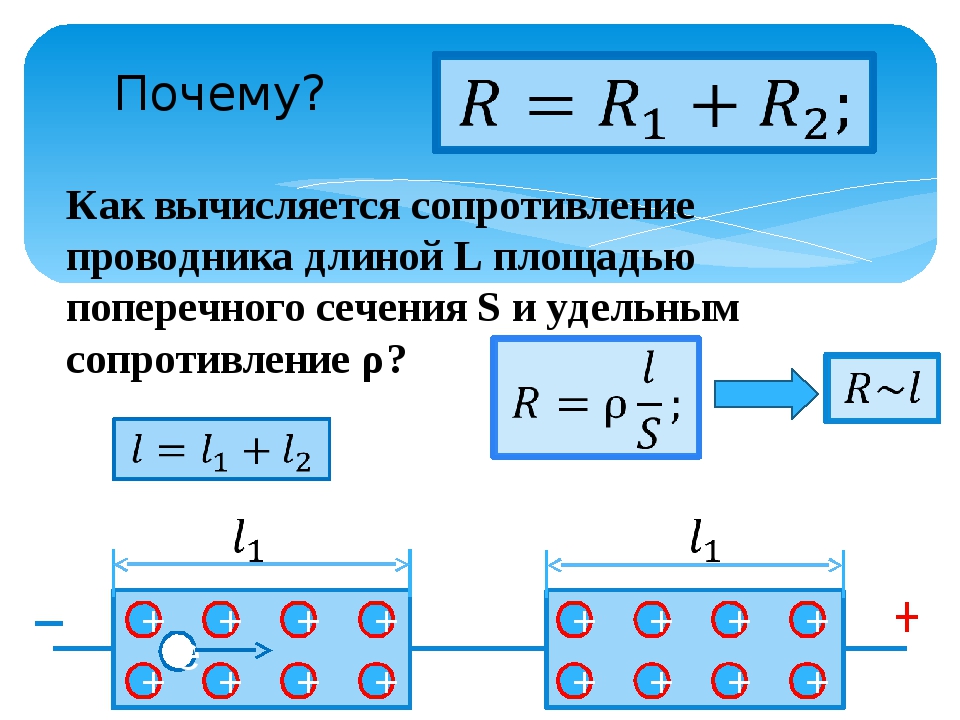
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.

- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.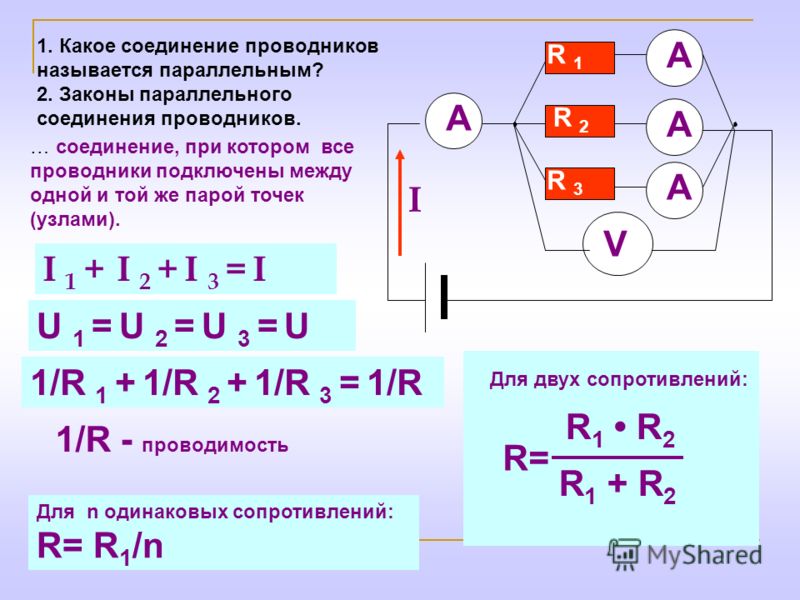
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой.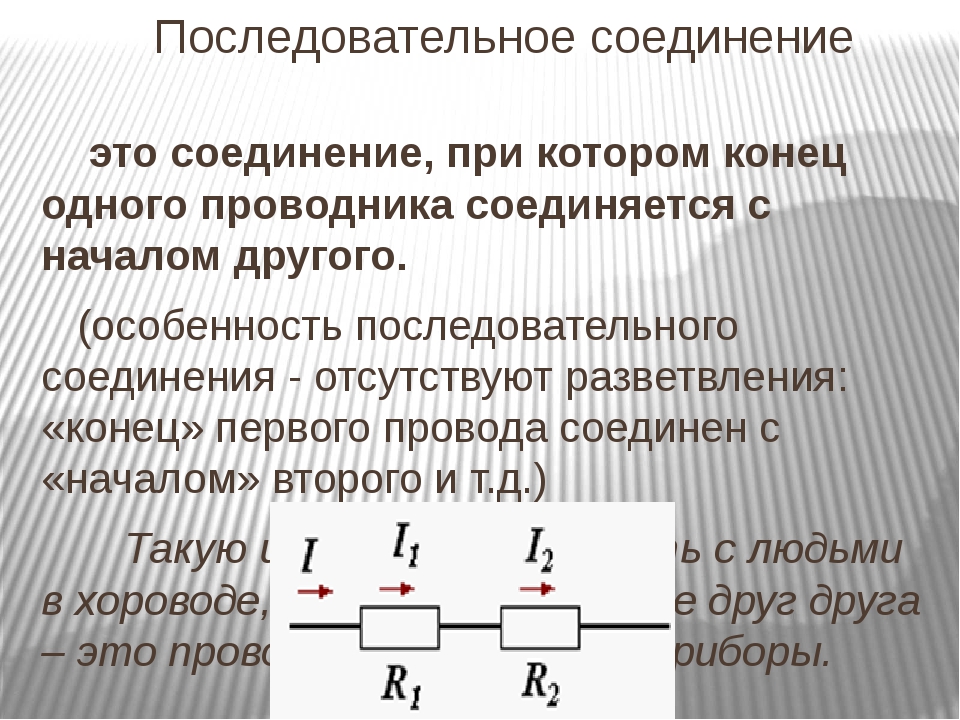 Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.

- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.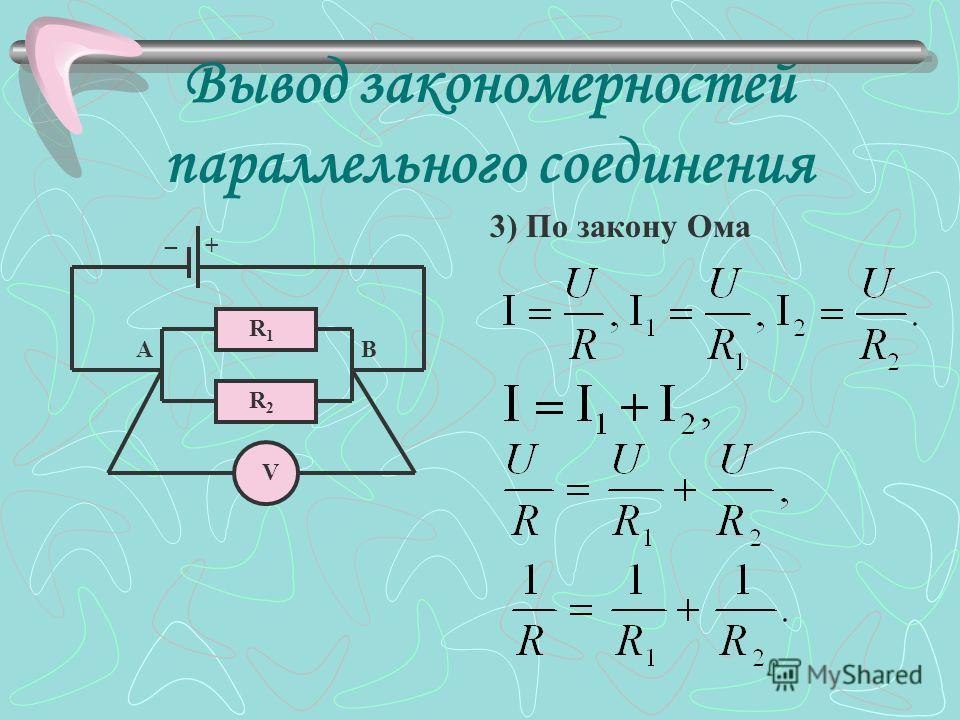
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
Применение последовательного и параллельного соединения проводников. Сопротивление последовательное и параллельное соединение, соединения проводников
Содержание:
Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы.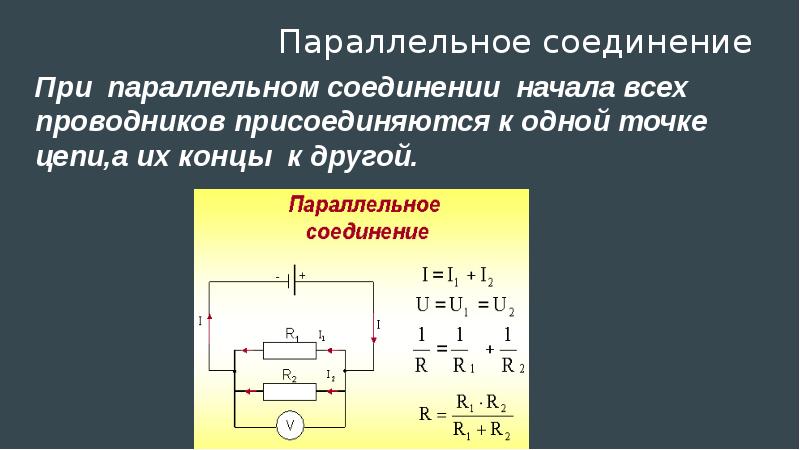 Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .
Данное свойство отражается формулой: R общ = R 1 + R 2 .
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.
Gif?x15027″ alt=»Общий вид»>
Общий вид
Особенности включения
Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.
Для такого включения типичны следующие особенности:
- Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
- Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.
В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.
Расчёт
Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).
Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:
I= U/R (одного из резисторов).
После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.
Типичные подключения
Пример №1
Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление.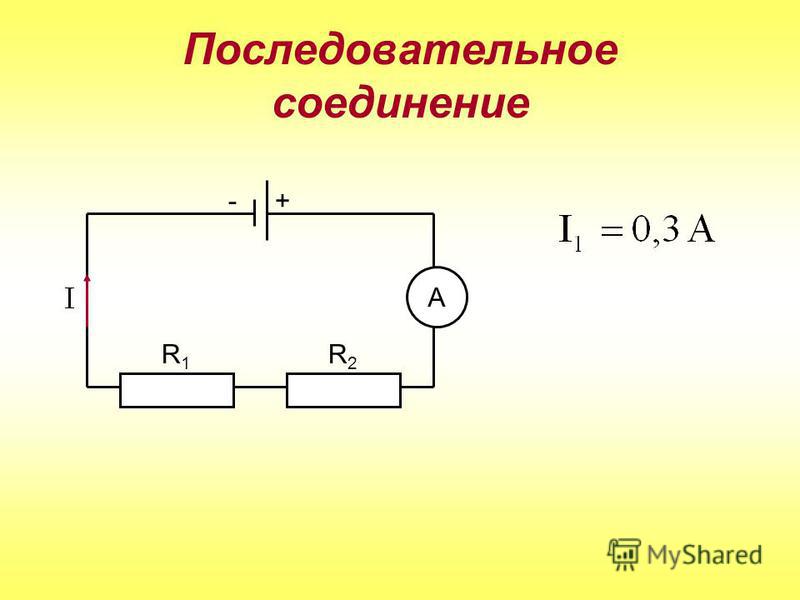 При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).
При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).
Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.
Из неё следует:
16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.
Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.
Пример №2
В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.
Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.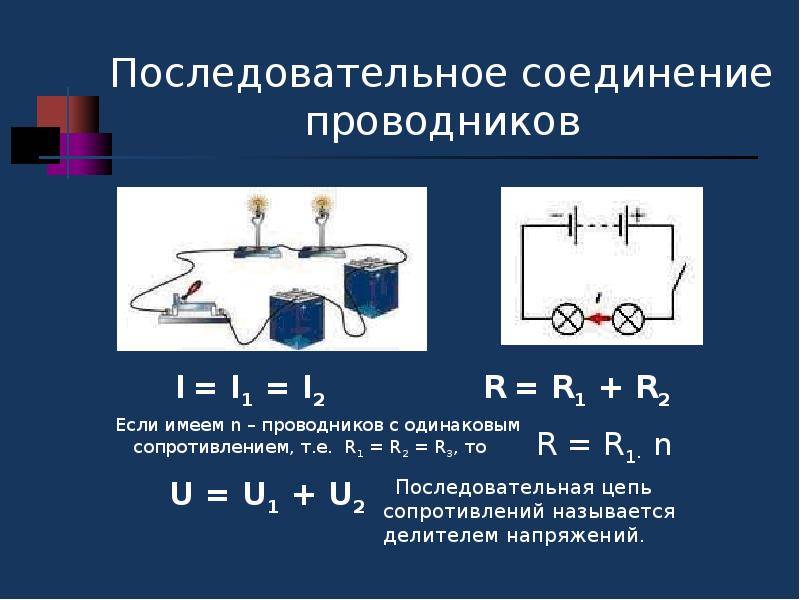
Gif?x15027″ alt=»Пример»>
В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:
1/R = 1/200+1/220+1/470 = 0,0117;
R=1/0,0117 = 85,67Ом.
В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.
Важно!
Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.
Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.
Расчёт комбинированных схем
Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.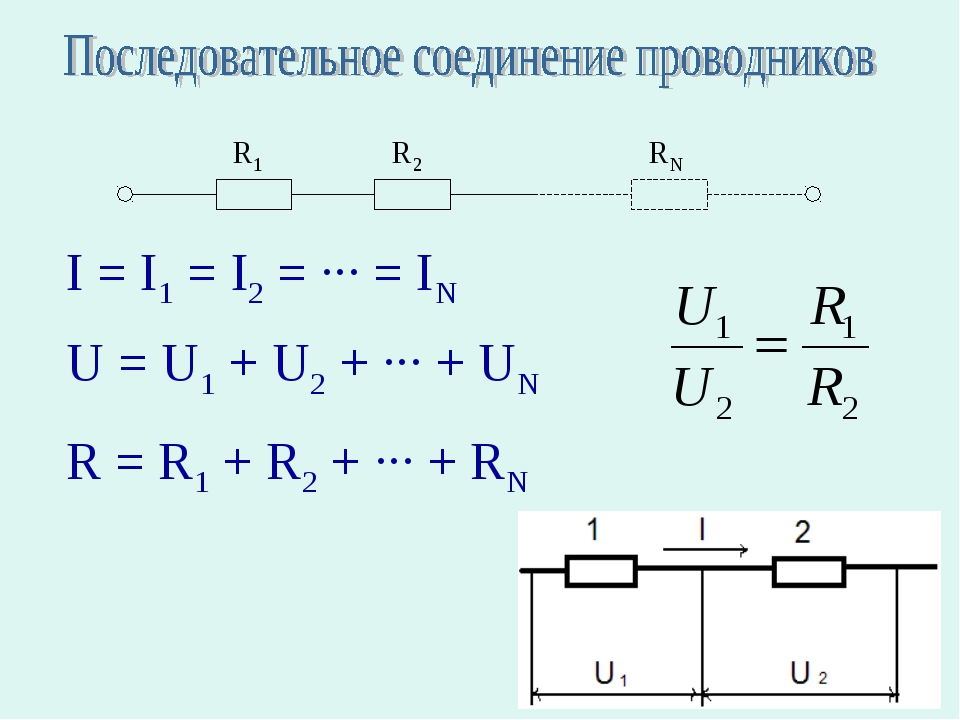
Gif?x15027″ alt=»Смешанная схема»>
Смешанная схема
Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.
Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.
В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R
. Этот закон, установленный экспериментально, называется закон Ома
(для участка цепи).
Закон Ома
для участка цепи
: сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника.
Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).
Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д
ва основных типа соединения проводников
: последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.
Последовательное соединение проводников
При последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова:
I 1 =
I 2 =
I
.
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений
: R 1 + R 2 = R
. Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: U 1 =
I*
R 1
, U 2 = I*R 2
. В таком случае общее напряжение равно U = I (
R 1 +
R 2)
. Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике
: U = U 1 + U 2
.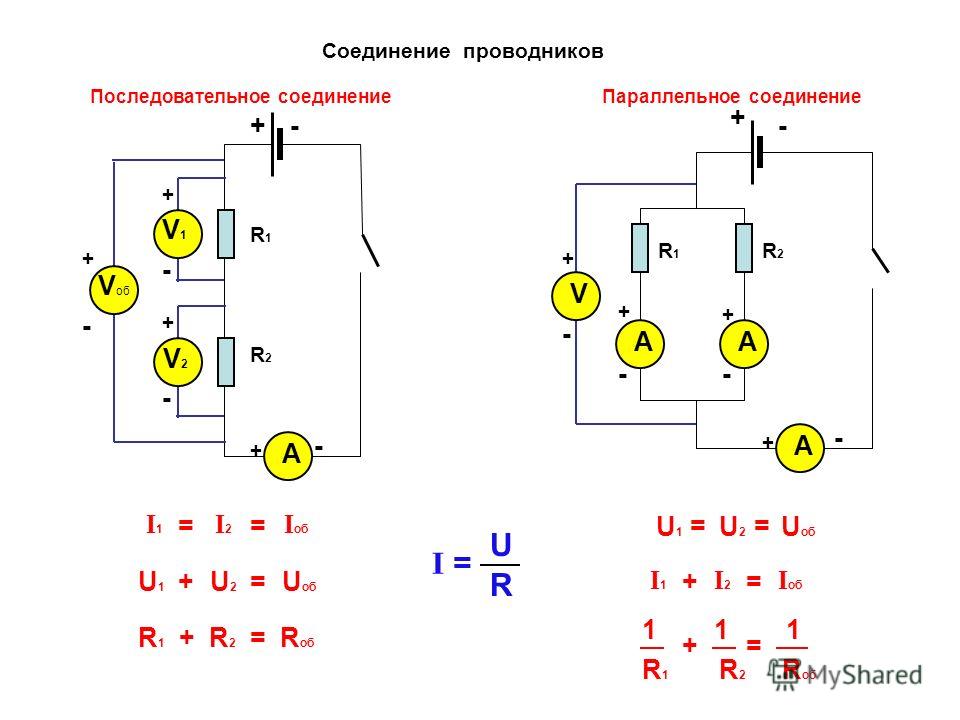
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
Для последовательного соединения проводников справедливы законы
:
1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводников
Примером параллельного соединения
проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U
В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U
.
При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I =
I 1 +
I 2
.
В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2
. Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2
, U = U 1 = U 2
,
1/R = 1/R 1 + 1/R
2
Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г
, то их общее сопротивление равно: R = г/2
. Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.
Для параллельного соединения проводников справедливы законы:
1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Сопротивление
проводников. Параллельное и последовательное
соединение проводников.
Электри́ческое
сопротивле́ние
—
физическая величина, характеризующая
свойства проводника препятствовать
прохождению электрического
тока и
равная отношениюнапряжения на
концах проводника к силе
тока,
протекающего по нему .
Сопротивление для цепей переменного
тока и для переменных электромагнитных
полей описывается понятиями импеданса и волнового
сопротивления. Сопротивлением (резистором)
также называют радиодеталь, предназначенную
для введения в электрические цепи
активного сопротивления.
Сопротивление
(часто обозначается буквой R
или r
)
считается, в определённых пределах,
постоянной величиной для данного
проводника; её можно рассчитать как
R
—
сопротивление;
U
— разность
электрических потенциалов (напряжение)
на концах проводника;
I
— сила
тока,
протекающего между концами проводника
под действием разности потенциалов.
При
последовательном соединении
проводников
(рис. 1.9.1) сила тока во всех проводниках
одинакова:
По закону
Ома, напряжения U
1 и U
2 на
проводниках равны
При
последовательном соединении полное
сопротивление цепи равно сумме
сопротивлений отдельных проводников.
Этот результат справедлив
для любого числа последовательно
соединенных проводников.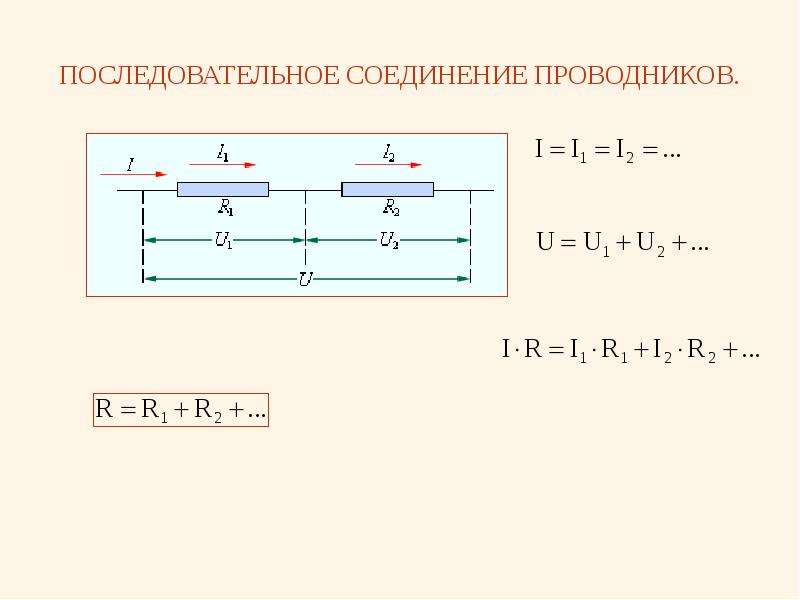
При
параллельном соединении
(рис. 1.9.2)
напряжения U
1 и U
2 на
обоих проводниках одинаковы:
Этот результат
следует из того, что в точках разветвления
токов (узлы A
и B
)
в цепи постоянного тока не могут
накапливаться заряды. Например, к
узлу A
за
время Δt
подтекает
заряд I
Δt
,
а утекает от узла за то же время
заряд I
1 Δt
+ I
2 Δt
.
Следовательно,I
= I
1 + I
2 .
Записывая на
основании закона Ома
При
параллельном соединении проводников
величина, обратная общему сопротивлению
цепи, равна сумме величин, обратных
сопротивлениям параллельно включенных
проводников.
Этот результат справедлив
для любого числа параллельно включенных
проводников.
Формулы для последовательного
и параллельного соединения проводников
позволяют во многих случаях рассчитывать
сопротивление сложной цепи, состоящей
из многих резисторов. На рис. 1.9.3
1.9.3
приведен пример такой сложной цепи и
указана последовательность вычислений.
Следует отметить, что
далеко не все сложные цепи, состоящие
из проводников с различными сопротивлениями,
могут быть рассчитаны с помощью формул
для последовательного и параллельного
соединения. На рис. 1.9.4 приведен пример
электрической цепи, которую нельзя
рассчитать указанным выше методом.
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение
– это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение
– это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение
– соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Цепи серии
— базовое электричество
Три закона для последовательных цепей
Существует три основных соотношения, касающихся сопротивления, тока и напряжения для всех последовательных цепей.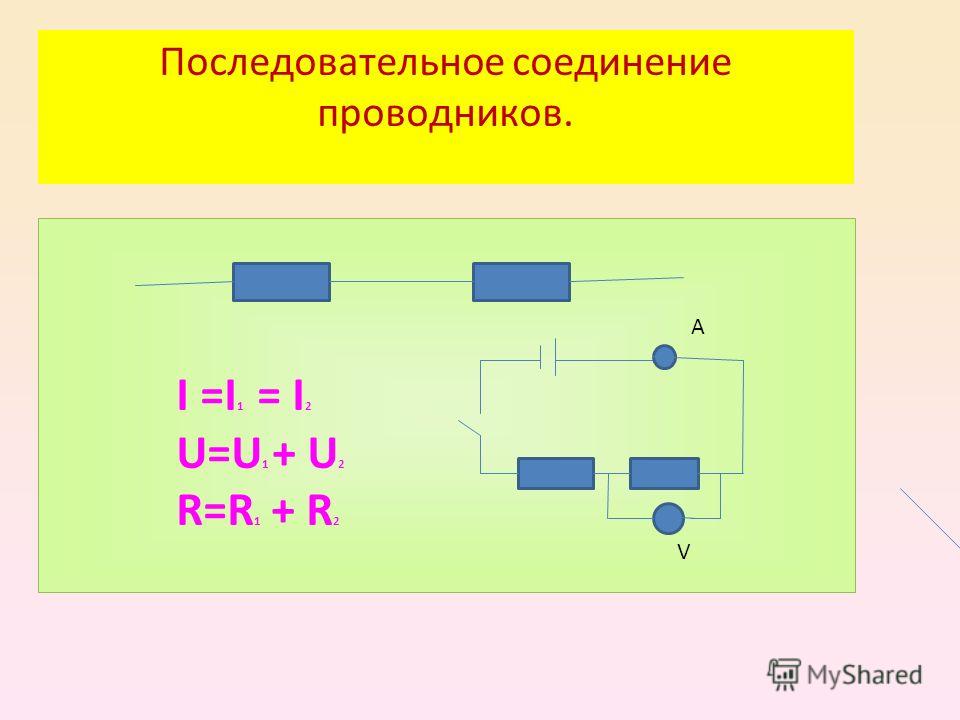 Важно, чтобы вы усвоили три основных закона для последовательных цепей.
Важно, чтобы вы усвоили три основных закона для последовательных цепей.
Сопротивление
Когда отдельные сопротивления подключаются последовательно, они действуют так же, как одно большое комбинированное сопротивление. Поскольку существует только один путь для протекания тока в последовательной цепи, и поскольку каждый из резисторов включен в линию, чтобы противодействовать этому протеканию тока, общее сопротивление является совокупным сопротивлением всех резисторов, установленных в линию.
Общее сопротивление последовательной цепи равно сумме всех отдельных сопротивлений в цепи .
Rt = R1 + R2 + R3…
Используя эту формулу, вы обнаружите, что полное сопротивление цепи равно:
RT = 15 Ом + 5 Ом + 20 Ом = 40 Ом
Рисунок 16. Последовательная схема
Текущая
Поскольку существует только один путь для электронного потока в последовательной цепи, ток имеет одинаковую величину в любой точке цепи.
Общий ток в последовательной цепи такой же, как ток через любое сопротивление цепи.
IT = I1 = I2 = I3…
Учитывая 120 В в качестве общего напряжения и определив общее сопротивление цепи как 40 Ом, теперь вы можете применить закон Ома для определения полного тока в этой цепи:
IT = 120 В / 40 Ом = 3 А
Этот общий ток цепи останется неизменным для всех отдельных резисторов цепи.
Напряжение
Прежде чем какой-либо ток будет проходить через сопротивление, должна быть доступна разность потенциалов или напряжение. Когда резисторы соединены последовательно, они должны «делить» общее напряжение источника.
Общее напряжение в последовательной цепи равно сумме всех индивидуальных падений напряжения в цепи.
Когда ток проходит через каждый резистор в последовательной цепи, он устанавливает разность потенциалов на каждом отдельном сопротивлении. Это обычно называется падением напряжения, и его величина прямо пропорциональна величине сопротивления. Чем больше значение сопротивления, тем выше падение напряжения на этом резисторе.
Это обычно называется падением напряжения, и его величина прямо пропорциональна величине сопротивления. Чем больше значение сопротивления, тем выше падение напряжения на этом резисторе.
ET = E1 + E2 + E3…
Используя закон Ома, вы можете определить напряжение на каждом резисторе.
3 А × 15 Ом = 45 В
3 А × 5 Ом = 15 В
3 А × 20 Ом = 60 В
Общее напряжение источника равно сумме отдельных падений напряжения:
45 В + 15 В + 60 В = 120 В
Обрыв в последовательной цепи
При появлении обрыва ток в цепи прерывается.Если нет тока, падение напряжения на каждом из резистивных элементов равно нулю. Однако разность потенциалов источника очевидна. Если вольтметр подключен через разомкнутый контур, показания такие же, как если бы он был подключен непосредственно к клеммам источника питания.
Рисунок 17. Обрыв цепи
Влияние обрыва линии и потери линии
Медь и алюминий используются в качестве проводников, потому что они мало препятствуют прохождению тока.Хотя сопротивлением часто пренебрегают при простом анализе цепей, в практических приложениях может возникнуть необходимость учитывать сопротивление линий.
Line Drop
Рисунок 18. Падение напряжения
Когда ток 10 А протекает через каждую линию с сопротивлением 0,15 Ом, на каждой линии появляется небольшое падение напряжения. Это падение напряжения на линейных проводниках обычно обозначается как линейное падение .
Поскольку есть две линии, общее падение составляет 2 × 1.5 В = 3 В. Напряжение сети на нагрузке (117 В) меньше напряжения источника.
В некоторых ситуациях может потребоваться использование более крупных проводов с меньшим сопротивлением, чтобы падение напряжения в линии не слишком сильно уменьшало напряжение нагрузки.
Потеря линии
Другой термин, связанный с проводниками, — потери в линии. Это потеря мощности, выраженная в ваттах, и связана с рассеянием тепловой энергии, когда ток течет через сопротивление проводов линии.Потери в линии рассчитываются с использованием одного из уравнений мощности.
Используя предыдущий пример:
P = I 2 × R
P = (10A) 2 × 0,3 Ом
P = 30 Вт
* Помните:
- Падение напряжения в линии выражается в вольтах.
- Потери в линии выражены в ваттах.
Атрибуция
ТОПОЛОГИЯ ЦЕПЕЙ И ЗАКОНЫ — Прикладное промышленное электричество
На этой странице мы изложим три принципа, которые вы должны понимать в отношении последовательных цепей:
Ток : величина тока одинакова для любого компонента в последовательной цепи.
Сопротивление : Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
Напряжение : Напряжение питания в последовательной цепи равно сумме индивидуальных падений напряжения.
Давайте взглянем на несколько примеров последовательных цепей, демонстрирующих эти принципы. Начнем с последовательной схемы, состоящей из трех резисторов и одной батареи:
Рисунок 3.1
Первый принцип, который нужно понять о последовательных схемах, заключается в следующем:
Величина тока в последовательной цепи одинакова для любого компонента в цепи.
Общий ток серии
[латекс] \ tag {3.1} I_ {Total} = I_1 = I_2 = … = I_n [/ latex]
Это связано с тем, что в последовательной цепи есть только один путь для прохождения тока. Поскольку электрический заряд проходит через проводники, как шарики в трубке, скорость потока (скорость мрамора) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.
По расположению 9-вольтовой батареи мы можем сказать, что ток в этой цепи будет течь по часовой стрелке от точки 1 к 2, к 3 к 4 и обратно к 1. Однако у нас есть один источник напряжения и три сопротивления. Как мы можем использовать здесь закон Ома?
Однако у нас есть один источник напряжения и три сопротивления. Как мы можем использовать здесь закон Ома?
Важная оговорка к закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны относиться друг к другу в одних и тех же двух точках в цепи. Мы можем увидеть эту концепцию в действии на примере схемы с одним резистором ниже.
Использование закона Ома в простой цепи с одним резистором
В схеме с одной батареей и одним резистором мы можем легко вычислить любое количество, потому что все они относятся к одним и тем же двум точкам в цепи:
[латекс] I \: = \ frac {E} {R} [/ латекс]
[латекс] I \: = \ frac {9V} {3k \ Omega} [/ латекс]
[латекс] \ pmb {I = 3 мА} [/ латекс]
Поскольку точки 1 и 2 соединены вместе проводом с незначительным сопротивлением, как и точки 3 и 4, мы можем сказать, что точка 1 электрически является общей с точкой 2, а точка 3 электрически общей с точкой 4. Поскольку мы знаем, что между точками 1 и 4 (непосредственно через аккумулятор) имеется электродвижущая сила 9 В, и поскольку точка 2 является общей для точки 1, а точка 3 — общей для точки 4, мы также должны иметь 9 В между точками 2. и 3 (прямо через резистор).
Поскольку мы знаем, что между точками 1 и 4 (непосредственно через аккумулятор) имеется электродвижущая сила 9 В, и поскольку точка 2 является общей для точки 1, а точка 3 — общей для точки 4, мы также должны иметь 9 В между точками 2. и 3 (прямо через резистор).
Следовательно, мы можем применить закон Ома ( I = E / R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все термины (E, I, R) относятся к одним и тем же двум точкам в цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.
Использование закона Ома в схемах с несколькими резисторами
В схемах, содержащих более одного резистора, мы должны соблюдать осторожность при применении закона Ома. В приведенном ниже примере схемы с тремя резисторами мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию R 1 , R 2 и R . 3 . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, какое напряжение есть на любом из этих резисторов по отдельности.
Цифра 9 вольт — это всего величин для всей цепи, тогда как цифры 3 кОм, 10 кОм и 5 кОм представляют собой отдельных величин для отдельных резисторов. Если бы мы включили цифру для общего напряжения в уравнение закона Ома с цифрой для отдельного сопротивления, результат не будет точно соответствовать какой-либо величине в реальной цепи.
Для R 1 закон Ома будет связывать величину напряжения на R 1 с током через R 1 , учитывая сопротивление R 1 , 3 кОм:
[латекс] I_ {R1} \: = \ frac {E_ {R1}} {R_1} [/ latex] или [латекс] E_ {R1} = I_ {R1} {(R_1)} [/ latex]
Но, поскольку нам неизвестно напряжение на R 1 (только полное напряжение, подаваемое батареей на комбинацию из трех последовательно соединенных резисторов), и нам не известен ток через R 1 , мы можем ‘ t делать какие-либо расчеты по любой из формул.То же самое касается R 2 и R 3 : мы можем применять уравнения закона Ома тогда и только тогда, когда все члены представляют свои соответствующие количества между одними и теми же двумя точками в цепи.
Итак, что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации R 1 , R 2 и R 3 , и мы знаем сопротивление каждого резистора, но поскольку эти величины не входят в В том же контексте мы не можем использовать закон Ома для определения тока в цепи.Если бы мы только знали, что такое общее сопротивление для цепи: тогда мы могли бы вычислить общий ток с нашей цифрой для общего напряжения ( I = E / R ).
Объединение нескольких резисторов в эквивалентный общий резистор
Это подводит нас ко второму принципу последовательной схемы:
Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
[латекс] \ tag {3.2} R_ {total} = R_1 + R_2 + … + R_n [/ латекс]
Это должно иметь интуитивный смысл: чем больше последовательно подключенных резисторов, через которые должен протекать ток, тем труднее будет протекать ток.
В примере задачи у нас были последовательно подключены резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:
[латекс] R_ {total} = R_1 + R_2 + R_3 [/ латекс]
[латекс] R_ {total} = 3 \ text {k} \ Omega + 10 \ text {k} \ Omega + 5 \ text {k} \ Omega [/ latex]
[латекс] \ pmb {R_ {total} = 18 \ text {k} \ Omega} [/ latex]
По сути, мы вычислили эквивалентное сопротивление R 1 , R 2 и R 3 вместе взятых.Зная это, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R 1 , R 2 и R 3 :
Расчет тока цепи с использованием закона Ома
Теперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9 вольт) и сопротивление между точками 1 и 4 (18 кОм):
[латекс] I_ {total} \: = \ frac {E_ {total}} {R_ {total}} [/ латекс]
[латекс] \: = \ frac {9V} {18k \ Omega} [/ латекс]
[латекс] \ pmb {I_ {total} = 500 мкА} [/ латекс]
Расчет напряжений компонентов по закону Ома
Зная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток через батарею), мы можем вернуться к нашей исходной принципиальной схеме и отметить ток через каждый компонент:
Теперь, когда мы знаем величину тока, протекающего через каждый резистор, мы можем использовать закон Ома для определения падения напряжения на каждом из них (применяя закон Ома в его надлежащем контексте):
[латекс] E_ {R1} = I_ {R1} {R_1} [/ латекс]
[латекс] = (500 мкА) {(3кОм)} [/ латекс]
[латекс] \ pmb {E_ {R1} = 1.5V} [/ латекс]
[латекс] E_ {R2} = I_ {R2} {R_2} [/ латекс]
[латекс] = (500 мкА) {(10 кОм)} [/ латекс]
[латекс] \ pmb {E_ {R2} = 5V} [/ латекс]
[латекс] E_ {R3} = I_ {R3} {R_3} [/ латекс]
[латекс] = (500 мкА) {(5 кОм)} [/ латекс]
[латекс] \ pmb {E_ {R3} = 2.5V} [/ латекс]
Обратите внимание на падение напряжения на каждом резисторе, и как сумма падений напряжения (1,5 + 5 + 2,5) равна напряжению батареи (источника питания): 9 вольт.
Это третий принцип последовательных цепей:
Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Общее последовательное напряжение
[латекс] E_ {total} = E_1 + E_2 + … E_n \ tag {3.3} [/ latex]
Анализ схем простых последовательностей с помощью «табличного метода» и закона Ома
Однако метод, который мы только что использовали для анализа этой простой последовательной схемы, можно упростить для лучшего понимания.Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:
Таблица 3.1
Правило для такой таблицы — применять закон Ома только к значениям в каждом вертикальном столбце. Например, E R1 только с I R1 и R 1 ; E R2 только с I R2 и R 2 ; и т.д. Вы начинаете свой анализ с заполнения тех элементов таблицы, которые даны вам с самого начала:
Таблица 3.2
Как видно из расположения данных, мы не можем подать 9 вольт ET (полное напряжение) ни на одно из сопротивлений (R 1 , R 2 или R 3 ) в любая формула закона Ома, потому что они находятся в разных столбцах. Напряжение батареи 9 В составляет , а не , приложенное непосредственно к R 1 , R 2 или R 3 . Однако мы можем использовать наши «правила» для последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило ряда сопротивлений для определения общего сопротивления из суммы отдельных сопротивлений:
Таблица 3.3
Теперь, введя значение общего сопротивления в крайний правый столбец («Общее»), мы можем применить закон Ома I = E / R к общему напряжению и общему сопротивлению, чтобы получить общий ток 500 мкА. :
Таблица 3.4.
Затем, зная, что ток распределяется поровну между всеми компонентами последовательной цепи (еще одно «правило» последовательной схемы), мы можем заполнить токи для каждого резистора из только что рассчитанного значения тока:
Таблица 3.5.
Наконец, мы можем использовать закон Ома для определения падения напряжения на каждом резисторе, по столбцу за раз:
Таблица 3.6
Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: все компоненты имеют одинаковый ток; сопротивления складываются, чтобы равняться большему общему сопротивлению; а падение напряжения в сумме равняется большему общему напряжению. Все эти правила находят корень в определении последовательной цепи. Если вы понимаете это определение полностью, то правила — не более чем сноски к определению.
- Компоненты в последовательной цепи имеют одинаковый ток:
[латекс] I_ {Всего} = I_1 = I_2 = I_3 =… = I_n [/ latex]
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений:
[латекс] R_ {Всего} = R_1 + R_2 + … + R_n [/ латекс]
- Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения:
[латекс] E_ {Всего} = E_1 + E_2 + … + E_n [/ латекс]
В этом разделе мы изложим три принципа, которые вы должны понимать в отношении параллельных цепей:
Напряжение: Напряжение одинаково на всех компонентах параллельной цепи.
Ток: Полный ток цепи равен сумме токов отдельных ответвлений.
Сопротивление: Отдельные сопротивления уменьшают , чтобы равняться меньшему общему сопротивлению, вместо прибавляют , чтобы получить общее.
Давайте взглянем на несколько примеров параллельных цепей, демонстрирующих эти принципы.
Начнем с параллельной схемы, состоящей из трех резисторов и одной батареи:
Рисунок 3.5
Напряжение в параллельных цепях
Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи . Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени.
[латекс] E_ {Total} = E_1 = E_2 = … = E_n \ tag {3.4} [/ latex]
Следовательно, в приведенной выше схеме напряжение на R 1 равно напряжению на R 2 , которое равно напряжению на R 3 , которое равно напряжению на батарее.
Это равенство напряжений можно представить в другой таблице для наших начальных значений:
Таблица 3.7.
Применение закона Ома для простых параллельных схем
Как и в случае с последовательными цепями, применяется то же предостережение для закона Ома: значения напряжения, тока и сопротивления должны быть в одном контексте, чтобы вычисления работали правильно.
Однако в приведенном выше примере схемы мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что мы знаем напряжение на каждом резисторе (9 вольт) и сопротивление каждого резистора:
[латекс] I_ {R1} \: = \ frac {E_ {R1}} {R_1} [/ латекс]
[латекс] \: = \ frac {(9V)} {(10kΩ)} [/ latex]
[латекс] \ pmb {I_ {R1} \: = 0.9mA} [/ латекс]
[латекс] I_ {R2} \: = \ frac {E_ {R2}} {R_2} [/ латекс]
[латекс] \: = \ frac {(9V)} {(2kΩ)} [/ латекс]
[латекс] \ pmb {I_ {R2} \: = 4,5 мА} [/ латекс]
[латекс] I_ {R3} \: = \ frac {E_ {R3}} {R_3} [/ латекс]
[латекс] \: = \ frac {(9V)} {(1kΩ)} [/ латекс]
[латекс] \ pmb {I_ {R3} = 9mA} [/ латекс]
Таблица 3.8
На данный момент мы еще не знаем, каков полный ток или полное сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому столбцу («Всего»). Однако, если мы внимательно подумаем о том, что происходит, должно стать очевидным, что общий ток должен равняться сумме всех токов отдельных резисторов («ответвлений»):
Рис. 3.6
По мере того, как полный ток выходит из положительного (+) вывода аккумуляторной батареи в точке 1 и проходит по цепи, часть потока разделяется в точке 2, чтобы пройти через R 1 , еще часть разделяется в точке 3, чтобы уйти. через R 2 , а оставшаяся часть идет через R 3 .Подобно реке, разветвляющейся на несколько более мелких ручьев, общий расход всех потоков должен равняться расходу всей реки.
То же самое происходит, когда токи через R 1 , R 2 и R 3 соединяются, чтобы течь обратно к отрицательному выводу батареи (-) к точке 8: поток тока из точки 7 к точке 8 должна равняться сумме токов (ответвлений) через R 1 , R 2 и R 3 .
Это второй принцип параллельных цепей: общий ток цепи равен сумме токов отдельных ветвей .
Используя этот принцип, мы можем заполнить место ИТ на нашей таблице суммой I R1 , I R2 и I R3 :
Таблица 3.9
Как рассчитать полное сопротивление в параллельных цепях
Наконец, применив закон Ома к крайнему правому столбцу («Всего»), мы можем вычислить полное сопротивление цепи:
Таблица 3.10
Уравнение сопротивления в параллельных цепях
Обратите внимание на кое-что очень важное.Общее сопротивление цепи составляет всего 625 Ом: на меньше , чем у любого из отдельных резисторов. В последовательной цепи, где общее сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть на больше, чем на , чем у любого из резисторов по отдельности.
Здесь, в параллельной цепи, все наоборот: мы говорим, что отдельных сопротивлений уменьшают , а не прибавляют , чтобы получить общее .
Этот принцип завершает нашу триаду «правил» для параллельных цепей, точно так же, как было обнаружено, что у последовательных цепей есть три правила для напряжения, тока и сопротивления.
Математически соотношение между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом:
Уравнение сопротивления в параллельных цепях
[латекс] R_ {total} = \ frac {1} {\ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n}} \ tag {3.5 } [/ латекс]
Три правила параллельных цепей
Таким образом, параллельная цепь определяется как цепь, в которой все компоненты подключены между одним и тем же набором электрически общих точек.Другими словами, все компоненты подключены друг к другу через клеммы.
Из этого определения следуют три правила параллельных цепей:
Все компоненты имеют одинаковое напряжение.
Сопротивления уменьшаются до меньшего общего сопротивления.
Токи ответвления в сумме равняются большему полному току.
Как и в случае с последовательными цепями, все эти правила находят корень в определении параллельной цепи. Если вы понимаете это определение полностью, то правила — не более чем сноски к определению.
- Компоненты в параллельной цепи имеют одинаковое напряжение:
[латекс] E_ {Всего} = E_1 = E_2 = … = E_n [/ латекс]
- Общее сопротивление в параллельной цепи на меньше , чем любое из отдельных сопротивлений:
[латекс] R_ {Total} = \ frac {1} {\ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n}} [/ латекс]
- Полный ток в параллельной цепи равен сумме токов отдельных ответвлений:
[латекс] I_ {Всего} = I_1 + I_2 +.2R} [/ латекс]
Этим легко управлять, добавив еще одну строку в нашу знакомую таблицу напряжений, токов и сопротивлений:
Таблица 3.11 Мощность
для любого конкретного столбца таблицы может быть найдена с помощью соответствующего уравнения закона Ома ( соответствует на основе цифр, представленных для E, I и R в этом столбце).
Интересное правило для общей мощности по сравнению с индивидуальной мощностью состоит в том, что оно является аддитивным для любой конфигурации цепи : последовательной, параллельной, последовательной / параллельной или другой.Мощность — это мера скорости работы, и поскольку рассеиваемая мощность должна равняться полной мощности, подаваемой источником (источниками) (в соответствии с Законом сохранения энергии в физике), конфигурация схемы не влияет на математику.
- Мощность складывается в любая конфигурация резистивной цепи:
[латекс] P_ {Всего} = P_1 + P_2 + … + P_n [/ латекс]
Напоминания при использовании закона Ома
Одна из наиболее распространенных ошибок, которые делают начинающие студенты-электронщики при применении законов Ома, — это смешивание контекстов напряжения, тока и сопротивления.Другими словами, ученик может ошибочно использовать значение I (ток) через один резистор и значение E (напряжение) через набор соединенных между собой резисторов, полагая, что они придут к сопротивлению этого резистора.
Не так! Помните это важное правило: переменные, используемые в уравнениях закона Ома, должны быть , общими для одних и тех же двух точек в рассматриваемой цепи. Я не могу переоценить это правило. Это особенно важно в последовательно-параллельных комбинированных схемах, где соседние компоненты могут иметь разные значения для падения напряжения и тока .
При использовании закона Ома для вычисления переменной, относящейся к отдельному компоненту, убедитесь, что напряжение, на которое вы ссылаетесь, относится только к этому единственному компоненту, а ток, который вы ссылаетесь, проходит исключительно через этот единственный компонент, а сопротивление, на которое вы ссылаетесь, равно исключительно для этого единственного компонента. Аналогичным образом, при вычислении переменной, относящейся к набору компонентов в цепи, убедитесь, что значения напряжения, тока и сопротивления относятся только к этому полному набору компонентов!
Хороший способ запомнить это — обратить пристальное внимание на две точки , , завершающие анализируемый компонент или набор компонентов, убедившись, что напряжение, о котором идет речь, проходит через эти две точки, что рассматриваемый ток является потоком электрический заряд от одной из этих точек до другой точки, что рассматриваемое сопротивление эквивалентно одному резистору между этими двумя точками, и что рассматриваемая мощность — это полная мощность, рассеиваемая всеми компонентами между этими двумя точками .
Примечания к «табличному» методу анализа цепей
«Табличный» метод, представленный как для последовательных, так и для параллельных цепей в этой главе, является хорошим способом сохранить контекст закона Ома правильным для любой конфигурации цепи. В таблице, подобной приведенной ниже, вам разрешено применять уравнение закона Ома только для значений одного вертикального столбца за раз:
Таблица 3.12
Получение значений по горизонтали по столбцам допустимо в соответствии с принципами последовательных и параллельных цепей:
Таблица 3.13
Таблица 3.14
«Табличный» метод не только упрощает управление всеми соответствующими величинами, но также облегчает перекрестную проверку ответов, упрощая поиск исходных неизвестных переменных другими методами или работая в обратном направлении для решения исходных данные значения из ваших решений. Например, если вы только что решили для всех неизвестных напряжений, токов и сопротивлений в цепи, вы можете проверить свою работу, добавив строку внизу для расчета мощности на каждом резисторе, чтобы посмотреть, добавляются ли все отдельные значения мощности. до полной мощности.Если нет, значит, вы где-то ошиблись! Хотя в этой технике «перекрестной проверки» вашей работы нет ничего нового, использование таблицы для упорядочивания всех данных для перекрестной проверки (-ий) приводит к минимуму путаницы.
- Примените закон Ома к вертикальным столбцам в таблице.
- Примените правила последовательного / параллельного горизонтального ряда в таблице.
- Проверьте свои расчеты, работая «в обратном направлении», чтобы попытаться прийти к первоначально заданным значениям (из ваших первых рассчитанных ответов), или решив величину, используя более одного метода (из разных заданных значений).
Что такое закон напряжения Кирхгофа (KVL)?
Принцип, известный как Закон напряжения Кирхгофа (открытый в 1847 году немецким физиком Густавом Р. Кирхгофом), можно сформулировать так:
«Алгебраическая сумма всех напряжений в контуре должна равняться нулю»
[латекс] E_ {T} = E_1 + E_2 + … + E_n = 0 [/ латекс]
Под алгебраическим я подразумеваю учет знаков (полярностей), а также величин.Под петлей я подразумеваю любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи и, наконец, обратно в исходную точку.
Демонстрация закона напряжения Кирхгофа в последовательной цепи
Давайте еще раз посмотрим на нашу примерную последовательную схему, на этот раз пронумеровав точки в цепи для опорного напряжения:
Рисунок 3.7
Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, измеритель зарегистрировал бы +45 вольт.Обычно знак «+» не отображается, а скорее подразумевается для положительных показаний на дисплеях цифровых счетчиков. Однако для этого урока очень важна полярность показаний напряжения, поэтому я покажу положительные числа явно: E 2-1 = + 45V
Когда напряжение указано с двойным нижним индексом (символы «2-1» в обозначении «E 2-1 »), это означает напряжение в первой точке (2), измеренное относительно второй точки. (1). Напряжение, указанное как «E cd », будет означать напряжение, указанное цифровым измерителем с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно «D».
Рис. 3.8.
Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего измерителя на точке впереди и черным измерительным проводом на точке сзади, получим следующие показания:
[латекс] E_ {3-2} = -10V [/ латекс]
[латекс] E_ {4-3} = -20 В [/ латекс]
[латекс] E_ {1-4} = -15V [/ латекс]
Рис. 3.9.
. Мы уже должны быть знакомы с общим принципом для последовательных цепей, согласно которому отдельные падения напряжения в сумме составляют общее приложенное напряжение, но при измерении падений напряжения таким образом и обращении внимания на полярность (математический знак) показаний обнаруживается другое. аспект этого принципа: все измеренные напряжения в сумме равны нулю:
В приведенном выше примере петля образована следующими точками в следующем порядке: 1-2-3-4-1.Не имеет значения, с какой точки мы начинаем или в каком направлении идем, отслеживая петлю; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем подсчитать напряжения в контуре 3-2-1-4-3 той же цепи:
Это может иметь больше смысла, если мы перерисуем наш пример последовательной схемы так, чтобы все компоненты были представлены в виде прямой линии:
Рисунок 3.10
Это все та же последовательная схема, только с компонентами, расположенными в другой форме.Обратите внимание на полярность падения напряжения резистора по отношению к батарее: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторе ориентированы в другую сторону: положительное слева и отрицательное справа. Это потому, что резисторы сопротивляются потоку электрического заряда, проталкиваемого батареей. Другими словами, «толчок», оказываемый резисторами против потока электрического заряда , должен, , происходить в направлении, противоположном источнику электродвижущей силы.
Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, черный провод слева и красный провод справа, как показано горизонтально:
Рисунок 3.11
Если бы мы взяли тот же вольтметр и измерили напряжение по комбинациям компонентов, начиная с единственного R 1 слева и продвигаясь по всей цепочке компонентов, мы увидим, как напряжения складываются алгебраически (до нуля):
Рисунок 3.12
Тот факт, что последовательные напряжения складываются, не должен быть загадкой, но мы заметили, что полярность этих напряжений сильно влияет на то, как складываются цифры. При считывании напряжения на R 1 —R 2 и R 1 —R 2 —R 3 (я использую символ «двойное тире» «-» для обозначения серии соединение между резисторами R 1 , R 2 и R 3 ), мы видим, как измеряемые напряжения последовательно увеличиваются (хотя и отрицательные) величины, потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (положительный левый , отрицательный справа).Сумма падений напряжения на R 1 , R 2 и R 3 равна 45 вольт, что соответствует выходу батареи, за исключением того, что полярность батареи противоположна падению напряжения на резисторе (отрицательный слева, положительный справа), поэтому мы получаем 0 вольт, измеренный на всей цепочке компонентов.
То, что мы должны получить ровно 0 вольт на всей струне, тоже не должно быть тайной. Глядя на схему, мы видим, что крайний левый угол струны (левая сторона R 1 : точка номер 2) напрямую соединен с крайним правым концом струны (правая сторона батареи: точка номер 2), так как необходимо для завершения схемы.Поскольку эти две точки соединены напрямую, они электрически общие, друг с другом. И, как таковое, напряжение между этими двумя электрически общими точками должно быть равным нулю.
Демонстрация закона напряжения Кирхгофа в параллельной цепи
Закон Кирхгофа о напряжении (иногда для краткости обозначаемый как KVL ) будет работать для любой конфигурации цепи вообще, а не только для простой серии. Обратите внимание, как это работает для этой параллельной цепи:
Рисунок 3.13
В параллельной схеме напряжение на каждом резисторе такое же, как и напряжение питания: 6 вольт. Суммируя напряжения вокруг контура 2-3-4-5-6-7-2, получаем:
Обратите внимание, как я обозначил конечное (суммарное) напряжение как E 2-2 . Поскольку мы начали нашу пошаговую последовательность в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E 2-2 ), которое, конечно, должно быть равно нулю. .
Действие закона Кирхгофа о напряжении независимо от топологии цепи
Тот факт, что эта схема является параллельной, а не последовательной, не имеет ничего общего с правомерностью закона Кирхгофа о напряжении. В этом отношении схема может быть «черным ящиком» — конфигурация ее компонентов полностью скрыта от нашего взгляда, с набором открытых клемм для измерения напряжения между ними — и KVL все равно останется верным:
Рис. 3.14.
Попробуйте выполнить любой порядок шагов с любого терминала на приведенной выше диаграмме, возвращаясь к исходному терминалу, и вы обнаружите, что алгебраическая сумма напряжений всегда равна нулю.
Более того, «петля», которую мы отслеживаем для KVL, даже не обязательно должна быть реальным током в прямом смысле этого слова. Все, что нам нужно сделать, чтобы соответствовать KVL, — это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между следующей и последней точкой. Рассмотрим этот абсурдный пример, отслеживая «петлю» 2-3-6-3-2 в той же параллельной цепи резистора:
Рисунок 3.15
Использование закона напряжения Кирхгофа в сложной цепи
KVL можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вокруг определенного «контура».В качестве примера возьмем следующую сложную схему (фактически две последовательные цепи, соединенные одним проводом внизу):
Рисунок 3.16
Чтобы упростить задачу, я опустил значения сопротивления и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют общий провод между собой (провод 7-8-9-10), что позволяет измерять напряжение между двумя цепями.
Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение KVL с напряжением между этими точками как неизвестным:
[латекс] E_ {4-3} + E_ {9-4} + E_ {8-9} + E_ {3-8} = 0 [/ латекс]
[латекс] E_ {4-3} + 12 В + 0 В + 20 В = 0 В [/ латекс]
[латекс] E_ {4-3} + 32V = 0 [/ латекс]
[латекс] \ pmb {E_ {4-3} = -32V} [/ латекс]
Рисунок 3.17 Рисунок 3.18 Рисунок 3.19 Рисунок 3.20
Обходя контур 3-4-9-8-3, мы записываем значения падения напряжения так, как их регистрировал цифровой вольтметр, измеряя с помощью красного измерительного провода на острие впереди и черного измерительного провода на точка позади, когда мы продвигаемся по петле. Следовательно, напряжение от точки 9 до точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» — в точке 4. Напряжение от точки 3 до точки 8 является положительным (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» — в точке 8.Напряжение от точки 8 до точки 9, конечно, равно нулю, потому что эти две точки электрически общие.
Наш окончательный ответ для напряжения от точки 4 до точки 3 — отрицательное (-) 32 вольта, что говорит нам, что точка 3 на самом деле положительна по отношению к точке 4, именно то, что цифровой вольтметр показал бы красным проводом в точке 4. и черный отрыв в точке 3:
Рис. 3.21.
Другими словами, первоначальное размещение наших «выводов счетчика» в этой проблеме KVL было «задом наперед».«Если бы мы сгенерировали наше уравнение KVL, начиная с E 3-4 вместо E 4-3 , шагая по той же петле с противоположной ориентацией измерительных проводов, окончательный ответ был бы E 3-4 = + 32 вольта:
Рис. 3.22
Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.
- Закон Кирхгофа о напряжении (KVL): «Алгебраическая сумма всех напряжений в контуре должна равняться нулю»
Что такое действующий закон Кирхгофа ?
Закон Кирхгофа о течениях, часто сокращаемый до KCL, гласит, что «алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю».
Этот закон используется для описания того, как заряд входит и покидает точку соединения или узел на проводе.
Вооружившись этой информацией, давайте теперь рассмотрим пример применения закона на практике, почему он важен и как он был получен.
Обзор параллельной цепи
Давайте внимательнее рассмотрим эту последнюю параллельную схему примера:
Рисунок 3.23 Таблица 3.15
Решение для всех значений напряжения и тока в этой цепи:
На данный момент мы знаем значение тока каждой ветви и полного тока в цепи. Мы знаем, что полный ток в параллельной цепи должен равняться сумме токов ответвления, но в этой цепи происходит нечто большее, чем просто это.Взглянув на токи в каждой точке соединения проводов (узле) в цепи, мы должны увидеть кое-что еще:
Рисунок 3.24
3.7. 3 тока на входе и выходе из узла
В каждом узле положительной «шины» (провода 1-2-3-4) у нас есть разделение тока от основного потока к каждому последующему резистору ответвления. В каждом узле отрицательной «шины» (провод 8-7-6-5) у нас есть ток, сливающийся вместе, чтобы сформировать основной поток от каждого последовательного резистора ответвления.Этот факт должен быть довольно очевиден, если вы подумаете об аналогии контура водопровода с каждым ответвлением, действующим как тройник, разделением или слиянием потока воды с основным трубопроводом, когда он движется от выхода водяного насоса к обратному каналу. резервуар или отстойник.
Если мы внимательно рассмотрим один конкретный узел «тройник», такой как узел 6, мы увидим, что ток, входящий в узел, равен по величине току, выходящему из узла:
Рисунок 3.25
Сверху и справа у нас есть два тока, входящие в соединение проводов, обозначенное как узел 6.Слева у нас есть единственный ток, выходящий из узла, равный по величине сумме двух входящих токов. Чтобы обратиться к аналогии с водопроводом: пока в трубопроводе нет утечек, поток, поступающий в фитинг, должен также выходить из фитинга. Это верно для любого узла («подгонки»), независимо от того, сколько потоков входит или выходит. Математически мы можем выразить это общее соотношение как таковое: [латекс] I_ {существующий} = I_ {ввод} [/ латекс]
Действующий закон Кирхгофа
г.Кирхгоф решил выразить его в несколько иной форме (хотя и математически эквивалентной), назвав его Текущий закон Кирхгофа (KCL):
.
[латекс] I_ {ввод} = -I_ {существующий} = 0 [/ латекс]
Текущий закон Кирхгофа, кратко изложенный в одной фразе, гласит:
«Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
[латекс] I_ {T} = I_1 + I_2 + … + I_n = 0 [/ латекс]
То есть, если мы присвоим каждому току математический знак (полярность), обозначающий, входят ли они (+) или выходят (-) из узла, мы можем сложить их вместе, чтобы гарантированно получить в сумме ноль.
Взяв наш пример узла (номер 6), мы можем определить величину тока, выходящего слева, задав уравнение KCL с этим током в качестве неизвестного значения:
[латекс] I_2 + I_3 + I_ {2 + 3} = 0 [/ латекс]
[латекс] 2 мА + 3 мА + I_ {2 + 3} = 0 [/ латекс]
[латекс] \ text {… решение для I …} [/ латекс]
[латекс] I = -2 мА-3 мА [/ латекс]
[латекс] \ pmb {I = -5mA} [/ латекс]
Отрицательный знак (-) на значении 5 миллиампер говорит нам, что ток на выходе из узла, в отличие от токов 2 миллиампер и 3 миллиампер, которые оба должны быть положительными (и, следовательно, входит в узел) .Независимо от того, обозначает ли отрицательное или положительное значение текущий вход или выход, совершенно произвольно, если они являются противоположными знаками для противоположных направлений и мы остаемся последовательными в наших обозначениях, KCL будет работать.
Вместе законы напряжения и тока Кирхгофа представляют собой прекрасную пару инструментов, полезных при анализе электрических цепей. Их полезность станет еще более очевидной в следующей главе («Сетевой анализ»), но достаточно сказать, что эти законы заслуживают того, чтобы их запомнил изучающий электронику не меньше, чем закон Ома.
- Текущий закон Кирхгофа (KCL): «Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
Учебное пособие по физике
: схемы серии
Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением. Когда все устройства соединены последовательным соединением, схема называется последовательной схемой .В последовательной цепи каждое устройство подключается таким образом, что существует только один путь, по которому заряд может проходить через внешнюю цепь. Каждый заряд, проходящий через контур внешней цепи, будет последовательно проходить через каждый резистор.
Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов к последовательной цепи приводит к довольно ожидаемому результату — увеличению общего сопротивления. .Поскольку в цепи есть только один путь, каждый заряд встречает сопротивление каждого устройства; поэтому добавление большего количества устройств приводит к большему общему сопротивлению. Это повышенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).
Эквивалентное сопротивление и ток
Заряды проходят через внешнюю цепь со скоростью, которая везде одинакова. В одном месте сила тока не больше, чем в другом.Фактическое количество тока обратно пропорционально общему сопротивлению. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Что касается батареи, которая нагнетает заряд, наличие двух последовательно соединенных резисторов с сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора с сопротивлением 12 Ом. Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом.А наличие четырех последовательно соединенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора 24 Ом.
Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи — это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в цепи. Для последовательных цепей математическая формула для вычисления эквивалентного сопротивления (R eq ) составляет
.
R экв = R 1 + R 2 + R 3 +…
, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, соединенных последовательно.
Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance , расположенного ниже. Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.
Ток в последовательной цепи везде одинаковый.Заряд НЕ накапливается и не начинает накапливаться в любом конкретном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами, поэтому в одном месте его меньше по сравнению с другим. Можно представить, что заряды движутся вместе по проводам электрической цепи и везде движутся с одинаковой скоростью. Ток — скорость, с которой течет заряд — везде одинаков. То же самое на первом резисторе, как на последнем резисторе, как в батарее.Математически можно написать
I аккумулятор = I 1 = I 2 = I 3 = …
, где I 1 , I 2 и I 3 — значения тока в точках расположения отдельных резисторов.
Эти значения тока легко вычислить, если известно напряжение батареи и отдельные значения сопротивления. Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление.А используя закон Ома (ΔV = I • R), можно определить ток в батарее и, следовательно, через каждый резистор, найдя соотношение напряжения батареи и эквивалентного сопротивления.
I аккумулятор = I 1 = I 2 = I 3 = ΔV аккумулятор / R экв
Разность электрических потенциалов и падения напряжения
Как обсуждалось в Уроке 1, электрохимическая ячейка цепи подает энергию на заряд, чтобы перемещать его через ячейку и устанавливать разность электрических потенциалов на двух концах внешней цепи.Элемент с напряжением 1,5 В создает разность электрических потенциалов во внешней цепи 1,5 В. Это означает, что электрический потенциал на положительной клемме на 1,5 В больше, чем на отрицательной клемме. Когда заряд движется по внешней цепи, он теряет 1,5 вольт электрического потенциала. Эта потеря электрического потенциала обозначается как падение напряжения . Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. Д.).) внутри резисторов или нагрузок. Если электрическая цепь, питаемая элементом на 1,5 В, оснащена более чем одним резистором, то совокупная потеря электрического потенциала составляет 1,5 В. На каждом резисторе есть падение напряжения, но сумма этих падений составляет 1,5 В — то же самое, что и номинальное напряжение источника питания. Эта концепция может быть выражена математически следующим уравнением:
ΔV аккумулятор = ΔV 1 + ΔV 2 + ΔV 3 +…
Чтобы проиллюстрировать этот математический принцип в действии, рассмотрим две схемы, показанные ниже на диаграммах A и B. Предположим, вас попросили определить два неизвестных значения разности электрических потенциалов между лампочками в каждой цепи. Чтобы определить их значения, вам нужно будет использовать приведенное выше уравнение. Батарея обозначается обычным схематическим символом, а рядом с ней указывается ее напряжение. Определите падение напряжения для двух лампочек, а затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.
Ранее в Уроке 1 обсуждалось использование диаграммы электрических потенциалов. Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.
Схема, показанная на схеме выше, питается от источника энергии 12 В.В цепи последовательно соединены три резистора, каждый из которых имеет собственное падение напряжения. Отрицательный знак разности электрических потенциалов просто означает потерю электрического потенциала при прохождении через резистор. Обычный ток направляется по внешней цепи от положительного вывода к отрицательному. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительного вывода, точка A на схеме находится на положительном выводе или выводе с высоким потенциалом.В точке A электрический потенциал 12 вольт, а в точке H (отрицательный вывод) — 0 вольт. Проходя через батарею, заряд приобретает электрический потенциал 12 вольт. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются в три этапа, каждый из которых соответствует прохождению через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда.Поскольку точки A и B разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через свой первый резистор, он теряет 3 В электрического потенциала и падает до 9 В в точке C. точка D отделена от точки C простым проводом, она имеет практически тот же электрический потенциал 9 В, что и C. Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает до 2 В в точке E Поскольку точка F отделена от точки E простым проводом, она имеет практически тот же электрический потенциал 2 В, что и E.Наконец, когда заряд проходит через свой последний резистор, он теряет 2 В электрического потенциала и падает до 0 В в точке G. схема снова. Прирост энергии обеспечивается аккумулятором при перемещении заряда с H на A.
В Уроке 3 закон Ома (ΔV = I • R) был представлен как уравнение, которое связывает падение напряжения на резисторе с сопротивлением резистора и током на резисторе.Уравнение закона Ома можно использовать для любого отдельного резистора в последовательной цепи. При объединении закона Ома с некоторыми принципами, уже обсужденными на этой странице, возникает большая идея.
В последовательных цепях наибольшее падение напряжения имеет резистор с наибольшим сопротивлением.
Поскольку в последовательной цепи ток везде одинаковый, значение I ΔV = I • R одинаково на каждом из резисторов последовательной цепи. Таким образом, падение напряжения (ΔV) будет изменяться с изменением сопротивления.Где бы сопротивление ни было наибольшим, падение напряжения будет наибольшим у этого резистора. Уравнение закона Ома можно использовать не только для прогнозирования того, что резистор в последовательной цепи будет иметь наибольшее падение напряжения, но и для расчета фактических значений падения напряжения.
| Δ В 1 = I • R 1 | Δ V 2 = I • R 2 | Δ V 3 = I • R 3 |
Математический анализ последовательных цепей
Приведенные выше принципы и формулы могут использоваться для анализа последовательной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в последовательной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R eq ), тока в батарее (I — ), а также падений напряжения и тока для каждого из трех резисторов.
Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.
R экв = R 1 + R 2 + R 3 = 17 Ом + 12 Ом + 11 Ом = 40 Ом
Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома.При использовании уравнения закона Ома (ΔV = I • R) для определения тока в цепи важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:
I tot = ΔV аккумулятор / R eq = (60 В) / (40 Ом) = 1,5 А
Значение тока 1,5 А — это ток в месте расположения батареи. Для последовательной цепи без точек разветвления ток везде одинаковый.Ток в месте расположения батареи такой же, как ток в каждом месте резистора. Впоследствии 1,5 ампер — это значение I 1 , I 2 и I 3 .
I аккумулятор = I 1 = I 2 = I 3 = 1,5 А
Осталось определить три значения — падение напряжения на каждом отдельном резисторе. Закон Ома снова используется для определения падения напряжения для каждого резистора — это просто произведение тока на каждом резисторе (вычисленное выше как 1.5 ампер) и сопротивление каждого резистора (указанное в постановке задачи). Расчеты показаны ниже.
| ΔV 1 = I 1 • R 1 ΔV 1 = (1,5 A) • (17 Ом) ΔV 1 = 25,5 В | ΔV 2 = I 2 • R 2 ΔV 2 = (1,5 A) • (12 Ом) ΔV 2 = 18 В | ΔV 3 = I 3 • R 3 ΔV 3 = (1.5 А) • (11 Ом) ΔV 3 = 16,5 В |
В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма падений напряжения для каждого отдельного резистора равна номинальному напряжению батареи. Другими словами, ΔV батареи = ΔV 1 + ΔV 2 + ΔV 3 ?
Является ли ΔV батареи = ΔV 1 + ΔV 2 + ΔV 3 ?
Это 60 В = 25.5 В + 18 В + 16,5 В?
60 В = 60 В?
Да !!
Математический анализ этой последовательной схемы включал смесь концепций и уравнений. Как это часто бывает в физике, отделение понятий от уравнений при принятии решения физической проблемы является опасным актом. Здесь необходимо учитывать концепции, согласно которым ток везде одинаков и что напряжение батареи эквивалентно сумме падений напряжения на каждом резисторе, чтобы завершить математический анализ.В следующей части Урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход сочетания концепций с уравнениями будет не менее важен для этого анализа.
Мы хотели бы предложить …
Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключать их так, как хотите. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение.Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Проверьте свое понимание
1. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:
а. Два последовательно включенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора сопротивлением 3 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора сопротивлением 5 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.
г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
ф. Три резистора с сопротивлением 12 Ом, 3 Ом и 21 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.
2. По мере увеличения количества резисторов в последовательной цепи общее сопротивление __________ (увеличивается, уменьшается, остается прежним) и ток в цепи __________ (увеличивается, уменьшается, остается прежним).
3. Рассмотрим следующие две схемы последовательных цепей. На каждой диаграмме используйте стрелки, чтобы указать направление обычного тока. Затем сравните напряжение и ток в обозначенных точках для каждой диаграммы.
4. Три одинаковые лампочки подключены к D-ячейке, как показано справа.Какое из следующих утверждений верно?
а. Все три лампочки будут иметь одинаковую яркость.
г. Лампа между X и Y будет самой яркой.
г. Лампа между Y и Z будет самой яркой.
г. Лампочка между Z и батареей будет самой яркой.
5. Три одинаковые лампочки подключены к батарее, как показано справа.Какие настройки можно внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все подходящие варианты.
а. Увеличьте сопротивление одной из лампочек.
г. Увеличьте сопротивление двух лампочек.
г. Уменьшите сопротивление двух лампочек.
г. Увеличьте напряжение аккумулятора.
e. Уменьшите напряжение аккумулятора.
ф. Удалите одну из луковиц.
6. Три одинаковые лампочки подключены к батарее, как показано справа. W, X, Y и Z обозначают места на трассе. Какое из следующих утверждений верно?
а. Разница потенциалов между X и Y больше, чем между Y и Z.
г. Разница потенциалов между X и Y больше, чем между Y и W.
г. Разница потенциалов между Y и Z больше, чем между Y и W.
г. Разница потенциалов между X и Z больше, чем между Z и W.
e. Разность потенциалов между X и W больше, чем на батарее.
ф. Разница потенциалов между X и Y больше, чем между Z и W.
7.Сравните схему X и Y ниже. Каждый питается от 12-вольтовой батареи. Падение напряжения на резисторе 12 Ом в цепи Y равно ____ падению напряжения на единственном резисторе в цепи X.
а. меньше чем
г. больше
г. то же, что
8. Аккумулятор на 12 В, резистор на 12 Ом и лампочка подключаются, как показано на схеме X ниже.Резистор на 6 Ом добавлен к резистору на 12 Ом и лампочке, чтобы создать цепь Y, как показано. Лампочка появится ____.
а. диммер в контуре X
г. диммер в контуре Y
г. одинаковая яркость в обеих цепях
9. Три резистора включены последовательно. При размещении в цепи с источником питания 12 В.Определите эквивалентное сопротивление, полный ток цепи, падение напряжения и ток на каждом резисторе.
Схемы простой серии | Последовательные и параллельные схемы
На этой странице мы изложим три принципа, которые вы должны понимать в отношении последовательных цепей:
- Ток : величина тока одинакова для любого компонента в последовательной цепи.
- Сопротивление : Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
- Напряжение : Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Давайте взглянем на несколько примеров последовательных цепей, демонстрирующих эти принципы.
Начнем с последовательной схемы, состоящей из трех резисторов и одной батареи:
Первый принцип работы с последовательными цепями заключается в следующем:
Величина тока в последовательной цепи одинакова для любого компонента в цепи.
Это связано с тем, что в последовательной цепи есть только один путь для прохождения тока. Поскольку электрический заряд проходит через проводники, как шарики в трубке, скорость потока (скорость мрамора) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.
Использование закона Ома в последовательных цепях
По расположению 9-вольтовой батареи мы можем сказать, что ток в этой цепи будет течь по часовой стрелке, от точки 1 к 2, к 3 к 4 и обратно к 1.Однако у нас есть один источник напряжения и три сопротивления. Как мы можем использовать здесь закон Ома?
Важная оговорка к закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны относиться друг к другу в одних и тех же двух точках в цепи. Мы можем увидеть эту концепцию в действии на примере схемы с одним резистором ниже.
Использование закона Ома в простой цепи с одним резистором
В схеме с одной батареей и одним резистором мы можем легко вычислить любое количество, потому что все они относятся к одним и тем же двум точкам в цепи:
Поскольку точки 1 и 2 соединены вместе проводом с незначительным сопротивлением, как и точки 3 и 4, мы можем сказать, что точка 1 электрически является общей с точкой 2, а точка 3 электрически общей с точкой 4.Поскольку мы знаем, что у нас есть 9 вольт электродвижущей силы между точками 1 и 4 (непосредственно через батарею), и поскольку точка 2 является общей для точки 1, а точка 3 — общей для точки 4, мы также должны иметь 9 вольт между точками 2 и 3. (прямо через резистор).
Следовательно, мы можем применить закон Ома (I = E / R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все термины (E, I, R) относятся к одним и тем же двум точкам в цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.
Использование закона Ома в схемах с несколькими резисторами
В схемах, содержащих более одного резистора, мы должны соблюдать осторожность при применении закона Ома. В приведенном ниже примере схемы с тремя резисторами мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию R 1 , R 2 и R . 3 . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, какое напряжение есть на любом из этих резисторов по отдельности.
Цифра 9 вольт — это всего величин для всей цепи, тогда как цифры 3 кОм, 10 кОм и 5 кОм представляют собой отдельных величин для отдельных резисторов. Если бы мы включили цифру для общего напряжения в уравнение закона Ома с цифрой для отдельного сопротивления, результат не будет точно соответствовать какой-либо величине в реальной цепи.
Для R 1 закон Ома будет связывать величину напряжения на R 1 с током через R 1 , учитывая сопротивление R 1 , 3 кОм:
Но, поскольку нам неизвестно напряжение на R 1 (только полное напряжение, подаваемое батареей на комбинацию из трех последовательно соединенных резисторов), и нам не известен ток через R 1 , мы можем ‘ t делать какие-либо расчеты по любой из формул.То же самое касается R 2 и R 3 : мы можем применять уравнения закона Ома тогда и только тогда, когда все члены представляют свои соответствующие количества между одними и теми же двумя точками в цепи.
Итак, что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации R 1 , R 2 и R 3 , и мы знаем сопротивление каждого резистора, но поскольку эти величины не входят в В том же контексте мы не можем использовать закон Ома для определения тока в цепи.Если бы мы только знали, каково общее сопротивление для цепи: тогда мы могли бы вычислить общий ток с нашей цифрой для общего напряжения (I = E / R).
Объединение нескольких резисторов в эквивалентный общий резистор
Это подводит нас ко второму принципу последовательной схемы:
Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
Это должно иметь интуитивный смысл: чем больше последовательно подключенных резисторов, через которые должен протекать ток, тем труднее будет протекать ток.
В примере задачи у нас были последовательно подключены резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:
По сути, мы вычислили эквивалентное сопротивление R 1 , R 2 и R 3 вместе взятых. Зная это, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R 1 , R 2 и R 3 :
Расчет тока цепи по закону Ома
Теперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9 вольт) и сопротивление между точками 1 и 4 (18 кОм):
Расчет напряжений компонентов по закону Ома
Зная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток через батарею), мы можем вернуться к нашей исходной принципиальной схеме и отметить ток через каждый компонент:
Теперь, когда мы знаем величину тока, протекающего через каждый резистор, мы можем использовать закон Ома для определения падения напряжения на каждом из них (применяя закон Ома в его надлежащем контексте):
Обратите внимание на падение напряжения на каждом резисторе и на то, как падает сумма напряжений (1.5 + 5 + 2,5) равно напряжению аккумулятора (питания): 9 вольт.
Это третий принцип последовательных цепей:
Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Анализ простых последовательных цепей с помощью «табличного метода» и закона Ома
Однако метод, который мы только что использовали для анализа этой простой последовательной схемы, можно упростить для лучшего понимания. Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:
Правило с такой таблицей — применять закон Ома только к значениям в каждом вертикальном столбце.Например, E R1 только с I R1 и R 1 ; E R2 только с I R2 и R 2 ; и т.д. Вы начинаете свой анализ с заполнения тех элементов таблицы, которые даны вам с самого начала:
Как вы можете видеть из расположения данных, мы не можем подать 9 вольт ET (полное напряжение) ни на одно из сопротивлений (R 1 , R 2 или R 3 ) ни при каких условиях. Формула закона Ома, потому что они находятся в разных столбцах.Напряжение батареи 9 В составляет , а не , приложенное непосредственно к R 1 , R 2 или R 3 . Однако мы можем использовать наши «правила» для последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило ряда сопротивлений для определения общего сопротивления из суммы отдельных сопротивлений:
Теперь, когда значение общего сопротивления вставлено в крайний правый столбец («Всего»), мы можем применить закон Ома I = E / R к общему напряжению и общему сопротивлению, чтобы получить общий ток 500 мкА:
Затем, зная, что ток распределяется поровну между всеми компонентами последовательной цепи (еще одно «правило» последовательной схемы), мы можем ввести токи для каждого резистора из только что рассчитанного значения тока:
Наконец, мы можем использовать закон Ома для определения падения напряжения на каждом резисторе, по столбцу за раз:
Проверка расчетов с помощью компьютерного анализа (SPICE)
Ради удовольствия, мы можем использовать компьютер для автоматического анализа этой самой схемы.Это будет хороший способ проверить наши расчеты, а также познакомиться с компьютерным анализом. Во-первых, мы должны описать схему компьютеру в формате, распознаваемом программным обеспечением.
Программа SPICE, которую мы будем использовать, требует, чтобы все электрически уникальные точки в цепи были пронумерованы, а размещение компонентов понималось по тому, какие из этих пронумерованных точек или «узлов» они разделяют. Для ясности я пронумеровал четыре угла схемы в нашем примере с 1 по 4. SPICE, однако, требует, чтобы где-то в схеме был нулевой узел, поэтому я перерисую схему, немного изменив схему нумерации:
Все, что я здесь сделал, это изменил нумерацию нижнего левого угла цепи на 0 вместо 4.Теперь я могу ввести несколько строк текста в компьютерный файл, описывающий схему в терминах, понятных SPICE, вместе с парой дополнительных строк кода, предписывающих программе отображать данные о напряжении и токе для нашего удовольствия от просмотра. Этот компьютерный файл известен как список цепей в терминологии SPICE:
последовательная цепь v1 1 0 г1 1 2 3к r2 2 3 10к r3 3 0 5k .dc v1 9 9 1 .print dc v (1,2) v (2,3) v (3,0) .конец
Теперь все, что мне нужно сделать, это запустить программу SPICE для обработки списка соединений и вывода результатов:
| версия 1 | в (1,2) | v (2,3) | v (3) | я (v1) |
|---|---|---|---|---|
| 9.000E + 00 | 1.500E + 00 | 5.000E + 00 | 2.500E + 00 | -5.000E-04 |
Эта распечатка сообщает нам, что напряжение аккумулятора составляет 9 вольт, а падение напряжения на R 1 , R 2 и R 3 составляет 1,5 В, 5 В и 2,5 В соответственно. Падения напряжения на любом компоненте в SPICE обозначаются номерами узлов, между которыми находится компонент, поэтому v (1,2) относится к напряжению между узлами 1 и 2 в цепи, которые являются точками, между которыми находится резистор R 1 . .
Порядок номеров узлов важен: когда SPICE выводит число для v (1,2), он учитывает полярность так же, как если бы мы держали вольтметр с красным измерительным проводом на узле 1 и черным измерительным проводом на узел 2. У нас также есть дисплей, показывающий ток (хотя и с отрицательным значением) на уровне 0,5 мА или 500 мкА. Итак, наш математический анализ подтвержден компьютером. Эта цифра отображается как отрицательное число в анализе SPICE из-за необычного способа обработки текущих вычислений SPICE.
Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: все компоненты имеют одинаковый ток; сопротивления складываются, чтобы равняться большему общему сопротивлению; а падение напряжения в сумме равняется большему общему напряжению. Все эти правила находят корень в определении последовательной цепи. Если вы понимаете это определение полностью, то правила — не более чем сноски к определению.
ОБЗОР:
- Компоненты в последовательной цепи имеют одинаковый ток: I Всего = I 1 = I 2 =.. . Я н
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: RTotal = R 1 + R 2 +. . . R n
- Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения E Всего = E 1 + E 2 +. . . En
Попробуйте наш Калькулятор закона Ома в разделе Инструменты .
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Ошибка разрыва связи
Приборная доска
Ресурсы по физике
Перейти к содержанию
Приборная доска
Авторизоваться
Панель приборов
Календарь
Входящие
История
Помощь
Закрывать
-
Мой Dashboard
- Физические ресурсы
- Домашняя страница
- Модули
- Руководства
- Лаборатории
- Часто задаваемые вопросы в лаборатории
- Проблемы
- Сочетания клавиш
- Видео по физике
- Интерактивные демонстрации лекций
К сожалению, вы обнаружили неработающую ссылку!
В чем разница между последовательными и параллельными схемами | ОРЕЛ
О нет! Почему не горят рождественские огни? О, вы думали, что было бы забавно вытащить одну из лампочек, а теперь все пошло прахом! Если вы одна из тех несчастных душ, которым удалось затемнить всю свою световую установку, не печальтесь, вы не одиноки.Каждый год миллионы огней по всему миру гаснут, чтобы получить один важный урок — научить вас различать между последовательными и параллельными цепями!
Во-первых, основы
Прежде чем мы углубимся в разницу между последовательными и параллельными цепями, давайте рассмотрим некоторые основные термины, которые мы будем обсуждать.
- Ток. У электричества есть работа, и когда электроны движутся по цепи, действует ток.
- Схема. Если это замкнутый непрерывный путь, то по нему будет течь электричество. На этом пути электричество может творить массу удивительных вещей, например, приводить в действие ваш смартфон или отправлять людей в космос!
- Сопротивление. Это то, с чем сталкивается электричество, когда оно течет по физическому материалу, будь то медный провод или простой старый резистор. Сопротивление ограничивает прохождение электрического тока.
Ниже вы найдете изображение простой схемы, которая включает батарею, выключатель и лампочку.
Самая простая из схем питания лампочки от аккумулятора.
Сезон сериала
Давайте вернемся к нашим рождественским огням, чтобы понять, как именно работает схема, соединенная последовательно. Скажем, у вас есть цепочка огней, соединенных одна за другой. Если вы посмотрите на схему, это будет выглядеть примерно так:
Ваши рождественские гирлянды последовательно, обратите внимание, что все гирлянды подключены друг за другом. (Источник изображения)
Что будет делать ток, когда мы подключим наш светильник к розетке? Давайте проследим за потоком:
- Включение. Когда мы включаем рождественские гирлянды в розетку, в розетке начинает течь ток.
- Плывёт. Затем он движется по жиле медной проволоки и сквозь наш рождественский свет, заставляя их ярко светиться.
- Возвращаюсь домой. Когда наш ток достигает конца нашей светящейся нити, он направляется к земле, чтобы немного отдохнуть, и цикл продолжается.
Неважно, какие компоненты вы размещаете в последовательной цепи, вы можете смешивать и сочетать конденсаторы, резисторы, светодиоды и несколько рождественских гирлянд вместе, и ток по-прежнему будет течь одинаково от одной части к другой. .
Вот здесь, как правило, гаснут рождественские огни. Что произойдет, если вы выдернете одну из этих лампочек в своей цепочке огней? Если ваши фары похожи на наши, то все они выключены! Почему это? Подумайте об этом: если ток течет от света к свету, и вы нарушаете эту связь, то вы перекрываете путь, по которому пытается течь электричество. Это называется обрыв цепи .
Ток и сопротивление в серии
Существует фундаментальный закон Вселенной, который следует помнить о том, как ток и сопротивление работают в последовательной цепи:
Чем больше работы (сопротивления) выполняет последовательная цепь, тем сильнее уменьшается ее ток.
Имеет смысл, правда? По мере того, как вы добавляете в цепь большее сопротивление, например, рождественские гирлянды или даже резистор, тем больше работы требуется для вашей схемы. Допустим, вы взяли схему, которую мы представили в начале этого блога, с одной лампочкой. Итак, что произойдет, если вы добавите еще один источник света в эту схему? Обе лампочки будут сиять так же ярко? Неа. Когда вы подключите вторую лампочку, она станет одинаково тусклой, потому что вы добавили в цепь большее сопротивление, что уменьшает ток.
Добавление еще одной лампочки последовательно уменьшает ток , потому что теперь у нашей батареи больше работы!
Но как узнать, какое сопротивление у вас в последовательной цепи? Вы просто складываете все различные значения сопротивления вместе. Например, в схеме ниже у нас есть два резистора, каждый по 10 кОм. Чтобы получить общее сопротивление в этой цепи, просто сложите все числа вместе. Это 10 кОм + 10 кОм, что составляет 20 кОм полного сопротивления.
Сложить наши резисторы в последовательную цепь очень просто, просто сложите каждый из них вместе.
И какой у вас будет ток в этой цепи, исходя из такого сопротивления? Вот как в этом разобраться.
- Используя наш проверенный треугольник закона Ома, мы получаем уравнение, которое нам нужно использовать: I = V / R или ток = напряжение, деленное на сопротивление.
- Подставляя известные нам числа, получаем I = 10V / 20k. Через нашу цепь проходит 0,5 миллиампер (мА)!
- Что, если бы мы вынули один из резисторов? Теперь наше уравнение I = 10 В / 10 кОм, и мы увеличили наш ток до 1 миллиампер (мА) за счет уменьшения сопротивления.
Параллельная работа
Итак, разве не было бы замечательно, если бы вы вытащили одну из лампочек в своей нити рождественских гирлянд, а остальные остались включенными? Если бы все ваши рождественские огни были соединены параллельно, то они вели бы себя именно так!
В параллельной цепи представьте, что все ваши световые нити соединены вместе. Но вместо того, чтобы каждую лампочку подключать одну за другой, все они подключаются отдельно в своих цепях, как на изображении ниже.Как видите, каждая лампочка имеет свою собственную мини-цепь, отдельную от другой, но все они работают вместе как часть более крупной цепи.
Ваши рождественские огни теперь параллельны, обратите внимание, как каждый свет имеет свою собственную цепь. (Источник изображения)
Но как протекает ток в такой цепи? Он не следует просто по одному пути; он следует за всеми одновременно! Вот почему это круто. Представьте, что вы выдергиваете одну из лампочек в такой схеме.Вместо того, чтобы останавливать всю работу рождественского света, остальная часть цепи будет продолжать движение, потому что каждый свет не зависит от источника света до или после него в качестве источника электричества.
Параллельный ток и сопротивление
Когда цепь соединена параллельно, ток и сопротивление начинают делать некоторые странные вещи, которых вы, возможно, не ожидали, вот что вам нужно запомнить:
В параллельных цепях, когда вы увеличиваете сопротивление, вы также увеличиваете ток, но в результате ваше сопротивление уменьшается вдвое.
Подождите, что? Звучит безумно! Но подумайте об этом в отношении рождественских огней. По мере того, как вы добавляете больше разноцветных огней в свою схему, вам нужно потреблять больше тока для питания всех этих огней, верно? И поэтому начинает происходить волшебство: чем больше огней вы добавляете, тем выше поднимается ваш ток, но этот увеличенный ток оказывает противоположное влияние на ваше сопротивление.
Это может быть немного сложно для понимания, поэтому давайте рассмотрим простой пример.Проверьте схему ниже:
Здесь мы имеем параллельную схему с двумя резисторами 10 кОм и батареей 10 В.
Здесь у нас есть аккумуляторный источник 10 В и два резистора 10 кОм, которые подключены параллельно. Теперь, поскольку каждый резистор имеет свою собственную схему, нам нужно выяснить, какой ток каждый будет использовать:
- Возвращаясь к нашему треугольнику закона Ома, мы знаем, что уравнение, которое нам нужно использовать, это I = V / R, или ток равен напряжению, деленному на сопротивление.
- И вставляя наши числа, мы получаем I = 10 В / 10 кОм, что составляет 1 мА.Но это только одна из двух схем резистора; Теперь нам нужно удвоить ток, чтобы получить общее значение для всей цепи, которое составляет 2 мА.
- Теперь, что происходит с нашим сопротивлением в два ампера? Мы можем использовать закон Ома, чтобы выяснить это с R = V / I, что составляет R = 10 В / 2 мА = 5 кОм. Поскольку мы удвоили наш ток, наши оригинальные резисторы 10 кОм теперь дают только половину сопротивления!
Да, все это довольно безумно, не так ли? Это просто один из тех законов Вселенной.
Как на самом деле работают рождественские огни
Так как же твои рождественские гирлянды на самом деле работают? Вот подсказка — они не на 100% последовательны или не на 100% параллельны, они оба! Эти умные инженерные эльфы решили, что самый эффективный способ заставить ваши рождественские огни работать — это соединить несколько серий огней параллельно. Посмотрите на изображение ниже, чтобы понять, что мы имеем в виду:
Многие из сегодняшних рождественских гирлянд соединены последовательно / параллельно.(Источник изображения)
Вот почему этот последовательный / параллельный гибрид хорош — если вы выдернете один свет, выключится только одна часть ваших фонарей, а не все. Это потому, что вы затронули только одну из последовательных цепей в вашей более крупной параллельной цепи. Но почему инженерные эльфы просто не сделали все огни параллельно? Для этого потребуется тонна проводов, и Санта должен следить за своими производственными затратами, как и мы!
Но подождите, вы можете вспомнить тот год, когда у вас перегорел свет, но остальные фонари продолжали работать, что там произошло? Вы можете поблагодарить этот небольшой фокус на так называемом шунте .Это маленькое устройство позволяет току продолжать движение по цепи даже после того, как лампа перегорела. Как же так? Давайте подробнее рассмотрим одну из ваших рождественских гирлянд ниже:
Шунтирующий провод поддерживает движение электричества даже после того, как лампа перегорела. (Источник изображения)
Видите этот провод, который обвивает нижнюю часть фонаря? Это шунт, и на нем есть покрытие, которое предотвращает прохождение электричества через него, пока свет работает правильно.Но когда верхний провод перегорает, повышение температуры приводит к плавлению покрытия шунтирующего провода, позволяя электричеству продолжать проходить от одного вывода к другому, и ваши рождественские огни продолжают работать!
Дар дарения
Вот тебе подарок на год! Теперь у вас есть новые знания о разнице между цепями, соединенными последовательно и параллельно, и о том, как они работают вместе, чтобы ваши рождественские огни сияли ярко.
Проще всего понять схемы, соединенные последовательно, поскольку ток течет в одном непрерывном и плавном направлении.И чем больше работы у вас будет выполнять последовательная цепь, тем больше будет уменьшаться ваш ток. Параллельные схемы немного сложнее, позволяя подключать несколько схем, работая индивидуально как часть более крупной схемы. Из-за этого интересного соединения, когда вы увеличиваете сопротивление в параллельной цепи, вы также увеличиваете ток!
Если вы все еще не можете осмыслить все это, то вот отличное видео от Bozeman Science, которое упрощает понимание:
А если вы все еще заблудились, то, возможно, вы исчерпали свой лимит на гоголь-моголь.Готовы разработать свои собственные схемы сегодня? Попробуйте Autodesk EAGLE бесплатно!
Инструменты и задачи обслуживания (интерактивные)
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению V. Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению : I V.
Это важное соотношение известно как закон Ома.Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Сопротивление и простые схемы
Если напряжение увеличивает ток, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением R. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток.Сопротивление обратно пропорционально току, или I.
Так, например, при удвоении сопротивления ток уменьшается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем I =.
Это соотношение также называется законом Ома. Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых действует закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах.Омические материалы имеют сопротивление R, которое не зависит от напряжения V и тока I. Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является Ом и обозначается символом Ω (заглавная греческая омега). Перестановка I = дает R = , поэтому единицы сопротивления: 1 Ом = 1 вольт на ампер: 1 Ом = 1.
На рисунке показана простая схема. Простая схема имеет один источник напряжения и один резистор.Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в R.
Простая электрическая цепь, в которой замкнутый путь прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Установление соединений: Соединения в реальном мире
Закон Ома (V = IR) — это фундаментальная зависимость, которая может быть представлена линейной функцией, в которой наклон линии представляет собой сопротивление.Сопротивление представляет собой напряжение, которое необходимо приложить к резистору для создания в цепи тока 1 А. График (на рисунке ниже) показывает это представление для двух простых схем с резисторами, которые имеют разное сопротивление и, следовательно, разные наклоны.
На рисунке показано соотношение между током и напряжением для двух разных резисторов. Наклон графика представляет значение сопротивления, которое составляет 2 Ом и 4 Ом для двух показанных линий.
Материалы, которые подчиняются закону Ома, имея линейную зависимость между напряжением и током, известны как омические материалы. С другой стороны, некоторые материалы демонстрируют нелинейную зависимость напряжения от тока и, следовательно, известны как неомические материалы. На рисунке ниже показаны соотношения между текущим напряжением для двух типов материалов.
Рисунок №. Показаны отношения между напряжением и током для омических и неомических материалов.
Очевидно, что сопротивление омического материала (показанного на (а)) остается постоянным и может быть рассчитано путем определения наклона графика, но это неверно для неомического материала (показанного на (b)).
Сопротивление может быть разным. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 1012 Ом или более. Сопротивление сухого человека может составлять 105 Ом, тогда как сопротивление человеческого сердца составляет около 103 Ом. Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10-5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны).Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление».
Дополнительную информацию можно получить, решив I = для V, что дает V = IR.
Это выражение для V можно интерпретировать как падение напряжения на резисторе, создаваемое током I. Для этого напряжения часто используется фраза IR drop . Например, фара в примере имеет падение ИК-излучения 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе.Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления. Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE = qΔV, и через каждую из них протекает одинаковое q.Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. Рисунок.)
Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Установление соединений: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму только с помощью резистора.Мы обнаружим, что сохранение энергии имеет другие важные применения в схемах и является мощным инструментом анализа схем.
Последовательные и параллельные резисторы
Большинство схем имеет более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела для потока заряда называется сопротивлением. Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Изображение показывает (а) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
При параллельном подключении резисторов от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Закон Джоуля
Мощность ассоциируется у многих с электричеством. Зная, что мощность — это скорость использования или преобразования энергии, каково выражение для электроэнергии? На ум могут прийти линии электропередач.Мы также думаем о лампочках с точки зрения их номинальной мощности в ваттах. Сравним лампочку на 25 Вт с лампой на 60 Вт. (См. Рисунок (a).) Поскольку оба работают от одного и того же напряжения, лампа мощностью 60 Вт должна потреблять больше тока, чтобы иметь большую номинальную мощность. Таким образом, сопротивление лампы на 60 Вт должно быть ниже, чем у лампы на 25 Вт. Если мы увеличиваем напряжение, мы также увеличиваем мощность. Например, когда лампочка мощностью 25 Вт, рассчитанная на работу от 120 В, подключена к 240 В, она на короткое время очень ярко светится, а затем перегорает.Как именно напряжение, ток и сопротивление связаны с электроэнергией?
Электрическая энергия зависит как от напряжения, так и от перемещаемого заряда. Проще всего это выражается как PE = qV , где q — это перемещенный заряд, а V, — напряжение (или, точнее, разность потенциалов, через которую проходит заряд). Мощность — это скорость перемещения энергии, поэтому электрическая мощность составляет P = =.
Учитывая, что ток равен I = ( обратите внимание, что Δt = t здесь), выражение для мощности становится P = IV.
Электрическая мощность ( P ) — это просто произведение тока на напряжение. Мощность имеет знакомые единицы ватт. Поскольку единицей СИ для потенциальной энергии (PE) является джоуль, мощность измеряется в джоулях в секунду или ваттах. Таким образом, 1 A⋅V = 1 Вт. Например, в автомобилях часто есть одна или несколько дополнительных розеток, с помощью которых можно заряжать сотовый телефон или другие электронные устройства. Эти розетки могут быть рассчитаны на 20 А, чтобы схема могла выдавать максимальную мощность P = IV = (20 А) (12 В) = 240 Вт.В некоторых приложениях электрическая мощность может быть выражена в вольт-амперах или даже киловольт-амперах 1 кА⋅В = 1 кВт.
Чтобы увидеть отношение мощности к сопротивлению, мы объединяем закон Ома с P = IV. Подстановка I = V / R дает P = () V = V 2 / R . Аналогично, замена V = IR дает P = I (IR) = I 2 R . Для удобства здесь собраны три выражения для электроэнергии:
P = IV
P = V 2 / R
P = I 2 R.
Обратите внимание, что первое уравнение всегда верно, тогда как два других можно использовать только для резисторов. В простой схеме с одним источником напряжения и одним резистором мощность, подаваемая источником напряжения, и мощность, рассеиваемая резистором, идентичны. (В более сложных схемах P может быть мощностью, рассеиваемой одним устройством, а не полной мощностью в цепи.)
Различные идеи можно получить из трех различных выражений для электроэнергии.Например, P = V 2 / R означает, что чем ниже сопротивление, подключенное к данному источнику напряжения, тем больше выдается мощность. Кроме того, поскольку напряжение возведено в квадрат в P = V 2 / R , эффект от приложения более высокого напряжения, возможно, больше, чем ожидалось.

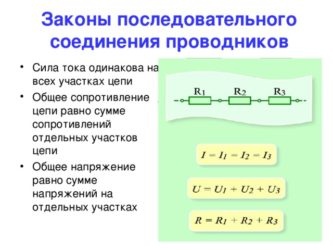


 На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
 Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.