Электричество и магнетизм
Применим закон Ампера для вычисления силы взаимодействия двух длинных прямолинейных проводников с токами I1 и I2, находящихся на расстоянии d друг от друга (рис. 6.26).
Рис. 6.26. Силовое взаимодействие прямолинейных токов:
1 — параллельные токи; 2 — антипараллельные токи
Видео 6.2. Взаимодействие двух параллельных проводников с током.
Проводник с током I1 создает кольцевое магнитное поле, величина которого в месте нахождения второго проводника равна
|
(6.23) |
Это поле направлено «от нас» ортогонально плоскости рисунка. Элемент второго проводника испытывает со стороны этого поля действие силы Ампера
|
(6. |
Подставляя (6.23) в (6.24), получим
|
(6.25) |
При параллельных токах сила F21 направлена к первому проводнику (притяжение), при антипараллельных — в обратную сторону (отталкивание).
Аналогично на элемент проводника 1 действует магнитное поле, создаваемое проводником с током I2 в точке пространства с элементом с силой F12. Рассуждая таким же образом, находим, что F12 = –F21, то есть в этом случае выполняется третий закон Ньютона.
Итак, сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников, рассчитанная на элемент длины проводника, пропорциональна произведению сил токов I1 и I2 протекающих в этих проводниках, и обратно пропорциональна расстоянию между ними. В электростатике по аналогичному закону взаимодействуют две длинные заряженные нити.
В электростатике по аналогичному закону взаимодействуют две длинные заряженные нити.
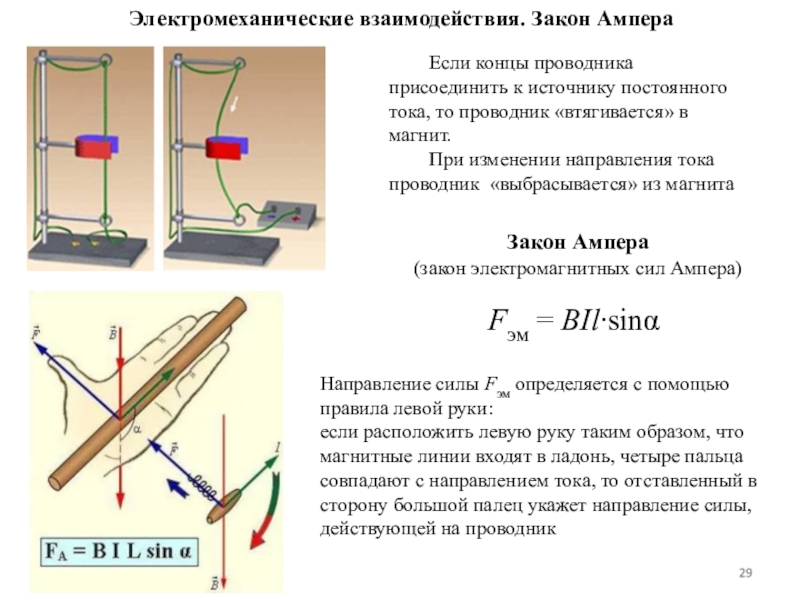
На рис. 6.27 представлен опыт, демонстрирующий притяжение параллельных токов и отталкивание антипараллельных. Для этого используются две алюминиевые ленты, подвешенные вертикально рядом друг с другом в слабо натянутом состоянии. При пропускании через них параллельных постоянных токов силой около 10 А ленты притягиваются. а при изменении направления одного из токов на противоположное — отталкиваются.
Рис. 6.27. Силовое взаимодействие длинных прямолинейных проводников с током
На основании формулы (6.25) устанавливается единица силы тока — ампер, являющаяся одной из основных единиц в СИ.
|
Ампер — это сила неизменяюшегося тока, который, протекая по двум длинным параллельным проводникам, расположенным в вакууме на расстоянии 1 м, вызывает между ними силу взаимодействия 2×10–7 Н на каждый метр длины провода. |
Пример. По двум тонким проводам, изогнутым в виде одинаковых колец радиусом R = 10 см, текут одинаковые токи I = 10 А в каждом. Плоскости колец параллельны, а центры лежат на ортогональной к ним прямой. Расстояние между центрами равно d = 1 мм. Найти силы взаимодействия колец.
Решение. В этой задаче не должно смущать, что мы знаем лишь закон взаимодействия длинных прямолинейных проводников. Поскольку расстояние между кольцами много меньше их радиуса, взаимодействующие элементы колец «не замечают» их кривизны. Поэтому сила взаимодействия дается выражением (6.25), куда вместо надо подставить длину окружности колец Получаем тогда
закон Ампера.взаимодействие параллельных токов
закон Ампера.взаимодействие параллельных токов
20)
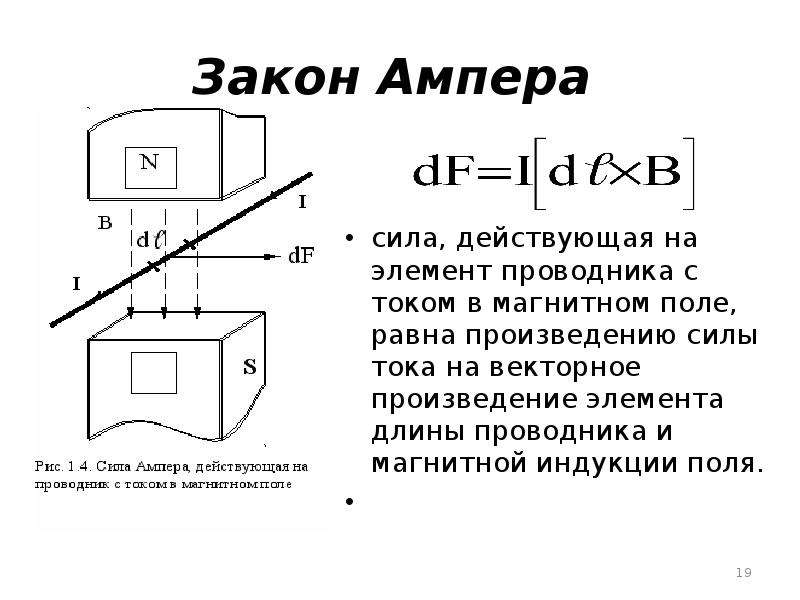
Закон Ампера — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент объёма dV проводника с током плотности , находящегося в магнитном поле с индукцией :
Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент объёма dV проводника с током плотности , находящегося в магнитном поле с индукцией :
.
Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный dl и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.
Модуль силы Ампера можно найти по формуле:
,
где α — угол между векторами магнитной индукции и тока.
Сила dF максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():
.
Два параллельных проводника
Два бесконечных параллельных проводника в вакууме
Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии r друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I1 и I2. Требуется найти силу, действующую на единицу длины проводника.
Бесконечный проводник с током I1 в точке на расстоянии r создаёт магнитное поле с индукцией:
(по закону Био — Савара — Лапласа).
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).
Модуль данной силы (r — расстояние между проводниками):
Интегрируем, учитывая только проводник единичной длины (пределы l от 0 до 1):
Закон Ампера для участка цепи – потребителя тока
Закон Ампера для участка
цепи – потребителя тока
Анализ законов электрического тока показал, что два
основных закона электродинамики — закон Ампера и закон Био – Савара – Лапласа недостаточно
полно описывают природу электрического тока.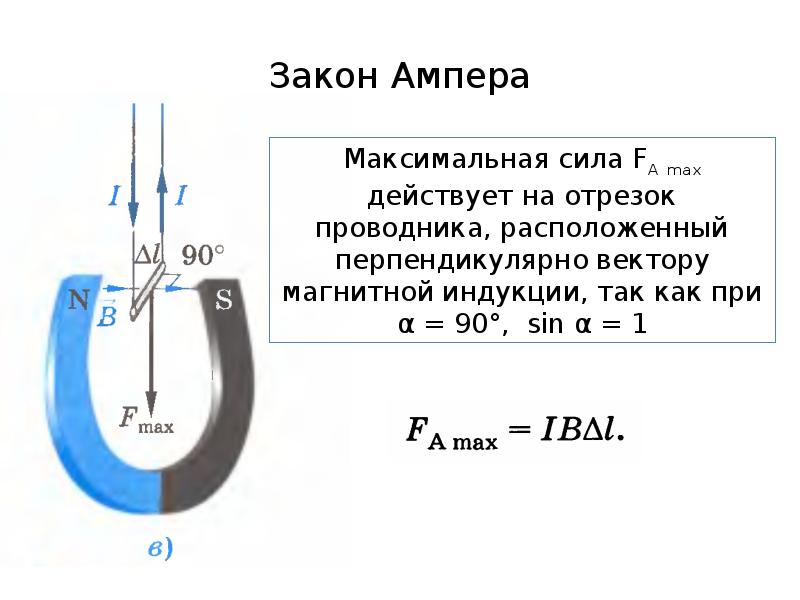 Они сформулированы только для
Они сформулированы только для
участка цепи – потребителя тока. Нет формул и формулировок этих законов для
участка цепи – источника тока и полной цепи электрического тока.
Другой проблемой электродинамики является безымянная
природа вектора, который переносит силовое взаимодействие – силы Ампера. Без
осознания физической природы силы Ампера невозможно дальнейшее
совершенствование устройств, использующих силу Ампера.
«Закон Ампера — закон механического взаимодействия
двух токов, текущих в малых отрезках проводников, находящихся на некотором
расстоянии друг от друга. Из закона Ампера следует, что параллельные проводники
с токами, текущими в одном направлении, притягиваются, а в противоположном —
отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой
магнитное поле действует на малый отрезок проводника с током». [8]
«Магнитное поле оказывает на рамку с током
ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой,
есть результат действия сил на отдельные её элементы. Обобщая результаты
Обобщая результаты
исследования действия магнитного поля на различные проводники с током, Ампер
установил, что сила ,
с которой магнитное поле действует на элемент проводника с
током, находящегося в магнитном поле, равна
,
(1)
где
—
вектор, по модулю равный и
совпадающий по направлению с током, —
вектор магнитной индукции.
Направление вектора может
быть найдено, согласно (6.1), по общим правилам векторного произведения, откуда
следует правило левой руки: если ладонь левой руки расположить так, чтобы в неё
входил вектор ,
а четыре вытянутых пальца расположить по направлению тока в проводнике, то
отогнутый большой палец покажет направление силы, действующей на ток». [1]
Сила Ампера
является одним из важнейших физических величин в электродинамике, и его
физическая природа должна быть определена.
В настоящее
время известен только закон Ампера для участка цепи – потребителя тока. Для
полной цепи и участка цепи – источника тока закон Ампера не сформулирован.
В теории электродинамики не нашло отражения
замечательное свойство электрического тока, которое позволяет более глубоко
понять физическую природу электрического тока. Это физическое явление реверса
силы Ампера при переходе участка цепи из режима потребления тока в режим
генерации тока.
Есть правила левой и правой руки, найденные из
экспериментально наблюдаемого поведения электрического тока. Эти правила
показывают, что сила Ампера меняет направление при переходе участка цепи из
потребителя в источник тока.
Теоретического объяснения этого факта нет, поскольку
все вектора, кроме безымянного радиус – вектора, остаются неизменными. В
классической электродинамике при переходе от правила левой руки к правилу
правой руки ничего не изменяется.
Не меняется направление вектора напряженности
магнитного поля ,
не меняется направление вектора напряжённости электрического поля .
Направление электрического тока также не меняется.
При наличии двух векторов, направление которых не
изменяется, в классической электродинамике нечем обосновать смену направления
третьего вектора — силы Ампера при переходе проводника с током из режима
двигателя в режим генератора.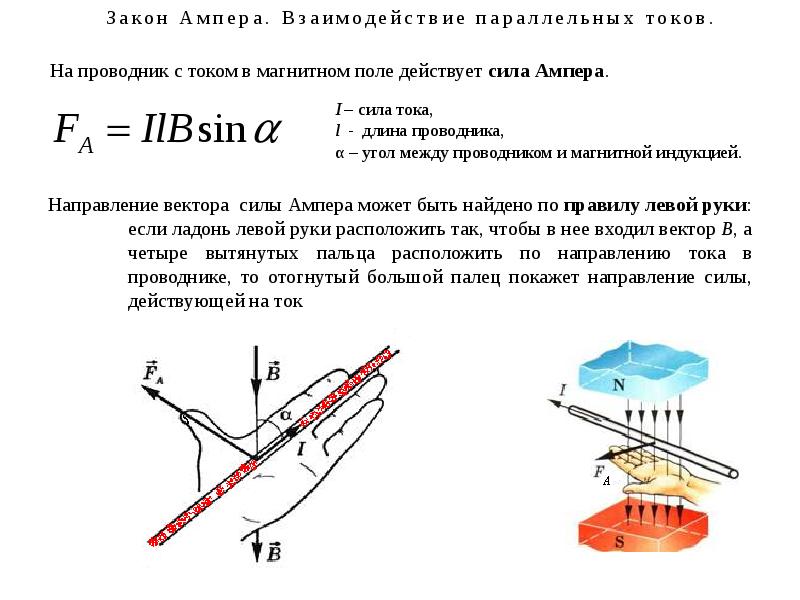
Найти ответ у этой теоретической загадки поможет
анализ правил левой и правой руки.
Литература
1. Трофимова Т. И. Курс Физики. «Высшая
школа». М.,1997.
2.
Дрюков В.М. О чём молчат физики. Тула, 2004.
3. http://www.sciteclibrary.ru/rus/avtors/d.html
4. / http://drjukow.narod.ru/
5. Дрюков В.М. Физика. Дополнительные материалы. Тула изд. ООО Аквариус. 2021
Применение действия силы Ампера в технике | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема:
Магнитостатика
Силы Ампера используются для преобразования энергии электрического тока в механическую энергию проводника. Такое преобразование применяется во многих электротехнических устройствах. Рассмотрим некоторые из них.
1. Электроизмерительные приборы магнитоэлектрической системы.
| Рис. 6.19. Строение измерительного прибора магнитоэлектрической системы |
Электроизмерительный прибор магнитоэлектрической системы состоит из постоянного магнита и проволочной рамки, которая находится между полюсами (рис. 6.19). Полюса магнита имеют специальные насадки, которые дают возможность получить такое магнитное поле, при котором поворачивание рамки в нем не приводит к изменению угла между магнитной индукцией и проводниками рамки. Этот угол остается всегда равным 90°. С рамкой соединены две спиральные пружины, которые подводят электрический ток к рамке. При прохождении электрического тока по рамке появляется сила Ампера, пропорциональная силе тока в рамке. Поворачивание рамки приводит к деформации пружин и возникновению силы упругости. Рамка прекратит поворачиваться тогда, когда момент силы Ампера станет равным моменту силы упругости.
Стрелка, связанная с рамкой, показывает угол ее поворота, при котором моменты уравновешиваются. Этот угол пропорциональный силе тока в рамке.
2. Электрический двигатель постоянного тока. Материал с сайта http://worldofschool.ru
| Рис. 6.20. Строение двигателя постоянного тока |
Электрический двигатель предназначен для непрерывного превращения энергии электрического тока в механическую. Принцип его действия такой же, как и электроизмерительного прибора, описанного выше. Но в его конструкции отсутствует пружина. Ток к рамке подводится через специальные скользящие контакты — щетки (рис. 6.20). При замыкании цепи рамка начинает взаимодействовать с магнитным полем постоянного магнита или электромагнита и поворачивается так, что ее плоскость становится перпендикулярной магнитной индукции. Непрерывность вращения рамки обеспечивается применением специального устройства — коллектора, которое периодически изменяет направление тока в рамке.
Непрерывность вращения рамки обеспечивается применением специального устройства — коллектора, которое периодически изменяет направление тока в рамке.
В современных электродвигателях постоянного тока подвижная часть (ротор) состоит из многих рамок, размещенных в пазах цилиндра из специальной электротехнической стали. Роль коллектора в них часто выполняет специальное электронное устройство.
На этой странице материал по темам:
Використання сили ампера в техніці
Применение силы ампера доклад
Применение силы ампера в жизни
Применение силы и ампера конспект
Сила ампера в техніці
МАЭ02 Режимы работы электрических источников питания, подстанций, сетей и систем
ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ
профессиональной направленности в магистратуру
Направление подготовки: 13. 04.02 — Электротехника, электромеханика и электротехнологии.
04.02 — Электротехника, электромеханика и электротехнологии.
Программа подготовки:
Режимы работы электрических источников питания, подстанций, сетей и систем (МАЭ02)
Кафедра, обеспечивающая преподавание программы: Электротехника и электрооборудование предприятий.
1. Особенности проведения вступительного испытания в магистратуру
1.1. Программы вступительного испытания сформирована на основе федерального государственного образовательного стандарта высшего образования по соответствующей программе бакалавриата.
1.2. Вступительное испытание проводятся в письменной форме в формате тестирования.
1.3. Вступительное испытание оценивается по 100-балльной шкале.
2. Перечень дисциплин, необходимых для освоения программы подготовки магистра и предусмотренных федеральным государственным образовательным стандартом подготовки бакалавров по данному направлению:
— Теоретические основы электротехники;
— Электрические машины;
— Электрический привод;
— Электрические и электронные аппараты.
3. Перечень вопросов для подготовки абитуриентов
3.1 Дисциплина «Теоретические основы электротехники»
Перечень вопросов:
1 Напряженность электростатического поля (ЭСП). Электрический потенциал. Градиент потенциала. Силовые линии и эквипотенциальные поверхности.
2 Поляризованность диэлектрика, электрическая индукция. Теорема Гаусса.
3 Раскрытие дивергенции в декартовой системе координат. Уравнения Пуассона и Лапласа.
4 Граничные условия. Методы расчета ЭСП.
5 Проводники в ЭСП. Электрическая емкость. Энергия и силы ЭСП.
6 Ток и плотность тока проводимости.
7 Закон Ома и Кирхгофа в дифференциальной форме.
8 Ток смещения.
9 Аналогия между ЭСП и электрическим полем постоянного тока (ЭППТ). Заземлители.
10 Магнитный поток и его непрерывность. Закон полного тока
11 Раскрытие ротора в декартовой системе координат
12 Законы Ампера и Био-Саварра-Лапласа.
13 Скалярный и векторный магнитные потенциалы магнитного поля постоянного тока (МППТ)
14 Сила Лоренца, электромагнитная индукция.
15 Индуктивность собственная и взаимная (в т.ч. многофазных линий).
16 Энергия и силы магнитного поля.
17 Магнитостатическое экранирование.
18 Аналогия ЭСП, ЭППТ и МППТ.
19 Система уравнений Максвелла.
20 Теорема Умова-Пойнтинга.
21 Поверхностный эффект и эффект близости.
22 Электромагнитное экранирование.
23 Метод конечных элементов. Система моделирования ELCUT
24 Элементы электрических цепей (ЭЦ), их условные обозначения и схемы замещения.
25 Идеализированные элементы ЭЦ и их параметры.
26 Двухполюсники. Передача энергии от активного двухполюсника к пассивному.
27 Законы Кирхгофа.
28 Метод контурных токов.
29 Теорема Телледжена, баланс мощностей.
30 Метод узловых потенциалов.
31 Эквивалентные преобразования активных ЭЦ
32 Теорема Тевенина и Нортона.
33 Метод наложения.
34 Метод эквивалентного генератора.
35 Получение синусоидального тока. Частота, период, фаза, мгновенное, амплитудное, действующее и среднее значения синусоидального тока.
36 Представление синусоидальных величин в виде проекций вращающихся векторов и комплексных чисел.
37 Резистивный, индуктивный и емкостный элементы в цепи синусоидального тока (их сопротивления, мощности, энергия, векторные диаграммы и диаграммы мгновенных значений, компонентные уравнения).
38 Неразветвленная цепь синусоидального тока. Резонанс напряжений.
39 Разветвленная цепь переменного тока. Резонанс токов.
40 Повышение коэффициента мощности электрических установок.
41 Круговые диаграммы. Фазовращатели.
42 Взаимная индуктивность (коэффициент индуктивной связи, индуктивность рассеяния).
43 Трансформатор воздушный.
44 Трансформатор с ферромагнитным сердечником.
45 Многофазные цепи. Получение трехфазной симметричной ЭДС.
Получение трехфазной симметричной ЭДС.
46 Индуктивность собственная и взаимная трехфазных линий. Индуктивные сопротивления трехфазных линий.
47 Соединения трехфазных цепей в звезду.
48 Соединение трехфазных цепей в треугольник.
49 Измерение мощности в трехфазных цепях.
50 Пульсирующее и вращающиеся магнитные поля.
51 Метод симметричных составляющих. Разложение фазных токов и напряжений на симметричные составляющие. Сопротивления прямой, обратной и нулевой последовательностей.
52 Фильтры симметричных составляющих. Фильтры тока и напряжения нулевой последовательности.
53. Расчет несимметричных режимов методом симметричных составляющих.
54 Причины переходных процессов. Законы коммутации.
55 Понятия о некорректной коммутации. Начальные условия.
56 Переходные процессы в RL- и RC-цепях.
57 Переходные процессы в RLC-цепи постоянного тока.
58 Переходные процессы в RLC-цепи переменного тока (режимы апериодический и периодические (сверхтоков и сверхнапряжений, резонанса и биений).
59 Операторный метод расчета переходных процессов (прямое преобразование Лапласа, его основные свойства и изображения простейших функций).
60 Обратное преобразование Лапласа. Формулы разложения.
61 Формулы включения.
62 Расчет переходных процессов при периодическом импульсном воздействии.
63 Импульсные и переходные характеристики.
64 Интегрирующие и дифференцирующие RC- и RL -цепи систем управления электроприводами (активные и пассивные).
65 Применение интеграла Дюамеля к анализу переходных процессов.
66 Нелинейные элементы и их характеристики. Методы анализа нелинейных ЭЦ.
67 Магнитные цепи (МЦ) электротехнических устройств.
68 Законы Ома и Кирхгофа для МЦ, методы анализа МЦ.
69 Расчет магнитной цепи (прямая и обратная задачи).
70 Расчет электромагнита переменного тока.
71 Влияние воздушного зазора на параметры катушки.
72 Дроссель насыщения, магнитный усилитель.
73 Феррорезонансные явления.
74 Переходные режимы в нелинейных цепях.
75 Причины возникновения несинусоидальных токов (НСТ), ЭДС, напряжений.
76 Разложение периодической несинусоидальной функции в ряд Фурье.
77 Частотный спектр.
78 Действующее и среднее значения и мощности НСТ.
79 Анализ ЭЦ с НСТ.
80 Высшие гармоники в трехфазных цепях.
81 Цифровые цепи и их характеристики.
82 Четырехполюсники (ЧП) их основные свойства.
83 Уравнения ЧП в Y, Z, A, B, H и G параметрах.
84 Коэффициент передачи ЧП.
85 Уравнения ЧП в гиперболической форме.
86 Входные и характеристические сопротивления ЧП.
87 Частотные электрические фильтры.
88 Пассивные RC- и RL-фильтры верхних и нижних частот.
89 Активные фильтры второго порядка.
90 «Электронные» индуктивности.
91 Первичные параметры однородной линии. Телеграфные уравнения.
92 Синусоидальный и переходный и режимы длинной линии.
3. 2 Дисциплина «Электрические машины»
2 Дисциплина «Электрические машины»
3.2.1 Раздел 1 «Машины постоянного тока»
Перечень вопросов:
1 Устройство и принцип действия машин постоянного тока. Конструкция машины постоянного тока.
2 Обмотки якоря машин постоянного тока: петлевые и волновые обмотки, шаги обмотки, схемы замещения, звезда фазовых ЭДС, параллельные ветви. ЭДС обмотки якоря.
3 Магнитная цель машины постоянного тока и расчет характеристики холостого хода.
4 Реакция якоря в машинах постоянного тока. Коммутация и пути ее улучшения.
6 Генераторы постоянного тока, их схемы. Энергетические диаграммы и рабочие характеристики.
7 Принцип обратимости электрических машин. Формула электромагнитного момента. Уравнения равновесия моментов и ЭДС в машинах постоянного тока.
8 Двигатели постоянного тока, их схемы, пусковые и рабочие характеристики, энергетическая диаграмма. Специальные машины постоянного тока.
3. 2.2 Раздел 2 «Трансфоматоры»
2.2 Раздел 2 «Трансфоматоры»
Перечень вопросов:
1 Устройство и принцип действия трансформатора, его уравнения. Приведенный трансформатор, его параметры, уравнения и схема замещения.
2 Режимы холостого хода трансформатора. Опыт холостого хода. Характеристики и векторные диаграммы холостого хода трансформатора.
3 Опыт короткого замыкания трансформатора. Характеристики и векторные диаграммы в опыте короткого замыкания трансформатора
4 Режим нагрузки трансформатора и векторные диаграммы трансформатора в режиме нагрузки.
5 Трехфазные трансформаторы. Групповые и трехстержневые трансформаторы. Группы соединения трехфазных трансформаторов.
6 Параллельная работа трансформаторов.
7 Трехобмоточные трансформаторы и автотрансформаторы.
8 Специальные трансформаторы. Измерительные трансформаторы. тока и напряжения. Сварочные трансформаторы.
3.2.3 Раздел 3 «Асинхронные машины»
Перечень вопросов:
1 Общие вопросы теории машин переменного тока. ЭДС обмотки машин переменного тока. Обмоточные коэффициенты однофазные и трехфазные обмотки машин переменного тока. Создание пульсирующих и вращающихся намагничивающих сил (НС) в машинах переменного тока.
ЭДС обмотки машин переменного тока. Обмоточные коэффициенты однофазные и трехфазные обмотки машин переменного тока. Создание пульсирующих и вращающихся намагничивающих сил (НС) в машинах переменного тока.
2 Устройство, принцип действия и режимы работы асинхронного двигателя. Приведенная асинхронная машина, ее параметры и схема замещения при заторможенном роторе.
3 Асинхронная машина при вращающемся роторе, ее схемы замещения, энергетическая диаграмма и выражение электромагнитного момента асинхронной машины через напряжения питающей сети.
4 Естественная механические характеристики асинхронного электродвигателя. Формула Клосса. Выражение момента через ток ротора и магнитный поток асинхронной машины.
5 Искусственные механические характеристики асинхронных электродвигателей.
6 Рабочие характеристики асинхронного двигателя.
7 Опыты холостого хода и короткого замыкания, круговая диаграмма асинхронной машины.
8 Пуск асинхронного двигателя. Двигатели с улучшенными пусковыми свойствами.
Двигатели с улучшенными пусковыми свойствами.
9 Понятия о регулировании частоты вращения асинхронного двигателя.
10 Специальные асинхронные машины. Микромашины автоматических устройств.
3.2.4 Раздел 4 «Синхронные машины»
Перечень вопросов:
1 Устройство и принцип действия синхронной машины. Реакция якоря синхронной машины. Рабочие характеристики синхронного генератора. U-образные характеристики синхронных генераторов.
2 Параллельная работа синхронных генераторов. Включение генераторов на параллельную работу.
3 Устройство и принцип действия синхронного двигателя (СД). Рабочие характеристики СД. Угловая характеристика СД.
4 Векторные диаграммы СД. U-образные характеристики СД и повышение коэффициента мощности сети с помощью СД.
5 Системы возбуждения синхронных машин.
6 Пуск синхронных электродвигателей.
3.3 Дисциплина «Электрический привод»
Перечень вопросов:
1 Электропривод (ЭП). Структурная схема ЭП. Классификация ЭП.
Структурная схема ЭП. Классификация ЭП.
2 Силовой канал ЭП. Механические характеристики механизмов.
3 Механические характеристики электромеханических преобразователей.
4 Обобщенная механическая модель ЭП совместные механические характеристики.
5 Динамический момент, статические режимы ЭП, статистическая устойчивость.
6 Динамические характеристики ЭП.
7 Приведение статических моментов и моментов инерции ЭП к валу электродвигателя.
8 Одномассовая модель механической части силового канала ЭП.
9 Двухмассовая модель механической части канала ЭП.
10 Классическое уравнение движения ЭП.
11 Естественная механическая характеристика двигателя постоянного тока независимого возбуждения (ДПТ НВ) в двигательном режиме.
12 Реостатные механические характеристики ДПТ НВ.
13 Семейство механических характеристик ДПТ НВ при изменении напряжения, подводимого к якорю.
14 Построение механических характеристик ДПТ НВ по паспортным данным в именованных единицах.
15 Построение механических характеристик ДПТ НВ по паспортным данным в относительных единицах.
16 Пуск ДПТ НВ
17 Основные требования к процессу пуска ДПТ НВ. Принципы расчета пусковых реостатов.
18 Графический метод пусковых реостатов
19 Тормозные режимы ДПТ НВ. Классификация, сравнительные оценки.
20 Рекуперативное торможение. Механические характеристики ДПТ НВ при рекуперативном торможении
21 Торможение ДПТ НВ при торможении противовключением
22 Динамическое торможение ДПТ НВ. Механические характеристики ДПТ НВ при динамическом торможении.
23 Механические характеристики двигателя последовательного возбуждения ДПТ НВ в двигательном режиме.
24 Тормозные режимы ДПТ НВ. Механические характеристики ДПТ НВ при торможении
25 Двигатели постоянного тока смешанного возбуждения.
26 Асинхронные двигатели (АД). Схема замещения и уравнение механической характеристики АД. Устойчивость АД.
27 Искусственные механические характеристики АД при изменении активного сопротивления ротора.
28 Искусственные механические характеристики АД при изменении амплитуды напряжения, подводимого к статору.
29 Искусственные механические характеристики АД при изменении частоты напряжения, подводимого к статору.
30 Построение механических характеристик АД по паспортным данным.
31 Пуск АД. Требования, предъявляемые к пуску АД.
32. Принципы расчета пусковых реостатов АД с фазным ротором.
33 Графический расчет пусковых реостатов АД.
34 Аналитический расчет пусковых реостатов АД.
35 Тормозные режимы АД. Классификация, сравнительные оценки.
36 Рекуперативное торможение АД. Механические характеристики АД при торможении противовключением.
37 Динамическое торможение АД. Механические характеристики АД при динамическом торможении.
38 Способы динамического торможения АД. Схемы динамического торможения АД, их сравнительная оценка.
39 Механические характеристики синхронных двигателей (СД) в двигательном режиме.
40 Схема замещения, векторная диаграмма и угловая характеристика СД. Устойчивость СД.
41 Пуск СД.
42 Торможение СД. Тормозные режимы СД.
43. Возбудители СД.
44 Форсировка возбуждения СД.
45 Электрическая часть силового канала ЭП. Структура, содержание
46 Классификация электрических преобразователей.
47 Электромеханические преобразователи в приводах постоянного тока. Механические характеристики системы генератор-двигатель.
48 Статические электрические преобразователи в ЭП постоянного тока. Классификация, структурные схемы.
49 Работа управляемого однополупериодного выпрямителя на активно индуктивную нагрузку. Регулирование характеристики управляемых выпрямителей.
50 Механические характеристики системы «управляемый статический преобразователь – двигатель постоянного тока».
51 Широтно-импульсный регулятор в электроприводах постоянного тока.
52 Электрическая часть силового канала ЭП переменного тока, функции, классификация.
53 Коммутационные устройства в электроприводах переменного тока.
54 Частотные преобразователи в ЭП переменного тока. Назначение, классификация.
55 Статические преобразователи частоты (СПЧ). Структурная схема и принцип действия СПЧ.
56 Автономные инверторы. Назначение, классификация.
57 Преобразователи частоты с промежуточным звеном постоянного тока.
58 Принципы частотного регулирования.
59 Механические характеристики ЭП с частотными преобразователями.
60 Автономные инверторы с широтно-импульсным регуляторованием
61 Автономные инверторы с широтно-импульсной модуляцией.
62 Информационный канал электропривода, состав, классификация.
63 Системы импульсно-фазового управления (СИФУ) структура, классификация.
64 Электромагнитные СИФУ, структура, назначение, функции.
65 Полупроводниковые синхронные СИФУ, структура, принцип действия.
66 Регулировочные характеристики полупроводниковых СИФУ.
67 Принципы скалярного управления ЭП.
68 Методы синтеза скалярного управления ЭП.
69 Принципы векторного управления ЭП.
70 Методы векторного управления.
3.4 Дисциплина «Электрические и электроные аппараты»
Перечень вопросов:
1 Назначение и классификация электрических и электронных аппаратов.
2 Требования, предъявляемые к электронным аппаратам.
3 Конструктивное исполнение электрических аппаратов: основные элементы, кинематические связи, принцип работы.
4 Приводы электрическ
ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ ПО ФИЗИКЕ
ФАКУЛЬТЕТ ФУНДАМЕНТАЛЬНОЙ
ФИЗИКО-ХИМИЧЕСКОЙ ИНЖЕНЕРИИ
Московский государственный университет имени М.В.Ломоносова
(физико-химический факультет)
Программа вступительного испытания по физике для поступающих в магистратуру факультета фундаментальной физико-химической инженерии по направлению 03.
 04.01 «Прикладные математика и физика»
04.01 «Прикладные математика и физика»
1. Законы Ньютона. Инерциальные и неинерциальные системы отсчета.
2. Принцип относительности Галилея и принцип относительности Эйнштейна. Инвариантность интервала между событиями.
3. Преобразование Лоренца. Относительность электрического и магнитного полей.
4. Законы сохранения энергии и импульса. Упругие и неупругие столкновения.
5. Уравнение движения материальной точки в релятивистской механике. Импульс и энергия материальной точки.
6. Закон всемирного тяготения и законы Кеплера. Движение тел в поле тяготения.
7. Закон сохранения момента импульса. Уравнение моментов. Вращение твердого тела вокруг неподвижной оси.
8. Течение идеальной жидкости. Уравнение непрерывности. Уравнение Бернулли.
9. Вязкое движение жидкости. Формула Пуазейля. Число Рейнольдса, его физический смысл.
10. Упругие деформации.
 Модуль Юнга и коэффициент Пуассона. Энергия упругой деформации.
Модуль Юнга и коэффициент Пуассона. Энергия упругой деформации.
11. Уравнение состояния идеального газа. Его интерпретация на основе молекулярно-кинетической теории. Уравнение Ван-дер-Ваальса.
12. Квазистатические процессы. Первое начало термодинамики. Количество теплоты и работа. Внутренняя энергия. Энтальпия.
13. Второе начало термодинамики. Цикл Карно. Энтропия. Закон возрастания энтропии.
14. Статистический смысл энтропии. Энтропия идеального газа. Флуктуации.
15. Термодинамические потенциалы. Условие равновесия систем.
16. Распределения Максвелла, Больцмана.
17. Равномерное распределение энергии по степеням свободы. Зависимость теплоемкости газов от температуры.
18. Фазовые переходы. Уравнение Клапейрона-Клаузиуса. Диаграммы состояний.
19. Явления переноса: диффузия, теплопроводность, вязкость. Коэффициент переноса в газах.
20. Броуновское движение.
 Соотношение Эйнштейна.
Соотношение Эйнштейна.
21. Закон Кулона. Теорема Гаусса в интегральной и дифференциальной формах. Теорема о циркуляции для электростатического поля. Потенциал. Уравнение Пуассона.
22. Электростатическое поле в веществе. Вектор поляризации, электрическая индукция. Граничные условия.
23. Магнитное поле постоянных токов в вакууме. Основные уравнения магнитостатики в вакууме. Закон Био-Савара. Сила Ампера. Сила Лоренца.
24. Магнитное поле в веществе. Основные уравнения магнитостатики в веществе. Граничные условия.
25. Электромагнитная индукция в движущихся и неподвижных проводниках. Э.Д.С. индукции. Само- и взаимоиндукция. Теорема взаимности.
26. Система уравнений Максвелла в интегральной и дифференциальной формах. Ток смещения. Материальные уравнения.
27. Закон сохранения энергии для электромагнитного поля. Вектор Пойнтинга. Импульс электромагнитного поля.
28. Квазистационарные токи.
 Свободные и вынужденные колебания в электрических цепях. Явления резонанса. Добротность колебательного контура. Ее энергетический смысл.
Свободные и вынужденные колебания в электрических цепях. Явления резонанса. Добротность колебательного контура. Ее энергетический смысл.
29. Понятие о спектральном разложении электрических сигналов. Спектры колебаний, модулированных по амплитуде и фазе.
30. Электрические флуктуации. Дробовой и тепловой шумы. Предел чувствительности электроизмерительных приборов.
31. Электромагнитные волны. Волновое уравнение. Уравнение Гельмгольца.
32. Электромагнитные волны в волноводах. Критическая частота. Объемные резонаторы.
33. Понятие о плазме. Дебаевское экранирование. Плазменная частота. Диэлектрическая проницаемость плазмы.
34. Интерференция волн. Временная и пространственная когерентность. Соотношение неопределенностей.
35. Принцип Гюйгенса-Френеля. Число Френеля, его физический смысл. Дифракция Френеля и Фраунгофера. Границы применимости геометрической оптики.
36. Дифракционный предел разрешения оптических и спектральных приборов.
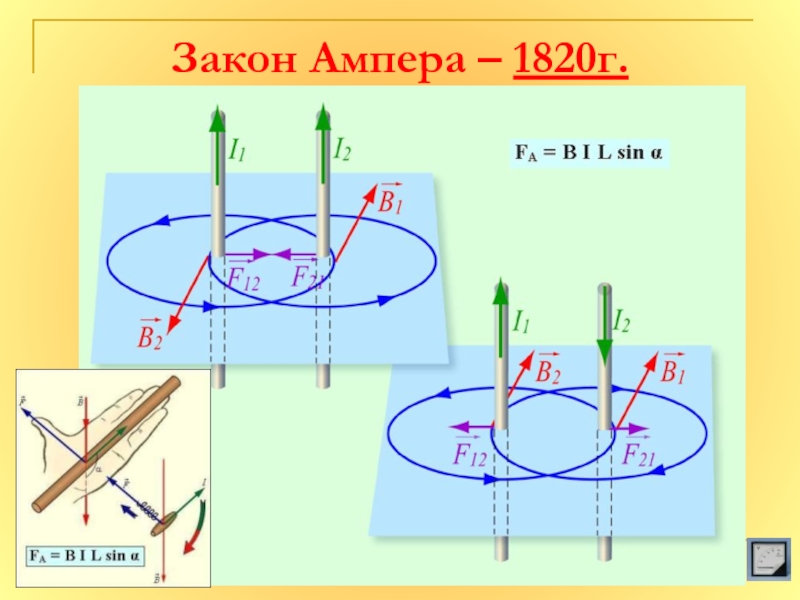 Критерий Рэлея.
Критерий Рэлея.
37. Пространственное Фурьепреобразование в оптике. Дифракция на синусоидальных решетках. Теория Аббе формирования изображения.
38. Принципы голографии. Голограмма Габора. Голограмма с опорным наклонным пучком. Понятие об объемных голограммах.
39. Волновой пакет. Фазовая и групповая скорость. Формула Рэлея. Классическая теория дисперсии. Нормальная и аномальная дисперсия.
40. Поляризация света. Угол Брюстера. Оптические явления в одноосных кристаллах.
41. Дифракция рентгеновских лучей. Формула ВульфаБрэгга. Показатель преломления вещества для рентгеновских лучей.
42. Квантовая природа света. Внешний фотоэффект. Уравнение Эйнштейна. Эффект Комптона.
43. Корпускулярно-волновой дуализм. Волны де Бройля. Опыты ДжермераДевиссона и Томсона по дифракции электронов.
44. Волновая функция, ее смысл. Операторы координаты и импульса. Средние значения физических величин. Соотношение неопределенностей для координат и импульса.
 Уравнение Шредингера.
Уравнение Шредингера.
45. Постулаты и принцип соответствия Бора. Энергетический спектр водородоподобных атомов. Радиус Бора. Атомная единица энергии.
46. Туннелирование частицы сквозь прямоугольный потенциальный барьер. Качественная теория альфараспада.
47. Опыты Штерна и Герлаха. Спин электрона, орбитальный и спиновый магнитный момент электрона.
48. Бозоны и фермионы. Принцип Паули. Периодическая система элементов Менделеева.
49. Атом в магнитном поле. Эффект Зеемана. Ядерный магнитный резонанс.
50. Радиоактивный распад атомного ядра. Различие энергетических спектров альфа- и бета- излучения. Нарушение закона сохранения пространственной четности в ядерном бета- распаде.
51. Соотношение неопределенностей для энергии и времени. Оценка времени жизни виртуальных частиц, радиусов сильного и слабого взаимодействий.
52. Резонансный характер ядерных реакций. Эффект Мёссбауэра.
53.
 Фундаментальные взаимодействия и фундаментальные частицы. Кварковая структура адронов.
Фундаментальные взаимодействия и фундаментальные частицы. Кварковая структура адронов.
54. Распределение Бозе-Эйнштейна. Фотонный газ. Основные законы равновесного излучения.
55. Спонтанное и вынужденное излучение. Методы создания инверсной заселенности. Принцип работы лазера.
56. Концепция фононов. Теплоемкость и теплопроводность кристаллической решетки в модели Дебая. Температура Дебая.
57. Распределение Ферми-Дирака. Вклад электронов в теплоемкость и теплопроводность кристаллов.
58. Электропроводность полупроводников. Электроны и дырки. Акцепторы и доноры. Электронно-дырочный переход.
59. Сверхпроводимость. Магнитные свойства сверхпроводников. Эффект Мейсснера. Критическое поле и критический ток. Куперовское спаривание. Квантование магнитного потока.
ЛИТЕРАТУРА
1. Сивухин Дмитрий Васильевич. Общий курс физики: [Учебное пособие в 5 томах], 3е издание, исправленное и дополненное.
 М.: Наука, 1989.
М.: Наука, 1989.
2. Киттель Ч. Элементарная физика твердого тела. М.: Наука, 1965.
3. Иванов А. А. Введение в квантовую физику систем из многих частиц. М.: МФТИ, 1993.
4. Ципенюк Ю. М. Физические основы сверхпроводимости. М.: МФТИ, 1995.
<< НАЗАД
© Факультет фундаментальной физико-химической инженерии 2006 — 2021
4.5: Закон Ампера — Physics LibreTexts
Магнитный аналог закона Гаусса для электричества
Мы уже говорили, что закон Гаусса для магнитного поля тривиален, так как нет магнитных монополей, но оказывается, что есть отдельный математический закон, который работает для магнитных источников так же, как закон Гаусса работает для электрических источников. Он включает в себя «закрытые» источники и позволяет нам использовать симметричные ситуации для решения полей с использованием методов, более простых, чем интегрирование закона Био-Савара.
Эта магнитная версия электрического закона Гаусса называется законом Ампера , и, поскольку он не может включать замкнутые точечные источники, вместо этого он имеет дело с линиями тока, которые либо вращаются сами по себе, образуя замкнутую цепь, либо бесконечно -long (и круг-назад на себя на бесконечность). Но как нам «заключить» линию тока? В случае заряда он был замкнутым, если не было возможности снять заряд с гауссовой поверхности, не пробив поверхность (т.е. на поверхности нет отверстий). В случае закона Ампера мы считаем, что ток проходит по воображаемому замкнутому контуру, называемому Amp è rian цепью — , а не по поверхности. Такой ток заключен, когда нет возможности вывести линию тока без разрыва цепи Ампера.
Рисунок 4.5.1 – Определение замкнутого тока
Существует два способа, при которых ток не будет замкнут: если на пути вокруг провода есть разрыв, так что провод может скользить по нему, или если отрезок провода имеет конечную длину и не образует замкнутый цикл. Если петля провода замкнута, то цепь Ампера «связана» с ней, и ток замыкается. Если провод бесконечно длинный, он точно так же не может выйти из цепи Ампера, не разорвав ее, поэтому его ток также замкнут. [ Математически мы обычно определяем ток как «окруженный» замкнутым путем, если он пронизывает каждую возможную поверхность, ограниченную замкнутым путем. Ясно, что есть растянутые поверхности, которые мы можем построить с замкнутым путем в качестве границы, которые не позволяют отрезку конечной длины проткнуть его. ]
Если петля провода замкнута, то цепь Ампера «связана» с ней, и ток замыкается. Если провод бесконечно длинный, он точно так же не может выйти из цепи Ампера, не разорвав ее, поэтому его ток также замкнут. [ Математически мы обычно определяем ток как «окруженный» замкнутым путем, если он пронизывает каждую возможную поверхность, ограниченную замкнутым путем. Ясно, что есть растянутые поверхности, которые мы можем построить с замкнутым путем в качестве границы, которые не позволяют отрезку конечной длины проткнуть его. ]
С этим определением замкнутого тока мы имеем закон Ампера:
\[\oint \limits_{\rm {path}}\overrightarrow B \cdot \overrightarrow {dl} = \mu_oI_{enclosed}\]
Интеграл выполняется по любой цепи Ампера, полностью охватывающей замкнутый ток, точно так же, как интеграл по закону Гаусса работает для любой замкнутой поверхности, окружающей заряд. Все свойства закона Гаусса аналогичны свойствам закона Ампера:
- Закрытый определяется с точки зрения способности снимать заряд/ток с поверхности/замкнутого пути без прорыва корпуса.

- Знак заряда внутри гауссовой поверхности связан с положительным направлением вектора площади. Если общий поток имеет отрицательное направление (противоположное ориентации площади), то заключенный заряд отрицателен. Точно так же мы определяем положительное направление циркуляции для цепи Ампера, и если направление магнитного поля тока имеет ту же ориентацию циркуляции, что и в цепи Ампера, то этот ток является «положительным», в противном случае он «отрицательный.»
- Могут быть как положительные, так и отрицательные заряды/токи, заключенные в поверхностный/замкнутый путь, и они объединяются, чтобы дать суммарный заряд/ток.
- Мы можем использовать симметрию для решения поля. Обычно это означает, что поле параллельно или перпендикулярно поверхности/замкнутому пути и что оно имеет постоянную величину на этой поверхности/замкнутом пути.
- Форма поверхности/замкнутого пути не имеет значения, пока он замкнут.
Рисунок 4. 5.2 – Сравнение закона Гаусса с законом Ампера
5.2 – Сравнение закона Гаусса с законом Ампера
Применение закона Ампера
Применение закона Ампера очень похоже на применение закона Гаусса – для вычисления полей используется симметрия. Прежде чем мы сделаем что-либо из этого, давайте подтвердим результат, который у нас уже есть – поле на оси круговой петли радиуса \(r\) (уравнение 4.4.10). Нам нужно выбрать полезную цепь — она должна охватывать ток, и она должна иметь направление, которое хорошо совпадает с направлением магнитного поля, которое мы знаем из симметрии.С этой целью мы выберем амперовский контур, который следует по оси \(z\) от \(-\infty\) до \(+\infty\), а оттуда обращается вокруг самого себя на бесконечности. Интеграл от этого бесконечно удаленного отрезка замкнутого пути будет равен нулю, потому что на этом расстоянии поле ослабевает до нуля, так что остается только интеграл по оси \(z\).
Рисунок 4.5.3 – Схема Ампера для контура
Магнитное поле на оси имеет то же направление, что и контур вдоль оси \(z\), и хотя мы не знаем угла между полем и направлением пути в другом месте, это не имеет значения, потому что поле исчезает. {+\infty} = \mu_oI\]
{+\infty} = \mu_oI\]
Поскольку замкнутый ток в этой цепи Ампера на самом деле является током в круговой петле, и поскольку этот ток имеет положительную ориентацию для этого замкнутого пути (он выходит за пределы страницы, а путь идет против часовой стрелки, что удовлетворяет правому -правило) для этого случая подтверждается закон Ампера.
Теперь давайте воспользуемся законом Ампера более традиционным способом – для вычисления магнитного поля в симметричной физической ситуации. Посмотрим на поле соленоида.Соленоид имеет высокую степень симметрии, главным образом благодаря нашему предположению, что его длина практически бесконечна. Рассмотрим направление поля внутри соленоида. Нет оснований ожидать, что она где-либо отклонится от параллельности оси, потому что тогда что может сделать точку, в которой происходит это расхождение, такой особенной? Это похоже на любую другую точку бесконечного соленоида, поэтому направление поля должно быть таким же, как и у любой другой точки соленоида.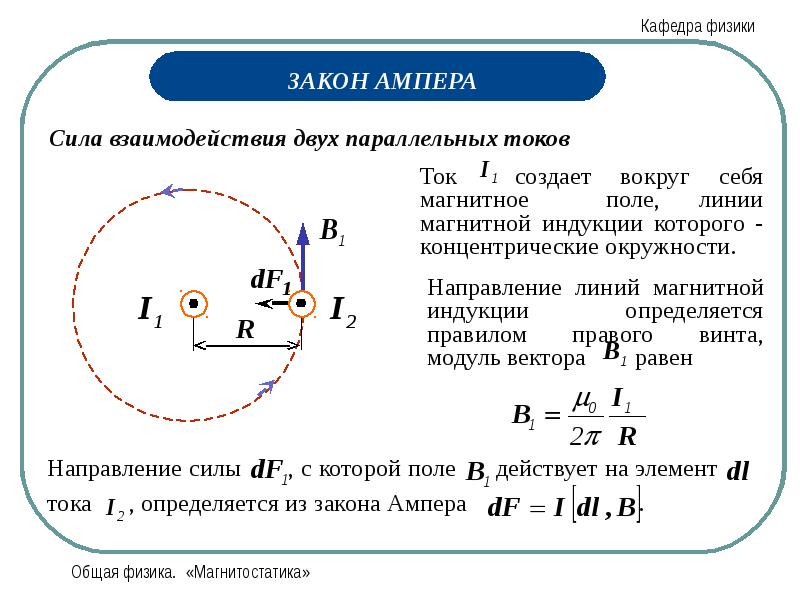 Более того, вдоль оси оно не должно усиливаться — почему поле в одной точке на оси должно быть большей величины, чем в любой другой?
Более того, вдоль оси оно не должно усиливаться — почему поле в одной точке на оси должно быть большей величины, чем в любой другой?
Конечно, знание того, что поле внутри соленоида везде параллельно оси и имеет одинаковую напряженность в зависимости от его положения вдоль оси внутри соленоида, не говорит нам, что напряженность поля также однородна в зависимости от расстояния от ось — возможно, она становится сильнее по мере приближения к проволочным виткам? Например, поле может выглядеть так:
.
Рис. 4.5.4 – Предположение о магнитном поле внутри соленоида
Мы можем проверить это предположение, используя закон Ампера. Мы делаем это, строя внутри соленоида прямоугольную цепь Ампера, две стороны которой параллельны полю, а две стороны перпендикулярны полю.
Рисунок 4.5.5 – Схема Ампера для внутренней части соленоида
Теперь применим закон Ампера. Во-первых, по этому замкнутому пути не протекает электрический ток, поэтому интеграл по пути будет равен нулю:
Во-первых, по этому замкнутому пути не протекает электрический ток, поэтому интеграл по пути будет равен нулю:
\[\oint \overrightarrow B \cdot \overrightarrow {dl} = \mu_oI_{enclosed} = 0\]
Во-вторых, магнитное поле перпендикулярно двум сторонам прямоугольника, поэтому скалярное произведение поля на смещения на этом участке цепи равно нулю, что дает нулевой интеграл вдоль вертикальных сегментов. И напряженность поля не меняется вдоль направления оси, а поле параллельно этим частям пути, поэтому скалярные произведения и интегралы выполняются легко:
\[\begin{array}{l} \int\limits_{vertical} \overrightarrow B \cdot \overrightarrow {dl} && = && 0 \\ \int\limits_{top} \overrightarrow B_{top} \cdot \ overrightarrow {dl} && = && \int \left(-B_{top}\;dl\right) && = && -B_{top}L \\ \int\limits_{bottom} \overrightarrow B_{bottom} \cdot \ overrightarrow {dl} && = && \int \left(+B_{bottom}\;dl\right) && = && +B_{bottom}L \end{массив}\]
Складывая все четыре вклада в интеграл и приравнивая его к нулю (отсутствие замкнутого тока), мы получаем, что \(B_{top} = B_{bottom}\), что означает, что напряженность поля на разных расстояниях от оси внутри соленоида на самом деле то же самое. Магнитное поле внутри соленоида совершенно однородно.
Магнитное поле внутри соленоида совершенно однородно.
Обратите внимание, что прямоугольная цепь Ампера, параллельная оси, проведенной вне соленоида, должна дать нам тот же результат: магнитное поле должно быть однородным и там. Но это означает, что поле той же силы бесконечно далеко от соленоида, как и сразу за его пределами. Естественно, поле равно нулю бесконечно далеко, а это означает, что мы можем заключить, что магнитное поле равно нулю везде вне соленоида.
Наконец, мы также можем использовать закон Ампера для определения напряженности однородного магнитного поля внутри соленоида, не проводя интегрирование бесконечного числа петель, как мы это делали в предыдущем разделе. Мы достигаем этого, строя прямоугольную цепь Ампера, параллельную оси с одной стороной внутри соленоида и другой снаружи его.
Рисунок 4.5.6 – Схема Ампера для расчета поля внутри соленоида
Как и ранее, мы видим, что вклады в интеграл от вертикальных сторон прямоугольного пути равны нулю, так как внутри соленоида поле перпендикулярно пути (а вне соленоида поле равно нулю).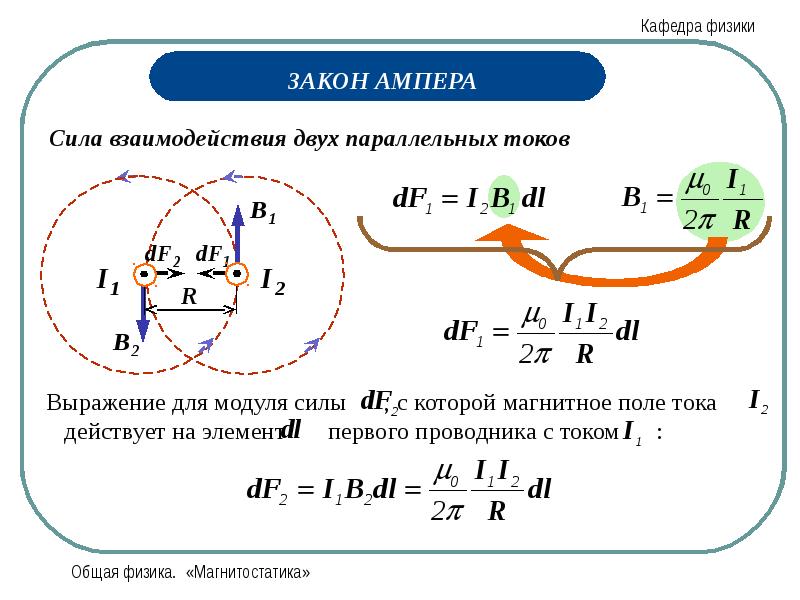 Однако на этот раз вклад одной из горизонтальных сторон (вне соленоида) также равен нулю, так как поля нет. Сторону прямоугольника внутри соленоида легко интегрировать, поэтому сложение их всех вместе по закону Ампера дает:
Однако на этот раз вклад одной из горизонтальных сторон (вне соленоида) также равен нулю, так как поля нет. Сторону прямоугольника внутри соленоида легко интегрировать, поэтому сложение их всех вместе по закону Ампера дает:
\[\mu_oI_{enclosed}=\oint \overrightarrow B \cdot \overrightarrow {dl} = BL\left(внутри\справа)+ 0 \left(вертикально\справа)+ 0 \left(снаружи\справа)\]
Теперь нам нужно определить закрытый ток. Из диаграммы мы можем видеть, используя правило правой руки для схемы Ампера, что ток, протекающий через страницу, положительный.На схеме показаны 6 закрытых проводов, но мы будем называть это более общим \(N\). Если ток, протекающий по проводу, равен \(I\), то замкнутый ток равен \(+NI\). Включение этого выше дает:
\[\mu_oNI = BL \;\;\;\Стрелка вправо\;\;\; B = \mu_o\dfrac{N}{L}I = \mu_o n I \]
Это соответствует результату, полученному ранее (уравнение 4.4.13). И, как и в случае с законом Гаусса для электрических полей, при использовании этого метода требуемая математическая гимнастика значительно сокращается.
Пример \(\PageIndex{1}\)
Рассмотрим тороидальный соленоид. Это соленоид конечной длины, ось которого изогнута таким образом, что два открытых конца замыкаются друг на друга, образуя классическую форму пончика (или рогалика). Когда мы смотрим на это устройство, с нашей точки зрения, ток проходит через провода, выходящие из страницы из центра тороида и входящие в страницу снаружи тороида (см. схему ниже). используйте закон Ампера, чтобы найти поле внутри и снаружи соленоида.
- Раствор
Лучше всего начать с просмотра поперечного сечения соленоида, разрезающего «бублик» параллельно плоскости страницы. Это показывает провода внутри с током, выходящим из страницы, и провода снаружи с током, входящим в страницу.
Из симметрии мы можем заключить, что магнитное поле на любом фиксированном расстоянии от центра имеет одинаковую величину, хотя напряженность поля может меняться при изменении этого расстояния.
 Кроме того, симметрия требует, чтобы направление поля было касательным к окружности в плоскости страницы и концентричным по отношению к центру тороида.
Кроме того, симметрия требует, чтобы направление поля было касательным к окружности в плоскости страницы и концентричным по отношению к центру тороида. Построение контура Ампера, представляющего собой круг в плоскости страницы, будет тогда параллельно любому полю, присутствующему где угодно, что упрощает вычисление интеграла. Если радиус кругового пути равен \(r\), то:
\[\oint \overrightarrow B \cdot \overrightarrow {dl} = \oint B\;dl = B\oint dl = B\left(2\pi r\right) \nonnumber\]
Если мы выберем цепь вне тороида (или внутри бублика), то замкнутый ток равен нулю, что говорит нам о том, что магнитное поле вне тороида равно нулю.Как и прямой соленоид, тороидальный соленоид ограничивает магнитное поле своей внутренней частью. Чтобы получить поле внутри соленоида, выберите радиус кругового пути так, чтобы он находился внутри соленоида:
На этот раз замкнутый ток равен общему количеству витков в соленоиде \(N\), умноженному на ток через провод \(I\), что дает нам поле внутри:
\[B\left(2\pi r\right) = \mu_o N I \;\;\;\Стрелка вправо\;\;\; B=\dfrac{\mu_o N I}{2\pi r} \nonumber\]
Обратите внимание, что это отличается от поля в прямом соленоиде двумя способами: во-первых, поле неоднородно внутри соленоида – оно сильнее ближе к центру, чем снаружи соленоида.
 И, во-вторых, именно общее число витков (которое теперь конечно), а не плотность витков определяет напряженность поля. Интересно, что плотность витков для тороида можно отрегулировать до «витков на радиан», а не оборотов на метр. Эта «угловая плотность поворота» просто \(\frac{N}{2\pi}\).
И, во-вторых, именно общее число витков (которое теперь конечно), а не плотность витков определяет напряженность поля. Интересно, что плотность витков для тороида можно отрегулировать до «витков на радиан», а не оборотов на метр. Эта «угловая плотность поворота» просто \(\frac{N}{2\pi}\).
Закон Ампера – University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как закон Ампера связывает магнитное поле, создаваемое током, со значением тока
- Рассчитайте магнитное поле длинного прямого провода, тонкого или толстого, по закону Ампера
Фундаментальное свойство статического магнитного поля заключается в том, что, в отличие от электростатического поля, оно не является консервативным.Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути.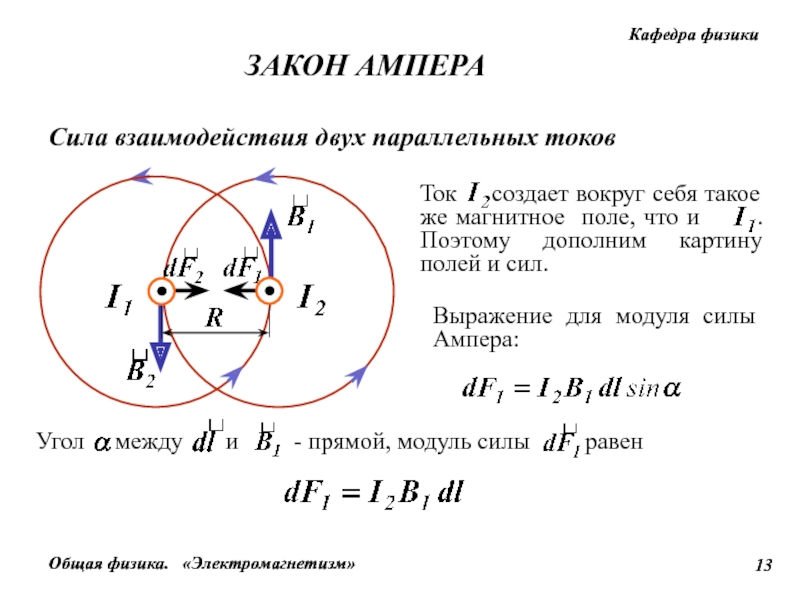 Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от и известен как закон Ампера. Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от и известен как закон Ампера. Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
(рисунок) показывает произвольную плоскость, перпендикулярную бесконечному прямому проводу, ток которого I направлен за пределы страницы. Линии магнитного поля представляют собой окружности, направленные против часовой стрелки и центрированные на проводе. Для начала рассмотрим замкнутые пути M и N . Обратите внимание, что один путь ( M ) охватывает провод, а другой ( N ) нет. Поскольку силовые линии круглые, это произведение B и проекции dl на окружность, проходящую через Если радиус этой конкретной окружности равен r , проекция равна и
Ток I длинного прямого провода направлен за пределы страницы.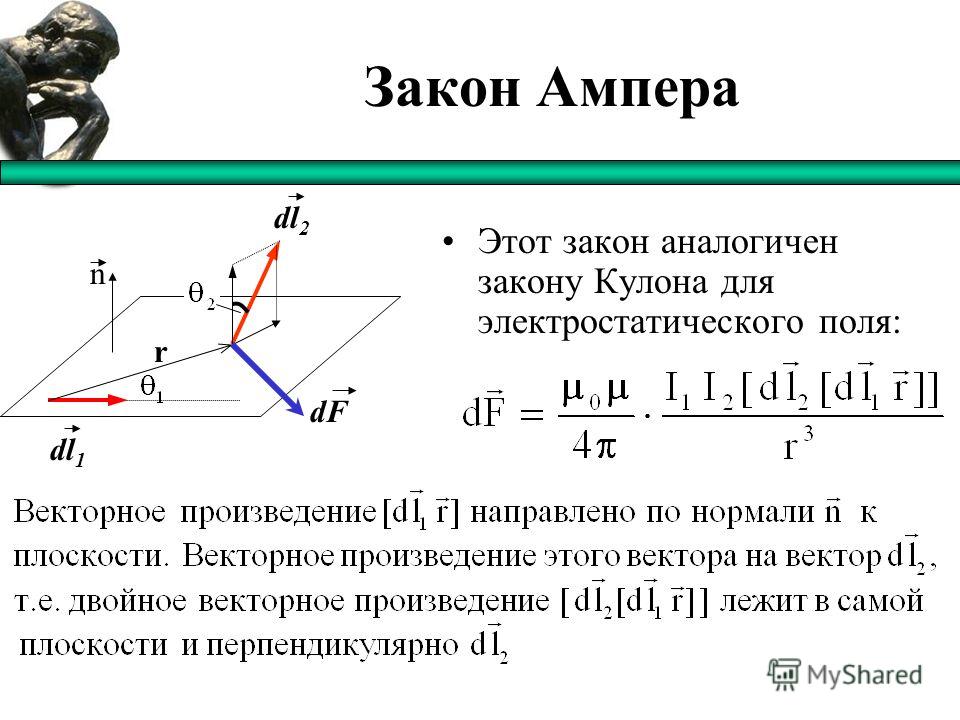 Интеграл равен и 0 соответственно для путей M и N .
Интеграл равен и 0 соответственно для путей M и N .
С учетом (Рисунок),
Для пути M , который циркулирует по проводу, и
Путь N , с другой стороны, циркулирует как по положительному (против часовой стрелки), так и по отрицательному (по часовой стрелке) (см. (Рисунок)), и поскольку он замкнут, Таким образом, для пути N ,
Распространение этого результата на общий случай есть закон Ампера.
Закон Ампера
По произвольному замкнутому пути,
, где I — это полный ток, проходящий через любую открытую поверхность S , периметр которой представляет собой путь интегрирования. Необходимо учитывать только токи внутри пути интегрирования.
Чтобы определить, является ли конкретный ток I положительным или отрицательным, согните пальцы правой руки в направлении пути интегрирования, как показано на (рис. ). Если I проходит через S в том же направлении, что и ваш вытянутый большой палец, I положительный; если I проходит через S в направлении, противоположном вашему вытянутому большому пальцу, это отрицательно.
). Если I проходит через S в том же направлении, что и ваш вытянутый большой палец, I положительный; если I проходит через S в направлении, противоположном вашему вытянутому большому пальцу, это отрицательно.
Стратегия решения проблем: закон Ампера
Чтобы рассчитать магнитное поле, создаваемое током в проводах, выполните следующие действия:
- Определите симметрию тока в проводе(ах). Если симметрии нет, используйте закон Био-Савара для определения магнитного поля.
- Определите направление магнитного поля, создаваемого проводом(ами), по правилу правой руки 2.
- Выберите петлю пути, в которой магнитное поле постоянно или равно нулю.
- Рассчитать ток внутри контура.
- Вычислите линейный интеграл вокруг замкнутого контура.
- Приравняйте и решите
Использование закона Ампера для расчета магнитного поля, создаваемого проводом Используйте закон Ампера для расчета магнитного поля, создаваемого постоянным током I в бесконечно длинном тонком прямом проводе, как показано на (рис. ).
).
Возможные компоненты магнитного поля B обусловлены током I , который направлен за пределы страницы.Радиальная составляющая равна нулю, потому что угол между магнитным полем и траекторией прямой.
Стратегия Рассмотрим произвольную плоскость, перпендикулярную проводнику, с током, направленным за пределы страницы. Возможные компоненты магнитного поля в этой плоскости и показаны в произвольных точках на окружности радиусом r с центром на проводе. Поскольку поле цилиндрически симметрично, оно не зависит от положения на этой окружности и не меняется. Также из симметрии радиальные линии, если они есть, должны быть направлены либо все внутрь, либо все наружу от провода.Это означает, однако, что должен существовать чистый магнитный поток через произвольный цилиндр, концентричный проводнику. Радиальная составляющая магнитного поля должна быть равна нулю, потому что мы можем применить закон Ампера к круговому пути, как показано.
Решение По этому пути постоянно и параллельно так
Таким образом, закон Ампера сводится к
Наконец, поскольку это единственный компонент, мы можем отбросить индекс и написать
Это согласуется с приведенным выше расчетом Био-Савара.
Значимость Закон Ампера работает хорошо, если у вас есть путь интегрирования, по которому можно получить результаты, которые легко упростить. Для бесконечного провода это легко работает с круговым путем вокруг провода, так что магнитное поле не учитывается при интегрировании. Если зависимость от пути кажется сложной, вы всегда можете вернуться к закону Био-Савара и использовать его для нахождения магнитного поля.
Расчет магнитного поля толстого провода по закону Ампера Радиус длинного прямого провода (рисунок) равен a , и по проводу течет ток, равномерно распределенный по его поперечному сечению.Найдите магнитное поле как внутри, так и снаружи провода.
(a) Модель провода с током радиусом a и током (b) Поперечное сечение того же провода радиусом a и петлей Ампера радиусом r .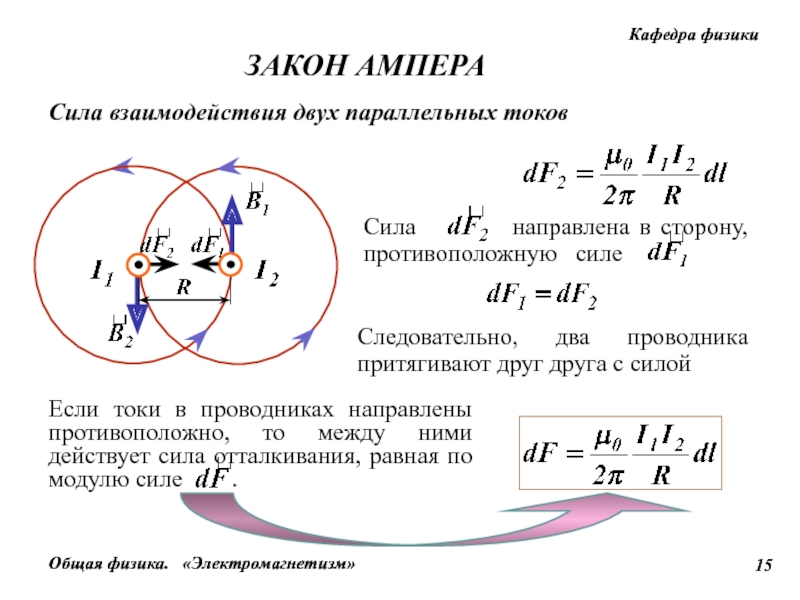
Стратегия
Эта задача имеет ту же геометрию, что и (рисунок), но замкнутый ток изменяется по мере того, как мы перемещаем путь интегрирования снаружи провода внутрь провода, где он не захватывает весь заключенный ток (см. (рисунок)).
Решение Для любого кругового пути радиусом r с центром на проводе
По закону Ампера это равно полному току, проходящему через любую поверхность, ограниченную путем интегрирования.
Сначала рассмотрим круговой путь внутри провода, например, показанный в части (a) на (Рисунок). Нам нужен ток I , проходящий через область, ограниченную путем. Она равна плотности тока Дж, умноженной на площади замкнутого пространства.Поскольку ток однороден, плотность тока внутри пути равна плотности тока во всем проводе, т.е. Следовательно, ток I , проходящий через область, ограниченную путем, равен
Мы можем учитывать это соотношение, потому что плотность тока Дж постоянна по площади провода. Следовательно, плотность тока на участке провода равна плотности тока на всей площади. Используя закон Ампера, получаем
Следовательно, плотность тока на участке провода равна плотности тока на всей площади. Используя закон Ампера, получаем
, а магнитное поле внутри провода равно
.
Вне провода ситуация идентична ситуации бесконечного тонкого провода из предыдущего примера; то есть
Вариант B с r показан на (Рисунок).
Изменение магнитного поля, создаваемого током в длинном прямом проводе радиусом a .
Значимость Результаты показывают, что по мере увеличения радиального расстояния внутри толстой проволоки магнитное поле увеличивается от нуля до известного значения магнитного поля тонкой проволоки. Вне провода поле падает независимо от того, толстый провод или тонкий.
Этот результат аналогичен тому, как закон Гаусса для электрических зарядов ведет себя внутри равномерного распределения зарядов, за исключением того, что закон Гаусса для электрических зарядов имеет равномерное распределение заряда по объему, тогда как закон Ампера здесь имеет однородную область распределения тока. Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
Проверьте свои знания Рассмотрите возможность использования закона Ампера для расчета магнитных полей конечного прямого провода и круглой проволочной петли. Почему это не полезно для этих расчетов?
В этих случаях интегралы вокруг петли Ампера очень сложны из-за отсутствия симметрии, поэтому этот метод бесполезен.
Резюме
- Магнитное поле, создаваемое током, следующим по любому пути, представляет собой сумму (или интеграл) полей, обусловленных сегментами вдоль пути (величина и направление, как для прямого провода), в результате чего возникает общая зависимость между током и полем, известная как зависимость Ампера.
 закон.
закон. - Закон Ампера можно использовать для определения магнитного поля от тонкой проволоки или толстой проволоки с помощью геометрически удобного пути интегрирования. Результаты согласуются с законом Био-Савара.
Концептуальные вопросы
Справедлив ли закон Ампера для всех замкнутых путей? Почему это обычно не полезно для расчета магнитного поля?
Закон Ампера действителен для всех замкнутых путей, но он бесполезен для расчета полей, когда создаваемое магнитное поле не имеет симметрии, которую можно использовать при соответствующем выборе пути.
Глоссарий
- Закон Ампера
- физический закон, утверждающий, что линейный интеграл магнитного поля вокруг электрического тока пропорционален току
Окружной закон Ампера
Окружной закон Ампера
Next: Магнитное поле
Вверх: Магнетизм
Предыдущий: Эффект Холла
Круговой закон Ампера
Рассмотрим длинный тонкий провод, по которому течет постоянный ток. Предположим, что
Предположим, что
Провод ориентирован так, что ток течет вдоль -оси.
Рассмотрим некоторую замкнутую петлю в плоскости -, которая окружает провод в
против часовой стрелки, если смотреть вниз по -оси. Предположим, что
— короткий прямолинейный элемент этой петли.
Составим скалярное произведение этого элемента с локальным магнитным полем
. Таким образом,
| (173) |
где угол, образуемый между направлением линейного элемента и
направление местного магнитного поля.Мы можем рассчитать
за
каждый элемент строки, из которого состоит цикл. Если суммировать все
значения, полученные таким образом, и принять предел в качестве
количество элементов стремится к бесконечности,
мы получаем линейный интеграл
| (174) |
Каково значение этого
интеграл? вообще сложный вопрос
отвечать.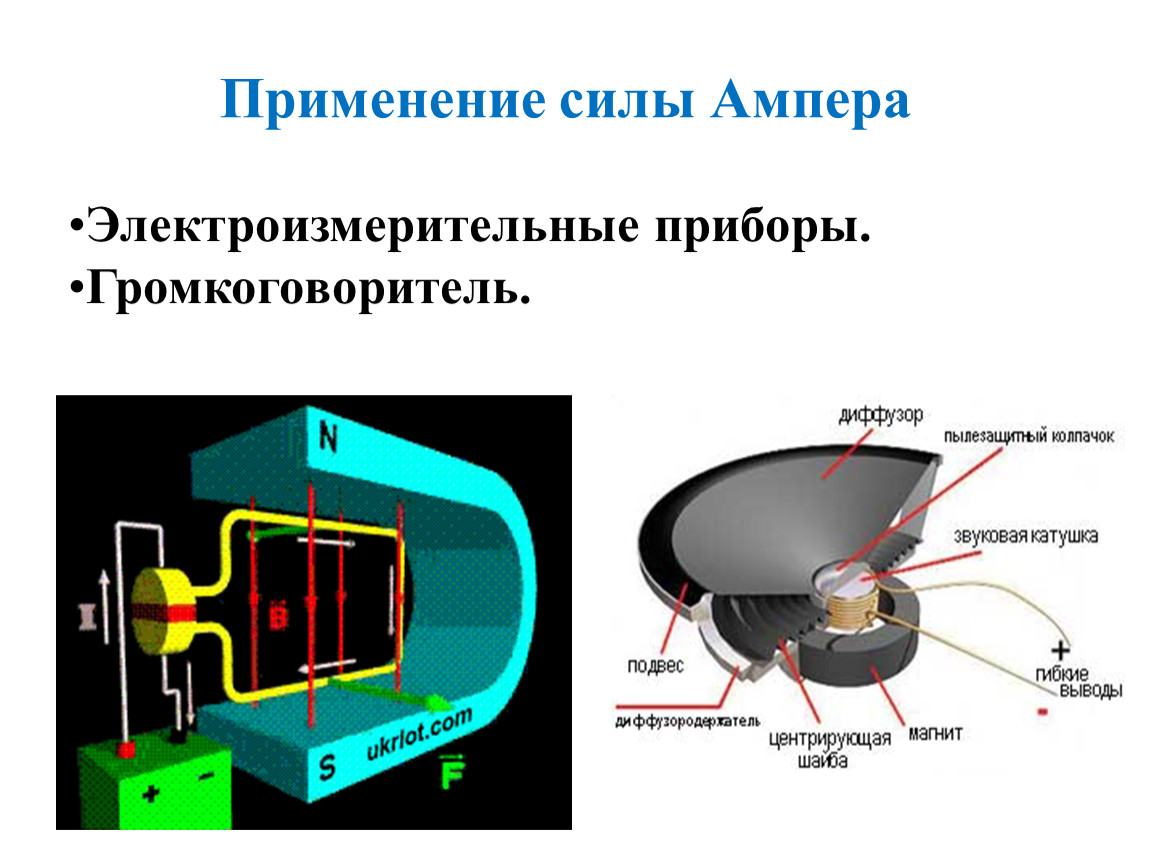 Однако рассмотрим частный случай. Предположим, что это круг
Однако рассмотрим частный случай. Предположим, что это круг
радиуса с центром на проводе.В этом случае напряженность магнитного поля
одинакова во всех точках цикла. По факту,
| (175) |
Более того, поле всюду параллельно элементам прямой, которые
составить петлю. Таким образом,
| (176) |
или
| (177) |
Другими словами, линейный интеграл магнитного поля вокруг некоторого
круглая петля с центром на проводе с током, и
в плоскости, перпендикулярной проводу, равен
раз больше тока, протекающего по проводу. Обратите внимание, что этот ответ не зависит от
Обратите внимание, что этот ответ не зависит от
радиус петли: т.е. , тот же результат
получается путем взятия линейного интеграла вокруг любых круговых петель с центром
на проводе.
В 1826 г. Ампер продемонстрировал, что уравнение (177) верно для любой замкнутой петли, которая
кружит вокруг любого распределения токов. Таким образом, круговой закон Ампера
можно написать:
Линейный интеграл магнитного поля вокруг некоторого замкнутого контура
равно произведению алгебраической суммы токов, проходящих через
петля.
При формировании алгебраической суммы токов, проходящих через контур, эти токи
вокруг которого петля вращается против часовой стрелки (смотря
против направления тока) считаются положительными токами, тогда как те
которую петля вращает по часовой стрелке (смотря
против направления тока) считаются отрицательными токами.
Контурный закон Ампера относится к магнитостатике (учение о магнитных полях
генерируются постоянными токами) то, что закон Гаусса для электростатики
(изучение электрических полей, создаваемых стационарными зарядами). Нравится
Нравится
Закон Гаусса, круговой закон Ампера особенно полезен в ситуациях
которые обладают высокой степенью симметрии.
Next: Магнитное поле
Вверх: Магнетизм
Предыдущий: Эффект Холла
2007-07-14
Закон Ампера
Закон Ампера
Ампер
закон
Закон Ампера представляет собой математическую формулировку соотношения
между токами и магнитными полями, которые они генерируют.это
таким образом, магнитный эквивалент закона Гаусса, который связывает заряды
к их электрическим полям. Закон Ампера сформулирован ниже для
ради любопытства, но пользоваться им не надо будет
по физике 232: формулы, которые нам нужны для
B поля соленоида и длинный
вместо этого можно принять на веру прямой провод.
Закон Ампера определяется в терминах произвольной поверхности и
замкнутый контур, образующий его границу. Таким образом, это напоминает
Закон Гаусса, который включает в себя объем и замкнутую поверхность, которые
образует его границу.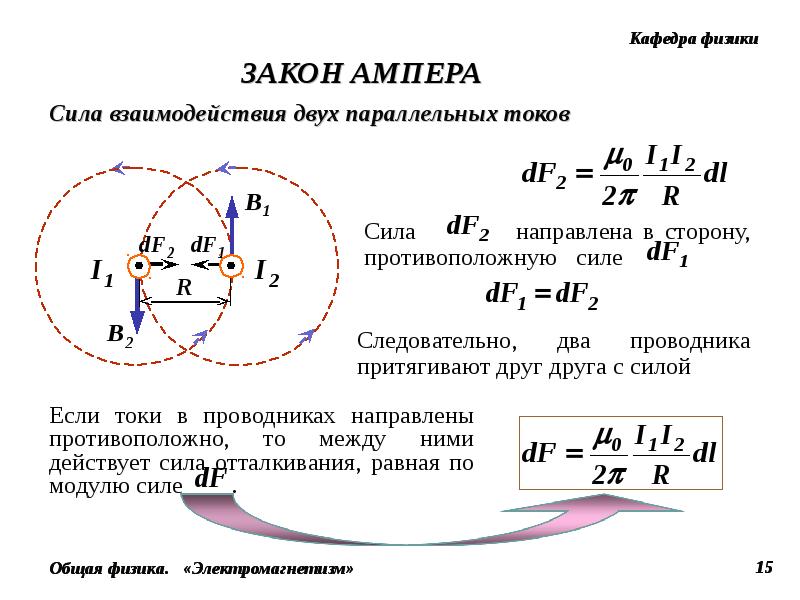 Рассмотрим замкнутый цикл, не обязательно
Рассмотрим замкнутый цикл, не обязательно
круг, разбитый на мелкие элементы длиной D L i
с магнитным полем Б и
у каждого элемента.
Закон Ампера гласит, что сумма по
элементы
составляющая магнитного поля вдоль направления
элемент, умноженный на длину элемента, пропорционален текущему
I который проходит через цикл:
Это общее утверждение закона Ампера.В случае с проводом петля может быть окружностью, очерченной вокруг
проволоки, а так как поле всегда касается окружности, cosq = 1.
Окружность круга радиусом r
равно 2p r , поэтому закон Ампера
дает
который является
выражение для магнитного поля провода, данное ранее.
Закон Ампера также позволит нам рассчитать магнитное поле
для соленоида.
Примеры
Указатель источников магнитного поля
Указатель лекций
Закон Ампера – Гиперучебник по физике
Обсуждение
Закон Био-Савара
Обычно с этим законом не очень интересно иметь дело, но это элементарная основа (самая примитивная формулировка) электромагнетизма.Жан-Батист Био и Феликс Савар.
| B = 9 = | |
| 4π | R 2 |
Давайте применим его к трем относительно простым ситуациям: прямой провод, одна петля провода и катушка провода со многими петлями (соленоид).
прямой провод
Имея бесконечно длинный прямой провод с током, используйте закон Био-Савара, чтобы определить напряженность магнитного поля на любом расстоянии r .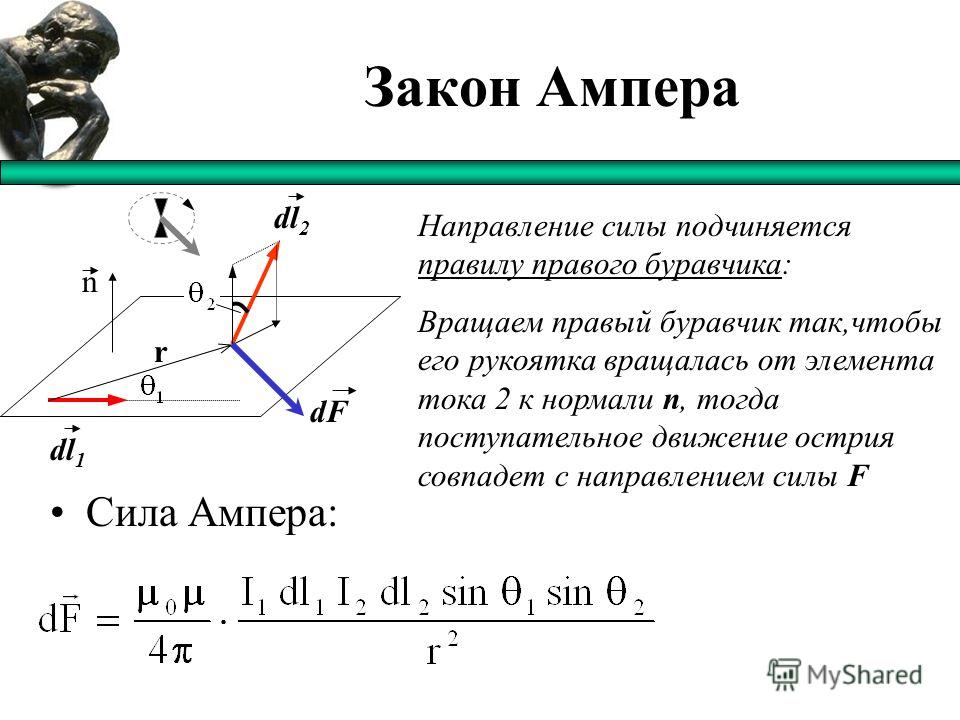
Начните с закона Био-Савара, потому что так говорит задача.
| = | μ 0 9 | ⌠ ⌡ |
| 4π | R 2 |
| +∞ | ||||
| Б строка = | мк 0 I | ⌠ ⌡ | y /√( x 2 + y 2 ) | дх к̂ |
| 4π | x 2 + у 2 | |||
| −∞ | ||||
| +∞ | ||||
| Б строка = | мк 0 I | ⌠ ⌡ | г | дх к̂ |
| 4π | ( x 2 + y 2 ) 3/2 | |||
| −∞ | ||||
| +∞ | |||||
| Б строка = | мк 0 I | ⎡ ⎢ ⎣ | х | ⎤ ⎥ ⎦ | к̂ |
| 4π | y ( x 2 + y 2 ) ½ | ||||
| −∞ | |||||
| Б строка = | мк 0 I | ⎡ ⎢ ⎣ | +1 | − | −1 | ⎤ ⎥ ⎦ | к̂ |
| 4π | г | г |
| Б строка = | мк 0 I | 2 | к̂ | |
| 4π | г |
одинарная проволочная петля
Для заданного контура провода с током радиусом a определите напряженность магнитного поля в любом месте вдоль его оси вращения на любом расстоянии x от его центра.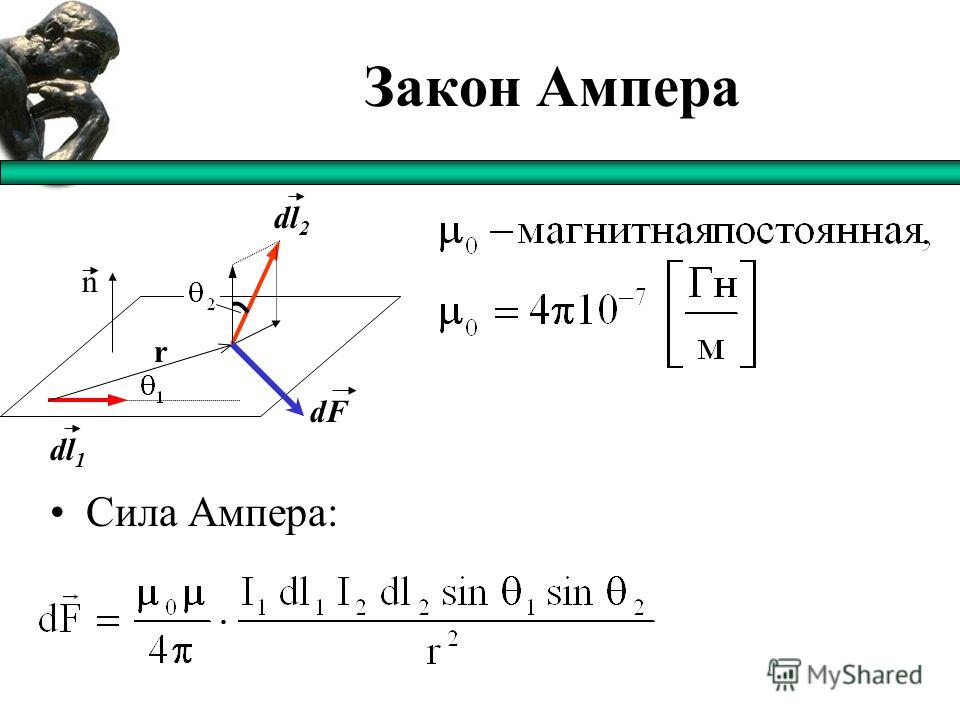
Начните с закона Био-Савара, потому что так говорит задача.
| = | μ 0 9 | ⌠ ⌡ |
| 4π | R 2 |
| 2π | ||||
| B петля = | мк 0 I | ⌠ ⌡ | a /√( x 2 + a 2 ) | и φ î |
| 4π | x 2 + a 2 | |||
| 0 | ||||
| 2π | |||||
| B петля = | мк 0 I | а 2 | ⌠ ⌡ | г φ î | |
| 4π | ( x 2 + a 2 ) 3/2 | ||||
| 0 | |||||
| B петля = | мк 0 I | а 2 | [2π − 0] → | |
| 4π | ( x 2 + a 2 ) 3/2 |
| B петля = | мк 0 I | а 2 | î | |
| 2 | ( x 2 + a 2 ) 3/2 |
| 9 = | 0 9059 9 | 9 2 |
| 2 | ( x 2 + A 2 ) 3/2 |
соленоид
Для данной катушки с бесконечным числом витков (бесконечный соленоид) определите напряженность магнитного поля внутри, если катушка имеет n витков на единицу длины.
[здесь находится изображение соленоида]
| B соленоид = | ⌠ ⌡ | d B петля |
Строго говоря, это не применение закона Био-Савара. На самом деле это просто приложение чистого исчисления. Что такое соленоид, как не набор катушек, а бесконечный соленоид — это бесконечный набор катушек. Исчисление любит бесконечность. Он ест его на завтрак.
| +∞ | ||||
| B соленоид = | мк 0 I | ⌠ ⌡ | а 2 | н дх î |
| 2 | ( x 2 + a 2 ) 3/2 | |||
| −∞ | ||||
| +∞ | ||||
| B соленоид = | мк 0 нИ | ⎡ ⎢ ⎣ | х | ⎤ ⎥ ⎦ |
| 2 | √( x 2 + a 2 ) | |||
| −∞ | ||||
| B соленоид = | мк 0 нИ | [(+1) — (-1)] → |
| 2 |
B 60547 Соленоид = μ 0 Ni î
0 = μ 0 9059 Ni
закон ампера
С законом Ампера все лучше (почти все).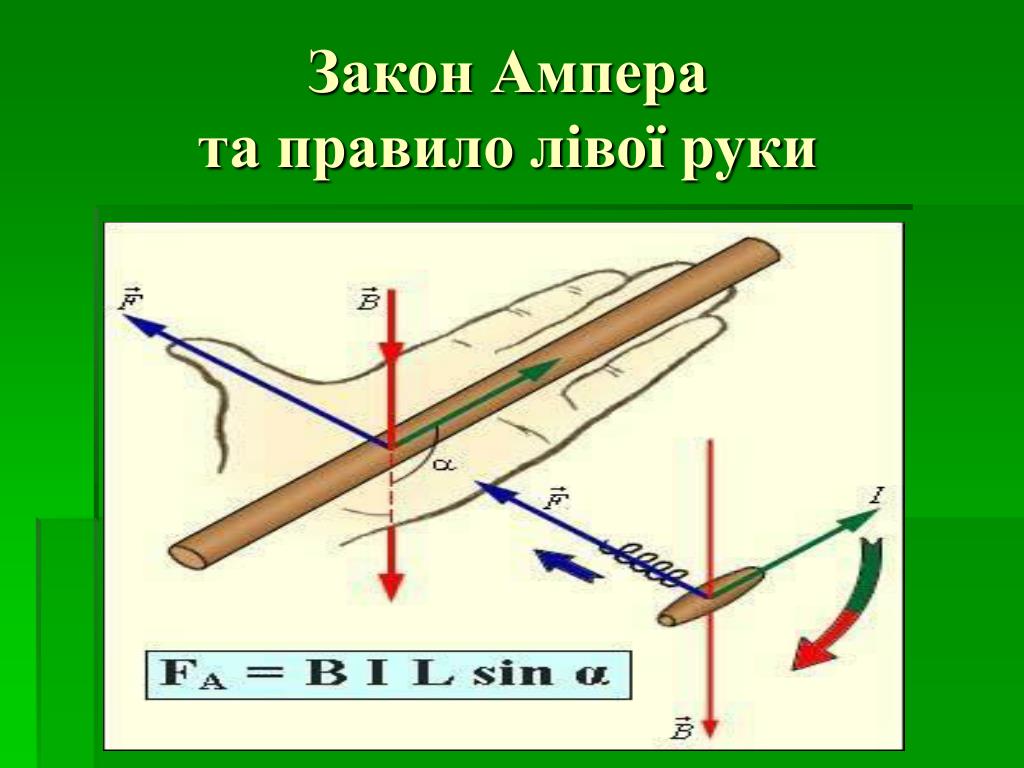
Андре-Мари Ампер (1775–1836) Франция
Закон в интегральной форме.
∮ B · d s = μ 0 I
Закон в дифференциальной форме.
∇ × B = μ 0 Дж
Эти формы закона неполные. Полный закон имеет дополнительный термин, называемый током смещения. Мы обсудим, что все это означает, в следующем разделе этой книги. А пока просто посмотрите на красивые символы.
| ∮ B · D S = μ 0 ε 0 0 | ∂Φ E 9 | + μ 0 I | ||||
| ∂ т |
| ∇ × 0 ε 0 ε 0 0 | ∂ E | + μ 0 J |
| ∂ T |
к прямому проводу, плоскому листу, соленоиду, тороиду и внутренней части провода.
прямой провод
Прямой провод. Посмотрите, как это просто.
[сюда идет прямой провод с амперной дорожкой]
Начните с закона Ампера, потому что это самый простой способ получить решение.
∮ B · d s = μ 0 I
B (2π r ) = μ 0 I
плоский лист
За прямым проводом лежит бесконечный лист.
[сюда идет бесконечный лист с амперовым путем]
Начните с закона Ампера, потому что это самый простой способ получить решение.
∮ B · d s = μ 0 I
B (2ℓ) = μ 0 σℓ
соленоид
Соленоид. Тоже удивительно просто.
[здесь идет соленоид с амперным путем]
Начните с закона Ампера, потому что это самый простой способ получить решение.
∮ B · d s = μ 0 I
Bℓ = μ 0 NI
B = мк 0 нИ
тороид
За соленоидом находится тороид.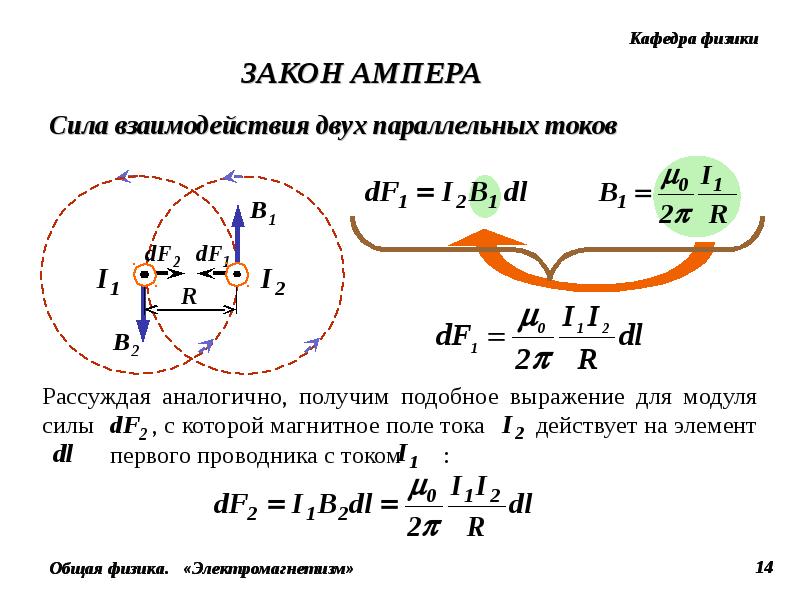
[тороид с амперной дорожкой идет сюда]
Посмотрите, как я вытаскиваю кролика из шляпы, начиная с закона Ампера, потому что это самый простой способ вытащить кролика из шляпы.
∮ B · d s = μ 0 I
B (2π r ) = μ 0 NI
внутренняя часть провода
Каково это оказаться внутри провода — внутри провода с суммарным током I ?
[здесь идет амперный путь внутри провода]
Начните с закона Ампера, потому что это самый простой способ найти решение.
∮ B · d s = μ 0 I
| B (2π r ) = μ 0 I | π р 2 |
| π R 2 |
Каково это оказаться внутри провода — внутри провода с плотностью тока ρ?
В последний раз вернемся к закону Ампера.
∮ B · d s = μ 0 I
B (2π r ) = μ 0 ρ(π r 2 )
ЗАКОН
АМПЕР ЗАКОН
АМПЕР
Магнитное поле на расстоянии r от очень длинного прямого провода, несущего
установившийся ток I, имеет величину, равную
(31.)
и направление, перпендикулярное r и I. Интеграл по путям по окружности
вокруг провода (см. рис. 31.1) равно
(31.2)
Здесь мы использовали тот факт, что магнитное поле является тангенциальным в любой точке
на круговой траектории интегрирования.
Рисунок 31.1. Магнитное поле, создаваемое током. Любой произвольный путь можно рассматривать как набор радиальных
сегменты (r изменяется, а [тета] остается постоянным) и круговые сегменты
([тета] изменяется, а r остается постоянным).Для радиальных сегментов магнитный
поле будет перпендикулярно смещению и масштабному произведению между
магнитное поле и смещение равны нулю. Рассмотрим теперь небольшой циркуляр
Рассмотрим теперь небольшой циркуляр
отрезок траектории вокруг провода (см. рис. 31.2). Интеграл по путям
вдоль этого кругового отрезка равно
(31.3)
Рисунок 31.2. Интеграл по путям по малому круговому пути. Уравнение (31.3) показывает, что вклад этого кругового
отрезок полного интеграла по траекториям не зависит от расстояния r и только
зависит от изменения угла [Delta][theta].Для замкнутого пути
общее изменение угла составит 2[pi], и уравнение (31.3) можно переписать как
(31.4)
Это выражение Закон Ампера :
» Интеграл от B по любому замкнутому математическому пути равен u 0
умножить ток, перехваченный областью, охватывающей путь »
Пример: Задача 31.5
Шесть параллельных алюминиевых проводов малого, но конечного радиуса лежат в
тот же самолет.Провода разделены равным расстоянием d, и они несут равные
токи I в том же направлении. Найдите магнитное поле в центре
первый провод. Предположим, что токи в каждом проводе распределены равномерно
Предположим, что токи в каждом проводе распределены равномерно
над его поперечным сечением.
Схематическое изображение задачи показано на рис. 31.3. Магнитное поле
генерируемое одним проводом, равно
(31.5)
где r — расстояние от центра провода.Уравнение (31.5)
правильно для всех точек за пределами провода, и поэтому может использоваться для определения
магнитное поле, создаваемое проводами 2, 3, 4, 5 и 6. Поле на
центр провода 1, благодаря току, протекающему по проводу 1, можно определить с помощью
по закону Ампера и равна нулю. Полное магнитное поле в центре
провод 1 можно найти векторным сложением вкладов каждого из шести
провода. Поскольку направление каждого из этих вкладов одинаково,
полное магнитное поле в центре провода 1 равно
(31.6)
Рисунок 31.3. Задача 31.5
Соленоид представляет собой устройство, используемое для создания однородного магнитного поля. Оно может
быть изготовлен из тонкой проводящей проволоки, намотанной на плотную спиральную катушку из многих витков.
Магнитное поле внутри соленоида можно определить суммированием магнитного
поля, генерируемые N отдельными кольцами (где N — число витков
соленоид). Мы ограничим наше обсуждение магнитного поля, создаваемого
соленоида к соленоиду, порожденному идеальным соленоидом бесконечной длины, и
имеет очень плотно намотанные катушки.
Идеальный соленоид обладает поступательной и вращательной симметрией. Однако, поскольку
силовые линии магнитного поля должны образовывать замкнутые петли, магнитное поле не может быть
направлена вдоль радиального направления (иначе линии поля были бы созданы или
разрушен на центральной оси соленоида). Поэтому делаем вывод, что
силовые линии в соленоиде должны быть параллельны оси соленоида. Величина
магнитного поля можно получить, применяя закон Ампера.
Рис. 31.4. Идеальный соленоид. Рассмотрим путь интеграции, показанный на рис. 31.4. Путь
интеграл магнитного поля вокруг этого пути интегрирования равен
(31.7)
где L — горизонтальная длина пути интегрирования.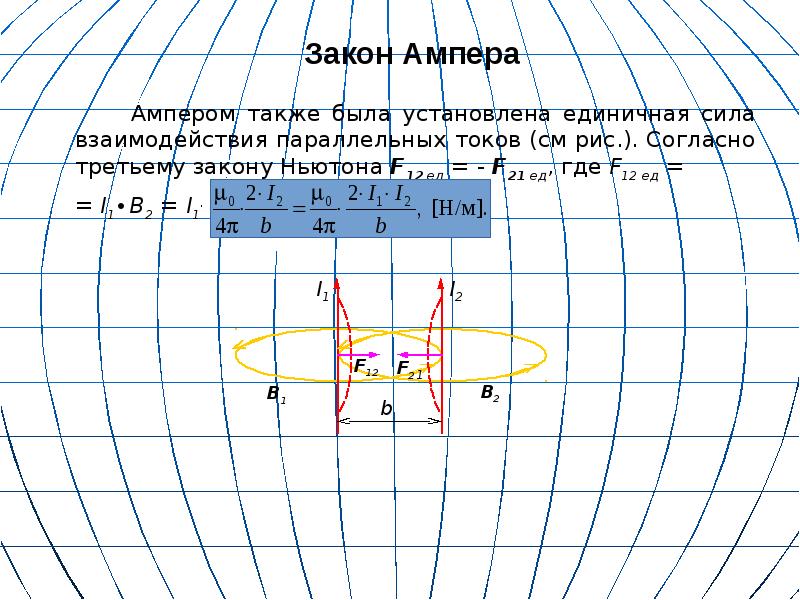 Текущий закрытый
Текущий закрытый
по пути интегрирования равно N . I 0 где N —
количество витков, заключенных в пути интегрирования, а I 0 — это
ток в каждом витке соленоида.Используя закон Ампера, мы заключаем, что
(31.8)
или
(31.9)
где n — число витков соленоида на единицу длины. Уравнение
(31.9) показывает, что магнитное поле B не зависит от положения внутри
соленоид. Мы заключаем, что магнитное поле внутри идеального соленоида равно
униформа.
Пример: Задача 31.14
По длинному соленоиду из n витков на единицу длины течет ток I, а
по длинному прямому проводу, лежащему вдоль оси этого соленоида, течет ток I’.Найдите чистое магнитное поле внутри соленоида на расстоянии r от оси.
Опишите форму силовых линий магнитного поля.
Магнитное поле, создаваемое соленоидом, является однородным, направленным параллельно
оси соленоида и имеет величину, равную
(31. 10)
10)
Магнитное поле длинного прямого провода, по которому течет ток I’, имеет
величина равна
(31.11)
и направлен перпендикулярно направлению r и I’.Направление
Таким образом, провод B перпендикулярен направлению
B соль . Суммарное магнитное поле внутри соленоида равно
векторная сумма B wire и B sol . Его величина равна
до
(31.12)
Угол a между направлением магнитного поля и осью z дан
по
(31.13)
Пример: Задача 31.15
Коаксиальный кабель состоит из длинного цилиндрического медного провода радиусом
r 1 окружен цилиндрической оболочкой с внутренним радиусом r 2
и внешний радиус r 3 (см. рис. 31.5). Проволока и оболочка несут
равные и противоположные токи I равномерно распределены по их объемам. Находить
формулы для магнитного поля в каждой из областей r < r 1 ,
r 1 < r < r 2 , r 2 < r <
r 3 и r > r 3 .
Силовые линии магнитного поля представляют собой окружности с центром на оси симметрии магнитного поля.
коаксиальный кабель. Сначала рассмотрим путь интегрирования с r < r 1 .
Континуальный интеграл B по этому пути равен
(31.14)
Ток, заключенный в этом пути интегрирования, равен
(31.15)
Применяя закон Фарадея, мы можем связать приложенный ток с путевым интегралом
В
(31.16)
Следовательно, магнитное поле В равно
(31.17)
Рисунок 31.5. Задача 31.15. В области между проволокой и оболочкой закрытый
ток равен I, а интеграл по пути магнитного поля определяется выражением
уравнение (31.14). Закон Ампера гласит, что
(31.18)
а магнитное поле определяется как
(31.19)
В третьей области (r 2 < r < r 3 ) континуальный интеграл
магнитного поля вдоль кругового пути с радиусом r определяется выражением
экв. (31.14). Приложенный ток равен
(31.14). Приложенный ток равен
(31.20)
Таким образом, магнитное поле равно
(31.21)
Ток, ограниченный путем интегрирования радиусом r > r 3
равен нулю (поскольку ток в проводе и в оболочке течет в
противоположные направления). Поэтому магнитное поле в этой области также
равен нулю.
Магнитная сила, действующая на частицу с зарядом q, движущуюся со скоростью v, равна
равно
(31.22)
Эта сила всегда перпендикулярна направлению движения частицы,
и поэтому изменит только направление движения, а не величину
скорости. Если заряженная частица движется в однородном магнитном
поле напряженностью B, перпендикулярное скорости v, то
величина магнитной силы определяется как
(31.23)
и его направление перпендикулярно v. В результате действия этой силы
частица будет совершать равномерное круговое движение.Радиус круга
определяется требованием равенства напряженности магнитной силы
центростремительная сила.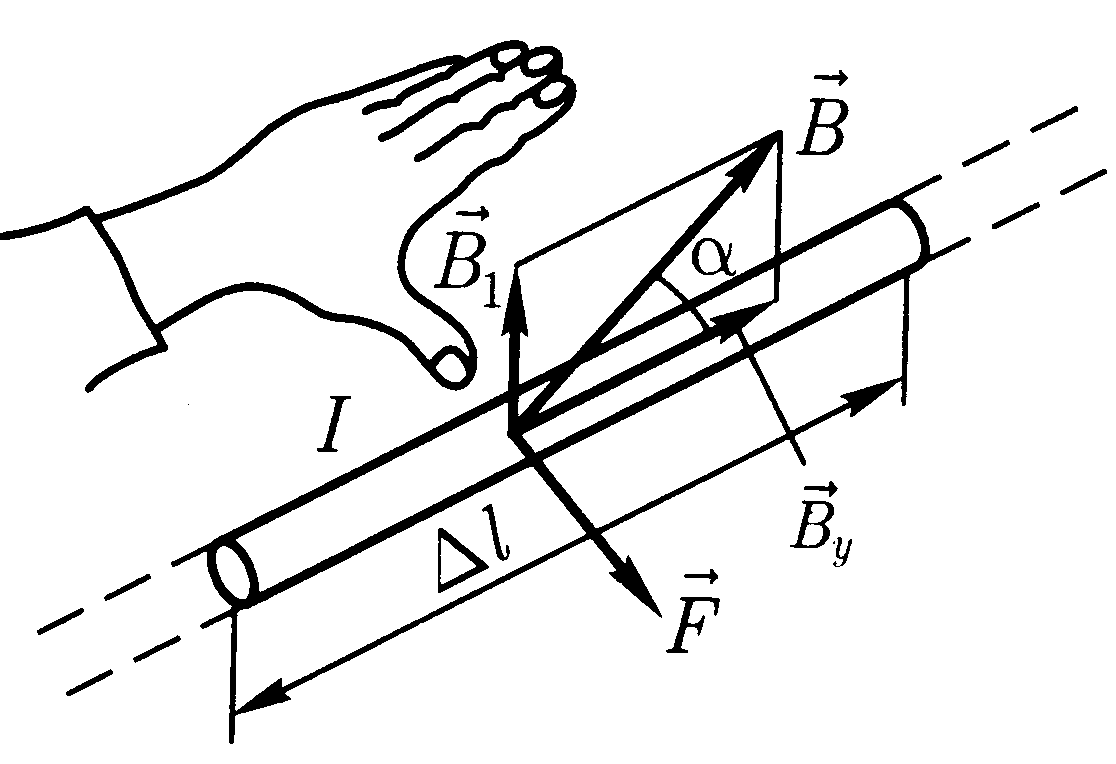 Таким образом,
Таким образом,
(31.24)
Радиус r орбиты равен
(31.25)
где р — импульс заряженной частицы. Расстояние, пройденное на
частица за один оборот равна
(31.26)
Время T, необходимое для совершения одного оборота, равно
.
(31.27)
Частота этого движения равна
(31.28)
и называется циклотронной частотой . Уравнение (31.28) показывает
что циклотронная частота не зависит от энергии частицы, и
зависит только от его массы m и заряда q.
Влияние магнитного поля на движение заряженной частицы можно использовать
определить некоторые его свойства. Одним из примеров является измерение
заряд электрона.Электрон, движущийся в однородном магнитном поле, будет
описывает круговое движение с радиусом, определяемым уравнением (31.25). Предположим,
электрон ускоряется потенциалом V 0 . Конечная кинетическая энергия
электрона определяется как
(31. 29)
29)
Импульс p электрона определяется его кинетической энергией
(31.30)
Таким образом, радиус кривизны траектории электрона равен
(31.31)
Уравнение (31.31) показывает, что измерение r можно использовать для определения
отношение массы к заряду электрона.
Другое применение влияния магнитного поля на движение
заряженная частица — циклотрон. Циклотрон состоит из вакуумированного резонатора.
помещенный между полюсами большого электромагнита. Полость разрезается на две
D-образные детали (называемые ди) с зазором между ними. Осциллирующий максимум
на пластины подается напряжение, генерирующее колеблющееся электрическое поле в
область между двумя деями.Заряженная частица, инжектированная в центр
циклотрон, будет совершать равномерное круговое движение в течение первой половины
один ход. Частота движения частицы зависит от ее массы, ее
заряд и напряженность магнитного поля. Частота генератора
выбирается таким образом, что каждый раз, когда частица пересекает зазор между дуантами, она
будет ускоряться электрическим полем. По мере увеличения энергии иона
По мере увеличения энергии иона
его радиус кривизны будет увеличиваться, пока он не достигнет края
циклотрон и экстрагируется.При движении в циклотроне ион будет
пересечь пропасть между деями много раз, и она ускорится до высоких
энергии.
До сих пор мы предполагали, что направление движения заряженного
частица перпендикулярна направлению магнитного поля. Если это
В этом случае будет происходить равномерное круговое движение. Если направление движения
ион не перпендикулярен магнитному полю, произойдет спиральное движение.
Скорость заряженной частицы можно разложить на две составляющие: одну
параллельно и одно перпендикулярно магнитному полю.Магнитная сила
действующее на частицу, будет определяться составляющей ее скорости
перпендикулярно магнитному полю. Проекция движения
частица в плоскости xy (предполагается, что она перпендикулярна магнитному полю)
будет круговой. Магнитное поле не повлияет на составляющую
движение параллельно полю, и эта составляющая скорости останется
постоянный. Конечным результатом будет движение по спирали.
Конечным результатом будет движение по спирали.
Заряженная частица, движущаяся в области с электрическим и магнитным полем, будет
испытать суммарную силу, равную
(31.32)
Эта сила называется силой Лоренца .
Рисунок 31.6. Заряженная частица движется в скрещенных E и B
поля. Рассмотрим частный случай, когда электрическое поле
перпендикулярно магнитному полю. Движение заряженной частицы в таком
регион может быть довольно сложным. Заряженная частица с положительным зарядом q
и скорость v движется в этом поле (см. рис. 31.6). Направление
частица, показанная на рисунке 31.6 перпендикулярна как электрическому полю, так и
магнитное поле. Электрическая сила, действующая на частицу, направлена
вдоль направления электрического поля и имеет величину, равную
(31.33)
Магнитная сила, действующая на заряженную частицу, направлена перпендикулярно
как v, так и B и имеет величину, равную
(31. 34)
34)
Суммарная сила, действующая на частицу, представляет собой сумму этих двух составляющих и имеет
величина равна
(31.35)
Если заряженная частица имеет скорость, равную
(31.36)
то результирующая сила будет равна нулю, а движение частицы будет
быть равномерным линейным движением. Устройство со скрещенными электрическим и магнитным полями
называется селектором скорости. Если щель расположена в соответствующем
позиции, он будет транспортировать только те частицы, скорость которых определена
величинами электрического и магнитного полей.
Рисунок 31.7. Ток в магнитном поле. Метод, используемый для определения плотности и знака заряда
носителей в металле основано на силе, действующей скрещенными полями E и B на
носители заряда. На схеме, показанной на рис. 31.7, показана металлическая полоса.
проводящий ток в указанном направлении и помещенный в однородный магнитный
поле с направлением магнитного поля, перпендикулярным
электрическое поле (генерирующее ток I). Предположим, что носители заряда в
Предположим, что носители заряда в
материала являются электроны, то электроны будут двигаться в направлении
противоположно току (см. рис. 31.7). Так как магнитное поле
перпендикулярно электрическому полю, оно также перпендикулярно направлению
движения электронов. Под действием магнитной силы электроны
отклоняются вниз, и на
нижняя часть полосы. В то же время дефицит отрицательного заряда будет
быть создан в верхней части полосы. Это распределение заряда создаст
электрическое поле, которое перпендикулярно внешнему электрическому полю и при
В условиях равновесия электрическая сила, создаваемая этим полем, нейтрализует
магнитная сила, действующая на электроны.Когда это происходит, внутренний
электрическое поле, E в , равно произведению электрона
скорость, v d , и напряженность магнитного поля, B. Как
В результате внутреннего электрического поля будет создана разность потенциалов.
между верхом и низом полосы. Если металлическая полоса имеет ширину w,
тогда разность потенциалов [Delta]V будет равна
(31. 37)
37)
Этот эффект называется эффектом Холла.
Скорость дрейфа электронов зависит от тока I в проводе, его
площадь поперечного сечения A и плотность электронов n (см. главу 28):
(31.38)
Объединяя уравнение (31.38) и уравнение (31.37), мы получаем следующее выражение для
[Дельта]В
(31.39)
Следовательно, для определения n можно использовать измерение ΔV.
Ток I, протекающий по проводу, эквивалентен совокупности зарядов
движущийся с некоторой скоростью v d вдоль провода.Количество
заряд dq, присутствующий на отрезке dL провода, равен
(31.40)
Если проволоку поместить в магнитное поле, то на нее будет действовать магнитная сила.
каждого из носителей заряда, и в результате на
провод. Предположим, что угол между направлением тока и направлением
поля равно [тета] (см. рис. 31.8). Магнитная сила, действующая
на отрезке dL провода равно
(31. 41)
41)
Суммарная сила, действующая на проводник со стороны магнитного поля, может быть найдена по формуле
интегрируя уравнение (31.41) по всей проволоке.
Рисунок 31.8. Магнитная сила на проводе.
Пример: Задача 31.33
Для измерения силы магнитного поля можно использовать весы.
Рассмотрим проволочную петлю, по которой течет точно известный ток, показанный на рис.
31.9, который частично погружен в магнитное поле. Сила, которую
магнитное поле, воздействующее на петлю, можно измерить с помощью весов, и это
позволяет рассчитать силу магнитного поля.Предположим, что
длина короткой стороны петли 10,0 см, сила тока в проводе 0,225
А, а магнитная сила равна 5,35 х 10 -2 Н. Какова сила
магнитное поле?
Рассмотрим три сегмента токовой петли, показанные на рис. 31.9.
погружены в магнитное поле. Магнитная сила, действующая на сегмент 1 и 3
имеют одинаковую величину, но направлены в противоположные стороны, а потому
отменить. Величина магнитной силы, действующей на сегмент 2, может быть
рассчитывается с использованием уравнения(31. 41) и равен
41) и равен
(31.42)
Эта сила измеряется с помощью весов и равна 5,35 х 10 -2 .
Н. Таким образом, напряженность магнитного поля равна
(31.43)
Рисунок 31.9. Токовая петля погружена в магнитное поле.
Если петля с током погружена в магнитное поле, результирующая магнитная сила будет
быть равным нулю. Однако крутящий момент на этом контуре в общем случае не будет
равен нулю.Предположим, что прямоугольная петля с током помещена в однородную
магнитное поле (см. рис. 31.10). Угол между нормалью тока
петля и магнитное поле равно [тета]. Магнитные силы, действующие на
верхняя и нижняя части текущего контура равны
(31.44)
где L — длина верхней и нижней кромки. Крутящий момент, действующий на
токовая петля относительно ее оси равна
(31.45)
Рисунок 31.10. Токовая петля помещена в однородное магнитное поле. Используя определение магнитного дипольного момента u, обсуждавшееся
в главе 30 уравнение (31. 45) можно переписать как
45) можно переписать как
(31.46)
где
(31.47)
Используя векторную запись, уравнение (31.45) можно переписать как
(31.48)
где направление магнитного момента определяется с помощью правой
правило.
Работа, которую необходимо совершить против магнитного поля, чтобы повернуть ток
петля на угол d[theta] равна — [tau] d[theta]. Изменение в
потенциальная энергия контура тока, когда он вращается между
[тета] 0 и [тета] 1 равно
(31.49)
Обычный выбор точки отсчета: [тета] 0 = 90 градусов. и
U([theta] 0 ) = 0 Дж. Если этот выбор сделан, мы можем переписать уравнение(31,50)
как
(31.50)
В векторной записи:
(31.51)
Потенциальная энергия токовой петли имеет минимум, когда u и B
параллельно и максимально, когда u и B антипараллельны.
Присылайте комментарии, вопросы и/или предложения по электронной почте wolfs@nsrl. rochester.edu и/или посетите домашнюю страницу Фрэнка Вольфса.
rochester.edu и/или посетите домашнюю страницу Фрэнка Вольфса.
12.5 Закон Ампера – University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как закон Ампера связывает магнитное поле, создаваемое током, со значением тока
- Рассчитайте магнитное поле длинного прямого провода, тонкого или толстого, по закону Ампера
Фундаментальное свойство статического магнитного поля заключается в том, что, в отличие от электростатического поля, оно не является консервативным.Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от [латекс]\stackrel{\to }{\textbf{B}}[/латекс] и известен как закон Ампера .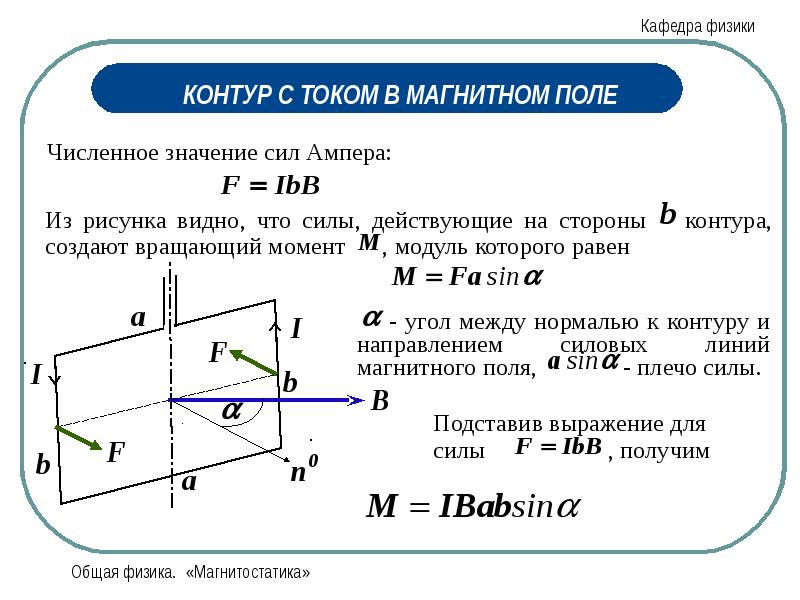 Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
На рис. 12.14 показана произвольная плоскость, перпендикулярная бесконечному прямому проводу, ток которого I направлен за пределы страницы. Линии магнитного поля представляют собой окружности, направленные против часовой стрелки и центрированные на проводе. Для начала рассмотрим [latex]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] над замкнутыми путями M и Н . Обратите внимание, что один путь ( M ) охватывает провод, а другой ( N ) нет.Поскольку силовые линии имеют круглую форму, [латекс]\stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] является произведением B и проекция dl на окружность, проходящую через [латекс]d\stackrel{\to }{\textbf{l}}.[/latex] Если радиус этой конкретной окружности равен r , проекция [латекс ]rd\theta,[/латекс] и
[латекс]\stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}=Br\phantom{\rule{0.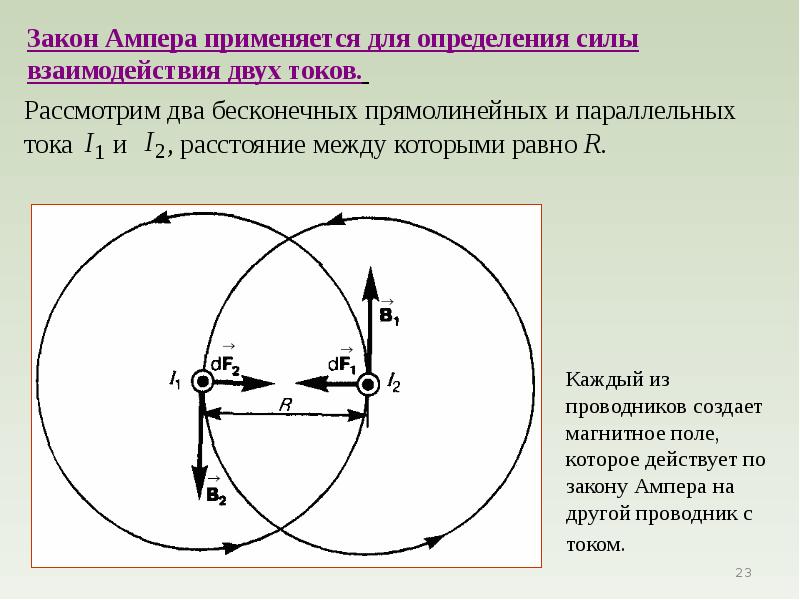 2em}{0ex}}d\theta .[/латекс]
2em}{0ex}}d\theta .[/латекс]
Рис. 12.14 Ток I длинного прямого провода направлен за пределы страницы. Интеграл [latex]\oint d\theta[/latex] равен [latex]2\pi[/latex] и 0 соответственно для путей M и N.
С [латексом]\stackrel{\to }{\textbf{B}}[/латекс], заданным уравнением 12.9,
[латекс]\мазь \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}=\мазь \left(\frac{{\mu}_{0 }I}{2\pi r}\right)\phantom{\rule{0.2em}{0ex}}r\phantom{\rule{0.2em}{0ex}}d\theta =\frac{{\mu} _{0}I}{2\pi}\oint d\theta .[/latex]
Для пути M , который циркулирует по проводу, [латекс]{\oint }_{M}d\theta =2\pi[/латекс] и
[латекс] {\ oint} _ {M} \ stackrel {\ to } {\ textbf {B}} · d \ stackrel {\ to } {\ textbf {l}} = {\ mu} _ {0} I .[/латекс]
Путь
N , с другой стороны, циркулирует как по положительному (против часовой стрелки), так и по отрицательному (по часовой стрелке) [латекс]d\тета[/латекс] (см. рис. 12.14), и, поскольку он замкнут, [латекс]{\ точка }_{N}d\theta =0.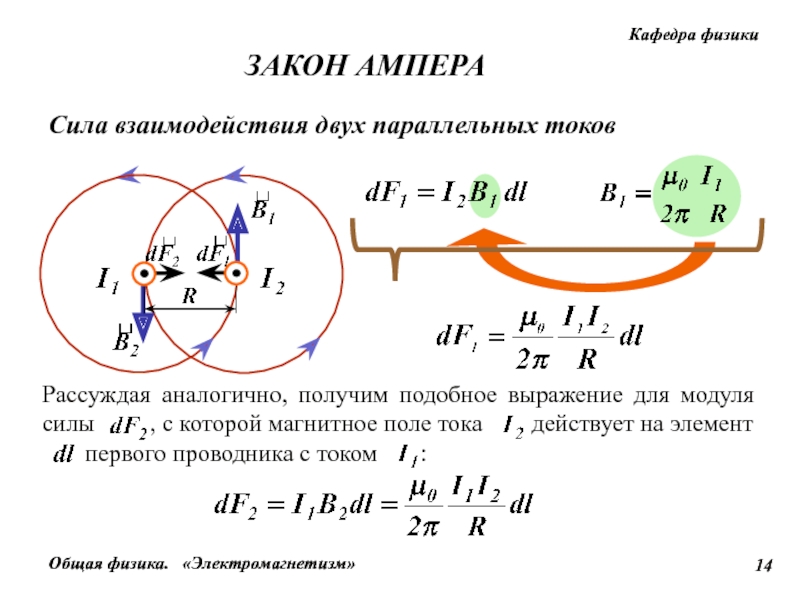 [/latex] Таким образом, для пути N ,
[/latex] Таким образом, для пути N ,
[латекс] {\ oint} _ {N} \ stackrel {\ to } {\ textbf {B}} · d \ stackrel {\ to } {\ textbf {l}} = 0. [/latex]
Распространение этого результата на общий случай есть закон Ампера.
Закон Ампера
По произвольному замкнутому пути,
[латекс]\мазь \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}={\mu}_{0}I[/latex]
, где I — полный ток, проходящий через любую открытую поверхность S , периметр которой представляет собой путь интегрирования.Необходимо учитывать только токи внутри пути интегрирования.
Чтобы определить, является ли конкретный ток I положительным или отрицательным, согните пальцы правой руки в направлении пути интегрирования, как показано на рисунке 12.14. Если I проходит через S в том же направлении, что и ваш вытянутый большой палец, I положителен; если I проходит через S в направлении, противоположном вашему вытянутому большому пальцу, это отрицательно.
Стратегия решения проблем: закон Ампера
Чтобы рассчитать магнитное поле, создаваемое током в проводах, выполните следующие действия:
- Определите симметрию тока в проводе(ах). Если симметрии нет, используйте закон Био-Савара для определения магнитного поля.
- Определите направление магнитного поля, создаваемого проводом(ами), по правилу правой руки 2.
- Выберите петлю пути, в которой магнитное поле постоянно или равно нулю.
- Рассчитать ток внутри контура.
- Вычислите линейный интеграл [латекс]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] вокруг замкнутого контура.
- Приравнять [латекс]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] к [латексу]{\mu}_{0 }{I}_{\text{enc}}[/latex] и найдите [латекс]\stackrel{\to }{\textbf{B}}.[/latex]
Пример
Использование закона Ампера для расчета магнитного поля, создаваемого проводом
Используйте закон Ампера для расчета магнитного поля, создаваемого постоянным током I в бесконечно длинном тонком прямом проводе, как показано на рисунке 12. 15.
15.
Рисунок 12.15 Возможные составляющие магнитного поля B, обусловленные током I, который направлен за пределы страницы. Радиальная составляющая равна нулю, потому что угол между магнитным полем и траекторией прямой.
Стратегия
Рассмотрим произвольную плоскость, перпендикулярную проводу, с током, направленным за пределы страницы. В произвольных точках окружности радиусом r по центру провода.Поскольку поле цилиндрически симметрично, ни [латекс]{B}_{r}[/латекс], ни [латекс]{В}_{\тета}[/латекс] не меняются в зависимости от положения на этой окружности. Также из симметрии радиальные линии, если они есть, должны быть направлены либо все внутрь, либо все наружу от провода. Это означает, однако, что должен существовать чистый магнитный поток через произвольный цилиндр, концентричный проводнику. Радиальная составляющая магнитного поля должна быть равна нулю, потому что 0.[/latex] Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке.
Решение
Показать ответ
По этому пути [latex]\stackrel{\to }{\textbf{B}}[/latex] является постоянным и параллельным [latex]d\stackrel{\to }{\textbf{l}} ,[/латекс] так
[латекс]\масло \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}={B}_{\theta}\oint dl={B} _{\тета}\влево(2\пи г\вправо).[/латекс]
Таким образом, закон Ампера сводится к
[латекс] {B} _ {\ theta} \ left (2 \ pi r \ right) = {\ mu } _ {0} I.[/латекс]
Наконец, поскольку [latex]{B}_{\theta}[/latex] является единственным компонентом [latex]\stackrel{\to }{\textbf{B}},[/latex] мы можем опустить индекс и напишите
[латекс] B=\frac{{\mu}_{0}I}{2\pi r}.[/latex]
Это согласуется с приведенным выше расчетом Био-Савара.
Значение
Закон Ампера хорошо работает, если у вас есть путь для интегрирования, по которому [латекс]\stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] результаты, которые легко упростить. Для бесконечного провода это легко работает с круговым путем вокруг провода, так что магнитное поле не учитывается при интегрировании. Если зависимость от пути кажется сложной, вы всегда можете вернуться к закону Био-Савара и использовать его для нахождения магнитного поля.
Для бесконечного провода это легко работает с круговым путем вокруг провода, так что магнитное поле не учитывается при интегрировании. Если зависимость от пути кажется сложной, вы всегда можете вернуться к закону Био-Савара и использовать его для нахождения магнитного поля.
Пример
Расчет магнитного поля толстой проволоки по закону Ампера
Радиус длинного прямого провода на рис. 12.16 равен a , и по проводу течет ток [латекс]{I}_{0}[/латекс], который равномерно распределен по его поперечному сечению.Найдите магнитное поле как внутри, так и снаружи провода.
Рисунок 12.16 (а) Модель провода с током радиуса а и тока [латекс]{I}_{0}.[/латекс] (б) Поперечное сечение того же провода, показывающее радиус а и петля Ампера радиуса r.
Стратегия
Эта задача имеет ту же геометрию, что и в примере 12.6, но замкнутый ток изменяется по мере того, как мы перемещаем путь интегрирования снаружи провода внутрь провода, где он не фиксирует весь заключенный ток (см. рисунок 12.16).
рисунок 12.16).
Решение
Показать ответ
Для любого кругового пути радиусом r с центром на проводе,
[латекс]\масло \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}=\oint Bdl=B\oint dl=B\left(2\ pi r\right).[/latex]
По закону Ампера это равно полному току, проходящему через любую поверхность, ограниченную путем интегрирования.
Сначала рассмотрим круговой путь, проходящий внутри проволоки [латекс]\левый(r\ле а\правый)[/латекс], такой как показан в части (а) на рис. 12.{2}}\phantom{\rule{0.2em}{0ex}}\left(r\le a\right).[/latex]
Вне провода ситуация идентична ситуации бесконечного тонкого провода из предыдущего примера; то есть
[латекс] B = \ frac {{\ mu } _ {0} {I} _ {0}} {2 \ pi r} \ phantom {\ rule {0.2em} {0ex}} \ left (r \ ge а\право).[/латекс]
Вариант B с r показан на рис. 12.17.
Рисунок 12.17 Изменение магнитного поля, создаваемого током [латекс]{I}_{0}[/латекс] в длинном прямом проводе радиусом a.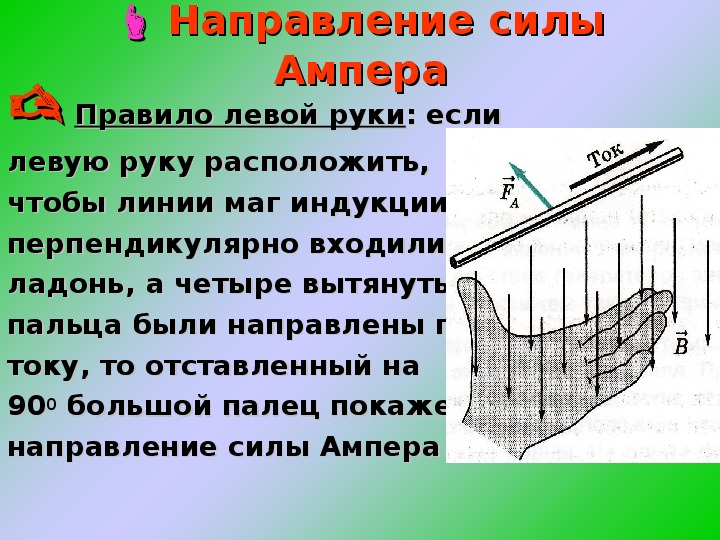
Значение
Результаты показывают, что по мере увеличения радиального расстояния внутри толстой проволоки магнитное поле увеличивается от нуля до известного значения магнитного поля тонкой проволоки. Вне провода поле падает независимо от того, толстый провод или тонкий.
Этот результат аналогичен тому, как закон Гаусса для электрических зарядов ведет себя внутри равномерного распределения зарядов, за исключением того, что закон Гаусса для электрических зарядов имеет равномерное распределение заряда по объему, тогда как закон Ампера здесь имеет однородную область распределения тока.Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
Пример
Использование закона Ампера с произвольными путями
Используйте закон Ампера для оценки [latex]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] для текущих конфигураций и путей в Рисунок 12. 18.
18.
Рисунок 12.18 Текущие конфигурации и пути для примера 12.8.
Стратегия
Закон Ампера гласит, что [латекс]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}={\mu}_{0}I[/ латекс], где I — полный ток, проходящий через замкнутый контур. Самый быстрый способ вычислить интеграл — вычислить [латекс]{\му}_{0}I[/латекс], найдя чистый ток через петлю. Положительные токи текут по большому пальцу правой руки, если ваши пальцы скручиваются в направлении петли.Это подскажет нам знак ответа.
Решение
Показать ответ
(a) Ток, протекающий вниз по контуру, равен току, выходящему из контура, поэтому чистый ток равен нулю. Таким образом, [латекс]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}=0.[/latex]
(b) В этой задаче нужно учитывать только ток 2 А, потому что это единственный ток внутри контура. Правило правой руки показывает нам, что ток, идущий вниз по контуру, имеет положительное направление. {\text{−6}}\text{T}\cdot \text{m/A}.[/латекс]
{\text{−6}}\text{T}\cdot \text{m/A}.[/латекс]
Значение
Если бы все токи закручивались так, что один и тот же ток входил бы в петлю и из петли, то суммарный ток был бы равен нулю и магнитного поля не было бы. Вот почему провода в электрическом шнуре расположены очень близко друг к другу. Токи, протекающие к устройству и от устройства по проводу, равны нулевому общему току, протекающему через петлю Ампера вокруг этих проводов. Следовательно, никакие блуждающие магнитные поля не могут присутствовать в проводах с током.
Проверьте свое понимание
Попробуйте использовать закон Ампера для расчета магнитных полей конечного прямого провода и круглой проволочной петли. Почему это не полезно для этих расчетов?
Показать решение
В этих случаях интегралы вокруг петли Ампера очень сложны из-за отсутствия симметрии, поэтому этот метод бесполезен.
Резюме
- Магнитное поле, создаваемое током, следующим по любому пути, представляет собой сумму (или интеграл) полей, обусловленных сегментами вдоль пути (величина и направление, как для прямого провода), что приводит к общему соотношению между током и полем, известному как Ампер.
 закон.
закон. - Закон Ампера можно использовать для определения магнитного поля от тонкой проволоки или толстой проволоки с помощью геометрически удобного пути интегрирования. Результаты согласуются с законом Био-Савара.
Концептуальные вопросы
Справедлив ли закон Ампера для всех замкнутых путей? Почему это обычно не полезно для расчета магнитного поля?
Показать решение
Закон Ампера действителен для всех замкнутых путей, но он бесполезен для расчета полей, когда создаваемое магнитное поле не имеет симметрии, которую можно использовать при соответствующем выборе пути.
Проблемы
Ток I течет по прямоугольной петле, показанной на прилагаемом рисунке. Оцените [latex]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] для путей A , B , C и D .
Показать решение
а. [латекс] {\ mu } _ {0} I; [/ латекс] б. 0; в. [латекс] {\ mu } _ {0} I; [/ латекс] d. 0
[латекс] {\ mu } _ {0} I; [/ латекс] d. 0
Оцените [латекс]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] для каждого из случаев, показанных на прилагаемом рисунке.
Катушка, поперечное сечение которой показано на прилагаемом рисунке, несет ток I и имеет N равномерно расположенных витков, распределенных по длине l. Оцените [latex]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}[/latex] для указанных путей.
Показать решение
а. [латекс] 3 {\ mu } _ {0} I; [/ латекс] б. 0; в. [латекс] 7 {\ mu } _ {0} I; [/ латекс] d. [латекс]\текст{−2}{\му }_{0}Я[/латекс]
Сверхпроводящий провод диаметром 0.25 см несет ток силой 1000 А. Каково магнитное поле сразу за проводом?
По длинному прямому проводу радиусом R протекает ток I , равномерно распределенный по поперечному сечению провода. На каком расстоянии от оси провода величина магнитного поля максимальна?
Показать решение
На прилагаемом рисунке показано поперечное сечение длинного полого цилиндрического проводника с внутренним радиусом [латекс]{r}_{1}=\text{3.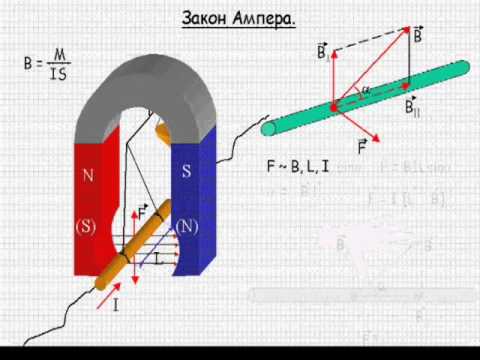 0 см}[/latex] и внешний радиус [латекс]{r}_{2}=\text{5,0 см}.[/latex] В страницу втекает ток силой 50 А, равномерно распределенный по поперечному сечению. Рассчитайте магнитное поле в точке [латекс]r=\text{2,0 см},\phantom{\rule{0,2em}{0ex}}r=4,0\phantom{\rule{0,2em}{0ex}}\text{см },\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}r=\text{6,0 см}.[/latex]
0 см}[/latex] и внешний радиус [латекс]{r}_{2}=\text{5,0 см}.[/latex] В страницу втекает ток силой 50 А, равномерно распределенный по поперечному сечению. Рассчитайте магнитное поле в точке [латекс]r=\text{2,0 см},\phantom{\rule{0,2em}{0ex}}r=4,0\phantom{\rule{0,2em}{0ex}}\text{см },\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}r=\text{6,0 см}.[/latex]
По длинному сплошному цилиндрическому проводнику радиусом 3,0 см течет ток силой 50 А, равномерно распределенный по его поперечному сечению.Постройте магнитное поле как функцию радиального расстояния r от центра проводника.
Показать решение
Часть длинного цилиндрического коаксиального кабеля показана на прилагаемом рисунке. Ток I течет по центральному проводнику, и этот ток возвращается во внешний проводник. Определить магнитное поле в областях (а) [латекс]r\le {r}_{1},[/latex] (б) [латекс]{r}_{2}\ge r\ge {r}_ {1},[/latex] (c) [латекс]{r}_{3}\ge r\ge {r}_{2},[/latex] и (d) [латекс]r\ge {r }_{3}.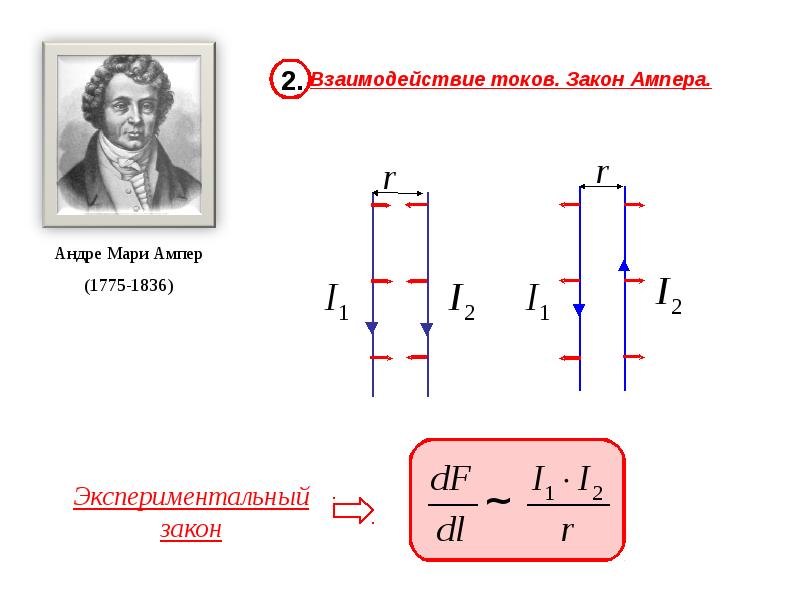 [/latex] Предположим, что ток распределен равномерно по сечениям двух частей кабеля.
[/latex] Предположим, что ток распределен равномерно по сечениям двух частей кабеля.
Глоссарий
- Закон Ампера
- физический закон, утверждающий, что линейный интеграл магнитного поля вокруг электрического тока пропорционален току
Лицензии и авторские права
Закон Ампера. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/12-5-amperes-law. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction
.

 24)
24)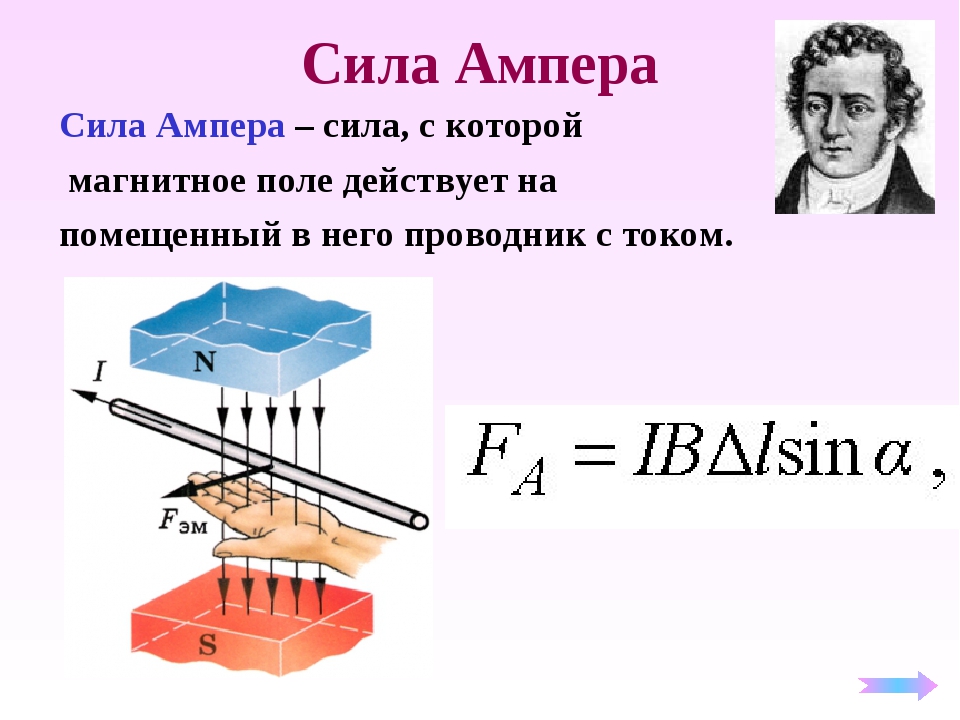
 Кроме того, симметрия требует, чтобы направление поля было касательным к окружности в плоскости страницы и концентричным по отношению к центру тороида.
Кроме того, симметрия требует, чтобы направление поля было касательным к окружности в плоскости страницы и концентричным по отношению к центру тороида.  И, во-вторых, именно общее число витков (которое теперь конечно), а не плотность витков определяет напряженность поля. Интересно, что плотность витков для тороида можно отрегулировать до «витков на радиан», а не оборотов на метр. Эта «угловая плотность поворота» просто \(\frac{N}{2\pi}\).
И, во-вторых, именно общее число витков (которое теперь конечно), а не плотность витков определяет напряженность поля. Интересно, что плотность витков для тороида можно отрегулировать до «витков на радиан», а не оборотов на метр. Эта «угловая плотность поворота» просто \(\frac{N}{2\pi}\). 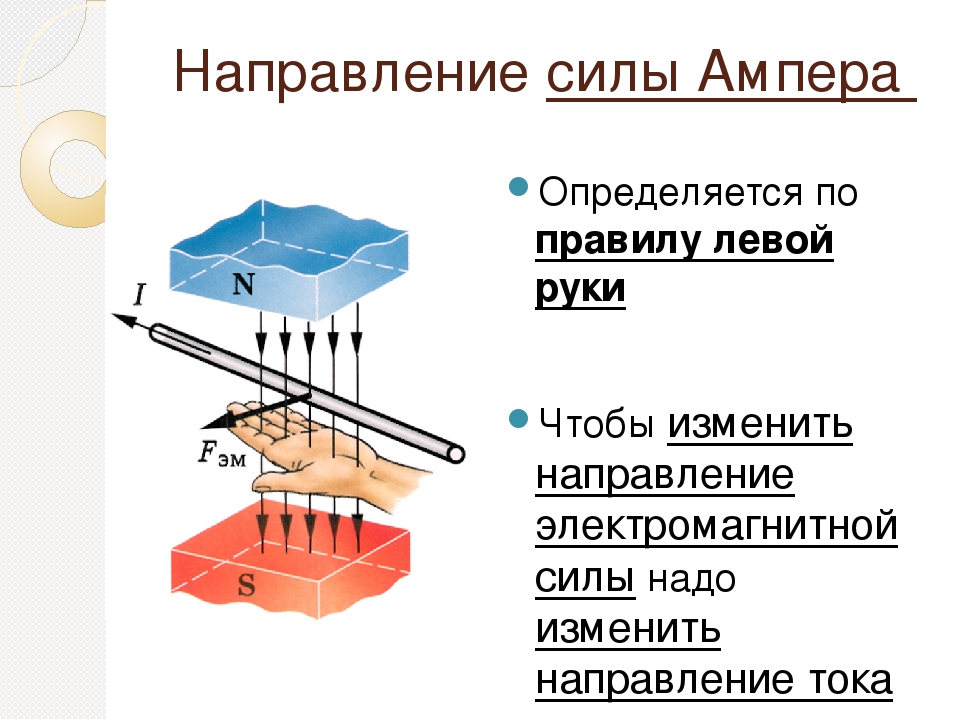 закон.
закон. закон.
закон.