Намагниченность — Физическая энциклопедия
НАМАГНИЧЕННОСТЬ — характеристика магн.
состояния макроскопич. тела; средняя плотность магн. момента M, определяется как магн. момент I единицы объёма: M
= I/V. Предел M = dI/dV
(dI — магн. момент физически бесконечно малого объёма dV)наз.
намагниченностью среды в точке. H. однородна в пределах рассматриваемого объёма,
если в каждой его точке M имеет одну и ту же величину и
направление. Единица H. в Международной системе единиц — ампер на метр (1 A/м
— H., при к-рой 1 м3 вещества обладает магн.
моментом 1 А.м2), в СГС системе единиц — эрг(Гс.см3).
H. вещества зависит от величины магн. поля и
темп-ры (см. Парамагнетизм, Диамагнетизм, Ферромагнетизм). Зависимость
Зависимость
M от напряжённости внеш. магн. поля H
выражается кривой намагничивания (см. Намагничивание, Гистерезис магнитный). H. тела зависит от напряжённости внеш. поля H, магн. свойств вещества
этого тела, его формы и расположения во внеш. поле. Между напряжённостью поля
в веществе HB и полем H существует соотношение:
НВ= Н — NM, где N — размагничивающий фактор .В
изотропных веществах направление M совпадает с направлением
H, в анизотропных — направление M и
H в общем случае различны.
Лит.: Вонсовский С. В., Магнетизм, M.,
1971; Пар-селл Э., Электричество и магнетизм, пер. с англ., 3 изд., M.,
1983.
Предметный указатель
>>
Сверхбыстрый переключатель для магнитной памяти нового поколения
Намагниченность материала можно представить как множество связанных между собой одинаково направленных микроскопических стрелок магнитных компасов. Ее направление относительно легко переключается с помощью различных внешних воздействий. Благодаря этому магнитные материалы нашли множество различных применений. Например, в привычных нам жестких дисках (HDD) информация записывается через переключение намагниченности в наноразмерных областях материала. Внешним воздействием служит импульс магнитного поля, создаваемый миниатюрной катушкой с током. При этом происходит разогревание устройства, и на его охлаждение приходится тратить энергию.
Ее направление относительно легко переключается с помощью различных внешних воздействий. Благодаря этому магнитные материалы нашли множество различных применений. Например, в привычных нам жестких дисках (HDD) информация записывается через переключение намагниченности в наноразмерных областях материала. Внешним воздействием служит импульс магнитного поля, создаваемый миниатюрной катушкой с током. При этом происходит разогревание устройства, и на его охлаждение приходится тратить энергию.
Повышение энергоэффективности — одна из фундаментальных проблем записи информации. Помимо этого необходимо увеличение емкости накопителя и повышение надежности хранения. Решить эту трилемму в рамках магнитного способа записи почти невозможно. Поэтому ученые и инженеры ищут ему альтернативу.
Перспективными материалами для новых элементов магнитной записи информации являются синтетические мультиферроики. Они представляют собой связанные друг с другом слои двух видов. Один из них — магнитный слой. Второй — сегнетоэлектрик, в котором упорядоченные электрические заряды создают электрическую поляризацию. Такой мультиферроик обладает одновременно намагниченностью и электрической поляризацией. Слои связаны между собой явлением магнитоупругости: направление намагниченности можно изменить при помощи механического воздействия. В синтетическом мультиферроике электрическая поляризация вызывает механическую деформацию. Она, в свою очередь, задает направление намагниченности. Стоит отметить, что синтетический мультиферроик может состоять из особых структур — магнитных доменов. Внутри каждого из них намагниченность ориентирована независимо от соседнего. Домены малого размера можно задействовать в качестве ячеек памяти в компьютерах нового поколения. Долгое время велись споры, возможно ли в них локально переключить намагниченность с помощью короткого лазерного импульса.
Один из них — магнитный слой. Второй — сегнетоэлектрик, в котором упорядоченные электрические заряды создают электрическую поляризацию. Такой мультиферроик обладает одновременно намагниченностью и электрической поляризацией. Слои связаны между собой явлением магнитоупругости: направление намагниченности можно изменить при помощи механического воздействия. В синтетическом мультиферроике электрическая поляризация вызывает механическую деформацию. Она, в свою очередь, задает направление намагниченности. Стоит отметить, что синтетический мультиферроик может состоять из особых структур — магнитных доменов. Внутри каждого из них намагниченность ориентирована независимо от соседнего. Домены малого размера можно задействовать в качестве ячеек памяти в компьютерах нового поколения. Долгое время велись споры, возможно ли в них локально переключить намагниченность с помощью короткого лазерного импульса.
«Оптический способ сверхбыстрого переключения намагниченности важен для реализации новых подходов к обработке и записи информации.Коллеги из Университета Аалто (Финляндия) приготовили для наших экспериментов синтетический мультиферроик, состоящий из магнитного слоя CoFeB и слоя сегнетоэлектрика BaTiO3 с полосовыми доменами. Мы же впервые изучили экспериментально, как реагирует намагниченность в отдельных доменах такого мультиферроика на воздействие лазерным импульсом длительностью менее 200 фемтосекунд»,— рассказывает Леонид Шелухин, младший научный сотрудник Физико-технического института имени А. Ф. Иоффе РАН (Санкт-Петербург).
Ученые обнаружили, что под воздействием фемтосекундного лазерного импульса в мультиферроике происходит очень быстрое и значительное ослабление магнитоупругой связи между его слоями (если сравнивать 1 фемтосекунду с 1 секундой, то это то же самое, как сравнить 1 секунду с 30 млн лет). Ослабление приводит к тому, что намагниченность слоя CoFeB начинает быстро менять свое
направление по определенной траектории. Физики показали, что такое изменение магнитоупругой связи связано с почти мгновенным тепловым воздействием лазера. Этот нагрев, однако, имеет импульсный характер, то есть происходит очень быстро. Поэтому нежелательное повышение температуры материала оказывается незначительным.
Этот нагрев, однако, имеет импульсный характер, то есть происходит очень быстро. Поэтому нежелательное повышение температуры материала оказывается незначительным.
Самым интересным оказалось то, что при определенных условиях движение намагниченности приводило к ее локальному переключению между двумя направлениями. Однако найти такие условия было очень сложно.
«Наши исследования нужно развивать дальше, подбирая слои для создания синтетического мультиферроика с нужной величиной магнитоупругой связи и деформаций в сегнетоэлектрике. Мы считаем, что это позволит создать материал, в котором будут реализованы оптимальные условия для быстрого и надежного переключения намагниченности одиночными лазерными импульсами»,— подытожил Леонид Шелухин.
Электричество и магнетизм
В присутствии магнетика вектор магнитной индукции равен сумме векторов магнитной индукции внешнего магнитного поля , создаваемого независимыми от магнетика токами, и магнитной индукции собственного поля магнетика
|
(7. |
Поле , создаваемое намагниченным магнетиком, разумеется, зависит от того, как намагничен магнетик, а намагничивается он суммарным полем , поэтому само является функцией : . Исключением в этом смысле может быть постоянный магнит, намагниченность которого не зависит, или практически не зависит от наличия или отсутствия внешнего магнитного поля, в частности, такое вещество, которое может оставаться намагниченным и в отсутствие внешнего — намагничивающего — поля.
Далее будет показано, что если магнитное поле вне магнетика параллельно его поверхности, то поле связано с магнитной индукцией в вакууме (то есть в отсутствие магнетика) соотношением
Безразмерная величина m называется магнитной проницаемостью. Все магнетики, в зависимости от характера влияния их собственного поля на суммарное магнитное поле, можно разделить на три группы:
В парамагнитных телах собственное поле увеличивает магнитный поток и, следовательно, парамагнитные тела притягиваются к магниту. В отличие от парамагнитных тел диамагнитные тела уменьшают магнитный поток. Это означает, как уже было сказано, что в диамагнитном теле под действием внешнего поля возникает собственное магнитное поле противоположное направлению внешнего магнитного поля. Следовательно, диамагнитные тела своим собственным магнитным полем отталкиваются от магнита.
В отличие от парамагнитных тел диамагнитные тела уменьшают магнитный поток. Это означает, как уже было сказано, что в диамагнитном теле под действием внешнего поля возникает собственное магнитное поле противоположное направлению внешнего магнитного поля. Следовательно, диамагнитные тела своим собственным магнитным полем отталкиваются от магнита.
Видео 7.1. Поведение пара- и диамагнетиков в неоднородном магнитном поле.
Как показывает опыт, вектор магнитной индукции собственного поля пара- и диамагнетика пропорционален вектору магнитной индукции внешнего поля B0
|
(7.2) |
Безразмерный коэффициент пропорциональности cm называется магнитной восприимчивостью вещества и является безразмерной величиной. У диамагнитных веществ магнитная восприимчивость является отрицательной величиной (cm < 0), у парамагнитных положительной (cm > 0). У ферромагнетиков магнитная восприимчивость cm зависит от величины магнитной индукции внешнего поля B0, поэтому в общем случае зависимость собственного поля ферромагнетика от внешнего нельзя считать линейной.
У диамагнитных веществ магнитная восприимчивость является отрицательной величиной (cm < 0), у парамагнитных положительной (cm > 0). У ферромагнетиков магнитная восприимчивость cm зависит от величины магнитной индукции внешнего поля B0, поэтому в общем случае зависимость собственного поля ферромагнетика от внешнего нельзя считать линейной.
Результирующее магнитное поле в присутствии магнетика равно:
|
(7.3) |
Сравнивая (7.3) с (7.1), получим
|
(7.4) |
Отсюда находим связь собственного поля с внешним
|
(7. |
аналогичную соответствующим выражениям для диэлектриков.
Для объяснения намагничивания тел Ампер предположил, что в атомах и молекулах вещества циркулируют особые круговые токи — молекулярные токи. Каждый такой ток создает в окружающем пространстве магнитное поле. В силу хаотической ориентации магнитных моментов отдельных молекулярных токов суммарный магнитный момент тела равен нулю. Под действием внешнего магнитного поля магнитные моменты молекулярных токов приобретают преимущественную ориентацию в одном направлении, вследствие чего вещество намагничивается — его суммарный магнитный момент становится отличным от нуля, возникает дополнительное поле (рис. 7.1).
Рис. 7.1. Молекулярные токи в магнетике
Наука в университете ИТМО
←
Все новости
Ученые Нового физтеха ИТМО Андрей Кудлис, Иван Шелых и Иван Иорш предложили новый способ сверхбыстрого переключения намагниченности в слоистых магнитных структурах. Полученные результаты могут быть использованы для эффективного управления ячейками памяти ― в частности, они открывают новые пути к полностью оптическим способам записи информации в двумерных материалах. Статья опубликована в Physical Review B, рецензируемом научном журнале, выпускаемом Американским физическим обществом.
Полученные результаты могут быть использованы для эффективного управления ячейками памяти ― в частности, они открывают новые пути к полностью оптическим способам записи информации в двумерных материалах. Статья опубликована в Physical Review B, рецензируемом научном журнале, выпускаемом Американским физическим обществом.
Электрон — это элементарная частица, которая обладает рядом свойств, в том числе имеет электрический заряд. Как его можно использовать для хранения информации? Например, держать в себе заряд может конденсатор. Заряженный конденсатор интерпретируется как двоичная единица или ноль, это зависит от договоренности. Разряженный же конденсатор будет восприниматься противоположным образом.
«А теперь представьте себе целый массив таких конденсаторов: часть из них может быть заряжена, часть нет, и в результате у нас получается цепочка из нулей и единиц — таким образом мы смогли закодировать некую информацию.
Этот же принцип используется при создании так называемой DRAM — динамической памяти с произвольным доступом», — объясняет Андрей Кудлис, один из авторов статьи, младший научный сотрудник Нового физтеха ИТМО.
<p>Источник: <a href=»https://depositphotos.com/home.html»>depositphotos.com</a></p>
Планки оперативной памяти энергозависимы. Со временем заряд с конденсатора по различным физическим причинам начинает стекать. Поэтому необходимо постоянно проверять, чтобы он не упал ниже некоторого критического значения. Также сама запись связана с зарядкой и разрядкой данных конденсаторов, для чего на практике необходимо много времени и энергии.
Чтобы решить эти проблемы, исследователи обратились к другому свойству электрона — спину. Спином, который был открыт еще в начале прошлого столетия, обладают и другие частицы. Это чисто квантово-механическое свойство частицы тесно ассоциировано с ее магнитным моментом. Помимо этого, сам спин квантован, то есть может принимать лишь дискретные значения, которые условно можно назвать «вверх» и «вниз», что с точки зрения приложения может трактоваться как бинарные единичка и нолик. Этот факт как раз и несет в себе потенциал для нужд хранения информации.
Помимо этого, сам спин квантован, то есть может принимать лишь дискретные значения, которые условно можно назвать «вверх» и «вниз», что с точки зрения приложения может трактоваться как бинарные единичка и нолик. Этот факт как раз и несет в себе потенциал для нужд хранения информации.
Однако работать только лишь с одним конкретным спином крайне трудно ― для удержания квантово-механического состояния рассматриваемой частицы нужны особые условия, в частности, сверхнизкие температуры.
Чтобы уйти от этой проблемы, представим, что у нас есть некий макроскопический объект, который включает в себя достаточно большое количество частиц, обладающих магнитным моментов. Такая система будет характеризоваться уже некоторым макропараметром, называемым намагниченностью, которая представляет из себя объемную плотность магнитного момента вещества.
«Есть такие материалы — ферромагнетики, они обладают так называемой спонтанной намагниченностью, которая обусловлена взаимодействием спинов системы, а не присутствием внешнего магнитного поля.
С их помощью тоже можно создавать определенные элементы памяти. В частности, магнитно-резистивную память: это своего рода слоистый пирог, состоящий из нанопленок. Например, две из них ферромагнитные, а посередине ― диэлектрическая. Но, в зависимости от того, как у слоев ферромагнетика ориентирована намагниченность, у слоя, расположенного посередине, будет разное электрическое сопротивление. Оно может быть огромным, а может быть, наоборот, очень низким», — говорит Андрей Кудлис.
<p>Андрей Кудлис. Фото из личного архива</p>
Одно из важнейших преимуществ такой памяти — ее энергонезависимость, так как тут нет необходимости постоянно подводить энергию для поддержания определенной намагниченности.
Более того, у ферромагнитной памяти (например, по сравнению с флеш-памятью) нет ограничений, связанных с числом актов записи информации. У флеш-памяти каждая перезапись наносит небольшой урон соответствующей структурной единице носителя (транзистор с плавающим затвором), поэтому твердотельные диски со временем выходят из строя. У ферромагнетиков такой проблемы нет.
У ферромагнетиков такой проблемы нет.
Итак, нижний слой может иметь постоянную намагниченность, а намагниченность верхнего слоя нужно уметь как-то переключать. Как это сделать? Например, в верхний слой ферромагнетика можно передавать ток поляризованных электронов.
«Если этот слой достаточно мал и если туда передавать ток поляризованных электронов, то он может изменить его намагниченность. То есть электронами переносится не только заряд, но еще и, например, передается поляризация. Таким образом, происходит переориентация намагниченности. Другой способ переключения намагниченности ― оптический. Вы берете лазер, который излучает поляризованный свет, и облучаете им образец. При определенных условиях намагниченность образца может быть переориентирована, таким образом чисто оптически мы можем повлиять на состояние ячейки памяти ― она будет иметь либо огромное, либо маленькое электрическое сопротивление», — продолжает Андрей Кудлис.
Что же подразумевается под «определенными условиями»? Помимо ферромагнитных свойств, облучаемый образец должен обладать уникальным набор оптических характеристик. Одним из таких материалов является слоистый иодид хрома III (CrI3). Это, с одной стороны, прямозонный полупроводник, обладающий большой энергией связи и силой осциллятора, а с другой ― двумерный ферромагнетик изинговского типа.
<p>Поведение различных проекций намагниченности, а также плотности экситонов, обладающих спинов «вверх», с течением времени. Исходное состояние соответствует отсутствию экситонов (электрон-дырочных пар) в системе, а намагниченность ориентирована вниз. После характерного времени перехода направление намагничивания меняется, а концентрация экситонов скачкообразно возрастает. Источник: статья в журнале Physical Review B / <a href=»https://journals.aps.org/prb/abstract/10.1103/PhysRevB.104.L020412″>journals.aps.org</a></p>
«Такие оптические свойства помогают с легкостью разрешать конкретные пики в оптических спектрах, что, конечно же, крайне удобно с точки зрения приложения.
Их комбинация с ферромагнитными особенностями данного материала позволяет менять ориентацию намагниченности оптическим образом. То есть мы начинаем светить лазерным излучением, которое обладает определенной поляризацией, и будем наблюдать, что в какой-то момент (что зависит, конечно же, от интенсивности накачки) намагниченность у этого материала переключается. Вот, пожалуйста, оптическое управление намагниченностью данного образца. Как это выглядит с точки зрения теории? В этом прямозонном полупроводнике при нерезонансной накачке могут создаваться некие эффективные комплексы, так называемые экситоны, представляющие из себя связанные электрон-дырочные пары. Они, в свою очередь, сами обладают неким эффективным спином. Мы будем разделять спин нашей электронной подсистемы — то есть обычных электронов и спин экситонов», — поясняет исследователь.
По словам Андрея Кудлиса, если представить двумерную структуру, то ее намагниченность, например, может быть усредненно направлена вниз. В случае, если на такой образец начать посылать свет с правой круговой поляризацией, то получается, что мы возбуждаем электроны с валентной зоны в зону проводимости, то есть создаем экситоны.
В случае, если на такой образец начать посылать свет с правой круговой поляризацией, то получается, что мы возбуждаем электроны с валентной зоны в зону проводимости, то есть создаем экситоны.
«Это приводит к созданию магнитного момента, который, если вы накачиваете достаточно сильно, может переориентировать намагниченность электронной подсистемы. И как раз этот механизм с помощью нашей модели мы и описываем», — отмечает Андрей Кудлис.
Please enable JavaScript to view the comments powered by Disqus.
Сверхбыстрый переключатель для магнитной памяти нового поколения
Ученые показали, что воздействие фемтосекундным лазерным импульсом позволяет изменять направление намагниченности синтетического мультиферроика. Этот эффект может оказаться полезен при создании устройств магнитной памяти нового поколения. Исследование поддержано грантом Российского научного фонда.
Намагниченность материала можно представить как множество связанных между собой одинаково направленных микроскопических стрелок магнитных компасов. Ее направление относительно легко переключается с помощью различных внешних воздействий. Благодаря этому магнитные материалы нашли множество различных применений. Например, в привычных нам жестких дисках (HDD) информация записывается через переключение намагниченности в наноразмерных областях материала. Внешним воздействием служит импульс магнитного поля, создаваемый миниатюрной катушкой с током. При этом происходит разогревание устройства, и на его охлаждение приходится тратить энергию.
Ее направление относительно легко переключается с помощью различных внешних воздействий. Благодаря этому магнитные материалы нашли множество различных применений. Например, в привычных нам жестких дисках (HDD) информация записывается через переключение намагниченности в наноразмерных областях материала. Внешним воздействием служит импульс магнитного поля, создаваемый миниатюрной катушкой с током. При этом происходит разогревание устройства, и на его охлаждение приходится тратить энергию.
Повышение энергоэффективности — одна из фундаментальных проблем записи информации. Помимо этого необходимо увеличение емкости накопителя и повышение надежности хранения. Решить эту трилемму в рамках магнитного способа записи почти невозможно. Поэтому ученые и инженеры ищут ему альтернативу.
Перспективными материалами для новых элементов магнитной записи информации являются синтетические мультиферроики. Они представляют собой связанные друг с другом слои двух видов. Один из них — магнитный слой. Второй — сегнетоэлектрик, в котором упорядоченные электрические заряды создают электрическую поляризацию. Такой мультиферроик обладает одновременно намагниченностью и электрической поляризацией. Слои связаны между собой явлением магнитоупругости: направление намагниченности можно изменить при помощи механического воздействия. В синтетическом мультиферроике электрическая поляризация вызывает механическую деформацию. Она, в свою очередь, задает направление намагниченности. Стоит отметить, что синтетический мультиферроик может состоять из особых структур — магнитных доменов. Внутри каждого из них намагниченность ориентирована независимо от соседнего. Домены малого размера можно задействовать в качестве ячеек памяти в компьютерах нового поколения. Долгое время велись споры, возможно ли в них локально переключить намагниченность с помощью короткого лазерного импульса.
Второй — сегнетоэлектрик, в котором упорядоченные электрические заряды создают электрическую поляризацию. Такой мультиферроик обладает одновременно намагниченностью и электрической поляризацией. Слои связаны между собой явлением магнитоупругости: направление намагниченности можно изменить при помощи механического воздействия. В синтетическом мультиферроике электрическая поляризация вызывает механическую деформацию. Она, в свою очередь, задает направление намагниченности. Стоит отметить, что синтетический мультиферроик может состоять из особых структур — магнитных доменов. Внутри каждого из них намагниченность ориентирована независимо от соседнего. Домены малого размера можно задействовать в качестве ячеек памяти в компьютерах нового поколения. Долгое время велись споры, возможно ли в них локально переключить намагниченность с помощью короткого лазерного импульса.
«Оптический способ сверхбыстрого переключения намагниченности важен для реализации новых подходов к обработке и записи информации. Коллеги из Университета Аалто (Финляндия) приготовили для наших экспериментов синтетический мультиферроик, состоящий из магнитного слоя CoFeB и слоя сегнетоэлектрика BaTiO3 с полосовыми доменами. Мы же впервые изучили экспериментально, как реагирует намагниченность в отдельных доменах такого мультиферроика на воздействие лазерным импульсом длительностью менее 200 фемтосекунд»,— рассказывает Леонид Шелухин, младший научный сотрудник Физико-технического института имени А. Ф. Иоффе РАН (Санкт-Петербург).
Коллеги из Университета Аалто (Финляндия) приготовили для наших экспериментов синтетический мультиферроик, состоящий из магнитного слоя CoFeB и слоя сегнетоэлектрика BaTiO3 с полосовыми доменами. Мы же впервые изучили экспериментально, как реагирует намагниченность в отдельных доменах такого мультиферроика на воздействие лазерным импульсом длительностью менее 200 фемтосекунд»,— рассказывает Леонид Шелухин, младший научный сотрудник Физико-технического института имени А. Ф. Иоффе РАН (Санкт-Петербург).
Ученые обнаружили, что под воздействием фемтосекундного лазерного импульса в мультиферроике происходит очень быстрое и значительное ослабление магнитоупругой связи между его слоями (если сравнивать 1 фемтосекунду с 1 секундой, то это то же самое, как сравнить 1 секунду с 30 млн лет). Ослабление приводит к тому, что намагниченность слоя CoFeB начинает быстро менять свое
направление по определенной траектории. Физики показали, что такое изменение магнитоупругой связи связано с почти мгновенным тепловым воздействием лазера. Этот нагрев, однако, имеет импульсный характер, то есть происходит очень быстро. Поэтому нежелательное повышение температуры материала оказывается незначительным.
Этот нагрев, однако, имеет импульсный характер, то есть происходит очень быстро. Поэтому нежелательное повышение температуры материала оказывается незначительным.
Самым интересным оказалось то, что при определенных условиях движение намагниченности приводило к ее локальному переключению между двумя направлениями. Однако найти такие условия было очень сложно.
«Наши исследования нужно развивать дальше, подбирая слои для создания синтетического мультиферроика с нужной величиной магнитоупругой связи и деформаций в сегнетоэлектрике. Мы считаем, что это позволит создать материал, в котором будут реализованы оптимальные условия для быстрого и надежного переключения намагниченности одиночными лазерными импульсами»,— подытожил Леонид Шелухин.
«Laser-Induced Magnetization Precession in Individual Magnetoelastic Domains of a Multiferroic Co40Fe40B20/BaTiO3 Composite»; L. A. Shelukhin, N. A. Pertsev, A. V. Scherbakov, D. L. Kazenwadel, D. A. Kirilenko, S. J. Hmlinen, S. van Dijken, A. M. Kalashnikova; журнал Physical. Review Applied, сентябрь 2020 г.
M. Kalashnikova; журнал Physical. Review Applied, сентябрь 2020 г.
Намагниченность — Справочник химика 21
Магнитная дефектоскопия. Магнитную порошковую дефектоскопию применяют для визуального неразрушающего контроля качества сварных соединений газотрубопроводов, емкостей, резервуаров и других стальных конструкций. Магнитная дефектоскопия основана на выявлении магнитного поля рассеяния над дефектом при помощи ферромагнитных частиц. Силовые линии в намагниченном изделии огибают дефект как препятствие с малой магнитной проницаемостью и образуют над ним магнитное поле рассеяния. [c.202]
Магнитная порошковая дефектоскопия основана на выявлении магнитного поля рассеяния над дефектом. При этом в качестве индикатора используются ферромагнитные частицы. Силовые линии в намагниченной детали огибают дефект как препятствие, имеющее малую магнитную проницаемость. Необходимым условием для выявления дефекта является перпендикулярное расположение дефекта к направлению магнитного поля. Поэтому деталь необходимо проверять в двух взаимно перпендикулярных направлениях. Магнитный порошок приготавливается из сухого мелко-размолотого железного сурика или из чистой железной окалины. Окалина измельчается в шаровой мельнице и просеивается. Мельчайшие частицы железного порошка, нанесенные на деталь пылевидным слоем (сухой метод) либо в виде водной или масляной суспензии (мокрый метод), концентрируются над трещиной и этим ее обнаруживают. При трещине шириной менее 10 м поле рассеяния не образуется. Аналогично, когда дефект располагается на глубине более 6 мм под поверхностью, поле рассеяния исчезает. [c.139]
Поэтому деталь необходимо проверять в двух взаимно перпендикулярных направлениях. Магнитный порошок приготавливается из сухого мелко-размолотого железного сурика или из чистой железной окалины. Окалина измельчается в шаровой мельнице и просеивается. Мельчайшие частицы железного порошка, нанесенные на деталь пылевидным слоем (сухой метод) либо в виде водной или масляной суспензии (мокрый метод), концентрируются над трещиной и этим ее обнаруживают. При трещине шириной менее 10 м поле рассеяния не образуется. Аналогично, когда дефект располагается на глубине более 6 мм под поверхностью, поле рассеяния исчезает. [c.139]
Отношение М /Нд обозначают символом х и называют магнитной восприимчивостью единицы объема. Объемная восприимчивость (безразмерная величина) связана с намагниченностью соотношением [c.130]
Намагниченность вещества характеризуется вектором намагниченности , численное значение которого равно магнитному моменту единицы объема [c. 139]
139]
Если больше, чем время, необходимое для удаления образца из поля, то избыточная заселенность спинов -Ь 1/2 сохранится, но они будут прецессировать вокруг направления суммарного локального поля на ядре, возникающего за счет спин-орбитального взаимодействия с соседними протонами. По всему образцу намагниченность равна нулю, но если этот образец вновь поместить в магнитное поле, то в образце одновременно возникает намагниченность, причем не придется ждать столько же времени, сколько необходимо для процесса Т . Эта ситуация изображена на рис. 14.8 в той части, которая помечена как образец повторно внесен в поле . Интенсивность намагниченности можно измерить немедленно после повторного внесения образца в магнитное поле, используя 90 -ный импульс и измеряя кривую СИС (рис. 14.8). Если период времени между удалением образца из поля и повторным его внесением туда достаточно велик по сравнению с то намагниченность будет падать по мере рандомизации спинов. [c.280]
Магнетики делятся на диа-пара- и ферромагнетики. Количественной характеристикой магнетиков является вектор намагниченности М (аналогичный вектору поляризации Р диэлектриков), определяемый выражением [c.38]
Количественной характеристикой магнетиков является вектор намагниченности М (аналогичный вектору поляризации Р диэлектриков), определяемый выражением [c.38]
При увеличении температуры ферромагнетика намагниченность его уменьшается, а при достижении некоторой критической температуры Тс (точки Кюри) он превращается в парамагнетик. [c.38]
Конструктивно оперативная память выполнена па магнитных кольцах диаметром 0,8 мм с прямоугольной петлей гистерезиса в виде блоков емкостью 64 Кбайт каждый. Использование магнитных колец в качестве запоминающего устройства основано на их способности находиться в двух устойчивых состояниях намагниченности и сохранять эти состояния неограниченно долго. Одно из состояний (например, положительная намагниченность) принимается как хранение единицы, а второе (отрицательная намагниченность) — хранение нуля. Очевидно, для хранения одного байта информации необходимо иметь девять таких колец (восемь информационных и один контрольный бит), объединенных общими проводами записи — считывания. Запись и считывание информации производятся под действием тока, пропускаемого по соответствующим проводам. При этом считывание производится обязательно с регенерацией. [c.182]
Запись и считывание информации производятся под действием тока, пропускаемого по соответствующим проводам. При этом считывание производится обязательно с регенерацией. [c.182]
Использование магнитных сердечников для хранения информации основано на том, что сердечник имеет два устойчивых состояния состояние положительной намагниченности (хранение единицы) и состояние отрицательной намагниченности (хранение нуля). Переход из одного состояния в другое осуществляется щ)д воздействием импульса тока. [c.18]
Магнитная поляризация (намагниченность). …………. /т Г гп т — у см г [c.43]
Явную форму вариаций энтропий фаз можно получить, пользуясь уравнением Гиббса, которое для изотропной среды в отсутствие электризации и намагниченности имеет вид [c.145]
Частные случаи термодинамического равновесия в гетерофазных системах. К частным случаям равновесия приводит различный характер взаимодействия рассматриваемой системы с окружающей средой, определяемый условиями изоляции системы. Будем рассматривать систему, которая состоит из двух изотропных фаз при отсутствии электризации и намагниченности. [c.145]
Будем рассматривать систему, которая состоит из двух изотропных фаз при отсутствии электризации и намагниченности. [c.145]
Магнитопорошковый метод заключается в том, что на поверхность сварного шва наносят суспензию флюоресцирующего порошка в керосине. Намагничивающее устройство создает переменное магнитное поле. Контролируемый участок освещается кварцевой лампой. Намагниченные частицы порошка скапливаются на полюсах потока рассеяния в дефектных местах, достаточно четко повторяя их форму. [c.294]
Для источников магнитного поля в виде намагниченных тел -постоянных магнитов плотность тока / = 0. В этом случае используются магнитожесткие материалы, т.е. материалы, имеющие больщую коэрцитивную силу и остаточную индукцию. К последним относятся ферритобариевые сплавы типа ЮНДК-24,. магнико, АЛИИ и др. [6]. Важнейшей характеристикой магнитных материалов служит максимальная удельная магнитная энергия, достигающая для сплавов 5шС05,з 128 кДж/м . [c.77]
[c.77]
Если подставить г/=7И, У=Н, где М — общая намагниченность и Н — напряженность магнитного поля, то получим [c.191]
С. Феррожидкости. Феррожидкости [40[ весьма перспективны для использования в качестве высокоэффективных теплоносителей. Специфическая температурная зависимость намагниченности благоприятствует хорошему их перемешиванию даже в отсутствие сил тяжести, поскольку на неодинаково нагретые объемы жидкости со стороны внешнего магнитного поля действуют различные силы. За счет неоднородных магнитных полей удается частично или полностью компенсировать силу тяжести в земных условиях, искусственно создавая в неизотермической среде ту или иную степень невесомости. [c.187]
Лекция 30. Магнитное поле в веществе. Намагниченность. Магнитная восприимчивость. Магнитная проницаемость среды. Напряженность магнитного поля. Атом в магнитном поле, диамагнетизм. [c.165]
Собственная остаточная намагниченность горных пород, возникающая в результате указанных выше процессов, сохраняется миллионы лет независимо от изменения магнитного поля Земли. [c.142]
[c.142]
За последние годы получил применение ядерный магнитный резонанс (ЯМР), который относится к радиоспектроскопическим методам. Явление ЯМР возникает под действием слабого радиочастотного поля, наложенного на сильное магнитное поле. ЯМР — это резонансный эффект изменения намагниченности вещества, который обнаруживают по возникновению электродвижущей силы индукции в катушке, окружающей образец исследуемого вещества. Спектр ЯРМ дает информацию о структуре соединения, о химической природе, пространственном расположении и числе атомов водорода в функциональной группе молекул, о ходе реакции, так как можно [c.230]
Величина вектора намагниченности, очевидно, аналогична вектору поляризации. Наличие вектора намагниченности означает, что элементарный объем горной среды, попадая во внешнее магнитное поле, создает свое собственное магнитное иоле. В первом приближении наблюдается прямо пропорциональная зависимость между векторами намагниченности и суммой напряженностей внешнего п собственного магнитных полей [c. 140]
140]
Экспериментально установлено, что снижение температуры горных пород во внешнем магнитном поле сопровождается появлением собственной остаточной намагниченности. В связи с этим основным источником высокой собственной намагниченности изверженных пород, видимо, являлись процессы их остывания во внешнем магнитном поле Земли. [c.142]
Природа неэкспоненциальной релаксации воды в гетерогенных системах. Спад намагниченности M(t) воды в гетерогенных системах иногда описывается многоэкспоненциальной функцией вида [c.232]
На ядрах Ю (/ = /2) намагниченность спадает как взвешенная сумма трех (/+7г) экспонент, причем одноэкспоненциальный спад наблюдается только при условии предельного сужения (ОоТс[c.233]
Вещества, молекулы или ионы которых имеют электроны с неспаренными спинами, обнаруживают способность втягиваться в магнитные поля. Магнитное поле упорядочивае 1 пространственную ориентацию неспаренных спинов и тем самым намагничивает вещество. Многие вещества, называемые парамагнитными, теряют намагниченность при их удалении из магнитного поля. Эти вещества содержат неспаренные электроны, и сила их втягивания в магнитное поле может использоваться для опреде- [c.524]
Многие вещества, называемые парамагнитными, теряют намагниченность при их удалении из магнитного поля. Эти вещества содержат неспаренные электроны, и сила их втягивания в магнитное поле может использоваться для опреде- [c.524]
Метод двойного резонанса с адиабатическим размагничиванием является новым методом в этой области. Рассмотрим образец с квадрупольным ядром в молекуле, в которой имеется несколько протонов. Если образец помещен в магнитное поле и мы ждем достаточно долго, чтобы наступило равновесие, то, как это обсуждалось в главе, посвященной ЯМР, будет существовать избыток протонных ядерных моментов, расположенных вдоль поля, которые участвуют в ларморовой прецессии и дают вклад в суммарную намагниченность. Если образец удалить из поля, то суммарная намагниченность упадет до нуля, поскольку индивидуальные моменты располагаются в соответствии со своими собственными локальными полями. Беспорядочная ориентация этих локальных полей в отсутствие внешнего поля приводит к нулевой суммарной намагниченности. Эта ситуация изображена на рис. 14.8 слева, в той части, которая помечена как образец удален из поля . [c.280]
Эта ситуация изображена на рис. 14.8 слева, в той части, которая помечена как образец удален из поля . [c.280]
Отмечают мелом направление центра тяжести детали от оси детали п, устанавливая на диаметрально протпвоположном направлении компенсирующие тарированные грузы (намагниченные куски железа, пластилин и др.), добиваются устранения дисбаланса (разбаланса). [c.124]
Такое уменьшение действительно было обнаружено [13] и использовано для измерения числа связей, образованных с металлом. Было показано, что при комнатной температуре хемосорбция одной молекулы С2Н4 производит то же воздействие на намагниченность N1, что и адсорбция одной молекулы Нг- Начало диссоциативной адсорбции С2Н4 было замечено около 100° С, когда 1 молекула С2Н4 становится эквивалентной ЗН2. [c.33]
По Селвуду [13], СаНе хемосорбируется на Ni при 27° С с разрывом в среднем трех связей на молекулу циклогексан при 150° С оказывает такое же действие на намагниченность Ni. как 4 молекулы Hj. Это объясняется разрывом четырех связей С—Н. — Прим. перев. [c.33]
как 4 молекулы Hj. Это объясняется разрывом четырех связей С—Н. — Прим. перев. [c.33]
Следует также отметить особый класс веществ — магнитные жидкости [29], которые представляют собой искусственные жидкие среды, обладающие одновременно намагниченностью и текучестью. Находясь в магнитном поле, они преобретают магнитный момент, лишь на порядок меньший магнитного момента твердах магнетиков. С помощью внешнего магнитного поля можно управлять свойствами и поведением магнитных жидкостей, что открывает новые возможности в химической технологии. [c.39]
Источниками электростатического поля в окружающем пространстве служат тела — проводники (электроды) или диэлектрики различной геометрической конфигурации, несущие электрический заряд. Источниками магнитного поля являются намагниченные тела или системы проводников с токами (катушки, соленоиды), р асполагаемые на маг-нитопроводах. [c.75]
Выбор класса функциональной зависимости, ашпроксимирующей матрш. (у данных, осуществляется из соображений сохранения физического соответствия математической модели реальному объекту. Таким образом, лгеханические параметры объекта могут быть определены по совокупности измеренных электрофизических параметров. качестве электрофизических параметров в математических моделях обычно выступают коэрцитивная сила Не, удельное электрическое сопротивление >, относительная магнитная проницаемость остаточная индукция Вг, намагниченность насыщения Ь и другие параметры. Но дая измерения совокупности этих параметров необходимо применение разнообразных приборов, установок и датчиков, что делает практически невозможным использование многопараметровой модели для экспресс-оценки техническ010 состояния оборудования в производственных условиях. Поэтому несомненный интерес [c.304]
(у данных, осуществляется из соображений сохранения физического соответствия математической модели реальному объекту. Таким образом, лгеханические параметры объекта могут быть определены по совокупности измеренных электрофизических параметров. качестве электрофизических параметров в математических моделях обычно выступают коэрцитивная сила Не, удельное электрическое сопротивление >, относительная магнитная проницаемость остаточная индукция Вг, намагниченность насыщения Ь и другие параметры. Но дая измерения совокупности этих параметров необходимо применение разнообразных приборов, установок и датчиков, что делает практически невозможным использование многопараметровой модели для экспресс-оценки техническ010 состояния оборудования в производственных условиях. Поэтому несомненный интерес [c.304]
Под объемной магнитной восприимчивостью м подразумевается коэффициент пропорциональности между намагниченностью (плотностью магнитного момента ) 1 единицы ббъсма газа или пера и напряженностью И магнитного паля в этом объеме, т. е. коэффициент в выражении Поскольку размерности величин I и Н одинаковы, величина А ,VI безразмерна и выражается п отвлеченных единицах. [c.580]
е. коэффициент в выражении Поскольку размерности величин I и Н одинаковы, величина А ,VI безразмерна и выражается п отвлеченных единицах. [c.580]
Магнитный момент, обусловливающий намагниченность, выражается в единицах, которые определяются через тапряженность магнитного поля, создаваемого этЯм моментом, но не через магнитную индукцию, [c.580]
Для правильного выбора метода намагничивания и его режима (величины тока) удобно пользоваться эталонами с истинными и ложными дефектами, которые могут встречаться на поверхности деталей поршневых 1 0м-прессоров. Эффективный контроль деталей компрессоров можно проводить с помощью дефектоскопов ДМП-2 и УМДЭ-2500. Для обеспечения удовлетворительной намагниченности необходим ток 16—32 А на 1 мм диаметра детали. [c.484]
Эти методы до некоторой степени аналогичны электроемкост-ным. Магнитометр достаточно малых размеров [98] погружают в кипящий слой и регистрируют изменения магнитного поля, вызванные перемещениями намагниченных или намагничивающихся в земном магнитном поле частиц.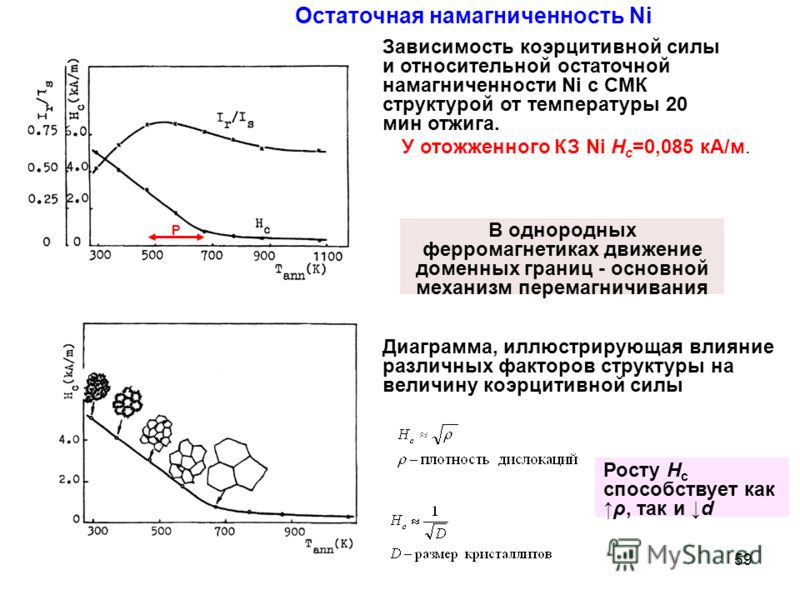 Совокупность нескольких таких магнитных локаторов может позволить следить за движением одной магнитно-помеченной частицы. При магнитной пометке некоторых частиц слоя — примеси — магнитометр измеряет изменение их концентрации в непосредственной близости от него и позволяет изучать перемешивание твердой фазы. При полной же пометке всех частиц, в принципе, можно измерять объемную плотность твердой фазы и ее колебания в области, прилегающей к датчику. Поскольку напряженность магнитного поля, создаваемая локально намагниченным участком, убывает пропорционально кубу расстояния, то магнитометрический датчик чувствителен к изменению в области, превышающей его по размерам в 2—3 раза (по объему в 10—30 раз). [c.83]
Совокупность нескольких таких магнитных локаторов может позволить следить за движением одной магнитно-помеченной частицы. При магнитной пометке некоторых частиц слоя — примеси — магнитометр измеряет изменение их концентрации в непосредственной близости от него и позволяет изучать перемешивание твердой фазы. При полной же пометке всех частиц, в принципе, можно измерять объемную плотность твердой фазы и ее колебания в области, прилегающей к датчику. Поскольку напряженность магнитного поля, создаваемая локально намагниченным участком, убывает пропорционально кубу расстояния, то магнитометрический датчик чувствителен к изменению в области, превышающей его по размерам в 2—3 раза (по объему в 10—30 раз). [c.83]
При контроле возможно появление ложных дефектов, так как скопление частиц может наблюдаться там, где есть риски, резкие границы различных структур. Иногда частицы оседают в местах изменения сечений деталей при завышенной напряженности поля. Для того чтобы отличить ложные дефекты, следует проводить повторный контроль. После проведения исследования необходимо снять остаточную намагниченность, так как остаточное магнитное поле может стать опасным. Намагниченные валы, например, могут способст-воиать попаданию металлических частиц в шарикоподшипники. [c.484]
После проведения исследования необходимо снять остаточную намагниченность, так как остаточное магнитное поле может стать опасным. Намагниченные валы, например, могут способст-воиать попаданию металлических частиц в шарикоподшипники. [c.484]
Среди парамагнетиков имеются вещества, обладающие ферромагнитными свойствами, для которых указанная прямая пропорциональная зависимость между векторами намагниченности и напряженности, строго говоря, не соблюдается. Для них характерен гистерезис намагничивания, который заключается в том, что с ростом напряженности внешнего иоля намагниченность растет, достигая насыщения. Однако при снятии напряженности внешнего поля намагниченность уменьшается ио другой, гнстеризисной кривой. Когда напряженность внешнего поля становится равной нулю, намагниченность не исчезает, а приобретает определенное для данного вещества значение, которое называется остаточной намагниченностью. [c.140]
Намагниченность горных сред обычно коррелирует с содержанием в ней ионов железа, титана, марганца, магния, алюминия, хрома и ванадия. Эти ионы — составная часть широко распространенных минералов. К ним относятся титаномагнетиты, гемати-тоильмениты,гидроокислы железа и пирротины. [c.140]
Эти ионы — составная часть широко распространенных минералов. К ним относятся титаномагнетиты, гемати-тоильмениты,гидроокислы железа и пирротины. [c.140]
Аналогичные явления происходят при механических напряжениях (деформациях) горных сред во внешнем магнитном поле. В зависимости от характера прикладываемых нагрузок собственная остаточная намагниченность называется пьезоостаточной либо динамической. Пьезоостаточная намагниченность возникает при статических нагрузках горных сред во внешнем магнитном поле. Динамическая намагниченность обусловлена действием переменных и ударных нагрузок. [c.142]
Физика и химия твердого состояния (1978) — [
c.287
]
Физикохимия полимеров (1968) — [
c.300
]
Физическая химия (1978) — [
c.495
]
Физикохимия полимеров Издание второе (1966) — [
c. 300
300
]
Физикохимия полимеров (1968) — [
c.300
]
Основы квантовой химии (1979) — [
c.4
]
Современная аналитическая химия (1977) — [
c.170
]
Современная неорганическая химия Часть 3 (1969) — [
c.3
,
c.24
]
Эластичные магнитные материалы (1976) — [
c.7
]
Введение в физическую химию и кристаллохимию полупроводников Издание 2 (1973) — [
c.243
]
Интерметаллические соединения редкоземельных металлов (1974) — [
c.211
]
Краткая химическая энциклопедия Том 2 (1963) — [
c.0
]
Структура и симметрия кристаллов (0) — [
c. 270
270
]
Термодинамика (0) — [
c.28
,
c.45
,
c.57
,
c.70
]
Биогенный магнетит и магниторецепция Новое о биомагнетизме Т.2 (1989) — [
c.41
,
c.43
,
c.134
,
c.139
,
c.143
,
c.178
,
c.180
,
c.181
,
c.183
,
c.184
,
c.186
,
c.197
,
c.198
,
c.199
,
c. 199
199
,
c.201
,
c.204
,
c.271
,
c.275
,
c.291
,
c.293
,
c.462
]
лекция Александра Королева в «Сириусе»
В «Сириусе» в рамках работы профильных инженерно-математических классов сочинским школьникам провел лекцию Александр Королев, кандидат физико-математических наук, ведущий научный сотрудник Института физики металлов имени М.Н. Михеева Уральского отделения РАН (ИФМ УрО РАН). Тема встречи – основы физики магнитных явлений и кривая намагничивания.
«Лекцию я начал с того, что многие ученые, прежде всего физики, говорят, что уровень цивилизации определяется уровнем потребляемой энергии», – отметил Александр Королев.
Метод измерения технологического развития цивилизации, основанного на количестве энергии, которое она может использовать для своих нужд, называют Шкалой Кардашева. Эта величина – явление чисто гипотетическое, даже спорное, однако оно отражает энергопотребление цивилизации в космической перспективе.
Эта величина – явление чисто гипотетическое, даже спорное, однако оно отражает энергопотребление цивилизации в космической перспективе.
«А физика магнитных явлений, о которой я рассказывал, – это научная область, которая обеспечила нам рывок в потреблении энергии. Чтобы энергию потреблять, ее надо еще и производить. Так вот, производство электроэнергии можно датировать XIX веком, временем открытия Фарадеем закона электромагнитной индукции – основы современного промышленного производства электричества и многих его применений», – продолжил ученый.
Из лекции Александра Королева школьники узнали, что такое магнитные весы Фарадея (индукционный магнитометр, предназначенный для измерения магнитных свойств материалов), обсудили основные идеи и опыты магнитной левитации (метод подъема объекта с помощью лишь магнитного поля) и подробно прошлись по понятиям диа- и парамагнетизма.
«Во времена английского физика Уильяма Гильберта и вплоть до научных открытий Фарадея вещества делили на магнитные (образец притягивается к магниту) и немагнитные (образец не притягивается к магниту). Фарадей показал, что все вещества являются магнитными и могут быть: а) диамагнитными (образец вещества отталкивается от магнита), б) парамагнитными (притягивается) и в) ферромагнитными (сильно притягивается)», – рассказал Королев.
Фарадей показал, что все вещества являются магнитными и могут быть: а) диамагнитными (образец вещества отталкивается от магнита), б) парамагнитными (притягивается) и в) ферромагнитными (сильно притягивается)», – рассказал Королев.
Измерить зависимость намагниченности или магнитной индукции от напряженности магнитного поля можно с помощью специальной кривой.
«Намагниченность может зависеть от разных факторов. И когда мы ее изучаем, причем с помощью самого простейшего графика, мы получаем массу информации. Например, о том, как сделать магнитный материал (он может быть разным и представлять из себя сплавы, химические соединения, жидкости, твердые вещества). Мы начнем понимать, как собрать генератор или двигатель. Возможности огромные», – отметил педагог.
По словам спикера, физику магнитных явлений можно считать не только существенной составляющей современных представлений о природе, но и основой технической оснащенности нашей цивилизации.
«Кривая намагничивания являлась и является добротным и универсальным инструментом для закладки фундамента и развития этой мощной науки», – подытожил Александр Королев.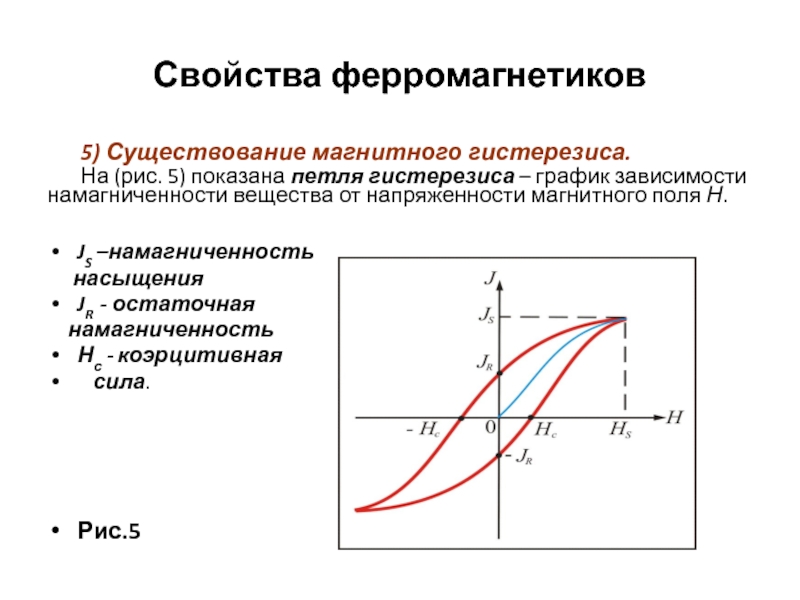
определение намагниченности по The Free Dictionary
Любой перегретый двигатель может, конечно, «заклинить» без предупреждения; но до нас дошло столько жалоб на несчастные случаи, подобные вашему, при съемке «Авроры», что мы склонны верить вместе с Лаваллем, что верхние слои «Северного сияния» представляют собой практически одну большую электрическую «утечку» и что паралич ваших двигателей был вызван до полного намагничивания всех металлических частей. Неожиданно было обнаружено, что намагниченность образца 4C была значительно ниже, чем намагниченность образца 2C, хотя содержание Со было одинаковым в каждом образце.В STT MRAM используются элементы памяти, в которых используется эффект, при котором ток, проходящий через магнитный материал, такой как магнитный туннельный переход (MTJ) (3), меняет направление намагниченности на противоположное (рис. 1). Первоначальные решения проблемы длительное время сбора данных для трехмерной визуализации FSE направлено на получение большего количества эхо-сигналов на импульс намагничивания (т. е. увеличение длины серии эхо-сигналов, ETL) и сокращение времени между последовательными импульсами намагничивания (уменьшение времени повторения, TR).Хотя интенсивность намагничивания, необходимая для обоих, почти одинакова, направления намагничивания различаются: значения составляют -74 и 172 градуса соответственно. Хотя во многих случаях физическое моделирование было ограничено свойствами, связанными с направлениями прокатки, использование Методы расчета в магнитных сердечниках требуют знания кривой намагничивания и петель гистерезиса в направлениях, отличных от направлений прокатки. Возможность определения поведения собственной намагниченности в монокристалле [001](110) Fe Si (GO) [001] и [0[бар.1]0] направлениях, поскольку на процесс намагничивания во всех других направлениях влияет геометрия образца (Fiorillo et al., 2002). Используя минимум математического «оборудования», охватывает классическое поле намагниченности, малые движения намагниченности, собственное демпфирование, флуктуации, изменение намагниченности в очень разбавленном массиве мелких частиц и изменение намагниченности в массивах частиц и сплошных средах.
е. увеличение длины серии эхо-сигналов, ETL) и сокращение времени между последовательными импульсами намагничивания (уменьшение времени повторения, TR).Хотя интенсивность намагничивания, необходимая для обоих, почти одинакова, направления намагничивания различаются: значения составляют -74 и 172 градуса соответственно. Хотя во многих случаях физическое моделирование было ограничено свойствами, связанными с направлениями прокатки, использование Методы расчета в магнитных сердечниках требуют знания кривой намагничивания и петель гистерезиса в направлениях, отличных от направлений прокатки. Возможность определения поведения собственной намагниченности в монокристалле [001](110) Fe Si (GO) [001] и [0[бар.1]0] направлениях, поскольку на процесс намагничивания во всех других направлениях влияет геометрия образца (Fiorillo et al., 2002). Используя минимум математического «оборудования», охватывает классическое поле намагниченности, малые движения намагниченности, собственное демпфирование, флуктуации, изменение намагниченности в очень разбавленном массиве мелких частиц и изменение намагниченности в массивах частиц и сплошных средах. Решатели для конкретных приложений можно использовать для проектирования вращающихся механизмов, сверхпроводящих магнитов, пучков частиц. , диэлектрическая изоляция и процессы намагничивания или размагничивания.Решатель, получивший название DEMAG, позволяет разработчикам оптимизировать конструкции оборудования путем точного моделирования как процесса намагничивания, так и последующих эффектов размагничивания, с которыми можно столкнуться. Шаг 1: Низкое намагничивание. Сигнал слабого магнитного поля обеспечивает широкий спектр данных, содержащих информацию как о геометрической, так и о магнитной деформации трубы. Материал Plastalloy можно намагничивать с использованием различных методов намагничивания, включая обычные, двухполюсные с каждой стороны, многополюсные или индивидуальное решение для подходит для многих медицинских и стоматологических приложений.Plastalloy™ от The Electrodyne Company можно намагничивать с использованием различных методов намагничивания, включая обычные, двухполюсные с каждой стороны, многополюсные или с помощью специальных схем намагничивания.
Решатели для конкретных приложений можно использовать для проектирования вращающихся механизмов, сверхпроводящих магнитов, пучков частиц. , диэлектрическая изоляция и процессы намагничивания или размагничивания.Решатель, получивший название DEMAG, позволяет разработчикам оптимизировать конструкции оборудования путем точного моделирования как процесса намагничивания, так и последующих эффектов размагничивания, с которыми можно столкнуться. Шаг 1: Низкое намагничивание. Сигнал слабого магнитного поля обеспечивает широкий спектр данных, содержащих информацию как о геометрической, так и о магнитной деформации трубы. Материал Plastalloy можно намагничивать с использованием различных методов намагничивания, включая обычные, двухполюсные с каждой стороны, многополюсные или индивидуальное решение для подходит для многих медицинских и стоматологических приложений.Plastalloy™ от The Electrodyne Company можно намагничивать с использованием различных методов намагничивания, включая обычные, двухполюсные с каждой стороны, многополюсные или с помощью специальных схем намагничивания.
Намагниченность
Намагниченность
Следующий: Магнитная восприимчивость и магнитная проницаемость
Up: Диэлектрические и магнитные среды
Предыдущий: Плотность энергии внутри
Вся материя состоит из атомов, а каждый атом состоит из
электроны в движении.Токи
связанные с этим движением
называются атомными токами . Каждый атомный ток
крошечная замкнутая цепь атомарных размеров, и поэтому может быть
правильно описывается как магнитный диполь. Если атомные токи
данного атома все текут в одной плоскости, тогда дипольный момент атома направлен нормально
плоскости (в смысле, заданном правилом правой руки), а его величина
является произведением полного циркулирующего тока и площади
текущая петля. В более общем случае, если
атомный ток
плотность в точке, то магнитный момент атома
является
| (856) |
где интеграл по объему атома. Если есть такие
Если есть такие
атомов или молекул на единицу объема, то намагниченность
( т.е. , магнитный дипольный момент на единицу объема) дается
от
. В более общем смысле,
| (857) |
где
средний магнитный дипольный момент
молекулы го типа в окрестности точки ,
и – среднее число таких молекул в единице объема при
.
Рассмотрим общую среду, состоящую из молекул,
поляризуемы и обладают чистым магнитным моментом.Легко показать, что любая циркуляция в поле намагниченности
приводит к эффективной плотности тока
в среде. По факту,
| (858) |
Эта плотность тока называется плотностью тока намагничивания ,
и обычно отличается от истинной плотности тока ,
, которая представляет собой конвекцию свободных зарядов в
средний. На самом деле существует третий тип тока, называемый поляризацией .
На самом деле существует третий тип тока, называемый поляризацией .
тока , что обусловлено кажущейся конвекцией связанных зарядов.Легко показать, что плотность тока поляризации
, дан кем-то
| (859) |
Таким образом, полная плотность тока в среде принимает вид
| (860) |
Следует подчеркнуть, что все слагаемые в правой части
приведенное выше уравнение представляет
реальные физические токи, хотя только первый член обусловлен движением
реальных зарядов (свыше атомных размеров).
Дифференциальная форма закона Ампера:
| (861) |
что тоже можно написать
| (862) |
где использовалось определение
. Приведенное выше выражение можно преобразовать, чтобы дать
Приведенное выше выражение можно преобразовать, чтобы дать
| (863) |
где
| (864) |
называется магнитной напряженностью и имеет те же размеры
как ( т.е. , магнитный дипольный момент на единицу объема).
В стационарной ситуации теорема Стокса говорит нам, что
| (865) |
Другими словами, линейный интеграл вокруг некоторой замкнутой кривой
равен потоку истинного тока через любую поверхность, присоединенную к этой
изгиб. В отличие от магнитного поля (которое определяет
сила
действующий на движущийся заряд
со скоростью ),
или намагниченность (магнитный дипольный момент
на единицу объема) напряженность магнитного поля не имеет четкого физического
значение. Единственная причина для его введения состоит в том, что он позволяет нам
Единственная причина для его введения состоит в том, что он позволяет нам
рассчитывать поля в присутствии магнитных материалов без
сначала необходимо знать распределение токов намагничивания.
Однако это возможно только при наличии определяющего соотношения
подключение и .
Следующий: Магнитная восприимчивость и магнитная проницаемость
Up: Диэлектрические и магнитные среды
Предыдущий: Плотность энергии внутри
2006-02-02
намагниченность — определение и значение
Во втором случае, когда намагниченность противоположна, все электроны «неправильные» в одном из двух магнитных слоев, так что общее сопротивление велико и препятствует протеканию электрического тока.
Нобелевская премия по физике 2007 г.
Эксперименты направлены на то, чтобы решить, вызвана ли эта перевернутая намагниченность переворотом магнитного поля Земли или сложным физическим или химическим процессом, происходящим в горных породах.
Патрик М.С. Блэкетт — Биография
Дополнительным приятным побочным эффектом является « намагничивание » клеток после включения наночастиц.
Научный блог — Научные новости прямо из источника
Дополнительным приятным побочным эффектом является « намагничивание » клеток после включения наночастиц.
Нанотехнологический провод
Дополнительным приятным побочным эффектом является « намагничивание » клеток после включения наночастиц.
инновации-отчет
Дополнительным приятным побочным эффектом является « намагничивание » клеток после включения наночастиц.
не определено
Дополнительным приятным побочным эффектом является « намагничивание » клеток после включения наночастиц.
инновации-отчет
Он вывел количественную зависимость напряженности магнитного поля от электрического тока (известную как теорема Ампера) и изучил процесс намагничивания железа .
Ампер, Андре Мари
Заявление может опровергнуть принятые физические пределы, установленные для намагниченности в веществе.
Профессор Миннесоты, возможно, нашел самое магнитное вещество в мире
Изменение направления намагниченности изменяет спиновую поляризацию вторичных или низкоэнергетических электронов, испускаемых веществом.
Разве мы не можем быть друзьями?
Намагниченность
Намагниченность
Магнитные материалы
Проблема:
Ферромагнетик — это тот, для которого намагниченность M ( r )
дана и плотность свободного тока j f = 0.
(a) Для этого случая запишите соответствующее значение Максвелла.
уравнения для магнитной индукции B и магнитного поля
Н дюймов
отсутствие переменного во времени электрического поля.
(b) Для этого ферромагнетика относятся B ,
Н и
М .
(c) Определите магнитный скалярный потенциал
Φ M и объясните, почему это
правильное понятие в данном случае.
(г) Покажите, что
∇ 2 Φ М
можно выразить через M уравнением Пуассона и дать его формальное
решение в отсутствие границ путем сравнения с решением электростатического уравнения Пуассона.
Решение:
- Концепты:
Магнитостатика, магнитные материалы - Рассуждение:
Исходя из уравнений Максвелла, получаем выражение для магнитного
скалярный потенциал для постоянных магнитов. - Детали расчета:
(а) ∇ ∙ В
= 0,
∇ × B = μ 0 j ,
j = j f +
й м ,
м м
знак равно
∇ × М .
Н = В /мк 0 —
М ,
∇ × Н =
j f .
Поскольку j f = 0, мы имеем
∇ ∙ Б
= 0,
∇ × Н = 0,
(б) H = B /мк 0 —
М .
(c) Ротор H везде равен нулю, поэтому мы можем написать
Х
= — ∇ Φ M .(г)
∇ ∙ Н =
∇ ∙ В /мк 0
— ∇ ∙ М .
Следовательно
∇ 2 Φ М
= ∇∙M .
В электростатике
решение уравнения Пуассона ∇ 2 Φ = -ρ/ε 0 в свободном пространстве равно
Φ( r ) = [1/(4πε 0 )]∫ρ( r ‘) dV’/| р —
р ‘|.
Те же уравнения имеют
те же растворы.
Φ M ( r ) = [-1/(4π)]∫ ∇∙M ( r ‘) dV’/| р —
р ‘|.
Проблема:
Сфера линейного магнитного
материал помещен в первоначально однородное магнитное поле магнитного поля B 0 .
Найдите новое поле внутри сферы.
Решение:
- Концепты:
Теорема единственности, граничные условия, B =
мк Н .
- Рассуждение:
Внешнее магнитное поле намагнитит шар. Магнитное поле
равномерно намагниченная сфера однородна внутри сферы ( B = 2 M μ 0 /3)
и чисто дипольное поле вне сферы. Предположим, что полное поле внутри
сфера является суперпозицией поля однородной намагниченной сферы и
постоянное внешнее поле B 0 . Суперпозиция этих
два поля удовлетворяют всем граничным условиям для B ,
( B 2 — B 1 ) · n 2
= 0, ( Б 2 —
В 1 )· т 2
= μ 0 k · n ,
на поверхности сферы.У нас есть уникальное решение, пока внутри B =
мк Н =
мк 0 (1 +
χ m ) H внутри
сфера.
B = μ H определяет
поверхностная плотность тока намагничивания. - Детали расчета:
B в = B 0 + 2 M μ 0 /3,
μ H в =
Б в ,
М = χ м Н в
= (χ м / мк) B в .
(1 — 2 мкм 0 х м /(3 мкм)) B в
= Б 0 . В в
= В 0 (3 + 3 х м )/(3 + х м ).
Магнитный момент шара равен м = (4πR 3 /3) М
= (4πR 3 /3)(χ m /μ) B в ,
где R — радиус сферы. Для R> R у нас
B OUT = B 0 + (μ 0 / 4π) [3 ( м × R ) R / R 5
— м /р 3 ].
Проблема:
Небольшая сферическая полость радиуса a сделана в постоянном магните
однородная намагниченность M . Находить
Б и
H в центре
полость.
Решение:
- Концепты:
Принцип суперпозиции - Рассуждение:
Уравнения Максвелла являются линейными уравнениями. Принцип
суперпозиция имеет место. Мы можем написать
Мы можем написать
B полость = B материал —
B равномерно
намагниченная сфера . - Детали расчета:
Для однородно намагниченной сферы имеем:
B out = чистое дипольное поле,
Б в =
униформа, по направлению М .
Пусть М = М к ,
м = (4/3)πa 3 М .
B вых = (μ 0 /4π)[3( m∙r ) r /r 5
— м /р 3 ].
B out_θ = (μ 0 /4π)(m/r 3 )sinθ,
B out_r = (μ 0 /4π)(2m/r 3 )cosθ.
В в = В в к .
B непрерывный
при р = а к .
B в = (μ 0 /4π)(2m/a 3 ) k
= (μ 0 /4π)(8/3)π M .
Таким образом, мы имеем B полость =
B материал — (μ 0 /4π)(8/3)π M .
B материал зависит от формы намагниченного материала.
H полость =
B полость /μ 0 .
Проблема:
Короткий цилиндр (длиной l и радиусом a) из железа намагничивается
вдоль оси цилиндра.Рассчитать H и
B на оси,
как внутри, так и снаружи.
Решение:
- Концепты:
Намагниченность M, плотности тока намагничивания,
поле соленоида
j m
знак равно
∇ × М ,
к м
знак равно
М × n . - Рассуждение:
Намагничивание всегда приводит к плотности тока намагничивания.
Равномерное намагничивание приводит к плотности поверхностного тока. Униформа
намагничивание цилиндра приводит к поверхностной плотности тока, подобной плотности
соленоид.
- Детали расчета:
Для соленоида имеем
B z = (μ 0 In/2)(cosθ 1
— cosθ 2 ).
(Мы выбираем осью симметрии ось z)(I*n) — ток на единицу длины, т.е.поверхностная плотность тока.
Поэтому для намагниченного цилиндра имеем на оси
B z = (μ 0 k m /2)(cosθ 1
— cosθ 2 ).
k m = M ( z /z) × ( ρ /ρ) = M ( φ /φ). B z = (μ 0 М/2)(cosθ 1
— cosθ 2 ).
Если центр цилиндра находится в начале координат, то
cosθ 1 = (z + l/2)/(a 2 + (z + l/2) 2 ) ½ , cosθ 2
= (z — l/2)/(a 2 + (z — l/2) 2 ) ½ .
H = B /μ 0 снаружи.
H = B /мк 0 —
М
внутри. H = k [(M/2)(cosθ 1
H = k [(M/2)(cosθ 1
— cosθ 2 ) — М] внутри.
При z = l/2 + e (e —> 0)
имеем H = k (M/2)cosθ 1 ,
H точек в положительном направлении z.
При г = 1/2 — е (е —> 0)
имеем H = k [(M/2)cosθ 1 — M],
H точек в отрицательном направлении оси Z.
H меняет направление на границе
Помните:
Одни и те же текущие распределения создают одни и те же поля.
Нормальный компонент
H не является непрерывным, ∇∙H ≠
0 вообще.
Проблема:
Катушка из N витков намотана на железное кольцо радиусом d
и поперечное сечение A (d >> A ½ ). Предположим,
постоянная магнитная проницаемость µ >> 1 для железа.
(a) Что такое магнитный поток
Φ = ∫ B∙ d A как функция
ток я?
(b) Если в
Кольцо, каков поток для того же тока I?
в) Какова энергия поля в железе и в зазоре?
(d) Чему равна собственная индуктивность при таком зазоре в кольце?
Решение:
- Концепты:
Закон Ампера для H ,
∮ Г
H∙ d l = I сквозной
Γ , H = B /μ 0 —
М ,
энергия магнитного поля, собственная индуктивность - Рассуждение:
Задача имеет достаточную симметрию, чтобы мы могли вычислить H из закона Ампера для H.
в одиночестве.
Железо не является жидким материалом, но мы предполагаем, что для заданной напряженности поля B
в задаче можно написать B = μ H .
После прорезания в кольце небольшого зазора воспользуемся граничными условиями
для B найти B и
H в разрыв. Мы используем энергию
плотности u = ½ B∙H , чтобы найти хранимую
энергия. - Детали расчета:
(a) H и B указывают на φ
направление, H = NI/(2πr), B =
мкНИ/(2πr).Если d >> A ½ , то B внутри катушки почти постоянна, B =
мкНИ/(2πд).
Флюс
Φ = ∫B n дА,
Φ = µN 2 IA/(2πd), Φ пропорционально I.
(b) Если b 2
<< А, затем Б железо
≈ B зазор = μ 0 H зазор ,
потому что нормальная составляющая B непрерывна.
H железо (2πd — b) + H зазор b = NI,
(B/μ)(2πd — b) + (B/μ 0 )b
= NI, из закона Ампера для H .
B = μμ 0 NI/[μ 0 (2πd — b)
+ мкб], Φ =
μμ 0 N 2 IA/[μ 0 (2πd — b)
+ мкб].
(c) Плотность энергии u = ½ B∙H =
(1/(2μ))B 2 .
Энергия поля в железе
U железо = A(2πd — b)(µ/2)(µ 0 NI/[µ 0 (2πd — b)
+ мкб]) 2 .
Энергия поля в зазоре
U зазор = Ab(μ 0 /2)(μNI/[μ 0 (2πd
— б) + мкб]) 2 .
U железо + U зазор = ½μμ 0 N 2 I 2 A/[μ 0 (2πd
— б) + мкб].
(d) Φ = LI или U = ½LI 2 выход L
= μμ 0 N 2 A/[μ 0 (2πd
— б) + мкб].Комментарий:
Когда вы сталкиваетесь с
с небольшим зазором между противоположными магнитными полюсами вы делаете то же самое
приближение, которое вы делаете, когда сталкиваетесь с небольшим разрывом между
большие противоположно заряженные пластины (конденсатор с параллельными пластинами). Вы предполагаете, что
Вы предполагаете, что
поле в промежутке однородно и пренебрегаем краевыми эффектами.
В этой задаче вы снова используете закон Ампера для
Х . Помните, что
нормальная составляющая B непрерывна, но нормальная составляющая
Х
не является.
Проблема:
Бесконечно длинный прямой провод, по которому течет постоянный ток.
I, лежит вдоль оси линейного парамагнитного цилиндра радиуса R и
проницаемость мк.
(a) Найдите H , B и
M внутри и снаружи цилиндра.
(b) Рассчитайте все связанные токи, протекающие в цилиндре.
Решение:
- Концепты:
Закон Ампера для H, ∮ Γ
H∙ г л
= I бесплатно через Γ , H =
В /мк 0 —
М - Обоснование:
Задача имеет цилиндрическую симметрию.Мы можем найти H из закона Ампера
в одиночестве.
Для линейных, изотропных, однородных (lih) магнитных материалов
имеем
М = Χ м Н ,
В = мк 0 ( Н +
M ) = μ 0 (1 + Χ m ) H = μ 0 κ m H
= μ H .
- Детали расчета:
(a) Пусть ток течет вдоль оси z в +z
направление.
Н
= I/(2πr)
( φ / φ) .
Для 0 < r < R, М
= (мк/мк 0
— 1)I/(2πr) ( φ /φ)
, Б =
мкI/(2πr) ( φ /φ) ,
Для r > R, M =
0, B = мк 0 I/(2πr)
( φ / φ)
(б)
м м
знак равно
∇ × М ,
к м
знак равно
М × n .
М = М φ ( φ /φ),
∇ × М =
к
(1/r)∂rM φ /∂r = 0,
∇ × M не определено при r = 0. I m
знак равно
∫ A ( ∇ × M ) ∙n dA = ∫ цикл M∙ д с
= (мк/мк 0
— 1) Я.
В дополнение к току I в проводе ток намагничивания (мк/мк 0
— 1) I течет в направлении k в центре.
Вдоль поверхности при r = R имеем поверхностный ток
к м
= (мк/мк 0
— 1)I/(2πR)
(- к ).
Ток намагничивания (мк/мкм) 0
— 1) I течет в направлении -k вдоль поверхности
магнитный материал.
Проблема:
Бесконечно длинный цилиндр из
радиус R несет «вмороженную» намагниченность, параллельную оси, M = kr, где
k является постоянным, а r является расстоянием от оси.
(a) Найдите B и H внутри и снаружи цилиндра.
(b) Найдите магнитный векторный потенциал внутри и снаружи цилиндра.
Решение:
- Концепты:
Токи намагничивания, закон Ампера для H - Рассуждение:
Пусть осью симметрии цилиндра будет ось z. Тогда объем
плотность тока намагничивания Дж м =
∇ × M есть
только компонент φ,
j mφ = -∂M/∂r
= -к.Плотность тока поверхностного намагничивания к м =
М
× n
также имеет только компонент φ, k mφ
= кР. - Детали расчета:
(a) Проблема эквивалентна проблеме набора бесконечно длинных,
вложенные катушки. Таким образом, мы знаем, что при r > R
Таким образом, мы знаем, что при r > R
Б =
H = 0. Для r < R Б и
H может иметь только z-компоненты, и мы можем решить проблему, используя Амперы
закон для H .Контурный интеграл тангенциальной составляющей
H вдоль закрытия
петля Γ должна быть нулевой, H = 0 везде.
Внутри намагниченного материала B =
мк 0 ( Н
+ М ), В = μ > 0 М .(б)
В = ∇ ×
А . Симметрия предполагает, что A можно выбрать так, чтобы он имел только компонент φ.
Теорема Стокса: ∫ площади S ( ∇ ×
A) ·n dS = ∫ B·n dS = ∫ Γ A· d r = ∫ Γ A φ 93
р d φ знак равно 2πrA φ .
Внутри: ∫ B·n dS = ∫ 0 r μ 0 kr
2πr dr = μ 0 2πk r 3 /3.
A φ = μ 0 k r 2 /3.
Снаружи: ∫ B·n dS = ∫ 0 R μ 0 kr
2πr dr = μ 0 2πk R 3 /3.
A φ = μ 0 k R 3 /(3r).
Проблема:
При насыщении, когда почти все атомы имеют свои магнитные моменты
выравнивается, магнитное поле в образце железа может быть 2 Тл.Если каждый
электрон вносит магнитный момент одного магнетона Бора, сколько электронов
на атом вносят вклад в поле насыщения железа?
(Железо: ~8,5*10 28 атомов/м 3 )
Решение:
- Концепты:
Намагниченность насыщения M sat , B =
мк 0 ( Н
+ М ). - Рассуждение:
M sat = Nm k , для магнитного поля, направленного в z
направление.Здесь m — величина магнитного момента каждого атома
N – число атомов в единице объема.
При насыщении B = μ 0 M насыщение .
- Детали расчета:
Намагниченность M определяется как магнитный дипольный момент на
объем единицы.
M = 8,5*10 28 атомов/м 3 *n*9,27*10 -24 Am 2 .
Здесь n — число электронов на атом, дающих вклад в насыщение
поле железа и 9.27*10 -24 Am 2 Бор
магнетон в единицах СИ.
2 T = 4π*10 -7 (Tm/A)*8,5*10 28 m -3 *n*9,27*10 -24 Am 2 ,
п = 2,
Вектор намагничивания — обзор
1.2.2 Магнитно-резонансная томография
Магнитно-резонансная томография (МРТ) представляет собой неинвазивные методы визуализации, используемые для получения изображений внутренней части тела. За последние 30 лет он стал одним из ключевых методов биовизуализации в медицине.Он обеспечивает патологические и физиологические изменения тканей организма, как ядерная медицина, в дополнение к структурным деталям органов, как КТ.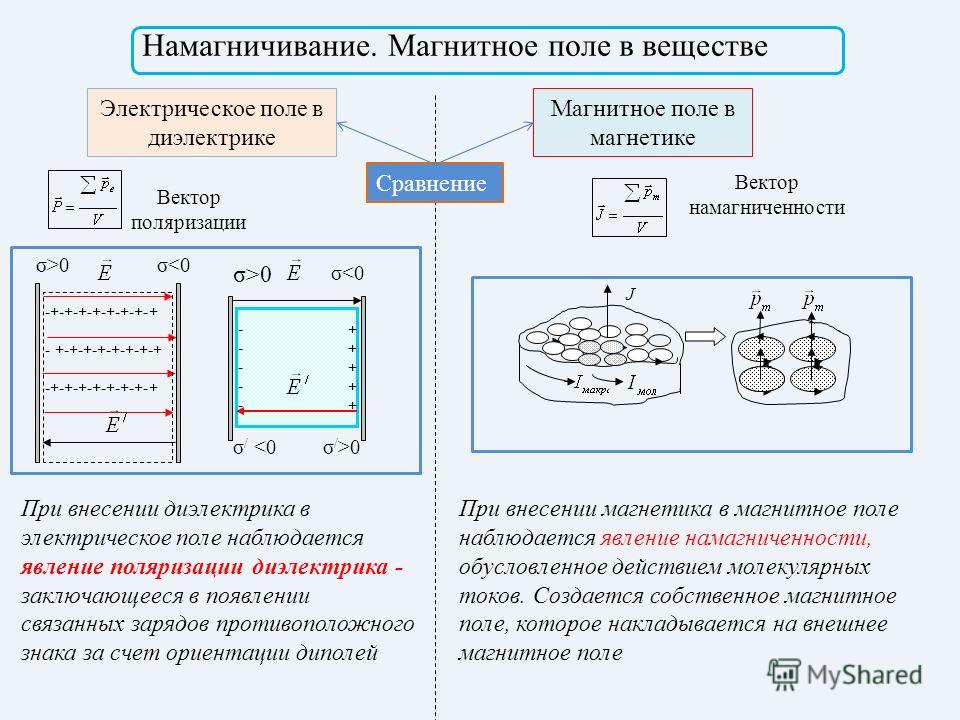
Сигнал МРТ возникает из-за ядерного магнетизма атомов водорода, находящихся в жире и воде человеческого тела, и основан на физическом принципе ядерного магнитного резонанса (ЯМР). ЯМР связан с зарядом и угловым моментом, которым обладают определенные ядра. Ядра имеют положительный заряд и в случае нечетного атомного номера или массового числа имеют угловой момент Φ.Имея спин, эти ядра являются ЯМР-активными. Каждое ядро, имеющее спин, также имеет микроскопическое магнитное поле. Когда приложено внешнее электрическое поле, спины стремятся выровняться с приложенным магнитным полем. Это свойство называется ядерным магнетизмом. Таким образом, спиновые системы становятся макроскопически намагниченными.
При МРТ мы изучаем макроскопическую намагниченность, рассматривая определенную спиновую систему (атомы водорода) в образце. «Образец» представляет собой небольшой объем ткани, т.е.д., воксель. При приложении постоянного магнитного поля B0 спиновая система становится намагниченной и может быть смоделирована объемным вектором намагниченности M. В невозмущенном состоянии M достигнет равновесного значения M0, параллельного направлению B0, см. рис. 1.9a.
В невозмущенном состоянии M достигнет равновесного значения M0, параллельного направлению B0, см. рис. 1.9a.
Очень важно отметить, что M(r,t) является функцией времени и трехмерной координаты r, которой можно управлять в пространстве с помощью внешних радиочастотных возбуждений и магнитных полей.
Для данного воксела значение МР-изображения характеризуется двумя важными факторами: свойствами ткани и протоколом сканирования.Наиболее важными свойствами ткани являются параметры релаксации T1 и T2, а также плотность протонов. Плотность протонов определяется как количество ядер-мишеней в единице объема. Программное и аппаратное обеспечение сканера манипулируют вектором намагниченности M во времени и пространстве на основе так называемой последовательности импульсов.
Далее мы сосредоточимся на конкретном вокселе и дадим уравнения движения для M(t) как функции времени t. Эти уравнения основаны на уравнениях Блоха и описывают прецессию вектора намагниченности вокруг внешнего приложенного магнитного поля с частотой ω0, известной как резонансная или ларморовская частота.
Вектор намагниченности M(t) состоит из двух компонентов:
- 1.
Продольная намагниченность определяется Mz(t), z-компонентой M(t).
- 2.
Вектор поперечной намагниченности Mxy(t), комплексная величина, объединяющая две ортогональные составляющие
(1.10)Mxy(t)=Mx(t)+jMy(t)
где ϕ угол комплексного числа Mxy, известный как фазовый угол, заданный как
(1.11)ϕ=tan-1MxMy
Поскольку M(t) является магнитным моментом, он будет иметь крутящий момент, если внешнее изменяющееся во времени магнитное поле B(t) применяется.Если это поле статично и ориентировано параллельно оси z, то B(t)=B0.
Вектор намагниченности M прецессирует, если он изначально ориентирован от B0. Спиновую систему также можно возбудить с помощью РЧ-сигналов, так что РЧ-сигналы генерируются на выходе стимулируемой системы. Это радиочастотное возбуждение достигается применением B1 на частоте Лармора, а не поддержанием ее постоянной, и позволяет отслеживать положение M(t). Однако прецессия не является вечной, и мы покажем, что есть два независимых механизма, которые гасят движение и вызывают исчезновение принятого сигнала: продольная и поперечная релаксация.
Однако прецессия не является вечной, и мы покажем, что есть два независимых механизма, которые гасят движение и вызывают исчезновение принятого сигнала: продольная и поперечная релаксация.
Под действием радиочастотного возбуждения M(t) смещается вниз под углом α к плоскости xy, если B1 находится в направлении оси y. При α=0 имеем Mz=0 и вектор намагниченности вращается в плоскости xy с частотой, равной ларморовской частоте. Импульс B1, необходимый для угла α = π/2, называется импульсом 90°. Вектор намагниченности возвращается в равновесное состояние и процесс релаксации описывается выражением
(1.12)Mz(t)=M01-exp-tT1
и зависит от времени продольной или спин-решеточной релаксации (T1), см. рис.1.8.
Рисунок 1.8. Вектор намагниченности M прецессирует вокруг оси z.
Поперечная или спин-спиновая релаксация — это эффект возмущений, вызванных другими соседними спинами, когда они меняют свою фазу относительно других. Эта расфазировка приводит к потере сигнала в антенне приемника. Результирующий сигнал называется затуханием свободной индукции (FID). Возврат поперечной намагниченности Mxy к равновесию описывается формулой
Результирующий сигнал называется затуханием свободной индукции (FID). Возврат поперечной намагниченности Mxy к равновесию описывается формулой
(1.13)Mxy(t)=Mx0y0exp-tT2
, где T2 — время спин-спиновой релаксации.T2 зависит от ткани и создает контраст на МР-изображениях. Однако принятый сигнал затухает быстрее, чем T2. Локальные возмущения статического поля B0 приводят к более быстрой постоянной времени T2∗, где T2∗ Рис. 1.9. (а) поперечная и (б) продольная релаксация. (1.14)1T2∗=1T2+1T2′ Важно отметить, что как T1, так и T2 зависят от ткани и для всех материалов T2≤T1. Ценную информацию можно получить при измерении временного хода процесса релаксации Т1/Т2 после применения последовательности РЧ-импульсов. Этот измеренный временной ход преобразуется из временной в частотную область на основе преобразования Фурье. Рис. 1.10. Преобразование измеренного временного хода в частотной области. Амплитуда в спектре проявляется на ларморовской частоте. Контраст между тканями можно увидеть, если измеренный сигнал в этих тканях отличается. Для достижения этого доступны две возможности: собственные свойства ЯМР, такие как PD, T1 и T2, и характеристики внешних возбуждений. Можно контролировать угол наклона кончика α и использовать сложные последовательности импульсов, такие как последовательность спинового эха.90-градусный импульс имеет период TR секунд (время повторения), за ним следует 180-градусный импульс через TE секунд (время эха). Этот второй импульс частично перефазирует спины и создает эхо-сигнал. На рис. 1.11 показано сканирование головного мозга в виде изображений, взвешенных по Т1, Т2 и плотности водорода. Рисунок 1.11. МРТ головного мозга показывает (a) T1, (b) T2 и (c) изображения, взвешенные по плотности водорода. Изображение предоставлено доктором А. Висмюллером, кафедра радиологии Мюнхенского университета. Под взвешенным значением понимается то, что различия в интенсивности, наблюдаемые между различными тканями, в основном вызваны различиями в T1, T2 и PD, соответственно, тканей.Основной способ создания контраста на основе вышеуказанных параметров представлен в таблице 1.2. Таблица 1.2. Основной способ создания контраста в зависимости от PD, T1 и T2. 7 Интенсивность пикселей I(x,y) МР-изображения, полученного с использованием последовательности спинового эха, определяется как (1. Изменение значений TR и TE будет управлять чувствительностью сигнала к T1/ Процесс T2-релаксации и будет создавать различные взвешенные контрастные изображения. Если, например, TR намного больше, чем T1 для всех тканей в области интереса, то член взвешивания T1 сходится к нулю, и сигнал не чувствителен к процессу T1-релаксации. То же самое верно для TE, намного меньшего, чем T2 для всех тканей. Когда обе чувствительности T1 и T2 уменьшаются, плотность пикселей зависит только от плотности протонов PD(x,y). Качество МР-изображения зависит не только от контрастности, но и от дискретизации и шума. Подводя итог, преимущества МРТ как инструмента визуализации заключаются в следующем: (1) отличные контрасты между различными органами и опухолями, необходимые для качества изображения, (2) трехмерный характер изображения и (3) контраст, обеспечиваемый Т1 и Механизм релаксации Т2 как один из наиболее важных методов визуализации. Важным методом МРТ является мультиспектральная магнитно-резонансная томография.Записывается последовательность трехмерных МРТ-изображений одной и той же области интереса при условии, что изображения зарегистрированы правильно. Этот тип визуализации позволяет различать различные типы тканей. Для дальнейшего усиления контраста между типами тканей используются контрастные агенты (КА) для управления временем релаксации. СА вводят внутривенно, и в это время достигается усиление сигнала для ткани с повышенной васкуляризацией. Функциональная магнитно-резонансная томография (фМРТ) представляет собой новый неинвазивный метод исследования когнитивных функций мозга [267].В основе этого метода лежит тот факт, что сигнал МРТ чувствителен к изменениям гемодинамических параметров, таких как кровоток, объем крови и оксигенация, которые возникают во время нервной активности. Наиболее часто используемым сигналом фМРТ является контраст, зависящий от уровня оксигенации крови (ЖИРНЫЙ). Двумя основными характеристиками гемодинамических эффектов являются пространственная и временная.В то время как сосудистая сеть в основном отвечает за пространственные эффекты, временные эффекты ответственны за вызванную задержку обнаруженных изменений МР-сигнала в ответ на нейронную активность и большую продолжительность дисперсии гемодинамических изменений. Временные аспекты накладывают два различных типа экспериментов фМРТ: «блочные» планы и «событийные» планы. Блочные конструкции характеризуются экспериментальной задачей, выполняемой в чередующейся последовательности блоков 20–60 с. В планах, связанных с событиями, множественные стимулы предъявляются случайным образом, и измеряется соответствующий гемодинамический ответ на каждый из них.Основная концепция этого типа эксперимента представляет собой почти линейную реакцию на множественные предъявления стимулов. Основными преимуществами этого метода являются: (1) неинвазивная запись сигналов головного мозга без риска облучения, как при КТ, (2) отличное пространственное и временное разрешение и (3) интеграция фМРТ с другими методами, такими как МЭГ и ЭЭГ. для изучения человеческого мозга. Основная функция фМРТ — визуализация активности мозга in vivo. Поэтому его применение заключается в диагностике, интерпретации и оценке лечения клинических нарушений когнитивных функций мозга.Наиболее важное клиническое применение заключается в предоперационном планировании и оценке риска при трудноизлечимой фокальной эпилепсии. В фармакологии фМРТ является ценным инструментом для определения того, как мозг реагирует на определенное лекарство. Помимо клинических применений, значение фМРТ для понимания неврологических и психических расстройств и уточнения диагноза постоянно растет. В процессе намагничивания и в процессе перемагничивания часть энергии в магнитных материалах будет необратимо преобразована в тепло и потеря энергии называется магнитными потерями.Следовательно, для магнитных материалов для магнитной гипертермии источником тепла являются магнитные потери. Магнитные потери Вт м включают потери на вихревые токи Вт и , гистерезисные потери Вт ч , а также другие потери, возникающие от остаточной магнитной релаксации или магнитного последействия 3 , то есть Вт м = Вт е + Вт ч + Вт r .В нормальных условиях магнитные потери в ферритах в основном представляют собой остаточные потери и гистерезисные потери; в металлических магнитных материалах в основном возникают потери на вихревые токи и потери на гистерезис. Для магнитопровода в переменном магнитном поле электромагнитная индукция может генерировать вихревые токи. Это приводит к тому, что напряженность магнитного поля H и интенсивность магнитной индукции B имеют неравномерное распределение амплитуды и фазы внутри материалов. Между тем, это приведет к отставанию фазы B от фазы H , что увеличит часть потерь энергии, известных как потери на вихревые токи.Экспериментальные исследования показывают, что для некоторых металлических магнитных материалов измеренные магнитные потери намного превышают сумму теоретических расчетов потерь на вихревые токи и квазистатических потерь. Разница между экспериментом и теорией, вызывающая дополнительные потери, называется аномальными потерями. Аномальные потери происходят как часть микровихревого тока, индуцируемого вблизи доменной стенки за счет электромагнитной индукции при движении доменной стенки; это также частично является результатом деформации доменных стенок или закрепления доменных стенок.Следует отметить, что аномальные потери составляют большую часть общих потерь в ряде металлических магнитных материалов (например, в листе кремнистой стали). Гистерезисные потери происходят из-за необратимого процесса намагничивания, существующего в магнитном материале (необратимое смещение доменной стенки и необратимое динамическое поведение магнитного домена). В квазистатическом магнитном случае потери на гистерезис пропорциональны площади петли гистерезиса. В средних и сильных переменных магнитных полях гистерезисные потери некоторых магнитных материалов на основе металлов соответствуют эмпирической формуле Штейнмеца Wh=ηBmnf, где f — частота, а η и n — константы, связанные с материалом.Например, для сплава 3%Si–Fe n≈1,6 и η≈1,2 Дж/(м3·Т). Остаточные потери означают все другие потери, кроме потерь на вихревые токи и потерь на гистерезис. Это обусловлено процессами магнитной релаксации в различных механизмах. В низкочастотных и слабых магнитных полях остаточные потери в основном представляют собой потери магнитного последействия и не имеют ничего общего с частотой. К высокочастотным остаточным потерям относятся потери, вызванные размерным резонансом, резонансом доменных стенок и собственным резонансом. Остаточные потери преобладают в ферритах. Остаточные потери, вызванные магнитным последействием, пропорциональны частоте, смещению доменных стенок и затуханию вращения вектора намагниченности. Эта потеря делится на две категории: тип Рихтера и тип Джордана. Первое связано с температурой и частотой; последний слабо зависит от температуры и частоты. Потери типа Рихтера в основном вызваны наведенной анизотропией, вызванной распространением примесей. Потери жорданового типа в основном вызваны тепловыми флуктуациями.Потери Рихтера в феррите обусловлены распространением валентных электронов между ионами. В области высоких и сверхвысоких частот на частоте 10 4 Гц и выше мнимая составляющая магнитной проницаемости на спектре феррита, связанная с магнитными потерями мк ″, может иметь несколько пиков поглощения в разных частотных областях. Они соответствуют резонансным потерям, которые также являются разновидностью релаксационных потерь. По мере увеличения частоты эти пики поглощения будут вызваны размерным резонансом, резонансом доменных стенок, естественным резонансом и естественным обменным резонансом. Исследования показали, что магнитные частицы диаметром примерно 10 нм в основном будут иметь релаксационные потери, демонстрируя более высокий SAR; и гистерезисные потери в основном возникают в магнитных частицах диаметром 100 нм–1 мкм, демонстрируя более низкую скорость SAR. Описаны два примера применения магнитной гипертермии. Шинкай и его коллеги использовали катионные липосомы (включая Fe 3 O 4 с размером частиц 10 нм) при гипертермии глиомы крыс. Опухоли более чем у 80% крыс полностью исчезли.Брусенцов и его коллеги использовали магнитную жидкость γ-Fe 2 O 3 , покрытую декстраном (включая γ-Fe 2 O 3 диаметром 10 нм) при гипертермии опухолей MX2 у крыс. Опухоли у 33% крыс полностью рецессии, срок выживания увеличился на 150%. Хотя использование наноматериалов способствовало развитию магнитной гипертермии, остается еще много проблем в применении магнитной гипертермии. Во-первых, необходимо улучшить нацеливание на гипертермию, SAR материалов и степень биобезопасности.Для достижения удовлетворительного эффекта его необходимо сочетать с другими методами лечения опухолей. Также необходимо учитывать, что магнитная жидкость должна иметь минимальный остаток в организме после завершения лечения. Как правило, наномагнитные материалы могут естественным образом выводиться из организма. Кроме того, мы можем воспользоваться преимуществами так называемой технологии управления магнитным полем, чтобы исключить потенциальный остаточный материал. Кроме того, после попадания магнитной жидкости в организм часть жидкости неизбежно найдет путь в клетки нормальных тканей.Нам также необходимо провести дальнейшие исследования воздействия наномагнитных материалов на нормальные ткани, то есть их побочных эффектов. Автор: Майк Гедеон, менеджер по рынку телекоммуникаций и серверов Когда магнитный материал помещается в магнитное поле, его магнитные диполи выравниваются, создавая ответную намагниченность, которая в сочетании с приложенным полем создает магнитную индукцию.Если бы ответ был линейным, это было бы легко вычислить. Однако отклик является нелинейным, что приводит к появлению кривых гистерезиса при циклическом изменении приложенного магнитного поля. Кривая намагничивания магнитного материала так же описывает магнитные свойства материала, как его кривая напряжения-деформации описывает его механические свойства. Точно так же, как основные свойства при растяжении можно найти на кривой напряжения-деформации, ключевые магнитные свойства также можно найти на кривой намагничивания. Прежде всего следует отметить, что существует два типа кривых намагничивания, генерируемых в ответ на приложенное поле. Кривые M-H сосредоточены на внутреннем отклике магнитного материала, а кривые B-H сосредоточены на магнитной индукции. Поэтому важно знать, на какой тип кривой вы смотрите, когда пытаетесь определить магнитные свойства. На рис. 1 схематически показано, что происходит, когда магнитное поле прикладывается к магнитному материалу.По мере увеличения напряженности поля магнитный момент материала ( также увеличивается, поскольку магнитные диполи начинают выравниваться с приложенным магнитным полем. То есть материал становится магнитно поляризованным . Поскольку M увеличивается, соответствующее магнитная индукция также увеличивается. В конце концов, когда магнитные диполи полностью выровнены с полем, больше не может увеличиваться. Это известно как намагниченность насыщения . Наклон кривой намагничивания представляет собой магнитную проницаемость (мк) материала.Обратите внимание, однако, что начальная намагниченность обычно не является прямой линией! Это означает, что магнитная проницаемость будет изменяться в зависимости от напряженности магнитного поля. Поэтому часто испытательные лаборатории сообщают о 3 значениях проницаемости. Это будут начальный (низкий наклон), промежуточный (максимальный наклон) и конечный (снова более низкий наклон). Поскольку самая длинная линейная часть кривой является максимальным наклоном, ее часто считают проницаемостью по умолчанию.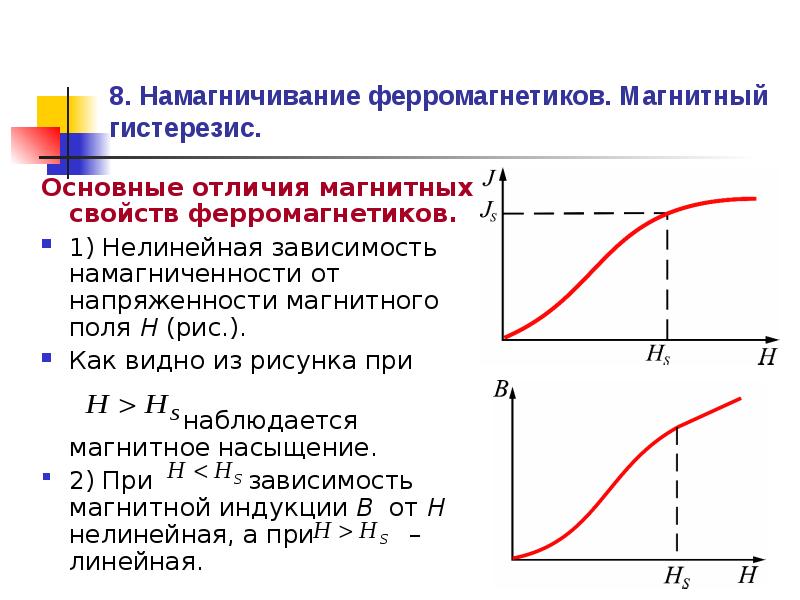 Амплитуда в спектре появляется на резонансной частоте нуклонов водорода в воде, см. рис. 1.10.
Амплитуда в спектре появляется на резонансной частоте нуклонов водорода в воде, см. рис. 1.10.
Contrast Параметры сканера PD длинные TR, прочитайте FID или использовать короткие TE T2 длинные TR, TE≈T2 T1 прочитайте FID или используйте короткое TE,TR≈T1  15)I(x,y)∝PD(x,y)1-exp-TRT1︸T1-взвешиваниеexp-TET2︸T2-взвешивание
15)I(x,y)∝PD(x,y)1-exp-TRT1︸T1-взвешиваниеexp-TET2︸T2-взвешивание
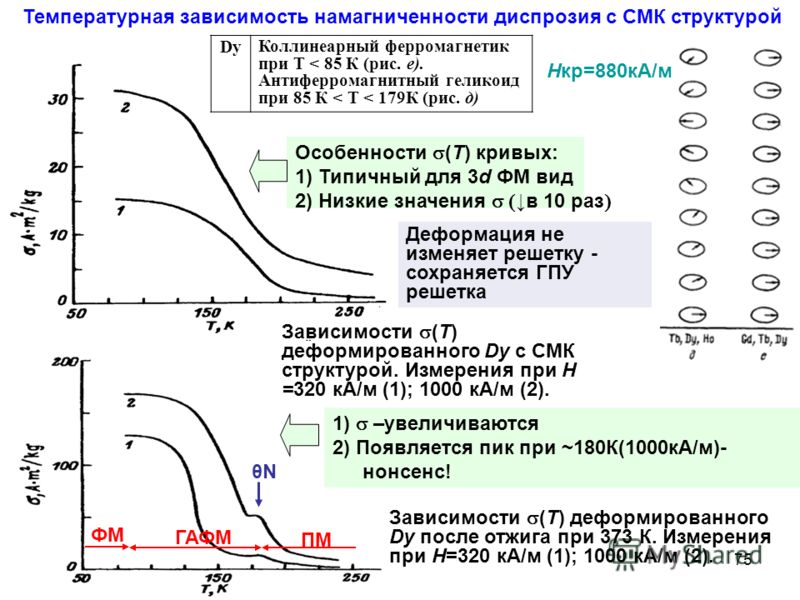 Жирный временной ответ изменяется, когда локальная концентрация дезоксигемоглобина снижается в области активности нейронов. Этот факт отражается на Т2*- и Т2-взвешенных МР-изображениях.
Жирный временной ответ изменяется, когда локальная концентрация дезоксигемоглобина снижается в области активности нейронов. Этот факт отражается на Т2*- и Т2-взвешенных МР-изображениях.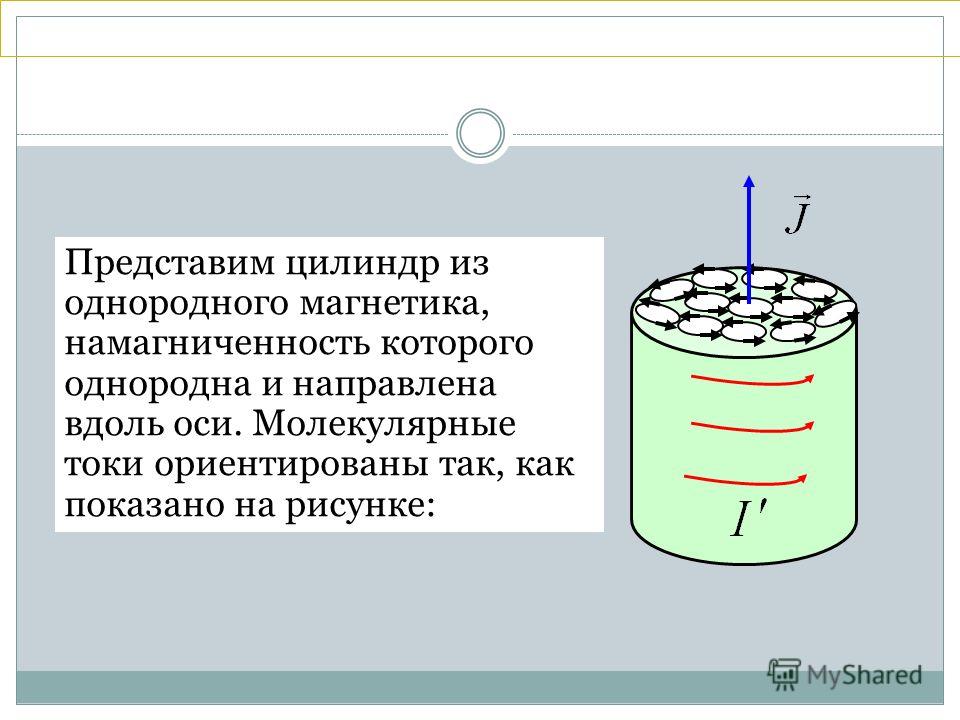 фМРТ с высоким временным и пространственным разрешением представляет собой мощный метод визуализации быстрых и тонких паттернов активации человеческого мозга. Функциональная локализация основана на явной корреляции между активностью нейронов и изменениями МР-сигнала. Как известно как из теоретических оценок, так и из экспериментальных результатов [266], вариация активированного сигнала на клиническом сканере очень мала.Это мотивирует применение методов анализа для определения формы волны отклика и связанных с ней активированных областей.
фМРТ с высоким временным и пространственным разрешением представляет собой мощный метод визуализации быстрых и тонких паттернов активации человеческого мозга. Функциональная локализация основана на явной корреляции между активностью нейронов и изменениями МР-сигнала. Как известно как из теоретических оценок, так и из экспериментальных результатов [266], вариация активированного сигнала на клиническом сканере очень мала.Это мотивирует применение методов анализа для определения формы волны отклика и связанных с ней активированных областей. Перемагничивание – обзор
9.6.4 Механизм термогенеза магнитных материалов для магнитной гипертермии
Кривые намагничивания и магнитные свойства
Рисунок 1 – Начальная кривая намагничивания. Когда магнитный материал помещается в магнитное поле, намагниченность (M) и связанная с ним индукция (B) увеличиваются. Скорость увеличения определяется магнитной проницаемостью материала.
На рис. 2 показана полная кривая гистерезиса для ферромагнитного материала. Я выбрал ферромагнитный материал, так как легко увидеть особенности кривой гистерезиса, но даже магнитомягкие материалы будут демонстрировать те же особенности, хотя кривая будет другой формы.
После первоначального намагничивания материала до насыщения магнитный файл обнуляется и переворачивается. Когда сила приложенного поля падает до нуля, в материале все еще остается остаточная намагниченность, что приводит к индукции, превышающей нуль. Эта остаточная намагниченность или индуктивность известна как остаточная намагниченность . На кривой B-H это будет обозначаться как . На кривой M-H это будет обозначаться как . Поскольку применяемое поле равно нулю, в единицах СИ и в единицах Гаусса (cgs).
Поскольку магнитное поле продолжает усиливаться в направлении, противоположном начальному насыщению, индукция будет продолжать падать и, в конце концов, изменится на противоположную. На пути вниз будет точка, где результирующая индукция равна нулю. (Здесь кривая B-H пересекает ось X). Сила приложенного магнитного поля, где это происходит, называется коэрцитивной силой (H C ) . В этот момент приложенное поле отрицательное, и оно точно уравновешивается оставшимся положительным магнитным моментом материала.
По мере того, как магнитное поле становится сильнее в отрицательном направлении, со временем магнитный момент также станет равным нулю. (Другими словами, здесь кривая M-H пересекает ось X.) Сила приложенного магнитного поля, где это происходит, называется собственной коэрцитивной силой (H Ci ) . Поскольку кривая гистерезиса пересекает ось X на кривой M-H вне того места, где она пересекается на кривой B-H, H Ci > H C .
В конце концов, насыщение будет достигнуто в другом направлении.Если поле снова изменить на обратное, материал вернется к насыщению по кривой, равной и противоположной кривой размагничивания. Другими словами, кривая перемагничивания будет равна кривой размагничивания, перевернутой симметрично по обеим осям.
Рисунок 2 – Кривая магнитного гистерезиса ферромагнитного материала. Остаточная магнитная намагниченность (Br) — это остаточная индукция, когда приложенное магнитное поле падает до нуля после достижения насыщения. (где петля гистерезиса пересекает ось Y (индукция).Коэрцитивная сила H c ) представляет собой силу обратного магнитного поля, необходимую для размагничивания насыщенного материала. Здесь петля гистерезиса пересекает ось X (приложенная напряженность поля).
Дополнительные статьи с техническими подробностями можно найти в нашем архиве технических сведений.
Другие товары
.

 Коллеги из Университета Аалто (Финляндия) приготовили для наших экспериментов синтетический мультиферроик, состоящий из магнитного слоя CoFeB и слоя сегнетоэлектрика BaTiO3 с полосовыми доменами. Мы же впервые изучили экспериментально, как реагирует намагниченность в отдельных доменах такого мультиферроика на воздействие лазерным импульсом длительностью менее 200 фемтосекунд»,— рассказывает Леонид Шелухин, младший научный сотрудник Физико-технического института имени А. Ф. Иоффе РАН (Санкт-Петербург).
Коллеги из Университета Аалто (Финляндия) приготовили для наших экспериментов синтетический мультиферроик, состоящий из магнитного слоя CoFeB и слоя сегнетоэлектрика BaTiO3 с полосовыми доменами. Мы же впервые изучили экспериментально, как реагирует намагниченность в отдельных доменах такого мультиферроика на воздействие лазерным импульсом длительностью менее 200 фемтосекунд»,— рассказывает Леонид Шелухин, младший научный сотрудник Физико-технического института имени А. Ф. Иоффе РАН (Санкт-Петербург).
 1)
1) 5)
5)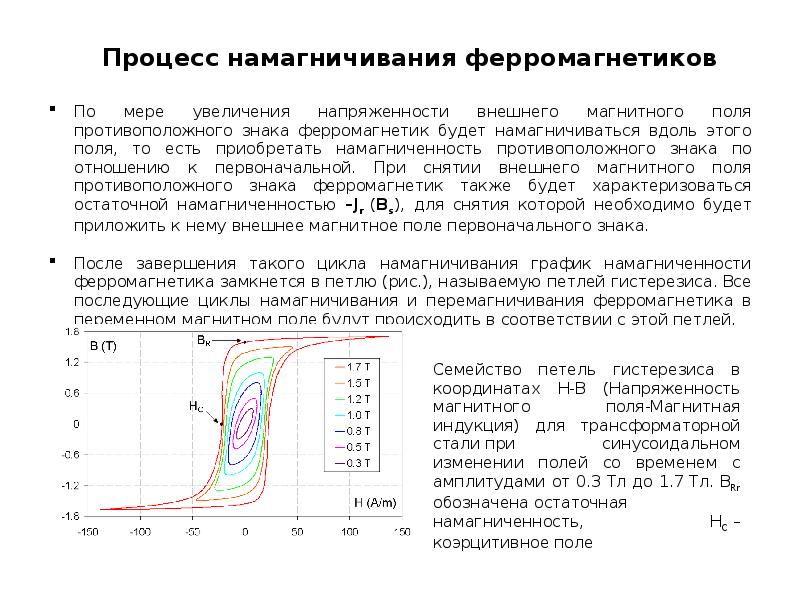 Этот же принцип используется при создании так называемой DRAM — динамической памяти с произвольным доступом», — объясняет Андрей Кудлис, один из авторов статьи, младший научный сотрудник Нового физтеха ИТМО.
Этот же принцип используется при создании так называемой DRAM — динамической памяти с произвольным доступом», — объясняет Андрей Кудлис, один из авторов статьи, младший научный сотрудник Нового физтеха ИТМО. С их помощью тоже можно создавать определенные элементы памяти. В частности, магнитно-резистивную память: это своего рода слоистый пирог, состоящий из нанопленок. Например, две из них ферромагнитные, а посередине ― диэлектрическая. Но, в зависимости от того, как у слоев ферромагнетика ориентирована намагниченность, у слоя, расположенного посередине, будет разное электрическое сопротивление. Оно может быть огромным, а может быть, наоборот, очень низким», — говорит Андрей Кудлис.
С их помощью тоже можно создавать определенные элементы памяти. В частности, магнитно-резистивную память: это своего рода слоистый пирог, состоящий из нанопленок. Например, две из них ферромагнитные, а посередине ― диэлектрическая. Но, в зависимости от того, как у слоев ферромагнетика ориентирована намагниченность, у слоя, расположенного посередине, будет разное электрическое сопротивление. Оно может быть огромным, а может быть, наоборот, очень низким», — говорит Андрей Кудлис.
 Их комбинация с ферромагнитными особенностями данного материала позволяет менять ориентацию намагниченности оптическим образом. То есть мы начинаем светить лазерным излучением, которое обладает определенной поляризацией, и будем наблюдать, что в какой-то момент (что зависит, конечно же, от интенсивности накачки) намагниченность у этого материала переключается. Вот, пожалуйста, оптическое управление намагниченностью данного образца. Как это выглядит с точки зрения теории? В этом прямозонном полупроводнике при нерезонансной накачке могут создаваться некие эффективные комплексы, так называемые экситоны, представляющие из себя связанные электрон-дырочные пары. Они, в свою очередь, сами обладают неким эффективным спином. Мы будем разделять спин нашей электронной подсистемы — то есть обычных электронов и спин экситонов», — поясняет исследователь.
Их комбинация с ферромагнитными особенностями данного материала позволяет менять ориентацию намагниченности оптическим образом. То есть мы начинаем светить лазерным излучением, которое обладает определенной поляризацией, и будем наблюдать, что в какой-то момент (что зависит, конечно же, от интенсивности накачки) намагниченность у этого материала переключается. Вот, пожалуйста, оптическое управление намагниченностью данного образца. Как это выглядит с точки зрения теории? В этом прямозонном полупроводнике при нерезонансной накачке могут создаваться некие эффективные комплексы, так называемые экситоны, представляющие из себя связанные электрон-дырочные пары. Они, в свою очередь, сами обладают неким эффективным спином. Мы будем разделять спин нашей электронной подсистемы — то есть обычных электронов и спин экситонов», — поясняет исследователь.
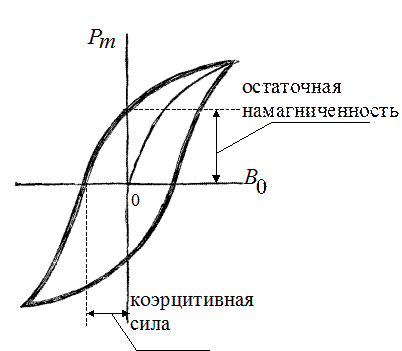

 Мы можем написать
Мы можем написать 

 H = k [(M/2)(cosθ 1
H = k [(M/2)(cosθ 1 

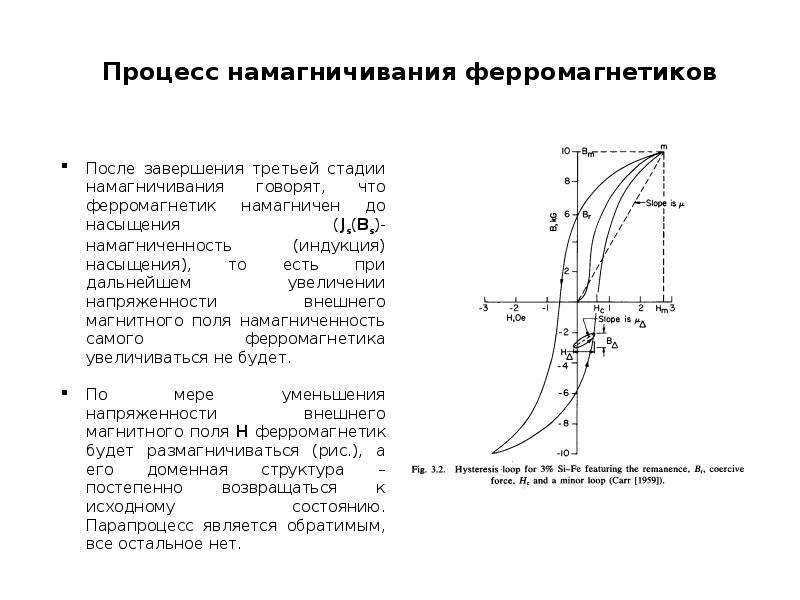 Вы предполагаете, что
Вы предполагаете, что

 Таким образом, мы знаем, что при r > R
Таким образом, мы знаем, что при r > R
