Действующее значение тока. Действующее значение напряжения
Господа, в прошлой статье мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока. Сегодня про него и поговорим!
Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения.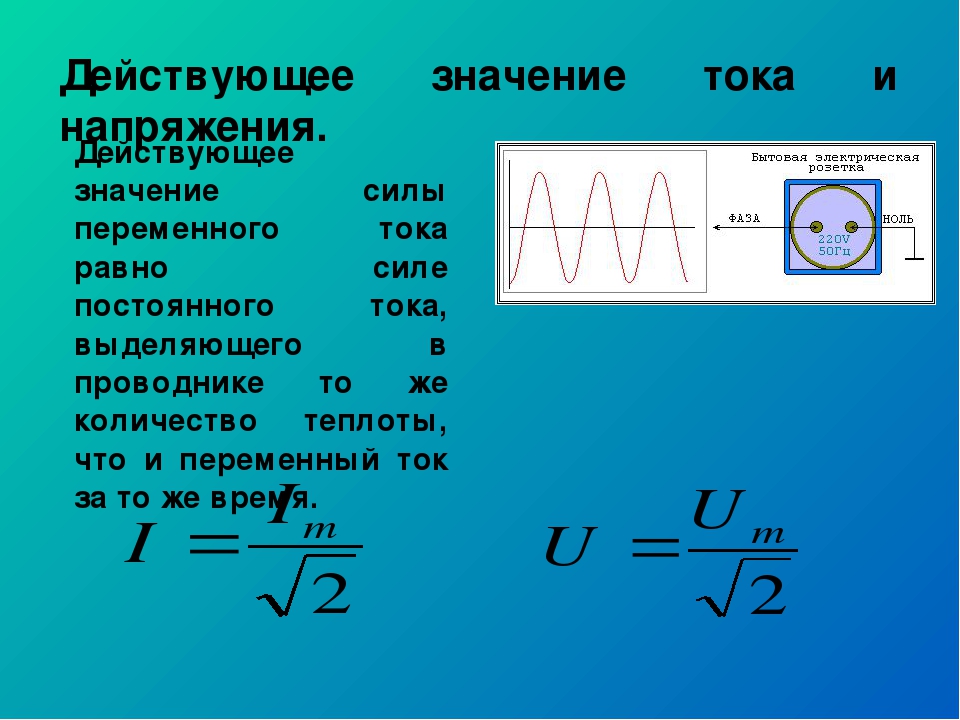 А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.
А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.
Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.
Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда Аm и период Tпериод (ну или частота f). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период Tпериод нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз. Допустим, мы насчитали, что за один период Tпериод синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время Tпериод выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?
Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?
Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье, закон изменения мощности переменного тока равен
Количество выделившейся энергии при работе тока за время Tпериод – соответственно, равно интегралу за время периода Tпериод:
Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .
А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .
Итак, как его нам брать? Ну, величины Im2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:
Погнали считать!
Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.
Итак, имеем
Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!
Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.
Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.
Итак, отбрасывая интеграл с косинусом, получаем
Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен
И, таким образом, получаем ответ
Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой Im в течении периода Tпериод. Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время Tпериод выделится то же самое количество энергии Q. Поэтому мы можем записать
Поэтому мы можем записать
Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца. А мы тем временем выразим действующее значение тока Iдейств. из этого выражения, предварительно сократив все, что можно
Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.
Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения. При этом у нас зависимость мощности от времени примет вот такой вид
Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно
Итак, действующее значение напряжения синусоидального тока равно
Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.
Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.
Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры, включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать
Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать
Отсюда получаем
Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.
Рисунок 1 – Закон изменения напряжения в розетках
И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.
ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.
Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)
На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна
Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна
Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.
На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Эффективное напряжение переменного тока. Действующие значения силы тока и напряжения
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? Действия тока не определяются ни амплитудным, ни мгновенным значениями. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? Действия тока не определяются ни амплитудным, ни мгновенным значениями. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Мощность P
постоянного тока I
, проходящего через сопротивление r
, будет
P
= I
2 × r
.
Мощность переменного тока выразится как средний эффект мгновенной мощности i
2 × r
за целый период или среднее значение от (I m
× sin ωt
) 2 × r
за то же время.
Пусть среднее значение i
2 за период будет M
. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем:
I
2 × r
= M
× r
,
Величина I
называется действующим значением переменного тока.
Среднее значение i
2 при переменном синусоидальном токе определим следующим образом. Построим синусоидальную кривую изменения тока (рисунок 1).
Построим синусоидальную кривую изменения тока (рисунок 1).
Рисунок 1. Действующее значение синусоидального тока
Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости i
2 от времени. Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i
) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием T
и площадью, равной площади, ограниченной кривой i
2 и горизонтальной осью. Высота прямоугольника M
будет соответствовать среднему значению i
2 за период. Это значение за период, вычисленное при помощи высшей математики, будет равно .
Следовательно,
Так как действующее значение переменного тока I
равно , то окончательно формула примет вид
Аналогично зависимость между действующим и амплитудным значениями для напряжения U
и E
имеет вид:
Действующие значения переменных величин, то есть действующее значение напряжения, тока и электродвижущей силы, обозначаются прописными буквами без индексов (U
, I
, E
).
На основании изложенного выше, можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующее значение тока и напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в раз. От этого расположение векторов на диаграмме не изменится.
В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.
Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток
.
- Переменный электрический ток
— это ток, сила и направление которого периодически меняются.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω
по синусоидальному или косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,
где u
– мгновенное значение напряжения, U
m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,
где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Исходя из этого можно дать еще такое определение:
- Переменный ток
– это электрический ток, который изменяется с течением времени по гармоническому закону.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п.
Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.
Генератор переменного тока
Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.
- Генератором переменного тока
называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.
ЭДС индукции генератора изменяется по синусоидальному закону
\(e={\rm E}_{m} \cdot \sin \omega \cdot t,\)
где \({\rm E}_{m} =B\cdot S\cdot \omega\) — амплитудное (максимальное) значение ЭДС.
При подключении к выводам рамки нагрузки сопротивлением R
, через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке
\(i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\)
где \(I_{m} = \dfrac{B\cdot S\cdot \omega }{R}\) — амплитудное значение силы тока.
Основными частями генератора являются (рис. 1):
- индуктор
— электромагнит или постоянный магнит, который создает магнитное поле; - якорь
— обмотка, в которой индуцируется переменная ЭДС; - коллектор со щетками
— устройство, посредством которого снимается с вращающихся частей или подается по ним ток.
Неподвижная часть генератора называется статором
, а подвижная — ротором
. В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.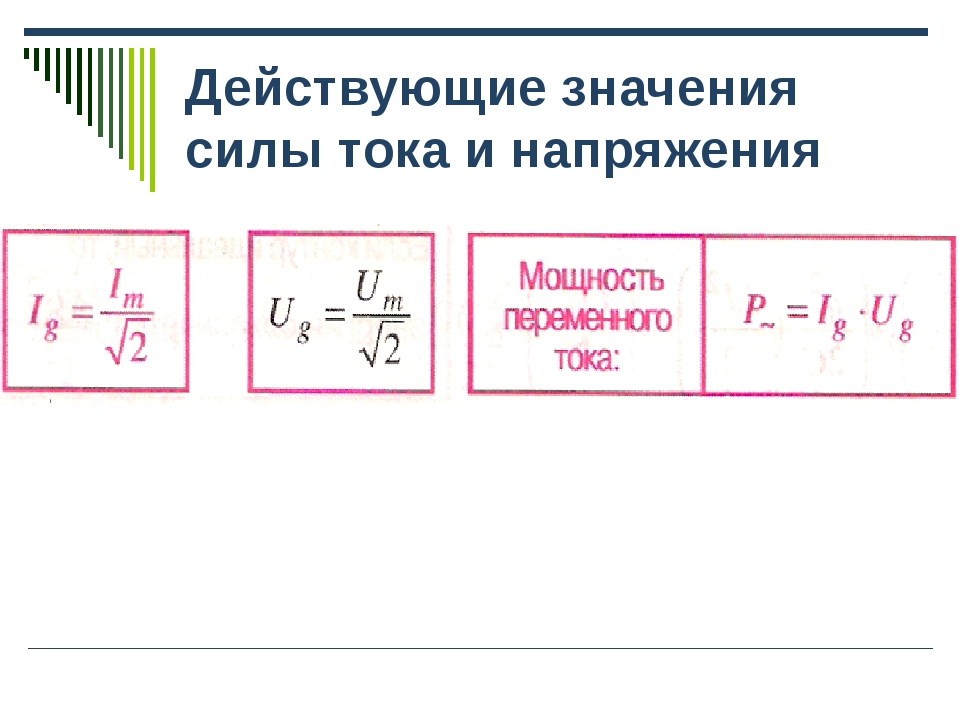
На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока. Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.
Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.
Из истории
. Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» — спросили его. Фарадей ответил: «Какая может быть польза от новорожденного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».
*Принцип действия
Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S
вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec{B}\) (см. рис. 1).
При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec{B}\) и нормали к плоскости рамки \(\vec{n}\) меняется со временем по линейному закону. Если в момент времени t
= 0 угол α 0 = 0 (см. рис. 1), то
\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)
где ω — угловая скорость вращения рамки, ν — частота ее вращения.
В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом
\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)
Тогда согласно закону Фарадея индуцируется ЭДС индукции
\(e=-\Phi «(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t. \)
\)
Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.
Действующие значения силы тока и напряжения
Пусть источник тока создает переменное гармоническое напряжение
\(u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)\)
Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R
, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)
где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины U m
, I m
называются амплитудными значениями напряжения и силы тока
. Зависящие от времени значения напряжения u
и силы тока i
называют мгновенными
.
Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения
.
- Действующим (эффективным) значением силы
переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буквой I
.
- Действующим (эффективным) значением напряжения
переменного тока называется напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буквой U
.
Действующие (I, U
) и амплитудные (I m , U m
) значения связаны между собой следующими соотношениями:
\(I = \dfrac{I_{m} }{\sqrt{2}}, \; \; \; U =\dfrac{U_{m} }{\sqrt{2}}.\)
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
\(P = U\cdot I = I^{2} \cdot R = \dfrac{U^{2}}{R}. {2}dt}}.}
{2}dt}}.}
Для синусоидального тока:
I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}
I m {\displaystyle I_{m}} — амплитудное значение тока.
Для тока треугольной и пилообразной формы:
I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}
Аналогичным образом определяются действующие значения ЭДС и напряжения.
Дополнительные сведения
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value
— эффективное значение. Также применяется аббревиатура RMS (rms) — root mean square
— среднеквадратичное (значение).
В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.
Источники
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики.
 А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5 - «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки
- Действующие значения тока и напряжения
- Среднеквадратичное значение
Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока
Мгновенное и максимальное значения.
Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями
этих величин и обозначают соответственно строчными буквами (e, i, u, p
).
Максимальным значением
(амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е
m , напряжения — U
m , тока — I
m .
Действующим (или эффективным)
значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.
Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.
Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.
По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:
E
m = E
· 1,41; U
m = U
· 1,41; I
m = I
· 1,41;
Среднее значение
= отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.
Под средним значением понимают среднеарифметическое ее значение за половину периода.
/ Среднее и действующие значения синусоидальных токов и напряжений
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
т. е. среднее значение синусоидального тока составляет от амплитудного. Аналогично,
Аналогично,
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным током,
Выделенная за то же время постоянным током теплота равна Приравняем их:
Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r
ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r
за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.
Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,
i | I | |||
При неизменном во времени токе энергия
W = I
2rT
Приравняв правые части
I
m
0,707I
m
.
Таким образом, действующее значение тока меньше амплитудного в √2 раз.
Аналогично определяют действующие значения ЭДС и напряжения:
Е =
E
m
/
√2, U = U
m
/
√2.
Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока
I
m
= √2I
= 1,41 10 = 14,1 A,
и мгновенное значение тока
i
= I
m
sin (ωt
+ ψ) = 14,1 sin (ωt
+ ψ).
При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):
T | ||||||||||
Е | Е | sin ωt d | |cos ωt | 0,637Е | ||||||
Аналогично можно найти средние значения тока и напряжения:
I
ср = 2I
т
/π; U
ср =
2U
т
/π.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения Действующее значение переменного тока Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока. Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r. Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время. Пусть среднее значение t2 за период будет М. Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени. Действующее значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √2,E= Em / √2 Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется. |
Список параметров напряжения и силы электрического тока
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Мгновенное значение
Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является (u (t) , i (t) {\displaystyle u(t)~,\quad i(t)}).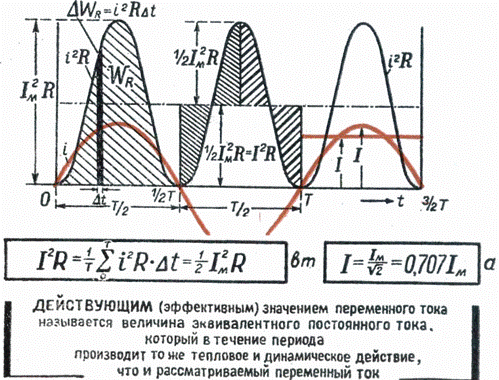 {2}(t)dt}}}
{2}(t)dt}}}
Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение
Среднее значение (смещение) — постоянная составляющая напряжения или силы тока
U = 1 T ∫ 0 T u (t) d t , I = 1 T ∫ 0 T i (t) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}
В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). {T}\mid i(t)\mid dt}
{T}\mid i(t)\mid dt}
На практике используется редко, однако большинство измерительных приборов переменного тока — магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
Коэффициенты пересчёта значений
- Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению.
 Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
- Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .
Параметры постоянного тока
- Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
- Справочник по радиоэлектронным устройствам
: В 2-х т. ; Под ред. Д. П. Линде — М.: Энергия, 1978
; Под ред. Д. П. Линде — М.: Энергия, 1978 - Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989
Нормативно-техническая документация
- ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
- ГОСТ 23875-88 Качество электрической энергии. Термины и определения
- ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения
Ссылки
- Электрические цепи постоянного тока
- Переменный ток. Изображение синусоидальных переменных
- Амплитудное, среднее, эффективное
- Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
- Системы тока и номинальные напряжения электроустановок
- Электричество
- Проблемы высших гармоник в современных системах электропитания
Какой физический смысл имеет действующее значение напряжения и тока
Александр титов
Действующее значение силы ПЕРЕМЕННОГО тока — это такое значение величины ПОСТОЯННОГО тока, действие которого произведёт ту же самую работу (или тепловой эффект) , что и действие переменного тока за время одного периода его действия.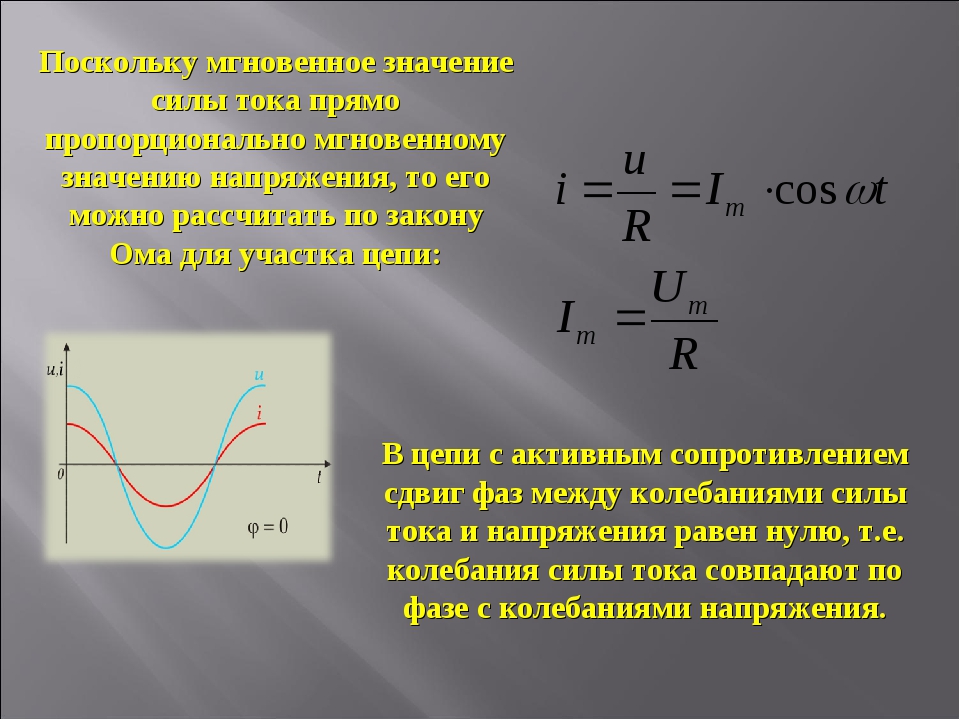 2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.
2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.
То же самое с действующим значением напряжения и ЭДС.
Vitas latish
можно грубо сказать
— напряжение — потенциальная энергия…. расческа- волосы…. напряжение = свечение, искорки, подъем волос… .
— ток это работа, действие, сила.. . тепло, горение, движение выплеск кенетической энергии
Физический смысл данных понятий примерно таков же, как физический смысл средней скорости или других величин, усредненных по времени. В различные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно лишь условно.
Вместе с тем совершенно очевидно, что различные токи имеют различные энергетические характеристики – они производят разную работу за один и тот же промежуток времени. Произведенная током работа принята за основу при определении действующего значения силы тока. Задаются определенным промежутком времени и рассчитывают работу, совершенную переменным током за этот промежуток времени. Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:
Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:
Откуда берется данная формула? Из хорошо известной формулы для мощности тока, выражаемой через квадрат его силы.
Действующие значения периодических и синусоидальных токов
Вычислять действующее значение для произвольных токов – занятие малопродуктивное. Зато для периодического сигнала данный параметр может оказаться весьма полезным. Известно, что любой периодический сигнал может быть разложен в спектр. То есть, представлен как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам нужно знать, как вычислять действующее значение простого синусоидального тока.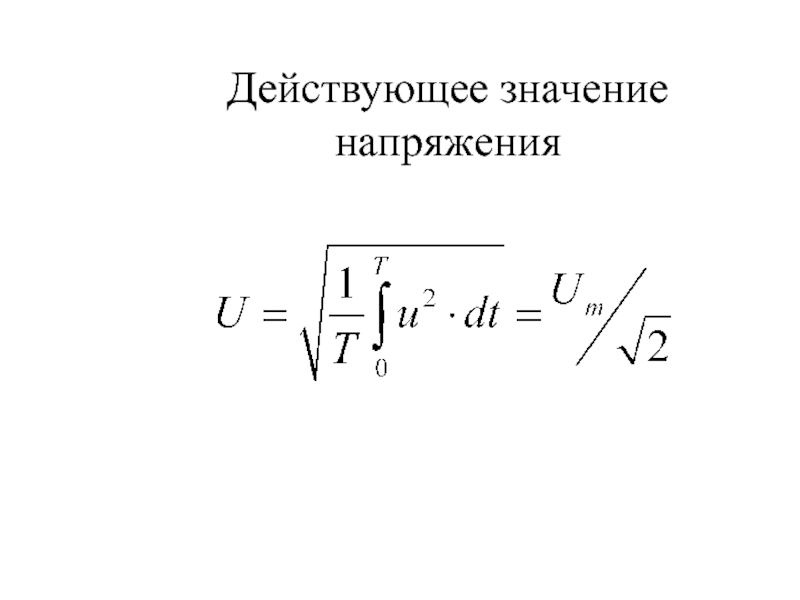 В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу.
В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу.
Силу переменного тока (напряжения) можно
охарактеризовать при помощи амплитуды.
Однако амплитудное значение тока
непросто измерить экспериментально.
Силу переменного тока удобно связать
с каким-либо действием, производимым
током, не зависящим от его направления.
Таковым является, например, тепловое
действие тока. Поворот стрелки амперметра,
измеряющего переменный ток, вызывается
удлинением нити, которая нагревается
при прохождении по ней тока.
Действующим
илиэффективным
значением
переменного тока (напряжения) называется
такое значение постоянного тока, при
котором на активном сопротивлении
выделяется за период такое же количество
теплоты, как и при переменном токе.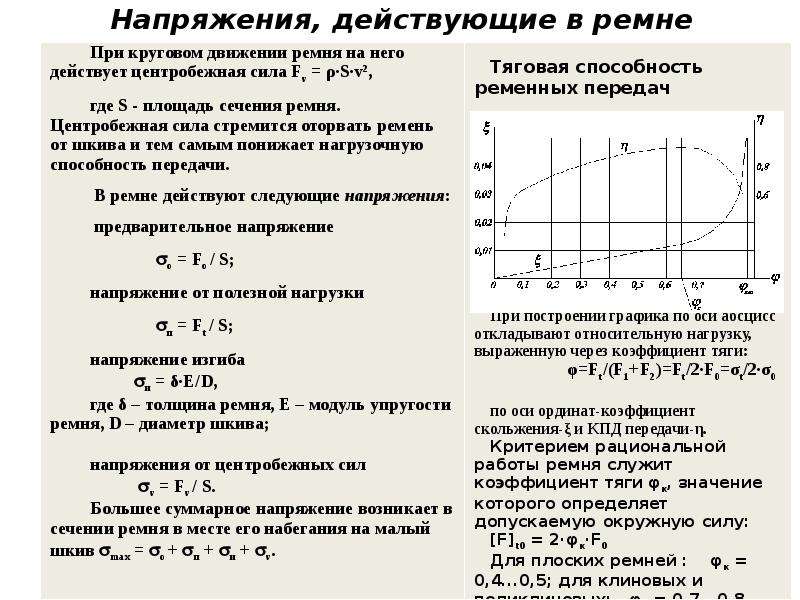
Свяжем
эффективное значение тока с его
амплитудным значением. Для этого
рассчитаем количество теплоты, выделяемое
на активном сопротивлении переменным
током за время, равное периоду колебаний.
Напомним, что по закону Джоуля-Ленца
количество теплоты, выделяющееся на
участке цепи cсопротивлениемприпостоянном
токеза время,
определяется по формуле
.
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени
.
Поделим период колебанийна очень большое число малых промежутков
времени
.
Количество теплоты
,
выделяемое на сопротивленииза время
:
.
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:
.
Сила тока в
цепи изменяется по синусоидальному
закону
,
.
Опуская
вычисления, связанные с интегрированием,
запишем окончательный результат
.
Если бы по
цепи шёл некоторый постоянный ток
,
то за время, равное,
выделилось бы тепло
.
По определению постоянный ток,
оказывающий такое же тепловое действие,
что и переменный, будет равен эффективному
значению переменного тока
.
Находим эффективное значение силы
тока, приравнивая теплоты, выделяемые
за период, в случаях постоянного и
переменного токов
(4.28)
Очевидно,
точно такое же соотношение связывает
эффективное и амплитудное значения
напряжения в цепи с синусоидальным
переменным током:
(4.29)
Например,
стандартное напряжение в сети 220 В –
это эффективное напряжение. По формуле
(4.29) легко посчитать, что амплитудное
значение напряжения в этом случае будет
равно 311 В.
4.4.5. Мощность в цепи переменного тока
Пусть на некотором участке цепи с
переменным током сдвиг фаз между током
и напряжением равен
,
т.е. сила тока и напряжение изменяются
по законам:
,
.
Тогда мгновенное
значение мощности, выделяемой на участке
цепи,
Мощность
изменяется со временем. Поэтому можно
говорить лишь о ее среднем значении.
Определим среднюю мощность, выделяемую
в течение достаточно длительного
промежутка времени (во много раз
превосходящего период колебаний):
С использованием
известной тригонометрической формулы
.
Величину
усреднять не нужно, так как она не зависит
от времени, следовательно:
.
За длительное
время значение косинуса много раз
успевает измениться, принимая как
отрицательные, так и положительные
значения в пределах от (1)
до 1. Понятно, что среднее во времени
значение косинуса равно нулю
,
поэтому
(4.30)
Выражая
амплитуды тока и напряжения через их
эффективные значения по формулам (4.28)
и (4.29), получим
. (4.31)
Мощность, выделяемая на участке цепи с
переменным током, зависит от эффективных
значений тока и напряжения и сдвига
фаз между током и напряжением
. Например,
если участок цепи состоит из одного
только активного сопротивления, то
и
.
Если участок цепи содержит только
индуктивность или только ёмкость, то
и
.
Объяснить среднее нулевое значение
мощности, выделяемой на индуктивности
и ёмкости можно следующим образом.
Индуктивность и ёмкость лишь заимствуют
энергию у генератора, а затем возвращают
её обратно. Конденсатор заряжается, а
затем разряжается. Сила тока в катушке
увеличивается, затем снова спадает до
нуля и т. д. Именно по той причине, что
на индуктивном и ёмкостном сопротивлениях
средняя расходуемая генератором энергия
равна нулю, их назвали реактивными. На
активном же сопротивлении средняя
мощность отлична от нуля. Другими словами
провод с сопротивлением
при протекании по нему тока нагревается.
И энергия, выделяемая в виде тепла, назад
в генератор уже не возвращается.
Если участок цепи содержит несколько
элементов, то сдвига фаз
может быть иным. Например, в случае
участка цепи, изображенного на рис. 4.5,
сдвиг фаз между током и напряжением
определяется по формуле (4.27).
Пример 4.7.
К генератору переменного
синусоидального тока подключён резистор
с сопротивлением.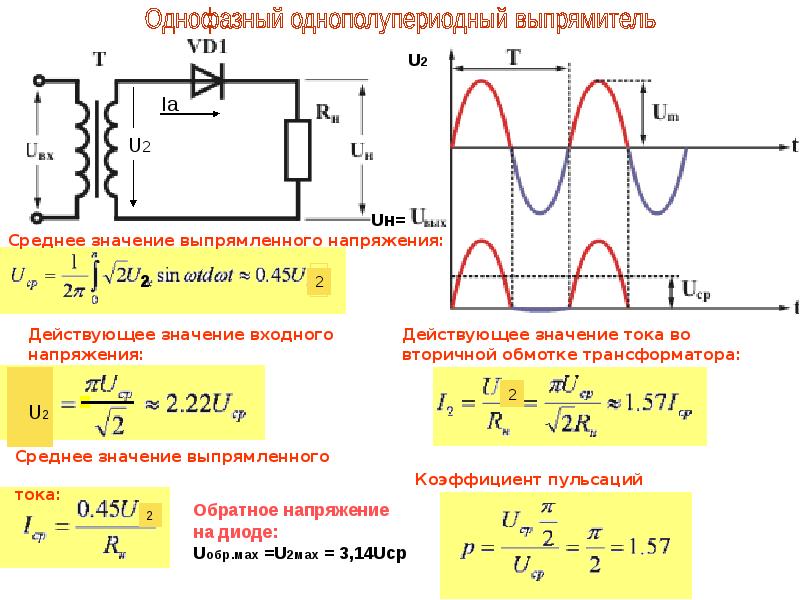
Во сколько раз изменится средняя
мощность, расходуемая генератором, если
к резистору подключить катушку с
индуктивным сопротивлением
а) последовательно, б) параллельно (рис.
4.10)? Активным сопротивлением катушки
пренебречь.
Решение.
Когда к генератору подключено
одно только активное сопротивление,
расходуемая мощность
(см. формулу (4.30)).
Рассмотрим цепь на рис. 4.10, а. В примере
4.6 было определено амплитудное значение
силы тока генератора:
.
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора
.
В результате средняя расходуемая
генератором мощность
.
Ответ: при
последовательном включении в цепь
индуктивности средняя мощность,
расходуемая генератором, уменьшится в
2 раза.
Рассмотрим цепь на рис. 4.10,б. В примере
4.6 было определено амплитудное значение
силы тока генератора
.
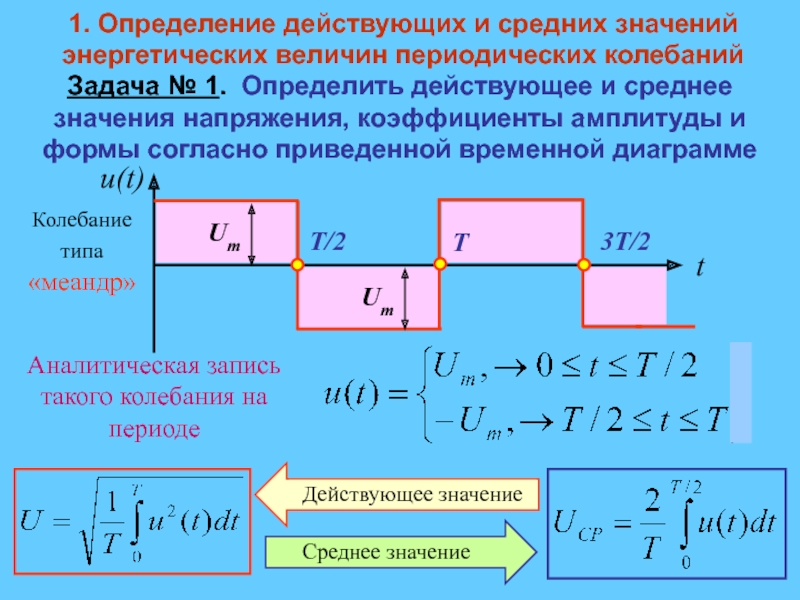
Из векторной диаграммы на рис. 4.11,б
определяем сдвиг фаз между током и
напряжением генератора
.
Тогда средняя
мощность, расходуемая генератором
Ответ: при
параллельном включении индуктивности
средняя мощность, расходуемая генератором,
не изменяется.
Метод измерения действующего значения напряжения с применением МК / Хабр
В данном посте речь пойдет об одном из вариантов измерения действующего значения напряжения и частоты сети на 8-ми битном микроконтроллере PIC18. При желании, можно метод перенести на любой другой МК, вплоть до всеми любимых ARDUINO (если они поддерживают реализацию прерываний по таймеру с частотой 5-10 кГц).
Также, рассматриваемый метод позволяет измерять частоту сетевого напряжения без использования внешних дополнительных средств, таких как компараторы. Но, при этом приходится жертвовать либо временными ресурсами МК, либо точностью измерения частоты.
Почему важно измерять действующее значение, а не какое либо другое, например, средневыпрямленное? Большинство “китайских” электронных вольтметров измеряют сетевое напряжение по средневыпрямленному значению. Методика измерения следующая: за период сетевого напряжения делается выборка из N значений амплитуды напряжения, результаты суммируются (без знака), делятся на N (усредняются), после чего полученный результат умножается на коэффициент
Методика измерения следующая: за период сетевого напряжения делается выборка из N значений амплитуды напряжения, результаты суммируются (без знака), делятся на N (усредняются), после чего полученный результат умножается на коэффициент
Указанный коэффициент определяет зависимость действующего значения синусоидального (!) сигнала от средневыпрямленного.
Такая методика измерения проста, не требует много ресурсов микроконтроллера (как временных, так и ресурсов памяти). Основным недостатком такой методики измерения является большая ошибка измерения на несинусоидальных сигналах.
Как все знают, изменение сигнала сетевого напряжения подчиняется синусоидальному закону (вследствие применения синхронных генераторов на электростанции), с частотой изменения сигнала 50 Гц (60 Гц). Однако, на практике вследствие влияния сторонних факторов (в основном подключение к сети мощных нелинейных нагрузок), а также применения инверторов с квазисинусоидальным выходным напряжением (см. рисунок), синусоида напряжения либо значительно искажается, либо заменятся прямоугольными импульсами. В таких случаях указанный выше метод измерения даст очень большую погрешность (например, в квазисинусоидальных инверторах выходное напряжение, измеренное “китайским» вольтметром может быть равно 180-200В, в то время как действующее напряжение будет равно 220В ).
рисунок), синусоида напряжения либо значительно искажается, либо заменятся прямоугольными импульсами. В таких случаях указанный выше метод измерения даст очень большую погрешность (например, в квазисинусоидальных инверторах выходное напряжение, измеренное “китайским» вольтметром может быть равно 180-200В, в то время как действующее напряжение будет равно 220В ).
Например, напряжение у меня дома
Почему важно измерять именно действующее значение напряжения (тока)? Потому что именно действующие (еще называют его эффективными) значения напряжения и тока определяют работу электрической системы (грубо говоря, электронагреватель выделяет тепло в прямой зависимости от действующих значений напряжения и тока сети).
Действующее значение измеряемой периодической величины рассчитывается по формуле
Или после дискретизации получим
Т.е. нам нужно делать выборку ряда значений за период сетевого напряжения, просуммировать значения квадратов точек выборки, поделить на количество точек за период (при определении количества точек выборки не забываем про теорему Котельникова-Шеннона), и взять квадратный корень из полученного результата.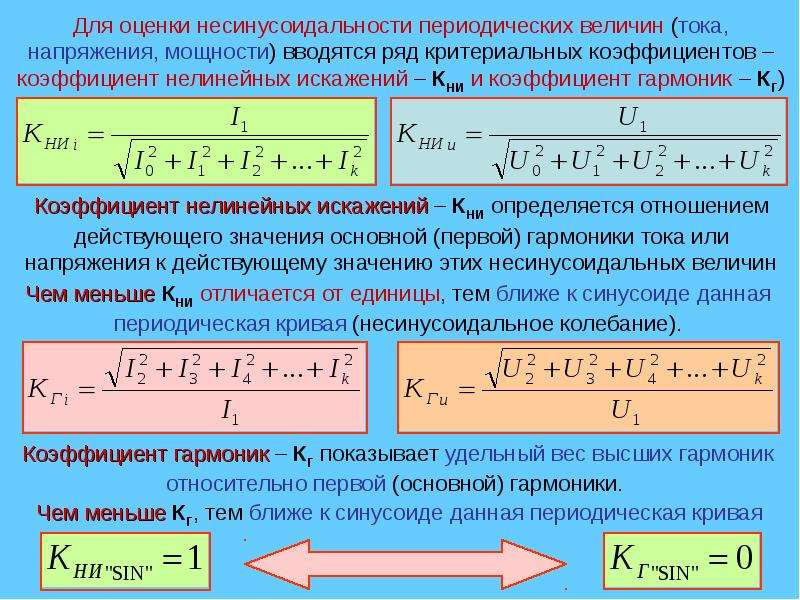
Вроде бы ничего сложного, если бы не но:
1) Каждый период точки выборки набираются заново, что увеличивает погрешность измерения;
2) В реальной сети, около нуля напряжения, могут встречаться как “нулевые полки”, так и повторные переходы через ноль напряжения, что значительно внесет погрешность в измерение.
С первым пунктом будем бороться измерением измерением суммы квадратов точек выборки за каждый полупериод, после чего суммируя n-ую сумму квадратов с (n+1)-й и откидывая (n-1)-ую.
Со вторым пунктом будем бороться введением зон нечувствительности по напряжению (введем границы напряжения перехода через ноль с положительной и отрицательной сторон) обычно 5-10 В в обе стороны, а также зон нечувствительности по частоте (ограничим допустимую частоту сигнала напряжения).
Таким образом, мы получим рассчитанное значение действующего значения сетевого напряжения за период на каждом полупериоде сетевого напряжения.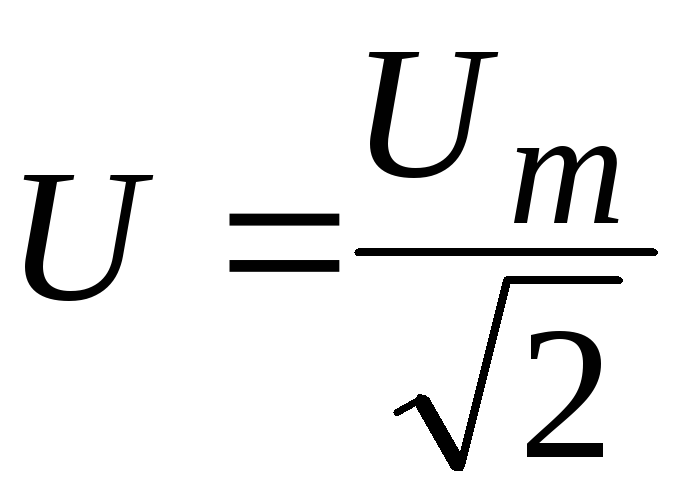 2/R) — чтобы не превышала допустимой мощности резисторов. Плечи дифференциального усилителя тоже делаем равными. Тогда, напряжение в точке 1 рассчитывается по формуле:
2/R) — чтобы не превышала допустимой мощности резисторов. Плечи дифференциального усилителя тоже делаем равными. Тогда, напряжение в точке 1 рассчитывается по формуле:
А напряжение в точке 1 будет иметь вид:
Также, половина опорного напряжения подается на один из каналов АЦП. Это позволяет в постоянном режиме (например, один раз за период) определять положение уровня нуля измеряемого напряжения.
Т.е. мы обошлись операционным усилителем с однополярным питанием, и наш входной сигнал в точке 1 изменяется от 0 до Uоп. Такой способ дает достаточно точные результаты, по сравнению, например, с выпрямлением напряжения с помощью диодов.
Расчет делителя и коэффициента АЦП сводится к следующему:
где A и В — замеры АЦП (за вычетом измеренного значения нуля сигнала — AN1) для текущего и предыдущего полупериодов; N1, N2 — число замеров для текущего и предыдущего полупериодов; Nadс — разрядность АЦП; U’оп — опорное напряжение за вычетом зон нелинейности (нечувствительности) операционного усилителя (обычно 0,6 В).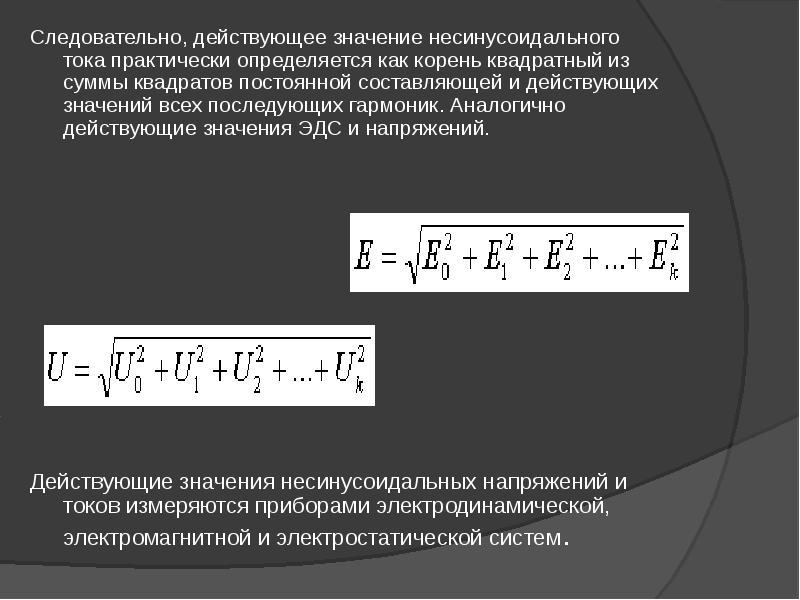
Расчет делителя удобно проводить считая сигнал постоянным, приведенным к амплитуде синусоидального, а не синусоидальным. Тогда действующее значение сигнала равно амплитудному и равно значению каждого замера.
Например, нужно рассчитать делитель для измерения максимального значения 420В переменного тока:
Сопротивление Ra выбирается в диапазоне от 500 кОм до 1500 кОм. По выбранному сопротивлению Ra рассчитывается Rb.
В итоге, алгоритм расчета действующего значения напряжения и частоты примет вид:
При этом часть затратных расчетов (деление, извлечение корня) можно перенести из прерывания в основную программу.
При расчете действующих значений на 8-ми битном МК целесообразно пользоваться целочисленными методами (с использованием масштабных коэффициентов) не прибегая к расчетам с плавающей запятой, а также упрощать по возможности арифметические операции (деление, изъятие квадратного корня и проч.). Это значительно экономит ресурсы МК.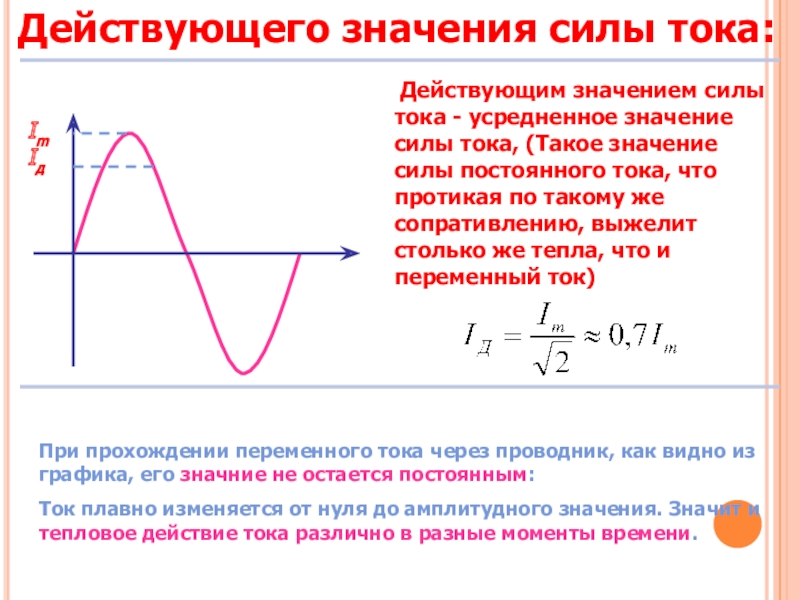
Напряжение действующее — Энциклопедия по машиностроению XXL
Если закон распределения нагрузки известен, то, пользуясь правилами нахождения закона распределения функций случайного аргумента (а вид этой функции крайне прост), можно найти закон распределения максимальных напряжений, действующих в конструкции/1 (S)
[c.6]
Напряжения, действующие в сечениях, могут быть записаны в виде [c.95]
Величина равнодействующей поверхностных сил определяется нормальным р и касательным а напряжениями, действующими на границах выделенного элемента. При этом нормальные на-.у—пряжения обусловливаются —— средними статическими дав- [c.36]
Во фланце в радиальном направлении действуют растягивающие напряжения стр, втягивающие фланец в отверстие матрицы, и сжимающие напряжения действующие в тангенциальном направлении и уменьшающие диаметральные размеры заготовки. При определенных размерах фланец заготовки может потерять устойчивость под действием сжимающих напряжений Стд, что приведет к образованию складок 6 (рис. 3.41, а). Складки могут появиться, если (D -d) > (18—20) S.
[c.107]
При определенных размерах фланец заготовки может потерять устойчивость под действием сжимающих напряжений Стд, что приведет к образованию складок 6 (рис. 3.41, а). Складки могут появиться, если (D -d) > (18—20) S.
[c.107]
Ультразвуковой метод основан на физическом явлении, связанном с изменением скорости прохождения ультразвуковых волн в зависимости от величины напряжений, действующих в металле. Метод дает хорошие результаты в случае однородного распределения напряжений или при необходимости определить среднеинтегральную величину напряжений по толщине сварного соединения. Однако с помощью данного метода невозможно определить характер распределения напряжений по толщине листа. [c.270]
На рис. 5.19 представлены зависимости коэффициента снижения реактивных напряжений т) г = ап/а%, где Or — максимальное реактивное напряжение в сечении, находящемся на расстоянии от границы шва заделки, равном j ад — собственные-реактивные напряжения, равные максимальным напряжениям, действующим на границе шва заделки) от относительного рас-
[c. 308]
308]
Таким образом, выполненный анализ реактивных напряжений в сочетании с имеющимися данными по распределению собственных ОСН в узлах, образованных типовыми сварными соединениями, позволяет принципиально определить напряженное состояние любого узла после окончания сварки конструкции в целом. Реактивные напряжения определяются на основе кривых представленных на рис. 5.15. 5-19. По известным размерам источников реактивных напряжений, действующих на рассматриваемый узел, определяются собственные реактивные напряжения каждого источника о . По известным расстояниям между рассматриваемым узлом и источником реактивных напряжений находятся коэффициенты снижения реактивных напряжений для каждого из источников. Зная и т) для всех соседних [c.309]
Размах напряжений, действующих на рассматриваемый узел, определяется режимом эксплуатационного нагружения конструкции, а максимальные напряжения в цикле равны суперпозиции реактивных напряжений с наибольшими в цикле эксплуатационными напряжениями. Таким образом, роль реактивных напряжений сводится к изменению асимметрии нагружения сварного узла.
[c.317]
Таким образом, роль реактивных напряжений сводится к изменению асимметрии нагружения сварного узла.
[c.317]
Расчетный анализ общих напряжений, действующих в районе клина при Т = 20 °С, был представлен в 6.2 (см. рис. 6.15). Следуя предложенной процедуре расчета и моделируя условия НТО аналогично изложенному выше, было изучено влияние НТО на общие напряжения, действующие в районе клина.
[c.359]
Циклическая прочность деталей сильно падает на участках ослаблений, резких переходов, входящих углов, надрезов и т. п., вызывающих местную концентрацию напряжений, максимальная величина которых может в 2-5 и более раз превышать средний уровень напряжений, действующих в этом сочетании. [c.293]
Сумма нормальных напряжений, действующих по двум взаимно перпендикулярным площадкам, постоянна и равна главному напряжению, т. е. Па + Ор = Д-
[c. 147]
147]
Максимальное касательное напряжение действует по площадке, параллельной главному напряжению Оз и составляющей угол 45° с направлениями а и Од. Величина этого напряжения равна полу-разности наибольшего и наименьшего из главных напряжений [c.150]
Чугун и другие хрупкие материалы, сравнительно плохо работающие на растяжение, разрушаются по винтовой поверхности, наклоненной к оси вала под углом 45°, т. е. по направлению действия максимальных растягивающих напряжений (рис, 135, б). Стальные валы чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении, [c.194]
При этих допущениях нормальные напряжения по площадке контакта распределяются по закону поверхности эллипсоида, площадка контакта имеет в общем случае форму эллипса, а максимальное напряжение действует в центре площадки контакта. [c.220]
Известный интерес, особенно при изучении пластических деформаций, представляет касательное напряжение, действующее по площадке, равнонаклоненной ко всем главным направлениям. Такая площадка называется октаэдрической, поскольку она параллельна грани октаэдра, который может быть образован из куба. Нормаль к этой площадке образует равные углы с главными направлениями
[c.174]
Такая площадка называется октаэдрической, поскольку она параллельна грани октаэдра, который может быть образован из куба. Нормаль к этой площадке образует равные углы с главными направлениями
[c.174]
Опуская в дальнейшем индекс при Q, установим связь между поперечной силой и напряжениями, действующими в рассматриваемом сечении. Из уравнения (3.30) [c.196]
Главное напряжение действует в направлении диагонали АС. Поэтому относительное удлинение е диагонали есть не что иное, как главное удлинение ei при плоском напряженном состоянии, представленном чистым сдвигом. Учитывая зависимость (8.4), из первой формулы (6.30) находим, что [c.199]
Максимальное касательное напряжение, действующее на периферии сечения стержня, [c.212]
Так, если материал плохо сопротивляется касательным напряжениям (действию сдвига), то первые трещины разрушения возникают [c.214]
Как указывалось выше, в зоне концентрации напряжения у отверстия малого диаметра, сделанного в пластинке, растягиваемой в одном направлении (рис. 234, а), значение максимальных растягивающих напряжений в точках т в три раза выше напряжений, действующих на контуре пластинки, т. е. а == 3.
[c.239]
234, а), значение максимальных растягивающих напряжений в точках т в три раза выше напряжений, действующих на контуре пластинки, т. е. а == 3.
[c.239]
Для балки прямоугольного поперечного сечения эпюры напряжений а и т приведены соответственно на рис. 253, бив. Кроме того, в каждой из этих точек по напряжениям о и т вычисляли главные напряжения растягивающие Tj и сжимающие Oj. Эти напряжения действуют на площадках, наклон которых к плоскости поперечного сечения изменяется от точки к точке. Изменение величины главных напряжений по высоте балки может быть представлено в виде эпюр Oj и g. Для той же балки эти эпюры приведены на рис. 253, г, д. [c.260]
| Рис. 1.1. Правило знаков для обобщенных нагрузок и напряжений, действующих на элемент балки. |
Для полного суждения о прочности материала необходимо уметь определять напряжения, действующие по любому наклонному сечению растянутого (сжатого) элемента (рис. II.26, а).
[c.53]
II.26, а).
[c.53]
Как уже было отмечено (см. 6), площадки, на которых нет касательных напряжений, называются главными площадками, а нормальные напряжения, действующие по главным площадкам,— главными напряжениями. Следовательно, нормальное напряжение в поперечном сечении растянутого или сжатого стержня есть главное напряжение. Поэтому оно обозначено 01, по-
[c.54]
Рассмотрим обратную задачу. Даны нормальные и касательные напряжения, действующие по граням элемента (рис. 11.28, а). Требуется определить положение главных площадок и значения главных напряжений. Рассмотрим равновесие трехгранной призмы с основанием DB (рис. 11.28, б). Примем, что о >Ор. Угол ф будем отсчитывать от направления большего напряже- [c.57]
Касательные напряжения действуют не только в поперечных сечениях стержня, но и (как это следует из закона парности касательных напряжений) в продольных (рис.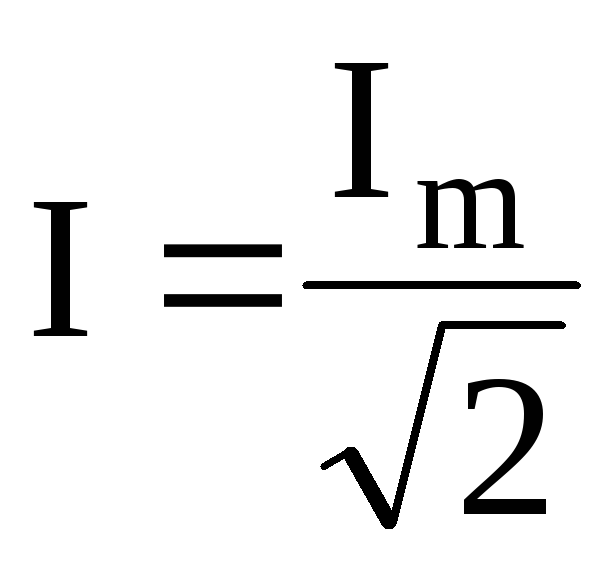 V. 10).
[c.116]
V. 10).
[c.116]
В некоторых случаях повышение стойкости швов против горячих трещин, наоборот, достигается повышением ликвирующих нримесей до концентраций, обеспечивающих получение при завершении кристаллизации сплошной пленки легкоплавкой эвтектики па поверхности кристаллита. Это может быть достигнуто легированием стали бором (0,3—1,5%). Повыи1епная литейная усадка и значительные растягивающие напряжения, действующие при затвердевании на сварочную ванну, также способствуют образовапию горячих трещин. Снижение действия силового фак- [c.287]
Выразим площадь поперечного сечения через изгибающий момент так, чтобы соблюдалось условие равнонадежности. Для этого запишем выражение для напряжений, действующих в сечениях балки, [c.95]
Учитывая изложенное, можно заключить, что экспериментальные методы измерения ОСН не могут дать полного представления о распределении напряжений по всему объему конструкции. Применение их ограничено случаями определения напряжений по какому-либо сечению узла (при этом известны только компоненты тензора напряжений, действующие в плоскости, перпендикулярной этому сечению), по поверхности изделия, а также оценкой средних по толщине соединения напряжений. Оценка локальных напряжений в высокоградиентных полях возможна как интегральная. Для детального исследования областей с высокоградиентньши полями напряжений целесообразно применять расчетные методы, а экспериментальные использовать для оценки корректности и применимости принятых в расчетах допущений.
[c.271]
Оценка локальных напряжений в высокоградиентных полях возможна как интегральная. Для детального исследования областей с высокоградиентньши полями напряжений целесообразно применять расчетные методы, а экспериментальные использовать для оценки корректности и применимости принятых в расчетах допущений.
[c.271]
С достаточной степенью точности ОСН исследуемого сварного узла конструкции могут быть оценены на основе предположения [88, 118], что предварительное напряженное состояние , возникающее после сварки соседних элементов конструкции, не влияет на формирование ОСН в рассматриваемом узле конструкции и что ОСН исследуемого узла конструкции определяются взаимодействием (при отсутствии пластического деформирования— суперпозицией) собственных ОСН, возникающих при сварке рассматриваемого узла, и напряжений, действующих от соседних сварных узлов (так называемых реактивных напряжений) — рис. 5.4. Отметим, что дифференцирование ОСН на собственные и реактивные является удобной инженерной схемати-
[c. 278]
278]
Ранее было введено понятие реактивных напряжений — напряжений, действующих от соседних сварных узлов на рассматриваемый узел. При таком определении собственные ОСН любого узла могут выступать в качестве реактивных в случае, если проводится анализ остаточной напряженности после сварки соседнего узла. Следовательно, для оиредблёния ОСН в конструкции в целом принципиально необходимо знать распределение собственных сварочных напряжений для всех сварных узлов. [c.297]
Здесь а%— радиальные реактивные напряжения, действующие на границе шва (о =Огг1г=дш), в дальнейшем будем называть их собственными реактивными напряжениями «п — коэффициент снижения реактивных напряжений. [c.304]
На первом этапе указанного анализа проведены расчетноэкспериментальные исследования ОСН в сварных толстолистовых конструкциях с многопроходными швами. Удобной инженерной схематизацией для расчета ОН в сложных сварных конструкциях является их дифференцирование на собственные и реактивные напряжения. В этом случае» ОСН сварного узла могут быть определены с помощью суперпозиции собственных ОСН, возникающих непосредственно при сварке рассматриваемого узла, и напряжений, действующих от соседних сварных узлов, названных реактивными напряжениями.
[c.326]
В этом случае» ОСН сварного узла могут быть определены с помощью суперпозиции собственных ОСН, возникающих непосредственно при сварке рассматриваемого узла, и напряжений, действующих от соседних сварных узлов, названных реактивными напряжениями.
[c.326]
Для тсплообмепнон аппаратуры характерны соединения труб с трубной решеткой. Сборку трубного пучка начинают со сборки каркаса, включающего трубпую решетку / и стяжки 2, на которых с помощью гаек закрепляют перегородки 3 (рис. 8.51). В собранный каркас последовательно заводят U-образпые трубки 4. Конструктивное оформление сварного соединения с трубной доской может быть различным (рис. 8.52, а—д). В большинстве случаев трубы пропускают через отверстия в трубных досках и приваривают круговыми швами с наружной стороны (рис. 8.52, а—в). Технологически это наиболее просто, однако при этом сварные швы оказываются в зоне максимальных рабочих напряжений, действующих в трубной доске. С целью облегчения условий выполнения сварного соединения и его работы в эксплуатации применяют приемы сварки по отбортовке-проточке (рис. 8.52, а) или с расплавлением специально проточенного в доске выступа (рис. 8.52, о), или же производят перед сваркой развальцовку концов труб (рис. 8.52, б). Варианты без пропуска труб через трубную доску (рис. 8.52, г, д) выводят сварные швы из зоны действия максимальных рабочих напряжений, но технология их выполнения сложнее
[c.282]
8.52, а) или с расплавлением специально проточенного в доске выступа (рис. 8.52, о), или же производят перед сваркой развальцовку концов труб (рис. 8.52, б). Варианты без пропуска труб через трубную доску (рис. 8.52, г, д) выводят сварные швы из зоны действия максимальных рабочих напряжений, но технология их выполнения сложнее
[c.282]
Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскостях поперечных сечений вала, имеют место касательные напряжения в продольных плоскостях. СЗни равны по величине парным напряжениям, но имеют противоположный знак (рис. 134). Таким образом, по граням элемента, ограниченного продольной и поперечной плоскостями сечения вала, действуют только касательные напряжения. Однако, как следует из формулы (9.22), на главных площадках, наклоненных к оси вала под углами 45° и 135°, действуют главные напряжения растягивающие Отах = т и сжимающие = —т (рис. 135, а), где х — касательные напряжения, действующие в продольном и поперечном сечениях. Величину нормальных и касательных напряжений в других площадках можно определить по формулам, приведенным в гл, 9.
[c.194]
Величину нормальных и касательных напряжений в других площадках можно определить по формулам, приведенным в гл, 9.
[c.194]
Обратная задача. В точке известны нормальные и касательные напряжения, действующие в двух взаимно перпендикулярных площадках, проходящих через данную точку требуется найти главные направления и главные напряжения. Иначе говоря, дан элемент Uibi idi (рис. 158) с действующими по его граням нормальными и касательными напряжениями нужно определить положение элемента abed, т. е. угол а,,, и найти главные напряжения.
[c.167]
Voltage Mode/Current Mode. Why a power supply can only regulate only one of these parameters at a time.
Источники питания высокого напряжения и информация о безопасности
Режим регулировки напряжения/Режим регулировки тока. Почему блок питания может одновременно регулировать только один из этих параметров
Большинство высоковольтных источников питания Spellman предлагают режим работы с регулировкой напряжения и тока с автоматическим переключением в зависимости от настроек и условий нагрузки. Для этого источник питания должен иметь два управляющих контура: регулировка напряжения и регулировка тока. Кроме того, каждому контуру требуется управляющий сигнал, предоставляемый пользователем, чтобы источник питания мог регулировать и ограничивать питание соответствующим образом.
Для этого источник питания должен иметь два управляющих контура: регулировка напряжения и регулировка тока. Кроме того, каждому контуру требуется управляющий сигнал, предоставляемый пользователем, чтобы источник питания мог регулировать и ограничивать питание соответствующим образом.
Режим регулировки напряжения
Большинство наших заказчиков используют наши источники питания в режиме регулировки напряжения. Когда источник питания работает в режиме регулировки напряжения, он ведет себя как источник напряжения. В этом случае блок питания эффективно регулирует выходное напряжение от 0 до 100 % от номинального выходного напряжения, в зависимости от выбранных настроек.
При этом выходной ток определяется величиной выходного напряжения и сопротивлением нагрузки на выходе источника питания. Большинство пользователей устанавливают ток на максимальное значение. В этом случае при коротком замыкании источник питания автоматически перейдет из режима регулировки напряжения в режим регулировки тока, установив ток на уровне 100 % от максимального номинального тока.
Режим регулировки тока
Намного реже наши заказчики используют источники питания в режиме регулировки тока. Когда источник питания работает в режиме регулировки тока, он ведет себя как источник тока. В этом случае блок питания эффективно регулирует выходной ток от 0 до 100 % от номинального выходного тока, в зависимости от выбранных настроек.
При этом выходное напряжение определяется величиной выходного тока и сопротивлением нагрузки на выходе источника питания. Большинство пользователей устанавливают напряжение на максимальное значение. В этой ситуации, если цепь разомкнута, источник питания автоматически перейдет из режима регулировки тока в режим регулировки напряжения, устанавливая напряжение на уровне 100 % от максимального номинального напряжения.
Программируемость Режима регулировки напряжения/Режима регулировки тока
В вышеуказанных ситуациях уровни напряжения и тока установлены на 100 % от номинальных значений, но их обычно можно регулировать в диапазоне от 0 до 100 % от номинальных значений, в соответствии с требованиями заказчика.
Регулировка только одного параметра
Как указано выше, стандартный высоковольтный источник питания может регулировать только один параметр (будь то напряжение или ток) одновременно. Если вы работаете в режиме регулировки напряжения, то на выходе у вас регулируемое напряжение и соответствующий ток. Если вы работаете в режиме регулировки тока, то на выходе у вас регулируемый ток и соответствующее напряжение. При этом основной момент заключается в том, что источник питания не может регулировать одновременно и напряжение, и ток. При работе в режиме регулировки напряжения (как работают в большинстве случаев) источник питания регулирует выходное напряжение, но ток, потребляемый источником питания, зависит от установленного напряжения и сопротивления нагрузки на выходе источника питания.
Эффективные значения силы тока и напряжения. Действующее значение напряжения
При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э.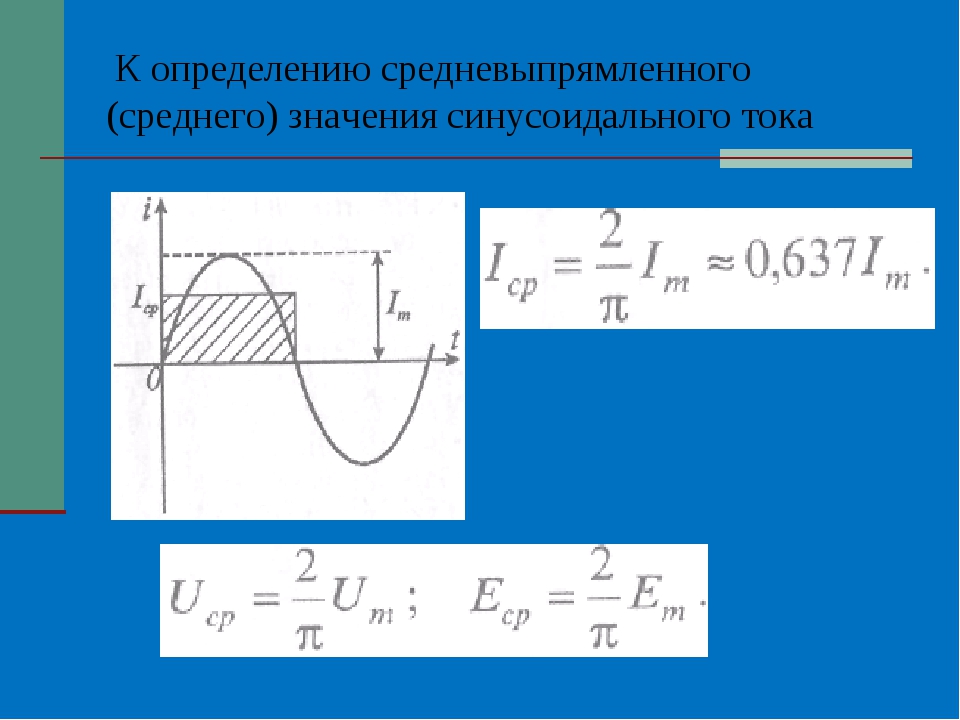 д. с.
д. с.
Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .
На шкалах измерительных приборов и технической документации также указываются действующие значения величин.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени
а за период переменного тока Т
Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:
Сократив общий множитель , получим действующее значение тока
Рис. 5-8. График переменного тока и квадрата тока.
На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока
Если ток изменяется по закону синуса, т. е.
е.
Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:
Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.
Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.
Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.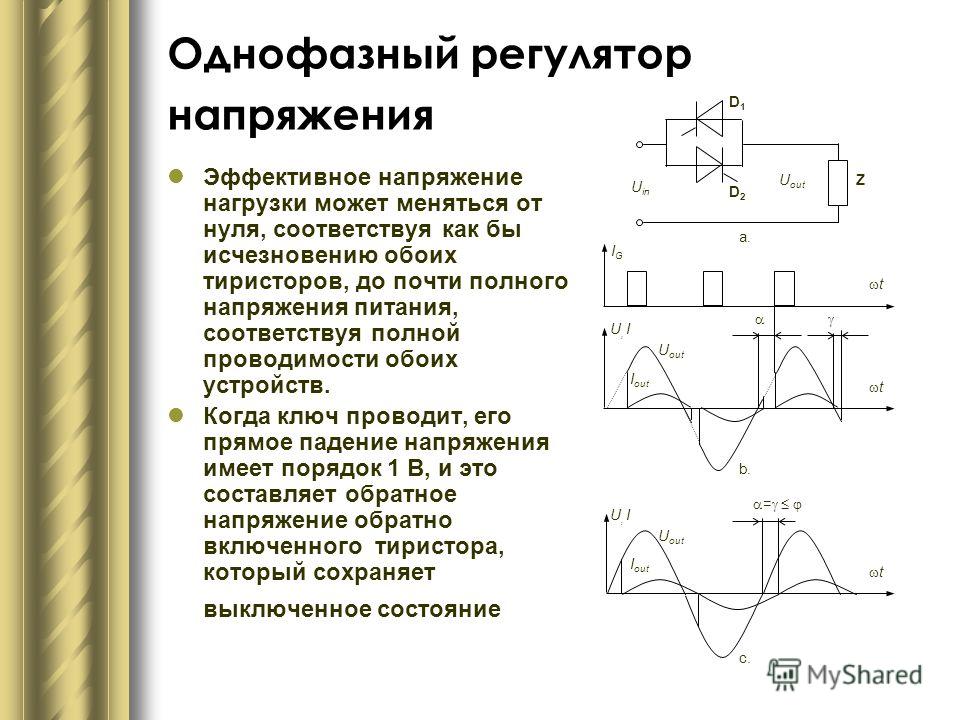
Рассмотрим следующую цепь.
Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.
Активное сопротивление
Сопротивление R
называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:
U = Um*cos(ω*t).
Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.
I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).
Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.
Действующее значение силы тока
Амплитуда силы тока определяется по следующей формуле:
Среднее значение квадрата силы тока за период вычисляется по следующей формуле:
Здесь Im есть амплитуда колебания силы тока. 2) = Um/√2.
2) = Um/√2.
Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:
Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.
Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.
Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.
>> Активное сопротивление. Действующие значения силы тока и напряжения
§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.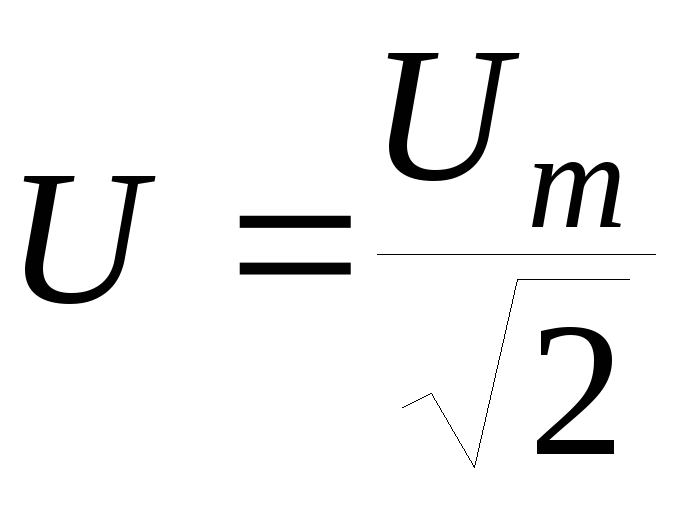
Сила тока в цени с резистором.
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством
Мощность в цепи с резистором.
В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.
Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
P = I 2 R. (4.18)
На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.
Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
P = i 2 R. (4.19)
Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение
График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t
Средняя мощность равна, таким образом, первому члену в формуле (4. 20):
20):
Действующие значения силы тока и напряжения .
Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:
Действующее значение силы переменного тока
равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:
Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем
Это закон Ома для участка цепи переменного тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:
P = I 2 R = UI.
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд. , перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
, перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков
Содержание урока
конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Дополнительные сведения
В англоязычной технической литературе для обозначения действующего значения употребляется термин «effective value
» — в дословном переводе «эффективная величина
»
В электротехнике приборы электромагнитной, электродинамической и тепловой систем реагируют на действующее значение.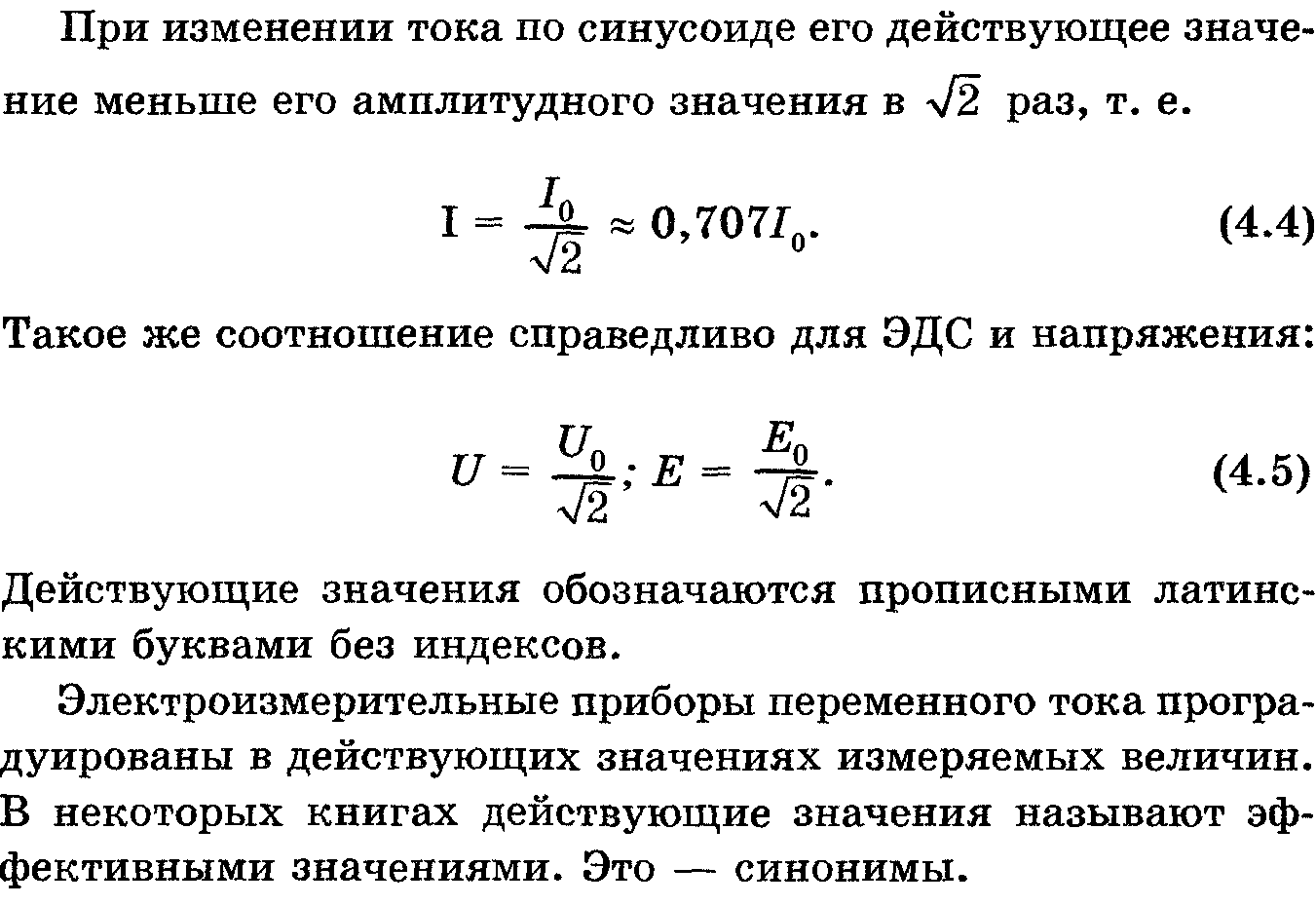
Источники
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки
См. также
- Список параметров напряжения и силы электрического тока
Wikimedia Foundation
.
2010
.
Смотреть что такое «Действующее значение переменного тока» в других словарях:
действующее значение переменного тока
эффективное значение переменного тока
— efektinė srovė statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas(ai) Grafinis formatas atitikmenys: angl. effective current; root mean square current vok. Effektivstrom, m rus. действующее значение… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
действующее значение тока
— Среднеквадратичное значение периодического электрического тока за период. Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… …
Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… …
В электротехнике среднее квадратичное за период значение переменного тока, напряжения, электродвижущей силы, магнитодвижущей силы, магнитного потока и т. п. Действующее значение синусоидального тока и напряжения в раз меньше их амплитудных… … Большой Энциклопедический словарь
— (электротехн.), среднее квадратичное за период значение переменного тока, напряжения, эдс, магнитодвижущей силы, магнитного потока и т. п. Действующие значения синусоидального тока и напряжения в √2 раз меньше их амплитудных значений. * * *… … Энциклопедический словарь
Ср. квадратичное за период значение переменного тока, напряжения, эдс, магнитодвижущей силы, магн. потока и т. п. Д. з. синусоидального тока и напряжения в кв. корень из 2 раз меньше их амплитудных значений … Естествознание. Энциклопедический словарь
ГОСТ Р МЭК 60252-2-2008: Конденсаторы для двигателей переменного тока.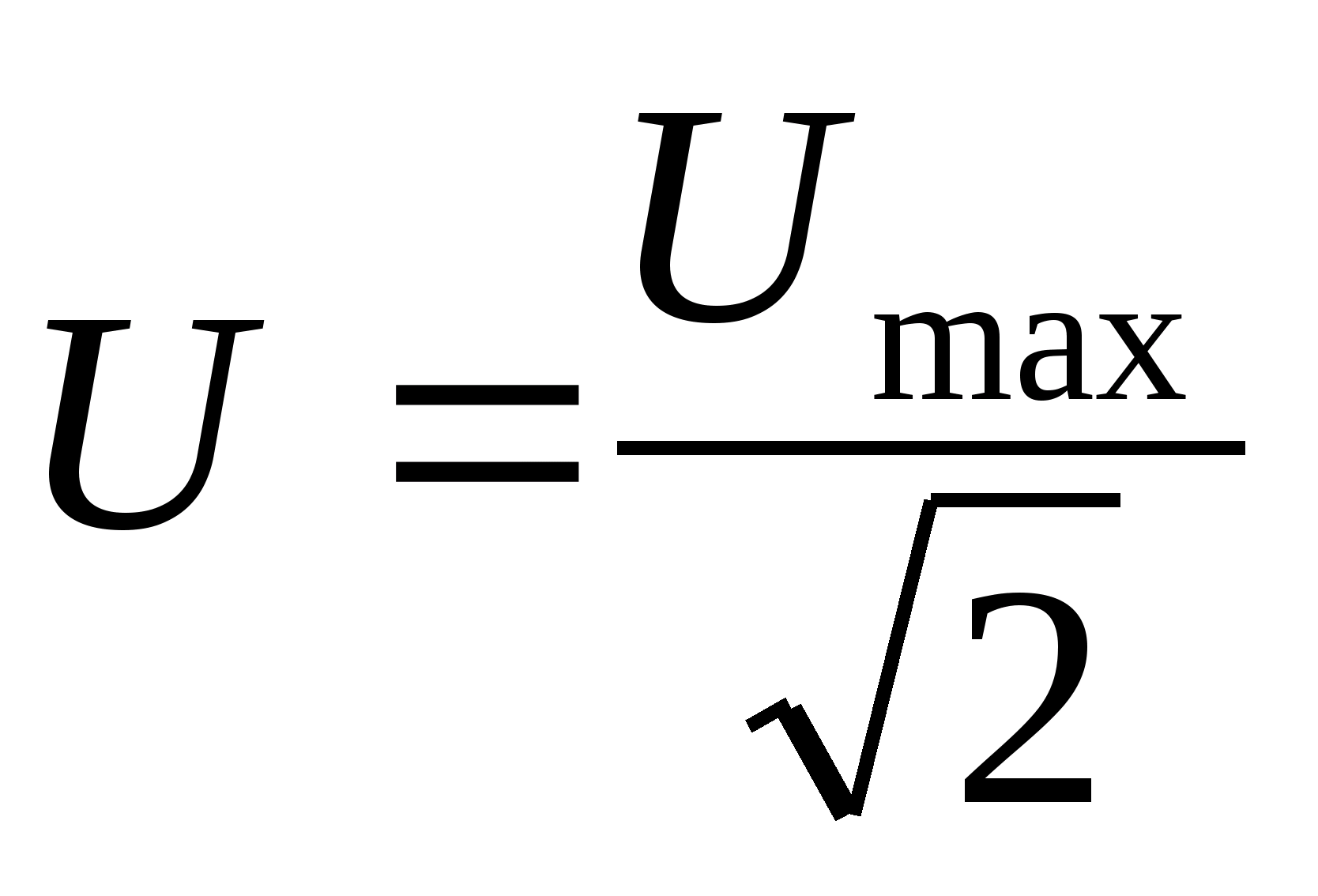 Часть 2. Пусковые конденсаторы
Часть 2. Пусковые конденсаторы
— Терминология ГОСТ Р МЭК 60252 2 2008: Конденсаторы для двигателей переменного тока. Часть 2. Пусковые конденсаторы оригинал документа: 1.3.11 длительность рабочего цикла (duty cycle duration): Общее время одного нагружения (подачи напряжения) и… … Словарь-справочник терминов нормативно-технической документации
истинное действующее значение
Справочник технического переводчика
истинное действующее значение
— [Интент] Прибор, измеряющий несинусоидальный электрический сигнал, например, имеющий форму импульсов или отрезков синусоиды, с учетом всех гармоник этого сигнала, является прибором, определяющим истинное действующее значение этого сигнала.… … Справочник технического переводчика
истинное действующее значение
— [Интент] Прибор, измеряющий несинусоидальный электрический сигнал, например, имеющий форму импульсов или отрезков синусоиды, с учетом всех гармоник этого сигнала, является прибором, определяющим истинное действующее значение этого сигнала. … … Справочник технического переводчика
… … Справочник технического переводчика
Мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока
. Сегодня про него и поговорим!
Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно.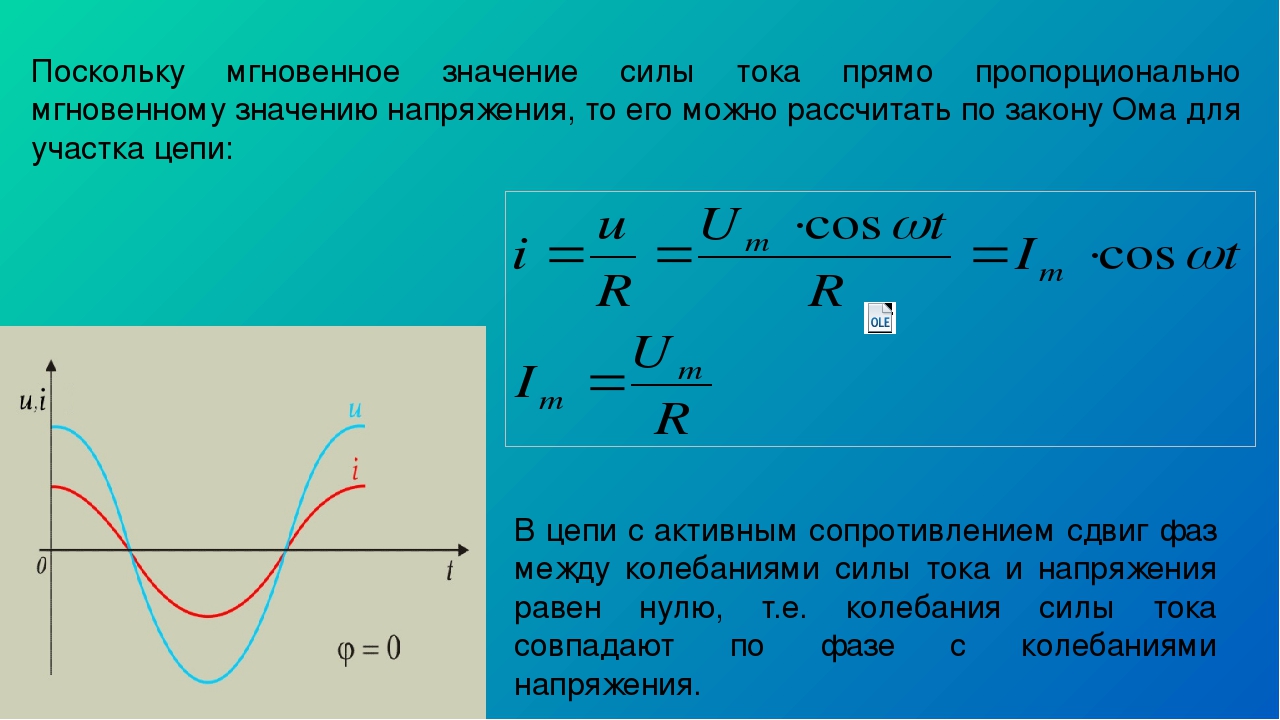 Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.
Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.
Итак, действующее (или среднеквадратичное) значение переменного тока — это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток.
Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.
Итак, у нас есть переменный ток. Допустим, синусоидальный.
Допустим, синусоидальный.
У него своя амплитуда А m
и период T период
(ну или частота f
). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R
и на этом резисторе выделяется энергия. За один период T период
нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз
. Допустим, мы насчитали, что за один период T
период синусоидального тока выделится Q
джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе
R за то же самое время
T период выделилось ровно такое же количество джоулей
Q.
Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока
И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока
. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?
Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье
, закон изменения мощности переменного тока равен
Количество выделившейся энергии при работе тока за время T период
— соответственно, равно интегралу за время периода T период
:
Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .
Итак, как его нам брать? Ну, величины I m 2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени
А для квадрата синуса нам надо применить формулу понижения степени
из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:
Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл — это площадь.
Итак, имеем
Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!
Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.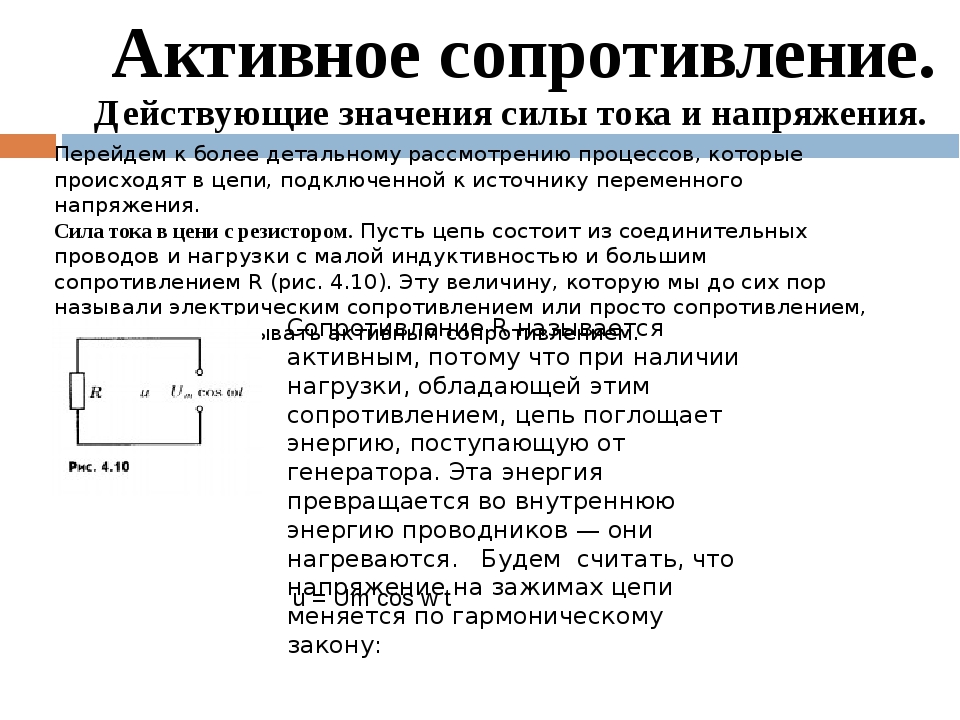
Итак, отбрасывая интеграл с косинусом, получаем
Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен
И, таким образом, получаем ответ
Это мы получили количество джоулей, которое выделится на резисторе
R
при протекании через него синусоидального тока амплитудой
I m
в течении периода
T период
. Теперь, чтобы найти чему в данном случае равен действующий ток
нам надо исходить из того, что на том же самом резисторе
R за то же самое время
T период выделится то же самое количество энергии
Q.
Поэтому мы можем записать
Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца
. А мы тем временем выразим действующее значение тока
I
действ
.
из этого выражения, предварительно сократив все, что можно
Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения.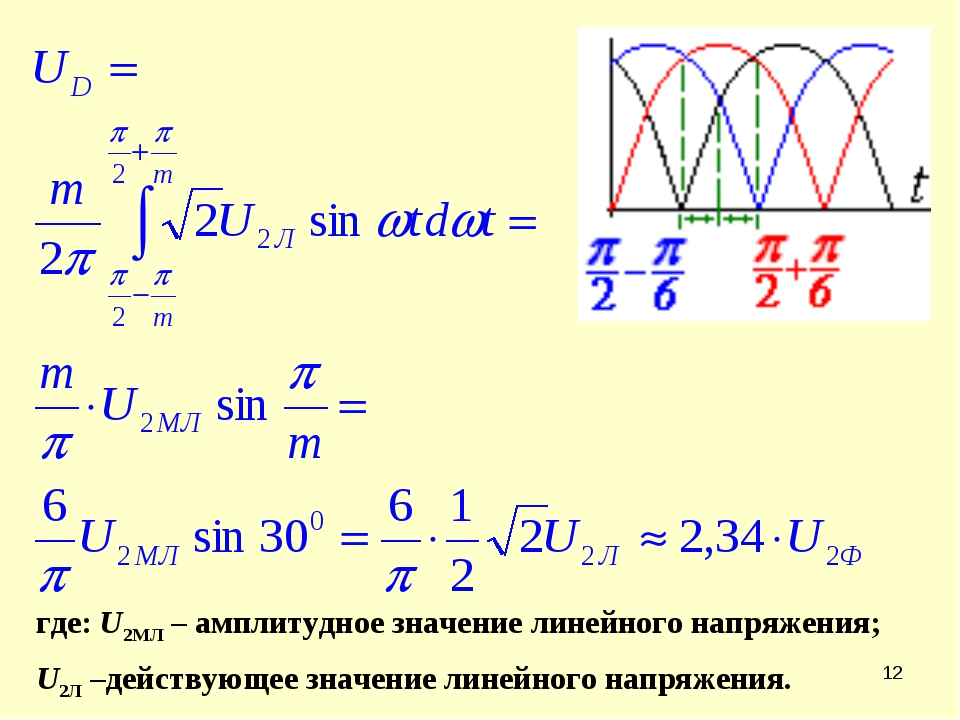
Хорошо запомните этот результат, это важный вывод.
Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения
. При этом у нас зависимость мощности от времени примет вот такой вид
Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно
Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.
Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.
Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В.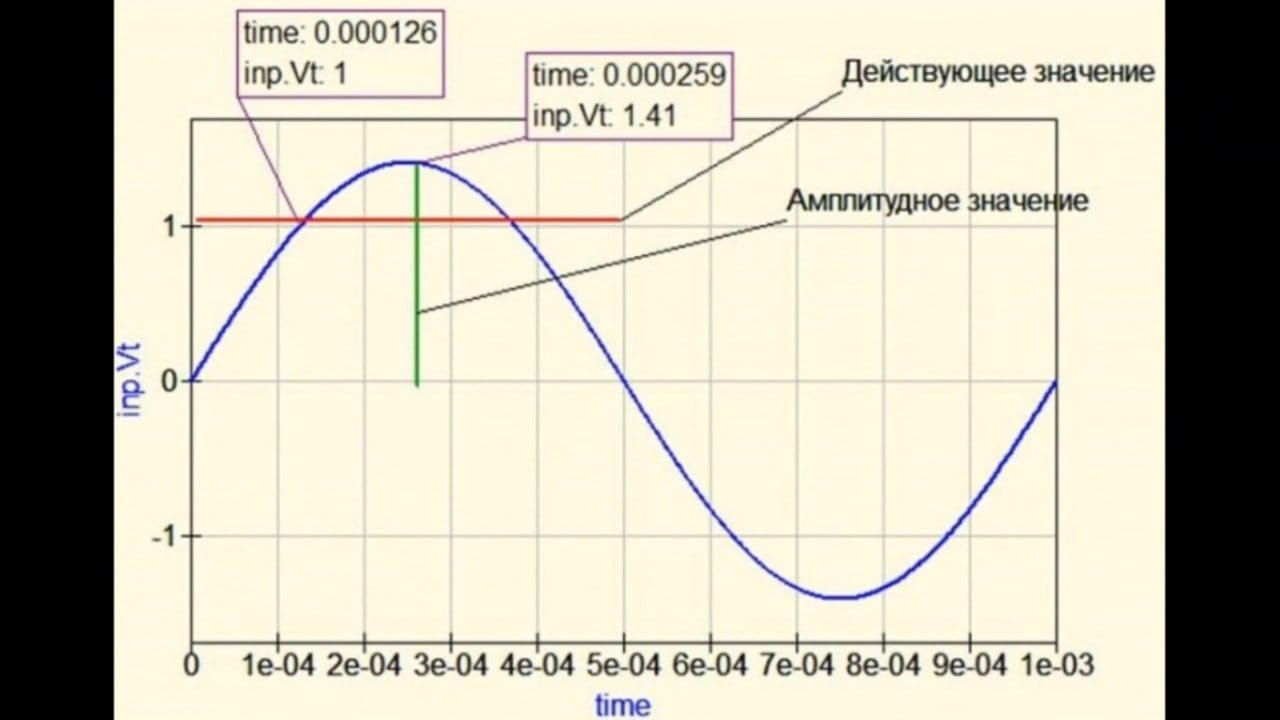 А каких вольт? У нас ведь теперь есть два термина — амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках — это действующее значение!
А каких вольт? У нас ведь теперь есть два термина — амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках — это действующее значение!
Вольтметры
и амперметры
, включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать
Отсюда получаем
Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.
Рисунок 1 — Закон изменения напряжения в розетках
И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа.
Смотрел я его через делитель напряжения
1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.
ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно!
Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением
есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления
, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.
Рисунок 2 — Осциллограмма напряжения в розетке (делитель 1:5)
На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота — ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна
Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.
На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!
Вступайте в нашу
Действующие значения тока и напряжения формулы. Эффективное, действующее напряжение, сила тока
Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.
При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.
Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.
В данное время в мировой промышленной практике широко распространен трехфазный переменный ток
, который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.
Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.
Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.
Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.
Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает
Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает
а) б)
Рис. 3.4. Пример трехфазной системы переменного тока
а) генератор трёхфазного тока; б) с тремя генераторами;
изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.
Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.
Соединение звездой
Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С
Начала обмоток принято обозначать буквами А, В, С
, а концы — X, Y, Z
. В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).
Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл
). Поскольку цепь трехфазная, то линейное напряжение будет в v3
раз больше фазного, т. е.: Uл = v3Uф.
Рассмотрим следующую цепь.
Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.
Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.
Активное сопротивление
Сопротивление R
называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:
U = Um*cos(ω*t).
Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.
I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).
Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.
Действующее значение силы тока
Амплитуда силы тока определяется по следующей формуле:
Среднее значение квадрата силы тока за период вычисляется по следующей формуле:
Здесь Im есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока. 2) = Um/√2.
2) = Um/√2.
Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:
Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.
Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.
Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.
,
После подстановки значения тока i
и последующих преобразований получим, что действующее значение переменного тока равно:
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.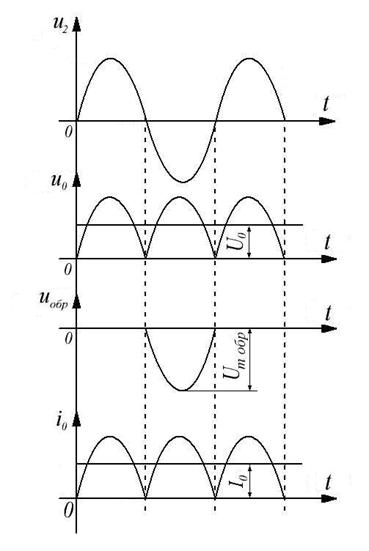
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U
Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
Действующее значение переменного тока
Теория
/
ТОЭ
/ Лекция N 3.
Представление синусоидальных величин с помощью векторов и комплексных чисел.
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими,
а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т.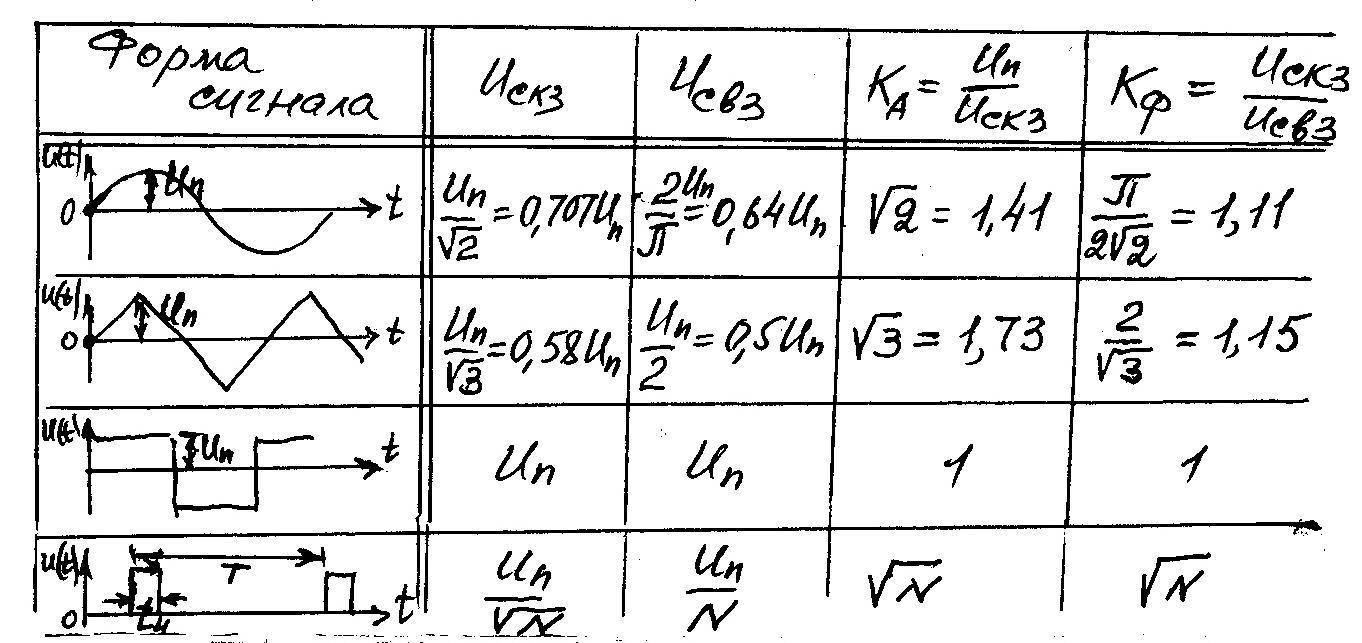
Для периодического тока имеем
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота
f
= 50Гц
.
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i
— мгновенное значение тока ;
u
– мгновенное значение напряжения ;
е
— мгновенное значение ЭДС ;
р
— мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m
).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением
периодического тока:
, |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е
1
и е
2
соответствуют уравнения:
Значения аргументов синусоидальных функций и называются фазами
синусоид, а значение фазы в начальный момент времени (t
=0):
и
— начальной фазой
(
).
Величину , характеризующую скорость изменения фазового угла, называют угловой частотой.
Так как фазовый угол синусоиды за время одного периода Т
изменяется на рад., то угловая частота есть , где f–
частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз
.
Для синусоидальных ЭДС е
1
и е
2
угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное
) с угловой частотой, равной w
. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е
1
и е
2
(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами.
3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами.
При построении векторных диаграмм векторы удобно располагать для начального момента времени (t
=0),
что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w
. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
Каждый из этих токов синусоидален и может быть представлен уравнением
Результирующий ток также будет синусоидален:
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt
Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt
=0.
При вращении этих векторов с одинаковой угловой скоростью w
их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .
Действующее и среднее значения переменного тока и напряжения.
Среднее или среднеарифметическое значение Fcp
произвольной функции времени f
(t
)за интервал времени Т
определяется по формуле:
Численно среднее значение Fср
равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f
(t
), осью t
и пределами интегрирования 0 – Т
(рис. 35).
35).
Для синусоидальной функции среднее значение за полный период Т
(или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т
или среднее значение за половину периода (Т
/2) между двумя нулевыми значениями (рис. 36) :
Ucp = Um∙
sinwt dt = 2R
. Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U
и тока I
. По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.
Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока.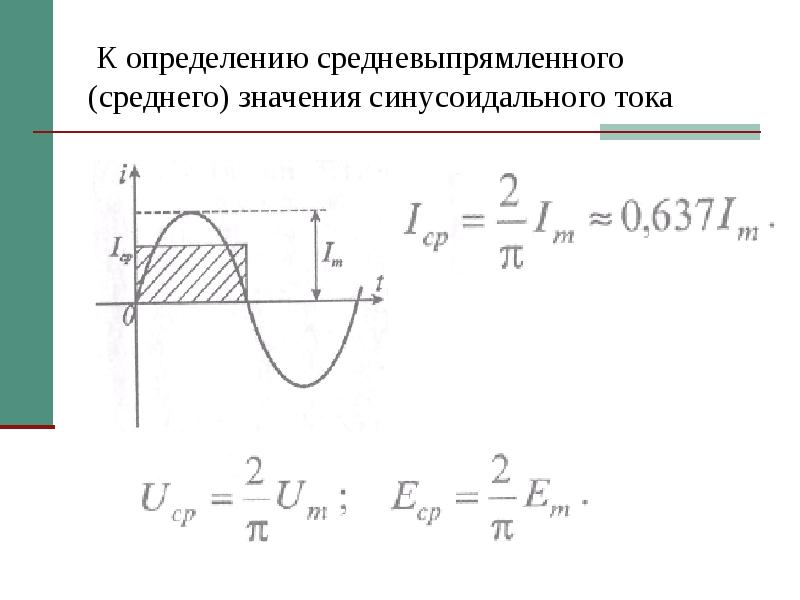 На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.
На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.
Что берется за действующее значение силы переменного тока и переменного напряжения
что берется за действующее значение силы переменного тока и переменного напряжения?
Боевое яйцо
Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.
Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.
Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.
Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.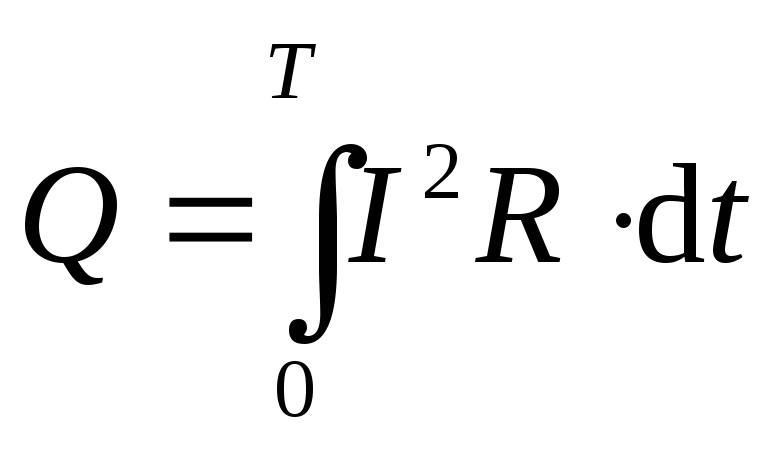
Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.
Вопрос: напряжение в электросети 220 В, что это значит?
Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.
Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.
Пример: Определить амплитуду напряжения электросети с напряжением 220 В.
Амплитуда равна 220 * 1,41=310,2 В.
Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)
Понятие эффективных (действующих) значений напряжения и силы тока
Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
Вашему вниманию подборка материалов: Действующее (эффективное) значение для сигналов стандартной формыСинусоидальный сигнал (синус, синусоида) Прямоугольный сигнал (меандр) Треугольный сигнал Закон Ома и мощность для действующих значений напряжения и силы токаЭффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах. Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом [Рассеиваемая на омической нагрузке мощность, Вт К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе. Если что-то непонятно, обязательно спросите! Еще статьи Микроконтроллеры — пример простейшей схемы, образец применения. Фузы (… Практика проектирования электронных схем. Самоучитель электроники…. Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить… Силовой резонансный фильтр для получения синусоиды от инвертора… Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Принцип работы, самостоятельное изготовление и наладка импульсного силового прео… Преобразователь однофазного напряжения в трехфазное. Принцип действия,… Электрическое напряжение. Амплитуда сигнала. Амплитудное. Вольт. Volt…. |
>> Активное сопротивление. Действующие значения силы тока и напряжения
§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.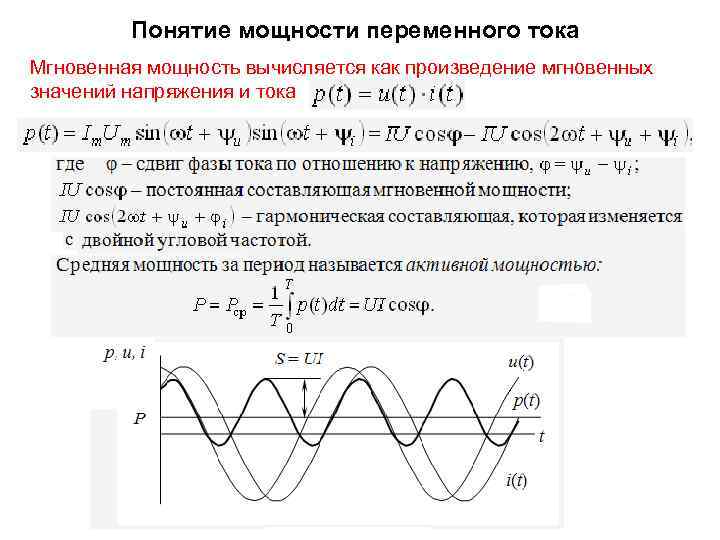
Сила тока в цени с резистором.
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством
Мощность в цепи с резистором.
В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.
Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
P = I 2 R. (4.18)
На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.
Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
P = i 2 R. (4.19)
Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение
График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t
Средняя мощность равна, таким образом, первому члену в формуле (4. 20):
20):
Действующие значения силы тока и напряжения .
Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:
Действующее значение силы переменного тока
равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:
Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем
Это закон Ома для участка цепи переменного тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:
P = I 2 R = UI.
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков
Содержание урока
конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Вконтакте
Одноклассники
Google+
Эффективное напряжение — обзор
В ранее упомянутых методах ШИМ трехфазные опорные напряжения модулируются индивидуально. В отличие от них, существует метод ШИМ, в котором используется другой подход, основанный на концепции пространственного вектора, называемый SVPWM. В методе SVPWM опорные значения трехфазного напряжения представлены в виде пространственного вектора vabc в комплексной плоскости, и этот опорный вектор напряжения модулируется векторами выходного напряжения, поступающими от инвертора.Метод SVPWM в настоящее время широко используется во многих приложениях с трехфазными инверторами, поскольку он создает основное выходное напряжение на 15,5 % больше, чем выходное напряжение, создаваемое методом SPWM, и обеспечивает меньшее гармоническое искажение тока нагрузки, меньшую пульсацию крутящего момента в двигателях переменного тока и меньшую коммутационные потери.
Концепция пространственного вектора, необходимая для этого метода ШИМ, обсуждалась в разделе 4.3. Для этого метода ШИМ, поскольку эталоны трехфазного напряжения задаются в виде пространственного вектора напряжения, возможные выходные напряжения инвертора также должны быть выражены в виде пространственного вектора.В разделе 7.1.4 мы видели, что в трехфазном инверторе существует восемь возможных состояний переключения. Векторы выходного напряжения Vo-V7, соответствующие восьми возможным состояниям переключения, показаны в таблице 7.3. Обратитесь к Примеру 3, который показывает, как получить эти векторы. На рис. 7.38 эти векторы выходного напряжения трехфазного инвертора изображены в комплексной плоскости.
Таблица 7.3. Векторы вывода напряжения, соответствующие коммутационным состояниям
| Стр. | ||||||||
|---|---|---|---|---|---|---|---|---|
| Напряжения фазы | Космический напряжение | |||||||
| SA | SB | SC | VAS | VBS | VCS | VN (N = 1 -7) | ||
| 0 | 0 | 0 | 0 | 0 | 0 | V0 = 0∠0 ° | ||
| 1 | 0 | 0 | 0 | 23vdc | — 13Vdc | -13Vdc V1 = 23Vdc∠0 ° | ||
| 1 1 | 0 | 13Vdc 13Vdc | -23Vdc V2 = 23Vdc∠60 ° | |||||
| 0 1 | 0 | 0 | -13VDC | 23VDC | -13VDC | V3 = 23VDC∠120 ° | ||
| 0 | 1 | 1 | -23VDC | 13VDC | 13VDC | |||
| 0 | 0 | 1 | -13VDC | -13VDC | 23VDC | V5 = 23VDC∠240 ° | ||
| 1 | 0 | 1 | 13VDC | -23VDC | 13VDC | V6 = 23VDC∠300 ° 7 = 23VDC∠300 ° 70038 | ||
| 1 | 1 | 1 | 0 | 0 | 0 | V7 = 0∠0 ° | ||
Рисунок 7.38. Векторы выходного напряжения в комплексной плоскости (или d–q осей стационарной системы отсчета).
Шесть из этих векторов, V1−V6, которые называются активным вектором напряжения или предлагают эффективное напряжение на нагрузке. Величина всех активных векторов равна 2Vdc/3. Однако они сдвинуты по фазе друг от друга на 60°. Напротив, два вектора, V0 и V7, называются вектором нулевого напряжения , который не может дать эффективное напряжение на нагрузке.
Пример 3
Выразите выходное фазное напряжение трехфазного инвертора в виде пространственного вектора.
Решение
В качестве примера найдем вектор напряжения V2 для состояния переключения Sa=1, Sb=1, Sc=0.
- •
Определение пространственного вектора напряжения:
V=23(vas+avbs+a2vcs)=vas+j13(vbs-vcs)
(Здесь, a=ej2π/3=−12+j32,a2 =ej4π/3=−12−j32)
- •
Фазные напряжения: vas=13 В пост. тока, vbs=13 В пост. тока, vcs=-23 В пост. 23Vdc∠60°
Мы можем получить векторы напряжения для остальных состояний переключения аналогично тому, как показано в Таблице 7.3.
7.2.4.1 Принцип метода широтно-импульсной модуляции пространственным вектором
Поскольку трехфазные эталоны напряжения изменяются со временем, эталонный вектор напряжения V* вращается против часовой стрелки в комплексной плоскости, как показано на рис. 7.39. Этот вектор совершает один оборот за электрический период опорного напряжения.
Рисунок 7.39. Вращение вектора напряжения.
В методе SVPWM опорное напряжение задается как пространственный вектор V*, и этот опорный вектор напряжения V* генерируется с использованием векторов выходного напряжения трехфазного инвертора.Используя два активных вектора напряжения, смежных с V*, и нулевые векторы среди доступных восьми векторов напряжения, метод SVPWM создает напряжение, которое имеет то же основное среднее значение вольт-секунды, что и заданный опорный вектор напряжения V*, за период модуляции Ts .
Теперь мы опишем, как генерировать опорный вектор напряжения. Предполагается, что опорный вектор напряжения V* находится внутри шестиугольника, который образован шестью векторами выходного напряжения трехфазного инвертора. Только когда это условие выполнено, опорный вектор напряжения может быть правильно модулирован.
Например, рассмотрим опорный вектор напряжения V*, заданный в секторе ① из шести сегментов шестиугольника, показанного на рис. 7.39. В этом случае инвертор не может генерировать требуемый опорный вектор напряжения напрямую, потому что нет выходного вектора инвертора, который имеет амплитуду и фазу, равные тем, что у опорного вектора напряжения. Таким образом, в качестве альтернативы из шести активных векторов два вектора напряжения, смежные с опорным вектором напряжения, и нулевые векторы используются для генерирования напряжения, которое имеет то же основное среднее значение вольт-секунд, что и заданный опорный вектор напряжения V*.Эта модуляция повторяется каждый период Ts модуляции в зависимости от частоты переключения.
Теперь рассмотрим этот процесс модуляции более подробно. Предполагается, что опорный вектор напряжения V* остается постоянным в течение периода модуляции Ts. Процесс синтеза векторов напряжения для генерации эталонного вектора V* состоит из трех шагов, как показано на рис. 7.40.
Рисунок 7.40. Процесс модуляции для генерации напряжения.
На первом этапе один из двух соседних активных векторов напряжения, V1, прикладывается первым в течение времени T1.В результате формируется выходное напряжение с величиной V1⋅(T1/Ts) в направлении вектора V1. Затем в течение времени T2 применяется другой вектор V2, чтобы соответствовать амплитуде и фазе опорного вектора напряжения V*. С помощью этих двух шагов можно генерировать то же самое выходное напряжение, что и опорный вектор напряжения, в течение периода модуляции Ts. Наконец, если T1+T2 Продолжительность (T1, T2 и T0) каждого вектора напряжения для создания заданного эталонного вектора V* можно рассчитать следующим образом.Вышеупомянутый процесс модуляции может быть выражен математически как (7,45)∫0TsV*dt=∫0TsVndt+∫T1T1+T2Vn+1dt+∫T1+T2TsV0,7dt Предполагая постоянное напряжение в звене постоянного тока в течение Ts, уравнение. (7.45) можно переписать как (7.46)V*⋅Ts=Vn⋅T1+Vn+1⋅T2 Например, если опорный вектор напряжения V* задан в первом секторе ① (0≤θ ≤60°), уравнение (7.46) можно разложить на две составляющие: (7.47){Ts⋅|V*|cosθ=T1⋅(23 В пост. тока)+T2⋅(23 В пост. тока)cos60°Ts⋅|V*|sinθ=T2⋅(23 В пост. тока) sin60° Решение уравнения.(7.47) дает времена длительности как (T1+T2) Здесь a=|V*|/23Vdc. Времена длительности опорного вектора напряжения в других секторах ②–⑥ можно рассчитать аналогичным образом. Рассмотрим достижимый диапазон выходного напряжения с помощью метода SVPWM. В методе SVPWM сумма времен длительности двух активных векторов напряжения не должна превышать периода модуляции, т.е.е., Т1+Т2≤Тс. Используя уравнения (7.48) и (7.49), величина опорного напряжения для удовлетворения этого требования может быть получена как Возможный диапазон опорного вектора напряжения V* находится внутри шестиугольника, образованного соединением концов шести активных векторов, как показано на рис. 7.41. Однако для опорного вектора напряжения в течение одного электрического периода диапазон опорного вектора напряжения должен находиться внутри вписанной окружности шестиугольника, чтобы получить равную величину.Следовательно, радиус вписанной окружности, Vdc/3, является максимальным основным фазным напряжением в методе SVPWM. Это значение примерно на 15,5% больше, чем у метода SPWM, и равно значению метода THIPWM. Значение соответствует 90,7% выходного напряжения в шестиступенчатом режиме. Рисунок 7.41. Возможный диапазон опорного вектора напряжения в SVPWM. В разделе 7.2.4.1 мы описали, как получить время продолжительности активного и нулевого векторов напряжения для создания заданного опорного вектора напряжения. Для заданных выбранных векторов и времени их длительности существует много способов разместить их в пределах интервала модуляции Ts. Расположение этих векторов не влияет на среднее значение выходного напряжения по интервалу Ts, но существенно влияет на диапазон линейной модуляции и гармонические характеристики выходного напряжения. В частности, важно размещение эффективных векторов напряжения.На рис. 7.42 сравнивается, как величина и частота пульсаций тока нагрузки могут изменяться в зависимости от размещения векторов действующего напряжения. На рис. 7.42А показан случай, когда эффективный вектор напряжения находится в середине интервала модуляции. По сравнению с рис. 7.42B, такое размещение приводит к меньшим пульсациям тока и более высокой частоте пульсаций. Таким образом, расположение, показанное на рис. 7.42А, может дать лучшие гармонические характеристики, чем на рис. 7.42В. Рисунок 7.42. Характеристики тока в зависимости от размещения активных импульсов напряжения.(А) в лучшем случае и (Б) в худшем случае. Д.Г. Холмс, Значение размещения нулевого пространственного вектора для схем ШИМ на основе несущей, IEEE Trans. Ind. Appl., 32 (5) (1996) 1122–1129. Было известно, что размещение эффективных векторов напряжения в центре интервала модуляции показывает превосходные гармонические характеристики, как показано на рис. 7.42A [8,9]. Техника SVPWM этой схемы размещения называется симметричной техникой SVPWM . Кроме того, это центрирование может дополнительно увеличить ширину импульса для модуляции эффективного напряжения, что приводит к расширению диапазона модуляции напряжения.Размещение векторов нулевого напряжения определяет положение эффективных векторов напряжения в пределах интервала модуляции Ts. Таким образом, в -симметричном методе SVPWM два нулевых вектора, V0 и V7, в течение равного времени T0/2 распределяются в начале и в конце интервала модуляции Ts, как показано на рис. 7.43. Кроме того, в этом случае для получения минимальной частоты переключения необходимо расположить последовательность переключений в следующем порядке: В 0 (000) → В 1 (100) → В 2 (110) → В 7 (111). Рисунок 7.43. Последовательность переключения. Для этой цели два нулевых вектора V0 и V7 используются поочередно в интервале Ts. В такой последовательности переключений переход от одного вектора к другому вектору может быть выполнен переключением только одного переключателя. В следующем интервале последовательность коммутации обращается, то есть, V 7 → V 2 → V 1 → V 0 Как показано на рис. 7,44 [9]. Этот интервал также требует только одного переключения для перехода.Такие чередующиеся последовательности переключения на каждом интервале модуляции позволяют уменьшить частоту переключения. Рисунок 7.44. Альтернативная последовательность переключения. На рис. 7.45 показаны последовательности переключений во всех шести секторах для симметричного метода SVPWM . Рисунок 7.45. Последовательности переключения в шести секторах. Для этой альтернативной последовательности переключения два интервала модуляции 2Ts становятся одним периодом переключения. Например, интервал модуляции Ts, равный 100 мкс, указывает на частоту переключения 5 кГц.Обычно интервал модуляции Ts относится к текущему периоду управления. Это связано с тем, что новое опорное напряжение задается в каждый период регулирования тока. Пример 4 Опишите полюсное напряжение для симметричного метода SVPWM. Из времени длительности вектора, рассчитанного для каждого сектора, как показано на рис. 7.45, мы можем получить полюсное и напряжение для метода SVPWM. Полюс напряжение для заданного командного вектора V* в первом секторе ① (0°≤θ≤60°) из уравнения.(7.48) и (7.49) равно van1=T1+T2Ts⋅Vdc2=32|V*|cos(π6−θ) Аналогичным образом полюсные напряжения для остальных секторов могут быть получены как: Сектор ② (60° ≤ θ ≤120°): van2=T1−T2Ts⋅Vdc2=32|V*|cos(π6−θ) 7.2.4.2 Метод широтно-импульсной модуляции с симметричным пространственным вектором
Решение
Сектор ③ (12003
≤180°):
van3=−T1−T2Ts⋅Vdc2=−32|V*|cos(π6−θ)
Сектор ④ (180°≤ θ ≤240°):
van −T1−T2Ts⋅Vdc2=−32|V*|cos(π6−θ)
Сектор ⑤ (240°≤ θ ≤300°):
van5=−T1+T2Ts⋅Vdc2=32| V*|cos(π6−θ)
Сектор ⑥ (300°≤ θ ≤360°):
van6=T1+T2Ts⋅Vdc2=32|V*|cos(π6−θ)
4
На следующем рисунке показано полюсное и напряжение, полученное во всех секторах для MI =1 (т.е., |V*|=Vdc/3).
Как видно из примера 4, интересно отметить, что напряжение на полюсе представляет собой не чисто синусоидальную волну, а форму волны, содержащую третью гармоническую составляющую, аналогичную форме волны модуляции метода THIPWM. В методе THIPWM мы видим, что добавление третьей гармоники к опорному напряжению может увеличить основную гармонику фазного напряжения. Поскольку метод SVPWM также использует третью гармоническую составляющую, можно также считать, что он расширяет диапазон линейной модуляции в большей степени, чем метод SPWM.
На рис. 7.46 сравниваются выходной крутящий момент и гармоническое искажение тока нагрузки для методов SPWM и SVPWM [7]. Легко видеть, что метод SVPWM допускает значение MI до 1,15 и может производить гармонические искажения ниже, чем у метода SPWM в высоком диапазоне модуляции.
Рисунок 7.46. Сравнение методов SPWM и SVPWM. (A) Квадрат среднеквадратичного значения гармоники тока и (B) гармоники крутящего момента.
Х.В. Ван Дер Брок и др., Анализ и реализация широтно-импульсного модулятора на основе пространственных векторов напряжения, IEEE Trans. Ind. Appl., 24 (1) (1988) 142–150.
В отличие от симметричного метода SVPWM, действующие напряжения в методе SPWM не размещаются в центре, в результате чего гармонические характеристики хуже, чем у симметричного метода SVPWM.
Гармонические порядки, содержащиеся в методе SVPWM, подобны порядкам метода SPWM, выраженным в уравнении. (7.42). Однако из рис.7.47 видно, что относительная величина гармоник частоты переключения для метода SVPWM меньше, чем для метода SPWM, а метод SVPWM эффективно распределяет свою энергию гармоник переключения в боковые полосы. Следовательно, THD метода SVPWM меньше, чем у метода SPWM, даже несмотря на то, что гармоника двойных частот переключения для метода SVPWM увеличивается.
Рисунок 7.47. Частотный спектр фазных напряжений для ШИМ и СВПЧ.
Недостатком метода SVPWM является то, что он требует тригонометрических расчетов и больших вычислительных затрат для расчета времени переключения активных векторов напряжения. Однако в настоящее время этот метод можно просто реализовать с помощью метода ШИМ на основе несущей с использованием напряжения смещения. Этот метод будет обсуждаться более подробно в разделе 7.4.
Описанный выше метод SVPWM использует метод симметричной модуляции, в котором два нулевых вектора распределяются в течение одинакового времени.В этом случае все переключатели в трех полюсах работают на каждом периоде модуляции. Таким образом, это называется трехфазной модуляцией или непрерывной модуляцией . Напротив, мы можем выбрать разное время длительности для двух нулевых векторов. В зависимости от выбора мы можем получить различные методы модуляции, которые различаются характеристиками модуляции, такими как характеристики гармоник, линейность напряжения и потери при переключении. Таким образом, размещение нулевых векторов является степенью свободы для модуляции в методе SVPWM.Типичным примером неравномерного распределения нулевых векторов является метод модуляции, в котором переключатели только двух из трех полюсов работают для уменьшения частоты переключения. Это называется двухфазной модуляцией или прерывистой модуляцией , при которой переключатели одной ветви остаются неактивными в интервале модуляции, как показано на рис. 7.48. В этом методе прерывистой модуляции используется только один нулевой вектор, либо T0, либо T7. Соответственно, это вызывает потерю симметрии в размещении эффективных векторов напряжения.Однако за счет включения только двух из трех полюсов общая частота переключения может быть снижена на 1/3 по сравнению с трехфазной модуляцией. В более высоком диапазоне модуляции прерывистая модуляция создает более низкие гармонические искажения из-за более высокой чистой частоты переключения. Однако в низком диапазоне модуляции из-за потери симметрии прерывистая модуляция имеет более высокое гармоническое искажение, чем непрерывная модуляция.
Рисунок 7.48. Последовательность переключения при двухфазной модуляции.
Объяснение действующих значений напряжения и тока
Переменный ток
Электричество и магнетизм
Объяснение среднеквадратичного значения напряжения и тока
Учебное руководство
за
14-16
Существует много способов объяснить среднеквадратичное (среднеквадратичное) напряжение и ток на разных уровнях сложности для учащихся продвинутого уровня.
- Для простейшего уровня скажем, что вы измеряете ток (или разность потенциалов) через небольшие промежутки времени. Возведите в квадрат каждое значение, сложите квадраты (все они положительные) и разделите на количество выборок, чтобы найти средний квадрат или средний квадрат. Затем извлеките из него квадратный корень. Это среднеквадратичное значение
(среднеквадратичное значение). - Для тех, кто знаком с графиками функций синуса и косинуса, можно попробовать следующий алгебраический метод.
- I = I 0 SINΩ T и I и 2 = 9 = I 0 2 Ω 2 Ω T
- Эффект нагрева зависит от I 2 R , поэтому требуется среднее значение I 2 , а не среднее значение I .
- Чтобы найти среднеквадратичное значение, вам нужно среднее значение sin 2 с течением времени.
- График sinω t и график cosω t выглядят одинаково, за исключением смещения начала координат. Так как это один и тот же шаблон, sin 2 ω t и cos 2 ω t имеют одно и то же среднее значение с течением времени.
- Но sin 2 ω t + cos 2 ω t = 1. Следовательно, среднее значение любого из них должно быть 1/2.
- Следовательно, среднеквадратичное значение I 0 sinω t должно быть I 0 √ 2
- Среднеквадратичное значение в 0,707 раз больше пикового значения, а пиковое значение в 1,41 раза больше значения, которое показывает вольтметр. Пиковое значение для сети 230 В составляет 325 В.
- В качестве альтернативы: Постройте график sin 2 θ. Разрежьте график пополам и переверните одну половину вверх ногами или скопируйте на прозрачную пленку и соедините вместе. Две половины точно совпадают, показывая, что среднее значение равно 1/2.
- Обратите внимание, что при использовании
несглаженного выпрямленного переменного тока
от простого источника питания оценка мощности, полученная путем умножения показаний вольтметра постоянного тока с подвижной катушкой и амперметра с подвижной катушкой, вероятно, будет почти на 20 % ниже. Это связано с тем, что каждый расходомер с подвижной катушкой измеряет простое среднее время пиков полупериода, а не среднеквадратичное значение. - размах напряжения = 6 квадратов от самой высокой точки до самой низкой, и каждый квадрат соответствует 10 В. Таким образом, размах напряжения = 60 В.
- пиковое напряжение (В или ) = половина пикового напряжения = 60/2 = 30 В
- В среднеквадратичное значение = среднеквадратическая разность потенциалов в вольтах, В
- В o = пиковое напряжение в вольтах, В
- I = среднеквадратичное значение тока в амперах, А
- I o = пиковый ток в амперах, А
- Максимальная средняя передаваемая мощность
- Напряжение и ток, среднеквадратичное значение
- Коэффициент мощности и полная мощность
- Треугольник мощности и комплекс мощности
- Обучение сохранению мощности переменного тока
Например, предположим, что есть 8 временных интервалов, как показано на диаграмме выше:
| Значения | 7 | 10 | 7 | 0 | -7 | -10 | 3 8 | |
| Квадраты | 49 | 100 | 49 | 0 | 49 | 100 | 30 | 89 |
Сумма квадратов = 396
Среднее число квадратов = 396/8 = почти 50
Квадратный корень ~ 7
При большем количестве интервалов среднеквадратичное значение оказывается равным
(пиковое значение) √ 2 = пиковое значение 1.41 = 0,707 пиковое значение
Среднеквадратичные значения тока и напряжения, умноженные вместе, дают фактическую мощность. Это жизненно важная часть при попытке провести количественные эксперименты с мощностью и энергией, такие как удельная теплоемкость.Значения составляют в лучшем случае только 80 % от значения.
Калькулятор среднеквадратичного значения напряжения
— от среднего значения, пикового и пикового значения до пикового значения
Калькулятор среднеквадратичного значения напряжения
Этот калькулятор можно использовать для расчета среднеквадратичного значения напряжения (V RMS ) синусоидального сигнала из различных связанных значений, таких как среднее значение (V AV ), пиковое или максимальное значение (V P или V MAX). ) и пиковое значение (V PP ).
Как рассчитать среднеквадратичное значение напряжения?
Как обсуждалось ранее о среднеквадратичном (RMS) или V RMS напряжении, это напряжение, эквивалентное постоянному току синусоиды i.е. если среднеквадратичное значение напряжения составляет 230 В переменного тока , вырабатывая 60 Вт тепла при подключении к нагревательному элементу, такому как резистор, такое же количество тепла может генерироваться источником постоянного напряжения 230 В постоянного тока при подключении к тому же нагревательному элементу, который был подключен ранее в цепи переменного тока.
Мы покажем различные уравнения для расчета среднеквадратичного напряжения с прикладными формулами и решенными примерами, как показано ниже.
Связанный калькулятор: Калькулятор значений 3-, 4-, 5- и 6-диапазонных резисторов
Уравнения для калькулятора среднеквадратичного значения
Поскольку калькулятор среднеквадратичного напряжения связан со средним значением (V AV ), пиковым или максимальным значением (VP или V MAX ) и значением размаха (V PP ), следующие связанные уравнения для калькулятора среднеквадратичного напряжения показаны на рис. 2.
Пиковое значение: В P или В МАКС
Максимальное значение, положительное или отрицательное, переменной величины (такой как напряжение или ток) известно как его амплитуда формы волны, максимальное значение или пиковое значение. Обозначается V P , I P или E MAX и I MAX .
В P = √2 x В СКЗ
Используя приведенную выше формулу, мы можем найти значение среднеквадратичного значения напряжения следующим образом:
В СКЗ = 0.7071 х В Р
Пример:
Предположим, что значение пикового напряжения составляет 325 В переменного тока, значение среднеквадратичного значения напряжения будет:
В СКЗ = 0,7071 x 325 В = 229,80 В СКЗ
Размах Значение (V PP )
Сумма положительных и отрицательных пиковых значений синусоидального сигнала известна как пиковое значение. Он выражается как I PP или V PP .
В ПП = 2√2 x В СКЗ
Используя приведенную выше формулу, мы можем найти значение среднеквадратичного значения напряжения следующим образом:
В СКЗ = 0,35355 x В PP
Пример:
Предположим, что значение пикового напряжения составляет 340 В переменного тока, значение среднеквадратичного значения напряжения будет:
В СКЗ = 0,35355 x 340 В = 120,2 В СКЗ
Связанные калькуляторы:
Среднее напряжение Значение (В AV )
Если мы преобразуем синусоиду переменного тока (AC) в волну постоянного тока (DC) через выпрямители, то преобразованное значение в постоянный ток известно как среднее значение этой синусоиды переменного тока.
Имейте в виду, что среднее значение напряжения полной синусоиды переменного тока равно нулю, потому что площадь, покрываемая положительными полупериодами, равна площади, покрываемой отрицательными полупериодами, которые компенсируют друг друга. Вот почему мы не можем использовать переменный ток для хранения батарей.
Мы используем только полуволну для измерения среднего значения напряжения или тока переменного тока.
В AV = (2√2) / π x В СКЗ
Используя приведенную выше формулу, мы можем найти значение среднеквадратичного значения напряжения следующим образом:
В СКЗ = 1.11 х В АВ
Пример:
Предположим, что среднее значение напряжения составляет 200 В переменного тока, значение среднеквадратичного значения напряжения будет:
В СКЗ = 1,11 x 200 В = 222 В СКЗ
Связанное сообщение:
Как определить среднеквадратичное напряжение в цепях переменного тока?
Введение
Среднеквадратичное значение любого изменяющегося во времени сигнала, как правило, связано с количеством тепла, выделяемого в цепи или на конкретном элементе цепи.Знаете ли вы, как рассчитать среднеквадратичное или среднеквадратичное значение напряжения синусоиды с учетом пикового напряжения? Здесь эта статья поможет вам рассчитать среднеквадратичное значение цепей переменного тока, а также предоставит процесс, который может помочь вам вывести формулу с использованием базовой математики и исчисления.
Что такое среднеквадратичное значение? | Самое простое объяснение
Каталог
Ⅰ Среднеквадратичное значение цепей переменного тока
Среднеквадратичное значение является важным термином в электротехнике. Каково точное значение среднеквадратичного значения? И почему это так важно? Это среднеквадратичное значение представляет собой действующее значение данного сигнала переменного тока, который будет производить такое же количество тепла (и, следовательно, мощности) на конкретном элементе, если он заменяется источником постоянного тока эквивалентной мощности.Физический смысл среднеквадратичного значения — это действующее значение напряжения сигнала переменного тока, то есть для выполнения работы в физике. Работа, совершаемая в процессе преобразования электрического тока в другие формы энергии, называется электрической работой, которая связана с током, напряжением и временем возбуждения. Чем выше напряжение, подаваемое на электроприборы, тем больше ток под напряжением, и чем дольше время включения, тем большую работу совершит ток. Среднеквадратичное значение также называют эффективным значением, которое рассматривается с точки зрения электромонтажных работ.Действующее значение переменного тока равно постоянному току/напряжению, при котором достигается такое же потребление мощности (нагрев) при том же сопротивлении. Поскольку это переменный ток, правильный результат должен быть получен после усреднения по времени (интегрирования), а мгновенное значение постоянного тока не должно использоваться для замены действующего значения. При статистическом анализе данных суммируется квадрат всех значений, затем вычисляется среднее значение и, наконец, извлекается квадратный корень для получения среднеквадратичного значения.
Рис. 1. Размах напряжения
В физике мы часто используем среднеквадратичное значение для анализа шума источника питания. Когда напряжение резистора равно напряжению переменного тока V(t), мощность V2/R изменяется со временем. Если энергию, потребляемую за цикл, разделить на количество циклов, это будет средняя мощность. Кроме того, если мощность постоянного напряжения, приложенного к тому же резистору, равна средней мощности переменного напряжения, эквивалентное постоянное напряжение является среднеквадратичным значением переменного напряжения.
Ⅱ Определение среднеквадратичного значения сигналов переменного тока
Буквально среднеквадратичное значение означает взять СУММУ, получить СРЕДНЕЕ, а затем взять КОРЕНЬ; в этом порядке, и вы получите среднеквадратичное значение. Как показано здесь, было получено общее уравнение для среднеквадратичного значения, которое можно использовать для нахождения среднеквадратичного значения любого изменяющегося во времени сигнала. Просто соблюдайте правила.
2.1 Синусоидальный сигнал
Следующие формулы применимы только к ЧИСТОМУ синусоидальному сигналу. В настоящее время многие электроприборы, например.г. приводы с регулируемой скоростью, как правило, вносят гармоники в электрическую систему. Следовательно, сигнал может больше не быть ЧИСТОЙ синусоидой.
Рассчитайте действующее значение из определения, т. е. переменный ток и постоянный ток соответственно проходят через один и тот же резистор. Если оба потребляют одинаковую электрическую энергию (или производят одинаковое джоулево тепло) за одно и то же время, то значение постоянного тока называется эффективным значением переменного тока. Накопление мощности сигнала с течением времени — это работа, совершаемая сигналом.Самый примитивный получен для синусоидальных волн, но на самом деле он применим ко всем формам волны.
Используйте определенный интеграл для расчета работы сигнала переменного тока в нагрузке R за один цикл. Он равен работе, совершаемой постоянной величиной (действующее значение) за один цикл нагрузки R.
VR:
Первоначальная мощность R:
Средняя мощность R:
Мощность стабильного постоянного напряжения Vdc равна , если эта мощность равна средней мощности переменного тока, то
Где Vdc называется среднеквадратичным значением сигнала переменного тока (Vrms)
Используя Vrms, рассчитайте среднюю мощность нагрузочного резистора R:
Расчет среднеквадратичного значения напряжения в конечном итоге используется для измерения средней продолжительной несущей способности сигнала.2 член), который затем суммируется (интегрирование) перед преобразованием обратно в напряжение с помощью операции извлечения квадратного корня. Зная среднеквадратичное значение напряжения, вы можете делать точные оценки фактической мощности, подаваемой с течением времени, независимо от полярности сигнала.
Проще говоря, например, сигнал прямоугольной формы с амплитудой 100В и скважностью 0,5, если рассчитывать по среднему значению, то его напряжение составляет всего 50В, а по среднеквадратичному значению — 70 .71В. Почему это? Например, есть набор 100-вольтовых батарейных блоков, которые будут останавливаться на 10 минут после каждой подачи питания на 10 минут, что означает, что рабочий цикл составляет половину. Если этот набор батарей управляет резистором 10 Ом, ток 10 А и мощность 1000 Вт будут генерироваться за 10 минут, а ток и мощность будут равны нулю во время сбоя питания.
Затем в течение 20 минут средняя мощность составляет 500 Вт, что эквивалентно мощности, генерируемой напряжением 70,71 В при прямой зарядке резистора 10 Ом.Напряжение 50 В постоянного тока может производить только 250 Вт мощности при зарядке резистора 10 Ом. Для двигателей и трансформаторов, пока среднеквадратический ток не превышает номинальный ток, они не сгорят, даже если будут перегружены в течение определенного периода времени.
2.2 Шаги уравнения для среднеквадратичного значения
Для расчета среднеквадратичного значения y(t) необходимо выполнить следующие шаги:
1) Вычислить квадрат y(t).
2) Возьмите среднее значение y2(t) за период.
3) Извлеките квадратный корень из среднего.
Пример:
(1) a 2 — константа, поэтому .
(2) cos(ωt) — полная косинусоидальная кривая.
(3)
2.3 Среднеквадратичное значение на мультиметре
В повседневной жизни обычные вольтметры масштабируются в соответствии с действующим значением синусоиды.
Действующее значение синусоиды U=максимум Um×0,707
Среднее значение обычно не используется, оно относится к среднему значению каждого мгновенного значения в положительном полупериоде или отрицательном полупериоде.
Среднее значение синусоиды Up=Maximum Um×(2/π)=0,637Um
Обратите внимание, что измерение переменного тока с помощью вольтметра и мультиметра основано на шкале эффективных значений. Если это несинусоидальная волна, такая как пульсовая волна, полученные показания счетчика не имеют смысла.
2.4 Другая форма волны
1) Полусинусоидальная форма волны
2) Прямоугольная волна
Когда мы хотим усреднить электрический сигнал, если процесс завершается за весь период или меньше, нам нужно указать точность.Для основных и симметричных сигналов переменного тока, независимо от частоты, пикового значения или периода, усреднение за полный период всегда дает 0 В. Поэтому целесообразнее усреднять эти сигналы в течение полупериода.
Короче говоря, среднее напряжение говорит вам, что ваше напряжение колеблется вокруг некоторого среднего значения, а среднеквадратичное напряжение показывает, насколько велико это колебание. Кроме того, квадрат RMS можно понимать как среднюю мощность на резисторе 1 Ом.
↪️Рекомендуемый инструмент для расчета среднеквадратичного значения: Калькулятор среднеквадратичного значения напряжения — от среднего значения, пикового и пикового до пикового значения
Часто задаваемые вопросы о расчете среднеквадратичного напряжения
1.Что означает РМС?
Среднеквадратичное значение
Среднеквадратичное значение или просто среднеквадратичное значение мощности в ваттах относится к непрерывной мощности динамика или сабвуфера или к тому, какую непрерывную мощность может выдавать усилитель. Значения RMS обычно ниже пиковых значений мощности, но они отражают то, на что устройство действительно способно.
2. Как рассчитать среднеквадратичное значение?
Возведите в квадрат каждое значение, сложите квадраты (все они положительные) и разделите на количество выборок, чтобы найти средний квадрат или средний квадрат.Затем извлеките из него квадратный корень. Это среднеквадратичное (rms) среднее значение.
3. Почему используется RMS?
Попытки найти среднее значение переменного тока сразу дадут вам нулевой ответ… Следовательно, используются среднеквадратичные значения. Они помогают найти действующее значение переменного тока (напряжения или тока). Это среднеквадратичное значение является математической величиной (используемой во многих областях математики), используемой для сравнения как переменного, так и постоянного тока (или напряжения).
4. Что такое среднеквадратичное значение шума?
RMS или среднеквадратичное значение определяется как среднее значение.С точки зрения шума, он определяется как процесс, используемый для определения средней выходной мощности (непрерывная форма волны) за длительный период времени.
5. Имеет ли значение среднеквадратичное значение? Значения RMS
, как правило, намного ниже, чем номинальная пиковая мощность, но они более точно отражают то, на что действительно способен усилитель или динамик. Думайте о RMS как об истинном рейтинге прослушивания. Хотя это и не идеальное средство сравнения, большинство рейтингов RMS сопоставимы, особенно при измерении среди продуктов известных брендов.
Альтернативные модели
| Часть | Сравнить | Производители | Категория | Описание | |
| ПроизводительНомер детали:KA7909TU | Сравните: Текущая часть | Производители: Fairchild | Категория: Регуляторы напряжения | Описание: Линейный регулятор напряжения FAIRCHILD SEMICONDUCTOR KA7909TU, 7909, фиксированный, от -35 В до -10 В на входе, -9 В и 1 А на выходе, TO-220AB-3 | |
| ПроизводительНомер детали: KA7909 | Сравните: KA7909TU VS KA7909 | Производители: Fairchild | Категория: | Описание: 3-контактный регулятор отрицательного напряжения 1 А | |
| ПроизводительНомер детали: TS7909CZ | Сравните: KA7909TU VS TS7909CZ | Производители: Тайваньский полупроводник | Категория: Линейные регуляторы | Описание: В РЭГ -9В, 7909, ТО-220-3; Тип регулятора напряжения: отрицательный фиксированный; Напряжение, вход Макс.: -11 В; Напряжение, макс. выход: -9…. | |
| № производителя: KA7909 | Сравните: KA7909TU VS KA7909 | Производители: Samsung | Категория: | Описание: Фиксированный отрицательный стандартный регулятор, 9 В, PSFM3 |
Пиковое напряжение переменного тока (AC), пиковое напряжение, среднеквадратичное (среднеквадратичное) напряжение
(DC) – постоянный ток
Элементы и батареи обеспечивают электрический ток, который всегда течет по цепи в одном и том же направлении, это называется постоянным током (DC).
(AC) – переменный ток
В Великобритании электрическая сеть подается при напряжении около 230 вольт и подается в виде (переменного) или переменного тока. Это означает, что ток течет в одном направлении, а затем в другом по цепи. Ток постоянно меняет направление (переменный), поэтому его называют (переменным) переменным током. В Великобритании частота сетевого электричества 50 Гц , это означает 50 циклов в секунду.
Сигналы переменного тока
Мы можем использовать осциллограф для представления сигнала переменного тока.
Мы можем использовать кривую осциллографа в качестве вольтметра, если знаем, какое значение коэффициента усиления по оси y установлено на осциллографе. Используя приведенную выше диаграмму и зная, что Y-усиление установлено на 10 В/дел, мы можем понять это;
Зная пиковое напряжение (V o ) и сопротивление (R) в цепи, мы можем рассчитать пиковый ток (I o ) , используя уравнение V=IR.
Среднеквадратичное значение (среднеквадратичное значение)
По мере того как p.d. и ток постоянно меняются в сигнале переменного тока, нам нужно представить среднее значение для p.d. и текущий.
Среднеквадратичные значения p.d. ( V rms ) и ток ( I rms ) представляют эффективное значение p.d. и ток в цепи переменного тока.
Простая формула RMS Напряжение и ток Цепь переменного тока
Идея эффективного значения возникает из-за необходимости измерять эффективность источника напряжения или тока при подаче мощности на резистивную нагрузку.Здесь мы изучим термин среднеквадратичное напряжение и ток.
Эффективное значение периодического тока представляет собой постоянный ток, который обеспечивает такую же среднюю мощность для резистора, как и периодический ток.
Сначала обязательно прочитайте, что такое цепь переменного тока.
Существует несколько типов мощности в цепи переменного тока:
90 Напряжение и ток переменного тока очень помогут вам при устройстве на работу инженером-электриком, так как их много можно найти на Jooble.Вы должны проверить это там, чтобы доказать то, что я сказал ранее о пользе изучения этой темы на продвинутом уровне.
Как рассчитать среднеквадратичное значение напряжения и тока
На рис. (1) цепь переменного тока (а), а цепь постоянного тока (б). Наша цель — найти I эфф , который будет передавать на резистор R ту же мощность, что и синусоида i .
| Рисунок 1. Найти эффективный ток: (A) Схема переменного тока, (b) Схема постоянного тока |
Средняя мощность, поглощенная резистором в цепи переменного тока, составляет
| (1) | (1) |
В то время как мощность, поглощенная резистором в цепи постоянного тока, составляет
| (2) |
, приравнивающий выражения в уравнениях.(1) и (2) и решив для I эфф , получим
| (3) |
9000. ; Это
4 |
Это указывает на то, что эффективное значение является (квадратный) корневой среднего уровня (или среднего) площадью периодического сигнал.
Таким образом, эффективное значение часто называют среднеквадратичным значением или краткосрочным значением ; А мы пишем
для любой периодической функции x (t) в целом, значение RMS задано
| (6 ) |
эффективное значение периодического сигнала представляет собой его среднеквадратичное (среднеквадратичное) значение.
Уравнение (6) утверждает, что для нахождения среднеквадратичного значения x(t) мы сначала находим его квадрат x 2 , а затем находим среднее значение, или
| (7) |
и квадратный корень (√) из этого среднего. Среднеквадратичное значение константы — это сама константа.
для синусоида I (T) = I м COS ΩT, эффективное или среднеквадратичное значение
| (8) |
| (9) |
| (10) |
| (11) |
Синусоидальное напряжение или ток часто указывается в терминах его максимального (или пикового) значения или среднеквадратичного значения, поскольку его среднее значение равно нулю.
Энергетика определяет векторные величины в терминах их среднеквадратичных значений, а не пиковых значений.
Например, 110 В, доступные в каждом домашнем хозяйстве, представляют собой среднеквадратичное значение напряжения от энергетической компании.
При анализе мощности удобно выражать напряжение и ток в их среднеквадратичных значениях.
Кроме того, аналоговые вольтметры и амперметры предназначены для непосредственного считывания среднеквадратичных значений напряжения и тока соответственно.
Примеры среднеквадратичного значения
Для лучшего понимания рассмотрим примеры ниже:
1.Определите среднеквадратичное значение формы волны тока на рис. (2). Если ток проходит через резистор сопротивлением 2 Ом, найти среднюю мощность, поглощаемую резистором.
Раствор:
Период формы волны составляет т = 4. За в течение периода, мы можем написать текущую форму волны как
Среднеквадратичное значение равно
Мощность, потребляемая резистором 2 Ом, составляет
2.Форма волны показана на рисунке. (3) представляет собой выпрямленную полупериодную синусоиду. Найдите среднеквадратичное значение и количество средней мощности, рассеиваемой на резисторе 10 Ом.
Решение:
Период формы волны напряжения представляет собой T = 2π, и
RMS Значение получено как
, но SIN 2 t = ½ (1 – cos 2 t ). Следовательно,
Средняя потребляемая мощность равна
Синусоидальные напряжения — Vpk, Vpk-pk, Vavg, Vrms
Синусоида определяется функцией тригонометрического синуса.При построении графика в виде зависимости напряжения (В) от фазы (θ)
он похож на рисунок справа. Форма волны повторяется каждые 2p
радиан (360°) и симметричен относительно оси напряжения (когда отсутствует смещение постоянного тока). Отображение напряжения и тока
циклическое поведение называется чередующимся; то есть переменный ток (AC). Здесь показан один полный цикл. Базовый
уравнение для синусоиды выглядит следующим образом:
Существует несколько способов определения амплитуды синусоидального сигнала, обычно в виде пикового напряжения (V pk
или V p ), размах напряжения (V pp или V pp или V pkpk или V pkpk ),
среднее напряжение (V avg или V avg ) и среднеквадратичное напряжение (V rms ).Пиковое напряжение
и размах напряжения очевидны, если посмотреть на график выше. Среднеквадратичное и среднее напряжение не так
очевидный.
См. также «Напряжения треугольной волны» и
Страницы напряжения прямоугольной формы.
Среднеквадратичное напряжение (В
действующее значение )
В виде
как следует из названия, V rms вычисляется путем извлечения квадратного корня из среднего квадрата
напряжения в правильно выбранном интервале.В случае симметричных сигналов, таких как синусоида, четверть периода
точно представляет все четыре четверти цикла сигнала. Поэтому допустимо выбирать первую четверть
цикл, который проходит от 0 радиан (0°) до p/2 радиан
(90°).
В среднеквадратичное значение — это значение, показываемое подавляющим большинством вольтметров переменного тока. Это значение, которое при применении
через сопротивление, производит такое же количество тепла, что и напряжение постоянного тока (DC) той же величины.
производить.Например, 1 В, приложенный к резистору 1 Ом, выделяет 1 Вт тепла. Синусоида 1 В rms
через резистор 1 Ом также выделяет 1 Вт тепла. Эта синусоида 1 В rms имеет пиковое напряжение √2 В (≈1,414
В) и размах напряжения 2√2 В (≈2,828 В).
Поскольку найти полный вывод формул для среднеквадратичного (V rms ) напряжения сложно,
сделано здесь для вас.
Итак,
≈ 0.


 А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5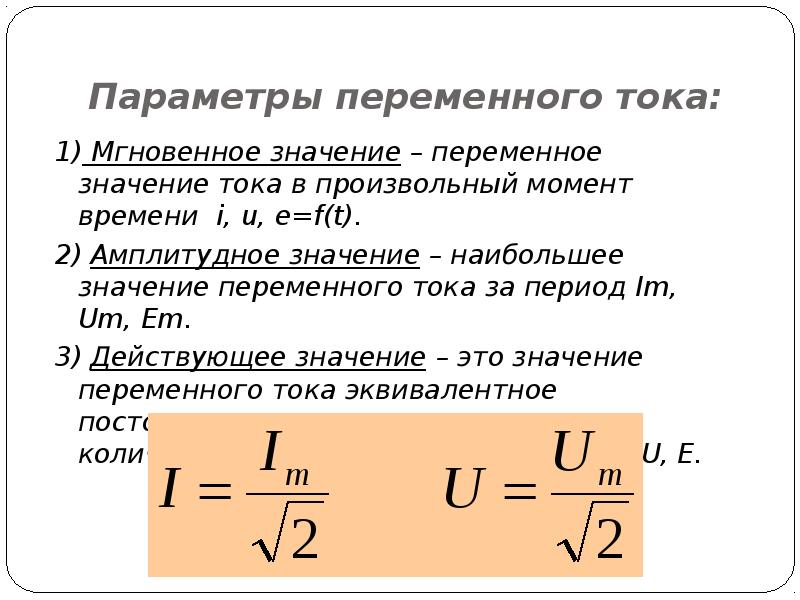
 Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M,
Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M,
 Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} . ; Под ред. Д. П. Линде — М.: Энергия, 1978
; Под ред. Д. П. Линде — М.: Энергия, 1978
 …
…