Замена параллельных ветвей, содержащих источники ЭДС и тока, одной эквивалентной. Замена источника тока источником эдс
Электротехника: Замена источников.
Рассмотрим замену источника напряжения источником тока преобразовав схему: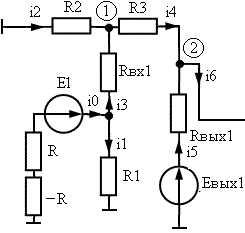
Рисунок 1 - Схема для преобразования
Последовательное соединение источника E1 и резистора R можно заменить параллельным соединением источника тока J и резистора R. Ток этого источника тока расчитывается по форуле:
Где E1 - напряжение источника напряжения E1, R - сопротивление резистора R.
Проводимость резистора соединённого параллельно с источником тока находится по формуле:
После преобразования схема будет выглядеть следующим образом:

Рисунок 2 - Преобразованая схема
Возможно и обратное преобразование когда параллельное соединение источника тока J (с значением тока равным J) и резистора заменяется последовательным соединением источника напряжения и резистора. В этом случае напряжение источника напряжения находится по формуле:
Или, если задана проводимость резистора G, по формуле:Где J - ток источника тока.
electe.blogspot.com
Эл-ка / 05 Лекции АВТ / UE_mod_2 / l 217
L. 217. «Электротехника» Аксютин В.А.
Эквивалентные преобразования электрических цепей.
Преобразование части электрической цепи является эквивалентным, если оно не изменяет значения токов и напряжений в не преобразованной части цепи.
Преобразование электрических цепей упрощает расчёт цепи. К основным видам можно отнести следующие преобразования:
Вынесение ЭДС за узел;
Замена последовательного, параллельного и смешанного соединения сопротивлений одним эквивалентным;
Замена реального источника тока эквивалентными источниками ЭДС;
Замена участка сложной цепи с параллельным соединением ветвей расположенных между двумя узлами;
Замена треугольника сопротивлений эквивалентной звездой и наоборот;
Замена сопротивления с известным током, зависимым источником ЭДС (теорема о компенсации).
Рассмотрим более подробно нижеприведенные преобразования.
Вынесение ЭДС за узел.
Это преобразование поясняется рис. 1. В каждую ветвь, подходящую к узлу рис. 1,а можно включить ЭДС E, направленные, например, от узла рис. 1,б. В ветви с исходным источником появляется две равных по модулю и разнонаправленных ЭДС, которые можно сократить. В результате преобразований эквивалентная цепь представлена на рис. 1,в.
E
E
E
E
E
E
E
E
E
а б в
Рис. 1
Замена последовательного, параллельного и смешанного соединения сопротивлений одним эквивалентным.
а б
в г
Рис. 2
Для всех случаев входной ток определим по закону Ома: I = U/RЭ,
где RЭ – входное сопротивление цепи
2.1. Последовательное соединение N резисторов рис. 2,а:
RЭ = R1 + R2 +…+ RN = Ri (1)
2.2. Параллельное соединение N резисторов рис. 2, б:
RЭ = 1/GЭ, (2)
где эквивалентная проводимость:
(3)
Входной ток определяется по закону Кирхгофа:
I =I1 + I2 + … +IN = Ii (4)
Токи в ветвях: Ii = U/Ri
2.3. Параллельное соединение двух резисторов рис. 2, в:
RЭ = 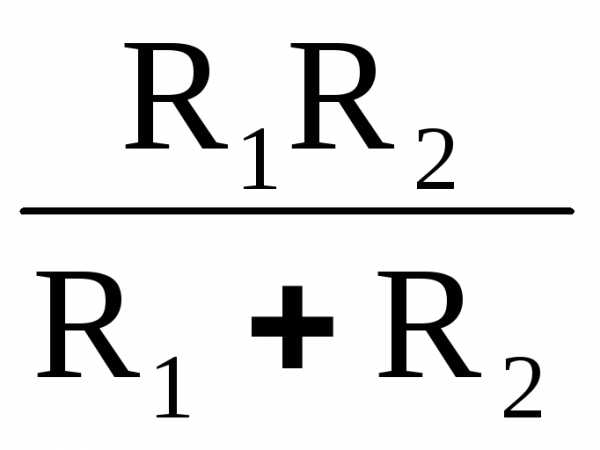 (5)
(5)
U = I RЭ = I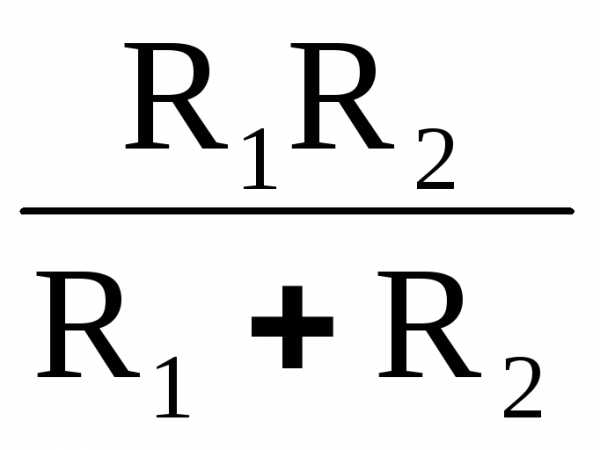
Токи в ветвях;
Ii = (6)
I2 = (7)
Соотношения (6) и (7) называют правилом рычага (разноса): ток в параллельной ветви равен произведению общего тока на сопротивление в противоположной ветви и делённое на сумму сопротивлений ветвей.
2.3. Параллельно-последовательное соединение трёх резисторов рис. 2, г:
RЭ = R+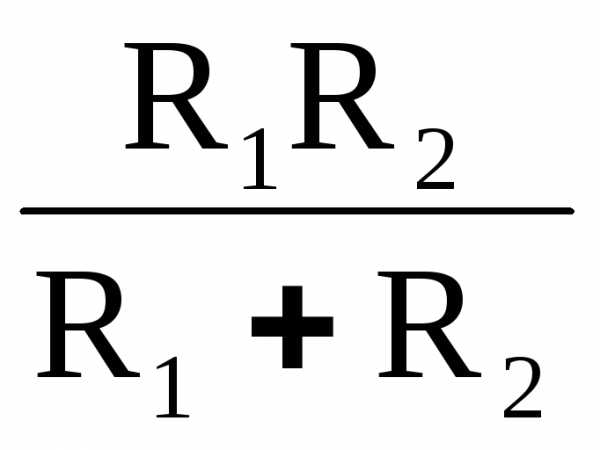 (8)
(8)
Токи в параллельных ветвях определим по (6) и (7):
Ii = 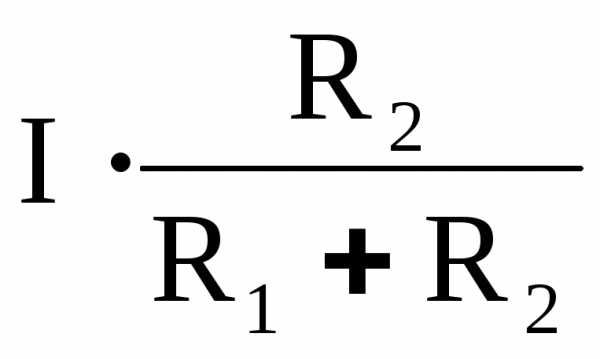 (9)
(9)
I2 =  (10)
(10)
Замена источника тока эквивалентными источниками ЭДС.
а б
Рис. 3
Рассмотрим фрагмент цепи, в который входит контур, содержащий источник тока и ряд ветвей (рис. 3,а). Источник тока можно преобразовать в источники ЭДС (рис. 3,б), если в каждую ветвь контура включить дополнительный источник ЭДС, равный произведению тока источника тока на сопротивление ветви. Направление обхода контура выбирается по направлению источника тока, а направление ЭДС задаётся на встречу обхода контура. Доказательство данного преобразования производится из аналогии уравнений метода контурных токов составленных для двух схем рис. 3,а и б.
Интерес представляет преобразование реального источника тока в источник ЭДС и наоборот. Порядок преобразования показан на рис. 4.
Рис. 4
Замена участка сложной цепи с параллельным соединением ветвей расположенных между двумя узлами.
а б
Рис. 5
На рис. 5,а изображён участок цепи, имеющий параллельное соединение нескольких ветвей. Применяя метод узловых потенциалов можно получить ветвь с эквивалентным сопротивлением и ЭДС рис. 5,б:
EЭ = 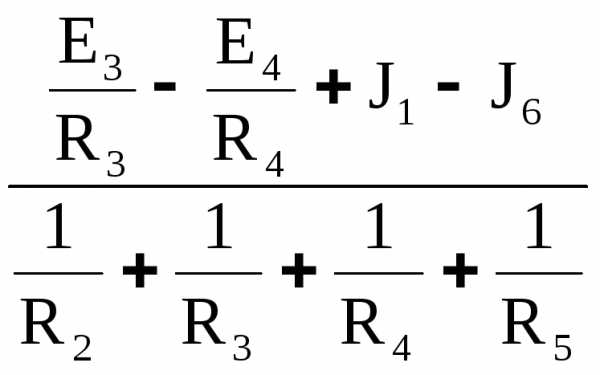 ; (11)
; (11)
RЭ =  . (12)
. (12)
В общем случае:
EЭ = 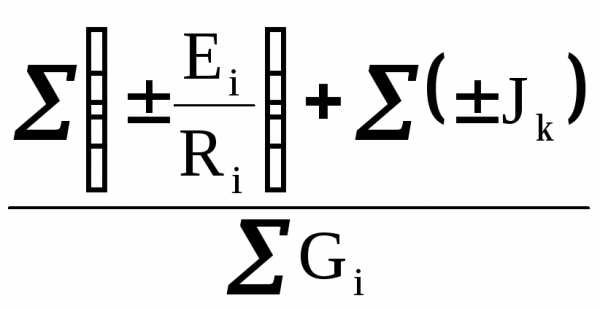 ; (13)
; (13)
RЭ =  . (14)
. (14)
Замена треугольника сопротивлений эквивалентной звездой и наоборот.
а б в
Рис. 6
а б в
Рис. 7
Трёхполюсник считается пассивным, если не содержит источников электрической энергии. Среди пассивных трёхполюсников наиболее часто встречаются «звезда» рис. 6 и «треугольник» сопротивлений рис. 7. Это основные схемы соединения элементов трёхфазных цепей.
Соединение в «звезду» – это соединение трёх сопротивлений, при котором они имеют общую точку и образуют три расходящихся луча. Обозначается Y (рис. 6).
Соединением в «треугольник» называют соединение, при котором элементы образуют геометрический треугольник. Обозначается  (рис. 7).
(рис. 7).
Существует вывод формул эквивалентной замены n-лучевой звезды m -сторонним многоугольником, причём m = 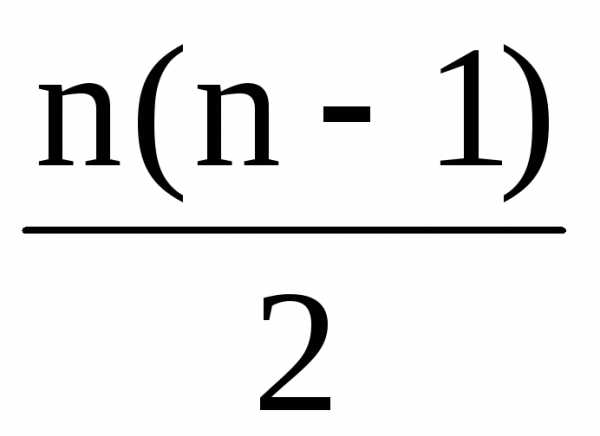 .
.
Однако обратное преобразование всегда возможно только при m = n = 3. Поэтому рассмотрим эквивалентное преобразование Y  . замена будет эквивалентной, если при одинаковых потенциалах одноименных полюсов звезды и треугольника токи, подходящие к этим полюсам, также одинаковы, то есть при одинаковых режимах работы сопротивления между одними и теми же парами полюсов звезды и треугольника равны.
. замена будет эквивалентной, если при одинаковых потенциалах одноименных полюсов звезды и треугольника токи, подходящие к этим полюсам, также одинаковы, то есть при одинаковых режимах работы сопротивления между одними и теми же парами полюсов звезды и треугольника равны.
При выводе соотношений полагаем, что внешние токи I1, I2, I3 и потенциалы φ1, φ2 и φ3 для Y и одинаковы. Для цепи рис 6,а запишем основные уравнения для определения токов в первой и второй ветвях, а также потенциала φ0:
Ii =  ; I2 =
; I2 = 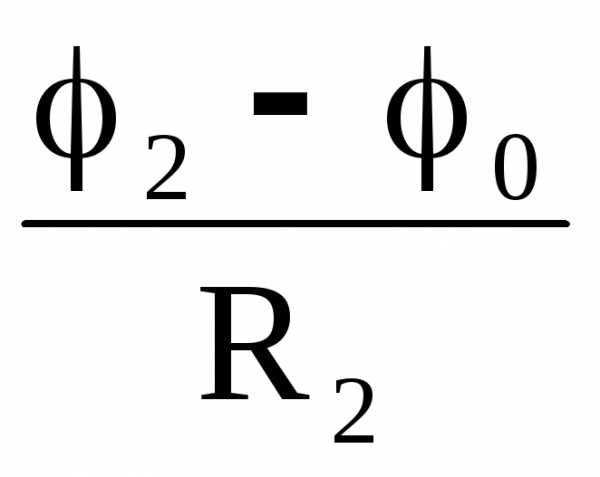 ; (15)
; (15)
; (16)
 ; (17)
; (17)
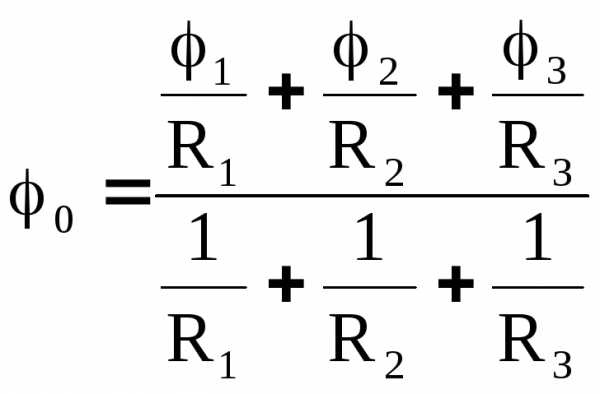
Обозначим: 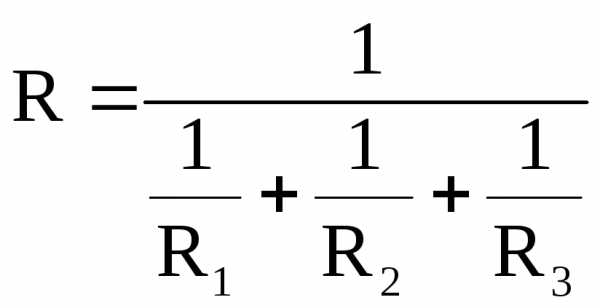
Подставим φ0 в (15) получим выражения для токов в «звезде»:
Ii = . (18)
I2 = . (19)
Для цепи рис 7,а запишем уравнения для токов в «треугольнике» :
I1 = I12 − I31 =  −
−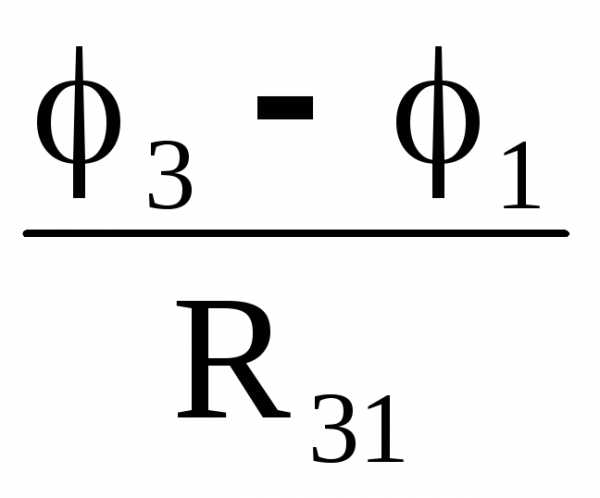 = ; (20)
= ; (20)
I2 = I23 − I12 =  −
−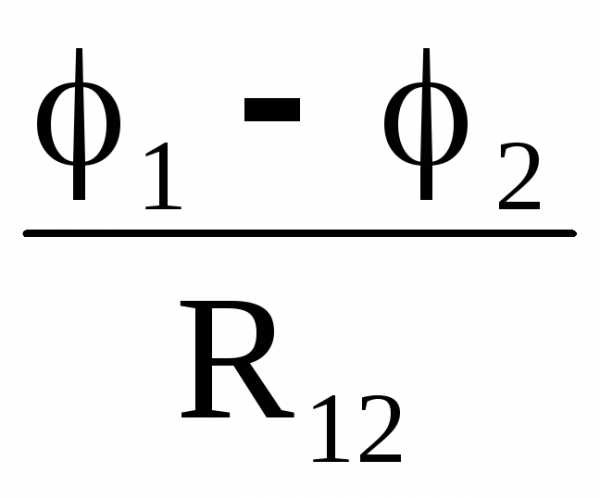 = (21)
= (21)
Приравняем коэффициенты при потенциалах φ2 и φ3 в (18) и (20) получим:
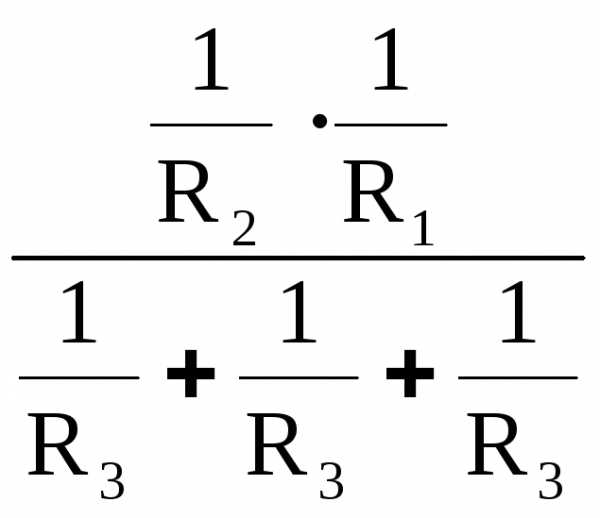 ..=..
..=.. ; (22)
; (22)
 ..=..
..=..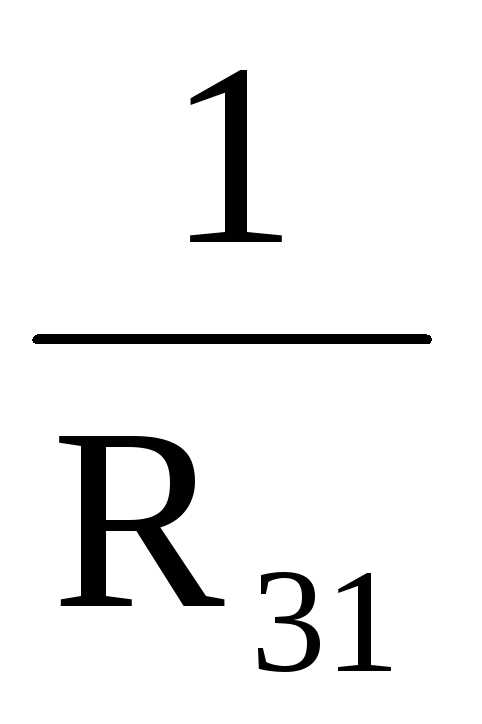 ; (23)
; (23)
Приравняем коэффициенты при потенциале φ3 в (19) и (21) получим:
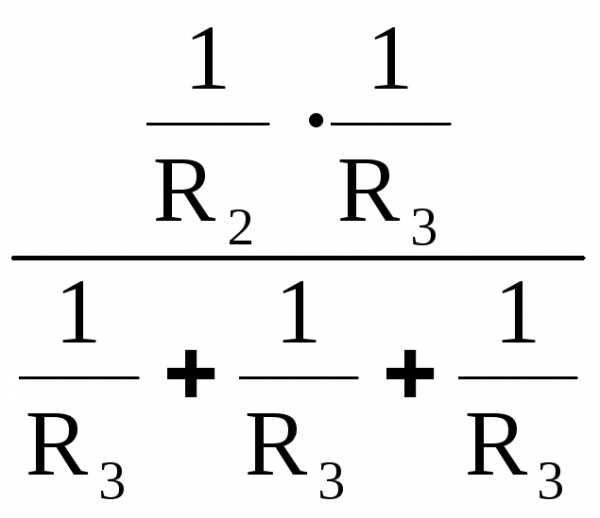 ..=..
..=..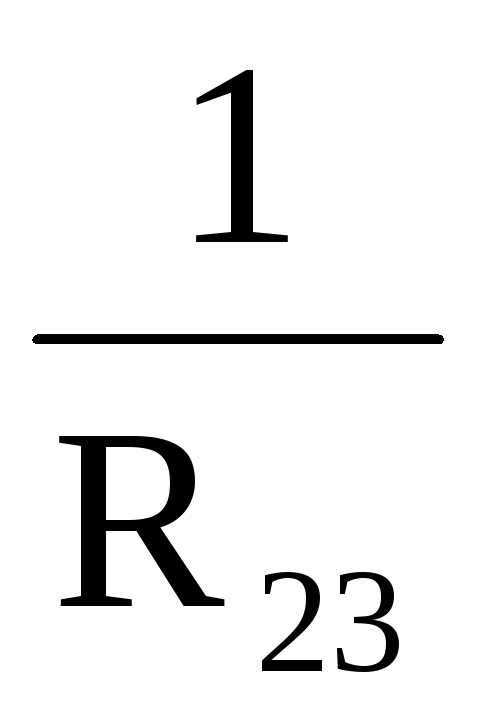 ; (24)
; (24)
Преобразовав (22), (23) и (24) получим следующие формулы взаимного преобразования соединения «звезда» рис. 6 и «треугольник» рис. 7:
| | |
| R1 = R2 = R3 = | R12 = R1 + R2 + R23 = R2 + R3 + R31 = R3 + R1 + |
Замена сопротивления с известным током, зависимым источником ЭДС (теорема о компенсации).
а б
Рис. 8
Согласно теореме о компенсации линейное сопротивление с известным током (рис. 8,а) можно заменить зависимым источником ЭДС, полярность которого совпадает с полярностью напряжения возникающего на зажимах сопротивления (рис. 8,б).
а б в
Рис. 9
Доказательство теоремы. В ветвь с линейным резистором рис. 9,а. включим два источника ЭДС E = I R, имеющих противоположное направление рис. 9,б. Так как напряжение на резисторе U=I R то разница потенциалов φ1 − φ3 = 0 и на схеме можно объединить точки 1 и 3 (на рис. 9,б показано пунктиром). В результате получим цепь рис. 9,в.
8
studfiles.net
Преобразование источника тока в эквивалентный источник эдс в реальных электрических схемах.
В схеме рис. 8 преобразовать источник тока в эквивалентный источник ЭДС и начертить эквивалентную схему.

Рис. 8. Электрическая схема
Прежде всего, следует выбрать путь, по которому проходит ток от источника тока . Пусть это будет контур adba. Обозначим этот путь штриховой линией.
Величина эквивалентного источника ЭДС равна произведению источника тока на величину параллельно включенного сопротивления :
, (7)
а направление стрелки источника ЭДС всегда против тока от источника тока , проходящего по резистору .

Рис. 9. Преобразованная электрическая схема
На рис. 9 показана эквивалентная схема, в которой источник тока заменен на эквивалентный источник ЭДС .
Токи , , те же самые, что и в исходной схеме рис. 8. Ток в эквивалентной схеме исчез. Теперь во всей ветви cba течет ток .
Рассмотрим более сложный случай, когда ток замыкается на два резистора.
В схеме рис. 10 преобразовать источник тока в эквивалентные источники ЭДС.
Рис. 10. Электрическая схема
Выберем путь, по которому проходит ток от источника тока, обозначенный штриховой линией на рис. 10.
Теперь в четвертой ветви вводится эквивалентный источник ЭДС
, а в пятой ветви вводится эквивалентный источник ЭДС
. Направления стрелок этих ЭДС против тока от источника тока , проходящего через резисторы и .
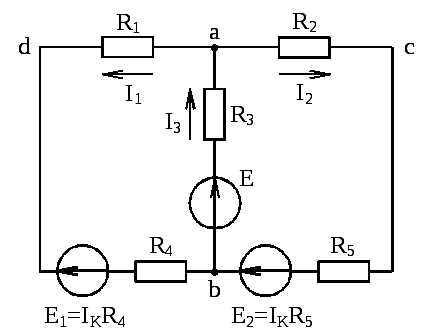
Рис. 11. Преобразованная электрическая схема
На рис. 11 показана эквивалентная схема. Токи , , те же самые, что и в исходной схеме рис. 10. Токи и в эквивалентной схеме исчезли. Ток теперь течет через резисторы и и источник ЭДС . Ток теперь течет через резисторы и и источник ЭДС .
Разветвленные и неразветвленные электрические цепи.
Электрические цепи подразделяются на неразветвленные и разветвленные. Схема рис. 6 представляет собой простейшую неразветвленную цепь, в которой все элементы включены последовательно и по которым протекает один и тот же ток. На рис. 8 и рис. 10 изображены разветвленные цепи, в которых имеется несколько ветвей. В каждой ветви течет свой ток. Ветвь можно определить как участок электрической цепи, образованный последовательно соединенными элементами и заключенный между двумя узлами.
Узел есть точка электрической цепи, в которой сходится не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена «жирная» точка (рис. 12а), то в этой точке есть электрическое соединение двух или нескольких ветвей. По этой причине узлы на электрической схеме обозначаются «жирными» точками.
а) б)
Рис. 12. Обозначение на схеме электрического соединения
Если «жирная» точка в месте пересечения не поставлена, то линии пересекаются без электрического соединения.
Электрическим контуром называется любой замкнутый путь в схеме. Ветвь с источником тока не учитывается при подсчете числа контуров. Так в схеме рис. 10 три контура: abda, acba, acbda.
Независимый электрический контур – это такой контур, в который входит хотя бы одна новая ветвь, не вошедшая в предыдущие контуры. Так в схеме рис. 10 два независимых контура abda и acba. Контур acbda не является независимым, так как все его ветви вошли в предыдущие независимые контуры.
В неразветвленной электрической цепи всегда только один контур. В разветвленной цепи всегда несколько контуров.
studfiles.net
как заменить источник тока источником эдс Видео
1 г. назад
В расчетах электрических цепей, кроме источников ЭДС, используют источники тока. Источник тока – это такой...
5 г. назад
Физика с Сергеем Рогиным. ЕГЭ, студентам. Все лекции здесь http://vk.com/physics_training. Задачи, разобранные в лекции...
4 г. назад
Приведены термины источника ЭДС и источника тока. Описаны в общих чертах простейшие схемы, в состав которых...
6 г. назад
Подписывайтесь на нашу группу Вконтакте — http://vk.com/chipidip, и Facebook — https://www.facebook.com/chipidip * Поведение конденса...
2 г. назад
Методы расчета сложных электрических цепей. Метод эквивалентного генератора. В данном видеоуроке произво...
6 мес. назад
Что такое электродвижущая сила? Объяснение закона Ома для полной (замкнутой) цепи. Урок №8. Катушка индуктив...
2 г. назад
В данном видео уроке производится расчет цепи методом наложения с двумя источниками, источником тока и...
3 г. назад
Суперпозиционные методы анализа цепей.
7 г. назад
Подписывайтесь на нашу группу Вконтакте — http://vk.com/chipidip, и Facebook — https://www.facebook.com/chipidip * Симистор это полупр...
8 г. назад
Подписывайтесь на нашу группу Вконтакте — http://vk.com/chipidip, и Facebook — https://www.facebook.com/chipidip * Эквивалентная схем...
6 г. назад
Подписывайтесь на нашу группу Вконтакте — http://vk.com/chipidip, и Facebook — https://www.facebook.com/chipidip * Как известно, многи...
5 г. назад
Подписывайтесь на нашу группу Вконтакте — http://vk.com/chipidip, и Facebook — https://www.facebook.com/chipidip * Одним из наиболее...
5 г. назад
Подписывайтесь на нашу группу Вконтакте — http://vk.com/chipidip, и Facebook — https://www.facebook.com/chipidip * При изготовлении...
8 мес. назад
Максимальный ток во вторичке был получен при расположении вторички в 1/12 и 11/12 первички. В ролике использова...
6 г. назад
VK: vk.com/mathemax2018 TG: t.me/mathemax. На примере цепи постоянного тока.
2 г. назад
Наш сайт http://www.faradej.ru/Основу химических источников тока составляют два электрода (отрицательно заряженный...
7 г. назад
Устранение искры размыкания при помощи диода и конденсатора.
2 г. назад
Электротехника. В данной лекции рассматриваем способ замены нескольких ветвей электрической цепи, содержа...
4 г. назад
В последние годы Московским государственным авиационным институтом (техническим университе том) - МАИ...
5 г. назад
В наших домах электроприемники питаются переменным электрическим током который является синусоидальным....
turprikol.com
1.5. Источник эдс и источник тока в электрических цепях
При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением величины внутреннего сопротивления r0 заменяют расчетным эквивалентным источником ЭДС или источником тока.
Рис. 1.14
Источник ЭДС (рис. 1.14) имеет внутреннее сопротивление r0, равное внутреннему сопротивлению реального источника. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС.
Для данной цепи запишем соотношение по второму закону Кирхгофа
(1.10)
E = U + Ir0 или E = U - Ir0.
Эта зависимость напряжения U на зажимах реального источника от тока I определяется его вольт-амперной или внешней характеристикой (рис. 1.15). Уменьшение напряжения источника U при увеличении тока нагрузки I объясняется падением напряжения на его внутреннем сопротивлении r0.
| Рис. 1.15 | Рис. 1.16 |
У идеального источника ЭДС внутреннее сопротивление r0 << Rн (приближенно r00). В этом случае его вольт-амперная характеристика представляет собой прямую линию (рис. 1.16), следовательно, напряжение U на его зажимах постоянно (U=E) и не зависит от величины сопротивления нагрузки Rн.
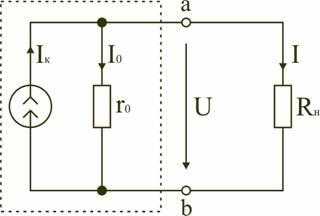 Рис. 1.17
Рис. 1.17
Источник тока, заменяющий реальный источник электрической энергии, характеризуется неизменным по величине током Iк, равным току короткого замыкания источника ЭДС , и внутренним сопротивление r0, включенным параллельно (рис. 1.17).
Стрелка в кружке указывает положительное направление тока источника. Для данной цепи запишем соотношение по первому закону Кирхгофа
Iк = I0 + I; .
В этом случае вольт-амперная (внешняя) характеристика I(U) источника тока определится соотношением
(1.11)
I = Iк - I0 = Iк - U/r0
и представлена на рис. 1.18.
| Рис. 1.18 | Рис. 1.19 |
Уменьшение тока нагрузки I при увеличении напряжения U на зажимах ab источника тока, объясняется увеличением тока Iо, замыкающегося в цепи источника тока.
В идеальном источнике тока r0>>Rн. В этом случае можно считать, что при изменении сопротивления нагрузки Rн потребителя Iо0, а IIк. Тогда из выражения (1.11) следует, что вольт-амперная характеристика I(U) идеального источника тока представляет прямую линию, проведенную параллельно оси абсцисс на уровне I = Iк = E/r0 (рис. 1.19).
При сравнении внешних характеристик источника ЭДС (рис. 1.15) и источника тока (рис. 1.18) следует, что они одинаково реагируют на изменение величины сопротивления нагрузки. Покажем, что в обоих случаях ток I в нагрузке определяется одинаковым соотношением.
Ток в нагрузке Rн для схем источника ЭДС (рис. 1.14) и источника тока (рис. 1.17) одинаков и равен .
Для схемы (рис. 1.14) это следует из закона Ома, т.к. при последователь-ном соединении сопротивления r0 и Rн складываются. В схеме (рис. 1.17) ток распределяется обратно пропорционально сопротивлениям r0 и Rн двух параллельных ветвей. Ток в нагрузке Rн
,
т.е. совпадает по величине с током при подключении нагрузки к источнику ЭДС. Следовательно, схема источника тока (рис. 1.17) эквивалентна схеме источника ЭДС (рис. 1.14) в отношении энергии, выделяющейся в сопротивлении нагрузки Rн, но не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания.
Каким из двух эквивалентных источников питания пользоваться, не играет существенной роли. Однако на практике, особенно при расчете электротехнических устройств, чаще используется в качестве источника питания источник ЭДС с внутренним сопротивлением r0 и величиной электродвижущей силы Е.
В тех случаях, когда номинальное напряжение или номинальный ток и мощность источника электрической энергии оказываются недостаточными для питания потребителей, вместо одного используют несколько источников. Существуют два основных способа соединения источников питания: последовательное и параллельное.
Последовательное включение источников питания (источников ЭДС) применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС (рис. 1.20).
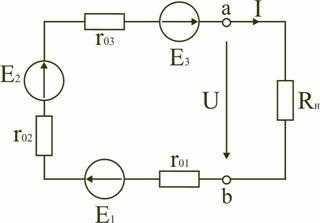
Рис. 1.20
Для этой цепи на основании второго закона Кирхгофа можно записать
E1 + E2 + E3 = I(r01 + r02 + r03 + Rн),
откуда
.
Таким образом, электрическая цепь на рис. 1.20 может быть заменена цепью с эквивалентным источником питания (рис. 1.21), имеющим ЭДС Eэ и внутреннее сопротивление rэ.
|
| Рис. 1.22 |
При параллельном соединении источников (рис. 1.22) соединяются между собой положительные выводы всех источников, а также их отрицательные выводы. Характерным для параллельного соединения является одно и то же напряжение U на выводах всех источников. Для электрической цепи на рис. 1.22 можно записать следующие уравнения:
I = I1 + I2 + I3; P = P1 + P2 + P3 = UI1 + UI2 + UI3 = UI.
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников. Параллельное соединение источников применяется в первую очередь тогда, когда номинальные ток и мощность одного источника недостаточны для питания потребителей. На параллельную работу включают обычно источники с одинаковыми ЭДС, мощностями и внутренними сопротивлениями.
studfiles.net
Режим гармонических колебаний. Частотные характеристики
Для удобства расчета электрических цепей иногда полезно производить замену источника ЭДС эквивалентным источником тока или выполнять обратную замену источника тока эквивалентным источником ЭДС.
Источники ЭДС и тока являются эквивалентными, если они обладают одной и той же внешней характеристикой (или ).
При присоединении к ним приемника с некоторым сопротивлением (или ) напряжение u (или ) и ток i (или ) в приемнике будут в обоих случаях одинаковы.
Уравнение внешней характеристики источника ЭДС имеет вид (или ).Запишем это уравнение иначе, а именно: (или). Уравнение внешней характеристики источника тока имеет вид (или). Эти внешние характеристики совпадут, если соблюдать условия
и или и .
По этим равенствам можно вычислить параметры и ( и ) источника тока, эквивалентного заданному источнику ЭДС, имеющему параметры е и rвн (и Zвн). Соответственно, из соотношений
и или и
можно получить параметры источника ЭДС, эквивалентного источнику тока. Эквивалентные замены могут быть произведены и для зависимых источников. Пусть в некоторой ветви pс проводимостью имеется зависимый, управляемый током ветви q источник тока . Согласно вышеприведенным формулам, можно преобразовать управляемый током источник тока в управляемый током источник ЭДС. Значение ЭДС будет равно и внутреннее сопротивление ZBH = Zp = 1/ Yр.
Преобразуем две параллельно соединенные ветви, содержащие источники ЭДС и и сопротивления Z1 =1/ Y1и Z2 =1/Y2(рис. 2.11), в одну эквивалентную ветвь.
Рис. 2.11. Преобразование двух параллельно соединенных ветвей в одну эквивалентную ветвь
Рассматривая параллельно соединенные на рис. 2.11 ветви как источники ЭДС и с внутренними сопротивлениями Z1 и Z2, заменим их эквивалентными источниками тока и с внутренними проводимостями Y1=1/Z1 и Y2=1/Z2 (рис. 2.11). Объединив эти два
источника тока в один с внутренней проводимостью Y= Y1+ Y2, перейдем от него к источнику ЭДС
с внутренним сопротивлением
Распространяя полученный результат на nпараллельно соединенных ветвей, найдем, что заменяющая их эквивалентная ветвь содержит источник ЭДС
и сопротивление
3ys.ru
Замена параллельных ветвей, содержащих источники ЭДС и тока, одной эквивалентной.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ ПО ДИСЦИПЛИНЕ
«ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ»
г. Волгодонск, 2015 г.
УДК 621.3.01
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ ПО ДИСЦИПЛИНЕ
«ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ»
Настоящие методические указания содержат рекомендации по решению и задания для выполнения контрольных работ по дисциплине «Теоретические основы электротехники». В начале разделов приводятся теоретические сведения, а так же примеры выполнения задач. / ВИТИ НИЯУ МИФИ. – Волгодонск, 2015. – 61 с.
© ВИТИ НИЯУ МИФИ, 2015
Содержание
Введение4
1 Задание №1. Цепи постоянного тока5
1.1 Теоретические положения7
1.2 Задача 118
1.3 Задача 221
1.4 Задача 323
1.5 Задача 425
2 Задание №2. Цепи однофазного синусоидального тока27
2.1 Теоретические положения27
2.2 Пример выполнения задания41
2.3 Задание на расчетно-графическую работу52
3 Расчет характеристик трехфазного трансформатора57
3.1 Методические указания к решению 3-ей задачи57
3.2 Задание на расчетно-графическую работу58
Список использованной литературы60
Введение
Данные методические указания предназначены для студентов очной и заочной формы обучения для выполнения контрольных работ по дисциплине «Теоретические основы электротехники».
Целью контрольной работы является ознакомление с основами электротехники и электроснабжения, изучение основных законов и методов упрощения электрических цепей и расчета их параметров.
Методические указания включают в себя 3 задания, а так же теоретические данные и примеры выполнения. Задания построены по вариантной схеме и состоят из таблиц вариантов и набора рисунков электрических цепей.
Задание №1. Цепи постоянного тока
Задачей расчета электрической цепи является определение токов в ее ветвях, потенциалов узлов, напряжений на отдельных участках (элементах) с последующей проверкой полученных результатов при помощи баланса мощностей. В процессе расчета часто применяют эквивалентные преобразования, которые заключаются в замене отдельных участков цепи более простыми. Замену осуществляют так, чтобы в остальной части цепи напряжения и токи не изменились. В результате эквивалентных преобразований упрощается исходная цепь и облегчается её расчет.
Электрической схемой называется графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов цепи.
Ветвью называется участок цепи, образованный одним или несколькими последовательно включенными элементами, по которым течет один и тот же ток.

Рисунок 1
Так, в схеме (рисунок 1) три ветви. Первая образована элементами Е, R1, R2; вторая – R3, J; третья – одним сопротивлением R4. Узлом называется место соединения трех и более ветвей (точки "а" и "b" в схеме рисунок 1). Пассивными называются ветви, не содержащие источников электрической энергии. Пример пассивного элемента – электрическое сопротивление R, в котором происходит преобразование электрической энергии в тепловую.
Ветви, содержащие источники энергии, называются активными. Источниками электрической энергии являются генерирующие устройства, в которых энергия того или иного вида преобразуется в электрическую. В процессе расчета электрических цепей пользуются идеальными и реальными источниками ЭДС и тока.
Идеальным источником ЭДС (рисунок 2) называется активный элемент с двумя выводами, напряжение на зажимах которого не зависит от тока, протекающего через источник, т. е Uab = Е.

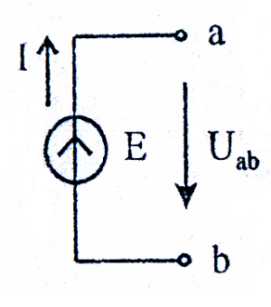 Идеальный источник ЭДС является источником бесконечной мощности, его внутреннее сопротивление равно нулю. Стрелка внутри источника указывает на направление возрастания потенциала. У реального источника ЭДС конечной мощности (рисунок 3) внутреннее сопротивление R0 не равно нулю. При увеличении тока, отдаваемого в нагрузку, происходит уменьшение напряжения Uab.
Идеальный источник ЭДС является источником бесконечной мощности, его внутреннее сопротивление равно нулю. Стрелка внутри источника указывает на направление возрастания потенциала. У реального источника ЭДС конечной мощности (рисунок 3) внутреннее сопротивление R0 не равно нулю. При увеличении тока, отдаваемого в нагрузку, происходит уменьшение напряжения Uab.
Рисунок 2 Рисунок 3
Идеальным источником тока (рисунок 4) называется активный элемент с двумя выводами, ток которого не зависит от напряжения Uab на его зажимах. Идеальный источник является источником бесконечной мощности. Его внутренняя проводимость равна нулю, а внутреннее сопротивление – бесконечно велико. Схема замещения реального источника тока конечной мощности приведена на рисунке 5
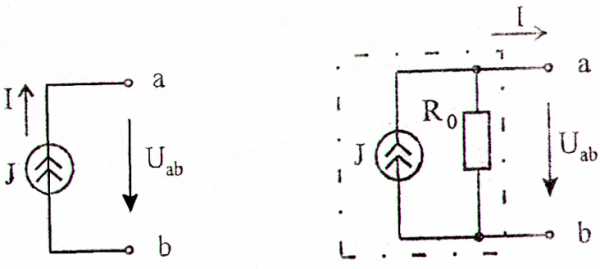 Рисунок 4 Рисунок 5
Рисунок 4 Рисунок 5
Теоретические положения
Закон Ома
Ток I и напряжение U на сопротивлении R связаны законом Ома следующим образом:
Законы Кирхгофа
Электрические цепи постоянного тока могут быть рассчитаны с помощью законов Кирхгофа.
Первый закон Кирхгофа:
Алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. Токи, направленные к узлу, условно принимаются положительными, а направленные от него – отрицательными (или наоборот).
Второй закон Кирхгофа:
Алгебраическая сумма ЭДС замкнутого контура равна алгебраической сумме падений напряжений в нём. Направление обхода контура выбирается произвольно; при записи левой части равенства ЭДС, направления которых совпадают с выбранным направлением обхода, принимаются положительными, а ЭДС, направленные против выбранного обхода – отрицательными. При записи правой части со знаком "+" берутся падения напряжения в тех ветвях, в которых положительное направление тока совпадает с направлением обхода, и со знаком " – " падения напряжения в тех ветвях, в которых положительное направление тока противоположно направлению обхода. Если цепь содержит Nв – ветвей, Nу – узлов, Nт – источников тока, то:
1) устанавливается число неизвестных токов: Nв - Nт;
2) число линейно-независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов без единицы: Nу - 1;
3) число уравнений, составляемых по второму закону Кирхгофа:
При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры (каждый из которых содержит по сравнению с предыдущим хотя бы одну новую ветвь), не содержащие источников тока. Так, для цепи Рисунок 1 система уравнений имеет вид:
Баланс мощностей
Пусть в электрической цепи имеются источники и приемники электрической энергии. Тогда условие баланса мощностей, являясь следствием закона сохранения энергии, формулируется следующим образом: суммарная мощность, генерируемая источниками энергии, равна суммарной мощности, потребляемой в цепи:
Где n – число ветвей, содержащих источники ЭДС;
m – число ветвей, содержащих источники тока;
UP – напряжение на зажимах источника тока;
q – число ветвей, содержащих сопротивления.
Мощность источника может быть положительной (если направления тока совпадает с направлением ЭДС Ek или напряжения UP) или отрицательной (направления тока и ЭДС противоположны или UP отрицательно). Отрицательный знак мощности означает, что соответствующий источник работает в режиме потребления энергии.
Так для цепи (рисунок 1) баланс мощностей имеет вид
1.1.4 Преобразование пассивных ветвей
Замена последовательно соединенных сопротивлений одним эквивалентным.Сопротивления соединены последовательно, если они обтекаются одним током (рисунок 6).
Рисунок 6
Эквивалентное сопротивление цепи, состоящее изn последовательно соединенных сопротивлений, равно сумме этих сопротивлений, т.е.
Замена параллельных сопротивлений одним эквивалентным.Сопротивления параллельны, если все они присоединены к одной паре узлов (рисунок 7).
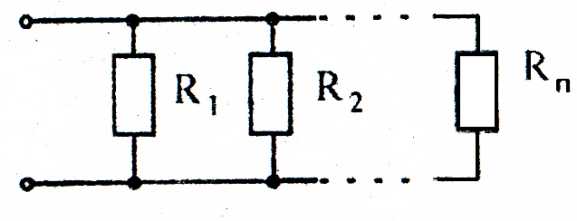
Рисунок 7
Эквивалентное сопротивление цепи, состоящей из n параллельно соединенных сопротивлений, есть величина, обратная сумме проводимостей отдельных ветвей.
,
где – проводимость k – й ветви.
В частном случае параллельного соединения двух и трех сопротивлений (рисунок 8) соответственно эквивалентные сопротивления:
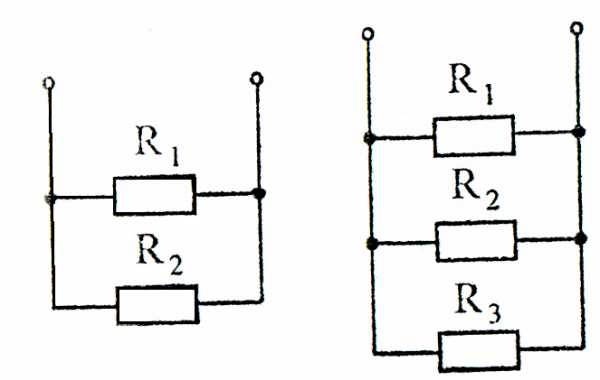
Рисунок 8
;
Замена смешанного соединения одним эквивалентным.Смешанное соединение – сочетание последовательного и параллельного соединений сопротивлений (рисунок 9):
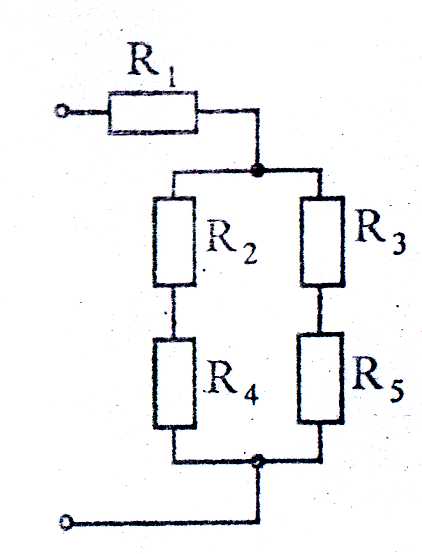
Рисунок 9
Пример 1.
Определить эквивалентное сопротивление цепи (рисунок 10а) между точками а и b при разомкнутом и замкнутом ключе. Дано: R1 = R2 = R3 = R4 = R5 = R6 = R7 = 10 Ом.
Решение
Заданная цепь при разомкнутом ключе изображена на рис.10 б.
а) б)
Рисунок 10
Искомое сопротивление определяем следующим образом:
;
;
Ом;
Ом;
Ом;
Ом.
При замкнутом ключе схема имеет вид, изображенный на рисунке 11.

Рисунок 11
Сопротивление цепи равно сумме двух сопротивлений, а именно:
;
;
;
Ом, Ом, Ом.
Формулы преобразования треугольника сопротивлений в эквивалентную звезду и наоборот (рисунок 12)
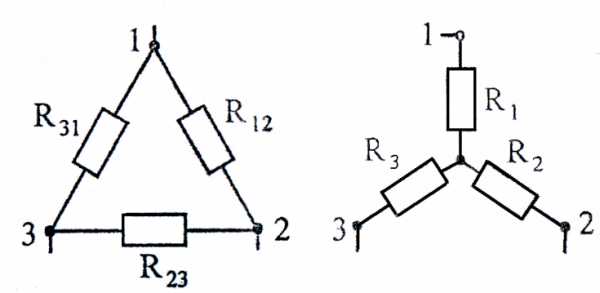
Рисунок 12
(1)
(2)
(3)
(4)
(5)
(6)
1.1.5 Преобразование активных ветвей
Замена ветви с несколькими источниками ЭДС ветвью с одной эквивалентной ЭДС. Условиями эквивалентности является равенство напряжений на зажимах (Uab, рисунок 13) исходной и эквивалентной ветвей, а также токов в ветвях.
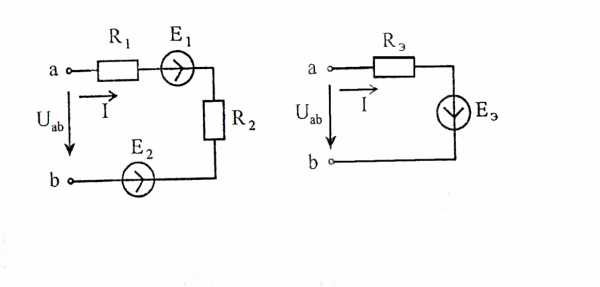
Рисунок 13
Величины ЕЭ, RЭ можно определить с помощью второго закона Кирхгофа. Так, для исходной ветви (рисунок 13)
(7)
для эквивалентной ветви
(8)
Сравнивая выражения (7) и (8), получим
; (9)
Формула (9) получена с учетом того, что направление эквивалентной ЭДС выбрано совпадающим с направлением тока в цепи. Отсюда следует простое правило расчета ЕЭ: если направление ЭДС источника в исходной цепи (E1, рисунок 13) совпадает с направлением тока, то она входит в правую часть формулы (9) со знаком плюс, иначе – минус (Е2, рисунок 13).
Задача 1
Определить эквивалентное сопротивление RЭ (рисунок 20, 21, 22) относительно указанных зажимов, если сопротивления равны 10 Ом. Данные взять из табл. 1-3 (номер варианта соответствует порядковому номеру студента в журнале).
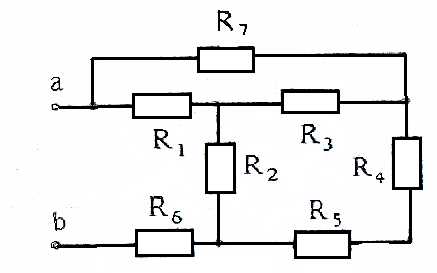
Рисунок 20
Таблица 1.
| № | ||||||||||
| R7=0 | R4=∞ | R3=∞ | R1=0 | R1=∞ | R2=0 | R2=∞ | R7=0 | R4=0 R5=0 | R7=∞ | |
| № | ||||||||||
| R3=0 | R4=0 | R5=∞ | R6=0 | R1=∞ | R2=0 R6=0 | R2=∞ R1=0 | R7=0 R2=∞ | R4=0 R5=0 | R7=∞ |
Таблица 1
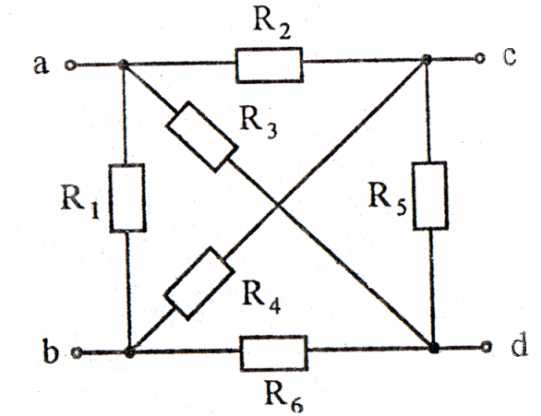
Рисунок 21
Таблица 2
| № | ||||||||||
| R5=0 | R5=∞ | R4=0 | R3=0 | R3=0 | R1=∞ | R5=0 | R2=0 | R4=0 | R2=0 | |
| Rab | Rab | Rab | Rcd | Rac | Rbd | Rac | Rcd | Rad | Rbc | |
| № | ||||||||||
| R3=∞ | R4=0 R6=∞ | R6=∞ | R6=0 | R1=∞ | R2=0 R6=0 | R2=∞ R1=0 | R7=0 R2=∞ | R4=0 R5=0 | R5=∞ R1=0 | |
| Rac | Rbd | Rac | Rcd | Rad | Rbc | Rab | Rab | Rab | Rcd |
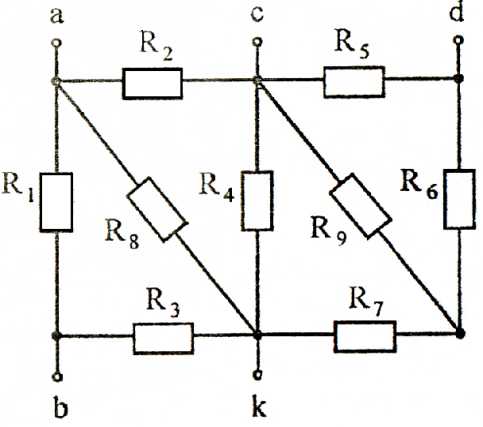
Рисунок 22
Таблица 3
| № | ||||||||||
| R9=0 | R4=∞ | R7=∞ | R8=0 | R8=0 R9=0 | R8=0 R9=∞ | R8=0 | R2=0 R7=0 | R6=∞ | R3=∞ R8=0 | |
| Rab | Rab | Rab | Rcd | Rac | Rkd | Rcd | Rcb | Rck | Rak | |
| № | ||||||||||
| R8=0 | R8=0 R9=0 | R8=0 R9=∞ | R8=0 | R2=0 R7=0 | R6=∞ | R3=∞ R8=0 | R9=0 | R4=∞ | R7=∞ | |
| Rab | Rab | Rab | Rcd | Rac | Rkd | Rcd | Rcb | Rck | Rak |
Задача 2
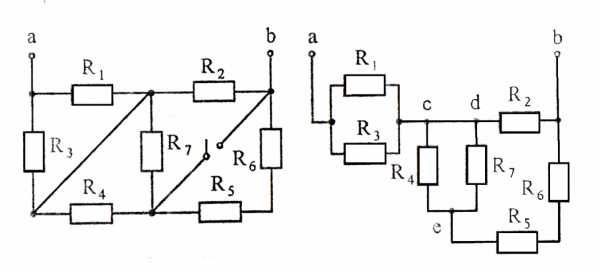
Используя преобразования параллельных ветвей, упростить схему до трёхконтурной. Составить уравнения по законам Кирхгофа для эквивалентной схемы. Номер схемы соответствует порядковому номеру студента в журнале (номеру 11 соответствует 1 схема, 12 – 2 схема, и т.д.).
Схемы к задаче 2:


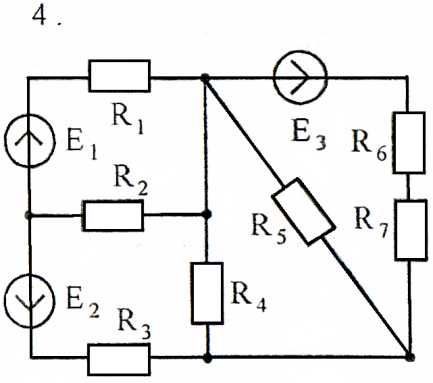

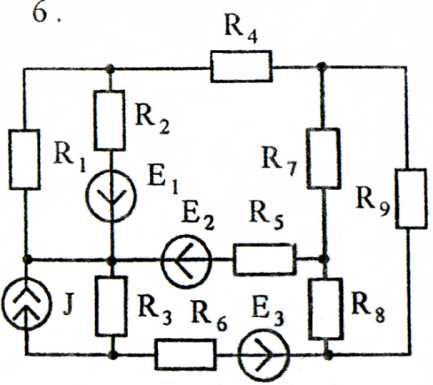

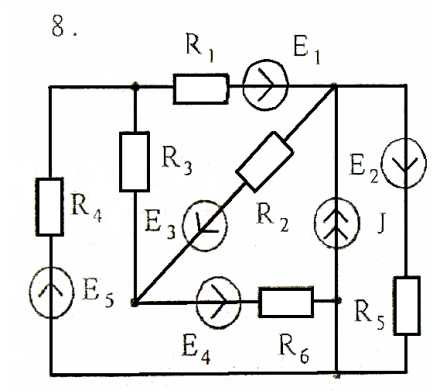
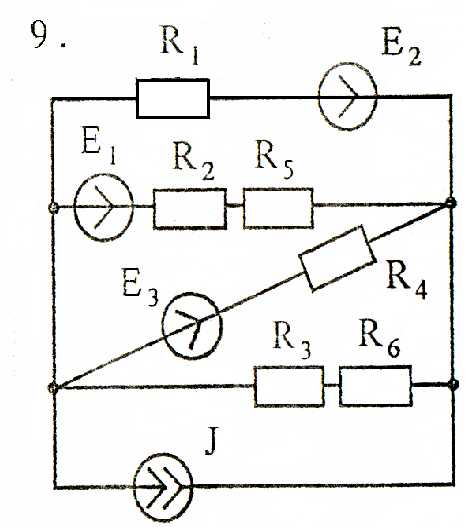
Задача 3
Используя взаимные преобразования активных треугольника и звезды, упростить схему до трёхконтурной. Номер схемы соответствует порядковому номеру студента в журнале (номеру 11 соответствует 1 схема, 12 – 2 схема, и т.д.).
Схемы к задаче 3:
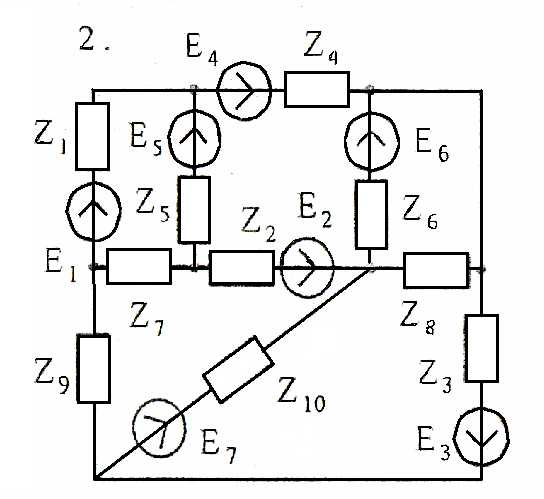
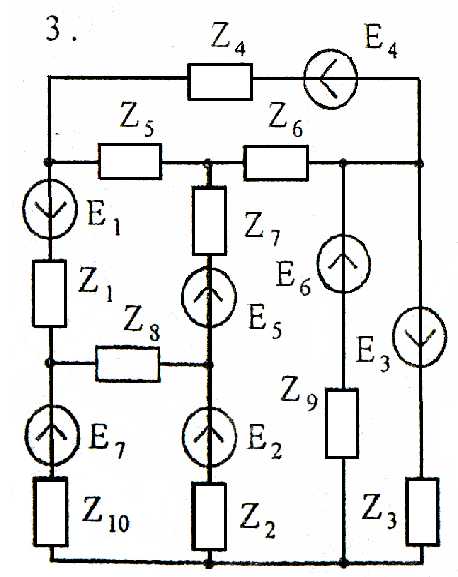
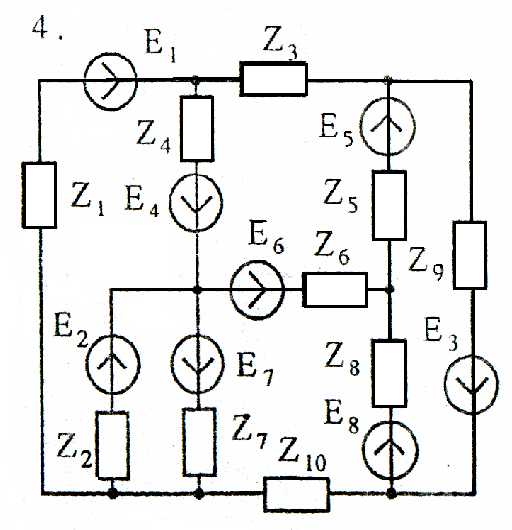
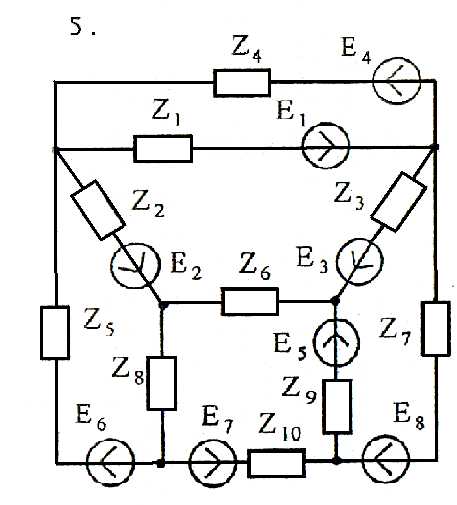

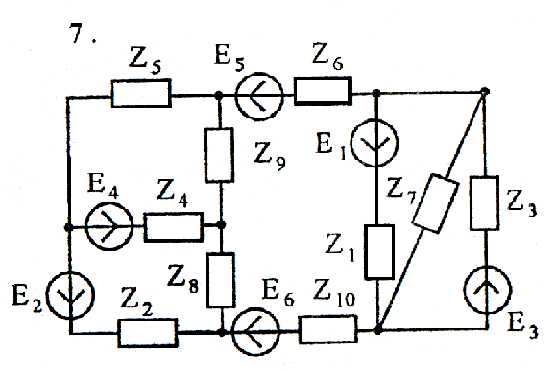
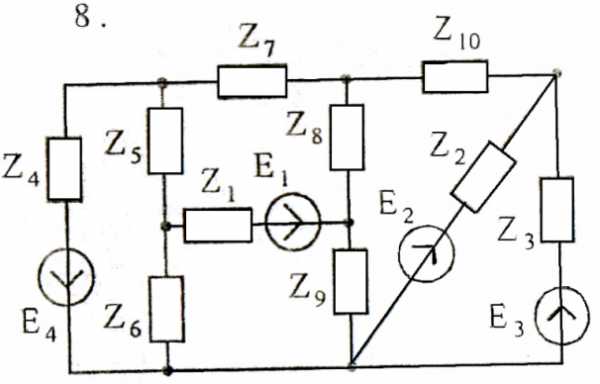


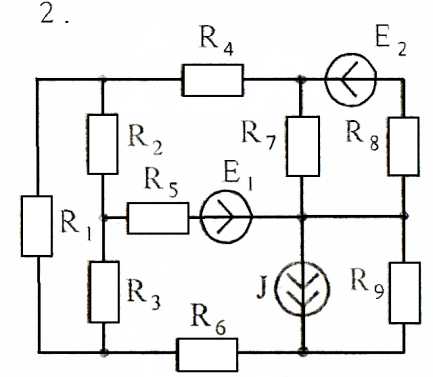
Задача 4
В цепи (рисунок 23) три источника питания, ЭДС которых равны E1,E2,E3; их внутренние сопротивления соответственно равны R01 = 0,1 Ом; R02 = 0,2 Ом; R03 = 0, 3 Ом. Отдельные ветви цепи могут быть разомкнуты при помощи рубильников P1, P2, P3, P4, P5, P6. Сопротивления в пассивных ветвях R1 = 1,5 Ом; R2 = 21 Ом; R3 = 2,5 Ом; R4 = 2 Ом; R5 = R6 = R7 = R8 = 3 Ом. Определить по методу непосредственного применения законов Кирхгофа токи во всех ветвях и режимы работы источников энергии. Составить баланс мощностей. Данные взять из табл. 4 (номер варианта соответствует порядковому номеру студента в журнале, номеру 11 соответствует 1 вариант, 12 – 2 вариант, и т.д.).

Рисунок 23
Таблица 4
| Вариант | Данные к задаче 4 | |||
| E1,В | E2,В | E3,В | Разомкнуты рубильники | |
| P4,P5,P6 | ||||
| P2,P5,P6 | ||||
| P2,P4,P5 | ||||
| P1,P4,P6 | ||||
| P2,P3,P6 | ||||
| P4,P5,P6 | ||||
| P2,P4,P5 | ||||
| P2,P3,P6 | ||||
| P1,P4,P6 | ||||
| P2,P5,P6 | ||||
| P4,P5,P6 | ||||
| P2,P5,P6 | ||||
| P2,P4,P5 | ||||
| P1,P4,P6 | ||||
| P2,P3,P6 | ||||
| P2,P3,P6 | ||||
| P1,P4,P6 | ||||
| P2,P5,P6 | ||||
| P4,P5,P6 | ||||
| P2,P5,P6 |
Задание №2. Цепи однофазного синусоидального тока
Задачей расчёта электрической цепи является определение токов в её ветвях, напряжений на участках цепи или потенциалов узлов. При этом задаются: конфигурация цепи, параметры ее элементов и ЭДС, источников. Для расчёта токов в сложных электрических цепях применяются методы уравнений Кирхгофа, контурных токов, узловых потенциалов, эквивалентного генератора.
Теоретические положения
Метод уравнений Кирхгофа
Расчёт линейных электрических цепей методом законов Кирхгофа сводится к решению систем алгебраических уравнений относительно неизвестных токов. Так как число неизвестных токов в заданной схеме равно числу ветвей n этой схемы, то система алгебраических уравнений должна иметь n-й порядок.
Пусть k – число узлов схемы. Из принципа непрерывности токов следует, что число линейно независимых уравнений, которые можно составить по первому закону Кирхгофа, равно (k-1).Недостающие уравнения, число которых [n-(k-1)], составляются по второму закону Кирхгофа для независимых контуров, не содержащих источников тока. Контуры являются независимыми, если в каждый из них входит ветвь, не входящая во все остальные.
Рассмотрим на примере расчёт токов в схеме (рисунок 24), которая содержит 6 ветвей, 4 узла и 3 независимых контура. Выберем произвольно направление токов в ветвях и направление обхода независимых контуров. Первые три уравнения (4 - 1 = 3) запишем по первому закону Кирхгофа, а оставшиеся три (6 - 3 = 3) – по второму закону Кирхгофа:
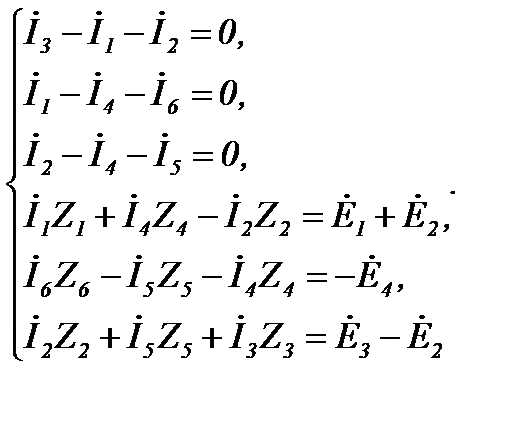

Рисунок 24
Решение полученной системы уравнений дает искомые токи. Если цепь содержит m ветвей с источниками тока, то число неизвестных токов уменьшается до (n-m). По первому закону Кирхгофа число уравнений остается без изменений (k-1), а по второму закону Кирхгофа она соответственно уменьшается на число ветвей с источниками тока [n-(k-1)-m].
Так, для схемы Рисунок 25, содержащей 6 ветвей и один источник тока, необходимо составить три уравнения по первому закону Кирхгофа и два – по второму.

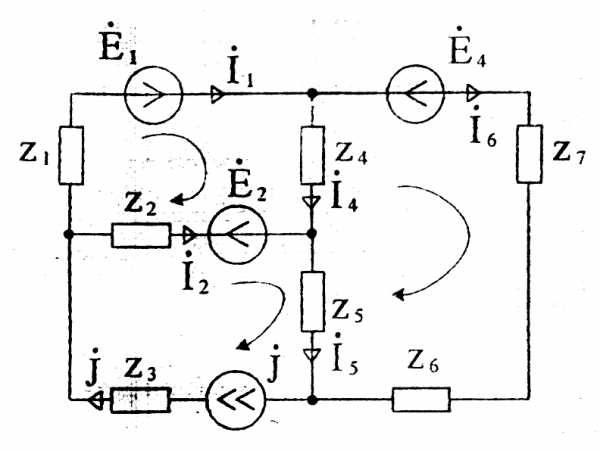
Рисунок 25
Если в результате расчётов какой-либо ток получился отрицательным, это значит, что его действительное направление противоположно выбранному.
К недостатку рассмотренного метода следует отнести высокий порядок системы уравнений для расчёта сложных электрических цепей.
Метод контурных токов
Расчёт разветвлённой цепи может быть сведён к решению всего [n-(k-1)] уравнений, составленных по второму закону Кирхгофа. Для этого цепь рассматривается как совокупность независимых соприкасающихся контуров и производится условная замена неизвестных токов в ветвях на токи, протекающие по замкнутым контурам. В уравнения, составленные по второму закону Кирхгофа, вводятся токи в независимых контурах – контурные токи.
Действительные токи в ветвях, принадлежащих только одному контуру, равны соответствующим контурным токам (но могут отличаться от них по направлению). Токи в общих для двух или нескольких контуров ветвях определяются как алгебраическая сумма соответствующих контурных токов. Первый закон Кирхгофа при этом будет выполняться автоматически. Направление контурных токов выбирается произвольно, а обход контуров условимся проводить в направлении контурных токов.
Для цепи с источниками ЭДС система уравнений, составленных для независимых контуров по второму закону Кирхгофа, содержит уравнения типа
где – контурные токи;
– сумма сопротивлений ветвей, образующих независимый m-й контур (контурное сопротивление), ;
– сумма ЭДС этого контура;
Zmq – сопротивление ветви, общей для m-го и q-контура (сопротивление связи).
Если в общих (смежных) ветвях направления контурных токов совпадают, то сопротивление связи берётся положительным, если токи направлены встречно, то – отрицательным. Контурные сопротивления всегда принимаются положительными.
При записи правой части уравнений ЭДС, направления которых совпадают с принятым направлением контурного тока (обхода), принимаются положительными, а при направленных противоположно – отрицательными.
Запишем систему уравнений по методу контурных токов для схемы Рисунок 26:
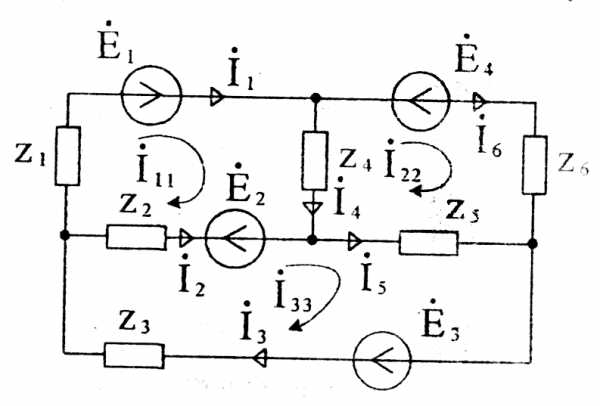
Рисунок 26

где

После решения системы уравнений относительно контурных токов находим токи в ветвях:
При наличии ветви с источником тока выбирается дополнительный контур, включающий эту цепь. Уравнение для дополнительного контура не составляется, т.к. контурный ток равен току источника. Падения напряжения на сопротивлениях связи с другими от источника тока (контурного тока) учитываются. Так, для цепи (рисунок 27) система уравнений имеет вид

Рисунок 27
где.
Метод узловых потенциалов
Если в разветвлённой электрической цепи число узловбез единицы меньше, чем число независимых контуров (k-1)<[n-(k-1)], удобно воспользоваться методом узловых потенциалов. Он сводится к составлению и решению системы алгебраических уравнений (k-1)-го порядка относительно неизвестных потенциалов (узловых потенциалов). При этом потенциал одного из узлов схемы полагают равным нулю.
Уравнения с узловыми потенциалами вытекают из первого закона Кирхгофа. После нахождения неизвестных потенциалов определяют токи в ветвях по закону Ома.
Уравнения, входящие в систему, являются однотипными и для m-го узла имеют следующий вид:
где – сумма проводимостей всех ветвей, сходящихся в m-ом узле, ;
– проводимость ветви, соединяющей узел m c узлом q. Если между какими-либо узлами нет ветви, то соответствующая проводимость равна нулю;
– ЭДС источников, расположенных в ветви между узлами m или q.
При этом ЭДС, направленные к узлу m (относительно которого составляется уравнение), берутся положительными, а направленные от этого узла – отрицательными.
Составим систему уравнений для схемы Рисунок 28, полагая :
где
Рисунок 28
После определения потенциалов находим токи по закону Ома:
Если ветвь содержит источник тока, то её проводимость равна нулю, т.к. внутреннее сопротивление источника тока равно бесконечности. Если к m-му узлу подтекает ток от источника тока, то он должен быть включен в правую часть уравнения со знаком «плюс», если утекает, то со знаком «минус». Так, для цепи (рисунок 29) система уравнений имеет вид при :


Рисунок 29
Баланс мощностей
В любой электрической цепи по закону сохранения энергии количество вырабатываемой за единицу времени энергии источников должно равняться мощности потребителей:
Рист=Рпотр, Qист=Qпотр.
Любое нарушение этих соотношений указывает на неточность проведённых вычислений.
Активную и реактивную мощности источников можно найти как действительную и мнимую части полной комплексной мощности источников:
где – сопряженный комплекс тока
Если направление тока совпадает с направлением источника ЭДС, то произведение входит в левую часть равенства со знаком «плюс», в противном случае – со знаком «минус».
Если электрическая цепь содержит источник тока j, то
где – напряжение на зажимах источника тока.
Активная мощность потребителей:
где Iq – действующее значение тока q-й ветви, содержащей активное сопротивление Rq.
Реактивная мощность потребителей:
Для индуктивности произведение I2XL входит в сумму со знаком «плюс», для емкости I2Xc – со знаком «минус».
Пример составления баланса мощности
В цепи (рисунок 30) с параметрами:
R1=15 Ом; R2=8 Ом; R3=20 Ом;
XL=20 Ом; XC1 =10 Ом; XC2 =15 Ом,
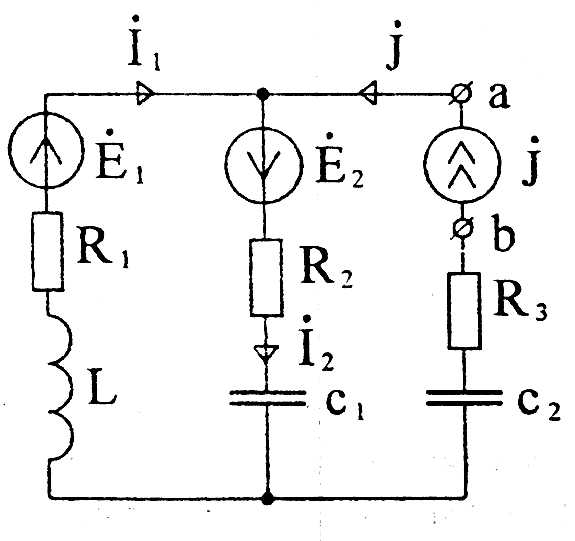
Рисунок 30
расчетным путем найдены токи:
Для составления баланса мощности найдем напряжение на зажимах источника тока (по второму закону Кирхгофа):
Тогда
Отсюда
Рист=8605,18 Вт; Qист=-2420,56 ВАр.
Найдём активную мощность потребителей:
Рпотр=13,7582 . 15+21,6952 . 8+102 . 20=8604,62 Вт.
Реактивная мощность потребителей:
Qпотр=13,7582 . 20 - 21,6952 . 10 - 102 . 15= -2421,08 BАp.
Баланс мощности выполняется в пределах допустимой погрешности расчета (до 3%).
Задание на расчетно-графическую работу
Шифр задания состоит из трех чисел – номеров строк из табл. 5-7. Все три числа шифра соответствуют порядковому номеру студента в журнале (номеру 11 соответствует 1 вариант, 12 – 2 вариант, и т.д.). При решении задачи необходимо:
1. Используя данные табл. 5, 6, найти все токи электрической цепи:
а) методом контурных токов;
б) методом узловых потенциалов.
2. Составить баланс мощности.
3. Рассчитать ток в одной из ветвей цепи методом эквивалентного генератора. Номер ветви выбирается по первой цифре шифра.
Таблица 5
Таблица 6
| Вариант | Z1, Ом | Z2, Ом | Z3, Ом | Z4, Ом |
cyberpedia.su
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
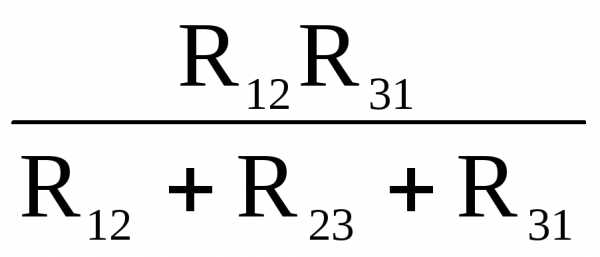 ;
;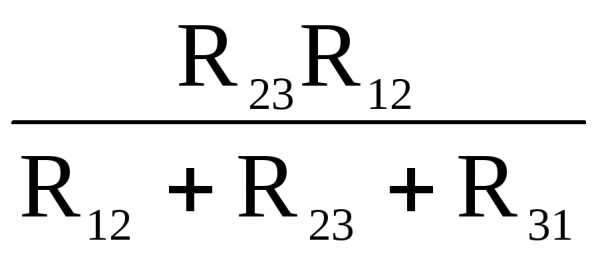 ;
;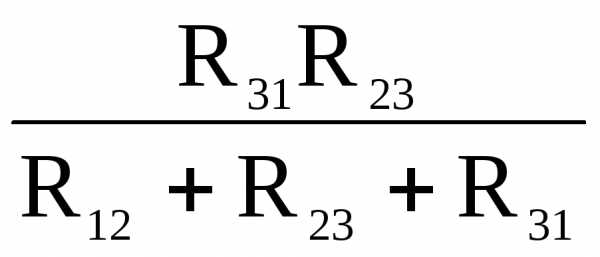 .
.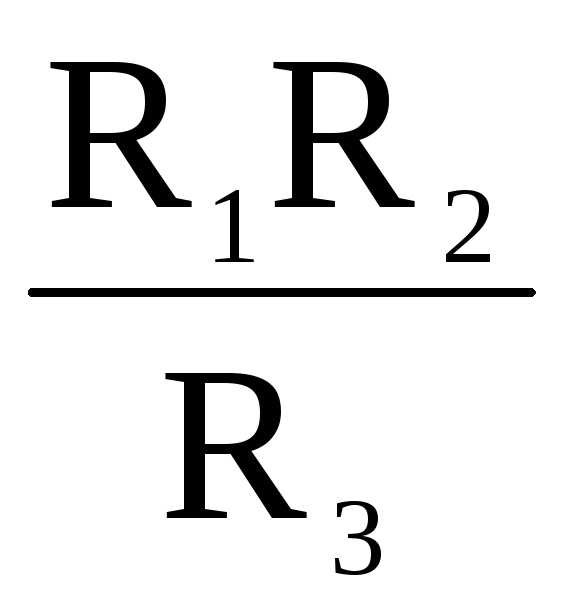 ;
;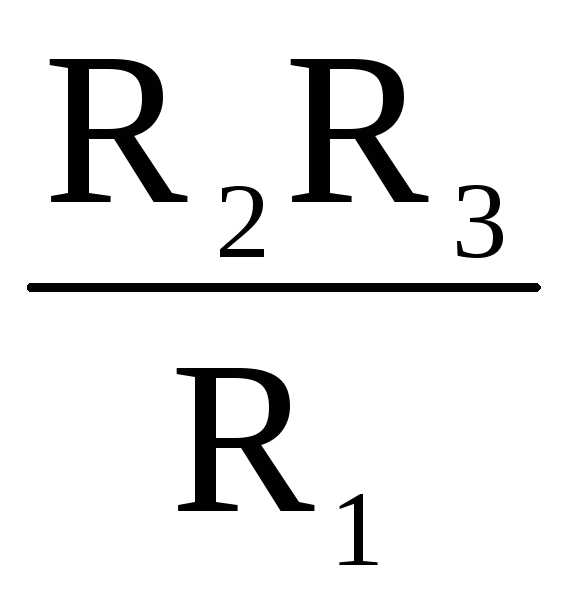 ;
; .
. Рис. 1.21
Рис. 1.21