Заряд и сила тока формула: Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца

Содержание

Конспект «Сила тока. Напряжение» — УчительPRO

«Сила тока. Напряжение»

Сила тока

Характеристикой тока в цепи служит величина, называемая силой тока (I). Сила тока – физическая величина, характеризующая скорость прохождения заряда через проводник и равная отношению заряда q, прошедшeгo через пoперeчное сечение проводника за промежуток времени t, к этому промежутку времени: I = q/t. Единица измерения силы тока – 1 ампер (1 А).

Определение единицы силы тока основано на магнитном действии тока, в частности на взаимодействии параллельных проводников, по которым идёт электрический ток. Такие проводники притягиваются, если ток по ним идёт в одном направлении, и отталкиваются, если направление тока в них противоположное.

За единицу силы тока принимают такую силу тока, при которой отрезки параллельных проводников длиной 1 м, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой 2*10^-7Н. Эта единица и называется ампером (1 А).

Зная формулу силы тока, можно получить единицу электрического заряда: 1 Кл = 1А * 1с.

Амперметр

Прибор, с помощью которого измеряют силу тока в цепи, называется амперметром. Его работа основана на магнитном действии тока. Основные части амперметра магнит и катушка. При прохождении по катушке электрического тока она в результате взаимодействия с магнитом, поворачивается и поворачивает соединённую с ней стрелку. Чем больше сила тока, проходящего через катушку, тем сильнее она взаимодействует с магнитом, тем больше угол поворота стрелки. Амперметр включается в цепь последовательно с тем прибором, силу тока в котором нужно измерить, и потому он имеет малое внутреннее сопротивление, которое практически не влияет на сопротивление цепи и на силу тока в цепи.

У клемм амперметра стоят знаки «+» и «—», при включении амперметра в цепь клемма со знаком «+» присоединяется к положительному пoлюсу источника тока, а клемма со знаком «—» к отрицательному пoлюсу истoчникa тока.

Напряжение

Источник тока создаёт электрическое поле, которое приводит в движение электрические заряды. Характеристикой источника тока служит величина, называемая напряжением. Чем оно больше, тем сильнее созданное им поле. Напряжение характеризует работу, которую совершает электрическое поле по перемещению электрического заряда.

Напряжение (U) — это физическая величина, равную отношению работы (А) электрического поля по перемещению электрического заряда к заряду (q): U = A/q.

Возможно другое определение понятия напряжения. Если числитель и знаменатель в формуле напряжения умножить на время движения заряда (t), то получим: U = At/qt. В числителе этой дроби стоит мощность тока (Р), а в знаменателе — сила тока (I). Получается формула: U = Р/I, т.е. напряжение — это физическая величина, равная отношению мощности электрического тока к силе тока в цепи.

Единица напряжения: [U] = 1 Дж/1 Кл = 1 В (один вольт).

Вольтметр

Напряжение измеряют вольтметром. Он имеет такое же устройство, что и амперметр и такой же принцип действия, но он подключается параллельно тому участку цепи, напряжение на котором хотят. Внутреннее сопротивление вольтметра достаточно большое, соответственно проходящий через него ток мал по сравнению с током в цепи.

У клемм вольтметра стоят знаки «+» и «—», при включении вольтметра в цепь клeмма со знаком «+» присоединяется к положительному полюсу источника тока, а клеммa со знаком «—» к отрицательному полюсу источника тока.

Формулы и определения.

1. Все проводники, используемые в электрических цепях, имеют условные обозначения для изображения на схемах и могут образовывать последовательные, параллельные и смешанные соединения.

2. Мощность тока – физическая величинa, хаpактеpизующая скорость превращения электрической энергии в другие её виды. Единица для измерения – 1 ватт (1 Вт). Измерительный прибор – ваттметр.

3. Сила тока – физическaя вeличина, характеpизующaя скоpость прохождения заряда через проводник и равная отношению заряда, пpoшедшего через попеpeчное сечение проводника, ко времени перемещения. Единица – 1 ампер (1 А). Измерительный прибор – амперметр (подключают последовательно).

4. Электрическое напряжение – физическaя вeличина, характеризующая электрическое поле, создающее ток, и равная отношению мощности тока к его силе. Единица – 1 вольт (1 В). Измерительный прибор – вольтметр (подключают параллельно)

5. Работа тока – физичeская величинa, хаpактеpизующая количество электроэнергии, превратившейся в другие виды энергии. Единица – 1 джоуль (1 Дж). Измерительный прибор – электрический счётчик, использующий единицу 1 киловатт-час (1 кВт·ч).

Конспект урока «Сила тока. Напряжение».

Следующая тема: «Электрическое сопротивление».

Электричество — Основные формулы

1. Электростатика

1.1 Закон Кулона

q₁, q₂ — величины точечных зарядов,
r — расстояние между зарядами.

1.2 Напряженность поля уединенного точечного заряда

q — величина уединенного точечного заряда,
r — расстояние от заряда.

1.3 Потенциал точки в поле точечного заряда

q — величина уединенного точечного заряда,
r — расстояние от заряда.

1.4 Потенциальная энергия заряда в электростатическом поле

φ — потенциал,
q₁ — величина заряда.

1.5 Потенциальная энергия заряда q₁ в поле точечного заряда

q — величина уединенного точечного заряда, который создает поле,
r — расстояние между зарядами.

1.6 Теорема Гаусса

N — поток вектора напряженности электрического поля через замкнутую поверхность,
q — полный заряд, находящийся внутри замкнутой поверхности.

1.7 Напряженность электрического поля вблизи от поверхности проводника

σ — поверхностная плотность заряда.

1.8 Емкость плоского кондесатора

q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.

1.9 Энергия плоского кондесатора

q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.

2. Постоянный электрический ток

2.1 Закон Ома для участка однородной цепи

U — напряжение на концах участка,
R — сопротивление участка цепи.

2.2 Закон Ома для замкнутой цепи с источником тока

— ЭДС (электродвижущая сила),
r — внутреннее сопротивление источника ЭДС.

2.3 Работа постоянного тока

U — напряжение на концах участка цепи,
t — время, за которое совершается работа.

2.4 Закон Джоуля-Ленца

Q — теплота,
R — сопротивление проводника,
t — время, за которое выделяется теплота.

2.5 Полная мощность, развиваемая источником тока

— ЭДС источника тока,
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.6 Полезная мощность

— ЭДС источника тока,
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.7 Коэффициент полезного действия источника тока

R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.8 Первое правило Кирхгофа

n — число проводников, сходящихся в узле;
I_k — сила тока в k-м проводнике.

2.9 Второе правило Кирхгофа

n — число неразветвленных участков в контуре;
m — число ЭДС в контуре.

Формула силы тока в физике

Определение и формула силы тока

Определение

Электрическим током называют упорядоченное движение носителей зарядов. В металлах таковыми являются электроны, отрицательно
заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.

Силой тока (током) через некоторую поверхность S называют скалярную физическую величину, которую обозначают I, равную:

где q – заряд, проходящий сквозь поверхность S, t – время прохождения заряда. Выражение (1) определяет величину силы тока в
момент времени t (мгновенное значение величины силы тока).

Некоторые виды силы тока

Ток носит название постоянного, если его сила и направление с течением времени не изменяются, тогда:

Формула (2) показывает, что сила постоянного тока равна заряду, который проходит сквозь поверхность S в единицу времени.

Если ток является переменным, то выделяют мгновенную силу тока (1), амплитудную силу тока и эффективную силу тока.
Эффективной величиной силы переменного тока (I_eff) называют такую силу постоянного тока, которая выполнит работу равную
работе переменного тока в течение одного периода (T):

Если переменный ток можно представить как синусоидальный:

то I_m – амплитуда силы тока ( – частота силы переменного тока).

Плотность тока

Распределение электрического тока по сечению проводника характеризуют при помощи вектора плотности тока
(). При этом:

где – угол между векторами
и
(
– нормаль к элементу поверхности dS),
j_n – проекция вектора плотности тока на направление нормали ().

Сила тока в проводнике определяется при помощи формулы:

где интегрирование в выражении (6) проводится по всему поперечному сечению проводника S

Для постоянного тока имеем:

Если рассматривать два проводника с сечениями S₁ и S₂ и постоянными токами, то выполняется соотношение:

Сила тока в соединениях проводников

При последовательном соединении проводников сила тока в каждом из них одинакова:

При параллельном соединении проводников сила тока (I) вычисляется как сумма токов в каждом проводнике (I_i):

Закон Ома

Сила тока входит в один из основных законов постоянного тока – закон Ома (для участка цепи):

где —
– разность потенциалов на концах, рассматриваемого участка,
— ЭДС источника, который входит в участок цепи, R – сопротивление участка цепи.

Единицы измерения силы тока

Основной единицей измерения силы тока в системе СИ является: [I]=A(ампер)=Кл/с

Примеры решения задач

Пример

Задание. Какой заряд (q) проходит через поперечное сечение проводника за промежуток времени от
t₁=2c до t₂=6c, если сила тока изменяется в соответствии с уравнением: I=2+t, где сила
тока в амперах, время в секундах?

Решение. За основу решения задачи примем определение мгновенной силы тока:

В таком случае, заряд, который проходит через поперечное сечение проводника, равен:

Подставим в выражение (1.2) уравнение для силы тока из условий задачи, примем во внимания границы изменения участка времени:

(Кл)

Ответ. q=24 Кл

Пример

Задание. Плоский конденсатор составлен из двух квадратных пластин со стороной A,
находящихся на расстоянии dдруг от друга. Этот конденсатор подключен к источнику постоянного напряжения U.
Конденсатор погружают в сосуд с керосином (пластины конденсатора вертикальны) со скоростью v=const. Какова сила тока,
которая будет течь по подводящим проводам в описанном выше процессе. Считать, что диэлектрическая проницаемость керосина равна
.

Решение. Основой для решения задачи станет формул для вычисления силы тока вида:

При погружении в керосин на глубину xописанной выше системы мы получаем два конденсатора, соединенных параллельно (над керосином и в керосине)
рис. 2. Для такой системы конденсаторов напряжение на каждом из них одинаково, поэтому уравнение для изменения заряда при движении
удобно искать в виде:

Емкость при параллельном соединении конденсаторов равна:

Формула для расчета емкостей C₁ и C₂ плоских конденсаторов имеет вид:

где ₀ – электрическая постоянная, переменной величиной при погружении
системы в керосин является площадь обкладок S:

Из выражений (2.4), (2.5) и условий задачи имеем:

Тогда подставив dC в формулу для силы тока (2.1) получаем:

Ответ.

Постоянный электрический ток. Сила тока. Напряжение. Электрическое сопротивление. Закон Ома для участка электрической цепи

1. Электрическим током называют упорядоченное движение заряженных частиц.

Для того чтобы в проводнике существовал электрический ток, необходимы два условия: наличие свободных заряженных частиц и электрического поля, которое создаёт их направленное движение.

При существовании тока в разных средах: в металлах, жидкостях, газах — электрический заряд переносится разными частицами. В металлах этими частицами являются электроны, в жидкостях заряд переносится ионами, в газах — электронами, положительными и отрицательными ионами.

Дистиллированная вода не проводит электрический ток, поскольку она не содержит свободных зарядов. Если в воду добавить поваренную соль или медный купорос, то в ней появятся свободные заряды, и она станет проводником электрического тока. В растворе поваренной соли в воде происходит электролитическая диссоциация — процесс разложения молекулы поваренной соли на положительный ион натрия и отрицательный ион хлора. Если в сосуд с раствором поваренной соли поместить две металлические пластины, соединённые с источником тока (рис. 79), то положительный ион натрия в электрическом поле будет двигаться к пластине, соединенной с отрицательным полюсом источника тока, называемым катодом, а отрицательный ион хлора — с положительным полюсом источника тока, называемым анодом.

Газы в обычных условиях тоже не проводят электрический ток, так как в них нет свободных зарядов. Однако если в воздушный промежуток между двумя металлическими пластинами, соединёнными с источником тока, внести зажжённую спичку или спиртовку, то газ станет проводником и гальванометр зафиксирует протекание тока но цепи. При внесении пламени в воздушный промежуток между пластинами происходит ионизация газа (рис. 80). При этом от атома «отрываются» электроны и образуется положительный ион. Во время движения электрон может присоединиться к нейтральному атому и образовать отрицательный ион. Положительные ионы движутся к отрицательному электроду, а отрицательные ионы и электроны — к положительному электроду.

2. Направленное движение зарядов обеспечивается электрическим полем. Электрическое поле в проводниках создаётся и поддерживается источником тока. В источнике тока совершается работа по разделению положительно и отрицательно заряженных частиц. Эти частицы накапливаются на полюсах источника тока. Один полюс источника заряжается положительно, другой — отрицательно. Между полюсами источника образуется электрическое поле, под действием которого заряженные частицы начинают двигаться упорядоченно.

В источнике тока совершается работа при разделении заряженных частиц. При этом различные виды энергии превращаются в электрическую энергию. В электрофорной машине в электрическую энергию превращается механическая энергия, в гальваническом элементе — химическая.

3. Электрический ток, проходя по цепи, производит различные действия. Тепловое действие электрического тока заключается в том, что при его прохождении по проводнику в нём выделяется некоторое количество теплоты. Пример применения теплового действия тока — электронагревательные элементы чайников, электроплит, утюгов и пр. В ряде случаев температура проводника нагревается настолько сильно, что можно наблюдать его свечение. Это происходит в электрических лампочках накаливания.

Магнитное действие электрического тока проявляется в том, что вокруг проводника с током возникает магнитное поле, которое, действуя на магнитную стрелку, расположенную рядом с проводником, заставляет её поворачиваться (рис. 81).

Благодаря магнитному действию тока можно превратить железный гвоздь в электромагнит, намотав на него провод, соединённый с источником тока. При пропускании по проводу электрического тока гвоздь будет притягивать железные предметы.

Химическое действие электрического тока проявляется в том, что при его прохождении в жидкости на электроде выделяется вещество. Если в стакан с раствором медного купороса поместить угольные электроды и присоединить их к источнику тока, то, вынув через некоторое время эти электроды из раствора, можно обнаружить на электроде, присоединённом к отрицательному полюсу источника (на катоде), слой чистой меди.

Это происходит потому, что между электродами существует электрическое поле, в котором ионы (положительно заряженные ионы меди и отрицательно заряженные ионы кислотного остатка) движутся к соответствующим электродам. Достигнув отрицательного электрода, ионы меди получают недостающие электроны, при этом восстанавливается чистая медь.

4. Характеристикой тока в цепи служит величина, называемая силой тока \( (I) \). Силой тока называют физическую величину, равную отношению заряда \( q \), проходящего через поперечное сечение проводника за промежуток времени \( t \), к этому промежутку времени: \( I=q/t \).

За единицу силы тока принимают такую силу тока, при которой отрезки параллельных проводников длиной 1 м, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой 2·10^-7 Н.

Эта единица называется ампером (1 А).

Зная формулу силы тока, можно получить единицу электрического заряда: 1 Кл = 1 А · 1 с.

5. Прибор, с помощью которого измеряют силу тока в цепи, называется амперметром. Его работа основана на магнитном действии тока. Основные части амперметра магнит и катушка. При прохождении по катушке электрического тока она в результате взаимодействия с магнитом, поворачивается и поворачивает соединённую с ней стрелку. Чем больше сила тока, проходящего через катушку, тем сильнее она взаимодействует с магнитом, тем больше угол поворота стрелки. Амперметр включается в цепь последовательно с тем прибором, силу тока в котором нужно измерить (рис. 82), и потому он имеет малое внутреннее сопротивление, которое практически не влияет на сопротивление цепи и на силу тока в цепи.

У клемм амперметра стоят знаки «+» и «-», при включении амперметра в цепь клемма со знаком «+» присоединяется к положительному полюсу источника тока, а клемма со знаком «-» к отрицательному полюсу источника тока.

6. Источник тока создаёт электрическое поле, которое приводит в движение электрические заряды. Характеристикой источника тока служит величина, называемая напряжением. Чем оно больше, тем сильнее созданное им поле. Напряжение характеризует работу, которую совершает электрическое поле по перемещению электрического заряда, равного 1 Кл.

Напряжением \( U \) называют физическую величину, равную отношению работы \( (A) \) электрического поля по перемещению электрического заряда к заряду \( (q) \): \( U=A/q \).

Возможно другое определение понятия напряжения. Если числитель и знаменатель в формуле напряжения умножить на время движения заряда \( (t) \), то получим: \( U=At/qt \). В числителе этой дроби стоит мощность тока \( (P) \), а в знаменателе — сила тока \( (I) \): \( U=P/I \), т.е. напряжение — физическая величина, равная отношению мощности электрического тока к силе тока в цепи.

Единица напряжения: \( [U]=[A]/[q] \); \( [U] \) = 1 Дж/1 Кл = 1 В (один вольт).

Напряжение измеряют вольтметром. Он имеет такое же устройство, что и амперметр и такой же принцип действия, но он подключается параллельно тому участку цепи, напряжение на котором хотят измерить (рис. 83). Внутреннее сопротивление вольтметра достаточно большое, соответственно проходящий через него ток мал по сравнению с током в цепи.

У клемм вольтметра стоят знаки «+» и «-», при включении вольтметра в цепь клемма со знаком «+» присоединяется к положительному полюсу источника тока, а клемма со знаком «-» к отрицательному полюсу источника тока.

7. Собрав электрическую цепь, состоящую из источника тока, резистора, амперметра, вольтметра, ключа (рис. 83), можно показать, что сила тока \( (I) \), протекающего через резистор, прямо пропорциональна напряжению \( (U) \) на его концах: \( I\sim U \). Отношение напряжения к силе тока \( U/I \) — есть величина постоянная. Если заменить резистор, включённый в цепь, другим резистором и повторить опыт, получим тот же результат: сила тока в резисторе прямо пропорциональна напряжению на его концах, а отношение напряжения к силе тока есть величина постоянная. Только в этом случае значение отношения напряжения к силе тока будет отличаться от отношения этих величин в первом опыте. Причиной этого является то, что в цепь включались разные резисторы. Следовательно, существует физическая величина, характеризующая свойства проводника (резистора), по которому течёт электрический ток. Эту величину называют электрическим сопротивлением проводника, или просто сопротивлением. Обозначается сопротивление буквой \( R \).

Сопротивлением проводника \( (R) \) называют физическую величину, равную отношению напряжения \( (U) \) на концах проводника к силе тока \( (I) \) в нём. \( R=U/I \).

За единицу сопротивления принимают Ом (1 Ом).

Один Ом — сопротивление такого проводника, в котором сила тока равна 1 А при напряжении на его концах 1 В: 1 Ом = 1 В/1 А.

Причина того, что проводник обладает сопротивлением, заключается в том, что направленному движению электрических зарядов в нём препятствуют ионы кристаллической решетки, совершающие беспорядочное движение. Соответственно, скорость направленного движения зарядов уменьшается.

8. Электрическое сопротивление \( R \) прямо пропорционально длине проводника \( (l) \), обратно пропорционально площади его поперечного сечения \( (S) \) и зависит от материала проводника. Эта зависимость выражается формулой: \( R=\rho\frac{l}{S} \). \( \rho \) — величина, характеризующая материал, из которого сделан проводник. Эта величина называется удельным сопротивлением проводника, её значение равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м².

Единицей удельного сопротивления проводника служит: \( [\rho]=\frac{[R][S]}{[l]} \); \( [\rho]=\frac{1Ом\cdot1м^2}{1м} \). Часто площадь поперечного сечения измеряют в мм², поэтому в справочниках значения удельного сопротивления проводника приводятся как в Ом·м, так и в \( \frac{Ом\cdotмм^2}{м} \).

Изменяя длину проводника, а следовательно его сопротивление, можно регулировать силу тока в цепи. Прибор, с помощью которого это можно сделать, называется реостатом (рис. 84).

9. Как показано выше, сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: \( I=\frac{U}{R} \). Этот закон, установленный экспериментально, называется законом Ома (для участка цепи): сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. На рисунке приведена схема электрической цепи, состоящей из источника тока, ключа и двух параллельно соединённых резисторов. Для измерения напряжения на резисторе \( R_2 \) вольтметр можно включить между точками

1) только Б и В
2) только А и В
3) Б и Г или Б и В
4) А и Г или А и В

2. На рисунке представлена электрическая цепь, состоящая из источника тока, резистора и двух амперметров. Сила тока, показываемая амперметром А₁, равна 0,5 А. Амперметр А₂ покажет силу тока

1) меньше 0,5 А
2) больше 0,5 А
3) 0,5 А
4) 0 А

3. Ученик исследовал зависимость силы тока в электроплитке от приложенного напряжения и получил следующие данные.

Проанализировав полученные значения, он высказал предположения:

А. Закон Ома справедлив для первых трёх измерений.
Б. Закон Ома справедлив для последних трёх измерений.

Какая(-ие) из высказанных учеником гипотез верна(-ы)?

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

4. На рисунке изображён график зависимости силы тока в проводнике от напряжения на его концах. Чему равно сопротивление проводника?

1) 0,25 Ом
2) 2 Ом
3) 4 Ом
4) 8 Ом

5. На диаграммах изображены значения силы тока и напряжения на концах двух проводников. Сравните сопротивления этих проводников.

1) \( R_1=R_2 \)
2) \( R_1=2R_2 \)
3) \( R_1=4R_2 \)
4) \( 4R_1=R_2 \)

6. На рисунке приведена столбчатая диаграмма. На ней представлены значения мощности тока для двух проводников (1) и (2) одинакового сопротивления. Сравните значения напряжения \( U_1 \) и \( U_2 \) на концах этих проводников.

1) \( U_2=\sqrt{3}U_1 \)
2) \( U_1=3U_2 \)
3) \( U_2=9U_1 \)
4) \( U_2=3U_1 \)

7. Необходимо экспериментально обнаружить зависимость электрического сопротивления круглого угольного стержня от его длины. Какую из указанных пар стержней можно использовать для этой цели?

1) А и Г
2) Б и В
3) Б и Г
4) В и Г

8. Два алюминиевых проводника одинаковой длины имеют разную площадь поперечного сечения: площадь поперечного сечения первого проводника 0,5 мм², а второго проводника 4 мм². Сопротивление какого из проводников больше и во сколько раз?

1) Сопротивление первого проводника в 64 раза больше, чем второго.
2) Сопротивление первого проводника в 8 раз больше, чем второго.
3) Сопротивление второго проводника в 64 раза больше, чем первого.
4) Сопротивление второго проводника в 8 раз больше, чем первого.

9. В течение 600 с через потребитель электрического тока проходит заряд 12 Кл. Чему равна сила тока в потребителе?

1) 0,02 А
2) 0,2 А
3) 5 А
4) 50 А

10. В таблице приведены результаты экспериментальных измерений площади поперечного сечения \( S \), длины \( L \) и электрического сопротивления \( R \) для трёх проводников, изготовленных из железа или никелина.

На основании проведённых измерений можно утверждать, что электрическое сопротивление проводника

1) зависит от материала проводника
2) не зависит от материала проводника
3) увеличивается при увеличении его длины
4) уменьшается при увеличении его площади поперечного сечения

11. Для изготовления резисторов использовался рулон нихромовой проволоки. Поочередно в цепь (см. рисунок) включали отрезки проволоки длиной 4 м, 8 м и 12 м. Для каждого случая измерялись напряжение и сила тока (см. таблицу).

Какой вывод можно сделать на основании проведённых исследований?

1) сопротивление проводника обратно пропорционально площади его поперечного сечения
2) сопротивление проводника прямо пропорционально его длине
3) сопротивление проводника зависит от силы тока в проводнике
4) сопротивление проводника зависит от напряжения на концах проводника
5) сила тока в проводнике обратно пропорциональна его сопротивлению

12. В справочнике физических свойств различных материалов представлена следующая таблица.

Используя данные таблицы, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) При равных размерах проводник из алюминия будет иметь меньшую массу и большее электрическое сопротивление по сравнению с проводником из меди.
2) Проводники из нихрома и латуни при одинаковых размерах будут иметь одинаковые электрические сопротивления.
3) Проводники из константана и никелина при одинаковых размерах будут иметь разные массы.
4) При замене никелиновой спирали электроплитки на нихромовую такого же размера электрическое сопротивление спирали уменьшится.
5) При равной площади поперечного сечения проводник из константана длиной 4 м будет иметь такое же электрическое сопротивление, что и проводник из никелина длиной 5 м.

Часть 2

13. Меняя электрическое напряжение на участке цепи, состоящем из никелинового проводника длиной 5 м, ученик полученные данные измерений силы тока и напряжения записал в таблицу. Чему равна площадь поперечного сечения проводника?

Ответы

Постоянный электрический ток. Сила тока. Напряжение. Электрическое сопротивление. Закон Ома для участка электрической цепи

5 (100%) 2 votes

Сила тока ?. Формула силы тока. Как обозначается ? единица измерения силы тока?

Автор Даниил Леонидович На чтение 5 мин. Просмотров 2.8k. Опубликовано 18 ноября

Электрический ток — это направленный поток отрицательно заряженных частиц. Величину электрического тока определяют по числу электронов, протекающих сквозь проводник с неким поперечным сечением за определенную единицу времени.

Однако в полной мере охарактеризовать ток только движением электронов невозможно. Он также имеет другие параметры. Действительно, объем электричества, равного одному кулону способно проходить через металлический проводник в течение одной секунды или другого промежутка времени.

Если принять во внимание временной промежуток как характеристику, то можно увидеть, что интенсивность потоков в разных случаях будет не одинаковой. Тот объем, который можно пропустить сквозь проводник за секунду именуют силой тока. В качестве обозначения используют Ампер, как международную единицу измерения.

Общее описание силы тока

Сила тока является объемом электрических зарядов, проходящих сквозь поперечные профили проводников в интервале времени, равному одной секунде. Как уже было выше сказано, что за единиц силы тока принимают Ампер, которая и принадлежит к Международной СИ, используемой во всех странах мира.

Один ампер равен силе изменения потока электричества при прохождении по параллельным, парным линейным проводникам бесконечной длины, имеют ничтожно малую площадь кругового сечения. Эти материалы находятся в вакууме друг от друга на расстоянии одного метра. Он вызывает силу взаимного влияние равную 2*10-7. Единица исчисления силы тока Ампер соответствует одному кулону, пройденному за одну секунду через поперечный профиль материала проводника.

В математическом исчислении характеристика выглядит как 1 А = 1 кулон/1 секунда. Величина показателя относительно большая, поэтому для бытовых электроприборов и микросхем применяют дополнительные единицы: 1 мА и 1 мкА, которые равны одной тысячной и одной миллионной части ампера.

Если известна величина электрозаряда, прошедшего сквозь проводник с нужным сечением за требуемый промежуток времени, то параметр можно выразить следующей формулой: l=q/t.

В замкнутой сети без ответвлений за одну секунду времени проходит одинаковое количество электронов в любом участке проводника. Поскольку заряды не могут накапливаться исключительно в одном участке электрической цепи, то его интенсивность не зависит от толщины и сечения кабеля.

Для более сложных цепей с ответвлениями такое утверждение также остается истинным. Но такое определение действует только для отдельных участков схемы, которые следует рассматривать как элементарная сеть.

Способы измерения силы тока

Для того чтобы узнать силу тока на требуемом участке цепи, одних теоретических вычислений не достаточно. Да, можно использовать формулы и узнать величину, но она будет приблизительной. Поскольку приборостроение, электроника и электрика — науки точные и не терпят погрешностей, был изобретен индукционный, а позднее электронный прибор, который способен показывать точные величины.

Амперметр предназначен для измерений силы тока на отдельных участках электрической цепи. Но значения, равные 1 Амперу и более можно увидеть только в силовых установках и сетях. Для снятия показаний с них используют специальные понижающие трансформаторы. Из курсов физики многие знают от чего зависит интенсивность действий электрического тока. Инициатором движения электронов является магнитное поле. От его силы зависит и мощность потока.

Ток подается на основные катушки, в которых создается индукция. С ее помощью во второстепенной катушке генерируется электричество меньшей величины. Показатель зависит от числа витков обмоток. Они прямо пропорциональны. Поэтому даже на крупных предприятиях, где напряжение достигает нескольких тысяч вольт применяют микроамперметры или миллиамперметры. Это связано, прежде всего, с безопасностью обслуживающего персонала.

Довольно часто в обиходе можно услышать термин мультиметр. Его отличие от амперметра заключается в возможности измерять несколько характеристик одновременно, тогда как амперметр является узкоспециализированным прибором.

Включают устройство в разрыв электрической цепи. При таком способе замеров, ток протекает через измеритель к потребителю. Следовательно, соединять прибор нужно до или после элемента нагрузки, так как в простой схеме без ответвлений он будет всегда одинаковым.

Существует ошибочное убеждение, что ток до потребителя и после не одинаковый, так как часть электричества тратится на компонента. Такое утверждение ошибочно, поскольку в ток представляет собой электромагнитный процесс, выполняемый в теле металлического проводника. Результатом становится упорядоченное движение электронов вдоль всей длины проводника. Но саму энергию переносят не электроны, а магнитное поле, которое окружает тело проводника.

Важно!
Через любой поперечный профиль металла простых электрических цепей проходит одинаковое количество электрического заряда. Сколько электронов вышло из положительного полюса источника питания, столько заходит в отрицательный полюс, пройдя через элемент нагрузки. В ходе движения электроны не могут расходоваться, как другие частицы материала. Они составляют единое целое с проводником и их количество всегда одинаковое.

Отличие напряжения от силы тока

Электричество, как и любая другая материя, имеет собственные характеристики, используемые для определения эффективности работы и контроля заданных параметров. В физике существуют такие понятия как «напряжение» и «сила тока». Они описывают одно и тоже явление, но сами по себе как показатели они отличаются друг от друга.

Такие различия заключены в принципе действия электричества. Под силой тока понимают объем потока электронов, способных пройти на расстояние одного метра за установленный интервал времени. Напряжение наоборот выражено в количестве потенциальной энергии. Оба понятия тесно связаны между собой. К внешним факторам влияния на них относят:

материал, из которого изготовлен проводник;
температура;
магнитное поле;
условия окружающей среды.

Отличия также заключаются в способах получения этих параметров. Когда на заряды проводника воздействует внешнее магнитное поле, формируется напряжение, которое генерирует поток между точками цепи. Так же специалисты выделяют отличия в энергопотреблении, называемым мощностью. Если напряжение характеризует параметры потенциальной энергии, то ток — кинетической.

Заключение

Сила тока является одним из важных параметров, характеризующих электричество. Он показывает, какой объем электрического заряда проходит через поперечный профиль металлического проводника. Данная характеристика широко применяется в электронике и энергетике.

формула формула мощности электрического тока

Электрический ток является физическим процессом. Если говорить упрощенно, то это упорядоченное движение заряженных частиц. Его протекание можно измерить и соответственно выразить в символьном и цифровом виде. Формула электрического тока, представляет собой выражение качественных и количественных параметров через сопротивление проводника, напряжение или разность потенциалов, а также через его силу. Так как любое перемещение чего-либо, подразумевает под собой совершение работы, то дополнительно можно вести разговор об электричестве используя формулу мощности электрического тока.

Основные понятия и формулы характеризующие электрический ток

Количественным параметром электрического тока является его сила, представляющая собой скалярную величину и выражающуюся в отношении заряда (принято обозначать буквой q) к периоду времени (t), за которое он пересекает сечение проводника. Следовательно, формула электрического тока, а если говорить правильно его сила, будет выглядеть следующим образом — I=q/t. Измеряется данный параметр в амперах. Так как скалярные величины являются действительными числами и определяются только значением, сила тока не может иметь отрицательный знак. С учетом того, что величина заряда не является постоянным параметром для разных электрических цепей, было введено понятие – плотность электрического тока (j), формула которой выглядят так – j=I/S, где S – площадь, пересекаемая зарядами. Следовательно, при увеличении силы тока и уменьшении поперечного сечения проводника плотность тока возрастает и наоборот. Как отмечалось выше, важными параметрами электричества, вернее электрической цепи являются напряжение в ней и сопротивление проводящих ток элементов.

Формула выражения силы электрического тока через сопротивление и напряжение

В отличие от фундаментальных исследований, в основе которых лежат теоретические выкладки данная зависимость была выведена практическим путем. Автором открытия является физик Ом, в честь которого закон и получил свое имя. По результатам своих опытов и экспериментов Ом пришел к выводу что сила тока (I) напрямую зависит от величины напряжения (U)и имеет обратную зависимость от сопротивления (R) элементов и деталей, включенных в электрическую цепь. Эту связь можно представить в виде – I=U/R. Путем несложных преобразований, формулы сопротивления и напряжения, выраженные через силу тока, будут выглядеть следующим образом – R=U/I и U=IxR, соответственно.

Формула силы электрического тока

Сопротивление электрического тока: формула

Формула напряжения электрического тока

Работа и мощность электрического тока

Формула мощности (Р) электрического тока напрямую зависит от его работы (А). Под работой тока подразумевается преобразование электрической энергии в механический, тепловой, световой или иной ее вид. Величина данного процесса напрямую зависит от времени его протекания, силы тока и напряжения в сети. Это можно выразить следующей формулой – А=IxUxt. Произведение (IxU) является ничем иным как мощностью. Следовательно, чем выше напряжение или сила тока в сети, тем большую мощность имеет электрический ток и большую работу он может совершить за единицу времени. Формула мощности электрического тока имеет следующий вид – Р=А/t или Р=IxU.

Работа электрического тока формула

Формула мощности электрического тока

Поэтому, если необходимо вычислить, какую работу производит ток, протекая по цепи в течение определенного времени, необходимо умножить мощность на временной промежуток, выраженный в секундах. Рассмотрим применение формул расчета работы и мощности электрического тока на примере электрического двигателя, подключенного к сети 220 В, а сила тока, измеренная амперметром для этого участка, составила 10А.

Р (мощность двигателя) = 10А (сила тока) х 220В (напряжение в сети) = 2200 Вт = 2,2 кВт.

Зная данный показатель, а также реальное или предполагаемое время функционирования электродвигателя можно определить какую работу он совершит за этот отрезок времени или другим словами сколько будет потрачено электроэнергии. Если двигатель был включен, например, 1 час, то можно найти искомое значение.

А (работа, совершенная двигателем) = 2,2 кВт (мощность) х 1 (время работы в часах) = 2,2 кВт ч. Именно этот показатель будет отражен на приборе учета расхода электроэнергии.

Исходя из того, что электрический ток является физическим процессом, то какой-либо его неизвестный параметр можно определить, зная его остальные характеристики. Приведем наиболее распространенные формулы для определения характеристик электрической цепи применяемые в электротехнике.

Напряжение или разность потенциалов

U = RxI
U = P/I
U = (P*R)^1/2

Сила электрического тока

Сопротивление

R = U / I
R = U²/ P
R = P / I²

Мощность

В заключение отметим, что приведенная информация справедлива для цепей с постоянным электрическим током. Формулы, применяемые для расчета характеристик переменного тока, будут отличаться за счет введения дополнительных переменных и характеристик свойственных данному типу электричества.

Заряд, ток и разница потенциалов

Символы цепей — вы встречали эти символы цепей в GCSE Physics.

Обычный ток течет по цепи от положительной (+) стороны ячейки к отрицательной (-). Однако электронов проходят по цепи в противоположном направлении от отрицательной (-) стороны ячейки к положительной (+).

Заряд, ток и разность потенциалов

Заряд (Q) — заряд измеряется в кулонах (Кл).

Один электрон несет заряд 1,6 x 10 ^-19 Кл.

Ток (I) — измеряется в амперах (А).

Ток — это скорость потока заряда . Ток в 1 А означает, что 1 кулон заряда проходит через точку в цепи каждую секунду. (1 A = 1 C s ^-1) Ток в цепи измеряется с помощью амперметра, который включен последовательно с интересующим компонентом в цепи.

I = ток в амперах, А
DQ = заряд в кулонах, К
Dt = время в секундах, с

Разность потенциалов (В) — измеряется в вольтах (В).

Потенциальная разница — это работа, выполненная на единицу оплаты . Разность потенциалов 1 В означает, что на один кулон заряда выполняется 1 джоуль работы. (1 В = 1 Дж C ^-1) Разность потенциалов в цепи измеряется с помощью вольтметра, который размещается параллельно с интересующим компонентом в цепи.

В = разность потенциалов в вольтах, В
Вт = выполненная работа или переданная энергия в джоулях, Дж
Q = заряд в кулонах, Кл

Сопротивление (Вт) — это отношение разности потенциалов на компоненте к току, протекающему через него, измеряется в омах (Вт).

R = сопротивление в Ом, Вт
В = разность потенциалов в вольтах, В
I = ток в амперах, А

Примеры;

Q1) Если все электроны несут заряд 1,6 x 10 ^-19 Кл, сколько электронов потребуется, чтобы получить общий заряд в один кулон?

Q2) Если ток 0.50 ампер протекает через цепь в течение 120 секунд. Сколько заряда будет передано в компонент в цепи?

Q3) Заряд в 4,0 кулонов был перемещен через разность потенциалов 24 вольт, сколько энергии было передано?

Q4) Разность потенциалов на компоненте составляет 12 вольт, а ток через него составляет 0,37 ампер. Какое сопротивление компонента?

Как рассчитать время зарядки аккумулятора и ток зарядки аккумулятора

Как рассчитать время зарядки и ток зарядки для зарядки аккумулятора?

Время простой зарядки аккумуляторов и формула тока зарядки аккумуляторов. (На примере аккумулятора 120 Ач).

Ниже приведены простые формулы тока зарядки аккумулятора и времени зарядки аккумулятора с решенным примером свинцово-кислотного аккумулятора емкостью 120 Ач.

Вот формула времени зарядки свинцово-кислотного аккумулятора.

Время зарядки аккумулятора = Аккумулятор Ач / Ток зарядки

T = Ач / А

Где,

Связанный пост: Разница между аккумулятором и конденсатором

Пример:

Предположим для 120 Аккумулятор Ач:

Прежде всего, рассчитаем зарядный ток для аккумулятора 120 Ач. Как известно, зарядный ток должен составлять 10% от номинальной емкости аккумулятора Ач.

Следовательно,

Зарядный ток для 120 Ач батареи = 120 Ач x (10/100) = 12 ампер.

Но из-за некоторых потерь мы можем взять 12-14 ампер для зарядки аккумуляторов вместо 12 ампер.

Предположим, мы взяли 13 А для зарядки, затем

Время зарядки 120 Ач батареи = 120/13 = 9,23 часа.

Но это был идеальный случай…

Практически было замечено, что 40% потерь происходит при зарядке аккумулятора.

Тогда 120 x (40/100) = 48….. (120 Ач x 40% потерь)

Следовательно, 120 + 48 = 168 Ач (120 Ач + потери)

Сейчас Время зарядки аккумулятора = Ач / ток зарядки

Ввод значений;

168/13 = 12,92 или 13 часов (в реальном случае)

Таким образом, для полной зарядки батареи 120 Ач потребуется 13 часов в случае необходимого зарядного тока 13A .

Похожие сообщения:

Разница между электрическим током и электрическим зарядом

Основная разница между зарядом и током

Электрический заряд и ток — это взаимосвязанные величины, но они отличаются друг от друга.

Основное различие между током и зарядом:

Ток: Это скорость потока заряда (обычно электронов). Ток (I) — это физическая величина, измеряемая в амперах (A).
Заряд: Это недостаток или избыток электронов на поверхности тела.Заряд (Q) — это физическое свойство материи, измеряемое в кулонах (C).

Связанные сообщения:

Что такое электрический заряд?

Известно, что недостаток или избыток электронов на материи — это электрический заряд. Типичная формула заряда следующая:

Q = It … или

Q = en

Где:

Q = заряд в кулонах
I = ток в амперах
т = время в секундах
e = количество электронов или протона
n = заряд одного избирательного или протона

Характерным символом заряда является «Q», а единицей измерения является кулон, выраженный «C», где один кулон:

Заряд 6.24 x 10 ¹⁸ электронов = 1C = Один кулон

или

Один кулон — это ток в один ампер в секунду, т.е. количество заряда, которое может перемещаться с помощью тока ампер из одной точки в другую за одну секунду времени, равно равняется одному кулону.

или

Один кулон — это количество заряда, когда он помещен в электрическое поле один вольт на метр (1 В / м), тогда на него будет приложена сила в один ньютон.

Один электрон имеет -1,602 x 10 ^-19 Кулоны заряда
Один протон имеет 1.602 x10 ^-19 Кулоны зарядов

Одни и те же заряды отталкивают друг друга, в то время как разные заряды притягиваются, т.е.

Выборы на выборы = отталкивание
Протоны на протоны = отталкивание
Электроны на протоны = притяжение

Сила притяжение или отталкивание между двумя заряженными частицами, расположенными на расстоянии «r», можно рассчитать по закону Кулона:

F = K (Q1 Q2 / r2)

Где:

F = Сила в ньютонах
K = Константа = 8.99 × 10 ⁹ м F ^-1.
Q1 = Первая заряженная частица
Q2 = Вторая заряженная частица
r = Расстояние между двумя заряженными частицами в метрах.

Есть три типа электрических зарядов.

Отрицательный заряд: избыток электронов на поверхности тела известен как отрицательно заряженная материя (избыток электронов, который в основном находится в нижней и внешней полосах или оболочке атома или молекулы).
Положительный заряд: Дефицит электронов на поверхности тела называется положительно заряженной материей (избыток протонов, которые в основном находятся в ядрышках атомов).
Нейтральный = равное количество электронов и протонов на частице делает ее нейтральной (нейтроны находятся в ядрышке атома).

Похожие сообщения:

Что такое электрический ток?

Электрический ток — это скорость потока заряда (обычно электронов), вызванная разностью потенциалов (напряжением). Сила тока обозначается символом «I» и измеряется в амперах с помощью символа «A».

Когда напряжение или ЭДС приложены к проводнику, возникает разность потенциалов, которая перемещает через него огромное количество электронов.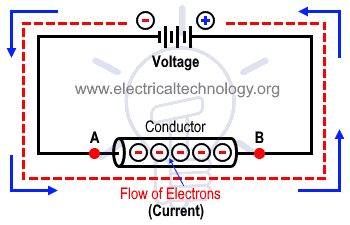

Ток — это физическая величина, которую можно измерить по следующей формуле:

I = Q / t … (в амперах)

Где:

I = ток в амперах
Q = заряд в Кулоны
t = Время в секундах

Есть два основных типа электрических токов, т.е.

Переменный ток: Поток заряда или выборы с изменяющимся направлением и величиной.
Постоянный ток: Поток заряда или выбора в одном направлении с постоянной величиной.

Ниже приведена сравнительная таблица тока и заряда с различными характеристиками.

Сравнение электрического заряда и тока

В следующей таблице показаны некоторые различия между зарядом и током.

Характеристики	Электрический ток	Электрический заряд
Определение	Ток — это скорость потока зарядов, обычно вызываемых ЭДС или напряжением.	Заряд — свойство вещества, проявляющее недостаток или избыток электронов на своей поверхности.
Символ	Ток, представленный символом «I».	Заряд обозначается символом «Q».
Единица	Единица измерения тока в системе СИ — Ампер, выраженная буквой «А».	Единица заряда в системе СИ — кулон, выраженная буквой «С».
Формула	I = Q / t I = dQ / dt	Q = It… или Q = en
Сила в полях	Ток создает как электрическое поле, так и магнитное поле.	Производит и поднимает только в электрическом поле.
Движение	Ток — это движение и поток заряда, как правило, электронов.	Заряд — это движение электронов, то есть недостаток или избыток электронов на теле.
Измерительный прибор	Амперметр (Амперметр)	Электрометр или баллистический гальванометр

Связанные сообщения:

Электрический заряд — формула, свойства, единицы, способы зарядки

- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
  BNAT
  Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 110003 CBSE
  Книги NCERT
  Книги NCERT для класса 5
  Книги NCERT, класс 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  NCERT Книги для класса 11
  NCERT Книги для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  9plar
  RS Aggarwal
  RS Aggarwal Решения класса 12
  RS Aggarwal Class 11 Solutions
  RS Aggarwal Решения класса 10
  Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  RD Sharma
  RD Sharma Class 6 Решения
  RD Sharma Class 7 Решения
  Решения RD Sharma класса 8
  Решения RD Sharma класса 9
  Решения RD Sharma класса 10
  Решения RD Sharma класса 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика
  Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Статистика
  9000 Pro Числа
  Числа
  9000 Pro Числа Тр Игонометрические функции
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убытки
  Полиномиальные уравнения
  Деление фракций
  Microology
  0003000
  FORMULAS
  Математические формулы
  Алгебраические формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000
  000 Калькуляторы
  000 Физические модели 900 Образцы документов для класса 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 1 1
  Образцы документов CBSE для класса 12
  Вопросники предыдущего года CBSE
  Вопросники предыдущего года CBSE, класс 10
  Вопросники предыдущего года CBSE, класс 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  HC Verma Solutions Класс 12 Физика
  Решения Лакмира Сингха
  Решения Лахмира Сингха класса 9
  Решения Лахмира Сингха класса 10
  Решения Лакмира Сингха класса 8
  9000 Класс
  9000BSE 9000 Примечания3 2 6 Примечания CBSE
  Примечания CBSE класса 7
  Примечания
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания 12 CBSE
  Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
  CBSE Примечания к редакции класса 10
  CBSE Примечания к редакции класса 11
  Примечания к редакции класса 12 CBSE
  Дополнительные вопросы CBSE
  Дополнительные вопросы по математике класса 8 CBSE
  Дополнительные вопросы по науке 8 класса CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Дополнительные вопросы по математике класса 9 CBSE Вопросы
  CBSE Class 10 Дополнительные вопросы по математике
  CBSE Class 10 Science Extra questions
  CBSE Class
  Class 3
  Class 4
  Class 5
  Class 6
  Class 7
  Class 8 Класс 9
  Класс 10
  Класс 11
  Класс 12
  Учебные решения
- Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для класса 11 по физике
  Решения NCERT для класса 11 Химия
  Решения NCERT для биологии класса 11
  Решение NCERT s Для класса 11 по математике
  NCERT Solutions Class 11 Accountancy
  NCERT Solutions Class 11 Business Studies
  NCERT Solutions Class 11 Economics
  NCERT Solutions Class 11 Statistics
  NCERT Solutions Class 11 Commerce
  NCERT Solutions for Class 12
  Решения NCERT для физики класса 12
  Решения NCERT для химии класса 12
  Решения NCERT для биологии класса 12
  Решения NCERT для математики класса 12
  Решения NCERT, класс 12, бухгалтерия
  Решения NCERT, класс 12, бизнес-исследования
  NCERT Solutions Class 12 Economics
  NCERT Solutions Class 12 Accountancy Part 1
  NCERT Solutions Class 12 Accountancy Part 2
  NCERT Solutions Class 12 Micro-Economics
  NCERT Solutions Class 12 Commerce
  NCERT Solutions Class 12 Macro-Economics
  NCERT Solut Ионы Для класса 4
  Решения NCERT для математики класса 4
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для математики класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для математики класса 6
  Решения NCERT для науки класса 6
  Решения NCERT для класса 6 по социальным наукам
  Решения NCERT для класса 6 Английский язык
  Решения NCERT для класса 7
  Решения NCERT для математики класса 7
  Решения NCERT для науки класса 7
  Решения NCERT для социальных наук класса 7
  Решения NCERT для класса 7 Английский язык
  Решения NCERT для класса 8
  Решения NCERT для математики класса 8
  Решения NCERT для науки 8 класса
  Решения NCERT для социальных наук 8 класса ce
  Решения NCERT для класса 8 Английский
  Решения NCERT для класса 9
  Решения NCERT для класса 9 по социальным наукам
  Решения NCERT для математики класса 9
  Решения NCERT для математики класса 9 Глава 1
  Решения NCERT для математики класса 9, глава 2
  Решения NCERT
  для математики класса 9, глава 3
  Решения NCERT для математики класса 9, глава 4
  Решения NCERT для математики класса 9, глава 5
  Решения NCERT
  для математики класса 9, глава 6
  Решения NCERT для математики класса 9, глава 7
  Решения NCERT
  для математики класса 9, глава 8
  Решения NCERT для математики класса 9, глава 9
  Решения NCERT для математики класса 9, глава 10
  Решения NCERT
  для математики класса 9, глава 11
  Решения
  NCERT для математики класса 9 Глава 12
  Решения NCERT
  для математики класса 9 Глава 13
  NCER Решения T для математики класса 9 Глава 14
  Решения NCERT для математики класса 9 Глава 15
  Решения NCERT для науки класса 9
  Решения NCERT для науки класса 9 Глава 1
  Решения NCERT для науки класса 9 Глава 2
  Решения NCERT для науки класса 9 Глава 3
  Решения NCERT для науки класса 9 Глава 4
  Решения NCERT для науки класса 9 Глава 5
  Решения NCERT для науки класса 9 Глава 6
  Решения NCERT для науки класса 9 Глава 7
  Решения NCERT для науки класса 9 Глава 8
  Решения NCERT для науки класса 9 Глава 9
  Решения NCERT для науки класса 9 Глава 10
  Решения NCERT для науки класса 9 Глава 12
  Решения NCERT для науки класса 9 Глава 11
  Решения NCERT для науки класса 9 Глава 13
  Решения NCERT
  для науки класса 9 Глава 14
  Решения NCERT для класса 9 по науке Глава 15
  Решения NCERT для класса 10
  Решения NCERT для класса 10 по социальным наукам
  Решения NCERT для математики класса 10
  Решения NCERT для класса 10 по математике Глава 1
  Решения NCERT для математики класса 10, глава 2
  Решения NCERT для математики класса 10, глава 3
  Решения NCERT для математики класса 10, глава 4
  Решения NCERT для математики класса 10, глава 5
  Решения NCERT для математики класса 10, глава 6
  Решения NCERT для математики класса 10, глава 7
  Решения NCERT для математики класса 10, глава 8
  Решения NCERT для математики класса 10, глава 9
  Решения NCERT для математики класса 10, глава 10
  Решения NCERT для математики класса 10 Глава 11
  Решения NCERT для математики класса 10 Глава 12
  Решения NCERT для математики класса 10 Глава ter 13
  Решения NCERT для математики класса 10 Глава 14
  Решения NCERT для математики класса 10 Глава 15
  Решения NCERT для науки класса 10
  Решения NCERT для класса 10 науки Глава 1
  Решения NCERT для класса 10 Наука, глава 2
  Решения NCERT для класса 10, глава 3
  Решения NCERT для класса 10, глава 4
  Решения NCERT для класса 10, глава 5
  Решения NCERT для класса 10, глава 6
  Решения NCERT для класса 10 Наука, глава 7
  Решения NCERT для класса 10, глава 8
  Решения NCERT для класса 10, глава 9
  Решения NCERT для класса 10, глава 10
  Решения NCERT для класса 10, глава 11
  Решения NCERT для класса 10 Наука Глава 12
  Решения NCERT для класса 10 Наука Глава 13
  NCERT S Решения для класса 10 по науке Глава 14
  Решения NCERT для класса 10 по науке Глава 15
  Решения NCERT для класса 10 по науке Глава 16
  Программа NCERT
  NCERT
- Commerce
  Class 11 Commerce Syllabus
  Учебный план класса 11
  Учебный план класса 11
  Учебный план экономического факультета 11
  Учебный план по коммерции класса 12
  Учебный план класса 12
  Учебный план класса 12
  Учебный план
  Класс 12 Образцы документов для торговли
  Образцы документов для предприятий класса 11
  Образцы документов для коммерческих предприятий класса 12
  TS Grewal Solutions
  TS Grewal Solutions Class 12 Accountancy
  TS Grewal Solutions Class 11 Accountancy
  Отчет о движении денежных средств 9 0004
  Что такое предпринимательство
  Защита прав потребителей
  Что такое основные средства
  Что такое баланс
  Что такое фискальный дефицит
  Что такое акции
  Разница между продажами и маркетингом
  03
  ICC
  Образцы документов ICSE
  Вопросы ICSE
  ML Aggarwal Solutions
  ML Aggarwal Solutions Class 10 Maths
  ML Aggarwal Solutions Class 9 Maths
  ML Aggarwal Solutions Class 8 Maths
  ML Aggarwal Solutions Class 7 Maths Решения Математика класса 6
  Решения Селины
  Решения Селины для класса 8
  Решения Селины для класса 10
  Решение Селины для класса 9
  Решения Фрэнка
  Решения Фрэнка для математики класса 10
  Франк Решения для математики 9 класса
  9000 4
  ICSE Class
  ICSE Class 6
  ICSE Class 7
  ICSE Class 8
  ICSE Class 9
  ICSE Class 10
  ISC Class 11
  ISC Class 12
- IC
- JEE4
- Образец статьи JEE
- Вопросник JEE
- Биномиальная теорема
- Статьи JEE
- Квадратное уравнение
NEET
Программа BYJU NEET
NEET 2020
NEET Eligibility
NEET Eligibility
NEET Eligibility 2020 Подготовка
NEET Syllabus
Support
Разрешение жалоб
Служба поддержки
Центр поддержки
Государственные советы
GSEB
GSEB Syllabus
GSEB Образец
003 GSEB Books
MSBSHSE
MSBSHSE Syllabus
MSBSHSE Учебники
MSBSHSE Образцы статей
MSBSHSE Вопросы
AP Board
AP Board
AP Board
9000
AP 2 Year Syllabus
MP Board
MP Board Syllabus
MP Board Образцы документов
MP Board Учебники
Assam Board
Assam Board Syllabus
Assam Board
Assam Board
Assam Board Документы
BSEB
Bihar Board Syllabus
Bihar Board Учебники
Bihar Board Question Papers
Bihar Board Model Papers
BSE Odisha
Odisha Board
Odisha Board
Odisha Board 9000
ПСЕБ 9 0002
PSEB Syllabus
PSEB Учебники
PSEB Вопросы и ответы
RBSE
Rajasthan Board Syllabus
RBSE Учебники
RBSE
RBSE
000 HPOSE
000 HPOSE
000
000 HPOSE
000
000 HPOSE
000
000
0003 Контрольные документы
JKBOSE
JKBOSE Syllabus
JKBOSE Образцы документов
Экзаменационные образцы JKBOSE
TN Board
TN Board Syllabus
9000 Papers 9000 TN Board Syllabus
9000 Книги
JAC
Программа обучения JAC
Учебники JAC
Вопросы JAC
Telangana Board
Telangana Board Syllabus
Telangana Board Textbook
Telangana Board
Учебник
Telangana Board
KSEEB
KSEEB Syllabus
KSEEB Model Question Papers
KBPE
KBPE Syllabus
Учебники KBPE
KBPE
0
9000 UPMS Board UPMS
Вопросы к Правлению UP
Совет по Западной Бенгалии
Учебный план Совета по Западной Бенгалии
Учебники по Совету по Западной Бенгалии
Вопросы по Совету по Западной Бенгалии
UBSE
TBSE
CBSE
Гоа Совет
MBSE
Meghalaya Board
Manipur Board
Haryana Board
Государственные экзамены
Банковские экзамены
Экзамены SBI
Экзамены IBPS
10 Экзамены IBPS
RbI Экзамены
SSC JE
SSC GD
SSC CPO
SSC CHSL
SSC CGL
Экзамены RRB
RRB JE
RRB NTPC
RRB Экзамены ALP
9102
RRB ALP
5
000 LIC ADO
UPSC CAPF
Список статей государственных экзаменов
Kids Learning
Class 1
Class 2
Class 3
Academic Questions
Вопросы по физике
Вопросы по физике
Вопросы по биологии
Вопросы по математике
Вопросы по естествознанию
Вопросы GK
Онлайн-обучение
Домашнее обучение
Полные формы
Общие полные формы
Физические науки
Физические науки
Биология Полные формы
Полные формы обучения
Полные формы банковского дела
Полные формы технологий
CAT
Программа BYJU CAT
Программа CAT
Экзамен CAT
Бесплатная подготовка CAT
Обзор экзамена CAT4 2020 CAT
КУПИТЬ КУРС
+919243500460
Физика
Вывод физических формул
Diff.Между в физике
Использование в физике
Типы и классификация
Взаимосвязь между в физике
Значение констант
Константы в физике
Статьи по физике
Physics Index Pages
Class 10 Physics Index 110004 Физический индекс
Класс 12 Физический индекс
Отрасли физики
Механика
Оптика
Электромагнетизм
Относительность
Акустический
Энергия движения
Энергия движения
Энергия движения
Ток электричества
Законы физики
Закон Ома
Законы движения Ньютона
Принцип Архимеда
Эффект Доплера
Закон Кирхгофа
Закон отражения
Закон отражения
0003 Принцип Бернулли
Закон Ленца
Список единиц СИ
Единица давления
Единица вязкости
Единица мощности
Единица плотности
Единица энергии
Единица силы
Единица измерения проводимости
Единица тока
Единица магнитного поля
Физические формулы
Физические формулы для класса 9
Физические формулы для класса 10
Физические формулы для класса 11
Физические формулы для класса 12
Калькуляторы по физике
Важные вопросы по физике
Важные вопросы для класса 11 по физике
Важные вопросы для класса 12 по физике
Важные вопросы по физике CBSE
Мудрые вопросы по физике
Учебный план по физике
Физика
.

Конспект «Сила тока. Напряжение» — УчительPRO

«Сила тока. Напряжение»

Сила тока

Амперметр

Напряжение

Вольтметр

Формулы и определения.

Электричество — Основные формулы

1. Электростатика

1.1 Закон Кулона

1.2 Напряженность поля уединенного точечного заряда

1.3 Потенциал точки в поле точечного заряда

1.4 Потенциальная энергия заряда в электростатическом поле

1.5 Потенциальная энергия заряда q1 в поле точечного заряда

1.6 Теорема Гаусса

1.7 Напряженность электрического поля вблизи от поверхности проводника

1.8 Емкость плоского кондесатора

1.9 Энергия плоского кондесатора

2. Постоянный электрический ток

2.1 Закон Ома для участка однородной цепи

2.2 Закон Ома для замкнутой цепи с источником тока

2.3 Работа постоянного тока

2.4 Закон Джоуля-Ленца

2.5 Полная мощность, развиваемая источником тока

2.6 Полезная мощность

2.7 Коэффициент полезного действия источника тока

2.8 Первое правило Кирхгофа

2.9 Второе правило Кирхгофа

Формула силы тока в физике

Определение и формула силы тока

Некоторые виды силы тока

Плотность тока

Сила тока в соединениях проводников

Закон Ома

Единицы измерения силы тока

Примеры решения задач

Постоянный электрический ток. Сила тока. Напряжение. Электрическое сопротивление. Закон Ома для участка электрической цепи

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

Часть 2

Ответы

Сила тока ?. Формула силы тока. Как обозначается ? единица измерения силы тока?

Общее описание силы тока

Способы измерения силы тока

Отличие напряжения от силы тока

Заключение

формула формула мощности электрического тока

Основные понятия и формулы характеризующие электрический ток

Формула выражения силы электрического тока через сопротивление и напряжение

Работа и мощность электрического тока

Напряжение или разность потенциалов

Сила электрического тока

Сопротивление

Мощность

Заряд, ток и разница потенциалов

Заряд, ток и разность потенциалов

Заряд (Q) — заряд измеряется в кулонах (Кл).

Ток (I) — измеряется в амперах (А).

Разность потенциалов (В) — измеряется в вольтах (В).

Сопротивление (Вт) — это отношение разности потенциалов на компоненте к току, протекающему через него, измеряется в омах (Вт).

Как рассчитать время зарядки аккумулятора и ток зарядки аккумулятора

Как рассчитать время зарядки и ток зарядки для зарядки аккумулятора?

Разница между электрическим током и электрическим зарядом

Основная разница между зарядом и током

Что такое электрический заряд?

Что такое электрический ток?

Сравнение электрического заряда и тока

Электрический заряд — формула, свойства, единицы, способы зарядки

0

alexxlab

Вам также может понравиться

Авр организация: Автоматика ввода резерва(АВР): схемы, назначение и требования

Передать показания водомеров: Передача показаний — ЕРКЦ

Составить принципиальную электрическую схему: Принципиальные схемы электрических цепей — Вольтик.ру

Добавить комментарий Отменить ответ

1.5 Потенциальная энергия заряда q₁ в поле точечного заряда