Зависимость частоты от тока: формула, взаимное влияние, нормы, характеристики

Содержание

формула, взаимное влияние, нормы, характеристики

Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы. Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы.

Нормируемые требования к показателям

В РФ требования к качеству работы энергосистемы стандартизированы.

В соответствии с ГОСТ 13109-97 частота в энергосистеме должна непрерывно поддерживаться на уровне f = 50 ± 0,2 Гц, при этом допускается кратковременное отклонение частоты до значения ∆f = 0,4 Гц.

Анализируя зависимость силы тока от частоты, можно сделать вывод, что если подключаемая нагрузка имеет чисто активный характер (к примеру, резистор), то в широком диапазоне сила тока от частоты иметь зависимость не будет. В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.

Другими словами, при варьировании частоты тока происходит изменение ёмкостного сопротивления, изменение которого, в свою очередь, приводит к изменению тока, протекающего по цепи.

То есть при повышении частоты, снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.

Математическое выражение зависимости будет иметь следующий вид: I = UCω;

Зависимость при учете активного сопротивления будет определяться следующим выражением: I (ω) = UCω √(R2 • C2 • ω2 + 1).

Влияние частоты тока на электроприборы

Далее рассмотрим влияние частоты электрического тока. Увеличение частоты до сравнительно невысоких величин (1 — 10 тыс. Гц), обычно является следствием исключительно повышения номинальной мощности электроаппаратуры, поскольку таким образом возрастает проводимость газовых промежутков. Для измерения частоты в системе используют частотомеры.

Паровая турбина разрабатываются и создаются таким образом, чтобы при номинальной скорости вращения (частоте) обеспечивалась максимальная выходная мощность на валу. При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.

Таким образом, наиболее экономичный режим работы достигается при оптимальной частоте.

Помимо этого, работа на пониженных частотах приводит к ускоренному износу рабочих лопаток и прочих частей и механизмов. Снижение частоты оказывает влияние на расход на собственные нужды станций.

ИССЛЕДОВАНИЕ ЗАВИСИМОМТИ АКТИВНОГО,ИНДУКТИВНОГО И ЕМКОСТНОГО СОПРОТИВЛЕНИЯ ОТ ЧАСТОТЫ ПЕРЕМЕННОГО ТОКА.ПРОВЕРКА ЗАКОНА ОМА ДЛЯ ПЕНИ ПЕРЕМЕННОГО ТОКА.

ЛАБОРАТОРНАЯ РАБОТА №1

ИССЛЕДОВАНИЕ ЗАВИСИМОМТИ АКТИВНОГО,ИНДУКТИВНОГО И ЕМКОСТНОГО СОПРОТИВЛЕНИЯ ОТ ЧАСТОТЫ ПЕРЕМЕННОГО ТОКА.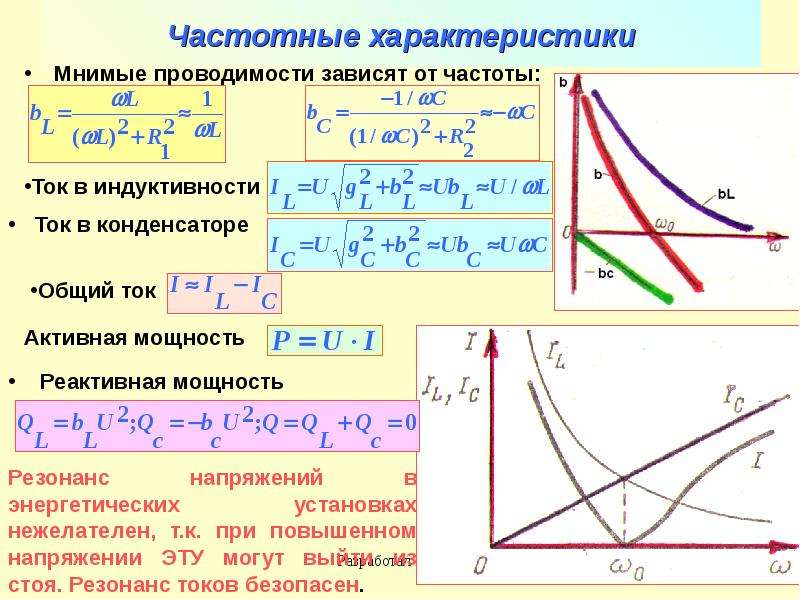 ПРОВЕРКА ЗАКОНА ОМА ДЛЯ ПЕНИ ПЕРЕМЕННОГО ТОКА.

Цель работы: выяснить зависимость сопротивлений от частоты.

Приборы и принадлежности:генератор звуковой частоты, амперметр, вольтметр, активное сопротивление, катушка индуктивности, конденсатор, провода.

КРАТКАЯ ТЕОРИЯ

Переменный электрический ток в электрических цепях является результатом возбуждения в них вынужденных электромагнитных колебаний. Эти вынужденные колебания создаются генераторами переменного тока, работающими на электростанциях.

Электрический генератор создает синусоидальное напряжение. Соответственно синусоидальным оказывается и ток.

Зависимость напряжения от времени можно записать в виде:

Если к сопротивлению R приложена разность потенциалов U, то по закону Ома:

где i, u — мгновенные значения напряжения и силы тока.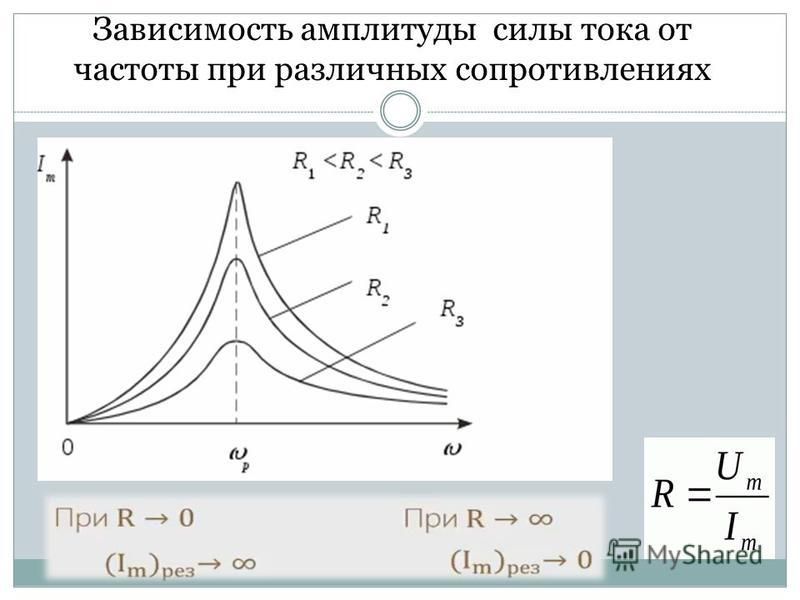

Потенциал периодически изменяется между

Величина называется амплитудным значением напряжения (или пиковым напряжением).

Амплитудное (пиковое) значение силы тока;

— циклическая частота.

, где

— частота тока.

Частота переменного тока в России равна 50 Гц.

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока.

I. Цепь, в которой разность потенциалов на реактивных сопротивлениях много меньше разности потенциалов на резисторе, будет являться цепью с активным сопротивлением.

Активным сопротивлением R называется физическая величина, определяемая отношением мощности Р переменного тока на участке электрической цепи к квадрату действующего значения силы тока на этом участке

Действующим значением силы переменного тока называют силу такого постоянного тока, при прохождении которого по той же цепи и за то же время выделяется такое же количество теплоты, как и при прохождении переменного тока.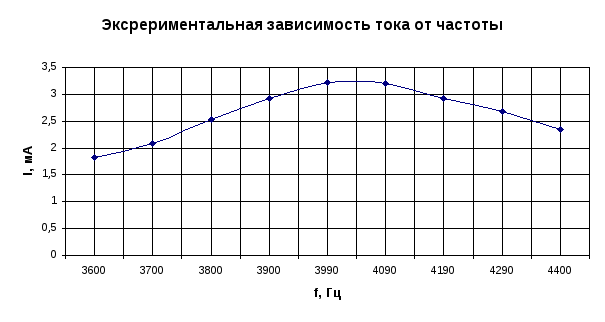

Выразим действующее значение силы тока I через амплитуду силы тока . Согласно определению, бесконечно малое количество теплоты, выделяемое постоянным током, равно такому же количеству теплоты, выделяемому переменным током.

На основании закона Джоуля — Ленца имеем:

Приравнивая значения и , получим:

Пусть теплота Q выделяется током в течение одного периода колебаний. Тогда, интегрируя данное выражение в пределах от 0 до Т получим:

Найдем значение интеграла:

Тогда ,откуда

Аналогично для действующих значений напряжений получим:

где действующее значение переменного напряжения U в раз меньше его амплитудного значения.

Колебания силы тока в цепи с активным сопротивлением происходят по закону:

где амплитуда силы тока

Частота и фаза переменного тока будут совпадать с частотой и фазой колебания напряжения (рис. 2,3).

На активном сопротивлении происходит преобразование электрической энергии во внутреннюю.

II.Рассмотрим цепь переменного тока с индуктивным сопротивлением, т.е. цепь, содержащую катушку.

Рис. 4

Произведение циклической частоты на индуктивность L называется индуктивным сопротивлением.

Через катушку идёт ток, изменяющийся по закону: ,

При этом в катушке возникает ток самоиндукции, а ЭДС самоиндукции будет

Приложенное к катушке напряжение должно в любой момент времени уравновешивать Э.Д.С. самоиндукции в катушке, если , то

Связь между амплитудой колебаний напряжения на концах проводника индуктивностью L с амплитудой колебаний силы тока в нем совпадает по форме с выражением закона Ома для участка цепи постоянного тока.

Хотя данное выражение совпадает по форме с выражением закона Ома для участка цепи , между ними имеются принципиальные отличия по существу. Электрическое сопротивление проводника при данной температуре является постоянной величиной, характеризующей проводник. Индуктивное сопротивление не является постоянной величиной, его значение прямо пропорционально частоте переменного тока.

Поэтому амплитуда колебаний силы тока в проводнике индуктивностью L при постоянном значении амплитуды колебаний напряжения убывает обратно пропорционально частоте

Индуктивное сопротивление энергию не потребляет. Из уравнений

видно, что сдвиг фаз между напряжением и током равен , колебания силы тока отстают от колебаний напряжения на четверть периода.

Индуктивное сопротивление выражают в омах, оно играет роль сопротивления в цепи переменного тока с катушкой индуктивности.

III. Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором.

При включении конденсатора в цепь переменного тока через диэлектрик, разделяющий обкладки конденсатора, электрические заряды проходить не будут. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в проводах, соединенных с его выводами появится переменный ток.

Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока, кажется горящей непрерывно, т.к. человеческий глаз не замечает периодического ослабления свечения нити лампы.

Ток в цепи с емкостным сопротивлением меняется по гармоническому закону

Напряжение на обкладках конденсатора ,

где

Ток в цепи

где

По закону Ома ,

где сопротивление конденсатора переменного тока, называемое емкостным сопротивлением.

;

При , напряжение будет максимальным

Отсюда следует, что

Как и индуктивное сопротивление катушки, емкостное сопротивление конденсатора не является постоянной величиной. Значение емкостного сопротивления обратно пропорционально частоте переменного тока.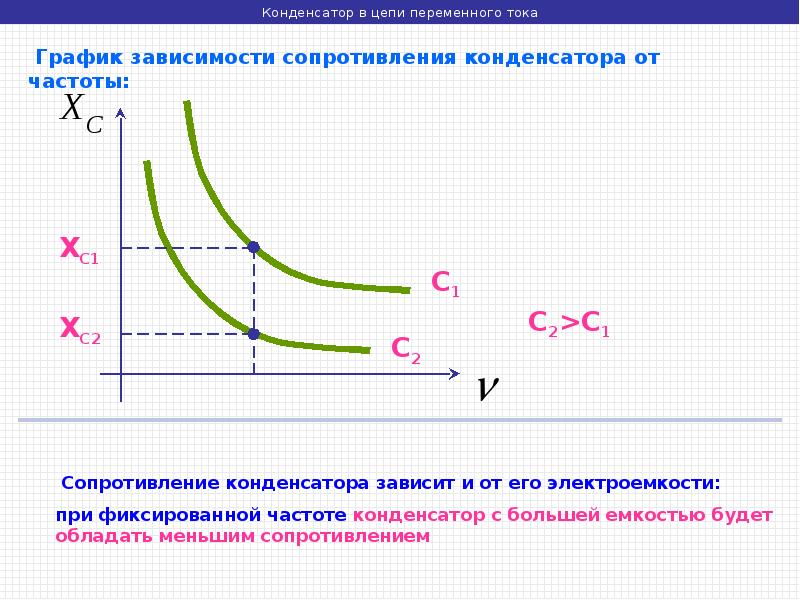

Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте .

Емкостное сопротивление энергию не потребляет, поэтому как и индуктивное является реактивным.

Сдвиг фаз между током и напряжением на конденсаторе, как видно из

формул

равен четверти периода, колебания силы тока опережают колебания внешнего напряжения по фазе на

IV. Рассмотрим полную цепь переменного тока, содержащую активное, индуктивное, емкостное сопротивления.

Ток на всех трёх участках один и тот же:

Разности потенциалов на всех трёх сопротивлениях имеют вид:

Частота колебаний результирующей разности потенциалов на клеммах генератора (совпадающей с его Э.Д.С.), равна частоте складываемых колебаний разности потенциалов.

Фаза результирующей разности потенциалов должна быть сдвинута по отношению к колебаниям силы тока в общем случае на угол

Для нахождения результирующей амплитуды напряжений (Э.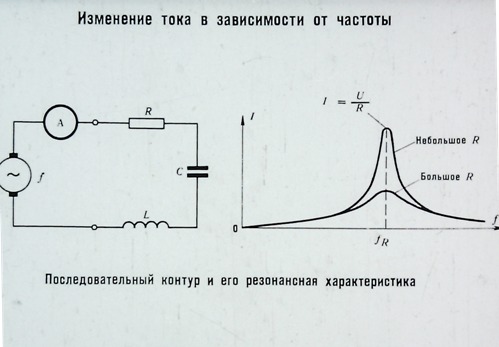 Д.С.) в цепи, построим векторную диаграмму цепи:

Так как сила тока в этом случае на всех участках цепи одинакова, то здесь в качестве базисного вектора выбирают вектор, изображающий амплитудное значение силы тока.

Векторы, изображающие амплитудные значения напряжений на отдельных участках строят под определенными углами к вектору силы тока. Эти углы равны сдвигам фаз на каждом из участков цепи. Результирующую амплитуду напряжений определяют как модуль результирующего вектора, который находят по правилу суммирования векторов, а фазу результирующего колебания просто измеряют соответствующим углом, отсчитанным в направлении против часовой стрелки от базисного вектора.

Из диаграммы видно:

Как видно, амплитуды колебаний силы тока и напряжения связаны соотношением

где величину Z , равную выражению называют полным сопротивлениемцепи переменного тока.

Выражение называется законом Ома для цепи переменного

тока.

Разделив левую и правую часть на получим, что закон справедлив и для действующих значений силы тока и напряжения.

Из формулы видно, что ток в цепи можно увеличить не меняя напряжение, а изменяя частоту.

При изменении частоты может наступить такой момент, когда и при одинаковой силе тока одинаковыми оказываются и амплитуды колебаний напряжения на конденсаторе и катушке.

Колебания напряжения на катушке и конденсаторе противоположны по фазе, поэтому сумма напряжений на них при в любой момент

времени = 0.

В результате напряжение на активном сопротивлении при резонансе оказывается равным полному напряжению , а сила тока

в цепи достигает максимального значения, т.е. наступает резонанс.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Упражнение 1.Собрать цепь с активным сопротивлением. Поддерживая напряжение постоянным, изменять частоту тока и отмечать значения силы тока.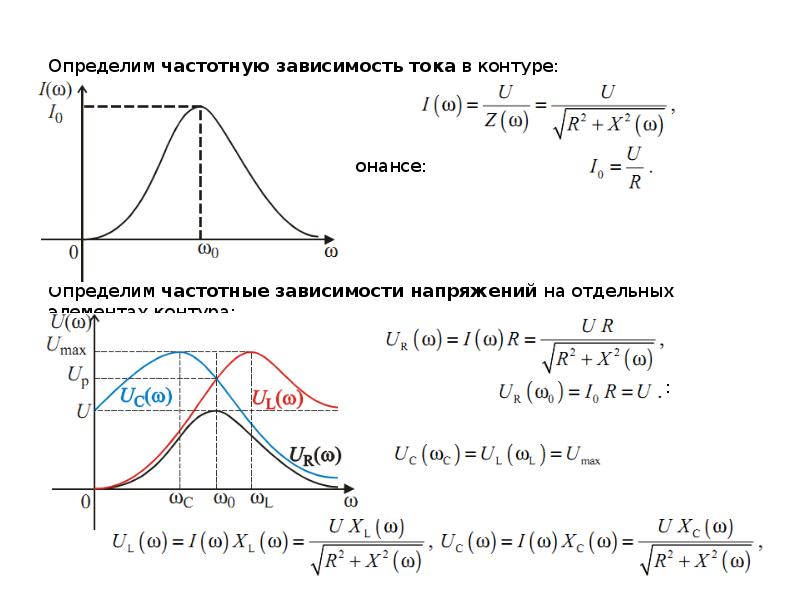 Результаты измерений занести в таблицу.

Построить график.

Упражнение 2. Собрать цепь с индуктивным сопротивлением, исследовать зависимость индуктивного сопротивления от частоты. Результаты занести в таблицу.

Построить график. Проверить результат опыта с теоретической формулой индуктивного сопротивления

Индуктивность указана на катушке. ( U = 458)

Упражнение 3.Проделать то же самое с емкостным сопротивлением (емкость конденсатора указана на конденсаторе).

Упражнение 4.Собрать цепь, состоящую из последовательно соединенных R, L, C. Изменяя частоту тока настроить цепь на резонанс. Измерить для этой частоты и Измерить напряжение во всей цепи и на каждом участке. Результаты занести в таблицу.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Как зависит индуктивность и индуктивное сопротивление от частоты, силы тока, напряжения?

2. Как зависит емкость и емкостное сопротивление от частоты, силы тока, напряжения?

3. Дайте понятие резонанса напряжений.

4. Дайте понятие резонанса токов.

5. Рассчитайте емкость конденсатора, необходимого для того, чтобы лампочку, рассчитанную на 12 В и ток 0,5 А, включить в цепь переменного тока напряжением 220 В.

6. Если трансформатор включить по ошибке в цепь постоянного тока, то он «сгорит». Почему?

7. Определите полное сопротивление катушки теоретически и практически. Результаты сравнить.

ЛАБОРАТОРНАЯ РАБОТА №2

ИЗУЧЕНИЕ ТРАНЗИСТОРА

Цель работы: изучение особенностей работы транзисторов по схеме с общим эмиттером ( снятие входной и выходной характеристики ), определение коэффициента усиления по току и входного сопротивления.

Приборы и принадлежности: транзистор типа МП 4 1, микроамперметр на 100 мка. миллиамперметр постоянного тока М45М. авометр, потенциометры сопротивлением 50-100 Ом. ключи замыкания, соединительные провода. источники питания.

КРАТКАЯ ТЕОРИЯ

Транзисторами называют активные полупроводниковые приборы, применяемые для усиления и генерирования электрических колебаний. Они подразделяются на биполярные и полевые ( униполярные ). Наиболее распространены транзисторы биполярные с двумя р — п-переходам и. Их работа основана на использовании носителей зарядов обоих знаков. Первые транзисторы были точечными, но они работали недостаточно устойчиво, в настоящее время изготовляются и применяются плоскостные транзисторы.

Устройство плоскостного биполярного транзистора показано на рис. I. Основной частью такого транзистора является тонкая монокристаллическая пластика германия 6 ( рис. I ), в которую со стороны больших граней вплавлены две капли индия 4 и 7. В результате в пластинке, имеющей сначала лишь электронную проводимость, образовались три различные области с чередующейся проводимостью: две крайние имеют дырочную проводимость ( р ) и называются эмиттером и коллектором, а средняя — электронную ( о ) и называется базой. На границе этих областей образовалось два электронно-дырочных перехода. Переход «эмиттер-база* называют Эмиттерным, а «база-коллектор* — коллекторным.

Каждый переход в отдельности ведет себя как обычный полупроводниковый диод. т. с. обладает односторонней проводимостью для электрического тока. Пластинка германия припаяна оловом к кристаллодержателю 5, который для лучшего теплообмена соединен с герметизированным металлическим корпусом 8. Вывод от эмиттера 2 и вывод от коллектора 9 проходит через стеклянные изоляторы 3. Вывод от базы I приварен к корпусу транзистора и расположен ближе к выводу эмиттера.

По типу проводимости транзисторы бывают п-р-п и р-п — р типа. 11риицип работы транзистора обоих типов одинаковый. Различие между ними заключается в том, что в транзисторе р-о-р — ток создается дырками, а в транзисторе п-р-п — электронами.

На рис. 2 изображена структура и условное обозначение транзисторов р-п-р и п-р-п типа. На условном графическом обозначении транзисторов р-п-р и п-р-п стрелка показывает условное ( от плюса к минусу ) направление тока в проводе эмиттера при прямом напряжении на эмиттерном переходе.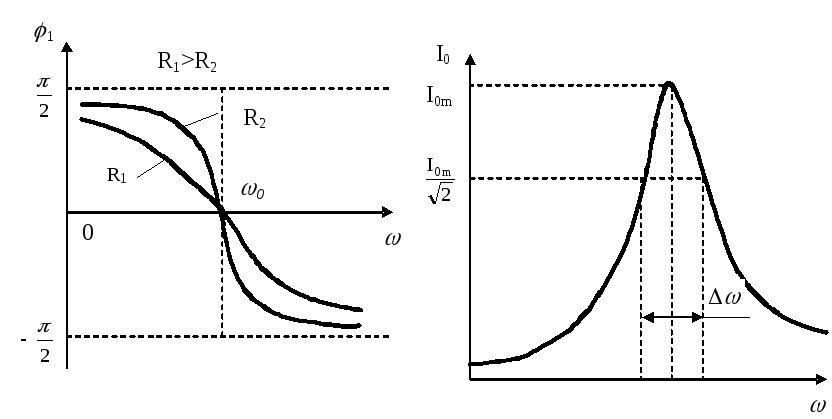 В схемах с транзисторами обычно образуются две цепи. Входная или управляющая цепь служит для управления работой транзистора. В входной или управляемой цепи получаются усиленные колебания. Источник усиливаемых колебаний включается во входную цепь, а в выходную включается нагрузка.

Физические процессы в биполярном транзисторе:

Рассмотрим работу транзистора типа п-р-п в режиме без нагрузки, когда включаем только источники постоянных питающих напряжений Е1 и Е2 ( рис.3 ) Транзистор включен по схеме с общим эмиттером, которая для транзисторов считается основной. Напряжение на эмиттерном переходе прямое, а на коллекторном — обратное. Прямое сопротивление эмиттерного перехода мало, поэтому все подводимое напряжение падает практически на высокоомном коллекторном переходе. Источник входного сигнала подключается к базе и эмиттеру» а усиленный сигнал снимают с коллектора и эмиттера. Принцип работы транзистора заключается в том. что прямое напряжение эмиттерного перехода, т. с. участка база-эмиттер

( Uб-э). Существенно влияет на токи эмиттера и коллектора: чем больше это напряжение, тем больше токи эмиттера и коллектора. При этом изменения тока коллектора лишь незначительно меньше изменений эмиттера. Таким образом, напряжение ( Uб-э). т. е. входное напряжение управляет током коллектора. Усиление электрических колебаний с помощью транзистора основано на этом явлении. Физические процессы в транзисторе происходят следующим образом: Под действием прямого напряжения, приложенного к эмиттерному переходу, электроны из области эмиттера переходят в область базы, а дырки из области базы переходят в область эмиттера. Ток, который при этом возникает, называют током эмиттера 1э. Большая часть этого тока переносится электронами, т. к. эмиттерная область имеет более высокую проводимость, чем дырочная область базы.

Электронный ток эмиттера течет в цепи базы и потому называется током базы 16. Одновременно с переходом электронов из области эмиттера в область базы во внешнюю цепь эмиттера уходит соответствующее число дырок, что приводит к образованию в области эмиттера новых электронов, и потому их число не убывает. Электроны, перешедшие из эмиттера в базу, движутся далее к коллекторному переходу. Это движение происходит в результате избытка концентрации их около эмиттерного перехода, а также под действием слабого электрического поля, существующего между эмиттером и коллектором транзистора. На пути к коллекторному переходу часть электронов рекомбинируется с дырками в области базы. В результате рекомбинации возникает ток базы, «тело дырок в базе должно быть изменённым. Вследствие рекомбинации каждую секунду сколько дырок исчезает, столько же новых дырок возникает за счет того, что из базы уходит в направлении к плюсу источника E1 такое же число электронов. Ток базы является бесполезным и даже вредным.

Ток коллектора получается меньше тока эмиттера, но в соответствии с первым законом «Кирхгофа» существует соотношение между токами: Iэ = Iк +I б. Обычно I б составляет малую маю эмиттера, т. е. I б « Iэ , а следовательно, ток коллектора незначительно меньше тока эмиттера и можно считать I б~ Iк. Именно для того, чтобы ток I б был как можно меньше, базу делают очень тонкой и уменьшит а ней концентрацию примесей, которая определяет концентрацию дырок, тогда метшее число электронов будет комбинировать в базе с дырками.

Если под действием входного напряжения во шик значительный ток эмиттера, то в область базы со стороны эмиттера поступает электроны. которые для данной области являются неосновными носителями. Не успевая комбинироваться с дырками при диффузии через баз. они доходят до коллекторного переход Чем больше тек эмиттера. тем больше электронов приходит к коллекторному переходу и тем меньше становятся его сопротивление. Соответственно увеличивается ток коллектора.

Зависимость между токами и напряжениями в транзисторах выражаются статическими вольт-амперными характеристиками транзисторов, снятыми при постоянном токе и отсутствии нагрузи в выходной цепи. Характеристики необходимы для рассмотрения свойств транзисторов a для практических расчетов транзисторных схем.

Наибольшее значение при применении транзисторов имеют два вида характеристик:

1)Входной характеристикой называют зависимость входного тока от входного напряжения при постоянном выходном напряжении:

Iб=f (Uб), при Uк-э=const

2)Выходной характеристикой называют зависимость выходного тоа от выходного напряжения при постоянном входом токе:

Iк =.f (Uk), Iб=const

Вид характеристик транзистора зависят от способа его включения, но для схем ОЭ и ОК они практически одинаковы, поэтому пользуются обычно входными я выходными характеристиками схем ОБ и ОЭ.

Статическим характеристики транзистора в схеме ОЭ. В этой схеме входной ток — ток базы 16, выходной — ток коллектора Iк, входное напряжение создастся между базой и эмиттером Uб-э, в выходное — между коллектором и эмиттером Uк-э.

Поскольку ток коллектора гораздо больше тока базы, а создаваемое им напряжение на нагрузке R в высокоомной выходной цепи значительно превышает напряжение во входной цепи. то, значит, схема ОЭ усиливает и ток, и напряжение и, следовательно, дает очень большое усиление мощности сигнала.

Выходные характеристики транзистора, включённого по схеме ОЭ. представляют собой зависимость тока коллектора от напряжения коллектор- эмиттер при постоянном токе базы. Выходные характеристики в схеме ОЭ — эта коллекторные характеристики характеристики

Входные характеристики транзистора, включённого во схеме ОЭ — это базовые характеристики, представляющие собой зависимость тока базы от напряжения база-эмиттер при постоянном напряжении коллектор-эмиттер.

ВЫПОЛНЕНИЕ РАБОТЫ

АСнятие входных статистических характеристик транзистора.

Упражнение 1. Подготовьте в тетради таблицу 1 для записи результатов измерений:

Таблица 1

Uк-э=0В	U-а=-ЗВ	Uк-э=4В	U=5В
Uб-э В	Iб, мкА	Uб-э ,В	Iб, мкм А	Uб-э,В	Iб,мкА	Uб-э,В	Iб,мкА

Упражнение 2. Соберите электрическую цепь по схеме, показанной на рис. 4. Прямое напряжение на эмиттерный подход подают от Еб=4.5В, а обратное напряжением на коллекторный переход Eк = 9В в контролируют вольтметром со шкалой 10В, силу тока базы измеряют микроамперметром со школой 100 мкА, а силу тока коллектора миллиамперметром со школой 7,5 А.

Предупреждение. В электрическую цепь включают сначала эмиттерный. а затем коллекторный переходы.

Упражнение 3. С помощью потенциометра R2 установите напряжение коллектор-эмиттер 3в. поддерживая его постоянным, измените напряжение между базой и эмиттером Uб-э от 0 до 0,2в через 0,02 В следите за показаниями прибора, измеряющего ток базы Uб результаты заносите в таблицу 1.

Упражнение 4. Установите напряжение Uk = 4В с помощью потенциометра R2 снимите

показания проборов аналогично заданию 3 и занесите их в таблицу 1.

Упражнение 5. С помощью потенциометра R2 установите напряжения Uk =5B и снимите

показания приборов аналогично заданию 3 в занесите их в таблицу 1.

Упражнение 6. На основами результатов наблюдений, записанных а таблице 1, постройте

семейство входных статистических характеристик транзистора.

Iб=f(Uб), при Uk=const.

БСнятие выходных статистических вольт-амперных характеристик транзистора

Упражнение 1. Подготовьте в тетради таблицу 2 для записи результатов измерений:

Таблица 2

IБ=10 мкА	IБ=15мкА	IБ= 20мкА	IБ=25мкА
Uk-э,В	Ik,мА	Uk-э,В	Ik,мА	Uk-э,В	Ik,мА	Uk-э,В	Ik,мА

Упражнение 2. Исследуйте зависимость силы тока коллектора oт напряжения между коллектором и эмиттером при постоянной силе тока базы ( рис. 4 ). Эти значения тока устанавливаются потенциометром R1 и поддерживаются в процессе наблюдений неизменными, соответственно 10, I5, 20, 25 мкА. Измеряйте для каждого значения Iб напряжение Uб-э с помощью вольтметра VI. Напряжение Uk измеряют с помощью потенциометра R2 от 0 до 7В через 1B и наблюдайте за показаниями прибора, измеряющим ток в цепи коллектора.

ЛАБОРАТОРНАЯ РАБОТА №3

КРАТКАЯ ТЕОРИЯ

Земля в целом представляет собой большой магнит и имеет два магнитных полюса: северный и южный. В любой точке пространства, окружающего Землю, и на ее поверхности обнаруживается действие магнитного поля. Магнитное поле представляет собой особую форму материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами. Подобно тому как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле, в пространстве, окружающем токи, возникает поле, называемое магнитным. Подобно электрическому полю, магнитное поле существует реально, независимо от нас, от наших знаний о нем.

Изучая пространственное распределение магнитного поля Земли, геологи получают сведения о строении земной коры, о местонахождении полезных

ископаемых/железной руды и пр./ Изучение магнитных бурь помогает понять закономерности явлений в ионосфере, влияющих на распространение радиоволн .Изучение земного магнетизма необходимо для правильного понимания основных вопросов происхождения Земли, Солнца и звезд. По вопросу о происхождении земного магнетизма работали ученые Гильберт/1600г./,Ломоносов/1352г./,Гаусе/1939/. Теория Гаусса дала возможность представить магнитное поле Земли в виде двух полей: поля, источники которого находятся внутри Земли, и поля, источники которого-вне Земли. Все существующие ныне теории земного магнетизма можно разделить на две группы.

Теории первой группы полагают, что главная часть магнитного поля Земли создается земной корой, содержащей в разных своих участках различное количество магнитных пород.

Теории второй группы полагают, что главная часть магнитного поля Земли создается электрическими токами, циркулирующими на больших глубинах в жидком ядре Земли.

В настоящее время известно, что наблюдаемое геомагнитное поле является суммой двух полей: постоянного и переменного. Чтобы изучить магнитное поле Земли, надо знать величину и направление напряженности в каждой точке этого поля .Обозначим через Т полную напряженность магнитного поля в какой-либо точке 0 северного полушария Земли. (Рис1.)

Рис.1.

Плоскость магнитного меридиана ОАВС. Плоскость географического меридиана ОВЕК.

Т;Нх;Ну;Нz;D;j;H -элементы земного магнетизма

Силовые линии магнитного поля лежат в плоскости магнитных меридианов. Магнитным меридианом называется дуга большого круга, проходящего через магнитные полюсы Земли. Магнитные полюсы Земли совпадают с ее географическими полюсами, вследствие чего между плоскостью магнитного меридиана, проходящего через данную точку 0 земной поверхности и плоскостью географического меридиана имеется некоторый угол Д/угол склонения/. Склонение может быть восточным или западным в зависимости от того, проходит ли магнитный меридиан к востоку или к западу от географического. Полную направленность Т можно разложить на две составляющие, лежащие в плоскости магнитного меридиана: напряженность Н/горизонтальная составляющая /в горизонтальном направлении напряженность Hz b вертикальном направлении /Вертикальная составляющая/. Нz считается , если она направлена вниз. В южном полушарии Нz отрицательна. Горизонтальная составляющая имеет максимальное значение на магнитном экваторе, равное 0,7 и постоянно уменьшается к полюсам. Вертикальная составляющая имеет максимальное значение вблизи магнитных полюсов/0,6-0,7/уменьшается на магнитном экваторе.

Горизонтальную составляющую можно разложить на две составляющие лежащие в горизонтальной плоскости, на северную Hx направленную вдоль географического меридиана и восточную Нy перпендикулярную к меридиану. Составляющая Нx считается положительной, если она направлена к северу, Н-составляющая считается положительной, если она направлена к востоку.

Магнитные элементы T, Н, Нx,Ну, Н, Дj связаны между собой простыми соотношениями, которые легко получить из рис 1

Нх= H cos D

Hy= H sin D

H z= H tg j

T= H cos j

H= Hx + Hy

Tg j= Hz\H

tg D= Hy\Hx

T= Hx+ Hy+ Hz

Целью настоящей работы является определение горизонтальной составляющей магнитного поля Н с помощью прибора, называемого тангенс-гальванометром и зная числовое значение горизонтальной напряженности и угла наклонения j найти полную напряженность магнитного поля Земли Т.

Тангенс-гальванометр представляет собой плоскую катушку большого радиуса. Плоскость катушки вертикальна: в центре ее находится короткая магнитная стрелка, расположенная горизонтально и могущая вращаться около вертикальной оси. Концы стрелки перемещаются по кругу /по лимбу/, разделенному на градусы. Такую магнитную стрелку с лимбом называют буссолью/рис.2/.

Плоскость витков катушки следует расположить в плоскости магнитного меридиана, которая определяется по направлению магнитной стрелки. На рис .4а пунктиром показано направление магнитного меридиана Земли, небольшие кружки Аи В-сечение одного витка горизонтальной плоскости, проходящей через центр катушки: магнитная стрелка.

При отсутствии ток в катушке на полюса магнитной стрелки действует только магнитное поле Земли Н/рис.4а/

Магнитное поле в центре витка большого витка радиуса перпендикулярно плоскости витка, направление его определяется направлением тока,

проходящего по витку .Напряженность поля, созданного током, на рис.4б обозначена через НТ.

Под действием двух полей Н и Нт — магнитная стрелка отклоняется на некоторый угол d :равновесие ее наступает тогда, когда она станет по направлению результирующего магнитного поля.

Из рис.46 видно что:

Tg d = Hт /Н

Напряженность магнитного поля в центре кругового тока определяется законом Лапласа: Нт= У\2ч

Если в катушке «н» витков, то

Нт= Ун/2ч

Подставляя полученное значение Н /2а/в формулу /I/,можно определят горизонтальную составляющую напряженности магнитного поля Земли:

Н= Ун/2ч tgd

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Упражнение 1. Определение горизонтальной составляющей земного магнитного поля.

Установка для экспериментального определения горизонтальной составлявшей напряженности земного магнитного поля Н дана на рис.5,где ТГ-тангенс-гальванометр, А-амперметр, R –реостат , К-ключ , Е-аккумулятор, К1-коммутатор тока в тангенс-гальванометре.

1.Ознакомившись с приборами и заготовив таблицу записей наблюдений, собирают приборы по схеме рис.5

рис.5

Амперметр необходимо поместить не ближе 1м от тангенс-гальванометра, т.к. магнитное поле амперметра может оказать сильное влияние на магнитную стрелку.

При проведении опыта нужно остерегаться так же влияния магнитного поля реостата. Коммутатор поставлен в сеть для того, чтобы иметь возможность менять направление тока в тангенс-гальванометре.

2. Очень часто т-г имеет установочные винты и уровень: буссоль снабжена эрретиром, для закрепления магнитной стрелки при переносе прибора. Освободив стрелку от арретира, при помощи установочных винтов добиваются того, чтобы она могла свободно вращаться, не задевая лимбы. Такая свободная стрелка довольно быстро устанавливается по магнитному меридиану, и будет сохранять его положение.

3. Вращают катушку около вертикальной оси и придают ей такое положение, при котором ее плоскость будет параллельна магнитной стрелке. Тогда плоскость катушки будет совмещена с плоскостью магнитного меридиана. В этом случае стрелка одним концом устанавливается на нулевое давление шкалы лимба.

4. Установите реостат на самое большое сопротивление и включив два витка прибора замыкают ключ К. Перемещением движка реостата увеличивают силу тока. Задавшись определенным углом отклонения стрелки / в пределах 35-55 / дают ей успокоится и производят отсчет ее положения по шкале лимба. Делать отсчет положения стрелки нужно обязательно по обоим ее концам: пусть эти отсчеты дают два значения угла d1 и d2. Записывают параметры Y.

5. Не меняя параметров цепи, коммутатором меняют направление тока в т-г. При той же (по абсолютной величине) силе тока делают еще два отсчета положения стрелки буссоли d1и d2.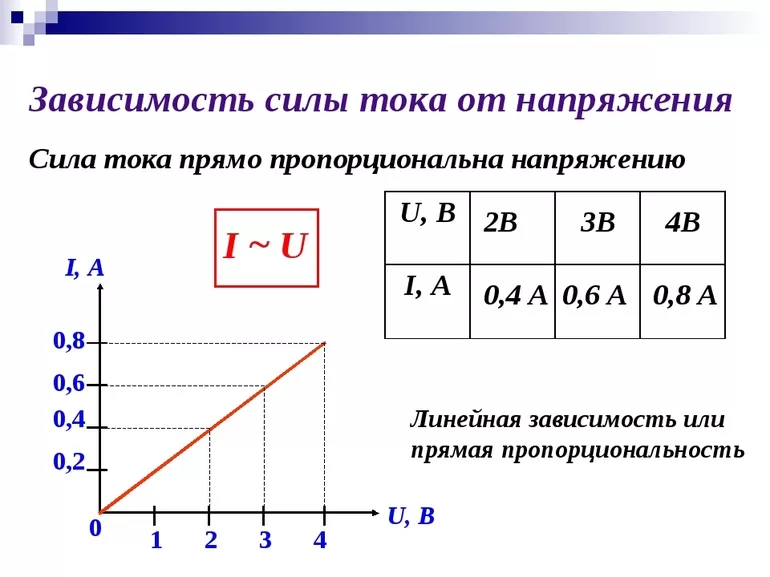

6. Аналогично проделывают несколько опытов при различных значениях тока, беря углы отклонения в пределах 35-55.

7.Измеряют миллиметровой линейкой диаметр витков и находят их радиус.

8.Повторить опыты с числом витков 4,6,8,10.

9 .Результаты измерений и вычислений записать в таблицу:

Существует ли зависимость напряжения от частоты?

Казалось бы, раскрыть зависимость напряжения от частоты просто. Стоит только обратиться с соответствующим запросом ко всезнающим поисковым системам и… убедиться, что ответа на этот вопрос попросту нет. Что же предпринять? Давайте разбираться вместе в этом непростом вопросе.

Напряжение или разность потенциалов?

Надо заметить, что напряжение и разность потенциалов — это одно и то же. По сути, это сила, которая способна заставить электрические заряды двигаться потоком. Не имеет значения, куда будет направлено это движение.

Разность потенциалов — просто другое выражение для напряжения. Оно нагляднее и, может быть, понятнее, но сути дела не меняет. Поэтому главный вопрос состоит в том, откуда берется напряжение, и от чего оно зависит.

В том, что касается домашней сети 220 Вольт, ответ простой. На гидростанции поток воды вращает ротор генератора. Энергия вращения трансформируется в силу напряжения. Атомная электростанция вначале превращает воду в пар. Он и крутит турбину. В бензоэлектростанции ротор вращает сила сгорающего бензина. Есть и другие источники, но суть всегда одна и та же: энергия превращается в напряжение.

Самое время задаться вопросом о зависимости напряжения от частоты. Но мы еще не знаем, откуда берется частота.

Что является источником частоты

Тот же самый генератор. Частота его вращения превращается в одноименное свойство напряжения. Вращайте генератор быстрее — частота будет больше. И наоборот.

Хвост не может «вилять» собакой. По той же причине частота не может изменить напряжение. Следовательно, выражение «зависимость напряжения от частоты тока» не имеет смысла?

Чтобы найти ответ, надо правильно сформулировать вопрос. Есть такая присказка про глупца и 10 ученых мужей. Он задавал неправильные вопросы, а они не могли ответить.

Если назвать напряжение другим определением, все встанет на свои места. Оно применяется для цепей, состоящих из множества разных сопротивлений. «Падение напряжения». Оба выражения часто считаются синонимами, что почти всегда неправильно. Потому что падение напряжения действительно может зависеть от частоты.

С чего бы напряжению падать?

Да просто потому, что не может не падать. Итак. Если на одном полюсе источника потенциал равен 220 Вольт, а на другом — ноль, то это падение могло произойти только в цепи. Закон Ома говорит о том, что, если в сети имеется одно сопротивление, то все напряжение на нем и упадет. Если два и больше — каждое падение будет пропорционально его величине, а их сумма равна исходной разности потенциалов.

Ну и что? Где здесь указание на зависимость напряжения от частоты тока? Пока что все зависит от величины сопротивления. Вот, если бы найти такой резистор, который меняет свои параметры при изменении частоты! Тогда и падение напряжения на нем менялось бы автоматически.

Есть такие резисторы

Их еще называют реактивными, в отличие от активных собратьев. На что же они реагируют, изменяя свою величину? На частоту! Существует 2 вида реактивных сопротивлений:

индуктивное;
емкостное.

Каждый вид связан со своим полем. Индуктивное — с магнитным, емкостное — с электрическим. На практике они представлены в первую очередь, соленоидами.

Они представлены на фото выше. И конденсаторами (ниже).

Их можно считать антиподами, потому что реакция на изменение частоты прямопротивоположная. Индуктивное сопротивление растет с частотой. Емкостное, наоборот, падает.

Теперь, учитывая особенности реактивных сопротивлений, в соответствии с законом Ома, можно утверждать, что зависимость напряжения от частоты переменного тока существует. Она может быть рассчитана с учетом величин реактивных сопротивлений в цепи. Только для ясности надо помнить, что речь идет именно о падении напряжения на элементе цепи.

И все-таки она существует!

Вопросительный знак в заголовке статьи превратился в восклицательный. «Яндекс» реабилитирован. Осталось только привести формулы зависимости напряжения от частоты для разных видов реактивных сопротивлений.

Емкостное: XC = 1/(w · C). Здесь w — угловая частота, C — емкость конденсатора.

Индуктивное: XL = w · L, где w — то же, что и в предыдущей формуле, L — индуктивность.

Как видно, частота влияет на величину сопротивления, изменяя его, следовательно, изменяет и падение напряжения. Если в сети имеется активное сопротивление R, емкостное XC и индуктивное XL, то сумма падений напряжений на каждом элементе будет равна разности потенциалов источника: U = U_r + U_xc+ U_xl.

Формула расчета периода переменных и постоянных токов в электротехнике

Изобретение электричества поставило человечество на новую грань развития. Технический прогресс опирался на два направления движения с использованием электроэнергии. В одном случае применялся постоянный ток, во втором – переменный. Внедрение источников электричества и электропотребителей вылилось в столетнюю войну между приверженцами двух видов энергии. В конце концов, победу одержали те, кто продвигал идею повсеместного использования её переменного вида.

Синусоида переменного электричества в системе координат

Общее понятие о переменном токе

В отличие от постоянного движения электронов в одном направлении, переменный ток меняет как направление, так и значение несколько раз за единицу времени. Изменения происходят по гармоническому закону. Если наблюдать подобный сигнал с помощью осциллографа, можно увидеть картинку в виде синусоиды.

Относительно оси ординат OY ток меняет своё направление с положительного на отрицательное и делает это периодически. Поэтому его мгновенное значение в первой позиции считается положительным, во второй – отрицательным.

Важно! Так как переменный ток – это алгебраическая величина, то говорить о его знаке заряда можно только для конкретного мгновенного значения, смотря, в каком направлении он протекает в этот момент.

Сигнал на экране осциллографа

Периодический переменный ток

Тот, который, изменяясь, успевает вернуться к своему исходному значению через одинаковые временные интервалы и при этом проходит весь цикл своих преобразований, называется периодическим. Его можно проследить на синусоиде, изображённой на экране осциллографа.

Период и амплитуда синусоидального колебания

Видно, что через одинаковые интервалы времени график повторяется без перемен. Эти интервалы обозначаются буквой Т и называются периодами. Частота, с которой в единицу времени укладывается определённое количество подобных периодов, – это частота тока переменного значения.

Её можно вычислить по формуле частоты переменного тока:

f = 1/T,

где:

f – частота, Гц;
T – период, с.

Частота равна количеству периодов в секунду и имеет единицу измерения 1 герц (Гц).

Внимание! Единица частоты в системе СИ носит имя Генриха Герца. 1 герц (Гц, Hz) = 1 с-1. К ней применимы кратные и дольные, выраженные стандартными приставками СИ, единицы.

Стандарты частоты

Для того чтобы обеспечить согласование работы источников переменного электричества, систем передач, приём и работу электропотребителей, применяются стандарты частоты. Используемая частота в электротехнике некоторых стран:

50 Гц – страны бывшего СССР, Прибалтики, страны Европы, Австралия, КНДР и другие;
60 Гц – стандарт, принятый в США, Канаде, Доминиканской республике, Тайвани, на Каймановых островах, Кубе, Коста-Рике, Южной Корее и ещё в некоторых странах.

В Японии используются обе частоты. Восточные регионы (Токио, Сендай, Кавасаки) используют частоту 50 Гц. Западные области (Киото, Хиросима, Нагоя, Окинава) применяют частоту 60 Гц.

К сведению. Железнодорожная инфраструктура Австрии, Норвегии, Германии, Швейцарии и Швеции по сей день применяет частоту 16,6 Гц.

Переменный синусоидальный ток

Это тот ток, который периодически меняется во времени, и его изменения подчиняются закону синусоиды. Это элементарное движение электрических зарядов, потому дальнейшему разложению на простые токи оно не подлежит.

Вид формулы такого переменного тока:

i = Im*sinωt,

где:

Im – амплитуда;
sinωt – фаза синусоидального тока, рад.

Здесь ω = const, называется угловой частотой переменного электричества, причём угол ωt находится в прямой временной зависимости.

Зная частоту f исходного тока, можно вычислить его угловую частоту, применив выражение:

ω = 2πf = 2π/Т.

Тут 2π – это выраженное в радианах значение центрального угла окружности:

Т = 2 π радиан = 3600;
Т/2 = π = 1800;
Т/4 = π/2 = 900.

Если выразить 1 рад в градусах, то он будет равен 57°17′.

Синусоидальное переменное движение электронов

Многофазный переменный ток

Для запуска и работы многих промышленных устройств и электрооборудования требуется не одна фаза, а несколько. В связи с этим рассматривают такие понятия, как двухфазный и трёхфазный переменные токи.

Трёхфазный ток

Этот вид электричества применяют в трёхфазной системе, в которую включены три однофазные цепи. Цепи имеют ЭДС переменной природы одной и той же частоты. Эти ЭДС сдвинуты по фазе относительно друг друга на ϕ = Т/3 = 2π/3. Такую систему называют трёхфазным током, а цепь – фазой.

Выработка, преобразование, доставка и потребление переменного электрического тока в основном происходят по трёхфазной системе электроснабжения.

Трёхфазный переменный ток

Двухфазный ток

Ещё в 1888 году Никола Тесла выполнил описание того, как можно на практике применить двухфазную сеть, и предложил разработанную им конструкцию двухфазного двигателя. Такие сети начали применять в начале 20 века. Они состояли из двух контуров.

Там напряжения контуров сдвигались по фазе на 900. Каждая фаза включала в себя два провода, у двухфазных генераторов было по два ротора, также конструктивно развёрнутые на угол 900.

Важно! Такие сети позволяли производить мягкий пуск двухфазных электродвигателей, практически с нулевого момента вращения. В то время как для запуска однофазного асинхронного двигателя требуется дополнительная пусковая обмотка или система запуска.

График двухфазного напряжения и схематический рисунок двухфазного генератора

Действующее значение синусоидального тока

Под действующим значением понимают его эффективность. Она равна такому значению постоянного тока, который выполнит ту же работу, что и переменный, за один период времени. Под работой здесь подразумевают его тепловую или электродинамическую направленность. Удобнее всего использовать среднеквадратичное значение переменного электричества.

Тогда действующее значение для синусоидального тока определяют по формуле:

I = * Im ≈ 0,707* Im,

где Im – величина амплитуды тока.

Действующее значение тока

Генерирование переменного тока

Кроме стандартных генераторов, для производства переменного тока применяются инверторы и фазорасщепители.

Инвертор

Это устройство, с помощью которого из постоянного тока получают его переменный вид. В процессе этого величина выходного напряжения тоже меняется. Схема устройства представляет собой электронный генератор синусоидального импульсного напряжения периодического характера. Есть варианты инверторов, работающих с дискретным сигналом. Инверторы применяют для автономного питания оборудования от аккумуляторов постоянного напряжения.

Инвертор 12/220 В, мощностью 1500 Вт

Фазорасщепитель

Ещё один способ получить несколько фаз из какого-либо сигнала – это выполнить его расщепление на несколько фаз. Это делается с помощью фазорасщепителя. Принудительная обработка сигналов цифрового или аналогового формата используется, как в радиоэлектронике, так и в силовой электротехнике.

Для электроснабжения трёхфазных асинхронных двигателей применяют выполненный на их же базе фазорасщепитель. Для этого обмотки трёхфазного двигателя соединяют не «звездой», а иначе. Две катушки присоединяют между собой последовательно, третью – подключают к средней точке второй обмотки. Двигатель запускают, как однофазный, после разгона в его третьей обмотке наводится ЭДС.

Интересно. В случае расщепления фаз подобным методом сдвиг фаз между 2 и 3 обмоткой составляет не 1200, как должно быть в идеале, а 900.

Сети переменного тока

По назначению и применению эти сети можно классифицировать следующим образом:

общие системы: питание объектов промышленного, транспортного, сельскохозяйственного и бытового назначения;
автономные сети: снабжение передвижных и стационарных автономных субъектов.

Общие сети переменного трёхфазного тока построены по четырёхпроводной схеме, где три провода – это «фаза», четвёртый – «ноль». Трансформаторные подстанции построены по схеме с глухо заземлённой нейтралью. Передача на дальние расстояния производится при высоком напряжении, которое затем понижается на подстанциях до напряжения 0,4 кВ и раздаётся потребителям.

Бытовые объекты подключаются по однофазной схеме. В этом случае требуются два провода: «фазный» и «нулевой».

Определение частоты и периода

Частота электрического тока – это величина физическая, она определяет количество колебаний за 1 секунду. Время, за которое происходит одно целое колебание, называется периодом.

Взаимосвязь частоты и работы электрооборудования

Частота тока – это один из параметров электроэнергии, который влияет на стабильную работу электроустановок и оборудования. При поставке энергии потребителю этот параметр строго контролируется, так же, как и напряжение.

Нить взаимосвязи выражается формулой номинального количества оборотов в минуту для вращающихся машин. КПД (коэффициент полезного действия) заложен в самой конструкции агрегатов. Он максимален при:

n = 60f/p,

где:

n – количество об./мин.;
f – частота;
p – количество пар полюсов.

Количество оборотов турбины генераторов напрямую связано с частотой вырабатываемого переменного тока, полученная частота отвечает за оптимальный режим вращения электродвигателя потребителя. При снижении частоты в сети обороты машины снижаются автоматически. Происходит перегрузка на валу, и страдает двигатель.

В то же время технологическая линия, в которую он передаёт энергию вращения, также терпит изменения в работе:

изменяется скорость движения конвейера, что влечёт за собой сбой технологического процесса и брак в итоге;
снижаются мощность и частота вращения насосов, вентиляторов, что приводит к нестабильной работе систем, в которых они установлены;
снижение частоты в энергосистеме на 1% приводит к падению общей мощности на нагрузке до 2%.

Для контроля этого важного электрического параметра применяют частотомеры.

Внимание! Снижение частоты на 10-15% вызывает падение производительности механизмов даже на самой электростанции до нуля. При частоте тока в сети 50 Гц (критической величиной являются 45 Гц) происходит лавинный спад.

Частотомер

Это прибор, предназначенный для измерения частоты и отображения полученного результата на экран. Для контроля в электросетях применяют приборы непосредственной оценки синусоидальных колебаний аналоговой конструкции.

Различают по методу установки:

стационарные;
щитовые;
переносные.

Частотомеры в современном исполнении имеют цифровое отображение результатов на электронном дисплее.

Токи высокой частоты

ТВЧ – такова их аббревиатура, используются для плавки металлов, закалки поверхности металлических изделий. ТВЧ – это токи, имеющие частоту более 10 кГц. В индукционных печах используют ТВЧ, помещая проводник внутрь обмотки, через которую пропускают ТВЧ. Под их воздействием возникающие в проводнике вихревые токи разогревают его. Регулируя силу ТВЧ, контролируют температуру и скорость нагрева.

Интересно. Расплавляемый металл может быть подвешен в вакууме с помощью магнитного поля. Для него не нужен тигель (специальный ковш для нагрева). Так получают очень чистые вещества.

Плюсы использования ТВЧ в разных случаях:

быстрый нагрев при ковке и прокате металла;
оптимальный температурный режим для пайки или сварки деталей;
расплав даже очень тугоплавких сплавов;
приготовление пищи в микроволновых печах;
дарсонвализация в медицине.

Получают ТВЧ с помощью установок, включающих в свой состав колебательный контур, или электромашинных генераторов. У статора и ротора генераторов на сторонах, обращённых друг другу, нанесены зубцы. Их взаимное движение порождает пульсацию магнитного поля. Частота на выходе тем больше, чем больше произведение числа зубцов ротора на частоту его вращения.

Период пульсаций и частота

Частота переменного тока может иметь другое название – пульсация. Периодом пульсации называют время единичной пульсации.

Интенсивность циклов

Для электросети с частотой 50 Гц период пульсации составит:

Т = 1/50 = 0,02 с.

При необходимости, зная эту зависимость, можно по времени цикла вычислить частоту.

Опасность разночастотных зарядов

Как постоянный, так и переменный ток при определённых значениях представляет опасность для человека. До 500 В разница в безопасности находится в соотношении 1:3 (42 В постоянного к 120 В переменного).

При значениях выше 500 В это соотношение выравнивается, причём константное электричество вызывает ожоги и электролизацию кожных покровов, изменяющееся – судороги, фибрилляцию и смерть. Тут уже частота пульсации имеет большое значение. Самый опасный интервал частот – от 40 до 60 Гц. Далее с повышением частоты риск поражения уменьшается.

Влияние частоты на пороговый ток

Частота переменного электричества – важный параметр. Она влияет не только на работу электроустановок потребителей, но и на человеческий организм. Изменяя частоту электрических колебаний, можно менять технологические процессы на производстве и качество вырабатываемой энергии.

Видео

Зависимость мощности от частоты формула

Нормируемые требования к показателям

В РФ требования к качеству работы энергосистемы стандартизированы.

В соответствии с ГОСТ 13109-97 частота в энергосистеме должна непрерывно поддерживаться на уровне f = 50 ± 0,2 Гц, при этом допускается кратковременное отклонение частоты до значения ∆f = 0,4 Гц.

То есть при повышении частоты, снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.

Математическое выражение зависимости будет иметь следующий вид: I = UCω;

Влияние частоты тока на электроприборы

Таким образом, наиболее экономичный режим работы достигается при оптимальной частоте.

Мощность — то, что характеризует скорость передачи с преобразованием электроэнергии. Какие есть нормы мощности в сети переменного тока и виды, что такое активная и реактивная мощность? Об этом и другом далее.

Нормы мощности в сети переменного тока

Напряжение и мощность — то, что нужно знать каждому человеку, живущему в квартире или частном доме. Стандартное напряжение сети переменного тока в квартире и частном доме выражается в количестве 220 и 380 ватт. Что касается определения количественной меры силы электрической энергии, необходимо сложить электрический ток с напряжением или же измерить необходимый показатель ваттметром. При этом чтобы сделать измерения последним аппаратом, нужно использовать щупы и специальные программы.

Мощность переменного тока определяется соотношением величины тока со временем, которая производит работу за определенное время. Обычный пользователь использует мощностный показатель, передаваемый ему поставщиком электрической энергии. Как правило, он равен 5-12 киловатт. Этих цифр хватает, чтобы обеспечить работоспособность необходимого бытового электрооборудования.

Этот показатель зависит от того, какие внешние условия поступления энергии в дом, какие поставлены ограничительные токовые устройства (автоматы или полуавтоматы), регулирующие момент поступления мощностных емкостей к потребительскому источнику. Это совершается на разных уровнях, от бытового электрощита до центрального устройства электрического распределения.

Характеристики

Переменный ток течет по цепи и меняет свое направление с величиной. Создает магнитное поле. Поэтому его нередко называют периодическим синусоидальным переменным электротоком. Согласно закону кривой линии, величина его меняется через конкретный промежуток времени. Поэтому он называется синусоидным. Имеет свои параметры. Из важных стоит указать период с частотой, амплитудой и мгновенным значением.

Период — это то время, на протяжении которого происходит изменение электротока, а затем оно повторяется вновь. Частота — период течение за секунду. Измеряется в герцах, килогерцах и миллигерцах.

Амплитуда — токовое максимальное значение с напряжением и эффективностью протекания на протяжении полного периода. Мгновенное значение — переменный ток или напряжение, возникающее за конкретное время.

Виды мощностей

Мощностью называется измеряемая физическая величина, которая равна скорости изменения с преобразованием, передачей или потреблением системной энергии. Согласно более узкому понятию, это показатель, который равен отношению затраченного времени на работы к самому периоду, который тратится на работу. Обозначается в механике символом N. В электротехнической науке используется буква P. Нередко можно увидеть также символ W, от слова ватт.

Мощность переменного тока -это произведение силы тока с напряжением и косинусом сдвига фаз. При этом беспрепятственно можно посчитать только активную и реактивную разновидность. Узнать полное мощностное значение можно через векторную зависимость этих показателей и площади.

Активная мощность

Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.

Реактивная мощность

Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов. Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значением.

Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.

Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания. Обе измеряются в ваттах и имеют большое значение в электромагнитном излучении, механической форме генератора или акустической волне. Активно применяются в промышленности.

Полная мощность

Полная — это сумма активной с реактивной мощностью. Равна сетевому мощностному показателю. Это произведение напряжения с током в момент игнорирования фазы угла между ними. Вся рассеиваемая с поглощаемой и возвращаемой энергией — это полная энергия.

Это произведение напряжения и тока, единица измерения которого это ватт, перемноженный на ампер. При активности цепи, полная равняется активной. Если речь идет об индуктивной или емкостной схеме, то полная больше, чем активная.

Комплексная мощность

Это сумма всех мощностных показателей фаз источника электроэнергии. Это комплексный показатель, модуль которого равняется полному мощностному показателю электроцепи. Аргументом является фазовый сдвиг между электротоком с сетевым напряжением. Может быть выражена уравнением, где суммарный мощностный показатель, который генерируют источники электроэнергии, равен суммарному мощностному показателю, который потребляется в электроцепи.

Обратите внимание! Вычисляется посредством использования соответствующей формулы. Так, необходимо комплексное напряжение перемножить на комплексны ток или же удвоенное значение комплексного тока перемножить на импеданс. Также можно удвоенное значение комплексного напряжения поделить на удвоенное значение импеданса.

Как узнать какая мощность в цепи переменного тока

Стоит указать, что это величина, которая прямо связывается с иными показателями. К примеру, она находится в прямой зависимости от времени, силы, скорости, вектора силы и скорости, модуля силы и скорости, момента силы и частоты вращения. Часто в формулах во время вычисления электромощности используется также число Пи с показателем сопротивления, мгновенным током, напряжением на конкретном участке электрической сети, активной, полной и реактивной силой. Непосредственно участник вычисления это амплитуда, угловая скорость и начальная сила тока с напряжением.

В однофазной цепи

Понять, какой мощностный показатель есть в однофазной цепи переменного тока, можно при помощи применения трансформатора тока. Для этого необходимо воспользоваться ваттметром, который включен через токовый трансформатор. Показания следует перемножить на трансформаторный коэффициент тока. В момент измерения мощности в высоком напряжении трансформатор тока необходим, чтобы заизолировать ваттметр и обеспечить безопасность пользователя. Параллельна цепь включается не непосредственным способом, а благодаря трансформатору напряжения. Вторичные обмотки с корпусами измерительных трансформаторных установок необходимо заземлять во избежание случайного изоляционного повреждения и попадания высокого напряжения на приборы.

Обратите внимание! Для определения параметров в сети необходимо амперметр перемножить на трансформаторный коэффициент тока, а цифры, полученные вольтметром, перемножить на трансформаторный коэффициент напряжения.

В трехфазной цепи

В цепи переменного тока мощностный показатель в трехфазной цепи определить можно, перемножив ток на напряжение. Поскольку это непостоянный электроток, он зависит от времени и других параметров, поэтому необходимо использовать другие проверенные схемы. Так, можно использовать ваттметр.

Измерение должно быть проведено только в одной фазе и по формуле умножено на три. Этот способ экономит приборы и уменьшает габариты измерения. Применяется для высокой точности измерения каждой фазы. В случае несимметричной нагрузки, нужно использовать соответствующую схему подключения ваттметра. Это более точный способ, но требует наличие трех ваттметров.

Обратите внимание! Если цепь не предусматривает наличие нулевого проводника, нужна также соответствующая схема.

Стоит указать, что сегодня измерить можно необходимые показатели не только аналоговым, но и цифровым прибором. Отличие второго в уменьшенных размерах и легкости. Кроме того, цифровые агрегаты способы осуществлять фиксацию тока с напряжением, косинусом сети и другим. Это позволяет на дистанции осуществлять отслеживание различных величин и передавать предупреждения, если есть отклонение. Это удобно, поскольку не нужно измерять ток с напряжением, а потом, используя формулы, все досконально просчитывать.

В целом, мощность — это величина, основное предназначение которой показывать силу работы конкретного прибора и во многих случаях скорость деятельности, взаимодействуя с ним. Она бывает механической, электрической, гидравлической и для постоянного с переменным током. Измеряется по международной системе в ваттах и киловаттах.

Экономия энергии и точное управление системами являются основными причинами применения преобразователей частоты в системах отопления, вентиляции и кондиционирования воздуха HVAC (Отопление, Вентиляция и Кондиционирование). Экономия энергии важна, так как небольшое уменьшение оборотов вентилятора или центробежного насоса имеет очень большое влияние на потребление им энергии.

КПД вентиляторов или насосов вместе с преобразователем частоты остается высоким на пониженных оборотах. КПД двигателя, однако, падает, поскольку двигатель становится недозагруженным. Изготовители преобразователей частоты предприняли попытки улучшить КПД двигателей на малых оборотах, используя ряд конструктивных решений. К сожалению, большинство из этих решений требует кропотливой ручной регулировки и все еще не может оптимизировать КПД двигателя во всех условиях.

Преобразователь частоты VLT HVAC Drive имеет уникальную функцию управления, называемую автоматической оптимизацией энергопотребления AEO (Automatic Energy Optimization). Благодаря этой функции преобразователь частоты автоматически увеличивает КПД двигателя до максимума в любых условиях работы.

Ниже рассматривается причина уменьшенного КПД двигателя при малых нагрузках и способ, которым функция AEO противодействует этой естественной тенденции. Рассматриваются также применение и ограничения данной функции.

Работа двигателя

В асинхронных электродвигателях переменного тока крутящий момент на валу двигателя создается магнитным полем внутри двигателя. Напряженность этого магнитного поля и возникающий в результате крутящий момент меняются вместе с требованием по нагрузке на двигателе. Более высокая нагрузка требует более высокого крутящего момента, что означает, что двигатель потребляет больше тока из линии питания. Хотя обороты двигателя остаются относительно постоянными, потребляемый ток может меняться существенно.

Если полный крутящий момент двигателя не требуется, то не требуется и полное магнитное поле. Ток, который создает чрезмерное магнитное поле, не дает положительного эффекта и генерирует реактивный ток, который тратит энергию и создает тепловое напряжение. Избыточный ток даже более очевиден на малом крутящем моменте, когда реактивный ток растет по сравнению с действительной составляющей тока. Это основная причина, почему малонагруженные двигатели демонстрируют низкий КПД, что и будет обсуждаться ниже более подробно.

Чтобы ограничить ток через двигатель, ограничивается подаваемое на двигатель напряжение. Хотя это и кажется простым, в действительности это не так. Слишком уменьшенное напряжение приводит к чрезмерному скольжению ротора двигателя, которое в свою очередь приводит к большому потреблению тока. Тепло, создаваемое этим током, может серьезно повредить двигатель. Поскольку слишком сильное неконтролируемое снижение напряжения может повредить двигатель, большинство изготовителей преобразователей частоты избегают уменьшения напряжения двигателя до оптимального уровня.

Зависимость напряжения от частоты

Для двигателей с нагрузками с постоянным крутящим моментом ток намагничивания двигателя должен оставаться постоянным во всем диапазоне управляемых преобразователем частоты оборотов. Поскольку индуктивное сопротивление (XL) обмоток статора двигателя пропорционально прилагаемой частоте, (XL = 2πfL), для поддержания постоянного тока двигателя требуется прямая зависимость между прилагаемым напряжением и частотой. Это прямая зависимость «напряжения от частоты» (U/F), является одним из способов управления двигателем при помощи преобразователя частоты.

Это относится к преобразователям частоты, которые рассчитаны на нагрузки при постоянном крутящем моменте, такие как конвейеры, лебедки и подобные промышленные установки. Постоянное значение В/Гц показано на Рисунке 1.

Когда преобразователь частоты с постоянной характеристикой U/f применяется при нагрузке с переменным крутящим моментом, полный ток намагничивания на малых оборотах больше, чем требуется самой нагрузкой. Это перенамагничивание, как было упомянуто, создает в двигателе избыточное тепло.

Решение заключается в определении, какое напряжение требуется двигателю для правильной работы. Поскольку для этого требуются специальные функции, некоторые изготовители преобразователей частоты просто игнорируют этот вопрос и их преобразователи частоты производят только постоянную характеристику U/f во всем диапазоне оборотов. Хотя такой подход не максимизирует КПД двигателя, он позволяет избежать перенамагничивания двигателя и образования чрезмерного скольжения ротора двигателя.

Поскольку нагрузки, требующие переменного крутящего момента, представляют собой совершенно другое, модель фиксированной характеристики U/f не будет работать для всех нагрузок. Когда производится попытка улучшить КПД двигателя, реальная настройка профиля U/f часто предоставляется конечному пользователю. При этом методе (представленном на Рисунке 2) от пользователя требуется определить промежуточную точку U/f в профиле преобразователя частоты. Для этого требуется большое количество экспериментов и оценок во всем диапазоне оборотов и нагрузки системы. Кроме того, если характеристики системы меняются, требуется повторить весь этот процесс настройки. Очевидно, что это не самое практичное решение.

Некоторые изготовители преобразователей частоты предлагают пользователю выбор из ряда предварительно заданных переменных профилей U/f. Хотя это и упрощает процедуру, все еще требуется вручную прогнать двигатель через весь диапазон оборотов и определить самый низкий профиль В/Гц, который будет воспринимать нагрузку без чрезмерного скольжения ротора двигателя или нагрева двигателя.

Характеристики нагрузки установки могут измениться из-за сезонных изменений или модернизации системы HVAC здания. В этом случае повторно должен быть осуществлен процесс ручной настройки. Из-за необходимости такой работы большинство пользователей просто выбирают высокий профиль U/f, зная, что это позволит справляться с нагрузкой. Это приводит к растрате дорогой энергии.

Функция автоматической оптимизации потребления энергии «Automatic Energy Optimization»

Лучшим решением для настройки напряжения в соответствии с кривой частоты/мощности стала бы ее автоматизация. Это именно то, что делает преобразователь частоты VLT HVAC Drive. Он использует уникальный процесс автоматической оптимизации энергопотребления «Automatic Energy Optimization», который без вмешательства пользователя автоматически гарантирует, что соотношение напряжения и частоты всегда оптимально для конкретной нагрузки двигателя.

Чтобы автоматически обеспечить правильное напряжение при любой рабочей частоте и нагрузке, преобразователь частоты непрерывно контролирует двигатель и реагирует на изменения. Уникальный процесс управленияVVC+ преобразователя частоты VLT HVAC Drive является основной частью. Ток контролируется таким образом, чтобы в любой момент можно было узнать показатели как активного тока (который меняется от нагрузки), так и реактивного тока (который намагничивает статор двигателя).

В результате, преобразователь частоты автоматически поддерживает максимальный КПД двигателя во всех условиях. Во время начального разгона подается до 110% выходного напряжения, чтобы обеспечить дополнительный крутящий момент на преодоление инерции нагрузки. Это также обеспечивает мягкий старт и плавное наращивание характеристик регулируемых преобразователей частоты, предназначенных для использования в системах HVAC. После того, как двигатель набирает заданные обороты, преобразователь частоты VLT HVAC Drive автоматически определяет уровень постоянной нагрузки и уменьшает выходное напряжение для максимизации КПД двигателя. Если нагрузка меняется, например, когда резко открывается клапан в системе накачки, частотный преобразователь определяет изменение нагрузки и немедленно увеличивает выходное напряжение, чтобы поддерживать управление двигателем.

Кроме того, функция Автоматической адаптации двигателя «Automatic Motor Adaptation (AMA)» преобразователя частоты VLT HVAC, которая точно определяет критические параметры двигателя, позволяет частотному преобразователю рассчитывать показатели тока, чтобы определить количество тока намагничивания, необходимого для конкретной нагрузки. В результате получаются исключительные характеристики двигателя при низкой нагрузке, в области, в которой большинство преобразователей частоты практически неэффективны. Преобразователь частотыVLT HVAC Drive может реально понизить реактивную часть тока двигателя. Этот компонент, часто составляющий 25% тока двигателя и больше при малой нагрузке, обычно игнорируется другими изготовителями преобразователей частоты.

Функция автоматической оптимизации энергопотребления «Automatic energy optimization (AEO)» позволяет преобразователю частоты VLT HVAC Drive управлять напряжением в широком диапазоне, чтобы настраивать выход частотного преобразователя на конкретную нагрузку. Диапазон напряжений, в котором работает функция AEO, представлен на Рисунке 3. Как видно, функция AEO позволяет преобразователю частоты в целях экономии энергии уменьшать напряжение на двигателе практически на 50%. Переменная характеристика U/f экономит еще 5% энергии в типовых установках HVAC.

Преимущества функции AEO

Основное преимущество применения функции автоматической оптимизации энергопотребления проявляется при нагрузках при переменном крутящем моменте. Поскольку обороты двигателя падают, нагрузка на двигатель существенно снижается. Если на двигатель подается постоянно соотношение U/f, это отрицательно влияет на КПД двигателя. Определить, насколько можно снизить напряжение на двигателе до того, как начнут снижаться характеристики двигателя, вручную довольно затруднительно. Функция AEO рассчитывает это автоматически и непрерывно. Если меняется профиль нагрузки, функция AEO реагирует на это изменение и настраивает напряжение, подаваемое на двигатель.

Рисунок 3. Рабочий диапазон функции AEO и экономия при использовании данной функции.

Даже без изменения оборотов функция AEO все еще экономит энергию. Чтобы обеспечить запас надежности функционирования и застраховать от проектных ошибок, большинство двигателей для систем HVAC имеют больший размер, чем требуется для работы с конкретной нагрузкой.

В результате, даже на полных оборотах, в условиях полного потока двигатель работает при неполной нагрузке. Без уменьшения напряжения, обеспечиваемого функцией AEO, двигатель работает неэффективно. С частотным преобразователем VLT HVAC Drive обычно следует отметить выходное напряжение с преобразователя частоты, которое меньше номинального значения, указанного на табличке с названием и номинальными данными двигателя, даже когда преобразователь частоты выдает полную частоту. Это скорее получаемая от функции AEO экономия, компенсирующая использование переразмеренного под конкретное применение двигателя, чем индикация неправильного состояния.

От применения функции AEO выигрывают также установки с переменными оборотами и постоянным объемом. Примером таких установок служит система вентилятора для чистой комнаты. В этом случае целью преобразователя частоты является поддержание постоянного потока воздуха, даже когда микрофильтр воздуха становится грязным. По мере того, как фильтр засоряется, частотный преобразователь автоматически увеличивает обороты вентилятора. ФункцияAEO гарантирует, что на валу двигателя всегда имеется достаточный крутящий момент, при этом поддерживается максимальный КПД двигателя.

Хотя максимизация КПД двигателя является основной целью функции AEO, имеются также и другие выгоды от ее применения. Тепловыделение в двигателе, основная причина отказа двигателей, сокращается. За счет уменьшения тепловых нагрузок в двигателе увеличивается срок службы двигателя. Уменьшенное выделение тепла в двигателе уменьшает также тепловую нагрузку от двигателя на окружающие элементы здания. В случаях установки больших двигателей в зонах с контролируемой температурой дополнительная экономия на затратах на охлаждение может быть существенной.

Уменьшенный ток также имеет дополнительную выгоду. Это отражается в снижении потерь энергии в преобразователе частоты и во всех других компонентах, подающих ток в двигатель, таких как трансформаторы или реакторы в линиях.

Работа нескольких двигателей

В установках, где имеется несколько работающих двигателей, но только один из них в каждый момент времени контролируется преобразователем частоты, таких как чередующиеся насосы, функция AEO будет максимизировать КПД того двигателя, который в данный момент работает. Метод динамического управления функции AEO автоматически реагирует на включенный двигатель и подает ток в соответствии с нагрузкой двигателя.

Поскольку функция AEO подстраивает выходное напряжение преобразователя частоты на конкретные требования конкретного двигателя, она не может работать надежно в установках с несколькими одновременно работающими двигателями. Если два или более двигателя одновременно подключаются к выходу регулируемого преобразователя частоты, функция AEO может только обеспечить выходное напряжение, которое корректно для среднего значения двигателей. В результате подаваемое на двигатели напряжение может оказаться слишком высоким для одного из двигателей и слишком низким для другого. Из-за проблем с возможным недонамагничиванием двигателя, этого следует избегать. Когда несколько двигателей одновременно управляются одним частотным преобразователем частоты, VLT HVAC Drive настраивается на предварительно запрограммированную кривую В/Гц для переменного крутящего момента.

Выводы

Двигатели в системах HVAC редко нагружаются полностью. Это связано с тем, что двигатели для конкретной установки обычно переразмерены, и потому, что нагрузка двигателя резко падает, когда уменьшается расход. Обычно на малых оборотах КПД двигателя небольшой.

Для улучшения КПД двигателя некоторые преобразователи частоты требуют наличия оператора системы, который регулирует выходные характеристики В/Гц. Эти ручные методы как обременительны, так и неточны. В результате, они используются редко. Кроме того, если изменяются требования к системе, оператор вынужден повторять настройки.

Уникальный алгоритм VVC+ частотного преобразователя VLT HVAC Drive детально контролирует потребности двигателя в токе. За счет этого регулируемый преобразователь частоты определяет нагрузку на двигатель, а функция автоматической оптимизации энергопотребления гарантирует, что двигатель в течение всего времени получает идеальное напряжение. Все это выполняется автоматически без необходимости вмешательства пользователя.

Простейшие цепи переменного тока — Электротехника — Учебные материалы — Каталог статей

Список всех статей на технические темы

Простая электротехника все статьи

Сначала читаем статью «Переменный ток — краткие сведения»

Все электротехнические устройства состоят из сопротивлений индуктивностей и емкостей

Соотношение индуктивности емкости в цепи переменного тока принципиально определяют свойства цепи переменного тока.

Активное сопротивление R — это такой элемент электрической цепи, который оказывает сопротивление току с выделением тепла. Ведет себя одинаково в цепях постоянного и переменного тока, хотя величина сопротивления несколько отличается, это придется учитывать в точных расчетах.

Индуктивность L –это такой элемент электрической цепи, который состоит из витков провода и при протекании тока создает магнитное поле, это магнитное поле противодействует изменениям тока.

При протекании постоянного тока индуктивность ведет себя как проволока и не считается сопротивлением. Сопротивлением она является только для переменного тока, чем больше частота переменного тока, тем больше сопротивление индуктивности.

Емкость C – это такой элемент электрической цепи, который накапливает заряд, и проводит ток, только пока заряжается, или разряжается, поэтому в цепях постоянного тока, тока не проводит, а в цепях переменного тока все время заряжается – разряжается и, значит, проводит ток. Сопротивление емкости переменному току тем меньше, чем выше частота переменного тока.

Емкость и индуктивность взаимно противоположные по свойствам элементы, значит, они могут снижать взаимное влияние в цепях переменного тока или совсем отключать друг друга. Емкость и индуктивность оказывают сопротивление переменному току, но не могут выделить тепла, поэтому на них не происходит прямых потерь мощности.

Активное сопротивление R в цепи переменного тока

Что нам интересно знать про простейшую электрическую цепь содержащую R ?

Какой ток протекает в ней, какое напряжение на ней действует? и какая мощность может быть получена.

Здесь изображены две синусоиды, которые нельзя сравнивать и говорить какая больше, какая меньше. Они разные для удобства рассмотрения. Красная синусоида изображает переменное напряжение, а синяя синусоида изображает переменный ток

Если через активное R сопротивление протекает переменный синусоидальный ток, то на нем действует переменное синусоидальное напряжение. Ток и напряжение имеют одинаковую частоту и совпадают по фазе.

Мощность на активном сопротивлении определяется как произведение тока и напряжения. Действующая мощность будет равна произведению действующего значения тока на действующее значение напряжения.

Черные полуволны показывают, что мощность выделяемая в цепи на активном сопротивление изменяется также по синусоидальному закону,

Только знак остается все время положительным, это значит, что поток мощности однонаправлен. Мощность получается как произведение каждой точки синусоиды тока на каждую точку синусоиды напряжения в один и тот же момент. Плюс напряжения на плюс тока даст нам плюс мощности. Минус напряжения на минус тока даст нам плюс мощности.

Это значит, что при протекании тока через активное сопротивление R, электрическая мощность приводит к выделению тепла.

P=UI U = Uа√2 ; I = Iа√2 P = UаIа/2

Средняя мощность за период равна постоянной составляющей мощности

Uа Iа/2

Физический смысл этого явления состоит в том, что активное сопротивление потребляет энергию от источника, выделяет энергию в виде тепла. Электрическая мощность, которая превращается в тепло, называется активной мощностью и обозначается, как и в цепях постоянного тока, буквой P

Активными сопротивлениями в цепях переменного тока являются нагревательные и осветительные приборы, а также резисторы в сигнальных схемах, кроме того, как активные сопротивления проявляют себя все устройства, на которых выделяется полезная мощность в любом виде. Например, электрический мотор, звуковые динамики и т. п.

Индуктивное сопротивление в цепи переменного тока

X_L= ωL

Чтобы сделать сосредоточенную индуктивность, кусок проволоки сматывают в катушку

Если к цепи с индуктивностью подключить переменное синусоидальное напряжение, то в ней должен протекать переменный синусоидальный ток.

Что же происходит в цепи с индуктивностью при протекании переменного тока.

Оказывается, ток и напряжение действуют не одновременно,

то есть, сдвинуты по фазе

На активном сопротивлении R, появление напряжения сразу – в тот же момент, вызывает появление тока, и они действуют в одной фазе.

На индуктивности так не получается.

Если напряжение от источника начинает нарастать, то ток за ним не успевает.

Почему? В индуктивности изменение тока, приводит к появлению ЭДС самоиндукции, а эта ЭДС направлена на встречу изменения тока. Напряжение растет, и ток хочет расти, но ЭДС самоиндукции препятствует нарастанию тока. Это примерно также, как сила инерции мешает разогнать тележку, когда мы сдвигаем ее с места.

Ток преодолевает сопротивление направленной навстречу ему ЭДС самоиндукции, и начинает нарастать, но это происходит, когда напряжение уже достигло максимального значения. Ток, наконец, достигает максимального значения, но напряжение в этот момент уже снизилось до нуля. Так и повторяется – ток все время отстает от напряжения на 90⁰то есть на π/2. Значит, фаза тока отрицательна и составляет — π/2

Откуда берется эта ЭДС самоиндукции, и почему она не мешает в цепи с сопротивлением R. Это связано с тем, что катушка индуктивности, в отличие от сопротивления R, создает сильное магнитное поле, благодаря большому количеству витков. Магнитное поле не может мгновенно изменяться, оно и рождает внутри провода ЭДС, которая препятствует изменению тока.

Более подробно об ЭДС самоиндукции смотри в статье Начальные представления об электромагнетизме

Красная синусоида напряжения пресекает ноль каждый раз раньше зеленой синусоиды тока на π/2

Вывод: В цепи с индуктивностью напряжение впереди тока на 90°.

Любое сопротивление ограничивает ток, но бывает активное сопротивление, бывает реактивное..

R — активное сопротивление — на нем выделяется тепло

X — реактивное сопротивление на нем не выделятся тепло

X_L – сопротивление индуктивности

X_L – сопротивление индуктивности L является реактивным, оно равно X_L=ωL, то есть, оно прямо пропорционально частоте ω и индуктивности L, чем больше индуктивность, тем больше реактивное сопротивление и чем выше частота тем больше реактивное сопротивление.

Индуктивность тем сильнее ограничивает ток, чем выше частота тока.

Индуктивность пропускает переменный ток тем лучше, чем меньше индуктивность и чем меньше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток индуктивность пропускает без всякого сопротивления

Мощность на индуктивности

Мощность определяется как произведение тока на напряжение. Для каждого момента времени точка синусоиды тока умножается на точку синусоиды напряжения и получается точка синусоида мощности. Синусоида мощности получается двунаправленной, положительные полупериоды сменяются отрицательными, значит, мощность пол периода выделяется и пол периода поглощается. Это значит, что индуктивность L полпериода накапливает энергию в магнитном поле, а затем полпериода возвращает ее в источник.

Частота синусоиды мощности вдвое больше частоты тока и напряжения.

На индуктивности не получается выделение тепла, и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на индуктивности, называется реактивной и обозначается не Р, а другой буквой – Q_L

Емкость в цепи переменного тока

X_C=1/ ωc

При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться. Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.

Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.

Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.

То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2

X_C — сопротивление емкости

X_C — сопротивление емкости является реактивным, оно равно X_C=1/ ωc, то есть оно обратно пропорционально частоте и емкости, чем больше емкость, тем меньше реактивное сопротивление и чем выше частота тем меньше меньше реактивное сопротивление.

Емкость пропускает переменный ток тем лучше, чем больше емкость и чем выше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток емкость вообще не пропускает.

Конденсатор часто ставят в участки цепей, в которых не должен проходить постоянный ток

Мощность в цепи с емкостью

Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.

Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник. Частота синусоиды мощности вдвое больше частоты тока и напряжения.

Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.

Реактивные сопротивления

Индуктивность и емкость проявляют себя в электрических цепях как сопротивления.

X_C – реактивное сопротивление емкости

X_L_{— реактивное сопротивление индуктивности}

Формулы сопротивлений позволяют их использовать для расчета задач по закону Ома для участка цепи.

Формула X_C=1/ ωc показывает, что сопротивление емкости зависит от частоты ω. Это означает, что емкость по-разному пропускает ток низкой и высокой частоты.

Емкость пропускает переменный ток тем лучше, чем выше частота.

Емкость вообще не пропускает постоянный ток, и это ее важнейшее свойство. Одно из главных применений емкости (конденсатора) состоит в том, что его ставят в те ветви схем, где запрещено протекание постоянного тока.

Формула X_L= ωL _{показывает, что сопротивление индуктивности зависит от частоты. Это означает, что индуктивность по-разному пропускает ток низкой и ток высокой частоты.}

Индуктивность хуже пропускает переменный ток высокой частоты

Чем больше частота. Тем труднее проходит переменный ток. Катушка индуктивности используется для ограничения переменного тока.

Конденсатор и катушка являются противоположностями.

Конденсатор пропускает переменный ток и не пропускает постоянный

Катушка пропускает постоянный ток и не пропускает переменный

Такие цепи содержат сопротивление R, индуктивность L, и ёмкость C.

Реальное сопротивление цепи, содержащей одновременно R, L и C, зависит от величины каждого элемента цепи, и от частоты переменного тока, который протекает в этой цепи.

Расчет цепей переменного тока по аналогии с расчетом цепей постоянного тока невозможен, потому, что необходимо учитывать фазовый сдвиг между током и напряжением.

Можно упростить цепи, если какой-то элемент: R, L или C пренебрежительно мал.

Задачи на переменный ток решаются методом векторных диаграмм.

Ток и напряжение являются векторными величинами.Их изображают как вращающиеся радиус -векторы, в этом смысле они отличаются от векторов сил и скоростей в механике, но правила сложения и вычитания векторов аналогичны.

Метод векторных диаграмм

Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.

В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.

Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.

Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.

Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.

Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.

Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.

Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.

На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.

Векторная диаграмма напряжений представляет собой векторный треугольник напряжений

Последовательное соединение L R.

Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.

Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.

Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,

Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.

Векторная диаграмма строится так.

Выберем фазу общего тока равной 0, вектор тока откладывается как горизонтальный вектор слева на право. Далее строим векторную диаграмму напряжений. Сначала откладывается вектор напряжения на сопротивлении R. Этот вектор, пойдет горизонтально, так как его фаза совпадает с фазой тока. Затем строят вектор напряжения на индуктивности L. Его надо откладывать под углом 90⁰ вверх, это потому, что напряжение на индуктивности впереди на 90⁰.

Второй вектор переносится из центра вращения. Прикладываем его к концу вектора напряжения на активном сопротивлении. Таковы правила сложения векторов.

Теперь остается построить вектор полного напряжения на обоих элементах. Это вектор суммы, он, как известно, строится из начала первого вектора к концу второго.

Получился прямоугольный треугольник. Любую сторону этого треугольника можно найти по теореме Пифагора.

Острый угол этого треугольника и есть реальный сдвиг фаз в этой цепи между током и общим напряжением. Он обязательно меньше 90 градусов, потому что только на идеально индуктивности он составляет 90 градусов. Активное сопротивление обязательно уменьшает сдвиг фаз.

Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление, обозначается Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и X_L

Z², = Rа² + X²_L

В цепи L R, в отличие от цепи только с L, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.

Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и Q_L

S² = Р^{2 +} Q²_L

Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников.

Последовательное соединение RC

Конденсаторы очень часто включают последовательно с сопротивлениями, но если даже специального сопротивления нет, любой конденсатор обладает определённой величиной активного сопротивления, которую необходимо учитывать в точных расчетах. Есть понятие «добротность» конденсатора, которая проявляет активную составляющую его сопротивления

При последовательном соединении, через все элементы цепи протекает один ток, который называем – общий.

Сначала откладываем вектор тока, фазу которого принимаем равной нулю. Вектор напряжения на активном сопротивлении, откладываем в том же направлении, так как на активном сопротивлении ток и напряжение совпадают по фазе.

К концу вектора напряжения на активном сопротивлении прикладываем начало вектора напряжения на емкости. Фаза напряжения на емкости отстает от фазы напряжения на активном сопротивлении на 90 градусов, а вектор отстающего напряжения откладывается вниз.

Векторная диаграмма напряжений представляет собой прямоугольный треугольник, который позволяет определить все составляющие по теореме Пифагора.

Активное сопротивление R включенное в цепь с катушкой или конденсатором уменьшает угол сдвига фаз.

Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление обозначается буквой Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и X_С

Z² = Rа² + X²_С

В цепи L C, в отличие от цепи только с C, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.

Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и Q_С

S² = Р^{2 +} Q²_С

Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников

Параллельное соединение RL

При параллельном соединении RL одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через катушку отстает по фазе от напряжения. на 90⁰. Общий ток отстает от напряжения меньше чем на 90⁰.

Для цепей с параллельным соединением элементов, гораздо удобнее использовать не сопротивления (активные и реактивные) а их обратные величины, которые называются проводимости. Вместо r используется g, вместо X_L используется b_L, вместо Xc используется b_c

Параллельное соединение RC

При параллельном соединении RС одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через конденсатор опережает по фазе от напряжения. на 90⁰. Общий ток опережает напряжение меньше чем на 90⁰

Значение Cos φ

Cos φ в практической электротехнике имеет очень важное значение. Реальные нагрузки, типа электромоторов и трансформаторов, имеют большую индуктивную составляющую сопротивления, то есть, фактически, представляют собой цепи RL. Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P).

Из формулы видно, что чем меньше Cos φ (Чем больше угол сдвига фаз), тем меньшую часть активная мощность составляет от полной мощности .

Только активная мощность является полезной, если источник затрачивает полную мощность, а от нагрузки мы можем получить только активную мощность, значит, Cos φ имеет смысл электротехнического КПД или коэффициента мощности.

В идеале источник должен отдавать такую мощность, которую будет потреблять нагрузка. Реальные устройства неизбежно содержат индуктивности (катушки, обмотки, и т.п.), значит, источник вынужден отдавать полную мощность, которая значительно больше, активной.

Проектирование устройств и электрических цепей должно иметь целью получить значение Cos φ как можно ближе к единице, то есть влияние индуктивности надо свести к минимуму. Плохие значения Cos φ приводят к большим неоправданным затратам электроэнергии.

Цепи RLC

Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.

В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.

RLC последовательно

Как будет выглядеть векторная диаграмма в общем случае?

При последовательном соединении сопротивлений на каждом сопротивлении действует своя часть напряжения. На большем сопротивлении будет большая часть напряжения.

На первой векторной диаграмме видно, что напряжение на конденсаторе U_c больше, чем на катушке U_L тогда суммарный вектор общего напряжения направлен вниз, и видно, xnj угол сдвига фаз отрицательный. На второй диаграмме видно, что напряжение на конденсаторе U_c, значительно меньше, чем U_L , и вектор общего напряжения оказался направленным вверх, угол сдвига фаз стал положительным.

В первом случае цепь имеет емкостный характер, во втором индуктивный.

На определенной частоте наступает равенство Uc = Ul, такое явление называется резонанс напряжений

Условие резонанса X_L = X_C

При резонансе напряжений Общее сопротивление цепи становится минимально, а ток становится максимальным, что может быть опасно для источника и требует надежной защиты.

RLC параллельно

Векторные диаграммы токов при параллельном соединении

При параллельно соединении элементов RLC напряжение на всех элементах действует одно и то же, а токи разные, чем меньше сопротивление ветви, тем больше ток. В первом случае ток катушки значительно больше тока конденсатора. Вектор общего тока направлен вниз. Во втором случае ток катушки значительно меньше тока конденсатора и вектор тока направлен вверх.

В первом случае цепь имеет индуктивный характер, во втором емкостный

На определенной частоте наступает равенство токов I_c = I_L такое явление называется резонанс токов.

При резонансе токов сопротивление цепи становится максимальным и ток уменьшается до величины, которая определяется сопротивлением R, которое остается в цепи.

Условия резонанса

Резонанс широко применяется в радиотехнических и различных электронных схемах.

XL = XC

Устройства для переменного тока и устройства для постоянного тока

Устройства. Которые включаются электрические цепи

Лампочки

Нагреватели

Электромоторы

Электроинструмент

Бытовые приборы

Электроника

И т. п.

Лампочки и нагреватели работают одинаково в цепях переменного и постоянного тока. В некоторых случаях разница может быть заметной, так как активное сопротивление в цепи постоянного тока (омическое) может отличаться от сопротивления в цепи переменного тока.

Электромоторы и электроинструмент рассчитанный на переменный ток, при подключении в цепь постоянного тока скорее всего сгорят, так как, у них пропадает индуктивное сопротивление и ток сильно возрастает.

Если моторы, и инструмент рассчитанные на постоянный ток, включены на переменный ток, они сильно потеряют мощность, так как появившееся индуктивное сопротивление и сильно ограничит потребляемый ток.

Анализ электронных схем: частотная характеристика

При анализе синусоидальных цепей мы научились находить напряжения и токи в цепи с источником постоянной частоты. Если мы оставим амплитуду синусоидального источника постоянной и изменим частоту, мы получим частотную характеристику схемы. Частотную характеристику можно рассматривать как полное описание синусоидального установившегося режима работы цепи как функции частоты.

Частотная характеристика схемы — это изменение ее поведения при изменении частоты сигнала.

Синусоидальные установившиеся частотные характеристики цепей важны для многих приложений, особенно в системах связи и управления. Особое применение — электрические фильтры, которые блокируют или устраняют сигналы с нежелательными частотами и пропускают сигналы с желаемыми частотами. Фильтры используются в радио, телевидении и телефонных системах для отделения одной частоты вещания от другой.

Мы начинаем эту главу с рассмотрения частотной характеристики простых схем с использованием их передаточных функций. Затем мы рассматриваем графики Боде, которые являются отраслевым стандартом для представления частотной характеристики. Мы также рассматриваем последовательные и параллельные резонансные цепи и сталкиваемся с важными понятиями, такими как резонанс, добротность, частота среза и полоса пропускания. Мы обсуждаем различные виды фильтров и масштабирование сети. В последнем разделе мы рассматриваем одно практическое применение резонансных цепей и два применения фильтров.

Передаточная функция — полезный аналитический инструмент для определения частотной характеристики цепи. Фактически, частотная характеристика схемы — это график передаточной функции схемы H (
ω размер 12 {ω} {}) по сравнению с
ω размер 12 {ω} {}, с
ω размер 12 {ω} {} от
ω = 0 размер 12 {ω = 0} {} до
ω = ∞ размер 12 {ω = бесконечность} {}.

Передаточная функция — это частотно-зависимое отношение принудительной функции к принудительной функции (или выхода к входу).Идея передаточной функции была неявной, когда мы использовали понятия импеданса и адмиттанса для связи напряжения и тока. В общем, линейная сеть может быть представлена блок-схемой, показанной в [ссылка].

Передаточная функция H (
ω размер 12 {ω} {}) схемы — это частотно-зависимое отношение выходного векторного сигнала Y (
ω размером 12 {ω} {}) (напряжение или ток элемента) на вход вектора X (
ω размер 12 {ω} {}) (напряжение или ток источника).

Таким образом,

H (ω) = Y (ω) X (ω) размер 12 {H \ (ω \) = {{Y \ (ω \)} над {X \ (ω \)}}} {}

при нулевых начальных условиях.Поскольку вход и выход могут быть либо напряжением, либо током в любом месте цепи, существует четыре возможных передаточных функции:

H (ω) = величина напряжения 12 {H \ (ω \) = ital «напряжение»} {}

усиление = V0 (ω) Vi (ω) размер 12 {ital «gain» = {{V rSub {size 8 {0}} \ (ω \)} над {V rSub {size 8 {i}} \ (ω \ )}}} {}

H (ω) = текущий размер 12 {H \ (ω \) = ital «текущий»} {}

усиление = I0 (ω) Ii (ω) размер 12 {ital «gain» = {{I rSub {size 8 {0}} \ (ω \)} над {I rSub {size 8 {i}} \ (ω \ )}}} {}

H (ω) = размер перевода 12 {H \ (ω \) = ital «transfer»} {}

импеданс = V0 (ω) Ii (ω) размер 12 {ital «импеданс» = {{V rSub {size 8 {0}} \ (ω \)} над {I rSub {size 8 {i}} \ (ω \ )}}} {}

H (ω) = размер перевода 12 {H \ (ω \) = ital «transfer»} {}

admittance = I0 (ω) Vi (ω) размер 12 {ital «admit» «tan» ital «ce» = {{I rSub {size 8 {0}} \ (ω \)} над {V rSub {size 8 { i}} \ (ω \)}}} {}

, где индексы i и o обозначают входные и выходные значения.Являясь сложной величиной, H (
ω размер 12 {ω} {}) имеет величину H (
ω размер 12 {ω} {}) и фаза
φ размер 12 {φ} {}; то есть
H (ω) = H (ω) ∠φ размер 12 {H \ (ω \) = H \ (ω \) ∠φ} {}.

Блок-схема, представляющая линейную сеть.

Чтобы получить передаточную функцию с помощью [link], мы сначала получаем эквивалент схемы в частотной области, заменяя резисторы, катушки индуктивности и конденсаторы их импедансами R, j
ω размер 12 {ω} {} L и 1 / j
ω размер 12 {ω} {} C. Затем мы используем любую схемотехнику, чтобы получить соответствующее количество в [ссылка].Мы можем получить частотную характеристику схемы, построив график амплитуды и фазы передаточной функции при изменении частоты. Компьютер реально экономит время при построении передаточной функции.

Передаточная функция H (
ω размера 12 {ω} {}) можно выразить через полином числителя N (
ω размер 12 {ω} {}) и многочлен знаменателя D (
ω размер 12 {ω} {}) как

H (ω) = N (ω) D (ω) размер 12 {H \ (ω \) = {{N \ (ω \)} над {D \ (ω \)}}} {}

Где N (
ω размер 12 {ω} {}) и D (
ω size 12 {ω} {}) не обязательно являются одними и теми же выражениями для входных и выходных функций соответственно.Представление H (
ω размер 12 {ω} {}) в [ссылка] предполагает, что числитель и знаменатель множители в H (
ω размер 12 {ω} {}) отменили, уменьшив соотношение до самых низких членов. Корни N (
ω size 12 {ω} {}) = 0 называются нулями H (
ω размер 12 {ω} {}) и обычно представлены как
jω = z1, z2, … размер 12 {jω = z rSub {размер 8 {1}}, z rSub {размер 8 {2}}, «.» «.» «.» } {} Аналогично корни D (
ω size 12 {ω} {}) = 0 — полюсы H (
ω размер 12 {ω} {}) и представлены как
jω = p1, p2 ,… размер 12 {jω = p rSub {размер 8 {1}}, p rSub {размер 8 {2}}, «.» «.» «.» } {}

Ноль в качестве корня полинома числителя — это значение, которое приводит к нулевому значению функции. Полюс, как корень полинома знаменателя, представляет собой значение, для которого функция бесконечна.

Чтобы избежать сложной алгебры, целесообразно заменить j
ω размер 12 {ω} {} временно с s при работе с H (
ω размера 12 {ω} {}) и заменим s на j
ω размер 12 {ω} {} в конце.

Не всегда легко получить быстрый график величины и фазы передаточной функции, как мы делали выше. Более систематический способ получения частотной характеристики — это графики Боде. Прежде чем мы начнем строить графики Боде, мы должны позаботиться о двух важных вопросах: об использовании логарифмов и децибел для выражения усиления.

Поскольку графики Боде основаны на логарифмах, важно помнить о следующих свойствах логарифмов:

logP1P2 = logP1 + logP2 размер 12 {«журнал» P rSub {размер 8 {1}} P rSub {размер 8 {2}} = «журнал» P rSub {размер 8 {1}} + «журнал» P rSub {размер 8 {2}}} {}
logP1 / P2 = logP1 − logP2 размер 12 {«журнал» {P rSub {размер 8 {1}}} косая черта {P rSub {размер 8 {2}} = «журнал» P rSub {размер 8 {1}} — » log «P rSub {размер 8 {2}}}} {}
logPn = nlogP размер 12 {«журнал» P rSup {размер 8 {n}} = n «журнал» P} {}
log1 = 0 размер 12 {«log» 1 = 0} {}

В системах связи коэффициент усиления измеряется в белах.Исторически сложилось, что Bel используется для измерения отношения двух уровней мощности или усиления мощности G; то есть

G = Количество лент = log10P2P1 размер 12 {G = ital «Number» {} cSup {} ital «of» {} cSup {} ital «bels» = «log» rSub {size 8 {«10»}} {{ P rSub {размер 8 {2}}} больше {P rSub {размер 8 {1}}}}} {}

Децибел (дБ) дает нам меньшую величину. это
1/10-й размер 12 {{1} косая черта {«10» rSup {размер 8 {ital «th»}}}} {} пояса и равен

GdB = 10log10P2P1 размер 12 {G rSub {size 8 {ital «dB»}} = «10» «log» rSub {size 8 {«10»}} {{P rSub {size 8 {2}}} больше {P rSub {размер 8 {1}}}}} {}

Когда
P1 = P2 размер 12 {P rSub {размер 8 {1}} = P rSub {размер 8 {2}}} {}, нет изменения мощности, и коэффициент усиления равен 0 дБ.Если
P2 = 2P1 размер 12 {P rSub {размер 8 {2}} = 2P rSub {размер 8 {1}}} {}, усиление составляет

GdB = 10log102 = 3 дБ размер 12 {G rSub {size 8 {ital «dB»}} = «10» «log» rSub {size 8 {«10»}} 2 = 3 ital «dB»} {}

А когда
P2 = 0,5P1 размер 12 {P rSub {размер 8 {2}} = 0 «.» 5P rSub {size 8 {1}}} {}, прирост

GdB = 10log100.5 = −3 дБ размер 12 {G rSub {size 8 {ital «dB»}} = «10» «log» rSub {size 8 {«10»}} 0 «.» 5 = — 3 итал. «ДБ»} {}

[ссылка] и [ссылка] показывают еще одну причину, по которой широко используются логарифмы: логарифм обратной величины количества просто отрицателен логарифмом этого количества.

В качестве альтернативы коэффициент усиления G может быть выражен через коэффициент напряжения или тока. Для этого рассмотрим сеть, показанную в [ссылка]. Если
P1 размер 12 {P rSub {size 8 {1}}} {} — входная мощность,
P2 размер 12 {P rSub {size 8 {2}}} {} — выходная мощность (нагрузка),
R1 размер 12 {R rSub {размер 8 {1}}} {} — входное сопротивление и
R2 размер 12 {R rSub {размер 8 {2}}} {} — сопротивление нагрузки, тогда
P1 = 0,5V12 / R1 размер 12 {P rSub {size 8 {1}} = 0 «.» 5 {V rSub {размер 8 {1}} rSup {размер 8 {2}}} косая черта {R rSub {размер 8 {1}}}} {} и
P2 = 0.5V22 / R2 размер 12 {P rSub {size 8 {2}} = 0 «.» 5 {V rSub {размер 8 {2}} rSup {размер 8 {2}}} косая черта {R rSub {размер 8 {2}}}} {}, и [ссылка] становится

GdB = 10log10P2P1 = 10log10V22 / R2V12 / R1 = 10log10 (V2V1) 2 + 10log10R1R2 размер 12 {G rSub {size 8 {ital «dB»}} = «10» «log» rSub {size 8 {«10»}} { {P rSub {размер 8 {2}}} больше {P rSub {size 8 {1}}}} = «10» «log» rSub {размер 8 {«10»}} {{V rSub {размер 8 {2 }} rSup {размер 8 {2}} / R rSub {размер 8 {2}}} больше {V rSub {размер 8 {1}} rSup {размер 8 {2}} / R rSub {размер 8 {1}} }} = «10» «log» rSub {размер 8 {«10»}} \ ({{V rSub {размер 8 {2}}} больше {V rSub {размер 8 {1}}}} \) rSup { размер 8 {2}} + «10» «журнал» rSub {размер 8 {«10»}} {{R rSub {размер 8 {1}}} больше {R rSub {размер 8 {2}}}}} { }
GdB = 20log10V2V1−10log10R2R1 размер 12 {G rSub {size 8 {ital «dB»}} = «20» «log» rSub {size 8 {«10»}} {{V rSub {size 8 {2}}} больше {V rSub {размер 8 {1}}}} — «10» «log» rSub {размер 8 {«10»}} {{R rSub {размер 8 {2}}} больше {R rSub {размер 8 {1 }}}}} {}

На случай, когда
R2 = R1 размер 12 {R rSub {размер 8 {2}} = R rSub {размер 8 {1}}} {}, условие, которое часто предполагается при сравнении уровней напряжения, [ссылка] становится

GdB = 20log10V2V1 размер 12 {G rSub {size 8 {ital «dB»}} = «20» «log» rSub {size 8 {«10»}} {{V rSub {size 8 {2}}} больше {V rSub {размер 8 {1}}}}} {}

Вместо этого, если
P1 = I12R1 размер 12 {P rSub {размер 8 {1}} = I rSub {размер 8 {1}} rSup {размер 8 {2}} R rSub {размер 8 {1}}} {} и
P2 = I22R2 размер 12 {P rSub {размер 8 {2}} = I rSub {размер 8 {2}} rSup {размер 8 {2}} R rSub {размер 8 {2}}} {}, для
R1 = R2 размер 12 {R rSub {размер 8 {1}} = R rSub {размер 8 {2}}} {}, получаем

GdB = 20log10I2I1 размер 12 {G rSub {size 8 {ital «dB»}} = «20» «log» rSub {size 8 {«10»}} {{I rSub {size 8 {2}}} больше {I rSub {размер 8 {1}}}}} {}

Соотношение напряжение-ток для четырехполюсной сети.

Из [link], [link] и [link] следует отметить три важных момента:

Эти 10 логарифмов используются для мощности, а 20 логарифмов используются для напряжения или тока из-за квадратного отношения между ними (
P = V2 / R = I2R размер 12 {P = {V rSup {размер 8 {2}}} косая черта {R} = I rSup {размер 8 {2}} R} {}).
Что значение в дБ является логарифмическим измерением отношения одной переменной к другой того же типа. Следовательно, он применяется при выражении передаточной функции H в [link] и [link], которые являются безразмерными величинами, но не при выражении H в [link] и [link].
Важно отметить, что мы используем только напряжение и величину тока в [link] и [link]. Отрицательные знаки и углы будут обрабатываться независимо, как мы увидим в разделе 4.

Имея это в виду, мы теперь применим концепции логарифмов и децибел для построения графиков Боде.

Получение частотной характеристики от передаточной функции, как мы делали в разделе 2, является сложной задачей. Частотный диапазон, необходимый для частотной характеристики, часто настолько широк, что неудобно использовать линейную шкалу для оси частот.Кроме того, существует более систематический способ определения важных характеристик амплитудных и фазовых графиков передаточной функции. По этим причинам стало стандартной практикой использовать логарифмическую шкалу для оси частот и линейную шкалу на каждом из отдельных графиков величины и фазы. Такие полулогарифмические графики передаточной функции, известные как графики Боде, стали отраслевым стандартом.

Графики Боде — это полулогарифмические графики амплитуды (в децибелах) и фазы (в градусах) передаточной функции в зависимости от частоты.

Графики

Боде содержат ту же информацию, что и нелогарифмические графики, обсуждавшиеся в предыдущем разделе, но их гораздо проще построить, как мы вскоре увидим.

Передаточную функцию можно записать как

H = H∠φ = Hejφ размер 12 {H = H∠φ = ital «He» rSup {size 8 {jφ}}} {}

Получаем натуральный логарифм от обеих сторон,

lnH = lnH + lnejφ = lnH + jφ размер 12 {«ln» H = «ln» H + «ln» e rSup {размер 8 {jφ}} = «ln» H + jφ} {}

Таким образом, действительная часть ln H является функцией величины, а мнимая часть — фазой.На графике величины Боде выигрыш

HdB = 20log10H размер 12 {H rSub {размер 8 {ital «dB»}} = «20» «log» rSub {size 8 {«10»}} H} {}

отображается в децибелах (дБ) в зависимости от частоты. [ссылка] предоставляет несколько значений H с соответствующими значениями в децибелах. На фазовом графике Боде
φ размер 12 {φ} {} показан в градусах в зависимости от частоты. И амплитудные, и фазовые графики построены на миллиметровой бумаге.

Удельное усиление и их значения в децибелах.
Величина H	20 log10H размер 12 {«log» rSub {размер 8 {«10»}} H} {} (дБ)
0.001	-60
0,01	-40
0,1	-20
0,5	-6
1/2 размера 12 {{1} косая черта {sqrt {2}}} {}	-3
1	0
2 размер 12 {sqrt {2}} {}	3
2	6
10	20
20	26
100	40
1000	60

Передаточная функция в форме [ссылка] может быть записана в терминах факторов, которые имеют действительную и мнимую части.Одно такое представление может быть

H (ω) = K (jω) ± 1 (1 + jω / z1) [1 + j2ζ1ω / ωk + (jω / ωk) 2] (1 + jω / p1) [1 + j2ζ2ω / ωn + (jω / ωn) 2 ] размер 12 {H \ (ω \) = {{K \ (jω \) rSup {size 8 {+ — 1}} \ (1 + jω / z rSub {size 8 {1}} \) \ [1+ j2ζ rSub {размер 8 {1}} ω / ω rSub {размер 8 {k}} + \ (jω / ω rSub {размер 8 {k}} \) rSup {размер 8 {2}} \]} над {\ (1 + jω / p rSub {размер 8 {1}} \) \ [1 + j2ζ rSub {размер 8 {2}} ω / ω rSub {размер 8 {n}} + \ (jω / ω rSub {размер 8 {n}} \) rSup {размер 8 {2}} \]}}} {}

, который получается делением полюсов и нулей в H (
ω размер 12 {ω} {}).Представление H (
ω размер 12 {ω} {}), как в [ссылка], называется стандартной формой. В этом частном случае H (
ω размер 12 {ω} {}) имеет семь различных факторов, которые могут появляться в различных комбинациях в передаточной функции. Это:

Коэффициент усиления K
полюс
(jω) −1 размер 12 {\ (jω \) rSup {size 8 {- 1}}} {} или ноль (j
ω размер 12 {ω} {}) в начале координат
простой столб
1 / (1 + jω / p1) размер 12 {{1} косая черта {\ (1+ {jω} косая черта {p rSub {размер 8 {1}} \)}}} {} или ноль
(1 + jω / z1) размер 12 {\ (1+ {jω} косая черта {z rSub {size 8 {1}} \)}} {}

При построении графика Боде мы наносим каждый фактор отдельно, а затем объединяем их графически.Факторы можно рассматривать по одному, а затем складывать аддитивно из-за логарифма, который делает графики Боде мощным инструментом проектирования.

Теперь мы построим прямолинейные графики факторов, перечисленных выше. Мы обнаружим, что эти прямолинейные графики, известные как графики Боде, аппроксимируют реальные графики с удивительной степенью точности.

Постоянный член : для коэффициента усиления K величина равна 20
log10 размер 12 {«log» rSub {размер 8 {«10»}}} {} K и фаза 00; оба постоянны с частотой.Таким образом, амплитуда и фазовые графики усиления показаны в [ссылка]. Если K отрицательно, величина остается 20
log10∣K∣ размер 12 {«log» rSub {size 8 {«10»}} lline K rline} {} но фаза
± 1800 размер 12 {+ — «180» rSup {размер 8 {0}}} {}.

Графики Боде для коэффициента усиления K: а) график величины, б) график фазы.

Полюс / ноль в начале координат : для нуля (j
ω размер 12 {ω} {}) в начале координат амплитуда 20
log10 размер 12 {«log» rSub {размер 8 {«10»}}} {} ω размер 12 {ω} {} и фаза 900.Они нанесены на [ссылка], где мы замечаем, что наклон графика амплитуды составляет 20 дБ / декаду, в то время как фаза постоянна с частотой.

Сюжеты Боде для полюса
(jω) −1 размер 12 {\ (jω \) rSup {size 8 {- 1}}} {} аналогичны, за исключением того, что наклон графика амплитуды составляет -20 дБ / декаду, в то время как фаза
−900 размер 12 {- «90» rSup {размер 8 {0}}} {}. В общем, для
(jω) N размер 12 {\ (jω \) rSup {size 8 {N}}} {} является целым числом, график амплитуды будет иметь наклон 20N дБ / декаду, а фаза — 90N градусов.

График Боде для нуля (jw) в начале координат: а) график величины, б) график фазы.

Простой полюс / ноль : для простого нуля
(1 + jω / z1) размер 12 {\ (1+ {jω} косая черта {z rSub {size 8 {1}} \)}} {}, величина
20log10 / 1 + jω / z1 / size 12 {«20» «log» rSub {size 8 {«10»}} lline 1+ {jω} косая черта {z rSub {size 8 {1}}} rline} {} и фаза
tan − 1ω / z1 size 12 {«tan» rSup {size 8 {- 1}} {ω} косая черта {z rSub {size 8 {1}}}} {}. Заметим, что

HdB = 20log10 / 1 + jωz1 / -> 20log101 = 0asω → 0 размер 12 {H rSub {size 8 {ital «dB»}} = «20» «log» rSub {size 8 {«10»}} lline 1+ {{jω} over {z rSub {size 8 {1}}}} rline drarrow «20» «log» rSub {size 8 {«10»}} 1 = 0 {} cSup {} ital «as» {} cSup {} ω rightarrow 0} {}
HdB = 20log10 / 1 + jωz1 / -> 20log10ωz1asω → ∞alignl {stack {
{} #
размер 12 {H rSub {size 8 {ital «dB»}} = «20» «log» rSub {size 8 {«10»}} lline 1+ {{jω} больше {z rSub {size 8 {1}} }} rline drarrow «20» «log» rSub {size 8 {«10»}} {{ω} over {z rSub {size 8 {1}}}} {} cSup {} ital «as» {} cSup { } ω правая стрелка бесконечность} {}
}} {}

, показывающий, что мы можем аппроксимировать величину как ноль (прямая линия с нулевым наклоном) для малых значений
ω размером 12 {ω} {} и прямой линией с крутизной 20 дБ / декада для больших значений
ω размер 12 {ω} {}.Частота
ω = z1 размер 12 {ω = z rSub {размер 8 {1}}} {}, где встречаются две асимптотические линии, называется частотой излома или частотой разрыва. Таким образом, приблизительный график величины показан в [ссылка] a, где также показан фактический график. Обратите внимание, что приблизительный график близок к реальному графику, за исключением частоты разрыва, где
ω = z1 размер 12 {ω = z rSub {size 8 {1}}} {} и отклонение равно
20log10 / 1 + j1 / = 20log102 = 3 дБ, размер 12 {«20» «log» rSub {size 8 {«10»}} lline 1 + j rSub {size 8 {1}} rline = «20» «log» rSub {size 8 {«10»}} sqrt {2} = 3 ital «dB»} {}.

В качестве линейного приближения положим
φ≈0 размер 12 {φ приблизительно 0} {} для
ω≤z1 / 10 размер 12 {ω <= {z rSub {size 8 {1}}} косая черта {"10"}} {}, φ≈450 размер 12 {φ приблизительно "45" rSup {размер 8 {0}}} {} для ω = z1 размер 12 {ω = z rSub {size 8 {1}}} {}, и φ≈900 размер 12 {φ приблизительно "90" rSup {размер 8 {0}}} {} для ω≥10z1 размер 12 {ω> = «10» z rSub {size 8 {1}}} {}. Как показано в [ссылка] b вместе с фактическим графиком, прямолинейный график имеет наклон
450 размер 12 {«45» rSup {размер 8 {0}}} {} за десятилетие.

График Боде нуля (1 + jw / z1): а) график величины, б) график фазы.

Сюжеты Боде для полюса
1 / (1 + jω / p1) размер 12 {{1} косая черта {\ (1+ {jω} косая черта {p rSub {размер 8 {1}} \)}}} {} аналогичны тем, что в [ссылка] за исключением того, что угловая частота находится на
ω = p1 размер 12 {ω = p rSub {size 8 {1}}} {}, величина имеет наклон — 20 дБ / декаду, а фаза имеет наклон
−450 размер 12 {- «45» rSup {размер 8 {0}}} {} на декаду

Квадрический полюс / ноль : величина квадратичного полюса
ωn) 21 + j2ς2ω / ωn + (jω / 1 / размер 12 {{1} косая черта {lbrace 1 + j2ς rSub {размер 8 {2}} {ω} косая черта {ω rSub {размер 8 {n}} + \ ({ jω} косая черта {ω rSub {размер 8 {n}} \) rSup {размер 8 {2}} rbrace}}}} {} — это
ωn) 21 + j2ς2ω / ωn + (jω / −20log10 размер 12 {- «20» «log» rSub {size 8 {«10»}} lline lbrace 1 + j2ς rSub {size 8 {2}} {ω} косая черта { ω rSub {размер 8 {n}} + \ ({jω} косая черта {ω rSub {размер 8 {n}} \) rSup {размер 8 {2}} rbrace}} rline} {} и фаза
−tan − 1 (2ς2ω / ωn) / 1 − ω2 / ωn) 2) размер 12 {- «загар» rSup {размер 8 {- 1}} {\ (2ς rSub {size 8 {2}} {ω} косая черта {ω rSub {размер 8 {n}} \)}} косая черта {1 — {ω rSup {размер 8 {2}}} косая черта {ω rSub {размер 8 {n}} \) rSup {размер 8 {2}} \)}}} {}.Но

HdB = −20log10 / 1 + j2ζ2ωωn + (jωωn) 2 / -> 0asω → ∞ размер 12 {H rSub {размер 8 {ital «дБ»}} = — «20» «log» rSub {размер 8 {«10»} } lline 1+ {{j2ζ rSub {size 8 {2}} ω} над {ω rSub {size 8 {n}}}} + \ ({{jω} над {ω rSub {size 8 {n}}}}) \) rSup {size 8 {2}} rline drarrow 0 {} cSup {} ital «as» {} rSup {} ω rightarrow infinity} {}

HdB = −20log10 / 1 + j2ζ2ωωn + (jωωn) 2 / -> — 40log10ωωnasω → ∞ размер 12 {H rSub {size 8 {ital «dB»}} = — «20» «log» rSub {size 8 {«10» }} lline 1+ {{j2ζ rSub {size 8 {2}} ω} над {ω rSub {size 8 {n}}}} + \ ({{jω} над {ω rSub {size 8 {n}}}) } \) rSup {размер 8 {2}} rline drarrow — «40» «log» rSub {размер 8 {«10»}} {{ω} больше {ω rSub {size 8 {n}}}} {} cSup {} ital «as» {} cSup {} ω rightarrow infinity} {}

Таким образом, график амплитуды состоит из двух прямых асимптотических линий: одна с нулевым наклоном для
ω <ωn размер 12 {ω <ω rSub {size 8 {n}}} {}, а другой с крутизной -40 дБ / декада для ω> ωn размер 12 {ω> ω rSub {размер 8 {n}}} {}, с размером ωn 12 {ω> ω rSub {размер 8 {n}}} {} в качестве угловой частоты.[ссылка] а показывает приблизительный и фактический графики амплитуд. Обратите внимание, что фактический график зависит от коэффициента демпфирования.
ς2 размер 12 {ς rSub {размер 8 {2}}} {}, а также угловую частоту
ωn размер 12 {ω rSub {размер 8 {n}}} {}. значительный пик в окрестности угловой частоты должен быть добавлен к прямолинейному приближению, если требуется высокий уровень точности. Однако для простоты мы будем использовать прямолинейное приближение.

Графики Боде квадратичного полюса 1 + j2ζ2ωωn + (jωωn) 2 размер 12 {H rSub {size 8 {ital «dB»}} = — «20» «log» rSub {size 8 {«10»}} lline 1+ {{ j2ζ rSub {размер 8 {2}} ω} над {ω rSub {размер 8 {n}}}} + \ ({{jω} над {ω rSub {размер 8 {n}}}}} \) rSup {размер 8 {2}} rline drarrow — «40» «log» rSub {size 8 {«10»}} {{ω} больше {ω rSub {size 8 {n}}}} {} cSup {} ital «as» { } cSup {} ω rightarrow infinity} {}
: а) график величины, б) график фазы.

Фазовый график представляет собой прямую линию с наклоном
900 размер 12 {«90» rSup {size 8 {0}}} {} за десятилетие, начиная с
ωn / 10 размер 12 {{ω rSub {size 8 {n}}} косая черта {«10»}} {} и заканчивается на
10ωn размер 12 {«10» ω rSub {размер 8 {n}}} {}, как показано в [ссылка] b. Мы снова видим, что разница между фактическим графиком и прямолинейным графиком связана с коэффициентом затухания. Обратите внимание, что прямолинейные аппроксимации для графиков амплитуды и фазы для квадратичного полюса такие же, как и для двойного полюса, т.е.е.
(1 + jω / ωn) −2 размер 12 {\ (1 + j {ω} косая черта {ω rSub {size 8 {n}} \) rSup {size 8 {- 2}}}} {}. Этого следует ожидать, потому что двойной полюс
(1 + jω / ωn) −2 размер 12 {\ (1 + j {ω} косая черта {ω rSub {size 8 {n}} \) rSup {size 8 {- 2}}}} {} равен полюсу квадрата
ωn) 21 + j2ς2ω / ωn + (jω / −1 размер 12 {lbrace 1 + j2ς rSub {size 8 {2}} {ω} косая черта {ω rSub {size 8 {n}} + \ ({jω} косая черта {ω rSub {размер 8 {n}} \) rSup {размер 8 {2}} rbrace}} rSup {размер 8 {- 1}}} {} когда
ς2 = 1 размер 12 {ς rSub {размер 8 {2}} = 1} {}.Таким образом, квадратичный полюс можно рассматривать как двойной полюс, как это касается приближения прямой линии.

Для квадратичного нуля
ωn) 21 + j2ς2ω / ωn + (jω / −2 размер 12 {lbrace 1 + j2ς rSub {размер 8 {2}} {ω} косая черта {ω rSub {размер 8 {n}} + \ ({jω} косая черта {ω rSub {size 8 {n}} \) rSup {size 8 {2}} rbrace}} rSup {size 8 {- 2}}} {}, графики в [ссылка] инвертированы, потому что график величины имеет наклон 40 дБ / декада, в то время как фазовый график имеет наклон
900 размер 12 {«90» rSup {размер 8 {0}}} {} за десятилетие.

[ссылка] представляет собой сводку графиков Боде для семи факторов. Чтобы набросать графики Боде для функции H (
ω размер 12 {ω} {}) в форме [ссылка], например, мы сначала записываем угловые частоты на миллиметровой бумаге полулогарифма, поочередно зарисовываем факторы, как описано выше, а затем аддитивно объединяем графики факторы. Комбинированный график часто строится слева направо с соответствующим изменением наклона каждый раз, когда встречается угловая частота.

Сводка прямолинейных графиков амплитуды и фазы по Боде.

Наиболее заметной особенностью частотной характеристики цепи может быть резкий пик (или резонансный пик), проявляющийся в ее амплитудной характеристике. Концепция резонанса применяется в нескольких областях науки и техники. Резонанс возникает в любой системе, имеющей комплексно сопряженную пару полюсов; это причина колебаний запасенной энергии из одной формы в другую. Это явление, которое допускает частотную дискриминацию в сетях связи.Резонанс возникает в любой цепи, имеющей хотя бы одну катушку индуктивности и один конденсатор.

эсонанс — это состояние в цепи RLC, в котором емкостное и индуктивное реактивные сопротивления равны по величине, что приводит к чисто реактивному импедансу.

Резонансные цепи (последовательные или параллельные) полезны для построения фильтров, поскольку их передаточные функции могут быть очень частотно-избирательными. Они используются в любых приложениях, таких как выбор нужных станций в радио- и ТВ-приемниках.

Рассмотрим последовательную схему RLC, показанную в [ссылка] в частотной области. Входное сопротивление

Z = H (ω) = VsI = R + jωL + 1jωC размер 12 {Z = H \ (ω \) = {{V rSub {size 8 {s}}} над {I}} = R + jωL + {{1 } больше {jωC}}} {}

или

Z = R + j (ωL − 1ωC) размер 12 {Z = R + j \ (ωL — {{1} над {ωC}} \)} {}

Резонанс возникает, когда мнимая часть передаточной функции равна нулю, или

Im (Z) = (ωL − 1ωC) = 0 размер 12 {«Im» \ (Z \) = \ (ωL — {{1} over {ωC}} \) = 0} {}

Стоимость
ω размером 12 {ω} {}, который удовлетворяет этому условию, называется резонансной частотой
ω0 размер 12 {ω rSub {размер 8 {0}}} {}.Таким образом, условие резонанса

ω0L = 1ω0C размер 12 {ω rSub {размер 8 {0}} L = {{1} больше {ω rSub {размер 8 {0}} C}}} {}

или

ω0 = 1LCrad / s размер 12 {ω rSub {size 8 {0}} = {{1} over {sqrt {ital «LC»}}} ital «rad» / s} {}

С
ω0 = 2πf0 размер 12 {ω rSub {размер 8 {0}} = 2πf rSub {размер 8 {0}}} {}.

f0 = 12πLCHz размер 12 {f rSub {size 8 {0}} = {{1} больше {2π sqrt {ital «LC»}}} ital «Hz»} {}

Последовательный резонансный контур.

Обратите внимание, что при резонансе:

1.Импеданс является чисто резистивным, таким образом, Z = R, другими словами, комбинация серии LC действует как короткое замыкание, и все напряжение проходит через R.

2. Напряжение
Vs размера 12 {V rSub {size 8 {s}}} {} и ток I синфазны, так что коэффициент мощности равен единице.

3. Величина передаточной функции H (
ω размер 12 {ω} {}) = Z (
ω размер 12 {ω} {}) минимален.

4. Напряжение индуктора и конденсатора может быть намного больше, чем напряжение источника.

Частотная характеристика текущей величины цепи

I = / I / = VmR2 + (ωL − 1ωC) 2 размер 12 {I = lline I rline = {{V rSub {size 8 {m}}} больше {sqrt {R rSup {size 8 {2}} + \ ( ωL — {{1} над {ωC}} \) rSup {размер 8 {2}}}}}} {}

Показано в [ссылка]; график показывает только симметрию, показанную на этом графике, когда ось частот является логарифмом. Средняя мощность, рассеиваемая цепью RLC, составляет

P (ω) = 12I2R размер 12 {P \ (ω \) = {{1} больше {2}} I rSup {размер 8 {2}} R} {}

Наибольшая рассеиваемая мощность происходит при резонансе, когда
I = Vrp / R размер 12 {I = {V rSub {size 8 {ital «rp»}}} косая черта {R}} {}, так что

P (ω0) = 12 Вм2R размер 12 {P \ (ω rSub {размер 8 {0}} \) = {{1} больше {2}} {{V rSub {размер 8 {m}} rSup {размер 8 {2 }}} более {R}}} {}

На определенных частотах
ω = ω1 = ω2 размер 12 {ω = ω rSub {размер 8 {1}} = ω rSub {размер 8 {2}}} {}, рассеиваемая мощность равна половине максимального значения; то есть

P (ω1) = P (ω2) = (Vm / 2) 22R = Vm24R размер 12 {P \ (ω rSub {size 8 {1}} \) = P \ (ω rSub {size 8 {2}} \) = {{\ (V rSub {размер 8 {m}} / sqrt {2} \) rSup {размер 8 {2}}} больше {2R}} = {{V rSub {размер 8 {m}} rSup {размер 8 {2}}} больше {4R}}} {}

Следовательно,
ω1 размер 12 {ω rSub {размер 8 {1}}} {} и
ω2 размером 12 {ω rSub {size 8 {2}}} {} называются частотами половинной мощности.

Зависимость амплитуды тока от частоты для последовательного резонансного контура, показанного на рисунке 7.

Частоты половинной мощности получают, задав Z равным
2R размер 12 {sqrt {2} R} {} и запись

R2 + (ωL − 1ωC) 2 = 2R размер 12 {sqrt {R rSup {размер 8 {2}} + \ (ωL — {{1} над {ωC}} \) rSup {размер 8 {2}}} = sqrt {2} R} {}

Решение для
ω размер 12 {ω} {}, получаем

ω1 = −R2L + (R2L) 2 + 1LC размер 12 {ω rSub {size 8 {1}} = — {{R} over {2L}} + sqrt {\ ({{R} over {2L}} \) rSup {размер 8 {2}} + {{1} больше {ital «LC»}}}} {}

ω2 = R2L + (R2L) 2 + 1LC размер 12 {ω rSub {size 8 {2}} = {{R} over {2L}} + sqrt {\ ({{R} over {2L}} \) rSup {size 8 {2}} + {{1} сверх {ital «LC»}}}} {}

Мы можем связать частоты половинной мощности с резонансной частотой.Из [ссылка] и [ссылка],

ω0 = ω1ω2 размер 12 {ω rSub {размер 8 {0}} = sqrt {ω rSub {размер 8 {1}} ω rSub {размер 8 {2}}}} {}

Решаем, что резонансная частота — это среднее геометрическое значений половинной мощности. Обратите внимание, что
ω1 размер 12 {ω rSub {размер 8 {1}}} {} и
ω2 размер 12 {ω rSub {размер 8 {2}}} {} в целом несимметричны относительно резонансной частоты
ω0 размер 12 {ω rSub {размер 8 {0}}} {}, поскольку частотная характеристика обычно не является симметричной. Однако, как будет вскоре объяснено, симметрия частот половинной мощности относительно резонансной частоты часто является разумным приближением.

Хотя высота кривой в [ссылка] определяется R, ширина кривой зависит от других факторов. Ширина кривой отклика зависит от полосы пропускания B, которая определяется как разница между двумя частотами половинной мощности,

B = ω2 − ω1 размер 12 {B = ω rSub {размер 8 {2}} — {}} {}

Это определение пропускной способности — лишь одно из нескольких, которые обычно используются. Строго говоря, B в [link] — это ширина полосы половинной мощности, потому что это ширина полосы частот между частотами половинной мощности.

«Резкость» резонанса в резонансном контуре количественно измеряется добротностью Q. При резонансе реактивная энергия в контуре колеблется между катушкой индуктивности и конденсатором. Коэффициент качества связывает максимальную или пиковую запасенную энергию с энергией, рассеиваемой в цепи за цикл колебаний:

Q = 2
π размер 12 {π} {} __________ Пиковая энергия, запасенная в контуре _____________

Энергия, рассеиваемая контуром за один период при резонансе

Он также считается мерой способности цепи накапливать энергию по отношению к ее способности рассеивать энергию.В последовательной цепи RLC пиковая запасенная энергия равна
12LI2 размер 12 {{{1} больше {2}} ital «LI» rSup {size 8 {2}}} {}, а энергия, рассеиваемая за один период, равна
12 (I2R) (1 / f) размер 12 {{{1} больше {2}} \ (I rSup {size 8 {2}} R \) \ ({1} косая черта {f \)}} {}. Следовательно,

Q = 2π12LI212I2R (1 / f) = 2πfLR размер 12 {Q = 2π {{{{1} over {2}} ital «LI» rSup {size 8 {2}}} over {{{1} over {2}) } I rSup {size 8 {2}} R \ (1 / f \)}} = {{2π ital «fL»} больше {R}}} {}

или

Q = ω0LR = 1ω0CR размер 12 {Q = {{ω rSub {размер 8 {0}} L} больше {R}} = {{1} больше {ω rSub {размер 8 {0}} курсив «CR»}} } {}

Обратите внимание, что коэффициент качества безразмерен.Взаимосвязь между полосой пропускания B и коэффициентом качества Q получается заменой [link] на [link] и использованием [link]

B = RL = ω0Q размер 12 {B = {{R} над {L}} = {{ω rSub {размер 8 {0}}} над {Q}}} {}

или
B = ω02CR размер 12 {B = ω rSub {размер 8 {0}} rSup {размер 8 {2}} ital «CR»} {}. Таким образом,

Добротность резонансного контура — это отношение его резонансной частоты к ширине полосы.

Имейте в виду, что [ссылка], [ссылка], [ссылка] и [ссылка] применимы только к последовательной цепи RLC.

Как показано в [ссылка], чем выше значение Q, тем более избирательна схема, но тем меньше ширина полосы. Избирательность схемы RLC — это способность схемы реагировать на определенную частоту и различать все другие частоты. Если полоса частот для выбора или отбраковки узкая, добротность резонансного контура должна быть высокой. Если полоса частот широкая, добротность должна быть низкой.

Резонансный контур предназначен для работы на своей резонансной частоте или вблизи нее.Считается, что это схема с высокой добротностью

20,5 Сравнение переменного и постоянного тока — College Physics

20,5 Сравнение переменного и постоянного тока — College Physics | OpenStaxSkip к контенту

Предисловие
1 Введение: Природа науки и физики
Введение в науку и область физики, физических величин и единиц
1.1 Физика: введение
1.2 Физические величины и единицы
1 .3 Точность, прецизионность и значимые цифры
1.4 Приближение
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
1. Введение в одномерную кинематику
2. 2.1 Смещение
3. 2.2 Векторы, скаляры и системы координат
4. 2.3 Время, скорость и скорость
5. 2.4 Ускорение
6. 2.5 Уравнения движения для постоянного ускорения в одном измерении
7. 2.6 Основы решения проблем для одномерной кинематики
8. 2.7 Падающие объекты
9. 2.8 Графический анализ одномерного движения
10. Глоссарий
11. Сводка раздела
12. Концептуальные вопросы
13. Задачи и упражнения
3 Двумерная кинематика
Введение в двумерную кинематику
3.1 Кинематика в двух измерениях: введение
3.2 Сложение и вычитание векторов: графические методы
3.3 Сложение и вычитание векторов: аналитические методы
3.4 Движение снаряда
3.5 Сложение скоростей
Глоссарий
Резюме раздела
Концептуальные вопросы
Задачи и упражнения
4 Динамика: сила и законы движения Ньютона
Введение в динамику: законы движения Ньютона
4.1 Развитие концепции силы
4.2 Первый закон движения Ньютона: инерция
4.3 Второй закон движения Ньютона: концепция системы
4.4 Третий закон движения Ньютона: симметрия сил
4.5 Нормальные, растягивающие и другие примеры сил
4.6 Стратегии решения проблем
4.7 Дальнейшие применения законов Ньютона движения
4.8 Расширенная тема: Четыре основных силы — Введение
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
5 Дальнейшее применение законов Ньютона: трение, сопротивление и эластичность
Введение: дальнейшие приложения законов Ньютона
5.1 Трение
5.2 Силы сопротивления
5.3 Упругость: напряжение и деформация
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
6 Равномерное круговое движение и гравитация
Введение в равномерное круговое движение и гравитацию
6.1 Угол вращения и угловая скорость
6.2 Центростремительное ускорение
6.3 Центростремительная сила
6.4 Фиктивные силы и неинерциальные системы координат: сила Кориолиса
6.5 Универсальный закон тяготения Ньютона
6.6 Спутники и законы Кеплера: аргумент в пользу простоты
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Проблемы и упражнения
7 Работа, энергия и энергетические ресурсы
Введение в Работа, энергия и энергетические ресурсы
7.1 Работа: научное определение
7.2 Кинетическая энергия и теорема работы-энергии
7.3 Гравитационная потенциальная энергия
7.4 Консервативные силы и потенциальная энергия
7.5 Неконсервативные силы
7.6 Сохранение энергии
7.7 Энергия
7.8 Работа, энергия и мощность у людей
7.9 Использование энергии в мире
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
8 Линейный импульс и столкновения
Введение в линейный импульс и столкновения
8.1 Линейный импульс и сила
8.2 Импульс
8.3 Сохранение импульса
8.4 Упругие столкновения в одном измерении
8.5 Неупругие столкновения в одном измерении
8.6 Столкновения точечных масс в двух измерениях
8.7 Введение в ракетное движение
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
1. Введение в статику и крутящий момент
2. 9.1 Первое условие равновесия
3. 9.2 Второе условие равновесия
4. 9.3 Стабильность
5. 9.4 Приложения статики, включая стратегии решения проблем
6. 9.5 Простые механизмы
7. 9.6 Силы и моменты в мышцах и суставах
8. Глоссарий
9. Краткое содержание раздела
10. Концептуальные вопросы
11. Задачи и упражнения
10 Вращательное движение и угловой момент
Введение во вращательное движение и угловой момент
10.1 Угловое ускорение
10.2 Кинематика вращательного движения
10.3 Динамика вращательного движения: вращательная инерция
10.4 Кинетическая энергия вращения: новый взгляд на работу и энергию
10,5 Угловой момент и его сохранение
10,6 Столкновения протяженных тел в двух измерениях
10.7 Гироскопические эффекты: векторные аспекты углового момента
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
1. Введение в статику жидкости
2. 11.1 Что такое жидкость?
3. 11.2 Плотность
4. 11.3 Давление
5. 11.4 Изменение давления по глубине в жидкости
6. 11.5 Принцип Паскаля
7. 11.6 Манометрическое давление, абсолютное давление и измерение давления
8. 11.7 Принцип Архимеда
9. 11.8 Когезия и адгезия в жидкостях : Поверхностное натяжение и капиллярное действие
10. 11.9 Давление в теле
11. Глоссарий
12. Краткое содержание раздела
13. Концептуальные вопросы
14. Проблемы и упражнения
12 Динамика жидкости и ее биологические и медицинские приложения
Введение в динамику жидкости и ее Биологические и медицинские приложения
12.1 Расход и его связь со скоростью
12.2 Уравнение Бернулли
12.3 Наиболее общие приложения уравнения Бернулли
12.4 Вязкость и ламинарный поток; Закон Пуазейля
12.5 Начало турбулентности
12.6 Движение объекта в вязкой жидкости
12.7 Явления молекулярного переноса: диффузия, осмос и связанные процессы
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Проблемы и упражнения
13 Температура, кинетическая теория и законы газа
Введение в температуру, кинетическую теорию и законы газа
13.1 Температура
13.2 Термическое расширение твердых тел и жидкостей
13.3 Закон идеального газа
13.4 Кинетическая теория: атомное и молекулярное объяснение давления и температуры
13.5 Фазовые изменения
13.6 Влажность, испарение и кипение
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
14 Методы теплопередачи и теплопередачи
Введение в методы теплопередачи
14.1 Тепло
14.2 Изменение температуры и теплоемкость
14.3 Фазовые изменения и скрытая теплота
14.4 Методы теплопередачи
14,5 Проводимость
14,6 Конвекция
14,7 Излучение
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Проблемы И упражнения
1. Введение в термодинамику
2. 15.1 Первый закон термодинамики
3. 15.2 Первый закон термодинамики и некоторые простые процессы
4. 15.3 Введение во второй закон термодинамики: тепловые двигатели и их эффективность
5. 15.4 Совершенный тепловой двигатель Карно: второй закон термодинамики заново
6. 15.5 Приложения термодинамики: тепловые насосы и холодильники
7. 15.6 Энтропия и второй закон термодинамики: Беспорядок и недоступность энергии
8. 15.7 Статистическая интерпретация энтропии и второй закон термодинамики: основное объяснение
9. Глоссарий
10. Краткое содержание раздела
11. Концептуальные вопросы
12. Задачи и упражнения
16 Колебательные движения и волны
Введение в колебательные движения и волны
16.1 Закон Гука: пересмотр напряжения и деформации
16.2 Период и частота колебаний
16.3 Простое гармоническое движение: особое периодическое движение
16.4 Простой маятник
16.5 Энергия и простой гармонический осциллятор
16.6 Равномерное круговое движение и простое Гармоническое движение
16,7 Затухающее гармоническое движение
16,8 Принудительные колебания и резонанс
16,9 Волны
16,10 Суперпозиция и интерференция
16.11 Энергия в волнах: интенсивность
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
1. Введение в физику слуха
2. 17.1 Звук
3. 17.2 Скорость звука, частота и длина волны
4. 17.3 Интенсивность звука и уровень звука
5. 17.4 Эффект Доплера и звуковые удары
6. 17.5 Звуковые помехи и резонанс: стоячие волны в воздушных столбах
7. 17.6 Слух
8. 17.7 Ультразвук
9. Глоссарий
10. Краткое содержание раздела
11. Концептуальные вопросы
12. Проблемы и упражнения
18 Электрический заряд и электрическое поле
Введение в электрический заряд и электрическое поле
18.1 Статическое электричество и заряд: сохранение заряда
18.2 Проводники и изоляторы
18.3 Закон Кулона
18.4 Электрическое поле: новое понятие поля
18.5 линий электрического поля: множественные заряды
18.6 Электрические силы в биологии
18.7 Проводники и электрические поля в статическом равновесии
18.8 Приложения электростатики
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Задачи и упражнения
19 Электрический потенциал и электрическое поле
Введение в электрический потенциал и электрическую энергию
19.1 Электрическая потенциальная энергия: разница потенциалов
19.2 Электрический потенциал в однородном электрическом поле
19.3 Электрический потенциал, вызванный точечным зарядом
19.4 Эквипотенциальные линии
19,5 Конденсаторы и диэлектрики
19,6 Последовательные и параллельные конденсаторы
19,7 Энергия, накопленная в конденсаторах
Глоссарий
Раздел Резюме
Концептуальные вопросы
Задачи и упражнения
20 Электрический ток, сопротивление и закон Ома
Введение в электрический ток, сопротивление и закон Ома
20.1 Ток
20,2 Закон Ома: сопротивление и простые схемы
20.3 Сопротивление и удельное сопротивление
20.4 Электроэнергия и энергия
20,5 Зависимость переменного тока от постоянного
20,6 Опасности поражения электрическим током и человеческое тело
20,7 Электрокардиограммы нервной проводимости
Глоссарий
Краткое содержание раздела
Концептуальные вопросы
Проблемы и упражнения
21 Цепи и приборы постоянного тока
Введение в схемы и приборы постоянного тока
21.1 Последовательные и параллельные резисторы
21.2 Электродвижущая сила: напряжение на клеммах
21.3 Правила Кирхгофа
21.4 Вольтметры и амперметры постоянного тока
21,5 Измерение нуля
21,6 Цепи постоянного тока, содержащие резисторы и конденсаторы
Глоссарий
Краткое содержание раздела
Концептуальный вид Вопросы
Задачи и упражнения
1. Введение в магнетизм
2. 22.1 Магниты
3. 22.2 Ферромагнетики и электромагниты
4. 22.3 Магнитные поля и линии магнитного поля
5. 22.4 Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле
6. 22,5 Сила на движущийся заряд в магнитном поле: примеры и приложения
7. 22,6 Холла Влияние
8. 22.7 Магнитная сила на токопроводящий проводник
9. 22.8 Крутящий момент на токовой петле: двигатели и измерители
10. 22.9 Магнитные поля, создаваемые токами: закон Ампера
11. 22.10 Магнитная сила между двумя параллельными проводниками
12. 22.11 Другие применения магнетизма
13. Глоссарий
14. Сводка раздела
15. Концептуальные вопросы
16. Проблемы и упражнения
23 Электромагнитная индукция, цепи переменного тока и электрические технологии
Введение в электромагнитную индукцию , Цепи переменного тока и электрические технологии
23.1 Индуцированная ЭДС и магнитный поток
23.2 Закон индукции Фарадея: Закон Ленца
23.3 ЭДС движения
23,4 Вихревые токи и магнитное демпфирование
23,5 Электрогенераторы
23,6 Обратная ЭДС

% PDF-1.3
%
1 0 obj
> поток

конечный поток
endobj
2 0 obj
>
endobj
6 0 obj
> / Rect [74.󣺸Xuw; M / _] nv? B ~ «? M.QQΪv8qqA ڼ

% PDF-1.3
%
1 0 obj
> поток

конечный поток
endobj
2 0 obj
>
endobj
6 0 obj
> / Rect [74.76 87,92 89,76 98,42] >>
endobj
5 0 obj
> / ProcSet [/ PDF / Text] / ColorSpace> / Font> / Свойства >>>
endobj
4 0 obj
> поток
h ެ ي d> J} B

! 8) ȃCuMax JwӮ + 4w t = _˿r ~ ú ~ sχoO / n9] ʹX> b * hBa9? XrÏ0WZLIW-2CH6 = yON \ Z [L, pEf83 `M͚ # PR # ѷIWgZvxB_!
\ ל yK: 2ȆM} I1ĺR $ .w ي fS & Y`P! 68w Ը
* [\ 2 /?} -H? E9Q7Fg @ ֩% 㗣 Пw} | 㫏> ~ zz | w> a + 9 — & @ [($ g (4

Переменный ток в сравнении с постоянным)

Переменный ток

Большинство рассмотренных до сих пор примеров, особенно те, которые используют батареи, имеют источники постоянного напряжения.Как только ток установлен, он также становится постоянным. Постоянный ток (DC) — это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) — это поток электрического заряда, который периодически меняет направление. Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока.Примеры включают коммерческую и бытовую энергетику, которая удовлетворяет многие наши потребности. На этом рисунке показаны графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.

(a) Напряжение и ток постоянного тока постоянны во времени после установления тока. (b) График зависимости напряжения и тока от времени для переменного тока частотой 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления.Частоты и пиковое напряжение источников переменного тока сильно различаются.

Разность потенциалов \ (В \) между клеммами источника переменного напряжения колеблется, как показано. Математическое выражение для \ (V \) дается \ (V = {V} _ {0} \ phantom {\ rule {0.20em} {0ex}} \ text {sin} \ phantom {\ rule {0.20em} {0ex}} \ text {2} \ pi \ text {ft} \).

На этом рисунке показана схема простой схемы с источником переменного напряжения. Напряжение между клеммами колеблется, как показано на рисунке: напряжение переменного тока определяется как

\ (V = {V} _ {0} \ phantom {\ rule {0.30em} {0ex}} \ text {sin} \ phantom {\ rule {0.30em} {0ex}} \ text {2} \ pi \ text {ft,} \)

где \ (V \) — напряжение в момент времени \ (t \) , \ ({V} _ {0} \) — пиковое напряжение, а \ (f \) — частота в герцах. Для этой простой цепи сопротивления \ (I = \ text {V / R} \), поэтому переменный ток равен

\ (I = {I} _ {0} \ phantom {\ rule {0.30em} {0ex}} \ text {sin 2} \ pi \ text {ft,} \)

где \ (I \) — ток в момент времени \ (t \), а \ ({I} _ {0} = {V} _ {0} \ text {/ R} \) — пиковый ток. В этом примере говорят, что напряжение и ток находятся в фазе, как показано на этом рисунке (b).

Ток в резисторе меняется взад и вперед, как управляющее напряжение, поскольку \ (I = \ text {V / R} \). Например, если резистор представляет собой люминесцентную лампочку, она становится ярче и тусклее 120 раз в секунду, когда ток постоянно проходит через ноль. Мерцание с частотой 120 Гц слишком быстро для ваших глаз, но если вы помашите рукой вперед и назад между лицом и флуоресцентным светом, вы увидите стробоскопический эффект, свидетельствующий о переменном токе. Тот факт, что световой поток колеблется, означает, что мощность колеблется.{2} \ phantom {\ rule {0.30em} {0ex}} \ text {2} \ pi \ text {ft} \), как показано на этом рисунке.

Установление соединений: домашний эксперимент — освещение переменного / постоянного тока

Проведите рукой между лицом и люминесцентной лампой. Вы наблюдаете то же самое с фарами своей машины? Объясните, что вы наблюдаете. Предупреждение: Не смотрите прямо на очень яркий свет .

Мощность переменного тока как функция времени. Поскольку напряжение и ток здесь синфазны, их произведение неотрицательно и колеблется от нуля до \ ({I} _ {0} {V} _ {0} \).Средняя мощность составляет \ ((1/2) {I} _ {0} {V} _ {0} \) _.

Чаще всего нас беспокоит средняя мощность, а не ее колебания — например, средняя потребляемая мощность лампы 60 Вт в настольной лампе составляет 60 Вт. Как показано на этом рисунке, средняя мощность \ ({P} _ {\ text {ave}} \) составляет

\ ({P} _ {\ text {ave}} = \ cfrac {1} {2} { I} _ {0} {V} _ {0}. \)

Это видно из графика, поскольку области над и под \ ((1/2) {I} _ {0} {V} _ {0} \) равны, но это также можно доказать с помощью тригонометрических тождеств.Точно так же мы определяем средний или действующий ток \ ({I} _ {\ text {rms}} \) и среднее или действующее напряжение \ ({V} _ {\ text {rms}} \) как соответственно

\ ({I} _ {\ text {rms}} = \ cfrac {{I} _ {0}} {\ sqrt {2}} \)

\ ({V} _ {\ text {rms}} = \ cfrac {{V} _ {0}} {\ sqrt {2}}. \)

, где среднеквадратичное значение означает среднеквадратичное значение, особый вид среднего. Как правило, для получения среднеквадратичного значения конкретная величина возводится в квадрат, определяется ее среднее значение (или среднее значение) и извлекается квадратный корень.Это полезно для переменного тока, так как среднее значение равно нулю. Теперь

\ ({P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}}, \)

, что дает

\ ({P} _ {\ text {ave}} = \ cfrac {{I} _ {0}} {\ sqrt {2}} \ cdot \ cfrac {{V} _ {0}} {\ sqrt {2} } = \ cfrac {1} {2} {I} _ {0} {V} _ {0}, \)

, как указано выше. Стандартной практикой является цитирование \ ({I} _ {\ text {rms}} \), \ ({V} _ {\ text {rms}} \) и \ ({P} _ {\ text {ave }} \), а не пиковые значения. Например, напряжение в большинстве домашних хозяйств составляет 120 В переменного тока, что означает, что \ ({V} _ {\ text {rms}} \) составляет 120 В.Обычный автоматический выключатель на 10 А прервет постоянный \ ({I} _ {\ text {rms}} \) более 10 А. Ваша микроволновая печь мощностью 1,0 кВт потребляет \ ({P} _ {\ text {ave} } = \ text {1.0 кВт} \) и так далее. Вы можете рассматривать эти среднеквадратичные и средние значения как эквивалентные значения постоянного тока для простой резистивной цепи.

Подводя итог, при работе с переменным током закон Ома и уравнения для мощности полностью аналогичны таковым для постоянного тока, но для переменного тока используются среднеквадратические и средние значения. Таким образом, для переменного тока закон Ома записывается

\ ({I} _ {\ text {rms}} = \ cfrac {{V} _ {\ text {rms}}} {R}.{2} R. \)

Пример: пиковое напряжение и мощность для переменного тока

(a) Каково значение пикового напряжения для источника переменного тока 120 В? (б) Какова пиковая потребляемая мощность лампочки переменного тока мощностью 60,0 Вт?

Стратегия

Нам говорят, что \ ({V} _ {\ text {rms}} \) составляет 120 В и \ ({P} _ {\ text {ave}} \) составляет 60,0 Вт. Мы можно использовать \ ({V} _ {\ text {rms}} = \ cfrac {{V} _ {0}} {\ sqrt {2}} \), чтобы найти пиковое напряжение, и мы можем манипулировать определением мощности найти пиковую мощность из заданной средней мощности.

Решение для (a)

Решение уравнения \ ({V} _ {\ text {rms}} = \ cfrac {{V} _ {0}} {\ sqrt {2}} \) для пиковое напряжение \ ({V} _ {0} \) и замена известного значения на \ ({V} _ {\ text {rms}} \) дает

\ ({V} _ {0} = \ sqrt { 2} {V} _ {\ text {rms}} = \ text {1} \ text {.} \ Text {414} (\ text {120 V}) = \ text {170 V}. \)

Обсуждение (a)

Это означает, что напряжение переменного тока меняется от 170 В до \ (\ text {–170 В} \) и обратно 60 раз в секунду. Эквивалентное постоянное напряжение составляет 120 В.

Решение для (b)

Пиковая мощность равна пиковому току, умноженному на пиковое напряжение. Таким образом,

\ ({P} _ {0} = {I} _ {0} {V} _ {0} = \ text {2} (\ cfrac {1} {2} {I} _ {0} {V} _ {0}) = \ text {2} {P} _ {\ text {ave}}. \)

Мы знаем, что средняя мощность составляет 60,0 Вт, поэтому

\ ({P} _ { 0} = \ text {2} (\ text {60} \ text {.} \ Text {0 W}) = \ text {120 W}.

формула, взаимное влияние, нормы, характеристики

Нормируемые требования к показателям

Влияние частоты тока на электроприборы

ИССЛЕДОВАНИЕ ЗАВИСИМОМТИ АКТИВНОГО,ИНДУКТИВНОГО И ЕМКОСТНОГО СОПРОТИВЛЕНИЯ ОТ ЧАСТОТЫ ПЕРЕМЕННОГО ТОКА.ПРОВЕРКА ЗАКОНА ОМА ДЛЯ ПЕНИ ПЕРЕМЕННОГО ТОКА.

Существует ли зависимость напряжения от частоты?

Напряжение или разность потенциалов?

Что является источником частоты

С чего бы напряжению падать?

Есть такие резисторы

И все-таки она существует!

Формула расчета периода переменных и постоянных токов в электротехнике

Общее понятие о переменном токе

Периодический переменный ток

Стандарты частоты

Переменный синусоидальный ток

Многофазный переменный ток

Трёхфазный ток

Двухфазный ток

Действующее значение синусоидального тока

Генерирование переменного тока

Инвертор

Фазорасщепитель

Сети переменного тока

Определение частоты и периода

Взаимосвязь частоты и работы электрооборудования

Частотомер

Токи высокой частоты

Период пульсаций и частота

Интенсивность циклов

Опасность разночастотных зарядов

Видео

Зависимость мощности от частоты формула

Нормируемые требования к показателям

Влияние частоты тока на электроприборы

Нормы мощности в сети переменного тока

Характеристики

Виды мощностей

Активная мощность

Реактивная мощность

Полная мощность

Комплексная мощность

Как узнать какая мощность в цепи переменного тока

В однофазной цепи

В трехфазной цепи

Работа двигателя

Преимущества функции AEO

Работа нескольких двигателей

Простейшие цепи переменного тока — Электротехника — Учебные материалы — Каталог статей

Активное сопротивление R в цепи переменного тока

Индуктивное сопротивление в цепи переменного тока

XL – сопротивление индуктивности

Мощность на индуктивности

Емкость в цепи переменного тока

XC — сопротивление емкости

Мощность в цепи с емкостью

Реактивные сопротивления

Задачи на переменный ток решаются методом векторных диаграмм.

Метод векторных диаграмм

Второй вектор переносится из центра вращения. Прикладываем его к концу вектора напряжения на активном сопротивлении. Таковы правила сложения векторов.

Теперь остается построить вектор полного напряжения на обоих элементах. Это вектор суммы, он, как известно, строится из начала первого вектора к концу второго.

Последовательное соединение RC

Параллельное соединение RL

Значение Cos φ

Цепи RLC

RLC последовательно

RLC параллельно

Условия резонанса

Анализ электронных схем: частотная характеристика

20,5 Сравнение переменного и постоянного тока — College Physics

Переменный ток в сравнении с постоянным)

Переменный ток

Установление соединений: домашний эксперимент — освещение переменного / постоянного тока

Пример: пиковое напряжение и мощность для переменного тока

alexxlab

Вам также может понравиться

Сип правила прокладки: Монтаж СИП: правила крепления, прокладки, подключения

Установка люминесцентных светильников: Подробная схема подключения люминесцентной лампы, устройство

Вести контроль: Бастрыкин взял под контроль расследование нападения на подростка под Калугой

Добавить комментарий Отменить ответ

X_L – сопротивление индуктивности

X_C — сопротивление емкости