Фильтрация и логические операторы | ПТИЦА-СЕКРЕТАРЬ
Как правило, в наших таблицах фигурируют или текстовые данные, или числовые. К каждому из них редактор Excel позволяет применить свои правила фильтрации, а также и правила логики, которые мы и рассмотрим в этой статье.
Для наглядности я немного дополнил исходную таблицу новыми сотрудниками:
Исходная таблица
Итак, допустим, по какой-то, неведомой обычному смертному причине, руководством была поставлена задача найти и представить пред светлы очи всех сотрудников, у которых фамилия созвучна имени Иван.
Чтобы не перебирать фамилии (пусть даже и отсортированные), а после выбирать нужные, можно выполнить следующие действия:
- В таблице сотрудников курсором мыши активируем кнопку фильтра и открываем меню фильтрации.
- Выбираем пункт меню Текстовые фильтры, в результате чего отобразится перечень команд, при помощи которого можно по разному отфильтровать текстовый столбец.

Меню фильтрации Excel
- Согласно поставленному условию наибольше подходит команда Начинается с…, на котором выполняем щелчок мышью.
- В открывшемся окне Пользовательский автофильтр уже указан столбец (Фамилия) и выведено условие фильтрации Начинается с….
Окно «Пользовательский автофильтр»
- В поле, которое расположено напротив этого условия, вписываем условие фильтрации согласно поставленной руководством задачи – “Иван”. Получается фраза: «Отобразить фамилии, которые начинаются с литер “Иван”.
- Нажимаем кнопку Ok.
- Фильтрация применяется к таблице, в результате чего мы видим только тех сотрудников, фамилии которых начинаются с литер “Иван”.
- Посылаем на печать результат работы и несем его руководству. Пусть вспоминает, зачем они ему нужны.
Результат фильтрации
Позвольте обратить Ваше внимание на переключатель И — ИЛИ, который стоит в окне Пользовательский автофильтр. При помощи него можно выполнять фильтрацию по двум условиям для одного столбца. В зависимости от того, какой логический элемент выбран (И либо ИЛИ), можно получить разные результаты. Разберемся, как работают эти элементы.
При помощи него можно выполнять фильтрацию по двум условиям для одного столбца. В зависимости от того, какой логический элемент выбран (И либо ИЛИ), можно получить разные результаты. Разберемся, как работают эти элементы.
Дабы не употреблять в объяснении умные термины, вроде слов множества или пересечение множеств, постараюсь несколько его упростить. Вспомним 1-й класс школы. 😀
Будем объединять при помощи логических операторов И – ИЛИ две кучки конфет. Допустим, в каждой кучке лежат конфеты отдельного наименования: 1 и 2. Но! К ним, в каждую кучку добавлены по несколько конфет наименования 3. Получаем в одной кучке конфеты 1 и 3, а в другой – конфеты 2 и 3.
Сложим обе кучки по правилам логического И. При этом мы получим в результирующей кучке только те конфеты, которые есть и в одной, и в другой кучках – конфеты наименования 3.
- Работа логического оператора И
Если сложить конфеты по правилам логического ИЛИ, то получим в результирующей кучке только те конфеты, которые попадаются или только в одной, или только в другой кучке – конфеты наименований 1 и 2.
- Работа логического оператора ИЛИ
Применительно к нашей таблице можно рассмотреть такой пример. Найдем фамилии всех сотрудников, которые или начинаются с Иван, или заканчиваются на ин.
Чтобы создать фильтр, позволяющий получить эти фамилии, следует для одноименного столбца вызвать окно Пользовательский автофильтр, в котором для условия фильтрации Начинается с… записываем текст Иван, а во втором условии фильтрации Заканчивается на… записываем текст ин. Для связи этих условий нужно использовать логическое ИЛИ.
После нажатия на кнопку Ok получим следующую таблицу:
- Соединение по условию ИЛИ
Если же использовать логическое И, то получим только одну фамилию, так как только она начинается с Иван и заканчивается на ин:
Соединение по условию И
Вот! Надеюсь этих примеров было достаточно, чтобы проиллюстрировать логику работы с операторами И и ИЛИ.
Это мы рассмотрели работу с текстовым столбцом. Работа с числовыми столбцами осуществляется так же, только по условиям оперирования с числовыми значениями. Тут в помощь пользователю предлагается пользовательский фильтр с операторами больше, меньше, меньше и пр. Все остальные действия очень похожи на те, которые были рассмотрены для работы с текстом, а операторы И и ИЛИ работают точно так же.
Фильтрация числовых значений
Вконтакте
Google+
|
Обзор логических математических инструментов (группа Math > Logical)—Справка
Доступно с лицензией Spatial Analyst.
Логические математические инструменты оценивают значения входных данных и определяют выходные значения на основании Булевой логики. Инструменты сгруппированы в четыре основные категории: Булевы, Комбинаторные, Логические и Относительные.
Инструменты сгруппированы в четыре основные категории: Булевы, Комбинаторные, Логические и Относительные.
Ниже приведен перечень всех инструментов каждой группы:
- Булевы:
Булев оператор And (Boolean And), Булев оператор Or (Boolean Or), Булев оператор XOr (Boolean XOr), Булев оператор Not (Boolean Not)
- Комбинаторные:
Комбинаторный оператор «And» (Combinatorial And, Комбинаторный оператор «Or» (Combinatorial Or), Комбинаторный оператор «XOr» (Combinatorial XOr)
- Относительные:
Равно (Equal To), Не равно (Not Equal), Больше (Greater Than), Больше или равно (Greater Than Equal), Меньше (Less Than), Меньше или равно (Less Than Equal)
- Логические:
Разницы (Diff), В списка (InList), Равно нулю (Is Null), Больше нуля (Over), Критерий (Test)
Булева логика обычно применяет двоичное условие к входным данным и оценивает двоичные условия для выходных данных. Двоичные условия могут быть выражены несколькими способами: «1» и «0», «True» (истина) и «False» (ложь), «yes» (да) и «no» (нет), «on» (вкл) и «off» (выкл) и так далее. В логических математических инструментах условие Ложь (False) представлено значением 0, а условие Истина (True) — значением, отличным от 0.
В логических математических инструментах условие Ложь (False) представлено значением 0, а условие Истина (True) — значением, отличным от 0.
Булевы инструменты оценивают входные данные только как Истина (True) или Ложь (False) и в качестве результата конкретного инструмента выдают Булево значение 1 или 0 (Истина или Ложь). Комбинаторные инструменты определяют уникальные комбинации входных значений на основе логики конкретного инструмента и выдают разные значения для каждой уникальной комбинации. Относительные инструменты сравнивают одно входное значение относительно другого и возвращают результат в виде Булева значения 1 или 0. Логические инструменты имеют разные способы применения Булевой логики, например, определение только тех входных ячеек, значение которых равны NoData, или использование нужного вам логического выражения для определения того, какие ячейки оцениваются как истинные.
В следующей таблице содержится перечень доступных логических математических инструментов по категории и дано краткое описание каждого:
Булева оценка
| Инструмент | Описание |
|---|---|
Булев оператор «And» (Boolean And) | Выполняет Булеву операцию И (AND) для значений ячеек двух входных растров. Если оба входных значения истинны (ненулевые), выходное значение будет 1. Если одно или оба входных значения ложны (нулевые), выходное значение будет 0. |
Булев оператор Not (Boolean Not) | Выполняет Булеву операцию Нет (Not) (дополнительно) для значений ячеек двух входных растров. Если входные значения истинны (ненулевые), выходное значение будет 0. Если входные значения ложные (нулевые), выходное значение будет 1. |
Булев оператор «Or» (Boolean Or) | Выполняет Булеву операцию Или (Or) для значений ячеек двух входных растров. Если одно или оба входных значений истинны (ненулевые), выходное значение будет 1. Если оба входных значения ложны (нулевые), выходное значение будет 0. |
Булев оператор «XOr» (Boolean XOr) | Выполняет Булеву операцию исключающего Или (XOr) для значений ячеек двух входных растров. Если одно входное значение истинно (ненулевое), а другое – ложное (нулевое), выходное значение – 1. Если оба входных значения истинны или оба ложны, выходное значение – 0. |
Булевы математические инструменты
Комбинаторная оценка
| Инструмент | Описание |
|---|---|
Комбинаторный оператор AND (Combinatorial And) | Выполняет Комбинаторную операцию И (AND) для значений ячеек двух входных растров. Если оба входных значения истинны (не-нулевые), выходное значение будет уникальным для каждой комбинации входных значений. Если одно или оба значения ложны (нулевые) – выходное значение – 0. |
Комбинаторный оператор Or (Combinatorial Or) | Выполняет Комбинаторную операцию Или (Or) для значений ячеек двух входных растров. Если какое-либо входное значение истинно (не-нулевое), выходное значение будет уникальным для каждой комбинации входных значений. Если оба значения ложны (нулевые) – выходное значение – 0. |
Комбинаторный оператор XOr (Combinatorial XOr) | Выполняет Комбинаторную операцию исключающего Или (XOr) для значений ячеек двух входных растров. Если одно входное значение истинно (не-нулевое), а другое – ложное (нулевое), выходное значение будет уникальным для каждой комбинации входных значений. Если оба входных значения истинные или оба входных значения ложные, выходное значение будет равно нулю. |
Комбинаторные математические инструменты
Относительная оценка
| Инструмент | Описание |
|---|---|
Равно (Equal To) | Выполняет относительную операцию "равно " (equal-to) для двух входных растров по принципу "ячейка-за-ячейкой ". Возвращает значение 1 для ячеек выходного растра, в которых значение ячейки первого входного растра равно значению соответствующей ячейки второго входного растра и значение 0 для ячеек, в которых значения не равны. |
Больше чем (Greater Than) | Выполняет относительную операцию "больше чем " (greater-than) для двух входных растров по принципу "ячейка-за-ячейкой ". Возвращает значение 1 для ячеек, в которых значение в первом растра больше, чем значение во втором растра и 0 для ячеек в которых значения первого растра меньше значений второго. |
Больше или равно (Greater Than Equal) | Выполняет относительную операцию "больше чем или равно " (greater-than-or-equal-to) для двух входных растров по принципу "ячейка-за-ячейкой ". Возвращает значение 1 для ячеек, в которых значение в первом растра больше или равно, чем значение во втором растра и 0 для ячеек в которых значения первого растра меньше значений второго. |
Оператор Меньше чем (Less Than) | Выполняет относительную операцию "меньше чем " (less-than) для двух входных растров по принципу "ячейка-за-ячейкой ". Возвращает значение 1 для ячеек, в которых значение в первом растре меньше, чем значение во втором растре и 0 для всех остальных ячеек. |
Меньше или равно (Less Than Equal) | Выполняет относительную операцию "меньше чем или равно " (less-than-or-equal-to) для двух входных растров по принципу "ячейка-за-ячейкой ". Возвращает значение 1 для ячеек, в которых значение в первом растра меньше или равно, чем значение во втором растра и 0 для остальных ячеек. |
Не равно (Not Equal) | Выполняет относительную операцию "не равно " (not-equal-to) для двух входных растров по принципу "ячейка-за-ячейкой ". Выдает значение 1 для ячеек, где значения на первом растре не равны значениям на втором растре и 0 для ячеек, значения которых равны. |
Относительные математические инструменты
Логическая оценка
| Инструмент | Описание |
|---|---|
Разность(Diff) |
Определяет, какие значения из первых входных данных логически отличаются от значений вторых входных данных на основе "ячейка-за-ячейкой ". Если значения двух входных растров разные, значения первого входного растра записываются в выходной растр. Если значения двух входных растров одинаковые, в соответствующей ячейке выходного растра будет 0. |
В списке (InList) | Определяет, какие значения из первых входных данных содержатся в наборе других входных данных на основе "ячейка-за-ячейкой ". Для каждой ячейки, если значение первого входного растра находится в списке других входных данных, это значение будет присвоено выходному растру. Если оно не найдено, выходным значением в ячейке будет значение NoData. |
Равно нулю (Is Null) | Определяет, какие значения из входного растра являются значениями NoData на основе "ячейка-за-ячейкой ". Возвращает значение 1, если входное значение – NoData и 0 для ячеек, значение которых не NoData. |
Больше нуля (Over) | Для ненулевых значений ячеек в первых входных данных, выходное значение будет значением первых входных данных. Если ячейки входного растра равны нулю, выходные значения для этих ячеек будут соответствовать ячейкам второго входного растра. |
Тест (Test) | Выполняет Булеву оценку входного растра с помощью логического выражения. Когда выражение оценивается как Истина, выходной ячейке присваивается значение 1. Если выражение ложно, выходной ячейке присваивается значение 0. |
Логические математические инструменты
Связанные темы
Отзыв по этому разделу?
Логические операторы | Python
Мы уже умеем писать функции, которые проверяют одиночные условия. Теперь научимся строить составные условия.
Хороший пример: проверка пароля. Предположим, что некий сайт при регистрации требует, чтобы пароль был длиннее восьми символов и короче двадцати символов. Да, ограничение выглядит странно, но бывает и такое.
В математике мы бы написали 8 < x < 20, но во многих языках программирования так сделать нельзя. К счастью, Python такие составные условия писать позволяет. И всё же на минутку мы забудем о такой возможности. Попробуем сделать два отдельных логических выражения и соединить их специальным оператором «И»:
Пароль длиннее 8 символов И пароль короче 20 символов.
Вот функция, которая принимает пароль и говорит, соответствует ли он условиям (True) или не соответствует (False):
def is_correct_password(password):
length = len(password)
return length > 8 and length < 20
print(is_correct_password('qwerty')) # => False
print(is_correct_password('qwerty1234')) # => True
print(is_correct_password('zxcvbnmasdfghjkqwertyui')) # => False
and — означает «И» (в математической логике это называют конъюнкцией). Всё выражение считается истинным, только если истинен каждый операнд — каждое из составных выражений. Иными словами, and означает «и то, и другое».
Приоритет этого оператора ниже, чем приоритет операторов сравнения, поэтому выражение length > 8 and length < 20 отрабатывает правильно без скобок.
Кроме and часто используется оператор or — «ИЛИ» (дизъюнкция). Он означает «или то, или другое, или оба». То есть выражение
Он означает «или то, или другое, или оба». То есть выражение a or b считается истинным, если хотя бы один из операндов (a или b или одновременно все операнды) является истинным. Иначе выражение ложное.
Операторы можно комбинировать в любом количестве и любой последовательности, но когда одновременно встречаются and и or, то приоритет лучше задавать скобками. Ниже пример расширенной функции определения корректности пароля:
def has_special_chars(str):
# проверяет содержание специальных символов в строке
def is_strong_password(password):
length = len(password)
# Скобки задают приоритет. Понятно что к чему относится.
return (length > 8 and length < 20) or has_special_chars(password)
Другой пример. Мы хотим купить квартиру, которая удовлетворяет условиям: площадь от 100 кв. метров и больше на любой улице ИЛИ площадь от 80 кв. метров и больше, но на центральной улице Main Street.
Напишем функцию, проверяющую квартиру. Она принимает два аргумента: площадь (число) и название улицы (строку):
def is_good_apartment(area, street):
return area >= 100 or (area >= 80 and street == 'Main Street')
print(is_good_apartment(91, 'Queens Street')) # => False
print(is_good_apartment(78, 'Queens Street')) # => False
print(is_good_apartment(70, 'Main Street')) # => False
print(is_good_apartment(120, 'Queens Street')) # => True
print(is_good_apartment(120, 'Main Street')) # => True
print(is_good_apartment(80, 'Main Street')) # => True
Область математики, в которой изучаются логические операторы, называется булевой алгеброй. Ниже показаны «таблицы истинности» — по ним можно определить, каким будет результат применения оператора:
И
and
| A | B | A and B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | False |
ИЛИ
or
| A | B | A or B |
|---|---|---|
| True | True | True |
| True | False | True |
| False | True | True |
| False | False | False |
Задание
Джон поручил Сэму реализовать автоматическое распознавание солдат Ланнистеров на видео.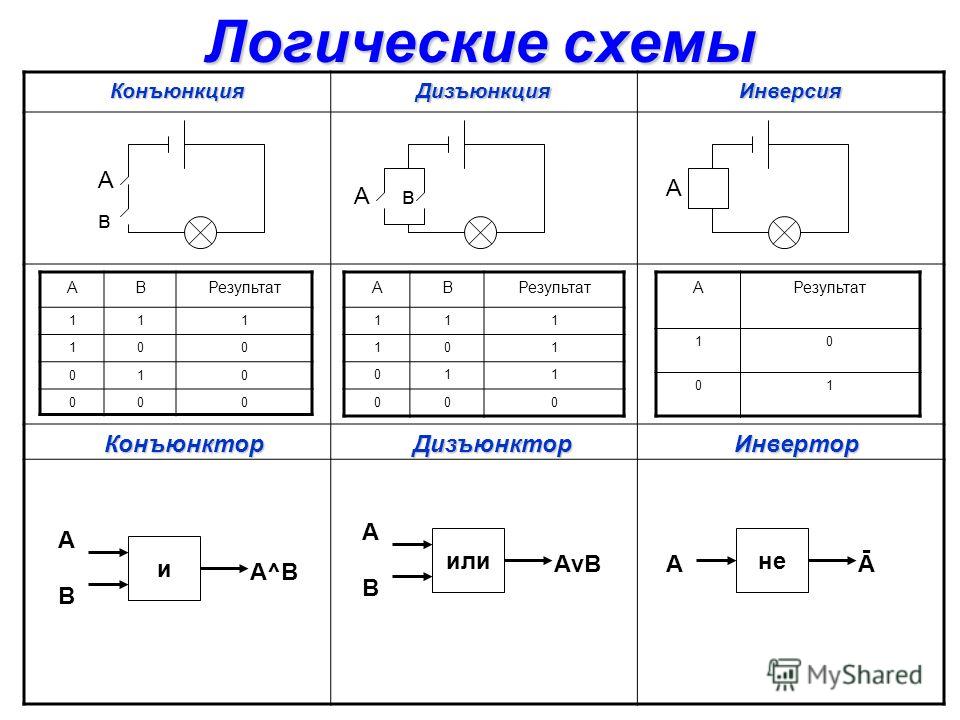 Идея автоматизировать дозор крепости казалась ему привлекательной. В процессе работы Сэму понадобилось написать функцию, которая определяет, Ланнистер ли перед ним или нет. Немного подумав, Сэм выделил следующие правила определения Ланнистера:
Идея автоматизировать дозор крепости казалась ему привлекательной. В процессе работы Сэму понадобилось написать функцию, которая определяет, Ланнистер ли перед ним или нет. Немного подумав, Сэм выделил следующие правила определения Ланнистера:
Если у солдата доспехи красного цвета И нет щита
ИЛИ
если у солдата есть щит с изображением льва
то это Ланнистер.
Напишите функцию is_lannister_soldier(), которая принимает на вход два аргумента:
- Цвет доспехов (строка). Если доспехи красные, то строка
red. None, если щита нет. Строкаlion, если щит есть, и на нём изображен лев.
Функция возвращает True, если распознан Ланнистер, и False, если не распознан.
Примеры вызова:
is_lannister_soldier('red', 'man') # False
is_lannister_soldier('blue', 'lion') # True
Когда будете проверять на равенство None, делайте так, как принято в настоящем коде на Python: shield is None — код будет выглядеть профессионально! Дело в том. что
что is работает быстрее в случае некоторых специальных значений вроде None, True и False.
Советы
Определения
Логические операторы — операторы «И» (
and), ИЛИ (or), позволяющие создавать составные логические условия.
Логические операции
Чаще всего используются следующие логические операции:
- инверсия (отрицание, логическое не),
- конъюнкция (логическое и),
- дизъюнкция (логическое или),
- импликация (следование),
- эквивалентность (тождество).
Рассмотрим каждую из них подробно. Для описания используем диаграммы Эйлера-Венна и таблицы истинности.
| Логическая операция/ соответствие в русском языке | Обозначение | Диаграмма Эйлера-Венна | Таблица истинности | ||
|---|---|---|---|---|---|
| инверсия (отрицание, логическое «НЕ»)/ «. | ¬ | A | ¬A | ||
| 0 | 1 | ||||
| 1 | 0 | ||||
| конъюнкция (логическое «И»)/ «…и…» | Λ, & | A | B | AΛB | |
| 0 | 0 | 0 | |||
| 0 | 1 | 0 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | |||
| дизъюнкция (логическое «ИЛИ») «. | V | A | B | AVB | |
| 0 | 0 | 0 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 1 | |||
| импликация (следование)/ «если…,то…», «когда. | → | A | B | A→B | |
| 0 | 0 | 1 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | |||
| эквивалентность (тождество) «тогда и только тогда, когда» | ↔, ≡ | A | B | A↔B | |
| 0 | 0 | 1 | |||
| 0 | 1 | 0 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | |||
Основные логические операции: инверсия, конъюнкция, дизъюнкция.
Остальные логические операции можно выразить через них:
A→B=¬AVB;
A↔B=(AΛB)V(¬AΛ¬B).
Порядок выполнения логических операций в выражении (от наибольшего приоритета к наименьшему):
инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
Пример:
AV¬BΛC→D↔E.
Порядок выполнения:
- ¬B
- (¬B)ΛC
- AV((¬B)ΛC)
- (AV((¬B)ΛC))→D
- ((AV((¬B)ΛC))→D)↔E
Перейти к решению задач на алгебру логики из демо ЕГЭ
Логические операторы — основы программирования
Кеннет Лерой Басби и Дэйв Брауншвейг
Обзор
Логический оператор — это символ или слово, используемое для соединения двух или более выражений, так что значение полученного составного выражения зависит только от значения исходных выражений и от значения оператора. Общие логические операторы включают AND, OR и NOT.
Обсуждение
В большинстве языков выражения, которые дают значения типа данных Boolean, разделены на две группы. Одна группа использует операторы отношения в своих выражениях, а другая группа использует логические операторы в своих выражениях.
Одна группа использует операторы отношения в своих выражениях, а другая группа использует логические операторы в своих выражениях.
Логические операторы часто используются для создания тестового выражения, контролирующего выполнение программы. Этот тип выражения также известен как логическое выражение, потому что при вычислении они создают логический ответ или значение. Есть три общих логических оператора, которые дают логическое значение, манипулируя другим логическим операндом (ами). Символы и / или названия операторов различаются в зависимости от языка программирования:
| Язык | И | ИЛИ | НЕ |
|---|---|---|---|
| С ++ | && | || | ! |
| С # | && | || | ! |
| Java | && | || | ! |
| JavaScript | && | || | ! |
| Python | и | или | не |
| Swift | && | || | ! |
Вертикальные черточки или символ трубопровода находятся на той же клавише, что и обратная косая черта \. Вы используете клавишу SHIFT, чтобы получить его. На большинстве клавиатур он находится чуть выше клавиши Enter. Это может быть сплошная вертикальная линия на некоторых клавиатурах и отображаться как сплошная вертикальная линия на некоторых печатных шрифтах.
Вы используете клавишу SHIFT, чтобы получить его. На большинстве клавиатур он находится чуть выше клавиши Enter. Это может быть сплошная вертикальная линия на некоторых клавиатурах и отображаться как сплошная вертикальная линия на некоторых печатных шрифтах.
В большинстве языков существуют строгие правила формирования правильных логических выражений. Пример:
6> 4 && 2 <= 14
6> 4 и 2 <= 14
Это выражение содержит два оператора отношения и один логический оператор. Используя приоритет правил операторов, два оператора «реляционного сравнения» будут выполняться перед оператором «логическое и».Таким образом:
true && true
True and True
Окончательная оценка выражения: истина.
Мы можем сказать это по-английски так: это правда, что шесть больше четырех, а два меньше или равно четырнадцати.
При формировании логических выражений программисты часто используют круглые скобки (даже если это технически не требуется), чтобы сделать логику выражения очень понятной. Рассмотрим переписанное выше сложное логическое выражение:
Рассмотрим переписанное выше сложное логическое выражение:
(6> 4) && (2 <= 14)
(6> 4) и (2 <= 14)
Большинство языков программирования распознают любое ненулевое значение как истинное.Это делает следующее выражение допустимым:
6> 4 && 8
6> 4 и 8
Но помните порядок действий. По-английски это шесть больше четырех, а восемь - не ноль. Таким образом,
true && true
True and True
Для сравнения 6 с 4 и 8 вместо этого будет записано как:
6> 4 && 6> 8
6> 4 и 6> 8
Это будет ложно как:
истина и ложь
истина и ложь
Таблицы истинности
Обычный способ показать логические отношения - это таблицы истинности.
| x | л | x и y |
| ложный | ложь | ложь |
| ложный | правда | ложь |
| истинное | ложь | ложь |
| истинное | правда | правда |
| x | л | x или y |
| ложный | ложь | ложь |
| ложный | правда | правда |
| истинное | ложь | правда |
| истинное | правда | правда |
| x | не x |
| ложный | правда |
| истинное | ложь |
Примеры
Я называю этот пример того, почему я ненавижу «и» и люблю «или».
Каждый день, когда я приходил из школы с понедельника по четверг; Я спрашивал маму: «Можно мне выйти на улицу поиграть?» Она отвечала: «Если ваша комната чистая и у вас сделана домашняя работа, вы можете выйти на улицу и поиграть». Я научился ненавидеть слово «и». Мне удалось выполнить одно из заданий и у меня было время поиграть до обеда, но оба… ну, я ненавидел «и».
В пятницу моя мать приняла более расслабленную точку зрения, и когда меня спросили, могу ли я выйти на улицу и поиграть, она ответила: «Если ваша комната чистая или ваша домашняя работа сделана, вы можете выйти на улицу и поиграть.«Я научился быстро убирать свою комнату в пятницу днем. Что ж, разумеется, я любил «или».
В качестве следующего примера представьте, что подросток разговаривает со своей матерью. Во время разговора мама говорит: «Ведь папа у тебя разумный!» Подросток говорит: «Разумно. (короткая пауза) Нет. "
Может быть, профессора колледжей подумают, что все их студенты готовились к экзамену. Ха-ха! Нет. Что ж, надеюсь, вы уловили суть.
Ха-ха! Нет. Что ж, надеюсь, вы уловили суть.
Примеры:
- 25 <7 || 15> 36
- 15> 36 || 3 <7
- 14> 7 && 5 <= 5
- 4> 3 && 17 <= 7
- ! ложь
- ! (13! = 7)
- 9! = 7 &&! 0
- 5> 1 && 7
Дополнительные примеры:
- 25 <7 или 15> 36
- 15> 36 или 3 <7
- 14> 7 и 5 <= 5
- 4> 3 и 17 <= 7
- не Ложь
- не (13! = 7)
- 9! = 7, а не 0
- 5> 1 и 7
Ключевые термины
- логический оператор
- Оператор, используемый для создания сложных логических выражений.
- таблицы истинности
- Распространенный способ показать логические отношения.
Список литературы
Полное руководство по логическим операторам в R | by Linda Ngo
Логические операторы позволяют нам изменять или сравнивать результаты сравнений, выполненных с использованием операторов отношения.
 Узнайте все, что вам нужно знать о них!
Узнайте все, что вам нужно знать о них!
Предположим, мы хотим изменить или сравнить результаты сравнений, выполненных с использованием операторов отношения. Как бы мы это сделали?
R делает это с помощью операторов AND , OR и NOT .
Логические операторы
- Оператор И
и - Оператор ИЛИ
| - НЕ оператор
!
Оператор И принимает два логических значения и возвращает ИСТИНА , только если оба значения сами ИСТИНА . Это означает, что TRUE & TRUE оценивается как TRUE , но что FALSE & TRUE , TRUE & FALSE и FALSE & FALSE оценивается как FALSE .
Только ИСТИНА и ИСТИНА дадут нам ИСТИНУ.
Вместо использования логических значений мы можем использовать результаты сравнений. Предположим, у нас есть переменная x , равная 12. Чтобы проверить, больше ли эта переменная 5, но меньше 15, мы можем использовать
Чтобы проверить, больше ли эта переменная 5, но меньше 15, мы можем использовать x больше 5 и x меньше 15.
x <- 12
x> 5 & x <15
Первая часть, x> 5 будет оценивать как TRUE , поскольку 12 больше 5. Вторая часть, x <15 также будет оценивать как TRUE , поскольку 12 также меньше 15.Итак, результатом этого выражения будет ИСТИНА , поскольку ИСТИНА и ИСТИНА равно ИСТИНА . Это имеет смысл, потому что 12 находится между 5 и 15.
Однако, если бы x было 17, выражение x> 5 & x <15 упростилось бы до ИСТИНА и ЛОЖЬ , что приводит к выражению ЛОЖЬ .
Для вас
Рассмотрим следующий вектор и переменную:
linkedin <- c (16, 9, 13, 5, 2, 17, 14)
last <- tail (linkedin, 1)
The linkedin vector представляет количество просмотров вашего профиля LinekdIn за последние семь дней. Переменная
Переменная last представляет последнее значение вектора linkedin .
Определите, находится ли переменная last между 15 и 20, исключая 15, но включая 20.
Решение
# Мы ищем R эквивалент 15last> 15 & last <= 20
Последняя переменная linkedin - 14, которая не находится между 15 и 20.
Для вас (2)
Рассмотрим следующие векторы:
linkedin <- c (16, 9, 13, 5, 2, 17 , 14)
facebook <- c (17, 7, 5, 16, 8, 13, 14)
Вектор linkedin представляет просмотры в вашем профиле LinkedIn за последние 7 дней, а вектор facebook представляет просмотры вашего профиля в Facebook за последние 7 дней.
Определите, когда просмотры в LinkedIn превысили 10 и просмотров Facebook не смогли достичь 10 за определенный день. Используйте векторы linkedin и facebook .
Решение
# linkedin превышает 10, но facebook меньше 10
linkedin> 10 & facebook <10
Только на третий день просмотров в LinkedIn было больше 10, а в Facebook меньше 10.
Для вас (3)
Рассмотрим следующую матрицу:
views <- matrix (c (linkedin, facebook), nrow = 2, byrow = TRUE)
Переменная linkedin и facebook соответствует тем же векторам в предыдущем для вас пытаться.
Матрица просмотров имеет первую и вторую строки, соответствующие векторам linkedin и facebook соответственно.
Определите, когда матрица просмотров равна числу от 11 до 14, исключая 11 и включая 14.
Решение
# Когда просмотры находятся между 11 (исключая) и 14 (включительно)?
просмотров> 11 & просмотров <= 14
В третий и последний день просмотры в LinkedIn были между 11 (исключая) и 14 (включительно).В шестой и последний день количество просмотров в Facebook было от 11 (исключая) до 14 (включительно).
Оператор ИЛИ (|) работает аналогично, но с той разницей, что только по крайней мере одно из логических значений должно быть равно ИСТИНА , чтобы вся операция ИЛИ оценивалась как ИСТИНА .
Это означает, что ИСТИНА | ИСТИНА равно ИСТИНА , но также ИСТИНА | ЛОЖНО и ЛОЖНО | ИСТИНА оценивается как ИСТИНА . Когда оба логических логических значения FALSE в операции ИЛИ, поэтому в случае FALSE | ЛОЖЬ , результат ЛОЖЬ .Помните, что операция OR не является исключительной операцией или or, поэтому TRUE | ИСТИНА также равно ИСТИНА .
С оператором И только ИСТИНА и ИСТИНА делает ИСТИНА , все остальное - ЛОЖЬ . С оператором OR только FALSE | ЛОЖЬ делает ЛОЖЬ , все остальное - ИСТИНА .
Так же, как и для операций И, мы можем использовать сравнения вместе с оператором ИЛИ. Предположим, у нас есть переменная y , равная 4.Чтобы узнать, меньше ли эта переменная 5 или больше 15, мы можем использовать следующее выражение:
y <- 4
y <5 | y> 15
R сначала выполнит сравнения, в результате чего TRUE | ЛОЖЬ , что, в свою очередь, приводит к ИСТИНА .
Теперь предположим, что y равно 14. Выражение y <5 | y> 15 теперь принимает значение FALSE | ЛОЖЬ . Ни одно из сравнений не дает ИСТИНА , поэтому результат ЛОЖЬ .
Для вас
Используя те же переменные из последнего, что вы можете попробовать, определите, находится ли last меньше 5 или больше 10.
linkedin <- c (16, 9, 13, 5, 2, 17 , 14)
last <- tail (linkedin, 1)
Solution
# Последний младше 5 или старше 10?
последняя <5 | last> 10
Последний элемент linkedin - 14, и хотя он меньше 5, он больше 10, что делает выражение истинным.
Для вас (2)
Рассмотрим те же векторы linkedin и facebook из предыдущих упражнений.
linkedin <- c (16, 9, 13, 5, 2, 17, 14)
facebook <- c (17, 7, 5, 16, 8, 13, 14)
Определить, когда один или оба социальных профиля посетили не менее 12 раз.
Решение
# Когда один или оба были посещены не менее 12 раз?
linkedin> = 12 | facebook> = 12
В дни 1, 3, 4, 6 и 7 один или оба социальных профиля были посещены не менее 12 раз.
Оператор НЕ, обозначенный восклицательным знаком ! , просто отменяет логическое значение, в котором он используется.То есть ! TRUE оценивается как FALSE , а ! FALSE оценивается как TRUE .
Так же, как операторы OR и AND, мы можем использовать оператор NOT в сочетании с логическими операторами. Это не всегда необходимо. Например, ! (X <5) совпадает с x> = 5 .
Однако в R бывают случаи, когда оператор NOT особенно удобен. Например, встроенная функция R, is.numeric () проверяет, является ли объект R числовым.Нет соответствующей встроенной функции, которая проверяет, не является ли это числовым. Чтобы проверить, нам нужно будет отрицать результат (! Is.). Итак, 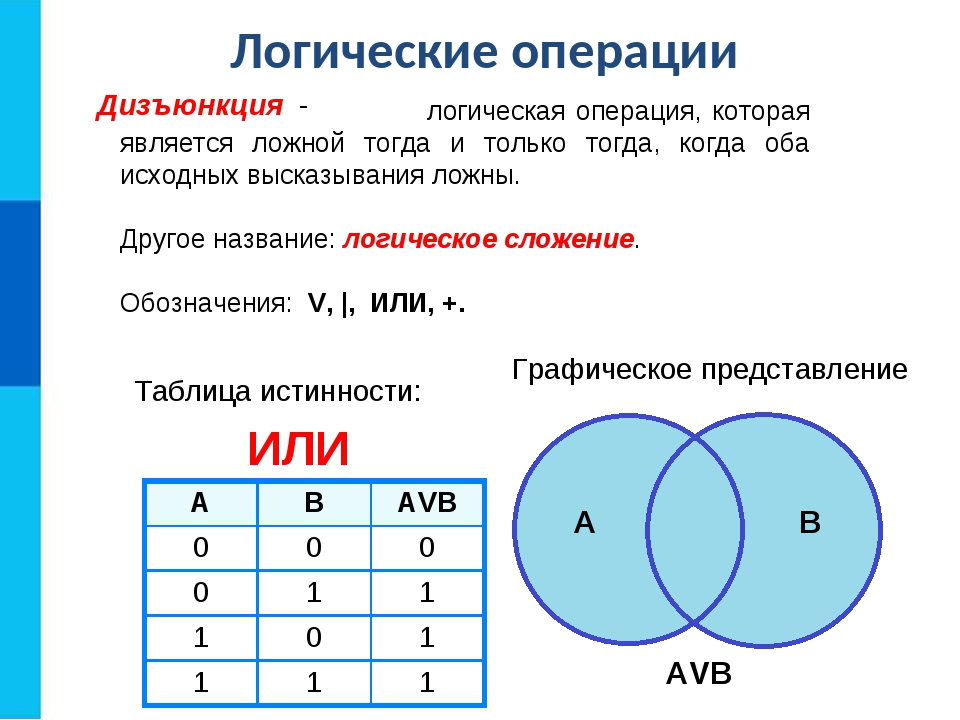 numeric ()
numeric () is.numeric (5) оценивается как ИСТИНА , поскольку 5 - это число. Если мы отрицаем этот результат с помощью оператора NOT (! Is.numeric (5) ), мы получим FALSE . Если, однако, мы используем is.numeric ("привет") , мы получим FALSE . Отрицание этого результата (! Is.numeric ("hello") ) дает нам ИСТИНА .
Теперь, как логические операторы работают с векторами и матрицами? Как и операторы отношения, они выполняют операции поэлементно. Рассмотрим эти два вектора:
c (ИСТИНА, ИСТИНА, ЛОЖЬ) & c (ИСТИНА, ЛОЖЬ, ЛОЖЬ)
Операция И над этими двумя векторами приводит к вектору с элементами ИСТИНА, , ЛОЖЬ, и НЕВЕРНО .
ИСТИНА ЛОЖЬ ЛОЖЬ
Первыми элементами в обоих векторах являются ИСТИНА , поэтому первый элемент результирующего вектора содержит ИСТИНА . Аналогично, для вторых элементов, где
Аналогично, для вторых элементов, где ИСТИНА и ЛОЖЬ дают ЛОЖЬ , а в третьих элементах, где ЛОЖЬ и ЛОЖЬ дают ЛОЖЬ .
То же самое происходит с оператором ИЛИ:
c (ИСТИНА, ИСТИНА, ЛОЖЬ) | c (ИСТИНА, ЛОЖЬ, ЛОЖЬ)
ИСТИНА | ИСТИНА дает ИСТИНА , ИСТИНА | FALSE также дает TRUE и FALSE | ЛОЖЬ дает ЛОЖЬ . Итак, мы получили бы результат:
ИСТИНА ИСТИНА ЛОЖЬ
Оператор НЕ также работает с каждым элементом вектора:
! C (ИСТИНА, ИСТИНА, ЛОЖЬ)
ИСТИНА преобразуются в ЛОЖЬ , и FALSE преобразуются в TRUE .Итак, мы получили бы результат
FALSE FALSE TRUE
Чтобы вы могли попробовать
Что вернет следующий набор выражений R:
x <- 5
y <- 7
! (! (X <4) & !!! (y> 12))
Решение
FALSE
Чтобы определить ответ, полезно разбить запрос на более мелкие выражения:
Сначала у нас есть левое выражение ! (x <4) внутреннего выражения (! (X <4) & !!! (y> 12)) .
-
x <4- посколькуxравно 5, а5 <4неверно, это утверждение оценивается какFALSE -
! (X <4)- Из вышеприведенного шага мы определил, чтоx <4оценивается какFALSE. Отрицание этого результата дает нам! FALSE, что соответствуетTRUE.
Далее у нас есть правильное выражение !!! (y> 12) внутреннего выражения (! (X <4) & !!! (y> 12)) .
-
y> 12- Поскольку y равно 7, а7> 12неверно, это выражение оценивается какFALSE. -
! (Y> 12)- Отрицая результат шага 1, мы получаем! FALSEилиTRUE. -
!! (y> 12)- Отрицая результат шага 2, мы получаем! TRUEилиFALSE. -
!!! (y> 12)- Отрицая результат шага 3, получаем! FALSEилиTRUE.
Итак, для внутреннего выражения (! (X <4) & !!! (y> 12)) оно оценивается как ИСТИНА и ИСТИНА , что равно ИСТИНА .
Внешний оператор НЕ ! отменяет это ИСТИНА , делая ! (! (X <4) & !!! (y> 12)) равным ! ИСТИНА или ЛОЖЬ .
В чем разница между одинарным и двойным амперсандом или вертикальной чертой? В R вы можете использовать как версию с одинарным знаком, так и версию с двойным знаком, но результат логической операции, которую вы выполняете, может быть другим.Наибольшая разница возникает, когда вы используете два типа операций над векторами.
c (ИСТИНА, ИСТИНА, ЛОЖЬ) & c (ИСТИНА, ЛОЖЬ, ЛОЖЬ)
Как мы видели ранее, приведенное выше выражение вычисляет вектор:
ИСТИНА ЛОЖЬ ЛОЖЬ
Однако, если мы используем двойной амперсанд , мы просто получаем ИСТИНА .
c (ИСТИНА, ИСТИНА, ЛОЖЬ) && c (ИСТИНА, ЛОЖЬ, ЛОЖЬ)
Это связано с тем, что операция двойного амперсанда проверяет только первых элементов каждого вектора. В этом случае первыми элементами являются
В этом случае первыми элементами являются ИСТИНА и ИСТИНА , поэтому выражение возвращает ИСТИНА .
Вы можете видеть аналогичные вещи, происходящие с оператором OR. Версия единого знака | возвращает и весь вектор. Версия с двойным знаком || возвращает результат операции ИЛИ для первого элемента каждого вектора.
Так что будьте внимательны при выполнении логических операций над векторами. Вероятно, вы захотите использовать версию с единым знаком.
2.1: Операторы и логические операторы
ПРЕДВАРИТЕЛЬНЫЙ ПРОСМОТР \ (\ PageIndex {1} \): Составные операторы
Математики часто разрабатывают способы построения новых математических объектов из существующих математических объектов. Можно сформировать новые утверждения из существующих утверждений, соединив утверждения такими словами, как «и» и «или», или путем отрицания утверждения. Логический оператор (или связующее ) в математических утверждениях - это слово или комбинация слов, которые объединяют одно или несколько математических утверждений для создания нового математического утверждения. Составной оператор - это оператор, содержащий один или несколько операторов. Поскольку некоторые операторы так часто используются в логике и математике, мы даем им имена и используем специальные символы для их представления.
Составной оператор - это оператор, содержащий один или несколько операторов. Поскольку некоторые операторы так часто используются в логике и математике, мы даем им имена и используем специальные символы для их представления.
- Конъюнкция операторов \ (P \) и \ (Q \) - это утверждение «\ (P \) и \ (Q \)», которое обозначается как \ (P \ wedge Q \). Утверждение \ (P \ wedge Q \) верно только тогда, когда оба \ (P \) и \ (Q \) верны.
- Дизъюнкция операторов \ (P \) и \ (Q \) является утверждением «\ (P \) или \ (Q \)» и обозначается как \ (P \ vee Q \).Утверждение \ (P \ vee Q \) истинно только тогда, когда истинно хотя бы одно из \ (P \) или \ (Q \).
- Отрицание ( утверждения ) утверждения \ (P \) является утверждением «, а не \ (P \)» и обозначается \ (\ urcorner P \). Отрицание \ (P \) истинно, только когда \ (P \) ложно, а \ (\ urcorner P \) ложно, только когда \ (P \) истинно.

- Импликация или условное - это утверждение « Если \ (P \) , то \ (Q \)» и обозначается \ (P \ to Q \).Утверждение \ (P \ to Q \) часто читается как «\ (P \) подразумевает \ (Q \)», и мы видели в разделе 1.1, что \ (P \ to Q \) ложно только тогда, когда \ (P \) истинно, а \ (Q \) ложно.
Несколько замечаний по поводу дизъюнкции.
Важно понимать использование оператора «или». В математике мы используем « включительно или », если не указано иное. Это означает, что \ (P \ vee Q \) истинно, когда оба \ (P \) и \ (Q \) истинны, а также когда истинно только одно из них.То есть \ (P \ vee Q \) истинно, если хотя бы одно из \ (P \) или \ (Q \) истинно, или \ (P \ vee Q \) ложно, только когда оба \ (P \ ) и \ (Q \) ложны.
Другое использование слова «или» - это « исключающее или ». Для исключающего или результирующий оператор является ложным, если оба утверждения верны. То есть, «\ (P \) эксклюзивное или \ (Q \)» истинно только тогда, когда истинно ровно одно из \ (P \) или \ (Q \). В повседневной жизни мы часто используем эксклюзивное или. Когда кто-то говорит: «На перекрестке поверните налево или идите прямо», этот человек использует исключительное или.
То есть, «\ (P \) эксклюзивное или \ (Q \)» истинно только тогда, когда истинно ровно одно из \ (P \) или \ (Q \). В повседневной жизни мы часто используем эксклюзивное или. Когда кто-то говорит: «На перекрестке поверните налево или идите прямо», этот человек использует исключительное или.
Некоторые комментарии по поводу отрицания . Хотя утверждение \ (\ urcorner P \) можно прочитать как «Это не тот случай, когда \ (P \)», часто есть лучшие способы сказать или написать это на английском языке. Например, мы обычно говорим (или пишем):
- Утверждение «391 простое» означает «391 не простое».
- Отрицание утверждения «\ (12 <9 \)» равно «\ (12 \ ge 9 \)».
- Для выписок
\ (P \): 15 - нечетное \ (Q \): 15 - простое
запишите каждое из следующих утверждений как английские предложения и определите, истинны они или ложны.
(а) \ (P \ клин Q \). (б) \ (P \ vee Q \). (c) \ (P \ клин \ urcorner Q \). (г) \ (\ urcorner P \ vee \ urcorner Q \).
(г) \ (\ urcorner P \ vee \ urcorner Q \). - Для заявлений
P: 15 нечетное R: 15 <17
запишите каждое из следующих утверждений в символической форме, используя операторы \ (\ wedge \), \ (\ vee \) и \ (\ urcorner \)
(a) 15 \ (\ ge \) 17. (b) 15 нечетно или 15 \ (\ ge \) 17.
(c) 15 четно или 15 <17. (г) 15 нечетно и 15 \ (\ ge \) 17.
ПРЕДВАРИТЕЛЬНЫЙ ПРОСМОТР \ (\ PageIndex {2} \): истинные значения утверждений
Мы будем использовать следующие два оператора для всего этого действия предварительного просмотра:
- \ (P \) - это высказывание «Идет дождь.”
- \ (Q \) - это утверждение «Дейзи играет в гольф».
В каждой из следующих четырех частей утверждениям \ (P \) и \ (Q \) будет присвоено значение истинности. Например, в вопросе (1) мы будем предполагать, что каждое утверждение истинно. В вопросе (2) мы будем предполагать, что \ (P \) истинно, а \ (Q \) ложно. В каждой части определите истинность каждого из следующих утверждений:
В каждой части определите истинность каждого из следующих утверждений:
(a) (\ (P \ wedge Q \)) Идет дождь, и Дейзи играет в гольф.
(b) (\ (P \ vee Q \)) Идет дождь или Дейзи играет в гольф.
(c) (\ (P \ to Q \)) Если идет дождь, значит, Дейзи играет в гольф.
(d) (\ (\ urcorner P \)) Дождя нет.
Какие из четырех утверждений [от (a) до (d)] верны, а какие - ложны в каждой из следующих четырех ситуаций?
1. Когда \ (P \) истинно (идет дождь) и \ (Q \) истинно (Дейзи играет в гольф).
2. Когда \ (P \) истинно (идет дождь) и \ (Q \) ложно (Дейзи не играет в гольф).
3. Когда \ (P \) ложно (дождь не идет) и \ (Q \) истинно (Дейзи играет в гольф).
4. Когда \ (P \) ложно (дождь не идет) и \ (Q \) ложно (Дейзи не играет в гольф).
В предварительных упражнениях этого раздела мы узнали о составных утверждениях и их истинностных значениях. Эта информация может быть сведена к таблицам истинности, как показано ниже.
| \ (П \) | \ (\ urcorner P \) |
|---|---|
| т | F |
| ф | т |
| \ (P \) | \ (Q \) | \ (P \ клин Q \) |
|---|---|---|
| т | т | т |
| т | F | F |
| ф | т | F |
| ф | F | F |
| \ (P \) | \ (Q \) | \ (P \ vee Q \) |
|---|---|---|
| т | т | т |
| т | F | т |
| ф | т | т |
| ф | F | F |
| \ (P \) | \ (Q \) | \ (P \ to Q \) |
|---|---|---|
| т | т | т |
| т | F | F |
| ф | т | т |
| ф | F | т |
Вместо того, чтобы запоминать таблицы истинности, для многих людей легче запомнить правила, приведенные в Таблице 2. 1.
1.
| Оператор | Символическая форма | Сводка истинных значений |
|---|---|---|
| Соединение | \ (П \ клин Q \) | Верно только тогда, когда оба \ (P \) и \ (Q \) верны |
| Дизъюнкция | \ (П \ Ви К \) | Ложь, только если оба \ (P \) и \ (Q \) неверны |
| Отрицание | \ (\ urcorner P \) | Значение противоположной истинности \ (P \) |
| условно | \ (P \ to Q \) | Ложь, только если \ (P \) истинно, а \ (Q \) ложно |
Другие формы условных отчетов
Условные утверждения чрезвычайно важны в математике, потому что почти все математические теоремы (или могут быть) сформулированы в форме условного утверждения в следующей форме:
Если «соблюдаются определенные условия», то «что-то происходит. ”
”
Крайне важно, чтобы все студенты, изучающие математику, досконально понимали значение условного утверждения и таблицы истинности условного утверждения.
Нам также необходимо знать, что в английском языке существуют другие способы выражения условного оператора \ (P \ to Q \), кроме «Если \ (P \), то \ (Q \)». Ниже приведены некоторые распространенные способы выражения условного оператора \ (P \ to Q \) на английском языке:
Проверка выполнения 2.1: Заявление «Только если»
Напомним, что четырехугольник - это четырехугольник.Пусть \ (S \) представляет следующее истинное условное утверждение:
Если четырехугольник квадрат, то это прямоугольник.
Запишите это условное выражение на английском языке, используя
.
- слово «всякий раз, когда»
- фраза «только если»
- фраза «необходимо»
- фраза «достаточно для»
- Ответ
Добавьте сюда текст.
 Не удаляйте сначала этот текст.
Не удаляйте сначала этот текст.
Построение таблиц истины
Таблицы истинности для составных утверждений могут быть построены с использованием таблиц истинности для основных связок. Чтобы проиллюстрировать это, мы построим таблицу истинности для. \ ((P \ клин \ urcorner Q) \ к R \). Первый шаг - определить необходимое количество строк.
- Для таблицы истинности с двумя разными простыми утверждениями необходимы четыре строки, поскольку есть четыре различных комбинации значений истинности для двух утверждений.Мы должны согласовываться с тем, как мы расставляем ряды. То, как мы сделаем это в этом тексте, - это пометить строки для первого оператора с помощью (T, T, F, F) и строки для второго оператора с помощью (T, F, T, F). Все таблицы истинности в тексте имеют эту схему.
- Для таблицы истинности с тремя разными простыми утверждениями необходимо восемь строк, поскольку существует восемь различных комбинаций значений истинности для трех утверждений.
 Наша стандартная схема для этого типа таблицы истинности показана в Таблице 2.2 .
Наша стандартная схема для этого типа таблицы истинности показана в Таблице 2.2 .
Следующим шагом является определение столбцов, которые будут использоваться. Один из способов сделать это - вернуться назад от формы данного оператора. Для \ ((P \ wedge \ urcorner Q) \ to R \) последний шаг - иметь дело с условным оператором \ ((\ to) \). Для этого нам нужно знать значения истинности \ ((P \ wedge \ urcorner Q) \) и \ (R \). Чтобы определить значения истинности для \ ((P \ wedge \ urcorner Q) \), нам нужно применить правила для оператора конъюнкции \ ((\ wedge) \), и нам нужно знать значения истинности для \ (P \ ) и \ (\ urcorner Q \).
Таблица 2.2 - это завершенная таблица истинности для \ ((P \ wedge \ urcorner Q) \ to R \) с номерами шагов, указанными внизу каждого столбца. Номера шагов соответствуют порядку заполнения столбцов.
| \ (П \) | \ (Q \) | \ (R \) | \ (\ urcorner Q \) | \ ((P \ клин \ urcorner Q) \) | \ ((P \ клин \ urcorner Q) \ to R \) |
|---|---|---|---|---|---|
| т | т | т | F | F | т |
| т | т | F | F | F | т |
| т | F | т | т | т | т |
| т | F | F | т | т | F |
| ф | т | т | F | F | т |
| ф | т | F | F | F | т |
| ф | F | т | т | F | т |
| ф | F | F | т | F | т |
| 1 | 1 | 1 | 2 | 3 | 4 |
- При заполнении столбца для \ (P \ wedge \ urcorner Q \) помните, что конъюнкция истинна только тогда, когда оба \ (P \) и \ (\ urcorner Q \) истинны.

- При заполнении столбца для \ ((P \ wedge \ urcorner Q) \ to R \) помните, что условное утверждение ложно только тогда, когда гипотеза \ ((P \ wedge \ urcorner Q) \) верна и заключение \ (R \) неверно.
Последний введенный столбец - это таблица истинности для утверждения \ ((P \ wedge \ urcorner Q) \ to R \), использующего настройку в первых трех столбцах.
Проверка выполнения 2.2: построение таблиц истинности
Создайте таблицу истинности для каждого из следующих утверждений:
- \ (P \ клин \ urcorner Q \)
- \ (\ urcorner (P \ клин Q) \)
- \ (\ urcorner P \ клин \ urcorner Q \)
- \ (\ urcorner P \ vee \ urcorner Q \)
Есть ли у любого из этих утверждений одна и та же таблица истинности?
- Ответ
Добавьте сюда текст.Не удаляйте сначала этот текст.
Двуусловное утверждение
Некоторые математические результаты сформулированы в форме «\ (P \) тогда и только тогда, когда \ (Q \)» или «\ (P \) необходимо и достаточно для \ (Q \)». Примером может быть: «Треугольник является равносторонним тогда и только тогда, когда его три внутренних угла совпадают». Символическая форма для биконусного утверждения «\ (P \) тогда и только тогда, когда \ (Q \)» есть \ (P \ leftrightarrow Q \). Чтобы определить таблицу истинности для двусмысленного утверждения, поучительно внимательно посмотреть на форму фразы «\ (P \) тогда и только тогда, когда \ (Q \)».Слово «и» предполагает, что это утверждение является союзом. На самом деле это сочетание утверждений «\ (P \), если \ (Q \)» и «\ (P \), только если \ (Q \)». Символическая форма этого соединения - \ ([(Q \ to P) \ wedge (P \ to Q] \).
Примером может быть: «Треугольник является равносторонним тогда и только тогда, когда его три внутренних угла совпадают». Символическая форма для биконусного утверждения «\ (P \) тогда и только тогда, когда \ (Q \)» есть \ (P \ leftrightarrow Q \). Чтобы определить таблицу истинности для двусмысленного утверждения, поучительно внимательно посмотреть на форму фразы «\ (P \) тогда и только тогда, когда \ (Q \)».Слово «и» предполагает, что это утверждение является союзом. На самом деле это сочетание утверждений «\ (P \), если \ (Q \)» и «\ (P \), только если \ (Q \)». Символическая форма этого соединения - \ ([(Q \ to P) \ wedge (P \ to Q] \).
Проверка выполнения 2.3: Таблица истинности для двояковыпуклого утверждения
Заполните таблицу истинности для \ ([(Q \ to P) \ wedge (P \ to Q] \). Используйте следующие столбцы: \ (P \), \ (Q \), \ (Q \ to P \ ), \ (P \ to Q \) и \ ([(Q \ to P) \ wedge (P \ to Q] \). Последний столбец этой таблицы будет истинным для \ (P \ leftrightarrow Q \ ).
- Ответ
Добавьте сюда текст. Не удаляйте сначала этот текст.
Другие формы двусмысленного заявления
Как и в случае с условным оператором, существует несколько распространенных способов выражения двусмысленного оператора, \ (P \ leftrightarrow Q \), на английском языке.
Пример
- \ (P \) есть и только если \ (Q \).
- \ (P \) необходимо и достаточно для \ (Q \).
- \ (P \) влечет \ (Q \), а \ (Q \) влечет \ (P \).
Тавтологии и противоречия
Определение: тавтология
Тавтология - это составное утверждение S, которое истинно для всех возможных комбинаций значений истинности составных утверждений, которые являются частью \ (S \). Противоречие - это составное утверждение, которое ложно для всех возможных комбинаций значений истинности составных утверждений, которые являются частью \ (S \).
То есть тавтология обязательно истинна при любых обстоятельствах, а противоречие обязательно ложно при любых обстоятельствах.
Проверка выполнения 2.4 (тавтологии и противоречия)
Для выписок \ (P \) и \ (Q \):
- Используйте таблицу истинности, чтобы показать, что \ ((P \ vee \ urcorner P) \) является тавтологией.
- Используйте таблицу истинности, чтобы показать, что \ ((P \ wedge \ urcorner P) \) противоречие.
- Используйте таблицу истинности, чтобы определить, является ли \ (P \ to (P \ vee P) \) тавтологией, противоречием или нет.
- Ответ
Добавьте сюда текст. Не удаляйте сначала этот текст.
Упражнения к разделу 2.1
- Предположим, что Дейзи говорит: «Если не пойдет дождь, я буду играть в гольф». Позже вы узнаете, что шел дождь, но Дейзи все еще играла в гольф. Было ли заявление Дейзи правдой или ложью? Поддержите свой вывод.

- Предположим, что \ (P \) и \ (Q \) - утверждения, для которых верно \ (P \ to Q \) и для которых верно \ (\ urcorner Q \).Какой вывод (если таковой имеется) можно сделать об истинности каждого из следующих утверждений?
(a) \ (P \)
(b) \ (P \ wedge Q \)
(c) \ (P \ vee Q \) - Предположим, что \ (P \) и \ (Q \) - утверждения, для которых \ (P \ to Q \) ложно. Какой вывод (если таковой имеется) можно сделать об истинности каждого из следующих утверждений?
(a) \ (\ urcorner P \ to Q \)
(b) \ (Q \ to P \)
(c) \ (P \ vee Q \) - Предположим, что \ (P \) и \ (Q \) - утверждения, для которых \ (Q \) ложно и \ (\ urcorner P \ to Q \) истинно (и неизвестно, если \ (R \) верно или неверно).Какой вывод (если таковой имеется) можно сделать об истинности каждого из следующих утверждений?
(a) \ (\ urcorner Q \ to P \)
(b) \ (P \)
(c) \ (P \ wedge R \)
(d) \ (R \ to \ urcorner P \) - Постройте таблицу истинности для каждого из следующих утверждений:
(a) \ (P \ to Q \)
(b) \ (Q \ to P \)
(c) \ (\ urcorner P \ to \ urcorner Q \)
(d) \ (\ urcorner Q \ to \ urcorner P \)Имеет ли какое-либо из этих утверждений одинаковую таблицу истинности?
- Постройте таблицу истинности для каждого из следующих утверждений:
(a) \ (P \ vee \ urcorner Q \)
(b) \ (\ urcorner (P \ vee Q) \)
(c) \ (\ urcorner P \ vee \ urcorner Q \)
(d) \ (\ urcorner P \ wedge \ urcorner Q \)Имеет ли какое-либо из этих утверждений одинаковую таблицу истинности?
- Постройте таблицу истинности для \ (P \ wedge (Q \ vee R) \) и \ ((P \ wedge Q) \ vee (P \ wedge R) \).
 Что вы наблюдаете.
Что вы наблюдаете. - Предположим, что каждое из следующих утверждений верно.
- Лаура учится в седьмом классе.
- - Лаура получила пятёрку за тест по математике или Сара получила пятёрку за тест по математике.
- �� Если Сара получила пятерку на тесте по математике, значит, Лора не учится в седьмом классе.
Если возможно, определите истинность каждого из следующих утверждений. Тщательно объясните свои рассуждения.
(a) Лаура получила пятёрку на тесте по математике.2 \) четное ». Выразите условное выражение \ (P \ to Q \) на английском языке, используя
(a) Форма условного оператора «if then»
(b) Слово «Implies»
(c) Форма «only if» выражения условное утверждение
(d) Фраза «необходимо для»
(e) Фраза «достаточно для» - Повторите упражнение (9) для условного оператора \ (Q \ to P \).
- Для утверждений \ (P \) и \ (Q \) используйте таблицы истинности, чтобы определить, является ли каждое из следующих утверждений тавтологией, противоречием или ни тем, ни другим.

(а) \ (\ urcorner Q \ vee (P \ to Q) \).
(b) \ (Q \ клин (P \ клин \ urcorner Q) \).
(c) \ ((Q \ клин P) \ клин (P \ to \ urcorner Q) \).
(d) \ (\ urcorner Q \ to (P \ клин \ urcorner P) \). - Для утверждений \ (P \), \ (Q \) и \ (R \):
(a) Докажите, что \ ([(P \ to Q) \ wedge P] \ to Q \) является тавтологией. Примечание : В символической логике это важная форма логического аргумента, называемая modus ponens .
(b) Докажите, что \ ([(P \ to Q) \ wedge (Q \ to R)] \ to (P \ to R) \) является автологией. Примечание : В символической логике это важная форма логического аргумента, называемая силлогизмом .Разведки и работы
- Работа с условными операторами. Заполните следующую таблицу:
Английская форма Гипотеза Заключение Условная форма Если \ (P \), то \ (Q \) \ (П \) \ (Q \) \ (от P \ до Q \) \ (Q \) только если \ (P \) \ (Q \) \ (П \) \ (Q \ к P \) \ (P \) необходимо для \ (Q \) \ (P \) достаточно для \ (Q \) \ (Q \) необходимо для \ (P \) \ (P \) подразумевает \ (Q \) \ (P \) только если \ (Q \) \ (P \) если \ (Q \) если \ (Q \), то \ (P \) если \ (\ urcorner Q \), то \ (\ urcorner P \) если \ (Q \), то \ (Q \ wedge R \) если \ (P \ vee Q \), то \ (R \) - Работа с истинностью утверждений.
 Предположим, что \ (P \) и \ (Q \) - истинные утверждения, что \ (U \) и \ (V \) - ложные утверждения, и что \ (W \) - утверждение, и неизвестно, если \ (W \) истинно или ложно.
Предположим, что \ (P \) и \ (Q \) - истинные утверждения, что \ (U \) и \ (V \) - ложные утверждения, и что \ (W \) - утверждение, и неизвестно, если \ (W \) истинно или ложно.Какие из следующих утверждений верны, какие ложны и для каких утверждений невозможно определить, истинно оно или ложно? Обоснуйте свои выводы.
(a) \ ((P \ vee Q) \ vee (U \ клин W) \) (f) \ ((\ urcorner P \ vee \ urcorner U) \ клин (Q \ vee \ urcorner V) \)
(b) \ (P \ клин (Q \ к W) \) (g) \ ((P \ клин \ urcorner Q) \ клин (U \ vee W) \)
(c) \ (P \ клин ( W \ к Q) \) (h) \ ((P \ vee \ urcorner Q) \ to (U \ wedge W) \)
(d) \ (W \ to (P \ wedge U) \) (i) \ ((P \ vee W) \ to (U \ wedge W) \)
(e) \ (W \ to (P \ wedge \ urcorner U) \) (j) \ ((U \ wedge \ urcorner V) \ to (P \ клин W) \)
- Ответ
Добавьте сюда текст.Не удаляйте сначала этот текст.
Логических функций в Excel: И, ИЛИ, XOR и НЕ
В учебном пособии объясняется сущность логических функций Excel И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ и НЕ, а также приводятся примеры формул, демонстрирующие их общее и изобретательное использование.
На прошлой неделе мы познакомились с логическими операторами Excel, которые используются для сравнения данных в разных ячейках. Сегодня вы увидите, как расширить использование логических операторов и построить более сложные тесты для выполнения более сложных вычислений.В этом вам помогут логические функции Excel, такие как AND, OR, XOR и NOT.
Логические функции Excel - обзор
Microsoft Excel предоставляет 4 логические функции для работы с логическими значениями. Это функции И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ и НЕ. Вы используете эти функции, когда хотите провести более одного сравнения в своей формуле или протестировать несколько условий вместо одного. Помимо логических операторов, логические функции Excel возвращают ИСТИНА или ЛОЖЬ при оценке их аргументов.
В следующей таблице приводится краткое описание того, что делает каждая логическая функция, чтобы помочь вам выбрать правильную формулу для конкретной задачи.
| Функция | Описание | Пример формулы | Описание формулы |
| И | Возвращает ИСТИНА, если все аргументы оцениваются как ИСТИНА. | = И (A2> = 10, B2 <5) | Формула возвращает ИСТИНА, если значение в ячейке A2 больше или равно 10, а значение в B2 меньше 5, в противном случае - ЛОЖЬ. |
| ИЛИ | Возвращает ИСТИНА, если какой-либо аргумент имеет значение ИСТИНА. | = ИЛИ (A2> = 10, B2 <5) | Формула возвращает ИСТИНА, если A2 больше или равно 10, или B2 меньше 5, или оба условия выполнены. Если ни одно из условий не выполнено, формула возвращает ЛОЖЬ. |
| XOR | Возвращает логическое исключающее ИЛИ всех аргументов. | = XOR (A2> = 10, B2 <5) | Формула возвращает ИСТИНА, если либо A2 больше или равно 10, либо B2 меньше 5.Если ни одно из условий не выполняется или выполняются оба условия, формула возвращает ЛОЖЬ. |
| НЕ | Возвращает обратное логическое значение своего аргумента. Т.е. Если аргумент ЛОЖЬ, то возвращается ИСТИНА, и наоборот.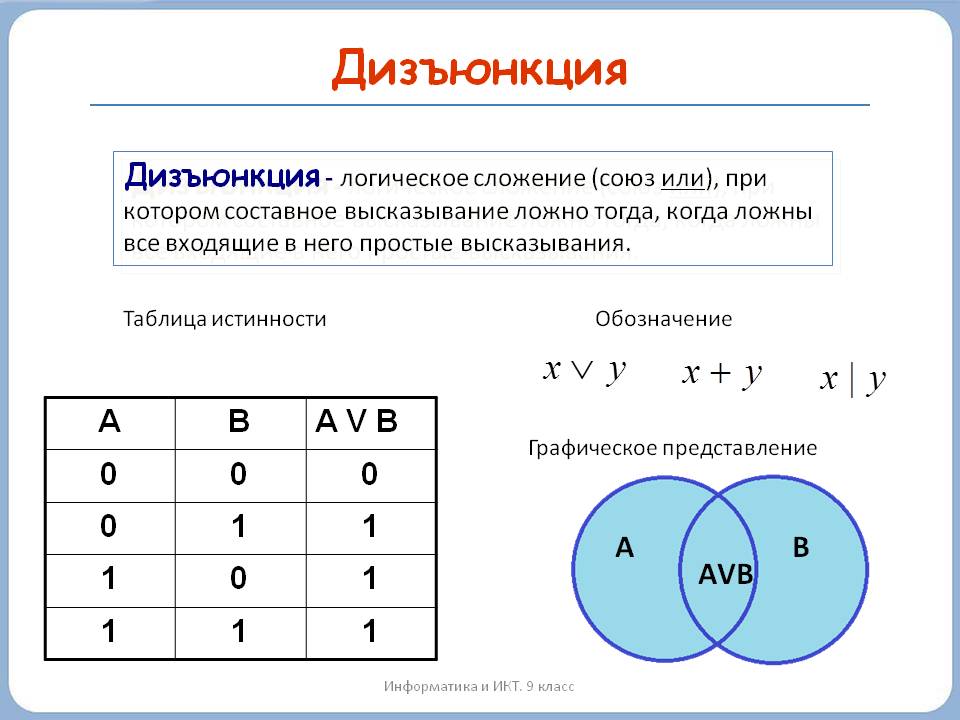 | = НЕ (A2> = 10) | Формула возвращает ЛОЖЬ, если значение в ячейке A1 больше или равно 10; В противном случае ИСТИНА. |
В дополнение к четырем логическим функциям, описанным выше, Microsoft Excel предоставляет 3 «условные» функции - ЕСЛИ, ЕСЛИОШИБКА и IFNA.
Логические функции Excel - цифры и факты
- В аргументах логических функций можно использовать ссылки на ячейки, числовые и текстовые значения, логические значения, операторы сравнения и другие функции Excel. Однако все аргументы должны соответствовать логическим значениям ИСТИНА или ЛОЖЬ либо ссылкам или массивам, содержащим логические значения.
- Если аргумент логической функции содержит пустых ячеек , такие значения игнорируются. Если все аргументы являются пустыми ячейками, формула возвращает # ЗНАЧ! ошибка.
- Если аргумент логической функции содержит числа, то ноль оценивается как ЛОЖЬ, а все другие числа, включая отрицательные числа, оцениваются как ИСТИНА.
 Например, если ячейки A1: A5 содержат числа, формула = AND (A1: A5) вернет ИСТИНА, если ни одна из ячеек не содержит 0, в противном случае - ЛОЖЬ.
Например, если ячейки A1: A5 содержат числа, формула = AND (A1: A5) вернет ИСТИНА, если ни одна из ячеек не содержит 0, в противном случае - ЛОЖЬ. - Логическая функция возвращает # ЗНАЧ! ошибка, если ни один из аргументов не дает логических значений.
- Логическая функция возвращает # ИМЯ? ошибка, если вы неправильно написали имя функции или попытались использовать функцию в более ранней версии Excel, которая ее не поддерживает.Например, функцию XOR можно использовать только в Excel 2016 и 2013.
- В Excel 2016, 2013, 2010 и 2007 вы можете включить до 255 аргументов в логическую функцию при условии, что общая длина формулы не превышает 8192 символа. В Excel 2003 и ниже вы можете указать до 30 аргументов, а общая длина вашей формулы не должна превышать 1024 символа.
Использование функции И в Excel
Функция И - самый популярный член семейства логических функций.Это удобно, когда нужно протестировать несколько условий и убедиться, что все они выполняются. Технически функция И проверяет указанные вами условия и возвращает ИСТИНА, если все условия оцениваются как ИСТИНА, в противном случае - ЛОЖЬ.
Технически функция И проверяет указанные вами условия и возвращает ИСТИНА, если все условия оцениваются как ИСТИНА, в противном случае - ЛОЖЬ.
Синтаксис функции И в Excel выглядит следующим образом:
И (логический1, [логический2],…)
Где логический - это условие, которое вы хотите проверить, которое может иметь значение ИСТИНА или ЛОЖЬ. Первое условие (логический1) является обязательным, последующие условия необязательны.
А теперь давайте рассмотрим несколько примеров формул, демонстрирующих, как использовать функции И в формулах Excel.
| Формула | Описание |
= И (A2 = "Бананы", B2> C2) | Возвращает TRUE, если A2 содержит "Bananas", а B2 больше, чем C2, в противном случае - FALSE. |
= И (B2> 20, B2 = C2) | Возвращает TRUE, если B2 больше 20, а B2 равно C2, в противном случае - FALSE. |
= И (A2 = "Бананы", B2> = 30, B2> C2) | Возвращает TRUE, если A2 содержит "Bananas", B2 больше или равно 30 и B2 больше C2, в противном случае - FALSE. |
Excel И функция - общее применение
Сама по себе функция И в Excel не очень интересна и имеет узкую полезность. Но в сочетании с другими функциями Excel И может значительно расширить возможности ваших листов.
Одно из наиболее распространенных применений функции И Excel в аргументе логический_тест функции ЕСЛИ для проверки нескольких условий вместо одного. Например, вы можете вложить любую из перечисленных выше функций И в функцию ЕСЛИ и получить результат, подобный этому:
= ЕСЛИ (И (A2 = «Бананы», B2> C2), «Хорошо», «Плохо»)
Дополнительные примеры формул ЕСЛИ / И можно найти в его учебнике: Функция ЕСЛИ в Excel с несколькими условиями И.
Формула Excel для условия МЕЖДУ
Если вам нужно создать формулу между в Excel, которая выбирает все значения между заданными двумя значениями, общий подход заключается в использовании функции ЕСЛИ с И в логическом тесте.
Например, у вас есть 3 значения в столбцах A, B и C, и вы хотите знать, находится ли значение в столбце A между значениями B и C. Чтобы составить такую формулу, все, что требуется, - это функция ЕСЛИ с вложенным И и пара операторов сравнения:
Чтобы составить такую формулу, все, что требуется, - это функция ЕСЛИ с вложенным И и пара операторов сравнения:
Формула для проверки, находится ли X между Y и Z включительно:
= ЕСЛИ (И (A2> = B2, A2 <= C2), «Да», «Нет»)
Формула для проверки, находится ли X между Y и Z, не включительно:
= ЕСЛИ (И (A2> B2, A2
Как показано на скриншоте выше, формула отлично работает для всех типов данных - чисел, дат и текстовых значений.При сравнении текстовых значений формула проверяет их посимвольно в алфавитном порядке. Например, в нем указано, что Яблоки не находятся между Абрикосом и Бананами , потому что вторая буква «p» в строке Яблоки стоит перед буквой «r» в строке Абрикос . Дополнительные сведения см. В разделе Использование операторов сравнения Excel с текстовыми значениями.
Как видите, формула ЕСЛИ / И проста, быстра и почти универсальна. Я говорю «почти», потому что это не относится к одному сценарию.Приведенная выше формула подразумевает, что значение в столбце B меньше, чем в столбце C, т.е. столбец B всегда содержит значение нижней границы, а C - значение верхней границы. По этой причине формула возвращает « № » для строки 6, где A6 имеет 12, B6 - 15 и C6 - 3, а также для строки 8, где A8 - 24 ноября, B8 - 26 декабря, а C8 - 21 окт.
Я говорю «почти», потому что это не относится к одному сценарию.Приведенная выше формула подразумевает, что значение в столбце B меньше, чем в столбце C, т.е. столбец B всегда содержит значение нижней границы, а C - значение верхней границы. По этой причине формула возвращает « № » для строки 6, где A6 имеет 12, B6 - 15 и C6 - 3, а также для строки 8, где A8 - 24 ноября, B8 - 26 декабря, а C8 - 21 окт.
Но что, если вы хотите, чтобы ваша промежуточная формула работала правильно, независимо от того, где находятся нижняя и верхняя границы значений? В этом случае используйте функцию МЕДИАНА Excel, которая возвращает медиану заданных чисел (т.е.е. число в середине набора чисел).
Итак, если вы замените И в логической проверке функции ЕСЛИ на МЕДИАНА, формула будет иметь вид:
= ЕСЛИ (A2 = МЕДИАНА (A2: C2), «Да», «Нет»)
И вы получите следующие результаты:
Как видите, функция МЕДИАНА отлично работает для чисел и дат, но возвращает # ЧИСЛО! ошибка для текстовых значений.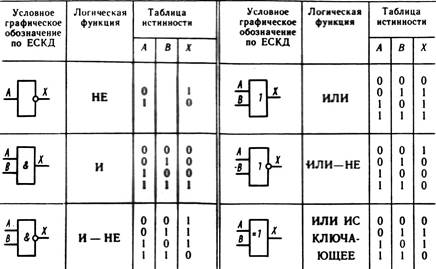 Увы, никто не идеален 🙂
Увы, никто не идеален 🙂
Если вам нужна идеальная формула Between, которая работает для текстовых значений, а также для чисел и дат, вам придется создать более сложный логический текст, используя функции И / ИЛИ, например:
= ЕСЛИ (ИЛИ (И (A2> B2, A2
Использование функции ИЛИ в Excel
Как и И, функция ИЛИ в Excel является базовой логической функцией, которая используется для сравнения двух значений или операторов.Разница в том, что функция ИЛИ возвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА, и возвращает ЛОЖЬ, если все аргументы ЛОЖЬ. Функция ИЛИ доступна во всех версиях Excel 2016–2000.
Синтаксис функции ИЛИ в Excel очень похож на И:
ИЛИ (логический1, [логический2],…)
Где логический - это то, что вы хотите проверить, которое может иметь значение ИСТИНА или ЛОЖЬ. Первое логическое значение является обязательным, дополнительные условия (до 255 в современных версиях Excel) необязательны.
А теперь давайте напишем несколько формул, чтобы вы почувствовали, как работает функция ИЛИ в Excel.
| Формула | Описание |
= ИЛИ (A2 = «Бананы», A2 = «Апельсины») | Возвращает ИСТИНА, если A2 содержит «Бананы» или «Апельсины», в противном случае - ЛОЖЬ. |
= ИЛИ (B2> = 40, C2> = 20) | Возвращает ИСТИНА, если B2 больше или равно 40 или C2 больше или равно 20, в противном случае - ЛОЖЬ. |
= ИЛИ (B2 = "", C2 = "") | Возвращает ИСТИНА, если либо В2, либо С2 пусто, либо оба значения; в противном случае - ЛОЖЬ. |
Наряду с функцией И в Excel, ИЛИ широко используется для расширения возможностей других функций Excel, выполняющих логические тесты, например функция ЕСЛИ. Вот лишь пара примеров:
Функция ЕСЛИ с вложенным ИЛИ
= ЕСЛИ (ИЛИ (B2> 30, C2> 20), «Хорошо», «Плохо»)
Формула возвращает « Хорошо, », если число в ячейке B3 больше 30 или число в C2 больше 20, в противном случае - « Плохо, ».
Excel Функции И / ИЛИ в одной формуле
Естественно, ничто не мешает вам использовать обе функции, И и ИЛИ, в одной формуле, если этого требует ваша бизнес-логика. Таких формул может быть бесконечное количество вариаций, которые сводятся к следующим основным схемам:
= И (ИЛИ (Cond1, Cond2), Cond3)
= И (ИЛИ (Cond1, Cond2), OR (Cond3, Cond4)
= ИЛИ (И (Cond1, Cond2), Cond3)
= ИЛИ (И (Cond1, Cond2), AND (Cond3, Cond4))
Например, если вы хотите узнать, какие партии бананов и апельсинов распроданы, т.е.е. Номер «В наличии» (столбец B) равен количеству «Продано» (столбец C), следующая формула OR / AND может быстро показать вам это:
= ИЛИ (И (A2 = «бананы», B2 = C2), AND (A2 = «апельсины», B2 = C2))
Функция ИЛИ в условном форматировании Excel
= ИЛИ ($ B2 = "", $ C2 = "")
Правило с приведенной выше формулой ИЛИ выделяет строки, содержащие пустую ячейку либо в столбце B, либо в столбце C, либо в обоих столбцах.
Дополнительные сведения о формулах условного форматирования см. В следующих статьях:
Использование функции XOR в Excel
В Excel 2013 Microsoft представила функцию XOR, которая представляет собой логическую функцию Exclusive OR .Этот термин определенно знаком тем из вас, кто имеет некоторое представление о любом языке программирования или информатике в целом. Тем, кто этого не делает, поначалу может быть сложно понять концепцию «Исключительное ИЛИ», но, надеюсь, поможет приведенное ниже объяснение, проиллюстрированное примерами формул.
Синтаксис функции XOR идентичен OR:
XOR (логический1, [логический2],…)
Требуется первый логический оператор (логическая 1), дополнительные логические значения необязательны.Вы можете проверить до 254 условий в одной формуле, и это могут быть логические значения, массивы или ссылки, которые оцениваются как ИСТИНА или ЛОЖЬ.
В простейшем варианте формула XOR содержит всего 2 логических оператора и возвращает:
- ИСТИНА, если любой из аргументов принимает значение ИСТИНА.

- ЛОЖЬ, если оба аргумента ИСТИНА или ни один из них не ИСТИНА.
Это может быть легче понять из примеров формул:
| Формула | Результат | Описание |
= XOR (1> 0, 2 <1) | ИСТИНА | Возвращает ИСТИНА, потому что 1-й аргумент - ИСТИНА, а 2 аргумент -й - ЛОЖЬ. |
= XOR (1 <0, 2 <1) | ЛОЖЬ | Возвращает ЛОЖЬ, потому что оба аргумента ЛОЖЬ. |
= XOR (1> 0, 2> 1) | ЛОЖЬ | Возвращает ЛОЖЬ, потому что оба аргумента ИСТИНА. |
При добавлении дополнительных логических операторов функция XOR в Excel приводит к:
- ИСТИНА, если нечетное количество аргументов оценивается как ИСТИНА;
- ЛОЖЬ, если общее количество ИСТИННЫХ операторов четное, или если все операторы ЛОЖЬ.
На скриншоте ниже показана точка:
Если вы не знаете, как применить функцию Excel XOR к реальному сценарию, рассмотрите следующий пример. Предположим, у вас есть таблица участников и их результатов за первые 2 игры. Вы хотите узнать, кто из плательщиков будет играть в игру 3 rd при следующих условиях:
Предположим, у вас есть таблица участников и их результатов за первые 2 игры. Вы хотите узнать, кто из плательщиков будет играть в игру 3 rd при следующих условиях:
- Участники, выигравшие игру 1 и игру 2, автоматически переходят в следующий раунд и не должны играть в игру 3.
- Участники, проигравшие обе первые игры, выбывают из игры и также не участвуют в третьей игре.
- Участники, победившие в Игре 1 или Игре 2, должны сыграть в Игру 3, чтобы определить, кто выйдет в следующий раунд, а кто нет.
Простая формула XOR работает именно так, как мы хотим:
= XOR (B2 = "выиграл", C2 = "выиграл")
И если вы вложите эту функцию XOR в логический тест формулы IF, вы получите еще более разумные результаты:
= ЕСЛИ (XOR (B2 = «Выигран», C2 = «Выигран»), «Да», «Нет»)
Использование функции НЕ в Excel
Функция НЕ является одной из простейших функций Excel с точки зрения синтаксиса:
НЕ (логический)
Вы используете функцию НЕ в Excel, чтобы изменить значение аргумента. Другими словами, если логический результат равен ЛОЖЬ, функция НЕ возвращает ИСТИНА, и наоборот. Например, обе приведенные ниже формулы возвращают ЛОЖЬ:
Другими словами, если логический результат равен ЛОЖЬ, функция НЕ возвращает ИСТИНА, и наоборот. Например, обе приведенные ниже формулы возвращают ЛОЖЬ:
.
= НЕ (ИСТИНА)
= НЕ (2 * 2 = 4)
Зачем нужно получать такие нелепые результаты? В некоторых случаях вам может быть интереснее узнать, когда определенное условие не выполняется, чем когда оно выполняется. Например, при просмотре списка одежды вы можете исключить какой-то цвет, который вам не подходит.Я не особо люблю черный цвет, поэтому использую эту формулу:
= НЕ (C2 = «черный»)
Как обычно, в Microsoft Excel есть несколько способов сделать что-либо, и вы можете добиться того же результата, используя оператор Not equal to: = C2 <> «черный».
Если вы хотите проверить несколько условий в одной формуле, вы можете использовать НЕ вместе с функцией И или ИЛИ. Например, если вы хотите исключить черный и белый цвета, формула будет выглядеть так:
= НЕ (ИЛИ (C2 = «черный», C2 = «белый»))
И если вы предпочитаете не черное пальто, а можете рассмотреть черный жакет или заднюю шубу, вам следует использовать НЕ в сочетании с функцией Excel И:
= НЕ (И (C2 = "черный", B2 = "пальто"))
Еще одно распространенное использование функции НЕ в Excel - изменение поведения какой-либо другой функции. Например, вы можете комбинировать функции NOT и ISBLANK, чтобы создать формулу ISNOTBLANK, которой нет в Microsoft Excel.
Например, вы можете комбинировать функции NOT и ISBLANK, чтобы создать формулу ISNOTBLANK, которой нет в Microsoft Excel.
Как известно, формула = ISBLANK (A2) возвращает ИСТИНА, если ячейка A2 пуста. Функция НЕ может изменить этот результат на FALSE: = NOT (ISBLANK (A2))
Затем вы можете сделать еще один шаг и создать вложенный оператор IF с функциями NOT / ISBLANK для реальной задачи:
= ЕСЛИ (NOT (ISBLANK (C2)), C2 * 0,15, «Без бонуса :(»)
В переводе на простой английский формула предписывает Excel выполнять следующие действия.Если ячейка C2 не пуста, умножьте число в C2 на 0,15, что даст 15% бонуса каждому продавцу, сделавшему дополнительные продажи. Если C2 пусто, появляется текст «Без бонуса :(».
По сути, так вы используете логические функции в Excel. Конечно, эти примеры лишь поверхностно затронули возможности AND, OR, XOR и NOT. Зная основы, теперь вы можете расширить свои знания, решая свои реальные задачи и составляя умные сложные формулы для своих рабочих листов.
Вас также может заинтересовать
Что такое логический вентиль (И, ИЛИ, XOR, NOT, NAND, NOR и XNOR)? Определение от WhatIs.com
Логический вентиль - это устройство, которое действует как строительный блок для цифровых схем. Они выполняют основные логические функции, которые являются фундаментальными для цифровых схем. В большинстве электронных устройств, которые мы используем сегодня, есть логические вентили. Например, логические вентили могут использоваться в таких технологиях, как смартфоны, планшеты или в устройствах памяти.
В схеме логические вентили будут принимать решения на основе комбинации цифровых сигналов, поступающих с их входов. Большинство логических вентилей имеют два входа и один выход.Логические вентили основаны на булевой алгебре. В любой момент каждый терминал находится в одном из двух двоичных состояний: ложно или истинно . Ложь представляет 0, а истина представляет 1. В зависимости от типа используемого логического элемента и комбинации входов двоичный выход будет отличаться. Логический вентиль можно представить себе как выключатель света, в котором в одном положении выход выключен - 0, а в другом - включен - 1. Логические вентили обычно используются в интегральных схемах (IC).
Логический вентиль можно представить себе как выключатель света, в котором в одном положении выход выключен - 0, а в другом - включен - 1. Логические вентили обычно используются в интегральных схемах (IC).
Базовые логические вентили
Существует семь основных логических вентилей: И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ, НЕ, ИЛИ, ИЛИ ИЛИ ИСКЛЮЧАЮЩЕЕ ИЛИ.
И | ИЛИ | XOR | НЕ | NAND | NOR | XNOR
Логический элемент И назван так потому, что, если 0 называется «ложным», а 1 называется «истинным», элемент действует так же, как логический оператор «И». На следующем рисунке и в таблице показаны символы схемы и логические комбинации для логического элемента И. (В символе входные клеммы находятся слева, а выходная клемма - справа.) Выходной сигнал «истина», когда оба входа «истина». В противном случае вывод будет «ложным». Другими словами, выход равен 1 только тогда, когда оба входа один И два равны 1.
И ворота
| Ввод 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Логический элемент ИЛИ получил свое название от того факта, что он ведет себя по образцу логического включающего "или". «Выход -« истина », если один или оба входа« истина ». Если оба входа« ложь », то выход« ложь ». Другими словами, для выхода должно быть 1, по крайней мере, вход 1 ИЛИ два должны быть 1.
«Выход -« истина », если один или оба входа« истина ». Если оба входа« ложь », то выход« ложь ». Другими словами, для выхода должно быть 1, по крайней мере, вход 1 ИЛИ два должны быть 1.
OR выход
| Ввод 1 | Ввод 2 | Выход |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
Логический элемент XOR ( исключающее ИЛИ ) вентиль действует так же, как логическое «или / или». «Выходной сигнал« истина », если один из входов, но не оба,« истина ». Выходной сигнал« ложь », если оба входа« ложь »или если оба входа« истина ». Другой способ взглянуть на это Схема должна следить за тем, чтобы на выходе было 1, если входы разные, и 0, если входы одинаковые.
«Выходной сигнал« истина », если один из входов, но не оба,« истина ». Выходной сигнал« ложь », если оба входа« ложь »или если оба входа« истина ». Другой способ взглянуть на это Схема должна следить за тем, чтобы на выходе было 1, если входы разные, и 0, если входы одинаковые.
вентиль XOR
| Ввод 1 | Ввод 2 | Выход |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Логический инвертор , иногда называемый логическим элементом НЕ , чтобы отличать его от других типов электронных инверторных устройств, имеет только один вход. Он меняет логическое состояние на обратное. Если на входе 1, то на выходе 0. Если на входе 0, то на выходе 1.
Он меняет логическое состояние на обратное. Если на входе 1, то на выходе 0. Если на входе 0, то на выходе 1.
Инвертор или НЕ вентиль
Логический элемент И-НЕ работает как логический элемент И, за которым следует вентиль НЕ. Он действует как логическая операция «и» с последующим отрицанием. На выходе будет «ложь», если оба входа «истина». В противном случае на выходе будет «истина».
Логический элемент NAND
| Ввод 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Логический элемент ИЛИ-НЕ представляет собой комбинацию логического элемента ИЛИ, за которым следует инвертор. Его выход будет «истина», если оба входа «ложь». В противном случае вывод будет «ложным».
Его выход будет «истина», если оба входа «ложь». В противном случае вывод будет «ложным».
NOR ворота
| Ввод 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |
Логический элемент XNOR (исключающее ИЛИ) - это комбинированный вентиль XOR, за которым следует инвертор. Его вывод «истина», если входы одинаковые, и «ложь», если входы разные.
Его вывод «истина», если входы одинаковые, и «ложь», если входы разные.
Вентиль XNOR
| Ввод 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Сложные операции могут выполняться с использованием комбинаций этих логических вентилей. Теоретически нет ограничений на количество ворот, которые могут быть объединены в одно устройство. Но на практике существует ограничение на количество ворот, которые могут быть упакованы в данное физическое пространство. Массивы логических вентилей находятся в цифровых ИС. По мере развития технологии ИС требуемый физический объем для каждого отдельного логического элемента уменьшается, и цифровые устройства того же или меньшего размера становятся способными выполнять все более сложные операции с постоянно увеличивающейся скоростью.
Теоретически нет ограничений на количество ворот, которые могут быть объединены в одно устройство. Но на практике существует ограничение на количество ворот, которые могут быть упакованы в данное физическое пространство. Массивы логических вентилей находятся в цифровых ИС. По мере развития технологии ИС требуемый физический объем для каждого отдельного логического элемента уменьшается, и цифровые устройства того же или меньшего размера становятся способными выполнять все более сложные операции с постоянно увеличивающейся скоростью.
Состав логических вентилей
Высокий или низкий двоичные состояния представлены разными уровнями напряжения.Логическое состояние терминала может и обычно часто изменяется по мере того, как схема обрабатывает данные. В большинстве логических вентилей низкое состояние составляет приблизительно ноль вольт (0 В), а высокое состояние - приблизительно пять вольт положительного напряжения (+5 В).
Логические вентили могут быть выполнены из резисторов и транзисторов или диодов. Резистор обычно можно использовать в качестве подтягивающего или понижающего резистора. Подтягивающие и понижающие резисторы используются, когда есть какие-либо неиспользуемые входы логического элемента для подключения к логическому уровню 1 или 0.Это предотвращает ложное переключение ворот. Подтягивающие резисторы подключены к Vcc (+ 5 В), а подтягивающие резисторы - к земле (0 В).
Резистор обычно можно использовать в качестве подтягивающего или понижающего резистора. Подтягивающие и понижающие резисторы используются, когда есть какие-либо неиспользуемые входы логического элемента для подключения к логическому уровню 1 или 0.Это предотвращает ложное переключение ворот. Подтягивающие резисторы подключены к Vcc (+ 5 В), а подтягивающие резисторы - к земле (0 В).
Обычно используются логические вентили TTL и CMOS. ИС TTL или транзисторно-транзисторной логики будут использовать биполярные переходные транзисторы типа NPN и PNP. КМОП, или дополнительные металл-оксидно-кремниевые ИС, построены из полевых транзисторов типа MOSFET или JFET. ИС TTL обычно обозначаются как микросхемы серии 7400, в то время как ИС КМОП часто могут быть обозначены как микросхемы серии 4000.
таблиц истинности пяти общих логических связок или операторов
В этом уроке мы построим пять (5) общих логических связок или операторов. Они считаются обычными логическими связками, потому что они очень популярны, полезны и всегда преподаются вместе.
Прежде чем мы начнем, я предлагаю вам просмотреть другой мой урок, ссылка на который приведена ниже.
Этот вводный урок о таблицах истинности содержит предварительные знания или информацию, которые помогут вам лучше понять содержание этого урока.
Введение в таблицы истины, утверждения и связки
Ле начинает с перечисления пяти (5) общих логических связок.
Пять (5) общих логических связок или операторов
- Логическое отрицание
- Логическое соединение (И)
- Логическое дизъюнкция (включающее ИЛИ)
- Логическое следствие (условное)
- Логическое биконусное (двойное следствие)
I. Таблица истинности логического отрицания
.
Отрицание утверждения также является утверждением, значение истинности которого прямо противоположно исходному утверждению.Например, отрицание утверждения символически записывается как
~ \ large {P} или \ large {\ neg P}.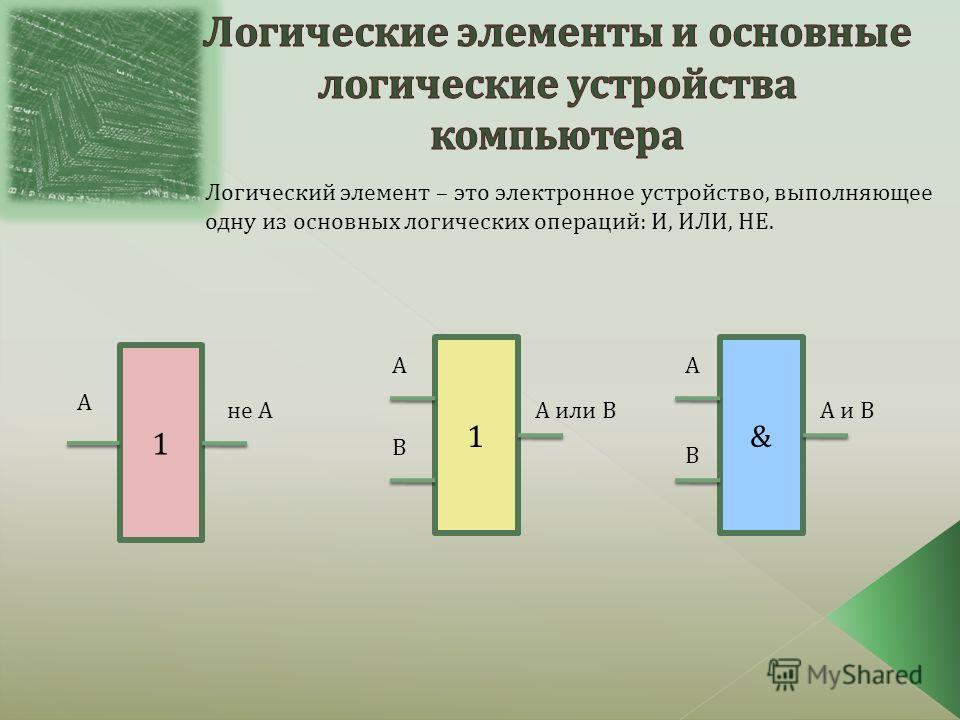
~ {P} или {\ neg P} читается как «не P.»
Помните: Оператор отрицания, обозначенный символом ~ или \ neg, принимает значение истинности исходного утверждения, а затем выводит значение, прямо противоположное его значению истинности. Другими словами, отрицание просто меняет значение истинности данного утверждения. Таким образом, если утверждение P истинно, то значение истинности его отрицания ложно.Таким же образом, если P ложно, истинное значение его отрицания истинно.
II. Таблица истинности логического соединения
Соединение - это тип составного оператора, который состоит из двух предложений (также известных как простые утверждения), соединенных оператором AND.
Символ, который используется для обозначения логического оператора AND или оператора конъюнкции, - \ color {red} \ Large {\ wedge}. Похоже на перевернутую букву V.
Если у нас есть два простых оператора P и Q, и мы хотим сформировать составной оператор, соединенный оператором AND, мы можем записать его как:
\ large {P \ wedge Q}.
{P \ wedge Q} читается как «P и Q».
Помните: Значение истинности составного утверждения P \ wedge Q истинно только в том случае, если значения истинности P и Q оба истинны. В противном случае P \ wedge Q ложно.
Обратите внимание в таблице истинности ниже, что, когда P истинно, а Q истинно, P \ wedge Q истинно. Однако остальные три комбинации предложений P и Q ложны.
III. Таблица истинности логической дизъюнкции
Дизъюнкция - это разновидность составного оператора, который состоит из двух простых операторов, образованных путем соединения операторов с помощью оператора OR.
В операторе дизъюнкции используется логическое ИЛИ. Это означает «одно или другое» или и то, и другое.
Символ, который используется для обозначения оператора ИЛИ или логической дизъюнкции, - \ color {red} \ Large {\ vee}. Он напоминает букву V алфавита.
Два предложения P и Q, соединенные оператором OR, чтобы сформировать составное утверждение, записываются как:
\ large {P \ vee Q}.
{P \ vee Q} читается как «P или Q».
Помните: Значение истинности составного утверждения P \ vee Q истинно, если значение истинности любого из двух простых утверждений P и Q истинно.Моресо, P \ vee Q также истинно, когда истинные значения обоих утверждений P и Q истинны. Однако единственный раз, когда оператор дизъюнкции P \ vee Q ложен, происходит, когда значения истинности P и Q ложны.
IV. Таблица истинности логического следствия
Импликация (также известная как условный оператор ) - это тип составного оператора, который формируется путем соединения двух простых операторов с помощью связки или оператора логической импликации.
Символ, который используется для представления оператора логического следования, - это стрелка, указывающая вправо, то есть стрелка вправо.
Когда два простых оператора P и Q соединяются оператором импликации, мы имеем:
\ Large {P \ to Q}.
- где P известна как гипотеза
- где Q известна как вывод
Есть много способов читать условное {P \ to Q}.Ниже приведены некоторые из немногих распространенных.
{P \ to Q} читается как «P подразумевает Q».
{P \ to Q} читается как «Если P, то Q».
{P \ to Q} читается как «P, только если Q».
{P \ to Q} читается как «Если P достаточно для Q».
{P \ to Q} читается как «Q необходимо для P».
{P \ to Q} читается как «Q следует из P».
{P \ to Q} читается как «Q, если P».
Помните: Значение истинности составного утверждения P \ to Q истинно, когда истинны оба простых утверждения P и Q.Более того, P \ to Q всегда верно, если P ложно. Единственный сценарий, в котором P \ to Q ложно, случается, когда P истинно, а Q ложно.
V. Таблица истинности логической биконусной или двойной импликации
Двойная импликация (также известная как двухусловный оператор ) - это тип составного оператора, который формируется путем соединения двух простых операторов с двухусловным оператором. Двуусловный оператор на самом деле представляет собой комбинацию условного оператора и его обратного.
Двуусловный оператор на самом деле представляет собой комбинацию условного оператора и его обратного.
Двузначный оператор обозначается двунаправленной стрелкой.
Когда вы соединяете два простых утверждения (также известных как молекулярные утверждения) с бикондиционным оператором, мы получаем:
\ Large {P \ leftrightarrow Q}
{P \ leftrightarrow Q} читается как «P тогда и только тогда, когда Q».
- где P известен как антецедент
- где Q известен как консеквент
Помните: Значение истинности биконусного утверждения P \ leftrightarrow Q истинно, когда оба простых утверждения P и Q истинны или оба ложны.В противном случае P \ leftrightarrow Q ложно.
Возможно, вас заинтересует:
Введение в таблицы истинности, утверждения и логические связки
Обратное, обратное и противоположное условному утверждению
Что такое логическая операция?
Обновлено: 16. 11.2019, компания Computer Hope
11.2019, компания Computer Hope
Логическая операция - это специальный символ или слово, которое соединяет две или более информационных фраз.Чаще всего он используется для проверки того, является ли определенная связь между фразами истинной или ложной.
В вычислениях логические операции необходимы, потому что они моделируют способ, которым информация течет через электрические цепи, например, внутри ЦП. Эти типы операций называются логическими операциями.
Элементы в схеме, которые ведут себя в соответствии с булевой логикой, называются логическими вентилями.
Фундаментальные логические операции
Следующие семь логических операций принимают входные данные, которые являются истинными (1) или ложными (0), и создают единственное выходное значение, которое также является истинным или ложным.
Большинство этих операций может принимать более двух входов, за исключением операции НЕ, которая принимает только один вход. Ниже приведены примеры использования только одного или двух входов, что обычно происходит внутри компьютера.
Операции перечислены ниже. Щелкните ссылку операции, чтобы узнать больше.
И
Логическая операция И возвращает истину, только если любой из ее входов верен. Если любой из входов ложен, выход также ложен.
В компьютерном программировании операция И обычно записывается как && (два амперсанда).
В булевой алгебре операция И для двух входов A и B может быть записана как AB .
Ниже приведена таблица истинности для операции И и принципиальная схема логического элемента И.
| И | ||
|---|---|---|
| А | В | AB |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
ИЛИ
Логическая операция ИЛИ возвращает истину, если любой из ее входов верен.Если все входы ложны, выход также ложен.
В компьютерном программировании операция ИЛИ обычно записывается как || (две вертикальные полосы).
В булевой алгебре значение ИЛИ двух входов A и B можно записать как A + B .
Примечание
Не путайте операцию ИЛИ с арифметическим сложением, даже если они оба используют символ « + ». Это разные операции.
Ниже приведена таблица истинности для операции ИЛИ и принципиальная схема логического элемента ИЛИ.
| ИЛИ | ||
|---|---|---|
| А | В | А + В |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
НЕ
Логическая операция НЕ возвращает истину, если ее вход ложен, и ложь, если ее вход истинен.
В компьютерном программировании операция НЕ обычно записывается как ! (восклицательный знак).
В булевой алгебре значение НЕ входа A может быть записано как A̅ (A с дополнительным знаком).
Ниже приведена таблица истинности для операции НЕ и принципиальная схема логического элемента НЕ.
NAND
Логическая операция И-НЕ (обозначающая «НЕ И») возвращает истину, если ее входы ложны, и ложь, если любой из ее входов истинен.
Подсказка
NAND Flash - это тип флэш-памяти, основанный на логических элементах NAND.
В булевой алгебре значение И-НЕ двух входов A и B может быть записано как (AB с лишним знаком).
NAND отличается тем, что является одним из двух «универсальных» логических вентилей, потому что любая другая логическая операция может быть создана с использованием только вентилей NAND. (Другой универсальный логический элемент - ИЛИ.)
Ниже приведена таблица истинности для операции И-НЕ и принципиальная схема логического элемента И-НЕ.
| NAND | ||
|---|---|---|
| А | В | ___ АВ |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
НОР
Логическая операция ИЛИ-ИЛИ (обозначающая «НЕ ИЛИ») возвращает истину, если ее входы ложны, и ложь, если любой из ее входов истинен.
Подсказка
NOR Flash - это тип флэш-памяти, основанный на логических вентилях NOR.
В булевой алгебре значение NOR двух входов A и B может быть записано как (A + B с лишним знаком).
NOR отличается тем, что является одним из двух «универсальных» логических вентилей, потому что любая другая логическая операция может быть создана с использованием только вентилей NOR. (Другой универсальный логический элемент - NAND.)
Ниже представлена таблица истинности для операции ИЛИ-НЕ и принципиальная схема логического элемента ИЛИ-НЕ.
| НОР | ||
|---|---|---|
| А | В | _____ А + Б |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
XOR
Логическая операция XOR (что означает «Исключающее ИЛИ») возвращает истину, если один из ее входов различается, и ложь, если все они одинаковы. Другими словами, если его входные данные представляют собой комбинацию истинного и ложного, вывод XOR будет истинным. Если все его входы истинны или все ложны, результат XOR ложен.
Другими словами, если его входные данные представляют собой комбинацию истинного и ложного, вывод XOR будет истинным. Если все его входы истинны или все ложны, результат XOR ложен.
В булевой алгебре значение XOR двух входов A и B может быть записано как A⊕B (символ XOR, ⊕, похож на знак плюса внутри круга).
Ниже приведена таблица истинности для операции XOR и ее принципиальная схема.
| XOR | ||
|---|---|---|
| А | В | A⊕B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
XNOR
Логическая операция XNOR (что означает «Исключающее НЕ ИЛИ») возвращает истину, если один из ее входов одинаков, и ложь, если любой из них отличается.Другими словами, если его входные данные представляют собой комбинацию истинного и ложного, на выходе XNOR будет ложно. Если все его входы истинны или все ложны, выход XNOR истинен.
Если все его входы истинны или все ложны, выход XNOR истинен.
В булевой алгебре значение XNOR двух входов A и B может быть записано как (символ XOR, ⊕, похож на знак плюса внутри круга с линией поверх всего).
Ниже приведена таблица истинности для операции XNOR и ее принципиальная схема.
| XNOR | ||
|---|---|---|
| А | В | _____ A⊕B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Аккумулятор, логическое значение, идемпотентность, оператор, условия программирования
.


 Если хотя бы одно из простых высказываний, связанных операцией И, будет ложным, то и составное высказывание будет ложным. Для записи логической операции И используют следующие обозначения: A И B, A AND B, A · B, A * B, A∧ B, A & B.
Если хотя бы одно из простых высказываний, связанных операцией И, будет ложным, то и составное высказывание будет ложным. Для записи логической операции И используют следующие обозначения: A И B, A AND B, A · B, A * B, A∧ B, A & B.  Для записи логической операции ИЛИ можно использовать следующие выражения: A ИЛИ B, A OR B, A + B, A∨ B, A | B.
Для записи логической операции ИЛИ можно использовать следующие выражения: A ИЛИ B, A OR B, A + B, A∨ B, A | B. 







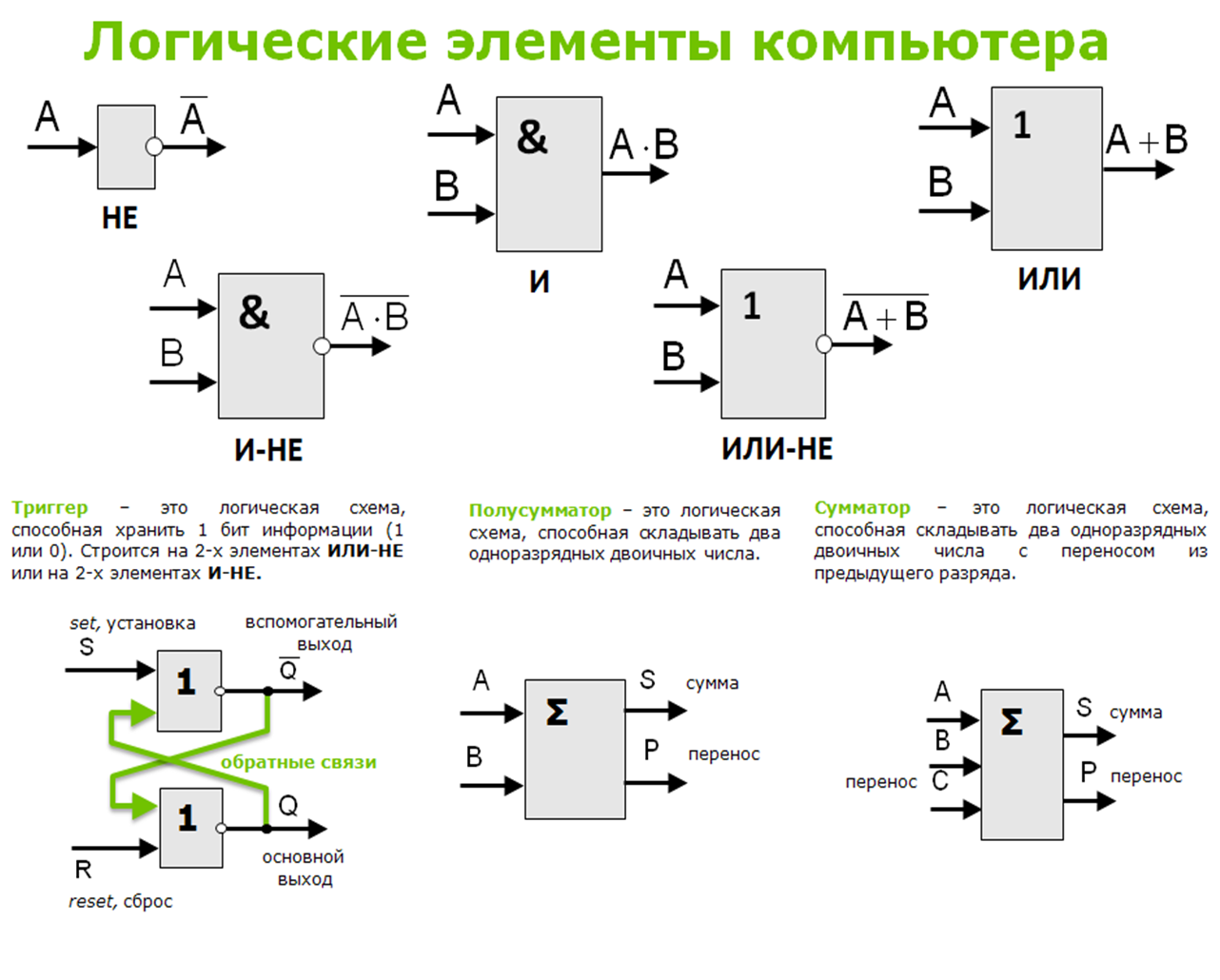
 ..не…», «неверно, что…»
..не…», «неверно, что…» ..или…», «…либо…»
..или…», «…либо…» .., тогда…»
.., тогда…»

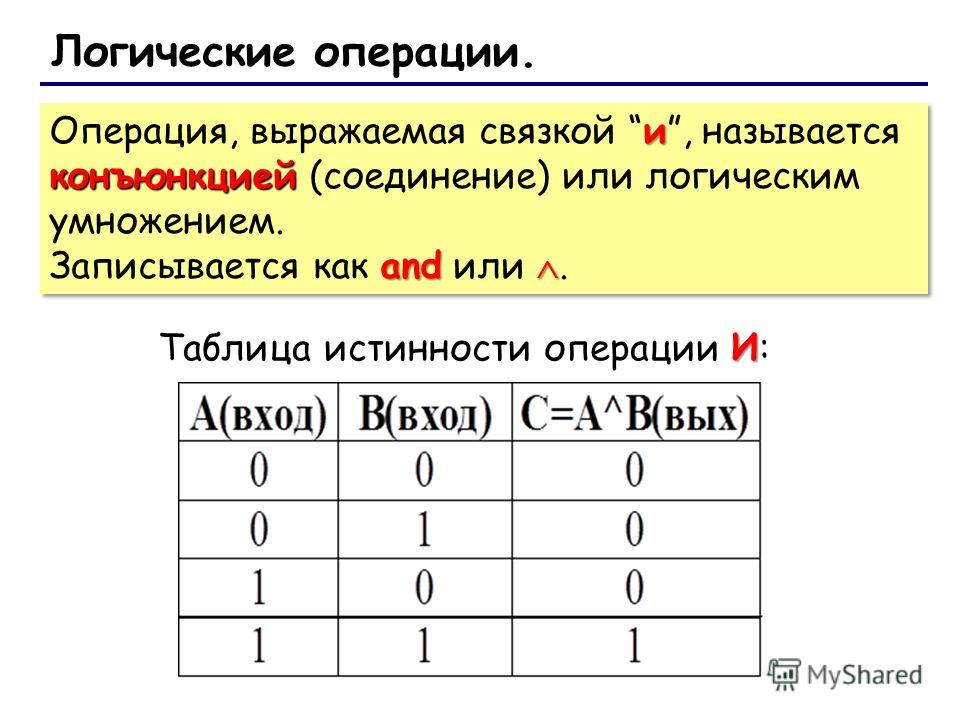 (г) \ (\ urcorner P \ vee \ urcorner Q \).
(г) \ (\ urcorner P \ vee \ urcorner Q \). Не удаляйте сначала этот текст.
Не удаляйте сначала этот текст. Наша стандартная схема для этого типа таблицы истинности показана в Таблице 2.2 .
Наша стандартная схема для этого типа таблицы истинности показана в Таблице 2.2 .
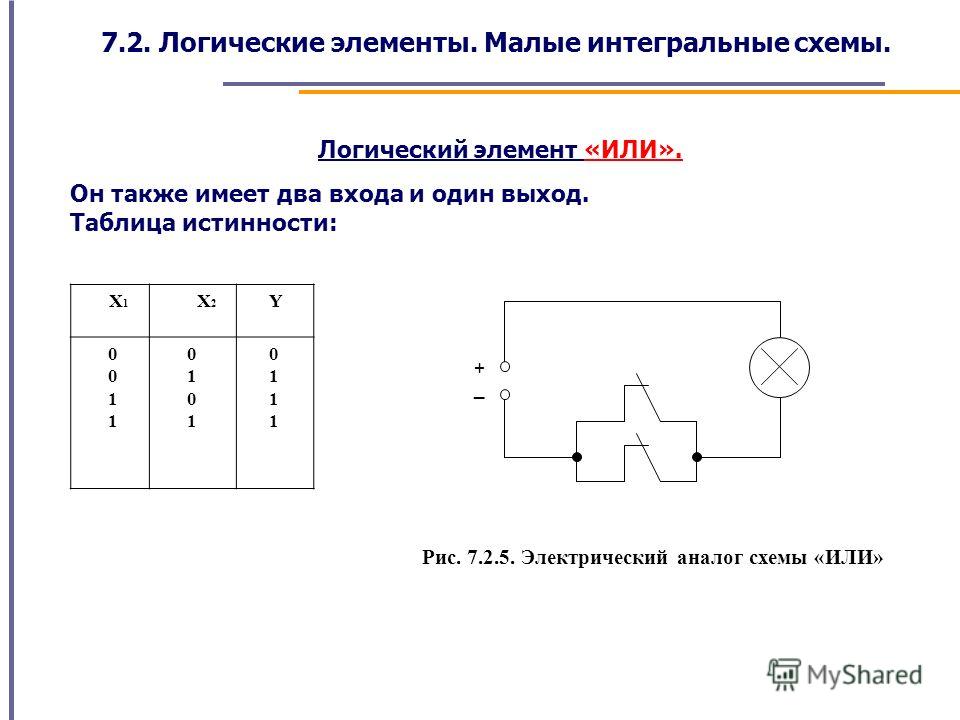
 Что вы наблюдаете.
Что вы наблюдаете.
 Предположим, что \ (P \) и \ (Q \) - истинные утверждения, что \ (U \) и \ (V \) - ложные утверждения, и что \ (W \) - утверждение, и неизвестно, если \ (W \) истинно или ложно.
Предположим, что \ (P \) и \ (Q \) - истинные утверждения, что \ (U \) и \ (V \) - ложные утверждения, и что \ (W \) - утверждение, и неизвестно, если \ (W \) истинно или ложно. Например, если ячейки A1: A5 содержат числа, формула = AND (A1: A5) вернет ИСТИНА, если ни одна из ячеек не содержит 0, в противном случае - ЛОЖЬ.
Например, если ячейки A1: A5 содержат числа, формула = AND (A1: A5) вернет ИСТИНА, если ни одна из ячеек не содержит 0, в противном случае - ЛОЖЬ.