Задание №4 ЕГЭ по математике базового уровня с решением
Преобразование выражений
Описание задания
В задании №4 ЕГЭ по математике базового уровня нам необходимо продемонстрировать умения работы с выражениями. В данных задачах необходимо выразить из заданного выражения нужную переменную и вычислить её, подставив значения.
Тематика заданий: преобразования выражений
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
Разбор типовых вариантов заданий №4 ЕГЭ по математике базового уровня
Вариант 4МБ1
Найдите v0 из равенства v = v0 + at, если v = 20, t = 2, a = 7.
Алгоритм выполнения:
- Подставить данные значения в выражение.
- Решить уравнение относительно неизвестной.
Решение:
Подставим все значения в данное выражение, получим:
20 = v0 + 7 · 2
Преобразуем:
20 = v0 + 14.
Найдем неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
v0 = 20 – 14
v0 = 6
Ответ: v0 = 6
Вариант 4МБ2
Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле . Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,9 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2.
Алгоритм выполнения:
- Подставить все значения в данную формулу.
- Произвести вычисления.
Решение:
По условию задания дана высота h=0,9 м и ускорение свободного падения g=9,8 м/с2. Подставим эти значения в формулу вычисления скорости v, получим:
Делаем умножение 1,8 на 9,8, имеем:
Примечание: При умножении в столбик десятичных дробей запятая записывается строго под запятой. В полученном результате справа отсчитывают столько знаков, сколько поле запятой в ОБЕИХ дробях ВМЕСТЕ.

и извлекаем из числа 17,64 квадратный корень:
м/с.
Ответ: 4,2 м/с.
Вариант 4МБ3
Энергия заряженного конденсатора W (в Дж) вычисляется по формуле , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью Ф, если заряд на его обкладке равен 0,019 Кл.
Алгоритм выполнения задания:
- Подставить все известные значения в данную формулу.
- Провести вычисления.
Решение:
Подставим в формулу энергии конденсатора значения q=0,019 Кл и C = Ф, получим:
Пояснения:
Если степень стоит за скобкой, а внутри скобки произведение, то степень относится к каждому из множителей. То есть (19 · 10-3)2 = 192 · 10-3·2.
Чтобы найти вторую степень числа нужно умножить число само на себя.
192 = 19 · 19 = 361
Умножить на число в отрицательной степени, значит разделить на это число, но только в положительной степени.
361 · 10-3 = 361/1000 = 0,361
Ответ: 0,361.
Вариант 4МБ4
Энергия заряженного конденсатора W (в Дж) вычисляется по формуле , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью Ф, если заряд на его обкладке равен 0,07 Кл.
Алгоритм выполнения:
- Подставить все известные значения в данную формулу.
- Провести вычисления.
Решение:
Подставим в формулу энергии конденсатора значения q=0,07 Кл и C = Ф, получим:
.
Пояснения:
Если степень стоит за скобкой, а внутри скобки произведение, то степень относится к каждому из множителей. То есть (7 · 10-2)2 = 72 · 10-2·2.
Чтобы найти вторую степень числа нужно умножить число само на себя.
72 = 7 · 7 = 49
Умножить на число в отрицательной степени, значит разделить на это число, но только в положительной степени.
49 · 10-1 = 49/10 = 4,9
Ответ: 4,9.
Вариант 4МБ5 (демо)
Найдите m из равенства F = ma, если F = 84 и a = 12.
Алгоритм выполнения:
- Подставить данные значения в выражение.
- Решить уравнение относительно неизвестной.
Решение:
Подставим все значения в данное выражение, получим:
84 = m ·12
2. Найдем неизвестный множитель. Чтобы найти неизвестный множитель нужно разделить произведение на известный множитель.
m = 84 : 12
m = 7
Ответ: 7 кг.
Вариант 4МБ6 (ЕГЭ 2017)
Найдите m из равенства F = ma , если F = 84 и a =12.
В начале выразим из формулы m, так как это множитель, то он равен произведению, деленному на второй множитель.
m=F/a
Теперь можем подставить числа из условия:
m=84/12=7
Ответ: 7
Вариант 4МБ7
Найдите v0 из равенства v = v0 + at , если v = 20 , t = 2 и a = 7 .
Аналогично выразим v0, перенеся at в левую часть:
v — at = v0
Подставим значения:
20 — 7 • 2 = 6 = v0
Ответ: 6
Вариант 4МБ8
Найдите S из равенства S = v0t + at2/2 , если v0 = 6 , t = 2 , a = −2.
В данном случае нам необходимо просто подставить числа и выполнить вычисления:
S = 6 • 2 + (-2) • 22/2 = 12 -4 = 8
Ответ: 8
Вариант 4МБ9
Перевести температуру из шкалы Фаренгейта в шкалу Цельсия позволяет формула , где tC – температура в градусах по шкале Цельсия, tF – температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Цельсия соответствует 95 градусов по шкале Фаренгейта?
Алгоритм выполнения
- Подставляем данное в условии для tF значение, равное 95, в формулу для tC.

- Выполняем числовые расчеты в формуле в такой последовательности: 1) вычитание в скобках; 2) внесение в числитель дроби 5/9 полученной в скобках разности; 3) сокращение 63 в числителе и 9 в знаменателе на 9; 4) нахождение конечного результата.
Решение:
Вычисляем вычитание в скобках:
95-32=63
Далее умножаем на 5/9, замечаем, что 63 делится на 9 — это 7, что и умножаем на 5, получаем 35!
Ответ: 35
Вариант 4МБ10
Кинетическая энергия (в джоулях) вычисляется по формуле , где m – масса тела (в килограммах), а v – его скорость (в м/с). Пользуясь этой формулой, найдите E (в джоулях), если v=4 м/с и m=10 кг.
Алгоритм выполнения
- Подставляем числовые данные из условия в формулу для Е.
- Производим вычисления. Сначала возводим v в квадрат (получаем 16). Затем сокращаем 16 в числителе и 2 в знаменателе на 2. Далее выполняем умножение.
Решение:
Возводим 4 в квадрат — это 16, умножаем на 10 — 160 и делим на 2 — 80 — вот и ответ!
Ответ:80
Вариант 4МБ11
Ускорение тела (в м/с2) при равномерном движении по окружности можно вычислить по формуле , где ω – угловая скорость вращения (в с–1), а R – радиус окружности (в метрах). Пользуясь этой формулой, найдите а (в м/с2), если R=4 м и ω=7 с–1.
Пользуясь этой формулой, найдите а (в м/с2), если R=4 м и ω=7 с–1.
Алгоритм выполнения
- Подставляем в формулу числовые значения для R и ω.
- Делаем вычисления в полученном числовом выражении: 1) возводим в квадрат 7; 2) выполняем умножение.
Решение:
Если R=4 и ω=7, то а = 72 · 4 = 49 · 4 = 196 (м/с2)
Ответ:196
Вариант 4МБ12
Мощность постоянного тока (в ваттах) вычисляется по формуле , где U – напряжение (в вольтах), R – сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R= 6 Ом и U=12 В.
Алгоритм выполнения
- Поскольку все числовые данные приведены в условии в соответствии с СИ, то просто подставляем эти числа в формулу для мощности.
- Вычисляем значение для Р: 1) в числителе 122 представляем как 12·12; 2) выполняем сокращение на 6; 3) находим произведение.
Решение:
Возводим 12 в квадрат — это 144, затем делим на 6 — это 24. Либо замечаем, что 12 можно сократить на 6 — это 2, тогда умножаем оставшуюся от квадрата 12 на 2 — снова получаем 24.
Либо замечаем, что 12 можно сократить на 6 — это 2, тогда умножаем оставшуюся от квадрата 12 на 2 — снова получаем 24.
Ответ:24
Вариант 4МБ13
Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s=nl, где n – число шагов, l – длина шага. Какое расстояние прошел человек, если l=50 см, n=1600? Ответ дайте в метрах.
Алгоритм выполнения
- Т.к. ответ требуется дать в метрах, то l тоже необходимо перевести в метры.
- Числовые данные подставляем в формулу для s.
- Производим умножение.
Решение:
l=50 см=0,5 м
Если l=0,5 n=1600, то s=0,5·1600=800 (м)
Ответ:800
Вариант 4МБ14
Закон Гука можно записать в виде F=kx, где F – сила (в ньютонах), с которой растягивают пружину, х – абсолютное удлинение пружины (в метрах), а k – коэффициент упругости. Пользуясь этой формулой, найдите х (в метрах), если F=51 Н и k=3 Н/м.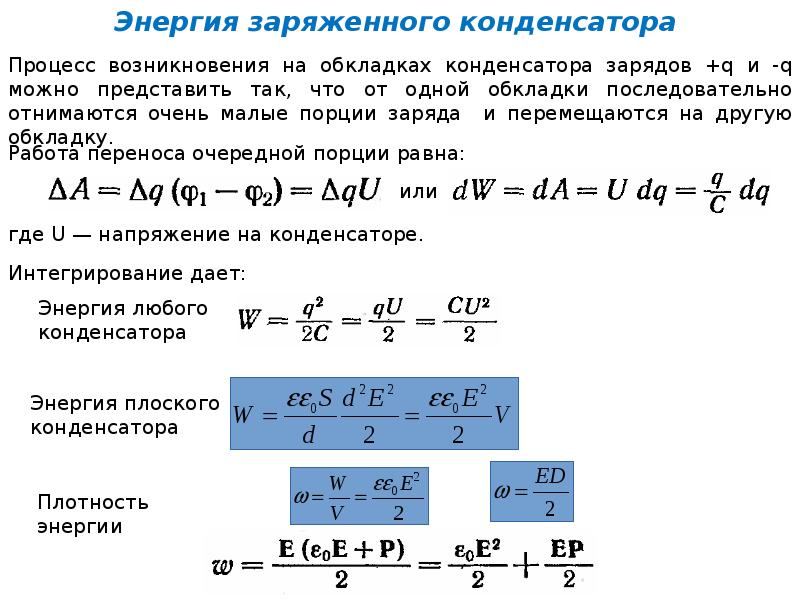
Алгоритм выполнения
- Из приведенной в условии формулы выражаем искомое удлинение х.
- В полученную формулу подставляем данные в условии числовые величины.
- Делаем вычисление.
Решение:
Искомое удлинение x находим как частное — F/k, так как x множитель.
Подставляя значения, получаем:
51/3=17
Ответ:17
Вариант 4МБ15
Работа постоянного тока (в джоулях) вычисляется по формуле, где I – сила тока (в амперах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t=5 с, I=2 А и R=13 Ом.
Алгоритм выполнения
- Подставляем в формулу приведенные в условии соответствующие числовые данные.
- Производим вычисления. Делаем это оптимальным способом: сначала находим I2, потом умножаем полученное число на значение для t, и уже затем множим это произведение на значение для R.
Решение:
Если I=2 А, R=13 Ом, t=5 с, то А=22·13·5=4·13·5=(4·5)·13=20·13=260 (Дж)
Ответ:260
Вариант 4МБ16
Сумма углов выпуклого многоугольника вычисляется по формуле , где n – количество его углов. Пользуясь этой формулой, найдите n, если ∑=15π.
Пользуясь этой формулой, найдите n, если ∑=15π.
Алгоритм выполнения
- Преобразовываем формулу и выражаем из нее искомое n.
- Подставляем в полученное уравнение формулу ∑=15π.
- Выполняем сокращение на π. Находим конечный результат.
Решение:
Из ∑=(n–2)π имеем: n–2=∑/π → n=∑/π+2.
Если ∑=15π, то получаем:
15π/π +2 = 17
Ответ:17
Вариант 4МБ17
Среднее геометрическое трех чисел a, b и c вычисляется по формуле . Вычислите среднее геометрическое чисел 2, 4, 27.
Алгоритм выполнения
- Подставляем в формулу числовые данные из условия.
- В подкоренном выражении представляем 4 как 22, а 27 как 33.
- Произведение 2·22 представляем как 23. Получаем две степени с показателем 3.
- Выносим степени из-под куб.корня. Получаем произведение оснований этих степеней. Вычисляем произведение.

Решение:
2 при умножении на 4 дает 2 в кубе, а 27 — это три в кубе. По свойству корней избавляемся от кубического корня и степеней для 2 и 3 поочередно (просто сокращая корень на степень), а затем выполняем умножение 2 на 3 — получаем 6.
Ответ:6
Вариант 4МБ18
Площадь треугольника вычисляется по формуле , где b и c – две стороны треугольника, а α – угол между ними. Пользуясь этой формулой, найдите площадь S, если b=18, c=16 и sinα=1/3.
Алгоритм выполнения
- Подставляем в формулу приведенные в условии числовые данные.
- Заводим 18 и 16 в числитель, получаем дробь с числителем и знаменателем в виде произведений, соответственно, чисел 18, 16 и 2,3.
- Сокращаем 18 и 3 на 3, а 16 и 2 на 2. Получаем в знаменателе 1, а в числителе произведение 6 и 8. Находим это произведение.
Ответ:48
Электроемкость конденсатора — формула и определение
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Электроемкость проводников
Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.
Электроемкость C = q/φ С — электроемкость [Ф] q — электрический заряд [Кл] φ — потенциал [В] |
Особенность этой величины в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости. Самая популярная — формула электроемкости шара.
Электроемкость сферы C = 4πεε0r С — электроемкость [Ф] ε — относительная диэлектрическая проницаемость среды [-] ε0 — электрическая постоянная ε0 = 8,85 × 10-12 Ф/м r — радиус шара [м] |
Конденсаторы
Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.
Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.
Конденсатор состоит из двух или более проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.
Когда заряд накапливается на обкладках, происходит процесс под названием зарядка конденсатора. Заряды на соседних обкладках равны по величине и противоположны по знаку.
Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:
Электроемкость конденсатора C = q/U С — электроемкость [Ф] q — электрический заряд [Кл] U — напряжение (разность потенциалов) [В] |
По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.
Так происходит разрядка конденсатора.
Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо сквозь диэлектрик. Такой конденсатор больше работать не будет.
Виды конденсаторов
Энергия конденсатора
У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.
Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.
Энергия электростатического поля Wp = qEd Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] E — напряженность электрического поля [В/м] d — расстояние от заряда [м] |
В случае с конденсатором d будет представлять собой расстояние между пластинами.
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.
Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.
В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.
Тогда энергия конденсатора равна:
Wp = qEd/2
Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:
U = Ed
Поэтому:
Wp = qU/2
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.
Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:
Энергия конденсатора Wp = qU/2 Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] U — напряжение на конденсаторе [В] |
Энергия конденсатора Wp = q2/2C Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] C — электроемкость конденсатора [Ф] |
Энергия конденсатора Wp = CU2/2 Wp — энергия электростатического поля [Дж] C — электроемкость конденсатора [Ф] U — напряжение на конденсаторе [В] |
Эти формулы справедливы для любого конденсатора.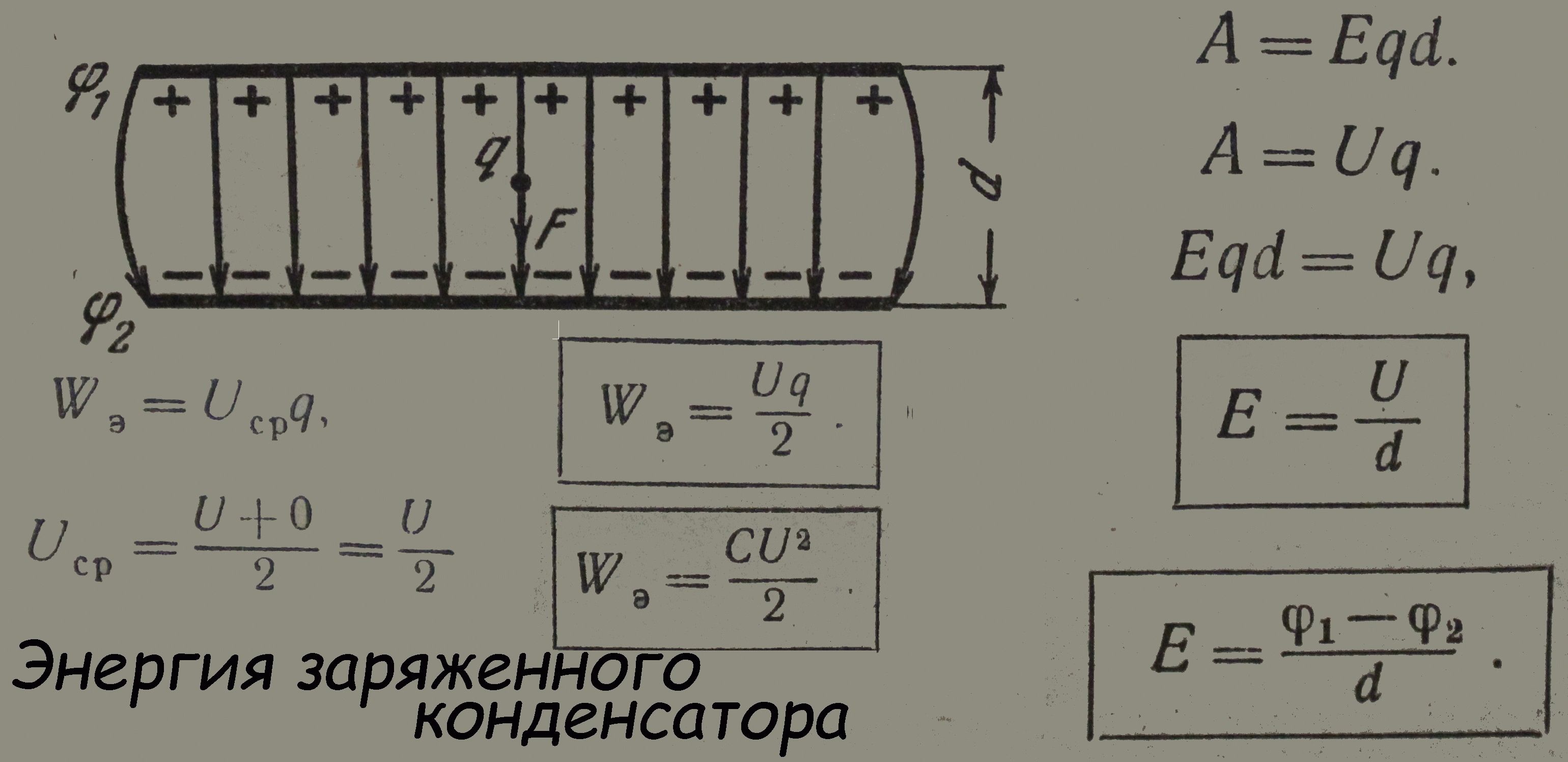
Применение конденсаторов
Конденсатор есть в каждом современном устройстве. Разберем два самых наглядных примера.
Пример раз — вспышка
Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.
Пример два — тачскрин
Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.
Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.
Но если поднести палец к металлической пластине, получится плохой конденсатор.
В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.
Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.
Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.
Изучать физику на примерах из реальной жизни может быть очень даже интересно. Попробуйте и убедитесь сами на классическом курсе по физике для 10 класса.
Попробуйте и убедитесь сами на классическом курсе по физике для 10 класса.
Определение начальной энергии частицы, заряда на пластинах конденсатора, его энергии и расстояние между пластинами конденсатора
Задание.
Ион 48BF2+
влетает в плоский конденсатор с начальной скоростью 500
км/с, под углом 10°
к положительно заряженной пластине на расстоянии 12 мм от отрицательно
заряженной пластины. Длина пластины (она имеет квадратную форму) 40 см, разность
потенциалов между пластинами 20 кВ, емкость конденсатора 0,1 нВ . Определить
начальную энергию частицы, заряд на пластинах конденсатора, его энергию и
расстояние между пластинами конденсатора. Построить графики аn(t) — зависимость нормального ускорения частицы от времени
полета в конденсаторе, V(x) — зависимость скорости
частицы от ее координаты “x”.
Исходные данные.
Параметры частицы:
Mr =48
q=1,6∙10-19 Кл
v0=500
км/с=5*105 м/с
h0=12
мм=0,012 м
a+=10°
Параметры конденсатора:
d=12мм=0,012м
l=50cм=0,5м
U=20 кВ=2*104
В
С=0,1 нВ=0,1*10-9
В
Основные теоретические положения.
Конденсатор — накопитель электрического
заряда.
Конденсатор представляет собой два близко расположенных
проводника (в данной задаче это тонкие пластины), разделенных слоем
диэлектрика.
Образующие конденсатор проводники называют обкладками
конденсатора.
Емкость — характеристика
конденсатора, количественная мера его способности удерживать электрический
заряд, под которой понимают величину, пропорциональную заряду q
и обратно пропорциональную разности потенциалов между обкладками U:
;
Энергией
заряженного конденсатора W называется полная
энергия системы двух проводников и вычисляется по формуле:
Энергия частицы,
обусловленная ее движением (скоростью), называется кинетической энергией
и вычисляется по формуле:
,
где m — масса частицы; v — скорость движения частицы.
На заряженную частицу со
стороны поля конденсатора действует сила:
,
где q — заряд конденсатора;-напряженность поля конденсатора.
Влетая в плоский
конденсатор, частица движется криволинейно и неравномерно.
Ускорение — харрактеристика
неравномерного движения; определяет быстроту изменения
скорости по модулю и направлению.
Составляющие
ускорения:
·
Тангенциальная — харрактеризует
быстроту изменения скорости по модулю
(направлена
по касательной к траектории) и обозначается аt:
·
нормальная — харрактеризует быстроту изменения
скорости по направлению
(направлена к центру
кривизны траектории) и определяется по формуле:
,
где R —
радиус кривизны траектории.
Полное ускорение при
криволинейном движении — геометрическая сумматангенциальной и
нормальной составляющих
Методика расчета.
1.
Начальная кинетическая энергия частицы.
Начальная кинетическая энергия частицы определяется по
формуле:
,
где v0-начальная скорость частицы,
m — масса иона 48BF2+,
которая вычисляется по формуле
,
Прототипы задания 13 «Расчеты по формулам».
 ОГЭ 2018
ОГЭ 2018
Задание 13 «Расчеты по формулам» ОГЭ 2018 Задание 13 «Расчеты по формулам» ОГЭ 2018
Вариант 1
Центростремительное ускорение при движении по окружности (в м/с 2) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с −1, а центростремительное ускорение равно 505,75 м/с2.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 147 Вт, а сила тока равна 3,5 А.
В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6500+4000n, где n — число колец, установленных в колодце.
 Пользуясь этой формулой, рассчитайте стоимость колодца из 13 колец. Ответ укажите в рублях.
Пользуясь этой формулой, рассчитайте стоимость колодца из 13 колец. Ответ укажите в рублях.
Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tC— температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует −1° по шкале Цельсия?
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 185° по шкале Фаренгейта?
Площадь четырёхугольника можно вычислить по формуле ,
где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 16, sinα =, a S=12,8.
Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 16, sinα =, a S=12,8.
Вариант 2
Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 7,5 с −1, а центростремительное ускорение равно 337,5 м/с2.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 423,5 Вт, а сила тока равна 5,5 А.
В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6500+4000n, где n — число колец, установленных в колодце.
 Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ укажите в рублях.
Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ укажите в рублях.
Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 73° по шкале Цельсия?
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 14° по шкале Фаренгейта?
Площадь четырёхугольника можно вычислить по формуле ,
где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 12, sinα =, a S=22,5.
Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 12, sinα =, a S=22,5.
Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле , где С — ёмкость конденсатора (в Ф), a U —
разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора ёмкостью 10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 13 В. Ответ дайте в джоулях.
Закон Кулона можно записать в виде , где F – сила
взаимодействия зарядов (в ньютонах), q1 и q2 – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Нм2/Кл2), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,004 Кл, r=3000 м, а F=0,016 Н.
Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле , где С — ёмкость конденсатора (в Ф), a U —
разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора ёмкостью 10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 8 В. Ответ дайте в джоулях.
Закон Кулона можно записать в виде , где F – сила
взаимодействия зарядов (в ньютонах), q1 и q2 – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Нм2/Кл2), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,006 Кл, r=300м, а F=5,4 Н.
Вариант 3
Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус окружности.
 Пользуясь этой формулой, найдите радиус R(в метрах), если угловая скорость равна 4 с −1, а центростремительное ускорение равно 96 м/с2.
Пользуясь этой формулой, найдите радиус R(в метрах), если угловая скорость равна 4 с −1, а центростремительное ускорение равно 96 м/с2.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 29,25 Вт, а сила тока равна 1,5 А.
В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6500+4000n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ укажите в рублях.
Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует −8° по шкале Цельсия?
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
 Скольким градусам по шкале Цельсия соответствует 210° по шкале Фаренгейта? Ответ округлите до десятых.
Скольким градусам по шкале Цельсия соответствует 210° по шкале Фаренгейта? Ответ округлите до десятых.
Площадь четырёхугольника можно вычислить по формуле ,
где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 6, sinα =, a S=3,75.
Вариант 4
Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 9 с −1, а центростремительное ускорение равно 243 м/с2.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах).
 Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 588 Вт, а сила тока равна 7 А.
Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 588 Вт, а сила тока равна 7 А.
В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6500+4000n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец. Ответ укажите в рублях.
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 55° по шкале Цельсия?
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует -40° по шкале Фаренгейта? Ответ округлите до десятых.

Площадь четырёхугольника можно вычислить по формуле ,
где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1 = 14, sinα =, a S=8,75.
Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле , где С — ёмкость конденсатора (в Ф), a U —
разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора ёмкостью 2∙10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 14 В. Ответ дайте в джоулях.
Закон Кулона можно записать в виде , где F – сила
взаимодействия зарядов (в ньютонах), q1 и q2 – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Нм2/Кл2), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,002 Кл, r=3000 м, а F=0,0016 Н.
Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,002 Кл, r=3000 м, а F=0,0016 Н.
Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле , где С — ёмкость конденсатора (в Ф), a U —
разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора ёмкостью 2 ∙10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 15 В. Ответ дайте в джоулях.
Закон Кулона можно записать в виде , где F – сила
взаимодействия зарядов (в ньютонах), q1 и q2 – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Нм2/Кл2), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,003 Кл, r=3000 м, а F=0,0027 Н.
Вариант 5
Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с −1, а центростремительное ускорение равно 289 м/с2.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 144,5 Вт, а сила тока равна 8,5 А.
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6000+4100n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 8 колец. Ответ укажите в рублях.
Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
 Скольким градусам по шкале Фаренгейта соответствует −15° по шкале Цельсия?
Скольким градусам по шкале Фаренгейта соответствует −15° по шкале Цельсия?
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 199° по шкале Фаренгейта? Ответ округлите до десятых.
Площадь четырёхугольника можно вычислить по формуле ,
где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 11, sinα =, a S=57,75.
Вариант 6
Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус окружности.
 Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 5,5 с −1, а центростремительное ускорение равно 60,5 м/с2.
Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 5,5 с −1, а центростремительное ускорение равно 60,5 м/с2.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 361,25 Вт, а сила тока равна 8,5 А.
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6000+4100n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец. Ответ укажите в рублях.
Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 124° по шкале Цельсия?
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
 Скольким градусам по шкале Цельсия соответствует 249° по шкале Фаренгейта? Ответ округлите до десятых.
Скольким градусам по шкале Цельсия соответствует 249° по шкале Фаренгейта? Ответ округлите до десятых.
Площадь четырёхугольника можно вычислить по формуле ,
где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1 = 9, sinα =, a S=56,25.
Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле , где С — ёмкость конденсатора (в Ф), a U —
разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора ёмкостью 10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 17 В. Ответ дайте в джоулях.
Закон Кулона можно записать в виде , где F – сила
взаимодействия зарядов (в ньютонах), q1 и q2 – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Нм2/Кл2), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,0007 Кл, r=500 м, а F=0,0504 Н.
Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,0007 Кл, r=500 м, а F=0,0504 Н.
Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле , где С — ёмкость конденсатора (в Ф), a U —
разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора ёмкостью 10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 19 В. Ответ дайте в джоулях.
Закон Кулона можно записать в виде , где F – сила
взаимодействия зарядов (в ньютонах), q1 и q2 – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Нм2/Кл2), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,008 Кл, r=300 м, а F=0,64 Н.
Вариант 7
Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 9 с −1, а центростремительное ускорение равно 405 м/с2.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 245 Вт, а сила тока равна 7 А.
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6000+4100n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 20 колец. Ответ укажите в рублях.
Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
 Скольким градусам по шкале Фаренгейта соответствует −44° по шкале Цельсия?
Скольким градусам по шкале Фаренгейта соответствует −44° по шкале Цельсия?
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 109° по шкале Фаренгейта? Ответ округлите до десятых.
Площадь четырёхугольника можно вычислить по формуле ,
где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 7, sinα =, a S=21.
Вариант 8
Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус окружности.
 Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 9,5 с −1, а центростремительное ускорение равно 180,5 м/с2.
Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 9,5 с −1, а центростремительное ускорение равно 180,5 м/с2.
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 6,75 Вт, а сила тока равна 1,5 А.
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6000+4100n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 10 колец. Ответ укажите в рублях.
Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
 Скольким градусам по шкале Фаренгейта соответствует 48° по шкале Цельсия?
Скольким градусам по шкале Фаренгейта соответствует 48° по шкале Цельсия?
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула tF=1,8tC+32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 41° по шкале Фаренгейта?
Площадь четырёхугольника можно вычислить по формуле ,
где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1 = 17, sinα =, a S=51.
Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле , где С — ёмкость конденсатора (в Ф), a U —
разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора ёмкостью 2∙10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 11 В. Ответ дайте в джоулях.
Найдите энергию конденсатора ёмкостью 2∙10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 11 В. Ответ дайте в джоулях.
Закон Кулона можно записать в виде , где F – сила
взаимодействия зарядов (в ньютонах), q1 и q2 – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Нм2/Кл2), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,0004 Кл, r=600 м, а F=0,005 Н.
Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле , где С — ёмкость конденсатора (в Ф), a U —
разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора ёмкостью 2∙10 − 4 Ф, если разность потенциалов на обкладках конденсатора равна 18 В. Ответ дайте в джоулях.
Ответ дайте в джоулях.
Закон Кулона можно записать в виде , где F – сила
взаимодействия зарядов (в ньютонах), q1 и q2 – величины зарядов (в кулонах), k – коэффициент пропорциональности (в Нм2/Кл2), а r – расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9 ∙109 Нм2/Кл2, q2=0,004 Кл, r=600 м, а F=0,4 Н.
Энергия заряженного конденсатора w в джоулях вычисляется
В заряженном конденсаторе обкладки име-ют разноименные заряды и взаимодейст-вуют между собой благодаря электричес-кому полю, которое сосредоточено в прост-ранстве между обкладками. О телах, между которыми существует взаимодействие, гово-рят, что они имеют потенциальную энер-гию. Следовательно, можно говорить и об энергии заряженного конденсатора
.
Обкладки заряженного конден-сатора взаимодействуют между собой.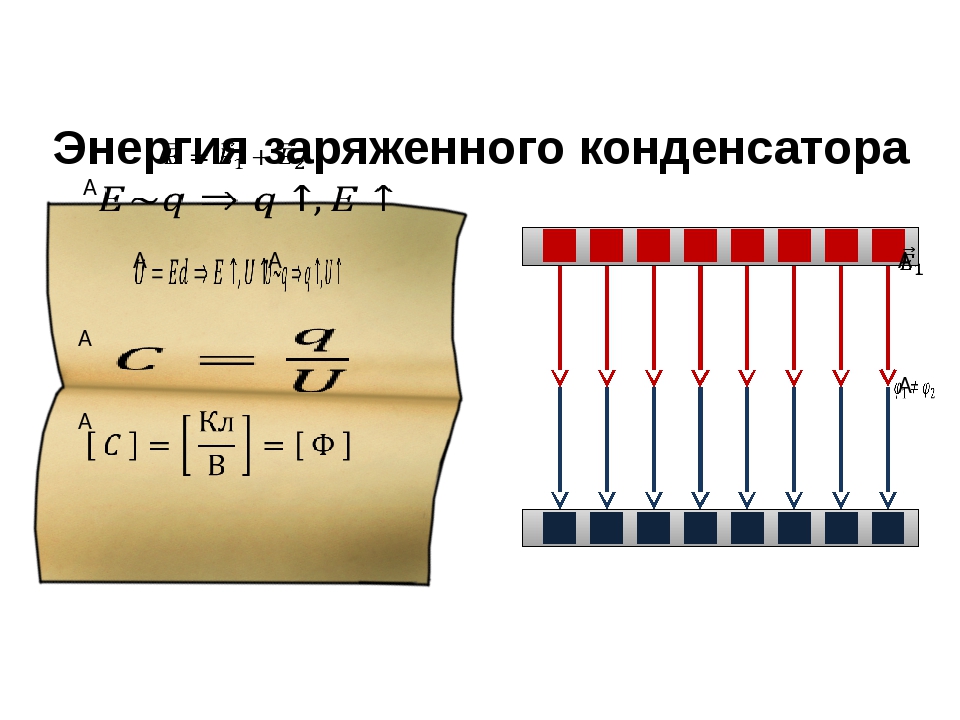
Наличие энергии
у заряженного конден-сатора можно подтвердить опытами.
Возьмем конденсатор достаточно боль-шой емкости, источник тока, лампочку на-кала и составим электрическую цепь, схема которой изображена на рис. 4.82. Переведем переключатель S
в положение 1 и зарядим конденсатор до определенной разности по-тенциалов от источника GB.
Если после этого перевести переключатель в положение 2, то можно наблюдать кратковременную вспышку света вследствие накала нити лам-почки. Наблюдаемое явление можно объяс-нить тем, что заряженный конденсатор имел энергию
, за счет которой была выполнена работа по накалу спирали лампочки.
В соответствии с законом сохранения энер-гии
работа, выполненная при разрядке кон-денсатора, равняется работе, выполненной при его зарядке. Расчет этой работы и, соответственно, потенциальной энергии кон-денсатора осложнен особенностями процес-са зарядки конденсатора. Пластины его за-ряжаются и разряжаются постепенно. Зави-симость заряда Q
Зави-симость заряда Q
конденсатора от времени при зарядке показана на графике (рис. 4.83). Заряд не только увеличивается постепенно, но и скорость его изменения не остается постоянной. Итак, вести расчеты на осно-вании формулы A =
qEd
нельзя, поскольку напряженность электрического поля не остается постоянной. Разность потенциалов также изменяется от нуля до максимально-го значения. На рис. 4.84 показано, что разность потенциалов изменяется про-порционально заряду конденсатора. Такая зависимость характерна для силы упругос-ти, которая зависит от удлинения пружины (рис. 4.85).
Воспользовавшись таким подобием, мож-но сделать вывод, что энергия заряженного конденсатора
будет равна
W =
Q
Δφ / 2.
Материал с сайта
Эта энергия
равна работе по зарядке конденсатора, которая численно равна пло-щади заштрихованного треугольника на гра-фике рис. 4.84.
Учитывая, что Q =
C
Δφ
, получим
W =
C(Δφ)
2 / 2.
А если учесть связь разности потенциалов с зарядом Δφ =
Q /
C
, то потенциальная энер-гия конденсатора может быть вычислена по формуле
W = (Q / 2) . (Q /
C) =
Q 2 / 2
C.
На этой странице материал по темам:
Энергия заряженного конденсатора шпора
Энергия заряженного конденсатора
Какие физические величины определяют энергию конденсатора
Самостоятельная работа по теме электроемкость плоского конденсатора
Як визначити енергію конденсатора за допомогою графіка
Вопросы по этому материалу:
Пусть потенциал обкладки конденсатора, на которой находится заряд равен а потенциал обкладки, на которой находится заряд , равен Тогда каждый из элементарных зарядов на которые можно разделить заряд находится в точке с потенциалом а каждый из зарядов, на которые можно разделить заряд , в точке с потенциалом .
Согласно формуле (28. 1) энергия такой системы зарядов равна
1) энергия такой системы зарядов равна
Воспользовавшись соотношением (27.2), можно написать три выражения для энергии заряженного конденсатора:
Формулы (29.2) отличаются от формул (28.3) только заменой на
С помощью выражения для потенциальной энергии можно найти силу, с которой пластины плоского конденсатора притягивают друг друга. Допустим, что расстояние между пластинами может меняться. Свяжем начало оси х с левой пластиной (рис. 29.1). Тогда координата х второй пластины будет определять зазор d между обкладками. Согласно формулам (27.3) и (29.2)
Продифференцируем это выражение по х, полагая заряд на обкладках неизменным (конденсатор отключен от источника напряжения). В результате получим проекцию на ось х силы, действующей на правую пластину:
Модуль этого выражения дает величину силы, с которой обкладки притягивают друг друга:
Теперь попытаемся вычислить силу притяжения между обкладками плоского конденсатора как произведение напряженности поля, создаваемого одной из обкладок, на заряд, сосредоточенный на другой. Согласно формуле (14.3) напряженность поля, создаваемого одной обкладкой, равна
Согласно формуле (14.3) напряженность поля, создаваемого одной обкладкой, равна
Диэлектрик ослабляет поле в зазоре в раз, но это имеет место только внутри диэлектрика (см. формулу (20.2) и связанный с нею текст). Заряды на обкладках располагаются вне диэлектрика и поэтому находятся под действием поля напряженности (29.4).
Умножив заряд обкладки q на эту напряженность, получим для силы выражение
Формулы (29.3) и (29.5) не совпадают. С опытом согласуется значение силы (29.3), получающееся из выражения для энергии. Это объясняется тем, что, кроме «электрической» силы (29.5), на обкладки действуют со стороны диэлектрика механические силы, стремящиеся их раздвинуть (см. § 22; отметим, что мы имеем в виду жидкий или газообразный диэлектрик). У края обкладок имеется рассеянное поле, убывающее по величине при удалении от краев (рис. 29.2). Молекулы диэлектрика, обладая дипольным моментом, испытывают дйствие силы, втягивающей их в область более сильного поля (см. формулу (9. 16)). В результате давление между обкладками повышается и появляется сила, ослабляющая действие силы (29.5) в раз.
16)). В результате давление между обкладками повышается и появляется сила, ослабляющая действие силы (29.5) в раз.
Если заряженный конденсатор с воздушным зазором частично погрузить в жидкий диэлектрик, наблюдается втягивание диэлектрика в пространство между пластинами (рис. 29.3). Это явление объясняется следующим образом. -Диэлектрическая проницаемость воздуха практически равна единице. Поэтому до погружения пластин в диэлектрик емкость конденсатора можно считать равной а энергию равной При частичном заполнении зазора диэлектриком конденсатор можно рассматривать как два параллельно включенных конденсатора, один из которых имеет площадь обкладки, равную — относительная часть зазора, заполненная жидкостью), и заполнен диэлектриком с второй с воздушным зазором имеет площадь обкладки, равную При параллельном включении конденсаторов емкости складываются:
Поскольку энергия будет меньше, чем (заряд q предполагается неизменным — перед погружением в жидкость конденсатор был отключен от источника напряжения). Следовательно, заполнение зазора диэлектриком оказывается энергетически выгодным. Поэтому диэлектрик втягивается в конденсатор и уровень его в зазоре поднимается. Это в свою очередь приводит к возрастанию потенциальной энергии диэлектрика в поле сил тяжести. В конечном итоге уровень диэлектрика в зазоре установится на некоторой высоте, соответствующей минимуму суммарной энергии (электрической и гравитационной). Рассмотренное явление сходно с капиллярным поднятием жидкости в узком зазоре между пластинками (см. § 119 1-го тома).
Следовательно, заполнение зазора диэлектриком оказывается энергетически выгодным. Поэтому диэлектрик втягивается в конденсатор и уровень его в зазоре поднимается. Это в свою очередь приводит к возрастанию потенциальной энергии диэлектрика в поле сил тяжести. В конечном итоге уровень диэлектрика в зазоре установится на некоторой высоте, соответствующей минимуму суммарной энергии (электрической и гравитационной). Рассмотренное явление сходно с капиллярным поднятием жидкости в узком зазоре между пластинками (см. § 119 1-го тома).
Втягивание диэлектрика в зазор между обкладками можно яснить также и с микроскопической точки зрения. У краев пластин конденсатора имеется неоднородное поле. Молекулы диэлектрика обладают собственным дипольным моментом либо приобретают его под действием поля; поэтому на них действуют силы, стремящиеся переместить их в область сильного поля, т. е. внутрь конденсатора. Под действием этих сил жидкость втягивается в зазор до тех пор, пока электрические силы, действующие на жидкость у края пластин, не будут уравновешены весом столба жидкости.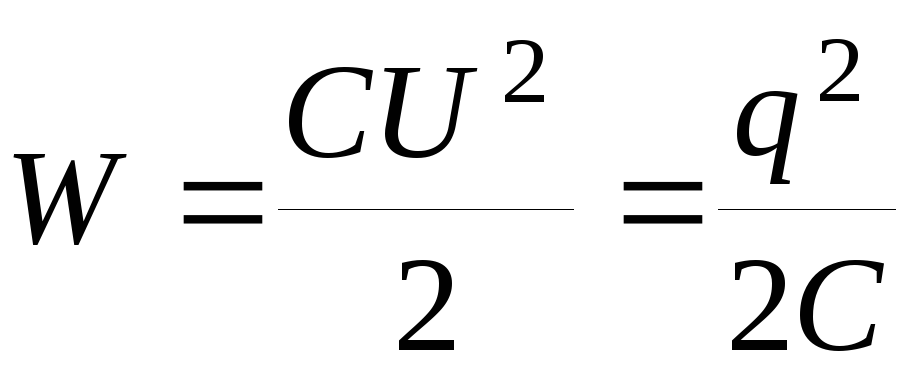
Электроемкостью
(емкостью) C уединенного изолированного
проводника называется физическая
величина, равная отношению изменения
заряда проводника q к изменению
его потенциала f:
C = Dq/Df.
Электроемкость
уединенного проводника зависит только
от его формы и размеров, а также
от окружающей его диэлектрической
среды (e).
Единица
измерения емкости в системе
СИ называется Фарадой. Фарада (Ф) —
это емкость такого уединенного проводника,
потенциал которого повышается на 1 Вольт
при сообщении ему заряда в 1 Кулон.
1 Ф =
1 Кл/1 В.
Конденсатором
называют систему двух разноименно
заряженных проводников, разделенных
диэлектриком (например, воздухом).
Свойство
конденсаторов накапливать и сохранять
электрические заряды и связанное
с ними электрическое поле характеризуется
величиной, называемой электроемкостью
конденсатора. Электроемкость конденсатора
равна отношению заряда одной из пластин
Q к напряжению между ними U:
C =
Q/U.
В
зависимости от формы обкладок,
конденсаторы бывают плоскими, сферическими
и цилиндрическими.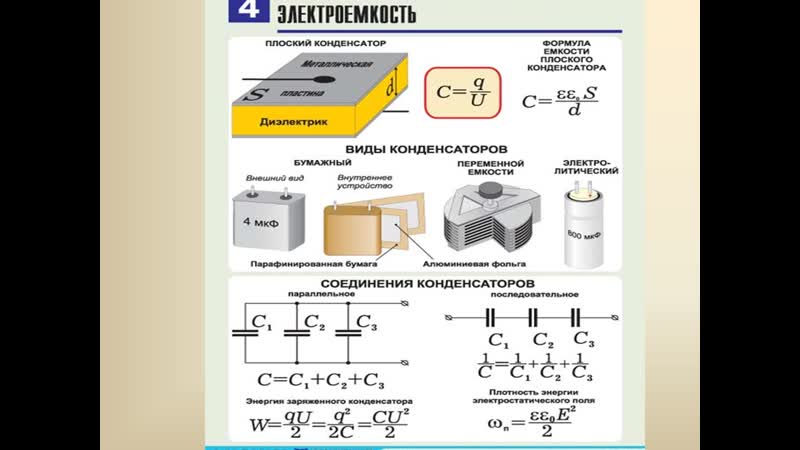 Формулы для расчета
Формулы для расчета
емкостей этих конденсаторов приведены
в таблице.
Соединение
конденсаторов в батареи.
На практике
конденсаторы часто соединяют в батареи —
последовательно или параллельно.
При
параллельном соединении напряжение
на всех обкладках одинаковое
U1 =
U2 = U3 = U = e, а емкость батареи
равняется сумме емкостей отдельных
конденсаторов C = C1 + C2 + C3.
При
последовательном соединении заряд
на обкладках всех конденсаторов
одинаков Q1 = Q2 = Q3, а напряжение
батареи равняется сумме напряжений
отдельных конденсаторов U = U1 + U2 +
U3.
Емкость
всей системы последовательно соединенных
конденсаторов рассчитывается
из соотношения:
1/C = U/Q = 1/C1 + 1/C2 +
1/C3.
Емкость
батареи последовательно соединенных
конденсаторов всегда меньше, чем емкость
каждого из этих конденсаторов
в отдельности.
Энергия электростатического
поля.
Энергия заряженного плоского
конденсатора Eк равна работе A, которая
была затрачена при его зарядке, или
совершается при его разрядке.
A =
CU2/2 = Q2/2С = QU/2 = Eк.
Поскольку
напряжение на конденсаторе может
быть рассчитано из соотношения:
U =
E*d,
где E — напряженность поля между
обкладками конденсатора,
d —
расстояние между пластинами
конденсатора,
то энергия заряженного
конденсатора равна:
Eк = CU2/2 =
ee0S/2d*E2*d2 = ee0S*d*E2/2 = ee0V*E2/2,
где V —
объем пространства между обкладками
конденсатора.
Энергия заряженного
конденсатора сосредоточена в его
электрическом поле.
Тип конденсатора | Формула для расчета | Примечания | Схематическое |
Плоский конденсатор | S — площадь пластины; | ||
Сферический конденсатор | C = 4pee0R1R2/(R2 — R1) | R2 и R1 — радиусы внешней | |
Цилиндрический | C = 2pee0h/ln(R2/R1) | h — высота цилиндров. |
Как
и любая система заряженных
тел, конденсатор
обладает
энергией. Вычислить энергию заряженного
плоского конденсатора с однородным
полем внутри него несложно.
Энергия
заряженного конденсатора.
Для
того чтобы зарядить конденсатор, нужно
совершить работу по разделению
положительных и отрицательных зарядов.
Согласно закону сохранения энергии эта
работа равна энергии конденсатора. В
том, что заряженный конденсатор обладает
энергией, можно убедиться, если разрядить
его через цепь, содержащую лампу
накаливания, рассчитанную на напряжение
в несколько вольт (рис.14.37
).
При разрядке конденсатора лампа
вспыхивает. Энергия конденсатора
превращается в тепло и энергию света.
Выведем
формулу для энергии плоского
конденсатора.
Напряженность поля, созданного зарядом
одной из пластин, равна Е/2
,
где Е
-напряженность
поля в конденсаторе. В однородном поле
одной пластины находится заряд q
,
распределенный по поверхности другой
пластины (рис. 2.
2.
Применение
конденсаторов
.
Зависимость электроемкости конденсатора
от расстояния между его пластинами
используется при создании одного из
типов клавиатур компьютера. На тыльной
стороне каждой клавиши располагается
одна пластина конденсатора, а на плате,
расположенной под клавишами, — другая.
Нажатие клавиши изменяет емкость
конденсатора. Электронная схема,
подключенная к этому конденсатору,
преобразует сигнал в соответствующий
код, передаваемый в компьютер.
Энергия конденсатора обычно не очень
велика — не более сотен джоулей. К тому
же она не сохраняется долго из-за
неизбежной утечки заряда. Поэтому
заряженные конденсаторы не могут
заменить, например, аккумуляторы в
качестве источников электрической
энергии.
Но это совсем не означает, что конденсаторы
как накопители энергии не получили
практического применения. Они имеют
одно важное свойство: конденсаторы
могут накапливать энергию более или
менее длительное время, а при разрядке
через цепь с малым сопротивлением они
отдают энергию почти мгновенно. Именно
Именно
это свойство широко используют на
практике.
Лампа-вспышка, применяемая в фотографии
,
питается электрическим током разряда
конденсатора, заряжаемого предварительно
специальной батареей. Возбуждение
квантовых источников света — лазеров
осуществляется с помощью газоразрядной
трубки, вспышка которой происходит при
разрядке батареи конденсаторов большой
электроемкости.
Однако основное применение конденсаторы
находят в радиотехнике.
Энергия конденсатора пропорциональна
его электроемкости и квадрату напряжения
между пластинами. Вся эта энергия
сосредоточена в электрическом поле.
Энергия поля пропорциональна квадрату
напряженности поля.
Энергия электрического поля
сегодня у нас последнее занятие по теории в дальнейшем мы будем решать задачи и писать тесты и контрольные работы итак тема урока энергия электрического поля энергия электрического поля домашнее задание на завтра конспект по учебнику мякишева параграф 101 и задачи пока что простенькие покере q для 10 класса задача с номерами 56 среднего уровня далее 124 достаточного уровня и все они находятся на странице 105 вот это домашнее задание на завтра но теперь слушайте и не говорите что вы не слышали сами знаете во время грозы последствия бывают очень разрушительны и от например разряда молнии значит откуда-то берется эта энергия которая обладает молния и вот сейчас мы этими вопросами как раз и займемся но мы не будем рассматривать с вами разряд молнии мы с вами рассмотрим более знакомую нам структуру плоский конденсатор и так пусть у нас имеется плоский конденсатор одну пластину которого мы зарядим положительно вторую пластину отрицательно таким же зарядом и давайте вторую пластину разместим почти вплотную к 1 то есть чтобы зазор между ними был очень-очень маленький и эту пластину мы покажем сейчас пунктирной линией вот так она несет на себе отрицательный заряд здесь заряд плюс q здесь минус q и теперь мы эту пластину отрицательно заряженную будем отодвигать от положительно заряженной пластины на какое-то расстояние d вот это расстояние на которое мы отодвигаем пластину площадь пластин и обозначим буквой s тут проводник который ни к чему не присоединен его использовали для того чтобы конденсатор зарядить и теперь конденсатор у нас подключен и вот мы понимаем что левая пластина и правая друг другу притягиваются ведь они разноименно заряженные давайте найдем с какой силой эти пластины друг дружке притягиваются для того чтобы ответить на этот вопрос поступим следующим образом будем считать левую пластину источником электрического поля а правую пластину заряженным телом которое в этом электрическом поле находится тогда напряженность поля создаваемая левой пластиной может быть найдено по формуле напряженности поля бесконечной плоскости напряженность поля левой пластины напряженность поля левой пластины обозначение и и один равняется сигма делить на 2 ну а дальше бы написали эпсилон нулевое но мы предполагаем что все это для общности происходит в среде с диэлектрической проницаемостью эпсилон тогда напряженность будет поля будет ок сила раз меньше то есть рядом с эпсилон нулевое появляются еще и диэлектрическая проницаемость что такое сигма в этой формуле поверхностная плотность заряда это отношение заряда на всей пластине к площади этой пластины сильно равняется заряд делить на площадь и вот левая пластина является источником поля а правая в этом поле находится поэтому на нее действует электрическая сила f электрическая и чтобы пластину удержать или чтобы эту пластину медленно отодвигать как мы сейчас с вами это сделаем нужно приложить внешнюю силу такую же точно по модулю вот эту силу мы обозначим f чтобы найти электрическую силу нужно умножить напряженность поля в котором находится заряд на величину заряда f электрическая равняется q умножить на е1 ну а теперь давайте в эту формулу подставим напряженность поля и тогда у нас получится что электрическая сила равняется q умножить на сигма делить на два ипсилон эпсилон 0 а теперь вспоминаем что сигма это отношения зарядок площади пластины равняется q умножить на q делить на 2 ip сила эпсилон 0 площадь пластин и и наконец сила которую мы прикладываем чтобы отодвинуть одну пластину другой она равна электрической силе по третьему закону ньютона f равняется эф электрическое я напоминаю что мы пластину отодвигаем медленно то есть мы не собираемся ей кинетическую энергию сообщать мы хотим просто переместить ее отсюда сюда поэтому эти силы одинаковы и можно написать что сила f равняется q квадрат на 2 эпсилон от тела 0 с q квадрат на 2 эпсилон эпсилон 0 чтобы отодвинуть пластину правую от левой нам нужно приложить такую силу но отодвигая эту пластину мы совершаем работу работа этой силы а равняется модулю силы f на расстояние пройденное пластины на d на модуль вектора перемещения пластины вы на косинус угла между направлением силой направлением перемещения мы перемещаем пластину в направлении действия силы так что тут не будет дополнительного косинуса и тогда остается что а равняется эф вот она q квадрат делить на 2 г по силам эпсилон нулевое с и здесь появляется множитель до посмотрите внимательно на эту формулу не просматривает ли в ней что-то знакомое электроемкость игорь правильно да давайте вспомним что емкость конденсатора c равняется эпсилон ип сила 0 с делить на д поэтому у нас вот здесь обратная емкость вот она тогда можно записать что работа по раздвигание у пластин равняется q квадрат на 2 c такую работу нужно совершить для того чтобы раздвинуть пластины конденсатора ну и какая работа зря не пропадает на что то это работа пошла как вы думаете на что это работа пошла нигде ничего мы не разгоняем значит кинетическая энергия нет нигде не приобретается телами за счет этой работы нигде ничего мы не нагреваем значит на внутреннюю энергию тоже эта работа не израсходовано на изменение внутренней энергии куда же она девалась а давайте подумаем о чем отличаются ситуация когда эти пластины были близко близко друг другу от ситуации когда эти пластины друга друга находятся на заметном расстояние ваня ну емкость изменилась до мы изменили потенциальную энергию потенциальную энергию чего пластин относительно друг друга хорошо значит это потенциальная энергия вот этой пластины в этой в поле этой пластины ну смотрите что было вот здесь когда правая пластина находилась в исходном положении вот здесь а поле было нет а теперь этот кусок пространства заполнен электрическим полем значит мы совершая работу создали электрическое поле в большей области пространства а это говорит о том что электрическое поле которое здесь появилась обладает энергией работа которую мы совершили пошла на создание электрического поля пространстве между пластинами конденсатора вот как получается здесь вверх электрическое поле и она обладает энергией и так работа которую мы совершили пошла на создание электрического поля и поэтому равна энергии электрического поля так что мы можем записать что энергия электрического поля сосредоточена в конденсаторе дуба льва электрическая равняется q квадрат делить на 2 c запомните эту формулу она нам не раз пригодится заряд на пластинах конденсатора измерять неудобно гораздо проще измерить напряжение между пластинами подключив конденсатору вольтметр поэтому давайте эту формулу немножко изменим запишем в другой форме а именно вспомним связь между зарядом на пластинах конденсатора и напряжение между пластинами по определению электроемкости емкость это величина равна и отношения заряда на пластинах конденсатора к напряжению между пластинами отсюда ку равняется цепь подставляем заряд в формулу для энергии у нас получается дуба левое электрическое равняется q квадрат то есть c квадрат квадрат делить на 2 c 1 степень емкости сокращается и мы получаем энергия электрического поля заряженного конденсатора равняется свою квадрат пополам вот так смотрите какая знакомая структура у этой формулы сколько уже энергии нам встречалось вычисляю щихся по такой формуле м в квадрат пополам и омега квадрат пополам что это такое это кинетическая энергия вращающегося тела к x квадрат пополам потенциальная энергия упругой деформированного тела и еще будут у нас впереди формулы такой же структуры для вычисления энергии но это будет немножко позже итак мы с вами умеем вычислять энергию электрического поля заряженного конденсатора но эта формула имеет эти две формулы имеют один недостаток создается впечатление что энергия обладает сам конденсатор но ведь на самом деле это не так что на самом деле обладает энергией поле которое сосредоточено между пластинами конденсатор это как сосуд для хранения электрического поля это как канистра она может быть пустой а может быть заполненной бензином точно также и конденсатор может быть разряжен а может быть заряжен то есть заполнен электрическим полем поэтому наверное с точки зрения науки будет правильней если мы выразим энергию электрического поля не через характеристики канистры в которой она храниться не через характеристики конденсатор а через характеристики самого электрического поля а какая величина характеризует электрическое поле напряженность ну давайте сейчас выразим энергию электрического поля через напряженность поля для этого поступим следующим образом возьмем вот эту формулу w электрическая равняется c у квадрат попала c это емкость конденсатора и мы только что с вами вспомнили что емкость конденсатора вычисляется пол вот такой формуле c равняется эпсилон эта сила 0 с делить на d воспользуемся этой формулой равняется эпсилон эпсилон нулевое с делить на 2d и на квадрат а теперь свяжем напряженность поля с электрическим напряжением между пластинами конденсатора напряжение у мы получим если напряженность поля е умножен на расстояние между пластинами на расстоянии отмеряем а я вдоль силовых линий в нашем случае это просто расстояние между пластинами конденсатора поскольку поле однородно внутри плоского конденсатора то эти можно пользоваться подставляем сюда равняется равняется капсулам хлеб сила нулевое теперь вместо у я пишу и квадрат b квадрат еще у нас с нужно не забыть на с и разделить на 2d вот так вы видите что одна степень d сокращается и у нас остается равняется давайте напишем так 1 2 ипсилон ипсилон 0 умножить на е квадрат умножить на с и на d посмотрите внимательно на эту формулу что вот это такое это объем между обкладками конденсатора это объем занимаем и электрическим полем поэтому можно написать что энергия электрического поля дабы левое электрическое равняется 1 2 эпсилон эпсилон 0 ед квадрат умножить на объем вот эту формулу мы сейчас в полную рамку брать не будем результат достаточно очевидны ясно что если поле данной напряженности занимает в два раза больший объем то она хранит и в два раза больше энергии поэтому энергия поля обязана быть прямо пропорционально объему ну понятно если это поле однородная но тогда имеет смысл ввести величину которых характеризует концентрацию энергии в пространстве назовем ее объемная плотность энергии объемная плотность энергии электрического поля обозначим эту величину маленькой буквой w и определим ее как отношение энергии электрического поля к объему в котором это поле сосредоточено понятно что это великого эта формула справедлива для однородного поля если поле неоднородно то объемная плотность меняется от точки к точке тогда если вы хотите задать объемную плотность надо взять небольшой объем но мы не будем усложнять ситуацию значит что такое объемная плотность энергии давайте запишем определение объемной плотностью энергии объемной плотностью энергии электрического поля объемной плотностью энергии электрического поля называется физическая величина равная называется физическая величина равная отношению энергии электрического поля к объему в котором это поле существует равное отношению энергии электрического поля к объему в котором это поле существует к объему в котором это поле существует эта формула справедлива для однородного поля у нас как раз такой случай тогда глядя вот сюда вы видите что множитель который перед объемом стоит это есть объемная плотность энергии электрического поля и так объемная плотность электрической ого поля вычисляется по формуле объемная плотность энергии эпсилон и описал им нулевое и квадрат вот эта формула более содержательно по сравнению с этими двумя потому что она выражает энергию поля через характеристики самого поля они того конденсатора который это поле внутри себя содержит это одна из фундаментальных формул физики она заслуживает особого места на доске и ваших конспектах запомните ее полезно помнить вот эту формулу она чаще всего при решении задач встречается но эта формула зато более важное ну что ж теперь когда вы знаете формулу для энергии электрического поля давайте посмотрим на практике как эта энергия себя проявляет для этого возьмем сосуд для электрического поля даже не один сосуд а много здесь у нас 6 конденсаторов емкость каждого конденсатора 22 тысячи микрофарад итак пример пример емкость равняется 6 умножить на 22 тысячи микро фарад ну или это можно посчитать 6 на 22 тысячи 6 умножить на 22 это 132 132 на 10 в 3 и на 10 в минус шестой так это будет 132 на 10 в 3 на 10 в минус шестой фраг или другими словами это будет 0 целых сто тридцать две сотых фарада внушительная электроемкости и вот сейчас мы с вами зарядим этот конденсатор от источника тока вот этот источник нужно обязательно соблюдать полярность потому как эти конденсаторы у нас электролитический вот здесь написано плюс минус надо положительных анод конденсаторов подключить вот сюда катод катодная пластины конденсатора подключить как минус так сейчас я разверну таким образом блок питания чтобы вам было крупно видно как происходит зарядка конденсатора и так вот перед вами источник тока положительный полюс источника отрицательны подключаем батарею конденсатора но перед этим проверим работает источник до стрелка отклоняется теперь подключаем конденсатор и смотрите что будет я буду плавно увеличивать напряжение а вы следите за показаниями амперметра давайте дадим крупнее амперметр и вольтметр напряжение увеличиваем чуть чуть поближе что было в фокусе вот так напряжение увеличиваем смотрим на амперметр ток течет напряжение растет то есть заряд все время накапливается на пластинах когда я перестаю увеличивает напряжение ток спадает до 0 а напряжение у нас оказывается равно 50 вольт а теперь смотрите я отключаю тумблер источника от сети вольтметра по-прежнему показывает 50 вольт конденсатор зарядился он хранит заряд отключим конденсатор пусть полежит на несколько часов если хороших конденсатор рода может и несколько дней так вот этот конденсатор заряженный а ну-ка давайте найдем какой же заряд этот конденсатор накопил ку равняется c умножить на u до какого напряжения мы зарядили конденсатор 50 вольт у нас у равняется 50 вольт и так зарядку равняется но и 132 парада умножить на 50 вольт фарад умноженный на вольт это кулон 0 , 132 умножить на 50 получается 6,6 6,6 кулонов ничего себе 6,6 урона если бы вот по одному кулону мы разместили на расстояние 1 метр они бы взаимодействовали силой 9 на 10 9 ньютона заряды противоположного знака а тут 6 кулон почти 7 кулон мирно уживаются внутри этого конденсатора отрицательные заряды на одной пластине диэлектрика положительное на другой почему потому что за пределами конденсатора поля нет это поле сосредоточена в тончайшим слоем диэлектрика в нашем случае окись алюминия но это мир на существующие электрическое поле обладает энергией мы сейчас не будем вычислять эту энергию а мы просто попробуем сейчас эту энергию освободить быстро разрядив конденсатор на например на напильник ну что рискнем нормально приварил а напильник видите ну чтож давайте рассчитаем какую же энергию накопил этот конденсатор и какова была мощность выделяющаяся при разряде конденсатора так ну что тема иди к доске поскольку ты вздрогнул сильнее всех посчитай пожалуйста какую энергию сосредоточила в себе поле этого конденсатор пользуясь вот этой формы ноль целых сто тридцать две сотых фарада умножить на 50 в квадрате сразу пишем 2500 вольт в квадрате и делим пополам так единицы измерения смотрите станет стороночку чуть-чуть вот туда на вольт можно вольт в квадрате можно разложить вольт умножить на вольт вольт на фарад это кулон кулон умноженный на вольт это джоуль ответ получается в джоулях продолжаю вот те калькулятор 100 65 джоулей 165 живой спасибо темам присаживать 165 джоулей но я всегда сравниваю эту энергию с работой по поднятию гири так 1 джоуль эта энергия которую нужно которую приобретает килограммовая гиря на высоте 10 сантиметров на метровой высоте 10 джоулей на 10-метровой высоте 100 джоулей а здесь энергия будет такая как если бы мы эту гирю поняли на высоту сто шестнадцать с половиной метров это где-то пятиэтажка а то и даже больше наверно даже больше но почему это сравнительно небольшая энергия так эффектно высвободилось как вы думаете короткий промежуток времени действительно оказывается что разряд конденсатора в нашем опыте длится примерно одну миллисекунду ты примерно 10 в минус 3 секунды по порядку величины конденсатор разряжается примерно за одну тысячную секунды тогда электрическая мощность п равна энергии электрического поля делить на время в течение которого эта энергия изменилась и мы получаем 165 джоулей делить на 10 в минус 3 секунды джоуль делить на секунду это что это в от 10 минус 3 в числителе даст нам 10 в 3 watt умножить на 10 3 это киловатт сто шестьдесят пять киловатт эта мощность потребляемая где-то 9 этаж кай примерно 165 киловатт что саша хотел спросить что-то очень просто это энергия выделилась в небольшом участке пространства сейчас я вам покажу что стало с напильником поскольку вся эта мощность выделилась в небольшом объеме то вот посмотрите что стало с напильником час наведем на резкость вот видите вот так конденсатор и прекрасно себя чувствуют чем хорош конденсатор его можно разряжать и заряжать большим током и он не портится от этого в отличие от химических источников тока для которого короткого замыкает замыкание губительно вот так вот такая огромная мощность кстати конденсаторы используют например в лампах вспышках в flash который на фотоаппаратах лампах вспышках там приблизительно мощность вспышки тоже порядка киловатт конденсаторы заряженные используют в лазерах импульсных лазеров для накопления энергии в импульсных лазеров накапливается куда больше энергии я вам уже рассказывал некоторые батареи конденсаторов состоят из тысяч конденсаторов заполняющих целое помещение так что с энергии электрического поля шутить иногда просто опасно ну давайте решим одну задачку она относится к грозовым явлением задача номер девять 19 гельфгат очень простенькая задача перед грозой напряженность электрического поля в воздухе достигает 50 кило вольт на метр какова при этом плотность энергии электрического поля перед грозой напряженность электрического поля в воздухе достигает я 50 кило вольт на метр найдем объемную плотность энергии эта задача просто на подстановку формулу но тем не менее давайте ее решим и так объемная плотность энергии равняется 1 2 эпсилон эпсилон нулевое ее квадрат гроза происходит в воздухе поэтому эпсилон равняется единице ип сила нулевое мы с вами помним давайте эту формулу используем непосредственно для расчетов энергию объемная плотность равняется 1 2 на восемь восемьдесят пять на десять в минус 12 фарад делить на метр это электрическая постоянная эпсилон 0 умножить на квадрат напряженности электрического поля 50 кило вольт на метр это 5 на 10 в какой степени вольт на метр 5 на 10 4 в квадрате это будет 25 на 10 8 так двадцать пять на десять в восьмой чего вольт в квадрате равняется вольт в квадрате на метр в квадрате правильно спасибо андрей вольт в квадрате на метр в квадрате так что у нас получается с единицами кубические метры видите вот тут знаменателя все в порядке фарад умножить на вольт в квадрате это джоуль значит получаются джоули на метр в квадрате на метр кубический ну теперь что делаем умножаем 885 умножить на 12 с половиной это примерно 110 110 а тут у нас 10 -12 10 в 8 значит 10 минус 4 10 минус 4 каких единиц джоулей на метр кубический или это получается 11 на 10 2 минус 2 джоулей на метр кубический это много или мало один кубический метр пространство под грозовым облаком обладает вот такой энергией ребята какого размера примерно грозовое облако километр а какой высоты промежут какую на какой высоте грозовые облака порядка километра тогда давайте посмотрим а какая же энергия сосредоточена в объеме километр на километр на километр в атмосфере под грозовым облаком пусть в равняется 1 километр кубических ребята сколько это кубических метров это 10 в девятой кубических метров тогда энергии электрического поля под грозовым облаком w электрическая равняется 11 на 10 в 7 до 10 минус 2 умножить на 10 9 на 10 в 7 джоулей наверное это впечатляющая цифра если вспомнить вот этот пример я сейчас не буду вычислять на какую высоту можно закинуть эту гирьку но она наверное не такая уже маленькая хотя почему не вычислить значит 100 джоулей это 10 метров так тысячи джоулей это 100 метров десять тысяч джоулей это километра а здесь тысячу раз больше 100 тысячи километров получается что-то очень много получается можно поднимать не только за счет этой энергии но и все посмотрели на team хорошо ребята на этом наш урок окончен отдыхая пьем чай утро на 5 играть
Время зарядки конденсатора формула.
 Накопление заряда на обкладках конденсатора
Накопление заряда на обкладках конденсатора
Вам понадобится
- — знание емкости или геометрических и физических параметров конденсатора;
- — знание энергии или заряда на конденсаторе.
Инструкция
Найдите напряжение между пластинами конденсатора, если известна текущая величина накопленной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C∙U²)/2, где C — емкость, а U — напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C).
Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (количества ) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q∙U/2 (где q — заряд). Следовательно, зная энергию и , можно вычислить напряжение между его пластинами по формуле: U=2∙W/q.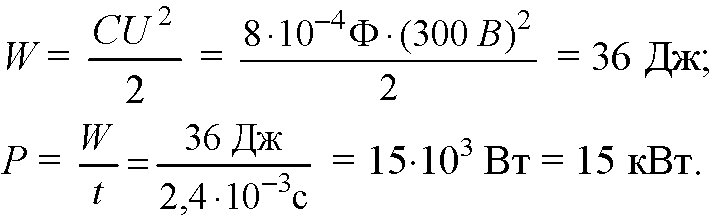 -12 Ф/м), ε — относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.
-12 Ф/м), ε — относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.
Обратите внимание
Для получения корректных результатов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ.
Для того чтобы знать, можно ли использовать в том или ином месте схемы конденсатор, следует определить его . Способ нахождения этого параметра зависит от того, каким образом он обозначен на конденсаторе и обозначен ли вообще.
Вам понадобится
- Измеритель емкости
Инструкция
На крупных конденсаторах
емкость
обычно обозначена открытым текстом: 0,25 мкФ или 15 uF. В этом случае, способ ее определения тривиален.
На менее крупных конденсаторах
(в том , SMD) емкость
двумя или тремя цифрами. В первом случае, она обозначена в пикофарадах. Во втором случае, первые две цифры емкость
Во втором случае, первые две цифры емкость
, а третья — в каких единицах она выражена:1 — десятки пикофарад;
2 — сотни пикофарад;
3 — нанофарады;
4 — десятки нанофарад;
5 — доли микрофарады.
Существует также система обозначения емкости, использующая сочетания латинских букв и цифр. Буквы обозначают следующие цифры:A — 10;
B — 11;
C — 12;
D — 13;
E — 15;
F — 16;
G — 18;
H — 20;
J — 22;
K — 24;
L — 27;
M — 30;
N — 33;
P — 36;
Q — 39;
R — 43;
S — 47;
T — 51;
U — 56;
V — 62;
W — 68;
X — 75;
Y — 82;
Z — 91.Полученное число следует умножить на число 10, предварительно возведенное в степень, равную цифре, следующей после . Результат будет выражен в пикофарадах.
Встречаются конденсаторы, емкость
на которых не обозначена вообще. Вы наверняка встречали их, в , в стартерах ламп дневного . В этом случае, измерить емкость
можно только специальным прибором.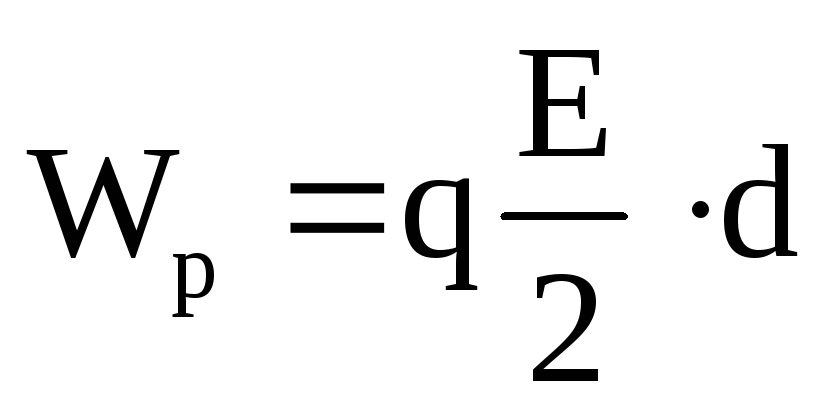 Они цифровыми и мостовыми.В любом случае, если конденсатор впаян в то или иное устройство, его следует обесточить, разрядить в нем конденсаторы фильтра и сам конденсатор, емкость
Они цифровыми и мостовыми.В любом случае, если конденсатор впаян в то или иное устройство, его следует обесточить, разрядить в нем конденсаторы фильтра и сам конденсатор, емкость
которого следует измерить, и лишь после этого выпаять его. Затем его необходимо подключить к прибору.На цифровом измерителе сначала выбирают самый грубый предел, затем переключают его до тех пор, пока он не покажет перегрузку. После этого переключатель переводят на один предел назад и читают показания, а по положению переключателя определяют, в каких единицах они выражены.На мостовом измерителе, последовательно переключая , на каждом из них прокручивают регулятор из одного конца шкалы в другой, пока звук из динамика не исчезнет. Добившись исчезновения , по шкале регулятора считывают результат, а единицы, в которых он выражен, также определяют по положению переключателя.Затем конденсатор устанавливают обратно в устройство.
Обратите внимание
Никогда не подключайте к измерителю заряженные конденсаторы.
Источники:
- Справочник по системам обозначения емкости
Найти значение электрического заряда
можно двумя способами. Первый – измерить силу взаимодействия неизвестного заряда
с известным и с помощью закона Кулона рассчитать его значение. Второй – внести заряд в известное электрическое поле и измерить силу, с которой оно действует на него. Для измерения заряда
протекающего через поперечное сечение проводника за определенное время измерьте силу тока и умножьте ее на значение времени.
Вам понадобится
- чувствительный динамометр, секундомер, амперметр, измеритель электростатического поля, воздушный конденсатор.
Инструкция
Измерение заряда
при его с известным зарядомЕсли известен одного тела, поднесите к нему неизвестный заряд и измерьте между ними в метрах. Заряды начнут взаимодействовать. С помощью динамометра измерьте силу их взаимодействия. Рассчитайте значение неизвестного заряда
— для этого квадрат измеренного расстояния умножьте на значение силы и поделите на известный заряд. 9)). Если заряды отталкиваются, то они одноименные, если же притягиваются – разноименные.
9)). Если заряды отталкиваются, то они одноименные, если же притягиваются – разноименные.
Измерение значения заряда
, внесенного в электрическое полеИзмерьте значение постоянного электрического поля специальным прибором (измеритель электрического поля). Если такого прибора нет, возьмите воздушный конденсатор, зарядите его, измерьте напряжение на его обкладках и поделите не расстояние между пластинами – это и будет значение электрического поля внутри конденсатора в вольтах на метр. Внесите в поле неизвестный заряд. С помощью чувствительного динамометра измерьте силу, которая на него действует. Измерение проводите в . Поделите значение силы на напряженность электрического поля. Результатом будет значение заряда
в Кулонах (q=F/Е).
Измерение заряда
, протекающего через поперечное проводникаСоберите электрическую цепь с проводниками и последовательно подключите к ней амперметр. Замкните ее на источник тока и измерьте силу тока с помощью амперметра в амперах.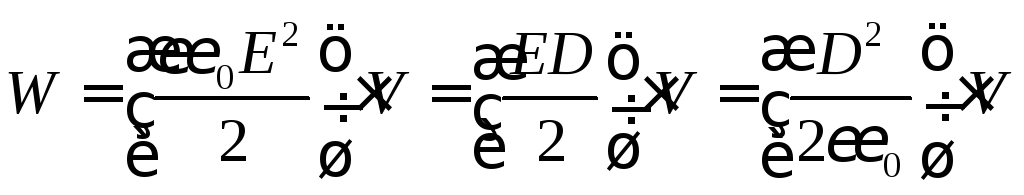 Одновременно секундомером засеките , в которого в цепи был электрический ток. Умножив значение силы тока на полученное время, узнайте заряд, через поперечное сечение каждого за это время (q=I t). При измерениях следите, чтобы проводники не перегревались и не произошло короткое замыкание.
Одновременно секундомером засеките , в которого в цепи был электрический ток. Умножив значение силы тока на полученное время, узнайте заряд, через поперечное сечение каждого за это время (q=I t). При измерениях следите, чтобы проводники не перегревались и не произошло короткое замыкание.
Конденсатором называется устройство, способное накапливать электрические заряды. Количество накапливаемой электрической энергии в конденсаторе характеризуется его емкостью
. Она измеряется в фарадах. Считается, что емкость в один фарад соответствует конденсатору, заряженному электрическим зарядом в один кулон при разности потенциалов на его обкладках в один вольт.
Инструкция
Определите емкость плоского конденсатора
по формуле С = S e e0/d, где S — площадь поверхности одной пластины, d — между пластинами, e — относительная диэлектрическая проницаемость , заполняющей пространство между пластинами (в вакууме она равна ), e0 — электрическая постоянная, равная 8,854187817 10(-12) Ф/м. Исходя из приведенной формулы, величина емкости будет зависеть от площади проводников, между ними и от материала диэлектрика. В качестве диэлектрика может применяться или слюда.
Исходя из приведенной формулы, величина емкости будет зависеть от площади проводников, между ними и от материала диэлектрика. В качестве диэлектрика может применяться или слюда.
Вычислите емкость сферического конденсатора
по формуле С = (4П e0 R²)/d, где П — число «пи», R — радиус сферы, d — величина зазора между его сферами.Величина емкости сферического конденсатора
прямо пропорциональна концентрической сферы и обратно пропорциональна расстоянию между сферами.
Рассчитайте емкость цилиндрического конденсатора
по формуле С = (2П e e0 L R1)/(R2-R1), где L — длина конденсатора
, П — число «пи», R1 и R2 — радиусы его цилиндрических обкладок.
Если конденсаторы в цепи соединены параллельно, рассчитайте их общую емкость по формуле С = С1+С2+…+Сn, где С1, С2,…Сn – емкости параллельно соединенных конденсаторов.
Вычислите общую емкость последовательно соединенных конденсаторов по формуле 1/С = 1/С1+1/С2+…+1/Сn, где С1, С2,…Сn — емкости последовательно соединенных конденсаторов.
Обратите внимание
На любом конденсаторе обязательно должна быть нанесена маркировка, которая может быть буквенно-цифровая или цветовая. Маркировка отражает его параметры.
Источники:
- Цветовая маркировка резисторов, конденсаторов и индуктивностей
Емкость – величина, в системе СИ выражаемая в фарадах. Хотя используются, фактически, лишь производные от нее – микрофарады, пикофарады и так далее. Что касается электроемкости плоского конденсатора, она зависит от зазора меж обкладок и их площади, от вида диэлектрика, в данном зазоре расположенного.
Инструкция
В том случае, если обкладки конденсатора имеют одинаковую площадь и имеют расположение строго одна над другой, рассчитайте площадь одной из обкладок – любой. Если же одна из них относительно другой смещена либо они разные , нужно рассчитывать площадь области, в которой обкладки друг дружку перекрывают.
При этом используются общепринятые формулы, рассчитывать площади таких геометрических фигур, как круг (S=π(R^2)), прямоугольника (S=ab), его частного случая – квадрата (S=a^2) – и других. (-12) Ф/м и является, по сути, диэлектрической проницаемостью вакуума.
(-12) Ф/м и является, по сути, диэлектрической проницаемостью вакуума.
Состоит из двух пластин (или обкладок), находящихся одна перед другой и сделанных из проводящего материала. Между пластинами находится изолирующий материал, называемый диэлектриком (рис. 4.1). Простейшими диэлектриками являются воздух, бумага, слюда и т. д.
Рис. 4.1
Зарядка конденсатора
Основным свойством конденсатора является его способность запасать электрическую энергию в виде электрического заряда.
На рис. 4.2(а) изображена схема, в которой конденсатор соединяется через ключ с источником питания. Когда ключ замкнут (рис. 4.2(б)), положительный полюс источника «откачивает» электроны с обкладки А, и она приобретает положительный заряд. Отрицательный полюс источника питания тем временем «поставляет» электроны на обкладку В, в результате чего она приобретает отрицательный заряд, по абсолютной величине равный положительному заряду обкладки А. Такой поток электронов называется током заряда.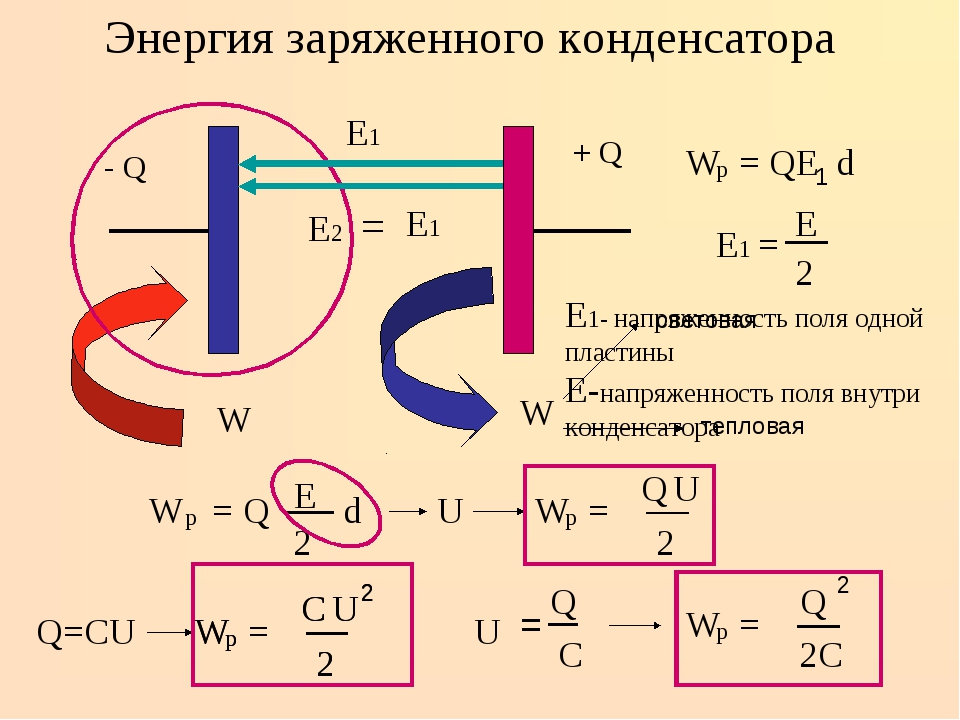 Он продолжает течь до тех пор, пока напряжение на конденсаторе не сравняется с ЭДС источника питания. В этом случае говорят, что конденсатор полностью заряжен. Электрический заряд обозначается буквой Q, а его величина измеряется в кулонах (Кл).
Он продолжает течь до тех пор, пока напряжение на конденсаторе не сравняется с ЭДС источника питания. В этом случае говорят, что конденсатор полностью заряжен. Электрический заряд обозначается буквой Q, а его величина измеряется в кулонах (Кл).
Рис. 4.2.
Когда конденсатор заряжен, между его обкладками возникает разность потенциалов, а следовательно, и электрическое поле.
Если в момент, когда конденсатор уже зарядился, разомкнуть ключ (рис. 4.2(в)), конденсатор будет хранить заряд. В этом случае внутри диэлектрика между обкладками возникает электрическое поле. При разряде конденсатора через сопротивление нагрузки (рис. 4.2(г)) электрическое ноле исчезает.
Емкость конденсатора
Способность конденсатора накапливать электрический заряд называется емкостью, а величина этой емкости обозначается буквой С и измеряется в фарадах (Ф). Фарада — очень большая единица емкости, и поэтому она практически не используется. Чаще используются дробные единицы:
1 микрофарада (мкФ) =
Ф = 10 -6 Ф,
1 пикофарада (пФ) =
мкФ =
10 -6 мкФ =
10 -12 Ф.
Емкость конденсатора возрастает с увеличением площади обкладок и убывает с увеличением расстояния между ними.
Например, при возрастании площади обкладок вдвое емкость также увеличивается в два раза. Если же увеличить вдвое расстояние между обкладками, емкость станет вдвое меньше.
Связь заряда, емкости и напряжения
Если конденсатор заряжен до разности потенциалов V , его заряд определяется формулой Q=CV
где С выражается в фарадах, V – в вольтах, а Q – в кулонах. Преобразовав эту формулу, получим:
Энергия заряженного конденсатора
Энергия W, запасенная конденсатором, определяется формулой
где W выражается в джоулях, С – в фарадах, а V — в вольтах.
Параллельное и последовательное соединение конденсаторов
Если два конденсатора, С1 и С2, соединены параллельно (рис. 4.3(а)), результирующая емкость СТ такого соединения равна сумме емкостей этих конденсаторов:
Если конденсаторы соединены последовательно (рис. 4.3(б)), результирующая емкость СТ оказывается меньше емкости любого из конденсаторов я выражается формулой
4.3(б)), результирующая емкость СТ оказывается меньше емкости любого из конденсаторов я выражается формулой
Например, если С1 = С2, то результирующая емкость СТ последовательного соединения равна половине емкости любого из конденсаторов:
Напряжение на последовательно соединенных конденсаторах
На схеме, показанной на рис. 4.4, конденсаторы С1 и С2 соединены последовательно и подключены к источнику постоянного напряжения VТ. Полное напряжение VТ будет поделено между С1 и С2 таким образом, что на конденсаторе меньшей емкости установится большее напряжение,
Рис. 4.3. Параллельное (а) и последовательное (б) соединение конденсаторов.
и наоборот.
Сумма V1 (напряжения на С1) и V2 (напряжения на С2) всегда равна полному напряжению VТ.
В общем случае, когда несколько конденсаторов, соединенных последовательно, подключено к источнику постоянного тока, напряжение на каждом из конденсаторов обратно пропорционально его емкости. При последовательном соединении двух конденсаторов напряжения на С1 и С2 соответственно равны
При последовательном соединении двух конденсаторов напряжения на С1 и С2 соответственно равны
Пример 1
Определим результирующую емкость цепи, изображенной на рис. 4.5. Результирующая емкость параллельного соединения равна
С2 + С3 = 10 + 20 = 30 пФ
Поскольку емкость С1 также равна 30 пФ, то результирующая емкость всей цепи равна ½*30 = 15 пФ.
Рис. 4.6.
Рис. 4.7.
Пример 2
откуда напряжение на С2 равно 30 – 20 = 10 В.
Рабочее напряжение
Любой конденсатор характеризуется некоторым максимальным напряжением, при превышении которого наступает пробой диэлектрика. Это напряжение называется рабочим, или номинальным, напряжением конденсатора, и подаваемое на конденсатор напряжение ни в коем случае не должно его превышать. При использовании конденсатора в цепях переменного тока амплитудное значение напряжения в цепи также не должно превышать рабочего напряжения конденсатора.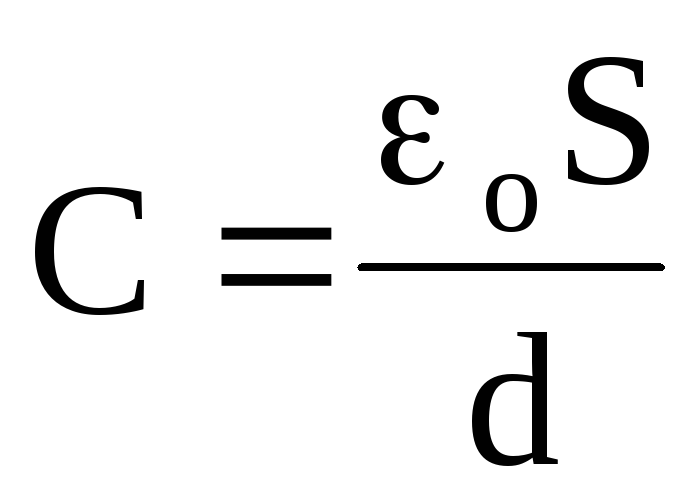 Рабочим напряжением для батареи конденсаторов, соединенных параллельно, является наименьшее из рабочих напряжений конденсаторов, входящих в схему, Например, рабочее напряжение для цепи, изображенной на рис. 4.7, равно 25 В.
Рабочим напряжением для батареи конденсаторов, соединенных параллельно, является наименьшее из рабочих напряжений конденсаторов, входящих в схему, Например, рабочее напряжение для цепи, изображенной на рис. 4.7, равно 25 В.
Для конденсаторов, соединенных последовательно, рабочее напряжение подбирать труднее. Рассмотрим схему на рис. 4.8. Конденсатор С1 (1 мкФ, рабочее напряжение Vраб = 25 В) соединен последовательно с конденсатором С2 (10 мкФ, Vраб = 10 В). Поскольку на конденсаторе С1, обладающем меньшей емкостью, установится большее напряжение, чем на С2, то при расчетах следует прежде всего иметь в виду рабочее напряжение конденсатора С1, равное 25 В. Таким образом, V1 = 25 В. соотношения V1/ V2 = С1/ С2 следует, что
Поскольку рабочее напряжение конденсатора С2 выше, чем V2, рабочее напряжение данной батареи конденсаторов равно 25 + 2,5 = 27,5 В.
Следует заметить, что если бы рабочее напряжение конденсатора было равно, например, 2 В, как показано на рис. 4.9, то он зарядился бы
Рис. 4.8. Рис. 4.9.
4.8. Рис. 4.9.
Рис. 4.10.
Рис. 4.11
. Катушка индуктивности
до уровня рабочего напряжения прежде, чем напряжение на конденсаторе С1 достигло бы 25 В. Вот расчет для этого случая:
V2 = 2 В, тогда.
Следовательно, рабочее напряжение такой батареи будет составлять 20 + 2 = 22 В.
Пример 3
Конденсаторы С1 и С2, изображенные на рис. 4.10, имеют каждый рабочее напряжение 60 В. Какое максимальное напряжение может быть приложено к этой схеме?
Решение
Поскольку на конденсаторе С1 установится более высокое напряжение, чем на конденсаторе С2, то напряжение на нем раньше достигнет уровня рабочего напряжения. При V1 = 60 В
Максимальное напряжение, которое может быть подано на данную схему, составляет 60 + 20 = 80 В.
В этом видео рассказывается о понятии конденсатора:
Темы кодификатора ЕГЭ
: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах
.
Но прежде введём понятие электрической ёмкости
.
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым
.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду
. Коэффициент пропорциональности принято обозначать , так что
Величина называется электрической ёмкостью
проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара, — его радиус. Отсюда ёмкость шара:
Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2)
и (3)
мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В
. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад
(Ф). Из определения ёмкости (1)
Из определения ёмкости (1)
видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
МкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2)
:
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Так легче запомнить, не правда ли?
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор
. Он состоит из двух параллельных металлических пластин (называемых обкладками
), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный
конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора
.
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:
На рис. 1
1
(слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.
Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1
справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4)
. Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты
: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора
как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В.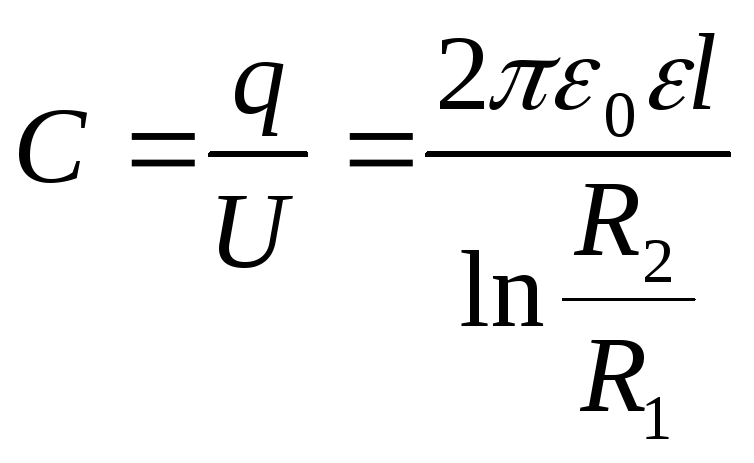 Формула (6)
Формула (6)
, таким образом, является модификацией формулы (1)
для случая системы двух проводников — конденсатора.
Из формул (6)
и (5)
легко находим ёмкость плоского воздушного конденсатора
:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4)
теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком
:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10)
: заполнение конденсатора диэлектриком увеличивает его ёмкость
.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины alt=»(d_2 > d_1)»>
, то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11)
и (7)
имеем:
Это можно переписать следующим образом:
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора
.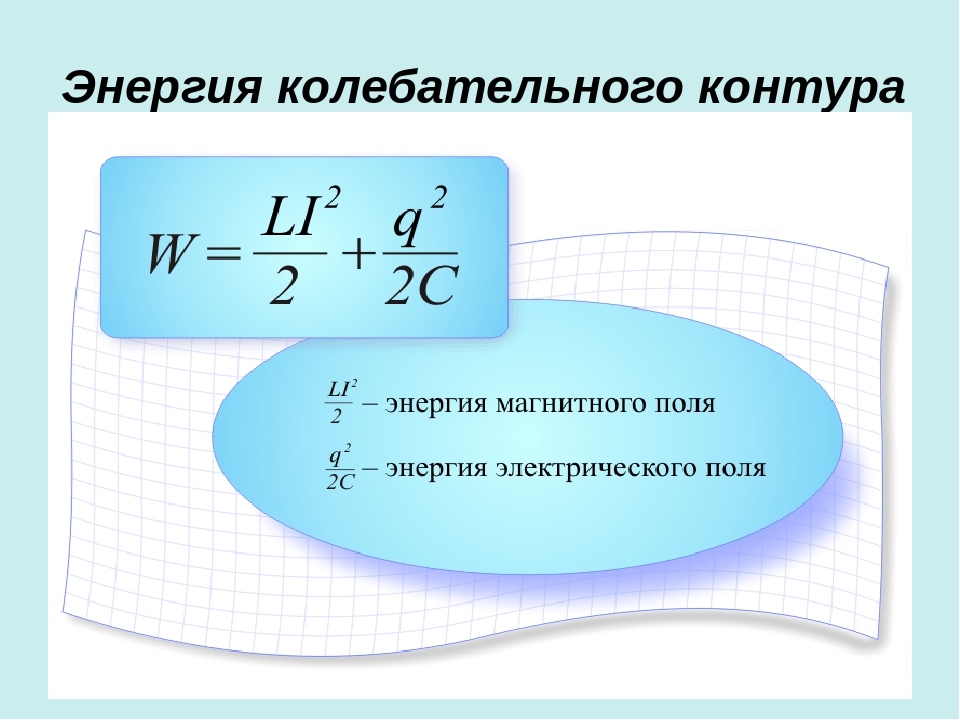
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12)
и (14)
.
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11)
получим:
При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12)
— (14)
останутся неизменными
. Ёмкость конденсатора в них теперь будет выражаться по формуле (10)
.
Итак, формулы (12)
— (14)
универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
Энергия электрического поля
Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.
Рассмотрим воздушный конденсатор и преобразуем формулу (14)
для его энергии:
Но — объём конденсатора. Получаем:
Получаем:
(15)
Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля
, сосредоточенного в некотором объёме .
Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.
Величина — энергия единицы объёма поля — называется объёмной плотностью энергии
. Из формулы (15)
получим:
(16)
В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.
Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15)
и (16)
будем иметь:
(17)
(18)
Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины;
– расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки;
– радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов (рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
ru.solverbook.com
Формула емкости конденсатора, С
Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:
называется емкостью конденсатора.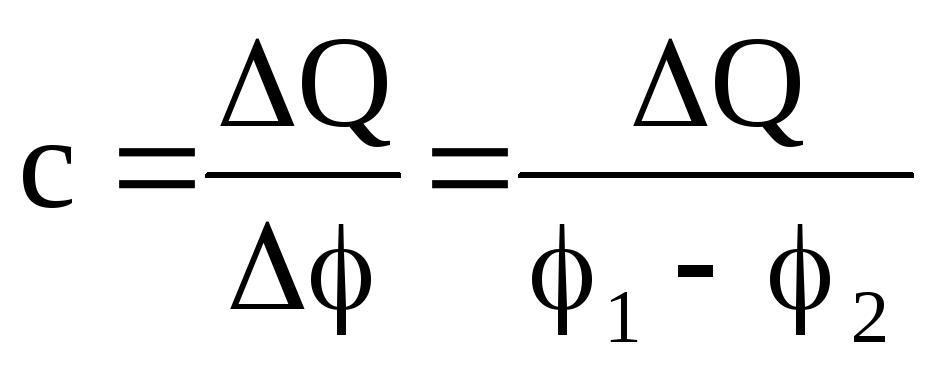 Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():
где – диэлектрическая проницаемость диэлектрика.
За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).
Формула электрической емкости плоского конденсатора
Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:
Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Формула электрической емкости цилиндрического конденсатора
Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:
Формула электрической емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком.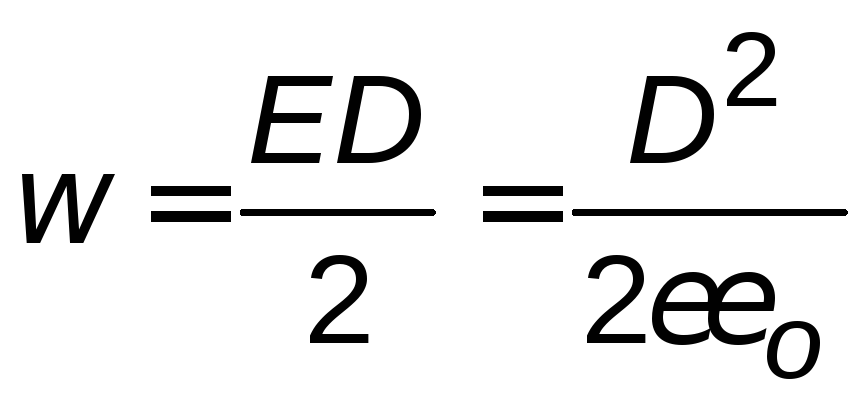 Емкость такого конденсатора находят как:
Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.
Примеры решения задач по теме «Емкость конденсатора»
ru.solverbook.com
Ёмкость конденсатора — Все формулы
Электрическая ёмкость — характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.
Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Конденсаторы можно классифицировать по следующим признакам и свойствам:
1) по назначению — конденсаторы постоянной и переменной емкости;
2) по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;
3) по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и т.д.
Так же есть:
Энергия конденсатора:
Ёмкость цилиндрического конденсатора:
Ёмкость плоского конденсатора:
Емкость сферического конденсатора:
В формуле мы использовали:
Электрическая ёмкость (ёмкость конденсатора)
Потенциал проводника (Напряжение)
Потенциал
Относительная диэлектрическая проницаемость
Электрическая постоянная
Площадь одной обкладки
Расстояние между обкладками
xn--b1agsdjmeuf9e.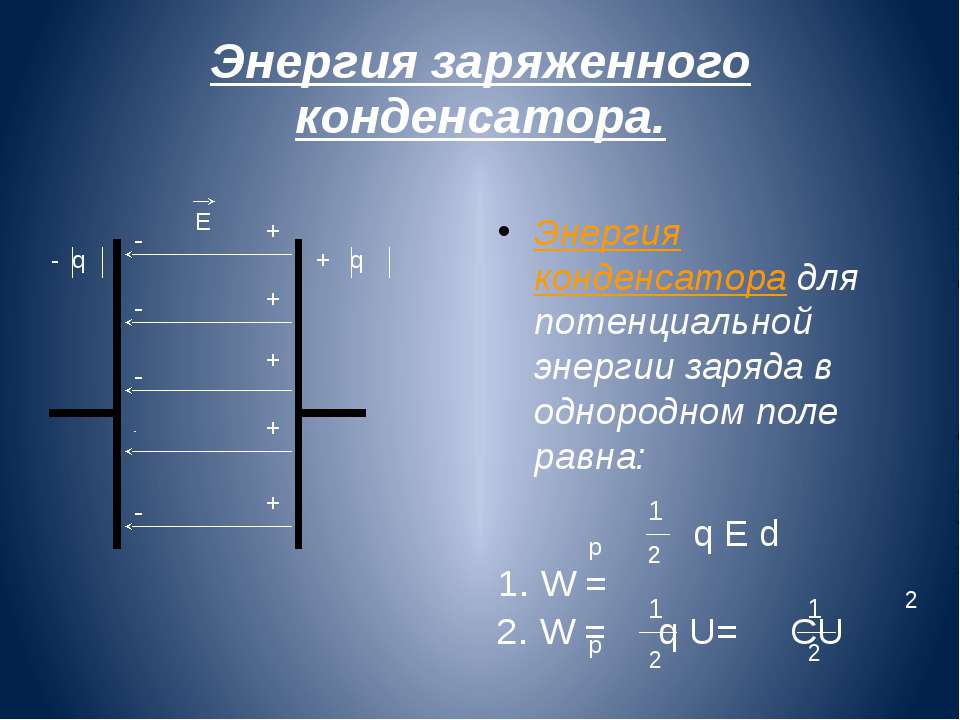 xn--p1ai
xn--p1ai
Заряд конденсатора, теория и примеры задач
Определение и заряд конденсатора
Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора – емкости (C).
По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов. Отличаются, также максимальные емкости и скорости зарядки и разряда конденсатора и батарейки.
Если к конденсатору присоединить источник напряжения (рис.1), то на одной из пластин конденсатора станут накапливаться отрицательные заряды (электроны), на другой положительные частицы (положительные ионы). Между обкладками конденсатора находится диэлектрик, вследствие этого, заряды не могут перебраться на противоположную пластину. Однако заметим, что электроны двигаются от источника тока до пластины конденсатора.
При первоначальном соединении конденсатора и источника тока на обкладках конденсатора много свободного места. Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.
Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.
Время, которое затрачивается на зарядку конденсатора от нулевого заряда (максимального тока) до полностью заряженного конденсатора (минимальная или нулевая сила тока) называют переходным периодом заряда конденсатора. На практике процесс зарядки конденсатора считают законченным, если сила тока уменьшилась до 1% от начальной величины.
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
Примеры решения задач
ru.solverbook.com
Формула электроемкости конденсатора
Обкладки должны иметь такую форму и быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально сосредоточено в ограниченной области пространства, между обкладками.
Назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.
Основной характеристикой конденсатора является электрическая емкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:
q – величина заряда на обкладке; – разность потенциалов между обкладками.
Электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. Если пространство между обкладками одного конденсатора заполнено диэлектриком с проницаемостью равной , а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в раз больше, чем емкость воздушного конденсатора ():
Формула электроемкости основных типов конденсаторов
При расчете электроемкости плоского конденсатора нарушением однородности поля около краёв обкладок обычно пренебрегают. Это становится возможным, если расстояние между пластинами существенно меньше, чем линейные размеры обкладок.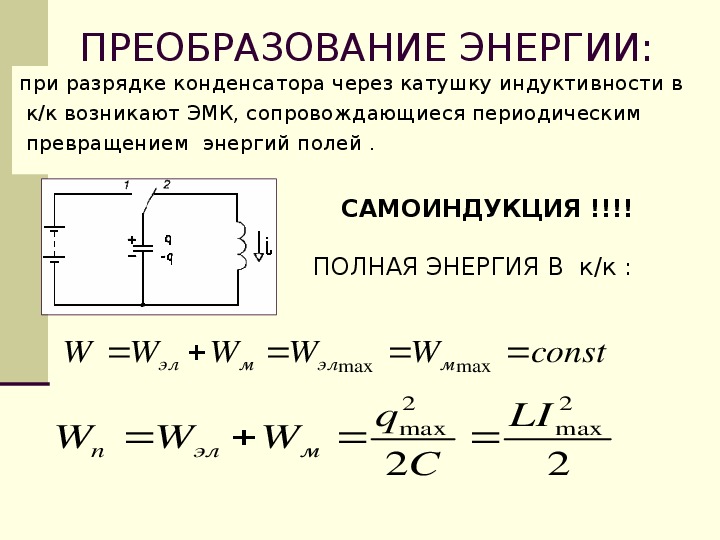 В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:
В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Если плоский конденсатор между обкладками имеет N слоев диэлектрика, при этом толщина каждого слоя равна , а диэлектрическая проницаемость , то его электрическую емкость рассчитывают при помощи формулы:
Цилиндрический конденсатор составляют две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполнено диэлектриком. При этом емкость цилиндрического конденсатора находят как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
У сферического конденсатора обкладками служат две концентрические сферические проводящие поверхности, пространство обкладками заполняет диэлектрик. Емкость сферического конденсатора вычисляют как:
где – радиусы обкладок конденсатора. Если , то можно считать, что , тогда, мы имеем:
Если , то можно считать, что , тогда, мы имеем:
так как – площадь поверхности сферы, и если обозначить , то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.
Электрическую емкость для линии из двух проводов находят как:
где d – расстояние между осями проводов; R – радиус проводов; l – длина линии.
Формулы для вычисления электрической емкости соединений конденсаторов
Если конденсаторы соединены параллельно, то суммарная емкость батареи (C) находится как сумма емкостей отдельных конденсаторов ():
При последовательном соединении конденсаторов емкость батареи вычисляют как:
Если последовательно соединены N конденсаторов, с емкостями то емкость батареи найдем как:
Сопротивление конденсатора
Если конденсатор включен в цепь с постоянного тока, то сопротивление конденсатора можно считать бесконечно большим.
При включении конденсатора в цепь переменного тока, его сопротивление носит название емкостного, и вычисляют его с помощью формулы:
где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.
Энергия поля конденсатора
Электрическое поле локализованное между пластинами конденсатора обладает энергией, которую можно вычислить при помощи формулы:
где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.
Энергия поля плоского конденсатора:
Примеры решения задач по теме «Электроемкость конденсатора»
ru.solverbook.com
Как найти заряд конденсатора 🚩 как определить величину заряда 🚩 Естественные науки
В обычном (без плагинов и модов) варианте Minecraft такого понятия, как конденсатор, не существует. Вернее, устройство, выполняющее его функции, имеется, но название у него совершенно другое — компаратор. Некоторая путаница в этом плане произошла еще в период разработки такого прибора. Сперва — в ноябре 2012-го — представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.
Сперва — в ноябре 2012-го — представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.
Подобное устройство существует для проверки заполненности расположенных позади него контейнеров. Таковыми могут быть сундуки (в том числе в виде ловушек), варочные стойки, раздатчики, выбрасыватели, печи, загрузочные воронки и т.п.
Помимо этого, его часто используют для сравнения двух сигналов редстоуна между собою — он выдает результат в соответствии с тем, как было запрограммировано в данной цепи, и с тем, какой режим выбран для самого механизма. В частности, компаратор может разрешить зажигание факела, если первый сигнал больше либо равен другому.
Также порой конденсатор-компаратор устанавливают рядом с проигрывателем, подключая его входом к последнему. Когда в звуковоспроизводящем устройстве проигрывается какая-либо пластинка, вышеупомянутый прибор будет выдавать сигнал, равный по силе порядковому номеру диска.
Скрафтить такой компаратор несложно, если имеется достаточно трудно добываемый ресурс — адский кварц. Его надо поставить в центральный слот верстака, над ним и по бокам от него установить три красных факела, а в нижнем ряду — такое же количество каменных блоков.
В большом количестве модов попадаются конденсаторы, имеющие самое разное предназначение. К примеру, в Galacticraft, где у геймеров есть возможность слетать на многие планеты для ознакомления с тамошними реалиями, появляется рецепт крафта кислородного конденсатора. Он служит для создания механизмов вроде коллектора и накопителя газа для дыхания, а также рамки воздушного шлюза. Для его изготовления четыре стальных пластины размещаются по углам верстака, в центре — оловянная канистра, а под нею — воздуховод. Остальные три ячейки занимают пластины из олова.
В JurassiCraft существует конденсатор потока — некий телепорт, позволяющий переместиться в удивительный игровой мир, кишащий динозаврами. Для создания такого прибора нужно поместить в два крайних вертикальных ряда шесть железных слитков, а в средний — два алмаза и между ними единицу пыли редстоуна. Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.
Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.
С модом Industrial Craft2 у игрока появляется возможность создавать как минимум два вида тепловых конденсаторов — красный и лазуритовый. Они служат исключительно для охлаждения ядерного реактора и для накопления его энергии и хороши для циклических сооружений такого типа. Остужаются они сами, соответственно, красной пылью или лазуритом.
Красный теплоконденсатор делается из семи единиц пыли редстоуна — их надо установить в виде буквы П и расставить под ними теплоотвод и теплообменник. Крафтинг же лазуритового устройства чуть посложнее. Для его создания четыре единицы пыли редстоуна расставляются по углам станка, в центр пойдет блок лазурита, по бокам от него — два красных тепловых конденсатора, сверху — теплоотвод реактора, а снизу — его же теплообменник.
В ThaumCraft, где сделан акцент на настоящем чародействе, конденсаторы тоже используются. Например, один из них — кристаллический — существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея — исследования, проводимого за специальным столом и с определенными приборами.
Например, один из них — кристаллический — существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея — исследования, проводимого за специальным столом и с определенными приборами.
Делается такой конденсатор из восьми тусклых осколков, в центр которых на верстаке помещается мистический деревянный блок. К сожалению, подобный прибор — равно как и его составляющие — просуществовал лишь до ThaumCraft 3, а в четвертой версии мода был упразднен.
www.kakprosto.ru
Соединение конденсаторов: формулы
Содержание:
- Последовательное соединение
- Онлайн калькулятор
- Смешанное соединение
- Параллельное соединение
- Видео
В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.
Последовательное соединение
При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.
В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.
Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.
Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.
Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.
Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.
Смешанное соединение
Параллельное соединение конденсаторов
Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.
Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.
В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.
Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.
electric-220.ru
Конденсатор — фундаментальный электронный компонент (наряду с резистором и катушкой индуктивности), предназначенный для накопления электрической энергии. Лучшей аналогией его работы будет сравнение с аккумуляторной батареей. Однако основой устройства последней являются обратимые химические реакции, а накопление заряда на обкладках конденсатора имеет исключительно электрическую природу.
Однако основой устройства последней являются обратимые химические реакции, а накопление заряда на обкладках конденсатора имеет исключительно электрическую природу.
Устройство и принцип работы
В простейшем варианте конструкция состоит из двух электродов в форме проводящих пластин
(называемых обкладками), разделённых диэлектриком, толщина которого ничтожно мала по сравнению с размерами обкладок. Практически применяемые радиоэлектронные компоненты содержат много слоёв диэлектрика и электродов. В качестве обозначения конденсатора на схеме используются два параллельных отрезка с пространством между ними. Они символизируют металлические пластины обкладок физического прибора, электрически разделённые между собой.
Многие считают Майкла Фарадея автором изобретения, но на самом деле это не так. Но он сделал главное — продемонстрировал первые практические примеры и способы использования этого прибора для хранения электрического заряда в своих экспериментах.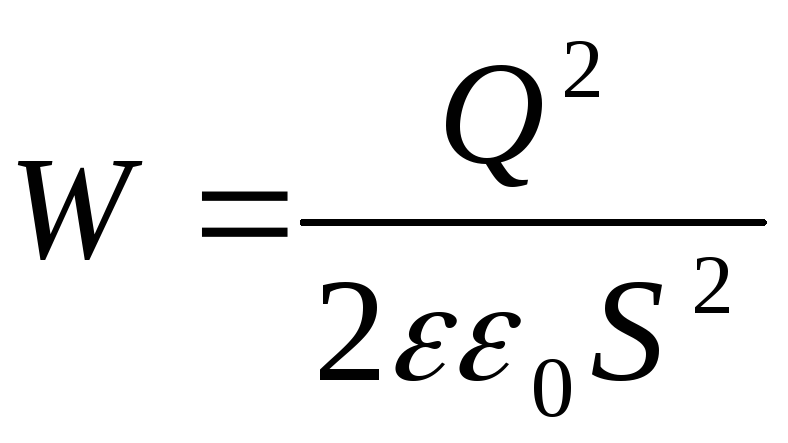 Благодаря Фарадею человечество получило способ измерять возможность накапливать заряд. Эта величина называется ёмкостью и измеряется в Фарадах.
Благодаря Фарадею человечество получило способ измерять возможность накапливать заряд. Эта величина называется ёмкостью и измеряется в Фарадах.
Работу конденсатора можно проиллюстрировать на примере событий, проходящих во вспышке цифровой фотокамеры за отрезок времени между нажатием кнопки и тем моментом, когда вспышка погаснет. Основой электронной схемы этого осветительного устройства является конденсатор, в котором происходит следующее:
- Зарядка. После нажатия кнопки поток электронов приходит в конденсатор и останавливается на одной из его пластин благодаря диэлектрику. Этот поток называется зарядным током.
- Накопление. Поскольку под действием электродвижущей силы всё больше и больше электронов будут поступать на обкладку и распределяться по ней, отрицательный заряд обкладки может расти до момента, пока накопленный потенциал не будет отталкивать поступающий избыточный поток электронов. Вторая пластина из-за дефицита электронов приобретает положительный заряд, по модулю равный отрицательному на первой.
 Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны.
Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны. - Сохранение. Поскольку обкладки заряжены противоположно, ионы и электроны будут притягиваться друг к другу, но не смогут соединиться из-за диэлектрической прослойки, создавая электростатическое поле. Благодаря этому полю конденсатор удерживает и сохраняет заряд.
- Разряд. Если в цепи появляется возможность для электронов протечь другим путём, то напряжение, накопленное между положительными и отрицательными зарядами обкладок, мгновенно реализуется в электрический ток, импульс которого в лампе вспышки преобразуется в световую энергию.
Таким образом в фотовспышке реализуется способность конденсатора накопить для импульса энергию из батареи питания.
Аккумулятор фотокамеры также является устройством, накапливающим энергию, но из-за химической природы накопления генерирует и отдаёт её медленно.
Ёмкость, заряд и напряжение
Свойство конденсатора сохранять заряд на пластинах в виде электростатического поля называется ёмкостью. Чем больше площадь обкладок и меньше расстояние между ними, тем большее количество заряда они способны накопить и, соответственно, обладают большей ёмкостью. При подаче напряжения на конденсатор отношение заряда Q к напряжению V даст значение ёмкости С. Формула заряда конденсатора будет выглядеть так:
Мера электрической ёмкости — фарад (Ф). Эта единица всегда положительная и не имеет отрицательных значений. 1 Ф равен ёмкости конденсатора, который способен сохранить заряд в 1 кулон на пластинах с напряжением в 1 вольт.
Фарад — очень большая единица измерения, для удобства использования применяют в основном её дольные меры:
- Микрофарад (мкФ): 1мкФ=1/1000000 Ф.

- Нанофарад (нФ): 1нФ=1/1000000000 Ф.
- Пикофарад (пФ): 1пФ=1/000000000000 Ф.
Кроме общего размера обкладок и расстояния между ними, существует ещё один параметр, влияющий на ёмкость — используемый тип изолятора. Фактор, по которому определяется способность диэлектрика повышать ёмкость конденсатора в сравнении с вакуумом, называется диэлектрической проницаемостью и описывается для разных материалов постоянной величиной от 1 и до бесконечности (теоретически):
- вакуум: 1,0000;
- воздух: 1,0006;
- бумага: 2,5-3,5;
- стекло: 3-10;
- оксиды металлов 6-20;
- электротехническая керамика: до 80.
Кроме конденсаторов с твёрдым диэлектриком (керамических, бумажных, плёночных) существуют также электролитические
. В последних используют алюминиевые или танталовые пластины с оксидным изолирующим слоем в качестве одного электрода и раствор электролита в качестве другого.
Главные особенности этой конструкции состоят в том, что она позволяет накапливать сравнительно внушительный заряд при небольших габаритах и является полярным электрическим накопителем.
То есть включается в электрическую цепь с соблюдением полярности.
Энергия, которую способны накопить большинство конденсаторов, обычно невелика — не больше сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому конденсаторы не могут заменить, например, аккумуляторные батареи в качестве источника питания. И хотя они способны эффективно выполнять только одну работу (сохранение заряда), их применение весьма многообразно в электрических цепях. Конденсаторы используются как фильтры, для сглаживания сетевого напряжения, в качестве устройств синхронизации и для других целей.
Какова формула энергии, запасенной в конденсаторе? – Rampfesthudson.com
Какова формула энергии, запасенной в конденсаторе?
Энергия, запасенная в конденсаторе, может быть выражена тремя способами: Ecap=QV2=CV22=Q22C E cap = QV 2 = CV 2 2 = Q 2 2 C , где Q — заряд, V — напряжение, C — емкость конденсатора. Энергия выражается в джоулях, если заряд – в кулонах, напряжение – в вольтах, а емкость – в фарадах.
Как найти энергию, запасенную в параллельном конденсаторе?
5:25Предлагаемый клип 98 секундКонденсаторы (10 из 11) параллельно, расчет накопленного заряда – YouTubeYouTubeНачало предложенного клипаКонец предложенного клипа
Каким образом должны быть подключены конденсаторы, чтобы получить максимальное количество энергии?
Конденсаторы, соединенные параллельно, суммируют свои емкости.Параллельная схема является наиболее удобным способом увеличения общего запаса электрического заряда.
Где хранится заряд в конденсаторе?
Конденсатор – это устройство для хранения энергии. Когда мы подключаем батарею к двум пластинам конденсатора, ток заряжает конденсатор, что приводит к накоплению зарядов на противоположных пластинах конденсатора. По мере накопления зарядов разность потенциалов на двух пластинах постепенно увеличивается.
Какой заряд хранится на каждом конденсаторе?
Следовательно, каждый конденсатор будет накапливать на своих пластинах одинаковое количество электрического заряда Q независимо от его емкости. Это связано с тем, что заряд, накопленный пластиной любого конденсатора, должен исходить от пластины соседнего конденсатора.
Это связано с тем, что заряд, накопленный пластиной любого конденсатора, должен исходить от пластины соседнего конденсатора.
Какой заряд хранится на каждом конденсаторе c1 и c2 в цепи, показанной ниже?
Таким образом, заряд каждого конденсатора равен Q=CeqV=32×9=6 мкФ.
Как увеличить емкость конденсатора?
Увеличение емкости, напряжения или того и другого увеличивает количество энергии, хранящейся в конденсаторе. В качестве альтернативы в конденсатор можно добавить диэлектрик.Диэлектрик представляет собой изолятор, помещенный между электродами. Это увеличивает емкость конденсатора без необходимости изменения его размеров.
Почему конденсатор подключен параллельно?
Конденсаторы — это устройства, используемые для хранения электрической энергии в виде электрического заряда. При параллельном подключении нескольких конденсаторов результирующая схема способна накапливать больше энергии, поскольку эквивалентная емкость представляет собой сумму индивидуальных емкостей всех задействованных конденсаторов.
Что произойдет, если конденсатор соединить последовательно?
При последовательном соединении конденсаторов емкостное сопротивление конденсатора действует как импеданс из-за частоты источника питания. Это емкостное реактивное сопротивление создает падение напряжения на каждом конденсаторе, поэтому последовательно соединенные конденсаторы действуют как сеть емкостного делителя напряжения.
Как последовательно соединить конденсаторы?
Когда конденсаторы соединены один за другим, говорят, что они соединены последовательно.Для конденсаторов, соединенных последовательно, общую емкость можно найти, сложив обратные величины отдельных емкостей и взяв обратную величину суммы.
Как рассчитать последовательные конденсаторы?
Когда конденсаторы соединены последовательно, общую емкость можно определить, взяв обратную величину емкости каждого конденсатора и сложив их вместе, чтобы получить обратную величину общей емкости.
Как решить проблему с конденсатором?
33:42Предлагаемый клип 120 секундКак решить любую проблему цепи с последовательными конденсаторами и …YouTubeНачало предложенного роликаКонец предложенного ролика
Могут ли конденсаторы повышать напряжение?
Поскольку конденсаторы накапливают энергию, они могут увеличивать кажущееся напряжение в некоторых цепях. Конденсаторы могут снизить потребление пикового тока в источниках питания, обеспечивая накопленную энергию во время пиковых нагрузок, которые могут привести к падению напряжения от источника питания.
Конденсаторы могут снизить потребление пикового тока в источниках питания, обеспечивая накопленную энергию во время пиковых нагрузок, которые могут привести к падению напряжения от источника питания.
Как рассчитать энергию, запасенную в заряженном конденсаторе
Шаги для расчета энергии, запасенной в заряженном конденсаторе
Шаг 1: Определите заряд, разность электрических потенциалов или емкость конденсатора, если они указаны.
Шаг 2: Подставьте известные значения переменных из шага 1 в одно из трех уравнений, чтобы найти электрическую потенциальную энергию, запасенную в конденсаторе.2}{2С}
$${экв}С
{/экв} – емкость конденсатора, {экв}В
{/eq} — разность электрических потенциалов, а {eq}q
{/eq} – это плата.
Давайте попрактикуемся в расчете энергии, запасенной в заряженном конденсаторе, на следующих двух примерах.
Пример задачи 1. Расчет энергии, запасенной в заряженном конденсаторе
Конденсатор емкостью {экв} 20\:{\rm F}
{/eq}, заряжается до потенциала {eq}100\:{\rm V}
{/экв}. 2}{2}
2}{2}
{/экв}.{-9}\:J}
{/экв} энергии хранится в этом конденсаторе.
Получите доступ к тысячам практических вопросов и пояснений!
РЕШЕНО:Уметь вычислять энергию заряженного конденсатора и понимать понятие энергии, связанное с электрическим полем.
Часть Д
Плоский конденсатор имеет площадь A и расстояние между пластинами d и заряжен до напряжения V. Используйте формулы из введения к задаче, чтобы получить формулу для энергии U конденсатора: Выразите ответ через A,d,V и соответствующие константы
Энергия заряженного конденсатора определяется выражением QV, где Q — заряд конденсатора, а V — разность потенциалов на конденсаторе: Энергия заряженного конденсатора может быть описана как энергия, связанная с электрическим полем, создаваемым внутри конденсатора:
AZd
Б
В этой задаче; выведете еще две формулы для энергии заряженного конденсатора; затем вы будете использовать конденсатор с плоскими пластинами в качестве носителя для получения формулы плотности энергии, связанной с электрическим полем: будет полезно вспомнить определение емкости, C Qiv и формулу для емкости
УУ
Отправить запрос Ответ
C = €A/d, где A — площадь каждой из пластин, а d — расстояние между пластинами.
 Как обычно, ¬o — это диэлектрическая проницаемость свободного пространства:
Как обычно, ¬o — это диэлектрическая проницаемость свободного пространства:
Вспомним теперь, что энергию конденсатора можно рассматривать как энергию электрического поля внутри конденсатора. Энергия электрического поля обычно описывается через плотность энергии
Плоский конденсатор является удобным устройством для получения формулы плотности энергии электрического поля, так как электрическое поле внутри него почти однородно. Тогда формулу для плотности энергии можно записать как u = 0
где U — энергия конденсатора, а V — объем конденсатора (а не напряжение).
Конденсаторы могут использоваться как «счетчики электрического заряда». Рассмотрим изначально незаряженный конденсатор емкостью $C$, его нижняя пластина заземлена, а верхняя пластина подключена к источнику электронов. (a) Если $N$ электронов течет на верхнюю пластину конденсатора, покажите, что результирующая разность потенциалов $V$ на конденсаторе прямо пропорциональна $N .(b)$ Предположим, что устройство измерения напряжения может точно определять изменения напряжения примерно на 1 $\mathrm{мВ}$ .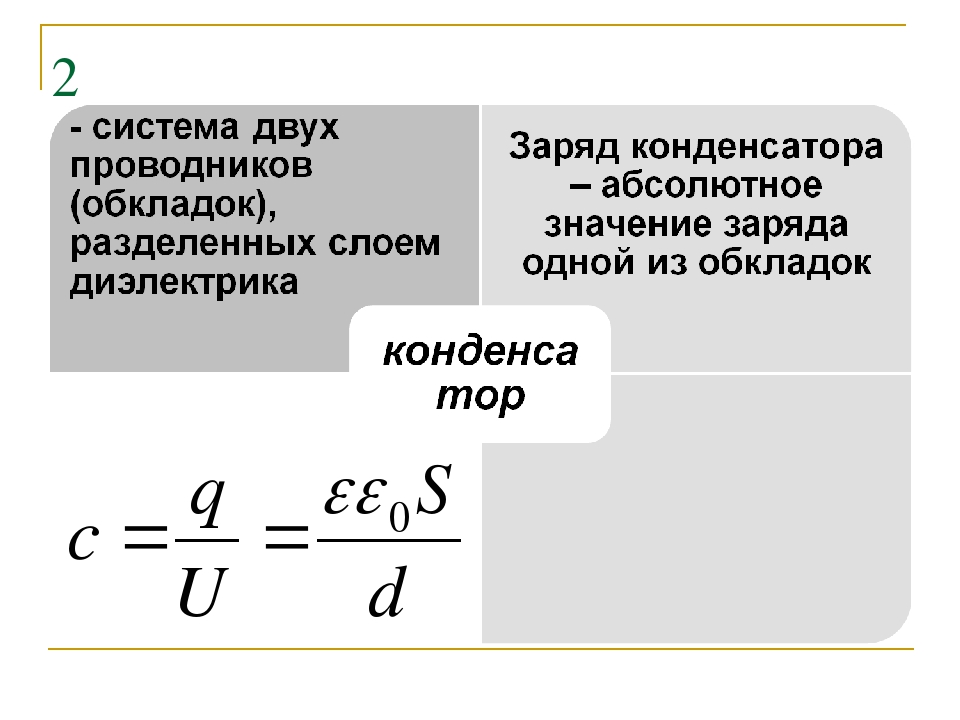 Какое значение $C$ потребуется для обнаружения каждого нового собранного электрона? (c) Используя современную полупроводниковую технологию, можно сконструировать конденсатор микронного размера с параллельными проводящими пластинами, разделенными изолирующим оксидом с диэлектрической проницаемостью $K=3$ и толщиной $d=100 \mathrm{нм}$ . Чтобы определить попадание отдельного электрона на пластину такого конденсатора, определите требуемое значение $\ell($ in $\mu \mathrm{m})$, предполагая квадратные пластины со стороной $\ell .$
Какое значение $C$ потребуется для обнаружения каждого нового собранного электрона? (c) Используя современную полупроводниковую технологию, можно сконструировать конденсатор микронного размера с параллельными проводящими пластинами, разделенными изолирующим оксидом с диэлектрической проницаемостью $K=3$ и толщиной $d=100 \mathrm{нм}$ . Чтобы определить попадание отдельного электрона на пластину такого конденсатора, определите требуемое значение $\ell($ in $\mu \mathrm{m})$, предполагая квадратные пластины со стороной $\ell .$
.
Электрическая потенциальная энергия (U) и электрический потенциал (В): (Примечания из C
Электрическая потенциальная энергия (U) и электрический потенциал
(V): ( Заметки от C.Erkals Лекции PHYS 221 )
Рассмотрим конденсатор с плоскими пластинами, который создает равномерную
электрическое поле между его большими пластинами.
Это достигается подключением каждой пластины к одному из выводов
источник питания (например, аккумулятор).
Рисунок 1: Электрическое поле создается заряженными пластинами
разделены расстоянием l. обвинения
на пластинах +Q и Q.
Рис. 2: Электрический заряд q перемещается из точки A в направлении
точка B с внешней силой T против электрической силы qE.
Рисунок 3, 4: Когда он перемещается на расстояние d, его
потенциальная энергия в точке B равна qEd относительно точки A.
Рисунок 5: При освобождении от B (T = 0) он ускорится
к нижней пластине. Как он движется
по направлению к нижней пластине ее потенциальная энергия уменьшается, а ее кинетическая энергия
увеличивается.Когда он достигает нижней
пластина (где мы можем выбрать Потенциальную энергию равной нулю), ее потенциал
энергия в точке A полностью преобразуется в кинетическую энергию в точке B:
Обратите внимание, что qEd — это работа, совершаемая полем в виде заряда.
движется под действием силы qE из В в А.
Здесь m — масса заряда q, а v — его скорость при достижении
точка А. Здесь мы предполагали, что электрические
поле однородное! Работа, выполненная полем E:
Давайте вспомним теорему о Кинетической Энергии-Работе (Рабочая Энергия
принцип):
, где мы ввели понятие потенциальной энергии и
консервативная сила (сила, под действием которой можно определить потенциальную энергию так,
что совершенная работа зависит только от разницы потенциальной энергии
функция оценивается в конечных точках).
Эмпирическое правило для принятия решения о том, является ли EPE
возрастание:
Если заряд движется в направлении, в котором он
нормально двигаться, его электрическая потенциальная энергия уменьшается. Если заряд перемещается в направлении, противоположном
чтобы он нормально двигался, его электрическая потенциальная энергия увеличивается. Эта ситуация аналогична ситуации
Эта ситуация аналогична ситуации
постоянное гравитационное поле (g = 9,8 м/с 2 ). Когда вы поднимаете предмет, вы
увеличивает свою гравитационную потенциальную энергию.Точно так же, когда вы опускаете объект, его гравитационная энергия
уменьшение.
Общая формула разницы потенциалов:
Работа, совершаемая полем E при воздействии на заряд q для перемещения
это из точки А в точку Б определяется как разность электрических потенциалов между
точки А и В:
Ясно, что потенциальная функция V может быть поставлена в соответствие каждому
точка в пространстве, окружающем распределение заряда (например, параллельная
тарелки).Приведенная выше формула обеспечивает
простой рецепт для расчета работы, совершаемой при перемещении заряда между двумя точками
где мы знаем величину разности потенциалов. Приведенные выше утверждения и формула справедливы независимо от
пути, по которому перемещается заряд.
Особый интерес представляет потенциал точечного заряда Q. Его можно найти, просто выполнив
интегрирование по простому пути (например, по прямой) из точки A
чье расстояние от Q равно r до бесконечности.Путь выбирается по радиальной линии так, что становится просто Edr.
Поскольку электрическое поле Q равно кОм/р 2 ,
Этот процесс определяет электрический потенциал точечной
обвинение. Обратите внимание, что потенциальная функция
скалярная величина, в отличие от электрического поля, являющегося векторной величиной. Теперь мы можем определить электрический потенциал
энергия системы зарядов или зарядовых распределений.Предположим, мы вычисляем работу, совершенную против
электрические силы при перемещении заряда q из бесконечности в точку на расстоянии r от
заряд Q. Работа дана:
Обратите внимание, что если q отрицательно, его знак должен использоваться в
уравнение! Таким образом, система
состоящий из отрицательного и положительного точечных зарядов, имеет отрицательный
потенциальная энергия.
Отрицательная потенциальная энергия означает, что необходимо совершить работу
против электрического поля при раздвигании зарядов!
Теперь рассмотрим более общий случай, связанный с
потенциал в окрестности ряда зарядов, как показано на рисунке
ниже:
Пусть r 1 ,r 2 ,r 3 —
расстояния зарядов до точки поля А, и r 12 , r 13 ,
r 23 представляют собой расстояние между зарядами.Электрический потенциал в точке А равен:
Пример:
Если мы принесем заряд Q из бесконечности и поместим его в точку А
проделанная работа будет:
Полная электрическая потенциальная энергия этой системы
зарядов, а именно работа, необходимая для приведения их в текущую позицию, может быть
рассчитывается следующим образом: сначала принесите q1 (ноль работы, так как нет заряда
вокруг еще), то в поле q1 вносим q2, то в поля q1 и q2
принести Q3. Добавьте всю работу, необходимую для
Добавьте всю работу, необходимую для
вычислить общую работу. Результат
будет:
Определение электрического поля по электрическому потенциалу:
Составляющая Е в любом направлении является отрицательной
скорость изменения потенциала с расстоянием в этом направлении:
Символ называется Градиент.
Электрическое поле – это градиент электрического потенциала.Линии электрического поля всегда
перпендикулярно эквипотенциальным поверхностям.
Эквипотенциальные поверхности:
Это воображаемые поверхности, окружающие заряд
распределение. В частности, если
распределение заряда сферическое (точечный заряд или равномерно заряженная сфера),
поверхности сферические, концентрические с центром заряда
распределение. Линии электрического поля
всегда перпендикулярны эквипотенциальным поверхностям.Уравнение подразумевает, что из-за
отрицательный знак, направление E противоположно направлению, в котором V
увеличивается; E направлена от высших к низшим уровням V (от высших
потенциал к более низкому потенциалу). Другой
Другой
Другими словами, градиент скаляра (в данном случае поля E) нормальен к поверхности
постоянного значения (эквипотенциальная поверхность) скаляра и в направлении
максимальная скорость изменения постоянного скаляра.
Помните об этом утверждении, когда будете проводить эксперимент.
Калькулятор энергии, запасенной в заряженном конденсаторе
Калькулятор энергии, запасенной в заряженном конденсаторе, рассчитает:
- Энергию, запасенную в заряженном конденсаторе, когда заданы величина заряда и разность потенциалов
- Энергия, запасенная в заряженном конденсаторе, когда количество заряда и емкость указаны
Обратите внимание, что для целей расчетов Калькулятор энергии, запасенной в заряженном конденсаторе, предполагает, что среда рассматривается как вакуум или воздух (ϵ = 1).
| Энергия, запасенная в заряженном конденсаторе, если заданы величина заряда и разность потенциалов, составляет Дж [Дж] |
| Энергия Дж [Джоулей] |
| Энергия, хранящаяся в заряженном конденсаторе, если заданы величина заряда и емкость W = × 2 2 / 2 |
|---|
| Энергия, накопленная в расчетах конденсатора |
| Вт = Q 2 / 90 165 2C W = 2 / 2 × 5 8 |
Энергетика, хранящаяся в заряженном конденсаторе калькулятор входных данных. |
| Электрический заряд (Q) C [Кулон] |
| Разница потенциала (ΔV) V [Volt] |
| емкость (C) F [Farad] |
Обратите внимание, что формула для каждого расчета вместе с подробными расчетами доступны ниже.Когда вы вводите конкретные коэффициенты каждой энергии, хранящейся в расчете заряженного конденсатора, калькулятор энергии, хранящейся в заряженном конденсаторе, автоматически вычисляет результаты и обновляет элементы формулы физики с каждым элементом энергии, хранящейся в расчете заряженного конденсатора. Затем вы можете отправить по электронной почте или распечатать эту энергию, хранящуюся в расчете заряженного конденсатора, для последующего использования.
Мы надеемся, что Калькулятор энергии, хранящейся в заряженном конденсаторе, был вам полезен при изучении физики. Если да, просим вас оценить этот калькулятор физики и, если у вас есть время, поделиться им в своей любимой социальной сети. Это позволяет нам распределять будущие ресурсы и сохранять эти калькуляторы по физике и учебные материалы бесплатными для всех по всему миру. Мы считаем, что у всех должен быть бесплатный доступ к учебным материалам по физике. Делясь с вами, вы помогаете нам охватить всех студентов-физиков и тех, кто интересуется физикой по всему миру.
Это позволяет нам распределять будущие ресурсы и сохранять эти калькуляторы по физике и учебные материалы бесплатными для всех по всему миру. Мы считаем, что у всех должен быть бесплатный доступ к учебным материалам по физике. Делясь с вами, вы помогаете нам охватить всех студентов-физиков и тех, кто интересуется физикой по всему миру.
★ ★ ★ ★ ★ ★ [Нет голосов]
[Нет голосов]
Разделы физики с учетом учебников
Раздел 1: Единицы и измерения
Раздел 15: Электродинамика
Формула и расчет
W = C × ΔV 2 2 / 2
W =
Q 2
/ / 2C
Электростатика Учебники физики, связанные с энергией Хранится в заряженном конденсаторе Калькулятор
Следующие учебные пособия по физике представлены в разделе «Электростатика» наших бесплатных учебных пособий по физике. Каждое учебное пособие по электростатике включает подробную формулу электростатики и пример того, как рассчитать и решить конкретные вопросы и проблемы электростатики. В конце каждого учебника по электростатике вы найдете вопросы по пересмотру электростатики со скрытым ответом, который открывается при нажатии. Это позволяет вам узнать об электростатике и проверить свои знания по физике, отвечая на вопросы теста по электростатике.
Каждое учебное пособие по электростатике включает подробную формулу электростатики и пример того, как рассчитать и решить конкретные вопросы и проблемы электростатики. В конце каждого учебника по электростатике вы найдете вопросы по пересмотру электростатики со скрытым ответом, который открывается при нажатии. Это позволяет вам узнать об электростатике и проверить свои знания по физике, отвечая на вопросы теста по электростатике.
Калькуляторы физики
Вам также могут пригодиться следующие калькуляторы физики.
Калькулятор заряда и энергии конденсатора
Легко рассчитать заряд и энергию любого конденсатора, зная его емкость и напряжение. Поддерживает несколько единиц измерения (мВ, В, кВ, МВ, ГВ, мФ, Ф и т. д.) для входных и выходных данных (Дж, кДж, МДж, кал, ккал, эВ, кэВ, Кл, кКл, мс и т. д.) .).
Быстрая навигация:
- Использование калькулятора заряда и энергии конденсатора
- Объяснение заряда конденсатора, энергии, емкости и напряжения
- Уравнения заряда конденсатора
- Формула энергии конденсатора
- Примеры расчета заряда конденсатора и энергии
Использование калькулятора заряда и энергии конденсатора
Этот инструмент работает как вычислитель заряда конденсатора и вычислитель энергии конденсатора , требуемые входные данные одинаковы в обоих случаях: емкость и напряжение, протекающие через конденсатор. Он поддерживает широкий диапазон входных и выходных единиц измерения. Просто введите два необходимых измерения и выберите единицы измерения для энергии и заряда (или используйте значения по умолчанию).
Он поддерживает широкий диапазон входных и выходных единиц измерения. Просто введите два необходимых измерения и выберите единицы измерения для энергии и заряда (или используйте значения по умолчанию).
Калькулятор использует известные уравнения (как описано ниже) и операции преобразования.
Объяснение заряда конденсатора, энергии, емкости и напряжения
Конденсатор состоит из двух параллельных проводящих (металлических) пластин, разделенных специальным изоляционным материалом, называемым «диэлектриком».Когда на пластины подается напряжение, одна пластина заряжается положительно по отношению к напряжению питания, а другая имеет равный и противоположный отрицательный заряд. Это приводит к уникальному свойству конденсатора содержать электрический заряд, подобно перезаряжаемой батарее. Электрический заряд 90 599 90 600, который может удерживать конденсатор, обозначается как 90 599 Q 90 600 (измеряется в кулонах (C)).
Напряжение (В) — это просто разность электрических потенциалов между двумя точками, измеряемая в вольтах (В). Способность конденсатора накапливать электрический заряд между его пластинами называется емкостью и обозначается C и измеряется в фарадах (Ф), что равно 1 Кулон/Вольт. Оно пропорционально размеру пластин и обратно пропорционально расстоянию между пластинами. Энергия (Э) — это количество работы, которую может выполнить накопленный заряд, и измеряется в джоулях, электрон-вольтах, калориях и т. д.
Способность конденсатора накапливать электрический заряд между его пластинами называется емкостью и обозначается C и измеряется в фарадах (Ф), что равно 1 Кулон/Вольт. Оно пропорционально размеру пластин и обратно пропорционально расстоянию между пластинами. Энергия (Э) — это количество работы, которую может выполнить накопленный заряд, и измеряется в джоулях, электрон-вольтах, калориях и т. д.
Уравнения заряда конденсатора
Из соотношений между зарядом (Q), емкостью (C) и напряжением (V) мы можем выразить формулу заряда емкости в виде следующих трех уравнений:
В первом показано, как найти емкость на основе заряда и напряжения, во втором — уравнение заряда конденсатора, а в третьем — уравнение напряжения конденсатора.
Формула энергии конденсатора
Энергия (или работа) конденсатора также может быть рассчитана, если известны его емкость (C) и напряжение (В), используя уравнение:
, где E — энергия (иногда пишется как W для работы).
Примеры расчета заряда конденсатора и энергии
Пример 1: Известно, что конденсатор на материнской плате компьютера имеет емкость 5 Фарад и известное напряжение 50 мВ.Чему равен заряд конденсатора в фарадах? Поскольку 1 кулон = 1 фарад-вольт, мы сначала преобразуем 50 мВ в 0,050 В, а затем применяем уравнение заряда конденсатора C = Q · V = 5 · 0,050 = 0,25 Кл.
Конечно, при использовании нашего калькулятора заряда конденсатора вам не нужно будет выполнять эти преобразования единиц измерения, так как они обрабатываются для вас на лету.
Пример 2: Конденсатор рассчитан на 0,1 Фарад, и известно, что напряжение составляет 10 Ват. Какова энергия конденсатора? Мы просто подставляем в уравнение энергии конденсатора выше: E = 0.1 · 10 2 / 2 = 10/2 = 5 Дж (Джоулей).
Ссылки
[1] Специальная публикация NIST 330 (2008 г.) — «Международная система единиц (СИ)», под редакцией Барри Н. Тейлора и Амблера Томпсона, с. 52
Тейлора и Амблера Томпсона, с. 52
[2] «Международная система единиц» (СИ) (2006 г., 8-е изд.). Bureau international des poids et mesures стр. 142–143. ISBN 92-822-2213-6
Как будет храниться энергия в полностью заряженном конденсаторе? – М.В.Организинг
Как будет храниться энергия в полностью заряженном конденсаторе?
Энергия, запасенная в конденсаторе, может быть выражена тремя способами: Ecap=QV2=CV22=Q22C E cap = QV 2 = CV 2 2 = Q 2 2 C , где Q — заряд, V — напряжение, C — емкость конденсатора.Энергия в джоулях для заряда в кулонах, напряжения в вольтах и емкости в фарадах.
Что такое параллельный пластинчатый конденсатор? Выведите выражение для энергии, запасенной в конденсаторе?
рассмотрим разделение d плоского конденсатора. Пусть U=12CV2 — энергия, запасенная в пространстве объемом V=A×d между пластинами. Это общее выражение, которое применимо к электрическим полям, обусловленным любой конфигурацией зарядов.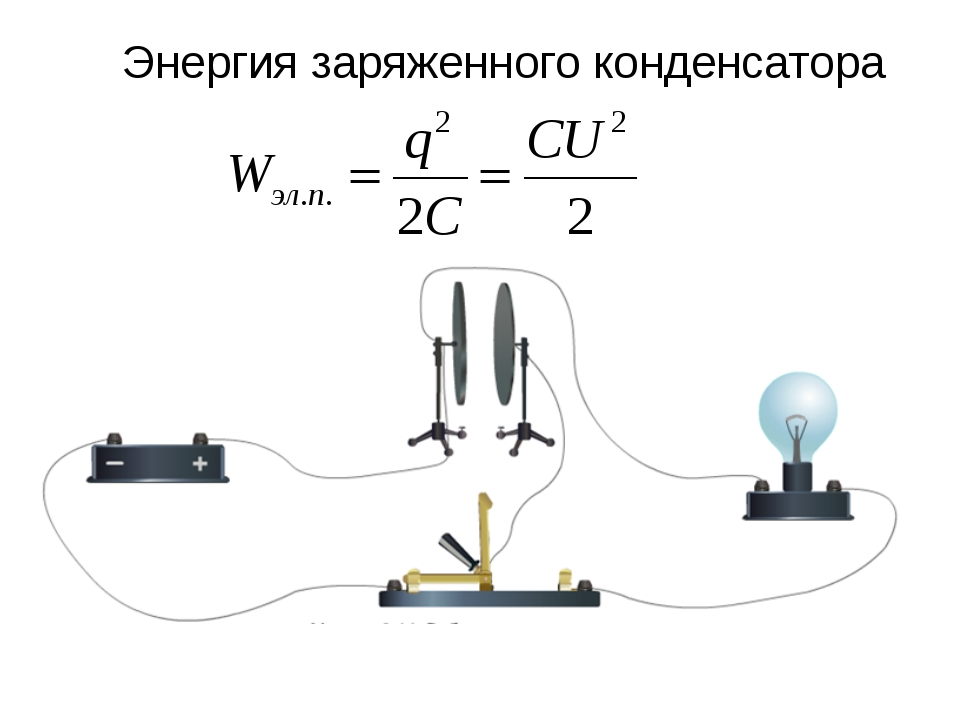
Как найти энергию плоского конденсатора?
Энергия, запасенная в конденсаторе, может быть рассчитана из эквивалентных выражений: Эта энергия запасается в электрическом поле.J. Исходя из определения напряжения как энергии на единицу заряда, можно было бы ожидать, что энергия, хранящаяся в этом идеальном конденсаторе, будет равна QV.
Что такое плотность энергии в конденсаторе?
Плотность энергии определяется как общая энергия на единицу объема конденсатора. Поскольку теперь для плоского конденсатора A × d = объем пространства между пластинами, которым ограничено электрическое поле E = V / d. Следовательно, Энергия запасается на единицу объема.
Какой аккумулятор имеет наибольшую плотность энергии?
Литий-ионный
Какова плотность энергии конденсатора и как в нем сохраняется энергия?
Плотность энергии конденсатора — это энергия, запасенная в единице объема.
Какова плотность заряда конденсатора?
Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.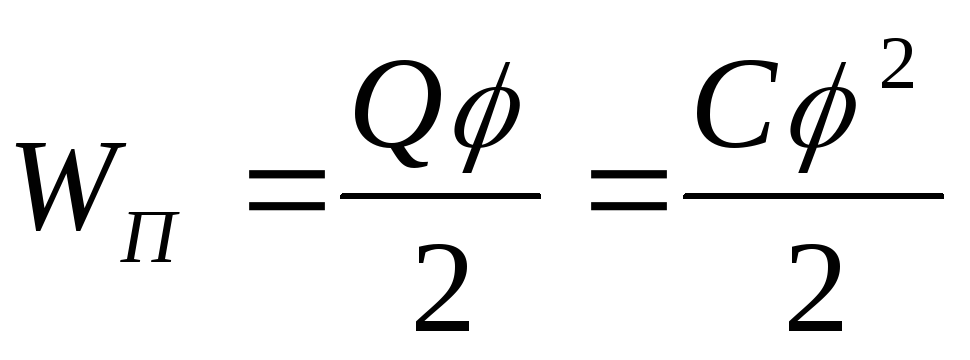 1F=1C1V. По определению, конденсатор емкостью 1,0 Ф способен сохранять заряд 1,0 Кл (очень большое количество заряда), когда разность потенциалов между его пластинами составляет всего 1,0 В.
1F=1C1V. По определению, конденсатор емкостью 1,0 Ф способен сохранять заряд 1,0 Кл (очень большое количество заряда), когда разность потенциалов между его пластинами составляет всего 1,0 В.
Как найти чистый заряд конденсатора?
Суммарный заряд на конденсаторе всегда равен нулю, потому что на пластинах есть одинаковые и разные заряды.Следовательно, конденсатор не является накопителем заряда. Это устройство для хранения электрической энергии. В конденсаторе любой формы накопленный заряд при зарядке напряжением V равен q=cv, где +cv хранится на одной пластине, а -cv хранится на другой пластине.
В чем разница между емкостью и конденсатором?
Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии. Он состоит как минимум из двух электрических проводников, разделенных расстоянием. Объем памяти в конденсаторе определяется свойством, называемым емкостью, о котором вы узнаете подробнее чуть позже в этом разделе.
Чему равна плотность заряда?
Плотность носителей заряда в проводнике равна количеству подвижных носителей заряда (электронов, ионов и т. д.) в единице объема. Плотность заряда в любой точке равна плотности носителей заряда, умноженной на элементарный заряд частиц.
Где самая высокая плотность заряда?
заряженный Г-образный проводник; в этих местах должна иметь место наибольшая плотность поверхностного заряда. Поле слабое во внутренних углах.Знаки зарядов на проводящих поверхностях можно вывести из того факта, что электрические поля направлены от положительных зарядов к отрицательным.
Что такое формула плотности заряда?
Формулы плотности заряда | Решенные примеры вопросов Плотность заряда является мерой того, сколько электрического заряда накапливается в определенном поле. В зависимости от природы формула плотности заряда может быть представлена следующим образом: (i) линейная плотность заряда; λ=ql, где q — заряд, а li — длина, по которой он распространяется.
Как рассчитать поверхностный заряд?
Поверхностная плотность заряда — это мера того, сколько электрического заряда накапливается на поверхности. Он рассчитывается как плата за единицу площади поверхности. Если q — заряд, а A — площадь поверхности, то плотность поверхностного заряда определяется выражением; σ=qA. Единицей плотности поверхностного заряда в системе СИ является См–2.
Что вызывает поверхностный заряд?
Свинцово-кислотные аккумуляторы инерционны и не могут быстро преобразовывать сульфат свинца в свинец и диоксид свинца во время зарядки.Это отсроченное действие приводит к тому, что большая часть активности заряда происходит на поверхностях пластин, что приводит к повышенному состоянию заряда (SoC) снаружи.
Что такое поверхностный заряд?
Поверхностный заряд — это двумерная поверхность с ненулевым электрическим зарядом. Эти электрические заряды ограничены этой двумерной поверхностью, а поверхностная плотность заряда, измеренная в кулонах на квадратный метр (Кл•м-2), используется для описания распределения заряда на поверхности.
Какова поверхностная плотность заряда Земли?
Поверхность земли имеет отрицательную поверхностную плотность заряда 10-9 см-2.Разность потенциалов в 400 кВ между верхним слоем атмосферы и поверхностью приводит (из-за низкой проводимости нижних слоев атмосферы) к току всего 1800 А по всему земному шару.
Как плотность заряда связана с электрическим полем?
Поскольку электрический заряд является источником электрического поля, электрическое поле в любой точке пространства может быть математически связано с присутствующими зарядами. Дивергенция электрического поля в точке пространства равна плотности заряда, деленной на диэлектрическую проницаемость пространства.…
Какая сила действует на поверхностный заряд?
∴ F= зарядов пусть поверхностная плотность заряда будет σ .ds для области ds. ∴F=2ϵ0kσ. σds. ⇒dsF=2ϵ0kσ2. ∴f=2ϵ0kσ2, которая называется механической силой на единицу площади.
Какова плотность поверхностного заряда на этой стороне монеты?
Ответы и ответы Поскольку электрическое поле находится прямо над лицевой стороной монеты, монету можно смоделировать как бесконечную плоскость заряда Eplane = η/(2ε0). Объединение этих уравнений даст Eplane = Q/(A⋅2⋅ε0).Преобразование этого уравнения для определения поверхностной плотности заряда будет (Q/A) = (Eplane⋅2⋅ε0).
Объединение этих уравнений даст Eplane = Q/(A⋅2⋅ε0).Преобразование этого уравнения для определения поверхностной плотности заряда будет (Q/A) = (Eplane⋅2⋅ε0).
Как называется сила, приходящаяся на единицу площади?
Давление определяется как сила на единицу площади.
Как рассчитать электростатическое давление?
Возьмем, таким образом, элемент поверхности dA с зарядом σdA. Как прекрасно объяснил Перселл, сила, действующая на такой элемент поверхности, определяется средним значением напряженности электрического поля внутри и снаружи. Поскольку поле внутри равно нулю, общая сила, действующая на элемент поверхности, равна dF=12σdA×4πR2σ4πϵ0ˆrR2=σ22ϵ0ˆrdA.
Как найти формулу силы?
Изучение формулы. Умножьте массу на ускорение. Сила (F), необходимая для перемещения объекта массой (m) с ускорением (a), определяется формулой F = m x a. Итак, сила = масса, умноженная на ускорение.
Какое выражение используется для нахождения силы правильно?
Ответ: Формула силы говорит, что сила равна массе (m), умноженной на ускорение (a). Если у вас есть любые две из трех переменных, вы можете найти третью.Сила измеряется в ньютонах (Н), масса – в килограммах (кг), а ускорение – в метрах в секунду в квадрате (м/с2).
Если у вас есть любые две из трех переменных, вы можете найти третью.Сила измеряется в ньютонах (Н), масса – в килограммах (кг), а ускорение – в метрах в секунду в квадрате (м/с2).
Где хранится энергия в конденсаторе?
Заряженный конденсатор запасает энергию в электрическом поле между своими пластинами. Когда конденсатор заряжается, электрическое поле нарастает. При отключении заряженного конденсатора от батареи его энергия остается в поле в пространстве между его пластинами.
Каково основное использование конденсатора?
Конденсаторы широко используются как части электрических цепей во многих распространенных электрических устройствах.В отличие от резистора, конденсатор не рассеивает энергию. Вместо этого конденсатор хранит энергию в виде электростатического поля между его пластинами.
Как найти заряд, накопленный в конденсаторе?
Заряд конденсатора, разделение пластин и напряжение Кроме того, чем большей емкостью обладает конденсатор, тем больший заряд будет нагнетаться данным напряжением. Это соотношение описывается формулой q=CV, где q — накопленный заряд, C — емкость, а V — приложенное напряжение.
Это соотношение описывается формулой q=CV, где q — накопленный заряд, C — емкость, а V — приложенное напряжение.
Какова формула для конденсаторов, включенных параллельно?
Каждый подключен непосредственно к источнику напряжения, как если бы он был один, поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы. CpV = C1V + C2V + C3V.
Какой заряд хранится на каждом конденсаторе?
Поскольку конденсаторы соединены последовательно, заряд каждого конденсатора равен Qdc=6 мкКл.
Когда конденсаторы соединены параллельно, что должно быть одинаковым для двух конденсаторов?
Когда конденсаторы соединены параллельно, что должно быть одинаковым для двух конденсаторов? Заряд в двух конденсаторах разный. Конденсаторы, соединенные параллельно, подключены к одним и тем же начальным и конечным точкам входа и выхода, поэтому имеют одинаковую разность потенциалов.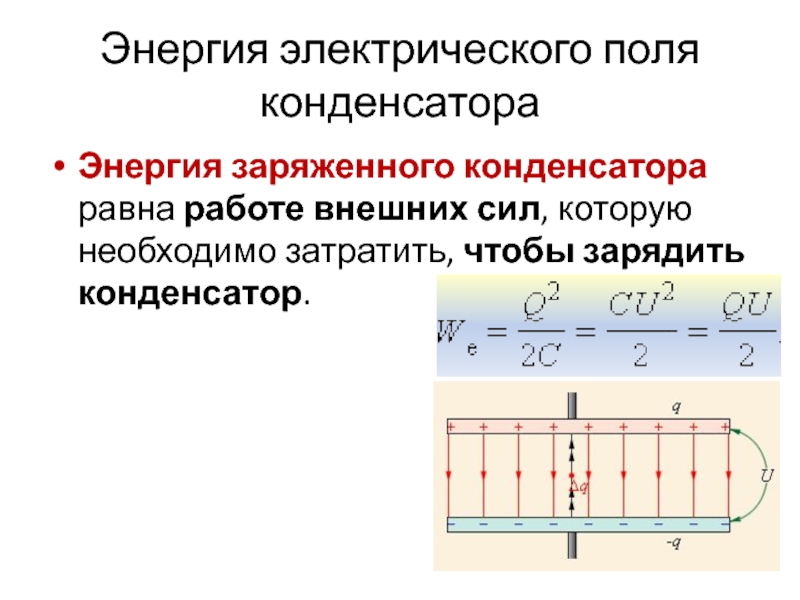
При параллельном соединении конденсаторов они одинаковые?
Когда конденсаторы соединены параллельно, общая емкость представляет собой сумму емкостей отдельных конденсаторов.Если два или более конденсатора соединены параллельно, общий эффект будет таким же, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.
Что происходит, когда конденсаторы соединены параллельно?
При параллельном соединении нескольких конденсаторов результирующая емкость цепи увеличивается и позволяет хранить больше энергии, поскольку эквивалентная емкость представляет собой сумму индивидуальных емкостей всех задействованных конденсаторов.
Имеют ли последовательно соединенные конденсаторы одинаковую энергию?
Также для конденсаторов, соединенных последовательно, все последовательно соединенные конденсаторы будут иметь одинаковый зарядный ток, протекающий через них, как iT = i1 = i2 = i3 и т. д.Два или более последовательно соединенных конденсатора всегда будут иметь одинаковый кулоновый заряд на своих обкладках.
Что такое постоянная параллельного конденсатора?
При параллельном соединении конденсаторов общая или эквивалентная емкость CT в цепи равна сумме всех отдельных конденсаторов, сложенных вместе. …
Как конденсаторы повышают напряжение?
Как увеличить напряжение с помощью двух конденсаторов
- Подсоедините положительный вывод одного конденсатора к отрицательному выводу другого конденсатора (для неполяризованных конденсаторов соедините любые два вывода вместе).
- Рассчитайте общую емкость Ct = (C1 x C2)/(C1 + C2).
- Подсоедините положительный щуп измерителя емкости к положительному свободному выводу комбинированного конденсатора.
Конденсаторы заряжаются быстрее последовательно или параллельно?
Параллельные конденсаторы имеют большую емкость, поэтому их зарядка займет больше времени. Так что заряжаясь одним и тем же током, они будут заряжаться быстрее. Последовательные конденсаторы имеют более высокое номинальное напряжение, поскольку общее напряжение распределяется по конденсаторам.
Когда конденсатор увеличивает площадь пластины?
Емкость пропорциональна площади пластины. Таким образом, любое увеличение площади пластины будет увеличивать емкость.
Влияет ли площадь пластины на напряжение?
Объяснение: Большая площадь пластин приводит к большему потоку поля (заряд, собранный на пластинах) при данной силе поля (напряжение на пластинах). РАСПОЛОЖЕНИЕ ПЛАСТИН: при прочих равных условиях большее расстояние между пластинами дает меньшую емкость; более близкое расстояние между пластинами дает большую емкость.
Пропустит ли конденсатор постоянный ток?
Конденсатор (также известный как конденсатор) представляет собой устройство с двумя металлическими пластинами, разделенными изолирующей средой, такой как фольга, ламинированная бумага, воздух и т. д. Имейте в виду, что конденсатор действует как разомкнутая цепь при постоянном токе, т. е. он работает только при переменном напряжении.
Какой конденсатор имеет самую высокую диэлектрическую проницаемость?
Answer Expert Verified Mica: обычно от 3 до 6.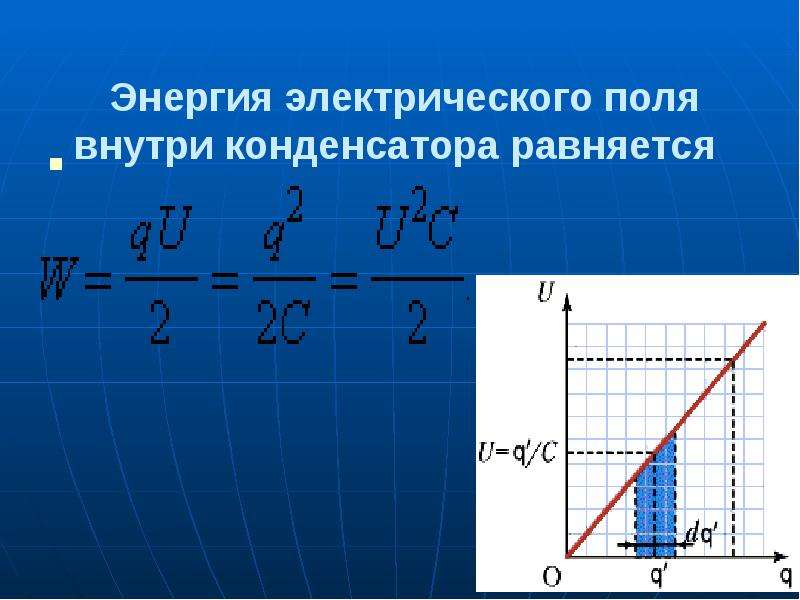




 Пользуясь этой формулой, рассчитайте стоимость колодца из 13 колец. Ответ укажите в рублях.
Пользуясь этой формулой, рассчитайте стоимость колодца из 13 колец. Ответ укажите в рублях. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ укажите в рублях.
Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ укажите в рублях.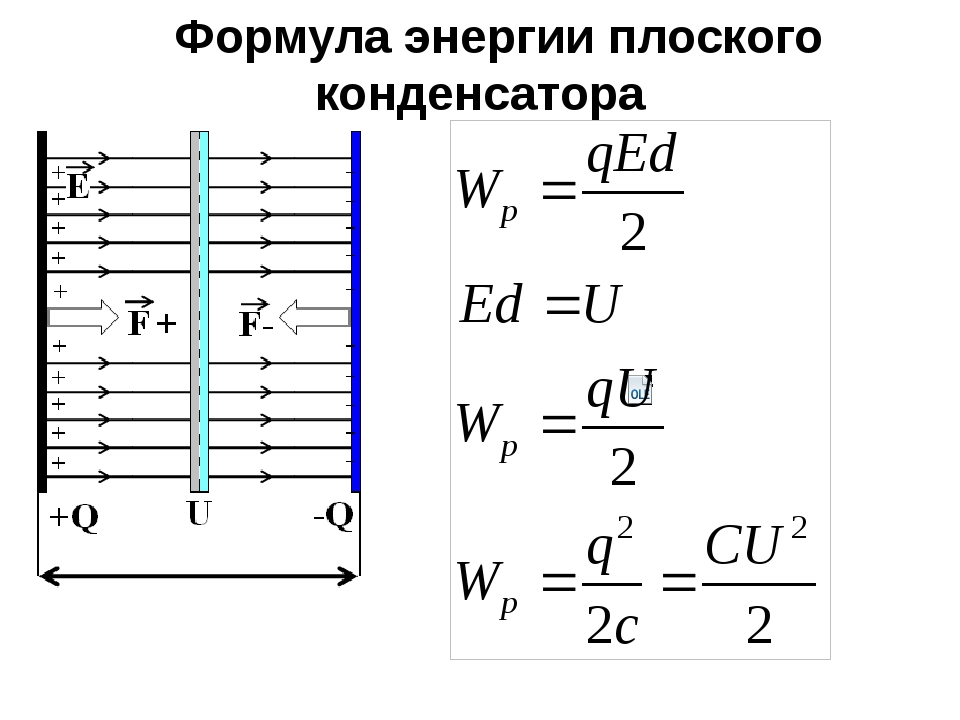 Пользуясь этой формулой, найдите радиус R(в метрах), если угловая скорость равна 4 с −1, а центростремительное ускорение равно 96 м/с2.
Пользуясь этой формулой, найдите радиус R(в метрах), если угловая скорость равна 4 с −1, а центростремительное ускорение равно 96 м/с2. Скольким градусам по шкале Цельсия соответствует 210° по шкале Фаренгейта? Ответ округлите до десятых.
Скольким градусам по шкале Цельсия соответствует 210° по шкале Фаренгейта? Ответ округлите до десятых. Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 588 Вт, а сила тока равна 7 А.
Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 588 Вт, а сила тока равна 7 А.
 Скольким градусам по шкале Фаренгейта соответствует −15° по шкале Цельсия?
Скольким градусам по шкале Фаренгейта соответствует −15° по шкале Цельсия? Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 5,5 с −1, а центростремительное ускорение равно 60,5 м/с2.
Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 5,5 с −1, а центростремительное ускорение равно 60,5 м/с2.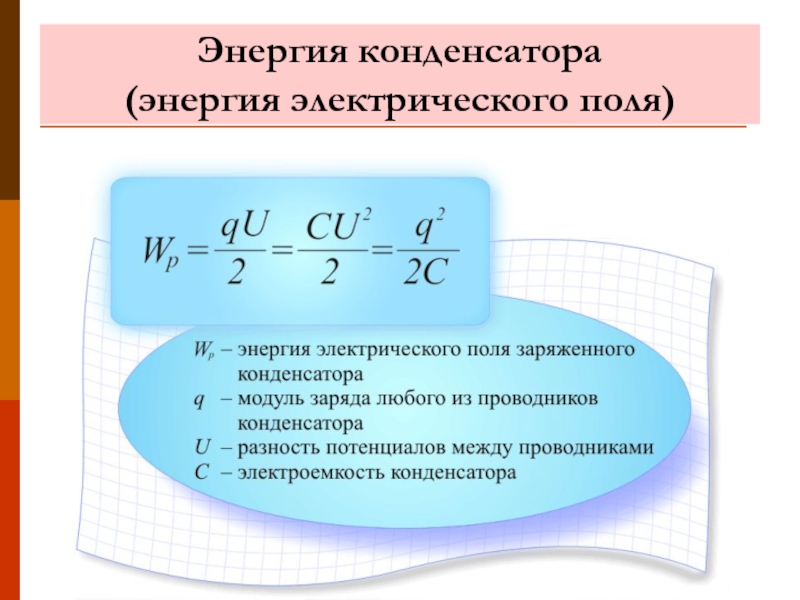 Скольким градусам по шкале Фаренгейта соответствует −44° по шкале Цельсия?
Скольким градусам по шкале Фаренгейта соответствует −44° по шкале Цельсия? Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 9,5 с −1, а центростремительное ускорение равно 180,5 м/с2.
Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 9,5 с −1, а центростремительное ускорение равно 180,5 м/с2. Скольким градусам по шкале Фаренгейта соответствует 48° по шкале Цельсия?
Скольким градусам по шкале Фаренгейта соответствует 48° по шкале Цельсия?
 Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны.
Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны. Аккумулятор фотокамеры также является устройством, накапливающим энергию, но из-за химической природы накопления генерирует и отдаёт её медленно.
Аккумулятор фотокамеры также является устройством, накапливающим энергию, но из-за химической природы накопления генерирует и отдаёт её медленно.
 То есть включается в электрическую цепь с соблюдением полярности.
То есть включается в электрическую цепь с соблюдением полярности.