|
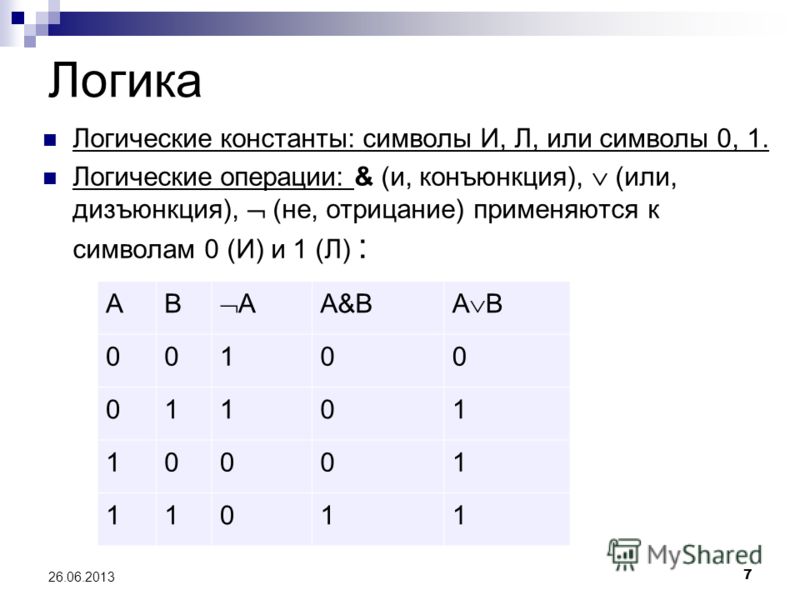
Логические связки, или логические операции — это символические конструкции логических языков (см. Язык формализованный), используемые для образования сложных высказываний (формул) из элементарных высказываний (см. Высказывание). Логическими связками называют также соответствующие этим символам союзы естественного языка (см. Язык). Обычно используются пять общеизвестных логических связок:
Из указанных логических связок отрицание называется одноместной (унарной) связкой; другие называются двухместными (бинарными) связками. В принципе, логические связки могут быть сколь угодно местными, но на практике более, чем бинарные, используются очень редко. В классической логике (см. Логика) любые многоместные логические связки выразимы через перечисленные. Некоторый практический смысл даёт также использование тернарной логической связки, называемой условной дизъюнкцией, связывающей три высказывания A, B и C и означающей, что «A в случае B, и C в случае не-B» или формально: (B ⊃ A) & (¬ B ⊃ C).
Классическая логика рассматривает логические связки экстенсионально (игнорируя содержательный смысл связываемых ими высказываний) как функции истинности, определяемые истинностными значениями связываемых ими высказываний. При двух имеющих место в этой логике истинностных значениях 1 (истинно) и 0 (ложно) высказывания A и B могут иметь четыре возможных набора упорядоченных истинностных значений: (1, 1), (1, 0), (0, 1), (0, 0).
Из четырёх одноместных функций интерес представляет только отрицание, меняющее значение высказывания на противоположное: когда A — истинно, ¬ A — ложно, и наоборот. Все другие унарные и бинарные классические функции могут быть выражены через представленные. Когда принятая в соответствующей семантике система логических связок позволяет дать определение всех остальных, её называют функционально полной.
Функции антидизъюнкция и антиконъюнкция, определимые соответственно как ¬ (A ∨ B) и ¬ (A & B), также представляют каждая в отдельности функционально полную систему связок. Это последнее обстоятельство было известно уже Ч.
Экстенсиональность логических связок придаёт им однозначность, упрощает проблему построения логических исчислений, даёт возможность решать для последних метатеоретические проблемы непротиворечивости, разрешимости, полноты. Однако в некоторых случаях истинностно-функциональная трактовка связок приводит к значительному несоответствию с тем, как они понимаются в естественном языке.
|
Основы алгебры логики в одной странице — Сайт учителя информатики Лосева А.В.
Скачать шпаргалку «Основы алгебры логики в одной странице»
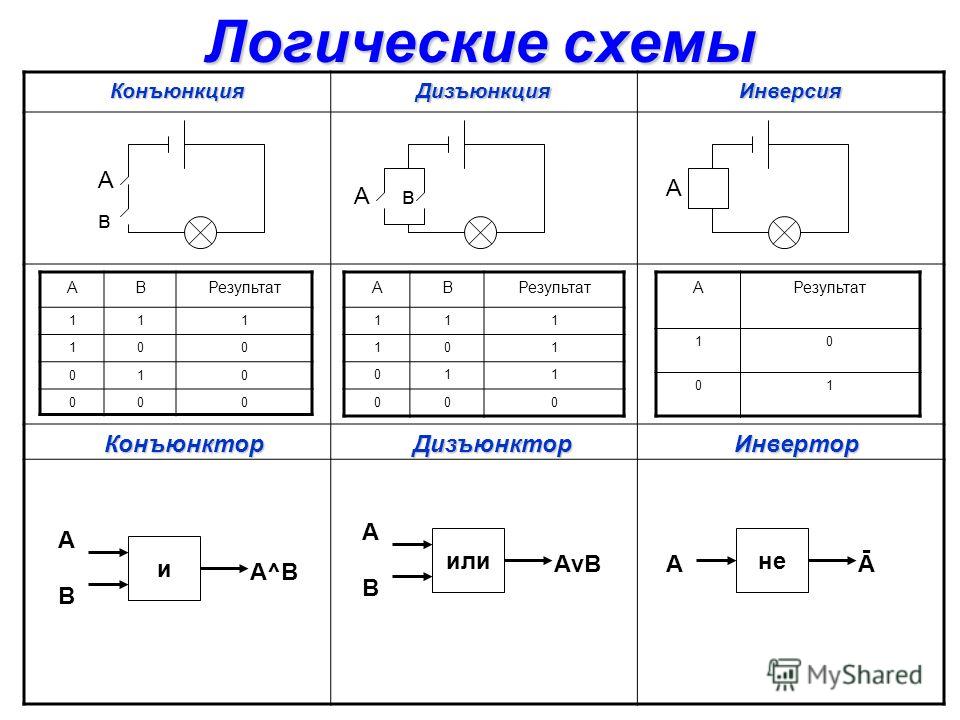
Логические операции
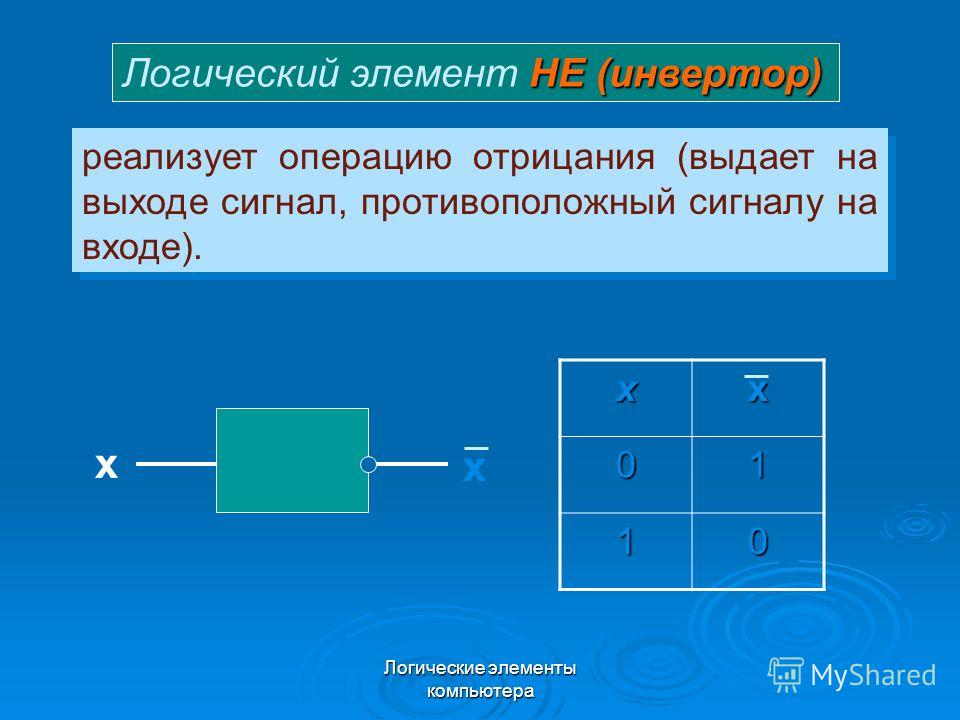
Инверсия (отрицание)
Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или .
Читается «НЕ» (например, «не А»).
Конъюнкция (логическое умножение)
Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б»)
Дизъюнкция (логическое сложение)
Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б»)
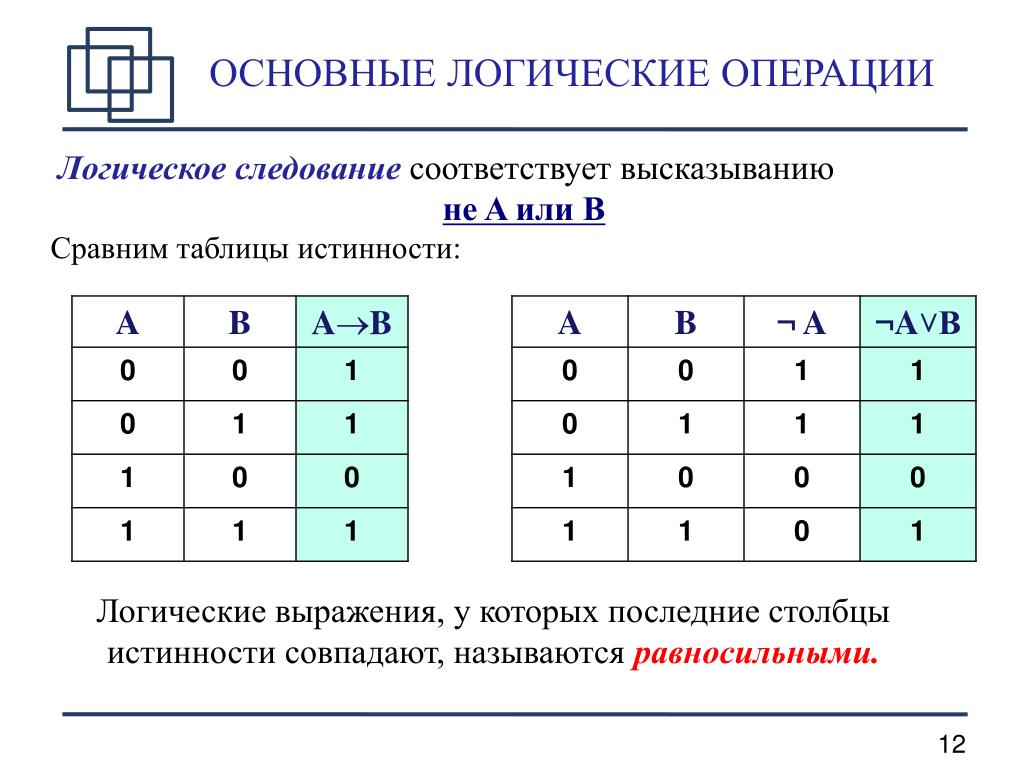
Импликация (следование)
Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ…ТО» (например, «если А, то Б»)
Эквивалентность (равнозначность)
Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
Таблицы истинности
Статью подготовил учитель информатики Лосев Антон Владимирович
|
1. |
Высказывание
|
1 |
|
2. 
|
Предложение
|
1 |
|
3. |
Приоритет логических операций
|
1 |
|
4. 
|
Способы решения логических задач
|
1 |
|
5. |
Скобки
|
2 |
|
6. 
|
Высказывания в геометрии
|
2 |
|
7. |
Логические операции
|
2 |
|
8. 
|
Как на ОГЭ
|
2 |
|
9. |
Высказывания в алгебре
|
2 |
|
10. 
|
Число строк в таблице
|
2 |
|
11. |
Логические элементы
|
2 |
|
12. 
|
Таблица истинности
|
4 |
|
13. |
Закон дистрибутивности
|
3 |
|
14. 
|
Упрощение
|
3 |
Высказывания — урок. Информатика, 8 класс.
Алгебра логики помогает нам понять внутреннее устройство компьютера. Ты уже знаешь, что компьютер обрабатывает информацию только в двоичном коде. Логика поможет тебе понять, как взаимодействуют между собой два состояния: \(0\) и \(1\). Процессор компьютера работает за счёт выполнения логических операций, но о них ты узнаешь позже.
Высказывание — это повествовательное предложение, о котором можно сказать, истинно оно или ложно.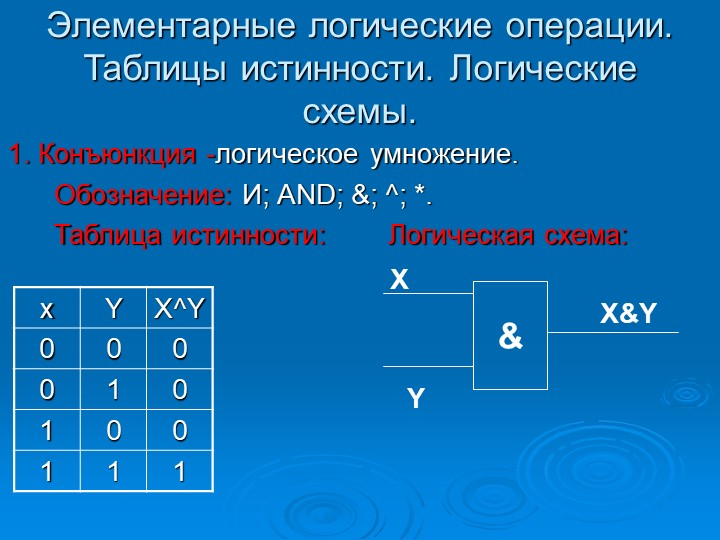
Например: 7×8=56, 26>4, «Осенние месяцы: сентябрь, октябрь, ноябрь», «Графический планшет — это устройство ввода информации» — это всё истинные высказывания.
«Земля имеет форму квадрата», «Монитор — это устройство для ввода информации», 3>21, 15−6=10 — это ложные высказывания.
Высказываниями не могут быть восклицательные и побудительные предложения, определения, уравнения (т. к. там есть переменные), односложные утверждения — «Он хороший» (не для всех непонятный он может быть хорошим).
В алгебре логики высказывания обозначаются латинскими буквами.
Для алгебры логики содержание высказывания не играет никакой роли, главным здесь является, истинно это высказывание или ложно.
Если высказывание истинно, то оно равно \(1\). Если ложно, то \(0\).
Например, \(A\) \(=\) «Монитор — это устройство для вывода информации» можно записать как A=1.
Высказывания могут быть простыми и сложными. Простые состоят из одного высказывания, а сложные — из нескольких высказываний, объединённых логическими операциями.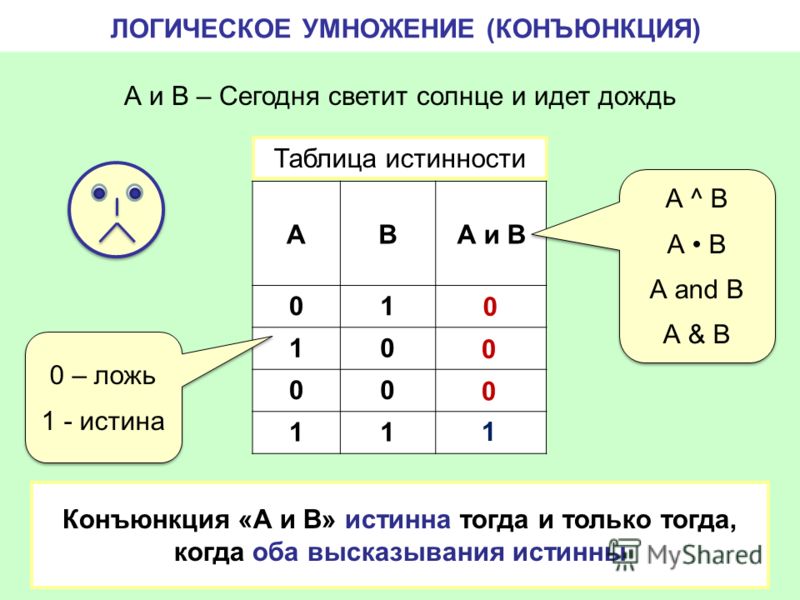
Например:
\(A\) \(=\) «Маша поёт в ансамбле»;
\(B\) \(=\) «Маша танцует народные танцы».
Если объединить эти два простых высказывания в одно сложное, можно получить следующее:
\(A\) или \(B\) \(=\) «Маша поёт в ансамбле ИЛИ Маша танцует народные танцы»;
\(A\) и \(B\) \(=\) «Маша поёт в ансамбле И Маша танцует народные танцы».
Подумай! Какая разница между первым и вторым сложными высказываниями?
Логические операции — урок. Информатика, 8 класс.
В алгебре логики, как и в математике, есть свои обозначения для операций (действий).
Рассмотрим основные логические операции.
1. Логическое отрицание.
Отрицание (инверсия) — это логическая операция, которая делает ложное высказывание истинным, а истинное — ложным.
Обозначение: НЕ \(A\), not \(A\), ¬A, A¯.
Таблица истинности для инверсии.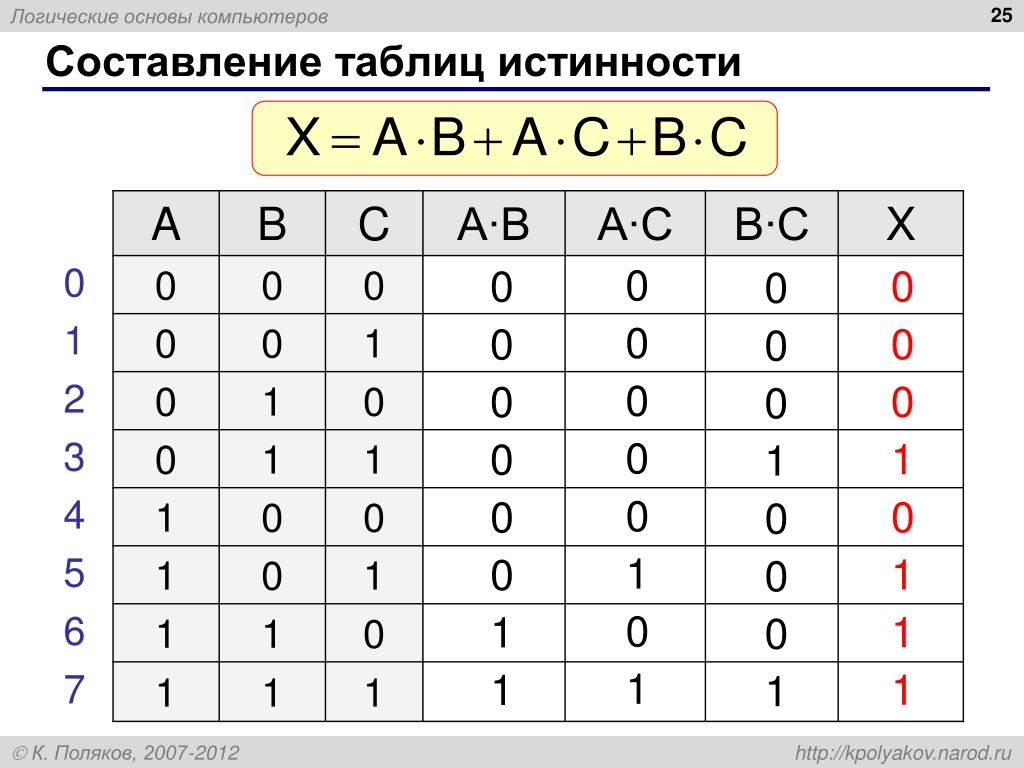
\(A\) | A¯ |
\(0\) | \(1\) |
\(1\) | \(0\) |
2. Конъюнкция (логическое умножение).
Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны.
Обозначение: И, and, &, \(×\), ∧.
Таблица истинности.
\(A\) | \(B\) | A∧B |
\(0\) | \(0\) | \(0\) |
\(0\) | \(1\) | \(0\) |
\(1\) | \(0\) | \(0\) |
\(1\) | \(1\) | \(1\) |
3. Дизъюнкция (логическое сложение).
Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны.
Обозначение: ИЛИ, or, \(+\), ∨.
Таблица истинности.
\(A\) | \(B\) | A∨B |
\(0\) | \(0\) | \(0\) |
\(0\) | \(1\) | \(1\) |
\(1\) | \(0\) | \(1\) |
\(1\) | \(1\) | \(1\) |
Приоритет выполнения логических операций:
- действия в скобках;
- инверсия;
- конъюнкция;
- дизъюнкция.
Основы логики. Логические операции и таблицы истинности
Содержание:
На данной странице будут рассмотренны 5 логических операций:
конъюнкция,
дизъюнкция,
инверсия,
импликация и
эквивалентность,
которых Вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных
логических выражениях и представим таблицы истинности для каждой логической операции. Советуем Вам
Советуем Вам
воспользоваться нашими программами для решения задач по математике,
геометрии и
теории вероятности.
Помоми большого количества программ для решения задач на сайте работает
форум, на котором Вы всегда можете
задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать
истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение
содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами,
обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать
одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или
нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда
оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из
простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат
отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова,
данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины
следует ложь.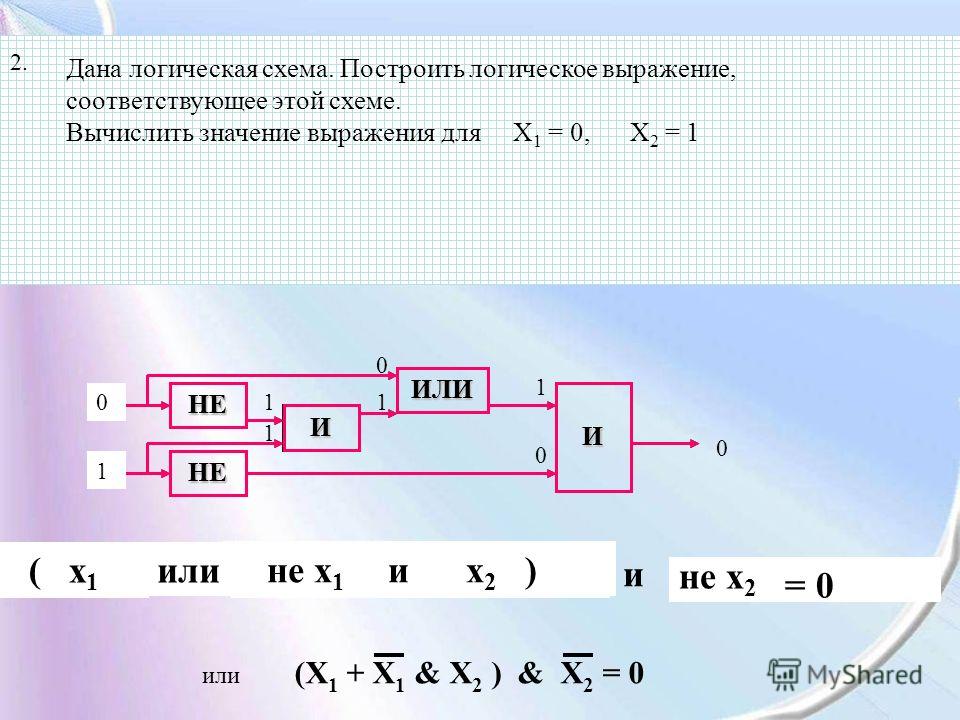 Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А),
Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А),
а второе (В) является следствием.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда
и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Слишком сложно?
Основы логики. Логические операции и таблицы истинности не по зубам? Тебе ответит эксперт через 10 минут!
Информатик БУ — Основы логики. Логические операции.
В математической логике операцией называется логическая связь между двумя высказываниями. Высказывание – это некое суждение, которое, как правило, может быть либо истинным, либо ложным. При этом ложью считается логический ноль (0), а истиной – логическая единица (1).
В алгебре логики существует пять основных операций: конъюнкция, дизъюнкция, импликация, эквиваленция и отрицание. Рассмотрим каждую из них.
Конъюнкция
Конъюнкция – это логическое умножение. Также принято называть её логическим «И». Обычно записывается в виде символов:
&, *, ˄
Приведем пример.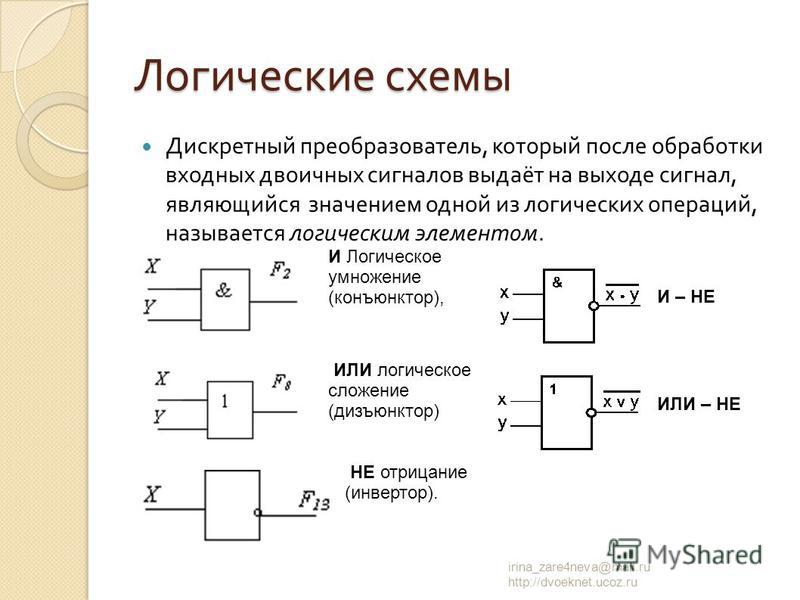
Чтобы поступить в вуз, нужно сдать ЕГЭ по русскому языку и математике. В данном случае, «сдать русский язык» и «сдать математику» — логические высказывания, а поступление в вуз – результат выражения. Обозначим высказывание «сдать русский язык» переменной А, высказывание «сдать математику» переменной Б, а результат выражения (т. е. поступление в вуз) переменной F:
A ˄ B = F
Таблица истинности для этого выражения будет выглядеть так:
| A | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
То есть, чтобы результат (поступление) был истинный (равен 1), обе переменные, связанные логическим умножением, должны быть истинны. Проще говоря, если вы, к примеру, сдадите математику, но завалите русский, вы никуда не поступите (результатом будет ложь).
Проще говоря, если вы, к примеру, сдадите математику, но завалите русский, вы никуда не поступите (результатом будет ложь).
Таким образом, конъюнкция истинна только в одном случае – когда обе переменные истинны.
Дизъюнкция
Дизъюнкция – это логическое сложение. Также принято называть её логическим «ИЛИ». Записывается в виде символов:
|, +, ˅
Приведем пример.
Чтобы поймать рыбу, рыбаку нужна перловка ИЛИ хлеб. В этом случае «есть перловка» и «есть хлеб» — логические высказывания, а результатом выражения может быть пойманная рыба. Обозначим высказывание «есть перловка» переменной А, а высказывание «есть хлеб» переменной B. Результат выражения – «рыба поймана» — переменной F.
А ˅ B = F
Таблица истинности для этого выражения будет выглядеть так:
| A | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Проще говоря, чтобы результат («рыба поймана») был истинный, рыбак может взять с собой или перловку, или хлеб, или и то, и другое.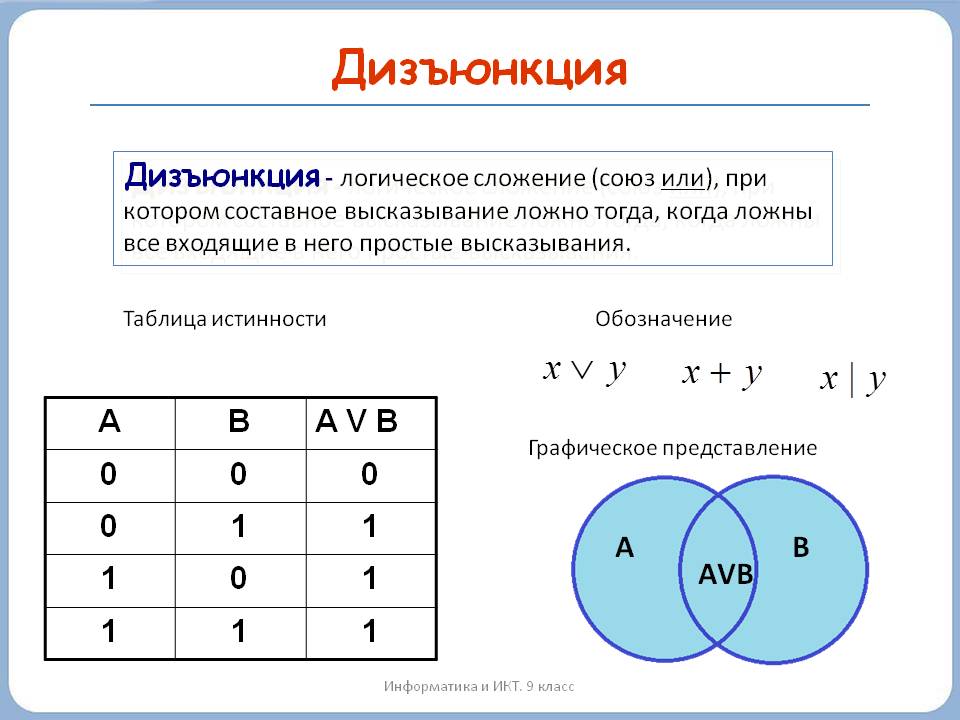 Но если он забудет взять наживку – рыбу он не поймает, то есть результатом выражения будет ложь.
Но если он забудет взять наживку – рыбу он не поймает, то есть результатом выражения будет ложь.
Таким образом, конъюнкция ложна только в одном случае – когда обе переменные ложны.
Импликация
Импликация – это логическое следование. Импликацию можно сравнить с о связкой «если…то». Записывается в виде горизонтальной стрелки, направленной вправо (→).
Импликацию можно обозначить как связь начальника и исполнителя. Приведём пример.
Предположим, учитель задал ученику задание. В этом случае «учитель задал» и «ученик сделал» — высказывания, а оценка будет являться результатом выражения. Обозначим высказывание «учитель задал» переменной A, высказывание «ученик сделал» — переменной B, а результат выражения (оценку) – переменной F.
A → B = F
Таблица истинности для этого выражения выглядит так:
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Если учитель ничего не задал, и ученик ничего не сделал – учитель двойку не поставит. Если учитель не задал, а ученик сделал – двойки также не будет. Если учитель задал, и ученик выполнил – оценка будет положительной. Но если учитель задал, а ученик не сделал – оценка будет отрицательной.
Если учитель не задал, а ученик сделал – двойки также не будет. Если учитель задал, и ученик выполнил – оценка будет положительной. Но если учитель задал, а ученик не сделал – оценка будет отрицательной.
Проще говоря, импликация ложна только в одном случае: если первое выражение истинно, а второе – ложно.
Эквиваленция
Эквиваленция – это логическое равенство (тождество) Обозначается «тройным» знаком равенства (≡). Результатом эквиваленции может быть истина только в том случае, если оба выражения, связанные эквиваленцией, равнозначны (эквивалентны).
Таблица истинности для выражения A≡B выглядит так:
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Инверсия
Инверсия – это логическое отрицание. Её также называют логическим «НЕ». Записывается в виде символов:
Её также называют логическим «НЕ». Записывается в виде символов:
!, ¬,
а также верхним подчеркиванием переменной.
Инверсия меняет значение переменной на противоположное, то есть:
логических уровней — learn.sparkfun.com
Введение
Мы живем в мире аналоговых сигналов. Однако в цифровой электронике есть только два состояния — ВКЛ или ВЫКЛ. Используя эти два состояния, устройства могут кодировать, транспортировать и контролировать большой объем данных. Логические уровни в самом широком смысле описывают любое конкретное дискретное состояние, которое может иметь сигнал. В цифровой электронике мы обычно ограничиваем наше исследование двумя логическими состояниями — двоичным 1 и двоичным 0.
рассматривается в этом учебном пособии
- Что такое логический уровень?
- Каковы общие стандарты логических уровней в цифровой электронике.
- Как взаимодействовать между различными технологиями.

- Перемещение по горизонтали
- Пониженно-повышающие регуляторы напряжения
Рекомендуемая литература
Это руководство основано на базовых знаниях в области электроники. Если вы еще этого не сделали, подумайте о прочтении этих руководств:
Что такое схема?
Каждый электрический проект начинается со схемы.Не знаю, что такое схема? Мы здесь, чтобы помочь.
двоичный
Двоичная система — это система счисления в электронике и программировании … поэтому важно научиться этому. Но что такое двоичный? Как это переводится в другие системы счисления, такие как десятичные?
Что такое логический уровень?
Проще говоря, логический уровень — это определенное напряжение или состояние, в котором может существовать сигнал.Мы часто называем два состояния в цифровой схеме ВКЛ или ВЫКЛ.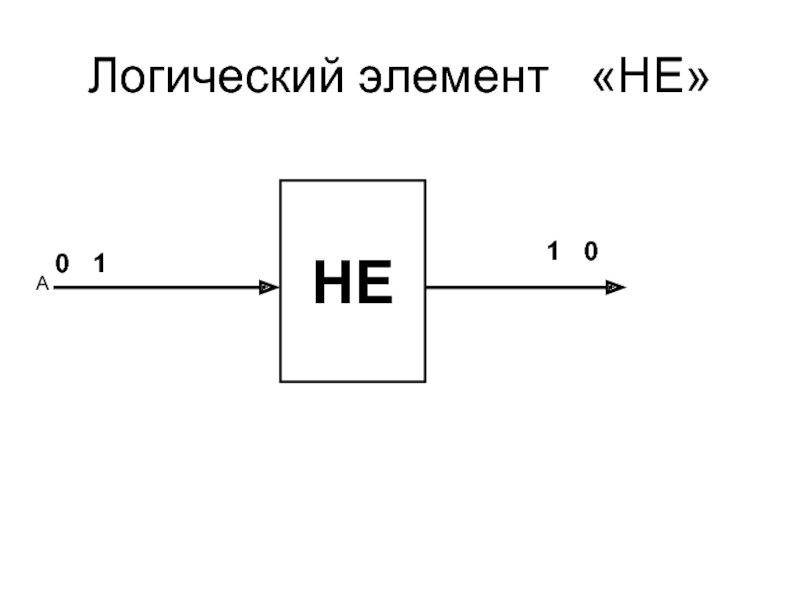 Представленное в двоичном формате, ON преобразуется в двоичную 1, а OFF переводится в двоичный 0. В Arduino мы называем эти сигналы HIGH или LOW соответственно. За последние 30 лет в электронике появилось несколько различных технологий для определения различных уровней напряжения.
Представленное в двоичном формате, ON преобразуется в двоичную 1, а OFF переводится в двоичный 0. В Arduino мы называем эти сигналы HIGH или LOW соответственно. За последние 30 лет в электронике появилось несколько различных технологий для определения различных уровней напряжения.
Логический 0 или Логический 1
Цифровая электроника использует двоичную логику для хранения, обработки и передачи данных или информации.Двоичная логика относится к одному из двух состояний — ВКЛ или ВЫКЛ. Обычно это переводится как двоичная 1 или двоичный 0. Двоичная 1 также называется сигналом HIGH, а двоичный 0 называется сигналом LOW.
Сила сигнала обычно описывается его уровнем напряжения. Как определяется логический 0 (LOW) или логическая 1 (HIGH)? Производители микросхем обычно определяют их в своих спецификациях. Наиболее распространенным стандартом является ТТЛ или транзисторно-транзисторная логика.
Активный-низкий и активный-высокий
При работе с микросхемами и микроконтроллерами вы, вероятно, столкнетесь с выводами, которые имеют активный низкий уровень и контакты, которые являются активными высокими. Проще говоря, это просто описывает, как активируется пин. Если это вывод с активным низким уровнем, вы должны «потянуть» этот вывод до НИЗКОГО уровня, подключив его к земле. Для активного высокого контакта вы подключаете его к ВЫСОКОМУ напряжению (обычно 3,3 В / 5 В).
Проще говоря, это просто описывает, как активируется пин. Если это вывод с активным низким уровнем, вы должны «потянуть» этот вывод до НИЗКОГО уровня, подключив его к земле. Для активного высокого контакта вы подключаете его к ВЫСОКОМУ напряжению (обычно 3,3 В / 5 В).
Например, предположим, что у вас есть регистр сдвига с выводом включения микросхемы CE. Если вы видите вывод CE в любом месте таблицы с линией, подобной этой, CE, то этот вывод активен на низком уровне. Для включения микросхемы контакт CE необходимо подтянуть к GND.Если, однако, на выводе CE нет линии, значит, он активен на высоком уровне, и его необходимо подтянуть до ВЫСОКОГО уровня, чтобы активировать вывод.
Многие ИС будут иметь контакты как с активным низким, так и с активным высоким уровнем. Только не забудьте дважды проверить имена контактов, над которыми есть линия. Линия используется для обозначения НЕ (также известного как полоса). Когда что-то ЗАМЕТАНО, оно переходит в противоположное состояние.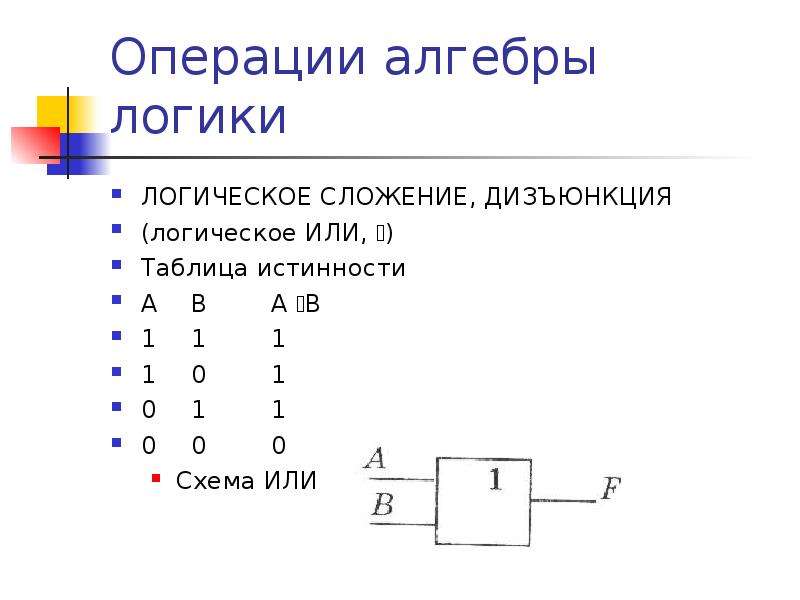 Таким образом, если вход с активным высоким уровнем отмечен NOTTED, то теперь он активен с низким уровнем. Просто как тот!
Таким образом, если вход с активным высоким уровнем отмечен NOTTED, то теперь он активен с низким уровнем. Просто как тот!
Логические уровни TTL
Большинство используемых нами систем полагаются на либо 3.Уровни TTL 3 В или 5 В. TTL — это аббревиатура от Transistor-Transistor Logic. Он основан на схемах, построенных на биполярных транзисторах, для переключения и поддержания логических состояний. Транзисторы в основном представляют собой переключатели с электрическим управлением. Для любого логического семейства необходимо знать несколько уровней порогового напряжения. Ниже приведен пример стандартных уровней TTL 5 В:
В OH — Минимальный уровень ВЫХОДНОГО напряжения, который устройство TTL обеспечивает для ВЫСОКОГО сигнала.
В IH — Минимальный уровень ВХОДНОГО напряжения должен считаться ВЫСОКИМ.
В OL — Максимальный уровень выходного напряжения, который устройство обеспечивает для НИЗКОГО сигнала.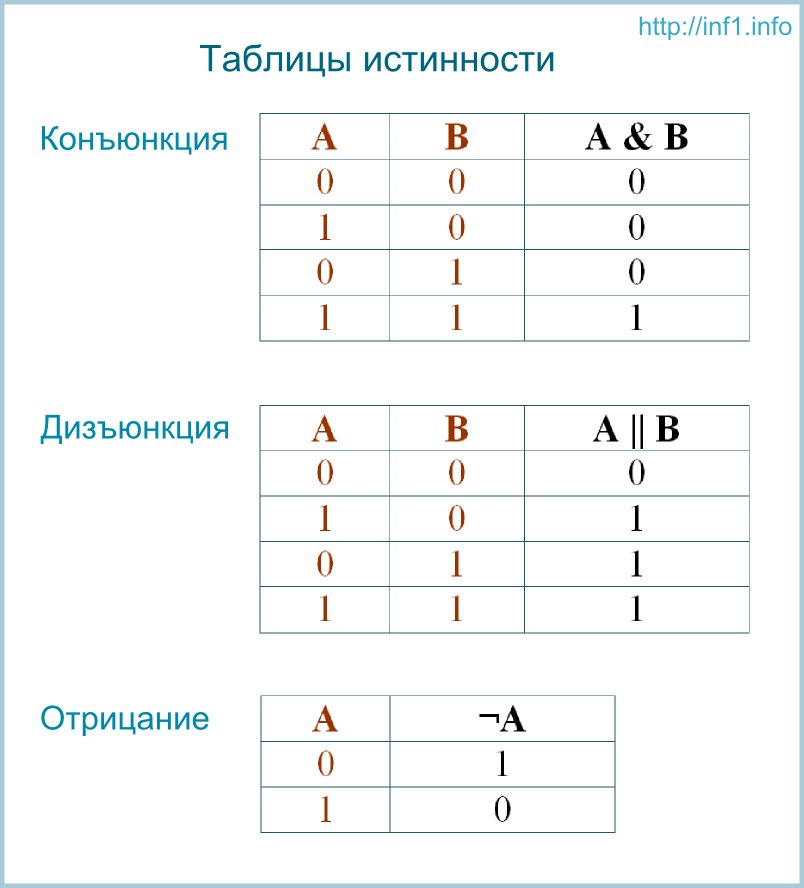
В IL — Максимальный уровень входного напряжения все еще считается НИЗКИМ.
Вы заметите, что минимальное выходное ВЫСОКОЕ напряжение (В OH ) составляет 2,7 В. В основном это означает, что выходное напряжение устройства, управляющего ВЫСОКИМ, всегда будет не менее 2,7 В. Минимальное входное ВЫСОКОЕ напряжение (В IH ) ) равно 2 В, или в основном любое напряжение, которое составляет не менее 2 В, будет считываться как логическая 1 (ВЫСОКАЯ) для устройства TTL.
Вы также заметите, что существует подушка 0,7 В между выходом одного устройства и входом другого. Иногда это называют запасом шума.
Аналогичным образом, максимальное выходное НИЗКОЕ напряжение (В OL ) составляет 0,4 В. Это означает, что устройство, пытающееся отправить логический 0, всегда будет ниже 0,4 В. Максимальное входное НИЗКОЕ напряжение (В IL ) составляет 0,8. V. Таким образом, любой входной сигнал ниже 0,8 В по-прежнему будет считаться логическим 0 (НИЗКИЙ) при считывании в устройство.
Что произойдет, если у вас напряжение между 0,8 В и 2 В? Что ж, ваше предположение не хуже моего. Честно говоря, этот диапазон напряжений не определен и приводит к недопустимому состоянию, часто называемому плавающим. Если выходной вывод на вашем устройстве «плавает» в этом диапазоне, нет уверенности в том, к чему приведет сигнал. Он может произвольно колебаться между HIGH и LOW.
Вот еще один способ взглянуть на допуски ввода / вывода для обычного устройства TTL.
3,3 В CMOS логические уровни
По мере развития технологий мы создали устройства, которые требуют более низкого энергопотребления и работают с более низким базовым напряжением ( В, = 3,3 В вместо 5 В). Для устройств на 3,3 В технология изготовления также немного отличается, что позволяет уменьшить занимаемую площадь и снизить общие затраты на систему.
Для обеспечения общей совместимости вы заметите, что большинство уровней напряжения почти такие же, как у устройств с напряжением 5 В. Устройство 3,3 В может взаимодействовать с устройством 5 В без каких-либо дополнительных компонентов. Например, логическая 1 (ВЫСОКИЙ) от устройства 3,3 В будет составлять не менее 2,4 В. Это по-прежнему будет интерпретироваться как логическая 1 (ВЫСОКИЙ) для системы 5 В, потому что оно выше V IH , равного 2 В.
Устройство 3,3 В может взаимодействовать с устройством 5 В без каких-либо дополнительных компонентов. Например, логическая 1 (ВЫСОКИЙ) от устройства 3,3 В будет составлять не менее 2,4 В. Это по-прежнему будет интерпретироваться как логическая 1 (ВЫСОКИЙ) для системы 5 В, потому что оно выше V IH , равного 2 В.
Однако следует предостеречь, когда идете в другом направлении и подключаете устройство с напряжением 5 В к устройству 3,3 В, чтобы устройство с напряжением 3,3 В было толерантным к 5 В. Спецификация, которая вас интересует, — это максимальное входное напряжение .На некоторых устройствах с напряжением 3,3 В любое напряжение выше 3,6 В приведет к необратимому повреждению микросхемы. Вы можете использовать простой делитель напряжения (например, 1 кОм и 2 кОм), чтобы снизить сигналы 5 В до уровня 3,3 В или использовать один из наших логических переключателей уровня.
Уровни логики Arduino
Глядя на таблицу ATMega328 (основной микроконтроллер, стоящий за Arduino Uno и Sparkfun RedBoard), вы можете заметить, что уровни напряжения немного отличаются.
Arduino построен на немного более прочной платформе. Наиболее заметное различие заключается в том, что недопустимая область напряжений составляет только от 1,5 В до 3,0 В. Запас шума больше на Arduino, и он имеет более высокий порог для НИЗКОГО сигнала. Это значительно упрощает создание интерфейсов и работу с другим оборудованием.
Ресурсы и дальнейшее развитие
Теперь, когда вы поняли суть одной из самых распространенных концепций в электронике, есть целый мир новых вещей, которые нужно изучить!
Хотите узнать, как микроконтроллер, такой как Arduino, может считывать аналоговое напряжение, создаваемое делителем напряжения? Вы можете сделать это с помощью нашего руководства по аналого-цифровым преобразователям.
Узнайте, как использовать различные уровни напряжения для управления другими устройствами, из нашего учебного пособия по широтно-импульсной модуляции.
Вам также может быть интересно использовать схемы делителей напряжения и преобразователи логических уровней для переключения с одного логического уровня на другой.
Последовательная связь
Концепции асинхронной последовательной связи: пакеты, уровни сигналов, скорости передачи, UART и многое другое!
Делители напряжения
Превратите большое напряжение в меньшее с помощью делителей напряжения.В этом руководстве рассказывается: как выглядит схема делителя напряжения и как она используется в реальном мире.
Руководство по подключению логического преобразователя уровня с однополярным питанием
Логический преобразователь с однополярным питанием позволяет вам двунаправленно транслировать сигналы от микроконтроллера 5 В или 3,3 В без необходимости во втором источнике питания! Плата обеспечивает выход как 5 В, так и 3,3 В для питания ваших датчиков. Он оснащен посадочным местом для резистора PTH для возможности регулировки регулятора напряжения на стороне низкого напряжения TXB0104 для 2.Устройства на 5 В или 1,8 В.
Он оснащен посадочным местом для резистора PTH для возможности регулировки регулятора напряжения на стороне низкого напряжения TXB0104 для 2.Устройства на 5 В или 1,8 В.
Или добавьте транзистор или реле для управления устройствами, работающими при более высоких напряжениях, как в руководствах, перечисленных ниже!
Подключение светодиодной панели
Краткий обзор светодиодных полосок SparkFun и несколько примеров, показывающих, как их подключить.
Транзисторы
Ускоренный курс по биполярным транзисторам.Узнайте, как работают транзисторы и в каких схемах мы их используем.
Руководство по эксперименту с Интернетом вещей
SparkFun ESP8266 Thing Dev Board — это мощная платформа для разработки, которая позволяет подключать ваши аппаратные проекты к Интернету.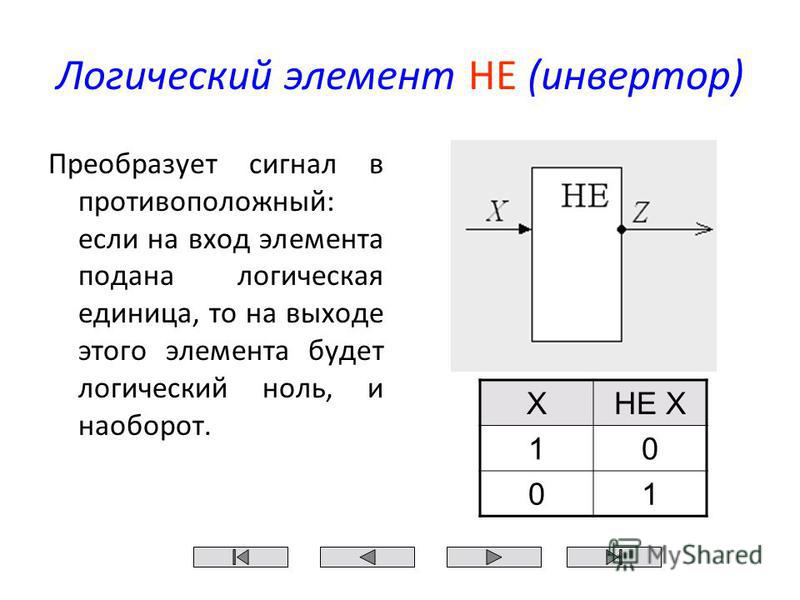 В этом руководстве мы покажем вам, как объединить некоторые простые компоненты для удаленной регистрации данных о температуре, отправки себе текстовых сообщений и управления освещением издалека.
В этом руководстве мы покажем вам, как объединить некоторые простые компоненты для удаленной регистрации данных о температуре, отправки себе текстовых сообщений и управления освещением издалека.
Список литературы
[решено] Если X = 0 в логическом уравнении, [X + Z {Y + (Z + X̅ Y)}] [Y
Законы булевой алгебры:
Все законы булевой алгебры показаны ниже
Имя | И Форма | ИЛИ Форма |
Закон о личности | 1.А = А | 0 + А = А |
Нулевой закон | 0.A = 0 | 1 + А = 1 |
Идемпотентный закон | A. | А + А = А |
Обратный закон | AA ’= 0 | A + A ’= 1 |
Коммутативный закон | AB = BA | А + В = В + А |
Ассоциативный закон | (AB) С | (А + В) + С = А + (В + С) |
Закон о распределении | А + ВС = (А + В) (А + С) | A (B + C) = AB + AC |
Закон об абсорбции | А (А + В) = А | А + АВ = А |
Закон Де Моргана | (AB) ’= A’ + B ’ | (A + B) ’= A’B’ |
Заявка:
Если положить X = 0, приведенное выше логическое уравнение становится
\ (\ Rightarrow \ left [{0 + Z \ left \ {{Y + \ left ({Z + Y} \ right)} \ right \}} \ right] \ left [{\ bar Y + \ left ( {Z + Y} \ right)} \ right] = 0 \)
\ (\ Rightarrow \ left [{Z \ left \ {{Y + Z} \ right \}} \ right] \ left [{1 + Z} \ right] = 0 \)
⇒ YZ + Z = 0
⇒ Z = 0
Ворота с несколькими входами | Логические ворота
Использование логического шлюза
Инверторы и буферы исчерпывают возможности схем с одним входом затвора. Что еще можно сделать с одним логическим сигналом, кроме как его буферизовать или инвертировать? Чтобы исследовать больше возможностей логических вентилей, мы должны добавить больше входных клемм в схемы.
Что еще можно сделать с одним логическим сигналом, кроме как его буферизовать или инвертировать? Чтобы исследовать больше возможностей логических вентилей, мы должны добавить больше входных клемм в схемы.
Добавление дополнительных входных клемм к логическому элементу увеличивает количество возможных состояний входа. С одним входным вентилем, таким как инвертор или буфер, может быть только два возможных состояния входа: либо вход «высокий» (1), либо он «низкий» (0).
Как упоминалось ранее в этой главе, двухвходной вентиль имеет четыре возможности (00, 01, 10 и 11).Трехвходовой вентиль имеет восемь возможностей (000, 001, 010, 011, 100, 101, 110 и 111) для состояний входа.
Количество возможных состояний входа равно двум в степени количества входов:
Это увеличение количества возможных входных состояний, очевидно, допускает более сложное поведение затвора. Теперь, вместо простого инвертирования или усиления (буферизации) одного «высокого» или «низкого» логического уровня, выходной сигнал логического элемента будет определяться любой комбинацией , единиц и нулей, присутствующей на входных клеммах.
Поскольку так много комбинаций возможно только с несколькими входными клеммами, существует много различных типов вентилей с несколькими входами, в отличие от вентилей с одним входом, которые могут быть только инверторами или буферами. В этом разделе будет представлен каждый базовый тип ворот, показывающий его стандартный символ, таблицу истинности и практическую работу. Фактическая схема TTL этих различных вентилей будет исследована в следующих разделах.
Ворота И
Один из самых простых для понимания логических элементов с несколькими входами — это элемент И, так называемый, потому что выход этого элемента будет «высоким» (1) тогда и только тогда, когда все входы (первый вход и второй вход и .. .) являются «высокими» (1). Если какой-либо вход (а) имеет «низкий» уровень (0), выход также гарантированно находится в «низком» состоянии.
Если вам интересно, логические элементы И сделаны с более чем тремя входами, но это менее распространено, чем простая разновидность с двумя входами.
Таблица истинности ворот И с двумя входами
Таблица истинности логического элемента И с двумя входами выглядит так:
И работа схемы выборки затвора
То, что эта таблица истинности означает на практике, показано в следующей последовательности иллюстраций, где логический элемент И с двумя входами подвержен всем возможностям входных логических уровней.Светодиод (светоизлучающий диод) обеспечивает визуальную индикацию выходного логического уровня:
Только когда все входы подняты до «высоких» логических уровней, выход логического элемента И становится «высоким», таким образом активируя светодиод только для одного из четырех состояний комбинации входов.
Ворота NAND
Вариант идеи логического элемента И называется вентилем И-НЕ.Слово «И-НЕ» является словесным сокращением слов НЕ и И.
По сути, вентиль И-НЕ ведет себя так же, как вентиль И с вентилем НЕ (инвертор), подключенным к выходному выводу. Чтобы обозначить эту инверсию выходного сигнала, символ логического элемента И-НЕ имеет пузырь на выходной линии.
Таблица истинности для логического элемента И-НЕ, как и следовало ожидать, в точности противоположна таблице истинности для логического элемента И:
Как и вентили И, вентили И-НЕ имеют более двух входов.В таких случаях применяется тот же общий принцип: выход будет «низким» (0) тогда и только тогда, когда все входы будут «высокими» (1). Если на каком-либо входе «низкий» (0), на выходе будет «высокий» (1).
Ворота OR
Наш следующий логический элемент, который нам предстоит исследовать, — это вентиль ИЛИ, так называемый, потому что выход этого логического элемента будет «высоким» (1), если какой-либо из входов (первый вход или второй вход или …) будет «высоким» ( 1). Выход логического элемента ИЛИ становится «низким» (0) тогда и только тогда, когда все входы «низкие» (0).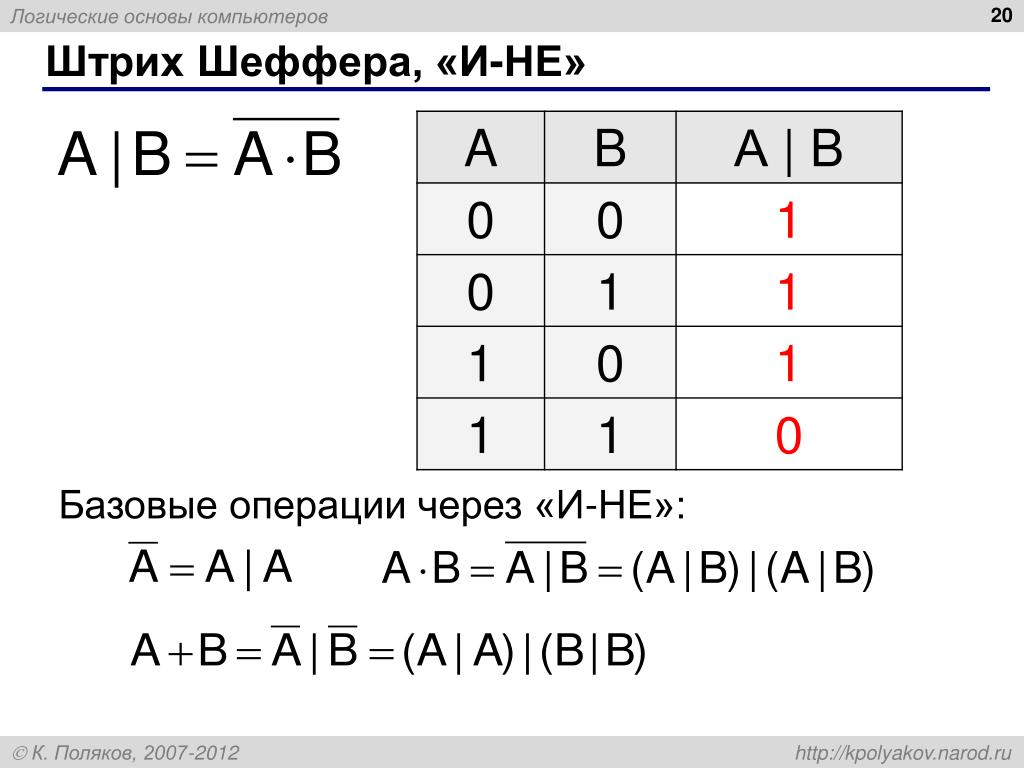
Таблица истинности ворот ИЛИ с двумя входами
Таблица истинности логического элемента ИЛИ с двумя входами выглядит так:
Работа схемы выборки логического элемента ИЛИ
Следующая последовательность иллюстраций демонстрирует функцию логического элемента ИЛИ, при этом 2 входа испытывают все возможные логические уровни. Светодиод (светоизлучающий диод) обеспечивает визуальную индикацию выходного логического уровня затвора:
Состояние любого входа, повышенного до «высокого» логического уровня, приводит к тому, что выход логического элемента ИЛИ становится «высоким», таким образом активируя светодиод для трех из четырех состояний комбинации входов.
Ворота NOR
Как вы могли догадаться, вентиль ИЛИ является логическим элементом ИЛИ с инвертированным выходом, точно так же, как вентиль И-НЕ является вентилем И с инвертированным выходом.
Вентили
NOR, как и все другие вентили с несколькими входами, которые мы видели до сих пор, могут быть изготовлены с более чем двумя входами. Тем не менее, применяется тот же логический принцип: выход становится «низким» (0), если какой-либо из входов становится «высоким» (1). Выход является «высоким» (1) только тогда, когда все входы «низкие» (0).
Ворота отрицательного И
Элемент «Отрицательное И» работает так же, как элемент И, со всеми его входами инвертированными (подключенными через элементы НЕ). В соответствии со стандартным условным обозначением логического элемента, эти перевернутые входы обозначаются пузырьками.
Вопреки первому инстинкту большинства людей, логическое поведение ворот «Отрицательное И» не совпадает с логическим поведением ворот И-НЕ. Его таблица истинности фактически идентична вентилю ИЛИ-НЕ:
Ворота отрицательного ИЛИ
Следуя той же схеме, вентиль отрицательного ИЛИ работает так же, как вентиль ИЛИ, со всеми его входами инвертированными. В соответствии со стандартным условным обозначением логического элемента, эти перевернутые входы обозначаются пузырьками. Поведение и таблица истинности логического элемента «Отрицательное ИЛИ» такие же, как и у логического элемента И-НЕ:
В соответствии со стандартным условным обозначением логического элемента, эти перевернутые входы обозначаются пузырьками. Поведение и таблица истинности логического элемента «Отрицательное ИЛИ» такие же, как и у логического элемента И-НЕ:
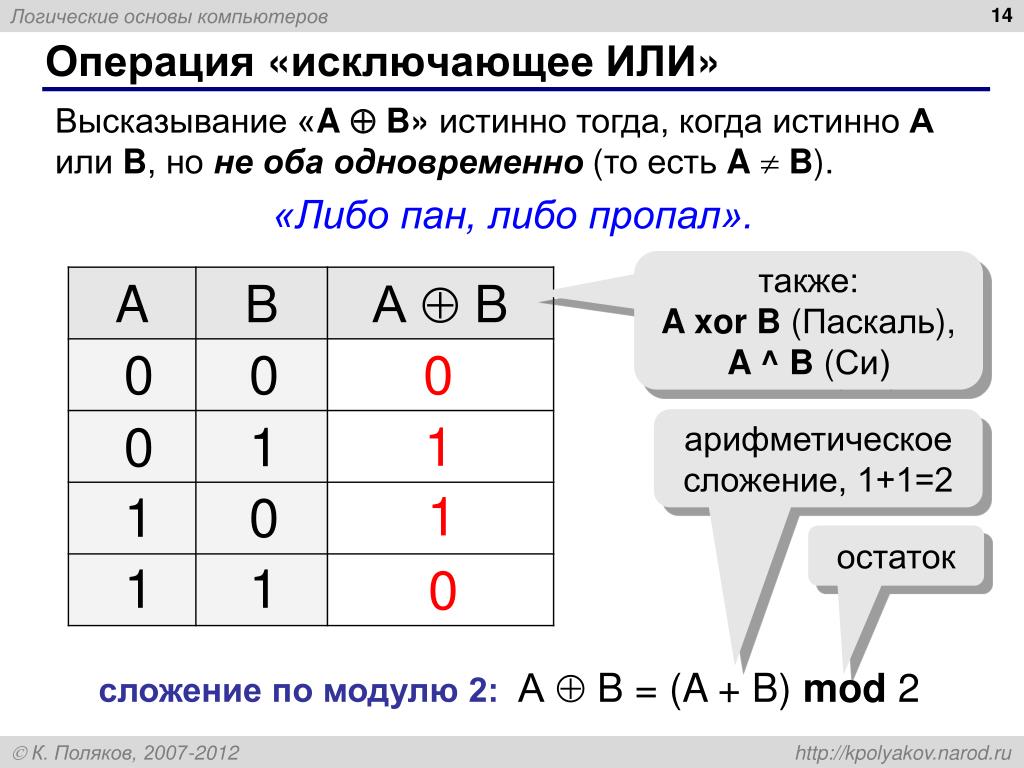
Ворота Эксклюзив-ИЛИ
Последние шесть типов ворот представляют собой довольно прямые вариации трех основных функций: И, ИЛИ и НЕ. Однако вентиль Exclusive-OR — это совсем другое.
Логические элементы
«Исключающее ИЛИ» выдают «высокий» (1) логический уровень, если входы находятся на разных логических уровнях, либо 0 и 1, либо 1 и 0.И наоборот, они выводят «низкий» (0) логический уровень, если входы имеют одинаковые логические уровни.
Шлюз Exclusive-OR (иногда называемый XOR) имеет как символ, так и шаблон таблицы истинности, который является уникальным:
Эквивалентные схемы XOR
Существуют эквивалентные схемы для логического элемента «Исключающее ИЛИ», состоящего из логических элементов «И», «ИЛИ» и «НЕ», как и для вентилей И-НЕ, ИЛИ-ИЛИ и вентилей с отрицательным входом.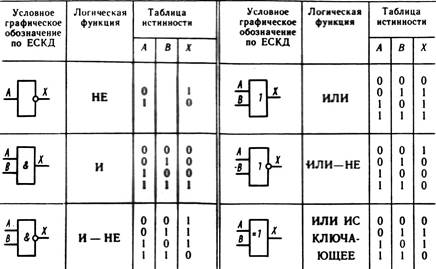 Довольно прямой подход к моделированию логического элемента «Исключающее ИЛИ» состоит в том, чтобы начать с обычного логического элемента ИЛИ, а затем добавить дополнительные вентили, чтобы запретить выходу на «высокий» уровень (1), когда оба входа «высокие» (1):
Довольно прямой подход к моделированию логического элемента «Исключающее ИЛИ» состоит в том, чтобы начать с обычного логического элемента ИЛИ, а затем добавить дополнительные вентили, чтобы запретить выходу на «высокий» уровень (1), когда оба входа «высокие» (1):
В этой схеме последний логический элемент И действует как буфер для выхода логического элемента ИЛИ всякий раз, когда на выходе логического элемента И-НЕ высокий уровень, то есть для первых трех комбинаций входных состояний (00, 01 и 10).Однако, когда оба входа имеют «высокий» (1), логический элемент И-НЕ выводит «низкий» (0) логический уровень, который заставляет последний логический элемент И выдавать «низкий» (0) выход.
Другая эквивалентная схема для элемента «Исключающее ИЛИ» использует стратегию двух элементов И с инверторами, настроенных для генерации «высоких» (1) выходов для входных условий 01 и 10. Последний элемент ИЛИ затем разрешает любой из элементов И. «Высокие» выходы для создания окончательного «высокого» выхода:
Логические элементы
Исключающее ИЛИ очень полезны для схем, в которых два или более двоичных числа должны сравниваться побитно, а также для обнаружения ошибок (проверка четности) и преобразования кода (двоичного в Грей и наоборот).
Ворота Exclusive-NOR
Наконец, нашим последним входом для анализа является вентиль Исключающее ИЛИ-НЕ, также известный как вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ. Это эквивалентно вентилю исключающего ИЛИ с инвертированным выходом. Таблица истинности для этих ворот прямо противоположна таблице истинности для ворот Исключающее ИЛИ:
Как указано в таблице истинности, цель логического элемента «Исключающее ИЛИ-ИЛИ» состоит в том, чтобы выводить «высокий» (1) логический уровень всякий раз, когда оба входа имеют одинаковые логические уровни (00 или 11).
ОБЗОР:
- Правило для логического элемента И: выход «высокий», только если первый вход и второй вход оба «высокий».
- Правило для логического элемента ИЛИ: выход «высокий», если вход A или , вход B «высокий».
- Правило для логического элемента И-НЕ: выход , а не «высокий», если и первый, и второй вход «высокий».

- Правило для логического элемента ИЛИ-ИЛИ: выход , а не «высокий», если первый или второй вход «высокий».”
- Вентиль «Отрицательное И» ведет себя как вентиль ИЛИ-НЕ.
- Логический элемент «отрицательное ИЛИ» ведет себя как логический элемент И-НЕ.
- Правило для логического элемента «Исключающее ИЛИ»: выход «высокий», если входные логические уровни различных .
- Правило для логического элемента «Исключающее ИЛИ-ИЛИ»: выход «высокий», если логические уровни входа равны и .
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Логические ворота
В
порядок, чтобы логическая схема «запоминала»
и сохраняют свое логическое состояние даже после
управляющий входной сигнал (ы) был
снято, необходимо для схемы
чтобы включить какую-либо форму обратной связи. Мы можем
Мы можем
начнем с пары инверторов, каждый из которых
его вход соединен с выходом другого.
Два выхода всегда будут иметь противоположные
логические уровни.
В
проблема в том, что у нас нет
любые дополнительные входы, которые мы можем использовать
чтобы изменить логические состояния, если мы хотим.Мы можем решить эту проблему, заменив
инверторы с воротами NAND или NOR,
и используя дополнительные строки ввода для управления
схема.
В
Схема, показанная ниже, представляет собой базовую защелку NAND. Входы обычно обозначаются буквой S.
Входы обычно обозначаются буквой S.
и «R» для «Set»
и «Сброс» соответственно. Так как
входы NAND обычно должны быть логическими
1, чтобы не повлиять на действие защелкивания,
входы считаются инвертированными
в этой схеме.
В
выходы любой однобитовой защелки или памяти
традиционно обозначаются Q и Q ‘.
В коммерческой схеме защелки либо
или оба из них могут быть доступны для
использование другими схемами.В любом случае
Сама схема составляет:
За
схема защелки NAND, оба входа должны
обычно находится на уровне логической единицы.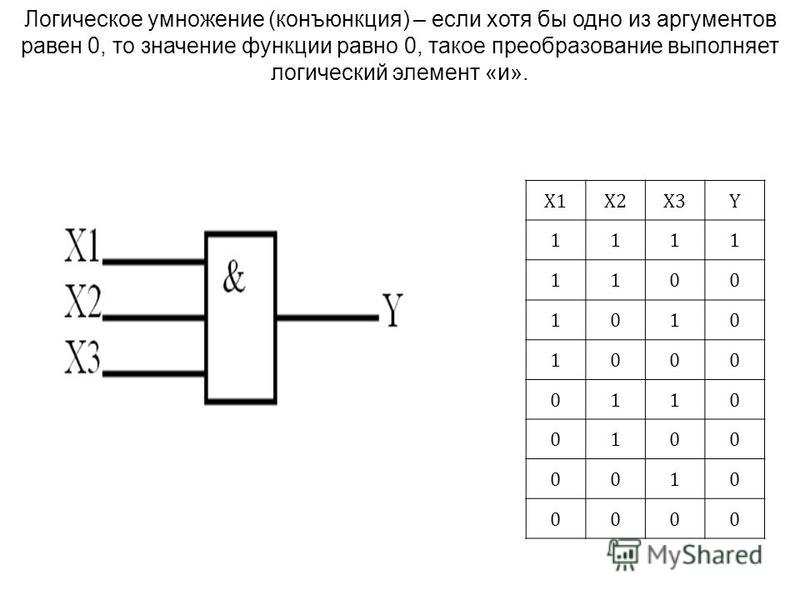 Изменение
Изменение
вход на уровень логического 0 заставит
который выводится на логическую 1.Та же логика
1 также будет применен ко второму входу
другого логического элемента NAND, что позволяет
выход упадет до уровня логического 0. Этот
в свою очередь, возвращается ко второму входу
оригинального гейта, заставляя его выход
чтобы оставаться в логике 1.
Применение
другой логический 0 вход в тот же вентиль
не будет иметь дальнейшего воздействия на эту схему.
Однако, применяя логический 0 к другому
ворота вызовут такую же реакцию в
другое направление, таким образом меняя состояние
цепи защелки в другую сторону.
Примечание
что запрещено иметь оба входа
на уровне логического 0 одновременно. Тот
состояние принудит оба выхода к логике
1, подавляя действие фиксации обратной связи.
В этом состоянии любой вход
к логике 1 сначала потеряет контроль, а
другой вход (все еще на логическом 0) управляет
итоговое состояние защелки.Если оба
входы переходят к логической 1 одновременно,
результат — состояние «гонки»,
и конечное состояние защелки не может
быть определенным заранее.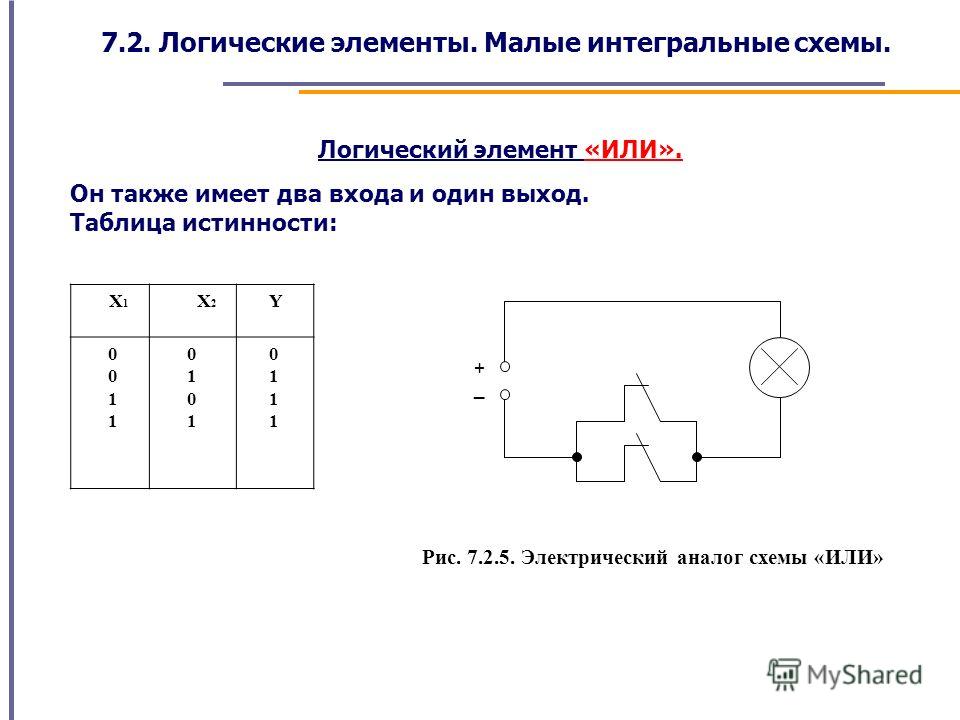
—
Защелка РС НОР —
Пока
большинство наших демонстрационных схем используют
Вентили NAND, те же функции могут также
выполняться с использованием ворот NOR.Несколько корректировок
необходимо сделать, чтобы учесть разницу
в логической функции, но логика задействована
очень похоже.
В
Схема, показанная ниже, является базовой защелкой NOR.
Входы обычно обозначаются буквой S.
и «R» для «Set»
и «Сброс» соответственно.Так как
входы ИЛИ-НЕ должны быть логическими.
0, чтобы избежать отмены действия фиксации,
входы в этой схеме не инвертированы.
Схема защелки на основе NOR:
За
цепи защелки ИЛИ-НЕ, оба входа должны
обычно находится на уровне логического 0.Изменение
вход на уровень логической 1 заставит
который выводится на логический 0. Та же логика
0 также будет применен ко второму входу
другого логического элемента ИЛИ-НЕ, позволяя этому выходу
подняться до уровня логической 1. Это в свою очередь
Это в свою очередь
возвращается ко второму входу
оригинальные ворота, заставляя их выход оставаться
при логическом 0 даже после внешнего входа
устранен.
Применение
еще один логический вход 1 в тот же вентиль
не будет иметь дальнейшего воздействия на эту схему.
Однако, применяя логику 1 к другому
ворота вызовут такую же реакцию в
другое направление, таким образом меняя состояние
цепи защелки в другую сторону.
Примечание
что запрещено иметь оба входа
на уровне логической 1 одновременно.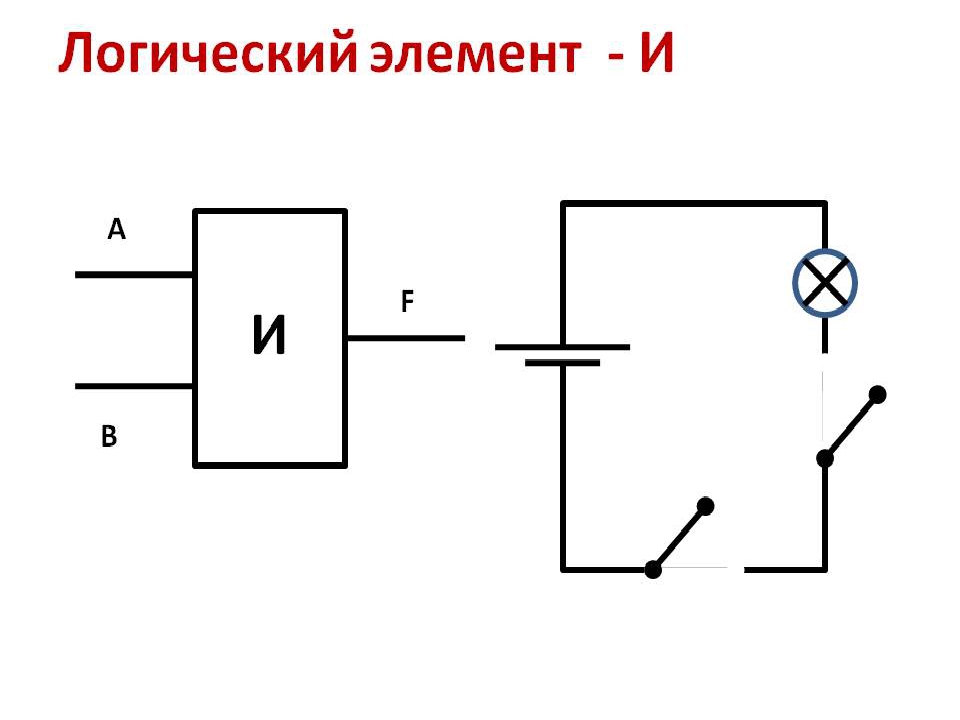 Тот
Тот
состояние принудит оба выхода к логике
0, подавляя действие фиксации обратной связи.
В этом состоянии любой вход
до логического 0 сначала потеряет контроль, а
другой вход (все еще на логической 1) управляет
итоговое состояние защелки.Если оба
входы переходят в логический 0 одновременно,
результат — состояние «гонки»,
и конечное состояние защелки не может
быть определенным заранее.
—
Тактовая защелка RS NAND —
От
добавление пары вентилей NAND ко входу
схемы защелки РС, выполняем
две цели: нормальная, а не перевернутая
входы, и третий вход, общий для обоих
ворота, которые мы можем использовать для синхронизации
эта схема с другими в своем роде.
В
тактовая защелка RS NAND показана ниже:
В
тактовая схема защелки RS очень похожа
в эксплуатации к основной защелке.S
и R входы обычно находятся на логическом 0,
и должен быть изменен на логику 1, чтобы изменить
состояние защелки. Однако с
третий ввод, новый фактор был
добавлен. Этот вход обычно обозначается
C или CLK, потому что он обычно контролируется
какой-то схемой часов, которая
используется для синхронизации некоторых из этих
схемы защелкивания друг с другом.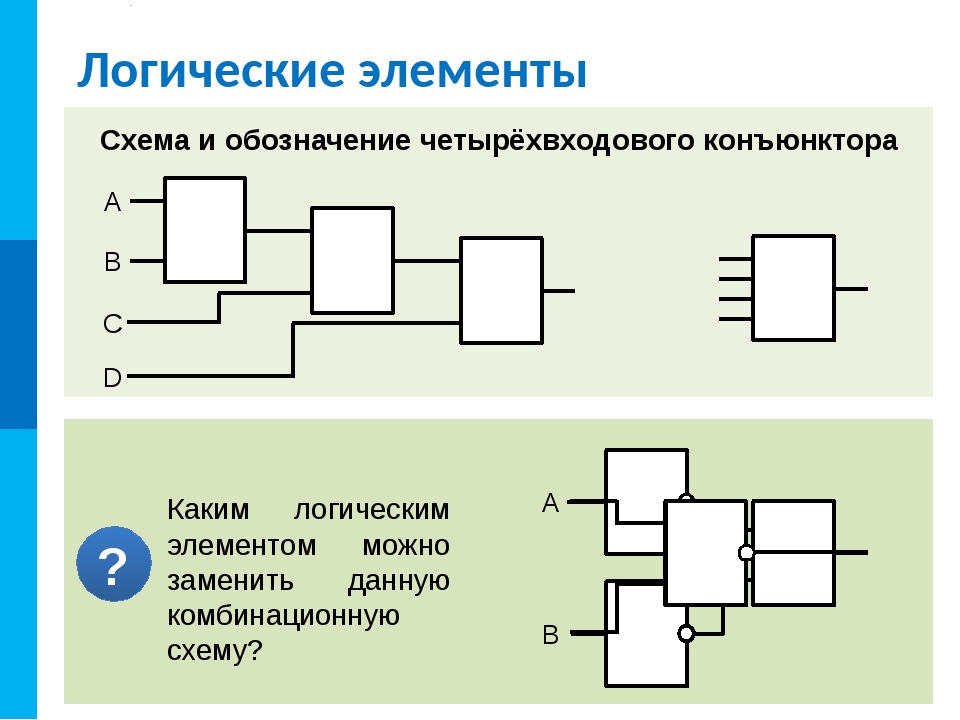 Выход
Выход
может только изменить состояние, пока вход CLK
является логикой 1. Когда CLK представляет собой логический 0,
Входы S и R не действуют.
В
то же правило не активировать оба
Входы S и R действуют одновременно:
если оба являются логической 1, когда часы
также логика 1, действие фиксации отключено
и оба выхода перейдут к логике 1.В
разница в этом случае в том, что если
Вход CLK сначала падает до логического 0, затем
нет вопросов и сомнений — настоящая гонка
состояние будет существовать, и вы не можете сказать
каким образом выходы остановятся.
Пример схемы на этой странице отражает
эта неопределенность.
За
правильная работа, выбранный R или S
вход должен быть доведен до логической 1, тогда
вход CLK должен иметь логическую 1 и
затем снова логический 0. Наконец, выбранный
вход должен быть возвращен к логическому 0.
В
тактовая защелка RS решает некоторые проблемы
базовой схемы защелки RS, и позволяет
более точный контроль за защелкиванием.
Однако это отнюдь не полный
решение.Остается серьезная проблема:
что эта схема защелки может легко испытать
изменение входных уровней S и R при
вход CLK все еще находится на уровне логической 1.
Это позволяет схеме изменять состояние
много раз, прежде чем вход CLK вернется
до логического 0.
Один
способ минимизировать эту проблему — сохранить
CLK на логическом 0 большую часть времени, и
чтобы разрешить только краткие изменения в логике 1.
Однако такой подход по-прежнему не может гарантировать
что защелка изменит только состояние
один раз, пока тактовый сигнал находится на уровне логики
1. Этот сигнал должен иметь определенную продолжительность.
Этот сигнал должен иметь определенную продолжительность.
чтобы все защелки успели
ответить на него, и за это время большинство
защелки могут реагировать на множественные изменения.
—
Триггер RS с синхронизацией по фронту —
К
отрегулируйте синхронизированную защелку RS для срабатывания фронта,
мы должны фактически объединить два одинаковых
тактовые схемы защелок, но есть они
работать на противоположных половинах часов
сигнал. Результирующая схема обычно
Результирующая схема обычно
называется триггером, потому что его выход
может сначала перевернуть в одну сторону, а потом снова повернуть
другой способ. Защелка RS с синхронизацией
также иногда называют триггером, хотя
это более правильно называть защелкой
схема.
В
двухсекционный триггер также известен как
триггер ведущий-ведомый, потому что
входная защелка работает как мастер-секция,
в то время как секция вывода подчинена
мастер в течение половины каждого тактового цикла.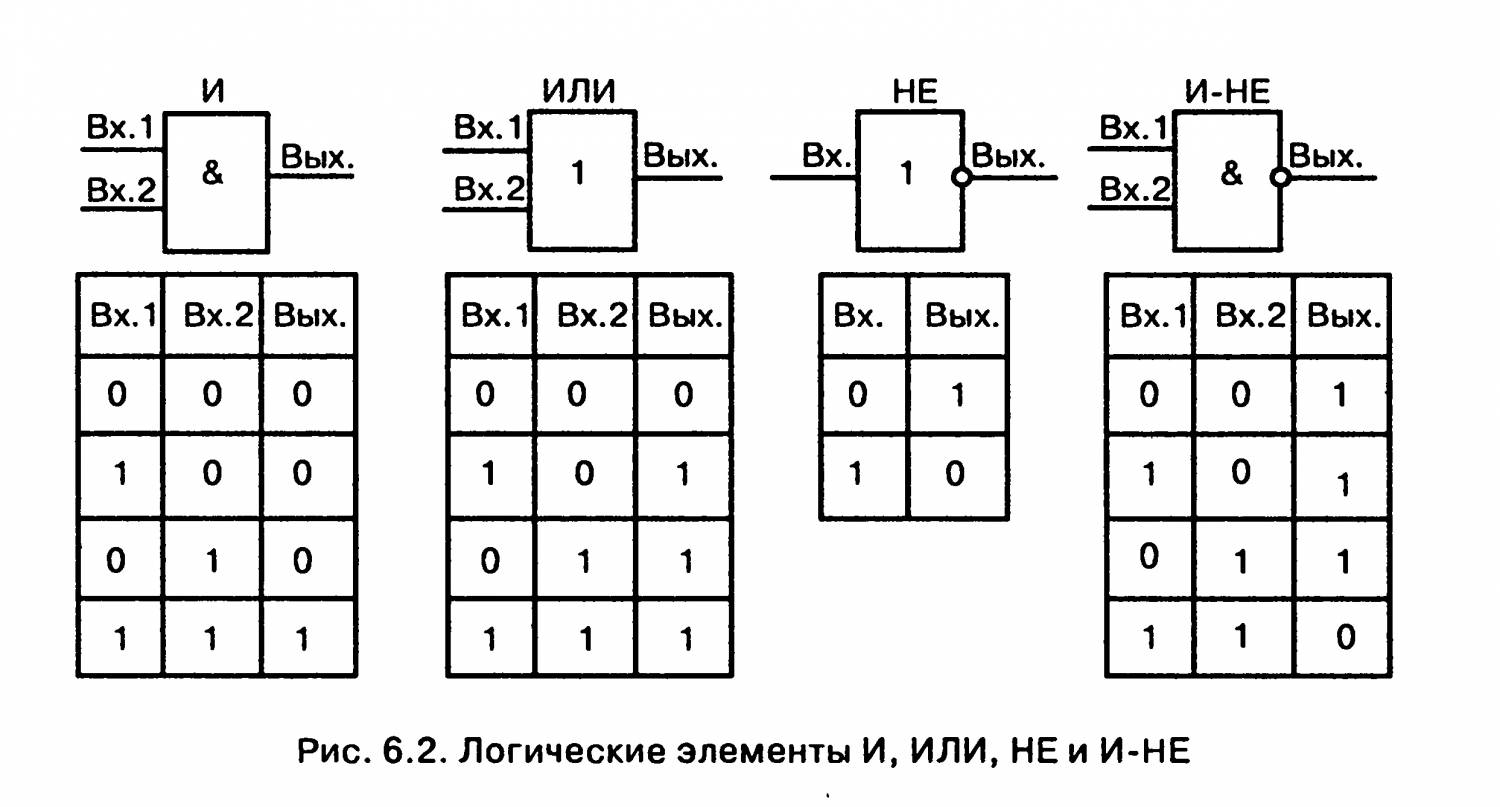
В
показан триггер RS NAND с синхронизацией по фронту
ниже:
В
RS-триггер, запускаемый по фронту, на самом деле состоит
двух идентичных схем защелки RS, как
показано выше.Однако инвертор подключил
между двумя входами CLK гарантирует, что
два раздела будут включены во время
противоположные полупериоды тактового сигнала.
Это ключ к работе этого
схема.
Если
мы начинаем с входа CLK на логическом 0
как первоначально изображено выше, S и
Входы R отключены от входа
(мастер) защелка. Поэтому любые изменения
Поэтому любые изменения
входных сигналов не может влиять на
состояние конечных выходов.
Когда
сигнал CLK переходит в логическую 1, сигнал S
и R-входы могут управлять состоянием
входной защелки, как и в случае одиночного
Схема защелки RS вы уже рассмотрели.Однако в то же время перевернутая
Сигнал CLK подается на выход (ведомый)
защелка предотвращает состояние входа
защелка не имеет никакого эффекта здесь. Следовательно,
любые изменения входных сигналов R и S
отслеживаются входной защелкой, в то время как CLK
находится на логической 1, но не отражается на
выходы Q и Q ‘.
Когда
CLK снова падает до логического 0, S и
Входы R снова изолированы от входа
защелка. В то же время перевернутый
Сигнал CLK теперь разрешает текущее состояние
входной защелки для достижения выхода
защелка.Следовательно, выходы Q и Q ‘
может изменить состояние только тогда, когда сигнал CLK
падает с логической 1 до логической 0. Это
известен как задний фронт CLK
сигнал; отсюда и обозначение с синхронизацией по фронту
резкий поворот.
—
Защелка D —
Один
очень полезная вариация на защелке RS
Схема представляет собой защелку данных или D-защелку
как это вообще называется. Как показано в
Как показано в
логическая схема ниже, D-защелка
построенный с использованием перевернутого входа S
в качестве входного сигнала R. Единственный оставшийся
вход обозначен буквой «D», чтобы различать
его работа от других типов защелок.
Не имеет значения, что вход R
сигнал эффективно синхронизируется дважды, так как
сигнал CLK либо разрешит сигналы
пройти оба ворот или нет.
За
для сравнения вы можете ознакомиться с RS NAND
схема защелки, если хотите.
В
защелка D, когда вход CLK является логическим
1, выход Q всегда будет отражать
логический уровень присутствует на входе D, нет
независимо от того, как это изменится.Когда CLK
вход падает до логического 0, последнее состояние
входа D улавливается и удерживается в
защелка для использования любыми другими цепями
может понадобиться этот сигнал.
Так как
одиночный вход D также инвертируется в
подать сигнал на сброс защелки,
эта схема защелки не может испытывать
состояние «гонки», вызванное всеми
входы одновременно находятся на логической 1. Следовательно, цепь D-защелки может быть безопасно
Следовательно, цепь D-защелки может быть безопасно
используется в любой схеме.
—
Символы триггера —
Несмотря на то что
внутренняя схема защелок и
на шлепанцы интересно смотреть
на индивидуальной основе, размещая все эти
логические символы на схеме, включающей несколько
шлепанцы быстро произведут так много
беспорядок, что общая цель
диаграмма будет потеряна.Чтобы избежать этой проблемы,
мы используем подход «черного ящика».
На самом деле это всего лишь один шаг вперед
что подход «черного ящика»
мы использовали при указании символов логического элемента
для представления конкретных кластеров электронных
компоненты — теперь мы используем один
символ для представления кластера логики
ворота соединены для выполнения определенного
функция.
Немного
Типичные символы триггеров показаны ниже:
Любой
этих символов могут быть изменены в соответствии с
к их фактическому использованию в более крупных
схема. Например, если только выход Q
Например, если только выход Q
используется, вполне может быть единственным выходом
показано. Некоторые шлепанцы включают мастер
входы предварительной настройки или сброса, которые обходят
часы и мастер-секция срабатывающего по фронту
триггер и принудительный вывод на немедленный
известное состояние.Это часто используется, когда
схема, состоящая из множества триггеров,
сначала включили, так что все цепи
начнется в известном состоянии.
Logic Level — обзор
9.2.3 Ограничения выводов
Первый вопрос, который приходит в голову при рассмотрении назначения выводов: «Почему бы не позволить инструментам FPGA назначать выводы?» Это частый вопрос, который задают дизайнеры, поскольку инструменты FPGA доверяют размещению и маршрутизации проекта. Однако есть несколько факторов, которые влияют на программно-управляемое назначение местоположения ресурса. Одна из основных директив размещения FPGA заключается в расширении функциональности во избежание перегрузки маршрутизации. Без четких указаний об обратном, инструменты обычно работают для распределения функциональности по доступным ресурсам. Например, инструменты FPGA могут испытывать трудности с идентификацией контактов, составляющих сигнальную шину, а также могут испытывать трудности с идентификацией управляющих сигналов, связанных с шиной.Без знания того, что сигналы образуют группу, инструменты не стремятся совмещать сигналы, даже если они могут выиграть от более близкого размещения. Хотя можно увеличить глобальные ограничения проекта, чтобы сигналы шины и связанные с ними управляющие сигналы располагались как группа, тогда группа разработчиков рискует чрезмерно ограничить проект. Это может значительно увеличить время размещения и маршрутизации программного обеспечения FPGA.
Однако есть несколько факторов, которые влияют на программно-управляемое назначение местоположения ресурса. Одна из основных директив размещения FPGA заключается в расширении функциональности во избежание перегрузки маршрутизации. Без четких указаний об обратном, инструменты обычно работают для распределения функциональности по доступным ресурсам. Например, инструменты FPGA могут испытывать трудности с идентификацией контактов, составляющих сигнальную шину, а также могут испытывать трудности с идентификацией управляющих сигналов, связанных с шиной.Без знания того, что сигналы образуют группу, инструменты не стремятся совмещать сигналы, даже если они могут выиграть от более близкого размещения. Хотя можно увеличить глобальные ограничения проекта, чтобы сигналы шины и связанные с ними управляющие сигналы располагались как группа, тогда группа разработчиков рискует чрезмерно ограничить проект. Это может значительно увеличить время размещения и маршрутизации программного обеспечения FPGA.
В конечном итоге команда разработчиков знает больше о желаемом потоке данных в процессе проектирования, чем об инструментах. Команда разработчиков должна быть в лучшем положении, чтобы направлять и влиять на реализацию проекта посредством информированного назначения контактов. Группе дизайнеров, использующей быстрый поток разработки, может потребоваться начать назначение ввода-вывода на очень ранних этапах цикла проектирования. Процесс назначения ввода / вывода более сложен, чем просто назначение сигналов доступным контактам пакета. В следующих параграфах будут представлены некоторые соображения, которые влияют на решения о назначении контактов.
Команда разработчиков должна быть в лучшем положении, чтобы направлять и влиять на реализацию проекта посредством информированного назначения контактов. Группе дизайнеров, использующей быстрый поток разработки, может потребоваться начать назначение ввода-вывода на очень ранних этапах цикла проектирования. Процесс назначения ввода / вывода более сложен, чем просто назначение сигналов доступным контактам пакета. В следующих параграфах будут представлены некоторые соображения, которые влияют на решения о назначении контактов.
Назначение сигналов уровня платы для ввода-вывода FPGA может иметь большое влияние на производительность системы.В идеальном мире критически важные функции FPGA уже были бы захвачены, скомпилированы и смоделированы несколько раз перед этапом назначения выводов, что позволило бы команде разработчиков определить оптимальное назначение выводов. Однако при типичной быстрой разработке системы контакты устройства назначаются на ранних этапах цикла проектирования. Раннее назначение может быть необходимо для поддержки ранней компоновки печатной платы. Возможно, что плата PCB уже разводится и находится в процессе сборки до того, как будет захвачен значительный процент функционального дизайна FPGA.Такая «фиксация выводов» может потребоваться для соблюдения жестких графиков проектирования и для того, чтобы разработка ПЛИС происходила параллельно с усилиями по сборке платы. Это приводит к максимальному продвижению по расписанию, а также к увеличению риска.
Возможно, что плата PCB уже разводится и находится в процессе сборки до того, как будет захвачен значительный процент функционального дизайна FPGA.Такая «фиксация выводов» может потребоваться для соблюдения жестких графиков проектирования и для того, чтобы разработка ПЛИС происходила параллельно с усилиями по сборке платы. Это приводит к максимальному продвижению по расписанию, а также к увеличению риска.
Важно отметить, что назначение выводов не критично для всех конструкций или всех выводов в конструкции. Конструкции со значительными запасами ввода / вывода или низкими рабочими скоростями могут не требовать тщательного назначения контактов. Однако назначение выводов может стать решающим фактором, если запас конструкции ограничен одним из следующих факторов проектирования ПЛИС:
- ▪
Доступность выводов ввода / вывода
- ▪
Логические ресурсы уровня матрицы FPGA
- ▪
Ресурсы маршрутизации на кристалле
- ▪
Требуемая логическая скорость в сравнении с максимальной скоростью FPGA
- ▪
Требуемая логическая скорость в зависимости от уровней логики, необходимых для реализации проекта
Назначение контактов
также могут стать критическими на уровне платы, когда сигналы требуют особых соображений по маршрутизации, таких как короткая длина трассы сигнала, согласованная длина линии или контролируемый импеданс.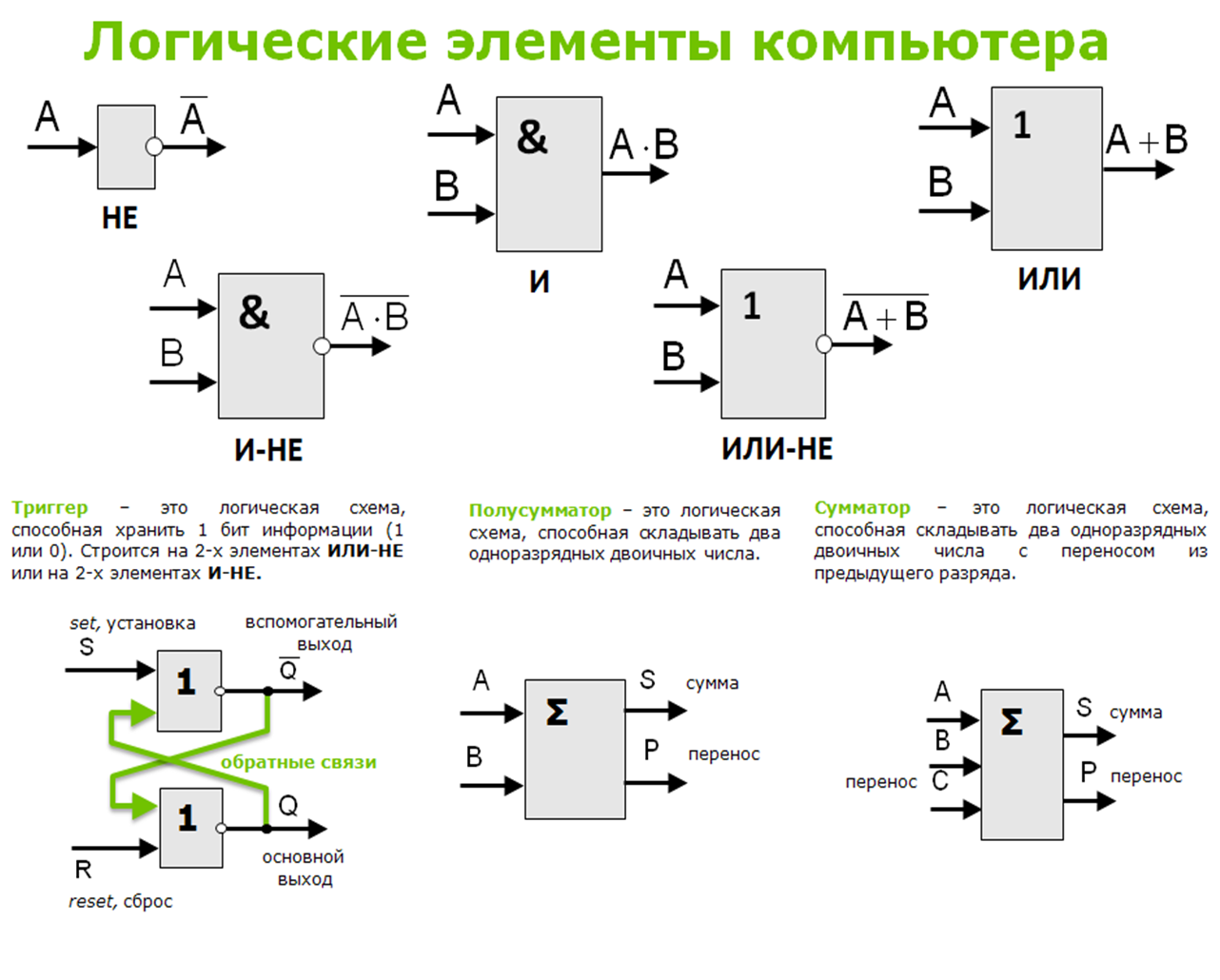 Эти требования могут быть результатом нагрузки сигнала, требований к скорости или требований к электромагнитным помехам.
Эти требования могут быть результатом нагрузки сигнала, требований к скорости или требований к электромагнитным помехам.
Большинство разработок попадают в группу кроссоверов, где назначение выводов не совсем критично, но также немаловажно для проектных характеристик. Практически любой дизайн может выиграть от хорошо реализованного назначения контактов. Можно повлиять на характеристики конструкции и улучшить их за счет продуманного назначения контактов. Конструктивные факторы, которые могут повлиять на назначение контактов, включают:
- ▪
Размер устройства
- ▪
Необходимый комплект устройства
- ▪
Класс скорости устройства
- ▪
Максимальная скорость, с которой может работать ПЛИС
- ▪
Время, необходимое для выполнения подпрограмм размещения и маршрутизации
- ▪
Количество слоев в печатной плате
- ▪
Количество переходных отверстий, необходимых для реализации кроссоверов сигналов в печатной плате
- ▪
Ширина дорожек и расстояние между печатными платами
- ▪
Размещение и ориентация компонентов на печатной плате
- ▪
Сложность и время, необходимое для разводки печатной платы
Назначение контактов часто не зависит от времени или времени нция, необходимая для реализации оптимизированного дизайна. Далее следуют несколько важных концепций назначения контактов.
Далее следуют несколько важных концепций назначения контактов.
Процесс назначения контактов является итеративным, и назначения контактов часто назначаются несколько раз в течение жизненного цикла проекта, когда происходят изменения и обновления конструкции.
Эффективное назначение выводов требует подробных знаний проектирования на уровне системы, в том числе:
- ▪
Взаимосвязи компонентов на уровне платы и детали интерфейса
- ▪
Целевая архитектура FPGA детали и предлагаемая реализация проекта на уровне FPGA
Назначение контактов может быть сложной задачей, потому что разработчик должен знать многие аспекты проекта.На назначение контактов влияют факторы как на уровне платы, так и на уровне фабрики устройства. Назначения должны производиться на основе сильного системно-ориентированного понимания потока данных проекта на всех уровнях. Эффективное назначение выводов требует детального знания сигнальных интерфейсов, входящих и исходящих из FPGA на уровне платы, а также понимания предлагаемых функциональных групп и интерфейсов внутри FPGA. Назначения также могут зависеть от деталей архитектуры семейства FPGA и структуры ввода-вывода, а также конфигурации банка ввода-вывода, установленной группой разработчиков.
Эффективное назначение выводов требует детального знания сигнальных интерфейсов, входящих и исходящих из FPGA на уровне платы, а также понимания предлагаемых функциональных групп и интерфейсов внутри FPGA. Назначения также могут зависеть от деталей архитектуры семейства FPGA и структуры ввода-вывода, а также конфигурации банка ввода-вывода, установленной группой разработчиков.
Поскольку компоненты FPGA бывают дискретных размеров, конструкции FPGA могут иметь «дополнительные» выводы ввода / вывода, которые не требуются для ввода или вывода критически важных для системы сигналов. Вместо того, чтобы просто оставлять эти штифты неиспользованными, следует приложить все усилия, чтобы использовать каждый из этих штифтов с умом. Контакты ввода / вывода, которые являются «запасными» после назначения требуемых сигналов, должны быть оценены для потенциального использования в качестве контрольных точек, вспомогательных вводов / выводов или определяемых пользователем заземлений. Рассмотрите функциональность платы с точки зрения системы.Какие функции могут быть добавлены в будущем? Какие сигналы потребуются для реализации будущих функций? Можно ли исправить ошибки на уровне платы внутри ПЛИС, если бы были доступны правильные сигналы? Могут ли быть обеспечены дополнительные функции состояния или управления путем маршрутизации определенных сигналов в ПЛИС? Что это за дополнительные сигналы?
Рассмотрите функциональность платы с точки зрения системы.Какие функции могут быть добавлены в будущем? Какие сигналы потребуются для реализации будущих функций? Можно ли исправить ошибки на уровне платы внутри ПЛИС, если бы были доступны правильные сигналы? Могут ли быть обеспечены дополнительные функции состояния или управления путем маршрутизации определенных сигналов в ПЛИС? Что это за дополнительные сигналы?
Еще одно важное применение неиспользуемых выводов — обеспечение доступа к внутренним узлам внутри ПЛИС для тестирования и отладки. Маршрутизация нескольких точек тестирования к заголовкам или разъему для легкого подключения к тестируемому оборудованию может значительно упростить этап проверки и отладки цикла проектирования.Также может быть полезно вывести несколько контактов на контактные площадки. Эти контактные площадки позволяют легко подключать белые провода, которые могут потребоваться для решения будущих проблем. Также следует рассмотреть возможность маршрутизации сигналов для поддержки функциональных возможностей разработки для тестирования (DFT) для поддержки перехода на ASIC в будущем.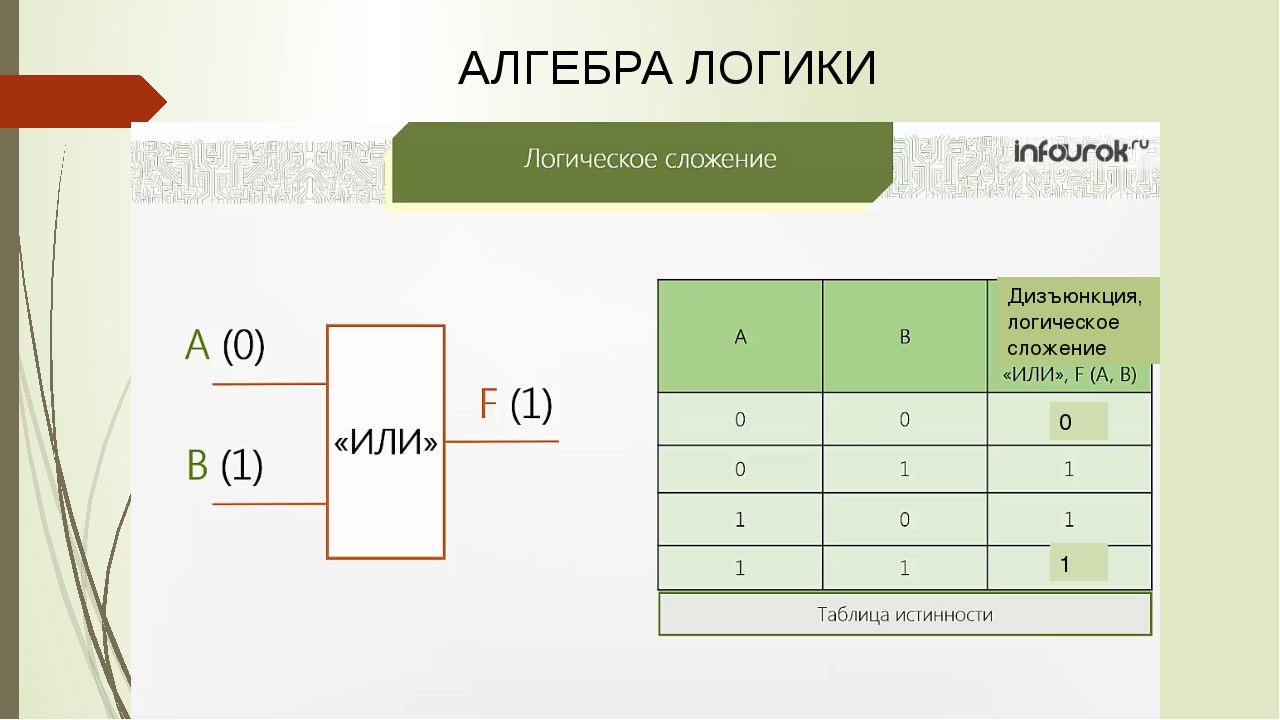
Следует рассмотреть возможность последовательного включения перемычек с нулевым сопротивлением с трассировками отладки и расширения относительно близко к корпусу FPGA. Размещение выводов подтягивающих и понижающих резисторов, а также подключения питания и заземления рядом с контактными площадками с нулевым сопротивлением также может быть реализовано для расширения возможностей проектирования в будущем.Эти дополнительные контактные площадки поддерживают доступ к иначе недоступным контактам ввода-вывода, что позволяет упростить добавление белых проводов для реализации обновлений дизайна, если требуются изменения интерфейса FPGA. Эти параметры поддерживают упрощенную отладку и потенциальное расширение дизайна в будущем, обеспечивая при этом максимальную гибкость дизайна в будущем. Хотя эти параметры могут быть очень полезны в средах прототипов и разработки, они менее подходят для плат массового производства.
Соображения по тактовой частоте при проектировании
Реализация сигналов синхронизации, маршрутизации, назначения выводов и управления синхронизацией может быть особенно сложной для проектирования ПЛИС.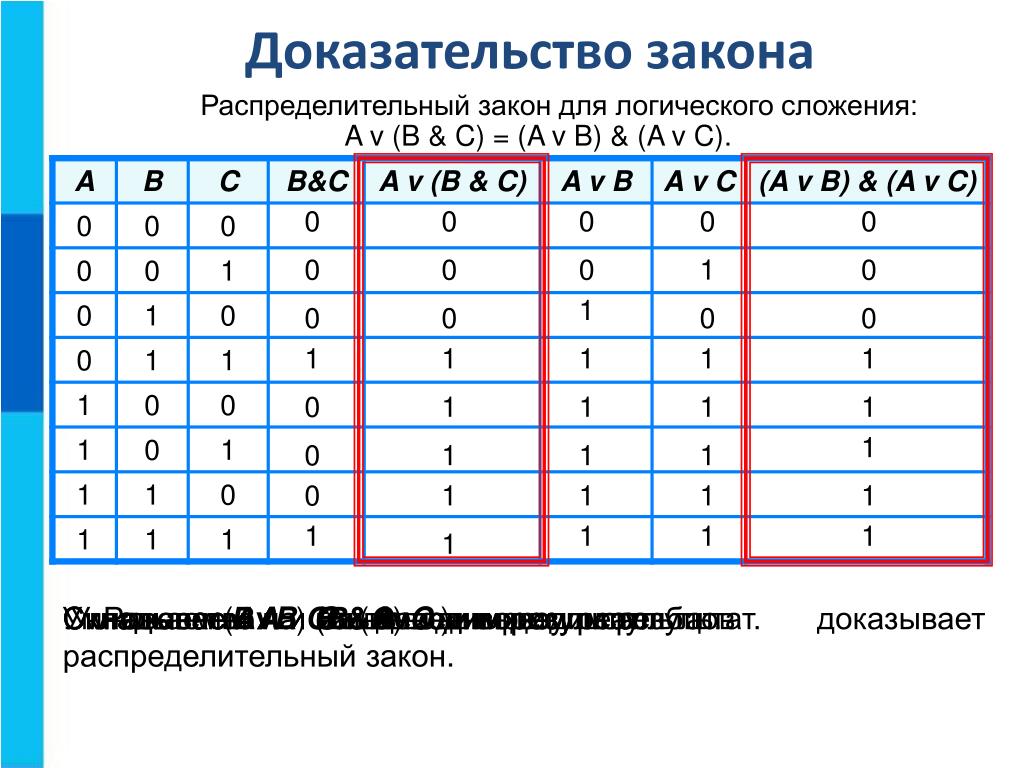 В этом разделе мы обсудим некоторые конструктивные факторы, связанные с реализацией часов. Например, возможно, что включение часов на конкретный выделенный вывод синхросигнала может ограничить использование или функциональность других выделенных выводов синхросигнала или использование внутренних глобальных ресурсов. Точно так же входы обратной связи по тактовому сигналу для компонента FPGA могут быть ограничены несколькими конкретными входными контактами тактового сигнала. Можно назначить сигнал общего назначения входному контакту обратной связи тактового сигнала, непреднамеренно блокируя доступ к этой функции FPGA.Ошибка в назначении выводов, связанных с часами, может серьезно ограничить функциональность реализации проекта. Очень важно, чтобы назначения часов были проверены и дважды сверены со всей доступной документацией, связанной с часами.
В этом разделе мы обсудим некоторые конструктивные факторы, связанные с реализацией часов. Например, возможно, что включение часов на конкретный выделенный вывод синхросигнала может ограничить использование или функциональность других выделенных выводов синхросигнала или использование внутренних глобальных ресурсов. Точно так же входы обратной связи по тактовому сигналу для компонента FPGA могут быть ограничены несколькими конкретными входными контактами тактового сигнала. Можно назначить сигнал общего назначения входному контакту обратной связи тактового сигнала, непреднамеренно блокируя доступ к этой функции FPGA.Ошибка в назначении выводов, связанных с часами, может серьезно ограничить функциональность реализации проекта. Очень важно, чтобы назначения часов были проверены и дважды сверены со всей доступной документацией, связанной с часами.
Эффективная реализация тактовой частоты для высокопроизводительных систем на базе FPGA выигрывает от разработки четко определенного плана реализации тактовой частоты.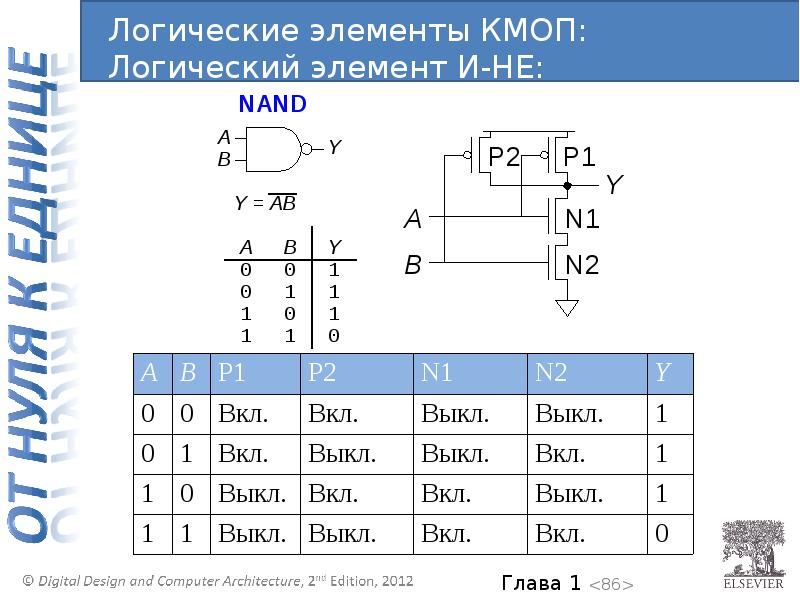 Конструкции ПЛИС обычно требуют высокого качества входной тактовой частоты и тщательного управления тактовой частотой и внутренней реализации ПЛИС.Факторы, которые могут ухудшить качество тактового сигнала, включают дрожание тактового сигнала, перекос тактового сигнала и искажение рабочего цикла.
Конструкции ПЛИС обычно требуют высокого качества входной тактовой частоты и тщательного управления тактовой частотой и внутренней реализации ПЛИС.Факторы, которые могут ухудшить качество тактового сигнала, включают дрожание тактового сигнала, перекос тактового сигнала и искажение рабочего цикла.
Эффекты джиттера тактовой частоты могут значительно снизить производительность реализованных систем. Влияние джиттера тактового сигнала включает уменьшение запаса временного бюджета и производительности. Смещение часов описывает разницу между временем прихода связанного сигнала и часов. Эффекты перекоса сигнала и тактовой частоты включают сбои времени удержания, ошибки данных и уменьшение запаса времени ввода / вывода. Искажение коэффициента заполнения тактового сигнала может привести к уменьшению длительности импульса, ошибкам данных и ненадежной работе схемы. Эффекты джиттера тактового сигнала, перекоса и искажения рабочего цикла могут влиять на все уровни производительности схем ПЛИС и должны тщательно контролироваться и контролироваться.
В следующих параграфах представлены некоторые рекомендации по проектированию часов FPGA.
- (1)
Разделите тактовые импульсы ПЛИС на группы приоритета. Используйте ограничения, чтобы более четко характеризовать часы для инструментов проектирования. Ограничения можно использовать для определения тактовых частот, фазовых соотношений и рабочих циклов.Ограничения также могут использоваться для связывания тактовых импульсов с высоким приоритетом со схемой, которой они управляют.
Группы приоритета часов
- ▪
Высокая частота с высоким разветвлением
- ▪
Средняя или низкая частота с высоким разветвлением
- ▪
Высокая частота с низким разветвлением
- ▪
Средняя или низкая частота с низким разветвлением
- (2)
Сначала назначьте тактовые частоты с наивысшим приоритетом.
 Двумя наиболее важными проблемами синхронизации FPGA являются высокая скорость и большое количество разветвлений. Часы с этими характеристиками следует отнести к более высокопроизводительным глобальным ресурсам. Количество высокопроизводительных буферов и ресурсов маршрутизации ограничено, поэтому ими следует тщательно управлять.
Двумя наиболее важными проблемами синхронизации FPGA являются высокая скорость и большое количество разветвлений. Часы с этими характеристиками следует отнести к более высокопроизводительным глобальным ресурсам. Количество высокопроизводительных буферов и ресурсов маршрутизации ограничено, поэтому ими следует тщательно управлять.- (3)
Назначьте ресурсы управления блоком часов. Тактовые блоки, такие как Digital Clock Manager (DCM) Xilinx, могут реализовывать расширенные функции тактовой схемы, включая частотное деление и умножение, фазовый сдвиг, регулировку на основе обратной связи и синхронную генерацию тактовых импульсов.Блоки синхронизации — это ограниченные ресурсы в компонентах FPGA. Команда разработчиков должна отслеживать и контролировать распределение этих ресурсов.
- (4)
Управление часами с более низким приоритетом. Хотя тактовые импульсы с более низким приоритетом могут быть реализованы на глобальных ресурсах полной FPGA, если они доступны, они также могут маршрутизироваться через стандартную матрицу маршрутизации FPGA.
 Можно разбить маршруты глобальных часов на несколько более мелких высокопроизводительных маршрутов часов.
Можно разбить маршруты глобальных часов на несколько более мелких высокопроизводительных маршрутов часов.
Примеры включают разбиение маршрута глобального тактового сигнала с возможностью подачи тактового сигнала на всю ПЛИС на более мелкие схемы, способные направлять тактовый сигнал на половину или четверть ПЛИС. Маршрутизация часов через глобальный маршрут подраздела может потребовать ввода часов на определенные контакты ввода / вывода. Это еще раз подчеркивает важность тщательного распределения контактов.
| (видео — базовая настройка логического анализатора) .Внутренние часы (режим синхронизации) : 100 Гц ~ 200 МГц . Память : 64 Мбит . Глубина памяти (на канал) 2 Мбит . Канал запуска : Интерфейс на базе 32-канального ПК . .Питание : USB 1.1 (2.0) . Запуск по протоколу пакета: параллельный, последовательный . Модуль запуска по длительности импульса: бесплатно | ||
| (видео — базовая настройка логического анализатора) .Внутренние часы (режим синхронизации) : 100 Гц ~ 200 МГц . Память : 4 Мбит . Глубина памяти (на канал) 128 Кбит . Канал запуска : Интерфейс на базе 32-канального ПК . .Питание : USB 1.  1 (2,0) 1 (2,0) | ||
| (видео — базовая настройка логического анализатора) .Внутренние часы (режим синхронизации) : 100 Гц ~ 200 МГц . Память : 4 Мбит Глубина памяти (на канал) 128 Кбит . Канал запуска : Интерфейс на базе 16-канального ПК . .Питание : USB 1.1 (2.0) | ||
| (видео — базовая настройка логического анализатора) .Внутренние часы (режим синхронизации) : 100 Гц ~ 200 МГц . Память : 1 Мбит . Глубина памяти (на канал) 64 Кбит . Канал запуска : Интерфейс на базе 16 ПК . .Питание : USB 1.  1 (2,0) 1 (2,0) | ||
| (видео — базовая настройка логического анализатора) .Внутренние часы (режим синхронизации) : 100 Гц ~ 200 МГц . Память : 512 Кбит Глубина памяти (на канал) 32 Кбит .Питание : USB 1.1 (2.0) | ||
| (видео — Logic Analyzer_basic setting) .Внутренняя частота дискретизации: 100 Гц ~ 200 МГц .Размер ОЗУ: 64 Мбит .Глубина памяти на канал: 2 Мбит .1 (2,0) для питания | ||
1.
 1 Логические операции
1 Логические операции
Математика обычно включает сочетание истинных (или гипотетически истинных)
утверждения различными способами для создания (или доказательства) новых истинных утверждений.
Начнем с разъяснения некоторых из этих фундаментальных идей.
Под предложением мы подразумеваем
утверждение, имеющее определенное значение истинности ,
истина (T) или ложь (F) — например,
«В 1492 году Колумб плавал по синему океану.» (T)
«Наполеон выиграл битву при Ватерлоо». (F)
В более общем смысле, формула означает
утверждение, возможно, с участием некоторых переменных, которое либо истинно, либо
false всякий раз, когда мы присваиваем определенные значения каждой из переменных.
Мы будем использовать заглавные буквы для обозначения формул. Если правда
формула зависит от значений, скажем, $ x $, $ y $ и $ z $, мы будем использовать
обозначение типа $ P (x, y, z) $ для обозначения формулы.
Пример 1.1.1. Если $ P (x, y) $ равно «$ x ^ 2 + y = 12 $», то $ P (2,8) $ и $ P (3,3) $ равны
истина, а $ P (1,4) $ и $ P (0,6) $ — ложь. Если $ Q (x, y, z) $ равно «$ x + y
Если $ Q (x, y, z) $ равно «$ x + y
Верно ли предложение или ложно, обычно зависит от того, что мы
говорят — одно и то же предложение может быть верным или ложным в зависимости от
по контексту; например, формула $ x | y $ означает `$ x $ делит
$ y $ ‘. То есть $ x | y $, если есть некоторый $ z $, так что $ y = x \ cdot z $. В настоящее время,
правда ли, что $ 3 | 2 $? Это зависит: если мы говорим о целых числах,
ответ — нет; если мы говорим о рациональных числах, ответ
да, потому что $ 2 = 3 \ cdot (2/3) $. (Конечно, если $ x \ not = 0 $ и $ y $ равны
любых рациональных чисел, затем $ x | y $, так что это не очень
полезное понятие.При нормальном использовании вид формулы
«$ x | y $» означает , что $ x $ и $ y $ являются целыми числами.)
Вселенная дискурса для определенной области математики — это набор, который
содержит все интересное по этой теме. Когда мы
изучение математических формул типа `$ x $ делит $ y $ ‘на переменные
предполагается, что они принимают значения в любой вселенной дискурса
подходит для конкретной темы. Вселенная дискурса
Вселенная дискурса
обычно это ясно из обсуждения, но иногда нам нужно
определите это явно для ясности.Универсум дискурса обычно обозначается $ U $.
Сложные предложения и формулы складываются из более простых,
используя небольшое количество логических операций . Просто горстка
этих операций позволят нам сказать все, что нам нужно сказать в
математика.
Если $ P $ — формула, то «not $ P $» — другое
формула, которую мы символически записываем как $ \ lnot P $. Конечно, $ \ lnot
P $ ложно, если $ P $ истинно, и наоборот — например,
«6 — не простое число» или «Неверно, что 6 — это простое число».
премьер » или
«$ \ lnot (\ hbox {6 простое число}) $ » (T)
«Рональд Рейган не был президентом.» (F)
Предположим, что $ P $ и $ Q $ — формулы. потом
«$ P $ и $ Q $» — это формула, записанная символически.
как $ P \ land Q $, называемое соединением
$ P $ и $ Q $. Для $ P \ land Q $ верны и $ P $, и $ Q $
должно быть истинным, в противном случае — ложным, например,
«5 долларов = 6 долларов и 7 долларов = 8 долларов». (F)
(F)
«Сиэтл находится в Вашингтоне, а Бойсе — в Айдахо». (T)
«Толстой был русским, а Диккенс —
Французский ». (F)
Если $ P $ и $ Q $ являются формулами, то формула «$ P $ или $ Q $» символически записывается как $ P \ lor Q $, называемая
дизъюнкция $ P $ и $ Q $.это
важно отметить, что это , включая , или, то есть, «либо
или оба». Итак, если $ P $, $ Q $ или и $ P $, и $ Q $ верны,
так и $ P \ lor Q $. Единственный способ, которым $ P \ lor Q $ может быть ложным, — это если оба $ P $
и $ Q $ ложны — например,
«Вашингтон находится в Канаде, а Лондон — в Англии». (T)
«$ 5
«Ленин был испанцем или Ганди был итальянцем». (F)
Если $ P $ и $ Q $ — формулы, то «если $ P $, то $ Q $»
или написано «$ P $ подразумевает $ Q $»
$ P \ подразумевает Q $, используя условный символ ,
$ \ подразумевает $.Не очевидно (по крайней мере, для большинства людей), при каких условиях
обстоятельства $ P \ подразумевают, что Q $ должно быть истинным. Отчасти это потому, что
Отчасти это потому, что
«if… then» используется более чем одним способом в обычном английском языке, однако
нам нужно исправить правило, которое позволит нам точно знать, когда $ P \ подразумевает
Q $ верно. Конечно, если $ P $ истинно, а $ Q $ ложно, $ P $ не может
следует $ Q $, поэтому $ P \ означает, что Q $ в этом случае неверно. Чтобы помочь нам с
в остальных случаях рассмотрим следующее утверждение:
«Если $ x $ меньше 2, тогда $ x $ меньше 4.»
Это утверждение должно быть верным независимо от значения $ x $.
(при условии, что вселенная дискурса является чем-то знакомым, например
целые числа). Если $ x $ равен 1, он оценивается как $ \ rm T \ implies T $, если $ x $
равно 3, оно становится $ \ rm F \ Impies T $, а если $ x $ равно 5, оно становится
$ \ rm F \ влечет F $. Таким образом, кажется, что $ P \ подразумевает, что Q $ истинно, если
$ P $ истинно, а $ Q $ ложно. Это правило, которое мы принимаем.
Наконец, с двумя условными обозначениями , записываемым $ \ Leftrightarrow $, соответствует
фраза «тогда и только тогда» или «если и только если»
коротко.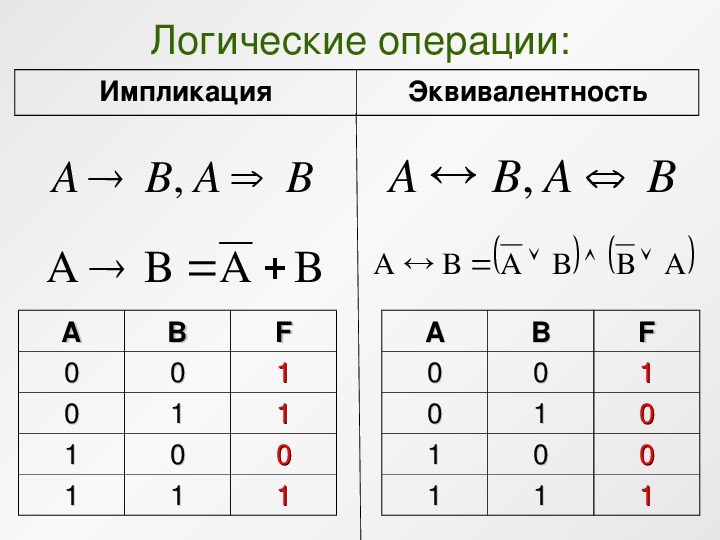 Итак, $ P \ Leftrightarrow Q $ истинно, когда и $ P $, и $ Q $
Итак, $ P \ Leftrightarrow Q $ истинно, когда и $ P $, и $ Q $
имеют то же значение истинности, в противном случае — ложь.
Пример 1.1.2. Предположим, что $ P (x, y) $ — это «$ x + y = 2 $», а $ Q (x, y) $
равно «$ xy> 1 $». Тогда, когда $ x = 1 $ и $ y = 1 $,
$ \ lnot P (x, y) $, $ P (x, y) \ land Q (x, y) $, $ P (x, y) \ lor Q (x, y) $,
$ P (x, y) \ влечет Q (x, y) $ и $ P (x, y) \ Leftrightarrow Q (x, y) $
имеют истинностные значения F, F, T, F, F, соответственно, и когда
$ x = 2 $ и $ y = 3 $ имеют значения истинности
T, F, T, T, F соответственно.
$ \ квадрат $
Используя операции $ \ lnot $, $ \ land $, $ \ lor $, $ \ implies $,
$ \ Leftrightarrow $, мы можем построить составные выражения , такие как
$$
(P \ land (\ lnot Q)) \ подразумевает ((\ lnot R) \ lor ((\ lnot P) \ land Q)).$$
Как показывает этот пример, иногда необходимо
включать много круглых скобок, чтобы термины были сгруппированы
в формуле ясно. Как и в алгебре, где
умножение имеет приоритет перед сложением, мы можем
убрать скобки
согласование определенного порядка, в котором логические
операции выполняются. Мы
Мы
будет применять операции в этом порядке, начиная с
от начала до конца: $ \ lnot $, $ \ land $, $ \ lor $, $ \ подразумевает $
и $ \ Leftrightarrow $. Так
$$ A \ подразумевает B \ lor C \ land \ lnot D
$$
это сокращение от
$$ A \ подразумевает (B \ lor (C \ land (\ lnot D))).$$
Как и в алгебре, часто имеет смысл включить
несколько дополнительных круглых скобок, чтобы убедиться, что предполагаемое значение ясно.
Большая часть информации, которую мы обсудили, может быть обобщена в таблицах истинности . Например, таблица истинности для
$ \ lnot P $ — это:
В этой таблице две строки, потому что есть только две возможности для
истинное значение $ P $. В других логических операциях используются две переменные, поэтому
им требуется 4 строки в своих таблицах истинности.
| $ P $ | $ Q $ | $ P \ land Q $ | $ P \ lor Q $ | $ P \ Rightarrow Q $ | $ P \ Leftrightarrow Q $ |
|---|---|---|---|---|---|
| T | T | T | T | T | T |
| F | T | F | T | T | F |
| T | F | F | T | F | F |
| F | F | F | F | T | T |
У любого составного выражения есть таблица истинности.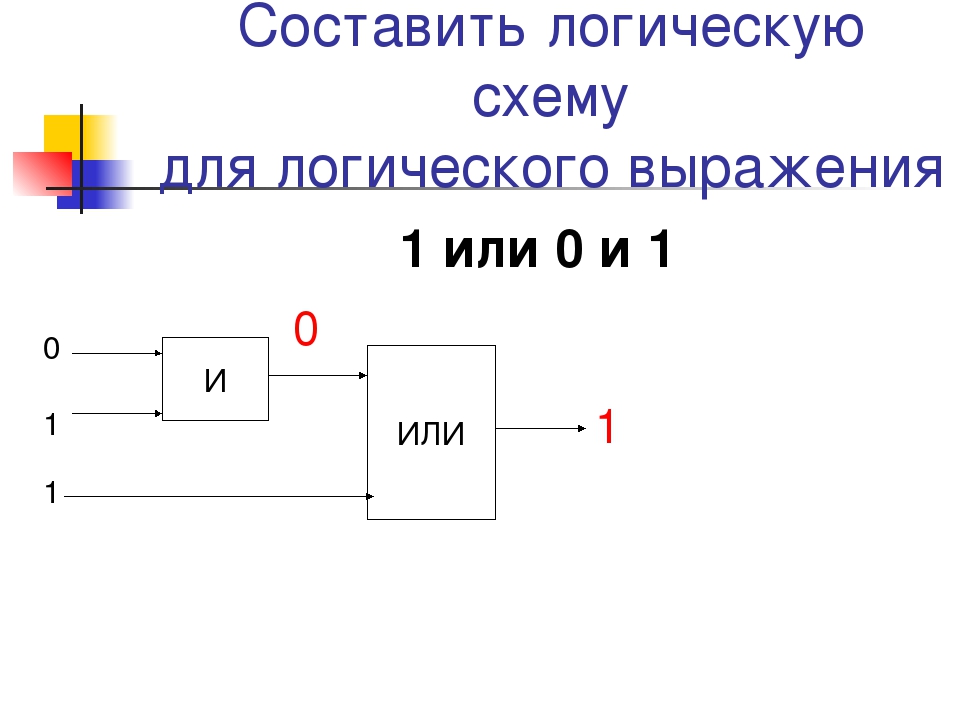 n $
n $
строк в таблице, потому что есть много разных способов назначить
Команды «T» и «F» для простых формул $ n $ в составном выражении.
Таблица истинности для $ (P \ land Q) \ lor \ lnot R $:
| $ P $ | $ Q $ | $ | $ P \ land Q $ | $ \ lnot R $ | $ (P \ land Q) \ lor \ lnot R $ |
|---|---|---|---|---|---|
| T | T | T | T | F | T |
| F | T | T | F | F | F |
| T | F | T | F | F | F |
| F | F | T | F | F | F |
| T | T | F | T | T | T |
| F | T | F | F | T | T |
| T | F | F | F | T | T |
| F | F | F | F | T | T |
Обратите внимание на то, как включение промежуточных шагов упрощает отображение таблицы.
рассчитывать и читать.
Тавтология — это логическое выражение, которое
всегда оценивается как T, то есть последний столбец своей таблицы истинности
состоит только из Т. Иногда говорят, что тавтология — это действительное ; хотя «действительный» используется в других контекстах как
что ж, это не должно вызывать путаницы. Например, $ (P \ land Q) \ lor
P \ Leftrightarrow P $ является тавтологией, поскольку ее таблица истинности:
| $ P $ | $ Q $ | $ P \ land Q $ | $ (P \ land Q) \ lor P $ | $ (P \ land Q) \ lor P \ Leftrightarrow P $ |
|---|---|---|---|---|
| T | T | T | T | T |
| F | T | F | F | T |
| T | F | F | T | T |
| F | F | F | F | T |
Мы перечислим несколько важных тавтологий в следующей теореме.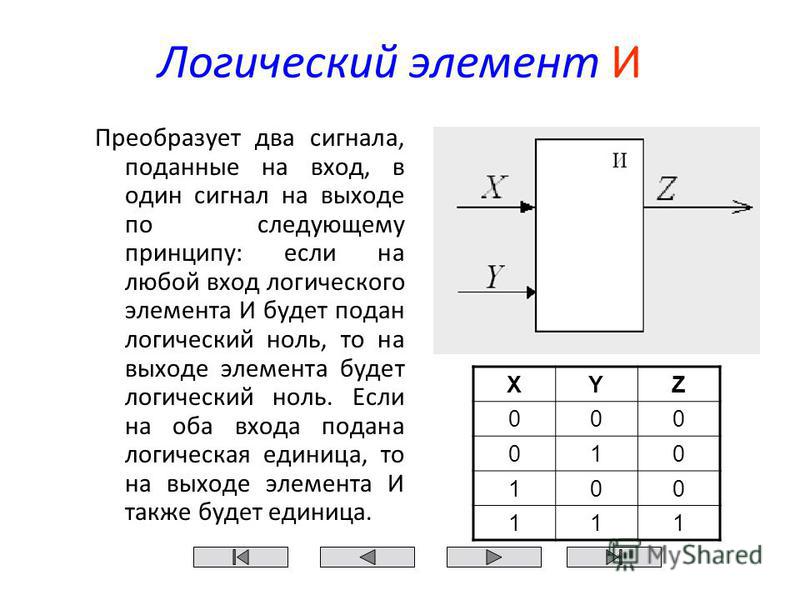
Теорема 1.1.3 Справедливы следующие утверждения.
а) $ P \ Leftrightarrow \ lnot \ lnot P $
б) $ P \ lor Q \ Leftrightarrow Q \ lor P $
c) $ P \ land Q \ Leftrightarrow Q \ land P $
d) $ (P \ land Q) \ land R \ Leftrightarrow P \ land (Q \ land R) $
e) $ (P \ lor Q) \ lor R \ Leftrightarrow P \ lor (Q \ lor R) $
f) $ P \ land (Q \ lor R) \ Leftrightarrow
(P \ земля Q) \ lor (P \ земля R) $
г) $ P \ lor (Q \ land R) \ Leftrightarrow (P \ lor Q) \ land (P \ lor R) $
ч) $ (P \ подразумевает Q) \ Leftrightarrow (\ lnot P \ lor Q) $
i) $ P \ подразумевает (P \ lor Q) $
j) $ P \ land Q \ подразумевает Q $
k) $ (P \ Leftrightarrow Q) \ Leftrightarrow ((P \ подразумевает Q) \ land
(Q \ влечет P)) $
l) $ (P \ подразумевает Q) \ Leftrightarrow (\ lnot Q \ подразумевает \ lnot P) $
Доказательство.
Доказательства оставлены как упражнения.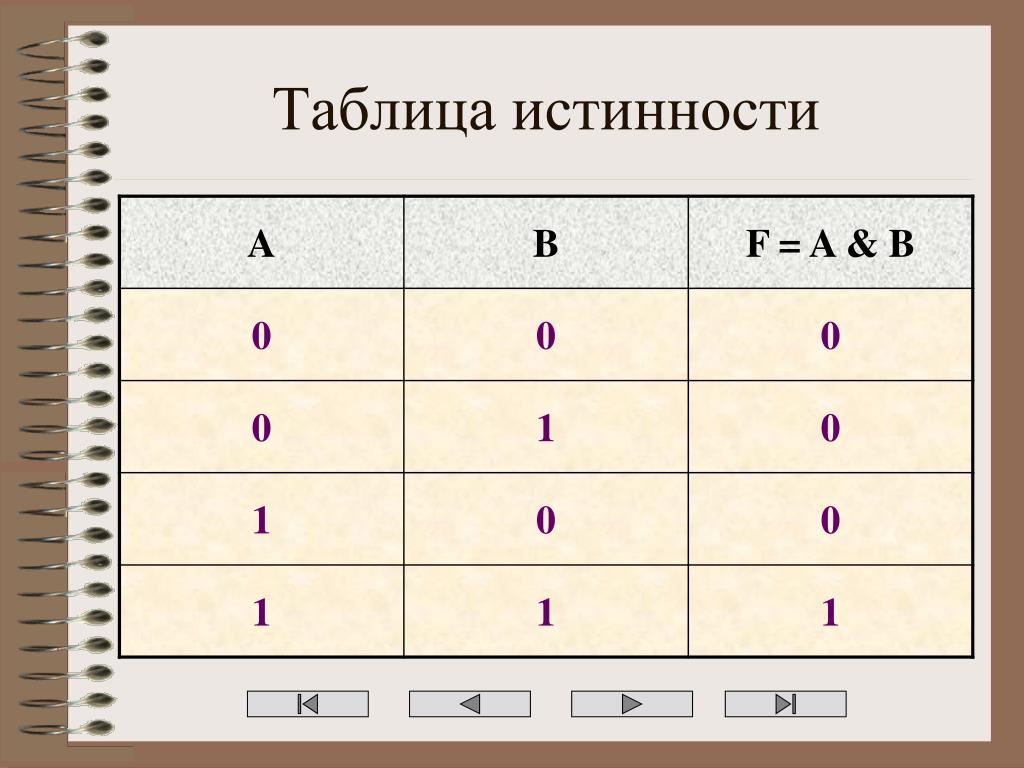
$ \ qed $
Заметим, что (b) и (c) — коммутативные законы, (d) и (e) —
ассоциативные законы и (f) и (g) говорят, что $ \ land $
и $ \ lor $ распределяются друг над другом. Это говорит о том, что существует
форма алгебры для логических выражений, аналогичных алгебре
для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений,
особенно в информатике.
Если две формулы всегда принимают одно и то же значение истинности, несмотря ни на что
элементы из вселенной дискурса мы заменяем различными
переменных, то мы говорим, что они эквивалентны .Стоимость эквивалента
формулы в том, что они говорят одно и то же. Это всегда правильный шаг
в доказательстве заменить некоторую формулу на эквивалентную. Кроме того,
многие тавтологии содержат важные идеи для построения доказательств. За
Например, (k) говорит, что если вы хотите показать, что $ P \ Leftrightarrow Q $, это
возможно (и часто желательно) разбить доказательство на два
частей, одна из которых доказывает импликацию $ P \ влечет Q $, а вторая
доказывая обратное , $ Q \ влечет P $.
Читая теорему 1.1.3 у вас может быть
заметил, что $ \ land $ и $ \ lor $ удовлетворяют многим аналогичным свойствам.
Эти понятия называются «двойственными» — для любого свойства
один, есть почти идентичное свойство, которому удовлетворяет другой,
при этом экземпляры двух операций поменялись местами. Это часто
означает, что когда мы доказываем результат, включающий одно понятие, мы получаем
соответствующий результат для его дуала без дополнительной работы.
Джордж Буль. логический
(1815–1864) имел только общее школьное образование, хотя учился
Греческий и латинский сами по себе.Он начал свою карьеру элементарным
школьный учитель, но решил, что ему нужно больше узнать о
математике, поэтому он начал изучать математику, а также
языки, необходимые для чтения современной литературы на
математика. В 1847 году он опубликовал небольшую книгу The Mathematical
Анализ Logic , который справедливо можно сказать, положил начало исследованию
математической логики. Ключевой вклад работы был в
Ключевой вклад работы был в
новое определение «математики», чтобы не означать просто «изучение чисел и
величина », но изучение символов и манипуляции с ними в соответствии с
к определенным правилам.Важность этого уровня абстракции для
будущее математики трудно переоценить. Наверное, на
Благодаря этой работе он перешел на работу в Куинс-колледж в Корке.
В Исследование законов мышления , опубликованном в 1854 году,
Буль установил настоящую формальную логику, развивая то, что сегодня называется
Булева алгебра, или иногда алгебра множеств . Он использовал символы для
сложение и умножение как операторы, но полностью абстрактно
смысл.Сегодня эти символы все еще иногда используются в логических
алгебры, хотя символы `$ \ land $ ‘и` $ \ lor $’, `$ \ cap $ ‘и
Также используются `$ \ cup $ ‘. Буль применил алгебраические манипуляции к
процесс рассуждения. Вот простой пример такого рода
манипуляции, которые он совершил: уравнение $ xy = x $ (которое сегодня можно было бы записать
$ x \ land y = x $ или $ x \ cap y = x $) означает, что `все, что удовлетворяет
$ x $ удовлетворяет $ y $, или, в наших терминах, $ x \ влечет y $. Если также $ yz = y $ (что
Если также $ yz = y $ (что
есть, $ y \ подразумевает z $), то замена $ y = yz $ на $ xy = x $ дает
$ x (yz) = x $ или $ (xy) z = x $.2 + bD + c = 0 $, лечение
$ D $ в виде числа предоставляет информацию о решениях для
дифференциальное уравнение.
Информация здесь взята из A History of Mathematics, by
Карл Б. Бойер, Нью-Йорк: Джон Вили и сыновья, 1968. Подробнее
информацию см. Лекций по десяти британским математикам , автор
Александр Макфарлейн, Нью-Йорк: John Wiley & Sons, 1916.
Упражнения 1.1
Пример 1.1.1
Постройте таблицы истинности для следующих логических выражений:
а) $ (P \ land Q) \ lor \ lnot P $
б) $ P \ подразумевает (Q \ land P) $
c) $ (P \ land Q) \ Leftrightarrow (P \ lor \ lnot R) $
d) $ \ lnot P \ подразумевает \ lnot (Q \ lor R) $
Пр. 1.1,2
Проверьте тавтологии теоремы 1.1.3.
Пример 1.1.3
Предположим, что $ P (x, y) $ — это формула «$ x + y = 4 $», а $ Q (x, y) $ — это
формула «$ x
$ P (x, y) \ land Q (x, y) $, $ \ lnot P (x, y) \ lor Q (x, y) $,
$ P (x, y) \ влечет \ lnot
Q (x, y) $, $ \ lnot (P (x, y) \ Leftrightarrow Q (x, y)) $,
используя значения:
| a) $ x = 1, y = 3 $ | c) $ x = 1, y = 2 $ |
| b) $ x = 3, y = 1 | d) $ x = 2, y = 1 $ |
Пр. 1.1,4
1.1,4
а) Найдите таблицы истинности для
$$
P \ land (\ lnot Q) \ land R, \ quad \ quad (\ lnot P) \ land Q \ land (\ lnot R)
$$
б) Используйте их, чтобы найти таблицу истинности для
$$
(П \ земля (\ lnot Q) \ земля R) \ lor ((\ lnot P) \ земля Q \ земля (\ lnot R))
$$
c) Используйте метод, предложенный в частях (a) и (b)
найти формулу со следующей таблицей истинности.
| $ P $ | $ Q $ | $ | $ R $ ??? |
|---|---|---|---|
| T | T | T | T |
| F | T | T | F |
| T | F | T | F |
| F | F | T | F |
| T | T | F | T |
| F | T | F | T |
| T | F | F | F |
| F | F | F | F |
г)
Используйте метод, предложенный частями (a) — (c), чтобы
объясните, почему любой список из $ 2 ^ n $ T и F является
последний столбец таблицы истинности для некоторой формулы с $ n $ буквами.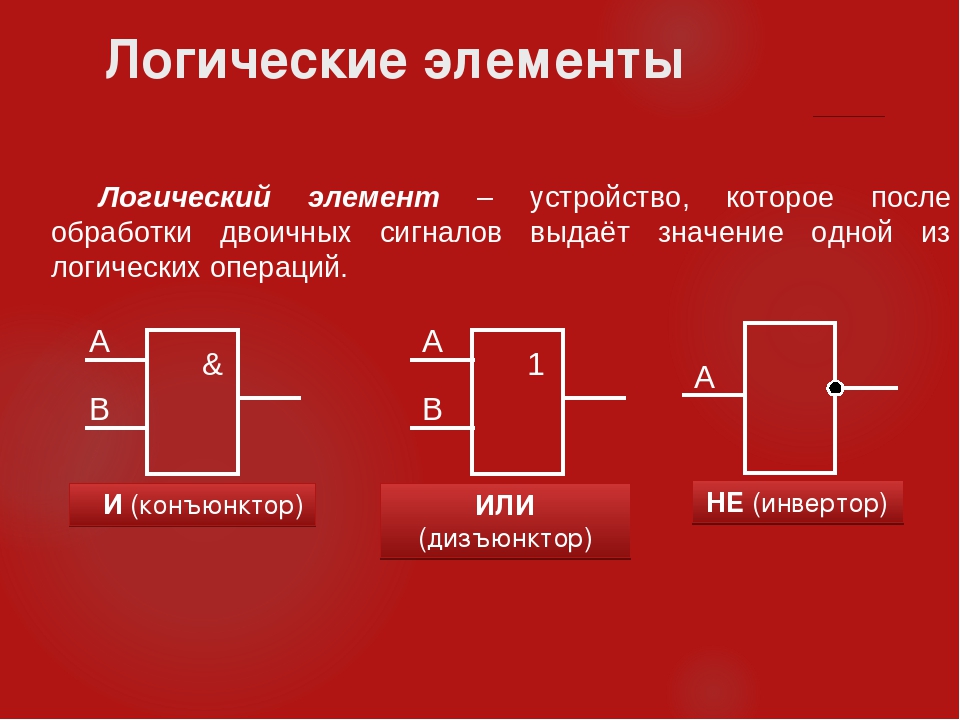

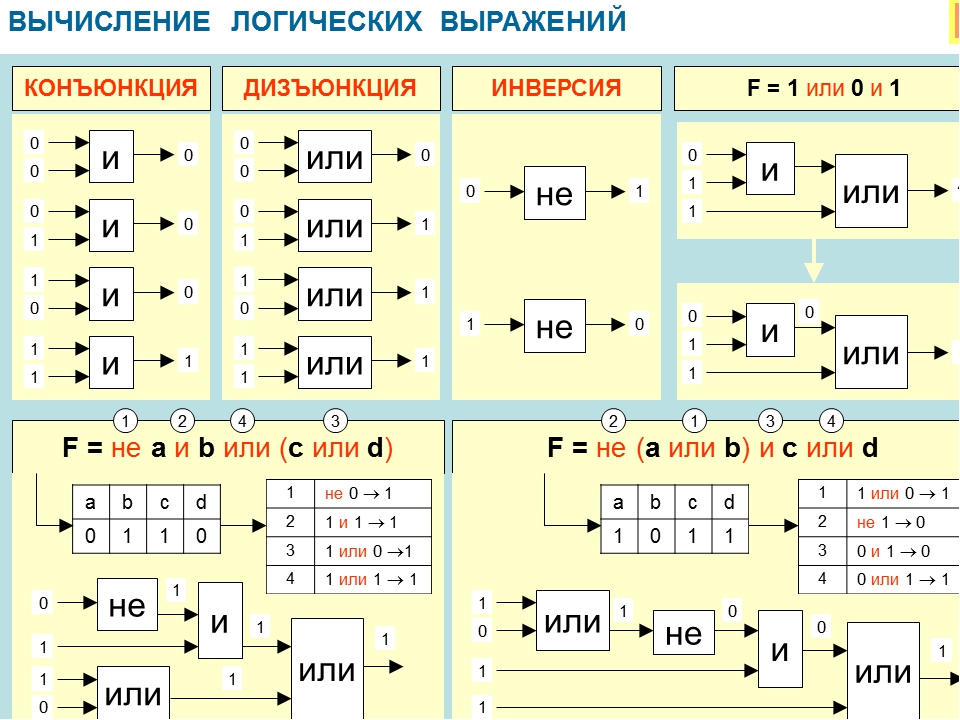
 Пропозициональная истинностная функция ставит в соответствие каждому перечисленному набору одно из значений истинности — 1 или 0. Всего таких функций 16. Конъюнкция приписывает выражению A & B значение 1 только в случае, когда как A, так и B истинны, то есть оба имеют значение 1, в остальных случаях значение A & B равно 0. Дизъюнкция Α ∨ B, напротив, ложна только в одном случае, когда ложны как A, так и B. Импликация A ⊃ B является ложной только при истинном (антецеденте) A и ложном (консеквенте) B. В остальных случаях A ⊃ B принимает значение 1.
Пропозициональная истинностная функция ставит в соответствие каждому перечисленному набору одно из значений истинности — 1 или 0. Всего таких функций 16. Конъюнкция приписывает выражению A & B значение 1 только в случае, когда как A, так и B истинны, то есть оба имеют значение 1, в остальных случаях значение A & B равно 0. Дизъюнкция Α ∨ B, напротив, ложна только в одном случае, когда ложны как A, так и B. Импликация A ⊃ B является ложной только при истинном (антецеденте) A и ложном (консеквенте) B. В остальных случаях A ⊃ B принимает значение 1. К полным системам в классической логике относятся, в частности, конъюнкция и отрицание; дизъюнкция и отрицание; импликация и отрицание. Конъюнкция и дизъюнкция определимы друг через друга за счёт эквивалентностей (A & B) ≡ ¬ (¬ A∨ ¬ B) и (A ∨ B) ≡ ¬ (¬ A & ¬ B), именуемых законами де Моргана, а также: (Α ⊃ Β) ≡ (¬ Α ∨ B), (A & B) ≡ ¬ (A ⊃ ¬ B), (Α ∨ B) ≡ (A ⊃ B) ⊃ A). Любая эквивалентность вида A ≡ B имеет силу только тогда, когда общезначима (всегда истинна) конъюнкция (A ⊃ B) & (B ⊃ A).
К полным системам в классической логике относятся, в частности, конъюнкция и отрицание; дизъюнкция и отрицание; импликация и отрицание. Конъюнкция и дизъюнкция определимы друг через друга за счёт эквивалентностей (A & B) ≡ ¬ (¬ A∨ ¬ B) и (A ∨ B) ≡ ¬ (¬ A & ¬ B), именуемых законами де Моргана, а также: (Α ⊃ Β) ≡ (¬ Α ∨ B), (A & B) ≡ ¬ (A ⊃ ¬ B), (Α ∨ B) ≡ (A ⊃ B) ⊃ A). Любая эквивалентность вида A ≡ B имеет силу только тогда, когда общезначима (всегда истинна) конъюнкция (A ⊃ B) & (B ⊃ A).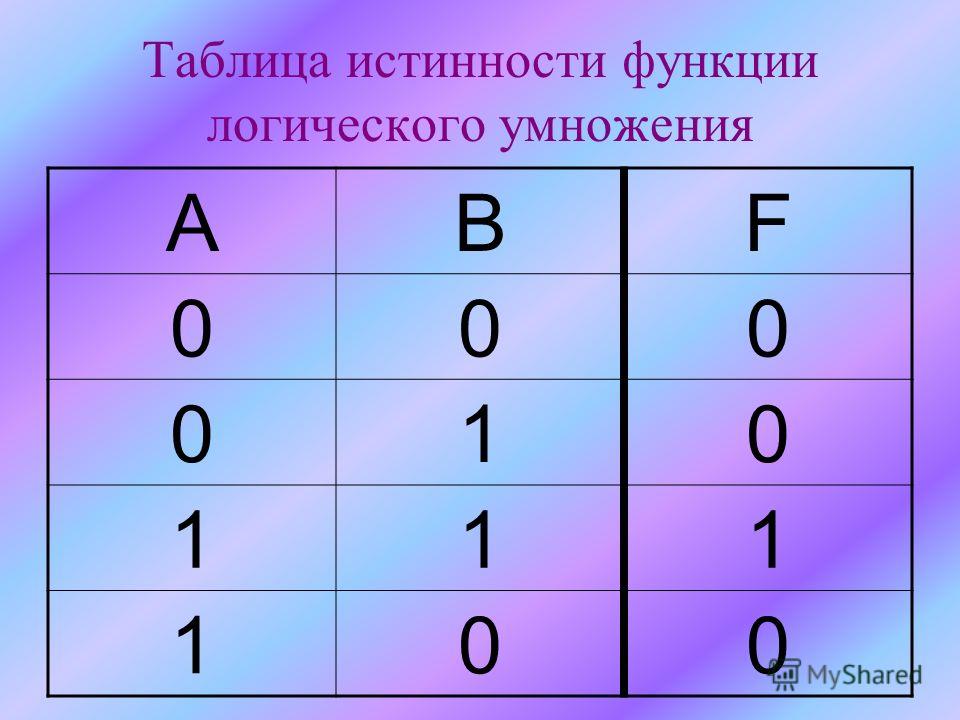 С. Пирсу (неопубликованная при его жизни работа 1880 года) и было переоткрыто X. Шеффером. Используя антидизъюнкцию как единственную логическую связку, Шеффер в 1913 построил полное исчисление высказываний. Антидизъюнкцию обозначают A∣B и называют штрихом Шеффера, читая данное выражение, как «не-A и не-B». Ж. Нико употребил то же обозначение для антиконъюнкции («Неверно, что одновременно A и B») и с помощью только этой связки в 1917 сформулировал полное исчисление высказываний с одной (всего!) аксиомой и одним правилом вывода. Таким образом, штрихом Шеффера называют по сути саму вертикальную черту, которая у разных авторов может обозначать как антидизъюнкцию, так и антиконъюнкцию.
С. Пирсу (неопубликованная при его жизни работа 1880 года) и было переоткрыто X. Шеффером. Используя антидизъюнкцию как единственную логическую связку, Шеффер в 1913 построил полное исчисление высказываний. Антидизъюнкцию обозначают A∣B и называют штрихом Шеффера, читая данное выражение, как «не-A и не-B». Ж. Нико употребил то же обозначение для антиконъюнкции («Неверно, что одновременно A и B») и с помощью только этой связки в 1917 сформулировал полное исчисление высказываний с одной (всего!) аксиомой и одним правилом вывода. Таким образом, штрихом Шеффера называют по сути саму вертикальную черту, которая у разных авторов может обозначать как антидизъюнкцию, так и антиконъюнкцию.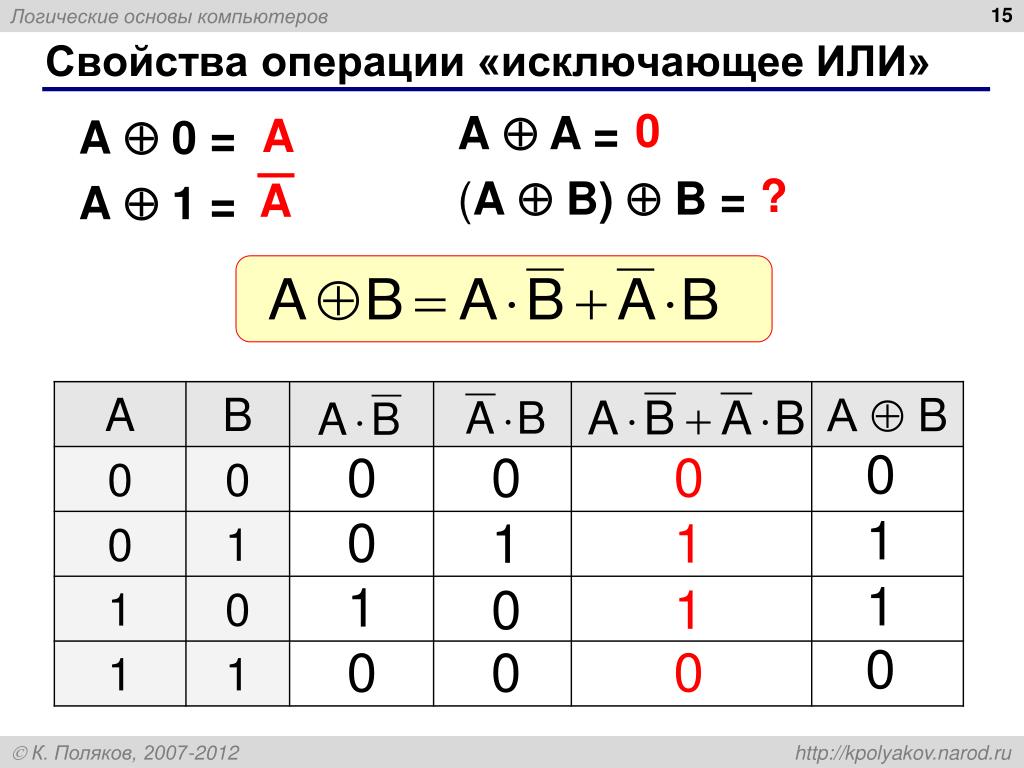 Так, указанная истинностная интерпретация импликации вынуждает признавать верными предложения вида «Если A, то B» даже в том случае, когда между высказываниями A и B (и, соответственно, событиями, о которых в них идёт речь) нет никакой реальной связи. Достаточно, чтобы A было ложным или B — истинным. Поэтому из двух предложений: «Если A, то B» и «Если B, то A», по крайней мере одно приходится признавать верным, что плохо сообразуется с обычным употреблением условной связки. Импликацию в данном случае специально называют «материальной», отличая её тем самым от условного союза, предполагающего, что между антецедентом и консеквентом истинного условного высказывания имеется действительная связь. При этом материальная импликация может прекрасно использоваться во многих контекстах, например, математических, когда при этом не забывают о её специфических особенностях. В некоторых случаях, однако, именно контекст не позволяет трактовать условный союз как материальную импликацию, предполагая взаимосвязь высказываний.
Так, указанная истинностная интерпретация импликации вынуждает признавать верными предложения вида «Если A, то B» даже в том случае, когда между высказываниями A и B (и, соответственно, событиями, о которых в них идёт речь) нет никакой реальной связи. Достаточно, чтобы A было ложным или B — истинным. Поэтому из двух предложений: «Если A, то B» и «Если B, то A», по крайней мере одно приходится признавать верным, что плохо сообразуется с обычным употреблением условной связки. Импликацию в данном случае специально называют «материальной», отличая её тем самым от условного союза, предполагающего, что между антецедентом и консеквентом истинного условного высказывания имеется действительная связь. При этом материальная импликация может прекрасно использоваться во многих контекстах, например, математических, когда при этом не забывают о её специфических особенностях. В некоторых случаях, однако, именно контекст не позволяет трактовать условный союз как материальную импликацию, предполагая взаимосвязь высказываний. Для анализа таких контекстов приходится строить специальные неклассические логики (например, релевантные логики), в язык которых вместо материальной импликации (или наряду с ней) вводятся другие импликации, которые понимаются интенсионально (содержательно) и верность которых не может быть обоснована истинностно-функционально. Интенсионально могут трактоваться также и другие логические связки.
Для анализа таких контекстов приходится строить специальные неклассические логики (например, релевантные логики), в язык которых вместо материальной импликации (или наряду с ней) вводятся другие импликации, которые понимаются интенсионально (содержательно) и верность которых не может быть обоснована истинностно-функционально. Интенсионально могут трактоваться также и другие логические связки.
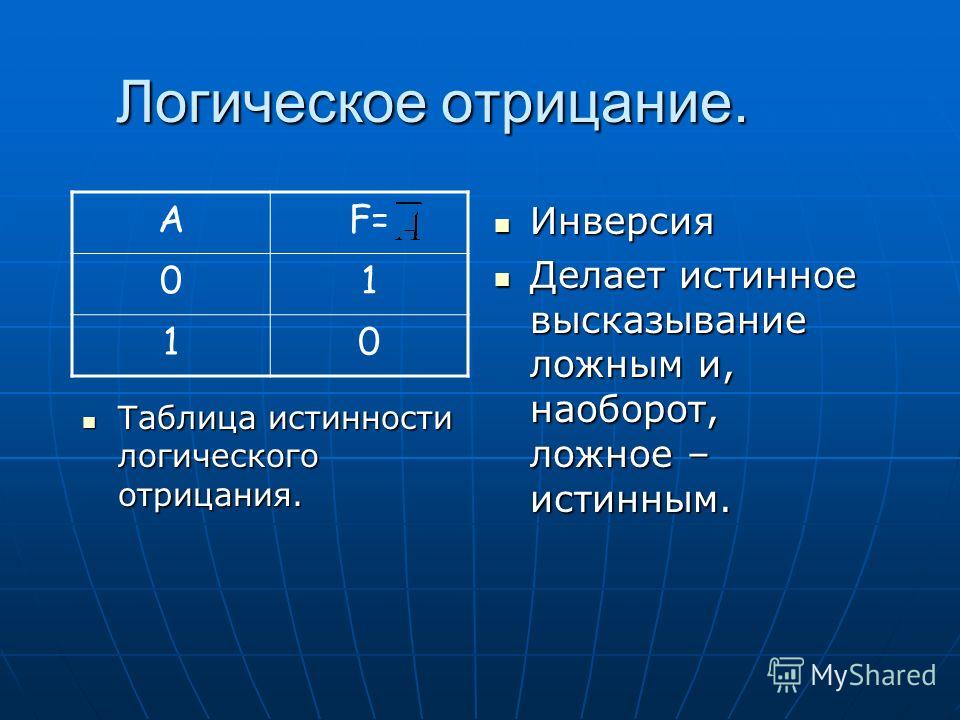 A = A
A = A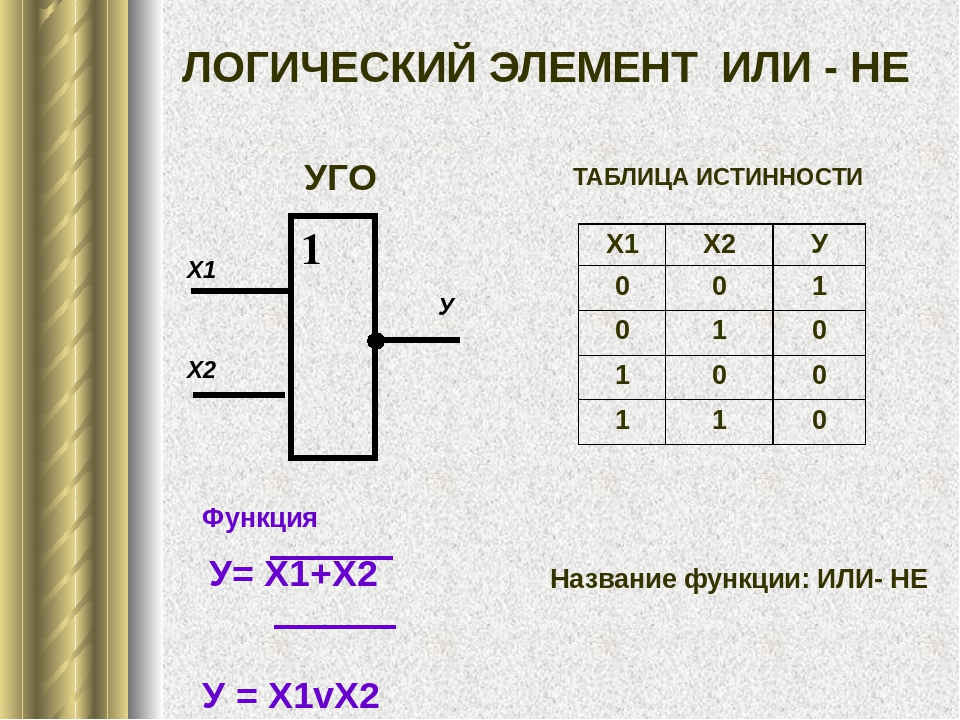
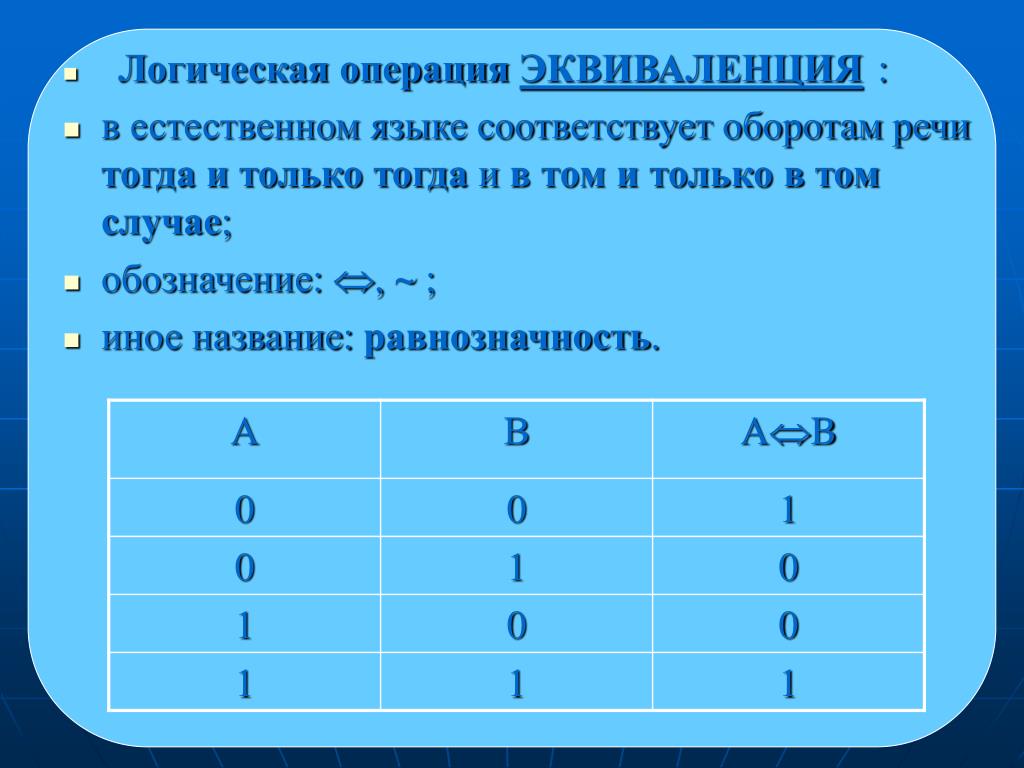 Двумя наиболее важными проблемами синхронизации FPGA являются высокая скорость и большое количество разветвлений. Часы с этими характеристиками следует отнести к более высокопроизводительным глобальным ресурсам. Количество высокопроизводительных буферов и ресурсов маршрутизации ограничено, поэтому ими следует тщательно управлять.
Двумя наиболее важными проблемами синхронизации FPGA являются высокая скорость и большое количество разветвлений. Часы с этими характеристиками следует отнести к более высокопроизводительным глобальным ресурсам. Количество высокопроизводительных буферов и ресурсов маршрутизации ограничено, поэтому ими следует тщательно управлять. Можно разбить маршруты глобальных часов на несколько более мелких высокопроизводительных маршрутов часов.
Можно разбить маршруты глобальных часов на несколько более мелких высокопроизводительных маршрутов часов.