| Fluke
Talk to a Fluke sales expert
Связаться с Fluke по вопросам обслуживания, технической поддержки и другим вопросам»
What is your favorite color?
Имя *
Фамилия *
Электронная почта *
FörКомпанияetag *
Номер телефона *
Страна * — Пожалуйста, выберите значение -United States (Estados Unidos)CanadaAfghanistanAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarticaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAzerbaijanBahamasBahrainBangladeshBarbadosБеларусь (Belarus)Belgien/Belgique (Belgium)BelizeBeninBermudaBhutanBoliviaBonaireBosnia and HerzegovinaBouvet IslandBotswanaBrasil (Brazil)British Indian Ocean TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCambodiaCameroonCape VerdeCayman IslandsCentral African RepublicČeská republika (Czech Republic)ChadChile中国 (China)Christmas IslandCittà Di VaticanCocos (Keeling) IslandsCook IslandsColombiaComorosCongoThe Democratic Republic of CongoCosta RicaCroatiaCyprusCôte D’IvoireDanmark (Denmark)Deutschland (Germany)DjiboutiDominicaEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEspaña (Spain)EstoniaEthiopiaFaroese FøroyarFijiFranceFrench Southern TerritoriesFrench GuianaGabonGambiaGeorgiaGhanaGilbralterGreeceGreenlandGrenadaGuatemalaGuadeloupeGuam (USA)GuineaGuinea-BissauGuyanaHaitiHeard Island and McDonald IslandsHondurasHong KongHungaryIcelandIndiaIndonesiaIraqIrelandIsraelIslas MalvinasItalia (Italy)Jamaica日本 (Japan)JordanKazakhstanKenyaKiribati대한민국 (Korea Republic of)KuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMéxico (Mexico)MicronesiaMoldovaMonacoMongoliaMontenegroMonserratMoroccoMozambiqueMyanmarNamibiaNauruNederland (Netherlands)Netherlands AntillesNepalNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorge (Norway)Norfolk IslandNorthern Mariana IslandsOmanÖsterreich (Austria)PakistanPalauPalestinePanamaPapua New GuineaParaguayPerú (Peru)PhilippinesPitcairn IslandPuerto RicoРоссия (Russia)Polska (Poland)Polynesia (French)PortugalQatarRepública Dominicana (Dominican Republic)RéunionRomânia (Romania)RwandaSaint HelenaSaint Pierre and MiquelonSaint Kitts and NevisSaint LuciaSaint Vincent and The GrenadinesSan MarinoSao Tome and PrincipeSaudi ArabiaSchweiz (Switzerland)SenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia and The South Sandwich IslandsSouth SudanSri LankaSudanSuomi (Finland)SurinameSvalbard and Jan MayenSverige (Sweden)SwazilandTaiwanTajikistanTanzaniaThailandTimor-LesteTokelauTogoTongaTrinidad and TobagoTunisiaTürkiye (Turkey)TurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUnited States Minor Outlying IslandsUruguayUzbekistanVanuatuVirgin Islands (British)Virgin Islands (USA)VenezuelaVietnamWallis and FutunaWestern SaharaWestern SamoaYemenZambiaZimbabwe
Почтовый индекс *
Интересующие приборы
iGLastMSCRMCampaignID
?Отмечая галочкой этот пункт, я даю свое согласие на получение маркетинговых материалов и специальных предложений по электронной почте от Fluke Electronics Corporation, действующей от лица компании Fluke Industrial или ее партнеров в соответствии с политикой конфиденциальности.
consentLanguage
Политика конфиденциальности
Законы Ома для участка цепи и для полной цепи
Автор Alexey На чтение 4 мин. Просмотров 11.3k. Опубликовано
Обновлено
В 1826 году немецкий ученый Георг Ом совершил открытие и описал
эмпирический закон о соотношении между собой таких показателей как сила тока, напряжение и особенности проводника в цепи. Впоследствии, по имени ученого он стал называться закон Ома.
В дальнейшем выяснилось, что эти особенности не что иное, как сопротивление проводника, возникающее в процессе его контакта с электричеством. Это внешнее сопротивление (R). Есть также внутреннее сопротивление (r), характерное для источника тока.
Закон Ома для участка цепи
Согласно обобщенному закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.
I = U/ R
Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника.
Беря во внимание вышеприведенную формулу, есть возможность найти неизвестные значенияUиR, сделав несложные математические операции.
U = I*R
R = U / I
Данные выше формулы справедливы лишь когда сеть испытывает на себе одно сопротивление.
Закон Ома для замкнутой цепи
Сила тока полной цепи равна ЭДС, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Замкнутая сеть имеет одновременно сопротивления внутреннего и внешнего характера. Поэтому формулы отношения будут уже другими.
I = E/ Rвн+r
Где E – электродвижущая сила (ЭДС), R- внешнее сопротивление источника, r-внутреннее сопротивление источника.
Закон Ома для неоднородного участка цепи
Замкнутая электрическая сеть содержит участки линейного и нелинейного характера. Участки, не имеющие источника тока и не зависящие от стороннего воздействия являются линейными, а участки, содержащие источник – нелинейными.
Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид:
I = U/ R = f1 – f2 + E/ R
Где f1 – f2 – разница потенциалов на конечных точках рассматриваемого участка сети
R – общее сопротивление нелинейного участка цепи
ЭДС нелинейного участка цепи бывает больше нуля или меньше. Если направление движения тока, идущего из источника с движением тока в электрической сети, совпадают, будет преобладать движение зарядов положительного характера и ЭДС будет положительная. В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС.
В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС.
Закон Ома для переменного тока
При имеющейся в сети емкости или инертности, необходимо учитывать при проводимых вычислениях, что они выдают свое сопротивление, от действия которого ток приобретает переменный характер.
Закон Ома для переменного тока выглядит так:
I = U/ Z
где Z – сопротивление по всей длине электрической сети. Его еще называют импеданс. Импеданс составляют сопротивления активного и реактивного характера.
Закон Ома не является основным научным законом, а лишь эмпирическим отношением, причем в некоторых условиях оно может не соблюдаться:
- Когда сеть обладает высокой частотой, электромагнитное поле меняется с большой скоростью, и при расчетах необходимо учитывать инертность носителей заряда;
- В условиях низкой температуры с веществами, которые обладают сверхпроводимостью;
- Когда проводник сильно нагревается проходящим напряжением, отношение тока к напряжению становится переменным и может не соответствовать общему закону;
- При нахождении под высоким напряжением проводника или диэлектрика;
- В светодиодных лампах;
- В полупроводниках и полупроводниковых приборах.

В свою очередь элементы и проводники, соблюдающие закон Ома, называются омическими.
Закон Ома может дать объяснение некоторым явлениям природы. Например, когда мы видим птиц, сидящих на высоковольтных проводах, у нас возникает вопрос – почему на них не действует электрический ток? Объясняется это довольно просто. Птицы, сидя на проводах, представляют собой своеобразные проводники. Большая часть напряжения приходится на промежутки между птицами, а та доля, что приходится на сами «проводники» не представляет для них опасности.
Но это правило работает лишь при единичном соприкосновении. Если птица заденет клювом или крылом провод или телеграфный столб, она неминуемо погибнет от огромного количества напряжения, которое несут в себе эти участки. Такие случаи происходят повсеместно. Поэтому в целях безопасности в некоторых населенных пунктах установлены специальные приспособления, защищающие птиц от опасного напряжения. На таких насестах птицы находятся в полной безопасности.
Закон Ома также широко применятся на практике. Электричество смертельно опасно для человека при одном лишь касании к оголенному проводу. Но в некоторых случаях сопротивление человеческого тела может быть разным.
Так, например, сухая и неповрежденная кожа обладает большим сопротивлением к воздействию электричества нежели рана или кожа, покрытая потом. В следствие переутомления, нервного напряжения и опьянения, даже при небольшом напряжении тока человек может получить сильный удар током.
В среднем, сопротивление тела человека – 700 Ом, значит, для человека является безопасным напряжение в 35 В. Работая с большим напряжением, специалисты используют специальные средства защиты.
Закон ома — формулировка простыми словами, определение,
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
- Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала. 2.
2.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
- Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Таблица удельных сопротивлений различных материалов
Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
Алюминий | 0,028 |
Бронза | 0,095 — 0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан ( сплав Ni-Cu + Mn) | 0,5 |
Латунь | 0,025 — 0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43 — 0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин ( сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром ( сплав никеля хрома железы и марганца) | 1,05 — 1,4 |
Олово | 0,12 |
Платина | 0. |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103 — 0,137 |
Титан | 0,6 |
Хромаль | 1,3 — 1,5 |
Цинк | 0,054 |
Чугун | 0,5-1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат. 2/м]
2/м]
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в Амперах, а подробнее о ней вы можете прочитать в нашей статье 😇
Давайте решим несколько задач на Закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом. 2/м
2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Таблица удельных сопротивлений различных материалов
Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
Алюминий | 0,028 |
Бронза | 0,095 — 0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан ( сплав Ni-Cu + Mn) | 0,5 |
Латунь | 0,025 — 0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43 — 0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин ( сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром ( сплав никеля хрома железы и марганца) | 1,05 — 1,4 |
Олово | 0,12 |
Платина | 0. |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103 — 0,137 |
Титан | 0,6 |
Хромаль | 1,3 — 1,5 |
Цинк | 0,054 |
Чугун | 0,5-1,0 |
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
- ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи I = ε/(R + r) I — сила тока [A] ε — ЭДС [В] R — сопротивление [Ом] r — внутреннее сопротивление источника [Ом] |
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
I = ε/(R + r)
Подставим значения:
I = 4/(3+1) = 1 A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
Последовательное соединение | Параллельное соединение | |
Схема | Резисторы следуют друг за другом | Между резисторами есть два узла Узел — это соединение трех и более проводников |
Сила тока | Сила тока одинакова на всех резисторах I = I1 = I2 | Сила тока, входящего в узел, равна сумме сил токов, выходящих из него I = I1 + I2 |
Напряжение | Общее напряжение цепи складывается из напряжений на каждом резисторе U = U1 + U2 | Напряжение одинаково на всех резисторах U = U1 = U2 |
Сопротивление | Общее сопротивление цепи складывается из сопротивлений каждого резистора R = R1 + R2 | Общее сопротивление для бесконечного количества параллельно соединенных резисторов 1/R = 1/R1 + 1/R2 + … + 1/Rn Общее сопротивление для двух параллельно соединенных резисторов R = (R1 * R2)/R1 + R2 Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов R = R1/n |
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала? Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой. Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного. |
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.
Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
Решение:
Общее сопротивление при параллельном соединении рассчитывается по формуле:
R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом
Ответ: общее сопротивление цепи равно 1 ⅓ Ом
Задачка три
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.
То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.
Задачка четыре со звездочкой
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. 2)/2R = R/2 = 10/2 = 5 Ом
2)/2R = R/2 = 10/2 = 5 Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
I = ε/(R + r)
R + r = ε/I
r = ε/I — R
Подставим значения:
r = 12/0,5 — 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Закон Ома для участка цепи и полной цепи: формулы и объяснение
Для электрика и электронщика одним из основных законов является Закон Ома. Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов. Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни. Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.
Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.
Историческая справка
Год открытия Закон Ома — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника. Позже выяснилось, что третья составляющая – это не что иное, как сопротивление. Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.
Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.
Закон Ома для участка цепи
Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:
I=U/R
Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.
Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.
Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.
Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:
f(x) = ky или f(u) = IR или f(u)=(1/R)*I
Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:
I=12 В/6 Ом=2 А
Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.
Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.
Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.
Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:
Rпровод=ρ(L/S)
Где ρ – удельное сопротивление в Ом*мм2/м, L – длина в м, S – площадь поперечного сечения.
Закон Ома для параллельной и последовательной цепи
В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:
I=I1=I2
U=U1+U2
R=R1+R2
Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток. При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:
Uэл=I*Rэлемента
Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:
I=I1+I2
U=U1=U2
1/R=1/R1+1/R2
Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.
Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.
Закон Ома для полной цепи
Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:
- напряжение, если это источник ЭДС;
- силу тока, если это источник тока;
Такой источник питания способен выдать любую мощность при неизменных выходных параметрах. В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.
Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:
I=ε/(R+r)
Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.
На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.
Закон Ома в дифференциальной и интегральной форме
Для однородного участка цепи приведенные выше формулы справедливы, для неоднородного проводника необходимо его разбить на максимально короткие отрезки, чтобы изменения его размеров были минимизированы в пределах этого отрезка. Это называется Закон Ома в дифференциальной форме.
Иначе говоря: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.
В интегральной форме:
Закон Ома для переменного тока
При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки Ra и реактивное сопротивление X (или Rr). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:
Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:
- Ток в цепи с индуктивностью не может измениться мгновенно.
- Напряжение в цепи с ёмкостью не может измениться мгновенно.
Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.
U=I*Z
XL и XC – это реактивные составляющие нагрузки.
В связи с этим вводится величина cosФ:
Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.
Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.
На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.
При этом сопротивление представляют в комплексной форме:
Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.
Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».
Как запомнить закон Ома
Чтобы запомнить Закон Ома – можно заучить формулировку простыми словами типа:
Чем больше напряжение – тем больше ток, чем больше сопротивление – тем меньше ток.
Или воспользоваться мнемоническими картинками и правилами. Первая это представление закона Ома в виде пирамиды – кратко и понятно.
Мнемоническое правило – это упрощенный вид какого-либо понятия, для простого и легкого его понимания и изучения. Может быть либо в словесной форме, либо в графической. Чтобы правильно найти нужную формулу – закройте пальцем искомую величину и получите ответ в виде произведения или частного. Вот как это работает:
Может быть либо в словесной форме, либо в графической. Чтобы правильно найти нужную формулу – закройте пальцем искомую величину и получите ответ в виде произведения или частного. Вот как это работает:
Вторая – это карикатурное представление. Здесь показано: чем больше старается Ом, тем труднее проходит Ампер, а чем больше Вольт – тем легче проходит Ампер.
Напоследок рекомендуем просмотреть полезное видео, в котором простыми словами объясняется Закон Ома и его применение:
Закон Ома – один из основополагающих в электротехнике, без его знания невозможна бОльшая часть расчетов. И в повседневной работе часто приходится переводить амперы в киловатты или по сопротивлению определять ток. Совершенно не обязательно понимать его вывод и происхождение всех величин – но конечные формулы обязательны к освоению. В заключении хочется отметить, что есть старая шуточная пословица у электриков: «Не знаешь Ома – сиди дома». И если в каждой шутке есть доля правды, то здесь эта доля правды – 100%. Изучайте теоретические основы, если хотите стать профессионалом на практике, а в этом вам помогут другие статьи из нашего сайта.
И если в каждой шутке есть доля правды, то здесь эта доля правды – 100%. Изучайте теоретические основы, если хотите стать профессионалом на практике, а в этом вам помогут другие статьи из нашего сайта.
Формула закона Ома в физике
Содержание:
Определение и формула закона Ома
Определение
Закон был получен Омом опытным путем. Построив вольт – амперную характеристику для проводника можно увидеть, что сила тока (I),
текущего через проводник пропорциональна напряжению (U) на нем $(I \sim U)$.
Закон Ома для участка цепи
Если на рассматриваемом участке цепи, содержащей проводник, источников ЭДС нет
$\left(U_{21}=\varphi_{1}-\varphi_{2}\right)$, то формула закона Ома является предельно простой:
$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}}{R}(1)$$
где R – сопротивление проводника (совокупности проводников, участка цепи).
Если источник тока в участок цепи включен и характеризуется при помощи ЭДС ($\varepsilon$), то формула закона Ома преобразуется к виду:
$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(2)$$
Закон Ома для замкнутой цепи
В том случае, если цепь является замкнутой, закон Ома принимает вид:
$$I=\frac{\varepsilon}{R}(3)$$
где под R=Rvnesh+rist понимают полное сопротивление цепи, которое включает так называемое внешнее
сопротивление (Rvnesh) и сопротивление источника ЭДС (rist).
Формула закона Ома в дифференциальной форме
Все выше приведенные формулы закона Ома были представлены в интегральной форме. Этот закон можно записать в дифференциальной форме,
которая характеризует электрическое состояние в точке.
$$\bar{j}=\sigma \bar{E}(4)$$
где $\sigma=\frac{1}{\rho}$ – удельная проводимость,
$\rho$ – удельное сопротивление,
$\bar{j}$ – вектор плотности тока,
$\bar{E}$ – вектор напряженности электрического поля. Векторы
$\bar{j}$ и $\bar{E}$ характеризуют одну точку проводящей среды.
В том случае, если среда изотропна, то $\bar{j} \uparrow \uparrow \bar{E}$.
Примеры решения задач
Пример
Задание. Пространство между пластинами плоского конденсатора заполняет неоднородное плохо проводящее вещество,
удельная проводимость которого изменяется в соответствии с линейным законом:
$\sigma(r)=\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d} r$ в направлении перпендикулярном пластинам.
d – расстояние между пластинами, S – площадь пластин конденсатора. {d} \frac{1}{\left(\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d}\right.} r\right) \frac{d r}{S}=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)}\left[\ln \left(d \sigma_{2}\right)-\ln \left(d \sigma_{1}\right)\right]= \\
{d} \frac{1}{\left(\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d}\right.} r\right) \frac{d r}{S}=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)}\left[\ln \left(d \sigma_{2}\right)-\ln \left(d \sigma_{1}\right)\right]= \\
=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)(1.2)
\end{array}
$$
Подставим найденное в (1.2) сопротивление в (1.1), получим искомую силу тока:
$I=\frac{U}{\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$
Ответ. $I=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$
Слишком сложно?
Формула закона Ома не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какой будет плотность тока в металлическом проводнике (удельное сопротивление считать равным
$\rho$) постоянного сечения, имеющем длину l, если напряжение,
которое приложено к проводу равно U?
Решение. Плотность тока для проводника, который имеет постоянное сечение S можно найти как:
Плотность тока для проводника, который имеет постоянное сечение S можно найти как:
$$j=\frac{I}{S}(2.1)$$
Силу тока можно вычислить, если использовать формулу Закона Ома для участка цепи не имеющего ЭДС:
$$I=\frac{U}{R}(2.2)$$
Сопротивление провода найдем, применяя формулу:
$$R=\rho \frac{l}{S}(2.3)$$
Подставим, необходимые величины в (2.1), получим:
$$j=\frac{U}{S R}=\frac{U S}{S \rho l}$$
Ответ. $j=\frac{U S}{S \rho l}$
Читать дальше: Формула мощности тока.
Закон Ома для участка цепи
Скажу сразу, что закон Ома – основной закон электротехники и применяется для расчета таких величин, как: ток, напряжение и сопротивление в цепи.
Рассмотрим электрическую цепь, приведенную на рисунке 1.
Рисунок 1. Простейшая цепь, поясняющея закон Ома.
Мы знаем, что электрический ток, то есть поток электронов, возникает в цепи между двумя точками (на рисунке А и Б) с разными потенциалами. Тогда следует считать, что чем больше разность потенциалов, тем большее количество электронов переместятся из точки с низким потенциалом (Б) в точку с высоким потенциалом (А). Количественно ток выражается суммой зарядов прошедших через заданную точку и увеличение разности потенциалов, то есть приложенного напряжения к резистору R, приведет к увеличению тока через резистор.
Тогда следует считать, что чем больше разность потенциалов, тем большее количество электронов переместятся из точки с низким потенциалом (Б) в точку с высоким потенциалом (А). Количественно ток выражается суммой зарядов прошедших через заданную точку и увеличение разности потенциалов, то есть приложенного напряжения к резистору R, приведет к увеличению тока через резистор.
С другой стороны сопротивление резистора противодействует электрическому току. Тогда следует сказать, что чем больше сопротивление резистора, тем меньше будет средняя скорость электронов в цепи, а это ведет к уменьшению тока через резистор.
Совокупность двух этих зависимостей (тока от напряжения и сопротивления) известна как закон Ома для участка цепи и записывается в следующем виде:
I=U/R
Это выражение читается следующим образом: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Следует знать что:
I – величина тока, протекающего через участок цепи;
U – величина приложенного напряжения к участку цепи;
R – величина сопротивления рассматриваемого участка цепи.
При помощи закона Ома для участка цепи можно вычислить приложенное напряжение к участку цепи (рисунок 1), либо напряжение на входных зажимах цепи (рисунок 2).
Рисунок 2. Последовательная цепь, поясняющая расчет напряжения на зажимах цепи.
В этом случае формула (1) примет следующий вид:
U = I *R
Но при этом необходимо знать ток и сопротивление участка цепи.
Третий вариант закона Ома для участка цепи, позволяющий рассчитать сопротивление участка цепи по известным значениям тока и напряжения имеет следующий вид:
R =U/I
Как запомнить закон Ома: маленькая хитрость!
Для того, что бы быстро переводить соотношение, которое называется закон Ома, не путаться, когда необходимо делить, а когда умножать входящие в формулу закона Ома величины, поступайте следующим образом. Напишите на листе бумаги величины, которые входят в закон Ома, так как показано на рисунке 3.
Рисунок 3. Как запомнить закон Ома.
Как запомнить закон Ома.
Теперь закройте пальцем, ту величину, которую необходимо найти. Тогда относительное расположение оставшихся незакрытыми величин подскажет, какое действие необходимо совершить для вычисления неизвестной величины.
Подробнее можно узнать в мультимедийном учебнике по основам электротехники и электроники.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
3. И снова Закон Ома! | 3. Электробезопасность | Часть1
3. И снова Закон Ома!
И снова Закон Ома!
Довольно часто нам приходится слышать такие фразы, как «Ударило током» или «Убило током», и ни какого упоминания о напряжении. Исходя из этого, у вас может сложиться впечатление, что для человека опасен ток, а не напряжение. Какой-то элемент истины здесь имеет место быть. Однако, если напряжение не представляет никакой опасности, то зачем пишутся предупреждающие таблички примерно такого содержания: «ОСТОРОЖНО — ВЫСОКОЕ НАПРЯЖЕНИЕ!»?
Однако, если напряжение не представляет никакой опасности, то зачем пишутся предупреждающие таблички примерно такого содержания: «ОСТОРОЖНО — ВЫСОКОЕ НАПРЯЖЕНИЕ!»?
По большому счету принцип «опасности тока» верен. Электрический ток вызывает ожоги тканей тела, блокирует мышцы и останавливает сердце, но он не может возникнуть сам по себе. Чтобы создать поток электронов через тело человека, к нему нужно приложить напряжение. При выполнении расчетов мы так же должны учесть сопротивление, которое тело человека оказывает электрическому току.
Если с помощью Закона Ома мы выразим силу тока через известные значения напряжения и сопротивления, то получим следующее уравнение:
Сила тока, проходящего через тело человека прямопропорциональна величине напряжения, приложенного к двум его точкам, и обратнопропрорциональна сопротивлению между этими точками. Очевидно, чем больше величина напряжения, создающего поток электронов, тем легче эти электроны будут проходить через конкретную величину сопротивления. Следовательно, высокое напряжение опасно для жизни, потому что оно создает большой ток, который может травмировать или убить человека. И наоборот, чем большее сопротивление оказывает тело электрическому току, тем медленнее будут течь через него электроны при заданной величине напряжения. Проще говоря, опасность того или иного напряжения зависит от величины сопротивления, оказываемого телом человека потоку электронов.
Очевидно, чем больше величина напряжения, создающего поток электронов, тем легче эти электроны будут проходить через конкретную величину сопротивления. Следовательно, высокое напряжение опасно для жизни, потому что оно создает большой ток, который может травмировать или убить человека. И наоборот, чем большее сопротивление оказывает тело электрическому току, тем медленнее будут течь через него электроны при заданной величине напряжения. Проще говоря, опасность того или иного напряжения зависит от величины сопротивления, оказываемого телом человека потоку электронов.
Сопротивление тела не является фиксированной величиной. Оно изменяется от человека к человеку, и время от времени. На измерении электрического сопротивления между пальцами рук и ног основывается метод определения процентного содержания жира в организме. Разные проценты содержания жира обеспечивают разные сопротивления, и это только одна из величин, влияющая на электрическое сопротивление тела человека. Чтобы метод работал точно, человек за несколько часов до теста должен регулировать потребление жидкости, а это говорит о том, что гидратация является еще одним фактором, влияющим на сопротивление человеческого тела.
Чтобы метод работал точно, человек за несколько часов до теста должен регулировать потребление жидкости, а это говорит о том, что гидратация является еще одним фактором, влияющим на сопротивление человеческого тела.
Сопротивление так же зависит от того, между какими частями тела мы его будем измерять: между руками, между ногами, между рукой и ногой и т.д. Необходимо учесть и тот фактор, что прекрасными проводниками электричества являются пот, богатый солями и минералами, а также кровь, с ее высоким содержанием проводящих химических элементов. Таким образом, контакт между проводом и потными руками или руками с кровоточащей раной будет обладать гораздо меньшим сопротивлением, чем контакт между проводом и руками с сухой, чистой кожей.
Измеряя сопротивление своего тела чувствительным измерительным прибором, путем сжимания его щупов пальцами рук, я получил значение 1 миллион Ом (1 МОм). При этом прибор показывает меньшее сопротивление, когда я плотно сжимаю щупы, и большее сопротивление — когда я ослабляю пальцы. Руки мои при этом чисты и сухи. Если бы я работал во влажной и грязной производственной среде, то сопротивление между моими руками было бы намного меньше, представляя большую угрозу поражения электрическим током.
Руки мои при этом чисты и сухи. Если бы я работал во влажной и грязной производственной среде, то сопротивление между моими руками было бы намного меньше, представляя большую угрозу поражения электрическим током.
Итак, какая же величина тока опасна для человека?. Ответ на этот вопрос зависит от нескольких факторов. Значительное влияние на то, как электрический ток воздействует на человека, оказывает химический состав его тела. Некоторые люди очень чувствительны к току, и поэтому испытывают непроизвольное сокращение мышц даже от разряда статического электричества, который другие люди могут и не почувствовать. Несмотря на эти различия, посредством тестов были выведены примерные значения тока (очень небольшие), которые могут оказать вредное воздействие на организм человека. Все значения в таблице даны в миллиамперах (миллиампер равен 1/1000 ампера):
«Гц» является сокращенным обозначением единицы измерения Герц, которая служит мерой скорости чередования направлений переменного тока. Эта мера иначе известна как частота. Так, заголовок «60 Гц АС» одного из столбцов таблицы означает что все значения этого столбца относятся к переменному току, который чередуется с частотой 60 циклов в секунду (1 цикл равен периоду времени, в течении которого поток электронов сначала движется в одном направлении, а потом в другом). Последняя колонка, с надписью «10 кГц АС», относится к переменному току, который совершает десять тысяч циклов в секунду.
Эта мера иначе известна как частота. Так, заголовок «60 Гц АС» одного из столбцов таблицы означает что все значения этого столбца относятся к переменному току, который чередуется с частотой 60 циклов в секунду (1 цикл равен периоду времени, в течении которого поток электронов сначала движется в одном направлении, а потом в другом). Последняя колонка, с надписью «10 кГц АС», относится к переменному току, который совершает десять тысяч циклов в секунду.
Следует иметь ввиду, что все вышеприведенные цифры являются приблизительными, поскольку реакция на ток людей с разным химическим составом тела будет различной. Существует предположение, что достаточно пропустить переменный ток величиной в 17 миллиампер через грудь человека, чтобы при определенных условиях вызвать у него аритмию сердца. Большинство данных таблицы, касающихся аритмии сердца, взяты из опытов над животными. И это естественно, ведь никто не будет проводить такие эксперименты на людях, в связи с чем имеющиеся данные весьма приблизительны. Если вас интересует вопрос, почему женщины более восприимчивы к электрическому току чем мужчины, то здесь мы вам не поможем — для нас это тоже загадка.
Если вас интересует вопрос, почему женщины более восприимчивы к электрическому току чем мужчины, то здесь мы вам не поможем — для нас это тоже загадка.
Теперь давайте предположим, что я взялся сухими и чистыми руками за контакты источника напряжения переменного тока частотой 60 Гц. Какое напряжение должно быть у этого источника, чтобы создать ток величиной 20 миллиампер (при таком токе я не смогу самостоятельно отпустить контакты источника)? Ответ на этот вопрос можно найти в Законе Ома (U = IR):
U = IR
U = (20 мA)(1 МОм)
U = 20,000 вольт, или 20 кВ
Имейте в виду, что это сценарий «лучшего случая» с точки зрения электробезопасности (чистая, сухая кожа), а полученная величина напряжения, с огромной долей вероятности, вызовет оцепенение человека. Гораздо меньшее напряжение потребуется для вызова болевых ощущений. Следует учесть так же и тот момент, что физиологические эффекты воздействия различных токов на разных людей могут значительно отличаться, поэтому наши расчеты являются только приблизительной оценкой действительности.
Следует учесть так же и тот момент, что физиологические эффекты воздействия различных токов на разных людей могут значительно отличаться, поэтому наши расчеты являются только приблизительной оценкой действительности.
Если я смочу пальцы своих рук водой, имитируя пот, то сопротивление моего тела между руками составит всего 17000 Ом (17 кОм). Обратите внимание, что в нашем случае с тонкими металлическими щупами измерительного прибора контактирует по одному пальцу каждой руки. Повторно вычислив напряжение, необходимое для получения тока величиной 20 мА, мы получим следующее значение:
U = IR
U = (20 мA)(17 kОм)
U = 340 вольт
В этом случае достаточно напряжения 340 вольт, чтобы создать ток 20 миллиампер через тело человека. Однако, смертельный удар током можно получить и от меньшего напряжения если увеличить площадь контакта, уменьшив тем самым его сопротивление. Примером такого контакта служит кольцо на пальце (золото обернутое вокруг пальца создает превосходный контакт для поражения электрическим током) или большой металлический предмет, такой как труба или ручка инструмента. Сопротивление организма при этом понизится до 1000 Ом (10 кОм), что создаст реальную угрозу поражения низкими значениями напряжения:
Примером такого контакта служит кольцо на пальце (золото обернутое вокруг пальца создает превосходный контакт для поражения электрическим током) или большой металлический предмет, такой как труба или ручка инструмента. Сопротивление организма при этом понизится до 1000 Ом (10 кОм), что создаст реальную угрозу поражения низкими значениями напряжения:
U = IR
U = (20 мA)(1 kОм)
U = 20 вольт
Таким образом, чтобы создать ток величиной 20 мА и вызвать оцепенение человека, достаточно напряжения 20 вольт. Ранее мы упомянули предположение, что сила тока 17 мА, пропущенная через грудь человека, при определенных условиях может вызвать аритмию сердца. Так вот, если сопротивление между руками человека будет равно 1 кОм, то для создания этого опасного условия потребуется всего 17 вольт:
U = IR
U = (17 мA)(1 kОм)
U = 17 вольт
В этих расчетах мы показали вам «наихудший» сценарий для напряжения переменного тока частотой 60 Гц и отличной проводимости человеческого тела.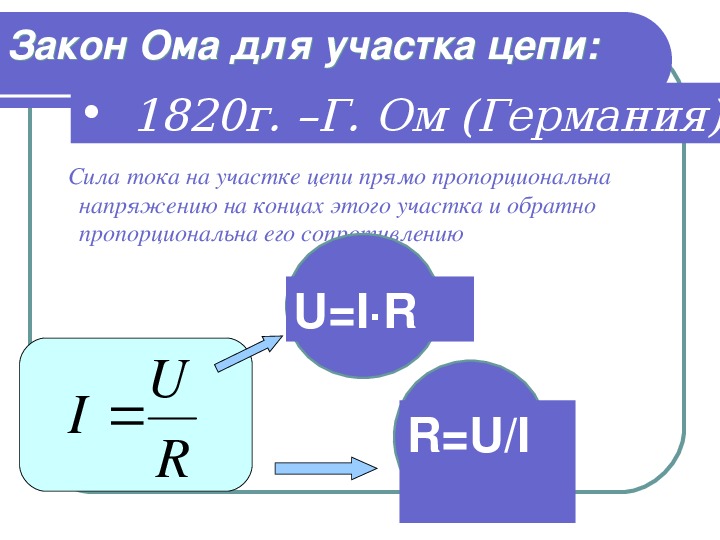 Данный пример дает наглядную картину опасности даже небольших значений напряжения.
Данный пример дает наглядную картину опасности даже небольших значений напряжения.
Понизить сопротивление человеческого тела до 1000 Ом можно не только путем воздействия рассмотренных выше экстремальных факторов (например плотным контактом золотого кольца с пальцем). Оно может уменьшиться при длительном воздействии напряжения (например, когда человек под действием тока не может разжать руку, и только крепче сжимает проводник). Одновременно с уменьшением сопротивления увеличивается сила тока при фиксированном напряжении.
Ниже приведены примерные значения сопротивлений точек контакта человека с различными предметами в различных условиях:
-
Контакт пальца с проводом: от 40 000 Ом до 1 000 000 Ом (сухой палец), от 4 000 Ом до 15 000 Ом (влажный палец). -
Контакт руки с проводом: от 15 000 Ом до 50 000 Ом (сухая рука), от 3 000 Ом до 5 000 Ом (влажная рука).
-
Контакт руки с металлическими плоскогубцами: от 5 000 Ом до 10 000 Ом (сухая рука), от 1 000 Ом до 3 000 Ом (влажная рука). -
Контакт с ладонью: от 3 000 Ом до 8 000 Ом (сухая ладонь), от 1 000 Ом до 2 000 Ом (влажная ладонь). -
Контакт (обхват) одной руки с 1,5-дюймовой металлической трубой: от 1 000 Ом до 3 000 Ом (сухая рука), от 500 Ом до 1 500 Ом (влажная рука). -
Контакт (обхват) двух рук с 1,5-дюймовой металлической трубой: от 500 Ом до 1 500 Ом (сухие руки), от 250 Ом до 750 Ом (влажные руки). -
Контакт руки, погруженной в проводящую жидкость, с этой жидкостью: от 200 Ом до 500 Ом. -
Контакт ноги, погруженной в проводящую жидкость, с этой жидкостью: от 100 Ом до 300 Ом.
Обратите внимание на значения сопротивлений в двух случаях с 1,5-дюймовой металлической трубой. Если трубу обхватить двумя руками, то сопротивление будет ровно в два раза меньше, чем при обхвате этой же трубы одной рукой.
Если трубу обхватить двумя руками, то сопротивление будет ровно в два раза меньше, чем при обхвате этой же трубы одной рукой.
Две руки, сжимающие металлическую трубу, увеличивают площадь контакта в два раза по сравнению с одной рукой. Это очень важное обстоятельство: электрическое сопротивление между любыми контактирующими объектами уменьшается с увеличением площади контакта при прочих равных условиях. В этом случае электроны текут из трубы в тело (или наоборот) по двум параллельным маршрутам.
Как вы увидите позже, общее сопротивление параллельной цепи всегда меньше (или равно) любого из сопротивлений этой цепи.
В промышленности пороговым значением опасного напряжения считается, как правило, напряжение величиной 30 вольт. Осторожный человек должен рассматривать любое напряжение, превышающее это значение, как опасное.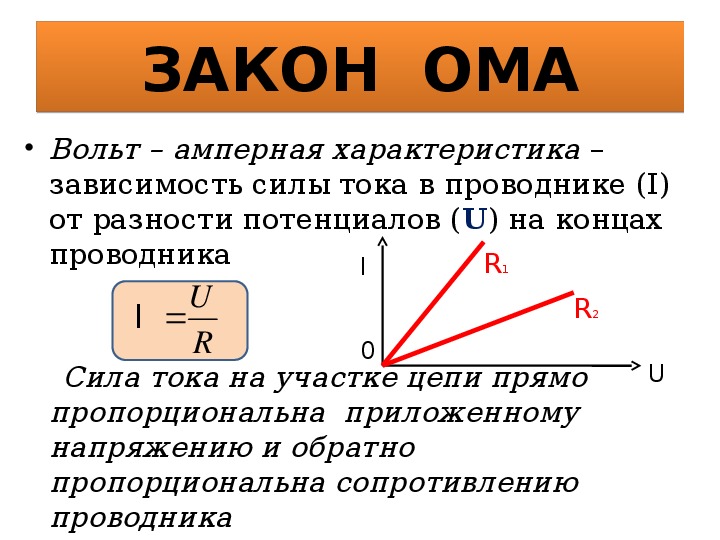 Работая с электричеством он должен содержать свои руки чистыми и сухими, а так же снять все металлические украшения, которые представляют опасность и при более низких значениях напряжения. Такие украшения, выступая в качестве контактов между двумя точками цепи, способны провести достаточный ток, чтобы сжечь кожу.
Работая с электричеством он должен содержать свои руки чистыми и сухими, а так же снять все металлические украшения, которые представляют опасность и при более низких значениях напряжения. Такие украшения, выступая в качестве контактов между двумя точками цепи, способны провести достаточный ток, чтобы сжечь кожу.
Опасными могут быть и напряжения менее 30 вольт, если они достаточны чтобы вызвать неприятные ощущения, в результате которых человек может совершить резкое движение и вступить в контакт с другим, более высоким напряжением или иным источником повышенной опасности. Автор статьи вспоминает, как однажды он ремонтировал свой автомобиль в жаркий летний день. По причине теплой погоды он был в шортах, и работая с аккумуляторной батареей прислонился оголенной частью ног к хромированному бамперу машины. Когда он коснулся металлическим ключом положительного контакта 12-вольтовой батареи, то почувствовал покалывание в точке контакта ноги с бампером. Таким образом, надежный контакт с металлом и потная кожа позволили почувствовать удар током от электрического потенциала значением всего-лишь 12 вольт.
К счастью, в этом случае ничего плохого не случилось. Но, если бы двигатель автомобиля был запущен, и воздействие тока почувствовала рука а не нога, то автор, возможно, рефлексивно дернул бы ее в сторону вращающегося вентилятора или уронил бы ключ на клеммы аккумулятора (вызвав тем самым короткое замыкание и сноп искр). Этот пример иллюстрирует еще один важный урок электробезопасности — электрический ток может послужить косвенной причиной травмирования.
Очень важное значение имеет путь, по которому ток течет через тело человека. Благодаря тому, что электрический ток оказывает влияние на все мышцы организма находящиеся на его пути, в том числе и на такие жизненно-важные, как сердце и легкие, наиболее опасным будет такой ток, который проходит через грудь человека. Это сценарий возможен в том случае, если человек соприкоснется с источником напряжения двумя руками.
В целях недопущения такого сценария, при работе со схемой (находящейся под напряжением) желательно использовать только одну руку, засунув вторую при этом в карман (чтобы случайно ничего ей не тронуть).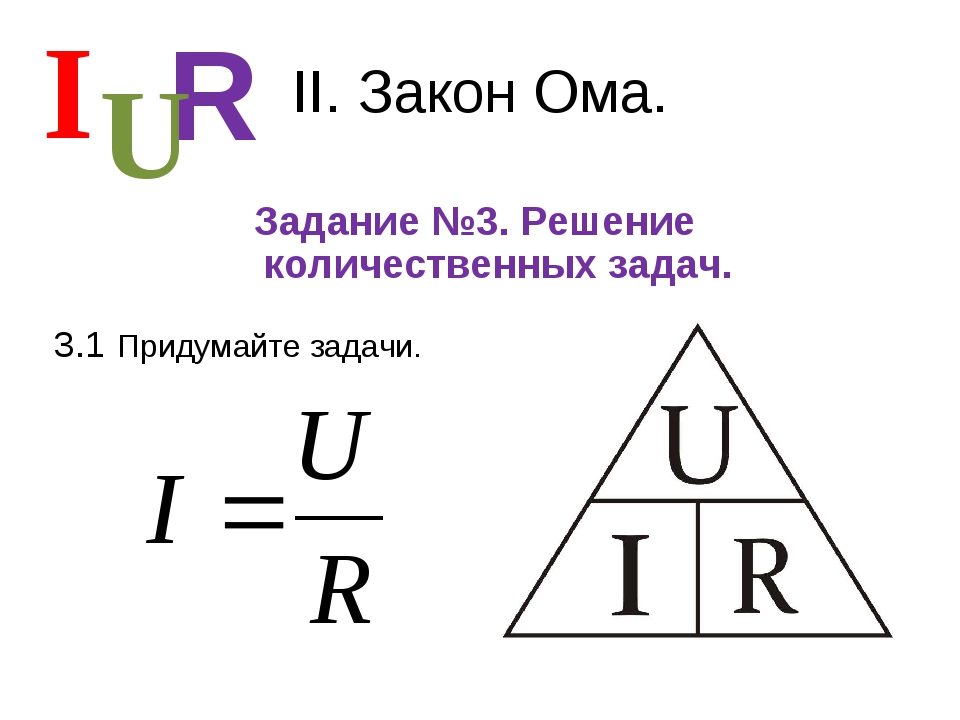 Конечно, безопаснее было бы работать с обесточенной схемой, но на практике это не всегда возможно. Если схема находится под напряжением, то работать с ней предпочтительнее правой рукой. А почему правой, спросите вы. Во-первых, если человек правша (каких большинство), то ему удобнее будет работать именно этой рукой, а во-вторых — сердце расположено в левой части грудной клетки.
Конечно, безопаснее было бы работать с обесточенной схемой, но на практике это не всегда возможно. Если схема находится под напряжением, то работать с ней предпочтительнее правой рукой. А почему правой, спросите вы. Во-первых, если человек правша (каких большинство), то ему удобнее будет работать именно этой рукой, а во-вторых — сердце расположено в левой части грудной клетки.
Лучшей защитой от удара электрическим током является сопротивление, которое может быть добавлено к телу при помощи изолированных инструментов, перчаток, сапог и других приспособлений. Как вы уже знаете, ток в цепи равен напряжению деленному на общее сопротивление потоку электронов. Наибольший эффект сопротивления будут иметь при расположении их таким образом, чтобы создать только один путь для потока электронов (подробнее на этом мы остановимся в последующих статьях):
Ниже представлена эквивалентная схема человека, экипированного перчатками и сапогами:
В этом случае суммарное (общее) сопротивление сапог, тела и перчаток потоку электронов будет больше, чем сопротивление каждого из компонентов по отдельности.
Безопасность является одной из причин, по которой электрические провода покрываются пластмассовой или резиновой изоляцией, которая значительно увеличивает сопротивление между проводником и прикоснувшемуся к нему человеком. Однако покрывать изоляцией высоковольтные провода линий электропередач слишком дорого, поэтому безопасность в этом случае достигается путем подвешивания их на столбы высоко над землей.
Краткий обзор:
-
Электрический ток оказывает вредное воздействие на организм человека. Чем больше напряжение, тем больший и опасный ток оно производит. Уменьшить силу тока может сопротивление. Высокое сопротивление является хорошей защитой от удара электрическим током. -
Напряжение величиной выше 30 вольт способно создать опасный ток. -
Не нужно надевать металлические украшения при работе с электрическими схемами. Кольца, ремешки часов, ожерелья, браслеты и другие подобные вещи обеспечивают отличный электрический контакт с телом человека и способны провести достаточный ток, чтобы вызвать ожог кожи даже при низких напряжениях.
Кольца, ремешки часов, ожерелья, браслеты и другие подобные вещи обеспечивают отличный электрический контакт с телом человека и способны провести достаточный ток, чтобы вызвать ожог кожи даже при низких напряжениях.
-
Опасность несет и такое низкое напряжение, которое непосредственно не может поразить человека. Его может быть достаточно, чтобы человек отдернул руку и вступил в контакт с другим, находящимся вблизи источником опасности. -
В целях предотвращения прохождения опасного тока через грудь человека, работать с запитанной схемой необходимо одной рукой (по возможности — правой).
Закон Ома и соотношение V-I-R
В физике есть определенные формулы, которые настолько мощны и распространены, что достигают уровня общеизвестных знаний. Студент-физик записывал такие формулы столько раз, что запоминал их, даже не пытаясь. Безусловно, для профессионалов в этой области такие формулы настолько важны, что остаются в их сознании. В области современной физики E = m • c 2 . В области ньютоновской механики F net = m • a.В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R.
В области современной физики E = m • c 2 . В области ньютоновской механики F net = m • a.В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R.
Преобладающим уравнением, которое пронизывает изучение электрических цепей, является уравнение
ΔV = I • R
Другими словами, разность электрических потенциалов между двумя точками в цепи ( ΔV ) эквивалентна произведению тока между этими двумя точками ( I ) и общего сопротивления всех электрических устройств, присутствующих между этими двумя точками ( R ).В остальной части этого раздела Физического класса это уравнение станет самым распространенным уравнением, которое мы видим. Это уравнение, часто называемое уравнением закона Ома , является мощным предсказателем взаимосвязи между разностью потенциалов, током и сопротивлением.
Закон Ома как предсказатель тока
Уравнение закона Ома можно переформулировать и выразить как
В качестве уравнения это служит алгебраическим рецептом для вычисления тока, если известны разность электрических потенциалов и сопротивление. Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение аккумулятора (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение аккумулятора (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
Приведенная ниже таблица иллюстрирует это соотношение как качественно, так и количественно для нескольких цепей с различными напряжениями и сопротивлением батарей.
Строки 1, 2 и 3 показывают, что удвоение и утроение напряжения батареи приводит к удвоению и утроению тока в цепи. Сравнение строк 1 и 4 или строк 2 и 5 показывает, что удвоение общего сопротивления служит для уменьшения вдвое тока в цепи.
Поскольку на ток в цепи влияет сопротивление, в цепях электроприборов часто используются резисторы, чтобы влиять на величину тока, присутствующего в ее различных компонентах.Увеличивая или уменьшая величину сопротивления в конкретной ветви схемы, производитель может увеличивать или уменьшать величину тока в этой ветви . Кухонные приборы, такие как электрические миксеры и переключатели света, работают, изменяя ток в нагрузке, увеличивая или уменьшая сопротивление цепи. Нажатие различных кнопок на электрическом микшере может переключить режим с микширования на взбивание, уменьшив сопротивление и позволив большему току присутствовать в миксере.Точно так же поворот ручки регулятора яркости может увеличить сопротивление его встроенного резистора и, таким образом, уменьшить ток.
На схеме ниже изображена пара цепей, содержащих источник напряжения (аккумуляторная батарея), резистор (лампочка) и амперметр (для измерения тока). В какой цепи у лампочки наибольшее сопротивление? Нажмите кнопку «Посмотреть ответ», чтобы убедиться, что вы правы.
Уравнение закона Ома часто исследуется в физических лабораториях с использованием резистора, аккумуляторной батареи, амперметра и вольтметра.Амперметр — это устройство, используемое для измерения силы тока в заданном месте. Вольтметр — это устройство, оснащенное датчиками, которых можно прикоснуться к двум точкам цепи, чтобы определить разность электрических потенциалов в этих местах. Изменяя количество ячеек в аккумуляторной батарее, можно изменять разность электрических потенциалов во внешней цепи. Вольтметр может использоваться для определения этой разности потенциалов, а амперметр может использоваться для определения тока, связанного с этим ΔV.К батарейному блоку можно добавить батарею, и процесс можно повторить несколько раз, чтобы получить набор данных I-ΔV. График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома.
График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома.
Величины, символы, уравнения и единицы!
Тенденция уделять внимание единицам — неотъемлемая черта любого хорошего студента-физика.Многие трудности, связанные с решением проблем, могут быть связаны с тем, что не уделялось внимания подразделениям. Поскольку все больше и больше электрических величин и их соответствующих метрических единиц вводится в этот раздел учебного курса «Физический класс», становится все более важным систематизировать информацию в своей голове. В таблице ниже перечислены некоторые из введенных на данный момент количеств. Для каждой величины также указаны символ, уравнение и соответствующие метрические единицы.Было бы разумно часто обращаться к этому списку или даже делать свою копию и добавлять ее по мере развития модуля. Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.
Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.
| Кол-во | Символ | Уравнение (я) | Стандартная метрическая единица | Другие единицы |
| Разность потенциалов (г.к.а. напряжение) | ΔV | ΔV = ΔPE / Q ΔV = I • R | Вольт (В) | J / C |
| Текущий | я | I = Q / t I = ΔV / R | Амперы (А) | Усилитель или К / с или В / Ом |
| Сила | п | P = ΔPE / т (еще предстоит) | Ватт (Вт) | Дж / с |
| Сопротивление | р | R = ρ • L / A R = ΔV / I | Ом (Ом) | В / А |
| Энергия | E или ΔPE | ΔPE = ΔV • Q ΔPE = P • t | Джоуль (Дж) | V • C или Вт • с |
(Обратите внимание, что символ C представляет собой кулоны.
)
В следующем разделе Урока 3 мы еще раз рассмотрим количественную мощность. Новое уравнение мощности будет введено путем объединения двух (или более) уравнений в приведенной выше таблице.
Мы хотели бы предложить …
Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Легко перетащите источник напряжения, резисторы и провода на рабочее место. Соедините их, и у вас будет схема. Добавьте амперметр для измерения тока и используйте датчики напряжения для определения падения напряжения. Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Проверьте свое понимание
1. Что из перечисленного ниже приведет к уменьшению тока в электрической цепи? Выберите все, что подходит.
а. уменьшить напряжение
г. уменьшить сопротивление
г. увеличить напряжение
г.увеличить сопротивление
2. Определенная электрическая цепь содержит батарею из трех элементов, провода и лампочку. Что из перечисленного может привести к тому, что лампа будет светить менее ярко? Выберите все, что подходит.
а. увеличить напряжение АКБ (добавить еще одну ячейку)
г. уменьшить напряжение аккумулятора (удалить элемент)
г.уменьшить сопротивление цепи
г.
увеличить сопротивление цепи
3. Вероятно, вас предупредили, чтобы вы не прикасались к электроприборам или даже к электрическим розеткам мокрыми руками. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____.
а.напряжение цепи должно быть выше
г. напряжение в цепи должно быть ниже
г. ваше сопротивление будет выше
г. ваше сопротивление должно быть ниже
e. ток через тебя будет ниже
4. Если бы сопротивление цепи было утроено, то ток в цепи был бы ____.
а. треть от
г. втрое больше
г. без изменений
г. … бред какой то! Сделать такой прогноз невозможно.
5. Если напряжение в цепи увеличить в четыре раза, то ток в цепи будет ____.
а.четверть от
г. в четыре раза больше
г. без изменений
г. … бред какой то! Сделать такой прогноз невозможно.
6. В схему подключены блок питания, резистор и амперметр (для измерения тока). Амперметр показывает значение тока 24 мА (миллиампер). Определите новый ток, если напряжение источника питания было…
а. … увеличилось в 2 раза, а сопротивление осталось постоянным.
г. … увеличилось в 3 раза, а сопротивление осталось постоянным.
г. … уменьшилось в 2 раза, а сопротивление осталось постоянным.
г. … оставалось постоянным, а сопротивление увеличивалось в 2 раза.
e. … оставалось постоянным, а сопротивление увеличивалось в 4 раза.
ф…. оставалось постоянным, а сопротивление уменьшалось в 2 раза.
г. … увеличилось в 2 раза, а сопротивление увеличилось в 2 раза.
ч. … увеличилось в 3 раза, а сопротивление уменьшилось в 2 раза.
и. … уменьшилось в 2 раза, а сопротивление увеличилось в 2 раза.
7.Используйте уравнение закона Ома, чтобы дать числовые ответы на следующие вопросы:
а. Электрическое устройство с сопротивлением 3,0 Ом позволит протекать через него току 4,0 А, если на устройстве наблюдается падение напряжения ________ Вольт.
г. Когда на электрический нагреватель подается напряжение 120 В, через нагреватель будет протекать ток 10,0 А, если сопротивление составляет ________ Ом.
г. Фонарик, который питается от 3 вольт и использует лампу с сопротивлением 60 Ом, будет иметь ток ________ ампер.
8. Используйте уравнение закона Ома, чтобы определить недостающие значения в следующих схемах.
9. См. Вопрос 8 выше. В схемах схем A и B какой метод использовался для контроля тока в схемах? А в схемах схем C и D какой метод использовался для контроля тока в цепях?
См. Вопрос 8 выше. В схемах схем A и B какой метод использовался для контроля тока в схемах? А в схемах схем C и D какой метод использовался для контроля тока в цепях?
Закон Ома
Закон Ома гласит, что
«ток через проводник между двумя точками прямо пропорционален разности потенциалов или напряжению между двумя точками, и обратно пропорционален сопротивлению между ними».
Закон Ома можно выразить как
I = U / R (1)
где
I = ток (ампер, А)
U = электрический потенциал (вольт, В)
R = сопротивление (Ом, Ом )
Пример — закон Ома
A 12-вольтная батарея подает питание на сопротивление 18 Ом . Ток в электрической цепи можно рассчитать как
I = (12 вольт) / (18 Ом)
= 0.67 ампер
Эквивалентные выражения закона Ома
Закон Ома (1) также можно выразить как
U = RI (2)
или
I (3)
Скачайте и распечатайте диаграмму закона Ома!
Пример — сопротивление электрической цепи
Ток силой 1 ампер протекает через электрическую цепь 230 В, . На приведенной выше диаграмме это означает сопротивление
На приведенной выше диаграмме это означает сопротивление
R ≈ 220 Ом
Его можно также рассчитать по закону Ома
R = (230 В) / (1 А)
= 230 Ом
Пример — Закон Ома и кратные и подмножители
Токи, напряжения и сопротивления в электрических цепях часто могут быть очень маленькими или очень большими, поэтому часто используются кратные и подкратные.
Требуемое напряжение, подаваемое на 3.Резистор 3 кОм для создания тока 20 мА можно рассчитать как
U = (3,3 кОм) (1000 Ом / кОм) (20 мА) (10 -3 А / мА)
= 66 В
Номограмма электрического сопротивления
Загрузите и распечатайте номограмму зависимости электрического сопротивления от вольт и ампер!
Значения по умолчанию на номограмме выше указывают 230 вольт , сопротивление 24 Ом и ток 10 ампер .
Мощность
Электрическая мощность может быть выражена как
P = UI
= RI 2
= U 2 / R (4)
48 где 49
P = электрическая мощность (Вт, Вт)
Пример — потребляемая мощность
Мощность, потребляемая в указанной выше электрической цепи 12 В , может быть рассчитана как
P = (12 вольт) 2 / ( 18 Ом)
= 8 Вт
Пример — мощность и электрическое сопротивление
Электрическая лампочка 100 Вт подключена к источнику питания 230 В и . Текущий ток можно рассчитать путем преобразования (4) в
Текущий ток можно рассчитать путем преобразования (4) в
I = P / U
= (100 Вт) / (230 В)
= 0,43 ампера
Сопротивление может быть вычислено путем реорганизации (4) в
R = U 2 / P
= (230 В) 2 / (100 Вт)
= 529 Ом
Номограмма электрической мощности
Эта номограмма может использоваться для оценки зависимости мощности отнапряжение и ампер.
Скачайте и распечатайте номограмму зависимости электрической мощности от вольт и ампер!
Значения по умолчанию на номограмме выше указывают 240 вольт , сопротивление 10 ампер и мощность 2,4 кВт для постоянного или однофазного переменного тока и 4 кВт для трехфазного переменного тока.
Калькулятор закона
Ом
Укажите любые 2 значения и нажмите «Рассчитать», чтобы получить другие значения в уравнениях закона Ома V = I × R и P = V × I.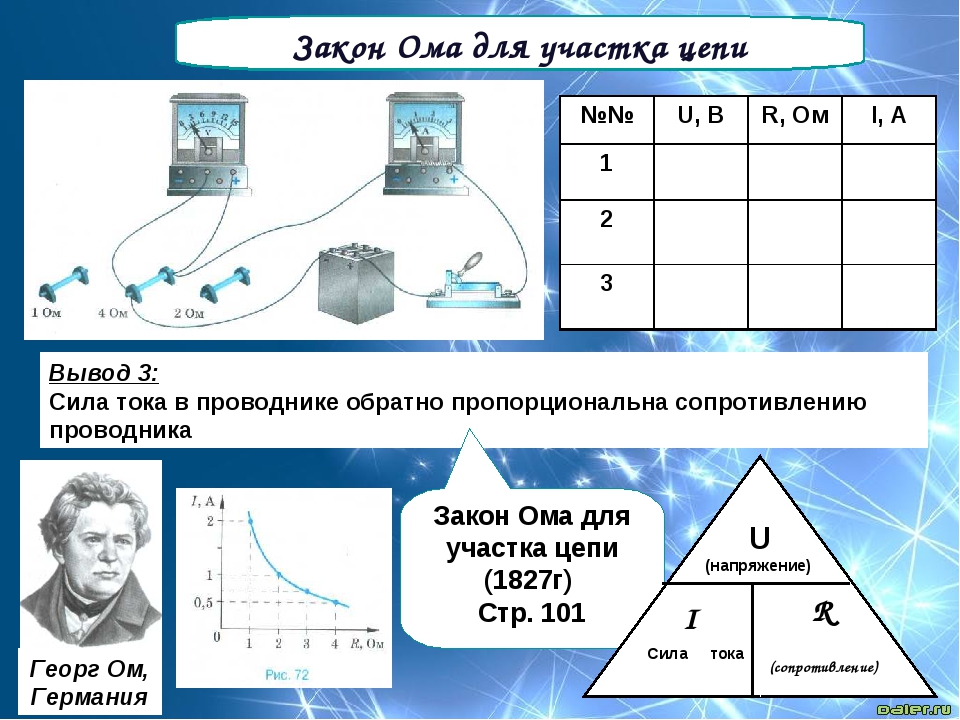
Связано: счетчик резисторов
Закон Ома
Закон
Ома гласит, что ток через проводник между двумя точками прямо пропорционален напряжению. Это верно для многих материалов в широком диапазоне напряжений и токов, а сопротивление и проводимость электронных компонентов, изготовленных из этих материалов, остаются постоянными. Закон Ома верен для цепей, содержащих только резистивные элементы (без конденсаторов или катушек индуктивности), независимо от того, является ли управляющее напряжение или ток постоянным (DC) или изменяющимся во времени (AC).Его можно выразить с помощью ряда уравнений, обычно всех трех вместе, как показано ниже.
Где:
В — напряжение в вольтах
R — сопротивление в Ом
I ток в амперах
Электроэнергетика
Мощность — это скорость, с которой электрическая энергия передается по электрической цепи за единицу времени, обычно выражается в ваттах в Международной системе единиц (СИ). Электроэнергия обычно вырабатывается электрическими генераторами и поставляется предприятиям и домам через электроэнергетику, но также может поставляться от электрических батарей или других источников.
Электроэнергия обычно вырабатывается электрическими генераторами и поставляется предприятиям и домам через электроэнергетику, но также может поставляться от электрических батарей или других источников.
В резистивных цепях закон Джоуля можно объединить с законом Ома для получения альтернативных выражений для количества рассеиваемой мощности, как показано ниже.
Где:
P — мощность в ваттах
Колесо формулы закона Ома
Ниже приведено колесо формул для соотношений по закону Ома между P, I, V и R. Это, по сути, то, что делает калькулятор, и представляет собой просто представление алгебраической манипуляции с уравнениями выше. Чтобы использовать колесо, выберите переменную для поиска в середине колеса, затем используйте соотношение для двух известных переменных в поперечном сечении круга.
Закон
Ома — Как соотносятся напряжение, ток и сопротивление | Закон Ома
Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться.Это непрерывное движение электрического заряда через проводники цепи называется током , и его часто называют «потоком», как поток жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» в цепи, называется напряжением . Напряжение — это особая мера потенциальной энергии, которая всегда относительна между двумя точками.
Когда мы говорим об определенном количестве напряжения, присутствующем в цепи, мы имеем в виду измерение того, сколько потенциальной энергии существует для перемещения носителей заряда из одной конкретной точки в этой цепи в другую конкретную точку.Без ссылки на , две конкретные точки , термин «напряжение» не имеет значения.
Ток имеет тенденцию проходить через проводники с некоторой степенью трения или сопротивления движению. Это противодействие движению правильнее называть сопротивлением . Сила тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующей прохождению тока.
Это противодействие движению правильнее называть сопротивлением . Сила тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующей прохождению тока.
Как и напряжение, сопротивление — это величина, относительная между двумя точками.По этой причине величины напряжения и сопротивления часто указываются как «между» или «поперек» двух точек в цепи.
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, мы должны уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любой другой вид физической величины. Для массы мы можем использовать единицы «килограмм» или «грамм».
Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия.Вот стандартные единицы измерения электрического тока, напряжения и сопротивления:
«Символ», присвоенный каждой величине, представляет собой стандартную буквенную букву, используемую для представления этой величины в алгебраическом уравнении. Подобные стандартизированные буквы распространены в физических и технических дисциплинах и признаны во всем мире.
Подобные стандартизированные буквы распространены в физических и технических дисциплинах и признаны во всем мире.
«Аббревиатура единицы» для каждой величины представляет собой алфавитный символ, используемый в качестве сокращенного обозначения для ее конкретной единицы измерения.И да, этот странно выглядящий символ «подкова» — это заглавная греческая буква Ω, просто символ иностранного алфавита (извинения перед читателями-греками).
Каждая единица измерения названа в честь известного экспериментатора в области электричества: amp в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта и Ом в честь немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение.«R» для сопротивления и «V» для напряжения говорят сами за себя, тогда как «I» для тока кажется немного странным. Считается, что буква «I» должна обозначать «интенсивность» (потока заряда), а другой символ напряжения, «E», означает «электродвижущую силу». Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «я».
Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «я».
Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах зарезервировано «E» для обозначения напряжения на источнике (таком как батарея или генератор) и «V» для обозначения напряжения на любом другом элементе.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (называемого «мгновенным» значением). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», в то время как пик напряжения при ударе молнии в тот самый момент, когда он попадает в линию электропередачи, скорее всего, будет обозначается строчной буквой «е» (или строчной буквой «v»), чтобы обозначить это значение как имеющееся в один момент времени.
То же самое соглашение о нижнем регистре справедливо и для тока, строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений постоянного тока (DC), которые стабильны во времени, будут обозначены заглавными буквами.
Однако большинство измерений постоянного тока (DC), которые стабильны во времени, будут обозначены заглавными буквами.
Кулон и электрический заряд
Одна основная единица измерения электрического тока, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, — это единица кулонов , которая представляет собой меру электрического заряда, пропорционального количеству электронов в несбалансированном состоянии.Один кулон заряда равен 6 250 000 000 000 000 000 электронов.
Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается заглавной буквой «C». Бывает так, что единица измерения тока, ампер, равна 1 кулону заряда, проходящего через заданную точку в цепи за 1 секунду. В этих терминах ток — это скорость движения электрического заряда по проводнику.
Как указывалось ранее, напряжение — это мера потенциальной энергии на единицу заряда , доступной для мотивации протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общая метрическая единица для энергии любого вида — джоулей , равная количеству работы, выполненной силой в 1 ньютон, приложенной при движении на 1 метр (в том же направлении).
Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общая метрическая единица для энергии любого вида — джоулей , равная количеству работы, выполненной силой в 1 ньютон, приложенной при движении на 1 метр (в том же направлении).
В британских подразделениях это чуть меньше 3/4 фунта силы, приложенной на расстоянии 1 фута. Проще говоря, требуется около 1 джоуля энергии, чтобы поднять гирю весом 3/4 фунта на 1 фут от земли или перетащить что-то на расстояние 1 фут, используя параллельную тяговую силу 3/4 фунта.В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленный на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Уравнение закона Ома
Принципиальное открытие
Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, прямо пропорциональна напряжению, приложенному к нему при любой заданной температуре. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя методы алгебры, мы можем преобразовать это уравнение в два варианта, решая для I и R соответственно:
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти уравнения могут работать, чтобы помочь нам анализировать простые схемы:
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа).Это позволяет очень легко применять закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы рассчитаем величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Какой ток (I) в этой цепи?
В этом втором примере мы рассчитаем величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Какое сопротивление (R) дает лампа?
В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):
Какое напряжение обеспечивает аккумулятор?
Техника треугольника закона Ома
Закон Ома — очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что серьезный студент должен запомнить его. Для тех, кто еще не знаком с алгеброй, есть уловка, чтобы запомнить, как найти любое количество, учитывая два других.
Он так часто используется при изучении электричества и электроники, что серьезный студент должен запомнить его. Для тех, кто еще не знаком с алгеброй, есть уловка, чтобы запомнить, как найти любое количество, учитывая два других.
Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
В конце концов, вам придется быть знакомым с алгеброй, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений.Если вы хорошо разбираетесь в алгебре, все, что вам нужно сделать, это зафиксировать E = IR в памяти и вывести из нее две другие формулы, когда они вам понадобятся!
ОБЗОР:
- Напряжение измеряется в вольт , обозначается буквами «E» или «V».

- Ток измеряется в ампер , обозначается буквой «I».
- Сопротивление измеряется в Ом , обозначается буквой «R».
- Закон Ома: E = IR; I = E / R; R = E / I
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Попробуйте наш калькулятор закона Ома в разделе «Инструменты».
Настроить CQ-Calling All Обзоры продуктов Рекламная информация | Основной закон Ома Здесь мы попытаемся объяснить закон Ома Закон Ома Что такое Ом Закон Ома составлен из Что такое напряжение? An , наполненный Что сейчас? По аналогии с , ведущие к крану. Что такое сопротивление? Аналогия Все три из них: напряжение, ток и сопротивление Информация: Закон Ома назван в честь баварцев. Закон Ома может быть I измеряется ток ампер R измеряется сопротивление в зависимости от размера труб и крана: В = I x Р = I = В / R (ток = Зная любые два значения цепи , Например, чтобы найти напряжение в Если в цепи есть ток 2 ампера, и (В = 2 ампера x 1 Ом = 2 Чтобы найти ток в той же цепи выше В этом третьем примере мы знаем ток (2 ампера) и Иногда очень полезно
Колесо наверху Вольт Чтобы использовать, просто Пример: Чтобы найти Вот Вы знаете Просто Вы
В указанном выше An Информация: Обычно закон Ома применяется только к Проводной
|
L3: Закон Ома — Физические вычисления
Содержание
- Закон Ома
- Связь закона Ома с нашими аналогами с водой
- Почему \ (I \), а не \ (C \)?
- Обязательно используйте базовые единицы
- Общие префиксы СИ
- Единицы преобразования
- Давайте проанализируем некоторые схемы!
- Пример 1: Решить для текущего
- Шаг 1: Определить известные
- Шаг 2: Применить известные
- Шаг 3: Решить для тока I
- Пример 2: Решить для тока снова (но с другим сопротивлением)
- Пример 3: Найти напряжение
- Пример 4: Найти сопротивление
- Пример 1: Решить для текущего
- Упражнение: Использование симулятора цепей
- Краткое содержание урока
- Ресурсы
- Следующий урок
В этом уроке мы узнаем о законе Ома , один из наиболее важных эмпирических законов в электрических цепях, который описывает, как связаны между собой ток , , напряжение , и сопротивление , . Хотя закон Ома невероятно полезен для анализа и понимания того, как работают схемы, как и многие «законы», он не всегда соблюдается (особенно для так называемых «неомических» устройств, таких как светодиоды или другие диоды). Но мы к этому еще вернемся.
Хотя закон Ома невероятно полезен для анализа и понимания того, как работают схемы, как и многие «законы», он не всегда соблюдается (особенно для так называемых «неомических» устройств, таких как светодиоды или другие диоды). Но мы к этому еще вернемся.
А теперь перейдем к закону Георга Ома!
Закон Ома
В 1827 году, после многих лет экспериментов, немецкий физик Георг Симон Ом опубликовал «Гальваническую цепь, исследованную математически, », которая стала основой закона Ома.Закон Ома гласит, что ток (\ (I \) в амперах) в проводнике прямо пропорционален приложенному напряжению (\ (V \) в вольтах) против сопротивления проводника (\ (R \) в омах) :
\ [I = \ frac {V} {R} \]
Таким образом, если мы удвоим напряжение в нашей цепи, например, соединив две батареи последовательно, то мы также удвоим ток. Закон Ома имеет большое значение для построения и использования схем с микроконтроллерами, включая делители напряжения и резистивные датчики.
Важно отметить, что вы увидите и будете использовать закон Ома во всех трех эквивалентных воплощениях (которые могут быть получены с помощью простой алгебры):
Если вы хотите найти ток в своей схеме, вы используете: \ (I = \ frac {V} {R} \)
Чтобы найти для напряжения , используйте: \ (V = I * R \)
Чтобы найти для сопротивления , используйте: \ (R = \ frac {V} {I } \)
Обратите внимание, как эти уравнения соотносятся с концепциями, которые мы объясняли в нашем первом уроке по напряжению, току и сопротивлению, к которым вы, возможно, захотите вернуться. Например, \ (I = \ frac {V} {R} \) ясно демонстрирует, что для увеличения тока мы можем либо увеличить напряжение , либо уменьшить сопротивление .
Например, \ (I = \ frac {V} {R} \) ясно демонстрирует, что для увеличения тока мы можем либо увеличить напряжение , либо уменьшить сопротивление .
Связь закона Ома с нашими аналогами с водой
Опять же, опираясь на наши гидравлические и электрические аналогии (которые мы подробно использовали в предыдущих уроках), мы можем выделить еще одно сходство. В 1840-х годах Пуазейль эмпирически показал, что скорость потока воды через трубу равна падению давления в трубе, деленному на сопротивление трубы — это называется закон Пуазейля .И это имеет смысл концептуально: большая разница давлений между двумя концами трубы создает большую силу, а меньшее сопротивление позволяет большему потоку воды.
Вам знакомо это уравнение? Должно. Это в точности закон Ома! Ток в цепи прямо пропорционален падению напряжения в цепи, деленному на ее сопротивление. См. Изображение ниже.
Рисунок.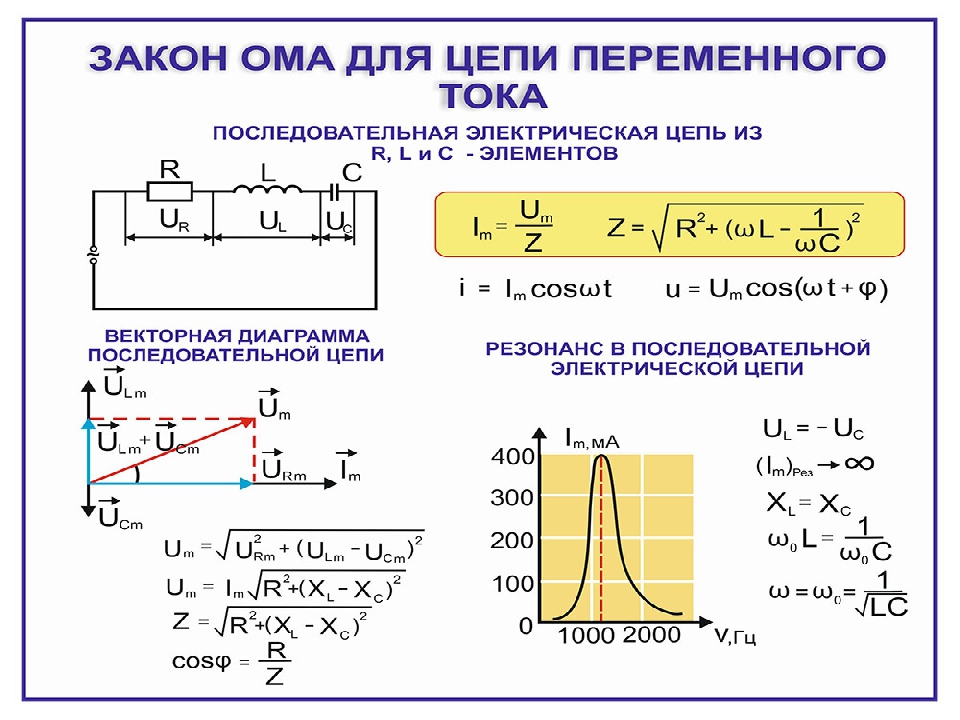 Закон Пуазейля для плавного течения жидкости и закон Ома для электрического тока аналогичны.Изображение основано на HyperPhysics в штате Джорджия и создано в PowerPoint. Изображения Пуазейля и Ома взяты из Википедии.
Закон Пуазейля для плавного течения жидкости и закон Ома для электрического тока аналогичны.Изображение основано на HyperPhysics в штате Джорджия и создано в PowerPoint. Изображения Пуазейля и Ома взяты из Википедии.
ПРИМЕЧАНИЕ:
Уравнение закона Пуазейля справедливо только для плавного (ламинарного, а не турбулентного) течения ньютоновской жидкости, такой как вода. Но такое условие не имеет отношения к электрическому току.
Почему \ (I \), а не \ (C \)?
Вы можете спросить: «Если \ (R \) — это сопротивление r в омах (Ом), а V — напряжение v в вольтах (В), то почему \ (I \) используется для обозначения c ток в амперах (A), а не в \ (C \)? » Две причины: во-первых, \ (C \) уже зарезервирован для единицы СИ, состоящей из столбцов (C), которая используется в самом определении ампер (напомним, что \ (1 \ A = 1 \ C / s \)) и таким образом, можно запутаться! Во-вторых, ампер назван в честь Андре-Мари Ампера, считающегося отцом электромагнетизма, который называл силу тока « i ntensité du courant» или « i ntensity of current». Итак, ток равен \ (I \), а не \ (C \).
Итак, ток равен \ (I \), а не \ (C \).
Обязательно используйте базовые блоки.
Распространенная проблема при применении закона Ома — или анализе цепей в целом — это испорченные базовые блоки. В цифровых схемах мы часто имеем дело с кОм (кОм), , что составляет 1000 Ом, миллиампер (мА), , что составляет \ (\ frac {1} {1000} \) (0,001) усилителя — или даже микроампер (мкА), что составляет одну миллионную (\ (\ frac {1} {1,000,000} \) или 0,000001) усилителя, и так далее. Нам нужно преобразовать эти единицы в базовые единицы , в вольтах (В), омах (Ом) и амперах (А) для выполнения нашего анализа.
Например, если схема содержит резистор 2,2 кОм с батареей 9 В, для расчета тока не следует по ошибке писать \ (I = \ frac {9V} {2.2Ω} A \), а вместо этого \ (I = \ frac {9V} {2200Ω} A \). Первый даст вам 4,1 А (большая сила тока и неправильный!), А второй даст правильное значение 0,0041 А, что составляет 4,1 мА.
Так что не забывайте дважды проверять свои устройства!
Общие префиксы SI
Ниже мы написали несколько общих префиксов SI, большинство из которых должно быть вам знакомо по другим измеряемым величинам. {-12} \)
{-12} \)
Таблица Эта диаграмма основана на веб-странице метрических префиксов SI NIST и рисунке 2.2 в книге Бартлетта.
Единицы преобразования
Для преобразования между префиксной единицей и базовой единицей мы умножаем на коэффициент преобразования. Чтобы преобразовать базовую единицу в единицу с префиксом, мы делим на коэффициент преобразования .
Так, например, чтобы преобразовать 2.{-6}} = 37 мкА \).
Разберем схемы!
Уф, хорошо, теперь мы готовы приступить к анализу некоторых схем. Мы начнем с простой схемы и перейдем к ней. Анализируя (или даже готовясь к созданию) схем, всегда полезно взять карандаш и бумагу. Итак, сделайте это сейчас.
Кроме того, полезно иметь возможность проверять нашу работу, что мы можем сделать в симуляторе схем. Мне нравится использовать CircuitJS, но я также использовал EveryCircuit и CircuitLab — последнее стоит денег.
Прежде чем мы начнем, давайте посмотрим это видео, в котором я строю простую резистивную схему в CircuitJS и вычисляю ее ток с учетом источника напряжения и резистора.
Видео Видео было создано с помощью симулятора CircuitJS. Прямая ссылка здесь.
Пример 1: Решить относительно тока
Представьте себе схему с батарейным питанием и одним резистором (базовым, да, но с педагогической точки зрения мощным!). Если нам заданы напряжение \ (9 В \) и сопротивление (\ (100 Ом \)), можем ли мы решить для тока \ (I \)?
Рисунок. Простая схема с питанием 9 В с одним резистором \ (100 Ом \). Можете ли вы, используя закон Ома, вычислить ток \ (I \)? Изображения сделаны в Fritzing и PowerPoint.
Шаг 1. Определите известных
Чтобы начать анализ, вам нужно определить все, что вы знаете об этой цепи.
Обратите внимание, что все провода, соприкасающиеся с положительной клеммой батареи , имеют одинаковый электрический потенциал (\ (9 В \)), который мы теперь отметили красным, и все провода, соприкасающиеся с отрицательной клеммой батареи , имеют одинаковый электрический потенциал. (\ (0V \)) — который мы отметили черным.Обратите внимание, что даже несмотря на то, что медные провода имеют некоторое сопротивление, оно настолько мало (особенно для длин в цифровой цепи), что мы можем смоделировать его как \ (0Ω \) (действительно, провода всегда предполагаются \ (0Ω \) в этом виде. схемотехнического анализа).
И поскольку мы вычисляем по току, нам нужно использовать формулировку закона Ома: \ (I = \ frac {V} {R} \). Более конкретно, поскольку напряжение всегда относительное — разность электрических потенциалов — мы используем \ (I = \ frac {V_1 — V_2} {R} \)
Рис. Все провода, соприкасающиеся с плюсовой клеммой аккумулятора, имеют одинаковое напряжение (9 В). Точно так же все провода, соприкасающиеся с отрицательной клеммой аккумулятора, имеют одинаковое напряжение (0 В). Изображения сделаны в Fritzing и PowerPoint.
Все провода, соприкасающиеся с плюсовой клеммой аккумулятора, имеют одинаковое напряжение (9 В). Точно так же все провода, соприкасающиеся с отрицательной клеммой аккумулятора, имеют одинаковое напряжение (0 В). Изображения сделаны в Fritzing и PowerPoint.
Шаг 2: Примените знания
Установив, что все провода наверху схемы (те, которые непосредственно подключены к положительной клемме) имеют одинаковый электрический потенциал, мы можем отметить это как один узел \ (V_1 \ ) . Точно так же все провода, соприкасающиеся с минусовой клеммой аккумулятора, можно назвать узлом \ (В_2 \) .
Теперь мы можем заменить \ (9V \) на \ (V_1 \) и \ (0V \) на \ (V_2 \). И мы также знаем, что \ (R = 100Ω \), что дает нам полное уравнение: \ (I = \ frac {9V — 0V} {100Ω} \)
Рис. Мы можем назвать все провода, соприкасающиеся с положительным клеммным узлом батареи \ (V_1 \), и все провода, соприкасающиеся с отрицательным клеммным узлом \ (V_2 \). Используя эту информацию, мы можем заменить \ (9V \) на \ (V_1 \) и \ (0V \) на \ (V_2 \). Изображения сделаны в Fritzing и PowerPoint.
Используя эту информацию, мы можем заменить \ (9V \) на \ (V_1 \) и \ (0V \) на \ (V_2 \). Изображения сделаны в Fritzing и PowerPoint.
Шаг 3: Решите для тока I
Наконец, мы готовы решить для тока \ (I = \ frac {9V — 0V} {100Ω} \ Rightarrow 0.09A \ Rightarrow 90mA \)
Сделали. Мы успешно применили закон Ома для определения тока!
Пример 2: Снова вычислить для тока (но с другим сопротивлением)
Давайте попробуем снова вычислить для тока с помощью аналогичной схемы. На этот раз сопротивление увеличено с \ (100 Ом \) до \ (4,7 кОм \).
Прежде чем делать что-либо еще: полезно подумать о концептуально , что произойдет?
Ток уменьшается, верно? И делает это пропорционально.
Действительно, ток идет от \ (90 мА \) с \ (100 Ом \) до \ (I = \ frac {9V} {4700 Ом} \ Rightarrow 0.0019𝐴 \ Rightarrow 1.9𝑚𝐴 \), что не очень много!
Рисунок. Как и ожидалось, ток \ (I \) уменьшается, когда сопротивление \ (R \) увеличивается.
Пример 3: Найти напряжение
Как отмечалось выше, мы можем использовать три различных формулировки закона Ома (\ (I = \ frac {V} {R} \), \ (V = I * R \), и \ (R = \ frac {V} {I} \)), чтобы помочь нам проанализировать различные неизвестные в схеме.
В этом случае давайте воспользуемся законом Ома, чтобы найти неизвестный источник напряжения . Предположим, что схема аналогична предыдущей: один источник напряжения (но неизвестного напряжения) с одним резистором размером \ (100 Ом \) и током \ (I = 50 мА \).
Поскольку мы вычисляем напряжение, мы должны использовать формулу \ (V = I * R \). Первое, что нам нужно сделать, это убедиться, что все наши измерения находятся в базовых единицах . Сила тока нет, поэтому измените его на силу тока (а не в миллиампер): \ (I = 50 мА \ Rightarrow 0.05А \).
Теперь мы можем легко найти \ (V = 0,05A * 100Ω = 5V \). Батарея является источником напряжения \ (5В \).
Рисунок. Используя формулировку \ (V = I * R \) закона Ома, мы можем найти напряжение при известном токе \ (I \) и известном сопротивлении \ (R \). Изображения сделаны в Fritzing и PowerPoint.
Используя формулировку \ (V = I * R \) закона Ома, мы можем найти напряжение при известном токе \ (I \) и известном сопротивлении \ (R \). Изображения сделаны в Fritzing и PowerPoint.
Пример 4: Решите для сопротивления
Готов поспорить, вы уже поняли это!
Наконец, вы можете использовать \ (R = \ frac {V} {I} \) для определения сопротивления, если известны \ (V \) и \ (I \).В этом случае давайте вернемся к нашей батарее \ (9 В \) и предположим, что у нас есть ток \ (1,32 мА \). Какой номинал резистора \ (R \)?
Опять же, первое, что нужно сделать, это преобразовать все единицы в базовые. Итак, \ (1.32mA \ Rightarrow 0.00132A \).
Теперь мы можем найти \ (R = \ frac {9V} {0.00132A} \ Rightarrow 6818.2Ω \ Rightarrow 6.8kΩ \)
Рис. Используя формулировку \ (R = \ frac {V} {I} \) закона Ома, мы можем найти сопротивление \ (R \) при известном напряжении \ (V \) и известном токе \ (I \ ).Изображения сделаны в Fritzing и PowerPoint.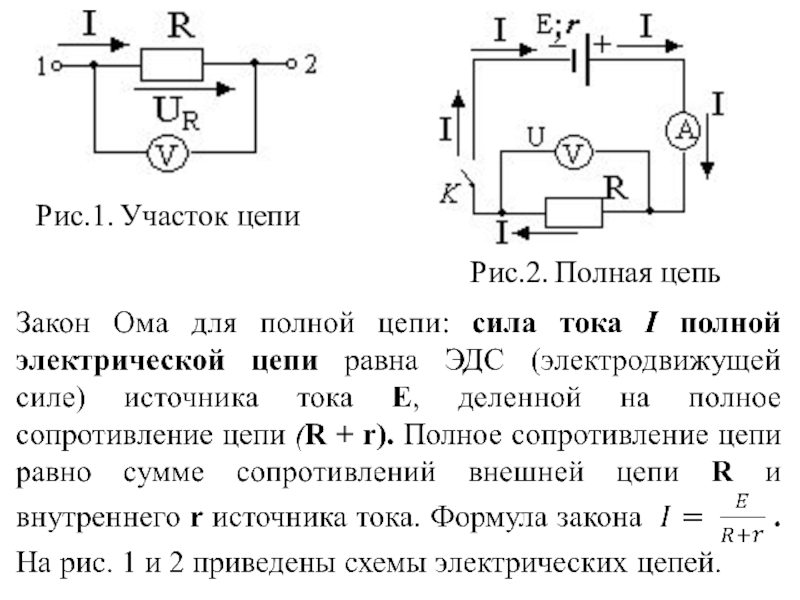
Упражнение: Использование симулятора схем
Теперь, когда мы получили начальное понимание закона Ома, пора построить и поиграть с некоторыми схемами в симуляторе схем.
Используя CircuitJS, постройте и проанализируйте пять различных типов резистивных цепей. Вы можете создавать любые схемы с некоторыми требованиями:
- Все схемы должны иметь только один источник питания
- Вы должны использовать только резисторы
- Вы можете использовать столько резисторов на схему, сколько хотите, но дважды щелкните по провода для отображения тока / напряжения
- Для каждой схемы сделайте снимок экрана и поместите его в журнал прототипирования вместе с кратким отражением того, что вы наблюдали / узнали.
Вы можете сохранить свои схемы одним из двух способов: (1) загрузить их локально (Файл -> Сохранить как) или (2) экспортировать их как общую ссылку (Файл -> Экспортировать как ссылку) — используйте последний вариант. для ваших журналов по прототипированию.
В свои журналы прототипирования включите снимок экрана каждой схемы CircuitJS вместе с кратким описанием того, что вы наблюдали, и прямой ссылкой на созданную вами схему CircuitJS.
Краткое содержание урока
В этом уроке мы узнали:
- Что существует эмпирический закон, называемый законом Ома, который описывает линейную зависимость между напряжением, током и сопротивлением
- В частности, закон Ома утверждает, что ток в цепь — это полное напряжение, деленное на полное сопротивление (\ (I = \ frac {V} {R} \)).Этот закон основан на концепциях и интуиции, которые мы развили в первом уроке этой серии.
- Мы также узнали, как применить закон Ома к некоторым простым схемам, чтобы найти неизвестные токи, напряжения и сопротивления. для новичков забывает преобразовать измерения в базовые единицы
- Затем мы поигрались со схемами в CircuitJS и сделали наблюдения.
Ресурсы
Следующий урок
В следующем уроке мы применим закон Ома к более сложным схемам — особенно тем, которые объединяют резисторы в серии и тем, которые объединяют их в параллельно .
Предыдущая: Схема Следующая: Последовательные и параллельные резисторы
Все материалы с открытым исходным кодом созданы лабораторией Makeability Lab и профессором Джоном Э. Фрелихом. Нашли ошибку? Отправьте сообщение о проблеме на GitHub.
Закон
Ом — обзор
8.2.2 Паразитная емкость
Закон Ома, как указано в уравнении. (8.1) не выполняется, когда модель устройства включает реактивные (емкостные или индуктивные) компоненты и учитываются изменяющиеся во времени напряжения / токи. В таких случаях обобщенная форма закона Ома, показанная в формуле.(8.4) описывает взаимосвязь между напряжением и током через понятие электрического импеданса Z .
(8,4) V = ZIwithZ = R + jX
Электрический импеданс Z представлен комплексным числом, действительная часть которого представляет собой сопротивление R , как определено ранее, тогда как мнимая часть X , называемое реактивным сопротивлением, учитывает реактивные эффекты.
Некоторые датчики несут информацию, относящуюся к измеряемым величинам, как в резистивных, так и в реактивных составляющих импеданса, поэтому интерфейсные схемы должны иметь возможность выполнять одновременную оценку R и X .С другой стороны, если полезная информация находится только в резистивном компоненте, как это обычно бывает с резистивными датчиками, реактивный компонент считается паразитным элементом, влияние которого следует минимизировать.
При работе с резистивными датчиками обычно основной паразитный вклад носит емкостной характер. В отличие от неидеальности большинства компонентов схемы, эти емкостные эффекты не могут быть компенсированы правильной калибровкой схемы, поскольку они зависят от конкретного датчика и условий эксплуатации.Если не принять во внимание надлежащим образом, такие эффекты могут вызвать ошибки в оценке сопротивления, как будет разъяснено в следующих разделах.
Одна из наиболее распространенных причин возникновения паразитных емкостных эффектов связана с производством датчиков. Если эффект восприятия достигается за счет определенных явлений, происходящих на поверхности датчика (например, с фотодетекторами и датчиками газа), обычным способом повышения чувствительности датчика является максимальное увеличение поверхностных эффектов путем реализации метода, основанного на встречно-штыревых электродах, как показано на Инжир.8.3. К сожалению, эта структура приводит к увеличению паразитной емкости между электродами C ee между электродами, как показано на рис. 8.3, которая становится еще более заметной по мере повторения встречно-штыревой структуры (Polese et al., 2017).
Если эффект восприятия достигается за счет определенных явлений, происходящих на поверхности датчика (например, с фотодетекторами и датчиками газа), обычным способом повышения чувствительности датчика является максимальное увеличение поверхностных эффектов путем реализации метода, основанного на встречно-штыревых электродах, как показано на Инжир.8.3. К сожалению, эта структура приводит к увеличению паразитной емкости между электродами C ee между электродами, как показано на рис. 8.3, которая становится еще более заметной по мере повторения встречно-штыревой структуры (Polese et al., 2017).
Рисунок 8.3. Паразитно-емкостный эффект в датчиках с встречно-штыревыми электродами.
Другая ситуация, в которой возникают паразитные емкостные эффекты, характерна для газовых датчиков. Некоторым устройствам для обнаружения газа необходимо работать при гораздо более высокой температуре, чем температура окружающей среды, и по этой причине они обычно снабжены встроенной нитью накала R h , которая действует как нагреватель (Samà et al. , 2017). Нить накала нагревателя представляет собой проводник, реализованный на той же подложке чувствительного компонента R s и разделенный диэлектрическим материалом, который электрически изолирует два компонента датчика. Однако небольшой размер реализованных устройств заставляет эти два компонента взаимодействовать друг с другом из-за емкостных эффектов, как показано на рис. 8.4.
, 2017). Нить накала нагревателя представляет собой проводник, реализованный на той же подложке чувствительного компонента R s и разделенный диэлектрическим материалом, который электрически изолирует два компонента датчика. Однако небольшой размер реализованных устройств заставляет эти два компонента взаимодействовать друг с другом из-за емкостных эффектов, как показано на рис. 8.4.
Рисунок 8.4. Паразитно-емкостный эффект в газовых сенсорах со встроенной нитью нагревателя.
Помимо этих возможных внутренних источников, емкостные эффекты могут возникать из-за внешних причин, таких как соединение между датчиком и измерительной системой, как показано на рис.8.5. Фактически, разъемы и провода, используемые для соединения датчика с электронной схемой, демонстрируют распределенную емкостную характеристику C c , которая, с точки зрения приборов, наблюдается параллельно с датчиком.
Рисунок 8.5. Паразитно-емкостный эффект из-за связи датчика с измерительной системой.
Расчет общего емкостного паразитного эффекта далеко не прост и часто требует полного понимания характеристик датчика, в том числе на микроскопическом уровне.По этой причине, когда необходимо учитывать паразитную емкость, обычно рассматривается упрощенная модель датчика, где паразитный конденсатор C с представлен параллельно с сопротивлением датчика R с. , с учетом всех возможных емкостных паразитных эффектов. Упрощенная модель датчика, используемая в следующих разделах, показана на рис. 8.6.
Рисунок 8.6. Упрощенная модель резистивного датчика с учетом паразитно-емкостных эффектов.
Следует отметить, что когда R с очень велико (напоминающее поведение, связанное с разомкнутой цепью) C с может преобладать, что приводит к значительным ошибкам в оценке сопротивления . В этих случаях (например, при работе с датчиками MOX) схемы интерфейса должны быть спроектированы таким образом, чтобы ограничить это возникновение.


 107
107 107
107 То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.
То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.
 Кольца, ремешки часов, ожерелья, браслеты и другие подобные вещи обеспечивают отличный электрический контакт с телом человека и способны провести достаточный ток, чтобы вызвать ожог кожи даже при низких напряжениях.
Кольца, ремешки часов, ожерелья, браслеты и другие подобные вещи обеспечивают отличный электрический контакт с телом человека и способны провести достаточный ток, чтобы вызвать ожог кожи даже при низких напряжениях.
 )
) увеличить сопротивление цепи
увеличить сопротивление цепи

 Мы предположим
Мы предположим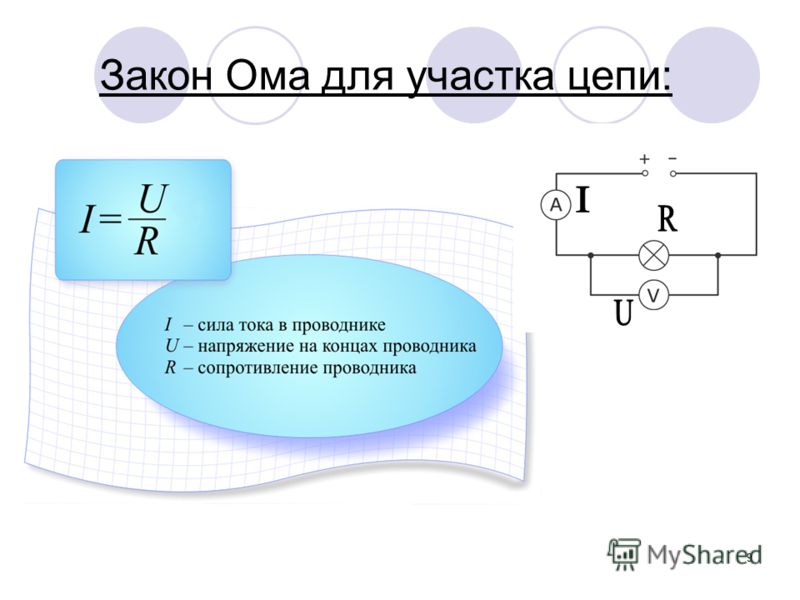 Срок
Срок


