Амплитудное значение силы тока: Амплитудное значение тока

Содержание

Амплитудное значение силы переменного тока в цепи Im=2,8 А. Чему равно действующее значение

По двох металевих паралельних рейках, нахилених під кутом α = 30 до горизонту, може ковзати горизонтальний провідник масою m = 0,5 кг і довжиною l = 0
…

,3 м. Уся система знаходиться в однорідному магнітному полі, вектор індукції якого спрямований вгору і дорівнює В = 0,2 Т. Рейки замикаються у верхній частині, конденсатором ємністю с =1,0 мкФ. Нехтуючи опором контуру, визначити прискорення, з яким буде рухатися провідник.

Почему автомобилю трудно двигаться по дороге во
время гололёда?

Помогите пожалуйста

Андрей занимается спринтерским бегом. К концу тренировки он устаёт и бежит стометровку
со скоростью 5 м/с, а на соревнованиях, со свежими силами
со ск
…

оростью 8 м/с.
Определите разницу
времени между результатами, Показанными Андреем
в тренировочном и соревновательном забегах. Ответ выразите в секундах и округлите до
десятых долей.
прошу помогите!!!!

Яка маса тіла, що втримується на похилій площині під кутом нахилу 45°, якщо коєфіцієнт тертя становить 0,4?
ПОЖАЛУЙСТА ЭТО КОНТРОЛЬНАЯ (

Допоможіть будь ласка! У закритому поршнем циліндрі знаходиться ідеальний газ.
Вкажіть, як зміниться внутрішня енергія газу, якщо його стискати:
А. зм
…

еншиться; Б. збільшиться;
В. спочатку збільшиться, потім зменшиться; Г. не зміниться;
Д. спочатку зменшиться, потім збільшиться.

Діаметр шийки краплі води в момент її відриву від скляної трубки можна вважати рівним діаметру трубки.Яку масу має падаюча крапля,якщо діаметр трубки
…

1 мм? Поверхневий натяг води рівний 7,28 10-²Н/м.

Вокруг прямого проводника с током существует магнитное поле, магнитные линии которого в точке A направлены так, как показано на рисунке. Определи напр
…

авление тока в проводнике.
Обрати внимание на то, что точка A находится перед проводником.
Из предложенных ответов выбери правильный.
Ток в проводнике не течёт.
Направление тока в проводнике определить невозможно.
Ток в проводнике направлен вниз.
Ток в проводнике направлен вверх.

На предоставленном рисунке ток течёт
справа налево.
слева направо.
в произвольном направлении.

Помогите пожалуйста!!!

Амплитудное значение — сила — ток

Cтраница 1

Амплитудное значение силы тока достигает при резонансе максимума, равного Uo / R, сдвиг фаз между напряжением и током отсутствует. Напряжения U L на индуктивности L и U c на емкости С равны по модулю и находятся в противофазе, так что полное напряжение на концах цепи U совпадает с напряжением U K на активном сопротивлении R. Напряжения на реактивных сопротивлениях могут по амплитуде значительно превышать приложенное напряжение.
[1]

Определим амплитудное значение силы тока и положение якоря относительно сердечника при различных величинах относительных воздушных зазоров.
[2]

Добычно амплитудным значением силы тока; если речь идет — г J3 о напряжении, то говорят об амплитудном значении напряжения. Во многих случаях эти величины являются очень важными. Так, например, при расчете изоляции какого-либо электрического аппарата приходится считаться именно с амплитудными значениями действующих в нем напряжений, так как в смысле пробоя наиболее опасными являются именно моменты максимума напряжения. Однако с точки зрения энергетических действий переменного тока, как — мы увидим ниже, оказывается более удобным характеризовать интенсивность тока иначе.
[4]

Чему равны амплитудные значения силы тока и напряжения IB цепи, если амперметр показывает 2 А, а вольтметр 120 В.
[6]

При этом в качестве расчетных необходимо прилимать амплитудные значения силы тока и напряжения.
[7]

Как видно из выражения ( 56), амплитудные значения силы тока во вторичной обмотке отличаются друг от друга коэффициентами, зависящими только от относительных величин воздушных зазоров.
[8]

На рис. 200 изображены графики / и 2 зависимости амплитудных значений силы тока /, в двух контурах от частоты ш вынужденных электромагнитных колебаний, происходящих в этих контурах. Резонанс в контуре с малым активным сопротивлением называют острым, а в контуре с большим активным сопротивлением — тупым.
[9]

В колебательном контуре с индуктивностью 0 40 Гн и емкостью 20 мкФ амплитудное значение силы тока равно 1 0 — Ю 1 А. Каким будет напряжение на конденсаторе в момент, когда энергия электрического и энергия магнитного полей будут равны.
[10]

Из уравнений ( 1) следует, что основное внимание нужно сосредоточить на нахождении амплитудного значения силы тока / 0 и сдвига фазы ф, ибо неизвестные амплитудное значение напряжения С / 0 и круговая частота ( о легко находятся из данных условия задачи.
[11]

Здесь вектор, изображающий напряжение, повернут относительно вектора тока на угол я / 2 в отрицательном направлении ( по часовой стрелке), / о и И с о — амплитудные значения силы тока и напряжения.
[12]

В сеть переменного тока с действующим значением напряжения 120В последовательно включены проводник с активным сопротивлением 10 Ом и катушка индуктивностью 0 1 Гн. Определить частоту v тока, если амплитудное значение силы тока в цепи равно 5 А.
[13]

УДАРНЫЙ ГЕНЕРАТОР — Синхронный генератор ( как правило, 3-фазного тока), предназнач. Применяется для испытаний элект-рич. Развиваемая мощность до неск. ГВ-А; амплитудное значение силы тока КЗ — неск.
[14]

Представляет собой 3-фазную синхронную машину, работающую в режиме 2 — и 3-фазных КЗ и рассчитанную на неск. КЗ через определенные промежутки времени ( напр. MB А и более; амплитудное значение силы тока КЗ — неск.
[15]

Страницы:

1

2

Связь действующего и амплитудного напряжения. Действующие значения силы тока и напряжения

Силу переменного тока (напряжения) можно
охарактеризовать при помощи амплитуды.
Однако амплитудное значение тока
непросто измерить экспериментально.
Силу переменного тока удобно связать
с каким-либо действием, производимым
током, не зависящим от его направления.
Таковым является, например, тепловое
действие тока. Поворот стрелки амперметра,
измеряющего переменный ток, вызывается
удлинением нити, которая нагревается
при прохождении по ней тока.

Действующим
илиэффективным
значением
переменного тока (напряжения) называется
такое значение постоянного тока, при
котором на активном сопротивлении
выделяется за период такое же количество
теплоты, как и при переменном токе.

.
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени

.
Поделим период колебанийна очень большое число малых промежутков
времени

.
Количество теплоты

,
выделяемое на сопротивленииза время

.
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:

Сила тока в
цепи изменяется по синусоидальному
закону

Опуская
вычисления, связанные с интегрированием,
запишем окончательный результат

Если бы по
цепи шёл некоторый постоянный ток
,
то за время, равное,
выделилось бы тепло

.
По определению постоянный ток,
оказывающий такое же тепловое действие,
что и переменный, будет равен эффективному
значению переменного тока

.
Находим эффективное значение силы
тока, приравнивая теплоты, выделяемые
за период, в случаях постоянного и
переменного токов

(4.28)

Очевидно,
точно такое же соотношение связывает
эффективное и амплитудное значения
напряжения в цепи с синусоидальным
переменным током:

(4.29)

Например,
стандартное напряжение в сети 220 В –
это эффективное напряжение. По формуле
(4.29) легко посчитать, что амплитудное
значение напряжения в этом случае будет
равно 311 В.

4.4.5. Мощность в цепи переменного тока

Пусть на некотором участке цепи с
переменным током сдвиг фаз между током
и напряжением равен
,
т.е. сила тока и напряжение изменяются
по законам:

Тогда мгновенное
значение мощности, выделяемой на участке
цепи,

Мощность
изменяется со временем. Поэтому можно
говорить лишь о ее среднем значении.
Определим среднюю мощность, выделяемую
в течение достаточно длительного
промежутка времени (во много раз
превосходящего период колебаний):

С использованием
известной тригонометрической формулы

Величину

усреднять не нужно, так как она не зависит
от времени, следовательно:

За длительное
время значение косинуса много раз
успевает измениться, принимая как
отрицательные, так и положительные
значения в пределах от (1)
до 1. Понятно, что среднее во времени
значение косинуса равно нулю

,
поэтому

(4. 30)

Выражая
амплитуды тока и напряжения через их
эффективные значения по формулам (4.28)
и (4.29), получим

. (4.31)

Мощность, выделяемая на участке цепи с
переменным током, зависит от эффективных
значений тока и напряжения и сдвига
фаз между током и напряжением
. Например,
если участок цепи состоит из одного
только активного сопротивления, то

.
Если участок цепи содержит только
индуктивность или только ёмкость, то

Объяснить среднее нулевое значение
мощности, выделяемой на индуктивности
и ёмкости можно следующим образом.
Индуктивность и ёмкость лишь заимствуют
энергию у генератора, а затем возвращают
её обратно. Конденсатор заряжается, а
затем разряжается. Сила тока в катушке
увеличивается, затем снова спадает до
нуля и т. д. Именно по той причине, что
на индуктивном и ёмкостном сопротивлениях
средняя расходуемая генератором энергия
равна нулю, их назвали реактивными. На
активном же сопротивлении средняя
мощность отлична от нуля. Другими словами
провод с сопротивлением
при протекании по нему тока нагревается.
И энергия, выделяемая в виде тепла, назад
в генератор уже не возвращается.

Если участок цепи содержит несколько
элементов, то сдвига фаз
может быть иным. Например, в случае
участка цепи, изображенного на рис. 4.5,
сдвиг фаз между током и напряжением
определяется по формуле (4.27).

Пример 4.7.
К генератору переменного
синусоидального тока подключён резистор
с сопротивлением.
Во сколько раз изменится средняя
мощность, расходуемая генератором, если
к резистору подключить катушку с
индуктивным сопротивлением

а) последовательно, б) параллельно (рис.
4.10)? Активным сопротивлением катушки
пренебречь.

Решение.
Когда к генератору подключено
одно только активное сопротивление,
расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере
4.6 было определено амплитудное значение
силы тока генератора:

.
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора

В результате средняя расходуемая
генератором мощность

Ответ: при
последовательном включении в цепь
индуктивности средняя мощность,
расходуемая генератором, уменьшится в
2 раза.

Рассмотрим цепь на рис. 4.10,б. В примере
4.6 было определено амплитудное значение
силы тока генератора

.
Из векторной диаграммы на рис. 4.11,б
определяем сдвиг фаз между током и
напряжением генератора

Тогда средняя
мощность, расходуемая генератором

Ответ: при
параллельном включении индуктивности
средняя мощность, расходуемая генератором,
не изменяется.

Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.

Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.

В данное время в мировой промышленной практике широко распространен трехфазный переменный ток
, который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода.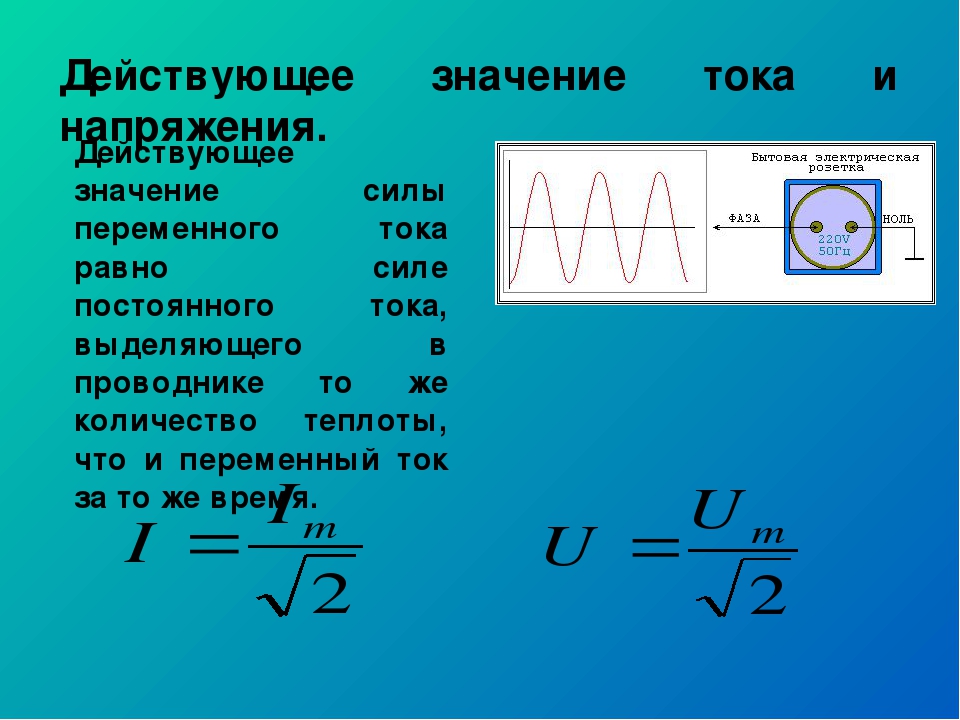 Каждая такая цепь называется фазой.

Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.

Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.

Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает

а) б)

Рис. 3.4. Пример трехфазной системы переменного тока

а) генератор трёхфазного тока; б) с тремя генераторами;

изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.

Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.

Соединение звездой

Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С
, а концы — X, Y, Z
. В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).

Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл
). Поскольку цепь трехфазная, то линейное напряжение будет в v3
раз больше фазного, т. е.: Uл = v3Uф.

Соединение треугольником.

Рисунок 3.6. Пример соединения треугольником

При использовании данного способа соединения конец X
первой обмотки генератора подключают к началу В
второй его обмотки, конец Y
второй обмотки — к началу С
третьей обмотки, конец Z
третьей обмотки — к началу А
первой обмотки. Пример соединения показан на рис. 3.6. При данном способе соединения фазных обмоток и подключении трехфазного генератора к трехпроводной линии линейное напряжение по своему значению сравнивается с фазным: Uф = Uл

Контрольные вопросы

1. Перечислите основные параметры, характеризующие переменный ток.

2. Дайте определение частоты и единицы её измерения.

3. Дайте определение амплитуды и единицы её измерения.

4. Дайте определение периода и единицы его измерения.

5. Отличие простейшего генератора трёхфазного тока от генератора однофазного тока.

6. Что такое фаза?

7. Что представляет собой ротор генератора трёхфазного тока?

8. Почему сдвинуты по фазе обмотки статора генератора трёхфазного тока?

9. Особенность симметричной системы трёх фаз.

10. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «звезда».

11. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «треугольник».

3.2. Виды сопротивлений в цепях переменного тока

В цепях переменного тока сопротивления разделяют на активные и реактивные.

В активных сопротивлениях

, включенных в цепь переменного тока, электрическая энергия преобразуется в тепловую. Активным сопротивлением R
обладают, например, провода электрических линий, обмотки электрических машин и т.д.

В реактивных сопротивлениях

электрическая энергия, вырабатываемая источником, не расходуется. При включении реактивного сопротивления в цепь переменного тока возникает лишь обмен энергией между ним и источником электрической энергии. Реактивное сопротивление создают индуктивности и ёмкости.

Если не учитывать взаимное влияние отдельных элементов электрической цепи, то в общем случае электрическая цепь синусоидального тока может быть представлена тремя пассивными элементами: активным сопротивлением R, индуктивностью L и емкостью C.

Активное сопротивление в цепи переменного тока
.

При включении в цепь переменного тока активного сопротивления, ток и напряжение совпадают по фазе (рис. 3.7) и изменяются по одному и тому же cинусоидальному закону: u=U m sinωt
. Они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 3.7.б).

Для цепи переменного тока, содержащей только активное сопротивление, закон Ома имеет такую же форму, как и для цепи постоянного тока: I=U/R.

Электрическая мощность р
в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i
и напряжения u
: p=ui
.

Рисунок 3.7. Схема включения в цепь переменного тока активного сопротивления R (a), кривые тока i
, напряжения u
и мощности p
(б) и векторная диаграмма.

Из графика видно, что изменение мощности происходит с двойной частотой по отношению к изменению тока и напряжения, т.е. один период изменения мощности соответствует половине периода изменения тока и напряжения.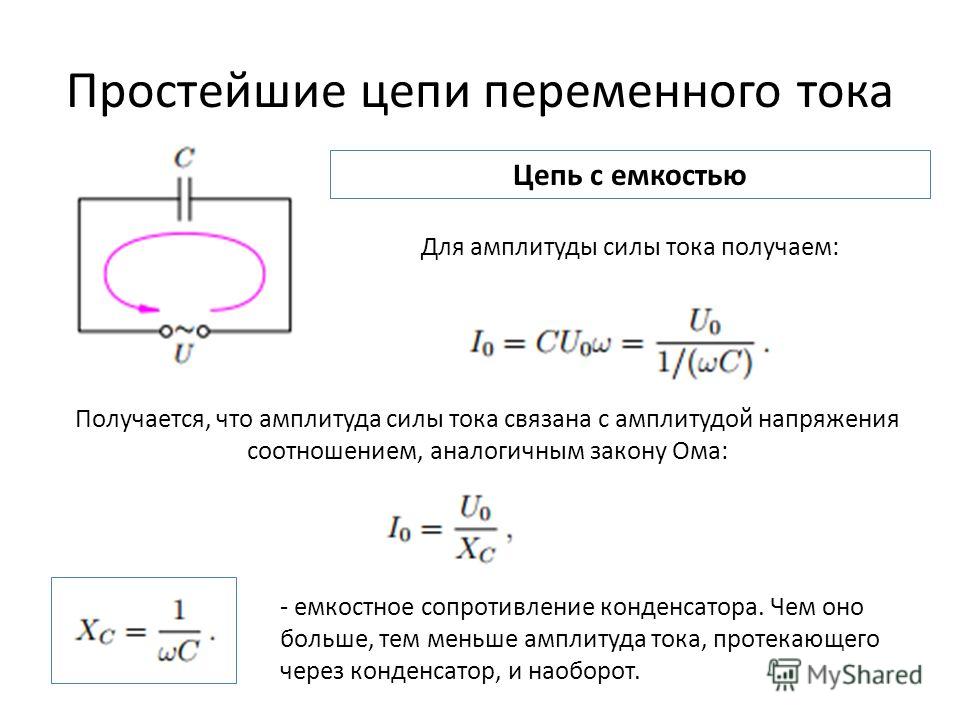 Все значения мощности положительные, это означает, что энергия передается от источника к потребителю.

Средняя мощность Рcp
, потребляемая активным сопротивлением, P=UI=I 2 R
– это и есть активная мощность.

Под индуктивностью L
будем понимать элемент электрической цепи (катушку индуктивности, потерями которой можно пренебречь), способный запасать энергию в своём магнитном поле, который не имеет активного сопротивления и ёмкостиС (рис.3.8).

При включении в цепь переменного тока индуктивности, изменяющийся ток непрерывно индуцирует в ней э.д.с. самоиндукции e L = LΔi/Δt,
где Δi/Δt
– скорость изменения тока.

Когда угол ωt
равен 90° и 270° скорость изменения тока Δi/Δt
=0, поэтому э.д.с. e L
=0.

Скорость изменения тока будет наибольшей, когда угол ωt
равен 0°, 180° и 360°. В эти минуты времени э.д.с. имеет наибольшее значение.

Кривая мощности представляет собой синусоиду, которая изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения. Мощность имеет положительные и отрицательные значения, т.е. возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью.

Рисунок 3.8. Схема включения в цепь переменного тока индуктивности (а), кривые тока i
, напряжения u
, э.д.с. e L
(б) и векторная диаграмма (в)

Э.д.с. самоиндукции согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. В первую четверть периода, когда ток увеличивается, э.д.с. имеет отрицательное значение (направлена против тока).

Во вторую четверть периода, когда ток уменьшается, э.д.с. имеет положительное значение (совпадает по направлению с током).

В третью четверть периода ток меняет своё направление и увеличивается, поэтому э.д.с. направлена против тока и имеет положительное значение.

В четвёртую четверть периода ток уменьшается и э.д.с. самоиндукции стремится поддержать прежнее положение тока и имеет отрицательное значение.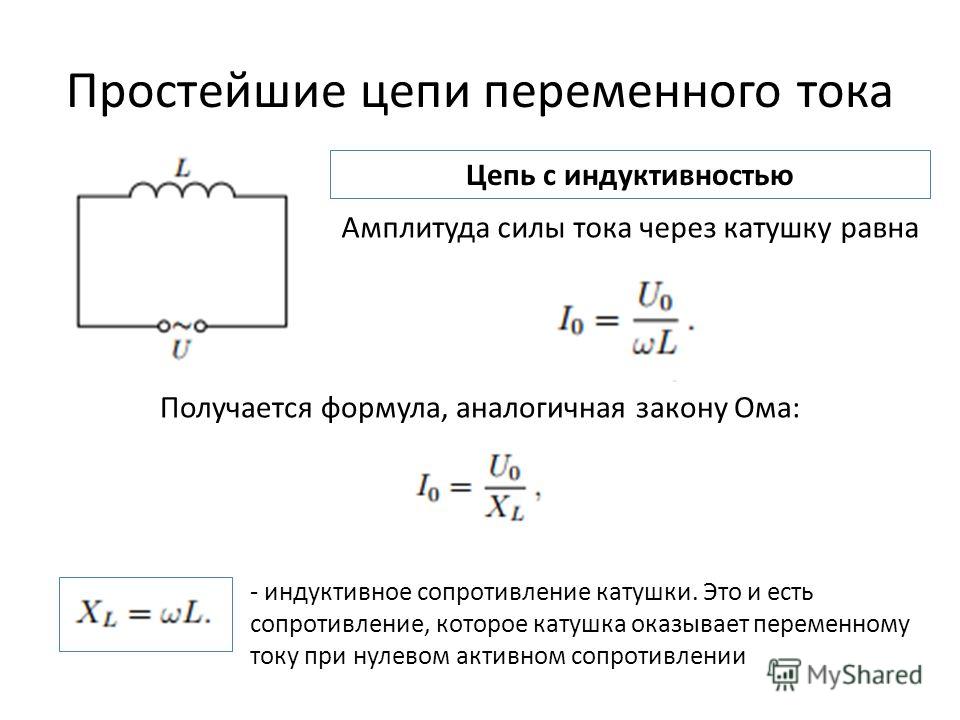 В результате ток отстает от напряжения по фазе на угол 90 О.

Сопротивление катушки или проводника переменному току, вызванное действием э.д.с. самоиндукции, называется индуктивным сопротивлением
Х L
[Ом]. Индуктивное сопротивление не зависит от материала катушки и от площади поперечного сечения проводника.

В цепях переменного тока катушки индуктивности соединяют последовательно и параллельно.

При последовательном соединении катушек эквивалентная индуктивностьLэ
и эквивалентное индуктивное сопротивление X L э
будут равны:

Lэ=L 1 +L 2 +… X L э=X L 1 +X L 2 +…

При параллельном соединении катушек:

1/Lэ=1/L 1 +1/L 2 +… 1/X L э=1/X L 1 +1/X L 2 +…

Контрольные вопросы

1. Какие виды сопротивления в цепях переменного тока Вы знаете?

2. Что значит активное сопротивление?

3. Что такое реактивное сопротивление?

4. Какие элементы цепи создают реактивное сопротивление?

5. Что такое активная мощность?

1. Дайте определение индуктивности.

2. Что происходит в первую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

3. Что происходит во вторую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

4. Дайте определение индуктивного сопротивления.

3.3. Конденсаторы. Ёмкость в цепи переменного тока

Конденсатор –
устройство, способное накапливать электрические заряды.

Простейший конденсатор представляет собой две металлические пластины (электроды), разделенные диэлектриком.

Каждый конденсатор характеризуется номинальной емкостью и допустимым напряжением. Напряжение конденсатора указывают на корпусе, и превышать его нельзя. Конденсаторы различаются формой электродов (плоский), типом диэлектрика и ёмкостью (постоянной и переменной).

Cтраница 2

Действующим значением силы тока I называется сила постоянного тока, выделяющего в проводнике за то же время такое же количество теплоты, что и переменный ток.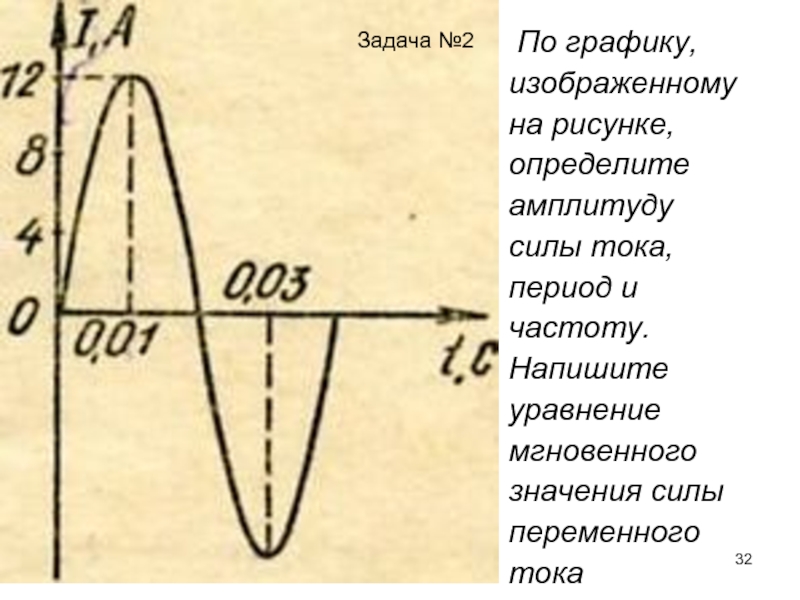

Как видно из рисунка, в каждый момент времени величины напряжения и силы тока принимают различные значения. Поэтому, чтобы судить о величине силы тока и напряжения переменного тока, пользуются действующим значением силы тока и напряжения. Чтобы определить действующее значение силы переменного тока, его приравнивают к силе постоянного тока, которое выделило бы в проводнике такое же количество тепла, как и переменный ток.

Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть переменного тока с действующим напряжением 220 В. Вторичная цепь трансформатора питает нагрузку с активным сопротивлением 50 Ом. Найти действующее значение силы тока во вторичной цепи, если падение напряжения во вторичной обмотке трансформатора, содержащей 165 витков, равно 50 В.

Таким образом, при замене операции извлечения корня сравнением время, за которое интегрируемый сигнал с ГЛИН станет равен интегралу от квадрата измеренной силы тока, пропорционально действующему значению силы тока. До этого К2 был открыт в течение времени т и пропускал на счетчик СИ импульсы с генератора тактовых импульсов ГТИ. Число импульсов TV / гтит записанное в СЧ, пропорционально действующему значению силы тока. Это число хранится в / 77, а по окончании цикла измерения отображается на ЦИ.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Рх o jjFr В слУчае т — н — СУХОЙ лампы применяют способ термометра, подвешиваемого вблизи генераторной лампы, и отмечают его показание. Затем, разрывая цепь колебательного контура генератора, дают на сетку генераторной лампы положительный потенциал до тех пор, пока термометр не по.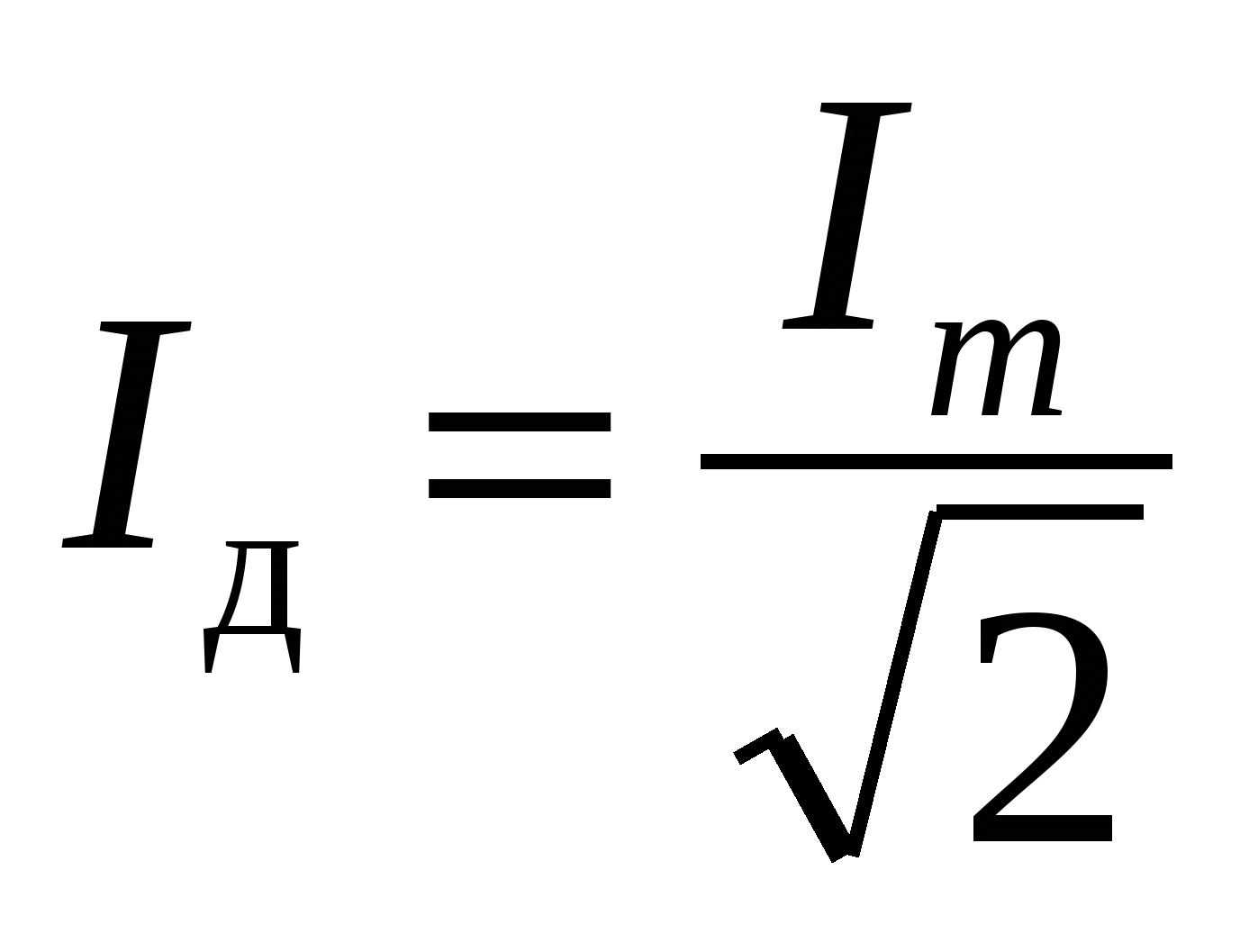 Беря в последнем случае величины 1а и Еа как исходные, определяем Рх из соотношения Рх1а Еа. Мощность в антенне определяется по ф-ле Рх — / /, где РЯ — мощность eW, ra — активное сопротивление антенны в Q и 1а — действующее значение силы тока в антенне в А. По скольку по современным международным нормам под мощностью передатчика принято понимать мощность в антенне, то упомянутая выше ф-ла определяет одновременно и мощность передатчика.

Тепловые измерители имеют наиболее широкое практич. Действие тепловых измерителей состоит в удлинении тонкой проволоки при нагревании ее проходящим по ней переменным током высокой частоты. Сам по себе эффект ограничивает пределы применимости таких измерителей токами от нескольких тА до 1 — 3 А в зависимости от материала тонкой проволоки, примененной в измерителе. Применяются сплавы серебра с платиной, платины с иридием и др. Если сплав применяется в виде проволоки, то она имеет диаметр сотых долей мм. При ленте толщина составляет 0 01 мм, ширина 3 мм и длина 25 — 30 мм. Удлинение нити нагреваемым током пропорционально квадрату действующего значения силы тока. Перемещение по шкале измерителя стрелки, связанной с той же проволокой с помощью особой подвижной системы, обычно пропорционально квадратному корню из действующей силы тока. Из-за этого шкалы тепловых измерителей имеют неравномерные интервалы между делениями.

В данном случае колебания тока являются гармоническими (график колебаний — синусоида) и вынужденными, поскольку параметры колебаний (частота, амплитуда) определяются внешним источником — генератором. Некоторые электротехнические устройства (например, колебательный контур) способны генерировать свободные гармонические колебания электрического тока. По левой ветви рамки — от нас и, поскольку в этом случае через клемму а течет ток в направлении, обратном показанному на рис. 12.1, ее полярность — минус. Поскольку при данном положении рамки сила тока имеет наибольшее значение, фаза колебаний может быть г / 2 или 3 / 2ir, в зависимости от того, какое направление тока в рамке мы принимаем за положительное. Сравнивая формулу (12.1) и заданную зависимость, нетрудно заметить, что 1т 10 А и ш 4тград / с. Далее, используя формулу (12.2), определяем частоту колебаний (отв. Используя закон Джоуля — Ленца (Q I2Rt), определяем действующее значение силы тока (отв.

Эффективные значения силы тока и напряжения

Работа с переменным током, в случае вынужденных колебаний, достаточно сложна. Но есть возможность привести сложное электромагнитное колебание к виду достаточно простого постоянного тока.

Основная идея: представим переменный ток в виде постоянного при условии равенства мощности постоянного тока и мощности переменного тока за один период колебания.

Итак:

для постоянного тока:

(1)

где
- — мощность постоянного тока,
- — сила постоянного тока,
- — напряжение в цепи постоянного тока.
для переменного тока

(2)

где
- — мощность переменного тока в момент времени ,
- — амплитудное (максимальное) значение силы тока,
- — амплитудное (максимальное) значение напряжение,
- — циклическая частота колебания,
- — начальная фаза колебания,
- — момент времени.

Проанализируем фразу «средняя мощность за период». Усреднение (2) приводит к вопросу об усреднении синуса, из математики:

, тогда средняя мощность переменного тока за период можно записать как:

(3)

Воспользуемся необходимым условием равенства мощностей (1) и (3):

(4)

где
- — эффективное значение силы тока,
- — эффективное значение напряжения.

Дальнейшая логика достаточно проста: т.к. сила тока и напряжение равнозначны, то запишем (4) в виде:

(5)

Таким образом:

(6)

Вывод: для расчёта параметров цепей переменного тока достаточно заменить её цепью постоянного тока при условии равенства мощностей за период. Выполнение данного условия приводит к использованию в цепи постоянного тока эффективных значений тока и напряжения (6). Т.е. все закономерности, характеризующие постоянный ток, будут справедливы и для переменного только при использовании эффективных значений.

Словесные обозначения:

- амплитудное, максимальное — , ,
- эффективное, действующее — , .

Поделиться ссылкой:

Twitter
Facebook
Telegram
WhatsApp

1. Мгновенное значение силы тока для фазы

Вариант
1

1. Мгновенное
значение силы тока для фазы П/6
равно 6А. Определите
амплитудное и действующее значения
силы тока.

2. Найдите
частоту вращения прямоугольной рамки
с числом витков
N
=
20 в магнитном поле с индукцией 0,5 Тл,
если амплитуда
индуцируемой ЭДС 10 В, а площадь рамки
равна 200 см².

3. К
источнику тока параллельно подключены
конденсатор емкостью
20 мкФ и катушка индуктивностью 0,02 Гн.
Напряжение на
конденсаторе 100 В, ток в катушке 2 А.
Затем источник отключают. Какой заряд
будет на конденсаторе, когда ток в
катушке равен
1А? (Потерями энергии на нагревание
проводов пренебречь.)

4. В
каких пределах должна изменяться
индуктивность катушки
колебательного контура, чтобы в контуре
происходили колебания
с частотой от 400 до 500 Гц? Емкость
конденсатора 10
мкФ.

5. Трансформатор
включен в сеть с переменным напряжением
U₁
= 220 В. Напряжение на зажимах вторичной
обмотки U₂=
20 В, ее
сопротивление г₂
= .1 (Ом), сила тока во вторичной обмотке
I₂=
2 А. Найдите коэффициент трансформации
и КПД трансформатора, пренебрегая
потерями в первичной обмотке и
сердечнике;

Вариант
2

1.
Амплитудное значение синусоидальной
ЭДС с частотой 50
Гц равно 10 В. Начальная фаза равна
нулю. Найдите величину ЭДС в момент
времени t.
=
1/300 с

2.
Прямоугольная рамка площадью 100 см²
вращается в горизонтальном
однородном магнитном поле с частотой
50 об/с. Магнитная
индукция поля 0,2 Тл. Найдите амплитуду
ЭДС, индуцируемую в рамке. Как изменится
эта амплитуда, если частоту вращения
рамки увеличить в 2 раза? Какая еще
величина изменится?

Действующее
значение напряжения на конденсаторе
в контуре
равно 100 В. Определите максимальное
значение энергии конденсатора
(электрическое поле) и катушки
(магнитное поле), если
электроемкость конденсатора равна
10 пФ.
Частота
колебаний электромагнитного
контура равна 30
кГц. Какой будет его частота, если
расстояние между пластинами
плоского конденсатора увеличить в
1,44 раза?

5. Первичная
обмотка трансформатора имеет 12000
витков и включена
в сеть переменного тока с напряжением
120 В. Какое число витков
должна иметь вторичная обмотка, если
ее сопротивление 0,5
(Ом)? Напряжение на вторичной обмотке
3,5 В при токе 1 А.

Амплитудное значение силы тока и напряжения. Действующее значение переменного тока и напряжения

После подстановки значения тока i
и последующих преобразований получим, что действующее значение переменного тока равно:

Аналогичные соотношения могут быть получены также для напряжения и ЭДС:

Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.

Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U
Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.

Действующее значение переменного тока

Теория
/
ТОЭ
/ Лекция N 3.
Представление синусоидальных величин с помощью векторов и комплексных чисел.

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими,
а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т.
Для периодического тока имеем

Диапазон частот, применяемых в технике: от сверхнизких частот (0. 01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота
f
= 50Гц
.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i
— мгновенное значение тока ;

u
– мгновенное значение напряжения ;

е
— мгновенное значение ЭДС ;

р
— мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m
).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением
периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е
1
и е
2
соответствуют уравнения:

Значения аргументов синусоидальных функций и называются фазами
синусоид, а значение фазы в начальный момент времени (t
=0):

и
— начальной фазой
(
).

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой.
Так как фазовый угол синусоиды за время одного периода Т
изменяется на рад., то угловая частота есть , где f–
частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз
.

Для синусоидальных ЭДС е
1
и е
2
угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное
) с угловой частотой, равной w
. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е
1
и е
2
(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами.
При построении векторных диаграмм векторы удобно располагать для начального момента времени (t
=0),
что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w
. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt
=0.
При вращении этих векторов с одинаковой угловой скоростью w
их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Действующее и среднее значения переменного тока и напряжения.

Среднее или среднеарифметическое значение Fcp
произвольной функции времени f
(t
)за интервал времени Т
определяется по формуле:

Численно среднее значение Fср
равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f
(t
), осью t
и пределами интегрирования 0 – Т
(рис. 35).

Для синусоидальной функции среднее значение за полный период Т
(или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т
или среднее значение за половину периода (Т
/2) между двумя нулевыми значениями (рис. 36) :

Ucp = Um∙
sinwt dt = 2R
. Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U
и тока I
. По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.

Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.

Что берется за действующее значение силы переменного тока и переменного напряжения

что берется за действующее значение силы переменного тока и переменного напряжения?

Боевое яйцо

Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.

Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.

Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.

Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.

Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.

Вопрос: напряжение в электросети 220 В, что это значит?

Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.

Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.

Пример: Определить амплитуду напряжения электросети с напряжением 220 В.

Амплитуда равна 220 * 1,41=310,2 В.

При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.

Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .

На шкалах измерительных приборов и технической документации также указываются действующие значения величин.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени

а за период переменного тока Т

Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:

Сократив общий множитель , получим действующее значение тока

Рис. 5-8. График переменного тока и квадрата тока.

На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока

Если ток изменяется по закону синуса, т. е.

Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:

Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.

Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.

Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.

Мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока
. Сегодня про него и поговорим!

Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.

Итак, действующее (или среднеквадратичное) значение переменного тока — это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток.
Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.

Итак, у нас есть переменный ток. Допустим, синусоидальный.
У него своя амплитуда А m
и период T период
(ну или частота f
). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R
и на этом резисторе выделяется энергия. За один период T период
нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз
. Допустим, мы насчитали, что за один период T
период синусоидального тока выделится Q
джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе
R за то же самое время
T период выделилось ровно такое же количество джоулей
Q.
Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока
. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?

Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье
, закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время T период
— соответственно, равно интегралу за время периода T период
:

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .

Итак, как его нам брать? Ну, величины I m 2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени
из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:

Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл — это площадь.

Итак, имеем

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.

Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе
R

при протекании через него синусоидального тока амплитудой
I m

в течении периода
T период
. Теперь, чтобы найти чему в данном случае равен действующий ток
нам надо исходить из того, что на том же самом резисторе
R за то же самое время
T период выделится то же самое количество энергии
Q.
Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца
. А мы тем временем выразим действующее значение тока
I

действ
.
из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения.
Хорошо запомните этот результат, это важный вывод.

Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения
. При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.

Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.

Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина — амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках — это действующее значение!
Вольтметры
и амперметры
, включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать

Отсюда получаем

Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 — Закон изменения напряжения в розетках

И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа.
Смотрел я его через делитель напряжения
1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.

ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно!
Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением
есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления
, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 — Осциллограмма напряжения в розетке (делитель 1:5)

На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота — ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.

На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!

Вступайте в нашу

Свяжем
эффективное значение тока с его
амплитудным значением. Для этого
рассчитаем количество теплоты, выделяемое
на активном сопротивлении переменным
током за время, равное периоду колебаний.
Напомним, что по закону Джоуля-Ленца
количество теплоты, выделяющееся на
участке цепи cсопротивлениемприпостоянном
токеза время,
определяется по формуле
.
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени
.
Поделим период колебанийна очень большое число малых промежутков
времени
.
Количество теплоты
,
выделяемое на сопротивленииза время
:
.
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:

Сила тока в
цепи изменяется по синусоидальному
закону

Опуская
вычисления, связанные с интегрированием,
запишем окончательный результат

Если бы по
цепи шёл некоторый постоянный ток
,
то за время, равное,
выделилось бы тепло
.
По определению постоянный ток,
оказывающий такое же тепловое действие,
что и переменный, будет равен эффективному
значению переменного тока
.
Находим эффективное значение силы
тока, приравнивая теплоты, выделяемые
за период, в случаях постоянного и
переменного токов

(4.28)

(4.29)

4.4.5. Мощность в цепи переменного тока

,
.

Тогда мгновенное
значение мощности, выделяемой на участке
цепи,

С использованием
известной тригонометрической формулы

Величину

усреднять не нужно, так как она не зависит
от времени, следовательно:

,
поэтому
(4. 30)

Выражая
амплитуды тока и напряжения через их
эффективные значения по формулам (4.28)
и (4.29), получим

. (4.31)

Решение.
Когда к генератору подключено
одно только активное сопротивление,
расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере
4.6 было определено амплитудное значение
силы тока генератора:

.
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора

В результате средняя расходуемая
генератором мощность

Рассмотрим цепь на рис. 4.10,б. В примере
4.6 было определено амплитудное значение
силы тока генератора

.
Из векторной диаграммы на рис. 4.11,б
определяем сдвиг фаз между током и
напряжением генератора

Тогда средняя
мощность, расходуемая генератором

Ответ: при
параллельном включении индуктивности
средняя мощность, расходуемая генератором,
не изменяется.

Переменный синусоидальный ток в течение периода имеет разные секундные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, также при электронных измерениях неловко воспользоваться моментальными либо амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Не считая того, об электронном эффекте временами изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Более комфортным оказалось введение понятий так именуемых действующих значений тока и напряжения
. В базу этих понятий положено термическое (либо механическое) действие тока, не зависящее от его направления.

— это значение неизменного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки деяния, производимого переменным током, мы сравним его деяния с термическим эффектом неизменного тока.

Мощность Р неизменного тока I
, проходящего через сопротивление r
, будет Р = Р 2
r
.

Мощность переменного тока выразится как средний эффект моментальной мощности I
2 r за целый период либо среднее значение от (Im
х sinωt

) 2 х r
за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность неизменного тока и мощность при переменном токе, имеем: I
2 r =
Mr, откуда I
= √
M
,

Величина I
именуется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим последующим образом.

Построим синусоидальную кривую конфигурации тока. Возведя в квадрат каждое секундное значение тока, получим кривую зависимости Р от времени.

Обе половины этой кривой лежат выше горизонтальной оси, потому что отрицательные значения тока (-i
) во 2-ой половине периода, будучи построены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное с помощью высшей арифметики, будет равно 1/2I 2 m
. Как следует, М =
1/2I 2 m

Потому что действующее значение I
переменного тока равно I
= √
M
, то совсем I = Im / √

Аналогично зависимость меж действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √

2
,
E= Em / √

Действующие значения переменных величин обозначаются строчными знаками без индексов (I
, U, Е).

На основании произнесенного выше можно сказать, что действующее значение переменного тока равно такому неизменному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, демонстрируют действующие значения тока либо напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √
2
раз. От этого размещение векторов на диаграмме не меняется.

Школа для электрика

действующие значения силы тока и напряжения

Рассмотрим следующую цепь. 2)*R = U*I.

Нужна помощь в учебе?

Предыдущая тема: Переменный электрический ток: формулы и примеры
Следующая тема:&nbsp&nbsp&nbspКонденсатор в цепи переменного тока: изменение силы тока в цепи

Что такое пиковый ток? — Sunpower UK

Sunpower Electronics имеет более чем 25-летний опыт торговли источниками питания, разрабатывая продукты для производства, чтобы предоставить нашим клиентам эффективные, мощные и долговечные решения. Если вы не уверены и нуждаетесь в поддержке по выбору правильного источника питания для вашего проекта, свяжитесь с нами сегодня. Мы предлагаем множество услуг, включая индивидуальные блоки питания, разработанные специально для ваших производственных проектов.

Что такое пиковый ток?

Пиковый ток — это максимальная величина тока, который выход может выдавать в течение коротких периодов времени.

При первом включении источника питания или электрического устройства в нагрузку протекает высокий начальный ток, начиная с нуля и возрастая до достижения пикового значения, известного как пиковый ток. Обычно он намного выше по сравнению с установившимся током. Затем ток будет постепенно уменьшаться от пикового значения тока до установившегося состояния, в котором он стабилизируется. (Для наших продуктов это количество будет указано в технических данных, которые вы сможете загрузить на страницах наших продуктов или по запросу.)

Разница между установившимся значением и пиковым током называется пусковым током. Это свойство, на которое дизайнеры должны обращать внимание при выборе компонентов. Пиковый ток должен быть в безопасных пределах и длиться непродолжительное время, чтобы избежать перегрузки компонентов, чрезмерного нагрева или повреждения.

Почему протекает пусковой ток?

Основной причиной пускового тока является зарядка больших развязывающих или сглаживающих конденсаторов в источниках питания.Другие причины включают ток, который питает индукторы или может быть в жестком диске и вентиляторах, а также низкое сопротивление компонентов, таких как нити лампы и другие, в холодном состоянии.

В это время, когда конденсаторы заряжаются или устройства выходят из холодного состояния, ток очень быстро увеличивается от нуля, повышаясь до пикового значения, а затем начинает постепенно уменьшаться до установившегося тока.

Пусковой ток на входе источника питания и относится к начальному значительному току, потребляемому из сети.Однако это также относится к величине тока, которую некоторые нагрузки, такие как жесткие диски, вентиляторы и другие устройства, потребляют от источника питания. В любом случае источник питания должен поддерживать пиковые токи как на входе, так и на выходе.

На выходе блок питания должен обеспечивать пиковый ток без отключения выходной цепи максимальной токовой защиты. Кроме того, схема источника питания должна иметь возможность различать пиковый ток и условия короткого замыкания или перегрузки по току.

Устойчивый, пусковой и пиковый ток при включении устройства — Кредит изображения

Источники питания пикового тока

Существуют блоки питания, специально разработанные для обеспечения высоких пиковых токов. Они обеспечивают токи от 200 до 300 процентов от максимального тока источника питания без необходимости перехода в состояние ограничения тока. Источники питания, которые обеспечивают высокий ток в течение короткого периода времени, обычно используются для таких нагрузок, как жесткие диски компьютеров, электродвигатели, насосы, приводы, вентиляторы и т. Д.

При разработке источника питания здесь, в Sunpower, мы понимаем и принимаем во внимание предполагаемые требования к нагрузке. Некоторые устройства, такие как дисководы, насосы, двигатели, головки принтера и другие, при первом включении всегда потребляют высокие пиковые токи. Если вам нужна поддержка в отношении источника питания для вашего проекта, свяжитесь с одним из наших специалистов сегодня и ознакомьтесь с нашим ассортиментом продукции.

В чем разница между пусковым током и пиковым током?

В чем разница между пусковым током и пиковым током?

Хотя пусковой ток имеет пиковое значение тока, термин «пусковой ток» обычно используется для описания тока, который требуется для подачи питания на устройство или изделие с питанием от переменного тока при первой подаче на него напряжения и питания.Это особенно верно для индуктивных нагрузок, таких как трансформаторы, индукторы и электродвигатели. Это также относится к источникам питания переменного / постоянного тока, в которых используется простой входной каскад выпрямителя / конденсатора. Эти начальные токи могут резко увеличиваться и быть немного выше нормального рабочего тока или так называемого «установившегося» тока. Пример пускового тока электродвигателя показан на рисунке 1. Он показывает, что пиковый ток для первого полупериода близок к 30 ампер, а затем уменьшается в течение последующих полупериодов по мере того, как двигатель раскручивается.

Другой пример пускового тока — это входной каскад переменного / постоянного тока, в котором используется выпрямитель, конденсаторная цепь, в которой конденсатор необходимо зарядить до его номинального напряжения, как показано на рисунке 2. В обоих случаях очевидно, что пусковой ток значительно больше, чем ток в установившемся режиме.

Пиковый ток с другой стороны применяется ко всем переменным токам, будь то пусковой или установившийся ток. Форма волны переменного тока имеет среднеквадратичное значение, представляющее эффективный или эквивалентный постоянный ток, но также имеет пиковое значение, как положительные, так и отрицательные пики, когда ток достигает максимального и минимального значения в течение каждого цикла.Абсолютное соотношение между среднеквадратичным значением и пиковым значением называется пик-фактором (CF). Для синусоидального тока, встречающегося при резистивной нагрузке, пик-фактор будет квадратным корнем из 2 или ~ 1,4142 к 1. Этот пик-фактор или отношение показано на рисунке 3.

Другие формы волн имеют разные пик-факторы, как показано в Таблице 1 ниже для некоторых других типичных форм волн переменного тока.

Почему это важно?

При использовании источника питания переменного тока для определения требуемого пускового тока для тестируемого устройства важно отметить, что источник переменного тока должен обеспечивать значительно больший ток в течение короткого периода времени, чем требуется для работы устройства в условиях испытание в устойчивом состоянии.В случае двигателей и индукторов пусковой ток может в 10–30 раз превышать номинальный ток. Для тороидальных индукторов это значение может быть до 50 раз больше номинального.

Ограничение тока источника может быть выражено как в отношении номинального тока RMS, так и номинального максимального тока. Для двигателей и индуктивных нагрузок пик-фактор пускового тока составляет всего 1,414, поэтому, если источник может поддерживать среднеквадратичный ток, будет поддерживаться и пиковое значение. Для входного оборудования с выпрямленным переменным током пик-фактор тока обычно намного выше 1.414, до 2 или 3 к 1, поэтому следует учитывать не только номинальное значение RMS, но и номинальный пиковый ток. Большинство доступных источников питания переменного тока будут поддерживать пик-факторы тока от 2,5 до 4 при максимальном среднеквадратичном выходном токе.

Эффекты ограничения тока

Если источник не может обеспечить требуемый пусковой ток, его все равно можно использовать для проверки нормальной работы, но требуемый пусковой ток не может быть определен, так как источник питания перейдет к пределу тока — либо среднеквадратичному значению, либо пику, либо обоим — и ограничит напряжение при этом.Это означает, что тестируемое устройство обычно по-прежнему запускается или включается, но не так быстро, как при работе от сети.

Искажение напряжения источника переменного тока

Высокие пиковые токи и искаженные формы волны тока также влияют на искажения источника питания переменного тока, поскольку они работают против выходного сопротивления источника питания. Чем ниже выходное сопротивление источника питания, тем меньше будет этот эффект. На рисунке 4 показано влияние сильно искаженного тока на искажение выходного напряжения.Когда ток достигает своего пика в верхней части формы волны напряжения, напряжение понижается, что приводит к появлению некоторого плоского максимума.

Чтобы смягчить этот эффект, на некоторых моделях источников переменного тока может быть предложена функция программируемого выходного импеданса, которая позволяет уменьшить выходное сопротивление. См. Сообщение в нашем блоге экспертов под названием «Что такое Prog Z для источника питания переменного тока и почему это важно» по адресу https://pacificpower.com/2017/03/programmable-z-ac-source-work-matter/

Что такое пиковое значение, среднее значение и среднеквадратичное значение? — определение и объяснение

Пиковое значение

Определение: Максимальное значение, достигаемое переменным количеством в течение одного цикла, называется его значением P eak .Он также известен как максимальное значение, амплитуда или пик. Синусоидальная переменная величина достигает своего пикового значения при 90 градусах, как показано на рисунке ниже.

Пиковые значения переменного напряжения и тока представлены E _m и I _m соответственно.

Среднее значение

Определение: Среднее значение всех мгновенных значений переменного напряжения и токов за один полный цикл называется средним значением .

Если мы рассмотрим симметричные волны, такие как синусоидальный ток или форма волны напряжения, положительный полупериод будет точно равен отрицательному полупериоду. Следовательно, среднее значение за полный цикл будет ноль .

Работа выполняется как по положительному, так и по отрицательному циклу, поэтому среднее значение определяется без учета знаков.

Итак, единственным положительным полупериодом считается определение среднего значения переменных величин синусоидальных волн.Давайте рассмотрим пример, чтобы понять это.

Разделите положительный полупериод на ( n ) количество равных частей, как показано на рисунке выше

Пусть i ₁, i ₂, i ₃ …… .. i _n — средние ординаты

Среднее значение тока I _ср = среднее значение средних ординат

R.M.S значение

Определение: Тот установившийся ток, который при прохождении через резистор с известным сопротивлением в течение заданного периода времени, в результате такое же количество тепла выделяется переменным током, когда он протекает через тот же резистор в течение того же периода времени. время называется р.M.S или действующее значение переменного тока.

Другими словами, значение R.M.S определяется как квадратный корень из средних квадратов мгновенных значений.

Пусть I будет переменным током, протекающим через резистор R в течение времени t секунд, который производит такое же количество тепла, как и постоянный ток (I _eff). База одного изменения делится на n равных частей, так что каждый интервал составляет t / n секунд, как показано на рисунке ниже.

Пусть i ₁, i ₂, i ₃, ………..in быть средними ординатами

Тогда тепло произведено в

Так как Ieff считается эффективным значением этого тока, то общее количество тепла, произведенного этим током, будет

Теперь, приравняв уравнение (1) и (2), получим

I _eff = квадратный корень из среднего квадратов мгновенных значений = среднеквадратичное значение

Среднеквадратичное значение — это фактическое значение переменной величины, которая говорит нам о способности источника переменного тока передавать энергию.

Амперметр регистрирует среднеквадратичное значение переменного тока, а вольтметр записывает среднеквадратичное значение переменного напряжения. Электропитание однофазного переменного тока в домашних условиях составляет 230 В, 50 Гц, где 230 В — это среднеквадратичное значение переменного напряжения.

Значения напряжения и тока в системе постоянного тока постоянны, поэтому нет проблем с оценкой их величин, но в системе переменного тока переменное напряжение и ток изменяются время от времени, и, следовательно, необходимо оценивать их величины.

Следующие три способа (пиковое значение, среднее значение и среднеквадратичное значение), приведенные выше, используются для выражения величины напряжения и тока.

AMCI: Advanced Micro Controls Inc :: Драйверы шагового двигателя: среднеквадратичное значение или пиковый ток?

Драйверы шагового двигателя

определяют величину тока, который они выводят на шаговый двигатель, в виде RMS или пикового тока. Насколько они разные?

В этом руководстве вы познакомитесь с разницей между двумя типами тока, используемыми при указании шаговых приводов и двигателей.Вы узнаете о взаимосвязи между среднеквадратичным значением и пиковым током и о том, почему это соединение важно при настройке систем шагового управления.

Изучив технические достоинства среднеквадратичного значения по сравнению с пиковым током, вы поймете, почему производители шаговых двигателей указывают кривые крутящего момента и максимальные значения только в среднеквадратичном токе, а не пиковом токе, при этом также используя драйвер шагового двигателя, указанный в среднеквадратичном токе. Какая для вас польза? Это упрощает согласование шагового двигателя с драйвером шагового двигателя в любом приложении.Следующие несколько абзацев проливают свет на это утверждение.

RMS, что означает среднеквадратическое значение, является основным измерением величины сигнала переменного тока (AC). Среднеквадратичное значение равно количеству постоянного тока (DC), необходимого для выработки эквивалентного количества тепла при нагрузке того же размера. Форма волны переменного тока переменного тока не важна. Значения RMS упрощают расчет средней мощности и энергии. Однако пиковые значения, которые дают только максимальное значение сигнала переменного тока, требуют дополнительной информации и могут сравниваться со среднеквадратичными значениями, только если форма сигнала известна.

Например, когда форма волны переменного тока является идеальной синусоидой, соотношение между среднеквадратичным значением и пиковым током будет следующим:

RMS-ток = Пиковый ток x 0,707 или Пиковый ток = RMS-ток x 1,414.

Соотношение между среднеквадратичным значением и пиковым током шагового двигателя зависит от конфигурации драйвера. Три общих режима работы драйверов шаговых двигателей включают в себя полный шаг, полушаговый режим и микрошаговый режим. Если вы посмотрите на осциллограф формы сигналов тока этих трех режимов, все они будут выглядеть по-разному, представляя соотношение между среднеквадратичным значением и пиковым током:

Идеальная форма волны полного шага (Рисунок A.)
Идеальный полушаговый форма волны (Рисунок B.)
Идеальный микрошаговый форма волны (Рисунок C.)

Все шаговые двигатели рассчитаны на среднеквадратичный ток, и при полном шаге, 200 шагов / оборот, нет никакой разницы в драйверах шаговых двигателей, которые выводят среднеквадратичный ток, и те, которые выводят пиковый ток. Драйвер шагового двигателя просто выводит значение тока, которое требуется двигателю. В следующем примере предположим, что 1.0 ампер RMS:

Рисунок A.

Однако при половинном шаге, 400 шагов / оборот, среднеквадратичный ток и пиковый ток не равны, как показано на рисунке B. Если пиковый драйвер не увеличит свой выходной ток на 15% (как показано на рисунке B.) двигатель будет не получает свой номинальный среднеквадратичный ток 1,0 А и, следовательно, не генерирует весь крутящий момент, который он способен обеспечить.

Рисунок B.

Микрошаговый сигнал показывает еще большую разницу между среднеквадратичным значением и пиковым током.В этом случае значение пикового тока должно быть увеличено примерно на 41% (как показано на рисунке С.), чтобы оно равнялось требуемому среднеквадратичному току двигателя 1,0 А.

Рисунок C.

RMS Приводы с управлением по току будут отправлять на двигатель выбранное среднеквадратичное значение тока независимо от формы сигнала тока. Это может быть не так с приводами, управляемыми пиковым током, которые выдают разные среднеквадратичные токи в зависимости от формы сигнала.

В заключение, поскольку шаговые двигатели определяют только кривые крутящего момента и максимальные номинальные значения в среднеквадратичном токе, использование шагового драйвера, который также указан в среднеквадратичном токе, вместо того, который указан в пиковом токе, упрощает согласование шагового двигателя с шаговым драйвером в любое приложение.

Для удобства AMCI указывает все свои шаговые приводы и двигатели как с номинальными значениями среднеквадратического, так и пикового тока (если применимо). Чистый результат = Гарантированная совместимость, производительность и надежность.

Пиковый ток драйверов изолированного затвора

Введение

Один общий вопрос, который задают при рассмотрении того, какой драйвер затвора использовать для приложения: какой пиковый ток может обеспечить драйвер? Пиковый ток — один из наиболее важных параметров в технических данных драйвера затвора.Эта метрика обычно используется в качестве основного показателя мощности драйвера затвора. Время для включения и выключения MOSFET / IGBT зависит от тока, который может подавать драйвер затвора, но не раскрывает всей картины. Термин «пиковый ток» настолько широко распространен в промышленности, что включен в заголовки многих технических паспортов драйверов затвора. Несмотря на это, его определение варьируется от части к части. В этой статье обсуждаются проблемы с использованием пикового тока в качестве решающего фактора при выборе драйвера затвора для конкретного приложения и сравниваются некоторые из наиболее распространенных представлений пикового тока в таблицах данных.Исследуется сравнение между драйверами затвора с аналогичными номерами пикового тока в их названиях и обсуждается сила возбуждения затвора.

Пример приложения

Изолированные драйверы затвора обеспечивают смещение уровня, изоляцию и мощность затвора для работы силовых устройств. Изолированная природа этих драйверов затвора позволяет управлять устройством с высокой и низкой стороны, а также обеспечивать барьер безопасности, если используется подходящее устройство. Пример приложения показан на рисунке 1.V _DD1 и V _DD2 имеют отдельные опорные точки заземления, и напряжения на каждом из них могут быть разными. Выводы 1–3 будут называться первичной стороной, а выводы 4–6 будут называться вторичной стороной в этой статье. Изоляция, обеспечиваемая драйверами затвора, может легко достигать сотен вольт, что позволяет использовать более высокие напряжения системной шины.

Подходящий изолированный драйвер затвора должен иметь возможность воспроизводить синхронизацию, представленную на первичной стороне, и управлять затвором силового устройства достаточно быстро, чтобы переходы переключения были приемлемыми.Более быстрое переключение может привести к меньшим потерям переключения, поэтому возможность быстрого переключения часто является востребованной чертой. Как правило, в рамках одного типа коммутационной технологии, чем большую мощность может выдержать силовое устройство, тем большую нагрузку оно представляет для драйвера затвора.

Рисунок 1. Типичное применение ADuM4120. Изолированные драйверы затвора

часто находят применение в полумостовых конфигурациях, таких как показано на рисунке 2. Драйвер верхнего плеча должен иметь возможность переключаться между заземлением системы и напряжением V _BUS, обеспечивая при этом необходимую мощность привода для силовое устройство, которым он управляет.

Рисунок 2. Типичное применение полумоста.

Расчет нагрузки

Время, необходимое для зарядки или разрядки затвора MOSFET / IGBT, определяет скорость переключения устройства. При фактическом использовании добавляется внешний последовательный резистор затвора для настройки времени нарастания / спада напряжения затвора и распределения рассеиваемой мощности с ИС драйвера затвора. Путем моделирования силового устройства в виде конденсатора и драйвера затвора с выходным каскадом MOSFET, проходящим через внешний последовательный резистор затвора, мы получаем RC-схему, как показано на рисунке 3.Уравнение пикового тока источника в этой упрощенной модели: I _{PK_SRC} = V _DD / (R _{DS (ON) _P} + R _EXT), а пиковый ток стока — I _{PK_SNK} = V _DD. / (R _{DS (ON) _N} + R _EXT). Для измерения пикового тока короткого замыкания R _EXT устанавливается на 0 Ом, но в приложении присутствует внешний последовательный резистор.

Рисунок 3. Упрощенная RC-модель зарядки и разрядки затвора.

Где:

R _{DS (ON) _N} — сопротивление включения драйвера затвора NMOS.

R _{DS (ON) _P} — сопротивление включения PMOS драйвера затвора.

R _EXT — это внешний последовательный резистор затвора.

C _{GATE_EQUIV} — эквивалентная емкость силового устройства.

Неоднозначность в заголовке таблицы данных

Пиковый ток предназначен для краткого сравнения силы возбуждения затвора, но представление значения варьируется от детали к детали и от производителя к производителю.На рис. 4 показаны кривые ВАХ, а также некоторые общие уровни, которые производители приводов затворов использовали для определения пикового значения тока. Уровни насыщения ВАХ конкретного МОП-транзистора широко варьируются в зависимости от процесса и температуры кремния, часто в ± 2 раза от типичного значения.

Во многих технических паспортах пиковый ток, указанный в технических характеристиках, является типичным током насыщения, который определяется путем замыкания выхода на относительно большую емкость или короткого замыкания драйвера на очень короткое время.Очень редко можно найти лист данных, который четко показывает минимальные и максимальные кривые ВАХ выходных драйверов в зависимости от температуры и изменений процесса, но если использовать типичное число насыщения в качестве значения пикового тока, будут части, которые не могут быть источником или потратить столько тока в реальном приложении. В некоторых таблицах данных указывается максимальное значение насыщенности, а в некоторых — минимальное значение насыщенности. Еще один метод описания доступного пикового тока в драйвере — это описание самого высокого тока, все еще находящегося в линейной области самой низкой кривой ВАХ или минимального линейного тока.Указав это число, пользователь может знать, что все части в приложении смогут получать или поглощать больше, чем это заданное значение. Это значение является консервативным, но пользователь может знать, что при правильном выборе размера внешнего последовательного резистора затвора выходные полевые транзисторы драйвера затвора не будут находиться в области насыщения при изменении температуры и технологического процесса.

Производственные испытания пикового тока часто очень трудны из-за ограничений по току на контакторах в тестовых средах. Нередко характеристики пикового тока в изолированных драйверах затвора гарантируются конструкцией и / или характеристиками.Различные производители могут указывать или не указывать минимальные или максимальные значения пикового тока. Таким образом, нет соглашения о том, какое выражение пикового тока использовать для сравнения между частями. Важно отметить, что пиковый ток не является постоянным или средним током. Если выход драйвера затвора работает правильно в линейной области выходных полевых транзисторов, пиковый ток существует только в самом начале переключения.

Рисунок 4. Пример ВАХ выходного драйвера на полевом транзисторе.

Хотя полные минимальные и максимальные кривые насыщения при изменении температуры и технологического процесса почти никогда не попадают в спецификации, некоторые производители изолированных драйверов затвора предоставляют типичную кривую I-V для выходного драйвера.Это может быть представлено в виде кривой I-V короткого замыкания или кривой с внешним последовательным сопротивлением затвора, чтобы более точно имитировать фактическое использование приложения. Если смотреть на ВАХ, которая включает внешнее последовательное сопротивление, ось напряжения обычно указывается в напряжении вторичной стороны, что означает, что график напряжения представляет собой напряжение V _DD2, распределяемое между внутренним R _{DS (ON)} и внешним. последовательный резистор затвора.

На рис. 5 показаны типичные ВАХ ADuM4121, указанные в листе технических данных.Следует отметить, что ADuM4121 упоминает мощность привода 2 А в заголовке таблицы данных, но типичные токи насыщения превышают 7 А. Это связано с тем, что в этом конкретном листе данных используется консервативное определение пикового тока в заголовке, сообщая пользователям, что Деталь определенно может подавать ток 2 А при любых изменениях температуры и процесса. Эта ВАХ также снята с внешним последовательным резистором затвора 2 Ом для имитации реальных характеристик приложения. Важно убедиться, что определение пикового тока, с которым пользователь сравнивает продукты, одинаково для разных частей, иначе при сравнении могут упустить ключевые факторы.

Рисунок 5. Таблица данных ADuM4121 I-V кривые.

Емкость по Миллеру

Хотя полевой МОП-транзистор или IGBT примерно представлены как емкостная нагрузка, существует нелинейность из-за динамической емкости затвор-сток, что приводит к области плато Миллера, где емкость изменяется во время включения (рисунок 6) и выключения. Зарядный ток для конденсатора затвора больше всего необходим в течение этого интервала плато Миллера. Пиковое значение тока не учитывает текущее значение в это время.Однако более высокий пиковый ток означает, что ток в области плато Миллера обычно будет больше.

Рисунок 6. Переход при включении IGBT, показывающий плато Миллера.

Рассеивание мощности: важное соображение

Чтобы зарядить и разрядить затвор силового устройства, необходимо затратить энергию. Если используется модель эквивалентной емкости и полная зарядка и разряд затвора происходит в каждом цикле переключения, мощность, рассеиваемая при переключении затвора, как для изолированных, так и для неизолированных драйверов затвора составляет:

Где:

P _DISS — мощность, рассеиваемая за один цикл переключения затвора.

C _EQ — эквивалентная емкость затвора.

В _DD2 — полный размах напряжения затвора силового устройства.

Q _{G_TOT} — общий заряд затвора силового устройства.

f _S — частота переключения системы.

Важно отметить, что эквивалентная емкость затвора C _EQ отличается от емкости C _ISS, указанной в технических паспортах силовых устройств. Это часто в 3-5 раз больше, чем C _ISS, и общий заряд затвора, Q _{G_TOT}, является более точным числом для использования.Следует также отметить, что последовательное сопротивление зарядки и разрядки не видно в этом уравнении, поскольку оно относится только к общей мощности, рассеиваемой при переключении, а не конкретно к мощности, рассеиваемой внутри IC драйвера затвора.

Из-за изолированного характера изолированных драйверов затвора стандарты требуют, чтобы различные области изоляции были разделены соответствующими расстояниями утечки и зазорами. Любые гальванические проводники на пути от первичной до вторичной области вычитаются из расстояний утечки и зазоров, и поэтому очень редко можно увидеть открытые контактные площадки или тепловые пробки для изолированных драйверов затвора.Это означает, что один из основных методов, помогающих снизить тепловое сопротивление интегральных схем, недоступен, что приводит к большей важности смещения рассеиваемой мощности за пределы изолированного блока драйвера затвора, чтобы обеспечить работу при более высоких температурах окружающей среды в данной рабочей точке.

Без возможности добавления теплового элемента к изолированным драйверам затвора тепловое сопротивление используемого корпуса примерно зависит от количества выводов, внутренней металлизации, соединений выводной рамки и размера корпуса.Для данного номера детали изолированного драйвера затвора при сравнении доступных деталей размер корпуса, количество выводов и часто распиновка будут одинаковыми, что приведет к примерно одинаковым числам тета-JA для конкурирующих деталей.

Рассеивание тепла внутри ИС драйвера затвора вызывает повышение температуры внутреннего перехода. Рассеиваемая мощность, вычисленная в уравнении 1, представляет собой общую рассеиваемую мощность при подъеме и опускании затвора силового устройства. Мощность, рассеиваемая в ИС драйвера затвора, распределяется между внутренними сопротивлениями полевых транзисторов выходного возбуждения, R _{DS (ON) _N} и R _{DS (ON) _P}, и внешним последовательным резистором затвора, R _EXT.Если драйвер затвора работает в основном в линейной области, коэффициент рассеяния мощности, который испытывает ИС драйвера затвора, составляет:

Если R _{DS (ON) _N} = R _{DS (ON) _P} = R _{DS (ON)}, уравнение 2 можно упростить до:

Общая мощность, которую ИС драйвера затвора получает от переключения силового устройства, затем становится уравнением 1, умноженным на уравнение 3:

Из уравнения 4 видно, что меньшее значение R _{DS (ON)} приводит к меньшей части рассеиваемой мощности, возникающей в изолированном драйвере затвора.Если желаемое время нарастания / спада должно быть соблюдено, постоянная RC для зарядки и разрядки затвора силового устройства должна быть сохранена. Сопротивление в константе RC представляет собой последовательную комбинацию внутреннего R _{DS (ON)} и внешнего последовательного резистора затвора. Другими словами, если два конкурирующих драйвера используются в приложении, чтобы иметь одинаковые скорости подъема и спада, драйвер с более низким R _{DS (ON)} позволяет использовать внешний последовательный резистор затвора большего размера, сохраняя при этом общее последовательное сопротивление одинаковым, Это означает меньшее рассеивание мощности внутри самой ИС драйвера затвора.

Сравнительный пример использования

Чтобы продемонстрировать, как определение пикового тока может варьироваться в зависимости от продукта, и чтобы показать преимущества более низкого R _{DS (ON)} в изолированном драйвере затвора, были выбраны три изолированных полумостовых драйвера с 4 А, упомянутыми в их названиях. Все три драйвера имели одинаковые схемы утечки, зазора, распиновки и заземления. Это позволило использовать общий макет для тестирования всех трех частей. Оценочная плата ADuM4221 использовалась в качестве тестовой платформы для сравнения ADuM4221 и двух частей, которые будут называться Competitor 1 и Competitor 2.Оценочная плата показана на рисунке 7.

Рисунок 7. Оценочная плата ADuM4221.

Требования к каждому из них приведены в таблице 1.

Таблица 1. Сравнение заявлений в технических паспортах
	Источник тока (А)	Потребляемый ток (А)
АДУМ4221	4	4
Конкурент 1	2	4
Конкурент 2	4	6

Если строго сравнивать значения, указанные в технических паспортах, может показаться, что Competitor 2 должен обеспечивать самый мощный привод затвора и, следовательно, самое быстрое время нарастания и спада для данной нагрузки.Чтобы упростить анализ, для нагрузки использовался дискретный керамический конденсатор, поэтому на осциллограммах не было плато Миллера. Кроме того, использовался только один выход драйверов двойного вывода.

Для первого условия испытания каждый драйвер был загружен конденсатором 100 нФ через внешний последовательный резистор затвора 0,5 Ом в конфигурации, показанной на Рисунке 3. Однократное включение и выключение драйверов было выполнено для сохранения рассеиваемой мощности в пределах допустимого диапазона. водитель низкий. Этот тест точно имитирует пиковый тест короткого замыкания.Результаты показаны на рисунках 8 и 9.

Рисунок 8. Тестирование при включении. 100 нФ с 0,5 Ом R _EXT. (а) Напряжение в зависимости от времени. (б) Текущее против времени. Рисунок 9. Тестирование выключения. 100 нФ с 0,5 Ом R _EXT. (а) Напряжение в зависимости от времени. (б) Текущее против времени.

Рисунок 8 показывает, что существует большая разница в скорости включения разных драйверов. Удивительно, но драйвер с самым высоким рыночным пиковым током имеет самое медленное время нарастания. Осциллограммы тока показывают, что все драйверы обеспечивают больше, чем обещанное текущее значение, но Конкурент 2 не выдерживает высокий ток.Общее время нарастания является функцией интеграла тока. Если посмотреть на время спада, показанное на рисунке 9, все три части работают относительно одинаково. В то время как пиковые токи одинаковы для разных продуктов, у Competitor 2 самые низкие устойчивые токи. В целом три части при тестировании на выключение работали одинаково. Из этого тестирования мы видим, что использование номера пикового тока в паспорте показывает, что более сильная часть спецификации демонстрирует более низкую мощность драйвера, чем другие.

Вторым условием тестирования было настроить все три драйвера так, чтобы время нарастания и спада было одинаковым, а затем задействовать детали с постоянной частотой переключения для оценки тепловых характеристик.Как показано на рисунке 8, ADuM4221 имеет самое быстрое время нарастания, что позволяет использовать более мощный внешний последовательный резистор затвора, чтобы соответствовать временам нарастания других драйверов. Было обнаружено, что внешний последовательный резистор затвора 1,87 Ом позволяет ADuM4221 иметь аналогичное время нарастания и спада по сравнению с конкурентом 1 с 0,91 Ом и конкурентом 2 с использованием внешнего последовательного резистора затвора 0,97 Ом для включения. Сопротивление выключения ADuM4221 было настроено на 0,97 Ом. Формы сигналов на входе и выходе показаны на рисунке 10.

Рисунок 10. Настроенный рост / падение всех трех драйверов. Канал 1 = вход, Канал 2 = ADuM4221, Канал 3 = Конкурент 1 и Канал 4 = Конкурент 2.

Если время нарастания и спада настроено на эквивалентность, интегралы сигналов тока сопоставимы, а потери при переключении видны на силовое устройство будет сопоставимо по применению. При использовании внешнего последовательного резистора затвора большего размера тепловая нагрузка может распределяться за пределами изолированного драйвера затвора. На Рис. 11, Рис. 12 и Рис. 13 показаны тепловые изображения работы трех драйверов, работающих при одинаковой температуре окружающей среды с частотой переключения 100 кГц, напряжением вторичной стороны 15 В и нагрузочной емкостью 100 нФ.

Рисунок 11. Тепловое изображение ADuM4221. Рис. 12. Тепловое изображение конкурента 1. Рис. 13. Тепловое изображение конкурента 2.

Прицельная сетка тепловизора — это выходная область изолированных драйверов затвора. Яркое пятно справа от каждого из них — это внешний последовательный резистор затвора. На рисунке 11 показано, что внешний последовательный резистор затвора более горячий, чем на двух других тепловизионных изображениях. Это ожидаемая операция, и она желательна. Все три теста работают с одинаковой частотой переключения и одинаковой емкостью нагрузки, поэтому общая рассеиваемая мощность одинакова.Чем больше мощности рассеивается на внешних резисторах, тем меньше мощности рассеивается внутри самой ИС драйвера затвора.

Competitor 1 работает с температурой поверхности ИС на 35,3⁰C выше, чем ADuM4221, что показывает тепловое ограничение со стороны конкурента из-за более высокого R _{DS (ON)}. Аналогичным образом, рассеяние мощности внутри Competitor 2 приводит к повышению температуры поверхности на 18,9 ° C по сравнению с ADuM4221, что приводит к большему нагреву драйвера затвора при тех же рабочих условиях.Это демонстрирует, что тепловые характеристики из-за более низкого внутреннего сопротивления важно учитывать при выборе драйвера затвора. Это повышение температуры важно при работе при более высоких температурах окружающей среды. Таблица 2 содержит табличные результаты тестирования.

Таблица 2. Сравнение тепловых характеристик: более низкая температура лучше
	R _{EXT_ON} (Ом)	R _{EXT_OFF} (Ом)	Температура IC (° C)
АДУМ4221	1.87	0,97	104,6
Конкурент 1	0,91	0,91	139,9
Конкурент 2	0,97	0,97	123,5

Заключение

Поскольку номинальные значения тока источника и потребителя сообщаются по-разному, формирование мнения о силе возбуждения различных частей на основе беглого взгляда на заголовок таблицы данных может ввести в заблуждение.Отсутствие прозрачности в определении пикового тока может привести к перепродаже или недооценке детали и существенно повлиять на ее шансы быть выбранными для конкретного применения до того, как она будет тщательно оценена со стороны потребителя. Убедиться, что пиковые токи, указанные в технических паспортах, сравниваются одинаково, необходимо для честного сравнения. При оценке изолированных драйверов затвора следует учитывать важность теплового запаса и низкого уровня R _{DS (ON)}. Хотя два драйвера затвора могут быть настроены на одинаковые значения подъема и спада, выбор драйвера с более низким R _{DS (ON)} позволяет получить больший тепловой запас и большую гибкость в скорости переключения.

Режим пикового тока и режим непрерывного тока Моделирование преобразователя постоянного тока и соображения при проектировании компенсации контура

Во многих приложениях, таких как вычислительная техника, требования к переходным нагрузкам шины питания становятся все более жесткими. Более того, поскольку он включает в себя сложные вычисления передаточной функции Лапласа, проектирование компенсации контура часто рассматривается многими инженерами как трудная и трудоемкая задача.

В этой статье, шаг за шагом, обсуждается моделирование среднего слабого сигнала широко используемых преобразователей постоянного тока в режимах пикового тока (PCM) и непрерывного тока (CCM).С помощью математической модели ADIsimPE / SIMPLIS от ADI используется инструмент моделирования коммутационных цепей, позволяющий свести к минимуму объем работы по сложным вычислениям. Затем показана упрощенная модель для более простого и быстрого проектирования и моделирования компенсации контура. Наконец, результаты тестирования оценочной платы ADP2386EVAL используются для подтверждения того, что частота кроссовера контура, запас по фазе и результаты моделирования переходной характеристики нагрузки хорошо согласуются с результатами тестирования.

Моделирование среднего слабого сигнала PCM

Как показано на рисунке 1, шесть блоков вносят вклад в функцию преобразователя постоянного тока в режим тока: резисторный делитель обратной связи, схема компенсатора, измерение и выборка тока, компаратор, силовой каскад и выходная сеть.В контуре сигнал линейного изменения тока катушки индуктивности сравнивается с выходным сигналом усилителя ошибки компенсатора, который является обратной связью с выходным напряжением. Сигнал PWM генерируется для управления переключателями для модуляции тока индуктора. Ток индуктора течет в выходной конденсатор и нагрузку. Из этих шести блоков силовой каскад является единственным нелинейным блоком и может быть самым сложным блоком для моделирования постоянного тока.

Рис. 1. Блок-схема понижающего преобразователя в токовом режиме.

Моделирование силового каскада как 3-контактного переключателя:

Активный режим переключения (A)
Общий режим (C)
Пассивный режим переключения (P), как показано на рисунке 2, мы получаем следующее уравнение 1:

Рисунок 2.Модель среднего слабого сигнала для 3-х полюсного переключателя.

Это средняя модель, действующая только в режиме постоянного тока, эквивалентная трансформатору с соотношением витков 1: d. Модель получает нас дифференциальное уравнение 2:

Слабые сигналы были использованы в средней модели, чтобы стать моделью среднего слабого сигнала (ASSM). С помощью этой модели силовой каскад можно линеаризовать для анализа.

По-прежнему используя понижающий преобразователь PCM CCM в качестве примера, весь регулятор был смоделирован в блок-схему передаточной функции Лапласа, как показано на рисунке 3.Есть два контура управления: контур напряжения и контур тока. В токовой петле ток катушки индуктивности измеряется RT и дискретизируется с линейным нарастанием на первом отрицательном входе компаратора. В контуре напряжения пульсации выходного напряжения регистрируются резистивным делителем с коэффициентом усиления K и дискретизируются в цепи компенсатора Av (s) как напряжение ошибки на положительном входе компаратора. С линейной компенсацией наклона в качестве второго отрицательного входного сигнала компаратор генерирует сигнал регулируемого рабочего цикла в модели среднего малого сигнала силового каскада для модуляции тока катушки индуктивности.

Рисунок 3. Блок-схема модели управления постоянным током CCM.

Функция усиления от тока индуктора к выходному напряжению показана в уравнении 3:

Функция усиления от рабочего цикла ШИМ до тока катушки индуктивности показана в уравнении 4:

Коэффициент усиления компаратора F _m показан в уравнении 5, S _n — наклон нарастания тока индуктора, S _e — компенсация наклона, T _s — период переключения:

Функция усиления эффекта дискретизации показана в уравнении 6:

Функция усиления от входного напряжения до тока катушки индуктивности показана в уравнении 7:

Функция усиления токовой петли показана в уравнении 8:

Функция усиления контура напряжения показана в уравнении 9:

Функция усиления контура показана в уравнении 10:

При проектировании целевого коэффициента усиления контура постоянного тока необходимо учитывать четыре фактора:

Высокое усиление контура постоянного тока для низкой ошибки постоянного тока
Широкая полоса пропускания контура для быстрой переходной характеристики
Наклон –20 дБ около частоты кроссовера для более высокого запаса по фазе (> 45 °)
Высокое затухание на высокой частоте для подавления шума

В контуре регулятора проектировщик настраивает только компенсатор Av (s) и резисторный делитель K обратной связи.Итак, в конструкцию петли включены два шага. Во-первых, отсоедините резисторный делитель от выхода, чтобы получить коэффициент усиления разомкнутого контура, как показано в уравнении 11:

Во-вторых, спроектируйте компенсатор Av (s) для компенсации нулей и полюсов усиления Goc (s) разомкнутого контура для достижения проектной цели усиления контура.

На рисунке 4 показан пример условий нормальной нагрузки, когда. В низкочастотной области есть один полюс (¹/₂ πRoCo) и один ноль (¹/₂ πRcCo) и один полюс 2-го порядка (1 / πfs) в высокочастотной области, вызванный за счет эффекта выборки He (s).Компенсатор Av (s) предназначен для увеличения частоты кроссовера, обеспечения наклона -20 дБ вблизи точки кроссовера и для получения запаса по фазе более 45 °. Компенсатор имеет два полюса и один ноль; один полюс используется для компенсации нулевого ESR конденсатора с разомкнутым контуром усиления, другой полюс функционирует как интегратор для увеличения усиления по постоянному току контура, а нулевой полюс компенсирует эффект нагрузки разомкнутого контура. Полюс второго порядка на высокой частоте (1 / πfs) полезен для ослабления шума.

Рисунок 4.PCM Этапы проектирования контура постоянного тока CCM.

Инструмент ADsimPE на базе SIMetrix / SIMPLIS — это симулятор схем для персонального использования, идеально подходящий для оценки линейных и коммутационных компонентов от Analog Devices. SIMetrix очень полезен для линейных схем, таких как операционные усилители, а SIMPLIS предназначен для коммутации компонентов, таких как преобразователи постоянного тока в постоянный и системы ФАПЧ. На рисунке 5 понижающая опорная схема CCM PCM была настроена в качестве эталона для проверки поведения схемы и точности модели. Это понижающий стабилизатор синхронизации PCM с 3.Вход 3 В, выход 1,2 В и частота коммутации 1,2 МГц.

Рис. 5. Эталонная схема понижения SIMPLIS PCM CCM.

Как показано на рисунке 6, в результатах расчета коэффициента усиления левого контура модели среднего слабого сигнала частота кроссовера составляет 50 кГц, а запас по фазе равен 90,35 °. Результат моделирования SIMPLIS, как видно на правой стороне рисунка 6, показывает запас по фазе 90,8 ° при частоте кроссовера 47,6 кГц. Это доказывает, что результат моделирования схемы переключения ADIsimPE / SIMPLIS совпадает со сложным расчетом ASSM, который предлагает разработчику быстрый способ проектирования контура.Однако схема, показанная на рисунке 5, не очень проста.

Рис. 6. Результат расчета ASSM и результат моделирования SIMPLIS.

Упрощенное моделирование среднего слабого сигнала PCM

Учитывая, что частота кроссовера в приложении намного больше, чем 1√LCo, оценка может быть выполнена для сложных уравнений. Для уравнения 4 функцию усиления от коэффициента заполнения ШИМ до тока катушки индуктивности можно упростить, как показано в уравнении 12:

Из рисунка 3 мы можем получить функцию усиления без обратной связи, которая представляет собой зависимость выходного напряжения компенсатора от тока катушки индуктивности, как показано в уравнении 13:

S _e — наклон положительного фронта компенсации крутизны.Возьми

А частота кроссовера намного больше, чем 1√LCo, поэтому функция усиления без обратной связи в уравнении 13 может быть дополнительно упрощена как уравнение 14:

Результатом является то, что ASSM без обратной связи может быть упрощен, как показано на рисунке 7, в источник тока с регулируемым выходным напряжением компенсатора, протекающий в сеть RLC, генерирующую ток катушки индуктивности. Эту модель гораздо проще использовать для моделирования или расчетов, чем исходные сложные уравнения.

Рис. 7. Упрощенная схема разомкнутого контура ASSM.

Используя эталонную схему на Рисунке 5, рассчитайте R _e и C _e, затем настройте упрощенную схему ASSM с обратной связью в ADSimPE, как показано на Рисунке 8. Результат моделирования SIMetrix показан в правой половине рисунка. 8 с частотой кроссовера 49 кГц и запасом по фазе 90,5 °, что соответствует результату расчета ASSM и результату моделирования SIMPLIS, показанному в разделе 2.

Рисунок 8.Упрощенная схема моделирования ASSM и результат.

ADP2386 Моделирование результатов моделирования и испытаний

ADP2386 — это синхронный понижающий стабилизатор PCM CCM от Analog Devices. Диапазон входного напряжения составляет от 20 В до выходного напряжения 0,6 В при выходном токе до 6 А, с диапазоном частот переключения от 200 кГц до 1,2 МГц. Универсальность устройства позволяет использовать его в понижающих и повышающих топологиях без дополнительных затрат и размеров. В этом разделе оценочная плата ADP2386EVAL будет использоваться для проверки результатов моделирования.Сравниваются два теста: тест контура и тест переходной нагрузки.

На рисунке 9 показана принципиальная схема ADP2386EVAL. Для тестирования плата настраивается в условиях, указанных в таблице 1, строка 1, ниже. Внутренняя компенсация наклона ADP2386 является адаптивной с периодом заполнения 0,6 фс, и уравнение 14 использовалось для получения упрощенных параметров ASSM, как показано в таблице 1, строка 2. Характеристики смещения постоянного тока выходного конденсатора падают примерно на 30% при 3,3 В, поэтому в упрощенном моделировании ASSM значение выходного конденсатора было изменено на 100 мкФ, а не на 147 мкФ на оценочной плате.

Таблица 1. Условия тестирования ADP2386EVAL и упрощенные параметры ASSM
V _IN	В _О	F _S	I _O	л	С	Компенсатор
12 В	3,3 В	600 кГц	3 А	2.2 мкГн	147 мкФ / 5 Ом	44,2 кОм, 1,2 н, 4,7 п
РТ	SE	S _n	S _f	R _e	C _e	G _м
123 мОм	0,2 В / мкс	0,49 В / мкс	0.18 В / мкс	2,51 Ом	128 нФ	580 мкСм

Рисунок 9. Схема ADP2386EVAL.

На рис. 10 показаны упрощенные результаты моделирования и тестирования ASSM контура ADP2386EVAL. Левая часть — моделирование ADIsimPD / SIMetrix — частота кроссовера 57 кГц, запас по фазе 71 °. Справа — результат теста AP модели 300 — частота кроссовера составляет 68,7 кГц, а запас по фазе — 59.3 °. Хотя есть разница между результатами испытаний и моделированием, мы знаем из технических данных ADP2386, что его коэффициент усиления усилителя ошибки варьируется от 380 мкСм до 580 мкСм, что связано с неточностью катушки индуктивности и выходного конденсатора. Так что разница между двумя результатами приемлема.

Рис. 10. Моделирование контура ADP2386EVAL и результаты испытаний.

Для испытания на переходную нагрузку включены два испытания. Тест 1 — это тест в условиях компенсатора Таблицы 1 с хорошим запасом по фазе и широкой частотой кроссовера.Тест 2 — это тест с компенсатором, измененным на 100 пФ / 1,2 нФ / 44,2 кОм, в котором частота кроссовера снижена до 39 кГц, а запас по фазе — до 36 °. На рисунке 11 показан переходный процесс нагрузки (от 0,5 A до 3 A, 0,2 A / мкс) Тест 1 и результат теста. Пик выброса был протестирован на уровне 67 мВ, а результат моделирования — 59 мВ, при этом переходные кривые хорошо согласованы. На рис. 12 показан переходный процесс нагрузки (от 0,5 А до 3 А, 0,2 А / мкс) Тест 2 и результат теста. Пик выброса испытан на 109 мВ, а результат моделирования — 86 мВ, причем кривые переходных процессов очень хорошо согласованы.

Рис. 11. Моделирование переходного режима нагрузки ADP2386EVAL и результаты теста 1.

Рис. 12. Моделирование переходных процессов нагрузки ADP2386EVAL и результаты испытаний 2.

Заключение

Компенсация контура часто рассматривается инженерами как очень сложная задача проектирования, особенно в приложениях с быстрыми переходными процессами нагрузки. В этой статье, основанной на широко используемом устройстве непрерывного понижения тока в режиме управления пиковым током, обобщены математическое моделирование среднего слабого сигнала и расчет контура, а также быстрый и простой метод моделирования ADISimPE / Simplis.Он также представил упрощенную модель среднего слабого сигнала и предложил упрощенный способ обработки конструкции компенсации контура. Результаты стендовых испытаний оценочной платы ADP2386EVAL и переходных процессов под нагрузкой подтвердили точность упрощенной модели и ее моделирования.

использованная литература

¹ ADP2386 Лист данных.

² ADP2386EVAL Руководство пользователя.

³ Брэд Брэнд и Мэриан К.Казимерчук. «Эффект выборки и удержания в преобразователях постоянного тока с ШИМ с контролем режима пикового тока ». 0-7803-8251-X 10.1109 / ISCAS.2004.1329944 Схемы и системы, 2004. ISCAS 2004.

Квалификация IP интерфейса для модели зарядного устройства на основе пикового тока

Электронное устройство подвержено повреждению электростатическим разрядом (ESD) в течение всего жизненного цикла, особенно после завершения обработки кремниевой пластины и до тех пор, пока устройство не будет собрано в системе.Шлифование обратной стороны пластин, распиловка пластин, упаковка, тестирование, а также сборка и пайка плат подвергают устройство опасности электростатического разряда. Чтобы избежать потери урожая из-за повреждения электростатическим разрядом, при производстве устройств принимаются обширные меры контроля для поддержания низких уровней электрического поля. С другой стороны, само устройство защищено от электростатического разряда встроенными сетями защиты от электростатического разряда, которые обеспечивают устойчивость к электростатическому разряду для всех открытых контактов устройства.

Существуют

испытательные модели и симуляторы ESD для оценки устойчивости устройства к электростатическому разряду.Чаще всего используются Модель человеческого тела (HBM) и Модель заряженного устройства (CDM). HBM [1] моделирует разряд заряженного человека, касающегося устройства, в то время как CDM моделирует быстрый разряд заряженного устройства на землю.

С момента своего появления в 1990-х годах различные стандарты CDM были определены JEDEC [2], ESDA [3], JEITA [4] и AEC [5]. Недавно ESDA и JEDEC выпустили совместный стандарт ANSI / ESDA / JEDEC JS-002-2018 [6], который заменяет существующие стандарты JEDEC и ESDA.

Все стандарты CDM имеют общую систему классификации, основанную на уровнях напряжения, см., Например, классификацию JS-002 в таблице 1.

Таблица 1: Уровни классификации устройств CDM ESD в соответствии с JS-002-2018

Разрядный (пиковый) ток, связанный с заданным уровнем напряжения CDM, не фиксирован, но зависит от характеристик тестируемого устройства (DUT), таких как размер кристалла, количество выводов, размер корпуса и другие. Следовательно, если блокировка IP интерфейса, т.е.грамм. хорошо известный интерфейс USB, DDR, HDMI, MIPI, Ethernet, SATA проходит квалификацию CDM для определенного целевого напряжения на тестовой микросхеме, нет гарантии, что этот IP-адрес пройдет тот же уровень напряжения при интеграции в продукт. Например, если продукт имеет больший размер кристалла или корпуса по сравнению с чипом квалификационного испытания IP, ток CDM при том же уровне квалификационного напряжения на продукте может быть выше, и IP может выйти из строя.

По этой причине для 3 сторонних IP-провайдеров ^rd по своей природе невозможно гарантировать, что спецификация напряжения CDM для IP будет интегрирована в еще неизвестный продукт; только цель CDM пик текущая цель должна использоваться, когда IP квалифицируется на тестовой микросхеме.

В следующем разделе описаны принципы метода тестирования CDM для понимания зависимости тока разряда CDM от устройства. Далее объясняется предлагаемая процедура квалификации CDM на основе пикового тока. Наконец, мы демонстрируем, как заказчик может оценить ожидаемый уровень прохождения напряжения CDM IP в продукте, используя текущую спецификацию CDM IP.

Тестирование в среде моделирования CDM

В оборудовании имитатора CDM ИУ размещается на изолирующем приспособлении штырями вверх («положение мертвого жука»), как показано на Рисунке 1.

Рисунок 1: Схема оборудования упрощенного тестера CDM

Генератор высокого напряжения используется для установки потенциала на полевой пластине и зарядки устройства до желаемого уровня напряжения, обычно в диапазоне от 125 В до 1000 В. Затем устройство разряжается через один из выводов устройства через заземленный пого-зонд, прикрепленный к манипулятору робота. Процедура повторяется для положительной и отрицательной полярности напряжения и для каждого вывода устройства последовательно. Затем применяются параметрические и функциональные тесты, чтобы определить, было ли повреждено ИУ.

Как показано на Рисунке 2, заряжается все ИУ, состоящее из матрицы, теплораспределителя, паяных выступов, контактов корпуса / шариков припоя, подложки и т. Д. Общая сумма заряда CDM зависит от свойств устройства.

Рисунок 2: Распределение заряда внутри DUT

Максимальный ток разряда тестируемого устройства пропорционален общему заряду и, следовательно, будет разным для каждого кристалла устройства и характеристик корпуса. Пиковый ток разряда при определенной настройке напряжения CDM не будет таким же во время фазы аттестации IP интерфейса по сравнению с аттестацией конечного продукта.

Когда заряженное ИУ заземлено через один из своих выводов, форма волны разрядного тока, среди прочего, характеризуется током первого пика (I _PEAK), как показано на рисунке 3.

Рисунок 3: Типичная форма кривой тока разряда CDM

Рисунок 4: Зависимость пикового тока CDM от площади корпуса BGA. Красные стрелки показывают пример показаний расчетного пикового тока для BGA 1225 мм2 при 250 В CDM.

На рисунке 4 показано, как ток CDM зависит от размера устройства.Пиковый ток разряда CDM измеряется для большого количества типов корпусов с шариковой решеткой (BGA) для напряжения CDM 500 В в зависимости от размера корпуса [7]. В зависимости от корпуса BGA, пиковый ток для разряда CDM 500 В может варьироваться от менее 4 А до более 10 А. Пиковые токи пропорциональны уровню напряжения CDM, что означает, что для 250 В максимальный пиковый ток обычно не превышает 6 А, как показано синей линией на рисунке 4.

Пиковый ток как проектный параметр для внутрикристальной сети ESD

Встроенная сеть ESD является частью интерфейса IP и включает в себя устройства ESD, такие как диоды, зажимы и межсоединения (металлические и контактные слои) в путях разряда.Основным параметром, определяющим уровень отказа этих устройств ESD и межсоединения, является ток разряда, поэтому пиковый ток CDM является ведущим параметром проектирования ESD для IP. Напряжение CDM, необходимое для достижения пикового тока, является просто производной характеристикой, которую нельзя определить без знания конечных свойств устройства. Допустимое отклонение напряжения CDM для конечного продукта неизвестно на ранних стадиях разработки, когда свойства кристалла и корпуса еще неизвестны, поэтому ток CDM является единственным возможным критерием для квалификации IP.По этой причине провайдеры IP должны использовать целевой пиковый ток CDM (I _TARGET) для проектирования CDM и квалификационных испытаний своих интерфейсных IP-решений.

Использование пикового тока для квалификации IP CDM интерфейса

Предлагаемый метод квалификации CDM для интерфейса IP состоит из двух этапов:

Определите корреляцию между напряжением CDM (V _CDM) и пиковым током (I _PEAK)
Выполните квалификацию IP при заданном пиковом токе (I _TARGET)

Шаг 1. Определите корреляцию между напряжением CDM ( В _CDM ) и пиковым током ( I _PEAK )

На этом этапе определяется квалификационное напряжение CDM (V _QUAL) DUT (в данном случае тестовая микросхема IP), которое соответствует целевому квалификационному пиковому току (I _TARGET).Неважно, какие уровни напряжения выбираются для тестирования, а также то, проходит ли устройство или выходит из строя при определенных уровнях напряжения CDM. Однако хорошей практикой является наличие точек считывания ниже и выше целевого напряжения CDM. Отношение пикового тока к напряжению CDM является линейной функцией, когда ИУ подвергается нагрузке на разных уровнях напряжения CDM, как показано на рисунке 5.

Рисунок 5: График l _PEAK относительно V _CDM используется для определения квалификационного уровня напряжения V _QUAL.На графике показан пример для I _TARGET = 6.0A

Для завершения шага 1:

Подайте напряжение на все выводы устройства (выводы ввода-вывода и выводы питания / заземления) при разных уровнях напряжения CDM;
Наблюдайте за формой волны пикового тока разряда и определяйте I _PEAK для каждого вывода;
Рассчитайте для каждого уровня напряжения CDM среднее значение I _PEAK для всех напряженных контактов;
Найдите линейную кривую зависимости напряжения CDM от среднего пикового тока; и
Используйте I _TARGET и график разрядного тока, см. Пример на рисунке 5, чтобы определить квалификационное напряжение CDM (V _QUAL).

Шаг 2: Проверьте квалификацию IP при целевом пиковом токе ( I _TARGET )

В соответствии со стандартами для квалификационного теста CDM используются три устройства. Для этого шага данные о прохождении / отказе имеют решающее значение и определяют результаты квалификации.

Для завершения шага 2:

Применение параметрических и функциональных предварительных нагрузочных тестов типа «годен / не годен»;
Используйте V _QUAL в качестве настройки напряжения в тестере CDM;
Напрягите все штыри на уровне V _QUAL CDM с помощью трех устройств; и
Примените пост-стрессовые параметрические и функциональные тесты типа «годен / не годен».
Фактическое значение I _TARGET определяется провайдером IP и должно соответствовать требованиям конечного продукта. Обратите внимание, что предварительным условием для метода квалификации IP является то, что размер тестового чипа достаточно велик, чтобы целевой пиковый ток достигался при напряжении CDM ниже практического предела
в 1000 В.

Оценка производительности IP CDM в конечном продукте

Существует два варианта оценки уровня напряжения IP CDM в конечном продукте на основе квалификационных данных IP по пиковому току:

Использовать корреляцию между напряжением CDM и I _PEAK предыдущих продуктов в аналогичной упаковке — наиболее удобный и точный вариант;
Если вариант один недоступен, оцените ожидаемый пиковый ток на основе размера корпуса, используя I _PEAK vs.соотношение размеров упаковки — показано на рисунке 4.

Внимание: Вариант № 2 может обеспечить только приблизительную оценку, поскольку конструкция корпусов BGA может сильно различаться в разных компаниях, а зависимость пикового тока BGA в целом может не совпадать с кривой, приведенной в упомянутой статье. Наиболее точным является измерение пикового тока для предыдущих продуктов в аналогичной упаковке.

Вопросы и ответы

Q-1: Я заметил, что спецификация модели человеческого тела (HBM) IP составляет 1 кВ, напряжение, как обычно.Почему вы сохраняете напряжение для HBM и переходите на ток для CDM?

A-1:  В случае HBM фактический ток разряда при заданном напряжении (например, 1 кВ) полностью определяется значением 100 пФ / 1500 Ом в тестере HBM и практически не зависит от свойств микросхемы и корпуса. IP, который проходит квалификацию HBM 1 кВ на тестовой микросхеме, также будет проходить проверку HBM на 1 кВ на продукте (при условии, что IP был правильно интегрирован в продукт). Поскольку для CDM ток, связанный с заданным уровнем напряжения напряжения (например,g., 250 В) могут сильно отличаться на тестовой микросхеме и продукте, только с (пиковым) током результаты теста могут быть спроецированы на продукт.

Q-2: Мой продукт соответствует спецификации CDM 250 В. Чип использует IP, который соответствует уровню пикового тока 6А CDM. Как мне узнать, соответствует ли IP-адрес моего продукта целевому показателю CDM 250 В? Чип будет собран в корпусе BGA1156 (35х35 мм, ^{, 2,}).

A-2: У вас есть аналогичный продукт в том же корпусе BGA1156? Если да, используйте этот продукт для измерения пикового тока разряда при 250 В CDM.Аналогичный пиковый ток можно ожидать и для нового продукта, поэтому, если пиковый ток меньше 6 А, ожидается, что IP-адрес будет пропускать 250 В.

Если предыдущий продукт не доступен в качестве эталона, используйте свойства продукта, чтобы оценить средний пиковый ток разряда при 250 В CDM. Воспользуйтесь графиком на Рисунке 4 и проверьте пиковый ток при 250 В для соответствующего размера корпуса, как указано. Для площади корпуса = 1225 мм ² и 250 В график CDM показывает 4,8 А, что меньше, чем пиковый ток квалификации IP, равный 6 А.

Заключение: По приблизительным оценкам, мы предполагаем, что IP в этом продукте будет соответствовать спецификации 250V CDM.

Резюме

Для CDM ток разряда при заданном уровне напряжения является функцией многих свойств устройства, особенно кристалла и размера корпуса. Поскольку фактический механизм отказа определяется током разряда, а не напряжением, уровни отказов для квалификации IP, измеренные на тестовой микросхеме, соответственно после интеграции в продукт, обычно будут совершенно другими.Это серьезно снижает ценность квалификаций IP с критерием напряжения CDM.

Чтобы решить эту проблему, мы ввели в этой статье критерий пикового тока (например, 6А) для квалификации IP по протоколу CDM. Квалификационные данные CDM вместе с основными характеристиками конечного продукта, такими как размеры упаковки, позволяют пользователю определить, будет ли IP, интегрированный в продукт, соответствовать квалификационному классу продукта CDM.

Список литературы

ANSI / ESDA / JEDEC JS-001-2017, «Модель человеческого тела (HBM) — уровень компонентов», май 2017 г.
Стандарт JEDEC JESD22-C101F, «Метод испытания модели индуцированного заряженного устройства для определения пороговых значений электростатического разряда для микроэлектронных компонентов», октябрь 2013 г., http: // www.jedec.org
EOS / ESD Association Inc., ANSI / ESD STM5.3.1-1999, «Уровень компонентов модели заряженного устройства (CDM)», 1999 г.
Стандарт JEITA CDM, CDM (EIAJ ED-4701 / 300-2, Метод испытаний 305A)
Совет по автомобильной электронике, AEC-Q100-011 Rev-B, «Испытание на электростатический разряд модели заряженного устройства», 2001 г.
ANSI / ESDA / JEDEC JS-002-2018, «Модель заряженного устройства (CDM) — Уровень устройства», январь x2019 г.
A. Jahanzeb, Y-Y. Лин, С. Марум, Дж. Шихл, К. Дуввери, «Изменения пикового тока CDM и влияние на пороги производительности CDM», Proc.Симпозиум EOS / ESD 2007, стр. 283-288

Питер К. де Йонг — специалист по ESD / LU в Synopsys, где он отвечает за решения ESD для широкого спектра системных интерфейсов. До прихода в Synopsis он проработал 20 лет в Philips Semiconductors Nijmegen (ныне NXP Semiconductors), где работал над защитой от электростатического разряда для библиотек ввода-вывода CMOS компании. де Йонг имеет степень магистра. степень в области технической физики в Делфтском технологическом университете, и можно связаться с питером[email protected].

Амплитудное значение силы переменного тока в цепи Im=2,8 А. Чему равно действующее значение

Амплитудное значение — сила — ток

Амплитудное значение — сила — ток

Связь действующего и амплитудного напряжения. Действующие значения силы тока и напряжения

4.4.5. Мощность в цепи переменного тока

Эффективные значения силы тока и напряжения

Поделиться ссылкой:

1. Мгновенное значение силы тока для фазы

Амплитудное значение силы тока и напряжения. Действующее значение переменного тока и напряжения

Действующее значение переменного тока

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Векторное изображение синусоидально изменяющихся величин

Действующее и среднее значения переменного тока и напряжения.

Что берется за действующее значение силы переменного тока и переменного напряжения

4.4.5. Мощность в цепи переменного тока

действующие значения силы тока и напряжения

Нужна помощь в учебе?

Что такое пиковый ток? — Sunpower UK

Что такое пиковый ток?

Почему протекает пусковой ток?

Источники питания пикового тока

В чем разница между пусковым током и пиковым током?

Что такое пиковое значение, среднее значение и среднеквадратичное значение? — определение и объяснение

Пиковое значение

Среднее значение

R.M.S значение

AMCI: Advanced Micro Controls Inc :: Драйверы шагового двигателя: среднеквадратичное значение или пиковый ток?

Пиковый ток драйверов изолированного затвора

Введение

Пример приложения

Расчет нагрузки

Неоднозначность в заголовке таблицы данных

Емкость по Миллеру

Рассеивание мощности: важное соображение

Сравнительный пример использования

Заключение

Режим пикового тока и режим непрерывного тока Моделирование преобразователя постоянного тока и соображения при проектировании компенсации контура

Моделирование среднего слабого сигнала PCM

Упрощенное моделирование среднего слабого сигнала PCM

ADP2386 Моделирование результатов моделирования и испытаний

Заключение

использованная литература

Квалификация IP интерфейса для модели зарядного устройства на основе пикового тока

alexxlab

Вам также может понравиться

Газокомпрессорные станции: Газокомпрессорная станция — Статьи — Горная энциклопедия

Диод как правильно подключить: Последовательное соединение светодиодов

Длинные лампы как называются: Как называются длинные лампы на потолке

Добавить комментарий Отменить ответ