Баланс мощностей в цепях синусоидального тока Баланс полной. Баланс мощностей в электрической цепи онлайн

Баланс мощностей

При решений электротехнических задач, часто нужно проверить правильность найденных значений. Для этого в науке ТОЕ, существует так называемый баланс мощностей.

Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность. 

Или

Проверим это соотношение на простом примере.

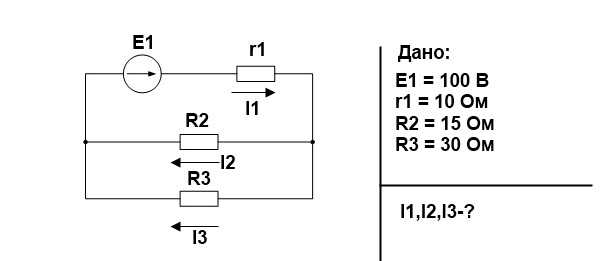
Для начала свернем схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.

 

Найдем по закону Ома ток источника и напряжение на R23, учитывая, что r1 и R23 соединены последовательно, следовательно, сила тока одинаковая. 

Найдем токи I2 и I3

Теперь проверим правильность с помощью баланса мощностей. 

Небольшое различие в значениях связано с округлениями в ходе расчета.

С помощью баланса мощностей, можно проверить не только простую цепь, но и сложную. Давайте проверим сложную цепь из статьи метод контурных токов.

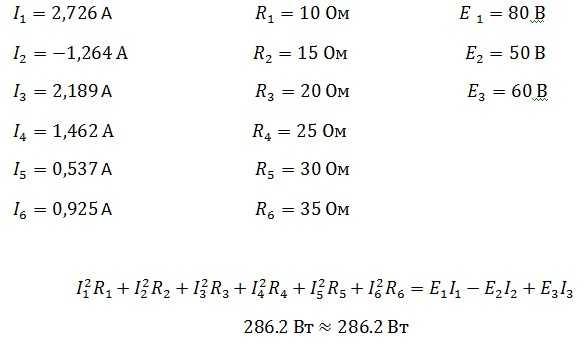
 Как видите независимо от сложности цепи, баланс сошелся, и должен сойтись в любой цепи!

Просмотров: 1300

electroandi.ru

Расчет электрической цепи постоянного тока. Расчетная часть. Общий баланс мощностей

методе контурных токов  уравнения составляют только по второму закону Кирхгофа для условных контурных токов. Количество контурных токов, как и количество уравнений должно быть равно числу независимых контуров рассматриваемой цепи.

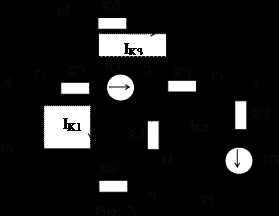
Порядок расчета методом контурных токов:

1.  Произвольно задают УНП неизвестных реальных токов в ветвях цепи.

2.  Произвольно задают УНП фиктивных контурных токов.

3.  Составляют уравнения по второму закону Кирхгофа  относительно контурных токов.

4.  Решают эти уравнения.

5.  Проверяют расчет.

Составим систему уравнений для данной электрической цепи:

.

Подставим в систему значения сопротивлений и ЭДС:

.

Решаем данную систему уравнений методом Крамера:

 А;

 А;

 А.

Выражаем реальные токи через известные контурные токи:

 А;

   А;

 А;

 А;

 А;

 А.

3.  Сделать проверку по первому закону Кирхгофа.

Сделаем проверку по первому закону Кирхгофа:

 ,       ;

,          ;

,         .

Проверка по первому закону сошлась. Токи ветвей рассчитаны правильно.

4.  Составить баланс мощностей.

Энергетический баланс мощностей составляют на основании закона сохранения энергии, согласно которому, энергия, выделившаяся в единицу времени в сопротивлениях схемы в виде тепла, должна быть равна энергии, вырабатываемой источниками за тот же промежуток времени.

.

Найдем мощность, вырабатываемую источником:

 Вт.

Найдем мощность, выделившуюся на нагрузке:

Найдем относительную погрешность нахождения баланса мощности:

Погрешность нахождения баланса мощности получилась меньше 2%, что соответствует условию нахождения баланса мощности.

5.  Рассчитать ток во второй ветви методом эквивалентного генератора.

В основе метода эквивалентного генератора лежит теорема об активном двухполюснике или об эквивалентном генераторе. Согласно этой теореме, сколь угодно сложную цепь относительно зажимов, выделенной ветви, можно представить активным двухполюсником или эквивалентным генератором. ЭДС этого генератора численно равна напряжению холостого хода на зажимах, выделенной ветви, а внутреннее сопротивление - эквивалентному сопротивлению цепи относительно тех же зажимов.

Порядок расчета методом эквивалентного генератора:

1.  Формируют схему в режиме холостого хода, разрывая ветвь с искомым током.

2.  Рассчитывают напряжение холостого хода между точками обрыва. Необходимые токи при этом рассчитывают любым известным методом в схеме в режиме холостого хода.

3.  Формируют схему для определения внутреннего сопротивления. При этом источники ЭДС выводят, учитывая их внутреннее сопротивление.

4.  Рассчитывают эквивалентное сопротивление относительно выделенных зажимов.

5.  По закону Ома для цепи с эквивалентным генератором рассчитывают ток искомой ветви.

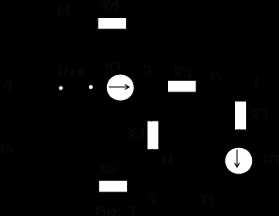
Найдем напряжение холостого хода разомкнутой ветви:

.

Найдем ток первой и шестой ветви. Воспользуемся методом свертывания цепи.

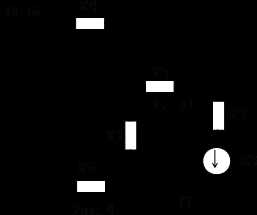
 Ом,

 А,

 A,

 A,

 А,

 B.

Рассчитаем внутреннее сопротивление генератора. Для чего треугольник (рис. 5)

 R1-R5-R3 преобразуем в звезду. Получим схему рис. 6.

 Ом,

 Ом,

 Ом.     

 Ом.

По закону Ома найдем ток ветви:

 А.

Ток второй ветви, найденный по методу эквивалентного генератора, равняется току второй ветви, найденному по методу контурных токов. Следовательно, расчет методом эквивалентного генератора выполнен, верно.

6.   Построить потенциальную диаграмму для любого контура.

Потенциальная диаграмма – это график изменения потенциала вдоль замкнутого контура или участка цепи. Построим потенциальную диаграмму для контура a-b-c-d. Заземлим одну из точек или узлов заданного контура. При этом полагают, что потенциал этой точки равен нулю.

Пусть , тогда

            В,

 В,

               В,

       В.

Рассчитаем суммарное сопротивление контура:

 Ом.

Построим потенциальную диаграмму.

Рис. 7

2.2.   Расчет электрической цепи переменного тока.

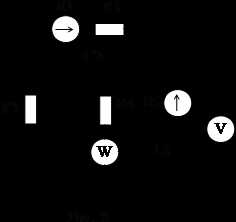
Исходные данные:

R1=10 Ом; C2=127 мкФ; R3=40 Ом; R4=50 Ом; L5=0.143 Гн,

 В,  В.

1. Составить систему уравнений по законам Кирхгофа в дифференциальной и комплексной формах (решать систему не надо).

Порядок составления полной системы уравнений по законам Кирхгофа:

1.  Произвольно задают УНП неизвестных реальных токов в ветвях цепи.

2.  Записывают по законам Кирхгофа систему линейных алгебраических уравнений относительно неизвестных токов.

Дифференциальная форма законов Кирхгофа:

1: ,

     2: ,

             I: ,

                          II: ,

         III: .

Законы Кирхгофа в комплексной форме:

1:  ,

     2:  ,

I:  ,

              II:  ,

III:  .

2.  Составить систему уравнений по методу узловых потенциалов. Решить систему, определить потенциалы узлов и токи ветвей.

Порядок расчета методом узловых потенциалов:

1. Задают УПН реальных токов в ветвях цепи.
2. Заземляют один узел, полагая его потенциал равным нулю.
3. Записывают уравнения относительно неизвестных потенциалов, используя первый закон Кирхгофа и закон Ома.
4. Решают эти уравнения.
5. По закону Ома рассчитывают реальные токи в ветвях цепи.
6. Проверяют расчет.

Найдем полные сопротивления ветвей:

 Ом,

 Ом,

 Ом,

 Ом,

 Ом.

Заземлим 3 узел, полагая потенциал этого узла равным нулю:

vunivere.ru

Баланс мощностей в цепях синусоидального тока Баланс полной

Баланс мощностей в цепях синусоидального тока Баланс полной мощности: Полная мощность источников: источники ЭДС Полная мощность потребителей: источники тока

Баланс активной мощности: Активная мощность источников: – угол нагрузки (угол между векторами напряжения и тока на комплексной плоскости) Активная мощность потребителей:

Баланс реактивной мощности: Реактивная мощность источников: Реактивная мощность потребителей:

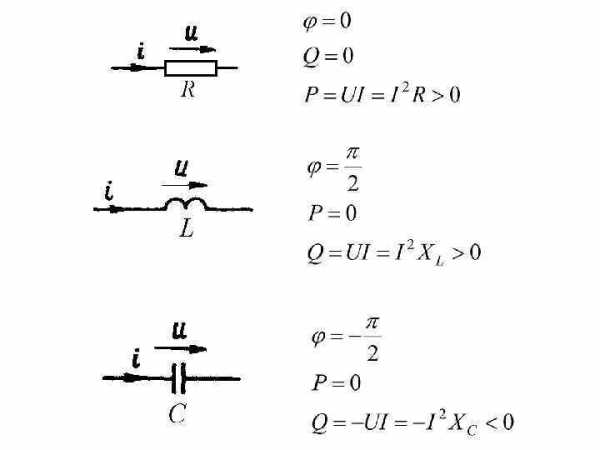
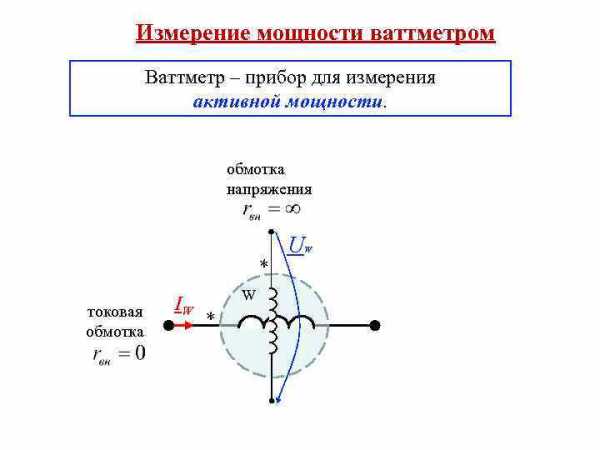Измерение мощности ваттметром Ваттметр – прибор для измерения активной мощности. обмотка напряжения * токовая обмотка IW W * W U W

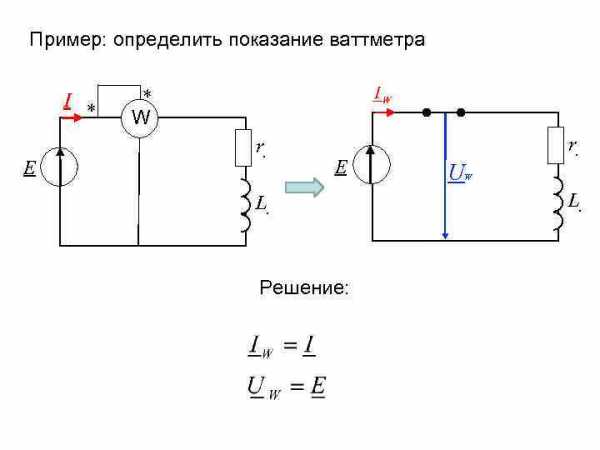Пример: определить показание ваттметра I E * * W r. E L. Решение: r. U W L.

При подключении ваттметра на вход схемы прибор измеряет всю активную мощность цепи. или

Резонансные явления в электрических цепях Резонансным режимом называют режим, при котором входное сопротивление (проводимость) является активным и входной ток совпадает со входным напряжением по фазе. резонанс напряжений резонанс токов

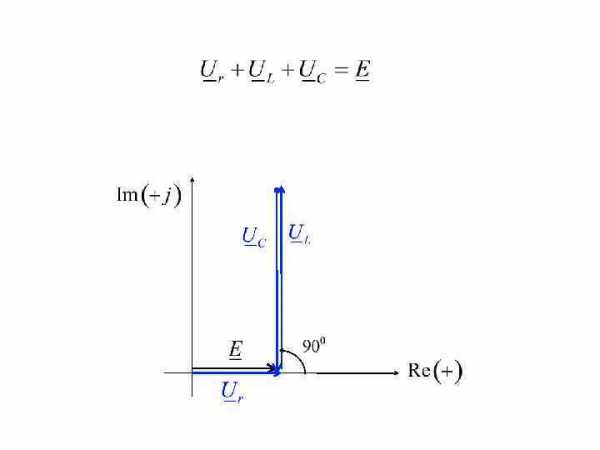
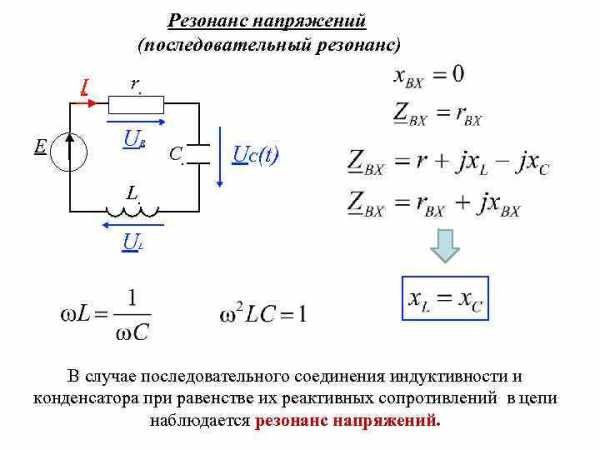Резонанс напряжений (последовательный резонанс) I E r. U R C. UC(t) L. U L В случае последовательного соединения индуктивности и конденсатора при равенстве их реактивных сопротивлений в цепи наблюдается резонанс напряжений.

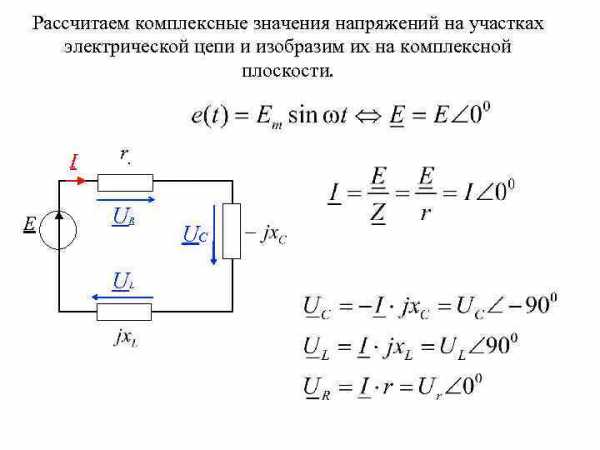Рассчитаем комплексные значения напряжений на участках электрической цепи и изобразим их на комплексной плоскости. I E r. U R U L UC

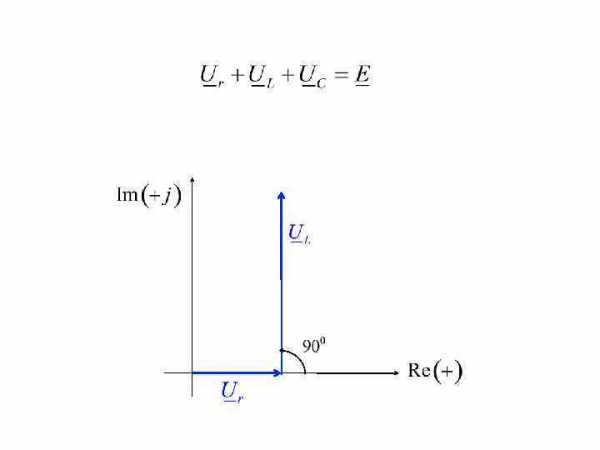
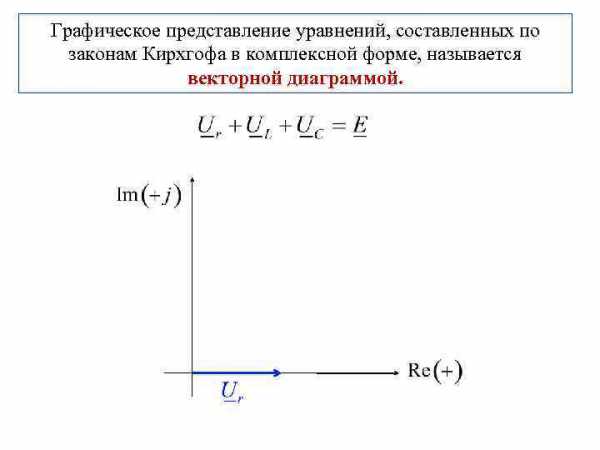Графическое представление уравнений, составленных по законам Кирхгофа в комплексной форме, называется векторной диаграммой.

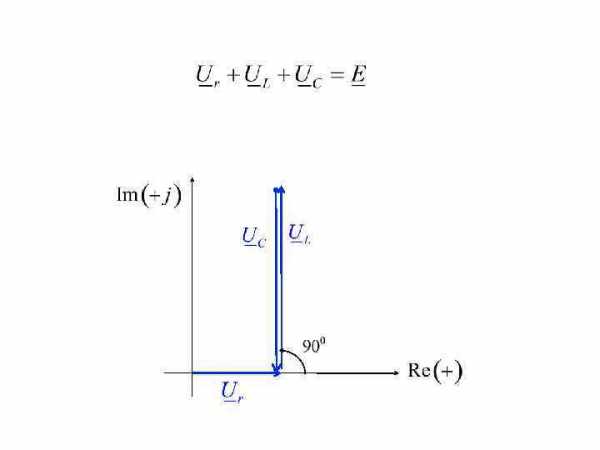
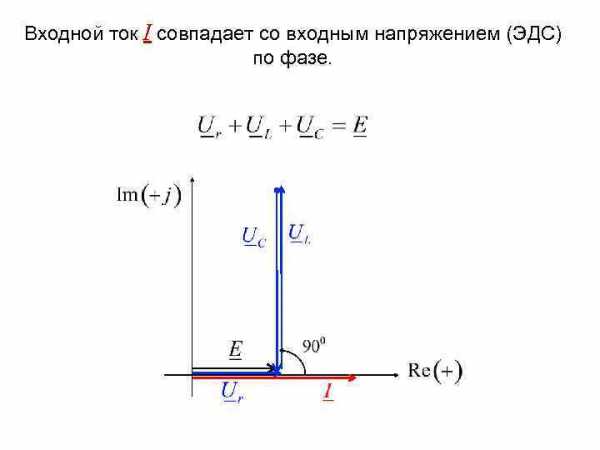Входной ток I совпадает со входным напряжением (ЭДС) по фазе.

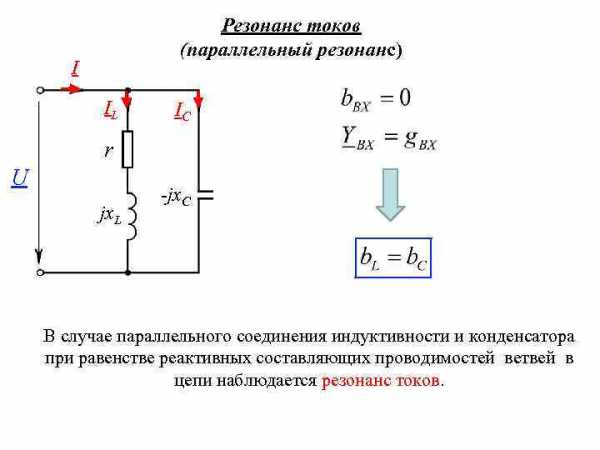Резонанс токов (параллельный резонанс) I IL IC r U jx. L -jx. C В случае параллельного соединения индуктивности и конденсатора при равенстве реактивных составляющих проводимостей ветвей в цепи наблюдается резонанс токов.

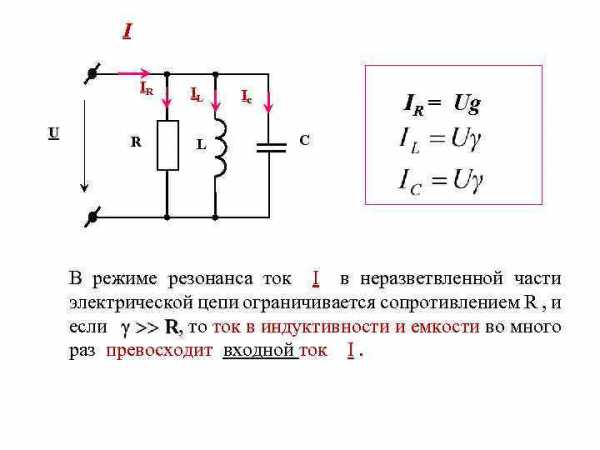I IR U R IL L Ic IR = Ug С В режиме резонанса ток I в неразветвленной части электрической цепи ограничивается сопротивлением R , и если , то ток в индуктивности и емкости во много раз превосходит входной ток I.

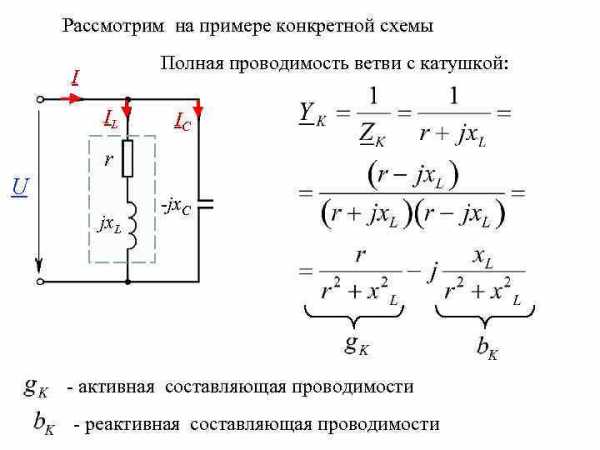Рассмотрим на примере конкретной схемы Полная проводимость ветви с катушкой: I IL IC r U jx. L -jx. C - активная составляющая проводимости - реактивная составляющая проводимости

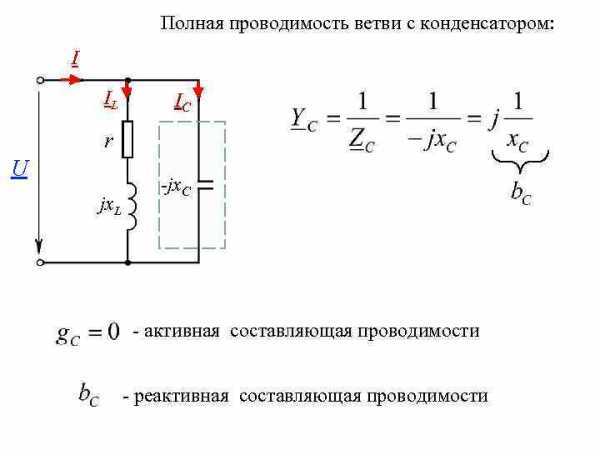Полная проводимость ветви с конденсатором: I IL IC r U jx. L -jx. C - активная составляющая проводимости - реактивная составляющая проводимости

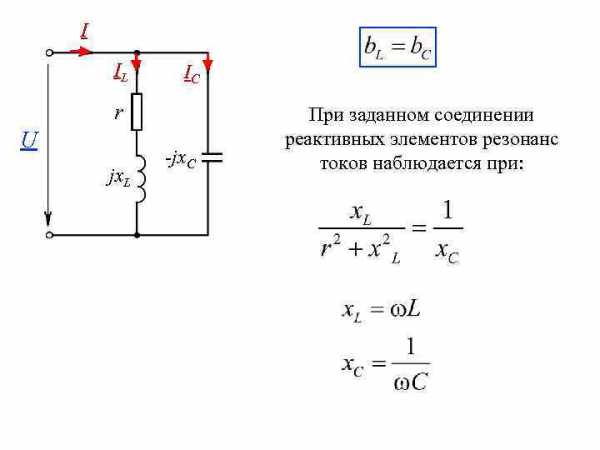I IL IC r U jx. L -jx. C При заданном соединении реактивных элементов резонанс токов наблюдается при:

Векторная диаграмма для случая резонанса токов. Уравнения, записанные по законам Кирхгофа для схемы: I IL r U jx. L IC U R -jx. C U L UC

Рассчитаем комплексные значения напряжений на участках электрической цепи и изобразим их на комплексной плоскости I IL r U jx. L IC U R -jx. C U L UC

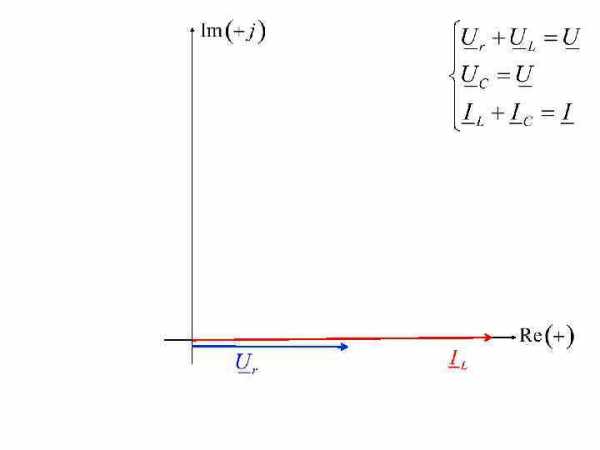
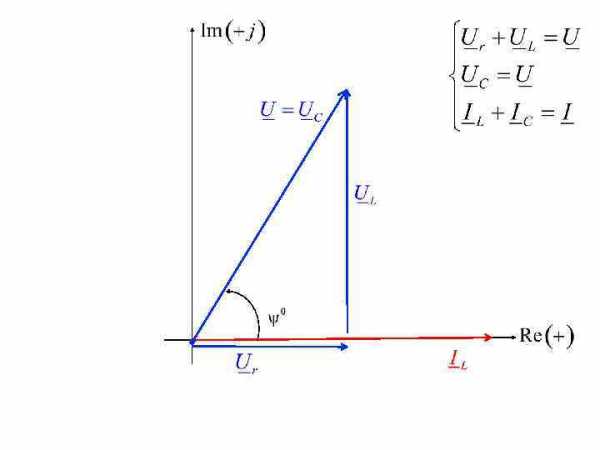
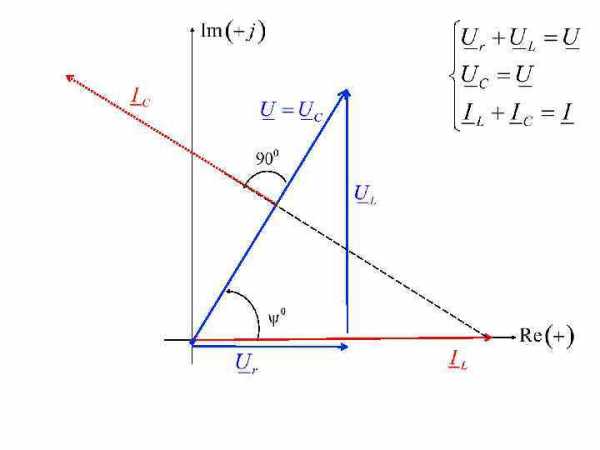
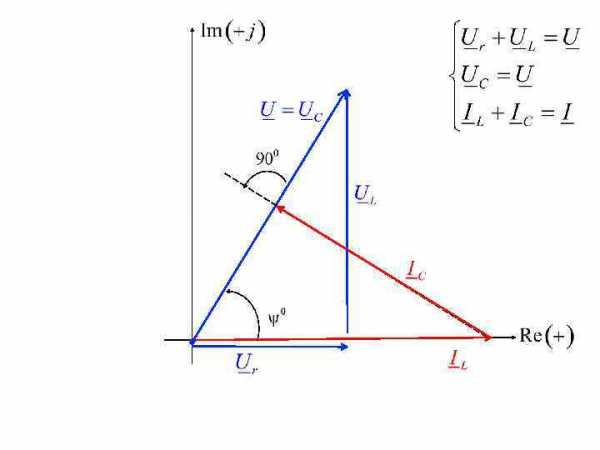
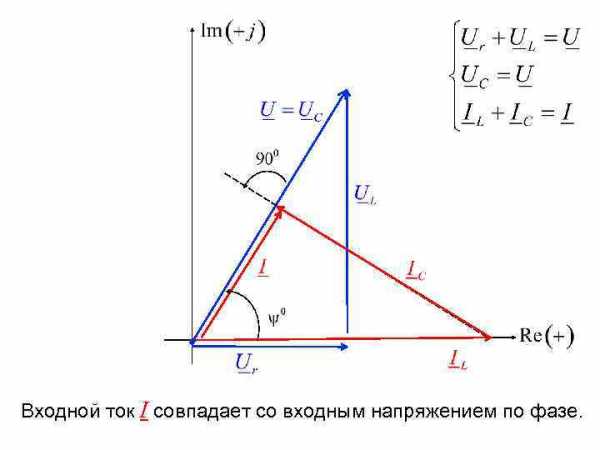Входной ток I совпадает со входным напряжением по фазе.

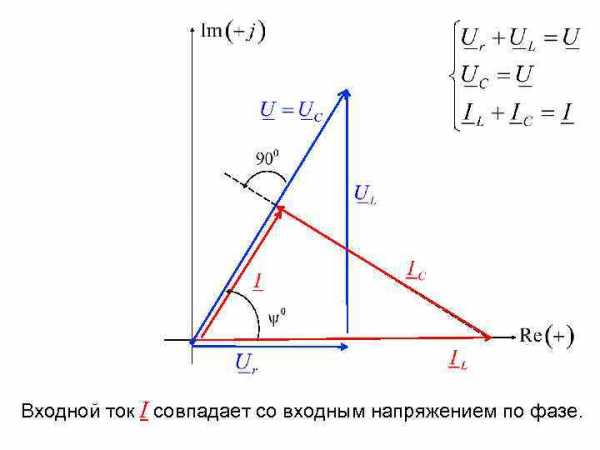Входной ток I совпадает со входным напряжением по фазе.

present5.com

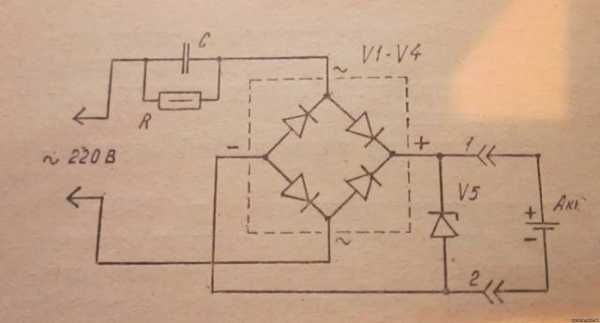
Баланс мощностей в электрической цепи

Если в рассматриваемойветви вместо резистора включен какой-либо другой преобразовательэлектромагнитной энергии в механическую или химическую, или другую формуэнергии (электрический мдвигатель, заряжающийся аккумулятор и т.п.), работу,проделанную током за время t, можно подсчитать в том случае, еслиизвестно напряжение на преобразователе.

Мощность, расходуемаяво всей внешней цепи, и мощность, отдаваемая генератором, одна и та жевеличина. Мощность, развиваемая генератором, всегда больше …

Согласно закону Джоуля—Ленца работа, совершаемая постоянным током в сопротивлении,

Если в рассматриваемой ветви вместо резистора включен какой-либо другой преобразователь электромагнитной энергии в механическую или химическую, или другую форму энергии (электрический двигатель, заряжающийся аккумулятор и т.п.), работу, проделанную током за время t, можно подсчитать в том случае, если известно напряжение на преобразователе.

В этом случае формула Джоуля—Ленца приобретает другой вид:

При постоянном токе мощность, поступающая в участок цепи с сопротивлением r, определяется выражением:

где I, U и r сохраняют тот же смысл, что и в формуле Джоуля—Ленца.

Мощность, расходуемая во всей внешней цепи, и мощность, отдаваемая генератором, одна и та же величина. Мощность, развиваемая генератором, всегда больше той, которую генератор отдает во внешнюю цепь, так как часть мощности расходуется на покрытие потерь внутри самого генератора.

Выражение баланса мощностей для одиночного замкнутого контура, содержащего генератор с э.д.с. Е и внутренним сопротивлением ri и резистор с сопротивлением r, можно получить из уравнения Кирхгофа.

Для этого контура

Если обе части этого равенства умножить на ток в цепи, то полученное уравнение и будет представлять собой баланс мощностей в данном контуре

Мощность, развиваемая генератором, равна сумме мощностей теряемой внутри генератора и отдаваемой во внешнюю цепь. Р0 = EI — мощность, развиваемая генератором, Pe = UI=I2r — мощность, отдаваемая генератором во внешнюю цепь, и Pi — I2ri — мощность, теряемая внутри самого генератора.

При выборе одинаковых положительных направлений тока через двухполюсник I и напряжения на двухполюснике U мощность, потребляемая двухполюсником, т. е. Произведение UI, должно быть положительно. Если же при этом окажется, что произведение UI отрицательно, это будет означать, что двухполюсник не потребляет электромагнитную энергию, а наоборот является генератором электромагнитной энергии и отдает эту энергию в электрическую цепь.

Если в электрической цепи ряд двухполюсников отдает электромагнитную энергию в цепь, то остальные эту энергию поглощают. В цепи при постоянном токе не может происходить накопления электромагнитной энергии. Поэтому сумма мощностей, расходуемых в пассивных двухполюсниках и мощностей, теряемых внутри генераторов, должна быть равна алгебраической сумме мощностей, развиваемых всеми генераторами, т. е. сумме произведений ЕкIк всех генераторов, действующих в цепи:

где n — число ветвей в цепи.

Уравнение баланса, полученное для простой цепи, содержащей один генератор, можно переписать, выразив мощность, расходуемую во внешней цепи, через мощность, развиваемую генератором, и мощность, теряемую внутри генератора:

10.12.2016 Без рубрики

talkipad.ru

---

• 
  Как сделать зарядное устройство для аккумулятора 12в из трансформатора
• 
  Какое наибольшее усилие на одну руку человека может приходиться при работе с измерительной штангой
• 
  Почему из крана холодной воды течет горячая вода
• 
  Как правильно научиться варить инверторной сваркой
• 
  Какая температура воды должна быть в батареях в отопительный сезон
• 
  Шестая планета от солнца это
• 
  Нагрузка трехфазная
• 
  Как подключить входной автомат
• 
  Токи обратной прямой и нулевой последовательности
• 
  В каких случаях требуется создание замкнутых схем эп
• 
  Двухполюсный автомат подключение