Частота в каких единицах измеряется: Единица измерения частоты, теория и онлайн калькуляторы

Формула циклической частоты. Циклическая частота – что и как? Непрямые методы измерения

ЧАСТОТА КОЛЕБАНИЙ, числоколебаний в 1 с. Обозначается.
Если T -периодот колебаний, то= 1/T; измеряется в герцах (Гц).Угловая
частотаколебаний= 2= 2/T
рад/с.

ПЕРИОД колебаний, наименьший промежуток
времени, через который совершающая
колебания системавозвращается в то же состояние, в котором
она находилась в начальный момент,
выбранный произвольно. Период -величина,
обратная частоте колебаний.Понятие»период» применимо, например, в
случае гармонических колебаний, однако
часто применяется и для слабо затухающих
колебаний.

Круговая или
циклическая частотаω

При изменении аргумента косинуса, либо
синуса на 2π эти функции возвращаются
к прежнему значению. Найдем промежуток
времени T, в течение которого фаза
гармонической функции изменяется на
2π .

ω(t + T) + α = ωt + α + 2π, или ωT = 2π.

Время T одного полного колебания
называется периодом колебания. Частотой
ν называют величину, обратную
периоду

Единица измерения частоты — герц (Гц),
1 Гц = 1 с -1 .

Круговая, или циклическая частоты ω в
2π раз больше частоты колебаний ν.
Круговая частота — это скорость изменения
фазы со временем. Действительно:

.

АМПЛИТУДА (от латинского amplitudo —
величина),
наибольшее отклонение от равновесного
значения величины, колеблющейся по
определенному, в том числе гармоническому,
закону; смотри такжеГармонические
колебания.

ФАЗА КОЛЕБАНИЙ аргумент функцииcos (ωt + φ), описывающей гармонический
колебательный процесс (ω — круговая
частота, t — время, φ — начальная
фаза колебаний, т. е. фаза колебаний вначальный
момент времениt = 0)

Смещение, скорость, ускорение колеблющейся системы частиц.

Энергия гармонических колебаний.

Гармонические колебания

Важным частным случаем периодических
колебаний являются гармонические
колебания, т.е. такие изменения физической
величины, которые идут по закону

где
.
Из курса математики известно, что
функция вида (1) меняется в пределах от
А до -А, и что наименьший положительный
период у нее.
Поэтому гармоническое колебание вида
(1) происходит с амплитудой А и периодом.

Не следует путать циклическую частоту
и
частоту колебаний.
Между ними простая связь. Так как,
а,
то.

Величина
называется
фазой колебания. При t=0 фаза равна,
потомуназывают
начальной фазой.

Отметим, что при одном и том же t:

где
—
начальная фаза.Видно, что начальная
фаза для одного и того же колебания
есть величина, определенная с точнотью
до.
Поэтому из множества возможных значений
начальной фазы выбирается обычно
значение начальной фазы наименьшее по
модулю или наименьшее положительное.
Но делать это необязательно. Например,
дано колебание,
то его удобно записать в видеи
работать в дальнейшем с последним видом
записи этого колебания.

Можно показать, что колебания вида:

где
имогут
быть любого знака, с помощью простых
тригонометрических преобразований
всегда приводится к виду (1), причем,,
ане
равна,
вообще говоря. Таким образом, колебания
вида (2) являются гармоническими с
амплитудойи
циклической частотой.
Не приводя общего доказательства,
проиллюстрируем это на конкретном
примере.

Пусть требуется показать, что колебание

будет гармоническим и найти амплитуду
,
циклическую частоту,
периоди
начальную фазу.
Действительно,

—

Видим, что колебание величины S удалось
записать в виде (1). При этом
,.

Попробуйте самостоятельно убедится,
что

.

Естественно, что запись гармонических
колебаний в форме (2) ничем не хуже записи
в форме (1), и переходить в конкретной
задаче от записи в данной форме к записи
в другой форме обычно нет необходимости.
Нужно только уметь сразу находить
амплитуду, циклическую частоту и период,
имея перед собой любую форму записи
гармонического колебания.

Иногда полезно знать характер изменения
первой и второй производных по времени
от величины S, которая совершает
гармонические колебания (колеблется
по гармоническому закону). Если
,
то дифференцирование S по времени t дает,.
Видно, что S» и S»» колеблются тоже по
гармоническому закону с той же циклической
частотой,
что и величина S, и амплитудамии,
соответственно. Приведем пример.

Пусть координата x тела, совершающего
гармонические колебания вдоль оси x,
изменяется по закону
,
где х в сантиметрах, время t в секундах.
Требуется записать закон изменения
скорости и ускорения тела и найти их
максимальные значения. Для ответа на
поставленный вопрос заметим, что первая
производная по времени от величины х
есть проекция скорости тела на ось х,
а вторая производная х есть проекция
ускорения на ось х:,.
Продифференцировав выражение для х по
времени, получим,.
Максимальные значения скорости и
ускорения:.

При изучении этого раздела следует иметь в виду, что колебания
различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.

Переходя к изучению электромагнитных волн нужно четко представлять, что
электромагнитная волна
— это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Таблица формул: колебания и волны

Физические законы, формулы, переменные	Формулы колебания и волны
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; α — начальная фаза; (ωt+α) — фаза.
Связь между периодом и круговой частотой:
Частота:
Связь круговой частоты с частотой:
Периоды собственных колебаний 1) пружинного маятника: где k — жесткость пружины; 2) математического маятника: где l — длина маятника, g — ускорение свободного падения; 3) колебательного контура: где L — индуктивность контура, С — емкость конденсатора.
Частота собственных колебаний:
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А 1 и А 2 — амплитуды составляющих колебаний, α 1 и α 2 — начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания
Уравнение затухающих колебаний: е = 2,71. .. — основание натуральных логарифмов.
Амплитуда затухающих колебаний: где А 0 — амплитуда в начальный момент времени; β — коэффициент затухания;
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура.
Частота затухающих колебаний ω:
Период затухающих колебаний Т:
Логарифмический декремент затухания:

Является герц (русское обозначение: Гц
; международное: Hz
), названный в честь немецкого физика Генриха Герца .

Частота обратно пропорциональна периоду колебаний : ν
= 1/T

.

Частота	1 мГц (10 −3 Гц)	1 Гц (10 0 Гц)	1 кГц (10 3 Гц)	1 МГц (10 6 Гц)	1 ГГц (10 9 Гц)	1 ТГц (10 12 Гц)
Период	1 кс (10 3 с)	1 с (10 0 с)	1 мс (10 −3 с)	1 мкс (10 −6 с)	1 нс (10 −9 с)	1 пс (10 −12 с)

В природе известны периодические процессы с частотами от ~10 −16 Гц
(частота обращения Солнца вокруг центра Галактики) до ~10 35 Гц
(частота колебаний поля, характерная для наиболее высокоэнергичных космических лучей).

Видео по теме

Круговая частота

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей: ω = 360°ν
.

Численно круговая частота равна числу колебаний (оборотов) за 2π
секунд. Введение круговой частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная круговая частота колебательного LC-контура равна
ω
L
C
=
1
/
L
C
,
{\displaystyle \omega _{LC}=1/{\sqrt {LC}},}
тогда как циклическая резонансная частота
ν
L
C
=
1
/
(2
π
L
C)
.
{\displaystyle \nu _{LC}=1/(2\pi {\sqrt {LC}}).}
В то же время ряд других формул усложняется. Решающим соображением в пользу круговой частоты стало то, что множители
2
π
{\displaystyle 2\pi }
и
1
/
2
π
{\displaystyle 1/2\pi }
, появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении круговой (угловой) частоты.

В механике при рассмотрении вращательного движения аналогом круговой частоты служит угловая скорость .

Частота дискретных событий

Частота дискретных событий (например, частота следования импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий — секунда в минус первой степени (русское обозначение: с −1
; международное: s −1
). Частота 1 с −1 равна такой частоте дискретных событий, при которой за время 1 с происходит одно событие .

Частота вращения

Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с −1
, s −1
), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.

Другие величины, связанные с частотой

Единицы измерения

В системе СИ единицей измерения циклической частоты является герц (Гц, Hz). Единица была первоначально введена в 1930 году
Международной электротехнической комиссией , а в 1960 году
принята для общего употребления 11-й Генеральной конференцией по мерам и весам , как единица СИ. До этого в качестве единицы циклической частоты использовался цикл в секунду
(1 цикл
в секунду = 1 Гц
) и производные (килоцикл в секунду, мегацикл в секунду, киломегацикл в секунду, равные соответственно килогерцу, мегагерцу и гигагерцу).

Метрологические аспекты

Для измерения частоты применяются частотомеры разных видов, в том числе: для измерения частоты следования импульсов — электронно-счётные и конденсаторные, для определения частот спектральных составляющих — резонансные и гетеродинные частотомеры, а также анализаторы спектра . Для воспроизведения частоты с заданной точностью используют различные меры — стандарты частоты (высокая точность), синтезаторы частот , генераторы сигналов и др. Сравнивают частоты компаратором частоты или с помощью осциллографа по фигурам Лиссажу .

Эталоны

Для поверки средств измерения частоты используются национальные эталоны частоты. В России к национальным эталонам частоты относятся:

• Государственный первичный эталон единиц времени, частоты и национальной шкалы времени ГЭТ 1-98 — находится во ВНИИФТРИ .
• Вторичный эталон единицы времени и частоты ВЭТ 1-10-82
  — находится в СНИИМ (Новосибирск).

Вычисления

Вычисление частоты повторяющегося события осуществляется посредством учета количества появлений этого события в течение заданного периода времени . Полученное количество делится на продолжительность соответствующего временного отрезка. К примеру, если на протяжении 15 секунд произошло 71 однородное событие, то частота составит

ν
=
71
15
s
≈
4.7
Hz
{\displaystyle \nu ={\frac {71}{15\,{\mbox{s}}}}\approx 4.7\,{\mbox{Hz}}}

Если полученное количество отсчетов невелико, то более точным приемом является измерение временного интервала для заданного числа появлений рассматриваемого события, а не нахождение количества событий в пределах заданного промежутка времени . Использование последнего метода вводит между нулевым и первым отсчетом случайную ошибку, составляющую в среднем половину отсчета; это может приводить к появлению средней ошибки в вычисляемой частоте Δν = 1/(2 T m
)
, или же относительной погрешности Δν
/ν
= 1/(2v
T m )

, где
T m — временной интервал, а ν
— измеряемая частота. Ошибка убывает по мере возрастания частоты, поэтому данная проблема является наиболее существенной для низких частот, где количество отсчетов
N мало.

Методы измерения

Стробоскопический метод

Использование специального прибора — стробоскопа — является одним из исторически ранних методов измерения частоты вращения или вибрации различных объектов. В процессе измерения задействуется стробоскопический источник света (как правило, яркая лампа, периодически дающая короткие световые вспышки), частота работы которого подстраивается при помощи предварительно откалиброванной хронирующей цепи. Источник света направляется на вращающийся объект, а затем частота вспышек постепенно изменяется. Когда частота вспышек уравнивается с частотой вращения или вибрации объекта, последний успевает совершить полный колебательный цикл и вернуться в изначальное положение в промежутке между двумя вспышками, так что при освещении стробоскопической лампой этот объект будет казаться неподвижным. У данного метода, впрочем, есть недостаток: если частота вращения объекта (x

) не равна частоте строба (y

), но пропорциональна ей с целочисленным коэффициентом (2x

, 3x

и т. п.), то объект при освещении все равно будет выглядеть неподвижным.

Стробоскопический метод используется также для точной настройки частоты вращения (колебаний). В этом случае частота вспышек фиксирована, а изменяется частота периодического движения объекта до тех пор, пока он не начинает казаться неподвижным.

Метод биений

Близким к стробоскопическому методу является метод биений . Он основан на том, что при смешивании колебаний двух частот (опорной ν

и измеряемой ν» 1

) в нелинейной цепи в спектре колебаний появляется также разностная частота Δν = |

ν −
ν» 1 |, называемая частотой биений (при линейном сложении колебаний эта частота является частотой огибающей суммарного колебания). Метод применим, когда более предпочтительным является измерение низкочастотных колебаний с частотой Δf

. В радиотехнике этот метод также известен под названием гетеродинного метода измерения частоты. В частности, метод биений используется для точной настройки музыкальных инструментов. В этом случае звуковые колебания фиксированной частоты (например, от камертона), прослушиваемые одновременно со звуком настраиваемого инструмента, создают периодическое усиление и ослабление суммарного звучания. При точной настройке инструмента частота этих биений стремится к нулю.

Применение частотомера

Высокие частоты обычно измеряются при помощи частотомера . Это электронный прибор , который оценивает частоту определенного повторяющегося сигнала и отображает результат на цифровом дисплее или аналоговом индикаторе. Дискретные логические элементы цифрового частотомера позволяют учитывать количество периодов колебаний сигнала в пределах заданного промежутка времени, отсчитываемого по эталонным кварцевым часам . Периодические процессы, которые не являются по своей природе электрическими (такие, к примеру, как вращение оси , механические вибрации или звуковые волны), могут быть переведены в периодический электрический сигнал при помощи измерительного преобразователя и в таком виде поданы на вход частотомера. В настоящее время приборы этого типа способны охватывать диапазон вплоть до 100 Гц; этот показатель представляет собой практический потолок для методов прямого подсчёта. Более высокие частоты измеряются уже непрямыми методами.

Непрямые методы измерения

Вне пределов диапазона, доступного частотомерам, частоты электромагнитных сигналов нередко оцениваются опосредованно, с помощью гетеродинов (то есть частотных преобразователей). Опорный сигнал заранее известной частоты объединяется в нелинейном смесителе (таком, к примеру, как диод) с сигналом, частоту которого необходимо установить; в результате формируется гетеродинный сигнал, или — альтернативно — биения , порождаемые частотными различиями двух исходных сигналов. Если последние достаточно близки друг к другу по своим частотным характеристикам, то гетеродинный сигнал оказывается достаточно мал, чтобы его можно было измерить тем же частотомером. Соответственно, в результате этого процесса оценивается лишь отличие неизвестной частоты от опорной, каковую следует определять уже иными методами. Для охвата ещё более высоких частот могут быть задействованы несколько стадий смешивания. В настоящее время ведутся исследования, нацеленные на расширение этого метода в направлении инфракрасных и видимо-световых частот (т. н. оптическое гетеродинное детектирование).

Примеры

Электромагнитное излучение

Полный спектр электромагнитного излучения с выделенной видимой частью

Видимый свет представляет собой электромагнитные волны , состоящие из осциллирующих электрических и магнитных полей, перемещающихся в пространстве. Частота волны определяет её цвет: 4×10 14 Гц
— красный цвет , 8×10 14 Гц
— фиолетовый цвет ; между ними в диапазоне (4…8)×10 14 Гц
лежат все остальные цвета радуги. Электромагнитные волны, имеющие частоту менее 4×10 14 Гц
, невидимы для человеческого глаза, такие волны называются инфракрасным (ИК) излучением . Ниже по спектру лежит микроволновое излучение и радиоволны . Свет с частотой выше, чем 8×10 14 Гц
, также невидим для человеческого глаза; такие электромагнитные волны называются ультрафиолетовым (УФ) излучением . При увеличении частоты электромагнитная волна переходит в область спектра, где расположено рентгеновское излучение , а при ещё более высоких частотах — в область гамма-излучения .

Все эти волны, от самых низких частот радиоволн и до высоких частот гамма-лучей, принципиально одинаковы, и все они называются электромагнитным излучением. Все они распространяются в вакууме со скоростью света .

Другой характеристикой электромагнитных волн является длина волны . Длина волны обратно пропорциональна частоте, так что электромагнитные волны с более высокой частотой имеет более короткую длину волны, и наоборот. В вакууме длина волны

λ
=
c
/
ν
,
{\displaystyle \lambda =c/\nu ,}

где с

— скорость света в вакууме. В среде, в которой фазовая скорость распространения электромагнитной волны c
′
отличается от скорости света в вакууме (c
′ = c/n

, где n

— показатель преломления), связь между длиной волны и частотой будет следующей:

λ
=
c
n
ν
.
{\displaystyle \lambda ={\frac {c}{n\nu }}.}

Ещё одна часто использующаяся характеристика волны — волновое число (пространственная частота), равное количеству волн, укладывающихся на единицу длины: k
= 1/λ
. Иногда эта величина используется с коэффициентом 2π
, по аналогии с циклической и круговой частотой k
s = 2π/λ
. В случае электромагнитной волны в среде

k
=
1
/
λ
=
n
ν
c
.
{\displaystyle k=1/\lambda ={\frac {n\nu }{c}}. }

k
s
=
2
π
/
λ
=
2
π
n
ν
c
=
n
ω
c
.
{\displaystyle k_{s}=2\pi /\lambda ={\frac {2\pi n\nu }{c}}={\frac {n\omega }{c}}.}

Звук

Свойства звука (механических упругих колебаний среды) зависят от частоты. Человек может слышать колебания с частотой от 20 Гц
до 20 кГц
(с возрастом верхняя граница частоты слышимого звука снижается). Звук с частотой более низкой, чем 20 Гц
(соответствует ноте ми

Гармонические колебания – колебания, совершаемые по законам синуса и косинуса. На следующем рисунке представлен график изменения координаты точки с течением времени по закону косинуса.

картинка

Амплитуда колебаний

Амплитудой гармонического колебания называется наибольшее значение смещения тела от положения равновесия. Амплитуда может принимать различные значения. Она будет зависеть от того, насколько мы сместим тело в начальный момент времени от положения равновесия.

Амплитуда определяется начальными условиями, то есть энергией сообщаемой телу в начальный момент времени. Так как синус и косинус могут принимать значения в диапазоне от -1 до 1, то в уравнении должен присутствовать множитель Xm, выражающий амплитуду колебаний. Уравнение движения при гармонических колебаниях:

x = Xm*cos(ω0*t).

Период колебаний

Период колебаний – это время совершения одного полного колебания. Период колебания обозначается буквой Т. Единицы измерения периода соответствуют единицам времени. То есть в СИ — это секунды.

Частота колебаний – количество колебаний совершенных в единицу времени. Частота колебаний обозначается буквой ν. Частоту колебаний можно выразить через период колебания.

ν = 1/Т.

Единицы измерения частоты в СИ 1/сек. Эта единица измерения получила название Герца. Число колебаний за время 2*pi секунд будет равняться:

ω0 = 2*pi* ν = 2*pi/T.

Частота колебаний

Данная величина называется циклической частотой колебаний. В некоторой литературе встречается название круговая частота. Собственная частота колебательной системы – частота свободных колебаний.

Частота собственных колебаний рассчитывается по формуле:

Частота собственных колебаний зависит от свойств материала и массы груза. Чем больше жесткость пружины, тем больше частота собственных колебаний. Чем больше масса груза, тем меньше частота собственных колебаний.

Эти два вывода очевидны. Чем более жесткая пружина, тем большее ускорение она сообщит телу, при выведении системы из равновесия. Чем больше масса тела, тем медленнее будет изменяться это скорость этого тела.

Период свободных колебаний
:

T = 2*pi/ ω0 = 2*pi*√(m/k)

Примечателен тот факт, что при малых углах отклонения период колебания тела на пружине и период колебания маятника не будут зависеть от амплитуды колебаний.

Запишем формулы периода и частоты свободных колебаний для математического маятника.

тогда период будет равен

T = 2*pi*√(l/g).

Данная формула будет справедлива лишь для малых углов отклонения. Из формулы видим, что период колебаний возрастает с увеличением длины нити маятника. Чем больше будет длина, тем медленнее тело будет колебаться.

От массы груза период колебаний совершенно не зависит. Зато зависит от ускорения свободного падения. При уменьшении g, период колебаний будет увеличиваться. Данное свойство широко используют на практике. Например, для измерения точного значения свободного ускорения.

Всё на планете имеет свою частоту. Согласно одной из версий, она даже положена в основу нашего мира. Увы, теория весьма сложна, чтобы излагать её в рамках одной публикации, поэтому нами будет рассмотрена исключительно частота колебаний как самостоятельное действие. В рамках статьи будет дано определения этому физическому процессу, его единицам измерений и метрологической составляющей. И под конец будет рассмотрен пример важности в обычной жизни обыкновенного звука. Мы узнаем, что он собой представляет и какова его природа.

Что называют частотой колебаний?

Под этим подразумевают физическую величину, которая используется для характеристики периодического процесса, что равен количеству повторений или возникновений определённых событий за одну единицу времени. Этот показатель рассчитывается как отношение числа данных происшествий к промежутку времени, за который они были совершены. Собственная частота колебаний есть у каждого элемента мира. Тело, атом, дорожный мост, поезд, самолёт — все они совершают определённые движения, которые так называются. Пускай эти процессы не видны глазу, они есть. Единицами измерений, в которых считается частота колебаний, являются герцы. Своё название они получили в честь физика немецкого происхождения Генриха Герца.

Мгновенная частота

Периодический сигнал можно охарактеризовать мгновенной частотой, которая с точностью до коэффициента является скоростью изменения фазы. Его можно представить как сумму гармонических спектральных составляющих, обладающих своими постоянными колебаниями.

Циклическая частота колебаний

Её удобно применять в теоретической физике, особенно в разделе про электромагнетизм. Циклическая частота (её также называют радиальной, круговой, угловой) — это физическая величина, которая используется для обозначения интенсивности происхождения колебательного или вращательного движения. Первая выражается в оборотах или колебаниях на секунду. При вращательном движении частота равняется модулю вектора угловой скорости.

Выражение этого показателя осуществляется в радианах на одну секунду. Размерность циклической частоты является обратной времени. В числовом выражении она равняется числу колебаний или оборотов, что произошли за количество секунд 2π. Её введения для использования позволяет значительно упрощать различный спектр формул в электронике и теоретической физике. Самый популярный пример использования — это обсчёт резонансной циклической частоты колебательного LC-контура. Другие формулы могут значительно усложняться.

Частота дискретных событий

Под этой величиной подразумевают значение, что равно числу дискретных событий, которые происходят за одну единицу времени. В теории обычно используется показатель — секунда в минус первой степени. На практике, чтобы выразить частоту импульсов, обычно применяют герц.

Частота вращения

Под нею понимают физическую величину, которая равняется числу полных оборотов, что происходят за одну единицу времени. Здесь также применяется показатель — секунда в минус первой степени. Для обозначения сделанной работы могут использовать такие словосочетания, как оборот в минуту, час, день, месяц, год и другие.

Единицы измерения

В чём же измеряется частота колебаний? Если брать во внимание систему СИ, то здесь единица измерения — это герц. Первоначально она была введена международной электротехнической комиссией ещё в 1930 году. А 11-я генеральная конференция по весам и мерам в 1960-м закрепила употребление этого показателя как единицы СИ. Что было выдвинуто в качестве «идеала»? Им выступила частота, когда один цикл совершается за одну секунду.

Но что делать с производством? Для них были закреплены произвольные значения: килоцикл, мегацикл в секунду и так далее. Поэтому беря в руки устройство, которое работает с показателем в ГГц (как процессор компьютера), можете примерно представить, сколько действий оно совершает. Казалось бы, как медленно для человека тянется время. Но техника за тот же промежуток успевает выполнять миллионы и даже миллиарды операций в секунду. За один час компьютер делает уже столько действий, что большинство людей даже не смогут представить их в численном выражении.

Метрологические аспекты

Частота колебаний нашла своё применение даже в метрологии. Различные устройства имеют много функций:

1. Измеряют частоту импульсов. Они представлены электронно-счётными и конденсаторными типами.
2. Определяют частоту спектральных составляющих. Существуют гетеродинные и резонансные типы.
3. Производят анализ спектра.
4. Воспроизводят необходимую частоту с заданной точностью. При этом могут применяться различные меры: стандарты, синтезаторы, генераторы сигналов и другая техника этого направления.
5. Сравнивают показатели полученных колебаний, в этих целях используют компаратор или осциллограф.

Пример работы: звук

Всё выше написанное может быть довольно сложным для понимания, поскольку нами использовался сухой язык физики. Чтобы осознать приведённую информацию, можно привести пример. В нём всё будет детально расписано, основываясь на анализе случаев из современной жизни. Для этого рассмотрим самый известный пример колебаний — звук. Его свойства, а также особенности осуществления механических упругих колебаний в среде, находятся в прямой зависимости от частоты.

Человеческие органы слуха могут улавливать колебания, которые находятся в рамках от 20 Гц до 20 кГц. Причём с возрастом верхняя граница будет постепенно снижаться. Если частота колебаний звука упадёт ниже показателя в 20 Гц (что соответствует ми субконтроктавы), то будет создаваться инфразвук. Этот тип, который в большинстве случаев не слышен нам, люди всё же могут ощущать осязательно. При превышении границы в 20 килогерц генерируются колебания, которые называются ультразвуком. Если частота превысит 1 ГГц, то в этом случае мы будем иметь дело с гиперзвуком. Если рассматривать такой музыкальный инструмент, как фортепиано, то он может создавать колебания в диапазоне от 27,5 Гц до 4186 Гц. При этом следует учитывать, что музыкальный звук не состоит только из основной частоты — к нему ещё примешиваются обертоны, гармоники. Это всё вместе определяет тембр.

Заключение

Как вы имели возможность узнать, частота колебаний является чрезвычайно важной составляющей, которая позволяет функционировать нашему миру. Благодаря ей мы можем слышать, с её содействия работают компьютеры и осуществляется множество других полезных вещей. Но если частота колебаний превысит оптимальный предел, то могут начаться определённые разрушения. Так, если повлиять на процессор, чтобы его кристалл работал с вдвое большими показателями, то он быстро выйдет из строя.

Подобное можно привести и с человеческой жизнью, когда при высокой частотности у него лопнут барабанные перепонки. Также произойдут другие негативные изменения с телом, которые повлекут за собой определённые проблемы, вплоть до смертельного исхода. Причём из-за особенности физической природы этот процесс растянется на довольно длительный промежуток времени. Кстати, беря во внимание этот фактор, военные рассматривают новые возможности для разработки вооружения будущего.

Конвертер частоты и длины волны • Фотометрия — свет • Компактный калькулятор • Онлайн-конвертеры единиц измерения

Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева

Период колебания волн у берегов Майами-Бич приблизительно равен 4 секундам.

Общие сведения

Частота

Частота — это величина, измеряющая как часто повторяется тот или иной периодический процесс. В физике с помощью частоты описывают свойства волновых процессов. Частота волны — количество полных циклов волнового процесса за единицу времени. Единица частоты в системе СИ — герц (Гц). Один герц равен одному колебанию в секунду.

Длина волны

Существует множество различных типов волн в природе, от вызванных ветром морских волн до электромагнитных волн. Свойства электромагнитных волн зависят от длины волны. Такие волны разделяют на несколько видов:

Резонансный магнетрон используется в микроволновых печах для подачи электромагнитной энергии в камеру печи.

• Гамма-лучи с длиной волны до 0,01 нанометра (нм).
• Рентгеновские лучи с длиной волны — от 0,01 нм до 10 нм.
• Волны ультрафиолетового диапазона, которые имеют длину от 10 до 380 нм. Человеческому глазу они не видимы.
• Свет в видимой части спектра с длиной волны 380–700 нм.
• Невидимое для людей инфракрасное излучение с длиной волны от 700 нм до 1 миллиметра.
• За инфракрасными волнами следуют микроволновые, с длиной волны от 1 миллиметра до 1 метра.
• Самые длинные — радиоволны. Их длина начинается с 1 метра.

Эта статья посвящена электромагнитному излучению, и особенно свету. В ней мы обсудим, как длина и частота волны влияют на свет, включая видимый спектр, ультрафиолетовое и инфракрасное излучение.

Электромагнитное излучение

Электромагнитное излучение — это энергия, свойства которой одновременно сходны со свойствами волн и частиц. Эта особенность называется корпускулярно-волновым дуализмом. Электромагнитные волны состоят из магнитной волны и перпендикулярной к ней электрической волны.

Энергия электромагнитного излучения — результат движения частиц, которые называются фотонами. Чем выше частота излучения, тем они более активны, и тем больше вреда они могут принести клеткам и тканям живых организмов. Это происходит потому, что чем выше частота излучения, тем больше они несут энергии. Большая энергия позволяет им изменить молекулярную структуру веществ, на которые они действуют. Именно поэтому ультрафиолетовое, рентгеновское и гамма излучение так вредно для животных и растений. Огромная часть этого излучения — в космосе. Оно присутствует и на Земле, несмотря на то, что озоновый слой атмосферы вокруг Земли блокирует большую его часть.

Атмосфера пропускает СВЧ-излучение в диапазоне частот C (с частотой от 4 до 8 Гц и с длиной волны от 7,5 до 3,75 сантиметров), которые используются для спутниковой связи

Электромагнитное излучение и атмосфера

Атмосфера земли пропускает только электромагнитное излучение с определенной частотой. Большая часть гамма-излучения, рентгеновских лучей, ультрафиолетового света, часть излучения в инфракрасном диапазоне и длинные радиоволны блокируются атмосферой Земли. Атмосфера поглощает их и не пропускает дальше. Часть электромагнитных волн, в частности, излучение в коротковолновом диапазоне, отражается от ионосферы. Все остальное излучение попадает на поверхность Земли. В верхних атмосферных слоях, то есть, дальше от поверхности Земли, больше радиации, чем в нижних слоях. Поэтому чем выше, тем опаснее для живых организмов находиться там без защитных костюмов.

Атмосфера пропускает на Землю небольшое количество ультрафиолетового света, и он приносит вред коже. Именно из-за ультрафиолетовых лучей люди обгорают на солнце и могут даже заболеть раком кожи. С другой стороны, некоторые лучи, пропускаемые атмосферой, приносят пользу. Например, инфракрасные лучи, которые попадают на поверхность Земли, используют в астрономии — инфракрасные телескопы следят за инфракрасными лучами, излучаемыми астрономическими объектами. Чем выше от поверхности Земли, тем больше инфракрасного излучения, поэтому телескопы часто устанавливают на вершинах гор и на других возвышенностях. Иногда их отправляют в космос, чтобы улучшить видимость инфракрасных лучей.

Этот осциллограф, который измеряет сетевое напряжение в розетке, показывает частоту в 59,7 герц и период колебаний 117 миллисекунд

Взаимоотношение между частотой и длиной волны

Частота и длина волны обратно пропорциональны друг другу. Это значит, что по мере увеличения длины волны частота уменьшается и наоборот. Это легко представить: если частота колебаний волнового процесса высокая, то время между колебаниями намного короче, чем у волн, частота колебаний которых меньше. Если представить волну на графике, то расстояние между ее пиками будет тем меньше, чем больше колебаний она совершает на определенном отрезке времени.

Чтобы определить скорость распространения волны в среде, необходимо умножить частоту волны на ее длину. Электромагнитные волны в вакууме всегда распространяются с одинаковой скоростью. Эта скорость известна как скорость света. Она равна 299&nbsp792&nbsp458 метрам в секунду.

Свет

Видимый свет — электромагнитные волны с частотой и длиной, которые определяют его цвет.

Длина волны и цвет

Самая короткая длина волны видимого света — 380 нанометров. Это фиолетовый цвет, за ним следуют синий и голубой, затем зеленый, желтый, оранжевый и, наконец, красный. Белый свет состоит из всех цветов сразу, то есть, белые предметы отражают все цвета. Это можно увидеть с помощью призмы. Попадающий в нее свет преломляется и выстраивается в полосу цветов в той же последовательность, что в радуге. Эта последовательность — от цветов с самой короткой длиной волны, до самой длинной. Зависимость скорости распространения света в веществе от длины волны называется дисперсией.

Радуга над рекой Ниагара

Радуга образуется похожим способом. Капли воды, рассеянные в атмосфере после дождя, ведут себя так же как призма и преломляют каждую волну. Цвета радуги настолько важны, что во многих языках существуют мнемоника, то есть прием запоминания цветов радуги, настолько простой, что запомнить их могут даже дети. Многие дети, говорящие по-русски, знают, что «Каждый охотник желает знать, где сидит фазан». Некоторые люди придумывают свою мнемонику, и это — особенно полезное упражнение для детей, так как, придумав свой собственный метод запоминания цветов радуги, они быстрее их запомнят.

Свет, к которому человеческий глаз наиболее чувствителен — зеленый, с длиной волны в 555 нм в светлой среде и 505 нм в сумерках и темноте. Различать цвета могут далеко не все животные. У кошек, например, цветное зрение не развито. С другой стороны, некоторые животные видят цвета намного лучше, чем люди. Например, некоторые виды видят ультрафиолетовый и инфракрасный свет.

Отражение света

Бриллиантовое кольцо

Цвет предмета определяется длиной волны света, отраженного с его поверхности. Белые предметы отражают все волны видимого спектра, в то время как черные — наоборот, поглощают все волны и ничего не отражают.

На первом рисунке: правильная огранка бриллиантов. Свет отражается вверх, по направлению к глазу и алмаз сверкает. На втором и третьем рисунках: неправильная огранка. Свет отражается в оправу и в стороны и алмазы выглядят тусклыми.

Один из естественных материалов с высоким коэффициентом дисперсии — алмаз. Правильно обработанные бриллианты отражают свет как от наружных, так и от внутренних граней, преломляя его, как и призма. При этом важно, чтобы большая часть этого света была отражена вверх, в сторону глаза, а не, например, вниз, внутрь оправы, где его не видно. Благодаря высокой дисперсии бриллианты очень красиво сияют на солнце и при искусственном освещении. Стекло, ограненное так же, как бриллиант, тоже сияет, но не настолько сильно. Это связано с тем, что, благодаря химическому составу, алмазы отражают свет намного лучше, чем стекло. Углы, используемые при огранке бриллиантов, имеет огромное значение, потому что слишком острые или слишком тупые углы либо не позволяют свету отражаться от внутренних стен, либо отражают свет в оправу, как показано на иллюстрации.

Спектроскопия

Для определения химического состава вещества иногда используют спектральный анализ или спектроскопию. Этот способ особенно хорош, если химический анализ вещества невозможно провести, работая с ним непосредственно, например, при определении химического состава звезд. Зная, какое электромагнитное излучение поглощает тело, можно определить, из чего оно состоит. Абсорбционная спектроскопия, являющаяся одним из разделов спектроскопии, определяет какое излучение поглощается телом. Такой анализ можно делать на расстоянии, поэтому его часто используют в астрономии, а также в работе с ядовитыми и опасными веществами.

Определение наличия электромагнитного излучения

Видимый свет, так же как и всё электромагнитное излучение — это энергия. Чем больше энергии излучается, тем легче эту радиацию измерить. Количество излученной энергии уменьшается по мере увеличения длины волны. Зрение возможно именно благодаря тому, что люди и животные распознают эту энергию и чувствуют разницу между излучением с разной длиной волны. Электромагнитное излучение разной длины ощущается глазом как разные цвета. По такому принципу работают не только глаза животных и людей, но и технологии, созданные людьми для обработки электромагнитного излучения.

Видимый свет

Люди и животные видят большой спектр электромагнитного излучения. Большинство людей и животных, например, реагируют на видимый свет, а некоторые животные — еще и на ультрафиолетовые и инфракрасные лучи. Способность различать цвета — не у всех животных — некоторые, видят только разницу между светлыми и темными поверхностями. Наш мозг определяет цвет так: фотоны электромагнитного излучения попадают в глаз на сетчатку и, проходя через нее, возбуждают колбочки, фоторецепторы глаза. В результате по нервной системе передается сигнал в мозг. Кроме колбочек, в глазах есть и другие фоторецепторы, палочки, но они не способны различать цвета. Их назначение — определять яркость и силу света.

Колбочки в сетчатке глаза чаек и многих других птиц содержит капли красного или желтого масла

В глазу обычно находится несколько видов колбочек. У людей — три типа, каждый из которых поглощает фотоны света в пределах определенных длин волны. При их поглощении происходит химическая реакция, в результате которой в мозг поступают нервные импульсы с информацией о длине волны. Эти сигналы обрабатывает зрительная зона коры головного мозга. Это — участок мозга, ответственный за восприятие звука. Каждый тип колбочек отвечает только за волны с определенной длиной, поэтому для получения полного представления о цвете, информацию, полученную от всех колбочек, складывают вместе.

У некоторых животных еще больше видов колбочек, чем у людей. Так, например, у некоторых видов рыб и птиц их от четырех до пяти типов. Интересно, что у самок некоторых животных больше типов колбочек, чем у самцов. У некоторых птиц, например у чаек, которые ловят добычу в воде или на ее поверхности, внутри колбочек есть желтые или красные капли масла, которые выступают в роли фильтра. Это помогает им видеть большее количество цветов. Подобным образом устроены глаза и у рептилий.

Этот инфракрасный термометр определяет температуру измеряемого объекта на расстоянии, по его тепловому излучению

Инфракрасный свет

У змей, в отличие от людей, не только зрительные рецепторы, но и чувствительные органы, которые реагируют на инфракрасное излучение. Они поглощают энергию инфракрасный лучей, то есть реагируют на тепло. Некоторые устройства, например приборы ночного видения, также реагируют на тепло, выделяемое инфракрасным излучателем. Такие устройства используют военные, а также для обеспечения безопасности и охраны помещений и территории. Животные, которые видят инфракрасный свет, и устройства, которые могут его распознавать, видят не только предметы, которые находятся в их поле зрения на данный момент, но и следы предметов, животных, или людей, которые находились там до этого, если не прошло слишком много времени. Например, змеям видно, если грызуны копали в земле ямку, а полицейские, которые пользуются прибором ночного видения, видят, если в земле были недавно спрятаны следы преступления, например, деньги, наркотики, или что-то другое. Устройства для регистрации инфракрасного излучения используют в телескопах, а также для проверки контейнеров и камер на герметичность. С их помощью хорошо видно место утечки тепла. В медицине изображения в инфракрасном свете используют для диагностики. В истории искусства — чтобы определить, что изображено под верхним слоем краски. Устройства ночного видения используют для охраны помещений.

Обыкновенная или зеленая игуана видит ультрафиолетовый свет. Фотография размещена с разрешения автора

Ультрафиолетовый свет

Некоторые рыбы видят ультрафиолетовый свет. Их глаза содержат пигмент, чувствительный к ультрафиолетовым лучам. Кожа рыб содержит участки, отражающие ультрафиолетовый свет, невидимый для человека и других животных — что часто используется в животном мире для маркировки пола животных, а также в социальных целях. Некоторые птицы тоже видят ультрафиолетовый свет. Это умение особенно важно во время брачного периода, когда птицы ищут потенциальных партнеров. Поверхности некоторых растений также хорошо отражают ультрафиолетовый свет, и способность его видеть помогает в поиске пищи. Кроме рыб и птиц, ультрафиолетовый свет видят некоторые рептилии, например черепахи, ящерицы и зеленые игуаны (на иллюстрации).

Человеческий глаз, как и глаза животных, поглощает ультрафиолетовый свет, но не может его обработать. У людей он разрушает клетки глаза, особенно в роговице и хрусталике. Это, в свою очередь, вызывает различные заболевания и даже слепоту. Несмотря на то, что ультрафиолетовый свет вредит зрению, небольшое его количество необходимо людям и животным, чтобы вырабатывать витамин D. Ультрафиолетовое излучение, как и инфракрасное, используют во многих отраслях, например в медицине для дезинфекции, в астрономии для наблюдения за звездами и другими объектами и в химии для отверждения жидких веществ, а также для визуализации, то есть для создания диаграмм распространения веществ в определенном пространстве. С помощью ультрафиолетового света определяют поддельные банкноты и пропуска, если на них должны быть напечатаны знаки специальными чернилами, распознаваемыми с помощью ультрафиолетового света. В случае с подделкой документов ультрафиолетовая лампа не всегда помогает, так как преступники иногда используют настоящий документ и заменяют на нем фотографию или другую информацию, так что маркировка для ультрафиолетовых ламп остается. Существует также множество других применений для ультрафиолетового излучения.

Цветовая слепота

Из-за дефектов зрения некоторые люди не в состоянии различать цвета. Эта проблема называется цветовой слепотой или дальтонизмом, по имени человека, который первый описал эту особенность зрения. Иногда люди не видят только цвета с определенной длиной волны, а иногда они не различают цвета вообще. Часто причина — недостаточно развитые или поврежденные фоторецепторы, но в некоторых случаях проблема заключается в повреждениях на проводящем пути нервной системы, например в зрительной коре головного мозга, где обрабатывается информация о цвете. Во многих случаях это состояние создает людям и животным неудобства и проблемы, но иногда неумение различать цвета, наоборот — преимущество. Это подтверждается тем, что, несмотря на долгие годы эволюции, у многих животных цветное зрение не развито. Люди и животные, которые не различают цвета, могут, например, хорошо видеть камуфляж других животных.

На этом изображении из диагностических таблиц для диагностики дальтонизма люди с нормальным зрением видят число 74

Несмотря на преимущества цветовой слепоты, в обществе ее считают проблемой, и для людей с дальтонизмом закрыта дорога в некоторые профессии. Обычно они не могут получить полные права по управлению самолетом без ограничений. Во многих странах водительские права для этих людей тоже имеют ограничения, а в некоторых случаях они не могут получить права вообще. Поэтому они не всегда могут найти работу, на которой необходимо управлять автомобилем, самолетом, и другими транспортными средствами. Также им сложно найти работу, где умение определять и использовать цвета имеет большое значение.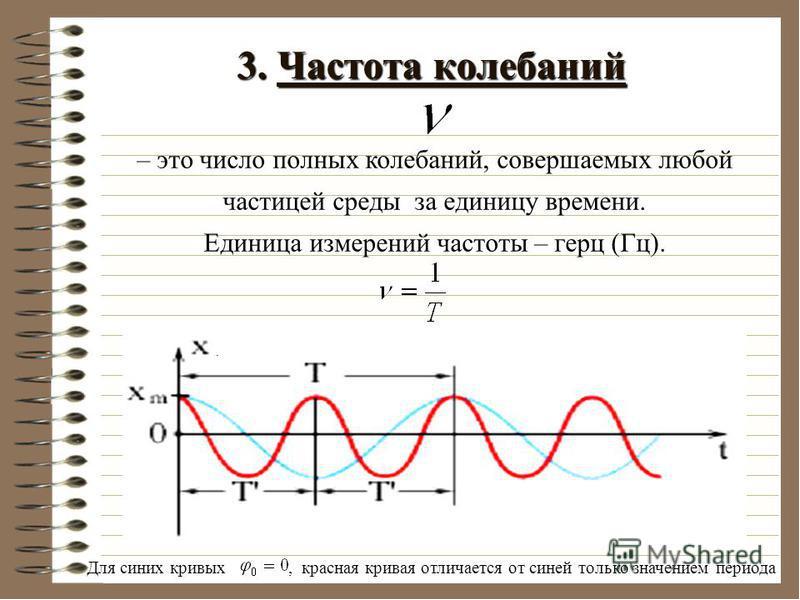 Например, им трудно стать дизайнерами, или работать в среде, где цвет используют, как сигнал (например, об опасности).

Проводятся работы по созданию более благоприятных условий для людей с цветовой слепотой. Например, существуют таблицы, в которых цвета соответствует знакам, и в некоторых странах эти знаки используют в учреждениях и общественных местах наряду с цветом. Некоторые дизайнеры не используют или ограничивают использование цвета для передачи важной информации в своих работах. Вместо цвета, или наряду с ним, они используют яркость, текст, и другие способы выделения информации, чтобы даже люди, не различающие цвета, могли полостью получить информацию, передаваемую дизайнером. В большинстве случаев люди с цветовой слепотой не различают красный и зеленый, поэтому дизайнеры иногда заменяют комбинацию «красный = опасность, зеленый = все нормально» на красный и синий цвета. Большинство операционных систем также позволяют настроить цвета так, чтобы людям с цветовой слепотой было все видно.

Цвет в машинном зрении

Машинное зрение в цвете — быстроразвивающаяся отрасль искусственного интеллекта. До недавнего времени большая часть работы в этой области проходила с монохромными изображениями, но сейчас все больше научных лабораторий работают с цветом. Некоторые алгоритмы для работы с монохромными изображениями применяют также и для обработки цветных изображений.

Камера Canon 5D автоматически находит человеческие лица и настраивается по одному из них на резкость

Применение

Машинное зрение используется в ряде отраслей, например для управления роботами, самоуправляемыми автомобилями, и беспилотными летательными аппаратами. Оно полезно в сфере обеспечения безопасности, например для опознания людей и предметов по фотографиям, для поиска по базам данных, для отслеживания движения предметов, в зависимости от их цвета и так далее. Определение местоположения движущихся объектов позволяет компьютеру определить направление взгляда человека или следить за движением машин, людей, рук, и других предметов.

Чтобы правильно опознать незнакомые предметы, важно знать об их форме и других свойствах, но информация о цвете не настолько важна. При работе со знакомыми предметами, цвет, наоборот, помогает быстрее их распознать. Работа с цветом также удобна потому, что информация о цвете может быть получена даже с изображений с низким разрешением. Для распознавания формы предмета, в отличие от цвета, требуется высокое разрешение. Работа с цветом вместо формы предмета позволяет уменьшить время обработки изображения, и использует меньше компьютерных ресурсов. Цвет помогает распознавать предметы одинаковой формы, а также может быть использован как сигнал или знак (например, красный цвет — сигнал опасности). При этом не нужно распознавать форму этого знака, или текст, на нем написанный. На веб-сайте YouTube можно увидеть множество интересных примеров использования цветного машинного зрения.

Обработка информации о цвете

Оптическая иллюзия с цветом

Фотографии, которые обрабатывает компьютер, либо загружены пользователями, либо сняты встроенной камерой. Процесс цифровой фото- и видеосъемки освоен хорошо, но вот обработка этих изображений, особенно в цвете, связана с множеством трудностей, многие из которых еще не решены. Это связано с тем, что цветное зрение у людей и животных устроено очень сложно, и создать компьютерное зрение наподобие человеческого — непросто. Зрение, как и слух, основано на адаптации к окружающей среде. Восприятие звука зависит не только от частоты, звукового давления и продолжительности звука, но и от наличия или отсутствия в окружающей среде других звуков. Так и со зрением — восприятие цвета зависит не только от частоты и длины волны, но и от особенностей окружающей среды. Так, например, цвета окружающих предметов влияют на наше восприятие цвета.

С точки зрения эволюции такая адаптация необходима, чтобы помочь нам привыкнуть к окружающей среде и перестать обращать внимание на незначительные элементы, а направить все наше внимание на то, что меняется в окружающей обстановке. Это необходимо для того, чтобы легче замечать хищников и находить пищу. Иногда из-за этой адаптации происходят оптические иллюзии. Например, в зависимости от цвета окружающих предметов, мы воспринимаем цвет двух тел по-разному, даже когда они отражают свет с одинаковой длиной волны. На иллюстрации — пример такой оптической иллюзии. Коричневый квадрат в верхней части изображения (второй ряд, вторая колонка) выглядит светлее, чем коричневый квадрат в нижней части рисунка (пятый ряд, вторая колонка). На самом деле, их цвета одинаковы. Даже зная об этом, мы все равно воспринимаем их, как разные цвета. Поскольку наше восприятие цвета устроено так сложно, программистам трудно описать все эти нюансы в алгоритмах для машинного зрения. Несмотря на эти трудности, мы уже достигли многого в этой области.

Литература

Автор статьи: Kateryna Yuri

Unit Converter articles were edited and illustrated by Анатолий Золотков

Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

Страница не найдена — ООО «АСМ Тесты и измерения»

Н О В О С Т И

С Наступающим Новым Годом и Рождеством!

---

Наш новый партнер Mecanum

В октябре наша компания подписала эксклюзивный договор с Канадской компанией Mecanum, которая является одним из крупных мировых производителей оборудования в области акустических испытаний материалов.

---

Наш новый партнер Teledyne Reson

Наша компания начала сотрудничать с датской фирмой Teledyne Reson, которая является ведущим поставщиком высококачественных решений для подводной акустики.

---

Ремонт портативных калибраторов акселерометров

Уважаемые клиенты! Если у Вас имеется портативный калибратор акселерометров HI-803, Endevco 28959FV или такой же калибратор другого производителя вы можете столкнуться с проблемой, что прибор выключается сразу после загрузки селфтеста.

---

Мониторы шума (Hlukové monitory)

Мониторы шума от Чешской компании «Hlukové monitory». Визуализация шума, для легкой и эффективной возможности его контролировать.

---

Сервисный центр

Сервисное обслуживание и ремонт измерительных приборов Bruel & Kjaer, Dewesoft, OnoSokki, LDS

---

Сергей Собянин предложил оборудовать дорожные камеры шумомерами

---

Распродажа оборудования со склада в Москве

---

Выставка PRO // Движение.Экспо

Приглашаем Вас посетить наш стенд на выставке PRO // Движение.Экспо, который будет находится в павильоне №1 в бизнес-лаунже № E7.8/1.

---

Новый партнер Microtech Gefell GmbH

Мы подписали эксклюзивное дистрибьюторское соглашение с компанией Microtech Gefell GmbH. Компания была основана в 1928 году в Германии и занимается производством микрофонов студийных и измерительных. В советское время эта компания была известна в нашей стране под брендом RFT, который был известен своим качеством и надежностью, и ни в чем не уступали другому известному бренду Bruel & Kjaer.

---

Представляем Вам нашего нового партнера — компания Dynalabs.

---

Первый сертифицированный бюджетный микрофон фирмы ACO (Япония)

---

Сертифицирована система поверки акселерометров 3629

---

Приглашаем на работу

---

ИДЕТ РЕГИСТРАЦИЯ НА СЕМИНАР

---

Амплитуда, частота, период колебаний — урок. Физика, 11 класс.

Рассмотрим величины, с помощью которых можно охарактеризовать колебания.

 

 

Сравним колебания двух качелей на рисунке — пустых качелей и качелей с мальчиком. Качели с мальчиком колеблются с большим размахом, т. е. их крайние положения находятся дальше от положения равновесия, чем у пустых качелей.

Наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия называется амплитудой колебаний.

Обрати внимание!

Амплитуда колебаний, как правило, обозначается буквой \(А\) и в СИ измеряется в метрах (м).

Пример:

На рисунке ниже амплитудой колебания мальчика на качелях является дуга ОА.

 

 

Обрати внимание!

Амплитуду можно измерять также в единицах плоского угла, например в градусах, поскольку дуге окружности соответствует определённый центральный угол, т. е. угол с вершиной в центре окружности.

Колеблющееся тело совершает одно полное колебание, если от начала колебаний проходит путь, равный четырём амплитудам.

Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.

Обрати внимание!

Период колебаний обозначается буквой \(Т\) и в СИ измеряется в секундах (с).

Пример:

Ударим по столу двумя линейками — металлической и деревянной. Линейки после этого начнут колебаться, но за один и тот же промежуток времени металлическая линейка (А) сделает больше колебаний, чем деревянная (В).

 

 

Число колебаний в единицу времени называется частотой колебаний.

Обрати внимание!

Обозначается частота греческой буквой ν («ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц).

Период колебания \(Т\) и частота колебаний ν связаны следующей зависимостью:

T=1ν.

Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы.

Любая колебательная система имеет определённую собственную частоту, зависящую от параметров этой системы. Например, собственная частота пружинного маятника зависит от массы груза и жёсткости пружины.

 

 

Рассмотрим колебания двух одинаковых пустых качелей на рисунке выше. В один и тот же момент времени красные качели из положения равновесия начинают движение вперед, а зеленые качели из положения равновесия движутся назад. Качели колеблются с одной и той же частотой и с одинаковыми амплитудами. Однако эти колебания отличаются друг от друга: в любой момент времени скорости качелей направлены в противоположные стороны. В таком случае говорят, что колебания качелей происходят в противоположных фазах.

Красные пустые качели и качели с мальчиком тоже колеблются с одинаковыми частотами. Скорости этих качелей в любой момент времени направлены одинаково. В этом случае говорят, что качели колеблются в одинаковых фазах.

Физическая величина, называемая фазой, используется не только при сравнении колебаний двух или нескольких тел, но и для описания колебаний одного тела.

Таким образом, колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой.

 

Источники:

Физика. 9 кл.: учебник / Перышкин А.В., Гутник Е.М. — М.: Дрофа, 2014. — 319 с.
www.ru.depositphotos.com, сайт «Фотобанк с премиум-коллекцией фотографий, векторов и видео»

www.mognovse.ru, сайт «Можно все»

Величины, характеризующие колебательное движение. Гармонические колебания :: Класс!ная физика

ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ КОЛЕБАТЕЛЬНОЕ

ДВИЖЕНИЕ

Любые колебания характеризуются следующими параметрами:

Смещение (х ) — отклонение

колеблющейся точки от положения равновесия в данный момент времени

[м].

Амплитуда колебаний – наибольшее смещение от положения равновесия

[м]. Если колебания незатухающие, то амплитуда постоянна.

Период колебаний ( Т )- время, за

которое совершается одно полное колебание. Выражается в секундах

[с].

Частота колебаний (v) — число

полных колебаний за единицу времени. В СИ измеряется в герцах (Гц).
Единица измерения названа так в честь известного немецкого физика

Генриха Герца (1857…1894).
1 Гц – это одно колебание в секунду. Примерно с такой частотой бьется человеческое сердце. Слово «херц» по-немецки означает «сердце».

Фаза колебаний — физическая величина,

определяющая смещение x в данный момент времени. Измеряется в радианах

(рад).

Период и частота колебаний связаны между собой обратно

пропорциональной зависимостью:

T = 1/v.

На нижеприведенном рисунке указаны значения частот

некоторых колебательных процессов

Рассматривая рисунок, вы обнаружите, что сердце

мыши сокращается гораздо чаще, чем

сердце кита. Точные значения этих величин соответственно – 600 и

15 ударов в минуту (в покое). Но, между прочим, и то и другое сердце

сокращается за свою жизнь около 750 миллионов раз.

Ученые считают,

что продолжительность жизни всех млекопитающих

(кроме человека), измеренная числом ударов сердца, примерно одинакова. Рисунок расскажет вам о частотных характеристиках

различных радиоволн, границах ультразвука и гиперзвука, о периодичности

морских волн и частоте смены кадров на экране телевизора. Может

возникнуть вопрос: почему показаны частоты обращения планет вокруг

Солнца? Потому что движения планет по своим орбитам – это периодические (повторяющиеся) процессы.

Источник: журнал «Наука и жизнь». Авт. В.

Лишевский.

Устали? — Отдыхаем!

Чем измеряется высота звука.

Единицы измерения высоты звука

ВЫСОТА
1. Вы видели высоту?
Вы видели высоту?
Бывали на ней хоть раз?
Ту высоту-красоту,
Где молнии возле глаз?
Ту высоту, где вдруг
Растут облаков грибы,
Где кружится пепел вьюг
И ветры сшибают лбы?
Вы слышали высоту?
Здесь рядом гуляет гром,
И, задевая звезду,
Птицы свистят

автора

Ильюшечкин Александр Александрович

Как уже упоминалось, поскольку высота звука является репрезентацией частоты звуковых колебаний, как правило, используются единицы измерения частоты — Герцы (Hz), где количество Герц, это количество колебаний в секунду:

Однако, используются и альтернативные системы измерения высоты звука, основанные на физиологическом (Барки) и психофизиологическом (Мелы) механизме его восприятия.

«Критические полосы» и Барки

Критическая полоса (ее также называют полосой равной разборчивости) — это минимальная полоса частот, которая возбуждает одну и ту же часть базилярной мембраны. В частотном промежутке от 0 до 16 кГц опытным путем были определены 24 критические полосы:

0-100 Гц,
100-200 Гц,
200-300 Гц,
300- 400 Гц,
400-510 Гц,
510-630 Гц,
630-770 Гц,
770-920 Гц,
920-1080 Гц,
1080- 1270 Гц,
1270-1480 Гц,
1480-1720 Гц,
1720-2000 Гц,
2000-2320 Гц,
2320- 2700 Гц,
2700-3150 Гц,
3150-3700 Гц,
3700-4400 Гц,
4400-5300 Гц,
5300- 6400 Гц,
6400-7700 Гц,
7700-9500 Гц,
9500-12 000 Гц
12 000-15 500 Гц

Звуковой сигнал в пределах одной и той же критической полосы как бы обобщается мозгом, создавая близкие слуховые ощущения. Если же звуковой сигнал переходит из одной критической полосы в другую, то слуховые ощущения в момент перехода заметно изменяются, потому что мозг анализирует информацию, полученную из разных критических полос, раздельно. Это не значит, что два тона, попавшие в одну критическую полосу, не различимы на слух, однако, слуховые ощущения внутри одной полосы очень близки, а в разных полосах — отличаются существенно. Участки базилярной мембраны, соответствующие критическим полосам, имеют приблизительно равную длину, которая составляет 1,2 мм на полосу.

Для удобства работы с критическими полосами существует специальная единица измерения частоты — Барк. В таблице приведены критические полосы и соответствующие им параметры:

Барк, № полосы	Критическая полоса (диапаз.), Гц	Ширина критической полосы, Гц	Центральная частота критической полосы, Гц

Измерение субъективного ощущения высоты и Мелы

На этой шкале равное изменение частоты в Мелах соответствует равному изменению ощущения высоты тона. Уже привычная нам шкала частот с единицей измерения “герц” такого свойства не имеет. Например, изменения частоты от 500 до 1000 Гц и от 1000 до 2000 Гц воспринимаются на слух слушателем, как неравные. В то же самое время звуковой сигнал с частотой 1000 мел кажется слушателю ровно в два раза “выше”, чем сигнал с частотой 500 мел, и в два раза “ниже”, чем сигнал с частотой 2000 мел. (Закон Вебера-Фехнера):

Итак, частотные параметры звука могут измеряться в Герцах, Мелах и Барках.

Герц
— это единица измерения, которой удобно пользоваться при проведении спектрального анализа.

Мел и Барк
— это психофизиологические акустические единицы измерения высоты тона, используемые в психоакустике при оценке субъективной высотой тона.

Как видно из графика, шкалы барков и мелов приблизительно совпадают, хотя некоторые расхождения наблюдаются в области средних частот:

В музыке используются другие шкалы для оценки высоты тона — музыкальные: полутоны, тоны, октавы и другие музыкальные интервалы. Следует отметить, что связь с психофизической шкалой высоты тона, построенной для чистых тонов, неоднозначна. До частоты примерно 5000 Гц увеличение высоты тона на октаву связано с удвоением частоты. Например, переход от ноты ля первой октавы к ноте ля второй октавы соответствует увеличению частоты от 440 до 880 Гц. Но выше частоты 5000 Гц это соответствие нарушается — чтобы получить ощущение увеличения высоты на октаву, надо увеличить соотношение частот почти в 10 раз, что следует иметь в виду при создании компьютерных композиций. Это дало основание некоторым ученым предложить две размерности высоты тона: психофизическую в мелах, пропорциональную в некоторых пределах логарифму частоты, установленную для чистых тонов (pitch height) и музыкальную, соответствующую названию нот (pitch chroma), которая может быть определена примерно до 5000 Гц. Следует отметить, что даже музыканты с абсолютным музыкальным слухом затрудняются в определении нот для звуков с частотой выше 5000 Гц. Это говорит о том, что механизмы восприятия высоты тона до 5000 Гц и выше — различны.
(И.
Алдошина)

Звуковые волны, как и другие волны, характеризуются такими объективными величинами, как частота, амплитуда, фаза колебаний, скорость распространения, интенсивность звука и другими. Но, кроме этого, они описываются тремя субъективными характеристиками. Это — громкость звука, высота тона и тембр.

Чувствительность человеческого уха различна для разных частот. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсивностью, но если эта интенсивность превышает определенный предел, то звук не слышен и вызывает только болевое ощущение. Таким образом, для каждой частоты колебаний существует наименьшая (порог слышимости
) и наибольшая (порог болевого ощущения
) интенсивность звука, которая способна вызвать звуковое ощущение. На рисунке 1 представлена зависимость порогов слышимости и болевого ощущения от частоты звука. Область, расположенная между этими двумя кривыми, является областью слышимости
. Наибольшее расстояние между кривыми приходится на частоты, к которым ухо наиболее чувствительно (1000-5000 Гц).

Если интенсивность звука — величина, объективно характеризующая волновой процесс, то субъективной характеристикой звука является громкость Громкость зависит от интенсивности звука, т.е. определяется квадратом амплитуды колебаний в звуковой волне и чувствительностью уха (физиологическими особенностями). Так как интенсивность звука , то чем больше амплитуда колебаний, тем громче звук.

Высота тона
— качество звука, определяемое человеком субъективно на слух и зависящее от частоты звука. Чем больше частота, тем выше тон звука.

Звуковые колебания, происходящие по гармоническому закону, с определенной частотой, воспринимаются человеком как определенный музыкальный тон
. Колебания высокой частоты воспринимаются как звуки высокого тона
, звуки низкой частоты — как звуки низкого тона
. Диапазон звуковых колебаний, соответствующий изменению частоты колебаний в два раза, называется октавой
. Так, например, тон «ля» первой октавы соответствует частоте 440 Гц, тон «ля» второй октавы — частоте 880 Гц.

Музыкальным звукам соответствуют звуки, издаваемые гармонически колеблющимся телом.

Основным тоном
сложного музыкального звука называется тон, соответствующий наименьшей частоте, которая имеется в наборе частот данного звука. Тоны, соответствующие остальным частотам в составе звука, называются обертонами
. Если частоты обертонов кратны частоте основного тона, то обертоны называются гармоническими, причем основной тон с частотой называется первой гармоникой
, обертон со следующей частотой — второй гармоникой
и т.д.

Музыкальные звуки с одним и тем же основным тоном различаются тембром, который определяется наличием обертонов — их частотами и амплитудами, характером нарастания амплитуд в начале звучания и их спадом в конце звучания.

При одной высоте тона звуки, издаваемые, например, скрипкой и пианино, отличаются тембром
.

Восприятие звука органами слуха зависит от того, какие частоты входят в состав звуковой волны.

Шумы
— это звуки, образующие сплошной спектр, состоящий из набора частот, т.е. в шуме присутствуют колебания всевозможных частот.

Звука, то есть от числа колебаний среды (обычно воздуха) в секунду, которые воздействуют на барабанную перепонку человека. С увеличением частоты колебаний растёт высота звука . В первом приближении субъективная высота звука пропорциональна логарифму частоты — согласно закону Вебера-Фехнера .

Основные сведения

Высота звука — субъективное качество слухового ощущения человека, наряду с громкостью и тембром , позволяющее располагать все звуки по шкале от низких к высоким. Для чистого тона (что это?)
она зависит главным образом от частоты (с ростом частоты высота звука повышается), но при субъективном восприятии — также и от его интенсивности (амплитуды?) — при возрастании интенсивности высота звука кажется ниже . Высота звука со сложным спектральным составом зависит от распределения энергии по шкале частот.

Частотные сигналы сложного спектра без основной частоты (первой гармоники в спектре) называются резидуальными
. Восприятие высоты частотного сигнала совпадает с восприятием высоты резидуальной версии такого же сигнала .

Напишите отзыв о статье «Высота звука»

Примечания

Литература

• Haynes B., Cooke P.R.
  Pitch // The New Grove Dictionary of Music and Musicians . London; New York, 2001.

См. также

Отрывок, характеризующий Высота звука

Источник этой необычайной силы прозрения в смысл совершающихся явлений лежал в том народном чувстве, которое он носил в себе во всей чистоте и силе его.
Только признание в нем этого чувства заставило народ такими странными путями из в немилости находящегося старика выбрать его против воли царя в представители народной войны. И только это чувство поставило его на ту высшую человеческую высоту, с которой он, главнокомандующий, направлял все свои силы не на то, чтоб убивать и истреблять людей, а на то, чтобы спасать и жалеть их.
Простая, скромная и потому истинно величественная фигура эта не могла улечься в ту лживую форму европейского героя, мнимо управляющего людьми, которую придумала история.
Для лакея не может быть великого человека, потому что у лакея свое понятие о величии.

5 ноября был первый день так называемого Красненского сражения. Перед вечером, когда уже после многих споров и ошибок генералов, зашедших не туда, куда надо; после рассылок адъютантов с противуприказаниями, когда уже стало ясно, что неприятель везде бежит и сражения не может быть и не будет, Кутузов выехал из Красного и поехал в Доброе, куда была переведена в нынешний день главная квартира.
День был ясный, морозный. Кутузов с огромной свитой недовольных им, шушукающихся за ним генералов, верхом на своей жирной белой лошадке ехал к Доброму. По всей дороге толпились, отогреваясь у костров, партии взятых нынешний день французских пленных (их взято было в этот день семь тысяч). Недалеко от Доброго огромная толпа оборванных, обвязанных и укутанных чем попало пленных гудела говором, стоя на дороге подле длинного ряда отпряженных французских орудий. При приближении главнокомандующего говор замолк, и все глаза уставились на Кутузова, который в своей белой с красным околышем шапке и ватной шинели, горбом сидевшей на его сутуловатых плечах, медленно подвигался по дороге. Один из генералов докладывал Кутузову, где взяты орудия и пленные.
Кутузов, казалось, чем то озабочен и не слышал слов генерала. Он недовольно щурился и внимательно и пристально вглядывался в те фигуры пленных, которые представляли особенно жалкий вид. Большая часть лиц французских солдат были изуродованы отмороженными носами и щеками, и почти у всех были красные, распухшие и гноившиеся глаза.
Одна кучка французов стояла близко у дороги, и два солдата – лицо одного из них было покрыто болячками – разрывали руками кусок сырого мяса. Что то было страшное и животное в том беглом взгляде, который они бросили на проезжавших, и в том злобном выражении, с которым солдат с болячками, взглянув на Кутузова, тотчас же отвернулся и продолжал свое дело.
Кутузов долго внимательно поглядел на этих двух солдат; еще более сморщившись, он прищурил глаза и раздумчиво покачал головой. В другом месте он заметил русского солдата, который, смеясь и трепля по плечу француза, что то ласково говорил ему. Кутузов опять с тем же выражением покачал головой.
– Что ты говоришь? Что? – спросил он у генерала, продолжавшего докладывать и обращавшего внимание главнокомандующего на французские взятые знамена, стоявшие перед фронтом Преображенского полка.
– А, знамена! – сказал Кутузов, видимо с трудом отрываясь от предмета, занимавшего его мысли. Он рассеянно оглянулся. Тысячи глаз со всех сторон, ожидая его сло ва, смотрели на него.
Перед Преображенским полком он остановился, тяжело вздохнул и закрыл глаза. Кто то из свиты махнул, чтобы державшие знамена солдаты подошли и поставили их древками знамен вокруг главнокомандующего. Кутузов помолчал несколько секунд и, видимо неохотно, подчиняясь необходимости своего положения, поднял голову и начал говорить. Толпы офицеров окружили его. Он внимательным взглядом обвел кружок офицеров, узнав некоторых из них.
– Благодарю всех! – сказал он, обращаясь к солдатам и опять к офицерам. В тишине, воцарившейся вокруг него, отчетливо слышны были его медленно выговариваемые слова. – Благодарю всех за трудную и верную службу. Победа совершенная, и Россия не забудет вас. Вам слава вовеки! – Он помолчал, оглядываясь.
– Нагни, нагни ему голову то, – сказал он солдату, державшему французского орла и нечаянно опустившему его перед знаменем преображенцев. – Пониже, пониже, так то вот. Ура! ребята, – быстрым движением подбородка обратись к солдатам, проговорил он.

Сила звука (интенсивность звука, определяющая его мощность) определяется как

Плотность звуковой энергии (Дж/м3) — определяет энергию звука, отнесенную к единице объема среды

Звуковая мощность — поток звуковой энергии W (Вт/м2)

Высота звука

Громкость звука

Тембр звука

Звуковое давление

Звуковое давление p — переменное избыточное давление, возникающее в среде при прохождении звуковой волны. Обычно звуковое давление мало по сравнению с постоянным давлением в среде. Звуковое давление следует отличать от давления звука.(см. табл.1)

отсюда 1 дБ — уровень звукового давления, для которого

Таблица 1. Уровни звукового давления (Муртазов А.К., 2007)

Высота звука

Высотой звука называется отражение в нашем сознании частоты колебания упругого тела. Мы воспринимаем как звук одного и того же названия не определенную частоту, а ряд близких частот. Например, как а1 мы воспринимаем колебательные движения не только с частотой 440 к/с, но и с частотами 435, 436, 437, 438, 439, 441, 442, 443, 444, 445 к/с (приблизительно). Таким образом, в нашем сознании частота перерабатывается в высоту.

Человек способен слышать весьма малые изменения высоты звука. Слуховой аппарат человека отмечает изменение высоты не одинаково в разных областях частот. Наиболее остро мы замечаем изменение высоты тонов в области от 500 до З 000 к/с. Для того, чтобы заметить эту разницу, требуется изменение в 5 центов (1/40 тона).

В низком регистре этот интервал увеличивается до 1/10 тона (например, в субконтроктаве).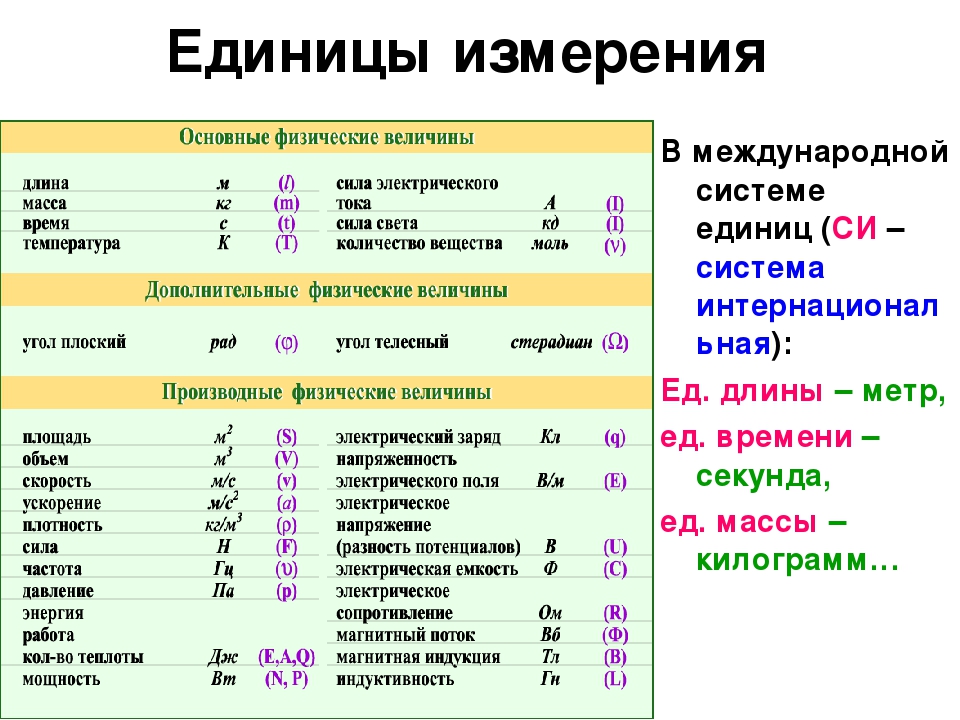 В высоком регистре, после З 000 к/с, интервал различения звуков по высоте также немного увеличивается. При одновременном слушании двух звуков можно заметить очень небольшую разницу между ними, благодаря биениям, которые отчетливо слышны, если слушать оба звука одним ухом. При слушании двух звуков, поочередно подводимых к разным ушам, разница, наоборот, увеличивается.

Если мы будем слушать короткие по времени звуки, постепенно уменьшая их длительность, то заметим, что значительное уменьшение длительности вызывает потерю ощущения высоты этих звуков.

Необходимо некоторое минимальное количество колебаний в секунду для того, чтобы человек мог судить о высоте звука. Исследования показали, что минимальная длительность звука, необходимая для определения его высоты, зависит от его частоты. (см.табл.2).

Таблица 2. Минимальная длительность звука, необходимая для определения его высоты

Из приведенной таблицы видно, что наиболее короткие звуки возможны в области частот от 700 до 3 200 к/с, т. е. от f2 до g4.

В низком регистре, в области субконтроктавы и контроктавы, длительность звука должна быть довольно большой.

Способность человека определять заданные музыкальные интервалы и воспроизводить их голосом, а также способность определять абсолютную высоту заданных звуков и воспроизводить их голосом являются свойствами музыкального слуха.

В первом случае, когда отношение между высотами звуков оценивается человеком как музыкальный интервал, как некоторое определенное качество, слух называется относительным.

Так как при некоторых изменениях между частотами звуков музыкальный интервал между ними сохраняет свою качественную определенность, то каждый интервал может иметь несколько количественных выражений.

Наличие относительного слуха совершенно необходимо для музыканта. Развитие его предусмотрено учебными планами музыкальных школ, училищ и консерваторий.

Во втором случае, т. е. при наличии способности определять абсолютную высоту заданных звуков (ступеней) или воспроизводить их голосом, слух называется абсолютным.

Обычно человек, обладающий абсолютным слухом, имеет также и относительный, но бывают случаи, когда при абсолютном слухе человек воспринимает музыкальные интервалы не как некоторое определенное качество, а лишь как сумму не связанных между собою звуков.

Абсолютный слух бывает двух типов — истинный и ложный. Для первого типа необходимо наличие у человека особых физиологических задатков. Второй тип абсолютного слуха требует постоянных и длительных упражнений.

Так, если истинный слух проявляется уже с самого раннего детства, то ложный слух можно выработать только в более зрелом возрасте. Критерием хорошего, истинного абсолютного слуха является способность быстро определять высоту заданного звука. Человек, обладающий ложным абсолютным слухом, обычно путем упражнений запоминает какой-либо один звук, например, б, а остальные звуки, он определяет, сравнивая их по высоте с этим звуком. Кроме того, встречаются лица, у которых абсолютный слух существует лишь по отношению к тому инструменту, на котором они играют. Но во всех случаях абсолютный слух способен определять и воспроизводить не частоту звука, а его высоту, т. е. его принадлежность к той или иной ступени.

Некоторые лица, не обладающие абсолютным слухом, могут определять высоту звуков, пользуясь какими-нибудь добавочными способами. Например, некоторые певцы определяют высоту звука, пользуясь ощущением напряжения голосовых связок.

Путем упражнений можно, безусловно, развить относительный слух. Что же касается превращения ложного абсолютного слуха в близкий к истинному, то это пока еще не доказано опытами.

Для музыканта большое значение имеет наличие внутреннего слуха — способность воображать высоту звуков и (в частности) созвучий. Внутренний слух позволяет исполнителю составить представление о музыкальном произведении до его прослушивания, а композитору дает возможность создавать произведение без помощи инструмента.

Для точного определения частоты колебаний звучащего тела применяются разнообразные приборы и методы.

Простейшим и наиболее старым методом является слуховое сравнение данного звука с другим, близким к нему по высоте звуком, частота колебаний которого точно известна, и последующий счет биений, возникающих между этими двумя звуками. Так например, если исследуемый звук дает с сравнительным звуком частоты 440 к/с полтора биения в секунду, а с другим сравнительным звуком частоты 444 к/с два с половиной биения в секунду, то частота его колебаний будет равна 141,5 к/c, и так далее.

Однако слуховой способ сравнения труден, так как требует специальной тренировки слуха исследователя. А если испытуемый звук дается человеком (например, голосом, на скрипке и т. п., на духовом инструменте), то он обычно инстинктивно подстраивается ко второму, слышимому им звуку измерительного прибора. Поэтому результаты сравнения получаются неточными.

Более точное определение частоты колебаний звучащих тел дает стробоскопический метод сравнения. При этом исследуемый звук превращается в световые импульсы (вспышки лампы с тлеющим разрядом), освещающие систему вращающихся дисков с чередующимися черными и белыми секторами, соотношения скоростей которых пропорциональны соотношениям между числами колебаний какой-либо музыкальной системы. При совпадении числа колебаний исследуемого звука с числом проходящих секторов на каком-либо из измерительных дисков, изображение на последнем покажется остановившимся. Это есть момент унисона двух колебательных процессов.

В существующих наиболее распространенных стробоскопических частотомерах применены комплекты из 12 измерительных дисков, скорости которых настроены по равномерно-темперированной музыкальной скале. Особое приспособление позволяет плавно изменять скорость вращения всех дисков одновременно в пределах ±3%, что соответствует изменению высоты звуков в пределах ± половины полутона. Указатель на шкале прибора дает возможность, в момент достижения унисона с исследуемым звуком, сразу прочесть высоту последнего относительно ближайшего, нормального темперированного звука, с точностью до 0,01 полутона (т. е. до одного цента).

Прибор очень чувствителен, не требует от оператора специальной тренировки слуха, и не издает никаких звуков, к которым мот бы подстраиваться исполнитель.

Получаемые на нем в музыкальных (логарифмических) единицах высоты звуков могут быть, при надобности, переведены в соответствующие частоты колебаний (герцы), при помощи специальных таблиц.

Рекомендуем также

Мощность в каких единицах измеряется

В чем измеряется мощность

Ещё в 18 веке мощность стали считать в лошадиных силах. До сих пор эта физическая величина употребляется для обозначения силы двигателей. Рядом с показателем мощности двигателя внутреннего сгорания в ваттах продолжают писать значение в л.с.

Мощность как физическая величина, формула мощности

Значение, показывающее, как быстро происходят преобразование, трансляция или потребление энергии в какой-либо системе, – мощность. Для характеристик энергетических условий важно, насколько быстро выполняется процесс. Работа, реализуемая в единицу времени, именуется мощностью:

P = А/t,

где:

Можно учитывать отдельно мощность в механике и электрическую мощность.

Чтобы получить ответ на вопрос: в чем измеряется механическая мощность, рассматривают действие силы на движущееся тело. Сила проделывает работу, мощность в таком случае определяется по формуле:

N = F*v,

где:

При вращательном движении эту величину определяют с учётом момента силы и частоты вращения, «об./мин.».

Зависимость между электрическим током и мощностью

Как рассчитать потребление электрической энергии

В электротехнике работой будет U – напряжение, которое перемещает 1 кулон, количество перемещаемых в единицу времени кулонов – это ток (I). Мощность электротока или электрическую мощность P получают, умножив ток на напряжение:

P = U*I.

Это полная работа, выполненная за 1 секунду.  Зависимость здесь прямая. Изменяя ток или напряжение, изменяют мощность, расходуемую устройством.

Одинакового значения Р добиваются, варьируя одну из двух величин.

Определение единицы измерения мощности тока

Единица измерения мощности тока носит имя Джеймса Ватта, шотландского инженера-механика. 1 Вт – это мощность, которую вырабатывает ток 1 А при разности потенциалов 1 В.

К примеру, источник при напряжении 3,5 В создаёт в цепи ток 0,2 А, тогда мощность тока получится:

P = U*I = 3,5*0,2 = 0,7 Вт.

Внимание! В механике мощность принято изображать буквой N, в электротехнике – буквой P. В чем измеряется n и P? Независимо от обозначения, это одна величина, и измеряется она в ваттах «Вт».

Ватт и другие единицы измерения мощности

Говоря о том, в чем измеряется мощность, необходимо знать, о чём идёт речь. Ватт – это величина, соответствующая 1 Дж/с. Она принята в Международной Системе Единиц. В каких единицах ещё измеряется мощность?  Раздел науки астрофизика работает с единицей под названием эрг/с. Эрг – очень маленькая величина, равная 10-7 Вт.

Ещё одна, поныне распространённая, единица из этого ряда – «лошадиная сила».  В 1789 году Джеймс Ватт подсчитал, что груз весом 75 кг из шахты может вытащить одна лошадь и сделать это со скоростью 1 м/с. Исходя из подсчёта такой трудоёмкости, мощность двигателей допускается измерить этой величиной в соотношении:

1 л.с. = 0,74 кВт.

Интересно. Американцы и англичане считают, что 1 л.с. = 745.7 Вт, а русские – 735.5 Вт. Спорить, кто прав, а кто нет, не имеет смысла, так как мера эта внесистемная и не должна быть использована. Международная организация законодательной метрологии рекомендует изъять её из обращения.

В России при расчёте полиса КАСКО или ОСАГО используют эти данные силового агрегата автомобиля.

Формула взаимосвязи между мощностью, напряжением и силой тока

В электротехнике работу рассматривают как некоторое количество энергии, отдаваемое источником питания на действие электроприбора в период времени. Поэтому электрическая мощность есть величина, описывающая быстроту трансформации или передачи электроэнергии. Её формула для постоянного тока выглядит так:

P = U*I,

где:

• U – напряжение, В;
• I – сила тока, А.

Для некоторых случаев, пользуясь формулой закона Ома, мощность можно вычислить, подставив значение сопротивления:

P = I*2*R, где:

• I – сила тока, А;
• R – сопротивление, Ом.

В случае расчётов мощности цепей переменного тока придётся столкнуться с тремя видами:

• активная её формула: P = U*I*cos ϕ, где – коэффициент угла сдвига фаз;
• реактивная рассчитывается: Q = U*I*sin ϕ ;
• полная представлена в виде: S = √P2 + Q2, гдe P – aктивная, а Q2 – реактивная.

Расчёты для однофазной и трёхфазной цепей переменного тока выполняются по разным формулам.

Важно! Потребители электроэнергии на предприятиях в большинстве асинхронные двигатели, трансформаторы и другие индуктивные приёмники. При работе они используют реактивную мощность, а та, протекая по линиям электропередач, приводит ЛЭП к дополнительной нагрузке. Чтобы повысить качество энергии, используют компенсацию реактивной энергии в виде конденсаторных установок.

Приборы для измерения электрической мощности

Провести измерения мощности позволяет ваттметр. У него две обмотки. Одна включается в цепь последовательно, как амперметр, вторая параллельно, как вольтметр. В установках электроэнергетики ваттметры определяют значения в киловатт-час «кВт*час». В измерениях нуждается не только электрическая, а также лазерная энергия. Приборы, способные измерять этот показатель, изготавливаются как стационарного, так и переносного исполнения. С их помощью оценивают уровень  лазерных излучений оборудования, применяющего этот вид энергии. Один из портативных измерителей – LP1, японского производителя. LP1 разрешает напрямую определять значения силы светового излучения, к примеру, в визуальном пятне оптических устройств проигрывателей DVD.

Прибор для измерения электрической мощности

Мощность в бытовых электрических приборах

Для нагрева металла нити накаливания лампочки, увеличения температуры рабочей поверхности утюга или иного бытового прибора, тратится определённое количество электроэнергии. Её величину, отбираемую нагрузкой за час, считают потребляемой мощностью этого аппарата.

Внимание! Если на лампочке написано «40 W, 230 V», это значит, что за 1 час она потребляет из сети переменного тока 40 Вт. Зная количество лампочек и параметры, подсчитывают, сколько энергии тратится на освещение комнат в месяц.

Как перевести ватты

Так как ватт – величина маленькая, в быту оперируют киловаттами, пользуются системой перевода величин:

• 1 Вт = 0,001 кВт;
• 10 Вт = 0,01 кВт;
• 100 Вт = 0,1 кВт;
• 1000 Вт = 1 кВт.

Мощность некоторых электрических приборов, Вт

Средние значения потребления электроэнергии бытовых устройств:

• плиты – 110006000 Вт;
• холодильники – 150-600 Вт;
• стиральные машины – 1000-3000 Вт;
• пылесосы – 1300-4000 Вт;
• электрочайники – 2000-3000 Вт.

Электрические параметры, указанные на бытовом приборе

Параметры каждого бытового прибора указываются в паспорте, а также обозначаются на корпусе. Там определены точные значения для информации потребителя.

Видео

Мощность (физика) — это… Что такое Мощность (физика)?

Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м. двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м., гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м., регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т.  п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]

— средняя мощность

— мгновенная мощность

Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.

Единицы измерения

В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.

Другой распространённой единицей измерения мощности является лошадиная сила.

Соотношения между единицами мощности

Единицы Вт кВт МВт кгс·м/с эрг/с л. с.

1 ватт	1	10-3	10-6	0,102	107	1,36·10-3
1 киловатт	103	1	10-3	102	1010	1,36
1 мегаватт	106	103	1	102·103	1013	1,36·103
1 килограмм-сила-метр в секунду	9,81	9,81·10-3	9,81·10-6	1	9,81·107	1,33·10-2
1 эрг в секунду	10-7	10-10	10-13	1,02·10-8	1	1,36·10-10
1 лошадиная сила[2]	735,5	735,5·10-3	735,5·10-6	75	7,355·109	1

Мощность в механике

Если на движущееся тело действует сила, то эта сила совершает работу.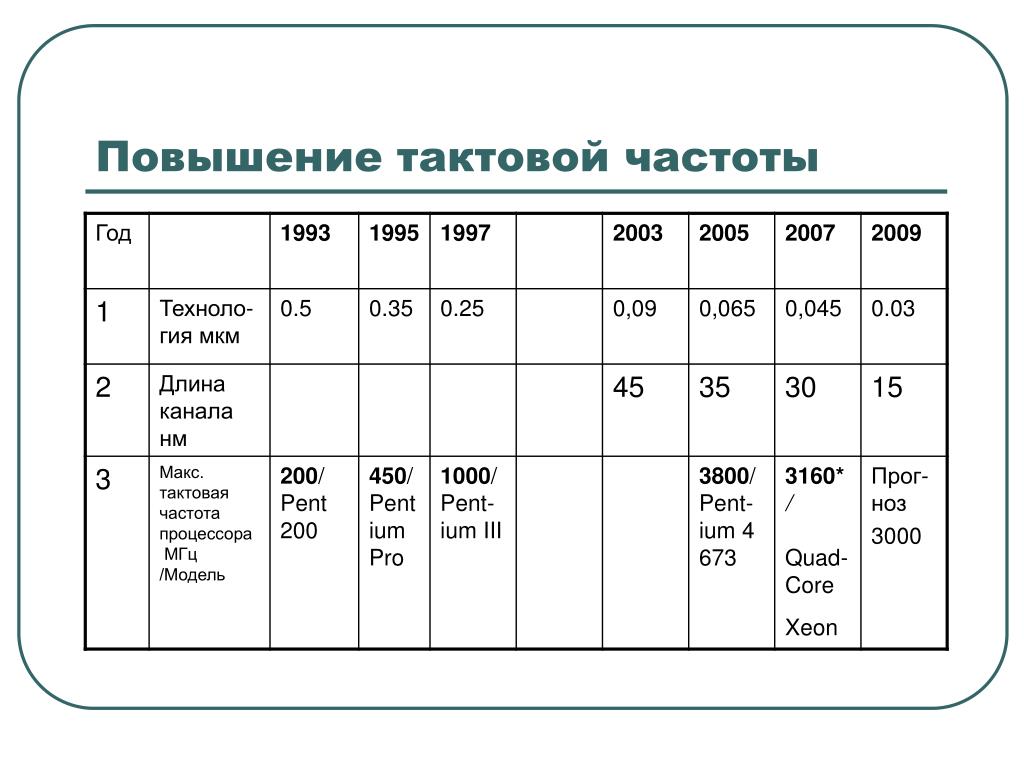 Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

F — сила, v — скорость, α — угол между вектором скорости и силы.

Частный случай мощности при вращательном движении:

M — момент,  — угловая скорость,  — число пи, n — частота вращения (об/мин).

Электрическая мощность

Основная статья: Электрическая мощность

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

S=P+jQ

S — Полная мощность, ВА

P — Активная мощность, Вт

Q — Реактивная мощность, ВАр

Приборы для измерения мощности

• Ваттметр
• Варметр
• Фазометр

Примечания

1. ↑ Большая Советская энциклопедия
2. ↑ «метрическая лошадиная сила»

См. также

Ссылки

Wikimedia Foundation. 2010.

Единицы измерения мощности

Программа КИП и А

Мощность — физическая величина, равная скорости изменения, преобразования, передачи или потребления энергии системы. Также мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Международная система единиц (СИ)

В Международной системе единиц (СИ) единицей измерения мощности является ватт [Вт],[W], равный одному джоулю [Дж],[J], делённому на секунду.   1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль. Таким образом, ватт является производной единицей измерения и связан с другими единицами СИ следующими соотношениями:

• Вт = Дж / с = кг·м²/с
• Вт = H·м/с
• Вт = В·А
• 1 Мегаватт [МВт] = 1000 кВт
• 1 Киловатт [кВт] = 1000 Вт
• 1 Вольт-ампер [В·А] = 1 Вт

Внесистемные единицы

• 1 Гигакалория в секунду [Гкал/с], [Gcal/s] = 4186.8 МВт
• 1 Килокалория в секунду [ккал/с], [kcal/s] = 4186.8 Вт
• 1 Калория в секунду [кал/с], [cal/s] = 4.1868 Вт
• 1 Гигакалория в час [Гкал/ч], [Gcal/h] = 1.163 МВт
• 1 Килокалория в час [ккал/ч], [kcal/h] = 1. 163 Вт
• 1 Калория в час [кал/ч], [cal/h] = 0.001163 Вт
• 1 Котловая лошадинная сила [hp(S)] = 9809.5 Вт
• 1 Электрическая лошадиная сила [hp(E)] = 746 Вт
• 1 Гидравлическая лошадиная сила [hp(H)] = 745.7 Вт
• 1 Механическая лошадиная сила [hp(I)] = 745.69987158227022 Вт
• 1 Метрическая лошадиная сила [hp(M)] = 735.49875 Вт
• 1 Килограмм·м/с [кг·м/с] = 9.80665 Вт
• 1 Джоуль в секунду [Дж·с]= 1 Вт
• 1 Джоуль в час [Дж·ч] = 0.0002777777777777 Вт
• 1 Эрг в секунду [эрг·с] = 0.0000001 Вт
• 1 Метрическая тонна охлаждения [RT] = 3861.15995 Вт

США и Британия

• 1 Американская тонна охлаждения [USRT] = 3.51686666 кВт
• 1 Британская термальная единица в секунду [BTU/s] = 1055.06 Вт
• 1 Британская термальная единица в минуту [BTU/m] = 17.584333 Вт
• 1 Британская термальная единица в час [BTU/h] = 0.293072224 Вт
• 1 Фунт на фут в секунду [ft·lbf/s] = 1.35581795 Вт

Мощность тока: единица измерения электрической величины, формулы для ее определения

Мощность является физическим показателем. Она определяет работу, производимую во временном отрезке и помогающую измерять энергетическое изменение. Благодаря единице измерения мощности тока легко определяется скоростное энергетическое течение энергии в любом пространственном промежутке.

Из-за прямой зависимости мощности от напряжения в сети и токовой нагрузки следует, что эта величина может появляться как от взаимодействия большого тока с малым напряжением, так и в результате возникновения значительного напряжения с малым током. Такой принцип применим для превращения в трансформаторах и при передаче электроэнергии на огромные расстояния.

Существует формула для расчета этого показателя. Она имеет вид P = A / t = I * U, где:

• Р является показателем токовой мощности, измеряется в ваттах;
• А — токовая работа на цепном участке, исчисляется джоулями;
• t выступает временным промежутком, на протяжении которого совершалась токовая работа, определяется в секундах;
• U является электронапряжением участка цепи, исчисляется Вольтами;
• I — токовая сила, исчисляется в амперах.

Электрическая мощность может иметь активные и реактивные показатели. В первом случае происходит преобразование мощностной силы в иную энергию. Ее измеряют в ваттах, так как она способствует преобразованию вольта и ампера.

Реактивный показатель мощности способствует возникновению самоиндукционного явления. Такое преобразование частично возвращает энергетические потоки обратно в сеть, из-за чего происходит смещение токовых значений и напряжения с отрицательным воздействием на электросеть.

Определение активного и реактивного показателя

Активная мощностная сила вычисляется путем определения общего значения однофазной цепи в синусоидальном токе за нужный временной промежуток. Формула расчета представлена в виде выражения Р = U * I * cos φ, где:

• U и I выступают в качестве среднеквадратичного токового значения и напряжения;
• cos φ является углом межфазного сдвига между этими двумя величинами.

Благодаря мощностной активности электроэнергия превращается в другие энергетические виды: тепловую и электромагнитную энергии. Любая электросеть с током синусоидального или несинусоидального направления определяет активность цепного участка суммированием мощностей каждого отдельного цепного промежутка. Электромощность трехфазного цепного участка определяется суммой каждой фазной мощности.

Аналогичным показателем активной мощностной силы считается величина мощности прохождения, которая рассчитывается путем разницы между ее падением и отражением.

Реактивный показатель измеряется в вольт-амперах. Он является величиной, применяемой для определения электротехнических нагрузок, создаваемых электромагнитными полями внутри цепи переменного тока. Единица измерения мощности электрического тока вычисляется умножением среднеквадратичного значения напряжения в сети U на переменный ток I и угол фазного синуса между этими величинами. Формула расчета выглядит следующим образом: Q = U * I * sin.

Если токовая нагрузка меньше напряжения, тогда фазное смещение носит положительное значение, если наоборот — отрицательное.

Величина измерения

Основной электротехнической единицей является мощность. Для того чтобы определить, в чем измеряется мощность электрического тока, нужно изучить основные характеристики этой величины. По законам физики ее измеряют в ваттах. В условиях производства и в быту величина переводится в киловатты. Вычисления крупных мощностных масштабов требуют перевода в мегаватты. Такой подход практикуется на электростанциях для получения электрической энергии. Работа исчисляется в джоулях. Величина определяется следующими соотношениями:

• 1 Джоуль равен 1 Ватту, умноженному на 1 секунду;
• 1 кДж = 1000 Дж;
• 1Мдж = 1000000 Дж;
• 1 ватт/час = 1 киловатт/час;
• 1 кВт * ч = 1000 Вт * 3600 с = 3600000 Дж.

Потребительская мощностная сила обозначается на самом электроприборе или в паспорте к нему. Определив этот параметр, можно получить значения таких показателей, как напряжение и электрический ток. Используемые показатели указывают, в чем измеряется электрическая мощность, они могут выступать в виде ваттметров и варметров. Реактивная сила показателя мощности определяется фазометром, вольтметром и амперметром. Государственным эталоном того, в чем измеряется мощность тока, считается частотный диапазон от 40 до 2500 Гц.

Примеры вычислений

Для расчета тока чайника при электромощности 2 КВт используется формула I = P / U = (2 * 1000) / 220 = 9 А. Для запитывания прибора в электросеть не используется длина разъема в 6 А. Приведенный пример применим только тогда, когда полностью совпадает фазное и токовое напряжение. По такой формуле рассчитывается показатель всех бытовых приборов.

Если цепь является индуктивной или имеет большую емкость, то рассчитывать мощностную единицу тока необходимо, используя другие подходы. К примеру, мощность в двигателе с переменным током определяется с помощью формулы Р = I * U * cos.

При подключении прибора к трехфазной сети, где напряжение будет составлять 380 В, для определения показателя суммируются мощности каждой фазы в отдельности.

В качестве примера можно рассмотреть котел из трех фаз мощностной вместимостью 3 кВт, каждая из которых потребляет 1 кВт. Ток на фазе рассчитывается по формуле I = P / U * cos φ = (1 * 1000) / 220 = 4,5 А.

На любом приборе обозначается показатель электромощности. Передача большого мощностного объема, применяемая в производстве, осуществляется по линиям с высоким напряжением. Энергия преобразовывается с помощью подстанций в электроток и подается для использования в электросети.

Благодаря несложным расчетам определяется мощностная величина. Зная ее значение, можно сделать правильный подбор напряжения для полноценной работы приборов бытового и промышленного предназначения. Такой подход поможет избежать перегорания электроприборов и обезопасить электросети от перепадов напряжения.



Частота, длина волны, амплитуда и скорость волны — Характеристики волн — National 4 Physics Revision

Вам необходимо знать об этих величинах, используемых в волнах — что они означают, используемые для них символы и единицы, используемые для их измерения.

Синусоидальная волна, показывающая пики, впадины и длину волны

Амплитуда (\ (a \)) волны — это расстояние от центральной линии (или неподвижного положения) до вершины гребня или до низа впадины . Будьте осторожны с этим количеством — центральная линия не всегда отображается на диаграмме.Амплитуда измеряется в метрах (\ (м \)). Чем больше амплитуда волны, тем больше энергии она несет.

Длина волны \ (\ lambda \) волны — это расстояние от любой точки на одной волне до той же точки на следующей волне. (Символ представляет собой греческую букву «лямбда».) Чтобы избежать путаницы, лучше всего измерять длину волны от вершины гребня до вершины следующего гребня или от нижней части впадины до нижней части следующего гребня. впадина. Длина волны также измеряется в метрах (\ (m \)) — в конце концов, это длина.

Частота (\ (f \)) волны — это количество волн, прошедших точку за определенное время. Обычно мы используем время в одну секунду, так что это дает частоту в единице герц (\ (Гц \)), поскольку один герц равен одной волне в секунду.

Не путайте это количество с частотой. Это не расстояние, пройденное волнами, и не скорость, хотя оно связано с обеими этими величинами. Для волн на воде и звуковых волн обычно достаточно единицы герц, но радио- и телевизионные волны имеют такую ​​высокую частоту, что килогерцы (\ (кГц \)) или даже мегагерцы (\ (МГц \)) являются лучшими единицами измерения.{-1} \)). Звук распространяется со скоростью около 340 метров в секунду.

Измерение частоты IP — Сервис CloudTesting ™

Frequency Measure IP — это алгоритм IP, который измеряет частоту и период периодического сигнала частотомером.
Используя этот IP, можно легко измерить и оценить следующие электрические характеристики целевых устройств.

• Измерение частоты выходных часов устройства
• Характеристика схемы ФАПЧ
• Характеристика цепи VCO
• Контроль качества кварцевого генератора

Кроме того, с помощью подключаемого модуля Multipoint Measurement можно легко измерить и оценить такие характеристики, как колебания значений нескольких измерений / максимальное значение / минимальное значение / среднее значение / вариация для вышеуказанного измерения.

Измененное содержание версии 2.03.00

Характеристики

• Может измерять частоту и период вывода, подключенного к каналу ввода / вывода.
• С помощью частотомера можно выполнить следующие измерения.

Тип измерения	Содержание измерений
Частота	Измерьте частоту (единицы: [Гц]) измеренного сигнала.
Period	Измерьте период (единицы: [с]) измеренного сигнала.

• Может измерять частоту / период для конкретного рабочего состояния, выполняя шаблон.

• Можно измерить, разомкнув контактное реле контакта ввода / вывода.

• Можно измерять, подавая напряжение VIH / VIL на контакты устройства.

• Значения измерений и результаты оценки могут быть сохранены в переменных путем промежуточной обработки.

• Может судить о результате выполнения шаблона.

• Может выполнить шаблон завершения.

• Может применять сигнал произвольной формы, синхронизированный с шаблоном с помощью подключаемого модуля применения произвольной формы сигнала .

• Может подавать питание от приборов внешнего источника питания, управляемых GPIB с помощью подключаемого модуля управления внешним источником питания .

• Cn измеряет несколько условий выполнения шаблона в одном элементе теста с помощью подключаемого модуля многоточечных измерений .Кроме того, можно судить о статистических значениях в каждой точке измерения.

• Может выполнять командные файлы в каждый момент времени последовательности измерений с помощью подключаемого модуля выполнения командных файлов .

• Путем подключения следующих IP-адресов он может оценивать и анализировать результаты измерений при изменении условий измерения.

Какие единицы используются для измерения звука? — Открытие звука в море

Науки включают количественное измерение свойств мира природы.Когда ученый проводит измерения, он должен сначала определить конкретные свойства, которые он будет измерять, как эти измерения будут проводиться и какие единицы они будут использовать. Например, если ученый измеряет свойство глубины воды, недостаточно сказать, что глубина воды составляет 250 единиц. Это может означать 250 футов, 250 метров или 250 морских саженей. Ученый должен указать единицы для этого значения.

Также важно понимать, как переводить единицы из одних единиц в другие.Большинство американцев знают, что 12 дюймов равны 1 футу, но может не быть известно, что 1 морская миля равна 1,85 километру. Хорошо известно, что 1 километр равен 1000 метрам, но не так хорошо известно, что 1 микрометр равен 10 ^-6 метрам.

Существуют фиксированные единицы измерения, такие как метры, и относительные единицы, такие как децибелы (дБ). Относительные единицы связаны с конкретными условиями. Например, децибелы в воде имеют другое относительное значение, чем децибелы в воздухе. Ученые согласились использовать 1 микропаскаль (мкПа) в качестве эталонного давления для подводного звука.Однако в воздухе ученые согласились использовать более высокое эталонное давление — 20 микропаскалей.

Таким образом, интенсивность звука, указанная в дБ в воде, отличается от интенсивности звука, выраженной в дБ в воздухе.

Ниже приведены некоторые общие единицы измерения звука под водой, их измерения и способы их преобразования друг в друга.

Общие единицы

Расстояние
1 метр (м) — единица расстояния; равно 3,28 фута
1 километр (км) = 1000 метров
1 сантиметр (см) = 0.01 метр (100 см = 1 м)
1 миллиметр (мм) = 0,001 метра (1000 мм = 1 м)
1 микрометр (мкм также 1 микрон) = 10 ^-6 метров

1 фут (ft) — единица расстояния; равно 12 дюймов

Вес / масса
1 грамм (г) — единица массы
1 килограмм (кг) = 1000 грамм = 2,2 фунта
1 метрическая тонна = 1000 килограммов

1 тонна — единица веса; равно 2000 фунтов (фунтов)

Время
1 секунда (сек) — единица времени
1 миллисекунда (мсек) = 0.001 секунда (10 ^-3 сек) (1000 мс = 1 сек)
1 микросекунда (мкс) = 0,000001 секунда (10 ^-6 сек) (1000000 мкс = 1 сек)

Температура
градусов Цельсия (° C) и Фаренгейта (° F) — единицы измерения температуры

Чтобы преобразовать градусы Цельсия (° C) в градусы Фаренгейта (° F):
(° F) = (° C x 1,8) + 32

Чтобы преобразовать градусы Фаренгейта (° F) в градусы Цельсия (° C):
(° C) = (° F — 32) ÷ 1,8

Соленость
1 часть на тысячу (ppt) = 1 грамм соли на литр раствора; единица пропорции, равная 0.001

Практические единицы солености (PSU или psu) = отношение проводимости пробы морской воды к стандартному раствору хлорида калия. Поскольку в соотношениях нет единиц, неверно, что 35 БП в точности равны 35 ppt.

Частота
1 Герц (Гц) = 1 цикл в секунду — единица частоты
1 килогерц (кГц) = 1000 Герц

Давление
1 паскаль (Па) — единица измерения давления
1 микропаскаль (мкПа) = 10 ^-6 Па — обычно используется при измерении звукового давления.
1 атмосфера (атм) = 14,7 фунтов / дюйм2 = 101,325 Па

Intensity
децибел (дБ) — мера силы звука; 1/10 бел.
Децибел — относительная единица, сравнивающая два давления; следовательно, также должно быть указано эталонное давление. В подводной акустике эталонное давление составляет 1 микропаскаль, поэтому истинная единица интенсивности подводного звука — дБ относительно 1 микропаскаль. В воздухе ученые согласились использовать более высокое эталонное давление — 20 микропаскалей.Следовательно, истинная единица интенсивности звуков в воздухе — это дБ относительно 20 микропаскалей. Поскольку в них используются разные эталонные давления, интенсивность звука, указанная в дБ в воде, не совпадает с интенсивностью звука, указанная в дБ в воздухе .

Дополнительные ссылки по DOSITS

Дополнительные ресурсы

единиц спектральных измерений

единиц спектральных измерений

---

Общий диапазон длин волн света, который мы можем измерить, охватывает невероятный диапазон почти
20 степеней десяти от самых коротких гамма-лучей до самых длинных радиоволн.Устройства, необходимые для измерения этих различных видов света, очень отличаются от
друг друга и были разработаны в разное время разными группами ученых.
Возможно, поэтому неудивительно, что соглашения, выработанные для каждой длины волны
диапазон, такой как единицы, используемые для описания длин волн или другой подобной номенклатуры,
варьируются от одной спектральной области к другой.

Демонстрируя наши личные предубеждения, может быть полезно снова обратиться к оптическому
область.{-10} метров, а видимый свет охватывает
колеблется от 4000 до 7000 Ангстрем (чуть меньше двух в относительном
длины волн). Для сравнения, ближний ультрафиолет обычно определяется как область
от 2000 Ангстрем до видимого диапазона дальний ультрафиолет опускается до 912 Ангстрем,
и крайний ультрафиолет простирается примерно до 50 ангстрем. Следовательно, ультрафиолет
свет распространяется примерно в 80 раз по относительной длине волны! (Я сказал вам
оптический диапазон составлял всего крошечных частей всего спектра!)

На длинах волн, превышающих оптический свет, единица Ангстрема становится все более и более
неловко.При 10000 Ангстрем астрономы обычно переходят в другую единицу измерения.
называется микроном, который составляет одну миллионную метра. (Следовательно, 10000 ангстрем =
1 микрон.) Похоже, это единица выбора для инфракрасного излучения. Например,
Инфракрасный астрономический спутник, известный как IRAS, наблюдал за всем небом.
в начале 1980-х на четырех длинах волн инфракрасного излучения: 12, 25, 60 и 100 микрон.
(Еще раз обратите внимание — инфракрасная область простирается более чем в 100 раз относительно
длины волн!)

В радиочасти спектра можно было измерить длины волн линейкой
или мерку — если бы вы видели свет радио! (И если бы вы могли получить световую волну
стоять на месте!) Самые короткие длины волн, обычно относящиеся к радиодиапазону:
около миллиметра, а самые длинные простираются до десятков и даже сотен метров,
относительная длина волны более чем в 100000 раз!

По историческим причинам радиоастрономы часто ссылаются на частоту
радиосвета вместо длины волны.Частота — это просто количество
длины волн
в секунду прохождение некоторой контрольной точки: чем короче длина волны, тем их больше
которые могут проходить контрольную точку за секунду (то есть чем больше частота).
Единица измерения длины волны 1 в секунду называется Гц, Гц.
(Гц). МНОГО длин волн в секунду может пройти контрольную точку, а радиоволны
измеряются в тысячах (килогерц или кГц, как в AM-радио), миллионах (мегагерц
или МГц, как FM-радио), или миллиарды (гигагерцы или ГГц) длин волн в секунду.Большинство длин волн, используемых в астрономии, находятся в диапазоне МГц и ГГц.

Для рентгеновского и гамма-излучения блок Ангстрем снова заброшен, потому что
длины волн становятся намного меньше одного Ангстрема! В этих регионах это
принято показывать спектры в масштабе единиц энергии вместо длин волн.
(Конечно, эти двое напрямую связаны, поэтому меняются только единицы.)
Выбранная единица энергии называется электрон-вольт .
(или эВ), с теми же префиксами, которые используются с Герцами, чтобы указать все больше и больше
энергии.Рентгеновское излучение колеблется от 0,1 до 100 килоэлектронвольт (кэВ), а гамма
лучи простираются вплоть до энергий гигаэлектронвольт (ГэВ). (Для сравнения,
оптический фотон имел бы энергию, выраженную всего в 2 электрон-вольта,
или около одной 500-миллионной типичного гамма-луча!)

Даже несмотря на то, что единицы измерения сильно различаются от региона к региону,
важно понимать, что все они измеряют одно и то же! Свет
просто свет, независимо от того, какая часть спектра ЭМ обсуждается, и это
просто характерная длина электромагнитной вибрации (или энергия
переносится каждым световым фотоном), который меняется по всему ЭМ-спектру!

Щелкните здесь, чтобы перейти к следующему разделу.

Вернитесь на главную страницу спектроскопии.

Билл Блэр ([email protected])

Как называется прибор для измерения частоты волны?

Роберт Дж.

задано • 31.08.16

Питер Т.
ответил • 31.08.16

Эффективный репетитор английского, испанского и элементарной математики.

Герц. это имя используется для волн и всего, что часто повторяется.

Все еще ищете помощь? Получите правильный ответ быстро.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и познакомьтесь онлайн.Никаких пакетов или подписок, платите только за необходимое время.

---

¢
€
£
¥
‰
µ
·
•
§
¶
SS
‹
›
«
»
< >
≤
≥
—
—
¯
‾
¤
¦
¨
¡
¿
ˆ
˜
°
—
±
÷
⁄
×
ƒ
∫
∑
∞
√
∼
≅
≈
≠
≡
∈
∉
∋
∏
∧
∨
¬
∩
∪
∂
∀
∃
∅
∇
*
∝
∠
´
¸
ª
º
†
‡
А
Á
Â
Ã
Ä
Å
Æ
Ç
È
É
Ê
Ë
Я
Я
Я
Я
Ð
Ñ
Ò
Ó
Ô
Õ
Ö
Ø
Œ
Š
Ù
Ú
Û
Ü
Ý
Ÿ
Þ
à
á
â
ã
ä
å
æ
ç
è
é
ê
ë
я
я
я
я
ð
ñ
ò
ó
ô
х
ö
ø
œ
š
ù
ú
û
ü
ý
þ
ÿ
Α
Β
Γ
Δ
Ε
Ζ
Η
Θ
Ι
Κ
Λ
Μ
Ν
Ξ
Ο
Π
Ρ
Σ
Τ
Υ
Φ
Χ
Ψ
Ω
α
β
γ
δ
ε
ζ
η
θ
ι
κ
λ
μ
ν
ξ
ο
π
ρ
ς
σ
τ
υ
φ
χ
ψ
ω
ℵ
ϖ
ℜ
ϒ
℘
ℑ
←
↑
→
↓
↔
↵
⇐
⇑
⇒
⇓
⇔
∴
⊂
⊃
⊄
⊆
⊇
⊕
⊗
⊥
⋅
⌈
⌉
⌊
⌋
〈
〉
◊

Частота, таблицы частот и уровни измерений — вводная статистика

Когда у вас есть набор данных, вам нужно будет организовать его так, чтобы вы могли анализировать, как часто каждый элемент данных встречается в наборе.Однако при расчете частоты вам может потребоваться округлить ответы, чтобы они были как можно более точными.

Ответы и округление

Самый простой способ округлить ответы — поставить окончательный ответ на один десятичный знак больше, чем было в исходных данных. Завершите только окончательный ответ. По возможности не округляйте промежуточные результаты. Если возникает необходимость округлить промежуточные результаты, доведите их как минимум до вдвое большего числа десятичных знаков, чем в окончательном ответе.Например, среднее значение четырех, шести и девяти баллов в трех тестах составляет 6,3 с округлением до ближайшей десятой, поскольку данные представляют собой целые числа. Большинство ответов будут округлены таким образом.

В этом курсе нет необходимости уменьшать большинство дробей. В главе о вероятностях, особенно в главе о вероятностях, полезно оставлять ответ в виде нередуцированной дроби.

Уровни измерения

Способ измерения набора данных называется его уровнем измерения.Правильные статистические процедуры зависят от того, знаком ли исследователь с уровнями измерения. Не каждую статистическую операцию можно использовать с каждым набором данных. Данные можно разделить на четыре уровня измерения. Их (от низшего до высшего уровня):

• Номинальный уровень шкалы
• Порядковый уровень шкалы
• Уровень интервальной шкалы
• Уровень шкалы отношения

Данные, измеренные по номинальной шкале: качественные (категориальные) .Категории, цвета, названия, этикетки и любимые блюда вместе с ответами «да» или «нет» являются примерами данных номинального уровня. Данные по номинальной шкале не заказываются. Например, бессмысленно пытаться классифицировать людей по их любимой еде. Ставить пиццу на первое место, а на второе — суши, не имеет смысла.

компаний по производству смартфонов — еще один пример данных номинального масштаба. Данные представляют собой названия компаний, производящих смартфоны, но нет согласованного порядка этих брендов, хотя у людей могут быть личные предпочтения.Данные номинального масштаба нельзя использовать в расчетах.

Данные, измеренные с использованием порядковой шкалы, аналогичны данным номинальной шкалы, но имеют большую разницу. Данные порядковой шкалы можно заказать. Примером данных по порядковой шкале является список пяти лучших национальных парков США. Пятерку лучших национальных парков США можно отнести к пяти, но мы не можем измерить различия между данными.

Другой пример использования порядковой шкалы — обзор круиза, где ответы на вопросы о круизе — «отлично», «хорошо», «удовлетворительно» и «неудовлетворительно».Эти ответы отсортированы от наиболее желаемого до наименее желаемого. Но разницу между двумя частями данных невозможно измерить. Как и данные номинальной шкалы, данные порядковой шкалы нельзя использовать в расчетах.

Данные, измеренные с использованием шкалы интервалов, аналогичны данным порядкового уровня, поскольку имеют определенный порядок, но между данными есть разница. Различия между данными шкалы интервалов можно измерить, хотя у данных нет отправной точки.

Температурные шкалы, такие как Цельсия (C) и Фаренгейта (F), измеряются с использованием шкалы интервалов. В обоих измерениях температуры 40 ° равно 100 минус 60 °. В различиях есть смысл. Но 0 градусов — нет, потому что в обеих шкалах 0 не является самой низкой температурой. Существуют такие температуры, как -10 ° F и -15 ° C, и они ниже 0,

.

Данные на интервальном уровне можно использовать в вычислениях, но нельзя выполнить одно сравнение. 80 ° C не в четыре раза жарче, чем 20 ° C (и 80 ° F в четыре раза больше, чем 20 ° F).Нет никакого смысла в соотношении 80 к 20 (или четыре к одному).

Данные, измеренные с использованием шкалы соотношений, решают проблему соотношения и предоставляют наиболее полную информацию. Данные шкалы соотношений аналогичны данным шкалы интервалов, но имеют нулевую отметку и могут быть вычислены соотношения. Например, четыре итоговых оценки за итоговый экзамен по статистике множественного выбора: 80, 68, 20 и 92 (из возможных 100). Экзамены выставляются на автоматическом уровне.

Данные могут быть упорядочены от самого низкого до самого высокого: 20, 68, 80, 92.

Различия между данными имеют смысл. Оценка 92 больше, чем оценка 68 на 24 балла. Коэффициенты можно рассчитать. Наименьшая оценка — 0. Таким образом, 80 — это четыре раза по 20. Оценка 80 в четыре раза лучше, чем оценка 20.

Частота

Двадцать студентов спросили, сколько часов они работают в день. Их ответы в часах следующие: 56332475235654435253.

(рисунок) перечисляет различные значения данных в порядке возрастания и их частоты.

Таблица периодичности рабочего времени студентов

ДАННЫЕ ЗНАЧЕНИЕ	ЧАСТОТА
2	3
3	5
4	3
5	6
6	2
7	1

Частота — это количество раз, когда значение данных встречается.Согласно (Рисунок), есть три студента, которые работают по два часа, пять студентов, которые работают по три часа, и так далее. Сумма значений в столбце частоты, 20, представляет общее количество учащихся, включенных в выборку.

Относительная частота — это отношение (доля или пропорция) количества раз, когда значение данных встречается в наборе всех результатов, к общему количеству результатов. Чтобы найти относительные частоты, разделите каждую частоту на общее количество студентов в выборке — в данном случае 20.Относительные частоты могут быть записаны в виде дробей, процентов или десятичных знаков.

Сумма значений в столбце относительной частоты на (Рисунок) равна, или 1.

Накопленная относительная частота — это накопление предыдущих относительных частот. Чтобы найти совокупные относительные частоты, добавьте все предыдущие относительные частоты к относительной частоте для текущей строки, как показано на (Рисунок).

Последняя запись в столбце совокупной относительной частоты — единица, указывающая на то, что накоплено сто процентов данных.

ПРИМЕЧАНИЕ

Из-за округления сумма в столбце относительной частоты не всегда может быть равна единице, а последняя запись в столбце совокупной относительной частоты может не быть единицей. Однако каждое из них должно быть близко к одному.

(рисунок) представляет рост в дюймах выборки из 100 полупрофессиональных футболистов-мужчин.

Данные в этой таблице были сгруппированы в следующие интервалы:

• от 59,95 до 61,95 дюймов
• 61.От 95 до 63,95 дюймов
• От 63,95 до 65,95 дюймов
• от 65,95 до 67,95 дюймов
• от 67,95 до 69,95 дюймов
• от 69,95 до 71,95 дюймов
• от 71,95 до 73,95 дюймов
• от 73,95 до 75,95 дюймов

Примечание

Этот пример снова используется в описательной статистике, где будет объяснен метод, используемый для вычисления интервалов.

В этом примере пяти игроков , чей рост попадает в интервал 59.95–61,95 дюймов, три игроков, рост которых находится в интервале 61,95–63,95 дюймов, 15 игроков, рост которых находится в интервале 63,95–65,95 дюймов, 40 игроков, рост которых находится в интервале 65,95–67,95 дюймов, 17 игроков, рост которых находится в интервале 67,95–69,95 дюймов, 12 игроков, рост которых находится в интервале 69,95–71,95, семь игроков, рост которых попадает в интервал 71.95–73.95 и — один игрок , рост которого находится в интервале 73.95–75.95. Все высоты попадают между конечными точками интервала, а не между конечными точками.

Из (Рисунок) найдите процент высот меньше 65,95 дюймов.

Если вы посмотрите на первый, второй и третий ряды, то увидите, что все высоты меньше 65,95 дюйма. Есть 5 + 3 + 15 = 23 игрока, рост которых меньше 65,95 дюйма. Процент высоты менее 65,95 дюймов составляет тогда или 23%.Этот процент представляет собой запись совокупной относительной частоты в третьей строке.

Попробуйте

(рисунок) показывает количество в дюймах годового количества осадков в выборке городов.

Из (Рисунок) найдите процент осадков, который составляет менее 9,01 дюйма.

Из (Рисунок) найдите процент высот между 61,95 и 65,95 дюймов.

Сложите относительные частоты во второй и третьей строках: 0.03 + 0,15 = 0,18 или 18%.

Попробуйте

Из (Рисунок) найдите процент осадков, который составляет от 6,99 до 13,05 дюйма.

Используйте рост 100 мужчин-полупрофессиональных футболистов (рисунок). Заполните пропуски и проверьте свои ответы.

1. Процент высот от 67,95 до 71,95 дюймов: ____.
2. Процент высот от 67,95 до 73,95 дюймов: ____.
3. Процент высот больше 65.95 дюймов это: ____.
4. Количество игроков в выборке с ростом от 61,95 до 71,95 дюймов: ____.
5. Какие данные есть высоты?
6. Опишите, как вы могли бы собрать эти данные (рост), чтобы эти данные были характерны для всех мужчин-полупрофессиональных футболистов.

Помните, вы считаете частоты . Чтобы найти относительную частоту, разделите частоту на общее количество значений данных. Чтобы найти накопленную относительную частоту, добавьте все предыдущие относительные частоты к относительной частоте для текущей строки.

1. 29%
2. 36%
3. 77%
4. 87
5. количественный непрерывный
6. получить списки из каждой команды и выбрать простую случайную выборку из каждой

Попробуйте

Из (Рисунок) найдите количество городов, в которых выпадает от 2,95 до 9,01 дюйма.

Совместное упражнение

Попросите кого-нибудь из вашего класса опросить количество братьев и сестер (братьев и сестер) у каждого ученика.Создайте частотную таблицу. Добавьте к нему столбец относительной частоты и столбец совокупной относительной частоты. Ответьте на следующие вопросы:

1. У какого процента учеников вашего класса нет братьев и сестер?
2. Какой процент студентов имеет от одного до трех братьев и сестер?
3. У какого процента студентов меньше трех братьев и сестер?

Девятнадцать человек спросили, сколько миль (с точностью до мили) они едут на работу каждый день. Данные следующие: 25732101815207101851213124510.(Рисунок) было произведено:

1. Таблица правильная? Если это не так, что не так?
2. Верно или неверно: три процента опрошенных людей добираются до трех миль. Если утверждение неверно, что это должно быть? Если таблица неверна, внесите исправления.
3. Какая доля опрошенных людей проезжает пять или семь миль?
4. Какая доля опрошенных людей проезжает 12 миль и более? Менее 12 миль? От пяти до 13 миль (не считая от пяти до 13 миль)?

1. No.В столбце частоты указано 18, а не 19. Не все совокупные относительные частоты верны.
2. Неверно. Частота на три мили должна быть одна; на две мили (оставленные) две. Столбец совокупной относительной частоты должен содержать: 0,1052, 0,1579, 0,2105, 0,3684, 0,4737, 0,6316, 0,7368, 0,7895, 0,8421, 0,9474, 1,0000.
4. «

Попробуйте

(рисунок) представляет количество в дюймах годового количества осадков в выборке городов. Какая доля опрошенных городов попадает между 11.03 и 13,05 дюйма осадков каждый год?

(рисунок) содержит общее количество погибших во всем мире в результате землетрясений за период с 2000 по 2012 год.

Год	Общее количество смертей
2000	231
2001	21 357
2002	11 685
2003	33 819
2004	228 802
2005	88 003
2006	6,605
2007	712
2008	88 011
2009	1,790
2010	320,120
2011	21 953
2012	768
Всего	823 856

Ответьте на следующие вопросы.

1. Какова частота смертей, измеренная с 2006 по 2009 годы?
2. Какой процент смертей произошел после 2009 года?
3. Какова относительная частота смертей, произошедших в 2003 году или ранее?
4. Каков процент смертей в 2004 году?
5. Что это за данные о количестве смертей?
6. Шкала Рихтера используется для количественной оценки энергии, производимой землетрясением. Примеры чисел по шкале Рихтера: 2,3, 4.0, 6.1 и 7.0. Что за данные эти числа?

1. 97118 (11,8%)
2. 41,6%
3. 67 092/823 356 или 0,081 или 8,1%
4. 27,8%
5. Количественный дискретный
6. Количественный непрерывный

Попробуйте

(рисунок) содержит общее количество дорожно-транспортных происшествий со смертельным исходом в США за период с 1994 по 2011 годы.

Год	Общее количество сбоев	Год	Общее количество сбоев
1994	36 254	2004	38 444
1995	37 241	2005	39 252
1996	37 494	2006	38 648
1997	37 324	2007	37 435
1998	37 107	2008	34 172
1999	37 140	2009	30 862
2000	37 526	2010	30 296
2001	37 862	2011	29 757
2002	38 491	Всего	653 782
2003	38 477

Ответьте на следующие вопросы.

1. Какова частота смертей, измеренная с 2000 по 2004 год?
2. Какой процент смертей произошел после 2006 года?
3. Какова относительная частота смертей, произошедших в 2000 году или ранее?
4. Каков процент смертей в 2011 году?
5. Какова совокупная относительная частота за 2006 г.? Объясните, что это число говорит вам о данных.

Обзор главы

Некоторые вычисления производят числа с искусственной точностью.Нет необходимости сообщать значение с точностью до восьми десятичных знаков, если меры, которые сгенерировали это значение, были точны только до ближайшей десятой. Округлите окончательный ответ до одного десятичного знака больше, чем было в исходных данных. Это означает, что если у вас есть данные, измеренные с точностью до десятых долей единицы, сообщайте окончательную статистику с точностью до сотых.

Помимо округления ответов, вы можете измерить свои данные, используя следующие четыре уровня измерения.

• Номинальный уровень шкалы: данные, которые нельзя заказать или использовать в расчетах
• Порядковый уровень шкалы: данных, которые можно заказать; разницу невозможно измерить
• Уровень интервальной шкалы: данных с определенным порядком, но без начальной точки; различия можно измерить, но нет такого понятия, как соотношение.
• Уровень шкалы соотношения: данных с начальной точкой, которую можно заказать; различия имеют смысл, и соотношения можно вычислить.

При организации данных важно знать, сколько раз встречается значение. Сколько студентов-статистиков изучают пять или более часов перед экзаменом? Какой процент семей в нашем квартале имеет двух домашних животных? Частота, относительная частота и совокупная относительная частота — это меры, которые отвечают на подобные вопросы.

Какой тип измерительной шкалы используется? Номинальный, порядковый, интервальный или коэффициентный.

1. Футболисты средней школы, классифицируемые по спортивным способностям: Высшее, Среднее, Выше среднего
2. Температура выпечки для различных основных блюд: 350, 400, 325, 250, 300
3. Цвета мелков в коробке с 24 мелками
4. Номера социального страхования
5. Доходы в долларах
6. Опрос удовлетворенности социальных веб-сайтов по номерам: 1 = очень доволен, 2 = в некоторой степени удовлетворен, 3 = не удовлетворен
7. Политическое мировоззрение: крайний левый, лево-центр, право-центр, крайний правый
8. Текущее время на аналоговых часах
9. Расстояние в милях до ближайшего продуктового магазина
10. Даты 1066, 1492, 1644, 1947 и 1944 годов
11. Рост женщин 21–65 лет
12. Распространенные буквенные классы: A, B, C, D и F

1. порядковый
2. интервал
3. номинальная
4. номинальная

Соотношение

6. порядковый номер
7. номинальная
8. интервал

Соотношение

10. интервал

Соотношение

12. порядковый номер

ДОМАШНИЕ

Пятьдесят студентов-заочников спросили, сколько курсов они изучают в этом семестре.(Неполные) результаты показаны ниже:

Нагрузки на курс для студентов-заочников

Количество курсов	Частота	Относительная частота	Накопленная относительная частота
1	30	0,6
2	15
3

1. Заполните пустые поля (рисунок).
2. Какой процент студентов посещает ровно два курса?
3. Какой процент студентов посещает один или два курса?

30% 90% ->

Шестьдесят взрослых с заболеваниями десен спросили, сколько раз в неделю они пользовались зубной нитью до постановки диагноза. (Неполные) результаты показаны на (Рисунок).

Частота чистки зубной нитью для взрослых с заболеваниями десен

# Чистка зубной нитью в неделю	Частота	Относительная частота	Кумулятивная относительная частота.
0	27	0,4500
1	18
3			0,9333
6	3	0,0500
7	1	0,0167

1. Заполните пустые поля (рисунок).
2. Какой процент взрослых пользуется зубной нитью шесть раз в неделю?
3. Какой процент чистки зубной нитью не более трех раз в неделю?

1. # Чистка зубной нитью в неделю	Частота	Относительная частота	Накопленная относительная частота
   0	27	0.4500	0,4500
   1	18	0,3000	0,7500
   3	11	0,1833	0,9333
   6	3	0,0500	0,9833
   7	1	0,0167	1

2. 5,00%
3. 93,33%

Девятнадцать иммигрантов в США спросили, сколько лет с точностью до ближайшего года они прожили в США.S. Данные следующие: 257221020150702051215124510.

(рисунок).

1. Исправьте ошибки в (Рисунок). Также объясните, как кто-то мог получить неправильные номера.
2. Объясните, что не так в этом утверждении: «47 процентов опрошенных людей жили в США в течение 5 лет».
3. Исправьте утверждение в b , чтобы сделать его правильным.
4. Какая часть опрошенных прожила в США пять или семь лет?
5. Какая часть опрошенных проживала в США.С. максимум 12 лет?
6. Какая часть опрошенных прожила в США менее 12 лет?
7. Какая часть опрошенных прожила в США от пяти до 20 лет включительно?

″> Частоты для 15 и 20 должны быть равны двум, а относительные частоты должны быть 2 19. Ошибка могла быть из-за неправильного копирования данных. Кумулятивная относительная частота за пять лет должна быть равна 0.4737. Ошибка связана с вычислением относительной частоты вместо кумулятивной относительной частоты. Кумулятивная относительная частота за 15 лет должна быть 0,8947. 47% — это кумулятивная относительная частота, а не относительная частота. 47% опрошенных прожили в США пять лет или меньше. 5 19 15 19 13 19 13 19 ->

Сколько времени нужно, чтобы добраться до работы? (Рисунок) показывает среднее время в пути по штату для работников в возрасте от 16 лет, которые не работают дома.Найдите среднее время в пути и правильно округлите ответ.

24,0	24,3	25,9	18,9	27,5	17,9	21,8	20,9	16,7	27,3
18,2	24,7	20,0	22,6	23,9	18,0	31,4	22,3	24,0	25,5
24.7	24,6	28,1	24,9	22,6	23,6	23,4	25,7	24,8	25,5
21,2	25,7	23,1	23,0	23,9	26,0	16,3	23,1	21,4	21,5
27,0	27,0	18,6	31,7	23,3	30.1	22,9	23,3	21,7	18,6

Сумма времени в пути 1 173,1. Разделите сумму на 50, чтобы вычислить среднее значение: 23,462. Поскольку время в пути в каждом штате измерялось до ближайшей десятой, округлите это вычисление до ближайшей сотой: 23,46.

Журнал Forbes опубликовал данные о лучших малых фирмах в 2012 году. Это были фирмы, акции которых торговались на бирже не менее года, их стоимость акций составляла не менее 5 фунтов стерлингов за акцию, а годовой доход составлял 5 миллионов фунтов стерлингов. и? 1 миллиард.(Рисунок) показывает возраст генеральных директоров первых 60 фирм.

Возраст	Частота	Относительная частота	Накопленная относительная частота
40–44	3
45–49	11
50–54	13
55–59	16
60–64	10
65–69	6
70–74	1

1. Какова частота генерального директора в возрасте от 54 до 65 лет?
2. Какой процент руководителей старше 65 лет?
3. Какова относительная частота лиц младше 50 лет?
4. Какова совокупная относительная частота генеральных директоров моложе 55 лет?
5. На каком графике показана относительная частота, а на каком — кумулятивная относительная частота?

26 (Это количество руководителей в категориях от 55 до 59 и от 60 до 64.) 12% (количество генеральных директоров в возрасте 65 лет и старше ÷ общее количество генеральных директоров) 14/60; 0,23; 23% 0,45 График A представляет совокупную относительную частоту, а график B показывает относительную частоту. ->

Используйте следующую информацию, чтобы ответить на следующие два упражнения: (рисунок) содержит данные об ураганах, которые нанесли прямые удары по США в период с 1851 по 2004 год. Урагану присваивается рейтинг категории силы, основанный на минимальной скорости ветра, создаваемой шторм.

Частота прямых попаданий ураганов

Категория	Количество прямых попаданий	Относительная частота	Кумулятивная частота
	Итого = 273
1	109	0.3993	0,3993
2	72	0,2637	0,6630
3	71	0,2601
4	18		0,9890
5	3	0,0110	1,0000

Какова относительная частота прямых попаданий ураганов категории 4?

1. 0,0768
2. 0.0659
3. 0,2601
4. Недостаточно информации для расчета

Какова относительная частота прямых попаданий, которые СОВЕРШЕННО были ураганом категории 3?

1. 0,3480
2. 0,9231
3. 0,2601
4. 0,3370

b ->

Глоссарий

Накопленная относительная частота

Термин применяется к упорядоченному набору наблюдений от наименьшего к наибольшему.Накопленная относительная частота — это сумма относительных частот для всех значений, которые меньше или равны заданному значению.

Частота

количество раз, когда значение данных встречается

Относительная частота

отношение количества раз, когда значение данных встречается в наборе всех результатов, к количеству всех результатов к общему количеству результатов

Как осциллограф измеряет частоту?

Осциллографы

измеряют напряжение электрического сигнала, которое затем графически отображается в виде сигналов.Однако осциллограф можно использовать для измерения в различных приложениях, одним из которых является частота. Но как именно осциллограф измеряет частоту? Что ж, есть простой ответ, а есть более сложный.

В большинстве современных цифровых осциллографов, если не во всех, вычисления выполняются за вас, поэтому вы сможете получить значение частоты во время измерения напряжения. Просто нажмите пару кнопок, чтобы увидеть частоту сигнала, который вы пытаетесь проверить, а также другие статистические данные, такие как стандартное отклонение и средняя частота.Однако есть способы определить частоту без помощи технологий.

Как рассчитать частоту

Вы можете легко измерить время и частоту, используя горизонтальную шкалу осциллографа. Если вы хотите обеспечить точность при измерении частоты, это поможет увеличить область сигнала на дисплее осциллографа — сделав ее больше, чтобы вам было легче преобразовать форму сигнала.

Во-первых, вам необходимо измерить время, используя горизонтальную шкалу на вашем осциллографе, а также подсчитать количество горизонтальных делений от одного конца волны до другого, где она пересекает центральную горизонтальную линию координатной сетки.Затем вы можете умножить количество горизонтальных делений на время / деление, чтобы найти период сигнала. Получив это, вы можете выполнить расчет частоты: деление единицы на период. Математически это может быть представлено как частота = 1 / период .

Автоматические измерения на цифровом осциллографе

Как упоминалось ранее, большинство высококачественных цифровых осциллографов выполняют измерения автоматически, а это означает, что вам не нужно выполнять вычисления. На осциллографах Tektronix измерения времени можно найти под значком «измерения» на дисплее.Это даст вам точное, живое значение частоты, которая будет меняться в зависимости от передаваемого сигнала.

Вы также можете получить доступ ко всем статистическим данным. Таким образом, вы можете увидеть стандартное отклонение, среднее значение, максимум и минимум частоты, что дает лучшее представление о том, как реагирует сигнал.

.