Что можно определить с помощью закона кулона: что можно определить с помощью закона кулона

Содержание

Закон Кулона в физике простыми словами

В данное статье описывается знаменитый закон из молекулярной физики — закон Кулона, название дано в честь ученого, который его открыл. Описывается также правило принципа суперпозиции и границы применимости закона кулоновского взаимодействия.

Закон Кулона определение и формула

Значительная доля явлений, которые совершаются в окружающем нас мире, пока что не имеет объяснения. Физики не сумели их разъяснить даже с помощью механики и молекулярной физики, однако некоторые такие явления можно объяснить силами, которые функционируют между предметами на расстояниях. Массы этих взаимодействующих тел абсолютно не оказывают влияния на конечное значение этих сил. То есть они никак не гравитационные. Эти силы привыкли именовать электромагнитными.

Электростатическое поле формируется покоящимися во времени электрическими зарядами, причем само оно также неизменно во времени.

Шарль Кулон

Закон Кулона — это фундаментальный закон, который открыл в свое время опытным путем ученый, инженер, естествоиспытатель Шарль Кулон. Данное физическое правило позволяет описывать связь двух заряженных предметов, сформулировано оно для абсолютно не двигающихся точечных зарядов в вакууме. Это основной закон электростатики.

Внимание! Точечные заряды — абстракция, в реальной жизни их нет. В физике под этим понятием свыклись иметь в виду заряды, физические размеры которых проигрывают в сравнении с длиной прямой, проведенной между ними.

Формулировка означает следующее: между двумя точечными электрическими зарядами в вакууме есть определенная сила. Она пропорциональна умножению их модулей, деленных на квадрат расстояния. Под расстоянием подразумевается длина прямой, соединяющей данные заряды. Эта сила считается силой взаимодействия, она направлена вдоль отрезка, соединяющего предметы. Кулоновская сила значится силой отталкивающей в случае совпадения знаков зарядов, и силой притяжения, если знаки зарядов являются разными. Заряды, как известно, бывают положительные и отрицательные. Положительный заряд получается путем трения стеклянной палочки о шелк, в то же время отрицательный достигается путем натирания эбонитовой палочки о шерсть.

Формула:

F=k⋅|q1|⋅|q2|/r2.

Иначе записать можно так, где коэффициент в знаменателе — это константа диэлектрической проницаемости.

Формула закона Кулона

Коэффициент пропорциональности в законе Кулона

Коэффициент k введен для того, чтобы обеспечить переход из гауссовой системы единиц в международную систему единиц (СИ). В гауссовой системе коэффициент равен 1. В международной — он обратно пропорционален 4-кратному произведению числа ПИ на электрическую постоянную. Электрическая постоянная — это константа, относится к числу фундаментальных физических постоянных. Ее значение примерно равно 8,85418781762⋅10⁻¹² Ф/м, где Ф — фарад. Записывается электрическая постоянная как E0.

Коэффициент пропорциональности в законе Кулона

Важно! В тех средах, где пространство заполнено бесконечным однородным диэлектрическим веществом, также добавляют диэлектрическую проницаемость.

Например, для воздуха диэлектрическая проницаемость равна 1,000594.

Коэффициент диэлектрической проницаемости

Значения диэлектрической проницаемости:

Вакуум	1
Воздух	1,000594
Керосин	2
Титанат бария	1200

Закон Кулона в векторной форме

В векторном виде выглядит так:

Закон Кулона в векторной форме

Пояснения: r₁₂ — радиус-вектор;

Сила кулоновского взаимодействия измеряется в Ньютонах. В системе СИ за единицу заряда принимают 1 Кл, то есть величину заряда, который протекает за 1 секунду в проводнике при силе тока 1 А. 1 Ньютон равен килограмму, помноженному на метр и все это деленное на секунду в квадрате.

Стоит отметить и закон сохранения заряда, который гласит, что алгебраическая сумма величин зарядов замкнутой электрической системы не меняется!

Векторная и скалярная форма закона Кулона

Что можно определить с помощью закона Кулона

Применив данный физический закон, возможно установить значение и направление силы, которая действует на точечный заряд со стороны иного заряда.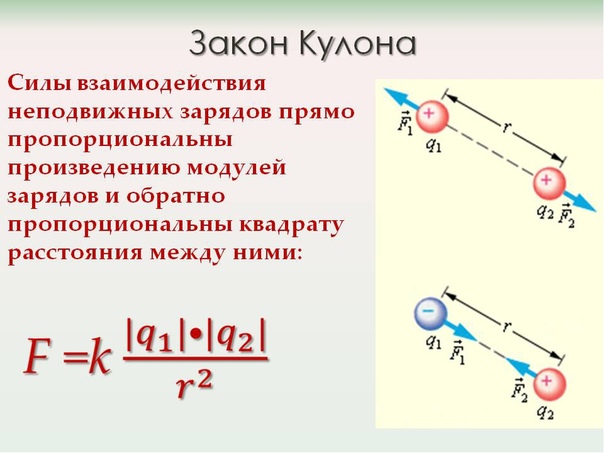 Также возможно вычислить величины точечных зарядов, значение радиус-вектора между ними.

Применение закона Кулона

Для каких заряженных тел справедлив закон

В идеале закон применяют только по отношению к точечным заряженным телам, однако в жизни он также справедлив для заряженных тел, расстояние между которыми превышает в несколько раз непосредственно размеры самих тел. Его применяют для сред, в которых нет свободных зарядов.

Точечно заряженные тела

Если заряды имеют форму сферы, то полагается, что весь заряд сконцентрирован в центре данной сферы.

Когда вынужденно применяют закон для заряженных тел, то их просто разбивают на множества заряженных точечных зарядов.

Также следует учесть тот факт, что заряды должны быть неподвижными. На те, которые движутся в электрическом поле, начинает действовать помимо силы Кулона еще сила Лоренца, к примеру. Данная сила придает заряженному телу дополнительное ускорение.

Границы применимости закона Кулона

Для того чтобы объяснить грамотно и максимально приближенно к истине поведение зарядов, находящихся в вакууме и являющихся точечными, используют закон Кулона. Тем не менее для реальных тел следует учесть следующие параметры:

объем и размеры рассматриваемых тел;
характеристики среды, в которой рассматривают заряженные тела;

Некоторые испытатели в экспериментах наблюдали, что если тело, которое несет небольшой заряд, поместить в электрическое поле другого тела с зарядом большим по значению, оно начинает притягиваться к последнему. В таком случае можно говорить о том, что кулоновское правило неприменимо, так как одноименные заряды должны отталкиваться, а не наоборот. То есть можно сказать, что в вышеописанном эксперименте не работают законы Кулона и сохранения электрического заряда. Скорее всего, физикам еще предстоит узнать, как именно и с помощью чего можно объяснить это явление.

Границы применимости закона Кулона

Также на очень маленьких расстояниях, порядка 10–18 м, появляются электрослабые эффекты. Кулоновские силы взаимодействия не работают. Но если внести небольшие поправки, то можно использовать закон Кулона. В сильных электромагнитных полях, к примеру около магнетронов, он также нарушается.

Закон Кулона в вакууме

Максимальное значение кулоновские силы достигают в вакууме. В других же средах добавляется в знаменатель сопротивление среды. Если проще, то чем больше значения зарядов, тем больше сила, если же расстояние между зарядами увеличить и поместить их в отличную от вакуума среду, то сила уменьшится.

Взаимодействие зарядов закон Кулона

Силы взаимодействия между зарядами по модулю принимают одинаковое значение, но отличаются по направлению. Таким образом, напрашивается вывод, что сила взаимодействия относится к тем силам, которые повинуются третьему закону Ньютона: у любой силы есть противодействующая сила, равная ей по модулю, но обратная по направлению.

Взаимодействие зарядов

Между электрическими зарядами одного знака действуют силы отталкивания, а между зарядами разных знаков — силы притяжения. Взаимодействие между зарядами лежит в основе всех фундаментальных законов электродинамики, электромагнетизма, электростатики.

Принцип суперпозиции закон Кулона

Вне зависимости от того, сколько зарядов в системе, можно использовать закон Кулона, чтобы высчитать силу взаимодействия между каждой парой. Отсюда следует принцип суперпозиции, который формулируется примерно так:

На заряд, который расположен в любой точке системы зарядов, действует сила. При этом заряды в системе объединены. Данная сила представляет собой векторную сумму сил, создающихся каждым зарядом системы по отдельности и действующих на заряд в данной точке. К слову, принцип суперпозиции распространяется на любые заряженные тела, не обязательно только на точечные заряды.

Принцип суперпозиции

Рисунок: F=F₂₁+F₃₁; F₂=F₁₂+F₃₂; F₃=F₁₃+F₂₃;

Пример: Есть две заряженные точки, которые действуют на третью точку силами: F1 и F2. Тогда система, состоящая из первой и второй точек, действует на третью точку с силой F = F1 + F2.

Также отсюда следует, что напряженность электрического поля, то есть силовая характеристика поля, складывается из суммы напряженностей, которые создаются обособленным зарядом поля.

Напряженность электрического поля

1) Напряженность равна результату деления кулоновской силы, действующей на заряд, на величину этого заряда.

[E] = Н/Кл = В/м

2) Величина пробного заряда не влияет на напряжённость.

3) Сила, которая действует на заряд от электрического поля, равняется произведению заряда на вектор напряженности в этой точке.

Напряженность электрического поля точечного заряда Q

Если рассмотреть с физической точки зрения, данное правило исходит из того, что покоящиеся заряды создают электростатическое поле. Иначе говоря, поля разных зарядов не влияют друг на друга, то есть суммарное поле системы зарядов складывается из векторной суммы электростатических полей, созданных каждым зарядом.

Важно! Следует учесть, что принцип суперпозиции не действует на очень малых или слишком больших расстояниях.

Принцип суперпозиции подразумевает тот факт, что на силы между двумя предметами (подразумеваются силы взаимодействия) не влияет присутствие других тел, обладающих каким-то количеством заряда. Но при этом должно быть задано распределение зарядов.

Задачи на закон Кулона с решением

Заряженный шарик приводят к тому, чтобы он соприкоснулся с точно таким же незаряженным шариком. Находясь на расстоянии r = 15r = 15 см, шарики отталкиваются с силой F = 1F = 1 мН. Какое значение было у первоначального заряда заряженного шарика?

Решение:

Так как заряд, когда соприкасается, делится на 2 ровные части из-за того, что шарики одинаковые, мы можем рассчитать заряды шаров после соприкосновения. Сила кулоновского взаимодействия нам известна.

Для начала необходимо перевести основные единицы в систему СИ:

Решение:

Получается, что до соприкосновения заряд заряженного шарика был вдвое больше:

Ответ:

Кл, что равно 10 мкКл.

Два одинаковых маленьких металлических шарика притягиваются с некоторой силой. Шарики привели в соприкосновение и раздвинули на расстояние в n = 2 раза большее, чем прежде. При этом модуль силы взаимодействия уменьшился в m = 5 раз. Найти величину заряда первого шарика до соприкосновения, если второй имел заряд q2 = 1,6 нКл.

Решение:

Сила кулоновского взаимодействия до того, как шары соприкоснулись:

Из условий задачи известно, что сила после соприкосновения уменьшилась в 5 раз:

Одновременно с этим заряды шаров изменились, то есть:

Одна и та же сила равна:

Следует ввести замену: q1 / q2 = t.

что равно

Решаем квадратное уравнение и находим два ответа:

Возвращаемся к замене:

Найдем q1:

Если считать по-другому:

Ответ:

Закон Кулона. Измерение электрического заряда.

В результате долгих наблюдений учеными было установлено, что разноименно заряженные тела притягиваются, а одноименно заряженные наоборот – отталкиваются. Это значит, что между телами возникают силы взаимодействия. Французский физик Ш. Кулон опытным путем исследовал закономерности взаимодействия металлических шаров и установил, что сила взаимодействия между двумя точечными электрическими зарядами будет прямопропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними:

Где k – коэффициент пропорциональности, зависящий от выбора единиц измерений физических величин, которые входят в формулу, а также и от среды, в которой находятся электрические заряды q₁ и q₂. r – расстояние между ними.

Отсюда можем сделать вывод, что закон Кулона будет справедлив только точечных зарядов, то есть для таких тел, размерами которых вполне можно пренебречь по сравнению с расстояниями между ними.

В векторной форме закон Кулона будет иметь вид:

Где q₁ и q₂ заряды, а r – радиус-вектор их соединяющий; r = |r|.

Силы, которые действуют на заряды, называют центральными. Они направлены по прямой, соединяющей эти заряды, причем сила, действующая со стороны заряда q₂ на заряд q₁, равна силе, действующей со стороны заряда q₁ на заряд q₂, и противоположна ей по знаку.

Для измерения электрических величин могут использоваться две системы счисления – система СИ (основная) и иногда могут использовать систему СГС.

В системе СИ одной из главных электрических величин является единица силы тока – ампер (А), то единица электрического заряда будет ее производной (выражается через единицу силы тока). Единицей определения заряда в СИ является кулон. 1 кулон (Кл) – это количество «электричества», проходящего через поперечное сечение проводника за 1 с при токе в 1 А, то есть 1 Кл = 1 А·с.

Коэффициент k в формуле 1а) в СИ принимается равным:

И закон Кулона можно будет записать в так называемой «рационализированной» форме:

Многие уравнения, описывающие магнитные и электрические явления, содержат множитель 4π. Однако, если данный множитель ввести в знаменатель закона Кулона, то он исчезнет из большинства формул магнетизма и электричества, которые очень часто применяют в практических расчетах. Такую форму записи уравнения называют рационализированной.

Величина ε₀ в данной формуле – электрическая постоянная.

Основными единицами системы СГС являются механические единицы СГС (грамм, секунда, сантиметр). Новые основные единицы дополнительно к вышеперечисленным трем в системе СГС не вводятся. Коэффициент k в формуле (1) принимается равным единице и безразмерным. Соответственно закон Кулона в не рационализированной форме будет иметь вид:

В системе СГС силу измеряют в динах: 1 дин = 1 г·см/с², а расстояние в сантиметрах. Предположим, что q = q₁ = q₂, тогда из формулы (4) получим:

Если r = 1см, а F = 1 дин, то из этой формулы следует, что в системе СГС за единицу заряда принимают точечный заряд, который (в вакууме) действует на равный ему заряд, удаленный от него на расстояние 1 см, с силой в 1 дин. Такая единица заряда называется абсолютной электростатической единицей количества электричества (заряда) и обозначается СГС_q. Ее размерность:

Для вычисления величины ε₀, сравним выражения для закона Кулона, записанные в системе СИ и СГС. Два точечных заряда по 1 Кл каждый, которые находятся на расстоянии 1 м друг от друга, будут взаимодействовать с силой (согласно формуле 3):

В СГС данная сила будет равна:

Сила взаимодействия между двумя заряженными частицами зависит от среды, в которой они находятся. Чтобы характеризовать электрические свойства различных, сред было введено понятие относительной диэлектрической проницательности ε.

Значение ε это различная величина для разных веществ – для сегнетоэлектриков ее значение лежит в пределах 200 – 100 000, для кристаллических веществ от 4 до 3000, для стекла от 3 до 20, для полярных жидкостей от 3 до 81, для неполярных жидкостей от 1,8 до 2,3; для газов от 1,0002 до 1,006.

Также от температуры окружающей среды зависит и диэлектрическая проницаемость (относительная).

Если учесть диэлектрическую проницаемость среды, в которую помещены заряды, в СИ закон Кулона примет вид:

Диэлектрическая проницаемость ε – величина безразмерная и она не зависит от выбора единиц измерения и для вакуума считается равной ε = 1. Тогда для вакуума закон Кулона примет вид:

Поделив выражение (6) на (5) получим:

Соответственно относительная диэлектрическая проницаемость ε показывает, во сколько раз сила взаимодействия между точечными зарядами в какой-то среде, которые находятся на расстоянии r друг относительно друга меньше, чем в вакууме, при том же расстоянии.

Для раздела электричества и магнетизма систему СГС иногда называют системой Гаусса. До появления системы СГС действовали системы СГСЭ (СГС электрическая) для измерения электрических величин и СГСМ (СГС магнитная) для измерения магнитных величин. В первой равной единице принималась электрическая постоянная ε₀, а второй магнитная постоянная μ₀.

В системе СГС формулы электростатики совпадают соответствующими формулами СГСЭ, а формулы магнетизма, при условии, что они содержат только магнитные величины – с соответствующими формулами в СГСМ.

Но если в уравнении одновременно будет содержаться и магнитные, и электрические величины, то данное уравнение, записанное в системе Гаусса, будет отличаться от этого же уравнения, но записанного в системе СГСМ или СГСЭ множителем 1/с или 1/с². Величина с равна скорости света (с = 3·10¹⁰ см/с) называется электродинамической постоянной.

Закон Кулона в системе СГС будет иметь вид:

Пример

На двух абсолютно идентичных каплях масла недостает по одному электрону. Силу ньютоновского притяжения уравновешивает сила кулоновского отталкивания. Нужно определить радиусы капель, если расстояния между ними значительно превышает их линейные размеры.

Решение

Поскольку расстояние между каплями r значительно больше их линейных размеров, то капли можно принять за точечные заряды, и тогда сила кулоновского отталкивания будет равна:

Где е – положительный заряд капли масла, равный заряду электрона.

Силу ньютоновского притяжения можно выразить формулой:

Где m – масса капли, а γ – гравитационная постоянная. Согласно условию задачи F_к = F_н, поэтому:

Масса капли выражена через произведение плотности ρ на объем V, то есть m = ρV, а объем капли радиуса R равен V = (4/3)πR³, откуда получаем:

В данной формуле постоянные π, ε₀, γ известны; ε = 1; также известен и заряд электрона е = 1,6·10^-19 Кл и плотность масла ρ = 780 кг/м³ (справочные данные). Подставив числовые значения в формулу получим результат: R = 0,363·10^-7 м.

Закон Кулона

Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.

Между электрическими зарядами действует сила. Как она зависит от величины зарядов и других факторов?

Этот вопрос исследовал в 1780-е годы французский физик Шарль Кулон (1736-1806). Он воспользовался
крутильными весами, очень похожими на те, которые применял Кавендиш для определения гравитационной постоянной.

Если к шарику на конце стержня, подвешенного на нити, подности заряд, стержень слегка отклоняется, нить закручивается,
и угол поворота нити будет пропорционален действующей между зарядами силе (крутильные весы).
С помощью этого прибора Кулон определил зависимость силы от величины зарядов и расстояния между ними.

В те времена еще не было приборов для точного определения величины заряда, но
Кулон сумел приготовить небольшие шарики с известным соотношением зарядов.
Если заряженный проводящий шарик, рассуждал он, привести в соприкосновение с точно таким же незаряженным шариком,
то имевшийся на первом заряд в силу симметрии распределится поровну между двумя шариками.

Это дало ему возможность получать заряды, составлявшие 1/2, 1/4 и т.д. от первоначального.

Несмотря на некоторые трудности, связанные с индуцированием зарядов, Кулону удалось доказать, что сила,
с которой одно заряженное тело действует на другое малое заряженное тело, прямо пропорциональна электрическому заряду каждого из них.
Другими словами, если заряд любого из этих тел удвоить, то удвоится и сила;
если же удвоить одновременно заряды обоих тел, то сила станет вчетверо больше. Это справедливо при условии, что расстояние
между телами остается постоянным.

Изменяя расстояние между телами, Кулон обнаружил, что действующая между ними сила обратно пропорциональна квадрату
расстояния: если расстояние, скажем, удваивается, сила становится вчетверо меньше.

Итак, заключил Кулон, сила, с которой одно малое заряженное тело (в идеальном случае -точечный заряд, т.е. тело, подобно материальной
точке не имеющее пространственных размеров) действует на другое заряженное тело, пропорциональна
произведению их зарядов Q₁ и Q₂ и обратно пропорциональна квадрату расстояния между ними:

Здесь k -коэффициент пропорциональности.

Это соотношение известно как закон Кулона; его справедливость подтверждена тщательными экспериментами,
гораздо более точными, чем первоначальные трудно воспроизводимые опыты Кулона.
Показатель степени 2 установлен в настоящее время с точностью 10^-16, т. е. он равен
2 ± 2×10^-16.

Коль скоро мы теперь имеем дело с новой величиной — электрическим зарядом, мы можем подобрать такую единицу измерения,
чтобы постоянная к в формуле равнялась единице.
И действительно, такая система единиц еще недавно широко использовалась в физике.

Речь идет о системе СГС (сантиметр-грамм-секунда), в которой используется электростатическая единица заряда СГСЭ. По определению два малых тела, каждое с зарядом 1 СГСЭ, расположенные на расстоянии 1 см друг от друга, взаимодействуют с силой 1 дина.

Теперь, однако, заряд чаще всего выражают в системе СИ, где его единицей является кулон (Кл).

Точное определение кулона через электрический ток и магнитное поле мы приведем позднее.

В системе СИ постоянная k имеет величину k = 8,988×10⁹ Нм²/Кл².

Заряды, возникающие при электризации трением обычных предметов (расчески, пластмассовой линейки и т. п.),
по порядку величины составляют микрокулон и меньше (1 мкКл = 10^-6 Кл).

Заряд электрона (отрицательный) приблизительно равен 1,602×10^-19 Кл.
Это наименьший известный заряд; он имеет фундаментальное значение и обозначается символом е, его часто называют элементарным зарядом.
е = (1,6021892 ± 0,0000046)×10^-19 Кл, или е ≈ 1,602×10^-19 Кл.

Поскольку тело не может приобрести или потерять долю электрона, суммарный заряд тела должен быть целым
кратным элементарного заряда. Говорят, что заряд квантуется (т.е. может принимать лишь дискретные
значения). Однако, поскольку заряд электрона е очень мал, мы обычно не замечаем дискретности макроскопических
зарядов (заряду 1 мкКл соответствуют примерно 10¹³ электронов) и считаем заряд непрерывным.

Формула Кулона характеризует силу, с которой один заряд действует на другой. Эта сила направлена вдоль линии, соединяющей заряды.
Если знаки зарядов одинаковы, то силы, действующие на заряды, направлены в противоположные стороны.
Если же знаки зарядов различны, то действующие на заряды силы направлены навстречу друг другу.

Заметим, что в соответствии с третьим законом Ньютона сила, с которой один заряд действует на другой,
равна по величине и противоположна по направлению силе, с которой второй заряд действует на первый.

Закон Кулона можно записать в векторной форме подобно закону всемирного тяготения Ньютона:

где F₁₂ — вектор силы, действующей на заряд Q1 со стороны заряда Q2,
— расстояние между зарядами,
— единичный вектор, направленный от Q2 к Q1.

Следует иметь в виду, что формула применима лишь к телам, расстояние между которыми значительно больше их собственных размеров.
В идеальном случае это точечные заряды. Для тел конечного размера не всегда ясно, как отсчитывать расстояние r между ними, тем
более что распределение заряда может быть и неоднородным.
Если оба тела — сферы с равномерным распределением заряда, то r означает расстояние между центрами сфер.
Важно также понимать, что формула определяет силу, действующую на данный заряд со стороны единственного заряда.
Если система включает несколько (или много) заряженных тел, то результирующая сила, действующая на данный заряд,
будет равнодействующей (векторной суммой) сил, действующих со стороны остальных зарядов.

Постоянная к в формуле Закона Кулона обычно выражается через другую константу, ε₀, так называемую
электрическую постоянную, которая связана с k соотношением k = 1/(4πε₀).
С учетом этого закон Кулона можно переписать в следующем виде:

где с наивысшей на сегодня точностью

или округленно

Запись большинства других уравнений электромагнитной теории упрощается при использовании ε₀,
поскольку 4π в окончательном результате часто сокращается. Поэтому мы будем обычно использовать Закон Кулона, считая, что:

Закон Кулона описывает силу, действующую между двумя покоящимися зарядами. Когда заряды движутся, между ними возникают дополнительные силы, и их мы обсудим в последующих главах. Здесь же рассматриваются только покоящиеся заряды; этот раздел учения об электричестве называется электростатикой.

Продолжение следует. Коротко о следующей публикации:

Электрическое поле

Электрическое поле — один из двух компонентов электромагнитного поля, представляющий собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, либо возникающий при изменении магнитного поля.

Альтернативные статьи: Электрический ток, Закон ома.

Замечания и предложения принимаются и приветствуются!

основной закон электростатики кратко и понятно

Содержание

Закон Кулона определение и формула

Шарль Кулон

Формула:

F=k⋅|q1|⋅|q2|/r2.

Иначе записать можно так, где коэффициент в знаменателе — это константа диэлектрической проницаемости.

Формула закона Кулона

Коэффициент пропорциональности в законе Кулона

Например, для воздуха диэлектрическая проницаемость равна 1,000594.

Коэффициент диэлектрической проницаемости

Значения диэлектрической проницаемости:

Вакуум	1
Воздух	1,000594
Керосин	2
Титанат бария	1200

Закон Кулона в векторной форме

В векторном виде выглядит так:

Закон Кулона в векторной форме

Пояснения: r₁₂ — радиус-вектор;

Векторная и скалярная форма закона Кулона

Что можно определить с помощью закона Кулона

Применение закона Кулона

Для каких заряженных тел справедлив закон

Точечно заряженные тела

Если заряды имеют форму сферы, то полагается, что весь заряд сконцентрирован в центре данной сферы.

Границы применимости закона Кулона

объем и размеры рассматриваемых тел;
характеристики среды, в которой рассматривают заряженные тела;

Границы применимости закона Кулона

Закон Кулона в вакууме

Взаимодействие зарядов закон Кулона

Взаимодействие зарядов

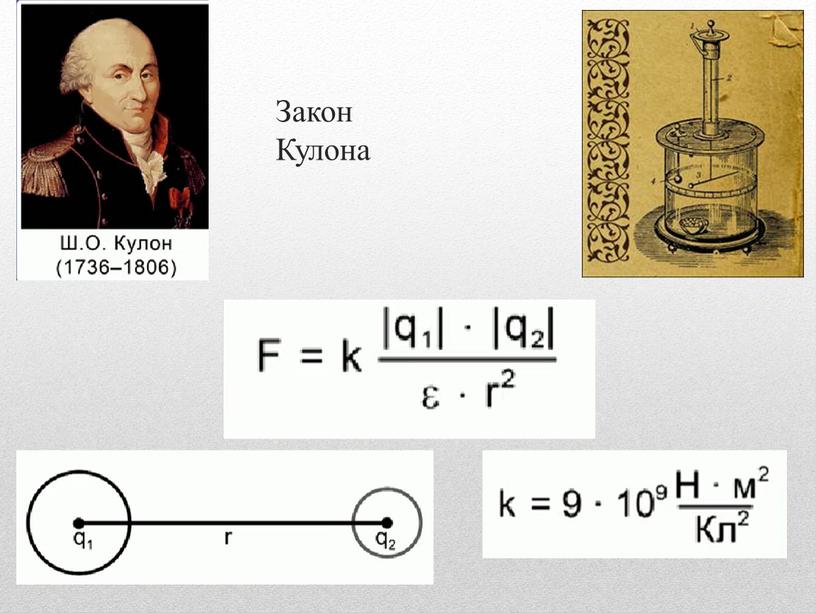
Принцип суперпозиции закон Кулона

Принцип суперпозиции

Рисунок: F=F₂₁+F₃₁; F₂=F₁₂+F₃₂; F₃=F₁₃+F₂₃;

Напряженность электрического поля

1) Напряженность равна результату деления кулоновской силы, действующей на заряд, на величину этого заряда.

[E] = Н/Кл = В/м

2) Величина пробного заряда не влияет на напряжённость.

Напряженность электрического поля точечного заряда Q

Задачи на закон Кулона с решением

Решение:

Для начала необходимо перевести основные единицы в систему СИ:

Решение:

Получается, что до соприкосновения заряд заряженного шарика был вдвое больше:

Ответ:

Кл, что равно 10 мкКл.

Решение:

Сила кулоновского взаимодействия до того, как шары соприкоснулись:

Из условий задачи известно, что сила после соприкосновения уменьшилась в 5 раз:

Одновременно с этим заряды шаров изменились, то есть:

Одна и та же сила равна:

Следует ввести замену: q1 / q2 = t.

Что равно

Решаем квадратное уравнение и находим два ответа:

Возвращаемся к замене:

Найдем q1:

Если считать по-другому:

Ответ:

Читайте также. Похожие записи.

Поделитесь статьей:

comments powered by HyperComments

Закон Кулона и его полевая трактовка

Историческая справка

Закон Кулона входит в число основных экспериментальных фактов, находящихся в основании теории б электричестве. {-12}\frac{Ф}{м}$.

Этот закон установлен Ш. Кулоном в 1785 г. экспериментально. Кулон измерял силы взаимодействия заряженных тел. Точность опытов была плохой, только аналогии с силами тяготения дала уверенность в том, что закон в виде (1) справедлив. С результатами эксперимента, обычно сравнивают следствия из закона Кулона, и на этой основе делается вывод о точности и границах применения данного закона. Первая проверка закона была проведена Кавендишем за 13 лет до Кулона. Кавендиш работ не публиковал, но надо отметить, что его метод был более точным, чем эксперименты Кулона. Позднее опыты по проверке закона Кулона проводил Максвелл. Эти опыты подтвердили справедливость закона Кулона с большой точностью. В соответствии с современными представлениями электромагнитные взаимодействия осуществляются посредством фотонов. Вследствие чего вопрос о справедливости закона Кулона сводится к вопросу о равенстве массы фотона нулю. Все частицы обладают корпускулярными и волновыми свойствами. Энергия фотона (${\varepsilon }_{\nu }=h\nu $) и ${\varepsilon }_{\nu }=m_{\nu }c^2$, где $m_{\nu }$ — масса фотона, $h$ — постоянная Планка.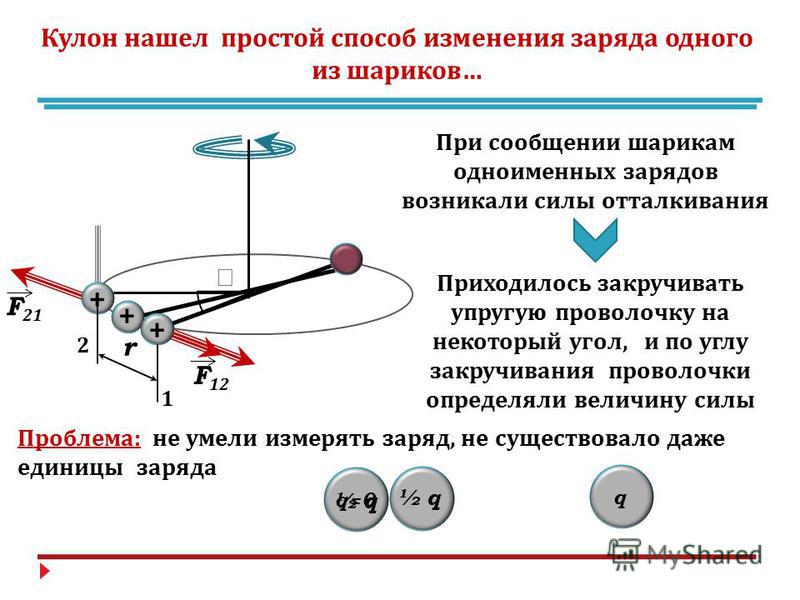 {-15}м$.

До работ Фарадея закон Кулона трактовался с позиций дальнодействия, то есть считалось, что одно тело действует на другое без посредников (действие на расстоянии). В первой половине 18 века сложился другой взгляд на механизм взаимодействия, в соответствии с которым существует посредник, осуществляющий непрерывную передачу сил.(теория близкодействия). Поначалу таким посредником назначили, так называемый Мировой эфир. Состояние которого характеризовали некоторыми механическими свойствами. Попытка математического описания механической картины передачи электрических взаимодействий была сделана Максвеллом. Он пытался представить электромагнитные силы в виде механических сил, которые вызываются натяжением и давлением в эфире. Позже Максвелл перешел к феноменологической формулировке взаимодействия и охарактеризовал состояние среды с помощью векторов: напряженности электростатического поля ($\overrightarrow{E}$), электрического смещения ($\overrightarrow{D}$), напряженности магнитного поля ($\overrightarrow{H}$), магнитной индукции ($\overrightarrow{B}$), которым не дал никакой механической интерпретации. В 1864 г. Максвелл сформулировал уравнения электромагнитного поля (уравнения Максвелла). Надежда на механическое толкование электромагнитных взаимодействий умерла. Поле стало основной сущностью, посредством которого осуществляется электромагнитное взаимодействие. Оно характеризуется величинами, которые не могут интерпретироваться в рамках механики. После того как Герц записал уравнения Максвелла в современном виде стало очевидно, что поле существует в пространстве и времени наряду с материей.

Полевая трактовка закона Кулона

Пусть мы имеем два точечных заряда $q_1\ (точка\ 1)\ $ и $q_2$(точка 2).Тогда ${\overrightarrow{F}}_{12}$- сила, с которой заряд $q_1$ действует на заряд $q_2$. ${\overrightarrow{F}}_{21}$- сила, с которой заряд $q_2$ действует на заряд $q_1$. ${\overrightarrow{r}}_{12}$- вектор из точки (1) в точку (2), ${\overrightarrow{r}}_{21}$ — вектор из точки (2) в точку (1). Исходя из принятых нами обозначений, запишем закон Кулона:

По своему физическому содержанию формулы (2) и (3) различны.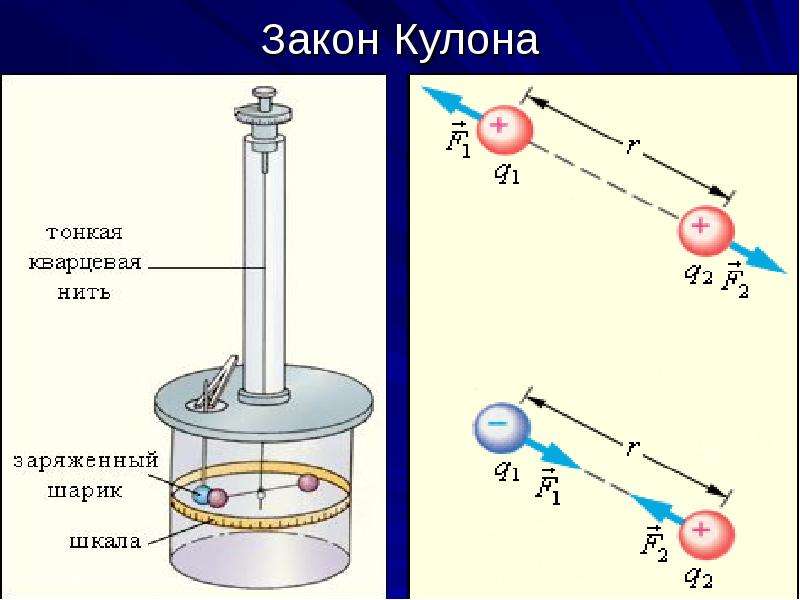 3}\ \left(11\right).\]

Пример 1

Задание: Три одинаковых точечных заряда величиной $q$ поместили в вершинах равностороннего треугольника. Найдите величину точечного заряда $Q$, который надо поместить в центр масс треугольника, чтобы система находилась в состоянии равновесия.

Решение:

Рис. 1

Для определенности допустим, что заряды в вершинах треугольника отрицательные, тогда на пересечении медиан (в центре масс) положительный.

Рассмотрим силы, которые действуют на заряд ${-q}_1$. Это будут три силы Кулона, две — отталкивания, со стороны зарядов в вершинах и одна — притяжения со стороны «центрального». Тогда условие равновесия сил запишем в виде:

\[\overrightarrow{F_{12}}+\overrightarrow{F_{13}}+\overrightarrow{F_{10}}=0\ \left(1.1\right).\]

Выберем ось OX, как указано на рис.1, найдем проекцию уравнения (1) на эту ось:

\[F_{12}{cos \left(\frac{\alpha }{2}\right)\ }+F_{13}{cos \left(\frac{\alpha }{2}\right)\ }-F_{10}=0\ \left(1. 7\frac{В}{м}$.

Глава 17. Взаимодействие электрических зарядов. Закон Кулона, принцип суперпозиции

Взаимодействие электрических зарядов описывается законом Кулона, который утверждает, что сила взаимодействия двух покоящихся точечных зарядов в вакууме равна

(17.1)

где и — модули зарядов, — расстояние между ними. Коэффициент пропорциональности в формуле (17.1) зависит от системы единиц. В международной системе единиц СИ этот коэффициент принято записывать в виде

(17.2)

где величина называется электрической постоянной, размерность величины сводится к отношению размерности длины к размерности электрической емкости (Фарада). Электрические заряды бывают двух типов, которые условно принято называть положительным и отрицательным. Как показывает опыт, заряды притягиваются, если они разноименные и отталкиваются, если одноименные.

В любом макроскопическом теле содержится огромное количество электрических зарядов, поскольку они входят в состав всех атомов: электроны заряжены отрицательно, протоны, входящие в состав атомных ядер — положительно. Однако большинство тел, с которыми мы имеем дело, не заряжены, поскольку количество электронов и протонов, входящих в состав атомов, одинаково, а их заряды по абсолютной величине в точности совпадают. Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.

Если заряды находятся в некоторой среде, которая занимает все пространство, то сила их взаимодействия ослабляется по сравнению с силой их взаимодействия в вакууме, причем это ослабление не зависит от величин зарядов и расстояния между ними, а зависит только от свойств среды. Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид

(17.3)

Если имеется не два, а большее количество точечных зарядов для нахождения сил, действующих в этой системе, используется закон, который называется принципомсуперпозиции¹. Принцип суперпозиции утверждает, что для нахождения силы, действующей на один из зарядов (например, на заряд ) в системе из трех точечных зарядов , и надо сделать следующее. Сначала надо мысленно убрать заряд и по закону Кулона найти силу, действующую на заряд со стороны оставшегося заряда . Затем следует убрать заряд и найти силу, действующую на заряд со стороны заряда . Векторная сумма полученных сил и даст искомую силу.

Принцип суперпозиции дает рецепт поиска силы взаимодействия неточечных заряженных тел. Следует мысленно разбить каждое тело на части, которые можно считать точечными, по закону Кулона найти силу их взаимодействия с точечными частями, на которое разбивается второе тело, просуммировать полученные вектора. Ясно, что такая процедура математически очень сложна, хотя бы потому, что необходимо сложить бесконечное количество векторов. В математическом анализе разработаны методы такого суммирования, однако в школьный курс физики они не входят. Поэтому, если такая задача и встретится, то суммирование в ней должно легко выполняться на основе тех или иных соображений симметрии. Например, из описанной процедуры суммирования следует, что сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы, равна нулю.

Кроме того, школьник должен знать (без вывода) формулы для силы, действующей на точечный заряд со стороны равномерно заряженной сферы и бесконечной плоскости. Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна

(17.4)

если точечный заряд находится снаружи сферы, и

(17.5)

если заряд находится внутри (причем не обязательно в центре). Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.

Если имеется очень большая плоскость с площадью , равномерно заряженная зарядом , и точечный заряд , то сила их взаимодействия равна

(17.6)

где величина имеет смысл поверхностной плотности заряда плоскости. Как следует из формулы (17. 6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.

Рассмотрим теперь решение данных в первой части книги задач.

Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов из задачи 17.1.1 выражается формулой

Заряды отталкиваются (ответ 2).

Поскольку капелька воды из задачи 17.1.2 имеет заряд ( – заряд протона), то она имеет в избытке электронов по сравнению с протонами. Значит при потере трех электронов их избыток уменьшится, и заряд капельки станет равен (ответ 2).

Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов при увеличении в раз расстояния между ними уменьшится в раз (задача 17.1.3 — ответ 4).

Если заряды двух точечных тел увеличить в раз при неизменном расстоянии между ними, то сила их взаимодействия, как это следует из закона Кулона (17.1), увеличится в раз (задача 17.1.4 — ответ 3).

При увеличении одного заряда в 2 раза, а второго в 4, числитель закона Кулона (17.1) увеличивается в 8 раз, а при увеличении расстояния между зарядами в 8 раз — знаменатель увеличивается в 64 раза. Поэтому сила взаимодействия зарядов из задачи 17.1.5 уменьшится в 8 раз (ответ 4).

При заполнении пространства диэлектрической средой с диэлектрической проницаемостью = 10, сила взаимодействия зарядов согласно закону Кулона в среде (17.3) уменьшится в 10 раз (задача 17.1.6 — ответ 2).

Сила кулоновского взаимодействия (17. 1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17.1.7 — ответ 3).

Похожая задача, но массы шариков разные. Поэтому при одинаковой силе ускорение шарика с меньшей массой в 2 раза больше ускорения шарика с меньшей массой , причем этот результат не зависит от величин зарядов шариков (задача 17.1.8 — ответ 2).

Поскольку электрон заряжен отрицательно, он будет отталкиваться от шара (задача 17.1.9). Но поскольку начальная скорость электрона направлена к шару, он будет двигаться в этом направлении, но его скорость будет уменьшаться. В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4).

В системе двух заряженных шариков, связанных нитью (задача 17.1.10), действуют только внутренние силы. Поэтому система будет покоиться и для нахождения силы натяжения нити можно использовать условия равновесия шариков. Поскольку на каждый из них действуют только кулоновская сила и сила натяжения нити, то из условия равновесия заключаем, что эти силы равны по величине.

Отсюда

где (ответ 1).

Система трех шариков в задаче 17.2.1 покоится, поэтому силы натяжения должны компенсировать силы кулоновского отталкивания крайних зарядов. Последние найдем по закону Кулона и принципу суперпозиции. Каждый крайний заряд отталкивается от центрального заряда и другого крайнего. Для суммы этих сил получаем

Этой величине и будет равна сила натяжения нитей (ответ 4). Отметим, что рассмотрение условия равновесия центрального заряда не помогло бы найти силу натяжения, а привело бы к заключению, что силы натяжения нитей одинаковы (впрочем, это заключение и так очевидно благодаря симметрии задачи).

Для нахождения силы, действующей на заряд — в задаче 17.2.2, используем принцип суперпозиции. На заряд — действуют силы притяжения к левому и правому зарядам (см. рисунок). Поскольку расстояния от заряда — до зарядов одинаковы, модули этих сил равны друг другу и они направлены под одинаковыми углами к прямой, соединяющей заряд — с серединой отрезка — . Поэтому сила, действующая на заряд — направлена вертикально вниз (вектор результирующей силы выделен жирным на рисунке; ответ 4).

Задача 17.2.3 похожа на предыдущую, но изменен знак одного из зарядов. Поэтому сила, действующая на заряд — со стороны правого заряда, не изменившись по величине, изменится по направлению (см. рисунок). Поэтому вектор результирующей силы будет направлен влево (вектор результирующей силы выделен жирным на рисунке; ответ 1).

На каждый заряд в задаче 17. 2.4 действуют силы отталкивания со стороны двух других зарядов (см. рисунок), причем значения этих сил одинаковы (из-за равенства величин всех зарядов и расстояний между ними) и равны

Из-за равенства значений сил-слагаемых параллелограмм сложения сил представляет собой ромб, и, следовательно, вектор результирующей силы направлен вдоль биссектрисы треугольника из зарядов (выделен жирным на рисунке). Поэтому угол, отмеченный на рисунке дугой равен 30°, а значение результирующей силы равно

(ответ 3).

Из формулы (17.6) заключаем, что правильный ответ в задаче 17.2.5 — 4. В задаче 17.2.6 нужно использовать формулу для силы взаимодействия точечного заряда и сферы (формулы (17.4), (17.5)). Имеем = 0 (ответ 3).

В задаче 17. 2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой

где . Поэтому и результирующая сила равна этому выражению (ответ 2)

В задаче 17.2.8 также следует использовать принцип суперпозиции. Если заряд поместить в точку , то силы, действующие на него со стороны зарядов и , направлены влево. Поэтому по принципу суперпозиции имеем для равнодействующей силы

где — расстояния от зарядов до исследуемых точек. Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу

В точке на заряд будут действовать силы, направленные направо, и потому

Из этих формул следует, что наибольшей сила будет в точке — ответ 1.

Пусть, для определенности, заряды шариков и в задаче 17.2.9 положительны. Так как шарики одинаковы, заряды после их соединения распределяться между ними равномерно и для сравнения сил, нужно сравнить друг с другом величины

(1)

которые представляют собой произведения зарядов шариков до и после их соединения. После извлечения квадратного корня сравнение (1) сводится к сравнению среднего геометрического и среднего арифметического двух чисел. А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1).

Задача 17.2.10 очень похожа на предыдущую, а ответ — другой. Непосредственной поверкой легко убедиться, что сила может как увеличиться, так и уменьшиться в зависимости от величин зарядов. Например, если заряды равны по величине, то после соединения шариков их заряды станут равны нулю, поэтому нулевой будет и сила их взаимодействия, которая, следовательно, уменьшится. Если один из первоначальных зарядов равен нулю, то после соприкосновения шариков заряд одного из них распределится между шариками поровну, и сила их взаимодействия увеличится. Таким образом, правильный ответ в этой задаче — 3.

1.2 Закон Кулона

Закон
взаимодействия электрических зарядов экспериментально установлен в 1785
г. французским ученым Ш. Кулоном. Природа вещей такова, что сила взаимодействия
между двумя небольшими заряженными шариками прямо пропорциональна произведению
величин их зарядов и обратно пропорциональна квадрату расстояния между ними.

Сила
взаимодействия зарядов — сила центральная,
т. е. направлена вдоль прямой, соединяющей заряды
(рис. 1.1). Для изотропной среды закон Кулона записывается следующим образом:

где k –
коэффициент пропорциональности; q₁
и q₂ — величины
взаимодействующих зарядов; r –
расстояние между ними; r – радиус-вектор, проведенный от
одного заряда к другому и направленный к тому из зарядов, на который действует
сила.

Формулировка закона Кулона: «Сила
электростатического взаимодействия между двумя точечными электрическими
зарядами прямо пропорциональна произведению величин зарядов, обратно
пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей
их прямой так, что одноименные заряды отталкиваются, а разноименные
притягиваются».

Следует отметить, что
закон Кулона применим для расчета взаимодействия точечных зарядов и тел
шарообразной формы при равномерном распределении заряда по их поверхности или
объёму.

Точечным зарядом называется заряженное тело, размерами которого
можно пренебречь по сравнению с расстояниями до других тел, несущих электрический
заряд.

Экспериментальные
исследования показали, что при прочих равных условиях сила электростатического
взаимодействия зависит от свойств среды, в которой
находятся заряды. Поэтому коэффициент пропорциональности k в законе Кулона представляют в виде k = k₁ / e, где k₁—
коэффициент, зависящий только от выбора системы единиц; e — безразмерная величина,
которая характеризует электрические свойства среды и называется относительной диэлектрической проницаемостью среды. Для вакуума e = 1.

В
системе единиц СИ единица заряда кулон (Кл) определяется через единицу силы
тока ампер (А) и единицу времени секунду (с), так что 1 Кл = 1 А×1 с. Коэффициент k₁ в этой системе определяется следующим образом: k₁= 1 / 4pe₀
= 8,988×10⁹
(Н×м²)
/ Кл², где e₀ = 8,85×10^–¹²
Кл² / (Н×м²)
и носит название электрической постоянной.

Таким образом,
закон Кулона для изотропной и однородной среды записывается в виде

(1.1)

Вопросы

1)
Запишите, сформулируйте и объясните закон Кулона

Сопоставьте силу кулоновского взаимодействия двух электронов с силой их
гравитационного взаимодействия

3)
Как изменится сила взаимодействия между двумя точечными
зарядами, если модуль заряда увеличить в четыре раза, а расстояние между
зарядами уменьшить вдвое?

наверх

Учебное пособие по физике: Закон Кулона

Взаимодействие между заряженными объектами — это неконтактная сила, действующая на некотором расстоянии друг от друга. Заряд, заряд и расстояние. Каждое электрическое взаимодействие включает в себя силу, которая подчеркивает важность этих трех переменных. Будь то пластиковая трубка для гольфа, притягивающая кусочки бумаги, два отталкивающих одинаково заряженных шара или заряженная пластина из пенополистирола, взаимодействующая с электронами в куске алюминия, всегда есть два заряда и расстояние между ними как три критических переменных, которые влияют на прочность. взаимодействия.В этом разделе Урока 3 мы исследуем важность этих трех переменных.

Сила как векторная величина

Электрическая сила, как и все силы, обычно выражается в единицах Ньютон. Как сила, сила электрического взаимодействия — это векторная величина, которая имеет как величину, так и направление. Направление электрической силы зависит от того, заряжены ли заряженные объекты одинаковым или противоположным зарядом, а также от их пространственной ориентации.Зная тип заряда на двух объектах, можно определить направление силы, действующей на любой из них, с небольшими рассуждениями. На приведенной ниже диаграмме объекты A и B имеют одинаковый заряд, заставляющий их отталкиваться друг от друга. Таким образом, сила на объект A направлена влево (от B), а сила на объект B направлена вправо (от A). С другой стороны, объекты C и D имеют противоположный заряд, заставляя их притягиваться друг к другу. Таким образом, сила, действующая на объект C, направлена вправо (к объекту D), а сила, действующая на объект D, направлена влево (к объекту C).Когда дело доходит до вектора электрической силы, возможно, лучший способ определить его направление — это применить фундаментальные правила взаимодействия зарядов (противоположности притягиваются, а любит отталкиваться), используя небольшие рассуждения.

Электрическая сила также имеет величину или силу. Как и в случае с большинством типов сил, на величину электрической силы влияет множество факторов. Два одинаково заряженных шара будут отталкивать друг друга, и силу их силы отталкивания можно изменить, изменив три переменных. Во-первых, количество заряда на одном из воздушных шаров влияет на силу отталкивающей силы. Чем больше заряжен воздушный шар, тем больше сила отталкивания. Во-вторых, количество заряда на втором воздушном шаре влияет на силу отталкивающей силы. Аккуратно натрите два шара шерстью животных, и они немного оттолкнутся. Сильно потрите два шара, чтобы передать им больше заряда, и они сильно оттолкнутся. Наконец, расстояние между двумя воздушными шарами будет иметь значительное и заметное влияние на силу отталкивания.Электрическая сила наиболее сильна, когда воздушные шары находятся максимально близко друг к другу. Уменьшение разделительного расстояния увеличивает силу. Величина силы и расстояние между двумя воздушными шарами составляет , обратно пропорционально .

Уравнение закона Кулона

Количественное выражение влияния этих трех переменных на электрическую силу известно как закон Кулона. Закон Кулона гласит, что электрическая сила между двумя заряженными объектами прямо пропорциональна произведению количества заряда на объектах и обратно пропорциональна квадрату разделительного расстояния между двумя объектами. В форме уравнения закон Кулона может быть записан как

, где Q ₁ представляет количество заряда на объекте 1 (в кулонах), Q ₂ представляет количество заряда на объекте 2 (в кулонах), а d представляет собой расстояние между два объекта (в метрах). Обозначение k — это константа пропорциональности, известная как константа закона Кулона. Значение этой постоянной зависит от среды, в которую погружены заряженные объекты.В случае воздуха это значение составляет приблизительно 9,0 x 10 ⁹ Н • м ² / C ². Если заряженные объекты присутствуют в воде, значение k может быть уменьшено в 80 раз. Стоит отметить, что единицы на k таковы, что при подстановке в уравнение единицы на зарядке (кулоны) и единицы расстояния (метры) будут отменены, оставив Ньютон в качестве единицы силы.

Уравнение закона Кулона дает точное описание силы между двумя объектами, когда объекты действуют как точечных зарядов . Заряженная проводящая сфера взаимодействует с другими заряженными объектами так, как будто весь ее заряд находится в ее центре. Хотя заряд равномерно распределен по поверхности сферы, центр заряда можно рассматривать как центр сферы. Сфера действует как точечный заряд, избыточный заряд которого находится в центре. Поскольку закон Кулона применяется к точечным зарядам, расстояние d в уравнении — это расстояние между центрами заряда для обоих объектов (а не расстояние между их ближайшими поверхностями).

Символы Q ₁ и Q ₂ в уравнении закона Кулона представляют количества заряда на двух взаимодействующих объектах. Поскольку объект может быть заряжен положительно или отрицательно, эти величины часто выражаются как значения «+» или «-». Знак заряда просто показывает, есть ли в объекте избыток электронов (отрицательно заряженный объект) или недостаток электронов (положительно заряженный объект).Может возникнуть соблазн использовать знаки «+» и «-» при вычислении силы. Хотя такая практика не рекомендуется, в этом нет никакого вреда. При использовании знаков «+» и «-» в расчете силы результат будет таков, что значение «-» для силы является признаком силы притяжения, а значение «+» для силы означает силу отталкивания. Математически значение силы будет положительным, если Q ₁ и Q ₂ имеют одинаковый заряд — либо оба «+», либо оба «-».И значение силы будет отрицательным, если Q ₁ и Q ₂ имеют противоположный заряд — один — «+», а другой — «-». Это согласуется с концепцией, что противоположно заряженные объекты обладают притягивающим взаимодействием, а одноименные заряженные объекты — отталкивающим. В конце концов, если вы мыслите концептуально (а не просто математически), вы сможете определить природу силы — притягивающую или отталкивающую — без использования знаков «+» и «-» в уравнении.

Расчеты по закону Кулона

В курсах физики закон Кулона часто используется как разновидность алгебраического рецепта для решения словесных задач физики. Здесь показаны три таких примера.

Пример A

Предположим, что два точечных заряда, каждый с зарядом +1,00 кулон, разделены расстоянием 1.00 метр. Определите величину электрической силы отталкивания между ними.

Это не самая сложная математическая задача, которую можно было выбрать. Он определенно был выбран не из-за его математической строгости. Используемая здесь стратегия решения проблем может показаться ненужной, учитывая простоту данных значений. Тем не менее, эта стратегия будет использована для иллюстрации ее полезности для решения любой проблемы закона Кулона.

Первым шагом стратегии является идентификация и перечисление известной информации в переменной форме.Здесь мы знаем заряды двух объектов (Q ₁ и Q ₂) и расстояние между ними (d). Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае проблема запрашивает информацию о силе. Так что F _elect — неизвестное количество. Результаты первых двух шагов показаны в таблице ниже.

Дано:

Q ₁ = 1.00 С
Q ₂ = 1,00 C
d = 1,00 м

Найти:

F _{избранный} = ???

Следующий и последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.

F _elect = k • Q ₁ • Q ₂ / d ²

F _elect = (9,0 x 10 ⁹ Н • м ² / C ²) • (1,00 C) • (1,00 C) / (1,00 м) ²

F _{электр.} = 9,0 x 10 ⁹ N

Сила отталкивания двух +1. 00 кулоновских зарядов, находящихся на расстоянии 1 метра друг от друга, составляет 9 миллиардов ньютонов. Это невероятно большая сила, по величине сопоставимая с массой более 2000 лайнеров.

Эта задача была выбрана в первую очередь из-за ее концептуального сообщения. Объекты просто не получают зарядов порядка 1,00 кулонов. Фактически, более вероятные значения Q составляют порядка 10 ^-9 или, возможно, 10 ^-6 кулонов. По этой причине греческий префикс часто используется перед кулоном в качестве единицы заряда. Заряд часто выражается в микрокулонах (мкКл) и нанокулонах (нКл). Если проблема указывает заряд в этих единицах, рекомендуется сначала преобразовать в кулоны перед подстановкой в уравнение закона Кулона.Следующие эквиваленты единиц измерения помогут в таком преобразовании.

1 кулон = 10 ⁶ микрокулон

1 кулон = 10 ⁹ нанокулон

Стратегия решения проблем, использованная в примере A, включала три этапа:

Определите и перечислите известную информацию в переменной форме.
Перечислите неизвестную (или желаемую) информацию в переменной форме.
Подставьте известные значения в уравнение закона Кулона и, используя соответствующие алгебраические шаги, найдите неизвестную информацию.(В некоторых случаях и для некоторых студентов может быть проще сначала выполнить алгебру, используя переменные, а затем выполнить замену в качестве последнего шага.)

Эта же стратегия решения проблем продемонстрирована в Пример B ниже.

Пример B

Два шара заряжаются одинаковым количеством и типом заряда: -6,25 нКл. Их разделяют на расстоянии 61.7 см. Определите величину электрической силы отталкивания между ними.

В задаче указано значение Q ₁ и Q ₂. Поскольку эти значения выражены в единицах нанокулонов (нКл), необходимо выполнить преобразование в кулоны. В задаче также указывается расстояние разделения (d). Поскольку расстояние указывается в сантиметрах (см), необходимо также выполнить преобразование в метры. Эти преобразования необходимы, поскольку единицами заряда и расстояния в постоянной Кулона являются кулоны и метры.Неизвестная величина — электрическая сила (F). Результаты первых двух шагов показаны в таблице ниже.

Дано:

Q ₁ = -6,25 нКл = -6,25 x 10 ^-9 С
Q ₂ = -6,25 нКл = -6,25 x 10 ^-9 C
d = 61,7 см = 0,617 м

Найти:

F _{избранный} = ???

Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для решения неизвестной информации. Эта подстановка и алгебра показаны ниже.

F _elect = k • Q ₁ • Q ₂ / d ²

F _elect = (9,0 x 10 ⁹ Н • м ² / C ²) • (6,25 x 10 ^-9 C) • (6,25 x 10 ^-9 C) / (0,617 м) ²

F _{электр.} = 9,23 x 10 ^-7 N

Обратите внимание, что знак «-» был удален из значений Q ₁ и Q ₂ до подстановки в уравнение закона Кулона.Как упоминалось выше, использование знаков «+» и «-» в уравнении приведет к положительному значению силы, если Q ₁ и Q ₂ одинаково заряжены, и отрицательному значению силы, если Q ₁ и Q ₂ заряжены противоположным образом. Полученные знаки «+» и «-» на F обозначают, является ли сила притягивающей (значение «-» F) или отталкивающей (значение «+» F).

Пример C

Два шара с зарядом +3. 37 µC и -8,21 µC притягивают друг друга с силой 0,0626 Ньютона. Определите расстояние между двумя воздушными шарами.

В задаче указано значение Q ₁ и Q ₂. Поскольку эти значения выражены в микрокулонах (мкКл), преобразование в кулоны будет выполнено. Проблема также указывает на электрическую силу (F). Неизвестная величина — это расстояние разделения (d). Результаты первых двух шагов показаны в таблице ниже.

Дано:

Q ₁ = +3,37 мкКл = +3,37 x 10 ^-6 С
Q ₂ = -8,21 мкКл = -8,21 x 10 ^-6 С
F _elect = -0,0626 Н (используйте — значение силы, так как оно привлекательное)

Найти:

d = ???

Как упоминалось выше, использование знаков «+» и «-» необязательно. Однако, если они используются, то они должны использоваться последовательно для значений Q и F. Их использование в уравнении показано в этой задаче.

Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для решения неизвестной информации. В этом случае сначала выполняется алгебра, а в последнюю — подстановка. Эта алгебра и подстановка показаны ниже.

F _elect = k • Q ₁ • Q ₂ / d ²

d ² • F _elect = k • Q ₁ • Q ₂

d ² = k • Q ₁ • Q ₂ / F _elect

d = SQRT (k • Q ₁ • Q ₂) / F _elect

d = КОРЕНЬ [(9.0 x 10 ⁹ Н • м ² / C ²) • (-8,21 x 10 ^-6 C) • (+3,37 x 10 ^-6 C) / (-0,0626 Н)]

d = Sqrt [+3,98 м ²]

d = +1,99 м

Сравнение электрических и гравитационных сил

Электрическая сила и гравитационная сила — это две бесконтактные силы, которые обсуждаются в учебном пособии по физике. Уравнение закона Кулона для электрической силы очень похоже на уравнение Ньютона для всемирной гравитации.

Эти два уравнения имеют очень похожую форму. Оба уравнения показывают обратную квадратичную зависимость между силой и разделительным расстоянием. И оба уравнения показывают, что сила пропорциональна произведению количества, вызывающего силу, — заряда в случае электрической силы и массы в случае силы тяжести. Тем не менее, между этими двумя силами есть поразительные различия.Во-первых, сравнение констант пропорциональности — k и G — показывает, что постоянная закона Кулона (k) значительно больше универсальной постоянной тяготения Ньютона (G). Впоследствии единица заряда будет притягивать единицу заряда со значительно большей силой, чем единица массы притягивает единицу массы. Во-вторых, гравитационные силы только притягивают; электрические силы могут быть как притягивающими, так и отталкивающими.

Обратное квадратичное соотношение между силой и расстоянием, вплетенное в уравнение, является общим для обеих бесконтактных сил. Это соотношение подчеркивает важность разделительного расстояния, когда речь идет об электрической силе между заряженными объектами. Этому и посвящен следующий раздел Урока 3.

Мы хотели бы предложить …

Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения по закону Кулона.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный закон Кулона позволяет учащемуся исследовать влияние заряда и разделительного расстояния на величину электрической силы между двумя заряженными объектами.

Проверьте свое понимание

Используйте свое понимание, чтобы ответить на следующие вопросы. По окончании нажмите кнопку, чтобы просмотреть ответы.

1. Q в уравнении закона Кулона означает _____.

а. масса заряженного объекта
г. # избыточных электронов на объекте
г. ток заряженного объекта
г. расстояние между заряженными объектами
e.заряд заряженного объекта

2. Символ d в уравнении закона Кулона обозначает расстояние от ___.

а. От A до B
г. От A до D
г.B по C
г. От B до D
e. C по D
ф. От A до G
г. От B до F
ч. C по E

3.Определите электрическую силу притяжения между двумя воздушными шарами с отдельными зарядами +3,5 x 10 ^-8 C и -2,9 x 10 ^-8 C при разделении на расстояние 0,65 м.

4. Определите электрическую силу притяжения между двумя воздушными шарами, заряженными противоположным типом заряда, но одинаковым количеством заряда. Заряд на воздушных шарах составляет 6.0 x 10 ^-7 C, и они разделены расстоянием 0.50 м.

5. Джоанна натерла шар шерстью, чтобы получить заряд -1,0 x 10 ^-6 C. Затем она достает пластиковую трубку для гольфа с зарядом +4,0 x 10 ^-6 C, локализованным в заданном месте. позиция. Она удерживает место заряда на пластиковой трубке для гольфа на расстоянии 50,0 см над воздушным шаром. Определите электрическую силу притяжения между трубкой для гольфа и воздушным шаром.

6. Баллон с зарядом 4,0 мкКл удерживают на расстоянии 0,70 м от второго баллона с таким же зарядом. Рассчитайте величину силы отталкивания.

7. На каком расстоянии разделения должны быть расположены два заряда размером 1,00 микрокулонов, чтобы сила отталкивания между ними была эквивалентна весу (на Земле) 1.00-кг масса?

Закон Кулона | Безграничная физика

Суперпозиция сил

Принцип суперпозиции (свойство суперпозиции) утверждает, что для всех линейных сил общая сила является векторной суммой отдельных сил.

Цели обучения

Примените принцип суперпозиции для определения чистой реакции, вызванной двумя или более стимулами

Основные выводы

Ключевые моменты

Принцип суперпозиции предполагает, что общий ответ в данном месте и в определенное время, вызванный двумя или более стимулами, представляет собой сумму ответов, которые были бы вызваны каждым стимулом индивидуально.
Полная кулоновская сила на испытательном заряде, создаваемая группой зарядов, равна векторной сумме всех кулоновских сил между испытательным зарядом и другими отдельными зарядами.
Суперпозиция сил не ограничивается кулоновскими силами. Это касается любых типов (или комбинаций) сил.

Ключевые термины

Сила Лоренца : Сила, действующая на заряженную частицу в электромагнитном поле.
единичный вектор : вектор длины 1.
электростатическая сила : электростатическое взаимодействие между электрически заряженными частицами; количество и направление притяжения или отталкивания между двумя заряженными телами.

Принцип суперпозиции (также известный как свойство суперпозиции) утверждает, что: для всех линейных систем чистый ответ в данном месте и времени, вызванный двумя или более стимулами, является суммой ответов, которые были бы вызваны каждым из них. стимул индивидуальный .2} [/ latex],

Сила Лоренца на движущейся частице : Сила Лоренца f на движущуюся заряженную частицу (с зарядом q) (мгновенная скорость v). Поле E и поле B различаются в пространстве и времени.

, где r — расстояние разделения, а ε ₀ — электрическая проницаемость. Если произведение q ₁ q ₂ положительное, сила между ними отталкивающая; если q ₁ q ₂ отрицательно, сила между ними притягивает.Принцип линейной суперпозиции позволяет расширить закон Кулона на любое количество точечных зарядов, чтобы получить силу, действующую на любой точечный заряд, путем векторного сложения этих индивидуальных сил, действующих только на этот точечный заряд. Результирующий вектор силы оказывается параллельным вектору электрического поля в этой точке с удаленным точечным зарядом.

Для расчета силы, действующей на небольшой испытательный заряд q в позиции [латекс] \ text {r} [/ latex], из-за системы из N дискретных зарядов:

[латекс] \ begin {align} \ boldsymbol {\ text {F} (\ text {r})} & = \ frac {\ text {q}} {4 \ pi ar \ epsilon_0} \ sum _ {\ text { i} = 1} ^ \ text {N} \ text {q} _ \ text {i} \ frac {\ boldsymbol {\ text {r} — \ text {r} _ \ text {i}}} {| \ boldsymbol {\ text {r} — \ text {r} _ \ text {i}} | ^ 3} \ & = \ frac {\ text {q}} {\ text {r} 4 \ pi ar \ epsilon_0} \ sum _ {\ text {i} = 1} ^ {\ text {N}} \ text {q} _ \ text {i} \ frac {\ boldsymbol {\ widehat {\ text {R} _ \ text {i}} }} {| \ boldsymbol {\ text {R} _ \ text {i}} | ^ 2} \ end {align} [/ latex],

, где q _i и r _i — величина и вектор положения i-го заряда, соответственно, и [latex] \ boldsymbol {\ widehat {\ text {R} _ \ text {i}}} [ / latex] — единичный вектор в направлении [латекс] \ boldsymbol {\ text {R}} _ {\ text {i}} = \ boldsymbol {\ text {r}} — \ boldsymbol {\ text {r} } _ \ text {i} [/ latex] (вектор, указывающий от зарядов q _i на q. )

Конечно, наше обсуждение суперпозиции сил применимо к любым типам (или комбинациям) сил. Например, когда заряд движется в присутствии магнитного поля, а также электрического поля, заряд будет ощущать как электростатические, так и магнитные силы. Полная сила, влияющая на движение заряда, будет векторной суммой двух сил. (В этом конкретном примере движущегося заряда сила, обусловленная наличием электромагнитного поля, в совокупности называется силой Лоренца (см.).

Сферическое распределение заряда

Распределение заряда вокруг молекулы имеет сферическую природу и создает своего рода электростатическое «облако» вокруг молекулы.

Цели обучения

Опишите форму кулоновской силы из сферического распределения заряда

Основные выводы

Ключевые моменты

Сила между двумя объектами обратно пропорциональна квадрату расстояния между двумя объектами.
Силы притяжения или отталкивания в сферическом распределении заряда сильнее ближе к молекуле и ослабевают по мере увеличения расстояния от молекулы.
Этот закон также учитывает силы, которые связывают атомы вместе с образованием молекул, и силы, которые связывают атомы и молекулы вместе с образованием твердых тел и жидкостей.

Ключевые термины

электростатическая сила : электростатическое взаимодействие между электрически заряженными частицами; количество и направление притяжения или отталкивания между двумя заряженными телами.

Благодаря работам ученых конца 18 века, основные характеристики электростатической силы — наличие двух типов зарядов, наблюдение, что подобные заряды отталкиваются, в отличие от зарядов притягиваются, и уменьшение силы с расстоянием — в конечном итоге были уточнены. , и выражается математической формулой.Математическая формула для электростатической силы называется законом Кулона в честь французского физика Шарля Кулона (1736–1806), который провел эксперименты и первым предложил формулу для ее расчета.

Распределение заряда в молекуле воды : Схематическое изображение внешнего электронного облака нейтральной молекулы воды. Электроны проводят больше времени рядом с кислородом, чем с водородом, обеспечивая постоянное разделение зарядов, как показано. Таким образом, вода является полярной молекулой.На него легче воздействуют электростатические силы, чем на молекулы с однородным распределением заряда.

Современные эксперименты подтвердили закон Кулона с большой точностью. Например, было показано, что сила обратно пропорциональна расстоянию между двумя объектами в квадрате (F∝1 / r ²) с точностью до 1 части на 1016. Никаких исключений не было обнаружено даже на малых расстояниях. внутри атома.

Закон Кулона действует даже внутри атомов, правильно описывая силу между положительно заряженным ядром и каждым из отрицательно заряженных электронов.Этот простой закон также правильно учитывает силы, которые связывают атомы вместе, чтобы образовать молекулы, и силы, которые связывают атомы и молекулы вместе, чтобы сформировать твердые тела и жидкости.

Обычно, когда расстояние между ионами увеличивается, энергия притяжения приближается к нулю, и ионная связь становится менее благоприятной. По мере увеличения величины противоположных зарядов увеличивается энергия, и ионная связь становится более благоприятной.

Электрическое поле — это векторное поле, которое связывает с каждой точкой пространства кулоновскую силу, которая испытывает испытательный единичный заряд.Учитывая электрическое поле, сила и направление силы F на количественный заряд q в электрическом поле E определяется электрическим полем. Для положительного заряда направление электрического поля направлено вдоль линий, направленных радиально от местоположения точечного заряда, а направление — в сторону для отрицательного заряда.

Это распределение вокруг заряженной молекулы имеет сферическую природу и создает своего рода электростатическое «облако» вокруг молекулы. Силы притяжения или отталкивания в сферическом распределении заряда сильнее ближе к молекуле и ослабевают по мере увеличения расстояния от молекулы.

На этом изображении показано внешнее электронное облако нейтральной молекулы воды. 2} [/ latex] r +.

Цели обучения

Объясните, когда можно использовать векторные обозначения закона Кулона

Основные выводы

Ключевые моменты

Векторные обозначения закона Кулона можно использовать в простом примере двух точечных зарядов, где только один из них является источником заряда.
Полная сила, действующая на полевой заряд для множественных зарядов точечных источников, является суммой этих отдельных сил.
Закон Кулона можно дополнительно упростить и применить к фиксированному количеству точек заряда.

Ключевые термины

закон Кулона : математическое уравнение, вычисляющее вектор электростатической силы между двумя заряженными частицами
электростатическая сила : электростатическое взаимодействие между электрически заряженными частицами; количество и направление притяжения или отталкивания между двумя заряженными телами.

Решение задач с векторами и законом Кулона

Электрическая сила между двумя точечными зарядами

Для решения проблемы электростатических сил между электрически заряженными частицами сначала рассмотрим две частицы с электрическими зарядами q и Q , разделенные в пустом пространстве расстоянием r. 3} [ / латекс]

В этом уравнении k равно [latex] \ frac {1} {4 \ pi \ varepsilon_0 \ varepsilon} [/ latex], где [latex] \ varepsilon_0 [/ latex] — диэлектрическая проницаемость свободного пространства, а [latex ] \ varepsilon [/ latex] — относительная диэлектрическая проницаемость материала, в который погружены заряды.Переменные [latex] \ mathbf {\ text {F} _ \ text {E}} [/ latex], [latex] \ mathbf {\ text {r}} _ \ text {q} [/ latex] и [ latex] \ mathbf {\ text {r}} _ \ text {Q} [/ latex] выделены жирным шрифтом, поскольку они являются векторами. Таким образом, нам нужно найти [latex] \ mathbf {\ text {r}} _ \ text {q} — \ mathbf {\ text {r}} _ \ text {Q} [/ latex], выполнив стандартное векторное вычитание. Это означает, что нам нужно вычесть соответствующие компоненты вектора [latex] \ mathbf {\ text {r}} _ \ text {Q} [/ latex] из вектора [latex] \ mathbf {\ text {r}} _ \ текст {q} [/ latex].

Это векторное обозначение можно использовать в простом примере двух точечных зарядов, только один из которых является источником заряда.

Применение закона Кулона : В простом примере можно использовать векторную запись закона Кулона, когда есть два точечных заряда, и только один из них является зарядом источника.

Электрическая сила на полевом заряде из-за фиксированного источника заряда

Предположим, что существует более одного заряда точечного источника, обеспечивающего силы на полевой заряд. На диаграмме показан довольно простой пример с тремя исходными зарядами (показаны зеленым и индексируются нижними индексами) и одним полевым зарядом (красным, обозначен q).Мы предполагаем, что исходные заряды фиксированы в пространстве, а на полевой заряд q действуют силы от исходных зарядов.

Множественные точечные заряды : Закон Кулона применяется к более чем одному точечному источнику заряда, создающему силы на полевом заряде.

Отметьте выбранную систему координат. Все заряды лежат в углах квадрата, и начало координат выбрано так, чтобы совмещаться с нижним правым исходным зарядом и совмещено с квадратом. 3} [/ латекс].3} [/ латекс]

Закон Кулона : В этом видео я продолжаю серию обучающих видео по электростатике. Он рассчитан на бакалавриат, и хотя он в основном нацелен на изучение физики, он должен быть полезен всем, кто проходит первый курс по электричеству и магнетизму, например инженерам и т. Д.

Общая физика II

Электрический
Поля

Помните, НЕДОСТАТОЧНЫЕ обвинения привлекают,

или

и LIKE заряды отражают,

или

От чего зависит величина этой электрической силы F?

Сила F прямо пропорциональна зарядам Q и
q,

ф.
Q q

Сила F обратно пропорциональна
квадрат расстояния
r между зарядами,

ф
1 / п ²

ф.
1 / п ²

Мы можем объединить их как

ф.
Кв / К ²

Пока
пропорции
хорош для качественных дискуссий и сравнений,
уравнения много
проще использовать для расчетов.Мы можем изменить это на
уравнение с
константа
пропорциональность , к.

F = k Q q / r ²

Эта коэффициент пропорциональности k зависит от единиц измерения
мы используем. Если мы измеряем силу F в ньютонах (Н), расстояние r в метрах
(m) и заряжает Q и q в кулонах (C), тогда k имеет значение
из

k = 9 x 10 ⁹ Н
м ² / C ²

Теперь мы должны спросить, а что такое кулон заряда,
так или иначе?

Электрический заряд электрона или протона обозначается буквой е.
и равно.. .

Закон Кулона описывает силу F между двумя электрическими
зарядов, Q и q, расстояние r друг от друга,

Какова сила между двумя положительными зарядами, 1
C
и 2 С,
когда их разделяет расстояние 1 м?

Помните, сила — это вектор .Закон Кулона позволяет нам
вычислить величину электрической силы, но мы должны
еще учтите, что сила это вектор!

Пример кулоновского
Закон .

Мы также когда-нибудь запишем эту «постоянную Кулона» как

, где «эпсилон-ноль»

и известна как «диэлектрическая проницаемость свободного пространства». Который
имя звучит зловеще, чем нужно. Это просто
еще одна форма «постоянной Кулона» — и не более того! Там
являются основными ситуациями или основными уравнениями, в которых мы получаем
фактор

, который в таком случае удобнее записать как

Возможно, вы смотрели на весы Кавендиша, когда
вы говорили о гравитации. Кавендиш использовал очень тонкий
баланс для измерения невероятно малых сил. Кулон при измерении
электрические силы имели большие силы для работы. Вот
эскиз весов, которые он использовал для измерения электрических сил и
определить характеристику по r-квадрату электрического
сила:

Закон Кулона — Веб-формулы

Согласно ученому Кулону, электрическая сила между двумя неподвижными полюсами прямо пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними.

Рассмотрим два неподвижных полюса, имеющих заряды q

₁ и q ₂ и разделенные расстоянием r, тогда электрическая сила (F) будет:

F œ q

₁ q ₂ и F œ 1 / r ²
F = K · q ₁ · q ₂ / r ²

Где
K = постоянная величина, равная 9 × 10 ⁹ Нм ² C ^-2
r = расстояние в метрах (м)
q _1, q ₂ = заряды в кулонах (Кл)
F = электрическая сила в Ньютонах (Н)

Предположим, мы рассматриваем вакуум как среду между двумя полюсами, тогда постоянная K заменяется на 1/4 π · ε

₀, где ε ₀ — электрическая диэлектрическая проницаемость свободного пространства. .

F = (1/4 π · ε

₀) · (q ₁ · q ₂ / r ²)

Закон Кулона используется для определения силы отталкивания, действующей между двумя электрическими зарядами. В случае наличия более двух электрических зарядов принцип суперпозиции в дополнение к закону Кулона применяется для расчета чистой электронной силы, действующей на любой один заряд.

Принцип суперпозиции определяется как когда на заряд действует более одной кулоновской силы, результирующая кулоновская сила, действующая на него, равна векторной сумме отдельных сил.

Короче говоря, кулоновская сила, действующая между двумя зарядами, не зависит от наличия другого заряда, что означает, что кулоновская сила — это сила двух тел.

Согласно закону Кулона, величина электрического поля (

E ), создаваемого одиночным точечным зарядом (q) на определенном расстоянии (R), определяется по формуле:

Где q — точечный заряд.

Напряженность электрического поля положительного точечного заряда направлена наружу в радиальном направлении и имеет величину, пропорциональную заряду и обратно пропорциональную квадрату расстояния от заряда. Это означает, что у нас есть электрическое поле, вызванное положительным точечным зарядом. Затем мы можем измерить напряженность этого поля на другом расстоянии, которое равно R. Чем дальше мы измеряем силу, тем больше становится R и тем меньше становится напряженность этого поля в конкретном месте.

Когда заряд не находится в центре координаты, мы можем использовать следующие уравнения:

начиная с

таким образом:

Расчет:
Пример 1: Сила, действующая между двумя частицами, равна равный весу одного из них.Две частицы имеют одинаковую массу 1,6 кг и заряд 1,6С. Посчитайте расстояние между ними. Значение K = 9 × 10 ⁹ и g = 10 мс ^-2.

K = 9 × 10 ⁹
g = 10 мс ^-2
q ₁ = q ₂ = 1,6C
m = 1,6 кг
F = масса одной из частиц = мг, что дает:
F = K · q ₁ · q ₂ / r ² = mg

Выделяя r из уравнения, получаем:
r ² = K · q ₁ · q ₂ / мг
r ² = 9 × 10 ⁹ × (1. 6 × 1,6) / (1,6 × 10)
r ² = 1,440 × 10 ⁹
r = 1,2 × 10 ³

Пример 2: Сила, действующая между двумя зарядами, находящимися на определенном расстоянии, равна A. Предположим, что величина зарядов уменьшена вдвое и расстояние между ними увеличивается вдвое, значит сила, действующая между ними?

а) А / 4
б) А / 16
в) А / 8
г) A

Мы знаем, что:
F = A
Сборы уменьшены вдвое = q ₁/2 q ₂/2
Расстояние удвоено = 2r

Вставляем значения в F = K · q ₁ · q ₂ / r ², получаем:
F _новый = K · (q ₁/2) · (q ₂/2) / (2r) ²
F _новый = K · q ₁ · q ₂ / ( 16 р ²)
И F _новый = F / 16, так как F = A, имеем:
F _новый = A / 16

youtube.com/v/Q0Sz1B3DiSA&hl=en_US&fs=1&color1=0x006699&color2=0x54abd6″ allowscriptaccess=»always» allowfullscreen=»true»>

Закон Кулона | Определение и факты

Закон Кулона , математическое описание электрической силы между заряженными объектами.Сформулированный французским физиком 18-го века Шарлем-Огюстеном де Кулоном, он аналогичен закону всемирного тяготения Исаака Ньютона.

Подробнее по этой теме

электричество: закон Кулона

Статическое электричество — это знакомое электрическое явление, при котором заряженные частицы передаются от одного тела к другому. Например, если …

И гравитационная, и электрическая силы уменьшаются пропорционально квадрату расстояния между объектами, и обе силы действуют вдоль линии между ними.Однако в законе Кулона величина и знак электрической силы определяются электрическим зарядом, а не массой объекта. Таким образом, заряд определяет, как электромагнетизм влияет на движение заряженных объектов. Заряд — это основное свойство материи. Каждый компонент материи имеет электрический заряд, значение которого может быть положительным, отрицательным или нулевым. Например, электроны заряжены отрицательно, а ядра атомов — положительно. Большая часть материи имеет равное количество положительного и отрицательного заряда и, следовательно, имеет нулевой чистый заряд.

Согласно Кулону, электрическая сила для покоящихся зарядов имеет следующие свойства:

Подобные заряды отталкиваются друг от друга; в отличие от обвинений привлекают. Таким образом, два отрицательных заряда отталкиваются друг от друга, а положительный заряд притягивает отрицательный.
Притяжение или отталкивание действует вдоль линии между двумя зарядами.
Величина силы изменяется обратно пропорционально квадрату расстояния между двумя зарядами. Следовательно, если расстояние между двумя зарядами увеличивается вдвое, притяжение или отталкивание становится слабее, уменьшаясь до одной четвертой от первоначального значения. Если заряды сближаются в 10 раз, величина силы увеличивается в 100 раз.
Размер силы пропорционален величине каждого заряда. Единица измерения заряда — кулон (С). Если бы было два положительных заряда, один из которых составлял 0,1 кулон, а второй — 0,2 кулона, они бы отталкивали друг друга с силой, которая зависит от произведения 0,2 × 0,1. Таким образом, если бы каждый из зарядов был уменьшен наполовину, отталкивание уменьшилось бы до четверти своего прежнего значения.

5.3 Закон Кулона — Университетская физика, Том 2

Цели обучения

К концу этого раздела вы сможете:

Опишите электрическую силу как качественно, так и количественно
Вычислить силу, с которой заряды действуют друг на друга
Определить направление электрической силы для различных источников заряда
Правильно описать и применить принцип суперпозиции для зарядов от нескольких источников

Эксперименты с электрическими зарядами показали, что если два объекта имеют электрический заряд, то они оказывают электрическую силу друг на друга. Величина силы линейно пропорциональна чистому заряду каждого объекта и обратно пропорциональна квадрату расстояния между ними. (Интересно, что сила не зависит от массы объектов.) Направление вектора силы вдоль воображаемой линии, соединяющей два объекта, и определяется знаками задействованных зарядов.

Пусть

q1, q2 = q1, q2 = чистые электрические заряды двух объектов;
r → 12 = r → 12 = векторное смещение от q1q1 к q2q2.

Электрическая сила F → F → на одном из зарядов пропорциональна величине его собственного заряда и величине другого заряда и обратно пропорциональна квадрату расстояния между ними:

F∝q1q2r122.F∝q1q2r122.

Эта пропорциональность становится равенством с введением константы пропорциональности. По причинам, которые станут понятны в следующей главе, используемая нами константа пропорциональности на самом деле представляет собой набор констант. (Мы вскоре обсудим эту константу.)

Закон Кулона

Величина электрической силы (или кулоновской силы) между двумя электрически заряженными частицами равна

| F12 | = 14πε0 | q1q2 | r122 | F12 | = 14πε0 | q1q2 | r122

5,1

Единичный вектор rr имеет величину 1 и указывает вдоль оси как заряды. Если заряды имеют один и тот же знак, сила в том же направлении, что и rr, показывая силу отталкивания. Если заряды имеют разные знаки, сила в направлении, противоположном rr, показывает силу притяжения.(Рисунок 5.14).

Рис. 5.14. Электростатическая сила F → F → между точечными зарядами q1q1 и q2q2, разделенными расстоянием r , задается законом Кулона. Обратите внимание, что третий закон Ньютона (каждая действующая сила создает равную и противоположную силу) применяется как обычно — сила, действующая на q1q1, равна по величине и противоположна по направлению силе, которую она оказывает на q2q2. а) подобные обвинения; (б) в отличие от обвинений.

Важно отметить, что электрическая сила непостоянна; это функция расстояния между двумя зарядами.Если либо пробный заряд, либо исходный заряд (или оба) движутся, то r → r → изменяется, и, следовательно, сила. Непосредственным следствием этого является то, что прямое применение законов Ньютона с этой силой может быть математически затруднено в зависимости от конкретной рассматриваемой проблемы. Это можно (обычно) сделать, но мы почти всегда ищем более простые методы вычисления любой интересующей нас физической величины (наиболее распространенным выбором является сохранение энергии).

Наконец, новая постоянная ε0ε0 в законе Кулона называется диэлектрической проницаемостью свободного пространства , или (лучше) диэлектрической проницаемостью вакуума.Это имеет очень важный физический смысл, который мы обсудим в следующей главе; пока что это просто эмпирическая константа пропорциональности. Его числовое значение (с точностью до трех значащих цифр) оказывается

ε0 = 8,85 · 10−12C2N · м2. ε0 = 8,85 · 10−12C2N · м2.

Эти единицы необходимы, чтобы дать силе в законе Кулона правильные единицы в ньютонах. Обратите внимание, что в законе Кулона диэлектрическая проницаемость вакуума составляет только часть константы пропорциональности. Для удобства мы часто определяем постоянную Кулона:

ke = 14πε0 = 8.99 × 109 Н · м2C2.ke = 14πε0 = 8,99 · 109 Н · м2C2.

Пример 5.1

Сила на электрон в водороде

Атом водорода состоит из одного протона и одного электрона. Протон имеет заряд + e + e, а электрон — −e − e. В «основном состоянии» атома электрон вращается вокруг протона на наиболее вероятном расстоянии 5,29 × 10–11 м 5,29 × 10–11 м (рис. 5.15). Вычислите электрическую силу протона, действующую на электрон.

Рис. 5.15. Схематическое изображение атома водорода, показывающее силу, действующую на электрон.Это изображение предназначено только для того, чтобы мы могли вычислить силу; атом водорода действительно не выглядит так. Вспомните рисунок 5.7.

Стратегия

В этом примере мы рассматриваем электрон и протон как две точечные частицы, каждая из которых имеет электрический заряд, и нам сообщают расстояние между ними; нас просят вычислить силу, действующую на электрон. Таким образом, мы используем закон Кулона.

Решение

Наши два заряда и расстояние между ними,
q1 = + e = + 1,602 × 10−19Cq2 = −e = −1. 602 × 10−19Cr = 5,29 × 10−11м. Q1 = + e = + 1,602 × 10−19Cq2 = −e = −1.602 × 10−19Cr = 5,29 × 10−11м.

Величина силы, действующей на электрон, равна

.
F = 14πϵ0 | e | 2r2 = 14π (8,85 × 10−12C2N · м2) (1,602 × 10−19C) 2 (5,29 × 10−11 м) 2 = 8,25 × 10−8N. F = 14πϵ0 | e | 2r2 = 14π (8,85 × 10–12C2N · м2) (1,602 × 10–19C) 2 (5,29 × 10–11 м) 2 = 8,25 × 10–8N.

Что касается направления, поскольку заряды двух частиц противоположны, сила притяжения; сила, действующая на электрон, направлена радиально прямо к протону везде на орбите электрона..

Значение

Это трехмерная система, поэтому электрон (и, следовательно, сила, действующая на него) может находиться где угодно в воображаемой сферической оболочке вокруг протона. В этой «классической» модели атома водорода электростатическая сила на электрон направлена во внутреннем центростремительном направлении, таким образом поддерживая орбиту электрона. Но обратите внимание, что квантово-механическая модель водорода (обсуждаемая в квантовой механике) совершенно другая.

Проверьте свое понимание 5.1

Что было бы иначе, если бы электрон также имел положительный заряд?

Заряды от нескольких источников

Анализ, который мы сделали для двух частиц, можно распространить на произвольное число частиц; мы просто повторяем анализ, по два заряда за раз.В частности, мы задаем вопрос: учитывая N зарядов (которые мы называем исходным зарядом), какова чистая электрическая сила, которую они оказывают на какой-либо другой точечный заряд (который мы называем тестовым зарядом)? Обратите внимание, что мы используем эти термины, потому что можем представить себе испытательный заряд, используемый для проверки силы силы, создаваемой исходными зарядами.

Как и все силы, которые мы видели до сих пор, чистая электрическая сила на нашем испытательном заряде — это просто векторная сумма каждой индивидуальной электрической силы, приложенной к нему каждым из отдельных исходных зарядов. i — смещения из положения i -го заряда в положение Q . Каждый из N единичных векторов указывает непосредственно от связанного с ним заряда источника в сторону испытательного заряда. Все это изображено на рис. 5.16. Обратите внимание, что между Q и qiqi нет никакой физической разницы; различие в ярлыках просто для ясного обсуждения, где Q — это заряд, на который мы определяем силу.

Рисунок 5.я. Знаки заряда источника и тестового заряда определяют направление силы на тестовом заряде.)

Однако есть одна сложность. Подобно тому, как каждый из зарядов источника оказывает силу на испытательный заряд, точно так же (по третьему закону Ньютона) испытательный заряд оказывает равную и противоположную силу на каждый из зарядов источника. Как следствие, каждый исходный заряд изменил бы положение. Однако согласно уравнению 5. 2 сила, действующая на испытательный заряд, является функцией положения; таким образом, при изменении положения исходных зарядов, результирующая сила на испытательном заряде обязательно изменяется, что изменяет силу, которая снова меняет положения.Таким образом, весь математический анализ быстро становится трудноразрешимым. Позже мы изучим методы работы с этой ситуацией, а пока мы сделаем упрощающее предположение, что исходные заряды каким-то образом фиксируются на месте, так что их положения постоянны во времени. (Испытательный заряд может перемещаться.) При наличии этого ограничения анализ зарядов известен как электростатический, где «статика» относится к постоянным (то есть статическим) положениям зарядов источника, а сила — к как электростатическая сила.

Пример 5.2

Чистая сила от двух источников заряда

Помещают три разных небольших заряженных объекта, как показано на рис. 5.17. Заряды q1q1 и q3q3 фиксируются на месте; q2q2 может двигаться свободно. )].)].

Мы не можем добавить эти силы напрямую, потому что они не указывают в одном направлении: F → 23F → 23 точки только в направлении — x , тогда как F → 21F → 21 точка только в направлении + y -направление. Чистая сила получается из применения теоремы Пифагора к его компонентам x и y :

где

Fx = −F23 = −14πε0q2q3r232 = — (8,99 × 109N · m2C2) (4.806 × 10−19C) (8,01 × 10−19C) (4,00 × 10−7 м) 2 = −2,16 × 10−14NFx = −F23 = — 14πε0q2q3r232 = — (8,99 × 109 Н · м2C2) (4,806 × 10−19C) (8.01 × 10−19C) (4,00 × 10−7м) 2 = −2,16 × 10−14N

Fy = F21 = 14πε0q2q1r212 = (8.99 × 109N · m2C2) (4.806 × 10−19C) (3.204 × 10−19C) (2.00 × 10−7m) 2 = 3.46 × 10−14N. Fy = F21 = 14πε0q2q1r212 = (8.99 × 109 Н · м2C2) (4,806 × 10−19C) (3,204 × 10−19C) (2,00 × 10−7 м) 2 = 3,46 × 10−14N.

Мы находим, что

F = Fx2 + Fy2 = 4,08 × 10−14NF = Fx2 + Fy2 = 4,08 × 10−14N

под углом

ϕ = tan − 1 (FyFx) = tan − 1 (3,46 × 10−14N − 2,16 × 10−14N) = — 58 °, ϕ = tan − 1 (FyFx) = tan − 1 (3,46 × 10−14N − 2,16 × 10−14N) = — 58 °,

, то есть на 58 ° 58 ° выше оси — x , как показано на схеме.

Значение

Обратите внимание, что при замене числовых значений зарядов мы не включали отрицательный знак ни для q2q2, ни для q3q3. Напомним, что отрицательные знаки векторных величин указывают на изменение направления рассматриваемого вектора. Но для электрических сил направление силы определяется типами (знаками) обоих взаимодействующих зарядов; мы определяем направления сил, учитывая, одинаковы ли знаки двух зарядов или противоположны.Если вы также включаете отрицательные знаки из отрицательных зарядов при замене чисел, вы рискуете математически изменить направление вычисляемой силы. Таким образом, самый безопасный способ сделать это — вычислить только величину силы, используя абсолютные значения зарядов, и определить направления физически.

Также стоит отметить, что единственная новая концепция в этом примере — это расчет электрических сил; все остальное (получение чистой силы от ее компонентов, разбиение сил на их компоненты, определение направления результирующей силы) аналогично силовым задачам, которые вы делали ранее. 2} \\
& = \ текст {9 000} \ текст {N}
\ end {выровнять *}

Эта сила отталкивающая, поскольку находится между двумя одинаковыми зарядами.

Вы должны заметить, что даже на таком большом расстоянии, как \ (\ text {1} \) \ (\ text {km} \), сила отталкивания значительна, потому что \ (\ text {1} \) \ (\ text {C} \) — это очень значительная сумма заряда.

Рассчитайте расстояние между двумя зарядами \ (\ text {+4} \) \ (\ text {nC} \) и \ (- \ text {3} \) \ (\ text {nC} \), если электростатический сила между ними равна \ (\ text {0,005} \) \ (\ text {N} \).2} \\
& = \ текст {8,67} \ текст {N}
\ end {выровнять *}

Далее отметим, что сила \ (Q_ {3} \) на \ (Q_ {2} \) отталкивающая, а сила \ (Q_ {1} \) на \ (Q_ {2} \) также отталкивающий. Итак, эти две силы действуют в одном направлении (вправо). Результирующая сила:

\ begin {align *}
F_ {eR} & = F_ {e1} + F_ {e2} \\
& = \ text {8,67} \ text {N} + \ text {0,1} \ text {N} \\
& = \ text {8,77} \ text {N} \ to \ the \ right.

Закон Кулона в физике простыми словами

Закон Кулона определение и формула

Коэффициент пропорциональности в законе Кулона

Закон Кулона в векторной форме

Что можно определить с помощью закона Кулона

Для каких заряженных тел справедлив закон

Границы применимости закона Кулона

Закон Кулона в вакууме

Взаимодействие зарядов закон Кулона

Принцип суперпозиции закон Кулона

Задачи на закон Кулона с решением

Закон Кулона. Измерение электрического заряда.

Пример

Решение

Закон Кулона

основной закон электростатики кратко и понятно

Закон Кулона определение и формула

Коэффициент пропорциональности в законе Кулона

Закон Кулона в векторной форме

Что можно определить с помощью закона Кулона

Для каких заряженных тел справедлив закон

Границы применимости закона Кулона

Закон Кулона в вакууме

Взаимодействие зарядов закон Кулона

Принцип суперпозиции закон Кулона

Задачи на закон Кулона с решением

Закон Кулона и его полевая трактовка

Историческая справка

Полевая трактовка закона Кулона

Глава 17. Взаимодействие электрических зарядов. Закон Кулона, принцип суперпозиции

1.2 Закон Кулона

Учебное пособие по физике: Закон Кулона

Закон Кулона | Безграничная физика

Суперпозиция сил

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Сферическое распределение заряда

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Решение задач с векторами и законом Кулона

Электрическая сила между двумя точечными зарядами

Электрическая сила на полевом заряде из-за фиксированного источника заряда

Общая физика II

Закон Кулона — Веб-формулы

Закон Кулона | Определение и факты

5.3 Закон Кулона — Университетская физика, Том 2

Цели обучения

Закон Кулона

Пример 5.1

Сила на электрон в водороде

Стратегия

Решение

Значение

Заряды от нескольких источников

Пример 5.2

Чистая сила от двух источников заряда

Значение

alexxlab

Вам также может понравиться

Пульт для подсветки диодной: Обзор светодиодной RGB-ленты Rubetek RL-3112 с Wi-Fi управлением | Светодиодные ленты | Обзоры

Электромагнитная проницаемость: МАГНИТНАЯ ПРОНИЦАЕМОСТЬ • Большая российская энциклопедия

Тв штекер для тв розетки: правила и варианту установки на стену

Добавить комментарий Отменить ответ