{2}}}},
а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля:
- D=εaE{\displaystyle \mathbf {D} =\varepsilon _{a}\mathbf {E} }
в рассматриваемой среде[1]. Вводятся абсолютная (а) и относительная (r, от англ. relative — относительный) проницаемости:
- εa=ε0εr{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon _{r}},
где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная[2]. Cам термин «диэлектрическая проницаемость» применяется и для εr{\displaystyle \varepsilon _{r}}, и для εa{\displaystyle \varepsilon _{a}}; ради краткости, одну из этих величин (в российской литературе чаще εr{\displaystyle \varepsilon _{r}}, в англоязычной εa{\displaystyle \varepsilon _{a}}) переобозначают как ε{\displaystyle \varepsilon } (из контекста всегда ясно, о чём идёт речь). Величина εr{\displaystyle \varepsilon _{r}} безразмерна, а εa{\displaystyle \varepsilon _{a}} по размерности совпадает с ε0{\displaystyle \varepsilon _{0}} (в Международной системе единиц (СИ): фарад на метр, Ф/м).
Проницаемость εr{\displaystyle \varepsilon _{r}} показывает, во сколько раз сила взаимодействия двух электрических зарядов в конкретной среде меньше, чем в вакууме, для которого εr=1{\displaystyle \varepsilon _{r}=1}. Отличие проницаемости от единицы обусловлено эффектом поляризации диэлектрика под действием внешнего электрического поля, в результате которой создаётся внутреннее противоположно направленное поле. В области низких частот ω{\displaystyle \omega } значение проницаемости реальных сред εr>1{\displaystyle \varepsilon _{r}>1}, обычно оно лежит в диапазоне 1—100, но для сегнетоэлектриков составляет десятки и сотни тысяч. Как функция частоты электрического поля величина εr(ω){\displaystyle \varepsilon _{r}(\omega )} слегка возрастает на участках вне линий поглощения данного материала, однако вблизи линий резко спадает, из-за чего высокочастотная диэлектрическая проницаемость ниже статической. Имеет место связь проницаемости и показателя преломления вещества: для немагнитной непоглощающей среды n2(ω)=εr(ω){\displaystyle n^{2}(\omega )=\varepsilon _{r}(\omega )}.
{-2}}
Ниже все формулы приводятся для СИ, а символ ε{\displaystyle \varepsilon } используется как замена εr{\displaystyle \varepsilon _{r}} (εa=ε0ε{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon }).
Эффект поляризации диэлектрика и проницаемость
Под воздействием электрического поля в диэлектрике имеет место поляризация — явление, связанное с ограниченным смещением зарядов или поворотом электрических диполей. Данное явление характеризует вектор электрической поляризации P{\displaystyle \mathbf {P} }, равный дипольному моменту единицы объёма диэлектрика. В отсутствие внешнего поля диполи ориентированы хаотично (см. верхний рис.), за исключением особых случаев спонтанной поляризации в сегнетоэлектриках. При наличии поля диполи в большей или меньшей степени поворачиваются (нижний рис.), в зависимости от восприимчивости χ(ω){\displaystyle \chi (\omega )} конкретного материала, а восприимчивость, в свою очередь, определяет проницаемость ε(ω){\displaystyle \varepsilon (\omega )}.
Помимо дипольно-ориентационного, имеются и другие механизмы поляризации. Поляризация не изменяет суммарного заряда в любом макроскопическом объёме, однако она сопровождается появлением связанных электрических зарядов на поверхности диэлектрика и в местах неоднородностей. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле, как правило, направленное против внешнего наложенного поля. В итоге тот факт, что εa≠ε0{\displaystyle \varepsilon _{a}\neq \varepsilon _{0}}, является следствием электрической поляризации материалов.
Роль диэлектрической проницаемости среды в физике
Относительная диэлектрическая проницаемость ε{\displaystyle \varepsilon } среды, наряду с её относительн
А Б В Г Д Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Я
| |
изделия)Дисперсия диэлектрической проницаемости — Циклопедия
Дисперсия диэлектрической проницаемости рассматривается в ряде фундаментальных работ по электродинамике [1][2][3], но наиболее подробно этот вопрос рассмотрен в работе [4].
На примере этой работы рассмотрим вопрос о том, каким образом решаются подобные задачи, когда для их решения вводится понятие вектора поляризации. Параграф 59 этой работы, где рассматривается этот вопрос, начинается словами: «Мы переходим теперь к изучению важнейшего вопроса о быстропеременных электрических полях, частоты которых не ограничены условием малости по сравнению с частотами, характерными для установления электрической и магнитной поляризации вещества» (конец цитаты). Эти слова означают, что рассматривается та область частот, где в связи с наличием инерционных свойств носителей зарядов поляризация вещества не будет достигать её статических значений. При дальнейшем рассмотрении вопроса делается заключение, что «в любом переменном поле, в том числе при наличии дисперсии вектор поляризации [math]{\bf{P}} = {\bf{D}} — {\varepsilon _0}{\bf{E}} [/math] (здесь и далее все цитируемые формулы записываются в системе СИ) сохраняет свой физический смысл электрического момента единицы объёма вещества» (конец цитаты).
2[/math]. (2)
Поэтому вывод о невозможности толкования формулы (1), как внутренней энергии электрических и магнитных полей в диспергирующих средах является правильным. Однако это обстоятельство заключается не в том, что такая интерпретация в рассмотренных средах является вообще невозможной. Она заключается в том, что для определения величины удельной энергии как термодинамического параметра в данном случае необходимо правильно вычислить эту энергию, и ниже будет показано, что для этого следует учесть не только электрическое поле, которое накапливает потенциальную энергию, но и ток электронов проводимости, которые, в связи с наличием массы, накапливают кинетическую энергию движения зарядов. Это покажем на примере диэлектрической проницаемости плазмоподобных сред. Бездиссипативными плазмоподобными средами считаются среды, в которых заряды могут двигаться без потерь [5]. К таким средам в первом приближении могут быть отнесены сверхпроводники, свободные электроны или ионы в вакууме (в дальнейшем проводники).
2}}}[/math], (6)
находим
[math]{{\bf{j}}_L} = \frac{1}{{{L_k}}}\int {{{\bf{E}}_{}}dt} [/math]. (7)
В данном случае величина [math] {L_k}[/math] представляет удельную кинетическую индуктивность носителей заряда [6]. Её существование связано с тем, что заряд, имея массу, обладает инерционными свойствами. Для случая гармонических полей [math] {\bf{E}} = {{\bf{E}}_0}\sin \omega t[/math] соотношение (7) запишется:
[math]{{\bf{j}}_L} = — \frac{1}{{\omega {L_k}}}{{\bf{E}}_0}\cos \omega t [/math]. (8)
Здесь и далее для математического описания электродинамических процессов будут в большинстве случаев, вместо комплексных величин, использоваться тригонометрические функции с тем, чтобы были хорошо видны фазовые соотношения между векторами, представляющими электрические поля и плотности токов. Из соотношения (7) и (8) видно, что [math] {{\bf{j}}_L}[/math] представляет индуктивный ток, т.к. его фаза запаздывает по отношению к напряжённости электрического поля на угол [math] \frac{\pi }{2}[/math] .
Если заряды находятся в вакууме, то при нахождении суммарного тока нужно учитывать и ток смещения
[math] {{\bf{j}}_\varepsilon } = {\varepsilon _0}\frac{{{\partial _{}}{\bf{E}}}}{{{\partial _{}}t}} = {\varepsilon _0}{{\bf{E}}_0}\cos \omega t[/math] .
Видно, что этот ток носит ёмкостной характер, т.к. его фаза на [math] \frac{\pi }{2}[/math] опережает фазу напряжённости электрического поля. Таким образом, суммарная плотность тока составит
[math]{{\bf{j}}_\sum } = {\varepsilon _0}\frac{{{\partial _{}}{\bf{E}}}}{{{\partial _{}}t}} + \frac{1}{{{L_k}}}\int {{{\bf{E}}_{}}dt} [/math] ,
или
[math]{{\bf{j}}_\Sigma } = {\left( {\omega {\varepsilon _0} — \frac{1}{{\omega {L_k}}}} \right)_{}}{{\bf{E}}_0}\cos \omega t [/math] . (9)
Если электроны находятся в материальной среде, то следует ещё учитывать и наличие положительно заряженных ионов. Однако при рассмотрении свойств таких сред в быстропеременных полях, в связи с тем, что масса ионов значительно больше массы электронов, их наличие не учитывается.
2}{L_k}}}[/math],
и есть, как указывает Ландау, зависящая от частоты диэлектрической проницаемостью плазмы, что и принято во всех существующих работах по физике плазмы. Если рассмотреть любую среду, в том числе и плазму, то плотность токов (в дальнейшем будем сокращённо говорить просто ток) будет определяться тремя составляющими, зависящими от электрического поля. Ток резистивных потерь будет синфазен электрическому полю. Ёмкостной ток, определяемый первой производной электрического поля по времени, будет опережать напряженность электрического поля по фазе на [math] \frac{\pi }{2}[/math] . Этот ток называется током смещения. Ток проводимости, определяемый интегралом от электрического поля по времени, будет отставать от электрического поля по фазе на [math] \frac{\pi }{2}[/math] . Все три указанные составляющие тока и будут входить во второе уравнение Максвелла и других составляющих токов быть не может. Причём все эти три составляющие токов будут присутствовать в любых немагнитных средах, в которых имеются тепловые потери.
2}}} + \frac{{{\mu _0}}}{{{L_k}}}{\bf{E}} = 0[/math] .
Для постоянных электрических полей можно записать:
[math]ro{t_{}}ro{t_{}}{\bf{E}} + \frac{{{\mu _0}}}{{{L_k}}}{\bf{E}} = 0 [/math] .
Следовательно, постоянные электрические поля проникают в сверхпроводник таким же образом, как и магнитные, убывая по экспоненциальному закону. Плотность же тока при этом растёт по линейному закону
[math]{{\bf{j}}_L} = \frac{1}{{{L_k}}}\int {{{\bf{E}}_{}}dt} [/math] .
Таким образом, получены данные, характеризующие процесс распространения электромагнитных волн в плазмоподобных средах.
- ↑ Гинзбург В. Л. Распространение электромагнитных волн в плазме. – М.: Наука. 1967 г. — 684 с.
- ↑ Ахиезер А. И. Физика плазмы М: Наука, 1974 – 719 с.
- ↑ Тамм И. Е. Основы теории электричества М.: Наука, 1989 – 504 с.
- ↑ Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред. М: Физматгиз, 1973.- 454 с.
- ↑ Александров А. Ф., Богданкевич Л. С.
, Рухадзе А. А. Колебания и волны в плазменных средах. Изд. Московского университета, 1990.- 272 с. - ↑ Менде Ф. Ф., Спицын А. И. Поверхностный импеданс сверхпроводников. Киев, Наукова думка, 1985.- 240 с. http://fmnauka.narod.ru/poverkhnostnyj_impedans_sverkhprovodnikov.pdf
, Рухадзе А. А. Колебания и волны в плазменных средах. Изд. Московского университета, 1990.- 272 с.Диэлектрическая проницаемость
Обратите внимание, что если вы щелкнете по диэлектрику (серый прямоугольник), вы сможете изменить его размер. Попробуйте заполнить пространство между пластинами диэлектриком.
Насколько эффективно диэлектрик позволяет конденсатору сохранять больше заряда, зависит от материала, из которого он сделан. Каждый материал имеет диэлектрическую проницаемость κ. Это отношение поля без диэлектрика (E o ) к чистому полю (E) с диэлектриком:
κ = E или / E
E всегда меньше или равно E o , поэтому диэлектрическая проницаемость больше или равна 1.Чем больше диэлектрическая проницаемость, тем больше заряда может храниться.
Полное заполнение пространства между пластинами конденсатора диэлектриком увеличивает емкость на коэффициент диэлектрической проницаемости:
C = κ C o , где C o — емкость без диэлектрика между пластинами.
Для конденсатора с параллельными пластинами, содержащего диэлектрик, полностью заполняющий пространство между пластинами, емкость определяется как:
C = κ ε o А / сут
Емкость становится максимальной, если диэлектрическая проницаемость максимальна, а пластины конденсатора имеют большую площадь и расположены как можно ближе друг к другу.
Если бы в качестве диэлектрика вместо изолятора использовался металл, поле внутри металла было бы нулевым, что соответствовало бы бесконечной диэлектрической проницаемости. Однако диэлектрик обычно заполняет все пространство между пластинами конденсатора, и, если бы это сделал металл, он закоротил бы конденсатор — поэтому вместо него используются изоляторы.
| Материал | Диэлектрическая проницаемость | Диэлектрическая прочность (кВ / мм) |
|---|---|---|
| Вакуум | 1.00000 | – |
| Воздух (сухой) | 1.00059 | 3 |
| Полистирол | 2,6 | 24 |
| Бумага | 3,6 | 16 |
| Вода | 80 | — |
Что такое диэлектрическая постоянная?
Диэлектрическая проницаемость — это отношение абсолютной диэлектрической проницаемости материала к абсолютной диэлектрической проницаемости вакуума.Техническое определение «диэлектрической проницаемости» или «относительной диэлектрической проницаемости» сложно и все еще обсуждается среди инженеров-электриков. Это связано с тем, что диэлектрическая проницаемость материала зависит от частоты приложенного напряжения.
Термин «статическая диэлектрическая проницаемость» используется для описания этого отношения при приложении постоянного тока или напряжения нулевой частоты.
Ученый со стаканами
Конденсаторы — это устройства, накапливающие электрические заряды.Они находят множество применений в электронике из-за своих уникальных характеристик. Они используются в качестве фильтров в источниках питания для устранения колебаний выходного напряжения, в качестве временных констант в схемах генератора и для блокировки напряжения постоянного тока (DC) при прохождении напряжения переменного тока (AC) в схемах усилителя.
Конденсатор имеет две пластины или ленты из проводящего материала, разделенные изолятором.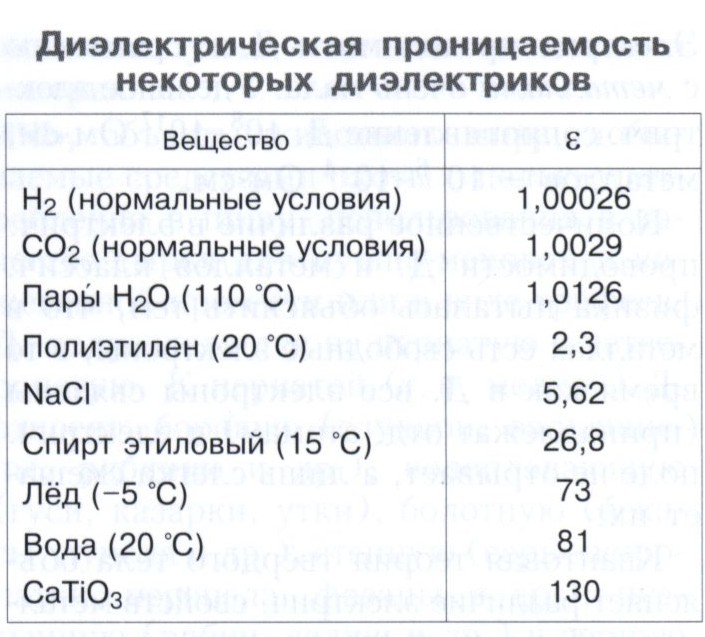
Когда через конденсатор подается постоянный ток, между пластинами накапливается заряд. Чтобы предотвратить потерю напряжения в зазоре между пластинами, между пластинами помещен изолятор. Этот изолятор известен как диэлектрик.
Термин «постоянная» вводит в заблуждение, когда речь идет о диэлектрической или диэлектрической проницаемости изолятора.При изменении применяемой частоты изменяется и диэлектрическая проницаемость. Термин, обычно используемый для частотно-зависимой диэлектрической проницаемости, — это «относительная диэлектрическая проницаемость».
С увеличением частоты относительная диэлектрическая проницаемость уменьшается.
В результате конденсаторы предназначены для работы в заданном диапазоне частот. Один диэлектрический материал может быть подходящим для использования с более низкими частотами, но он может не работать должным образом при воздействии высокочастотного напряжения. Конденсаторам в высокочастотных цепях нужны изоляторы с гораздо более высокой диэлектрической проницаемостью.
Некоторые диэлектрические изоляторы действительно способствуют образованию электрического поля в конденсаторе.Они делают это, помогая сконцентрировать и выровнять электрическое поле. Эта характеристика, наряду с изолирующей способностью материала, определяет диэлектрическую проницаемость или относительную диэлектрическую проницаемость данного материала.
Диэлектрическая проницаемость обычных материалов
Диэлектрик из различных материалов
Диэлектрическая постоянная (диэлектрическая проницаемость) — это количество электрической энергии, запасенной в изоляторе, когда на него накладывается электрическое поле.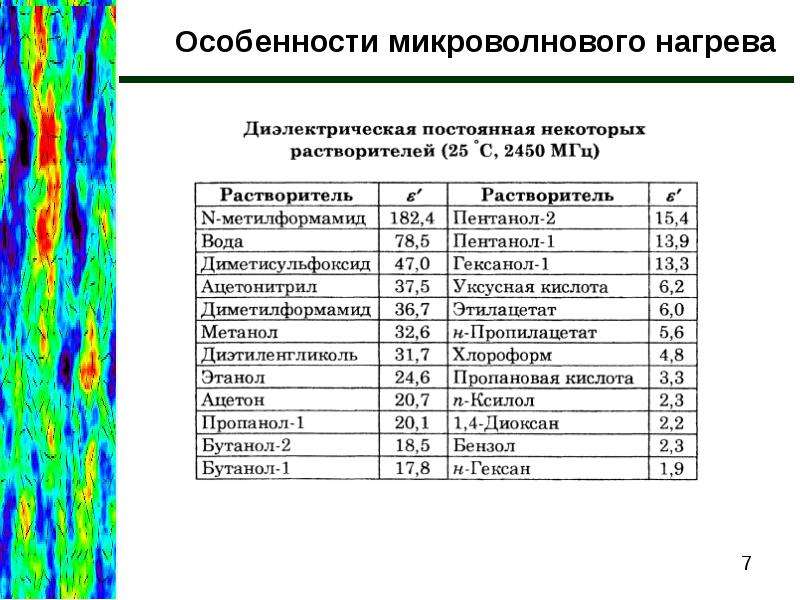
Диэлектрическая проницаемость выражается отношением к диэлектрической проницаемости в вакууме или (1.000000). При прочих равных условиях большая диэлектрическая проницаемость диэлектрика дает большую емкость; меньшая диэлектрическая проницаемость диэлектрика дает меньшую емкость.
В следующей таблице перечислены диэлектрические постоянные различных распространенных материалов:
Диэлектрическая постоянная (диэлектрическая проницаемость)
| Материал | Диэлектрик |
Акрил (оргстекло) | 2.7 — 4,5 |
Акрилонитрилбутадиенстирол (ABS) | 2,87 |
Ацеталь (Делрин) | 3,6 |
Воздух | 1. 000585 |
Глинозем | 9,3 — 11,5 |
Асбест | 3.0–4,8 |
Бакелит | 3,5-5,0 |
Пчелиный воск | 2,6–3,0 |
Целлулоид | 3,3-11 |
Эпоксидная смола (литая) | 3,6 |
Formica | 3.6–6 |
FR-4 | 4,3 — 5,0 |
Слюда | 5,4 |
Micarta | 3,2 — 5,5 |
Неопрен | 6-9 |
Нейлон | 4. 0–5,0 |
Бумага (чистая) | 3,0 |
Парафиновый воск | 2,1–2,5 |
Фенольная смола | 4,9 |
Полиамид | 2,5–2,6 |
Поликарбонат (Lexan®) | 2.9-3.0 |
Полиэфирная пленка (майлар) | 2,8 — 4,5 |
Полиэтилен | 2,27–2,5 |
Полипропилен | 2,25 |
Полистирол | 2,4–2,6 |
Поливинилхлорид (ПВХ) | 2. 8-3,4 |
Фарфор | 5,1-6,0 |
Стекло Pyrex | 4,3 — 5,0 |
Кварц | 4,2 |
Резиновый цемент | 2,7–2,9 |
Кремний | 11.0–12 |
Силиконовое масло | 2,2–2,9 |
Силиконовая резина | 3,2-9,8 |
шелк | 2,5–3,5 |
Стирол (ABS) | 2,8 |
Тефлон (PTFE) | 2. 1 |
Тефлон (стекловолокно) | 2,2–2,8 |
Вода (дистиллированная) | 76,5 — 80 |
воск | 2,4-6,5 |
Древесина, сухая | 2-6 |
Древесина влажная | 10-30 |
Диэлектрическая проницаемость
Диэлектрическая постоянная измеряет степень концентрации электростатического потока в материале и также известна как относительная статическая диэлектрическая проницаемость, статическая диэлектрическая постоянная и относительная диэлектрическая проницаемость.
Это важно при определении того, можно ли использовать вещество в конденсаторах или в различных химических и физических приложениях. Значение диэлектрической проницаемости материала необходимо знать, прежде чем использовать его для изготовления оптических волокон или коаксиальных кабелей. Хотя этот термин широко используется, он может иметь различные математические коннотации в зависимости от контекста его применения. Диэлектрическая проницаемость относится к статической или частотно-зависимой относительной диэлектрической проницаемости.
Как рассчитать диэлектрическую проницаемость
Шаг 1 — Определите диэлектрическую проницаемость материала, которая представляет собой отношение статической проницаемости исследуемого материала к статической проницаемости вакуума.Формула: er = es / e0, где er обозначает диэлектрическую проницаемость, es обозначает статическую диэлектрическую проницаемость исследуемого материала, а e0 — статическая диэлектрическая проницаемость вакуума, которая по определению имеет значение 1.
Шаг 2 — Обратите внимание на единицы диэлектрической проницаемости, которые представляют собой число, представляющее отношение es и e0.
Шаг 3 — Измерьте емкость конденсатора с помощью испытательного материала, помещенного между пластинами, и присвойте это значение Cx. Повторите этот процесс с вакуумом между пластинами и присвойте значение C0.
Шаг 4 — Разделите Cx на Co, чтобы определить диэлектрическую проницаемость. Если электромагнитное поле изменяется с течением времени, значение определяется на основе частоты изменения и чаще называется относительной диэлектрической проницаемостью.
Шаг 5 — Следующая формула определяет диэлектрическую проницаемость из статической электрической восприимчивости: er = 1 + Xe. Хе — это статическое электричество восприимчивости исследуемого материала.
Диэлектрическая проницаемость
Мы знаем, что диэлектрическая проницаемость материала связана с
к (1) скорости распространения электромагнитной волны через материал, и (2) энергии, запасенной
Электрическое поле в материале.
-11 [Ф / м]. Ну это не особо
легко запомнить. Кроме того, нас действительно волнует только отношение диэлектрической проницаемости материала к диэлектрической проницаемости свободного пространства.
Это говорит нам, среди прочего, о замедлении скорости света в материале, а также о соответствующем уменьшении длины волны.
для электромагнитной волны в материале.
Отношение диэлектрической проницаемости материала (скажем, задаваемое)
к диэлектрической проницаемости свободного пространства (написано) — диэлектрическая проницаемость.То есть:
| [Уравнение 1] |
|---|
Таким образом, можно обнаружить, что материал FR4 имеет диэлектрическую проницаемость 4. Это почти заставляет задуматься, что означает 4 в FR4.
Таким образом, гораздо проще обсуждать диэлектрики по их диэлектрической проницаемости, а не по их диэлектрической проницаемости.
Обратите внимание, что диэлектрическая проницаемость свободного пространства (вакуума) написана, потому что это самая низкая диэлектрическая проницаемость в природе.
Любой другой материал (включая воздух) будет иметь (по крайней мере, несколько) более высокую диэлектрическую проницаемость.
Я завершу эту страницу таблицей общих диэлектрических постоянных.
Таблица I. Диэлектрические постоянные обычных материалов
| Материал | Диэлектрическая проницаемость |
|---|---|
| Вакуум | 1,0 |
| Воздух | 1.0006 |
| Резина | 2,1 |
| Резина | 2,8 |
| Бумага | 3,0 |
| Кокаин | 3.1 |
| Кварц | 4,2 |
| Стекло | 7,8 |
| Циркон | 12 |
| Этиловый спирт | 24 |
| Вода (212 ° F) | 55,3 |
| Вода (32 град. F) | 88 |
Определения антенн
Учебное пособие по антенне (домашняя)
Вверху: диэлектрическая постоянная
Эта страница, посвященная диэлектрической проницаемости, защищена авторским правом.
Никакая часть не может быть воспроизведена без разрешения автора.
Авторское право 2009-2012 antenna-theory.com. Диэлектрическая постоянная.
5.1.2 Диэлектрическая проницаемость
5.1.2 Диэлектрическая проницаемость
Диэлектрическая проницаемость, также называемая диэлектрической проницаемостью.
описывает отношение
между электрическим смещением и напряженностью поля. Для общего случая это
тензор зависит от частоты и внешних воздействий, таких как магнитные поля.В изотропных материалах этот тензор сводится к скаляру. Диэлектрическая проницаемость
обычно дается как произведение безразмерной относительной диэлектрической проницаемости
а диэлектрическая проницаемость вакуума
.
Особый интерес представляет статическая диэлектрическая проницаемость.
а также
высокочастотная диэлектрическая проницаемость
.
Пока статический диэлектрик
постоянная входит в уравнение Пуассона, а также в модели для нескольких
механизмов рассеяния, обе константы используются при описании полярных
оптическое рассеяние.
Статическая диэлектрическая проницаемость теллурида свинца необычно высока и составляет
зависит от температуры, как показано на рис. 5.1.
Экспериментальные данные в основном доступны для диапазона низких температур.
[198,199,200]. Значения для комнатной температуры и выше
приведены в [200,194], но их недостаточно, чтобы дать нам
четкая картина зависимости
в этом диапазоне. Низкий
данные о температуре от Nishi [198], Tennant
[200], а Дашевский [201] может
моделироваться простым степенным законом
| (5.2) |
Однако данные Dalven [194] предполагают линейную
зависимость, моделируемая
| (5,3) |
Выражение для
в Pb
Sn
Те в диапазоне
является
приведено в [202].
Кроме того, экспериментальные данные для низкого
диапазон температур предоставлен Ниши в [198].
Высокочастотная диэлектрическая проницаемость составляет около
раз ниже, чем
статическая диэлектрическая проницаемость [194,203].
| (5.4) |
Линейные модели (5.3) и (5.4) применяются для
моделирование методом Монте-Карло, представленное в разделе 5.4 для
высокотемпературный диапазон.
М. Вагнер: Моделирование термоэлектрических устройств
.
