Анализ сложных электрических цепей постоянного тока. Электрическая цепь сложная

Сложные электрические цепи постоянного тока. Сложные электрические цепи

Метод законов Кирхгофа

Сложной электрической цепью принято называть разветвленную цепь, содержащую несколько источников, расположенных в разных ветвях. Пример сложной цепи постоянного тока приведен на рис. 22.

Рис. 22. Пример сложной цепи постоянного тока

Истинные направления токов в ветвях сложной электрической цепи, как правило, неизвестны. Поэтому анализ сложной цепи начинается с выбора так называемых положительных направлений токов в ветвях схемы. На схеме положительные направления токов в ветвях обозначают стрелками с символами тока I . Пример выбора условных положительных направлений токов в ветвях схемы показан на рис. 22.

Если в результате анализа цепи получается, что ток в ветви положителен, то истинное направление тока будет совпадать с выбранным положительным направлением тока. Если в результате расчета окажется, что ток в ветви отрицателен, то истинное направление тока противоположно выбранному положительному направлению тока. Т.е. в ходе анализа электрической цепи токи в ветвях рассматриваются как алгебраические величины.

Наиболее общий подход к анализу сложных электрических цепей основан на использовании законов Кирхгофа. С помощью законов Кирхгофа составляется система линейных алгебраических уравнений относительно неизвестных токов. Число неизвестных токов равно числу ветвей схемы. Обозначим это число через m . Следовательно, с помощью законов Кирхгофа необходимо составить систему из m уравнений с m неизвестными токами.

При составлении уравнений по законам Кирхгофа необходимо придерживаться следующего правила. Если в схеме n узлов, то с помощью первого закона Кирхгофа составляется (n – 1) независимое уравнение. (Уравнение для последнего узла будет зависимым). Оставшиеся [m –(n –1)] уравнения составляются с помощью второго закона Кирхгофа для так называемых независимых контуров.

Независимый контур – это такой контур, при обходе которого появляется хотя бы одна новая ветвь по сравнению с ранее рассмотренными контурами.

В разветвленной цепи число независимых контуров всегда меньше общего количества контуров. Поэтому при выборе независимых контуров имеется определенная свобода выбора. Однако число независимых контуров в схеме всегда регламентировано. Схема рис. 22, например, содержит

[m – (n – 1)] = = 3

независимых контура.

В результате составления (n – 1) уравнения по первому закону Кирхгофа и [m – (n – 1)] уравнения по второму закону Кирхгофа образуется система из m уравнений относительно неизвестных токов ветвей. Решение этой системы позволяет определить токи ветвей.

Схема рис. 22 состоит из шести ветвей. Выбранные положительные направления токов в ветвях указаны на схеме стрелками с символами тока I 1 , I 2 , I 3 , I 4 , I 5 , I 6 . Для расчета токов в ветвях этой схемы с помощью законов Кирхгофа необходимо составить систему из шести уравнений.

Схема содержит четыре узла (n = 4). По первому закону Кирхгофа необходимо составить три уравнения. Условимся при составлении уравнений по первому закону Кирхгофа токи, выходящие из рассматриваемого узла, брать со знаком «плюс», а входящие в узел, – со знаком «минус».

В узел а входит ток I 1 , а выходят токи I 2 и I 3 . Тогда для узла a уравнение первого закона Кирхгофа будет иметь вид

Из узла b выходят токи I 1 , I 4 , I 6 . Уравнение первого закона Кирхгофа для уз

electrician-i.ru

Сложные электрические цепи

В электрических цепях довольно часто встречается смешанное соединение , представляющее собой комбинацию последовательного и параллельного соединений. Если взять, например, три прибора, то возможны два варианта смешанного соединения. В одном случае соединяются два прибора параллельно, а к ним последовательно подключается третий (рис. 1, а).

Такая цепь имеет два последовательно включенных участка, один из которых представляет собой параллельное соединение. По другой схеме соединены последовательно два прибора, а параллельно к ним подключен третий (рис. 1, б). Эту цепь следует рассматривать как параллельное соединение, в котором одна ветвь сама является последовательным соединением.

При большем количестве приборов могут быть различные, более сложные схемы смешанного соединения. Иногда встречаются более сложные цепи, содержащие несколько источников ЭДС.

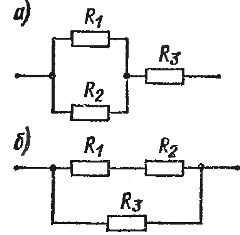
Рис. 1. Смешанное соединение резисторов

Для расчета сложных цепей существуют различные методы. Наиболее общим из них является применение . В самом общем виде этот закон гласит, что во всяком замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений.

Необходимо брать алгебраическую сумму потому, что ЭДС, действующие навстречу друг другу, или падения напряжения, созданные противоположно направленными токами, имеют разные знаки.

При расчете сложной цепи в большинстве случаев бывают известны сопротивления отдельных участков цепи и ЭДС, включенных источников. Чтобы найти токи, следует в соответствии со вторым законом Кирхгофа составить для замкнутых контуров уравнения, в которых токи являются неизвестными величинами. К этим уравнениям надо добавить уравнения для точек разветвления, составленные по первому закону Кирхгофа. Решая эту систему уравнений, определим токи. Конечно, для более сложных цепей этот метод получается довольно громоздким, так как приходится решать систему уравнений с большим числом неизвестных.

Применение второго закона Кирхгофа можно показать на следующих простейших примерах.

Пример 1. Дана электрическая цепь (рис. 2). ЭДС источников равны Е1= 10 В и Е2 = 4 В, а г1 = 2 Ом и r2 = 1 Ом соответственно. ЭДС источников действуют навстречу. Нагрузочное сопротивление R = 12 Ом. Найти ток I в цепи.

Рис. 2. Электрическая цепь с двумя источниками, включенными навстречу друг другу

Решение. Так как в данном случае имеется лишь один замкнутый контур, то составляем одно единственное уравнение: E 1 - E 2 = IR + Ir 1 + Ir 2 .

В левой его части имеем алгебраическую сумму ЭДС, а в правой части - сумму падений напряжений, создаваемых током I

wiregid.ru

Сложные электрические цепи

К сложным электрическим цепям относят цепи, содержащие несколько источников электрической энергии, включенных в разные ветви. Ниже на рисунке изображены примеры таких цепей.Для сложных электрических цепей неприменима методика расчета простых электрических цепей. Упрощение схем невозможно, т.к. нельзя выделить на схеме участок цепи с последовательным или параллельным соединением однотипных элементов. Иногда, преобразование схемы с ее последующим расчетом все-таки возможно, но это скорее исключение из общего правила.

Для полного расчета сложных электрических цепей обычно используют следующее методы:

1. Применение законов Кирхгофа (универсальный метод, сложные расчеты системы линейных уравнений).
2. Метод контурных токов (универсальный метод, расчеты немного проще чем в п.1)
3. Метод узловых напряжений (универсальный метод, расчеты немного проще чем в п.1)
4. Принцип наложения (универальный метод, несложные расчеты)
5. Метод эквивалентного источника (удобен когда необходимо произвести не полный расчет электрической цепи, а найти ток в одной из ветвей).
6. Метод эквивалентного преобразования схемы (применим довольно редко, простые расчеты).

Особенности применения каждого метода расчета сложных электрических цепей более подробно изложены в соответсвующих подразд

К простым относят электрические цепи, которые содержат либо один источник электрической энергии, либо несколько находящихся в одной ветви электрической цепи. Ниже изображены две схемы простых электрических цепей. Первая схема содержит один источник напряжения, в таком случае электрическая цепь однозначно относится к простым цепям. Вторая содержит уже два источника, но они находятся в одной ветви, следовательно это также простая электрическая цепь.Расчет простых электрических цепей обычно производят в такой последовательности:

1. Сначала упрощают схему последовательно преобразовав все пассивные элементы схемы в один эквивалентный резистор. Для этого необходимо выделять участки схемы, на которых резисторы соединены последовательно или параллельно, и по известным формулам заменять их эквивалентными резисторами (сопротивлениями). Цепь постепенно упрощают и приводят к наличию в цепи одного эквивалентного резистора.
2. Далее подобную процедуру проводят с активными элементами электрической цепи (если их количество более одного источника). По аналогии с предыдущим пунктом упрощаем схему до тех пор, пока не получим в схеме один эквивалентный источник напряжения.
3. В итоге мы приводим любую простую электрическую схему к следующему виду: Теперь есть возможность применить закон Ома - соотношение (1.22) и фактически определить значение тока протекающего через источник электрической энергии.
4. Теперь поэтапно эквивалентную схему преобразовывают к начальному виду. После каждого пункта "усложнения" схемы используя законы Ома и Кирхгофа определяют токи и напряжения на отдельных участках схемы. Фактически выполняются действия, обратные описанным в пункте 1 и 2. По окончании этого пункта получаем полный расчет электрической цепи.

 

Дата добавления: 2015-07-14; просмотров: 525 | Нарушение авторских прав

mybiblioteka.su - 2015-2018 год. (0.009 сек.)

mybiblioteka.su

Сложные электрические цепи

1. Цепи постоянного тока(состав и особенности элементов цепи, область применения)

Электрическая цепь состоит из трех основных элементов:

источника электрической энергии;

приемника электрической энергии;

соединительных проводов.

Источники электрической энергии - превращают химическую, механическую, тепловую, световую или энергию других видов в электрическую энергию.

Основное назначение источника энергии - создать и поддерживать в цепи разность потенциалов, разность электрических уровней; создать как бы электрический напор, под воздействием которого образуется упорядоченное движение электрических зарядов, то есть ток.

Принято зажим высшего потенциала источника обозначать знаком "+", зажим низшего потенциала знаком "-".

Разность электрических потенциалов количественно определяется величиной, которая называется электродвижущей силой, или коротко ЭДС.

Внешней характеристикой называется функциональная зависимость напряжения на клеммах источника от величины тока, протекающего через источник.

Приемник электрической энергии - электрическая энергия преобразуется тепловую, световую, механическую и другие виды энергии.

Это могут быть электрические лампы, нагревательные приборы, электродвигатели и другие устройства.

Вольтамперной характеристикой называется функциональная зависимость напряжения на зажимах нагрузки от тока, протекающего через нагрузку.

Линейным элементом, или нагрузкой, называют такой, сопротивление которого R при любых значениях тока через него остается постоянным, а вольтамперная характеристика представляет собой прямую линию.

Нелинейным элементом называют такой, сопротивление которого R непостоянно и зависит от величины тока, проходящего через него, а вольтамперная характеристика представляет собой кривую линию.

Только линейные элементы подчиняются закону Ома.

Соединительные провода - они обеспечивают передачу электрической энергии, транспортируют энергию от источника к нагрузке.

Их назначение передать электрическую энергию потребителю с минимальными потерями.

Область применения цепи постоянного тока: в технике, электронных схемах.

2. Эквивалентные преобразования в цепях постоянного тока при последовательном, параллельном и смешанном соединениях сопротивлений.

При последовательном:

При параллельном соединение:

Два наиболее встречающихся на практике случая:

a)Параллельное соединение n одинаков сопротивлений.

б)Параллельное соединение двух сопротивлений.

Преобразование в смешанном соед

electric-school.ru

Смешанное соединение и сложные электрические цепи. Сложные электрические цепи

В сложной электрической цепи постоянного тока (Таблица 2)

определить токи на всех участках цепи. Задачу решить двумя любыми методами

Таблица 2

Вариант №	Данные для расчётов	Схема электрической цепи
	Е 1 =136В; Е 2 =80В; R 1 = 194 Ом; R 2 =76 Ом; R 3 = 240 Ом; R 4 =120 Ом. . r 1 = 6 Ом; r 2 = 4 Ом.	Рис.12
	Е 1 =150В; Е 2 =170В; R 1 = 29,5Ом;R 2 =24 Ом; R 3 = 40 Ом; r 1 = 0,5 Ом; r 2 = 1 Ом.	Рис.13
	Е 1 =68В; Е 2 =40В; R 1 = 97Ом;R 2 =38Ом; R 3 = 120 Ом; R 4 =60Ом; r 1 = 3 Ом; r 2 = 2 Ом.	Рис.14
	Е 1 =45В; Е 2 =60В; R 1 = 2 Ом;R 2 =14.5 Ом; R 3 = 15 Ом; R 4 =5 Ом 5 r 1 = 0,5 Ом; r 2 = 0,5Ом.	Рис.15
	Е 1 =30В; Е 2 =40В; R 1 =10Ом;R 2 =2 Ом; R 3 = 3Ом; R 4 = R 5 =12Ом; r 1 = 2Ом; r 2 = 1Ом.	Рис.16
Вариант №	Данные для расчётов	Схема электрической цепи
	Е 1 =90В; Е 2 =120В; R 1 = 4Ом;R 2 =29 Ом; R 3 = 30 Ом; R 4 =10Ом; r 1 = 1Ом; r 2 = 1Ом.	Рис.17
	Е 1 =120В; Е 2 =144В; R 1 = 3,6Ом;R 2 =6,4 Ом; R 3 = 6 Ом; R 4 =4 Ом r 1 = 0,4 Ом; r 2 = 1,6 Ом.	Рис.18
	Е 1 =160В; Е 2 =200В; R 1 = 9Ом;R 2 =19 Ом; R 3 = 25 Ом; R 4 =100Ом; r 1 = 1Ом;r 2 = 1 Ом.	Рис.19
	Е 1 =60В; Е 2 =72В; R 1 = 1,8Ом;R 2 =3,2 Ом; R 3 = 3 Ом; R 4 =2Ом; r 1 = 0,2Ом; r 2 = 0,8 Ом.	Рис.20
	Е 1 =80В; Е 2 =100В; R 1 = 9Ом;R 2 =19 Ом; R 3 = 25 Ом; R 4 =100Ом; r 1 = 1Ом; r 2 = 1 Ом.	Рис. 21

Решение задачи 2 требует знаний методов расчёта сложной электрической цепи и ее участков, законов Кирхгофа, методики определения эквивалентно­го сопротивления цепи. Перед решением задачи изучите методики расчётов сложных электрических цепей постоянного тока и рассмотрите соответствующие им типовые при­меры.

Методические указания к решению задачи 2:

2.1. Метод наложения токов

Метод наложения является одним из методов расчета сложных цепей с несколькими источниками.

Сущность расчета цепей методом наложения сводится к следующему:

1. В каждой ветви рассматриваемой цепи направление тока выбирается произвольно.

2. Количество расчетных схем цепи равно количеству источников в исходной схеме.

3. В каждой расчетной схеме действует только один источник, а остальные источники заменяются их внутренним сопротивлением.

4. В каждой расчетной схеме методом свертывания определяют частичные токи в каждой ветви. Частичным называется условный ток, протекающий в ветви под действием только одного источника. Направление частичных токов в ветвях вполне определенно и зависит от полярности источника.

5. Искомые токи каждой ветви рассматриваемой схемы определяются как алгебраическая сумма частичных токов для этой ветви. При этом частичный ток, совпадающий по направлению с искомым, считается положительным, а несовпадающий - отрицательным. Если алгебраическая сумма имеет положительный знак, то направление искомого тока в ветви совпадает с произвольно выбранным, если отрицательный, то направление тока противоположно выбранному.

Пример 2.1. Метод наложения токов

Определить токи во всех ветвях цепи, схема которой приведена на рисунке 22, если задано Е 1 = 40 В; Е 2 = 30 В; R 01 = R 02 = 0,4 Ом; R 1 = 30 Ом; R 2 =R 3 = 10 Ом; R 4 =R 5 = 3,6 Ом.

Рисунок 22 Рисунок 23

Рисунок 24

Устанавливается, что количество ветвей и соответственно различных токов в цепи (рисунок 22) равно пяти, и произвольно выбирается направление этих токов.

Количество расчетных схем две, так как в цепи два источника.

Вычисляются частичные токи, созданные в ветвях первым источником (I’) Для этого изображается та же цепь, только вместо Е 2 - его внутреннее сопротивление (R 02). Направление частичных токов в ветвях указаны в схеме (рисунок 23).

Вычисление этих токов производится методом свертывания

Тогда первые частичные токи в цепи (рисунок 23), имеют следующие значения:

Вычисляются частичные токи, созданные вторым источником (I’’). Для этого изображается исходная цепь, заменив в ней первый источник (Е 1) его внутренним сопротивлением (R 01). Направления этих частичных токов в ветвях указаны на схеме (рисунок 24).

Вычислим эти токи, пользуясь методом свертывания.

Вторые частичные токи в цепи (рисунок 24) имеют следующие значения:

Следовательно, искомые токи в рассматриваемой цепи (рисунок 22) определяются алгебраической суммой частичных токов (см. рисунок 22, 23 и 24) и имеют следующие значения:

Ток I АБ имеет знак «-», следовательно, его направление противоположно произвольно выбранному, т.е. I АБ направлен из точки А в точку Б.

2.2. Метод узлового напряжения

Расчет сложных разветвленных электрических цепей с несколькими источниками можно осуществить методом узлового напряжения, если в этой цепи имеются только два узла. Напряжение между этими узлами и называется узловым. U АБ - узловое напряжение схемы (рисунок 25).

Величина узлового напряжения определяется отношением алгебраическ

electriciastudio.ru

Анализ сложных электрических цепей постоянного тока.

Метод законов Кирхгофа

Сложной электрической цепью принято называть разветвленную цепь, содержащую несколько источников, расположенных в разных ветвях. Пример сложной цепи постоянного тока приведен на рис. 22.

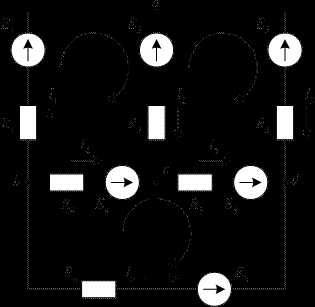
Рис. 22. Пример сложной цепи постоянного тока

Истинные направления токов в ветвях сложной электрической цепи, как правило, неизвестны. Поэтому анализ сложной цепи начинается с выбора так называемых положительных направлений токов в ветвях схемы. На схеме положительные направления токов в ветвях обозначают стрелками с символами тока I. Пример выбора условных положительных направлений токов в ветвях схемы показан на рис. 22.

Если в результате анализа цепи получается, что ток в ветви положителен, то истинное направление тока будет совпадать с выбранным положительным направлением тока. Если в результате расчета окажется, что ток в ветви отрицателен, то истинное направление тока противоположно выбранному положительному направлению тока. Т.е. в ходе анализа электрической цепи токи в ветвях рассматриваются как алгебраические величины.

Наиболее общий подход к анализу сложных электрических цепей основан на использовании законов Кирхгофа. С помощью законов Кирхгофа составляется система линейных алгебраических уравнений относительно неизвестных токов. Число неизвестных токов равно числу ветвей схемы. Обозначим это число через m. Следовательно, с помощью законов Кирхгофа необходимо составить систему из m уравнений с m неизвестными токами.

При составлении уравнений по законам Кирхгофа необходимо придерживаться следующего правила. Если в схеме n узлов, то с помощью первого закона Кирхгофа составляется (n – 1) независимое уравнение. (Уравнение для последнего узла будет зависимым). Оставшиеся [m–(n –1)] уравнения составляются с помощью второго закона Кирхгофа для так называемых независимых контуров.

Независимый контур – это такой контур, при обходе которого появляется хотя бы одна новая ветвь по сравнению с ранее рассмотренными контурами.

В разветвленной цепи число независимых контуров всегда меньше общего количества контуров. Поэтому при выборе независимых контуров имеется определенная свобода выбора. Однако число независимых контуров в схеме всегда регламентировано. Схема рис. 22, например, содержит

[m – (n – 1)] = [6 – (4 – 1)] = 3

независимых контура.

В результате составления (n – 1) уравнения по первому закону Кирхгофа и [m – (n – 1)] уравнения по второму закону Кирхгофа образуется система из m уравнений относительно неизвестных токов ветвей. Решение этой системы позволяет определить токи ветвей.

Схема рис. 22 состоит из шести ветвей. Выбранные положительные направления токов в ветвях указаны на схеме стрелками с символами тока I1, I2, I3, I4, I5, I6. Для расчета токов в ветвях этой схемы с помощью законов Кирхгофа необходимо составить систему из шести уравнений.

Схема содержит четыре узла (n = 4). По первому закону Кирхгофа необходимо составить три уравнения. Условимся при составлении уравнений по первому закону Кирхгофа токи, выходящие из рассматриваемого узла, брать со знаком «плюс», а входящие в узел, – со знаком «минус».

В узел а входит ток I1, а выходят токи I2 и I3. Тогда для узла a уравнение первого закона Кирхгофа будет иметь вид

Из узла b выходят токи I1, I4, I6. Уравнение первого закона Кирхгофа для узла b имеет вид

В узел c входят токи I2 и I4, а выходит ток I5. Поэтому для узла c можно записать

Уравнения первого закона Кирхгофа, составленные для узлов а, b, c, включают в себя токи всех шести ветвей рассматриваемой схемы. Суммируя уравнения, составленные по первому закону Кирхгофа для узлов а, b, c, получаем следующее уравнение:

Это уравнение отличается от уравнения первого закона Кирхгофа для узла d только знаками, а именно:

То есть, уравнение первого закона Кирхгофа для узла d зависимое.

По второму закону Кирхгофа для рассматриваемой схемы необходимо составить три уравнения для трех независимых контуров. В качестве независимых контуров можно рассматривать, например, левый контур, составленный из первой, второй и четвертой ветвей, правый контур, составленный из второй, третьей и пятой ветвей, и нижний контур, составленный из четвертой, пятой и шестой ветвей.

При составлении уравнения второго закона Кирхгофа для каждого независимого контура необходимо придерживаться следующего правила. Если выбранное положительное направление тока в ветви совпадает с направлением обхода контура, то падение напряжения на соответствующем элементе R в левой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если выбранное положительное направление тока в ветви противоположно направлению обхода контура, то падение напряжения на соответствующем элементе R в левой части уравнения второго закона Кирхгофа берется со знаком «минус». Если направление действия источника ЭДС, указанное на схеме стрелкой, совпадает с направлением обхода контура, то соответствующая ЭДС Е в правой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если направление действия источника ЭДС, указанное на схеме стрелкой, противоположно направлению обхода контура, то соответствующая ЭДС Е в правой части уравнения второго закона Кирхгофа берется со знаком «минус».

Направления обхода независимых контуров на схеме рис. 22 выберем по часовой стрелке. Эти направления обхода указаны на схеме стрелками, замыкающимися вдоль каждого из независимых контуров.

Рассмотрим поочередно каждый из независимых контуров. В левом контуре токи I1 и I2 совпадают с направлением обхода контура. Падения напряжений R1I1, R2I2 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «плюс».Ток I4 имеет направление, противоположное направлению обхода левого контура. Падение напряжения R4I4 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «минус». Направление действия источника ЭДС Е1 совпадает с направлением обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е1 необходимо взять со знаком «плюс». Направления действия источников ЭДС Е2 и Е4 противоположны направлению обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е2 и Е4 необходимо взять со знаком «минус». Таким образом, для левого независимого контура справедливо следующее уравнение второго закона Кирхгофа:

Аналогично для правого и нижнего независимых контуров схемы рис. 22 получаем следующие уравнения второго закона Кирхгофа:

При объединении уравнений, составленных по первому и второму законам Кирхгофа для схемы рис. 22, получается следующая система линейных алгебраических уравнений:

Решение этой системы позволяет найти токи I1, I2, I3, I4, I5, I6. По известным токам можно найти падения напряжений на элементах схемы, мощности и так далее.

Изложенный метод анализа сложных электрических цепей носит название метода законов Кирхгофа. Метод законов Кирхгофа – это наиболее общий подход к анализу электрических цепей.

Для анализа сложных электрических цепей могут использоваться и другие методы, например, метод контурных токов, метод узловых потенциалов, метод наложения, метод эквивалентного генератора. Эти методы строятся на основе законов Кирхгофа, закона Ома, принципа наложения. Поэтому они справедливы для линейных цепей. Исключение составляет метод эквивалентного генератора, который предполагает, что ветвь с искомым током может быть и нелинейной. Многообразие методов анализа сложных электрических цепей позволяет в каждом конкретном случае выбрать тот метод, который дает наиболее простой алгоритм расчета.

В частности, метод контурных токов и метод узловых потенциалов подобно методу законов Кирхгофа сводятся к решению систем линейных алгебраических уравнений. Однако количество искомых величин, а, следовательно, и порядок систем линейных алгебраических уравнений в этих методах меньше, чем в методе законов Кирхгофа.

Для решения систем линейных алгебраических уравнений используются известные математические методы. При малом количестве уравнений в системе можно использовать метод определителей (правило Крамера). При достаточно большом количестве уравнений в системе целесообразно использовать метод последовательного исключения неизвестных Гаусса с выбором главного элемента или итерационные методы решения систем линейных алгебраических уравнений, например, метод Зейделя.

Проверку правильности полученного решения можно выполнить путем подстановки найденных значений токов ветвей в систему уравнений, составленную по законам Кирхгофа, или путем составления баланса мощностей (смотри ниже).

Рассмотрим поочередно основные методы анализа электрических цепей. Но предварительно рассмотрим общий вопрос, касающийся геометрической структуры электрических цепей.

 

Похожие статьи:

poznayka.org

Сложные электрические цепи постоянного тока

Метод законов Кирхгофа

Сложной электрической цепью принято называть разветвленную цепь, содержащую несколько источников, расположенных в разных ветвях. Пример сложной цепи постоянного тока приведен на рис. 22.

Рис. 22. Пример сложной цепи постоянного тока

Истинные направления токов в ветвях сложной электрической цепи, как правило, неизвестны. Поэтому анализ сложной цепи начинается с выбора так называемых положительных направлений токов в ветвях схемы. На схеме положительные направления токов в ветвях обозначают стрелками с символами тока I . Пример выбора условных положительных направлений токов в ветвях схемы показан на рис. 22.

Если в результате анализа цепи получается, что ток в ветви положителен, то истинное направление тока будет совпадать с выбранным положительным направлением тока. Если в результате расчета окажется, что ток в ветви отрицателен, то истинное направление тока противоположно выбранному положительному направлению тока. Т.е. в ходе анализа электрической цепи токи в ветвях рассматриваются как алгебраические величины.

Наиболее общий подход к анализу сложных электрических цепей основан на использовании законов Кирхгофа. С помощью законов Кирхгофа составляется система линейных алгебраических уравнений относительно неизвестных токов. Число неизвестных токов равно числу ветвей схемы. Обозначим это число через m . Следовательно, с помощью законов Кирхгофа необходимо составить систему из m уравнений с m неизвестными токами.

При составлении уравнений по законам Кирхгофа необходимо придерживаться следующего правила. Если в схеме n узлов, то с помощью первого закона Кирхгофа составляется (n – 1) независимое уравнение. (Уравнение для последнего узла будет зависимым). Оставшиеся [m –(n –1)] уравнения составляются с помощью второго закона Кирхгофа для так называемых независимых контуров.

Независимый контур – это такой контур, при обходе которого появляется хотя бы одна новая ветвь по сравнению с ранее рассмотренными контурами.

В разветвленной цепи число независимых контуров всегда меньше общего количества контуров. Поэтому при выборе независимых контуров имеется определенная свобода выбора. Однако число независимых контуров в схеме всегда регламентировано. Схема рис. 22, например, содержит

[m – (n – 1)] = = 3

независимых контура.

В результате составления (n – 1) уравнения по первому закону Кирхгофа и [m – (n – 1)] уравнения по второму закону Кирхгофа образуется система из m уравнений относительно неизвестных токов ветвей. Решение этой системы позволяет определить токи ветвей.

Схема рис. 22 состоит из шести ветвей. Выбранные положительные направления токов в ветвях указаны на схеме стрелками с символами тока I 1 , I 2 , I 3 , I 4 , I 5 , I 6 . Для расчета токов в ветвях этой схемы с помощью законов Кирхгофа необходимо составить систему из шести уравнений.

Схема содержит четыре узла (n = 4). По первому закону Кирхгофа необходимо составить три уравнения. Условимся при составлении уравнений по первому закону Кирхгофа токи, выходящие из рассматриваемого узла, брать со знаком «плюс», а входящие в узел, – со знаком «минус».

В узел а входит ток I 1 , а выходят токи I 2 и I 3 . Тогда для узла a уравнение первого закона Кирхгофа будет иметь вид

Из узла b выходят токи I 1 , I 4 , I 6 . Уравнение первого закона Кирхгофа для узла b имеет вид

В узел c входят токи I 2 и I 4 , а выходит ток I 5 . Поэтому для узла c можно записать

Уравнения первого закона Кирхгофа, составленные для узлов а , b , c , включают в себя токи всех шести ветвей рассматриваемой схемы. Суммируя уравнения, составленные по первому закону Кирхгофа для узлов а , b , c , получаем следующее уравнение:

Это уравнение отличается от уравнения первого закона Кирхгофа для узла d только знаками, а именно:

То есть, уравнение первого закона Кирхгофа для узла d зависимое.

По второму закону Кирхгофа для рассматриваемой схемы необходимо составить три уравнения для трех независимых контуров. В качестве независимых контуров можно рассматривать, например, левый контур, составленный из первой, второй и четвертой ветвей, правый контур, составленный из второй, третьей и пятой ветвей, и нижний контур, составленный из четвертой, пятой и шестой ветвей.

При составлении уравнения второго закона Кирхгофа для каждого независимого контура необходимо придерживаться следующего правила. Если выбранное положительное направление тока в ветви совпадает с направлением обхода контура, то падение напряжения на соответствующем элементе R в левой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если выбранное положительное направление тока в ветви противоположно направлению обхода контура, то падение напряжения на соответствующем элементе R в левой части уравнения второго закона Кирхгофа берется со знаком «минус». Если направление действия источника ЭДС, указанное на схеме стрелкой, совпадает с направлением обхода контура, то соответствующая ЭДС Е в правой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если направление действия источника ЭДС, указанное на схеме стрелкой, противоположно направлению обхода контура, то соответствующая ЭДС Е в правой части уравнения второго закона Кирхгофа берется со знаком «минус».

Направления обхода независимых контуров на схеме рис. 22 выберем по часовой стрелке. Эти направления обхода указаны на схеме стрелками, замыкающимися вдоль каждого из независимых контуров.

Рассмотрим поочередно каждый из независимых контуров. В левом контуре токи I 1 и I 2 совпадают с направлением обхода контура. Падения напряжений R 1 I 1 , R 2 I 2 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «плюс».Ток I 4 имеет направление, противоположное направлению обхода левого контура. Падение напряжения R 4 I 4 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «минус». Направление действия источника ЭДС Е 1 совпадает с направлением обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е 1 необходимо взять со знаком «плюс». Направления действия источников ЭДС Е 2 и Е 4 противоположны направлению обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е 2 и Е 4 необходимо взять со знаком «минус». Таким образом, для левого независимого контура справедливо следующее уравнение второго закона Кирхгофа:

Аналогично для правого и нижнего независимых контуров схемы рис. 22 получаем следующие уравнения второго закона Кирхгофа:

При объединении уравнений, составленных по первому и второму законам Кирхгофа для схемы рис. 22, получается следующая система линейных алгебраических уравнений:

Решение этой системы позволяет найти токи I 1 , I 2 , I 3 , I 4 , I 5 , I 6 . По известным токам можно найти падения напряжений на элементах схемы, мощности и так далее.

Изложенный метод анализа сложных электрических цепей носит название метода законов Кирхгофа. Метод законов Кирхгофа – это наиболее общий подход к анализу электрических цепей.

Для анализа сложных электрических цепей могут использоваться и другие методы, например, метод контурных токов, метод узловых потенциалов, метод наложения, метод эквивалентного генератора. Эти методы строятся на основе законов Кирхгофа, закона Ома, принципа наложения. Поэтому они справедливы для линейных цепей. Исключение составляет метод эквивалентного генератора, который предполагает, что ветвь с искомым током может быть и нелинейной. Многообразие методов анализа сложных электрических цепей позволяет в каждом конкретном случае выбрать тот метод, который дает наиболее простой алгоритм расчета.

В частности, метод контурных токов и

top-electrician.ru

---

• 
  Какой компрессор нужен для покраски авто
• 
  24 вольта источник питания
• 
  Система управления замкнутая
• 
  Сопротивление проверить
• 
  Подсветка аквариумная
• 
  4G антенны мимо
• 
  Нет отопления куда жаловаться
• 
  Цена деления шкалы весов 10 г с какой погрешностью взвешивают ими продукты
• 
  Что лучше латунь или никель
• 
  В лампах энергосберегающих есть ртуть
• 
  Муп дюртюлинские электрические и тепловые сети