Электронные цепи: правила расчета для определения силы тока

Электрическая цепь. Чем прозвонить основные элементы

   В электротехнике рассматривается устройство и принцип действия основных электротехнических устройств, используемых в быту и промышленности. Чтобы электротехническое устройство работало, должна быть создана электрическая цепь, задача которой передать электрическую энергию этому устройству и обеспечить ему требуемый режим работы.

   Электрическая цепь, схема эксперимента

   Электрическая цепь — это совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении. Для анализа и расчета электрическая цепь графически представляется в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения.

   Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы:

1) Источники электрической энергии (питания).

   Общим свойством всех источников питания является преобразование какого-либо вида энергии в электрическую. Источники, в которых происходит преобразование неэлектрической энергии в электрическую, называются первичными источниками. Вторичные источники – это такие источники, у которых и на входе, и на выходе – электрическая энергия (например, выпрямительные устройства).

2) Потребители электрической энергии.

   Общим свойством всех потребителей является преобразование электроэнергии в другие виды энергии (например, нагревательный прибор). Иногда потребители называют нагрузкой.

3) Вспомогательные элементы цепи: соединительные провода, коммутационная аппаратура, аппаратура защиты, измерительные приборы и т.д., без которых реальная цепь не работает.

   Когда электрический прибор внезапно перестает работать, то у его владельца появляется желание самостоятельно разобраться с неисправностью и устранить ее. Для этого необходимо убедиться в целостности электрической схемы, качестве подключения соединительных проводов, исправности переключателей, коммутационных аппаратов и других элементов.  Такая проверка заключается в измерении электрического сопротивления цепи. На языке электриков ее называют «прозвонкой».

Электрическая цепь, как происходит замер сопротивления

   Проверка сопротивления любой электрической схемы основана на действии закона Ома для участка цепи, через который пропускают ток и замеряют его величину. На вход проверяемой схемы подают стабилизированное напряжение. Обычно для этого используют химические источники тока:

• гальванические батарейки
• аккумуляторы

   Электрическая цепь, как происходит замер сопротивления в электрической цепи

   Реже применяют выпрямленное напряжение от сети переменного тока. Если схема целая и в ней отсутствуют обрывы, то ток преодолеет полное сопротивление цепи, а его величина выразится соотношением I=U/R

Самодельные приборы-прозвонки

   Простейшие устройства, которыми пользуются электрики для проверки сопротивления, называют «прозвонками». Самую простую из них можно сделать самостоятельно, исходя из приведенного ниже описания.

   К одному концу батарейки припаивают цоколь лампочки от карманного фонаря, а к другому — гибкий электрический провод в изоляции с зажимом-крокодилом на конце. На второй контакт лампочки крепится медная проволока 2,5 квадрата, выполняющая роль щупа. Если посадить крокодил на щуп, то цепь прозвонки замкнется и через нее потечет ток. Его величина достаточна для разогрева нити накала и свечения лампочки. Яркость света зависит от:

• состояния батарейки (при большом разряде напряжение снижается)
• величины сопротивления участка цепи

   Если между щупом и крокодилом поместить резистор, то величина его сопротивления скажется уменьшением свечения лампочки. Например, номинальный ток нити накала величиной 100 мА создается при прямом подключении к новой батарейке. Когда при проверке резистора ток снизится до 80 мА, то свечение будет хорошо заметно. При значительном же увеличении сопротивления или разрыве цепи лампочка потухнет.

   Таким простым методом электрики проверяют целостность проводов и других участков схемы с величиной сопротивления до нескольких десятков Ом. При этих замерах в проверяемой цепи не должно присутствовать напряжение от посторонних источников, которыми могут быть:

• заряженные конденсаторы
• наводки от соседних электротехнических устройств
• параллельно подключенные цепочки со своим питанием

 

Внимание! Принцип отсутствия напряжения от постороннего источника на проверяемой схеме должен выполняться при замере сопротивления любым прибором. Иначе не только проявится увеличенная погрешность, но может выйти из строя измерительный прибор.

   Если электрики по ошибке подключают такие прозвонки к фазному и нулевому проводникам в действующей электропроводке, то нить накала лампочки от проходящего тока мгновенно получает тепловой удар, от которого стеклянный баллон взрывается и разлетается мелкими осколками.  Аналогичные ошибки при замерах омметрами и мультиметрами приводят к перегоранию токопроводящих пружин измерительных головок или компонентов схем у новых электронных моделей. Только дорогие приборы ведущих производителей снабжаются защитой от коротких замыканий, возникающих при подобных ситуациях. Но стоит ли их проверять таким способом? Основной недостаток самодельных прозвонок такого типа — это отсутствие возможности определения высокоомных сопротивлений. Поэтому их используют только при проверках токовых низкоомных цепей.

Многофункциональные индикаторы напряжения-отвертки

   Такие устройства сейчас массово выпускаются промышленностью. Они позволяют выполнять 5 основных функций при работе с электричеством. Одна из них — замер сопротивления, который осуществляется подключением контролируемого участка через цепь, созданную между пальцами человека.

   В конструкции подобных многофункциональных приборов для замера сопротивления используются:

• элементы питания с общим напряжением 3 вольта
• биполярный транзистор, усиливающий сигнал тока индикации
• светодиод, свечение которого свидетельствует о прохождении тока через проверяемый участок цепи
• наконечник отвертки, служащий контактной площадкой

   Маломощные источники напряжения этих приборов способны выдать в схему только токи низких значений, которые при усилении транзистором достигают всего десятка миллиампер.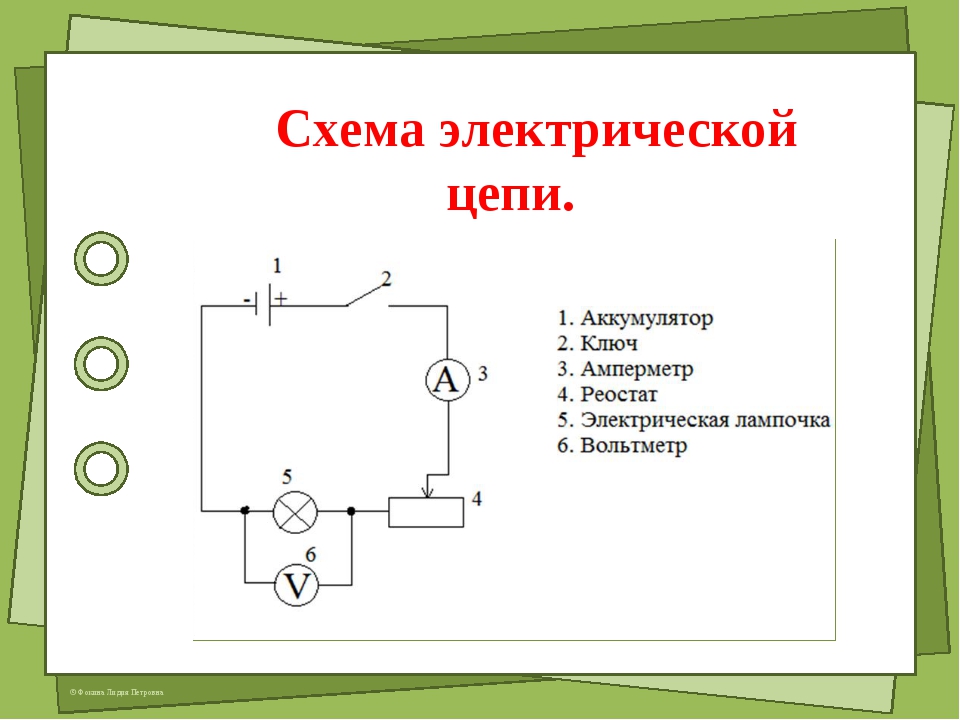 Этого вполне достаточно для свечения светодиода. Однако, проверять ими можно целостность предохранителей, нитей накала лампочек и подобных простых устройств. При измерениях в сложных схемах многофункциональные индикаторы работают некорректно потому, что способны прозвонить высокоомные участки, созданные заниженным сопротивлением окружающей среды. Этот их основной недостаток часто вводит в заблуждение электриков.

Омметры

   Их массовое производство в СССР началось с 1940 года. В конструкцию прибора входят:

• эбонитовый корпус с клеммными выводами для подключения проводов к измеряемому сопротивлению
• батарейка на 4,5 вольта, размещаемая в отсеке питания с контактными пластинами
• амперметр, проградуированный в Омах
• регулировочное сопротивление для калибровки напряжения, подаваемого в схему

   На корпусе прибора около выходных контактов знаками «+» и «—» промаркирована полярность подаваемого на схему напряжения.  Такой омметр измеряет активное сопротивление от 20 до 2000 Ом. На практике электрикам приходится работать не только в этом диапазоне, а с более высокими и низкими значениями. С этой целью выпускают:

• мегаомметры различной мощности, выдающие повышенное напряжение в проверяемую схему
• измерительные мосты, позволяющие делать точные замеры малоомных сопротивлений

Мультиметры, тестеры

   Для удобства выполнения электрических замеров на базе омметра работают комбинированные приборы, позволяющие оценивать величины сопротивлений на шкалах:

• Омов
• килоОмов
• мегаОмов

   Они имеют одну точную измерительную головку, которая с помощью шунтов или добавочных сопротивлений, подключаемых системой различных режимных переключателей, может работать в качестве:

• омметра
• амперметра
• вольтметра

   Для каждого режима на общей шкале нанесена собственная цифровая градуировка в соответствующих единицах.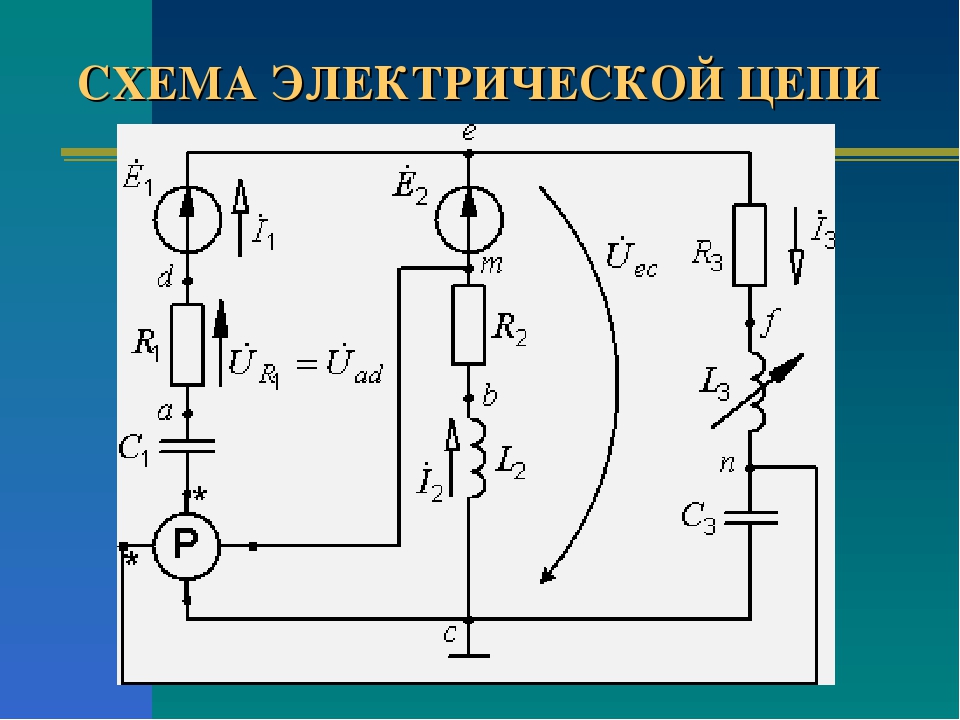 Три объединенных функции измерения сопротивления, тока и напряжения послужили поводом называть такие приборы:

• мультиметром (образовано от слов «много» и «мерить»)
• авометром (сокращение от «ампер», «вольт», «ом», «измерение»)
• тестером (обозначает возможность проведения «тестов»)

   Современные приборы работают как на основе обработки аналоговых величин, так и с применением цифровых технологий. Они у большинства моделей снабжены дисплеем, на который сразу выводится значение измеряемого параметра. Это удобно потому, что:

• облегчается снятие показании
• не требуется разбираться с градуировкой шкалы
• отпадает необходимость заниматься дополнительными математическими вычислениями

   Однако, принцип подачи напряжения на измеряемый участок цепи и замер величины тока, протекающего через сопротивление, остался прежним во всех устройствах. Электрик, хорошо понимающий, как работает закон Ома, всегда разберется с назначением переключателей и способами отображения информации на любой приборе, выполнит правильно замер сопротивления.

Электрическая цепь, как проверить исправность прибора

   Основное правило точного определения сопротивления — это грамотная подготовка измерительного оборудования к работе и использование его по назначению.

   Электрическая цепь, проверка целостности электрической цепи

   На производственных предприятиях все электроизмерительные приборы, включая омметры, должны своевременно проверяться на:

• целостность изоляции и иметь штамп испытательной лаборатории, подтверждающий разрешение на эксплуатацию в действующих электроустановках
• правильность работы в заявленном классе точности и иметь клеймо поверителя

   У бытовых приборов этими вопросами должен заниматься владелец, сдавая свой тестер в соответствующие лаборатории.  Перед каждым замером сопротивления необходимо:

• выставить стрелочный прибор в горизонтальной плоскости и зафиксировать его
• проверить предварительную установку стрелки на ноль
• выполнить градуировку источника напряжения
• перевести все переключатели прибора в соответствующий режим измерения
• оценить исправность подключения соединительных проводов и их целостность, для чего замкнуть концы и проверить реакцию стрелки или цифрового отображения сопротивления на дисплее

   И всегда помните о проверке отсутствия напряжения на тестируемом участке до начала измерений.

Электрическая цепь, как вызвонить основные элементы электрической схемы

   При контроле величины сопротивления любого участка цепи проверяемый компонент подключается на выходные клеммы измерительного прибора, переведенного в режим омметра.

Провода и кабели

   Исправная металлическая жила обладает сопротивлением, близким к нулю, а изоляционный слой на ней — стремящимся к бесконечности. Это правило взято за основу проверки проводов и кабелей. Внутри электропроводки встречаются кабельные линии и провода, соединенные различными способами. До начала замера каждый кабель и провод необходимо разъединить с двух сторон, иначе могут возникнуть ошибки из-за дополнительно подключенных цепочек. Если необходимо оценить сборку электрической схемы, то проверяют:

• целостность жил
• отсутствие посторонних цепочек, которые могут возникнуть при нарушениях изоляции

   В первом случае работают омметром, а во втором — мегаомметром определенного напряжения и мощности. Когда на одну жилу подается напряжение с омметра, то измерительная головка на исправном проводе покажет «0» Ом. Действующие кабели, которые подлежат прозвонке, могут быть проложены в земле и протянуты на несколько сотен метров. Такое удаление противоположных концов осложняет замер. Выход из создавшейся ситуации состоит в удлинении измерительного провода за счет:

• использования заранее проверенной и промаркированной жилы
• подключения одного конца омметра и противоположной стороны провода к контурам заземления для создания пути тока через землю

   При поиске повреждений изоляции, приведшей к коротким замыканиям в сети лучше работать мегаомметром и последовательно замерять сопротивление каждой жилы относительно всех остальных и землей.  У кабелей разного назначения нормируемое сопротивление изоляции может колебаться от 0,5 до нескольких мегаом. При выявлении мест нарушения изоляции провода бракуют и выводят из эксплуатации.

Предохранитель

   Поскольку этот элемент представляет собой короткий отрезок проволоки, помещенный в диэлектрический корпус, то его исправное состояние будет соответствовать показанию 0 на шкале омметра, а оборванное — ∞.

Резистор

   Его изготавливают для работы в схемах с различными значениями электрического сопротивления, которое может быть от долей Ома до нескольких мегаом. Поэтому при проверках резисторов пользуются всеми режимами омметра.

Диод

   Основное назначение этого полупроводникового элемента состоит в пропускании тока в одну сторону и блокировании в другую. Поскольку омметр при подключении к схеме выдает ток определенной полярности, то у исправного диода при прямом подключении прибора будет 0 Ом, а при обратном — ∞. Если при прямом и обратном включении омметр показывает 0 или ∞, то диод пробит или перегорел.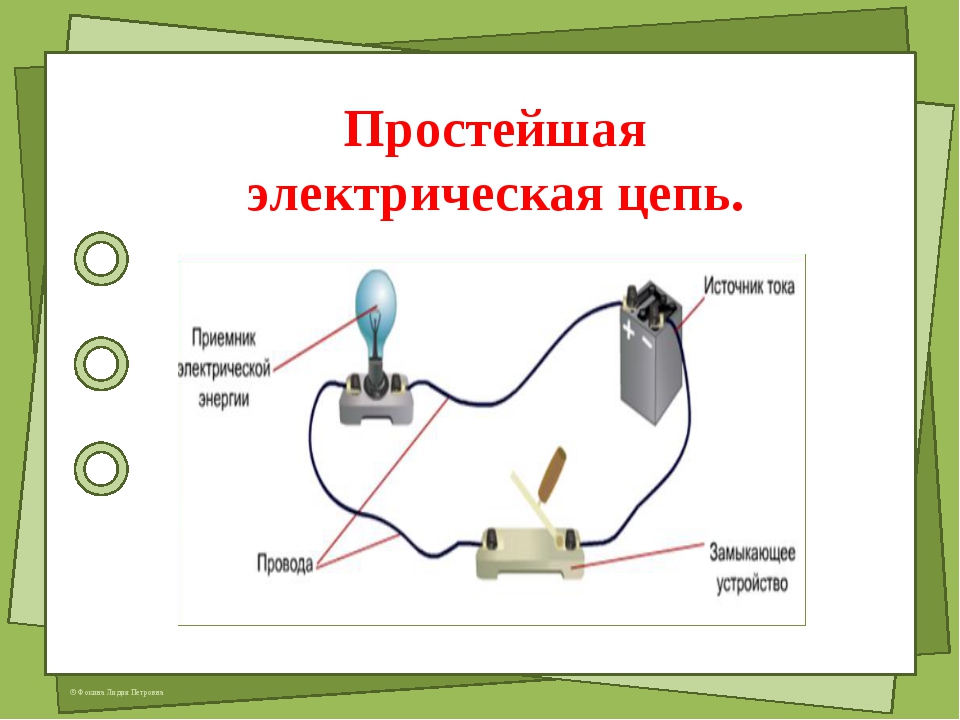 Его необходимо менять.

Светодиод

   В практической электротехнике встречаются как единичные, так и комплексные светодиодные конструкции. Они работают по принципу обычного диода, дополнительно излучающего свет при прохождении тока через него. Когда ток заблокирован, то свечения не будет. На первый взгляд технология проверки светодиода ничем не отличается от предыдущего способа. Но здесь есть особенность: ток номинального свечения большинства светодиодов составляет порядка 10 мА. Если омметр выдает значительно меньшую величину, то свечения просто не будет видно. Это чаще всего присуще современным экономным и дорогим мультиметрам. Значительно превышать ток через светодиод самодельной прозвонкой тоже не рекомендуется. Полупроводниковый слой может не выдержать увеличенный тепловой режим. Поэтому при таких проверках необходимо знать технические возможности измерительного прибора и ограничивать время испытаний. Лучше всего для проверки светодиода использовать регулируемый источник с возможностью плавного увеличения тока до 10 мА.

Катушка индуктивности, трансформатор, электродвигатель, дроссель

   Эти устройства выполняют намоткой изолированного провода на катушку, которая размещается внутри магнитопровода. Каждый виток обмотки при прохождении тока создает вокруг себя электромагнитное поле, которое складывается с полями остальных витков. Если изоляция проводов между витками будет нарушена, то возникает электрический контакт (межвитковое замыкание), которое резко уменьшает суммарную индуктивность. При прозвонке таких обмоток их активное сопротивление меняется так незначительно, что выявить подобную неисправность замером омметром невозможно. Межвитковые замыкания определяют:

• включением под нагрузку в цепях переменного тока
• снятием вольтамперной характеристики

   Методом омметра можно только определить обрыв провода или нарушение контактного соединения в обмотке.

ТЭН

   Теплонагревательные элементы работают в электрочайниках, электрических котлах отопления, обогревателях.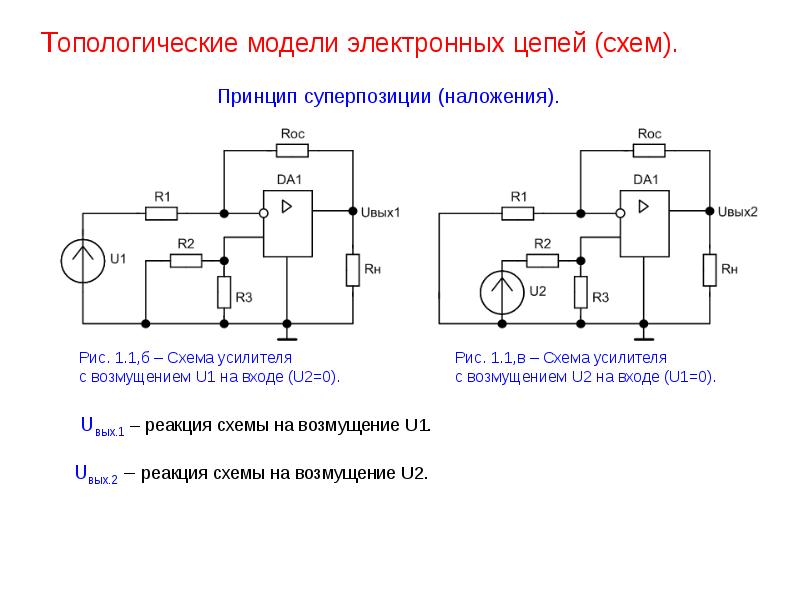 Они изготовлены из нихромовой проволоки, помещенной в металлический корпус и подсоединенной к контактным ножкам. При замере исправного ТЭНа показание сопротивления на омметре будет иметь небольшое значение, которое может составлять от нескольких единиц до десятков Ом (зависит от конструкции). Обрыв нити проявится индикацией ∞. У мощных обогревателей используют несколько ТЭНов, которые подключают параллельно, а клеммы располагают рядом. В таких случаях надо внимательно разобраться с принадлежностью клеммных выводов. При прозвонке ТЭНа надо дополнительно замерять мощным мегаомметром сопротивление изоляции между нихромовой нитью и корпусом. Если оно пробито, то обогреватель надо браковать, иначе при его работе будет присутствовать потенциал напряжения на корпусе.

Лампа накаливания

   Ее нить тоже состоит из нихромовой проволоки, которая расположена между центральным и боковым контактами и обладает в холодном состоянии сопротивлением от 3 до 200 Ом. Обрыв же часто можно увидеть визуально.

Люминесцентная лампа

   Стеклянная герметичная трубчатая колба заполнена инертным газом, а по обоим торцам расположены по 2 контактных вывода, подключенные к нитям накала. Их надо прозвонить с каждой стороны. Если одна из них оборвана, то лампа неисправна и светить не будет.

Энергосберегающие и светодиодные лампы

   Компактные люминесцентные лампы имеют такое же устройство, как и обычные, только у них электронная схема запуска вмонтирована внутри корпуса цоколя. Подключиться к колбе для выполнения замера без демонтажа конструкции не получится. Поэтому такие лампы, как и светодиодные, проверяют подачей напряжения, а разборкой схемы занимаются только при ремонте.

Будем рады, если подпишетесь на наш Блог!

[wysija_form id=»1″]

Механическая модель электрических цепей / Хабр

Здесь даже можно будет замоделировать трансформатор и операционный усилитель, но все по порядку.

Электрические цепи можно описать следующими уравнениями:

• для катушки
• для конденсатора
• для резистора

(Напряжение падения на катушке равно минус ЭДС)

В механике есть следующие уравнения:

• для массивного тела
• для пружины
• для вязкого трения

(Внешняя сила, действующая на пружину равна минус силе состороны пружины, если в точке приложение силы нет массы)

Как вы наверно догадались, электрические и механические величины можно сопоставить двумя способами:

электро	мех. 1	мех.2
U	F	v
I	v	F
Ф	p	x
Q	x	p
L	m	1/k
C	1/k	m
R

Обычно, когда пытаются провести электро-механическую аналогию, используют первый способ, хотя кое-где можно встретить и второй, им-то мы и воспользуемся.

Но мы будем моделировать во вращательной механике, где каждую поступательную величину мы заменим соответствующим моментом или угловой величиной:

Но для простоты обозначать будем как в поступательной механике:
Так как в электричестве есть понятия потенциал (в точке) и напряжение (между точками), потенциал мы будем моделировать скоростью вращения вала, а напряжение — разностью скоростей двух валов. Ее можно получить при помощи дифференциала (как в автомобиле), у которого один из боковых валов инвертирован:

Выше были изложены пространные теоретические рассуждения, почему мы будем делать именно так. Дальше будет непосредственно описано, как мы это будем делать.

Перейдем к моделированию электрических компонентов:

Источник напряжения

Можно моделировать как вал, вращающийся с постоянной скоростью (который ну ни как невозможно остановить), и подключенный к разностному входу дифференциала. С двух других его концов можно снимать напряжение (они крутятся друг относительно друга с постоянной скоростью).

Источник тока

То же самое, но только используется вал, выдающий постоянный крутящий момент. Такой вал без нагрузки будет разгонятся до бесконечно большой скорости вращения.

Резистор я бы замоделировал так:

От дифференциала идут лопасти и опускаются в стакан с жидкостью.

Чем более вязкая жидкость — тем больше проводимость, тем меньше сопротивление. Между несоединенными валами бесконечное сопротивление. А у резистора, у которого заклинило лопасти — сопротивление нулевое. Можно пофантазировать о напряжении пробоя, и трении между валом и его держателями, но по моему это сходство как-то не очень.

Конденсатор — маховик, присоединенный к дифференциалу

Так же как и в идеальном конденсаторе нет тока утечки, также и в его модели совсем нет трения. Так же как сила тока заряжает конденсатор, так же момент сил между валами разгоняет маховик. В таком конденсаторе на одной пластине всегда заряд , а на другой – .

Также емкостью может обладать одиночная сфера (или проводник другой формы). Если он заряжен зарядом Q, то на его поверхности будет потенциал . Их отношение и будет емкостью этого проводника. Это можно замоделировать маховиком без дифференциала.

Катушка — пружинкой, присоединенной к дифференциалу

(«Заземлением» будем обозначать неподвижные части конструкции)

Где v — разность скоростей двух валов, а x — их относительное смещение.

Если считать, что жесткость пружинки достаточно велика, а момент сил, передаваемый из одного вала в другой, достаточно мал, то катушку можно замоделировать так:

Если пофантазировать, то можно провести аналогию между петлей гистерезиса ферромагнетиков и неупругой деформацией пружинки. Правда в ферромагнетиках нет аналога усталости металла.

А также, модель катушки можно использовать как модель амперметра, если присоединить стрелку к выходу дифференциала.

Ее направление отклонения от положения равновесия будет свидетельствовать о том, в какую сторону вал №1 толкает вал №2. А ее величина — о моменте сил, с которым один вал воздействует на другой, т.е. о силе тока через моделируемую катушку.

И из казалось бы самого простого закона получается, что минус [ЭДС катушки] = [напряжению падения на ней] = разности скоростей валов = производной по времени относительного смещения двух валов. В катушке, которая ни к чему не подключена всегда ток =0, а в ее модели пружина не деформирована. Но если в катушке есть ток, а потом ее накоротко замкнуть (сверхпроводником), то ток в ней так и останется, а ее модель так и будет оставаться в деформированном состоянии.

В принципе в катушке можно обойтись без дифференциала, но в трансформаторе, который содержит в себе пару катушек, так уже не получится.

Рассмотрим парочку переходных процессов.

Источник напряжения, ключ, резистор, (изначально незаряженный) конденсатор.

Изначально конденсатор не заряжен.

Включаем ключ (после этого ), и на резисторе оказывается напряжение питания, через него начинает течь ток и заряжать конденсатор, что эквивалентно тому, что на конденсаторе начинает расти напряжение, а на резисторе соответственно падать, и ток соответственно тоже начинает падать. Если через некоторое время ключ разомкнуть, то конденсатор так и останется заряженным, а напряжение на резисторе упадет до 0.

Изначально маховик покоится.

Включаем ключ (после этого сумма скоростей маховика и лопастей резистора равна скорости источника напряжения), маховик в начальный момент покоится, а лопасти резистора (невесомые) начинают вращаться, но из-за трения возникает момент сил, который разгоняет маховик.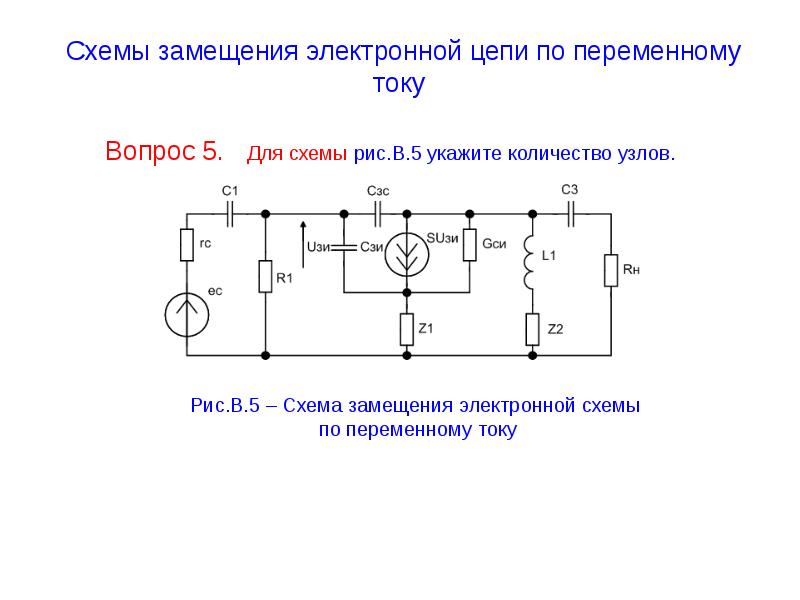 Чем быстрее крутится маховик, тем медленнее крутятся лопасти резистора, и тем с меньшей силой вращают маховик. Если через некоторое время ключ разомкнуть, то маховик продолжит вращаться не меняя своей скорости, а скорость лопастей резистора упадет до 0.

Источник напряжения, ключ, резистор, катушка.

Вначале ток равен нулю. Мы включаем ключ (после этого ), и на катушку подается напряжение питания, и оно начинает постепенно разгонять ток через катушку. По мере увеличения тока, увеличивается напряжение падения на резисторе, а значит напряжение, разгоняющее ток в катушке, падает, а значит ток постепенно перестает расти. Если через некоторое время ключ разомкнуть, то в результате практически мгновенной остановки тока на катушке будет очень короткий всплеск ЭДС, полярность которого будет обратна полярности источника напряжения.

Вначале пружинка не растянута. Мы включаем ключ (после этого сумма скоростей деформации пружинки и лопастей резистора равна скорости источника напряжения), и пружинка начинает растягиваться так, как будто в самый начальный момент сопротивление резистора =0.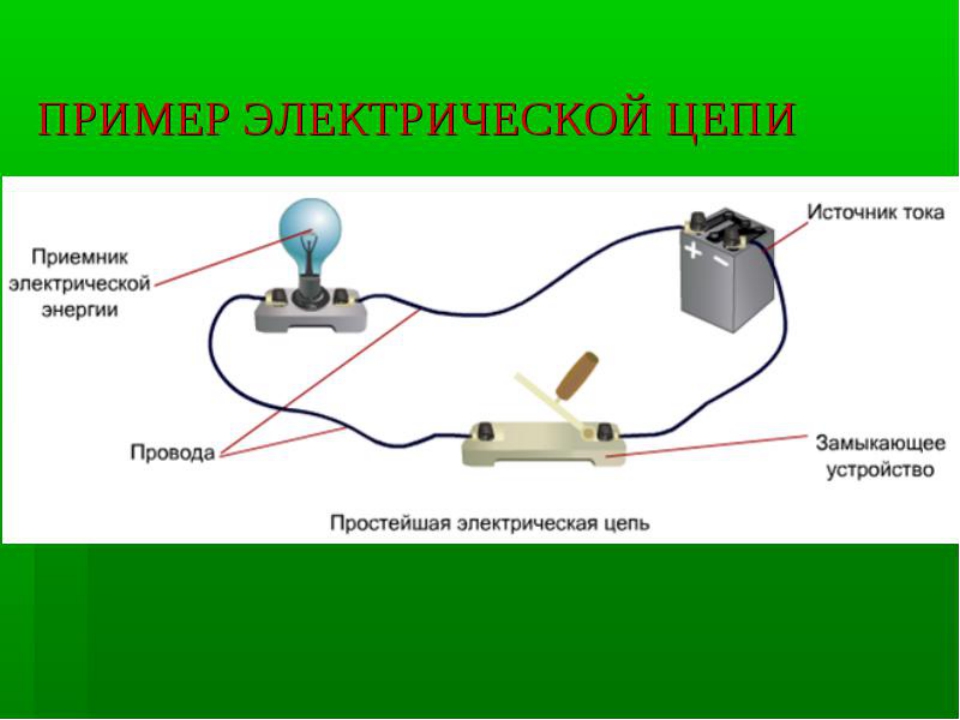 Уже растянутая пружинка начинает оказывать силу на резистор, в результате чего в резисторе возникает разность скоростей, а в пружинке разность скоростей начинает уменьшаться. Чем больше пружинка натянута, тем большую силу она оказывает на резистор, тем больше разность скоростей в резисторе, и тем меньше разность скоростей в катушке (вернее в ее модели), и тем медленнее растягивается пружинка катушки дальше. Если через некоторое время ключ разомкнуть, то в результате практически мгновенного падения нагрузки на пружинку, она очень быстро сожмется в исходное положение.

Механическую модель можно упростить, представив себе покоящуюся на воде невесомую лодку, к которой прикреплена пружинка, а другой конец пружинки внезапно начинают тянуть с постоянной скоростью. Вначале лодка покоится. Потом пружинка начинает натягиваться, и чем больше натягивается, тем больше увлекает за собой лодку, и тем меньше разность между скоростями двух концов пружинки. А если пружинку отпустить (масса кораблика и масса пружинки =0), то кораблик тут же остановится, а пружинка тут же сожмется.

И, наконец, механическая модель трансформатора.

Сам трансформатор описывается также как катушка:
где
Иначе говоря трансформатор описывается системой уравнений:

И чтобы получить механическую модель трансформатора, достаточно взять механические модели двух катушек, и соединить их пружинкой через рычаг:

Можно все поступательные пружинки заменить на вращательные, а рычаг заменить на редуктор:

Найдем уравнения, описывающие эту систему.

Предположим, что нижнее плечо сместилось вверх на (в месте крепления пружины) под действием силы , а верхнее сместилось вверх на (в месте крепления пружины) под действием силы . Записав вторые законы Ньютона для обоих невесомых плеч, идущих от дифференциалов, получим систему:

что тоже самое с

ее можно разрешить относительно и :

где

Сравнивая эту систему с (1) получается, что матрицу

следует сопоставлять с матрицей

И если у нас есть трансформатор, у которого все витки одинаковые по форме и сечению, на 1й обмотке витков, на второй — , и — доля от магнитного потока, создаваемого 1й катушкой, которая проходит через 2ю катушку (или наоборот — они совпадают) (Если катушки находятся на большом расстоянии, то и это фактически две разные катушки.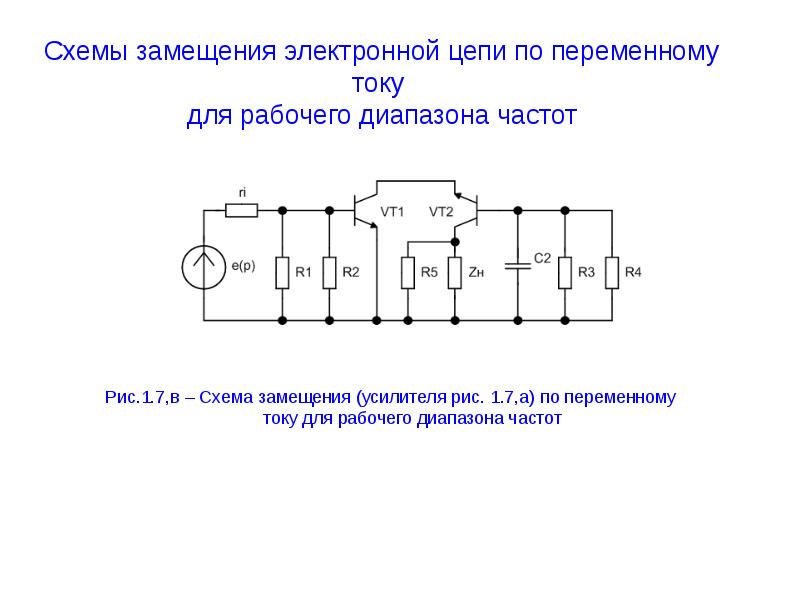 А если катушки близко друг к другу и к тому же соединены сердечником, то .), то матрица индуктивностей будет выглядеть так:

где — коэффициент, зависящий от размеров трансформатора и материала сердечника.

Если в его модели взять , то из соотношений

отношения жесткостей пружин будут выглядеть так:

а матрица индуктивностей модели так:
т.к. , то =>

то соотношения жесткостей тоже >0 (если исключить из модели рычаг, т.е. b=1, то одно из этих соотношений окажется отрицательным, а пружин с отрицательной жесткостью не бывает).

И обратно: при любых соотношения жесткостей пружин

и при любом соотношении плеч рычага b>0

При и модели катушек становятся практически независимыми.

При и модели катушек становятся жестко соединены через рычаг без пружинки. А индуктивности начинают стремится к

Для примера работы трансформатора рассмотрим схему: источник переменного напряжения, трансформатор, резистор

и рассчитаем ее

->
пусть

тогда

последнее уравнение можно переписать в виде
OPOC:
Этот вклад будет виден только сразу после включения схемы, потом затухнет и не будет участвовать в установившемся режиме трансформации.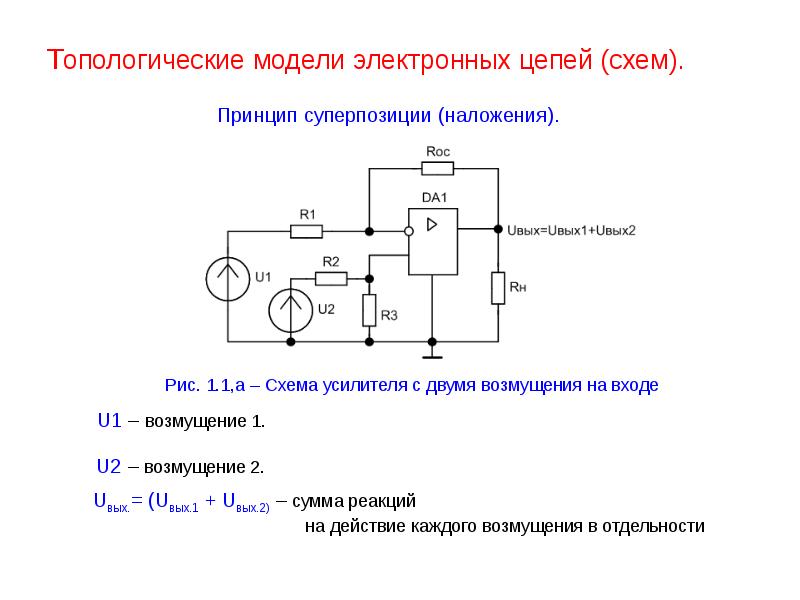

Если изменить уравнение так:

и искать ЧРНС в виде , то придем к алгебраическому уравнению
=>

т.к. , то

В случае с механической моделью этой схемы

где величины в квадратных скобках следует заменить их механическими аналогами.

Как и ожидалось, жесткость первой пружинки ни какой роли не играет (при любом c).

Если упростить механический аналог этой схемы, то у нас получится невесомый кораблик на воде, через пружинку привязанный к берегу, и который через другую пружинку и рычаг двигают туда-сюда по гармоническому закону.

Нелинейные элементы

Из нелинейных элементов диод можно храповиком замоделировать, операционный усилитель (который работает так: если напряжение на входе + больше чем напряжение на входе -, то он выдает +U, а если наоборот, то -U) — как на картинке, а транзистор — я не придумал как.

Вместо заключения

В моделях резистора, диода и одиночной катушки можно обойтись без дифференциала. Если пофантазировать, трение валов в креплениях можно интерпретировать как ток утечки через изолятор провода, деформацию валов — как паразитную индуктивность проводов, а момент инерции валов — как паразитную емкость. А вот модели проводов в себе не содержат сопротивления — они сверхпроводящие.

Было бы прикольно, если б кто-нибудь в реальности что-нибудь такое сделал (например из лего-техника, или на 3d принтере напечатал), да на ютуб выложил.

5. Радиотехнические цепи. Радиотехнические цепи и сигналы. Учебное пособие

5.1. Классификация радиотехнических цепей

5.2. Характеристики линейных радиотехнических цепей

5.3. Инерционные линейные цепи

5.4. Методы анализа преобразования сигналов линейными цепями

5.4.1. Классический метод

5.4.2. Временной метод

5.4.3. Спектральный метод

5.4.4. Операторный метод

5.5. Простейшие радиотехнические цепи

5.5.1. Пассивные апериодические цепи

5.5.2. Пассивные частотно-избирательные цепи

5.5.3. Активные линейные цепи

5. 1. Классификация радиотехнических цепей

При рассмотрении обобщённой структурной схемы радиотехнической информационной системы было показано, что передача сообщений сопровождается цепочкой преобразований сигналов. Преобразования сопровождаются различными радиотехническими устройствами, которые представляют собой совокупность физических объектов, между которыми существуют определённые взаимодействия. Отдельный объект, осуществляющий то или иное преобразование сигналов, называется радиотехнической цепью.

Радиотехническая цепь имеет вход, на который подаётся исходный сигнал, и выход, откуда снимается преобразованный сигнал. Такая цепь как физическая система является одномерной. Если цепь имеет несколько входов и выходов, то она называется многомерной. В дальнейшем будут рассматриваться только одномерные системы.

Если неизвестны внутренние процессы преобразования сигналов, то радиотехническую цепь можно представить в виде т.н. “чёрного ящика” (рис. 5.1), где оператор преобразования. Вместе с тем, в ряде случаев рассматривают и внутренние состояния радиотехнической цепи. К характеристикам состояния можно отнести напряжения и токи на различных элементах(резисторах, емкостях, индуктивностях) цепи. Если цепь характеризуется только одним состоянием, то она называется цепью первого порядка. Если же в качестве состояний рассматриваются токи или напряжения на n элементах цепи, то цепь является цепью n—го порядка. Порядок цепи оказывает существенное влияние на вид оператора преобразования .

Таким образом, результат преобразования входного сигнала радиотехнической цепью с оператором можно записать следующим образом

(5.1)

Рис. 5.2

Это обобщённое выражение позволяет провести классификацию радиотехнических цепей (рис. 5.2).

В первую очередь, отметим, что оператор преобразования с течением времени может оставаться постоянным, либо изменяться. Поскольку оператор преобразования целиком определяется параметрами цепи, то очевидно, неизменный во времени оператор характеризуется постоянными параметрами и цепи называются цепями с постоянными параметрами. Если же оператор изменяется во времени, то выходной сигнал описывается выражением

, (5.2)

а цепь называется цепью с переменными параметрами или параметрической цепью.

По виду оператора преобразования цепи делятся на линейные и нелинейные. Если оператор удовлетворяет условиям

, (5.3)

, (5.4)

то он является линейным оператором и цепь соответственно является линейной. В противном случае цепь относится к нелинейным цепям.

Условия (5.3) и (5.4) отражают фундаментальный принцип суперпозиции, который состоит в том, что реакция, т.е. выходной отклик цепи на сумму сигналов равен сумме откликов на эти сигналы, поступившие на вход цепи по отдельности. Простейшие линейные цепи (резисторный делитель напряжения и RC-цепь) изображены на рис. 5.3. Если выходной сигнал радиотехнической цепи в некоторый момент времени определяется только значением входного сигнала в тот же момент времени, то такая цепь называется безынерционной. Если же выходной сигнал зависит не только от значения входного сигнала в данный момент времени , но и от значений в предыдущие моменты времени, то такая цепь является инерционной. Очевидно, резисторный делитель (рис. 5.3, а) является безынерционной. Инерционность цепи определяется наличием в её составе ёмкостей и индуктивностей, поэтому RC-цепь, изображённая на рис. 5.3, б является инерционной цепью.

Завершим классификацию цепей по признаку наличия в составе цепи источника энергии. Если источник энергии в составе цепи отсутствует, такая цепь называется пассивной. Приведённые выше линейные цепи являются пассивными. При наличии же источника энергии в составе цепи цепь является активной. В качестве активных элементов радиотехнических цепей выступают электронные лампы, транзисторы и т. д. С этой точки зрения усилитель электрических сигналов является активной цепью.

5.2. Характеристики линейных радиотехнических цепей

При рассмотрении радиотехнических сигналов было установлено, что сигнал может быть представлен как во временной (динамическое представление), так и в частотной (спектральное представление) областях. Очевидно, при анализе процессов преобразования сигналов цепи также должны иметь соответствующие описания временными или частотными характеристиками.

Начнём с рассмотрения временных характеристик линейных цепей с постоянными параметрами. Если линейная цепь осуществляет преобразование в соответствии с оператором и на вход цепи подаётся сигнал в виде дельта-функции (на практике очень короткий импульс), то выходной сигнал (реакция цепи)

(5.5)

называется импульсной характеристикой цепи. Импульсная характеристика составляет основу одного из методов анализа преобразования сигналов, который будет рассмотрен ниже.

Если на вход линейной цепи поступает сигнал , т.е. сигнал вида “единичный перепад”, то выходной сигнал цепи

(5.6)

называется переходной характеристикой.

Между импульсом и переходной характеристикой существует однозначная связь. Так как дельта-функция (см. подраздел 1.3):

,

то подставляя это выражение в (5.5), получим:

. (5.7)

В свою очередь переходная характеристика

. (5.8)

Перейдём к рассмотрению частотных характеристик линейных цепей. Применим к входному и выходному сигналам прямое преобразование Фурье

,

.

Отношение комплексного спектра выходного сигнала к комплексному спектру входного сигнала называется комплексным коэффициентом передачи

(5.9)

Из этого следует, что

. (5.10)

Таким образом, оператором преобразования сигнала линейной цепью в частотной области служит комплексный коэффициент передачи.

Представим комплексный коэффициент передачи в виде

, (5.11)

где и соответственно модуль и аргумент комплексной функции . Модуль комплексного коэффициента передачи как функция частоты называется амплитудно-частотной характеристикой (АЧХ), а аргумент – фазочастотной характеристикой (ФЧХ). Амплитудно-частотная характеристика является чётной, а фазочастотная характеристика – нечётной функцией частоты .

Врменные и частотные характеристики линейных цепей связаны между собой преобразованием Фурье

, (5.12)

, (5.13)

что вполне объяснимо, поскольку они описывают один и тот же объект – линейную цепь.

5.3. Инерционные линейные цепи

Как уже отмечалось ранее, если выходной сигнал цепи определяется не только значениями входного сигнала в рассматриваемый момент времени , но и значениями входного сигнала в предыдущие моменты, то такая цепь называется инерционной. Если к этому же оператор преобразования линейный, то радиотехническая цепь является линейной инерционной цепью.

Линейные инерционные цепи (их ещё называют динамическими) нашли широкое распространение в радиотехнике. К ним относятся простейшие RC и RL цепи, колебательные контура и т.д. Как правило, линейные инерционные цепи описываются линейными дифференциальными уравнениями.

В качестве примера рассмотрим простейшую RC-цепь, изображённую на рис. 5.3, б. Согласно закону Кирхгофа можно записать

, (5.14)

где и — напряжения на соответствующих элементах цепи. Но напряжение является выходным сигналом цепи, т.е. . С другой стороны, напряжение на резисторе

,

где – ток, протекающий в цепи. Так как в цепь включена ёмкость, то ток протекающий в цепи:

,

.

Подставляя эти выражения в выражение (5.14), получим:

. (5.15)

Таким образом, простейшая RC-цепь описывается линейным дифференциальным уравнением первого порядка. Отметим, что состояние цепи характеризуется только напряжением на ёмкости, поэтому данная цепь является цепью первого порядка. Отсюда следует, что порядок дифференциального уравнения соответствует порядку цепи.

В общем случае линейная инерционная цепь описывается линейным дифференциальным уравнением n-ого порядка

(5.16)

или в компактной записи

, (5.17)

где и — коэффициенты уравнения.

Если известно дифференциальное уравнение (5.16), описывающее линейную цепь, можно найти характеристики цепи. Применим к обеим частям уравнения (5.16) прямое преобразование Фурье. Тогда, с учётом (2.47) можно записать

,

откуда следует

. (5.18)

Для рассмотренной выше RC-цепи уравнение (5.15) можно представить в виде

,

где , ; .

Тогда комплексный коэффициент передачи цепи в соответствии с (5.18) будет иметь вид

Теперь, зная , можно определить импульсную характеристику, используя (5.13), а также переходную характеристику (5.8), АЧХ и ФЧХ цепи.

5.4. Методы анализа преобразования сигналов линейными цепями

Основной задачей анализа является определение реакции (выходного) сигнала цепи при действии на её входе сигнала известной формы. При этом, входной сигнал может быть описан как во временной, так и в частотной области. В связи с этим различают следующие методы анализа: классический, временной (или метод интеграла наложения), спектральный и операторный. Выбор того или иного метода зависит от структуры цепи, вида воздействующего на неё сигнала, формы представления (временная или частотная) входного сигнала.

5.4.1. Классический метод

Классический метод основывается на решении дифференциального уравнения вида (5.16), описывающего линейную цепь. Решение этого уравнения представляет собой сумму двух слагаемых

, (5.19)

где первое слагаемое представляет собой общее решение однородного дифференциального уравнения

, (5.20)

а второе слагаемое – частотное решение (5.16) при , где – правая часть уравнения (5.16). Физически – свободная составляющая полного отклика (выходного сигнала), представляет собой реакцию цепи на отключение(или включение) входного сигнала и характеризует переходные процессы в цепи. Второе слагаемое – вынужденная составляющая, является реакцией цепи после окончания переходных процессов и характеризует установившейся(стационарный) режим преобразования цепью входного сигнала. Обычно, классический метод используется для изучения переходных процессов, что приводит к необходимости решения уравнения (5.20). Общее решение однородного уравнения (5.20) имеет вид

, (5.21)

где , ,…, – постоянные коэффициенты, определяемые начальными условиями,

, ,…, – корни характеристического уравнения:

. (5.22)

Это уравнение имеет ровно n корней, при этом корни могут быть либо вещественными, либо комплексными, что определяет характер переходных процессов. Что же касается , то если входной сигнал является постоянным или периодическим, то после окончания переходных процессов выходной сигнал принимает форму входного сигнала. Так, если представляет собой гармонический сигнал, то также будет гармоническим, отличаясь от входного сигнала амплитудой и начальной фазой.

В качестве примера рассмотрим, что собой представляет отклик RC-цепи (рис. 5.3,8) на входной сигнал вида .

Дифференциальное уравнение цепи (5.15) перепишем в виде

,

где – постоянная времени.

Поскольку дифференциальное уравнение имеет порядок n=1, решение однородного уравнения

согласно (5.21), запишется в виде

,

где – корень характеристического уравнения

,

откуда следует . Тогда

.

До поступления входного сигнала ёмкость С разряжена. В момент поступления входного сигнала (скачка) ёмкость не может мгновенно зарядиться до , это произойдёт по мере перехода к установившемуся режиму. Очевидно в установившемся режиме

.

Таким образом, суммарный выходной сигнал

.

Коэффициент найдём из начальных условий. Начальными условиями при исследовании линейных цепей называют значения токов в индуктивностях и напряжений на емкостях в момент времени . Так как в этот момент времени , то можно записать

,

Откуда следует . Тогда окончательно суммарный выходной сигнал

.

На рис. 5.4. изображены эпюры напряжений на входе и выходе исследуемой RC-цепи.

5.4.2. Временной метод

Временной метод (метод интеграла положения, метод интеграла Дюамеля) основывается на представлении входного сигнала цепи в виде суммы элементарных сигналов вида единичного скачка или очень короткого импульса ( – функции). Тогда, зная отклик линейной цепи на каждый элементарный сигнал и суммируя их можно получить в соответствии с принципом суперпозиции (наложения) полный отклик цепи на входной сигнал сложной формы.

Выберем в качестве элементарного сигнала – функцию. Тогда входной сигнал в соответствии с (1.19) можно записать следующим образом

.

Очевидно, выходной сигнал

.

Так как оператор не зависит от времени, его можно внести под знак интеграла. Тогда, с учётом (5.5)

. (5.23)

Если момент появления входного сигнала , то с учётом того, что выходной сигнал не может появиться ранее входного, выражение (5.23) принимает вид

. (5.24)

Таким образом, сигнал на выходе линейной цепи представляет собой свёртку входного сигнала с импульсной характеристикой цепи. Линейная цепь с постоянными параметрами при преобразовании проводит операцию взвешенного суммирования всех мгновенных значений входного сигнала, начиная с момента и заканчивая текущим моментом времени . Роль весовой функции выполняет импульсная характеристика цепи.

Выражение (5.24) носит название интеграла Дюамеля. Это выражение было получено в предположении, что входной сигнал представлен в виде суммы элементарных сигналов вида – функций. Если входной сигнал представить в виде (1.15) комбинаций сигналов вида единичного скачка, то можно получить другие формы интеграла Дюамеля, в частности

. (5.25)

Здесь – переходная характеристика цепи.

Итак, для использования метода интеграла наложения необходимо знать импульсную характеристику или переходную характеристику . Эти характеристики можно определить несколькими способами. Прямой (непосредственный способ состоит в решении дифференциального уравнения (5.20) в предположении, что входной сигнал является очень коротким импульсом(для определения импульсной характеристики) или сигналом вида единичного скачка( для определения переходной характеристики).

В выше приведённом примере было решено дифференциальное уравнение и найден отклик RC-цепи на воздействие сигнала

.

Очевидно, форма отклика не изменится, если входной сигнал будет единичным скачком, при этом масштаб отклика изменится в раз. Тогда выходной сигнал

, (5.26)

поскольку реакция цепи на единичный скачок является переходной характеристикой. В соответствии с (5.7) определяется импульсная характеристика

(5.27)

Второй способ определения импульсной или переходной характеристики, назовём его косвенным, состоит в использовании однозначного соответствия между импульсной характеристикой и комплексным коэффициентом передачи.

5.4.3. Спектральный метод

При рассмотрении характеристик линейной цепи было получено соотношение (5.10), связывающее спектральные характеристики входного и выходного сигнала с комплексным коэффициентом передачи цепи. Это соотношение лежит в основе спектрального анализа. Если задачей анализа является определение частотных характеристик выходного сигнала, то при известных и использование (5.10) полностью решает эту задачу. В ряде случаев сигнал представлен во временной области и требует найти отклик цепи как функцию времени. При этом использование метода интеграла наложения может быть затруднено сложностью нахождения импульсной характеристики цепи. В то же время комплексный коэффициент передачи найти достаточно просто. Тогда спектральный метод анализа сводится к следующим операциям:

— для входного сигнала прямым преобразованием Фурье находится комплексный спектр ;

— определяется комплексный коэффициент передачи цепи ;

— в соответствии с (5.10) определяется комплексный спектр выходного сигнала ;

— обратным преобразованием Фурье вычисляется форма сигнала на выходе цепи.

Итак, важнейшим условием использования спектрального метода является знание комплексного коэффициента передачи исследуемой цепи. Найти комплексный коэффициент передачи можно, используя методы теории цепей (метод узловых потенциалов или метод контурных токов). Если известно аналитическое описание цепи дифференциальным уравнением (5.16), то комплексный коэффициент передачи находится в соответствии с (5.18). Наконец, цепь можно представить в виде делителя напряжения, элементами которого являются комплексные сопротивления

; ; .

Проиллюстрируем последний подход на примере уже рассматривавшейся выше RC-цепи. Если представить цепь как делитель напряжения, то выходной сигнал представляет собой напряжение на ёмкости С. Тогда, если комплексный ток, протекающий в цепи, то

,

и комплексный коэффициент передачи

,

что совпадает с результатом, полученным в подразделе 5.3.

5.4.4. Операторный метод

Операторный метод является обобщением спектрального метода. В основе метода лежит преобразование Лапласа. Рассмотрим некоторый сигнал , определённый на интервале времени (0, ). Умножим этот сигнал на и полученный новый сигнал подвергнем преобразованию Фурье

.

Обозначая через , получим

. (5.28)

Выражение (5.28) называется односторонним преобразованием Лапласа функции . При этом, называют оригиналом, а изображением.

Нетрудно убедиться, что при выражение (5.28) преобразуется к виду

,

что соответствует преобразованию Фурье. Таким образом если преобразование Фурье представляет собой спектральное разложение сигнала по гармоническим составляющим , то преобразование Лапласа – разложение сигнала по экспоненциально – косинусным составляющим . Действительно, представим

.

Здесь использована формула Эйлера

.

С другой стороны

,

где .

Тогда окончательно

представляет собой экспоненциально – косинусную функцию.

Переход от изображения к оригиналу осуществляется при помощи обратного преобразования Лапласа

. (5.29)

Для значительной части функций широко используемых при описании оригиналов были рассчитаны изображения по Лапласу. Некоторая часть оригиналов и изображений приведена в таблице 5.1.

Поскольку преобразование Лапласа является обобщением преобразования Фурье, то оно обладает теми же свойствами, что и преобразование Фурье. Остановимся на некоторых из них, которые будем использовать в дальнейшем. Пару преобразований (прямое и обратное) будем обозначать следующим образом

.

1. Линейность преобразований Лапласа

(5.30)

2. Свойство временного сдвига

(5.31)

3. Операция дифференцирования

; (5.32)

4. Операция интегрирования

. (5.33)

Применим к обеим частям уравнения (5.16) прямое преобразования Лапласа. Тогда с учётом (5.32), получим

(5.34)

откуда следует

. (5.35)

Это отношение называется передаточной функцией цепи или её операторным коэффициентом. Таким образом, передаточная функция является оператором преобразования линейной цепью в базисе экспоненциально – косинусных сигналов.

Сравним выражение комплексного коэффициента передачи (5.18) с выражением (5.35). Из этого сравнения следует, что комплексный коэффициент передачи является частным случаем при , т.е.

(5.36)

Таким образом, если известна передаточная функция цепи, то операторный метод поиска отклика цепи состоит в следующем:

— находится изображение по Лапласу входного сигнала

; (5.37)

— находится изображение выходного сигнала как произведение

; (5.38)

— определяется оригинал выходного сигнала

. (5.39)

Установим связь между временными характеристиками и передаточной функцией. Произведя в (5.12) замену на , получим

.

Таким образом, передаточная функция и импульсная характеристика связаны между собой преобразованием Лапласа

.

Что касается переходной характеристики, то применяя к (5.8) преобразование Лапласа и учитывая (5.33), получим

.

В заключение отметим, что операторный метод позволяет сводить линейные дифференциальные уравнения вида (5.16) к алгебраическим уравнениям (5.34), что позволяет в ряде случаев упростить анализ цепей. Помимо этого, учитывая широкое распространение таблиц преобразований Лапласа для большого числа функций, можно исключить громоздкие вычисления, непосредственно обращаясь к этим таблицам.

Рассмотрим применение операторного метода на примере анализа определения отклика RC-цепи на входной сигнал вида . Эта задача была решена классическими временными методами. Спектральным методом был найден комплексным коэффициент передачи. Заменив в выражении для цепи на , получим передаточную функцию цепи

.

Следуя операторному методу найдём изображение по Лапласу входного сигнала, воспользовавшись при этом таблицей 5.1

.

Далее, в соответствии с (5.38), определим изображение выходного сигнала

.

И наконец, по таблице 5.1 (позиция 5) находим оригинал

,

что совпадает с полученными ранее результатами.

5.5. Простейшие радиотехнические цепи

5.5.1. Пассивные апериодические цепи

При классификации радиотехнических цепей было отмечено, что по признаку наличия в цепи источника энергии цепи подразделяются на пассивные и активные. Начнем с рассмотрения пассивных цепей первого порядка, т.е. цепей содержащих один реактивный элемент (емкость или индуктивность). На основе этих цепей строятся как простейшие активные цепи, так и более сложные радиотехнические устройства.

Выше в качестве примера линейной цепи при рассмотрении методов анализа приводилась RC-цепь, которая получила название интегрирующей цепи. Рассмотрим еще одну RC-цепь, называемую дифференцирующей цепью, определим ее характеристики и сравним с характеристиками интегрирующей цепи.

Определение характеристик цепей можно проводить любым из рассмотренных выше методов. Так, например, при определении частотных характеристик цепей в данном случае удобно представить ту или иную цепь в виде делителя напряжения, в состав которого входят комплексные сопротивления и . Временные характеристики (переходную и импульсную) можно рассчитать как методом интеграла наложения, так и операторным методом.

В таблице 5 представлены схемы интегрирующей и дифференцирующей цепи, дифференциальные уравнения, которыми описываются цепи, аналитические выражения комплексного коэффициента передачи , амплитудно-частотных , фазо-частотных , а также переходных и импульсных характеристик и их графические изображения.

Анализ графиков АЧХ цепей показывает, что интегрирующая цепь пропускает нижние частоты и задерживает верхние, т.е. является фильтром нижних частот (ФНЧ). Дифференцирующая цепь наоборот пропускает верхние частоты и тем самым является фильтром верхних частот (ФВЧ).

Форма временных (переходной и импульсной) характеристик определяет характер переходных процессов. Для рассматриваемых цепей переходные характеристики представляют собой монотонно возрастающую (для интегрирующей цепи) и монотонно убывающую (для дифференцирующей цепи) функции. Это определило название цепей как апериодических.

Обратимся к выражению для комплексного коэффициента передачи интегрирующей цепи. При комплексный коэффициент передачи

.

Так как входной и выходной сигналы связаны соотношением

,

то при указанном условии

. (5.40)

Но оператор является оператором интегрирования. Тогда применяя обратное преобразование Фурье, получим

,

т.е. цепь выполняет функцию интегрирования входного сигнала.

Аналогично для дифференцирующей цепи при

и (5.41)

Таблица 5

Как известно, оператор – это оператор дифференцирования. Очевидно, обратное преобразование Фурье обеих частей (5.41) дает

.

Таким образом, рассмотренные простейшие RC-цепи осуществляют соответственно приближенное интегрирование и дифференцирование входных сигналов.

В заключение отметим, что в качестве интегрирующих и дифференцирующих цепей могут выступать и RL-цепи, где реактивными элементами являются индуктивности. Схемы этих цепей также представляют собой делители напряжения, с той лишь разницей, что в интегрирующей цепи выходной сигнал снимается с резистора, а в дифференцирующей – с индуктивности.

5.5.2. Пассивные частотно-избирательные цепи

К пассивным частотно-избирательным цепям относятся колебательные контуры. Простейший колебательный контур содержит резистор R, индуктивность L и емкость C. Если в контуре элементы R, L и C соединены последовательно, то такой контур называется последовательным, а если соединены параллельно – параллельным колебательным контуром.

Рис.5.6

Один из вариантов последовательного колебательного контура изображен на рис. 5.6. Так же, как и предыдущие цепи, рассматриваемый контур можно представить как делитель напряжения. Тогда

комплексный коэффициент передачи контура

,

или с учетом того, что , и :

. (5.42)

Из этого выражения следует, что комплексный коэффициент передачи имеет максимум при

, (5.43)

т.е. последовательный колебательный контур из совокупности сигналов разных частот выделяет один, который имеет частоту . Это явление, как известно, называется резонансом, а частота – резонансной частотой.

Резонансная частота определяется из условия (5.43):

или . (5.44)

Рассмотрим основные характеристики последовательного колебательного контура.

Характеристическим сопротивлением называется значение сопротивления одного из реактивных элементов (индуктивности или емкости) при резонансной частоте

. (5.45)

Добротностью контура называется отношение характеристического сопротивления к резистивному

. (5.46)

Поясним физический смысл добротности. Из (5.42) при имеем

.

Тогда с учетом (5.46) можно записать

. (5.47)

Таким образом, добротность показывает во сколько раз напряжение на индуктивности или емкости (выходной сигнал) больше, чем приложенное входное напряжение. Затуханием контура называется безразмерная величина, обратная добротности

.

Постоянная времени контура

, (5.48)

характеризует инерционность контура. Очевидно, чем больше (чем больше ), тем медленнее протекают переходные процессы в контуре.

Возвратимся к (5.42) и представим это выражение с учетом (5.44) в виде

.

Обозначая

,

после несложных преобразований получим

.

Рассмотрим поведение комплексного коэффициента передачи в окрестности резонансной частоты, т.е. при . Тогда величина :

, (5.49)

где – абсолютная расстройка, представляет собой так называемую удвоенную относительную расстройку. С учетом этого выражение для комплексного коэффициента передачи можно представить как функцию удвоенной относительной расстройки в следующем виде

. (5.50)

Амплитудно-частотная характеристика

, (5.51)

а фазо-частотная характеристика

. (5.52)

На рис. 5.7 изображены графики АЧХ и ФЧХ рассматриваемого колебательного контура в окрестности резонансной частоты.

Рис. 5.7

Полосой пропускания контура называется диапазон частот, в пределах которого . Очевидно, равенство в этом выражении соответствует граничным частотам и полосы пропускания. Эти частоты находятся в результате решения уравнения

. (5.53)

Решение этого уравнения дает

, ,

или с учетом (5.49)

, .

Тогда полоса пропускания контура определяется по формуле

. (5.54)

В заключение составим дифференциальное уравнение последовательного колебательного контура. Напряжение, приложенное к контуру:

, (5.55)

где – напряжение на резисторе, – напряжение на индуктивности, – напряжение на конденсаторе. Но напряжение на конденсаторе является выходным сигналом . С другой стороны напряжение на резисторе , а напряжение на индуктивности . Ток, протекающий через контур, можно выразить через напряжение на конденсаторе

.

Тогда напряжение на индуктивности

,

и на резисторе

.

Подстановка этих выражений в (5.55) дает соотношение

.

Разделим обе части этого уравнения на . Тогда уравнение принимает вид

, (5.56)

где – коэффициент затухания.

Применив к обеим частям уравнения (5.56) преобразование Лапласа, можно получить выражение для передаточной функции

. (5.57)

Нетрудно заметить, что замена в (5.57) на приводит к выражению (5.42).

Параллельный колебательный контур представляет собой параллельное соединение , и элементов (рис. 5.8). Входным сигналом такого контура является ток , а выходным – напряжение на элементах контура. Согласно закону Ома комплексное значение напряжения на элементах контура

.

В свою очередь комплексное сопротивление есть величина, обратная комплексной проводимости. При параллельном соединении , и комплексная проводимость равна

, (5.58)

или

. (5.59)

Проводя суммирование дробей, и вычисляя обратное значение суммы, получим

. (5.60)

Как и в последовательном контуре, резонанс в параллельном колебательном контуре, как это следует из (5.60), имеет место при условии .

Характеристическое сопротивление контура описывается выражением (5.45). Что касается добротности , то в отличие от (5.46) для параллельного контура она определяется выражением

. (5.61)

Отсюда постоянная времени контура

. (5.62)

Вводя параметр и проводя аналогичные рассуждения, как и в случае последовательного контура, после несложных преобразований получим выражение для в окрестности резонансной частоты:

. (5.63)

Очевидно, амплитудно-частотная характеристика

, (5.64)

носит такой же характер, как и для последовательного контура (5.51). Поэтому график АЧХ параллельного контура совпадает по форме с кривой рис. 5.7а. Фазо-частотная характеристика имеет вид

. (5.65)

На рис. 5.9 приведен график ФЧХ параллельного контура. Полоса пропускания и граничные частоты и определяются аналогично этим же параметрами последовательного контура. При составлении дифференциального уравнения следует учесть, что входной сигнал – ток

, (5.66) где ; ; – токи, протекающие через соответствующие элементы, – напряжение на контуре, являющееся выходным сигналом .

Подстановка этих выражений в (5.65) дает

.

Дифференцирование левой и правой частей приводит к результату

, (5.67)

где – коэффициент затухания.

Передаточная функция параллельного контура описывается выражением

. (5.68)

5.5.3. Активные линейные цепи

Типичным примером активной цепи является усилитель, собранный на n-p-n транзисторе с общим эмиттером. Если нагрузкой усилителя служит R-цепь, то такой усилитель является апериодической активной цепью, а если нагрузкой служит колебательный контур – частотно-избирательной активной цепью.

Рис. 5.10

На рис. 5.10 представлена упрощенная принципиальная схема частотно-избирательной активной цепи. При достаточно малой амплитуде входного сигнала такую цепь можно считать линейной (линейным усилителем малых сигналов). Этот случай мы и рассмотрим.

Для определения характеристик рассматриваемой активной цепи составим ее эквивалентную схему. Транзистор можно представить в

виде источника тока управляемого напряжением . Величина тока в этом случае составит

, (5.69)

где – крутизна характеристики транзистора (крутизна управления), имеющая размерность . Как известно, источник тока можно представить как параллельное соединение идеального источника и внутреннего сопротивления, в качестве которого выступает внутреннее сопротивление транзистора . Тогда эквивалентная схема рассматриваемой цепи принимает вид (рис. 5.11).

Рис.5.11

Так же, как и для пассивной цепи (параллельного контура) комплексный коэффициент передачи:

.

совпадает с комплексным сопротивлением . Вместе с тем, для рассматриваемой цепи комплексная проводимость определяется выражением

, (5.70)

где – эквивалентное сопротивление контура с учетом внутреннего сопротивления транзистора. Сравнение (5.70) с (5.59) показывает, что комплексный коэффициент передачи рассматриваемой цепи описывается выражением (5.60) с той лишь разницей, что вместо собственного сопротивления параллельного контура здесь выступает

. (5.71)

Очевидно, исходя из эквивалентной схемы, добротность рассматриваемого усилителя составит величину

. (5.72)

Так как , то включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности, что объясняется шунтирующим свойством транзистора.

Аналогично комплексный коэффициент передачи как функция удвоенной относительной расстройки ε описывается выражением

, (5.73)

а амплитудно-частотная и фазо-частотная характеристики – соответственно выражениями:

, (5.74)

. (5.75)

Полоса пропускания рассматриваемого усилителя определяется в соответствии с (5.54), где вместо фигурирует

. (5.76)

Очевидно, так как включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности до , это в свою очередь обуславливает расширение полосы пропускания.

Цепь RL — RL circuit

Электрическая цепь, состоящая из резистивных и индуктивных элементов, без емкостных элементов.

Резистор-индуктора цепи ( RL цепи ), или RL — фильтр или сеть RL , является электрическая цепь состоит из резисторов и катушек индуктивности с приводом от напряжения или источника тока . Схема RL первого порядка состоит из одного резистора и одной катушки индуктивности и представляет собой простейший тип схемы RL.

Схема RL первого порядка является одним из простейших аналоговых электронных фильтров с бесконечной импульсной характеристикой . Он состоит из резистора и катушки индуктивности, подключенных последовательно от источника напряжения или параллельно работающих от источника тока.

Введение

Основными пассивными элементами линейной цепи являются резистор (R), конденсатор (C) и индуктор (L). Эти элементы схемы могут быть объединены в электрическую цепь четырьмя различными способами: RC-цепь , RL-цепь, LC-цепь и RLC-цепь с сокращениями, указывающими, какие компоненты используются. Эти схемы демонстрируют важные типы поведения, которые являются фундаментальными для аналоговой электроники . В частности, они могут действовать как пассивные фильтры . В этой статье рассматривается схема RL как последовательно, так и параллельно, как показано на схемах.

На практике, однако, конденсаторы (и RC-цепи) обычно предпочтительнее катушек индуктивности, поскольку их легче изготовить и, как правило, они физически меньше, особенно для компонентов с более высокой стоимостью.

Обе цепи RC и RL образуют однополюсный фильтр. В зависимости от того, находится ли реактивный элемент (C или L) последовательно с нагрузкой или параллельно с нагрузкой, будет зависеть, является ли фильтр низкочастотным или высокочастотным.

Часто цепи RL используются в качестве источников питания постоянного тока для усилителей RF, где индуктивность используется для пропускания постоянного тока смещения и блокировки возврата RF в источник питания.

Эта статья основана на знании комплексного импеданса представления индукторов и на знании частотной области представления сигналов .

Комплексное сопротивление

Комплексное сопротивление Z _L (в омах ) от индуктора с индуктивностью L (в генри ) является

ZLзнак равноLs.{\ Displaystyle Z_ {L} = Ls \ ,.}

Комплексная частота s — это комплексное число ,

sзнак равноσ+jω,{\ displaystyle s = \ sigma + j \ omega \ ,,}

где

Собственные функции

В комплекснозначными собственные функции любого линейного времени инвариантной системы (LTI) имеют следующие формы:

V(т)знак равноАеsтзнак равноАе(σ+jω)тАзнак равноАеjϕ⇒V(т)знак равноАеjϕе(σ+jω)тзнак равноАеσтеj(ωт+ϕ). {\ sigma t} \ cos (\ omega t + \ phi) \ ,.}

Синусоидальное установившееся состояние

Синусоидальное установившееся состояние — это особый случай, когда входное напряжение состоит из чистой синусоиды (без экспоненциального затухания). Как результат,

σзнак равно0{\ displaystyle \ sigma = 0}

и оценка s становится

sзнак равноjω.{\ displaystyle s = j \ omega \ ,.}

Последовательная схема

Рассматривая схему как делитель напряжения , мы видим, что напряжение на катушке индуктивности составляет:

VL(s)знак равноLsр+LsVяп(s),{\ Displaystyle V_ {L} (s) = {\ frac {Ls} {R + Ls}} V _ {\ mathrm {in}} (s) \ ,,}

а напряжение на резисторе равно:

Vр(s)знак равнорр+LsVяп(s).{\ Displaystyle V_ {R} (s) = {\ frac {R} {R + Ls}} V _ {\ mathrm {in}} (s) \ ,.}

ток

Ток в цепи везде одинаковый, так как цепь включена последовательно:

я(s)знак равноVяп(s)р+Ls.{\ Displaystyle I (s) = {\ frac {V _ {\ mathrm {in}} (s)} {R + Ls}} \ ,. {- {\ frac {t} {\ tau}}} \ ,.}

Рекомендации по частотной области

Это выражения в частотной области . Их анализ покажет, какие частоты схемы (или фильтры) пропускают, а какие отклоняют. Этот анализ основан на рассмотрении того, что происходит с этими коэффициентами усиления, когда частота становится очень большой и очень маленькой.

При ω → ∞ :

граммL→1а такжеграммр→0.{\ displaystyle G_ {L} \ to 1 \ quad {\ mbox {and}} \ quad G_ {R} \ to 0 \ ,.}

При ω → 0 :

граммL→0а такжеграммр→1.{\ displaystyle G_ {L} \ to 0 \ quad {\ mbox {and}} \ quad G_ {R} \ to 1 \ ,.}

Это показывает, что если выходной сигнал поступает через катушку индуктивности, высокие частоты пропускаются, а низкие частоты ослабляются (отклоняются). Таким образом, схема ведет себя как фильтр верхних частот . Однако, если выходной сигнал поступает через резистор, высокие частоты отклоняются, а низкие частоты пропускаются. В этой конфигурации схема ведет себя как фильтр нижних частот . Сравните это с поведением выхода резистора в RC-цепи , где все наоборот.

Диапазон частот, который пропускает фильтр, называется его полосой пропускания . Точка, в которой фильтр ослабляет сигнал до половины его нефильтрованной мощности, называется его частотой среза . Это требует, чтобы коэффициент усиления схемы был уменьшен до

граммLзнак равнограммрзнак равно12.{\ displaystyle G_ {L} = G_ {R} = {\ frac {1} {\ sqrt {2}}} \ ,.}

Решение вышеуказанного уравнения дает

ωcзнак равнорL рад / силижcзнак равнор2πL Гц,{\ displaystyle \ omega _ {\ mathrm {c}} = {\ frac {R} {L}} {\ mbox {rad / s}} \ quad {\ mbox {или}} \ quad f _ {\ mathrm {c }} = {\ frac {R} {2 \ pi L}} {\ mbox {Hz}} \ ,,}

это частота, которую фильтр будет ослаблять до половины своей исходной мощности.

Ясно, что фазы также зависят от частоты, хотя в целом этот эффект менее интересен, чем изменение коэффициента усиления.

При ω → 0 :

ϕL→90∘знак равноπ2 радианыа такжеϕр→0. {\ circ} = — {\ frac {\ pi} {2} } {\ mbox {радианы}} \ ,.}

Таким образом, при постоянном токе (0  Гц ) напряжение резистора находится в фазе с напряжением сигнала, в то время как напряжение катушки индуктивности опережает его на 90 °. По мере увеличения частоты напряжение на резисторе запаздывает на 90 ° относительно сигнала, а напряжение на катушке индуктивности становится синфазным с сигналом.

Замечания во временной области

Этот раздел основан на знании e , натуральной логарифмической константы .

Самый простой способ получить поведение во временной области — использовать преобразования Лапласа из выражений для V _L и V _R, приведенных выше. Это эффективно преобразует jω → s . Предполагая ступенчатый вход (т.е. V _in = 0 перед t = 0, а затем V _in = V после):

Vяп(s)знак равноV⋅1sVL(s)знак равноV⋅sLр+sL⋅1sVр(s)знак равноV⋅рр+sL⋅1s.{\ displaystyle {\ begin {align} V _ {\ mathrm {in}} (s) & = V \ cdot {\ frac {1} {s}} \\ V_ {L} (s) & = V \ cdot { \ frac {sL} {R + sL}} \ cdot {\ frac {1} {s}} \\ V_ {R} (s) & = V \ cdot {\ frac {R} {R + sL}} \ cdot {\ frac {1} {s}} \,. {- t {\ frac {R} {L}}} \ right) \,. \ end {align}}}

Таким образом, напряжение на катушке индуктивности с течением времени стремится к 0, в то время как напряжение на резисторе стремится к V , как показано на рисунках. Это согласуется с интуитивно понятной точкой зрения, что на катушке индуктивности будет напряжение только до тех пор, пока ток в цепи изменяется — когда схема достигает своего установившегося состояния, дальнейшее изменение тока и, в конечном итоге, отсутствие напряжения на катушке индуктивности.

Эти уравнения показывают, что у последовательной цепи RL есть постоянная времени, обычно обозначаемая τ =L/р время, за которое напряжение на компоненте падает (на катушке индуктивности) или повышается (на резисторе) с точностью до 1/еего окончательного значения. То есть τ — это время, за которое V _L достигает V (1/е) и V _R для достижения V (1 -1/е) .

Скорость изменения дробная 1 -1/ена τ . Таким образом, при переходе от t = Nτ к t = ( N + 1) τ напряжение переместится примерно на 63% от своего уровня при t = Nτ к своему конечному значению. Таким образом, напряжение на катушке индуктивности упадет примерно до 37% после τ и практически до нуля (0,7%) примерно через 5 τ . Закон Кирхгофа подразумевает, что напряжение на резисторе будет расти с той же скоростью. Когда затем источник напряжения заменяется коротким замыканием, напряжение на резисторе падает экспоненциально с t от V до 0. Резистор разряжается примерно до 37% после τ и практически полностью разряжается (0,7%) примерно через 5 τ. . Обратите внимание, что ток I в цепи ведет себя так же, как напряжение на резисторе, в соответствии с законом Ома .

Задержка нарастания или спада в цепи в этом случае вызвана противо-ЭДС от катушки индуктивности, которая, когда ток, протекающий через нее, пытается измениться, предотвращает рост тока (и, следовательно, напряжения на резисторе). или падает намного быстрее, чем постоянная времени цепи. Поскольку все провода имеют некоторую самоиндукцию и сопротивление, все цепи имеют постоянную времени. В результате, когда источник питания включен, ток не мгновенно достигает своего установившегося значения,V/р. Вместо этого для завершения подъема требуется несколько постоянных времени. Если бы это было не так, и ток был достичь устойчивого состояния немедленно, очень сильные индукционные электрические поля будут генерируемым резким изменением в магнитном поле — это привело бы к разрушению воздуха в цепи и электрическую дуге , возможно повреждение компонентов (и пользователей).

Эти результаты также могут быть получены путем решения дифференциального уравнения, описывающего схему:

Vяпзнак равнояр+LdяdтVрзнак равноVяп-VL.{\ displaystyle {\ begin {align} V _ {\ mathrm {in}} & = IR + L {\ frac {dI} {dt}} \\ V_ {R} & = V _ {\ mathrm {in}} -V_ {L} \,. \ End {выровнено}}}

Первое уравнение решается с помощью интегрирующего множителя и дает ток, который необходимо дифференцировать, чтобы получить V _L ; второе уравнение простое. {- 1} \ left ({\ frac {\ omega L} {R}} \ right) \ right)}

Параллельная схема

Параллельная цепь RL обычно менее интересна, чем последовательная цепь, если она не питается от источника тока. Это в значительной степени связано с тем, что выходное напряжение V _out равно входному напряжению V _in — в результате эта схема не действует как фильтр для входного сигнала напряжения.

Со сложными сопротивлениями:

ярзнак равноVяпряLзнак равноVяпjωLзнак равно-jVяпωL.{\ displaystyle {\ begin {align} I_ {R} & = {\ frac {V _ {\ mathrm {in}}} {R}} \\ I_ {L} & = {\ frac {V _ {\ mathrm {in} }}} {j \ omega L}} = — {\ frac {jV _ {\ mathrm {in}}} {\ omega L}} \,. \ end {выровнено}}}

Это показывает, что катушка индуктивности отстает от тока резистора (и источника) на 90 °.

Параллельная схема видна на выходе многих схем усилителя и используется для изоляции усилителя от эффектов емкостной нагрузки на высоких частотах. Из-за фазового сдвига, вносимого емкостью, некоторые усилители становятся нестабильными на очень высоких частотах и ​​имеют тенденцию к колебаниям. Это влияет на качество звука и срок службы компонентов (особенно транзисторов), и этого следует избегать.

Смотрите также

Ссылки

DiscoverCircuits.com был запущен в 2002 году Бесплатные электронные схемы

Добро пожаловать в DiscoverCircuits — онлайн с 2002 года Discover Circuits — это жизненно важный онлайн-ресурс для инженеров, любителей, изобретателей и консультантов. Сборник информации на сайте поможет вам быстро найти дизайнерских идей для задач электронного проектирования. пожалуйста свяжитесь со мной с любыми вопросами, комментариями или предложениями.Спасибо.
	Последнее обновление 22.12.2017 06:37
Есть дизайн? Пожалуйста, напишите , если вы хотите, чтобы я на ссылался на и / или на отправил свой оригинальный дизайн . Спасибо.
Другие веб-сайты Дэйва, которые стоит посетить: сборник ресурсов для изобретателей, любителей, ученых и инженеров информационный портал о возобновляемых, альтернативных или устойчивых источниках энергии Dave Johnson & Associates консультационные услуги для новых продуктов от концепции до производство или повышение стоимости и производительности существующих продуктов
Предыдущие выпуски журнала DC Magazine Примечание: Если специально не указано имя, Дэвид Джонсон не проектировал схемы, перечисленные на этом сайте, и не сможет ответить на вопросы о них. Вопросы задавайте разработчику схемы.

Электронные устройства и схемы — Что такое электроника

The
слово «электроника» происходит от слова «электронная механика»,
средства для изучения поведения электрона при различных
условия применяемых электрических
поле.

Электроника
определение

Филиал
техника, в которой поток и контроль электронов в
вакуум или полупроводник называется электроникой.Электронику также можно определить как отрасль техники.
в котором электронные устройства и их использование
учился.

The
движение электронов через проводник дает нам электрический
текущий. Этот электрический ток можно получить с помощью
аккумуляторов и генераторов.

The
устройство, управляющее потоком электронов, называется
электрическое устройство.Эти устройства являются основным корпусом
блоки электронных схем.

Электроника
имеют различные отрасли, включая цифровую электронику, аналоговую
электроника, микроэлектроника, наноэлектроника,
оптоэлектроника, интегральные схемы и полупроводники
устройство.

История
электроники

Диод
вакуумная лампа была первым электронным компонентом, изобретенным
Дж.А. Флеминг. Позже Ли Де Форест разработал триод,
трехэлементная вакуумная лампа с возможностью усиления напряжения.
Вакуумные лампы сыграли важную роль в области микроволнового излучения.
и передачи высокой мощности, а также телевизионные приемники.

В
1947 г. — лаборатории Bell разработали первый транзистор на основе
об исследованиях Шокли, Бардина и Браттейна.Однако,
транзисторные радиоприемники не разрабатывались до конца 1950-х гг.
из-за существующего огромного запаса электронных ламп.

В
В 1959 году Джек Килби из Texas Instruments разработал первый
Интегральная схема. Интегральные схемы содержат большое количество
полупроводниковых устройств, таких как диоды и транзисторы в
очень маленькая территория.

Преимущества
электроники

Электронные устройства проигрывают
главная роль в повседневной жизни.Различные электронные
устройства, которые мы используем в повседневной жизни, включают

Сегодня,
компьютеры используют везде. Дома используются компьютеры
за игры, просмотр фильмов, исследования, оплату
счета и бронирование билетов на ж / д и авиалинии.
В школе учащиеся используют компьютеры для выполнения своих
задания.

мобильный
телефоны используются для различных целей, например для отправки
текстовые сообщения, голосовые вызовы, серфинг в Интернете, игры
игры и песни для прослушивания.

Банкомат
электронное телекоммуникационное устройство, которое используется
для вывода денег в любое время из любого места. Стойки для банкоматов
для банкомата. Клиент может снять
деньги до определенного лимита в любое время дня или
ночь.

Ручка
диск особенно используется для хранения большого количества данных
а также используется для передачи данных с одного устройства на
еще один.Например, данные, хранящиеся в компьютере, могут быть
перенесен на флешку. Данные, хранящиеся в этой ручке
диск можно получить в любое время.

Телевидение
электронное устройство, в основном используемое для развлечений и
знания. Он используется для просмотра фильмов в развлекательных целях,
новости для знаний, мультики для детей.

Цифровой
камера — это камера, используемая для съемки фото и видео.Этот
изображения и видео сохраняются для последующего воспроизведения.

Базовые электронные компоненты

Электронный
компоненты являются основными строительными блоками электронного
схема, электронная система или электронное устройство.Oни
контролировать поток электронов в электронной системе или
Электронная схема.

Электронный
компоненты очень маленькие. Следовательно, их легко носить с собой.
из одного места в другое. Стоимость электронных
компонентов также невысокий. Электронные компоненты состоят из двух
или более терминалов.

Когда
а
группа электронных компонентов соединена вместе в
электронная плата, такая как печатная плата (PCB), полезная
электронная схема сформирована.Каждый электронный компонент в
Схема выполняет определенную задачу.

Типы
электронных компонентов

The
электронные компоненты обычно делятся на два типа:

Пассивный
компоненты

Активный
компоненты

Пассивный
компонент

The
электронный компонент, потребляющий энергию
в виде напряжения
из источника, но не производит и не поставляет энергию
называется пассивным электронным компонентом.

1. пассивный
   компоненты не могут контролировать поток электронов или электрического
   ток через цепь, но они ограничивают поток
   электроны или электрический ток.
2. Пассивный
   компоненты не могут усиливать или увеличивать мощность
   электрический сигнал.
3. Пассивный
   компоненты временно сохраняют электрическую энергию в
   форма статического электрического поля или магнитного поля.
4. Пассивный
   компоненты не зависят от внешнего источника энергии или
   напряжение для выполнения определенной операции.

Разные типы
пассивных компонентов

The
различные типы пассивных компонентов включают резисторы,
конденсаторы и катушки индуктивности.

Резисторы

Резисторы
являются обычно используемыми компонентами электронных схем.А
резистор — это электронный компонент, ограничивающий электрическую
ток или поток электронов до определенного уровня. Это состоит из
два терминала.

Как
резистор снижает или ограничивает электрический ток
зависит от величины сопротивления резистора. Резисторы
с большим значением сопротивления уменьшит большое количество
электрический ток, тогда как резисторы с меньшим сопротивлением
значение уменьшит меньшее количество электрического тока.

The
электрический ток, уменьшенный или ограниченный резистором,
измеряется в омах и обозначается символом Ω.
Размер резисторов очень маленький.

Конденсаторы

Конденсаторы
являются наиболее широко используемыми электронными компонентами после
резисторы. Конденсаторы временно хранят электрическую энергию
в виде статического электричества
поле.

Конденсаторы состоят из двух
параллельные электрические проводники, разделенные непроводящей
или изоляционный материал, называемый диэлектриком. Диэлектрические материалы
не позволяйте электричеству течь через них.

Катушки индуктивности

An
индуктор — это пассивный двухконтактный электронный компонент, который
временно сохраняет электрическую энергию в виде
магнитное поле.Он состоит из катушки из медных проводов или
электропроводящие провода. Когда электрический ток
проходит через катушку, создается магнитное поле и
хранится в катушке из медных проводов.

Активный
компонент

The
электронный компонент, который потребляет энергию в виде
напряжение или ток и производит или поставляет энергию в форме
электрического тока или напряжения называется активной составляющей.

1. An
   активный компонент не только контролирует поток электронов или
   электрический ток, но также усиливает или увеличивает мощность
   электронного сигнала.
2. Активный
   компоненты зависят от внешнего источника энергии или
   напряжение для выполнения определенной операции.
3. Когда
   активные компоненты потребляют достаточно напряжения, они запускаются
   операционная.

Различные типы активных
компоненты

различные типы активных компонентов включают диоды,
транзисторы и интегральные схемы (ИС).

Диод

А
диод — полупроводник
компонент, пропускающий большую часть электрического тока или
потоки электронов в одном направлении (прямое направление), в то время как
блокирует большую часть электрического тока в противоположном направлении
(обратное направление).Он состоит из двух клемм или
электроды: катодный и анодный. Материал p-типа диода
действует как анод, а материал n-типа действует как катод.

Когда напряжение подается на диод таким образом, чтобы
положительный вывод подключен к аноду, а отрицательный
клемма подключается к катоду, диод позволяет
электрический ток.

Когда
напряжение подается на диод таким образом, чтобы
положительный вывод подключен к катоду, а отрицательный
клемма подключена к аноду, диод блокирует
электрический ток.

Транзистор

Транзистор — это полупроводниковый компонент, который усиливает или
увеличивает электронные сигналы.Три ученых назвали
Уолтер Браттейн, Уильям Шокли и Дж. Бардин изобрели
транзистор в 1947 году в Bell Laboratories. Транзисторы
изготовлены из полупроводниковых материалов, таких как кремний и
германий.

интегрированный
цепь

An
Интегральная схема представляет собой небольшой полупроводниковый чип, на котором
миллионы электронных компонентов, таких как конденсаторы,
резисторы и транзисторы изготавливаются.Цена
Интегральная схема меньше по сравнению с дискретными компонентами
потому что в интегральной схеме все компоненты
изготовлены на единой микросхеме.

Это
может работать как микропроцессор, усилитель и счетчик. В
изобретение ИС изменило мир электроники.

Что такое электронная схема?

2. Программирование
3. Электроника
4. Компоненты
5. Что такое электронная схема?

Дуг Лоу

Электронная схема — это полный набор проводников, по которым может проходить ток.Цепи обеспечивают путь для прохождения тока. Чтобы быть цепью, этот путь должен начинаться и заканчиваться в одной и той же точке. Другими словами, схема должна образовывать петлю. Электронная схема и электрическая цепь имеют одинаковое определение, но электронные схемы, как правило, являются цепями низкого напряжения.

Например, простая схема может включать в себя два компонента: аккумулятор и лампу. Схема позволяет току течь от батареи к лампе, через лампу, а затем обратно к батарее. Таким образом, схема образует законченный цикл.

Конечно, схемы могут быть более сложными. Однако все схемы можно свести к трем основным элементам:

• Источник напряжения: Источник напряжения заставляет ток течь, например, как батарея.

• Нагрузка: Нагрузка потребляет электроэнергию; он представляет собой фактическую работу, выполняемую схемой. Без нагрузки в цепи нет особого смысла.

  Нагрузка может быть такой же простой, как одиночная лампочка.В сложных схемах нагрузка представляет собой комбинацию компонентов, таких как резисторы, конденсаторы, транзисторы и т. Д.

• Токопроводящий путь: Токопроводящий путь обеспечивает путь, по которому течет ток. Этот маршрут начинается у источника напряжения, проходит через нагрузку и затем возвращается к источнику напряжения. Этот путь должен образовывать петлю от отрицательной стороны источника напряжения к положительной стороне источника напряжения.

В следующих параграфах описывается несколько дополнительных интересных моментов, которые следует иметь в виду, когда вы размышляете о природе основных схем:

• Когда цепь замкнута и образует петлю, которая позволяет току течь, цепь называется замкнутой схемой. Если какая-либо часть цепи отключена или прервана, так что петля не образуется, ток не может течь. В этом случае цепь называется разомкнутая цепь .

  Обрыв цепи — это оксюморон. В конце концов, чтобы считаться схемой, компоненты должны образовывать полный путь. Если путь открыт, это не кругооборот. Следовательно, разомкнутая цепь чаще всего используется для описания цепи, которая вышла из строя либо намеренно (с помощью переключателя), либо из-за какой-либо ошибки, такой как слабое соединение или поврежденный компонент.

• Короткое замыкание относится к цепи, не имеющей нагрузки. Например, если лампа подключена к цепи, но имеется прямое соединение между отрицательной клеммой аккумулятора и ее положительной клеммой.

  Ток при коротком замыкании может быть опасно высоким. Короткое замыкание может привести к повреждению электронных компонентов, вызвать взрыв аккумулятора или вызвать возгорание.

  Короткое замыкание иллюстрирует важный момент, касающийся электрических цепей: возможно — даже обычное — для цепи может быть несколько путей прохождения тока.Ток может протекать через лампу, а также через путь, который напрямую соединяет две клеммы батареи.

  Ток течет везде, где только может. Если в вашей цепи есть два пути, по которым может течь ток, ток не выбирает один из них; он выбирает оба. Однако не все пути равны, поэтому ток не течет одинаково по всем путям.

  Например, ток будет легче проходить через короткое замыкание, чем через лампу. Таким образом, лампа не будет гореть, потому что почти весь ток будет проходить в обход лампы в пользу более легкого пути через короткое замыкание.Даже в этом случае через лампу будет протекать небольшой ток.

Об авторе книги

У Дуга Лоу до сих пор есть набор экспериментатора электроники, который дал ему отец, когда ему было 10 лет. Хотя он стал программистом и написал книги по различным языкам программирования, Microsoft Office, веб-программированию и компьютерам (в том числе 30+ книг для чайников), Дуг никогда не забывал свою первую любовь: электронику.

Электронные схемы

Электронные схемы

Электронные схемы

---

Вот несколько изящных схем, которые вы, возможно, захотите попробовать.Схемы и образцы печатных плат являются файлами GIF и могут отображаться по-разному в некоторых браузерах. Возможно, вы захотите сохранить изображения (особенно шаблоны печатной платы) на жесткий диск, загрузить их в редактор фотографий (Photoshop, Paint Shop Pro, GIMP и т. Д.) И отрегулировать размер перед переносом рисунка на доску. . Возможны варианты печатных плат. Эта страница постоянно дорабатывается, и время от времени будут появляться новые дополнения. Некоторые из этих схем были разработаны мной, большинство — нет.По возможности я старался указать автора схемы, но поскольку многие из этих схем взяты из моей личной коллекции, которую я собирал в течение многих лет, эта информация не всегда доступна.

Вы можете ранжировать схемы в зависимости от того, насколько они вам нравятся, щелкнув значки с изображением молнии. Эти ранги могут основываться на том, насколько вам нравится схема, работает она или не работает для вас, или насколько полезной вы нашли схему.Кроме того, вы можете добавить свои собственные комментарии внизу каждой схемы, заполнив форму.

Цепи делятся на категории, как указано ниже.

Рядом с некоторыми схемами в этом списке есть маленькие маркеры риска (*), которые дают основную информацию о том, была ли схема разработана, протестирована или модифицирована веб-мастером.

Маркер	Описание
*	Схема не тестировалась мной.Поэтому я не буду предлагать гарантии, что они будут работать.
*	Эта схема была разработана мной.
*	Эта схема была разработана не мной, а была изменена мной.

Самые популярные схемы сегодня, вчера и за все время можно найти ниже.

Детальный вид: Вкл. / Выкл.
Контур	Автор	Просмотры	Рейтинг	Комментарии	Маркер
Драйвер люминесцентной лампы 12 В постоянного тока		426,778		63	*
3-канальный анализатор спектра		206 083		20
Инвертор люминесцентных ламп 40 Вт	Барт Милнс	314 858		60	*
Регулируемый стробоскоп		290 948		36
Черный свет		256 211		29
Цвет (звук) Орган		273,122		36
Электронные кости НОВИНКА!		174 237		10	*
Fantastic Atom Expander		187 385		25
Триггер ведомого вспышки		205 022		18	*
Infa-Red Пульт дистанционного управления		614 782		216	*
ИК-удлинитель дистанционного управления НОВИНКА!		116 764		2	*
IR Remote Jammer	Карл	246 809		110	*
ИК пульт дистанционного управления НОВО!		144 596		9	*
ЛАЗЕРНЫЙ передатчик / приемник		392 572		92
Светодиодный охотник		428 828		83	*
Светодиодный метроном НОВИНКА!		90 586		3	*
Светодиодный термометр		194 581		22	*
Детектор света / темноты		293 205		90	*
Простой цветной орган		126 761		10	*
Стробоскоп		261,195		27	*
Диммер TRIAC		534 356		55

Детектор воды

отстойника / трюмной помпы

Детальный вид: Вкл. / Выкл.
Контур	Автор	Просмотры	Рейтинг	Комментарии	Маркер
7-сегментный светодиодный счетчик		899 206		214	*
Регулятор скорости двигателя переменного тока		368 885		29	*
Детектор воздушного потока		238,856		54	*
Кодовый замок цифровой клавиатуры		184 201		20
Сигнализация низкого напряжения		213 706		58	*
Pine Racecar Victory Judge		92,533		1	*
Управление двигателем постоянного тока с широтно-импульсной модуляцией		632,160		94
Датчик дождя		291 725		112	*
Простой детектор лжи		544 706		323
Простой тестер полярности	Дадли Леру	151 267		13	*
Простой сервоконтроллер		207 127		22	*
Простой сенсорный выключатель НОВИНКА!		156 846		5	*
Простой двухскоростной контактор Контроллер двигателя постоянного тока		192,171		21	*
Контроллер шагового двигателя		722 258		120	*
Реле задержки времени		540,369		88
Реле задержки времени II	jawaharlal @ excite.com	229 635		39	*
Сенсорный переключатель		275 969		51	*
Реле с активацией видео		110 351		8	*
Удаление стабилизатора видео / MacroVision	Антти Паарлахти	166 439		10	*
с регулятором		139 307		18	*
Тревога контура провода	Алекс Миден	193 649		27	*

Детальный вид: Вкл. / Выкл.
Контур	Автор	Просмотры	Рейтинг	Комментарии	Маркер
Преобразователь постоянного / постоянного тока с 12 В на 24 В NEW!		296 827		25	*
Преобразователь от 12 В до 120 В переменного тока		1,474,437		689
Преобразователь 6В в 12В		504 805		121
Автоматическое зарядное устройство для свинцово-кислотных аккумуляторов 12 В		911 586		248
Автоматический переключатель мощности с измерением нагрузки		152,448		16	*
Автомобильное зарядное устройство		862 228		159	*
Источник питания с двойной полярностью		356 576		84	*
Источник питания с фиксированным напряжением		295,726		52	*
Сильноточный источник питания		320,196		66	*
Высоковольтный сильноточный источник питания		238,998		35	*
Источник питания LASER		279 121		28
Адаптер для портативного CD-плеера для автомобиля		197 817		12	*
Блок питания		718 574		259	*
Твердотельная катушка Тесла НОВИНКА!		132,537		4
Твердотельная катушка Тесла / генератор высокого напряжения		421 087		50
Бестрансформаторный источник питания		446 631		117	*
Преобразователь напряжения		319 486		51	*
Преобразователь напряжения II		188 247		19	*

Детальный вид: Вкл. / Выкл.
Контур	Автор	Просмотры	Рейтинг	Комментарии	Маркер
Усилитель звука мощностью 22 Вт		568 831		182
FM-передатчик мощностью 3 Вт	Rae XL Ткачик	317,195		83	*
Усилитель мощностью 50 Вт		489 924		74
8 Note Tune Player		129,550		12	*
8-ваттный аудиоусилитель		354 450		67	*
Приемник бортовой радиосвязи		260 239		49	*
Crystal Radio		149,335		53	*
Цифровой регулятор громкости		317 283		47	*
Электронный стетоскоп		296 362		141	*
Аудиомикшер на полевых транзисторах		326,526		41
FM-передатчик		973,411		420
Guitar Fuzz Effect		229 744		52	*
Микрофонный микшер	Анатолий И.Шихатов	235 987		26	*
Синтезатор моно в стерео	или	118 951		18	*
Одноламповый регенеративный радиоприемник NEW!		121 652		4	*
Операционный усилитель Радио		368 022		80	*
Однокристальный AM-радио НОВИНКА!		89 869		2	*
Одночиповое FM-радио НОВИНКА!		156 482		1	*
Измеритель уровня звука		326,434		51	*
Ламповый стереоусилитель	Уэсли Кинслер	253 413		15	*
Тональный контроль		292 142		31
Орган транзистор		183 462		28

---

Вернуться на страницу электроники | Напишите мне | Поиск

---

Все материалы, отмеченные как «мои», являются собственностью Аарона Кейка.Однако вы можете распространять его сколько хотите, с указанием мне или без него. Только не претендуйте на это самостоятельно, и было бы неплохо, если бы вы добавили ссылку на мою страницу. Все остальные материалы являются собственностью их авторов.

Электронные схемы FC

Архив схем FC Новые и обновленные проекты Контроллеры заряда солнечных батарей, темный свет, LVD, метры Светодиодные схемы Светодиодное освещение, 13 цветов, светодиодная радуга Радиолюбительские схемы и радиомаяки, плавный боковой сигнал, антенный тюнер, трубка QRP Music and Audio Circuits: ревербераторы, ламповые усилители, ламповый фузз, ламповый фазер, панорамирование Micro Power FM Broadcasting Circuits FM-стереомодулятор, антенны, моды FM10, жучок на солнечной батарее Схемы широтно-импульсного модулятора (ШИМ), регуляторы скорости двигателя, регуляторы света Телефонные цепи телефонный кран Цепи управления загрузкой компьютера Сброс RS-232, автоматический запуск ПК Цепи испытательного оборудования логический зонд, индикатор осьминога, калибратор частоты Цепи счетчика Гейгера, счетчики, числовой счетчик, восстановление зонда Видеосхемы двигателя удаленной камеры, миниатюрной камеры и телевизора Разные схемы: Программное обеспечение Некоторые из моих Свободное программное обеспечение может быть полезно при работе над электронными проектами. Также см. Мой список Кросс-ассемблеры Linux и связанные проекты. Продажа комплектов солнечной энергии Некоторые из 12-вольтных цепей солнечной энергии, представленных на этом сайте доступны на моем предприятии по производству комплектов, CirKits.com. Вы можете поддержать этот сайт, купив указанные ниже комплекты.

Обзор Архив схем FC содержит множество электронных схем, которые у меня есть разработан и задокументирован. Я попытался включить несколько необычных схем, с упором на полезные приложения вместо простых игрушечных схем.Большинство этих проектов могут быть построены с доступными дискретными составные части. Лишь некоторые схемы здесь основаны на микропроцессорах. Micros может значительно увеличить мощность небольшого устройства, но специализированные инструменты разработки могут сделать проект недоступным для многих любителей и системы разработки обычно устаревают в короткие сроки. Преодолевая эту тенденцию, платформа Arduino — это простая в освоении микропроцессорная платформа с бесплатной разработкой программного обеспечения среда, которая настолько популярна, что должна существовать долгие годы.Есть ряд небольших, недорогих и полнофункциональных компьютеров. платформы, которые можно использовать в качестве контроллеров, к ним относятся Raspberry Pi, BeagleBone и ODROID. Большинство схем на этом сайте нарисованы с открытым исходным кодом. и кросс-платформенный XCircuit программа для рисования схем. Я большой поклонник операционной системы Linux. Если у вас есть запасной компьютер, я рекомендую изучить ряд различных дистрибутивов Linux. Linux Mint с рабочим столом Mate хорошо работает на старом оборудовании.Mint — это производная от Ubuntu. Fedora — еще один популярный дистрибутив, есть много дистрибутивов на выбор. Большой выбор бесплатных приложений для электронного, аудио, видео и любительского радио. доступны в различных дистрибутивах Linux. alexxlab Посмотреть все записи автора alexxlab → Вам также может понравиться Оплата электроэнергии в ленобласти: Оплата онлайн 04.01.202124.11.2020 Размерность напряжения: Единица измерения напряжения, теория и онлайн калькуляторы 30.10.197027.12.2021 Обучение по электробезопасности: Обучение по электробезопасности — очное и дистанционное обучение в области электробезопасности 02.10.197104.01.2022 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт