Электропроводность металлов это: Электропроводность — Физическая энциклопедия

Физический класс | Электронная теория проводимости металлов «

В 1900 году немецкий физик П. Друде создал теорию электропроводности металлов. В основе этой теории лежат следующие допущения:

1. Свободные электроны в металлах ведут себя подобно молекулам идеального газа. Электронный газ подчиняется законам идеального газа.
2. Движение свободных электронов подчиняется законам Ньютона.
3. Свободные электроны в процессе хаотического движения сталкиваются только с ионами кристаллической решетки.
4. При столкновении электронов с ионами электроны передают ионам свою кинетическую энергию полностью.

Согласно данной модели, на отрезке проводника свободные электроны совершают хаотическое тепловое движение. Действующее в проводнике электрическое поле перемещает электроны с небольшой скоростью (скорость дрейфа электронов ~ 0,1 мм/с) вдоль проводника.

Сила тока в проводнике:

I=en<v>S

где n – концентрация свободных электронов в проводнике

<v> – средняя скорость дрейфа электронов

S – поперечное сечение проводника.

С позиции электронной проводимости металлов удалось объяснить причину нагревания проводников при прохождении электрического тока.

Электронная теория проводимости металлов экспериментально подтверждена в 1913 году российскими физиками Л.И. Мандельштамом и Н.Д. Папалекси и в 1916 году американскими физиками Т. Стюартом и  Р. Толменом.

Направление электрического тока в проводнике выбрано в сторону движения положительно заряженных частиц.

Отношение заряда, переносимого через поперечное сечение проводника за интервал времени, к этому интервалу времени называется силой тока.

В СИ [I] = 1 А (Ампер)

Для поддержания электрического тока в проводнике необходимо электрическое поле. Его действие характеризуется электрическим напряжением.

В СИ [U] = 1 В (Вольт)

Для поддержания постоянного направленного движения заряженных частиц в проводнике электрическое поле должно совершать работу. Эту работу принято называть работой электрического тока.

Работа сил электрического поля или работа электрического тока на участке цепи сопротивлением R и за время t равна:

В СИ [A] = 1 Дж (Джоуль)

При нагревание проводника растет его температура, следовательно, увеличивается внутренняя энергия. С прекращением роста температуры проводника он начинает передавать окружающим телам некоторое количество теплоты, равное работе электрического тока. Таким образом, формула A=IUt определяет количество теплоты, переданное проводником другим телам.

Для последовательного соединения проводников удобнее воспользоваться формулой:

При параллельном соединении удобно использовать формулу:

Для характеристики электрических приборов удобнее пользоваться физической величиной, получившей название мощность тока.

Мощность электрического тока равна:

В СИ [P] = 1 Вт (Ватт)

Назад

Удельное сопротивление и электропроводимость: формулы и объяснение

В данной статье мы подробно разберем что такое удельное сопротивление и электропроводность, ясно опишем все формулы с помощью примеров задач, а так же дадим вам таблицу удельных сопротивлений некоторых проводников.

Описание

Закон Ома гласит, что, когда источник напряжения (V) подается между двумя точками в цепи, между ними будет протекать электрический ток (I), вызванный наличием разности потенциалов между этими двумя точками. Количество протекающего электрического тока ограничено величиной присутствующего сопротивления (R). Другими словами, напряжение стимулирует протекание тока (движение заряда), но это сопротивление препятствует этому.

Мы всегда измеряем электрическое сопротивление в Омах, где Ом обозначается греческой буквой Омега, Ω. Так, например: 50 Ом, 10 кОм или 4,7 МОм и т. д. Проводники (например, провода и кабели) обычно имеют очень низкие значения сопротивления (менее 0,1 Ом), и, таким образом, мы можем пренебречь ими, как мы предполагаем в расчетах анализа цепи, что провода имеют ноль сопротивление. С другой стороны, изоляторы (например, пластиковые или воздушные), как правило, имеют очень высокие значения сопротивления (более 50 МОм), поэтому мы можем их игнорировать и для анализа цепи, поскольку их значение слишком велико.

Но электрическое сопротивление между двумя точками может зависеть от многих факторов, таких как длина проводников, площадь их поперечного сечения, температура, а также фактический материал, из которого он изготовлен. Например, давайте предположим, что у нас есть кусок провода (проводник), который имеет длину L, площадь поперечного сечения A и сопротивление R, как показано ниже.

Электрическое сопротивление R этого простого проводника является функцией его длины, L и площади поперечного сечения A. Закон Ома говорит нам, что для данного сопротивления R ток, протекающий через проводник, пропорционален приложенному напряжению, поскольку I = V / R. Теперь предположим, что мы соединяем два одинаковых проводника вместе в последовательной комбинации, как показано на рисунке.

Здесь, соединив два проводника вместе в последовательной комбинации, то есть, к концу, мы фактически удвоили общую длину проводника (2L), в то время как площадь поперечного сечения A остается точно такой же, как и раньше. Но помимо удвоения длины, мы также удвоили общее сопротивление проводника, дав 2R как: 1R + 1R = 2R.

Таким образом , мы можем видеть , что сопротивление проводника пропорционально его длину, то есть: R ∝ L. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально больше, чем оно длиннее.

Отметим также, что, удваивая длину и, следовательно, сопротивление проводника (2R), чтобы заставить тот же ток I, чтобы течь через проводник, как и раньше, нам нужно удвоить (увеличить) приложенное напряжение I = (2 В) / (2R). Далее предположим, что мы соединяем два идентичных проводника вместе в параллельной комбинации, как показано.

Здесь, соединяя два проводника в параллельную комбинацию, мы фактически удвоили общую площадь, дающую 2А, в то время как длина проводников L остается такой же, как у исходного одиночного проводника. Но помимо удвоения площади, путем параллельного соединения двух проводников мы фактически вдвое сократили общее сопротивление проводника, получив 1 / 2R, поскольку теперь каждая половина тока протекает через каждую ветвь проводника.

Таким образом, сопротивление проводника обратно пропорционально его площади, то есть: R 1 / ∝ A или R ∝ 1 / A. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально меньше, чем больше его площадь поперечного сечения.

Кроме того, удваивая площадь и, следовательно, вдвое увеличивая суммарное сопротивление ветви проводника (1 / 2R), для того же тока, чтобы I протекал через параллельную ветвь провода, как раньше, нам нужно только наполовину уменьшить приложенное напряжение I = (1 / 2V) / (1 / 2R).

Н

ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ

ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ

Специально поставленные опыты показали, что при прохождении электрического тока масса металлических проводников остается постоянной, не изменяется и их химический состав. На этом основании можно предположить, что в создании электрического тока в металлах участвуют только электроны. Предположение об электронной природе электрического тока в металлах подтверждено опытами Мандельштама и Папалекси (1913г.) и Стюарта и Толмена (1916г.). Идея этих опытов состоит в том, что поскольку электрон имеет массу, то он должен обладать соответствующей инерцией движения. Следовательно, если проводник из металла привести в движение, то при внезапной его остановке электроны по инерции будут продолжать движение, в результате чего создается эффект электрического тока, который может быть измерен соответствующими достаточно чувствительными приборами. Таким образом, было доказано, что носителями электрического тока в металлах являются свободные электроныили электроны проводимости.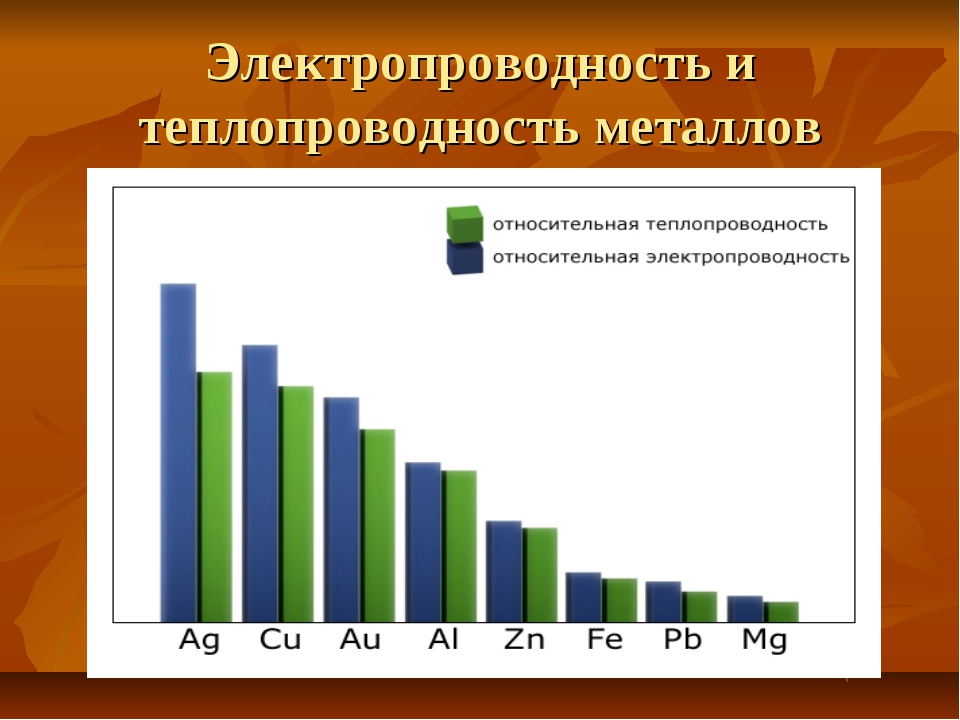

Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий, согласно электронной теории металлов, свойствами идеального газа.

Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. По классической теории Друде-Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории, можно найти среднюю скорость теплового движения электронов

,

которая при Т =300К равна 1,1×10⁵м/с. Тепловое движение электронов, являясь хаотичным, не может привести к возникновению тока.

При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т.е. возникает электрический ток. среднюю скорость упорядоченного движения электронов можно оценить согласно формуле для плотности тока:

.

Выбрав допустимую плотность тока, например для медных проводов 10⁷ А/м², получим, что при концентрации носителей тока n = 8×10²⁸ м^-3 средняя скорость упорядоченного движения электронов равна 7,8×10^-4м/с. Следовательно, << , т.е. даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающего электрический ток, значительно меньше их скорости теплового движения.

Полученный результат, казалось бы, противоречит факту практически мгновенной передачи электрических сигналов на большие расстояния. А дело в том, что замыкание электрической цепи влечет за собой распространение электрического поля со скоростью с ( с = 3×10⁸м/с ). Через время ( l – длина цепи) вдоль цепи установится стационарное электрическое поле и в этой цепи начнется упорядоченное движение электронов. Поэтому электрический ток возникает в цепи практически одновременно с ее замыканием.

Итак, электрический ток в металлах – это поток движущихся электронов. Движение электронов обусловлено существованием электрического поля в проводнике. Так как сила, с которой воздействует поле на электроны, зависит от напряженности Е электрического поля, то можно предположить, что плотность тока j зависит от напряженности Е.

Опыт показывает, что в случае слабых полей для большинства проводников хорошо соблюдается пропорциональность между плотностью тока и напряженностью внешнего поля:

(1)

Данное соотношение носит название закона Ома в дифференциальной форме для плотности тока. Коэффициент пропорциональности l называетсяудельной электропроводностью.

Выражение (1) получено как в классической теории электропроводности металлов Друде-Лоренца, так и в квантовой теории. Однако, хотя формулы для коэффициента электропроводности l в обеих теориях подобны друг другу, значения l существенно различаются. По классической теории удельная электропроводность обратно пропорциональна корню из абсолютной температуры, т.е. λ ~ , а опыт дает λ ~ .

Трудность возникла при оценке длины свободного пробега электронов в металле . Чтобы, пользуясь формулой для электропроводности l, вытекающей из классической теории, получить такие значения l, которые не расходились бы с опытными данными, нужно принять среднюю длину свободного пробега в сотни раз большей, чем период решетки металла. Иными словами, приходится предполагать, что электрон проходит без соударений с ионами решетки сотни межузельных расстояний, что противоречит классической теории Друде-Лоренца.

Выход из этого затруднения был найден в квантовой теории металлов, когда была учтена волновая природа электронов. Квантовая теория рассматривает электрон как частицу, обладающую волновыми свойствами, а движение электронов проводимости в металле как процесс распространения электронных волн.

Совершенно правильная (идеальная) кристаллическая решетка, в узлах которой находятся неподвижные частицы, не должна рассеивать электронные волны. Пучок свободных электронов должен двигаться в ней беспрепятственно, такая решетка не должна оказывать сопротивления прохождению электрического тока. Рассеяние электронных волн возникает лишь с появлением в решетке центров рассеяния неоднородностей (искажений), по размеру превосходящих длину электронных волн. Такими центрами являются, в первую очередь, искажения решетки, возникающие вследствие тепловых колебаний узлов решетки, – флуктуации плотности.При беспорядочном направлении колебаний среди огромного числа ионов, образующих кристаллическую решетку металла, всегда найдутся такие, которые в данный момент двигаются навстречу друг другу. Рассеяния между ними в этот момент окажутся меньше расстояния между узлами в неподвижной решетке, а плотность вещества в микрообъемах, охватывающих эти ионы, – выше средней плотности вещества. В соседних областях возникают микрообъемы, в которых плотность вещества будет ниже среднего ее значения. Подобные местные отступления от среднего значения и представляют собой флуктуации плотности.

Таким образом, вследствие теплового движения узлов решетки твердое тело в каждый момент времени является микроскопически неоднородным: при переходе от одного микрообъема к другому его плотность меняется. Это изменение проявляется тем резче, чем меньшее число ионов охватывают микрообъемы. Как правило, размер таких микрообъемов превосходит длину электронных волн свободных электронов, вследствие чего они являются эффективными центрами рассеяния этих волн. Рассеяние электронных волн на этих центрах, соответствующее соударениям электронов с кристаллической решеткой, и является причиной электрического сопротивления чистых металлов. Чем выше температура металла, тем интенсивнее и чаще возникают флуктуации плотности, тем большее будет рассеяние электронных волн и тем большее будет его сопротивление, а электропроводность – меньшая.

Для зависимости удельной электропроводности от температуры квантовая теория дает хорошо согласующиеся с опытом результаты, а именно λ ~ . Таким образом, удельная электропроводность металла уменьшается с повышением температуры, а это значит, что сопротивление его увеличивается с повышением температуры.

Дата добавления: 2015-10-30; просмотров: 161 | Нарушение авторских прав

mybiblioteka.su — 2015-2020 год. (0.008 сек.)

Почему металлы являются хорошими проводниками электричества?

Здесь мы объяснили характеристики металлов, которые делают их очень хорошими проводниками.

Давайте сначала выясним, в чем разница между хорошим и плохим проводником электричества. Хорошим проводником электричества является любой материал, который позволяет электричеству легко проходить через него без особого сопротивления. С другой стороны, плохой проводник электричества — это тот, который препятствует свободному протеканию электрического тока через него.Другими словами, хороший проводник имеет высокую проводимость и низкое сопротивление, тогда как плохой проводник имеет низкую проводимость и высокое сопротивление.

Свойства металлов

Хотите написать для нас? Что ж, мы ищем хороших писателей, которые хотят распространять информацию. Свяжитесь с нами, и мы поговорим …

Давайте работать вместе!

Все мы знаем, что самая маленькая единица всех элементов — это атом. Атом — это нейтральная частица с положительно заряженным ядром в центре и отрицательно заряженными электронами, движущимися по ряду орбит вокруг ядра.Электропроводность элемента определяется его атомной структурой. В куске металла несколько миллионов атомов. Каждый атом металлического элемента имеет два или три электрона на своей внешней орбите, которые также известны как валентные электроны.

Атомы образуют металлическую связь друг с другом, давая металлу плотноупакованную стабильную структуру. Во время образования этих связей валентные электроны, присутствующие на самой внешней орбите, полностью отделяются от своего родительского атома и могут свободно перемещаться в пространстве, которое находится в решетчатой ​​структуре металла.Когда нет электрического поля, электроны рассеянно перемещаются в разных направлениях. При приложении электрического поля электроны начинают переходить от одного конца металла к другому. Таким образом, большое количество свободно текущих электронов ответственны за проведение электричества через металл. Они действуют как носители заряда и переносят электричество через структуру металла.

Теперь поговорим о том, почему металлы обладают теплопроводностью. Опять же, ответ заключается в том, что в них много свободно движущихся электронов.Благодаря этим свободным электронам тепло легко передается через металлы. Когда к металлу прикладывается тепло, свободные электроны вблизи источника тепла получают много энергии и начинают быстро двигаться. Поскольку металл имеет плотноупакованную структуру, возбужденные свободные электроны сталкиваются с другими соседними электронами. Это помогает мгновенно передать вибрацию на прилегающую территорию. Таким образом, тепло передается через металлические вещества с большой скоростью.

Какие металлы являются хорошими проводниками электричества?

Почти все существующие металлические элементы являются проводниками электричества, хотя проводимость зависит от элемента.Химические элементы, которые считаются очень хорошими проводниками, следующие:

• Медь
• Серебро
• Алюминий
• Золото
• Никель
• Хром
• Утюг
• Магний
• Меркурий
• Титан
• Молибден

Несмотря на то, что проводимость или передача электричества происходит через все металлы одинаково, их уровень электропроводности неодинаков.Другими словами, способность передавать электрический ток у каждого металла разная. Лучшим проводником электричества считается серебро, за ним идет медь, а затем и золото. Когда дело доходит до использования металлов в электротехнике, медь используется более широко, чем серебро. Это потому, что серебро дороже меди. Поэтому низкая стоимость меди делает ее более целесообразным вариантом для практического использования в различном электрическом и электрическом оборудовании.

металлоконструкций

Точки плавления и кипения

Металлы имеют тенденцию к высоким температурам плавления и кипения из-за прочности металлической связи.Прочность связи варьируется от металла к металлу и зависит от числа электронов, которые каждый атом делокализует в море электронов, и от упаковки.

Металлы группы 1, такие как натрий и калий, имеют относительно низкие температуры плавления и кипения, главным образом потому, что каждый атом имеет только один электрон, вносящий вклад в связь, но есть и другие проблемы:

• Элементы группы 1 также неэффективно упакованы (с 8 координатами), поэтому они не образуют столько связей, сколько большинство металлов.

• У них относительно большие атомы (это означает, что ядра находятся на некотором расстоянии от делокализованных электронов), что также ослабляет связь.

Электропроводность

Металлы проводят электричество. Делокализованные электроны могут свободно перемещаться по структуре в трехмерном пространстве. Они могут пересекать границы зерен. Даже несмотря на то, что узор может быть нарушен на границе, пока атомы соприкасаются друг с другом, металлическая связь все еще присутствует.

Жидкие металлы также проводят электричество, показывая, что, хотя атомы металла могут свободно перемещаться, делокализация остается в силе до тех пор, пока металл не закипит.

Теплопроводность

Металлы — хорошие проводники тепла. Тепловая энергия улавливается электронами в качестве дополнительной кинетической энергии (это заставляет их двигаться быстрее). Энергия передается по всему остальному металлу движущимися электронами.

Прочность и технологичность

Ковкость и пластичность

Металлы описываются как ковкий (можно раскалывать на листы) и пластичный (можно вытягивать на проволоку).Это происходит из-за способности атомов перемещаться друг по другу в новые позиции без разрыва металлической связи.

Если приложить небольшое напряжение к металлу, слои атомов начнут катиться друг по другу. Если напряжение снова будет снято, они вернутся в исходное положение. В этих условиях металл считается эластичным по шкале .

Если приложить большее напряжение, атомы перекатываются друг на друга в новое положение, и металл навсегда изменяется.

Твердость металлов

Этому катанию слоев атомов друг на друга препятствуют границы зерен, потому что ряды атомов не выстраиваются должным образом. Отсюда следует, что чем больше имеется границ зерен (чем меньше отдельные кристаллические зерна), тем тверже становится металл.

В противоположность этому, поскольку границы зерен — это области, где атомы не находятся в таком хорошем контакте друг с другом, металлы имеют тенденцию к разрушению на границах зерен.Увеличение количества границ зерен не только делает металл тверже, но и делает его более хрупким.

Контроль размера кристаллических зерен

Если у вас чистый кусок металла, вы можете контролировать размер зерен с помощью термообработки или обработки металла.

При нагревании металла атомы встряхиваются в более правильное расположение — уменьшается количество границ зерен и, таким образом, металл становится мягче.Если стучать по металлу в холодном состоянии, образуется много мелких зерен. Таким образом, холодная обработка делает металл более твердым. Чтобы восстановить его работоспособность, вам необходимо повторно нагреть его.

Вы также можете нарушить регулярное расположение атомов, вставив в структуру атомы немного другого размера. Сплавы , такие как латунь (смесь меди и цинка), тверже, чем исходные металлы, поскольку неоднородность структуры помогает предотвратить скольжение рядов атомов друг по другу.

Удельное электрическое сопротивление и проводимость — Infogalactic: ядро ​​планетарных знаний

Удельное электрическое сопротивление (также известное как удельное электрическое сопротивление , удельное электрическое сопротивление или объемное удельное сопротивление ) является внутренним свойством, которое количественно определяет, насколько сильно данный материал противостоит прохождению электрического тока. Низкое удельное сопротивление указывает на материал, который легко пропускает электрический ток. Удельное сопротивление обычно обозначается греческой буквой ρ (ро).Единицей измерения удельного электрического сопротивления в системе СИ является ом · метр (Ом · м) ^{[1] [2] [3]} , хотя также используются другие единицы, такие как ом · сантиметр (Ом · см). Например, если твердый куб материала размером 1 м × 1 м × 1 м имеет контакты листов на двух противоположных гранях, а сопротивление между этими контактами составляет 1 Ом, то удельное сопротивление материала составляет 1 Ом · м.

Электропроводность или Удельная проводимость является величиной, обратной удельному электрическому сопротивлению, и измеряет способность материала проводить электрический ток.Обычно он обозначается греческой буквой σ (сигма), но иногда также используются κ (каппа) (особенно в электротехнике) или γ (гамма). Его единица СИ — сименс на метр (См / м), а единица CGSE — обратная секунда (с ^-1 ).

Другой родственной величиной, широко используемой в литературе по физике плазмы, является коэффициент магнитной диффузии, определяемый как где — магнитная проницаемость. Единицей измерения коэффициента магнитной диффузии в СИ является.

Определение

Резисторы или проводники постоянного сечения

Кусок резистивного материала с электрическими контактами на обоих концах.

Многие резисторы и проводники имеют однородное поперечное сечение с равномерным течением электрического тока и изготовлены из одного материала. (См. Диаграмму справа.) В этом случае удельное электрическое сопротивление ρ (греч. Rho) определяется как:

где

R — электрическое сопротивление однородного образца материала (измеряется в Ом, Ом)

— длина отрезка материала (в метрах, м)

A — площадь поперечного сечения образца (измеряется в квадратных метрах, м ² ).

Причина, по которой удельное сопротивление определяется таким образом, заключается в том, что оно делает сопротивление внутренним свойством , в отличие от сопротивления. Все медные провода, независимо от их формы и размера, имеют примерно одинаковое сопротивление , но длинный тонкий медный провод имеет намного большее сопротивление , чем толстый короткий медный провод. Каждый материал имеет свое собственное удельное сопротивление — например, удельное сопротивление резины намного больше, чем удельное сопротивление меди.

В гидравлической аналогии прохождение тока через материал с высоким сопротивлением похоже на проталкивание воды по трубе, заполненной песком, тогда как прохождение тока через материал с низким сопротивлением похоже на проталкивание воды через пустую трубу.Если трубы одинакового размера и формы, у трубы, заполненной песком, будет более высокое сопротивление потоку. Однако сопротивление не только определяется наличием или отсутствием песка. Это также зависит от длины и ширины трубы: короткие или широкие трубы имеют меньшее сопротивление, чем узкие или длинные.

Приведенное выше уравнение можно транспонировать, чтобы получить закон Пуйе (названный в честь Клода Пуйе):

Сопротивление данного материала увеличивается с увеличением длины, но уменьшается с увеличением площади поперечного сечения.Из приведенных выше уравнений удельное сопротивление выражается в единицах СИ в оммометрах. Также иногда используются другие единицы измерения, такие как ом⋅см или ом⋅дюйм.

Формулу можно использовать для интуитивного понимания значения удельного сопротивления. Например, если и (образующий куб с идеально проводящими контактами на противоположных гранях), то сопротивление этого элемента в омах численно равно удельному сопротивлению материала, из которого он сделан, в ом-метрах. Аналогичным образом, материал 1 Ом · см будет иметь сопротивление 1 Ом при контакте с противоположными гранями куба 1 см × 1 см × 1 см.

Электропроводность σ (греч. Сигма) определяется как величина, обратная удельному сопротивлению:

Электропроводность в системе СИ — сименс на метр (См / м).

Общее определение

Приведенное выше определение относится к резисторам или проводникам с одинаковым поперечным сечением, где ток течет через них равномерно. Более основное и общее определение начинается с того факта, что электрическое поле внутри материала заставляет электрический ток течь.Удельное электрическое сопротивление ρ определяется как отношение электрического поля к плотности создаваемого им тока:

где

ρ — удельное сопротивление материала проводника (измеряется в Ом⋅метрах, Ом⋅м),

E — величина электрического поля (в вольт на метр, В⋅м ⁻¹ ),

J — величина плотности тока (в амперах на квадратный метр, A⋅m ⁻² ),

, в котором E и J находятся внутри проводника.

Электропроводность обратная:

Например, резина — это материал с большим ρ и малым σ , потому что даже очень большое электрическое поле в резине почти не вызывает протекания тока через него. С другой стороны, медь представляет собой материал с малым размером ρ и большим σ , потому что даже небольшое электрическое поле пропускает через него большой ток.

Причины проводимости

Упрощенная теория полос

Квантовая механика утверждает, что электроны в атоме не могут принимать произвольное значение энергии.Напротив, электроны должны занимать фиксированные уровни энергии, и значения между этими уровнями невозможны. Когда большое количество таких разрешенных энергетических уровней расположены близко друг к другу (в энергетическом пространстве) — то есть имеют схожие (незначительно отличающиеся) — энергии, мы можем говорить об этих энергетических уровнях вместе как об «энергетической зоне». В материале может быть много таких энергетических зон, в зависимости от атомного номера {числа электронов (если атом нейтрален)} и их распределения (помимо внешних факторов, таких как изменение энергетических зон окружающей средой).

Электроны материала стремятся минимизировать общую энергию материала, переходя в состояния с низкой энергией; однако принцип исключения Паули означает, что все они не могут перейти в самое низкое состояние. Вместо этого электроны «заполняют» зонную структуру, начиная снизу. Характерный энергетический уровень, до которого заполнились электроны, называется уровнем Ферми. Положение уровня Ферми относительно зонной структуры очень важно для электропроводности: только электроны на энергетических уровнях вблизи уровня Ферми могут свободно перемещаться, поскольку электроны могут легко перепрыгивать между частично занятыми состояниями в этой области.Напротив, состояния с низкой энергией все время жестко заполнены фиксированным числом электронов, а состояния с высокой энергией всегда пусты.

В металлах есть много уровней энергии вблизи уровня Ферми, а это означает, что существует много электронов, которые могут двигаться. Это причина высокой электронной проводимости металлов.

Важная часть теории зон состоит в том, что могут существовать запрещенные зоны по энергии: интервалы энергии, которые не содержат уровней энергии.В изоляторах и полупроводниках количество электронов оказывается как раз достаточным для заполнения определенного целого числа низкоэнергетических зон точно до границы. В этом случае уровень Ферми попадает в запрещенную зону. Поскольку вблизи уровня Ферми нет доступных состояний, а электроны не могут свободно перемещаться, электронная проводимость очень мала.

Металлы

Металл состоит из решетки атомов, каждый из которых имеет внешнюю оболочку из электронов, которые свободно отделяются от своих родительских атомов и перемещаются по решетке.Это также известно как положительная ионная решетка. ^[4] Это «море» диссоциируемых электронов позволяет металлу проводить электрический ток. Когда на металл подается разность электрических потенциалов (напряжение), возникающее электрическое поле заставляет электроны дрейфовать к положительному выводу. Фактическая скорость дрейфа электронов очень мала, порядка метра в час. Однако, поскольку электроны плотно упакованы в материале, электромагнитное поле распространяется через металл со скоростью света. ^[5] Механизм аналогичен передаче количества движения шарикам в люльке Ньютона. ^[6]

Металлы обладают стойкостью при температуре около комнатной. Основная причина этого сопротивления — столкновение электронов с атомами, составляющими кристаллическую решетку. Это действует, чтобы рассеять электроны и потерять свою энергию при столкновениях, а не при линейном движении через решетку. В металлах с примесями также вносят вклад в сопротивление возникающие дефекты решетки. ^[7]

Чем больше площадь поперечного сечения проводника, тем больше электронов на единицу длины может переносить ток. В результате сопротивление меньше в проводниках с большим поперечным сечением. Количество случаев рассеяния, с которыми сталкивается электрон, проходящий через материал, пропорционально длине проводника. Следовательно, чем длиннее проводник, тем выше сопротивление. На сопротивление также влияют разные материалы. ^[8]

В полупроводниках и изоляторах

Основные статьи: Полупроводник и изолятор (электричество)

В металлах уровень Ферми лежит в зоне проводимости (см. Зонную теорию выше), давая начало свободным электронам проводимости.Однако в полупроводниках положение уровня Ферми находится внутри запрещенной зоны, примерно на полпути между минимумом зоны проводимости и максимумом валентной зоны для собственных (нелегированных) полупроводников. Это означает, что при 0 градусах Кельвина свободных электронов проводимости нет, а сопротивление бесконечно. Однако сопротивление продолжает уменьшаться по мере увеличения плотности носителей заряда в зоне проводимости. В примесных (легированных) полупроводниках атомы примеси увеличивают концентрацию основных носителей заряда, отдавая электроны в зону проводимости или принимая дырки в валентной зоне.Для обоих типов донорных и акцепторных атомов увеличение плотности примеси снижает сопротивление. Следовательно, высоколегированные полупроводники ведут себя металлически. При очень высоких температурах вклад термически генерируемых носителей преобладает над вкладом атомов легирующей примеси, и сопротивление экспоненциально уменьшается с температурой.

В ионных жидкостях / электролитах

Основная статья: Проводимость (электролитическая)

В электролитах электрическая проводимость осуществляется не зонными электронами или дырками, а движущимися целыми частицами атомов (ионами), каждый из которых несет электрический заряд.Удельное сопротивление ионных жидкостей сильно различается в зависимости от концентрации — в то время как дистиллированная вода является почти изолятором, соленая вода является разумным проводником электричества. В биологических мембранах токи переносятся ионными солями. Небольшие отверстия в мембранах, называемые ионными каналами, избирательны по отношению к определенным ионам и определяют сопротивление мембраны.

Сверхпроводимость

Основная статья: Сверхпроводимость

Удельное электрическое сопротивление металлического проводника постепенно уменьшается при понижении температуры.В обычных проводниках, таких как медь или серебро, это уменьшение ограничено примесями и другими дефектами. Даже вблизи абсолютного нуля реальный образец нормального проводника показывает некоторое сопротивление. В сверхпроводнике сопротивление резко падает до нуля, когда материал охлаждается ниже критической температуры. Электрический ток, протекающий в петле из сверхпроводящего провода, может сохраняться бесконечно без источника питания. ^[9]

В 1986 году исследователи обнаружили, что некоторые керамические материалы из купрата и перовскита имеют критическую температуру выше 90 К (-183 ° C). ^{[необходима ссылка ]} Такая высокая температура перехода теоретически невозможна для обычного сверхпроводника, поэтому исследователи назвали эти проводники высокотемпературными сверхпроводниками . Жидкий азот кипит при 77 К, что облегчает выполнение многих экспериментов и применений, которые менее практичны при более низких температурах. В обычных сверхпроводниках электроны удерживаются вместе парами за счет притяжения, связанного с решеточными фононами. Лучшая доступная модель высокотемпературной сверхпроводимости все еще довольно груба.Существует гипотеза, что спаривание электронов в высокотемпературных сверхпроводниках обеспечивается короткодействующими спиновыми волнами, известными как парамагноны. ^[10]

Плазма

Основная статья: Плазма (физика)

Молния — это пример плазмы, присутствующей на поверхности Земли. Обычно молния разряжает 30 000 ампер при напряжении до 100 миллионов вольт и излучает свет, радиоволны, рентгеновские лучи и даже гамма-лучи. ^[11] Температура плазмы при молнии может приближаться к 28 000 Кельвинов (28 000 ° C) (50 000 ° F), а плотность электронов может превышать 10 ²⁴ м ⁻³ .

Плазма — очень хорошие электрические проводники, и электрические потенциалы играют важную роль. Потенциал, существующий в среднем в пространстве между заряженными частицами, независимо от того, как его можно измерить, называется потенциалом плазмы или потенциалом пространства . Если электрод вставлен в плазму, его потенциал обычно значительно ниже потенциала плазмы из-за того, что называется оболочкой Дебая. Хорошая электропроводность плазмы делает ее электрические поля очень маленькими.Это приводит к важной концепции квазинейтральности , согласно которой плотность отрицательных зарядов примерно равна плотности положительных зарядов в больших объемах плазмы ( n _e = n _i ), но на шкале длины Дебая может быть дисбаланс заряда. В особом случае, когда образуются двойные слои , разделение зарядов может увеличиваться на несколько десятков длин Дебая.

Величина потенциалов и электрических полей должна определяться другими способами, кроме простого определения чистой плотности заряда.Типичный пример — предположить, что электроны удовлетворяют соотношению Больцмана:

Дифференциация этого отношения дает возможность вычислить электрическое поле по плотности:

Возможно получение не квазинейтральной плазмы. Электронный луч, например, имеет только отрицательные заряды. Плотность ненейтральной плазмы обычно должна быть очень низкой или очень маленькой. В противном случае отталкивающая электростатическая сила рассеивает его.

В астрофизической плазме дебаевское экранирование предотвращает прямое воздействие электрических полей на плазму на больших расстояниях, т. Е. Больших, чем длина Дебая. Однако наличие заряженных частиц заставляет плазму генерировать магнитные поля и воздействовать на них. Это может вызвать и действительно вызывает чрезвычайно сложное поведение, такое как образование двойных слоев плазмы, объекта, который разделяет заряд на несколько десятков длин Дебая. Динамика плазмы, взаимодействующей с внешними и самогенерируемыми магнитными полями, изучается в академической дисциплине магнитогидродинамика.

Плазма часто называют четвертым состоянием вещества, после твердого тела, жидкостей и газов. ^{[12] [13]} Он отличается от этих и других низкоэнергетических состояний материи. Хотя он тесно связан с газовой фазой в том смысле, что он также не имеет определенной формы или объема, он отличается во многих отношениях, включая следующее:

Имущество	Газ	Плазма
Электропроводность	Очень низкий : Воздух является отличным изолятором до тех пор, пока он не распадется на плазму при напряженности электрического поля выше 30 киловольт на сантиметр. [14]	Обычно очень высокая : Для многих целей проводимость плазмы можно рассматривать как бесконечную.
Самостоятельно действующие виды	One : Все частицы газа ведут себя одинаково, под действием силы тяжести и столкновений друг с другом.	Два или три : Электроны, ионы, протоны и нейтроны можно различать по знаку и величине их заряда, так что они ведут себя независимо во многих обстоятельствах, с разными объемными скоростями и температурами, что допускает такие явления, как новые типы волн и нестабильность.
Распределение скоростей	Максвелловский : Столкновения обычно приводят к максвелловскому распределению скоростей всех частиц газа с очень небольшим количеством относительно быстрых частиц.	Часто не максвелловский. : Столкновительные взаимодействия часто бывают слабыми в горячей плазме, и внешнее воздействие может увести плазму далеко от локального равновесия и привести к значительной популяции необычно быстрых частиц.
Взаимодействия	Двоичный : Столкновения двух частиц являются правилом, столкновения трех тел крайне редки.	Коллективный : Волны или организованное движение плазмы очень важны, потому что частицы могут взаимодействовать на больших расстояниях посредством электрических и магнитных сил.

Удельное сопротивление и проводимость различных материалов

Основная статья: Удельное электрическое сопротивление элементов (страница данных)

• Металлический проводник имеет высокую проводимость и низкое удельное сопротивление.
• Изолятор, подобный стеклу, имеет низкую проводимость и высокое сопротивление.
• Электропроводность полупроводника обычно является промежуточной, но сильно варьируется в зависимости от различных условий, таких как воздействие на материал электрических полей или определенных частот света, и, что наиболее важно, от температуры и состава полупроводникового материала.

Степень легирования полупроводников имеет большое значение для проводимости. В некотором смысле, большее количество легирования приводит к более высокой проводимости. Электропроводность водного раствора сильно зависит от концентрации растворенных в нем солей и других химических веществ, которые ионизируются в растворе.Электропроводность образцов воды используется в качестве индикатора того, насколько образец не содержит соли, ионов или примесей; чем чище вода, тем ниже проводимость (тем выше удельное сопротивление). Измерения электропроводности в воде часто обозначаются как удельная проводимость по отношению к проводимости чистой воды при 7002298150000000000 25 ° C. ЕС-метр обычно используется для измерения проводимости в растворе. Приблизительное резюме выглядит следующим образом:

В этой таблице показаны удельное сопротивление, проводимость и температурный коэффициент различных материалов при 20 ° C (68 ° F, 293 K)

Материал	ρ (Ом · м) при 7002293150000000000 ♠ 20 ° C	σ (См / м) при 7002293150000000000 ♠ 20 ° C	Температура Коэффициент [примечание 1] (K -1 )	Номер ссылки
Углерод (графен)	6992100000000000000 ♠ 1.00 × 10 −8	7008100000000000000 ♠ 1,00 × 10 8	-0,0002	[15]
Серебристый	0000000159″> 699215 00000000 ♠ 1,59 × 10 −8	7007630000000000000 ♠ 6,30 × 10 7	0,0038	[16] [17]
Медь	6992167999999999999 ♠ 1,68 × 10 −8	7007596000000000000 ♠ 5.96 × 10 7	0.003862	[18]
Отожженная медь [примечание 2]	6992172000000000000 ♠ 1,72 × 10 −8	7007580000000000000 ♠ 5.80 × 10 7	0,00393	[19]
Золото [примечание 3]	6992244000000000000 ♠ 2,44 × 10 −8	7007410000000000000 ♠ 4,10 × 10 7	0,0034	[16]
Алюминий [примечание 4]	0000000282″> 6992282000000000000 ♠ 2.82 × 10 −8	7007350000000000000 ♠ 3,50 × 10 7	0,0039	[16]
Кальций	6992335999999999999 ♠ 3,36 × 10 −8	7007298000000000000 ♠ 2,98 × 10 7	0,0041
Вольфрам	6992560000000000000 ♠ 5.60 × 10 −8	700717 00000000 ♠ 1,79 × 10 7	0,0045	[16]
цинк	69925 000000000 ♠ 5.90 × 10 −8	700716 00000000 ♠ 1,69 × 10 7	0,0037	[20]
Никель	699269 00000000 ♠ 6,99 × 10 −8	43E7″> 7007143000000000000 ♠ 1,43 × 10 7	0,006
Литий	6992928000000000000 ♠ 9,28 × 10 −8	7007108000000000000 ♠ 1,08 × 10 7	0,006
Утюг	6993100000000000000 ♠ 1.00 × 10 −7	7007100000000000000 ♠ 1.00 × 10 7	0,005	[16]
Платина	6993106000000000000 ♠ 1,06 × 10 −7	7006943000000000000 ♠ 9,43 × 10 6	0,00392	[16]
Олово	699310 00000000 ♠ 1,09 × 10 −7	7006917000000000000 ♠ 9,17 × 10 6	0. 0045
Углеродистая сталь (1010)	6993143000000000000 ♠ 1,43 × 10 −7	700669 00000000 ♠ 6,99 × 10 6		[21]
Свинец	6993220000000000000 ♠ 2,20 × 10 −7	7006455000000000000 ♠ 4.55 × 10 6	0,0039	[16]
Титан	6993420000000000000 ♠ 4,20 × 10 −7	7006238000000000000 ♠ 2.38 × 10 6	0,0038
Электротехническая сталь с ориентированной зернистостью	6993459999999999999 ♠ 4,60 × 10 −7	7006217000000000000 ♠ 2,17 × 10 6		[22]
Манганин	000000482″> 6993482000000000000 ♠ 4,82 × 10 −7	7006206999999999999 ♠ 2,07 × 10 6	0,000002	[23]
Константан	6993489999999999999 ♠ 4.90 × 10 −7	7006204000000000000 ♠ 2,04 × 10 6	0,000008	[24]
Нержавеющая сталь [примечание 5]	69936 000000000 ♠ 6,90 × 10 −7	7006145000000000000 ♠ 1,45 × 10 6		[25]
Меркурий	6993979999999999999 ♠ 9.80 × 10 −7	7006102000000000000 ♠ 1.02 × 10 6	0.0009	[23]
Нихром [примечание 6]	0000011″> 6994110000000000000 ♠ 1,10 × 10 −6	7005670000000000000 ♠ 6,7 × 10 5	6996400000000000000 ♠ 0,0004	[16]
GaAs	6997100000000000000 ♠ 1,00 × 10 −3 до 7008100000000000000 ♠ 1,00 × 10 8	6992100000000000000 ♠ 1,00 × 10 −8 до 7003100000000000000 ♠ 10 3		[26]
Углерод (аморфный)	6996500000000000000 ♠ 5.От 00 × 10 −4 до 6996800000000000000 ♠ 8,00 × 10 −4	7003125000000000000 ♠ 1,25 × 10 3 до 7003200000000000000 ♠ 2 × 10 3	-0,0005	[16] [27]
Углерод (графит) [примечание 7]	5E-6″> 6994249999999999999 ♠ 2,50 × 10 −6 до 6994499999999999999 ♠ 5,00 × 10 −6 // базальная плоскость 6997300000000000000 ♠ 3,00 × 10 −3 ⊥ базальная плоскость	7005200000000000000 ♠ 2.00 × 10 5 до 7005300000000000000 ♠ 3,00 × 10 5 // базисная плоскость 7002330000000000000 ♠ 3,30 × 10 2 ⊥ базальная плоскость		[28]
ПЕДОТ: PSS	6997100000000000000 ♠ 1.00 × 10 −3 до 69900000000000 ♠ 1.00 × 10 −1	7001100000000000000 ♠ 1 × 10 от 1 до 7003460000000000000 ♠ 4,6 × 10 3	?	[29]
Германий [примечание 8]	6999459999999999999 ♠ 4.60 × 10 −1	2,17	-0,048	[16] [17]
Морская вода [примечание 9]	6999200000000000000 ♠ 2,00 × 10 -1	8″> 7000480000000000000 ♠ 4.80		[30]
Вода для плавательного бассейна [примечание 10]	6999333000000000000 ♠ 3,33 × 10 −1 до 6999400000000000000 ♠ 4,00 × 10 −1	6999250000000000000 ♠ 0.От 25 до 6999300000000000000 0,30		[31]
Питьевая вода [примечание 11]	7001200000000000000 ♠ 2,00 × 10 от 1 до 7003200000000000000 ♠ 2,00 × 10 3	6996500000000000000 5,00 × 10 −4 до 6998500000000000000 ♠ 5,00 × 10 −2		[необходима ссылка ]
Кремний [примечание 8]	7002640000000000000 ♠ 6.40 × 10 2	6997156000000000000 ♠ 1,56 × 10 −3	3001250000000000000 ♠ −0,075	[16]
Дерево (влажное)	7003100000000000000 ♠ 1.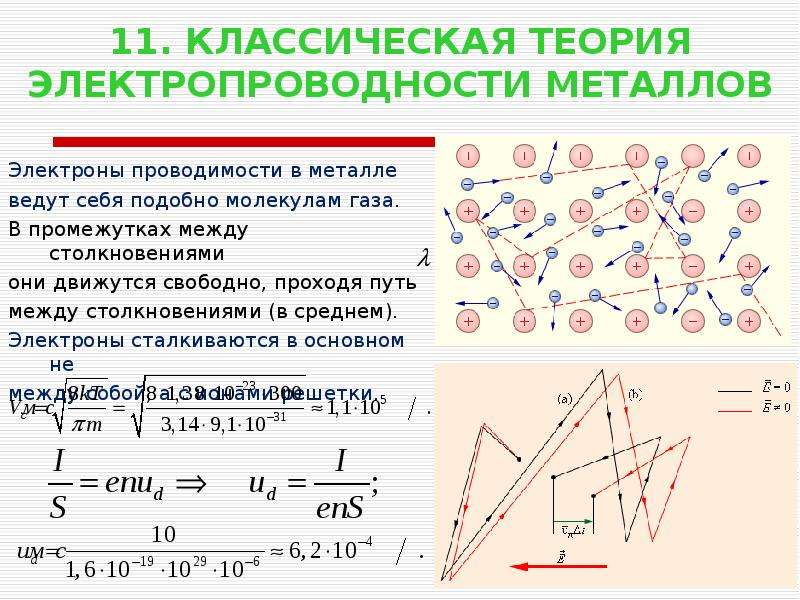 00 × 10 3 до 7004100000000000000 ♠ 1.00 × 10 4	6996100000000000000 ♠ 10 −4 до 6997100000000000000 ♠ 10 −3		[32]
Деионизированная вода [примечание 12]	7005180000000000000 ♠ 1.80 × 10 5	6994550000000000000 ♠ 5,50 × 10 −6		[33]
Стекло	7011100000000000000 ♠ 1.00 × 10 11 до 7015100000000000000 ♠ 1.00 × 10 15	6985100000000000000 ♠ 10 −15 до 69800000000000 ♠ 10 −11	?	[16] [17]
Твердая резина	7013100000000000000 ♠ 1.00 × 10 13	6986100000000000000 ♠ 10 −14	?	[16]
Древесина (сушка в духовке)	7014100000000000000 ♠ 1. 00 × 10 14 до 7016100000000000000 ♠ 1,00 × 10 16	6984100000000000000 ♠ 10 −16 до 6986100000000000000 ♠ 10 −14		[32]
сера	7015100000000000000 ♠ 1.00 × 10 15	6984100000000000000 ♠ 10 −16	?	[16]
Воздух	7016130000000000000 ♠ 1,30 × 10 16 до 7016330000000000000 ♠ 3.30 × 10 16	6985300000000000000 ♠ 3 × 10 −15 до 6985800000000000000 ♠ 8 × 10 −15		[34]
Углерод (алмаз)	7012100000000000000 ♠ 1.00 × 10 12	~ 6987100000000000000 ♠ 10 −13		[35]
Плавленый кварц	5E17″> 7017750000000000000 ♠ 7,50 × 10 17	6982130000000000000 ♠ 1,30 × 10 −18	?	[16]
ПЭТ	7021100000000000000 ♠ 1.00 × 10 21	69799999999999 ♠ 10 −21	?
Тефлон	7023100000000000000 ♠ 1.00 × 10 23 до 7025100000000000000 ♠ 1.00 × 10 25	6975100000000000000 ♠ 10 −25 до 6977100000000000000 ♠ 10 −23	?

Эффективный температурный коэффициент зависит от температуры и степени чистоты материала. Значение 20 ° C является приблизительным при использовании при других температурах.Например, для меди коэффициент становится ниже при более высоких температурах, а значение 0,00427 обычно указывается как 7002273149999999999 0 ° C. ^[36]

Чрезвычайно низкое удельное сопротивление (высокая проводимость) серебра характерно для металлов. Джордж Гамов аккуратно резюмировал природу взаимодействия металлов с электронами в своей научно-популярной книге One, Two, Three … Infinity (1947): «Металлические вещества отличаются от всех других материалов тем, что внешние оболочки их атомов связаны довольно слабо и часто позволяют одному из своих электронов уйти на свободу.Таким образом, внутренняя часть металла заполнена большим количеством непривязанных электронов, которые бесцельно путешествуют, как толпа перемещенных лиц. Когда на металлическую проволоку действует электрическая сила, приложенная к ее противоположным концам, эти свободные электроны устремляются в направлении силы, образуя, таким образом, то, что мы называем электрическим током ». С технической точки зрения, модель свободных электронов дает базовое описание потока электронов. в металлах.

Древесина широко считается чрезвычайно хорошим изолятором, но ее удельное сопротивление чувствительно зависит от содержания влаги, при этом влажная древесина является как минимум в 7010100000000000000 ♠ 10 ¹⁰ худшим изолятором, чем высушенная в печи.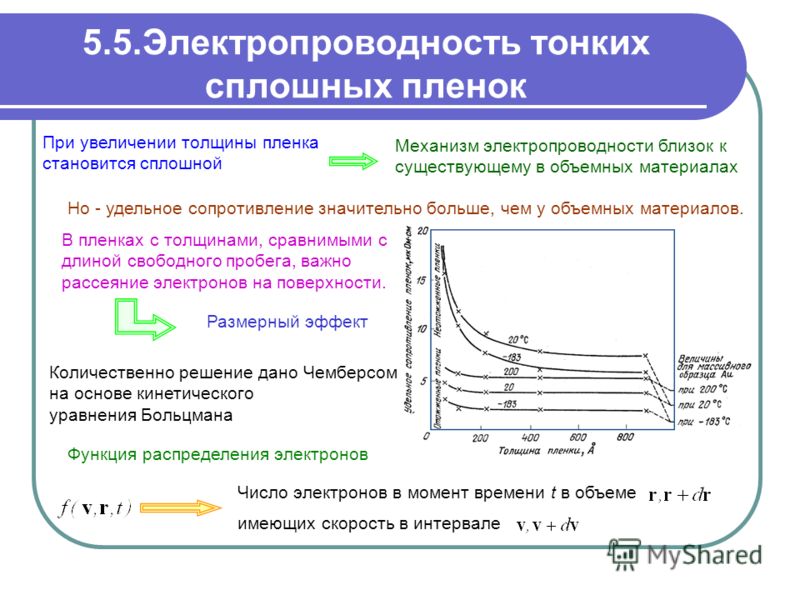 ^[32] В любом случае достаточно высокое напряжение — например, при ударах молнии или некоторых высоковольтных линиях электропередач — может привести к пробою изоляции и риску поражения электрическим током даже при явно сухой древесине.

Температурная зависимость

Линейное приближение

Удельное электрическое сопротивление большинства материалов изменяется в зависимости от температуры. Если температура T не слишком сильно меняется, обычно используется линейное приближение:

, где называется температурным коэффициентом удельного сопротивления , — это фиксированная эталонная температура (обычно комнатная температура) и удельное сопротивление при температуре.Параметр представляет собой эмпирический параметр, подобранный на основе данных измерений. Поскольку линейное приближение является только приближением, оно отличается для разных эталонных температур. По этой причине принято указывать температуру, которая была измерена при помощи суффикса, например, и соотношение сохраняется только в диапазоне температур вокруг эталона.