ОПРЕДЕЛЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЕМКОСТИ КОНДЕНСАТОРА БАЛЛИСТИЧЕСКИМ МЕТОДОМ. Емкость конденсатора определение

определение емкости конденсатора_Панферов

Чтобы внешние поля не оказывали влияния на ёмкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле заряда обкладок было сосредоточено только между ними. Этому условию удовлетворяют две пластины, расположенные близко друг к другу, два коаксиальных цилиндра и две концентрические сферы. Соответственно бывают плоские, цилиндрические и сферические конденсаторы.

Электроёмкость конденсатора зависит от геометрических размеров и формы обкладок, расстояния между ними и диэлектрической проницаемости среды между обкладками. Для плоского конденсатора она равна

где S – площадь обкладки,d – расстояние между обкладками.

Помимо ёмкости, каждый конденсатор характеризуется предельным напряжением Umax, которое выдерживает конденсатор без пробоя диэлектрика. Пробой диэлектрика происходит в результате разрядки конденсатора, диэлектрик при этом теряет свои диэлектрические свойства и конденсатор выходит из строя.

V.Контрольные вопросы

1.Какова цель работы?

2.Как выглядит электрическая схема экспериментальной установки?

3.Какова программа работы?

4.Какие величины задаются постоянными?

5.Какие величины определяются прямыми и косвенными измерениями?

6.Какие нужно построить графики?

7.Что называется электроёмкостью уединённого проводника?

8.В каких единицах измеряется электроёмкость?

9.От чего зависит величина электроёмкости?

10.Что такое конденсатор? Для чего он служит?

11.От чего зависит ёмкость конденсатора?

12.Как рассчитать погрешность измерения напряжения?

13.Как рассчитать погрешность измерения времени?

14.Как оценить погрешность определения ёмкости?

15.Какой вид должен иметь график зависимости напряжения конденсатора от времени при разрядке?

16.Расчёт ёмкости проводящего шара (формула).

17.Расчёт ёмкости плоского конденсатора (формула).

18.Что называется электрическим током?

19.Какой ток является постоянным, а какой квазистационарным?

20.Что называется силой тока?

21.Что называется разностью потенциалов, э.д.с. и напряжением?

22.Что измеряет вольтметр – напряжение или разность потенциалов?

23.Формулы закона Ома для однородного и неоднородного участков цепи и для всей замкнутой цепи.

24.Что такое узел в разветвлённой цепи? Как записывается первое правило Кирхгофа? Следствием какого закона оно является?

studfiles.net

ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА — КиберПедия

С ПОМОЩЬЮ ВОЛЬТМЕТРА

Цель работы: определение емкости конденсаторов и проверка законов последовательного и параллельного соединений конденсаторов.

Приборы и оборудование: источник питания, вольтметр, потенциометр (R), эталонный конденсатор (Сэт), исследуемые кон­денсаторы (Сх1 и Сх2), переключатели.

 

Теоретические сведения

 

Опытным путем было установлено, что в природе существует два типа электрических зарядов, условно названных положительными и отрицательны­ми. Одноименные заряды отталкиваются друг от друга, разноименные притя­гиваются.

Р. Милликен доказал, что электрический заряд дискретен, т.е. величина за­ряда любого тела составляет целое число, кратное элементарному электриче­скому заряду е (e=1,6∙10-19 Кл). Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.

В результате обобщения опытных данных был сформулирован фундамен­тальный закон природы - закон сохранения заряда: алгебраическая сумма элек­трических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри нее.

Единица электрического заряда, 1 кулон (Кл), - это электрический заряд, проходящий через поперечное сечение проводника при силе тока в 1 А за время, рапное 1с :

1Кл=1 А∙1с.

Закон взаимодействия неподвижных точечных электрических зарядов был открыт Кулоном: сила взаимодействия F двух точечных зарядов прямо пропор­циональна величине зарядов q1 и q2 и обратно пропорциональна квадрату расстояния г между ними:

∙ (1)

где =8,85×10-12 Ф/м - электрическая постоянная; - диэлектрическая проницаемость среды (безразмерная величина).

Напряженность электрического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в эту точку:

. (2)

Направление вектора совпадает с направлением силы, действующей на положительный заряд. Выражение для определения единицы напряжен­ности электрического поля:

(3)

Графически электростатическое поле изображают с помощью линий нап­ряженности (силовых линий), которые проводят так, чтобы касательные к ним в каждой точке пространства совпадали по направлению с вектором напряженно­сти (рис. I).

Величина

называется потоком вектора напряженности через площадку dS. Здесь - вектор, модуль которого равен dS, а направление совпадает с нор­малью n к площадке dS ( ).

Электростатические поля подчиняются принципу суперпозиции: напря­женность результирующего поля, созданного системой зарядов, равна гео­метрической сумме напряженностей полей, созданных в данной точке каждым из зарядов в отдельности:

(4)

где - напряженность электростатического поля, созданного i-м зарядом.

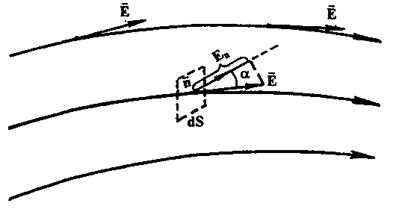
Рис. 1

 

Теорема Остроградского-Гаусса для электростатического поля в вакууме звучит так: поток вектора напряженности электростатического поля через про­извольную замкнутую поверхность в вакууме равен алгебраической сумме за­ключенных внутри этой поверхности зарядов, деленной на e0:

(5)

Из теоремы Гаусса следует, что напряженность электростатического поля между двумя бесконечными параллельными и разноименно заряженными плоскостями в вакууме будет равна

, (6)

где - поверхностная плотность заряда плоскостей.

Если между заряженными плоскостями находится изолятор с диэлектриче­ской проницаемостью , то напряженность поля внутри него уменьшается в раз (рис. 2):

(7)

Электростатическое поле является полем консервативных сил, т.е. работа, совершаемая силами поля по перемещению электрического заряда из одной точки пространства в другую, не зависит от траектории движения заряда, а оп­ределяется только его начальным и конечным положениями. Для такого рода полей можно ввести понятие потенциальной энергии заряда, численно равной работе, совершаемой силами электростатического поля по перемещению его из данной точки пространства в другую (ту, в которой потенциальная энергия заряда равна нулю).

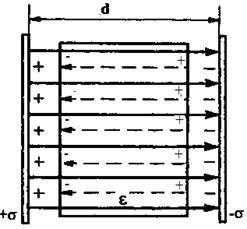
Рис. 2

 

Как правило, потенциальная энергия заряда, удаленного в бесконечность, считается равной нулю. Поэтому она будет равна

, (8)

где - радиус-вектор; - кулоновская сила; - напряжен­ность электростатического поля; q0 - электрический заряд.

Если заряд q0 перемещается из первой точки во вторую(определяются со­ответственно радиус-векторами и то работу, совершаемую силами по­ля, можно найти как разность работ

A (9)

где и ; и - работы, совершаемые силами поля при пе­ремещении заряда из первой и второй точек в бесконечность.

Потенциал – физическая величина, определяемая работой сил поля по пе­ремещению единичного положительного заряда из данной точки в беско­нечность:

. (10)

Единица потенциала - вольт (В): 1 В - потенциал такой точки поля, в ко­торой заряд в 1Кл обладает потенциальной энергией в 1 Дж:

.

Поскольку , то

(11)

 

 

Отсюда

 

(12)

Зная потенциал в каждой точке пространства можно найти напряженность электростатического поля:

(13)

Знак «минус» указывает на то, что вектор напряженности Ё направлен в сторону убывания потенциала.

Потенциал уединенного проводника прямо пропорционален его заряду;

При этом величину (14)

называют электроемкостью уединенного проводника. Единица электроемкости - фарад (Ф): 1 Ф - емкость такого уединенного проводника, потенциал которо­го изменяется на 1В при сообщении ему заряда в 1Кл, т.е.

. (15)

Для накопления значительных зарядов служат конденсаторы, состоящие из двух проводников (обкладок), разделенных диэлектриком. В зависимости от формы обкладок конденсаторы подразделяются на плоские, цилиндрические и сферические. Под емкостью конденсатора понимается физическая величина, равная отношению накопленного заряда q к разности потенциалов между обкладками:

(16)

где напряжение между обкладками. Плоский конденсатор обладает емкостью

(17)

где - диэлектрическая проницаемость изолятора; - электрическая постоян­ная; S - площадь обкладки; d - расстояние между обкладками.

Для увеличения емкости и варьирования ее возможных значений конден­саторы соединяют в батареи параллельно или последовательно. У параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна см рис. 3.

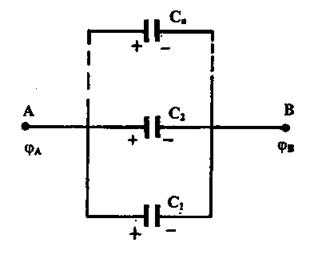
Рис. 3

 

Если емкости отдельных конденсаторов то их заряды равны со­ответственно

 

(18)

а заряд батареи конденсаторов-

Полная емкость батареи –

, (19)

т.е. при параллельном соединении конденсаторов она равна сумме емкостей от­дельных конденсаторов.

У последовательно соединенных конденсаторов заряды всех обкладок рав­ны по модулю, а разность потенциалов на зажимах батареи, см. рис. 4, равна

. (20)

Причем для любого из рассматриваемых конденсаторов

.

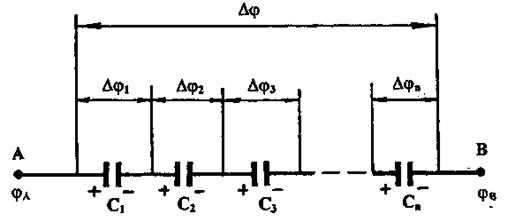
Рис. 4

С другой стороны,

(21)

откуда , (22)

т.е. при последовательном соединении конденсаторов суммируются обратные величины емкостей.

Если дана емкость эталонного конденсатора Сэт, то неизвестную емкость другого конденсатора Сх можно определить следующим образом.

Сначала конденсатор Сэт зарядить от источника постоянного тока (рис.5а). При этом накапливается заряд q. С помощью вольтметра измерить напряже­ние на обкладках конденсатора:

Тогда

.

Отсюда

. (23)

Затем эталонный конденсатор отключить от источника питания и к нему параллельно присоединить конденсатор неизвестной емкости Сх (рис. 5б). Электрический заряд q распределится по конденсаторам Сэт и Сх.

Согласно закону сохранения зарядов в замкнутой системе

(24)

где q1, q2- электрические заряды на конденсаторах Сэти Сх.

 

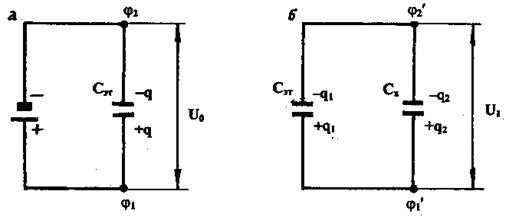
Рис. 5, а Рис. 5, б

 

После этого измерить напряжение на обкладках конденсаторов, причем

и .

Отсюда

и . (25)

Поэтому

В результате (26)

 

Порядок выполнения работы

 

1. Тумблером S1 включить установку собранную по схеме (рис. 6).

2. Переключателем S2 включить напряжение от источника питания на эталонном конденсаторе.

3. Установить движком потенциометра R напряжение U0=(1±0,2) В. Снять показания вольтметра.

4. Переключателем S2 отключить эталонный конденсатор от источника питания.

5. Соединить проводниками Сэт и Сх1 параллельно и снять показания вольтметра U1.

6. Тумблером S3 разрядить конденсаторы.

7. Подавая на эталонный конденсатор напряжение от 1 В до 3 В, провести измерения 3 раза. Данные занести в таблицу.

8. Для каждой пары значений напряжений U0 и U1 найти электроемкость по формуле

.

Затем определить среднюю величину электроемкости Сх1(ср). Результаты вычислений занести в таблицу.

9. По п.п. 3-9 найти электроемкость Сх2.

Таблица

U0	U1	Cx1	U0	U2	Cx2	U0	Uпар	Cпосл	U0	Uпосл	Cпар

 

10. Соединить конденсаторы Сх1 и Сх2 последовательно (рис. 7).

11. По п.п. 3-9 найти электроемкость батареи Спосл.

12. Соединить конденсаторы Сх1 и Сх2 параллельно (рис. 8).

13. По п.п. 3-9 найти электроемкость батареи Спар.

По формулам и вычислить емкость батареи последовательно и параллельно соединенных конденсаторов и сравнить результаты с экспериментальными значениями.

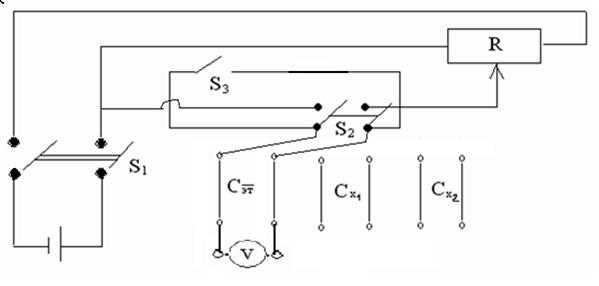
Рис. 6

 

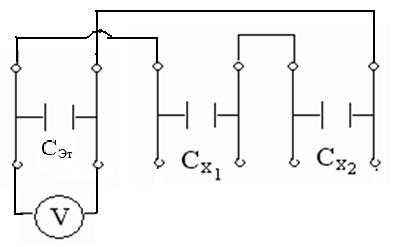Последовательно   Рис. 7

 

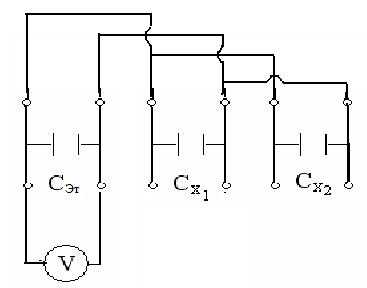Параллельно   Рис. 8

 

=1000 мкФ.

Контрольные вопросы

1. Как взаимодействуют электрические заряды? Закон кулона. Единица электрического заряда в системе СИ.

2. Закон сохранения электрического заряда.

3. Что такое напряженность электрического поля, силовые линии электростатического поля, поток вектора напряженности? В чем состоит принцип суперпозиции электрических полей.

4. Сформулировать теорему Остроградского-Гаусса для электростатического поля в вакууме. Как определяется напряженность электрического поля между двумя бесконечными параллельными и разноименно заряженными плоскостями?

5. Что такое потенциальная энергия электрического заряда, потенциал данной точки электростатического поля? Как найти работу, совершаемую силами поля по перемещению электрического заряда из одной точки в другую? единица потенциала и напряжения в системе СИ.

6. Какова связь между потенциалом и напряженностью электрического поля в данной точке?

7. Чему равна электроемкости уединенного проводника и конденсатора? Единица электроемкости в системе СИ.

8. Рассказать о параллельном и последовательном соединении конденсаторов. Вывести формулы.

 

ЛАБОРАТОРНАЯ РАБОТА 5

 

cyberpedia.su

Характеристики конденсаторов Основные параметры Ёмкость

Основной характеристикой конденсатора является его ёмкость, характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад.

Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположена на расстоянии d друг от друга, в системе СИ выражается формулой: , где—диэлектрическая проницаемость среды, заполняющая пространство между пластинами (в вакууме равна единице), —электрическая постоянная, численно равная 8,854187817·10−12 Ф/м. Эта формула справедлива, лишь когда d намного меньше линейных размеров пластин.

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.

или

Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.

При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна

или

Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.

Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.

Индуктивность.

Свойство проводника влиять на ток в цепи и изменении его значения называют индуктивностью, а катушки, в которых наиболее сильно проявляется это свойство - катушками самоиндукции или индуктивности. Чем больше число витков и размеры катушки, тем больше ее индуктивность, тем значительнее влияет она на ток в электрической цепи. 

Итак, катушка индуктивности препятствует как нарастанию, так и убыванию тока в электрической цепи. Еще она находится в цепи постоянного тока, и влияние ее сказывается только при включении и выключении тока. В цепи же переменного тока, где беспрерывно изменяются ток и его магнитное поле, ЭДС самоиндукции катушки действует все время, пока течет ток. Это электрическое явление и используется в генераторах - основных элементах колебательного контура - катушке индуктивности.

studfiles.net

Упражнение 1. Определение емкости конденсаторов с помощью мостика Сотти Краткая теория

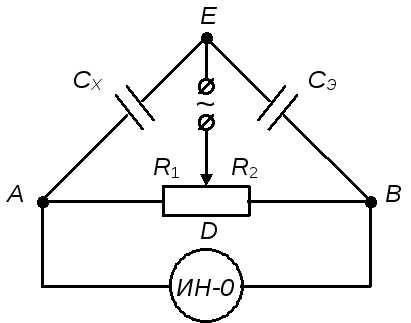
Рис.1.

Для определения ёмкости конденсаторов можно воспользоваться мостовой схемой (рис.1). На схеме:Сэ- конденсатор известной емкости,Сx- исследуемый конденсатор,ИН-0- индикатор нуля (вольтметр переменного тока или электронный осциллограф).

Напряжение со звукового генератора подводится к одной диагонали моста (DE), а в другую диагональ моста (AB) включается индикатор нуля. Принцип измерения основан на нахождении такого положения движка реостата, при котором потенциалы точекАиВодинаковы (А = В), ток в индикаторе нуля отсутствует, а мост находится в равновесии.

Выведем условие электрического равновесия моста. Рассмотрим электрическую ветвь моста DAE. Найдем зарядdq, прошедший по этой ветви за времяdt:

,

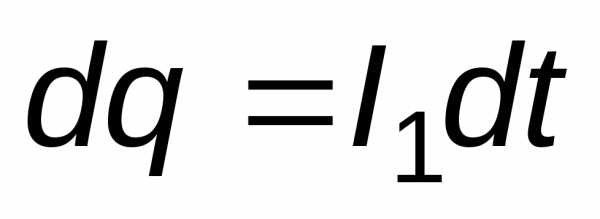где ток .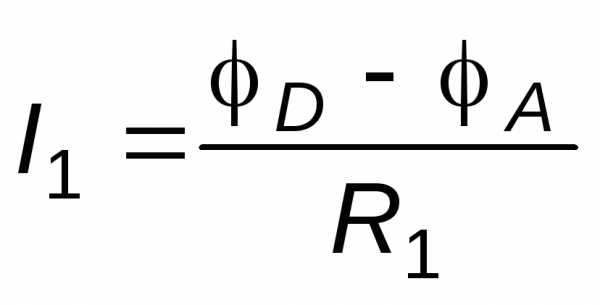

Из определения ёмкости конденсатора следует, что

dq = Cx(A - E).

Тогда получим:

.

Аналогичное выражение имеет место для ветви DBE:

.

Из последних двух формул, учитывая, что A=B, можно записать:

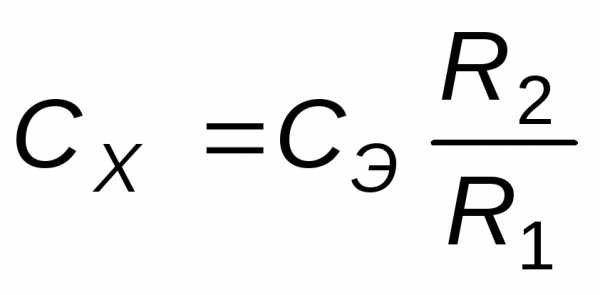. (1)

Порядок выполнения

1. Собрать установку по схеме рис.1.

2. В качестве реохорда использовать реостат на 500 Ом (Сопротивление реостата указано ориентировочно). Эталонный конденсатор имеет емкость 0,25 мкФ..

3. Подать на схему напряжение со звукового генератора (U10 В,f1 кГц) и, передвигая движок реостата, добиться наличия одинаковых потенциалов в точкахАиВ, т.е. добиться равновесия моста. При равновесии моста на экране электронного осциллографа наблюдается минимальный по амплитуде сигнал.

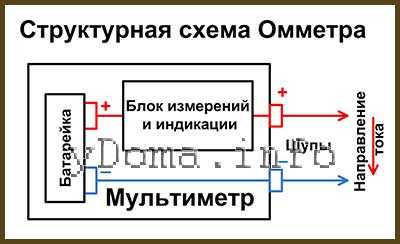
4. Отключив предварительно реостат от установки, с помощью мультиметра (в режиме омметра) измерить сопротивления R1 и R2 и, по формуле (1), определить ёмкость двух конденсаторов с неизвестной ёмкостью.

5. Определить результирующую ёмкость этих же двух конденсаторов при их параллельном и последовательном соединении.

6. По известным формулам вычислить электроёмкость последовательного и параллельного соединения неизвестных конденсаторов и сравнить и расчеты с экспериментальными данными.

7. Оценить погрешность измерения.

8. Результаты работы оформить в виде таблицы.

Упражнение 2. Определение емкости конденсатора методом куметра Краткая теория

Метод куметраоснован на том, что измеряемая ёмкость входит в состав колебательного контура с малым затуханием (с большой добротностьюQ). Собственная частота колебательного контура, как это следует из теории свободных колебаний, определяется выражением:

,

где 02=1/LC, а=R/2L - коэффициент затухания.

Подставив значения 0и, получим:

.

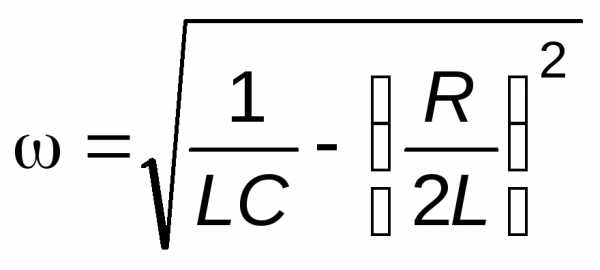Если контур обладает малым затуханием (сопротивление Rочень мало), то вторым членом в выражении под радикалом можно пренебречь и записать:

.

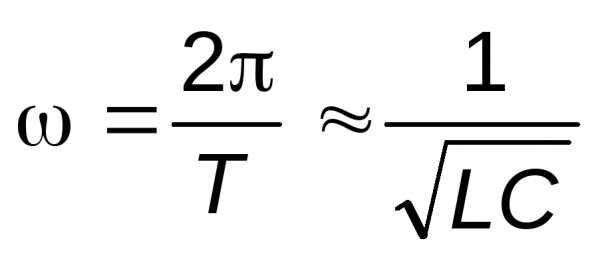Освобождаясь от радикала, получим:

,

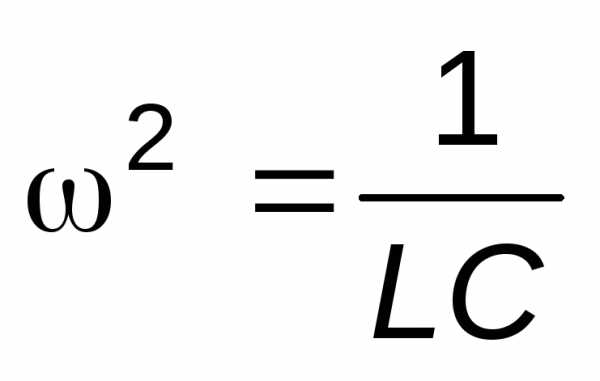откуда следует:

.

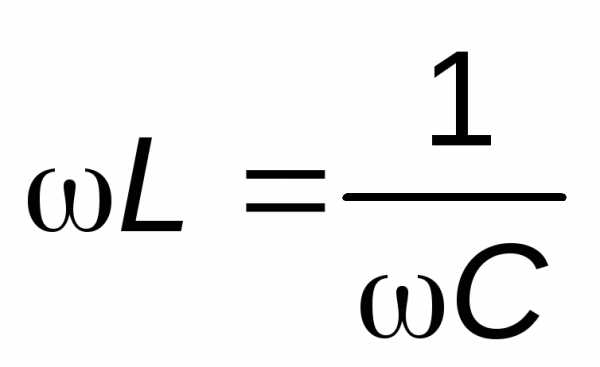Таким образом, собственная частота колебаний контура с малым затуханием определяется из равенства индуктивного и ёмкостного сопротивлений. Если резонанс в контуре достигнут, то для нахождения Сx достаточно знать величиныиL. Резонанса добиться можно, изменяя либоL, либо.

Рис.2.

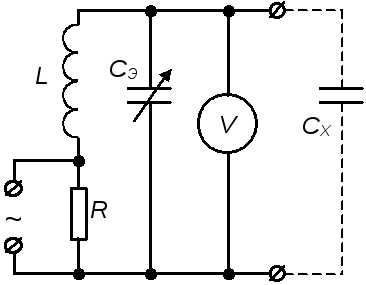Существует, однако, более простой способ достижения резонанса путем включения параллельно измеряемому конденсаторуСxградуированного конденсатораСэпеременной ёмкости (рис.2).

Вначале ёмкостьСx отключена. Изменяя ёмкость эталонного конденсатора до значенияСэ=С1, добиваются резонанса, который можно зафиксировать по максимальному показанию вольтметраV. Для этого случая будет справедливо соотношение:

.

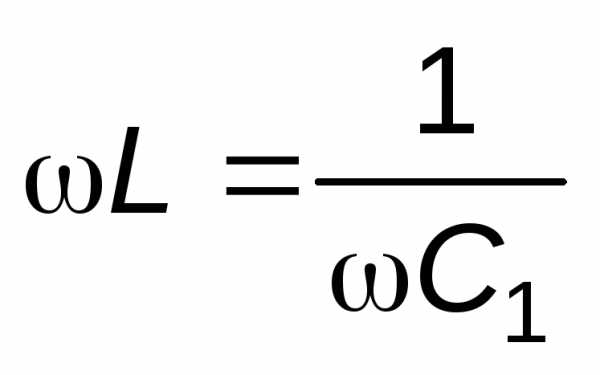Затем подключают измеряемый конденсатор Сxи вновь добиваются резонанса при значенииСэ=С2. Для данного случая будет справедливо соотношение:

.

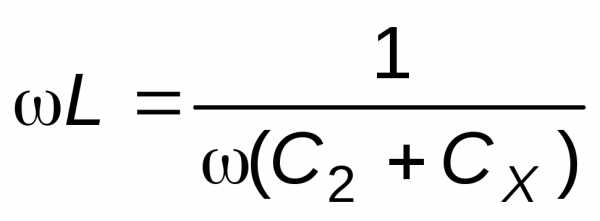Из последних двух уравнений получаем:

Сx=С1-С2.

Если градуированного конденсатора переменной ёмкости нет в распоряжении, то резонанса добиваются путем изменения частоты. Опыт производится в такой последовательности. Вначале ёмкость Сxотключена. Устанавливают эталонную ёмкость определенной величиныСэ=С= const и путем изменения частоты добиваются резонанса:

.

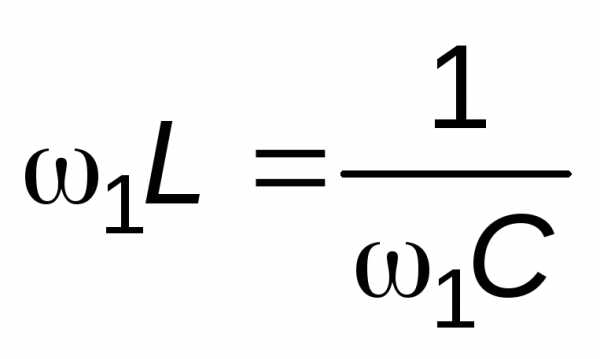Затем подключают измеряемый конденсатор Сxи вновь добиваются резонанса при той же ёмкости эталонного конденсатора:

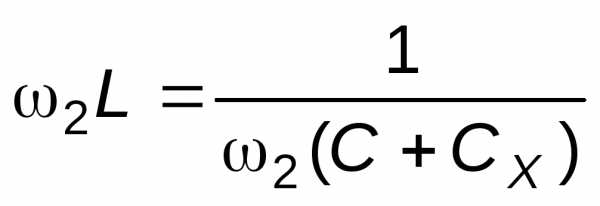
Из последних двух уравнений получаем:

.

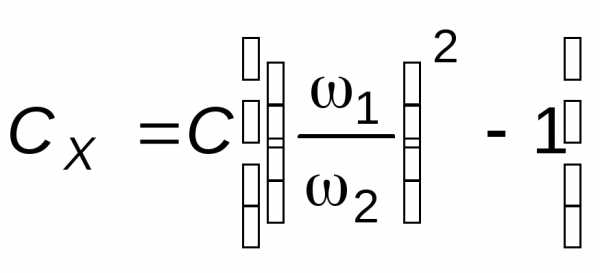Данное упражнение следует провести по второму варианту.

Порядок выполнения

1. Подготовить измерительную схему в соответствии с рис.2. Эталонную ёмкость следует взять величиной 1000 пФ. В качестве вольтметра использовать осциллограф.

2. Рассчитать (и установить на звуковом генераторе) резонансную частоту контура, пользуясь соотношением . Эталонная электроёмкость рассчитывается по следующей формуле:Сэ= (1000 пФ +С0) = 1130 пФ, гдеС0= 130 пФ – ёмкость монтажа эталонного конденсатора. Значение индуктивностиLуказано на катушке.

3. Подать со звукового генератора напряжение (не более 10 В) на контур с эталонным конденсатором, уточнить частоту резонанса.

4. Подключив конденсатор с неизвестной ёмкостью, определить её значение, добиваясь резонанса изменением частоты генератора.

5. Оценить погрешность измерения.

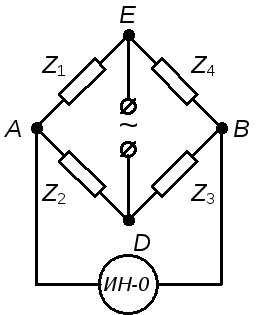
Рис.3.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Пользуясь схемой, изображённой на рис.3, выведите условие равновесия моста переменного тока в комплексной формеZ1Z3=Z2Z4, гдеZk= (Rk+iXk) – сопротивление (импеданс) одного из плеч моста.

2. Подставляя, в соответствии с реальной схемой (рис.1), в выражение Z1Z3=Z2Z4 вместо сопротивленийZkих значения, выраженные черезRkиХk, и приравнивая их действительные и мнимые части, найдите два уравнения, которые являются условиями равновесия моста переменного тока. Пользуясь этими уравнениями, найдите условие равновесия мостика Сотти.

3. В чем заключается физическая основа применения метода куметра для измерения электроёмкости конденсаторов?

4. Какой тип резонанса (токов или напряжений) возникает в использованном колебательном контуре?

5. Чем ограничивается диапазон измерений ёмкостей в рассмотренных методах?

Лабораторная работа №8

Измерение мощности переменного тока и сдвига фаз между током и напряжением

Цельработы:измерение мощности переменного тока и сдвига фаз между током и напряжением для различных нагрузок с помощью ваттметра.

Приборы и принадлежности:источник питания, ваттметр, реостат, набор сопротивлений нагрузки.

studfiles.net

Измерение емкости электрического конденсатора

Цель работы: изучение метода наименьших квадратов на примере измерения емкости электрического конденсатора.

Приборы и принадлежности: электронный осциллограф, генератор гармонических колебаний, электрический конденсатор с неизвестной емкостью, резистор.

Электрический конденсатор - устройство, состоящее их двух проводящих электродов (обкладок), разделенных диэлектриком или вакуумом. Способность конденсатора накапливать электрический заряд характеризуется физической величиной, называемой электроемкостью или просто емкостью С. Она связывает между собой заряд конденсатора q и напряжение между его обкладками q:

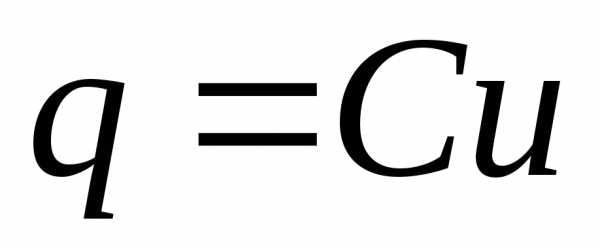(43)

Величина емкости определяется диэлектрической проницаемостью материала диэлектрика, формой и геометрическими размерами конденсатора.

Единица измерения емкости в системе СИ - 1 фарад [Ф], имеющий размерность, согласно формуле (43), {Кл/В]. Из-за того, что заряд в 1 Кл очень велик, емкость в 1 Ф также велика. Поэтому на практике используют в основном доли этой единицы: 1 микрофарад (1 мкФ (10-6 Ф), 1 пикофарад [пФ] 10-12 Ф) и т.п.

Через конденсатор постоянный ток протекать не может. Однако в цепи, содержащей источник переменной электродвижущей силы, происходят периодические зарядка и разрядка конденсатора, то есть имеет место движение зарядов - электрический ток. Пусть напряжение на конденсаторе изменяется по гармоническому закону

, (44)

где Um - амплитуда колебаний напряжения. Подставляя (44) в (43), получим:

(45)

Мгновенное значение силы электрического тока, текущего через конденсатор, равно производной заряда по времени:

(46)

Сопоставляя выражения (41) и (43), можно сделать вывод, что колебания силы тока опережают колебания напряжения на конденсаторе на /2. Это означает, что в то время, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. Выражение (46) может быть представлено в виде:

(47)

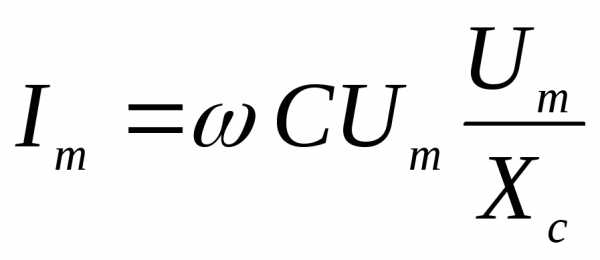(48)

где Im- амплитуда колебаний тока.

Сравнение (48) с классической формулой закона Ома для участка цепи приводит к выводу, что величина имеет размерность электрического сопротивления. Поэтому ее называют емкостным сопротивлением конденсатора переменному току.

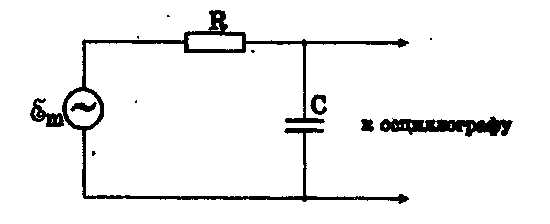
Рис. 12

Если собрать цепь, электрическая схема которой показана на рис. 12, то амплитуда колебаний ЭДС источника 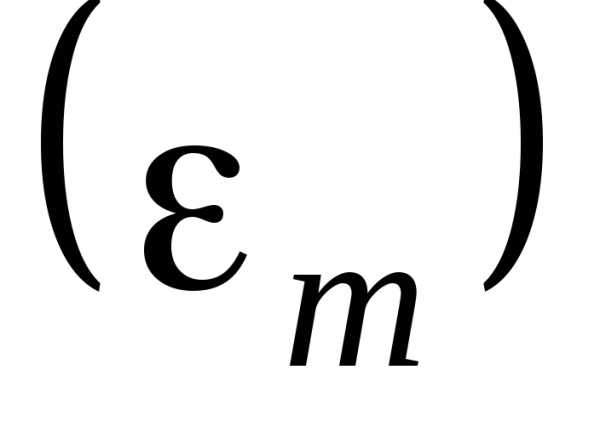и амплитуда переменного тока, протекающего через электрическую цепь, будут связаны соотношением:

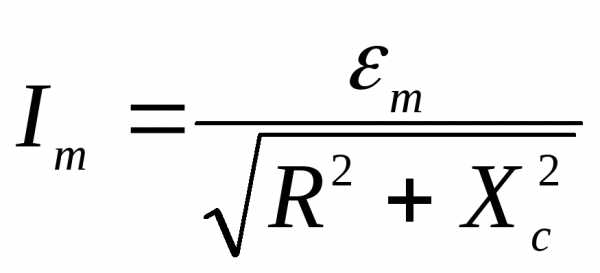(49)

Регистрируемая осциллографом амплитуда колебаний напряжения на конденсаторе равна:

(50)

Подбирая частоту колебаний и величину сопротивления, можно добиться выполнения условия. Тогда формулу (50) можно представить в виде:

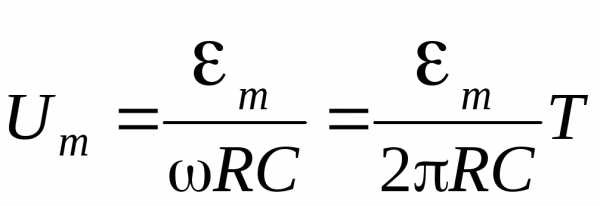, (51)

где Т=1/f - период колебаний.

Если выполняется неравенство , существует прямо пропорциональная зависимость амплитуды колебаний напряжения на конденсаторе от периода колебаний. На данном обстоятельстве и основан метод определения емкости конденсатора.

Представляя выражение (51) в ви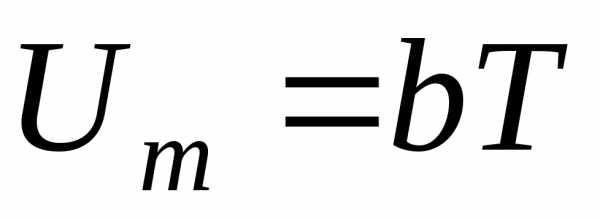де , где 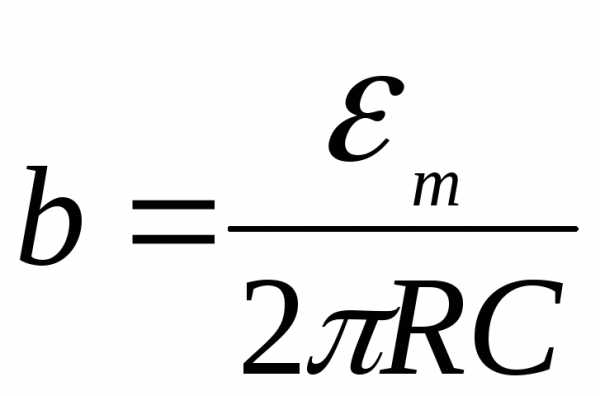задачу измерения неизвестной емкости С можно свести к определению величины коэффициента пропорциональности b по экспериментально зафиксированной зависимости 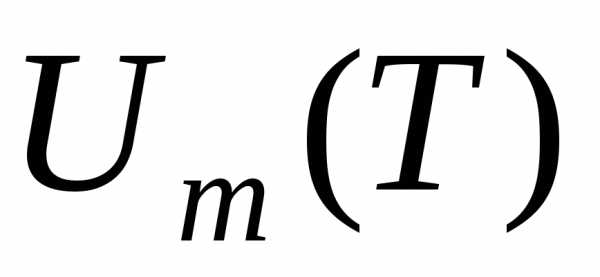при условии, что имеется информация о величинахR и 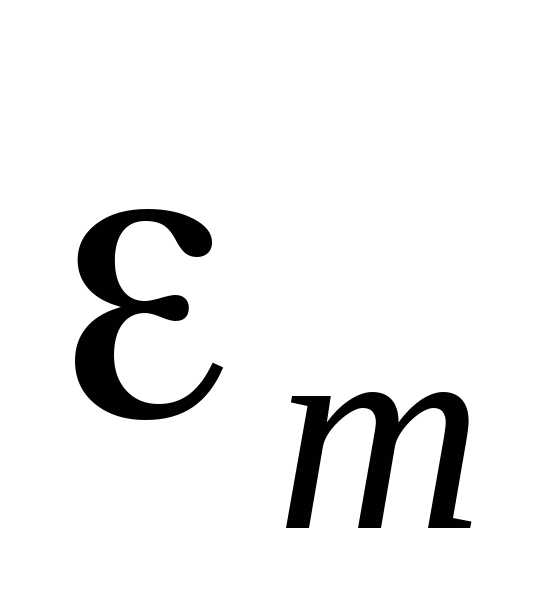. Коэффициент пропорциональностиb определим с помощью метода наименьших квадратов согласно формуле (15), в которую вместо xi и уi, следует подставить экспериментально измеренные значения периода и соответствующие им амплитуды колебаний напряжения. Величина емкости конденсатора определяется соотношением:

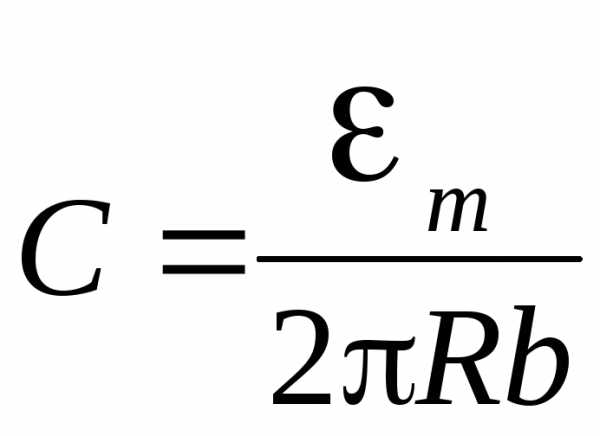(52)

Амплитуда колебаний ЭДС источника 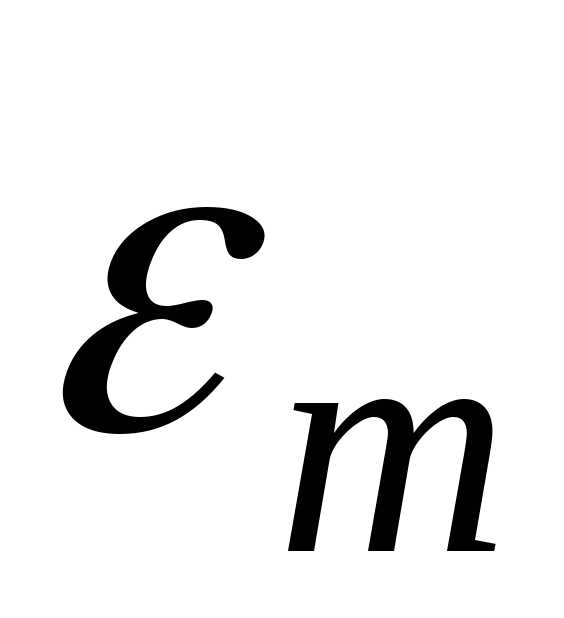измеряется путем непосредственного подключения источника к осциллографу, а величина сопротивленияR указана.

Поскольку определение емкости с помощью формулы (52) представляет собой задачу косвенных измерений, то погрешность С следует вычислять по правилу (6), формально рассматривая емкость конденсатора кА функцию величин 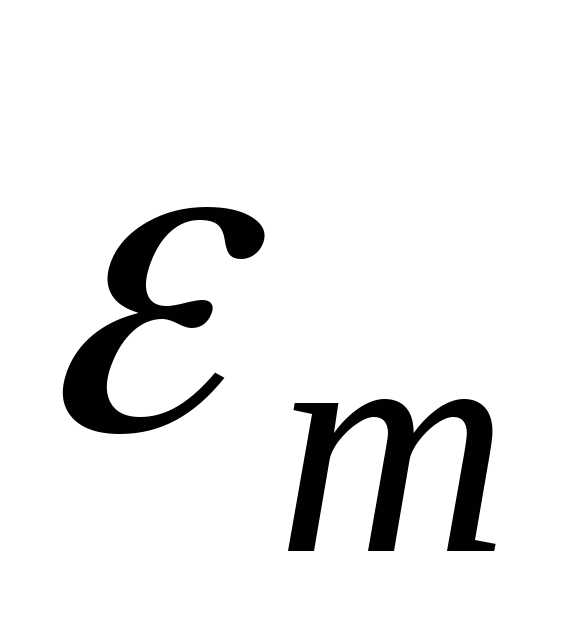,R и b.

studfiles.net

Физика дать определение что такое конденсатор и емкость конденсатора

Конденсатор состоит из двух металлических пластин (обкладок) , изолированных одна от другой прослойкой воздуха или каким-либо другим диэлектриком (слюдой, бумагой и т. д.) . Если одной из пластин сообщить положительный заряд, а другой — отрицательный, т. е. противоположно зарядить их, то заряды пластин, взаимно притягиваясь, будут удерживаться на пластинах. Это позволяет сосредоточить на пластинах гораздо большее количество электричества, чем если бы заряжать их в удалении одна от другой. Следовательно, конденсатор может служить устройством, запасающим на своих обкладках значительное количество электричества. Иначе говоря, конденсатор — это накопитель электрической энергии. Емкость конденсатора равна: С = еS / 4&#960;l где С — емкость; е - диэлектрическая проницаемость диэлектрика; S — площадь одной пластины в см2, &#960; — постоянное число, равное 3,14; l — расстояние между пластинами в см. Источник: <a rel="nofollow" href="http://electricalschool.info/main/osnovy/419-jelektricheskoe-pole.html" target="_blank" >Электрическое поле, электростатическая индукция, емкость и конденсаторы</a>

Конденса&#769;тор (от лат. condense — «уплотнять» , «сгущать» ) — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками) , разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Ёмкость выражай из определения.

Конденсатор, в народе именуемый кондером, является средством накопления электроэнергии в электрических цепях. Типичной областью применения являются: сглаживающие фильтры в источниках электропитания; цепи межкаскадовых связей; фильтрация помех. Основной характеристикой является емкость. Измеряют емкость в МикроФарадах (Мкф) (1*10-6 Фарада) , Пикофарадах (Пф) (1*10-9 Фарада) и НаноФарадах (Нф) (1*10-12 Фарада) . Если вы разберете конденсатор, то увидите там обкладки. Емкость конденсатора пропорционально увеличивается с площадью обкладок и уменьшается с расстоянием между ними. Еще одной важным параметром конденсатора является рабочее напряжение. Напряжение это не с потолка берется, а характеризуется максимальным напряжением при превышении которого наступает пробой диэлектрика и смерть кондера.

конденсатор- представляет собой два проводника (обкладки) , разделённые тонким слоем диэлектрика (в часности воздуха)

touch.otvet.mail.ru

ОПРЕДЕЛЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЕМКОСТИ КОНДЕНСАТОРА БАЛЛИСТИЧЕСКИМ МЕТОДОМ

КРАТКАЯ ТЕОРИЯ. Электрической емкостью называется физическая величина, показывающая заряд, который способно накапливать тело при приложении к нему потенциала в 1В:

.

Конденсатор – тело, способное накапливать достаточно большой заряд. Простейший конденсатор представляет собой два проводника (обкладки), разделенные слоем диэлектрика.

Под электроемкостью конденсатора понимают физическую величину, показывающую заряд, который способен накапливать конденсатор при приложении к нему напряжения в 1 В.

. (1)

Виды конденсаторов:

1. По электроемкости: конденсаторы постоянной емкости; конденсаторы переменной емкости.

2. По виду диэлектрика: воздушные; керамические; бумажные и т.д.

3. По форме обкладок: плоские; сферические и т. д.

Конденсаторы соединяются в батареи.

Виды соединения конденсаторов:

А) последовательное;

Б) параллельное.

Общая емкость при последовательном соединении конденсаторов:

,

где n – число конденсаторов.

Для двух конденсаторов получим:

. (2)

Общая электроемкость при параллельном соединении конденсаторов:

. (3)

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения емкости конденсатора пользуются схемой, приведенной на рис.1, где ИП - исто­чник постоянного напряжения, V - вольтметр, Сх- исследуе­мый конденсатор, Кн - перек­лючатель, позволяющий под­ключать конденсатор к источ­нику питания или к гальванометру Г. Параллельно гальванометру подключен ключ Кл, который замыкают на короткое время перед измерением для установки светово­го луча ("зайчика") в начальное положение.

Как следует из (1), нахождение значения электроемкости связано с определением заряда Q на обкладках и напряжения U, которое определяется вольтметром V. Заряд Q можно измерить при помощи баллистического гальванометра. Главной частью гальванометра (рис. 2) является подвешенная на вертикальной нити Т рамка F, помещенная в поле постоянного магнита М. Скрепленное с рамкой зеркальце L служит для изме­рения угла поворота рамки гальвано­метра в магнитном поле при прохожде­нии по ней электрического тока. Заряд Q, протекающий через рамку, пропорционален первому отбросу светового луча:

,

где А - постоянная гальванометра, N - число делений шкалы для первого отброса светового луча. Значение пос­тоянной А можно определить, разряжая через гальванометр конденсатор известной ёмкости С, заряженный до напряжения U, тогда заряд конденсатоpa равен:

, и . (4)

ИЗМЕРЕНИЯ. 1. Собрать схему (рис. 1), подключить конденсатор известной емкости и зарядить его до напряжения, при котором во время разряда конденсатора "зайчик" по шкале гальванометра отклонится на 0,7….0,8 длины шкалы. Далее, определив средний отброс "зайчика" из 5 опытов по разрядке известного конденсатора, найти постоянную гальванометра А, используя (4).

2. Определить емкости двух конденсаторов С1 и C2 по известной постоянной гальванометра А. Для этого подключают вместо образцового сначала конденсатор С1, потом C2. Изменяя напряжение на конденсаторе, добиться отклонения "зайчика" на 0,7...0,8 длины шкалы. Определив средний отброс "зайчика" из 5 опытов, находят значения емкостей C1и C2 из формулы (4).

3. Определить емкость батареи из двух конденсаторов при параллельном и последовательном соединении. Сравнить результаты опыта с результатами вычисления емкости батареи по формулам (2) и (3).

РЕЗУЛЬТАТЫ

С, мкФ	U, В	N1	N2	N3	N4	N5	Nср.	А, мкФ×В

 

№ опыта	U, В	N1	N2	N3	N4	N5	Nср.	C, мкФ

 

ЛАБОРАТОРНАЯ РАБОТА № 4э

ОПРЕДЕЛЕНИЕ ЭДС ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ

МЕТОДОМ КОМПЕНСАЦИИ

КРАТКАЯ ТЕОРИЯ. При протекании электрического тока в замкнутой цепи, состоящей из проводника и источника тока (электрической батареи), оказывается, что внутри источника тока положительные заряды должны перемещаться против сил электростатического поля. Это возможно только в том случае, если на заряды действуют силы неэлектрического происхождения, так называемые сторонние силы. Работа сторонних сил по перенесению 1 Кл заряда между теми точками цепи, где они действуют, называется электродвижу­щей силой (ЭДС): . ЭДС измеряется в вольтах.

Согласно закону Ома для полной цепи:

, (1)

где e - ЭДС, i - сила тока, r - внутреннее сопротивление источника, U - напряжение на полюсах источника тока. Из формулы (1) видно, что обычные токопроводящие вольтметры непригодны для точного определения ЭДС.

При отсутст­вии тока ЭДС равна напряжению на полюсах источника. Из этого следует, что принципиально возможно измерить ЭДС электро­статическим или электронным вольтметром (вольтметрами, не потребляю­щими тока). Наиболее точным методом измерения ЭДС является метод ком­пенсации.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Принципиальная схема компенсационного метода измерения ЭДС изображе­на на рис. 1. Вспомогательная ба­тарея с ЭДС, заведомо превосходящей ЭДС ис­следуемого элемента, поддерживает ток в цепи реохорда АВ0. Исследуемый источник ЭДС одним полюсом присоединен к точке А, а другим - через гальванометр G и сопро­тивление R к движку реохорда D. Компенсация ЭДС возможна только в том случае, если вспомогательная батарея и исследуемый элемент включены одноименными полюсами навстречу друг другу. Напряжение на реохорде больше, чем , поэтому всегда можно подобрать участок реохорда AD дли­ной (сопротивлением Rx), чтобы напряжение на нем равнялось . При этом сила тока через гальванометр будет равна нулю ( уравновешивается напряжением ). В уравновешенной таким образом цепи согласно за­кону Кирхгофа для контура AD А можно написать:

. (2)

Для того, чтобы исключить из уравнения (2) силу тока, вместо неизвест­ного элемента переключателем К подключают к цепи нормальный элемент Вестона (рис.1) с известной ЭДС . Компенсация ЭДС произойдет при но­вом положении движка (при длине AD равной lN и сопротивления этого уча­стка RN).

Условие компенсации выразится равенством: . (3)

Из (2) и (3) имеем: (4)

или . (5)

Таким образом, измерение ЭДС сводится к измерению длин участков реохорда. В рассматриваемом методе гальванометр применяется не для из­мерения тока, а для констатации его отсутствия. Для этих целей применяются приборы, у которых нуль расположен посередине шкалы. Точность измерения ЭДС по схеме на рис. 1 невелика, так как при отсчете длины делаются погрешности более 0,5 мм. Кроме того, в процессе эксплуата­ции проволока стирается, и ее сопротивление по длине делается неоднород­ным. Монтажная схема установки изображена на рис. 2. Сопротивление R (порядка 104 Ом) служит для ограничения тока, те­кущего через гальванометр. Нормальный и исследуемый элемент подключа­ются к схеме с помощью ключа К2. В опытах батарея , элементы и ex подключаются только на короткое время нажатием - двой­ного ключа К2 для того, чтобы не перегревалась проволока рео­хорда. При измерениях рекомендуется производить компенсацию дважды: до и после компенсации ЭДС нормального элемента. Из двух значений длин реохорда следует взять среднее, которое подставляется в формулу (5). Значение берется из паспорта =1.018 В.

ЗАДАНИЕ. 1. Собрать схему (рис. 2) и поставить рукоятку тумблера К1 в такое положе­ние, чтобы был включен элемент . Замкнуть ключ К2, перемещая контакт D реохорда, добиться того, чтобы стрелка гальванометра установилась на нуль. Запи­сать в таблицу длину между А и D – Nx.

2. Перекинуть рукоятку тумблера К1 и включить элемент . Проделать для этого элемента все, что указано в пункте 1, и записать в таблицу. Опыт проделать 3 раза. По результатам измерений по формуле: рассчитать ЭДС. Опыты повторить с вторым элементом и обоими элементами, вклю­ченными последовательно. Результат представить в виде:

.

РЕЗУЛЬТАТЫ

№ опыта	Nx, дел.	Nn, дел.	DNx, дел.	DNn, дел.	ex, В	Dex, В

 

ЛАБОРАТОРНАЯ РАБОТА № 6э

ИЗУЧЕНИЕ ЗАВИСИМОСТИ МОЩНОСТИ ИСТОЧНИКА ТОКА ОТ СОПРОТИВЛЕНИЯ НАГРУЗКИ

КРАТКАЯ ТЕОРИЯ. В электрической цепи, содержащей источник тока с ЭДС e и внутренним сопротивлением r, на резисторе R (рис.1) будет выделяться полезная мощность:

, (1)

где I - сила тока. Согласно закону Ома для замкнутой цепи:

. (2)

Из (1) и (2) следует что:

. (3)

Ток I протекает так же и внутри источника, и поэтому в нем выделяется мощность

.

Полная мощность источника:

. (4)

Полезная мощность источника изменяется от нуля при R = 0, проходит через максимум при

, (5)

а затем убывает, стремясь к нулю при . Максимальное значение полезной мощности:

. (6)

ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ

1. Собрать цепь, состоящую из источника тока, ключа, магазина резисторов R согласно рис.1.

2. Снять зависимость тока I от сопротивления R. Результаты записать в виде таблицы. Изменение R с помощью декадных переключателей магазина производить при разомкнутом ключе. Ключ замыкается только на время проведения измерения.

3. Рассчитать полезную мощность по формуле (1) и вычертить график зависимости Рп (R).

4. По графику определить r, Pпmaх и, используя (6), рассчитать ЭДС источника тока e.

ЛАБОРАТОРНАЯ РАБОТА № 13э



infopedia.su

---

• 
  Бесперебойник apc
• 
  Сухой газ
• 
  Светодиодные лампы под люминесцентные светильники
• 
  Электрическая схема кран балки с описанием
• 
  Как проверить галогеновую лампу мультиметром
• 
  Усилители тока
• 
  Вектор магнитной индукции от чего зависит
• 
  Индикатор 220 вольт на светодиоде
• 
  Передать показания счетчика газа черкассы
• 
  Контур повторного заземления
• 
  Как не платить за свет в частном доме