Емкостное реактивное сопротивление: Реактивное сопротивление

Реактивное сопротивление

Итак, катушки индуктивности и конденсаторы препятствуют протеканию переменного тока. Такое сопротивление по переменному току носит название реактивного сопротивления Х и измеряется в омах. Реактивное сопротивление зависит как от величины индуктивности и емкости, так и от частоты сигнала.

Катушка индуктивности имеет индуктивное реактивное сопротивление VL равное

где f — частота в герцах, a L — индуктивность в генри.
Так как ω = 2πf, то можно записать XL = ωL. Например, реактивное сопротивление катушки с индуктивностью 10 мГн, на которую подается сигнал частотой 1 кГц, равно

XL = 2π*1*103*10 *10-3 = 62,8 Ом.

Реактивное сопротивление катушки индуктивности возрастает с увеличением частоты сигнала (рис. 4.26).
Конденсатор имеет емкостное сопротивление XC равное

где С — емкость в фарадах. Например, реактивное сопротивление конденсатора емкостью 1 мкФ, на который подается сигнал частотой 10 кГц, равно

Рис. 4.26. Зависимость индуктивного                                            Рис. 4.27.
сопротивления от частоты.

Рис. 4.28. Векторная сумма емкостного (XC)

и индуктивного (XL) сопротивлений.

                                                                                                                                         Рис. 4.29.
(а) Катушка индуктивности, соединенная последовательно с резистором R.
(б) Векторное представление R, XL и их векторной суммы Z

Реактивное сопротивление конденсатора уменьшается с увеличением частоты сигнала (рис. 4.27).
Результирующее сопротивление цепи, включающей в себя емкостное сопротивление XC и индуктивное сопротивление XL, равно векторной сумме XC и XL. Векторы XC и XL, как видно из рис. 4.28(б), находятся в противофазе, т. е. разность фаз между ними равна 1800. Поэтому результирующее сопротивление просто равно разности между XC и XL. Например, пусть XL = 100 Ом, а XC = 70 Ом. Тогда результирующее реактивное сопротивление Х = 100 – 70 = 30 Ом и является индуктивным так как XL больше, чем XС.

Импеданс
Результирующее сопротивление цепи, содержащей как активное, так и реактивное (индуктивное либо емкостное) сопротивление, носит название импеданса или полного сопротивления цепи.
Импеданс Z является векторной суммой реактивного сопротивления Х и активного сопротивления R.
Рассмотрим, например, схему, изображенную на рис. 4.29. Она включает в себя индуктивное сопротивление XL соединенное последовательно с резистором R. Как видно из рис. 4.29(б), вектор XL опережает вектор R на 90°. Импеданс равен

Если XL = 400 Ом и R = 300 Ом, то Z = 500 Ом.

Добавить комментарий

Ёмкостное сопротивление. Индуктивное сопротивление

Физика
– какая ёмкость слова,

Физика
для нас не просто звук,

Физика
– опора и основа,

Всех
без исключения наук!

Задача
1.
В цепи переменного тока с частотой 50 Гц при напряжении 220 В возникает сила
тока 4 А. Известно, что в эту цепь включена катушка с ничтожно малым активным
сопротивлением. Какова индуктивность катушки?

Ответ:
175 мГн.

Задача
2.
. При увеличении частоты от 50 Гц до 60 Гц, ёмкостное сопротивление конденсатора
с постоянной ёмкостью уменьшилось на 10 Ом.  Найдите электроёмкость
конденсатора.

Ответ:
53 мкФ.

Задача
3.
Известно, что через катушку, включенную в цепь переменного тока с частотой 200 Гц,
проходит ток не более 3 А. Найдите напряжение на катушке, в момент времени
t = 0,2 мс,
если в начальный момент времени оно максимально. Индуктивность катушки равна 5 мГн.

Ответ:
18,3 В.

Задача
4.
Докажите, что если частота переменного тока равна собственной частоте, то по
катушке индуктивности и конденсатору будет протекать одинаковый ток, а также на
катушке и на конденсаторе будет одинаковое напряжение.

Ответ:
доказано.

Сопротивления | Цепи переменного тока

Введем теперь ряд величин, характеризующих цепь синусоидального тока.
Отношение комплексного напряжения к комплексному току называется комплексным сопротивлением:

где — отношение действующего или амплитудного напряжения соответственно к действующему или амплитудному току называется полным сопротивлением. Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т. е.
Комплексное сопротивление можно представить в виде

где — действительная часть комплексного сопротивления, называется активным сопротивлением; — значение мнимой части комплексного сопротивления, называется реактивным сопротивлением.
Очевидно, что

Из ( 3.23а) следует, что для последовательного контура (см. рис. 3.8) комплексное сопротивление

причем реактивное сопротивление

где

называются соответственно индуктивным и емкостным сопротивлениями.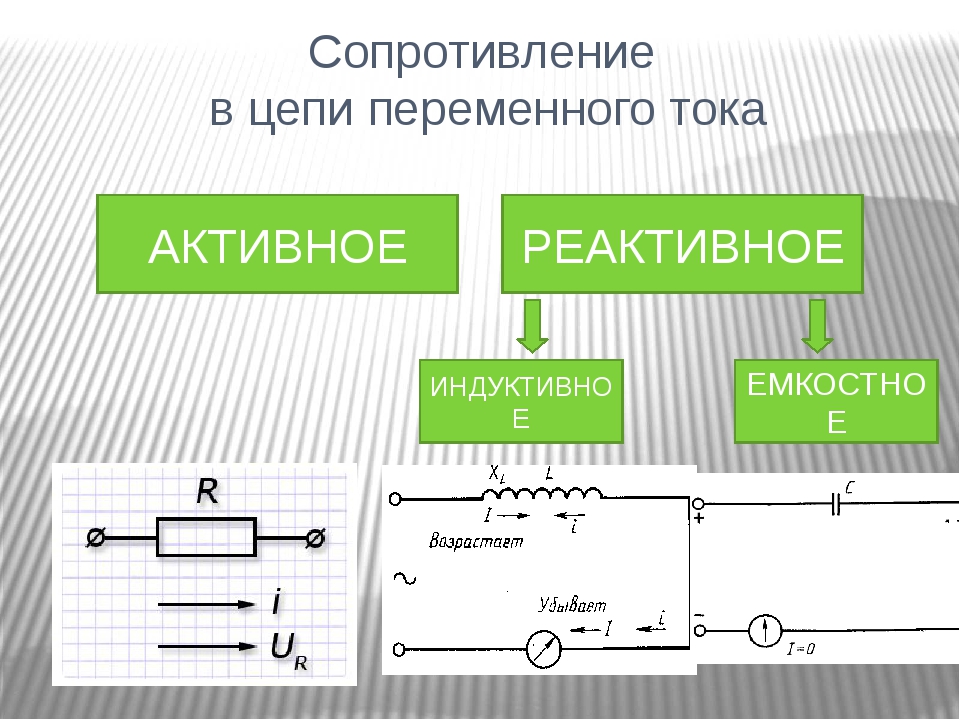
Из ( 3.15) и ( 3.19) видно, что индуктивное сопротивление связывает между собой амплитуды или действующие значения напряжения на индуктивности и тока:

Индуктивное сопротивление прямо пропорционально частоте тока. Это объясняется тем, что напряжение на индуктивном элементе пропорционально скорости изменения тока:
Емкостное сопротивление, как следует из ( 3.16) и ( 3.20), связывает между собой амплитуды или действующие значения напряжения на емкости и тока:

Емкостное сопротивление обратно пропорционально частоте тока. Эту зависимость от частоты легко пояснить, если считать заданным напряжение на емкостном элементе, а искомой величиной ток: . Ток прямо пропорционален скорости изменения напряжения на емкостном элементе, и, следовательно, емкостное сопротивление обратно пропорционально частоте напряжения.
Напряжения на последовательно соединенных индуктивности и емкости противоположны по фазе; поэтому в (3.27) для реактивного сопротивления х сопротивления входят с различными знаками. Напряжения на индуктивности и на емкости сдвинуты по фазе относительно напряжения на сопротивлении соответственно на π/2 и —π/2. Поэтому эти сопротивления входят в Z как .
Следует обратить внимание на то, что индуктивное и емкостное сопротивления являются величинами арифметическими — положительными, а реактивное сопротивление — величина алгебраическая и может быть как больше, так и меньше нуля.
Для ветви, содержащей только индуктивность, реактивное сопротивление х равно индуктивному сопротивлению , а реактивное сопротивление х ветви, содержащей только емкость, равно емкостному сопротивлению, взятому со знаком минус, т. е. .
Заметим также, что для ветвей, каждая из которых содержит только сопротивление r, только индуктивность L или только емкость С, комплексные сопротивления соответственно равны:

Если ветвь содержит несколько последовательно соединенных резистивных, индуктивных и емкостных элементов, то при вычислении сопротивления и тока их можно заменить тремя элементами:

Реактивное сопротивление

Реактивное сопротивление – это сопротивление прохождению переменного электрического тока в электрической цепи, обусловленное наличием в ней индуктивности или конденсатора.

Дело в том, что для постоянного тока индуктивность является обычным проводником и поэтому сопротивление его прохождению в цепи ничтожно мало. Конденсатор при тех же условиях для постоянного тока является диэлектриком – его электрическое сопротивление бесконечно велико.

Если же мы имеем дело с переменным током, то в этом случае сопротивление его прохождению по цепи индуктивности  или конденсатора зависит от множества факторов: частоты самого тока, емкости конденсатора или индуктивности катушки.

Очень часто конденсатор и индуктивность из-за наличия в них реактивного сопротивления называют реактивными элементами или реактивными электронными компонентами.

Чем обусловлено реактивное сопротивление

В катушке

При протекании переменного электрического тока через катушку, он создает в ее витках магнитное поле, а оно в свою очередь обуславливает создание электродвижущей силы. Эта ЭДС направлена против внешнего тока, поэтому препятствует ему, то есть создает сопротивление. Как правило, реактивное сопротивление индуктивности называют еще индуктивным.

В конденсаторе

При протекании переменного тока через цепь конденсатора происходят процессы накопления и отдачи электрического заряда, связанные с действием в цепи электрического поля. Его действие также противоположно по направлению к внешнему току и поэтому создает для него сопротивление. Это сопротивление еще называют емкостным.

Интересно

Реактивное сопротивление катушки с увеличением ее индуктивности (количества витков) будет увеличиваться. В конденсаторе же рост емкости (увеличение площади электродов) приводит к прямо противоположному эффекту – уменьшению реактивного сопротивления.

Глава 17. Резонансные цепи . Введение в электронику

ЦЕЛИ

После изучения этой главы студент должен быть в состоянии:

• Написать формулы для определения емкостного и индуктивного сопротивления.

• Описать, как реагируют на переменный ток и напряжение конденсаторы и катушки индуктивности.

• Дать определение реактивного сопротивления последовательной цепи и уметь определить характер цепи (индуктивный или емкостный).

• Дать определение термина импеданс.

• Уметь вычислять импеданс, который содержит как резистивную, так и емкостную или индуктивную составляющие.

• Объяснить, как должен быть модифицирован закон Ома перед использованием его для цепей переменного тока.

• Уметь вычислять Х_с, X_L, X, Z и I_т в последовательных RLC цепях.

• Уметь вычислять I_c, I_L, I_x, I_R и I_z в параллельных RLC цепях.

В предыдущих главах сопротивление, емкость и индуктивность в цепях переменного тока рассматривались по отдельности. В этой главе исследуется комбинация сопротивления, емкости и индуктивности в цепи переменного тока. Рассматриваемые вопросы не являются новым материалом, но применяют все изложенные ранее принципы.

Когда реактивное сопротивление катушки индуктивности равно реактивному сопротивлению конденсатора в цепи, возникает резонанс. Резонансные цепи широко используются в электронике.

17-1. РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ

Емкостное реактивное сопротивление — это противодействие, которое конденсатор оказывает переменному току. Оно измеряется в омах и обозначается символом Х_с. Емкостное реактивное сопротивление вычисляется по формуле:

Х_с = 1/2πfC

Заметим, что при использовании этой формулы емкость должна быть выражена в фарадах (а не в долях фарады).

Индуктивное реактивное сопротивление — это противодействие, которое катушка индуктивности оказывает переменному току. Оно измеряется в омах и обозначается символом X_L. Индуктивное реактивное сопротивление вычисляется по формуле:

X_L = 2πfL.

Заметим, что при использовании этой формулы индуктивность должна быть выражена в генри (а не в долях генри).

Емкостное реактивное сопротивление служит причиной того, что ток опережает по фазе напряжение. Индуктивное реактивное сопротивление служит причиной того, что ток отстает по фазе от напряжения. Емкостное и индуктивное реактивные сопротивления прямо противоположны по создаваемым эффектам и, следовательно, когда в цепи присутствуют и индуктивность и емкость, общий эффект определяется разностью их значений. Эта разность называется реактивным сопротивлением и обозначается символом X. Реактивное сопротивление может быть выражено следующими формулами:

X = Х_с — X_L или X = X_L — Х_с.

_{ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 10 генри (рис. 17-1), работающей на частоте 60 герц?}

_{Рис. 17-1}

_Дано:

_{f = 60 Гц; L = 10 Гн; С = 1 мкФ}

_{Х =?}

_{Решение:} 

_{Хс = 1/2πfC} 

_{Хс =1/(6,28)(60)(0,000001)}

_{Хс =2654 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(10)}

_{XL = 3768 Ом}

_{X = XL- XC = 3768–2654}

_{X = 1114 Ом (индуктивное).}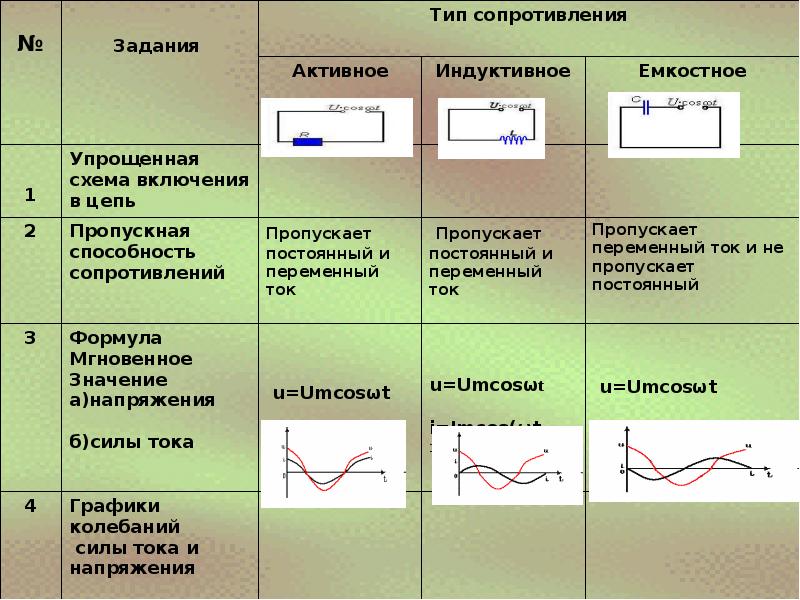

_{ПРИМЕР: Чему равно реактивное сопротивление цепи, содержащей конденсатор емкостью 1 мкФ, соединенный последовательно с индуктивностью 1 генри (рис. 17-2), работающей на частоте 60 герц?}

_{Рис. 17-2} 

 _Дано:

_{f = 60 Гц; L = 1 Гн; С = 1 мкФ}

_{Х =?}

_{Решение:} 

_{Хс = 1/2πfC} 

_{Хс = 1/(6,28)(60)(0,000001)}

_{Хс =2654 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(1)}

_{XL = 376,8 Ом}

_{X = XC — XL = 2654 — 376,8}

_{X = 2277,2 Ом (емкостное).}

Эти примеры иллюстрируют важный момент. Когда емкостное и индуктивное реактивные сопротивления соединены последовательно, меньшее значение всегда вычитается из большего. Получающееся в результате реактивное сопротивление характеризуется большим значением.

17-1. Вопросы

1. Каково фазовое соотношение между током и напряжением на конденсаторе?

2. Каково фазовое соотношение между током и напряжением на катушке индуктивности?

3. По какой формуле определяется полное реактивное сопротивление последовательной цепи, когда известны значения Х_с и X_L?

4. Какова величина полного реактивного сопротивления (X) последовательной цепи, содержащей Х_с = 50 ом и X_L = 20 ом? Укажите, является X емкостным или индуктивным.

17-2. ИМПЕДАНС

Реактивное сопротивление, как емкостное, так и индуктивное, противодействует протеканию тока в цепях переменного тока. Активное сопротивление также препятствует протеканию тока в цепи. Комбинированное противодействие реактивного и активного сопротивлений называется импедансом и обозначается символом Z.

И активное, и реактивное сопротивления измеряются в омах. Следовательно, кажется логичным сложить эти сопротивления для того, чтобы получить импеданс. Однако этого делать нельзя, поскольку активное и реактивное сопротивления — величины векторные. В цепях переменного тока, содержащих только активное сопротивление, ток и напряжение находятся в фазе. И ток, и напряжение достигают своих максимальных значений одновременно.

Как упоминалось ранее, в цепях переменного тока, содержащих только реактивные сопротивления, ток будет либо опережать, либо отставать от напряжения на 90 градусов. Следовательно, напряжение в чисто реактивной цепи будет отличаться по фазе на 90 градусов от напряжения в чисто резистивной цепи.

Когда цепь содержит и активное, и реактивное сопротивление, импеданс будет больше любого их них. Кроме того, ток в такой цепи будет не в фазе с напряжением. Сдвиг по фазе будет в пределах от нуля до 90 градусов.

Для того чтобы найти импеданс, используется векторная диаграмма — прямоугольный треугольник сопротивлений. Это может быть сделано потому, что ток через резистор находится в фазе с напряжением на нем, а ток через реактивную нагрузку сдвинут по фазе на 90 градусов относительно напряжения на ней. Они находятся под прямым углом друг к другу.

ПРИМЕР: Чему равен импеданс последовательно соединенных резистора сопротивлением 150 ом и индуктивного реактивного сопротивления 100 ом?

В качестве первого шага нарисуем основание треугольника, представляющее резистор 150 ом. Далее нарисуем линию под углом 90 градусов к основанию, представляющую индуктивное сопротивление 100 ом. После этого соединим концы линий, образуя гипотенузу треугольника. Гипотенуза представляет импеданс цепи (рис. 17-3).

Рис.  17-3. Векторная диаграмма.

Теорема Пифагора утверждает:

с² = а² + Ь²,

где с — гипотенуза, а и b — катеты.

Графически это представлено на рис. 17-4.

Рис. 17-4. Векторная диаграмма, показывающая связь активного сопротивления, реактивного индуктивного сопротивления и импеданса в последовательной цепи.

Если импеданс, активное и реактивное сопротивления заменить соответствующими символами, то формула будет выглядеть следующим образом:

Z² = R² + X².

Вернемся к определению импеданса последовательной комбинации резистора 150 ом и индуктивного сопротивления 100 ом.

Дано:

R = 150 Ом; X_L = 100 Ом.

Решение:

Z² = R² + X²

Z² =(150)² + (100)² = 32500

Z = √(32500) = 180,28 Ом.

Если вместо индуктивного в цепи находится емкостное сопротивление, то линию, представляющую емкостное сопротивление, обычно рисуют направленной вниз. Это показывает, что оно действует в направлении противоположном индуктивному сопротивлению, которое рисуют направленным вверх.

В последовательной цепи с емкостным реактивным сопротивлением формула для вычисления импеданса будет выглядеть следующим образом:

Z² = R² + Х²_С.

_{ПРИМЕР: Чему равен импеданс цепи, содержащей резистор сопротивлением 220 ом, соединенный последовательно с конденсатором, имеющим емкостное реактивное сопротивление 270 ом?}

_Дано:

_{R = 220 Ом; Xc = 270 Ом.}

_{Решение:}

_{Z² = R² + X²c}

_{Z² = (220)² + (270)² = 121300}

_{Z = √(121300) = 348,28 Oм.}

_{Z = 348,28 Ом.}

_{Если последовательная цепь содержит индуктивное и емкостное реактивные сопротивления, а также активное сопротивление, необходимо найти полное реактивное сопротивление (X). Реактивное сопротивление может быть либо индуктивным, либо емкостным. Следовательно, может быть использована одна из следующих формул:} 

_{Z² = R² + X²L;}

_{Z² = R² + Х²с.}

17-2. Вопросы

1. Как называется полное противодействие в цепи переменного тока?

2. Какая формула используется для вычисления величины полного противодействия в последовательной цепи?

3. Чему равно значение Z в последовательной цепи переменного тока, где Х_с = 3 Ом, X_L = 6 Ом, a R = 4 Ом?

17-3 ЗАКОН ОМА

Закон Ома не может быть применен в цепях переменного тока потому, что он не учитывает реактивное сопротивление. Модифицируя закон Ома путем учета импеданса, можно получить общий закон, который применим к цепям переменного тока.

I = E/R преобразуется в I = E/Z

Эта формула применима к переменному току, текущему в любой цепи.

_{ПРИМЕР: Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 250 ом и емкостное сопротивление 150 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?}

_Дано:

_{R = 510 Ом; XL = 250 Ом; Xc = 150 Ом; E = 120 В}

_{Решение:}

_{X = ХL + Хc = 250–150}

_{X = 100 Ом (индуктивное)}

_{Z² = R² + X²}

_{Z² =(510)² +(100)²}

_{Z = √(270100)}

_{Z = 519,71 Ом}

_{I = E/Z = 120/519,71}

_{I = 0,23 А или 230 мА.}

17-3. Вопросы

1. Каким образом модифицируется закон Ома, чтобы его можно было применить к цепям переменного тока для определения напряжения и тока?

2. Последовательная цепь содержит резистор сопротивлением 510 ом, индуктивное сопротивление 300 ом и емкостное сопротивление 375 ом. Какой ток течет по цепи, если к ней приложено напряжение 120 вольт?

17-4. ЦЕПИ RLC

Материал, изложенный до сих пор, применим ко всем цепям переменного тока. В приведенных примерах рассматривались последовательные цепи. Понятия, рассмотренные в этом параграфе, не содержат нового материала, но используют все принципы, изложенные ранее.

_{ПРИМЕР: На рис. 17-5 показана последовательная RLC цепь. Необходимо вычислить Хс, XL, X, Z и IT.}

_{Рис. 17-5. Последовательная цепь RLC.}

_{Сначала вычислим Хс, XL и X.}

 _Дано:

_{f = 60 Гц; С = 470 мкФ; L = 27 мГн.}

_{Решение:}

_{Xc = 1/2πfC}

_{Xc = 1/(6,28)(60)(0,000470)}

_{XC = 5,65 Ом}

_{XL = 2πfL}

_{XL = (6,28)(60)(0,027)}

_{XL = 10,17 Ом}

_{X = XL — Xc = 10,17 — 5,65}

_{X = 4,52 Ом (индуктивное).}

_{Используем значение X для вычисления Z.}

 _Дано:

_{X = 4,52 Ом; R = 10 Ом.}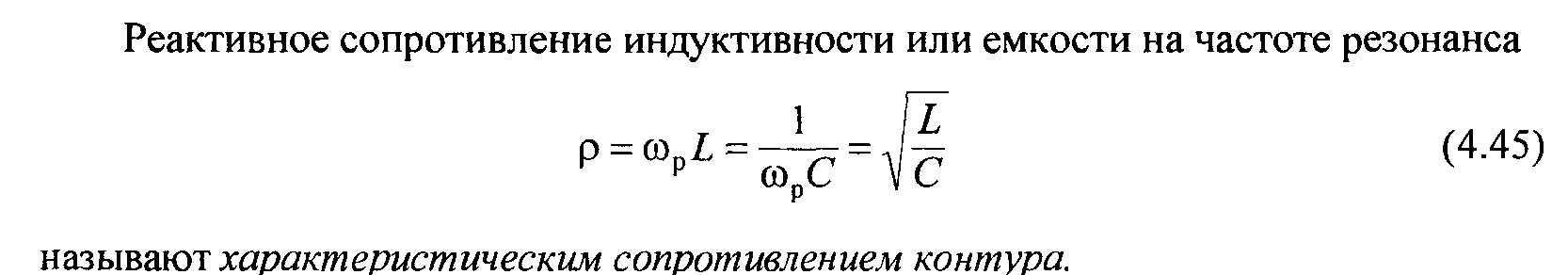

_{Решение:}

_{Z² = R² + X²}

_{Z² = (10)² + (4,52)² = 120,43}

_{Z = √(120,43) = 10,97 Ом.}

_{Это значение Z может быть использовано для вычисления полного тока (IT).}

_Дано:

_{Z = 10,97 Ом; E = 120 В.}

_{Решение:}

_{IT = E/Z = 120/10,97}

_{IT = 10,94 A.} 

Помните, что во всех частях последовательной цепи течет один и тот же ток.

Если элементы в цепях соединены параллельно, то следует учесть одно главное различие между последовательными и параллельными цепями. При последовательном соединении по всей цепи течет один и тот же ток, а в параллельной цепи к каждой ветви приложено одинаковое напряжение. Вследствие этой разницы полный импеданс параллельной цепи должен вычисляться на основе тока в цепи.

В последовательной цепи RLC для вычисления реактивного сопротивления и импеданса используются следующие формулы:

X = Х_с — X_L или X = X_L — Х_с, Z² = R² + X².

В случае параллельных цепей должны использоваться следующие формулы:

I_X = I_с — I_L или I_X = I_L — I_X; I²_Z = (I_R)² + (I_X)²

Импеданс параллельной цепи находится с помощью формулы:

I_Z = E/Z

Замечание: Если неизвестно напряжение (Е), приложенное к цепи, то для вычисления I_c, I_L, I_x, I_R и I_Z можно использовать любое значение Е. То же значение напряжения должно использоваться для вычисления импеданса.

_{ПРИМЕР: Найти значение Z для цепи, показанной на рис. 17-6.}

_{Рис. 17-6. Параллельная цепь RLC.}

_Дано:

_{Е = 120 В; R = 60 Ом; Хс = 75 Ом; XL = 50 Ом.}

_{Решение:}

_{Первым шагом в вычислении Z является вычисление токов отдельных ветвей.}

_{IR = E/R = 120/60 = 2 A} 

_{Ix = E/Xc = 120/75 = 1,6 A}

_{IL = E/XL = 120/50 = 2,4 A}

_{Используя значения IR, Ic, IL, вычислим Ix и Iz}

_{IX = IL — Ic = 2,4 – 1,6}

_{Ix = 0,8 А (индуктивный)}

_{I²z = (IR)^{2 +} (Ix)²}

_{I²z = (2)² + (0,8)² = 4,64}

_{Iz = √(4,64) = 2,15 A.}

_{Используя значение Iz, вычислим Z.}

_{Iz = E/Z}

_{2,15 = 120/Z} 

_{Z = 120/2,15 = 55,8 Ом}

В завершение этой главы отметим, что мы рассмотрели все блоки, из которых строятся электрические цепи. При изложении материала использовались ранее изученные понятия и соотношения.

17-4. Вопрос

1. Чем отличаются вычисления импеданса для последовательной цепи переменного тока и для параллельной цепи?

РЕЗЮМЕ

• Конденсатор в цепи переменного тока оказывает противодействие любому изменению напряжения, так же как он это делает в цепи постоянного тока.

• Ток опережает по фазе напряжение на конденсаторе на 90 градусов.

• Противодействие, оказываемое конденсатором переменному току, называется емкостным реактивным сопротивлением. Оно обозначается Х_с и вычисляется по формуле:

X_C = 1/2πfC

• Катушка индуктивности в цепи переменного тока противодействует любому изменению тока, так же как она это делает в цепи постоянного тока.

• На катушке индуктивности ток отстает по фазе от напряжения на 90 градусов.

• Противодействие, оказываемое катушкой индуктивности переменному току, называется индуктивным реактивным сопротивлением. Оно обозначается X_L и вычисляется по формуле

X_L = 2πfL.

• Полное реактивное сопротивление последовательной цепи переменного тока определяется формулами X = X_C — X_L или X = X_L — X_C.

• Полное реактивное сопротивление последовательной цепи переменного тока является либо емкостным, либо индуктивным, в зависимости от того, какая величина больше, Х_C или X_L.

• В параллельной цепи реактивное сопротивление определяется с помощью формул

I_Z = E/Z

где I_z определяется формулой I_z² = (I_R)² + (I_X)², а I_х вычисляется по формуле I_X = I_C — I_L или I_X = I_L — I_C.

• Реактивное сопротивление параллельной цепи также может быть емкостным или индуктивным, в зависимости то того, какая величина больше I_C или I_L.

• Полное сопротивление цепи переменного тока называется импедансом. Он обозначается символом Z. В последовательной цепи Z² = R² + X². В параллельной цепи I²_Z = (I_R)² + (I_X)² и

I_Z = E/Z

• Получена формула для закона Ома, который можно применять для пеней переменного тока:

I = E/Z

Глава 17. САМОПРОВЕРКА

1. Чему равны значения Х_С, X_L, X, Z и I_T для цепи, изображенной на рис. 17-7?

Рис. 17-7. Последовательная цепь RLC.

2.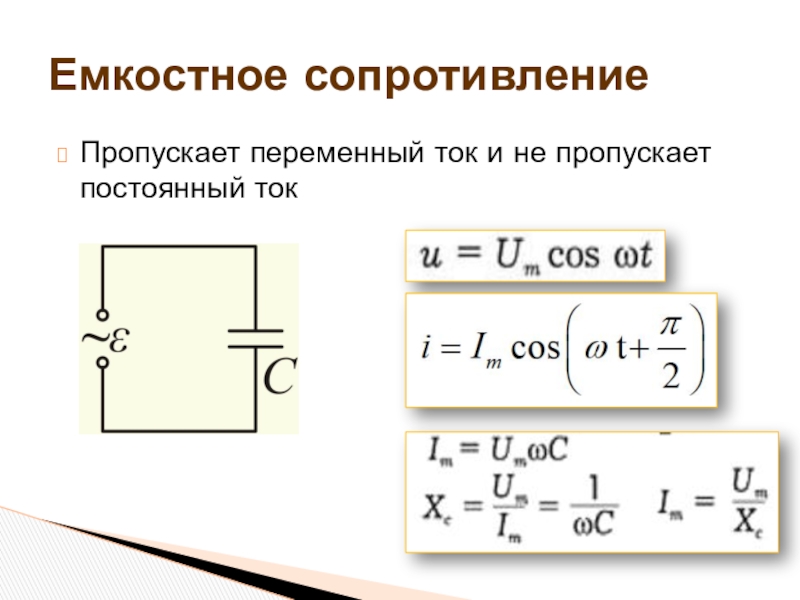  Чему равны значения I_C, I_L, I_X, I_R и I_Z для цепи, изображенной на рис. 17-8?

Рис. 17-8. Параллельная цепь RLC.

Основные понятия сопротивления и реактивного сопротивления — Знания

1. Импеданс

В цепи с сопротивлением, индуктивностью и емкостью (цепь RLC) блокирующее воздействие на переменный ток называется импедансом; сопротивление обычно обозначается как Z, единица измерения Ом; полное сопротивление состоит из сопротивления, индуктивного сопротивления и емкостного сопротивления, но не трех. Для конкретной цепи полное сопротивление не является постоянным, а изменяется в зависимости от частоты; в последовательной цепи резисторов, катушек индуктивности и конденсаторов сопротивление цепи обычно больше, чем сопротивление.

2. Реактивность

Блокирующее воздействие конденсаторов и катушек индуктивности на переменный ток в цепи вместе называется реактивным сопротивлением, выраженным в X, в омах. Реактивное сопротивление изменяется при изменении частоты цепи переменного тока, вызывая изменение фазы тока и напряжения в цепи.

3. Соотношение между сопротивлением, реактивным сопротивлением, емкостным сопротивлением и индуктивным сопротивлением

Сопротивление, сумма сопротивления и реактивного сопротивления, математически выражается как:

Z — полное сопротивление в омах

R сопротивление в омах

X — реактивное сопротивление в омах

j — мнимая единица

Когда X> 0, это называется индуктивным сопротивлением

Когда X = 0, реактивное сопротивление равно 0

Когда X 0,>

Для идеального чисто индуктивного или емкостного компонента реактивного сопротивления с нулевым сопротивлением сила сопротивления равна величине реактивного сопротивления.

Общее реактивное сопротивление типичной цепи равно: X = XL? Xc

Где XL — индуктивное сопротивление цепи, а Xc — емкостное сопротивление цепи.

3.1 Смысл сопротивления

Индуктивное реактивное сопротивление (XL) обычно обусловлено наличием в цепи индуктивного контура (такого как катушка), и результирующее электромагнитное поле создает соответствующую электрическую силу, которая блокирует поток тока. Чем больше изменение тока, то есть, чем больше частота цепи, тем больше индуктивное сопротивление; когда частота становится равной 0, то есть когда она становится постоянным током, индуктивное сопротивление также становится равным нулю. Индуктивное реактивное сопротивление вызывает разность фаз между током и напряжением. Индуктивное сопротивление можно рассчитать по следующей формуле:

XL = ωL = 2 × π × f × L

XL — индуктивное сопротивление, единица измерения Ом, Ом

ω — угловая частота в радианах в секунду, рад / с

f — частота в герцах, Гц

3.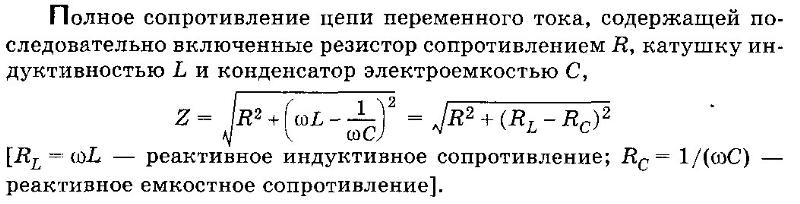 2 емкостное сопротивление

Концепция емкостного реактивного сопротивления (Xc) отражает характеристику того, что переменный ток может проходить через конденсатор. Чем выше частота переменного тока, тем меньше емкостное сопротивление, то есть меньше блокирующий эффект конденсатора. Емкостное сопротивление также вызывает разность фаз между током и напряжением на конденсаторе. Емкостное сопротивление можно рассчитать по следующей формуле:

Xc = 1 / (ω × C) = 1 / (2 × π × f × C)

Xc — емкостное сопротивление в Ом, Ом

ω — угловая частота в радианах в секунду, рад / с

f — частота в герцах, Гц

C — емкость в Фаразе F 1 раз

Что такое активное и реактивное сопротивление. Ёмкостное сопротивление. | Электроника, ESP32, Arduino

Изучать электротехнику всегда лучше на конкретных примерах. Соберем схему состоящую из резистора, двух светодиодов и подадим на нее переменное напряжение.

Резистор — активная нагрузка в цепи переменного тока

Резистор — активная нагрузка в цепи переменного тока

Переменный ток с частотой 50Гц меняет направление 100 раз в секунду

Переменный ток с частотой 50Гц меняет направление 100 раз в секунду

Первый 10 миллисекунд горит верхний светодиод, вторые 10 миллисекунд горит нижний светодиод

Первый 10 миллисекунд горит верхний светодиод, вторые 10 миллисекунд горит нижний светодиод

Если в эту цепь вместо светодиодов подключить амперметр и построить график изменения тока в зависимости от напряжения с выхода источника переменного тока, то они будут совпадать по времени

Активным называют сопротивление участка, если оно уменьшает ток в цепи, препятствует движению зарядов и одновременно отбирает у них часть мощности. Понятие «активное сопротивление» понадобилось именно потому, что есть элементы электрических цепей, которые оказывают сопротивление току, но мощности при этом не отбирают. О таких элементах говорят что у них реактивное сопротивление.

События на участке с активным сопротивлением беспрекословно подчиняются закону Ома в том виде, в каком он был установлен для постоянного тока. В такой цепи максимум тока будет наблюдаться в тот же момент, что и максимум напряжения.

Емкостное сопротивление — один из примеров реактивного сопротивления. Сам конденсатор ни какой мощности от генератора не потребляет. В какие-то моменты, правда, генератор, затрачивает усилия на то чтобы зарядить конденсатор, но конденсатор честно возвращает полученную энергию в момент разряда. Конденсатор напоминает пружину, которая что берет то и отдает.

Соберем еще одну схему:

Первая пара светодиодов подключена через резистор, вторая через конденсатор

Первая пара светодиодов подключена через резистор, вторая через конденсатор

Ток для первой пары светодиодов, ограничен резистором, для второй пары светодиодов конденсатором.

Резистивное и емкостное сопротивление

Резистивное и емкостное сопротивление

В цепи переменного тока происходит постоянная зарядка/разрядка конденсатора и поэтому светодиоды светятся.

А вот высокоскоростная камера дает более интересную картину происходящего:

Резистивное и емкостное сопротивление, максиму тока наблюдается в разные периоды времени.

Резистивное и емкостное сопротивление, максиму тока наблюдается в разные периоды времени.

Ток проходящий через конденсатор не совпадет по значению с током проходящим через резистор.

Переход через 0. Ток через резистор равен нулю, ток в цепи конденсатора максимальный

Переход через 0. Ток через резистор равен нулю, ток в цепи конденсатора максимальный

Амплитудное значение напряжения. Ток в цепи резистора максимальный, в цепи конденсатора равен нулю.

Амплитудное значение напряжения. Ток в цепи резистора максимальный, в цепи конденсатора равен нулю.

Если перерисовывать график изменения яркости светодиодов, получится картинка из старой советской книжки.

Синусоидальное напряжение создаёт синусоидальный ток через конденсатор. Ток опережает напряжение на 90 градусов. Это не нужно понимать так, будто ток появляется раньше, чем мы прикладываем к конденсатору напряжение; подобное не возможно. Просто амплитуда тока наступает на четверть периода раньше, чем амплитуда напряжения.

Свойство конденсатора сдвигать фазу, часто используют для подключения трехфазных электродвигателей в однофазную сеть. В одной из следующих статей обязательно соберем такой визуальный макет.

Полный список всех статей канала доступен по этой ссылке:

Всем удачи!

реактивное сопротивление | электроника | Britannica

реактивное сопротивление , в электричестве, мера сопротивления, которое цепь или часть цепи оказывает электрическому току, поскольку ток изменяется или переменный. Постоянные электрические токи, протекающие по проводникам в одном направлении, испытывают сопротивление, называемое электрическим сопротивлением, но не реактивное сопротивление. Реактивное сопротивление присутствует в дополнение к сопротивлению, когда по проводникам течет переменный ток. Реактивное сопротивление также возникает в течение коротких промежутков времени, когда постоянный ток изменяется по мере приближения к установившемуся потоку или отклонения от него, например, когда выключатели замкнуты или разомкнуты.

Реактивное сопротивление бывает двух типов: индуктивное и емкостное. Индуктивное реактивное сопротивление связано с магнитным полем, которое окружает провод или катушку с током. Переменный ток в таком проводнике или индукторе создает переменное магнитное поле, которое, в свою очередь, влияет на ток и напряжение (разность потенциалов) в этой части цепи. Катушка индуктивности по существу противостоит изменениям тока, заставляя изменения тока отставать от изменений напряжения. Ток нарастает, когда управляющее напряжение уже уменьшается, имеет тенденцию оставаться на максимальном значении, когда напряжение меняет свое направление на обратное, падает до нуля, когда напряжение увеличивается до максимума в противоположном направлении, и меняет свое направление и нарастает в в том же направлении, что и напряжение, даже если напряжение снова падает. Индуктивное реактивное сопротивление, мера этого противодействия току, пропорционально как частоте f переменного тока, так и свойству катушки индуктивности, называемому индуктивностью (обозначаемой как L и зависящей, в свою очередь, от размеров катушки индуктивности, расположения, и окружающую среду). Индуктивное сопротивление X _L равно произведению частоты тока и индуктивности проводника, умноженному на 2π, просто X _L = 2π f Индуктивное сопротивление выражается в омах. (Единицей частоты является герц, а индуктивности — генри.)

Емкостное сопротивление, с другой стороны, связано с изменением электрического поля между двумя проводящими поверхностями (пластинами), отделенными друг от друга изолирующей средой. Такой набор проводников, конденсатор, по существу противостоит изменениям напряжения или разности потенциалов на его пластинах. Конденсатор в цепи замедляет протекание тока, заставляя переменное напряжение отставать от переменного тока, что в отличие от индуктора. Емкостное реактивное сопротивление, мера этого противодействия, обратно пропорционально частоте f переменного тока и свойству конденсатора, называемому емкостью (обозначается C и зависит от размеров конденсатора, расположения и изолирующей среды). ). Емкостное сопротивление X _C равно обратному произведению 2π, частоты тока и емкости этой части цепи, просто X _C = 1/(2 π f C ).Емкостное сопротивление измеряется в омах. (Емкость измеряется в фарадах.)

Поскольку индуктивное сопротивление X _L заставляет напряжение опережать ток, а емкостное сопротивление X _C заставляет напряжение отставать реактивное сопротивление X — их разность, то есть X = X _L — X _C . Величина, обратная реактивному сопротивлению, 1/ X , называется проводимостью и выражается в единицах обратного ома, называемого мхо ( ом пишется наоборот).

Емкостное реактивное сопротивление

• Изучив этот раздел, вы сможете описать:
• •Емкостное реактивное сопротивление.
• •Взаимосвязь между реактивным сопротивлением, частотой и емкостью.
• •Графическое представление емкостного сопротивления.

В конденсаторе с постоянным напряжением, модуль 4.2 показано, что текущий поток падает до нуля после начального переходного периода. Однако при приложении переменного напряжения любой заметной частоты ток течет сначала в одном направлении, а затем в другом. Конденсатор сначала заряжается, а затем разряжается, поэтому при условии, что частота подаваемого переменного тока достаточно высока, конденсатор никогда не достигает своего полностью заряженного состояния с нулевым током ни при какой полярности, и ток продолжает течь все время. Величина протекающего тока будет зависеть от угловой скорости приложенного напряжения и от емкости конденсатора

Рис. 6.2.1 Емкостное реактивное сопротивление X

_C

Чем ниже частота приложенного напряжения, тем больше времени конденсатор должен достичь полностью заряженного состояния с нулевым током, прежде чем напряжение изменит свою полярность и снова начнет разряжать конденсатор. Таким образом, конденсатор проводит больше времени полностью заряженным и пропуская гораздо меньший ток, поэтому среднее значение протекающего тока меньше на низких частотах. Когда применяется более высокая частота, конденсатор переходит от заряда к разряду раньше на своей кривой заряда и остается дальше от своего полностью заряженного состояния.Как следствие, больше тока течет. Таким образом, сопротивление протеканию тока в любом конденсаторе заданного размера уменьшается с увеличением частоты. Это зависящее от частоты сопротивление протеканию тока в конденсаторе называется ЕМКОСТНОЙ РЕАКТИВНОЙ АКТИВНОСТЬЮ (X _C ).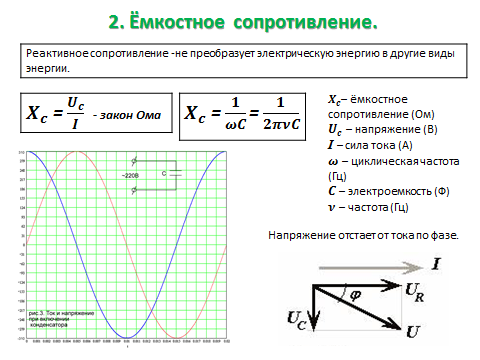 Формула емкостного сопротивления:

На рис. 6.2.1 показан график зависимости емкостного сопротивления от частоты для заданной емкости конденсатора, при этом емкостное сопротивление (X _C ) обратно пропорционально частоте (X _C уменьшается по мере увеличения частоты).

Реактивное сопротивление также обратно пропорционально величине емкости, и значение X _C на любой конкретной частоте будет меньше в больших конденсаторах, чем в меньших. Все конденсаторы будут иметь бесконечно высокие значения реактивного сопротивления при 0 Гц (т.е. ток не течет при постоянном токе), но в больших конденсаторах реактивное сопротивление падает до низкого уровня на гораздо более низких частотах, чем в меньших конденсаторах. По этой причине конденсаторы большей емкости используются в низкочастотных устройствах.

Расчет емкостного сопротивления

• Изучив этот раздел, вы сможете описать:
• • Расчеты с учетом емкостного сопротивления.
• • Многоэтапные расчеты реактивного сопротивления и сопротивления.

Для расчетов, основанных на емкостном реактивном сопротивлении, вам в первую очередь нужно подумать об информации на странице «Реактивное сопротивление и сопротивление» и оценить разницу между реактивным сопротивлением и сопротивлением и двумя типами реактивного сопротивления. Для расчетов вы можете выбрать, какую формулу использовать для емкостного сопротивления: 1/2πƒC или 1/ωC, но чаще используется 1/2πƒC (одна из причин заключается в том, что в научных калькуляторах в основном есть клавиша π, но нет клавиши ω!) .

Помните, что некоторые проблемы, которые вам могут понадобиться для решения, не обязательно будут иметь очевидное решение, например, просто вычисление реактивного сопротивления компонента. Например, если вас просят рассчитать напряжение питания, необходимое для получения определенного протекающего тока, или напряжения на компоненте, могут потребоваться два или более шагов, используя ответ из одного расчета, чтобы предоставить информацию для второго расчета, прежде чем достичь окончательный ответ.

Прежде чем начать, подумайте над следующими советами; они облегчат проблемы, если вы будете внимательно следовать им.

1. Подготовьте ответы с помощью карандаша и бумаги; перерисуйте схему, над которой вы работаете.

2. Перечислите информацию, которую вы получили, и то, что вам нужно найти для ответа. Это поможет вам решить, можно ли найти ответ за один шаг или вам понадобится промежуточный ответ.

3. После того, как вы перечислите информацию на шаге 2, вам нужно будет решить, какую подходящую формулу (или формулы) использовать. Запишите и это.

4. Конечно, ответ — это не просто число, если это определенное число Ом (или любая другая единица измерения), не забудьте указать правильную единицу измерения (например, Ом, кОм или МОм), иначе ваш ответ бессмысленный.

5. Когда вы вводите значения в свой калькулятор, преобразуйте все большие или малые (Мэг, микро и т. д.) значения в их основные единицы (вольты, омы и т. д.) с помощью клавиши EXP. Здесь легко ошибиться и получить действительно глупые ответы, в тысячи раз большие или слишком маленькие.

Все эти действия поначалу могут показаться трудоемкими, но выработайте привычку, и они облегчат ваши расчеты, потому что вы будете следовать знакомому методу.Они также будут более надежными, потому что, когда вам нужно выполнить многоэтапные вычисления, вам нужно быть организованным. Так легко ошибиться на полпути к своей работе, потому что вы забыли, где именно вы находитесь в расчетах. Однако, если вы записали каждую проблему, это позволит вам вернуться назад и увидеть, где вы ошиблись, чтобы не повторять одни и те же ошибки.

Зачем лезть во все эти хлопоты, когда в Интернете есть множество калькуляторов, которые сделают расчеты за вас?

Многие электронные и веб-калькуляторы превосходны, просто введите данные и нажмите, чтобы получить ответ.Но вам все равно нужно инстинктивно знать, какую формулу использовать, когда и почему.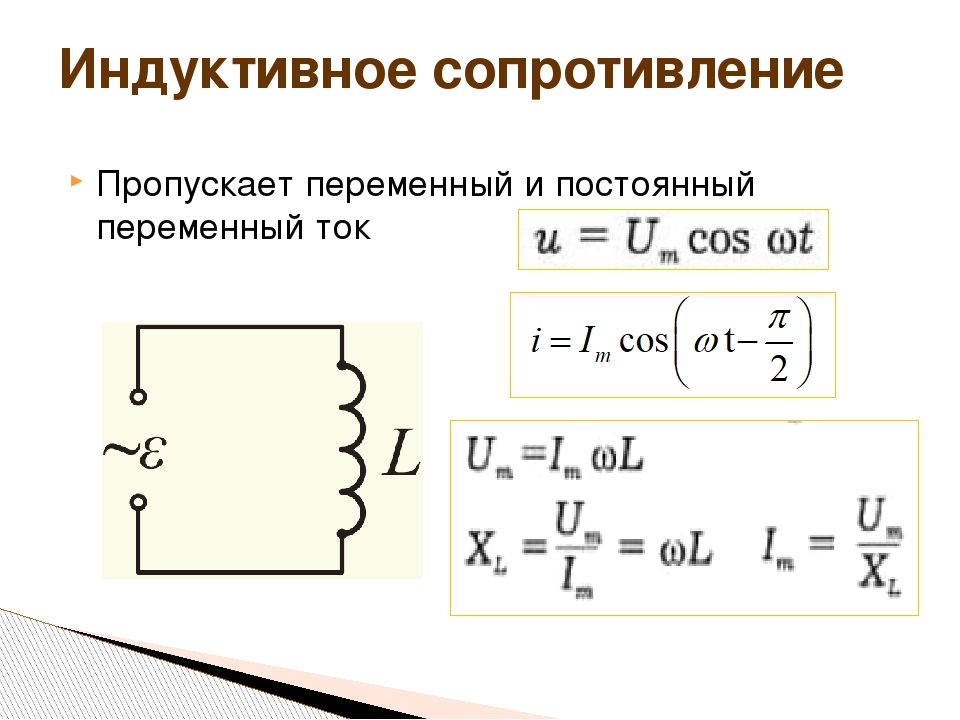 Чтобы быть достаточно знакомым, чтобы сделать это хорошо, вам нужно знать, как работают различные формулы. Лучший способ сделать это — начать с решения некоторых задач вручную, тогда вы найдете многие калькуляторы, предлагаемые на веб-сайтах, гораздо более полезными.

Чтобы помочь вам на правильном пути, почему бы не загрузить нашу брошюру «Советы по математике», в которой показано, как использовать калькулятор с показателями степени и техническими обозначениями для работы с этими единицами измерения и каждый раз получать правильный ответ.

Нет научного калькулятора? В буклете «Советы по математике» объясняется, что вам нужно (и что вам не нужно, чтобы не тратить деньги напрасно). Если вы не хотите покупать научный калькулятор, вы всегда можете взять его бесплатно на сайте www.calculator.org/download.html. Пользователи ПК могут попробовать Calc98.

Какой бы калькулятор вы ни выбрали, помните, что вы должны прочитать инструкции, чтобы ознакомиться с методами работы, которые вы должны использовать, поскольку они различаются от калькулятора к калькулятору.

Итак, вы прочитали эти инструкции и готовы начать. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.

Рис. 6.4.1 Пример емкостного реактивного сопротивления

Примеры реактивного сопротивления.

Проблема, показанная на рис. 6.4.1, является типичным примером, когда необходимо найти ряд связанных величин, включая реактивное сопротивление конденсатора. Другие значения, такие как среднеквадратичное напряжение (V _RMS ) и среднеквадратичное значение тока (I _RMS ), описаны в Модуле 1.2

Примечание. Если вы используете Calc98 для своих расчетов, вам необходимо установить в меню «Просмотр»> «Параметры»> «Отображение» значение «Инженерное» (в разделе «Десятичные числа»), и было бы неплохо, пока вы находитесь в этом меню, выбрать 2 из Раскрывающийся список Decimals для установки количества цифр после запятой. Это округлит ваш ответ до двух знаков после запятой, что является достаточно точным для большинства применений, и предотвратит получение глупых ответов, таких как 75,666666666667Ω, которые были бы слишком точными для большинства целей.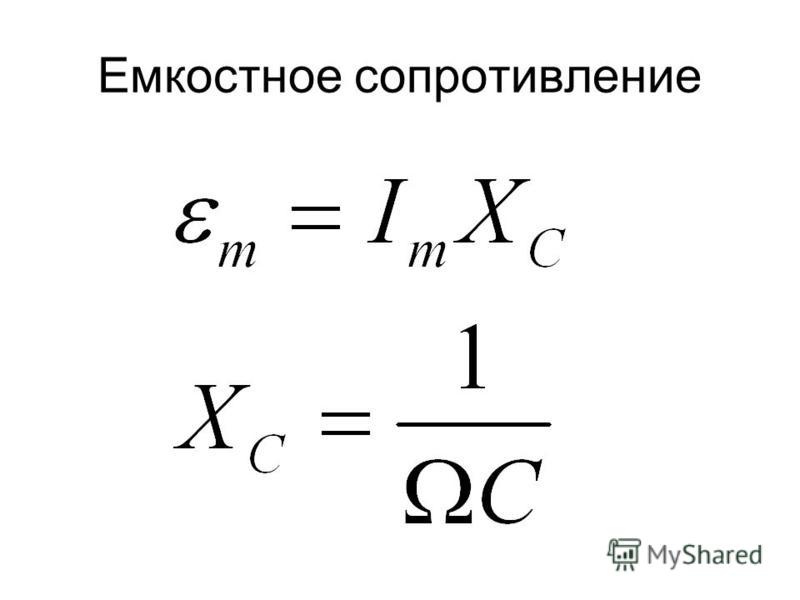

Емкость и емкостное реактивное сопротивление — Inst Tools

Конденсаторы

Изменение переменного напряжения, приложенного к конденсатору, заряд конденсатора и ток, протекающий через конденсатор, представлены на рисунке 3.

Рисунок 3: Напряжение, заряд и ток в конденсаторе

Ток, протекающий в цепи, содержащей емкость, зависит от скорости изменения напряжения.Течение на рис. 3 максимально в точках a, c и e. В этих точках напряжение изменяется с максимальной скоростью (т. е. проходит через ноль).

Между точками a и b напряжение и заряд увеличиваются, а ток поступает в конденсатор, но его значение уменьшается. В точке b конденсатор полностью заряжен, а ток равен нулю. От точек b к c напряжение и заряд уменьшаются по мере разрядки конденсатора, а его ток течет в направлении, противоположном напряжению.От точек с до d конденсатор начинает заряжаться в обратном направлении, а напряжение и ток снова в одном направлении.

В точке d конденсатор полностью заряжен, и ток снова равен нулю. От точек d до e конденсатор разряжается, и протекание тока противоположно напряжению. На рис. 3 ток опережает приложенное напряжение на 90°. В любой чисто емкостной цепи ток опережает приложенное напряжение на 90°.

Емкостное реактивное сопротивление

Емкостное реактивное сопротивление – это сопротивление конденсатора или емкостной цепи протеканию тока.Ток, протекающий в емкостной цепи, прямо пропорционален емкости и скорости изменения приложенного напряжения. Скорость изменения приложенного напряжения определяется частотой источника питания; поэтому, если частота емкости данной цепи увеличивается, ток увеличивается.

Можно также сказать, что если частота или емкость увеличиваются, сопротивление току уменьшается; следовательно, емкостное реактивное сопротивление, которое противодействует протеканию тока, обратно пропорционально частоте и емкости.

Емкостное реактивное сопротивление X _C измеряется в омах, как и индуктивное реактивное сопротивление.

Приведенное ниже уравнение является математическим представлением емкостного реактивного сопротивления.

где

f = частота (Гц)
π = ~3,14
C = емкость (фарады)

Приведенное ниже уравнение представляет собой математическое представление емкостного реактивного сопротивления, когда емкость выражается в микрофарадах (мкФ).

Приведенное ниже уравнение представляет собой математическое представление тока, протекающего в цепи только с емкостным реактивным сопротивлением.

, где
I = эффективный ток (А)
E = эффективное напряжение на емкостном реактивном сопротивлении (В)
X _C = емкостное реактивное сопротивление (Ом)

Пример:

Конденсатор емкостью 10 мкФ подключен к источнику питания 120 В, 60 Гц (см. рис. 4). Найти емкостное сопротивление и силу тока в цепи. Нарисуйте векторную диаграмму.

Рисунок 4: Схема и векторная диаграмма

Решение:

1. Емкостное реактивное сопротивление

X _C = 1 000 000 / [ (2)(3,14)(60)(10)]

X _C = 1 000 000 / 3768 = 265,4 Ом

2. Ток, протекающий в цепи

I = 120/265,4 = 0,452 А

3. Векторная диаграмма, показывающая опережение тока по напряжению на 90°, представлена ​​на рисунке 4b.

Рабочий лист емкостного реактивного сопротивления — электрические цепи переменного тока

Пусть сами электроны дадут вам ответы на ваши «учебные задачи»!

Примечания:

По моему опыту, ученикам требуется много практики с анализом цепей, чтобы стать профессионалом.С этой целью преподаватели обычно дают своим ученикам множество практических задач для решения и дают ответы, чтобы студенты могли проверить свою работу. Хотя этот подход позволяет учащимся хорошо разбираться в теории цепей, он не дает им полного образования.

Студентам нужна не только математическая практика. Им также нужны настоящие практические занятия по построению схем и использованию тестового оборудования. Итак, я предлагаю следующий альтернативный подход: студенты должны построить свои собственные «практические задачи» с реальными компонентами и попытаться математически предсказать различные значения напряжения и тока.Таким образом, математическая теория «оживает», и учащиеся получают практические навыки, которые они не получили бы, просто решая уравнения.

Другая причина для следования этому методу практики состоит в том, чтобы научить студентов научному методу : процессу проверки гипотезы (в данном случае математических предсказаний) путем выполнения реального эксперимента. Студенты также разовьют реальные навыки устранения неполадок, поскольку они время от времени допускают ошибки при построении схемы.

Потратьте несколько минут вместе с классом на изучение некоторых «правил» построения схем до того, как они начнутся.Обсудите эти вопросы со своими учениками в той же сократовской манере, в которой вы обычно обсуждаете вопросы из рабочих листов, а не просто говорите им, что они должны и не должны делать. Я не перестаю удивляться тому, как плохо студенты усваивают инструкции, представленные в формате типичной лекции (монолога инструктора)!

Отличный способ познакомить учащихся с математическим анализом реальных цепей — предложить им сначала определить значения компонентов (L и C) на основе измерений напряжения и тока переменного тока.Самая простая схема, конечно же, представляет собой один компонент, подключенный к источнику питания! Это не только научит студентов правильно и безопасно настраивать цепи переменного тока, но также научит их измерять емкость и индуктивность без специального контрольно-измерительного оборудования.

Примечание по реактивным компонентам: используйте качественные конденсаторы и катушки индуктивности, а для питания старайтесь использовать низкие частоты. Небольшие понижающие силовые трансформаторы хорошо работают с катушками индуктивности (не менее двух катушек индуктивности в одном корпусе!), если напряжение, подаваемое на любую обмотку трансформатора, меньше номинального напряжения этого трансформатора для этой обмотки (во избежание насыщения сердечника). ).

Примечание для тех инструкторов, которые могут жаловаться на «потерянное впустую» время, необходимое для того, чтобы студенты строили реальные схемы, а не просто математически анализировали теоретические схемы:

С какой целью студенты изучают ваш курс?

Если ваши учащиеся будут работать с реальными схемами, им следует по возможности учиться на реальных схемах. Если ваша цель — обучить физиков-теоретиков, то обязательно придерживайтесь абстрактного анализа! Но большинство из нас планирует, чтобы наши ученики делали что-то в реальном мире с образованием, которое мы им даем.«Потерянное» время, потраченное на построение реальных схем, окупится огромными дивидендами, когда им придет время применить свои знания для решения практических задач.

Кроме того, когда студенты создают свои собственные практические задачи, они узнают, как выполнять первичные исследования , что дает им возможность самостоятельно продолжить свое образование в области электротехники/электроники.

В большинстве наук реалистичные эксперименты гораздо сложнее и дороже поставить, чем электрические цепи. Профессора ядерной физики, биологии, геологии и химии хотели бы, чтобы их студенты применяли передовую математику в реальных экспериментах, не представляющих угрозы безопасности и стоящих меньше, чем учебник.Они не могут, а вы можете. Воспользуйтесь удобством, присущим вашей науке, и заставьте ваших учеников практиковать математику на множестве реальных схем!

Емкостное реактивное сопротивление Xc — Engineer-Educators.com

Эффективность конденсатора в прохождении потока переменного тока зависит от емкости цепи и применяемой частоты. В какой степени конденсатор пропускает поток переменного тока, во многом зависит от значения емкости конденсатора, указанного в фарадах (f).Чем больше емкость конденсатора, тем большее число электронов, измеряемое в кулонах, необходимо для приведения конденсатора в полностью заряженное состояние. Как только конденсатор приближается или фактически достигает полностью заряженного состояния, полярность конденсатора будет противодействовать полярности приложенного напряжения, по существу действуя как разомкнутая цепь. Чтобы дополнительно проиллюстрировать эту характеристику и то, как она проявляется в цепи переменного тока, рассмотрим следующее. Если конденсатор имеет большое емкостное значение, что означает, что ему требуется относительно большое количество электронов, чтобы привести его в полностью заряженное состояние, то ток довольно высокой частоты может чередоваться через конденсатор, при этом конденсатор никогда не достигает полного заряда.В этом случае, если частота достаточно высока, а емкость настолько велика, что конденсатор никогда не успевает полностью зарядиться, вполне возможно, что конденсатор может оказывать очень малое сопротивление току или вообще не оказывать его. Однако, чем меньше емкость, тем меньше электронов требуется, чтобы довести его до полного заряда, и более вероятно, что конденсатор будет накапливать достаточно противоположного заряда, чтобы он мог оказывать большое сопротивление току, если не до такой степени, что ведет себя как разомкнутая цепь.Между этими двумя крайними состояниями лежит континуум возможностей токовой оппозиции в зависимости от комбинации применяемой частоты и выбранной емкости. Ток в цепи переменного тока можно контролировать, изменяя емкость цепи таким же образом, как сопротивление может управлять током. Фактическое реактивное сопротивление переменного тока Xc, как и сопротивление, измеряется в омах (Ом). Емкостное реактивное сопротивление Xc определяется следующим образом: 

Пример задачи:
Предполагается последовательная цепь, в которой приложенное напряжение составляет 110 вольт при 60 имп/с, а емкость конденсатора составляет 80 Мф.Найти емкостное сопротивление и ток.

Решение:
Чтобы найти емкостное реактивное сопротивление, используется уравнение Xc = 1/(2 p f C). Сначала емкость, 80 Мф, переводят в фарады путем деления 80 на 1 000 000, так как 1 миллион микрофарад равен 1 фараду. Это частное равно 0,000080 фарад. Это подставляется в уравнение и

После определения реактивного сопротивления можно использовать закон Ома так же, как он используется в цепях постоянного тока для определения тока.

22.4 Емкостное реактивное сопротивление

22.4 Емкостное реактивное сопротивление

Переменный ток

В цепи постоянного тока нет тока через конденсатор
— или через эту простую схему, содержащую конденсатор.

Однако в цепи переменного тока через это соединение будет протекать ток.
простая схема конденсатора. Конденсатор начнет накапливать
заряд, и противонапряжение, а затем переменное напряжение изменится
и конденсатор разрядится и начнет наращивать противоположное
обвинение.

В простой цепи резистора мы определили сопротивление R
к

В = ИР

Мы хотели бы сделать что-то с похожей формой для этого
конденсаторная цепь. Аналогичным образом мы можем написать

.

В _С = I Х _С

, где V _C — максимальное напряжение на
конденсатор, а I — максимальный ток в цепи.
X _C называется «емкостным реактивным сопротивлением»; это аналог сопротивления
а также измеряется в омах (). Количество тока через эту цепь и, следовательно, значение
емкостное реактивное сопротивление — зависит от частоты переменного тока
поставка. Низкочастотное переменное напряжение быстро зарядит конденсатор.
много, что будет очень мало тока. Конечно, напряжение постоянного тока
предельный случай или предельная низкая частота и тогда ток отсутствует при
все. Высокочастотное переменное напряжение начнет заряжать конденсатор только до того, как
он меняет направление и разряжает конденсатор, так что будет больше
Текущий.То есть у емкостное сопротивление будет
большой для низких частот и маленький для высоких частот . Емкостный
реактивное сопротивление определяется как

В отличие от случая с резистором, напряжение и ток в этом
простая схема конденсатора не в фазе. То есть они делают
не имеют своих максимальных значений одновременно и они не идут
до нуля одновременно.