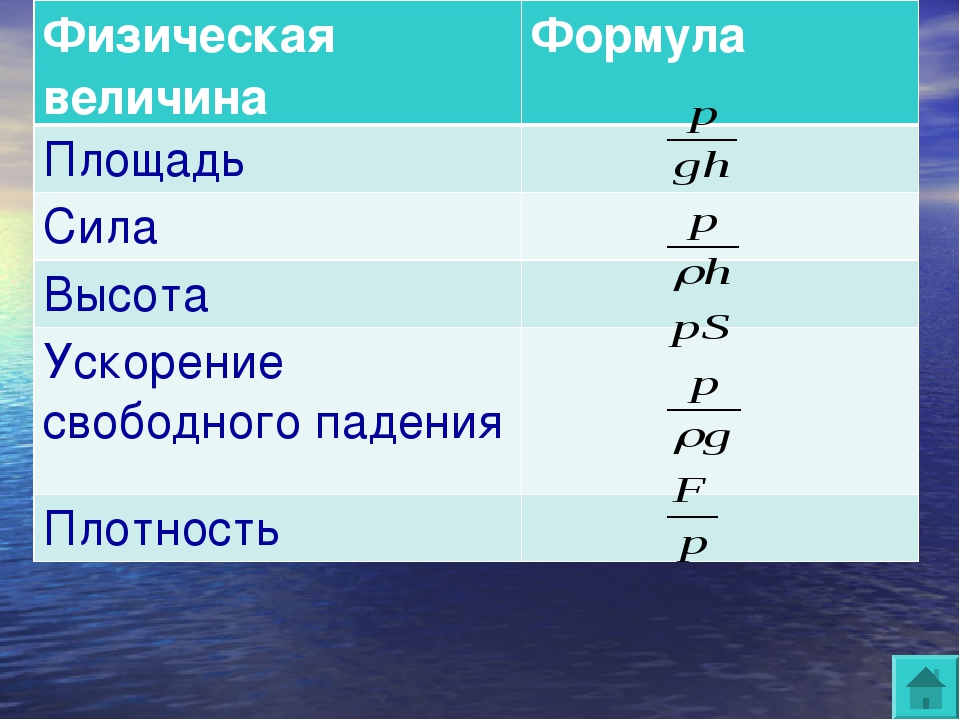
Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачать PDF со всеми формулами и определениями по физике за 7 класс.
Скачать PDF со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины. Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения. |
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
при прямом измерении результат можно увидеть непосредственно на шкале инструмента;
при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).
Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики. |
Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени.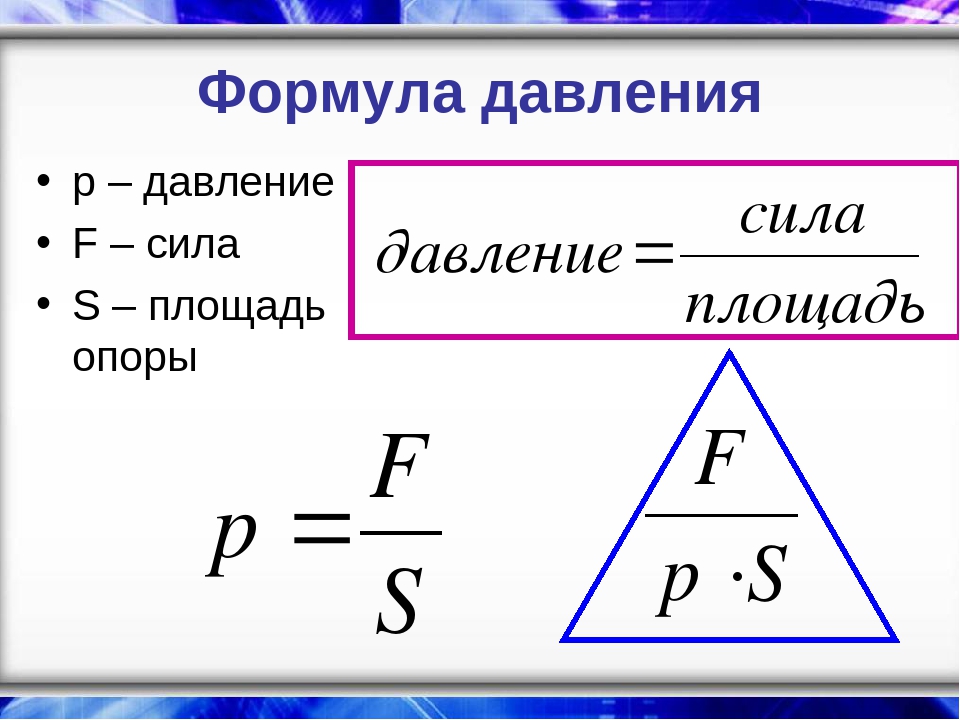 Это составляющие системы отсчета.
Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.
Траектория движения — мысленная линия, вдоль которой перемещается тело.
Путь — длина траектории тела от начальной до конечной точки.
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние. |
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.
Формула скорости равномерного криволинейного движения:
где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с2.
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес. |
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Fтяж = mg
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему. |
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз. Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы. |
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.
Уравнение равновесия рычага:
F1 × l1 = F2 × l2
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.
Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l. |
Формула момента силы:
M = F × l, где F — модуль силы, l — длина плеча.
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.
Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении. |
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
М1 + М2 + Мn + … = 0
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности. Сила давления направлена перпендикулярно поверхности. |
Формула давления:
p = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
1 Па = 1 Н/м2
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.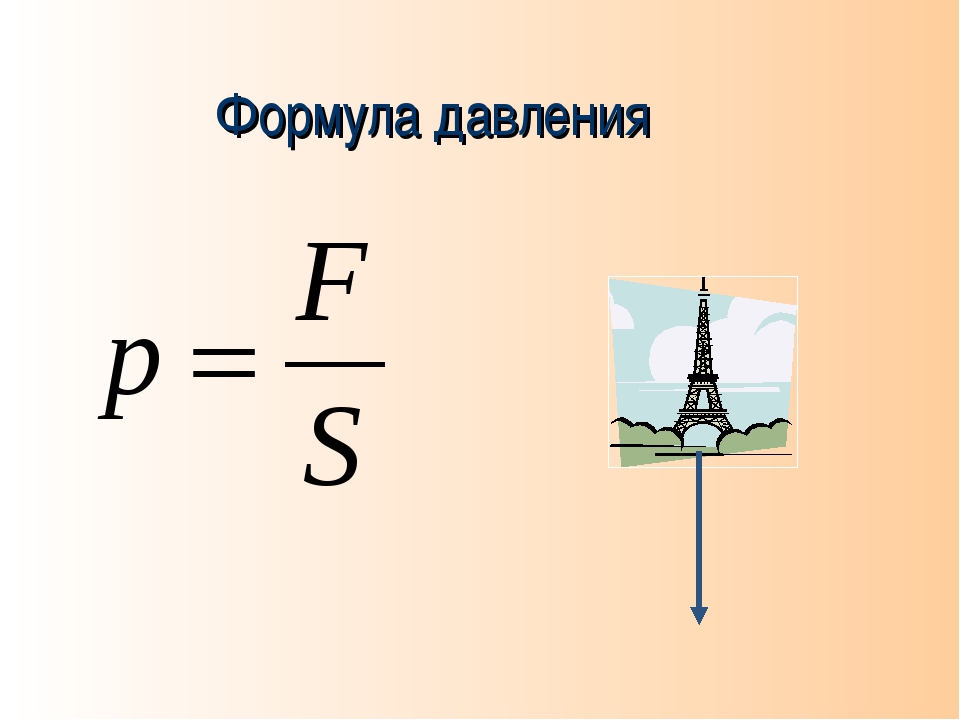
Формулу для расчета силы давления вывести несложно:
F = p × S
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.
g = 9,8 м/с2
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления. |
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
p = F / S, где F — модуль силы, S — площадь поверхности.
Сообщающиеся сосуды
Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения. |
Если ρ1 = ρ2, то h1 = h2 и ρ1gh1 = ρ2gh2, где:
p — плотность жидкости,
h — высота столба жидкости,
g = 9,8 м/с2.
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.). |
Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Следовательно,
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
Сила выталкивания тела, погруженного в жидкость или газ, равна весу данной жидкости или газа в таком же объеме, как у этого тела. |
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с2.
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
если плотность тела выше плотности среды, оно уйдет на дно;
если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение. |
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения. |
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
Кинетическая энергия | Пропорциональна массе тела и квадрату его скорости. | Ek = mv2/2 |
Потенциальная энергия | Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания. | Ep= mgh |
Полная механическая энергия | Складывается из кинетической и потенциальной энергии. | E = Ek+Ep |
Сохранение и превращение энергии | Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу. | Ek+ Ep= const |
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии. |
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
Удачи на экзаменах!
Давление атмосферное, гидростатическое. Закон Паскаля, сила. Сообщающиеся сосуды, применение
Тестирование онлайн
Давление. Основные понятия
Механика жидкостей
Давление
Это физическая скалярная величина, которая определяется по формуле
Атмосферное давление
Атмосфера — это воздушная оболочка Земли, которая удерживается гравитационными силами. Атмосфера имеет вес и давит на все тела на Земле. Давление атмосферы составляет около 760 мм.рт.ст. или 1 атм., или 101325Па. Миллиметр ртутного столба, атмосфера — это различные внесистемные единицы измерения давления. Атмосферное давление уменьшается на 1 мм.рт.ст. при поднятии над Землей на каждые 11м.
Атмосферное давление уменьшается на 1 мм.рт.ст. при поднятии над Землей на каждые 11м.
Что такое давление в 1 атм? Рукопожатие крепкого мужчины составляет 0,1 атм, удар боксера составляет несколько атмосферных единиц. Давление каблука-шпильки составляет 100 атмосфер. Если на ладонь положить гирю в 100 кг, то получим неравномерное давление в одну атмосферу, при погружении на 10 м под воду получим равномерное давление в 1 атмосферу. Равномерное давление легко переносится человеческим организмом. Нормальное атмосферное давление, которое действует на каждого человека, компенсируется внутренним давлением, поэтому его мы совершенно не замечаем, несмотря на то, что оно является достаточно существенным.
Закон Паскаля
Давление на жидкость или газ передается во всех направлениях одинаково.
Давление внутри жидкости (газа) на одной и той же глубине одинаково во всех направлениях (влево вправо, вниз и вверх!)
Гидростатическое давление
Это давления столбика жидкости на дно сосуда. Какая сила создает давление? Жидкость обладает весом, который давит на дно.
Какая сила создает давление? Жидкость обладает весом, который давит на дно.
Давление жидкости на дно
Давление на дно сосуда не зависит от формы сосуда, но зависит от площади его дна. При этом сила давления на дно может быть и больше и меньше силы тяжести жидкости в сосуде. В этом заключается «гидростатический парадокс».
На стенку сосуда гидростатическое давление распределено неравномерно: у поверхности жидкости оно равно нулю (без учета атмосферного давления), внутри жидкости изменяется прямо пропорционально глубине и на уровне дна достигает значения . Это переменное давление можно заменить средним давлением
Сообщающиеся сосуды
Это сосуды, которые имеют общий канал внизу.
Однородная жидкость устанавливается в сообщающихся сосудах на одном уровне независимо от формы сосудов, как видно на фотографии.
Разнородные жидкости устанавливаются в сообщающихся сосудах согласно формуле
Гидравлический пресс
Гидравлический пресс состоит из двух сообщающихся сосудов цилиндрической формы.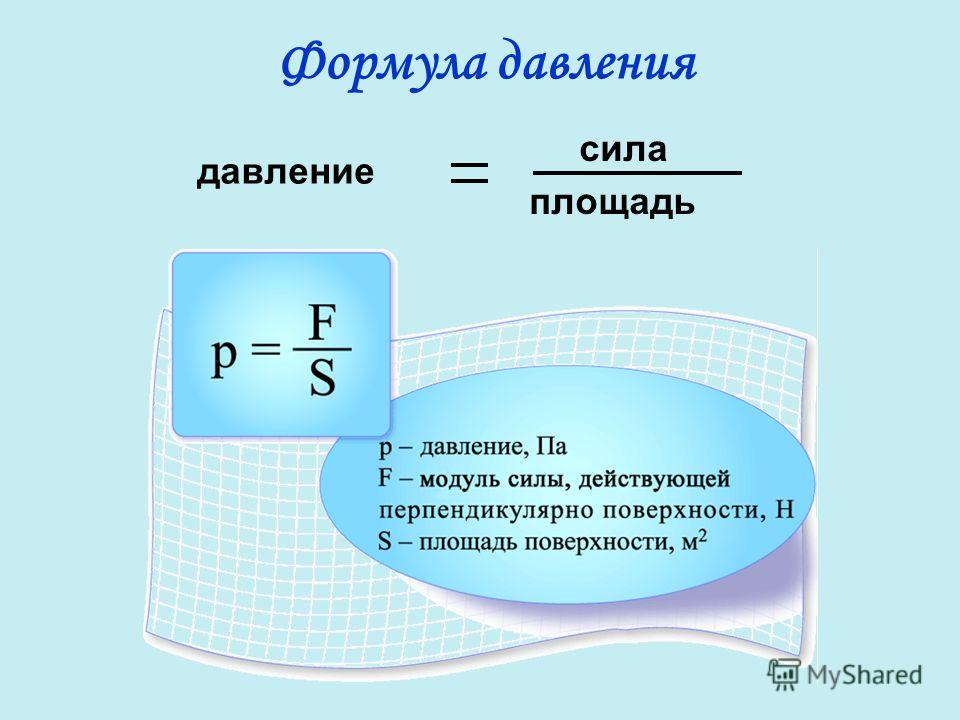 В сосудах двигаются поршни с площадями S1 и S2. Цилиндры заполнены техническим маслом.
В сосудах двигаются поршни с площадями S1 и S2. Цилиндры заполнены техническим маслом.
Объем жидкости, вытесненный малым поршнем поступает в большой цилиндр.
Гидравлический пресс дает выигрыш в силе во столько раз, во сколько площадь большего поршня больше площади меньшего. Выигрыша в работе гидравлический пресс не дает.
На практике вследствие наличия трения:
Если сила направлена под углом к нормали (перпендикуляру), то давление определяется по формуле
Газы и жидкости, находящиеся под давлением, нашли широкое применение в промышленной технике.
Например, пневматический отбойный молоток. При помощи сжатого воздуха работают также двери в автобусах и метро, тормоза поездов и грузовых автомобилей.
Встречаются также механизмы, работающие при помощи сжатой жидкости. Они называются гидравлическими. Например, устройство гидравлического пресса.
Численное значение атмосферного давления было определено опытным путем в 1643 году итальянским ученым Э. Торричелли.
Торричелли.
Стеклянную трубку длиной около метра, запаянную с одного конца, наполняют доверху ртутью. Затем, плотно закрыв отверстие пальцем, трубку переворачивают и опускают в чашу со ртутью, после чего палец убирают. Ртуть из трубки начинает выливаться, но не вся: остаётся «столб» » 76 см высотой, считая от уровня в чаше. Примечательно, что эта высота не зависит ни от длины трубки, ни от глубины её погружения.
Атмосферное давление уравновешивает гидростатическое давление столбика ртути. Согласно закону Паскаля давление атмосферы давит вверх на столбик ртути. А столбик ртути давит вниз своим весом. Ртуть перестает опускаться, когда эти давления одинаковые. Вычислив гидростатическое давление ртути известной высоты, определили давление атмосферы.
Трубка Торричелли с линейкой является простейшим барометром – прибором для измерения атмосферного давления
Для измерения атмосферного давления используют также барометр-анероид.
Поскольку атмосферное давление уменьшается по мере удаления от поверхности Земли, то шкалу анероида можно проградуировать в метрах.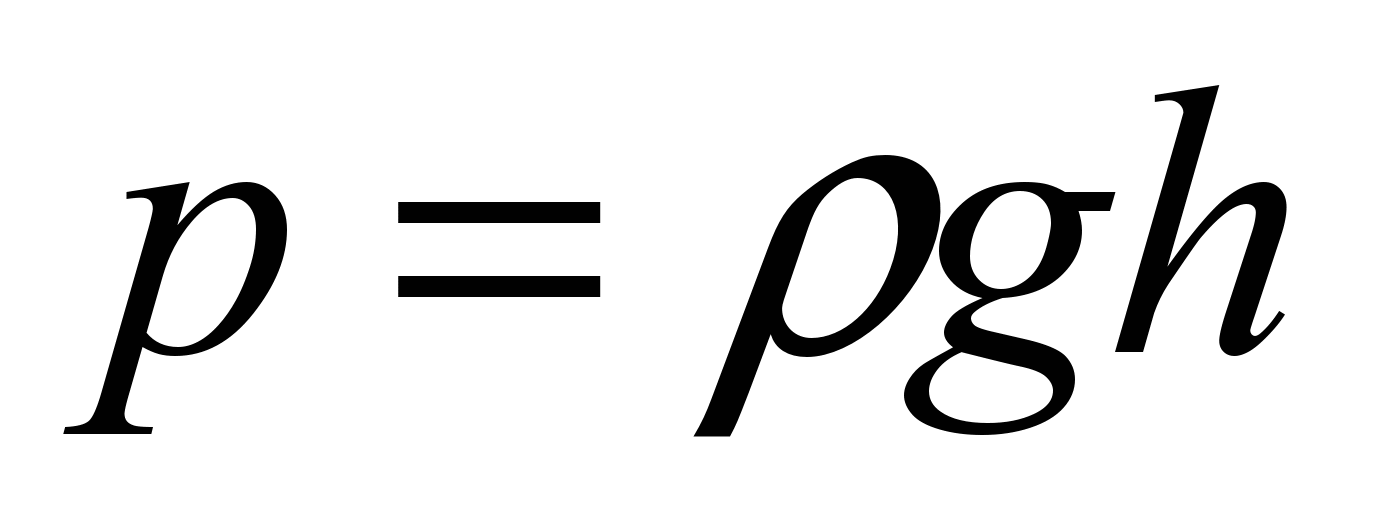 В этом случае он называется альтиметром.
В этом случае он называется альтиметром.
Пусть прямоугольный металлический брусок площадью основания S и высотой h лежит на дне сосуда, в который налита вода до высоты H, H>h. Как определить силу давления бруска на дно сосуда?
Возможны два случая! Пусть брусок неплотно прилегает ко дну сосуда, тогда снизу на брусок действует сила давления жидкости. Эта сила больше силы давления жидкости сверху, поэтому возникает сила Архимеда. Сила Архимеда — результат разницы силы гидростатического давления на нижнюю грань бруска и верхнюю грань, зависит от высоты бруска и площади основания.
Используем 2 закон Ньютона:
Рассмотрим второй возможный случай. Пусть брусок прилегает ко дну так плотно, что жидкость под него не подтекает. Снизу отсутствует давление жидкости, следовательно сила Архимеда равна нулю. Сверху же на брусок действует сила давления жидкости и атмосферы.
Используем 2 закон Ньютона для этого случая:
p0 — атмосферное давление,
p — гидростатическое давление столба жидкости высотой H-h.
Формула расчета давления воздуха, пара, жидкости или твердого тела. Узнаем как находить давление (формула расчета)?
Давление – это физическая величина, которая играет особую роль в природе и жизни человека. Это незаметное глазу явление не только влияет на состояние окружающей среды, но и очень хорошо ощущается всеми. Давайте разберемся, что это такое, какие виды его существуют и как находить давление (формула) в разных средах.
Что называется давлением в физике и химии
Данным термином именуется важная термодинамическая величина, которая выражается в соотношении перпендикулярно оказываемой силы давления на площадь поверхности, на которую она воздействует. Это явление не зависит от размера системы, в которой действует, поэтому относится к интенсивным величинам.
В состоянии равновесия, по закону Паскаля, давление одинаково для всех точек системы.
В физике и химии оное обозначается с помощью буквы «Р», что является сокращением от латинского названия термина – pressūra.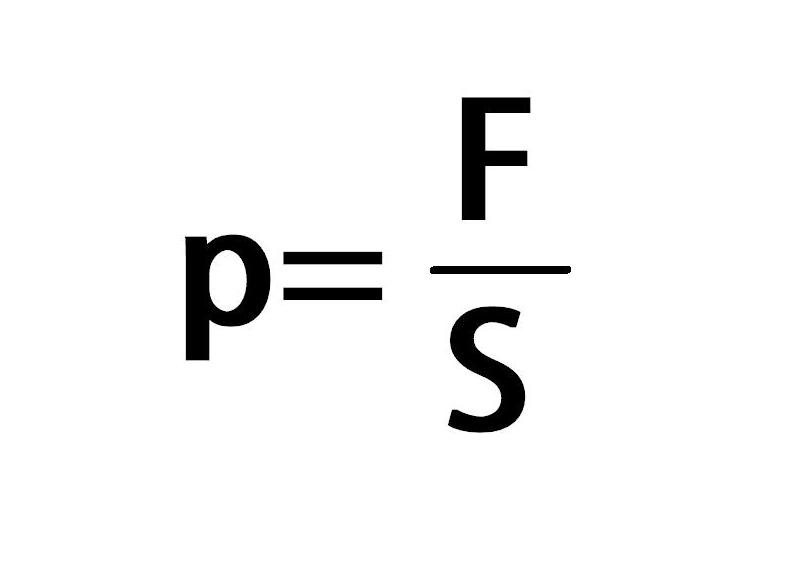
Если речь идет об осмотическом давлении жидкости (равновесие между давлением внутри и снаружи клетки), используется буква «П».
Единицы давления
Согласно стандартам Международной системы СИ, рассматриваемое физическое явление измеряется в паскалях (кириллицей – Па, латиницей — Ра).
Исходя из формулы давления получается, что один Па равен одному Н (ньютон — единица измерения силы) разделенному на один квадратный метр (единица измерения площади).
Однако на практике применять паскали довольно сложно, поскольку эта единица очень мала. В связи с этим, помимо стандартов системы СИ, данная величина может измеряться по-другому.
Ниже приведены наиболее известные ее аналоги. Большинство из них широко используется на просторах бывшего СССР.
- Бары. Один бар равен 105 Па.
- Торры, или миллиметры ртутного столба. Приблизительно один торр соответствует 133, 3223684 Па.
- Миллиметры водяного столба.
- Метры водяного столба.

- Технические атмосферы.
- Физические атмосферы. Одна атм равна 101 325 Па и 1,033233 ат.
- Килограмм-силы на квадратный сантиметр. Также выделяются тонна-сила и грамм-сила. Помимо этого, есть аналог фунт-сила на квадратный дюйм.
Общая формула давления (физика 7-го класса)
Из определения данной физической величины можно определить способ ее нахождения. Выглядит он таким образом, как на фото ниже.
В нем F – это сила, а S – площадь. Иными словами, формула нахождения давления – это его сила, разделенная на площадь поверхности, на которую оно воздействует.
Также она может быть записана так: Р = mg / S или Р = pVg / S. Таким образом, эта физическая величина оказывается связанной с другими термодинамическими переменными: объемом и массой.
Для давления действует следующий принцип: чем меньше пространство, на которое влияет сила – тем большее количество давящей силы на него приходится. Если, же площадь увеличивается (при той же силе) – искомая величина уменьшается.
Формула гидростатического давления
Разные агрегатные состояния веществ, предусматривают наличие у них отличных друг от друга свойств. Исходя из этого, способы определения Р в них тоже будут другими.
К примеру, формула давления воды (гидростатического) выглядит вот так: Р = pgh. Также она применима и к газам. При этом ее нельзя использовать для вычисления атмосферного давления, из-за разности высот и плотностей воздуха.
В данной формуле р – плотность, g – ускорение свободного падения, а h – высота. Исходя из этого, чем глубже погружается предмет или объект, тем выше оказываемое на него давление внутри жидкости (газа).
Рассматриваемый вариант является адаптацией классической примера Р = F / S.
Если вспомнить, что сила равна производной массы на скорость свободного падения (F= mg), а масса жидкости – это производная объема на плотность (m = pV), то формулу давление можно записать как P = pVg / S. При этом объем – это площад, умноженная на высоту (V = Sh).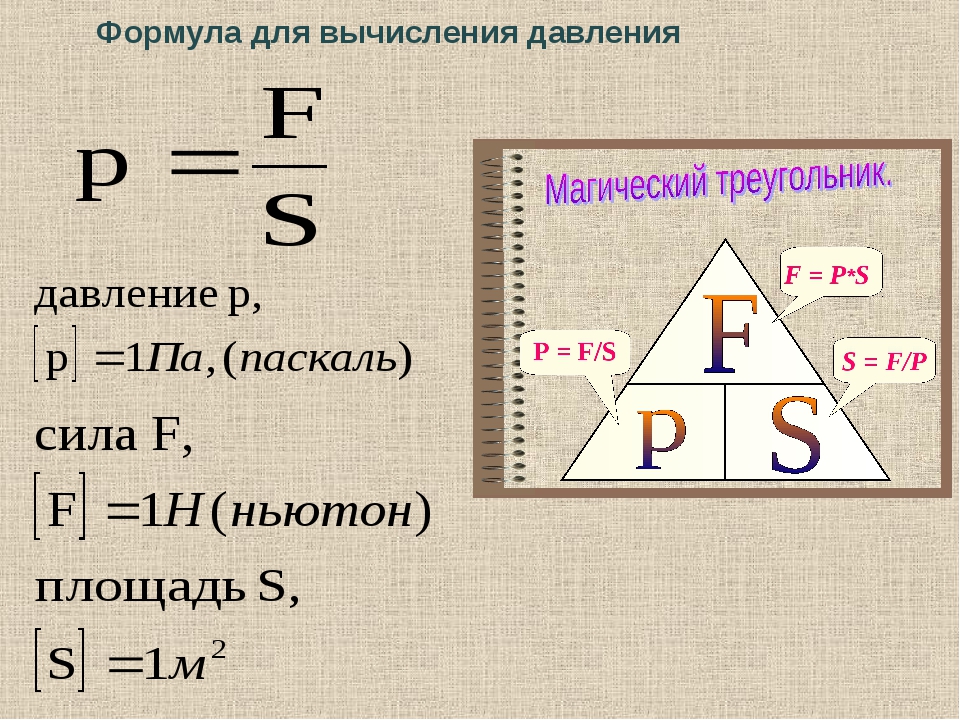
Если вставить эти данные, получится, что площадь в числителе и знаменателе можно сократить и на выходе — вышеупомянутая формула: Р = pgh.
Рассматривая давление в жидкостях, стоит помнить, что, в отличие от твердых тел, в них часто возможно искривление поверхностного слоя. А это, в свою очередь, способствует образованию дополнительного давления.
Для подобных ситуаций применяется несколько другая формула давления: Р = Р0 + 2QH. В данном случае Р0 – давление не искривленного слоя, а Q – поверхность натяжения жидкости. Н – это средняя кривизна поверхности, которую определяют по Закону Лапласа: Н = ½ (1/R1+ 1/R2). Составляющие R1 и R2 – это радиусы главной кривизны.
Парциальное давление и его формула
Хотя способ Р = pgh применим как для жидкостей, так и для газов, давление в последних лучше вычислять несколько другим путем.
Дело в том, что в природе, как правило, не очень часто встречаются абсолютно чистые вещества, ведь в ней преобладают смеси. И это касается не только жидкостей, но и газов. А как известно, каждый из таких компонентов осуществляет разное давление, называемое парциальным.
И это касается не только жидкостей, но и газов. А как известно, каждый из таких компонентов осуществляет разное давление, называемое парциальным.
Определить его довольно просто. Оно равно сумме давления каждого компонента рассматриваемой смеси (идеальный газ).
Из этого следует, что формула парциального давления выглядит таким образом: Р = Р1+ Р2+ Р3… и так далее, согласно количеству составляющих компонентов.
Нередки случаи, когда необходимо определить давление воздуха. Однако некоторые по ошибке проводят вычисления только с кислородом по схеме Р = pgh. Вот только воздух — это смесь из разных газов. В нем встречаются азот, аргон, кислород и другие вещества. Исходя из сложившейся ситуации, формула давления воздуха — это сумма давлений всех его составляющих. А значит, следует приметь вышеупомянутую Р = Р1+ Р2+ Р3…
Наиболее распространенные приборы для измерения давления
Несмотря на то что высчитать рассматриваемую термодинамическую величину по вышеупомянутым формулам не сложно, проводить вычисление иногда попросту нет времени. Ведь нужно всегда учитывать многочисленные нюансы. Поэтому для удобства за несколько столетий был разработан ряд приборов, делающих это вместо людей.
Ведь нужно всегда учитывать многочисленные нюансы. Поэтому для удобства за несколько столетий был разработан ряд приборов, делающих это вместо людей.
Фактически почти все аппараты такого рода являются разновидностями манометра (помогает определять давление в газах и жидкостях). При этом они отличаются по конструкции, точности и сфере применения.
- Атмосферное давление измеряется с помощью манометра, именуемого барометром. Если необходимо определить разряжение (то есть давление ниже атмосферного) — применяются другая его разновидность, вакуумметр.
- Для того чтобы узнать артериальное давление у человека, в ход идет сфигмоманометр. Большинству он более известен под именем неинвазивного тонометра. Таких аппаратов существуют немало разновидностей: от ртутных механических до полностью автоматических цифровых. Их точность зависит от материалов, из которых они изготавливаются и места измерения.
- Перепады давления в окружающей среде (по-английски — pressure drop) определяются с помощью дифференциальных манометров или дифнамометров (не путать с динамометрами).

Виды давления
Рассматривая давление, формулу его нахождения и ее вариации для разных веществ, стоит узнать о разновидностях этой величины. Их пять.
- Абсолютное.
- Барометрическое
- Избыточное.
- Вакуумметрическое.
- Дифференциальное.
Абсолютное
Так называется полное давление, под которым находится вещество или объект, без учета влияния других газообразных составляющих атмосферы.
Измеряется оно в паскалях и являет собою сумму избыточного и атмосферного давлений. Также он является разностью барометрического и вакуумметрического видов.
Вычисляется оно по формуле Р = Р2 + Р3 или Р = Р2 — Р4.
За начало отсчета для абсолютного давления в условиях планеты Земля, берется давление внутри емкости, из которой удален воздух (то есть классический вакуум).
Только такой вид давления используется в большинстве термодинамических формул.
Барометрическое
Этим термином именуется давление атмосферы (гравитации) на все предметы и объекты, находящие в ней, включая непосредственно поверхность Земли. Большинству оно также известно под именем атмосферного.
Его причисляют к термодинамическим параметрам, а его величина меняется относительно места и времени измерения, а также погодных условий и нахождения над/ниже уровня моря .
Величина барометрического давления равна модулю силы атмосферы на площади единицу по нормали к ней.
В стабильной атмосфере величина данного физического явления равна весу столпа воздуха на основание с площадью, равной единице.
Норма барометрического давления — 101 325 Па (760 мм рт. ст. при 0 градусов Цельсия). При этом чем выше объект оказывается от поверхности Земли, тем более низким становится давление на него воздуха. Через каждый 8 км оно снижается на 100 Па.
Благодаря этому свойству в горах вода в чайниках закивает намного быстрее, чем дома на плите. Дело в том, что давление влияет на температуру кипения: с его снижением последняя уменьшается. И наоборот. На этом свойстве построена работа таких кухонных приборов , как скороварка и автоклав. Повышение давления внутри их способствуют формированию в посудинах более высоких температур, нежели в обычных кастрюлях на плите.
И наоборот. На этом свойстве построена работа таких кухонных приборов , как скороварка и автоклав. Повышение давления внутри их способствуют формированию в посудинах более высоких температур, нежели в обычных кастрюлях на плите.
Используется для вычисления атмосферного давления формула барометрической высоты. Выглядит она таким образом, как на фото ниже.
Р – это искомая величина на высоте, Р0 – плотность воздуха возле поверхности, g – свободного падения ускорение, h – высота над Землей, м – молярная масса газа, т – температура системы, r – универсальная газовая постоянная 8,3144598 Дж⁄(моль х К), а е – это число Эйклера, равное 2.71828.
Часто в представленной выше формуле давления атмосферного вместо R используется К – постоянная Больцмана. Через ее произведение на число Авогадро нередко выражается универсальная газовая постоянная. Она более удобна для расчетов, когда число частиц задано в молях.
При проведении вычислений всегда стоит брать во внимание возможность изменения температуры воздуха из-за смены метеорологической ситуации или при наборе высоты над уровнем моря, а также географическую широту.
Избыточное и вакуумметрическое
Разницу между атмосферным и измеренным давлением окружающей среды называют избыточным давлением. В зависимости от результата, меняется название величины.
Если она положительная, ее называют манометрическим давлением.
Если же полученный результат со знаком минус – его именуют вакуумметрическим. Стоит помнить, что он не может быть больше барометрического.
Дифференциальное
Данная величина является разницей давлений в различных точках измерения. Как правило, ее используют для определения падения давления на каком-либо оборудовании. Особенно это актуально в нефтедобывающей промышленности.
Разобравшись с тем, что за термодинамическая величина называется давлением и с помощью каких формул ее находят, можно сделать вывод, что это явление весьма важно, а потому знания о нем никогда не будут лишними.
Расчет давления жидкостей. 7-й класс
Тип урока: урок изучения нового материала.
Вид урока: урок – беседа.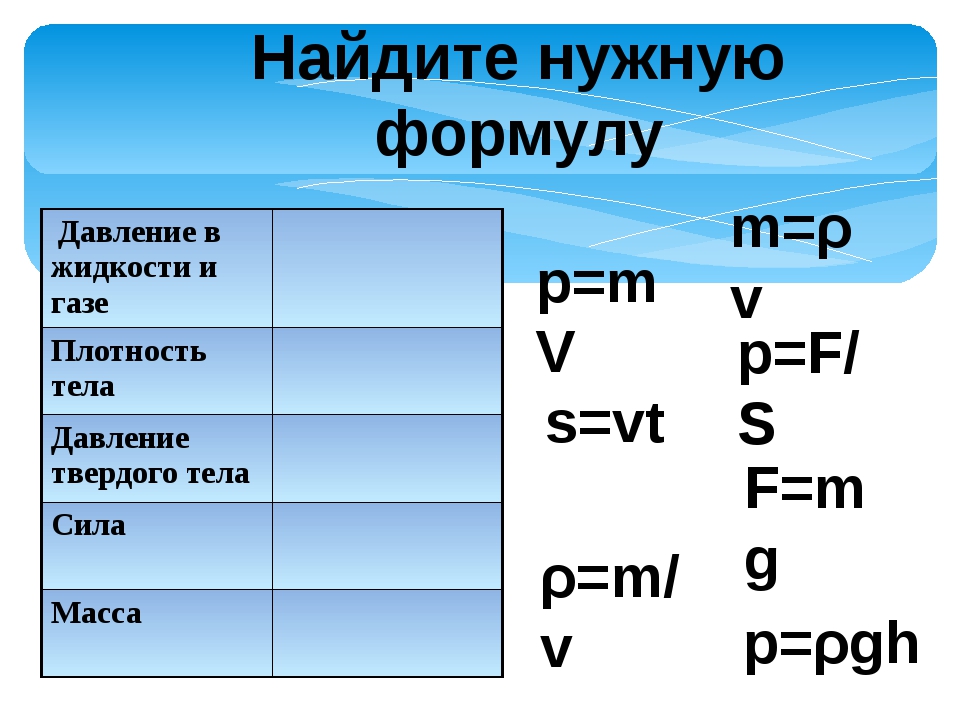
Межпредметная связь: с математикой,
астрономией, психологией.
Цели:
1) вывести формулу для расчета давления
жидкости;
2) выразить величины из формулы;
3) научить рассчитывать давление жидкостей;
4) научить анализировать зависимость величин;
5) развить логическое мышление;
6) привитие интереса к предмету.
Оборудование: сосуды различного сечения с
водой; сосуды с различными жидкостями; небольшая
коробка с резиновым дном, соединенная с
манометром; модель солнечной системы; таблица
“Ускорения свободного падения на различных
планетах” [ 4] (приложение).
План урока:
- Организационный момент. (1 мин)
- Актуализация опорных знаний. (3 мин)
- Мотивация обучения. (2 мин)
- Объяснение нового материала. (5 мин)
- Закрепление нового материала.
 (2 5 мин)
(2 5 мин) - Итог урока. Оценки. Рефлексия. (3 мин)
- Домашнее задание. (1 мин)
Ход урока
1.Организационный момент.
Учитель. Сегодня нам предстоит трудная
работа.
Выполним упражнение. Массаж ушных мочек.
(Стимулирует работу головного мозга).
Готовы?
2. Актуализация опорных знаний.
1)Как изменится давление воздуха в шинах
автомобиля при его разгрузке? [ ]
2)Объясните назначение наперстка, надеваемого
на палец при шитье иглой.
3)Как увеличить давление человека в 2 раза?
(встать на одну ногу)
4)Что ответила давящая сила, равная одному
ньютону и действующая перпендикулярно
поверхности, когда один полураздавленный
квадратный метр этой поверхности смущенно
спросил ее: “Дорогая, как ты ко мне относишься?”
Ответ. Сила покраснела и, опустив ресницы,
шепнула: “Милый, мое отношение к тебе равно
одному паскалю” [2 , №131 ]
3.
 Мотивация изучения нового материала.
Мотивация изучения нового материала.
Как рассчитать давление жидкостей?
От каких величин зависит давление жидкостей?
Одинаково ли давление жидкостей на дно сосуда?
Демонстрация. Сосуды различной формы и
сосуды с различными жидкостями (вода чистая, вода
соленая, масло растительное).
Зависит ли давление от глубины погружения?
Демонстрация. Гидростатическое давление на
разной глубине.
4. Объяснение нового материала.
Вывод формулы коллективно. Рисунок 2.
P = F / S = m g / s = p v g / s = p s h g / s = p g h
Учитель. От каких величин зависит давление
жидкости? (плотности жидкости, высоты, ускорения
свободного падения)
Учитель. Чем плотность жидкости больше, тем
давление …. ? (больше)
Учитель. Зависимость – прямо –
пропорциональная.
Учитель. Чем высота больше, тем давление … ?
Зависимость? (больше, прямо – пропорциональная,)
Учитель. Чем ускорение свободного падения больше,
Чем ускорение свободного падения больше,
тем давление … ? Зависимость? (больше, прямо –
пропорциональная)
Чем p >, тем Р > . Чем g >, тем Р >. Чем h > ,
тем Р >
Одинаково ли давление жидкости на дно сосудов
различной формы? Рисунок 1 [ 3, № 417 ]
| h 1 = h 2 = h 3 = h 4 | |
| p 1 = p 2 = p3 = p 4 | P1 = P2 = P3 = P4 |
| g 1 = g 2 = g3 = g4 |
Давление не зависит от массы жидкости, формы
сосуда.
Учитель: Устали? Впереди нас ждут великие
дела. Выполним упражнение:
Массаж кончиков пальцев на обеих руках
(стимуляция работы головного мозга)
5.
 Закрепление.
Закрепление.
Решение задач.
1)Вывод неизвестного множителя:
h = P / g p ; g = P / h p ; p = P / h g
2)Эксперимент. Рассчитать давление воды на дно
стакана. Изменится ли давление если: в воду
опустить деревянный брусок, воду перелить в
более широкую емкость?
3)На какую глубину должен быть погружен в море
батискаф, чтобы давление на его поверхность
стало равным 6 1 9 0 к Па ?
4)Какая жидкость налита в стакан, если ее
давление на дно равно 1350 Па, а высота равна 15
см?
5) На Луне вода в сосуде высотой 1 м оказывает
давление 1 6 2 3 Па. Определить ускорение
свободного падения.
Учитель. Мы с вами хорошо поработали.
Погладьте себя по макушке. Похвалите .
Работа с учебником.
Рассмотреть рисунки, вопросы.
6. Рефлексия.
Игра – “Крокодил”. (Пантомима)
Изобразить: давление жидкости; дно сосуда,
испытывающее давление жидкостей разных
плотностей, разных высот и на разных планетах.
7. Домашнее задание.
§ 38, задание 8.
Придумать задачи на применение формул для
расчета высоты, давления.
Сообщение “Подготовка водолазов, дайверов”.
Литература:
- Учебник “Физика 7 класс” А.В. Перышкин, Москва,
“Дрофа”, 2008 г. - “Физика”. Григорий Остер. Москва, “Росмен” 1994,
№131 - Сборник задач по физике В.И. Лукашик, 7-8 кл,
Москва, “Просвещение”, 1995. - Справочник по физике и технике, А.С. Енохович,
Москва, “Просвещение”,1990.
Приложение
Тест по физике «Давление жидкости и газа» (7 класс)
Физический диктант. Урок « Решение задач по теме «Давление. Сила давления.» 7кл
Тест. «Давление жидкости и газа». Вариант 1.
1. Единицы измерения силы давления.
2. Формула механического давления.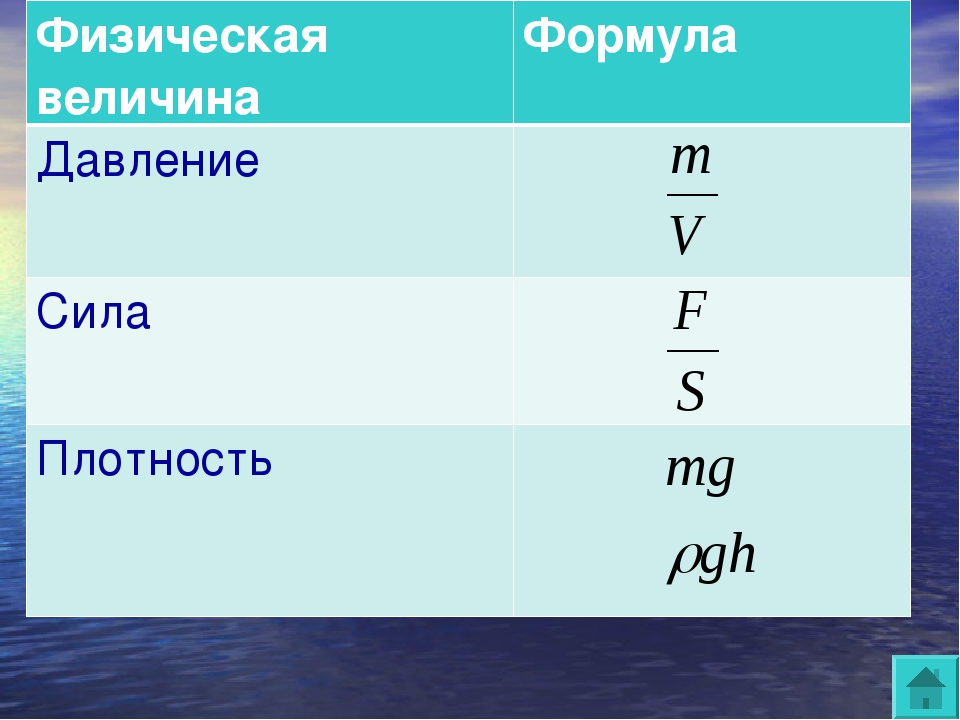
3. Чем обусловлено давление газа на стенки сосуда?
4. Сформулируйте закон Паскаля.
5. Как изменится давление газа, если увеличить его температуру?
6. Как изменится давление газа, если увеличить объем сосуда?
7. Формула гидростатического давления.
8. Выразите высоту столба жидкости из предыдущей формулы.
9. В два одинаковых сосуда, до одного и того же уровня налили воду и нефть. Какая из жидкостей будет оказывать на дно большее давление.
10. Сравните давление газа на дно и крышку сосуда.
Тест. «Давление жидкости и газа». Вариант 2.
1. Единицы измерения давления.
2. Формула силы давления.
3. От чего зависит давление газа на стенки сосуда?
4. Сформулируйте закон Паскаля.
5. Как изменится давление газа, если уменьшить его температуру?
6. Как изменится давление газа, если уменьшить объем сосуда?
7. Формула гидростатического давления.
8. Выразите плотность жидкости из предыдущей формулы.
9. В два одинаковых сосуда, до одного и того же уровня налили воду и серную кислоту. Какая из жидкостей будет оказывать на дно большее давление.
10. Сравните давление газа на дно и крышку сосуда.
Тест. «Давление жидкости и газа». Вариант 3.
1. Единицы измерения давления.
2. Формула силы давления.
3. От чего зависит давление жидкости на дно сосуда?
4. Сформулируйте закон Паскаля.
5. Как изменится давление газа, если уменьшить его температуру в 3 раза?
6. Как изменится давление газа, если уменьшить объем сосуда в 2 раз?
7. Формула гидростатического давления.
8. Выразите плотность жидкости из предыдущей формулы.
9. В два одинаковых сосуда, до одного и того же уровня налили воду и серную кислоту. Какая из жидкостей будет оказывать на дно большее давление и во сколько раз?
10. Сравните давление жидкости на дно и стенку сосуда.
Тест. «Давление жидкости и газа». Вариант 4.
1. Единицы измерения давления.
2. Формула механического давления.
3. От чего зависит давление газа на стенки сосуда?
4. Сформулируйте закон Паскаля.
5. Как изменится давление газа, если увеличить его температуру в 2 раза?
6. Как изменится давление газа, если уменьшить объем сосуда в 3раза ?
7. Формула гидростатического давления.
8. Выразите плотность жидкости из предыдущей формулы.
9. В два одинаковых сосуда, до одного и того же уровня налили воду и серную кислоту. Какая из жидкостей будет оказывать на дно большее давление.
10. Сравните силу давления жидкости на дно и стенку сосуда, если их площадь одинакова.
Давление газа
Отвечая на первый, из поставленных выше, вопрос, предположим, что давление газов на стенки сосуда объясняется ударами молекул.
Для того, чтобы в процессе поиска расчетной формулы этого давления ограничиться знаниями элементарной математики и физики, введем некоторые упрощения.
- Форма, строение молекул достаточно сложны. Но попробуем представить их в виде маленьких шариков. Это позволит нам применить к описанию процесса удара молекул о стенки сосуда законы механики, в частности, второй закон Ньютона.
- Будем считать, что молекулы газа находятся на достаточно большом расстоянии друг от друга, так, что силы взаимодействия между ними пренебрежимо малы. Если между частицами отсутствуют силы взаимодействия, соответственно, равна нулю и потенциальная энергия взаимодействия. Назовем газ, отвечающий этим свойствам, идеальным.
- Известно, что молекулы газа движутся с разными скоростями. Однако, усредним скорости движения молекул и будем считать их одинаковыми.
- Предположим, что удары молекул о стенки сосуда абсолютно упругие (молекулы ведут себя при ударе подобно резиновым мячикам, а не подобно куску пластилина). При этом скорости молекул изменяются лишь по направлению, а по величине остаются прежними.
 Тогда изменение скорости каждой молекулы при ударе равно –2υ.
Тогда изменение скорости каждой молекулы при ударе равно –2υ.
Введя такие упрощения, рассчитаем давление газа на стенки сосуда.
|
|
|
Сила действует на стенку со стороны множества молекул. Она может быть рассчитана как произведение силы, действующей со стороны одной молекулы, на число молекул, движущихся в сосуде в направлении этой стенки. Так как пространство трехмерно и каждое измерение имеет два направления: положительное и отрицательное, можно считать, что в направлении одной стенки движется одна шестая часть всех молекул (при большом их числе): N = N0 / 6.
Так как пространство трехмерно и каждое измерение имеет два направления: положительное и отрицательное, можно считать, что в направлении одной стенки движется одна шестая часть всех молекул (при большом их числе): N = N0 / 6.
Сила, действующая на стенку со стороны одной молекулы, равна силе, действующей на молекулу со стороны стенки. Сила, действующая на молекулу со стороны стенки, равна произведению массы одной молекулы на ускорение, которое она получает при ударе о стенку:
Ускорение же – это физическая величина, определяемая отношением изменения скорости ко времени, в течение которого это изменение произошло: a = Δυ / t.
Изменение скорости равно удвоенному значению скорости молекулы до удара: Δυ = –2υ.
Если молекула ведет себя подобно резиновому мячику, нетрудно представить процесс удара: молекула, ударяясь, деформируется. На процесс сжатия и разжатия затрачивается время. Пока молекула действует на стенку сосуда, о последнюю успевает удариться еще некоторое число молекул, находящихся от нее на расстояниях не дальше l = υt. (Например, условно говоря, пусть молекулы имеют скорость 100 м/с. Удар длится 0,01 с. Тогда за это время до стенки успеют долететь и внести свой вклад в давление молекулы, находящиеся от нее на расстояниях 10, 50, 70 см, но не далее 100 см).
(Например, условно говоря, пусть молекулы имеют скорость 100 м/с. Удар длится 0,01 с. Тогда за это время до стенки успеют долететь и внести свой вклад в давление молекулы, находящиеся от нее на расстояниях 10, 50, 70 см, но не далее 100 см).
Будем рассматривать объем сосуда V = lS.
Подставив все формулы в исходную, получаем уравнение:
|
|
где:
– масса одной молекулы,
– среднее значение квадрата скорости молекул, N – число молекул в объеме V.
Сделаем некоторые пояснения по поводу одной из величин, входящих в полученное уравнение.
Так как движение молекул хаотично и преимущественного движения молекул в сосуде нет, их средняя скорость равна нулю. Но ясно, что это не относится к каждой отдельной молекуле.
Но ясно, что это не относится к каждой отдельной молекуле.
Для вычисления давления идеального газа на стенку сосуда используется не среднее значение x-компоненты скорости молекул
а среднее значение квадрата скорости
Чтобы введение этой величины было более понятным, рассмотрим численный пример.
Пусть четыре молекулы имеют скорости 1, 2, 3, 4 усл. ед.
Квадрат среднего значения скорости молекул равен:
|
|
Среднее значение квадрата скорости равно:
|
|
Если скорости молекул равны +1, –2 , –3 , +4 усл.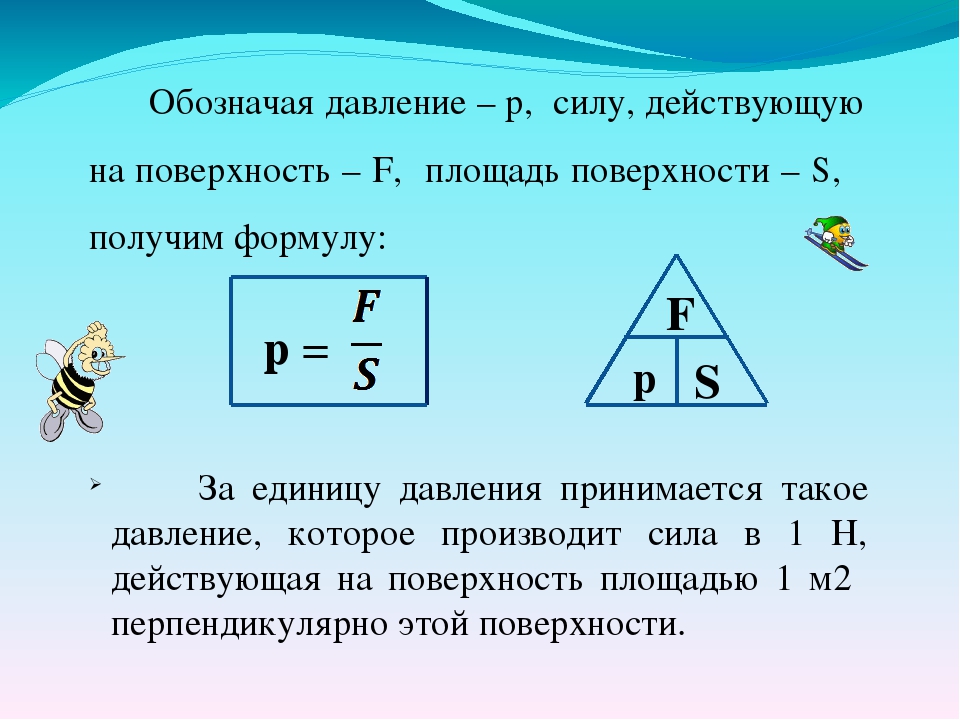 ед., то квадрат среднего значения скорости равен:
ед., то квадрат среднего значения скорости равен:
|
|
Среднее значение квадрата скорости равно:
|
|
Средние значения проекций квадрата скорости на оси x, y, z связаны со средним значением квадрата скорости соотношением:
|
|
Если извлечь квадратный корень из
то получим величину, которая называется средней квадратичной скоростью молекул.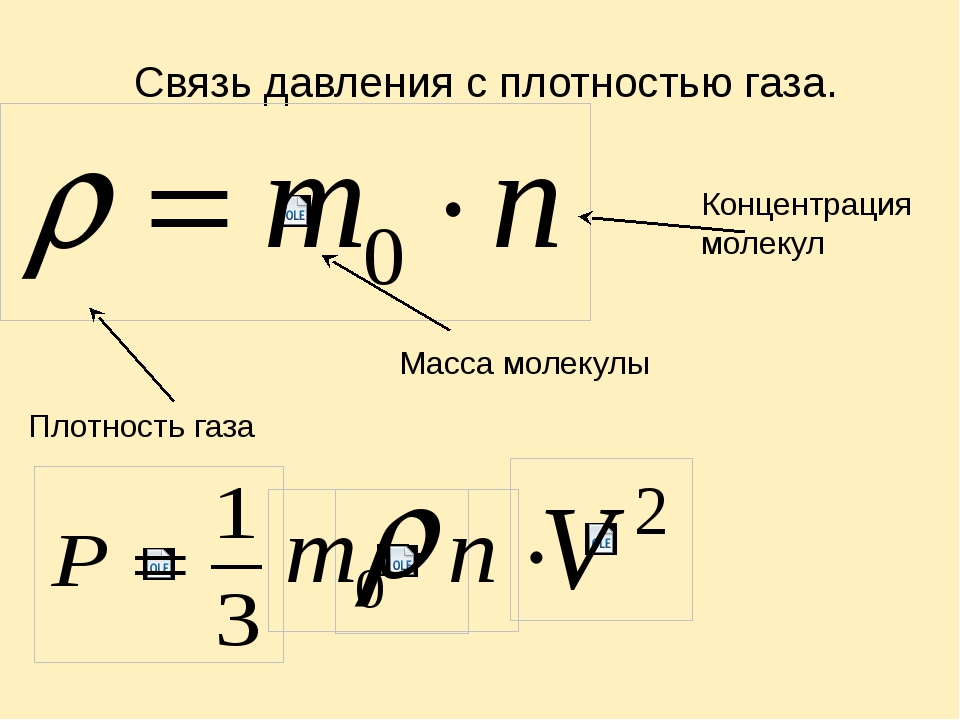
Величина, определяемая отношением числа частиц к объему, в котором они находятся, называется концентрацией (обозначается буквой n).
Величина же
– это средняя кинетическая энергия каждой молекулы газа.
С учетом этого полученное уравнение можно переписать в виде:
|
|
Уравнения связывают макропараметры газа – его давление и объем (p, V) с микропараметрами – массой молекул и их скоростью (m0, υ), или энергией
Последнее уравнение читается следующим образом: давление идеального газа на стенки сосуда прямо пропорционально концентрации молекул в сосуде и их средней кинетической энергии.
Расчет давления жидкости на дно и стенки сосуда
Рассмотрим, как можно рассчитать давление жидкости на дно и стенки сосуда. Решим сначала задачу с числовыми данными. Прямоугольный бак наполнен водой (рис. 96). Площадь дна бака 16 м2, высота его 5 м. Определим давление воды на дно бака.
Решим сначала задачу с числовыми данными. Прямоугольный бак наполнен водой (рис. 96). Площадь дна бака 16 м2, высота его 5 м. Определим давление воды на дно бака.
Сила, с которой вода давит на дно сосуда, равна весу столба воды высотой 5 м и площадью основания 16 м2, иначе говоря, эта сила равна весу всей воды в баке.
Чтобы найти вес воды, надо знать ее массу. Массу воды можно вычислить по объему и плотности. Найдем объем воды в баке, умножив площадь дна бака на его высоту: V= 16 м2*5 м=80 м3. Теперь определим массу воды, для этого умножим ее плотность p = 1000 кг/м3 на объем: m = 1000 кг/м3 * 80 м3 = 80 000 кг. Мы знаем, что для определения веса тела надо его массу умножить на 9,8 Н/кг, так как тело массой 1 кг весит 9,8 Н.
Следовательно, вес воды в баке равен P = 9,8 Н/кг * 80 000 кг ≈ 800 000 Н. С такой силой вода давит на дно бака.
Разделив вес воды на площадь дна бака, найдем давление p:
p = 800000 H/16 м2 = 50 000 Па = 50 кПа.
Давление жидкости на дно сосуда можно рассчитать, пользуясь формулой, что значительно проще. Чтобы вывести эту формулу, вернемся к задаче, но только решим ее в общем виде.
Обозначим высоту столба жидкости в сосуде буквой h, а площадь дна сосуда S.
Объем столба жидкости V= Sh.
Масса жидкости т = pV,или m = pSh.
Вес этой жидкости P = gm, или P = gpSh.
Так как вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, то, разделив вес P на площадь S, получим давление р:
p = P/S, или p = gpSh/S
т. е.
p = gph.
Мы получили формулу для расчета давления жидкости на дно сосуда. Из этой формулы видно, что давление жидкости на дно сосуда прямо пропорционально плотности и высоте столба жидкости.
По этой формуле можно вычислять и давление на стенки, сосуда, а также давление внутри жидкости, в том числе давление снизу вверх, так как давление на одной и той же глубине одинаково по всем направлениям.
При расчете давления по формуле:
p = gph
надо плотность p выражать в килограммах на кубический метр (кг/м3), а высоту столба жидкости h — в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в, паскалях (Па).
Пример. Определить давление нефти на дно цистерны, если высота столба нефти 10 м, а плотность ее 800 кг/м3.
Вопросы. 1. От каких величин зависит давление жидкости на дно сосуда? 2. Как зависит давление жидкости на дно сосуда от высоты столба жидкости? 3. Как зависит давление жидкости на дно сосуда от плотности жидкости? 4. Какие величины надо знать, чтобы рассчитать давление жидкости на стенки сосуда? 5. По какой формуле рассчитывают давление жидкости на дно и стенки сосуда?
Упражнения. 1. Определите давление на глубине 0,6 м в воде, керосине, ртути. 2. Вычислите давление воды на дно одной из глубочайших морских впадин, глубина, которой 10 900 м, Плотность морской воды 1030 кг/м3. 3. На рисунке 97 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на нее — гиря массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.
3. На рисунке 97 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на нее — гиря массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.
Задания. 1. Возьмите высокий сосуд. В боковой поверхности его по прямой, на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и налейте в сосуд до верха воды. Откройте отверстия и проследите за струйками вытекающей воды (рис. 98). Ответьте на вопросы: почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной? 2. Прочтите в конце учебника параграфы «Гидростатический парадокс. Опыт Паскаля», «Давление на дне морей и океанов. Исследование морских глубин».
14.1 Жидкости, плотность и давление – Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Назовите различные фазы вещества
- Описать характеристики фаз материи на молекулярном или атомарном уровне
- Различать сжимаемые и несжимаемые материалы
- Определение плотности и связанных с ней единиц СИ
- Сравните и сопоставьте плотности различных веществ
- Определение давления и связанных с ним единиц СИ
- Объясните взаимосвязь между давлением и силой
- Расчет силы по давлению и площади
Вещество чаще всего существует в виде твердого тела, жидкости или газа; эти состояния известны как три общие фазы материи. В этом разделе мы подробно рассмотрим каждый из этих этапов.
В этом разделе мы подробно рассмотрим каждый из этих этапов.
Характеристики твердых тел
Твердые тела твердые, имеют определенную форму и определенный объем. Атомы или молекулы в твердом теле находятся в непосредственной близости друг от друга, и между этими молекулами существует значительная сила. Твердые тела примут форму, определяемую характером этих сил между молекулами. Хотя настоящие твердые тела не являются несжимаемыми, тем не менее для изменения формы твердого тела требуется большая сила.В некоторых случаях сила между молекулами может заставить молекулы организоваться в решетку, как показано на рисунке. Структура этой трехмерной решетки представлена молекулами, соединенными жесткими связями (смоделированными как жесткие пружины), что дает ограниченную свободу движения. Даже большая сила вызывает лишь небольшие смещения атомов или молекул решетки, и твердое тело сохраняет свою форму. Твердые тела также сопротивляются силам сдвига. (Сдвиговые силы — это силы, действующие по касательной к поверхности, как описано в разделе «Статическое равновесие и упругость». )
)
Характеристики жидкостей
Жидкости и газы считаются жидкостями , потому что они поддаются силам сдвига, тогда как твердые тела сопротивляются им. Подобно твердым телам, молекулы жидкости связаны с соседними молекулами, но таких связей гораздо меньше. Молекулы в жидкости не зафиксированы на месте и могут двигаться относительно друг друга. Расстояние между молекулами аналогично расстоянию в твердом теле, поэтому жидкости имеют определенные объемы, но форма жидкости изменяется в зависимости от формы ее сосуда.Газы не связаны с соседними атомами и могут иметь большие расстояния между молекулами. Газы не имеют ни определенной формы, ни определенных объемов, так как их молекулы движутся, чтобы заполнить сосуд, в котором они находятся (рис.).
Рис. 14.2 (а) Атомы в твердом теле всегда находятся в тесном контакте с соседними атомами, удерживаясь на месте силами, представленными здесь пружинами. б) Атомы в жидкости также находятся в тесном контакте, но могут скользить друг по другу. Силы между атомами сильно сопротивляются попыткам сжатия атомов.в) Атомы в газе свободно перемещаются и разделены большими расстояниями. Газ необходимо держать в закрытом контейнере, чтобы предотвратить его свободное расширение и утечку.
Силы между атомами сильно сопротивляются попыткам сжатия атомов.в) Атомы в газе свободно перемещаются и разделены большими расстояниями. Газ необходимо держать в закрытом контейнере, чтобы предотвратить его свободное расширение и утечку.
Жидкости легко деформируются при воздействии нагрузки и не возвращаются к своей первоначальной форме после прекращения действия силы. Это происходит потому, что атомы или молекулы в жидкости могут свободно скользить и менять соседей. То есть жидкости текут (поэтому они являются типом жидкости), а молекулы удерживаются вместе за счет взаимного притяжения. Когда жидкость помещается в контейнер без крышки, она остается в контейнере.Поскольку атомы плотно упакованы, жидкости, как и твердые тела, сопротивляются сжатию; для изменения объема жидкости необходима чрезвычайно большая сила.
Напротив, атомы в газах разделены большими расстояниями, и поэтому силы между атомами в газе очень слабы, за исключением случаев, когда атомы сталкиваются друг с другом.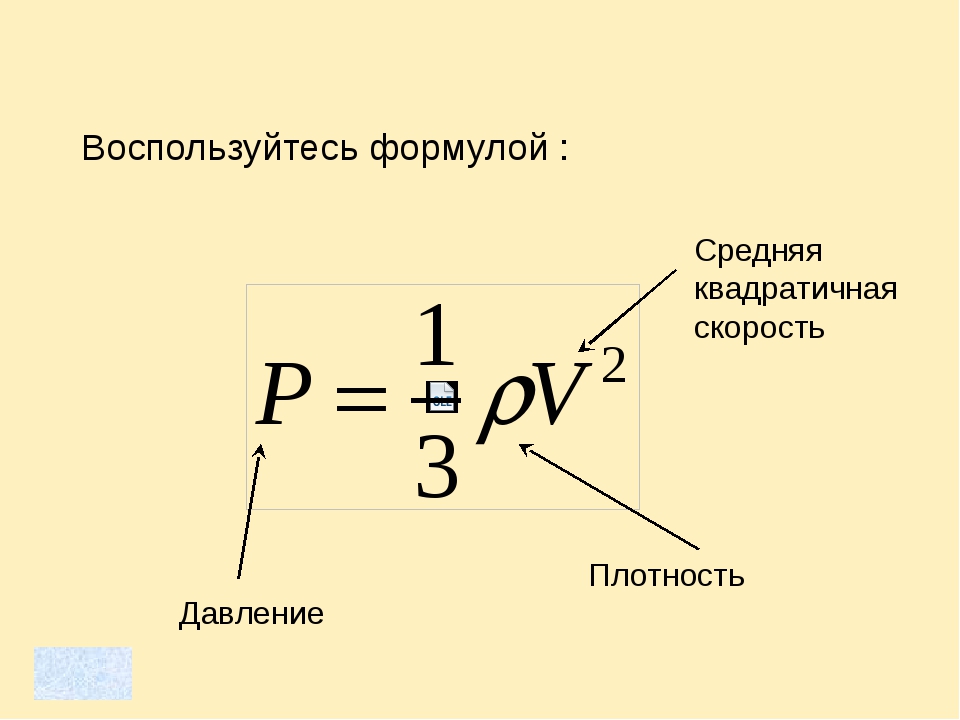 Это делает газы относительно легко сжимаемыми и позволяет им течь (что делает их жидкостями). При помещении в открытый контейнер газы, в отличие от жидкостей, будут выходить наружу.
Это делает газы относительно легко сжимаемыми и позволяет им течь (что делает их жидкостями). При помещении в открытый контейнер газы, в отличие от жидкостей, будут выходить наружу.
В этой главе мы обычно называем и газы, и жидкости просто жидкостями, проводя различие между ними только тогда, когда они ведут себя по-разному. Существует еще одна фаза вещества — плазма, существующая при очень высоких температурах. При высоких температурах молекулы могут диссоциировать на атомы, а атомы диссоциировать на электроны (с отрицательными зарядами) и протоны (с положительными зарядами), образуя плазму. Плазма не будет подробно обсуждаться в этой главе, потому что плазма имеет очень отличные свойства от трех других распространенных фаз материи, обсуждаемых в этой главе, из-за сильных электрических сил между зарядами.
Плотность
Предположим, что брусок из латуни и брусок дерева имеют одинаковую массу. Если оба бруска бросить в резервуар с водой, почему дерево всплывет, а латунь утонет (рисунок)? Это происходит потому, что латунь имеет большую плотность, чем вода, а древесина имеет меньшую плотность, чем вода.
Рисунок 14.3 (a) Блок из латуни и блок из дерева имеют одинаковый вес и массу, но блок из дерева имеет гораздо больший объем. (b) При помещении в аквариум, наполненный водой, латунный куб тонет, а деревянный брусок всплывает.(Деревянный брусок на обеих картинках одинаков; он был перевернут на бок, чтобы соответствовать масштабу.)
Плотность является важной характеристикой веществ. Это имеет решающее значение, например, при определении того, тонет ли объект в жидкости или плавает.
Плотность
Средняя плотность вещества или объекта определяется как его масса в единице объема,
[латекс]\rho =\frac{m}{V}[/латекс]
, где греческая буква [латекс]\ро[/латекс] (ро) — символ плотности, m — масса, а V — объем.{3}[/латекс]
Как видно из рисунка, плотность объекта может помочь определить его состав. Плотность золота, например, примерно в 2,5 раза больше плотности железа, что примерно в 2,5 раза больше плотности алюминия. Плотность также раскрывает кое-что о фазе материи и ее подструктуре. Обратите внимание, что плотности жидкостей и твердых тел примерно сопоставимы, что согласуется с тем фактом, что их атомы находятся в тесном контакте.{3}[/латекс]
Плотность также раскрывает кое-что о фазе материи и ее подструктуре. Обратите внимание, что плотности жидкостей и твердых тел примерно сопоставимы, что согласуется с тем фактом, что их атомы находятся в тесном контакте.{3}[/латекс]
Плотность вещества не обязательно постоянна по всему объему вещества. Если плотность вещества постоянна во всем веществе, говорят, что это однородное вещество . Твердый железный брусок является примером однородного вещества. Плотность постоянна на всем протяжении, а плотность любого образца вещества равна его средней плотности. Если плотность вещества непостоянна, говорят, что это гетерогенное вещество .Кусок швейцарского сыра является примером гетерогенного материала, содержащего как твердый сыр, так и пустоты, заполненные газом. Плотность в определенном месте в неоднородном материале называется локальной плотностью и определяется как функция местоположения [латекс]\rho =\rho (x,y,z)[/латекс] (рисунок).
Рисунок 14.4 Плотность может варьироваться в зависимости от гетерогенной смеси. Локальная плотность в точке получается делением массы на объем в малом объеме вокруг данной точки.
Локальная плотность может быть получена с помощью процесса ограничения, основанного на средней плотности в небольшом объеме вокруг рассматриваемой точки, принимая предел, когда размер объема приближается к нулю,
[латекс]\rho =\underset{\Delta V\to 0}{\text{lim}}\frac{\Delta m}{\Delta V}[/latex]
где [латекс]\ро[/латекс] — плотность, м — масса, а V — объем.
Поскольку газы могут свободно расширяться и сжиматься, плотность газов значительно зависит от температуры, тогда как плотность жидкостей зависит от температуры незначительно.Поэтому плотности жидкостей часто считают постоянными, при этом плотность равна средней плотности.
Плотность — это размерное свойство; поэтому при сравнении плотностей двух веществ необходимо учитывать единицы. По этой причине для сравнения плотностей часто используют более удобную безразмерную величину, называемую удельным весом. Удельный вес определяется как отношение плотности материала к плотности воды в [латексе]4.{3}[/latex]), но его удельный вес составляет 2,7, независимо от единицы плотности. Удельный вес — особенно полезная величина в отношении плавучести, которую мы обсудим позже в этой главе.
По этой причине для сравнения плотностей часто используют более удобную безразмерную величину, называемую удельным весом. Удельный вес определяется как отношение плотности материала к плотности воды в [латексе]4.{3}[/latex]), но его удельный вес составляет 2,7, независимо от единицы плотности. Удельный вес — особенно полезная величина в отношении плавучести, которую мы обсудим позже в этой главе.
Давление
Вы, несомненно, слышали слово «давление», используемое по отношению к крови (высокое или низкое кровяное давление) и по отношению к погоде (погодные системы высокого и низкого давления). Это только два из многих примеров давления в жидкостях. (Вспомните, что мы ввели понятие давления в книге «Статическое равновесие и упругость» в контексте объемного напряжения и деформации.)
Давление
Давление ( p ) определяется как нормальная сила F на единицу площади A , к которой приложена сила, или [латекс]p=\frac{F}{A}. [/latex]
[/latex]
Чтобы определить давление в конкретной точке, давление определяется как сила dF , действующая со стороны жидкости на бесконечно малый элемент площадью dA , содержащий точку, что приводит к [латекс]p=\frac{dF}{ дА}[/латекс].
Действие одной и той же силы может существенно различаться в зависимости от площади, на которую она воздействует.{2}.[/latex] Вот почему острая игла способна проткнуть кожу при приложении небольшого усилия, но приложение такого же усилия пальцем не прокалывает кожу (рисунок).
Рисунок 14.5 (a) Человек, которого тыкают пальцем, может испытывать раздражение, но сила не имеет длительного эффекта. (b) Напротив, той же силы, приложенной к участку размером с острый конец иглы, достаточно, чтобы сломать кожу.
Обратите внимание, что хотя сила является вектором, давление является скаляром. Давление является скалярной величиной, поскольку по определению оно пропорционально величине силы, действующей перпендикулярно площади поверхности. {2}.[/латекс]
{2}.[/латекс]
Для давления используются несколько других единиц измерения, которые мы обсудим позже в этой главе.
Изменение давления с глубиной в жидкости постоянной плотности
Давление определяется для всех состояний вещества, но особенно важно при обсуждении жидкостей. Важной характеристикой жидкостей является отсутствие значительного сопротивления компоненту силы, приложенной параллельно поверхности жидкости. Молекулы жидкости просто текут, приспосабливаясь к горизонтальной силе.Сила, приложенная перпендикулярно поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что в каждой точке внутри жидкости в направлении наружу возникает сила реакции, уравновешивающая силу, действующую на молекулы на границе.
Рассмотрим жидкость постоянной плотности, как показано на рисунке. Давление на дне контейнера обусловлено давлением атмосферы [латекс]({p}_{0})[/латекс] плюс давление, обусловленное весом жидкости. Давление жидкости равно весу жидкости, деленному на площадь. Вес жидкости равен произведению ее массы на ускорение свободного падения.
Вес жидкости равен произведению ее массы на ускорение свободного падения.
Рисунок 14.6 Дно этого контейнера выдерживает весь вес жидкости в нем. Вертикальные стороны не могут воздействовать на жидкость восходящей силой (поскольку она не может противостоять сдвигающей силе), поэтому дно должно поддерживать все это.
Поскольку плотность постоянна, вес можно рассчитать, используя плотность:
[латекс]w=mg=\rho Vg=\rho Ahg.[/latex]
Таким образом, давление на дне сосуда равно атмосферному давлению, добавленному к весу жидкости, деленному на площадь:
[латекс]p={p}_{0}+\frac{\rho Ahg}{A}={p}_{0}+\rho hg.[/латекс]
Это уравнение годится только для давления на глубине для жидкости постоянной плотности.
Давление на глубине для жидкости постоянной плотности
Давление на глубине в жидкости постоянной плотности равно атмосферному давлению плюс давление от веса жидкости, или
[латекс]p={p}_{0}+\rho hg,[/latex]
Где p — давление на определенной глубине, [латекс]{р}_{0}[/латекс] — атмосферное давление, [латекс]\ро[/латекс] — плотность жидкости, г — ускорение свободного падения, ч — глубина.
Рисунок 14.7 Плотина «Три ущелья», воздвигнутая на реке Янцзы в центральном Китае в 2008 г., создала массивное водохранилище, в котором было перемещено более миллиона человек. (кредит: «Le Grand Portage»/Flickr)
Пример
Какую силу должна выдерживать плотина?
Рассмотрим давление и силу, действующие на плотину, удерживающую водоем (рис.). Предположим, что ширина плотины составляет 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? б) Рассчитайте силу, действующую на плотину.
Среднее давление p из-за веса воды является давлением на средней глубине h 40,0 м, так как давление линейно возрастает с глубиной. Сила, действующая на плотину со стороны воды, равна среднему давлению, умноженному на площадь контакта, [латекс]F=pA.[/латекс]
решение
- Среднее давление из-за веса жидкости
[латекс]р=ч\ро г.[/латекс]
Введите плотность воды из рисунка и примите ч за среднюю глубину 40.
 {13}\text{N}[/latex] вес воды в резервуаре. На самом деле это всего лишь 0,0800% веса.
{13}\text{N}[/latex] вес воды в резервуаре. На самом деле это всего лишь 0,0800% веса.Проверьте свое понимание
Если бы водохранилище на рисунке занимало вдвое большую площадь, но сохраняло бы ту же глубину, нужно ли было бы перепроектировать плотину?
Показать решение
Давление, найденное в части (а) примера, полностью не зависит от ширины и длины озера; он зависит только от его средней глубины у плотины. Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не от горизонтальной протяженности водохранилища.На диаграмме обратите внимание, что толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличивающегося давления.
Давление в статической жидкости в однородном гравитационном поле
Статическая жидкость — это жидкость, которая не находится в движении. В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке будет реагировать на результирующую силу и ускоряться.

Давление в любой точке статической жидкости зависит только от глубины в этой точке.Как обсуждалось, давление в жидкости вблизи Земли меняется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности. Это разумное приближение для таких жидкостей, как вода, где требуются большие силы для сжатия жидкости или изменения объема. В плавательном бассейне, например, плотность приблизительно постоянна, и вода на дне очень мало сжимается под весом воды наверху.Однако путешествие в атмосферу — это совсем другая ситуация. Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли.
Чтобы вывести формулу для изменения давления с глубиной в резервуаре, содержащем жидкость с плотностью ρ на поверхности Земли, мы должны начать с предположения, что плотность жидкости непостоянна. Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, расположенная ближе к поверхности, из-за веса жидкости над ней.
 Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.Представьте себе тонкий элемент жидкости на глубине ч , как показано на рисунке. Пусть элемент имеет площадь поперечного сечения A и высоту [латекс]\Delta y[/латекс]. Силы, действующие на элемент, обусловлены давлением p ( y ) над ним и [латекс]р(у+\Delta y)[/латекс] под ним. Вес самого элемента также показан на диаграмме свободного тела.
Рисунок 14.8 Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела.
Поскольку элемент жидкости между y и [латекс]y+\Delta y[/латекс] не ускоряется, силы уравновешены. Используя декартову ось y , ориентированную вверх, мы находим следующее уравнение для y -компоненты:
[латекс]p(y+\Delta y)A-p(y)A-g\Delta m=0(\Delta y \gt 0).[/latex]
Обратите внимание, что если бы элемент имел ненулевую y -компоненту ускорения, правая часть не была бы равна нулю, а вместо этого была бы массой, умноженной на y -ускорение.
 Массу элемента можно записать через плотность жидкости и объем элементов:
Массу элемента можно записать через плотность жидкости и объем элементов:[латекс]\Delta m=|\rho A\Delta y|=\text{−}\rho A\Delta y\text{ }(\Delta y \gt 0).[/latex]
Поместив это выражение для [латекс]\Delta m[/latex] на рисунок, а затем разделив обе части на [latex]A\Delta y[/latex], мы находим
[латекс]\frac{p(y+\Delta y)-p(y)}{\Delta y}=\text{-}\rho g.[/latex]
Беря предел бесконечно малому элементу [латекс]\Delta y\к 0[/латексу], мы получаем следующее дифференциальное уравнение, которое дает изменение давления в жидкости:
[латекс]\frac{dp}{dy}=\text{−}\rho g.[/латекс]
Это уравнение говорит нам, что скорость изменения давления в жидкости пропорциональна плотности жидкости. Решение этого уравнения зависит от того, постоянна плотность ρ или изменяется с глубиной; то есть функция ρ ( y ).
Если диапазон анализируемых глубин не слишком велик, плотность можно считать постоянной. Но если диапазон глубин достаточно велик для заметного изменения плотности, как, например, в случае с атмосферой, плотность существенно меняется с глубиной.
 {\ text {−} h} \ rho gdy \ hfill \\ \ hfill p-{p} _ {0} & = \ hfill & \ rho gh \ hfill \\ \ hfill p& =\ hfill & {p}_ {0}+\rho gh.\hfill \end{массив}[/латекс]
{\ text {−} h} \ rho gdy \ hfill \\ \ hfill p-{p} _ {0} & = \ hfill & \ rho gh \ hfill \\ \ hfill p& =\ hfill & {p}_ {0}+\rho gh.\hfill \end{массив}[/латекс]Следовательно, давление на глубине жидкости на поверхности Земли равно атмосферному давлению плюс ρgh , если плотность жидкости постоянна по высоте, как мы нашли ранее.
Обратите внимание, что давление в жидкости зависит только от глубины от поверхности, а не от формы сосуда. Таким образом, в сосуде, где жидкость может свободно перемещаться в различных частях, жидкость остается на одном уровне в каждой части, независимо от формы, как показано на рисунке.
Рисунок 14.9 Если жидкость может свободно течь между частями сосуда, она поднимается на одинаковую высоту в каждой части. В изображенном контейнере давление на дне каждой колонны одинаково; если бы это было не то же самое, жидкость текла бы до тех пор, пока давления не сравнялись бы.
Изменение атмосферного давления с высотой
Особый интерес представляет изменение атмосферного давления с высотой.
 Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна.(Мы обсудим закон идеального газа в следующей главе, но мы предполагаем, что вы знакомы с ним из средней школы и химии.) Пусть p ( y ) будет атмосферным давлением на высоте y . Плотность [латекс]\ро[/латекс] при y , температура T по шкале Кельвина (К) и масса m молекулы воздуха связаны с абсолютным давлением идеального газа закон, по форме
Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна.(Мы обсудим закон идеального газа в следующей главе, но мы предполагаем, что вы знакомы с ним из средней школы и химии.) Пусть p ( y ) будет атмосферным давлением на высоте y . Плотность [латекс]\ро[/латекс] при y , температура T по шкале Кельвина (К) и масса m молекулы воздуха связаны с абсолютным давлением идеального газа закон, по форме[латекс] p = \ rho \ frac {{k} _ {\ text {B}} T} {m} \, \ text {(атмосфера),} [/latex]
, где [латекс]{к}_{\текст{В}}[/латекс] — постоянная Больцмана, которая имеет значение [латекс]1.{-23}\text{J/K}[/latex].
Возможно, вы встречали закон идеального газа в форме [латекс]pV=nRT[/латекс], где n — число молей, а R — газовая постоянная.
 Здесь тот же закон записан в другой форме, с использованием плотности [латекс]\ро[/латекс] вместо объема V . Следовательно, если давление p изменяется с высотой, то и плотность [латекс]\ро .[/латекс] Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как
Здесь тот же закон записан в другой форме, с использованием плотности [латекс]\ро[/латекс] вместо объема V . Следовательно, если давление p изменяется с высотой, то и плотность [латекс]\ро .[/латекс] Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как[латекс]\frac{dp}{dy}=\text{-}p(\frac{mg}{{k}_{\text{B}}T}),[/latex]
, где в скобках указано постоянное количество.{y}\hfill \\ \hfill \text{ln}(p)-\text{ln}({p}_{0})& =\hfill & \text{−}\alpha y\hfill \\ \ hfill \text{ln}(\frac{p}{{p}_{0}})& =\hfill & \text{−}\alpha y\hfill \end{массив}[/latex]
Это дает решение
[латекс]p(y)={p}_{0}\text{exp}(\text{−}\alpha y).[/latex]
Таким образом, атмосферное давление экспоненциально падает с высотой, поскольку ось y направлена вверх от земли, а y имеет положительные значения в атмосфере над уровнем моря.Давление падает в [латекс]\фрак{1}{е}[/латекс], когда высота равна [латекс]\фрак{1}{\альфа},[/латекс], что дает нам физическую интерпретацию для [латекс]\альфа[/латекс]: Константа [латекс]\фрак{1}{\альфа }[/латекс] — это шкала длины, которая характеризует изменение давления с высотой и часто называется высотой шкалы давления.

Мы можем получить приблизительное значение [латекс]\альфа[/латекс], используя массу молекулы азота в качестве прокси для молекулы воздуха. При температуре [латекс]\текст{27 °С,}[/латекс] или 300 К находим
[латекс] \ alpha = — \ frac {mg} {{k} _ {\ text {B}} T} = \ frac {4.{-23}\,\text{J/K}\times \text{300 K}}=\frac{1}{8800\,\text{m}}.[/latex]
Следовательно, на каждые 8800 метров атмосферное давление падает в 1/ e раз, или примерно на одну треть своего значения. Это дает нам лишь грубую оценку реальной ситуации, поскольку мы предполагали и постоянную температуру, и постоянную g на столь больших расстояниях от Земли, ни одно из которых в действительности не верно.
Направление давления в жидкости
Давление жидкости не имеет направления, будучи скалярной величиной, тогда как силы, вызванные давлением, имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности.Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига.
 Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке показано давление воздуха на стенки покрышки и воды на тело пловца.
Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке показано давление воздуха на стенки покрышки и воды на тело пловца.Рисунок 14.10 (a) Давление внутри этой шины действует перпендикулярно ко всем поверхностям, с которыми она контактирует.Стрелки представляют направления и величины сил, действующих в различных точках. (b) Давление оказывается перпендикулярно всем сторонам этого пловца, так как вода потекла бы в пространство, которое он занимает, если бы его там не было. Стрелки представляют направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы внизу больше из-за большей глубины, что дает сеть вверх или выталкивающую силу. Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.

Атмосферное давление — Видео по физике от Brightstorm
Итак, давайте поговорим об атмосферном давлении, давлении, связанном с атмосферой воздуха, которая окружает нас повсюду. Что ж, воздух — это жидкость, это то, что может менять свою форму и размер без особого давления. Это означает, что мы сидим здесь, погруженные в воздух, и это означает, что мы поддерживаем вес всего воздуха над нами, а это означает, что мы испытываем давление. Итак, мы готовы, верно? Давление жидкости, давление жидкости, вот оно, плотность жидкости, умноженная на g, умноженная на высоту.Хорошо, что мы используем для плотности воздуха, я имею в виду, что мы знаем, какая плотность здесь внизу, но плотность воздуха становится меньше, когда мы поднимаемся вверх, так что мы должны использовать в этой формуле и как насчет h? Что мы должны использовать для высоты атмосферы? Что вы думаете? Я не знаю, и на самом деле эти две вещи связаны друг с другом. Так что это своего рода проблема, мы не можем использовать эту формулу, поэтому нам нужно сделать что-то еще, и что мы собираемся сделать, так это просто измерить ее напрямую.
 Итак, мы возьмем трубку, полную ртути, погрузим ее в ванну с ртутью, а затем поднимем трубку вот так, хорошо.
Итак, мы возьмем трубку, полную ртути, погрузим ее в ванну с ртутью, а затем поднимем трубку вот так, хорошо.Внутри трубки не было воздуха, значит, ртуть немного упадет вниз, а там ничего нет. Так что давление здесь 0, поддерживать нечего. Здесь, с другой стороны, у нас вся атмосфера давит вниз. Так что это означает, что разница в давлении между атмосферным давлением и 0 поддерживает эту высоту столбика ртути. И теперь мы можем использовать плотность, умноженную на g, умноженную на час, потому что плотность ртути почти постоянна, и мы можем измерить высоту.Таким образом, атмосферное давление определяется плотностью ртути, умноженной на 9,8 метра в секунду в квадрате, умноженной на любую высоту столба ртути. Итак, это атмосферное давление пропорционально высоте ртутного столба. И это приводит к одному из самых ранних измерений одной из первых единиц измерения давления миллиметру ртутного столба.
Теперь, когда мы проводим стандартные измерения, мы обнаруживаем, что атмосферное давление составляет всего около 760 миллиметров ртутного столба.
 Теперь у нас есть определение того, что мы подразумеваем под стандартной атмосферой, так что давайте посмотрим сюда.Одна стандартная атмосфера равна 760 торр. Этот торр — это единица, которая должна была быть похожа на миллиметр ртутного столба, но названа в честь физика по имени Торр Чарли, который много работал над давлением в 1600-х годах. Итак, если вы на самом деле посмотрите на то, что на самом деле это в миллиметрах ртутного столба, это 763,3, так что это близко, но не совсем одно и то же. Что ж, для стандартной единицы в Соединенных Штатах люди часто используют фунты PSI на квадратный дюйм. Одна атмосфера в фунтах на квадратный дюйм составляет примерно 14,7 фунтов на квадратный дюйм. Так что это значит?
Теперь у нас есть определение того, что мы подразумеваем под стандартной атмосферой, так что давайте посмотрим сюда.Одна стандартная атмосфера равна 760 торр. Этот торр — это единица, которая должна была быть похожа на миллиметр ртутного столба, но названа в честь физика по имени Торр Чарли, который много работал над давлением в 1600-х годах. Итак, если вы на самом деле посмотрите на то, что на самом деле это в миллиметрах ртутного столба, это 763,3, так что это близко, но не совсем одно и то же. Что ж, для стандартной единицы в Соединенных Штатах люди часто используют фунты PSI на квадратный дюйм. Одна атмосфера в фунтах на квадратный дюйм составляет примерно 14,7 фунтов на квадратный дюйм. Так что это значит?Ну, это значит, что на каждый квадратный дюйм твоего лица, дюйм, дюйм что-то вроде этого, у меня 14.7 фунтов на каждый квадратный дюйм. Вот почему я не просто падаю в обморок, ну, я вдыхаю воздух, который находится под таким же давлением. Таким образом, воздух выталкивается наружу, воздух снаружи проталкивается внутрь, и коже не нужно слишком много поддерживать.
 Те же самые идеи используются аквалангистами, которые ныряют глубоко и вдыхают сжатый воздух, так что они получают более высокое давление, и тогда их кожа не должна выдерживать такую большую разницу давлений между водой. океан и их внутренние органы, их легкие и их кровь и все такое.Так или иначе, это просто небольшое примечание.
Те же самые идеи используются аквалангистами, которые ныряют глубоко и вдыхают сжатый воздух, так что они получают более высокое давление, и тогда их кожа не должна выдерживать такую большую разницу давлений между водой. океан и их внутренние органы, их легкие и их кровь и все такое.Так или иначе, это просто небольшое примечание.Чтобы записать это в единицах СИ, потому что, конечно, мы всегда использовали единицы СИ, это будет записано как 101 325 Паскалей, так что это одна атмосфера, и опять же это стандартное определение. Когда кто-то говорит о стандартной атмосфере, это то, что они имеют в виду. Но это просто стандартная атмосфера. Итак, давайте продолжим и используем эту идею для решения проблемы.Так что, когда я сосу через соломинку, по сути, я делаю то же самое, что мы видели здесь с этой ртутной колонкой. Я удаляю часть воздуха из верхней части соломинки, так что теперь давление внутри моего рта меньше, чем давление, создаваемое атмосферой. Так что эта разница в давлении заставляет столб воды, газировки или чего бы то ни было, что я пью, поднимается в соломинке.
 Итак, теперь у меня есть вопрос к вам, какова максимальная высота воды, которую вы можете поддерживать в соломинке? Итак, если вы будете сосать изо всех сил, насколько высоко может подняться эта колонка? Может ли он стать бесконечно высоким?
Итак, теперь у меня есть вопрос к вам, какова максимальная высота воды, которую вы можете поддерживать в соломинке? Итак, если вы будете сосать изо всех сил, насколько высоко может подняться эта колонка? Может ли он стать бесконечно высоким?Ну, вот идея, как и раньше, у вас есть столб воды, и на самом деле то, что поддерживает его, — это атмосферное давление.Так что лучшее, что вы можете сделать, это то, что мы видели с ртутным барометром. 0 давление в верхней части, теперь вы не можете на самом деле сделать это, вы можете попробовать, но это будет своего рода идеализированным лучшим, что вы можете себе представить, делая 0 давление там наверху. А потом у вас здесь атмосферное давление, и оно должно поддерживать этот столб воды. Итак, что мы собираемся сделать, так это сказать, что p атмосферное равно плотности воды, умноженной на ускорение под действием силы тяжести, умноженное на высоту. И это та высота, которую мы ищем, верно? Ну, теперь это просто очень просто, мне просто нужно решить и подставить числа, пока все в единицах СИ, я готов к работе.
 Таким образом, h будет равно p атмосферы 101 325 при плотности воды 10 в третьей, g 9,8, и когда вы все это посчитаете, вы обнаружите, что это около 10,34. Какой будет единица? Ну, все в единицах СИ, так что все в единицах СИ, это высота, это метры. Это означает, что максимальная высота столба воды, которую вы можете поддерживать на земле, составляет 10,34 метра.
Таким образом, h будет равно p атмосферы 101 325 при плотности воды 10 в третьей, g 9,8, и когда вы все это посчитаете, вы обнаружите, что это около 10,34. Какой будет единица? Ну, все в единицах СИ, так что все в единицах СИ, это высота, это метры. Это означает, что максимальная высота столба воды, которую вы можете поддерживать на земле, составляет 10,34 метра.Вы хотите поддерживать больше, чем это, вы должны давить сильнее, вы не можете просто позволить атмосфере делать вашу работу за вас. Хорошо, конечно, если это более плотная жидкость, такая как ртуть, максимальная высота, которую вы можете поддерживать, будет 763.3 миллиметра, что немного меньше примерно 75% 76,33% метра, хорошо, так что это намного меньше, и это потому, что ртуть намного плотнее воды. Итак, давайте продолжим и рассмотрим некоторые другие типы проблем, которые вас могут попросить решить, связанные с этим. Некоторые из них довольно странные, там нет ничего сложного, но вы, возможно, не подумали, что делать, хорошо.
 Итак, вопрос, каков общий вес атмосферы? Какой-то странный вопрос, да? Вы смотрите на этот вопрос, и вы как что? Откуда мне это знать? Хорошо, вес атмосферы, помните, мы говорили, что давление, связанное с атмосферой, на самом деле связано с ее весом.Итак, я знаю давление, а как насчет веса? Ну, вес будет, это сила, так что вес будет давлением, умноженным на площадь.
Итак, вопрос, каков общий вес атмосферы? Какой-то странный вопрос, да? Вы смотрите на этот вопрос, и вы как что? Откуда мне это знать? Хорошо, вес атмосферы, помните, мы говорили, что давление, связанное с атмосферой, на самом деле связано с ее весом.Итак, я знаю давление, а как насчет веса? Ну, вес будет, это сила, так что вес будет давлением, умноженным на площадь.Ну, я знаю, что такое атмосферное давление, какая площадь? Ну а атмосфера действует на всю планету. Таким образом, это давление действует на площадь поверхности всей планеты. Хорошо, какова площадь поверхности всей планеты? Ну, это 4 пи, умноженное на радиус всей планеты в квадрате, 4 пи в квадрате, как мы знаем из геометрии, верно? Так что теперь все, что мне нужно сделать, это подставить числа, радиус Земли составляет около 6370 километров, хорошо.Итак, мы собираемся записать это снова как 101 325. Я собираюсь игнорировать единицы, потому что я знаю, какие единицы будут в конце, пока все в единицах СИ, я в порядке.
 Таким образом, p атмосферы 4 pi равно 12,54, а затем у нас есть радиус, он должен быть в единицах СИ. Я сказал 6370 километров, мне нельзя использовать километры. Я должен сказать 6,37 умножить на 10 на 6 метров, и я возьму это в квадрат. И когда я подставляю все эти числа в калькулятор, я получаю вес 5,17 умноженный на 19, хорошо, теперь какая единица? Это вес, то есть сила, и в единицах СИ, выраженных в ньютонах, это довольно большой вес.
Таким образом, p атмосферы 4 pi равно 12,54, а затем у нас есть радиус, он должен быть в единицах СИ. Я сказал 6370 километров, мне нельзя использовать километры. Я должен сказать 6,37 умножить на 10 на 6 метров, и я возьму это в квадрат. И когда я подставляю все эти числа в калькулятор, я получаю вес 5,17 умноженный на 19, хорошо, теперь какая единица? Это вес, то есть сила, и в единицах СИ, выраженных в ньютонах, это довольно большой вес.Но это вся атмосфера земли и заметьте, насколько она проста на самом деле. Это прямо следует из того, что значит вес, что значит давление и что значит площадь? А потом просто умножьте числа, хорошо, вот как это происходит. Хорошо, давайте посмотрим на это последнее, какова масштабная высота атмосферы при постоянной плотности. Хорошо, так что это займет минуту, чтобы понять, что я имею в виду. Помните, в начале мы хотели использовать плотность, умноженную на ускорение под действием силы тяжести, умноженную на высоту, чтобы определить давление на поверхности земли во всей атмосфере.
 Но мы сказали, что есть пара проблем, плотность не была постоянной, и мы не знали, что использовать по высоте или для высоты. Итак, в этой задаче от нас требуется принять постоянную плотность и просто взять плотность на уровне моря. А затем определите, какая высота, подходящая высота, которая даст нам давление, которое мы измеряем.
Но мы сказали, что есть пара проблем, плотность не была постоянной, и мы не знали, что использовать по высоте или для высоты. Итак, в этой задаче от нас требуется принять постоянную плотность и просто взять плотность на уровне моря. А затем определите, какая высота, подходящая высота, которая даст нам давление, которое мы измеряем.Хорошо, так что давай сделаем это, потому что это будет интересный ответ. Итак, мы скажем, что p атмосферы равно плотности gh, я хочу h, поэтому мы будем иметь h равно p атмосферы 101 325, а плотность воздуха на уровне моря составляет около 1.3 килограмма на кубический метр. Итак, у меня будет 1,3, 9,8, и когда вы все это проработаете, вы получите 7,9 километра. Теперь это довольно сумасшедшие 7,9 километров на самом деле не очень высоко, все в порядке. На самом деле это меньше, чем высота полета большинства самолетов. Хорошо, по крайней мере, когда они проходят большие расстояния, и поэтому над этим должен быть воздух, и это прямо указывает нам на то, что плотность воздуха должна измениться, потому что, если бы она была просто постоянной, весь путь вверх по атмосфере тоже заканчивается.
 низкий. Ладно, это атмосферное давление.2)}\]
низкий. Ладно, это атмосферное давление.2)}\]Пример
Давление 280 Па действует под углом 90° на площадь 0,04 м 2 . Какая сила действует под углом 90° к площади?
Сначала измените уравнение, чтобы найти силу, нормальную к площади поверхности:
сила, нормальная к площади поверхности = давление × площадь этой поверхности
Затем подставьте значения в уравнение:
сила = 280 × 0,04
сила = 11.2 N
- Вопрос 2f0dlj3wqjm.0.0.0.1:0.1.0.$0.$1.$9.1″>
- Показать ответ
Сначала преобразовать 150 кПа в Па:
150 × 1,000 = 150,000
Затем подставьте значения в уравнение: = 150 000 × 180
сила = 27 000 000 Н
Жидкость оказывает давление 150 кПа под прямым углом к стене площадью 180 м 2 .Рассчитайте силу, действующую на стену.
Сила определяется давлением и площадью
р=Ж/Д
Свойства материи
Сила определяется давлением и площадью
Рассказ о физике
за
11-14Расчет силы
Итак, если вы держите голову под водой, вы можете определить давление окружающей воды ушами.
 (Ваша барабанная перепонка действует как
(Ваша барабанная перепонка действует как детектор разницы давлений
. Бомбардирующие молекулы воды воздействуют на открытые участки барабанных перепонок. Частицы воздуха в вашем ухе бомбардируют внутреннюю часть и также оказывают воздействие. Результат этих двух сил это то, что вы чувствуете.) Величина этой силы определяется простым соотношением: сила = давление × площадь.Вы всегда можете
выровнять давление
, зажав нос, зажав рот и выдыхая, в результате чего внутрь попадет больше частиц.Вероятно, вы можете отрегулировать давление так, чтобы сила, действующая внутри, и сила, действующая снаружи, были одинаковыми, по крайней мере, в бассейне.Вот точный способ записи, чтобы каждый термин был просто числом:
силаньютон = давлениеньютон/метр 2 × площадьметр 2
Вы также можете написать (записывая для себя единицы измерения) как сила в ньютонах = давление в ньютонах/метрах 2 × площадь в метрах 2
Первая форма более краткая и точная, так как каждый термин сводится к простому числу: число × единица, деленная на единицу, оставляет просто число.

(Помните, что физическая величина — это число, умноженное на единицу измерения.)
Перестановки
Вы можете изменить это, чтобы сделать давление субъектом формулы, но отношение останется тем же.
Можно написать, достаточно полно, (записывая про себя единицы):давление в ньютонах/метрах 2 = сила в ньютонахплощадь в метрах 2
Или даже выразить это довольно кратко:
давление = площадь силы
Наиболее лаконично можно написать:
P = F A
Вам нужно будет сопоставить выбранное вами представление с имеющимися у вас классами, чтобы они могли понять взаимосвязь.
Другими словами, большой давление в воде создаст большую силу, действующую на открытый участок барабанной перепонки. Если давление слишком велико, вы можете получить перфорацию барабанной перепонки из-за действия силы.
Калькулятор давления и формула — Академия калькуляторов
Введите общую силу и площадь приложения силы для расчета общего давления на объект или систему.

Формула давления
Формула давления следующая:
П = Ф/А
- Где P — давление
- F — сила
- A — площадь
Давление также является мерой потенциальной энергии системы. Это сила, действующая на площадь, поэтому, если эта сила действует на некотором расстоянии, система может выполнять работу над другим объектом или системой. Посредством обработки уравнения давление можно рассчитать следующим образом:
Давление (P) = Работа / Объем
Определение давления
Давление — это сила, приложенная к объекту, перпендикулярная поверхности объекта и равномерно распределенная по этой площади.2). Давление также измеряется в атмосферах (атм), что является давлением атмосферы Земли на уровне моря.
Как рассчитать давление
В физике давление известно как сила на единицу площади. В результате уравнение для силы может быть записано так, как показано выше. То есть P = F/A. Давайте взглянем на реальный физический пример того, как можно рассчитать давление, приложенное к объекту.
 В этом примере мы рассмотрим круглую пластину, на всю поверхность которой действует сила в равной степени со стороны жидкости, находящейся под сжатием.2
В этом примере мы рассмотрим круглую пластину, на всю поверхность которой действует сила в равной степени со стороны жидкости, находящейся под сжатием.2 - Наконец, проанализируйте свои результаты и посмотрите, совпадают ли они с ожидаемыми результатами.
Часто задаваемые вопросы
Что такое давление?
Давление — это мера силы на единицу площади.
Давление | Encyclopedia.com
ПОНЯТИЕ
Давление – это отношение силы к площади поверхности, на которую она воздействует. Хотя твердые тела оказывают давление, самые интересные примеры давления связаны с жидкостями, то есть газами и жидкостями, и в частности с водой и воздухом.Давление играет ряд важных ролей в повседневной жизни, в том числе его роль в работе насосов и гидравлических прессов. Поддержание обычного атмосферного давления имеет важное значение для здоровья и благополучия человека: тело идеально приспособлено к обычному атмосферному давлению, и если это давление значительно изменится, у человека могут возникнуть вредные или даже фатальные побочные эффекты.
КАК ЭТО РАБОТАЕТ
Сила и площадь поверхности
Когда сила приложена перпендикулярно площади поверхности, она оказывает давление на эту поверхность, равное отношению F к A, , где F — сила и A площадь поверхности.Следовательно, формула для давления ( p ) такова: p = F / A. Одним интересным следствием этого отношения является тот факт, что давление может увеличиваться или уменьшаться без какого-либо изменения силы, другими словами, если поверхность становится меньше, давление становится больше, и наоборот.
Если бы одна чирлидерша держала на плечах другую чирлидершу, а девушка сверху стояла бы на лопатках девушки снизу, то ноги верхней девушки оказывали бы определенное давление на плечи нижней девушки.Это давление будет равно весу верхней девушки ( F, , что в данном случае является ее массой, умноженной на нисходящее ускорение под действием силы тяжести), деленному на площадь поверхности ее ступней. Предположим, что верхняя девушка выполняет сложное акробатическое движение, поднимая левую ногу и упираясь в правое колено, так что только ее правая нога оказывает всю силу своего веса. Теперь площадь поверхности, на которую действует сила, уменьшилась вдвое, и, таким образом, давление на нижнее плечо девушки увеличилось в два раза.
Предположим, что верхняя девушка выполняет сложное акробатическое движение, поднимая левую ногу и упираясь в правое колено, так что только ее правая нога оказывает всю силу своего веса. Теперь площадь поверхности, на которую действует сила, уменьшилась вдвое, и, таким образом, давление на нижнее плечо девушки увеличилось в два раза.
По той же причине, а именно по той причине, что уменьшение площади поверхности увеличивает чистое давление, хорошо поставленный удар карате намного эффективнее, чем шлепок открытой ладонью. Если бы кто-то ударил ладонью прямо по доске, единственным вероятным результатом была бы сильная жалящая боль в руке. Но если вместо этого нанести удар по доске, держа руку перпендикулярно — при условии, конечно, что вы являетесь знатоком карате, — доска может расколоться надвое. В первом случае площадь приложения силы велика, а чистое давление на доску относительно невелико, тогда как в случае удара карате площадь поверхности намного меньше, а, следовательно, давление намного больше.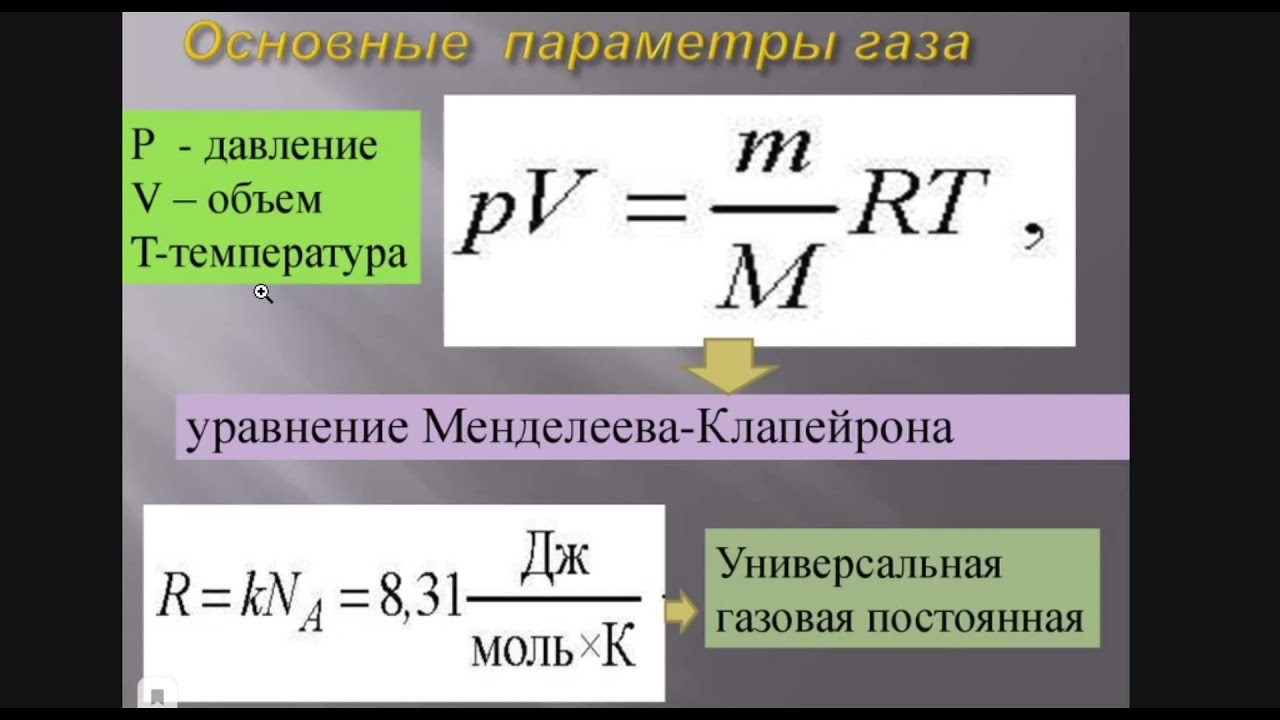
Иногда предпочтительна большая площадь поверхности. Таким образом, снегоступы гораздо эффективнее для ходьбы по снегу, чем обычные туфли или ботинки. Обычная обувь ненамного больше поверхности стопы и идеально подходит для ходьбы по тротуару или траве. Но при глубоком снегу эта относительно небольшая площадь поверхности увеличивает давление на снег и заставляет ноги тонуть. Снегоступы, поскольку их площадь поверхности значительно больше, чем у обычной обуви, уменьшают отношение силы к площади поверхности и, следовательно, снижают чистое давление.
Тот же принцип применим к зимним лыжам и водным лыжам. Как и снегоступы, лыжи позволяют лыжнику оставаться на поверхности.
снегу, но, в отличие от снегоступов, лыжи длинные и тонкие, что позволяет лыжнику более эффективно скользить по заснеженному склону. Что касается катания на воде, то люди, имеющие опыт в этом виде спорта, могут кататься босиком, но это сложно. Большинству новичков требуются водные лыжи, которые еще раз уменьшают чистое давление, оказываемое весом лыжника на поверхность воды.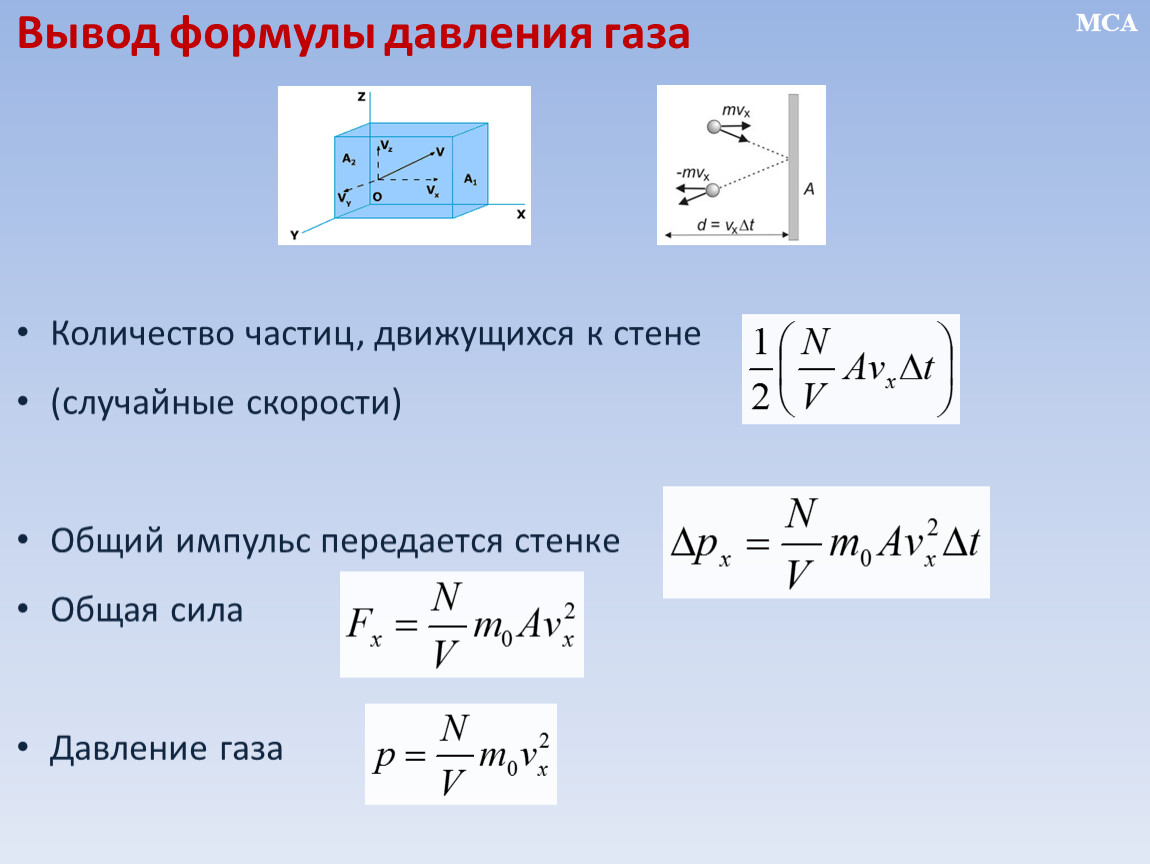
Измерение давления
Давление измеряется рядом единиц в английской и метрической, или, как это называется в научном сообществе, системе СИ. Поскольку p = F / A , все единицы давления представляют собой некоторое отношение силы к площади поверхности. Основная единица СИ называется паскаль (Па) или 1 Н/м 2 . Ньютон (Н), единица силы в СИ, равен силе, необходимой для ускорения 1 килограмма массы со скоростью 1 метр в секунду в квадрате.Таким образом, Паскаль равен давлению в 1 ньютон на поверхности площадью 1 квадратный метр.
В английской или британской системе давление измеряется в фунтах на квадратный дюйм, сокращенно lbs./in 2 . Это равно 6,89 · 10 3 Па, или 6890 Па. Ученые — даже в США, где преобладает британская система единиц, — предпочитают пользоваться единицами СИ. Однако британская единица давления является знакомой частью повседневной жизни американского водителя, потому что давление в шинах в Соединенных Штатах обычно измеряется в фунтах на квадратный дюйм.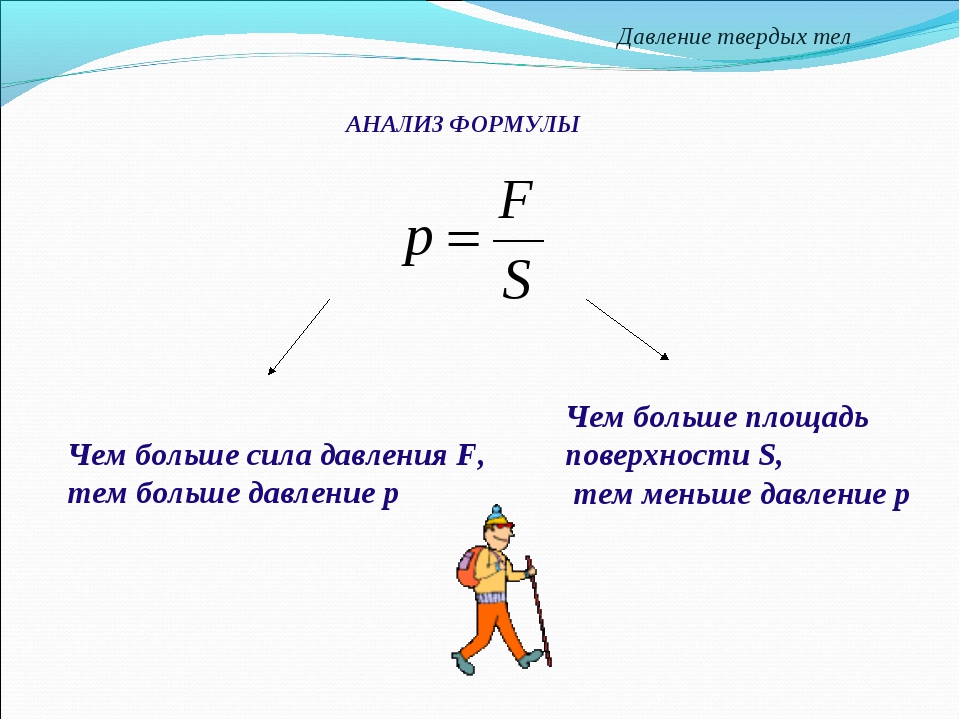 (Рекомендуемое давление в шинах для автомобилей среднего размера обычно составляет 30–35 фунтов/дюйм 2 .)
(Рекомендуемое давление в шинах для автомобилей среднего размера обычно составляет 30–35 фунтов/дюйм 2 .)
Другой важной мерой давления является атмосфера (атм), представляющая собой среднее давление воздуха на уровне моря. В английских единицах это равно 14,7 фунта/дюйм 2 , а в единицах СИ 1,013 · 10 5 Па, т. е. 101 300 Па. В системе СИ есть еще две специализированные единицы измерения давления. : бар, равный 10 5 Па, и торр, равный 133 Па.Метеорологи, ученые, изучающие погодные условия, используют миллибар (мб), который, как следует из его названия, равен 0,001 бар. На уровне моря атмосферное давление составляет примерно 1013 мб.
БАРОМЕТР.
Торр, ранее известный как «миллиметр ртутного столба», равен давлению, необходимому для поднятия столба ртути (химический символ ртутного столба) на 1 мм. Он назван в честь итальянского физика Эванджелисты Торричелли (1608-1647), который изобрел барометр, прибор для измерения атмосферного давления.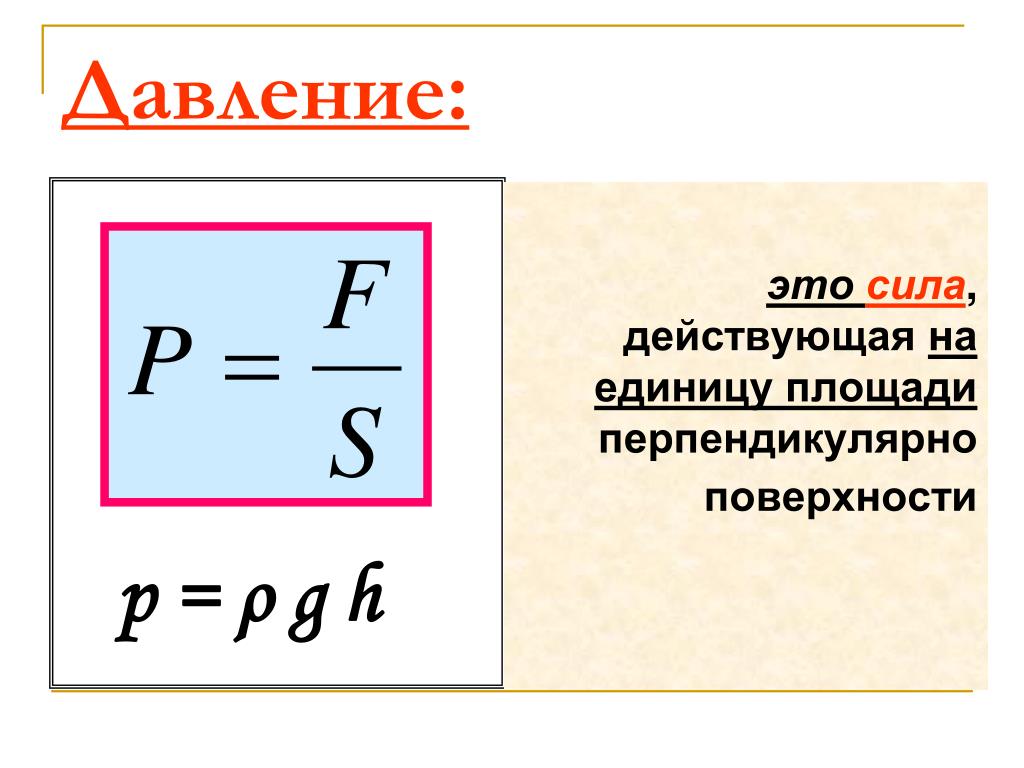
Барометр, сконструированный Торричелли в 1643 году, состоял из длинной стеклянной трубки, наполненной ртутью. Трубка была открыта с одного конца и перевернута вверх дном в чашу, содержащую больше ртути: следовательно, открытый конец был погружен в ртуть, а закрытый конец наверху представлял собой вакуум, т. е. область, в которой давление значительно ниже 1 атм.
Давление окружающего воздуха давило на поверхность ртути в чаше, а вакуум в верхней части трубки создавал область практически без давления, в которую могла подниматься ртуть.Таким образом, высота, на которую поднималась ртуть в стеклянной трубке, представляла собой нормальное давление воздуха (т. е. 1 атм.). Торричелли обнаружил, что при нормальном атмосферном давлении столбик ртути поднимается до 760 миллиметров.
Таким образом, значение 1 атм было установлено равным давлению, оказываемому на столбик ртути высотой 760 мм при температуре 0°C (32°F). Более того, изобретение Торричелли со временем стало неотъемлемой частью обеих научных лабораторий.
и домохозяйств. Поскольку изменения атмосферного давления влияют на погодные условия, сегодня многие домашние и наружные термометры также включают барометр.
Давление и жидкости
С точки зрения физики и газы, и жидкости называются жидкостями, то есть веществами, которые соответствуют форме своего сосуда. Таким образом, давление воздуха и давление воды являются особыми предметами под более широким заголовком «давление жидкости». Жидкость реагирует на давление совершенно иначе, чем твердое тело. Плотность твердого тела делает его устойчивым к небольшим приложениям давления, но если давление увеличивается, оно испытывает растяжение и, в конечном счете, деформацию.Однако в случае жидкости напряжение заставляет ее течь, а не деформироваться.
Существуют три важные характеристики давления, оказываемого на жидкости контейнером. Во-первых, жидкость в сосуде, не испытывающая внешнего движения, прикладывает силу, перпендикулярную стенкам сосуда. Точно так же стенки контейнера воздействуют на жидкость, и в обоих случаях сила всегда перпендикулярна стенкам.
В каждой из этих трех характеристик предполагается, что емкость конечна: другими словами, жидкости некуда больше деваться.Отсюда второе утверждение: внешнее давление, действующее на жидкость, передается равномерно. Обратите внимание, что предыдущее утверждение было квалифицировано термином «внешнее»: сама жидкость оказывает давление, составляющая силы которого равна ее весу. Следовательно, жидкость на дне имеет гораздо большее давление, чем жидкость наверху, из-за веса жидкости над ней.
В-третьих, давление на любую маленькую поверхность жидкости одинаково, независимо от ориентации этой поверхности. Другими словами, область жидкости, перпендикулярная стенкам контейнера, испытывает такое же давление, как и область, параллельная или расположенная под углом к стенкам.Может показаться, что это противоречит первому принципу, согласно которому сила перпендикулярна стенкам сосуда. На самом деле сила является векторной величиной, что означает, что она имеет как величину, так и направление, тогда как давление является скаляром, что означает, что оно имеет величину, но не имеет определенного направления.
ПРИМЕНЕНИЕ В РЕАЛЬНОЙ ЖИЗНИ
Принцип Паскаля и гидравлический пресс
Три характеристики давления жидкости, описанные выше, имеют ряд следствий и приложений, среди которых так называемый принцип Паскаля.Как и единица давления в системе СИ, принцип Паскаля назван в честь французского математика и физика Блеза Паскаля (1623–1662), сформулировавшего второе из трех утверждений: внешнее давление, приложенное к жидкости, передается равномерно по всему объему тела. эта жидкость. Принцип Паскаля лег в основу одной из важнейших когда-либо разработанных машин — гидравлического пресса.
Простой гидравлический пресс, используемый для подъема автомобиля в автомастерской, обычно состоит из двух больших цилиндров, расположенных рядом.Каждый цилиндр содержит поршень, и цилиндры соединены в нижней части каналом, содержащим жидкость. Клапаны регулируют поток между двумя цилиндрами. Когда кто-то прикладывает усилие, нажимая на поршень в одном цилиндре (входном цилиндре), это дает равномерное давление, которое вызывает выход в
второй цилиндр, толкая вверх поршень, который поднимает автомобиль.
В соответствии с принципом Паскаля давление во всем гидравлическом прессе одинаково и всегда будет равно отношению силы к давлению.Пока это соотношение одинаково, значения F и A могут различаться. В случае автомобильного домкрата входной цилиндр имеет относительно небольшую площадь поверхности, и, следовательно, сила, которая должна быть приложена, также относительно невелика. Выходной цилиндр имеет относительно большую площадь поверхности и, следовательно, прилагает относительно большую силу для подъема автомобиля. Это, в сочетании с разницей в высоте между двумя цилиндрами (обсуждаемой в контексте механических преимуществ в другом месте этой книги), позволяет поднимать тяжелый автомобиль с относительно небольшим усилием.
ГИДРАВЛИЧЕСКИЙ ТАРАНТ.
Автомобильный домкрат представляет собой простую модель гидравлического пресса в действии, но на самом деле принцип Паскаля имеет гораздо больше применений. Среди них гидравлический цилиндр, используемый в различных машинах, от бульдозеров до гидравлических подъемников, используемых пожарными и коммунальными службами для подъема на высоту.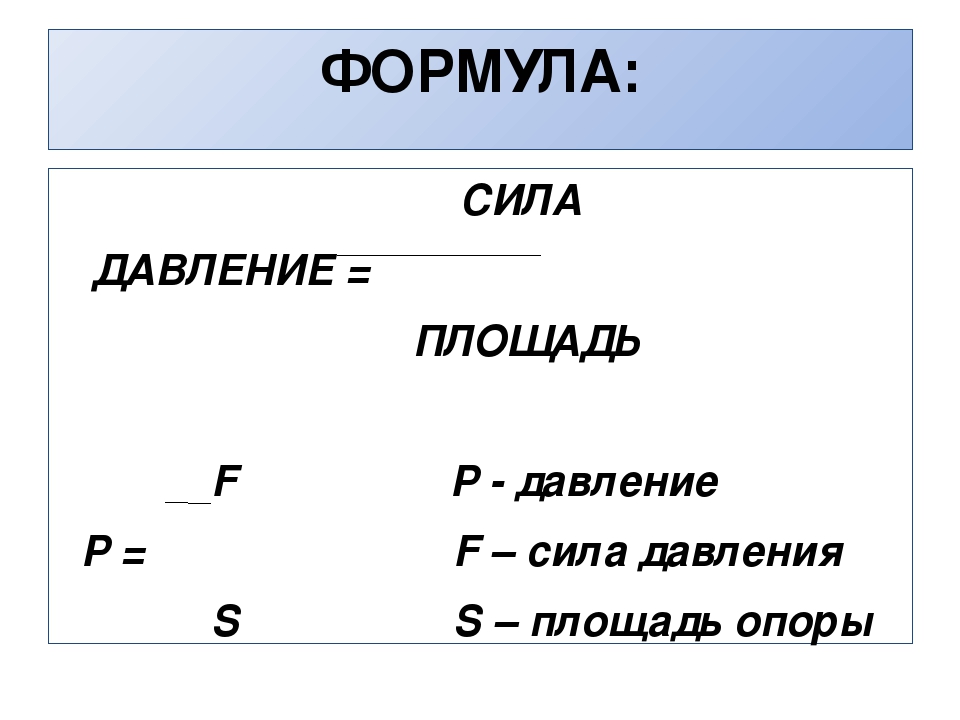 Однако в гидроцилиндре характеристики входного и выходного цилиндров противоположны характеристикам автомобильного домкрата.
Однако в гидроцилиндре характеристики входного и выходного цилиндров противоположны характеристикам автомобильного домкрата.
Входной цилиндр, называемый главным цилиндром, имеет большую площадь поверхности, тогда как выходной цилиндр (называемый рабочим цилиндром) имеет небольшую площадь поверхности.Кроме того, хотя опять же, это фактор, связанный с механическим преимуществом, а не с давлением как таковым, главный цилиндр короткий, а рабочий цилиндр высокий. Из-за большей площади поверхности главного цилиндра по сравнению с рабочим цилиндром гидроцилиндр не считается эффективным с точки зрения механического преимущества: другими словами, входная сила намного больше, чем выходная сила.
Тем не менее, гидроцилиндр так же хорошо подходит для своей цели, как автомобильный домкрат.В то время как домкрат предназначен для подъема тяжелого автомобиля на короткое расстояние по вертикали, гидравлический цилиндр перемещает гораздо более легкий груз (обычно всего одного человека) на гораздо большее расстояние по вертикали — например, на вершину дерева или здания.
Использование разницы давлений
НАСОСЫ.
В насосе используется принцип Паскаля, но вместо того, чтобы удерживать жидкость в одном контейнере, насос позволяет жидкости вытекать. В частности, насос использует разницу давлений, заставляя жидкость перемещаться из области более высокого давления в область более низкого давления.Очень простым примером этого является сифонный шланг, используемый для забора бензина из бензобака автомобиля. Всасывание на одном конце шланга создает область низкого давления по сравнению с областью относительно высокого давления бензобака. В конце концов, бензин выйдет из конца шланга низкого давления. (И если повезет, человек, перекачивающий воду, сможет это предвидеть, чтобы не получить полный рот бензина!)
Поршневой насос, более сложный, но все же довольно простой, состоит из вертикального цилиндра, вдоль которого расположен поршень. поднимается и опускается.Рядом с дном цилиндра расположены два клапана: впускной клапан, через который жидкость поступает в цилиндр, и выпускной клапан, через который жидкость вытекает из него.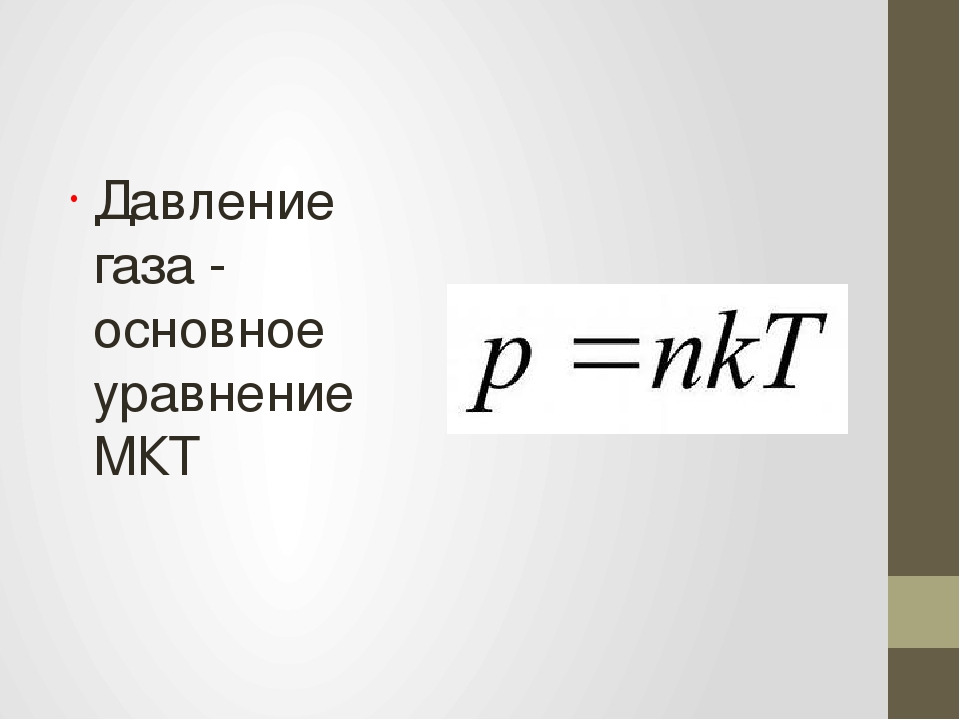 На такте всасывания, когда поршень движется вверх, впускной клапан открывается и позволяет жидкости поступать в цилиндр. При ходе вниз впускной клапан закрывается, а выпускной клапан открывается, и давление, создаваемое поршнем на жидкость, выталкивает ее через выпускной клапан.
На такте всасывания, когда поршень движется вверх, впускной клапан открывается и позволяет жидкости поступать в цилиндр. При ходе вниз впускной клапан закрывается, а выпускной клапан открывается, и давление, создаваемое поршнем на жидкость, выталкивает ее через выпускной клапан.
Одним из наиболее очевидных применений поршневого насоса является двигатель автомобиля.В этом случае, конечно, перекачиваемой жидкостью является бензин, который толкает поршни, обеспечивая серию контролируемых взрывов, создаваемых воспламенением газа от свечи зажигания. В другой разновидности поршневых насосов, используемых для накачивания баскетбольных мячей или велосипедных шин, перекачиваемой жидкостью является воздух. Затем есть насос для воды, который качает питьевую воду из-под земли. Его также можно использовать для удаления желаемой воды из места, где она является помехой, например, со дна лодки.
ПРИНЦИП БЕРНУЛЛИ.
Хотя Паскаль дал ценные сведения об использовании давления для выполнения работы, мыслителем, первым сформулировавшим общие принципы взаимосвязи между жидкостями и давлением, был швейцарский математик и физик Даниэль Бернулли (1700–1782). Бернулли считается отцом гидромеханики, изучения поведения газов и жидкостей в состоянии покоя и в движении.
Бернулли считается отцом гидромеханики, изучения поведения газов и жидкостей в состоянии покоя и в движении.
Проводя эксперименты с жидкостями, Бернулли заметил, что при уменьшении диаметра трубы вода течет быстрее.Это навело его на мысль, что какая-то сила должна действовать
на воду сила, как он рассуждал, должна возникать из-за разности давлений. В частности, более медленно движущаяся жидкость в более широкой части трубы имеет большее давление, чем часть жидкости, движущейся через более узкую часть трубы. В результате он пришел к выводу, что давление и скорость обратно пропорциональны, другими словами, при увеличении одного уменьшается другое.
Отсюда он сформулировал принцип Бернулли, который гласит, что при всех изменениях движения сумма статического и динамического давления в жидкости остается неизменной.Жидкость в состоянии покоя оказывает статическое давление, которое обычно подразумевается под «давлением», как и под «давлением воды». Однако когда жидкость начинает двигаться, часть статического давления, пропорциональная скорости жидкости, преобразуется в так называемое динамическое давление или давление движения. В цилиндрической трубе статическое давление действует перпендикулярно поверхности сосуда, а динамическое давление параллельно ей.
В цилиндрической трубе статическое давление действует перпендикулярно поверхности сосуда, а динамическое давление параллельно ей.
Согласно принципу Бернулли, чем больше скорость потока в жидкости, тем больше динамическое давление и меньше статическое давление: другими словами, более медленно движущаяся жидкость оказывает большее давление, чем более быстро движущаяся.Открытие этого принципа в конечном итоге сделало возможным создание самолета.
При движении жидкости из более широкой трубы в более узкую объем этой жидкости, перемещающейся на заданное расстояние за заданный период времени, не изменяется. Но поскольку ширина более узкой трубы меньше, жидкость должна двигаться быстрее (то есть с большим динамическим давлением), чтобы переместить то же количество жидкости на то же расстояние за то же время. Один из способов проиллюстрировать это — понаблюдать за поведением реки: в широкой, свободной области она течет медленно, но если ее поток сужается стенами каньона, то она резко ускоряется.
Принцип Бернулли в конечном итоге стал основой аэродинамического профиля, конструкции крыла самолета, если смотреть с торца. Аэродинамический профиль имеет форму асимметричной капли, лежащей на боку, «толстым» концом к воздушному потоку. Когда воздух попадает на переднюю часть аэродинамического профиля, воздушный поток разделяется, часть его проходит над крылом, а часть проходит под ним. Однако верхняя поверхность аэродинамического профиля изогнута, тогда как нижняя поверхность намного прямее.
В результате воздуху, протекающему сверху, приходится преодолевать большее расстояние, чем воздуху, протекающему под крылом.Поскольку жидкости имеют тенденцию компенсировать все объекты, с которыми они вступают в контакт, воздух вверху будет течь быстрее, чтобы встретиться с воздухом внизу в задней части крыла. Более быстрый поток воздуха, как продемонстрировал Бернулли, указывает на более низкое давление, а это означает, что давление на нижнюю часть крыла удерживает самолет в воздухе.
Плавучесть и давление
За сто двадцать лет до первого успешного полета на самолете братьев Райт в 1903 году другая пара братьев — французские гольфисты — разработали еще одно средство полета.Это был воздушный шар, который опирался на совершенно другой принцип отрыва от земли: плавучесть или стремление объекта, погруженного в жидкость, всплывать. Однако, как и в случае с принципом Бернулли, понятие плавучести связано с давлением.
В третьем веке до нашей эры греческий математик, физик и изобретатель Архимед (ок. 287–212 до н. э.) открыл так называемый принцип Архимеда, согласно которому выталкивающая сила объекта, погруженного в жидкость, равна вес жидкости, вытесненной телом.Вот почему корабли плавают: потому что их выталкивающая, или подъемная, сила меньше, чем равна весу вытесняемой ими воды.
Корпус корабля предназначен для вытеснения или перемещения количества воды, вес которого превышает вес самого судна. Вес вытесненной воды, то есть ее масса, умноженная на нисходящее ускорение, вызванное силой тяжести, равна выталкивающей силе, действующей на корабль со стороны океана. Если корабль весит меньше, чем вытесняемая им вода, он будет плавать; но если он будет весить больше, он утонет.
Если корабль весит меньше, чем вытесняемая им вода, он будет плавать; но если он будет весить больше, он утонет.
Факторы, связанные с принципом Архимеда, зависят от плотности, гравитации и глубины, а не от давления. Однако чем больше глубина внутри жидкости, тем больше давление, которое давит на объект, погруженный в жидкость. Кроме того, общее давление на заданной глубине в жидкости частично связано как с плотностью, так и с силой тяжести, составляющими выталкивающей силы.
ДАВЛЕНИЕ И ГЛУБИНА.
Давление, которое жидкость оказывает на дно сосуда, равно dgh, , где d — плотность, g — ускорение свободного падения и h — глубина сосуда.Для любой порции жидкости ч равно ее глубине внутри контейнера, а это означает, что
чем глубже человек идет, тем больше давление. Кроме того, полное давление внутри жидкости равно dgh + p внешнее, , где p внешнее — давление, оказываемое на поверхность жидкости. В поршне-цилиндровом узле это давление исходит от поршня, а в воде — из атмосферы.
В поршне-цилиндровом узле это давление исходит от поршня, а в воде — из атмосферы.
В этом контексте океан можно рассматривать как своего рода «контейнер».На ее поверхность воздух оказывает направленное вниз давление, равное 1 атм. Плотность самой воды однородна, как и ускорение вниз под действием силы тяжести; тогда единственной переменной является ч, или расстояние под поверхностью. … В самых глубоких частях океана давление невероятно велико — намного больше, чем может выдержать любой человек. Это огромное давление толкает вверх, сопротивляясь нисходящему давлению объектов на его поверхности. В то же время, если лодка вес правильно распределяется вдоль его корпуса, корабль увеличивает площадь и минимизирует силу, тем самым оказывая нисходящее давление на поверхность воды, которое меньше, чем восходящее давление самой воды.Следовательно, он плавает.
Давление и тело человека
ДАВЛЕНИЕ ВОЗДУХА.
Монгольфы использовали принцип плавучести не для того, чтобы плыть по воде, а для того, чтобы парить в небе на корабле легче воздуха. Подробности этого достижения обсуждаются в другом месте в контексте плавучести; но тема полета легче воздуха предполагает еще одну концепцию, которая несколько раз упоминалась в этом эссе: атмосферное давление.
Подробности этого достижения обсуждаются в другом месте в контексте плавучести; но тема полета легче воздуха предполагает еще одну концепцию, которая несколько раз упоминалась в этом эссе: атмосферное давление.
Точно так же, как давление воды самое большое на дне океана, давление воздуха самое большое на поверхности Земли, которая фактически находится на дне «океана» воздуха.И давление воздуха, и давление воды являются примерами гидростатического давления — давления, которое существует в любом месте тела жидкости из-за веса жидкости над ним. В случае атмосферного давления воздух тянется вниз силой земного притяжения, а воздух вдоль поверхности испытывает большее давление из-за веса (функция силы тяжести) воздуха над ним. Однако на больших высотах над поверхностью Земли сила гравитации уменьшается, и, следовательно, атмосферное давление намного меньше.
При обычном опыте тело человека подвергается внушительному давлению.Учитывая значение атмосферного давления, обсуждавшееся ранее, если вытянуть руку — предполагая, что поверхность составляет около 20 дюймов 90 771 2 90 710 (0,129 м 90 771 2 90 710 ) — сила воздуха, действующая на нее, составляет почти 300 фунтов (136 кг).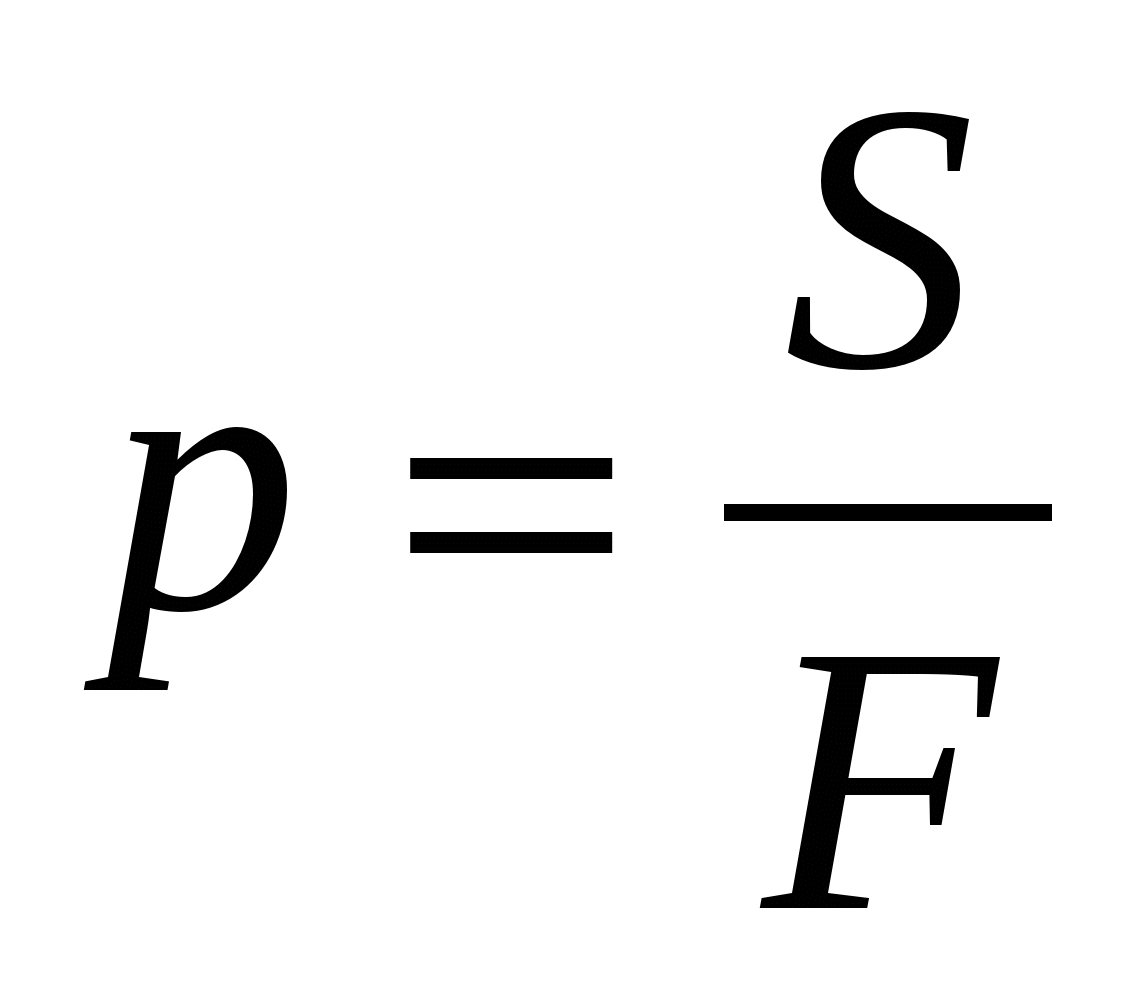 )! Как же это
)! Как же это
руку не раздавит весь этот вес? Причина в том, что само человеческое тело находится под давлением, и что внутренняя часть тела оказывает давление, равное давлению воздуха.
РЕАКЦИЯ НА ИЗМЕНЕНИЯ ДАВЛЕНИЯ ВОЗДУХА.
Человеческое тело приспособлено к нормальному атмосферному давлению в 1 атм, и если это внешнее давление изменяется, в организме происходят изменения, которые могут быть вредными или даже фатальными.Незначительным примером этого является «хлопанье» в ушах, которое происходит, когда кто-то едет через горы или едет в самолете. С изменением высоты меняется давление, и, следовательно, давление в ушах также меняется.
Как отмечалось ранее, на больших высотах атмосферное давление снижается, что затрудняет дыхание. Поскольку воздух — это газ, его молекулы имеют тенденцию не притягиваться: другими словами, когда давление низкое, они стремятся удалиться друг от друга, и в результате человеку, находящемуся на большой высоте, трудно достичь цели. достаточное количество воздуха в его легкие.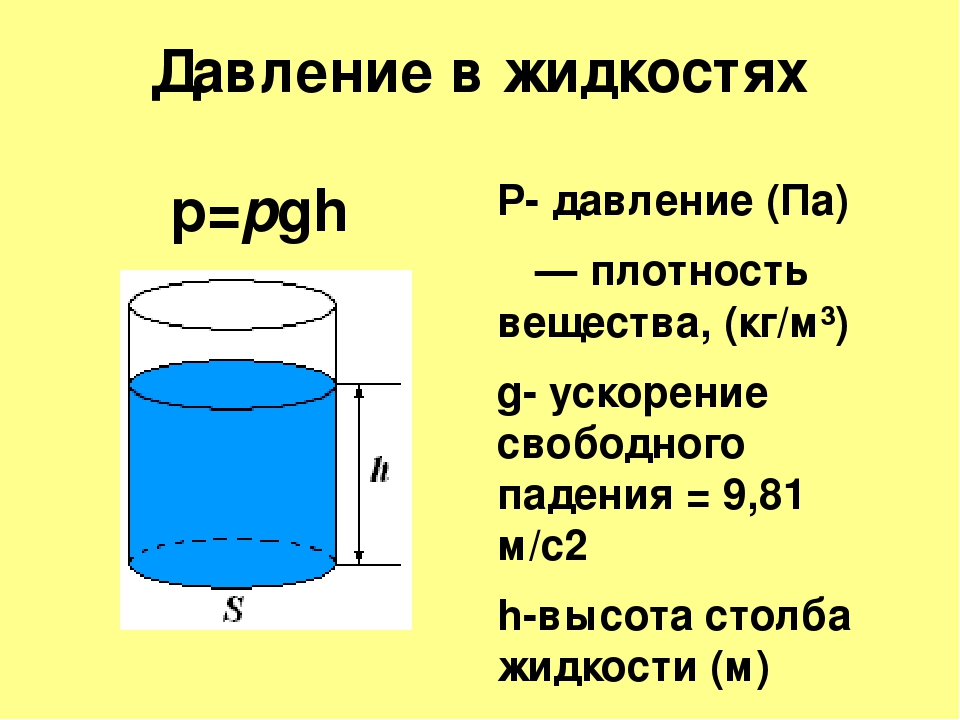 Бегуны, участвовавшие в Олимпийских играх 1968 года в Мехико, городе в горах, должны были тренироваться в высокогорных условиях, чтобы они могли дышать во время соревнований. Для бейсбольных команд, соревнующихся в Денвере, штат Колорадо (известном как «Город на высоте мили»), этот недостаток дыхания компенсируется тем фактом, что пониженное давление и сопротивление позволяют бейсбольному мячу легче двигаться по воздуху.
Бегуны, участвовавшие в Олимпийских играх 1968 года в Мехико, городе в горах, должны были тренироваться в высокогорных условиях, чтобы они могли дышать во время соревнований. Для бейсбольных команд, соревнующихся в Денвере, штат Колорадо (известном как «Город на высоте мили»), этот недостаток дыхания компенсируется тем фактом, что пониженное давление и сопротивление позволяют бейсбольному мячу легче двигаться по воздуху.
Если человек вырос в такой высокогорной среде, конечно, он привыкает дышать в условиях низкого атмосферного давления.В перуанских Андах, например, люди всю жизнь проводят на высоте, более чем в два раза превышающей денверскую, но человеку из низкогорной местности следует посещать такие места только после принятия мер предосторожности. На очень больших высотах, конечно, человек не может дышать: поэтому кабины самолетов герметизированы. Большинство самолетов оснащены кислородными масками, которые падают с потолка, если внутри салона происходит перепад давления. Без этих масок все в салоне погибли бы.
КРОВЯНОЕ ДАВЛЕНИЕ.
Другим аспектом давления и человеческого организма является кровяное давление. Точно так же, как идеальное зрение 20/20, врачи рекомендуют целевое кровяное давление «120 на 80» — но что это значит? Когда у человека измеряют артериальное давление, на плечо на уровне сердца наматывают надувную манжету. В то же время стетоскоп помещают вдоль артерии в нижней части руки для контроля звука кровотока. Манжета надувается, чтобы остановить кровоток, затем давление
высвобождается до тех пор, пока кровь снова не начнет течь, производя булькающий звук в стетоскопе.
Давление, необходимое для остановки кровотока, известно как систолическое давление, которое равно максимальному давлению, создаваемому сердцем. После того, как давление на манжету уменьшается до тех пор, пока кровь не начнет нормально течь, что отражается в прекращении булькающего звука в стетоскопе, снова измеряется давление в артерии. Это диастолическое давление, или давление, существующее в артерии между ударами сердца. Для здорового человека систолическое давление должно быть 120 торр, а диастолическое давление 80 торр.
Для здорового человека систолическое давление должно быть 120 торр, а диастолическое давление 80 торр.
ГДЕ УЗНАТЬ БОЛЬШЕ
«Атмосферное давление: сила, действующая под действием веса воздуха» (веб-сайт).
Бейсер, Артур. Физика, 5-е изд. Чтение, Массачусетс: Addison-Wesley, 1991.
«Кровяное давление» (веб-сайт).
Кларк, Джон Оуэн Эдвард. Атмосфера. Нью-Йорк: Gloucester Press, 1992.
Кобб, Аллан Б. Супернаучные проекты об океанах. New York: Rosen, 2000.
«Физика подводного плавания: урок давления» (веб-сайт).
Провензо, Юджин Ф. и Астери Бейкер Провензо. 47 простых классических экспериментов. Иллюстрации Питера А. Зорна-младшего. Нью-Йорк: Dover Publications, 1989.
Нью-Йорк: Dover Publications, 1989.
«Понимание атмосферного давления» USA Today (веб-сайт).
Зубровски, Берни. Воздушные шары: изготовление и эксперименты с надувными игрушками. Иллюстрировано Роем Доти. New York: Morrow Junior Books, 1990.
КЛЮЧЕВЫЕ ТЕРМИНЫ
АТМОСФЕРА:
Мера давления, обозначаемая аббревиатурой «атм» и равная среднему давлению воздуха на уровне моря. В английских единицах это равно 14,7 фунтов на квадратный дюйм, а в единицах СИ — 101 300 паскалей.
БАРОМЕТР:
Форма прибора для измерения атмосферного давления.
ПЛАВУЧОСТЬ:
Тенденция объекта, погруженного в жидкость, плавать.
ЖИДКОСТЬ:
Любое вещество, будь то газ или жидкость, которое соответствует форме своего сосуда.
МЕХАНИКА ГИДРОИЗОЛЯЦИИ:
Изучение поведения газов и жидкостей в состоянии покоя и в движении.
ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ:
давление, существующее в любом месте тела жидкости из-за веса жидкости над ним.
ПАСКАЛЬ:
Основная СИ или метрическая единица давления, сокращенно «Па» и равная 1 Н/м 2 .
ПРИНЦИП ПАСКАЛЯ:
Утверждение, сформулированное французским математиком и физиком Блезом Паскалем (1623-1662), согласно которому внешнее давление, воздействующее на жидкость, передается равномерно по всему телу этой жидкости.
ДАВЛЕНИЕ:
Отношение силы к площади поверхности, когда сила приложена в направлении, перпендикулярном этой поверхности.Формула давления ( p ) выглядит следующим образом: p = F / A , где F — сила, а A — площадь поверхности.
Дока Брауна Часть 2 Еще Более продвинутые идеи с участием Основы теории частиц и свойства газов, Субиндекс для части 2: Другие расчеты см. И молярный объем газа Максвелл Дока Брауна 4.Поведение идеального газа и Введение в модель кинетических частиц идеального газа
В прошлом было проведено множество измерений. Однако до этого, если посмотреть на эти Поэтому так же, как и установленный К = или С + 273 Некоторые примеры приведены ниже, а
Некоторые известные температуры указаны ниже
Немного странно говорить, что у твоего тела есть НАЧАЛО СТРАНИЦЫ 5.
Подробнее о расчетах давления и объема газа 4а. Закон Бойля для объема и газа
НАЧАЛО СТРАНИЦЫ Расчеты 4б. Закон Шарля/Закон Гей-Люссака для давления/объема и и комбинированный
Комбинированный газовый закон
НАЧАЛО СТРАНИЦЫ ДРУГИЕ ПОЛЕЗНЫЕ СТРАНИЦЫ Передовой См. также расчеты газа Моли и молярный объем газа, закон Авогадро Объем реагирующего газа Все остальные расчетные страницы
|








 (2 5 мин)
(2 5 мин) Тогда изменение скорости каждой молекулы при ударе равно –2υ.
Тогда изменение скорости каждой молекулы при ударе равно –2υ. {13}\text{N}[/latex] вес воды в резервуаре. На самом деле это всего лишь 0,0800% веса.
{13}\text{N}[/latex] вес воды в резервуаре. На самом деле это всего лишь 0,0800% веса.
 Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.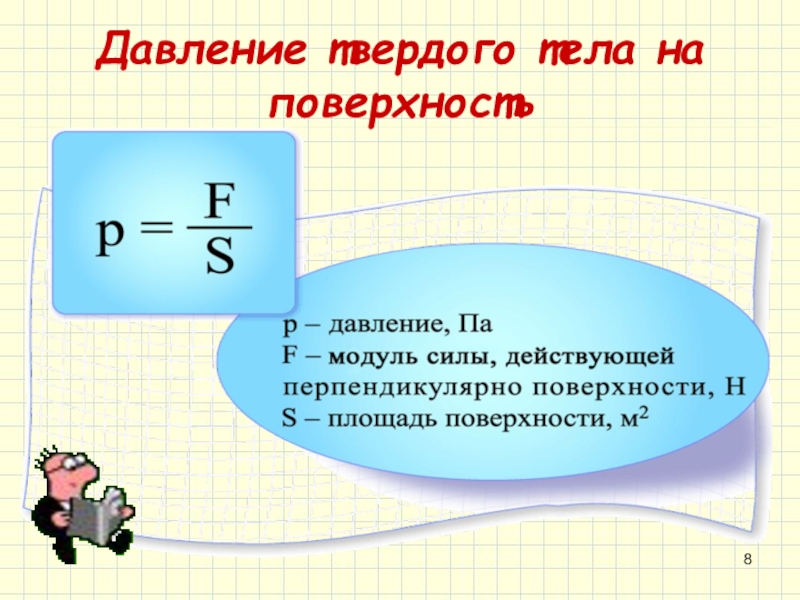 Массу элемента можно записать через плотность жидкости и объем элементов:
Массу элемента можно записать через плотность жидкости и объем элементов: {\ text {−} h} \ rho gdy \ hfill \\ \ hfill p-{p} _ {0} & = \ hfill & \ rho gh \ hfill \\ \ hfill p& =\ hfill & {p}_ {0}+\rho gh.\hfill \end{массив}[/латекс]
{\ text {−} h} \ rho gdy \ hfill \\ \ hfill p-{p} _ {0} & = \ hfill & \ rho gh \ hfill \\ \ hfill p& =\ hfill & {p}_ {0}+\rho gh.\hfill \end{массив}[/латекс]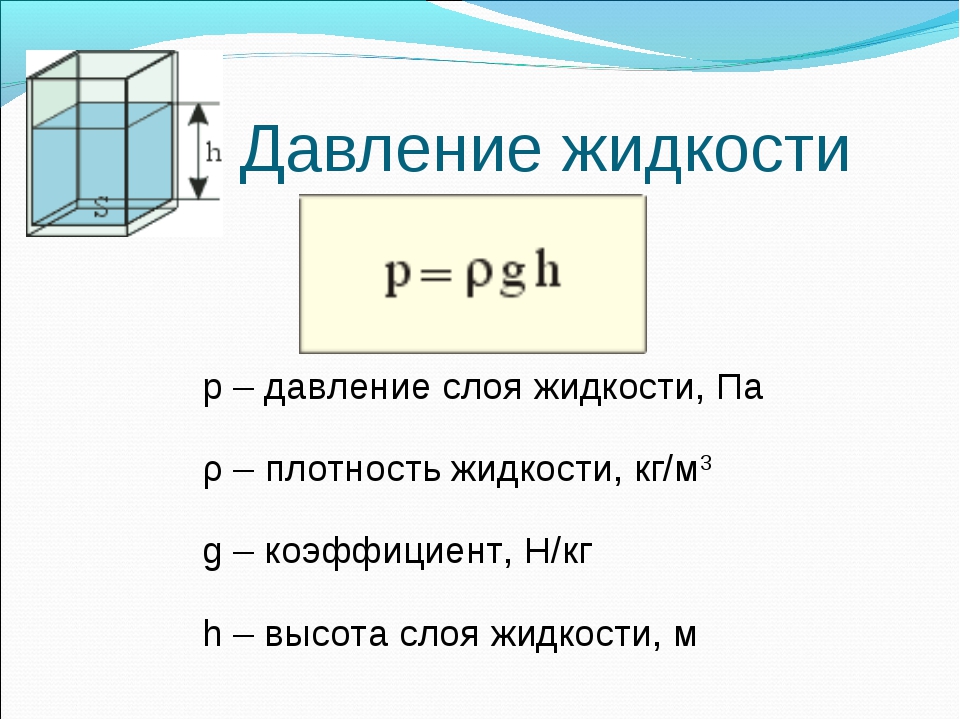 Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна.(Мы обсудим закон идеального газа в следующей главе, но мы предполагаем, что вы знакомы с ним из средней школы и химии.) Пусть p ( y ) будет атмосферным давлением на высоте y . Плотность [латекс]\ро[/латекс] при y , температура T по шкале Кельвина (К) и масса m молекулы воздуха связаны с абсолютным давлением идеального газа закон, по форме
Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна.(Мы обсудим закон идеального газа в следующей главе, но мы предполагаем, что вы знакомы с ним из средней школы и химии.) Пусть p ( y ) будет атмосферным давлением на высоте y . Плотность [латекс]\ро[/латекс] при y , температура T по шкале Кельвина (К) и масса m молекулы воздуха связаны с абсолютным давлением идеального газа закон, по форме Здесь тот же закон записан в другой форме, с использованием плотности [латекс]\ро[/латекс] вместо объема V . Следовательно, если давление p изменяется с высотой, то и плотность [латекс]\ро .[/латекс] Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как
Здесь тот же закон записан в другой форме, с использованием плотности [латекс]\ро[/латекс] вместо объема V . Следовательно, если давление p изменяется с высотой, то и плотность [латекс]\ро .[/латекс] Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как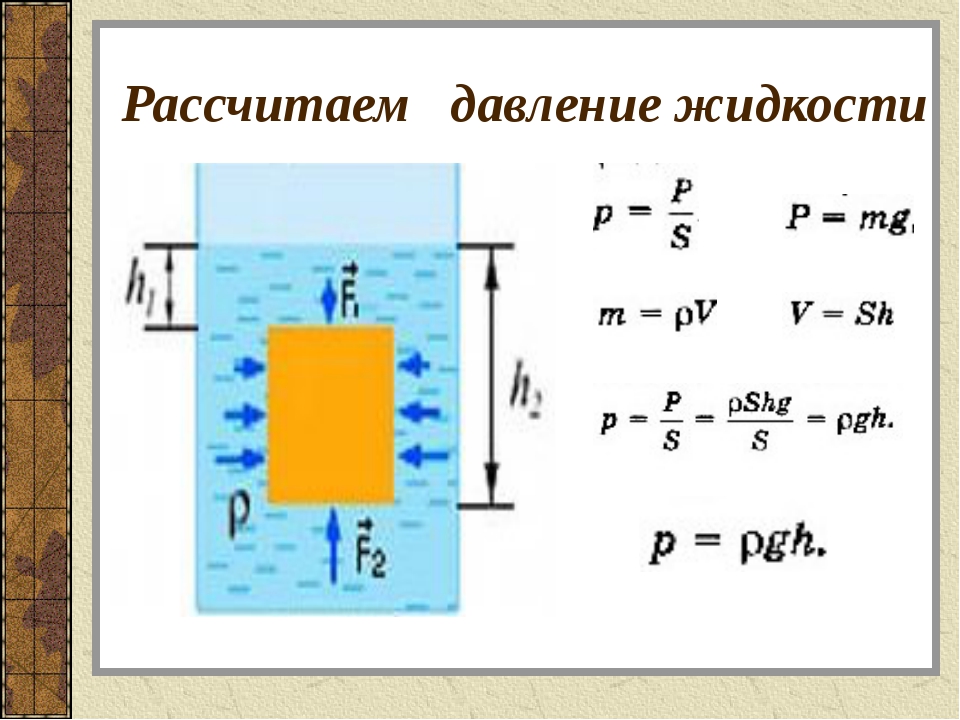
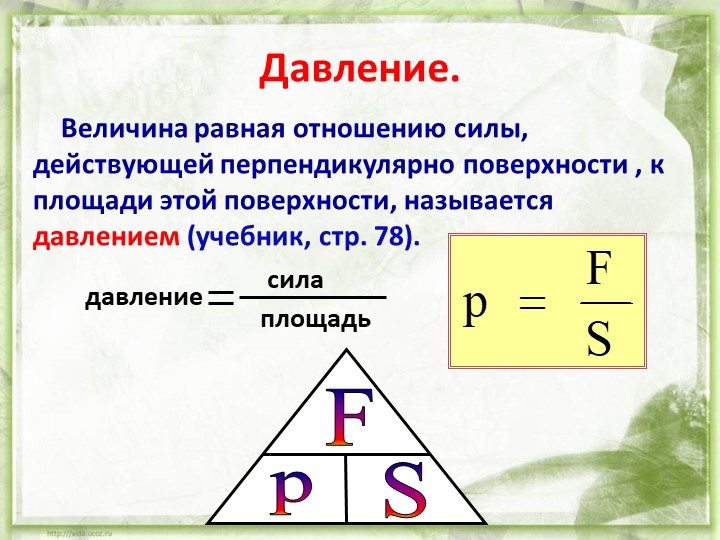 Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке показано давление воздуха на стенки покрышки и воды на тело пловца.
Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке показано давление воздуха на стенки покрышки и воды на тело пловца.
 Итак, мы возьмем трубку, полную ртути, погрузим ее в ванну с ртутью, а затем поднимем трубку вот так, хорошо.
Итак, мы возьмем трубку, полную ртути, погрузим ее в ванну с ртутью, а затем поднимем трубку вот так, хорошо. Теперь у нас есть определение того, что мы подразумеваем под стандартной атмосферой, так что давайте посмотрим сюда.Одна стандартная атмосфера равна 760 торр. Этот торр — это единица, которая должна была быть похожа на миллиметр ртутного столба, но названа в честь физика по имени Торр Чарли, который много работал над давлением в 1600-х годах. Итак, если вы на самом деле посмотрите на то, что на самом деле это в миллиметрах ртутного столба, это 763,3, так что это близко, но не совсем одно и то же. Что ж, для стандартной единицы в Соединенных Штатах люди часто используют фунты PSI на квадратный дюйм. Одна атмосфера в фунтах на квадратный дюйм составляет примерно 14,7 фунтов на квадратный дюйм. Так что это значит?
Теперь у нас есть определение того, что мы подразумеваем под стандартной атмосферой, так что давайте посмотрим сюда.Одна стандартная атмосфера равна 760 торр. Этот торр — это единица, которая должна была быть похожа на миллиметр ртутного столба, но названа в честь физика по имени Торр Чарли, который много работал над давлением в 1600-х годах. Итак, если вы на самом деле посмотрите на то, что на самом деле это в миллиметрах ртутного столба, это 763,3, так что это близко, но не совсем одно и то же. Что ж, для стандартной единицы в Соединенных Штатах люди часто используют фунты PSI на квадратный дюйм. Одна атмосфера в фунтах на квадратный дюйм составляет примерно 14,7 фунтов на квадратный дюйм. Так что это значит?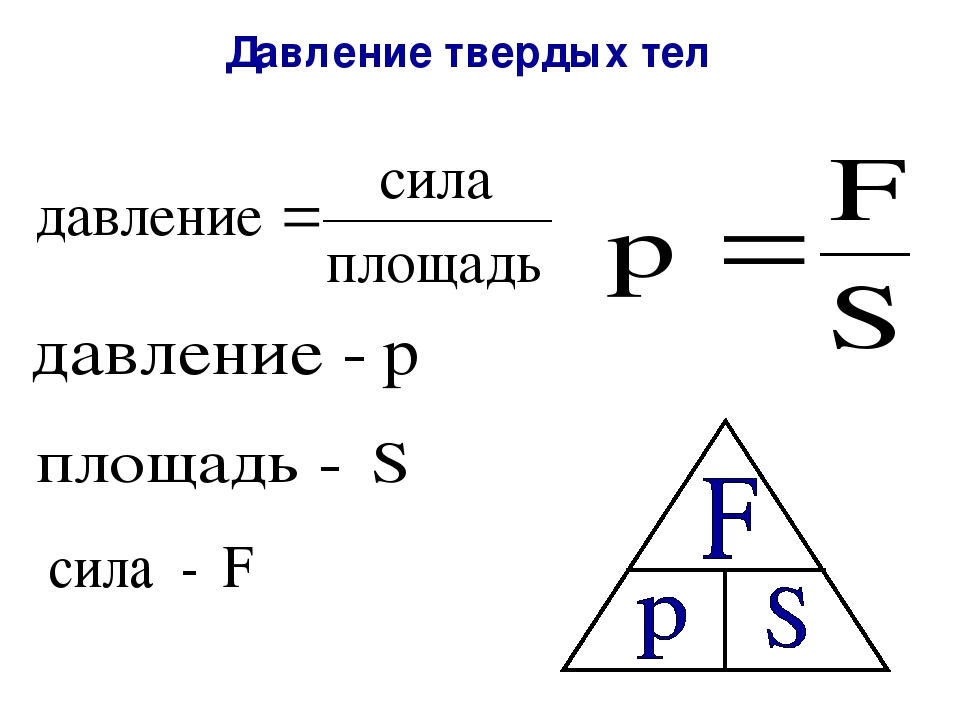 Те же самые идеи используются аквалангистами, которые ныряют глубоко и вдыхают сжатый воздух, так что они получают более высокое давление, и тогда их кожа не должна выдерживать такую большую разницу давлений между водой. океан и их внутренние органы, их легкие и их кровь и все такое.Так или иначе, это просто небольшое примечание.
Те же самые идеи используются аквалангистами, которые ныряют глубоко и вдыхают сжатый воздух, так что они получают более высокое давление, и тогда их кожа не должна выдерживать такую большую разницу давлений между водой. океан и их внутренние органы, их легкие и их кровь и все такое.Так или иначе, это просто небольшое примечание. Итак, теперь у меня есть вопрос к вам, какова максимальная высота воды, которую вы можете поддерживать в соломинке? Итак, если вы будете сосать изо всех сил, насколько высоко может подняться эта колонка? Может ли он стать бесконечно высоким?
Итак, теперь у меня есть вопрос к вам, какова максимальная высота воды, которую вы можете поддерживать в соломинке? Итак, если вы будете сосать изо всех сил, насколько высоко может подняться эта колонка? Может ли он стать бесконечно высоким? Таким образом, h будет равно p атмосферы 101 325 при плотности воды 10 в третьей, g 9,8, и когда вы все это посчитаете, вы обнаружите, что это около 10,34. Какой будет единица? Ну, все в единицах СИ, так что все в единицах СИ, это высота, это метры. Это означает, что максимальная высота столба воды, которую вы можете поддерживать на земле, составляет 10,34 метра.
Таким образом, h будет равно p атмосферы 101 325 при плотности воды 10 в третьей, g 9,8, и когда вы все это посчитаете, вы обнаружите, что это около 10,34. Какой будет единица? Ну, все в единицах СИ, так что все в единицах СИ, это высота, это метры. Это означает, что максимальная высота столба воды, которую вы можете поддерживать на земле, составляет 10,34 метра.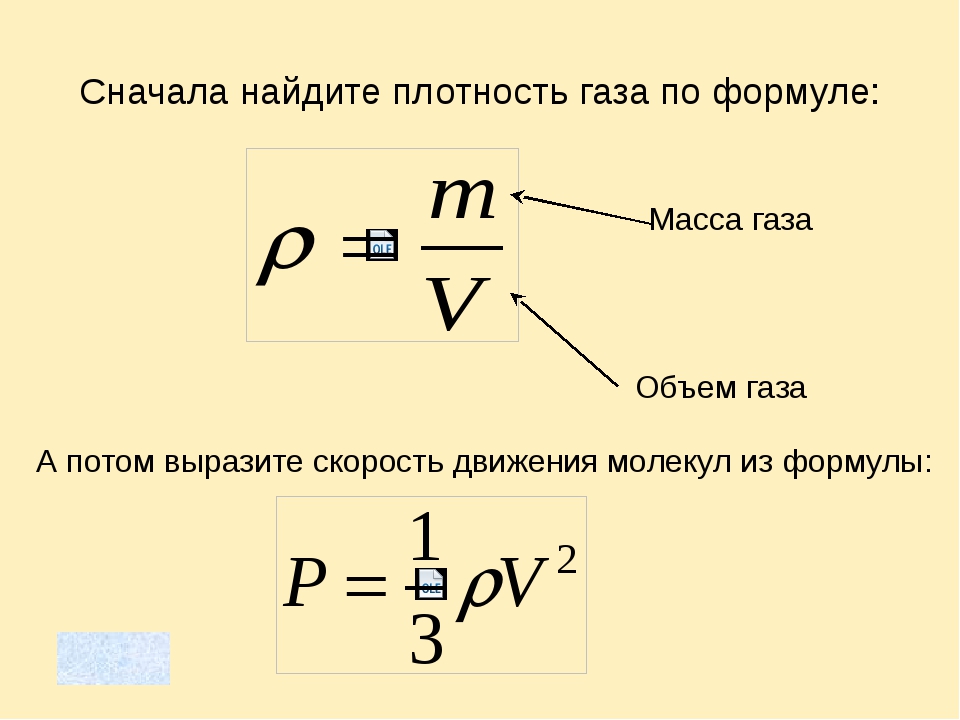 Итак, вопрос, каков общий вес атмосферы? Какой-то странный вопрос, да? Вы смотрите на этот вопрос, и вы как что? Откуда мне это знать? Хорошо, вес атмосферы, помните, мы говорили, что давление, связанное с атмосферой, на самом деле связано с ее весом.Итак, я знаю давление, а как насчет веса? Ну, вес будет, это сила, так что вес будет давлением, умноженным на площадь.
Итак, вопрос, каков общий вес атмосферы? Какой-то странный вопрос, да? Вы смотрите на этот вопрос, и вы как что? Откуда мне это знать? Хорошо, вес атмосферы, помните, мы говорили, что давление, связанное с атмосферой, на самом деле связано с ее весом.Итак, я знаю давление, а как насчет веса? Ну, вес будет, это сила, так что вес будет давлением, умноженным на площадь. Таким образом, p атмосферы 4 pi равно 12,54, а затем у нас есть радиус, он должен быть в единицах СИ. Я сказал 6370 километров, мне нельзя использовать километры. Я должен сказать 6,37 умножить на 10 на 6 метров, и я возьму это в квадрат. И когда я подставляю все эти числа в калькулятор, я получаю вес 5,17 умноженный на 19, хорошо, теперь какая единица? Это вес, то есть сила, и в единицах СИ, выраженных в ньютонах, это довольно большой вес.
Таким образом, p атмосферы 4 pi равно 12,54, а затем у нас есть радиус, он должен быть в единицах СИ. Я сказал 6370 километров, мне нельзя использовать километры. Я должен сказать 6,37 умножить на 10 на 6 метров, и я возьму это в квадрат. И когда я подставляю все эти числа в калькулятор, я получаю вес 5,17 умноженный на 19, хорошо, теперь какая единица? Это вес, то есть сила, и в единицах СИ, выраженных в ньютонах, это довольно большой вес. Но мы сказали, что есть пара проблем, плотность не была постоянной, и мы не знали, что использовать по высоте или для высоты. Итак, в этой задаче от нас требуется принять постоянную плотность и просто взять плотность на уровне моря. А затем определите, какая высота, подходящая высота, которая даст нам давление, которое мы измеряем.
Но мы сказали, что есть пара проблем, плотность не была постоянной, и мы не знали, что использовать по высоте или для высоты. Итак, в этой задаче от нас требуется принять постоянную плотность и просто взять плотность на уровне моря. А затем определите, какая высота, подходящая высота, которая даст нам давление, которое мы измеряем. низкий. Ладно, это атмосферное давление.2)}\]
низкий. Ладно, это атмосферное давление.2)}\] (Ваша барабанная перепонка действует как
(Ваша барабанная перепонка действует как 

 В этом примере мы рассмотрим круглую пластину, на всю поверхность которой действует сила в равной степени со стороны жидкости, находящейся под сжатием.2
В этом примере мы рассмотрим круглую пластину, на всю поверхность которой действует сила в равной степени со стороны жидкости, находящейся под сжатием.2 Газовые законы, касающиеся давления, объема и
Газовые законы, касающиеся давления, объема и

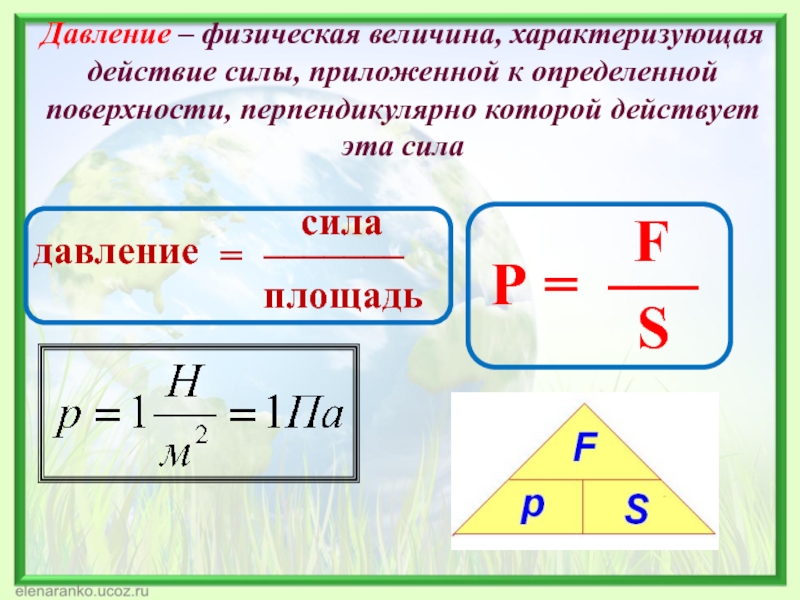 е. KE (J)
е. KE (J) Это привело
Это привело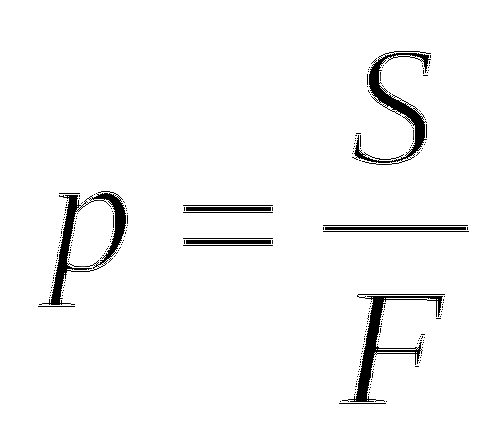
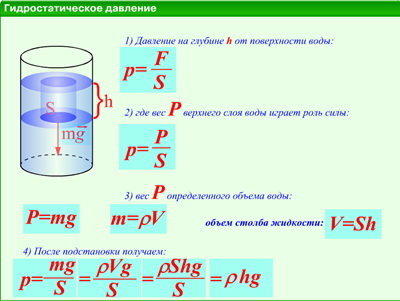 5 или С
5 или С  Модель частиц газа — движение и давление газа
Модель частиц газа — движение и давление газа 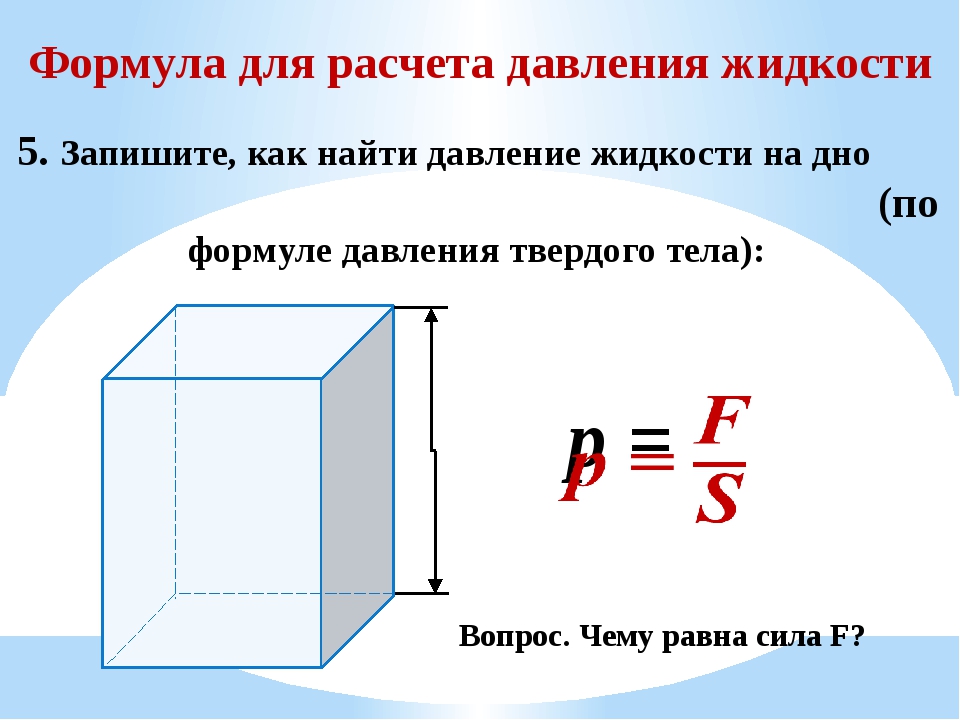


 г. кислород для больниц, может быть
г. кислород для больниц, может быть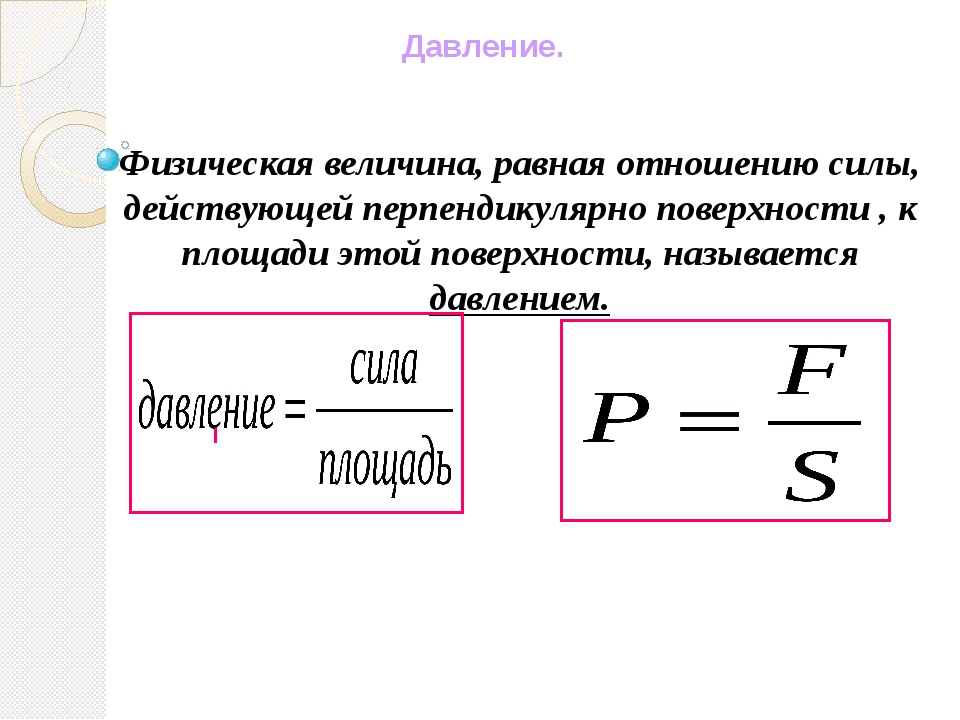 Q4a 2
Q4a 2  Q4a 4
Q4a 4 
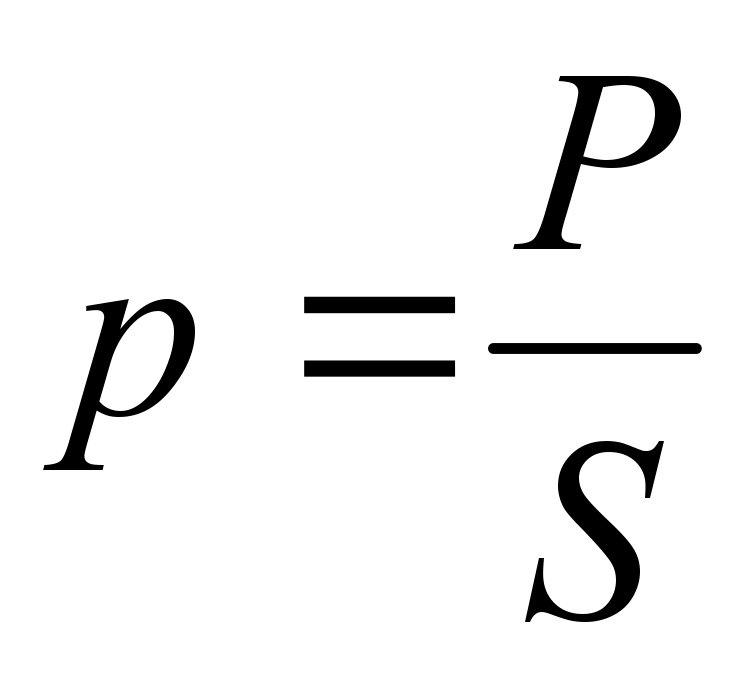

 ..
..

 4b Q2
4b Q2  Объем углекислого газа, собранного за 5 минут в
Объем углекислого газа, собранного за 5 минут в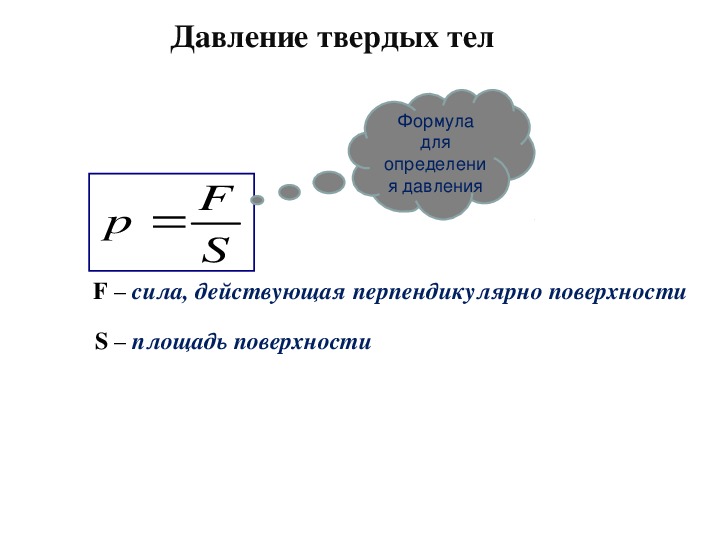 0 см 3 , Т 1 = 273 + 27 = 300К, Т 2 = 273 +
0 см 3 , Т 1 = 273 + 27 = 300К, Т 2 = 273 +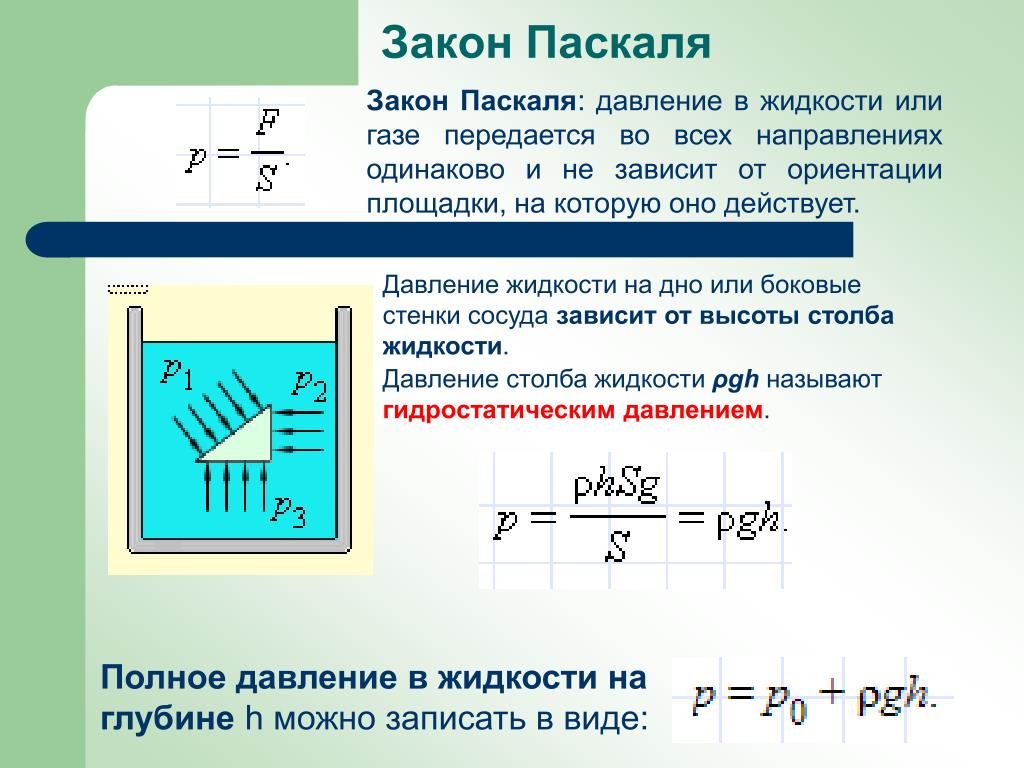 е. 27 или С)
е. 27 или С)
 01 х 25 х 308)/(15 х 298) = 1,74 атм
01 х 25 х 308)/(15 х 298) = 1,74 атм 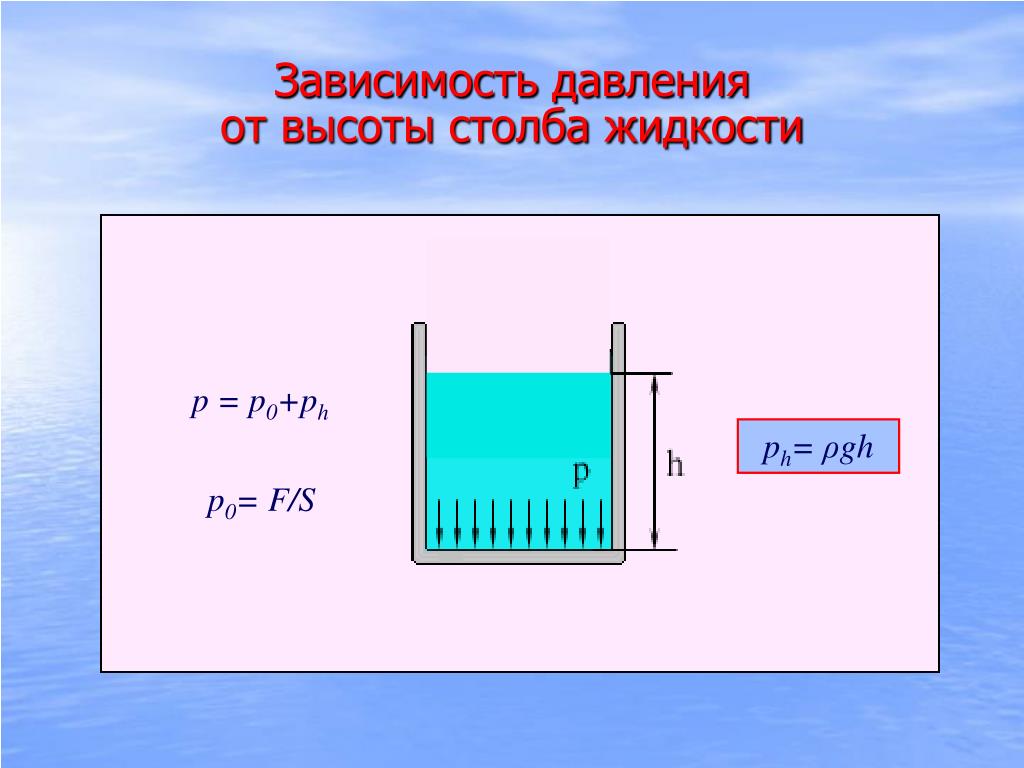
 314 Дж на кельвин на моль ( Дж К -1
314 Дж на кельвин на моль ( Дж К -1